Amor romántico
“Sin el animal que habita dentro de nosotros somos ángeles castrados.”
Hermann Hesse.
“Amor: un juego en el cual hay dos que pierden, el hombre y la mujer, y uno sólo que gana: la especie.”
Abate Prévost.
“El enamoramiento es un estado de miseria mental en que la vida de nuestra conciencia se estrecha, empobrece y paraliza.”
José Ortega y Gasset.

El amor romántico no es fácil de definir. Nada menos que catorce acepciones aparecen en el Diccionario de la Lengua (por cierto, la última afirma que así se conoce el cadillo, una planta que se considera mala hierba). Quizá nos ayude la definición que ha publicado Tiffany Field, de la Universidad de Miami:
“Amor es un sentimiento profundo de afecto y cuidado que implica intimidad, compromiso y pasión, que nutre como el aire, el agua, las palabras y el tacto, y que tiene características típicas en la conducta, la fisiología y la bioquímica de las personas.”
El amor integra, por tanto, conductas, pensamientos, emociones y moléculas asociadas con el deseo de iniciar y mantener una relación con otra persona.
Parece que el amor incluye tres componentes: sexo, unión emocional e intimidad, y compromiso en el cuidado mutuo y de los hijos. Podemos resumir y concretar que el amor romántico es un compromiso para formar pareja con pasión, intimidad y cuidados. Es universal y aparece en todas las culturas. De manera inmediata suspende, en los que forman la pareja, la búsqueda de otras parejas. Tiene características propias en las emociones, en las conductas, en hormonas como la oxitocina o la testosterona, y en las respuestas neuropsicológicas de las zonas del cerebro relacionadas, ante todo, con los circuitos cerebrales de recompensa.
El amor tiene efectos beneficiosos para los individuos, con emociones positivas, felicidad y satisfacción vital, aunque también supone estrés, celos, a veces ruptura con tristeza y sensación de vergüenza, incluso depresión. Golpea a todos por lo menos una vez en la vida. En encuestas publicadas en Estados Unidos, Sandra Langeslag y Jan van Strien, de las universidades de Missouri y de Maryland, afirman que el porcentaje de individuos que padecen, o gozan, del amor romántico casi llega al 100%.
Hay varias hipótesis sobre el amor romántico. Garth Fletcher y sus colegas, de la Universidad Victoria de Wellington, en Nueva Zelanda, plantean tres propuestas conectadas entre sí. En primer lugar, el amor romántico es una conducta de compromiso para motivar la formación de la pareja en nuestra especie. En segundo lugar, la formación de la pareja facilita el peculiar ciclo vital de homínidos que implica dedicar una enorme y duradera inversión en tiempo y recursos para criar los hijos nacidos con un desarrollo muy temprano. Y, finalmente, el amor romántico ayuda a gestionar la pareja a largo plazo, incluyendo las relaciones familiares, y facilita la evolución de la inteligencia social y de las herramientas de cooperación dentro del grupo, clan o familia tan típicos en nuestra especie.
Según la revisión que hacen Fletcher y su grupo, los datos que se conocen son coherentes con la propuesta de que el amor romántico es una conducta de compromiso para formar la pareja. Hay referencias específicas de este objetivo en la conducta de ambos sexos, en la presencia de hormonas y en la aparición de mecanismos psicológicos peculiares del amor. Además, el amor romántico supone una ventaja pues da mejor salud y mayor supervivencia en los adultos y en las crías, o sea, en los niños.
Sin embargo, también hay conductas contrarias para el mantenimiento de la pareja y el cuidado de los hijos. Son, por ejemplo, los matrimonios arreglados y obligatorios, la poligamia, la separación, el divorcio y, en general, la infidelidad. Por el contrario, también hay mecanismos que regulan y controlan la relación y, sobre todo, la fidelidad por lo que implica de evitar la crianza de los genes de otro. Algunos autores sugieren que cada vez hay más evidencias de que, cuando nuestra especie surgió hace unos 150000 años, la conducta habitual en la reproducción era la monogamia. Cuando aparecieron los cazadores recolectores, la relación se complicó con la formación de clanes familiares, aunque siempre a partir de parejas.

En las primeras fases del amor romántico aparecen los síntomas típicos de las adicciones, sean a sustancias o a conductas. Hay euforia, deseo, tolerancia, dependencia física y emocional, abandonos, desintoxicaciones y recaídas. Helen Fisher y su grupo, de la Universidad de Indiana en Bloomington, proponen que el amor romántico es una adicción natural, y resultado de la selección natural pues es, casi siempre, positiva para la reproducción. Fisher afirma que ha evolucionado desde hace miles de años como mecanismo de supervivencia para buscar pareja y para el éxito reproductor.
El escaneo del cerebro de las personas enamoradas revela que se activan las zonas relacionadas con la recompensa y, en concreto, lugares con dopamina, el neurotransmisor conocido como recompensa química cerebral. Son las mismas zonas que funcionan con varias adiciones hacia sustancias o conductas como, por ejemplo, las armas de fuego en Estados Unidos, las autocaravanas en sus dueños, los pastelitos, la cocaína, las anfetaminas o el fútbol en los hinchas. O, en este último caso, es así para los seguidores del Oporto o del Coimbra, de la Primera División de Portugal, como declaran los 56 voluntarios del estudio de Isabel Duarte y su grupo, de la Universidad de Coimbra. Como definen los autores, este apego a un equipo de fútbol es un amor no romántico, pero con una atracción específica a su equipo y una motivación para seguirlo que se sienten premiadas por los circuitos cerebrales de recompensa. En concreto, los autores lo llaman amor tribal. O sea, al grupo, al clan, a la familia.
También el grupo de Zhiling Zou, de la Universidad del Sudoeste en Chongqing, en China, estudia el amor romántico como adicción en su primera fase y relatan que, cuando la relación amorosa progresa, los síntomas de adicción se atenúan y, poco a poco, desaparecen. Se pasa de una conducta de adicción a una conducta prosocial no adictiva.
De nuevo, como en el estudio de Helen Fisher (y en la afición al fútbol), el escaneo del cerebro revela la activación del área de recompensa y, además, de la red de emociones entre personas y con el entorno social. De nuevo, están la oxitocina y la dopamina.

Esta profunda implicación de hormonas, determinadas áreas del cerebro y neurotransmisores en el amor ha llevado a proponer que no es una emoción sino una necesidad fisiológica como el hambre, la sed, el sueño o el sexo. Así lo escribe Enrique Burunat, de la Universidad de La Laguna, cuando afirma que el amor es una conducta resultado de la selección natural para conseguir un mayor éxito en la reproducción. Los que desarrollan amor y, por tanto, compromiso para la cría de los hijos, tienen más descendencia y transmiten los genes de esa conducta a las siguientes generaciones. Los que no tienen amor, tienen menos descendencia y van desapareciendo. Así, después de miles de años, sea seleccionado la mejor conducta para el éxito en la reproducción. Y es una necesidad fisiológica y conductual inevitable. Por ello, el 100% de los humanos sienten o han sentido el amor en algún momento de su vida.
Por cierto, esta adicción al amor romántico es un poco especial. Los estudios del grupo de Jordane Boudesseul, de la Universidad de Grenoble, en Francia, demuestran que quien está enamorado cree más en el amor romántico, lo que se antoja coherente, pero, además, quien está enamorado cree en el libre albedrío aunque, también, acepta que la vida, quizá su enamoramiento en concreto, tiene un fuerte sentido determinista. Está, a la vez y sin ser consciente de ello, convencido de que se enamora obligatoriamente de quien quiere.
Para terminar, el amor romántico también tiene, a veces, un final, una ruptura que, como se dice, rompe el corazón. Nos cuenta Tiffany Field, aquella que nos definió el amor, que existe un síndrome del corazón roto. Una ruptura sentimental reproduce algo parecido a un ataque al corazón, aunque sin arterias ocluidas ni daños permanentes. Estas rupturas provocan hasta el mal funcionamiento del sistema inmune, con aumento general de la inflamación, lo que también influye en el corazón, y disminución de las defensas.
Referencias:
Boudesseul, J. et al. 2016. Free love? On the relation between belief in free will, determinism, and passionate love. Conciousness and Cognition 46: 47-59.
Burunat, E. 2016. Love is not an emotion. Psychology 7: 1883-1910.
Buss, D.M. 1996. La evolución del deseo. Alianza Ed. Madrid. 417 pp.
Duarte, I.C. et al. 2017. Tribal love: the neural correlates of passionate engagement in football fans. Social Cognitive and Affective Neuroscience doi: 10.1093/scan/nsx003
Field, T. 2016. Romantic love. International Journal of Behavioral Research & Psychology 4: 185-190.
*Fisher, H. 2004. Por qué amamos. Naturaleza y química del amor romántico. Santillana Ed. Madrid. 348 pp.
Fisher, H.E. et al. 2016. Intense, passionate, romantic love: A natural addiction? How the fields that investigate romance and substance abuse can inform each other. Frontiers in Psychology doi: 10.3389/fpsyg.2016.00687
Fletcher, G.J.O. et al. 2015. Pair-bonding, romantic love, and evolution: The curious case of Homo sapiens. Perspectives in Psychological Science 10: 20-36.
Langeslag, S.J.E. & J.W. van Strien. 2016. Regulations of romantic love feelings: preconceptions, strategies, and feasibility. PLOS ONE 11: e01611087
Song, S. et al. 2016. Romantic love is associated with enhanced inhibitory control in an emotional stop-signal task. Frontiers in Psychology doi: 10.3389/fpsyg.2016.01574
Zou, Z. et al. 2016. Romantic love vs. drug addiction may inspire a new treatment for addiction. Frontiers in Psychology doi: 10.3389/fpsyg.2016.01436
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Amor romántico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Naukas Bilbao 2017 – Carolina Jiménez: Ciencia y cine, avanzando de la mano
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

El cine no es más que la combinación del arte de la narrativa y el avance tecnológico. Lo sabe y lo explica como nadie Carolina Jiménez, artista de efectos especiales digitales para el cine que ha participado y participa en algunas de las superproducciones más conocidas de los últimos años.
Carolina Jiménez: Ciencia y cine, avanzando de la manoEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Carolina Jiménez: Ciencia y cine, avanzando de la mano se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Álex Méndez: Luz de luna
- Naukas Bilbao 2017 – Teresa Valdés-Solís: Limpia, fija y da esplendor
- Naukas Bilbao 2017 – Ignacio López-Goñi: Las bacterias también se vacunan
Una fibra óptica de plástico actúa como concentrador solar luminiscence
Un equipo de investigación de la UPV/EHU ha desarrollado un fibra óptica con dopantes híbridos que concentra la luz solar con un rendimiento alto y un coste bajo. Hasta ahora nunca se había utilizado como concentrador solar una fibra óptica de plástico que combina componentes orgánicos e inorgánicos.

Imagen: Itxaso Parola / UPV/EHU
Los resultados muestran que el rendimiento de la fibra al concentrar y transportar luz solar es alto, y que, conectado a células fotovoltaicas, resulta ser un sistema muy apropiado para suministrar electricidad a pequeños dispositivos.
Tan solo un 3 % de la energía consumida en 2017 proviene de sistemas eólicos, solares y de biomasa; los expertos, sin embargo, creen que actualmente la obtención de energía solar tiene las mayores perspectivas de crecimiento. No cabe duda de que siempre dispondremos de energía solar, y además de aprovecharla utilizando huertos solares, también se pueden utilizar sistemas más pequeños integrados en diversos espacios (en casas, tejados, etc.).
A nivel mundial se están llevando a cabo muchos estudios de mejora de células solares fotovoltaicas. Las células fotovoltaicas más avanzadas hasta el momento son las de silicio, pero son muchos los aspectos que necesitan ser mejorados: las fuentes de silicio son limitadas; las instalaciones requieren de grandes superficies; son necesarios sistemas de seguimiento solar, así como luz solar directa; su rendimiento disminuye mucho en días nublados o con luz difusa, etc. En definitiva, todavía resulta caro disponer de la energía solar.
Precisamente, en una investigación llevada a cabo por los departamentos de Física Aplicada I e Ingeniería de Comunicaciones de la UPV/EHU, en colaboración con el grupo Applied Organic Materials de la Universidad Técnica de Brunswick, han conseguido una fibra óptica de plástico con dopante híbrido que servirá para producir energía a pequeña escala. Para mejorar las características de la fibra óptica han añadido al polímero un dopante compuesto por substancias tanto orgánicas como inorgánicas. “Podrá utilizarse con células fotovoltaicas que alimenten pequeños dispositivos o sensores, y podría tener una gran potencialidad en el mercado de la fotovoltaica integrada en edificios o edificación verde —explica Itxaso Parola, autora de la investigación—. Además, conectada a fibras pasivas, se puede transportar la luz desde un extremo al otro de la fibra, y así, servir para alimentar dispositivos alejados de la fuente de energía”.
“La fibra óptica de plástico con dopante híbrido funciona como un concentrador solar luminiscente: absorbe la luz solar y la emite a una mayor longitud de onda; transporta la luz al extremo de la fibra, por reflexión interna total, y en el extremo de la fibra se coloca la célula fotovoltaica —explica Parola—. Es la primera vez que se utilizan para ese fin fibras ópticas de plástico que combinan componentes orgánicos e inorgánicos”. Asimismo, la investigadora de la UPV/EHU ha destacado que, como otros concentradores luminiscentes, este también resulta muy apropiado para obtener energía solar en espacios situados en sombra y en días nublados.
Según los resultados de las medidas llevadas a cabo, una fibra de 6 cm de longitud puede llegar a concentrar un tercio de la luz que emite el sol un día soleado de verano, y en opinión de la investigadora “ese resultado es muy bueno”. Han medido el rendimiento de la fibra en diversas condiciones ambientales y de iluminación, y “hemos observado que tiene un buen rendimiento en todos los casos, aunque el rendimiento es incluso algo mayor cuando la luz no incide directamente en la fibra. Esa característica es muy positiva teniendo en cuenta que el rendimiento de las células de silicio es muy pequeño en días nublados o de luz difusa”, comenta. Aunque la investigadora ha reconocido que cuando la fibra es muy larga la luz que se transporta por el interior se debilita, “con una sola fibra de 6 m de longitud hemos conseguido concentrar una intensidad de luz 1,3 veces mayor que la luz directa del sol”, detalla.
Tal como afirma la investigadora, es mucho más barato preparar sistemas como este que utilizar mayores superficies de células de silicio. De todas formas, Parola reconoce que es necesario investigar más en este campo para arrojar luz sobre varios aspectos: “Nosotros hemos realizado experimentos utilizando una única fibra, pero se necesitarían haces de fibras para poder cubrir el área activa de una célula fotovoltaica. Por otra parte, la superficie de las células fotovoltaicas es cuadrada, y al cubrir esa superficie con fibras cilíndricas siempre quedarán pequeñas zonas que no obtendrán luz. Ahora, estamos probando con diferentes diámetros de fibra; cuando la fibra es más gruesa pierde flexibilidad, pero, al mismo tiempo, absorbe más luz. Todavía tenemos mucho que investigar, pero los resultados son muy prometedores”.
Referencia:
I. Parola, D. Zaremba, R. Evert, J. Kielhorn, F. Jakobs, M. A. Illarramendi, J. Zubia, W. Kowalsky, Hans-Hermann Johannes (2018) “High performance fluorescent fiber solar concentrators employing double‐doped polymer optical fibers” Solar Energy Materials and Solar Cells. DOI: 10.1016/j.solmat.2018.01.013
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Una fibra óptica de plástico actúa como concentrador solar luminiscence se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Hidrógeno a partir de composites de fibra de carbono
- Cómo incorporar nanotubos de carbono a un plástico de aviación
- La óptica se hace atómica: la lente más pequeña del mundo
La Criatura de “La forma del agua”
Usar el cine para hablar de ciencia es algo que suelo hacer habitualmente, y muchas películas se prestan a ser analizadas desde un punto de vista biológico, y eso es lo que vamos a hacer hoy con La forma del agua. Lo primero que me gustaría comentar sobre ella es que he quedado maravillado con esta nueva película del director mexicano Guillermo del Toro, y me ha recordado a lo mucho que disfruté con su obra El laberinto del fauno. Y es que como se oye mucho por ahí, los monstruos de este cineasta son maravillosos. Si encima me dan la excusa para poder hablar de biología, pues ya tenemos la película perfecta. Pocos Premios de la Academia para mi gusto ha ganado. Cabe recordar que La forma del agua se ha llevado el Oscar a la mejor película, al mejor director, a la mejor banda sonora y al mejor diseño de dirección; un total de cuatro estatuillas de las trece nominaciones que tenía.

Cartel de la forma del agua
Pero empecemos por el principio. ¿De qué trata está película? Si hay que hacer un resumen, tenemos que decir que va sobre el amor, el amor en sus múltiples facetas. Es una oda al amor, claramente. Un precioso cuento de amor en el que uno queda atrapado desde que empiezan las primeras palabras a narrar la historia, acompañadas de unas bellas imágenes cuidadas al máximo. Y es que está claro que ese es otro de los puntos fuertes de la película, la fotografía, que junto con la magnífica banda sonora, terminan de conformar esta maravillosa historia que ha cautivado a tanta gente.

El inicio de la película
Intentaremos que no haya spoilers en el post, pero está claro que tengo que contar algunos detalles, así que si alguien no quiere que le adelante algún detalle tiene que dejar de leer aquí, aunque me voy a centrar solo en la parte biológica que concierne a la criatura y no en la historia que se relata. Y es que esta criatura me ha cautivado a muchos niveles, y nos va a dar pie para que hablemos de detalles biológicos interesantes, que podemos conocer a lo largo del metraje de la película.

La criatura de La forma del agua
Muchos, al verla la primera vez, no hemos podido evitar acordarnos de otro de los monstruos clásicos del cine, La criatura de la Laguna Negra, de la película homónima de 1954 (Creature from the Black Lagoon), que fue titulada en español La mujer y el monstruo. Y es que el propio director, Guillermo del Toro, ha reconocido que esta película marcó su vida cuando la vio de pequeño.
“Tenía seis años cuando vi El Monstruo de la Laguna Negra en la televisión y hubo tres cosas que despertó en mí, la primera que no revelaré; la segunda fue la imagen más hermosa que había visto, me sentí abrumado por la belleza; y la tercera cosa fue que en realidad esperaba que terminaran juntos y no lo hicieron…”

La Criatura de la Laguna Negra
Tengo que reconocer que la primera frase que se nos puede pasar a la mayoría por la cabeza cuando vemos a la criatura es: – Vaya bicho más feo -, pero yo tuve la sensación contraria, me parecía una criatura de gran belleza, magnífica, digna de admiración, por lo que ahí coincido con las palabras de Del Toro, que no había leído hasta que me he puesto a buscar información para escribir esta reseña. Y es que el monstruo está perfectamente diseñado, con un cuidado extremo de todos los detalles, para que nos guste; lo que contrasta muchísimo con el disfraz, mas bien cutre, de la película de 1954, cosa que por otro lado es normal. Los monstruos de las películas antiguas nos suelen parecer mas feos casi siempre.

Comparativa
Según se narra al inicio de la película, cuando traen al monstruo a un laboratorio secreto del Gobierno, se habla de que lo encontraron en Sudamérica, del mismo modo que la Criatura de la Laguna Negra fue encontrado por un paleontólogo en el Amazonas, por lo que ambas tienen el mismo origen. El ser tiene aspecto de anfibio, y desde el primer momento se deja ver su piel húmeda y suave, aunque en algunas partes de la película se pueden intuir algo parecido a escamas, más o menos de gran tamaño que me hicieron dudar de la naturaleza de dicha criatura. Es más, atendiendo a ciertas características, podemos dudar de si estamos ante un anfibio estricto o si es un paso intermedio en la escala evolutiva entre este grupo y el de los reptiles. O incluso un espécimen intermedio entre anfibios y peces, todo ello complicado por la forma claramente antropomórfica del ser.

¿Pez, anfibio o reptil?
Desde el principio de la película nos dejan muy claro que la criatura necesita agua salada, por lo que tenemos que empezar hablando de ósmosis, que es un fenómeno físico que ocurre cuando tenemos dos disoluciones separadas por una membrana semipermeable, es decir una superficie que permite el paso de ciertas sustancias de forma selectiva. En el caso que nos interesa vamos a considerar que la membrana semipermeable permite el paso del agua, pero no de las sustancias que lleve disuelta, esto es, permite el paso del disolvente, pero no de los solutos. La ósmosis, se produce cuando dos disoluciones de diferentes concentraciones se encuentran separadas por una membrana de este tipo.
En este caso, el agua atravesará la membrana desde donde hay menor concentración de solutos hasta donde hay mayor concentración. La lógica y la experiencia nos dice que esto ocurre hasta que las dos disoluciones se igualan, y ambas presenten la misma concentración. A la disolución que tiene mayor concentración de solutos se le llama hipertónica, mientras que a la que tiene menos se le llama hipotónica. Cuando las dos se igualan, tras pasar el líquido desde el medio hipotónico al hipertónico, los dos medios pasan a convertirse en isotónicos, es decir, tienen la misma concentración. A partir de esto se define por ejemplo, la presión osmótica, pero no vamos a entrar en más conceptos físicos, sino que nos vamos a quedar en la aplicación biológica de este proceso. Sobre ósmosis y criaturas de este tipo nos habló magistralmente mi admirado Sergio Palacios en este post.
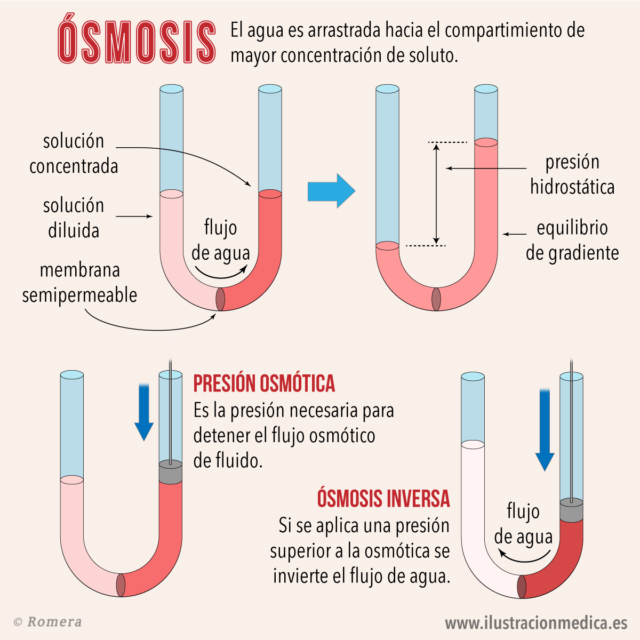
Ósmosis
Al igual que los peces, nuestra criatura cuenta con adaptaciones que le permiten sobrevivir a determinada concentración de sales en el agua, y debido a ello pueden vivir en el océano. Pero aquí nos encontramos el primer problema, que ahora comentaremos mientras repasamos algunas escenas de diálogo de la película, en las que se habla del origen de la criatura en los siguientes términos:
“… Sí, y lo sé bien. Yo saqué a esa bestia inmunda del fango de un río en Sudamérica y la arrastré hasta aquí. Y por el camino no congeniamos mucho.
Bien, esa criatura puede parecerles humana, porque se yergue sobre dos piernas, pero Dios nos creó a su imagen y semejanza. No creerán que Dios se parece a eso, ¿no?”
(Lo dice el Coronel Strickland hablando con las limpiadoras del laboratorio).

El actor Michael Shannon interpretando magistralmente a Strickland
Vale, tenemos una criatura marina, que dice que fue sacada del fango de un río sudamericano… No cuadra mucho, pero sigamos buscando pistas, a ver si podemos averiguar qué río era. El mismo Strickland, suelta más adelante la siguiente frase:
“Los indígenas del Amazonas lo veneraban como un Dios.”
Se trata del río Amazonas, que por cierto es el mismo río donde se hallaba la criatura de la película de 1954. Pero, ¿es el Amazonas un río de agua salada? Nada más lejos de la realidad. La consideración de agua dulce, que es como se entiende que es la de los ríos, se hace teniendo en cuenta que la salinidad esté entre un 0 y un 0,05 %, por lo que no parece muy lógico que esta criatura pueda vivir en el río Amazonas, excepto que lo haga en su desembocadura. En esa zona se mezclan los dos tipos de agua, dulce y salada, por lo que no sería extraño que los encuentros entre la criatura y los indígenas, y el lugar donde atraparon a este ser fuera la desembocadura del río Amazonas.

Delta del Amazonas
La concentración salina en los mares es de entre 33 y 35 g/l, es decir, de aproximadamente un 3,5 %, a causa de la sal común, el cloruro sódico, que hay disuelta en este medio. Sin embargo, la concentración de los fluidos corporales de los peces teleósteos, que son la mayoría de los peces que viven en medios marinos, es mucho menor, por lo que estos animales nadan en un medio hipertónico o hiperosmótico. Debido a esto, el agua tenderá a salir desde el interior de las células hacia dicho medio, por lo que corren el riesgo de morir, literalmente, deshidratados a pesar de vivir rodeados del líquido elemento. Para compensarlo no tienen mas remedio que beber.
Cabe suponer que nuestra criatura tenga las adaptaciones que los peces marinos: Al beber agua salada, está introduciendo en sus cuerpos una gran cantidad de sales que van disueltas en el agua, por lo que necesita algún mecanismo para expulsar este exceso salino. Y este mecanismo consiste en eliminar las sales mediante unas células especializadas de las branquias, y mediante una orina escasa, pero muy concentrada.
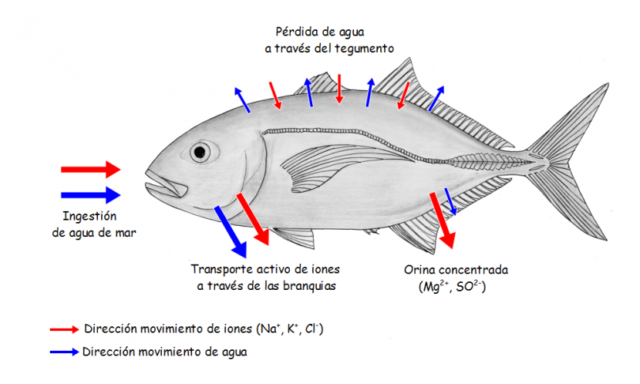
Osmorregulación en peces de agua salada
Existen peces que pueden vivir en los dos medios, es decir, los llamados peces diádromos, que viajan entre los ríos y los mares o viceversa. Hay peces que se aparean y nacen en los ríos, pero que pasan la mayor parte de su vida adulta en el mar, son los llamados peces anádromos, cuyo ejemplo más conocido quizás sean los salmones, entre los que destaca la especie Salmo salar, el salmón común o salmón del Atlántico. Entre los peces catádromos, también uno de los ejemplos más conocidos es el de las anguilas, Anguilla anguilla. Estos curiosos peces con forma alargada, nacen en el Océano Atlántico, en el conocido mar de los Sargazos, donde pasaran unos meses en forma de larva, llamadas larvas leptocéfalas, que arrastradas por las corrientes llegan hasta las costas de Europa, donde remontan los ríos para crecer y vivir en ellos durante muchos años. De adultos viajan río abajo para volver al mar de los Sargazos, donde nacieron, y reproducirse, llevando a cabo la puesta en dicho lugar.
En ambos casos, el problema está en que la osmorregulación debe adaptarse al medio en el que se encuentran en cada momento y para ello las estructuras celulares de las branquias deben cambiar acomodándose a la salinidad del medio. Cuando están en agua dulce, medio hipotónico, el epitelio branquial es capaz de absorber sales, mientras que en agua salada, medio hipertónico, las células de las branquias expulsan sal activamente. El control de la diferenciación y de la actividad de estas células se realiza mediante hormonas, así por ejemplo, el cortisol y la hormona del crecimiento activan este epitelio en la transición de los ríos al mar, mientras que la prolactina lo hace cuando ocurre el paso contrario.
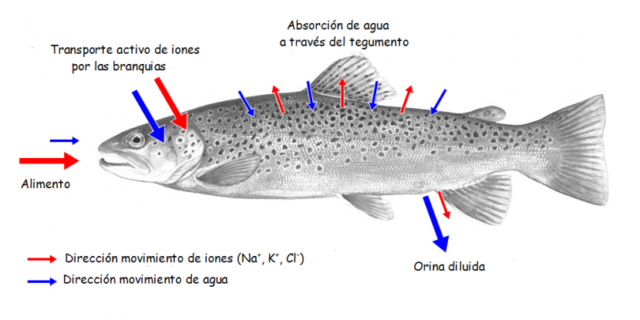
Osmorregulación en peces de agua dulce
Y para complicar aún más el asunto existen algunas especies de peces llamados anfídromos, que se mueven entre el mar y el agua dulce, o entre los ríos y el agua salada, aunque no lo hacen por causas reproductivas, como los anteriores, sino para alimentarse o a causa de cambios estacionales. Un ejemplo de ellos son las lisas, Mugil cephalus, un pez carroñero muy habitual en las desembocaduras de los ríos, ya que es muy adaptable a distintas condiciones de salinidad e incluso a la contaminación. Creo que en un caso parecido a éste nos encontraríamos a nuestra criatura, que vive en el océano y que sube a la desembocadura de los ríos en busca de alimentos, más aún cuando en la película se cita que los indígenas le lanzaban flores, frutas y otros presentes. En varias escenas vemos como le encanta comer huevos cocidos, una fuente de proteína, ofrecidos por personajes humanos.

Los huevos, fuente de proteínas…
De nuevo nos encontramos otro problema de coherencia en los diálogos de la película que llegué a pensar que era un error cuando lo escuché la primera vez, y que me ha hecho buscar la versión original para ver si era un fallo de traducción. Se trata de lo que el Dr. Robert Hoffstetler le dice a Elisa, una de las limpiadoras, durante uno de los momentos más importantes del metraje:
“El agua debe tener entre un 5 y un 8 % de salinidad. Vale con sal común.”

El actor Michael Stuhlbarg con el doctor Robert Hoffstetler
¿Cómo? una salinidad mucho mayor que la media del agua del mar… ¿pero no habíamos quedado en que era una criatura marina que podía moverse a la desembocadura del río Amazonas? En un principio pensé que ahí se habían pasado con el porcentaje, quizás para enfatizar el problema de sacar a la criatura del laboratorio y hacer ver una necesidad o dependencia mayor del agua salada. Uno de los sitios más salados de nuestro planeta es el mar Muerto, cuya salinidad es variable, pero puede rondar entre un 22 y un 28 % de salinidad. El Gran Lago Salado norteamericano tiene una salinidad entre un 5 y un 22 % y muchos lagos salados sudamericanos tienen una salinidad variable entre el 3 y el 25 %. Pero nuestra criatura no vive en un lago, ni en el Mar Muerto.
Podemos aceptar que la criatura puede adaptarse a rangos variables de salinidad, lo que sumado a que también vemos que el agua del tanque del laboratorio y la bañera tienen que tener un producto (que no se menciona qué es), que le da un aspecto verdoso, y que me recordaba en todo momento a las aguas eutrofizadas. Todo ello nos da las pistas necesarias para que podamos concluir que su hábitat es una zona en la desembocadura de un río que está sufriendo este proceso de eutrofización. Esto consiste en que en un cuerpo de agua cerrado o casi cerrado, con poca corriente, los nutrientes que ingresan masivamente al sistema generan una gran biomasa de organismos de vida efímera. Al morir, toda esta masa biológica se acumula sobre el fondo al no ser totalmente consumidos por organismos descomponedores, sobre todo bacterias. Estos procesos naturales de eutrofización se pueden observar en las lagunas formadas por los cauces antiguos de ríos que se transforman en pantanos y posteriormente se cubren de vegetación. En el Amazonas, por supuesto, también ocurre esto. Por fin dimos con la clave del posible sitio de origen de nuestra misteriosa criatura.

Tanque de agua de la criatura
Cuando la criatura sale del laboratorio y tiene que pasar un tiempo en una bañera, además de lo que supone un espacio tan pequeño para un ser más alto que un humano medio, lo pasa muy mal suponemos que por no haber controlado exactamente la concentración salina del agua de la bañera, que seguramente se haya quedado corta. Gran parte de los problemas que tiene en esos momentos se deben a la necesidad de un hábitat natural amplio y acondicionado para que sobreviva, con una concentración salina adecuada.

La criatura en una bañera “eutrofizada” artificialmente
Hasta ahora, en todo momento hemos hablado de peces, pero dijimos al principio que nuestra criatura protagonista posiblemente se tratara de un anfibio, por lo que pasemos ahora a hablar de por qué pensamos esto, teniendo en cuenta las adaptaciones a la vida acuática y terrestre que vemos en la criatura, que son las típicas de este tipo de seres en la ficción.
En primer lugar atendamos a su aspecto general, con un color verdoso muy habitual en muchos grupos de anfibios, como ranas, sapos y tritones. El patrón de colores ondulado es muy característico y llamativo visto así, pero en el medio acuático eutrofizado que comentábamos antes debe significar un buen camuflaje para la criatura. La piel del tritón jaspeado, Triturus marmoratus, o las escamas del pez león, Pterois antennata, presenta patrones parecidos.

Tritón jaspeado y pez león
Es cierto que en el nuevo monstruo de Del Toro nos encontramos con la producción de luz en algunas células de la piel, lo que es una novedad frente a monstruos más clásicos. La bioluminiscencia es la producción de luz por parte de organismos vivos. Bioquímicamente hablando, se trata de una reacción en la que interviene una enzima llamada luciferasa, que hace que el oxígeno oxide a la proteína llamada luciferina, que da lugar a la oxiluciferina, produciéndose también agua y luz. Se trata de una transformación directa de energía química en energía lumínica. En la vida real las funciones de esta bioluminiscencia pueden ser múltiples, desde atraer a posibles presas, servir para comunicación entre individuos, camuflaje o distracción o como señal de advertencia. Para nuestra criatura no sabemos cual es la función en libertad, pero en la película vemos que está asociada con la regeneración de tejidos.

Bioluminiscencia
No hay anfibios bioluminiscentes que conozcamos, aunque recientemente se encontró una rana que brilla en la oscuridad, pero lo hace por fluorescencia que es diferente a la bioluminiscencia. Se trata de una rana sudamericana, la rana puntuada, o Hypsiboas punctatus, una especie que vive en montañas, pantanos, marismas y bosques tropicales y subtropicales, de varios países de Sudamérica, como Argentina, Bolivia, Brasil o Colombia, y que es capaz de brillar en la oscuridad. Lo que si tienen los anfibios es una capacidad increíble para regenerar los tejidos, así que la capacidad del monstruo para hacerlo también tiene su punto de justificación científica.

Hypsiboas punctatus
El ajolote mexicano y otras especies de salamandras y tritones presentan la capacidad de regenerar sus tejidos. Si se lesionan una extremidad o la cola son capaces de regenerarla, pero lo más asombroso es que también pueden hacerlo con partes de sus órganos vitales, como el corazón o el cerebro. Básicamente, lo que hacen estos animales es revertir sus células hasta el estado de células madre, para poder reparar los tejidos renovando todas las células que hagan falta. Al igual que nuestra bestia protagonista tiene esta capacidad para curar, estos anfibios están siendo usados para investigar posibles tratamientos de regeneración en pacientes amputados y curación de algunas enfermedades.
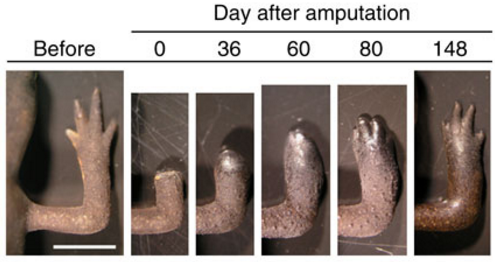
Regeneración en anfibios
Otra característica evidente en la criatura es su modo de respiración. Desde el principio se ven unas agallas grandes en el cuello entre las que suponemos entrever varias hendiduras branquiales, que dan acceso a las branquias que usa para respirar dentro del agua. Así mismo parece claro que cuenta con pulmones, que le permiten respirar en tierra. Hay varias referencias a ello en la película:
“Absorción de oxígeno e intercambio de dióxido de carbono. ¿Qué demonios es esto hijo?”
(Lo dice el general Hoyt hablando con el coronel Strickland)
“Esta criatura puede alternar entre dos mecanismos de respiración totalmente diferentes.”
(La intervención del Dr. Robert Hoffstetler matiza datos sobre la respiración de la criatura)

Detalle de diseño de la criatura. Se ven los repliegues branquiales en la cara y el cuello

Detalle del tórax de la criatura durante una sesión de maquillaje
Strickland apostilla a la intervención anterior con una frase que dice: – “El pez del fango también.”-, en referencia a los peces del género Periophthalmus, también llamados saltarines del fango. Estos fascinantes seres viven en manglares tropicales y tienen la capacidad de respirar aire en un modo de vida anfibio. Tienen capacidad para respirar a través de la piel, su mucosa bucal y faringe. Esto solo es posible en condiciones de mucha humedad, limitándolos a permanecer en el área fangosa. Éste tipo de respiración cutánea es muy similar al de los anfibios, por lo que el comentario de Strickland no está tan fuera de lugar.
Otra importante adaptación para ayudar a respirar aire es la existencia de grandes cámaras branquiales que actúan como un depósito de oxígeno, lo cual les sirve mientras están en tierra. La habilidad de enterrarse en profundos hoyos de sedimentos fangosos, les ayuda en su termorregulación, y también a evitar depredadores. Además, pueden utilizar esta capacidad para desovar en estos agujeros en el fango. Gracias a la cámara branquial pueden respirar cuando están enterrados y el agua tiene poca concentración de oxígeno.

Periophthalmus barbarus
Volviendo a la película, el propio Strickland vuelve a hacer otro comentario en referencia a los pulmones de la criatura:
“¿Ve eso que tiene a lo largo del pecho? Esta criatura tiene un cartílago articulado que separa los pulmones primarios de los secundarios. (…)”
En nuestro mundo real, los anfibios usan varios sistemas de respiración, como son la cutánea, la branquial, la pulmonar y la respiración a través de la cavidad oral. La respiración cutánea la utilizan cuando están sumergidos, por ejemplo para reproducirse, y de esta manera pueden respirar también a través de la piel mientras ésta se mantenga húmeda en el exterior. Tengamos en cuenta que los anfibios fueron los primeros vertebrados que salieron del agua para llevar a cabo gran parte de su vida fuera del agua, aunque no se independizaron totalmente de ella. Su reproducción los ata al agua, ya que sus huevos, sin cáscara, necesitan ser depositado en lugares muy húmedos o masas de agua para que no se desequen.
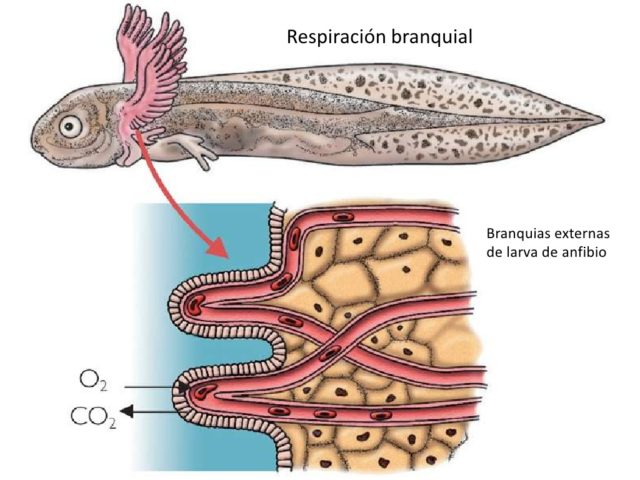
Respiración branquial en renacuajos
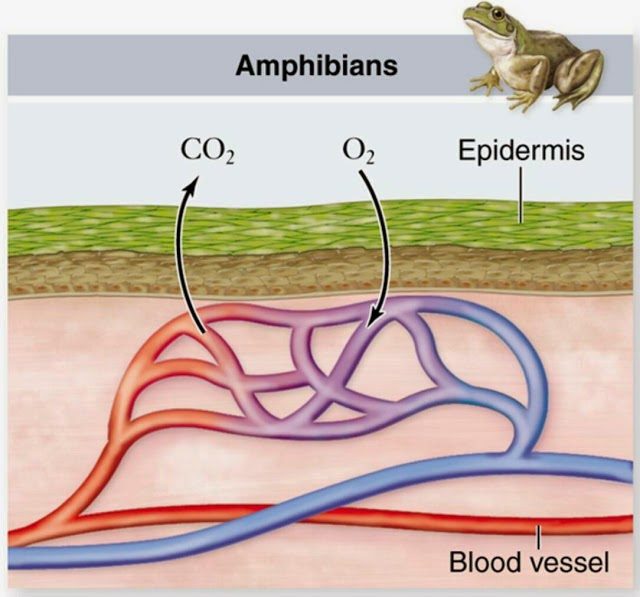
Respiración cutánea en anfibios adultos
Los primeros peces que desarrollaron la capacidad de salir del agua para sobrevivir cierto tiempo en tierra, la adquirieron gracias al desarrollo de pulmones, aunque estos fueran rudimentarios y menos efectivos que los de reptiles, aves y mamíferos. Los pulmones de las salamandras y tritones son unos simples sacos de paredes lisas bien vascularizadas, mientras que los de ranas y sapos son un poco más complejos con pliegues y cámaras, lo que aumenta la capacidad respiratoria. Estos primeros pulmones que tuvieron los anfibios derivan de la vejiga natatoria de los peces.
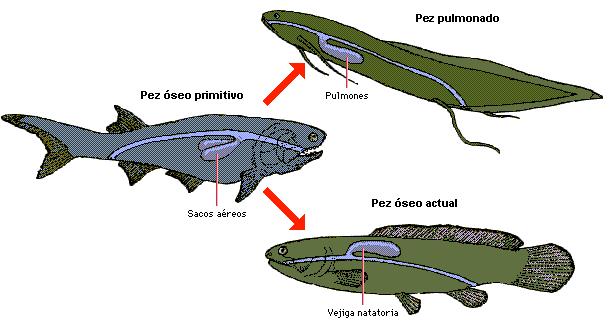
Vejiga natatoria
En cuanto a la respiración branquial, en los renacuajos y larvas de los anfibios es la forma más usual de respirar, y, normalmente, tras la metamorfosis, al llegar a adultos, sustituyen estas estructuras por los pulmones y pasan de tener respiración branquial a tener respiración pulmonar. De todas maneras, el tipo de respiración depende de la especie. Por ejemplo los ajolotes adultos pueden conservar la respiración branquial, mientras algunos tipos de salamandras, como las del género Bolitoglossa, carecen de respiración pulmonar y lo hacen exclusivamente por respiración cutánea.

Bolitoglossa mexicana
Nuestra criatura, es un ser alto y galante, para este papel, Guillermo del Toro ha utilizado al actor Doug Jones, que también hizo del Fauno en su famosa película. Este actor no es la primera vez que se mente en la piel de un hombre-anfibio, bastante parecido a éste, puesto que ya lo hizo en otra de las películas del cineasta mexicano. En Hellboy hacía el papel Abe Sapien, aunque este personaje es descrito más como un hombre-pez. En cualquier caso el parecido de ambas criaturas es más que razonable.

Abe Sapien
El propio Guillermo Del Toro dice que para los movimientos del monstruo quería la fluidez del Silver Surfer de los 4 Fantásticos, al que por cierto también interpretó Jones en su versión cinematográfica. Para que el diseño de la criatura fuera atractivo, el director se llevaba frecuentemente el traje a su casa para pedir opinión femenina en cuestiones como el abdomen más o menos marcado, el trasero o la anchura del pecho y los hombros. Doug Jones necesitaba cuatro horas de preparación y maquillaje para terminar teniendo el aspecto de la criatura. El resultado era una piel con todas las imperfecciones y detalles que un híbrido entre humano y anfibio debería tener: en el cuello y repliegues de la piel hay imperfecciones, hoyuelos, líneas, arrugas, cicatrices, vasos sanguíneos y pliegues. En cuanto a los colores también se ven diferentes tonos y variaciones según el ángulo de observación, la sombra, el medio en el que esté y la iluminación.

Doug Jones durante una sesión de preparación del traje y el maquillaje
Se pueden ver en las extremidades de la criatura estructuras a modo de aletas, aunque no demasiado grande para primar el aspecto antropomórfico sobre el anfibio. Llama poderosamente la atención la creta dorsal que presenta a lo largo de su espalda, siguiendo la línea de la columna vertebral, que puede ser una referencia a su condición de macho. Los machos de los tritones desarrollan este tipo de crestas dorsales en su espalda y en su cola como un signo de dimorfismo sexual que se usa para hacerlos más llamativos en el cortejo.

La cresta en la espalda de la criatura
La condición de macho de nuestro espécimen queda clara desde el principio, pero se hace referencia varias veces a su entrepierna, que se observa bastante plana, sin señal de la presencia de ningún pene u órgano copulador. Es la protagonista de la película, Elisa, la que en un momento dado explica a su amiga si la criatura tiene pene o no, y es aquí donde, debido a su condición de muda, lo hace mediante gestos. Atendiendo a como lo explica, la imagen que me hice de como era la estructura del pene de la criatura me recordó a la de un animal acuático, pero que precisamente no es un anfibio, ya que la mayoría de ellos carecen de pene, sino a la de los cocodrilos, que son reptiles.

Detalle del cuerpo completo de la criatura

Un juguete sexual inspirado en el supuesto órgano copulador de la criatura
El aligátor americano, también conocido como caimán americano, Alligator mississipiensis, es un tipo de cocodrilo que habita en Estados Unidos. Estos animales tienen un extraño pene blancuzco y con aspecto blando, que está continuamente en erección pero retraído en el interior de la cloaca, y que solo es impulsado al exterior por un reflejo muscular, al estimularse los nervios adecuados. En nuestra criatura el pene también se mantiene en el interior del cuerpo de ésta, hasta que no es necesaria su presencia, lo que coincide un poco con la explicación de Elisa y con la entrepierna plana que vemos en pantalla. Al no depender de sangre ni de ningún tipo de mecanismo hidráulico para su funcionamiento son los músculos los que se encargan de producir su salida, y la estructura elástica de un tendón es la que hace que se retraiga de nuevo, como si de una goma elástica se tratara.
En cuanto la musculatura de la cloaca se relaja y se abre, éste se libera. Los propios científicos encargados de su estudio comparan la eyección del pene del aligátor con la salida del contenido de un tubo de pasta de dientes, para que nos hagamos una idea. Si esto es así con la criatura de La forma del agua no lo sabemos, pero a mí es lo que se me vino a la mente. De esta característica reptiliana hablaba al principio del post, cuando dudábamos de su naturaleza.
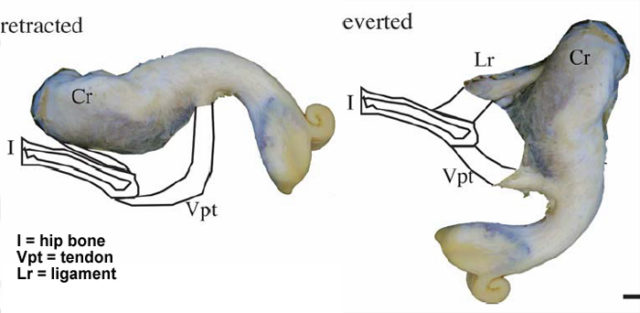
El pene siempre erecto de un aligátor
Otro de los aspectos importantes es el rostro, pues Doug Jones se tiene que expresar, y una máscara habría sido un estorbo para ello. El rostro de la criatura está conseguido con prótesis para las agallas y repliegues, que se manipulaban externamente y se movían por control remoto. Se esforzaron por crear un rostro no demasiado extraño y una boca que fuera besable, por lo que los labios son bastante humanos. Su nariz es casi inexistente, reduciéndose a dos pequeñas fosas nasales y son sus grandes ojos lo que más destaca en su rostro. Estos parpadean de una curiosa forma, en horizontal en vez de en vertical, y es debido a que posee una membrana nictitante o tercer párpado, que es transparente y sirve para protegerlo del agua cuando se sumerge. De hecho vemos como estos párpados se le cierran en algunas escenas justo cuando se está hundiendo en el agua.

Los ojos de la criatura
Son muchos los detalles que hemos analizado de esta criatura, y aún así estoy seguro de que podríamos profundizar mucho más en cada uno de ellos o en otros que se nos hayan pasado, como por ejemplo la forma de alimentación, pero queda claro que disfrutar del cine añadiendo un punto de vista científico hace que una película, ya de por sí magnífica, mejore aún más.
Este post ha sido realizado por Carlos Lobato (@BiogeoCarlos) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias científicas y más información:
Kelly, D. A. (2013). Penile anatomy and hypotheses of erectile function in the American alligator (Alligator mississippiensis): muscular eversion and elastic retraction. The Anatomical Record, 296(3), 488-494.
Salas, R., Cruz, S. J. M., Castillo, E. B., & Guzmán, C. T. (2018). Análisis morfométrico y batimétrico de la laguna de Huamanpata, región Amazonas. INDES Revista de Investigación para el Desarrollo Sustentable, 2(2), 30-38.
Jackson, D. C. (1987). HOW DO AMPHIBIANS BREATHE BOTH. Comparative physiology: Life in water and on land, 9, 49.
Daniels, C. B., & Orgeig, S. (2003). Pulmonary surfactant: the key to the evolution of air breathing. Physiology, 18(4), 151-157.
España, M. D. C. M., Martinez, J. M., Moreira-Turcq, P., Bonnet, M. P., Villar, R. E., de Gamundi, A. V., … & Seyler, P. Monitoreo espacial y temporal del estado trófico de los lagos de planicies de inundación en la Amazonía central mediante sensores remotos.
Brainerd, E. L., & Owerkowicz, T. (2006). Functional morphology and evolution of aspiration breathing in tetrapods. Respiratory physiology & neurobiology, 154(1-2), 73-88.
La “osmótica” criatura de la Laguna Negra
Pero mira como osmorregulan los peces en el río
Descubrieron un arrecife de coral en el río Amazonas
Descubren inmenso arrecife en la desembocadura del río Amazonas
Wikipedia: Ósmosis
Wikipedia: Osmorregulación
La salinización de los ríos es un problema medioambiental en todo el planeta
El artículo La Criatura de “La forma del agua” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los animales que respiran en agua
- La distribución del agua animal y el curioso caso del potasio
- La forma de las hojas
Crónica de la 2ª jornada “Las pruebas de la educación”
Después el éxito de la primera edición de la jornada “Las pruebas de la educación”, el pasado 2 de febrero tuvo lugar la segunda edición de ésta jornada que nuevamente completó aforo.
La jornada busca generar debate sobre cuestiones que afectan a la educación, desde el sistema educativo hasta los métodos de aprendizaje en auge, pasando por los problemas de aplicación de los distintos programas o las técnicas y herramientas con los que hacer frente a los problemas cognitivos de los alumnos. Y todo ello basándose en la evidencia científica disponible al respecto.

Problemas de aprendizaje
El encargado de abrir la jornada fue José Ramón Alonso, quien trató el tema del autismo en la educación. Tras explicar que el déficit de la interacción social y los patrones de comportamiento restringidos y repetitivos son las principales características de los trastornos del espectro autista, el ponente pasó a dar una serie de consejos para los profesores de estos alumnos.
Entre ellos, ayudar al niño a desarrollar estrategias y habilidades para comunicarse o adaptar la enseñanza a las peculiaridades del aprendizaje del niño. Dirigirse al niño en primera persona e individualmente o hacer preguntas cerradas en lugar de abiertas son algunas de las adaptaciones que el profesorado puede aplicar para facilitar el día a día a los alumnos con trastorno del espectro autista.
Por otro lado, un trastorno de aprendizaje común en el aula es la dislexia, que crea dificultades de lectura en los alumnos que lo padecen. Joana Acha describió la base fonológica del trastorno acreditada por la neurociencia. En la actualidad hay muchos métodos que aseguran ayudar con la dislexia: el método Tomatis, el Brain Gym, el método Doman o la kinesiología. Ninguno de ellos está avalado por la evidencia científica.
En el caso de la dislexia lo probado científicamente es de base fonológica, ya que se ha demostrado que trabajar habilidades como el conocimiento fonológico, la asociación sonido-letra o la adquisición del léxico visual, entre otras, tienen un efecto positivo.
Deberes, evaluación y eficacia
¿Sirven para algo los deberes? ¿Qué utilidad tienen las evaluaciones? Son dos de las cuestiones a la orden del día en el ámbito educativo y que han provocado posturas muy encontradas, hasta llegar a la huelga de deberes. La psicóloga Marta Ferrero fue la encargada de presentar las pruebas científicas al respecto.
Y lo cierto es que, pese a la mala fama que tienen últimamente, las pruebas científicas avalan tanto los deberes como las evaluaciones. Según las investigaciones, la evaluación no solo sirve para valorar, sino que favorece el aprendizaje y fomenta el estudio: cuantas más evaluaciones (recuperación de información, no solo exámenes con nota) más sesiones de estudio. No solo eso, también ayuda a detectar las lagunas de conocimiento en el aprendizaje.
En el caso de los deberes la conclusión es clara: los deberes aportan beneficios a todos los alumnos. Pero no cualquier tipo de deberes. Según explicó la ponente, los deberes han de mandarse con un propósito y también es importante que en los hogares se cree un espacio y una rutina para hacerlos. Finalmente, Ferrero presentó las dificultades deseables1 (concepto enmarcado en la Teoría del Desuso, de Bjork y Bjork2) como método de enseñanza.
Este método está basado en el funcionamiento de la memoria, que es precisamente el tema que trató el psicólogo Joaquín Morís. Al principio de su ponencia el psicólogo sentó la base de que todo aprendizaje implica memoria y que memoria no es igual a aprender de memoria.
Según explicó Moris, cuanto más accesible una habilidad, menor aprendizaje. Y es que entra en juego la ilusión de la fluidez: “si estoy haciendo bien la tarea, cómo no voy a estar aprendiendo”. De ahí que las dificultades deseables sean un método para mejorar el aprendizaje.
Por supuesto, el aprendizaje se da en el contexto de un sistema educativo concreto que también influye. La filóloga Inger Enkvist presentó el caso del sistema educativo sueco, que instauró la escuela educativa única o de base. En ella los profesores tenían 5 consignas: motivación, actividad, concreción, individualización y colaboración. El sistema concatenó reformas y leyes educativas y en la década de los ochenta prácticamente desaparecieron las notas, un alumno recibía su primera nota a los 15 años. Se trata de un sistema que, según la ponente, además de no contar con el beneplácito del profesorado, no obtuvo los resultados esperados.
Además del sistema educativo, los distintos centros también tienen un gran impacto en la educación. Es de lo que trató la ponencia de Beronika Azpillaga, quien forma parte de un grupo que investiga la eficacia de distintos centros escolares en el País Vasco y analiza las características de aquellos con mejores resultados.
Entre las claves de los centros eficaces destacó el seguimiento y las tutorías fuertes, la atención a la diversidad y la importancia de un buen equipo humano. En esta ocasión trajo la segunda parte de la investigación que junto a Luis Lizasoain presentó en la anterior edición de la jornada.
En la charla-coloquio final se pusieron de manifiesto algunos de los problemas a los que se enfrenta la educación en la actualidad. Entre ellos destacó la distancia existente entre la investigación y la docencia y la dificultad del profesorado para acceder e interpretar correctamente investigaciones científicas relevantes de su campo. Debido a este cisma, es frecuente que los profesores se dejen llevar por metodologías que se ponen de moda a pesar de carecer de base científica y que, preocupantemente, en muchas ocasiones provienen de fuentes fiables.
De ahí que se subrayase la importancia de dotar a los profesores de las aptitudes y herramientas adecuadas para que puedan discernir entre metodologías eficaces y científicamente probadas y metodologías sin base alguna.
Referencias:
1Bjork, R.A. (1994) Memory and metamemory considerations in the training of human beings. In J. Metcalfe &A. Shimamura (Eds.), Metacognition: Knowing about Knowing (pp. 185-205) Cambridge, MA:MIT Press.
2 Bjork, E. L., & Bjork, R. A. (2014). Making things hard on yourself, but in a good way: Creating desirable difficulties to enhance learning. In M. A. Gernsbacher and J. Pomerantz (Eds.), Psychology and the real world: Essays illustrating fundamental contributions to society (2nd edition). (pp. 59-68). New York: Worth.
Sobre la autora: Ziortza Guezuraga, periodista, es colaboradora de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Crónica de la 2ª jornada “Las pruebas de la educación” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Crónica de la 1ª jornada “Las pruebas de la educación”
- Las pruebas de la educación 2018: El coloquio
- Cómo destruir un buen sistema de educación. El ejemplo sueco
La ciencia y la tentación de la narrativa
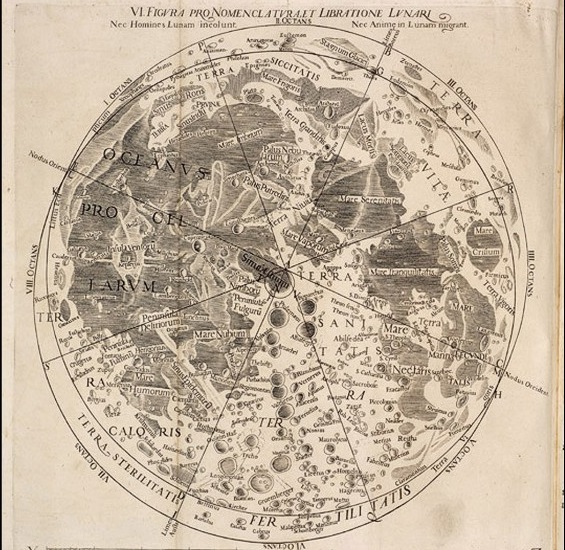
La publicación en 1610 del “Sidereus nuncius” de Gaileo contenía mapas de la Luna con montañas y planicies que echaban por tierra la visión del universo aristotélica y las narrativas asociadas. En 1651 Franceso Grimaldi dibujaba este mapa a las órdenes de Giovanni Battista Riccioli, sacerdote jesuita, en el que éste bautizaba los accidentes geográficos lunares con nombres que aún se usan hoy día.
La gran tragedia de la ciencia, decía Thomas Henry Huxley con considerable ironía, es el asesinato de una hermosa hipótesis a manos de un repugnante dato. Y es algo mucho más común de lo que imaginamos: innumerales, intrincadas, preciosas y espectacularmente explicativas hipótesis resultan cada día dañadas, heridas o destruidas por la súbita aparición en escena de un feo y aparentemente insignificante dato que sin embargo se convierte en su victimario y ejecutor. Porque no importa lo atractiva que pueda parecer una hipótesis ni la potencia de su capacidad explicativa, no hay explicación o teoría de funcionamiento de un fenómeno natural que pueda resistir a la imposibilidad de explicar un dato fehaciente.
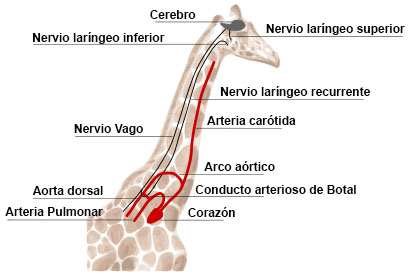
El fenómeno está especialmente extendido en biología por culpa de la inagotable y feroz creatividad chapucera de la evolución por selección natural. Es común que un intrincado y complejo fenómeno que se podría explicar por la elegante interacción de un puñado de reglas comprensibles y sencillas resulte funcionar a base de ad hocs, como una sucesión de parches colocados unos sobre otros empleando los materiales menos convenientes y usando las combinaciones menos elegantes. La naturaleza suele utilizar lo que funciona y tiene a mano aunque la solución no sea la más económica o racional, y así es común que las redes genéticas que controlan un fenómeno usen absurdas combinaciones y extraños ciclos de control, o que una adaptación morfológica provoque situaciones carentes de lógica como el nervio faríngeo recurrente de la jirafa, que llega a alcanzar los 5 m de longitud para cubrir una distancia mucho menor. Ante este tipo de datos y hechos reales cualquier hipótesis alambicada y hermosa puede resultar más que perjudicada.
En el fondo se trata de uno de los muchos problemas que traen ’de fábrica’ los cerebros humanos a la hora de entender el universo que nos rodea; esos defectos del intelecto que tanto nos dificultan pensar con absoluta claridad. Porque para nuestra forma de pensar no hay nada más intoxicador y atrayente que una buena historia; nos gusta tanto una narrativa clara, elegante y sencilla que somos incapaces de resistirnos a la tentación y no sólo creemos en ella, sino que si es necesario la ‘ajustamos’ un poco si no encaja con los datos.
Las narrativas, las buenas historias, actúan sobre la mente humana como un virus: la colonizan, la invaden y la emplean para reproducirse transmitiéndose a otras mentes. Los cuentos y las narraciones nos gustan tanto que existen industrias multimillonarias dedicadas a ellos, desde los medios al cine, y la creación y mantenimiento de narrativas forma parte clave de nuestra política y de nuestra sociedad. El periplo del héroe, también llamado el monomito, es el arquetipo básico de buena parte de nuestras historias y su ubicuidad y persistencia demuestra la potencia que la narración tiene sobre nosotros. Las buenas historias, que cuanto están bien narradas son capaces de esconder sus propios fallos y debilidades, ejercen tan poderosa influencia sobre nuestra mente como para resultar peligrosas.
Este peligro se refiere sobre todo a la interacción entre las historias y la realidad, algo que ocurre en ciencia todo el tiempo. Los científicos son humanos por tanto sus mentes funcionan con historias; una buena teoría o una buena hipótesis no es más que una buena historia que explica una serie de fenómenos y los integra en un todo comprensible. Cualquier estudiosos de la realidad tenderá a construir una narrativa con lo que contempla, una historia que le ayude a comprender de qué manera aspectos aparentemente diferentes son en realidad facetas distintas de un fenómeno subyacente más fácil de comprender. En ese sentido la emisión de hipótesis y la creación de teorías no se diferencia en exceso de la creación de mitos o de narraciones; teorizar no está tan lejos de la literatura o del arte como pudiésemos imaginar.
Pero en la ciencia hay un paso más que resulta vital: confrontar nuestras preciosas narrativas hipotéticas, esas creaciones del intelecto cargadas de lógica y elegancia, con la cruda realidad. Donde a menudo las bellas hipótesis que podrían explicarlo todo de un modo sencillo y elegante resultan evisceradas porque a pesar de todo su poder explicativo resultan ser incapaces de explicar un simple dato. Toda la creatividad humana, toda la estructura del viaje heroico, todo el afán de simplicidad belleza de una hermosa hipótesis quedan en nada cuando esa explicación no es capaz de enfrentarse a un hecho. La narración nada tiene que hacer si la historia que estamos contando no puede explicar lo que de verdad sucede en ese experimento, en ese detalle anatómico, en ese detector.
Y de este modo las más bellas narrativas de la ciencia se pierden y desaparecen, y carreras científicas enteras llegan a un brusco final cuando aparecen datos que masacran sin piedad su capacidad explicativa. Porque los cerebros de los humano somos muy vulnerables al poder de las historias, pero en ciencia una buena narración no es suficiente.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La ciencia y la tentación de la narrativa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Los vacíos cósmicos y la estructura del universo

Imagen en infrarrojo del espacio profundo tomada por el Telescopio Espacial Hubble
Cuando pensamos en el universo en su conjunto imaginamos una cantidad enorme de galaxias. De hecho, las galaxias son lo más estudiado por los astrónomos para comprender el universo en su conjunto. Sin embargo, los investigadores están descubriendo que hay mucho que aprender de los vacíos cósmicos: franjas de espacio mayormente vacío, tan grandes que la luz tarda cientos de millones de años en atravesarlos.
La temperatura y la presión del gas presente en los huecos podría, por ejemplo, proporcionar pistas sobre cómo la energía circula a través del cosmos. Un equipo de investigadores encabezado por David Alonso, de la Universidad de Oxford (Reino Unido), han dado uno de los primeros pasos para determinar estas propiedades del gas mediante el análisis de cómo el gas distorsiona la luz del Universo primitivo.
El fondo cósmico de microondas (FCM) es la primera luz que se libera en el universo, aproximadamente 380,000 años después del Big Bang. El gas intergaláctico aumenta la energía de los fotones del FCM, y esta distorsión es una poderosa herramienta para estudiar los cúmulos de galaxias. Pero nadie la ha usado para estudiar los vacíos cósmicos. El equipo de Alonso combinó mapas del FCM con imágenes de 774 vacíos cósmicos. A partir de ahí los investigadores dedujeron las propiedades del gas en cada vacío comparando de la energía medida de los fotones del FCM con modelos de la presión electrónica en los vacíos.
De esta forma los astrofísicos descubrieron que la presión es menor que el promedio cósmico. Este resultado no es sorprendente, dado que poco se puede esperar que suceda en un vacío, y puede significar que los vacíos evolucionaron pasivamente conforme aumentaba la edad del Universo.
Pero hay indicios en los datos de que el gas podría estar más caliente de lo esperado. Si este hallazgo se confirmase, podría ser una señal de que los poderosos chorros emitidos por los agujeros negros supermasivos bombeen energía al gas intergaláctico y ayuden de esta manera a dar forma al universo. La resolución de este problema tendrá que esperar varios años hasta que se disponga de telescopios más potentes, como el Observatorio Simons en Chile.
Referencia:
David Alonso, J. Colin Hill, Renée Hložek, and David N. Spergel (2018) Measurement of the thermal Sunyaev-Zel’dovich effect around cosmic voids Physical Review D doi: 10.1103/PhysRevD.97.063514
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Los vacíos cósmicos y la estructura del universo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los vacíos cósmicos y la relatividad general
- La estructura del universo como una interferencia cuántica
- La estructura en común de estrellas de neutrones y aparcamientos
Alexandre Grothendieck, el genio rebelde
En una conversación matemática, alguien sugirió a Grothendieck que debería considerar un número primo particular. “¿Te refieres a un número concreto?”, contestó Grothendieck. La otra persona replicó “Sí, un número primo concreto”. Grotendieck sugirió: “De acuerdo, tomemos el 57”.
Allyn Jackson en [2], página 1196.
El 57 se conoce desde entonces como “el número primo de Grothendieck”: por cierto, no es primo, ya que 57 = 3 x 19…

Alexandre Grothendieck. Fuente: Wikimedia Commons.
Alexandre Grothendieck nació el 28 de marzo de 1928. Su madre, Hanka Grothendieck (1900-1957), era periodista, y su padre, Sascha Schapiro (1889-1942), un fotógrafo ruso, judío y militante anarquista.
Entre 1934 y 1939, Hanka y Sascha se unieron a los anarquistas en la Guerra Civil Española, dejando a su hijo a cargo de unos conocidos en Hamburgo. Tras reunirse con sus padres en el sur de Francia, Sascha fue recluido en el campo de internamiento de Vernet y transferido después al de Auschwitz, en el que fue asesinado. Hanka y Alexandre fueron enviados al campo de internamiento de Rieucros, después al de Brens en 1942. Con ayuda de una asociación protestante cuya misión era la de salvar niños judíos, se evadieron para evitar la deportación y la muerte.
Al acabar la guerra, Alexandre comenzó sus estudios de matemáticas en Montpellier. Laurent Schwartz (1915-2002) y Jean Dieudonné (1906-1992) fueron sus directores de tesis (Produits tensoriels topologiques et espaces nucleaires, 1953). Al conocerle, entregaron a su nuevo alumno un listado de catorce problemas que consideraban como un vasto programa de trabajo para varios años, y le pidieron que eligiera uno de ellos. Algunos meses más tarde, Alexandre fue a ver a sus directores habiendo resuelto los catorce problemas: la leyenda acababa de comenzar.
En la primera parte de su carrera, Grothendieck trabajó en análisis funcional y, a pesar de los grandes aportes en esta área, sus posteriores trabajos en geometría algebraica, teoría K y álgebra homológica son los que le dieron la fama.
En 1966 fue galardonado con la Medalla Fields, pero por razones políticas se negó a acudir a Moscú a recoger su premio. Fue el primero de una serie de reconocimientos y posicionamientos políticos que le alejaron sin remedio de la comunidad científica. En 1977 se le concedió la Medalla Émile Picard de la Academia de Ciencias de París, que subastó para donar el dinero al gobierno de Vietnam del Norte. En 1988 se le concedió el Premio Crafoord de la Real Academia Sueca de Ciencias (junto a su alumno Pierre Deligne) y lo rechazó, argumentando que no necesitaba ni el dinero ni los honores.

Carta en la que Grothendieck renuncia a toda utilización comercial de sus obras, 2010. Fuemte: Secret Blogging Seminar
Apátrida, pacifista, ecologista, y muy influenciado por el movimiento hippy, Alexandre Grothendieck fue un genio de las matemáticas, con una personalidad indomable. Falleció el 13 de noviembre de 2014. En las referencias recomendadas puede conocerse más sobre su vida y su obra.
Como topóloga, no he podido resistirme a reproducir estas palabras de Alexandre Grothendieck extraídas de su Récoltes et Semailles, Réflexions et témoignage sur un passé de mathématicien. Eneste largo texto, producto de profundas meditaciones realizadas durante años y nunca publicado, el matemático pasaba revista a su obra científica y analizaba el entorno matemático con, en algunas ocasiones, una mirada muy crítica.
La noción de “espacio” es sin duda uno de las más antiguas en matemáticas. Es tan fundamental en nuestra aprehensión “geométrica” del mundo que ha permanecido más o menos tácita durante más de dos milenios. Es a lo largo del pasado siglo cuando esta noción ha conseguido desprenderse, gradualmente, del dominio tiránico de la percepción inmediata (de un único y mismo “espacio” que nos rodea), y de su teorización tradicional (“euclidiana”) para adquirir su autonomía y su dinámica propias. Hoy en día, es una de las pocas nociones universales y más comúnmente utilizadas en matemáticas, sin duda familiar para cualquier matemático sin excepción. Además, es una noción proteiforme donde las haya, con cientos y miles de caras, dependiendo del tipo de estructuras que se incorporen a estos espacios, desde las más ricas (como las venerables estructuras “euclidianas” o las estructuras “afines” y “proyectivas”, o también las estructuras “algebraicas” de las “variedades” del mismo nombre, que las generalizan y suavizan) hasta las más simples: aquellas en las que cualquier elemento de información “cuantitativo” de cualquier tipo parece haber desaparecido sin posibilidad de retorno, y donde solo queda la quintaesencia cualitativa de la noción de “proximidad” o la de “límite”, y la versión más elusiva de la intuición de la forma (llamada “topológica”). La más pobre de todas estas nociones, la que hasta ahora, y durante el último medio siglo, había tomado el lugar de una especie de amplio marco conceptual común para abarcar a todas las demás, era la del espacio topológico. El estudio de estos espacios constituye una de las ramas más fascinantes, la más persistente, de la geometría: la topología.
Récoltes et Semailles, La topologie ou l’arpentage des brumes, 51-52.
Más información:
[1] Philippe Douroux, Alexandre Grothendieck. Un voyage à la poursuite des choses évidentes, Images des Mathématiques, CNRS, 2012
[2] Allyn Jackson, Comme Appelé du Néant-As If Summoned from the Void. The Life of Alexandre Grothendieck (parte 1 y parte 2), Notices AMS, vol. 51 (9) (2004) 1038-1056 y vol. 51 (10) (2004) 1196-1212
[3] Winfried Scharlau, Who Is Alexander Grothendieck?, Notices AMS, vol. 55 (8) (2008) 930-941
[4] Javier Fresán, Un congreso de geometría algebraica celebra la figura de Grothendieck, genio, apátrida y ermitaño, Público, 2009
[5] Francisco R. Villatoro, La obra de Alexander Grothendieck (1928-2014),La ciencia de la mula Francis, 16 noviembre 2014
[6] Textos de Alexandre Grothendieck, recopilación de Juan Antonio Navarro González
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Alexandre Grothendieck, el genio rebelde se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Wolfgang Döblin, un genio perdido
- Alexandre Yersin: el rango que otorga la ciencia
- El genio de Ampère
Relaciones hídricas y salinas de los animales: fundamentos

Los líquidos corporales de los animales se distribuyen en tres espacios o compartimentos, principalmente: celular (líquido intracelular), espacios entre las células (líquido intersticial) y, de haberlas, cavidad general del cuerpo y sistema vascular (líquido celómico, plasma sanguíneo, hemolinfa o equivalente). Como vimos aquí, el líquido intersticial y el plasma pueden ser considerados conjuntamente líquido extracelular (o medio interno). En los animales sin sistema vascular la razón de esa identidad es obvia. En los animales con sistema circulatorio abierto no hay discontinuidad alguna entre la hemolinfa y el líquido que baña las células. Y en los de sistema cerrado, los capilares tienen poros (entre las células endoteliales o, incluso, atravesando tales células) a través de los cuales se establece una continuidad casi absoluta entre ambos sistemas; las únicas sustancias que no atraviesan la barrera que representa el endotelio capilar son ciertas moléculas, como proteínas plasmáticas, cuyo gran tamaño impide su salida del capilar hacia los espacios intercelulares. Por lo tanto, el líquido intersticial y el plasma (o equivalente) tienen la misma concentración osmótica y casi idéntica composición iónica. Sin embargo, aunque los líquidos extra e intracelular tengan también la misma concentración osmótica, la composición de iones y de ciertas moléculas orgánicas es muy diferente en ambos fluidos.
Por las razones dadas, desde un punto de vista funcional, resulta útil reducir las subdivisiones anteriores a dos: medio intracelular y medio interno. Ambos medios se encuentran separados por la membrana celular que, dada su carácter semipermeable, ejerce de barrera para con ciertos solutos (Na+, Cl–, sustancias orgánicas) pero no para con el K+ ni para con el agua. Y por otro lado, el medio interno y el medio exterior también se encuentran separados por el tegumento, que normalmente hace función de barrera.
Los animales han de preservar su contenido hídrico dentro de ciertos márgenes, porque de ese contenido depende la existencia de los fluidos corporales y que esos fluidos tengan características compatibles con las funciones animales. Al fin y al cabo, todas las estructuras internas se hallan bañadas por fluidos, que son el ambiente inmediato de células, orgánulos celulares y moléculas. Su composición es el contexto en el que funcionan aquellas. Las concentraciones de los iones a los que nos referiremos enseguida dependen del volumen de los fluidos en los que se encuentran disueltos. Y además, de ese volumen depende el de las células y tejidos.
Los animales también han de mantener en un rango restringido de valores la concentración intracelular de los iones inorgánicos. El K+, principal catión intracelular, ha de mantener una concentración relativamente alta, pues así lo requiere la estabilidad e integridad funcional de las proteínas. Del mismo modo, han de mantener a niveles reducidos la concentración de Na+ y Cl– dentro de las células, porque incluso concentraciones moderadas de esos iones desestabilizan las proteínas celulares. Además, las concentraciones intra y extracelulares de esos tres iones puede determinar (dependiendo de la permeabilidad relativa de la membrana celular para con cada uno de ellos) la diferencia de potencial eléctrico entre los lados interno y externo de la membrana, lo que resulta crucial desde el punto de vista de la transmisión del impulso nervioso en las neuronas y de la contracción muscular.
Por todo lo apuntado hasta aquí, desde el punto de vista de los equilibrios que han de mantener los animales en materia de contenido hídrico y concentración interna de solutos, la capacidad para ejercer un cierto control sobre los movimientos de agua y sales a través de esas barreras es esencial en la mayor parte de las especies. Aunque ese control se ejerce de forma diferente en las dos barreras mencionadas (membrana celular y tegumento corporal) dependiendo del tipo de relación que cada especie mantiene con el medio en el que se encuentra.
Los animales, como es sabido, ocupan medios acuáticos y el medio terrestre. En lo relativo a los medios acuáticos, estos pueden tener muy diferentes concentraciones salinas. No obstante, la división fundamental es la que existe entre el agua de mar y las aguas dulces. El agua marina tiene una concentración osmótica de 1000 mOsm (miliosmolar), que corresponde a unos 35 g kg-1 (g de sales por kg de agua). Las aguas dulces varían dentro de un rango relativamente estrecho, de entre 0,15 y 15 mOsm; en términos de masas, su concentración de sales se encuentra entre 0,1 y 0,2 g kg-1, aunque se consideran aguas dulces todas aquellas cuya concentración gravimétrica es inferior a 0,5 g kg-1. Los iones principales del agua de mar son Na+ (470 mM), Cl– (548 mM), Mg+2 (54 mM), SO4-2 (28 mM), Ca+2 (10 mM) y K+ (10 mM). Las concentraciones de esas sustancias en aguas dulces, aunque muy bajas, pueden variar considerablemente entre unas masas de aguas y otras. No obstante, las siguientes pueden considerarse típicas del agua dulce: Na+ (0,35 mM), Cl– (0,23 mM), Mg+2 (0,21 mM), SO4-2 (0,19 mM), Ca+2 (0,75 mM) y K+ (0,08 mM).
Por otra parte, también hay importantes volúmenes de agua cuya concentración salina se encuentra entre la del mar y la del agua dulce: son las aguas salobres. Son relativamente normales en zonas costeras en las que el aporte de agua dulce continental diluye el agua marina, especialmente en los estuarios. Y también hay aguas hipersalinas, normalmente en lagos que experimentan una fuerte evaporación; son las aguas cuya concentración supera claramente la del agua de mar.

Flamencos en el lago salino y alcalino de Bogoria (Kenya). En primer plano emergencia de agua caliente.
En lo que se refiere a los medios terrestres, no existen medios que puedan ser diferenciados de forma tan nítida como las aguas saladas y las aguas dulces. La variable relevante en este caso es la presión parcial de vapor de agua en la atmósfera, porque esa variable, como veremos, afecta directamente a la pérdida de agua de un animal por evaporación. La presión de vapor de agua es la porción de la presión atmosférica que es debida al gas vapor de agua y tiene la peculiaridad, por comparación con otros gases, de que tiene un valor límite que no puede superar. Ese valor, que es la presión de saturación, varía con la temperatura: cuanto más alta es esta, mayor es la presión de vapor de saturación: a 0ºC, la presión de saturación del vapor de agua es 4,6 mmHg (0,61 kPa) y a 40ºC es 55,3 mmHg (7,37 kPa).
El agua que puede perder por evaporación un animal depende (1) de la presión parcial de vapor de agua en la atmósfera en la que se encuentra y de lo próxima o alejada que se encuentre esa presión de la de saturación (cuanto mayor sea la diferencia entre la presión de saturación y la presión parcial de vapor de agua, mayor será la pérdida), (2) de la renovación del aire en la proximidad del tegumento, (3) de la temperatura corporal del animal (por razones que no detallaremos aquí), (4) del grosor de la barrera que separa de la atmósfera el fluido corporal que se evapora y (5) de la permeabilidad del tegumento para con el agua. Por lo tanto, los factores ambientales que más inciden en la pérdida potencial de agua por evaporación son la presión parcial de vapor del agua, el viento, la temperatura del ambiente (porque de ella depende la presión de saturación) y la temperatura del animal. El agua se puede perder por otras vías, pero no nos ocuparemos aquí de ellas pues no guardan relación directa con los factores ambientales, que son los que ahora nos interesan. Por lo mismo, tampoco nos ocuparemos de los mecanismos para adquirir agua.
Los animales pueden desarrollar tres tipos de regulación: osmótica, iónica y de volumen. La regulación osmótica (osmorregulación) consiste en el mantenimiento en niveles constantes o casi constantes la concentración osmótica del medio interno. Cuando se define de esta forma la osmorregulación, normalmente se asume que tal capacidad se ejercita en el contexto de variaciones ambientales en la concentración osmótica del medio externo. Pero eso no tiene por qué ser así. También cabe hablar de osmorregulación en aquellos casos en que los animales mantienen concentraciones osmóticas internas constantes (o casi constantes) y diferentes de la del medio externo. Incluso si nos referimos a un animal terrestre que vive en un medio no acuático y que, por tanto, no puede ser caracterizado en términos de concentración osmótica, también podemos considerarlo osmorregulador si es capaz de mantener constante la concentración osmótica del medio interno en un contexto, por ejemplo, de variaciones en la disponibilidad de agua o bajo regímenes alimenticios de variables contenidos salinos.
Los animales que no regulan la concentración osmótica de su medio interno son osmoconformadores, lo que quiere decir que, si ocupan medios acuáticos la concentración osmótica de su medio interno se asemeja a la del medio externo y que si se trata de animales terrestres, varía en función de las condiciones ambientales.
La regulación iónica, por su parte, consiste en la capacidad para mantener constante la concentración de iones inorgánicos en el medio interno. En este caso no cabe hablar de una capacidad de regulación iónica general, sino que tal capacidad siempre se refiere a un ión concreto puesto que cada ión cuya concentración está regulada está sujeto a procesos específicos. También en relación con los iones inorgánicos recurrimos al término conformador para denominar al animal que no regula la composición de alguno de ellos; como en el caso de la regulación, también aquí la incapacidad para regular la concentración de un ión es específica para ese ión.
Nos interesa también la capacidad –o su ausencia- para regular el volumen del medio interno. Si un animal dispone de tal capacidad diremos que es un regulador del volumen, y que es conformador del volumen si carece de ella.
Para terminar, interesa valorar qué consecuencias tiene para el medio intracelular que un animal sea o no capaz de regular las magnitudes anteriores. Dado que las membranas celulares son permeables al agua, la concentración osmótica del medio intracelular es la misma que la de su medio interno; por lo tanto, un animal que regule este, mantendrá aquel igualmente regulado. Si, por el contrario, no regulase osmóticamente su medio interno, el medio intracelular experimentará una variación tendente a igualar su concentración con la de aquel, y dado que los iones inorgánicos han de ser mantenidos en un rango estrecho de concentraciones, ello podría provocar cambios en el volumen de las células debidas a flujo osmótico de agua.
En lo que a la concentración de iones inorgánicos se refiere, es importante que los ya señalados Na+, Cl– y K+ se mantengan dentro de un margen relativamente estrecho de concentraciones propias de los medios interno e intracelular. Las variaciones que se produzcan en el medio interno no deberían ser importantes ni incidir en lo que ocurra dentro de las células. De lo contrario, y como ya se ha señalado, la estructura de las proteínas (enzimas, principalmente) y, por ende, su integridad funcional se vería amenazada.
En lo que al volumen se refiere, la capacidad o incapacidad para regular el volumen del medio interno no debería afectar al volumen del medio intracelular si no se producen cambios en la osmolaridad. No obstante, en el caso de que un cambio en el volumen del medio interno ocurriese a la vez que una variación en su concentración osmótica, el volumen celular podría verse afectado como ya se ha dicho antes. No obstante, muchos animales han desarrollado la capacidad de realizar ajustes de la concentración intracelular de osmolitos orgánicos gracias a los cuales pueden mantener constante su volumen celular (regularlo) aunque cambie la concentración osmótica fuera (y dentro) de las células. Gracias a esa capacidad, a la que nos referimos aquí, se evita el flujo osmótico de agua hacia o desde el interior celular y el volumen permanece constante. A esa capacidad se la denomina regulación isosmótica del volumen celular.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Relaciones hídricas y salinas de los animales: fundamentos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Las ecuaciones de campo de la relatividad general
La teoría general de la relatividad hemos visto que se basa, de forma análoga a la especial, en dos principios básicos: el de equivalenvia y el de covariancia. También hemos podido apreciar lo fácil e intuitivo que es enunciarlos. Otra cosa muy diferente es expresarlos matemáticamente y las consecuencias que se derivan de ellos son impresionantes, paradójicas y no fácilmente aprehensibles. Por ello, aunque la tentación sea obviar todo el aspecto matemático, no podemos dejar de pasar muy por encima por él y tener una idea de, al menos, el aspecto que tienen las llamadas ecuaciones del campo de Einstein [1][2].
Einstein empleó varios años y muchas discusiones y trabajos con matemáticos, especialmente Marcel Grossman y David Hilbert, para poder lograr la expresión matemática de sus ideas. Aunque Einstein ya dispuso de un primer esbozo en 1911 no sería hasta finales de 1915 que encontrase la forma definitiva [3]. La ecuaciones de campo se presentaron a la Academia Prusiana de Ciencias en noviembre de 1915. La idea general es que las soluciones a estas ecuaciones indican cómo el espaciotiempo y la masa-energía se influyen el uno a la otra y viceversa. Por ejemplo, cómo afecta al espaciotiempo la presencia de una masa como la del Sol, y cómo este espaciotiempo afecta al movimiento de una masa menor en las proximidades del Sol, como la de un planeta; o qué le pasa al espaciotiempo cuando una estrella masiva colapsa sobre sí misma hasta crear un punto de densidad infinita.
La dificultad matemática que encontró Einstein estriba en expresar cuantitativamente que el espaciotiempo se curva y cómo lo hace. Para conseguirlo tuvo que aprender las bases toda una rama de las matemáticas: el cálculo tensorial.
El espaciotiempo se curva en presencia de masa-energía. Imagen: ESA–C.Carreau
El espaciotiempo se curva
Si cortas una naranja por la mitad, quitas la pulpa del interior, e intentas aplanar el hemisferio de piel resultante, terminas rajándolo. Si tratas de aplanar algo con la forma de una silla de montar, como una patata frita (de las de bolsa) revenida, te encuentras con el problema contrario: hay “demasiada” superficie y se te forman pliegues. Si coges, sin embargo, un rollo de papel de cocina y deseas aplanarlo, no hay nada más fácil, con desenrollarlo, listo. Las superficies como las esferas se dice que están curvadas positivamente, las que tienen la forma de una silla de montar que lo están negativamente, y las que son como el papel de cocina son, simplemente, planas (démonos cuenta que son planas en este sentido aunque no estén en un plano). Esto es así porque la curvatura se define en términos de “geometría intrínseca” de una superficie, en la que la distancia se mide en función de los caminos que están dentro de la superficie.
Hay varias formas de hacer precisa esta noción de curvatura y hacerla cuantitativa, de tal manera que a cada punto de la superficie se pueda asociar un número que diga “cómo de curvada” está en ese punto. Para poder hacer esto es necesario que se cumplan determinadas condiciones matemáticas que permitan determinar las longitudes de los caminos, es lo que se llama una métrica riemanniana. La noción de curvatura puede ser generalizada a un mayor número de dimensiones, de tal forma que se habla de la curvatura en un punto en una variedad riemanniana de d dimensiones. Sin embargo, cuando la dimensión es mayor de dos, es decir, no es un plano lo que se curva sino un espacio, las posibilidades de curvatura en un punto se hacen tan complicadas que ya no pueden ser expresadas por un número sino por algo llamado el tensor de Ricci.
Un tensor no es más que la extensión del concepto de vector a dimensiones adicionales. Un escalar, un número, aparece en un gráfico como un punto, un objeto de cero dimensiones. Un vector, que tiene magnitud y dirección, aparecería en un gráfico como una línea, es decir, como un objeto de una dimensión. El tensor extiende esta idea a las dimensiones adicionales. Esto podemos interpretarlo como un conjunto de vectores relacionados, moviéndose en múltiples direcciones en un plano.
Lo veremos mejor de otra manera. En vez de pensar en un vector como un conjunto de coordenadas, lo podemos considerar una operación, es decir, un vector lo que haría es asociar una dirección a un número. Lo importante desde el punto de vista matemático es que la operación es lineal y homogénea. Gracias a esto, un vector queda completamente determinado por sus proyecciones en d direcciones, donde d es el número de dimensiones del espacio en el que se define. Por tanto, un vector se puede expresar como un conjunto de números que son en realidad sus proyecciones en un sistema de ejes coordenados.
Un vector es realmente un tensor de rango 1, asocia 1 dirección a un número. Un escalar, es un tensor de rango 0, asocia 0 direcciones a un número. Por tanto un tensor de rango 2 (un tensor ya por derecho propio), asocia dos direcciones arbitrarias a un número. Si quisiéramos expresarlo en términos de las coordenadas, como se hace con los vectores, necesitaríamos d x d números. Para un tensor de rango q, por tanto, necesitaríamos nq números.
Las ecuaciones de campo
Veamos ahora desde el punto de vista formal las ecuaciones de campo de la relatividad general. Si has llegado leyendo hasta aquí no te asustará demasiado, después de todo no es más que una igualdad tensorial en la que se relacionan un conjunto de tensores 4 x 4 (simétricos, pero en esto no vamos a entrar ahora), para un espaciotiempo de 4 dimensiones.
![]()
Donde Rμν es el tensor de curvatura de Ricci del que hablábamos más arriba, R es la curvatura escalar (simplificando, la curvatura entendida en el sentido que hablábamos más arriba, un número asociado a un punto del espacio), gμν es el tensor métrico (una generalización del campo gravitatorio y principal objeto de interés), G es la constante gravitacional de Newton, c la velocidad de la luz en el vacío y Tμν el tensor de energía-impulso.
Los índices en los tensores son etiquetas, es una forma de llamarlos. En este caso se emplea la notación abstracta de Penrose. Se puede usar cualquier símbolo conveniente para los índices de los tensores. Tradicionalmente, las letras latinas se usan para indicar que se están usando coordenadas espaciales (x, y, z), mientras que las griegas se emplean para indicar coordenadas espaciotemporales (x, y, z, t).
Notas:
[1] Esta entrega de la serie puede saltarse sin pérdida de continuidad.
[2] En lo que sigue nos basamos mayormente en nuestro nuestro “Einstein y…la pizarra del Observatorio del Monte Wilson” Experientia docet 17/12/2010
[3] La importancia de la cronología puede apreciarse en nuestro Desviación de la luz y falsabilidad
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las ecuaciones de campo de la relatividad general se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La primera imagen de Sagitario A* podría ser la prueba “definitiva” de la relatividad general
- La relatividad del tiempo (y 3)
- La relatividad de la masa
¿Quién llorará por los animales feos cuando desaparezcan?

El pez gota ostenta el dudoso honor de ser considerado el animal más feo del mundo (Fuente: FishesOfAustralia)
Hace apenas unos días murió Sudán, el último rinoceronte blanco del norte macho. Es una de las cinco especies de rinocerontes que hay en el mundo, y con la muerte del último macho, podemos darla oficialmente por extinta. Quedan con vida aun dos hembras, una hija y una nieta de Sudán, y se espera que utilizando técnicas de fecundación in vitro haya una posibilidad, aunque sea pequeña, de recuperar algún día la especie.
Pero la muerte de Sudán es un símbolo de nuestro fracaso en la conservación de la biodiversidad. La hemos fastidiado, queridos congéneres, y Sudán es la última prueba que nos ha llegado, un mensaje alto y claro. Ojalá sirva como toque de atención y nos pongamos las pilas con esto. La Tierra es hogar de millones de especies y nosotros somos la única con conciencia y responsabilidad para preservarla para todas las demás.

Sudan, el último rinoceronte blanco del norte macho, vivió sus últimos años custodiado para protegerle de los cazadores furtivos (Fuente: Ol Pejeta Conservancy)
Y digo todas. Insisto en ello porque cuando pensamos en conservación de especies solemos pensar en lindos koalas, gorilas imponentes, tigres majestuosos o simpáticos delfines. Y aunque es loable querer proteger a los cetáceos, ¿quién se acuerda de todas esas otras especies, las feas, las antipáticas, las despeluchadas, las viscosas, las patéticas? ¿Es que no merece el pez gota, nombrado una vez el animal más feo del mundo, sobrevivir igual que lo merece el lince o el águila imperial?
¿Puede el marketing salvar a los animales poco conmovedores?
Bob Smith es director del Instituto Durrell de Conservación y Ecología de la Universidad de Kent. En un artículo publicado en The Conversation a medias con Diogo Verissimo, de la Universidad de Oxford, comentaba que “nosotros como científicos conservacionistas queríamos comprobar si quizá el marketing podría salvar a estas otras especies. Si las empresas consiguen vender productos como fregonas y otros productos monótonos, ¿por qué no íbamos a poder recaudar dinero para salvar al poco glamuroso topo dorado gigante, incluso aunque parezca un pequeño cojín peludo con una pequeña nariz pegada?”.
Así que Smith y Verissimo compararon dos estrategias de recaudación de fondos para la conservación de especies, una de WWF y otra de la Sociedad Zoológica de Londres a través de su programa EDGE of Existence (al borde de la existencia). Ambas campañas eran muy diferentes: la de WWF trataba de recaudar dinero para un amplio abanico de proyectos que iban desde hacer frente al cambio climático y el comercio ilegal de animales salvajes a la conservación de los océanos y los bosques, mientras que la de EDGE estaba centrada en salvar a 100 mamíferos en peligro de extinción.
“Dado los diferente de ambas campañas queríamos ver si el marketing suponía alguna diferencia”, explican los autores, y para eso había que tener en cuenta qué animales se utilizaban como reclamo y cuál era su grado de atractivo, algo que depende de distintas cosas, como por ejemplo de si son bonitos, adorables, grandes o famosos.
Para crear una escala de atractivo animal se eligió a 850 personas involucradas en la conservación y se les enseñó una selección de imágenes, escogidas al azar, de entre las que ambas campañas estaban utilizando, y se les pidió que las clasificasen.
Comenzaron por la campaña de WWF, que recauda dinero a través de la adopción de los animales. Cuando la gente dona dinero, otorgan su apoyo a especies bien conocidas, y a cambio consiguen un animal de peluche, fotos de esos animales y certificados de adopción. El dinero donado va a acciones y proyectos que no solo benefician a los animales adoptados, sino a todo el ecosistema en general.

¿Cómo no iba a conmovernos la penosa situación de los adorables pandas? Solo un corazón de hielo se resistiría a intentar salvarlos (Fuente: Wikipedia Commons)
Los científicos determinaron que dos factores en concreto influían las elecciones de los donantes a WWF: el atractivo del animal y el grado de amenaza de extinción que sufrieran. “Las campañas de marketing no tenían ningún efecto. Daba igual como estuviesen descritas o presentadas, las especies más atractivas siempre reciben más donaciones, probablemente porque la gente ya las conoce y le gustan”.
Es posible salvar a ratas y murciélagos si sabes cómo
El programa EDGE funciona de forma diferente. Aunque apoya algunas especies mundialmente conocidas, como el elefante asiático, muchas otras son mucho menos atractivas, incluyendo un amplio grupo de ratas y murciélagos. Cada una de estas especies aparece en su web y los usuarios pueden aprender cuanto quieran sobre ellas.
En este caso, los resultados de Smith y Verissimo muestran que si bien la gente en general se muestra más interesada por donar para especies atractivas, en este caso las estrategias de marketing sí que influyen en la decisión. Los animales a los que se daba más visibilidad y se promocionaba conseguían más atención de los donantes.

No es tan lindo como un koala, pero ¿es que acaso el jerbo orejudo no merece nuestra ayuda? (Fuente: Wikipedia Commons)
Al comparar las dos campañas, los resultados muestran que entre 2011 y 2017 los animales que más dinero recaudaron en la web de WWF fueron el oso polar, el oso panda, el tigre y el leopardo de las nieves, mientras que en la web de EDGE fueron el delfín chino de río (ya extinto), el jerbo orejudo, el loris esbelto rojo y el murciélago de hocico de cerdo.
Los autores creen por tanto que utilizar técnicas de marketing con habilidad puede ayudar a recaudar fondos no solo para los animales que a todos nos derriten el corazón, sino también para los que no querríamos encontrarnos trepando por la pared de nuestra casa. Para estimar el impacto que podrían tener esas técnicas de marketing, crearon un modelo matemático basado en los datos recogidos del proyecto EDGE, una ecuación capaz de predecir las donaciones basándose en el atractivo del animal (algo que es fijo) y si fue o no promocionado por la organización en su web (algo que es variable).
Utilizando esa fórmula simularon distintas situaciones para los 10 animales más atractivos y los 10 menos atractivos según la clasificación hecha por los voluntarios del estudio. Si el marketing no intervenía, el modelo estimaba que las especies más adorables recaudarían hasta diez veces más que las más desagradables o feas. Pero al introducir el marketing que podía llevar a cabo la organización (situar las diez especies menos atractivas en las zonas destacadas de su web), el modelo predecía que las donaciones se multiplicarían por 26.

Sin un poquito de ayuda, un topo dorado gigante nunca tendrá el éxito de recaudación de un delfín, un tigre o un águila (Foto: Globalspecies.org)
Esto quiere decir, aseguran los dos autores del artículo, que las especies feas, al menos en lo que se refiere a ratones, murciélagos y similares, no lo tienen todo perdido y que hay mucho trabajo que los activistas y conservacionistas pueden hacer para echarles una mano.
Pero eso no es todo. El éxito de una campaña de marketing para salvar una especie, o un entorno, depende también de otros factores. El estudio Asignación Óptima de Recursos entre Especies Amenazadas: un Protocolo de Priorización de Proyectos, publicado en 2009, analizaba cuál es la mejor forma de gestionar el dinero dedicado a conservación, que por desgracia nunca es suficiente, para que sea lo más eficiente posible. “La literatura académica dedicada a la asignación sistemática de prioridades normalmente recomienda hacer un ranking de especies basándose en varios criterios, incluyendo el nivel de amenaza y el valor de esa especie en términos de distinción evolutiva, importancia ecológica y significado social. Pero este enfoque ignora dos aspectos cruciales: el coste del proyecto y las probabilidades de que el proyecto sea un éxito”.
Aclaran Smith y Verissimo que su estudio no analizó si una u otra estrategia de marketing sirvió para aumentar el número total de donaciones, pero sí que fue muy útil para aumentar el número de especies que la población reconoce y en cuya supervivencia se implica. No solo los gorilas o los osos panda tienen derecho a sobrevivir, ¿o es que nadie llorará al pez gota cuando desaparezca, igual que estamos todos ahora llorando por Sudán?
Referencias:
Increased conservation marketing effort has major fundraising benefits for even the least popular species. Diogo Verissimo, Robert J. Smith et al. Biological Conservation, Julio 2017.
Asignación Óptima de Recursos entre Especies Amenazadas: un Protocolo de Priorización de Proyectos. Liana N. Joseph, Richard F. Maloney, Hugh P. Possingham. Conservation Biology. Marzo 2009.
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo ¿Quién llorará por los animales feos cuando desaparezcan? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El tamaño relativo de los órganos animales
- Las actividades animales
- Los animales que respiran en agua
Umami

Saccharina japonica
En 1909 el profesor de química Kikunae Ikeda publicó en japonés un artículo en el que propuso la existencia de un sabor básico no reconocido antes como tal: el umai (sabroso en japonés). Hasta ese momento se pensaba que los seres humanos teníamos receptores sensoriales gustativos específicos para los sabores dulces, salados, ácidos y amargos. Esos eran los considerados cuatro sabores básicos, cada uno con su receptor. El umai es muy característico del caldo (dashi) que preparan en Japón con bonito deshidratado y konbu, que es el nombre común del alga marrón Saccharina japonica. Ikeda denominó umami al nuevo sabor básico; el sufijo mi en japonés significa esencia.
Mediante un procedimiento de extracción que constaba de trenta y ocho pasos, Ikeda obtuvo del alga una sustancia cuyos cristales tenían su mismo sabor; la identificó como ácido glutámico. Su sal de sodio -el glutamato sódico- fue la forma del compuesto que proporcionó el mejor y más intenso sabor a umami. El ácido glutámico es un aminoácido, una de las sustancias de las que están formadas las proteínas, solo que este cumple, además, otras funciones en los seres vivos. Ocupa una posición central como intermediario en numerosas vías metabólicas. Y es un importante neurotransmisor (molécula que transmite información entre neuronas), el más abundante en el sistema nervioso de los vertebrados.
El glutamato está presente en muchos alimentos ricos en proteínas, como la carne. Además, somos capaces de detectar su presencia en la comida incluso en concentraciones ínfimas, por lo que es un indicador excelente de su valor nutricional. Pero hay más alimentos ricos en este aminoácido, como el tomate cocinado y ciertos alimentos fermentados, como el queso. Y la leche humana tiene 10 veces más concentración de glutamato que la de vaca, lo que da una idea de la gran importancia que este aminoácido tiene para los seres humanos ya desde que nacemos.
Tras el hallazgo del papel e importancia gustativa del glutamato, un discípulo de Ikeda extrajo del bonito deshidratado otra sustancia, el inosinato, que también contribuye al umai propio del dashi. El inosinato es un nucleótido cuya presencia en el alimento refuerza el efecto del glutamato. El mismo efecto ejerce el guanilato -otro nucleótido- que fue extraído de levaduras algunos años después por otro investigador japonés. El guanilato se encuentra en vegetales y hongos, y además de en las levaduras, pueden extraerse cantidades importantes de setas shitaki deshidratadas. Tanto el inosinato como el guanilato son, como lo es el glutamato, indicadores del valor nutricional del alimento; por esa razón tenemos receptores específicos para esas sustancias.
Tras su descubrimiento, Ikeda patentó un método para producir glutamato monosódico y desde entonces ha sido muy utilizado como potenciador de sabor. En la actualidad se extrae del konbu. Con ese propósito se cosechan anualmente dos mil quinientos millones de toneladas del alga en las costas de China. Entre el 2 y el 3% de la masa seca de Saccharina japonica es glutamato. Tan alto contenido es debido a que su presencia en el interior de las células del alga permite a estas igualar su concentración interna de solutos con la del agua de mar y evitar así la deshidratación. Lo interesante de ese fenómeno es que hay animales marinos que acumulan en sus tejidos glutamato y otros aminoácidos exactamente por la misma razón que lo hacen las algas: impiden así que el agua salga de su interior debido al efecto osmótico. He aquí un hermoso capricho de la naturaleza: ante un mismo problema, animales y vegetales recurren a una misma solución, solución que, además, encierra el secreto de nuestra predilección por ciertos alimentos.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Este artículo fue publicada en el diario Deia el 17 de diciembre de 2017.
El artículo Umami se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cuando las algas rojas no pueden gestionar los radicales libres
- Los invasores
- Identificada la proteína que provoca la inflamación tras un ictus
Naukas Bilbao 2017 – Déborah García Bello: Saboer
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

El grafiti es un arte efímero que para poder saborearlo hay que saber. Deborah García Bello conseguirá que lo mires de otra manera en apenas 10 minutos.
Deborah García: SaboerEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Déborah García Bello: Saboer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Mónica Lalanda: Una muerte de cómic
- Naukas Bilbao 2017 – Álex Méndez: Luz de luna
- Naukas Bilbao 2017 – Laura Morrón: La gran divulgadora
Salud ósea en estudiantes universitarios

La osteoporosis es una enfermedad asociada habitualmente con la edad y la mujer, aunque cada vez hay más varones que la padecen. Esta enfermedad se trata farmacológicamente en el momento en que se detecta. Sin embargo, la prevención en la juventud es una estrategia a tener en cuenta para llegar a la madurez con huesos bien mineralizados y de calidad.
Un estudio llevado a cabo por un grupo de investigación de los departamentos de Fisiología y Enfermería de la UPV/EHU ha analizado la salud ósea de 156 estudiantes de entre 18 y 21 años. Esta es una de las escasas investigaciones realizadas sobre la calidad del hueso de personas adultas que aún no han llegado al punto álgido de madurez ósea (21-30 años). Hasta ahora lo que se han realizado son principalmente estudios retrospectivos de los factores que se cree que son determinantes de la calidad ósea.
Idoia Zarrazquin, una de las autoras, explica que “la mayoría de los estudios realizados hasta el momento están centrados en la edad adulta y en el inicio de la decadencia ósea, traducida en osteoporosis, sobre todo entre las mujeres a partir de los 50 años. Nosotras consideramos que es importante hacer estos estudios previos para conocer qué influye positivamente en la calidad del hueso, porque el margen de mejora es más amplio ya que por delante hay más de una década para incrementar la mineralización lo antes posible”.
Ejercicio y nutrición equilibrados
En este estudio, se ha analizado la actividad y condición física, la composición corporal y la nutrición de sujetos jóvenes (61 varones y 95 mujeres) desde septiembre de 2016 hasta mayo de 2017. Se registraron sus características antropométricas, el consumo dietético, la capacidad aeróbica, la fuerza muscular y la actividad física que realizan habitualmente. Además, se midió su estado óseo mediante ultrasonidos, una técnica no invasiva y sencilla de utilizar.
El conjunto de jóvenes estudiantes que ha participado en la investigación presentan en general una buena calidad ósea. Son estudiantes que en su mayoría realizan deporte: de forma más vigorosa los varones, de manera más moderada las mujeres. Respecto al calcio, los hombres consumen una media de 1.080 mg/día, es decir, por encima de las recomendaciones de la Organización Mundial de la Salud (1000 mg/día), mientras que las mujeres no llegan a este valor (814 mg/día). En cuanto a la vitamina D, ni varones (3,88 mg/día) ni mujeres (3,10 mg/día) alcanzan lo recomendado por la OMS (5mg/día).
Actividad física sí, pero sin pasarse
Aunque los jóvenes analizados presentan una buena calidad ósea general, ésta puede ser mejorable para ralentizar la disminución ósea que se dará con la edad. En este sentido, Gotzone Hervás, primera firmante del estudio, concreta que el conocer los factores que ayudan a la formación ósea puede servir para prevenir estas enfermedades. “Sabemos que la actividad física mejora el músculo y fortalece el hueso. Existe una interconexión entre ellos y, si la actividad es intensa, ambos mejoran, resistirán mejor el paso de los años y afrontarán mejor la decadencia ósea”.
Por tanto, la actividad moderada-intensa y los deportes de impacto son recomendables, pero hay que equilibrarlos con la adecuada nutrición otra de las autoras, Fátima Ruiz-Litago. “La tensión y fuerza muscular mejora la mineralización del hueso, pero eso no significa que cuanto más mejor, porque está demostrado que deportistas de élite también sufren osteoporosis. Es decir, la actividad física tiene que ser moderadamente intensa, sin sobrepasarse; sobre todo, entre las mujeres. Cuando el ejercicio es muy intenso las necesidades nutricionales también son muy elevadas y, en el caso de las mujeres deportistas, muy difíciles de cubrir por sus propias características físicas y hormonales. Es por ello que es más habitual de lo pensado que entre deportistas de élite se den casos de osteoporosis”.
En definitiva, los investigadores de la UPV/EHU concluyen que, además de una correcta nutrición en calcio y vitamina D, la actividad física contribuye a acumular minerales óseos de manera que al llegar a la madurez el índice de rigidez ósea sea alto y se contrarreste la decadencia que se produce a partir de los 30/35 años y sobre todo a partir de los 50. “Las futuras recomendaciones para prevenir la osteoporosis también pasarán por favorecer la fuerza muscular”, asegura Idoia Zarrazquin.
Referencia:
Hervás, G.; Ruiz-Litago, F.; Irazusta, J.; Fernández-Atutxa, A.; Fraile-Bermúdez, A.B.; Zarrazquin, I. (2018) Physical Activity, Physical Fitness, Body Composition, and Nutrition Are Associated with Bone Status in University Students Nutrients doi: 10.3390/nu10010061
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Salud ósea en estudiantes universitarios se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La sorprendente densidad ósea de los atletas kenianos
- La gestión de la salud y seguridad en el trabajo de las mujeres
- El método Feldenkreis y las personas con discapacidad intelectual
¿Qué permitió las increíbles fosilizaciones de Burgess Shale?

Hace algo más de una década, una joven Chenoa cantaba aquello de “Estoy cansada de cuerpos duros”. Probablemente, escribió la letra de la canción pensando en todos aquellos paleontólogos que se dedican al estudio de organismos (o parte de ellos) fósiles que no tenían ninguna parte dura.
Y es que si eres una almeja tendrás muchas más posibilidades de pasar al registro fósil, esa suerte de posteridad geológica que hoy usamos para completar el árbol de la vida, que una grácil medusa gracias precisamente a esos cuerpos duros y mineralizados de los que se quejaba amargamente la cantante marplatense.
Bromas aparte, el registro fósil tiene un sesgo de conservación brutal hacia la preservación de las partes duras de los organismos, como pueden ser los huesos o las conchas, mientras que los organismos formados exclusivamente por partes blandas suelen descomponerse mucho antes de fosilizar sin dejar rastro alguno de su existencia.
Figura 1. Este pariente de la avispa lo tuvo realmente difícil para fosilizar, pero tras su muerte cayó en un ambiente muy favorable para su fosilización.
Afortunadamente para nosotros, existe lo que conocemos como Lagerstätte, un grupo de yacimientos fosilíferos entre los que se encuentran aquellos que permiten una preservación excepcional de los organismos, tanto de sus partes blandas, como de organismos completos.
Uno de los detalles que hoy día desconocemos con exactitud es que permite precisamente la existencia de este tipo de yacimientos: ¿Será un rápido enterramiento de los fósiles? ¿Tendrá que ver con la mineralogía existente? ¿Influirá el tamaño de grano de la roca? ¿O quizás hay algún factor que no hemos tenido en cuenta hasta ahora?
En las últimas décadas se ha puesto mucho énfasis en la búsqueda de biomarcadores3, moléculas orgánicas complejas formadas por la actividad de los organismos vivos, que podemos encontrar en las rocas y que atestigüen la presencia de vida no solo en nuestro planeta sino, por ejemplo, en Marte, donde cada vez somos capaces de enviar instrumentos más sensibles, capaces de caracterizar con gran detalle la composición química de las rocas.
No sabemos si se desarrolló o existe vida en otros lugares más allá de nuestro planeta. Pero si esto ocurrió en algún momento, es probable que también comenzase su andadura con cuerpos blandos, sin mineralizaciones.
Si fuésemos capaces de conocer las condiciones, los procesos y los ambientes que permitieron en nuestro planeta la aparición de las Lagerstätte, podríamos comenzar a buscar esta suerte de geomarcadores1 también en otros puntos del Sistema Solar, con vistas a decidir los lugares de aterrizaje de futuras misiones que tengan la posibilidad de estudiar la existencia de vida en el pasado.
Un nuevo estudio2 llevado a cabo por científicos de distintas universidades británicas y norteamericanas ha abordado este problema estudiando una de las mejores Lagerstätte conocidas, la de Burgess Shale, que toma su nombre de un yacimiento Canadiense descubierto a principios del siglo XX y que data de hace unos 500 millones de años, en el Cámbrico, momento en el que ocurre una gran diversificación evolutiva en el reino animal.
Gracias a este tipo de yacimientos, de los que se conocen varias docenas en todo el mundo, se ha podido completar de una manera mucho más exhaustiva el árbol de la vida en el Cámbrico ya que sin estos, más del 80% de los organismos aparecidos en este periodo, no habrían dejado rastro alguno en el registro fósil.
¿Qué hace a este tipo de yacimientos tan especiales que permiten la excepcional preservación de las partes blandas?
Desde hace un par de décadas, sabemos que algunas arcillas son capaces de facilitar la fosilización ya que son capaces de adherirse a cierto tipo de enzimas encargadas de romper la célula tras la muerte del organismo, dejándolas inactivas y por lo tanto ralentizando la descomposición.
Pero en los últimos años, diversos experimentos han mostrado como la presencia de arcillas como la caolinita y la bertierina son capaces de interferir en el crecimiento de algunas bacterias encargadas de la putrefacción de los organismos muertos… ¿Podría la presencia de cierto tipo de arcillas tener una relación fundamental con la aparición de yacimientos del tipo de Burgess Shale?.
Para resolver esta cuestión, este equipo de científicos ha analizado en detalle la mineralogía de más de 200 muestras de fósiles del Cámbrico provenientes de 19 yacimientos de cuatro continentes, de las cuales 131 correspondieron a fosilizaciones del tipo de Burgess Shale, y 82 en las que solo aparecen restos mineralizados.
Los resultados muestran que los fósiles de partes blandas se conservan mejor en rocas que contienen bertierina, que en estudios anteriores ya se había demostrado su efecto contra las bacterias que provocan la putrefacción de los tejidos.
Hoy en día esta arcilla se forma principalmente en ambientes tropicales, con aguas ricas en hierro, lo que probablemente sirva como indicador para interpretar que el ambiente en el que vivieron estos organismos también fue las aguas de algún mar u océano tropical del Cámbrico.
Aunque este nuevo análisis mineralógico consigue predecir con una tasa de éxito de alrededor del 80% la posibilidad de fosilización de tipo Burguess Shale en rocas sedimentarias de grano fino formadas durante el Cámbrico, es manifiesto que hay otros factores que también son importantes para una buena preservación, como puede ser un enterramiento rápido, la presencia de aguas pobres en oxígeno o la composición de las aguas.
Este estudio abre la puerta a la búsqueda de nuevos yacimientos de tipo Burgess Shale en nuestro planeta que hayan podido pasar desapercibidos, pero quizás pueda ser también el pistoletazo de salida para localizar rocas favorables a la fosilización en lugares como Marte, donde sabemos que hubo un ambiente mucho más adecuado para el desarrollo de la vida al principio de su historia, y de haber existido esta, quien sabe si también quedó registrada en las rocas como ocurrió en con la que habitaba aquellos mares tropicales del Cámbrico.
Este artículo lo ha escrito Nahum Méndez Chazarra y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU
Referencias:
[1] J. Martinez-Frias, E. Lázaro, A. Esteve-Núñez, and C. M. B. L. Beard. Biogeochemical cycling of iron isotopes. Science. CrossRef PubMedJohnson, Geomarkers versus Biomarkers: Paleoenvironmental and Astrobiological Significance, vol. 36. 2009.
[2] R. P. Anderson, N. J. Tosca, R. R. Gaines, N. M. Koch, and D. E. G. Briggs, “A mineralogical signature for Burgess Shale – type fossilization,” vol. 46, no. 4, pp. 2–5, 2018.
[3] M. Gargaud and W. M. Irvine, Encyclopedia of Astrobiology. 2015.
El artículo ¿Qué permitió las increíbles fosilizaciones de Burgess Shale? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La aparición de los tejidos musculares y el registro fósil
- Del zumo de naranja a la selva, un ejemplo de reciclaje extremo
- Las cartas de Darwin: ¡La geología por encima de todo!
Catástrofe Ultravioleta #23 TOTALIDAD

Catástrofe Ultravioleta #23 TOTALIDAD
El pasado 21 de agosto de 2017 tuvo lugar uno de los eclipses totales de Sol más seguidos de la historia. Millones de personas pudieron contemplar aquel apasionante momento y desde Catástrofe Ultravioleta no quisimos quedarnos atrás. Aprovecharemos este eclipse para conocer infinidad de curiosidades sobre nuestra estrella y descubrir qué fenómenos ocurren durante los mágicos minutos en los que el Sol queda oculto tras la Luna. Un viaje que nos llevará desde los descubrimientos de Galileo hasta las futuras misiones espaciales.
Agradecimientos: Carolina Jiménez (OKinfografia), José Miguel Viñas (Divulgameteo), Miquel Serra-Ricart (IAC), Expedición Sheilos, GOAT (Grupo de Observadores Astronómicos de Tenerife), Alejandra Godell, Héctor Socas (IAC), José Carlos del Toro Iniesta (IAA)
** Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) con el patrocinio parcial de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.
El artículo Catástrofe Ultravioleta #23 TOTALIDAD se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Preparados para una Catástrofe Ultravioleta
- Catástrofe Ultravioleta #13 LEVIATÁN
- Catástrofe Ultravioleta #01 Expedición
El falso pan integral tiene los días contados

assortment of baked bread on wood table
El pan integral es una opción más saludable que el pan blanco, sin embargo, no todos los panes que lucen la palabra integral en su etiquetado son realmente integrales. La normativa vigente lo permite, cosa que no ocurre en otros países. Desde el Ministerio de Agricultura y Pesca, Alimentación y Medio Ambiente (Mapama) se ha presentado un borrador que pretende derogar la normativa actual para que llamemos a cada cosa por su nombre y no nos sigan vendiendo, al amparo de la ley, falso pan integral.
Diferencias entre harina integral y refinada
Las harinas integrales son aquellas que se fabrican moliendo el cereal entero. Los cereales tienen tres partes: la cáscara del cereal es el salvado, donde está la mayor parte de la fibra, la parte central es el endospermo, compuesto mayoritariamente por almidón, y el núcleo es el germen, donde se concentra la fracción grasa del cereal.
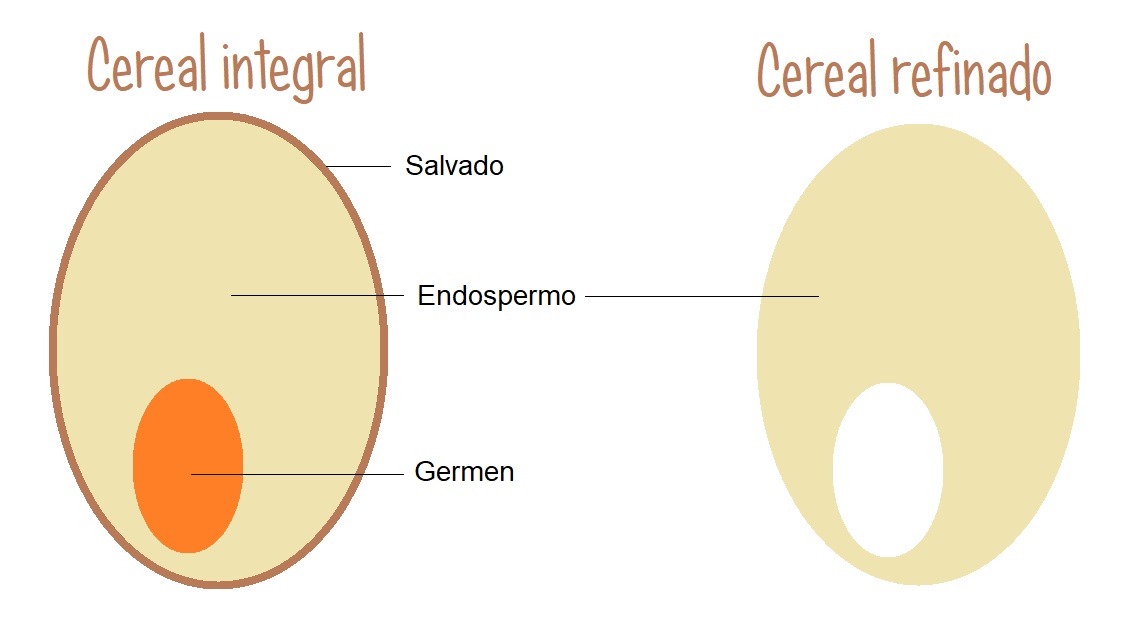
Las harinas integrales de mayor calidad son las que se muelen a la piedra. La razón es que no se desperdicia ni se separan las diferentes partes del grano. Estas harinas pueden tamizarse para separar parte de salvado y así elaborar una semi-integral.
Según el tipo de molienda que se utilice, obtendremos harinas con diferente tasa de extracción. La tasa de extracción indica los kilos de harina que se obtienen moliendo 100 kilos de cereal. Así, una harina con tasa de extracción del 100% es una harina 100% integral, con el grano entero, y una harina con una tasa de extracción del 70% será, para los panaderos, una harina refinada.
En cambio, la mayor parte de las harinas que encontramos en el mercado suele ser fruto de un tipo de molienda por fases. Normalmente en cada una de estas fases se separan las diferentes partes del grano. Por un lado conseguimos una harina blanquísima que solo contiene endospermo, una harina oscura hecha con el salvado y, por otro lado, el germen, que suele retirarse porque su contenido graso hace que la harina se ponga rancia con más facilidad.
Las harinas integrales fabricadas a partir de molienda en fases se fabrican mezclando en la proporción deseada la harina blanca con la harina de salvado. A veces están tan poco logradas que las fases pueden separarse utilizando un colador. Los panaderos suelen llamar a estas harinas de mezcla ‘falsa integral’. Algunos fabricantes de harina integral lo indican en el envase como dos ingredientes: harina y salvado.

Los panaderos la prefieren integral
Los panaderos que elaboran el pan de forma tradicional, empleando masa madre, suelen usar harinas integrales. La razón es que las levaduras se encuentran en mayor proporción en el salvado. Estas levaduras rompen el almidón en azúcares simples y los fermentan formando las características burbujas del pan.
En cambio, al hacer pan con harina integral, la fibra absorbe más agua y esto obstaculiza el desarrollo del gluten, es decir, se tarda más en conseguir una masa elástica.
El manejo de harinas integrales para elaborar pan requiere más destreza que el manejo de harinas refinadas. No obstante, la complejidad de la elaboración del pan integral repercute en un producto con mejores cualidades nutricionales.
El pan integral es más saludable que el pan blanco
Las harinas integrales contienen todas la vitaminas y nutrientes del cereal completo, siendo especialmente interesante para nuestra salud su alto contenido en fibra. La fibra favorece el tránsito intestinal y además hace que el pan sea más saciante.
El pan integral tiene las mismas calorías que el pan refinado, así que es un mito eso de que ‘engorda menos’, pero al resultar más saciante necesitaremos comer menos cantidad.
La fibra también hace que el pan integral tenga menor índice glucémico, es decir, hace que metabolicemos los carbohidratos lentamente y que no nos suba la glucosa en sangre. Por el contrario, los panes blancos tienen alto índice glucémico, lo que significa que se metabolizan muy rápido dando elevados y repentinos picos de glucosa en sangre y, en consecuencia, picos de insulina. Este es el motivo por el que el pan blanco es poco saciante y por el que las personas con diabetes limitan su consumo.
La ley actual permite llamar integral a casi cualquier pan
En la normativa vigente sobre fabricación y comercio del pan, el pan integral se define como «el elaborado con harina integral», sin especificar el porcentaje que debe llevar este producto para ser considerado integral. La harina integral, por su parte, «es el producto resultante de la molturación del grano de cereal y cuya composición corresponde con la del grano del cereal íntegro», sin indicar qué porcentaje de grano entero debe llevar.
Así, un pan con un bajo contenido de harina integral puede llevar en su envase la palabra integral. La normativa se lo permite. También puede indicar «fuente de fibra» si contiene más de 3 g de fibra por cada 100 g de producto, o «alto contenido en fibra» si tiene 6 g de fibra. Tenemos que tener en cuenta que 100 g de pan elaborado con 100% harina integral de trigo contendrá más de 8 g de fibra.
Existe, por tanto, una especie de vacío legal respecto a la denominación integral del pan. Algunos productos lucen en su etiqueta la frase «elaborado con harina 100% integral», cuando en realidad llevan un porcentaje ínfimo de harina integral. Claro que no es lo mismo decir «elaborado con harina 100% integral» que «elaborado con 100% harina integral». El primero solo dice que contiene harina integral (y que esa parte de harina integral es 100% integral) y el segundo dice que el 100% de la harina empleada es integral.
Una nueva normativa para los panes integrales
El Gobierno quiere acabar con estas tretas y por eso ha propuesto un cambio de normativa a través de un proyecto presentado por el Ministerio de Agricultura y Pesca, Alimentación y Medio Ambiente (Mapama). El objetivo es, entre otros, proporcionar una información adecuada al consumidor que facilite su elección de compra. Este proyecto se ha escrito a semejanza del de los países nórdicos, donde ya está regulado que solo pueden denominar pan integral a aquel que contenga más del 80% de harina integral.
La futura normativa concretará las características que deberá tener el pan integral y unificará criterios: «Se denominarán ‘pan 100% integral’ o ‘pan integral’ los panes elaborados con harina exclusivamente integral, excluyendo de dicho porcentaje las harinas procesadas/malteadas. Los panes en los que la harina utilizada en la elaboración no sea exclusivamente integral incluirán en la denominación la mención ‘elaborado con harina integral X%’». Si el porcentaje es inferior al 100%, el porcentaje exacto deberá figurar en el frontal del envase con la misma tipografía, tamaño y color que la palabra integral.
Los panes elaborados con harinas diferentes al trigo, como espelta, kamut, centeno, etc. podrán denominarse ‘pan de…’ siempre y cuando contengan al menos un 50% de ese cereal.
Cómo saber si el pan que compramos es realmente integral
Hasta que la nueva normativa se aplique, todavía nos encontraremos panes en el mercado que se llaman integrales aun cuando contienen cantidades irrisorias de harina integral. A veces contienen semillas que los hacen parecer integrales.
Como en todos los alimentos envasados, la realidad del producto no esta en los eslóganes del frontal del envase, sino en la lista de ingredientes y en la tabla nutricional. Tenemos que prestar atención a la lista de ingredientes.
Los ingredientes van ordenados de mayor a menor cantidad en el producto. Así, un pan cuyo primer ingrediente contenga la palabra integral o grano entero, quiere decir que el ingrediente mayoritario sí es una harina integral. Además, entre paréntesis lucirá el porcentaje exacto de harina integral.

En los ejemplos mostrados en la imagen superior encontramos tostadas de pan con diferentes contenidos de harina integral, a pesar de que en el frontal todos se denominan integrales. En el primer producto el ingrediente principal es harina integral. Es, por tanto, el ingrediente mayoritario, aunque solo sea un 58% del producto. El ingrediente que le sigue es «harina de trigo», es decir, harina refinada. En el segundo producto, el ingrediente mayoritario es «harina de trigo», es decir, harina refinada. La integral es solo un 46%. En el tercer producto el ingrediente mayoritario sí es harina integral y en un porcentaje elevado: 88%. Además, el resto de los ingredientes son semillas, levadura, sal… No contiene ni azúcares ni harinas refinadas.
Para conocer la realidad de un pan integral debemos buscar un producto cuyo primer ingrediente sea «integral» o «grano entero». Si indica el porcentaje, será mejor cuanto mayor sea. Lo ideal es que tenga al menos un 80% de integral. Si en el resto de los ingredientes no aparecen ni azúcares ni otras harinas, estaremos ante una buena opción de compra.
Conclusión
La normativa actual permite llamar pan integral a cualquier pan que contenga harina integral, sea cual sea esa cantidad. El proyecto presentado por el Mapama pretende cambiar la normativa para que solo se pueda denominar integral al pan elaborado con un 100% de harina integral. Hasta que la normativa no cambie tendremos que seguir fijándonos en la lista de ingredientes. Y, si compramos pan fresco sin envasar, le preguntaremos a los panaderos.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo El falso pan integral tiene los días contados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El mejor lacón con grelos tiene su ciencia
- El buen turrón tiene su ciencia
- La pantalla de tu móvil solo tiene tres colores
Destruyendo asteroides con bombas atómicas

Ilustración: Elena Khavina
Un numeroso equipo de físicos e ingenieros encabezados por A. Y. Arasova, del Instituto de Investigación Científica de Física Experimental Panruso (VNIIEF), el principal centro de investigación del complejo militar-industrial de Rusia en armas nucleares, ha modelado el impacto de una explosión nuclear en un asteroide que amenazase la Tierra. Para ello se fabricaron asteroides en miniatura y los bombardearon con un láser. La técnica de modelado desarrollada en este estudio es una forma de evaluar experimentalmente los criterios de destrucción de asteroides, así como la energía de la explosión necesaria para eliminar un objeto peligroso en curso de colisión con la Tierra.
Los asteroides son cuerpos celestes compuestos principalmente de carbono, silicio, metales y, algunas veces, hielo. Habitualmente se clasifican los objetos de más de 1 metro como asteroides, aunque este límite inferior aún está en discusión. En el otro extremo de la escala, los asteroides alcanzan los 900 kilómetros de diámetro. Viajando a 20 kilómetros por segundo, estos gigantes representan una amenaza creíble de aniquilar toda la vida en la Tierra.
Hay dos opciones básicas cuando se trata de proteger el planeta de la colisión con un asteroide: o se le desvía o se vuela en pedazos de tal manera que la mayoría n impacte con la atmósdfera y, los que lo hagan, se quemen en ella de tal modo que lleguen a la superficie sin causar daños catastróficos. Los autores de este estudio se han centrado en la segunda opción, creando un modelo experimental con el que comprobar los efectos de una poderosa onda de choque liberada por una explosión nuclear en la superficie del asteroide. El equipo de investigación demuestra que un breve pulso láser dirigido a una réplica en miniatura de un asteroide produce efectos destructivos similares a los de una explosión nuclear en una roca espacial real. Las distribuciones de calor y presión predichas para el evento real generalmente coinciden con las medidas en el experimento de laboratorio.
Para que el modelo de láser fuera preciso, los investigadores se aseguraron de que la densidad y rigidez del asteroide de laboratorio, e incluso su forma, imitaran las reales. Gracias a esta correspondencia precisa, los investigadores obtuvieron una forma de calcular directamente la energía requerida de una explosión nuclear en el asteroide real a partir de la energía de un pulso láser que destruye su réplica en miniatura.
La composición de los asteroides artificiales para las pruebas se corresponde a la de los meteoritos condríticos (básicamente de carbono), que representan aproximadamente el 90 por ciento de los restos de asteroides que alcanzan la superficie de la Tierra. Las réplicas se hicieron usando los datos sobre el meteorito recuperado del fondo del lago Chebarkul. Es el fragmento más grande del asteroide que entró en la atmósfera de la Tierra en febrero de 2013, explotando sobre el Óblast de Cheliábinsk, Rusia. El material del asteroide se fabricó usando una combinación de sedimentación, compresión y calentamiento, imitando el proceso de formación natural. A partir de muestras cilíndricas se hicieron asteroides de prueba esféricos, elipsoidales y cúbicos.

Estela del bólido de Cheliábinsk fotografiado desde Ekaterimburgo
Para estimar los criterios de destrucción de asteroides, los investigadores analizaron los datos disponibles del meteorito de Cheliábinsk. Ingresó a la atmósfera de la Tierra como un asteroide de 20 metros y se fracturó en pequeños fragmentos que no causaron daños catastróficos. Por lo tanto, tiene sentido afirmar que un asteroide de 200 metros ha sido eliminado si se fractura en pedazos con diámetros 10 veces más pequeños y masas 1.000 veces más pequeñas que la roca inicial. Por razones obvias, esta conclusión solo se cumple para un asteroide de 200 metros que entra en la atmósfera en un ángulo similar y para fragmentos que viajan a lo largo de trayectorias similares a la del meteoro de Cheliábinsk.
Los experimentos indican que para eliminar un asteroide de 200 metros, la bomba necesita liberar la energía equivalente a 3 megatones de TNT. A este dato se llegua porque los investigadores midieron que es necesario un pulso láser de 500 julios para destruir un modelo de 8-10 milímetros de diámetro. Para poner el dato en perspectiva, 3 megatones vendría a ser equivalente a la energía de todas y cada una de las bombas detonadas durante la Segunda Guerra Mundial, incluidas las bombas atómicas que se lanzaron sobre Hiroshima y Nagasaki; por otro lado tampoco es tanto: el explosivo más poderoso jamás detonado, la bomba Zar, construida por la Unión Soviética en 1961, liberó 58,6 megatones (aunque los números varían algo según las fuentes; este dato es el oficioso ruso); las bombas de hidrógeno estadounidenses de la Guerra Fría se estima que liberaban 25 megatones.
El equipo de investigación ahora planea expandir el estudio experimentando con réplicas de asteroides de diferentes composiciones, incluidas las que contienen hierro, níquel y hielo. También pretenden identificar con mayor precisión cómo la forma del asteroide y la presencia de cavidades en su superficie afectan el criterio de destrucción general.
De momento no hay amenazas inminentes de asteroides, por lo que el equipo tiene tiempo de perfeccionar esta técnica para evitar un desastre planetario.
Referencia:
Aristova, E.Y., Aushev, A.A., Baranov, V.K. et al. (2018) J. Exp. Theor. Phys. doi 10.1134/S1063776118010132
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Destruyendo asteroides con bombas atómicas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Choques de asteroides, arte islámico y cuasicristales
- Asteroides, ¿de la amenza a la oportunidad?
- Los meteoritos ya no son lo que eran desde hace 466 millones de años
Ilustraciones artísticas de un matemático
El año 1990 la American Mathematical Society (Sociedad Matemática Americana) publicó un curioso libro que, bajo el título de Mathematical Impressions, recogía más de ochenta ilustraciones artísticas del matemático ruso Analoty T. Fomenko.

Portada del libro “Mathematical Impressions” del matemático A.T. Fomeko
Mi primer contacto con A. T. Fomenko fue a través de sus libros de Geometría Diferencial y Topología Algebraica, relacionados con mi área de investigación. Libros como Modern Geometry. Methods and Applications (1984, 1985 y 1990), Symplectic Geometry. Methods and Applications (1988) o Homotopic topology (1986), entre muchos otros.
El matemático ruso Anatoly Timofeevich Fomenko, que nació el 13 de marzo de 1945 en la ciudad ucraniana de Donetsk, por aquel entonces Stalino (URSS), fue un conocido topólogo y geómetra diferencial de la Universidad Estatal de Moscú, así como miembro de la Russian Academy of Sciences (Academia Rusa de Ciencias).
En 1969 publicó en ruso, junto con Dimitry B. Fuchs y Victor L. Gutenmacher, su libro Homotopic topology, que sería traducido al inglés en 1987. Las personas que leyeron este libro matemático se quedaron sorprendidas al encontrarse en el mismo una serie de ilustraciones artísticas en blanco y negro, y del tamaño de una página, que pretendían explicar visualmente algunos conceptos matemáticos muy complejos, pero que, al mismo tiempo, utilizando una estética oscura y expresionista, tenían un marcado carácter artístico. Una versión moderna de ese libro fue publicada en 2016 por Springer (GMT 273).
Veamos algunas de las ilustraciones que formaron parte de este libro. La primera de ellas, que inicia el libro es Esfera con cuernos de Alexander (1967), que ilustra un concepto topológico extraño como son las esferas con cuernos de Alexander (véase la entrada James Waddell Alexander de Marta Macho, para más información).

“Esfera con cuernos de Alexander” (1967), ilustración perteneciente al libro “Homotopic Topology”, que también fue recogida en el libro “Mathematical Impressions”

“Zoo topológico” (1967), ilustración perteneciente al libro “Homotopic Topology”, que también fue recogida en el libro “Mathematical Impressions”
La segunda ilustración de arriba es Zoo topológico (1967). La explicación que acompaña a la misma dice así:
“En este espacio cavernoso, la galería de un gran castillo austero, tres seres observan desde arriba como otras criaturas pasan el tiempo en una colección de magníficas formas matemáticas, cada una siendo una perturbación diferente del espacio físico. Arriba a la derecha, un poliedro animado cobra vida y comienza a descomponerse en sus componentes, las conchas, como escorpiones, de las que está hecho. Observe la cola del aparente escorpión, arqueándose hacia arriba y hacia la cabeza de las conchas, revelando intuitivamente las facetas de la estructura y forma del objeto. Vea cómo las conchas finalmente se unen para crear un único poliedro infinito. Mientras tanto, en el centro del gran hall, un enorme toro, es decir, un objeto con forma de donuts, se está dando la vuelta (el interior pasa a ser exterior, y al revés), transformándose a sí mismo y al espacio que lo rodea. Curiosamente, a pesar de que el toro, que ha sido cortado o perforado, se retuerce en el espacio y se está dando la vuelta, el nuevo objeto sigue siendo un toro, aunque las superficies interna y externa se han intercambiado.
En la parte inferior izquierda, a la sombra de un gran pilar, yace un objeto llamado el collar de Antoine, bastante familiar en topología. A su derecha, descansa una película de jabón, que se extiende a través de un cable circular. Compuesto por la unión de una banda normal de Moebius con una banda triple de Moebius, esta superficie minimal es notable ya que puede contraerse continuamente a lo largo de su límite sin romperse. Incluso se puede transformar en otro objeto, conocido en topología como una casa de Bing con un agujero. Finalmente, en el centro hay un solenoide 2-adico.”
Para las personas que el anterior texto solamente les parece un cúmulo de términos matemáticos incomprensibles, diremos que es una galería de imágenes de superficies topológicas interesantes. Entre los términos mencionados están “el collar de Antoine” del que podéis leer en la entrada Louis Antoine y su fabuloso collar, de Marta Macho, la famosa “banda de Moebius”, sobre la que podéis ver el video La banda de Moebius, de la sección Una de Mates del programa de TV Órbita Laika, o las películas de jabón, que son superficies minimales, sobre las que podéis ver este otro video Matemáticas con jabón, de Una de Mates.
Otra ilustración en la que se intenta explicar un proceso matemático es la siguiente, cuyo título es ¿Es posible darle la vuelta (el interior pasa a ser exterior, y al revés) a una esfera (de dimensión 2) en el espacio euclídeo tridimensional ambiente dentro de la clase de las inmersiones diferenciables (“suaves”)? (1985, aparece en la versión inglesa).

“¿Es posible darle la vuelta (el interior pasa a ser exterior, y al revés) a una esfera (de dimensión 2) en el espacio euclídeo tridimensional ambiente dentro de la clase de las inmersiones diferenciables (“suaves”)?” (1985), ilustración perteneciente al libro “Homotopic Topology”, que también fue recogida en el libro “Mathematical Impressions”
Para visualizar el proceso de darle la vuelta (el interior pasa a ser exterior, y el exterior pasa a ser interior) a una esfera (de dimensión 2) en el espacio euclídeo tridimensional, que se ilustra en la anterior imagen, puede verse el siguiente video… How to turn a sphere inside out:
Disfrutemos de un par de ejemplos más de ilustraciones de la publicación Homotopic Topology. La primera (aunque de su versión más moderna) tiene el título Fantasía sobre el tema de los fractales, análogos a los conjuntos de Cantor, y dimensión de Hausdorff no entera (1986).

“Fantasía sobre el tema de los fractales, análogos a los conjuntos de Cantor, y dimensión de Hausdorff no entera” (1986), ilustración perteneciente al libro “Homotopic Topology”, que también fue recogida en el libro “Mathematical Impressions”
Y la última ilustración que incluimos de Homotopic Topology tiene el enigmático título, para aquellas personas de fuera del mundo de las matemáticas, o más concretamente, de la topología algebraica, El problema de un algoritmo efectivo de cálculo de los grupos de homotopía de las esferas no está resuelto (ya aparece en la publicación de 1986).

“El problema de un algoritmo efectivo de cálculo de los grupos de homotopía de las esferas no está resuelto”, ilustración perteneciente al libro “Homotopic Topology”, que también fue recogida en el libro “Mathematical Impressions”
El matemático ruso continuó trabajando en la misma línea durante los siguientes años, llegando a realizar al menos 280 ilustraciones artísticas de conceptos y resultados matemáticos, no solamente de geometría y topología, sino también de otros tópicos como estadística, probabilidad o teoría de números.
En el libro Mathematical Impressions, publicado por la American Mathematical Society, en 1990, se incluyeron 84 ilustraciones, 23 de las cuales eran en color.
En la introducción de este libro A. T. Fomenko escribe: “Pienso en mis dibujos como si fueran fotografías de un mundo extraño, pero real, y la naturaleza de este mundo, uno de objetos y procesos infinitos, no se conoce bien. Claramente, existe una conexión entre el mundo matemático y el mundo real…. Esta es la relación que yo veo entre mis dibujos y las matemáticas.“
A continuación, mostraremos algunas ilustraciones incluidas en este libro tan especial, que es Mathematical Impressions.

“Una superficie algebraica de Kummer y sus puntos singulares” (1971), del libro “Mathematical Impressions”, de A. T. Fomenko
Las superficies de Kummer son superficies algebraicas que tienen dieciséis puntos singulares. El ejemplo de Fomenko tiene 8 puntos singulares reales, como la superficie cuyo modelo físico (del Touch Geometry Project) mostramos a continuación.

Modelo físico de una superficie der Kummer con 8 puntos dobles reales, del proyecto Touch Geometry Project, de la Universidad Nacional de V. N. Kazarin Kharkiv
La siguiente obra recibe el título Fantasía geométrica sobre el tema de las funciones analíticas (1971).

“Fantasía geométrica sobre el tema de las funciones analíticas” (1971), del libro “Mathematical Impressions”, de A. T. Fomenko
También nos encontramos con una representación del infinito en la obra Infinito matemático (1977). El texto que acompaña la imagen es el siguiente:
“Miles de caras en una multitud gritan, rodeando una sola cabeza ominosa. De hecho, esta imagen refleja las meditaciones de los matemáticos sobre el infinito, un concepto que acompaña a muchas teorías y que aparece de diferentes maneras en geometría, lógica, teoría de números y muchas otras áreas. Infinito potencial y real, paradojas de lógica, problemas irresolubles, la hipótesis del continuo y sus diversas versiones, matemáticas constructivas, intuicionismo (en el espíritu de Poincaré) -todos estos cobran vida mediante la existencia del infinito matemático, cuyo estudio presenta fascinantes problemas filosóficos sobre el conocimiento del mundo que nos rodea. En cuanto a las personas, un homeomorfismo adecuado puede identificar a diferentes seres humanos desde un punto de vista geométrico, comenzando con un único sujeto ideal. Todo esto también recuerda a los muchos artistas medievales que trataron de reflejar sus interpretaciones de infinitos físicos y morales sobre lienzos dedicados a los sufrimientos de Jesucristo.”

“Infinito matemático” (1977), del libro “Mathematical Impressions”, de A. T. Fomenko
También realizó ilustraciones relacionadas con la probabilidad, como esta obra titulada Procesos aleatorios en probabilidad (1985).

“Procesos aleatorios en probabilidad” (1985), del libro “Mathematical Impressions”, de A. T. Fomenko
También reflexiones visuales sobre los importantes números irracionales π y e, como la obra Los remarcables números π y e (1985), en la que vemos los primeros decimales del número π (3,1415926535 8979323846 2643383279…), en la cara frontal del edificio, y los del número e (2,7182818284 5904523536 0287471352…), en la cara lateral.

“Los remarcables números π y e (1985)”, del libro “Mathematical Impressions”, de A. T. Fomenko
Y terminemos, casi, con dos ilustraciones con títulos incomprensibles para las personas que no trabajan en estos temas.

“Espines de dos variedades hiperbólicas cerradas compactas de dimensión 3” (1987), del libro “Mathematical Impressions”, de A. T. Fomenko

“Puntos singulares de campos de vectores y la capa frontera en el flujo de un líquido alrededor de un cuerpo rígido” (1980), del libro “Mathematical Impressions”, de A. T. Fomenko
Y para terminar, esta vez sí, una obra relacionada también con temas no matemáticos.

“La tentación de San Antonio” (1979), del libro “Mathematical Impressions”, de A. T. Fomenko
Bibliografía
1.- Anatoly T. Fomenko, Mathematical Impressions, AMS, 1990.
2.- B. A. Dubrovin, S. P. Novikov, A. T. Fomenko, Modern Geometry. Methods and Applications. Springer-Verlag, GTM 93 (Part 1), 1984; GTM 104 (Part 2), 1985; GTM 124 (Part 3) 1990.
3.- A. T. Fomenko Symplectic Geometry. Methods and Applications. Gordon and Breach, 1988.
4.- A. T. Fomenko, D. B. Fuchs, V. L. Gutenmacher, Homotopic topology, Akademiai Kiadó, 1986.
5.- Anatoly Fomeko, Dimitry Fuchs, Homotopical Topology, Akademiai Kiadó, 1989 (Springer, GTM 273, 2016).
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Ilustraciones artísticas de un matemático se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Variaciones artísticas del teorema de Napoleón
- Pierre Fatou, un matemático poco (re)conocido
- El problema matemático de las cartas extraviadas
Respuesta de los sistemas respiratorio y cardiovascular al ejercicio físico
Cuando el organismo humano pasa de encontrarse en condiciones de reposo a desarrollar una actividad física intensa, sus sistemas respiratorio y cardiovascular modifican sus prestaciones para dar respuesta a las demandas metabólicas elevadas que impone la actividad física. Ya vimos aquí como se regula la respiración, y aquí y aquí, la circulación sanguínea, que son las dos funciones que permiten ajustar el suministro de oxígeno a las necesidades. Veremos a continuación cuáles son las magnitudes propias del funcionamiento del sistema respiratorio y del sistema cardiovascular en condiciones de reposo, primero, y de actividad intensa después.
Reposo
En condiciones de reposo respiramos entre unas catorce y dieciséis veces (ciclos completos de inspiración y espiración) por minuto; o sea, nuestra frecuencia respiratoria (fr) se encuentra entre 14 y 16 min-1. Un hombre inspira en cada ocasión (VC: volumen corriente) alrededor de 0,5-0,6 l y una mujer 0,4-0,5 l; en otras palabras, en cada una de esas inspiraciones introducimos alrededor de medio litro de aire nuevo en los pulmones. Por lo tanto, el volumen de medio respiratorio inspirado y espirado por unidad de tiempo (V: tasa ventilatoria) es de unos 7,5 l min-1.
No obstante, a los 300 millones de alveolos (similares a microburbujas de 0,3 mm de diámetro y cuya superficie total equivale a 100 m2) no llegan los 7,5 l-1, sino 5,4 l min-1, ya que la diferencia corresponde al volumen inspirado que llena los conductos (bronquios y bronquiolos) que no participan en el intercambio respiratorio y son, por lo tanto, espacio muerto.
Por otro lado, en caso de necesidad, pueden introducirse mayores volúmenes de aire en los pulmones (VIR: volumen inspiratorio de reserva): hasta tres litros (VIR = 3 l) los hombres y dos litros (VIR = 2 l) las mujeres. También pueden expulsarse mayores volúmenes en la espiración. Ese volumen adicional que puede ser exhalado (VER: volumen espiratorio de reserva) es de 1,2 l, en los hombres, y 0,8 l, en las mujeres, aproximadamente. Pero hay un volumen residual (VR) que no es posible desalojar: 1,2 l y 1 l en hombres y mujeres, respectivamente. La capacidad pulmonar total (CPT) masculina es de 6 l y la femenina de 4,2, aproximadamente.
El aire inspirado tiene una presión parcial de oxígeno (pO2) de 158,8 mmHg pero la del oxígeno de los alveolos se encuentra entre 100 mmHg y 105 mmHg.
En condiciones de reposo a la sangre pasan 0,3 l min-1 en los hombres. Esa es su tasa de consumo de oxígeno (VO2 = 0,3 l min-1) en reposo.
En esas condiciones, el corazón late setenta veces por minuto (frecuencia cardiaca: fh= 70 min-1) y el volumen impulsado en cada latido (volumen sistólico: VS) es de 71 ml. El gasto cardiaco –volumen de sangre impulsado por el corazón por unidad de tiempo- es de 5 l min-1. Como tienen alrededor de 5 l de sangre, necesitan alrededor de un minuto para hacer pasar toda su sangre por el corazón. Esas cifras corresponden a hombres sin entrenar; si se trata de atletas de resistencia, VS rondaría los 100 ml y fh sería de unos 50 min-1, aunque puede ser incluso inferior.
La tensión parcial de oxígeno en la sangre arterial (tO2A) es de unos 95 mmHg, y la de la que llega procedente de los tejidos (tO2V), de unos 40 mmHg, y la diferencia entre las concentraciones arterial y venosa de oxígeno (CA –CV) es de 0,06 l O2 por litro de sangre.

Actividad intensa
Durante la realización de ejercicio físico intenso la frecuencia respiratoria puede pasar de 16 min-1 a 40-60 min-1, dependiendo del individuo y de la intensidad del esfuerzo.
El volumen inspiratorio puede llegar a valores máximos de 2 l (en reposo era de 0,5 l), y la tasa ventilatoria pasa de los 7,5 l min-1 del estado de reposo a valores de entre 90 y 120 l min-1 en condiciones de intensa actividad. En esas condiciones el consumo de oxígeno (VO2)puede llegar a 3 o 4 l min-1 en hombres jóvenes no entrenados, y a 5 l min-1 en jóvenes con entrenamiento de resistencia.
La presión parcial de oxígeno en condiciones de actividad intensa puede aumentar hasta pO2 = 115 mmHg dependiendo del nivel de actividad y, por lo tanto, de demanda metabólica; cuanto mayor es la demanda más alta es la presión parcial alveolar porque, como hemos visto, la frecuencia respiratoria y tasa ventilatoria aumentan, elevándose de esa forma la renovación de aire y, en consecuencia, su presión parcial de oxígeno.
Para poderlo sostener, el corazón puede bombear hasta 20 l min-1 (en hombres jóvenes no entrenados) y para ello, ha de latir a frecuencias cardiacas que pueden alcanzar los 190 latidos por minuto (min-1), y el volumen sistólico pasar a unos 105 ml. Los hombres con entrenamiento de resistencia pueden alcanzar valores de gasto cardiaco de 35 l min-1, con frecuencias cardiacas (fh) similares o algo inferiores a las de los hombres no entrenados, pero volúmenes sistólicos (VS) de cerca de 180 ml.
Conforme aumenta la demanda de oxígeno por parte de la musculatura esquelética, la diferencia entre las concentraciones de oxígeno de la sangre arterial y la sangre venosa (CA –CV) aumenta de los 0.06 l por litro de sangre de las condiciones de reposo a máximos de 0,14 l O2 por litro de sangre para consumos de oxígeno de 5 l min-1.
Bajo condiciones de reposo los músculos reciben muy poca sangre, pero en condiciones de trabajo máximo, 1 kg de músculo esquelético puede llegar a recibir 2,5 l min-1. Dado que esa cifra representa más de un 10% del gasto cardiaco, no es posible mantener más de 10 kg de músculo (la tercera parte de toda la musculatura) trabajando a máximo nivel, puesto que hay que seguir irrigando e encéfalo y el corazón, en primer lugar, y otros órganos y tejidos aunque estos recibiendo muy poca sangre. Aquí puedes encontrar una descripción detallada de cómo se reorganiza el flujo sanguíneo al pasar de reposo a la actividad intensa.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Respuesta de los sistemas respiratorio y cardiovascular al ejercicio físico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El flujo sanguíneo se reorganiza en respuesta a las necesidades
- La curva de disociación de un pigmento respiratorio
- Regulación de la circulación (1): control del sistema cardiovascular

