Los secretos de ‘La joven de la perla’

La joven de la perla
Hay obras de arte que dibujan un rostro en nuestra imaginación con tan sólo escuchar su nombre. Entre ellas está La joven de la perla, pintada hacia 1665 por Johannes Vermeer. No hay duda de que, a día de hoy, la joven sigue siendo una influencer en toda regla que ha inspirado libros y películas. Por eso, todo tema relacionado con este cuadro despierta un gran interés y el radar de KimikArte no podía pasar por alto el estudio técnico realizado en el Mauritshuis, el museo donde se aloja la obra. Un equipo internacional liderado por Abbie Vandivere ha examinado cada detalle del óleo y ella misma se ha encargado de elaborar un fabuloso blog que reúne toda la información recogida. Como quizás no tengáis tiempo para leer las 20 entradas que ha escrito, a continuación os hago un resumen de los hallazgos más interesantes, no sin antes agradecer a su autora y al museo el permiso para emplear este material*.
La vida de la joven
Se ha especulado mucho sobre quién era La joven de la perla, pero en este artículo no intentaremos despejar esa incógnita. Tampoco nos centraremos en la figura del padre de la criatura, envuelta asimismo en un halo de misterio. Vermeer, uno de los pintores más admirados del siglo XVII, no tuvo tal reputación en su época y fue un pintor poco prolífico. Por lo menos eso es lo que indica el escaso número de obras (34 reconocidas) que han llegado a nuestros días. En las siguientes líneas nos centraremos exclusivamente en su más célebre creación, de ahí que nos interese conocer qué pasó con ella una vez que el neerlandés le dio la última pincelada.
Por mucho que su nombre indique lo contrario, nuestra protagonista tiene ya más de 350 años y ha tenido tiempo de vivir unas cuantas desventuras. No se sabe nada sobre su paradero hasta 1881 cuando un tal Arnoldus Andries des Tombe le echó el ojo en una subasta de La Haya. Como experto en arte enseguida reconoció la calidad de la obra, y debió ser el único, ya que se la llevó por lo que hoy equivaldría a unos 30 euros. Una auténtica ganga, vamos. El afortunado comprador hizo entelar la obra en Amberes y la mantuvo en su poder durante toda su vida. Cuando murió, en 1902, legó el cuadro al Mauritshuis, donde todavía hoy se puede disfrutar.

Imagen 1. La joven de la perla (44×39 cm) de Vermeer (ca. 1665) en una fotografía de catálogo de 1924. Fuente: Imagen cedida por el Mauritshuis.
Durante el s. XX la obra fue sometida a unos cuantos tratamientos de limpieza y a otros tantos barnizados, entre los que cabe destacar los procesos de restauración y conservación llevados a cabo en los años sesenta. La obra se volvió a reentelar, se eliminaron retoques previos y barnices y se le aplicó un nuevo barniz coloreado. En este momento tenemos que puntualizar que, pese a que a día de hoy este último paso sería impensable, los criterios de conservación y restauración han ido cambiado con el tiempo y en aquella época algunos consideraban que los barnices amarillentos dignificaban la obra. En cualquier caso, y con motivo de una exposición dedicada a Vermeer, dicho barniz se eliminó en 1994. Ésta es la última restauración a la que se ha sometido la pieza y en dicho proceso se realizaron dos interesantes hallazgos: el barniz había ocultado el brillo de los labios de la joven y uno de los brillos de la archiconocida perla no era tal. Concretamente, lo que se pensaba que era una pincelada de Vermeer para resaltar la perla no era más que un trocito de pintura que accidentalmente se había dado la vuelta engañando a los expertos durante años (Imagen 2). Así que la obra perdió un detalle, pero, a cambio, ganó otro.

Imagen 2. En la fotografía de la derecha se señala el brillo “falso” descubierto en la perla.
Lo que el ojo no ve
Como ya hemos visto en entradas anteriores, hay diferentes técnicas que nos permiten explorar detalles que a simple vista no podemos percibir. Me refiero a las radiografías, la fotografía infrarroja, la fluorescencia ultravioleta o la luz rasante. En la Imagen 3 podéis ver qué diferentes son las imágenes logradas con algunas de estas técnicas.

Imagen 3. Radiografía (A), fotografía de fluorescencia ultravioleta (B) y fotografía de luz rasante (C) (René Gerritsen). Fuente: Imágenes cedidas por el Mauritshuis.
En la radiografía (Imagen 3A) se puede ver que algunas zonas son más claras. Esto se debe a la presencia de compuestos con átomos que absorben más los rayos X (al igual que nuestros huesos se ven blancos en una radiografía médica debido al calcio). Gracias a ello podemos observar los clavos del marco o las zonas pintadas con pigmentos que contienen átomos pesados como puede ser el blanco de plomo (lo entenderéis mejor si observáis los ojos y la perla). La radiografía también nos permite apreciar mejor el entramado del lienzo, lo que el equipo científico ha empleado para calcular el número de hilos de lino y comparar los resultados con el de otras obras de Vermeer.
La luz ultravioleta (Imagen 3B) nos permite ver la fluorescencia de ciertos materiales. Podéis observar que toda la obra tiene cierta fluorescencia y eso se debe al barniz que la cubre. Los barnices tradicionales, al envejecer, se vuelven fluorescentes lo que permite identificar intervenciones posteriores a su aplicación. Por ejemplo, la mancha oscura en el ojo corresponde a un retoque realizado en 1994. También cabe destacar la fluorescencia acentuada en los labios, que nos indica que Vermeer empleó alguna laca orgánica fluorescente para lograr ese espectacular efecto.
Por último, y aunque en este caso no se necesite ninguna tecnología especial, el empleo de la luz rasante nos ayuda a apreciar la tridimensionalidad del cuadro (Imagen 3C). Así se aprecia mejor la pincelada de Vermeer y, sobre todo, las craqueladuras, esas grietas surgidas a lo largo de los años por el envejecimiento de los materiales y las tensiones provocadas por los cambios de condiciones ambientales.
Los materiales
Puede que Vermeer no fuese un pintor de éxito, pero el hecho de vivir en una ciudad como Delft le facilitó el acceso a materiales de primerísima calidad. Recordemos que las Provincias Unidas eran el centro comercial por excelencia de Europa, además de una referencia en la manufactura de numerosos productos, entre ellos los lienzos. Ya hemos mencionado que el artista empleó un lienzo de lino, pero no hemos dicho que ese soporte no es adecuado para pintar directamente y por eso es necesario cubrirlo con una capa preparatoria que ofrezca una superficie regular: la imprimatura. La imprimatura la podía realizar el propio pintor, pero en aquella época era habitual comprar los soportes ya preparados. Las estratigrafías de la obra han permitido cuantificar que la imprimatura de La joven tiene un grosor de unos 0,2 mm y está compuesta por blanco de plomo, pigmentos ocres y creta. La creta es una roca blanquecina de carbonato cálcico y origen orgánico formada por fósiles de ciertas algas. De hecho, en la Imagen 4 se pueden apreciar algunos de estos fósiles “durmiendo” bajo capas de pinturas.

Imagen 4. Estratigrafía con la preparación y capas de pintura (Rod Erdmann). A la izquierda se distinguen unos cocolitos. La mitad derecha de la imagen corresponde a fotografía de fluorescencia ultravioleta y la de la izquierda a fotografía de luz visible. En este enlace se puede observar la imagen interactiva. Fuente: Imagen cedida por el Mauritshuis.
Otro de los materiales indispensables en un óleo es el aceite empleado como aglutinante. Los análisis de cromatografía de gases han confirmado que el aceite empleado por Vermeer era de linaza, el más habitual en esta técnica pictórica, y que se obtiene de las semillas de la misma planta con la que se elabora el lienzo. Estos análisis también han desvelado que el artista empleó un aceite previamente tratado para contralar su secado, un factor crítico a la hora de pintar al óleo. Curiosamente también se ha detectado aceite de colza, pero lo más probable es que su presencia se deba a una contaminación en el molino en el que se elaboraban los aceites. Lógicamente una sección dedicada a los materiales artísticos no estaría completa sin hablar de los pigmentos que, debido a su relevancia, trataremos en un apartado diferenciado.
Los pigmentos de Vermeer
Empezaremos por uno de los pigmentos que menos destaca en la composición, pero que no por ello es menos importante: el rojo. A priori sólo lo observamos en los labios que, como ya hemos dicho, están realizados con una laca orgánica. Los análisis mediante cromatografía líquida han confirmado que se trata de carmín, un colorante obtenido de las cochinillas y que también se emplea en la industria alimentaria y, paradójicamente, en productos cosméticos como los pintalabios. Pero no es este el único rojo del óleo. Empleando fluorescencia de rayos X se realizó un mapeo de la presencia de ciertos elementos químicos, entre ellos el mercurio, y se observó que era muy abundante en los labios y, en menor medida, en la piel (Imagen 5). La explicación es que Vermeer empleó cinabrio (HgS) entre sus pigmentos rojos. Probablemente pintó los labios con este pigmento y luego lo cubrió con la laca roja para obtener el efecto deseado. Por otra parte, la presencia de mercurio en el rostro de la chica (en la que también se ha detectado carmín) es debida a que Vermeer añadió este pigmento a la pintura para lograr el color deseado para realizar la piel.

Imagen 5. Mapeo de mercurio obtenido mediante fluorescencia de rayos X (detalle). Fuente: Imagen cedida por el Mauritshuis.
Al hablar de la radiografía hemos mencionado un pigmento blanco: el blanco de plomo (o albayalde). Este compuesto destaca, obviamente, en todos aquellas partes del retrato pintadas de dicho color: la blusa, los ojos, la perla, etc. Pero si volvemos la vista a la radiografía de la Imagen 2 veremos que hay una zona de la cara que es mucho más blanquecina de la otra. Eso quiere decir que en esas áreas Vermeer añadió más pigmento blanco a su pintura como recurso para lograr una mayor claridad. Así, uno de los culpables de los fabulosos juegos de luz de la obra es el albayalde.
Y del blanco pasemos al negro. En este caso los análisis químicos han revelado la presencia de dos pigmentos diferentes: el negro de carbón y el negro de hueso. El primero ofrece un tono más azulado y el segundo un tono más marrón, de ahí que Vermeer los combinase y mezclase para lograr las tonalidades deseadas. En cualquier caso, el negro que más llama la atención es el del propio fondo. Pero, ¡oh sorpresa!, esta zona no estaba pintada de tal color originalmente. Es cierto que el neerlandés aplicó una capa de pintura negra sobre la imprimatura, pero encima depositó una veladura de color verde formada por dos lacas de origen vegetal: índigo (azul) y gualda (amarillo). Estas lacas se degradan bajo la exposición lumínica y son sensibles a otros factores ambientales, por lo que el paso del tiempo ha hecho mella en ellas y nos han dejado un fondo más oscuro que el que pintó Vermeer.
Dejemos el fondo a un lado y volvamos a la ropa de nuestra protagonista. ¿De qué color es la chaqueta que viste? ¿Amarilla? ¿Marrón? De hecho no hay una única respuesta, ya que Vermeer usó diferentes pigmentos amarillentos, rojizos y marrones. La fluorescencia de rayos X ha revelado que las ropas contienen una gran cantidad de hierro, lo que indica la presencia de una familia de pigmentos conocida como tierras: ocre amarillo (FeO(OH)·nH2O), ocre rojo (Fe2O3), siena, etc. Estos compuestos son muy habituales en la naturaleza y dibujan, a su manera, paisajes tan espectaculares como los del Roussillon francés.
Y si hablamos de los ropajes, no podemos pasar por alto la prenda más llamativa: el turbante. A los ya mencionados colores amarillos se les une aquí el azul. Un azul que es, incluso, más exótico que el turbante al que le da el color: el azul ultramar. Ya hemos explicado en otra ocasión que este pigmento se traía desde Afganistán y que era increíblemente caro. En La joven de la perla, Vermeer no sólo lo usa en el turbante, sino que lo emplea mezclado con otros pigmentos (por ejemplo en la chaqueta). Resulta sorprendente que, sin ser un pintor de primerísimo orden en su época, tuviese acceso a un producto tan exclusivo. Pero son muchas las cosas que desconocemos de este genio que, además de esta obra maestra, nos ha regalado joyas como Vista de Delft o La lechera.
La firma
Como si se tratase de un cuadro, acabaremos este artículo con la firma. La de Vermeer, por supuesto. Hoy en día es un rastro apenas invisible en la esquina superior izquierda que se confunde con el fondo degradado. Pero, una vez más, la fluorescencia de rayos X (en este caso la de calcio) nos permite ver con mayor claridad, y distinguir así el llamativo monograma que dejó el artista (Imagen 6). Si os apetece curiosear, aquí podéis ver las diferentes firmas que empleó a lo largo de su carrera, que son casi tantas como las obras que pintó.
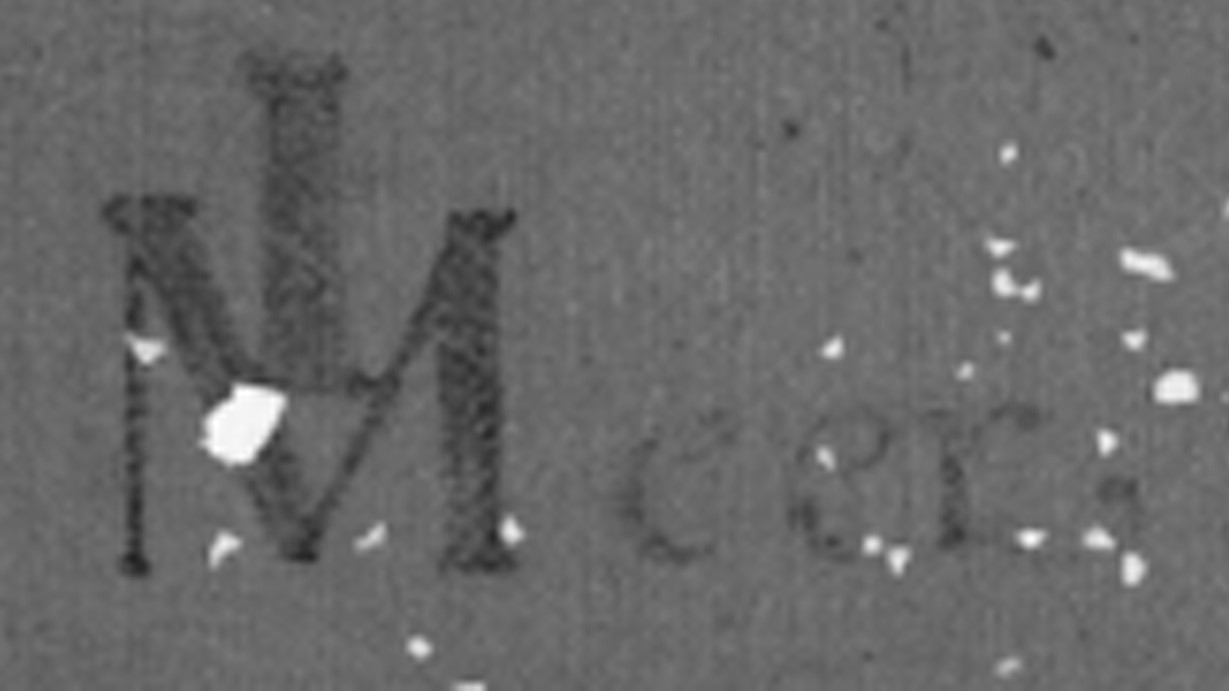
Imagen 6. El monograma de Vermeer identificado gracias al mapeo de calcio con fluorescencia de rayos X (Annelies van Loon). Fuente: Imagen cedida por el Mauritshuis.
*N. del A. Me gustaría expresar mi más sentido agradecimiento al museo Mauritshuis por facilitarme el acceso a las imágenes obtenidas durante el proyecto The girl in the spotlight
Para saber más
Girl with a blog de Abbie Vandivere.
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo Los secretos de ‘La joven de la perla’ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Códigos secretos en la primera guerra mundial
- “Los siete mares de la divulgación” por Pilar Perla
- Secretos
La curva de la atención, ¿una leyenda urbana?
Juan C. Ripoll

Una curva de la atención es una representación gráfica de cómo evoluciona la atención a lo largo del tiempo que dura una actividad. Pero con “la curva de la atención” me estoy refiriendo a algo más concreto: un modelo que indica que la atención de los alumnos a lo largo de una clase disminuye rápidamente, de tal forma que entre 10 y 20 minutos después de que el profesor comience una explicación, la atención del alumnado es mínima y, consecuentemente, también su aprovechamiento.
Recientemente me llegó una lista de consejos para enseñar a leer de una manera respetuosa con la forma de aprender del cerebro. En esa lista encontré una tabla con indicaciones acerca del tiempo que se podía dedicar a la instrucción directa según el curso de los alumnos, desde los 5 a 8 minutos de 1º y 2º de primaria hasta los 12 a 15 minutos para los alumnos de últimos cursos de la secundaria y el bachillerato. Esta tabla iba acompañada por una referencia a Jensen (2005). El libro de Jensen incluye una tabla con estas recomendaciones pero, a diferencia de lo que hace con otras propuestas, no va acompañada por ninguna referencia.
Podría ser algo anecdótico, pero este modelo de la evolución de la atención se está utilizando como base para proponer modificaciones en la forma de enseñar. Por ejemplo, tenemos esta entrevista a Francisco Mora publicada en el diario El País (Torres, 2017), en la que declara:
“nos estamos dando cuenta, por ejemplo, de que la atención no puede mantenerse durante 50 minutos, por eso hay que romper con el formato actual de las clases. Más vale asistir a 50 clases de 10 minutos que a 10 clases de 50 minutos. En la práctica, puesto que esos formatos no se van a modificar de forma inminente, los profesores deben romper cada 15 minutos con un elemento disruptor: una anécdota sobre un investigador, una pregunta, un vídeo que plantee un tema distinto… Hace unas semanas la Universidad de Harvard me encargó diseñar un MOOC (curso online masivo y abierto) sobre Neurociencia. Tengo que concentrarlo todo en 10 minutos para que los alumnos absorban el 100% del contenido. Por ahí van a ir los tiros en el futuro.”
En otro ejemplo, del blog Escuela con cerebro (Guillén, 2012) encontramos esto:
“existen ciclos clave de nuestro cerebro que oscilan entre 90 y 110 minutos y nos permiten mantener la atención. Diversos estudios demuestran que la atención sostenida sólo puede mantenerse durante cortos períodos de tiempo que no superan los 15 minutos. Aparece el factor temporal como una variable decisiva en el aprendizaje y es que, además, a nivel neuronal, se requiere tiempo para fortalecer las sinapsis y no tener que responder a otros estímulos generados. Como el aprendizaje de nuevos conceptos o destrezas requiere un tiempo de procesamiento y asimilación, los docentes deberíamos organizar nuestros contenidos en bloques que no superaran los 20 minutos. Después de cada bloque, para facilitar el aprendizaje y optimizar los ciclos de atención, deberíamos invertir unos minutos en reflexionar sobre lo explicado o en descansar.”
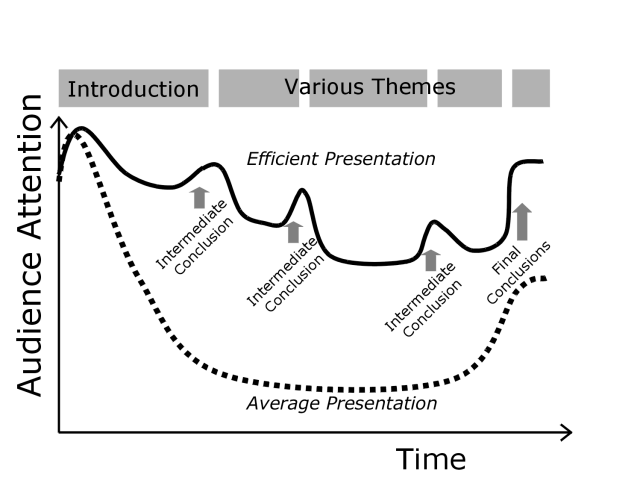
Curvas de atención promedio (discontinua) y presuntamente optimizada (continua).
¿Una leyenda urbana?
Personalmente, cuando me encuentro con este tipo de propuestas, me surgen bastantes dudas. La primera es si no se han considerado las influencias del contexto al medir la evolución de la atención durante una exposición del profesor. ¿Influyen en la la concentración del alumnado el contenido de la exposición, su dificultad, o los recursos retóricos que emplea el profesor para explicarlo? ¿Influye el momento del día o la cantidad de clases que haya habido previamente? Pero la mayor duda que se me plantea es ¿cómo han medido la atención del alumnado a lo largo de la clase y cómo hicieron para que esas medidas no afectaran a la atención, que era el objeto de estudio?
Aparentemente, el modelo de la curva de la atención tiene varios elementos en común con las leyendas urbanas: nos llega de fuentes que no lo han comprobado directamente, pero aseguran conocer datos fiables. Sin embargo, cuando comenzamos a analizar esos datos, la cuestión se enreda y empezamos a encontrar más referencias indirectas y distintas formas de contar la historia. Basta con hacer una búsqueda de imágenes referentes a la “curva de la atención” o “attention curve” para empezar a encontrar diferentes representaciones. La mayoría de ellas comienzan con un aumento rápido de la atención, seguido por una brusca caída, una fase baja (estable o ligeramente decreciente) y un repunte posterior. Sin embargo, las alturas relativas, y las pendientes que se muestran pueden ser bastante diferentes. Algunas van acompañadas por referencias de tiempo y otras no. Las que incluyen estas referencias suelen representar intervalos de 40 a 60 minutos y suelen situar el declive de la atención entre los 15 y los 30 minutos.
Durante esta búsqueda superficial encontré que algunas de las imágenes proporcionaban referencias a manuales dirigidos a mejorar la eficacia de las clases, por ejemplo Gibbs (1992) o Bligh (1998; la primera edición de este manual es de 1971).
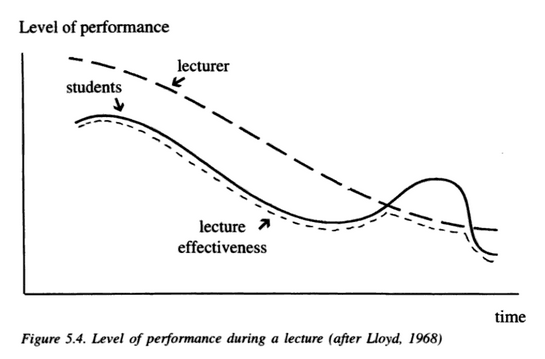
Figura de la página 56 de Bligh (1998)
Se puede acceder parcialmente al manual de Bligh a través de Google Books y es muy ilustrativo ver la imagen que incluye en la página 56. Lo primero que me chocó es que la curva que se representa es mucho más plana que las curvas de Bligh que había encontrado buscando imágenes en internet y, también, que la representación se plantea como una interacción entre la receptividad de los alumnos y la actuación del profesor. Esta segunda parte no la había visto en ninguna de las representaciones que había estado consultando.
Y ahora, otro salto en el tiempo. Bligh referencia la representación que incluye en su manual a Lloyd (1968). Cuanto más retrocedemos en el tiempo (y ya van 50 años) más difícil me resulta consultar las fuentes, y no he podido acceder a este artículo de Lloyd. Sin embargo, en el intento, he encontrado una revisión que describe su contenido y que ofrece información interesante sobre la curva de la atención.
Pero antes de continuar con esa revisión, sí que me gustaría indicar que hay intentos de representar la fluctuación de la atención del alumnado bastante más antiguos, por ejemplo el de Philpott (1934). En realidad, este modelo no tomaba datos sobre la atención de los alumnos durante las explicaciones, sino en la realización de actividades como cálculos aritméticos. Lo curioso es que trata de representarla mediante una curva que representa la evolución de la atención a lo largo de 15 minutos. El propio Philpott menciona otros intentos anteriores de representar los cambios en la atención, así que no parece que sea el modelo más antiguo.
Una revisión
Ahora sí, me centro en la revisión que he presentado en la sección anterior, publicada por Wilson y Korn (2007). Es muy breve y se puede encontrar en internet, así que recomiendo su lectura directa, pero también me gustaría destacar algunos puntos.
Wilson y Korn también encontraron que existe una especie de acuerdo tácito que indica que la atención de los alumnos durante una explicación solo se mantiene durante unos 10 o 15 minutos. Para ver qué respaldo tiene esa idea, examinaron las referencias que daban algunos manuales de pedagogía en los que la encontraron.
En esta búsqueda encontraron que varias de las fuentes que se citaban no eran estudios empíricos, sino que se basaban en otras fuentes o en observaciones e impresiones personales. En ese tirar del hilo localizaron unos pocos estudios empíricos, en los que la atención de los alumnos se medía según la cantidad de apuntes que tomaban durante la clase, a partir de la observación de su comportamiento, el recuerdo de los contenidos explicados, medidas de autoinforme y medidas fisiológicas (tasa cardíaca).
Varios de estos estudios tienen problemas metodológicos como que no se haya evaluado la fiabilidad de los observadores o que no quede clara la relación entre la variable medida y la atención (por ejemplo, los alumnos pueden dejar de tomar apuntes porque se distraen, pero también por otros motivos, como que perciban que el profesor repite ideas, que las consideren poco importantes o algo ya sabido). Además, en algunas ocasiones no hay consistencia entre las medidas de observación y las medidas de aprendizaje o entre los resultados de distintos estudios.
No olvido que esta revisión hablaba de la curva de la atención de Lloyd (1968), la más antigua que he localizado sobre atención a una explicación. Wilson y Korn (2007) indican que el modelo que propone Lloyd no se construyó a partir de datos empíricos, sino de sus experiencias y observaciones como profesor.
Algo más reciente, por favor
Esta revisión de Wilson y Korn ya tiene unos cuantos años, de modo que es posible que en ese tiempo la investigación haya aportado datos a favor de las miniclases de 10 o 15 minutos, o quizá no…
Bradbury (2016) también ha realizado una revisión, ahora más reciente sobre este tema. Sus conclusiones son muy similares a las de Wilson y Korn (2007), pero realiza algunas aportaciones interesantes. Bradbury sitúa el origen del mito de los 15 minutos de atención en un informe sobre la toma de apuntes, publicado en 1978, aunque ya hemos visto cómo Lloyd (1968) ya había expuesto la idea del declive de la atención tras los primeros minutos de clase. Entre los estudios que revisa Bradbury hay uno posterior a 2007, en el que se empleó una medida de autorregistro con pulsadores inalámbricos y en el que se vio como la atención de los alumnos (universitarios que hacían un curso de química) fluctuaba a lo largo de la clase, pero sin seguir una pauta.
Su conclusión es que el límite de 10 a 15 minutos para la duración de las explicaciones no está respaldado por evidencias. También indica que, según los estudios revisados, parece que la mayor fuente de variabilidad en la atención de los alumnos es el profesor, no el formato de la clase. Me imagino que no se trata del profesor en sí, sino de sus habilidades para comunicar los contenidos y mantener el interés de la clase.
Para intentar mantener el rigor, habría que tener en cuenta que las dos revisiones que he presentado no son sistemáticas y, por ejemplo, esta de Bradbury omite estudios como el de Risko, Anderson, Sarwal, Engelhardt y Kingstone (2012) o el de Farley, Risko y Kingstone (2013), sin que sepamos si se trata de una omisión accidental o de algo intencionado porque los participantes no seguían clases presenciales sino grabadas en vídeo.
Concluyendo
La idea de que el funcionamiento de la atención humana hace recomendable no prolongar las explicaciones más allá de un intervalo entre 10 y 20 minutos está bastante extendida. A veces se presenta como una aportación de la “neurodidáctica”, pero no se trata de una novedad ya que se puede encontrar como algo ya establecido a partir de la segunda mitad del siglo XX. Sin embargo, resulta difícil identificar su origen y también localizar un conjunto de evidencias que respalden esta creencia.
Los datos que he aportado aquí para cuestionarla no son especialmente rigurosos: algunas apreciaciones sobre las distintas formas en que se presenta y la facilidad con la que se da por cierta basándose en referencias a fuentes no empíricas. No obstante, no olvidemos que es responsabilidad de quienes plantean modificaciones en la forma de estructurar las clases el aportar las evidencias que respalden sus propuestas. Mi objetivo era, sencillamente, poner de manifiesto que quizá no existan esas evidencias.
La atención del alumnado a las lecciones o explicaciones es un asunto complejo en el que probablemente influyen el nivel de desarrollo, la motivación, los recursos del profesor, el contenido de la explicación, la fatiga, la presencia o ausencia de distractores y otras variables. Explicar esa atención a las explicaciones únicamente en función de su duración es, quizá, demasiado simplista. Buena parte de los estudios sobre el tema se han realizado con alumnado universitario, no de etapas escolares. Esto merecería una exploración más profunda ya que no es extraño que el profesorado de educación primaria y secundaria combine a lo largo de una sesión lectiva explicaciones, intervenciones del alumnado, actividades y corrección de las actividades, de manera que podríamos estar tratando de solucionar un problema poco habitual (largas explicaciones que el alumnado no es capaz de aprovechar).
Sería un exceso de confianza realizar modificaciones generales de la estructura o duración de las clases dando por supuesto que este modelo es válido, sin comprobar que realmente lo es y comunicar claramente a los implicados (alumnado, familias, profesorado y responsables del sistema educativo) la evidencia disponible para promover estos cambios.
Referencias:
Bligh, D. (1998). What’s the use of lectures (5ª ed.). Exeter: Intellect.
Bradbury, N. A. (2016). Attention span during lectures: 8 seconds, 10 minutes, or more? Advances in Physiology Education, 40(4), 509-513.
Gibbs, G. (1992). Improving the quality of student learning. Bristol: Technical & Educational Services Ltd.
Farley, J., Risko, E. F. y Kingstone, A. (2013). Everyday attention and lecture retention: the effects of time, fidgeting, and mind wandering. Frontiers in Psychology, 4, 619.
Guillén, J. C. (2012). La atención: un recurso limitado. Disponible en https://escuelaconcerebro.wordpress.com/2012/03/04/la-atencion-un-recurso-limitado/
Jensen, E. (2005). Teaching with the mind in brain (2ª ed.). Alexandria (EEUU): ASCD.
Lloyd, D. H. (1968). A concept of improvement of learning response in taught lesson. Visual Education, 23-25.
Philpott, S. J. F. (1934). A theoretical curve of fluctuations of attention. British Journal of Psychology, 25(2), 221-255.
Risko, E. F., Anderson, N., Sarwal, A., Engelhardt, M. y Kingstone, A. (2012). Everyday attention: Variation in mind wandering and memory in a lecture. Applied Cognitive Psychology, 26(2), 234-242.
Torres, A. (2017). Hay que acabar con el formato de clases de 50 minutos. Disponible en https://elpais.com/economia/2017/02/17/actualidad/1487331225_284546.html
Wilson, K. y Korn, J. H. (2007). Attention during lectures: Beyond ten minutes. Teaching and Psychology, 34(2), 85-89.
Sobre el autor: Juan Cruz Ripoll es maestro de primaria y doctor en educación.
El artículo La curva de la atención, ¿una leyenda urbana? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un chip de ADN para el diagnóstico de TDAH (trastorno por déficit de atención e hiperactividad)
- La leyenda del cuervo y el búho
- La curva de disociación de un pigmento respiratorio
Ciencia grande, ciencia pequeña

Una fracción de los investigadores y técnicos que trabajan con el detector CMS del CERN.
En los últimos tiempos está de moda la ciencia grande. Los organismos de investigación y quienes financian la ciencia favorecen los proyectos macro, con participación internacional, objetivos enormes y plantillas ingentes. Grandes coaliciones de múltiples laboratorios o centros de investigación, grandes problemas a resolver y grandes ambiciones, a ser posible con grandes instrumentos en proyectos que cuestan grandes cantidades y se alargan en grandes periodos temporales. En algunos casos, como cuando se trata de obtener financiación europea, es obligatorio buscar la cooperación de equipos de investigación externos porque el objetivo no es sólo fomentar la ciencia, sino forzar la cooperación paneuropea. En otros disponer de un socio, incluso extracomunitario, aumenta las posibilidades de conseguir dinero por razones de política internacional.
En otras ocasiones es forzoso que el proyecto sea de gran tamaño, porque el instrumental necesario lo es: si tu trabajo implica usar un macrotelescopio, o un acelerador de partículas, o diseñar e integrar un instrumento en un satélite necesariamente tendrás que integrarte en un gran equipo internacional. Lo cual tiene dos inconvenientes graves, en lo que se refiere a la práctica científica desde el punto de vista personal; dos cuestiones que demasiadas veces no se tienen en cuenta a la hora de pensar en una carrera profesional, o en la ciencia en su conjunto.
Por una parte nadie entrena de modo formal a los científicos para formar parte de, y mucho menos para dirigir, grandes equipos. Las habilidades y capacidades necesarias para integrarse en (o liderar) un gran consorcio internacional, o para gestionar desde el punto de vista práctico un laboratorio, no están en el temario de las carreras de ciencias. Coordinar equipos internacionales, gestionar el suministro de consumibles, pedir permisos de excavación o solicitar becas o financiación de proyectos no es algo que se aprenda durante una carrera de ciencias físicas, biológicas o matemáticas. No hablemos ya de la gestión de personal, una tarea que en las empresas tiene departamentos especializados y que en un entorno científico se ve complicada por el hecho de que no siempre es posible ‘fichar’ a la persona que se desea; a la hora de contratar un técnico de laboratorio, supongamos, es posible que haya que convocar un concurso público que nos traerá a una persona cualificada, sí, pero a la que quizá no conocemos. Y teniendo en cuenta que además la tarea del líder del equipo incluirá definir líneas de investigación para sus becarios y postdoc pensando en las necesidades del equipo propio, pero también en sus carreras profesionales futuras, y la plasmación de todo esto en publicaciones y tesis; otra tarea compleja y que no se enseña de modo reglado sino que se aprende (con suerte) en el ejercicio profesional.
En lo que se refiere a la ciencia esta querencia, o moda, de los estamentos financiadores por los megaproyectos fuerza a los científicos a buscar determinado tipo de problemas como objetivo de sus investigaciones, dejando de lado otros más pequeños, pero no por ello menos interesantes. Es por eso que resulta mucho más sencillo obtener fondos para proyectos de Big Data que para caracterizar la flora y fauna de una región, por ejemplo; o para realizar grandes campañas de geomorfología a gran escala que para caracterizar la geoquímica local. Se organizan consorcios internacionales de miles de investigadores y cientos de laboratorios para luchar contra el cáncer o para crear y operar el Gran Colisionador de Hadrones, pero es mucho más difícil encontrar financiación para otro tipo de ciencia más pequeña, con menos necesidad de grandes equipos o instrumentos y con resultados menos llamativos, aunque no por ello de menor importancia. Y con ello perdemos datos que son también importantes pero que no se capturan, porque iniciar un proyecto para hacerlo es un suicidio a la hora de conseguir un respaldo a tu investigación.
Como en cualquier área los científicos deben escoger entre erigir catedrales y pintar cuadros. El constructor de catedrales necesita grandes equipos de gente, mucho tiempo, capacidades de gestión y paciencia, pero a cambio puede construir enormes edificios que desafiarán a los siglos. Para ello debe tener todas esas cualidades y además debe renunciar a controlar hasta el último detalle de su creación; necesariamente tendrá que delegar en el maestro cantero para que talle los capiteles o en el ebanista para que se ocupe del coro, por lo que la obra final no será tan personal; sólo un Justo Gallego puede construir una catedral él solo (y así le ha salido). En cambio el pintor tiene que renunciar a las obras inmensas más allá de la Capilla Sixtina o los grandes frescos, ya que la capacidad de trabajo de un humano tiene sus límites. Pero a cambio hasta el último detalle del resultado estará bajo su control; si lo desea cada brillo, cada sombra y cada color del cuadro resultante serán su obra. Son dos modos diferentes de enfocar el acto creativo y dos maneras de enfrentarse al trabajo necesario.
El peligro es que concentrándonos demasiado en las catedrales nos olvidemos de pintar cuadros. No sólo no estamos formando a los científicos para el tipo de trabajo que hoy se les exige, sino que además estamos abandonando otro tipo de ciencia más callada, solitaria y de alcance quizá más limitado en principio, pero sin la cual los macroproyectos tampoco pueden llegar muy lejos. Ayudemos a los constructores de catedrales, pero apoyemos también los proyectos menos ambiciosos, más personales y también necesarios. Porque de lo contrario la ciencia grande se comerá a la pequeña, y saldremos todos perdiendo.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo Ciencia grande, ciencia pequeña se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La forma de las charcas árticas

A veces, para crear un modelo de algún fenómeno natural aparentemente complejo bastan tan solo dos parámetros. Un ejemplo típico es el movimiento de una bandada de estorninos. Otro ha resultado ser la forma de las charcas de agua marina formadas al derretirse el hielo del Ártico. Y esto puede ser muy importante para conocer nuestro futuro a medio plazo.
El cambio climático ha alterado drásticamente el Ártico, con el hielo marino derritiéndose más rápido de lo que predecían los modelos a gran escala. En parte esta subestimación se debe a la falta de una comprensión completa de las charcas que aparecen a partir del hielo que se derrite. Un nuevo modelo geométrico de charcas árticas puede reproducir las distribuciones observadas tanto de los tamaños como de las formas de las charcas. Debido a su simplicidad, el modelo puede resultar práctico para predecir cómo un mayor calentamiento podría afectar a los casquetes polares.
Cuando el hielo marino del Ártico se derrite, se forman charcas de agua de varias formas y tamaños en la superficie del hielo. Las charcas tienen un impacto enorme en el transporte de energía, ya que el agua es menos reflectante y absorbe más la energía solar que el hielo o la nieve. Esta propiedad conduce a un mecanismo de retroalimentación positiva: cuantos más charcas se forman, más luz solar se absorbe y mayor cantidad de hielo se funde. Es por esto que los investigadores se esfuerzan en formular modelos de charcas que les permitan incorporar estos efectos de retroalimentación de pequeña escala en modelos climáticos a gran escala. Pero, para que esta incorporación sea posible, los modelos de charcas deben ser simples además de eficaces.
Un equipo de investigadores encabezado por Predrag Popović, de la Universidad de Chicago (EE.UU.), ha ideado un modelo de charca simple que se basa en dibujar círculos aleatoriamente en un plano y suponer que se forman charcas de hielo derretido en los huecos entre los círculos. El modelo tiene solo dos parámetros de entrada: el radio medio del círculo y la fracción del área superficial cubierta por huecos (la conectividad).
El equipo afinó estos parámetros para que los huecos exhiban las mismas correlaciones espaciales que las observadas en las charcas de hielo derretido. Utilizando esta parametrización, los autores demuestran que el modelo reproduce con precisión otras características de las charcas, como la caracterización fractal de sus formas y la abundancia de charcas como función de la superficie.
Adicionalmente se analizaron las funciones de correlación de las charcas en varias fechas. Sorprendentemente resulta que la escala de las charcas y su conectividad son constantes en diferentes años y tipos de hielo.
Estos resultados demuestran que la geometría y la abundancia de las charcas de hielo derretido árticas se pueden describir de forma sencilla, lo que puede aprovecharse en futuros modelos que mejorarían las predicciones de la respuesta del hielo marino al calentamiento del Ártico.
Predrag Popović, B. B. Cael, Mary Silber, and Dorian S. Abbot (2018) Simple Rules Govern the Patterns of Arctic Sea Ice Melt Ponds Physical Review Letters doi: 10.1103/PhysRevLett.120.148701
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo La forma de las charcas árticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La presencia de sales podría hacer que exista una tectónica de placas en Europa
- ¿Y si el Sol estuviese cambiando de forma fundamental?
- Cómo dejar de usar petróleo y seguir consumiendo sus derivados de forma barata
Andrew Wiles: de conjetura a teorema
Quizás la mejor manera de describir mi experiencia haciendo matemáticas sea comparándola con entrar en una mansión oscura. Entras en la primera habitación, y está oscura, completamente a oscuras. Vas dando tumbos, tropezando con los muebles. Poco a poco aprendes donde está cada mueble, y finalmente, después de más o menos seis meses, encuentras el interruptor de la luz y lo conectas. De repente todo se ilumina, y puedes ver exactamente dónde estás. Entonces entras en la siguiente habitación oscura…
Andrew Wilesi

Andrew Wiles en 1995. Fuente: Wikimedia Commons.
El matemático británico Andrew Wiles nació el 11 de abril de 1953. En su 65 cumpleaños quería recordarle a través de dos propuestas teatrales, una didáctica y otra musical.
Pero empecemos por el principio. En 1993, Andrew Wiles deslumbró a la comunidad matemática al revelar que había demostrado del Último Teorema de Fermat, el famoso problema matemático enunciado por Pierre de Fermat en 1637. Recordemos que Fermat escribió en el margen de su copia de la Arithmetica de Diofanto, en el problema que trata sobre la división de un cuadrado como suma de dos cuadrados, lo siguiente:
Es imposible dividir un cubo en suma de dos cubos, o un bicuadrado en suma de dos bicuadrados, o en general, cualquier potencia superior a dos en dos potencias del mismo grado; he descubierto una demostración maravillosa de esta afirmación. Pero este margen es demasiado angosto para contenerla.
Durante siglos, nadie consiguió demostrar este enunciado, hasta que en 1993, durante unos cursos de verano en la Universidad de Cambridge, Wiles anunció que la conjetura había pasado a teorema: después de siete años de afanosa entrega, había probado la conjetura de Taniyama-Shimura, de la que se seguía la conjetura de Fermat según un trabajo previo del matemático Kenneth A. Ribet. A finales del verano de 1993, uno de los especialistas que estaban comprobando el documento con la demostración de Wiles encontró un error en una parte del razonamiento. Wiles repasó la demostración con la ayuda de su entonces alumno Richard Taylor, hasta concluir la prueba definitiva en otoño de 1994.
Las dos propuestas escénicas que recuerdo en estas líneas tratan sobre Wiles y la demostración del teorema de Fermat. La primera de ellas, la más reciente, El misterio de Fermat (2017), es una obra de teatro de la compañía Teatre de l’Enjòlit con texto y dirección de Albert Alemany.

Cartel de “El misterio de Fermat”.
La obra persigue acercar las matemáticas al público más joven a través de este misterio que permaneció sin solución durante más de trescientos cincuenta años: en su resolución participaron numerosas mentes brillantes, que solventaron algunos casos particulares y desarrollaron herramientas matemáticas complejas antes de que Andrew Wiles publicara su demostración.
El misterio de Fermat lleva a escena una apasionante historia de descubrimientos, pasiones, errores y logros por medio de escenas cortas y de continuos saltos en el tiempo involucrando veinticinco personajes históricos. Algunos de ellos son Pierre de Fermat (1601-1665) –que no aparece representado por ningún actor, pero es nombrado continuamente, reforzando el misterio al que alude el título de la obra–, Marin Mersenne (1588-1648) –que tuvo una nutrida correspondencia con Fermat–, René Descartes (1596-1650), Blaise Pascal (1623-1662) –que intercambió con Fermat numerosas cartas analizando los juegos de dados, debido a su común interés por la teoría de la probabilidad–, Leonhard Euler (1707-1783) –que demostró el último teorema de Fermat en el caso n=3. Además, gran parte de los primeros trabajos de Euler en teoría de números se basan en estudios de Fermat: probó el pequeño teorema de Fermat, el teorema de Fermat sobre la suma de dos cuadrados y también comprobó la falsedad de algunas de las conjeturas de Fermat–, Sophie Germain (1776-1831) –cuyas importantes aportaciones en teoría de números permitieron avanzar en la prueba del último teorema de Fermat–, Carl Friedrich Gauss (1777-1855), Ernst Kummer (1810-1893) –que probó el último teorema de Fermat para una clase considerable de exponentes primos–, los matemáticos Yutaka Taniyama (1927-1958) y Goro Shimura (1930) –que enunciaron la conjetura de Taniyama-Shimura, un caso especial de la cual fue demostrada en 1995 por Wiles y Richard Taylor (1962), suficiente para demostrar el último teorema de Fermat– y, por supuesto, Andrew Wiles.
El misterio de Fermat pretende entretener, mostrar una parte esencial de la historia de las matemáticas, enseñar algunos conceptos matemáticos sencillos, hablar de la manera en la que ‘se fraguan’ las matemáticas y de la pasión que se siente al recorrer este camino. A través de los personajes que atraviesan la obra, se intenta transmitir el amor por la ciencia, la belleza de las matemáticas, y el valor del esfuerzo y la pasión personalizados en la figura de Andrew Wiles.
La segunda propuesta es el musical Fermat’s last tango (2001) de Joshua Rosenblum y Joanne Sydney Lessner

Cartel de “Fermat’s last tango”.
Este musical –que mezcla estilos variados como rocanrol, jazz o tango– transcurre en la época en que se ha descubierto un error en la demostración del Wiles del teorema de Fermat.
Andrew Wiles está encarnado por un personaje ficticio, el profesor Daniel Keane. La obra comienza con una conferencia de prensa en la que se anuncia la conclusión de la prueba del Teorema de Fermat. Pronto aparece el fantasma de Fermat afirmando que él ya había demostrado su famoso teorema, y mofándose de la complicada demostración de Keane. Como aliados de Fermat para burlarse de Keane aparecen Pitágoras (c. 569 a. C.–c. 475 a. C.), Euclides (ca. 325 a. C.-ca. 265 a. C.), Carl Friedrich Gauss e Isaac Newton (1643-1727), que llegan desde el Aftermath, el lugar en el que viven los matemáticos inmortales. Menosprecian al joven matemático que, en su opinión, usa métodos oscuros y complicados.
Fermat anuncia a Keane que su prueba contiene un error, en una sarcástica canción:
But your proof contains a flaw, Profesor Keane. It destroys the whole fundation of your finely tunned machine. I hate to be a spoilsport. I know it was your Goal. But your proof contains a big fat hole.ii
Keane, aterrado, comprueba que el error efectivamente existe y comienza, ofuscado, a repasar su prueba. Se origina un complicado triángulo entre Anna, la esposa de Keane, que desea que su marido deje de obsesionarse, el propio Keane y Fermat, que sigue burlándose del joven matemático. El resto de la obra es una lucha entre lo viejo y lo nuevo: Fermat desea mantener a toda costa su fama y desanima a Keane en cada uno de sus progresos. En un socarrón concurso en el que se nombra a muchos famosos matemáticos, Fermat y los miembros del Aftermath presionan implacablemente a Keane para que intente encontrar la demostración. Anna, a su vez, sigue intentando que Daniel – que se pasa la vida encerrado en el ático trabajando– reaccione. En un dramático tango –en el que se canta el tema que da título a la obraiii–, el matemático francés y Anna se disputan a Keane como pareja de baile.
Finalmente, los Aftermath se dan cuenta del valor y la dificultad del trabajo de Keane, de la brillantez de los métodos modernos por él utilizados y terminan apoyándole y dándole la bienvenida a su selecto grupo. Tras un arduo trabajo, Keane encuentra finalmente la demostración del teorema, recibiendo la aprobación de su admirado Fermat…
Debajo dejamos el video de una de las representaciones.
Referencias:
-
Dossier sobre la obra El misterio de Fermat, Teatre de l’Enjòlit
-
Marta Macho Stadler, El misterio de Fermat, Teatre de l’Enjòlit, DivulgaMAT, Teatro y matemáticas, abril 2018
-
R. Osserman, Fermat’s Last Tango, Notices of the AMS, vol. 48, núm. 11, 1330-1332, 2001
-
Marta Macho Stadler, Fermat’s Last Tango, DivulgaMAT, Teatro y matemáticas, noviembre 2008
Notas:
iExtraída del documental de S. Singh y John Lynch “Fermat’s Last Theorem” Programa Horizon, BBC, 1997. La traducción es de Capi Corrales Rodrigáñez de su “Un paseo por el siglo XX de la mano de Fermat y Picasso”.
ii Minuto 32:20 del video que acompaña a esta entrada.
iiiMinuto 59:45 del video que acompaña a esta entrada.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Andrew Wiles: de conjetura a teorema se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (y 4): ¿Podemos creer la prueba de la conjetura?
- El teorema de Marion (Walter)
- Euler y el último teorema de Fermat
La regulación osmótica de los animales de agua dulce

Carassius auratus
Como vimos aquí, solo los invertebrados marinos y, entre los vertebrados, los peces bruja tienen ancestros exclusivamente marinos. Por esa razón sus medios internos tienen la misma concentración osmótica que el agua de mar –no necesitan regularla- y una composición iónica que no difiere demasiado de la de aquél, aunque esta sí la deben regular. Todos los demás vertebrados tienen en sus linajes ancestros dulceacuícolas. En la actualidad, un buen número de invertebrados viven en aguas dulces, al igual que numerosas especies de peces teleósteos, algunas de peces elasmobranquios y otros vertebrados (anfibios y reptiles, principalmente). Pues bien, todos los animales que viven en aguas dulces regulan la concentración osmótica de su medio interno, manteniéndola muy por encima de la del medio externo. Son, por lo tanto, reguladores hiperosmóticos.
Estos animales han de hacer frente a dos posibles problemas para mantener constante la concentración interna. Por un lado el agua tiende a entrar en sus organismos a favor de gradiente osmótico. Si no consiguiesen contrarrestar fisiológicamente esa tendencia, el organismo se llenaría de agua, el medio interno (plasma y fluido intersticial) en primera instancia y, como consecuencia, el medio intracelular también, lo que provocaría la deformación de las células y, eventualmente, su ruptura. El segundo problema sería la pérdida de los solutos internos a favor de gradiente electroquímico.
Una característica común de los animales de agua dulce es que la concentración osmótica de su medio interno (y, por lo tanto, también intracelular) es muy inferior a la de los animales marinos osmoconformadores (u osomoconcordantes). Así pues, la adaptación a un medio muy diluido conllevó una reducción en la concentración osmótica de su medio interno, de manera que el gradiente que habían de mantener los miembros de los linajes que protagonizaron la transición del mar a los ríos es muy inferior al que habría sido de no haberse producido tal reducción. Ha de entenderse que esa reducción no constituye la respuesta de un individuo a un cambio de salinidad del medio, sino que consistió en un cambio de base genética que requirió de plazos de tiempo muy prolongados. Para que nos hagamos una idea de la magnitud de la reducción, sirvan los siguientes valores de osmolaridad (mOsm) del medio interno de diferentes géneros:
Dulceacuícolas (concentración osmótica del agua dulce: 0,5-10): Spongilla (Porifera): 55; Chlorohydra (Cnidaria): 45; Asplachna (Rotifera): 81; Anodonta (Mollusca): 66; Viviparus (Mollusca): 80; Hirudo (Annelida): 200; Astacus (Arthropoda, Crustacea): 477; Potamotrygon (Chordata, Chondrichthyes): 308; Carassius (Chordata, Actinopterygii): 392; Rana (Chordata, Amphibia): 234.
Marinas (concentración osmótica del agua de mar: 1000): Aurelia (Cnidaria): 1050; Asterias (Echinodermata): 1015; Loligo (Mollusca): 1003; Arenicola (Annelida): 1020; Homarus (Arthropoda, Crustacea): 1035; Myxine (Chordata, Cyclostomi): 1152; Squalus (Chordata, Chondrichthyes): 1000; Latimeria (Chordata, Sarcopterygii): 954; Opsanus (Chordata; Actinopterygii): 392; Fejervarya (Chordata, Amphibia): 830.
Pero incluso habiendo reducido considerablemente el gradiente de concentraciones osmóticas entre el medio interno y el externo, sigue habiendo una fuerte tendencia del agua a entrar en el organismo y de las sales a salir. Por esa razón, el tegumento de estos animales suele ser poco permeable, aunque el grado de permeabilidad es muy diferente en unos grupos y en otros. Esa baja permeabilidad del tegumento es considerada la primera barrera frente a la dilución.
La baja permeabilidad general del tegumento, no obstante, no evita los movimientos de agua y de sales. Hay epitelios que no se pueden impermeabilizar. Las superficies respiratorias son el enclave que mejor ilustra esa imposibilidad. Un epitelio impermeable no permitiría el intercambio de gases. Y con el digestivo pasa algo parecido; no obstante, hay que decir que los reguladores hiperosmóticos evitan beber, por lo que el agua que pueda introducirse a través de los epitelios digestivos es solo la que se incorpora con el alimento. Por las razones dadas, los animales de agua dulce han de contar con mecanismos que contrarresten esos flujos pasivos. Y aquí entra en juego la segunda barrera frente a la dilución, que se explica a continuación.

Rana clamitans
Evitan la invasión de agua produciendo grandes volúmenes de orina. El cangrejo de río Astacus fluviatilis elimina un 8% de su masa corporal en forma de orina; en el anfibio Rana clamitans y el pez Carassius auratus ese porcentaje es del 33%, en el sapo Xenopus laevis es del 58% y en el caracol dulceacuícola Viviparus viviparus, puede variar entre el 36% y el 131%. Esa tarea corre a cargo del órgano excretor.
Y además de eliminar una gran cantidad de agua en forma de orina, los animales de agua dulce deben reducir en la medida de lo posible la concentración de sales en la orina. La concentración osmótica de la orina representa, con respecto a la del medio interno, un 20% en Viviparus, un 16% en Xenopus, un 14% en Carassius y un 10% en Astacus. De no proceder de ese modo, la orina tendría la misma concentración osmótica que el medio interno (sería isosmótica) por lo que el trasiego constante de agua dulce hacia el interior y su eliminación como orina isosmótica con el medio interno, provocaría una fuerte pérdida de sales. Sería como si se produjese un lavado permanente del medio interno, lo que anularía la posibilidad de mantener una concentración osmótica constante y diferente de la del medio externo. El órgano excretor debe hacer, por lo tanto, una doble tarea, producir orina abundante, por un lado, y por el otro reabsorber la mayor cantidad posible de iones de esa orina antes de su evacuación. Ese trabajo, no obstante, requiere gastar energía, pues los iones que se reabsorben han de transportarse gastando ATP en el proceso. Nada es gratis.
Pues bien, para los reguladores hiperosmóticos no es suficiente con producir orina abundante y diluida. Porque por baja que sea su concentración osmótica, nunca lo es tanto como el medio externo. Así pues, la eliminación del agua que entra a favor de gradiente osmótico siempre conlleva una cierta pérdida de sales. Parte de las sales que se pierden pueden recuperarse a través del sistema digestivo, porque se absorben junto con el alimento. Y la otra parte ha de incorporarse a través de otras vías extrarrenales, como son la piel en anfibios, la vejiga urinaria en tortugas o las branquias en peces y crustáceos. La incorporación extrarrenal de sales es la tercera barrera frente a la dilución. Los enclaves en los que tiene lugar pueden ser diferentes dependiendo de la especie, pero los mecanismos básicos son similares, ya que conllevan el transporte activo de las sales que tienden a perderse -Na+ y Cl– en mayor medida- y, por lo tanto, de nuevo con importante gasto de energía en forma de ATP.
Así pues, un buen número de grupos animales se han adaptado a vivir en aguas dulces. Esa adaptación ha conllevado una reducción importante en la concentración osmótica del medio interno, un alto grado de impermeabilización de los tegumentos, la producción de altos volúmenes de orina de la que se recupera la mayor cantidad de sales posible, y la incorporación extrarrenal de las sales necesarias para mantener constante su concentración en el medio interno. Para estos procesos se requieren dispositivos tales como eficaces órganos excretores, así como transportadores de sales en determinados enclaves. La osmorregulación conlleva un importante coste de energía, porque transportar iones contra gradiente electroquímico es caro. Pero está claro que ese coste es compensados por las ventajas que comporta ocupar los nichos que ofrecen las aguas dulces. De otra forma no habría habido linajes que, desde los océanos, “se aventurasen” a colonizar esos nuevos medios.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La regulación osmótica de los animales de agua dulce se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Animales en equilibrio osmótico: invertebrados marinos y peces bruja
- Relaciones hídricas y salinas de los animales
- La distribución del agua animal y el curioso caso del potasio
Comprobaciones experimentales de la relatividad general (y 2)

Titulares de The New York Times del 10 de noviembre de 1919 (izquierda) e infografía del Illustrated London News del 22 de noviembre de 1919 (derecha), que recogen el resultado de Eddington.
Sin duda la predicción que hizo famosa la teoría general de la relatividad y cuya comprobación lanzó al estrellato a la teoría y, con ella, a Einstein fue que el espaciotiempo se curva. La famosa medición de la “desviación de la luz” en las proximidades de un objeto masivo como el Sol por parte de Arthur Eddington en forma de cambio de la posición aparente de una estrella ocupó las portadas de la prensa mundial en 1919. Sn embargo, el concepto de que la luz se “desvía” es erróneo, porque asume un espacio absoluto, newtoniano. Para comprender la magnitud de la predicción de Einstein y el mérito del experimento de eddington, tendremos que hacer un poco de historia.
Ya en otra parte hemos explicado que la predicción de que la luz sufre una desviación al pasar cerca de un objeto masivo está presente en la mecánica newtoniana. Tanto es así que tanto Henry Cavendish en 1784 (en un manuscrito que, fiel a su costumbre, no publicó) como Johan Georg von Soldner [1] realizaron cálculos de la magnitud de esa desviación. El manuscrito de von Soldner, titulado “Sobre la desviación de un rayo de luz de su movimiento rectilíneo por la atracción de un cuerpo celeste del que pasa cerca”, escrito en 1801 y publicado en 1804, contenía los resultados de éste.
En 1911 Einstein publicaba el artículo “Sobre la influencia de la gravedad en la propagación de la luz” [2], ampliación de uno de 1908, en el que obtenía, atención, los valores de von Soldner pero, eso sí, basándose únicamente en el principio de equivalencia. Tal era la coincidencia numérica que Philipp Lénárd tuvo base para acusar después a Einstein de plagio.
Avanzada la teoría general de la relatividad, Einstein se dio cuenta de algunos errores, y corrigió sus cálculos en 1915 obteniendo los datos (la suma de los efectos clásicos y de la dilatación temporal gravitacional) que después Eddington daría por confirmados en 1919.
Diferencias de modelo
Sin embargo, lo importante es la diferencia de modelo. Mientras que Cavendish y Soldner asumen que la luz es una partícula con masa y, por tanto, debe ser atraída por el Sol según la ley gravitatoria de Newton, lo que Einstein afirma es que el espaciotiempo se curva por la presencia de la masa del Sol y que la luz, que viaja en “línea recta”, nos “da la impresión” de que se desvía. Pero hemos de ser conscientes de lo que línea “recta” significa en un espaciotiempo: si el espaciotiempo se curva, la luz se curva.
Quizás un ejemplo de algo aparentemente no relacionado pero que es fácil que hayamos visto alguna vez nos puede servir para aprehender lo que decía Einstein. Está relacionado con los conceptos de campo, en concreto con el de campo magnético. Gilbert describió la acción de la piedra imán diciendo que tenía una “esfera de influencia” alrededor de ella. Con esto quería decir que cualquier otro objeto magnético que entrase en esta “esfera” sería atraído por la piedra imán. Además, la intensidad de la fuerza atractiva sería mayor cuanto más cercano estuviese del imán. En términos actuales diríamos que la piedra imán está rodeada por un campo magnético.
Experimentalmente podemos visualizar fácilmente un campo magnético o, más precisamente, la parte del mismo que intersecta el plano de un papel, colocando debajo de éste un imán (idealmente con una forma regular) y esparciendo limaduras de hierro alrededor, como en la imagen que sigue:
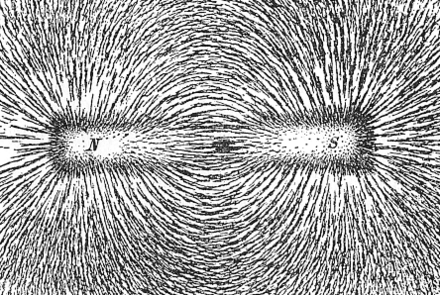
El campo magnético se suele representar en forma de líneas que representan la fuerza y dirección del campo, como en esta otra imagen:
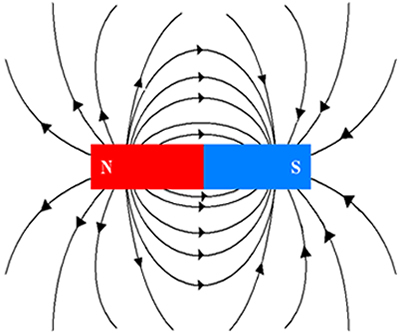
Así es como solemos pensar cuando hablamos de campos, a saber, como líneas de fuerza que existen en el espacio y en el tiempo.
Tengamos en mente que las imágenes anteriores corresponden a un campo magnético en dos dimensiones (la parte del campo que intersecta el plano del papel) porque asumimos que vivimos en un espacio absoluto de 3 dimensiones. Una región del espaciotiempo (que, recordemos, tiene cuatro dimensiones) donde existe un objeto masivo, podemos representarla con una dimensión menos para poder visualizarla de la siguiente forma (asumiendo la perspectiva como una dimensión) según la teoría general de la relatividad:
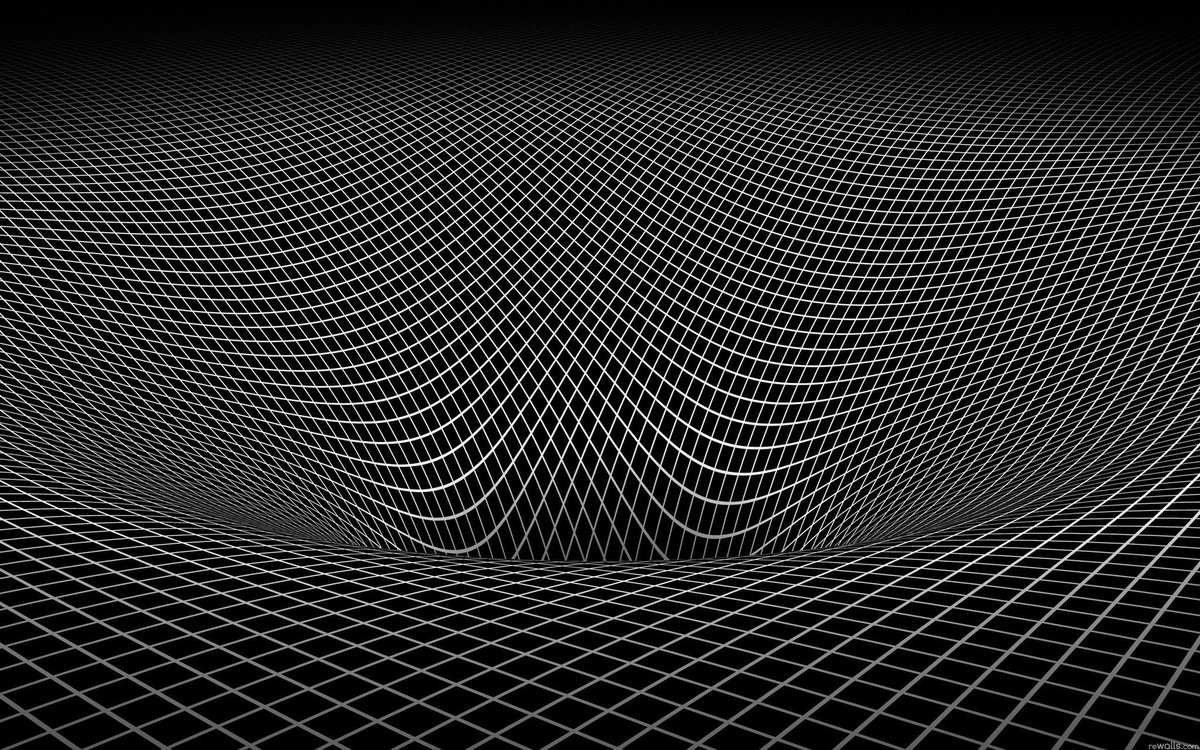
Las líneas nos pueden parecer las de un campo como las del campo magnético, pero hay una diferencia crucial: estas líneas no representa un campo en el espacio y en el tiempo, estas líneas representan el espaciotiempo mismo y su curvatura. De hecho lo que ves en la imagen es, estrictamente hablando (descartando la perspectiva), bidimensional y representa un “corte” del espaciotiempo cuatridimensional.
Por tanto, en un diagrama de este tipo si un objeto, o la luz, viaja por el espaciotiempo en una región en la que hay un objeto masivo, el camino más corto entre dos puntos será una línea curva. En geometría diferencial estas líneas se llaman geodésicas y no son más que la generalización del concepto de línea recta a espacios curvos.
La observación de Eddington
Decíamos más arriba que tanto la vieja teoría de la gravedad de Newton como la nueva de Einstein predecían que la luz no viaja necesariamente en líneas rectas, sino que puede ser desviada cuando pasa cerca de algo tan pesado como el Sol. Sin embargo Einstein predecía que la desviación aparente sería mayor: lo suficiente como para que las posiciones aparentes de las estrellas detrás del Sol se desplazasen de forma detectable con respecto a las posiciones conocidas y verdaderas.
Un eclipse solar total ocurre cada par de años, pero son solamente visibles desde las regiones ecuatoriales. El eclipse solar del 29 de mayo de 1919 tendría lugar por suerte frente a una brillante constelación de estrellas y daba la oportunidad perfecta para comprobar experimentalmente la nueva teoría Einstein.
Desde Oxford, Arthur Eddington observó cuidadosamente la posición de las estrellas en enero y febrero de 1919. El eclipse sería visible desde ambos lados del Atlántico por lo que, para asegurarse buen tiempo en al menos en un punto de observación, Frank Dyson, el Astrónomo Real, mandó un equipo de observación a Sobral (Brasil) y a Eddington a Príncipe (São Tomé e Príncipe). Los cielos estuvieron despejados en ambas localizaciones y, durante cinco minutos en total, ambos equipos se las arreglaron para tomar varía fotografías nítidas de las estrellas.
Cuando Eddington volvió a casa y comparó las posiciones aparentes de las estrellas detrás del Sol con las reales, ambos conjuntos de datos eran consistentes con la teoría de Einstein. El descubrimiento fue publicado oficialmente en Philosophical Transactions of the Royal Society [3]. Para entonces Einstein ya era una celebridad mundial.
Notas:
[1] J. G. von Soldner (1804) “Über die Ablenkung eines Lichtstrals von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkörpers, an welchem er nahe vorbei geht”, Berliner Astronomisches Jahrbuch, pp. 161-172
[2] A. Einstein (1911) “Einfluss der Schwerkraft auf die Ausbreitung des Lichtes”, Annalen der Physik 35: 898–908.
[3] Dyson, F., Eddington, A., & Davidson, C. (1920). A Determination of the Deflection of Light by the Sun’s Gravitational Field, from Observations Made at the Total Eclipse of May 29, 1919 Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character (1896-1934), 220 (1), 291-333 DOI: 10.1098/rsta.1920.0009
El atento lector se habrá fijado que en el título de este artículo de Eddington et al. se habla de “gravitational field” un concepto que aún es newtoniano, como no puede ser de otra manera ya que esa es la teoría (paradigma, diría alguno) imperante en ese momento.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Comprobaciones experimentales de la relatividad general (y 2) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Comprobaciones experimentales de la relatividad general (1)
- Las ecuaciones de campo de la relatividad general
- El principio de relatividad (y 4): la versión de Einstein
Nanokomik#2, cómic participativo de nanoficción
Acercar la nanotecnología en un formato atractivo para los jóvenes es el objetivo del proyecto nanoKOMIK, desarrollado por los centros de investigación CIC nanoGUNE y Donostia International Phyisics Center (DIPC) y que ha contado con la ayuda de Fundación Española para la Ciencia y la Tecnología (FECYT). NanoKOMIK es una herramienta para dar a conocer los avances que se dan en el campo de la nanociencia y la nanotecnología, a través de un cómic participativo de nanoficción.
En 2017 se ha llevado a cabo la segunda edición del proyecto. En esta segunda edición han participado 240 personas que se han adentrado en el mundo de los nanopoderes de personajes diversos. Parte de los resultados de esta edición se han publicado en el cómic Nanokomik#2, donde se recogen tres historietas en las que han participado los ganadores de la categoría adulta del desafío nanoKOMIK 2017. El cómic está disponible en euskera, castellano, francés e inglés en la página: www.nanokomik.com.

Imagen: Portada del cómic NanoKOMIK#2.
Tomando como referencia las mejores ideas de los cómics presentados al desafío y en colaboración con los ganadores de la categoría adulta, se ha dado forma a las nuevas historietas: Domi(nano)ción del mundo, Míster Llamas y Entre Plantas. En estas divertidas historias se cuentan las aventuras de una ingeniosa neuro-nano-científica que otorga el poder de la ubicuidad a una política corrupta, de un amante de los viajes espaciales que salva una misión a punto de estallar y del científico inmerso en la creación de un nanohíbrido capaz de reproducir el proceso fotosintético de las plantas de manera artificial.
Las historietas del cómic divulgativo recogen las ideas más originales presentadas al desafío. En la recreación han participado los dibujantes Aśka, Rubén Molina y Jöse Sénder, y las coordinadoras del proyecto Amaia Arregi (DIPC) e Itziar Otegui (nanoGUNE). La obra completa está disponible bajo licencia creative commons en euskera, castellano, francés e inglés, tanto en papel como en su versión digital en la web www.nanokomik.com.
El artículo Nanokomik#2, cómic participativo de nanoficción se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Mónica Lalanda: Una muerte de cómic
- Las matemáticas en el cómic Ken Games
- Un cómic de hace dos mil años a todo color
El pueblo que hablaba con las ballenas, ¿podría enseñarnos su idioma a los demás?

Un inuit (o esquimal) otea el horizonte en busca de ballenas. Fotograma de la película “Arctic Currents. A year in the life of the bowhead whale” del Museo del Norte de la Universidad de Alaska.
Arqueólogos y antropólogos no tienen muy claro en qué momento el ser humano desarrolló la tecnología necesaria para cazar ballenas, pero en general está aceptado que en el Ártico esta actividad comenzó en las costas de Canadá entre el año 600 y el 800. Durante miles de años antes los pobladores del Ártico sobrevivieron cazando focas, caribús y morsas en las orillas del mar helado.
Cuenta Krista Langois en este reportaje de la revista Hakai, que uno de esos grupos, conocidos como los Dorset, o los Tunit en la tradición oral Inuit, son legendarios por el gran tamaño y la fuerza de sus miembros, a los que se consideraban gigantes, además de estar perfectamente adaptados a su entorno. Pero a pesar de sus míticas capacidades de supervivencia, los Tunit desaparecieron hace unos mil años.

Esquimales arponeando una ballena en 1939. Wikimedia Commons
Una teoría sobre su desaparición es que apareció otro grupo de población, los Inuit (que nosotros llamamos esquimales), proveniente de Alaska, que supo adaptarse mejor que ellos y que creó tecnología conveniente y eficaz, comiéndoles el terreno. Parte de esa tecnología pudieron ser sus barcas hechas con piel de foca, que les permitieron alejarse de la costa mar adentro para cazar ballenas: cada primavera, ballenas boreales de más de 54.000 kilos se adentraban en ese mar de hielo y los nuevos pobladores conseguían cazar alguna con habilidad, talento, y mucha suerte.
Las ballenas articulan la vida social
Cazar ballenas cambió para siempre el modo de vida en el Ártico. Por primera vez, era posible conseguir carne de una sola vez suficiente alimento para dar de comer a un pueblo entero, así que empezaron a surgir asentamientos permanentes aquellos lugares a los que las ballenas volvían con regularidad. Con ello evolucionaron también las organizaciones sociales: los cazadores de éxito hicieron fortuna y se situaron en la cima de las nuevas jerarquías. Muy pronto la caza de ballenas se convirtió en el centro de la vida cotidiana pero también de la vida cultural y espiritual.

Familia esquimal en torno a 1900. Wikipedia Commons
Una vida que fascinaba a los europeos. En la literatura medieval se representaba el Ártico como una tierra de peces monstruosos y personas que podían convocarlos en la costa utilizando magia y murmurando hechizos. Incluso cuando siglos después los primeros exploradores volvieron contando en qué consistía realmente la caza, despiece y cocinado de una ballena, nada muy diferente de cazar un esturión excepto por la escala del animal, el misticismo seguía presente. En 1938, la antropóloga Margaret Lantis describió a los Inuit y otros pueblos emparentados, como los Inupiat, como parte de un “culto a las ballenas”.
Lantis se basaba en tabús muy extendidos y en rituales diseñados para fortalecer la relación entre los humanos y las ballenas: en muchos sitios, a una ballena recién cazada se le dejaba agua fresca, comida e incluso bolsas de viaje para asegurarle una vuelta segura al hogar de su espíritu. Cada cazador tenía su propia canción para atraer a las ballenas hacia él, los chamanes realizaban ceremonias en el interior de círculos hechos con huesos de ballena y amuletos hechos con reliquias de ballena pasaban de padres a hijos dentro de las familias de cazadores.
Para cualquier observador externo, todo resultaba misterioso y desconocido, especialmente para arqueólogos y biólogos, para los que toda esta actitud chocaba frontalmente con los valores científicos occidentales, que evitaban cualquier aspecto que se acercase al antropomorfismo, es decir, a dar a los animales cualidades y emociones humanas.

Un sonajero esquimal con forma de ballena fabricado en torno a 1900. Wikimedia Commons
Unos valores que, según cuenta Erica Hill, zooaequeóloga de la Universidad del Sudeste de Alaska, en el mencionado reportaje de la revista Hakai, han limitado el conocimiento que los arqueólogos tienen hoy de la prehistoria en el Ártico: los amuletos y esos círculos de huesos se han descrito como parte de un ritual sin explorar o explicar apenas qué querían decir en realidad para las personas que los hicieron. En vez de eso, los científicos que los han estudiado se han centrado en la información tangible que ofrecían: qué comían esas personas, cuántas calorías consumían y cómo sobrevivían.
¿Puede ser útil mirar a las ballenas como las miraban los inuit?
Ahora, un grupo creciente de arqueólogos están utilizando información etnográfica e historias orales para reexaminar esos artefactos bajo una luz nueva y reinterpretarlos de un modo menos occidental para conocer algo más sobre la historia de sus antepasados.
Pero hay otro motivo por el que este enfoque arqueológico puede ser interesante: porque permite acometer desde otro punto de vista, y por tanto completar, las investigaciones que tratan de determinar si algunos animales, entre ellos los cetáceos, tienen sistemas comunicativos que se acercan en complejidad al de los humanos. Algunas de esas investigaciones están ayudando a confirmar algunos de esos rasgos y habilidades que los habitantes del Ártico atribuían a las ballenas hace más de mil años.
Uno de esos biólogos es Hal Whitehead, profesor de la Universidad Dalhousie de Nueva Escocia, y él argumenta que los cetáceos tienen su propia cultura, algo que siempre ha quedado reservado para las sociedades humanas.
Según su definición, una cultura es un conocimiento social que va pasando de una generación a la siguiente. Bien, pues algo así ha sido señalado en varios estudios recientes, incluido uno que las ballenas boreales que viven en el Norte del Pacífico, cerca de la costa de Alaska, y las que viven en el Atlántico, cerca de Groenlandia, cantan canciones diferentes igual que los humanos hablamos distintos idiomas o tenemos distintos estilos musicales. Igualmente, manadas de orcas que habitan al sur de la isla de Vancouver, y otras que viven hacia el norte de la misma isla, se saludan entre sí mostrando comportamientos diferentes, a pesar de que genéticamente son grupos casi idénticos y viven en territorios que se solapan.
Además, sabemos que las crías pasan años con sus madres, desarrollando fuertes relaciones materno-filiales que sirven precisamente para la transmisión de esa información cultural, y que las ballenas boreales viven suficiente tiempo como para acumular una información y conocimiento que merece la pena transmitir a las generaciones siguientes.
Por otro lado, otros mitos están demostrando ser menos fantasiosos de lo que una vez parecieron. Durante años, los biólogos pensaron que las ballenas no poseían sentido del olfato, a pesar de que los cazadores Inupiat aseguraban que el olor del humo las ahuyentaba, hasta que en 2010 el científico Hans Thewissen descubrió el sistema olfativo perfectamente funcional al analizar el cráneo y cerebro de varias ballenas. También la vieja creencia de los Yupik de que las beluga una vez caminaron por la tierra ha resultado ser cierta: hace 50 millones de años, un ancestro de las ballenas modernas caminó por la tierra, y por eso los fetos de ballena desarrollan patas durante un breve periodo de tiempo antes de perderlas de nuevo.
Imitar sonidos no es hablar… pero ¿nos acerca un paso?
Nada de todo esto quiere decir que las ballenas conversasen con los cazadores o que se entregasen a ellos cuando eran convocadas. Pero sí que es verdad que una vez que terminemos de descubrir en qué consiste el complejo sistema cultural de las ballenas y cómo lo utilizan, será más fácil entender sus señales y aprender hasta qué punto sería posible una comunicación entre especies.
Estamos aún lejos de esa comunicación, pero algunos estudios recientes permiten vislumbrar de qué estamos hablando. Por ejemplo, el caso de Wikie, una orca que vive en el acuario Marineland en Antibes, Francia, y que demostró cómo estos animales son capaces de imitar el habla humana cuando aprendió a decir con su chirriante voz las palabras “hello”, “goodbye”, “one”, “two”, “three” y “Amy”, el nombre de su entrenadora. Las grabaciones de audio demuestran que sin un aparato fonador como el nuestro algunos sonidos no son sencillos, pero que sin duda Wikie era capaz de imitar y repetir dichas palabras. Como curiosidad, Wikie no solo aprendió a imitar palabras, también otros sonidos poco familiares para las orcas, como una pedorreta.
Este avance sirve para entender mejor cómo unos grupos de ballenas se comunican con canciones diferentes a las de otros grupos: el origen estaría precisamente en sus habilidades de imitación, que habrían ido causando poco a poco que cada grupo evolucione su habla en direcciones diferentes. Otro ejemplo de esa cultura de los cetáceos que nos fascina a todos, científicos o no, y que quizá podamos entender mejor si tomamos nota de lo que sabían aquellos primeros hombres que susurraban a las ballenas.
Referencias:
When men and whales talk – Krista Langlois. Hakai Magazine.
Cultura Dorset – Wikipedia.
Alaskan Eskimo Ceremonialism – Margaret Lantis. Univerisdad de Michigan.
Cultural lifes of whales and dolphins – Hal Whitehead y Luke Rendell.
Olfaction and brain size in the bowhead whale (Balaena mysticetus) – J. G. M. Thewissen, John George, Cheryl Rosa, Takushi Kishida. Marine Mammal Science.
Imitation of novel conspecific and human speech sounds in the killer whale (Orcinus orca) – José Z. Abramson, Mª Victoria Hernández-Lloreda, Lino García, et al. Proceedings of the Royal Society B: Biological Sciences.
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo El pueblo que hablaba con las ballenas, ¿podría enseñarnos su idioma a los demás? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Eran nuestras ballenas
- Cómo usar a las ballenas como detectores de radiación
- Los enigmas que nos cantan desde el fondo del océano
La filoxera y sus delitos

Hoja de una vid afectada de filoxera.
Las primeras vides afectadas lo fueron en Pujault (Gard, Francia) en 1863. La plaga siguió extendiéndose por ese país y algo más tarde por el resto de Europa. Cinco años después el botánico Jules-Émile Planchon identificó al culpable. Era un insecto diminuto (de entre 0,3 y 1,4 mm) cuyo nombre científico actual es Daktylosphaera vitifoliae, conocido vulgarmente como filoxera. En las viñas europeas el insecto se introduce bajo tierra y ataca a las raíces, alimentándose de su savia y secretando un producto que impide el cierre de los orificios practicados por el parásito. La planta no solo sufre la pérdida de savia sino que, además, queda expuesta al contagio de hongos y bacterias, y desarrolla nudosidades y tuberosidades (tumores) que son las que acaban provocando su muerte. Al principio es una planta la que se marchita; luego lo hacen las de alrededor; poco después sucumben todas las viñas de una misma zona. La planta atacada muere tres años después del contagio. La filoxera procedía de América, de donde había llegado gracias a la rapidez con que los barcos de vapor hacían el viaje a través del Atlántico. Hasta la sustitución de los veleros por los barcos más modernos impulsados por vapor los insectos no sobrevivían a la travesía oceánica.
En sus zonas de procedencia los machos y las hembras de Daktylosphaera copulan en verano y la hembra pone un único huevo sobre el tronco de la planta. La eclosión de ese huevo se produce en primavera y da lugar a una hembra (sin alas) que se reproduce de forma partenogenética, o sea, sin haber sido fecundada por un macho. Tras tres mudas, que se producen en apenas tres semanas, pone entre cuarenta y cien huevos. Cada uno de ellos da lugar a una nueva hembra partenogenética y el proceso se repite otras cinco o seis veces. De esa forma pueden surgir en poco tiempo millones de nuevas hembras de filoxera que pueden instalarse en las hojas o en las raíces, aunque también pueden migrar de una a otra ubicación. Las hembras partenogenéticas de la última generación, tras una muda adicional, se transforman en ninfas que son las que producen los ejemplares (alados) de los que nacen los machos y hembras que se reproducen sexualmente tras copular. Estos no se alimentan y viven tan solo unos pocos días. En Europa las cosas son diferentes, porque rara vez se reproducen sexualmente y cuando lo hacen su descendencia no sobrevive.
Los efectos de la plaga fueron devastadores. Numerosas zonas vitivinícolas europeas se vieron afectadas durante el último tercio del siglo XIX y primeras décadas del XX. Aunque se han ensayado diferentes técnicas para combatir la plaga, a la postre el procedimiento más efectivo ha resultado ser el de los injertos de cepas europeas en troncos de vides americanas. Estas sufren el ataque del insecto, que se alimenta de su savia, pero no provoca su muerte.
Francia fue el país europeo en el que la plaga tuvo un impacto económico más profundo: miles de familias fueron a la ruina y, como consecuencia, el sistema económico en su conjunto sufrió los efectos de la epidemia. Además, sus consecuencias no se limitaron a la esfera puramente económica: en las zonas afectadas se cometieron, en promedio, un 22% más de delitos contra la propiedad, porque muchas personas perdieron el que había sido su modo de vida tradicional y optaron por recurrir al robo. Pero curiosamente en esas mismas zonas se produjeron un 13% menos de crímenes violentos porque a la vez que se redujo la producción de vino también descendió su consumo.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 14 de enero de 2018.
El artículo La filoxera y sus delitos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Naukas Bilbao 2017 – Aitor Sánchez: Si Donald Trump fuese nutricionista
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Aitor Sánchez desarma la pirámide alimentaria y sus aberraciones en 10 minutos. Y sí, sale Trump.
Aitor Sánchez: Si Donald Trump fuese nutricionistaEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Aitor Sánchez: Si Donald Trump fuese nutricionista se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- Naukas Bilbao 2017 – Mónica Lalanda: Una muerte de cómic
- Naukas Bilbao 2017 – Laura Morrón: La gran divulgadora
La estrella individual más lejana jamás vista

Un equipo internacional, en el que ha participado Tom Broadhurst, investigador Ikerbasque en la UPV/EHU, ha identificado la estrella individual más lejana jamás vista. Una enorme estrella azul bautizada como Ícaro. Normalmente hubiera sido imposible apreciar este fenómeno, incluso con los telescopios más grandes del mundo, pero gracias a una carambola de la naturaleza, que ha permitido amplificar enormemente el débil brillo de la estrella, los astrónomos que utilizan el Telescopio Espacial Hubble de la NASA han podido localizarla y establecer un nuevo récord de distancia. Asimismo, la identificación de Ícaro ha permitido descartar una de las teorías sobre la materia oscura.
La estrella está localizada en una galaxia espiral tan distante que su luz ha tardado 9 mil millones de años en llegar a la Tierra. De lo que se deduce que surgió cuando el universo tenía aproximadamente el 30 por ciento de su edad actual.El descubrimiento de Ícaro a través de lentes gravitacionales abre un nuevo camino para que los astrónomos estudien estrellas individuales en galaxias distantes. Tom Broadhurst, investigador Ikerbasque en la UPV/EHU, es un experto mundial en el campo de las lentes gravitacionales, método que proporciona una mirada excepcional y detallada de cómo evolucionan las estrellas, especialmente las estrellas más luminosas. “Esta es la primera vez que vemos una estrella individual magnificada”, explicó el líder del estudio, Patrick Kelly, de la Universidad de Minnesota, Twin Cities. “Puedes ver galaxias individuales, pero esta estrella está al menos 100 veces más lejos que la siguiente estrella individual que podemos estudiar, excepto en los casos de explosiones de supernovas”.
La peculiaridad cósmica que hace visible a esta estrella es un fenómeno llamado “lente gravitacional”. La gravedad de un cluster masivo de galaxias actúa como una lente natural en el espacio, doblando y amplificando la luz. A veces, la luz de un solo objeto de fondo aparece como imágenes múltiples. La luz se puede magnificar mucho, de forma que objetos extremadamente tenues y distantes sean lo suficientemente brillantes como para que puedan ser vistos.
Tom Broadhurst es uno de los líderes mundial en el campo de las lentes gravitacionales y se dio cuenta de que este evento es una estrella enormemente ampliada en un universo lejano. En este caso, un cluster de galaxias llamado MACS J1149 + 2223 ubicado entre la Tierra y la galaxia que contiene a Ícaro crea una “lupa” natural. Al combinar la fuerza de esta lente gravitacional con la extraordinaria resolución y sensibilidad del Hubble, los astrónomos pueden ver y estudiar Ícaro. La estrella se ha llamado “Ícaro” por el personaje mitológico griego que voló demasiado cerca del sol y cuyas alas de plumas y cera se derritieron. (Su nombre oficial es MACS J1149 + 2223 Lensed Star 1.) Al igual que Ícaro, la estrella solo alcanzó una gloria fugaz vista desde la Tierra, cuando por un instante se multiplicó 2.000 veces su verdadero brillo.
El equipo de investigadores había estado utilizando el Hubble para monitorizar una supernova en la lejana galaxia espiral cuando, en 2016, detectaron un nuevo punto de luz no lejos de la supernova magnificada. Sabían que no se trataba de otra supernova porque no se calentaba, no explotaba. La luz simplemente llegaba porque estaba magnificada. Cuando analizaron los colores de la luz que provenía de este objeto, descubrieron que era una estrella supergigante azul. Este tipo de estrellas es mucho más grande, más masivo, más caliente y posiblemente cientos de miles de veces más brillante que nuestro Sol, pero a esta distancia, todavía estaba demasiado lejos para ser vista sin ser observada a través de lentes gravitacionales.
Detectar la amplificación de una única estrella de fondo puntual proporciona una oportunidad única para probar la naturaleza de la materia oscura. La materia oscura es un material invisible que compone la mayor parte de la masa del universo. Los resultados de esta investigación rechazan la teoría de que la materia oscura está formada por una gran cantidad de agujeros negros creados en el nacimiento del universo, ya que las fluctuaciones leves de las estrellas de fondo, monitorizadas con Hubble durante 13 años, se verían diferentes si hubiera un enjambre de agujeros negros intermedios. Cuando se ponga en órbita el Telescopio Espacial James Webb de la NASA, los astrónomos esperan encontrar muchas más estrellas como Ícaro. La extraordinaria sensibilidad de Webb permitirá una medición más detallada, incluso en el caso de que las estrellas distantes estén girando.
Referencia:
Patrick L. Kelly et al (2018) Extreme magnification of an individual star at redshift 1.5 by a galaxy-cluster lens Nature Astronomy doi: 10.1038/s41550-018-0430-3
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La estrella individual más lejana jamás vista se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La luz polarizada de la estrella más brillante de Leo
- #Naukas15 Fantasía en la divulgación: una estrella para Cervantes
- HR, la estrella de los diagramas en astrofísica
Se vende invasora a buen precio
Existe un amplio consenso científico al respecto de las invasiones biológicas: no solo son una de las mayores preocupaciones a nivel ecológico, sino que constituyen un factor clave en lo que denominamos cambio global. Esto es especialmente grave ya que el transporte de especies exóticas aumenta más y más cada día[1].
Mascotas raras que nadie que tú conozcas tiene y que te dan esa sensación de ser alguien especial —más especial cuanto más difícil sea encontrar un veterinario que pueda atenderla— o la sensación de tener el mejor jardín porque has puesto una planta nueva que nadie de tu vecindario parece tener, se suman a las modas que este o aquel famoso promueven al aparecer en televisión hablando de lo que mola su nueva cotorra o el charlatán de turno que dice curar el cáncer con hojas de Kalanchoe daigremontiana, planta con alto potencial invasor, ya que es capaz de reproducirse de forma clonal con una facilidad asombrosa[2].
En algunos países, como Australia o Nueva Zelanda, las políticas son extraordinariamente restrictivas y no se permite la introducción de especies foráneas. Pero en España y en Europa, de momento, adolecemos de medidas preventivas adecuadas. No solo eso, sino que aceptamos la introducción incluso desde entidades públicas. El lector únicamente tiene que pasear por un parque urbano de su ciudad. Que me avise si encuentra un parque que esté dominado por robles, encinas, hayas, alcornoques o cualesquiera especies nativas; cuando aparecen éstas en los parques, solo ocupan puestos anecdóticos. Sin embargo, no entraña gran dificultad observar con asombro parques llenos de acacias, ailantos, castaños de indias, arces y demás flora de diversa procedencia.

Ailanto (Ailanthus altissima)
Es importante remarcar el detalle de que algunas de las plantas que vemos en esos parques, como el ailanto (Ailanthus altissima) o la acacia mimosa (Acacia dealbata) son especies invasoras que están reguladas por la autoridad hipotéticamente competente[3]. Y no solo eso. Se siguen encontrando algunas de estas especies en los viveros[4]. Esto es grave. Por un lado, desde la ciencia se intenta predecir qué especies tienen el potencial de convertirse en invasoras, con el fin de regular su comercio y evitar su dispersión[5], y por el otro lado, nos encontramos con plantas cuyo comercio ya está regulado, que se siguen vendiendo en viveros y plantando en parques y jardines.
Recientemente, la industria ha adquirido una tendencia hacia la existencia de un número menor de productores pero más grandes, y están surgiendo nuevos canales de distribución, en particular el comercio por Internet [6]. Vender y comprar plantas por eBay, a través de foros o por cualquier otro recurso electrónico tiene grandes ventajas tanto para el cliente como para el vendedor. El segundo ya no está limitado a los clientes locales; puede vender prácticamente a cualquier parte del mundo sin tener que asumir grandes costes, y el comprador puede optar a una mayor cantidad de distribuidores, que no tienen que estar necesariamente cerca de él.
El comercio de plantas por internet no solo aumenta el intercambio global de plantas sino que aumenta la dificultad de control, haciendo que sea más fácil eludir los controles fronterizos y la normativa al respecto[7]. De hecho, se ha demostrado que 13 de las 35 especies de plantas que encontramos en la lista de 100 de las especies exóticas invasoras más dañinas del mundo[8] se encontraron sin dificultad en eBay. Es más, casi el 40% de las especies de plantas que se venden en la plataforma son invasoras[9].
Teniendo en cuenta que solo una minoría de las especies de plantas son invasoras, este dato demuestra la existencia de una excesiva representación de las especies invasoras respecto a las que no lo son.
Ejemplo de especies invasoras a la venta en eBay
A pesar de los grandes esfuerzos que se están realizando en el control de las invasiones biológicas, en la erradicación de las especies invasoras en las excepcionales ocasiones en que eso es posible, y en los trabajos de predicción y prevención de futuras invasiones, aún se están ofreciendo a diario, tanto en viveros como en Internet muchas especies exóticas invasoras. Hay quienes opinan que es necesario reforzar las medidas de control y vigilancia de comercio a este respecto para revertir esta peligrosa situación. Hay otros que piensan que deben instalarse sistemas de vigilancia en línea que rastreen este tipo de comercio con el fin de regularlo. Probablemente ambos tengan razón, pero un punto esencial es también la concienciación.
Y es que al fin y al cabo, si algo se vende es porque hay alguien que lo compra. Es muy importante que la gente conozca las especies invasoras, sea consciente del daño que hacen, no solo a nivel medioambiental, sino también a nosotros mismos. Y es que hay especies invasoras que dañan nuestras cosechas, las hay que atacan a nuestro ganado, que destruyen nuestras infraestructuras e incluso que nos hacen enfermar, poniendo en riesgo nuestra propia salud. Hoy he hablado sobre todo de plantas, pero también existen animales, hongos y microorganismos invasores.
Como he dicho, si algo se vende es porque hay alguien que lo compra. La concienciación es muy importante. Que la gente conozca la lista de especies invasoras de su país[10],[11], y rechace activamente la compra de esas especies puede ser una forma más de luchar contra este problema en ocasiones tan olvidado, pero que está muy presente. Si conseguimos que la gente no las compre, tal vez los distribuidores dejen de venderlas.
Este post ha sido realizado por Alvaro Bayón (@VaryIngweion) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias y más información:
[1] Hulme, P.E., 2009. Trade, transport and trouble: managing invasive species pathways in an era of globalization. Journal of Applied Ecology 46. https://doi.org/10.1111/j.1365-2664.2008.01600.x
[2] Guerra-García, A., Golubov, J., C. Mandujano, M., 2014. Invasion of Kalanchoe by clonal spread. Biological Invasions 17, 1615–1622. https://doi.org/10.1007/s10530-014-0820-0
[3] BOE, 2013. Real Decreto 630/2013, de 2 de agosto, por el que se regula el Catálogo español de especies exóticas invasoras. BOE 185, 56764–56786. https://www.boe.es/diario_boe/txt.php?id=BOE-A-2013-8565
[4] Cronin, K., Kaplan, H., Gaertner, M., Irlich, U.M., Hoffman, M.T., 2017. Aliens in the nursery: assessing the attitudes of nursery managers to invasive species regulations. Biol Invasions 19, 925–937. https://doi.org/10.1007/s10530-016-1363-3
[5] Roy, H.E., European Commission, Directorate-General for the Environment, CEH (Centre of Ecology & Hydrology), 2015. Invasive alien species: prioritising prevention efforts through horizon scanning: final report. Publications Office, Luxembourg. http://ec.europa.eu/environment/nature/invasivealien/docs/Prioritising%20prevention%20efforts%20through%20horizon%20scanning.pdf
[6] Dehnen-Schmutz, K., Holdenrieder, O., Jeger, M.J., Pautasso, M., 2010. Structural change in the international horticultural industry: Some implications for plant health. Scientia Horticulturae 125, 1–15. https://doi.org/10.1016/j.scienta.2010.02.017
[7] Giltrap, N., Eyre, D., Reed, P., 2009. Internet sales of plants for planting – an increasing trend and threat? EPPO Bulletin 39, 168–170. https://doi.org/10.1111/j.1365-2338.2009.02283.x
[8] Lowe, S., Browne, M., Boudjelas, S., De Poorter, M., 2000. 100 of the world’s worst invasive alien species: a selection from the global invasive species database. Invasive Species Specialist Group Auckland. https://s3.amazonaws.com/academia.edu.documents/33655728/100_world_worst_invasive_alien_species_English.pdf?AWSAccessKeyId=AKIAIWOWYYGZ2Y53UL3A&Expires=1521221921&Signature=ZB%2FR1BrlyaYpyD0eaedZOPu6lfA%3D&response-content-disposition=inline%3B%20filename%3D00_OF_THE_WORLDS_WORST_INVASIVE_ALIEN_SP.pdf
[9] Humair, F., Humair, L., Kuhn, F., Kueffer, C., 2015. E-commerce trade in invasive plants. Conservation Biology 29, 1658–1665. https://doi.org/10.1111/cobi.12579
[10] Sanz Elorza, M., Dana Sánchez, E.D., Sobrino Vesperinas, E. (Eds.), 2004. Atlas de las Plantas Alóctonas Invasoras en España. Dirección General para la Biodiversidad, Madrid. http://www.animalrecord.net/Atlas_Plantas_Aloctonas_Espana.pdf
[11] BOE, 2013. Real Decreto 630/2013, de 2 de agosto, por el que se regula el Catálogo español de especies exóticas invasoras. BOE 185, 56764–56786. https://www.boe.es/diario_boe/txt.php?id=BOE-A-2013-8565
El artículo Se vende invasora a buen precio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Cómo llegó el darwinismo a España? 06. Los introductores – Odón de Buen
- #Naukas15 Odón de Buen
- Del zumo de naranja a la selva, un ejemplo de reciclaje extremo
Muchos adultos son incapaces de realizar operaciones financieras básicas
John Jerrim
![]()
 

“No sé ni cuánto me va a costar esto”. Imagen: Shutterstock
Supongamos que un litro de cola cuesta 3.15 €. Si compras un tercio de litro de cola, ¿cuánto pagarías?
La anterior puede parecer una pregunta bastante básica. ¿Algo que quizás esperarías que la gran mayoría de adultos pueda responder? Especialmente si se les permite usar una calculadora.
Desafortunadamente, la realidad es que una gran cantidad de adultos en todo el mundo tienen dificultades incluso con un problema financiero tan básico (la respuesta correcta es 1.05 dólares, por cierto).
Utilizando datos del Programa para la Evaluación Internacional de las Competencias de los Adultos (PIAAC, por sus siglas en inglés) de la Organización para la Cooperación y el Desarrollo Económicos (OCDE), mis coautores y yo hemos analizado cómo responden los adultos de 31 países a cuatro preguntas financieras relativamente simples.
Además de la pregunta anterior, a los participantes se les hicieron preguntas como: “Supongamos que en tu visita al supermercado compras cuatro tipos de paquetes de té: té de manzanilla (4.60 €), té verde (4.15 €), té negro (EE.UU. 3.35 €) y té de limón (1.80 €). Si pagases por todos estos artículos con un billete de 20 €, ¿cuánto cambio recibirías? “
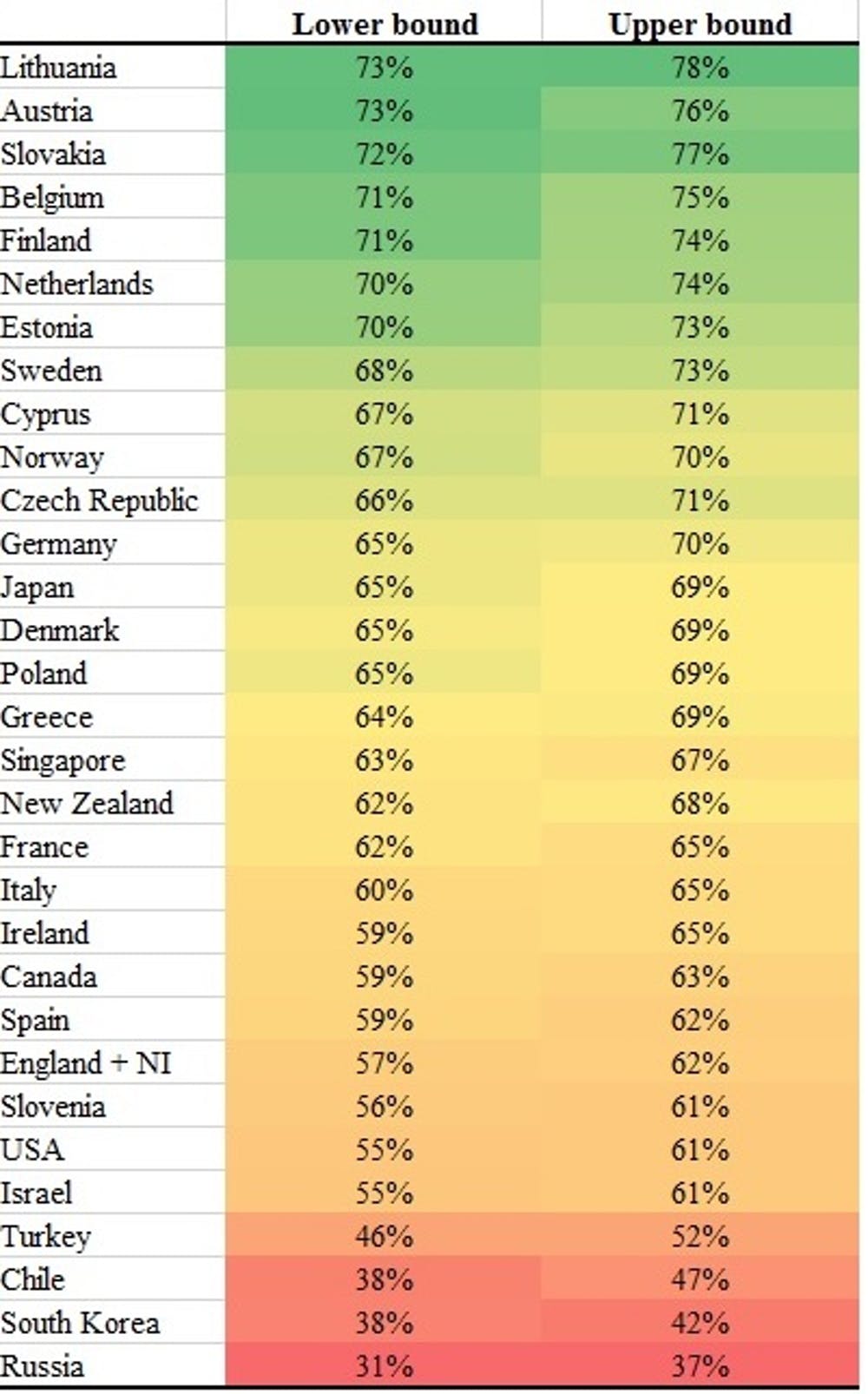
Los resultados (como se ve en la tabla) nos permitieron crear un rango estimado para el porcentaje de la población adulta que podría responder la pregunta de la cola correctamente. Estos resultados se basan en una muestra aleatoria de adultos de cada país.
Encontramos que Lituania, Austria y Eslovaquia tuvieron más éxito, pero incluso en estos países uno de cada cuatro adultos no pudo dar la respuesta correcta.
En muchos otros países, la situación es aún peor. Cuatro de cada diez adultos en lugares como Inglaterra, Canadá, España 0 EE. UU. no pueden hacer este cálculo simple, incluso cuando tenían una calculadora a mano. Del mismo modo, menos de la mitad de los adultos en lugares como Chile, Turquía o Corea del Sur pueden obtener la respuesta correcta.
Cálculos básicos
Por supuesto, no todos los grupos dentro de cada país lo hacen tan mal, y existen diferencias notables en las habilidades de alfabetización financiera entre diferentes grupos demográficos.
En las cuatro preguntas financieras que se hicieron a los adultos, en la mayoría de los países, los varones tendían a desempeñarse un poco mejor que las mujeres. Los jóvenes (particularmente los de 25 a 34 años) también obtuvieron mejores resultados que los mayores de 55 años.

Muchos adultos tienen dificultades con tareas financieras básicas, como determinar el mejor precio real [2] en el supermercado. Imagen: Shutterstock
Las diferencias más marcadas se vieron por grupo de educación. Volviendo a la primera pregunta anterior, en muchos países los adultos con un nivel de educación “bajo” (el equivalente a completar la educación secundaria) tenían menos del 50% de posibilidades de responder la pregunta correctamente. En lugares como Canadá o Estados Unidos, esto se redujo a tan solo el 25%.
Dolor de cabeza financiero
Nuestros resultados ponen de relieve claramente la cantidad de adultos que están mal equipados para tomar decisiones financieras clave. Y cómo, de hecho, muchos tienen dificultades para hacer frente incluso a tareas financieras muy simples.
A largo plazo, esto destaca la necesidad crítica de que la alfabetización financiera se enseñe en las escuelas, para garantizar que los jóvenes estén equipados para las complejas decisiones financieras a las que se enfrentarán en el mundo real.
Sin embargo, de manera más inmediata, dado el bajo nivel de habilidades financieras entre muchos adultos, es vital que la información que se suministre con los productos financieros sea tan simple y sencilla de interpretar como sea posible. Y en la era de los préstamos exprés [1] y las tarjetas de crédito de alto interés, también debe haber disponible asesoramiento y orientación adecuados cuando sea necesario. Porque de lo contrario existe un peligro real de que una gran proporción de la población corra el riesgo de cometer graves errores financieros.
Notas del traductor:
[1] Traducimos el “payday loan” original por “préstamo exprés”, una figura más común en la economía altamente bancarizada de Europa continental; el “préstamo nómina” no es exactamente lo mismo porque implica un análisis del riesgo de la operación, mientras que en los anteriores no existe (son préstamos “preconcedidos”). El “payday loan” originalmente era un avance de dinero en efectivo que se realizaba a cambio del cheque de la paga que tenía una fecha de vencimiento posterior, de ahí su nombre.
[2] Traducimos “value” por “mejor precio real” porque se trata de determinar cuánto cuesta un producto por unidad de medida, independientemente del precio de la unidad de venta. Así, por ejemplo, la oferta del supermercado a 0,99 € por un envase de 100 g de producto es en realidad más cara que el aparentemente más caro envase de 125 g que se vende a 1,10 € (0,88 € por 100 g).
Referencia:
Aditi Bhutoria, John Jerrim , Anna Vignoles (2018) The financial skills of adults across the world. New estimates from PIAAC. PIAAC_Working_Report_March_2018
Sobre el autor:
John Jerrim es profesor de economía y estadística social en el University College de Londres (Reino Unido)
Texto traducido y adaptado por César Tomé López a partir del original publicado por The Conversation el 15 de marzo de 2018 bajo una licencia Creative Commons (CC BY-ND 4.0)
El artículo Muchos adultos son incapaces de realizar operaciones financieras básicas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Uno, dos, muchos
- La pubertad está comenzando antes para muchos niños; la educación sexual debería afrontar esta realidad
- Modelos en ciencia: la sinapsis tripartita no existe en adultos
De la sal «sin gluten» al champú «sin gluten»: no solo marketing

Hace unos días comenzó a anunciarse en televisión el champú «sin gluten» de un conocido laboratorio cosmético. En el supermercado nos encontramos alimentos «sin gluten» que de serie no lo contienen, como por ejemplo la sal o los garbanzos. Podríamos pensar que estamos ante dos torticeras estrategias de marketing, pero eso sería quedarnos en la superficie. La realidad del asunto es más compleja y está en los hechos, sobre todo en los hechos científicos.
¿Son necesarios los productos sin gluten?
Las personas con enfermedad celiaca no pueden consumir alimentos con gluten. Es una enfermedad sistémica crónica autoinmune. Esto quiere decir que el organismo de las personas que padecen esta enfermedad reacciona ante algunas sustancias que componen el gluten como si fuesen tóxicas, generando inflamación y ocasionando lesiones intestinales. Puede terminar por dañar cualquier órgano o tejido. Afecta a personas que presentan una predisposición genética. Entre el 1 y el 2% de la población padece esta enfermedad.
La enfermedad celiaca no es exactamente una intolerancia ni una alergia, aunque suele explicarse así para hacerla comprensible, realmente es una enfermedad autoinmune. Las personas que padecen esta enfermedad pueden estar en contacto con el gluten porque éste no atraviesa la piel, sin embargo, no pueden ingerirlo.
Esta enfermedad puede provocar complicaciones de salud muy graves. Su tratamiento consiste en el seguimiento de una dieta estricta sin gluten durante toda la vida. Por este motivo sí es necesario que existan alimentos sin gluten para ellos.
¿Los alimentos sin gluten son mejores para todos?
El gluten es un conjunto de proteínas que está naturalmente presente en muchos cereales como el trigo, la espelta, la cebada, el centeno o el kamut, y les confiere un mayor interés culinario. El gluten es el responsable de la elasticidad de la masa de harina y de la consistencia y esponjosidad de los panes y masas horneadas. También es apreciado por su poder espesante. Durante el horneado, el gluten es el que retiene los gases de la fermentación en el interior de la masa, haciendo que esta suba y quede esponjosa. Después de la cocción, la coagulación del gluten es responsable de que el bollo no se desinfle una vez cocido.
Los panes, bollos y masas hechos con harinas sin gluten, como las de trigo sarraceno, arroz, maíz o garbanzo, son difíciles de manejar precisamente porque no contienen gluten.
Las personas que padecen la enfermedad celiaca, si quieren consumir panes, bollos o pastas, tienen que optar por fórmulas con harinas sin gluten. Desgraciadamente en muchos casos esto va en detrimento del sabor y la textura de los alimentos, además resultan más caros que los productos análogos fabricados con harinas con gluten, debido al mayor coste de las materias primas y a la mayor complejidad del proceso de fabricación.
Las personas que no padecen esta enfermedad no tienen ninguna razón por la que seguir una dieta sin gluten. Comer sin gluten no es ni más sano ni ayuda a perder peso, como muchas veces se ha dado a entender. Sin embargo, nos encontramos que las ventas de productos «sin gluten» ha aumentado a pesar de que no haya más personas con enfermedad celiaca. Algunas dietas se ponen de moda por muy absurdas que sean.
Una dieta sin gluten se basa en evitar una serie de cereales concretos. Nada más. En el caso de las personas con enfermedad celiaca además tienen que cuidar que no haya contaminación cruzada, es decir, que los alimentos no se hayan fabricado y cocinado donde también se fabrican y cocinan los alimentos con gluten. Para ellos seguir una dieta sin gluten es complicado. Si no tienes la enfermedad celiaca, no te compliques la vida.
Sal sin gluten: parece absurdo, pero no lo es
En el año 2000 la Federación de Asociaciones de Celíacos de España (FACE) emprendió la esforzada tarea de solicitar a la industria alimentaria, tanto a fabricantes como a distribuidores, que incluyeran algún tipo de distintivo en sus productos para ayudar a las personas con enfermedad celiaca a diferenciar entre los productos que podían consumir y los que no. Algunos productos, sobre todo procesados, pueden incluir en su composición harinas con gluten por motivos tecnológicos y puede resultar complicado ver cuáles son. Por aquel entonces la legislación vigente todavía no contemplaba las normas de etiquetado que hoy en día conocemos como «sin gluten» o «bajo en gluten». De ahí la petición.

En el año 2002, Mercadona ya ofrecía 50 referencias de productos «sin gluten» que fueron incluidos en la lista de productos aptos para celíacos en FACE. Mercadona sacó su propio sello «sin gluten», incluyéndolo en todos los alimentos libres de gluten, tanto si eran susceptibles de contenerlo como si no. Por este motivo encontramos alimentos con este sello, incluida la sal, el arroz, los garbanzos… alimentos que jamás lo han contenido. Este sello no respondía a una ridícula estrategia de marketing, sino a satisfacer la demanda de los consumidores y la petición de FACE. Otros muchos fabricantes y grandes distribuidores como Eroski o Carrefour se han sumado a esta iniciativa. En la actualidad ofrecen cientos referencias de alimentos sin gluten que habrían sido susceptibles de contenerlo. Tenemos más oferta de alimentos sin gluten que nunca.
El cambio en la normativa tardó algo más en llegar. Gracias a la iniciativa de los grandes distribuidores del sector alimentario, y a una propuesta del Ministerio de Sanidad y Consumo español, desarrollada a través de la Agencia Española de Seguridad Alimentaria y Nutrición (AESAN), y presentada a la Comunidad Europea en enero de 2008, se estableció que el límite de cantidad de gluten que debe figurar en la composición de todos los alimentos para ser considerados «sin gluten» ha de ser inferior a 20 mg/kg y para ser considerados «bajos en gluten» ha de ser inferior a 100 mg/kg. Esta propuesta se incluyó en el reglamento en 2009 y se mantiene en el reglamento vigente. En la actualidad existen varios sellos que certifican que los alimentos son «sin gluten».
Cosméticos sin gluten: parece absurdo y casi siempre lo es
Una conocida marca de cosméticos anuncia en televisión un nuevo champú «sin gluten». El envase del producto luce en su frontal el «sin gluten» como si se tratase de un eslogan comercial. Esto suscita chascarrillos y enfados a partes iguales. Hace un par de años se hacían bromas con el famoso «champú creador de materia» sin embargo, para sorpresa de muchos resultó que en aquel producto había mucha más ciencia de la que imaginábamos. Podríamos pensar que el champú sin gluten correrá la misma suerte, pero no, con ese eslogan nos están tomando el pelo, nunca mejor dicho.

Por un lado, el gluten no suele formar parte de los productos cosméticos porque no cumple ninguna función en ellos. Podríamos encontrar cantidades ínfimas en algún producto que contuviese avena o extractos de cereales con gluten. Según los estudios, incluso estos cosméticos contienen un máximo de 10 mg/kg de gluten; están por debajo de la cantidad de gluten que pueden contener los alimentos «sin gluten». Tendríamos que comernos dos labiales de cacao con avena para superar este límite. Obviamente el problema no sería ingerir gluten, sino comer barras de labios.
Por otro lado, el gluten no penetra en el organismo a través de la piel. Así que, aunque un cosmético contuviese gluten, éste no afectaría en nada a las personas con enfermedad celíaca. No obstante, hay que tener cuidado si entra en contacto con mucosas, heridas, o si se trata de productos infantiles, ya que los niños podrían ingerirlos accidentalmente durante el aseo. A las personas con enfermedad celiaca se les aconseja no utilizar labiales con ingredientes susceptibles de contener gluten, porque obviamente es más fácil ingerirlo, o cremas hidratantes de manos que podrían contaminar la comida. Aun así, la probabilidad de ingerir una cantidad nociva de gluten a través del uso de un cosmético es remota.

Hay un tipo de dermatitis que guarda cierta relación con el gluten. Se trata de la dermatitis herpetiforme. Esta enfermedad comúnmente aparece asociada a la enfermedad celiaca. Sin embargo, no se desarrolla por contacto por vía tópica con el gluten, sino tras su ingesta, así que los cosméticos sin gluten tampoco son necesarios para las personas con esta clase de dermatitis.
La Federación de Asociaciones de Celíacos de España (FACE) se ha puesto en contacto con el laboratorio que vende el champú para que retire el reclamo de «sin gluten». La razón que alegan es que este tipo de estrategia publicitaria banaliza la enfermedad celiaca, induce miedo a los consumidores y además de perpetúa los mitos en torno al gluten.
A título individual no pongo en duda las cualidades de este champú. Con total certeza será un buen producto cosmético. La estrategia publicitaria no solo se basa en el «sin gluten», pero desde luego sí ha acaparado toda la atención. Por eso solicito a estos laboratorios que retiren el «sin gluten» de su publicidad. No lo necesitan. Además, las personas que no estén bien informadas, que estén especialmente sensibilizadas con el tema del gluten porque tienen hijos con enfermedad celiaca, son un blanco fácil. Bastante fastidiado lo tienen con la alimentación como para preocuparse por chorradas.
Conclusión
Los cosméticos no llevan gluten porque éste no cumple ninguna función. Indicarlo como reclamo publicitario es un error. Causa inquietud en los consumidores, banaliza la enfermedad celiaca, perpetúa mitos y no responde a ninguna necesidad real. Además, si un cosmético tuviese gluten, las personas con enfermedad celiaca podrían utilizarlo sin problema.
En cambio, los alimentos sin gluten son necesarios para las personas que padecen la enfermedad celiaca. Las personas que no padecen la enfermedad celiaca no tienen por qué seguir una dieta sin gluten. Ni es más sana, ni sirve para perder peso.
La Federación de Asociaciones de Celíacos de España solicitó a fabricantes y distribuidores que todos los productos que no contienen gluten llevasen algún tipo de distintivo. Incluidos los productos que de forma natural no deberían contener gluten. No hubo una intención perversa por parte de la industria alimentaria. Todo lo contrario. Tanto es así que la industria se adelantó y propició un cambio de normativa que ahora nos permite distinguir más fácilmente qué alimentos llevan gluten y cuáles no.
Es tan vago creer que los alimentos sin gluten son más sanos como creer que la única intención de la industria es engañarnos. Suspicacias la justas.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo De la sal «sin gluten» al champú «sin gluten»: no solo marketing se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La pantalla de tu móvil solo tiene tres colores
- En busca de los genes de la enfermedad celíaca
- El peligro de saber sólo un poco
Una teoría cinética para los sistemas financieros

Ya operan en los mercados financieros roboadvisors, asesores automatizados para las inversiones, además de sistemas automatizados basados en algoritmos de toda clase y condición que pueden tomar y ejecutar miles de decisiones por minuto. Además existen sistemas de análisis cuantitativo que han convertido a matemáticos, físicos, estadísticos y expertos en computación, como los propietarios de Renaissance Technologies, en multimillonarios.
Para que nos hagamos una idea de la potencia de estos modelos, en 2008, el año de la gran crisis financiera, en el que el S&P 500, el índice que recoge a las 500 mayores empresas de los Estados Unidos, cayó un 38,5 %, el fondo Medaillon* de Renaissance, basado en el algoritmo Baum-Welch, que se emplea en ingeniería eléctrica, pero mejorado por el espeialista en álgebra James Ax, ganó un increíble 98,2 %. Esto es, la posibilidad de modelar eficaz y eficientemente el mercado existe, pero es una información secreta y solo la conocen algunos de los 290 propietarios-inversores de Renaissance.
Los altibajos de los mercados financieros parecen impredecibles, pero los físicos han demostrado que los modelos estocásticos aleatorios pueden captar la dinámica del mercado a gran escala, como los cambios en el índice Dow Jones. Lo que faltaba hasta ahora era un modelo, publicado en abierto, que describiese las interacciones a escalas más pequeñas, a nivel de operadores del mercado, los llamados traders.
Eso es precisamente lo que ha conseguido un grupo de investigadores encabezado por Kiyoshi Kanazawa, del Instituto Tecnológico de Tokio, un modelo que describe lo que ocurre a pequeña escala, utilizando para ello datos sobre traders individuales que operan en el mercado de divisas, el mayor mercado del mundo y en el que se opera con una frecuencia muy alta. Los investigadores comprobaron que el modelo podía usarse para desarrollar una teoría macroscópica que capturase con precisión la distribución de precios y otros indicadores del mercado.
¿Una partícula de polen en un vaso de agua o el par yen-dólar un día de mercado cualquiera?
El comportamiento estocástico, como el movimiento browniano de las partículas en un fluido, se puede entender con la llamada teoría cinética. En este enfoque, se comienza con un modelo de interacciones (o colisiones) microscópicas, moleculares, y se termina construyendo un modelo macroscópico que puede observarse casi a simple vista en el caso del movimiento browniano. El resultado final es una ecuación que describe la evolución de la posición de la partícula, la temperatura o alguna otra variable estadística a gran escala. Los “econofísicos” han intentado desarrollar una teoría cinética para los sistemas financieros, pero faltaban datos fiables sobre el comportamiento microscópico de los traders individuales.
Kanazawa y sus colaboradores analizaron las transacciones de alta frecuencia de cinco días entre dólares y yenes (cinco días puede parecer poco pero este es un mercado gigantesco, con millones de transacciones semanales). Hicieron un seguimiento del comportamiento de los traders, tanto en sus “ofertas” (bids, en el argot) como en los “precios de venta” (asks). Los traders envían pedidos cada pocos segundos, pero una transacción solo ocurre cuando el precio de venta de un trader coincide con el precio de oferta de otro trader.
Kanazawa et al. descubrieron que los operadores respondían a cada transacción ajustando sus precios de oferta /demanda según los cambios en el precio de transacción del mercado. Modelaron este “seguimiento de la tendencia” y encontraron que conducía a una ecuación similar a la de Boltzmann para el movimiento global de los precios. Esta ecuación macroscópica podría reproducir observaciones a gran escala del mercado de divisas.
* Como curiosidad: el nombre Medaillon viene del hecho de que el fundador de Renaissance James Simmons fue ganador del premio Veblen (1976) de geometría y James Ax del Cole (1967) de teoría de números.
Referencia:
Kiyoshi Kanazawa, Takumi Sueshige, Hideki Takayasu, and Misako Takayasu (2018) Derivation of the Boltzmann Equation for Financial Brownian Motion: Direct Observation of the Collective Motion of High-Frequency Traders Physical Review Letters doi: 10.1103/PhysRevLett.120.138301
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Una teoría cinética para los sistemas financieros se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La teoría cinética y la segunda ley de la termodinámica
- Los antecedentes de la teoría cinética
- La criticalidad de los mercados financieros
El origen poético de los números de Fibonacci
Un tema que ya se está convirtiendo en clásico en la sección Matemoción del Cuaderno de Cultura Científica es la sucesión de Fibonacci. Ya que como decía Marta Macho en una de sus últimas entradas ¡Nos encanta Fibonacci!.
Como seguramente sabrán las personas que estén leyendo esta entrada, la conocida como sucesión de Fibonacci fue introducida por el matemático italiano Leonardo de Pisa (1170-1241), a quien se le conocía como Fibonacci, esto es, hijo de Bonaccio, en su libro “Liber Abaci” (1202, El libro del Ábaco), como solución a uno de los problemas de ingenio que se planteaban en el mismo.

Caricatura de Fibonacci, realizada por el dibujante Enrique Morente para la exposición El Rostro Humano de las Matemáticas
Recordemos el problema en cuestión:
“Consideremos una familia de conejos con la característica de que tardan un mes en ser fértiles. Cuando han alcanzado la fertilidad, cada pareja se aparea teniendo al mes siguiente (cada hembra) una pareja de crías (un macho y una hembra) que de nuevo tardarán en ser fértiles un mes y entonces se aparearán. ¿Cuántas parejas de conejos habría al cabo de un tiempo dado, por ejemplo, un año?”

Número de parejas de conejos durante los primeros meses
No es difícil darse cuenta que la sucesión de parejas de conejos, suponiendo que estos no se mueran, que hay cada mes es la siguiente:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…
que tiene la propiedad de que cada número der la sucesión, Fn, es igual a la suma de los dos números anteriores, Fn = Fn – 1 + Fn – 2, para n = 1, 2, 3, …
En la sección Una de Mates del Cuaderno de Cultura Científica, que recoge los videos de esta sección dentro del programa de TV Orbita Laika, en su segunda temporada, podéis ver la explicación del problema de Fibonacci.
La sucesión de Fibonacci no solo es interesante dentro de las matemáticas, sino que juega un papel fundamental en el estudio de la morfología de las plantas, en concreto, en la filotaxis, siendo el número de espirales de las cabezas de los girasoles, las piñas o el romanescu, números de dicha sucesión, también nos la encontramos en el arte, como en las obras del artista italiano Mario Merz (1925-2003), o en la literatura, como en el poema Alfabeto (1981) de poeta danesa Inger Christensen (1935-2009).

Números de Fibonacci en el edificio Mole Antonelliana de Turín (Italia), del artista Mario Merz. Wikimedia (Felpe Cadoná)
Sin embargo, en esta entrada no vamos a hablar de las propiedades matemáticas de la sucesión de Fibonacci o de la presencia de esta en la naturaleza y la cultura, sino que vamos a viajar hasta la India, unos cuantos siglos antes de que el matemático italiano Fibonacci escribiera su libro Liber Abaci, para descubrir la presencia de los números de Fibonacci en la poesía en sánscrito.
En 1985, el matemático indio Parmanad Singh, del Raj Narain College de la India, publicó en la revista Historia Mathematica el artículo The so-called Fibonacci Numbers in Ancient and Medieval India (Los así llamados números de Fibonacci en la India antigua y medieval), en el cual mostraba el origen indio de los números de Fibonacci y su conexión con la poesía en la lengua sánscrita.
En la poesía en sánscrito, lengua antigua de la India, existen los poemas en los cuales hay un número fijo de sílabas por verso (los llamados varna-vrttas) y aquellos en los que hay un número fijo de “moras” por verso (llamados matra-vrattas). Para los que no sabíamos que es la “mora”, esta es “la unidad que mide el peso silábico, es decir, la duración de los segmentos fonológicos que componen la sílaba” (según la Wikipedia). En sánscrito hay dos tipos de sílabas, unas cortas (llamadas laghu), de una mora o instante silábico, y otras largas (llamadas guru), de dos moras.
El latín, como las lenguas clásicas indias, el sánscrito y el prácrito, o el griego, también constaba de dos tipos de sílabas, cortas y largas. Las sílabas podían tener una sola mora, como aquellas sílabas acabadas en vocal breve, ya que en latín se distinguía entre vocales breves y largas, y las que tenían dos moras, que eran el resto de sílabas, las terminadas en vocales largas o en consonante. Una misma palabra podía tener dos significados distintos en función de que la vocal fuese corta o larga, así la “a” de “mălus” era una vocal corta y la palabra significaba “malo”, mientras que en “mālus” la vocal era larga y el significado era “manzano”, o también “mástil”. La primera palabra tenía dos sílabas con tres moras, mientras que la segunda tenía dos sílabas con cuatro moras. Otro ejemplo de palabra con dos significados en función de si la vocal es corta o larga es “solum”, con vocal corta “sŏlum” significaba “suelo”, mientras que tenía el significado de “solo” con la vocal larga, “sōlum”.
Volviendo al sánscrito, un verso de tipo varna-vrttas, que recordemos que en este tipo de métrica se mantiene el número de sílabas de cada verso, con tres sílabas posee 8 posibilidades, en relación a las moras que componen el mismo. Si llamamos C a una sílaba corta, con una mora, y L a una sílaba larga, con dos moras, las posibles estructuras, en relación a las moras, son 8: CCC, LCC, CLC, CCL, CLL, LCL, LLC y LLL. Aunque el número de sílabas se mantiene constante, el número de moras varía de unas estructuras a otras, la primera tiene 3 moras, las tres siguientes 4 moras, las tres con dos silabas largas tienen 5 moras y la última tiene 6 moras.
Sin embargo, si consideramos un verso de tipo matra-vrttas, que recordemos que en este tipo de métrica se mantiene el número de moras de cada verso, con tres moras, existen solamente 3 estructuras posibles CCC, CL y LC, siendo ahora variable el número de sílabas, la primera con tres sílabas y las otras con dos.

Fragmento del texto sagrado “Rig Veda”, escrito en sánscrito, que es el texto más antiguo de la India, probablemente escrito entre el 1.500 y 1.200 a.c., y que constaba de una serie de himnos compuestos para los dioses
Pero… ¿qué tienen que ver los poemas en sánscrito con los números de Fibonacci?
Para dar respuesta a esta pregunta vamos a centrarnos en la métrica matra-vrttas. Veamos cuántas posibles estructuras existen de versos con 1, 2, 3, 4 o 5 moras.
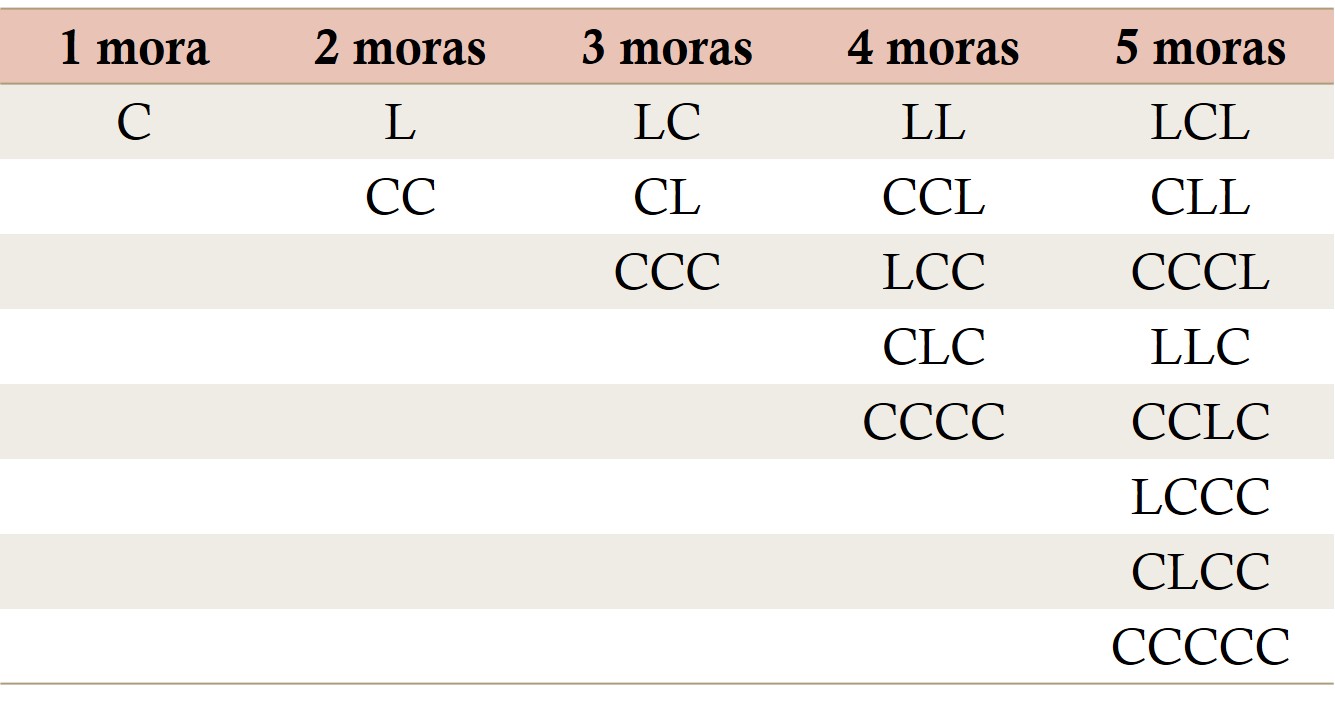
El número de variaciones posibles, para versos con 1, 2, 3, 4 o 5 moras, son 1, 2, 3, 5 y 8, que como podemos observar son números de Fibonacci. Pero fijémonos, por ejemplo, en las estructuras de los versos con 4 moras, los podemos dividir en dos tipos, los que terminan en una sílaba larga (L), que son las dos estructuras con 2 moras (L y CC) a las que se ha añadido dos moras mediante una sílaba larga (LL y CCL), y los que terminan en una sílaba corta (C), que son las tres estructuras con 3 moras (LC, CL y CCC) a las que se ha añadido una mora mediante una sílaba corta (LCC, CLC y CCCC). En consecuencia, hay 2 + 3 = 5 posibles estructuras con 4 moras.
Si ahora quisiéramos ver cuántas estructuras diferentes existen para los versos de la métrica matra-vrttas con 6 moras, obtendremos que son 13, los generados a partir de los de 4 moras al añadirle una sílaba larga (L), que son 5, y los generados a partir de los de 5 moras al añadirles una sílaba corta (C), que son 8, luego en total 5 + 8 = 13. En concreto, LLL, CCLL, LCCL, CLCL y CCCCL, junto con LCLC, CLLC, CCCLC, LLCC, CCLCC, LCCCC, CLCCC y CCCCCC.
Por lo tanto, lo que estamos diciendo es que el número de estructuras posibles con m moras es igual a la suma del número de estructuras con m – 1 y m – 2 moras, que es el motivo por el que salen los números de Fibonacci. En resumen,
¡¡la cantidad de estructuras posibles para versos matra-vrttas con m moras es igual al número de Fibonacci Fm+1!!
Si tenemos en cuenta que una sílaba corta (C) es 1 tiempo y una sílaba larga (L) son 2 tiempos, podemos escribir el anterior resultado como un resultado matemático.
Teorema: El número de Fibonacci Fm+1 es igual al número de formas de obtener el número m como sumas de 1s y 2s, donde el orden sí importa.
Por ejemplo, arriba hemos visto que el número 4 se puede obtener como cinco sumas diferentes con 1s y 2s, a saber, 2 + 2, 1 + 1 + 2, 2 + 1 + 1, 1 + 2 + 1 y 1 + 1 + 1 + 1, siguiendo el orden del cuadro anterior.
Ya hemos visto la relación que tiene la poesía en sánscrito con los números de Fibonacci, pero la pregunta ahora es si en la India eran conscientes de esta relación. Veamos lo que nos dice Parmanand Singh en su artículo.
Según este autor, Acarya Pingala (que vivió entre el 700 a.c. y el 100 d.c.), quien fue la primera autoridad en el estudio de la métrica en la India, pudo tener conocimiento de estos números, los conocidos como números de Fibonacci. Sin embargo, no existe una evidencia directa de esto, sino que en los comentarios de su obra realizados en el siglo X por el comentador Yadava, este habla de la regla de Pingala “misrau ca” (algo así como “y los dos juntos”) para explicar la expansión de los matra-vrttas combinando las expansiones de las dos métricas anteriores al añadir un guru (L) y un laghu (C), respectivamente. Y algo similar ocurre con otra autoridad antigua en la métrica de la India, Acarya Bharata, quien pudo vivir entre el 100 a.c. y el 350 d.c.
Sin embargo, la primera autoridad en el estudio de la métrica en la India que menciona explícitamente la regla de la formación de los números de variaciones de matra-vrttas fue Acarya Virahanka, quien vivió entre los siglos sexto y octavo. Puede leerse en una de sus obras algo así “Juntando las variaciones de las dos métricas anteriores, se obtiene la cantidad. Este es un método para conocer el número (de variaciones) de la siguiente matra-vrtta”.
Y el primer autor que menciona explícitamente los números de Fibonacci, mientras analiza y comenta la obra de Acarya Virahanka, es Gopala, cuyo comentario manuscrito de la obra del anterior está datado entre los años 1133 y 1135.
Otra autoridad que menciona explícitamente la regla de la creación de los matra-vrttas y los números de Fibonacci fue el poeta y estudioso de la métrica Acarya Hemacandra, en su estudio sobre la métrica Chandonusasana (1150). La regla de Hemacandra puede ser traducida algo así “la suma de los números [de variaciones] del último y anteúltimo, da lugar al del siguiente matra-vrtta”, y explícitamente menciona, como lo hizo Gopala, “1, 2, 3, 5, 8, 21, 34 y se continua de esta forma”.
Parmanand Singh menciona otra obra famosa sobre la métrica en la cual se dan algunas reglas sobre los números de Fibonacci, Prakrta Paingala, publicada posiblemente en el siglo XIV.
Todos estos estudios sobre la métrica de los matra-vrttas pertenecen al campo de la ciencia de la métrica, pero el primer estudio matemático en India de la sucesión de Fibonacci fue la obra Ganita Kaumudi (1356) del matemático Narayana Pandita, posterior a la obra del matemático italiano Fibonacci. En esta obra se estudian más sucesiones de números, además de la de Fibonacci, como la conocida como sucesión de las vacas de Narayana, de la que hablamos en la entrada Las vacas de Narayana, la versión hindú de los conejos de Fibonacci.
Obra “La secuencia de Fibonacci” del artista venezolano Rafael Araujo
Bibliografía
1.- Mario Livio, La proporción áurea, La historia de phi, el número más sorprendente del mundo, Ariel, 2006.
2.- Parmanad Singh, The so-called Fibonacci Numbers in Ancient and Medieval India, Historia Mathematica 12, n. 3, p. 229 – 244 (1985).
3.- Página web del artista Rafael Araujo.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El origen poético de los números de Fibonacci se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los números (y los inversos) de Fibonacci
- ¡Nos encanta Fibonacci!
- Una conjetura sobre ciertos números en el ‘sistema Shadok’
Animales en equilibrio osmótico: invertebrados marinos y peces bruja

Pez bruja del Pacífico o mixino morado (“Eptatretus stoutii”)
Los animales surgieron en el océano y allí se produjo su mayor radiación evolutiva; quizás por esa razón no hay ningún otro medio con más diversidad de grandes grupos. De hecho, en el mar están representados todos los filos y gran parte de las clases de animales, lo que no ocurre ni en las aguas dulces ni en el medio terrestre. Posiblemente eso explique por qué todos los invertebrados que son exclusivamente marinos son osmoconformadores; esto es, tienen la misma concentración osmótica que el agua de mar (alrededor de 1000 mOsm) y no hacen trabajo alguno para ajustar esa concentración1: sencillamente se encuentran en equilibrio osmótico con el medio externo, son isosmóticos2.
Como vimos aquí, de los tres grandes grupos en que puede clasificarse la fauna del planeta de acuerdo con la composición de sus medios interno e intracelular, los invertebrados marinos no solo se caracterizan por tener un medio interno con la misma concentración osmótica que el medio en el que viven sino que, además, tiene una composición iónica similar, aunque no idéntica, a la del agua de mar. Por las razones que dimos aquí, el medio intracelular, sin embargo, no tiene la misma composición de solutos ya que una parte muy importante de ellos son sustancias orgánicas, aunque mantienen, lógicamente, la misma concentración osmótica total.
Dado que la composición iónica del medio interno y la del agua marina no son idénticas, los invertebrados marinos han de recurrir a procesos activos de regulación iónica para mantener esas diferencias. Sus superficies corporales suelen ser muy permeables, lo que conlleva que los iones se muevan libremente entre ambos medios (interno y externo) a favor de gradiente electroquímico. Por ello, aquellos iones que se encuentran más concentrados en el plasma o líquido interno tienden a salir al exterior. Para contrarrestar el efecto de la pérdida, estos animales recurren al transporte activo desde el exterior, lo que conlleva un cierto gasto energético, y a incorporar los iones del agua ingerida con el alimento. Los órganos excretores también juegan un papel importante en estos procesos. En crustáceos y moluscos, por ejemplo, aunque la orina suele ser isosmótica con el plasma, el órgano excretor modifica la composición iónica, recuperando activamente los iones que tienden a perderse con mayor facilidad a través del tegumento o del epitelio respiratorio.
La mayor parte de las especies de esponjas, cnidarios, anélidos, moluscos, equinodermos, artrópodos y otros grupos menores que viven en los océanos pertenecen a linajes que no han abandonado nunca el medio marino. Eso explica el hecho de que sean isosmóticos y que algunos sean, además estenohalinos3, o sea, que no sean capaces de tolerar variaciones ambientales de salinidad. Los equinodermos son estenohalinos, carecen de representantes en aguas dulces; y casi todos los cnidarios también lo son4.
Las aproximadamente sesenta especies de mixines o peces bruja que viven en la actualidad han de incluirse también con los invertebrados marinos osmoconformadores de los que nos hemos ocupado aquí. Pueden considerarse una excepción, ya que son vertebrados, pero su presencia en este grupo no puede considerarse en absoluto anecdótica. Los mixines son muy interesantes. Carecen de mandíbula; o sea, son de los pocos representantes del grupo que retiene la condición agnata. Son, con toda probabilidad, el único grupo de vertebrados con ancestros exclusivamente marinos. Los otros vertebrados agnatos vivientes en la actualidad son las lampreas, algunos de cuyos representantes son de agua dulce. Por esa razón no es anecdótica su presencia aquí junto con los invertebrados marinos, ya que sus linajes son exclusivamente marinos. Eso explica que sus medios internos hayan retenido una concentración osmótica prácticamente idéntica a la del agua de mar en la que surgieron y han evolucionado, y que la composición de solutos del medio interno, aunque no sea la misma que la del medio externo, se le asemeje de forma notable y, lo que es más importante, que esté basada principalmente en sales inorgánicas.
Notas:
1Conviene advertir de que algunos invertebrados marinos ocupan medios de agua salobre o de concentración salina variable, como áreas estuarinas o lagunas costeras, y algunos han desarrollado una cierta capacidad para regular la concentración de su medio interno; pero no nos ocuparemos aquí de ellos por el momento.
2Isosmótico significa “de la misma concentración osmótica”.
3 El prefijo “esteno” indica que no tolera variaciones de algún factor. El opuesto a ese rasgo es la tolerancia amplia, que viene expresada por el prefijo “euri”. Así, estenohalino indica que no tolera variaciones de la salinidad y eurihalino, que tolera amplias variaciones de ese factor. Tanto “esteno” como “euri” se utilizan para caracterizar el rango de tolerancia para con otros factores.
4De las aproximadamente 10.000 especies del filo, menos de 40 son de agua dulce; la inmensa mayoría son marinas.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Animales en equilibrio osmótico: invertebrados marinos y peces bruja se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Relaciones hídricas y salinas de los animales
- La respiración de los invertebrados terrestres
- Efectores osmóticos
Comprobaciones experimentales de la relatividad general (1)
Cuando la teoría general de la relatividad se publicó en 1916 vino a explicar algunas observaciones astronómicas, hasta ese momento sin explicación satisfactoria, y realizó varias predicciones que se irían confirmando a lo largo del siglo siguiente, la última de ellas, las ondas gravitacionales, detectadas en 2016.
Hemos de aclarar que explicación, en filosofía de la ciencia, tiene un sentido minimalista. Simplificando, se dice que una teoría explica un conjunto de datos conocidos de una observación, si estos datos podrían haberse predicho usando la teoría. En cierto sentido una explicación es una predicción retroactiva.
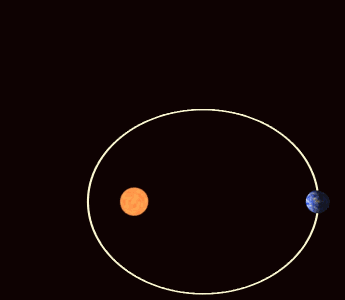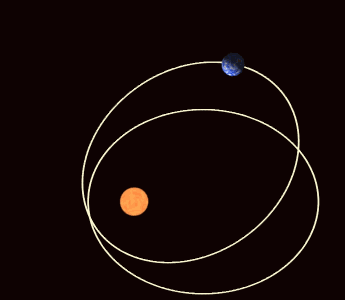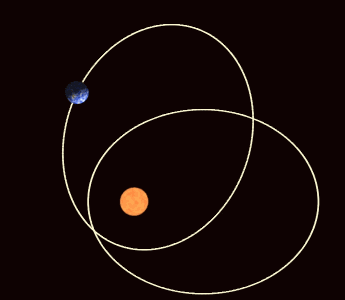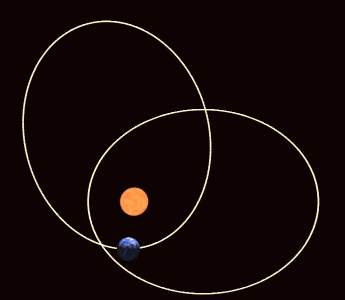
Precesión de la órbita de un planeta.
Pues bien, a comienzos del siglo XX se había venido observando durante décadas, desde que lo describiese Urbain le Verrier en 1859, que la órbita de Mercurio tenía ciertas peculiaridades. Los planetas se supone que siguen órbitas elipsoidales, con el Sol en uno de los focos de la elipse, tal y como había descrito Kepler y explicado (en el sentido que usamos esta palabra) Newton. Resulta que el punto de la órbita más cercano al Sol, el perihelio, se supone que es fijo pero se había observado que se desplazaba ligeramente de lo previsto, lo suficiente como para poder medirse consistentemente, rotando alrededor del Sol; este fenómeno se conoce como precesión de la órbita y ocurre en todos los planetas no solo en Mercurio, algo que solo pudo medirse mucho después en los demás debido a lo pequeño del efecto. La teoría de Newton podía explicar el fenómeno, pero en ningún caso la magnitud de la precesión de la órbita de Mercurio.
Para explicarlo se aventuraron multitud de hipótesis, entre ellas la existencia de un planeta más próximo al Sol que el propio Mercurio, al que llamaron Vulcano. En el artículo que publicó Einstein en 1916 demostraba que sus ecuaciones “predecían” y, por tanto, explicaban, que el perihelio de Mercurio debía avanzar cada año y que la magnitud del avance se correspondía con los valores observados. Un punto a favor de la teoría, pero en ningún caso definitivo. Curiosamente Paul Gerber había llegado a la misma fórmula final para la magnitud de la precesión en 1898, pero se había basado en la teoría electromagnética de Weber (ya superada por la de Maxwell), y la consistencia lógica de la derivación era dudosa, por lo que se descartó la idea.

Corrimiento al rojo gravitacional o de Einstein
Einstein también recogía en su artículo de 1916 que, si la relatividad general es correcta, entonces la longitud de onda de la luz que se aleja del origen de un campo gravitatorio muy fuerte debería presentar un desplazamiento al rojo cuando se observa desde un punto muy alejado del origen. De nuevo esto es algo que ya predice Newton y que ya estudiaron John Michell en 1783 y Pierre Simon de Laplace en 1796 usando la teoría corpuscular de la luz newtoniana.
El problema del planteamiento newtoniano es que llegaría un momento en que la luz no podría escapar de una estrella lo suficientemente masiva, pero el hecho es que escapa. La teoría ondulatoria vino a remediar esta paradoja, pero fue necesaria la teoría de Einstein para explicar el desplazamiento al rojo que ve un observador externo y que se debe, no a que la longitud de onda de la luz se altere, sino a que relojes en diferentes puntos miden diferentes tiempos. El corrimiento al rojo que predice Einstein no es fácil de medir, pero los experimentos realizados a lo largo del siglo XX confirman que la magnitud observada se corresponde con las predicciones, no solo en la luz que escapa de púlsares y estrellas, sino en la que escapa de la propia Tierra donde el efecto es mucho menor.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Comprobaciones experimentales de la relatividad general (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las ecuaciones de campo de la relatividad general
- El principio de relatividad (y 4): la versión de Einstein
- Confirmación experimental de la teoría de la relatividad especial (y 2)
Juguetes y hormonas sexuales

A lo largo de la vida hay distintos momentos en los que se elevan los niveles de hormonas sexuales en la sangre. Uno de esos momentos es el periodo perinatal. Poco antes del nacimiento y durante unos pocos meses posteriores al mismo se produce una elevación transitoria de los niveles de testosterona en los niños y de los de estrógenos en las niñas. La siguiente subida tiene lugar en la pubertad y esa ya no es transitoria, puesto que a partir de ese momento y hasta su muy posterior declive, bien avanzada la madurez, esos niveles se mantienen altos.
La elevación puberal de los niveles de hormonas sexuales induce y acompaña la maduración sexual, así como la aparición de los caracteres sexuales secundarios. Pero si bien sabemos cuál es la función de esa elevación, no tenemos el mismo conocimiento acerca de la subida transitoria perinatal. Dado que esa elevación no antecede ni va acompañada de ningún cambio anatómico o fisiológico -al menos evidente-, se ha postulado que en ese momento el tejido diana de esas hormonas es el cerebral y que podrían ser responsable de la configuración de algunas de las diferencias existentes en el comportamiento de niños y niñas.
En un trabajo publicado hace unos años, un equipo de psicólogas de Texas A & M University dieron cuenta de los resultados obtenidos en una investigación acerca de los condicionantes del comportamiento de niños y niñas y, más en concreto, del modo en que se ve afectado por estereotipos de sexo presentes en la sociedad o por factores de naturaleza biológica.
A la edad de tres años chicos y chicas muestran diferencias en sus preferencias de juego. Los chicos tienden a jugar más que las chicas con pelotas, vehículos y juguetes de construcción, y prefieren jugar con grupos más numerosos que las chicas. En qué medida estas diferencias son debidas a una suerte de programación biológica o son el resultado de la presión social es materia de intenso debate. Aunque parece ser que la exposición uterina a distintos niveles hormonales podría inducir la preferencia por unos u otros tipos de juguetes, no se ha investigado aún cuáles pueden ser el efecto de la elevación perinatal de los niveles de hormonas sexuales en el comportamiento infantil.
Las psicólogas de la universidad tejana trabajaron con bebés de 3 y 4 meses y encontraron que, si bien el comportamiento de las niñas no parecía verse afectado por la exposición pre o postnatal a distintos niveles hormonales, en los niños sí se observó una relación. Los niños con niveles más altos de testosterona mostraban una mayor preferencia por grupos de figuras que por figuras individuales. Y la mayor preferencia por animaciones con una pelota que por animaciones con un muñeco se relacionaba con la exposición prenatal a la testosterona.
No cabe extrapolar conclusiones definitivas de estos resultados al comportamiento en edades posteriores, cuando ya se manifiestan con claridad las diferencias por unos u otros juguetes. Pero si los factores hormonales condicionan algunos aspectos del comportamiento infantil temprano, bien cabe suponer que tal condicionamiento se extienda hacia edades mayores, con todo lo que ello comporta.
Fuente:
Gerianne Alexander, Teresa Wilcox y Mary Elizabeth Farmer (2009): “Hormone–behavior associations in early infancy” Hormones and Behavior 56: 498-502; DOI: 101016/j.yhbeh.2009.08.003
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Juguetes y hormonas sexuales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Gradualismo o saltacionismo… en evolución lingüística
- Ciencia express: Qué son las hormonas
- ¿Nacidos para creer?

