No habrá solución sin más conocimiento
 Foto: Claudio Schwarz / Unsplash
Foto: Claudio Schwarz / UnsplashSegún todos los indicios nos enfrentamos a la mayor crisis de salud pública que ha conocido la población occidental actual. Su causante, la pandemia COVID-19 no solo va a tener efectos directos sobre la salud y la vida de miles de personas. Los tendrá también de otra naturaleza, más difusos pero de más largo alcance.
La llamada gripe española de 1918 no nos sirve para anticipar cuáles pueden ser las consecuencias de orden social de la pandemia actual. Hay, por un lado, una gran incertidumbre con relación a la incidencia y letalidad de ambas, aquella gripe y esta pandemia. Habrá de pasar más tiempo para tener datos fiables de COVID-19. Por otro lado, hoy sabemos mucho más que hace un siglo y contamos con medios muy superiores para combatir la enfermedad. Y por último, en muchos países la pandemia de gripe española no dejó la huella social que podría haber dejado de no haber coincidido con la Gran Guerra.
En una época en la que las guerras ocurren ya lejos de nuestras fronteras y en una zona geográfica en la que no se producen grandes catástrofes naturales, COVID-19 revela un flanco vulnerable de nuestras sociedades. Por primera vez para muchas generaciones de europeos, una amenaza real se cierne sobre nuestro modo de vida. Incluso aunque la letalidad del virus SARS-CoV-2 sea inferior al 1% de los contagiados, se transmite con tal facilidad que puede acabar infectando a millones de personas (las autoridades alemanas barajan cifras del 70% de la población). Y como sabemos, un porcentaje nada desdeñable de los infectados enferman de gravedad y requieren cuidados intensivos. Por eso, los sistemas de salud se encuentran en riesgo y su eventual insuficiencia podría provocar problemas adicionales y una gran crisis de confianza en el modelo. A lo anterior hay que añadir los efectos económicos que ya se están produciendo sobre sectores que, como el turístico en España, crean riqueza y mantienen muchos puestos de trabajo.
Es difícil evaluar las consecuencias que tendría un trauma sociosanitario en sociedades habituadas a la tranquilidad que proporciona el contar con un buen sistema de salud, pero sus efectos no serán inocuos en términos sociopolíticos. Por ello, los países que no acierten a la hora de contener la extensión rápida del virus y mitigar los efectos sobre la salud pública experimentarán, seguramente, inestabilidad política.
Por otro lado, las epidemias son caldo de cultivo de la xenofobia. Las restricciones al movimiento de personas entre diferentes países o zonas geográficas quizás sean útiles para contener la expansión de la enfermedad, pero también influyen en la percepción que tiene la gente de los extranjeros. Así ha sido durante milenios y no hay razones para pensar que ahora será diferente.
Y a la par que afrontamos serias amenazas, también hay datos para el optimismo. El esfuerzo que están haciendo las potencias científicas del mundo para conocer el virus y la forma de combatirlo no tiene parangón. Nunca se había compartido tanta información entre equipos de diferentes países. Probablemente no se había hecho antes un esfuerzo colectivo de tal magnitud. Esta es una buena noticia para la humanidad porque la solución a largo plazo solo puede venir del conocimiento. Estamos mejor que hace un siglo porque hoy sabemos más que entonces. Y para resolver el problema, deberemos aprender más aún. En el futuro nos esperan otras pandemias, quizás de nuevos virus o de superbacterias. Y otros desafíos nos aguardan, unos de orden sanitario y otros de diferente índole. No bastará con la ciencia y la tecnología para resolverlos, pero sin ciencia y tecnología no serán resolubles.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo No habrá solución sin más conocimiento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Terremotos en la gran pantalla: algunas verdades y diversas mentiras
Los fósiles, los minerales o las rocas son, entre otras cosas, en lo primero que pensamos al hablar de geología, pero lo cierto es que la física es un ámbito científico que difícilmente se puede desvincular de la geología. Y es que el fundamento físico resulta clave a la hora de explicar algunos procesos geológicos que suceden tanto en el océano como en la superficie terrestre.
Con el fin de poner sobre la mesa la estrecha relación entre la geología y la física, los días 27 y 28 de noviembre de 2019 se celebró la jornada divulgativa “Geología para poetas, miopes y despistados: La Geología también tiene su Física”. El evento tuvo lugar en la Sala Baroja del Bizkaia Aretoa de la UPV/EHU en Bilbao.
La segunda edición de esta iniciativa estuvo organizada por miembros del grupo de investigación de Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Geoparque de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

Volver a ver una película con un especialista al lado puede ser una experiencia de lo más enriquecedora. En este caso la película es San Andreas (2015) y el especialista Arturo Apraiz, profesor del departamento de geodinámica de la Universidad del País Vasco, UPV/EHU. En esta charla se repasan escenas y diálogos de la película, con sus aciertos y errores geológicos, y Apraiz aprovecha para aclarar conceptos y profundizar en algunos aspectos más desconocidos de los terremotos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Terremotos en la gran pantalla: algunas verdades y diversas mentiras se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La eternidad en un grano de arena
- Geotermia urbana
- Los ecos del fondo submarino: imágenes de las estructuras geológicas.
El efecto de los microplásticos en los ríos
 Foto: Landsil / Unsplash
Foto: Landsil / UnsplashLa preocupación por la contaminación producida por los microplásticos es cada vez mayor; debido a su abundancia, ubicuidad y persistencia en el tiempo, los microplásticos representan un riesgo potencial para los organismos y los ecosistemas. Sin embargo, los estudios sobre su distribución en sistemas de agua dulce, tanto en lagos como en ríos, y sus efectos sobre los organismos de estas aguas son escasos, y hay muy poca información sobre su potencial influencia en el funcionamiento de estos ecosistemas.
En este contexto, el grupo de investigación Stream Ecology de la UPV/EHU, en colaboración con el Museo Nacional de Ciencias Naturales (CSIC) de Madrid, ha estudiado “los efectos de los microplásticos en los ecosistemas de agua dulce y en dos de los grupos más importantes de organismos que viven en ellos: los anfibios y los invertebrados”, explica Naiara López Rojo, investigadora del grupo de la UPV/EHU. Para ello han realizado experimentos de laboratorio, en los que han replicado las condiciones de los ríos y lagunas donde viven estos animales, y los han expuesto a diferentes concentraciones de microplásticos fluorescentes: “Réplicas sin microplásticos (control), a baja concentración, a concentración intermedia y a alta, siendo el resto de características idénticas (iluminación, temperatura, etc)”.

De esta manera, el grupo ha estudiado, por una parte, el efecto de los microplásticos en la supervivencia, alimentación y el crecimiento de los renacuajos, así como la ingestión y la egestión de los mismos. Además, “hemos analizado si los microplásticos se adhieren al perifiton (conjunto de organismos microscópicos que crece sobre las rocas del lecho y principal fuente de alimentación de estos renacuajos) y si alteran su productividad, pues eso demostraría una alteración del funcionamiento de los ecosistemas de agua dulce”, afirma la investigadora. Por otra parte, han examinado los efectos de los microplásticos en la descomposición de la hojarasca (uno de los procesos más importantes de los ecosistemas fluviales) y en la supervivencia y crecimiento de los organismos que se alimentan de ella (invertebrados detritívoros); asimismo, han estudiado el grado de adhesión de los microplásticos a la hojarasca y el grado de ingestión y egestión de los detritívoros, evaluando así los mecanismos de la transferencia trófica de los microplásticos.
Los resultados demuestran que “los microplásticos causan mortalidad a los detritívoros en todas las concentraciones (en la concentración más alta la mortalidad es nueve veces mayor), pero no afectan a su crecimiento. En el caso de los renacuajos, hemos visto que mueren en la concentración más alta de microplásticos; en las otras concentraciones, no hemos observado letalidad, pero sí un descenso en el crecimiento de los anfibios”, añade López-Rojo.
Los estudios de fluorescencia realizados a los renacuajos indican, según la investigadora, “una presencia de microplásticos en los organismos, en sus heces y en el perifiton. Y esto sugiere que los microplásticos pueden ser estresores importantes para los anfibios, al igual que otros contaminantes, el cambio climático, la pérdida de hábitat, etc. Además, los anfibios pueden ser una importante vía de transmisión de los microplásticos del agua dulce a los ecosistemas terrestres”. En el caso de los invertebrados, los análisis sugieren que los microplásticos también fueron ingeridos (muy probablemente a través de la ingestión de partículas adheridas a la hojarasca) y parte de ellos, excretados. La descomposición de la hojarasca se redujo en función del incremento de la concentración de los microplásticos. “Estos resultados aportan nuevas evidencias de los efectos perjudiciales de este contaminante en los insectos acuáticos y en el funcionamiento de los ecosistemas fluviales, y pone en evidencia la necesidad de estandarizar los métodos a utilizar en futuros experimentos con microplásticos, para poder hacer comparaciones”, concluye la investigadora del Departamento de Biología Vegetal y Ecología de la UPV/EHU.
López Rojo remarca la necesidad de seguir investigando el efecto de este tipo de contaminante en los ecosistemas de agua dulce: “Estamos viendo que la respuesta depende del tipo de organismo que analices, del tiempo de exposición, etc. Se tendría que estudiar una exposición más prolongada, porque precisamente los plásticos persisten mucho más que 15 días. Sería interesante, también, estudiar el efecto de este contaminante junto con otro tipo de estresores, a los que también están sujetos tanto los ríos como las lagunas. Porque, probablemente, la interacción entre varios estresores puede resultar más perjudicial todavía”.
Referencias:
Naiara López-Rojo, Javier Pérez, Alberto Alonso, Francisco Correa-Araneda, Luz Boyero (2020) Microplastics have lethal and sublethal effects on stream invertebrates and affect stream ecosystem functioning Environmental Pollution doi: 10.1016/j.envpol.2019.113898
Luz Boyero, Naiara López-Rojo, Jaime Bosch, Alberto Alonso, Francisco Correa-Araneda, Javier Pérez (2020) Microplastics impair amphibian survival, body condition and function Chemosphere DOI: 10.1016/j.chemosphere.2019.125500
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El efecto de los microplásticos en los ríos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La contribución global de los ríos intermitentes al ciclo del carbono
- Verdín, eucaliptos y cambio climático
- Todo lo que se puede medir en un río
La emoción de las escalas musicales
 Foto: Darya Tryfanava / Unsplash
Foto: Darya Tryfanava / UnsplashNo hace falta ser un experto en música. Si alguna vez has oído hablar de “el modo menor”, probablemente haya sido asociado a su poder para evocar tristeza. En cambio, su luminoso hermano “el Modo Mayor”, suele llegar anunciando la alegría.
Esto es así… en general, hasta cierto y siempre dentro del contexto de la música occidental. A fin de cuentas, para componer la tristeza no existe una receta fácil, ni ingredientes mágicos. Pero incluso en algo tan aparentemente convencional como el uso de una escala musical y su asociación emocional, podemos encontrar las huellas de la voz humana.
La aparente bipolaridad de la música Mayor-menor, es relativamente reciente, para empezar. Incluso dentro de la tradición occidental, existen siete modos distintos que se vienen utilizando desde tiempos de la Antigua Grecia —y puede que incluso antes: existen indicios de que la música sumeria ya utilizaba un sistema similar basado en escalas de siete notas. Cada uno de estos modos, tradicionalmente, se ha asociado a distintos usos con sus propias connotaciones emocionales. Y, si nos alejamos un poquito de Europa y su legado, el abanico se amplía aún más: encontramos escalas pentatónicas, octatónicas, escalas con microtonos o escalas que dividen el rango sonoro en más o menos unidades iguales (como la escala cromática occidental, de 12 semitonos).
Sólo hay una cosa común dentro de toda esta diversidad: allá donde uno vaya, los sistemas musicales utilizan escalas. Y allá donde se utilizan escalas, estas suelen asociarse a distintas emociones. Esto no es un detalle menor. A priori, el espectro sonoro es un continuo: existen sonidos de 440 Hz, de 441 Hz… y también los infinitos sonidos cuyas frecuencias se pueden definir entre estas dos. El hecho de que para cantar, decidamos quedarnos sólo con “algunos” de estos sonidos posibles es una de las características más universales de la música. Y, también, una de las características que más fácilmente nos ayudan a distinguirla del habla humana (al hablar normalmente, nuestro uso del sonido no está discretizado… a menos que estemos queriendo imitar a un robot).
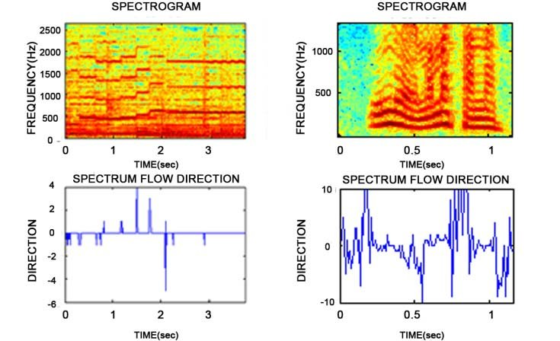 Espectrogramas de sonidos musicales (izquierda) y habla (derecha). Fuente: Speech detection on broadcast audio
Espectrogramas de sonidos musicales (izquierda) y habla (derecha). Fuente: Speech detection on broadcast audio
Podemos pensar en las notas de una escala como una limitación deliberada de los sonidos disponibles para hacer música. En esa misma línea, el ritmo podría entenderse como una limitación de los cuándos posibles disponibles. Quizás, ambas restricciones sean simplificaciones necesarias para poder cantar coordinadamente con otros seres humanos y para poder recordar esas melodías1. Ritmo y escalas forman una especie de matriz, como la cuadrícula de un papel pautado, que nos sirve de plantilla. Si los sonidos musicales y los momentos fuesen infinitos, la probabilidad de cantar las mismas frecuencias, al mismo tiempo, con otras personas, sería despreciable. Sin notas y figuras rítmicas, todas las melodías se emborronarían en una gaussiana de probabilidad en torno a alguna frecuencia siempre variable y mal definida. Todos los coros disonarían, todos los auditorios se llenarían de desconciertos…
Si bien la utilización de escalas puede obedecer a cuestiones adaptativas, su asociación emocional resulta más difícil de desentrañar. Pero parece claro que las escalas son unos de los ingredientes que, sin saberlo, utilizamos para interpretar una pieza musical. Su sonido define el molde sobre el que se construye cada canción y esto, a su vez, nos permite generar ciertas expectativas. Bastan unos pocos compases de música para hacernos a una idea de qué sonidos vamos a escuchar, en qué orden, con qué frecuencia… durante toda la pieza. Estas expectativas pueden cumplirse, o no, lo que a su vez nos mantiene involucrados en la escucha, en un constante devenir de sorpresas, sospechas y deseos cumplidos.
Los sonidos de un modo o una escala, por su parte, le dan su propia sonoridad característica. Se podría decir que la escala es a la música lo que la paleta de color es a un cuadro ─curiosamente, raga, la palabra que designa los modos melódicos de la música indica, significa literalmente “lo que colorea la mente”. Pero establecer qué colecciones de colores son “los alegres” o “los tristes” depende de muchos factores, algunos de ellos puramente culturales. La escala menor, por ejemplo, con su innegable fama de triste, se utiliza en la tradición folklórica búlgara asociada a otro tipo de emociones.
O, sin irse tan lejos: ¿os acordáis de Despacito? La canción del verano más bailada en las discotecas de medio mundo está escrita en modo menor. En este caso, muchos otros aspectos de la canción ─especialmente, su ritmo─ son capaces de eliminar la posible tristeza que habitualmente asociamos a su modo. Aún así… basta cambiarla a modo mayor para que el carácter cambie por completo. Os presento a Luis Fonsi, el éxito del tíovivo:
Otras alegrías célebres escritas en modo menor incluyen Aserejé, It’s raining men y hasta el tema de El Hormiguero. Happy de Pharrell Williams, una canción que lleva la alegría hasta en el título, literalmente, no está escrita en modo menor sino en modo dórico pero podría argumentarse que los dos se parecen bastante.
Por otra parte, haciendo melancólico al modo Mayor, encontramos el precioso Adagio del concierto para piano de Ravel, el tema principal de la banda sonora de Memorias de África de John Barry, o Wish you were here de Pink Floyd.
Si bien la asociación del modo menor con la tristeza es culturalmente dependiente y matizable de muchas maneras, esto no significa que sea una asociación arbitraria. Existen motivos por los probablemente, percibimos el modo menor como más triste que su contraparte, el modo Mayor. Y todo podría radicar, precisamente, en la comparación inconsciente que hacemos entre ambos y en su paralelismo con ciertos aspectos de la prosodia humana. Pero este asunto tiene su propia enjundia y merece su propio post.
Nota:
1The Origins of Musicality. Edited by Henkjan Honing
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo La emoción de las escalas musicales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La cuadratura del cuadrado: en busca del santo grial
Una de mis pasiones dentro de las matemáticas es el estudio de aquellos pequeños problemas matemáticos o de ingenio que surgieron dentro de la matemática recreativa como sencillos divertimentos matemáticos, pero que fueron creciendo con el interés de muchos matemáticos que dedicaron su tiempo a pensar sobre ellos y que se acabaron convirtiendo en hermosos diamantes, con una interesante investigación matemática a su alrededor.
Sobre algunos de estos problemas matemáticos clásicos hemos hablado en el Cuaderno de Cultura Científica, como El problema de las estudiantes de Kirkman, El problema de los sellos de Sylvester, El problema de la plantación de árboles en fila, El problema de las cartas extraviadas, El teorema de los cuatro colores, El problema de Malfatti, o El problema de pesas de Bachet de Méziriac, entre otros.
En esta entrada de la sección Matemoción vamos a hablar de otro de estos problemas clásicos, el conocido como problema de la cuadratura del cuadrado, del que ya hemos hablado brevemente en otras dos entradas, Blanche Descartes y la cuadratura del cuadrado y Teselaciones rítmicas perfectas.
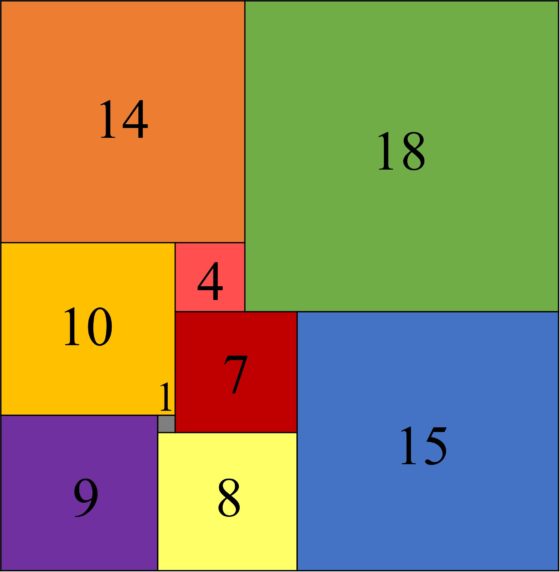 División de un rectángulo de dimensiones 32 x 33 en 9 cuadrados de distintos tamaños, de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18. Construcción de Zbigniew Moron (1925)
División de un rectángulo de dimensiones 32 x 33 en 9 cuadrados de distintos tamaños, de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18. Construcción de Zbigniew Moron (1925)El problema, enunciado de forma sencilla, sería el siguiente:
Problema de la cuadratura del cuadrado (o rectángulo): Dividir un cuadrado (o rectángulo) en un número finito de cuadrados más pequeños, todos de distintos tamaños.
Vayamos con algunos conceptos que vamos a utilizar a lo largo de esta entrada. La cuadratura, o disección, de un rectángulo (en particular, de un cuadrado) en cuadrados más pequeños, todos de distintas dimensiones, como se plantea en el problema, se denomina perfecta. A la cuadratura de un rectángulo que contiene la cuadratura de algún sub-rectángulo se le llama compuesta, mientras que si no existe un sub-rectángulo tal, diremos que es simple. Se llama orden de la cuadratura al número de cuadrados que se han utilizado en la cuadratura del rectángulo. La cuadratura del rectángulo de la imagen anterior es perfecta y simple.
Por otra parte, los lados de los cuadrados pequeños tienen que ser múltiplos racionales de los lados del cuadrado (o del rectángulo) grande, por lo tanto, podemos trabajar con cuadrados tales que sus lados tengan longitud entera, así como los lados del rectángulo grande.
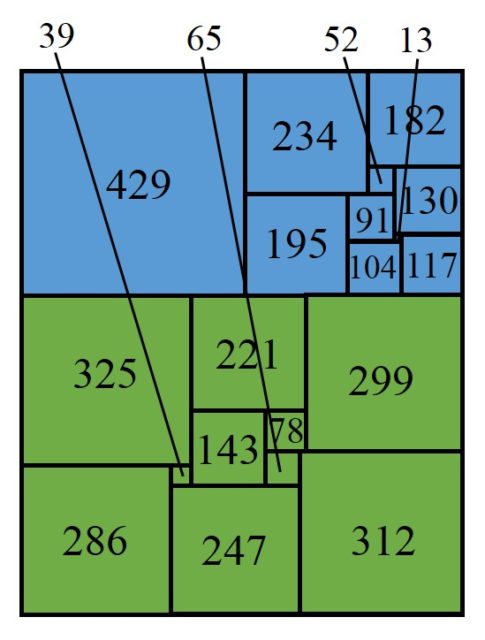 Cuadratura perfecta, pero compuesta, de un rectángulo de dimensiones 845 x 1.040 en 20 cuadrados de distintos tamaños. Esta cuadratura de un rectángulo forma parte de la construcción de Roland Sprague de 1939, que se verá más adelante. Obsérvese que esa descomposición contiene cuadraturas de dos sub-rectángulos, el azul y el verde en la imagen
Cuadratura perfecta, pero compuesta, de un rectángulo de dimensiones 845 x 1.040 en 20 cuadrados de distintos tamaños. Esta cuadratura de un rectángulo forma parte de la construcción de Roland Sprague de 1939, que se verá más adelante. Obsérvese que esa descomposición contiene cuadraturas de dos sub-rectángulos, el azul y el verde en la imagen
En la página Sources in recreational mathematics, an annotated bibliography, el matemático estadounidense David Singmaster menciona que la primera persona que publica, que se tenga constancia de ello, sobre algún problema relacionado con la cuadratura del cuadrado es el matemático recreativo inglés Henry E. Dudeney (1857-1930). En su conocido libro Los acertijos de Canterbury, publicado en 1907, publica el problema El joyero de Lady Isabel, que decía lo siguiente.
El joyero de Lady Isabel: La joven prima y pupila de Sir Hugh, Lady Isabel de Fitzarnulph, era conocida por todo el mundo como “Isabel la Bella”. Entre sus tesoros había un joyero, cuya tapa superior tenía la forma de un perfecto cuadrado. La tapa del joyero estaba incrustada con trozos de madera y una franja de oro de 10 pulgadas* de largo por un cuarto de pulgada de ancho.
Cuando los jóvenes empezaron a pedir la mano de Lady Isabel, Sir Hugh prometió que daría su consentimiento a aquel que consiguiese decirle las dimensiones de la tapa del joyero con solo los siguientes datos: que había una franja rectangular de oro de 10 pulgadas de largo por 1/4 de pulgada de ancho; y el resto de la tapa estaba incrustado exactamente con trozos de madera, cada uno de los cuales era un cuadrado perfecto y no había dos piezas del mismo tamaño. Muchos jóvenes fracasaron, pero uno de ellos finalmente tuvo éxito. El rompecabezas no es uno de los fáciles, pero las dimensiones del rectángulo de oro, junto con las otras condiciones, determinan completamente el tamaño de la tapa del joyero.
[* Recordemos que una pulgada es una medida de longitud inglesa equivalente a 25,4 milímetros]
 Ilustración que acompaña el problema El joyero de Lady Isabel, que aparece en el libro Los acertijos de Canterbury, de Henry Dudeney
Ilustración que acompaña el problema El joyero de Lady Isabel, que aparece en el libro Los acertijos de Canterbury, de Henry Dudeney
El propio Henry Dudeney decía en la solución al problema que este no era precisamente un rompecabezas sencillo. La solución, única, era que la tapa del joyero era un cuadrado de 20 pulgadas de lado, como se muestra en la imagen.
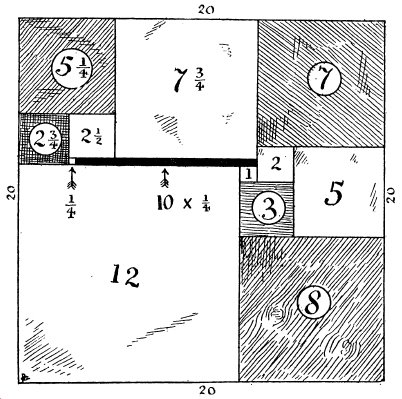 Ilustración con la solución al problema El joyero de Lady Isabel, que aparece en el libro Los acertijos de Canterbury, de Henry Dudeney
Ilustración con la solución al problema El joyero de Lady Isabel, que aparece en el libro Los acertijos de Canterbury, de Henry Dudeney
Aunque este rompecabezas ya había sido publicado, como comenta David Singmaster, por Henry Dudeney en enero de 1902, en el número 584 de la revista The London Magazine. En cualquier caso, el problema de Dudeney no era realmente una cuadratura del cuadrado, ya que incluía un rectángulo en la disección del mismo, aunque se le aproximaba mucho y sugería un interés en el problema de la cuadratura del cuadrado.
El problema de la cuadratura del cuadrado (o del rectángulo) debía de interesar ya desde tiempo atrás, puesto que en 1903 el matemático alemán Max Dehn (1878-1952), que era estudiante del matemático alemán David Hilbert (1862-1943) y que en su habilitación de 1900 había resuelto el tercer problema de los famosos problemas del milenio del propio Hilbert, publicó el primer trabajo matemático sobre la “disección de un rectángulo en cuadrados más pequeños”. Demostró que un rectángulo podía ser diseccionado en cuadrados más pequeños si y sólo si la proporción entre su altura y su anchura era un número racional.
En la obra póstuma del jugador de ajedrez y matemático recreativo estadounidense Sam Loyd (1841-1911) Cyclopedia of 5000 Puzzles (Los acertijos de Sam Loyd), publicada en 1914, se incluía el rompecabezas de la colcha de retazos (the patch quilt puzzle), que planteaba dividir una colcha cuadrada con 13 x 13 cuadraditos pequeños en retales cuadrados de una, o más piezas. Es decir, el problema de diseccionar un cuadrado en cuadrados más pequeños, aunque sin importar que se repitan los tamaños de estos.
 Ilustración que acompaña el problema El rompecabezas de la colcha de retazos, que aparece en el libro Los acertijos de Sam Loyd
Ilustración que acompaña el problema El rompecabezas de la colcha de retazos, que aparece en el libro Los acertijos de Sam Loyd
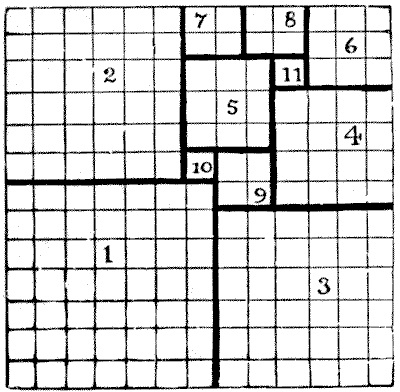 Ilustración con la solución al problema El rompecabezas de la colcha de retazos, que aparece en el libro Los acertijos de Sam Loyd. Esta formada por retales cuadrados cuyos lados son 7, 6 (dos retales cuadrados), 4, 3 (dos retales), 2 (tres retales) y 1 (dos cuadrados)
Ilustración con la solución al problema El rompecabezas de la colcha de retazos, que aparece en el libro Los acertijos de Sam Loyd. Esta formada por retales cuadrados cuyos lados son 7, 6 (dos retales cuadrados), 4, 3 (dos retales), 2 (tres retales) y 1 (dos cuadrados)
David Singmaster menciona que este rompecabezas había sido publicado previamente, en 1907, por Sam Loyd en la revista Our Puzzle Magazine. Además, también aparecería en el libro de Henry Dudeney Amusements in Mathematics (1917), con el nombre La colcha de la señora Perkins. Por este motivo el problema de diseccionar un cuadrado en cuadrados más pequeños, permitiendo que estos tengan el mismo tamaño se conoce como el problema de la colcha de la señora Perkins.
Aunque recordemos que en esta entrada estamos interesados en el problema de la cuadratura perfecta del cuadrado, es decir, la disección de un cuadrado, o rectángulo, en cuadrados más pequeños todos de distintos tamaños, y no en el problema de la colcha de la señora Perkins.
Los primeros ejemplos de rectángulos con cuadraturas perfectas y, además, simples, fueron publicados en 1925 por el matemático polaco Zbigniew Moron (1904-1974), en el artículo O Rozkladach Prostokatow Na Kwadraty (Sobre la disección de un rectángulo en cuadrados). Eran el rectángulo de tamaño 33 x 32 dividido en 9 cuadrados distintos (orden 9), cuyos lados eran 1, 4, 7, 8, 9, 10, 14, 15 y 18, que aparece en la primera imagen de esta entrada y el rectángulo de tamaño 65 x 47, dividido en 10 cuadrados distintos (orden 10), con lados 3, 5, 6, 11, 17, 19, 22, 23, 24 y 25, que mostramos a continuación.
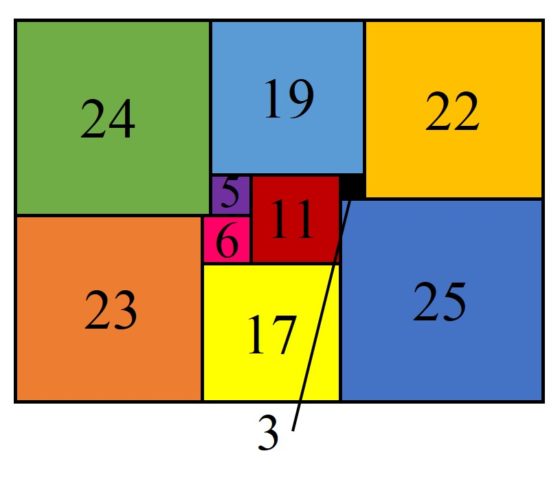 Cuadratura perfecta y simple de un rectángulo de dimensiones 65 x 47 en 10 cuadrados de distintos tamaños, de lados 3, 5, 6, 11, 17, 19, 22, 23, 24 y 25. Construcción de Zbigniew Moron (1925)
Cuadratura perfecta y simple de un rectángulo de dimensiones 65 x 47 en 10 cuadrados de distintos tamaños, de lados 3, 5, 6, 11, 17, 19, 22, 23, 24 y 25. Construcción de Zbigniew Moron (1925)
En los años 1930 el problema de descomponer un cuadrado en un número finito de cuadrados de distintos tamaños fue añadido, por el matemático polaco Stanislaw Ruziewicz -que era quien le había hablado a Zbigniew Moron del problema de la cuadratura del rectángulo- al Cuaderno escocés, como el problema número 59. Un grupo de matemáticos polacos, conocidos como La escuela matemática de Lwow (entre los matemáticos relacionados con esta escuela estaban Stephan Banach, Marek Mac, Kazimierz Kuratowski, Stanisław Mazur, Hugo Steinhaus o Stanislaw Ulam, entre otros), se reunían en el Café Escocés de Lwow para hablar de problemas matemáticos. Solían escribir con lápiz sobre el mármol de las mesas, pero al final del día las mesas se limpiaban y se perdían los problemas y discusiones que habían tenido. Por este motivo, a partir de 1935 decidieron recoger los problemas y soluciones en un cuaderno que sería conocido como Cuaderno Escocés. El último problema, número 193, es de 1941.
 Postal de la Plaza Academia, en Lwow, Polonia, antes de la Segunda Guerra Mundial (en la actualidad la ciudad pertenece a Ucrania). En el edificio de la derecha estaba el Café Escocés, donde se reunían los matemáticos de La escuela matemática de Lwow
Postal de la Plaza Academia, en Lwow, Polonia, antes de la Segunda Guerra Mundial (en la actualidad la ciudad pertenece a Ucrania). En el edificio de la derecha estaba el Café Escocés, donde se reunían los matemáticos de La escuela matemática de Lwow
Poco tiempo después, el matemático japonés Michio Abe construyó más de 600 rectángulos perfectos simples, que recogió en el artículo Covering the square by squares without overlapping (Recubriendo un cuadrado con cuadrados que no se solapan) publicado en 1930 en la revista Journal of Japan Mathematical Physics. Además, en un segundo artículo publicado en 1931 mostró la construcción de una serie infinita de rectángulos perfectos compuestos, construidos a partir de un rectángulo perfecto simple de tamaño 195 x 191.
¿Y qué ocurría con la cuadratura perfecta del cuadrado? Por un lado, sabemos que alrededor del año 1930, el gran matemático húngaro Paul Erdös (1913-1996) había conjeturado que cualquier disección de un cuadrado en cuadrados más pequeños tenía que contener, al menos, dos cuadrados del mismo tamaño, luego no podía ser perfecta. Por otra parte, existía en ese tiempo una conjetura del matemático ruso Nikolai N. Luzin (1883-1950), la conjetura de Luzin, según la cual era imposible diseccionar un cuadrado en un número finito de cuadrados distintos. El matemático belga Maurice Kraitchik (1882-1957), en su libro La mathématique des jeux ou Récréations mathématiques (1930), afirmaba que en una comunicación personal el matemático Luzin le había hablado de esa conjetura. Quizás la conjetura de Luzin llegó a oídos de Erdös o ambos conjeturaron lo mismo de forma independiente, pero lo cierto es que en los años 1930 se creía que la cuadratura (perfecta) del cuadrado era imposible.
 Los cuatro del Trinity -Leonard Brooks, Cedric Smith, Arthur Stone y William Tutte- en Cambridge, en 1938
Los cuatro del Trinity -Leonard Brooks, Cedric Smith, Arthur Stone y William Tutte- en Cambridge, en 1938
Pero la historia continúa. Como cuenta el matemático británico William Th. Tutte (1917 – 2002) en su artículo Squaring the square (Cuadrando el cuadrado), publicado por Martin Gardner en su columna de juegos matemáticos de la revista Scientific American, su colega Arthur H. Stone (1916-2000), cuando aún eran estudiantes en la Universidad de Cambridge (Gran Bretaña), quedó intrigado por la supuesta imposibilidad de descomponer un cuadrado en cuadrados más pequeños distintos, relacionada con el problema planteado por Dudeney en Los acertijos de Canterbury. Entonces intentó probar, sin éxito, dicha imposibilidad, aunque acabó construyendo una disección perfecta de un rectángulo de dimensiones casi cuadradas, 177 x 176, en 11 cuadrados más pequeños.
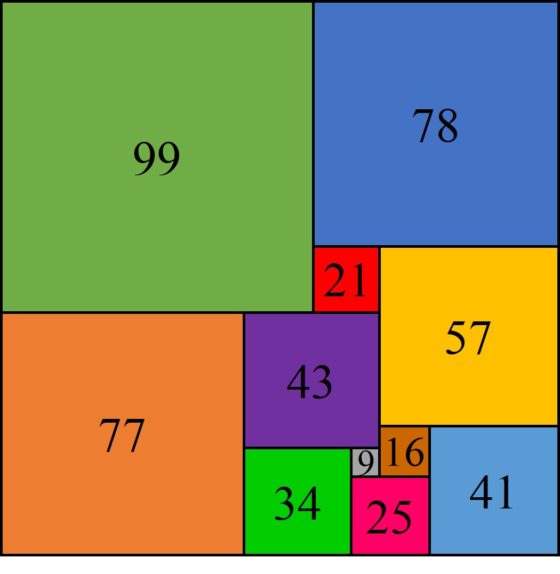 Disección perfecta de un rectángulo, de tamaño 177 x176, en 11 cuadrados distintos, de lados 9, 16, 21, 25, 34, 41, 43, 57, 77, 78 y 99
Disección perfecta de un rectángulo, de tamaño 177 x176, en 11 cuadrados distintos, de lados 9, 16, 21, 25, 34, 41, 43, 57, 77, 78 y 99
El método empleado para construir este rectángulo es sencillo. Se parte de un rectángulo que se divide en rectángulos más pequeños, por ejemplo, como aparece en la siguiente imagen que contiene 11 rectángulos. Se asume que ese diagrama nos da realmente una descomposición en cuadrados de un rectángulo, pero asumiendo que hemos dibujado mal la descomposición cuadrada del rectángulo, es decir, el rectángulo grande sí es un rectángulo, aunque quizás de dimensiones distintas a las que aparece en el dibujo, y los rectángulos pequeños son realmente cuadrados mal dibujados. Se empieza dando valor a los lados de dos de los pequeños cuadrados (en la imagen rectángulos) que estén juntos, de valores x e y, y se van calculando los valores de los lados de los demás cuadrados pequeños, en relación a estos, con sencillas expresiones algebraicas. Por ejemplo, el cuadrado debajo de los cuadrados de lados x e y, sería un cuadrado de lado x + y, el pequeño cuadrado a la derecha de los de dimensiones x y x + y tendrá lado 2 x + y, y así con el resto de cuadrados. De esta manera, todos los cuadrados encajan bien, unos con otros, salvo quizás los que están a ambos lados de la línea AB de la imagen, por lo que hay que elegir valores de x e y para que ahí también encajen, es decir, 14 y – 3 x = (3 x – 3 y) + (3 x + y). Despejando, 16 y = 9 x. Y tomando x = 16 e y = 9 se obtiene la cuadratura perfecta de un rectángulo de dimensiones 177 x 176, encontrada por Stone.
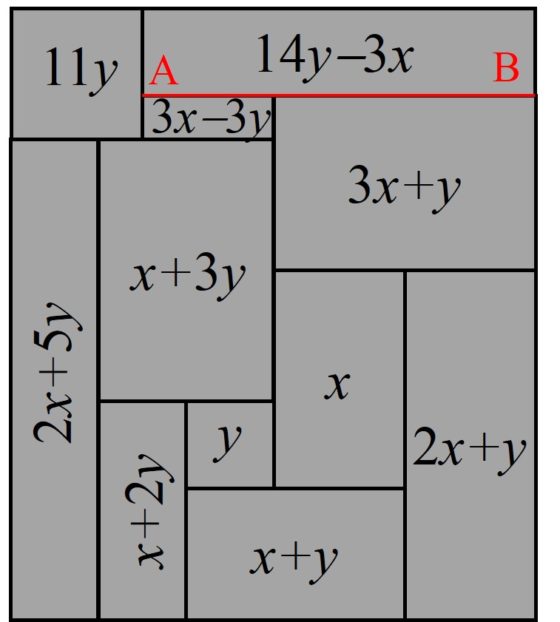 Método algebraico para construir una cuadratura perfecta de un rectángulo
Método algebraico para construir una cuadratura perfecta de un rectángulo
Entonces, el joven Arthur Stone y sus tres compañeros, también estudiantes del Trinity College de la Universidad de Cambridge, Rowland L. Brooks (1916-1993), Cedric A. B. Smith (1917-2002) y William Th. Tutte, los cuatro de Trinity, empezaron a construir rectángulos con disecciones perfectas mediante cuadrados utilizando el anterior método algebraico y a discutir sobre el problema de la cuadratura del cuadrado y el rectángulo. Entonces, relacionaron el problema de las disecciones cuadradas de los rectángulos con la teoría de las redes eléctricas de Kirchhoff (de lo que hablaremos en mi siguiente entrada en la sección Matemoción del Cuaderno de Cultura Científica), lo que les llevó finalmente a poder construir ejemplos de cuadraturas perfectas de cuadrados, tanto compuestas (es decir, con su-rectángulos perfectos), como simples.
En el artículo The Dissection of Rectangles into Squares (La disección de rectángulos en cuadrados), publicado en Duke Math. J. en 1940 se recoge toda esta investigación sobre las redes eléctricas, algunos de los ejemplos obtenidos y, en particular, el primer ejemplo de cuadratura perfecta y simple de un cuadrado de lado 5.468, de orden 55. Así mismo, se demuestra que el menor orden posible para la cuadratura perfecta de un rectángulo es 9 y que existen dos rectángulos con disecciones perfectas de orden 9.
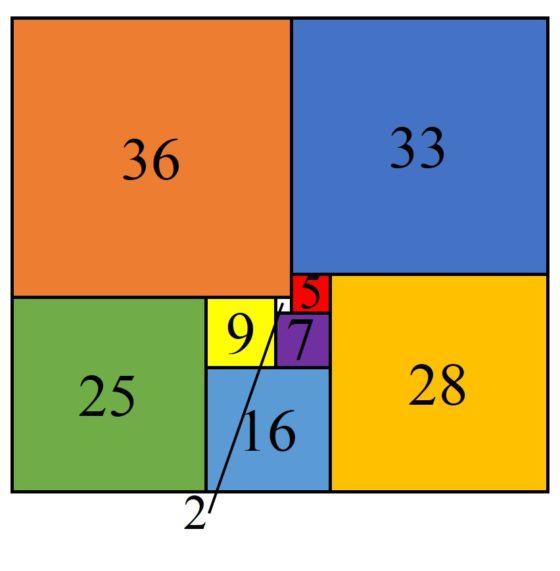 : Una de las dos cuadraturas perfectas simples de orden 9 de un rectángulo que existen, la otra es la que hemos mostrado al principio de esta entrada
: Una de las dos cuadraturas perfectas simples de orden 9 de un rectángulo que existen, la otra es la que hemos mostrado al principio de esta entrada
David Singmaster recoge en Sources in recreational mathematics, an annotated bibliography que en las actas del Encuentro 203 de la Sociedad Matemática del Trinity (Cambridge) de marzo de 1939, Arthur Stone anunció, en el artículo de su conferencia Squaring the square, que Rowland Brooks había obtenido un ejemplo de cuadratura perfecta del cuadrado, de orden 39, que sería el primer ejemplo que demostraba que la conjetura de Luzin era errónea. Y en las actas del encuentro número 204, abril de 1939, Cedric Smith anunciaba que William Tutte había encontrado el primer cuadrado perfecto simple, de orden 55. Estos ejemplos se recogían en el artículo de 1940 de los cuatro de Trinity.
Aunque el primer artículo publicado con un contraejemplo a la conjetura de Luzin fue anterior al artículo de Brooks, Smith, Stone y Tutte de 1940, ya que fue publicado en la revista Mathematische Zeitschrift en 1939, por el matemático alemán Roland P. Sprague (1894-1967). Sprague construyó, a partir de los ejemplos de Zbigniew Moron, un rectángulo perfecto simple de orden 12 y otros cinco cuadrados, un cuadrado con una cuadratura perfecta, pero compuesta, de orden 55.
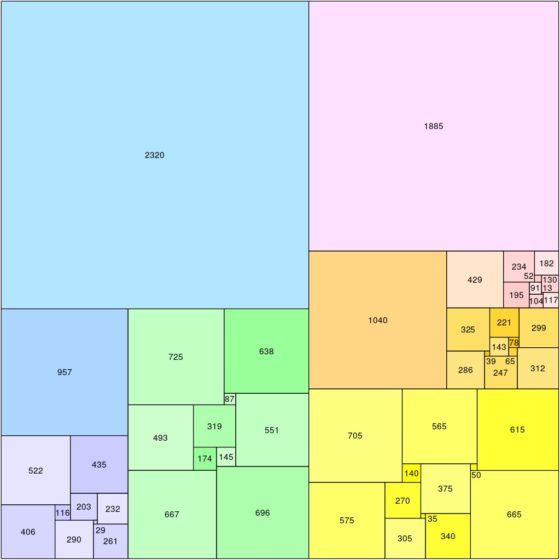 Cuadratura perfecta, compuesta, de orden 55 de un cuadrado de lado 5.205, obtenida por Roland Sprague en 1939. Imagen de Wikimedia Commons, cedida por Cmglee
Cuadratura perfecta, compuesta, de orden 55 de un cuadrado de lado 5.205, obtenida por Roland Sprague en 1939. Imagen de Wikimedia Commons, cedida por Cmglee
Poco a poco se fueron construyendo más ejemplos de cuadraturas perfectas de cuadrados, tanto compuestas, como simples. Por ejemplo, en 1948 el matemático británico Theophilus H. Willcocks (1912-2014) construyó una cuadratura perfecta de un cuadrado de orden 24, es decir, con tan solo 24 cuadrados, aunque era compuesta (véase la siguiente imagen). Durante mucho tiempo fue el orden más pequeño encontrado de una cuadratura perfecta de un cuadrado, de hecho, el orden 24 es el más pequeño posible para el caso de las cuadraturas compuestas.
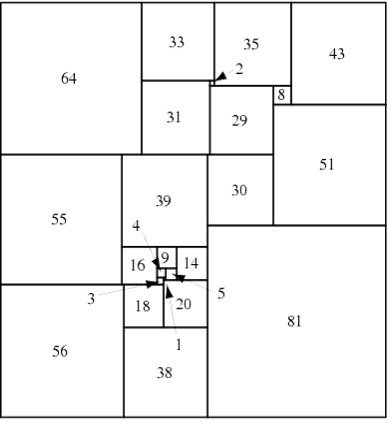 Cuadratura perfecta, compuesta, de orden 24 de un cuadrado de lado 175, obtenida por Theo Willcocks en 1948. Imagen de Wolfram MathWorld
Cuadratura perfecta, compuesta, de orden 24 de un cuadrado de lado 175, obtenida por Theo Willcocks en 1948. Imagen de Wolfram MathWorld
La llegada de los ordenadores cambió la investigación del problema de la cuadratura del cuadrado, permitiendo búsquedas más exhaustivas y la clasificación de todas las cuadraturas en función del orden. Es de destacar en esta nueva etapa la investigación de los matemáticos neerlandeses Christoffel J. Bouwkamp (1915 – 2003) y Adrianus J. W. Duijvestijn (1927-1998). En 1978, Duijvestijn descubrió la única cuadratura perfecta simple del cuadrado del orden más bajo posible, 21.
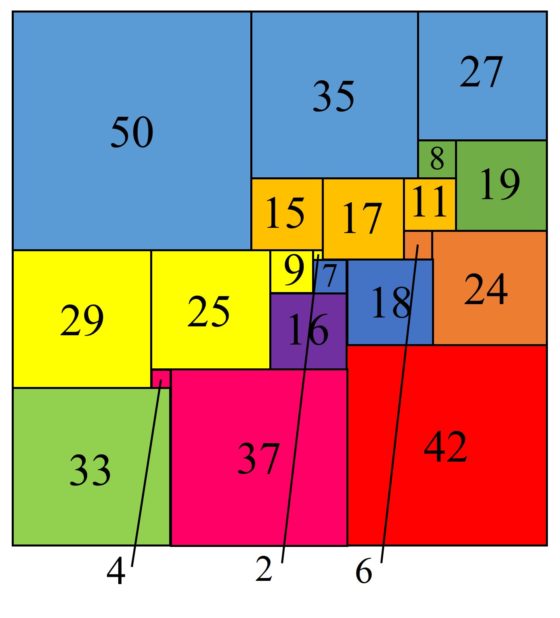 Cuadratura perfecta simple de orden 21 de un cuadrado de lado 112, obtenida por Arie Duijvestijn en 1978. Hemos coloreado los cuadrados para observar los cuadrados que van juntos en el código de Bouwkamp que se describe a continuación
Cuadratura perfecta simple de orden 21 de un cuadrado de lado 112, obtenida por Arie Duijvestijn en 1978. Hemos coloreado los cuadrados para observar los cuadrados que van juntos en el código de Bouwkamp que se describe a continuación
Antes de terminar esta entrada, expliquemos una notación sencilla, llamada código de Bouwkamp, que existe para describir las cuadraturas mediante cuadrados. En esta notación, se utilizan corchetes para incluir los cuadrados adyacentes que tienen el lado superior a la misma altura (horizontal) y los grupos de corchetes se van escribiendo desde el lado superior del cuadrado (o rectángulo) grande hacia abajo. Por ejemplo, la cuadratura perfecta simple del cuadrado de orden 21 descrita en la imagen anterior tiene el código de Bouwkamp [50, 35, 27], [8, 19], [15, 17, 11], [6, 24], [29, 25, 9, 2], [7, 18], [16], [42], [4, 37], [33].
Además, el número de cuadraturas perfectas del cuadrado de orden n, para n mayor o igual que 21, es la sucesión 1, 8, 12, 26, 160, 441, 1.152, 3.001, 7.901, … que en la Enciclopedia on-line de sucesiones de números enteros es la sucesión OEIS A006983.
Para terminar esta entrada del Cuaderno de Cultura Científica sobre el problema de la cuadratura (perfecta) del cuadrado, vamos a pensar en una disección muy particular, aquella en la que los lados de los cuadrados pequeños recorren todos los números naturales desde 1 hasta uno dado m. ¿Existirá una cuadratura como esta?
Si existiese esa cuadratura, el área del cuadrado grande, que será un número cuadrado N2, sería la suma de las áreas de los cuadrados pequeños, que como están todos los lados desde 1 hasta m, sería la suma de los cuadrados de los cuadrados de los primeros m números naturales, es decir,
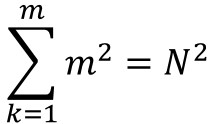
La suma de los cuadrados de los primeros números naturales es la sucesión de números que se conoce como números piramidales cuadrados (la sucesión OEIS A000330, de la Enciclopedia on-line de sucesiones de números enteros), pero solo hay un número piramidal cuadrado que sea el cuadrado de un número natural,´distinto de 1, el número 4.900 = 702, que es la suma de los cuadrados de los 24 primeros números naturales. Sin embargo, en 1974 se demostró, realizando una búsqueda exhaustiva por ordenador, que es imposible colocar los 24 cuadrados con lados de todos los tamaños entre 1 y 24 de manera que formen un cuadrado de lado 70.
Bibliografía
1.- Wolfram MathWorld: Perfect Square Dissection.
2.- Stuart Anderson, Tiling by squares
3.- David Singmaster, Sources in recreational mathematics, an annotated bibliography
4.- Henry Dudeney, Los acertijos de Canterbury, RBA, 2011.
5.- Sam Lyod, Los acertijos de Sam Loyd, RBA, 2011.
6.- Wikipedia: Scottish book
7.- Slanislaw Ulam, tradución al inglés del Scottish book
8.- Martin Gardner, The 2nd Scientific American Book of Mathematical Puzzles and Diversions, University of Chicago Press, 1987. Contiene el capítulo de W. Th. Tutte Squaring the square.
9.- Hallard T. Croft, Kenneth J. Falconer, Richard K. Guy, Unsolved Problems in Geometry, Springer-Verlag, 1991.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La cuadratura del cuadrado: en busca del santo grial se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Blanche Descartes y la cuadratura del cuadrado
- Motivar a los alumnos: el «santo grial» de la educación
- Un cuadrado mágico ‘papal’
El misterio de la temperatura constante
 Foto: Aaron Burden / Unsplash
Foto: Aaron Burden / UnsplashDe forma tradicional se dice que la materia aparece en uno de tres estados o fases: sólido, líquido o gaseoso (vapor) [1]. De acuerdo con la teoría cinético-molecular [2], un factor que distingue cada uno de estos estados es la cantidad de energía distribuida entre las moléculas que componen el material. En el estado gaseoso las moléculas tienen la mayor cantidad de energía y en el estado sólido la menor. Las transiciones de un estado a otro se pueden conseguir agregando o extrayendo energía en forma de calor.
Pero no es tan fácil. Existe un hecho misterioso que puede comprobarse con un recipiente con agua y un termómetro. El hecho es que, a pesar de aportar energía, por ejemplo, para evaporar el agua, la temperatura de ésta no cambia en absoluto mientras se produce el cambio de fase. Dicho de otra manera, en cada transición de un estado a otro, ¡la cantidad de energía térmica parece desaparecer (si vamos a estados de temperatura más alta) o aparece sin que haya pérdida de energía en otro lugar (si vamos a estados de temperatura más baja)!
Nos vemos obligados, pues, a incluir un concepto adicional [3], el concepto de entropía, que da una idea del nivel de desorden [4].
Para ver el proceso básico que conduce a la formación de un sólido tomemos el agua como sustancia ejemplo. Comenzamos con agua líquida, que enfriaremos extrayendo energía como calor. A medida que el agua se enfría, la variación de su temperatura, ΔT, está relacionada con la cantidad de la energía neta transferida como calor, ΔQ, por la relación ΔQ = m·c·ΔT , donde m es la masa de agua y c es el calor específico del agua líquida, que en este caso es 1 caloría por gramo y por grado centígrados. A medida que continuamos enfriando el agua, alcanzamos una temperatura a la cual el líquido experimenta un cambio de fase de líquido a sólido. Todos los líquidos terminan transformándose en sólidos, pero lo hacen a temperaturas muy diferentes. El agua a presión atmosférica comenzará a congelarse a 0 °C (273 K), pero el helio líquido no se congela hasta que alcanza los 4 K, muy cerca del cero absoluto.
En este punto, observamos el hecho misterioso: a medida que “extraemos calor”, el líquido continúa congelándose formando hielo, pero la temperatura se mantiene igual. ¿De dónde sale la energía que estamos extrayendo? La energía extraída parece haber estado «oculta» en el líquido y estar asociada con la formación del sólido, el hielo. Este “calor oculto» se llama calor latente [5]. Para el agua, tiene un valor de aproximadamente 80 calorías por gramo de agua.
Pero ¿qué es este calor latente y qué tiene que ver con la transformación de un líquido en un sólido? Dado que el proceso de enfriamiento implica la extracción de energía del material, las moléculas comienzan a organizarse en un estado de energía mínima. Esto se logra a medida que las moléculas se agrupan en una disposición lo más ordenada y estructurada posible. El estado de energía mínima tendrá el orden más alto, lo que significa que tiene la entropía más baja. El cambio en la entropía, ΔS, se define como la energía neta transferida como calor, ΔQ, ganada o perdida por el sistema, dividida por la temperatura absoluta (en kelvin) del sistema: ΔS = ΔQ/T .
Vemos pues que el calor latente que se extrae del agua a medida que se congela, ΔQ, está directamente asociado con la disminución de la entropía de las moléculas de agua a medida que forman la estructura ordenada del hielo sólido.
Por supuesto, si la energía térmica se introduce nuevamente en el sistema la entropía comenzará a aumentar a medida que las moléculas comiencen a vibrar más y más rápido. Finalmente podrán romper los enlaces que la convierten en un sólido. Esto es lo que llamamos fusión. Nuevamente, la temperatura permanece constante mientras el sólido se derrite mientras se aporta energía térmica. Durante este proceso, la energía térmica entrante se vuelve latente una vez más, ya que la temperatura no cambia, pero la entropía aumenta y la disposición ordenada dentro del sólido se rompe, formando un charco de agua donde una vez tuvimos un cubo de hielo ordenado.
Notas:
[1] Existen varios más, pero ese conocimiento no nos aporta nada ahora.
[2] Para repasar algunos conceptos básicos de esta teoría pueden consultarse las entregas 18 y siguientes de nuestra serie La dinámica del calor.
[3] Lo mismo pasa con la energía o materia oscuras, con la diferencia de que en este caso sabemos explicar el origen del mismo, mientras que en estas cosas oscuras no tenemos las ideas muy claras todavía (discúlpese el mal juego de palabras).
[4] Quizás sea conveniente señalar en este punto que gran parte de la comprensión básica de las transiciones de fase y la formación de la materia sólida se desarrolló alrededor del año 1900, pero fue necesaria la mecánica cuántica en las décadas posteriores para una comprensión completa, y algunos aspectos de estos complicados procesos son aun objeto de intensa investigación.
[5] “Latente” es una forma culta de decir “escondido, oculto”, culta por aquello de que latente es oculto en latín (discúlpese el mal juego de palabras).
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El misterio de la temperatura constante se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los experimentos de Joule
- La primera ley de la termodinámica
- Se intuye la conservación de la energía (1)
Conflictos de intereses en la ciencia
 Foto: CDC / Unsplash
Foto: CDC / UnsplashComo cualquier otra actividad humana, la práctica científica no está exenta de dilemas éticos. Los intereses, normalmente económicos, constituyen un incentivo muy poderoso para actuar de forma incorrecta. Por esa razón no es difícil incurrir en conflictos de intereses, que son los que enfrentan la búsqueda libre de la verdad con el deseo de satisfacer los deseos o intereses del agente que financia la investigación. En esos casos, no obstante, se pueden producir situaciones de diferente gravedad desde el punto de vista ético. La situación más justificable es la que se produce cuando de manera inconsciente de toman decisiones erróneas que favorecen el resultado supuestamente deseado por quien patrocina la investigación. Las malas decisiones pueden ser metodológicas, principalmente de índole estadística (aunque raramente si son inconscientes) o pueden obedecer a sesgos cognitivos como razonamiento motivado u otros. En teoría, si el investigador declara la posible existencia de un conflicto de intereses, su responsabilidad quedaría a salvo o, al menos, eso es lo que aceptamos socialmente.
Estas situaciones se pueden producir, por ejemplo, en el sector farmacéutico, ámbito en el que confluyen la actividad científica y los intereses de un sector empresarial poderoso. Ya en el año 2000 la industria farmacéutica destinaba del orden de mil quinientos millones de dólares a la financiación de programas universitarios. Esos fondos sirvieron para impulsar importantes proyectos de investigación, pero la posibilidad de que se lleguen a hacer públicos resultados negativos acerca de la efectividad de algún tratamiento disminuye si quien los ha obtenido depende económicamente de la empresa que financia el estudio o, incluso, gran parte de la investigación que desarrolla (Agin, 2007). En tales casos, ni siquiera viene a cuento plantear la cuestión de los conflictos de intereses porque, aunque obviamente existen, no han de declararse dado que no se llegan a publicar los resultados.
Por otra parte, no está en absoluto garantizada la efectividad de buen número de los medicamentos que se aprueban y se lanzan al mercado. A modo de ejemplo, un estudio publicado en octubre de 2017 en el British Medical Journal puso de manifiesto que 33 de 68 nuevos fármacos anticancerosos aprobados por la Agencia Europea del Medicamento entre 2009 y 2013 no habían demostrado mejorar la calidad de vida o extender la supervivencia de los pacientes. Ni siquiera está claro si sus bases farmacológicas son fiables. Y por si lo anterior era poco, los que sí arrojaban resultados mejores que tratamientos ya existentes o que el placebo, a menudo tenían un efecto solo marginal.
Lo cierto es que los ensayos clínicos se pueden prestar a serias interferencias, con potenciales consecuencias graves. Esa es la razón por la que los investigadores están obligados a declarar los conflictos de intereses que pudieran darse en el contexto de la investigación que da lugar a los resultados que se publican. Por eso, es muy grave que un investigador omita esa declaración, máxime cuando la materia acerca de la cual se investiga y se publica puede conducir a la aprobación o comercialización de un medicamento. Hace unos meses se dio a conocer el caso del oncólogo Josep Baselga, director médico del Memorial Sloan Kettering Cancer Center de Nueva York, que no dio a conocer en sus artículos publicados en revistas tan importantes como The New England Journal of Medicine o The Lancet, el haber recibido importantes cantidades de dinero procedentes de empresas farmacéuticas.
La revista Prescrire , publicada por una asociación independiente de profesionales sanitarios, informa con regularidad de los problemas relacionados con fármacos aprobados por las autoridades. Cada año actualiza la lista de los que producen más daño que beneficio. Y en general hace un examen crítico de la información disponible acerca de los medicamentos e informa de su efectividad, y posibles problemas. El simple hecho de su existencia y su amplia difusión en el mundo sanitario de diferentes países (cuenta con una edición internacional en inglés, además de publicarse originalmente nen francés) son muestra de los problemas de los que adolece el sistema farmacéutico.
Hay casos en los que a la existencia de conflictos de intereses que pueden verse alimentados por motivaciones más o menos inconscientes, se suma un deseo de obtener beneficios económicos a cambio del aval “científico” a productos que, o bien carecen de los efectos que se predican o pueden, incluso, ser perjudiciales para la salud.
En el primer caso se encuentra la actitud de científicos que avalan productos comerciales cuyos supuestos efectos beneficiosos no han sido demostrados y que, de hecho, no cuentan con la aprobación de la EFSA, la Agencia Europea de Salud Alimentaria. El bioquímico José M López Nicolás (2016) ha ilustrado esta forma de proceder por parte de científicos del CSIC que han avalado un producto comercial (revidox), por sus supuestos efectos antienvejecimiento, aunque no haya pruebas de que tal producto ejerza los efectos que se le atribuyen.
De mayor gravedad es el aval científico al consumo de alcohol (aunque sea a dosis bajas) por sus supuestos efectos beneficiosos para la recuperación física tras la práctica de alguna actividad deportiva. Cada vez hay más pruebas de que el consumo de alcohol es potencialmente dañino para la salud a cualquier dosis. Sin ir más lejos, el último gran estudio, cuyos resultados fueron publicados en The Lancet, ha llegado a esa conclusión, aunque desde hace unos años ya se dispone de datos que indican que desde dosis realmente bajas, el consumo de alcohol está asociado con la posibilidad de desarrollar varios tipos de cáncer. También sabemos ahora que el consumo incluso de bajas dosis de alcohol durante el embarazo, puede tener efectos negativos duraderos sobre el feto. Y son de sobra conocidos los efectos muy dañinos que provoca la adicción al alcohol, tanto de salud, como de convivencia y de seguridad. Por todo ello, resulta difícilmente comprensible que científicos se presten a avalar los beneficios del consumo de cerveza, por ejemplo.
Por último, cabe atribuir la máxima gravedad a la actitud de científicos que han realizado informes fraudulentos y ocultado de forma voluntaria información relevante en asuntos con graves implicaciones de salud. Nos referimos, en concreto, a los efectos del consumo de tabaco sobre la salud de fumadores (activos y pasivos).
Durante la segunda mitad del siglo pasado se fueron acumulando pruebas de la peligrosidad del tabaco. Tanto por el potente efecto adictivo de la nicotina como por la toxicidad de las numerosas sustancias que contiene, el tabaco causa un daño grave a los fumadores. Sin embargo, las compañías tabacaleras desarrollaron numerosas tácticas para contrarrestar el impacto negativo de los científicos y médicos que alertaban acerca de los males que causa el tabaco (Agin, 2007). Y entre esas tácticas, una de ellas fue la de contratar prestigiosos científicos cuyo papel fue el de obtener datos que sirviesen para sembrar dudas acerca de la vinculación entre el tabaco y el cáncer.
Las compañías de tabaco realizaron también estudios demoscópicos para conocer la opinón de la ciudadanía y poder diseñar mejores campañas de desinformación. Editaron folletos e informes para los médicos, medios de comunicación y, en general, los responsables de tomar medidas políticas y público en general; el mensaje era que no había ningún motivo de alarma. La industria sostenía que no había «ninguna prueba» de que el tabaco fuese malo y en ese quehacer contaron con el apoyo de científicos de alto nivel. Su papel en todo este asunto es hoy bien conocido y ha sido expuesto por Oreskes y Conway (2018).
Fuentes:
Agin, D (2007): Ciencia basura. Starbooks, Barcelona.
López Nicolás, J M (2016): Vamos a contar mentiras. Cálamo, Madrid.
Oreskes, N y Conway, E N (2018): Mercaderes de la duda. Cómo un puñado de científicos oscurecieron la verdad sobre cuestiones que van desde el humo del tabaco al calentamiento global. Capitán Swing, Madrid.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Conflictos de intereses en la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sesgos ideológicos que aquejan a la ciencia
- El ethos de la ciencia
- El fraude y las malas prácticas en ciencia
La prensa y el medio ambiente
Eduardo Angulo
 Imagen: Pixabay
Imagen: PixabayA finales de 2004, conocimos un artículo, firmado por Ilhami Kiziroglu y sus colegas, de la Universidad de Hacettepe de Ankara, en Turquía. Era un estudio de la presencia de noticias sobre medio ambiente en la prensa turca. Analizaban el contenido de diez periódicos turcos de gran tirada en los años 2002 y 2003. Contaban el número de artículos con estas temáticas y calculaban la media por día. El periódico con más noticias ambientales llegaba al 2.16% del total de noticias publicadas ese día. El que menos se quedaba en el 0.25%, y había tres diarios que no publicaban ninguna noticia. La conclusión era que había interés por los problemas ambientales en los medios impresos de Turquía pero, sin embargo, la frecuencia de publicación era muy baja.
Por entonces, comenzábamos a analizar las noticias sobre ambiente en los medios dentro de la asignatura Percepción Social de la Contaminaci ón: Literatura, Cine y Medios de Comunicación, incluida en el programa del Máster Contaminación y Toxicología Ambientales de la UPV/EHU, que se imparte en la Estación Marina de Plentzia (PIE). El trabajo para terminar la asignatura es un estudio del análisis de la prensa, con una metodología sencilla y rápida que permite obtener datos fiables en el tiempo que dura la asignatura, diez semanas en total. Ahora ya hay datos desde 2006 a 2019.
El análisis de las noticias se hace sobre cinco ejemplares del diario elegido por cada grupo. Corresponden a cinco días laborables de una misma semana, la misma para todos los grupos de alumnos para facilitar la comparación de los resultados. Hay que evitar elegir una semana en la que no hay grandes noticias relacionadas con el medio ambiente: desastres, accidentes, Fukushima o Chernobyl, incendios forestales, informes o reuniones del ICPP, … Esos días no reflejan el comportamiento habitual de la prensa en relación con el ambiente.
En general, los cinco días elegidos corresponden a diciembre o enero, por las fechas en que se imparte la asignatura, entre finales de octubre y principios de febrero. Los grupos son de 2-3 alumnos que forman ellos mismos y, también, eligen el periódico que van a estudiar, según sus preferencias, y todos los grupos deben elegir periódicos diferentes. Es recomendable que los elijan según su tirada, distribución geográfica e ideología.
El método que aplicamos consiste en medir la superficie de una página del diario y multiplicar por el número total de páginas y, así, obtener la superficie total del ejemplar. A continuación, se localizan las noticias relacionadas con el medio ambiente, se mide su superficie, se divide por la superficie total del ejemplar y se obtiene el porcentaje respecto del total. Se hace el cálculo con los cinco días laborables de la semana elegida y, en último término, se obtiene el porcentaje del diario completo para la semana. La cifra final es fácil de manejar y comparar entre periódicos en años sucesivos.
Además del cálculo del porcentaje, es importante incluir un resumen de las noticias y debatir su clasificación como de medio ambiente. Para Rogelio Fernández Reyes, de la Universidad de Sevilla, y en un artículo en que revisa lo que se considera periodismo ambiental, lo define como el “especializado que atiende la información generada por la interacción del hombre o de los seres vivos con su entorno, o del entorno en sí”. También ayuda a concretar la temática ambiental de las noticias la Ley 27/2006 de 18 de julio, por la que se regulan los derechos de acceso a la información, de participación pública y de acceso a la justicia en materia de medio ambiente, como sugiere Inés Rodríguez Cruz, de la Universidad de Sevilla, en 2012.
Decidir si una determinada noticia trata del medio ambiente o no provoca muy interesantes debates entre los alumnos del Máster. En 2018, dos alumnas, Estefanía Pereira y Raquel Catalán, presentaron una propuesta para clasificar las noticias como de medio ambiente. La transcribo a continuación:
Para clasificar una noticia como medioambiental es necesario que esta cumpla una serie de bases. De este modo, se ha establecido que debe satisfacerse alguno de los siguientes requisitos para que una noticia pueda ser clasificada en esta temática:
1. La noticia deberá versar, de alguna manera, sobre los componentes químicos, físicos, biológicos o geológicos que constituyen el medioambiente.
2. El suceso tratará los posibles perjuicios, peligros o, finalmente, el deterioro del entorno físico sobre el que se asienta un ecosistema.
3. La noticia discutirá los daños y detrimentos a los organismos que forman parte de un determinado ecosistema.
4. La crónica hablará sobre un proyecto que beneficie al mantenimiento del biotopo y la biocenosis en su estado natural o más saludable, así como la recuperación de este.
5. El artículo tratará la reducción o racionalización del consumo de energía como mecanismo para un desarrollo medioambiental sostenible, así como versará sobre energías limpias y renovables que, con su utilización, provoquen una mejora en el presente o el futuro del medioambiente respecto a las energías convencionales.
En el curso actual, 2019-2020, los alumnos Mikel Arenaza, Alicia Cano y Julia Montilla han añadido tres nuevos criterios que presento aquí para contribuir al debate.
6. La reducción o racionalización del consumo de productos (bienes materiales, alimentos, medicamentos, etc.) para minimizar la cantidad de residuos como mecanismo para un desarrollo medioambiental sostenible.
7. Movimientos sociales con el objetivo de concienciar a la ciudadanía.
8. Actos o decisiones políticas relacionadas con la reducción del cambio climático y de la contaminación, así como con cualquier suceso medioambiental.
En los años en que se ha hecho el estudio, se han revisado 14 periódicos pero, para obtener porcentajes para la comparación entre ellos, solo se han utilizado los que se han analizado seis años o más. Así quedan siete diarios: Berria, Deia, El Correo, El Mundo, El País, Gara y La Razón.
Berria, Gara y Deia son periódicos de distribución local. También lo es El Correo, pero pertenece a una cadena, Vocento, de distribución nacional. Los tres restantes se editan en Madrid y tienen cobertura nacional: El País, El Mundo y La Razón.
No es fácil determinar con precisión la ideología de estos diarios pues incluso puede variar y ajustarse al entorno político y social del momento, tanto en cuanto a las ventas como a quienes estén en el gobierno. En cuanto a su tirada, el Estudio General de Medios y otras encuestas parecidas los colocan, de mayor a menor, con El País, El Mundo, El Correo, La Razón, Deia y Berria. De Gara no tengo datos.
Los porcentajes muestran que el máximo lo marca Berria, con el 3.59% de media para 9 años, seguido de El País, con 2.07% para 11 años, y El Correo, con 1,83% para 15 años. El mínimo está en La Razón, con el 0.94% para 9 años.
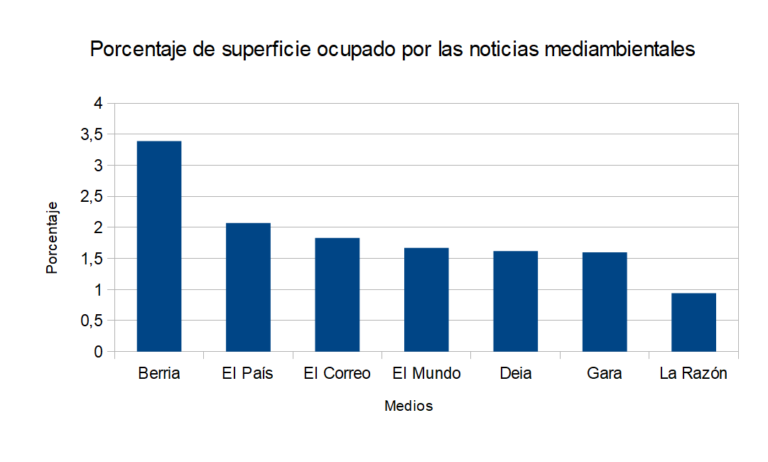
En primer lugar, un diario local, Berria; en segundo lugar, el periódico de mayor tirada, El País; y, en tercer lugar, el periódico local de mayor tirada y de una cadena nacional, El Correo. Todos ellos son diarios cercanos al centro, en su ideología, tanto desde la izquierda como desde la derecha.
Sorprende el bajo porcentaje de noticias ambientales, con el máximo del 3.39% en Berria. Es un tema polémico y, se supone, que interesa a la ciudadanía y, en concreto, a los lectores de cada diario. Por ejemplo, el CIS en 2010, encontraba que solo el 3% de los encuestados colocaba el medio ambiente como el asunto más importante. Y, en segundo lugar, lo hacía el 5%. En 2005 era del 2%. Sin embargo, en esas fechas, el 72.6% de los encuestados considera que “la conservación del medio ambiente ha de plantearse como un problema inmediato y urgente.” En la encuesta de la Unión Europea de 2018, el 94% considera importante proteger el medio ambiente. Todas son cifras muy dispares, aunque el medio ambiente preocupa más si no se pregunta por otros problemas considerados por la población como más importantes.
Sin embargo, los periódicos tienen un espacio limitado y la mayoría, quizá por tradición o por costumbre, lo ocupan con temas más conocidos como la política, la economía o el fútbol. Inés Rodríguez Cruz, en las conclusiones de su estudio, comienza afirmando que, en 2008, el medio ambiente es un tema marginal y no forma parte de los asuntos de cobertura obligada en los medios de comunicación. Por ejemplo, para El País y en 2008, el porcentaje de noticias sobre medio ambiente fue de 1,86% respecto del total de noticias. En nuestros datos era del 2,92% para ese año. Incluso el último año y en diciembre, con la celebración de la COP25 en Madrid, en El País se publicaron unos 30 artículos, el 3% del tráfico total de esos días.
Incluso en revisiones más extensas los resultados son parecidos. En el estudio de Schäfer y sus colegas, de la Universidad de Hamburgo, con datos de 27 países tomados entre 1996 y 2010, la conclusión es que el cambio climático es un tema relevante para los medios en todos los países. Y, a continuación, se afirma que supone el 0.62% de los artículos publicados entre 1997 y 2009 en los 37 periódicos revisados. Schäfer añade que, en esos años, el interés sobre el cambio climático ha aumentado en todos los países.
En la gráfica que publican referente a España, el porcentaje está siempre, de 1996 a 2010, por debajo del 2.5%. En concreto, es del 0.17% entre 1997 y 2000, del 0.23% de 2001 a 2005, y del 0.80% de 2006 a 2009. Todo ello coincide, más o menos, con los resultados del Máster.
En conclusión, el medio ambiente es importante para los ciudadanos, tal como las encuestas de opinión apuntan, pero, en general, es un tema apenas visible en el contenido de los medios de comunicación. Por ahora no se adivina en los medios un propósito claro y evidente de poner sistemáticamente la atención en los problemas ambientales.
Referencias:
Barkemeyer, R. et al. 2008. Media coverage of climate change: An international comparison. Environment and Planning C: Politics and Space DOI: 101177/0263774X16680818.
Bailey, A. et al. 2014. How gramatical choice shapes media representations of climate (un)certainty. Environmental Communication 8: 197-215.
Cortés, B. et al. 2004. La construcción de problemas ambientales a través de la prensa española. Cuestiones metodológicas y resultados preliminares. Medio Ambiente y Comportamiento Humano 5: 71-87.
Ecotropía. 2002. Análisis de la información medioambiental en la prensa española. Ecotropía 8.
El País. 2019. El pulso de la emergencia climática en las noticias. El País. 20 diciembre.
Fernández Reyes, R. 2003. En torno al debate sobre la definición del periodismo ambiental. Ámbitos 9-20: 143-151.
Fernández Reyes, R. & I. Jiménez Gómez. 2019. Spanish newspaper coverage of climate change or global warming, 2000-2019. Media and Climate Change Observatory Data Sets. Universidad de Sevilla, Universidad Complutense de Madrid and Center for Science and Technology Policy Research. Cooperative Institute for Research in Environmental Sciences, University of Colorado. DOI: 1025810/37f9-1j65
Kiziroglu, I. et al. 2004. The extent of environmental-related discussions in the Turkish printed media. Fresenius Environmental Bulletin 13: 1109-1111.
Martínez Valdés, V. 2003. Medios de comunicación y medio ambiente. Hiper-textos 7: 11 pp.
Ramos Rodríguez, J.M. et al. 2011. Prensa regional y medio ambiente: cobertura informativa en cuatro diarios de Puebla. Revista Iberoamericana de Comunicación 21: 41-60.
Rodríguez Cruz, I. 2012. Análisis cuantitativo de la información sobre medio ambiente en la prensa española. III Congreso Internacional de Investigación de la Comunicación, Tarragona, 18-20 enero 2012. 20 pp.
Rodríguez Cruz, I. & J. Bezunartea Valencia. 2016. Capacidad movilizadora de la información sobre medio ambiente: la importancia de la calidad periodística para promover una actitud proambiental. Estudios sobre el Medio Periodístico 22: 517-530.
Schäfer, M.S. et al. 2012. Media attention for climate change around the world: Data from 27 countries. International Conference “Culture, Politics, and Climate Change”, University of Colorado Boulder, September 13-15. 35 pp.
Torres, M.A. 2003. El medio ambiente, ¿un tema en el ostracismo? Revista Comunicación y Ciudadanía 2003: 38-51.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo La prensa y el medio ambiente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Patrimonio geológico: la otra mitad del ambiente
- Modelado matemático: del legado de Galileo al ambiente, la medicina y la tecnología
- El petróleo, los desastres y la prensa
La eternidad en un grano de arena
Los fósiles, los minerales o las rocas son, entre otras cosas, en lo primero que pensamos al hablar de geología, pero lo cierto es que la física es un ámbito científico que difícilmente se puede desvincular de la geología. Y es que el fundamento físico resulta clave a la hora de explicar algunos procesos geológicos que suceden tanto en el océano como en la superficie terrestre.
Con el fin de poner sobre la mesa la estrecha relación entre la geología y la física, los días 27 y 28 de noviembre de 2019 se celebró la jornada divulgativa “Geología para poetas, miopes y despistados: La Geología también tiene su Física”. El evento tuvo lugar en la Sala Baroja del Bizkaia Aretoa de la UPV/EHU en Bilbao.
La segunda edición de esta iniciativa estuvo organizada por miembros del grupo de investigación de Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Geoparque de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

¿Cómo podemos conocer la antigüedad de un elemento geológico? Una de las formas es por las características físicas de sus componentes. Miren del Val, técnico del laboratorio de datación por luminiscencia en el Centro Nacional de Investigación sobre Evolución Humana (CENIEH, Burgos), nos introduce en el apasionante mundo de la geocronología física.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo La eternidad en un grano de arena se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Geotermia urbana
- Los ecos del fondo submarino: imágenes de las estructuras geológicas.
- Otra mirada al planeta: arte y geología
El azúcar del ADN caracterizado átomo a átomo por espectrometría de microondas

Un trabajo de investigación llevado a cabo por el Grupo de Espectroscopía del Departamento de Química Física de la UPV/EHU y del Instituto Biofisika ha conseguido determinar con resolución atómica la estructura de los azúcares que forman parte del ADN, la 2-desoxirribosa. Se trata de “una resolución sin precedentes; hemos podido posicionar en el espacio cada uno de los átomos de este azúcar”, tal como describe el líder del grupo, Emilio J. Cocinero. El trabajo es portada de ACS Central Science.
Cocinero considera este resultado como la culminación de un trabajo que les ha llevado más de diez años: “Este resultado ha sido posible gracias al aumento de la sensibilidad del espectrómetro de microondas que tenemos en nuestro grupo, que hemos diseñado, construido y modificado nosotros mismos, y que ahora mismo está entre los 3 mejores aparatos de este tipo en el mundo”.
Una de las principales dificultades que tuvieron que superar fue la gran variabilidad y flexibilidad entre las diferentes formas o conformaciones que pueden adoptar las moléculas de 2-desoxirribosa. Los átomos que conforman estas moléculas de azúcar se pueden organizar formando anillos de cinco miembros, o formando anillos de seis miembros. “En la naturaleza, las formas biológicas presentan anillos de cinco miembros, pero en los experimentos, al aislar completamente el azúcar, y apartarlo de cualquier disolvente y sin interactuar con el resto de elementos que conforman el ADN y condicionan su configuración, la forma más estable de azúcares que conseguíamos era la de anillos de seis miembros”, explica Cocinero.
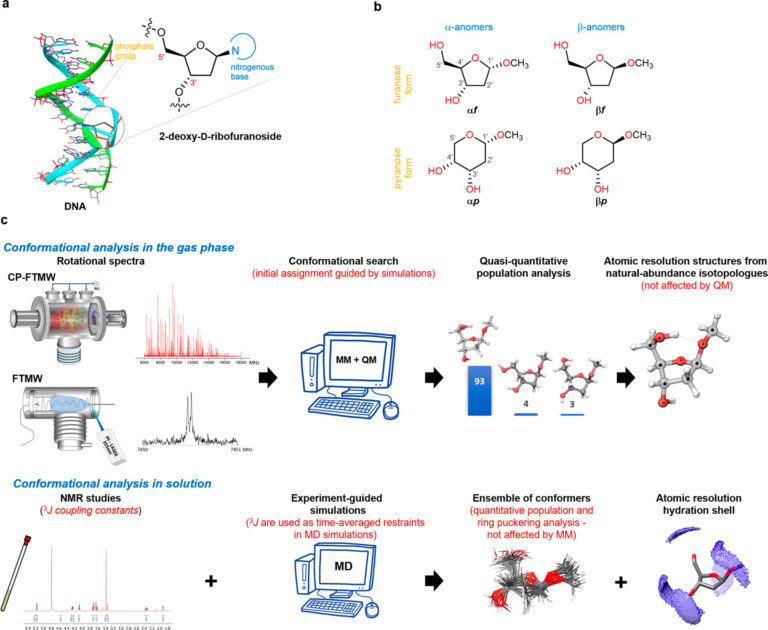
Para dar solución a esta situación, contaron con la colaboración de investigadores del Departamento de Química de la Universidad de Oxford, quienes les ayudaron en la síntesis de las cuatro formas que pueden adoptar las 2-desoxirribosas, tanto en las formas biológicas como las que no aparecen en la naturaleza, y las bloquearon, «añadiendo un grupo metilo a los azúcares para que no se interconvirtieran unas formas en otras, y poder estudiar cada una de ellas de forma individual”, detalla el investigador.
Así, han podido caracterizar la estructura de todas ellas a escala atómica, de forma aislada, y después, con ayuda de investigadores de la Universidad de La Rioja, han podido analizar cómo cambia la estructura de estas formas al entrar en contacto con el disolvente, el agua, “que se asemeja más al medio natural en el que se suelen encontrar. Hemos visto las diferencias entre unas formas y otras, y las hemos caracterizado”.
Asimismo, este análisis les ha permitido hipotetizar sobre “porqué la forma que se observa en la naturaleza es la que se observa y no otra. Según hemos visto, la forma de anillos de cinco miembros es más flexible, y la conformación que toma en la cadena del ADN favorece el enlazamiento de los consecutivos nucleótidos”, relata.
Ahora, con el desarrollo instrumental conseguido, van a abordar “el estudio de moléculas más grandes, tratando de construir sistemas que se acerquen cada vez más a las formas biológicas reales, para dar mejores respuestas. Buscamos el límite de la técnica instrumental”, concluye Emilio J. Cocinero.
Referencia:
Camilla Calabrese, Iciar Uriarte, Aran Insausti, Montserrat Vallejo-López, Francisco J. Basterretxea, Stephen A. Cochrane, Benjamin G. Davis, Francisco Corzana, and Emilio J. Cocinero (2020)Observation of the Unbiased Conformers of Putative DNA-Scaffold Ribosugars ACS Central Science 6 (2), 293-303 doi: 10.1021/acscentsci.9b01277
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El azúcar del ADN caracterizado átomo a átomo por espectrometría de microondas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Azúcar moreno, ¿mejor que el azúcar blanco?
- ¿Azúcar moreno o azúcar milagro?
- La importancia del agua en un biomarcador contra el cáncer
¿Qué dice la investigación sobre el aula invertida?
Marta Ferrero
El aula o clase invertida (en inglés, flipped classroom) es un modelo de enseñanza en el que las actividades que los alumnos han solido realizar fuera de clase (por ejemplo, practicar la solución de problemas) se incorporan al trabajo dentro del aula, mientras que las actividades que tradicionalmente se han hecho dentro del aula (por ejemplo, la transmisión de información por parte del profesor) se realizan fuera del horario escolar y como paso previo al trabajo en el aula (Låg & Grøm, 2019; van Alten, Phielix, Janssen, Kester, 2019). Dicho de otra forma, los alumnos aprenden por su cuenta mediante diversos recursos fuera del aula y realizan actividades interactivas y colaborativas en las horas de clase (Cheng, Ritzhaupt, & Antonenko, 2018; Mok, 2014). A esta definición básica, algunos autores añaden otros ingredientes fundamentales como, por ejemplo, las vídeo-conferencias como recurso pedagógico fuera del aula (Bishop, 2014) o la realización de proyectos y otras actividades de aprendizaje activo en grupo (como los debates o el role-playing) dentro del aula (Foldnes, 2016; Bishop & Verleger, 2013).
Los defensores del aula invertida señalan que algunas de las principales ventajas de este modo de enseñar son una mayor personalización del proceso de enseñanza-aprendizaje (Bergmann & Sams, 2012; O’Flaherty & Phillips, 2015), un aprendizaje más profundo por el carácter más atractivo de las actividades (Chi & Wylie, 2014), el uso más aprovechado del tiempo en el aula y el empleo más flexible de las nuevas tecnologías (Herreid, Schiller, Herreid, & Wright, 2014), la mayor responsabilidad del estudiante sobre su propio aprendizaje (O’Flaherty & Phillips, 2015) o un mayor poder de decisión sobre el ritmo de aprendizaje que adoptar (Abeysekera & Dawson, 2015) o su mayor participación en clase (DeLozier & Rodhes, 2017). Ante un modelo en el que los alumnos tienen más tiempo para realizar actividades significativas, que les permiten a su vez pensar sobre y regular su propio aprendizaje, lo esperable sería que el resultado final fuera mejor que el alcanzado mediante métodos “tradicionales”. Pero, ¿qué dice la investigación? La síntesis que se presenta a continuación se apoya principalmente en dos de los meta-análisis más recientes y completos que se han hecho sobre el aula invertida hasta el momento, en estudiantes universitarios (Cheng et al., 2018; Låg y Grøm, 2019) y de secundaria (van Alten et al., 2019).
 Imagen: StockSnap / Pixabay
Imagen: StockSnap / PixabayHallazgos principales
Aunque el modelo de aula invertida se remonta al año 2000, tuvieron que pasar diez años hasta que la comunidad científica investigara su impacto en el aprendizaje de forma sistemática (Cheng et al., 2018). Como resultado, a día de hoy contamos con numerosas revisiones y meta-análisis sobre el efecto que tiene el modelo de aula invertida en los estudiantes. Antes de seguir, conviene señalar que la gran mayoría de estas revisiones se han hecho con estudiantes universitarios, principalmente en el área de ciencias de la salud. Volveremos sobre esta cuestión y sus implicaciones más adelante. En términos generales, los resultados indican que el aula invertida tiene un impacto positivo en el aprendizaje de los estudiantes y que este impacto es superior al de la clase tradicional, centrada en el profesor, y donde el conocimiento se transfiere principalmente de éste a sus alumnos mediante clases magistrales (Cheng et al., 2018; Låg & Grøm, 2019; van Alten et al., 2019). El tamaño de este efecto, es decir, la cantidad de beneficio que el aula invertida tiene en los alumnos varía en función de la calidad de los estudios. Concretamente, cuanto mejor están hechos los estudios (por ejemplo, muestras más amplias, asignación al azar del grupo experimental y control) menor es el impacto que tiene la clase invertida en el aprendizaje de los estudiantes. Considerando estos estudios mejor diseñados, el aula invertida provoca mejoras muy pequeñas, incluso triviales, en el rendimiento del alumnado en comparación con la clase tradicional (Cheng et al., 2018; Låg & Grøm, 2019).
Junto con estos resultados generales, la investigación aporta también otros datos de interés. En primer lugar, todo parece indicar que la clase invertida no es igual de eficaz en todas las materias. Concretamente, este modelo resultaría más eficaz en Artes y Humanidades que en materias relacionadas con las STEM (Cheng et al., 2018; Låg & Grøm, 2019) o con los estudios de Ingeniería, donde los resultados son en algunos casos negativos (Cheng et al., 2018). En segundo lugar, parece que el aula invertida arroja mejores resultados cuanto más breve en su duración total (Cheng et al., 2018). En tercer lugar, parece que el aula invertida tiene poca influencia en la satisfacción de los estudiantes, incluso aunque su aprendizaje haya sido superior bajo este mismo (Låg & Grøm, 2019; van Alten et al., 2019). En cuarto lugar, el componente social que tienen muchas de las actividades propias del aprendizaje activo (por ejemplo, el trabajo colaborativo) no parece moderar los efectos del aula invertida sobre el rendimiento del alumnado (Låg & Grøm, 2019).
¿Qué falta por saber?
Debido a la gran heterogeneidad que presentan los estudios que analizan el efecto de la clase invertida en el aprendizaje, resulta muy difícil determinar qué elementos son claves para lograr una intervención eficaz. Entre los posibles moderadores del éxito de la clase invertida que se han estudiado, solamente la evaluación de los conocimientos previos de los alumnos y el tiempo de clase “cara a cara” parecen tener influencia en los resultados. En concreto, todo parece indicar que pasar un cuestionario a los alumnos antes de las sesiones de aula invertida contribuye a un mayor rendimiento académico, bien porque aumenta la motivación de los alumnos bien por el efecto ya conocido que tiene la evaluación en los aprendices (Låg & Grøm, 2019; van Alten et al., 2019). Además, mantener la duración habitual de la clase presencial (no reducirla en favor de las actividades que se hacen fuera) también contribuye a mejorar la eficacia del aula invertida (van Alten et al., 2019). Este hecho deja en el aire la pregunta sobre qué otros moderadores no considerados hasta el momento presente explican el impacto de la clase invertida en el aprendizaje.
Junto con esto, hay otros interrogantes a los que la investigación existente aún no ha dado respuesta pero que resultan de vital importancia para decidir cuándo adoptar o no el modelo de clase invertida. En relación a los alumnos, aún no existen suficientes datos sobre la eficacia de este enfoque en función de la edad y características de los alumnos. La gran mayoría de los estudios se han realizado con estudiantes universitarios, con unos conocimientos previos, capacidad de autorregulación y habilidades de trabajo en grupo que, con toda seguridad, son muy superiores a las que presenta un estudiante de educación primaria o incluso de secundaria. Dado que todos estos elementos son centrales en el modelo de aula invertida, sería esperable que el aula invertida no tuviera los mismos resultados en alumnos noveles o en alumnos con dificultades de aprendizaje. En relación al profesorado, aún no se sabe cuánto peso tiene la formación previa (por ejemplo, sobre el diseño de actividades y materiales o el trabajo cooperativo) en el éxito del modelo de aula invertida. En relación al centro escolar y al perfil de las familias, sería preciso determinar el peso que tiene disponer de los recursos necesarios fuera del aula, bien en el colegio bien en casa, (por ejemplo, acceso a internet o un espacio y condiciones de estudio adecuados) para completar las actividades previas que exige el modelo de aula invertida.
¿Qué implicaciones tienen estos resultados en el día a día en las aulas?
Teniendo en cuenta que el impacto del aula invertida en el rendimiento académico no es el mismo en todas las asignaturas, es conveniente que el profesorado valore el nivel de exigencia que impone este modelo en cada materia antes de tomar ninguna decisión. Por poner un ejemplo, aquellas materias que requieren de mucha práctica e interacción para su dominio pueden desbordar al alumnado si éste tiene que hacer un trabajo independiente previo (Cheng et al., 2018).
Para que el aula invertida resulte eficaz, es crucial que el alumno sea capaz de adquirir conocimientos de forma autónoma antes de entrar en clase. Este autoaprendizaje exige a su vez que el alumno tenga un control sobre su propio proceso de aprendizaje, es decir, que pueda autorregularse. Todo docente que se plantee adoptar el modelo de aula invertida debe cerciorarse de que el alumnado está adquiriendo por su cuenta los conocimientos previos necesarios para que la clase presencial sea exitosa. Para ello, puede recurrir a diversas herramientas como usar cuestionarios on-line o revisar los apuntes hechos por sus alumnos durante el estudio personal (Cheng et al., 2018).
El aula invertida exige que el profesorado invierta una cantidad de tiempo considerable en la elaboración y selección de recursos con los que el alumno debe trabajar antes de la clase presencial (vídeos y otro tipo de materiales). Dado el impacto tan pequeño que el aula invertida parece tener en el rendimiento del alumnado, los docentes deben valorar con detenimiento el coste de oportunidad que supone adoptar este modelo de aprendizaje (Cheng et al., 2018).
Conclusiones
El modelo de aula invertida desplaza fuera de ésta las explicaciones más teóricas, magistrales por parte del docente y, por tanto, permite que el tiempo en clase se destine a actividades más desafiantes para el alumnado, donde los conocimientos, feedback y modelado del docente se hacen realmente imprescindibles y enriquecedores. En definitiva, donde cobran todo el sentido. Además, el aula invertida favorece que el alumno se responsabilice de su propio proceso de aprendizaje y participe más durante las sesiones presenciales.
Ahora bien, antes de adoptar este modelo es conveniente tener presente algunas consideraciones. En primer lugar, la investigación existente es aún escasa, muy heterogénea, presenta en general importantes limitaciones metodológicas (falta de aleatorización de la muestra o falta de información sobre la implementación específica del modelo, entre otras) y se centra principalmente en alumnado universitario. En segundo lugar, y ligado al punto anterior, para que el aula invertida sea exitosa el alumnado ha de ser capaz de adquirir conocimientos de forma autónoma fuera del aula así como disponer de las condiciones necesarias para hacerlo. Por tanto, el aula invertida puede no ser aconsejable para todo tipo de alumnos, en cuanto a nivel de habilidades y capacidad como de situación social. En tercer y último lugar, los beneficios del aula invertida parecen ser muy pequeños en comparación con el modelo de clase tradicional. Sin embargo, los costes que supone a nivel de tiempo e inversión en la elaboración de materiales pueden ser muy altos.
Referencias:
Abeysekera, L., & Dawson, P. (2015). Motivation and cognitive load in the flipped classroom: Definition, rationale and a call for research. Higher Education Research and Development, 34, 1-14.
Bergmann, J., & Sams, A. (2012). Flip your classroom: Reach every student in every class every day. Eugene, OR: International Society for Technology in Education.
Bishop, J. L. (2014). A controlled study of the flipped classroom with numerical methods for engineers (Doctoral dissertation). Recuperado de: Proquest Dissertations and Theses Global Database (UMI. No. 3606852)
Bishop, J. L., & Verleger, M. A. (2013, June 23–26). The flipped classroom: A survey of the research. Manuscrito presentado en the ASEE Annual Conference and Exposition, Atlanta, GA. Recuperado de: https://peer.asee.org/22585
Cheng, L., Ritzhaupt, A. D., & Antonenko, P. (2018). Effects of the flipped classroom instructional strategy on students’ learning outcomes: A meta-analysis. Educational Technology Research & Development, 67, 793-824.
Chi, M. T. H., & Wylie, R. (2014). The ICAP framework: Linking cognitive engagement to active learning outcomes. Educational Psychologist, 49, 219-243.
DeLozier, S. J., & Rhodes, M. G. (2017). Flipped classrooms: A review of key ideas and recommendations for practice. Educational Psychology Review, 29, 141-151.
Foldnes, N. (2016). The flipped classroom and cooperative learning: Evidence from a randomised experiment. Active Learning in Higher Education, 17, 39-49.
Herreid, C. F., Schiller, N. A., Herreid, K. F., & Wright, C. B. (2014). A chat with the survey monkey: Case studies and the flipped classroom. Journal of College Science Teaching, 44, 75-80.
Hew, K. F., & Lo, C. K. (2018). Classroom improves student learning in health professions education: A meta-analysis. BMC Medical Education, 18:38
Karabulut-Ilgu, A., Jaramillo Cherrez, N., & Jahren, C. T. (2018). A systematic review of research on the flipped learning method in engineering education. British Journal of Educational Technology, 49, 398-411.
Låg, T., & Sæle, R. G. (2019). Does the flipped classroom improve student learning and satisfaction? A systematic review and meta-analysis [Dataset]. Dataverse. doi:10.18710/QA8WBZ
Mok, H. N. (2014). Teaching tip: The flipped classroom. Journal of Information Systems Education, 25, 7-11.
O’Flaherty, J., & Phillips, C. (2015). The use of flipped classrooms in higher education: A scoping review. The Internet and Higher Education, 25, 85-95.
van Alten, D. C. D., Phielix, C., Janssen, J., & Kester, L. (2019). Effects of flipping the classroom on learning outcomes and satisfaction: A meta-analysis. Educational Research Review, 28, 100281.
Sobre la autora: Marta Ferrero es doctora en psicología e investigadora de la Universidad de Deusto
El artículo ¿Qué dice la investigación sobre el aula invertida? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Autismo y educación: problemas y pautas en el aula
- De cómo la ludificación del aula prepara a los niños para vivir en un estado policial
- Un estudio dice que…
Una información paradójica
Accromαth es una revista bianual editada por el Institut des sciences mathématiques y el Centre de recherches mathématiques, centros de investigación matemática ubicados en Montreal, Canadá. Sus artículos están orientados a la divulgación de las matemáticas y pensados principalmente para profesorado y alumnado de enseñanza secundaria.
Desde hace años la sigo con interés, sobre todo sus secciones Glanures mathématico-littéraires –Recolecciones matemático-literarias, con fragmentos de textos procedentes de la literatura en los que las matemáticas “se cuelan” de alguna manera– y Rubrique des paradoxes –Sección de paradojas–. Jean-Paul Delahaye es el responsable de este último apartado. Propone en cada número de la revista una paradoja relacionada de alguna manera con las matemáticas y la resuelve en el siguiente número, planteando una nueva para pensarla durante los seis meses que siguen. Algunas de ellas no son nada sencillas de resolver.
Delahaye es matemático de formación y profesor emérito de informática en la Universidad de Lille (Francia). Su investigación se centra en teoría de la complejidad computacional. Dedicado también a la divulgación de la ciencia, recibió en 1998 el Premio d’Alembert (nombrado en honor a Jean le Rond d’Alembert) otorgado por la Société Mathématique de France por el conjunto de sus trabajos de divulgación matemática.
En el segundo número de Accromath de 2019, Delahaye proponía un problema L’information paradoxale –La información paradójica– cuya solución se explica en el primer número de la revista de 2020.
Damos a continuación el enunciado del problema y la solución –ambas enunciadas y explicadas por Delahaye– tal y como aparecen en los dos números consecutivos de Accromath.
 Imagen 1: Diseñada partir de una imagen de Pixabay.
Imagen 1: Diseñada partir de una imagen de Pixabay.
Esta paradoja precisa paciencia para ser resuelta… o la ayuda de un ordenador.
Se eligen cinco números enteros distintos entre 1 y 10: a, b, c, d y e –están ordenados en orden creciente–. A un grupo de cuatro personas se les dan distintas informaciones para que adivinen de que números se trata: A Patricia se le dice cuál es su producto P, a Silvia su suma S, a Cristian la suma de sus cuadrados C=a2+b2+c2+d2+e2, y a Vicente la cantidad V=(a+b+c)(d+e).
Una hora después de haberles planteado el problema, las cuatro personas –a las que se pregunta de manera simultánea– responden a la vez: «Desconozco cuales son los números a, b, c, d y e.».
Tras haber transcurrido otra hora, las cuatro personas –a las que se pregunta de nuevo a la vez– responden conjuntamente: «Desconozco cuales son los números a, b, c, d y e.».
Se continúa de esta manera, hora a hora, obteniendo exactamente la misma respuesta hasta que han pasado veintitrés horas tras la formulación del problema. En ese momento las cuatro personas –a las que se pregunta simultáneamente por la solución– responden a la vez: «Desconozco cuales son los números a, b, c, d y e.». Tras esta contestación conjunta –la vigésimo tercera, idéntica a las anteriores–, las cuatro personas sonríen y exclaman al mismo tiempo: «¡Ya está! Ahora sé cuáles son los números a, b, c, d y e.».
Parece paradójico que la repetición –veintitrés veces– de la misma afirmación de ignorancia por parte de las cuatro personas lleve oculta una información significativa.
Ahora ya sabes lo suficiente para adivinar los cinco números a, b, c, d y e. Intenta entender la razón y ármate de paciencia, porque la solución llega tras realizar unos largos cálculos…
Así plantea Delahaye esta paradoja. Si deseas pensar en la respuesta, no mires aún la solución…
Hay 252 quíntuples posibles (a, b, c, d, e) que solucionan el problema: son las combinaciones sin repetición de diez elementos tomados de cinco en cinco, es decir, el número combinatorio C(10,5).
Algunos de esos quíntuples poseen una suma S que permitiría adivinar (a, b, c, d, e). Por ejemplo si S = 15, esta es la menor suma posible y necesariamente se tendría a = 1, b = 2, c = 3, d = 4 y e = 5. Como en el primer paso Silvia indicó que desconocía la solución, eso significa que la familia de números propuesta no puede ser (1, 2, 3, 4, 5). Esto sucede para otras sumas. De la misma manera, algunos productos P sólo pueden obtenerse de una manera y sucede lo mismo con las cantidades C y V.
Por medio de un largo cálculo a mano –o un poco más corto usando un ordenador– se llega a demostrar que la eliminación de esos quíntuples –cuyas cantidades S, P, C o V solo se pueden conseguir de una manera– reduce las posibilidades iniciales a 140. Patricia, Silvia, Cristian y Vicente realizan este razonamiento de eliminación durante la primera hora que sigue a la propuesta del problema.
A partir de esas 140 posibilidades para (a, b, c, d, e) cada persona puede volver a razonar de la misma manera. Si Silvia indica que no es capaz de decir cuál es la lista (a, b, c, d, e), eso indica que en esa nueva lista de 140 quíntuples se pueden eliminar las correspondientes a sumas S que solo aparecen una vez en esa lista. Lo mismo puede hacerse para P, C y V. Así, se llega a una lista de 100 posibles soluciones.
Razonando de este modo hora a hora, la reducción de posibles soluciones proporciona, paso a paso, posibilidades cada vez menos numerosas. De hecho, a lo largo de estas reducciones se obtienen posibles quíntuples candidatos en estas cantidades: 85, 73, 64, 62, 60, 57, 54, 50, 47, 44, 40, 36, 33, 31, 28, 24, 19, 13, 8, 4.
 Imagen 2: Diseñada partir de una imagen de Pixabay.
Imagen 2: Diseñada partir de una imagen de Pixabay.
La consideración de la última información dada en la etapa vigésimo tercera permite a las cuatro personas llegar a la solución única: S = 28, P = 3360, C = 178 y V = 195. Y, de este modo, terminan por deducir que a = 2, b = 5, c = 6, d = 7 y e = 8.
Referencias:
Jean-Paul Delahaye, Rubrique des paradoxes : L’information paradoxale, Accromath. Volume 14.2 – été-automne 2019
Jean-Paul Delahaye, Solution du paradoxe précédent: L’information paradoxale, Accromath. Volume 15.1 – hiver-printemps 2020
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Una información paradójica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Falsos positivos, o la importancia de comprender la información
- Cartogramas, una herramienta de información visual
- Uno, dos, muchos
¿Más allá de la mecánica cuántica?
 Foto: Tim Mossholder / Unsplash
Foto: Tim Mossholder / UnsplashLa idea de que la solución de la ecuación de Schrödinger es una onda que representa, no una onda física, sino la probabilidad de encontrar la partícula asociada en algún estado concreto de movimiento ha tenido un gran éxito. De hecho, cada experimento ideado hasta ahora para probar esta interpretación ha confirmado estos resultados [1]. Sin embargo, a muchos científicos todavía les resulta difícil aceptar la idea de que es imposible saber exactamente qué está haciendo una partícula. [2]
El más destacado de estos incrédulos fue Einstein. En una carta a su amigo y colega Max Born, escrita en 1926, comentó:
La mecánica cuántica es ciertamente imponente. Pero una voz interior me dice que no es todavía la auténtica. La teoría dice mucho, pero no nos aproxima un ápice al secreto del “viejo”. Yo, en cualquier caso, estoy convencido de que él no lanza dados.
Por lo tanto, Einstein estaba de acuerdo con la utilidad y el éxito de la mecánica cuántica, pero se negaba a aceptar leyes basadas en la probabilidad como el nivel final de explicación en física. El comentario sobre no creer que Dios jugase a los dados (una expresión que usó muchas veces más tarde) expresaba la fe [3] de Einstein de que aún se deben encontrar leyes más básicas y deterministas. Con esto quería decir que si se conociesen todas las condiciones de un sistema aislado y se conociesen las leyes que describen las interacciones, entonces debería ser posible predecir con precisión, de acuerdo con la «causalidad estricta», lo que sucederá a continuación, sin ninguna necesidad de probabilidad [4].
Algunos científicos estuvieron y están de acuerdo con Einstein, pero todos los científicos están de acuerdo en que, como teoría, la mecánica cuántica funciona en la práctica. Da las respuestas correctas a muchas preguntas en física; unifica ideas y sucesos que alguna vez estuvieron desconectados; ha producido muchos experimentos y conceptos nuevos de enorme utilidad práctica, abriendo la puerta a muchos avances tecnológicos, desde transistores, microprocesadores y superconductores, hasta láseres y las últimas técnicas de imagen médica, por mencionar algunos.
Por otro lado, todavía hay discusiones acaloradas [5] sobre el significado básico de la mecánica cuántica. Produce funciones de probabilidad, no trayectorias precisas. Algunos científicos ven en este aspecto de la teoría una indicación importante de la naturaleza del mundo. Para otros científicos, el mismo hecho indica que la mecánica cuántica aún está incompleta. [2] Algunos en este segundo grupo están tratando de desarrollar una teoría más fundamental y no estadística. Para un modelo así, la mecánica cuántica actual sería solo un caso especial. Como en otros campos de la ciencia, los mayores descubrimientos aquí pueden ser los que aún no se han hecho. [6]
Notas:
[1] Los que vean esto como prueba falsacionista irrefutable tendrán motivo para la reflexión leyendo La falsación ya no es lo que era y los enlaces que contiene.
[2] Visto [1], también comprenderán que haya quien insista en encontrar variables ocultas. Véase adicionalmente Los dados de Dios.
[3] Incluso los científicos que desprecian la filosofía, lo que no era el caso de Einstein precisamente, parten de una cosmovisión que prejuzga; muchas veces esta cosmovisión no explícita tiene una base filosófica o religiosa y, en algunos casos, es pura ideología. Véase Sesgos ideológicos que aquejan a la ciencia.
[4] Este convencimiento entronca con el concepto de verdad; la ciencia es coherentista, aunque muchos la consideren correspondiente, como Einstein. Sobre esto véase Verdad verdadera.
[5] Entendamos que el acaloramiento es un término relativo, sobre todo si tenemos en cuenta que la discusión se sustancia en forma de artículos subidos a arXiv u otros repositorios.
[6] Más sobre este asunto en nuestra serie Incompletitud y medida en física cuántica
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo ¿Más allá de la mecánica cuántica? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Construyendo la mecánica cuántica
- La interpretación de Copenhague de la mecánica cuántica
- La probabilidad en mecánica cuántica
Parte de la investigación científica es quizás irrelevante
 Foto: Gabriel Sollmann / Unsplash
Foto: Gabriel Sollmann / UnsplashLa actividad investigadora no ha dejado de crecer en el mundo. Cada vez son más los países que dedican importantes volúmenes de recursos a sostenerla. Y como consecuencia de ello, cada vez hay más resultados que publicar. Por otro lado, no dejan de surgir disciplinas o subdisciplinas, y es normal que la aparición de esas disciplinas venga acompañada por la creación de una o varias revistas científicas en las que se publica los trabajos de aquellas. Además, como se ha señalado antes, los profesionales de la ciencia y quienes aspiran a formar parte de la profesión se encuentran cada vez más presionados para publicar artículos con los resultados de su trabajo. Y por otro lado, las revistas científicas cada vez imponen más restricciones a las dimensiones de cada publicación. Por todo ello, se publican infinidad de artículos científicos cada día, miles, de todo tipo de temas, cada vez más y, en promedio, cada vez más breves.
Una parte importante de esos artículos no son leídos por nadie. Según estimaciones relativamente antiguas, un 55% de los artículos científicos no se citan nunca, y muchos otros son consultados y, a veces, citados, en muy pocas ocasiones (Hamilton, 1990; Pendlebury, 1991). Las cosas, sin embargo, no parecen alcanzar extremos tan alarmantes (Van Noorden, 2017) para las alrededor de 12.000 revistas referenciadas en la Web of Science. Al parecer no llega al 10% el porcentaje de artículos no citados en las revistas de esa base de datos, aunque es probablemente bastante más alto en los miles de revistas no recogidas y que, sin embargo, figuran en el currículo de muchísimos investigadores y en la producción de muchos centros de investigación.
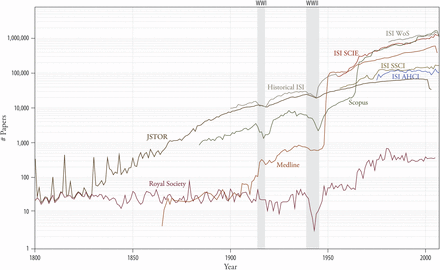 Variación del número de artículos científicos publicados en el mundo de acuerdo con diferentes bases de datos bibliográficas. Fuente: Shiffrin et al (2018) PNAS 115 (11): 2632-2639
Variación del número de artículos científicos publicados en el mundo de acuerdo con diferentes bases de datos bibliográficas. Fuente: Shiffrin et al (2018) PNAS 115 (11): 2632-2639Un 4% de todos los artículos publicados en revistas biomédicas, un 8% de los de química y un 11% de los de física no había sido citado diez años después. Si se excluyen las autocitas, o sea, las ocasiones en que un investigador cita su propio trabajo, el porcentaje de artículos no citados sube de manera considerable (en algunas especialidades hasta un 50%). Esas son las disciplinas en las que los porcentajes de artículos no citados son los más bajos. Los artículos no citados llegan a ser el 24% en ingeniería y tecnología, mucho más alto que en las ciencias naturales. Considerando la literatura científica en su conjunto (39 millones de artículos de todas las disciplinas regogidas en la Web of Science) desde 1990 hasta 2016, un 21% no habían recibido ninguna cita. La mayor parte de esos artículos no citados se habían publicado en revistas poco conocidas. Esa es la razón por la que hay razones para pensar que el porcentaje de artículos no citados es aún mayor en las revistas no recogidas en esa base documental.
En otra categoría se encuentran las revistas de humanidades. El 65% de los artículos de ese campo no habían sido citados en 2006, lo que puede deberse, en parte al menos, a que en la investigación en humanidades hay quizás menor dependencia del saber acumulado que en las ciencias naturales. Aunque también ocurre que en la Web of Science no están bien representadas esas disciplinas, porque ignora muchas revistas y libros.
La diferencia entre las estimaciones de 1990 y 1991, por un lado, y la de 2006 por el otro, se debe, en parte, a que las primeras incluían cartas al editor, respuestas, editoriales y, en general, todas las piezas publicadas por las revistas, mientras que la última solo valoraba las de los artículos de investigación publicados. Pero otra razón es que a lo largo de los años se ha producido un descenso en el porcentaje de artículos no citados y es descenso obedece, también en parte, a que en cada artículo se incluyen cada vez más citas.
Por último, los especialistas en cienciometría advierten acerca del hecho de que hay más artículos que son citados una o dos veces que los que no son citados. Y si se tiene en cuenta lo superficiales que son muchas de las citas, el diagnóstico del fenómeno no es nada halagüeño. Hay muchísima investigación que tiene un impacto mínimo o que lo tiene nulo.
Puede resultar aventurado considerar muchos de esos artículos carentes de todo interés. La trayectoria de un artículo puede ser muy azarosa y acabar teniendo suficiente impacto muchos años después de su publicación aunque en los inmediatamente siguientes su influencia haya sido nula. Pero no es verosímil que eso ocurra con la mayoría de los artículos que no se citan o se citan mínimamente. La cruda conclusión es que mucha investigación realizada (a la vista de los datos anteriores cabría hablar quizás de un 20%, aproximadamente) no interesa a nadie, y quizás un porcentaje similar interesa a algunos, pero interesa poco. En otras palabras, una parte muy importante de la investigación no es relevante a juicio de la propia comunidad científica, por lo que es desconocida y el esfuerzo que se le ha dedicado, es un esfuerzo baldío.
Una derivación extrema y, cabría decirse, patológica, de este estado de cosas, es el fenómeno de las revistas depredadoras de acceso abierto. Como puede atestiguar cualquier investigador en ejercicio, hay empresas que organizan congresos científicos y editoriales que publican revistas supuestamente especializadas que ofrecen la posibilidad de presentar comunicaciones (en los congresos) o publicar artículos (en las revistas) previo pago de importantes cantidades de dinero. Jeffrey Beall, bibliotecario de la Universidad de Colorado en Denver (EEUU), ha confeccionado una lista de ese tipo de revistas, que puede consultarse aquí (actualizada en 2015) y Antonio Martínez Ron ha tratado el fenómeno en Vozpópuli.
Existen esas revistas y se celebran esos congresos porque hay investigadores que los alimentan con sus contribuciones. No solamente carecen de la más mínima credibilidad en la comunidad científica; no tienen, además, ningún interés para nadie. Se publican porque el sistema de publicaciones ha perdido su función original y ha pasado a satisfacer los requerimientos de una comunidad necesitada de acreditar logros para estabilizarse o progresar en la carrera académica. Las revistas de calidad, al menos, ejercen un cierto control aunque sus publicaciones tengan eco escaso o nulo. Las depredadoras no llegan ni a cubrir esos mínimos. Pero no debemos engañarnos, todo ello es consecuencia de un sistema que ha pervertido sus objetivos primordiales.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Parte de la investigación científica es quizás irrelevante se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- No todas las personas tienen las mismas oportunidades de dedicarse a la actividad científica
- Science + : 1 – La carrera científica I: el doctorado y la investigación académica”
- La ciencia quizás tenga valores… pero no sabemos cuáles son
Así nos hizo la Iglesia: Individualistas, independientes y prosociales si no es personal
 Fuente: Dickinson College
Fuente: Dickinson CollegeEn el año 506 la Iglesia de Occidente, en un concilio celebrado en la localidad de Agda, Francia, tomó una decisión de profundas consecuencias para el devenir de Europa y por ello, aunque de forma indirecta, el de la humanidad. Con el fin de acabar con el incesto, prohibió el matrimonio entre primos, y a partir de aquella decisión adoptó una serie de normas que ampliaron la prohibición de casamiento entre miembros de una misma familia. A comienzos del segundo milenio, la prohibición alcanzó a los primos en sexto grado. Se proscribió el matrimonio con familiares adoptivos, así como con parientes políticos. La Iglesia promovió también los casamientos “por elección” de los cónyuges en contra de la práctica tradicional de matrimonios acordados, y a menudo requería que los recién casados se estableciesen en una residencia independiente de la de sus progenitores (residencia neolocal). Igualmente, prohibió la adopción legal, las segundas nupcias, cualquier forma de poligamia y el concubinato.
Pues bien, de acuerdo con un estudio basado en el análisis de un ingente volumen de datos y cuyas conclusiones se han publicado recientemente, esa decisión, a través de sus efectos sobre la estructura social, ha propiciado en las poblaciones occidentales una psicología diferente de la del resto de poblaciones en lo relativo al grado de individualismo, confianza, conformidad y pensamiento analítico de sus miembros.
Según los autores de la investigación, como consecuencia de las medidas tomadas por la Iglesia, hacia el año 1500 gran parte de Europa se caracterizaba por una configuración social basada en débiles relaciones de parentesco, con unidades familiares monógamas, descendencia bilateral, matrimonio tardío y residencia neolocal. Esa estructura social se diferenciaba con claridad de la que caracterizaba a la mayor parte del resto de sociedades, al menos hasta que recibieron el influjo europeo.
Las instituciones basadas en el parentesco han sido las estructuras en torno a las cuales se ha organizado la vida social a lo largo de la historia humana. Además, desde el comienzo del Neolítico, con la aparición de la agricultura, y mediante un proceso de evolución cultural, se ampliaron y reforzaron las normas de parentesco intensivo, como el matrimonio entre primos, la formación de clanes familiares y la convivencia de familias extensas en una misma residencia. Todo ello promovía la cohesión social, la interdependencia y la cooperación dentro del grupo.
Dado que las normas sociales moldean las motivaciones, emociones y percepciones de la gente, quienes se educan y conviven en sociedades con instituciones basadas en fuertes vínculos de parentesco desarrollan unos rasgos psicológicos que les facilitan adaptarse a las demandas del entorno colectivista propio de su densa red social. Las normas de parentesco intensivo recompensan la conformidad, la obediencia y la lealtad intragrupal, a la vez que desincentivan el individualismo, la independencia y las motivaciones impersonales que promueven la justicia y la cooperación.
Por todo ello, en las sociedades occidentales, al haberse difuminado la estructura social basada en los vínculos de parentesco, la gente tiende a ser más individualista, independiente y prosocial de una forma impersonal, a la vez que muestra menor conformidad y lealtad para con el grupo al que pertenecen. Son las sociedades denominadas “WEIRD”, acrónimo inglés de white (blanca), educated (educada), industrialized (industrializada), rich (rica), democratic (democrática). De ser correctas la conclusiones de este estudio, bien podría ser que un propósito de la Iglesia tan modesto como era el de acabar con el incesto, haya estado en el origen, al menos en parte, de la extraña prosperidad de que gozan los países occidentales. No por casualidad, además del acrónimo dicho, weird en inglés significa extraño.
Fuente: Jonathan F. Schulz, Duman Bahrami-Rad, Jonathan P. Beauchamp and Joseph Henrich (2019): The Church, intensive kinship, and global psychological variation. Science 366 (6466), eaau5141. DOI: 10.1126/science.aau5141.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Así nos hizo la Iglesia: Individualistas, independientes y prosociales si no es personal se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Geotermia urbana
Los fósiles, los minerales o las rocas son, entre otras cosas, en lo primero que pensamos al hablar de geología, pero lo cierto es que la física es un ámbito científico que difícilmente se puede desvincular de la geología. Y es que el fundamento físico resulta clave a la hora de explicar algunos procesos geológicos que suceden tanto en el océano como en la superficie terrestre.
Con el fin de poner sobre la mesa la estrecha relación entre la geología y la física, los días 27 y 28 de noviembre de 2019 se celebró la jornada divulgativa “Geología para poetas, miopes y despistados: La Geología también tiene su Física”. El evento tuvo lugar en la Sala Baroja del Bizkaia Aretoa de la UPV/EHU en Bilbao.
La segunda edición de esta iniciativa estuvo organizada por miembros del grupo de investigación de Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Geoparque de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

Las técnicas geotérmicas permiten aprovechar temperaturas tan bajas como 25ºC y hasta 15ºC. Iñigo Arrizabalaga, director general de Telur Geotermia y Agua S.A. (Durango), nos introduce en esta energía renovable.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Geotermia urbana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los ecos del fondo submarino: imágenes de las estructuras geológicas.
- Geología: la clave para saber de dónde venimos y hacia dónde vamos
- Geología, ver más allá de lo que pisamos
Magnetosomas para el tratamiento del cáncer
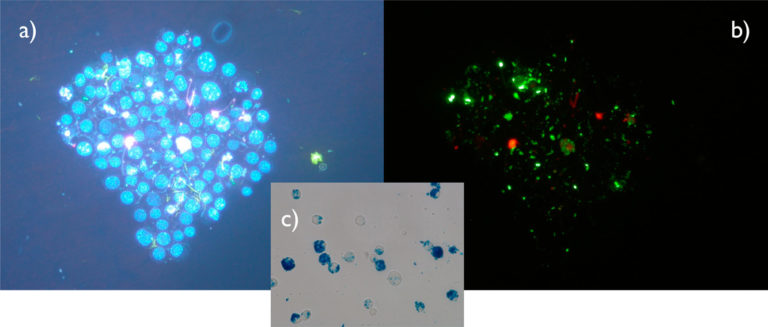 Magnetosomas internalizados por macrófagos, bajo diferentes filtros. Fuente: A. Muela et al (2016)
Magnetosomas internalizados por macrófagos, bajo diferentes filtros. Fuente: A. Muela et al (2016)Las nanopartículas magnéticas han permitido en los últimos años explorar modos de actuación alternativos a las terapias actualmente en uso en la lucha contra el cáncer. Una ventaja notable de las nanopartículas magnéticas es que pueden emplearse como agentes teranósticos (elementos que participan tanto en la terapia como en el diagnóstico) y entre los diferentes tipos destacan los magnetosomas, nanopartículas magnéticas sintetizadas por un tipo concreto de bacterias denominadas bacterias magnetotácticas.
Estos nanosistemas no solo se pueden usar en el transporte de fármacos sino que también presentan notables propiedades físicas y magnéticas para poder emplearlos en hipertermia —aumento de la temperatura corporal—, así como en el transporte guiado de fármacos. “El presente trabajo se centra en el estudio del potencial terapéutico de los magnetosomas en tratamientos de hipertermia magnética, una técnica que aprovecha la energía térmica producida por nanopartículas magnéticas bajo la acción de un campo magnético alterno para eliminar las células cancerígenas”, señala David Muñoz Rodríguez, investigador del Departamento de Inmunología, Microbiología y Parasitología de la UPV/EHU.
“Los magnetosomas, al contrario que las nanopartículas magnéticas de síntesis química, poseen de manera natural una membrana lipoproteica que los protege, evitando a la vez su aglomeración. Además, pueden funcionalizarse, es decir, ciertos fármacos o agentes antitumorales pueden adherirse a la membrana para poder guiarlos de forma eficiente hasta la masa tumoral. Las nanopartículas magnéticas emiten en forma de calor la energía que absorben del campo magnético alterno que se les aplica desde el exterior, provocando así un aumento de temperatura en los tumores y combatiéndolos”, indica Muñoz.
“Los magnetosomas presentan gran capacidad de producir calor (mayor que las nanopartículas magnéticas de síntesis química) y su eficiencia en la hipertermia queda demostrada al ver que el 80 % de las células morían en los experimentos realizados”, comenta David Muñoz. Además, “la hipertermia magnética tiene la ventaja de ser una terapia local, sin provocar efectos secundarios severos en el organismo. El campo magnético no debe aplicarse en cualquier zona del cuerpo, ni de cualquier manera: hay que aplicarlo solo a la zona afectada por el tumor, alcanzando una temperatura que oscile entre los 43 y 46 ºC ,ya que en este intervalo de temperatura las células entran en lo que se llama apoptosis —muerte celular programada—. Hemos demostrado que la hipertermia magnética usando magnetosomas proporciona un aumento de temperatura suficiente para reducir la viabilidad celular de forma estadísticamente significativa, induciendo a las células a que entren en apoptosis y mueran”, subraya el autor del trabajo.
El investigador ha destacado que «el uso de magnetosomas en este tipo de terapias podría tener un futuro prometedor y ser una alternativa válida a los tratamientos antitumorales convencionales”. Sin embargo, Muñoz afirma que “sería fundamental conocer la distribución de dichas partículas magnéticas en el organismo. Es decir, una vez han actuado, ¿dónde van a parar? Algunos estudios señalan que el propio organismo podría metabolizar los magnetosomas; otros dicen que suelen acumularse en órganos como el hígado, riñón, el bazo… Ahí está el hándicap”.
Referencias:
Muela, A.; Muñoz, D.; Martín-Rodríguez, R.; Orue, I.; Garaio, E.; Abad Díaz de Cerio, A.; Alonso, J.; García, J. Á.; Fdez-Gubieda, M. L. Optimal Parameters for Hyperthermia Treatment Using Biomineralized Magnetite Nanoparticles: Theoretical and Experimental Approach. (2016) J. Phys. Chem. C, 120, 24437– 24448, doi: 10.1021/acs.jpcc.6b07321
Huizar-Felix, A. M.; Munoz, D.; Orue, I.; Magen, C.; Ibarra, A.; Barandiaran, J. M.; Muela, A.; Fdez-Gubieda, M. L. Assemblies of magnetite nanoparticles extracted from magnetotactic bacteria: A magnetic study. (2016) Appl. Phys. Lett. , 108, 063109, doi: 10.1063/1.4941835
Lourdes Marcano, David Muñoz, Rosa Martín-Rodríguez, Iñaki Orue, Javier Alonso, Ana García-Prieto, Aida Serrano, Sergio Valencia, Radu Abrudan, Luis Fernández Barquín, Alfredo García-Arribas, Alicia Muela, and M. Luisa Fdez-Gubieda (2018) Magnetic Study of Co-Doped Magnetosome Chains The Journal of Physical Chemistry C 122 (13), 7541-7550 doi: 10.1021/acs.jpcc.8b01187
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Magnetosomas para el tratamiento del cáncer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lo mejor de dos mundos para avanzar en el tratamiento del cáncer
- Implante de factores de crecimiento en nanoesferas para el tratamiento de alzhéimer y párkinson
- Nanopartículas para reducir la metástasis hepática del cáncer de colon
El genio cegado por su propia teoría
Nos situamos en 1873. James Clerk Maxwell era uno de los miembros más distinguidos de la Royal Society de Londres, ya que, unos años antes había demostrado que electricidad y magnetismo son dos caras del mismo fenómeno, y que viajan de la mano en forma de onda a la velocidad de la luz. Ese mismo año publicó su magnum opus: el Tratado de Electricidad y Magnetismo, un compendio de todo su trabajo que predecía que la luz es, de hecho, una onda electromagnética.
Pero aquel tratado predecía otro fenómeno quizás más sorprendente: al igual que una masa empuja a otra masa al chocar con ella, las ondas electromagnéticas, por el mero hecho de ser ondas que transportan energía, serían capaces de transmitir movimiento al incidir en un objeto, de empujarlo. No en vano, hoy en día sabemos que este es el principio por el que funcionan las velas solares.
Por aquel entonces, William Crookes, que era químico y un gran experimentador, tenía fama por su gran habilidad creando tubos de vacío: tubos de vidrio de los que se extraía casi todo el aire con diferentes propósitos. De hecho, ha pasado a la historia por ser el creador del tubo de rayos catódicos: un tubo de vacío con dos electrodos que, años más tarde, se utilizó para descubrir los electrones y los rayos-X, e incluso sirvió para inventar el televisor.
Pero a pesar de su habilidad técnica, también tenía fama de no ser muy buen científico. O, al menos, en la Royal Society no estaba muy bien considerado, puesto que, como buen caballero victoriano, era espiritista. De hecho, durante aquel año, el buen hombre se hallaba buscando “fuerzas psíquicas”… Para ello, estaba realizando unas medidas de masa muy delicadas con talio dentro de uno de sus tubos de vacío cuando se dio cuenta de que, cuando el sol incidía en el dispositivo, las medidas salían distintas.
¿Cómo podía ser posible? Crookes lo vio claro: estaba ante una prueba empírica de la teoría de Maxwell. Esto le llevó a concebir el artilugio que conocemos como “molinillo de luz” o “radiómetro de Crookes”. Consta, cómo no, de un tubo de vacío, normalmente en forma de bombilla. En su interior hay unas aspas, con una cara negra y otra reflectante, unidas a un capuchón de vidrio que pende sobre una aguja, para evitar al máximo el rozamiento. Según Crookes, la teoría de Maxwell establece que la luz interactúa de forma diferente con la parte negra y la reflectante, lo que resulta en una fuerza neta que impulsa las aspas. Y lo cierto es que, cuando pones el molinillo a la luz… ¡las aspas giran!
 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons
Maxwell recibió el artículo de Crookes que describía el experimento y se quedó maravillado con la elegancia de la prueba de su propia teoría. Alabó su trabajo, perdonando su pasado espiritista, y recomendó su inmediata publicación. Se realizó una presentación del artilugio en la Royal Society por todo lo alto, y las crónicas contaron que “la ciencia había hecho un agujero en el infinito”.
Pero finalmente resultó que uno de los mayores genios científicos de la historia, cegado por su propia teoría, seducido por la supuesta elegancia de la demostración, cayó presa de su propio sesgo. Y es que la teoría electromagnética, efectivamente, establece que la luz interacciona de forma distinta con las caras de las aspas, pero más concretamente dice que la parte reflectante recibe el doble de presión que la parte negra. Y, por tanto, ¡gira al revés!, ¡debería girar para el otro lado!
Ni que decir tiene que, a partir de ese momento, empezó una carrera para investigar el verdadero funcionamiento del molinillo. Entre otras cosas, se vio que, cuando había mucho aire dentro, no giraba; cuando había demasiado poco, tampoco; cuando se enfriaba, giraba en el otro sentido… todo parecía indicar que algo tenía que ver el poco aire que quedaba dentro del tubo de vacío.
Se especuló mucho hasta que Osborne Reynolds, en 1879, dio finalmente con la solución: se trata de un fenómeno denominado transpiración térmica. Resulta que, en las condiciones del tubo de vacío, las poquitas moléculas de aire que quedan en su interior ya no interaccionan entre ellas, lo que se denomina gas enrarecido. La cara negra de las aspas se calienta más que la cara reflectante, porque absorbe la radiación, y así se calienta el aire circundante. Lo que sucede entonces es que el aire frío tiende a trepar por el borde del aspa y pasa al lado caliente, y así se produce un empuje neto hacia el otro lado.
 Simulación de la transpiración térmica en un molinillo de luz, por Moritz Nadler
Simulación de la transpiración térmica en un molinillo de luz, por Moritz NadlerComo epílogo, Reynolds escribió un artículo con esta explicación que revisó… Maxwell de nuevo. Pero Maxwell, quizás herido en su orgullo, decidió paralizar la publicación y escribir su propio artículo para criticar a Reynolds. Entonces Reynolds quiso publicar una crítica de la crítica de Maxwell al primer artículo suyo rechazado. Pero, entretanto, lamentablemente Maxwell murió, y de nuevo Reynolds se quedó sin publicación, esta vez por respeto al recién fallecido. Hoy en día, el molinillo es una baratija que se suele vender en tiendas de museos científicos como curiosidad.
Sobre el autor: Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute.
El artículo El genio cegado por su propia teoría se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La teoría de la invariancia
- ¿La teoría de la invariancia es física o metafísica?
- La teoría cinética y la segunda ley de la termodinámica
La ecuación de las ciudades oscuras
Las ciudades oscuras es una serie de novelas gráficas, publicadas originalmente en francés, del dibujante belga François Schuiten y el guionista francés Benoît Peeters, cuyo primer álbum Las murallas de Samaris fue publicado en 1983 y que sigue publicándose en la actualidad. En el momento en el que escribo estas líneas cuenta con doce álbumes: Las murallas de Samaris, La fiebre de Urbicande, La Torre, La ruta de Armilia, Brüsel, La chica inclinada, La sombra de un hombre, La Frontera Invisible (doble), La teoría del grano de arena (doble), Recuerdos del eterno presente.
En la colección de novelas gráficas Las ciudades oscuras nos encontramos ante una serie de historias entre fantásticas y surrealistas que transcurren en diferentes ciudades de un continente imaginario que se encuentra situado en el planeta Antichton, o Anti-Tierra. Este hipotético planeta fue inventado por el filósofo y matemático pitagórico Filolao (aprox. 470 – 380 a.n.e.) cuando describió un sistema cosmológico, no geocéntrico, en el que había un fuego central distinto del Sol y un planeta situado en la posición diametralmente opuesta a la Tierra, respecto a dicho fuego central, la anti-Tierra.
La arquitectura y el diseño urbanístico de las ciudades oscuras son protagonistas principales de esta serie de novelas gráficas, pero también la política, la sociedad, la ciencia, las creencias o las relaciones humanas., entre muchos otros
 Nueve portadas de la serie de novelas gráficas Las ciudades oscuras de François Schuiten (dibujo) y (Benoît Peters), publicadas por Norma Editorial. Imágenes de la página web de Norma Editorial
Nueve portadas de la serie de novelas gráficas Las ciudades oscuras de François Schuiten (dibujo) y (Benoît Peters), publicadas por Norma Editorial. Imágenes de la página web de Norma EditorialEn esta entrada del Cuaderno de Cultura Científica vamos a centrarnos en uno de los álbumes de la serie titulado La fiebre de Urbicande (1985). El protagonista de esta historia es Eugen Robick, el “urbatecto” (unión de urbanista y arquitecto) oficial de la ciudad de Urbicande, que está preocupado por el diseño urbanístico de la ciudad y su falta de simetría. La ciudad de Urbicande está dividida por su río en dos zonas. La zona sur, en la que vive la alta sociedad, sería una ciudad geométrica, con avenidas rectas, que se intersecan perpendicularmente, sobre la que se han diseñado, de forma racional, edificios rectos y simétricos, mientras que la zona norte, en la que vive la parte de la sociedad que la clase alta quiere mantener alejada, posee un desarrollo urbanístico irregular.
Sin embargo, un inesperado acontecimiento cambiará las preocupaciones de Eugen Robick y de los habitantes de la ciudad de Urbicande, la aparición de un misterioso cubo encontrado en unas obras y que se convertirá en el desencadenante de los acontecimientos futuros de la ciudad.
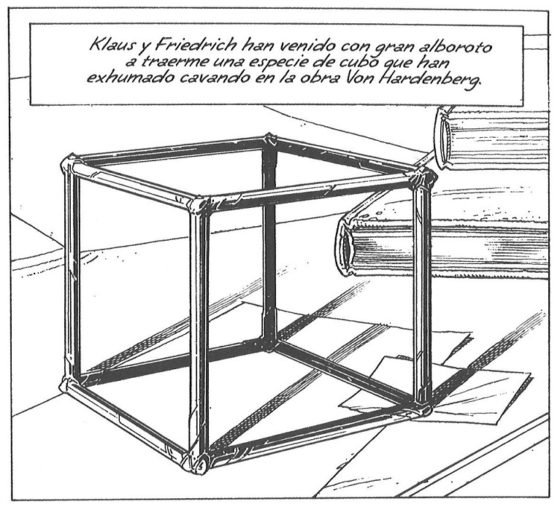 Viñeta de la novela gráfica La fiebre de Urbicande, de Scuiten-Peeters, en el cual vemos el cubo que se convertirá en protagonista de esta historia
Viñeta de la novela gráfica La fiebre de Urbicande, de Scuiten-Peeters, en el cual vemos el cubo que se convertirá en protagonista de esta historia
Aparentemente el cubo no posee un gran interés, salvo que está construido con un material extremadamente duro. El urbatecto Eugen Robick lo describe así en las primeras páginas.
“Klaus y Friedrich han venido con gran alboroto a traerme una especie de cubo que han exhumado cavando en la obra Von Hardenberg.
El objeto habría quebrado la pala de una grúa, debido a su gran solidez.
Al observarla fríamente, no tiene sin embargo nada de demasiado extraño. Es una simple estructura cúbica totalmente vacía cuyas aristas no deben de superar los quince centímetros.”
Lo curioso es que, poco tiempo después, del cubo han surgido unas prolongaciones que extendían los lados del mismo, con un crecimiento constante, hasta generar un nuevo cubo en cada una de las caras del hexaedro regular original. De forma que en esta primera etapa se ha creado una pequeña red con 7 cubos. Además, al tiempo que iba ocurriendo esto, el tamaño del cubo original ha ido creciendo también, así en un día el tamaño de las aristas del cubo, de los cubos, ha pasado de 15 a 20 centímetros. El grosor de las aristas también ha ido creciendo paulatinamente.
 Viñeta de la novela gráfica La fiebre de Urbicande, de Scuiten-Peeters, en el cual vemos el momento en que se está terminando la primera etapa de desarrollo del cubo original, convirtiéndose en una pequeña red de 7 cubos, el central y uno en cada cara del mismo
Viñeta de la novela gráfica La fiebre de Urbicande, de Scuiten-Peeters, en el cual vemos el momento en que se está terminando la primera etapa de desarrollo del cubo original, convirtiéndose en una pequeña red de 7 cubos, el central y uno en cada cara del mismo
Como el proceso no para, la red de cubos va creciendo poco a poco, en tamaño y en número de ortoedros que lo conforman. En la siguiente etapa de crecimiento, en cada cara de los cubos que forman la red surgen nuevos cubos, luego de 7 cubos pasa a 25. Y en la siguiente etapa, la red de cubos, que tendrá la forma de un octaedro (es decir, una doble pirámide, hacia arriba y hacia abajo), estará formada por 63 cubos. Después, 129, 231, etcétera.
 Viñetas de la novela gráfica La fiebre de Urbicande, de Scuiten-Peeters, en las cuales vemos al urbatecto Robick estudiar la estructura y calcular el número de cubos que tendrá en cada etapa de crecimiento
Viñetas de la novela gráfica La fiebre de Urbicande, de Scuiten-Peeters, en las cuales vemos al urbatecto Robick estudiar la estructura y calcular el número de cubos que tendrá en cada etapa de crecimiento
Eugen Robick, que era matemático de formación según se comenta en la parte de La leyenda de la red, empieza a estudiar la estructura reticular que se genera. En particular, obtiene una fórmula, que veremos más adelante, que le da el número de cubos que tendrá la estructura en cada paso. Pero estudiemos nosotros esa sucesión de números que nos da la cantidad de cubos que posee la red octaédrica que aparece en la novela gráfica.
Empecemos pensando el problema en dimensión 2. Supongamos que nuestra estructura original es un cuadrado, que va creciendo y formando una red de cuadrados de forma similar a como la red de cubos de Urbicande (véase la siguiente imagen). En cada lado del cuadrado original se forma un nuevo cuadrado y sobre los lados de los nuevos cuadrados irán creciendo nuevos cuadrados.
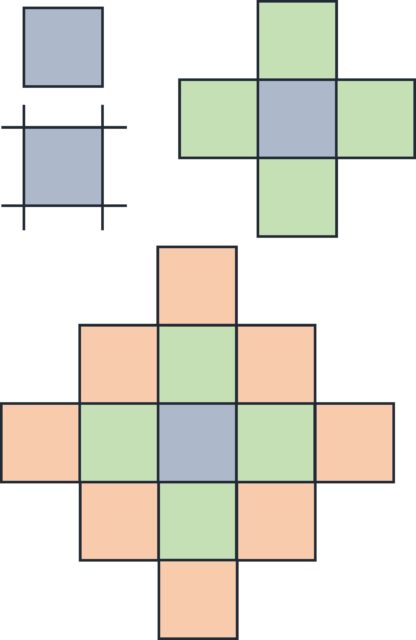
Primero, en el momento cero tenemos 1 cuadrado (c0), del que surgen 4 más, luego 5 (c1) en total. En la segunda etapa se incorporan 8, luego 13 (c2) en total… y así continúa. Pero, veamos cuantos cuadrados se incorporan en cada momento. Si nos fijamos en la anterior imagen, en la segunda etapa (c2), los cuadrados que se incorporan forman un cuadrado grande (rojo) con 3 cuadrados en cada lado, luego tiene (4 x 3 – 4 = 4 x (3 – 1) = 4 x 2 = 8 cuadrados, es decir, cuatro veces los cuadrados que hay en cada lado menos 4, de los vértices, que contábamos dos veces). En general, en el paso n-ésimo se incorporarán, a los anteriores cubos, 4 x n cubos más. Por lo tanto, se obtiene la siguiente fórmula:
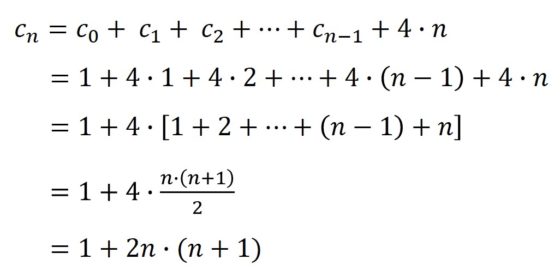
Donde hemos utilizado, en el ante-último paso, la fórmula de la suma de los n primeros números (véase la entrada Matemáticas para ver y tocar ).
 Página de la novela gráfica La fiebre de Urbicande, de Scuiten-Peeters, en la cual vemos al urbatecto Robick dentro de la estructura reticular que cada vez va creciendo más
Página de la novela gráfica La fiebre de Urbicande, de Scuiten-Peeters, en la cual vemos al urbatecto Robick dentro de la estructura reticular que cada vez va creciendo más
 Estructura reticular con cubos, que adopta la forma de un octoedro, después de tres etapas, luego con 25 cubos, que he realizado con el material de construcción Zometool
Estructura reticular con cubos, que adopta la forma de un octoedro, después de tres etapas, luego con 25 cubos, que he realizado con el material de construcción Zometool
El razonamiento que hemos desarrollado en el plano, para cuadrados, no solo nos ayuda a entender el problema en dimensión tres, para cubos, sino que nos permite obtener fácilmente una fórmula para la cantidad de cubos de cada etapa de la red. Esto se debe a que en la etapa n-ésima la cantidad de cubos de la zona/capa central de la red octaédrica es igual a la cantidad de cuadrados de la etapa n-ésima de los cuadrados planos (cn), ya que solo nos fijamos en los cubos que están a la misma altura, en la misma capa horizontal. En la capa de arriba de la central, y también en la de abajo, hay tantos cubos como cuadrados había en la etapa anterior, luego (n – 1)-ésima de los cuadrados planos (c(n – 1)), y así con el resto. Veamos los primeros pasos. En la primera etapa hay 5 cubos en la zona central y 1 arriba y otro abajo, en total, 7 cubos. En la segunda etapa hay 13 cubos en la zona central, 5 en la zona que está justo encima y 5 en la que está justo debajo, y 1 cubo arriba del todo y 1 abajo del todo, en total 13 + 2 x 5 + 2 x 1 = 25 cubos.
Es decir, tenemos la fórmula general para la cantidad de cubos de la red de Urbicande dada en función de los anteriores números:
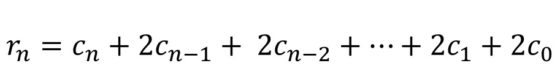
Pero sustituyendo el valor de los números de cuadrados (cn) calculados anteriormente, se obtiene:
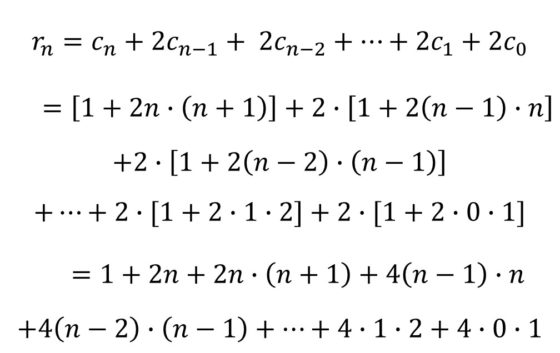
Observemos que en la segunda igualdad hemos sumado primero los 1s de los corchetes, obteniendo el número 1 + 2n del inicio.
Hemos obtenido así una primera fórmula para el cálculo del número de cubos de la red. Si vais dando valores a n = 0, 1, 2, 3, 4, 5, … obtendréis la cantidad de hexaedros regulares de cada etapa 1, 7, 25, 63, 129, 231, …
Vamos a intentar obtener una fórmula más sencilla de manejar. Si denotamos como Tn a los números triangulares, es decir, la suma de los n primeros números, Tn = 1 + 2 + … + n, que sabemos que es igual a n (n + 1) / 2, podemos demostrar que la anterior fórmula es igual a:
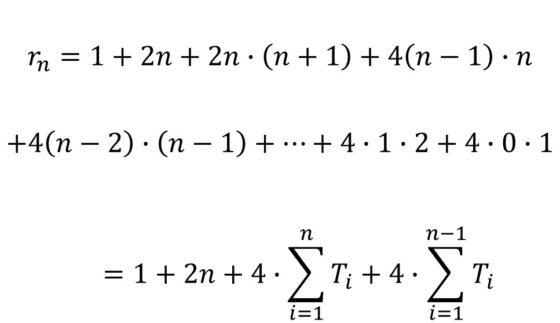
Para seguir avanzando necesitamos la fórmula de la suma de los números triangulares. En la siguiente imagen podéis ver dicha fórmula, con la demostración sin palabras que publicó Monte J. Zerger en Mathematics Magazine (diciembre, 1990) y que aparece también en el libro Demostraciones sin Palabras, de Roger B. Nelsen.
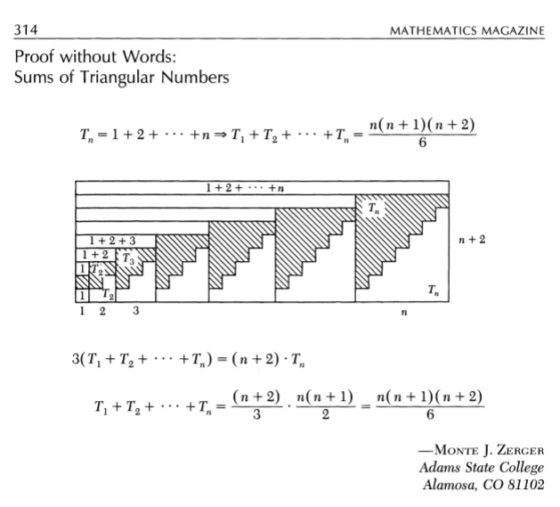 Demostración sin palabras que publicó Monte J. Zerger en Mathematics Magazine (diciembre, 1990) de la suma de los números triangulares
Demostración sin palabras que publicó Monte J. Zerger en Mathematics Magazine (diciembre, 1990) de la suma de los números triangulares
Ahora, haciendo uso de la anterior fórmula se obtiene la siguiente fórmula para la sucesión de cubos que conforman la red octaédrica de La fiebre de Urbicande:
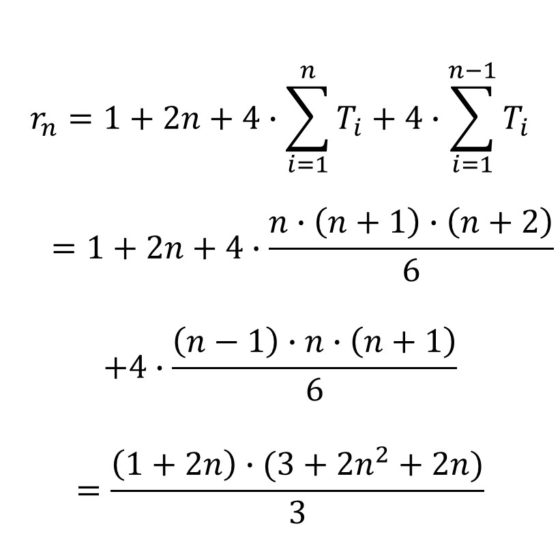
 Robick y Sofía, una mujer a la que conoce nuestro protagonista y de la que se enamora, disfrutando del paisaje de la estructura reticular, de la que se ve la pirámide superior, mientras que la inferior está ya bajo tierra
Robick y Sofía, una mujer a la que conoce nuestro protagonista y de la que se enamora, disfrutando del paisaje de la estructura reticular, de la que se ve la pirámide superior, mientras que la inferior está ya bajo tierra
Si volvemos a la novela gráfica de Schuiten-Peeters, podemos observar que la fórmula que he obtenido coincide con una de las dos que aparecen en la misma. Una de ellas es la fórmula de Robick y la otra la que aparece en el opúsculo El misterio de Urbicande “de un tal R. de Brok”, dentro de la parte denominada La leyenda de la red, que es un documento perteneciente a los Archivos de “las ciudades oscuras”.
 Página extraída del opúsculo El misterio de Urbicande, anotada por Eugen Robick, en la que podemos ver las dos fórmulas matemáticas para el número de cubos de la estructura reticular, la fórmula de Robick y la fórmula de R. de Brok (que aparece descrita como “Mi fórmula”)
Página extraída del opúsculo El misterio de Urbicande, anotada por Eugen Robick, en la que podemos ver las dos fórmulas matemáticas para el número de cubos de la estructura reticular, la fórmula de Robick y la fórmula de R. de Brok (que aparece descrita como “Mi fórmula”)
El razonamiento que utiliza Eugen Robick es diferente al mío y por eso la fórmula que obtiene es diferente. Podemos decir que yo cuento los cubos de cada capa horizontal de la estructura reticular, mientras que Robick cuenta los cubos en columnas verticales.
Expliquemos brevemente la idea de Robick. En la etapa n-ésima del desarrollo de la red la “columna central” de la estructura con forma de octaedro (pirámide doble) tiene 2n + 1 cubos, que es el número que aparece en primer lugar en su fórmula. Después divide la pirámide doble, menos la columna central, en cuatro partes iguales (en la siguiente imagen observamos la partición en lo que sería la vista desde arriba de la red) y calcula la cantidad de cada parte, que es la expresión que aparece multiplicando al 4.
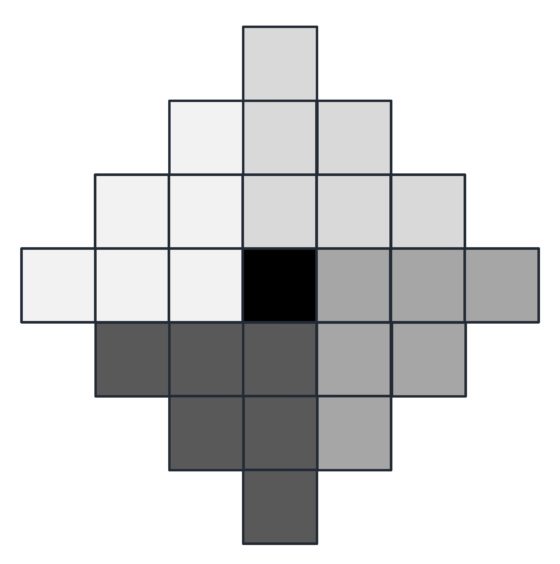 Vista desde arriba de la estructura reticular, con la columna central que se corresponde con el cuadrado negro y las cuatro zonas de la retícula octaédrica en las que Robick divide la estructura
Vista desde arriba de la estructura reticular, con la columna central que se corresponde con el cuadrado negro y las cuatro zonas de la retícula octaédrica en las que Robick divide la estructura
Ahora razonemos visualmente (en la siguiente imagen) cómo obtiene Robick la fórmula del cálculo de los cubos de cada una de esas cuatro partes.
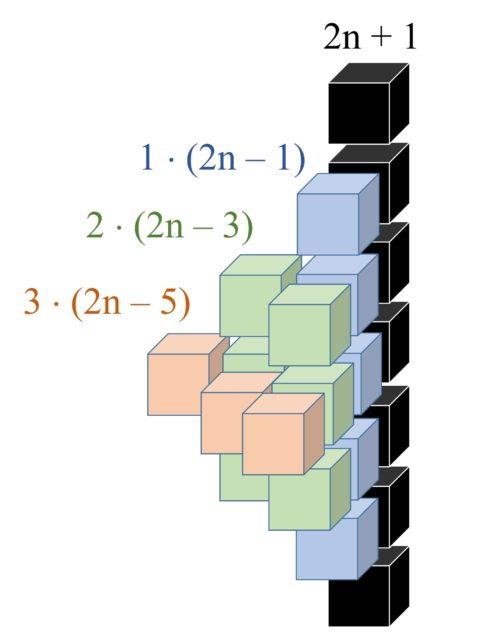 Ilustración, para la etapa n = 3 del crecimiento de la red, de la columna central de cubos, en la que hay 2n +1 elementos, más una de las cuatro partes en las que Robick divide la retícula. Se indican con diferentes colores los cubos que cuenta juntos, que van por alturas
Ilustración, para la etapa n = 3 del crecimiento de la red, de la columna central de cubos, en la que hay 2n +1 elementos, más una de las cuatro partes en las que Robick divide la retícula. Se indican con diferentes colores los cubos que cuenta juntos, que van por alturas
Juntando todo lo anterior se obtiene la fórmula de Robick:
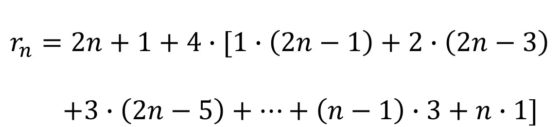
No hemos entrado en el trasfondo social y político de la historia que se cuenta en La fiebre de Urbicande, pero eso dejo que lo descubráis en vuestra propia lectura de la novela gráfica.
 Viñeta de La fiebre de Urbicande, de Schuiten-Peeters, en la que vemos el momento en el que la red ya solo tiene un cubo alrededor de la ciudad, por lo que ya no interfiere en la vida de la misma. La red de hexaedros regulares seguirá creciendo, primero superando la ciudad, luego el continente, después el planeta y seguirá creciendo en la galaxia
Viñeta de La fiebre de Urbicande, de Schuiten-Peeters, en la que vemos el momento en el que la red ya solo tiene un cubo alrededor de la ciudad, por lo que ya no interfiere en la vida de la misma. La red de hexaedros regulares seguirá creciendo, primero superando la ciudad, luego el continente, después el planeta y seguirá creciendo en la galaxia
Finalizamos la entrada animando a la lectura de la serie de novelas gráficas de François Schuiten y Benoît Peeters, Las ciudades oscuras, y con la imagen de la contraportada de La fiebre de Urbicande de la edición en castellano de Norma editorial en 2015, con tres de los protagonistas de la historia, Eugen, Sofía y el misterioso cubo.
 Contraportada de La fiebre de Urbicande, Schuiten-Peeters, Norma editorial, 2015
Contraportada de La fiebre de Urbicande, Schuiten-Peeters, Norma editorial, 2015
Bibliografía
1.- Francois Schiten, Benoit Peeters, La fiebre de Urbicande (Las ciudades oscuras), Norma Editorial, 2015.
2.- Roger B. Nelsen, Demostraciones sin palabras (ejercicios de pensamiento visual), Proyecto Sur, 2001.
3.- Jean-Paul Van Bendegem, A short explanation of «Le Mystère d’Urbicande», Alta plana, the impossible & infinite encyclopedia of the world created by Schuiten & Peeters
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La ecuación de las ciudades oscuras se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Triangulando: Pascal versus Sierpinski
- Buscando las soluciones del cubo de Anda
- Locura instantánea, un rompecabezas con cubos de colores
La interpretación de Copenhague de la mecánica cuántica
 Sede del Instituto de Física Teórica de la Universidad de Copenhague construida y constituido, respectivamente, en 1921 con Niels Bohr como director. Popularmente conocido como Instituto Bohr, adoptó oficialmente ese nombre en 1965. Fuente: Niels Bohr Institutet
Sede del Instituto de Física Teórica de la Universidad de Copenhague construida y constituido, respectivamente, en 1921 con Niels Bohr como director. Popularmente conocido como Instituto Bohr, adoptó oficialmente ese nombre en 1965. Fuente: Niels Bohr InstitutetEl principio de complementariedad de Bohr es una afirmación de una enorme importancia, porque significaba que lo que observamos en nuestros experimentos no es lo que la naturaleza realmente es cuando no la estamos observando. Pero ahondemos sobre esto, porque la afirmación choca con el sentido común [1], lo que puede hacer más difícil asimilar lo que aquí se está diciendo [2].
De hecho, la naturaleza no favorece ningún modelo específico cuando no estamos observando; si algo podemos afirmar es que la naturaleza es una mezcla de las muchas posibilidades que podría ser hasta que observamos [3]. Al establecer un experimento, seleccionamos el modelo que exhibirá la naturaleza y decidimos si los fotones, electrones, protones e incluso las pelotas de tenis (si se mueven lo suficientemente rápido) se comportarán como corpúsculos o como ondas.
En otras palabras, según Bohr, ¡el experimentador se convierte en parte del experimento! Al hacerlo, el experimentador interactúa con la naturaleza, de tal modo que nunca podemos observar todos los aspectos de la naturaleza como realmente es “en sí” [4]. De hecho, esta expresión, si bien es atractiva, no tiene un significado operativo. En cambio, deberíamos decir que solo podemos conocer la parte de la naturaleza que nuestros experimentos ponen de manifiesto. [5] La consecuencia de este hecho, a nivel cuántico, decía Bohr, es el principio de incertidumbre, que coloca una limitación cuantitativa sobre lo que podemos aprender sobre la naturaleza en cualquier interacción dada; y la consecuencia de esta limitación es que debemos aceptar la interpretación de probabilidad de los procesos cuánticos individuales. De aquí que al principio de incertidumbre a menudo también se le llame principio de indeterminación.
No hay forma de evitar estas limitaciones, según Bohr, mientras la mecánica cuántica siga siendo una teoría válida. Estas ideas, por supuesto, están totalmente en desacuerdo con el sentido común, como apuntábamos antes. Asumimos que la naturaleza existe de manera completamente independiente de nosotros y que posee una realidad y un comportamiento definidos, incluso cuando no la estamos observando. Así, supones que el mundo fuera del lugar donde estás todavía existe más o menos como fue la última vez que lo observaste. No cabe duda de que la naturaleza se comporta así en nuestra experiencia cotidiana, y esta visión es una suposición fundamental de la física clásica. Incluso tiene un nombre filosófico; se llama «realismo», y para los fenómenos y objetos en el rango de la experiencia ordinaria es perfectamente apropiado. Pero, como Bohr a menudo enfatizó, tenemos que estar preparados para esperar que el mundo cuántico no sea como el mundo cotidiano en el que vivimos.
Parte de la dificultad viene del lenguaje que empleamos. Nuestra lengua común no puede expresar adecuadamente lo que las matemáticas consiguen hacer de manera muy eficiente. Max Born, uno de los fundadores de la mecánica cuántica, lo expresó así (nuestro énfasis):
El origen último de la dificultad radica en el hecho (o principio filosófico) de que estamos obligados a usar las palabras del lenguaje común cuando deseamos describir un fenómeno, no mediante un análisis lógico o matemático, sino mediante una imagen atractiva para la imaginación. El lenguaje común ha crecido con la experiencia cotidiana y nunca puede superar estos límites. La física clásica se ha limitado al uso de conceptos de este tipo; al analizar los movimientos visibles, ha desarrollado dos formas de representarlos mediante procesos elementales: partículas en movimiento y ondas. No hay otra forma de dar una descripción pictórica de los movimientos: tenemos que aplicarlo incluso en la región de los procesos atómicos, donde la física clásica se descompone. [6]
Juntos, el principio de complementariedad de Bohr, el principio de incertidumbre de Heisenberg y la interpretación de probabilidad de Born forman una interpretación lógicamente coherente del significado de la mecánica cuántica. Dado que esta interpretación se desarrolló en gran medida en el instituto de Bohr en la Universidad de Copenhague, se la conoce como la Interpretación de Copenhague de la mecánica cuántica. Los resultados de esta interpretación tienen profundas consecuencias científicas y filosóficas que se siguen estudiando y debatiendo. [7]
Notas:
[1] La ciencia se empeña en demostrar que el sentido común no deja de ser una colección de sesgos antropocéntricos y, por lo tanto, si bien útiles para el día a día en muchos casos, no necesariamente ciertos.
[2] Por eso es interesante fijarse en las palabras en cursiva, que están cuidadosamente seleccionadas.
[3] Este es el principio de superposición cuántico, sobre el que reflexionamos en La teoría superpositiva.
[4] Esto del “en sí” está entrecomillado porque es más un concepto filosófico que físico. Está relacionado con la caracterización de la sustancia de la época racionalista de la filosofía. Recordemos, por ejemplo, que Spinoza en la definición tercera del libro primero de la Ética decía “Por substancia entiendo aquello que es en sí y se concibe por sí, esto es, aquello cuyo concepto, para formarse, no precisa del concepto de otra cosa.”
[5] Y aquí hay que reflexionar mínimamente. Esto no es una invitación al misticismo, como algunos se apresuran a adoptar. Fijémonos en que, al fin y al cabo, conocemos incluso a nuestro mejor amigo solo a través de un mosaico de encuentros, conversaciones y actividades repetidas, en muchas circunstancias diferentes.
[6] A este respecto puede resultar interesante nuestro La verdadera composición última del universo (y IV): Platónicos, digitales y pansiquistas
[7] Una introducción a los elementos del debate puede encontrarse en nuestra serie Incompletitud y medida en mecánica cuántica
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La interpretación de Copenhague de la mecánica cuántica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Construyendo la mecánica cuántica
- La probabilidad en mecánica cuántica
- El principio de complementariedad

