¿Que puede aportar (y qué no) la neurociencia a la educación?
Érase una vez… en el País Vasco, un congreso tan oportuno y tan útil, y tan bien recibido en Bilbao y en Donostia-San Sebastián, que muchos pensaron que tenía que viajar a más lugares. Así que la Cátedra de Cultura Científica y la Fundación Promaestro se pusiron de acuerdo y, con la ayuda de EduCaixa, lo llevaron a Madrid: casi un centenar de personas con espíritu crítico y bien informadas llenaron el pasado 2 de abril la modesta y acogedora sala de CaixaForum en la que se celebró.

Así como toda (buena) historia tiene un (buen) principio, toda (buena) práctica tiene un (buen) fundamento. Un fundamento, una justificación, una razón, una prueba. Lo más importante es que nuestras prácticas educativas estén sostenidas por evidencias científicas. Su nombre da igual. Da igual, ¿o no?
“Que algo lleve el prefijo «neuro» no significa que contenga más verdad, pero –apostilla el profesor Juan Lupiáñez en su ponencia– la neurociencia le presta estatus a la psicología”. Sorprendentemente, aportaciones teóricas ya clásicas de la psicología son tenidas más en cuenta por el público cuando provienen de la neurociencia. El catedrático de la Universidad de Granada presenta estudios que demuestran que la gente comprende y recuerda mejor aquellos datos y teorías en los que aparecen términos e imágenes relacionadas con el cerebro.
Es decir, que las palabras también importan y, precisamente por eso, tenemos que ser especialmente cuidadosos con ellas y evitar que nos obnubilen: ¿Cuántos siguen creyendo en neuromitos, en el brain gym y en la teoría del cerebro derecho e izquierdo, por ejemplo? ¿Cuántos hablan de educar al cerebro y olvidan que el objetivo de la escuela es educar a la persona? Entender el cerebro, repite el ponente, “es mucho más complicado que entender el comportamiento, que ya es complicado”, y además “éste no es una máquina: no podemos cambiar sus conexiones como cambiamos las bujías de un coche”.
Es muy recomendable escuchar a los neurocientíficos –afirma en su conclusión Lupiáñez– pero, en lo que se refiere a evidencias educativas, “siempre es mejor ampliar su búsqueda más allá de un solo campo”.
Edición realizada por César Tomé López a partir de materiales suministrados por Fundación Promaestro
El artículo ¿Que puede aportar (y qué no) la neurociencia a la educación? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las ideas erróneas sobre educación entre el profesorado: prevalencia, causas y soluciones
- Autismo y educación: problemas y pautas en el aula
- Educación basada en la evidencia: retos y propuestas de mejora
Cómo conservar mejor los alimentos con una iluminación inteligente
![]()
Raquel Esteban, José Ignacio García Plazaola y Víctor Resco de Dios
 Ernest Brillo / Unsplash
Ernest Brillo / UnsplashEl otoño ha dejado paso al invierno. Y con él, se van los colores propios de la estación que hemos despedido: el verde que cubría a los árboles de hoja caduca se transforma en un abanico de colores, que va desde el ocre hasta el naranja.
Los pigmentos responsables de estos colores son imprescindibles para la salud humana. Además, la calidad de los alimentos está relacionada con la preservación de estos compuestos y, por lo tanto, conocer su funcionamiento ayuda a disminuir el desperdicio de alimentos.
A través de las nuevas tecnologías podemos lograr mejoras sustanciales en dos aspectos: la calidad nutricional y la preservación de los vegetales vegetales.
Los pigmentos de las plantas, nuestras vitaminas
Tanto el color verde como la gama de colores típicamente otoñales se deben a las propiedades físico-químicas de los pigmentos de las hojas:
- Las clorofilas son los pigmentos responsables de los tonos verdes.
- Los carotenoides de los colores amarillo-naranja.
Estos pigmentos son clave en el funcionamiento y la supervivencia vegetal. Participan en procesos tan importantes como la fotosíntesis y la tolerancia a las condiciones adversas.
¿Recuerda cuando su abuela le decía que comiera zanahorias para preservar la vista? Pues llevaba parte de razón. Los carotenoides son imprescindibles para la vista.
El beta caroteno, el mayoritario de la zanahoria, es la provitamina A, que forma parte de la retina de los ojos. Los amarillos como la luteína y la zeaxantina están en la mácula y son los responsables de disipar las especies reactivas de oxigeno de nuestros ojos
Además, debido a sus propiedades antioxidantes, estos pigmentos aportan otros beneficios a la salud, como la mejora de la capacidad cognitiva y la prevención de enfermedades degenerativas.
Al ser los humanos incapaces de sintetizar carotenoides, los debemos incorporar en la dieta mediante la ingesta de frutas, verduras y legumbres, principalmente. Forman parte de las vitaminas.
 Las zanahorias contienen carotenoides beneficiosos para la vista.
Las zanahorias contienen carotenoides beneficiosos para la vista.Voltamax/Pixabay
Así cambia el valor nutritivo de los vegetales
Una cualidad que define a las plantas es que, aunque las cosechemos, siguen vivas. Es decir, continúan realizando procesos fisiológicos como la fotosíntesis y la respiración.
Todos los vegetales que vemos en los expositores de los supermercados están vivos. Esto se debe a la característica modular de sus órganos y a su habilidad para mantener una autonomía fisiológica.
Aunque aparentemente estén inactivos, en realidad su maquinaria está completamente activa. Responden a las condiciones ambientales que se dan desde que se recolectan hasta que acaban en la nevera de nuestros hogares.
El contenido de carotenoides y, por lo tanto, de las vitaminas o compuestos antioxidantes, es muy variable. Va a responder a las condiciones a las que están expuestos los productos, aumentando o disminuyendo su concentración.
Dicho de otra forma: el contenido nutricional de un vegetal (basándonos en el contenido de carotenoides) varía a lo largo del día.
Por ejemplo, el carotenoide zeaxantina –relacionado, junto con la luteína, con la disminución del riesgo de padecer degeneración macular asociada a la edad– presenta valores máximos durante el día y mínimos por la noche.
El papel de los frigoríficos
Los frigoríficos, ya sea en nuestra casa, o en un supermercado, suelen mantener los alimentos bajo condiciones de oscuridad continua o de luz continua.
En los hogares, por ejemplo, suele suceder lo primero: el vegetal no ve la luz, salvo por los pocos segundos en los que abrimos la puerta. En muchos supermercados, sin embargo, la iluminación es continua y el producto en el expositor nunca experimenta la oscuridad.
 En los supermercados, los vegetales se conservan en condiciones de luz.
En los supermercados, los vegetales se conservan en condiciones de luz.Matheus Cenali/Pexels
Nuestros estudios indican que guardar las verduras bajo estas condiciones tan extremas de luz acorta su vida.
Los carotenoides y demás pigmentos foliares se degradan más rápidamente bajo estos ritmos de luz artificial, lo que provoca cambios visuales (cambios de color en las hojas de verde a amarillento). Disminuye la calidad de los alimentos y hace que se desperdicien con más facilidad.
Si incorporamos ciclos de luz/oscuridad en los sistemas de refrigeración, de forma que reproduzcamos los ciclos de día/noche que el vegetal experimenta cuando crece en el campo, lograremos mejoras sustanciales en la preservación de los alimentos.
Medir los contenidos de carotenoides
Para entender mejor el valor nutricional de los vegetales, y para mejorar su preservación, necesitamos cuantificar cuántos carotenoides y clorofilas tienen los alimentos que comemos.
La técnica más precisa, pero a la vez costosa, de cuantificación es el análisis mediante cromatografía en un laboratorio. Este es un procedimiento caro y complejo.
Una alternativa mucho más sencilla es el uso de técnicas basadas en al análisis de la reflectancia de la luz. Consisten en evaluar la cantidad de cada tipo de luz reflejada por la superficie del alimento en cuestión, es decir, en cuantificar el color. Este será proporcional a su contenido de pigmentos.
Estos métodos no son tan precisos, pero sí más económicos. Solo se necesita el aparato de medición y generalmente existe en versión portátil.
En una investigación reciente, hemos aplicado estas técnicas en una simulación de un ambiente de supermercado. Hemos conseguido determinar el contenido aproximado de los carotenoides a partir de la medida de sus características ópticas. Este hecho abre una interesante línea para el futuro y nos dirige hacia los supermercados 2.0.
En un futuro cercano será posible medir los antioxidantes de nuestros alimentos tan solo apretando un botón. Incluso, la tecnología de los supermercados podría incluir drones con sensores que nos indiquen el valor aproximado de esos compuestos.![]()
Sobre los autores: Raquel Esteban y José Ignacio García Plazaola son profesores de fisiología vegetal en la Universidad del País Vasco / Euskal Herriko Unibertsitatea y Víctor Resco de Dios es profesor de incendios forestales y cambio global en la Universitat de Lleida.
Este artículo fue publicado originalmente en The Conversation. Artículo Original.
El artículo Cómo conservar mejor los alimentos con una iluminación inteligente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un espectrómetro Raman portátil mide el punto óptimo de maduración del tomate
- ¿Cómo llegan bacterias resistentes y residuos de antibióticos a los alimentos?
- El azúcar oculto en los alimentos
¿Y si la bolsa de plástico fuese más sostenible que las de papel o algodón?
 Foto: Karina Tess / Unsplash
Foto: Karina Tess / UnsplashLas bolsas de plástico son las que peor reputación tienen. Esto sucede porque a menudo se juzga la sostenibilidad de las bolsas y su impacto medioambiental solo en función de si el material es fácilmente biodegradable. Sale ganando la bolsa de papel porque imaginamos que, si la tirásemos en el monte o al mar, se biodegradaría en poco tiempo. Sin embargo, este análisis es superficial e incompleto. No se está teniendo el cuenta el ciclo de vida de la bolsa: qué impacto medioambiental tiene su fabricación, cuánta energía se usa en su producción y transporte, cómo se conserva, si se reutiliza, cuánto tiempo de vida útil tiene…
Todos estos parámetros se han analizado científicamente y, para sorpresa de muchos, las bolsas de algodón y de papel no salen mejor paradas que las de plástico.
El análisis de ciclo de vida, ACV (LCA en inglés) es un balance ecológico con el que se evalúa el impacto ambiental de un producto durante todas las etapas de su existencia, desde la extracción de materias primas, la producción, la distribución, el uso, la posible reutilización, el reciclaje, la valorización y la gestión de residuos.
Las bolsas de plástico de polietileno surgieron en los años 60 como una alternativa sostenible a las bolsas de papel que se usaban tradicionalmente. El coste energético de fabricación es irrisorio en comparación con el papel, se usa una fracción residual de petróleo que no es útil como combustible, no implica tala de árboles, es más resistente y pesa diez veces menos que el papel, por lo que la huella de carbono derivada del transporte también se reduce diez veces. Todo parecían ventajas. Lo que no se esperaba es que se usasen de forma tan irresponsable.
Cada persona gasta de media 180 bolsas de plástico al año. En 2008 la media en España era de 300 bolsas por habitante y año, dato que se ha reducido más del 60% gracias a la reutilización, principalmente animada por campañas de concienciación medioambiental y por el cobro obligatorio de las bolsas.
El plástico es un material inerte y duradero, lo que en principio es ventajoso. Pero la realidad es que el 80% de los residuos que llegan al mar son plásticos. Cada año llegan al mar unos ocho millones de toneladas de plástico. China, Indonesia y Filipinas encabezan la clasificación de los países que más cantidad arrojan, y los 20 primeros –todos en Asia y África, excepto Estados Unidos y Brasil– son responsables del 83% del plástico mal gestionado que puede acabar en el mar. De todo el plástico que llega al mar, el 1,5% se ha convertido en microplásticos, se ha ido fragmentando hasta transformarse en pedazos tan pequeños que son muy difíciles de eliminar.
El plástico llega al mar porque no se está reciclando ni destruyendo como es debido. En España solo el 66,5% del plástico se recicla y el 12% se incinera para obtener energía.
Con respecto al la influencia sobre el cambio climático podemos hacer un cálculo que nos permite saber la cantidad de CO2 emitido por el uso de bolsas de plástico, incluyendo su incineración. Una bolsa de plástico tiene una masa de entre 4 y 8 g. Cada persona gasta unas 180 bolsas de plástico al año, mayoritariamente de polietileno. Haciendo los cálculos estequiométricos, el uso de bolsas de plástico supone un aporte de 340 g de CO2 al año por individuo. En comparación con el transporte esto es muy poco: desplazarse en coche sólo 3 o 4 km (dependiendo del modelo) también produce 340 g de CO2.
 Fábrica de pasta de celulosa en Finlandia. Fuente: Wikimedia Commons
Fábrica de pasta de celulosa en Finlandia. Fuente: Wikimedia CommonsHaciendo el análisis del ciclo de vida (ACV) de las bolsas de plástico convencionales comparadas con las de papel, sale ganado ampliamente la bolsa de plástico. La producción y consumo de papel tienen un fuerte impacto ambiental y social sobre el planeta. La industria papelera y de celulosa ocupa el quinto lugar del sector industrial en consumo mundial de energía, y utiliza más agua por cada tonelada producida que cualquier otra industria. También, la industria papelera se encuentra entre los mayores generadores de contaminantes del aire y del agua, así como gases de efecto invernadero responsables del cambio climático. Tendríamos que reutilizar la bolsa de papel tres veces para que su impacto medioambiental sea equivalente al de una bolsa de plástico convencional. Es decir, usar y tirar una bolsa de plástico tiene un impacto medioambiental tres veces menor que hacerlo con una de papel. Si además reutilizamos la bolsa de plástico una sola vez, aunque solo sea para contener basura, el impacto será 6 veces menor que el de la bolsa de papel.
Si analizamos el ciclo de vida (ACV) de las bolsas de algodón, su impacto medioambiental es el más dañino de todos. El algodón se cultiva de forma intensiva, necesita de mucho terreno, un importante gasto energético y su transformación en tejido emite, entre otras sustancias nocivas, gases de efecto invernadero. Producir 1 kg de tejido de algodón requiere más de 40.000 litros de agua en promedio, una sed mucho mayor que la de cualquier vegetal e incluso la mayoría de las carnes. A diferencia del papel, también hay que tener en cuenta que el algodón no se recicla en la mayoría de los países.
 Cosecha y empaquetamiento sobre el terreno de algodón en Texas (EE.UU.). Fuente: Wikimedia Commons
Cosecha y empaquetamiento sobre el terreno de algodón en Texas (EE.UU.). Fuente: Wikimedia CommonsA esto hay que añadir que las bolsas de algodón son la opción menos higiénica. El algodón es un material que puede ser colonizado por microorganismos patógenos, por lo que no debería ponerse en contacto directo con alimentos, y debería lavarse con la misma asiduidad y a la misma temperatura que los trapos de cocina. El gasto energético y el impacto medioambiental derivado de su uso es sustancial.
En comparación, una bolsa de algodón habría que utilizarla 131 veces para que su impacto medioambiental fuese equiparable al de la bolsa de plástico convencional.
La única forma en la que una bolsa de tela es más sostenible que una de papel es usándola muchas veces a lo largo de mucho tiempo. Y tener dos o tres bolsas de algodón, no decenas. Lo mismo podría decirse de las bolsas de papel. Sin embargo, las bolsas de papel no resisten tantas reutilizaciones, principalmente porque se contaminan, no son lavables y se descomponen con la humedad.
Analizando toda la evidencia científica de la que disponemos, las bolsas de plástico son la opción más sostenible. Si además las reutilizamos y las llevamos al contenedor adecuado (en España es el contenedor amarillo), el impacto medioambiental será todavía menor. En la actualidad ya hay superficies comerciales en las que ofrecen bolsas reutilizables de plástico de poliéster para frutas y verduras, más sostenibles que las habituales de polietileno de baja densidad.
 Bolsa de plástico de poliéster. Foto: Deborah García Bello
Bolsa de plástico de poliéster. Foto: Deborah García Bello
La opción más sostenible de todas es la que engloba las bondades del plástico y las del uso responsable que solemos hacer con las de algodón, que se prestan a un mayor número de reutilizaciones. Las bolsas de rafia, por ejemplo, que son un tejido de plástico de polietileno y propileno, son muy resistentes, estéticas e higiénicas. También lo son las de poliéster, como la «puto plástico» de la foto que, irónicamente también es de plástico.
Fuentes:
Lewis, H., Verghese, K., & Fitzpatrick, L. (2010). Evaluating the sustainability impacts of packaging: the plastic carry bag dilemma. Packaging Technology and Science: An International Journal, 23(3), 145-160.
Edwards, C., & Fry, J. M. (2011). Life cycle assessment of supermarket carrier bags. Environment Agency, Horizon House, Deanery Road, Bristol, BS1 5AH.
Bell, K., & Cave, S. (2015). Comparison of Environmental Impact of Plastic, Paper and Cloth Bags. Research and Library Service Briefing Note, Northern Ireland Assembly
Interim Review os the Plastic Shopping Bags Ban. ACT Government. 2012.
Hyder Consulting, LCA of shopping bag alternatives: Final report, Zero Waste South Australia, August 2009, p.3
Daniel Montoya. Plastic bags: an update. NSW Parliamentary Research Service April 2013
The Danish Environmental Protection Agency (2018). Life Cycle Assessment of grocery carrier bags.
Brian Halweil y Lisa Mastny. Informe anual del Worldwatch Institute sobre progreso hacia una sociedad sostenible. Ed. Icaria, Noruega, 2004.
Advancing Sustainable Materials Management: 25Fact Sheet Assessing Trends in Material Generation, Recycling, Composting, Combustion with Energy Recovery and Landfilling in the United States July 2018
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo ¿Y si la bolsa de plástico fuese más sostenible que las de papel o algodón? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Adiós a las microesferas de plástico en los cosméticos
- Si hacer fármacos fuese como jugar a Lego, la pieza más guay se llamaría carbino
- Corales, ciencia y plástico.
Composición nº1, la historia de X gobernada por el azar
Una tirada de dados jamás abolirá el azar.
Stéphane Mallarmé
Un Coup de Dés jamais n’abolira le Hasard –Una tirada de dados jamás abolirá el azar– es el título de un poema de Stéphane Mallarmé (1842-1898) publicado en 1897. Compuesto en forma de versos libres, es uno de los primeros poemas tipográficos de la literatura francesa.
El título de este poema, junto a su autor, aparece en el colofón del libro Composición n01 de Marc Saporta (1923-2009) en su traducción al castellano publicada por la editorial Capitán Swing en 2012. La primera versión, en francés, fue publicada en 1962 por la editorial Le Seuil.
Composición n01 es una novela compuesta por 150 hojas no encuadernadas, no numeradas, escritas por una única cara e introducidas al azar en una caja.
 Foto: Marta Macho Stadler.
Foto: Marta Macho Stadler.
En el prefacio, el autor explica las ‘instrucciones de uso’ de su novela y proporciona algunas claves sobre la lectura:
Se ruega al lector que mezcle estas páginas como una baraja. Que las corte, si lo desea, con la mano izquierda, igual que una echadora de cartas. El orden en el que salgan las hojas después de hacerlo orientará el destino de X.
Porque el tiempo y el orden de los acontecimientos regulan la vida más que la naturaleza de estos acontecimientos. Sin duda, la Historia impone un marco: la pertenencia de un hombre al maquis y su paso por las tropas de ocupación en Alemania pertenecen a una época determinada. Asimismo, los hechos que marcaron su infancia no pueden presentarse como vividos en la edad adulta.
No obstante, no es indiferente saber si conoció a su amante, Dagmar, antes o después de su matrimonio; si abusó de la pequeña Helga durante su adolescencia o su madurez; si el robo que cometió tuvo lugar bajo el abrigo de la Resistencia o en tiempos menos turbulentos; si el accidente del que fue víctima carece de relación con el robo (o la violación) o si tuvo lugar durante la huida.
Del encadenamiento de las circunstancias depende que la historia acabe bien o mal. Una vida se compone de elementos múltiples. Pero el número de composiciones posibles es infinito.
El libro de Saporta ‘cuenta’ una historia de un personaje misterioso. Una, y no la historia, porque el relato transcurre dependiendo del orden en el que se colocan las hojas tras barajarlas, como indica el autor en el prefacio. Cada página corresponde a un episodio procedente de los recuerdos del personaje X. Este narrador aparece como un ladrón y un violador. De hecho, dos de las páginas de Composición n01 se dedican a citar algunos artículos –entiendo que eran los que estaban vigentes en Francia cuando Saporta publicó su texto, en 1962– relativos a los delitos de robo y violación.
Al recorrer las páginas de esta singular novela, la historia va incorporando diferentes personajes, algunos de los cuales son recurrentes: Marianne –la esposa de X–, Dagmar –su amante– o Helga –una joven a la que X viola– aparecen en numerosas ocasiones, mientras que otros personajes solo son citados en una de las páginas. Cada una de las hojas corresponde a un marco espacio-temporal que cambia continuamente. El lugar elegido –una ciudad ocupada por el ejército alemán, el patio de una escuela o el apartamento de alguno de los personajes– depende de lo que el azar dispone tras barajar las páginas del libro.
Aunque pienses que estoy intentando ‘destripar’ la versión de Composición n01 que he leído, no pasa nada; es bastante improbable que, tras barajar las páginas del libro, la versión que tú vas a leer sea la misma que la mía…
 Foto: Marta Macho Stadler.
Foto: Marta Macho Stadler.
El prefacio de Marc Saporta termina con la frase: Pero el número de composiciones posibles es infinito. En realidad, Composición n01 no contiene infinitas versiones de la historia de X. Aunque es cierto que contiene muchas. De hecho, al haber 150 páginas que pueden ordenarse de manera aleatoria, el número de novelas distintas que podemos leer es la factorial de 150 –son las permutaciones sin repetición de 150 elementos–.
Para hacernos una idea de esa cantidad de versiones, el factorial de 150 es el número:
57133839564458545904789328652610540031895535786011264182548375833179829124845398393126574488675311145377107878746854204162666250198684504466355949195922066574942592095735778929325357290444962472405416790722118445437122269675520000000000000000000000000000000000000,
número que está formado por 263 cifras y finaliza con 37 ceros. Redondeando, el factorial de 150 es aproximadamente 5,7 x 10262. Y, efectivamente, es un número muy, muy grande… pero no infinito.
Referencias
-
Una tirada de dados jamás abolirá el azar de Stéphane Mallarmé (Una propuesta estético-filosófica de Juan David García Bacca, incluida en su obra «Necesidad y Azar. Parménides y Mallarmé», Editorial Antrophos, Barcelona, 1985), Revista aesthethika 12 (2), septiembre 2016. Caos e invención, pág. 53-54
-
Marc Saporta, Composición no1, Capitán Swing, 2012
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Composición nº1, la historia de X gobernada por el azar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ‘La Historia es la ciencia de la desgracia de los hombres’
- El teorema de los cuatro colores (1): una historia que comienza en 1852
- Ciegos ante el azar
El comportamiento ondulatorio de los electrones
 Una imagen por difracción de electrones parecida a esta pero tomada en 1982 terminó dándole el premio Nobel de química a Dan Shechtman en 2011 por el descubrimiento de los cuasicristales. Fuente: Wikimedia Commons
Una imagen por difracción de electrones parecida a esta pero tomada en 1982 terminó dándole el premio Nobel de química a Dan Shechtman en 2011 por el descubrimiento de los cuasicristales. Fuente: Wikimedia CommonsEn 1923, Louis de Broglie sugirió que la dualidad onda-corpúsculo que se aplica a los fotones, a la radiación electromagnética, también podría aplicarse a los electrones y otras partículas atómicas. Quizás, dijo, la dualidad onda-corpúsculo es una propiedad fundamental de todos los procesos cuánticos. Si es así, las partículas que siempre se consideraron corpúsculos materiales pueden, en algunas circunstancias, actuar como ondas. De Broglie buscó una expresión para la longitud de onda que podría estar asociada con el comportamiento ondulatorio de un electrón. Encontró la expresión con un argumento muy simple.
El momento lineal de un fotón de longitud de onda λ es p = h/λ o, dicho de otra forma, la longitud de onda del fotón es λ = h/p. De Broglie pensó que esta relación también podría aplicarse a los electrones que se mueven con velocidad v y, por tanto, con un momento lineal p = mv. Sugirió audazmente que la longitud de onda de un electrón es λ = h/mv, donde m es la masa del electrón y v su velocidad.
Pero, ¿qué significa decir que un electrón tiene una longitud de onda igual a la constante de Planck dividida por su mometo lineal? Como hemos visto, si esta afirmación tiene algún significado físico debe ser posible comprobarla mediante algún tipo de experimento. En este caso, se debería poder medir alguna propiedad ondulatoria del electrón. La primera de esas propiedades que se pudo medir fue la difracción.
De la relación λ = h/mv se deduce que las longitudes de onda asociadas a los electrones serán muy cortas, incluso para electrones bastante lentos. Un electrón acelerado a través de una diferencia de potencial de solo 100 V tendría una longitud de onda de solo 10-10 m. Una longitud de onda tan pequeña no daría efectos de difracción mensurables al encontrar incluso un objeto microscópicamente pequeño (digamos, de una micra, 10-6 m). No podía manipularse un objeto así en la época. Había que buscar algo del tamaño de la longitud de onda que pudiese usarse.
En 1920 estaba bien establecido que los cristales tienen una estructura reticular regular. La distancia entre los planos de átomos en un cristal es de aproximadamente 10-10 m. Tras proponer De Broglie que los electrones podían tener propiedades de onda, varios físicos sugirieron que la existencia de ondas de electrones podría mostrarse usando cristales como rejillas de difracción. Los experimentos iniciados en 1923 por C.J. Davisson y L.H. Germer encontraron patrones de difracción similares a los obtenidos anteriormente para los rayos X.
El experimento de Davisson-Germer demostraba dos cosas. Primero, los electrones tienen propiedades de onda, de lo contrario no podrían mostrar el patrón de difracción de las ondas. Se podría decir que un electrón se mueve siguiendo el camino que toma la onda de Broglie que está asociada al electrón. En segundo lugar, las longitudes de onda de los electrones están dadas correctamente por la relación de de Broglie, λ = h/mv .
 Patrón de difracción obtenido al hacer incidir un haz de electrones en aluminio policristalino (una masa de aluminio compuesta de multitud de cristales diminutos orientados al azar). G.P. Thomson encontró un patrón similar usando una lámina de oro. Fuente: Cassidy Physics Library.
Patrón de difracción obtenido al hacer incidir un haz de electrones en aluminio policristalino (una masa de aluminio compuesta de multitud de cristales diminutos orientados al azar). G.P. Thomson encontró un patrón similar usando una lámina de oro. Fuente: Cassidy Physics Library.Estos resultados fueron confirmados en 1927 cuando G.P. Thomson [1] hizo pasar un haz de electrones a través de una delgada lámina de oro. Thomson encontró un patrón como el que se muestra en la imagen 1. Se asemeja a los patrones de difracción producidos por los haces de luz que atraviesan hojas finas de materiales. Para 1930 la difracción que se producía en los cristales había permitido demostrar el comportamiento ondulatorio incluso de los átomos de helio y de las moléculas de hidrógeno. [2]
Los experimentos que confirmaban la hipótesis de De Broglie indicaban que la dualidad onda-corpúsculo es una propiedad general no solo de la radiación sino también de la materia.
Notas:
[1] Sí, el hijo de J.J. Thomson.
[2] Se puede decir que Joseph John Thomson demostró que el electrón es una partícula y que su hijo George Paget Thomson que es una onda. J.J. recibió el Nobel en 1906 y G.P. en 1937.
El artículo El comportamiento ondulatorio de los electrones se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El comportamiento corpuscular de la luz: el efecto Compton
- El comportamiento corpuscular de la luz: momento lineal del fotón
- La realidad de los estados estacionarios
El ethos de la ciencia
 Lise Meitner con unas estudiantes estadounidenses (Sue Jones Swisher, Rosalie Hoyt y Danna Pearson McDonough) en las escaleras del edificio de química del Bryn Mawr College (Pennsylvania, EE.UU.) en abril de 1959. Meitner, de origen judío, nació en Austria, trabajó en Alemania y finalmente se refugió en Suecia debido a la persecución nazi. Participó notablemente en el descubrimiento de la fisión nuclear. Su compañero de equipo Otto Hahn recibió el premio Nobel (1944), pero no ella cuando era igualmente merecedora, si no más.
Lise Meitner con unas estudiantes estadounidenses (Sue Jones Swisher, Rosalie Hoyt y Danna Pearson McDonough) en las escaleras del edificio de química del Bryn Mawr College (Pennsylvania, EE.UU.) en abril de 1959. Meitner, de origen judío, nació en Austria, trabajó en Alemania y finalmente se refugió en Suecia debido a la persecución nazi. Participó notablemente en el descubrimiento de la fisión nuclear. Su compañero de equipo Otto Hahn recibió el premio Nobel (1944), pero no ella cuando era igualmente merecedora, si no más.Dado que lo que aquí nos interesa es la cuestión de los males que afligen a la empresa científica, nos parece conveniente partir de una exposición de los valores de la ciencia, puesto que, en general, los males son rasgos que se oponen a aquellos. Empezaremos por los valores o normas enunciadas por el sociólogo Robert K. Merton en la primera mitad del siglo pasado, para pasar, en la anotación siguiente, a otras visiones de esta misma cuestión.
Las consideraciones éticas no son ajenas al desempeño científico. La investigación se rige por un código de comportamiento que asumimos como propio quienes nos dedicamos a esa actividad. En 1942, el sociólogo Robert K. Merton postuló la existencia de un “ethos científico”, un conjunto de valores que deben impregnar o inspirar la actividad científica. Sin ellos la ciencia, como empresa colectiva, perdería su misma esencia. Según él, la palabra «ciencia» hace referencia a diferentes cosas, aunque relacionadas entre sí. Normalmente se utiliza para denotar: (1) un conjunto de métodos característicos mediante los cuales se certifica el conocimiento; (2) un acervo de conocimiento acumulado que surge de la aplicación de estos métodos; (3) un conjunto de valores y normas culturales que gobiernan las actividades científicas; (4) cualquier combinación de los elementos anteriores.
En expresión de Merton (1942), “el ethos de la ciencia es ese complejo, con resonancias afectivas, de valores y normas que se consideran obligatorios para el hombre de ciencia. Las normas se expresan en forma de prescripciones, proscripciones, preferencias y permisos. Se las legitima sobre la base de valores institucionales. Estos imperativos, trasmitidos por el precepto y el ejemplo, y reforzados por sanciones, son internalizados en grados diversos por el científico, moldeando su conciencia científica. Aunque el ethos de la ciencia no ha sido codificado, se lo puede inferir del consenso moral de los científicos tal como se expresa en el uso y la costumbre, en innumerables escritos sobre el espíritu científico y en la indignación moral dirigida contra las violaciones del ethos”.
Para Merton (1942), el fin institucional de la ciencia es el crecimiento del conocimiento certificado. Y los métodos empleados para alcanzar ese fin proporcionan la definición de conocimiento apropiada: enunciados de regularidades empíricamente confirmados y lógicamente coherentes (que son, en efecto, predicciones). Los imperativos institucionales (normas) derivan del objetivo y los métodos. Toda la estructura de normas técnicas y morales conducen al objetivo final. La norma técnica de la prueba empírica adecuada y confiable es un requisito para la constante predicción verdadera; la norma técnica de la coherencia lógica es un requisito para la predicción sistemática y válida. Las normas de la ciencia poseen una justificación metodológica, pero son obligatorias, no solo porque constituyen un procedimiento eficiente, sino también porque se las cree correctas y buenas. Son prescripciones morales tanto como técnicas.
Merton (1942) propuso cuatro conjuntos de imperativos institucionales: el universalismo, el comunalismo, el desinterés y el escepticismo organizado, como componentes del ethos de la ciencia moderna.
Si la comunidad científica comparte un proyecto común –la construcción de un cuerpo de conocimiento certificado o fiable acerca del mundo y de cómo funciona-, las normas que Merton (1942) identificó son algo parecido a los valores compartidos por esa comunidad, valores que son considerados esenciales. Una interpretación actualizada de las normas mertonianas, es la que propone el físico John Ziman (2000), y que se presenta a continuación.
- Lo importante en la ciencia no es quién la practica, sino su contenido, los conocimientos que adquirimos acerca del mundo y de los fenómenos que ocurren en él. Todos pueden contribuir a la ciencia con independencia de su raza, nacionalidad, cultura o sexo.
- El conocimiento certificado debería ser compartido por el conjunto de la comunidad científica, con independencia de qué parte de los descubrimientos ha sido hecha por unos u otros científicos. Así pues, todos deberían tener el mismo acceso a los bienes científicos y debería haber un sentido de propiedad común al objeto de promover la colaboración. El secretismo es lo opuesto a esta norma, puesto que el conocimiento que se oculta, que no se hace público, no es de ninguna ayuda en el cumplimiento del objetivo de la comunidad, que el conocimiento certificado crezca.
- Desinterés. Se supone que los científicos actúan en beneficio de una empresa común, más que por interés personal. No obstante, no debe confundirse este “desinterés” con altruismo. De lo que se trata es de que el beneficio que pueda reportar los descubrimientos científicos, sin dejar de resultar beneficiosos para quien los realice, no entorpezca o dificulte la consecución del objetivo institucional de la ciencia: la extensión del conocimiento científico.
- Escepticismo organizado El escepticismo quiere decir que las declaraciones o pretensiones científicas deben ser expuestas al escrutinio crítico antes de ser aceptadas. Este es el valor que compensa el universalismo. Todos los miembros de la comunidad científica pueden formular hipótesis o teorías científicas, pero cada una de ellas debe ser evaluada, sometida al filtro de la prueba o la refutación para comprobar si se sostiene. Las propuestas que superan esa prueba con éxito pasan a formar parte del bagaje universal de conocimiento científico. El escepticismo es el valor que permite que funcione el del desinterés, porque sin escepticismo es más fácil caer en la tentación de anteponer el interés personal al del conjunto de la comunidad científica.
A los científicos no se nos da un manual con esas normas. Se supone que las adquirimos prestando atención a lo que hacen otros científicos en nuestra comunidad, los comportamientos que se castigan y los que se premian. En otras palabras, no es necesariamente lo que los científicos hacemos habitualmente; porque a veces lo que hacemos no satisface lo que pensamos que deberíamos hacer.
Hace unos años MacFarland & Cheng (2008) analizaron en qué medida los miembros de la academia hacen suyas en la actualidad las normas mertonianas y comprobaron que la norma que menos apoyo recibe es el desinterés. Interpretan ese menor apoyo como una consecuencia de la tendencia creciente a alinear los intereses de investigación con las oportunidades de financiación. Y cabe plantearse si el menor apoyo al ideal del desinterés constituye una disfunción del sistema científico o, por el contrario, es simplemente muestra de una concepción de la empresa científica diferente de la que en su día concibió Robert Merton.
No obstante, creo que el conjunto de valores aquí expuesto sería suscrito como deseable por la mayoría de científicos, por lo que me parece un buen punto de partida para evaluar la medida en que esos valores impregnan la práctica de la investigación científica que realmente se hace. Por esa razón, me ha parecido adecuado denominar “males de la ciencia” a aquellos comportamientos que no se ajustan a esos principios o aquellas formas de funcionar del sistema científico que impiden o dificultan su cumplimiento.
Fuentes:
Merton, R K (1942): “Science and Technology in a Democratic Order” Journal of Legal and Political Sociology1: 115-126. [Traducción al español como “La estructura normativa de la ciencia” en el volumen II de “La Sociología de la Ciencia” Alianza Editorial 1977, traducción de The Sociology of Science – Theoretical and Empirical Investigations, 1973]
Ziman, J (2000): Real Science: What It Is and What It Means. Cambridge University Press.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo El ethos de la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El ethos de la ciencia y las normas de Merton
- La ciencia no tiene valores… ¿o sí los tiene?
- La hostilidad a la ciencia
Ha llegado el frío
 Foto: Talgat Baizrahmanov / Unsplash
Foto: Talgat Baizrahmanov / UnsplashPara mantener la temperatura corporal constante cuando llega el frío, un animal homeotermo necesita reponer mediante el metabolismo el calor que pierde. Esa pérdida depende de la diferencia entre la temperatura del organismo y la del ambiente, por un lado, y del grado de aislamiento, por el otro. Por esa razón y si dejamos al margen a los hibernantes, el modo en que los mamíferos responden a la bajada invernal de temperatura tiene dos componentes principales. Por un lado, aumentan el grado de aislamiento con el exterior. Y por el otro, si la temperatura ambiental baja mucho, también elevan la actividad metabólica; producen así más calor y compensan la mayor pérdida.
El aislamiento se puede modificar de varias formas: cambiando la postura corporal para exponer una menor o mayor superficie al exterior, limitando la circulación sanguínea por la periferia de las extremidades y dejando que se enfríen, o actuando sobre el pelaje para cambiar el grosor de la capa de aire que aísla la superficie del cuerpo del exterior. Pero por debajo de cierta temperatura esas respuestas no bastan y hay que gastar más energía, como se ha dicho, elevando el metabolismo. Por eso es importante contar con alimento abundante cuando llega el frío o, en su defecto, con depósitos de reservas.
Pero los seres humanos somos especiales. Somos homeotermos, sí, pero nuestra especie surgió en África y nuestro linaje homínido es africano. Evolucionamos en la sabana y muchas de nuestras características son claro reflejo de nuestra procedencia. Durante esa evolución nos quedamos prácticamente desnudos y desarrollamos una gran capacidad para sudar y refrigerarnos de una manera muy eficiente evaporando el sudor sobre la superficie corporal. De hecho, el desplazamiento a zonas frías nos obligó a vestir ropas con una capacidad de aislamiento adecuado a la temperatura de cada zona. Y a pesar de todo, la vida en lugares verdaderamente fríos nos ha exigido esfuerzos considerables para disponer de habitación confortable (gastando en calefacción), vestir ropas de abrigo y conseguir el alimento necesario para comer más.
Cuando los sensores de temperatura que tenemos repartidos por diferentes lugares del cuerpo detectan la bajada térmica, informan al hipotálamo, una estructura nerviosa en el interior del encéfalo. Y este responde dando las órdenes debidas, tanto al sistema endocrino como al nervioso. Ciertas órdenes provocan cambios en la circulación sanguínea periférica y en la disposición del pelaje, de manera que se aumenta el grado de aislamiento. Y otras elevan la actividad metabólica. En esos ajustes intervienen hormonas tales como la adrenalina, la noradrenalina y las tiroideas, que provocan un aumento del metabolismo. Quienes tienen grasa parda llevan ventaja, porque es un tejido cuya única función es producir calor. Y llegado el caso, tiritamos también.
Los mamíferos de zonas frías están, lógicamente, bien adaptados a la vida en entornos helados. Una cría de oso polar mantiene su metabolismo constante hasta 0ºC, y se estima que solo llegaría a multiplicarlo por tres a 60ºC bajo cero. Los zorros árticos, perros esquimales y demás grandes mamíferos árticos prácticamente no necesitan elevar su metabolismo salvo a temperaturas verdaderamente extremas, como 25 o 30ºC bajo cero. Pero a los seres humanos, como no hemos dejado de ser primates de sabana, todo eso nos sale muy caro. Un individuo desnudo empieza a elevar su metabolismo al descender la temperatura de 26ºC, aproximadamente, y a 8ºC lo triplica.
De lo anterior se extrae una triste conclusión. El frío es especialmente cruel con los pobres de solemnidad: no solo no tienen recursos para calentar el entorno en el que viven, tampoco los tienen para calentar su propio interior.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Ha llegado el frío se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:1969: el año en el que llegamos a la Luna e inventamos Internet

El año 1969 marcó un antes y un después. Fue el año en el que el ser humano pisó por primera vez un astro distinto al que nos vio nacer: la Luna. Fue, sin ninguna duda, un momento histórico. Pero, pocos meses después sucedería algo que cambiaría nuestro mundo por completo: un grupo de ingenieros en los Estados Unidos consiguió que dos ordenadores de distintos fabricantes se hablaran entre ellos, estableciendo así el germen de lo que sería Internet. Ese hecho pasó desapercibido en esos momentos, pero para muchos fue un hito mucho más relevante que lo que supuso nuestra llegada a la Luna.
Javier Pedreira, divulgador científico en el blog Microsiervos donde firma como Wicho, repasa en esta charla cómo fueron y que significaron estos dos hitos históricos.
Pedreira es responsable de Informática de los Museos Científicos Coruñeses desde hace ya casi 15 años y cofundador Microsiervos, uno de los blogs sobre ciencia y tecnologías más leídos en español en el mundo. Además, es colaborador habitual en varios medios de comunicación.
Esta charla se enmarca en el ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
Edición realizada por César Tomé López
El artículo 1969: el año en el que llegamos a la Luna e inventamos Internet se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Álex Méndez: Luz de luna
- Naukas Bilbao 2017 – Ángel Gómez Roldán: Tras la sombra de la Luna
- Coloquios escépticos: ¿Fuimos a la Luna?, con Eugenio Manuel Fernández Aguilar
Un aislante topológico intrínsecamente magnético
 Un cristal de telururo de bismuto y manganeso, el primer aislante topológico magnético predicho y confirmado. Foto: A. Isaeva, TU Dresden/IFW Dresden
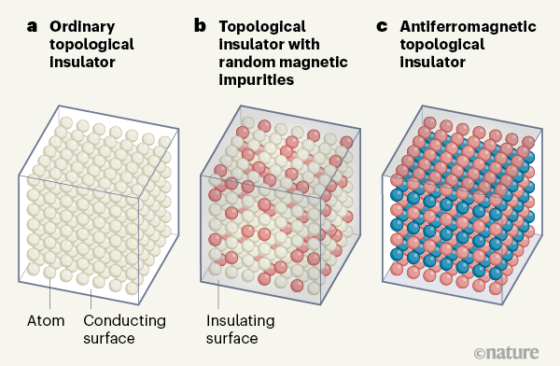
Un cristal de telururo de bismuto y manganeso, el primer aislante topológico magnético predicho y confirmado. Foto: A. Isaeva, TU Dresden/IFW DresdenLos materiales llamados aislantes topológicos son aquéllos que no dejan pasar la corriente eléctrica en su volumen, pero sí sobre su superficie. A diferencia de los conductores habituales, como los metales, la corriente no sufre ninguna pérdida de energía al circular en la superficie de un aislante topológico. Esta propiedad abre grandes posibilidades de aplicación en electrónica, pues facilitaría la fabricación de dispositivos más eficientes y rápidos, propiedades muy deseables habida cuenta del rápido avance de la demanda energética mundial asociada a la electrónica. No es de extrañar, por tanto, que el descubrimiento de los aislantes topológicos hace aproximadamente una década causase que la investigación en nanotecnología y en física de la materia condensada dedicase buena parte de sus recursos a ellos.
Uno de los retos durante estos años de intensa investigación, por las aplicaciones tecnológicas que podría tener en las tecnologías de la información, por ejemplo, ha sido la creación de un aislante topológico magnético. Hasta hace poco el magnetismo se introducía en los aislantes topológicos no-magnéticos exclusivamente por la llamada vía extrínseca, que consiste en añadir átomos que confieren propiedades magnéticas. Sin embargo, gracias al esfuerzo de un grupo de investigadores del Centro de Física de Materiales (CFM, centro mixto CSIC-UPV/EHU), el Donostia International Physics Center (DIPC) y la Universidad del País Vasco (UPV/EHU) ahora ya es posible fabricar un aislante topológico magnético intrínseco, esto es, que tiene propiedades magnéticas por su propia naturaleza. Los resultados se han publicado en Nature y han merecido un análisis en News & Views.
 Fuente: Nature
Fuente: NatureEl equipo formado por los investigadores Mikhail Otrokov, Evgueni Chulkov, María Blanco Rey y Pedro M. Etxenike, ha logrado predecir teóricamente el primer aislante topológico magnético, el telururo de bismuto y manganeso, de fórmula química MnBi2Te4. El investigador Ikerbasque y líder del estudio, Mikhail Otrokov, afirma que «el trabajo previo desde diferentes enfoques nos llevó a la conclusión de que la ruta intrínseca era la única viable hoy en día. Entonces dirigimos nuestros esfuerzos a encontrar un aislante topológico magnético intrínseco basándonos en experiencias previas, gracias a las cuales supimos qué estructura cristalina y composición atómica debía tener tal material».
La confirmación experimental de la predicción ha sido un trabajo que ha involucrado a investigadores expertos en distintas áreas de centros de investigación de referencia de Rusia, Azerbaiyán, Alemania, Austria, Japón, Italia y los EE.UU, coordinados por los investigadores de los centros vascos. Otrokov ha explicado que para la confirmación experimental la primera tarea fue la síntesis de los cristales del compuesto por parte de los expertos en síntesis química. Una vez sintetizadas, las muestras fueron sometidas a multitud de experimentos de caracterización estructural, magnética, electrónica, de transporte, de composición atómica, etc. que han permitido verificar las características predichas.
«El MnBi2Te4 además de ser un aislante topológico con propiedades magnéticas intrínsecas, ha resultado ser un material antiferromagnético, tal y como habíamos calculado», explica Blanco. El antiferromagnetismo consiste en un orden magnético a escala atómica tal que el material carece de magnetización neta. Por ello estos materiales son mucho más robustos frente a perturbaciones por imanes.
El telururo de bismuto y manganeso tiene un gran potencial tanto a nivel fundamental como a nivel tecnológico. Es extraordinariamente rico en propiedades exóticas, como, por ejemplo, varios efectos de Hall, incluido el efecto Hall cuántico, algunos de los cuales se utilizan en la calibración de constantes físicas por su excepcional precisión. El MnBi2Te4 también se puede usar para la creación de los llamados fermiones de Majorana. Un tipo de partícula que se ha llegado a considerar la piedra angular de la computación cuántica. Asimismo, el MnBi2Te4 es el primer material intrínseco para el que se predice una respuesta electromagnética muy similar a la de un axión, una hipotética partícula postulada en el marco de la cromodinámica cuántica, que es buena candidata para resolver el problema de la materia oscura. Por ello se están diseñado muchos experimentos dirigidos precisamente a la detección de señales de un comportamiento de tipo axión en la familia de este compuesto.
Los resultados del estudio, que ya habían sido publicados en arXiv y difundidos en charlas impartidas por los autores en congresos internacionales, han sido bien recibidos por la comunidad científica internacional. A día de hoy el MnBi2Te4 y otros materiales basados en él se están estudiando en decenas de centros de investigación, siendo los radicados en EE.UU. y China los que muestran una actividad más intensa.
Ya se han patentado ya varios dispositivos basados en los aislantes topológicos magnéticos. Así, el MnBi2Te4 puede ser utilizado en las interconexiones quirales de los circuitos integrados, que prometen un rendimiento superior a las conexiones de cobre ordinarias que se emplean actualmente en los circuitos disponibles comercialmente. Otras aplicaciones incluyen moduladores ópticos, sensores de campo magnético y elementos de memoria.
Los investigadores, junto a su red de colaboradores internacionales, esperan poder observar en el MnBi2Te4 algunas de las exóticas propiedades mencionadas y descubrir nuevos aislantes topológicos magnéticos intrínsecos con características incluso superiores que las del propio MnBi2Te4.
Referencia:
M. M. Otrokov, I. I. Klimovskikh, H. Bentmann, D. Estyunin, A. Zeugner, Z. S. Aliev, S. Gaß, A. U. B. Wolter, A. V. Koroleva, A. M. Shikin, M. Blanco-Rey, M. Hoffmann, I. P. Rusinov, A. Yu. Vyazovskaya, S. V. Eremeev, Yu. M. Koroteev, V. M. Kuznetsov, F. Freyse, J. Sánchez-Barriga, I. R. Amiraslanov, M. B. Babanly, N. T. Mamedov, N. A. Abdullayev, V. N. Zverev, A. Alfonsov, V. Kataev, B. Büchner, E. F. Schwier, S. Kumar, A. Kimura, L. Petaccia, G. Di Santo, R. C. Vidal, S. Schatz, K. Kißner, M. Ünzelmann, C. H. Min, Simon Moser, T. R. F. Peixoto, F. Reinert, A. Ernst, P. M. Echenique, A. Isaeva and E. V. Chulkov.(2019) Prediction and observation of an antiferromagnetic topological insulator. Nature doi: 10.1038/s41586-019-1840-9
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un aislante topológico intrínsecamente magnético se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La teoría de bandas de los sólidos se hace topológica
- Superelasticidad nanométrica
- Trayectorias de las partículas cargadas en un campo magnético
La ciencia de llorar a gusto
Composers have a gift, as Barber did, for confirming with music what we already know—sad music intensifies sadness, and in that intensity, solace is somehow provided. [*]
The saddest music ever written, Thomas Larson, 2010.

Los humanos somos unos monos muy raros. A veces, cuando nos duele algo, goteamos. Pongamos que se nos ha muerto un cactus, que nuestro gato nos deja, que nos pillamos un dedo con la puerta. Entonces, una glándula de la región externa del ojo empieza a liberar un líquido salado lleno de proteínas, agua, moco y grasa. Este líquido, más conocido como lágrimas, fluye por la superficie del ojo y se desprende desde las pestañas hasta que, además de goteras, tenemos la cara roja, la nariz congestionada, el rímel como si lo hubiese aplicado Jackson Pollock…
A priori, no parece una reacción especialmente provechosa y, para colmo, los humanos somos la única especie que produce las llamadas lágrimas psíquicas o emocionales1. En su tercer libro sobre teoría evolutiva, La Expresión de las Emociones en el Hombre y los Animales (1872), Charles Darwin llegó a afirmar que este tipo de lágrimas son “inútiles”. Por suerte, algo hemos aprendido desde entonces.
Para empezar, hoy sabemos que no todas las lágrimas son iguales. Las lágrimas emocionales son solo un tipo. Las producimos cuando sentimos emociones intensas, principalmente dolor, pero también con la risa y la felicidad. Existen además lágrimas reflejas o irritativas, que son las que derramamos al ver sufrir a una cebolla o si se nos mete algo en el ojo. Y aunque desde fuera puedan parecer iguales, al microscopio las diferencias se vuelven evidentes. Si bien todas contienen lípidos, metabolitos, electrolitos y enzimas, las lágrimas emocionales tienen además una mayor cantidad de proteínas y hormonas que no se encuentran en el caso de las reflejas. En concreto, se encuentran sustancias relacionadas con la respuesta al estrés y al dolor, como la Encefalina (un anestésico natural) y la Adrenocorticotropa (un trabador de lenguas artificial), que podrían tener un efecto autorregulador. Eso explicaría por qué a veces uno se encuentra mejor después de una buena llorera.
Y para el profesor David Huron explicaría también, por qué disfrutamos de la música triste2: “Cuando una persona está en un estado triste, esta hormona llamada prolactina se libera y tiene un efecto psicológico de consuelo”. Es como si nuestro cuerpo tuviese un mecanismo para que la tristeza y el dolor no se agudicen demasiado, no alcancen ciertos límites que nos incapaciten. Ahora bien, es posible sentir esta sensación de alivio incluso en situaciones donde no existe ningún duelo real. Y una de esas situaciones se da cuando escuchamos música. “La música triste nos pone en un estado de duelo. Pero al final del día, ¡nada terrible ha sucedido!”, no se nos ha muerto el cactus, no nos ha dejado el gato, no hay restos de dedo en ninguna puerta. Por ello, afirma Huron, “sí es posible llorar a gusto, gracias a la música”.
Sin embargo, esta hipótesis sobre el llanto no es la única ni tampoco la más explicativa3. Si bien las lágrimas desencadenan una respuesta fisiológica, su función principal es actuar como señal. Los ojos con goteras, la nariz congestionada, la cara hinchada y salpicada como un Pollock… todos estos síntomas combinados comunican a otros Sapiens un mensaje claro y directo: “Socorro, necesito ayuda”.
En ese sentido, el llanto es muy distinto de la apacible tristeza. Mientras la tristeza deja ver indicios que pueden llegar a confundirse con otros estados fisiológicos (como el cansancio), el llanto es una señal explícita, su función es comunicar y por ello se vale de varios canales, para resultar más evidente e inequívoca. Cuando lloramos, no sólo goteamos; también vocalizamos de una manera muy peculiar: nuestra garganta se tensa, nuestra voz se agudiza, emitimos sonidos vibrantes y ruidosos, a veces sostenidos en el tiempo —notas largas que languidecen y se rinden hacia el grave—, otras veces, entrecortados en forma de sollozo. Nada que ver con los sonidos de la tristeza.
Algunos estudios muestran que, cuando vemos a alguien llorar, se activa en nosotros automáticamente una respuesta de empatía y compasión por los demás. ¿Quizás sucede lo mismo cuando oímos a un violín llorar?
Referencias:
1Asmir Gračanin, Lauren M. Bylsma, Ad J. J. M. Vingerhoets. “Why Only Humans Shed Emotional Tears”. Humane Nature, 2018.
2David Huron. “Why is sad music pleasurable? A possible role for prolactin”. Musicae Scientiae, 2011.
3Michael Trimble. “Why humans like to cry: Tragedy, evolution and the brain”. 2012
Nota:
[*] Los compositores tienen un don, como lo tenía Barber, para confirmar con música lo que ya sabemos; la música triste intensifica la tristeza, y en esa intensidad, de alguna manera, se proporciona consuelo. [Traducción de César Tomé López]
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo La ciencia de llorar a gusto se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El arte contemporáneo que mira al Tangram
En la octava edición del FIG Bilbao, Festival Internacional de Grabado y Arte sobre Papel, que tuvo lugar el pasado mes de noviembre en Bilbao, descubrí una serie de interesantes grabados del artista madrileño Javier Abad Alonso, co-fundador del estudio de grabado y galería Arco Tijera, relacionada con el Tangram, el clásico rompecabezas de tipo geométrico.
 Fotografía de la mesa de la galería Arco Tijera durante la celebración del festival FIG Bilbao, en la que podemos ver dos fotolitografías del artista Javier Abad Alonso de la serie que relaciona el rompecabezas Tangram con el cosmos. Imagen de la página de Facebook de Arco Tijera
Fotografía de la mesa de la galería Arco Tijera durante la celebración del festival FIG Bilbao, en la que podemos ver dos fotolitografías del artista Javier Abad Alonso de la serie que relaciona el rompecabezas Tangram con el cosmos. Imagen de la página de Facebook de Arco Tijera
El Tangram es un rompecabezas geométrico de origen chino, aunque de antigüedad desconocida (véase más sobre su historia en la entrada Tangram), formado por 7 piezas poligonales –5 triángulos, 1 cuadrado y 1 paralelogramo de tipo romboide (que pueden verse en la siguiente imagen) – con las cuales se puede formar la figura básica, que es un cuadrado, o una enorme familia de figuras, tanto figurativas (animales, personas, objetos, números, letras, etc), como geométricas (figuras poligonales convexas, etc), además de poder ser utilizado de forma didáctica para aprender matemáticas (teorema de Pitágoras, áreas, ángulos, etc).
 Las siete piezas del Tangram formando la figura básica del cuadrado
Las siete piezas del Tangram formando la figura básica del cuadradoEste rompecabezas geométrico nos permite incluso jugar con algunas paradojas, es decir, dos figuras formadas por las siete piezas del Tangram, de igual aspecto, salvo que aparentemente una de ellas es una “extensión” (tiene un añadido) de la otra. La paradoja más conocida es la que consiste en dos monjes y que aparece en el libro Amusements in Mathematics (1917), del matemático recreativo Henry Dudeney (1857-1930). Otras dos conocidas paradojas pertenecen a la persona que popularizó el Tangram, el jugador de ajedrez y matemático recreativo Sam Loyd (1841-1911), que las incluye en su libro The Eighth Book of Tan (1903). En la siguiente imagen mostramos la paradoja de la taza mágica.
 Paradoja de la taza mágica, de Sam Loyd, que consiste en tres tazas similares, aparentemente una de ellas con más superficie que las otras dos. Imagen de Wikimedia Commons
Paradoja de la taza mágica, de Sam Loyd, que consiste en tres tazas similares, aparentemente una de ellas con más superficie que las otras dos. Imagen de Wikimedia Commons
Pero regresemos a la serie de grabados de Javier Abad Alonso, que recibe el nombre “Supremus, el cerebro del hombre también es el cosmos”. Este artista toma como punto de partida las ideas del movimiento artístico Suprematismo y en particular de su cofundador Kazimir Malevich (1879-1935), recogiendo además la idea de imitar la naturaleza utilizando módulos geométricos, como explica el propio artista en el texto del proyecto. Así mismo, explica que una referencia fundamental en su trabajo es la pintura icónica de Kazimir Malevich Cuadrado negro (1915-1930):
“El espíritu revolucionario del cuadro de Malévich más de un siglo después de ser exhibido por primera vez sigue manteniendo intacto su espíritu transgresor y aún resulta controvertida para la mayor parte de la sociedad actual, el debate que genera, es algo que aún no ha sido superado y su vigencia es mi punto de partida. Modificar el color negro por paisajes extraídos de un observatorio astronómico e ir deconstruyendo el cuadrado con la ayuda de un juego geométrico siguiendo las reglas suprematistas expuestas de su manifiesto.”
Para esta serie de fotolitografías (como se explica en el Diccionario de Historia del Arte, la fotolitografía es un proceso de impresión litográfico que utiliza una imagen formada a través de medios fotográficos), este artista del grabado utilizada por una parte fotografías del cielo estrellado, tomadas con el telescopio de un observatorio astronómico, y el rompecabezas geométrico más conocido, el Tangram.
A través de una serie de ejemplos concretos de sus fotolitografías, que mostraremos a continuación, podemos observar el uso que hace este artista del grabado de este versátil rompecabezas geométrico.
En el primer grabado, que forma parte de un grupo de cinco fotolitografías de la serie Supremus, El cráneo del hombre también es el cosmos con las que este artista ganó el primer premio de la 17 Edición «Gran Canaria Series de Obra Gráfica» (2019), podemos observar la imagen de un trozo de cielo estrellado dividida en siete zonas poligonales, en concreto con la forma de las siete piezas del Tangram. Además, la imagen que configuran las siete piezas, que es la imagen del cielo estrellado, tiene la forma de una figura poligonal convexa, un hexágono irregular, que es una de las 13 configuraciones poligonales convexas (un polígono convexo es un polígono cuyos ángulos interiores miden menos de 180º, es decir, no hay zonas que externas metidas hacia dentro) que puedes realizarse con las piezas del Tangram.
 Fotolitografía de la serie “El cráneo del hombre también es el cosmos”, de Javier Abad Alonso, serie ganadora del primer premio de la 17 Edición «Gran Canaria Series de Obra Gráfica» (2019). Imagen de la página de Facebook de Arco Tijera
Fotolitografía de la serie “El cráneo del hombre también es el cosmos”, de Javier Abad Alonso, serie ganadora del primer premio de la 17 Edición «Gran Canaria Series de Obra Gráfica» (2019). Imagen de la página de Facebook de Arco TijeraEn los dos siguientes grabados, pertenecientes al tríptico que este artista madrileño ha expuesto durante la VIII Bienal Iberoamericana de obra gráfica ciudad de Cáceres (2019), vemos dos fotolitografías, cuyas imágenes son cuadradas, del cielo estrellado y divididas, de nuevo, en las piezas de un rompecabezas geométrico.
Si nos fijamos bien, en la primera litografía la mitad superior es la imagen de una fotografía recortada por las siete piezas del Tangram formando un rectángulo (de proporciones 1:2), mientras que el rectángulo de la mitad inferior es un giro de 180 grados de la pieza de arriba alrededor del centro de la imagen global. Por lo tanto, en esta composición las piezas de arriba y abajo son las mismas en forma e imagen.
Sin embargo, en la segunda litografía la mitad superior está formada por la imagen de una fotografía recortada por las siete piezas del Tangram formando un triángulo (también de proporciones, 1:2), pero ahora el triángulo de abajo es la imagen especular (de tipo espejo) del triángulo de arriba. Por lo cual, ahora las piezas de abajo y arriba son las mismas en forma, las siete piezas del Tangram (bueno, la pieza romboide volteada), pero realmente no en imagen, ya que la imagen de cada pieza de abajo la imagen de espejo respecto de la de arriba.
 Fotolitografía 1 del tríptico de Javier Abad Alonso expuesto en la VIII Bienal Iberoamericana de obra gráfica ciudad de Cáceres (2019). Imagen de la página de Facebook de Arco Tijera
Fotolitografía 1 del tríptico de Javier Abad Alonso expuesto en la VIII Bienal Iberoamericana de obra gráfica ciudad de Cáceres (2019). Imagen de la página de Facebook de Arco Tijera
 Fotolitografía 2 del tríptico de Javier Abad Alonso expuesto en la VIII Bienal Iberoamericana de obra gráfica ciudad de Cáceres (2019). Imagen de la página de Facebook de Arco Tijera
Fotolitografía 2 del tríptico de Javier Abad Alonso expuesto en la VIII Bienal Iberoamericana de obra gráfica ciudad de Cáceres (2019). Imagen de la página de Facebook de Arco Tijera
En los ejemplos que hemos comentado hasta ahora podemos observar como Javier Abad utiliza configuraciones convexas del Tangram, distintas del cuadrado básico, como son el hexágono irregular, el rectángulo 1:2 y el triángulo 1:2. En la siguiente fotolitografía utiliza un trapecio isósceles, en las partes derecha e izquierda de la imagen, que son una la imagen especular de la otra.
 Fotolitografía 3 del tríptico de Javier Abad Alonso expuesto en la VIII Bienal Iberoamericana de obra gráfica ciudad de Cáceres (2019). Imagen de la página de Facebook de Arco Tijera
Fotolitografía 3 del tríptico de Javier Abad Alonso expuesto en la VIII Bienal Iberoamericana de obra gráfica ciudad de Cáceres (2019). Imagen de la página de Facebook de Arco Tijera
Y en la siguiente obra utiliza la configuración convexa de un trapecio rectangular. Sin embargo, en esta fotolitografía, aunque las piezas que aparecen se corresponden también con dos juegos enteros del rompecabezas Tangram, no ocurre, como en los ejemplos anteriores, que una parte es simétrica a la otra, sino que las dos configuraciones (derecha e izquierda) son dos imágenes celestes distintas.
 Fotolitografía de la serie “El cráneo del hombre también es el cosmos”, de Javier Abad Alonso, serie ganadora del primer premio de la 17 Edición «Gran Canaria Series de Obra Gráfica» (2019). Imagen de la página de Facebook de Arco Tijera
Fotolitografía de la serie “El cráneo del hombre también es el cosmos”, de Javier Abad Alonso, serie ganadora del primer premio de la 17 Edición «Gran Canaria Series de Obra Gráfica» (2019). Imagen de la página de Facebook de Arco TijeraAunque Javier Abad no siempre utiliza configuraciones convexas como puede verse en alguna de las obras que hay en la página de Facebook de Arco Tijera, o incluso maneja las piezas de dos juegos completos del rompecabezas Tangram creando una nueva configuración con las 14 piezas, como en la siguiente fotolitografía, donde además ya no se trata de una imagen del cielo “duplicada”, sino una única imagen.
 Fotolitografía de la serie “El cráneo del hombre también es el cosmos”, de Javier Abad Alonso, serie ganadora del primer premio de la 17 Edición «Gran Canaria Series de Obra Gráfica» (2019). Imagen de la página de Facebook de Arco Tijera
Fotolitografía de la serie “El cráneo del hombre también es el cosmos”, de Javier Abad Alonso, serie ganadora del primer premio de la 17 Edición «Gran Canaria Series de Obra Gráfica» (2019). Imagen de la página de Facebook de Arco TijeraSin embargo, Javier Abad Alonso no es el único artista contemporáneo que ha utilizado, o utiliza, el rompecabezas geométrico Tangram, como se mostrará a lo largo de esta entrada del Cuaderno de Cultura Científica.
Vamos a continuar este pequeño paseo por el arte contemporáneo que mira al Tangram por el artista italiano, aunque en la actualidad reside en Grecia, Francesco Moretti, quien cultiva varios formatos, como la pintura, la escultura, el video, el diseño interior o los libros artísticos (como puede verse en su página web), pero también el grabado. De hecho, tiene varias series de maravillosos grabados en los que hace uso del rompecabezas Tangram y algunas de las configuraciones que pueden realizarse con sus piezas.
La primera serie de grabados de Francesco Moretti lleva el título de Tangram game. Estas obras son algunas de las configuraciones conocidas del Tangram (hombre cayendo, avión, pez, cisne, caballo, gato, flecha o conejo). Cada pieza del Tangram tiene un diseño geométrico diferente. Además, en cada grabado todas las piezas son del mismo color o cada una tiene un color distinto.
 Conejo (2018), de Francesco Moretti. Linograbado con 7 colores, de tamaño 50 x 70 cm. Imagen extraída de la página del artista Francesco Moretti
Conejo (2018), de Francesco Moretti. Linograbado con 7 colores, de tamaño 50 x 70 cm. Imagen extraída de la página del artista Francesco Moretti Gato (2018), de Francesco Moretti. Linograbado con 7 colores, de tamaño 50 x 70 cm. Imagen extraída de la página del artista Francesco Moretti
Gato (2018), de Francesco Moretti. Linograbado con 7 colores, de tamaño 50 x 70 cm. Imagen extraída de la página del artista Francesco MorettiTiene una segunda serie dedicada a las mujeres, titulada Tangram Ladies, en la cual utiliza para cada obra dos impresiones en color de la imagen que ha diseñado, las cuales son cortadas en tiras y “entrelazadas como si fueran hilos de lana en un tejido”. Las configuraciones del Tangram utilizadas son, por supuesto, de figuras femeninas. El resultado es de una gran belleza.
 Mujer Tangram 01 (2018), de Francesco Moretti. Linograbado con 2 impresiones, de tamaño 50 x 70 cm. Imagen extraída de la página del artista Francesco Moretti
Mujer Tangram 01 (2018), de Francesco Moretti. Linograbado con 2 impresiones, de tamaño 50 x 70 cm. Imagen extraída de la página del artista Francesco Moretti
La siguiente serie de grabados, denominada Closed forms (formas cerradas), está formada por algunas de las 13 configuraciones convexas que existen para este rompecabezas geométrico. Además, en cada figura incluye líneas paralelas con la forma de la misma figura, que nos recuerdan a algunas de las obras del artista abstracto y minimalista norteamericano Frank Stella (véase la entrada Frank Stella, la forma del lienzo).
 Forma cerrada 03 (2018), de Francesco Moretti. Linograbado en 2 colores, de tamaño 50 x 50 cm. Imagen extraída de la página del artista Francesco Moretti
Forma cerrada 03 (2018), de Francesco Moretti. Linograbado en 2 colores, de tamaño 50 x 50 cm. Imagen extraída de la página del artista Francesco MorettiEn la última serie de grabados en los que utiliza este rompecabezas geométrico, que recibe el nombre de Tangram óptico, utiliza diferentes configuraciones de animales del Tangram (camello, gallina, oso, ardilla y tejón). Por otra parte, sobre las piezas diseña una serie de líneas que crean cierto efecto óptico y a que, a diferencia de los anteriores diseños, las líneas se continúan de unas piezas a otras ya dentro de la configuración realizada.
 Oso (2018), de Francesco Moretti. Linograbado de tamaño 50 x 70 cm. Imagen extraída de la página del artista Francesco Moretti
Oso (2018), de Francesco Moretti. Linograbado de tamaño 50 x 70 cm. Imagen extraída de la página del artista Francesco Moretti
Pero la utilización del Tangram que realiza este artista italiano no se limita al grabado, sino que también realiza una serie de potentes esculturas inspiradas en el rompecabezas, realizadas tanto en madera, como en acero.
 Cisne (2018), de Francesco Moretti. Madera. Tamaño 43 x 19 x 45 cm. Imagen extraída de la página del artista Francesco Moretti
Cisne (2018), de Francesco Moretti. Madera. Tamaño 43 x 19 x 45 cm. Imagen extraída de la página del artista Francesco Moretti
En el año 2016, la galería Espacio Líquido de Gijón en su nueva propuesta por difundir la obra de artistas del entorno organizó una muestra titulada Estructura primitiva, que unía el trabajo de dos creadores como Jorge Nava (Gijón, 1980) y Job Sánchez (A Coruña, 1979). La propuesta del artista gallego Job Sánchez fue su serie Tangram, en la que se utilizaban algunas configuraciones convexas del rompecabezas. Por ejemplo, en cuatro collages de papel y vinilo sobre papel (con los títulos Tangram 1, 2, 3, 4) se utilizaban cuatro de estas configuraciones. Aunque quizás la propuesta más impactante fue el mural, de acrílico y grafico sobre la pared, de un tamaño de 135 x 180 cm, que vemos a la derecha en la siguiente imagen.
 Imagen de la exposición Estructura Primitiva en la Galería Espacio Líquido, en 2016. A la derecha, Sin título (2016), del artista Job Sánchez, perteneciente a la serie Tangram. Acrílico y grafico sobre la pared, de un tamaño de 135 x 180 cm. Imagen de la página de la revista cultural online LaEscena
Imagen de la exposición Estructura Primitiva en la Galería Espacio Líquido, en 2016. A la derecha, Sin título (2016), del artista Job Sánchez, perteneciente a la serie Tangram. Acrílico y grafico sobre la pared, de un tamaño de 135 x 180 cm. Imagen de la página de la revista cultural online LaEscena
 Imagen de la exposición Estructura Primitiva en la Galería Espacio Líquido, en 2016. Tangram 1, 2, 3, 4 (2016), collage de papeles y vinilo sobre papel, y Sin título (2016), tangram de madera pegado y pintado, con vinilo en la pared, del artista Job Sánchez, perteneciente a la serie Tangram. Imagen de la página de la revista cultural online LaEscena
Imagen de la exposición Estructura Primitiva en la Galería Espacio Líquido, en 2016. Tangram 1, 2, 3, 4 (2016), collage de papeles y vinilo sobre papel, y Sin título (2016), tangram de madera pegado y pintado, con vinilo en la pared, del artista Job Sánchez, perteneciente a la serie Tangram. Imagen de la página de la revista cultural online LaEscena
Otra artista que utiliza el Tangram es la artista francesa, afincada en Aarhus (Dinamarca), Lucie Payoux. Tiene dos obras en las que utiliza la configuración básica del cuadrado, del Tangram, en las cuatro posiciones obtenidas al rotar 90 grados esa configuración básica. Y cada pieza tiene su propio diseño.
 Tangram (2019), de la artista Lucie Payoux. Acrílico y óleo sobre madera. Tamaño de 55 x 55 cm. Imagen de la página web de la artista
Tangram (2019), de la artista Lucie Payoux. Acrílico y óleo sobre madera. Tamaño de 55 x 55 cm. Imagen de la página web de la artistaEl artista holandés Daan Roukens también utiliza las cuatro rotaciones de 90 grados de la configuración básica del cuadrado en su graffiti sobre madera On the Wall / Sobre el muro (2010), que realizó para el Artpie 2010, en Ámsterdam, en el que se van repitiendo las cuatro imágenes de forma periódica.
 On the Wall / Sobre el muro (2010), del artista Daan Roukens, para el Artpie 2010, en Ámsterdam. Grafitti sobre madera. Tamaño de 1 x 16 metros. Imagen de la página web del artista
On the Wall / Sobre el muro (2010), del artista Daan Roukens, para el Artpie 2010, en Ámsterdam. Grafitti sobre madera. Tamaño de 1 x 16 metros. Imagen de la página web del artistaLa francesa Françoise Bergaglia ha desarrollado un interesante trabajo como ceramista en los últimos años. Como ella misma ha comentado en su página La galerie des Tangram, este rompecabezas geométrico le fascina, sus siete piezas y la infinidad de configuraciones posibles que existen. En La galerie des Tangram tiene más de 50 piezas, de diferentes tamaños, realizadas en terracota sobre configuraciones del Tangram.
 Variaciones rojo y azul sobre fondo pintado, de Françoise Bergaglia. Imagen de su página La galerie des Tangram
Variaciones rojo y azul sobre fondo pintado, de Françoise Bergaglia. Imagen de su página La galerie des TangramSigamos con el diseño. La compañía de diseño 22 Studio Room de Taipei (Taiwan) realizó la escultura Ciudad Tangram que vemos en la siguiente imagen tomando como base la configuración cuadrada del Tangram.
 Escultura Ciudad Tangram, diseñada por la compañía 22 Studio Room de Taipei (Taiwan). Imagen de la página The Journal Shop
Escultura Ciudad Tangram, diseñada por la compañía 22 Studio Room de Taipei (Taiwan). Imagen de la página The Journal ShopTambién podemos encontrar ejemplos dentro de la arquitectura. El estudio de arquitectura de Barcelona del arquitecto Carlos Ferrater, OAB – Office of Architecture in Barcelona, diseño en el año 2013 el proyecto de Casa Tangram, de Borja Ferrater y Carlos Ferrater, para ser construida en Angelo Drive, Beverly Hills.
El estudio OAB explica así la relación del rompecabezas geométrico con su diseño arquitectónico:
“La relación entre el rompecabezas y nuestro proyecto se ha vuelto casual pero con un alcance muy significativo. Nuestro propósito de simplificar el proyecto destacando sus aspectos más importantes nos llevó a relacionar el proyecto con esta brillante, pero a la vez simple idea del juego de rompecabezas, que nos permite representar múltiples formas desde el punto de partida.
Tangram utiliza siete figuras geométricas y con cada una de ellas podemos crear múltiples posibilidades. Nuestro proyecto comenzó con unas premisas muy claras desde el primer día, tales como la relación natural con el paisaje existente, una perfecta organización del programa arquitectónico y un objeto bellamente terminado diseñado para ser visto desde diferentes lugares.
Siempre hemos querido convertir estos tres temas principales en una solución muy clara y potente, tomando como creencia fundamental la fuerza de abstracción en la arquitectura.
Queríamos simplificar la forma mientras transmitíamos estos conceptos importantes con formas geométricas. Este tipo de lógica y pensamiento está bien relacionado con la abstracción, rigor y austeridad que se han utilizado en la arquitectura moderna a lo largo del siglo XX, teniendo California como un magnifico epicentro.”
En la página web del estudio OAB puede encontrarse la descripción completa del proyecto.
 Imágenes del proyecto Casa Tangram, de Borja Ferrater y Carlos Ferrater, para ser construida en Angelo Drive, Beverly Hills
Imágenes del proyecto Casa Tangram, de Borja Ferrater y Carlos Ferrater, para ser construida en Angelo Drive, Beverly Hills
Y vamos a terminar este pequeño paseo con una hermosa obra del diseñador gráfico e ilustrador Hugo Giner.
 Ilustración de Hugo Giner. Imagen de su Instagram, a través de su página web
Ilustración de Hugo Giner. Imagen de su Instagram, a través de su página web
Bibliografía
1.- Página web del artista Javier Abad Alonso
2.- Javier Abada Alonso, Supremus, el cerebro del hombre también es el cosmos [comunicación personal]
3.- Diccionario de Historia del Arte: fotolitografía
4.- Página web del artista Francesco Moretti
5.- Página web del artista Job Sánchez
6.- Página web de la artista Lucie Payoux
7.- Página web del artista Daan Roukens
8.- Página web de la ceramista Françoise Bergaglia
9.- Página web de la compañía de diseño 22 Studio Room
10.- Página web del estudio OAB – Office of Architecture in Barcelona
11.- Página web del diseñador gráfico e ilustrador Hugo Giner
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El arte contemporáneo que mira al Tangram se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El comportamiento corpuscular de la luz: el efecto Compton
 Foto: Bessi / Pixabay
Foto: Bessi / PixabayHemos visto que el momento lineal del fotón es inversamente proporcional a su longitud de onda, p = h/λ. ¿Tiene sentido físico definir el momento lineal de un fotón de esta manera?
Consideremos un haz de luz (visible o de rayos X) que incide sobre los átomos de una objeto diana, una delgada lámina de metal, por ejemplo. Según la teoría electromagnética clásica, la luz se dispersará en varias direcciones, pero su frecuencia no cambiará. La absorción de luz de cierta frecuencia por un átomo puede ser seguida por la reemisión de luz de una frecuencia diferente. Pero si la onda de luz simplemente se dispersa, entonces, según la teoría clásica, la frecuencia no debería cambiar.
Según la teoría cuántica, sin embargo, la luz está compuesta de fotones. Según la teoría de la relatividad, los fotones tienen momento lineal. Si esto es así, en una colisión entre un fotón y un átomo debería aplicarse la ley de conservación del momento, una consecuencia directa de la tercera ley de Newton. Según esta ley cuando un cuerpo de masa pequeña choca con un objeto de masa mucho mayor en reposo, simplemente o rebota hacia atrás o se desvía; experimenta muy poca pérdida de velocidad y los cambios en su energía son mínimos. Pero si las masas de los dos objetos que chocan no son muy diferentes sí se puede transferir una cantidad significativa de energía en la colisión.
Arthur Compton calculó cuánta energía debería perder un fotón en una colisión con un átomo si el momento del fotón fuese h/λ. Llegó a la conclusión de que el cambio en la energía es demasiado pequeño como para poder observar el efecto mecánico de un fotón en algo tan grande comparativamente como un átomo completo. Pero si un fotón golpeara un electrón, que tiene una masa significativamente más pequeña, el fotón debería transferir una cantidad significativa de energía al electrón.
En 1923, Compton pudo demostrar que los rayos X se comportan de hecho como corpúsculos con momento lineal p = h/λ cuando chocan con electrones. Compton midió la longitud de onda (o la frecuencia) de los rayos X incidentes y una vez dispersados y, de esta manera, pudo determinar el cambio en el momento lineal del fotón de rayos X. Al medir por separado el momento lineal del electrón tras la dispersión, pudo verificar que p = h/λ utilizando la ley de conservación del momento. Por este trabajo Compton recibió el Premio Nobel en 1927.
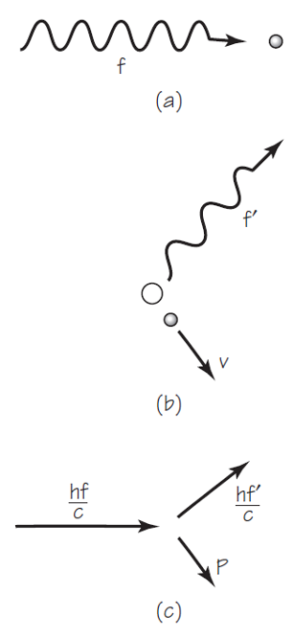 Efecto Compton. (a) Un fotón de frecuencia f incide sobre un electrón en reposo; (b) el fotón es dispersado tras la colisión con una frecuencia diferente f ‘, mientras que el electrón adquiere una velocidad v; (c) la ley de conservación del momento lineal establece que el momento lineal antes de la colisión debe ser igual al momento lineal tras la colisión (recuerda que es una suma vectorial, por lo que en la imagen se representan la dirección y sentido con flechas y se anota la magnitud; p en este caso es el producto de la masa del electrón por la velocidad adquirida v).
Efecto Compton. (a) Un fotón de frecuencia f incide sobre un electrón en reposo; (b) el fotón es dispersado tras la colisión con una frecuencia diferente f ‘, mientras que el electrón adquiere una velocidad v; (c) la ley de conservación del momento lineal establece que el momento lineal antes de la colisión debe ser igual al momento lineal tras la colisión (recuerda que es una suma vectorial, por lo que en la imagen se representan la dirección y sentido con flechas y se anota la magnitud; p en este caso es el producto de la masa del electrón por la velocidad adquirida v).Por lo tanto, el experimento de Compton demuestra que un fotón puede considerarse como una partícula con un momento lineal (p = h/λ) y una energía (E = hc/λ = hf) definidos. También demuestra que las colisiones entre fotones y electrones obedecen las leyes de conservación del momento lineal y la energía.
La explicación de Eisntein del efecto fotoeléctrico ya apuntaba a que la luz tiene propiedades similares a las de los corpúsculos. La expresión matemática del momento lineal y el efecto Compton proporcionaron pruebas adicionales de este hecho. Debe quedarnos claro, sin embargo, que los fotones no son como corpúsculos ordinarios, aunque solo sea porque los fotones no existen a velocidades diferentes a la de la luz [*]. Pero en lo demás, como en su comportamiento durante la dispersión, los fotones actúan de manera muy parecida a las corpúsculos de materia; de entrada, tienen momento lineal y energía.
Sin embargo, también sabemos que la luz, los fotones por tanto, actúa como una onda, teniendo frecuencia y longitud de onda. En otras palabras, la radiación electromagnética en algunos experimentos exhibe un comportamiento similar a lo que se considera un comportamiento de corpúsculo, y en otros experimentos su comportamiento es similar a lo que se considera un comportamiento de onda. Este patrón de comportamiento se suele llamar dualidad onda-corpúsculo de la radiación.
¿Es un fotón una onda o un corpúsculo? La única respuesta, señaló Bohr, es que puede actuar como una u otro, dependiendo de lo que se haga con él.
Nota:
[*] No puede haber fotones en reposo y, por lo tanto, no hay masa en reposo para los fotones. Véanse La velocidad de las ondas electromagnéticas y la naturaleza de la luz y El principio de constancia de la velocidad de la luz.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El comportamiento corpuscular de la luz: el efecto Compton se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El comportamiento corpuscular de la luz: momento lineal del fotón
- El dilema del efecto fotoeléctrico
- La explicación de Einstein del efecto fotoeléctrico
Las publicaciones científicas
 Foto: Nationale Bank van Belgie – Banque Nationale de Belgique / flickr
Foto: Nationale Bank van Belgie – Banque Nationale de Belgique / flickrUn componente clave de la empresa científica es el sistema de publicaciones, pues sin él no sería posible exponer al escrutinio crítico las conclusiones del trabajo de cada uno.
Ya desde los albores de la ciencia moderna las cosas funcionaban de ese modo. Copérnico, Kepler y Galileo, cada uno a su manera, publicaron los resultados de sus observaciones o experimentos (en el caso de Galileo experimentos mentales, algunos de ellos). Lo propio hizo Harvey, por ejemplo, y otros reconocidos pioneros de la ciencia tal y como la conocemos hoy. Además, algunos también operaron de una forma algo diferente. Algunos miembros de la Royal Society acostumbraban, en sus primeros años, a realizar experimentos y demostraciones ante sus compañeros. El contraste era directo; al hacerlos testigos de la forma en que se había obtenido algún resultado de interés, la validación o refutación del resultado era inmediata. Pero ya la misma Royal Society, en 1665 (cinco años después de su creación) comenzó a publicar la Philosophical Transactions of the Royal Society. Ese mismo año, algo antes, se había empezado a publicar en París Le Journal des Sçavans, considerada la primera revista científica de la historia.Andando el tiempo las ciencias de la naturaleza han alcanzado unas dimensiones tales que ya no sería posible recurrir a las demostraciones directas para dar fe de la validez de los resultados obtenidos. Por eso, el aumento de la actividad científica ha venido acompañado por un crecimiento paralelo del sistema de publicaciones científicas.
Los primeros artículos científicos tenían un estilo narrativo más literario y con un hilo argumental biográfico, el autor contaba cómo había ido haciendo el descubrimiento. Posteriormente (se suele citar a Pasteur como el principal impulsor de la idea) el hilo narrativo se centra en la reproducibilidad del descubrimiento, independientemente de la historia que llevo a hacerlo. Hoy día esa estructura (resumen, introducción, materiales y métodos, resultados, discusión, conclusiones y referencias) se ha hecho universal. En el lado positivo, esta estructura permite una alta densidad de información, a cambio los trabajos son difíciles de leer y más aún de escribir.
En principio, las revistas científicas se publican para dar a conocer los resultados de las investigaciones. De otra forma no sería posible poner al alcance de todos los resultados obtenidos ni, por lo tanto, podrían someterse a crítica general. Y por otro lado, la publicación de los resultados supone también un bien en sí mismo, dado que en la medida a que obliga a los investigadores a sistematizar y ordenar los resultados, y a elaborar un argumento que les dé coherencia y los enmarque en el curso general del desarrollo científico, también sirve de ayuda para mejorar los conocimientos y sentar las bases de su progreso. Hay, de hecho, quien argumenta que las publicaciones científicas constituyen el conocimiento científico propiamente dicho, dado que son el archivo de todo lo investigado y conocido.
Pero las publicaciones científicas, además de las señaladas, han pasado a cumplir otras funciones que tienen poco que ver con ellas. Se han convertido en uno de los medios más utilizados para evaluar la productividad y la calidad de investigadores e instituciones científicas y académicas. Por ello, han pasado a formar parte de las herramientas métricas básicas que se utilizan para, en función de las evaluaciones, decidir el acceso a puestos de trabajo de personal investigador, su posterior promoción profesional y, en general, asignar los recursos públicos en el marco de la política científica de gobiernos y universidades.
Por todo ello, desde el punto de vista de los intereses de investigadores e instituciones, las publicaciones científicas no se consideran solo como un elemento de prestigio, el distintivo que señala al buen investigador o la institución de alto nivel. Han pasado a ser una herramienta de promoción profesional e institucional e, incluso, de mera supervivencia en el sistema científico. Ello genera una presión muy grande sobre científicos y centros.
El método que siguen las editoriales para seleccionar los artículos merecedores de ser publicados es someterlos a la consideración de especialistas de reconocido nivel. Es lo que se denomina revisión por pares. El término par, como sinónimo de igual, hace referencia al hecho de que los revisores son investigadores como los autores de los trabajos. Así pues, los evaluadores son colegas de los autores y, en principio, se encuentran al mismo nivel que aquellos. Se supone que este procedimiento garantiza que los trabajos que se publican cumplen los requisitos exigibles para aceptar que un trabajo sea dado a conocer. Normalmente cuanto mayor es el nivel de las revistas y más son los investigadores que les remiten sus trabajos para publicación, y de esa forma se genera un circuito de retroalimentación positiva que funciona de acuerdo con la siguiente secuencia: cuantos más son los trabajos remitidos a una revista, más son los rechazados, por lo que como solo se seleccionan los muy buenos, la calidad de los que se publican es cada vez mayor; ello actúa como incentivo para publicar en esa revista, con lo que la remisión de trabajos aumentará, y así sucesivamente. Esa es la teoría.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Las publicaciones científicas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Hacia un nuevo sistema de publicaciones científicas
- #Naukas15 De publicaciones científicas
- #Naukas14 Acceso abierto a las publicaciones científicas
Las angulas se van a China
Menú de Sabino Arana en la Nochebuena de 1895 en la cárcel de Larrínaga, en Bilbao:
“Ostras, chirlas, alubias, bacalao, angulas, besugo, bermejuelas, merluza y caracoles; de postre, compota de manzana, pastel, mazapán y turrón de Jijona; y de bebida, vino de Aranburuzabala, txakoli, jerez, oporto y chartreuse.”
 Angulas. Fuente: Wikimedia Commons
Angulas. Fuente: Wikimedia CommonsLlega la Navidad. Llegan las felicitaciones, las compras, la espectacular iluminación, el Nacimiento y el Árbol de Navidad, los Reyes Magos, Santa Klaus y el Olentzero, la familia, los amigos, las comidas y las cenas y, en el recuerdo, un lejano recuerdo, las angulas. Uno descubre que va perdiendo la memoria, quizá por los años, sobre todo por los años que han pasado desde que comió angulas por última vez, y ha olvidado hasta su sabor. Pero, seguro que no pasa lo mismo en Shanghai, punto de destino de 40 kilos de angulas vivas requisadas en el Aeropuerto de Loiu a finales de abril de 2017. Al año siguiente, se desmanteló otra red en España, Portugal y Marruecos, preparada para enviar media tonelada de angulas a China. En febrero de 1918, la Guardia Civil entregó 310 kilos de angulas, incautadas en Barajas, a la Diputación de Gipuzkoa para repoblar los ríos Oiartzun y Oaria.
El tráfico ilegal de angulas viene de años atrás, y, por ejemplo, en 2012, el SEPRONA incautó tonelada y media de angulas, valoradas en millón y medio de euros. Iban, también, a China, para su crecimiento y venta como anguilas. Y en 2016 fueron 2.5 toneladas. Los contrabandistas llegan a pagar las angulas hasta a 2800 euros el kilo. Entran unas 3000 angulas en cada kilo, y aunque algunas mueren durante los traslados, el negocio es muy rentable. Por cada kilo de angulas se obtienen 1260 kilos de anguilas, y ya sin cabeza, ahumadas y envasadas, se venden en Asia a 40 euros el kilo. Por tanto, por un kilo de angulas a 2800 euros se obtienen 50000 euros de anguilas. Los 40 kilos de Loiu podrían haber alcanzado los 74000 euros en China. Se ha escrito que el contrabando de angulas es más rentable que el tráfico de cocaína.
En la red más organizada de contrabando de angulas, que se desmanteló a principios de marzo de 2017, la Guardia Civil recuperó angulas capturadas en el Guadalquivir, la Albufera de Valencia y el Delta del Ebro. De allí, en camión frigorífico y en cubetas de agua, se transportaban hasta el Aeropuerto de Atenas, donde embarcaban en avión con destino a Hong Kong. Se calcula que los beneficios de esta organización eran unos siete millones de euros al año.
La primera condena por contrabando de angulas, en junio de 2019, supuso seis millones de euros de multa y seis años de cárcel.
En el País Vasco se comían angulas (Anguilla anguilla), y ya he contado mis recuerdos o, mejor, la pérdida de mis recuerdos (y también los de Sabino Arana), pero, según Estibaliz Díaz y María Korta, de la Fundación AZTI, las capturas han disminuido enormemente en los últimos 30 años, según testimonios de anguleros veteranos y según sus propios datos obtenidos entre 2003 y 2009. Hace medio siglo, las capturas de angulas llegaron a las 20000 toneladas, y ahora son unas 5000 toneladas.
 Anguilla anguilla. Fuente: Wikimedia Commons
Anguilla anguilla. Fuente: Wikimedia CommonsYa que la angula es la fase juvenil de la anguila que llega de los Sargazos a los ríos para crecer hasta anguila adulta, si faltan las angulas, también escasearán las anguilas. El grupo de Loreto García Arberas, de la UPV/EHU de Leioa, ha estudiado la presencia de la anguila en los ríos de Bizkaia y, más en concreto, en el río Barbadún. La abundancia, desde la década de los ochenta hasta 2009, disminuye, aunque en los 2000, con la construcción de depuradoras y menos contaminación, la población se mantiene y parece que comienza a recuperarse.
Algo parecido ocurre en toda la Península, con datos de población y, además, con la aparición de la acuicultura de la anguila. Según Luis Pérez y sus colegas, de la Universidad Politécnica de Valencia, desde la década de los sesenta, las capturas de angulas y de anguilas disminuyen, por diversas causas y, entre ellas, la sobreexplotación y la alteración del hábitat por la construcción de embalses y la contaminación.
La anguila europea se distribuye por el Mediterráneo y el Atlántico, desde Marruecos hasta Escandinavia. En España, hasta la década de los noventa, era mayor el número de anguilas procedentes de la pesca que de la acuicultura. Pero en los 2000, las anguilas de los ríos disminuyeron y la especie se incluyó en las listas de especies en peligro de extinción. Comienzan a dominar en el mercado las anguilas procedentes de la acuicultura, con 411 toneladas en el 2000, frente a las 71 toneladas de la pesca directa. El total llegó a las 100000 toneladas de la acuicultura en la década de los 2000, aunque ahora ha bajado a unas 70000 toneladas. Como ejemplo sirve la Albufera de Valencia, con 17 toneladas de angulas de la pesca directa en 1960 a casi cero en 1994.
 Distribución de la angula europea Anguilla anguilla. Fuente: Wikimedia Commons
Distribución de la angula europea Anguilla anguilla. Fuente: Wikimedia CommonsLas anguilas adultas salen de los ríos europeos cuando alcanzan de 5 a 15 años y viajan hasta el Mar de los Sargazos, donde se reproducen y vuelven a las costas europeas en un viaje de 280 días como máximo, según la investigación de Raymonde Leconte-Finiger, de la Universidad de Perpignan. Pero, sabemos poco del viaje de ida a las Sargazos y, todavía menos conocemos el viaje de vuelta. Ni siquiera sabemos si las larvas se dejan arrastrar o si controlan el movimiento o, quizá, si el control aumenta según maduran.
 Larvas de anguila. Fuente: Wikimedia Commons
Larvas de anguila. Fuente: Wikimedia CommonsSabemos que cambian de profundidad según el día y la noche. En las últimas investigaciones, como la del grupo de Lewis Naisbett-Jones, de la Universidad de Carolina del Norte, se ha propuesto y ensayado con modelos que las angulas y anguilas se orientan en su viaje oceánico con el campo magnético de la Tierra, por lo menos hasta llegar a la Corriente del Golfo que, se supone, las transporta hasta los Sargazos. Es una hipótesis en estudio.
El viaje de ida se completa normalmente en la misma temporada, aunque el trabajo de David Righton, del Laboratorio Cefas de Suffolk, en Inglaterra, demuestra que hay ejemplares que llegan al año siguiente.
Los investigadores marcan con localizadores a 707 angulas de 20 ríos de la fachada atlántica europea y del Mediterráneo. Siguen a las anguilas en su viaje hasta las islas Azores, en camino a los Sargazos, aunque para llegar quedan todavía unos 5000 kilómetros. Consiguen datos de 80 anguilas. Viajan entre 3 y 47 kilómetros al día, con cambios de profundidad, en el fondo de día y más a la superficie de noche. Con estas cifras, los autores suponen que hay, como decía, anguilas que llegarán al año siguiente. Pero, como dice Pérez Iglesias, las anguilas inician el viaje cuando se les atrofia el sistema digestivo y no se pueden alimentar y, si tardan más de un año en llegar a las Sargazos, reproducirse y morir, se plantea el enigma de su nutrición durante el viaje de ida. Además, con modelos de su distribución en los Sargazos, se ha propuesto que la mayoría mueren durante el primer año de vida y ni siquiera inician la vuelta.
 Reconstrucción de las migraciones de las anguilas a partir de los datos de radiotrazado. Imagen: Righton et al (2016)
Reconstrucción de las migraciones de las anguilas a partir de los datos de radiotrazado. Imagen: Righton et al (2016)Fue el oceanógrafo danés Johannes Schmidt quien, en 1922, descubrió este extraordinario viaje de las anguilas para la reproducción. Es curioso que en el mismo Mar de los Sargazos se reproducen también las anguilas (Anguilla rostrata) de la costa atlántica de Norteamérica. Son especies parecidas y difíciles de distinguir. Los especialistas utilizan el número de vértebras de su columna vertebral: 110-119 vértebras en la anguila europea, y 103-110 vértebras en la especia americana. Parece que, en el viaje de vuelta a su continente, los errores no llegan al 1%.
O, esto lo sabemos seguro, pueden acabar en China. Allí se las suelta para que crezcan en el agua de los arrozales. Y, como ocurre con otras especies invasoras en otros ambientes, terminarán escapando y no se conoce el efecto que producirán sobre la especie de anguila asiática (Anguilla japónica), aunque la especie europea se cría en acuicultura, sobre todo en el Japón, desde hace años.
Referencias:
Aranburu, A. et al. 2016. Glass eel recuitment and exploitation in a South European estuary (Oria, Bay of Biscay). ICES Journal of Marien Science 73: 111-121.
Díaz, E. & M. Korta. 2010. Pesquería de la angula en el País Vasco. I Jornadas Españolas de la Anguila. Donostia-San Sebastián. P. 67-69.
Europa Press. 2018. Entregan a Gipuzkoa 310 kilos de angulas incautadas en Barajas para repoblar ríos. 10 febrero.
Europa Press. 2018. El SEPRONA desmantela una red criminal instalada en España dedicada a la exportación ilegal de angulas a China y Japón. 6 abril.
García Arberas, L. et al. 2010. Anguilas en los ríos de Bizkaia: poblaciones y condiciones de hábitat. I Jornadas Españolas de la Anguila. Donostia-San Sebastián. P. 84-87.
Lecomte-Finiger, R. 1994. The early life of the European eel. Nature 370: 424.
Naisbett- Jones, L.C. et al. 2017. A magnetic map leads juvenile European eels to the Gulf Stream. Current Biology 27: 1236-1240.
Núñez-Villaveirán, L. 2018. Contrabando de angulas, más rentable que la cocaína. El Mundo 10 junio.
Pérez, L. et al. 2004. Producción de anguilas: pasado, presente y futuro.. Revista AquaTIC 20: 51-78.
Pérez Iglesias, J.I. 2016. Peces escurridizos. Cuaderno de Cultura Científica. 30 octubre.
Planelles, M. 2017. El viaje ilegal de las angulas del Guadalquivir a los mercados de China. El País 8 marzo.
Righton, D. et al. 2016. Empirical observations of the spawning migration of European eels: The long and dangerous road to the Sargasso Sea. Science Advances 2: e1501694
van Ginneken, V.J.T. & G.E. Maes. 2005. The European eel (Anguilla anguilla, Linnaeus), its lifecycle, evolution and reproduction: a literature review. Reviews in Fish Biology and Fisheries 15: 367-398.
Westerberg, H. et al. 2017. Modeling the drift of European (Anguilla anguilla) and American (Anguilla rostrata) eel larvae during the year of spawning. Canadian Journal of Fisheries and Aquatic Sciences 75: 224-234.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Las angulas se van a China se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Peces escurridizos
- ¿Puede China salvar a los elefantes africanos? Pronto lo descubriremos
- Hace 16 años ya: el hundimiento del Prestige
Percepción del arte a través de la neurobiología, la psicología y la crítica del arte

Hay obras de arte que a unos les fascinan y a otros les espantan. Hay algunas que pasan inadvertidas, y hay otras que enfadan o que, por el contrario, despiertan buenas sensaciones o incluso emocionan. Lo mismo ocurre con los espacios. Hay lugares en los que da gusto estar, y hay lugares que sentimos que nos expulsan.
La organización del espacio nos afecta indudablemente, y nuestra casa, nuestro barrio y nuestras ciudades determinan de alguna forma la persona que hoy por hoy somos. Pero, ¿cómo actúa nuestra percepción frente a estos espacios? ¿Qué determina que una obra de arte o un espacio nos agrade o no?
El ciclo de conferencias “Ciencia y arte a pie de calle” aborda esta y otras cuestiones relacionadas con seis expertos de seis áreas de conocimiento diferentes. Arte y ciencia se entrelazaron en este ciclo de conferencias en dos jornadas, los pasados 19 y 27 de junio en la Biblioteca Bidebarrieta de Bilbao.
El evento se enmarca en el ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta con el propósito de promover y difundir el conocimiento científico.
La primera jornada multidisciplinar que analiza la relación que existe entre el arte, la neurobiología y la psicología, y que cuneta con la participación de la neurobióloga Conchi Lillo, la psicóloga Patri Trezanos y la crítica de arte Elena Vozmediano. Deborah García Bello ejerce de anfitriona.
Conchi Lillo es bióloga y doctora en neurociencias por la USAL y profesora titular en la Facultad de Biología de Salamanca desde el año 2011. Investiga en el área de la neurobiología de la visión en el INCYL (Instituto de Neurociencias de Castilla y León), está adscrita en IBSAL (Instituto de Investigación Biomédica de Salamanca). Dirige el Servicio de Microscopía Electrónica de la Universidad de Salamanca. Ha publicado más de 60 artículos científicos y colabora con las plataformas de divulgación científica Naukas y Desgranando Ciencia.
Patri Tezanos es psicóloga especializada en neurociencia y divulgadora científica en el canal “Antroporama” de Youtube. Compagina su actividad de divulgación con la investigación en el campo de la neurociencia en el Instituto Cajal del CSIC en Madrid.
Elena Vozmediano, licenciada en Historia del Arte por la Universidad Complutense de Madrid y crítica de Arte que colabora semanalmente en el suplemento El Cultural. Es miembro del Instituto de Arte Contemporáneo (IAC). Ha sido galardonada con el Premio GAC 2012 a la Crítica de Arte, que otorgan las asociaciones de galerías de arte catalanas, y con el Reconocimiento del Arte Contemporáneo 2014, del IAC.
Edición realizada por César Tomé López
El artículo Percepción del arte a través de la neurobiología, la psicología y la crítica del arte se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia, arte y cultura callejera: física y música
- Arte & Ciencia: Analogías entre el arte y la ciencia como formas de conocimiento
- Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte
La estadística nos recuerda que los seres humanos no son cometas
 Foto: Clarisse Meyer / Unsplash
Foto: Clarisse Meyer / UnsplashEn la representación del siglo XIV de abajo vemos a la diosa Fortuna, ciega, manejando una rueda de azar cuyo resultado es desconocido para el ser humano. Es la diosa de los caprichos del destino. Enfrente está Sapientia, la diosa de la sabiduría, orgullosa, llena de luz, de claridad, ante un espejo que demuestra su capacidad de autoconocimiento y reflexión.

Asociamos sabiduría con certeza, ciencia, seguridad y tranquilidad. La incertidumbre, con la fortuna, lo oscuro, lo desconocido y el futuro incierto. Sin embargo, como decía Ciceron, “la fortuna, no la sabiduría, gobierna la vida”.
En la ambición de conocer qué deparaba el futuro, los gobernantes han mirado más a Fortuna que a Sapientia. Para ello consultaban a videntes los resultados de la rueda del azar. En la antigua Grecia, las pitonisas del oráculo de Delfos atendían a preguntas formuladas por quien pudiera pagar las correspondientes tasas. La influencia del místico ruso Rasputin alcanzó a casi toda la familia Románov. El actual presidente de Brasil tiene como asesor a Olavo de Carvalho, un filósofo new age y astrólogo.
Sin embargo, también desde tiempos remotos se ha entendido la importancia del conocimiento para tomar decisiones de Estado sobre el futuro, en la convicción de que sus consecuencias no son tan azarosas.
Por ello, no es de extrañar que la palabra estadística proceda etimológicamente de la palabra Estado, por la utilidad de la sistematización de datos en las grandes decisiones.
Faraones y cometas
Los faraones del antiguo Egipto daban gran importancia a la recopilación de datos. Guillermo el Conquistador ordenó en 1066 un censo considerado el primer compendio estadístico de Inglaterra.
Gaspar Neumann (1648 –1715) trabajó en las primeras tablas de mortalidad, que usó para combatir la creencia popular de que los años terminados en 7 eran fatídicos y con una mortalidad mayor.
Edmund Halley (1656-1742), que ya barruntaba la idea de que los cometas vistos en 1531, 1607 y 1682 eran el mismo objeto, utilizó los métodos de Neumann para predecir la reaparición del cometa a finales de 1758 o principios de 1759.
El cometa reapareció el 25 de diciembre de 1758 en medio de una gran expectación. Por desgracia, Halley había muerto años antes y no pudo contemplar ese momento. La humanidad estaba aprendiendo el manejo de la rueda de la diosa Fortuna.
En esa época se inició el estudio del cálculo de probabilidades, relegado al análisis de los juegos de azar y con poca repercusión en el resto de disciplinas.
Las ciencias experimentales seguirían en la búsqueda del conocimiento certero, determinista, que interpretaba la incertidumbre como un fallo, no como parte intrínseca del conocimiento.
“Si tu experimento necesita estadística, hubiera sido necesario hacer un experimento mejor”, decía el físico Ernest Rutherford (1871-1937).
“Dios no juega a los dados con el universo”, afirmaba Einstein (1879-1955) en su crítica a la mecánica cuántica.
No había sitio para la rueda del azar en el conocimiento científico.
 Foto: Riho Kroll / Unsplash
Foto: Riho Kroll / UnsplashNace la estadística moderna
Todo cambiaría a lo largo del siglo XX a partir de los trabajos de matemáticos como Ronald Fisher (1890-1962), Karl Pearson (1857-1936), su hijo Egon (1895-1980) y Jerzy Neyman (1894-1981).
Se establecieron las bases de lo que conocemos como la inferencia estadística, que nos abrieron las puertas para obtener conclusiones generales sobre poblaciones a partir de una muestra de datos representativos.
Además, podemos reducir los márgenes de error de nuestras conclusiones a medida que aumentamos el tamaño de la muestra, contrastar la validez de nuestras hipótesis de partida y la capacidad de ajuste de nuestros modelos.
Si a esto unimos la modelización dinámica de las trayectorias inciertas, con la formalización del patrón de probabilidades de Norbert Wiener (1894-1964) y la axiomática de Andrei Kolmogorov (1903-1987), hemos desarrollado una batería inmensa de técnicas que nos permiten obtener intervalos de confianza a lo largo del tiempo, acotar los umbrales de incertidumbre y predecir los escenarios futuros más probables.
A finales del siglo XX, en todas las ramas de la ciencia se utilizaban modelos que incorporaban la incertidumbre y la probabilidad. Desde entonces la estadística se ha consolidado como un área científica común y casi imprescindible.
Buscando un límite estricto a la duda
Ya de lleno en el siglo XXI, la capacidad de trabajar con grandes bases de datos y de simular muchísimas réplicas de las dinámicas de las variables nos ha llevado a creer que podemos dar respuesta al personaje de Guía del autoestopista galáctico (Douglas Adams, 1979) que gritaba “¡Demandamos áreas estrictamente delimitadas de duda e incertidumbre!”. ¿Es así?
El editor de la revista Wired, Chris Anderson (1961), afirma en su libro El fin de la teoría que con datos y algoritmos de autoaprendizaje no necesitamos modelos ni teoría para predecir los comportamientos futuros.
“Olvídense de la taxonomía, de la ontología y de la psicología. ¿Quién sabe por qué la gente hace lo que hace? Lo importante es que lo hace y que lo podemos rastrear y medir con una fidelidad sin precedentes”.
Basta una buena base de datos y técnicas estadísticas adecuadas y podremos diseñar el modelo de negocio de una empresa, seleccionar personal con criterios objetivos y realizar inversiones financieras.
Si Halley pudo predecir la reaparición del cometa en el siglo XVIII, en el siglo XXI parece que podamos predecir casi cualquier evento sobre el que tengamos muchos datos disponibles.
El mundo real es complejo
Hemos hecho grandes avances en el conocimiento de la incertidumbre, expresión que no deja de ser paradójica. Debemos utilizar este conocimiento con mucha cautela. No olvidemos las dos condiciones esenciales para predecir en estadística: disponer de buena información y poder extrapolarla.
La predicción del paso del cometa Halley se basó en los datos pasados y en el hecho de que la trayectoria del cometa era previsible a partir de los mismos. Esta condición no se cumple siempre, y menos cuando se trata de predecir preferencias sociales, habilidades personales y eventos nunca antes observados.
Además, recordemos que las personas no funcionamos como un cometa. A veces podemos modificar nuestra trayectoria después de conocer las medidas que forman nuestra órbita. La realidad social es muy compleja. Como diría la gran dama de la estadística Gertrude Cox (1900-1978), los polinomios son notoriamente poco fiables cuando se extrapolan.
Hay tres ejemplos que ilustran esta complejidad.
Antes de la crisis financiera de 2007, las agencias de calificación tenían datos sobre los activos basados en hipotecas de alto riesgo. Los habían evaluado con la más alta calificación crediticia, AAA, y así se pusieron en circulación con gran éxito. ¿Cómo pudo ser? No había precedentes de peligro, ya que los datos no registraban ninguna morosidad. Cuando la morosidad comenzó, lo hizo en una gran cascada. Las consecuencias son por todos conocidas.
 Foto: Vladimir Solomyani / Unsplash
Foto: Vladimir Solomyani / UnsplashNokia tenía que apostar por un nuevo modelo de negocio en 2011. Además de tensiones internas, Tricia Wang explica que parte de su debacle se debió a la miopía de Nokia al basarse únicamente en los datos de usuarios de los teléfonos móviles en circulación. Estos no predecían las preferencias de los teléfonos que estaban por llegar.
Amazon diseñó un algoritmo de selección de personal para desarrollar software usando patrones que podían observarse en los currículos presentados a la empresa durante una década. En 2015 lo dejaron de usar: no amaba a las mujeres. En la base de datos apenas había ejemplos femeninos de los que el algoritmo pudiera aprender a reclutar mujeres.
Estos ejemplos nos recuerdan que entender el contexto es esencial y que no debemos caer en la prepotencia de manejar grandes bases de datos y algoritmos sofisticados renunciando a combinar otro tipo de conocimientos sobre la evolución de la variable que queremos estudiar.
Decía Eduardo Chillida (1942-2002) que cuando era joven dibujaba muy bien, representaba perfectamente lo que veía, pero que eso no le aportaba nada. Se le ocurrió comenzar a dibujar con la mano izquierda para forzar que su mano fuera más despacio que su cabeza.
Uso esta anécdota para aconsejar a mis estudiantes que usen las técnicas y los programas informáticos a su disposición con su mano izquierda. Hacer estadística no es solo recopilar datos, diseñar algoritmos e intervalos de confianza. Yo me quedo con la descripción del brillante estadístico contemporáneo Winfried Stute, que define la estadística como “el arte de ponderar información”.![]()
Sobre la autora: Eva Ferreira García es catedrática de estadística, especializada en modelos dinámicos bajo incertidumbre, en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La estadística nos recuerda que los seres humanos no son cometas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- 50 años modificando genes (en seres humanos)
- Investigación con medicamentos en seres humanos: del laboratorio a la farmacia
- El aprendizaje continuo mejora la interacción de robots con humanos en lenguaje natural
Oro parece, plátano es
 Comedian (2019). Maurizio Cattelan. Imagen: EFE/EPA/RHONA WISE
Comedian (2019). Maurizio Cattelan. Imagen: EFE/EPA/RHONA WISE
Aunque este plátano fuese de oro no costaría 120.000 dólares.
El oro es una representación plástica del dinero. Porque el dinero es una abstracción. Por eso el inodoro de Maurizio Cattelan es de oro. El oro también es la representación de la luz sagrada, por eso los iconos religiosos se pintan y se cubren con oro. Por eso el Cristo Pantocrátor de Sicilia está repleto de oro. «Yo soy la luz del mundo».
El oro representa tanto los gustos profanos, el privilegio económico, como la divinidad y la trascendencia. El oro es un material que apela tanto a la voluntad de poder como a la voluntad de sentido. Ningún otro material abarca significados en principio tan opuestos.
Sobre todo en arte contemporáneo, el oro puede significar las dos cosas. Lo terrenal y lo divino. Si hay una línea que separa estos mundos, los artistas la han trazado con oro.
Las obras contemporáneas con oro son tremendamente sugerentes. Con los ojos del poder se leen de una manera, y con los del sentido se leen de otra. A veces las dos lecturas no son tan diferentes.
 Danae riceve la pioggia d’oro (1560-1565). Tiziano. Óleo sobre lienzo. 129,8 x 181,2 cm. Imagen: Wikimedia Commons
Danae riceve la pioggia d’oro (1560-1565). Tiziano. Óleo sobre lienzo. 129,8 x 181,2 cm. Imagen: Wikimedia CommonsLa obra Dánae (1959) de Vadim Zakharov es una revisión contemporánea de la Danáe de Tiziano. En ninguna de las dos obras se usa oro, sino la representación del oro. Porque el oro no es solo un material. El oro es un color.
En la obra de Tiziano aparece Dánae, que había sido encerrada por su padre, para evitar que se cumpliese la profecía de que un nieto le asesinase. Pero Zeus, el pretendiente de Dánae, se transforma en una nube de oro que penetra en la celda de Dánae y la fecunda.
Unos 450 años después, Vadim Zakhaorov rescata esta historia y la convierte en una performance. Diseñó unas monedas doradas que caen a un patio al que solo pueden acceder mujeres. Protegidas con paraguas, las mujeres pueden recoger las monedas con un cubo. En la performance, igual que en la pintura de Tiziano en su tiempo, el oro significa la divisa del género y del poder.
 Dánae (2013). Vadim Zakharov. Materiales variados, dimensiones variables. Imagen: Financial Times
Dánae (2013). Vadim Zakharov. Materiales variados, dimensiones variables. Imagen: Financial TimesLa obra El beso (1907-1908) de Gustav Klimt contiene oro. Ocho variedades de pan de oro que el artista manipuló para lograr diferentes efectos.
El oro ofrece una lectura tanto espiritual como terrenal. El lugar es de oro. Los ropajes son de oro. Los cuerpos no. Ahí está la línea que separa lo trascendente de lo mundano. Como si el sentido de un beso fuese sobrenatural. No el acto en sí, sino el mundo místico que surge a través de él. Es un mundo especial, alejado de lo cotidiano. Klimt nos está diciendo con oro: puedes tocar lo que amas.
 El beso (1907-1908). Gustav Klimt. Óleo, pan de oro y plata sobre lienzo. 180 x 180 cm. Imagen: Wikimedia Commons
El beso (1907-1908). Gustav Klimt. Óleo, pan de oro y plata sobre lienzo. 180 x 180 cm. Imagen: Wikimedia CommonsEl oro es un metal raro. Raro en toda la extensión de la palabra. Es raro porque se encuentra libre en la naturaleza. Otros metales se combinan con oxígeno, forman rocas, como sulfatos, sulfuros o carbonatos. El oro no. El oro es de color dorado. No se altera con el tiempo porque no se oxida. No deja de brillar. Es raro porque hay poco. Esa es una de las razones por las que se atesora como dinero. Su precio también fluctúa, como el del dinero. Es dinero con lustre.
Para los científicos, el color del oro y su escasa reactividad en gran medida siguen siendo un enigma. Para describir su color recurrimos a efectos relativistas. Cuando un elemento tiene tantos electrones (y por tanto tantos protones en su núcleo) ocurren fenómenos extraños desde el punto de vista de la física clásica. Los electrones se mueven a tal velocidad, con tanta energía, que tenemos recurrir a la relatividad. El salto de energía que se produce entre los electrones más externos, los de los orbitales 5 y 6, es tan pequeño que los electrones se disponen en configuraciones teóricamente anómalas. El color dorado implica que el oro absorbe energía en torno al azul. Es decir, absorbe energía de la región visible. Los orbitales 5 y 6 están tan próximos que la energía de la luz azul es suficiente.
 Configuración electrónica del oro. Imagen: Wikimedia Commons
Configuración electrónica del oro. Imagen: Wikimedia CommonsExisten varios métodos en arte para trabajar el oro y para cubrir objetos con oro. El que tiene más tradición en arte es el uso de pan de oro. El oro es un metal muy dúctil —que se deforma fácilmente aplicando presión— y maleable —fácilmente modelable y transformable en láminas—. Gracias a eso podemos transformarlo en pan de oro. Se bate con un martillo hasta obtener una lámina de metal con el grosor de una micra, incluso menos. Con 130 g de oro podemos fabricar hasta 10.000 láminas de pan de oro de 8 x 8 cm.
La artista Roni Horn creó en los años 80 una obra hecha exclusivamente con oro: Campo de oro. Esta obra es 1 kg de oro puro en una lámina de una centésima de milímetro de espesor. Esta lámina, tan etérea que parece ingrávida, se expone directamente en el suelo.
 Gold field (1982). Roni Horn. Oro. 124,5 x 152,4 x 0,002 cm. Imagen: (c) Roni Horn / Houser & Wirth/ The New York Times
Gold field (1982). Roni Horn. Oro. 124,5 x 152,4 x 0,002 cm. Imagen: (c) Roni Horn / Houser & Wirth/ The New York TimesA Roni Horn, más que el uso histórico del oro, su peso cultural o su sentido metafórico, le interesa su relación con la luz desde un punto de vista empírico. La luz incide en la lámina de oro dando la impresión de queda atrapada allí, como si emanase de su interior una misteriosa irradiación.
El oro es un material valioso y que dota de valor. Es un material que puede significar lo divino y puede significar lo lujoso. La palabra glamur está escrita con letras de oro. Con oro se pintan ángeles y cúpulas. Con oro se visten los mercados. La bisutería de latón se chapa con oro para parecer.
El oro puede resultar precioso y chabacano al mismo tiempo. Es excesivo, ostentoso y hortera. La cultura hip hop bajó el oro a la tierra. El oro representa el poder de la forma más frívola que puede entenderse el poder.
Piensa en el objeto cotidiano más ordinario y vulgar y hazlo de oro macizo. Y llámalo América.
 Instalación de América de Maurizio Cattelan en el Solomon Guggenheim de Nueva York. Imagen: Guggenheim
Instalación de América de Maurizio Cattelan en el Solomon Guggenheim de Nueva York. Imagen: GuggenheimAmérica (2016) es el inodoro de oro del artista Maurizio Cattelan. Está hecho de oro macizo de 18 quilates. El quilate designa la pureza del oro. Un quilate (símbolo K o kt) representa una veinticuatroava (1/24) parte de la masa total de la aleación que compone el metal. Una pieza de 24 quilates está hecha de 24/24 partes de oro y por lo tanto es de oro puro. El inodoro de oro, al ser de 18 quilates, su aleación está hecha de 18/24 (o 3/4) partes de oro. Es decir, tiene una pureza del 75%.
El inodoro de Cattelan tiene una masa de 103 kg. El precio del oro hoy es de 1.462,48 dólares por onza. Haciendo los cálculos obtenemos que solo el material de la obra costaría casi 4 millones de dólares. Hoy en día forma parte de la colección del Guggenheim y se estima su valor en 6 millones de dólares.
Hasta hace unos meses la obra estuvo instalada en uno de los baños del museo Guggeheim de Nueva York. Los visitantes podían usarlo como un retrete ordinario. Recientemente fue instalado en el Palacio de Blenheim en Reino Unido, donde estaba disponible para su uso como parte de una exposición de las obras de Cattelan. Se colocó en lugar de un inodoro utilizado anteriormente por Winston Churchill. Sorprendentemente, el 14 de septiembre de 2019 robaron la escultura y se supone que todavía está en paradero desconocido. La obra ya era famosa, pero con el robo ganó todavía más protagonismo. Después de la piedra robada de Yoko Ono, el inodoro de oro es la Mona Lisa robada de este siglo.
 La fuente (1917). Marcel Duchamp. Imagen: SFMOMA
La fuente (1917). Marcel Duchamp. Imagen: SFMOMAEl inodoro de Cattelan es como el urinario de Marcel Duchamp de nuestro tiempo. Es una copia de Duchamp, pero de oro. Una crítica intelectualmente vaga sobre la voluntad de poder, el lujo y las apariencias. Una crítica manida del mercado del arte. Es espectáculo, pero de oro. Es frivolidad, pero de oro. Sin embargo, ha sido la obra conceptual que, de manera más concisa y directa, ha retratado la obscenidad del poder.
Cattelan dice que «la risa y el humor es un caballo de Troya para entrar en contacto directo con el inconsciente, golpear la imaginación y desencadenar reacciones viscerales pero sin violencia».
 Un día perfecto (1999). Maurizio Cattelan. Imagen: Armin Linke / Perrotin
Un día perfecto (1999). Maurizio Cattelan. Imagen: Armin Linke / PerrotinYa en 1999 Cattelan sujetó a una pared de una galería, con cinta adhesiva, a Massimo de Carlo, su marchante de arte de Milán. Tituló la obra A Perfect Day, Un día perfecto. No tuvo tanto eco mediático como su reciente plátano pegado a la pared con cinta americana en el Art Basel de Miami. El plátano se titula Comedian, comediante. Es una suerte de autorretrato.
No es la primera vez que en el arte se usa el plátano para significar mofa. Ya lo hizo Andy Warhol o Guerrilla Girls. «Vivo en un planeta donde los hombres resbalan con cáscaras de plátanos», canta Mucho Muchacho en «Buah!».
 Autorretrato comiendo un plátano (1982). Andy Warhol. Imagen: Pinterest
Autorretrato comiendo un plátano (1982). Andy Warhol. Imagen: PinterestComedian es una bufonada sin mayor interés que ha conseguido captar la atención, no tanto la del mundo del arte, sino la de fuera.
Se supone que ha vendido tres copias de la pieza por 120.000 dólares cada una. Oro parece, plátano es. Algunos medios de comunicación cubrieron la noticia. Un escándalo. Llegados a este punto hace falta recordar que el precio es lo que alguien esté dispuesto a pagar. Un plátano y un trozo de cinta americana tienen un coste de producción que no llega ni a un dólar. Si el plátano fuese de oro macizo, el coste de producción rondaría los 7.000 dólares. No es lo mismo coste que precio. Ni en arte, ni en prácticamente nada.
El artista David Datuna arrancó el plátano de la pared y se lo comió. Otro día el plátano estaba tan maduro que se cayó al suelo y los galeristas lo reemplazaron por otro. Noticias súper importantes.
El Art Basel es una de las ferias de arte más relevantes, sin embargo, algunos medios de comunicación sólo prestaron atención al dichoso plátano. Una anécdota trivial para el mundo del arte convertida en circo mediático. También hay quien habrá leído este articulo hasta el final gracias a un maldito plátano. Si hay un problema con esto, ¿dónde está en realidad?
Para saber más:
Oskar González (2019) La tabla periódica en el arte: Oro kimikArte / Cuaderno de Cultura Científica
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Oro parece, plátano es se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Por qué si nunca hemos vivido mejor que ahora el mundo nos parece cada vez peor?
- Saber y saber que se sabe
- Las dietas detox ni desintoxican ni adelgazan
Infinitos
Puedo contar… hasta el infinito…
Eugène Ionesco, La lección
Cuando hablamos de manera informal, aludimos al infinito al referirnos a algo “muy grande”, a algo inalcanzable o lejano, a algo que no termina…
El concepto de infinito aparece en matemáticas, en filosofía y en otras ramas de la ciencia. Muchas paradojas relacionadas con la lógica están vinculadas con el infinito. De algunas de ellas hemos hablado en ¿Cuántas bolas contiene el jarrón al mediodía?, Una paradoja del infinito: ¿riqueza o ruina?, Una paradoja del infinito: la oferta del diablo, Infinitos monos o La paradoja de Tristram Shandy.
La idea de infinito es difícil de aprehender. Porque no hay un único infinito. Por ejemplo, los números enteros y los reales son infinitos, pero los primeros son numerables y los segundos no. Son conjuntos infinitos pero “de distinto tamaño”. Pero no hay que dejarse llevar por la apeirofobia, es mejor intentar entender lo que significa el infinito en cada momento… y disfrutar.
El cosmólogo John Barrow (1952) escribió en 2005 el libro de divulgación The infinity book: A Short Guide To The Boundless, Timeless, and Endless en el que hablaba del significado del infinito a lo largo de la historia, y de lo que este concepto ha influido en nuestro conocimiento y percepción del mundo. Y después escribió el libreto de Infinities, obra de teatro basada en este libro, estrenada en marzo de 2002 en Milán, representada por el Piccolo Teatro y dirigida por Luca Ronconi. Unos meses más tarde, se escenificó en La Nau de Valencia.

La obra se representa en una nave industrial dividida en cinco escenarios, con 65 actrices y actores involucrados. Cada escenario presenta el concepto de infinito desde un punto de vista diferente. El público va entrando en grupos de entre 60 y 80 personas; se mueven a través de los cinco escenarios, por turnos, permaneciendo en cada uno de ellos unos 15 minutos. La obra parece de este modo “infinita” al repetirse cada escena sin cesar.
Escenario 1: ¡Bienvenidos al Hotel infinito!
Trata del famoso Hotel infinito de Hilbert –que posee una cantidad numerable de habitaciones, es decir, ordenadas del modo 1, 2, 3, 4, 5, etc.–. El recepcionista tiene como misión alojar a cualquier visitante que llegue al hotel, a pesar de que se encuentre lleno. Un actor explica las recolocaciones que deben realizarse en las habitaciones para conseguir alojar a todos los huéspedes. Utiliza un monitor que aclara las operaciones matemáticas necesarias para lograrlo.
Por ejemplo, si llega un forastero, basta con desplazar el huésped de la habitación número n a la habitación n+1, y así la habitación número 1 queda libre para el recién llegado.
 Recolocaciones cuando llega un forastero. Imagen: Marta Macho Stadler.
Recolocaciones cuando llega un forastero. Imagen: Marta Macho Stadler.
Incluso si llegan infinitos –en cantidad numerable– nuevos visitantes, el recepcionista encontrará sitio para ellos: el huésped de la habitación número n pasará a la habitación 2n, y así todas las estancias impares quedarán libres para alojar a los recién llegados. En este último caso, la propiedad que entra en juego es la que afirma que el cardinal de los números naturales, pares e impares, ¡es el mismo!
 Recolocaciones cuando llegan infinitos forasteros. Imagen: Marta Macho Stadler.
Recolocaciones cuando llegan infinitos forasteros. Imagen: Marta Macho Stadler.
Escenario 2: La vida eterna
El público accede a una gran caja negra llena de personas ancianas que leen, abatidas, en sus sillas. Visten viejas ropas de época. La atmósfera es asfixiante. Los largos monólogos crean un ambiente de monotonía que conduce irremediablemente a la idea de eternidad. Se plantean diversas cuestiones. ¿Es realmente apetecible la vida eterna? ¿Qué consecuencias personales provocaría? ¿No es mejor una vida limitada, pero única e intensa?
Escenario 3: La replicación infinita
Este escenario teatraliza la Biblioteca de Babel de Jorge Luis Borges, esa biblioteca que lo alberga todo. Este fragmento del libro de Borges describe esa biblioteca:
A cada uno de los muros de cada hexágono corresponden cinco anaqueles; cada anaquel encierra treinta y dos libros de formato uniforme; cada libro es de cuatrocientas diez páginas; cada página de cuarenta renglones; cada renglón de unas ochenta letras. […] La biblioteca es total y en sus anaqueles se registran todas las posibles combinaciones de los veintitantos símbolos ortográficos, o sea, todo lo que es dable expresar. Todo: la historia minuciosa del porvenir, las autobiografías de los arcángeles, el catálogo fiel de la biblioteca, miles y miles de catálogos falsos, la demostración de la falacia de esos catálogos, el evangelio gnóstico de Basílides, el comentario de ese evangelio, el comentario del comentario, la relación verídica de tu muerte.
 La biblioteca de Babel. Imagen: Wikimedia Commons.
La biblioteca de Babel. Imagen: Wikimedia Commons.
Mediante juegos de espejos se produce la fantasía de ‘biblioteca infinita’. El público recorre esos pasillos mientras las voces de los actores resuenan a su alrededor. Los protagonistas visten igual y llevan máscaras idénticas, no es posible distinguirlos. Parece que cada vez hay más y más sobre el escenario. Con estas incesantes replicaciones se sugiere la imposibilidad de individualidad.
Este escenario simboliza la vida en un universo donde nada comienza. Todo se rehace incesantemente. Ninguna idea es nueva. Nada se realiza por primera vez ni por última. Nada es único. Cada persona posee réplicas ilimitadas de sí misma.
En un universo de este tipo, infinito, todo aquello que posee una probabilidad no nula de suceder ocurriría infinitas veces. En ese mundo existiría, en cada instante, un número infinito de reproducciones de cada uno de nosotros realizando nuestras mismas acciones, y otro número infinito de copias haciendo cualquier otra cosa. De hecho, habría una infinidad de copias de nosotros mismos realizando cualquier actividad con probabilidad no nula… ¡Realmente inquietante!
Escenario 4: El infinito no es un gran número
Este escenario habla acerca del famoso conflicto entre los matemáticos Georg Cantor y Leopold Kronecker acerca de la naturaleza del infinito. Según Kronecker, las matemáticas sólo podían construirse perfectamente si recurrían exclusivamente a los números enteros y a un número finito de operaciones. Las revolucionarias ideas de Cantor sobre el infinito fueron sistemáticamente rechazadas por Kronecker.
 Leopold Kronecker y Georg Cantor. Imagen: Wikimedia Commons.
Leopold Kronecker y Georg Cantor. Imagen: Wikimedia Commons.
En este escenario, la convulsa vida de Cantor –que sufrió numerosas depresiones a lo largo de su vida– se presenta a través de un actor inmovilizado en una silla de ruedas y vendado. Mientras tanto Kronecker –que es quien retiene a su alumno en esa silla– le da lecciones, desvariando, en una simulada aula en la que el público participa como parte del alumnado.
Escenario 5: ¿Es posible viajar en el tiempo?
En este escenario el público entra en un gran espacio abierto. Una anciana atraviesa la estancia vacilando. En cierto momento aparece su nieto que lleva una silla de ruedas hacia ella –aludiendo a la famosa paradoja de la abuela–. La idea de viaje en el tiempo se muestra a través de un tren con mesas, donde los pasajeros se sientan en ambas direcciones, sugiriendo un recorrido de ida y vuelta.
Pueden verse imágenes de esta obra en la referencia [5]. Sin duda, se trata de una inspiradora manera de hablar sobre el infinito, porque…
Un país sin teatro es un país sin espejos.
Rodolfo Usigli
Referencias
[1] R. Hoffmann and S. Coyaud, Infinite ideas. A theatrical contemplation of infinity makes full use of industrial space, Nature 416, 585, 11 abril 2002
[2] Marta Macho Stadler, Infinities de John Barrow, DivulgaMAT, 2009
[3] Marcus de Sautoy, To infinity and beyond, The Guardian, 5 noviembre 2003
[4] K. Shepherd-Barr, Hilbert’s Hotel, Other Paradoxes, Come to Life in New «Math Play», SIAM News 36 (7), septiembre 2003
[5] Algunas fotografías de la representación en Milán, Piccolo Teatro
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Infinitos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Infinitos monos
- El problema de la plantación de árboles en filas (2)
- ¿Cuántas bolas contiene el jarrón al mediodía?
El comportamiento corpuscular de la luz: momento lineal del fotón
 Foto: Johannes Plenio / Pixabay
Foto: Johannes Plenio / PixabayEl descubrimiento del cuanto de energía en los primeros años del siglo XX proporcionó una explicación del efecto fotoeléctrico y permitió el éxito del modelo cuántico del átomo de Bohr. Este modelo y los otros éxitos de la época contribuyeron a lo que se conoce como «teoría cuántica».
Sin embargo, la existencia del cuanto de energía, ya sea en la luz o en los átomos, planteaba un serio problema para la física, ya que era incompatible con la mecánica de Newton y la teoría de ondas electromagnéticas de Maxwell. En estas teorías, la energía es siempre continua e infinitamente divisible. Pero estas teorías «clásicas» se construyeron sobre la base de eventos que ocurren en el mundo visible a escala humana, desde planetas y estrellas hasta objetos microscópicos. No debería sorprendernos que la naturaleza pueda comportarse de manera diferente cuando nos adentramos en territorios muy alejados de la experiencia cotidiana, como el interior de los átomos o la estructura submicroscópica de cantidades minúsculas de luz.
A mediados de la década de 1920, la comunidad científica tenía claro que los primeros modelos cuánticos, realmente un pastiche de conceptos cuánticos y clásicos, eran fundamentalmente inadecuados y que se necesitaba una nueva teoría para abarcar el mundo cuántico que existía a nivel subatómico, una nueva mecánica cuántica en la que el cuanto estuviese integrado en los cimientos mismos de la física desde el principio. La clave para el desarrollo de la nueva mecánica provino del estudio pormenorizado de los conceptos cuánticos de corpúsculo y onda. Empecemos con el primero.
La hipótesis de Einstein de cuantos de luz creaba un dilema. Si bien el trabajo de Einstein indicaba que la luz se comporta como corpúsculos en experimentos como el efecto fotoeléctrico, la luz se comportaba claramente como ondas en el importante experimento de doble rendija de Young. Cuando un rayto de luz incide en dos rendijas estrechas cercanas, la luz que emerge de cada una de las rendijas interfiere y forma en una pantalla bandas alternas brillantes y oscuras que son características de la interferencia de las ondas. Los corpúsculos no pueden formar este patrón. Además, la teoría electromagnética de Maxwell explicaba la radiación electromagnética como un fenómeno ondulatorio, idea esta apoyada por el experimento de Young y muchos otros.
Por otro lado, la descripción de Einstein del efecto fotoeléctrico mostraba que la luz se comporta como si consistiera en cuantos de luz parecidos a corpúsculos, más tarde llamados «fotones». Cada fotón tiene energía E = hf, donde h es la constante de Planck y f es la frecuencia de la luz. El propio Einstein señaló que, dado que los fotones transportan energía, esta energía, mientras el fotón se mueve a la velocidad de la luz, c, es equivalente a una cierta cantidad de masa, de acuerdo con su famosa fórmula E = mc2. Esta cantidad de masa equivalente es, por tanto, m = E/c2.
Pero si el fotón tiene energía, y la energía es equivalente a una cantidad de masa, ¿significa esto que el fotón tiene momento lineal? Elaboremos un poco.
En física newtoniana el momento lineal, p, también llamado cantidad de movimiento, de un cuerpo se define como el producto de la masa de ese cuerpo por su velocidad, esto es, p = m·v [1]. Podemos sustituir m por su equivalente [2], lo que nos da p = Ev/c2, una ecuación para el momento en la que no aparece la masa directamente. Si la aplicamos al fotón, que se desplaza a la velocidad de la luz, v = c, resulta que p = E/c .
El efecto fotoeléctrico no dice nada del momento del fotón pero sí de su energía, como hemos mencionado antes, E = hf. De donde resulta que podemos expresar el momento lineal de un fotón de frecuencia f como p = hf/c.
También sabemos que frecuencia y longitud de onda son inversamente proporcionales, y la constante de proporcionalidad es la velocidad, esto es, f = v/λ, y, en el caso del fotón, f = c/λ. De donde resulta que el momento lineal del fotón es inversamente proporcional a su longitud de onda, p = h/λ.
Todo esto está muy bien y queda muy bonito pero no deja de ser prestidigitación matemática. La cuestión es: ¿tiene sentido físico definir el momento lineal de un fotón de esta manera? Diremos que tiene sentido físico si permite comprender algún resultado experimental. El primer uso con éxito de esta expresión para el momento lineal fue en el análisis de un fenómeno descubierto por Arthur H. Compton. Será lo que veamos a continuación.
Notas:
[1] Velocidad y momento son vectores, es decir, aparte de su magnitud tenemos que especificar su dirección y sentido. A los efectos de esta discusión los tratamos como escalares (solo magnitud) porque consideramos siempre dirección y sentido el de la propagación de la luz.
[2] La equivalencia E = mc2 aplica a cualquier cuerpo.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El comportamiento corpuscular de la luz: momento lineal del fotón se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ley del gas ideal a partir del modelo cinético
- La fe en las leyes de conservación
- La realidad de los estados estacionarios
El marco en el que se desarrolla la ciencia
 El globo de la ciencia y la innovación. CERN (Ginebra, Suiza). Fuente: geneve.com
El globo de la ciencia y la innovación. CERN (Ginebra, Suiza). Fuente: geneve.comCon esta anotación damos comienzo a una serie en la que trataremos un conjunto de temas que pueden englobarse bajo la denominación genérica de “males de la ciencia”. Entendemos por males de la ciencia todas aquellos rasgos o prácticas de la empresa científica que, de una u otra forma, socavan su integridad, limitan su credibilidad o dificultan un desarrollo adecuado. Pero antes de tratar esos “males” conviene saber de qué hablamos cuando hablamos de ciencia y cuál es el marco en que se desenvuelve.
Una descripción mínima de la ciencia
Quienes nos dedicamos a la investigación científica queremos desentrañar los secretos de la naturaleza, conocerla, entender los mecanismos subyacentes a lo que estudiamos. Observamos los fenómenos que nos interesan, buscamos regularidades en ellos, y si las encontramos tratamos de elaborar modelos que los representen, que nos ayuden a explicar las observaciones y, si es posible, a hacer predicciones. La medida de nuestro éxito viene determinada por nuestra capacidad para alumbrar nociones antes desconocidas, para generar nuevo conocimiento. A los científicos nos mueve la curiosidad, el interés por desvelar misterios, por arrojar luz allí donde antes había oscuridad. Aunque también puede interesarnos resolver algún problema práctico, crear algún producto nuevo, diseñar un nuevo procedimiento; en este segundo supuesto las cosas cambian algo, pero no demasiado. La curiosidad se dirige a resolver un problema concreto y el conocimiento es en este caso un conocimiento práctico.
En el pasado la mayoría de quienes se dedicaban a la ciencia lo hacían en solitario. Establecían normalmente relaciones epistolares con otros científicos o participaban en reuniones o demostraciones públicas en el marco de sociedades o academias. Pero el trabajo, la investigación, la hacían por su cuenta. Así trabajaron Galileo, Newton o Darwin, por ejemplo. Pero esa forma de trabajar prácticamente ha desaparecido. En la actualidad la ciencia es mucho más una tarea colectiva realizada por científicos profesionales trabajando en instituciones (e intensiva en financiación) que una vocación personal realizada de forma aislada por personas cuyo sustento no dependía de su actividad científica. Hoy, por el contrario, está altamente institucionalizada y requiere, además, de fuertes aportaciones económicas. Son esos dos elementos los que abordaremos a continuación.
Las instituciones científicas
Las primeras instituciones específicamente científicas fueron las sociedades científicas y las academias. Las más antiguas son la italiana Academia de los linces (1603), la Leopoldina o Academia alemana de las ciencias naturales (1652), la británica Royal Society (1660) y la Academia de Ciencias de Francia (1666). Originalmente, eran instituciones dedicadas a desarrollar actividades científicas y, sobre todo, a intercambiar y transmitir conocimiento. En la actualidad, las actividades y objetivos dependen de sus estatutos, pero sobre todo se dedican a transmitir conocimiento y a asesorar a gobiernos e instituciones públicas y entidades privadas. Pero no están consideradas agentes activos en investigación científica.
En la actualidad las instituciones científicas por excelencia, además de las universidades, son entidades de carácter público. Normalmente tienen una adscripción disciplinar concreta, o agrupa a varios centros de diversa filiación, y abarcan un amplio espectro de campos de conocimiento, incluidos de ciencia básica y de ciencia aplicada. En esas entidades desempeña su labor personal científico profesional que ha sido contratado con ese propósito. La medida en que desempeñan su tarea viene dada por la calidad y cantidad de los logros científicos alcanzados.
La investigación es una actividad esencial del personal de muchas universidades y, por lo tanto, la investigación científica lo es del profesorado de las disciplinas científicas. Esto no quiere decir que en todas las universidades se haga investigación, pero sí en prácticamente todas las herederas de la tradición alemana (humboldtiana) y también de las que se adscriben al modelo anglosajón de universidades investigadoras (research universities). Se justifica su dedicación a la investigación porque se supone que la práctica investigadora cualifica a su profesorado, lo que redunda en una mejor práctica docente. Y además, son las universidades, al otorgar el título de doctor, las instituciones encargadas de formar al personal investigador que desempeña su actividad en otras instituciones. También en estas instituciones, el nivel de desempeño del profesorado en esta faceta viene dado por la calidad y cantidad de los logros científicos.
Las universidades no son las únicas entidades en las que se realiza investigación a la vez que desempeñan otras actividades, a veces con carácter principal. Si en las universidades se compagina docencia e investigación, en los hospitales, por ejemplo, se compagina la práctica clínica con actividad investigadora en el campo sanitario. Y dependiendo del país de que se trate, pueden darse situaciones equivalentes también en otras instituciones de carácter público. Normalmente se trata de agencias gubernamentales que prestan un servicio de asesoramiento e información de carácter técnico muy especializado y en las que una parte de los recursos se destinan a la investigación.
Muchas empresas son también agentes activos en la creación de conocimiento. Lo pueden ser, además, de dos formas diferentes. Pueden contar con sus propias unidades y personal o, alternativamente, pueden contratar los servicios de otros agentes. El objetivo de la investigación empresarial es el desarrollo de nuevos productos, nuevos procesos o métodos que permitan mejorar la rentabilidad de los productos que lanza al mercado. Es, salvo raras excepciones, lo que se conoce como investigación aplicada. Por eso, el nivel de desempeño se cifra en el grado de adecuación de los resultados a las necesidades u objetivos de la empresa. Esa actividad puede plasmarse en productos que cuenten, posteriormente, con protección comercial, aunque no necesariamente ocurre así.
La financiación de la investigación
El otro elemento clave para el desarrollo de la ciencia es su financiación, puesto que sin recursos que sostengan una actividad de alto coste, como es la investigación científica, esta no es posible, no al menos con las dimensiones y alcance con que cuenta actualmente.
Francis Bacon (1561-1626) acuñó la expresión Knowledge is power, not mere ornament nor argument. Esa idea en apariencia tan simple y obvia, no lo era tanto en la época en que la formuló. De hecho, uno de los rasgos que diferencia la ciencia medieval de la moderna es que en esta última la búsqueda sistemática de conocimiento se ve como una forma de generar riqueza y poder. En la mente de Bacon, el conocimiento debía ser puesto al servicio de la nación. Tenía, pues, importancia política. Y por esa razón entendía que la Corona debía sostener su búsqueda sistemática; también entendía que con ese propósito debían crearse instituciones dedicadas a la búsqueda de conocimiento. Al principio no tuvo demasiado éxito en sus pretensiones, pero la idea de Bacon se ha acabado abriendo paso, y unos gobiernos antes y otros después -la mayor parte de ellos entrados ya en el siglo XX- han hecho suya la noción de que la actividad científica proporciona conocimiento susceptible de generar riqueza y proporcionar poder y, por lo tanto, que merece la pena dedicar recursos a sostener dicha actividad.
El desarrollo de la bomba atómica en EEUU durante la segunda guerra mundial –en el marco del denominado Proyecto Manhattan- se considera el hito que abrió la era de la “ciencia de estado”. Puso de manifiesto que con una financiación importante y contando con la participación de muchos científicos, un proyecto orientado a la consecución de un objetivo prefijado daba frutos muy valiosos. Tras el éxito de este proyecto se reconoce explícitamente (Venavar Bush) el valor de la ciencia para el estado, y se generaliza la financiación de la actividad científica al estilo del proyecto Manhattan, dinero público para proyectos con objetivos bien establecidos y duraciones limitadas.
En la actualidad en la mayor parte de los países avanzados es la administración pública la principal financiadora de la actividad científica y lo hace a través de muy diferentes programas [1]. Por esa razón, son los gobiernos los que toman las principales decisiones relativas a la orientación que ha de dársele. En definitiva, son los poderes públicos los que determinan las áreas en las que se debe investigar y las líneas que deben desarrollarse [2].
Como se ha dicho antes, otra parte de la investigación es la que tiene como objetivo el desarrollar nuevos productos o nuevos servicios, y se hace en o para empresas que, legítimamente, persiguen obtener beneficios económicos de esa forma. Las empresas que financian esa investigación no suelen estar interesadas en que sus resultados se den a conocer. El conocimiento que se genera en ellas es, lógicamente, de su propiedad, porque lo protegen.
La tecnociencia
Javier Echeverría (2019) ha reflexionado acerca del hecho de que precisamente a partir del Proyecto Manhattan antes mencionado la tecnología y, en particular, las tecnologías de la información y la comunicación, se han convertido en una mediación indispensable para el progreso científico. Ha denominado tecnociencia a esa hibridación entre ciencia y tecnología.
Según su visión, la tecnociencia no consiste únicamente en esa hibridación. Los grandes proyectos tecnocientíficos (Proyecto Manhattan, ENIAC, la Conquista del Espacio, los National Institutes of Health, el telescopio Hubble, los superaceleradores de Brookhaven y CERN europeo, el proyecto Genoma Humano, las grandes infraestructuras de investigación y tratamiento en los centros sanitarios, las empresas biofarmacéuticas, etc.) requieren un gran apoyo financiero, político, empresarial y, en algunos casos, también militar. Como conclusión, en lugar de las comunidades científicas, que son las que hacen ciencia, el agente de la tecnociencia es estructuralmente plural e incluye como mínimo a científicos, ingenieros, técnicos, políticos, inversores, empresarios, juristas, publicitarios y, con mucha frecuencia, también instituciones militares que toman a su cargo o participan activamente en determinados proyectos de investigación, así como desarrollando aplicaciones (I+D militar)
Fuente:
Tanto en este como en sucesivas entregas de esta serie, solo se consignarán aquí las fuentes no enlazadas directamente en el texto.
Echeverría, J (2019): Valores y mundos digitales (en prensa).
Notas:
[1]Normalmente más de la mitad del gasto en I+D se hace con cargo a fondos provenientes de diferentes administraciones; si a esas cantidades se le restase lo que no se gasta en investigación científica propiamente dicha, la contribución relativa de las administraciones sería mayor.
[2]Aunque lógicamente ello no es óbice para que en sus decisiones no tengan una influencia muy importante diferentes grupos de interés.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo El marco en el que se desarrolla la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- «Los blogs universitarios de divulgación científica en el marco de la Ley de la Ciencia» por José Manuel López Nicolás
- En la ciencia todo se desarrolla vigoroso, obvio y estupendo como en un cuento de hadas
- La hostilidad a la ciencia

