¿Por qué los átomos tienen el tamaño que tienen?
 Imagen: Berndthaller / Wikimedia Commons
Imagen: Berndthaller / Wikimedia CommonsA escala atómica el principio de incertidumbre se usa principalmente en argumentos generales sobre la teoría atómica más que en problemas numéricos concretos. Por ejemplo, el principio de incertidumbre ayuda a responder una pregunta fundamental que los pensadores se han planteado desde que apareció el concepto de átomo: ¿por qué los átomos tienen el tamaño que tienen? [1]
Los átomos en realidad están compuestos principalmente de espacio vacío. En el centro de cada átomo hay un núcleo muy pequeño, en el que se concentra toda la carga positiva y casi toda la masa del átomo. Alrededor del núcleo hay una cantidad de electrones igual a la carga positiva del núcleo. Los electrones están dispuestos en varias órbitas cuánticas. La más baja se llama el «estado fundamental». Pero incluso la órbita del estado fundamental todavía está lejos del núcleo. En la mayoría de los átomos, el radio del estado fundamental es de unos 10-8 cm, mientras que el radio del núcleo es de unos 10-12 cm. Esto significa que un núcleo ocupa solo una pequeña fracción del espacio dentro de un átomo; el resto está vacío (a excepción de unos pocos electrones que podemos considerar de tamaño puntual) [2].
El modelo de Rutherford, basado en un modelo planetario del átomo, es inestable, ya que el átomo debería colapsar en el núcleo, porque los electrones deberían irradiar su energía y girar en espiral hacia el núcleo. Bohr intentó explicar por qué esto no sucede al postular la existencia de estados cuánticos estacionarios, mientras que la mecánica cuántica asocia dichos estados con ondas estacionarias, teniendo el estado fundamental la onda de electrónica estacionaria más pequeña posible en esa órbita. Pero es el principio de incertidumbre el que explica por qué no podemos tener estados más bajos y por qué los electrones negativos no pueden existir dentro de o sobre el núcleo positivo. Bueno, para ser estrictos, el principio de incertidumbre combinado con el principio de constancia de la velocidad de la luz de la teoría de la relatividad.
Una aplicación simple de la relación de incertidumbre para la posición y el momento (Δx·Δpx≥h/4π) muestra que si un electrón está confinado a un espacio de 10-8 cm, el tamaño de un átomo promedio en centímetros, entonces la incertidumbre en su velocidad es menor que la velocidad de la luz. Pero si se limita a un espacio mucho más pequeño, o incluso al tamaño del núcleo, la incertidumbre en su velocidad excedería la velocidad de la luz, que es, redondeando, 3·1010 cm/s. Pero nada puede superar a la velocidad de la luz [3], ninguna partícula material puede exceder la velocidad de la luz. Por lo tanto, el espacio dentro del átomo entre el núcleo y el primer estado cuántico debe permanecer vacío. [4]
Ya tenemos un tamaño mínimo para el átomo dado por la combinación de incertidumbre y relatividad. ¿Existe algún límite al tamaño máximo?
Para aumentar el tamaño de un átomo, tendríamos que llevar electrones a estados cuánticos mucho más altos. Además de requerir la inyección de una gran cantidad de energía, los estados energéticos más altos no están espaciados uniformemente, sino que están cada vez más separados. Por lo tanto, la probabilidad aumenta enormemente de que los electrones en estos estados superiores puedan escapar del átomo y liberarse, por lo que dicho átomo no existiría durante mucho tiempo debido a la menor atracción electrostática del núcleo, lo que significa que en la práctica la mayoría de los átomos que se pueden estudiar tienen un tamaño de aproximadamente 10-8 cm.
Veremos en su momento que el hecho de que los átomos tengan un tamaño del orden de 10-8 cm ayuda a explicar muchas de las propiedades de la materia que vemos a nuestro alrededor.
Notas:
[1] Veremos que para responder a esta pregunta tendremos que echarmano de lo que hemos visto hasta ahora de Átomos y Cuantos.
[2] Implícitamente estamos considerando el aspecto corpuscular de los electrones. Esta interpretación es la que nos conviene en esta explicación, pero no debemos olvidar la dualidad onda-corpúsculo.
[3] Véase nuestra serie La teoría de la invariancia, una teoría popularmente llamada con un nombre que da lugar a equívocos: teoría de la relatividad.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo ¿Por qué los átomos tienen el tamaño que tienen? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El tamaño del átomo de hidrógeno
- La estructura de la tabla periódica se deduce de la estructura de capas de los átomos
- El tamaño de las moléculas
Ciencia Patológica
 Irving Langmuir. Imagen: Wikimedia Commons
Irving Langmuir. Imagen: Wikimedia CommonsAdemás del fraude, hay otros comportamientos por parte de quienes realizan investigación de vanguardia que pueden conducir a obtener –y en ocasiones anunciar o publicar- conclusiones erróneas o insostenibles. El que da lugar a la denominada “ciencia patológica” es uno de ellos.
La expresión “ciencia patológica” fue acuñada por Irvin Langmuir, químico y físico estadounidense que fue premio Nobel de química en 1932. Se movió entre la ciencia experimental y la teórica, y fue presidente de la Asociación Química Americana.
En la conferencia “Coloquio en el Laboratorio de Investigación Knolls de la General Electric”, impartida el 18 de Diciembre de 1953, Langmuir describió la “ciencia de las cosas que no son”, más tarde conocida como “ciencia patológica”. Esa denominación no hace referencia a una forma particular de pseudociencia, pues esta no tiene pretensión alguna de seguir el denominado “método científico”, sino a un tipo de investigación científica afectada por sesgos inconscientes y efectos subjetivos.
En su conferencia, Langmuir previno contra los peligros del autoengaño y dio cuenta de varios casos famosos, entre ellos: Los Rayos N, (Blondlot, 1903), una prueba experimental contraria a la Teoría de la Relatividad (Kaufmann, 1906), las radiaciones mitogenéticas o rayos Gurwitsch (1923), una verificación prematura del ”corrimiento al rojo” gravitacional (Adams, 1924), y los experimentos dudosos sobre rayos canales de Rupp (1926)*. J M Barandiarán (2017) incluye también en esa relación el caso de Percival Lowell y los “canales” marcianos, a los que dedicó la mayor parte de su actividad en el observatorio (privado) de Flagstaff (Arizona).
La ciencia patológica es un fenómeno que presenta los siguientes rasgos relativos a un supuesto descubrimiento científico:
- El efecto observable máximo es producido por un agente causante de intensidad apenas perceptible, y la magnitud del efecto es sustancialmente independiente de la intensidad de la causa.
- La magnitud del efecto es cercana al límite de la detectabilidad, o muchas medidas son necesarias debido a la baja relevancia estadística de los resultados. Suele ocurrir que el investigador encuentre excusas en estos casos para descartar datos convenientemente.
- Hay afirmaciones de gran exactitud.
- Se proponen teorías fantásticas contrarias a la experiencia.
- Las críticas se resuelven con excusas ad hoc.
- La proporción de partidarios frente a los críticos aumenta y después cae gradualmente al olvido. Los críticos no pueden reproducir los experimentos, sólo pueden los que son partidarios. Al final no se salva nada. De hecho, nunca hubo nada.
Como regla general la ciencia patológica trabaja en los límites difusos, no hay pretensión de fraude, simplemente es mala ciencia, que se practica por no saber reconocer las limitaciones epistemológicas del investigador, sus instrumentos y sus diseños experimentales. Hay mucha más de lo que sería deseable, sobre todo en algunos campos nuevos y de moda. El caso más sonado de ciencia patológica es, quizás, el de la supuesta “fusión fría”.
Si pensamos que para los investigadores constituye un fuerte incentivo la posibilidad de realizar descubrimientos cruciales, nos encontraríamos, paradójicamente, ante un caso en el que el reconocimiento por los hallazgos –que compensa, supuestamente, el carácter desinteresado de la actividad científica-, actuaría como factor principal de esta variedad de mal. Se trata de un efecto similar al de la segunda modalidad de fraude científico. También en este caso, es el escepticismo, la virtud mertoniana que queda en entredicho, no tanto porque se impida su ejercicio, sino porque no se actúa conforme a lo que tal virtud exige.
El contenido de esta anotación se ha basado, sobre todo, en esta otra de César Tomé López (2013) en el Cuaderno de Cultura Científica, y en la de J M Barandiarán (2017) en la web de BC Materials.
Nota:
[*] Rupp tuvo que admitir finalmente que sus extraordinarios resultados se debían, en parte, a una falsificación de datos.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Ciencia Patológica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ni ciencia, ni pseudociencia, ciencia patológica.
- Ciencia a presión: Ciencia patológica y patología editorial
- El fraude y las malas prácticas en ciencia
El efecto hoy en día
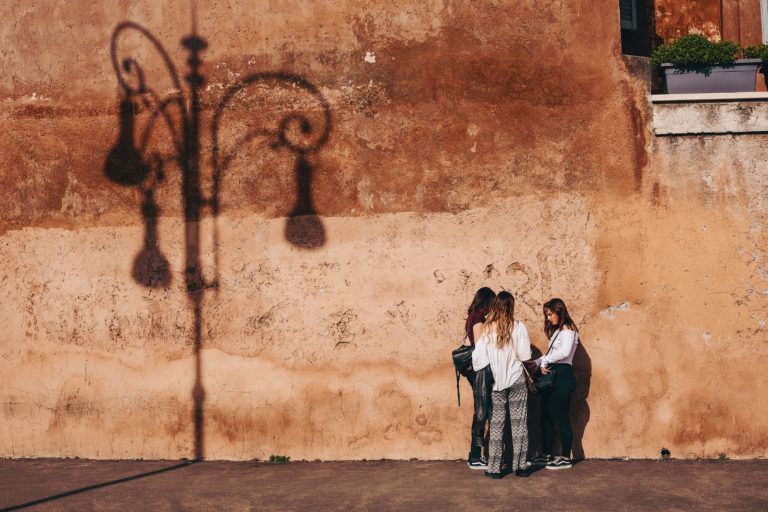 Foto: Cristina Gottardi / Unsplash
Foto: Cristina Gottardi / Unsplash“Ahora los chicos aman el lujo. Tienen malas maneras, desprecian la autoridad; no respetan a los mayores y prefieren la cháchara al ejercicio”. Las personas mayores decimos cosas semejantes con frecuencia. Y eso no es de ahora; se han dicho, al menos, desde que tenemos registros escritos de lo que pensaban nuestros antepasados. La cita entrecomillada con la que se abre este texto, en concreto, se atribuye a Sócrates. Pero si eso fuera cierto, si los jóvenes fuesen cada vez más disolutos, mas irrespetuosos, más holgazanes o más alocados, por citar solo algunos de los defectos que se les suelen atribuir, la juventud y con ella el resto de la humanidad, habría degenerado de una forma difícilmente soportable. Algo falla en esas expresiones.
Una investigación cuyas conclusiones se han dado a conocer recientemente ha abordado este asunto, indagando acerca del fenómeno denominado “efecto hoy en día” (these days effect en inglés). Y para ello ha pulsado la opinión de las personas mayores acerca de cómo han evolucionado tres rasgos en concreto desde nuestros años mozos hasta la juventud de hoy en día. Los rasgos son el respeto a las personas mayores, la inteligencia y el gusto por la lectura.
La conclusión general del estudio es que hay, efectivamente, una tendencia general a hablar mal de la juventud en lo relativo al respeto a los mayores y el gusto por la lectura. Y también una tendencia a valorar de forma negativa a la gente joven en aquellos rasgos en los que uno destaca o cree destacar; esta tendencia es común a los tres rasgos investigados. O sea, cuando una persona adulta es muy respetuosa con la autoridad, tiende a pensar que la gente joven de ahora respeta a los mayores menos que los jóvenes de su época. Y lo propio ocurre con la inteligencia y con la afición a leer. El efecto es, sobre todo, específico de cada rasgo, porque, por ejemplo, alguien muy aficionado a la lectura pero que valora poco la autoridad, no tiende a pensar que los jóvenes de hoy en día no respetan a los mayores como se les respetaba antes. En otras palabras, ese “efecto hoy en día” no consiste en una minusvaloración o mala opinión general de la juventud sino que se circunscribe a dominios relativamente específicos.
Los autores del trabajo identificaron dos mecanismos que subyacen al efecto. Por un lado, observaron que la gente que destaca en algún rasgo tiene una especial tendencia a percibir los fallos en ese mismo rasgo de los demás, tanto en los jóvenes como en los adultos. Y por otra parte, tienden a proyectar sus características actuales hacia el pasado, incurriendo en el error de pensar que cuando eran jóvenes tenían las mismas virtudes o rasgos favorables que en el presente. Por eso se comparan tal y como se ven a sí mismos hoy con los jóvenes, sin caer en la cuenta de que ellos no son ahora como eran hace cuarenta años. Este mismo sesgo ha podido estar actuando durante milenios, con lo que ello implica.
Si llevamos siglos valorando de forma negativa a los “jóvenes de hoy en día”, es muy improbable que los mayores dejemos de hacerlo en adelante. Por esa razón, cuando oiga a sus familiares o colegas, o incluso, se descubra a sí mismo diciendo que los jóvenes de ahora son indisciplinados, no respetan a sus mayores, no leen, antes llegaban mejor preparados a la universidad, o cosas semejantes, antes de asentir o de seguir con la diatriba piense que eso mismo decían los griegos hace casi veinticinco siglos.
Fuente:
John Protzko and Jonathan W. Schooler (2019): Kids these days: Why the youth of today seem lacking Science Advances: 5 (10) eaav5916 DOI: 10.1126/sciadv.aav5916
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El efecto hoy en día se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- No duermas, hay leones
- El efecto escenario: por qué la gente elige la opción de en medio
- El desajuste adolescente
Energía… ¿oscura?

¿Podemos predecir el destino del Universo? Aunque parezca sorprendente, al parecer sí que se puede. Sin embargo, en el intento nos hemos encontrado con el efecto de la llamada ‘energía oscura’. ¿Podemos entender de dónde viene la energía oscura y cuál es su efecto, o debemos simplemente aceptar su existencia?
Ciertamente, nos encontramos ante grandes incógnitas. Para abordar estas cuestiones y reflexionar sobre ellas, el ciclo de conferencias Bidebarrieta Científica acogió la charla titulada “Energía… ¿oscura?” de la mano de Marcos Pellejero Ibáñez, investigador postdoctoral en el Donostia International Physics Center, el pasado 29 de enero de 2020.
Marcos Pellejero habló sobre el Universo y el vacío en esta conferencia del ciclo Bidebarrieta Científica, iniciativa impulsada por la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta y que en esta ocasión se celebrará en el marco de la tercera edición del ciclo de cine y ciencia organizado por la Filmoteca Vasca, el Donostia International Physics Center (DIPC) y el Festival de Cine de San Sebastián.
Edición realizada por César Tomé López
El artículo Energía… ¿oscura? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Prótesis biocompatibles por impresión 3D
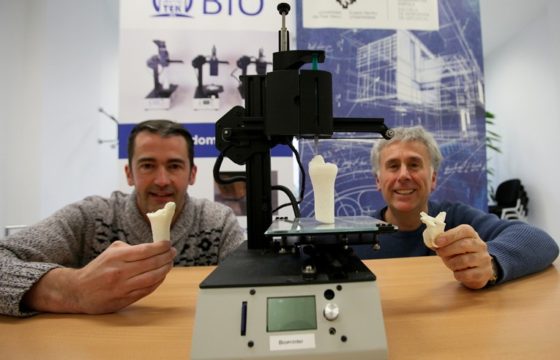 Koldo Artola de Domotek y Pedro Guerrero de Biomat. Foto: Nagore Iraola -UPV/EHU.
Koldo Artola de Domotek y Pedro Guerrero de Biomat. Foto: Nagore Iraola -UPV/EHU.La impresión en tres dimensiones (3D) ha constituido un gran avance en la medicina personalizada al desarrollar biomodelos que facilitan en gran medida la labor del profesional de la salud. Un nuevo paso en este camino es el trabajo colaborativo llevado a cabo entre el grupo Biomat de la Universidad del País Vasco y la empresa Domotek que ha permitido la obtención de biomodelos personalizados de colágeno nativo. Gracias a los avances en la obtención de biomateriales procesables por impresión 3D, desarrollados por Biomat, y en la adquisición y procesado de datos para impresoras 3D, llevados a cabo por Domotek, los productos fabricados pueden ser utilizados como piezas de utillaje o prótesis gracias a su biocompatibilidad.
“A partir de imágenes médicas tomadas al paciente, principalmente mediante Tomografía Axial Computarizada (TAC) o Imagen por Resonancia Magnética (MRI), se pueden obtener modelos digitales 3D de gran precisión -explica Pedro Guerrero, investigador del grupo Biomat-. Estos modelos digitales se pueden transformar en datos que pueden ser procesados por las impresoras 3D para imprimir réplicas exactas (biomodelos) de la anatomía del paciente. Estos biomodelos sirven al médico para verificar los procedimientos quirúrgicos y mejoran la comunicación de los médicos con el paciente, mostrándole el biomodelo al paciente para que este comprenda mejor la intervención a realizar. En la actualidad, los implantes personalizados hacen posible la reconstrucción del defecto sin alterar la anatomía del paciente, consiguiéndose una mejora en la eficiencia de la cirugía y reduciendo la duración y los costes de la misma”.
Las impresoras 3D pueden reproducir los biomodelos en plástico o resina, pero estos materiales presentan riesgos de infección o rechazo, por ello el desarrollo de nuevos materiales es clave. “Con el desarrollo llevado a cabo por Biomat y Domotek, los biomodelos se pueden fabricar con colágeno nativo tipo I, un material biocompatible, biodegradable, poroso, adecuado para la adhesión celular y que no presenta citotoxicidad. Por tanto, estos biomodelos fabricados con materiales basados en colágeno nativo pueden ser las prótesis del mañana, ya que, gracias a sus propiedades, pueden comportarse como sustitutos temporales del tejido dañado mientras este se regenera. En el caso de los implantes, la biodegradabilidad es muy importante ya que evita una segunda cirugía para eliminar el implante”, aclara el profesor Guerrero.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Prótesis biocompatibles por impresión 3D se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Polímeros biocompatibles para integrar dispositivos electrónicos en nuestro cuerpo
- Cómo regular la velocidad de disolución de los biometales de las prótesis
- Control adaptativo de robots para rehabilitación
El efecto escenario: por qué la gente elige la opción de en medio

Ante una lista de opciones o elementos similares colocados en fila, los humanos tendemos a descartar los extremos y quedarnos con aquellos situados en medio. Sucede con números, con imágenes e incluso con concursantes de un programa de televisión1. El efecto de preferencia central (“center stage effect” o “centrality preference” en la literatura en inglés) ha sido estudiado por la psicología desde hace décadas y presenta una robusta evidencia23. Los motivos de esta curiosa preferencia no terminan de estar claros 4: podría tratarse de una cuestión perceptiva56 (fijamos nuestra mirada en el centro por lo que tendemos a elegir cosas situadas ahí), cultural7 (el prestigio y la autoridad asociados a una posición central), o una estrategia para reducir el esfuerzo mental que supone elegir8. De un modo u otro, las implicaciones de este efecto resultan de lo más variopintas. Aquí van algunas:
Servicios públicos
En un artículo publicado en 19959, Nicholas Christenfeld presentó una serie de experimentos sobre este curioso sesgo: en uno de ellos, examinó las preferencias de los playeros de California a la hora de ir a mear. Como hubiese sido un poco violento plantarse en la puerta de los servicios públicos a contar visitantes, Christenfeld usó una medida indirecta. Con ayuda del personal de limpieza, registró el uso de papel higiénico de cada una de las cabinas. El resultado confirmó la sospecha: los playeros utilizaban los retretes centrales con bastante más frecuencia de la que cabía esperar por puro azar. Así que la próxima vez, ya sabes… si quieres usar el retrete más limpio, deberías optar por los extremos. No sólo estarán menos usados, además tendrás más posibilidades de encontrar papel higiénico.
¡Compra, compra!
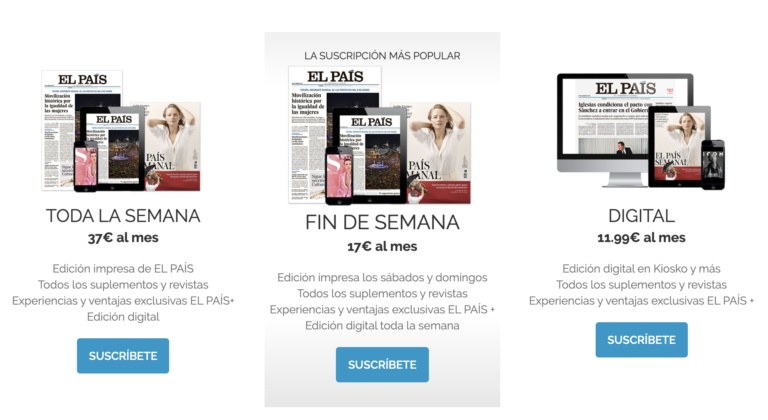
Objetos similares colocados en fila. Está claro que nuestra preferencia por la centralidad tiene muchas ocasiones de salir a relucir cada día. Pero quizás la más clara es la que nos sitúa como compradores ante una colección de productos. Esta colección puede tomar distintas formas: puede ser un escaparate, perfectamente ordenado tras un cristal. También puede tratarse de un catálogo, la balda del supermercado, o las bebidas en la nevera al final de un buffet. Y, claro está, también puede darse en internet: desde la galería de amazon a cualquier página web de venta online. En todos estos casos, los clientes tienden a elegir y gastar más dinero en los elementos situados hacia el centro de su campo visual. Es algo que saben quienes disponen los productos en tiendas físicas y también quienes crean páginas web. De hecho, si recientemente has contratado alguna suscripción o servicio online, es probable que esta distribución te resulte sospechosamente familiar:
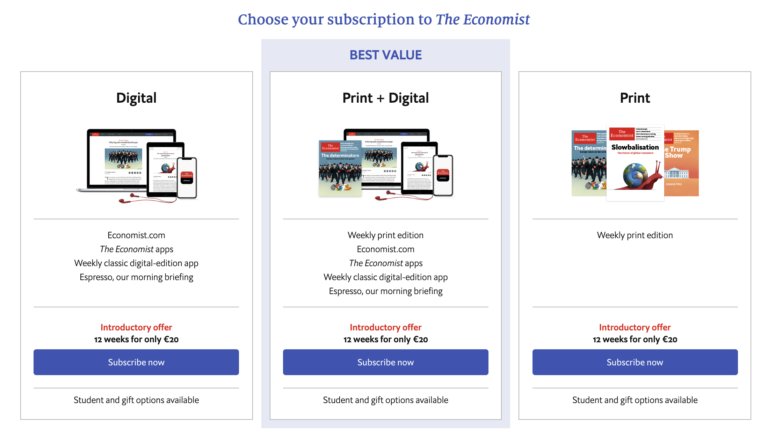
Esta es una captura de la página de suscripción a The Economist. Pero la idea no es precisamente original. La misma idea se repite una y otra vez. Sencillamente, porque funciona.

Exámenes tipo test
El MIR es, quizás, una de las pruebas más exigentes a las que se enfrenta todo médico durante su carrera. Sin embargo, hasta hace algunos años, los estudiantes recién salidos de la facultad podían contar con una pequeña ventaja. Si algún concepto sobre anatomía humana se les escapaba, siempre podían jugársela con la psicología: debido a los sesgos de quienes habían diseñado el examen, no todas las respuestas eran correctas con igual probabilidad. Según me cuentan los doctores Elena Alvar y Julián Palacios (especialistas en anestesiología y cardiología, respectivamente), este hecho era ampliamente conocido por los estudiantes y se contaba en algunos cursos de preparación a las pruebas. Las respuestas correctas seguían una distribución muy similar a las de las carreras de tortugas. Los examinadores, sin saberlo, tendían a colocar las respuestas correctas con mayor probabilidad hacia el centro. Los estudiantes, incluso sin haberlo sabido, hubiesen optado por ellas también: el sesgo funciona en ambos sentidos y quienes se someten en este tipo de tests, tienden a buscar la respuesta correcta lejos de los extremos.
Esta colaboración no buscada entre examinadores y examinados tiende a darse en todas las pruebas de elección múltiple10. Pero en el caso del MIR tuvo su fin hacia 2010. Desde ese año y hasta 2014, el Ministerio hizo un esfuerzo deliberado por equilibrar la distribución de aciertos entre las 5 respuestas posibles. En 2015, los exámenes pasaron a tener cuatro alternativas en lugar de 5 y parece que los resultados han vuelto a perder el equilibrio favoreciendo ligerísimamente las opciones de en medio. El margen es tan leve que nadie se va a librar de estudiar. Pero ante la duda… siempre mejor quedarse con la segunda o tercera tortuga.
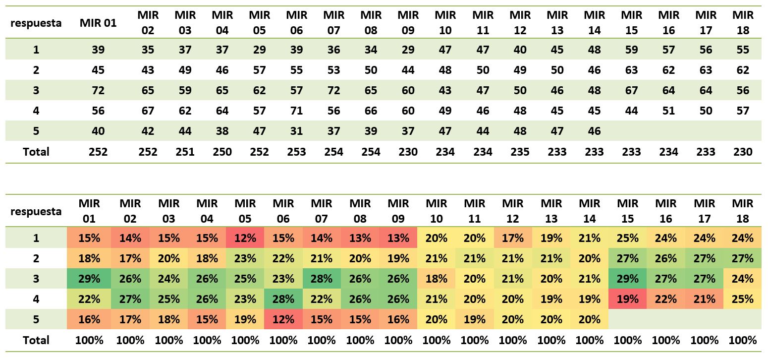 Distribución de las respuestas correctas, según su posición, en las pruebas del MIR, año a año. Fuente.
Distribución de las respuestas correctas, según su posición, en las pruebas del MIR, año a año. Fuente.Referencias:
1Raghubir, P. & Valenzuela. (2006). Centre-of-inattention: Position biases in decision-making. Organisational Behaviour and Human Decision Processes, 99, 66-80
2Paul Rodway Astrid Schepman & Jordana Lambert (2011). Preferring the One in the Middle: Further Evidence for the Centre‐stage Effect. Applied cognitive Psychology.
3Maya Bar-Hillel (2015). Position Effects in Choice From Simultaneous Displays: A Conundrum Solved. Perspectives on Psychological Science.
4Paul Rodway, Astrid Schepman, Volker Thoma (2015). Reachability Does Not Explain the Middle Preference: A Comment on Bar-Hillel
5Benjamin W. Tatler (2007). The central fixation bias in scene viewing: Selecting an optimal viewing position independently of motor biases and image feature distributions. Journal of Vision.
6 A. Selin Atalay, H. Onur Bodur, and Dina Rasolofoarison (2012). Shining in the Center: Central Gaze Cascade Effect on Product Choice. Journal of Consumer Research.
7Valenzuela, Ana & Raghubir, Priya. (2009). Position-based beliefs: The center-stage effect. Journal of Consumer Psychology,
8Jerry I. Shaw, Jon E. Bergen, Chad A. Brown & Maureen E. Gallagher (2000) Centrality Preferences in Choices Among Similar Options, The Journal of General Psychology,
9Nicholas Christenfeld (1995). Choices from Iden tical Options. Psychological Science,
10Attali, Yigal & Bar-Hillel, Maya (2003). Guess Where: The Position of Correct Answers in Multiple‐Choice Test Items as a Psychometric Variable. Journal of Educational Measurement.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El efecto escenario: por qué la gente elige la opción de en medio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Estas Navidades no engordarás medio kilo
- Los números feos de la lotería
- ¿Cuánta gente ha vivido en la Tierra?
Las curvas del espirógrafo
En mi anterior entrada del Cuaderno de Cultura Científica Guía matemática para el cómic ‘Promethea’, sobre las referencias matemáticas que aparecen en Promethea (1999-2005), del guionista Alan Moore y el dibujante James H. Williams III, mencioné que en algunas partes del mismo aparecían “curvas hipotrocoides dibujadas con un espirógrafo”, como las que se pueden ver en la siguiente imagen.
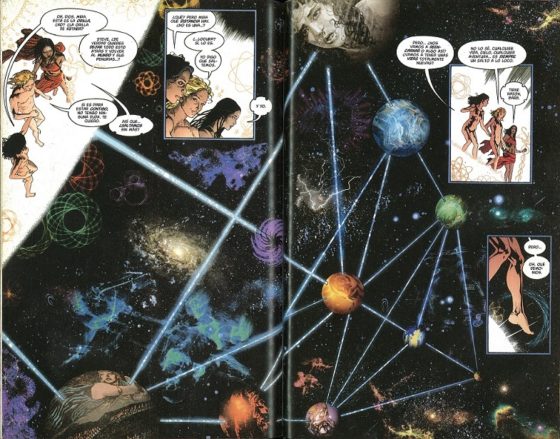 Doble página del cómic Promethea, de Alan Moore (guion) y J.H. Williams III (dibujo)
Doble página del cómic Promethea, de Alan Moore (guion) y J.H. Williams III (dibujo)
Si nos fijamos en las curvas que aparecen dibujadas en el cómic es posible que nos recuerden a los diseños geométricos realizados con un juguete llamado espirógrafo, con el que tal vez jugamos en nuestra infancia. Diseños geométricos como los que aparecen en la siguiente imagen.

O también los dibujos de esta otra imagen.
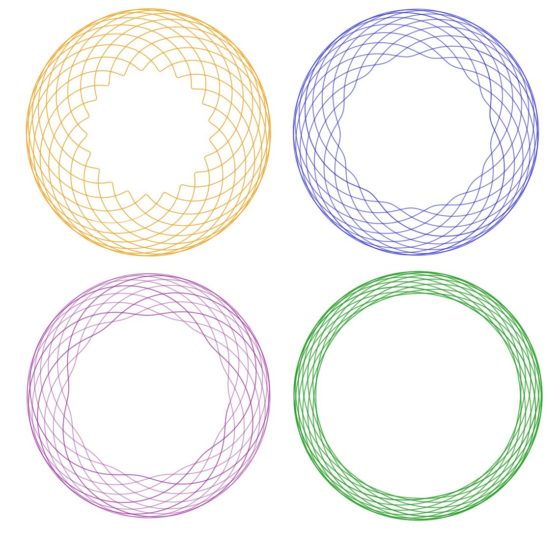
Estos diseños geométricos los he realizado con el Inspirograph, que es una réplica digital del espirógrafo desarrollada por el ingeniero canadiense Nathan Friend.
“Kate conocía a todos los tenderos y se llevaba bien con ellos. La verdulería la llevaban Eric y su mujer Mavis. No tenían hijos, pero eran amables con Kate y todas las navidades le compraban un regalo con el que –era increíble– siempre daban en el clavo. El año pasado le habían comprado un espirógrafo, y Kate lo había utilizado para confeccionar un logotipo para sus tarjetas de visita.”
[Katherine O Flynn, Lo que perdimos, Alfaguara, 2009]
El espirógrafo es un juguete con el que dibujar diseños geométricos que consisten en curvas cíclicas, en concreto, las curvas conocidas con los nombres de hipotrocoides (como los primeros dibujos que hemos trazado) y epitrocoides (como los segundos dibujos), que describiremos matemáticamente más adelante. Este juguete consiste en una serie de engranajes o ruedas dentadas –círculos o coronas circulares en la versión original y más sencilla, pero con formas más complejas en la actualidad–, de tal forma que al girar una rueda dentada sobre la otra, que permanece fija, se producen los diseños geométricos. El dibujo se realiza con un lápiz o rotulador cuya punta se coloca en uno de los agujeros que tiene el interior de la rueda dentada que se hace girar. La rueda dentada fija puede ser tanto una corona circular dentada, de forma que se puede girar la otra rueda dentada tanto por el exterior (generando las curvas epitrocoides), como por el interior (generando las curvas hipotrocoides), de las que solía haber dos en el juego, o un círculo dentado de diferentes tamaños sobre el que solo se puede hacer girar la otra por el exterior (generando hipotrocoides).
 Versión del juguete espirógrafo fabricada por Palitoy y vendida en Gran Bretaña en la década de los años 1980. Imagen: Multicherry / Wikimedia Commons
Versión del juguete espirógrafo fabricada por Palitoy y vendida en Gran Bretaña en la década de los años 1980. Imagen: Multicherry / Wikimedia Commons
El espirógrafo fue creado por el ingeniero británico Denys Fisher (1918-2002) en los primeros años de la década de 1960. Animado por su familia y amigos, el ingeniero británico fundó Denys Fisher Toys (que en 1970 compraría la empresa Palitoy, la cual acabaría formando parte de Hasbro en 1991) y empezó a comercializar el juguete. Se presentó en la Feria Internacional de Juguetes de Nurenberg en 1965 y fue declarado juguete británico del año en 1967. Fue patentado en 16 países. La siguiente imagen es de la patente de 1966 en Estados Unidos.
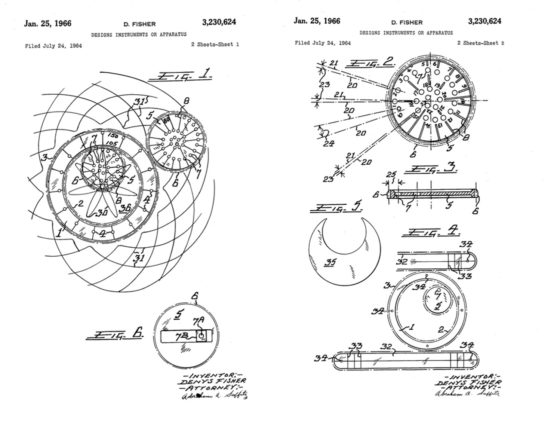 Imágenes pertenecientes a la patente en EEUU del espirógrafo de Denys Fisher, US32230624
Imágenes pertenecientes a la patente en EEUU del espirógrafo de Denys Fisher, US32230624
El juego fue todo un éxito. Además, evolucionó rápidamente incluyendo engranajes de formas variadas, que permitían diseños geométricos cada vez más sofisticados y originales. En 2013 la compañía de juguetes Kahootz relanzó el espirógrafo y ganó varios premios, como el Astra Best Toys for Kids de 2013, así mismo fue finalista a juguete del año en 2014.
Pero mencionemos algunos antecedentes de la creación del ingeniero británico Denys Fisher. En 1827 el ingeniero y arquitecto británico Peter Hubert Desvignes (1804-1883) diseñó un mecanismo que llamó “speiragraph” y que servía para dibujar complejas curvas de tipo espiral. El objetivo de este mecanismo era crear diseños que ayudasen a evitar las falsificaciones de los billetes.
 Carpeta con 26 hojas de papel que contienen dibujos realizados con el “speiragraph” de Peter Hubert Desvignes, perteneciente al Science Museum Group. A la izquierda se observa una hoja con una serie de dibujos horizontales de curvas de tipo espiral, mientras que a la derecha hay una hoja con un dibujo de tipo circular de una curva espiral
Carpeta con 26 hojas de papel que contienen dibujos realizados con el “speiragraph” de Peter Hubert Desvignes, perteneciente al Science Museum Group. A la izquierda se observa una hoja con una serie de dibujos horizontales de curvas de tipo espiral, mientras que a la derecha hay una hoja con un dibujo de tipo circular de una curva espiral
El matemático, ingeniero eléctrico e inventor polaco Bruno Abakanowicz (1852-1900), quien inventaría mecanismos como el intégrafo, para representar la integral de una función definida gráficamente, y el parabológrafo, para trazar parábolas, inventó otro mecanismo con el nombre de “spirograh” (espirógrafo), entre 1881 y 1900, que también debía trazar curvas de tipo espiral (spiro + graph), aunque no he podido encontrar ninguna referencia directa del mismo.
El primer juguete precursor del espirógrafo fue el llamado “The Marvelous Wondergraph” con el que realizar diseños geométricos de curvas espirales, pero que pasó bastante desapercibido. En la publicación The Boy Mechanic apareció en 1913 un artículo explicando cómo construir tu propio wandergraph.
 Juguete The Marvelous Wondergraph, perteneciente al The Children’s Museum of Indianapolis
Juguete The Marvelous Wondergraph, perteneciente al The Children’s Museum of Indianapolis
En la década de los años 1930 se comercializó otro juguete para trazar diseños geométricos de curvas, llamado “Hoot-Nanny, The Magic Desiner”, que tuvo más éxito que el anterior y se vendió hasta la década de los años 1950. En la siguiente imagen vemos las instrucciones originales del juguete, con algunas de las curvas que podían trazarse con el mismo. Además, hay un simulador en la red del Hoot-Nanny, con el que podéis divertiros trazando curvas curiosas.
 Instrucciones originales del juguete Hoot-Nanny
Instrucciones originales del juguete Hoot-Nanny
Aunque el juguete espirógrafo del ingeniero británico Denys Fisher fue el que más éxito alcanzó, quizás por la sencillez de su diseño y su manejo, por lo que también trazaba curvas más sencillas, o tal vez porque en los años 60 la sociedad estaba más abierta a este tipo de imágenes geométricas, ya que era el tiempo de la psicodelia y del arte pop.
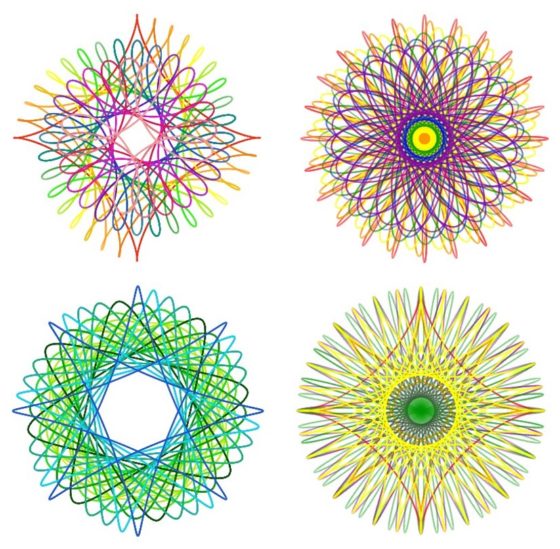 Diseños geométricos realizados con el espirógrafo digital Inspirograph
Diseños geométricos realizados con el espirógrafo digital Inspirograph
Pero vayamos a las curvas geométricas que dibuja el espirógrafo, las hipotrocoides y epitrocoides, que son dos tipos particulares de curvas cíclicas o “ruletas”. Las curvas cíclicas son las curvas planas descritas por la trayectoria de un punto que pertenece a una curva plana (o relacionado con ella) que rueda, sin deslizarse, sobre otra curva plana. A la familia de las curvas cíclicas pertenecen la cicloide, las trocoides, las epicicloides, las hipocicloides, epitrocoides, hipotrocoides y las involutas.
La cicloide es la curva que describe un punto que está en el borde de una rueda circular, es decir, el punto de una circunferencia, que rueda, sin deslizarse, a lo largo de una recta.
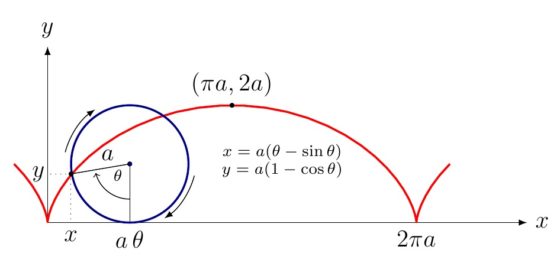 Imagen de una de los arcos de la curva cicloide, en rojo, generada por un punto de la circunferencia –azul– que gira, sin deslizarse, sobre la recta horizontal – eje x del plano coordenado–. Imagen de Herman Jaramillo para la web StakExchange
Imagen de una de los arcos de la curva cicloide, en rojo, generada por un punto de la circunferencia –azul– que gira, sin deslizarse, sobre la recta horizontal – eje x del plano coordenado–. Imagen de Herman Jaramillo para la web StakExchange
Esta curva, como las demás que se citan aquí, ya era conocida en la antigüedad, pero fue ampliamente estudiada en el siglo XVII por grandes matemáticos como el francés Marin Mersenne (1588-1648), quien dio la primera definición matemática precisa, el italiano Galileo Galilei (1564-1642), quien estudió la curva durante cuarenta años y a quien le debemos su nombre (que viene de las palabras griegas kuklos, de la que deriva ciclo y que significa círculo, y eidos, que significa forma o imagen), el francés Gilles de Roverbal (1602-1675), quien calculó el área debajo de la curva, el italiano Evangelista Torricelli (1607-1647), Blaise Pascal (1623-1662), que tiene una curiosa relación con la cicloide (puede leerse en la entrada Blaise Pascal, Dios y la cicloide), Christiaan Huygens (1629-1695), quien descubriría que la cicloide es la curva tautócrona, es decir, aquella para la cual el tiempo que tarda una bola en recorrer la cicloide invertida, sin deslizamiento, hasta llegar al punto más bajo de la curva es independiente de la altura desde la que se dejó caer la bola, y utilizó esta propiedad para construir el péndulo cicloidal, el francés Girard Desargues (1591-1661), el matemático alemán Gottfried Wilhelm Leibniz (1646-1716), o el matemático suizo Johann Bernoulli (1667-1748), quien descubrió que la cicloide era la curva braquistócrona, es decir, la curva de recorrido más rápido de una bola que se desplaza de un punto a otro más bajo por el efecto de la gravedad, entre muchos otros.
 Experimento del Technoseum, Mannheim, Alemania, demostrando que la cicloide es la curva braquistócrona, de los cuatro caminos que unen la parte superior con la inferior, el que tiene la forma de cicloide es el más rápido, es decir, el camino por el cual la bola llega antes a su destino
Experimento del Technoseum, Mannheim, Alemania, demostrando que la cicloide es la curva braquistócrona, de los cuatro caminos que unen la parte superior con la inferior, el que tiene la forma de cicloide es el más rápido, es decir, el camino por el cual la bola llega antes a su destino
Una cita literaria conocida en la que se menciona a la cicloide y su condición de curva tautócrona es Moby Dick (1851), del escritor estadounidense Hermann Melville (1819-1891):
Algunos marineros viejos y cínicos acostumbran, durante las guardias de noche, introducirse en ellas [las dos ollas de la refinería del barco] y enrollarse en su interior para dormir un rato. Mientras están dedicados a la tarea de lustrarlas –un hombre en cada olla, hombro con hombro– se transmiten muchas comunicaciones confidenciales, por encima de los labios de hierro. El sitio es propicio, también, para la meditación matemática profunda. En la olla izquierda del Pequod, mientras hacía circular dirigentemente la esteatita frente a mí, me sorprendió indirectamente el hecho notable de que en geometría todos los cuerpos que se deslizan en el cicloide, mi esteatita por ejemplo, descienden de cualquier punto exactamente en el mismo tiempo.
Por otra parte, se denomina curva trocoide a la curva que describe un punto conectado con una rueda circular, ya sea porque pertenece al interior de la misma, a su circunferencia o siendo exterior al círculo está conectado con este, que rueda, sin deslizarse, sobre una línea recta. Por lo tanto, la cicloide es una curva trocoide (término que viene de las palabras griegas trhokos, que significa rueda, y eidos, que significa forma o imagen) en la que el punto está sobre la circunferencia de la rueda circular. Si el punto es interior se habla de cicloide reducida y si es exterior de cicloide alargada.
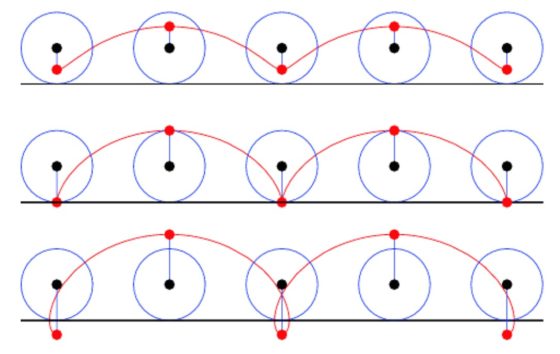 Imagen de los tres tipos de curvas trocoides, la cicloide reducida, la cicloide y la cicloide alargada. Imagen de Wolgram MathWorld
Imagen de los tres tipos de curvas trocoides, la cicloide reducida, la cicloide y la cicloide alargada. Imagen de Wolgram MathWorld
En el espirógrafo clásico hay dos piezas muy alargadas de forma que la parte central es recta, por lo cual, al girar una de las ruedas dentadas por esta parte se obtiene una cicloide reducida.
 Diferentes cicloides reducidas obtenidas trabajando con una de las piezas alargadas y una rueda dentada en el espirógrafo digital Inspirograph
Diferentes cicloides reducidas obtenidas trabajando con una de las piezas alargadas y una rueda dentada en el espirógrafo digital InspirographLa curva epicicloide es la trayectoria de un punto de una circunferencia que rueda, sin deslizarse, por el exterior de una circunferencia fija. En función de la relación que existe entre los radios de ambas circunferencias se obtendrán diferentes curvas. Por ejemplo, si ambos radios son iguales se obtiene una cardioide, si el radio de la circunferencia que rueda es la mitad (1/2) del radio de la rueda fija, la curva es una nefroide.
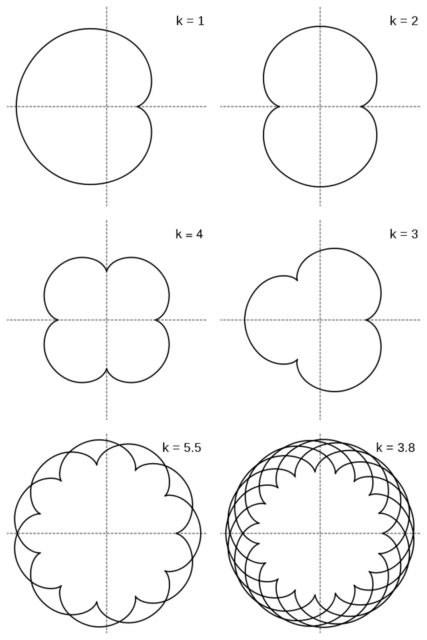 Algunos ejemplos de epicicloides en función de la proporción entre los radios de ambas circunferencias, que incluyen a la cardioide y la nefroide, los dos primeros ejemplos. Imagen de Wikimedia Commons
Algunos ejemplos de epicicloides en función de la proporción entre los radios de ambas circunferencias, que incluyen a la cardioide y la nefroide, los dos primeros ejemplos. Imagen de Wikimedia Commons
Por otra parte, si la circunferencia que rueda lo hace por el interior de la cincunferencia fija la curva que se obtiene es una hipocicloide. Si la relación entre los radios de las circunferencias pequeña –la que rueda– y grande –la que esta fija– es 1/3 se obtiene la curva denominada deltoide, si es 1/4 la curva generada es una astroide y de nuevo en función de esa relación se obtienen diferentes curvas.
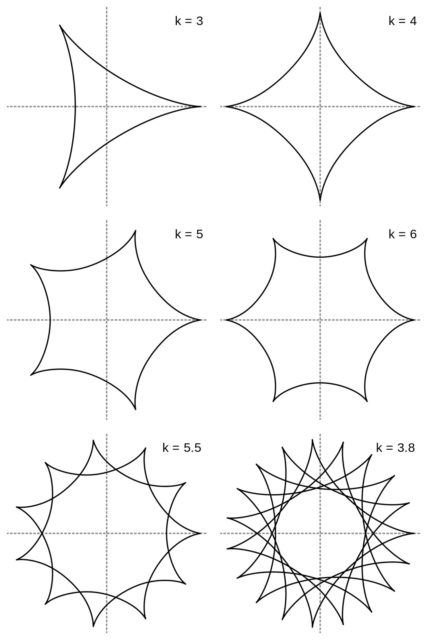 Algunos ejemplos de hipocicloides en función de la proporción entre los radios de ambas circunferencias, que incluyen a la deltoide y la astroide, los dos primeros ejemplos. Imagen de Wikimedia Commons
Algunos ejemplos de hipocicloides en función de la proporción entre los radios de ambas circunferencias, que incluyen a la deltoide y la astroide, los dos primeros ejemplos. Imagen de Wikimedia Commons
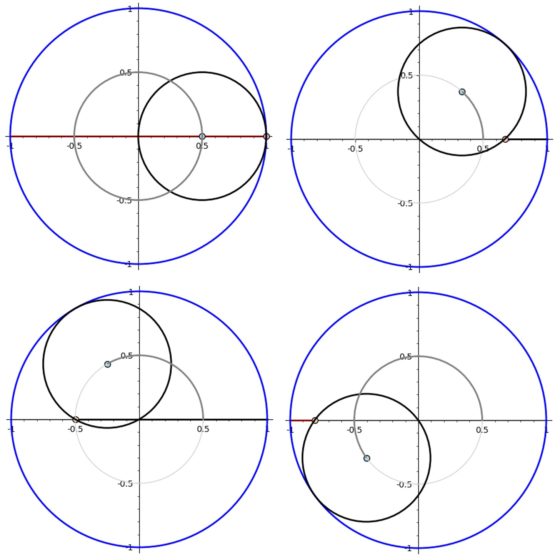
No hemos mencionado intencionadamente cual es la curva que se obtiene cuando la relación entre los radios de ambas circunferencias es 1/2, ya que esta es una recta, conocida con el nombre de “línea de La Hire”, y que es una forma de obtener un movimiento lineal a partir de un movimiento circular. Como se ve en la siguiente imagen, cuando la circunferencia móvil recorre la mitad del camino, el punto de la circunferencia que gira (color crema en la imagen) recorre el diámetro de la circunferencia fija, y lo vuelve a recorrer en la otra mitad del giro.
En la antigüedad la humanidad pensaba que la circunferencia era una figura geométrica perfecta, relacionada con lo divino, por lo que postularon que el movimiento de los planetas era circular alrededor de la Tierra. Dos de los grandes defensores de este modelo fueron Aristóteles (384–322 a.n.e) y Claudio Ptolomeo (aprox. 100-170). Sin embargo, muchos pensadores postularon que el Sol era el centro natural –el primero en proponerlo fue Aristarco de Samos (aprox. 310-230 a.n.e.)– y se dieron cuenta de que entonces, según las observaciones astronómicas, el movimiento de los planetas alrededor del Sol no podía ser circular. Por lo tanto, introdujeron las curvas epicicloides e hipocicloides para producir curvas que se adaptaran al movimiento observado de los planetas. Y como estos tampoco acababan de describir perfectamente los movimientos, empezaron a introducir curvas más complejas relacionadas con las anteriores. Las dos teorías sobre el movimiento de los planetas, circular o mediante curvas derivadas de epicicloides e hipociclodides, fueron rivales hasta que Johannes Kepler (1571-1630) demostró, a partir de las observaciones de Tycho Brahe (1546-1601), que la órbita de Marte era elíptica, con el Sol en uno de sus focos. Posteriormente, Isaac Newton (1643-1727) demostraría matemáticamente que la órbita de un cuerpo alrededor de un campo gravitatorio son secciones de cónicas.
El estudio de las epicicloides e hipocicloides se reinició en el Renacimiento. Estas curvas fueron estudiadas por Alberto Durero (1471-1528), Girard Desargues, Christian Huygens, Gottfried Wilhelm Leibniz, Isaac Newton, Jacob Bernoulli (1654-1705), Phillipe de La Hire (1640-1718), Johann Bernoulli, Daniel Bernoulli (1700-1782) o Leonhard Euler (1707-1783), que también estudiarían las siguientes curvas que vamos a mostrar en esta entrada del Cuaderno de Cultura Científica.
Las últimas curvas cíclicas que vamos a mostrar aquí son las generadas por el espirógrafo clásico, las epitrocoides e hipotrocoides. Una curva epitrocoide es la trayectoria que describe un punto, conectado a un círculo que rueda, sin deslizamiento, sobre el exterior de una circunferencia fija. Si el punto está en el interior del círculo que rueda se obtiene una epitrocoide como algunas de las obtenidas en el espirógrafo clásico (primera curva de la siguiente imagen), si el punto está en la circunferencia es una epicicloide (segunda curva de la imagen), mientras que si el punto es exterior al círculo que rueda (que podemos considerar conectado al centro por un segmento fijo para que ruede con el círculo) se obtiene una epitrocoide que podemos dibujar fácilmente con el ordenador, pero no con el espirógrafo clásico (tercera curva de la imagen).
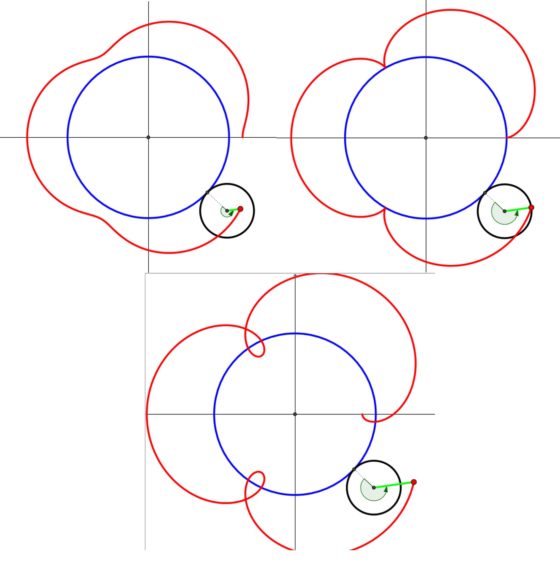 Tres curvas epitrocoides en las que varía que el punto que describe la curva esté en el interior del círculo que rueda, en su circunferencia o en el exterior. Imagen obtenida del GeoGebra, de la página web GeoGebra Tutorial Movie Bank
Tres curvas epitrocoides en las que varía que el punto que describe la curva esté en el interior del círculo que rueda, en su circunferencia o en el exterior. Imagen obtenida del GeoGebra, de la página web GeoGebra Tutorial Movie Bank
En la siguiente imagen podemos ver una epitrocoide dibujada con el espirógrafo clásico, con una rueda dentada rodando alrededor de otra rueda dentada fija.
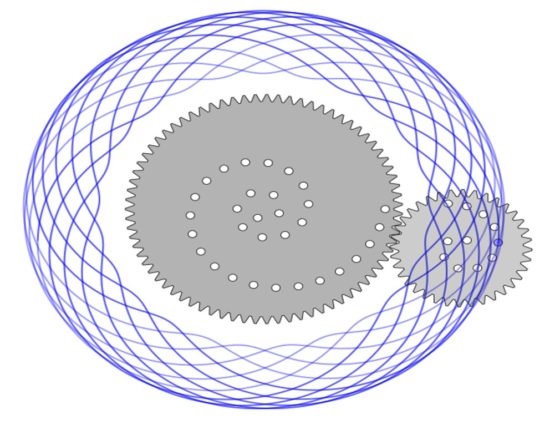 Epitrocoide realizada con el espirógrafo digital Inspirograph, en la que hemos dejado las ruedas dentadas para comprobar que es una epitrocoide, obtenida al hacer rodar una rueda dentada –la pequeña en la imagen– alrededor de una rueda dentada fija –la grande en la imagen–
Epitrocoide realizada con el espirógrafo digital Inspirograph, en la que hemos dejado las ruedas dentadas para comprobar que es una epitrocoide, obtenida al hacer rodar una rueda dentada –la pequeña en la imagen– alrededor de una rueda dentada fija –la grande en la imagen–
Mientras que una curva hipotrocoide es la trayectoria que describe un punto, conectado a un círculo que rueda, sin deslizamiento, sobre el interior de una circunferencia fija. De nuevo el punto conectado al círculo que rueda puede ser interior, de la circunferencia o exterior.
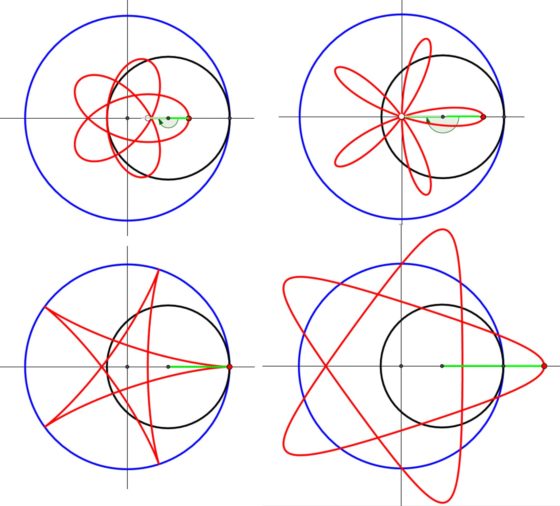 Cuatro curvas hipotrocoides en las que varía que el punto que describe la curva esté en el interior del círculo que rueda (las dos primeras), en su circunferencia o en el exterior. Imagen obtenida del GeoGebra, de la página web GeoGebra Tutorial Movie Bank
Cuatro curvas hipotrocoides en las que varía que el punto que describe la curva esté en el interior del círculo que rueda (las dos primeras), en su circunferencia o en el exterior. Imagen obtenida del GeoGebra, de la página web GeoGebra Tutorial Movie Bank
De la misma forma que antes, podemos ver una hipotrocoide dibujada con el espirógrafo clásico, con una rueda dentada rodando en el interior de una corona circular dentada fija.
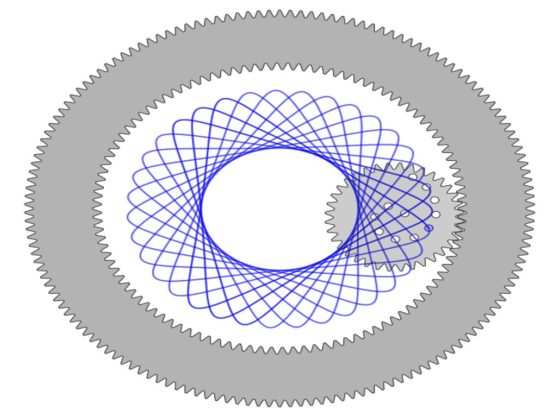 Hipotrocoide realizada con el espirógrafo digital Inspirograph, en la que hemos dejado las ruedas dentadas para comprobar que es una hipotrocoide, obtenida al hacer rodar una rueda dentada –la pequeña del interior en la imagen– en el interior de una corona circular dentada fija –la grande alrededor de la pequeña en la imagen–
Hipotrocoide realizada con el espirógrafo digital Inspirograph, en la que hemos dejado las ruedas dentadas para comprobar que es una hipotrocoide, obtenida al hacer rodar una rueda dentada –la pequeña del interior en la imagen– en el interior de una corona circular dentada fija –la grande alrededor de la pequeña en la imagen–
Un ejercicio bonito, relacionado con todas estas curvas cíclicas, es la obtención de las ecuaciones paramétricas de las mismas. Por ejemplo, las ecuaciones paramétricas de las hipotrocoides son:
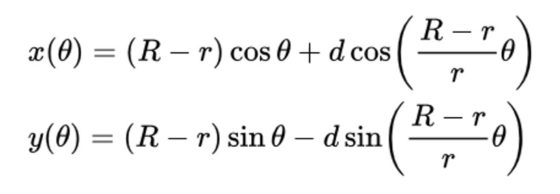
donde R es el radio de la circunferencia fija exterior, r el radio del círculo interior que rueda y d la distancia al centro del círculo que gira del punto cuya trayectoria estamos considerando (que describe la hipotrocoide). Sin embargo, no lo resolveremos en esta entrada, lo dejaremos para aquellas personas a las que les apetezca enfrentarse al mismo.
Para terminar, mencionaremos que también existen artistas contemporáneos, como ocurrió con Alan Moore y James H. Williams III, autores del cómic Promethea, que han quedado fascinados por la belleza de los diseños de las curvas cíclicas generadas con el espirógrafo. Un ejemplo es la artista estadounidense Robin P. Schlacter, quien utiliza hipotrocoides en muchas de sus obras.
 Robin P. Schlacter, Casting Pearls (2013). Imagen de la página web de Robin Schlacter
Robin P. Schlacter, Casting Pearls (2013). Imagen de la página web de Robin Schlacter
Bibliografía
1.- Wikipedia: Spirograph .
2.- Wolfram Mathworld: Spirograph
3.- Nathan Friend, Inspirograph
4.- Toy tales: Spirograph
5.- J. Dennis Lawrence, A catalog of special plane curves, Dover Publications, 1972.
6.- José Manuel Álvarez Pérez, Curvas en la historia 1 y 2, Nivola, 2006.
7.- Wikipedia: Hypotrochoid
8.- Wikipedia: Epitrochoid
9.- Raúl Ibáñez, Construcción de curvas planas, Un paseo por la Geometría 1997/1998.
10. Página web de la artista Robin P. Schlacter.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Las curvas del espirógrafo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La materia oscura auto-interactuante y las curvas de rotación de las galaxias
- Un dulce problema de Paul Erdös
- Construye tu propia calculadora de sumas y restas
El carácter fundamental de las relaciones de incertidumbre
 Foto: Franck V / Unsplash
Foto: Franck V / UnsplashEl principio de incertidumbre y las relaciones de incertidumbre resultantes son válidas para cualquier objeto, incluso para un automóvil. Pero las limitaciones que impone el principio de incertidumbre no tienen consecuencias prácticas para objetos tan con tanta masa como coches o pelotas de béisbol que se mueven a velocidades normales para nuestra experiencia humana diaria. Esto se debe a que los valores de incertidumbre involucrados son demasiado pequeños como para ser percibidos. Las limitaciones se hacen evidentes e importantes solo a escala atómica.
Debido a esta discrepancia entre lo que ocurre en el día a día humano y lo atómico es muy importante comprender que las incertidumbres que establece el principio de Heisenberg no son debidas a un defecto del experimentador ni de los instrumentos que usa. Esto debe quedar diáfanamente claro [1]: Nunca, jamás, podremos construir instrumentos para sortear las incertidumbres recíprocas en las mediciones impuestas por las relaciones de incertidumbre.
Esto se debe a que las relaciones de incertidumbre de Heisenberg son una consecuencia directa de la mecánica cuántica y la dualidad onda-partícula. Pero su validez no está completamente ligada a la de la mecánica cuántica. Efectivamente, la mecánica cuántica podría ser sustituida por otro modelo para describir la realidad cuántica [2] y las relaciones de incertidumbre, que emanan de la existencia misma de los cuantos, son más fundamentales que la propia mecánica cuántica.
Desarrollemos esto mínimamente.
Hemos visto el papel que juega la constante h de Planck en la definición del cuanto de luz y en la descripción de los estados estacionarios en el átomo de Bohr. Además, la constante h aparece en las dos ecuaciones básicas para la energía y el momento lineal del fotón, E = hf y p = h/λ, y también en muchas otras ecuaciones cuánticas. También aparece en las relaciones de incertidumbre. Si h fuera 0, eso significaría que la cantidad de energía sería cero, por lo que no habría cuantos de luz, solo ondas continuas.
El momento lineal del fotón también sería cero, y las relaciones de incertidumbre serían Δx·Δpx = 0 o Δt· ΔE = 0 [3]. Por tanto no habría incertidumbres recíprocas en posición y momento, tiempo y energía, y podríamos medir simultáneamente las características de onda y corpúsculo de los objetos cuánticos sin ningún problema.
Pero aunque sea muy pequeña, la constante de Planck no es cero [4], el cuanto existe, nos enfrentamos a la dualidad onda-partícula, la mecánica cuántica sigue siendo un modelo aceptado, y la naturaleza es tal que limita la precisión de nuestras mediciones a escala atómica al nivel más fundamental.
Notas:
[1] Lo que sigue es el tipo de afirmación categórica que los relativistas y postmodernistas varios que en el mundo son prejuzgan como prepotencia de la ciencia. Su postura, como decimos prejuiciosa, se basa en supuestos y asunciones filosóficas, sin contraste con la realidad física. Es este contraste continuo con la realidad el que permite a la ciencia afirmar cosas como esta en estos términos. Los posmodernos optan por la ignorancia. Son indiscernibles de una persona religiosa, a saber, tratan sus afirmaciones como no falsables.
[2] Recordemos: la mecánica cuántica es un modelo teórico para describir los resultados de los experimentos. La realidad de los cuantos es experimental. Podrá cambiar la teoría, pero los hechos son tozudos.
[3] Hay muchísimas relaciones de incertidumbre. Nosotros, para lo que nos interesa, con estas dos para ilustrarlas nos basta y nos sobra.
[4] Su valor está fijado, por ser una de las constantes fundamentales de la naturaleza, desde 2019: 6,62607015·10−34 J·s. El kilogramo se define en función de este valor de h.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El carácter fundamental de las relaciones de incertidumbre se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El principio de incertidumbre, cuantitativamente
- El principio de incertidumbre, cualitativamente
- Construyendo la mecánica cuántica
El fraude y las malas prácticas en ciencia
Fraude y malas prácticas ha habido desde hace mucho tiempo. Hay documentados multitud de casos, incluso entre los científicos más famosos. Hay fundadas sospechas de que Ptolomeo hizo pasar por suyos datos astronómicos que en realidad eran de Aristarco de Samos. Recientemente ha ingresado en prisión Dong-Pyou Han, un investigador en vacunas, condenado por inventar datos en experimentos sobre la vacuna contra el VIH. Los casi 2000 años que separan estos sucesos han estado salpicados de otros muchos casos. Parece ser que Millikan eliminaba de su cuaderno de laboratorio las observaciones que no le interesaban, Mendel y sus guisantes también han resultado polémicos, incluso hay dudas sobre si Galileo realizó realmente los experimentos que relata en sus textos. Hay casos clásicos, como el del hombre de Pitdown, un fósil que se hizo pasar por el eslabón perdido en la evolución entre el hombre y el mono cuando realmente era un engendro creado con trozos de cráneo humano y de chimpancé. Hay multitud de casos bien documentados y diversas compilaciones, como la recientemente publicada por Ángel Abril-Ruiz que, además, se puede consultar en línea.
Resulta especialmente escandaloso oír hablar de fraude en una profesión dedicada fundamentalmente a la búsqueda de la verdad. Ese escándalo ayuda a hacerse un modelo mental de la situación en el que la inmensa mayoría de los científicos son “normales” (totalmente honrados) y una pequeña fracción son “manzanas podridas” (totalmente deshonestos). Sin embargo la realidad dista bastante de este modelo. Según algunos estudios (Fanelli (2009) y resumidas también por uno de nosotros en 2015, aquí), más de dos tercios de los científicos admite realizar algún tipo de malas prácticas y uno de cada 50 admite falsificar o inventar resultados, una de las peores prácticas imaginables. Es interesante notar que cuando se pregunta por las malas prácticas que uno conoce de los compañeros los números salen bastante más altos que cuando se pregunta por las propias.
Fischer y Zigmond (2002) incluyen entre las prácticas abiertamente fraudulentas la fabricación o falsificación de datos, el plagio, y lo que podríamos denominar el cocinado de datos (selección, manipulación y manejo). Pero también consideran como malas prácticas otras formas de proceder entre las que se encuentran lo que denominan –un tanto eufemísticamente- autoría honoraria, el no reconocimiento expreso de las fuentes, la opacidad en la metodología, la publicación fragmentada y la publicación duplicada de los mismos resultados en diferentes artículos. E incluyen malos comportamientos no solo de los autores de los trabajos, sino también de los revisores; entre estas están las revisiones sesgadas de los originales remitidos para su publicación y el uso de información privilegiada tomada de esos originales, entre otros.
De mala práctica debe ser calificada también la pesca de datos o p-hacking. Consiste en ir seleccionando datos o combinaciones de datos hasta que se acaba consiguiendo que los análisis estadísticos arrojen el resultado buscado porque los efectos que interesa destacar alcanzan el nivel de significación estadístico preestablecido. La significación estadística de un efecto se establece sobre la base del valor de p, que normalmente se establece en 0.05. En otras palabras, se considera que se produce un determinado efecto si, asumiendo la hipótesis nula, la probabilidad de obtener los datos que se tienen es inferior al 5%. Las malas prácticas consisten en descartar valores extremos por ser considerados anómalos; también se pueden agrupar de formas diferentes; o modificar el tipo de tratamiento estadístico. Una vez se alcanza el resultado “deseado”, ese es el que se publica. Judith Rich Harris, en su libro The Nurture Hypothesis ha diseccionado de forma brillante un buen número de estas prácticas que han servido para “demostrar” que la educación que proporcionan los padres a sus hijos en el hogar ejerce efectos duraderos sobre el comportamiento de estos en la vida adulta.
Podríamos ordenar un listado de prácticas cuestionables de las más graves a las que apenas suponen un problema. Entre estas últimas tendríamos cuestiones como la autoría honoraria, la opacidad metodológica o el plagio de una frase. Es a la luz de una escala de gravedad de las malas prácticas como pueden entenderse los datos de los estudios antes citados sobre la prevalencia del fraude. Muchos científicos, si no todos, podemos incurrir en malas prácticas de bajo nivel, siendo mucho menos frecuentes las prácticas moralmente más reprobables. En todo caso, cada científico deberá situar sobre una escala de prácticas cuestionables el nivel con el que se siente cómodo, el umbral de lo aceptable. Mientras ese umbral se mantenga dentro de unos márgenes socialmente aceptables, no denominamos propiamente fraude a esas prácticas. Lo que se considera opacidad metodológica, el nivel de lo estadísticamente significativo o el tamaño mínimo de una muestra, por poner algunos ejemplos concretos, son elementos convencionales que pueden variar con el tiempo, y lo que se considerarían niveles intolerables en el pasado pueden ser normales hoy (o viceversa).
Federico di Trochio (1993) estableció dos categorías de fraude, dos motivaciones muy diferentes para que un científico incurra en comportamientos mucho más allá del umbral de lo socialmente aceptable. Curiosamente, se trata de dos categorías provocadas por motivaciones que casi se podrían calificar de opuestas pero que no es extraño que concurran en los miembros de una misma comunidad. Como se ha señalado antes, a quienes nos dedicamos a la ciencia nos mueve el ánimo de ensanchar los límites del conocimiento, de descubrir nuevos hechos y de asignar a esas hechos explicaciones que les otorguen algún sentido; nos hacemos preguntas y aspiramos a responderlas, de una forma tal que las respuestas son el origen de nuevas preguntas. Pues bien, inmersos en esa dialéctica no es difícil anteponer el hallazgo de una “buena” respuesta, de una “buena” explicación o “buena” teoría al cumplimiento de los necesarios estándares de rigor. Cuando eso ocurre se abre una vía por la que no es difícil llegar cada vez más lejos, pues la tolerancia para con las trampas que hace uno mismo es mayor cuantas más hace. Es pues la obnubilación por lo que se cree una buena teoría lo que causa en última instancia esta categoría de fraude. Otro posible resultado de esa obnubilación por el propio resultado es la perseveración empecinada en el mismo incluso cuando las pruebas en su contra son ya clamorosas. A esto se le ha llamado “ciencia patológica” y se describirá en detalle más adelante.
La segunda modalidad se refiere al hecho de que la de científico es una profesión, y como tal dispone de los correspondientes sistemas de acceso, estabilización laboral y promoción. Se trata, además, de una profesión muy exigente en muchos casos, pues la necesidad de obtener resultados y de publicarlos puede llegar a ser muy acuciante. A esa necesidad obedece la expresión “publicar o perecer”, y ante esa perspectiva se puede flaquear y relajar los estándares éticos llegando al fraude en toda regla.
En resumen, en vez de asumir un modelo de manzanas podridas para el fraude, la idea de una gradación de comportamientos cuestionables y un umbral de lo aceptable (socialmente establecido) resulta más adecuada y ayuda a entender los datos sobre incidencia de malas prácticas que muestran los diferentes estudios.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo El fraude y las malas prácticas en ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Fraude científico (III). Profundizando en los dos tipos de fraude
- Fraude científico (II). La difusa frontera de la deshonestidad
- #Naukas13 Malas gráficas
Genocidio
Genocidio: “Exterminio o eliminación sistemática de un grupo por motivos de raza, etnia, religión, política o cionalidad».
Diccionario de la lengua española / RAE.
“El Nacionalsocialismo no es otra cosa que Biología Aplicada”.
Rudolf Franz Ferdinand Höss, comandante de Auschwitz.
 Fotos de las fichas de niños judíos en Auschwitz. Fuente: DeAgostini / Getty Images vía history.com
Fotos de las fichas de niños judíos en Auschwitz. Fuente: DeAgostini / Getty Images vía history.comEl genocidio, como concepto, definición y delito, es una creación moderna, aunque los antecedentes han acompañado a nuestra especie en toda su historia evolutiva. El término lo utilizó por primera vez el jurista polaco Rafael Lemkin, y lo describió como un crimen de extermino. Tomó carácter oficial en los procesos de Nuremberg a los dirigentes nazis al terminar la Segunda Guerra Mundial. Aparece entre los delitos del acta de acusación de Nuremberg el 8 de octubre de 1945. Cuenta Manuel Ollé Sesé, de la Universidad Complutense, que el Convenio para la Prevención y Sanción del Delito de Genocidio se aprobó en la Asamblea General de las Naciones Unidas con fecha de 9 de diciembre de 1948, y entró en vigor el 12 de enero de 1951. El artículo 607 del Código Penal español establece que los delitos de genocidio tienen “el propósito de destruir total o parcialmente un grupo nacional, étnico, racial, religioso o determinado por la discapacidad de sus integrantes”, según Ley Orgánica aprobada el 23 de noviembre de 1995. Hay que recordar que un grupo, sean cuales sean las razones para que sea un grupo, tiene derecho a existir como una colectividad.
E s más, tal como escribió Hannah Arendt en su crónica sobre el juicio a Eichmann, “el genocidio es un ataque a la diversidad humana como tal, es decir, a una de las características de la “condición humana”, sin la cual los términos “humanidad” y “género humano” carecerían de sentido”. Llega a proponer, como término más adecuado que genocidio, que se denomine “matanza administrativa”.
El concepto de genocidio lo amplió el profesor Baruk, en 1967, cuando añadió que es la destrucción de “todo gen, de toda posibilidad de reproducción, de persistencia, de un pueblo”.
Según solicita Xaimán Aizenstadt, de la Universidad Francisco Marroquín de Guatemala, la definición de genocidio no se debe considerar cerrada sino que debe ser tan flexible e imaginativa como la capacidad humana para el mal.
Aunque el concepto, la definición y la jurisprudencia sobre genocidio comenzó después de la Segunda Guerra Mundial, la historia de nuestra especie está llena de genocidios. Sin entrar en detalles, centraremos el texto en el genocidio nazi, pero hay que recordar la destrucción de Cartago, los anasazi del suroeste del actual Estados Unidos, la cruzada albigense en la Francia del siglo XIII, el exterminio de los armenios al principio del siglo XX, las matanzas de Ruanda o Bosnia … Y, además, aún sin nombre ni concepto, la idea del genocidio viene de lejos en el tiempo y acompaña desde siempre nuestra historia. Y, también, la historia de la evolución biológica. Solo hay que recordar el título completo del libro de Charles Darwin: “Sobre el origen de la especies por medio de la selección natural, o la preservación de razas favorecidas en la lucha por la vida”.
La violación se reconoció como delito de genocidio en el Tribunal Internacional de Ruanda para hechos ocurridos en 1993 y 1994 contra refugiados tutsis. Todo acto de violencia sexual, incluyendo embarazos forzosos, pueden constituir genocidio cuando son cometidos con la intención de destruir un grupo nacional, étnico, racial o religioso.
El Tercer Reich fue un periodo en el que la violencia masiva organizada, a una escala inigualada en la historia moderna, se canalizó contra millones de seres humanos que, según la sociobiología nazi, eran política, racial, étnica y económicamente inferiores. Escribió Zygmunt Bauman que el genocidio nazi no fue un proceso bárbaro sino moderno y civilizado. Los nazis utilizaron muchos de los logros y herramientas de la era industrial –la fábrica, el tren, los productos químicos sintéticos y la organización administrativa de todo el proceso- con efectos letales, confiando en la ciencia moderna y la planificación racional, en la que todo se subordina a un único objetivo limitado y definido. Pelagia Lewinska, comunista polaca que estuvo internada en Auschwitz y sobrevivió, declaró años después que “no me queda otro remedio que admirar la habilidad con que los alemanes habían introducida en la organización de la vida del campo de Auschwitz la ciencia moderna. Habían aplicado no solo un sistema de condiciones materiales que aniquilaba a la gente, sino que empleaban también con precisión la psicología para desorganizar el alma humana, para destruir moralmente al ser racional”.
Los hombres corrientes de la Alemania nazi participaron en el genocidio porque creían que los judíos debían morir, que su aniquilación era socialmente deseable, que eran una raza inferior de infrahumanos. Para los ciudadanos corrientes, el exterminio de los judíos no era un crimen. Era la culminación del antisemitismo que existía desde hace siglos en Europa central.
Kurt Gerstein: El Espía de Dios
 Kurt Gerstein. Fuente: history.com
Kurt Gerstein. Fuente: history.comNació en 1905 en Munster y murió en París en 1945. Ingeniero de minas, se afilió al Partido Nazi el 12 de mayo de 1933, y a las SS y fue destinado al Instituto de Higiene de las SS.
Por su preparación técnica fue destinado a la unidad encargada de la Solución Final y presenció las primeras ejecuciones con gas en agosto de 1942. Fue testigo del exterminio judío en los campos de Sobibor, Belzec y Treblinka y decidió transmitir la información de lo que ocurría a los aliados y a la Iglesia Católica. En Belzec, Gerstein vio morir a 5000 judíos en 1942. El texto que redactó, conocido como Informe Gerstein, fue utilizado en los juicios de Nuremberg. Por su profunda fe religiosa fue conocido como El Espía de Dios. Toda su vida, desde su afiliación al partido, fue una constante lucha entre su fe religiosa y su ideología nazi.
Protestó por la absorción de los movimientos juveniles protestantes en las Juventudes Hitlerianas. Lo hizo ante Baldur von Schirach, líder de las Juventudes, y Monseñor Müller, obispo protestante. En otra ocasión, en 1935, durante el estreno de una obra de teatro pronazi, y con un explícito mensaje anticristiano, protestó en el teatro y recibió una paliza que le costó tres dientes.
También tuvo algún enfrentamiento con las Gestapo por la organización de campamentos juveniles que mezclaban religión y nazismo. Por todo ello, en 1936 fue detenido y expulsado del Partido. Al comenzar la guerra, en 1940, se alistó voluntario en las SS.
Pasó información a diplomáticos a Suecia y Suiza, a la resistencia holandesa, autoridades religiosas e, incluso, intentó una entrevista con el Nuncio de la Santa Sede en Berlín y no lo consiguió. Nadie le creía por lo terrible de lo que contaba. Apuntaba todo lo que veía y sus notas fueron la base del Informe Gerstein.
Fue uno de los encargados de transportar el Zyklon B utilizado en las cámaras de gas. El Zyklon B lo suministraban a los campos de exterminio las empresas Degesch y Testa de I.G. Farben Konzern, y contenía ácido prúsico o ácido cianhídrico, componente esencial de insecticidas que fabricaba desde 1924. Para envenenar a una persona bastaban 0.12 miligramos por litro de aire. La muerte es casi instantánea.
En 1943, las empresas suministraron 12174,09 kilogramos y obtuvieron un beneficio de 127985,79 marcos. Se ha calculado que Gerstein, por su trabajo en el Servicio de Higiene, que incluía los gases tóxicos, suministró 3790 kilogramos de Zyklon B a los campos de Auschwitz y Oranienburg. Bastaban para matar a 450000 personas solo en Auschwitz.
Los crematorios de los campos de concentración los suministró la empresa J.A. Topf & Sohne, de Wiesbaden, que años después, el 5 de enero de 1953, obtuvo en la República Federal Alemana la patente nº 861731 para un “Procedimiento y dispositivo para la incineración de cuerpos, cadáveres y partes de los mismos”.
Desertó al final de la guerra y se entregó a los aliados el 22 de abril de 1945. Ingresó en la prisión de Cherche-Midi, en París, acusado del delito de genocidio. Apareció ahorcado en su celda el 25 de julio de 1945. En 1965 fue rehabilitado en Alemania como resistente por el Canciller Kurt Georg Kiesinger.
Y todo el esfuerzo, por lo menos en los primeros años del régimen nazi, fue contra judíos y gitanos. Ya en enero de 1939, meses antes del inicio de la Segunda Guerra Mundial, Hitler mencionó como objetivo “la destrucción de la raza judía en Europa”.
Más adelante, con la invasión de Rusia, se extendió a los eslavos. Las órdenes incluían ejecutar a los comisarios soviéticos.
De nuevo Pelagia Lewinska nos ofrece sus reflexiones cuando explica que, en Auschwitz, los alemanes “internaban a todos: a los que les parecían inútiles; a los que consideraban como un peso muerto en la obra creadora de la gran Alemania; a los que juzgaban peligrosos; a los que podían constituir una amenaza para el Estado hitleriano; o cuya muerte se hacía necesaria para proveer de oro al Tesoro alemán y procurar a los alemanes bienes y comodidades como era el caso de los judíos … Al lado de los detenidos políticos estaban gentes recogidas en la calle, en los cines, en las iglesias, en los cafés, en los trenes, en el mercado negro y en los lugares de placer. Los había que no eran culpables de actividades políticas conscientes ni contrarios al hitlerismo”.
Para Stephen Chorover, profesor del MIT y judío que perdió a gran parte de su familia en el genocidio nazi, las ideas sociobiológicas ya existentes desempeñaron una función doblemente influyente en el proceso de exterminio. En primer lugar, suministraron el aparato conceptual que médicos y científicos necesitaban para concebir, planificar y realizar la “destrucción de las vidas carentes de valor” o, si se quiere, para la eutanasia de degenerados, desviados, enfermos, … En segundo lugar, ayudaron a construir y ratificar la tesis nazi según la cual la calidad racial es el criterio para juzgar el valor de individuos y países.
Esas ideas habían comenzado con Charles Darwin y su “Origen de las especies”, Herbert Spencer y su naturaleza de “dientes y garras”, Francis Galton y la eugenesia, y tantos otros en Europa y Estados Unidos. Y, no hay que olvidar, que, desde la biología, el genocidio es siempre agresión intraespecífica, o sea, entre individuos de la misma especie.
Konrad Lorenz: El pasado del Premio Nobel
 Konrad Lorenz. Fuente: nobelprize.org
Konrad Lorenz. Fuente: nobelprize.orgNació en Viena en 1903 y murió en Alterberg, Austria, en 1989. Estudió medicina en la Universidad Columbia de Nueva York, y se doctoró en la Universidad de Viena. La lectura de las aventuras de Nils Holgerson, de la autora sueca Selma Lagerlof, le llevó, como a tantos otros, al interés por los animales, las aves en concreto, y al estudio de la zoología. Acepta estudiar medicina para contentar a su padre, y el contacto con los profesores Ferdinand Hochstetter, de anatomía, y Karl Buhler, de psicología, le llevan a utilizar el método comparativo para estudiar el comportamiento. Una vez graduado, en 1939, fue nombrado profesor de psicología con orientación biológica en la Universidad de Konigsberg, en Alemania.
En 1938 se afilió al Partido Nazi, Escribió, en su petición de afiliación, que “puedo decir que todo mi trabajo científico está dedicado a las ideas de los nacionalsocialistas”. Sus escritos de la época apoyaban la ideología nazi de la higiene racial con el apoyo de la terminología científica. Por ejemplo, en junio de 1940, apareció un artículo de Lorenz titulado, en traducción “Alteraciones del comportamiento propio de la raza causadas por la domesticación”. Escribe que “de la amplia analogía biológica de la relación entre el cuerpo y la úlcera cancerosa por una parte, y de un pueblo y sus miembros convertidos en asociales por deficientes por otra, se deducen grandes paralelismos, salvando las naturales diferencias … Todo intento de reconstrucción de los elementos destruidos en relación con la totalidad es, por tanto, desesperado. Por suerte, su extirpación es más fácil para el médico del cuerpo social, y para el organismo supraindividual menos peligrosa que la operación del cirujano en el cuerpo individual”. Terminaba con “la idea racial como base de nuestro estado ya ha logrado mucho en este sentido”. Lorenz jamás escondió esta publicación y repitió las ideas que escribió en muchos de sus libros.
Loren Eisenberg, de la Universidad de Harvard, añade que Lorenz fue explícito en la defensa de los conceptos nazis de pureza racial y, por ejemplo, justificó las restricciones legales al matrimonio con no-arios como medida social para corregir “la degeneración inducida por la domesticación”. Algo similar escribía Lorenz en su libro, publicado en 1975, y titulado “Los ocho pecados mortales de la Humanidad” y, sobre todo, en el capítulo titulado “Decadencia genética”, uno de los “pecados mortales” del título. Menciona que, en un péndulo de ideologías y conductas, en un extremo está que todos los hombres son iguales desde su nacimiento y, en el otro extremo, coloca, literalmente, a ”Eichmann, Auschwitz, la eutanasia y el odio racista”. Para Lorenz, en este péndulo en medio está la virtud o, si se quiere, todos los hombres no son iguales pero ello no nos debe llevar a Eichmann o Auschwitz.
En 1941, una vez comenzó la guerra, fue movilizado como médico militar destinado en Poznan, en Polonia, como neurólogo y psiquiatra, y, en 1944, enviado al frente oriental. Capturado por los rusos, fue su prisionero durante seis años. Allí conoció de primera mano el adoctrinamiento marxista y lo comparó con el nazismo, que conocía en detalle.
Hasta febrero de 1948 no pudo regresar a Austria y declaró su arrepentimiento por su afiliación al Partido Nazi. En principio, negó haber pertenecido al Partido, hasta que se demostró que era cierto. También negó haber conocido el alcance del genocidio, a pesar de su puesto como psicólogo en la Oficina de Política Racial.
Con una financiación escasa y muchos problemas, organizó, en 1949, la estación de investigación de Altenberg. Marchó a Alemania, a la estación de Buldeon, donde fundó el Instituto Max Planck de Fisiología del Comportamiento. En este centro, a comienzos de los sesenta, desarrolló su teoría del comportamiento que unía la evolución, lo innato y lo aprendido. Por todo ello, en 1973 recibió el Premio Nobel.
En su autobiografía, publicada en 1988, Lorenz recordó que, en aquellos años, “estaba asustado, como todavía lo estoy, por la idea de que procesos genéticos de deterioro puedan estar funcionando en la humanidad civilizada. Movido por este miedo, hice algo muy poco aconsejable poco después de que los alemanes invadieran Austria: escribí sobre los peligros de la domesticación y, para ser entendido, expresé mis escritos en la peor terminología nazi. No quiero presentar atenuantes de estos escritos. En realidad, creía que algo bueno vendría del nuevo gobierno … Ninguno sospechaba que la palabra “selección”, utilizada por estos gobernantes, significaba asesinato”.
La Universidad de Salzburgo le retiró, en 2015, el título de Doctor Honoris Causa, concedido en 1983. La universidad argumentó que fue la difusión, por Lorenz, de las ideas nacionalsocialista y, por declarar en aquellos años, que era “siempre un nacionalista”, y utilizar su trabajo para difundir “elementos básicos de la ideología racista del nacionasocialismo”.
Lo había definido Adolf Hitler años antes: “Hemos de crear una técnica de despoblación. Si me pregunta usted lo que entiendo yo por despoblación, le diré a usted que veo la liquidación de unidades raciales, y lo haré, puesto que veo en ella, a grandes rasgos, mi misión fundamental. La Naturaleza es cruel y, por este motivo, también nosotros podemos ser crueles. Si mando a lo mejor del pueblo alemán a la guerra sin lamentos, en ningún momento, el derramamiento de la valiosa sangre alemana en el infierno de la guerra, también tengo el derecho de destruir millones de hombres de razas inferiores, que se multiplican como los parásitos”. Detrás de estas declaraciones está la biología de la época, está el genocidio. Ya lo había expuesto Hitler en 1925 en su libro Mi lucha. Hitler trataba de crear, en el este de Europa, un “espacio vacío”, que era el lugar donde viviría la raza de señores que debía ser creada y organizada por Himmler. Es lo que afirmaba Erich Koch, comisario del Reich y responsable de la administración nazi en Ucrania: “Somos un pueblo de señores que ha de tener en cuenta que el obrero alemán más bajo es mil veces mejor, desde el punto de vista racial y biológico, que cualquier exponente de la población local”.
Detrás de esta ideología supremacista estaba lo que Alfred Rosenberg, ideólogo del Partido Nazi, declaró en el juicio de Nuremberg que “… y finalmente en Munich me especialicé en los estudios de la nueva investigación biológica”. Afirmó que el sentimiento de humanidad iba “contra el proceso de selección natural”. Por ello, consigue que el genocidio se base en la evolución. El mismo Rosenberg escribió que la humanidad trata del individuo y olvida al Estado y al pueblo. Es un concepto que niega las diferencias nacionales y raciales y considera la Humanidad sin diferencias.
Como explicó Heinrich Himmler en una conferencia en enero de 1937, la biología, según los nazis, estaba en el centro de su limpieza étnica, y “no hay mejor ilustración de las leyes de la herencia y de la raza … que un campo de concentración. En el se encuentran hidrocéfalos, bizcos, contrahechos, semijudíos y un número incalculable de productos de razas inferiores”. O, más en extenso y en un lenguaje científico y proponiendo los campos de trabajo, Hans Reiter, médico nazi con cargos en la administración y en el campo de concentración de Buchenwald, declaró en 1941 que “la legislación biológica-hereditaria se preocupa de suprimir, poco a poco, la creación de nuevas generaciones de individuos asociales … El estudio biológico del rendimiento humano debe conducir y reconducir, sin duda, a disponer en la medida de lo posible de esa mano de obra, de manera a desarraigar de una ocupación estéril o de la ociosidad para conducirla por la fuerza a un trabajo real y enteramente provechoso al pueblo y al Estado”. Antes de comenzar la guerra ya se habían esterilizado entre 350000 y 400000 personas.
Para organizar la solución final y eliminar a los judíos de Europa, Reinhard Heydrich, jefe de la Oficina Central de Seguridad del Reich, convocó a los jefes de servicio de las SS y a algunos cargos del Gobierno a una conferencia en el Lago Wannsee. Se celebró el 20 de enero de 1942. Asistieron 14 altos cargos y la presidió Heydrich. Allí se decidió la deportación al este, los trabajos forzados y el exterminio. Una de las conclusiones de Heydrich fue que “sin dudarlo, una gran parte perecerá a consecuencia de la natural disminución. Los que queden y que al final puedan resistir todo esto, que serán los más resistentes, deben ser tratados convenientemente ya que estas personas, resultado de la selección natural, son el embrión básico de un nuevo desarrollo judío”.
Adolf Eichmann: Funcionario leal
 Adolf Eichman. Fuente: Wikimedia Commons
Adolf Eichman. Fuente: Wikimedia CommonsCuando ya estaba en la cárcel israelí, en 1960, escribió:
“Me llamo Karl Adolf Eichmann, nací en Solingen el 19 de marzo de 1906, pertenezco a la raza aria y al gran Reich alemán.
No hay acontecimientos importantes en mi niñez, ni en mi primera juventud; mi verdadera vida empezó cuando, en 1931, entré a formar parte del gran Partido Nazi, para la salvación de Alemania, con el número de inscripción 899895, y más adelante ingresé en el cuerpo escogido de las SS …”.
Entró en el Partido Nazi por la amistad de su padre con Ernst Kaltebrunner, jefe del Servicio de Seguridad del Reich a partir de 1942, juzgado en Nuremberg, condenado a muerte y ahorcado en 1946. Eichmann se afilió el 1 de abril de 1932 y el mismo día entró en las SS.
Casado en 1932, tuvo cuatro hijos, el último de ellos en Argentina.
Después de su traslado a Berlín en 1934, comenzó su carrera de buen funcionario cuando le encargaron, en 1937, organizar el éxodo de los judíos de Austria, con la ayuda de organizaciones sionistas, hacia Palestina. En Solingen, en casa de un amigo judío, había aprendido yidish y hebreo, y estaba preparado para cumplir las órdenes. Consiguió el traslado de hasta 100000 judíos al mes hacia el extranjero. Para conseguirlo viajó como periodista a Palestina, desde Austria, en 1937, y conoció al Gran Mufti de Jerusalén y se convirtió en su gran amigo personal, aunque Hannah Arendt no da crédito a esta historia.
Al comenzar la guerra, en 1939, los órdenes fueron concentrar los judíos europeos en guetos en Polonia, para crear un estado judío en Europa oriental y, más adelante, llevarlos a la isla de Madagascar. Pero en septiembre de 1940 cambió el plan y comenzó el exterminio. Fue la Sección B4 de la Gestapo, dirigida por Eichmann, la que organizó las deportaciones masivas y el traslado de judíos a los campos de exterminio. En la conferencia de Wannsee, en 1942, estaba Eichmann como encargado de los transportes.
Eichmann era un hombre ordenado y, en medio de una de las tareas más terribles, siempre conservó su espíritu burocrático. Tenaz y organizado, Eichmann cumplía su deber, según las órdenes recibidas. Según declaró, era un ejecutor de órdenes superiores. Alcanzó el rango de teniente coronel de la SS. En 1944, en Budapest, comentó a un colega de las SS que “el número de judíos muertos alcanza casi los seis millones; pero esto es un secreto de Estado”.
Al terminar la guerra, Eichmann fue capturado con una identidad falsa y consiguió huir. Pasó por Austria, Suiza e Italia, y consiguió un pasaporte falso que le permitió viajar a Argentina. Llegó el 14 de julio de 1950. Su familia llegó en 1952 y, después de pasar por varias ciudades, se instalaron en Buenos Aires. Trabajó en una fábrica de Mercedes Benz.
Pero el 11 de mayo de 1960 fue capturado por el servicio secreto israelí en Buenos Aires. Fue descubierto por un judío alemán ciego, Lothar Hermann, emigrado desde 1938, y cuya hija era amiga del hijo menor de Eichmann. El Mossad, servicio secreto israelí, no dio crédito a que un ciego hubiera descubierto a Eichmann. Confirmaron la noticia y planearon su captura y transporte inmediato a Israel. Uno de los miembros del Mossad que lo capturó, lo describió como “un hombrecito suave y pequeño, algo patético, y normal, no tenía la apariencia de haber matado a millones de los nuestros … pero él organizó la matanza”. El 20 de mayo lo trasladaron a Israel.
En el juicio, Eichmann alegó, en su defensa, que actuó por obediencia debida a sus superiores. Declaró que “no perseguí a los judíos con avidez ni placer. Fue el gobierno quien lo hizo. La persecución, por otra parte, solo podía decidirla un gobierno, pero en ningún caso yo. Acuso a los gobernantes de haber abusado de mi obediencia. En aquella época era exigida la obediencia …”.
Hannah Arendt escribió que Eichmann no era un supervillano y, para ella, lo más impactante fue que, cualquier persona, en determinadas circunstancias y en el entorno adecuado, puede ser tremendamente malvado porque crea que es su obligación o, si se quiere, su trabajo a cumplir.
Fue condenado a muerte por genocidio y ejecutado, en la prisión de Ramla, en la madrugada del 1 de junio de 1962.
Sus últimas palabras fueron “Larga vida a Alemania. Larga vida a Austria. Larga vida a Argentina. Estos son los países con los que más me identifico y nunca los voy a olvidar. Tuve que obedecer las reglas de la guerra y las de mi bandera. Estoy listo”.
Más adelante, además de judíos y gitanos, otros muchos entraron en la lista de exterminio de los nazis. Himmler declaró que “lo que le suceda a un ruso o a un checo no me importa lo más mínimo. Lo que las naciones puedan ofrecernos en forma de buena sangre de nuestro tipo lo tomaremos, si es necesario secuestrando a sus hijos y educándolos con nosotros”.
En la primavera de 1942, del 75% al 80% de las que serían víctimas del genocidio nazi estaban vivas, pero menos de un año después, en la primavera de 1943, la mayoría habían muerto. Después de la Conferencia de Wansee, el genocidio tuvo una primera ola de crímenes corta e intensiva.
Pelagia Lewinska: Veinte meses en Auschwitz
 Mujeres supervivientes de Auschwitz. Fuente: Holocaust Encyclopedia
Mujeres supervivientes de Auschwitz. Fuente: Holocaust EncyclopediaNació en 1907 y murió en 2004. Fue activista del Partido Comunista polaco en el que alcanzó cargos importantes en el área de Educación y en el movimiento scout de Polonia.
Durante le guerra pertenecía a la resistencia y fue capturada y encerrada en el campo de Auschwitz. Estuvo en un barracón con otras mujeres, gitanas, polacas, checas, rusas, francesas, incluso algunas alemanas, todas en la suciedad y la mugre del campo de exterminio.
El 23 de enero de 1943, un grupo de mujeres de la prisión de Cracovia fue trasladado a Auschwitz “después del suplicio y la tortura de los interrogatorios en las oficinas de la Gestapo”. Eran 16 mujeres del grupo de Pelagia Lewinska y 160 mujeres en total. Además, en los vagones de ganado en que las llevarían al campo montaron casi 500 hombres, sobre todo judíos. En su recuerdo está que llegaron a Auschwitz. Se detuvo el tren. Los hombres de la Gestapo las bajaron a culatazos. Orden de marcha en filas de a cinco. A lo lejos, las luces del campo sobre alambradas y torres de vigilancia. Un olor terrible sobre el paisaje. Las frauen de las SS les robaron las joyas. Y el tatuaje del número en el antebrazo sería la identidad de cada una en el campo. El de Pelagia Lewinska era 32292.
El 28 de enero fue la primera noche en el campo. Frío y oscuridad. Como literas, andamios de madera de tres alturas. Arriba, el tejado; abajo, tierra apisonada. En el bloque 26, todas mujeres judías, murieron 1800 en tres meses. Prohibido poseer cualquier cosa. Antes del amanecer, la llamada.
El bloque 25 era el de la muerte. Se cargaban camiones con mujeres. Iban y venían desde los hornos crematorios. Una y otra vez.
En Auschwitz murieron tres millones de personas. Entre las mujeres, en enero de 1943, el promedio de defunciones era de 100 mujeres al día. En febrero y marzo de 1944, un año después, el promedio llegaba a las 800, sobre una población total casi idéntica de unas 15000 detenidas. Era imposible evacuar el enorme número de cadáveres. De las 100000 mujeres tatuadas hasta agosto de 1944, solo vivían unas 11000.
“La más veterana de las internadas recorría la formación distribuyendo golpes con una porra. Los cráneos crujían, ensordecían los oídos y se hinchaban los ojos. Pero nadie podía moverse. Era indispensable permanecer inmóvil. El procedimiento de la lista no había terminado”.
En la tercera noche desde la salida de Cracovia, una gitana se puso de parto en el barracón. Una médico checa le atendió. Extrañó a las nuevas que no llegara ayuda de la enfermería del campo. Una veterana comentó que “eso no tiene importancia”.
La comida era unas patatas mal cocidas y una sopa con tronchos de berza como una piedra. Comprendieron que estaba permitido morir de hambre. Las veteranas explicaban que “esto es la tumba”.
Los médicos del campo designaban a quien debía morir.
“Todas las enfermas, verdaderos esqueletos ambulantes, desfilaban dormidas ante el, para que escogiese y designase a aquellas para quienes no había ni tiempo ni sitio adecuado para una lenta agonía. Convenía que muriesen enseguida…”
Las alambradas eléctricas fueron la liberación para muchas prisioneras. Cada mañana, un grupo de detenidas recogía cadáveres de las alambradas o, como decían, “cosechaban liberadas”.
“La verdad es que Auschwitz fue un lugar de exterminio en masa de seres humanos. Cinco trenes diarios llegaban e iban a la cámara de gas. La tierra de Auschwitz se abonaba con las cenizas de los gentes de toda Europa y daba magníficas cosechas”.
En un discurso del 4 de octubre de 1943 a altos cargos de las SS, Himmler declaró:
“La mayoría de vosotros sabéis lo que significa ver cien cadáveres yaciendo juntos, quinientos cadáveres, o mil. Habéis pasado por esto y … salvo algunas excepciones, ejemplo de debilidad humana … seguir siendo decentes, esto es lo que nos ha curtido. Esta es una página gloriosa de nuestra historia que nunca se ha escrito y nunca se escribirá”.
La evolución trata de nosotros y los otros, de altruismo y de xenofobia. Pero, además, está la cultura y la educación para modular lo que la evolución selecciona y, también, la propia evolución selecciona la cultura y la educación como bases de la flexibilidad de la especie humana. Su falta provoca rigidez en las conductas que deben ser flexibles para la adaptación a entornos nuevos y cambiantes.
Para terminar con cierta esperanza, identificar las raíces evolutivas que llevan al genocidio permitirá no tomarlo como un destino inevitable de la especie humana, sea cual sea su base cultural y sociobiológica.
Y, recordar que Jerry Fowler publicó en 2004 que el primer genocidio del siglo XXI está documentado en Darfur, en el Sudán.
Referencias:
Abad, J.J. 1976. La selección de la raza aria (Lebensborn). Círculo de Amigos de la Historia. Madrid. 286 pp.
Abos, A. 2012. Eichmann en la horca. El País 31 mayo.
Aizenstadt Leistenschneider, X.A. 2007. Origen y evolución del concepto de genocidio. Revista de Derecho Universidad Francisco Marroquín 25: 11-22.
Arendt, H. 2018. Eichmann en Jerusalén. Un estudio acerca de la banalidad del mal. Penguin Random House. Barcelona. 440 pp.
Armstrong, K. 2015. Campos de sangre. La religión y la historia de la violencia. Paidós. Barcelona. 575 pp.
Bauman, Z. 2010. Modernidad y holocausto. Ed. Sequitur. Madrid. 272 pp.
Brannigan, A. 1998. Criminology and the Holocaust: Xenophobia, evolution, and genocide. Crime & Delinquency 44: 257-276.
Brayard, F. 2002. L’humanité versus Zyklon B. L’ambiguité du choix de Kurt Gerstein. Vingtième Siècle. Revue d’Histoire 73: 15-25.
Chorover, S.L: 1985. Del Génesis al genocidio. La sociobiología en cuestión. Ed. Orbis. Barcelona. 280 pp.
Deschmann, U., 1996. Biologists under Hitler. Harvard University Press. Cambridge and London. 468 pp.
Eisenberg, L. 1972. The human nature of human nature. Science 176: 123-128.
Eisenberg, L. 2005. Which image for Lorenz? American Journal of Psychiatry 162: 1760.
Friedman, T.L. 1995. Foreign Affairs; Allies. New York Times June 7.
Fowler, J. 2004. Beyond humanitarian bandages – confronting genocide in Sudan. New England Journal of Medicine 351: 2574-2576.
Hébert, V. 2006. Disguised resistance? The story of Kurt Gerstein. Holocaust and Genocide Studies 20: 1-33.
Heydecker, J.J. & J. Leeb. 1962. El proceso de Nuremberg. Ed. Bruguera. Barcelona. 512 pp.
Jiménez Lozano, J. 2005. La historia de un espía. ABC 21 mayo.
Klopfer, P. 1994. Konrad Lorenz and the National Socialists: On the politics of Ethology. International Journal of Comparative Psychology 7: 202-208.
Lorenz, K. 1975. Los ocho pecados mortales de la humanidad. Plaza & Janés. Nabrcelona. 128 pp.
Manvell, R. 1975. SS Gestapo. Dominación por terror. Ed. San Martín. Madrid. 160 pp.
Mulisch, H. 1961. El juicio a Eichmann. Causa Penal 40/61. Titivillus. ePub base r1.2. 141 pp.
Müller-Hill, B. 1985. Ciencia mortífera. La segregación de judíos, gitanos y enfermos mentales (1933-1945). Ed. Labor. Barcelona. 272 pp.
Ollé Sesé, M. 2015. El crimen de genocidio (1): Génesis y evolución legislativa nacional e internacional. Serie Working Papers 01/2015. Fundación Internacional Baltasar Garzón. 14 pp.
Sax, B. 2007. Konrad Lorenz and the mythology of science. En “What are animals to us: Approaches from science, religión, folklore, literatura and art”, p. 269-276. Ed. por D. Aftandilian et al. University of Tennessee. Knoxville.
Staub, E. & D. Bar-Tal. 2003. Genocide, mass killing, and intractable conflicto. En “Oxford handbook of political psychology”, p. 710-751. Ed. por D.O. Sears et al. Oxford University Press. Oxford.
Stern, B. & P. Lewinska. 1960. Eichmann. Su vida. Sus víctimas. Fomento Internacional de Cultura. Barcelona. 286 pp.
Ternon, Y. & S. Helman. 1971. Historia de la Medicina SS o El mito del racismo biológico. Fomento de Cultura Ed. Valencia. 408 pp.
Wiesenthal, S. 1989. Justicia, no venganza. Ed. B. Barcelona. 441 pp.
Wikipedia. 2017. Kurt Gerstein. 20 diciembre.
Wikipedia. 2018. Pelagia Lewinska. 16 agosto.
Wikipedia. 2018. Genocidios en la historia. 29 septiembre.
Wikipedia. 2018. Konrad Lorenz. 1 octubre.
Wikipedia. 2018. Adolf Eichmann. 4 October.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Genocidio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Desmitificando: Las rubias son “tontas”
- Historias de la malaria: El charlatán y caballero Sir Robert Talbor
- Ingredientes para la receta: El kiwi
Neandertales y Cro-mañones: dos humanidades, dos destinos

Vivimos un momento inaudito en el curso de la evolución humana. Durante cientos de miles de años han sido varias las especies humanas que han habitado la Tierra. Sin embargo, actualmente es nuestra especie (Homo sapiens) la única del linaje humano que vive en la superficie terrestre.
Los Neandertales habitaron el viejo continente durante casi medio millón de años, para después dejar paso a nuestra especie, que llegó hace apenas 45.000 años a Europa. Estas dos especies se cruzaron en Oriente Medio, durante miles de años tuvieron tecnologías semejantes y presentaron rasgos culturales similares. Ambas dejaron su huella en el País Vasco. En una época de retos como la actual, con problemas de la envergadura del cambio climático, no está de más recordar que la extinción no es algo ajeno al linaje humano.
Asier Gómez Olivencia aborda las diferencias y similitudes de estas dos especies en esta conferencia, pronunciada en el marco del ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad. Esta conferencia, en concreto, fue la primera sesión de “Bidebarrieta Científica” del 2020, año en el que además la Cátedra de Cultura Científica celebra su décimo aniversario.
Asier Gómez Olivencia es doctor en Paleontología Humana. Ha investigado en la Universidad de Cambridge y en el Museo Nacional de Historia Natural de Francia. Es investigador del programa Ramón y Cajal y en 2014 se incorporó al Departamento de Estratigrafía y Paleontología de la UPV/EHU como investigador Ikerbasque. Ha participado en grupos de investigación internacionales como investigador y como director de grupo. Entre las investigaciones que ha dirigido destaca la realizada para investigar la presencia de renos durante el Pleistoceno en la Península Ibérica o la reconstrucción del tórax de un neandertal en 3D, con los restos fósiles del yacimiento de Kebara (Israel).
Edición realizada por César Tomé López
El artículo Neandertales y Cro-mañones: dos humanidades, dos destinos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Neandertales ¿crónica de una muerte anunciada?, por María Martinón-Torres
- Los neandertales respiraban de otra manera
- Prevenir y tratar la enfermedad de Alzheimer: Una visión moderna
Biomimética cuántica: átomos y fotones como seres vivos
![]()
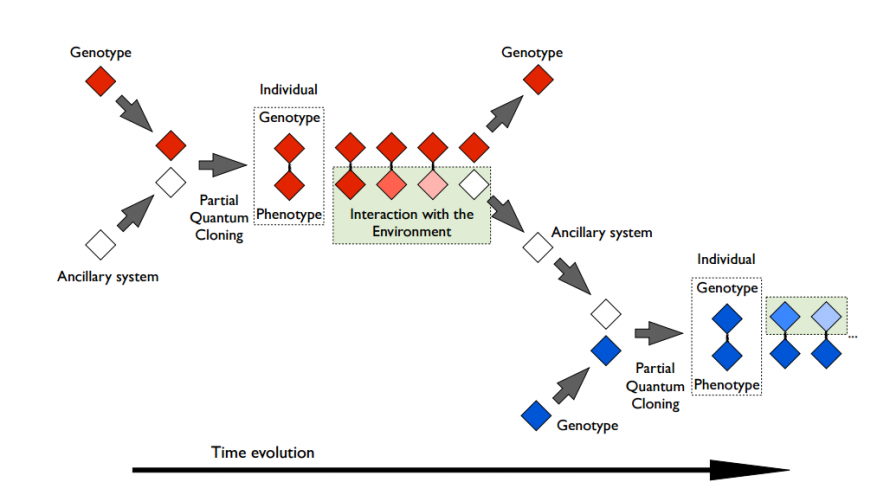
El ecólogo Thomas S. Ray decidió dejar funcionando toda la noche el programa que acababa de desarrollar. Era finales de 1989 y los ordenadores tenían una capacidad muy limitada. Ray había escrito una serie de pequeños programas muy sencillos que trataban de competir por la memoria y el tiempo de procesado.
El científico encontró a la mañana siguiente algo totalmente inesperado. Sus sencillos programas se habían replicado, mutado y recombinado sucesivamente hasta formar estructuras complejas y evolucionadas.
Este sencillo juego, que Ray denominó Tierra, dio a luz una rama fundamental de la biología computacional denominada dinámica ecológica y de evolución.
Las posibilidades de la tecnología cuántica
Los ordenadores cuánticos, que usan propiedades únicas como la superposición y el entrelazamiento para incrementar la potencia computacional, podrán realizar en el futuro cálculos fuera del alcance de los ordenadores actuales o clásicos.
Sin embargo, los recursos computacionales con los que cuentan actualmente los chips cuánticos son escasos, con solo unos pocos bits cuánticos disponibles que son poco fiables.
En los últimos años hemos trabajado en una línea de investigación pionera en vida artificial cuántica que denominamos biomimética cuántica. Tratamos de conseguir que los átomos y fotones muestren características propias de los sistemas biológicos.
El primer paso fue desentrañar el mecanismo de reproducción de la información, un proceso muy sutil, ya que la clonación cuántica está prohibida por los fundamentos de la mecánica cuántica.
Después, atacamos el problema del número mínimo de componentes con los que debe contar un individuo cuántico para llevar a cabo las funciones más básicas, como la reproducción o la mutación.
La conclusión es que dos átomos o fotones son suficientes: uno que codifica la información del genotipo y el otro que juega el papel de fenotipo y envejece por interacción con el ambiente. Este resultado es sorprendente porque tendemos a asociar comportamientos biológicos con la emergencia de la complejidad en sistemas macroscópicos.
Seres artificiales en la nube
Posteriormente, hemos comprobado los modelos desarrollados para estas dinámicas en la nube en un ordenador cuántico de IBM que constaba de cinco bits cuánticos. Este trabajo supuso la primera implementación de vida artificial cuántica en un ordenador cuántico, es decir, que simulamos vida cuántica en un sistema físico inerte.
Actualmente estamos investigando la introducción de factores más complejos como, por ejemplo, reemplazar la reproducción asexual por la sexual, mediante el uso de diferentes géneros, que ayude a aumentar la complejidad del sistema.
También estamos considerando estudiar las características de los depredadores y las presas para simular las dinámicas de interacción entre ambos que se dan en la naturaleza, descritas por las ecuaciones de Lotka-Volterra. En definitiva, tenemos la versión cuántica del juego Tierra de Thomas S. Ray al alcance de la mano.
En esta situación, el acceso a ordenadores cuánticos nos permite contar con nuevas reglas de juego (las de la física cuántica) que producirán sin duda resultados incluso más sorprendentes que los de su versión clásica gracias a la existencia de superposición y entrelazamiento cuánticos.
Afortunadamente para nosotros, como mentes científicas curiosas, estos trabajos sugieren preguntas profundas sobre el surgimiento de la complejidad biológica, la conservación de la información y las consecuencias de la interacción entre entes biológicos.![]()
Sobre el autor: Mikel Sanz es investigador del grupo Quantum Technologies for Information Science (QUTIS) de la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Biomimética cuántica: átomos y fotones como seres vivos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo de cuánticos son los fenómenos cuánticos en los seres vivos
- Una puerta cuántica robusta y ultrarrápida
- Cómo acabar con el desprecio a los fotones
Vidas salvadas por la cloración del agua
 Foto: Mukesh Sharma / Unsplash
Foto: Mukesh Sharma / Unsplash«El empleo de cloro en la potabilización del agua es probablemente el avance en salud pública más significativo del milenio». Esto lo publicó la revista Life en 1997. Se calcula que, desde 1919 se han salvado 177 millones de vidas gracias a la cloración del agua.
A lo largo de la historia hemos ido desarrollando métodos cada vez más eficaces para garantizar la seguridad del agua que consumimos. Algunos tienen más de 4000 años de antigüedad, empezando por la decantación y la filtración, y terminando por la cloración, que nos permitió minimizar el riesgo de contagio de cólera, tifus, disentería y polio.
-
Empezamos a filtrar y decantar el agua
Hay registrados métodos para mejorar el sabor y el olor del agua 4.000 años antes de Cristo. Se han encontrado escritos griegos en los que se hablaba de métodos de tratamiento de aguas por filtración a través de carbón, exposición a los rayos solares y ebullición.
En el antiguo Egipto el agua se decantaba. Se dejaba reposar en vasijas de barro hasta que precipitasen las impurezas, quedándose con la parte superior del agua. También añadían alumbre para favorecer la precipitación de las partículas suspendidas en el agua. A este proceso se le llama coagulación y es el origen de las técnicas que se emplean en las potabilizadoras modernas.
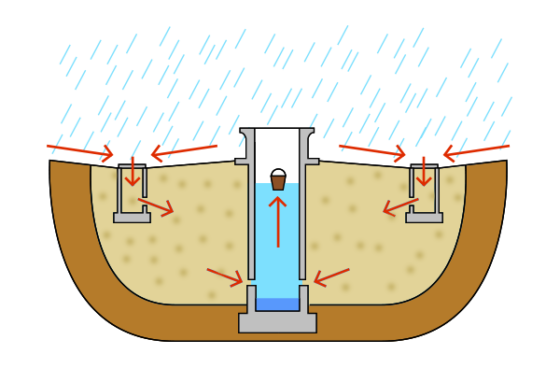 Funcionamiento de las cisternas filtradoras de Venecia. Imagen: playandtour.com
Funcionamiento de las cisternas filtradoras de Venecia. Imagen: playandtour.comUno de los primeros ejemplos de potabilización de agua a gran escala lo encontramos en Venecia. Allí se recogía y almacenaba el agua de lluvia. Para ello se construyeron cisternas bajo las plazas y otros espacios públicos, donde el agua llegaba a través de desagües en los que se colocaron filtros de arena de mayor a menor gradación. El acceso al agua potable se hacía hasta finales del XIX a través de pozos instalados en las plazas. Hoy en día son visibles, aunque están clausurados con tapas de metal.
 Pozo clausurado de Venecia. Imagen: playandtour.com
Pozo clausurado de Venecia. Imagen: playandtour.comEn Italia, el médico Luca Antonio Porzio es considerado el artífice de los primeros sistemas de filtrado de agua a través de arena y posterior decantación. En Francia Joseph Amy por su parte diseñó filtros para el agua a pequeña y gran escala con esponjas, lana y carbón.
Poco después de que Joseph Amy consiguiera en 1749 la primera patente para un filtro de agua emitida en el mundo, el londinense James Peacock obtuvo la primera patente británica. La filtración se realizaba a través de arena dispuesta por tamaño creciente y por ascenso en lugar de por descenso. El filtro de Peacock fue un fracaso, no obstante, marcó el comienzo de un período de experimentación que dio como resultado los filtros lentos de arena que se usan en la actualidad.
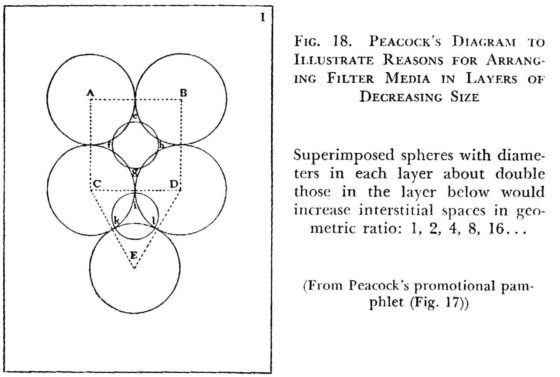 Imagen: thisdayinwaterhistory.wordpress.com
Imagen: thisdayinwaterhistory.wordpress.com-
Descubrimos los microbios
A finales del siglo XIX, a medida que se realizaban mejoras en los sistemas de filtración, también se estableció la Teoría microbiana de la enfermedad. Es una teoría científica que propone que los microorganismos son la causa de una amplia gama de enfermedades. Antes de aquello no sabíamos de la existencia de microorganismos. Resultaba impensable que unos pequeños seres vivos conviviesen con nosotros, estuviesen por todas partes y fuesen el germen de muchas enfermedades.
La teoría microbiana fue un descubrimiento científico realizado por Louis Pasteur y posteriormente probado por Robert Koch. Consiguió reemplazar antiguas creencias como la teoría miasmática o la teoría de los humores, por las que se pensaba que las enfermedades las causaban una suerte de efluvios malignos. Aunque la teoría microbiana fue muy controvertida cuando se propuso, obviamente fue fundamental para entender y combatir la propagación de enfermedades.
-
Cloro para acabar con los microorganismos patógenos
Aunque los suministros municipales de agua se multiplicasen a lo largo del siglo XIX, las condiciones sanitarias y de salud no comenzaron a mejorar radicalmente hasta la introducción de la desinfección con cloro a principios del siglo XX.
Por ejemplo, en 1900 había más de 3.000 sistemas de suministro municipal de agua en los Estados Unidos, pero en ocasiones, en lugar de mejorar la salud y la seguridad, contribuyeron a expandir enfermedades. Este fue el caso de la epidemia de cólera de 1854 en el barrio del Soho en Londres, en el que murieron más de 700 personas en una semana en un área de apenas medio kilómetro de diámetro. El médico John Snow, precursor de la epidemiologia moderna, relacionó el brote con una bomba que suministraba agua proveniente de un pozo contaminado con heces.
Para tratar de erradicar la desinfección, Snow optó por utilizar cloro. A principios del siglo XX, el uso de cloro empezó a popularizarse como técnica de desinfección también en Europa.
El ejemplo más antiguo que se conoce es el de Middelkerke, Bélgica, donde en 1902 se puso en marcha la primera planta de cloración. Antes de la filtración se añadía cloruro de calcio y percloruro de hierro. En Reino Unido se implantó en 1905, cuando un filtro de arena lento y defectuoso y un suministro de agua contaminado causaron una grave epidemia de tifus en Lincoln. Alexander Cruickshank Houston utilizó la cloración del agua para detener la epidemia. Emplearon hipoclorito de calcio.
En Estados Unidos comenzaron a desinfectar el agua con agentes clorados en 1908, en Boonton Reservoir, que sirvió de suministro para Nueva Jersey. El proceso de tratamiento con hipoclorito de calcio fue concebido por John L. Leal, y la planta de cloración fue diseñada por George Warren Fuller. En los años siguientes, la desinfección con cloro utilizando cloruro de cal (hipoclorito de calcio) se instaló rápidamente en los sistemas de agua potable de todo el mundo. En 1914, más de 21 millones de personas recibían agua tratada con cloro en los Estados Unidos, y en 1918, más de 1.000 ciudades de América del Norte ya estaban usando cloro para desinfectar su suministro de agua, que llegaba aproximadamente a 33 millones de personas.
En España la cloración llegó a la mayor parte de las ciudades en 1925 mediante el uso de hipoclorito. Uno de los episodios más graves sucedidos antes de la cloración ocurrió en la ciudad de A Coruña. En 1854 una epidemia de cólera provocó la muerte de 2026 personas en tan solo 20 días. El 20% de la población coruñesa falleció.
Las redes de abastecimiento de agua a domicilio llegarían a Coruña en 1908. En 1915 se implantaron los primeros sistemas de saneamiento mediante filtrado con arena, y en 1918 se implantó la cloración.
 Capilla de San Amaro, A Coruña. Imagen: César Quián en La Voz de Galicia.
Capilla de San Amaro, A Coruña. Imagen: César Quián en La Voz de Galicia.
En el cementerio coruñés de San Amaro existe una capilla bajo la que se encuentra la fosa común en la que fueron enterrados los fallecidos por aquella epidemia de cólera.
-
Así funciona la cloración
La cloración es un método de desinfección y potabilización del agua. Su papel no es eliminar contaminantes —esto se hace por otras vías en las plantas de tratamiento de aguas—, sino destruir microorganismos patógenos.
Para ello se añade cloro al agua a tratar. El cloro puede suministrarse de varias maneras. Si se añade cloro gas (Cl2), el cloro reacciona con el agua formando diferentes especies según el pH del agua: perclorato, hipoclorito, ácido clorhídrico, ácido hipocloroso… También pueden utilizarse directamente compuestos clorados como dióxido de cloro o hipoclorito. Todos ellos son sustancias oxidantes
La cloración causa alteraciones en la pared celular de las células bacterianas. Con cloro suficiente, se destruyen proteínas y ADN de las células. Ese es el mecanismo por el que el cloro acaba con los microorganismos, afectando a sus funciones vitales hasta llevarlos a la muerte, por lo que son incapaces de producir enfermedades. Estos compuestos clorados son oxidantes. Esto hace que además sean germicidas, eliminando mohos, algas y otros microorganismos además de bacterias.
Actualmente conocemos otros muchos oxidantes con cualidades similares, como otros halógenos, el permanganato o el ozono. Pero el más empleado sigue siendo el cloro. La razón es que, aunque haya otros métodos de desinfección, cuando el agua sale de la planta de tratamiento circulará por tuberías donde sigue habiendo riesgo de contaminación. Por eso se aplica una post-cloración, es decir, se añade una cierta cantidad extra de cloro que garantiza el viaje seguro del agua potable por las tuberías hasta el grifo de nuestra casa.
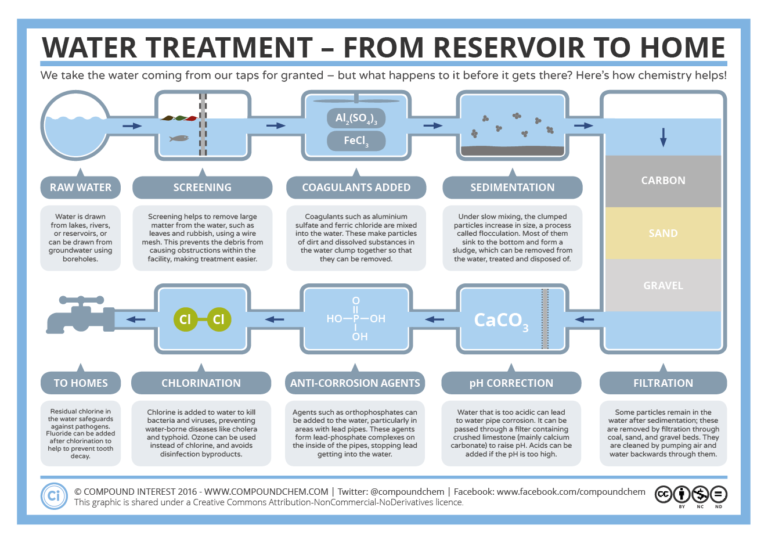 Imagen: compoundchem.com
Imagen: compoundchem.comHoy en día, en las estaciones de tratamiento de agua potable (ETAP) se realizan los procesos necesarios para que el agua natural procedente de embalses y otras captaciones se transforme en agua potable. En ellas se llevan a cabo procesos físicos, químicos y biológicos complejos capaces de lograr un agua segura, con buen olor y sabor. Además de tratar el agua, ésta se analiza periódicamente, es decir, se mide su calidad y su composición química y biológica.
-
Subproductos de la cloración
El cloro puede reaccionar con compuestos orgánicos que se encuentran naturalmente en el suministro de agua para producir compuestos conocidos como subproductos de desinfección (DBP). Los DBP más comunes son los trihalometanos (THM).
Químicamente los trihalometanos son moléculas de metano (CH4) en las que tres de sus hidrógenos han sido sustituidos por halógenos (flúor, cloro, bromo o yodo). Se forman al reaccionar compuestos oxidantes de cloro con moléculas orgánicas pequeñas fruto de la descomposición de materia orgánica. La materia orgánica que el agua arrastra de forma natural, como restos vegetales, se descompone en el agua dando lugar a moléculas orgánicas sencillas como aminoácidos y azúcares. Estas moléculas simples son las que pueden llegar a transformarse en trihalometanos tras los procesos de cloración.
Según varios estudios, la exposición a trihalometanos a largo plazo podría aumentar las probabilidades de desarrollar cáncer de vejiga. Esto se ha extrapolado de experimentos en animales. Es una de las razones por la que el reglamento europeo establece un límite máximo de trihalometanos en 100 microgramos por litro de agua. Según el Sistema de Información Nacional de Aguas de Consumo, en España tenemos un promedio de 27,35 microgramos de trihalometanos por litro, casi cuatro veces inferior a los niveles estimados como seguros por la Organización Mundial de la Salud. Con lo cual, a pesar del alarmismo promovido por algunos medios de comunicación, los trihalometanos no son un motivo de preocupación.
-
Así eliminamos los subproductos de la cloración
Periódicamente se hace un control de presencia de trihalometanos en aguas de consumo para garantizar que nunca se haya sobrepasado el límite marcado por la normativa.
Además, conocemos varios mecanismos que nos permiten minimizar la presencia de trihalometanos. En algunas plantas de tratamiento de aguas se utilizan otros oxidantes diferentes al cloro como tratamiento previo a la cloración, reduciendo la formación de trihalometanos. Las aguas también se someten a procesos de filtración y separación previos usando membranas, arena y carbón activo que eliminan gran parte de la materia orgánica antes de que el agua llegue a la fase de cloración. También se usan cloraminas que previenen la formación de trihalometanos. No obstante, hay técnicas más económicas y eficientes fundamentadas en la naturaleza química de los trihalometanos.
Los trihalometanos son compuestos volátiles. Esto quiere decir que tienen tendencia a pasar a fase gas y evaporarse del agua. Así, a medida que el agua avanza por las tuberías, la cantidad de trihalometanos va disminuyendo. La solubilidad también se ve afectada por la temperatura, así que habrá menos trihalometanos en aguas cálidas que en aguas frías.
Por tanto, se trata de establecer un balance entre materia orgánica, cloro añadido y tiempo de aireación del agua antes de destinarla a consumo.
-
Reflexión final
La cloración del agua ha sido uno de los aportes de la química más importantes de la historia de la humanidad. Un hito en materia de salud pública. Gracias a la cloración del agua hemos evitado epidemias de cólera, tifus o polio que se habrían llevado por delante millones de vidas.
 Imagen: Unicef
Imagen: UnicefA pesar de llevar más de un siglo clorando el agua, no hemos conseguido que esta solución tan eficaz, fácil de aplicar y económica, llegue a todo el mundo. La escasez de agua potable es la causa principal de enfermedades en el mundo. Una de cada seis personas no tiene acceso a agua potable. La mortandad en la población infantil es especialmente elevada. Unos 4.500 niños mueren a diario por carecer de agua potable y de instalaciones básicas de saneamiento. En los países en vías de desarrollo, más del 90% de las muertes por diarrea a causa de agua no potable se producen en niños menores de cinco años.
La cloración del agua salva miles de vidas al año, y lo hemos logrado recorriendo un largo camino de desarrollo e investigación científica. Pero para que la cloración salve vidas en todo el mundo, además de ciencia, hace falta mucho más.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Vidas salvadas por la cloración del agua se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Agua cruda, la nueva moda antiprogreso del primer mundo
- Sal de la piscina si te pican los ojos y no mezcles lejía con amoniaco
- La importancia del agua en un biomarcador contra el cáncer
El gato de Arnold
Las matemáticas son parte de la física. La física es una ciencia experimental, una de las ciencias naturales. Las matemáticas son la parte de la física en la que los experimentos son baratos.
Vladimir I. Arnold, en [1].
 Vladímir Ígorevich Arnold. Imagen: Wikimedia Commons.
Vladímir Ígorevich Arnold. Imagen: Wikimedia Commons.
Con esta contundente afirmación sobre la educación matemática comenzaba su artículo el prolífico matemático ruso Vladímir Ígorevich Arnold (1937-2010). El científico era muy crítico con la manera de enseñar matemáticas debido al nivel de abstracción que estaban alcanzando en aquella época. El grupo Bourbaki impulsó en Francia esta alta conceptualización de las matemáticas que fue posteriormente adoptada en otros países. Arnold opinaba que esta elección tenía un impacto negativo en la educación matemática, que había otra manera más natural y satisfactoria de introducir conceptos y problemas. Lamentaba que, en este intento por construir una “matemática pura” siguiendo el método axiomático-deductivo, se había llegado a rechazar el esquema clásico en física («experiencia – modelo – estudio del modelo – conclusiones – verificación por la experiencia») para reemplazarlo por el esquema «definición – teorema – demostración».
En [1], Arnold comentaba con sorna:
A la pregunta «¿Cuánto son 2+3?» un alumno de escuela francés ha contestado «3+2 porque la suma es conmutativa.». ¡Ni siquiera sabía a qué era igual esta suma, ni siquiera entendía lo que le estaban preguntando!
¿Exageraba Arnold o tenía razón en sus contundentes afirmaciones? Supongo que habrá opiniones variadas. Así que dejamos aparte las opiniones de Arnold para centrarnos en su gato…
En la teoría de sistemas dinámicos, la «aplicación gato de Arnold» es un ejemplo de difeomorfismo de Anosov sobre el toro. Para aquellas personas que deseen conocer la definición y propiedades de esta aplicación, dejamos algunas referencias al final de esta anotación. Dicho de manera sencilla, la «aplicación gato de Arnold» es una transformación del toro en sí mismo inducida por una aplicación lineal sobre el plano.
Recordemos, antes de seguir, que el toro puede obtenerse como el cociente de un cuadrado con las identificaciones mostradas en la figura:
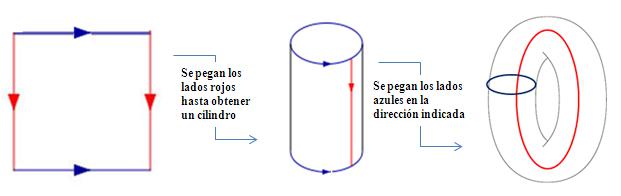 El toro como cociente de un cuadrado. Imagen: Marta Macho Stadler.
El toro como cociente de un cuadrado. Imagen: Marta Macho Stadler.
Siguiendo su máxima de experimentar, Arnold mostró los efectos de esta aplicación usando la imagen de un gato dibujada sobre un toro, de allí el nombre de esta aplicación. ¿Y cómo lo hizo? Colocó la imagen de un gato sobre un cuadrado –teniendo en cuenta las identificaciones indicadas anteriormente, la imagen puede pensarse sobre un toro– la deformó siguiendo la definición de la «aplicación gato de Arnold» y recortó la imagen resultante en trozos para recomponerla de manera adecuada sobre el cuadrado –y por lo tanto sobre el toro, tras cocientar–.
 Imagen de un gato transformado por la aplicación gato de Arnold. Imagen: Wikimedia Commons.
Imagen de un gato transformado por la aplicación gato de Arnold. Imagen: Wikimedia Commons.
Este proceso se puede repetir. Es decir, a la imagen obtenida se le puede volver a aplicar la «aplicación gato de Arnold» y observar cómo evoluciona este sistema.
Existe un análogo discreto de la «aplicación gato de Arnold». Al tratarse de una transformación biyectiva de una imageni, sabemos que existe un menor número entero, k, de manera que realizando k veces la transformación se vuelve a obtener la imagen original.
La imagen de debajo –de 150 por 150 píxeles– representa a un gato –no pertenece a Arnold; es del autor de la imagen, Claudio Rocchini–. Podemos observar el efecto de la transformación tras 1, 3, 132, 155, 157, 200, 211, 240, 275, 299 y 300 iteraciones, momento en el que la imagen original reaparece. Es decir, el número entero k aludido antes es de 300 para una imagen de 150 por 150 píxeles.
 Imagen de un gato transformado por la aplicación gato de Arnold. Imagen: Wikimedia Commons.
Imagen de un gato transformado por la aplicación gato de Arnold. Imagen: Wikimedia Commons.
A continuación puede verse una simulación de cómo evoluciona la «aplicación gato de Arnold» discreta sobre una imagen de 74 por 74 píxeles. En este caso el número entero k es 114, es decir, se recupera la imagen original tras 114 iteraciones. Observar, además que en la iteración 57 aparece la imagen original, pero girada 180 grados.
 Imagen: Wikimedia Commons
Imagen: Wikimedia Commons
Sin duda sorprende recuperar la imagen de partida tras este aparente comportamiento caótico. Estas sorpresas forman parte de la belleza de las matemáticas.
Por cierto, si te apetece experimentar con tus propias imágenes, en las referencias [4] y [5] puedes hacerlo online.
Referencias
[1] Vladimir I. Arnold, «Sur l’éducation mathématique», Gazette de Mathématiciens 78 (1998), 19-29 (traducido del ruso por J.- M. Kantor)
[2] Arnold’s cat map, Wikipedia (consultado el 18 de enero de 2020)
[3] David D. Nolte, Vladimir Arnold’s Cat Map, Galileo Unbound, 16 junio 2019
[5] Jason Davies, Arnold’s Cat Map, 2012
Nota:
i Una transformación biyectiva de una imagen de n por m píxeles es una modificación de esta imagen sobre sí misma: cada pixel se desplaza de su lugar a otro –y el que ocupa ese lugar se mueve a otro sitio–. Ningún pixel desaparece, sólo cambia de posición. En matemáticas se habla de una permutación de los estos píxeles. El conjunto P de las permutaciones sobre un conjunto finito forma un grupo –el grupo simétrico, que en este caso, además, es un grupo finito–. Puede demostrarse que si P es una permutación de este tipo, existe un número entero k tal que si P se aplica k veces se recupera la transformación identidad –la permutación que no cambia nada–.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo El gato de Arnold se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Tales de Mileto y el caso del gato que venía del cielo
- Visualizando la hiperesfera a través de la fibración de Hopf
- Un gato de Cheshire cuántico
El principio de incertidumbre, cuantitativamente
 Foto: Sailer / Unsplash
Foto: Sailer / UnsplashNuestras consideraciones cualitativas del principio de incertidumbre pueden resumirse así:
Es imposible medir la posición y el momento lineal de un corpúsculo subatómico en el mismo instante con una precisión ilimitada. Cuanto más precisa es la medición del momento lineal, menos precisa es la medición de la posición en ese instante, y viceversa.
Esta conclusión se recoge formalmente en el principio de incertidumbre, establecido por Werner Heisenberg en 1927. El principio de incertidumbre se puede expresar cuantitativamente [1] en dos expresiones matemáticas simples, conocidas como relaciones de incertidumbre, que son conclusiones necesarias extraídas de experimentos sobre mediciones que involucran objetos cuánticos.
Vamos a llamar Δx a la incertidumbre en la medida de la posición del objeto y llamaremos Δpx a la incertidumbre en la medida del momento lineal del objeto en la dirección x en ese mismo instante. El principio de incertidumbre de Heisenberg dice que el producto de estas dos incertidumbres debe ser igual o mayor que la constante de Planck dividida por 4π. O sea, Δx·Δpx≥h/4π. Existen relaciones similares para las coordenadas y y z. Veamos qué quiere decir.
Esta relación de incertidumbre dice que si usamos un fotón de longitud de onda corta en un intento de medir la posición de un electrón con una precisión muy alta, de modo que Δx sea muy pequeña, entonces la incertidumbre en la medición del momentoΔpx debe ser al menos h/(4π· Δx) . Esto significa que a medida que Δx se hace más pequeña, Δpx tiene que hacerse más grande. El efecto Compton nos sirve para entender qué ocurre: el electrón rebota con más velocidad (con mayor momento lineal) cuanto más corta sea la longitud de onda (mayor energía, por tanto) del fotón de medición.
De hecho, si medimos la posición con tanta precisión que no hay incertidumbre en absoluto en la posición, entonces Δx sería cero.Pero para hacer esto nos hubiéramos visto obligados a usar un fotón cuya longitud de onda fuese cero. Y un fotón así tendría una energía infinita. En este caso, la incertidumbre en el momento lineal del electrón sería infinita o, mejor, indefinida.
Por otro lado, si permitimos que la incertidumbre en la medición de la posición sea muy grande, entonces la incertidumbre en la medición del momento se volvería muy pequeña, ya que el fotón tendría una longitud de onda larga (momento lineal bajo). Si Δx se hace tan grande que fuese infinita, o indefinida, entonces Δpx se convertiría en cero. Podríamos medir el momento lineal en ese instante con absoluta precisión. Pero no podemos medir tanto la posición como el impulso con absoluta precisión al mismo tiempo. La relación de incertidumbre nos obliga a una compensación. Cuando la precisión de una variable aumenta, la otra debe disminuir, y viceversa.
De igual manera que esta relación de incertidumbre afecta al par de variables posición y momento lineal, existe otra análoga [2] que afecta al par energía y tiempo. Si llamamos Δt a la incertidumbre en la medición del tiempo y ΔE a la incertidumbre en la medición de la energía de un objeto cuántico en un instante dado, entonces el principio de incertidumbre de Heisenberg dice que Δt· ΔE≥h/4π.
Como hemos visto, esta relación se puede resumir en:
Es imposible medir el tiempo y la energía de un objeto cuántico en el mismo instante con una precisión ilimitada. Cuanto más precisa es la medición del tiempo, menos precisa es la medición de la energía en ese instante, y viceversa.
Nota:
[1] Si no es cuantitativo no es física, sino filosofía.
[2] Aunque mucho menos popular.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El principio de incertidumbre, cuantitativamente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El principio de incertidumbre, cualitativamente
- Se establece el principio de conservación de la energía
- Las ondas electrónicas y la estructura atómica
No todas las personas tienen las mismas oportunidades de dedicarse a la actividad científica
 Foto: Sharon McCutcheon / Unsplash
Foto: Sharon McCutcheon / UnsplashSería deseable que todas las personas con capacidad para ello pudiesen, si esa es su voluntad, participar en la empresa científica. Sin embargo, no ocurre eso; no todas las personas tienen las mismas oportunidades de dedicarse a la actividad científica. La participación en la ciencia es, por tanto, desigual, lo que va en contra o limita su deseable carácter universal.
Para empezar, hay grandes diferencias entre los ciudadanos de unos países y otros en las posibilidades de practicar ciencia. La mayor parte de los habitantes de regiones o países con menos recursos tienen prácticamente vedado el acceso a la actividad científica. Hay dos razones para ello. La más evidente es que los países pobres disponen de pocos recursos y, en teoría, suelen dedicarlos a satisfacer necesidades acuciantes o, al menos, la ciencia no se encuentra entre sus prioridades de gasto.
La segunda razón es que la práctica científica requiere de un adiestramiento muy prolongado, para lo que se necesitan largos periodos de formación. Pero en los países más pobres la escolarización es muy baja, y la permanencia en el sistema educativo es relativamente breve. Bajo esas circunstancias es realmente muy difícil iniciarse en la carrera científica. Esa es una de las razones por las que, según T. Ferris [Timothy Ferris (2010): The Science of Liberty: Democracy, Reason and the Laws of Nature. Harper Collins], existe un vínculo entre desarrollo científico y grado de libertad en un país, porque, según él, los países interesados en promover la ciencia se ven obligados a proporcionar educación al conjunto de la población y esa educación es también la base de una ciudadanía más crítica y exigente.
De un modo similar, las diferencias socioeconómicas en el seno de un mismo país también pueden representar una limitación para el acceso universal a la ciencia. Los chicos y chicas de extracción sociocultural más baja encuentran en la práctica más dificultades para acceder a altos niveles de formación y, por lo tanto, al desempeño de profesiones científicas.
Las posibilidades de participar en el desarrollo de la ciencia también se ven perjudicadas cuando el acceso a la financiación de proyectos no se rige de acuerdo con criterios meritocráticos. Por ejemplo, quienes forman parte de las comisiones que evalúan propuestas de financiación de proyectos de investigación o de concesión de becas o puestos de trabajo, no siempre deciden de acuerdo con criterios meritocráticos. En un estudio ya clásico, Wenneras y Wold (1997) encontraron que los miembros de comités en Suecia que asignaban puestos posdoctorales favorecían a las personas con las que tenían alguna relación. Diez años después Sandstrom y Hallsten (2008) hicieron un nuevo análisis con la misma metodología y vieron que el favoritismo hacia las amistades persistía. De estudios realizados en un único país no pueden extraerse conclusiones universales firmes, pero no se trata de asignar carácter universal al problema, sino de señalar que en algunos sistemas existe y que, por lo tanto, es un mal que puede afectar potencialmente al resto de sistemas científicos.
Por otra parte, en todos los países en que se ha estudiado, se han observado diferencias en el desarrollo de una carrera científica por parte de hombres y de mujeres. Se tiende a pensar que esas diferencias tienen su origen en las preferencias de chicos y chicas por diferentes tipos de estudios. Sin embargo, ese no es siempre el caso. Así, en nuestro entorno son similares los números de chicos y de chicas que cursan una carrera universitaria de ciencias. También son similares los porcentajes de quienes hacen un doctorado. Las diferencias se producen en las carreras de ingeniería (con muchos más chicos) y de ciencias de la salud (con muchas más chicas). Y dentro de las carreras científicas, la presencia femenina es menor en física y geología, y mayor en química y en ciencias de la vida. Leslie et al (2015) han puesto de manifiesto que, de hecho, las preferencias en función del género no obedecen a una hipotética divisoria que separaría las carreras científico-tecnológicas del resto de estudios, sino a las expectativas de brillantez considerada necesaria para cursar con éxito unos estudios y otros. Así, cuanto mayor es la brillantez que se supone necesaria (porque así se le atribuye) para cursar con éxito unos estudios, menor es el porcentaje de mujeres que los escogen. Se trata, por lo tanto, de un efecto de base cultural y, por ello, susceptible de ser corregido o atenuado.
Donde se producen la diferencia importante entre hombres y mujeres es en el progreso en la carrera científica. Y es a esa diferencia a la que obedece la escasa presencia femenina en los niveles más altos del escalafón. Este fenómeno se manifiesta de formas diversas y sus causas pueden ser también variadas.
En el estudio antes citado de Wenneras y Wold (1997), además del favoritismo para con las amistades, también encontraron que había un claro sesgo a favor de las solicitudes de financiación presentadas por hombres, aunque el estudio de Sandstrom y Hallsten (2008), hecho con la misma metodología, concluyó que había desparecido el sesgo sexista. Otros autores (Head et al, 2013) han confirmado (en el Reino Unido) que no hay sesgo antifemenino en la concesión de financiación para puestos de trabajo o proyectos del Wellcome Trust o el Medical Research Council. Sin embargo, las mujeres reciben menores cantidades para sus proyectos y la diferencia tiene que ver con el estatus científico (laboral) de quienes solicitan la financiación. Además, las diferencias no han variado en los 14 años que han sido analizados (Head, 2017).
Por otro lado, Van den Besselaar P & Sandstrom U (2016) han analizado cómo afectan las diferencias de género en el desempeño investigador y su impacto en las carreras científicas y han encontrado que parte de las diferencias en la contratación de investigadores e investigadoras pueden explicarse por diferencias en el grado de desempeño (medido a partir de los cv), pero que, además, también opera un sesgo antifemenino en las decisiones de contratación. Creen esos autores, por otro lado, que las diferencias en el desempeño pueden ser también, en última instancia, el resultado del efecto que decisiones igualmente sesgadas ejercen sobre la actitud de las mujeres ante su trabajo. El conocido como “estudio de Jennifer y John” ilustra bien a las claras de qué tipo de decisiones se trata: en los procesos de selección y promoción del personal científico opera un sesgo en virtud del cual a las mujeres se las valora menos y se les ofrecen peores condiciones en dichos procesos.
Al efecto de los sesgos citados se añaden las dificultades añadidas que experimentan las mujeres por la maternidad o en razón de su mayor implicación en la atención a la familia. Cech & Blair-Loy (2019) han encontrado que el 43% de las investigadoras norteamericanas de disciplinas STEM que tienen su primer hijo abandonan su empleo a tiempo completo; unas dejan la vida profesional por completo, otras cambian de actividad profesional y otras pasan a desempeñar trabajos a tiempo parcial. El porcentaje de hombres que hace lo propio es de un 23%.
A lo anterior habría que añadir que tal y como ocurre con ciertos ámbitos profesionales, la progresión en el mundo de la ciencia exige una actitud y una dedicación que, por comparación con los hombres, muchas mujeres no están dispuestas a asumir porque tienen otras prioridades personales. Los efectos conjuntos de los factores citados acaban provocando una menor presencia femenina en las autorías de artículos de investigación, de manera que se genera un círculo vicioso que tiende a mantener el status quo, neutralizando incluso las medidas que se toman para favorecer la progresión de las mujeres en el cursus honorus de la ciencia. Sin excluir la incidencia de sesgos similares a los comentados aquí, la menor presencia de mujeres en los puestos de alto nivel junto con su menor producción de literatura científica, explicaría también el minúsculo porcentaje de mujeres que han sido otorgado el premio Nobel u otros equivalentes.
Algunos de los factores citados comprometen el carácter universal de la empresa científica, pues limitan el acceso de las mujeres a los niveles profesionales más altos y a las posibilidades de logros profesionales que tales niveles brindan. Y aunque tampoco cabe descartar una cierta autoselección negativa (derivada de las diferentes prioridades y actitudes personales), habría que preguntarse si es beneficioso que las reglas del juego –las que propician el alto grado de competitividad del mundo científico- se mantengan tal y como están, porque en su actual configuración el sistema científico está prescindiendo de la aportación de muchas mujeres de talento.
Para cerrar este apartado, nos referiremos a quienes pertenecen a los colectivos identificados mediante las siglas LGTBQ. Son personas que han experimentado y experimentan exclusión y acoso también en el mundo de la ciencia, si bien es cierto que su situación ha mejorado en los últimos años, principalmente en Europa Occidental, América y Australia. Sin embargo, siguen siendo acosados y perseguidos en los países musulmanes, en Rusia y en parte de Asia (Waldrop, 2014), por lo que no tienen acceso a la práctica científica en igualdad de condiciones con el resto. Por otro lado, aunque en los países occidentales los científicos pertenecientes a los colectivos LGTBQ se sienten más aceptados en sus entornos de trabajo que quienes se dedican a otras profesiones (Broadfoot, 2015), también son peor tratados en sus centros que las demás personas (Gibney, 2016); a ese tipo de razones atribuye Guglielmi (2018) el hecho de que los estudiantes pertenecientes a las minorías citadas de carreras científicas abandonen sus estudios en una mayor proporción que el resto de estudiantes. Como señala Waldrop (2014), la aceptación de la condición LGTBQ –para la que su visibilización es imprescindible- es necesaria para que quienes pertenecen a esos colectivos puedan desempeñar su actividad con normalidad, lo cual es bueno para la propia empresa científica en sí. Y como señala Javier Armentia el “visibilizar la ciencia LGTBIQ sirve para ayudar a muchas personas. Y sirve para la misma ciencia (en general), para mostrar que la herramienta que está cambiando el mundo también trabaja para permitir un mundo inclusivo y más justo con la diversidad”. O sea, para conseguir un mundo mejor.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo No todas las personas tienen las mismas oportunidades de dedicarse a la actividad científica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Actividad de la Cátedra de Cultura Científica (UPV/EHU) en 2010/2011
- Ageing-On: Promoviendo un envejecimiento saludable y estimulante para todas las personas
- Actividad de la Cátedra de Cultura Científica (UPV/EHU) en 2012
Todos los pasos que des
 Foto: Atanas Dzhingarov / Unsplash
Foto: Atanas Dzhingarov / UnsplashSabemos que muchas enfermedades crónicas y muertes prematuras están asociadas con la inactividad física. Y disponemos cada vez de más datos que sugieren que el sedentarismo puede provocar consecuencias similares. Hasta hace poco, las mismas personas cuyo estado de salud era objeto de estudio eran las que proporcionaban la información sobre el nivel de actividad física que se utilizaba en las investigaciones. Pero ese procedimiento se presta a errores. Porque así es fácil que se subestime la intensidad real de las asociaciones observadas, y es difícil determinar cómo cambia el estado de salud en respuesta a diferentes niveles de actividad física, sobre todo cuando esta es de baja intensidad.
Con objeto de superar esas limitaciones, un estudio reciente ha combinado información procedente de 8 investigaciones que, en conjunto, abarcaron 36 383 personas mayores de 40 años de edad y a las que, durante unos 6 años (de media), se les midió la actividad que desarrollaban. Así es; en esas investigaciones el nivel de actividad física no se había establecido a partir de la información de los participantes, sino que se había medido haciendo uso de acelerómetros; de esa forma se excluyó la subjetividad y los errores propios de los estudios anteriores. Del total de participantes, 2 149 (5,9%) murieron durante el estudio. Y fue precisamente la probabilidad de morir durante el periodo de seguimiento, la variable que se utilizó para establecer la influencia de la actividad física sobre el estado de salud general.
Los resultados de este metaanálisis –así se denominan los estudios que combinan datos procedentes de varias investigaciones para ganar seguridad en las conclusiones- confirmaron, en parte, lo que ya se sabía, pero aportaron información adicional valiosa.
Para empezar, la magnitud del efecto de la actividad física sobre el riesgo de muerte, tal y como se ha establecido en este estudio, duplica la que se había estimado antes con los estudios en los que se preguntaba a los participantes cuánta actividad recordaban haber desplegado.
En cuanto a los resultados, se comprobó que sea cual sea la intensidad de la actividad física, esta se asocia con una reducción sustancial del riesgo de morir. Ahora bien, también se observó que cuanto mayor es la actividad que se desarrolla, menor es el riesgo de muerte; en otras palabras: proporciona más beneficios hacer mucha actividad que hacer poca. Y la relación entre mortalidad y actividad es especialmente acusada cuando esta es de baja intensidad; por encima de un cierto tiempo e intensidad de desempeño físico, el riesgo de muerte se mantiene prácticamente constante. De hecho, la mayor reducción en el riesgo de muerte se produce hasta llegar a algo más de 6 horas diarias realizando una actividad física de muy baja intensidad, unas 5 horas si la intensidad es moderadamente baja, hora y media para una intensidad moderadamente alta, y media hora si la intensidad del ejercicio físico es muy alta.
Por último, hábitos de vida sedentarios también conllevan un mayor riesgo de muerte, y ese aumento del riesgo se produce con claridad cuando se pasa más de nueve horas y media diarias levantándose muy pocas veces del asiento.
Este estudio no ha buscado caracterizar las causas de muerte. Se ha limitado a constatar la existencia de un fuerte vínculo entre mortalidad e inactividad física. Y sus conclusiones son claras: es muy importante no pasar demasiado tiempo sentados, trabajando o viendo la televisión, y mantenerse lo más activos posible; pero si no podemos desarrollar mucha actividad, eso no debe ser motivo para no hacer ninguna, porque todos los pasos que demos, aunque sean unos pocos, reportan beneficios.
Fuente: U. Ekelund et al (2019): Dose-response associations between accelerometry measured physical activity and sedentary time and all cause mortality: systematic review and harmonised meta-analysis. British Medical Journal 366: I4570
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Todos los pasos que des se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Pero dónde diablos están todos?
- Todos los rojos son chillones
- Cómo alertar del peligro de los pasos de cebra y patentarlo
Motivar a los alumnos: el «santo grial» de la educación
Érase una vez… en el País Vasco, un congreso tan oportuno y tan útil, y tan bien recibido en Bilbao y en Donostia-San Sebastián, que muchos pensaron que tenía que viajar a más lugares. Así que la Cátedra de Cultura Científica y la Fundación Promaestro se pusiron de acuerdo y, con la ayuda de EduCaixa, lo llevaron a Madrid: casi un centenar de personas con espíritu crítico y bien informadas llenaron el pasado 2 de abril la modesta y acogedora sala de CaixaForum en la que se celebró.

Juan Pedro Núñez aporta en esta conferencia más evidencias sobre el incierto recorrido de muchas tecnologías en las aulas, debido a los procesos de habituación a los que está sometida la atención. En otras palabras: usar un día las tablets en el aula es divertido y funciona, pero si las usas todos los días es imposible que tengan el mismo efecto. Por otra parte, explicaba el profesor de la Universidad Pontificia Comillas, “el interés que debería tener el sistema educativo es educar personas con motivaciones a largo plazo. Motivar a corto plazo es muy sencillo».
Hemos pasado en muy poco tiempo de un sistema educativo «cuyo lema era «la letra con sangre entra», donde la memorización pasiva, el esfuerzo por parte del alumno y el ejercicio de la disciplina por parte del profesor eran los elementos básicos, a un sistema cuyo lema es «divertirse aprendiendo», que promueve la creatividad como competencia principal y que deja al profesor la labor de conseguir que los alumnos estén eternamente motivados». Además de que esto último supone un esfuerzo ímprobo, el acelerado cambio de sistema ha traído nuevos mitos, creencias y mantras educativos que se repiten sin cesar, y Núñez es tajante al referirse a uno de ellos: “Miente quien dice que «todo el mundo es capaz de hacer cualquier cosa» y educar sobre falsedades no es educar”. “¿Entrenamos para la frustración en el aula?”, se pregunta el psicoterapeuta al hilo de esta cuestión, incidiendo en que “para que alguien pueda soportar el frio, tiene que pasar frío. Del mismo modo, para que alguien sea capaz de gestionar su frustración tiene que padecer frustración. Y en un contexto controlado y educativo es donde una persona mejor puede aprender a gestionar su frustración”.
Sin embargo, subraya el ponente, «la «frustración» es una palabra maldita que no aparece nunca en la investigación aplicada”. Así, en sus conclusiones, Núñez coincide también con Juan Lupiáñez al recomendar “buscar evidencias en diversas áreas; los últimos artículos de un campo concreto no nos van a abrir los ojos a todo lo que se sabe de un proceso o realidad compleja”.
Edición realizada por César Tomé López a partir de materiales suministrados por Fundación Promaestro
El artículo Motivar a los alumnos: el «santo grial» de la educación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las pruebas de la educación 2018: El coloquio
- Cómo destruir un buen sistema de educación. El ejemplo sueco
- ¿Que puede aportar (y qué no) la neurociencia a la educación?
La microglía es un sensor de mortalidad neuronal
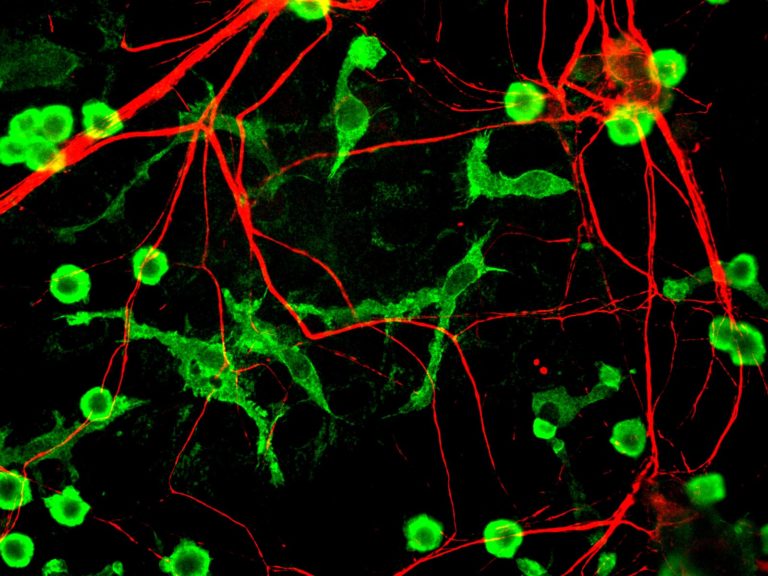 Microglías (verde) y neuronas (rojo). Fuente: Wikimedia Commons
Microglías (verde) y neuronas (rojo). Fuente: Wikimedia CommonsLa muerte neuronal, que generalmente asociamos al envejecimiento del cerebro y las enfermedades neurodegenerativas, también afecta a las neuronas jóvenes. Las neuronas recién nacidas mueren de manera frecuente durante el desarrollo del cerebro de manera programada, controlada mediante un mecanismo de suicidio celular llamado “apoptosis”. Para evitar convertirse en un cementerio, el cerebro tiene un mecanismo muy eficaz de eliminación de cadáveres: las células de microglía. La microglía, descubierta hace 100 años por el vallisoletano Pío del Río Hortega, es la encargada de “comerse” las células muertas mediante el proceso de “fagocitosis”.
Sin embargo, la fagocitosis no es simplemente la retirada pasiva de residuos para evitar el daño de las neuronas circundantes, como demuestra un estudio internacional liderado por Jorge Valero y Amanda Sierra, del centro vasco de neurociencias Achúcarro, la fundación Ikerbasque, y la Universidad del País Vasco UPV/EHU. Por el contrario, la fagocitosis de neuronas muertas es un proceso activo que repercute directamente en la salud y la función de las neuronas supervivientes.
Del mismo modo que tras la muerte de una cebra en la sabana, los buitres y otros carroñeros eliminan el cadáver, y sus deposiciones sirven para nutrir el suelo y que crezcan plantas que alimentan a otras cebras, la microglía también cierra el ciclo vital de las neuronas.
Para estudiar este proceso, los investigadores se centraron en la producción de nuevas neuronas o neurogénesis, que se produce en un área del cerebro adulto muy importante para los procesos de memoria y aprendizaje, el hipocampo. En esta región, la mayor parte de las neuronas recién nacidas se suicida a los pocos días de nacer, y son inmediatamente englobadas y eliminadas por la microglía. La primera pista de que el proceso de fagocitosis participaba de manera activa en la regulación de la neurogénesis la obtuvo el investigador del grupo Iñaki París, que utilizó distintos modelos genéticos de bloqueo de la fagocitosis proporcionados por colaboradores del Instituto Salk en California y del Instituto de Medicina Experimental de Budapest. En estos ratones, la reducción de la fagocitosis de células apoptóticas estaba acompañada de cambios en la producción de nuevas neuronas, lo que sugería la existencia de algún tipo de señal de comunicación entre la microglía fagocítica y las células recién nacidas.
La respuesta a esta hipótesis la obtuvo la investigadora del grupo Irune Díaz-Aparicio. Utilizando un modelo en cultivo en el que la microglía era “alimentada” con células apoptóticas, observó que lejos de ser un proceso pasivo de retirada de residuos, la fagocitosis era en realidad un proceso extraordinariamente activo y que alteraba a la microglía en todos los niveles, desde genéticos hasta metabólicos. Parte de estos cambios implicaban al secretoma, que es el conjunto de moléculas secretadas o liberadas por la microglía fagocítica, y que contenía señales que instruían a las células recién nacidas para continuar dividiéndose o diferenciarse en neuronas. Este secretoma era la señal entre la microglía fagocítica y las células recién nacidas en el hipocampo, y es por tanto el responsable de cerrar el ciclo vital de las neuronas.
Los investigadores proponen por tanto que la microglía actúa como un sensor de mortalidad. Cuando la microglía detecta mucha muerte de células recién nacidas indica al sistema de producción de neuronas que se están generando demasiados excedentes y debe frenar la producción. Por el contrario, cuando detecta pocas muertes, el hipocampo podría admitir más neuronas nuevas y se ha de retirar el freno. Por tanto, la conclusión principal de este estudio es que la microglía fagocítica ayuda a frenar la producción de nuevas neuronas mediante su secretoma contribuyendo al equilibrio entre vida y muerte.
Estos estudios tienen importantes implicaciones para nuestra comprensión de cómo se defiende el cerebro ante la muerte neuronal en el envejecimiento y las enfermedades neurodegenerativas, como la enfermedad de Alzheimer, la de Parkinson, el infarto cerebral o la epilepsia. En estas enfermedades, potenciar la fagocitosis puede ser una nueva estrategia neuroprotectora, no solamente para acelerar la limpieza del tejido de los restos de células muertas, si no para que el secretoma de la microglía contribuya a regenerar el tejido dañado.
Referencia:
Irune Diaz-Aparicio, Iñaki Paris, Virginia Sierra-Torre, Ainhoa Plaza-Zabala, Noelia Rodríguez-Iglesias, Mar Márquez-Ropero, Sol Beccari, Paloma Huguet, Oihane Abiega, Elena Alberdi, Carlos Matute, Irantzu Bernales, Angela Schulz, Lilla Otrokocsi, Beata Sperlagh, Kaisa E. Happonen, Greg Lemke, Mirjana Maletic-Savatic, Jorge Valero and Amanda Sierra (2020) Microglia actively remodel adult hippocampal neurogenesis through the phagocytosis secretome Journal of Neuroscience, 0993-19; doi: 10.1523/JNEUROSCI.0993-19.2019
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La microglía es un sensor de mortalidad neuronal se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La hiperactividad neuronal impide que las microglías realicen su trabajo
- La ineficiencia de las microglías causa del 100 % de mortalidad de un hongo multirresistente
- Más allá de las neuronas
Los números feos de la lotería

Existen pocos tesoros más buscados que un billete de lotería ganador. Sin embargo, en el último sorteo de Navidad, la administración Ormaetxea de Bilbao (tan popular como podría serlo “Doña Manolita” en Madrid) tuvo que devolver dos series completas de billetes agraciados con el tercer y quinto premio. El motivo: al tratarse de “números feos”, nadie había querido comprarlos.
Preguntado sobre el asunto, Sergio Etxebarria, gerente de la Lotería bilbaína se explaya: «Nadie lo ha querido, no se han atrevido con él. Como tenía dos ceros por delante la gente lo descarta. Los más maniáticos creen incluso que si les ofreces uno tan bajo les quieres engañar». Los adefesios, en este caso, eran el 00750 (tercer premio), 06293 (quinto). Por su culpa, este año, Bilbao ha sacrificado 360.000 € a su ideal colectivo de belleza numérica. «Y esto que nos ha pasado a nosotros habrá pasado en muchas administraciones de España porque los números bajos cuesta mucho venderlos». Pero el comienzo en 0 no es el único criterio que parecen guiar este caprichoso sentido estético: “La gente busca aquellos que cree bonitos. Se piden mucho impares, en 5 o 7, el 69… números que se asocian a buena suerte».
No se trata, sin embargo, de una simple superstición. Las personas somos torpes reconociendo el azar y aún lo somos más a la hora de generarlo1. En general, sospechamos de números o combinaciones en las que leemos demasiadas casualidades, demasiada “intención”, como dos ceros seguidos a la izquierda, y curiosamente, buscando el azar, lo ordenamos inadvertidamente. En un estudio de 20122, se pedía a 20 sujetos que generasen secuencias aleatorias de 300 números. Los resultados no sólo no eran aleatorios desde un punto de vista matemático: una vez analizados, resultaban casi 3 veces más predecibles y diferenciables según el sujeto que los había generado.
Los azares imperfectos afectan a otros sorteos, no solo a la lotería de Navidad. En La Primitiva, los jugadores deben hacer ocho apuestas en las que eligen 6 números entre el 1 y el 49. La gente tiende a elegir números no consecutivos porque sospecha de las secuencias. Como afirma Antonio S. Chinchón, el autor de este interesante estudio basado en datos de Loterías del Estado (y de un blog maravilloso), “pensamos que tenemos más posibilidades de volvernos ricos eligiendo 4-12-23-25-31-43 en lugar de 3-17-18-19-32-33, por ejemplo”. El autor (y yo misma), se incluye dentro de esta percepción, si bien las secuencias que contienen números consecutivos son prácticamente igual de probables (P=0.4952) que las que los contienen. A fin de cuentas, es lo que caracteriza a los sesgos: no basta con conocerlos para poder evitarlos. En este caso, además, donde las ganancias se reparten entre los ganadores, una estrategia que quisiera maximizar el valor de las apuestas debería combatirlos activamente.
Puede pensarse que los números están impregnados de un simbolismo y unas asociaciones culturales difíciles de esquivar. Pero nuestra búsqueda de azar resulta imperfecta también cuando nos alejamos de ellos. Para explicarlo os propongo, antes de seguir leyendo, que contestéis a esta sencilla encuesta:
¿Crees que en una encuesta la posición de las respuestas importa?
— Almudena M. Castro (@puratura) January 14, 2020
…
¿Ya?
Si el experimento funciona (aunque con el azar, nunca se sabe…), lo más probable es que hayas elegido la tercera o la segunda respuesta. Es más, cuantos más participantes haya, la distribución de los resultados debería ir pareciéndose cada vez más a los de esta curiosa carrera, un twit que suma más de 68 mil respuestas:
It’s a turtle race
just tap a turtle and retweet pls
— ᴊᴜʟs⁷ (@deservebts) June 19, 2019
No es un caso aislado, resultados muy parecidos reaparecen cada vez que alguien saca a las tortugas a correr. El motivo es que, ante una secuencia de elementos (objetos u opciones, colocados en fila), tendemos a evitar los de los extremos, quizás porque leemos demasiada “intención” en ellos, como en un número de lotería “demasiado bajo”. Es lo que se conoce como “center stage effect” o “centrality preference”3 y afecta no solo a las tortugas olímpicas, sino también a los productos que cogemos de la balda del supermercado, a las respuestas que damos en un test multiopción e incluso al baño en el que nos metemos cuando tenemos una urgencia en un lugar público. Quizás algo a tener en cuenta la próxima vez antes de descartar un número de lotería “feo” —al menos para saber que todos lo son; improbables en la misma medida— o plantear una encuesta a través de Twitter —los curiosos sin una respuesta clara tenderán a sesgar los resultados.
Referencias:
1N. Ginsburg, P. Karpiuk (1994). Random Generation: Analysis of the Responses. Perceptual and Motor Skills, 1994
2Marc-André Schulz, Barbara Schmalbach, Peter Brugger, Karsten Witt. Analysing Humanly Generated Random Number Sequences: A Pattern-Based Approach. Plos One, 2012.
3 Paul Rodway Astrid Schepman & Jordana Lambert (2011). Preferring the One in the Middle: Further Evidence for the Centre‐stage Effect. Applied cognitive Psychology,.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Los números feos de la lotería se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Aprendiendo técnicas para contar: lotería primitiva y bombones
- El secreto de los números que no querían ser simétricos
- ¿Te tocó ayer la lotería? Da lo mismo, eres la persona más rica del mundo

