Las cárcavas marcianas y los ciclos de oblicuidad
Hay términos que a priori pueden parecer poco relacionados con la geología -al menos en un sentido estricto- pero que son capaces de condicionar, por ejemplo, el clima de un planeta, y con ello su dinámica externa, dejando una impronta en procesos erosivos y deposicionales, hasta el punto de que podemos aproximarnos a la historia climática de un planeta como puede ser la Tierra o Marte a través de su geomorfología o de su sedimentología. La palabra en cuestión que hoy nos trae aquí es oblicuidad, o lo que es lo mismo, la inclinación del eje de rotación de un planeta con respecto al plano orbital, y de la que podemos decir que cuanto mayor sea el ángulo, más extremas serán las estaciones, aunque con sus particularidades para cada zona del planeta.
Podríamos pensar que los planetas mantienen estable a lo largo del tiempo esta inclinación del eje de rotación, pero lo cierto es que no es así, sino que hay ciclos en los cuales este valor va cambiando entre momentos de mayor y menor oblicuidad. En nuestro planeta estos cambios son relativamente pequeños -entre 22,1º y 24,5º -, pero en Marte su oblicuidad puede oscilar en ocasiones entre valores cercanos a los 10º, periodos de baja oblicuidad, a otros en los que su eje se inclina por encima de los 40º.
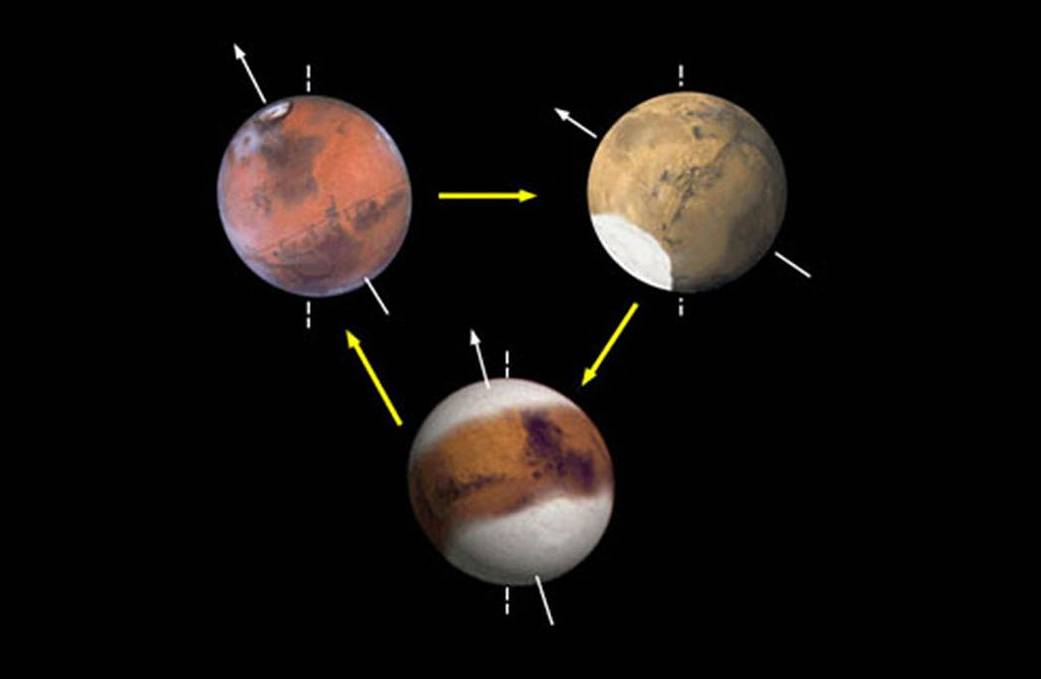 Recreación de como podrían ser de extremos los ciclos de oblicuidad en Marte. En la actualidad estaría en una situación similar a la de la imagen superior izquierda. Cortesía de la NASA/JPL-Caltech.
Recreación de como podrían ser de extremos los ciclos de oblicuidad en Marte. En la actualidad estaría en una situación similar a la de la imagen superior izquierda. Cortesía de la NASA/JPL-Caltech.Los momentos en los que Marte tuviese una mayor oblicuidad serían perfectos para que hubiese una transferencia importante de masa de los polos a la atmósfera, es decir, que una parte del dióxido de carbono que se encuentra formando hielo en estos depósitos polares, acabase sublimándose y permitiese un aumento de la presión atmosférica, pudiendo llegar a valores que duplican la actual presión atmosférica, algo que facilitaría alcanzar mayores temperaturas así como unas condiciones de mayor estabilidad para la presencia de agua líquida en la superficie.
Pero regresemos a la geología. En Marte aparecen una serie de pequeños barrancos que en nuestro planeta conocemos como cárcavas y que en la Tierra suelen estar formados por la erosión fluvial en zonas con pendiente, donde la fuerza del agua y a veces la poca competencia de los materiales -o incluso una baja proporción de materiales consolidados- permite que se produzca una incisión y el transporte de materiales ladera abajo.
 Cárcavas en la Tierra, en este caso en la provincia de Guadalajara. Imagen cortesía del Centro Nacional de Información Geográfica (CNIG)
Cárcavas en la Tierra, en este caso en la provincia de Guadalajara. Imagen cortesía del Centro Nacional de Información Geográfica (CNIG)Además, algunas de estas cárcavas observadas en Marte parecen relativamente recientes en tiempo geológico, algo que se aprecia porque conservan todavía muy bien su forma y no han sido alteradas en gran medida por otros procesos y porque no acumulan una gran cantidad de cráteres de impacto. Pero, si las condiciones actuales no permiten la presencia de agua líquida en la superficie -al menos no en los lugares ni en la cantidad para generar las poblaciones más recientes de cárcavas-, ¿cómo han podido formarse?.
Algunos estudios sugerían que estas estarían formadas por el hielo de dióxido de carbono, que durante su sublimación -el paso de sólido a gaseoso sin pasar por el líquido- provocaría que los materiales sobre -o debajo- de los que se encuentra se desestabilicen y caigan ladera abajo, a veces ayudados por el propio dióxido de carbono en estado gaseoso que serviría como una especie “lubricante” que facilitaría su transporte. Este mecanismo podría ser incluso funcional en la actualidad, especialmente durante la primavera y el verano marcianos en laderas iluminadas por el Sol.
Este proceso repetido a lo largo del tiempo daría lugar las cárcavas que observamos, como por ejemplo se describe en Pilorget et al. (2016). De algún modo podríamos decir que esta erosión sería “en seco”, ya que no necesita agua para explicar la formación de las cárcavas. Pero lo cierto es que hoy día, al menos en el tiempo que hemos podido observar el planeta rojo y estudiar los cambios que se producen en su superficie, las cárcavas no muestran una gran actividad, por lo que podrían ser una herencia de otros momentos de la historia de Marte más que representar una forma del modelado actual.
En este artículo nos referimos únicamente a las cárcavas que aparecen en las laderas de algunas montañas y cráteres, que parecen tener un origen diferente a aquellas que se forman en las dunas de zonas polares y donde parece que el agente erosivo es exclusivamente el dióxido de carbono a causa de los ciclos estacionales y que son más representativas del clima actual.
Un nuevo estudio publicado en la revista Science por Dickson et al. (2023) vuelve a poner en el punto de mira al agua como agente formador de las cárcavas. Hoy día, con la actual inclinación del eje de rotación de Marte, los lugares donde existen estas cárcavas no cumplen las condiciones de presión y temperaturas necesarias para que el hielo de agua que existe en el regolito u otros almacenes geológicos cercanos a la superficie pueda derretirse y permitir al agua bajar ladera abajo, pero cuando la oblicuidad del planeta se encuentra alrededor de los 35º, las condiciones serían favorables para la fusión del hielo y para que el agua se mantuviese estable en la superficie el tiempo suficiente de generar los procesos erosivos y el depósito de los sedimentos que observamos.
 Cárcavas en Marte capturadas por el instrumento HiRISE. La pendiente de la imagen iría de izquierda -más alto- a derecha -más bajo-. Además, se puede apreciar como al final de las cárcavas aparecen una serie de “abanicos” como consecuencia de los materiales arrastrados por el agua. Cortesía de NASA/JPL-Caltech/UArizona.
Cárcavas en Marte capturadas por el instrumento HiRISE. La pendiente de la imagen iría de izquierda -más alto- a derecha -más bajo-. Además, se puede apreciar como al final de las cárcavas aparecen una serie de “abanicos” como consecuencia de los materiales arrastrados por el agua. Cortesía de NASA/JPL-Caltech/UArizona.Para llegar a esta conclusión, los científicos han desarrollado un modelo climático en el cual han podido marcar las localizaciones de las poblaciones de cárcavas más recientes y ver en que momentos y bajo que condiciones la formación de estas podría darse de una manera más o menos simultánea, algo que parece explicarse muy bien mediante los ciclos de oblicuidad marcianos. De hecho, estos procesos formadores de las cárcavas podrían haberse repetido en los últimos millones de años, siendo la última vez hace aproximadamente unos 630.000 años.
Este descubrimiento tiene muchas repercusiones. El primero de cara a la exploración planetaria, ya que nos permitiría acceder a depósitos de hielo para su estudio, pero también de cara a la astrobiología, porque la presencia de agua líquida -aunque sea en momentos más o menos efímeros- podría ser importante para la vida en Marte si esta existiese, suponiendo estos intervalos de tiempo en los que hay agua líquida en superficie una especie de puente entre las condiciones frías y secas y otras que amplíen el rango de espacios habitables en el planeta.
Pero, sin lugar a dudas, estudios como estos ponen de manifiesto lo difícil que es a veces la interpretación de la geología en otros lugares diferentes a la Tierra. Es por ello que se necesitan aproximaciones multidisciplinares que nos permitan comprender un poco mejor la historia de los planetas y otros cuerpos del Sistema Solar.
Referencias:
Dickson, J. L., A. M. Palumbo, J. W. Head, L. Kerber, C. I. Fassett, y M. A. Kreslavsky. «Gullies on Mars Could Have Formed by Melting of Water Ice during Periods of High Obliquity». Science 380, n.º 6652 (30 de junio de 2023): 1363-67. https://doi.org/10.1126/science.abk2464.
Dickson, James L., y James W. Head. «The Formation and Evolution of Youthful Gullies on Mars: Gullies as the Late-Stage Phase of Mars’ Most Recent Ice Age». Icarus 204, n.º 1 (noviembre de 2009): 63-86. https://doi.org/10.1016/j.icarus.2009.06.018.
Dundas, Colin M., Serina Diniega, Candice J. Hansen, Shane Byrne, y Alfred S. McEwen. «Seasonal Activity and Morphological Changes in Martian Gullies». Icarus 220, n.º 1 (julio de 2012): 124-43. https://doi.org/10.1016/j.icarus.2012.04.005.
Dundas, Colin M., Alfred S. McEwen, Serina Diniega, Candice J. Hansen, Shane Byrne, y Jim N. McElwaine. «The Formation of Gullies on Mars Today». Geological Society, London, Special Publications 467, n.º 1 (enero de 2019): 67-94. https://doi.org/10.1144/SP467.5.
Treiman, Allan H. «Geologic Settings of Martian Gullies: Implications for Their Origins». Journal of Geophysical Research 108, n.º E4 (2003): 8031. https://doi.org/10.1029/2002JE001900.
Pilorget, C., y F. Forget. «Formation of Gullies on Mars by Debris Flows Triggered by CO2 Sublimation». Nature Geoscience 9, n.º 1 (enero de 2016): 65-69. https://doi.org/10.1038/ngeo2619.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Las cárcavas marcianas y los ciclos de oblicuidad se ha escrito en Cuaderno de Cultura Científica.
Por qué los humanos tenemos un extra inesperado de energía (y para qué sirve)
energía
 Foto: Jordan McQueen / Unsplash
Foto: Jordan McQueen / UnsplashEl metabolismo es el conjunto de transformaciones mediante las cuales, a partir de materia orgánica (la comida), agua y oxígeno, construimos nuestro cuerpo y generamos energía para todo proceso vital. Gastamos energía cuando hacemos ejercicio. Pero también al dormir, manteniendo y reparando el cuerpo. O pasando una agradable tarde de lectura: no olvidemos que mantener el cerebro “le cuesta” a un adulto el 20 % de toda su energía diaria.
El modo en que obtenemos y gastamos energía los humanos ha sido objeto de discusión en las ciencias y las humanidades. Más aún desde que se ha descubierto que contamos con un extra de energía inesperado. Comparados con otros primates, empleamos más energía de la que podría parecer necesaria por nuestras características físicas.
¿Por qué necesitamos los humanos ese extra de energía? Y ¿cómo la conseguimos?
Una de las respuestas más apasionantes a ambas preguntas tiene que ver con nuestra naturaleza biocultural.
La paradoja energética humanaDurante nuestra evolución hemos desarrollado rasgos que nos diferencian de nuestros parientes vivos más cercanos: crecemos más lentamente, desarrollamos un cerebro más grande, nos reproducimos más, vivimos más años y somos más resistentes en el ejercicio físico que chimpancés, bonobos y gorilas.
Estos rasgos son energéticamente caros, y hacerlos posibles a lo largo de nuestra vida es lo que se ha llamado la paradoja energética humana.
Hasta hace unos años, sorprendentemente nadie había comparado el gasto energético total entre humanos y grandes simios. El primero en hacerlo fue el biólogo experimental Herman Pontzer, que propuso que los humanos estamos metabolicamente “acelerados”. Esto significa que el linaje humano ha experimentado una aceleración en la tasa metabólica a lo largo de la evolución, proporcionando energía para cerebros más grandes y una reproducción más rápida sin sacrificar el mantenimiento del organismo y la longevidad. Pontzer lo describió como el extra inesperado de energía humana: gastamos más energía por unidad de masa que nuestros parientes más cercanos. Y eso se acompaña de un metabolismo particularmente acelerado.
La energía la distribuye el corazónSi seguimos el rastro del gasto energético, el camino nos lleva directos al corazón, el órgano que ha encarnado la esencia de la vida a lo largo y ancho de nuestra historia. Siempre ha sido protagonista, desde la representación prehistórica en la Cueva del Pindal en Asturias hasta el énfasis actual en una buena salud cardiaca, pasando por su pesaje en el viaje al más allá en el antiguo Egipto, o su transformación en jaguar tras la muerte para los Waorani amazónicos.
El corazón provee a todo el cuerpo de la energía necesaria para toda la actividad fisiológica. Podemos cuantificar este suministro con el gasto cardiaco, que es el producto de la cantidad de sangre que bombeamos en un latido por el número de latidos por minuto.
Este flujo tiene un valor medio aproximado de cinco litros por minuto. Así mantenemos la circulación de materias primas (oxígeno y nutrientes) y de deshecho (dióxido de carbono, agua) de nuestro metabolismo, lo que nos lleva a la paradoja energética humana. Si comparados con otros grandes simios estamos metabólicamente acelerados (empleamos más energía por unidad de masa), podemos esperar que nuestro gasto cardiaco por unidad de masa también sea mayor.
Una manera de estudiarlo es midiendo el diámetro de la “tubería” por la cual sale del corazón toda la sangre de un latido. A partir de ecocardiografías en grandes simios vivos observamos que nuestra aorta es similar a la de los gorilas, que nos pueden duplicar en tamaño. De hecho, controlando por el peso tenemos una aorta mayor por unidad de masa que los gorilas. Para alimentar nuestro metabolismo acelerado tenemos un gasto cardiaco mayor por unidad de masa: una aorta de gorila en un cuerpo de humano.
Reproducción biocultural¿Y bien? ¿Cómo sostenemos el sistema? ¿Cómo logramos esa energía extra que permite desarrollar un cerebro voraz o parir más que cualquier otro primate?
Una respuesta a estas preguntas la encontramos en nuestra naturaleza biocultural.
Pensemos en un ingrediente de la paradoja: nuestro gran cerebro. Termina de crecer en volumen aproximadamente a los seis años de edad, en un proceso tan costoso que frena el crecimiento corporal y emplea nada menos que el 40 % de la energía total diaria de los niños (y más del 65 % de la energía en reposo). De hecho, en la infancia tenemos un gasto cardiaco y quemamos más energía por unidad de masa que de adultos.
Pensemos ahora en otro ingrediente de la paradoja: nos reproducimos más. Las madres humanas tienen la capacidad de tener bebes a un ritmo mayor que otros grandes simios. Las humanas destetan a la cría para quedarse embarazada de nuevo cuando aquella todavía es dependiente y quema energía a una tasa muy elevada. Esto sólo es posible gracias a la provisión de cuidados y de comida nutritiva y procesada que proporciona la comunidad, una característica exclusivamente humana: no criamos solas.
Como sugiere el biólogo humano Barry Bogin, una clave es que los humanos practicamos una reproducción biocultural. En nuestra especie, el cuidado y provisión de las crías no es solo asunto de los progenitores. En esa tarea es fundamental el papel de abuelas, abuelos, hermanos y hermanas mayores, y otros familiares. Pero también el papel de otras personas del grupo cuyo vínculo se define culturalmente, más allá de la genética (las “tías” y “tíos” de la infancia, en realidad amigos cercanos de nuestros padres). Otra característica exclusivamente humana.
Siguiendo esta senda energética biocultural, se ha propuesto que, durante nuestra evolución, una de las soluciones para la búsqueda de alimento nutritivo fue el desarrollo de la caza y recolección y de la horticultura. Estas habilidades sociales, de grupo, nos permitieron mejorar nuestra tasa de retorno energético.
Mediante un proceso social complejo, intenso y costoso pero rentable, obtenemos más calorías en menos tiempo que los demás grandes simios. Así alimentamos la máquina.
La supervivencia del más amistosoLa reproducción biocultural y el aumento del retorno energético no se explican sin un aumento continuado de nuestra sociabilidad a lo largo de la evolución. Un aumento que seguramente se produjo en una retroalimentación que incluyó a otros hitos como el fuego, el lenguaje y el cocinado de los alimentos.
Tan llamativa es nuestra sociabilidad que se ha sugerido que nuestra evolución es un proceso de autodomesticación, de “supervivencia del más amistoso”.
Regresando a la perspectiva fundamental de los ciclos de materia y energía, los corazones y cerebros forman parte de metabolismos individuales entretejidos en un grupo social. Al fin y al cabo, forman parte de una matriz biocultural evolutiva capaz de costear nuestra paradoja energética.
El ensayo del recientemente fallecido Nuccio Ordine La utilidad de lo inútil expresa la profundidad de estos vínculos. En él, Ordine escribe: “La necesidad de imaginar, de crear, es tan fundamental como lo es respirar”. Así, según Ordine: “Esta respiración […] expresa el excedente de la vida respecto de la vida misma […], energía que circula de forma invisible y que va más allá de la vida, aún siendo inmanente a ella”.
Una evocadora reflexión para dar respuesta al inesperado extra de energía humana.![]()
Sobre el autor: Luis Ríos Frutos es Profesor de Antropología en la Universidad Complutense de Madrid
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Por qué los humanos tenemos un extra inesperado de energía (y para qué sirve) se ha escrito en Cuaderno de Cultura Científica.
El mono que desafió la sincronía

Cómo influyen los parásitos en el comportamiento de los animales, cómo se modifica la conducta de las madres mamífero o cuáles son las enfermedades que nos afectan y desde cuándo hemos desarrollado comportamientos funerarios ante la muerte son algunos de los aspectos que se analizarán en la V Jornada Nacional sobre Evolución y Neurociencias.
Especialistas en ambas materias se reunieron el 11 y 12 de mayo en una nueva edición conducida por Eva Garnica y Pablo Malo, psiquiatras y miembros de la Red de Salud Mental de Bizkaia, y organizada por esa misma entidad y la Cátedra de Cultura Científica de la UPV/EHU.
La jornada, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolucionista y divulgar de un modo accesible para todos los públicos.
A la hora de entender las psicopatologías y su tratamiento el conocimiento del hecho evolutivo tiene mucho que aportar, especialmente para asumir que no somos más que primates enamorados de los símbolos que nos alegramos con lo bueno u odiamos al otro en sincronía.
Julio Sanjuán Arias es coordinador de la Unidad de Primeros Episodios Psicóticos del Hospital Clínico Universitario de Valencia, investigador principal de la línea de Psiquiatría y enfermedades Neurodegenerativas del INCLIVA y profesor Titular de Psiquiatría en la Universidad de Valencia.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo El mono que desafió la sincronía se ha escrito en Cuaderno de Cultura Científica.
La natalidad es solo un número
 Foto: Luana Azevedo / Unsplash
Foto: Luana Azevedo / UnsplashLa demografía es una ciencia de sumas y restas, pero si queremos entender su lógica matemática es preciso incorporar la dimensión temporal y analizar los efectos que ejerce la estructura demográfica en su propia dinámica. Cifras de nacimientos como las recientemente publicadas por Eustat deben, por tanto, contextualizarse. Destacar las bajas cifras de nacimientos sin ponerlas en su contexto es quedarse en una visión muy simplificada de la realidad. El número total de nacimientos es cada vez más bajo, pero es solo un número. Si no lo relativizamos, no podremos interpretarlo. Si lo comparamos con la población total, a través de la tasa bruta de natalidad, el resultado son valores cada vez más bajos. Pero, como también se está reduciendo el número de mujeres en edad fértil, si lo medimos a través del índice sintético de fecundidad, nos da valores que superan los de hace tres décadas1.
La natalidad no es el único factor demográficoAdemás, gozamos de mayor eficiencia reproductiva que en el pasado. Lo que MacInnes y Pérez Díaz (2009)2 denominan la revolución reproductiva nos ha conducido a que menores índices de fecundidad por mujer deriven en mayores volúmenes de población. Un menor número de hijos, pero con más medios para su cuidado y educación, lleva a una supervivencia mucho mayor y a un incremento notable de la esperanza de vida. Una sociedad con mayores niveles educativos será también más productiva, por lo que el volumen de población activa necesario para garantizar la sostenibilidad de las pensiones será menor. Asimismo, si se alarga la esperanza de vida, se llega con mejor salud a la vejez y se retrasan el resto de las etapas vitales, no resulta tampoco tan insensato retrasar la edad de jubilación y mantener activo un capital humano que puede aportar experiencia y know-how.
Por otro lado, ¿cómo establecer el número óptimo de nacimientos, tratándose de una decisión individual, un proyecto de vida que cada cual puede o debería poder elegir? Porque, aunque tradicionalmente la demografía ha situado en 2,1 el número de hijos por mujer necesario para que se produzca el reemplazo generacional, esa cifra no incorpora el impacto de las migraciones ni del incremento de la longevidad ni de los nuevos modelos familiares. Es, por tanto, un valor discutible, como lo es considerar que una pérdida de población sea siempre negativa y, por ende, preocuparse más por la cantidad de habitantes que por la calidad de vida de dichos habitantes.
El mayor logro demográfico de los países desarrolladosNo nos percatamos de que gozamos de mejor calidad de vida que nuestros antepasados y que convertirse en sociedades envejecidas es el mayor logro demográfico de los países desarrollados. La pirámide de población de amplia base de los países en vías de desarrollo recoge su pujante natalidad, pero también es el reflejo de una mortalidad por edades relativamente alta y de un marcado descenso de individuos entre una cohorte de edad y la siguiente. Nuestras pirámides, bastante más alargadas y que han perdido hace tiempo su característica forma triangular, indican, por el contrario, un continuo incremento de la esperanza de vida. Sin embargo, en lugar de destacar que los índices de supervivencia de las sucesivas generaciones son cada vez más positivos, los titulares periodísticos se centran en los efectos negativos del envejecimiento de la población y en la baja natalidad.
Aunque ampliamente compartida, presentar el bajo número de nacimientos como algo negativo no deja de ser una valoración subjetiva. Además, gran parte de las alarmas demográficas no se sostienen en fundamentos científicos, sino que se impregnan de ideologías políticas o religiosas que ponen a la familia como núcleo central de organización de la sociedad y otorgan a la mujer el rol de garante de la natalidad. Nos enfrentamos a un cambio en el modelo reproductivo, no solo a nivel individual, sino también como sociedad, que consigue que la población siga creciendo a pesar de que la natalidad se reduzca.
Esa reducción se puede explicar en base al coste de oportunidad que supone tener hijos. En el pasado, tener una prole abundante significaba una probabilidad más alta de que sobreviviesen a la infancia en mayor número y pudiesen contribuir a edades tempranas a la economía familiar e, incluso, garantizasen el cuidado de los padres en la vejez. En la actualidad, las familias que deciden tener hijos se enfrentan a altos costes tanto económicos como medidos en términos de tiempo, lo que lleva a muchas de ellas a replantearse esa decisión.
La maternidad pasa facturaEspecialmente en el caso de las mujeres, la maternidad pasa factura. Son ellas quienes disfrutan en mayor medida de reducciones de la jornada laboral o de excedencias por cuidado de hijos o familiares. A medida que el número de hijos aumenta, presentan mayor probabilidad de abandonar el mercado laboral3, reduciendo también su empleabilidad futura. Por esos y otros motivos, se retrasa la edad de la maternidad y con frecuencia no se tienen los hijos que se desean.
Ese hecho sí debería ser objeto de preocupación por parte de las políticas públicas. Políticas de igualdad que garanticen una sociedad más equitativa, políticas laborales que reduzcan la precariedad laboral y permitan la conciliación de la vida personal y laboral o políticas de vivienda que faciliten el acceso a la misma y favorezcan la emancipación temprana de los jóvenes tendrán una incidencia importante en la decisión de abordar la maternidad/paternidad.
En cambio, las políticas pronatalistas, que hacen un uso ideológico de las estadísticas demográficas, se muestran ineficientes en el fomento de la natalidad. Ayudas coyunturales y no progresivas como son los cheques bebé universales, aunque mejoren la situación de familias en situación de vulnerabilidad, no serán tampoco relevantes en la decisión reproductiva. Probablemente, patrones de parentalidad compartida y una corresponsabilidad real contribuirán en mucha mayor medida a reducir la distancia existente entre expectativas y realidad reproductiva.
Notas y Referencias:
1 Según los Indicadores para el análisis de los fenómenos demográficos (Eustat, 2022), en 1990/1991, el índice sintético de fecundidad de Euskadi era de 0,97 hijos por mujer mientras que en 2020/2021, se sitúa en 1,25 hijos por mujer. En ese mismo periodo, según las Estadísticas de nacimientos, la tasa bruta de natalidad se ha reducido, pasando de 7,7 a 6,5 nacimientos por cada mil habitantes, mientras que el número total de nacimientos ha disminuido también en algo menos de 2.000.
2 MacInnes, J., y Pérez Díaz, J. (2009). ‘The Reproductive Revolution’. The Sociological Review, vol. 57, nº. 2, págs. 262–284. https://doi.org/10.1111/j.1467-954X.2009.01829.x
3 En España, según datos de la Encuesta de Población Activa (INE, 2022), en el caso de los hombres entre 25 y 49 años, presentan una mayor tasa de empleo si tienen hijos que si no tienen hijos (89,7 frente a 83,6), mientras que en las mujeres de esa misma edad se reduce la empleabilidad (en el caso de ser madres, 69,7 frente a 74,7 si no tienen hijos). Pero llama especialmente la atención la distancia existente en el caso de que el número de hijos sea superior a 3, ya que en los hombres la tasa de empleo alcanza el 84,2 (superior incluso a la que presentan cuando no tienen hijos), y en las mujeres es de 53,4 (más de 20 puntos inferior a la que presentan si no son madres).
Sobre la autora: Itziar Aguado es Profesora del Área de Geografía Humana en la Facultad de Letras de la UPV/EHU
Una versión de este texto apareció originalmente en campusa.
El artículo La natalidad es solo un número se ha escrito en Cuaderno de Cultura Científica.
Geología en el Tour
arqueas
Reconozco que, de siempre, me ha encantado seguir las grandes vueltas ciclistas veraniegas, pero no por el deporte en sí, sino por la gran oportunidad de ver unos paisajes increíbles que caracterizan los países por los que pasa la serpiente multicolor. Y el Tour de Francia de este año me está encantando, porque no paran de subir unas montañas míticas. Así que esta semana os voy a hablar de la geología del Tour de Francia, pero no como os lo estáis imaginando.
 Maillot del equipo ciclista Arkéa Samsic en el Tour de Francia 2023. Imagen tomada de www.letour.fr
Maillot del equipo ciclista Arkéa Samsic en el Tour de Francia 2023. Imagen tomada de www.letour.frSi estáis siguiendo la ronda gala, os habréis encontrado con un equipo francés llamado Arkéa Samsic. Pues cada vez que veo las letras Arkéa bien grandes en los maillots, lo que menos pienso es en una empresa de finanzas o en un grupo ciclista. Lo que me viene a la mente es en el origen de la vida en nuestro planeta.
Hoy en día, toda la vida del planeta se puede dividir en tres grandes grupos, llamados Dominios: Archaea (más conocidas en el argot popular como arqueas), Bacteria (creo que estas no necesitan traducción) y Eucarya (o células eucariotas). Los dos primeros grupos son organismos unicelulares sin núcleo diferenciado (lo que en mi época de estudiante se llamaban procariotas y formaban el Reino Monera), mientras que el último está compuesto por organismos con células que tienen un núcleo verdadero.
Arquea es una palabra de origen griego que significa “antiguo”, ya que, hasta no hace mucho, a estos organismos se les consideraba como las formas de vida más antiguas de nuestro planeta. Además, se creía que eran todos extremófilos, es decir, que habitaban ambientes considerados actualmente como muy extremos para la vida: unas arqueas se alimentaban de metano, otras se desarrollaban en medios de alta salinidad y un tercer grupo vivían en condiciones de temperaturas muy elevadas.
Pero todo esto ha cambiado en los últimos años. Recientemente, se han descubierto arqueas en ambientes muy normalitos, por decirlo de alguna manera, como el agua del mar o el fango del suelo continental. Incluso, se pone en duda que realmente sean los organismos vivos más primitivos de la Tierra. Así que vamos a viajar en el tiempo, a ver si nos situamos un poco en toda esta historia… Aunque no va a ser tan fácil como os podéis imaginar, porque la ausencia de un registro fósil tan antiguo nos obliga a trabajar con edades estimadas a partir del estudio genético de actuales grupos de arqueas, bacterias y eucariotas.
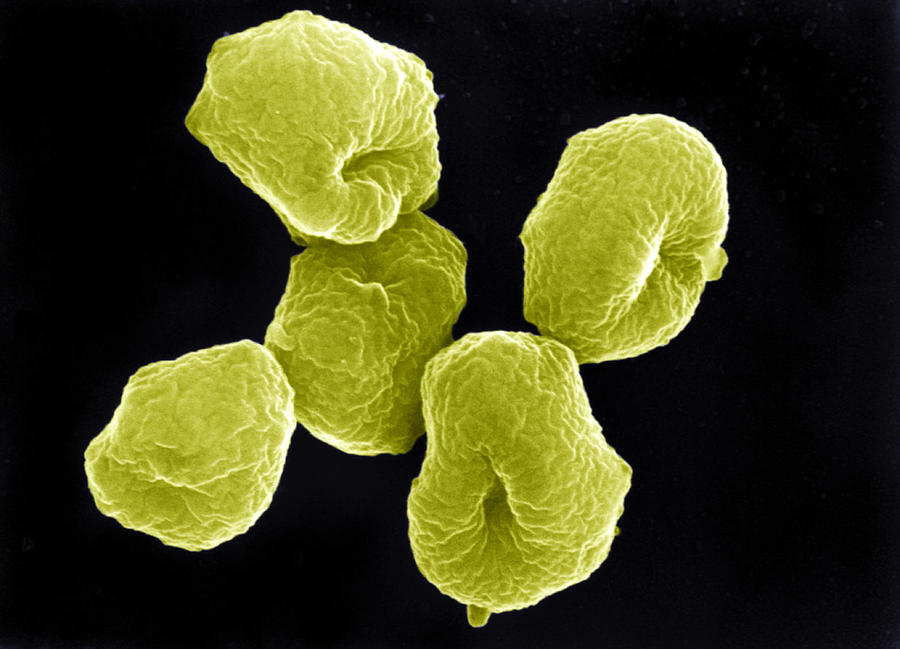 Fotografía coloreada de Microscopio Electrónico de Barrido (SEM) de una arquea Sulfolobus, un grupo de organismos extremófilos que habita en medios acuáticos de agua caliente con abundante azufre disuelto. Cada célula mide, aproximadamente, 0,002 mm. Imagen de Oliver Meckes EYE OF SCIENCE /Pixels
Fotografía coloreada de Microscopio Electrónico de Barrido (SEM) de una arquea Sulfolobus, un grupo de organismos extremófilos que habita en medios acuáticos de agua caliente con abundante azufre disuelto. Cada célula mide, aproximadamente, 0,002 mm. Imagen de Oliver Meckes EYE OF SCIENCE /PixelsHoy en día se acepta que nuestro planeta tiene unos 4570 millones de años de edad, millón de años arriba, millón de años abajo. Pues se considera que las primeras formas de vida verdaderas, es decir, células sin núcleo que incluían moléculas de ADN en su interior, aparecieron hace unos 4350 millones de años. Como dice el grupo de música heavy Nightwish en su canción Greatest Show on Earth, que entre LUCA. Estas siglas significan Last Universal Common Ancestor, que se puede traducir como el Último Ancestro Común Universal. Lo primero, no era un organismo en singular, sino un grupo de organismos evolucionados a partir de la unión de los ladrillos de la vida, moléculas de ARN libres que se combinaron para secuenciar ADN.
Pero, ¿qué tipo de organismos eran LUCA? Hasta no hace mucho se consideraban como las primeras arqueas. Actualmente, se ha llegado al consenso de que se trata de un grupo primitivo de bacterias. Por tanto, los organismos más antiguos de nuestro planeta no son el grupo cuyo nombre significa, precisamente, antiguo, sino que lo son las bacterias. Aunque la diferenciación entre los dos dominios pudo producirse muy rápido, hace entre 3800 y 4100 millones de años, dando lugar a dos clados muy diferenciados.
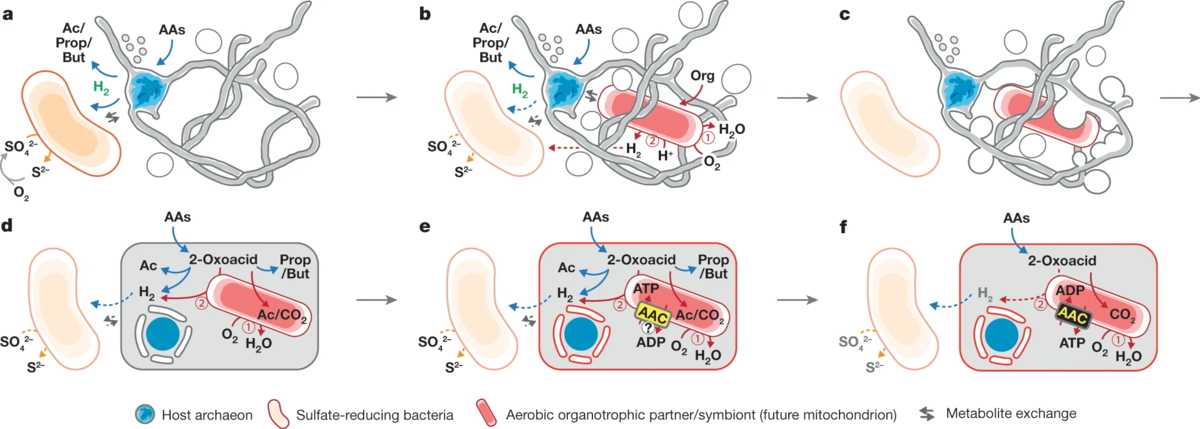 Mecanismo simbiótico propuesto entre las arqueas y las bacterias para dar origen a los organismos eucariotas. Imagen tomada de Imachi et al. (2020) Isolation of an archaeon at the prokaryote–eukaryote interface. Nature volume 577, pages 519–525
Mecanismo simbiótico propuesto entre las arqueas y las bacterias para dar origen a los organismos eucariotas. Imagen tomada de Imachi et al. (2020) Isolation of an archaeon at the prokaryote–eukaryote interface. Nature volume 577, pages 519–525¿Y los eucariotas? Pues parece que tardaron un poquito más en aparecer, estimándose su presencia más antigua hace unos 2300 millones de años. Estudios recientes han llegado a la conclusión de que este último dominio surgió de un grupo de arqueas primitivas que pudieron hacer simbiosis con bacterias más evolucionadas. Estos primeros eucariotas debieron ser unicelulares, pero rápidamente evolucionaron, dando lugar a organismos pluricelulares hace entre 1900 y 2100 millones de años. Es decir, que los dos grupos primigenios unieron fuerzas para generar la vida compleja en nuestro planeta.
Todo esto que os he contado parecen simples curiosidades biológicas, pero es algo mucho más complejo, porque tanto la aparición como la evolución de las primeras formas de vida provocaron cambios en nuestro planeta que lo condicionaron todo. Los primeros seres vivos aparecieron en un mundo sometido al bombardeo continuo de cuerpos extraterrestres, con una atmósfera reductora y mares repletos de hierro disuelto en el agua. La evolución de estos organismos primitivos dio lugar a las cianobacterias hace entre 3400 y 3700 millones de años, los seres fotosintéticos más antiguos, que llegaron a provocar un cambio desde una atmósfera reductora a una débilmente oxidante. Llegando hace unos 2400 millones de años a producirse el Gran Evento Oxidativo, a partir del cual disfrutamos de una atmósfera totalmente oxidante, lo que aceleró aún más la evolución biótica. Unos cambios ambientales radicales gracias a los cuales los seres humanos estamos aquí hoy.
Espero que, a partir de ahora, sigáis las etapas ciclistas de otra manera. Y cuando algún miembro del equipo Arkéa tome protagonismo con una escapada, os acordéis de la importancia evolutiva de estos pequeños organismos. Incluso, que veáis a un eucarionte con arqueas y bacterias en simbiosis con su organismo para permitirle hacer esos titánicos esfuerzos subiendo esas preciosas montañas, fruto de millones de años de evolución de nuestro planeta.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Geología en el Tour se ha escrito en Cuaderno de Cultura Científica.
Martha Betz Shapley, la “Primera Dama del Observatorio de Harvard”
En mi tercer año [en la Universidad de Missouri] conocí a una morena llamada Martha Betz, de Kansas City, y nunca me separé de ella, ni quise hacerlo. Nos conocimos en una clase de matemáticas: ella se sentaba en primera fila y conocía todas las respuestas. Era una mujer inteligente… Hizo cinco cursos completos y obtuvo las mejores calificaciones en todos ellos.
 Martha Betz Shapley. Fuente: MacTutor.
Martha Betz Shapley. Fuente: MacTutor.
Martha Betz nació el 3 de agosto de 1890 en Kansas City, Missouri (Estados Unidos). Era la tercera de las siete hijas e hijos de Carl Betz y Louise Wittig Betz. El abuelo paterno de Martha, John G. Betz había nacido en Hannover (Alemania) y emigrado a Estados Unidos junto a su esposa en 1863. Contó a su nieta que había visto una vez en las calles de Hannover a la astrónoma Caroline Lucretia Herschel (1750-1848). Aunque ella recordaba esta anécdota de su abuelo, en aquel momento, Martha no sospechaba que dedicaría toda su vida a estudiar las estrellas.
Carl Betz era maestro de música en varias escuelas de Kansas City y transmitió su pasión por la música a su prole; tocar música fue uno de los mayores pasatiempos de Martha a lo largo de su vida.
De maestra a astrónomaComo su madre y dos de sus hermanas, y con solo 15 años, Martha se convirtió en maestra de escuela primaria tras completar su formación secundaria. A los 18 comenzó sus estudios en la Universidad de Missouri, donde obtuvo una licenciatura en educación, y se convirtió en profesora de matemáticas de secundaria en 1912. En 1914, se casó con el astrónomo Harlow Shapley (1885-1972) al que había conocido durante sus estudios en la universidad. Lo hicieron después de que Shapley finalizara su tesis doctoral en Princeton. De hecho, según confirma su nieta Deborah Shapley, Martha ayudó a Harlow realizando algunos cálculos para su tesis que trataba sobre sistemas binarios eclipsantes.
El matrimonio se trasladó al Observatorio Mount Wilson donde comenzaron a trabajar como astrónomos profesionales. Mientras él estudiaba las estrellas variables cefeidas, Martha se centró en el análisis de las binarias eclipsantes que, como ya hemos comentado, habían sido el tema de investigación doctoral de su marido. Redactó una serie de artículos dedicados al cálculo de los elementos y la variación de los períodos de los sistemas eclipsantes que fueron contribuciones destacadas en su época. Entre estos trabajos destacan The period of U Cephei(1916) o The Light Curve and Orbital Elements of the Eclipsing Binary Y Leonis (1918).
También colaboró varias veces en la investigación de Shapley, algunas ocasiones como coautora. Algunos de esos trabajos son The Light Curve of XX Cygni(1915) o Studies Based on the colors and magnitudes in stellar clusters (1919).
En 1921 Harlow Shapley fue nombrado director del Observatorio de Harvard. Martha lo acompañó en su nuevo puesto y continuó su trabajo sobre binarias eclipsantes durante un tiempo, aunque pronto su familia de cinco hijos (Mildred, Willis, Alan Horace, Lloyd Stowell y Carl Betz) se convirtió en el centro de su atención.
Durante la Segunda Guerra Mundial, los Shapley participaron en actividades humanitarias, encontrando hogar para muchas familias judías que habían huido de Europa. Además, Martha se unió a Zdeněk Kopal (1914-1993) y otros astrónomos de Harvard que estaban trabajando para la División de Cooperación Industrial en el Instituto Tecnológico de Massachusetts. Sus habilidades matemáticas fueron esenciales para calcular trayectorias de proyectiles para la Armada y las Fuerzas Aéreas. Tras finalizar la contienda, continuó colaborando con el mismo grupo, midiendo posiciones y calculando órbitas de meteoros.
Cuando sus hijos e hija abandonaron el hogar familiar, Martha Shapley regresó a sus investigaciones astronómicas. Su última contribución a la astronomía fue Catalogue of the Elements of Eclipsing Binaries (1956) en colaboración con Zdeněk Kopal.
Primera Dama del Observatorio de HarvardDurante los 32 años en los que Harlow Shapley fue director del Observatorio de la Universidad de Harvard, a Martha se la conocía como la Primera Dama del Observatorio. El matrimonio era muy apreciado por su hospitalidad con “la familia astronómica de Harvard” (personal fijo y personas que trabajaban temporalmente o visitaban el Observatorio), y Martha era una anfitriona entregada en las reuniones que organizaban en su casa.
Tres de sus hijos también se dedicaron a la astronomía y las matemáticas: Mildred Shapley Matthews (1915-2016) se convirtió en una destacada astrónoma; Willis Shapley (1917-2005) trabajó como administrador de la NASA; y Lloyd Shapley (1923-2016) fue un brillante matemático que recibió el Premio Nobel de Economía el año 2012 junto a Alvin E. Roth (citamos a estos dos investigadores en Matemática discreta y trasplantes cruzados de riñones).
Martha Shapley falleció el 24 de enero de 1981, a los 90 años de edad.
La Sra. Shapley lamenta no haber hecho más por su cuenta. No es el tipo de mujer que se conforma con el mérito de haber ayudado a su marido. Cree que una mujer nacida con aptitudes, y ella evidentemente las tenía, tiene la obligación de utilizarlas, y no sólo en su calidad de esposa y madre.
Referencias
-
John J O’Connor and Edmund F. Robertson, Martha Betz Shapley, MacTutor History of Mathematics Archive, University of St Andrews
-
Barbara L. Welther, Guilt by Association: How Mrs. Harlow Shapley Lost Her Job, Bulletin of the American Astronomical Society 18 (1986) 1055
-
Zdeněk Kopal, Obituary – Shapley, Martha-Betz 1890-1981, Astrophysics and Space Science 79 (1981) 261-264
-
Deborah Shapley, Martha Shapley – Astronomer, Harlow Shapley Project, 8 marzo 2023
-
Martha Betz Shapley, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Martha Betz Shapley, la “Primera Dama del Observatorio de Harvard” se ha escrito en Cuaderno de Cultura Científica.
Los invasores: Los hipopótamos del narco Escobar
Es la especie animal invasora más grande del mundo, tal como titulan su artículo Jonathan Shurin y sus colegas, de la Universidad de California San Diego de La Jolla. Mide entre tres y cinco metros de la cabeza a la punta de la cola, con metro y medio de altura hasta los hombros. El peso medio es de 1500 a 1800 kilos, aunque puede llegar a los 3000. Es el hipopótamo común, de nombre científico Hippopotamus amphibius. Habita el África subsahariana hasta Sudáfrica y es una especie invasora en Colombia por los caprichos de un célebre narcotraficante, Pablo Escobar.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsLa portada y el primer capítulo de Historia de las especies invasoras, del biólogo Ángel León Panal, libro publicado en 2021, están dedicados a los hipopótamos de Colombia y al narco Pablo Escobar. Dirigía en 1978 el Cártel de Medellín. Visitaba el curso medio del valle del río Magdalena, en el centro de Colombia. En la zona compró varias fincas con selva, agua y montaña y fundó la Hacienda Nápoles, en el municipio de Puerto Triunfo, Departamento de Antioquía, así llamada en homenaje a su admirado Al Capone, nacido en Napolés.
En la finca mostraba su colección de automóviles y practicaba varios deportes, entre ellos el tenis. Pero el mayor atractivo era el Zoológico. Se informó de las especies que se adaptarían al clima de aquella zona de Colombia y, por medio de intermediarios de Estados Unidos, compró, por ejemplo, cebras, elefantes, rinocerontes, jirafas, hipopótamos y más especies que, poco a poco, iban llegando a la hacienda. En total llegaron a ser unos mil doscientos animales.
Los hipopótamos primero fueron cuatro, tres hembras y un macho, en 1981, y pronto llegaron a seis con la compra de otros ejemplares (quizá, no está claro, eran entre dos y seis los ejemplares del grupo inicial). Tras la muerte de Pablo Escobar a los 44 años, en 1993 y acribillado a balazos por la policía colombiana, los hipopótamos y otros animales quedaron en la Hacienda Nápoles. Eran muchos hipopótamos y en 2016 llegaban a 30 ejemplares y, para 2020, se calculó que había entre 60 y 80 individuos. Viven, de media, unos 40 años en estado silvestre y las hembras tienen unas 25 crías. Las proyecciones para el futuro hablan de 800-1400 individuos en Colombia para 2040.
Las últimas previsiones publicadas hace unas semanas por Amanda Subalusky y sus colegas, de la Universidad de Florida en Gainesville, estiman que el crecimiento de la población de hipopótamos es del 9.6% al año, lo que supone 230 individuos para 2032. Incluso el cálculo de crecimiento de la población, según D.N. Castelblanco-Martínez y su grupo, del Consejo Nacional de Ciencia y Tecnología de Ciudad de México, podría llegar a los 800 individuos en 2034. Todos estos datos suponen que, según la estrategia de control que adopte el Gobierno de Colombia, hay hipopótamos en el país por unos 50-100 años.
En conclusión, es el único grupo de hipopótamos en estado salvaje y viable que se puede encontrar fuera de África.
Algunos ejemplares abandonaron la Hacienda Nápoles y siguieron el curso del río Magdalena hacia el norte hasta, por ahora y con datos confirmados, unos 150 kilómetros de la finca, aunque las citas más al norte parecen que están a unos 400 kilómetros. Para los habitantes de los márgenes del río es un asunto difícil pues los hipopótamos son agresivos y peligrosos. En África causan más muertes al año que leones, elefantes, búfalos y rinocerontes juntos, como escribe Ángel León Panal. Además, pueden transmitir enfermedades como la tuberculosis, la brucelosis, la leptospirosis, el ántrax y la salmonelosis.
Ingenieros de ecosistemasSon los hipopótamos lo que se denomina ingenieros de ecosistemas, pues pueden modificar los hábitats en que se encuentran. Es un herbívoro que transporta nutrientes desde las plantas de las que se alimenta hasta las zonas acuáticas donde libera sus heces. Algo así como una tonelada de carbono y otros compuestos al año y por individuo. En los ecosistemas acuáticos en que vive puede provocar la eutrofización por exceso de nutrientes por la acumulación de los componentes de las heces. Según el resumen de Jonathan Shurin y sus colegas, los hipopótamos importan al hábitat acuático materia orgánica y nutrientes con un impacto apreciable en el metabolismo del ecosistema y en la estructura de la comunidad.
Por cierto, desde 2012 y por orden judicial está prohibida la caza de hipopótamos en Colombia. Y en 2014, el Gobierno optó por la conservación de los hipopótamos, controló su reproducción y exportó algunos ejemplares a zoológicos de otros países como Ecuador y Uruguay. Sin embargo, en 2021, la Unión Internacional para la Conservación de la Naturaleza envió una carta de intervención al Gobierno de Colombia recomendando iniciar un programa para eliminar la población de hipopótamos. Y en sentido opuesto, el hipopótamo fue declarado legalmente como especie invasora hace poco más de un año, el 24 de marzo de 2022.
El control de la población de hipopótamos en Colombia ha planteado varios problemas. En 2018 revisaron los métodos Santiago Monsalve, de la Corporación Universitaria Lasallista, y Alejandro Ramírez, de la Universidad de Durham. Se han propuesto los anticonceptivos para las hembras y la castración química en los machos. Pero faltan datos sobre su eficacia. Ninguno de estos métodos parece funcionar con ella tal y como se propone su aplicación según D.N. Castelblanco-Martínez y su grupo. Para la aplicación de estas técnicas se necesita controlar la agresividad de los hipopótamos, también poco estudiada y difícil de evitar por su tamaño y peso. También la población ha crecido en tal cantidad que la captura y entrega a zoológicos ya no es posible. La caza y eliminación de individuos ha provocado un gran debate con ONGs y la sociedad en general por lo que, por ahora, se ha abandonado.
La conservación compasiva de los hipopótamos no es una opciónComo resumen final valen los comentarios de Amanda Subalusky y sus colegas, de la Universidad de Yale, publicados en 2021. El hipopótamo es un ingeniero de ecosistemas que puede tener efectos profundos en los entornos terrestre y acuático y afectar la biodiversidad original de la cuenca del río Magdalena. Los hipopótamos también son agresivos y representan una amenaza para los habitantes de la región del río Magdalena aunque, por otra parte, también podrían generar beneficios económicos por el turismo. Sin embargo, se necesita más investigación para cuantificar el tamaño y la distribución de la población de hipopótamos y para predecir los efectos ecológicos, sociales y económicos que pueden provocar. Pero el conocimiento debe equilibrarse con la consideración de las preocupaciones sociales y culturales al desarrollar estrategias de manejo apropiadas para la introducción de una especie invasora.
Además, en este debate sobre cómo manejar una especie invasora, Colombia depende en gran medida del negacionismo científico: varios participantes en debates públicos tergiversan el trabajo y las opiniones de los científicos y cuestionan su ética y motivos. Destacan la necesidad y la confianza en la acción basada en la ciencia, proponen participar en discusiones sobre las preocupaciones éticas, y deben superar falsos dilemas, a menudo poco argumentados. La “conservación compasiva”, que valora los derechos e intereses de los individuos de una especie exótica carismática, no puede prevalecer sobre (1) los derechos e intereses de los individuos de las especies nativas y (2) la conservación de poblaciones, ecosistemas y servicios que suponen las especies nativas. Como proponen Sebastián Restrepo y Carlos Daniel Cadenas, de las universidades Javeriana y de los Andes, de Bogotá, sin una acción decisiva por parte de las autoridades ambientales de Colombia, con una variedad de medidas que incluyen la matanza selectiva bajo estándares humanitarios de bienestar animal, las poblaciones de hipopótamos continuarán expandiéndose a expensas de los ecosistemas que sustentan a comunidades humanas vulnerables y las especies nativas.
Referencias:
Castaño, J.A. 2008. Dos hipopótamos tristes. Letras Libres junio: 22-25.
Castelblanco-Martínez, D.N.et al. 2021. A hippo in the room: Predicting the persistence and dispersion of an invasive mega-vertebrate in Colombia, South America. Biological Conservation 253: 108923.
Dembitzer, J. 2018. The case for hippos in Colombia. Israel Journal of Ecology & Evolution doi: 10.1163/22244662-06303002.
León Panal, A.L. 2021. Historia de las especies invasoras. Guadalmazán. Córdoba. 425 pp.
Monsalve Buriticá, S. & A. Ramírez Guerra. 2018. Estado actual de los hipopótamos (Hippopotamus amphibius) en Colombia: 2018. Revista CES Medicina Veterinaria y Zootecnia 13: 338-346.
Resolución nº 0346, de 24 marzo 2022, Por la cual se modifica el artículo 1º de la Resolución Nº 848 de 2008, adicionando la especie Hippopotamus amphibius (Hipopótamo común) y se toman otras determinaciones. El Ministro de Ambiente y Desarrollo Sostenible. Colombia.
Restrepo, S. & C.D. Cadena. 2021. Science denialism limits management of invasive hippos in Colombia. Frontiers in Ecology and the Environment 19: 323-325.
Shurin, J.B. et al. 2020. Ecosystem effects of the world’s largest invasive animal. Ecology e02991.
Subalusky, A.L. et al. 2021. Potential ecological and socio-economic effects of a novel megaherbivore introduction: the hippopotamus in Colombia. Oryx 55: 105-113.
Subalusky, A.L. et al. 2023. Rapid population growth and high management costs have created a narrow window for control of introduced hippos in Colombia. Scientific Reports 13: 6193.
Wikipedia. 2023. Hippopotamus amphibius. 12 mayo.
Para saber más:
Catástrofe Ultravioleta #18 INVASORES
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Los invasores: Los hipopótamos del narco Escobar se ha escrito en Cuaderno de Cultura Científica.
ChatGPT puede inventarse artículos médicos y hacerte creer que son auténticos
Los chatbots generados por inteligencia artificial (IA) han experimentado una auténtica revolución entre la población general en el último año, con ChatGPT como su máximo exponente. Centenares de millones de personas alrededor del mundo usan, con más o menos frecuencia, estas tecnologías para diversos fines como resolver dudas o como complemento en el trabajo para redactar textos o para programar. Sin embargo, esta herramienta, que usa el procesamiento del lenguaje natural para generar textos equivalentes a los escritos por los humanos, puede ser tan convincente a la hora de dar información cierta como cuando arroja otra que es totalmente falsa.
 Foto: Levart_Photographer / Unsplash
Foto: Levart_Photographer / UnsplashUn equipo de investigadores de la Universidad Carolina de Praga ha puesto a prueba la capacidad de ChatGPT, desarrollado por la empresa OpenAI, para crear un artículo médico falso, desde cero. Los resultados de su experimento, que se han publicado en la revista Journal of Medical Internet Research, son preocupantes. En tan solo una hora y sin ninguna formación previa del usuario, esta tecnología generó un artículo científico sobre neurocirugía que parecía verídico para los no expertos en la materia. Los autores crearon el documento mediante una serie de preguntas e indicaciones a la IA para ir mejorando progresivamente la calidad de sus respuestas. Posteriormente, expertos en el campo de la neurocirugía, de la psiquiatría y de la estadística evaluaron el artículo falso comparándolo con artículos reales similares.
En apariencia, el artículo científico generado por ChatGPT es idéntico a uno convencional. Reúne los diferentes apartados propios de estos documentos (resumen, introducción, métodos, resultados y discusión), muestra datos y tablas y utiliza las palabras apropiadas con una estructura coherente y lógica. No obstante, las personas expertas podían detectar múltiples errores como imprecisiones en el uso de ciertas palabras o en la redacción de referencias científicas: algunas presentaban detalles incorrectos, mientras que otras directamente eran inventadas. En cualquier caso, el profesor de neurocirugía encargado de evaluarlo explica que «en general, el artículo generado mostró un gran nivel de competencia técnica y autenticidad».
La creación de artículos científicos falsos no es un problema nuevo. En el mundo académico existe una gran presión para que los investigadores sean prolíficos a la hora de publicar si desean avanzar profesionalmente o incluso sobrevivir, un fenómeno conocido en el mundillo como «Publica o muere». Esto lleva a que algunos científicos, escasos de ética, publiquen a toda costa, aunque sea mediante artículos falsos. La demanda de artículos inventados ha llegado a tal nivel que existen empresas, conocidas como «fábricas de artículos», que se encargan de generar artículos falsos por encargo de científicos para así inflar su curriculum y progresar en su carrera. Se estima que casi el 22 % de los artículos retirados de revistas científicas en 2021 fueron por este tipo de engaño.
Las revistas depredadoras añaden más leña al fuego del fraude científico. Estas publicaciones basan su modelo de negocio en cobrar por publicar artículos, pero sin contar con los procesos adecuados de revisión por pares que caracterizan a las revistas científicas. El resultado es que resulta muy fácil colar artículos inventados o de muy poca calidad en este tipo de revistas. Se estima que existen unas 8.000 revistas depredadoras que, en su conjunto, publican cada año 420.000 papers con escasa o nula garantía de calidad. , lo que supone el 20 % de la publicación científica anual mundial, que gira en torno a los 2,5 millones de artículos.
La irrupción de la IA como generadora de artículos falsos, en medio de este panorama, complica aún más la situación porque facilita en gran medida todo el proceso de fraude para las personas sin escrúpulos. Además, dada la capacidad que tiene esta tecnología de perfeccionarse a sí misma, es posible que en un futuro próximo la redacción automática de artículos inventados y creíbles sea una cuestión de minutos sin apenas esfuerzo por parte de una persona. Quizás, la IA podría llegar a un nivel de refinamiento que hiciera difícil incluso para los expertos en la materia distinguir los artículos científicos reales de los falsos.
La tentación de usar la IA para tomar el camino fácil y progresar en el mundo académico puede ser demasiado poderosa para algunos científicos. Por esta razón, los autores sostienen que se necesita mayor vigilancia y mejores métodos de detección para luchar contra la IA en la investigación científica. No obstante, esta herramienta puede aportar valor, al ayudar en la preparación del manuscrito, el análisis de los resultados y la edición del texto de un artículo científico genuino.
En el estudio se recalca la importancia de desarrollar e implantar guías éticas y de buenas prácticas para el uso de esta herramienta en la investigación y en la escritura científica. Por otro lado, obligar a los investigadores a ser transparentes en cuanto al uso de la IA (para que declaren cuánto de su texto se ha generado por esta tecnología) podría echar para atrás a aquellos que contemplen utilizarla para inventarse parcial o totalmente un artículo científico.
Sea como sea, la IA ha llegado para quedarse. Al igual que un cuchillo, esta herramienta se puede usar tanto para el bien como para el mal. Será necesario detectar, desincentivar y castigar a aquellos que tengan la tentación de usar la IA con malos propósitos para evitar que el fraude en la ciencia se convierta en un problema mucho mayor en un futuro próximo.
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo ChatGPT puede inventarse artículos médicos y hacerte creer que son auténticos se ha escrito en Cuaderno de Cultura Científica.
La buena literatura ayuda a ponernos en el lugar de los otros
 Foto: Matias North / Unsplash
Foto: Matias North / UnsplashLeer buena literatura mejora nuestra capacidad para empatizar con los otros y para entenderlos, para interpretar mejor su comportamiento; en definitiva, para ponernos en su lugar. Expresado en términos algo más técnicos y con pocas palabras, mejora nuestra «teoría de la mente» (TM), que es la capacidad para asignar pensamientos, intenciones y emociones a otras personas. Dentro de ella se diferencia la afectiva (TMa), que es la que se refiere a las emociones, y la cognitiva (TMc), que es la relativa a los pensamientos e intenciones.
La conclusión general presentada en el párrafo anterior ha sido obtenida a partir de experimentos diseñados para valorar el posible efecto que tienen diferentes tipos de lectura sobre la capacidad para ponernos en el lugar de los demás. Proporcionaron a grupos formados por diferentes personas textos breves tomados de libros seleccionados y, tras su lectura, a las personas de cada grupo les pasaron test para evaluar diferentes indicadores de TM. En todos los experimentos se valoró también el grado de familiaridad de los participantes con la literatura, para lo que se utilizó un test de reconocimiento de autores. En el primer experimento compararon el efecto de leer ficción literaria con el de leer lo que se denomina no ficción. Y a continuación, en una serie de otros cuatro experimentos, compararon el efecto de leer ficción literaria con el de leer lo que ellos denominan ficción popular que, a los efectos de esta anotación, podemos llamar “superventas” (best sellers).[1]
Citaré, a modo de ejemplo, dos de los test utilizados. En el denominado de “lectura de la mente en los ojos”, considerado el test prototípico de TM afectiva, se pedía a los participantes que asignasen estados emocionales a las expresiones faciales que se les mostraban en imágenes centradas en los ojos. Y en el denominado “test de Yoni”, debían deducir estados emocionales (para TMa) o pensamientos (para TMc) a partir de claves lingüísticas y visuales mínimas. Aunque los autores también utilizaron un test de falsa suposición –del tipo de Sally & Anne–[2] para valorar la teoría de la mente cognitiva, no dio ningún resultado.
El primer experimento mostró que la lectura de ficción literaria mejora la teoría de la mente afectiva por comparación con la lectura de textos de no ficción. De los siguientes experimentos se concluyó que el efecto es específico de la ficción literaria, y que, por lo tanto, no se extiende a la ficción popular. Como el test de falsa suposición no funcionó, lo autores recurrieron al test de Yoni al que me he referido antes, que es bastante más exigente que el de falsa suposición y que, como hemos visto, sirve para determinar ambas modalidades de TM, la afectiva y la cognitiva. Los resultados de los experimentos en que se utilizó este test mostraron que el efecto de la lectura de ficción literaria no se limitaba a la TM afectiva, sino que se extienden también a la TM cognitiva.
De acuerdo con tres de los cinco experimentos, la familiaridad con la literatura sí ejerce efectos positivos sobre la TM, pero ese efecto no se verificó en los otros dos experimentos. Los investigadores sugieren que ese aspecto debe ser investigado de forma más específica, pues las referencias anteriores indicaban que, en efecto, la familiaridad con la literatura de ficción es un factor que afecta de forma positiva a la teoría de la mente. Y lo cierto es que hay razones para que así ocurra, ya que la ficción amplía nuestro conocimiento de las vidas de otros y nos ayuda a reconocer nuestras semejanzas y diferencias con ellos.
Sin embargo, los autores, sin descartar que eso sea así, creen que la relación entre la teoría de la mente y la familiaridad con la literatura puede deberse a características del texto más sutiles que la simple caracterización de los personajes. Ellos proponen que la ficción puede cambiar no sólo lo que pensamos de los demás, sino lo que pensamos de uno mismo. Según su planteamiento, la ficción afecta a los procesos propios de la TM al obligarnos a implicarnos en la lectura de la mente de los personajes. Y eso es algo que no valdría para cualquier forma de ficción. Solo la literaria llevaría al lector a implicarse en los procesos propios de la teoría de la mente.
Sostienen que la ficción literaria es más polifónica y más rica tras la interpretación del lector que reelabora lo leído y que, por ello, le permite adquirir las claves necesarias para comprender a los personajes. En ese sentido, se parecería más a la vida real que la ficción popular, pues está llena de personajes complejos cuyas vidas no son fácilmente discernibles. Por comparación con la vida real, la ventaja de la ficción es que en ésta no se corre ningún peligro personal por implicarse en la trama. Es más, mientras que muchas de nuestras relaciones sociales habituales están gobernadas por estereotipos y convenciones, las que se presentan en las obras de ficción literaria no se ajustan a nuestras expectativas en muchas ocasiones. Por eso, los lectores de ficción literaria deben hacer uso de recursos interpretativos más flexibles para poder inferir los sentimientos y pensamientos de los personajes. O lo que es lo mismo, deben recurrir a los procesos mentales propios de la teoría de la mente. La llamada «ficción popular», por el contrario, tiende a describir el mundo y las personas de una forma mucho más coherente y predecible; de esa forma, reafirma las expectativas de los lectores y no tiene por qué mejorar la teoría de la mente.
Los resultados de los experimentos confirman, según los autores, lo anterior, y sugieren que las explicaciones que se basan en el contenido concreto de la ficción no podrían dar cuenta de aquellos. De hecho, los textos utilizados trataban asuntos muy diferentes. Además, no les parece verosímil que los lectores pudiesen aprender mucho acerca de los demás leyendo unos textos tan breves. Por otro lado, era específicamente la ficción literaria la que ejercía efecto sobre la TM. Por todo ello, los investigadores proponen que es la adopción de un papel activo para representar los estados subjetivos de los personajes la que hace que la lectura de ficción literaria promueva la teoría de la mente.
En otro orden de cosas, y a pesar de que los resultados relativos al efecto de la familiaridad con la literatura no fueron concluyentes, sostienen que es muy probable que leer ficción literaria de manera frecuente conduzca a mejoras estables en la teoría de la mente. Por otra parte, no creen que los efectos benéficos de la buena literatura se limiten a los procesos de la TM, sino que seguramente produzca también beneficios de otro tipo, tanto de índole cognitiva como afectiva, y es muy posible que dichos efectos sean generalizables a la ficción en general, no sólo a la literaria.
Fuente:
David Comer Kidd y Emanuele Castano (2013): «Reading Literary Fiction Improves Theory of Mind» Science 342: 377-380.
Notas:
[1] Las obras de ficción literaria seleccionadas por los autores de este trabajo habían recibido algún tipo de galardón literario de prestigio, y los superventas fueron tomados de la lista de libros más vendidos de Amazon.
[2] En su versión original, en este test se muestra al sujeto una escena en la que hay dos muñecas, Sally y Anne. Sally coge una canica (o cualquier otro objeto de pequeño tamaño) y lo coloca en su cesta. A continuación sale de la escena. Entonces, Anne coge la canica de la cesta de Sally y la pone en su propia cesta. Regresa Sally a la escena y se le hace al sujeto la pregunta clave: “¿Dónde buscará Sally la canica?” El sujeto supera el test si responde que en la cesta de Sally, pues de esa forma aplicará la misma lógica que aplicaría Sally. Ello quiere decir que se pone en el lugar de Sally, que adopta su perspectiva. Los sujetos incapaces de ponerse en el lugar del otro y anticipar sus actos, responden de acuerdo con la información con que cuentan, esto es, que la canica se encuentra en la cesta de Anne, donde ella la ha puesto. Quienes superan el test entienden que Sally tiene sus propias suposiciones que pueden no corresponder a la realidad, y ese es precisamente el requerimiento nuclear de la teoría de la mente.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La buena literatura ayuda a ponernos en el lugar de los otros se ha escrito en Cuaderno de Cultura Científica.
El origen de la cultura de la muerte en el linaje humano

Cómo influyen los parásitos en el comportamiento de los animales, cómo se modifica la conducta de las madres mamífero o cuáles son las enfermedades que nos afectan y desde cuándo hemos desarrollado comportamientos funerarios ante la muerte son algunos de los aspectos que se analizarán en la V Jornada Nacional sobre Evolución y Neurociencias.
Especialistas en ambas materias se reunirán el 11 y 12 de mayo en una nueva edición conducida por Eva Garnica y Pablo Malo, psiquiatras y miembros de la Red de Salud Mental de Bizkaia, y organizada por esa misma entidad y la Cátedra de Cultura Científica de la UPV/EHU.
La jornada, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolucionista y divulgar de un modo accesible para todos los públicos.
Por muy diferentes que puedan parecer las diferentes poblaciones humanas en el mundo hay algo que comparten a nivel fundamental: la cultura funeraria o cultura de la muerte. ¿Cómo se desentraña el origen de esta cultura de la muerte del registro arqueológico? Esto es lo que nos explica Nohemí Sala en esta charla.
Nohemí Sala es investigadora del CENIEH. Geóloga de formación y doctora en Paleontología por la Universidad Complutense de Madrid, su investigación está enfocada en los procesos de formación de los yacimientos paleontológicos y arqueológicos, desde un punto de vista geológico y tafonómico (la tafonomía es la parte de la paleontología que estudia los procesos de fosilización y la formación de los yacimientos de fósiles).
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo El origen de la cultura de la muerte en el linaje humano se ha escrito en Cuaderno de Cultura Científica.
Hogares en fosa en un yacimiento mesolítico ibérico
Un estudio sobre los sedimentos arqueológicos del Arenal de la Virgen, un yacimiento al aire libre situado en un sistema dunar junto a la Laguna de Villena (Alicante), revela la existencia de campamentos con hogares durante el Mesolítico. El objetivo de este trabajo era aclarar el origen antrópico (producido o modificado por la actividad humana) de un tipo de evidencia arqueológica común pero poco estudiada en yacimientos mesolíticos de principios del Holoceno localizada en contextos dunares semiáridos de Europa: los conocidos como hogares en fosa o ‘hearth-pits’.
“En la Península Ibérica es la primera vez que se estudia este tipo de estructuras de manera detallada aplicando una metodología sistemática con el fin de determinar su formación, comprender mejor su función específica y evaluar las alteraciones sufridas tras la ocupación y el abandono del yacimiento”, señala Ana Polo-Díaz, investigadora del Departamento de Geografía, Prehistoria y Arqueología de la Universidad del País Vasco, miembro del Grupo de Investigación en Prehistoria de la UPV/EHU (Gizapre) y primera firmante del artículo.
Como novedad, para llevar a cabo ese trabajo, los investigadores han aplicado una novedosa metodología de arqueología científica interdisciplinar que integra el análisis estratigráfico y textural, la química del suelo, la micromorfología, la petrografía y la luminiscencia ópticamente estimulada y termoluminiscencia .
“Los resultados obtenidos permiten confirmar el origen antrópico de las estructuras investigadas, cuya cronología se asocia dos fases de ocupación diferentes: la más lejana, con una antigüedad de entre 9.300 y 9.100 años, mientras que la más reciente tiene una antigüedad de entre 8.700 y 8.400 años”, explica Javier Fernández López de Pablo.

En cuanto a la fase más antigua de ocupación se han descubierto restos de estructuras correspondientes a un posible horno en cubeta, así como a una zona anexa dedicada a la acumulación de residuos de combustión procedentes de dicho horno y con un uso puntual. Por lo que respecta a la fase más reciente, se han identificado áreas de actividad de mayor extensión en superficie respecto a la fase más antigua, en las que además de evidencia de fuego, se han documentado residuos de la ocupación de un asentamiento que se extendió entre 200 y 400 años.
Los datos obtenidos evidencian condiciones climáticas favorables de habitabilidad durante el periodo de tiempo específico en el que tuvo lugar el asentamiento en el Arenal de Virgen, durante el Holoceno Antiguo. “Esas condiciones ambientales se caracterizaron por un incremento en la humedad ambiental, la temperatura y la cubierta vegetal, en contraste a una significativa mayor aridez detectada en los momentos anteriores y posteriores a la ocupación del sitio durante el Pleistoceno y el Holoceno Medio, respectivamente”, indican los autores del artículo.
Los resultados de esta investigación abren nuevas perspectivas para la investigación de los asentamientos al aire libre de los últimos grupos de cazadores-recolectores de la Prehistoria en la Península Ibérica, en un momento crucial en la evolución humana, tras el final de la última gran glaciación y el comienzo del periodo climático en el que nos encontramos en la actualidad, el Holoceno.
Referencia:
Ana Polo-Díaz, Jose Ramón Rabuñal, Guillaume Guérin & Javier Fernández-López de Pablo (2023) Mesolithic hearth-pits and formation processes: a geoarchaeological investigation of sediments from El Arenal de la Virgen site (SE Iberia) Archaeological and Anthropological Sciences doi: 10.1007/s12520-023-01794-5
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Hogares en fosa en un yacimiento mesolítico ibérico se ha escrito en Cuaderno de Cultura Científica.
La catenaria: sensores (3/4)
Desde los años sesenta, la tecnología ferroviaria ha desarrollado multitud de sensores que ayudan, de una forma u otra, a la operación. Sensores de cajas calientes para determinar la temperatura de los ejes de un tren y evitar roturas y descarrilamientos. Detectores de caída o arrastre de objetos por la vía. Medidores de viento lateral, cruciales en los grandes viaductos. Detectores de incendios en túneles. La alimentación eléctrica en sí misma está controlada en los puntos donde se toma de la red de alta tensión de propósito general y se transforma para la alimentación óptima de los trenes. En estas ubicaciones, llamadas subestaciones de tracción, no faltan dispositivos capaces de cortar la corriente en milisegundos en caso de detectar cualquier problema.
Sin embargo, la propia integridad y desempeño mecánico de la catenaria ha tardado mucho más en disponer de sensores propios que los demás elementos de la infraestructura ferroviaria. Esto ha sido así por la particular dificultad que reviste instalar electrónica sensible en un entorno de alta tensión. Las elevadas corrientes, y por tanto los intensos campos electromagnéticos, pueden dañar cualquier circuitería que no esté muy protegida o suficientemente alejada.
 Vías de salida de la estación Madrid-Puerta de Atocha-Almudena Grandes. Foto: Iván RiveraSensores para la catenaria
Vías de salida de la estación Madrid-Puerta de Atocha-Almudena Grandes. Foto: Iván RiveraSensores para la catenaria
¿Qué es lo más interesante a la hora de monitorizar el comportamiento de la catenaria? La integridad de los aisladores, el movimiento de los contrapesos que regulan la tensión mecánica de los hilos o la respuesta dinámica del hilo de contacto al paso de un pantógrafo son todas ellas posibles respuestas. Esta última, la respuesta dinámica del hilo de contacto al paso del pantógrafo de un tren en marcha, es particularmente compleja de dilucidar. Los pantógrafos son sistemas mecánicos con suspensiones taradas para ejercer cierta fuerza vertical contra el hilo de contacto. Pero esta fuerza no puede ser, como en la historia de Ricitos de Oro, ni muy pequeña ni muy grande. Si la fuerza es demasiado leve, existe el riesgo de que el pantógrafo se despegue por momentos del hilo de contacto ante cualquier mínima irregularidad. La elevada corriente eléctrica que fluye entre este hilo y los frotadores montados sobre la mesilla del pantógrafo no se interrumpe inmediatamente. Antes bien, la aparición de un pequeño hueco provoca la descarga de un arco voltaico: un pequeño rayo que ioniza el aire circundante y eleva las temperaturas tanto del hilo como del material del frotador (habitualmente grafito, por sus especiales características conductoras y autolubricantes).
 Arcos voltaicos en el contacto pantógrafo-catenaria. Fuente: [Zhou 2022]Este flash térmico, reiterado, provoca un desgaste temprano de los frotadores y del hilo. En casos extremos, tanto el hilo como el propio pantógrafo pueden romperse, provocando un fenómeno conocido como enganchón. En este caso, el pantógrafo dañado arrastra el hilo de contacto, provocando daños ulteriores en el tren y en la infraestructura. Si el tren circulaba a una velocidad elevada, puede destruir varios kilómetros de hilos antes de detenerse por completo. El tráfico ferroviario queda cortado durante horas o días en tanto se repara la catenaria y se hace necesario remolcar el tren afectado.
Arcos voltaicos en el contacto pantógrafo-catenaria. Fuente: [Zhou 2022]Este flash térmico, reiterado, provoca un desgaste temprano de los frotadores y del hilo. En casos extremos, tanto el hilo como el propio pantógrafo pueden romperse, provocando un fenómeno conocido como enganchón. En este caso, el pantógrafo dañado arrastra el hilo de contacto, provocando daños ulteriores en el tren y en la infraestructura. Si el tren circulaba a una velocidad elevada, puede destruir varios kilómetros de hilos antes de detenerse por completo. El tráfico ferroviario queda cortado durante horas o días en tanto se repara la catenaria y se hace necesario remolcar el tren afectado.
 Incidente de arrastre de hilo de contacto en Cetina, línea Madrid-Barcelona-Frontera francesa. (Autor desconocido)
Incidente de arrastre de hilo de contacto en Cetina, línea Madrid-Barcelona-Frontera francesa. (Autor desconocido)El caso contrario, el de un exceso de fuerza de empuje por parte del pantógrafo, también es susceptible de dañar la instalación, por un procedimiento inicialmente distinto. La fuerza de empuje para un pantógrafo extendido se ajusta en el taller, y por tanto en condiciones estáticas. Circular a velocidades elevadas, sin embargo, puede alterar esta fuerza debido a fenómenos de sustentación: la mesilla del pantógrafo se comporta como un alerón y, en función de pequeñas variaciones de su ángulo de ataque respecto de la dirección de avance, puede sufrir un empuje extra hacia arriba o hacia abajo.
El conjunto de efectos que aparecen en la práctica sobre la interfaz pantógrafo-catenaria hace muy deseable el registro de lo que ocurre en condiciones dinámicas. Tal es así, que tanto la fuerza ejercida por los pantógrafos como un parámetro relacionado y de medida más sencilla, el desplazamiento vertical del hilo de contacto, están limitados por una normativa específica. Sin embargo, realizar la medida necesaria para asegurar su cumplimiento de un modo comercialmente práctico ha estado fuera de las capacidades de la tecnología ferroviaria hasta hace relativamente poco tiempo. ¿Y cuál es el reto? Nada menos que registrar cambios en la altura del hilo de contacto de pocos centímetros que pueden suceder tan rápido como un milisegundo. Naturalmente, mientras fluyen por él intensas corrientes eléctricas y sin que el tren, que pasa justo por debajo, ni su pantógrafo, que está por definición rozando el hilo, perturben la medida o dañen el equipo.
Medida potenciométricaLa primera tecnología que se aplicó a la medida dinámica del comportamiento del hilo fue la de los sensores potenciométricos lineales. Estos dispositivos transforman una distancia en una diferencia de potencial eléctrico mediante una resistencia variable giratoria conectada a un circuito divisor de tensión; en la jerga técnica, decimos que son un tipo de transductor. El giro del potenciómetro cambia el valor de su resistencia eléctrica, de modo que, si se alimenta la entrada del circuito con una tensión constante, la salida es proporcional al ángulo total girado (por ejemplo, dos vueltas serían 720 grados).
El potenciómetro, montado en un bastidor fijo, se acopla por su eje de giro solidariamente con un carrete que aloja un cable flexible enrollado en una ranura helicoidal. El cable sale del dispositivo por una abertura. En su extremo, se acopla al elemento móvil cuya distancia se desee medir: el cambio en la longitud se traslada al giro del potenciómetro y, por tanto, a la tensión eléctrica de salida del equipo. Por último, todo el conjunto se acopla por su eje a un resorte espiral para que el sistema tienda a volver a su posición inicial. El funcionamiento mecánico es algo similar, así, al de un flexómetro, una cinta métrica de las que todos tenemos en casa.
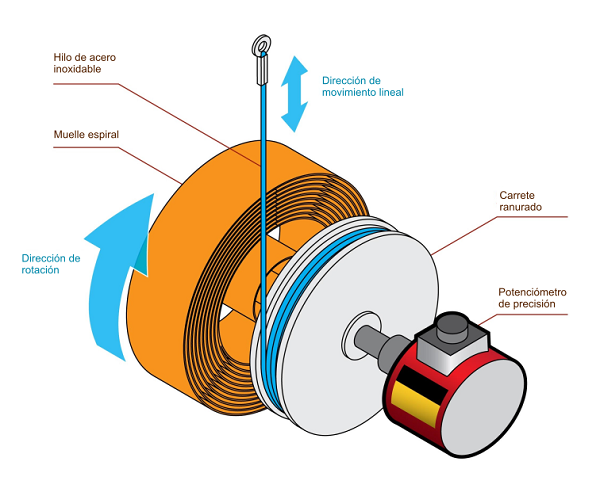 Sensor potenciométrico lineal. Adaptado de [FUTEK 2023])
Sensor potenciométrico lineal. Adaptado de [FUTEK 2023])
Existen más posibilidades técnicas muy similares para realizar este mismo montaje (por ejemplo, sustituir el potenciómetro por un encoder o codificador rotativo óptico bidireccional), pero todas adolecen de los mismos problemas: por un lado, la unión entre el hilo de contacto y el carrete es flexible, con lo que trabaja a tracción, pero no a compresión. El pantógrafo, al elevar el hilo de contacto, comprime y destensa el cable del sensor, que depende de la inercia del resorte espiral para recuperar la tensión de trabajo. El resultado será una señal de potencial eléctrico de salida que no reflejará fielmente el movimiento del hilo. Tanto menos cuanto más rápido sea este movimiento. Aunque solo vayamos a registrar la máxima cota vertical alcanzada, puede que no sea todo lo precisa que debería. Hasta ahora estos sensores se han utilizado a velocidades relativamente bajas, pero por los efectos aerodinámicos que afectan al pantógrafo, las velocidades altas, en el entorno de los 300 kilómetros por hora, son tanto o más interesantes.
El segundo problema es más evidente. El hilo de contacto tiene que estar unido físicamente al sensor, con lo que existe un riesgo de derivación eléctrica. En el mejor de los casos destruiría el equipo de medida. En función de la arquitectura concreta de la catenaria, este riesgo puede ser o no aceptable dependiendo de si es o no posible instalar el equipo sensor y todos sus elementos auxiliares en la zona con riesgo eléctrico, y extraer la señal de medida para su transmisión y procesado mediante un sistema de acoplamiento óptico en infrarrojos. El administrador de infraestructuras ferroviarias español, Adif, está probando este tipo de sensores en vías de alta velocidad.
Medida por visión artificialTodos los problemas de la medida potenciométrica se soslayarían con un sistema que pudiera hacer la medida a distancia. La respuesta es, claramente, la visión artificial. En este caso hay que colocar una cámara de resolución suficiente apuntada hacia el hilo de contacto por un lateral. Los algoritmos del sistema, bastante sencillos, detectarán el hilo como una línea horizontal en el campo de visión, cuya altura cambiará al pasar el pantógrafo por debajo. Es necesario calibrar el sistema con un montaje de laboratorio: cada píxel que se desplace la línea del hilo corresponderá a una longitud real, cuyo valor exacto dependerá de la distancia horizontal desde la cámara al hilo, la óptica de la cámara y el sensor, similar al de cualquier cámara fotográfica actual, que digitaliza la imagen captada. Para garantizar la toma de imágenes las veinticuatro horas del día, el sistema tendrá que funcionar en el infrarrojo (el cobre del hilo es un buen reflector), con su propia iluminación [Logytel 2023].
Esta aproximación a la medida viene, sin embargo, con sus propios problemas. La niebla densa y, sobre todo, la lluvia, perjudican la visión en infrarrojo, ya que las gotas de agua también son buenas reflectoras. La imagen captada se llena de ruido y, por tanto, se hace más complicado extraer una medida fiable. En cualquier caso, el mayor problema de este tipo de soluciones es su elevado coste. Un sensor de este tipo, junto a sus sistemas auxiliares, puede suponer para la administración ferroviaria desembolsos por encima del centenar de miles de euros.
En el último capítulo de esta serie exploraremos una tecnología cuya novedosa aplicación al comportamiento del contacto pantógrafo-catenaria permitirá superar gran parte de las limitaciones de los sensores actuales.
Bibliografía
[FUTEK 2023] String potentiometer sensor. FUTEK Advanced Sensor Technology Inc. (2023). https://www.futek.com/string-potentiometer
[Logytel 2023] Detector del Comportamiento dinámico del pantógrafo (DCDP). Logytel. (2023). http://logytel.es/soluciones/ferrocarriles/detectores-sensorizacion/detector-del-comportamiento-dinamico-del-pantografo-dcdp/
[Zhou 2022] Zhou, H., Duan, F., Liu, Z., Chen, L., Song, Y., & Zhang, Y. (2022). Study on electric spark discharge between pantograph and catenary in Electrified Railway. IET Electrical Systems in Transportation, 12(2), 128–142. https://doi.org/10.1049/els2.12043
Del mismo autor:
Los límites del Hyperloop
El camión solar: ¿una posibilidad real?
Sobre el autor: Iván Rivera es ingeniero especializado en proyectos de innovación de productos y servicios para ferrocarriles.
El artículo La catenaria: sensores (3/4) se ha escrito en Cuaderno de Cultura Científica.
Las estadísticas del médico que era un asesino en serie
médico
La editorial Capitán Swing no suele publicar muchos libros de matemáticas, pero cuando lo hace suelen ser verdaderas joyas, como Apología de un matemático (del famoso matemático británico Godfrey Harold Hardy), un libro que suelo recomendar habitualmente, Armas de destrucción matemática (de la matemática estadounidense Cathy O’Neil, autora del blog mathbabe.org) o Y me llevo una (del matemático Joseángel Murcia, autor del blog Tocamates, matemáticas y creatividad, junto a la ilustradora Cristina Daura). Hace poco han publicado un nuevo libro, El arte de la estadística, cómo aprender de los datos, del matemático británico David Spiegelhalter, uno de esos interesantes libros construido a partir de ejemplos reales. En palabras de su autor “este libro utiliza problemas del mundo real como punto de partida para la enseñanza de la estadística”.
 Portada del libro El arte de la estadística, cómo aprender de los datos, del matemático británico David Spiegelhalter, publicado recientemente por la editorial Capitán SwingUn médico de familia
Portada del libro El arte de la estadística, cómo aprender de los datos, del matemático británico David Spiegelhalter, publicado recientemente por la editorial Capitán SwingUn médico de familia
El libro El arte de la estadística cayó en mis manos a través de la periodista científica Eva Caballero, directora del programa de divulgación científica La mecánica del caracol, de Radio Euskadi. Ella me pidió que realizase una reseña del mismo en mi colaboración quincenal en su programa. El libro me enganchó desde las primeras páginas, ya que comparto con el autor la filosofía de que se puede responder a preguntas profundas, por ejemplo, qué son las matemáticas y para qué sirven, o en el caso de este libro, la estadística, utilizando ejemplos concretos y reales.
El estadístico británico y miembro del Churchill College (Cambridge), David Spiegelhalter, utiliza ejemplos reales ya desde la primera página del libro. Ante la pregunta que abre la introducción, ¿Por qué necesitamos la estadística?, nos contesta con el ejemplo de la importancia que tuvo la aplicación de la misma en la investigación del caso de Harold Shipman. Este fue un médico de familia británico, considerado el asesino en serie con un mayor número de muertes confirmadas de la historia, motivo por el cual fue apodado “doctor muerte”.
Entre los años 1975 y 1998 inyectó a un mínimo de 218 pacientes (en el primer informe sobre este caso – véase The Shipman Inquiry / La investigación Shipman – se estableció una cantidad de 215 víctimas, que en un informe posterior se elevó a las 218 que son las que se consideran confirmadas en la actualidad), aunque la cifra real se estima que podría estar entre 250 y 509, mayoritariamente ancianos, debidas a “una sobredosis masiva de opiáceos”.
Este médico estuvo asesinando a muchas personas sin que nadie se percatara de ello, hasta que cometió un error, que fue lo que destapó esta enorme serie de asesinatos. En 1998 falsificó el testamento de una de sus víctimas, Kathleen Grundy, de 81 años y exalcaldesa de Hyde (condado de Gran Manchester), para quedarse con todo su dinero, lo cual hizo que la hija de la víctima, que era abogada, empezase a sospechar que había algo raro en la muerte de su madre y en el hecho de que le dejara todo su dinero a su médico. Se exhumó y se analizó el cadáver de Kathleen Grundy y se hallaron rastros de diamorfina (es decir, heroína). Entonces, se siguió investigando. De entre las pacientes que no habían sido incineradas se exhumaron los restos de 15 (incluida Kathleen Grundy), que habían fallecido entre 1995 y 1998, y se encontraron también niveles letales de diamorfina.
Un análisis forense posterior del ordenador de Shipman mostró además que había modificado el historial de algunas de sus pacientes para que pareciesen más enfermas de lo que realmente estaban. Aunque el médico era un apasionado de la tecnología no se percató de que esas modificaciones quedaban registradas, los datos estaban ahí solo había que buscarlos.
En 1999 se le llevó a juicio por el asesinato de esas 15 pacientes, Marie West, Irene Turner, Lizzie Adams, Jean Lilley, Ivy Lomas, Jermaine Ankrah, Muriel Grimshaw, Marie Quinn, Kathleen Wagstaff, Bianka Pomfret, Naomi Nuttall, Pamela Hillier, Maureen Ward, Winifred Mellor, Joan Melia y Kathleen Grundy. El 31 de enero de 2000, el jurado encontró culpable de asesinato a Harold Shipman y el juez le condenó a quince cadenas perpetuas consecutivas y recomendó que nunca fuese liberado: “Usted ha cometido horrendos crímenes. Asesinó a cada una de sus pacientes con una calculada y helada perversión de su capacidad médica. Usted era, antes que nada, el médico de estas personas”.
Era el 13 de enero de 2004, el médico asesino Harold Shipman, con 57 años de edad, se suicidó en su celda, ahorcándose con las sábanas de su cama.
 Fotos de Harold Shipman en prisión
Fotos de Harold Shipman en prisiónDurante el juicio el médico decidió no defenderse y no dijo absolutamente nada, salvo declararse inocente. La cuestión de qué había pasado y el alcance de sus acciones quedó sin resolver, por este motivo se abrió una investigación para intentar conocer cuántos crímenes había cometido realmente. El autor del libro El arte de la estadística, David Spiegelhalter, fue uno de los expertos en estadística que fue convocado en dicha investigación. Se pudo establecer que había asesinado al menos a 218 pacientes y posiblemente a 45 más, aunque podrían ser incluso más aún. Se baraja una cifra entre 250 y 500 personas asesinadas, aunque solo estén confirmadas 218.
Hora de la muerteDavid Spiegelhalter nos muestra algunos estudios estadísticos que proporcionan cierta información sobre el caso del médico asesino Harold Shipman.
Empecemos por una cuestión sencilla que se puede descubrir mirando únicamente al certificado de defunción, la hora del día a la que fallecieron los pacientes del doctor Shipman, y que es un buen ejemplo de cómo un sencillo análisis estadístico puede ayudar a detectar una anomalía, que en este caso escondía una terrible realidad. Se realizó un estudio de la hora a la que murieron los pacientes de este médico y se comparó con las horas a las que morían los pacientes de otros médicos de familia locales. El gráfico que aparece en el libro es contundente.
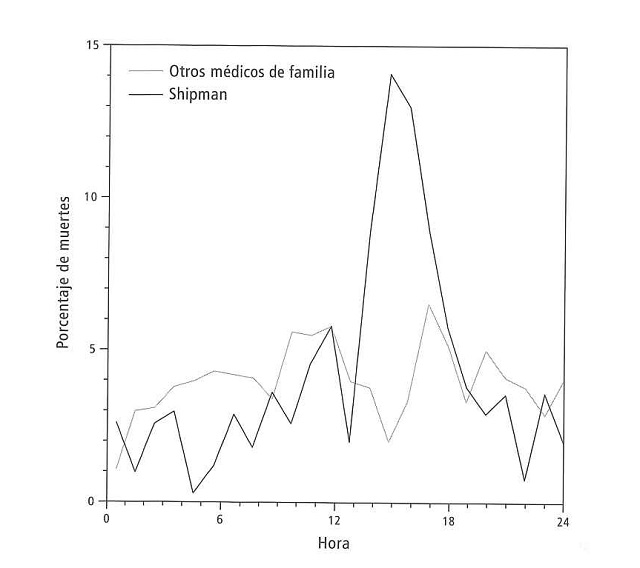 Hora de la muerte de los pacientes del médico Harold Shipman, comparada con las horas en las que murieron los pacientes de otros médicos de familia locales. Imagen del libro El arte de la estadística (Capitán Swing, 2023), de David Spiegelhalter
Hora de la muerte de los pacientes del médico Harold Shipman, comparada con las horas en las que murieron los pacientes de otros médicos de familia locales. Imagen del libro El arte de la estadística (Capitán Swing, 2023), de David SpiegelhalterSi se mira el porcentaje de muertes en las diferentes horas del día de los pacientes de otros médicos de familia locales nos encontramos la típica gráfica que parece una montaña, con subidas y bajadas, pero que están en un rango de entre el 3% y el 6%, a lo largo de todas las horas del día. Por ejemplo, a las 12:00 del mediodía se produce el 5% de las muertes de los médicos locales, mientras que a las 15:00 solo se producen un 2%. Sin embargo, si miramos a la gráfica de los pacientes de Shipman se observa una gran elevación. Entre las 13:30 y las 18:00 el porcentaje de muertes de sus pacientes está entre el 6% y el 14%, es decir, un porcentaje anormalmente alto, si lo comparamos con los otros médicos de familias locales, de las muertes de sus pacientes ocurrían a esas horas.
Los datos hablaban de que ahí había un hecho anómalo, pero no explicaban qué era lo que ocurría, por qué había un pico de muertes a esas horas. Una investigación posterior reveló que el doctor Shipman realizaba visitas a domicilio después de comer, cuando podía estar a solas con sus pacientes ancianos. Les ofrecía una inyección, que supuestamente les ayudaría a estar mejor o no tener dolores, pero que realmente era una dosis letal de diamorfina. Después de que el paciente muriese el médico cambiaba el historial médico del paciente para que pareciese una muerte natural esperada. Aunque una simple autopsia hubiese desvelado que la causa de la muerte era la diamorfina, lo cierto es que la avanzada edad de sus pacientes y que supuestamente habían muerto por causas naturales hizo que dichas autopsias no se llevaran a cabo.
Victimología y año del asesinatoOtro análisis estadístico que muestra David Spiegelhalter respondía a la cuestión de qué tipo de personas asesinó Harold Shipman y cuando las asesinó, en qué año. En el libro se incluye un análisis de dispersión que muestra la edad y el año de la muerte de las 215 víctimas inicialmente confirmadas. Es decir, la edad y el año de la muerte de cada víctima es un punto y podemos analizar cómo se agrupan dichos puntos, que además son oscuros si la víctima era mujer y claros si era hombre.
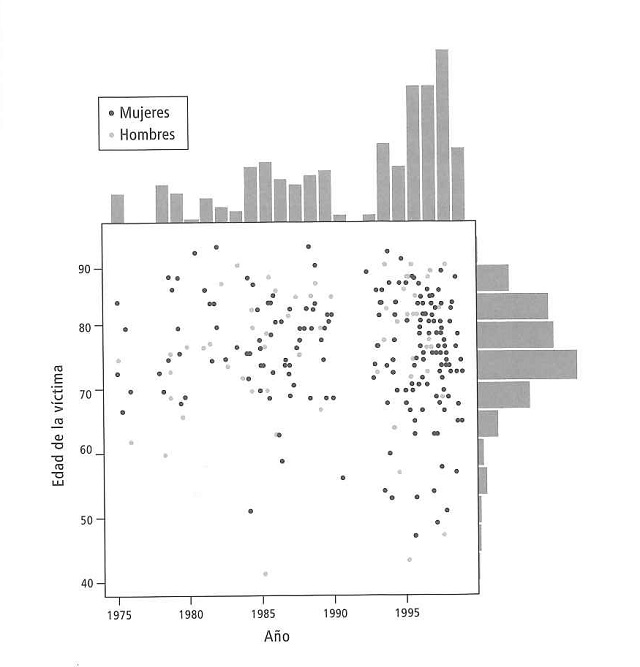
Algunas conclusiones que se podían extraer del diagrama de dispersión eran las siguientes.
i) La mayoría de las víctimas eran mujeres, ya que claramente hay más puntos oscuros.
ii) Las víctimas eran personas mayores, la mayoría de ellas tenía entre 65 y 90 años, pero sobre todo estaban entre los 70 y 85 años.
iii) En el diagrama se puede observar que alrededor del año 1992 hay un periodo en el que no hay víctimas, que luego sigue con un periodo con mucha intensidad, hay una gran acumulación de víctimas y además empieza a asesinar a gente más joven, entre los 42 y 65 años, aunque la mayoría siguen siendo personas ancianas. Este último periodo seguramente coincide con el hecho de que montase una consulta privada, ya que antes compartía consulta con otros médicos.
iv) Hay dos periodos con muchas víctimas, entre 1984 y 1990, y sobre todo el último periodo, que hemos comentado, desde 1993 hasta que lo cogieron.
En este ejemplo la estadística ayudó a extraer información sobre el caso del doctor muerte, a conocer mejor lo que había ocurrido. David Spiegelhalter añade que además “el análisis estadístico formal podía haber ayudado a atrapar antes a Shipman”. De hecho, en el capítulo 10, titulado Responder preguntas y reivindicar descubrimientos, hay un apartado titulado ¿Podría haberse atrapado antes a Harold Shipman?
¿Podría haberse atrapado antes a Harold Shipman?El autor del libro menciona que habría bastado mirar a los certificados de defunción para observar que había algo anómalo. Ya hemos comentado el estudio comparativo entre las horas de los fallecimientos de los pacientes del doctor Shipman y de los pacientes de otros médicos de familia locales, del periodo que va desde 1977 hasta 1998, extraído simplemente de los certificados de defunción. Aunque un análisis estadístico básico era, y así lo hicieron, el estudio comparativo de la cantidad acumulada de defunciones (simplemente contar el número de certificados de defunción) de los pacientes del doctor Shipman y de los pacientes de otros médicos de familia locales (que en la siguiente gráfica se ha separado además también por sexo), desde el año 1977. Se descubrió que la variación entre la mortalidad acumulada (desde 1977) para todos los médicos locales (en la siguiente gráfica la barra horizontal del cero marca la referencia de la mortalidad acumulada de los médicos locales) y la mortalidad acumulada del doctor Shipman, iba creciendo con el paso de los años, cada vez más y especialmente en las mujeres, como se puede observar en la siguiente gráfica, extraída del libro, que es, de nuevo, contundente.
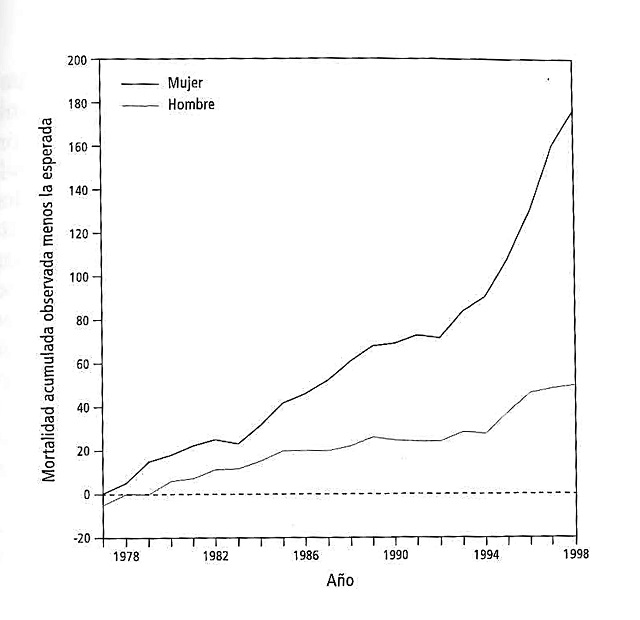 Número acumulado de certificados de defunción firmados por Harold Shipman para pacientes de 65 años o más y que murieron en su casa o en su clínica. Imagen del libro El arte de la estadística (Capitán Swing, 2023), de David Spiegelhalter
Número acumulado de certificados de defunción firmados por Harold Shipman para pacientes de 65 años o más y que murieron en su casa o en su clínica. Imagen del libro El arte de la estadística (Capitán Swing, 2023), de David SpiegelhalterImaginemos que todos los años se hubiese realizado una comparación entre las tasas de defunción de cada médico de familia local, con la tasa esperada de todos ellos. La cuestión que se plantea el autor del libro es ¿cuándo se podría haber dado la voz de alarma? En 1979 ya se observaba una variación de la tasa de mortalidad significativa, pero David Spiegelhalter y su equipo buscaban una variación que garantizara que no había ninguna duda y crearon una serie de márgenes de error (que no explicaremos aquí y que pueden leerse, perfectamente explicados, en el texto El arte de la estadística) y que mostraban que en 1984, con total seguridad, podía afirmarse que se estaban cometiendo asesinatos de pacientes del doctor Shipman, al menos, que algo extraño estaba ocurriendo, y haber iniciado una investigación para dilucidar qué provocaba esas variaciones.
Si se hubiese realizado esta supervisión de los médicos de familia se habría llegado a detener al doctor Shipman en 1984, evitando la muerte de unas 175 personas.
Después de este caso se realizó una supervisión de los médicos de familia, la cual desveló la existencia de otro médico con tasas de mortalidad muy altas, y que, por lo tanto, se investigó. La investigación desveló que se trataba de un médico que ejercía en una ciudad costera con muchas residencias de la tercera edad, con muchas personas mayores, y que no había nada anómalo en su comportamiento. Esto nos muestra que la estadística suele detectar los resultados atípicos, y que luego hay que analizar el motivo por el cual son atípicos. O de otra forma, como dice el autor del libro, “cuidado con los algoritmos”.
 David Spiegelhalter, autor del libro El arte de la estadística, cómo aprender de los datos (Capitán Swing, 2023)
David Spiegelhalter, autor del libro El arte de la estadística, cómo aprender de los datos (Capitán Swing, 2023)Bibliografía
1.- David Spiegelhalter, El arte de la estadística, cómo aprender de los datos, Capitán Swing, 2023.
2.- Mónica G. Álvarez, Harold Shipman, el afable médico adicto al crimen: “Soy un ser superior”, La Vanguardia, 3 de abril de 2020.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Las estadísticas del médico que era un asesino en serie se ha escrito en Cuaderno de Cultura Científica.
Los microbios ganaron poderes fotosintéticos gracias a una bomba de protones
bomba de protones
Una nueva investigación revela cómo los microbios marinos usan una membrana adicional que alguna vez tuvo funciones digestivas para aumentar su rendimiento de la fotosíntesis.
Un artículo de Saugat Bolakhe. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Los diversos microbios acuáticos de formas intrincadas llamados diatomeas son extraordinariamente efectivos para convertir el dióxido de carbono en moléculas orgánicas a través de la fotosíntesis. Fuente: Steve Gschmeissner/Science Source; modificado por Quanta Magazine
Los diversos microbios acuáticos de formas intrincadas llamados diatomeas son extraordinariamente efectivos para convertir el dióxido de carbono en moléculas orgánicas a través de la fotosíntesis. Fuente: Steve Gschmeissner/Science Source; modificado por Quanta MagazineUna densa selva tropical u otra vegetación terrestre verde puede ser lo primero que viene a la mente al mencionar la fotosíntesis. Sin embargo las nubes de fitoplancton que llenan los océanos son las principales impulsoras de ese proceso en la naturaleza. Los microbios acuáticos unicelulares similares a plantas generan más del 50 % del oxígeno de la atmósfera y absorben casi la mitad del dióxido de carbono, convirtiéndolo en glucosa, grasas, proteínas y otras moléculas orgánicas que nutren la red alimentaria de los océanos. .
Un estudio publicado recientemente en Current Biology ha determinado finalmente la fuente de esta eficiencia fotosintética sin precedentes, que ha desconcertado a los científicos durante mucho tiempo. La nueva investigación descubrió que algunos fitoplánctones están equipados con una membrana interna adicional que lleva una enzima «bomba de protones» que potencia su capacidad para convertir el dióxido de carbono en otras sustancias. Las mejoras debidas a esta modificación de proteína parecen contribuir a la producción de casi el 12% del oxígeno del aire y hasta el 25% de todo el carbono «fijado» (bloqueado en compuestos orgánicos) en el océano.
Sorprendentemente, esta innovación fotosintética parece haber evolucionado por casualidad a partir de una proteína de membrana que se utilizó originalmente para la digestión en el ancestro del fitoplancton. Además de explicar la eficiencia de las células en la fotosíntesis, el nuevo trabajo ayuda a confirmar la teoría de que ese fitoplancton surgió a partir de una alianza simbiótica entre un protozoo y una resiliente alga roja.
«Me parece asombroso que una enzima de protones que conocemos desde hace tantas décadas sea responsable de mantener un fenómeno tan crucial en la Tierra», afirma Dennis Brown, biólogo celular de la Escuela de Medicina de Harvard que estudia las funciones de las proteínas de membrana y no ha estado involucrado en el estudio.
Los investigadores sabían que ciertas clases de fitoplancton (diatomeas, dinoflagelados y cocolitóforos) destacan por sus excepcionales habilidades fotosintéticas. Estas células son extremadamente hábiles en absorber dióxido de carbono de su entorno y dirigirlo a sus cloroplastos para la fotosíntesis, pero los detalles de por qué son tan buenas en esto no estaban muy claros. Sin embargo, una característica exclusiva de esos tres grupos de fitoplancton es que tienen una membrana extra alrededor de sus cloroplastos.
Hace siete años, el microbiólogo Daniel Yee, el primer autor del nuevo estudio, estaba estudiando diatomeas para su doctorado en la Institución Scripps de Oceanografía de la Universidad de California en San Diego. La fotosíntesis no era su objetivo; buscaba comprender cómo las diatomeas regulan su acidez interna para ayudar con el almacenamiento de nutrientes y construir su resistente pared celular de sílice. Pero notaba repetidamente la característica membrana adicional alrededor de sus cloroplastos.
Aprendió que la membrana adicional era ampliamente considerada por los investigadores como un remanente de un antiguo acto fallido de digestión. Los científicos habían planteado la hipótesis de que, hace unos 200 millones de años, un protozoo depredador había tratado de darse un festín con un alga fotosintética unicelular. Envolvió a la resiliente alga en una estructura membranosa llamada vacuola alimenticia para digerirla pero, por razones desconocidas, la digestión no ocurrió. En cambio, el alga sobrevivió y se convirtió en una compañera simbiótica del protozoo, alimentándolo con los frutos de su fotosíntesis. Esta asociación se hizo más profunda a lo largo de las generaciones hasta que el nuevo organismo dos-en-uno evolucionó hasta convertirse en las diatomeas que conocemos hoy. Pero la capa de membrana adicional que había sido una vacuola alimenticia no desapareció.
A fines de la década de 1990, algunos científicos plantearon la hipótesis de que era probable que la antigua vacuola alimenticia todavía poseyese una proteína transmembranal llamada bomba de protones. Las bombas de protones son moléculas muy versátiles que pueden especializarse para diversas tareas en los organismos, desde la digestión hasta la regulación de la acidez de la sangre y ayudar a las neuronas a enviar señales, explica el microbiólogo Martin Tresguerres, coautor principal del nuevo estudio y antiguo director de tesis de Yee en la UCSD. En los mamíferos, un tipo de bomba de protones puede crear condiciones ácidas altamente corrosivas dentro de áreas de los huesos para descomponer su estructura mineralizada y disolverla con el tiempo.
Yee descubrió que la misma bomba de protones también ayuda a las diatomeas a fabricar su resistente caparazón de sílice. Pero considerando la versatilidad de la bomba de protones y su asociación directa con el cloroplasto, estaba convencido de que hacía aún más.
Usando una combinación de técnicas de biología molecular, Yee y su equipo confirmaron que la membrana adicional alrededor del cloroplasto del fitoplancton contiene una bomba de protones activa y funcional, una llamada VHA, que a menudo cumple una función digestiva en las vacuolas alimenticias. Incluso fusionaron la bomba de protones con una proteína fluorescente para poder verla funcionar en tiempo real. Sus observaciones respaldaron la teoría endosimbiótica de cómo las diatomeas adquirieron la membrana adicional alrededor de sus cloroplastos.
Yee, Tresguerres y sus colegas también tenían curiosidad sobre cómo la bomba de protones podría afectar a la actividad fotosintética del cloroplasto. Para averiguarlo, utilizaron un fármaco inhibidor, la concanamicina A, para detener el funcionamiento de la bomba de protones mientras controlaban cuánto carbono seguía el fitoplancton incorporando formando carbonatos y produciendo oxígeno. Encontraron que la inhibición de la bomba de protones disminuyó significativamente tanto la fijación de carbono como la producción de oxígeno en las células.
Trabajo adicional les ayudó a comprender que la bomba mejoraba la fotosíntesis al concentrar el carbono cerca de los cloroplastos. La bomba transfería protones desde el citoplasma al espacio entre la membrana extra y el cloroplasto. El aumento de la acidez en este compartimento provocaba que más carbono (en forma de iones bicarbonato) se difundiera en él para neutralizarlo. Las enzimas convirtían el bicarbonato nuevamente en dióxido de carbono, que estaba entonces convenientemente cerca de las enzimas fijadoras de carbono del cloroplasto.
Usando estadísticas sobre la distribución de las diatomeas y otro fitoplancton con la membrana adicional en todo el océano global, los investigadores extrapolaron que este aumento en la eficiencia de la proteína de membrana VHA representa casi el 12% del oxígeno atmosférico de la Tierra. También aporta entre el 7% y el 25% de todo el carbono oceánico fijado cada año. Eso es al menos 3.500 millones de toneladas de carbono, casi cuatro veces más de lo que emite anualmente la industria de la aviación mundial. En el extremo superior de la estimación de los investigadores VHA podría ser responsable de retener hasta 13.500 millones de toneladas de carbono al año.
Los científicos ahora pueden agregar este factor a otras consideraciones al estimar los efectos del cambio climático en la rapidez con la que el dióxido de carbono atmosférico se fija en moléculas orgánicas, lo que determina la rapidez con la que el planeta continuará calentándose. También se relaciona con las discusiones sobre si los cambios en la acidez del océano tendrán un impacto directo en las tasas de fijación de carbono y producción de oxígeno. Yee afirma que los científicos también pueden comenzar a preguntarse si las soluciones biotecnológicas basadas en el mecanismo recién descubierto podrían mejorar el proceso de secuestro de carbono para limitar el cambio climático.
Yee, que ahora es becario postdoctoral en el Laboratorio de Fisiología Celular y Vegetal del Centro Nacional Francés de Investigación Científica en Grenoble, se enorgullece de que su equipo haya podido proporcionar un nuevo mecanismo sobre cómo ocurre la fotosíntesis en una forma de vida tan importante desde el punto de vista ecológico.
“Pero también nos damos cuenta”, concluye, “que cuanto más aprendemos, menos sabemos”.
El artículo original, Microbes Gained Photosynthesis Superpowers From a ‘Proton Pump’, se publicó el 5 de julio de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo Los microbios ganaron poderes fotosintéticos gracias a una bomba de protones se ha escrito en Cuaderno de Cultura Científica.
El núcleo de Marte
núcleo de marte
Para la geología es fundamental el conocer como son y en qué estado se encuentran las distintas capas que conforman el interior de los distintos cuerpos del Sistema Solar, ya que eso puede aportarnos pistas sobre su formación, composición y grado de actividad. Aunque a grandes rasgos y gracias a las medidas indirectas desde la órbita y a cada vez mejores modelos numéricos empezamos a conocer como son los planetas -y otros cuerpos- por dentro, necesitamos misiones que nos permitan ver detalles más finos. Gracias a misiones como la InSight, que llegó a Marte en noviembre de 2018 y concluyó su misión en diciembre de 2022, estamos empezando a conocer mucho mejor el interior del planeta rojo. Probablemente durante años veamos aparecer nuevos artículos con interpretaciones de los datos y modelos sobre el interior que nos ayuden a comprender por qué este planeta evolucionó de una manera tan diferente a la Tierra.
 En esta representación artística podemos ver el módulo de aterrizaje de la misión InSight, junto con el “topo” introducido en el suelo marciano -a la derecha- y a la izquierda el instrumento SEIS, del que no vemos directamente el sismómetro, sino que apreciamos la cúpula que le sirve para mantenerse aislado de los cambios de temperatura y el impacto del viento. Imagen cortesía de la NASA/JPL.
En esta representación artística podemos ver el módulo de aterrizaje de la misión InSight, junto con el “topo” introducido en el suelo marciano -a la derecha- y a la izquierda el instrumento SEIS, del que no vemos directamente el sismómetro, sino que apreciamos la cúpula que le sirve para mantenerse aislado de los cambios de temperatura y el impacto del viento. Imagen cortesía de la NASA/JPL.Dos de sus instrumentos, SEIS -un sismómetro e instrumento principal de la misión- y RISE -un experimento que aprovecha el sistema de comunicaciones de la sonda para conocer mejor la rotación y el “bamboleo” del planeta- han demostrado con creces ser muy sensibles y útiles para ayudarnos a conseguir una “radiografía” del planeta y estudiar distintos procesos geológicos que van desde los terremotos y la posible actividad volcánica hasta la redistribución de masas entre la superficie del planeta y la atmósfera debido a la transferencia del dióxido de carbono que ocurre a causa de las estaciones.
Lo importante de tener dos instrumentos como estos de manera simultánea sobre el planeta es que, aunque usen metodologías muy diferentes, nos permiten comprobar si efectivamente los modelos de su interior generados a partir de ambos instrumentos se parecen y son comparables… algo que efectivamente ha sido así y que vamos a intentar explicar que se ha visto exactamente y que implicaciones tiene.
Empecemos por los datos de SEIS. Como decíamos anteriormente, SEIS es un sismómetro muy sensible, capaz de detectar las ondas sísmicas provocadas por los terremotos o el impacto de los meteoritos, entre otros eventos. Las ondas sísmicas, cuando viajan por el interior del planeta desde el punto donde ha ocurrido el terremoto -y que llamamos hipocentro- ven su velocidad y trayectoria alterada por el cambio de propiedades y composición de los materiales que van atravesando, ya que el interior de los planetas no suele ser homogéneo.
Para poder detectar mediante este instrumento la capa más interna de Marte, en este caso el núcleo del planeta, SEIS necesitaba detectar terremotos que hubiesen ocurrido lo suficientemente lejos como para que las ondas sísmicas que le llegasen hubiesen tenido que atravesar el núcleo o haber rebotado en la interfaz entre el manto y el núcleo.
Esto, a priori, y dado el grado de actividad geológica de Marte, podría resultar complicado en el tiempo que durara la misión, ya que tendrían que ocurrir terremotos de suficiente magnitud a una distancia importante y que fuesen detectados por la InSight -no podemos dejar de lado que una de las grandes zonas potenciales donde podría haber terremotos en Marte se encuentra, con respecto a la InSight, en lo que denominamos como zona de sombra sísmica-, pero todo cambió entre los soles 976 y 1000 -hablamos de eventos sísmicos ocurridos en 2021-, cuando un terremoto y el impacto de un cuerpo contra la superficie del planeta permitieron al sismómetro detectar las ondas atravesando el núcleo del planeta rojo.
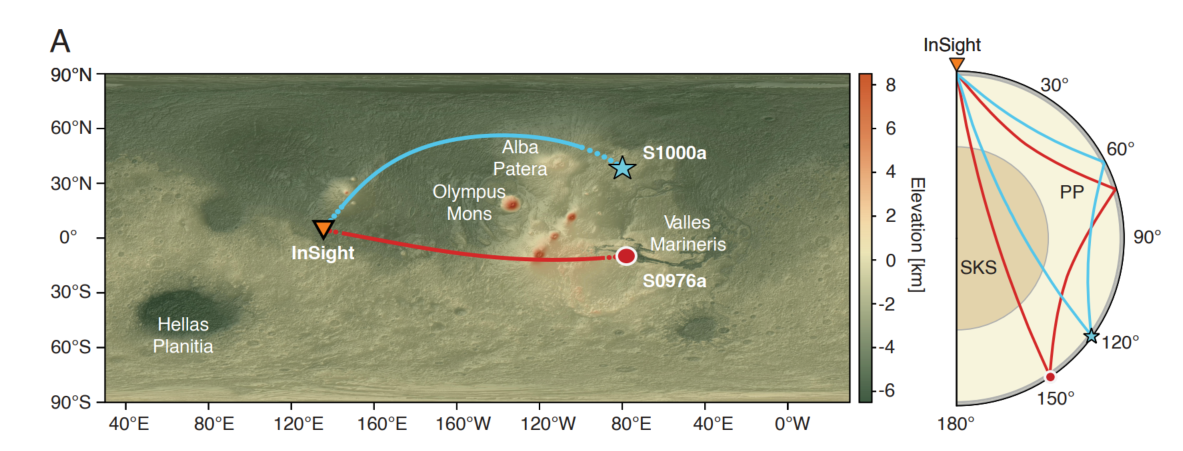 Imagen la que podemos ver la localización de la InSight sobre un mapa topográfico de Marte y la localización de los dos epicentros de los terremotos detectados. También, a la derecha, podemos ver las fases sísmicas que llegaron al sismómetro y que permitieron reconocer el núcleo interno, como es en este caso la fase SKS. Imagen cortesía de Irving et al. (2023).
Imagen la que podemos ver la localización de la InSight sobre un mapa topográfico de Marte y la localización de los dos epicentros de los terremotos detectados. También, a la derecha, podemos ver las fases sísmicas que llegaron al sismómetro y que permitieron reconocer el núcleo interno, como es en este caso la fase SKS. Imagen cortesía de Irving et al. (2023).Para que nos hagamos una idea de la distancia, el epicentro del terremoto estaría localizado a una distancia entre los 7424 y los 8468 kilómetros, mientras que el impacto ocurrió a una distancia de unos 7300 kilómetros. La diferencia en la precisión en la localización entre el terremoto y el impacto se debe a un factor: mientras que el lugar del impacto ha sido observado directamente por la Mars Reconaissance Orbiter, y por lo tanto, establecer unas coordenadas muy precisas, calcular el epicentro de un terremoto requiere de que tengamos un modelo a priori del interior del planeta que nos permita establecer el comportamiento de las ondas sísmicas, lo que en el caso de Marte tiene mucha incertidumbre.
En 2021, Stähler et al. ya publicaron las primeras estimaciones del tamaño del núcleo de Marte basándose en las ondas reflejadas en la interfaz manto-núcleo, y obteniendo un valor de unos 1830±40 kilómetros, pero estos datos, aunque importantes no son suficientes… y es que, ¿de qué está compuesto y en que estado está el núcleo de Marte? Si bien es cierto que en este artículo ya se tratan algunas de las cuestiones fundamentales, era preciso el poder observar las ondas atravesando el núcleo para poder confirmar algunas de las sospechas que tenían los científicos, como los que aportan el artículo de Irving et al. (2023).
El primer detalle que salta a la vista es que el núcleo de Marte contiene, además del hierro, alrededor de un 20% de elementos ligeros como el azufre, el oxígeno el hidrógeno y el carbono, una diferencia importante si lo comparamos con la Tierra, donde el núcleo externo, por ejemplo, tiene aproximadamente un 10% de elementos ligeros.
El segundo es que no se ha observado, de momento, un núcleo interno sólido como tiene nuestro planeta y que, si existe, debería de tener un radio menor de los 750 kilómetros, y probablemente, para cerrar esta cuestión de una manera definitiva, se necesiten de nuevas misiones en superficie.
Como decíamos al principio, hay otro instrumento, en este caso RISE, capaz de aportarnos pistas de una manera más indirecta del interior del planeta. Y es que este instrumento es capaz de medir el efecto Doppler resultante de minúsculas variaciones que ocurren tanto en la rotación de Marte como en la orientación de su eje, y para lo que tenemos que imaginarnos al planeta Marte como una peonza girando.
 Representación artística del interior de Marte en la que podemos apreciar los epicentros y trayectoria de las ondas de los terremotos detectados por la InSight y el tamaño de la corteza, manto y núcleo marcianos. Imagen cortesía de NASA/JPL-Caltech/University of Maryland.
Representación artística del interior de Marte en la que podemos apreciar los epicentros y trayectoria de las ondas de los terremotos detectados por la InSight y el tamaño de la corteza, manto y núcleo marcianos. Imagen cortesía de NASA/JPL-Caltech/University of Maryland.Pues bien, de este experimento se ha deducido un radio para el núcleo de Marte de unos 1835±55 kilómetros, un valor dentro del rango de los anteriores estudios y que muestra que los cálculos entre diferentes estudios son coherentes entre sí, pero con una diferencia: en este modelo, por ejemplo, no habría cabida para un núcleo sólido, sino que todo se encontraría en estado líquido. Este último dato podría apuntar a que la inexistencia de un núcleo sólido fuese una de las causas del fin del campo magnético global de Marte.
Este modelo también está de acuerdo con el porcentaje aproximado de un 20% de elementos ligeros en el núcleo que también aparece en Irving et al. (2023), donde el más abundante de los ligeros sería el azufre -con un 15±2% en peso-, seguido del oxígeno -con un 2.5±0.5%-, el carbono -con un 1.5±0.5%- y por último el hidrógeno con alrededor del 1%.
Por último, gracias a los datos de RISE se ha descubierto una ligera tendencia al acortamiento de los días de la que se desconoce su origen, pero que podría ser debida o bien a la dinámica climática y a la transferencia de materia entre los casquetes polares y la atmósfera -y viceversa- o a factores internos.
Sin duda, misiones como la InSight, y que a simple vista nos pueden parecer menos atractivas que otras mucho más complejas y espectaculares como las que llevan a cabo los rovers sobre Marte, ponen de manifiesto que podemos aprender todavía mucho más sobre el interior de Marte igual que a principios del siglo XX empezamos a hacer en nuestro propio planeta gracias al avance de la sismología.
Referencias:
Irving, Jessica C. E., Vedran Lekić, Cecilia Durán, Mélanie Drilleau, Doyeon Kim, Attilio Rivoldini, Amir Khan, et al. «First Observations of Core-Transiting Seismic Phases on Mars». Proceedings of the National Academy of Sciences 120, n.º 18 (2 de mayo de 2023): e2217090120. doi: 10.1073/pnas.2217090120.
Le Maistre, Sébastien, Attilio Rivoldini, Alfonso Caldiero, Marie Yseboodt, Rose-Marie Baland, Mikael Beuthe, Tim Van Hoolst, et al. «Spin State and Deep Interior Structure of Mars from InSight Radio Tracking». Nature, 14 de junio de 2023. doi: 10.1038/s41586-023-06150-0.
Stähler, Simon C., Amir Khan, W. Bruce Banerdt, Philippe Lognonné, Domenico Giardini, Savas Ceylan, Mélanie Drilleau, et al. «Seismic Detection of the Martian Core». Science 373, n.º 6553 (23 de julio de 2021): 443-48. doi: 10.1126/science.abi7730.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El núcleo de Marte se ha escrito en Cuaderno de Cultura Científica.
Crecen los efectos nocivos de la contaminación lumínica en la astronomía
contaminación lumínica
La luz artificial nocturna, el despliegue de constelaciones de satélites y las interferencias de radio están impactando negativamente en las observaciones astronómicas, limitando los descubrimientos científicos, nuestras conexiones culturales con el cielo nocturno y las posibilidades del astroturismo.
 Cielo nocturno desde el destino turístico Starlight Pampa Joya (Antofagasta, Chile). Foto: Braham Millal (foto premiada en el V Maratón de Fotografía Starlight en la temática «Contaminación lumínica»)
Cielo nocturno desde el destino turístico Starlight Pampa Joya (Antofagasta, Chile). Foto: Braham Millal (foto premiada en el V Maratón de Fotografía Starlight en la temática «Contaminación lumínica»)A lo largo de la historia de la humanidad, mirar al cielo estrellado ha sido una fuente de inspiración para la humanidad. Así nació la astronomía, como un elemento común en todas las culturas que, desde antiguo, se ha utilizado para establecer calendarios, navegar, descubrir nuevas tierras e impulsar muchas investigaciones científicas.
Pero en las últimas décadas la comunidad astronómica, tanto de profesionales como de aficionados, ha comprobado que cada vez es más difícil desarrollar su labor debido a la creciente contaminación lumínica y otras nuevas amenazas: las nuevas constelaciones de satélites y las interferencias de radio.
Hasta hace solo un par de años nuestra principal preocupación se centraba en la pérdida progresiva del cielo nocturno debido al creciente aumento de la contaminación lumínica, con aproximadamente un 10 % de crecimiento al año y una cuarta parte de la superficie del planeta ya contaminada.
Fuimos los astrónomos los primeros en advertir de este problema y los que señalamos que este deterioro tenía serias implicaciones, no solo en la ciencia sino también en el medioambiente (existe una relación entre sobreiluminación y cambio climático que el público desconoce), en la biodiversidad, la salud, el patrimonio cultural asociado al cielo nocturno y en el desarrollo socioeconómico sostenible a través del astroturismo.
Pero en los últimos años hemos visto despuntar nuevas y muy serias amenazas para la astronomía profesional y amateur. El despliegue de un gran número de satélites en órbita terrestre baja (LEO) ha tenido un impacto imprevisto. Al darnos cuenta, ya los teníamos sobre nuestras cabezas.
Cuando se lanzó un lote prototipo de 60 naves de este tipo en mayo de 2019, los astrónomos se sorprendieron por lo brillantes que parecían desde el suelo. Entre el 5 y el 10 % de estos satélites están presentes sobre lugares astronómicos en un momento dado, y una proporción de ellos está iluminada por el Sol en un cielo oscuro.
 Estrella Albireo en la constelación del Cisne tomada el 26 de diciembre de 2019. Dos de las diez exposiciones de 2,5 minutos grabaron satélites Starlink moviéndose por el campo. Foto: Rafael Schmall
Estrella Albireo en la constelación del Cisne tomada el 26 de diciembre de 2019. Dos de las diez exposiciones de 2,5 minutos grabaron satélites Starlink moviéndose por el campo. Foto: Rafael SchmallCon planes de hasta 400.000 satélites en estas constelaciones para 2030, miles serán visibles desde cada lugar en cualquier momento. Hasta el 30 % de las exposiciones de campo amplio en un gran telescopio se perderían durante las primeras horas de la tarde y antes del amanecer, y casi el 50 % de las exposiciones crepusculares estarían contaminadas.
Uno de los proyectos que se verán fuertemente afectados serán los estudios automatizados en busca de objetos en movimiento como asteroides potencialmente peligrosos.
El tercer problema son las interferencias de radio. La radioastronomía consiste en observar el universo en longitudes de onda que también son utilizadas por las radiocomunicaciones generadas por el hombre. Hemos convivido con ellas y con acuerdos internacionales que permitían definir bandas de radio protegidas.
Pero el incremento del ancho de banda y de la potencia de transmisión de las radiocomunicaciones ha provocado un aumento de las interferencias de radiofrecuencia en las observaciones astronómicas.
El despliegue de constelaciones LEO también producirá cientos de fuentes de radiointerferencias brillantes en rápido movimiento, visibles para los radiotelescopios a cualquier hora del día.
España es pionera en la conservación del cieloLa contaminación lumínica cuenta ya con regulaciones eficaces y tecnología para su disminución y ya se están dando algunos pasos en algunos países como en España que ha sido pionero en la preservación del cielo con la Ley del Cielo de 1988 de Canarias, pero me temo que el riesgo por las megaconstelaciones avanza muy rápidamente y es demoledor.
Los primeros satélites (década de 60 y hasta ahora) no eran maniobrables, pero el avance en la tecnología espacial ha contribuido a construir satélites cada vez más resistentes y maniobrables. Estos ya disponen de sistemas de propulsión que les permiten cambiar su órbita, así como desviarse de trayectorias de objetos entrantes y evitar colisiones, consiguiendo así misiones más largas.
La proliferación de pequeños satélites eleva los riesgos de colisión, especialmente en la órbita baja que ya está densamente poblada y, por tanto, aumentan el riesgo de colisión y de generar basura espacial. Estos impactos pueden poner en peligro satélites de observación, de vigilancia terrestre y para comunicaciones, cruciales para nuestra seguridad entre otros aspectos.
Por otra parte, están los satélites Starlink (operados por la compañía Space X de Elon Musk), equipados con sistemas de propulsión que pueden utilizarse para maniobrarlos fuera del camino de posibles colisiones. Esto podría ayudar a reducir el riesgo de colisiones y evitar aumentar aún más la cantidad de desechos en el espacio. Pero su creciente número no hará sino aumentar este riesgo y el espacio será cada vez menos sostenible.
Amenaza para la astronomía profesional y amateurEsta contaminación lumínica, en su conjunto, amenaza los observatorios astronómicos profesionales, que se localizan precisamente en lugares remotos del planeta por contar con cielos muy oscuros. Cualquier resplandor del cielo puede saturar la débil señal de los objetos astronómicos, impidiendo su detección.
Sin embargo, las observaciones astronómicas terrestres impulsan importantes descubrimientos de gran repercusión en astrofísica y física fundamental y, a menudo, son esenciales para interpretar las observaciones de los telescopios espaciales. Actualmente existen más de 40 telescopios ópticos terrestres con espejos de 3 metros o más de diámetro.
Por su parte, la astronomía amateur también está fuertemente amenazada por la también llamada luz artificial de la noche (ALAN) y las megaconstelaciones de satélites LEO, especialmente en los ámbitos de los programas de investigación con científicos profesionales, la astrofotografía y el astroturismo.
 Ejemplo de contaminación lumínica, sobre todo por el uso de leds blancos y azules y el escaso blindaje de las luminarias. Cielo nocturno fotografiado desde la isla de Sálvora, en el Parque Nacional de las Islas Atlánticas en Galicia, certificado como Destino Turístico Starlight. Foto: Fernando Rey
Ejemplo de contaminación lumínica, sobre todo por el uso de leds blancos y azules y el escaso blindaje de las luminarias. Cielo nocturno fotografiado desde la isla de Sálvora, en el Parque Nacional de las Islas Atlánticas en Galicia, certificado como Destino Turístico Starlight. Foto: Fernando ReyAproximadamente un millón de personas se dedican a la astronomía amateur, dos órdenes de magnitud más que el número de astrónomos profesionales. Los aficionados utilizan cámaras y telescopios con campos de visión más amplios que los grandes telescopios, por lo que es más probable que sus imágenes contengan estelas de satélites artificiales.
Los astrónomos aficionados descubren cometas, buscan supernovas en las galaxias, realizan campañas de seguimiento de estrellas variables y meteoritos, y confirman candidatos a exoplanetas.
Estas operaciones son especialmente vulnerables a la contaminación lumínica porque este colectivo no tiene acceso a los recursos económicos y tecnológicos necesarios para mitigar sus efectos. El incremento de la luz artificial nocturna y las megaconstelaciones satelitales compromete seriamente estas actividades, que serán prácticamente imposibles en la próxima década si se mantienen las tendencias actuales.
Asimismo, la demanda de certificación y formación en astroturismo ha crecido más de un 300 % en los últimos cinco años, atrayendo a decenas de miles de visitantes y proporcionando un retorno económico de más de cien millones de dólares en múltiples territorios, crecimiento que también se ve amenazado por el aumento de la contaminación lumínica.
En busca de solucionesEs absolutamente necesario que trabajemos juntos y coordinadamente las partes interesadas (observatorios, industria, comunidad astronómica, organismos de financiación de la ciencia, responsables políticos nacionales e internacionales) sobre las medidas técnicas y políticas necesarias para limitar el impacto de la contaminación lumínica, radiofrecuencias y megaconstelaciones en la astronomía.
Respecto a estos últimos, las observaciones astronómicas se beneficiarían enormemente si las constelaciones de satélites planificadas utilizaran el menor número posible de naves espaciales (siendo el número óptimo cero) y mantuvieran las órbitas de los satélites bajas para que entraran en la sombra de la Tierra poco después de la puesta de sol.
También se necesitan establecer estrictasregulaciones y normativas nacionales e internacionales y vigilar su cumplimiento. En este sentido es esperanzador el papel que desempeña el recientemente creado Centro para Protección del Cielo (CPS) oscuro y silencioso de interferencias de megaconstelaciones de la Unión Astronómica Internacional (IAU).
Es necesario un pacto mundial en defensa del cielo. Esto implica educar y concienciar a la sociedad en su conjunto, algo que hacemos desde la Fundación Starlight a través de la difusión de la astronomía y el desarrollo socioeconómico local de las comunidades locales a través del astroturismo.
También sumando adhesiones a la Declaración Mundial de La Palma en Defensa del cielo Nocturno y el Derecho a la Luz de las Estrellas, y dando un paso más, defendiendo ante Naciones Unidas junto con la asociación de mujeres empresarias y profesionales BPW Spain, que el cielo sea un objetivo de desarrollo sostenible, porque sin cielo no hay planeta.
Referencia:
Varela Perez, A. (2023) The increasing effects of light pollution on professional and amateur astronomy Science doi: 10.1126/science.adg0269
Sobre la autora: Antonia M. Varela Pérez es investigadora de Instituto de Astrofísica de Canarias (IAC) y directora de la Fundación Starlight
Este texto apareció originalmente en SINC.
El artículo Crecen los efectos nocivos de la contaminación lumínica en la astronomía se ha escrito en Cuaderno de Cultura Científica.
¿Qué nos enferma a los humanos?

Cómo influyen los parásitos en el comportamiento de los animales, cómo se modifica la conducta de las madres mamífero o cuáles son las enfermedades que nos afectan y desde cuándo hemos desarrollado comportamientos funerarios ante la muerte son algunos de los aspectos que se analizarán en la V Jornada Nacional sobre Evolución y Neurociencias.
Especialistas en ambas materias se reunirán el 11 y 12 de mayo en una nueva edición conducida por Eva Garnica y Pablo Malo, psiquiatras y miembros de la Red de Salud Mental de Bizkaia, y organizada por esa misma entidad y la Cátedra de Cultura Científica de la UPV/EHU.
La jornada, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolucionista y divulgar de un modo accesible para todos los públicos.
Nunca estamos sanos al 100 % sanos, ni al borde de la muerte estás completamente enfermo. La salud es un espectro en el que nos movemos continuamente. ¿Qué es lo que hace que nos movamos hacia la enfermedad? Sari Arponen apunta algunas pautas.
Sari Arponen es doctora en Ciencias Biomédicas por la Universidad Complutense de Madrid, profesora universitaria en la Universidad Camilo José Cela y experta en microbiota. Licenciada en Medicina por la Universidad de Murcia, se especializó en Medicina Interna en el Hospital Universitario de la Princesa de Madrid. Es autora de varios libros.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo ¿Qué nos enferma a los humanos? se ha escrito en Cuaderno de Cultura Científica.
¿Se puede oler el párkinson?
párkinson
 Foto: Pexels / Pixabay
Foto: Pexels / PixabayPor curioso que parezca, ciertas enfermedades se pueden relacionar con distintos olores característicos. Por ejemplo, la diabetes puede hacer que el aliento huela a manzanas podridas; la insuficiencia renal, que lo haga a amoníaco u orina; mientras que la enfermedad hepática grave se ha relacionado con el olor del aliento a moho, ajo y huevos podridos. Las personas con esquizofrenia pueden tener un aroma corporal característico que recuerda al del moho.
Quizás se pregunte: ¿por qué cambia el olor de una persona cuando está enferma? Resulta que nuestros cuerpos expulsan constantemente sustancias volátiles al aire que respiramos, mediante el aliento, sudoración, excreciones, etc. El aroma de estas sustancias puede variar dependiendo de la edad, el estilo de vida y la dieta, pero también si una enfermedad produce alteraciones en nuestro organismo.
La mujer que puede oler el párkinsonLa escocesa Joy Milne acudió con su marido Les, diagnosticado con párkinson, a una conferencia sobre esta patología. Unos años antes de que Les fuese diagnosticado, Joy notó que el olor de su esposo había cambiado: se había vuelto más almizclado, parecido al de la madera. Pero la sorpresa llegó cuando Joy reconoció ese mismo olor en la conferencia, donde la sala estaba llena de personas afectadas por párkinson.
En una posterior conferencia, realizada en Escocia en 2012, Joy, nerviosa ante la mirada de los espectadores, se lo comentó al ponente de la conferencia, el investigador de la Universidad de Edimburgo Tilo Kunath. Este contactó con la química analítica de la Universidad de Mánchester, Perdita Barran, para conocer su opinión al respecto.
Aunque Kunath estaba esperanzado, Barran se encontraba algo escéptica. Finalmente hicieron una prueba a ciegas, donde le dieron a oler seis camisetas usadas por personas con párkinson y otras seis de controles sanos. Joy consiguió identificar las prendas de las personas enfermas y, además, marcó la prenda de uno de los controles sanos como si tuviese la dolencia. Un buen porcentaje de acierto que intrigó aún más a los investigadores cuando la persona supuestamente sana fue diagnosticada con párkinson nueve meses después.
¿Sirve el olfato para hacer diagnósticos precoces?Tras este trabajo piloto, se siguió investigando, y en 2019 se publicó un estudio, dirigido por Barran y financiado por Parkinson’s UK y la Michael J. Fox Foundation, donde participaron 64 personas, 21 controles y 43 pacientes. En él pasaban una gasa por la parte trasera del cuello y la parte superior de la espalda para analizar los componentes presentes en el sebo, un biofluido ceroso que contiene compuestos volátiles olorosos y es rico en lípidos.
El sebo es excretado por las glándulas sebáceas de la piel y su sobreproducción, conocida como seborrea, es un síntoma de la enfermedad de Parkinson. Un momento, pero ¿por qué obtenían la muestra de sebo de esas zonas y no de alguna otra parte corporal? Pues porque Joy decía que ahí era donde más olor a párkinson encontraba en las camisetas.
Sigamos con el estudio. Se llevaron a cabo dos pruebas con sendas técnicas: la espectrometría de masas, un método analítico para identificar compuestos en una muestra, y el agudo sentido del olfato de Joy (conocido como hiperosmia). En este trabajo observaron diferencias entre los compuestos volátiles presentes en el sebo de los controles y de los pacientes, encontrando el aldehído perílico disminuido y el icosano aumentado en personas con párkinson.
Siguieron investigando y se centraron en estudiar los lípidos presentes en el sebo. Ya en un estudio publicado en 2021 encontraron diferencias entre las personas afectadas por la enfermedad neurodegenerativa y los controles. En otro trabajo publicado posteriormente, en 2022, desarrollaron una nueva técnica no invasiva para analizar muestras de sebo de forma mucho más rápida (2-3 minutos) y accesible.
David Krestin y las observaciones olvidadasNo obstante, estos estudios sobre el sebo no son nuevos. En 1927, el cardiólogo David Krestin se percató de que las personas con párkinson presentaban seborrea en la cara y que esto se podría utilizar para diagnosticar la enfermedad. Sin embargo, al ser Krestin cardiólogo, la comunidad científica no tuvo en cuenta sus observaciones y el sebo se quedó en el olvido hasta que Joy hizo prender la mecha.
Estas antiguas observaciones y los recientes estudios liderados por Barran confirman el potencial del sebo en el diagnóstico precoz de la enfermedad de Parkinson. Se puede obtener mediante técnicas no invasivas y puede ser adecuado para la búsqueda de biomarcadores de las enfermedades.
La importancia de encontrar nuevos biomarcadoresUn biomarcador es una sustancia cuya alteración podría indicar la presencia de alguna enfermedad. La búsqueda de biomarcadores cobra mayor importancia en patologías difíciles de diagnosticar como el párkinson.
Esta enfermedad neurodegenerativa es diagnosticada cuando aparecen los síntomas motores característicos que todos relacionamos con el párkinson: temblores, movimientos lentos, rigidez muscular, etc. El problema es que para cuando llega el diagnóstico, ya se han perdido el 60 % de las neuronas que producen dopamina en la sustancia negra, área afectada en esta enfermedad.
Encontrar biomarcadores podría abrir las puertas al diagnóstico temprano de la dolencia. Al igual que un test de embarazo dice si una mujer está embarazada o no, o con un alcoholímetro podemos saber si alguien ha bebido, el análisis de biomarcadores en distintas muestras como el sebo podría convertirse en un gran indicador de presencia de párkinson.
Por lo tanto, es de suma importancia que se siga financiando este tipo de estudios para hallar señales tempranas de esta enfermedad, de la que se espera que afecte a más de 12 millones de personas para el 2040.
Este artículo resultó ganador de la III edición del certamen de divulgación joven organizado por la Fundación Lilly y The Conversation España.![]()
Sobre la autora: Maider Zubelzu Irazusta, Estudiante de doctorado en Farmacología, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Se puede oler el párkinson? se ha escrito en Cuaderno de Cultura Científica.
Geocine de verano
 Afloramiento de rocas graníticas en Salamanca, España
Afloramiento de rocas graníticas en Salamanca, EspañaAhora que llega el buen tiempo y los días de vacaciones, también regresa una costumbre muy arraigada en muchas localidades de nuestra geografía, el cine de verano. No hay nada mejor que sentarse a la fresca durante el atardecer en la plaza del pueblo, con tu familia y amistades, viendo una película gratuita en pantalla grande mientras cenas un buen bocadillo con una ensalada. Y, si encima aprendemos un poco de Geología mientras nos divertimos con esa película, la experiencia se convierte en algo mucho más gratificante.
Hoy voy a hablaros de una de esas películas con las que podemos conocer un poquito más el trabajo de las personas profesionales de las Ciencias de la Tierra. Pero no creo que sea una de las que os estaréis imaginando ahora mismo, porque no trata de desastres naturales en donde un héroe de camisa vaquera arremangada salva el mundo, o de bichos prehistóricos gigantes atacando ciudades, ni tampoco de aventuras en selvas, desiertos o cuevas buscando minerales preciosos. Es una película que no creo que pongan en los cines de verano, salvo en la “hora golfa”, porque es un clásico del cine de terror de finales del siglo XX. Me estoy refiriendo a “Tremors”.
 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons“Tremors”, traducida al castellano como “Temblores”, es una película de terror y ciencia ficción norteamericana estrenada en 1990. En una sinopsis rápida, el film está ambientado en un pequeño pueblo en mitad del desierto de Nevada, Estados Unidos, donde su minúscula población se ve atacada por unas extrañas criaturas subterráneas y deben buscar la manera de sobrevivir ante esta amenaza. Hasta aquí la parte sin destripar la película.
Os estaréis preguntando que dónde está la Geología en todo esto. Pues en que es, precisamente, el conocimiento teórico y práctico en esta ciencia lo que salva a la población. Y aquí empieza la parte con destripe de este artículo.
Justo al principio de la película se introduce a una de las protagonistas, una estudiante de Geología que se presenta a sí misma como sismóloga. La sismología es una de las disciplinas de las Ciencias de la Tierra y se encarga de estudiar los terremotos, esos movimientos del terreno debidos a la liberación de energía del interior de la Tierra en forma de ondas. Uno de los mecanismos que se utiliza para monitorizar terremotos son los sismógrafos o sismómetros, unos aparatos que consisten en un tambor cilíndrico forrado de papel que va girando con un periodo de tiempo determinado, sobre el que se sitúa un péndulo con un peso y un punzón que va escribiendo en dicho papel. Cuando se produce un movimiento del terreno todo el aparato vibra, excepto el péndulo, que se mantiene quieto por el peso, lo que hace que el dibujo reflejado por el punzón pase de una línea recta a una serie de picos oscilatorios de lado a lado. Este registro gráfico en papel de los terremotos se denomina sismograma.
 Sismógrafo del Departamento del Interior de Estados Unidos, en el que se aprecia la señal gráfica que dejan las vibraciones del terreno en el sismograma. Fuente: Wikimedia Commons
Sismógrafo del Departamento del Interior de Estados Unidos, en el que se aprecia la señal gráfica que dejan las vibraciones del terreno en el sismograma. Fuente: Wikimedia CommonsEn la película vemos cómo la geóloga está instalando los medidores de vibraciones en la zona de estudio, unos pequeños bloques metálicos que entierra en el suelo a poca profundidad y que se conectan por cables al sismógrafo. Y también cómo se marcan en el papel los movimientos del terreno al pasar las criaturas cerca de los aparatos. De hecho, las lecturas que hace la chica de los sismogramas obtenidos por varios sismómetros que tiene distribuidos por todo el valle en el que se asienta el pueblo, le permiten saber cuántos organismos hay y hacia donde se mueven: directos a por la población para darse un buen festín.
Pero la parte geológica no termina aquí. Cuando consiguen acabar con uno de los bichos y se ponen a estudiarlo, se dan cuenta de que es una especie de gusano sin ojos, con tentáculos y una extraña boca. Entonces la gente le pregunta a la geóloga sobre el origen del organismo, que para eso es la científica del grupo y debería saberlo. Obviamente responde que no tiene ni idea de lo que es, pero que no existe nada similar en el registro fósil, así que hipotetiza que puede tratarse de un organismo más antiguo que el propio registro fósil en sí, llegando a tener más de 2200 millones de años de antigüedad. Una estimación de edad muy acertada para ser 1990, pero hoy en día se han descubierto fósiles más antiguos, unos estromatolitos de hace entre 3700 y 3500 millones de años, así que la prota se quedó corta por más de 1000 millones de años. Y en cuanto al origen, cualquier friki de la ciencia ficción como yo sabe que estos bichos están basados en los gusanos de arena del planeta Arrakis de las novelas Dune de F. Herbert, que a su vez se basan en los chthonians, unas criaturas gusanoides imaginadas por H. P. Lovecraft dentro de su bestiario de criaturas del terror cósmico.
 Reconstrucción del aspecto ambiental que tendría nuestro planeta hace unos 3500-3700 millones de años, durante el Eón Arcaico, con mares poco profundos colonizados por estromatolitos. Ilustración de Christian Jegou Publiphoto Diffusion. Fuente
Reconstrucción del aspecto ambiental que tendría nuestro planeta hace unos 3500-3700 millones de años, durante el Eón Arcaico, con mares poco profundos colonizados por estromatolitos. Ilustración de Christian Jegou Publiphoto Diffusion. FuentePero sigamos con la película. Al descubrir que los organismos no tienen ojos, la geóloga comenta que no los necesitan porque viven bajo tierra, por lo que su manera de orientarse se basa en detectar con los tentáculos las vibraciones que se transmiten por el interior del terreno. Es así como localizan a las presas que caminan sobre el suelo. Esto la empuja a plantear la manera de escapar de la amenaza, comentando al resto de la gente que, textualmente, “debemos evitar los aluviones del Pleistoceno”. Cuando todo el mundo se la queda mirando sin entender lo que ha dicho, explica que se refiere a que tienen que alejarse del suelo blando que cubre todo el valle en el que se asienta el pueblo, escapando hacia las montañas de granito puro que les rodea, ya que son rocas muy duras que no pueden atravesar los gusanos. Esto hace que otro protagonista grite, en un momento de la película, “las rocas pueden salvarnos”.
Me voy a quedar con esta frase y no voy a desvelar más sobre la película. Aunque sea de terror y del subgénero de “bichos comiéndose a la gente”, apenas tiene sangre ni escenas desagradables. Pero lo que sí la diferencia de otras similares es que todas las decisiones que toman a lo largo de la trama están basadas en el conocimiento geológico del terreno, así que se salvan gracias a la Geología. Por mi parte, os la recomiendo encarecidamente, porque podéis aprender Ciencias de la Tierra mientras pasáis un rato entretenido este verano.
Más películas geológicas:
El aperitivo preferido de los Comerrocas
65, ¿un título acertado?
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Geocine de verano se ha escrito en Cuaderno de Cultura Científica.
Marie Crous, la matemática que introdujo el punto en la notación decimal
Marie Crous fue una matemática francesa del siglo XVII. Se desconocen sus datos biográficos, en particular las fechas de su nacimiento y fallecimiento.
Fue la maestra de escritura y preceptora de la joven aristócrata Charlotte de Caumont La Force (1650-1724). Tuvo como mecenas a otra mujer, a Madame de Combalet duquesa de Aiguillon (1604-1675), sobrina del cardenal Richelieu. Aunque su protectora conocía a Marin Mersenne (1588-1648), Marie Crous no fue reconocida por el entorno científico de Mersenne y no figura en la lista de las eruditas célebres de su tiempo.
En 1636, y posteriormente en 1641, publicó dos manuales de aritmética que proporcionaron un estudio sobre el sistema de numeración decimal muy innovador en su época.
 Portadas de los dos escritos de Marie Crous. Fuente: Institut de France.
Portadas de los dos escritos de Marie Crous. Fuente: Institut de France.
Solo existe una copia conocida de estos dos escritos (encuadernados juntos). Se encontró en la antigua colección de la biblioteca personal del cardenal Giulio Raimondo Mazarino (1602-1661), protegido de Richelieu, mecenas de las artes y coleccionista de libros.
El primer escrito matemático de Marie CrousEl escrito Avis de Marie Crous aux filles exerçant l’arithmétique : sur les dîmes ou dixième du sieur Stevin. Contenant plusieurs avertissements démonstrations, et propositions : en lesquelles est declaré comment elles se peuvent servir de la partition des dîmes, sans le changement des divisions des monnaies, poids, et mesures : par le moyen de cinq tables y contenues.. Le tout renvoyé à mon abrégé pour y être très utile (París, 1636) va mucho más allá de lo que puede encontrarse en los manuales elementales de iniciación al cálculo.
Crous dedicó este trabajo a su alumna Charlotte de Caumont La Force.
 Dedicatoria a Charlotte de Caumont La Force. Fuente: Institut de France.
Dedicatoria a Charlotte de Caumont La Force. Fuente: Institut de France.
Este trabajo incluye una presentación de las fracciones decimales, reproducida a partir de De Thiende (1585, traducida ese mismo año al francés como La Disme) de Simon Stevin (1548-1620). Marie Crous introduce en esta obra un cambio importante respecto a Stevin: el punto (hoy la coma en España y otros países) para separar la mantisa de la parte decimal.
También reemplaza las unidades decimales que faltan con ceros: un cambio fundamental que dio a la numeración decimal su forma actual.
El segundo escrito matemático de Marie CrousEn su escrito Abbregé recherché de Marie Crous pour tirer la solution de toutes propositions d’aritmetique, dependantes des reigles y contenuës : avec quelques propositions sur les changes, escontes, interests, compagnies, associations, payemens, departemens de deniers, meslanges, bureau des monnoyes, & thoisages. Divisé en trois parties. Ensemble un advis sur les dixmes, ou dixiesmes du sieur Stevin (París, 1641), Crous desarrolló un texto completo de matemáticas comerciales. Esta obra comienza con una epístola dedicada a su protectora, la duquesa de Aiguillon.
 Dedicatoria a Madame de Combalet. Fuente: Institut de France.
Dedicatoria a Madame de Combalet. Fuente: Institut de France.
En la primera parte (páginas 1 a 32) Crous introduce demostraciones (así las denomina ella, aunque no incluye ningún razonamiento) en las que muestra cómo deben realizarse las diferentes operaciones basándose en las cuatro reglas. La autora indica, entre otros muchos ejemplos, cómo hacer varias operaciones simultáneamente; por ejemplo, 956 menos 784 más 230 o 9 por 472 más 683.
 Algunos ejemplos de operaciones. Fuente: Institut de France.
Algunos ejemplos de operaciones. Fuente: Institut de France.
En la segunda parte (páginas 39 a 69) incluye métodos para la realización de cálculo mental, en particular para fracciones decimales y para la realización de la regla de tres y sus aplicaciones en el intercambio comercial.
Y en la tercera parte, propone diferentes aplicaciones de las dos primeras del Abbregé.
La intención de sus escritosEstos libros de aritmética estaban dirigidos a las mujeres “para tratar de aliviar a aquellas que ejercen esta ciencia tanto por las necesidades de sus asuntos como
por el placer de su mente”. Crous cita explícitamente en sus tratados la compra de joyas o el forrado de tapices, pero también la comparación de valores económicos procedentes de la compra de terrenos o la constitución de una renta vitalicia con una suma determinada.
La historia de Marie Crous me recuerda a la de la matemática y maestra de niñas María Andresa Casamayor de La Coma (1720-1780), cuyo Tyrocinio arithmetico, Instrucción de las quatro reglas llanas también fue un manual de aritmética para aprender de manera directa el empleo de las cuatro reglas básicas, tan necesaria en las transacciones comerciales de la época.
¿Cuántas Marie o María Andresa habrán existido?
Referencias
-
Orly Terquem et Camille-Christophe Gerono, Notice bibliographique sur le calcul décimal en Nouvelles annales de mathématiques, vol. 12, 1853 [el artículo habla sobre Simon Stevin y Marie Crous, la parte de Crous está en las páginas 200-205].
-
Catherine Goldstein, Neither public nor private: mathematics in early modern France, preprint, 2003
-
Catherine Goldstein, Les fractions décimales : un art d’ingénieur ? (2010). ffhal-00734932v2
-
Hannah Wills, Sadie Harrison, Erika Jones, Rebecca Martin, and Farrah Lawrence-Mackey (ed.), Women in the History of Science. A source book, UCL Press, 2023 (páginas 112-120)
-
Marie Crous, Wikipédia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Marie Crous, la matemática que introdujo el punto en la notación decimal se ha escrito en Cuaderno de Cultura Científica.

