El núcleo de Marte
núcleo de marte
Para la geología es fundamental el conocer como son y en qué estado se encuentran las distintas capas que conforman el interior de los distintos cuerpos del Sistema Solar, ya que eso puede aportarnos pistas sobre su formación, composición y grado de actividad. Aunque a grandes rasgos y gracias a las medidas indirectas desde la órbita y a cada vez mejores modelos numéricos empezamos a conocer como son los planetas -y otros cuerpos- por dentro, necesitamos misiones que nos permitan ver detalles más finos. Gracias a misiones como la InSight, que llegó a Marte en noviembre de 2018 y concluyó su misión en diciembre de 2022, estamos empezando a conocer mucho mejor el interior del planeta rojo. Probablemente durante años veamos aparecer nuevos artículos con interpretaciones de los datos y modelos sobre el interior que nos ayuden a comprender por qué este planeta evolucionó de una manera tan diferente a la Tierra.
 En esta representación artística podemos ver el módulo de aterrizaje de la misión InSight, junto con el “topo” introducido en el suelo marciano -a la derecha- y a la izquierda el instrumento SEIS, del que no vemos directamente el sismómetro, sino que apreciamos la cúpula que le sirve para mantenerse aislado de los cambios de temperatura y el impacto del viento. Imagen cortesía de la NASA/JPL.
En esta representación artística podemos ver el módulo de aterrizaje de la misión InSight, junto con el “topo” introducido en el suelo marciano -a la derecha- y a la izquierda el instrumento SEIS, del que no vemos directamente el sismómetro, sino que apreciamos la cúpula que le sirve para mantenerse aislado de los cambios de temperatura y el impacto del viento. Imagen cortesía de la NASA/JPL.Dos de sus instrumentos, SEIS -un sismómetro e instrumento principal de la misión- y RISE -un experimento que aprovecha el sistema de comunicaciones de la sonda para conocer mejor la rotación y el “bamboleo” del planeta- han demostrado con creces ser muy sensibles y útiles para ayudarnos a conseguir una “radiografía” del planeta y estudiar distintos procesos geológicos que van desde los terremotos y la posible actividad volcánica hasta la redistribución de masas entre la superficie del planeta y la atmósfera debido a la transferencia del dióxido de carbono que ocurre a causa de las estaciones.
Lo importante de tener dos instrumentos como estos de manera simultánea sobre el planeta es que, aunque usen metodologías muy diferentes, nos permiten comprobar si efectivamente los modelos de su interior generados a partir de ambos instrumentos se parecen y son comparables… algo que efectivamente ha sido así y que vamos a intentar explicar que se ha visto exactamente y que implicaciones tiene.
Empecemos por los datos de SEIS. Como decíamos anteriormente, SEIS es un sismómetro muy sensible, capaz de detectar las ondas sísmicas provocadas por los terremotos o el impacto de los meteoritos, entre otros eventos. Las ondas sísmicas, cuando viajan por el interior del planeta desde el punto donde ha ocurrido el terremoto -y que llamamos hipocentro- ven su velocidad y trayectoria alterada por el cambio de propiedades y composición de los materiales que van atravesando, ya que el interior de los planetas no suele ser homogéneo.
Para poder detectar mediante este instrumento la capa más interna de Marte, en este caso el núcleo del planeta, SEIS necesitaba detectar terremotos que hubiesen ocurrido lo suficientemente lejos como para que las ondas sísmicas que le llegasen hubiesen tenido que atravesar el núcleo o haber rebotado en la interfaz entre el manto y el núcleo.
Esto, a priori, y dado el grado de actividad geológica de Marte, podría resultar complicado en el tiempo que durara la misión, ya que tendrían que ocurrir terremotos de suficiente magnitud a una distancia importante y que fuesen detectados por la InSight -no podemos dejar de lado que una de las grandes zonas potenciales donde podría haber terremotos en Marte se encuentra, con respecto a la InSight, en lo que denominamos como zona de sombra sísmica-, pero todo cambió entre los soles 976 y 1000 -hablamos de eventos sísmicos ocurridos en 2021-, cuando un terremoto y el impacto de un cuerpo contra la superficie del planeta permitieron al sismómetro detectar las ondas atravesando el núcleo del planeta rojo.
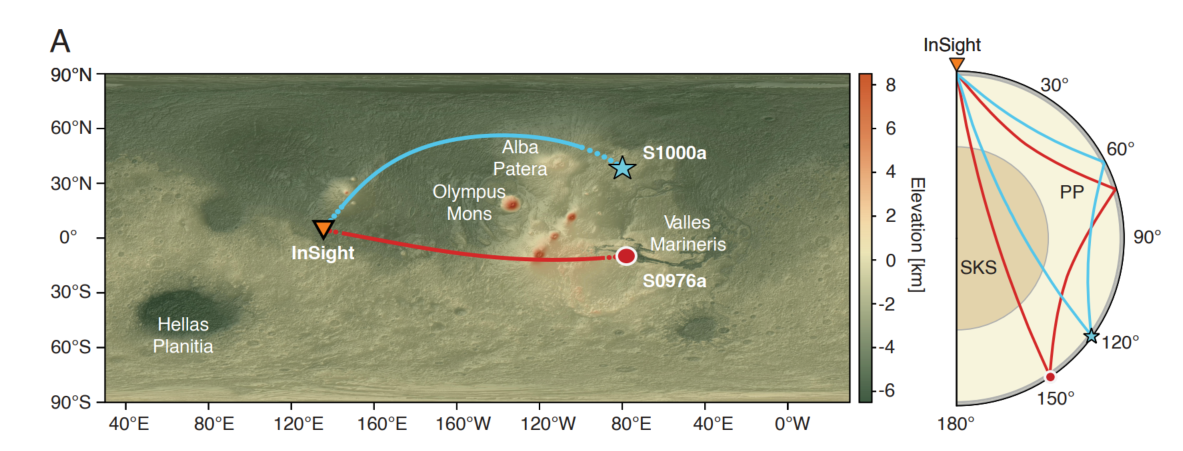 Imagen la que podemos ver la localización de la InSight sobre un mapa topográfico de Marte y la localización de los dos epicentros de los terremotos detectados. También, a la derecha, podemos ver las fases sísmicas que llegaron al sismómetro y que permitieron reconocer el núcleo interno, como es en este caso la fase SKS. Imagen cortesía de Irving et al. (2023).
Imagen la que podemos ver la localización de la InSight sobre un mapa topográfico de Marte y la localización de los dos epicentros de los terremotos detectados. También, a la derecha, podemos ver las fases sísmicas que llegaron al sismómetro y que permitieron reconocer el núcleo interno, como es en este caso la fase SKS. Imagen cortesía de Irving et al. (2023).Para que nos hagamos una idea de la distancia, el epicentro del terremoto estaría localizado a una distancia entre los 7424 y los 8468 kilómetros, mientras que el impacto ocurrió a una distancia de unos 7300 kilómetros. La diferencia en la precisión en la localización entre el terremoto y el impacto se debe a un factor: mientras que el lugar del impacto ha sido observado directamente por la Mars Reconaissance Orbiter, y por lo tanto, establecer unas coordenadas muy precisas, calcular el epicentro de un terremoto requiere de que tengamos un modelo a priori del interior del planeta que nos permita establecer el comportamiento de las ondas sísmicas, lo que en el caso de Marte tiene mucha incertidumbre.
En 2021, Stähler et al. ya publicaron las primeras estimaciones del tamaño del núcleo de Marte basándose en las ondas reflejadas en la interfaz manto-núcleo, y obteniendo un valor de unos 1830±40 kilómetros, pero estos datos, aunque importantes no son suficientes… y es que, ¿de qué está compuesto y en que estado está el núcleo de Marte? Si bien es cierto que en este artículo ya se tratan algunas de las cuestiones fundamentales, era preciso el poder observar las ondas atravesando el núcleo para poder confirmar algunas de las sospechas que tenían los científicos, como los que aportan el artículo de Irving et al. (2023).
El primer detalle que salta a la vista es que el núcleo de Marte contiene, además del hierro, alrededor de un 20% de elementos ligeros como el azufre, el oxígeno el hidrógeno y el carbono, una diferencia importante si lo comparamos con la Tierra, donde el núcleo externo, por ejemplo, tiene aproximadamente un 10% de elementos ligeros.
El segundo es que no se ha observado, de momento, un núcleo interno sólido como tiene nuestro planeta y que, si existe, debería de tener un radio menor de los 750 kilómetros, y probablemente, para cerrar esta cuestión de una manera definitiva, se necesiten de nuevas misiones en superficie.
Como decíamos al principio, hay otro instrumento, en este caso RISE, capaz de aportarnos pistas de una manera más indirecta del interior del planeta. Y es que este instrumento es capaz de medir el efecto Doppler resultante de minúsculas variaciones que ocurren tanto en la rotación de Marte como en la orientación de su eje, y para lo que tenemos que imaginarnos al planeta Marte como una peonza girando.
 Representación artística del interior de Marte en la que podemos apreciar los epicentros y trayectoria de las ondas de los terremotos detectados por la InSight y el tamaño de la corteza, manto y núcleo marcianos. Imagen cortesía de NASA/JPL-Caltech/University of Maryland.
Representación artística del interior de Marte en la que podemos apreciar los epicentros y trayectoria de las ondas de los terremotos detectados por la InSight y el tamaño de la corteza, manto y núcleo marcianos. Imagen cortesía de NASA/JPL-Caltech/University of Maryland.Pues bien, de este experimento se ha deducido un radio para el núcleo de Marte de unos 1835±55 kilómetros, un valor dentro del rango de los anteriores estudios y que muestra que los cálculos entre diferentes estudios son coherentes entre sí, pero con una diferencia: en este modelo, por ejemplo, no habría cabida para un núcleo sólido, sino que todo se encontraría en estado líquido. Este último dato podría apuntar a que la inexistencia de un núcleo sólido fuese una de las causas del fin del campo magnético global de Marte.
Este modelo también está de acuerdo con el porcentaje aproximado de un 20% de elementos ligeros en el núcleo que también aparece en Irving et al. (2023), donde el más abundante de los ligeros sería el azufre -con un 15±2% en peso-, seguido del oxígeno -con un 2.5±0.5%-, el carbono -con un 1.5±0.5%- y por último el hidrógeno con alrededor del 1%.
Por último, gracias a los datos de RISE se ha descubierto una ligera tendencia al acortamiento de los días de la que se desconoce su origen, pero que podría ser debida o bien a la dinámica climática y a la transferencia de materia entre los casquetes polares y la atmósfera -y viceversa- o a factores internos.
Sin duda, misiones como la InSight, y que a simple vista nos pueden parecer menos atractivas que otras mucho más complejas y espectaculares como las que llevan a cabo los rovers sobre Marte, ponen de manifiesto que podemos aprender todavía mucho más sobre el interior de Marte igual que a principios del siglo XX empezamos a hacer en nuestro propio planeta gracias al avance de la sismología.
Referencias:
Irving, Jessica C. E., Vedran Lekić, Cecilia Durán, Mélanie Drilleau, Doyeon Kim, Attilio Rivoldini, Amir Khan, et al. «First Observations of Core-Transiting Seismic Phases on Mars». Proceedings of the National Academy of Sciences 120, n.º 18 (2 de mayo de 2023): e2217090120. doi: 10.1073/pnas.2217090120.
Le Maistre, Sébastien, Attilio Rivoldini, Alfonso Caldiero, Marie Yseboodt, Rose-Marie Baland, Mikael Beuthe, Tim Van Hoolst, et al. «Spin State and Deep Interior Structure of Mars from InSight Radio Tracking». Nature, 14 de junio de 2023. doi: 10.1038/s41586-023-06150-0.
Stähler, Simon C., Amir Khan, W. Bruce Banerdt, Philippe Lognonné, Domenico Giardini, Savas Ceylan, Mélanie Drilleau, et al. «Seismic Detection of the Martian Core». Science 373, n.º 6553 (23 de julio de 2021): 443-48. doi: 10.1126/science.abi7730.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El núcleo de Marte se ha escrito en Cuaderno de Cultura Científica.
Crecen los efectos nocivos de la contaminación lumínica en la astronomía
contaminación lumínica
La luz artificial nocturna, el despliegue de constelaciones de satélites y las interferencias de radio están impactando negativamente en las observaciones astronómicas, limitando los descubrimientos científicos, nuestras conexiones culturales con el cielo nocturno y las posibilidades del astroturismo.
 Cielo nocturno desde el destino turístico Starlight Pampa Joya (Antofagasta, Chile). Foto: Braham Millal (foto premiada en el V Maratón de Fotografía Starlight en la temática «Contaminación lumínica»)
Cielo nocturno desde el destino turístico Starlight Pampa Joya (Antofagasta, Chile). Foto: Braham Millal (foto premiada en el V Maratón de Fotografía Starlight en la temática «Contaminación lumínica»)A lo largo de la historia de la humanidad, mirar al cielo estrellado ha sido una fuente de inspiración para la humanidad. Así nació la astronomía, como un elemento común en todas las culturas que, desde antiguo, se ha utilizado para establecer calendarios, navegar, descubrir nuevas tierras e impulsar muchas investigaciones científicas.
Pero en las últimas décadas la comunidad astronómica, tanto de profesionales como de aficionados, ha comprobado que cada vez es más difícil desarrollar su labor debido a la creciente contaminación lumínica y otras nuevas amenazas: las nuevas constelaciones de satélites y las interferencias de radio.
Hasta hace solo un par de años nuestra principal preocupación se centraba en la pérdida progresiva del cielo nocturno debido al creciente aumento de la contaminación lumínica, con aproximadamente un 10 % de crecimiento al año y una cuarta parte de la superficie del planeta ya contaminada.
Fuimos los astrónomos los primeros en advertir de este problema y los que señalamos que este deterioro tenía serias implicaciones, no solo en la ciencia sino también en el medioambiente (existe una relación entre sobreiluminación y cambio climático que el público desconoce), en la biodiversidad, la salud, el patrimonio cultural asociado al cielo nocturno y en el desarrollo socioeconómico sostenible a través del astroturismo.
Pero en los últimos años hemos visto despuntar nuevas y muy serias amenazas para la astronomía profesional y amateur. El despliegue de un gran número de satélites en órbita terrestre baja (LEO) ha tenido un impacto imprevisto. Al darnos cuenta, ya los teníamos sobre nuestras cabezas.
Cuando se lanzó un lote prototipo de 60 naves de este tipo en mayo de 2019, los astrónomos se sorprendieron por lo brillantes que parecían desde el suelo. Entre el 5 y el 10 % de estos satélites están presentes sobre lugares astronómicos en un momento dado, y una proporción de ellos está iluminada por el Sol en un cielo oscuro.
 Estrella Albireo en la constelación del Cisne tomada el 26 de diciembre de 2019. Dos de las diez exposiciones de 2,5 minutos grabaron satélites Starlink moviéndose por el campo. Foto: Rafael Schmall
Estrella Albireo en la constelación del Cisne tomada el 26 de diciembre de 2019. Dos de las diez exposiciones de 2,5 minutos grabaron satélites Starlink moviéndose por el campo. Foto: Rafael SchmallCon planes de hasta 400.000 satélites en estas constelaciones para 2030, miles serán visibles desde cada lugar en cualquier momento. Hasta el 30 % de las exposiciones de campo amplio en un gran telescopio se perderían durante las primeras horas de la tarde y antes del amanecer, y casi el 50 % de las exposiciones crepusculares estarían contaminadas.
Uno de los proyectos que se verán fuertemente afectados serán los estudios automatizados en busca de objetos en movimiento como asteroides potencialmente peligrosos.
El tercer problema son las interferencias de radio. La radioastronomía consiste en observar el universo en longitudes de onda que también son utilizadas por las radiocomunicaciones generadas por el hombre. Hemos convivido con ellas y con acuerdos internacionales que permitían definir bandas de radio protegidas.
Pero el incremento del ancho de banda y de la potencia de transmisión de las radiocomunicaciones ha provocado un aumento de las interferencias de radiofrecuencia en las observaciones astronómicas.
El despliegue de constelaciones LEO también producirá cientos de fuentes de radiointerferencias brillantes en rápido movimiento, visibles para los radiotelescopios a cualquier hora del día.
España es pionera en la conservación del cieloLa contaminación lumínica cuenta ya con regulaciones eficaces y tecnología para su disminución y ya se están dando algunos pasos en algunos países como en España que ha sido pionero en la preservación del cielo con la Ley del Cielo de 1988 de Canarias, pero me temo que el riesgo por las megaconstelaciones avanza muy rápidamente y es demoledor.
Los primeros satélites (década de 60 y hasta ahora) no eran maniobrables, pero el avance en la tecnología espacial ha contribuido a construir satélites cada vez más resistentes y maniobrables. Estos ya disponen de sistemas de propulsión que les permiten cambiar su órbita, así como desviarse de trayectorias de objetos entrantes y evitar colisiones, consiguiendo así misiones más largas.
La proliferación de pequeños satélites eleva los riesgos de colisión, especialmente en la órbita baja que ya está densamente poblada y, por tanto, aumentan el riesgo de colisión y de generar basura espacial. Estos impactos pueden poner en peligro satélites de observación, de vigilancia terrestre y para comunicaciones, cruciales para nuestra seguridad entre otros aspectos.
Por otra parte, están los satélites Starlink (operados por la compañía Space X de Elon Musk), equipados con sistemas de propulsión que pueden utilizarse para maniobrarlos fuera del camino de posibles colisiones. Esto podría ayudar a reducir el riesgo de colisiones y evitar aumentar aún más la cantidad de desechos en el espacio. Pero su creciente número no hará sino aumentar este riesgo y el espacio será cada vez menos sostenible.
Amenaza para la astronomía profesional y amateurEsta contaminación lumínica, en su conjunto, amenaza los observatorios astronómicos profesionales, que se localizan precisamente en lugares remotos del planeta por contar con cielos muy oscuros. Cualquier resplandor del cielo puede saturar la débil señal de los objetos astronómicos, impidiendo su detección.
Sin embargo, las observaciones astronómicas terrestres impulsan importantes descubrimientos de gran repercusión en astrofísica y física fundamental y, a menudo, son esenciales para interpretar las observaciones de los telescopios espaciales. Actualmente existen más de 40 telescopios ópticos terrestres con espejos de 3 metros o más de diámetro.
Por su parte, la astronomía amateur también está fuertemente amenazada por la también llamada luz artificial de la noche (ALAN) y las megaconstelaciones de satélites LEO, especialmente en los ámbitos de los programas de investigación con científicos profesionales, la astrofotografía y el astroturismo.
 Ejemplo de contaminación lumínica, sobre todo por el uso de leds blancos y azules y el escaso blindaje de las luminarias. Cielo nocturno fotografiado desde la isla de Sálvora, en el Parque Nacional de las Islas Atlánticas en Galicia, certificado como Destino Turístico Starlight. Foto: Fernando Rey
Ejemplo de contaminación lumínica, sobre todo por el uso de leds blancos y azules y el escaso blindaje de las luminarias. Cielo nocturno fotografiado desde la isla de Sálvora, en el Parque Nacional de las Islas Atlánticas en Galicia, certificado como Destino Turístico Starlight. Foto: Fernando ReyAproximadamente un millón de personas se dedican a la astronomía amateur, dos órdenes de magnitud más que el número de astrónomos profesionales. Los aficionados utilizan cámaras y telescopios con campos de visión más amplios que los grandes telescopios, por lo que es más probable que sus imágenes contengan estelas de satélites artificiales.
Los astrónomos aficionados descubren cometas, buscan supernovas en las galaxias, realizan campañas de seguimiento de estrellas variables y meteoritos, y confirman candidatos a exoplanetas.
Estas operaciones son especialmente vulnerables a la contaminación lumínica porque este colectivo no tiene acceso a los recursos económicos y tecnológicos necesarios para mitigar sus efectos. El incremento de la luz artificial nocturna y las megaconstelaciones satelitales compromete seriamente estas actividades, que serán prácticamente imposibles en la próxima década si se mantienen las tendencias actuales.
Asimismo, la demanda de certificación y formación en astroturismo ha crecido más de un 300 % en los últimos cinco años, atrayendo a decenas de miles de visitantes y proporcionando un retorno económico de más de cien millones de dólares en múltiples territorios, crecimiento que también se ve amenazado por el aumento de la contaminación lumínica.
En busca de solucionesEs absolutamente necesario que trabajemos juntos y coordinadamente las partes interesadas (observatorios, industria, comunidad astronómica, organismos de financiación de la ciencia, responsables políticos nacionales e internacionales) sobre las medidas técnicas y políticas necesarias para limitar el impacto de la contaminación lumínica, radiofrecuencias y megaconstelaciones en la astronomía.
Respecto a estos últimos, las observaciones astronómicas se beneficiarían enormemente si las constelaciones de satélites planificadas utilizaran el menor número posible de naves espaciales (siendo el número óptimo cero) y mantuvieran las órbitas de los satélites bajas para que entraran en la sombra de la Tierra poco después de la puesta de sol.
También se necesitan establecer estrictasregulaciones y normativas nacionales e internacionales y vigilar su cumplimiento. En este sentido es esperanzador el papel que desempeña el recientemente creado Centro para Protección del Cielo (CPS) oscuro y silencioso de interferencias de megaconstelaciones de la Unión Astronómica Internacional (IAU).
Es necesario un pacto mundial en defensa del cielo. Esto implica educar y concienciar a la sociedad en su conjunto, algo que hacemos desde la Fundación Starlight a través de la difusión de la astronomía y el desarrollo socioeconómico local de las comunidades locales a través del astroturismo.
También sumando adhesiones a la Declaración Mundial de La Palma en Defensa del cielo Nocturno y el Derecho a la Luz de las Estrellas, y dando un paso más, defendiendo ante Naciones Unidas junto con la asociación de mujeres empresarias y profesionales BPW Spain, que el cielo sea un objetivo de desarrollo sostenible, porque sin cielo no hay planeta.
Referencia:
Varela Perez, A. (2023) The increasing effects of light pollution on professional and amateur astronomy Science doi: 10.1126/science.adg0269
Sobre la autora: Antonia M. Varela Pérez es investigadora de Instituto de Astrofísica de Canarias (IAC) y directora de la Fundación Starlight
Este texto apareció originalmente en SINC.
El artículo Crecen los efectos nocivos de la contaminación lumínica en la astronomía se ha escrito en Cuaderno de Cultura Científica.
¿Qué nos enferma a los humanos?

Cómo influyen los parásitos en el comportamiento de los animales, cómo se modifica la conducta de las madres mamífero o cuáles son las enfermedades que nos afectan y desde cuándo hemos desarrollado comportamientos funerarios ante la muerte son algunos de los aspectos que se analizarán en la V Jornada Nacional sobre Evolución y Neurociencias.
Especialistas en ambas materias se reunirán el 11 y 12 de mayo en una nueva edición conducida por Eva Garnica y Pablo Malo, psiquiatras y miembros de la Red de Salud Mental de Bizkaia, y organizada por esa misma entidad y la Cátedra de Cultura Científica de la UPV/EHU.
La jornada, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolucionista y divulgar de un modo accesible para todos los públicos.
Nunca estamos sanos al 100 % sanos, ni al borde de la muerte estás completamente enfermo. La salud es un espectro en el que nos movemos continuamente. ¿Qué es lo que hace que nos movamos hacia la enfermedad? Sari Arponen apunta algunas pautas.
Sari Arponen es doctora en Ciencias Biomédicas por la Universidad Complutense de Madrid, profesora universitaria en la Universidad Camilo José Cela y experta en microbiota. Licenciada en Medicina por la Universidad de Murcia, se especializó en Medicina Interna en el Hospital Universitario de la Princesa de Madrid. Es autora de varios libros.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo ¿Qué nos enferma a los humanos? se ha escrito en Cuaderno de Cultura Científica.
¿Se puede oler el párkinson?
párkinson
 Foto: Pexels / Pixabay
Foto: Pexels / PixabayPor curioso que parezca, ciertas enfermedades se pueden relacionar con distintos olores característicos. Por ejemplo, la diabetes puede hacer que el aliento huela a manzanas podridas; la insuficiencia renal, que lo haga a amoníaco u orina; mientras que la enfermedad hepática grave se ha relacionado con el olor del aliento a moho, ajo y huevos podridos. Las personas con esquizofrenia pueden tener un aroma corporal característico que recuerda al del moho.
Quizás se pregunte: ¿por qué cambia el olor de una persona cuando está enferma? Resulta que nuestros cuerpos expulsan constantemente sustancias volátiles al aire que respiramos, mediante el aliento, sudoración, excreciones, etc. El aroma de estas sustancias puede variar dependiendo de la edad, el estilo de vida y la dieta, pero también si una enfermedad produce alteraciones en nuestro organismo.
La mujer que puede oler el párkinsonLa escocesa Joy Milne acudió con su marido Les, diagnosticado con párkinson, a una conferencia sobre esta patología. Unos años antes de que Les fuese diagnosticado, Joy notó que el olor de su esposo había cambiado: se había vuelto más almizclado, parecido al de la madera. Pero la sorpresa llegó cuando Joy reconoció ese mismo olor en la conferencia, donde la sala estaba llena de personas afectadas por párkinson.
En una posterior conferencia, realizada en Escocia en 2012, Joy, nerviosa ante la mirada de los espectadores, se lo comentó al ponente de la conferencia, el investigador de la Universidad de Edimburgo Tilo Kunath. Este contactó con la química analítica de la Universidad de Mánchester, Perdita Barran, para conocer su opinión al respecto.
Aunque Kunath estaba esperanzado, Barran se encontraba algo escéptica. Finalmente hicieron una prueba a ciegas, donde le dieron a oler seis camisetas usadas por personas con párkinson y otras seis de controles sanos. Joy consiguió identificar las prendas de las personas enfermas y, además, marcó la prenda de uno de los controles sanos como si tuviese la dolencia. Un buen porcentaje de acierto que intrigó aún más a los investigadores cuando la persona supuestamente sana fue diagnosticada con párkinson nueve meses después.
¿Sirve el olfato para hacer diagnósticos precoces?Tras este trabajo piloto, se siguió investigando, y en 2019 se publicó un estudio, dirigido por Barran y financiado por Parkinson’s UK y la Michael J. Fox Foundation, donde participaron 64 personas, 21 controles y 43 pacientes. En él pasaban una gasa por la parte trasera del cuello y la parte superior de la espalda para analizar los componentes presentes en el sebo, un biofluido ceroso que contiene compuestos volátiles olorosos y es rico en lípidos.
El sebo es excretado por las glándulas sebáceas de la piel y su sobreproducción, conocida como seborrea, es un síntoma de la enfermedad de Parkinson. Un momento, pero ¿por qué obtenían la muestra de sebo de esas zonas y no de alguna otra parte corporal? Pues porque Joy decía que ahí era donde más olor a párkinson encontraba en las camisetas.
Sigamos con el estudio. Se llevaron a cabo dos pruebas con sendas técnicas: la espectrometría de masas, un método analítico para identificar compuestos en una muestra, y el agudo sentido del olfato de Joy (conocido como hiperosmia). En este trabajo observaron diferencias entre los compuestos volátiles presentes en el sebo de los controles y de los pacientes, encontrando el aldehído perílico disminuido y el icosano aumentado en personas con párkinson.
Siguieron investigando y se centraron en estudiar los lípidos presentes en el sebo. Ya en un estudio publicado en 2021 encontraron diferencias entre las personas afectadas por la enfermedad neurodegenerativa y los controles. En otro trabajo publicado posteriormente, en 2022, desarrollaron una nueva técnica no invasiva para analizar muestras de sebo de forma mucho más rápida (2-3 minutos) y accesible.
David Krestin y las observaciones olvidadasNo obstante, estos estudios sobre el sebo no son nuevos. En 1927, el cardiólogo David Krestin se percató de que las personas con párkinson presentaban seborrea en la cara y que esto se podría utilizar para diagnosticar la enfermedad. Sin embargo, al ser Krestin cardiólogo, la comunidad científica no tuvo en cuenta sus observaciones y el sebo se quedó en el olvido hasta que Joy hizo prender la mecha.
Estas antiguas observaciones y los recientes estudios liderados por Barran confirman el potencial del sebo en el diagnóstico precoz de la enfermedad de Parkinson. Se puede obtener mediante técnicas no invasivas y puede ser adecuado para la búsqueda de biomarcadores de las enfermedades.
La importancia de encontrar nuevos biomarcadoresUn biomarcador es una sustancia cuya alteración podría indicar la presencia de alguna enfermedad. La búsqueda de biomarcadores cobra mayor importancia en patologías difíciles de diagnosticar como el párkinson.
Esta enfermedad neurodegenerativa es diagnosticada cuando aparecen los síntomas motores característicos que todos relacionamos con el párkinson: temblores, movimientos lentos, rigidez muscular, etc. El problema es que para cuando llega el diagnóstico, ya se han perdido el 60 % de las neuronas que producen dopamina en la sustancia negra, área afectada en esta enfermedad.
Encontrar biomarcadores podría abrir las puertas al diagnóstico temprano de la dolencia. Al igual que un test de embarazo dice si una mujer está embarazada o no, o con un alcoholímetro podemos saber si alguien ha bebido, el análisis de biomarcadores en distintas muestras como el sebo podría convertirse en un gran indicador de presencia de párkinson.
Por lo tanto, es de suma importancia que se siga financiando este tipo de estudios para hallar señales tempranas de esta enfermedad, de la que se espera que afecte a más de 12 millones de personas para el 2040.
Este artículo resultó ganador de la III edición del certamen de divulgación joven organizado por la Fundación Lilly y The Conversation España.![]()
Sobre la autora: Maider Zubelzu Irazusta, Estudiante de doctorado en Farmacología, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Se puede oler el párkinson? se ha escrito en Cuaderno de Cultura Científica.
Geocine de verano
 Afloramiento de rocas graníticas en Salamanca, España
Afloramiento de rocas graníticas en Salamanca, EspañaAhora que llega el buen tiempo y los días de vacaciones, también regresa una costumbre muy arraigada en muchas localidades de nuestra geografía, el cine de verano. No hay nada mejor que sentarse a la fresca durante el atardecer en la plaza del pueblo, con tu familia y amistades, viendo una película gratuita en pantalla grande mientras cenas un buen bocadillo con una ensalada. Y, si encima aprendemos un poco de Geología mientras nos divertimos con esa película, la experiencia se convierte en algo mucho más gratificante.
Hoy voy a hablaros de una de esas películas con las que podemos conocer un poquito más el trabajo de las personas profesionales de las Ciencias de la Tierra. Pero no creo que sea una de las que os estaréis imaginando ahora mismo, porque no trata de desastres naturales en donde un héroe de camisa vaquera arremangada salva el mundo, o de bichos prehistóricos gigantes atacando ciudades, ni tampoco de aventuras en selvas, desiertos o cuevas buscando minerales preciosos. Es una película que no creo que pongan en los cines de verano, salvo en la “hora golfa”, porque es un clásico del cine de terror de finales del siglo XX. Me estoy refiriendo a “Tremors”.
 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons“Tremors”, traducida al castellano como “Temblores”, es una película de terror y ciencia ficción norteamericana estrenada en 1990. En una sinopsis rápida, el film está ambientado en un pequeño pueblo en mitad del desierto de Nevada, Estados Unidos, donde su minúscula población se ve atacada por unas extrañas criaturas subterráneas y deben buscar la manera de sobrevivir ante esta amenaza. Hasta aquí la parte sin destripar la película.
Os estaréis preguntando que dónde está la Geología en todo esto. Pues en que es, precisamente, el conocimiento teórico y práctico en esta ciencia lo que salva a la población. Y aquí empieza la parte con destripe de este artículo.
Justo al principio de la película se introduce a una de las protagonistas, una estudiante de Geología que se presenta a sí misma como sismóloga. La sismología es una de las disciplinas de las Ciencias de la Tierra y se encarga de estudiar los terremotos, esos movimientos del terreno debidos a la liberación de energía del interior de la Tierra en forma de ondas. Uno de los mecanismos que se utiliza para monitorizar terremotos son los sismógrafos o sismómetros, unos aparatos que consisten en un tambor cilíndrico forrado de papel que va girando con un periodo de tiempo determinado, sobre el que se sitúa un péndulo con un peso y un punzón que va escribiendo en dicho papel. Cuando se produce un movimiento del terreno todo el aparato vibra, excepto el péndulo, que se mantiene quieto por el peso, lo que hace que el dibujo reflejado por el punzón pase de una línea recta a una serie de picos oscilatorios de lado a lado. Este registro gráfico en papel de los terremotos se denomina sismograma.
 Sismógrafo del Departamento del Interior de Estados Unidos, en el que se aprecia la señal gráfica que dejan las vibraciones del terreno en el sismograma. Fuente: Wikimedia Commons
Sismógrafo del Departamento del Interior de Estados Unidos, en el que se aprecia la señal gráfica que dejan las vibraciones del terreno en el sismograma. Fuente: Wikimedia CommonsEn la película vemos cómo la geóloga está instalando los medidores de vibraciones en la zona de estudio, unos pequeños bloques metálicos que entierra en el suelo a poca profundidad y que se conectan por cables al sismógrafo. Y también cómo se marcan en el papel los movimientos del terreno al pasar las criaturas cerca de los aparatos. De hecho, las lecturas que hace la chica de los sismogramas obtenidos por varios sismómetros que tiene distribuidos por todo el valle en el que se asienta el pueblo, le permiten saber cuántos organismos hay y hacia donde se mueven: directos a por la población para darse un buen festín.
Pero la parte geológica no termina aquí. Cuando consiguen acabar con uno de los bichos y se ponen a estudiarlo, se dan cuenta de que es una especie de gusano sin ojos, con tentáculos y una extraña boca. Entonces la gente le pregunta a la geóloga sobre el origen del organismo, que para eso es la científica del grupo y debería saberlo. Obviamente responde que no tiene ni idea de lo que es, pero que no existe nada similar en el registro fósil, así que hipotetiza que puede tratarse de un organismo más antiguo que el propio registro fósil en sí, llegando a tener más de 2200 millones de años de antigüedad. Una estimación de edad muy acertada para ser 1990, pero hoy en día se han descubierto fósiles más antiguos, unos estromatolitos de hace entre 3700 y 3500 millones de años, así que la prota se quedó corta por más de 1000 millones de años. Y en cuanto al origen, cualquier friki de la ciencia ficción como yo sabe que estos bichos están basados en los gusanos de arena del planeta Arrakis de las novelas Dune de F. Herbert, que a su vez se basan en los chthonians, unas criaturas gusanoides imaginadas por H. P. Lovecraft dentro de su bestiario de criaturas del terror cósmico.
 Reconstrucción del aspecto ambiental que tendría nuestro planeta hace unos 3500-3700 millones de años, durante el Eón Arcaico, con mares poco profundos colonizados por estromatolitos. Ilustración de Christian Jegou Publiphoto Diffusion. Fuente
Reconstrucción del aspecto ambiental que tendría nuestro planeta hace unos 3500-3700 millones de años, durante el Eón Arcaico, con mares poco profundos colonizados por estromatolitos. Ilustración de Christian Jegou Publiphoto Diffusion. FuentePero sigamos con la película. Al descubrir que los organismos no tienen ojos, la geóloga comenta que no los necesitan porque viven bajo tierra, por lo que su manera de orientarse se basa en detectar con los tentáculos las vibraciones que se transmiten por el interior del terreno. Es así como localizan a las presas que caminan sobre el suelo. Esto la empuja a plantear la manera de escapar de la amenaza, comentando al resto de la gente que, textualmente, “debemos evitar los aluviones del Pleistoceno”. Cuando todo el mundo se la queda mirando sin entender lo que ha dicho, explica que se refiere a que tienen que alejarse del suelo blando que cubre todo el valle en el que se asienta el pueblo, escapando hacia las montañas de granito puro que les rodea, ya que son rocas muy duras que no pueden atravesar los gusanos. Esto hace que otro protagonista grite, en un momento de la película, “las rocas pueden salvarnos”.
Me voy a quedar con esta frase y no voy a desvelar más sobre la película. Aunque sea de terror y del subgénero de “bichos comiéndose a la gente”, apenas tiene sangre ni escenas desagradables. Pero lo que sí la diferencia de otras similares es que todas las decisiones que toman a lo largo de la trama están basadas en el conocimiento geológico del terreno, así que se salvan gracias a la Geología. Por mi parte, os la recomiendo encarecidamente, porque podéis aprender Ciencias de la Tierra mientras pasáis un rato entretenido este verano.
Más películas geológicas:
El aperitivo preferido de los Comerrocas
65, ¿un título acertado?
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Geocine de verano se ha escrito en Cuaderno de Cultura Científica.
Marie Crous, la matemática que introdujo el punto en la notación decimal
Marie Crous fue una matemática francesa del siglo XVII. Se desconocen sus datos biográficos, en particular las fechas de su nacimiento y fallecimiento.
Fue la maestra de escritura y preceptora de la joven aristócrata Charlotte de Caumont La Force (1650-1724). Tuvo como mecenas a otra mujer, a Madame de Combalet duquesa de Aiguillon (1604-1675), sobrina del cardenal Richelieu. Aunque su protectora conocía a Marin Mersenne (1588-1648), Marie Crous no fue reconocida por el entorno científico de Mersenne y no figura en la lista de las eruditas célebres de su tiempo.
En 1636, y posteriormente en 1641, publicó dos manuales de aritmética que proporcionaron un estudio sobre el sistema de numeración decimal muy innovador en su época.
 Portadas de los dos escritos de Marie Crous. Fuente: Institut de France.
Portadas de los dos escritos de Marie Crous. Fuente: Institut de France.
Solo existe una copia conocida de estos dos escritos (encuadernados juntos). Se encontró en la antigua colección de la biblioteca personal del cardenal Giulio Raimondo Mazarino (1602-1661), protegido de Richelieu, mecenas de las artes y coleccionista de libros.
El primer escrito matemático de Marie CrousEl escrito Avis de Marie Crous aux filles exerçant l’arithmétique : sur les dîmes ou dixième du sieur Stevin. Contenant plusieurs avertissements démonstrations, et propositions : en lesquelles est declaré comment elles se peuvent servir de la partition des dîmes, sans le changement des divisions des monnaies, poids, et mesures : par le moyen de cinq tables y contenues.. Le tout renvoyé à mon abrégé pour y être très utile (París, 1636) va mucho más allá de lo que puede encontrarse en los manuales elementales de iniciación al cálculo.
Crous dedicó este trabajo a su alumna Charlotte de Caumont La Force.
 Dedicatoria a Charlotte de Caumont La Force. Fuente: Institut de France.
Dedicatoria a Charlotte de Caumont La Force. Fuente: Institut de France.
Este trabajo incluye una presentación de las fracciones decimales, reproducida a partir de De Thiende (1585, traducida ese mismo año al francés como La Disme) de Simon Stevin (1548-1620). Marie Crous introduce en esta obra un cambio importante respecto a Stevin: el punto (hoy la coma en España y otros países) para separar la mantisa de la parte decimal.
También reemplaza las unidades decimales que faltan con ceros: un cambio fundamental que dio a la numeración decimal su forma actual.
El segundo escrito matemático de Marie CrousEn su escrito Abbregé recherché de Marie Crous pour tirer la solution de toutes propositions d’aritmetique, dependantes des reigles y contenuës : avec quelques propositions sur les changes, escontes, interests, compagnies, associations, payemens, departemens de deniers, meslanges, bureau des monnoyes, & thoisages. Divisé en trois parties. Ensemble un advis sur les dixmes, ou dixiesmes du sieur Stevin (París, 1641), Crous desarrolló un texto completo de matemáticas comerciales. Esta obra comienza con una epístola dedicada a su protectora, la duquesa de Aiguillon.
 Dedicatoria a Madame de Combalet. Fuente: Institut de France.
Dedicatoria a Madame de Combalet. Fuente: Institut de France.
En la primera parte (páginas 1 a 32) Crous introduce demostraciones (así las denomina ella, aunque no incluye ningún razonamiento) en las que muestra cómo deben realizarse las diferentes operaciones basándose en las cuatro reglas. La autora indica, entre otros muchos ejemplos, cómo hacer varias operaciones simultáneamente; por ejemplo, 956 menos 784 más 230 o 9 por 472 más 683.
 Algunos ejemplos de operaciones. Fuente: Institut de France.
Algunos ejemplos de operaciones. Fuente: Institut de France.
En la segunda parte (páginas 39 a 69) incluye métodos para la realización de cálculo mental, en particular para fracciones decimales y para la realización de la regla de tres y sus aplicaciones en el intercambio comercial.
Y en la tercera parte, propone diferentes aplicaciones de las dos primeras del Abbregé.
La intención de sus escritosEstos libros de aritmética estaban dirigidos a las mujeres “para tratar de aliviar a aquellas que ejercen esta ciencia tanto por las necesidades de sus asuntos como
por el placer de su mente”. Crous cita explícitamente en sus tratados la compra de joyas o el forrado de tapices, pero también la comparación de valores económicos procedentes de la compra de terrenos o la constitución de una renta vitalicia con una suma determinada.
La historia de Marie Crous me recuerda a la de la matemática y maestra de niñas María Andresa Casamayor de La Coma (1720-1780), cuyo Tyrocinio arithmetico, Instrucción de las quatro reglas llanas también fue un manual de aritmética para aprender de manera directa el empleo de las cuatro reglas básicas, tan necesaria en las transacciones comerciales de la época.
¿Cuántas Marie o María Andresa habrán existido?
Referencias
-
Orly Terquem et Camille-Christophe Gerono, Notice bibliographique sur le calcul décimal en Nouvelles annales de mathématiques, vol. 12, 1853 [el artículo habla sobre Simon Stevin y Marie Crous, la parte de Crous está en las páginas 200-205].
-
Catherine Goldstein, Neither public nor private: mathematics in early modern France, preprint, 2003
-
Catherine Goldstein, Les fractions décimales : un art d’ingénieur ? (2010). ffhal-00734932v2
-
Hannah Wills, Sadie Harrison, Erika Jones, Rebecca Martin, and Farrah Lawrence-Mackey (ed.), Women in the History of Science. A source book, UCL Press, 2023 (páginas 112-120)
-
Marie Crous, Wikipédia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Marie Crous, la matemática que introdujo el punto en la notación decimal se ha escrito en Cuaderno de Cultura Científica.
Política y ciencia
Hace casi un siglo, en 1927, el genetista y biólogo evolutivo, y marxista convencido, J.B.S. (John Burdon Sanderson) Haldane publicó, en su libro Mundos posibles, un capítulo titulado Política y ciencia. Apareció, traducido a nuestro idioma, en 1947. Comentaba el autor que de vez en cuando le preguntaban si no había pensado nunca en intervenir en política. Afirma que es curioso que la misma pregunta se suele hacer a quienes son capaces de hablar seguido durante unos veinte minutos. Haldane había respondido que, en ocasiones, la política no es propia de un hombre honrado.
Si seguimos con lo que escribieron otros conocidos científicos y políticos sobre esta relación entre ciencia y política, podemos citar a Carl Sagan, que veía que debían estar más relacionadas de lo habitual. En 1996 avisaba de que vivimos en una sociedad basada en la ciencia y la tecnología y, sin embargo, en la que casi nadie entiende nada de ciencia y tecnología. Y es una mezcla inflamable de ignorancia y poder que, tarde o temprano, nos va a estallar en la cara. Además, Michel Polanyi afirma que nos negamos a aceptar una prueba científica si no prueba lo que queremos creer.
 Foto: Pelayo Arbués / UnsplashOficina C
Foto: Pelayo Arbués / UnsplashOficina C
Ahora vamos a tratar hechos concretos de la relación entre ciencia y política. La Oficina de Ciencia y Tecnología del Congreso de los Diputados español tiene como principal objetivo proveer a la Cámara de evidencias científicas sobre determinados temas de interés, con objeto de contribuir a la toma de decisiones informadas según el conocimiento científico disponible. La actividad de la Oficina la ofrece por el Congreso de los Diputados en colaboración con la Fundación Española para la Ciencia y la Tecnología, según el convenio suscrito por ambas partes el 5 de marzo de 2021. En la web del Congreso aparece como Oficina C.
Selecciona para el Congreso la evidencia científica sobre temas de interés y facilita el diálogo entre la comunidad científica y los diputados y diputadas, y así ayuda en la búsqueda de decisiones informadas según el conocimiento científico. Las evidencias se obtienen de artículos científicos publicados en revistas científicas, entrevistas con investigadores, científicos y expertos y de otras fuentes relacionadas con la actividad de la ciencia. Todo ello se analiza y resume en informes, denominados C, según un proceso estándar aceptado. Estos informes son públicos y están a disposición de diputados, diputadas y del público.
Desde la Oficina C consideran que su labor busca un nuevo ecosistema en el que los diputados y diputadas estén informados del conocimiento científico interdisciplinar y en el que su labor parlamentaria y las políticas públicas que desarrollen sean más capaces de abordar los grandes retos actuales. Con ello, las instituciones democráticas se ven fortalecidas. Y la comunidad científica conocerá mejor la labor parlamentaria y podrá contribuir de manera más estructurada a la formulación de políticas públicas. Además, el conocimiento mutuo aumenta la conexión y la confianza entre los actores implicados (diputados y diputadas, comunidad científica y sociedad).
Los cuatro primeros Informes C ya son públicos, en español e inglés, y tratan del hidrógeno verde como combustible, la inteligencia artificial y la salud, los avances en el tratamiento del cáncer y la ciberseguridad.
Decía Ortega que…Escriben Andreu Climent y Lorenzo Melchor que, hace un siglo, José Ortega y Gasset aseguró que el progreso de la civilización humana se debe fundamentalmente a dos razones:
-
La democracia, la adquisición de derechos sociales y civiles y el establecimiento y consolidación de instituciones que trasciendan generaciones humanas.
-
La generación del conocimiento en su sentido más amplio y el desarrollo científico y tecnológico.
Para conseguir y mantener lo primero es fundamental la política. Para conseguir y mantener lo segundo resulta crucial la ciencia. Se pueden identificar tres grupos que intervienen en este proceso, según Julián Briz e Isabel de Felipe, de la Universidad Politécnica de Madrid. En primer lugar están los científicos y académicos que estudian e investigan. En segundo lugar intervienen los que deciden y ejecutan desde el Gobierno y la Administración, o sea, los que toman las decisiones políticas. Y, en una democracia, los medios de comunicación que difunden lo anterior. Es evidente que la coordinación entre estos tres grupos es necesaria para la eficacia de todo el sistema.
Sin embargo y en general, los que se dedican a la política no están formados en ciencia. José Antonio Lozano mencionaba en 2013 que, en el Congreso de Estados Unidos, solo el 2% de sus miembros tenían una formación científica profesional. Y muchos de los representantes declaraban que en sus estudios universitarios huían de las materias científicas.
Sin embargo, Andreu Climent, afirmaba en 2018, que aunque la ciencia no es infalible, la toma de decisiones políticas informadas en el conocimiento existente aumenta las posibilidades de acertar.
¿Tiene sentido la ciencia para quienes los hechos les son indiferentes?Como hizo Max Weber hace un siglo debemos preguntarnos si tiene sentido la aportación de la ciencia para aquellos a quienes los hechos les son indiferentes y para aquellos que solo consideran la toma de posición en la práctica. Que es lo que hacen, o deben hacer, los políticos. Para Weber, lo primero es aceptar los hechos que resultan incómodos. Pero los hechos pueden ser verdaderos incluso aunque no sean bellos, ni sagrados, ni buenos, y formar parte de la sabiduría de todos los días. Pero el científico ofrece lo que tiene de la ciencia, no algo más. Como apoyaría Weber, el científico no es un caudillo, es un profesional de la ciencia. Podemos volver a J.B.S. Haldane cuando escribía en 1947 que, mientras la política no sea una disciplina de la ciencia hay que suponer que las reformas políticas, sociales y económicas son más bien experimentos.
Desde la Universidad de Chicago, Martha Nussbaum plantea el debate desde un enfoque diferente, a primera vista, incluso contrario. La actual crisis viene de la educación, promovida desde gobiernos y poderes económicos, de la que se eliminan las artes y las humanidades. Pero, añade, también desaparece el enfoque humanístico de las ciencias que incluye la imaginación, la creatividad o el rigor en el pensamiento crítico. Queda la rentabilidad a corto plazo con el cultivo del máximo utilitarismo y de las prácticas prioritarias para generar más riqueza.
El manifiesto publicado en octubre de 2020, firmado por 55 sociedades científicas y enviado al Presidente del Gobierno de España y a los Presidentes de las 17 comunidades autónomas, llevaba el título de “En la salud, ustedes mandan pero no saben”. Era un decálogo y ya en el punto primero los firmantes pedían que para enfrentarse a la pandemia las decisiones dominantes deben basarse en la mejor evidencia científica disponible, desligada por completo del continuo enfrentamiento político. Sin embargo, como ocurre a menudo, el manifiesto provocó que se considerase la pandemia no solo como cuestión médica, que sin duda lo es, sino además, como escribía Lina Gálvez en elDiario.es, también política.
Pero los científicos, afirmaba en 2017 José Cervera y como proclama Hannah Arendt, “son partidarios de los hechos y los datos sobre las emociones … a la hora de tomar decisiones, y también cuando se trata de cómo gobernar un grupo humano”. O sea, si hablamos de política. Incluso añadía Cervera que “la política no es un simple asunto de toma de decisiones racional y basado en datos”.
Más adelante continuó el debate sobre la importancia de los datos de la ciencia en las decisiones políticas. En julio de 2022, Daniel Innerarity, de la UPV/EHU, publicó en El Correo un artículo de opinión que, en la entradilla, pedía que “habría que ponderar y equilibrar las justificaciones tecnológicas, la validez de los datos, igual que hacemos con las diferencias ideológicas o de intereses”. En el texto concluye que los algoritmos, o sea, la tecnología basada en los algoritmos, no toman decisiones, pero lo ignoramos o, quizá por comodidad, lo consentimos. Propone politizar los procedimientos técnicos. Para ello debe haber ámbitos donde se discutan datos, algoritmos y artefactos. Es politizar la digitalización. Y la solución viene en acomodar los algoritmos entre los distintos intereses y visiones presentes una sociedad. Arendt rebatiría con su afirmación de que los hechos no cambian y en la ciencia aprendemos de los hechos.
Científicos, aprendan políticaNo pasó mucho tiempo, menos de un mes, en que no solo se pide un ámbito para debatir la ciencia (la tecnología en este caso) sino que pide, directamente, que la solución es que los científicos aprendan política. Como dirían los representantes elegidos para el Congreso de Estados Unidos, hay que huir de la ciencia y que sean los científicos los que sepan de política. El autor, Braulio Gómez, escribe que “da más miedo que nos acaben dominando los científicos que desprecian a los políticos que cualquier forma de inteligencia artificial”. El título de su columna resume su conclusión cuando pide “Científicos, aprendan política”. Supongo que el actual debate sobre Doñana entre políticos y científicos enseñará que los hechos a veces no cambian aunque los políticos, como dice Braulio Gómez, “tenían que ser negociados para cuidar otros intereses presentes en la sociedad que ellos [los científicos] consideraban menores”. El agua existe o no existe, esto son hechos.
Propone Jon Irazusta, de la UPV/EHU, que la solución del debate entre ciencia y política viene del diálogo, de la colaboración que ayude a encontrar la mejor solución en los problemas que se deben afrontar. Ni ciencia ni política, más bien la negociación entre ambas. Y, al contrario de lo que conocemos del Congreso de Estados Unidos, Irazusta pide, para los científicos, que se ilustren en temas alejados de su especialidad concreta o, si se quiere, que se interesen por las Humanidades, como pedía Martha Nussbaum.
Debemos retomar el debate que plantearon Carl Mitcham y Adam Briggle, de las universidades de Colorado, en Estados Unidos, y de Twente, en Holanda, sobre hasta donde se debería permitir que la política o la ética deben influir en la investigación científica, sea cual sea la relación entre ellas o sobre la formación en política y ciencia de quien toma las decisiones. Debate abierto para ahora, por ejemplo con el cambio climático, y para el futuro, en mi opinión, sobre biomedicina.
Además, como explica Santiago Iñiguez de Onzoño, de la IE University de Madrid, Emmanuel Kant, en su texto breve Teoría y Práctica, dice que no hay una diferencia sustancial entre teoría y práctica, solo que hay buena y mala investigación. Escribía Kant que “tal vez eso sea correcto en teoría, pero no sirve para la práctica” pues la teoría sin práctica es simple juego intelectual. La primera, la buena teoría, es real y compatible con los problemas aplicados, es decir, con la práctica. Solo nos falta decidir, entre ciencia y política, cuál es la teoría y cuál es la práctica. Y, en consecuencia, cuál funciona y cuál no es compatible con la realidad. ¿Quizá la política, sobre todo los programas electorales, son teoría, y la ciencia es práctica? De nuevo queda el debate abierto.
Referencias:
BOE 15 abril 2021. Anuncio de la Fundación Española para la Ciencia y la Tecnología F.S.P. (FECYT) por el que se publica el extracto del Convenio de colaboración entre el Congreso de los Diputados y la Fundación Española para la Ciencia y la Tecnología F.S.P., para el desarrollo de la Oficina de Ciencia y Tecnología del Congreso de los Diputados. P. 23452.
Briz Escribano, J. & I. de Felipe Boente. 2023. El valor del conocimiento académico en las decisiones políticas sobre alimentación. The Conversation 26 abril
Cervera, J. 2017. Ciencia y política: el papel de la verdad. Cuaderno de Cultura Científica 11 mayo.
Climent, A. & L. Melchor. 2018. Cómo acercar ciencia y política para mejorar la sociedad de hoy (y de mañana). The Conversation 8 noviembre.
Gálvez, L. 2020. Ciencia y política: ustedes saben mucho, pero no de todo. elDiario.es 5 octubre.
Gómez, B. 2022. Científicos, aprendan política. El Correo 19 agosto.
Haldane, J.B.S. 1947. Mundos posibles. José Janés Ed. Barcelona. 218 pp.
Innerarity, D. 2022. Un parlamento para los algoritmos. El Correo 24 julio.
Iñiguez de Onzoño, S. 2023. Cómo formar a directivos ilustrados. The Conversation 10 mayo.
Irazusta, J. 2022. Ciencia y humanidades: una relación aún sin resolver. Campusa 24 febrero.
Kant, I. 2006. Teoría y práctica. Ed. Tecnos. Madrid. 65 pp.
Lozano Teruel, J.A. 2013. ¿Son compatibles ciencia y política? ADC Alternativas de Comunicación. Murcia. 380 pp.
Manifiesto de 55 sociedades científicas. 2020. Octubre.
Mitcham, C. & A. Briggle. 2007. Ciencia y política: perspectiva histórica y modelos alternativos. Revista CTS 8: 143-158.
Nussbaum, M. 2010. Sin fines de lucro. Por qué la democracia necesita de las humanidades. Katz Eds. Buenos Aires. 199 pp.
Polanyi, M. 1962. The republic of science: Its political and economic theory. Minerva 1: 54-73.
Weber, M. 1979. El político y el científico. Alianza Ed. Madrid. 231 pp.
Para saber más:
Ciencia, ideología y práctica política
Ciencia, política y hechos
Ciencia, creencias, política y matar al mensajero
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Política y ciencia se ha escrito en Cuaderno de Cultura Científica.
Superolfateadoras
olfato
 Foto: Richárd Ecsedi / Unsplash
Foto: Richárd Ecsedi / UnsplashLos seres humanos somos animales visuales. Exceptuando a los ciegos, la vida cotidiana de las personas gira principalmente en torno al sentido de la vista, mientras que el resto de los sentidos desempeñan un papel secundario. Nuestro olfato, por ejemplo, en comparación con el de muchos otros animales, es pobre y tiene una función mucho menos vital que la vista o el oído. Sin embargo, con la pandemia de COVID-19 este menospreciado sentido cobró un protagonismo inusitado. Multitud de personas a lo largo del mundo notaron que habían perdido parcial (hiposmia) o totalmente su capacidad olfatoria (anosmia) tras la infección por el SARS-CoV-2. Como consecuencia, muchas de ellas tenían menos apetito, al tener dificultades para oler los alimentos o para degustarlos. Esto se debe a que el olfato también interviene, junto con el gusto, en el reconocimiento del sabor de los alimentos.
Más allá de los papeles más obvios del olfato como son el disfrute de los alimentos y evitar la inhalación de sustancias que puedan ser tóxicas para las personas, este sentido influye en otros muchos aspectos de nuestra vida que pueden pasar desapercibidos: potencia la evocación de recuerdos, interviene en la selección de pareja sexual, modula la frecuencia cardíaca, la presión arterial y la percepción del dolor, provoca cambios en el estado de ánimo o de alerta…
Aunque el sentido del olfato del Homo sapiens no destaque especialmente por su capacidad para detectar olores débiles ni por su habilidad para distinguir sutiles diferencias entre aromas, existe una importante variabilidad entre individuos… y entre sexos. Por lo general, las mujeres tienen el olfato más desarrollado que los hombres en todos los aspectos. Por un lado, su umbral olfativo es más bajo, es decir, necesitan una menor concentración de una sustancia en el aire para detectar su olor. Por otro, también tienen una capacidad mayor para identificar olores concretos y distinguirlos entre ellos.
Un estudio, publicado en 2014 en la revista PLOS ONE, aportó una posible explicación a por qué la que las mujeres suelen tener un mejor olfato: ellas tienen más células en el bulbo olfatorio (hasta un 50 % más), la zona del cerebro encargada de recibir y procesar la información sobre los olores que recibe del nervio olfatorio. No obstante, es preciso aclarar que las diferencias entre las habilidades olfatorias de hombres y mujeres son relativamente pequeñas. Así, hay varones que pueden tener más olfato que ciertas mujeres, pues la agudeza olfatoria entre personas del mismo sexo puede variar en gran medida. De hecho, las personas con hiperosmia (incremento de la sensibilidad olfatoria) destacan por su capacidad para percibir olores imperceptibles para la gran mayoría y por sentir con mucha mayor intensidad aquellos aromas que todos huelen. Tanto es así que la habilidad olfatoria de estos individuos puede estar varios órdenes de magnitud por encima de la gente con un sentido del olfato corriente.
Sin duda, la hiperosmia supone una notable ventaja para ciertos colectivos profesionales como perfumistas, sumilleres y catadores, pero en el día a día este don puede convertirse en un verdadero castigo al entrar a zonas con hedores muy intensos. Por ejemplo, el fuerte olor a «humanidad» del metro en hora punta es un lugar extremadamente hostil para una persona con hiperosmia que puede llegar a experimentar las mismas reacciones que un individuo con un sentido normal del olfato en una cloaca inmunda: vómitos, náuseas, mareos y hasta desmayos. Por esa razón, las personas con hiperosmia procuran evitar todos aquellas áreas que supongan una tortura olfatoria, lo que puede afectarles en su esfera social.
La hiperosmia es una condición relativamente rara, pero las causas que pueden provocarlo son muy variadas. Hay personas que nacen con esta característica, mientras que otras pueden adquirirla, a veces de forma transitoria, a lo largo de la vida. Ciertas enfermedades, como migrañas, epilepsia del lóbulo temporal, párkinson o trastornos autoinmunitarios pueden desencadenar una hiperosmia, pero también el consumo de ciertas sustancias (como anfetaminas). En la actualidad, existe bastante debate científico sobre si realmente los cambios hormonales que se producen durante el embarazo pueden provocar hiperosmia o si, en realidad se trata de otra cosa: una percepción distorsionada de los olores, con la aparición, incluso, de olores fantasma (que no existen), o una reacción mayor a los olores, con una sensibilidad olfatoria que no varía.
Más allá de catar refinados vinos o deleitarse con exquisitos perfumes, contar con un olfato extraordinario puede darte un poder inesperado: detectar a personas que sufren párkinson por su característico olor. Los científicos descubrieron hace años que la escocesa Joy Milne es capaz de detectar ciertas moléculas que liberan los afectados por esta enfermedad neurológica, incluso mucho antes de que se manifiesten los primeros signos. Milne descubrió esta extraña habilidad con su marido, cuyo olor cambió 12 años antes de padecer párkinson. Su habilidad se puso a prueba en diversos estudios: la mujer con hiperosmia podía reconocer con gran precisión a los pacientes con párkinson con tan solo oler sus camisetas e incluso reconoció a una persona como afectada por párkinson, cuando su diagnóstico médico llegó 8 meses más tarde.
Ahora los científicos están trabajando en un método objetivo para detectar específicamente aquellas moléculas asociadas al párkinson, probablemente liberadas por las glándulas sebáceas de la piel. El caso de Milne refleja, una vez más, la hiperosmia tanto como una maldición, como un don. En la vida diaria, la escocesa puede oler a personas que podrían padecer párkinson en un futuro próximo, pero no puede informarles por razones éticas, aconsejada por expertos en la materia.
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo Superolfateadoras se ha escrito en Cuaderno de Cultura Científica.
Virtudes de la nostalgia
 Photo by Jon Tyson on Unsplash
Photo by Jon Tyson on Unsplash
El pasado es la referencia de la nostalgia, pero su ámbito psicológico puede extenderse hacia el futuro. Los sentimientos de nostalgia son universales, y resulta que, por comparación con la evocación de episodios ordinarios, elevan el optimismo o, al menos, generan expresiones de optimismo.
Esa es la conclusión principal de una serie de cuatro estudios en los que, utilizando diferentes procedimientos que no detallaré, se ha analizado la medida en que los sentimientos de nostalgia producen un estado de optimismo, así como los procesos mentales que intermedian en esa relación. Los estudios se han realizado con hombres y mujeres de distintas edades y de tres nacionalidades, estadounidenses, daneses e ingleses.
El primero de los estudios sirvió para identificar la posible existencia de la relación. El segundo ilustró que la inducción experimental de sentimientos de nostalgia hace que aumente el optimismo de las personas. El tercero reprodujo los hallazgos del anterior, utilizando, para ello, la exposición a canciones nostálgicas y, como control, a canciones normales. Este tercer estudio puso de manifiesto el papel mediador de la autoestima en el efecto de la nostalgia sobre el optimismo. Esto es, los sentimientos de nostalgia mejoran la autoestima y es esta última la que, al parecer, eleva el optimismo. Esta observación es coherente con hallazgos anteriores, según los cuales los recuerdos del propio pasado ayudan a mantener los sentimientos de amor propio; pero, además, extiende ese conocimiento hacia el futuro, en el sentido de que los sentimientos de autoestima provocados por la nostalgia pueden ayudarnos a mejorar nuestras perspectivas de futuro. El cuarto estudio ayudó a clarificar en mayor medida estos procesos, exponiendo a las personas que participaron en los experimentos a letras de canciones nostálgicas y, como control, a letras de canciones normales. Mediante este cuarto estudio se estableció una secuencia causal más extensa para la relación entre los sentimientos nostálgicos y la autoestima, al incluir como mediador de dicha relación la sensación de conectividad social.
Así pues, la nostalgia promueve la sensación de conectividad social; ésta, a su vez, eleva la autoestima, y como consecuencia de una mayor autoestima, aumenta el optimismo. O, dicho de otra forma, el aumento en la autoestima que experimentan los participantes es la consecuencia de un más intenso sentimiento de conectividad social que se deriva del ensueño nostálgico; y esa mayor autoestima es, por su parte, la que hace que aumente el optimismo.
Es sabido que el optimismo proporciona bienestar y beneficios en términos de salud. Por ello, y a tenor de los resultados obtenidos en estos experimentos, la nostalgia puede ser una vía muy adecuada hacia el bienestar, favoreciendo comportamientos saludables y éxito en las relaciones. Además, como se da la circunstancia de que el recurso a los recuerdos nostálgicos suele acentuarse en periodos de tristeza, soledad, aburrimiento o dudas existenciales, los resultados obtenidos en este trabajo implican que la nostalgia, al promover el optimismo, podría ayudar a las personas a hacer frente a la adversidad psicológica. La nostalgia, según los autores del trabajo, puede, en definitiva, ser un catalizador para conectar el pasado, presente y futuro de una persona, proporcionándole un sentido de continuidad.
Utilizando palabras casi textuales (pero traducidas) de los autores, la conclusión de este trabajo es que “la nostalgia no es una vieja fotografía en sepia guardada bajo llave en un cajón. Su poder, de largo alcance, puede iluminarnos el camino a seguir.”
Fuente: Wing-Yee Cheung, Tim Wildschut, Constantine Sedikides, Erica G. Hepper, Jamie Arndt y Ad J. J. M. Vingerhoets (2013): “Back to the Future: Nostalgia Increases Optimism” Pers Soc Psychol Bull 39: 1484.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Virtudes de la nostalgia se ha escrito en Cuaderno de Cultura Científica.
Adicción, ¿el hambre de toda la vida?

Cómo influyen los parásitos en el comportamiento de los animales, cómo se modifica la conducta de las madres mamífero o cuáles son las enfermedades que nos afectan y desde cuándo hemos desarrollado comportamientos funerarios ante la muerte son algunos de los aspectos que se analizarán en la V Jornada Nacional sobre Evolución y Neurociencias.
Especialistas en ambas materias se reunirán el 11 y 12 de mayo en una nueva edición conducida por Eva Garnica y Pablo Malo, psiquiatras y miembros de la Red de Salud Mental de Bizkaia, y organizada por esa misma entidad y la Cátedra de Cultura Científica de la UPV/EHU.
La jornada, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolucionista y divulgar de un modo accesible para todos los públicos.
El fenómeno de la adicción (a lo que sea) se basa en mecanismos que hemos desarrollado a lo largo de la evolución para sobrevivir, pero que entran en funcionamiento para otras cosas. Si lo pensamos un momento, la adicción funciona como el hambre de toooda la vida. Esta es la tesis que expone en esta charla Gerardo Sabio.
Gerardo Sabio es psicólogo clínico y director técnico de la Asociación Ferrolana de Drogodependencias (ASFEDRO).
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Adicción, ¿el hambre de toda la vida? se ha escrito en Cuaderno de Cultura Científica.
Ondas gravitacionales gigantescas detectadas usando púlsares
Astrofísicos de varias asociaciones internacionales, valiéndose de algunos de los más grandes radiotelescopios en el mundo, han encontrado evidencia de ondas gravitacionales gigantescas, que oscilan con períodos que van de años a décadas. Estos resultados han sido posibles gracias a una precisa observación de un conjunto de púlsares (relojes cósmicos) en nuestra galaxia.
 Imagen desde el telescopio del Chinese Pulsar Timing Array. Fuente: NAOC of CAS
Imagen desde el telescopio del Chinese Pulsar Timing Array. Fuente: NAOC of CAS
La señal de ondas gravitacionales se ha podido observar a través de los datos tomados por el Observatorio Norteamericano de Nanohercios para Ondas Gravitacionales (NANOGrav) del Physics Frontiers Center (PFC) durante 15 años. Esta colaboración, de más de 190 científicos, en su mayoría de EE. UU. y Canadá, financiada por la National Science Foundation (NSF) americana, utiliza los púlsares (una estrella de neutrones que gira muy rápidamente sobre su eje, emitiendo en cada giro un ‘pulso’ de radio) para identificar la presencia de las ondas gravitacionales. Las colaboraciones internacionales que utilizan telescopios en Europa, India, Australia y China han mostrado resultados similares de forma independiente.
Si bien resultados anteriores de NANOGrav descubrieron una misteriosa señal temporal en todos los púlsares que se observaron, esta señal era demasiado débil para revelar su origen. Los datos hechos públicos hoy de los 15 años de observación demuestran que la señal es consistente con la presencia de ondas gravitacionales de ondulación lenta que atraviesan nuestra galaxia. «Esta es una evidencia clave de las ondas gravitacionales a frecuencias muy bajas», según el Dr. Stephen Taylor de la Universidad de Vanderbilt, actual investigador principal de esta colaboración internacional «Después de años de trabajo, NANOGrav está abriendo un camino nuevo en el universo de las ondas gravitacionales».
A diferencia de las fugaces ondas gravitacionales de alta frecuencia observadas por instrumentos terrestres como LIGO (el Observatorio de ondas gravitacionales por interferometría láser), esta señal continua de baja frecuencia solo puede percibirse con un detector mucho más grande que la Tierra. Para ello, los astrónomos convirtieron nuestro sector de la Vía Láctea en una enorme antena de ondas gravitacionales usando estrellas exóticas llamadas púlsares. NANOGrav ha obtenido datos de 68 púlsares durante 15 años lo que le ha permitido formar un tipo de detector llamado “Conjunto de sincronización de púlsares” (Pulsar Timing Array en su descripción en inglés).
Un púlsar es el remanente ultradenso del núcleo de una estrella masiva después de su desaparición en una explosión de supernova. Los púlsares giran rápidamente, emitiendo pulsos de ondas de radio que barren el espacio a su alrededor de manera similar a los pulsos de luz de un faro en la costa. Estas estrellas, por tanto, parecen «latir» cuando se observan desde la Tierra. Los más rápidos de estos objetos, llamados púlsares de milisegundos, giran cientos de veces cada segundo. Sus pulsos son muy estables, lo que los hace útiles como relojes cósmicos precisos.
La teoría de la relatividad General de Einstein predice de manera precisa cómo las ondas gravitacionales deberían afectar las señales de estos púlsares. Al estirar y comprimir la estructura del espaciotiempo a su paso, las ondas gravitacionales afectan al ritmo de cada pulso, de manera leve pero predecible, retrasando algunos de ellos y adelantando a otros. Estos desfases están correlacionados para todos los pares de púlsares de acuerdo a la distancia que separa a las dos estrellas en el cielo. Los datos obtenidos por NANOGrav son perfectamente compatibles con lo que predice la teoría de la relatividad.
Comparando estas predicciones teóricas con los datos presentados hoy podemos asegurar que, el conjunto de datos más reciente de NANOGrav muestra evidencias de la presencia de ondas gravitacionales con períodos que abarcan de años a décadas. Estas ondas podrían surgir de los agujeros negros más masivos de todo el Universo: miles de millones de veces más masivos que el Sol, con tamaños superiores a la distancia entre la Tierra y el Sol. Los estudios futuros de esta señal abrirán un nuevo camino en el universo de ondas gravitacionales, proporcionando información sobre los agujeros negros titánicos que se fusionan en el corazón de galaxias distantes, entre otras fuentes exóticas.
En palabras de Jose Juan Blanco-Pillado, Investigador Ikerbasque en la UPV/EHU y miembro asociado de NANOGrav: “Estos resultados marcan un hito en la historia de la detección de ondas gravitacionales y nos permiten observar el universo desde una nueva perspectiva. En el futuro esperamos que este tipo de observaciones nos ayuden a entender procesos astrofísicos conocidos e identificar o descubrir otros fenómenos que han permanecido ocultos hasta ahora. »
“En particular la investigación que realizamos en la UPV/EHU se centra en identificar nuevos procesos en el universo primordial que puedan dar una señal detectable por este tipo de observatorios de ondas gravitacionales. La detección de este tipo de señales de forma inequívoca nos daría una información muy valiosa de como evolucionó el universo en sus primeros instantes.”
Astrofísicos de todo el mundo han estado persiguiendo esta señal de ondas gravitacionales. Varios documentos publicados hoy por las colaboraciones de Parkes Pulsar Timing Array en Australia, Chinese Pulsar Timing Array y European Pulsar Timing Array/Indian Pulsar Timing Array muestran indicios de la misma señal en sus datos. A través del consorcio International Pulsar Timing Array, las colaboraciones regionales están trabajando juntas para combinar sus datos a fin de caracterizar mejor la señal y buscar nuevos tipos de fuentes, convencidas de la importancia y necesidad de la colaboración internacional.
Para saber más:
Ondas gravitacionales: una nueva era para la humanidad
Cosmología de ondas gravitacionales en 29 órdenes de magnitud
Comprimiendo la luz para detectar mejor ondas gravitacionales
Referencia:
Gabriella Agazie et al (2023) The NANOGrav 15 yr Data Set: Evidence for a Gravitational-wave Background The Astrophisical Journal Letters. doi: 10.3847/2041-8213/acdac6
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Ondas gravitacionales gigantescas detectadas usando púlsares se ha escrito en Cuaderno de Cultura Científica.
La catenaria: una introducción a su mantenimiento (2/4)
mantenimiento
Another flaw in the human character is that everybody wants to build and nobody wants to do maintenance. (Otra falta de la condición humana es que todo el mundo quiere construir, pero nadie quiere hacer el mantenimiento.)—Kurt Vonnegut
 Foto: Catherine / Unsplash
Foto: Catherine / UnsplashEl mantenimiento es el conjunto de procesos necesarios para conservar la funcionalidad de cualquier sistema tecnológico en su nivel de diseño. Como todo proceso industrial, el mantenimiento tiene un coste asociado en capital, trabajo y huella medioambiental. Además, el mantenimiento lleva aparejado cierto nivel de indisponibilidad de los sistemas mantenidos. Estos periodos de parada o funcionamiento degradado suponen pérdidas que se pueden contabilizar en el propio proceso de mantenimiento. Reducirlas al mínimo imprescindible es un reto interesante, en el que juegan un papel fundamental las políticas de mantenimiento.
Al igual que los elementos materiales que comprenden toda tecnología, las políticas de mantenimiento también han experimentado una evolución con el tiempo. La primera y elemental es «cuando algo se rompe, se repara», también llamado mantenimiento correctivo. Esta aproximación, por sí sola, es inviable cuando tratamos con sistemas de los que depende la seguridad de las personas. Pronto se percibió que la indisponibilidad del sistema afectado, desde la avería hasta su puesta en funcionamiento, suponía por sí misma una fuente de costes considerable. Esto aparejó la creación de la política «revisamos el sistema a intervalos regulares», o mantenimiento preventivo. El objetivo es «cazar» los fallos antes de que sucedan, algo más fácil de decir que de hacer y que supone de por sí toda una nueva disciplina de la técnica.
Naturalmente, los fallos aún ocurren, ora porque escapen a los mecanismos de detección cuando aún son «prefallos», ora por puro azar. Un intervalo de inspección muy pequeño detectará un número creciente de fallos en desarrollo, y viceversa para tiempos crecientes. El propio acto de la inspección tiene un coste. Esto introduce su frecuencia en la fórmula del objetivo que deseamos optimizar. La práctica totalidad de los mantenimientos son todavía una combinación, ajustada para buscar un coste mínimo a mano o mediante herramientas estadísticas sencillas, de prevención y corrección.
 Una herramienta especializada de mantenimiento ferroviario, el tren esmerilador de carriles de Metro de Madrid, estacionado en una vía de apartado de la estación de Almendrales (línea 3). Foto: Iván RiveraUn mundo ideal
Una herramienta especializada de mantenimiento ferroviario, el tren esmerilador de carriles de Metro de Madrid, estacionado en una vía de apartado de la estación de Almendrales (línea 3). Foto: Iván RiveraUn mundo ideal
Dos tipos de avances tecnológicos han permitido soñar con una política ideal, que podríamos denominar «cambiamos la pieza justo antes de que falle», o mantenimiento predictivo. Si, de algún modo, logramos retrasar las acciones de mantenimiento hasta un momento arbitrariamente cercano al del fallo, pero siempre anticipándolo, habremos eliminado la indisponibilidad por avería a la vez que espaciamos al máximo las intervenciones. El coste teórico de este mantenimiento es, por tanto, el mínimo posible para nuestro nivel de servicio deseado. ¿Cuáles son los avances que habilitan este salto conceptual?
En primer lugar, la disponibilidad masiva y barata de potencia de cálculo. Los ordenadores actuales son capaces de simular sistemas físicos de gran complejidad. Aunque estimar las solicitaciones sobre una catenaria flexible requiere realizar cálculos mecánicos, eléctricos y térmicos de forma simultánea, esto está al alcance de computadoras con un precio razonable.
Pero los cálculos no lo son todo. Cualquier sistema físico más complejo que la proverbial vaca esférica carece de soluciones analíticas. Es decir: no existen ecuaciones sencillas y fáciles de calcular que lo representen. Hay que recurrir a métodos numéricos iterativos: un conjunto de fórmulas más o menos simplificadas que se ejecuta, recurrentemente, para momentos sucesivos de un tiempo en el que consideramos una subdivisión básica. No importa cuál: horas, segundos, milésimas de segundo. Cualquiera de ellas establecerá una contrapartida entre la precisión obtenida y el tiempo real en el que obtendremos respuestas. Disponer de ordenadores más rápidos no evita la existencia de este dilema, solo lo desplaza a un punto de equilibrio diferente. Además, el tipo de matemáticas que suele ser necesario resolver provoca que doblar la potencia de cálculo no suponga, en general, dividir por dos el tiempo de proceso o multiplicar por dos la precisión, sino considerablemente menos. Cada iteración calculada tendrá un error que irá, inevitablemente, a alimentar la entrada de la siguiente. En un número de ciclos que depende de cada sistema simulado, la deriva de las respuestas respecto de la realidad será tan grande como para hacer inútil todo el ejercicio.
Es aquí donde entra en juego el segundo avance: los sensores. Hoy es mucho más sencillo y barato conocer valores para las variables de estado de un sistema real gracias a la miniaturización de la electrónica. Quien mide, sabe (aunque medir también es un arte de la ingeniería, sujeto a sus propios balances entre precisión y exactitud). Si en una simulación introducimos periódicamente correcciones derivadas de lecturas de sensores en un sistema real, podemos controlar el error y, por tanto, la deriva.
 Equipos de alimentación eléctrica y control en una subestación de tracción de Serveis Ferroviaris de Mallorca. Foto: Iván Rivera«Mellizos digitales»
Equipos de alimentación eléctrica y control en una subestación de tracción de Serveis Ferroviaris de Mallorca. Foto: Iván Rivera«Mellizos digitales»
Lo que tenemos entre manos pretende ser un «gemelo digital»: un sistema simulado capaz de ofrecer respuestas concretas ante todo tipo de cuestiones. ¿Qué efecto tendría sobre la catenaria duplicar el tráfico de trenes? Podríamos «copiar y pegar» series de datos registrados en los sensores para hacernos una idea. ¿Y si queremos conocer el efecto de un aumento de la temperatura en un verano particularmente duro? Podríamos simular la dilatación extra sobre el metal.
Ni que decir tiene que un auténtico gemelo digital es una quimera, tanto por las limitaciones de los métodos y la capacidad de cálculo como por las imprecisiones —inevitables— cometidas por los sensores. O por su ausencia, ya que no será económicamente viable llenar de artefactos de medida toda la infraestructura. Medio en broma, podríamos decir que lo que obtendremos de la fusión de simuladores físicos y sensores será un «mellizo digital». Algo razonablemente parecido al sistema real. Lo suficiente como para poder hacer predicciones fiables sobre su rendimiento y sobre las diferentes necesidades del mantenimiento. Esta es la teoría, pero ¿y la práctica?
En una instalación industrial genérica, una vez determinados los puntos de medida necesarios, debemos garantizar tanto la alimentación eléctrica de los sensores como su conectividad. Para lo que podríamos llamar «instalación concentrada», esto no es un problema serio. La alimentación está garantizada por una red de distribución de baja tensión convencional. En lo que respecta a la conectividad, podremos encontrar alternativas de todo tipo, inalámbricas y cableadas.
 Salida sur de la estación de Valladolid Campo Grande. Foto: Iván RiveraEl problema de las instalaciones lineales
Salida sur de la estación de Valladolid Campo Grande. Foto: Iván RiveraEl problema de las instalaciones lineales
Pero la catenaria no es una instalación industrial concentrada: es una instalación lineal distribuida a lo largo de decenas, centenares, miles de kilómetros de red férrea. A pesar de que la catenaria transporta energía eléctrica, lo hace en unas condiciones en las que resulta particularmente oneroso transformarla entre su forma de consumo para el ferrocarril (en España, corriente continua a 3 kilovoltios o alterna a 25 kilovoltios) en una alimentación adecuada para los sensores y su circuitería asociada, generalmente 12 o 24 voltios en continua. Este problema se puede solventar, evitando kilómetros de red de distribución en baja tensión, mediante el uso de placas fotovoltaicas y baterías.
Los problemas de conectividad pueden soslayarse con el uso de la red celular 3G/4G, y si la cobertura resulta ser defectuosa, con agregadores y radioenlaces punto a punto u otras alternativas. Las redes específicas de baja potencia y largo alcance, como LoRaWAN o SigFox, diseñadas específicamente para ofrecer conectividad a sensores son interesantes siempre que la cantidad de datos a transferir por unidad de tiempo sea lo suficientemente pequeña; la experiencia muestra, sin embargo, que esta suposición resulta ser problemática para un buen número de prototipos de sensores asociados a la operación ferroviaria. La solución, el despliegue generalizado de las nuevas redes celulares 5G y sus sucesoras (6G está a la vuelta de la esquina), es cuestión de tiempo. A esto nos referimos los ingenieros de teleco cuando hablamos de «la Internet de las Cosas».
Suele decirse que, sin salir del planeta, los requisitos más estrictos de resistencia y durabilidad frente a los elementos están en el entorno militar, y justo después en la industria del transporte, donde la ferroviaria destaca por méritos propios. El ferrocarril tiene instalaciones extendidas a lo largo de centenares de kilómetros, expuestas a la intemperie, cruzando estepas, desiertos o selva, bajo temperaturas extremas y variables, en ambientes húmedos, salinos o contaminados por partículas en suspensión, con poca o ninguna vigilancia activa. ¿Cómo lograr hacer de una instalación como la catenaria una infraestructura monitorizada del siglo XXI?
Del mismo autor:
Los límites del Hyperloop
El camión solar: ¿una posibilidad real?
Sobre el autor: Iván Rivera es ingeniero especializado en proyectos de innovación de productos y servicios para ferrocarriles.
El artículo La catenaria: una introducción a su mantenimiento (2/4) se ha escrito en Cuaderno de Cultura Científica.
El recorrido del caballo de Vandermonde
Me encanta que hoy en día cuando estamos estudiando sobre un tema, por ejemplo, el problema del recorrido del caballo sobre el tablero de ajedrez (tema al que hemos dedicado varias anotaciones en el Cuaderno de Cultura Científica, como El problema del recorrido del caballo en el tablero de ajedrez, El problema del recorrido del caballo en el tablero de ajedrez (II) o ¿Existen recorridos mágicos del caballo en el tablero de ajedrez?), podamos acudir a las fuentes originales y comprobar, por nosotros mismos, lo que está escrito en las ellas, gracias a que muchos textos clásicos ya están digitalizados. Esto es lo que me ha pasado con el método de Vandermonde para construir un recorrido cerrado del caballo. En varios textos nos encontrábamos comentarios sobre el mismo, pero no se explicaba cómo funcionaba.
 Primera página del trabajo Remarques sur les problèmes de situation / Comentarios sobre los problemas de la situación (1771) del matemático francés Alexandre-Théophile VandermondeEl problema del recorrido del caballo
Primera página del trabajo Remarques sur les problèmes de situation / Comentarios sobre los problemas de la situación (1771) del matemático francés Alexandre-Théophile VandermondeEl problema del recorrido del caballo
Empecemos recordando el enunciado del problema del recorrido del caballo.
Problema del recorrido del caballo: Buscar un recorrido de la figura del caballo (con su característico salto en forma de L) sobre el tablero de ajedrez que consista en mover esta pieza del juego, desde una casilla inicial, de forma sucesiva a través de todas las casillas del tablero, pasando una sola vez por cada una de ellas, y terminando en la casilla inicial (recorrido cerrado) o en otra casilla distinta (recorrido abierto).
En las mencionadas entradas, en concreto en la entrada El problema del recorrido del caballo en el tablero de ajedrez (II), se mostraron algunos métodos para construir recorridos como el sencillo método del matemático francés Abraham de Moivre (1667-1754), el ingenioso método del matemático suizo Leonhard Euler (1707-1783), la ingeniosa y elegante técnica del matemático alemán H. C. von Warnsdorff (1780-1858) o la hermosa construcción el médico, matemático, físico, teólogo y lexicólogo británico Peter Mark Roget (1779-1869). En la anotación de hoy vamos a abordar un nuevo método de construcción de recorridos cerrados del caballo sobre el tablero de ajedrez, el método de Vandermonde.
Si buscamos información sobre este método, podremos leer, por ejemplo, en el libro clásico de matemática recreativa Mathematical Recreations and Essays, de W. W. Rouse Ball, H. S. M. Coxeter, lo siguiente:
El siguiente intento de especial interés se debe a Vandermonde, que redujo el problema a la aritmética. Su idea era cubrir el tablero por dos o más rutas independientes tomadas al azar, y luego conectarlas. Definió la posición de una casilla mediante una fracción x/y, cuyo numerador x es el número de la casilla desde un lado del tablero, y cuyo denominador y es su número desde el lado adyacente del tablero; esto equivale a decir que x e y son las coordenadas de una casilla.
Y se explican algunas cuestiones más, por ejemplo, como afecta el movimiento del caballo a la nueva notación, y se muestra el recorrido concreto expresado mediante las fracciones, pero no se explica cómo se obtiene ese recorrido, ni por qué el método es aritmético. Por suerte podemos acudir al texto original y ver qué nos dice el mismo.
El método de VandermondeAlexandre-Theophile Vandermonde (1735-1796), fue un el músico, matemático y químico francés, cuyo nombre a muchos nos hace recordar nuestra época de estudiantes, cuando aprendimos el conocido determinante de Vandermonde. En matemáticas tan solo escribió cuatro trabajos, uno sobre la resolución de ecuaciones, otro sobre el problema del recorrido del caballo, otro sobre combinatoria y el último sobre la teoría de los determinantes. El problema del recorrido del caballo sobre el tablero de ajedrez lo abordó en su segundo trabajo Remarques sur les problèmes de situation / Comentarios sobre los problemas de la situación (1771), que es uno de los textos fundacionales de la rama de las matemáticas denominada Topología (véase la anotación La topología modifica la trayectoria de los peces).
Como el texto está en francés tendremos que traducirlo, o nosotros mismos o con la ayuda de alguien, incluido algún traductor online.
Empecemos por la forma en la que Vandermonde denota las diferentes casillas del tablero de ajedrez. Cada casilla se denota con una fracción de la forma x/y, donde x denota la fila en la que se encuentra esa casilla en el tablero (empezando por el lado inferior) e y la columna en la que se encuentra la casilla (empezando por el lado izquierdo), para x e y con valores entre 1 y 8. Así, como vemos en la siguiente imagen, la casilla de abajo a la izquierda es la casilla 1/1, la de abajo a la derecha 1/8, etcétera.
En otras palabras, la notación de las casillas es un sistema para describir la posición de las mismas en el tablero de ajedrez y nada tiene que ver con el número racional x/y.
La siguiente cuestión a analizar es cómo afecta el movimiento del caballo a la notación utilizada. Como el caballo realiza un salto en forma de L, dos casillas “hacia delante” y una “hacia un lado”, entonces si el caballo está en una casilla x/y, puede saltar a alguna de las casillas siguientes x + 2/y + 1, x + 1/y + 2, x – 1/y + 2, x – 2/y + 1, x – 2/y – 1, x – 1/y – 2, x + 1/y – 2, x + 2/y – 1, siempre que sea posible (por ejemplo, de 1/1, que es una casilla de la esquina, solo puede ir a 3/2 y 2/3, o de 5/1, que es una casilla de un lateral, solo puede ir a 7/2, 6/3, 4/3 y 3/2), como se muestra en la siguiente imagen.
Por lo tanto, encontrar un recorrido del tablero de ajedrez consiste en reordenar los 64 valores de las fracciones que describen las casillas 1/1, 1/2, 1/3, 1/4, …, 2/1, 2/2, 2/3, 2/4, …, 3/1, 3/2, 3/3, 3/4, …, 8/5, 8/6, 8/7, 8/8, de manera que de cada casilla del reordenamiento se pasa a la siguiente mediante alguno de los movimientos anteriores (correspondientes con el salto del caballo), así después de 5/5 puede ir 4/3, pero no 7/2. Además, si el recorrido es cerrado, la última fracción de la reordenación deberá continuarse con la primera, mediante alguno de esos movimientos.
Después, Vandermonde plantea que “la búsqueda de la solución se simplifica tratando de aproximar el recorrido del caballo a una forma simétrica”. Además, “el recorrido del caballo formará una figura simétrica si cuando, en la expresión mediante fracciones del recorrido, se intercambian los números 8 por 1, 7 por 2, 6 por 3, 5 por 4, y viceversa, ya sea solo en los números de los numeradores, solo en los números de los denominadores o en ambos a la vez, no cambia la expresión total (el recorrido)”.
Por lo tanto, si antes se buscaba un recorrido (del caballo) con 64 movimientos (el recorrido es cerrado, y de la última casilla se salta a la primera), ahora basta encontrar 16 movimientos, es decir, 16 términos (casillas) de la sucesión 1/1, 1/2, 1/3, 1/4, …, 2/1, 2/2, 2/3, 2/4, …, 3/1, 3/2, 3/3, 3/4, …, 8/5, 8/6, 8/7, 8/8, de manera que si se intercambian los números 8 y 1, 7 y 2, 6 y 3, 5 y 4, en el numerador, no se consigue ningún término de los 16 anteriores (notemos que al realizar esos cambios en el numerador se obtiene un recorrido que es simétrico al primero –con 16 términos- respecto a la recta horizontal que pasa por el centro del tablero), si se cambian en el denominador tampoco coinciden los nuevos términos con los anteriores (notemos que al realizar esos cambios en el denominador se obtiene un recorrido que es simétrico al primero –con 16 términos- respecto a la recta vertical que pasa por el centro del tablero), ni tampoco si se cambian tanto en el numerador, como en el denominador.
Con el objetivo de obtener esos 16 términos, pero de manera que al intercambiar los números 8 y 1, 7 y 2, 6 y 3, 5 y 4, en el numerador y/o el denominador no se repiten términos se procede de la siguiente manera. Se empieza escribiendo los 64 términos que describen las casillas:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Y se toma, de forma aleatoria, un primer término, por ejemplo, 5/5 (hemos elegido el mismo que Vandermonde para obtener el mismo ejemplo que él obtiene en su trabajo). Para construir los cuatro recorridos simétricos se toman los cinco términos equivalentes (utilizando que podemos intercambiar 4 y 5), que son 5/5, 4/5, 5/4 y 4/4, que serán los primeros términos de los cuatro recorridos simétricos que se van a construir.

Como estos cuatro términos ya los hemos utilizado, los quitamos del conjunto de las fracciones (casillas) a elegir, quedando ahora las restantes:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Ahora, se toma un segundo término para el recorrido, de entre los que nos quedan (arriba), que sea continuación de 5/5. Entre los ocho posibles términos que continuarían a 5/5 (mediante el movimiento del salto del caballo), elegimos el 4/3. Entonces, este nuevo término 4/3, junto con sus transformados 5/3, 4/6 y 5/6, los colocamos a continuación de los anteriores.

Y se eliminan los cuatro nuevos términos de las posibilidades de elección, quedando ahora:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
A continuación, elegimos otro término para el recorrido. Nos habíamos quedado en 4/3, que se podría continuar, a priori, con 2/2, 2/4, 3/1, 3/5, 5/1, 5/5, 6/2, 6/4, aunque 5/5 ya no es posible, luego tomamos 2/4, que, junto con sus transformados, 7/4, 2/5 y 7/5, añadimos a continuación de los anteriores.

Eliminando los cuatro nuevos términos del listado de elegibles:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Para continuar debemos de tener en cuenta que nos hemos quedado en el 2/4 y que nos quedan los términos anteriores para continuar (ya se han eliminado 12 términos de los 64 iniciales). El 2/4 se podría continuar, a priori, con una de las seis opciones siguientes 1/2, 1/6, 3/2, 3/6, 4/3 y 4/5, pero de estas ya no son elegibles 4/3 y 4/5, luego podríamos continuar con 1/2. Entonces, se añade 1/2 y sus transformados 8/2, 1/7 y 8/7.

Veamos en la siguiente imagen esos cuatro primeros términos de nuestro recorrido y sus simétricos, cada uno de un color distinto (en azul el primero, que empieza en 5/5; en rojo el segundo, que empieza en 4/5 y, como se ve, es simétrico al azul, respecto a la recta horizontal que pasa por el centro del tablero; el tercero, que empieza en 5/4, en verde, y que es simétrico al azul respecto a la recta vertical que pasa por el centro del tablero; y en amarillo oro el cuarto recorrido, que empieza en 4/4 y que es simétrico horizontalmente al verde y verticalmente al rojo).
De nuevo, eliminaríamos los cuatro últimos términos del listado de posibles términos:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Ahora, tenemos que seguir desde el término (casilla) 1/2, que solo podría seguir a 2/4, 3/1 y 3/3, pero el 2/4 no es posible, luego elegimos uno de los otros dos, por ejemplo, 3/1, que, junto a sus transformados, 6/1, 3/8 y 6/8, añadimos a los anteriores. De esta forma podríamos continuar hasta terminar los cuatro recorridos simétricos:

Y podemos representar esos cuatro recorridos simétricos (azul, rojo, verde y amarillo oro) que hemos obtenido mediante nuestro procedimiento.
A continuación, tenemos que unir esos cuatro recorridos parciales, que pasan por 16 casillas cada uno, para obtener el recorrido cerrado final, que pase por las 64 casillas del tablero.
Si observamos las cuatro sucesiones de fracciones que hemos creado (véase imagen un poco más arriba), podremos darnos cuenta de que la primera se puede continuar con la cuarta, puesto que la primera termina en 3/6 y la cuarta empieza en 4/4, y es una continuación permitida (ya que se corresponde con el salto del caballo, 3+1/6 – 2 = 4/4). De esta forma creamos un recorrido parcial que es la unión del primero con el cuarto (en el tablero, los recorridos azul y amarillo oro, que dejamos en azul oscuro en la siguiente imagen donde los representamos). Mientras que la segunda sucesión, que termina en 6/6, se puede continuar con la tercera, que empieza por 5/4 (= 6 – 1/6 – 2), creando así otro recorrido parcial fruto de unir los recorridos segundo y tercero (en el tablero, los recorridos rojo y verde, que dejamos en verde oscuro en la siguiente imagen donde los representamos).
Por lo tanto, los dos recorridos parciales son:

Y representados, con colores, sobre el tablero nos quedarían como se muestra en la imagen.
Para finalizar hay que unir esos dos recorridos que nos han quedado. Como no se puede continuar un recorrido con el otro, puesto que el último elemento de uno de los recorridos no se puede conectar con un movimiento válido con el primer elemento del otro (por ejemplo, el 6/3 del primero no se puede conectar con el 4/5 en el segundo, ni el 3/3 del segundo con el 5/5 del primero), esto obliga a romper la simetría y buscar otra forma de unirlos. Si nos fijamos en el primer recorrido parcial, tenemos que entre los elementos 2/4 y 1/2 podemos intercalar el otro recorrido, ya que de 2/4 pasamos a 4/5 y de 3/3 a 1/2. Por lo tanto, el orden final de las 64 fracciones quedaría:

Y sobre el tablero el recorrido cerrado del caballo que se ha construido es el siguiente.
Podemos observar en el trabajo original de Vandermonde, que este es efectivamente el recorrido que construyó con su método.
 Anteúltima página del trabajo Remarques sur les problèmes de situation / Comentarios sobre los problemas de la situación (1771) del matemático francés Alexandre-Théophile Vandermonde, en la que se muestra el recorrido cerrado del caballo construido con el método descrito en el trabajo
Anteúltima página del trabajo Remarques sur les problèmes de situation / Comentarios sobre los problemas de la situación (1771) del matemático francés Alexandre-Théophile Vandermonde, en la que se muestra el recorrido cerrado del caballo construido con el método descrito en el trabajoPara finalizar os animo a que iniciéis la construcción en otro elemento distinto a 5/5 y construyáis vuestro propio recorrido cerrado.
Bibliografía
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
2.- W. W. Rouse Ball, H. S. M. Coxeter, Mathematical Recreations and Essays, Dover Publications, 1987 (originalmente publicada por W. W. R. Ball en 1892 –la versión original puede encontrarse en el Proyecto Gutenberg – y extendida por el geómetra H. S. M. Coxeter en 1974)
3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
4.- A. T. Vandermonde, Remarques sur les problèmes de situation, Histoire de l’Académie Royale des Sciences, avec les Mémoires de mathématiques et de physique, 1771, pp. 566-574.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El recorrido del caballo de Vandermonde se ha escrito en Cuaderno de Cultura Científica.
La clave de la diversidad de especies podría estar en sus similitudes
diversidad
Un nuevo trabajo de modelado sugiere por qué la naturaleza es más diversa de lo que predice la teoría ecológica basada en nichos.
Un artículo de Veronique Greenwood. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Allison Li / Quanta Magazine
Ilustración: Allison Li / Quanta MagazineHace más de cuatro décadas los ecólogos de campo se propusieron cuantificar la diversidad de árboles en una parcela boscosa en la isla de Barro Colorado en Panamá, una de las extensiones de bosque más intensamente estudiadas del planeta. Comenzaron a contar cada árbol con un tronco de más de un centímetro de diámetro. Identificaron las especies, midieron los troncos y calcularon la biomasa de cada individuo. Pusieron escaleras en los árboles, examinaron los árboles jóvenes y lo registraron todo en hojas de cálculo cada vez mayores.
Mientras observaban los datos que se acumulaban año tras año, comenzaron a notar algo extraño en ellos. Con más de 300 especies, la diversidad de árboles en la pequeña isla de 15 kilómetros cuadrados era asombrosa. Pero la distribución de los árboles entre esas especies también estaba muy desequilibrada, ya que la mayoría de los árboles pertenecían a unas pocas especies.
Desde esos primeros estudios, ese patrón sobrecargado y altamente desigual se ha visto repetidamente en los ecosistemas de todo el mundo, particularmente en las selvas tropicales. El ecólogo Stephen Hubbell de la Universidad de California, Los Ángeles, quien formó parte del equipo de las mediciones en Barro Colorado, estima que menos del 2% de las especies de árboles en el Amazonas representan la mitad de todos los árboles individuales, lo que significa que el 98 % de las especies son poco comunes.
Una biodiversidad tan alta va en contra de las predicciones hechas por una importante teoría de la ecología, que dice que en un ecosistema estable cada nicho o rol debe ser ocupado por una especie. La teoría de nichos sugiere que no hay suficientes nichos para permitir que todas las especies que los ecólogos observaron existan de manera estable. La competencia por los nichos entre especies similares debería haber llevado a las poco comunes a la extinción.
Un nuevo artículo sobre modelado ecológico en Nature de James O’Dwyer y Kenneth Jops de la Universidad de Illinois, Urbana-Champaign explica al menos parte de esta discrepancia. Han descubierto que las especies que aparentemente deberían ser competidoras frente a frente pueden compartir un ecosistema si los detalles de sus historias de vida, como cuánto tiempo viven y cuántos descendientes tienen, se alinean de la manera correcta. Su trabajo también ayuda a explicar por qué una de las formas con más exito de modelar ecologías a menudo llega a resultados precisos, aunque pasa por alto casi todo lo que sabemos sobre cómo funcionan los organismos.
 El biólogo de plantas James O’Dwyer de la Universidad de Illinois, Urbana-Champaign quería entender cómo los modelos basados en la teoría neutral de la ecología pueden reproducir tan bien los patrones naturales de la biodiversidad cuando ignoran los detalles de cómo viven e interactúan las especies. Fuente: Universidad de Illinois / Michelle Hassel
El biólogo de plantas James O’Dwyer de la Universidad de Illinois, Urbana-Champaign quería entender cómo los modelos basados en la teoría neutral de la ecología pueden reproducir tan bien los patrones naturales de la biodiversidad cuando ignoran los detalles de cómo viven e interactúan las especies. Fuente: Universidad de Illinois / Michelle HasselEn 2001, la paradójicamente alta biodiversidad en la isla de Barro Colorado inspiró a Hubbell a proponer la revolucionaria teoría neutral de la ecología. La teoría de la ecología tradicional enfatizaba la competencia por los nichos entre las especies. Pero Hubbell señaló que las especies podrían no importar realmente en esa ecuación porque, en efecto, los individuos también compiten por los recursos con miembros de su propia especie. Sugirió que los patrones de diversidad en los ecosistemas podrían ser en gran parte productos de procesos aleatorios.
Para una teoría que se ocupaba de la biodiversidad, la teoría neutral de Hubbell era escasa. Ignoró las variaciones en las esperanzas de vida, las peculiaridades nutricionales y otros detalles que distinguen a una especie de otra. En los modelos basados en la teoría cada individuo en un ecosistema teórico es idéntico. Una vez que se empieza a contar el tiempo el ecosistema evoluciona estocásticamente, con individuos compitiendo y reemplazándose entre sí al azar. La teoría estaba completamente en desacuerdo con los enfoques de la ecología basados en especies, y provocó un apasionado debate entre los ecólogos porque parecía muy contraria a la intuición.
Sin embargo, sorprendentemente, a medida que avanzaban las caminatas aleatorias en los modelos neutrales, se reproducían características clave de lo que Hubbell y sus colegas habían visto en sus datos de la isla de Barro Colorado y lo que otros han visto en otros lugares. En este modelado que casi perversamente no reconoce diferencias, hay destellos del mundo real.
Esa tensión entre los modelos y la realidad ha interesado a O’Dwyer durante mucho tiempo. ¿Por qué la teoría neutral parecía funcionar tan bien? ¿Había alguna manera de incorporar información sobre cómo funcionan las especies para obtener resultados que pudieran parecer aún más realistas?
 Antes de unirse al laboratorio de O’Dwyer como estudiante de posgrado, Kenneth Jops había estudiado formas en las que las historias de vida podrían usarse para predecir la vulnerabilidad de las especies de plantas a la extinción. Foto: Dra. Hannah Scharf
Antes de unirse al laboratorio de O’Dwyer como estudiante de posgrado, Kenneth Jops había estudiado formas en las que las historias de vida podrían usarse para predecir la vulnerabilidad de las especies de plantas a la extinción. Foto: Dra. Hannah ScharfUna de las cosas que hace que los modelos neutrales sean atractivos, afirma O’Dwyer, es que realmente hay profundas universalidades entre muchos seres vivos. Si bien las especies animales no son idénticas, son notablemente similares a nivel de, digamos, el sistema circulatorio. Los mismos números relacionados con la fisiología surgen una y otra vez en animales y plantas, reflejando quizás las limitaciones de su historia evolutiva compartida. De acuerdo con un principio llamado ley de Kleiber, por ejemplo, la tasa metabólica de un animal generalmente aumenta con su tamaño, escalando como una ley de potencias, la misma ley de potencias, sin importar la especie. (Se han ofrecido varias teorías sobre por qué la ley de Kleiber es verdadera, pero la respuesta aún se debate).
Dados esos signos del orden subyacente, O’Dwyer se preguntó si algunos detalles de cómo viven los organismos importan más que otros para determinar el éxito con el que las especies competirán y sobrevivirán durante el tiempo evolutivo. Tomemos nuevamente el metabolismo: si un ecosistema puede verse como una expresión de los metabolismos de sus habitantes, entonces los tamaños de los organismos son números especiales y significativos. El tamaño de un individuo puede ser más útil para modelar su destino a lo largo del tiempo que cualquier otro detalle sobre su dieta o identidad de especie.
O’Dwyer se preguntó si uno de esos factores cruciales y privilegiados podría ser capturado por la historia de vida, un concepto que combina estadísticas de especies como el número promedio de descendientes, el tiempo hasta la madurez sexual y la esperanza de vida. Imagina una parcela de 50 plantas individuales. Cada una tiene su propia esperanza de vida, su propio patrón de reproducción. Después de tres meses, una planta puede producir 100 semillas, mientras que otra similar produce 88. Tal vez el 80% de sus semillas germine, produciendo la próxima generación, que pasará por su propia versión de este ciclo. Incluso dentro de una especie, el número de plantas individuales variará, a veces un poco, a veces mucho, un fenómeno llamado ruido demográfico. Si esta variación es aleatoria, a la manera de la teoría neutral de Hubbell, ¿qué patrones surgirán en las generaciones sucesivas?
O’Dwyer sabía que había encontrado a alguien que podía ayudarlo a explorar esa pregunta cuando Jops se unió a su laboratorio como estudiante de posgrado. Jops había estudiado previamente si los modelos que usaban historias de vida podían predecir si una especie de planta vulnerable sobreviviría o si estaba a punto de desaparecer. Juntos, comenzaron a elaborar las matemáticas que describirían lo que sucede cuando la historia de vida se encuentra con la competencia.
En el modelo de Jops y O’Dwyer, como en los modelos neutrales, la estocasticidad, la influencia de los factores aleatorios en las interacciones deterministas entre las especies, es importante. Las historias de vida de las especies, sin embargo, pueden amplificar o reducir los efectos de esa aleatoriedad. “La historia de vida es una especie de lente a través de la cual funciona el ruido demográfico”, explica O’Dwyer.
Cuando los investigadores permitieron que su modelo progresara a lo largo del tiempo, poniendo a prueba a cada individuo simulado, descubrieron que ciertas especies podían persistir una junto a la otra durante largos períodos a pesar de que competían por los mismos recursos. Al profundizar en los números en busca de una explicación, Jops y O’Dwyer encontraron que un término complejo llamado tamaño efectivo de la población parecía útil para describir un tipo de complementariedad que podría existir entre las especies. Encapsulaba el hecho de que una especie podría tener una mortalidad alta en un punto de su ciclo de vida, luego una mortalidad baja en otro, mientras que una especie complementaria podría tener una mortalidad baja en el primer punto y una mortalidad alta en el segundo. Cuanto más similar era este término para dos especies, más probable era que una pareja pudiera vivir una junto a la otra a pesar de competir por el espacio y la nutrición.
“Experimentan el ruido demográfico con la misma amplitud”, explica O’Dwyer. “Esa es la clave para que vivan juntos mucho tiempo”.
 Estas cuatro especies de plantas herbáceas perennes (en el sentido de las agujas del reloj desde la parte superior izquierda: Eryngium cuneifolium, Polygonella robusta, Lechea deckertii y Lechea cernua) coexisten en las comunidades de Florida en lugar de llevarse unas a otras a la extinción. Como predice la nueva investigación, las cuatro especies tienen historias de vida excepcionalmente similares. Fuentes: South Florida Listed Species USFWS y Bob Peterson (fila de arriba); Jay Horn.
Estas cuatro especies de plantas herbáceas perennes (en el sentido de las agujas del reloj desde la parte superior izquierda: Eryngium cuneifolium, Polygonella robusta, Lechea deckertii y Lechea cernua) coexisten en las comunidades de Florida en lugar de llevarse unas a otras a la extinción. Como predice la nueva investigación, las cuatro especies tienen historias de vida excepcionalmente similares. Fuentes: South Florida Listed Species USFWS y Bob Peterson (fila de arriba); Jay Horn.Los investigadores se preguntaron si prevalecían patrones similares en el mundo real. Se basaron en la base de datos COMPADRE, que alberga detalles sobre miles de especies de plantas, hongos y bacterias tomados de una variedad de estudios y fuentes, y se concentraron en plantas perennes que vivían juntas en las mismas parcelas de investigación. Descubrieron que, como había predicho su modelo, las especies de plantas que vivían juntas tenían historias de vida muy parecidas: los pares de especies que viven en el mismo ecosistema tienden a ser más complementarios que los pares creados al azar.
Los hallazgos sugieren maneras en que las especies que no están necesariamente en competencia directa podrían funcionar bien juntas sin recurrir a nichos distintos, afirma Annette Ostling, profesora de biología en la Universidad de Texas, Austin. “Lo mejor es que señalan que estas ideas… pueden extenderse a especies que son bastante diferentes pero complementarias”, comenta.
Para William Kunin, profesor de ecología en la Universidad de Leeds en Inglaterra, el artículo sugiere una razón por la cual el mundo natural, a pesar de toda su complejidad, puede parecerse a un modelo neutral: los procesos ecológicos pueden tener una forma de anularse entre sí, por lo que que lo que parece una variedad infinita puede tener un resultado simple que describe como «neutralidad emergente». Hubbell, por su parte, agradece la ampliación de su obra inicial. “Ofrece algunas ideas sobre cómo generalizar modelos neutrales, modificarlos para incluir un poco de diferencias específicas, expandirse y contraerse para ver qué sucede con la diversidad en una comunidad local”, dijo.
Sin embargo, este es solo una parte del problema de comprender cómo surge la biodiversidad y por qué persiste. “En ecología, luchamos con la relación entre patrón y proceso. Muchos procesos diferentes pueden producir el mismo patrón”, explicao Ostling. O’Dwyer espera que, en los próximos años, más datos sobre el mundo real puedan ayudar a los investigadores a discernir si el tamaño efectivo de la población es capaz de explicar la coexistencia de manera consistente.
Kunin espera que el artículo inspire a otros a seguir trabajando con ideas de la teoría neutral. En un campo donde las cualidades únicas de los individuos, en lugar de sus puntos en común, han prevalecido durante mucho tiempo, la teoría neutral ha obligado a los ecólogos a ser creativos. “Nos sacó de nuestras rutinas mentales y nos hizo pensar en qué cosas realmente importan”, afirma.
Hubbell, quien planteó la teoría neutral sobre la ecología hace tantos años, se pregunta si conjuntos de datos verdaderamente inmensos sobre bosques reales podrían producir el tipo de detalle necesario para aclarar la relación entre la historia de la vida y la biodiversidad. “Este es el tipo de construcción sobre la teoría neutral que esperaba que sucediera”, comenta sobre el nuevo artículo. “Pero es solo un pequeño paso hacia la comprensión real de la diversidad”.
El artículo original, The Key to Species Diversity May Be in Their Similarities, se publicó el 26 de junio de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo La clave de la diversidad de especies podría estar en sus similitudes se ha escrito en Cuaderno de Cultura Científica.
La evolución del interior de la luna Europa
Europa, el satélite de Júpiter, es uno de los lugares de nuestro Sistema Solar en los que pensamos hay un mayor potencial astrobiológico debido a la posible existencia de un océano de agua líquida debajo de su corteza helada. Algo que esperamos que en la próxima década confirmen misiones como la europea JUICE, que despegó a mediados del mes de abril de este año, o la norteamericana Europa Clipper, cuya fecha de despegue prevista es octubre de 2024, y cuyo ensamblaje se encuentra en una fase muy avanzada.
Europa es un satélite algo más pequeño que nuestra Luna -unos 3100 kilómetros de diámetro frente a 3474 kilómetros- pero a pesar de eso su superficie atestigua que hay una actividad geológica capaz de rejuvenecerla desde dentro, e incluso, como hablamos en “Una tectónica de placas más allá de la Tierra” en diciembre de 2022, podría tener una tectónica de placas, y esto significa que hay alguna fuente de energía interna capaz de provocar estos procesos.
 Europa observada por la sonda JUNO en septiembre de 2022. Obsérvese la relativa juventud de su superficie por la escasez de cráteres de impacto que se pueden observar. Imagen cortesía de NASA/JPL-Caltech/SwRI/MSSS/Kevin M. Gill.
Europa observada por la sonda JUNO en septiembre de 2022. Obsérvese la relativa juventud de su superficie por la escasez de cráteres de impacto que se pueden observar. Imagen cortesía de NASA/JPL-Caltech/SwRI/MSSS/Kevin M. Gill.Por si esto fuese poco, en 2013 se anunció el descubrimiento de posibles géiseres de agua -capaces de llegar a los cien kilómetros de altura- a partir de datos del Telescopio Espacial Hubble, agua, aunque cuyo origen no sabemos si procede de bolsas de agua existentes en el interior de la corteza o del océano, un fenómeno que sería similar al observado en Encélado, satélite de Saturno, y que añade, si cabe, más interés al estudio de Europa, ya que estudiando el agua que sale despedida en estos fenómenos, podemos intentar averiguar su procedencia, y en el caso de ser del interior de Europa, conocer mejor ese posible océano.
Pero, ¿cómo es Europa por dentro y cómo ha sido su evolución? Un artículo recién publicado en Science Advances aporta un nuevo modelo sobre su estructura interna y la evolución que ha tenido a lo largo del tiempo, algo fundamental de cara a conocer qué fuentes de energía serían las responsables de mantener un océano de agua líquida desde su formación o si el océano en realidad se formó posteriormente.
En las últimas décadas, muchos de los estudios científicos han apuntado a una rápida evolución del interior de Europa tras su formación. Es decir, que los procesos de diferenciación planetaria, aquellos que dan lugar a la estructura por capas de los planetas y otros cuerpos, ocurrieron muy pronto en la historia de Europa, procesos para los que generalmente se necesita mucho calor para fundir total o parcialmente, en este caso Europa, y que los elementos más pesados se hundan hacia el fondo y los más ligeros vayan hacia la superficie.
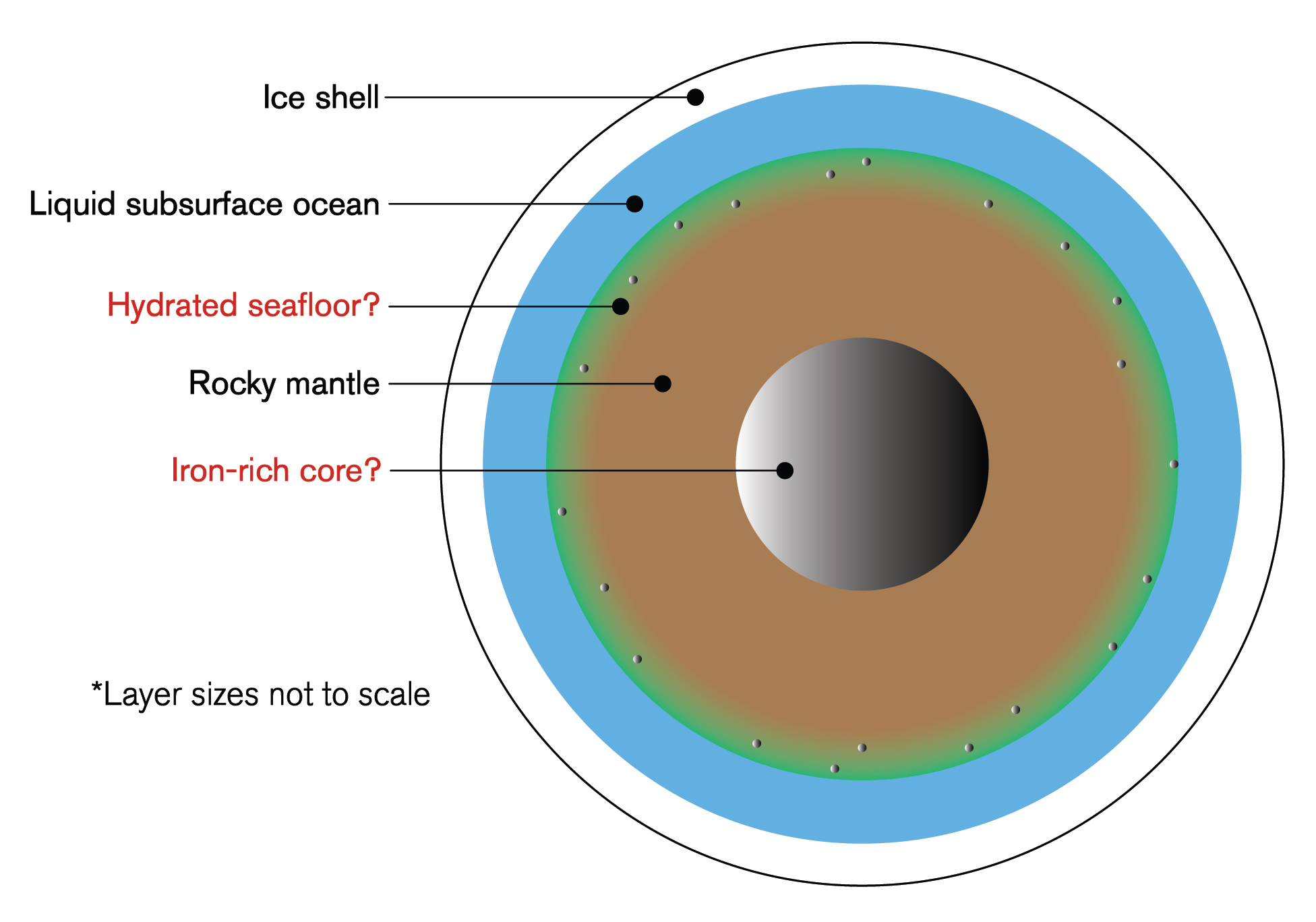 Posible estructura interna de Europa. En rojo y con interrogantes, algunas de las dudas planteadas por el estudio, especialmente sobre un núcleo bien desarrollado. Cortesía de Kevin Trinh/ASU.
Posible estructura interna de Europa. En rojo y con interrogantes, algunas de las dudas planteadas por el estudio, especialmente sobre un núcleo bien desarrollado. Cortesía de Kevin Trinh/ASU.Por los datos que tenemos hasta el momento, la estructura de Europa, a grandes rasgos, estaría formada por una corteza de hielo de unos 15 a 25 kilómetros de potencia, un océano subterráneo de entre 60 y 150 kilómetros de espesor, un manto rocoso y un núcleo metálico.
Este nuevo estudio propone que Europa se formó como una mezcla más o menos homogénea de roca, hielo y elementos metálicos que lentamente fue segregándose en las distintas capas, tardando en formarse el núcleo interno -si está formado completamente- a lo largo de miles de millones de años. La existencia o no de este núcleo y su estado nos podría dar pistas sobre el calor interno que todavía se genera en Europa.
Además, proponen que la deshidratación de los minerales silicatados -fruto del calor procedente de la desintegración radioactiva- presentes en Europa -algunos silicatos pueden contener moléculas de agua o grupos hidroxilo en su estructura cristalina- podría haber sido la responsable de la formación del océano y de la capa de hielo, ya que el agua iría migrando desde zonas más profundas hacia las más superficiales, primero formando la corteza de hielo, y después permitiendo, bajo esta, la existencia de un océano.
 Posibles caminos evolutivos del interior de Europa. Dependiendo de la cantidad de calor disponible para Europa, podría no existir una diferenciación completa de su interior. Imagen cortesía de Kevin Trinh/ASU
Posibles caminos evolutivos del interior de Europa. Dependiendo de la cantidad de calor disponible para Europa, podría no existir una diferenciación completa de su interior. Imagen cortesía de Kevin Trinh/ASUHay algo más. Este modelo es ciertamente desfavorable, ya que predice que la actividad geológica en la interfaz entre el océano y el manto rocoso podría ser muy poca, limitando mucho la existencia de fenómenos hidrotermales o volcánicos en su interior en la actualidad, lo que limitaría de una manera importante el potencial astrobiológico del satélite joviano, algo que también podría explicar la menor actividad que hemos observado con respecto a Encélado.
A pesar de esto, los científicos reconocen que, aunque sus modelos son muy detallados y muestran distintos escenarios evolutivos para Europa, todavía se necesitan más datos para confirmar si realmente están en lo cierto o si incluso pueden estar ocurriendo otro tipo de fenómenos -como el calentamiento por mareas- que mantengan un interior más activo de lo predicho por ellos.
Sea como fuere, probablemente tengamos que esperar todavía hasta la llegada de las misiones JUICE y Europa Clipper en la próxima década para tener más datos que nos permitan conocer un poco mejor el interior de Europa y sentar si es el mundo habitable que todos esperamos o si, por el contrario, las condiciones no son tan favorables como pensábamos anteriormente.
Referencia:
Kevin T. Trinh et al. (2023) Slow evolution of Europa’s interior: metamorphic ocean origin, delayed metallic core formation, and limited seafloor volcanism. Sci. Adv. doi: 10.1126/sciadv.adf3955
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo La evolución del interior de la luna Europa se ha escrito en Cuaderno de Cultura Científica.
La ecuación trascendente de la txalaparta
 Txalaparta en La menor: idiófono basado en tablones tallados sobre caballetes y bastones para interpretación por parejas a cuatro manos
Txalaparta en La menor: idiófono basado en tablones tallados sobre caballetes y bastones para interpretación por parejas a cuatro manosLa txalaparta es un antiguo idiófono original de Vasconia, cuya peculiaridad como instrumento de percusión y su enigmática historia ha despertado mucho interés entre los musicólogos e historiadores. La primera referencia histórica a la txalaparta aparece en 1882 en un libro sobre la producción de sidra en el País Vasco ([1], p. 129), aunque existen menciones anteriores a las toberas (una variante metálica de la txalaparta): la primera de ellas en un documento legal de 1688 ([2], pp. 52-53). Se sabe muy poco sobre la práctica de la txalaparta antes del siglo XX, pero antropólogos, historiadores, músicos y otros científicos han colocado el instrumento en una novedosa vía de crecimiento, utilización y actualización cultural de gran interés internacional:
Las hermanas Sara y Maika Gómez (Ttukunak) en el Festival de Primavera de Budapest, Palacio de las Artes, 2017
La txalaparta ordinaria consta de unos tablones de madera colocados de forma horizontal sobre dos soportes, y golpeados a cuatro manos por bastones también de madera. Debido al origen rural del instrumento, es muy habitual utilizar tablones de maderas de árboles locales como el roble, castaño o aliso, y bastones de fresno, similares a los mangos cortos de las herramientas del campo.
Modelado matemático de la txalapartaLa vibración transversal de los tablones se puede modelar matemáticamente mediante la conocida teoría de vigas o barras de Euler-Bernoulli. Dado que los listones sonoros de la txalaparta están libres sin sujeción a ambos extremos, estas condiciones de contorno restringen las frecuencias permitidas para vibrar. Así, las tablas de la txalaparta solamente pueden sonar según los modos de vibración soluciones de una preciosa ecuación trascendente (no algebraica).
Esta ecuación trascendente se expresa como cosh(kL)cos(kL)=1, donde k es el número de onda de los infinitos modos de vibración y L es la longitud del tablón.
Esta ecuación no puede resolverse de forma analítica sino por medios numéricos o gráficos, y los infinitos modos de vibración de cada tablón siguen una serie inarmónica musical, muy diferente a la serie armónica que resulta en las cuerdas vibrantes de las guitarras, violines o pianos, o en las columnas de aire de las flautas, oboes o clarinetes.
Así pues, si calculamos el modo fundamental de vibración de una tabla golpeada, y resolvemos con métodos numéricos la ecuación trascendente de la txalaparta, resulta que las notas musicales que corresponden a cada tablón siguen una serie de frecuencias sonoras muy poco armónicas: f1, f2=2.76f1, f3=5.40f1, f4=8.94f1, f5=13.35f1,…
Si terminamos los cálculos, podemos también representar la distribución espacial de los primeros modos vibratorios de cada listón sonoro, tal y como se muestra en la figura siguiente. Como el primer modo de vibración es el más importante en cada tabla, la txalaparta apoya sus tablones en las líneas nodales de este primer modo, para dejarlos vibrar con total libertad. Como puede observarse en la figura, el apoyo óptimo del instrumento se encuentra en puntos simétricos cercanos a ¼ de la longitud de cada tabla, si damos preferencia al primer modo de vibración.
 Vibraciones transversales de un tablón golpeado en una txalaparta. Se incluyen los cinco primeros modos de vibración, la tabla horizontal en color marrón y sus dos soportes situados en las dos líneas nodales del primer modo: a 22.4% de la longitud del tablón, desde sus extremos izquierdo y derecho. Fuente: cálculo computacional del autor.
Vibraciones transversales de un tablón golpeado en una txalaparta. Se incluyen los cinco primeros modos de vibración, la tabla horizontal en color marrón y sus dos soportes situados en las dos líneas nodales del primer modo: a 22.4% de la longitud del tablón, desde sus extremos izquierdo y derecho. Fuente: cálculo computacional del autor.
El movimiento oscilatorio de este primer modo de vibración se puede visualizar en la animación mostrada a continuación. Los modos superiores, cada uno a su propia frecuencia fn, efectúan movimientos vibratorios similares. Los n+1 puntos nodales de cada modo se mantienen inmóviles y sus n máximos y mínimos móviles corresponden con puntos ventrales de la vibración. Notemos que en la figura anterior se pueden localizar los nodos de cada modo mediante la intersección de las gráficas con la tabla horizontal trazada en color marrón. Los puntos ventrales de cada modo se encuentran entre sus puntos nodales, y corresponden con zonas de máxima flexión de las tablas.
 Animación del primer modo de vibración transversal de las tablas golpeadas con condiciones de contorno libres a ambos extremos. Fuente: Wikimedia Commons
Animación del primer modo de vibración transversal de las tablas golpeadas con condiciones de contorno libres a ambos extremos. Fuente: Wikimedia Commons
Observamos que la txalaparta es un instrumento de percusión que incluye una serie inarmónica musical. En instrumentos de percusión cromática como los modernos xilófonos o marimbas, las barras sonoras se afinan tallando las maderas para poder conseguir instrumentos con toda la escala cromática ([3], pp 628-629). Aunque la txalaparta no es de naturaleza cromática, es posible construir un instrumento afinado y mejorar su serie armónica y propiedades musicales.
La txalaparta bien afinadaPara construir una txalaparta bien afinada, basta con tallar las tablas eliminando madera en su parte central-inferior. Existen dos razones para realizar este tallado inferior de los tablones: por un lado, alcanzar la afinación de nota (frecuencia) deseada para el primer modo de cada barra sonora del instrumento, y por otro, conseguir notas cercanas a una serie armónica para los principales modos superiores de cada uno de sus elementos vibrantes. Cada tablón se esculpe para ajustar selectivamente la frecuencia y forma de un modo normal de vibración que se pretende, sintonizando la masa y la rigidez de la madera. La eliminación de madera en una zona de flexión pronunciada reduce la rigidez más que la masa de la tabla, de modo que la frecuencia disminuye. Por otro lado, la supresión de madera en una zona de poca flexión reduce la masa más que la rigidez, de forma que la frecuencia aumenta. Esta técnica escultórica permite perfectamente construir una txalaparta musical y afinada.
 Proceso de eliminación de madera en la parte central-inferior de uno de los tres tablones de roble de la txalaparta fabricada por el autor.
Proceso de eliminación de madera en la parte central-inferior de uno de los tres tablones de roble de la txalaparta fabricada por el autor.Aunque no existe un modelo estándar de txalaparta, dependiendo de los estilos musicales o interés de los intérpretes, es común emplear típicamente entre 1 y 5 tablones. Un ajuste básico para poder emitir acordes tonales requiere al menos tres notas simultáneas, que pueden ejecutarse golpeando tres tablas. Utilizando tres robustos listones de roble de longitud 123cm, anchura 16cm y grosor 5 cm, como el mostrado en la fotografía, es sencillo tallar estas barras como hemos indicado y generar potentes y armónicos elementos sonoros. En este caso concreto los tablones han sido esculpidos de manera que sus modos fundamentales vibren a 110 Hz (La1), 131 Hz (Do2), 165 Hz (Mi2): esto nos permite denominar el instrumento como una txalaparta en La menor. Además, el golpeo de los tablones en zonas intermedias, excitan los modos de vibración superiores, que han sido ajustados en una serie armónica. Por todo ello, una buena pareja ejecutante en esta txalaparta afinada puede extraer del instrumento verdadera recóndita armonía.
Hutsun en las calles de Aviñón (Francia)
Referencias
[1] Severo de Aguirre-Miramon (1882) Fabricación de la sidra en las provincias vascongadas. Hijos de I.R. Baroja, San Sebastian, p. 129.
[2] Manuel de Lekuona (1920) Las toberas. Revista de cultura vasca, Euskalerriaren Alde n. 194, pp: 52-53.
[3] Neville H. Fletcher and Thomas D. Rossing (1998) The Physics of Musical Instruments (2nd Edition), ISBN-9780387983745, Springer, New York, pp: 628-629.
Del mismo autor:
Lutería y acústica (serie)
Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo La ecuación trascendente de la txalaparta se ha escrito en Cuaderno de Cultura Científica.
Psicodelia y tratamientos psiquiátricos, notas clínicas y evolucionistas

Cómo influyen los parásitos en el comportamiento de los animales, cómo se modifica la conducta de las madres mamífero o cuáles son las enfermedades que nos afectan y desde cuándo hemos desarrollado comportamientos funerarios ante la muerte son algunos de los aspectos que se analizarán en la V Jornada Nacional sobre Evolución y Neurociencias.
Especialistas en ambas materias se reunirán el 11 y 12 de mayo en una nueva edición conducida por Eva Garnica y Pablo Malo, psiquiatras y miembros de la Red de Salud Mental de Bizkaia, y organizada por esa misma entidad y la Cátedra de Cultura Científica de la UPV/EHU.
La jornada, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolucionista y divulgar de un modo accesible para todos los públicos.
En los años noventa del siglo pasado se produjo el resurgimiento de la investigación en psicodelia, abriendo todo un mundo de tratamientos psiquiátricos y un mejor conocimiento de las bases evolutivas en las que se basa el efecto de estos fármacos, como nos cuenta Luis Caballero en esta charla.
Luis Caballero es psiquiatra, jefe de la Sección de Psiquiatría del Hospital Universitario Puerta de Hierro y Profesor Asociado del Departamento de Psiquiatría de la Universidad Autónoma de Madrid.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Psicodelia y tratamientos psiquiátricos, notas clínicas y evolucionistas se ha escrito en Cuaderno de Cultura Científica.
Una batería biodegradable para móviles
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsActualmente no seríamos capaces de realizar nuestras tareas diarias sin los teléfonos móviles y otros aparatos electrónicos. Pero, desgraciadamente, la esperanza de vida de estos dispositivos es bastante limitada. En España se desechan anualmente más de 20 millones de dispositivos de telefonía móvil.
Detrás de esta cifra está, por un lado, la obsolescencia programada, tanto por incompatibilidad de hardware como por falta de actualización en el sistema operativo. Otro aspecto clave en este tipo de dispositivos es la batería, normalmente basada en tecnología de iones de litio. Estas baterías cuentan normalmente con una vida útil inferior a las 1 000 cargas.
Así, los teléfonos inteligentes tienen una media de uso de 18 meses, y en muy raras ocasiones se emplean durante más de cuatro o cinco años.
Una de las estrategias para solventar estos problemas sería el desarrollo de baterías transitorias (transient, en inglés), basadas en materiales abundantes que se degraden en subproductos no tóxicos. Todo ello, manteniendo los altos estándares de funcionamiento que poseen las baterías convencionales de iones de litio. Pero ¿es esto realmente posible?
Economía circular, una solución parcialLa solución actualmente más extendida consiste en adoptar patrones circulares que se alejen del sistema de producción lineal. Es decir, transitar desde “producir, consumir, tirar” a nuevos hábitos de manera que puedan volver a reutilizarse los dispositivos móviles, o parte de ellos, en otras aplicaciones.
Si consideramos una perspectiva circular, las alternativas de reutilización o remanufactura deben ser preferentes sobre el reciclaje. Una posible opción son los sistemas de garantía extendida, los sistemas de recogida y los mercados de segunda mano.
Existen empresas que, tras una recogida selectiva, reacondicionan teléfonos móviles para posteriormente venderlos a menor coste. Iniciativas como estas generan grandes beneficios ambientales, sociales y económicos.
Otra opción es el reciclaje de las baterías. Mediante diversos tratamientos químicos y térmicos, es posible extraer los materiales económicamente relevantes de las baterías, que serán utilizados posteriormente para fabricar nuevas baterías. De este modo, se limitan los posibles efectos nocivos de materiales como el litio, el cobalto o el manganeso, y se evita la necesidad de procesos de extracción de metales de la minería tradicional.
Pero ¿qué ocurre con los dispositivos electrónicos que no puedan ser tratados?
Los móviles que no se recogenDebemos tener en cuenta que los teléfonos móviles son los aparatos electrónicos con los índices de recogida más bajos. A pesar de los esfuerzos que desarrollan diversas entidades públicas, como por ejemplo la instalación de puntos limpios móviles no asistidos, existe un altísimo riesgo de que gran cantidad de teléfonos móviles se pierdan en el medio ambiente.
Únicamente el 17,4 % de los residuos electrónicos se recogen, tratan y reciclan adecuadamente. El restante no se documenta, y gran parte acaba en destinos de lo más variados, desde vertederos, a bosques, ríos o mares. Ello implica que gran cantidad de materiales no biodegradables y altamente tóxicos, como son el cobalto, el níquel, el manganeso y los electrolitos orgánicos acaben contaminando los suelos, el aire, el agua y los seres vivos; incluidos los humanos.
Por ejemplo, las sustancias tóxicas que forman parte de las baterías convencionales de iones de litio pueden filtrarse en las aguas subterráneas, donde pueden influir en las especies acuáticas y terrestres. La Organización Mundial de la Salud estima que la exposición a los residuos electrónicos puede provocar alteraciones de las funciones pulmonares y problemas respiratorios, especialmente en niños y adolescentes, entre otros efectos.
Baterías compostables, otra posible soluciónEn un reciente estudio desarrollado por la Universidad del País Vasco/Euskal Herriko Unibertsitatea, la Escuela Politécnica Federal de Zúrich y la Universidad de Nueva Gales del Sur, hemos demostrado que es posible fabricar baterías compostables que además sean competitivas en cuanto a rendimiento.
La tecnología transitoria busca el desarrollo de materiales, dispositivos o sistemas que experimenten procesos de degradación controlada tras un periodo de funcionamiento estable, dejando tras de sí residuos inocuos.
Así, primero identificamos elementos no tóxicos, abundantes y biodegradables, que ofrecieran unas características físicas, mecánicas y electroquímicas mínimas.
Tras una extensa búsqueda, identificamos y aplicamos las siguientes opciones:
- Polímeros de origen natural como la celulosa y la agarosa para el electrolito.
- La polidopamina, un material natural con alta capacidad de reducción-oxidación, para el desarrollo del cátodo.
- Un ánodo de zinc, metal biodegradable y biocompatible que permite fabricar electrolitos basados en agua.
 Fotografías que muestran la degradación de los componentes individuales de la pila transitoria en el tiempo.
Fotografías que muestran la degradación de los componentes individuales de la pila transitoria en el tiempo.Author provided
El trabajo dio como resultado una batería recargable que combina compostabilidad con un rendimiento electroquímico sobresaliente. De hecho, se observó una pérdida de peso del 49,9 ± 2,9 % tras 63 días en condiciones de compostaje industrial.
También se ha demostrado que estas baterías pueden cargarse a lo largo de más de 10 000 ciclos, el equivalente a 27 años continuados considerando una carga diaria. Gracias nuestro prototipo, el sueño de una batería compostable que también cumpla la función completa de un dispositivo de almacenamiento de energía desde el punto de vista electroquímico es una realidad.![]()
Sobre el autor: Erlantz Lizundia, Profesor de Ecodiseño y Economía Circular, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Para saber más:
Por qué la tecnología deja de funcionar
Basura electrónica y economía circular
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Una batería biodegradable para móviles se ha escrito en Cuaderno de Cultura Científica.
¿Existe el Antropoceno con mayúsculas?
Seguro que todo el mundo, en un contexto u otro, ha oído hablar del término Antropoceno y, rápidamente, lo ha asociado con Geología. También lo habréis visto reflejado en llamativas ilustraciones del tiempo geológico como la parte más moderna y actual del mismo. Incluso, podéis encontrar una entrada en el diccionario de la Real Academia Española (la RAE), en la cual la primera acepción dice textualmente: “adj. Geol. Dicho de una época: Que es la más reciente del período cuaternario, abarca desde mediados del siglo XX hasta nuestros días y está caracterizada por la modificación global y sincrónica de los sistemas naturales por la acción humana”.
Con estos precedentes, es más que factible pensar que Antropoceno realmente es un término geológico que define el momento actual en el que vivimos dentro de la historia de la Tierra. Pero, ¿esto es así? Para comprobarlo, tenemos que acudir a una vieja amiga de la que ya os he hablado anteriormente, la tabla cronoestratigráfica internacional o tabla de los tiempos geológicos. La única referencia válida, desde el punto de vista geológico, para darle nombre a las diversas fases por las que ha pasado nuestro planeta a lo largo de su dilatada historia. Y si nos fijamos en la versión más actualizada de la tabla, no aparece por ningún lado la palabra “Antropoceno”. Estamos viviendo en el Piso Megalayense, de la Época Holoceno, dentro del Periodo Cuaternario.
 Ilustración de la obra “Cruisin’ the Fossil Coastline”, del artista Ray Troll del año 2017, donde refleja la existencia del Antropoceno como la época geológica más moderna. Fuente: Ray Troll
Ilustración de la obra “Cruisin’ the Fossil Coastline”, del artista Ray Troll del año 2017, donde refleja la existencia del Antropoceno como la época geológica más moderna. Fuente: Ray TrollEntonces, ¿de dónde procede la idea de que el Antropoceno representa, geológicamente hablando, el momento actual? Pues vamos a bucear en la historia para descubrirlo. Corría el año 2000 cuando el químico atmosférico neerlandés Paul Crutzen gritó, de manera espontánea, durante una conferencia sobre la situación de nuestro planeta que no estábamos en el Holoceno, que vivíamos en el Antropoceno, término procedente de dos palabras griegas: anthropos – ser humano y kainos – nuevo. Esta interrupción tan gratuita, así como el nombre tan llamativo que acuñó Crutzen, favorecieron la aceptación de su concepción por parte del público allí congregado. El químico desarrolló entonces esta idea, buscando pruebas científicas que evidenciasen esta influencia humana en el medio natural en época reciente. Y la conclusión fue demoledora: un incremento sin igual de la presencia de gases de efecto invernadero en la atmósfera, un aumento exponencial del consumo de recursos naturales, una aceleración en la subida de la temperatura y del nivel del mar, mayor velocidad en la pérdida de biodiversidad, eventos climáticos cada vez más extremos y recurrentes y un largo etcétera que sólo podían significar una cosa, que el ser humano había sido capaz de alterar los ciclos biogeoquímicos naturales de nuestro planeta en las últimas décadas.
Incluso, se le ha podido dar una fecha de inicio a todos estos problemas, mediados del siglo XX. En concreto, a partir de 1950 todos esos indicadores socioeconómicos y ambientales experimentaron un crecimiento exponencial, lo cual, unido a las pruebas con bombas nucleares que dejaron un marcador temporal por todo el mundo, este año se considera como el comienzo oficial del Antropoceno.
 Versión más actualizada (abril de 2023) de la tabla de los tiempos geológicos, en la que no aparece la palabra Antropoceno como división temporal dentro del Cuaternario. Fuente: stratigraphy.org
Versión más actualizada (abril de 2023) de la tabla de los tiempos geológicos, en la que no aparece la palabra Antropoceno como división temporal dentro del Cuaternario. Fuente: stratigraphy.orgMientras que gran parte de la comunidad científica ha aceptado las propuestas de Crutzen, llegando a afirmar con rotundidad que nos encontramos en una época diferente a las anteriores, ¿qué opina el ámbito geológico? Pues aquí tenemos un bonito enfrentamiento. Por un lado, el geólogo británico Jan Zalasiewicz es un firme defensor del Antropoceno como una nueva época geológica dentro del Cuaternario, llegando a contar con cientos de especialistas que secundan su propuesta, habiendo constituido un grupo de trabajo sobre esta cuestión dentro de la Unión Internacional de Ciencias Geológicas (IUGS por sus siglas en inglés). Por otro lado, gran parte de las personas que conforman el resto de comisiones de la IUGS son reacias a su consideración.
El principal problema que se esgrime actualmente para definir una nueva época geológica es el concepto tiempo. Un evento que apenas tiene unas décadas de duración y cuya permanencia en el registro geológico dentro de miles o millones de años está seriamente cuestionada, no tiene suficiente entidad, dentro de las normativas formales actuales de la IUGS, para poder ser considerada como una nueva división temporal dentro de la tabla de los tiempos geológicos.
Aunque esta discusión entre especialistas de Geología sigue su curso, el antropoceno, y esta vez lo escribo con minúsculas, no supone ninguna división temporal formal de la historia de la Tierra. Al menos, de momento. Por lo que esa definición de la RAE que os ponía al principio es más que errónea.
 Detalle de una roca denominada “beachrock” o playa cementada, formada por escorias de fundición, fragmentos de ladrillos refractarios y restos de plásticos, formada en la playa de Gorrondatxe (Getxo, Bizkaia). Foto: Iranzu Guede Sagastizabal.
Detalle de una roca denominada “beachrock” o playa cementada, formada por escorias de fundición, fragmentos de ladrillos refractarios y restos de plásticos, formada en la playa de Gorrondatxe (Getxo, Bizkaia). Foto: Iranzu Guede Sagastizabal.Obviamente no estoy diciendo que la influencia humana en el medio natural no esté dejando una huella más que evidente. Si queréis un ejemplo muy llamativo y relativamente cercano de esto, podéis visitar la playa de Gorrondatxe, en Bizkaia, donde encontraréis unas rocas formadas hace menos de doscientos años por la cementación de los residuos de las industrias metalúrgicas de Bilbao vertidos al mar en la desembocadura del Nervión: escorias de fundición, ladrillos refractarios, vidrios, plásticos, latas de aluminio… pero el Antropoceno, como concepto temporal en la escala geológica, no existe. Lo que existe es el antropoceno como definición de nuestra inconsciencia a la hora de consumir, de manera desmedida, los recursos de nuestro planeta. Así que no confundamos términos y sigamos viviendo en el Holoceno, hasta que la IUGS nos diga lo contrario.
Para saber más:
Geología, Antropoceno y cambio climático
¿Son las ‘beachrocks’ una prueba del Antropoceno?
¿Comenzó el Antropoceno con la era nuclear?
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿Existe el Antropoceno con mayúsculas? se ha escrito en Cuaderno de Cultura Científica.
Kathleen Booth, la matemática pionera en programación que creó el primer lenguaje ensamblador
Andrew era una figura muy extrovertida… mientras que Kathleen era muy tranquila y trabajaba en segundo plano. Así que no me sorprende en absoluto que gran parte del crédito por sus logros conjuntos se le dé a Andrew. Pero admitirían que trabajaron juntos constantemente.
La matemática Kathleen Booth contribuyó con su trabajo pionero al desarrollo de las primeras computadoras. Codiseñó uno de los primeros ordenadores operativos, escribió uno los primeros libros sobre diseño y programación de computadoras, creó el primer lenguaje ensamblador, investigó sobre la traducción del lenguaje natural y las redes neuronales, y cocreó el conocido como algoritmo de multiplicación de Booth. Como ha sucedido a otras muchas investigadoras, una figura masculina, aun sin pretenderlo, la eclipsó.
 Kathleen Booth. Fuente: Microsoft.
Kathleen Booth. Fuente: Microsoft.
Kathleen Hylda Valerie Britten (1922-2022) nació en Stourbridge (Inglaterra); era la segunda de los tres hijos de Gladys May Kitchen y Frederick John Britten, un inspector de impuestos.
En 1944 obtuvo un grado en ciencias con especialidad en matemáticas en el Royal Holloway College, centro en el que pudo estudiar gracias a una beca concedida por tres años.
Como a otras muchas mujeres, la Segunda Guerra Mundial le proporcionó una oportunidad de trabajo basado en la ciencia al margen de la enseñanza, a la que se las limitaba profesionalmente. Así, comenzó a trabajar como oficial científica junior en el Royal Aircraft Establishment en Farnborough; en este centro de investigación colaboró en la realización de pruebas estructurales en materiales que se utilizaron posteriormente en la fabricación de aeronaves.
Los tediosos cálculos cristalográficosEn 1946 Kathleen se unió a un grupo de investigación en cristalografía de rayos X en el Birkbeck College. El equipo estaba dirigido por el cristalógrafo John Desmond Bernal (1901-1971), secundado por el físico Andrew Donald Booth (1918-2009).
Desde 1943 Booth trabajaba en la determinación de estructuras cristalinas usando datos obtenidos por difracción de rayos X. Estas investigaciones requerían cálculos numéricos excesivamente largos y pesados por lo que decidió intentar automatizar el proceso desarrollando una computadora analógica. Kathleen se incorporó al equipo matemáticos de Booth en el Birkbeck College, trabajando con las imágenes obtenidas mediante cristalografía de rayos X y que contribuyeron al descubrimiento de la forma de doble hélice del ADN.
Kathleen y Andrew iniciaron una larga colaboración científica que duraría toda su vida. Britten obtuvo su doctorado en matemática aplicada en el King’s College de Londres en 1950 y, ese mismo año, se casó con Andrew Booth. El matrimonio tuvo un hijo y una hija.
 Andrew Booth y Kathleen Britten. Fuente: International Union of Crystallography (Creative Commons).Diseñando y programando ordenadores
Andrew Booth y Kathleen Britten. Fuente: International Union of Crystallography (Creative Commons).Diseñando y programando ordenadores
Kathleen y Andrew colaboraron en la construcción y programación de tres computadoras. Como físico e ingeniero electrónico, él se encargaba del diseño y ella, con una profunda formación matemática, de la parte de programación.
Booth diseñó entre 1947 y 1948 una computadora electromecánica, la ARC (Automatic Relay Calculator). No era un ordenador de propósito general; fue diseñado específicamente para hacer la síntesis de Fourier, uno de los pasos esenciales para determinar la estructura de un cristal. Aunque Andrew lo diseñó, fue Kathleen quien lo construyó y probó junto a la asistente de investigación Xenia Sweeting.
En esa época Kathleen creó un lenguaje simbólico para simplificar el proceso de programación de la máquina; lo denominó Contracted Notation (en General Considerations in the Design of an All-purpose Electronic Digital Computer, 1947). Se reconoce como el primer lenguaje ensamblador del mundo. Esta propuesta, que traduce unos y ceros en instrucciones legibles por seres humanos, supuso un gran avance en la programación de computadoras, que hasta ese momento se realizaba introduciendo bits individuales e incluso conectando y desconectando cables.
También diseñaron la máquina SEC (Simple Electronic Computer) entre 1948 y 1949.
En esa época Andrew y Kathleen crearon el llamado algoritmo de multiplicación de Booth, de interés en el estudio de la arquitectura de ordenadores.
Su máquina más conocida fue la APEC (All-Purpose Electronic Computer), diseñada en 1949. En 1951, la empresa British Tabulating Machine Company usó sus circuitos de hardware como base para el diseño de su computadora HEC 1 (Hollerith Electronic Computer).
 Kathleen Britten y Xenia Sweeting. Fuente: International Union of Crystallography (Creative Commons).
Kathleen Britten y Xenia Sweeting. Fuente: International Union of Crystallography (Creative Commons).
Todo este trabajo llevó a Andrew y Kathleen Booth a publicar el libro Automatic digital calculators (1953).
Kathleen lideró el desarrollo de programas para la traducción automática en Birkbeck; en aquel momento se trataba de una propuesta pionera para unas máquinas que estaban pensadas para realizar cálculos numéricos. El 11 de noviembre de 1955, el Laboratorio de Computación de Birkbeck realizó una demostración pública de traducción automática. Kathleen Booth escribió en su computadora (en francés):
C’est un exemple d’une traduction fait par la machine à calculer installée au laboratoire de Calcul de Birkbeck College, Londres.
(Este es un ejemplo de traducción realizada por la máquina de cálculo instalada en el laboratorio de computación de Birkbeck College, Londres).
Y la computadora imprimió (en inglés):
This is an example of a translation made by the machine for calculation installed at the laboratory of computation of Birkbeck College, London.
En 1958 Kathleen publicó el libro Programming for an automatic digital calculator.
La etapa canadienseEl matrimonio Booth realizó un trabajo sobresaliente en Birkbeck College, aunque pensaban que no se les estaba dando el crédito que merecían. Andrew solicitó en varias ocasiones que se creara una Cátedra permanente en Ciencias de la Computación, pero se la denegaron, a pesar de tener incluso una fuente de financiación concedida para sostenerla. Por ese motivo, en 1962, ambos renunciaron a sus puestos en ese centro y decidieron emprender una nueva vida en Canadá.
Comenzaron enseñando e investigando en la Universidad de Saskatchewan hasta 1972 y después en la Universidad de Lakehead hasta su jubilación en 1978.
Kathleen se mantuvo activa en su investigación sobre redes neuronales y, en 1993, publicó el artículo Using neural nets to identify marine mammals junto a su hijo Ian. Fue su último trabajo publicado; tenía 71 años.
Andrew Booth falleció en noviembre de 2009, con 91 años. Kathleen lo hizo casi trece años después, con 100 años de edad. Hizo historia en la teoría de la computación aunque su nombre apenas sea conocido.
Referencias
-
John J. O’Connor and Edmund F. Robertson, Kathleen Booth. MacTutor History of Mathematics archive, University of St Andrews
-
Sue Gee, Computer Pioneer Kathleen Booth Dies At Age 100, i-programmer, 30 octubre 2022
-
Chris Putnam, Remembering a USask computing pioneer, College of Arts and Science, University of Saskatchewan, 6 diciembre 2022
-
Kathleen Booth, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Kathleen Booth, la matemática pionera en programación que creó el primer lenguaje ensamblador se ha escrito en Cuaderno de Cultura Científica.

