Yamnaya
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsHace cinco mil trescientos años, en el ocaso de la Edad del Cobre y los albores de la del Bronce, surgió, al norte de los mares Negro y Caspio, la que hoy denominamos cultura yamna, también llamada “del sepulcro”. El grupo humano que la desarrolló experimentó una gran expansión geográfica; los yamnaya se extendieron hacia el este hasta el territorio de la actual Mongolia y hacia el oeste por todo el subcontinente europeo. A la Península Ibérica llegaron hace, aproximadamente, cuatro mil trescientos años, diez siglos después de su aparición. Su legado genético se encuentra hoy en prácticamente toda Europa y parte de Asia. Tan grande fue su éxito demográfico.
Hasta hace relativamente poco tiempo, la mayor parte de la información relativa a esta cultura se había obtenido de investigaciones arqueológicas, por su característico método de enterramiento; de ahí el nombre “cultura del sepulcro”. Hacían las inhumaciones en túmulos (kurganes), unos sepulcros excavados en el suelo en los que se colocaba el cadáver boca arriba y con las rodillas dobladas. Además, los cuerpos eran cubiertos con ocre.
En algunos enterramientos se han hallado restos de animales domesticados y, por otro lado, los restos más antiguos de carros con ruedas se han encontrado en Europa Oriental en un kurgán en Ucrania perteneciente a la cultura yamna, precisamente. A partir de esos elementos, a los yamnaya se les ha considerado nómadas o seminómadas, que se desplazaban en carros de dos ruedas o vagones de cuatro, pastoreaban ganado y adquirieron la capacidad para consumir leche. A esas adquisiciones se les ha atribuido su fenomenal éxito demográfico.
Las dudas que pudiera haber acerca de los elementos que impulsaron su expansión se han empezado a disipar tras la publicación reciente de los resultados de una investigación. En ella han examinado el sarro de los dientes de restos humanos procedentes del periodo inmediatamente anterior al comienzo de la expansión yamnaya, durante su inicio y tras haberse producido. Han estudiado restos dentales de 56 individuos que vivieron en un periodo de tiempo que va desde hace unos 6600 a 3700 años. Y el examen ha consistido en la caracterización de los restos de proteínas presentes en ese sarro y la determinación de su origen.
Diez de los once individuos procedentes del final de la Edad del Cobre carecían de rastros de haber consumido leche o productos lácteos. Solo uno presentaba restos de proteínas lácteas, debido quizás a su consumo ocasional. Sin embrago, en quince de los dieciséis individuos procedentes del comienzo de la Edad del Bronce, la dentadura contenía abundantes restos lácteos, prueba fiable de su consumo habitual.
Además, algunas de las muestras analizadas en los restos de individuos procedentes del comienzo de la Edad del Bronce contenían proteínas de leche de yegua. Ese dato, junto con otras evidencias arqueológicas, sugiere que los yamnaya no solamente consumían leche de vacas, ovejas y cabras, sino que, además, domesticaron el caballo, lo utilizaron para cabalgar y tirar de carros de dos ruedas, y llegaron incluso a consumir leche de yegua.
Todos estos elementos refuerzan la idea de que la domesticación del caballo y el pastoreo de rebaños de diferentes especies fueron los elementos que impulsaron una transición demográfica muy intensa que permitió la expansión de los jinetes de las estepas hacia Mongolia, el norte del subcontinente indio y el extremo occidental del europeo. El genetista David Reich sostiene que los varones yamnaya llegaron incluso a sustituir la práctica totalidad de los varones de otros linajes en la Península Ibérica hace unos cuatro mil quinientos años. De ser cierta esa conjetura, pocos linajes habrían tenido un éxito tan “arrollador”.
Fuente: Wilkin, S., Ventresca Miller, A., Fernandes, R. et al. Dairying enabled Early Bronze Age Yamnaya steppe expansions. Nature (2021).
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Yamnaya se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Sergio Pérez Acebrón – El comienzo más difícil
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.
Las probabilidades de que una concepción termine resultando en un nacimiento son muchísimo más bajas de los que te imaginas. Sergio Pérez Acebrón nos presenta qué ocurre en las primeras 6 semanas del embarazo, esos momentos en que ni siquiera muchas mujeres sospechan que pueden estar embarazadas,
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Sergio Pérez Acebrón – El comienzo más difícil se ha escrito en Cuaderno de Cultura Científica.
En busca de El Dorado (en los alimentos)
Ivan Gomez-Lopez, Maitane González-Arceo y María P. Portillo
Durante el cocinado los alimentos son susceptibles de sufrir muchos cambios de color, olor y/o sabor. Estos cambios se deben a la formación de diferentes sustancias químicas que no siempre son beneficiosas, como es el caso de la acrilamida. Ésta se forma gracias a la reacción de Maillard, que se da a altas temperaturas en presencia del aminoácido asparagina e hidratos de carbono. Por ello, los alimentos en los que se puede encontrar mayor cantidad de acrilamida son los elaborados a base de patata y cereales, además del café, entre otros. Este compuesto está clasificado como probable cancerígeno por la Agencia Internacional de Investigación contra el Cáncer (IARC, International Agency for Research on Cancer), pudiendo producir efectos negativos sobre la salud. La única manera de reducir su ingesta es previniendo la formación de la misma, ya que es fácil de identificar debido al cambio de color que producen los alimentos. No obstante, cabe destacar que, siguiendo una dieta variada y equilibrada, su ingesta no debería suponer una preocupación mayor.
 Foto: Leti Kugler / Unsplash
Foto: Leti Kugler / UnsplashIntroducción
La mayoría de los alimentos que consumimos hoy en día sufren una serie de procesos que modifican muchas de sus características. Estos procesos no solo se dan en la industria alimentaria; el cocinado de los alimentos que realizamos en el hogar es un procesamiento térmico con el que se producen cambios en características como el olor, el color, la textura y/o el sabor. También se puede reducir el valor nutricional de los alimentos, por ejemplo, por pérdida de vitaminas. No obstante, también se producen efectos positivos como la eliminación de microorganismos patógenos [1].
Durante el cocinado de los alimentos se dan una serie de reacciones químicas que, en ciertos casos, desencadenan en la formación compuestos tóxicos. A veces estos compuestos son fácilmente detectables a simple vista ya que van asociados a cambios de color de los alimentos. Este es el caso de la acrilamida, una sustancia química que se crea de forma natural en los productos alimenticios que contienen almidón durante procesos culinarios cotidianos a altas temperaturas, como la fritura, el tostado, el asado u otros procesos térmicos a más de 120 ºC y a baja humedad [2]. ¿Quién no ha oído decir que una tostada quemada o la carne muy hecha provoca “cáncer”? Pero, ¿Hasta qué punto es esto cierto?
¿Cómo se forma la acrilamida?
Mientras se da el procesamiento térmico de un alimento, los colores del mismo tienden a pardearse, debido a la reacción de Maillard. Esta reacción es la responsable de la formación de compuestos que dan color, sabor y olor al alimento cocinado a temperaturas altas. Además de estos cambios que hacen atractivos y apetecibles los alimentos, se puede generar, entre otros compuestos, la acrilamida. Para la formación de la acrilamida, el alimento debe tener una serie de características. En primer lugar, es necesario que el alimento sea rico en hidratos de carbono y en segundo lugar, se requiere la presencia del aminoácido asparagina (Figura 1). Cabe destacar, que la formación de este compuesto va asociado al tiempo y temperatura de cocción [3]. Cuanto más tiempo cocinamos una patata frita, particularmente mediante fritura y en menor grado en el caso del horneado, más oscura se vuelve, formándose mayor cantidad de acrilamida.
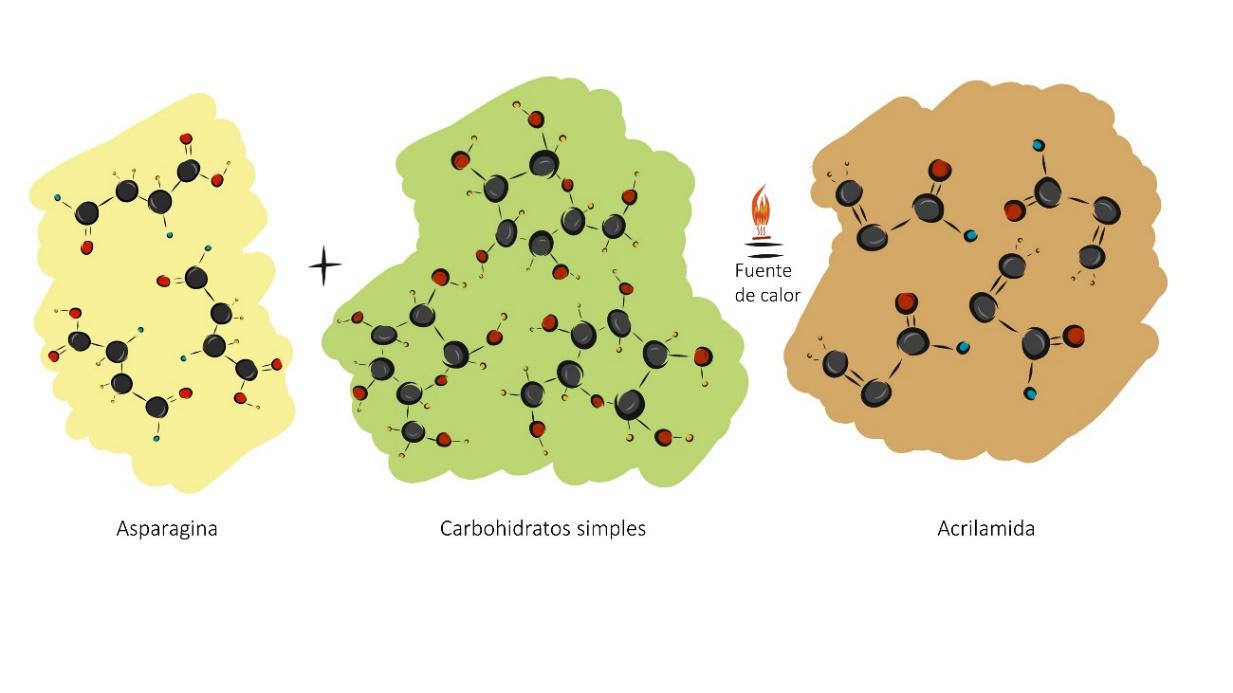 Figura 1. Representación de formación de la acrilamida. Fuente: Los autores.
Figura 1. Representación de formación de la acrilamida. Fuente: Los autores.
¿En qué alimentos se puede encontrar y qué presencia tiene la acrilamida en nuestra dieta?
Las fuentes más comunes de acrilamida son las patatas fritas o los productos fritos a base de patata, cereales y sus derivados como galletas, bizcochos y pan y el café tostado. En un reciente estudio de la AESAN (Agencia Española de Seguridad Alimentaria y Nutrición) se muestra que la patata y sus derivados son los alimentos que más contribuyeron a la ingesta de acrilamida en adultos, adolescentes y niños mayores de 1 año, representando un 49-62% de la exposición. En bebés menores de un año, los principales contribuyentes son los alimentos que no provienen ni de patata ni de cereales (Figura 2) [2].
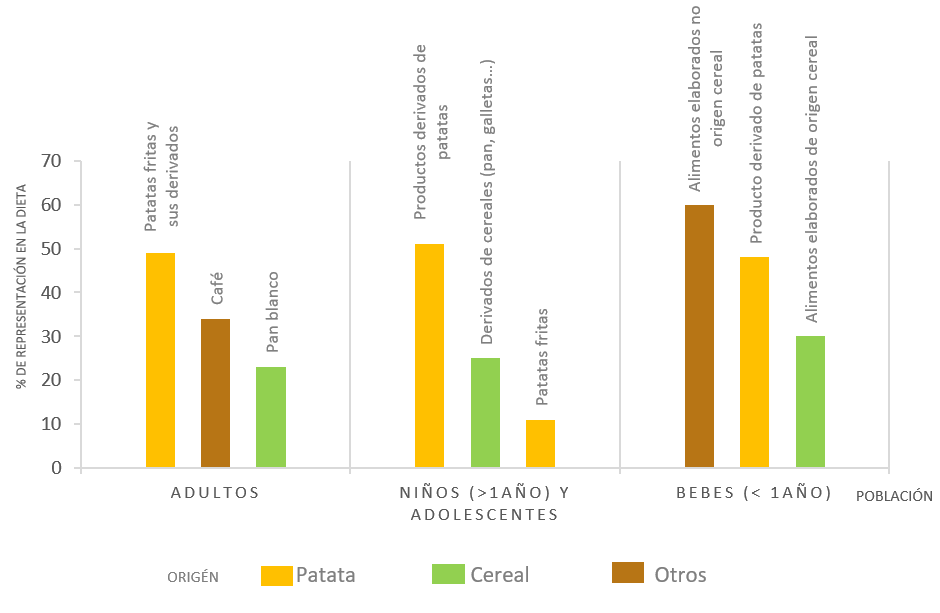 Figura 2. Porcentaje de contribución de diversos alimentos a la ingesta de acrilamida según edad. Datos obtenidos de la Agencia Española de Seguridad Alimentaria y Nutrición, 2020. Fuente: Los autores.
Figura 2. Porcentaje de contribución de diversos alimentos a la ingesta de acrilamida según edad. Datos obtenidos de la Agencia Española de Seguridad Alimentaria y Nutrición, 2020. Fuente: Los autores.
¿Cuáles son los efectos negativos de la acrilamida?
La Agencia Internacional de Investigación contra el Cáncer (IARC, International Agency for Research on Cancer) ha clasificado la acrilamida como “probable cancerígeno para los humanos” [4].Pero, hasta el momento, el potencial carcinógeno (que produce cáncer o favorece su aparición) y genotóxico (que daña el ADN) de la acrilamida solo ha sido demostrado en modelos animales. Dado que en humanos sólo se han realizado unos pocos estudios epidemiológicos, no se puede establecer una clara asociación entre la exposición a la acrilamida mediante la dieta y el desarrollo del cáncer. Otros estudios preclínicos apuntan que la acrilamida tiene efectos sobre la reproducción, el sistema nervioso y el hígado [5].
Aunque es importante hacer hincapié en que estos efectos tóxicos solo se han demostrado en animales, sin embargo, es preferible actuar con precaución y tratar de reducir la exposición a la acrilamida, por ejemplo, minimizando su presencia en los alimentos.
¿Existe una “dosis tolerable” de acrilamida?
Puesto que cualquier nivel de exposición a una sustancia genotóxica puede dañar el ADN y contribuir a la aparición de cáncer, los científicos de la Autoridad Europea de Seguridad Alimentaria (EFSA, European Food Safety Authority) concluyen que no se puede establecer una ingesta diaria tolerable de acrilamida en alimentos [6]. Por ello, deberíamos reducir su ingesta lo máximo posible. La Organización de las Naciones Unidas para la Agricultura y la Alimentación (FAO, Food and Agriculture Organization) publicó en 2009 un Código de Prácticas para intentar reducir el contenido de acrilamida en los alimentos [7].
¿Cómo podemos reducir la formación e ingesta de acrilamida?
Entre otras, la Administración de Medicamentos y Alimentos de Estados Unidos (FDA, Food and Drug Administration) hace una serie de recomendaciones que se pueden seguir en casa a la hora de cocinar alimentos para minimizar la formación de acrilamida [8]:
-
Reducir el tiempo de fritura y controlar la temperatura en la medida de lo posible.
-
En el caso concreto de las patatas, se recomienda guardarlas en un lugar seco y oscuro y evitar la nevera.
-
El color es un buen indicador de la cantidad de acrilamida, por lo que se deben retirar los alimentos de la fuente de calor cuando tienen un color dorado, y evitar las tonalidades marrones oscuras (Figura 3).
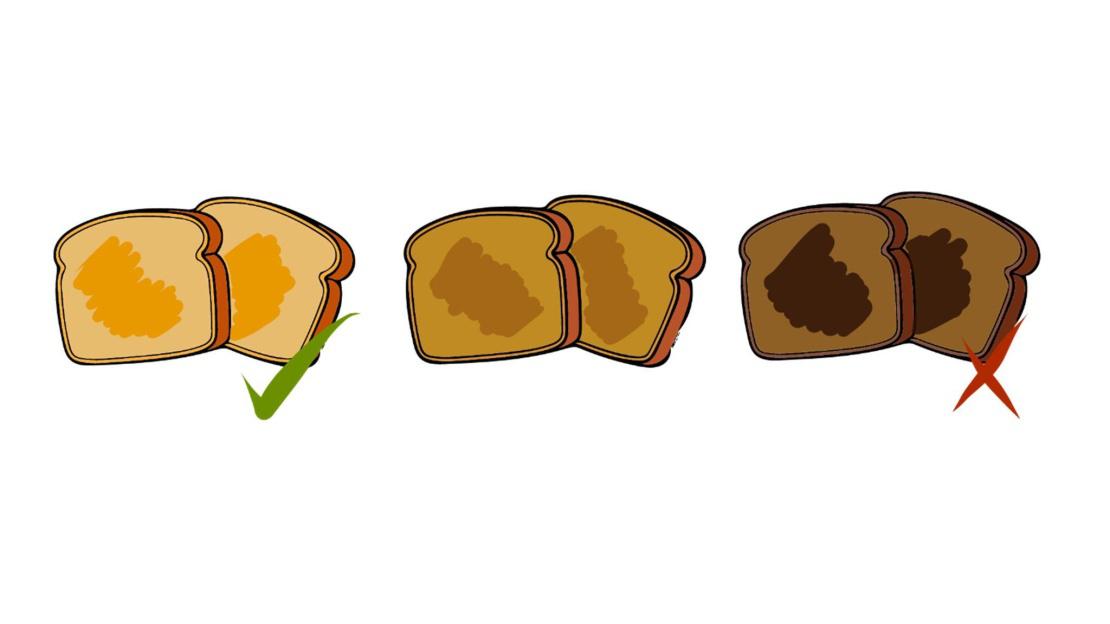 Figura 3. Representación de los diferentes colores de tostado obtenido según el tiempo de cocinado del pan. Siendo la más oscura la que mayor cantidad de acrilamida alberga. Fuente: Los autores.
Figura 3. Representación de los diferentes colores de tostado obtenido según el tiempo de cocinado del pan. Siendo la más oscura la que mayor cantidad de acrilamida alberga. Fuente: Los autores.
Como conclusión, cabe destacar que, aunque los alimentos citados en el presente artículo puedan contener una gran cantidad de acrilamida, dado que si llevamos una dieta variada y equilibrada no van suponer la base de nuestra alimentación, la ingesta de acrilamida no debería preocuparnos en exceso.
Bibliografía
- Rifai L y Saleh FA. A Review on Acrylamide in Food: Occurrence, Toxicity, and Mitigation Strategies. International Journal of Toxicology, 39(2):93-102 (2020). doi: 10.1177/1091581820902405
-
Aesan (Agencia Española de Seguridad Alimentaria y Nutrición). Con la acrilamida no desentones, elige dorado, elige salud. (21/12/2020).
-
Teodorowicz M, van Neerven J, y Savelkoul H. Food Processing: The Influence of the Maillard Reaction on Immunogenicity and Allergenicity of Food Proteins. Nutrients, 9(8), 835 (2017). doi: 10.3390/nu9080835
-
Agencia Internacional para la Investigación en Cáncer (IARC). IARC monographs on the evaluation of carcinogenic risk to humans. Some industrial chemicals. Volumen 60 (1994).
-
Perera DN, Hewavitharana GG y Navaratne SB. Comprehensive Study on the Acrylamide Content of High Thermally Processed Foods. BioMed Research International (2021). doi: 10.1155/2021/6258508
-
Autoridad europea de seguridad alimentaria (EFSA). Scientific Opinion on acrylamide in food. EFSA Journal 13(6):4104 (2015).
-
Organización de las Naciones Unidas para la Agricultura y la Alimentación (FAO). Código de prácticas para reducir el contenido de acrilamida en los alimentos. CAC/RCP 67-2009 (2009).
-
FDA (Food and Drug Administration). You Can Help Cut Acrylamide in Your Diet (14/03/2016).
Sobre los autores:
Ivan Gomez-Lopez 1,2 , Maitane González-Arceo1, María P. Portillo1,3
1 Grupo de Nutrición y Obesidad, Departamento de Farmacia y Ciencias de los Alimentos, Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU)
2 Grupo de fitoquímica y funcionalidad de productos vegetales, Departamento de Biotecnología y Microbiología de los Alimentos, Instituto de investigación en ciencias de la alimentación (CIAL) (CSIC-UAM)
3 Centro de Investigación Biomédica en Red de la Fisiopatología de la Obesidad y Nutrición (CiberObn)
El artículo En busca de El Dorado (en los alimentos) se ha escrito en Cuaderno de Cultura Científica.
Pokepaleontología
En la primera generación de videojuegos de Pokémon nos encontrábamos con unos objetos curiosos cuando visitábamos la región de Kanto: un par de fósiles y un fragmento de ámbar o resina fósil. Hasta aquí podíamos considerarlo una anécdota, pero venía acompañada por una parte más fantasiosa. Una vez que conseguíamos esos objetos, podíamos acudir con ellos a un laboratorio científico para que reviviesen a los Pokémon que habían dejado esos restos fósiles. En el último caso, incluso, extrayendo una muestra de ADN preservado en el ámbar, al más puro estilo de la novela de Michael Crichton “Parque Jurásico”.
Esta idea de completar nuestra colección de Pokémon con ejemplares extintos reanimados por la ciencia tuvo una fantástica acogida entre los fanáticos de esta saga, de tal manera que los diseñadores decidieron incluir más fósiles en casi todas las nuevas generaciones de videojuegos. Pero el diseño de estas criaturas fósiles no surgió simplemente de una imaginación desbordada, sino que tiene una base científica sólida. Así que vamos a sacar nuestra Pokédex paleontológica y analicemos esos organismos tan particulares, considerando primero los invertebrados para pasar, a continuación, a los vertebrados.
 Diseño de las cartas del juego de mesa Pokémon Trading Card Game con una agrupación de restos fósiles inidentificados y con los científicos que se dedican a buscar y revivir Pokémon fósiles. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.
Diseño de las cartas del juego de mesa Pokémon Trading Card Game con una agrupación de restos fósiles inidentificados y con los científicos que se dedican a buscar y revivir Pokémon fósiles. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.Uno de los primeros Pokémon fósiles que podíamos revivir era Kabuto, cuya morfología responde a una mezcla entre un cangrejo herradura y un trilobites, un grupo de artrópodos marinos extintos hace unos 250 millones de años.
También podíamos hacernos con Anorith, criatura casi calcada a los Anomalocaris, un grupo de organismos relacionados con los artrópodos que poblaron los mares cámbricos hace entre 510 y 530 millones de años.
 Aspecto del Pokémon Anorith. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.
Aspecto del Pokémon Anorith. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.Por otro lado, nos encontrábamos con Omanyte, Pokémon directamente basado en unos cefalópodos marinos también extintos llamados ammonites.
 Aspecto del Pokémon Omanyte. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.
Aspecto del Pokémon Omanyte. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.Pero un ejemplar que podía confundirnos sobre su grupo taxonómico de origen era Lileep. Considerado de tipo planta, además de roca, lo conseguíamos a partir del fósil raíz, lo que nos hacía pensar que se trataría de algún tipo de vegetal pretérito. Pero su morfología está basada en los crinoideos, un grupo de equinodermos marinos comúnmente conocidos como “lirios de mar” porque de un simple vistazo recuerdan a una planta, pero se trata de animales.
El primer Pokémon fósil vertebrado lo encontrábamos a partir de ese ADN antiguo conservado en ámbar, ya que revivíamos a un Aerodactyl, cuyo nombre y forma recuerdan enormemente a Pterodactylus, un género de reptiles voladores mesozoicos.
En cuanto a los reptiles acuáticos, podíamos hacernos con Tirtouga, que está basado en el género extinto de tortugas marinas cretácicas Protostega, la segunda tortuga de mayor tamaño de la historia, solo superadas por el género Archelon, extintas también a finales del Cretácico. Y sí, la evolución de Tirtouga, Carracosta, mucho más grande y fuerte, tiene su inspiración precisamente en este último género de tortugas gigantes.
Por supuesto, no podían faltar los Pokémon originados a partir de géneros extintos de dinosaurios. Por un lado, revivíamos a Cranidos, una criatura similar a los paquicefalosáuridos, un grupo que tenía fusionados los huesos frontal y parietal, lo que le aportaba una resistente protuberancia ósea en la cabeza. Por su parte, Shieldon se inspira en los ceratópsidos, un grupo de dinosaurios que desarrollaron una estructura ósea en la parte trasera de la cabeza a modo de collar protector. Y no podía faltar el Pokémon basado en el Tyrannosaurus rex, Tyrunt.
 Aspecto del Pokémon Cranidos. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.
Aspecto del Pokémon Cranidos. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.Con Amaura también podíamos equivocarnos en su clasificación faunística, como en el caso de Lileep. Y es que revivía a partir del fósil aleta, por lo que nos podríamos imaginar que está inspirado en algún tipo de reptil marino. Pero, en realidad, su desarrollo está basado en la especie Amargasaurus cazaui, un dinosaurio saurópodo que tenía una hilera de espinas dorsales desde la cabeza hasta la punta de la cola.
Finalmente encontramos a Archen, la versión Pokémon de Archaeopteryx, género considerado como una forma de transición entre los dinosaurios y las aves.
 Aspecto del Pokémon Archen. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.
Aspecto del Pokémon Archen. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.Pero estas criaturas no son las únicas herramientas didácticas de paleontología aparecidas en la saga de videojuegos. En la región de Hoenn descubrimos un Pokémon que se creía extinto y al que consideran un fósil viviente, Relicanth. Esta criatura es un homenaje a los celacantos, un grupo de peces que se consideraban extintos desde finales del Cretácico ya que no se tenían evidencias ni de restos fósiles más modernos ni de su presencia en la actualidad, al habitar aguas profundas y de difícil acceso, hasta que se capturó un ejemplar vivo hace décadas.
Y el último guiño geológico lo aportan los juegos de octava generación. Aquí podemos combinar fósiles en grupos de dos piezas para revivir Pokémon híbridos. Así conseguimos un Dracozolt, que es mitad un dromeosáurido, dinosaurio de baja estatura y con el cuerpo emplumado, y mitad un estegosáurido, dinosaurio con placas óseas dorsales. Arctozolt es la combinación de un dromeosáurido y un plesiosaurio, un reptil marino. Por su parte, Dracovish representa una mezcla entre un Dunkleosteus, un género de peces acorazados de la Era Paleozoica, y un estegosáurido. Y, por último, podemos revivir a un Arctovish, parte Dunkleosteus y parte plesiosaurio.
Esta mezcla de géneros y grupos faunísticos rememora los comienzos de la paleontología de vertebrados, cuando los naturalistas de finales del s. XVIII y comienzos del s. XIX se empeñaban en montar esqueletos completos en cada yacimiento fósil, incluso mezclando restos de especies y géneros diferentes, dando lugar a formas que nunca existieron en la naturaleza.
Sin duda, la saga de videojuegos Pokémon es una manera de lo más divertida de aprender paleontología. Ahora sólo nos queda hacernos con todos los fósiles que aparecen en los mismos.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Pokepaleontología se ha escrito en Cuaderno de Cultura Científica.
El proyecto «Código Dickens»: descifrando la «carta de Tavistock»
Charles Dickens (1812-1870) fue el autor de títulos tan conocidos como Oliver Twist, David Copperfield, Historia de dos ciudades o Cuento de Navidad. El escritor inglés era aficionado a los acertijos, llegando a inventar un código propio, basado en la braquigrafía, con el que «redactó» algunos textos aún no descifrados. De hecho, Dickens usó de manera frecuente la taquigrafía como herramienta en informes parlamentarios, redacción de cartas y toma de notas, aunque se desconoce el sistema que utilizó.
El proyecto Código Dickens intenta descifrar estos documentos taquigrafiados del escritor inglés. Claire Wood, profesora de Literatura Victoriana en la Universidad de Leicester (Reino Unido), dirige este proyecto en el que colabora también Hugo Bowles, profesor de Inglés en la Universidad de Foggia (Italia).
Uno de los textos estudiados en este proyecto es la «carta Tavistock», depositada en la Biblioteca y Museo Morgan de Nueva York, llamada de esta manera por estar escrita en un papel con membrete de la casa Tavistock en la que Dickens y su familia vivieron entre 1851 y 1860.
 Charles Dickens (Wikimedia Commons) y la «carta Tavistock» (The Dickens Code)
Charles Dickens (Wikimedia Commons) y la «carta Tavistock» (The Dickens Code)A finales de 2021, Wood y Bowles hicieron un llamamiento internacional para intentar descubrir el significado de esta misteriosa misiva. Ofrecían un premio en metálico a quien ayudara a aclarar total o parcialmente el significado de esta carta, guardada en el museo durante más de 150 años sin que nadie descubriera su clave. Numerosas personas de todos los lugares del mundo atendieron esta solicitud, y las aportaciones recibidas han conseguido resolver parcialmente el rompecabezas. Y hago alusión a un puzle, porque aproximadamente el 70 % del contenido se ha completado uniendo las piezas que cada persona ha ido aportando. Diferentes «descifradores amateurs» han ido proponiendo trozos de texto traducido, ayudando a que el significado escondido haya tomado forma. Se han identificado en la «carta Tavistock» expresiones como «Día de la Ascensión», «la próxima semana», «anuncio», «rechazado», «devuelto», «falso e injusto» o «en audiencia pública». Todas ellas forman parte de esas piezas que han ido encajando poco a poco y que han ayudado a descubrir, entre otras, la fecha de la carta en la que Dickens aludía a algún manuscrito que alguna revista o periódico le había rechazado.
Esta hipótesis se ha visto reforzada tras encontrar en un museo de Nueva York una carta de 1859, escrita por el gerente de The Times, Mowbray Morris,en la que el directivo pedía disculpas a Dickens por la decisión de un empleado, que había rechazado el anuncio del escritor, temeroso de sus posibles consecuencias legales.
El anuncio era urgente para el escritor ya que concernía a la disolución de una sociedad: Dickens era copropietario y editor de una revista semanal llamada Household Words. El escritor había entrado en conflicto con los editores de esta publicación, Bradbury & Evans, y Dickens decidió crear una nueva revista de la que sería el único propietario y editor, y de la que tendría el control total: All The Year Round. Para él era prioritario conseguir que la transición entre las dos publicaciones fuera lo más rápida posible y, por supuesto, al mismo tiempo, pretendía atraer a los lectores de Household Words hacia su nuevo proyecto.
 Portadas de Household Words y All The Year Round (Wikimedia Commons).
Portadas de Household Words y All The Year Round (Wikimedia Commons).
Descontento por la respuesta negativa del empleado, el 6 de mayo de 1859 el escritor se había dirigido al editor del periódico The Times, J.T. Delane, pidiendo su intervención. Y habría guardado una copia críptica de esa misiva, posiblemente por razones legales: esa es la «carta Tavistock».
Delane pasó la carta de Dickens a Mowbray Morris, quien se hizo responsable del malentendido al haber ordenado a sus empleados rechazar anuncios que consideraran conflictivos de alguna manera. El 9 de mayo escribió una carta de disculpa al escritor, la encontrada en el museo de Nueva York, y procedió a ordenar la publicación del anuncio de Dickens.
La comprensión, aunque sea parcial, de esta carta puede ayudar a entender mejor el método taquigráfico de Dickens, su vida y su obra. Aún quedan muchos manuscritos cifrados del autor por traducir. Esta labor detectivesca, realizada con precisión matemática, probablemente se vaya realizando gracias a las investigaciones de personas procedentes de la Academia y la colaboración de un voluntariado ávido por descubrir.
La carta de Tavistock nos da una idea de los tratos comerciales de Dickens: los otros manuscritos podrían incluir extractos de libros en los estantes de Dickens, discursos improvisados o incluso un cuento desconocido.
Claire Wood
Referencias
-
Descubierto en Handiwork, Futility Closet, 11 febrero 2022
-
The Dickens Code: Enduring mystery of Dickens shorthand letter solved with crowd-sourced research, The University of Leicester, 2 febrero 2022
-
Claire Wood, Decoding the Tavistock letter, or, Dickens and the ‘dark arts of Victorian media management’, The Dickens Code, 7 febrero 2022
-
Transcripción de la «carta Tavistock», The University of Leicester y Università di Foggia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo El proyecto «Código Dickens»: descifrando la «carta de Tavistock» se ha escrito en Cuaderno de Cultura Científica.
Las neuronas pueden vivir más que el cuerpo que las alberga
Si tu encéfalo pudiese conseguir un cuerpo nuevo, ¿durante cuánto tiempo podría seguir viviendo? Y si ese cuerpo fuese biónico, esa ilusión que llamas yo, ¿viviría indefinidamente? En lo que sigue no encontrarás respuestas concluyentes a estas preguntas, sino los resultados de un experimento que nos dan pistas de cuáles podrían ser.
La senescencia replicativa es un proceso por el cual las células de los mamíferos sufren el acortamiento de las cadenas de los telómeros, las repeticiones de secuencias de ADN que están al final de los cromosomas y que protegen a estos durante el proceso de replicación. La longitud de los telómeros es una forma molecular de reloj biológico, reflejando el historial de las divisiones de la célula y la edad biológica de tejidos y órganos.
Pero, si esto es así, ¿qué edad biológica atribuimos a las neuronas? Porque las neuronas no se dividen. Estarán sujetas a otros factores de envejecimiento pero no a la senescencia replicativa. Por tanto, ¿cuánto puede vivir una neurona? Esta es la pregunta que un grupo de investigadores encabezado por Lorenzo Magrassi, de la Universidad de Pavía (Italia) ha intentado empezar a responder en un experimento con ratones y ratas. Los investigadores han encontrado que efectivamente las neuronas pueden vivir más tiempo que el cuerpo en el que nacieron, tanto como su organismo huésped.
El experimento, de manera muy simplificada, consistió en trasplantar precursores neuronales del cerebelo de ratones (tomados cuando estos ratones aún eran fetos) en los cerebros de unas ratas que viven más tiempo por término medio. Las neuronas trasplantadas sobrevivieron en sus huéspedes hasta tres años, el doble de la vida media del ratón.
Este resultado sugeriría que la supervivencia neuronal y el envejecimiento en un mamífero son procesos coincidentes pero separables. La primera consecuencia es que si conseguimos alargar la vida (entendemos sana, obviamente) del organismo, el sistema nervioso central la va a acompañar, las neuronas de su encéfalo seguirían activas lo que dure el cuerpo. Alargar la vida se podría conseguir siguiendo pautas específicas en lo que a dieta y comportamiento (evitar zonas contaminadas, hacer ejercicio, etc.) se refiere además de la ingestión adecuada de fármacos. En otras palabras, si se extrapolan los datos a los humanos (con todas las reservas pertinentes), las neuronas podrían aguantar hasta unos 150-160 años si, como es lógico, no media ninguna enfermedad.
Habrá quien argumente que sobrevivir no lo es todo, que también es importante cómo se sobrevive. La muerte neuronal no ocurre solo por el envejecimiento del encéfalo. Así, las neuronas del cerebelo sufren una pérdida sustancial de ramas dendríticas, espinas y sinapsis en el envejecimiento normal. ¿Qué ocurre entonces en una neurona trasplantada? Una parte de las neuronas trasplantadas por los investigadores fueron células de Purkinje para estudiar precisamente si la densidad de espinas disminuía como en los ratones donantes o como en las ratas huésped. Encontraron que la pérdida de espinas en las células trasplantadas sigue un ritmo menor del típico en ratones y más parecido al de las ratas.
Por lo tanto, si se consiguen superar los problemas inmunológicos (rechazo) las neuronas trasplantadas pueden vivir toda la vida de su huésped.
Independientemente de las oportunidades que se abrirían para los transhumanistas, entendiendo el término en sentido amplio, a largo plazo, existirían posibilidades farmacológicas muy interesantes a medio plazo si se consiguiesen desentrañar los mecanismos moleculares responsables del distinto comportamiento de las neuronas en un entorno (ratón) y otro (rata). Por otra parte, el que el envejecimiento sea algo en lo que las células no son autónomas podría tener su relevancia desde un punto de vista evolutivo o, incluso, epidemiológico.
Referencia:
Magrassi, L., Leto, K., & Rossi, F. (2013). Lifespan of neurons is uncoupled from organismal lifespan Proceedings of the National Academy of Sciences, 110 (11), 4374-4379 DOI: 10.1073/pnas.1217505110
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 3 de abril de 2013.
El artículo Las neuronas pueden vivir más que el cuerpo que las alberga se ha escrito en Cuaderno de Cultura Científica.
Negacionismo, anticiencia y pseudociencias: ¿en qué se diferencian?
Antonio Diéguez Lucena
 Shutterstock / Maclevan
Shutterstock / Maclevan
A raíz de la pandemia de covid-19 se han hecho de uso común algunos términos técnicos, muchos provenientes de la medicina, que no siempre han sido utilizados con conocimiento de causa. Lo mismo ha sucedido con términos provenientes de la filosofía, sobre todo de la epistemología. Hay tres que han resultado particularmente socorridos y sobre los que, sin embargo, sigue habiendo una gran incorrección en su uso: negacionismo, anticiencia y pseudociencia.
Son tres conceptos muy relacionados y, de hecho, tienden a solaparse en ocasiones. De ahí que las actitudes de algunas personas puedan ser encajadas en más de uno de ellos. Es importante usarlos con precisión porque, como estamos viendo estos días, un uso abusivo de alguno de ellos termina por diluir su significado.
No todo el mundo es negacionista
En el ámbito académico el término negacionismo lleva tiempo cristalizando. No es tan amplio como para incluir toda crítica a los resultados científicos, puesto que esto convertiría absurdamente en un negacionista a cualquier científico que cuestionara, con buena base argumental o fáctica, una hipótesis ampliamente aceptada. Tampoco es tan estrecho como para referirse solo a los que rechazan la evidencia histórica sobre el Holocausto (aunque ese fuera su origen).
Los negacionismos más extendidos hoy se refieren al cambio climático, a la existencia del virus del sida o de la covid-19, y a la efectividad de las vacunas en general.
Los negacionistas suelen defenderse diciendo que ellos representan el sano escepticismo y actitud crítica que debe predominar en la ciencia. Sin embargo, esto es una maniobra de despiste. El negacionismo no debe confundirse con el escepticismo organizado que, como señaló hace décadas el sociólogo Robert K. Merton, constituye un atributo característico de la ciencia.
A diferencia de este, no pretende poner en cuestión hipótesis científicas que no han sido suficientemente contrastadas, sino que promueve más bien un rechazo dogmático y poco razonando, frecuentemente por motivaciones emocionales e ideológicas, de tesis científicas bien establecidas acerca de determinados fenómenos.
Una de las mejores caracterizaciones que se han dado por ahora del negacionismo está en un breve artículo de 2009 de Pascal Diethelm, un economista especializado en salud, y Martin McKee, un médico que enseña sobre salud pública.
Según ellos, el negacionismo consistiría en un rechazo del consenso científico con argumentos ajenos a la propia ciencia, o sin argumento alguno. Esto genera la impresión de que hay debate donde realmente no lo hay. Está ligado a cinco rasgos:
- el recurso a ideas conspiracionistas.
- el recurso a falsos expertos y el desprecio por los expertos reales
- la selección a conveniencia de los datos y análisis.
- la formación de expectativas imposibles sobre lo que la ciencia puede realmente proporcionar.
- el uso de falacias lógicas.
Anticiencia por la tierra plana o contra la evolución
También en la anticiencia encontramos la impugnación de hipótesis científicas o de hechos bien establecidos por la ciencia, pero hay en ella una actitud con un carácter más general.
No se limita a negar un aspecto concreto o una explicación específica de ciertos mecanismos naturales, sino que rechaza una teoría completa o incluso avances científicos fundamentales.
Dos ejemplos muy claros serían el terraplanismo y el repudio de la teoría de la evolución por parte de los creacionistas radicales. Obviamente, en la medida en que los negacionismos comportan casi siempre, al menos de forma indirecta, una oposición a teorías o hechos bien asentados por la práctica científica, asumen una actitud anticientífica, aunque no siempre sea así.
Puede haber casos de personas que nieguen esos hechos o teorías y lo hagan convencidos de que la buena ciencia es la que lleva necesariamente a dicha negación.
Sería el caso, por ejemplo, de los negacionistas del cambio climático que se aferran a ese pequeño porcentaje de climatólogos que niegan solo que el cambio climático esté causado por la actividad del ser humano.
Del mismo modo, una persona antivacunas que rechace las vacunas de ARN porque cree que pueden producir cambios en el genoma del vacunado estaría manteniendo una actitud anticientífica, puesto que esa creencia choca con lo que nos dice la ciencia.
Una persona que desconfíe de las vacunas contra la covid-19 porque considera que todavía no se conocen posibles efectos secundarios a largo plazo no necesariamente estaría comprometida con actitudes anticientíficas, aunque cabría preguntarse si no estaría llevando sus recelos más allá de lo prudente.
Uno de los pioneros en el estudio de la anticiencia ha sido el historiador de la ciencia Gerald Holton. Ya a comienzos de los 90 del pasado siglo nos avisaba del peligro de que despertara “esa bestia que dormita en el subsuelo de nuestra civilización”. Parece que la bestia ha despertado, puesto que las actitudes anticientíficas empiezan a hacerse cada vez más notables incluso en países con un nivel educativo relativamente alto.
Se ha constatado mediante diversos estudios que los negacionismos y las actitudes anticiencia van ligados por lo habitual a la aceptación de teorías conspirativas y de los llamados “hechos alternativos”. Es este un eufemismo para referirse a hechos que en realidad nunca se han producido, pero son asumidos por conveniencia.
Si alguien se opone al consenso de la ciencia sin tener genuinos argumentos científicos o datos fiables, debe articular algún tipo de explicación conspiracionista para justificar por qué existe ese consenso.
El recurso más fácil es pensar que los científicos están comprados por las grandes empresas farmacéuticas, o por las industrias biotecnológicas, o por el poder político o militar.
Esas teorías conspirativas han sido llevadas al paroxismo por movimientos como QAnon, cuya creencia en que una élite satánica y pedófila quiere controlarnos a todos e impedir que Donald Trump triunfe, y para ello utilizan cualquier medio a su alcance, incluyendo las vacunas, hace replantearse la definición del ser humano como animal racional.
Pseudociencia: falsedades disfrazadas de ciencia
Las pseudociencias son disciplinas o teorías que pretenden ser científicas sin serlo realmente. Eso les lleva inevitablemente a chocar con teorías científicas aceptadas.
Ejemplos populares hoy en día serían la astrología, la homeopatía, la parapsicología y la “medicina cuántica” (aunque esta recibe otros nombres y tiene diversas ramificaciones).
Conviene aclarar que, por mucho que a veces se confunda la homeopatía con la medicina naturista y con el herbarismo, no son la misma cosa. En estas últimas el paciente recibe al menos sustancias que tienen un efecto químico sobre su organismo. El problema aquí sería el control de las dosis.
La homeopatía, en cambio, se basa en la idea de que el poder curativo de una sustancia viene dado, entre otras cosas, por la dilución extrema con la que se administra. Pero las diluciones son tan extremas que es imposible que el paciente reciba una sola molécula del principio activo.
Para justificar esto, los defensores de la homeopatía recurren a una teoría carente por completo de base científica, por no decir simplemente contraria a la ciencia, como es la de la “memoria del agua”. Según esta teoría, el agua que ha estado en contacto con el principio activo guarda memoria de sus propiedades químicas y esa “información” es la que se mantiene en el preparado homeopático y cura al paciente.
Lo curioso es que, en la mayor parte de los casos, lo que el paciente recibe no es un tarrito con agua, sino una pastilla de azúcar.
Contra lo que algunos parecen creer, fiándose demasiado de Popper, las pseudociencias no son infalsables. Es decir, sus tesis pueden ser puestas a prueba mediante contrastación empírica. De hecho, muchas de las afirmaciones de las pseudociencias están falsadas, puesto que la ciencia ha mostrado que son falsas. Las pseudociencias pueden alegar, y de hecho lo hacen, que cuentan en su haber con muchas “confirmaciones” (en el sentido de predicciones cumplidas), lo cual puede ser cierto, pero obviamente eso no las hace científicas.
Ilustremos todo lo que acabamos de decir con el ejemplo de la pandemia:
- El que niega que exista la pandemia o el virus que la causa es un negacionista.
- El que rechaza las vacunas en general y, por ello mismo, también estas vacunas contra la covid-19, por creer que están hechas para dañar o para controlar a la gente es alguien que mantiene actitudes anticientíficas.
- Los diversos remedios que se han propuesto contra la infección como si estuvieran apoyados en la ciencia sin estarlo realmente, como los homeopáticos, son pseudociencia.

Sobre el autor: Antonio Diéguez Lucena es catedrático de Lógica y Filosofía de la Ciencia en la Universidad de Málaga
Este artículo fue publicado originalmente en The Conversation. Artículol original.
El artículo Negacionismo, anticiencia y pseudociencias: ¿en qué se diferencian? se ha escrito en Cuaderno de Cultura Científica.
Alubias, garbanzos y lentejas contra el cambio climático
 Campo de alfalfa en Ribera de Navarra (España). Foto: David Soba
Campo de alfalfa en Ribera de Navarra (España). Foto: David Soba
Según las previsiones del Panel Intergubernamental del Cambio Climático para los próximos años, se espera que los cultivos del futuro crezcan en ambientes más secos y cálidos.
Los estreses ambientales (descenso en la precipitación, incremento en la temperatura, etc.) son factores clave en la producción y calidad de los cultivos. Por eso será necesario un mayor esfuerzo en el desarrollo de variedades mejor adaptadas a condiciones adversas para alcanzar la creciente demanda de alimentos.
La cara y la cruz de los fertilizantes
Junto con el desarrollo de variedades mejor adaptadas, en las últimas décadas se ha optado por aumentar el uso de fertilizantes nitrogenados. De esta forma se consigue incrementar la producción de manera efectiva y económica. Esto es así porque, en general, la respuesta del cultivo suele ser proporcional al nitrógeno aportado y este es relativamente barato. Tal es su éxito, que el uso global de fertilizantes nitrogenados ha aumentado casi un 800 % desde 1961.
Otro dato que da fe de nuestra actual dependencia: se estima que los abonos sintéticos permiten alimentar a la mitad de la población mundial. O dicho de otra forma, la mitad de las calorías que consumimos han sido producidas gracias a este tipo de fertilizantes.
Frente a estas indudables ventajas, existen inconvenientes.
En el mejor de los casos, solo el 50 % del nitrógeno aplicado es tomado por los cultivos. ¿El resto? Parte acaba en las aguas, tanto superficiales como subterráneas, en forma de nitrato, parte se pierde a la atmósfera en forma de óxido nitroso. La principal fuente de emisión de este gas, con un potencial de calentamiento casi 300 veces mayor que el CO₂, son los abonos nitrogenados. Por lo tanto, el uso de estos abonos participa activamente en el calentamiento global.
Leguminosas al rescate
No todos los cultivos tienen la misma dependencia del nitrógeno sintético. Hay una familia de cultivos que es capaz de aprovechar el nitrógeno atmosférico, formando para ello una relación simbiótica con ciertas bacterias presentes en el suelo. Son las leguminosas: desde las lentejas a la alfalfa pasando por alubias y garbanzos.
Esta relación tiene lugar en unos tejidos subterráneos específicos. Son los nódulos. En ellos, la planta huésped (en este caso las leguminosas) suministra al nódulo la fuente de carbono (energía) en forma de fotoasimilados. La bacteria, a cambio, le suministra el nitrógeno fijado, que puede ser usado por la planta, por ejemplo, para formar proteínas. Esto hace a las leguminosas prácticamente independientes del aporte de nitrógeno sintético.
Así, esta singular característica de las leguminosas puede ayudarnos a combatir el cambio climático de dos maneras:
- evitando el uso de abonos nitrogenados y la consiguiente emisión de óxido nitroso;
- reduciendo las emisiones de CO₂ asociadas a la producción de fertilizantes (se estiman en el 1,8 % del total de emisiones).
Además, los residuos que deja el cultivo de leguminosas (ricos en nitrógeno) enriquecen el suelo y fertilizan el cultivo siguiente de forma natural.
Entonces, ¿cuál es el problema?
Con todas estas ventajas, pueden pensar que su uso debería estar extendido. Sin embargo, aunque a nivel global ocupan el 15 % de la superficie cultivada, solo por detrás de los cereales, su éxito es mucho menor en Europa. Concretamente se cultivan en el 1,5 % de la superficie agraria europea. Esto es debido, principalmente, a tres causas:
- Falta de aceptación por parte de los consumidores. Pese a ser un alimento arraigado en la cultura mediterránea, su consumo ha descendido por la introducción de nuevos patrones de consumo.
- Alta especialización de la agricultura europea en la producción de cereales y oleaginosas (girasol y colza). Esto provoca una dependencia de los abonos nitrogenados y de las importaciones de materias primas proteicas (Europa importa el 70 %, principalmente soja).
- Poco atractivo para los agricultores. Esto es debido a los bajos precios y a que su producción (en gran parte condicionada por su capacidad para fijar nitrógeno) se ve fuertemente afectada por estreses ambientales, muchos de ellos asociados al cambio climático.
El problema limita la solución
Como hemos indicado, su independencia de los abonos nitrogenados y su baja huella de carbono hacen de los distintos cultivos de leguminosas una gran herramienta para reducir el impacto de la agricultura en el cambio climático. Sin embargo, al mismo tiempo, la producción de leguminosas se ve fuertemente condicionada por los factores climáticos adversos asociados al mismo.
Es en este punto cuando la investigación entra en escena. El funcionamiento del nódulo está estrechamente relacionado con el estado fisiológico de la planta huésped. Por lo tanto, factores ambientales que afecten a la planta lo harán también a la fijación de nitrógeno por el nódulo y, en definitiva, a la producción. Es preciso incrementar nuestros conocimientos sobre los mecanismos que condicionan la fijación de nitrógeno atmosférico y su potenciación como herramienta de fertilización natural en un contexto de cambio climático.
El trabajo continuo y cooperativo de distintos grupos de investigación (como el nuestro) está permitiendo identificar y comprender estos mecanismos. Esta información nos permite identificar las variedades y perfiles fisiológicos y moleculares implicados en una producción más sostenible en condiciones de crecimiento adversas.
 Instalaciones para estudiar el efecto del CO₂ en plantas leguminosas imitando condiciones reales. Departamento de Agricultura de Estados Unidos (Alabama, EE. UU.).
Instalaciones para estudiar el efecto del CO₂ en plantas leguminosas imitando condiciones reales. Departamento de Agricultura de Estados Unidos (Alabama, EE. UU.).David Soba, Author provided
Potenciar su producción y consumo
Como hemos visto, es imprescindible optimizar la gestión de los cultivos para alcanzar el objetivo fijado por la UE de reducir las pérdidas de nutrientes en un 50 % y el uso de fertilizantes sintéticos en un 20 % para 2030. Al mismo tiempo, estos deben satisfacer las demandas de una población creciente y con hábitos de consumo cambiantes. Todo ello bajo unas condiciones de cambio climático.
Con este fin, aprovechar las ventajas agronómicas y ambientales que nos ofrecen las leguminosas es clave. Para ello, es vital comprender el efecto que el calentamiento global tendrá sobre estos cultivos y, con esta información, seleccionar variedades más eficientes en condiciones climáticas futuras. Pero estas acciones, irremediablemente, deben ir unidas a otras medidas como incentivos al cultivo de leguminosas a través de la política agraria comunitaria y aquellas encaminadas a aumentar su consumo entre la población.![]()
Sobre los autores: David Soba Hidalgo es investigador postdoctoral e Iker Aranjuelo Michelena, científico titular, en el Instituto de Agrobiotecnología (IdAB – CSIC – Gobierno de Navarra)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Alubias, garbanzos y lentejas contra el cambio climático se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Ignacio López Goñi – Me han dichooooooo, que hay un bichooooooo
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

Ahora que España está saliendo de la sexta ola es un estupendo ejercicio intelectual echar la vista atrás, a septiembre del año 2021, antes de ómicron y la sexta ola, y recordar esta charla de Ignacio López Goñi sobre la biología del SARS-cov-2, un virus que ha mutado miles de veces. Los virus son nubes de mutantes, pero eso no tiene que llevar a la histeria, porque las vacunas… funcionan. Advertencia a quienes empleen auriculares: Nacho canta en este vídeo.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Ignacio López Goñi – Me han dichooooooo, que hay un bichooooooo se ha escrito en Cuaderno de Cultura Científica.
Regla de modestia
Hoy se celebra el Día Internacional de la Mujer y la Niña en la Ciencia. En la Cátedra de Cultura Científica de la UPV/EHU este año hemos dirigido la mirada hacia el efecto que ejercen ciertos estereotipos a la hora de orientar la elección de estudios por parte de chicos y chicas.

Como señalamos aquí en su día, si se consideran en conjunto las disciplinas científicas, no hay excesivas diferencias en los números de hombres y de mujeres que cursan una carrera universitaria de ciencias. También se asemejan los porcentajes de quienes hacen un doctorado. No obstante, existen diferencias en lo relativo a las preferencias de chicos y chicas por ciertas carreras. Las más importantes se dan en las de ingeniería (con muchos más chicos) y de ciencias de la salud (con muchas más chicas). Y dentro de las carreras estrictamente científicas, la presencia femenina es menor en física y mayor en las biociencias.
Los factores que subyacen a esas diferencias no son conspicuos, no resultan evidentes, son sutiles. Así, con carácter general, las chicas no suelen optar por profesiones para cuyo desempeño se requiere una competencia intensa (tal y como se documenta, p. ej. aquí y aquí, y revisados aquí junto con otros estudios) entre sus practicantes. Ese factor, junto al efecto de ciertos estereotipos, puede estar en la base, por ejemplo, del cambio que se produjo en 2012 en los estudios de matemáticas. Antes de esa fecha se asociaban con la docencia, una actividad profesional muy común entre las mujeres, pero a partir de entonces aumentó la demanda de profesionales en matemáticas para puestos en el área tecnológica y empresarial, trabajos a los que se atribuye una mayor competitividad. El menor atractivo de esos estudios para las jóvenes sería consecuencia, así, de estereotipos de género y, además, los reforzaría.
Por otro lado, las preferencias en la elección de estudios de posgrado en función del género no parecen ajustarse a una hipotética divisoria que separaría los estudios científicos y tecnológicos del resto, sino al efecto de otros factores. Entre ellos están las expectativas del grado de brillantez considerado necesario para cursar con éxito unos y otros. Cuanto mayor es la brillantez que se supone necesaria (porque así se le atribuye) para cursar con éxito unos estudios, menor es el porcentaje de mujeres que los escogen. Y es probable que ese mismo fenómeno se produzca a la hora de elegir los estudios de grado.

Que las chicas tiendan a inclinarse por estudios para los que creen que no es necesario ser una persona “tan brillante” tiene, al parecer, origen en la niñez, a partir de los seis años, aproximadamente. A esa edad las niñas empiezan a dudar que sean tan inteligentes como los niños. Comienzan entonces a evitar actividades que se consideran propias de personas “verdaderamente inteligentes”. Parece ser que esos estereotipos se construyen en el entorno familiar y que en su génesis incide la denominada “regla de modestia”, por la que se enseña a las niñas, desde bebés, a no alardear de sus habilidades y, por el contrario, se anima a hacerlo a los niños. Se trataría, por lo tanto, de un efecto de base cultural.
A los factores anteriores, cabe añadir el efecto de lo que se denomina “incongruencia de roles” (role incongruity) y “falta de ajuste” (lack of fit). Consiste en la identificación de los rasgos propios de las personas que son consideradas buenas científicas con las características estereotípicamente masculinas (agencia, competitividad…), mientras que a las mujeres se les atribuyen rasgos que se identifican menos con los que se supone adornan a aquellas, como el carácter cooperativo (comunal), principalmente.
En definitiva, en la elección de estudios universitarios operan estereotipos ligados a la autopercepción y a la competencia que se atribuyen las chicas a sí mismas. Actúan en varias instancias en la vida académica y profesional, y contribuyen a socavar las posibilidades de desarrollo y progreso en la vida académica de las científicas. Se trata de barreras que obstaculizan el acceso de las mujeres a determinados estudios de ciencia y tecnología, por lo que, en la práctica, no gozan de las mismas oportunidades que los hombres.
El vídeo al que acompaña este texto pretende dar a conocer la existencia de esas barreras, no por sutiles poco efectivas, porque en la Cátedra de Cultura Científica pensamos que es necesario poner de relieve la existencia de los factores –esos u otros– que limitan el acceso de las mujeres a ciertos estudios. Solo así, conociéndolos, estaremos en condiciones de actuar para que dejen de existir. Lo hacemos hoy, mediante este vídeo, y lo hacemos el resto de los días del año también, a través de las publicaciones en Mujeres con Ciencia. Porque para la Cátedra de Cultura Científica de la UPV/EHU todos los días del año son días de la mujer y la niña en la ciencia.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
Más sobre el 11 de febrero- Juan Ignacio Pérez, Hoy es el día de la mujer y la niña en la ciencia, todos lo son, 11 febrero 2017.
- Juan Ignacio Pérez, No es una percepción, 11 febrero 2018.
- Juan Ignacio Pérez, Mi hija quiere ser ingeniera, 11 febrero 2019.
- Juan Ignacio Pérez, Motivos para un día internacional, 11 de febrero 2020.
- Juan Ignacio Pérez, La historia de June Almeida, 11 de febrero de 2021.
El artículo Regla de modestia se ha escrito en Cuaderno de Cultura Científica.
La distancia a las estrellas (II)
A pesar de no poder pagar las facturas que han llegado hasta su playa, el náufrago de nuestro relato se encuentra de muy buen humor. Gracias a todos esos nuevos números desperdigados sobre la arena, ahora entiende mucho mejor cómo son los continentes y países que rodean a su pequeña isla. Sin embargo, aún hay un detalle que le falta concretar. La preocupa la distancia que tendrá que recorrer para poder huir de la isla a nado. Bueno, eso y los tiburones, claro. Pero contra los tiburones tiene un buen repelente (y espera que funcione).
Para intentar calcular las distintas que le separan de otros mundos al otro lado del océano, el náufrago empieza a anotar el número de botellas que llegan a su playa en cada dirección. Se trata de un dato fácil de medir y además parece muy prometedor. Es razonable pensar que cuanto más cerca se encuentre un país, más botellas suyas alcanzarán la la isla desierta. Pero para hacer esa inferencia, hay una variable que el náufrago necesita conocer, y es el tamaño y poderío económico de las naciones que envían todos esos mensajes. Lógicamente, los países más grandes y activos económicamente generarán muchas más facturas. De modo que un país grande y relativamente lejano, podría acabar arrojando muchas más botellas en la arena que un país cercano pero chiquitín.
Volviendo a la astronomía, el problema es equivalente al de comparar la magnitud absoluta de una estrella con su magnitud aparente. La magnitud absoluta es el brillo intrínseco de la estrella, su poderío energético (el número de botellas que envía), mientras que la aparente es la luz que llega hasta nosotros. Conociendo estas dos magnitudes, es posible calcular la distancia que nos separa de ella. Lógicamente, cuanto más lejos se sitúa una estrella, menor es su magnitud aparente. La cuestión es ¿cómo podemos calcular su magnitud absoluta?
Esta pregunta permaneció sin respuesta hasta finales del siglo XIX. Fue entonces cuando Henrietta Swan Leavitt, otra de las astrónomas de Harvard, empezó a fijarse en unas curiosas estrellas intermitentes situadas en la Nube de Magallanes. Eran las llamadas estrellas variables o cefeidas, unas estrellas entre cuatro y veinte veces más masivas que el Sol, que se encienden y apagan regularmente. Sus periodos suelen estar comprendidos entre unas pocas horas a meses1, y aunque ya habían sido descritas con anterioridad, fue Leavitt quien observó por primera vez que las más brillantes eran las que tenían los periodos más largos.
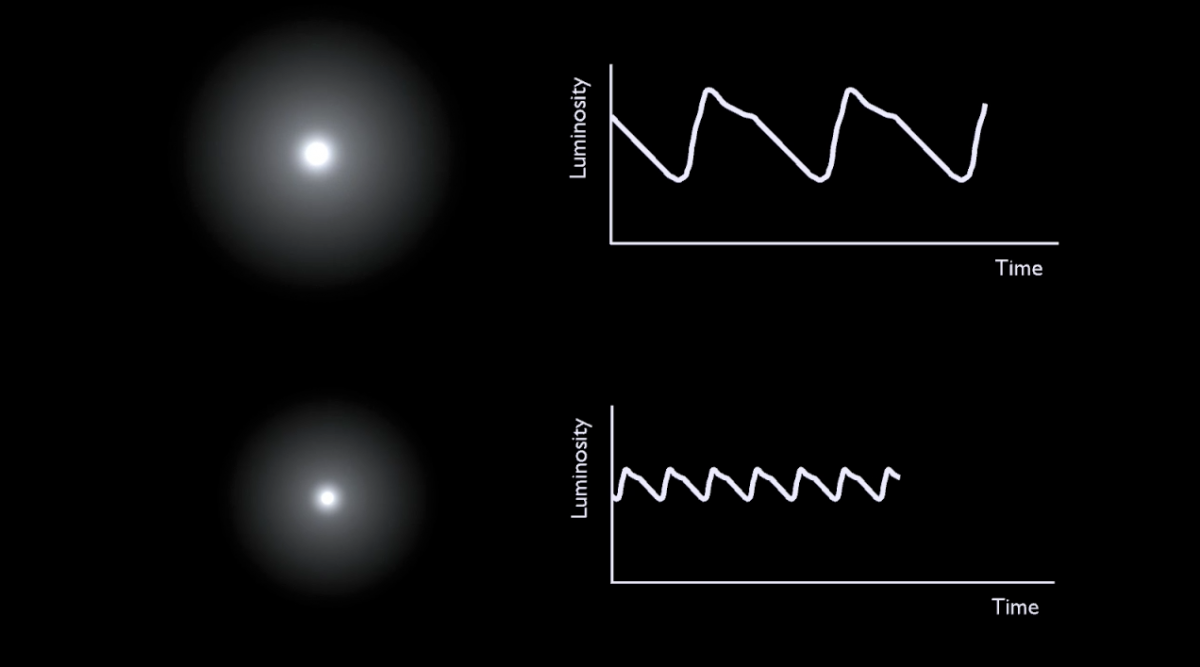 Curvas de luz de estrellas cefeidas. Fuente: El diario secreto de Henrietta S. Leavitt
Curvas de luz de estrellas cefeidas. Fuente: El diario secreto de Henrietta S. Leavitt
Si bien la astrónoma no podía saberlo en aquel momento, esta relación no era un accidente, ni una mera casualidad. La variación de la luminosidad de las cefeidas tiene su origen en el equilibrio de fuerzas que caracterizan a toda estrella. En estas inmensas bolas de plasma, la gravedad tiende a contraer la materia y a empujarla hacia el interior. En cambio, las reacciones nucleares liberan energía y aumentan la presión de radiación dentro de la estrella, de modo que empujan la masa hacia el exterior. En la mayoría de las estrellas estas dos fuerzas se encuentran en equilibrio. Sin embargo, cuando esto no sucede, cuando una estrella se desvía respecto a su radio ideal, puede empezar a oscilar, como un corazón de luz. En estos casos, el tamaño de la estrella es lo que determina el periodo de la oscilación o “pulsación”. Cuanto más grande es la estrella, más lentos son sus latidos.
Esta fue la relación que descubrió Henrietta Leavitt mientras analizaba las estrellas de las Nubes de Magallanes2. En 1912 publicó un artículo en el que analizaba los periodos de veinticinco cefeidas. Las más luminosas eran, precisamente, las que oscilaban más lentamente. Como se suponía que todas ellas estaban a una distancia similar de la Tierra, esto significaba que cada latido estaba directamente relacionado con la magnitud absoluta de su estrella. Bastaba con estimar la distancia a la que se encontraba alguna Cefeida cercana (un elemento necesario para “calibrar” la nueva regla de medir) para empezar a situar galaxias, nebulosas y todo tipo de formaciones astronómicas sobre la profundidad inabarcable del cielo.
El texto de 1912 estaba firmado por Pickering, como casi todos los trabajos que salían del Observatorio, pero en el primer párrafo se aclara que el estudio ha sido elaborado por Leavitt. En apenas tres páginas, la astrónoma abría el camino para resolver uno de los puzzles más antiguos de la astronomía: la clave para medir distancias en el universo.
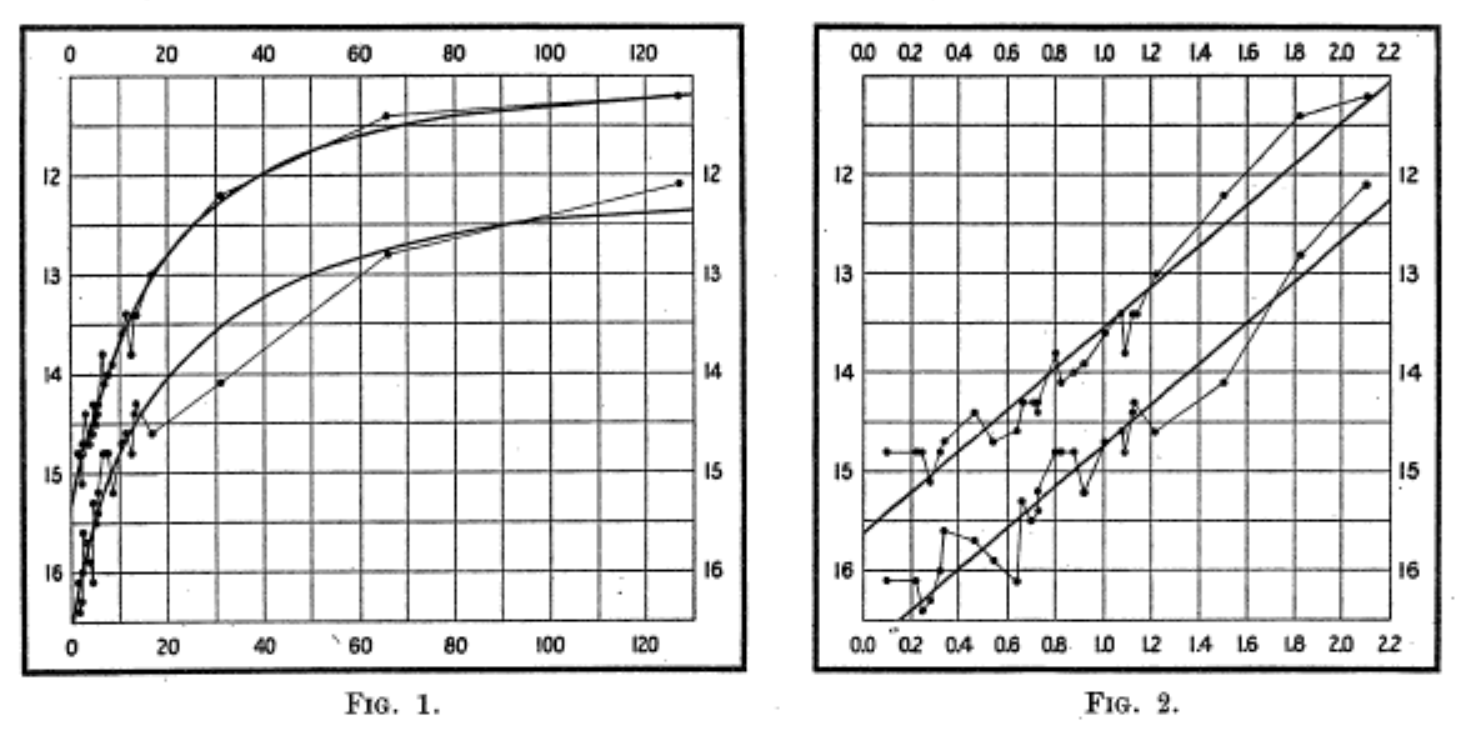
Henrietta S. Leavitt, 19122. Las gráficas representas la magnitud aparente de veinticinco cefeidas en función de su periodo. En la segunda gráfica utiliza una escala logarítmica.
Referencias:
1IAA-CSIC/FECYT. “Una regla para medir el universo”. El extraño caso de Henrietta Leavitt y Erasmus Cefeido, Instituto de Astrofísica de Andalucía, 5 de diciembre de 2012. Consultado el 6 de febrero de 2022.
2Leavitt, Henrietta Swan, and Edward Charles Pickering. “Periods of 25 Variable Stars in the Small Magellanic Cloud.” Harvard College Observatory Circular, vol. 173, 1912, pp. 1-3, https://adsabs.harvard.edu/full/1912HarCi.173….1L.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo La distancia a las estrellas (II) se ha escrito en Cuaderno de Cultura Científica.
En busca de la banda de Moebius más corta posible
La banda de Moebius es un sorprendente objeto topológico, una superficie con una sola cara y un solo borde, con propiedades muy curiosas (véanse el video La banda de Moebius de la sección Una de Mates del programa de televisión Orbita Laika; el libro La banda de Moebius, de Clifford Pickover; el libro Festival mágico-matemático de Martin Gardner; o algunas de las entradas de la sección Matemoción, del Cuaderno de Cultura Científica, que mencionamos en la bibliografía; por citar algunas referencias) que ha cautivado a muchísimas personas, tanto de dentro como de fuera de las matemáticas.
 Cinta de Moebius bicolor (2017), del artista y ceramista catalán Joan Puyal. Imagen de la página del ICRE – Institut Català per a la Recerca en Escultura
Cinta de Moebius bicolor (2017), del artista y ceramista catalán Joan Puyal. Imagen de la página del ICRE – Institut Català per a la Recerca en Escultura
A pesar de que es el objeto topológico por excelencia, en la entrada de hoy vamos a fijarnos en un problema geométrico relacionado con su construcción con una tira de papel.
Para empezar, una banda de Moebius es una banda retorcida que podemos construir de forma sencilla de la siguiente forma. Si tomamos una tira de papel y pegamos los extremos se obtiene una banda normal con dos caras y dos bordes, pero si primero giramos uno de los extremos del papel media vuelta y después juntamos los extremos se obtiene la banda de Moebius, una superficie que solo tiene una cara y un solo borde.
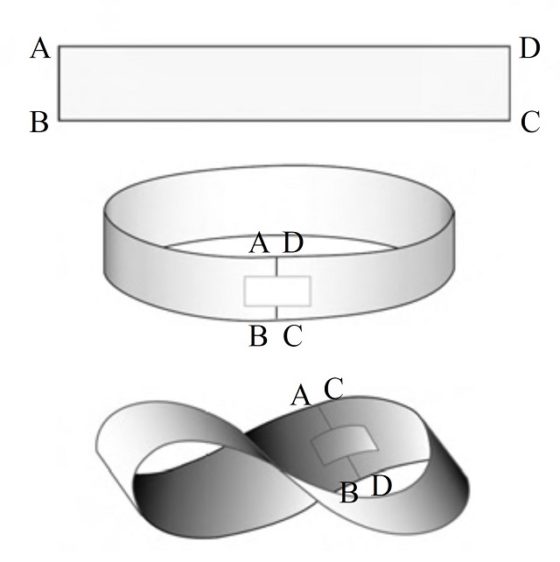
El problema geométrico consiste en construir una banda de Moebius con una tira de papel lo más corta posible. Es decir, dada una tira de papel (como la de la siguiente imagen) que tiene una anchura a y una largura b, se trata de construir una banda de Moebius con una largura b lo más corta posible (dejando fija la anchura a).
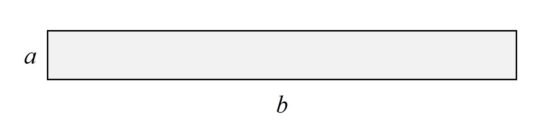
Si la tira de papel es bastante larga, como la de la imagen anterior (podemos construir en casa una tira como la de la imagen que, para una anchura de 10 cm, tendría una largura de 96 cm –o también, para una anchura de 2cm, la largura es de 19,2 cm–), entonces la cinta de Moebius que se construye con ella es bastante holgada, con lo cual podemos recortarla en largura (hacerla más corta) y seguir construyendo nuestra superficie de una sola cara. La cuestión es hasta dónde podríamos ir recortando en la largura.
La banda de Moebius que hemos construido la podemos “aplanar” de la forma en la que aparece en esta imagen, que tiene una forma de tipo triangular (que nos recuerda al símbolo del reciclaje).
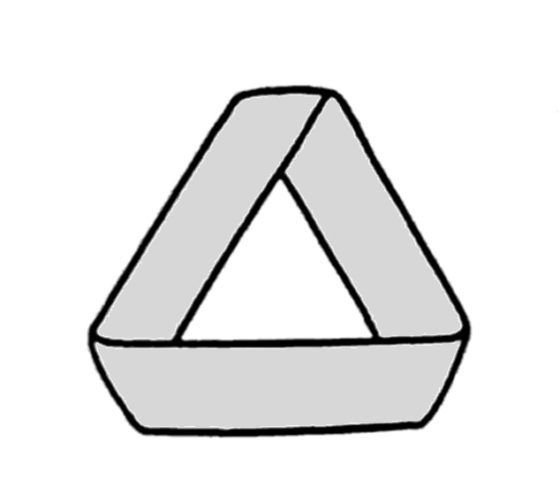
Vemos que efectivamente tiene holgura, hay espacio en el centro. Entonces, si vamos recortando la largura de la banda iremos cerrando ese hueco central, como se muestra en la siguiente imagen, hasta llegar el momento en que se cierre el hueco. Además, como podemos observar, en ese momento final lo que ocurre es que tenemos un hexágono.
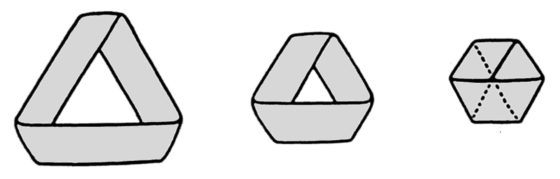
En concreto, nuestra banda de Moebius “recogida” está formada por nueve triángulos equiláteros, como se muestra en la siguiente imagen. Los pares de triángulos equiláteros de papel 2 y 3, 5 y 6, así como 8 y 9, están superpuestos, uno encima del otro, en nuestra banda retorcida, mientras que los triángulos equiláteros 1, 4 y 7 están solos.
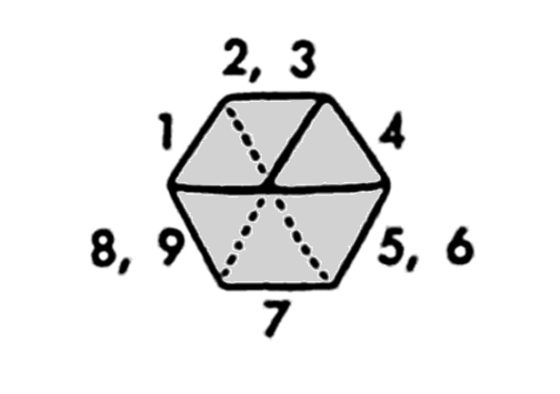
Para conocer cuánto hemos acortado nuestra tira de papel, o más bien, hasta que longitud (respecto de la anchura) hemos acortado, vamos a separar/cortar de nuevo nuestra tira y desplegarla. Tendremos en ella los nueve triángulos equiláteros que, si cortamos en la banda de Moebius justo por el medio de uno de ellos, quedan distribuidos en la tira como se muestra en la imagen.

Para calcular, a partir de la imagen anterior, la relación de la largura (b) respecto a la anchura (a), vamos primero a calcular el lado de cada triángulo equilátero, en función de la anchura a. Para ello vamos a utilizar el teorema de Pitágoras sobre el triángulo rectángulo de la izquierda, que es la mitad del triángulo equilátero. Si llamamos x a la longitud del lado del triángulo equilátero, tendremos el siguiente esquema.
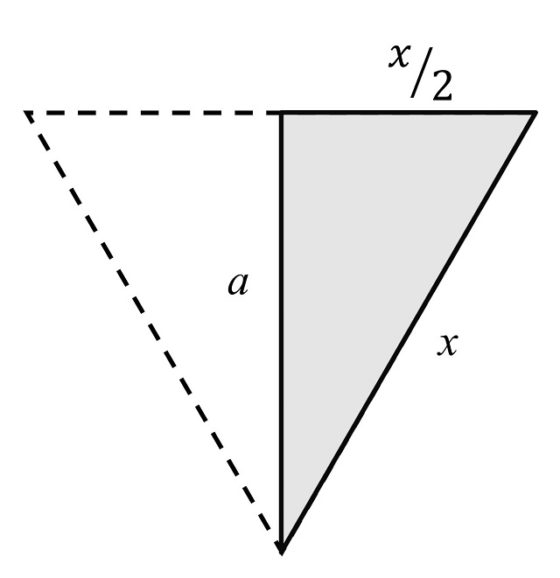
Luego, por el teorema de Pitágoras (la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa):
![]()
Y despejando x, en función de a, se obtiene que:

Por lo tanto, si tenemos en cuenta que la tira de papel que hemos obtenido tiene una largura (b) que es 4,5 veces el lado del triángulo equilátero (x), como se puede observar en una de las imágenes anteriores, entonces se tiene que la largura de la tira es igual a:
![]()
La largura es aproximadamente 5, 2 veces la anchura (ajustando un poco más, 5,196). Es decir, si nuestra tira de papel tuviese una anchura de 10 centímetros, la largura sería de 51,96 centímetros (recordemos que la inicial tenía una anchura de 10 cm y una largura de 96 cm).
 Silla de Moebius (2005), diseño de una silla de Acapulco con forma de cinta de Moebius, del artista mexicano Pedro Reyes. Imagen de la publicación digital Patio Productions
Silla de Moebius (2005), diseño de una silla de Acapulco con forma de cinta de Moebius, del artista mexicano Pedro Reyes. Imagen de la publicación digital Patio Productions
El matemático Stephen Barr, en su interesante libro Experiments in Topology, nos cuenta que es posible reducir la largura de la tira de papel a la tercera parte.
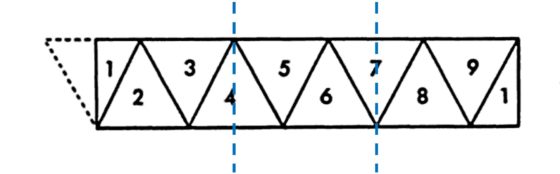
Veamos cómo construir la banda de Moebius a partir de la tercera parte de la banda de nueve triángulos equiláteros. Ahora nos quedamos con un trozo de tira de papel con tres triángulos equiláteros, por ejemplo, los tres de la izquierda de la imagen anterior, dos enteros en el centro y dos mitades en los laterales.
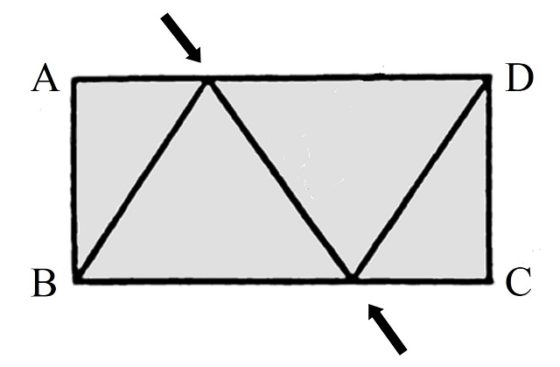
Para construir la banda de Moebius debemos pegar el lateral AB con el lateral opuesto, después de dar media vuelta, es decir, con CD. En particular, el punto A se pega con el punto C y B con D. Para ello, primero doblamos por el lado común de los dos triángulos equiláteros enteros (marcado con las flechas en la imagen), de forma que el triángulo equilátero de la derecha queda sobre el de la izquierda, como se ve en la siguiente imagen.
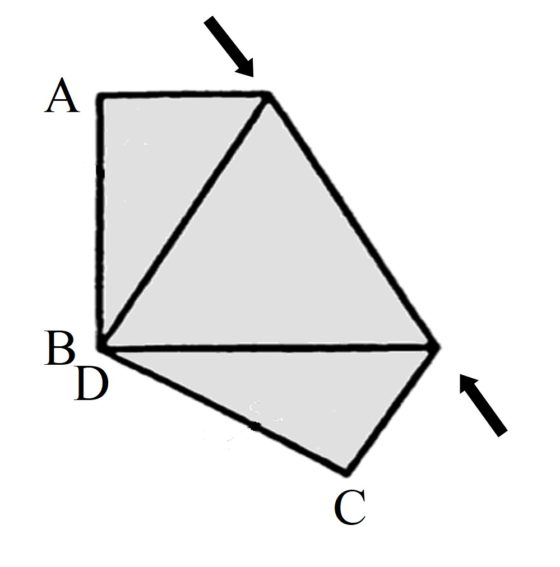
Ahora, doblamos las dos mitades laterales de triángulo equilátero (que son triángulos rectángulos), la que tiene al lado AB y la que tiene al lado CD, colocándolas encima del triángulo equilátero entre ellos (formado por la superposición de los anteriores triángulos equiláteros), como se muestra en la imagen.
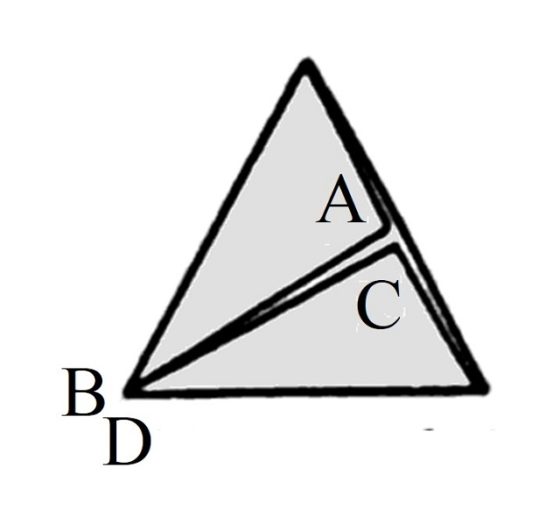
Entonces, se pegan los lados AB y CD obteniéndose una banda de Moebius. A las personas que estáis leyendo esta entrada del Cuaderno de Cultura Científica os animo a que realicéis esta construcción en vuestra casa, o donde deseéis claro.
¿Cuánto se ha reducido ahora la largura (respecto de la anchura)? Como habíamos dicho anteriormente, se reduce a la tercera parte de la anterior reducción, es decir, ahora la largura (b) es igual a:
![]()
Por ejemplo, nuestra tira original de 10 cm de anchura y 96 cm de largura, la habíamos reducido a una largura de 51,96 cm, que ahora la hemos reducido a 17,32 cm (la raíz de tres es igual a 1,732).
En el libro Experiments in Topology se plantea la cuestión de si se podría realizar una banda de Moebius, con una tira de papel cuadrada. Si consideramos la tira de papel anterior, de 10 cm de anchura, sería una largura de también 10 cm. El propio Stephen Barr nos muestra la solución.
Si partimos de una tira de papel ABCD cuadrada, como la de la imagen, se empieza doblando por una de las diagonales.
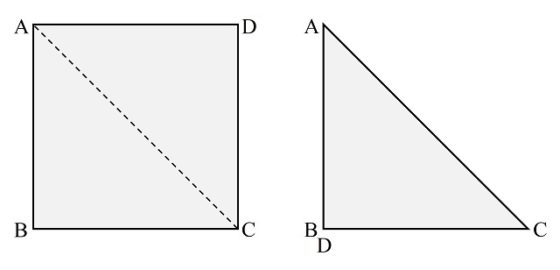
A continuación, se dobla por la otra diagonal, quedando un triángulo (isósceles y rectángulo) que es la cuarta parte del cuadrado original.
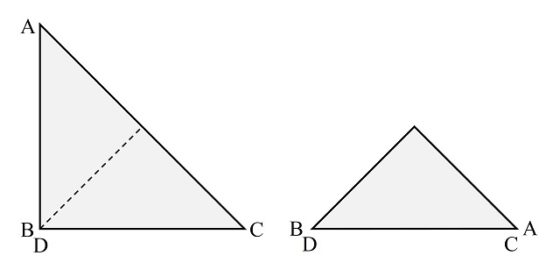
Entonces, se pegan los lados AB con CD para formar la banda de Moebius. Hemos de tener cuidado, ya que los lados a pegar están en la base del triángulo obtenido, pero en distintas capas. El lado AB está en la capa de arriba, mientras que el lado CD está en la tercera capa empezando por arriba (o en la segunda empezando por abajo). Por este motivo, si hacemos esta construcción en nuestra casa, tenemos que tener un poco de cuidado cuando vayamos a poner el celo para pegar esos lados.
 Escultura Cinta sin fin (1953-56), del artista y diseñador suizo Max Bill. Escultura en el Middelheim Museum (Amberes, Bélgica)
Escultura Cinta sin fin (1953-56), del artista y diseñador suizo Max Bill. Escultura en el Middelheim Museum (Amberes, Bélgica)
A pesar de estos ingeniosos métodos de Stephen Barr para crear bandas de Moebius para tiras de papel que son bastante cortas –el caso del cuadrado es significativo- como para intentar dar medio giro a un lado y pegarlo con el opuesto, el gran divulgador de las matemáticas, el estadounidense Martin Gardner (1914-2010), en una de sus columnas de Juegos matemáticos de la revista Scientific American (recogida en el libro The Sixth Scientific American Book of Mathematical Puzzles and Diversions, publicado por vez primera en 1971), plantea el problema de hacer una banda de Moebius para tiras más cortas aún, por ejemplo, si es el doble de ancha que larga.
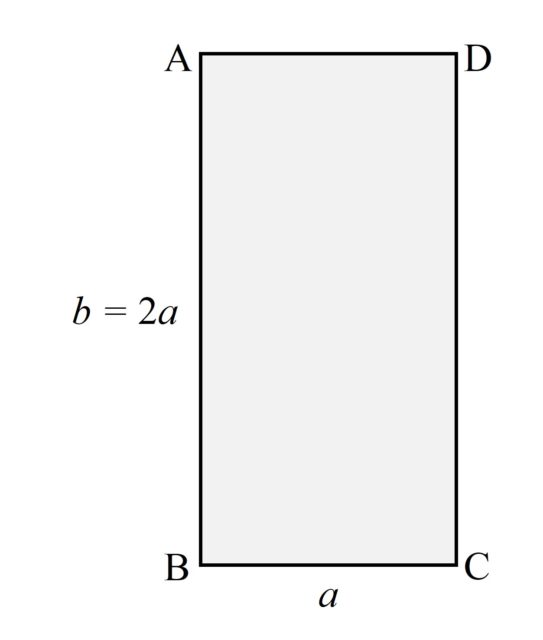
De nuevo, deberíamos de pegar el lado AB con su opuesto, después de girar este media vuelta, es decir, con el lado CD. El problema evidente es que el una tira de papel muy corta, necesitaríamos una mayor largura para poder pegar los lados opuestos –después de girar uno media vuelta-.
La genial idea de Martin Gardner fue conseguir que la anchura “fuese más corta aún”, de manera que con esa nueva anchura la largura nos permita girar la banda media vuelta y pegar los extremos. ¿Cómo conseguir reducir la anchura, sin modificar las dimensiones reales de nuestra tira de papel? La idea es ingeniosa. Se trata de realizar una cantidad de pliegues horizontales –igualmente espaciados- a nuestra tira de papel de forma que se generen una cantidad impar de zonas plegadas iguales.
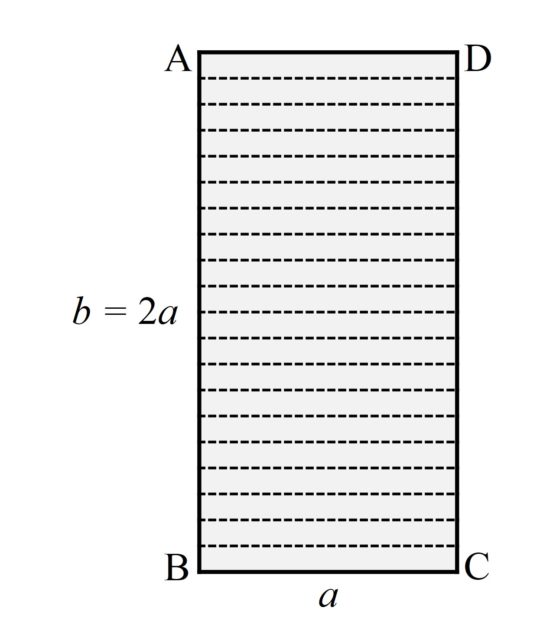
En la anterior imagen hemos realizado 20 pliegues, que generan 21 zonas, que se pliegan en acordeón formando una tira de papel cuya anchura se ha reducido en relación a la largura.
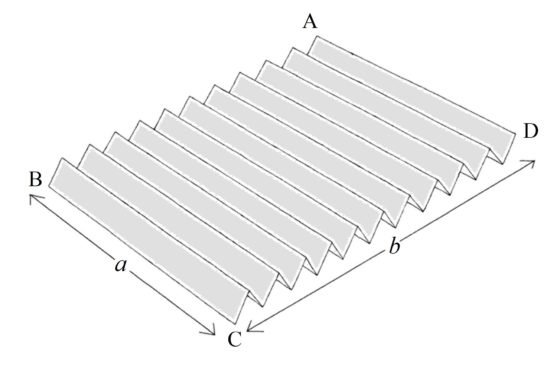
La “nueva” tira, después de realizar completamente estos pliegues, tiene una largura suficiente (aunque recordemos que está formada por 21 capas de papel, que se han generado al realizar los pliegues) como para poder girarla media vuelta y pegar los lados plegados, AB con CD (como se muestra en la siguiente imagen, sacada del libro de Martin Gardner).
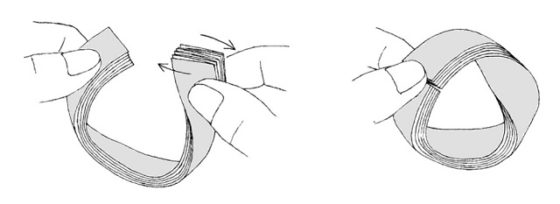
¡Qué maravilla de construcción de bandas de Moebius a partir de tiras de papel muy cortas!
Bibliografía
1.- Clifford A. Pickover, La banda de Möbius, Almuzara, 2009.
2.- Martin Gardner, Festival mágico-matemático, Alianza editorial, 1984.
3.- Marta Macho, Poesía retorcida sobre la banda de Moebius, Cuaderno de Cultura Científica, 2016.
2.- Marta Macho, Otto Spiegel, de la simetría a la teoría del caos, Cuaderno de Cultura Científica, 2019.
3.- Raúl Ibáñez, De menú para hoy, dos novelas gráficas negras con salsa matemática, Cuaderno de Cultura Científica, 2019.
4.- Raúl Ibáñez, Guía matemática para el cómic ‘Promethea’, Cuaderno de Cultura Científica, 2020.
5.- Raúl Ibáñez, Arte Moebius (I), Cuaderno de Cultura Científica, 2020.
6.- Raúl Ibáñez, Arte Moebius (II), Cuaderno de Cultura Científica, 2020.
7.- Stephen Barr, Experiments in Topology, Dover, 1989.
8.- Martin Gardner, The Sixth Scientific American Book of Mathematical Puzzles and Diversions, Simon & Schuster, 1971.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo En busca de la banda de Moebius más corta posible se ha escrito en Cuaderno de Cultura Científica.
El futuro de hace 10 años
Hace casi diez años, el 25 de julio de 2012, publiqué este artículo en Experientia docet hablando sobre las posibilidades que podría traer el futuro. El mensaje fundamental es la importancia de lo imprevisible, cosa que desarrollé algo más en la conferencia que di en Naukas Valladolid 2021 y que aparece al final. Creo que es un ejercicio interesante echar la vista atrás, contrastar, y aprender para el futuro.

El 15 de abril de 2010 volvía a casa después de asistir a una demostración de un nuevo equipo industrial en una ciudad del centro de Suecia. Cuando llegamos mi compañero y yo al aeropuerto de Estocolmo nos encontramos con el caos. Al parecer un volcán en Islandia, el Eyjafjallajökull, había entrado en erupción y las cenizas que arrojaba a a la atmósfera obligaban a cerrar el espacio aéreo por tiempo indefinido. Nuestro vuelo a Madrid aún no estaba cancelado aunque sí muchos otros. Yo, siguiendo un instinto de supervivencia peculiar, entré en la bien surtida librería a comprarme un par de libros.
Nuestro vuelo fue el último en despegar de Estocolmo antes del cierre del espacio aéreo sueco y nuestro piloto nos llevó a España dando un rodeo por Polonia. En ese tiempo comencé a leer uno de los libros que más me ha hecho pensar en los dos últimos años: The Black Swan, The Impact of the Highly Improbable, de Nassim Nicholas Taleb.
Un cisne negro, citando a Taleb, es un acontecimiento que reúne tres características. Primero, es completamente inesperado, ya que nada en el pasado puede apuntar de forma convincente a esa posibilidad. Segundo, tiene un impacto enorme. Tercero, a pesar de ser inesperado, nuestra capacidad humana para la racionalización a posteriori hace que lo veamos como algo explicable y predecible.
Los cisnes negros son el tipo de acontecimientos que marcan las revoluciones científico-técnicas; pensemos en el descubrimiento de los rayos X o en la penicilina o, y perdonad que aquí cite una afición, los cuasicristales. En las próximas décadas serán los cisnes negros los que marquen la evolución de la ciencia y la técnica concretas. Por definición no podemos saber cuáles serán. Nosotros, en lo que sigue, no vamos a intentar predecir qué desarrollos concretos habrá en la ciencia y la técnica en lo que queda de siglo, ya dejamos a otros que se equivoquen en eso, sino que vamos a explorar brevemente, y sin ánimo de ser exhaustivos, las áreas en las que podrían producirse esos avances. Puede que te sorprendan.
La instrumentalización de la química y el recorrido limitado de la física.
La química, como ciencia que permite conocer el universo, está agotada. No habrá sorpresas químicas relevantes, si bien cabe esperar de ella una enorme variedad de contribuciones prácticas. La química es como una lengua que cuesta dominar: a lo largo de los siglos hemos ido aprendiendo su gramática, su vocabulario, sus modismos, cada uno de estos descubrimientos permitiéndonos conocer más el universo y a nosotros. Pero un idioma, una vez dominado, sirve para expresar ideas. Este es el futuro papel de la química, un instrumento sofisticado que facilitará mucho de lo que sigue.
La física sólo es un poco más estimulante desde esta perspectiva que hablamos. Aunque aún haya mucho que aprender acerca de la estructura fundamental del universo, las máquinas necesarias para realizar esta exploración son cada vez más grandes y caras. Existe un concepto económico crítico para estas situaciones, el de rendimientos decrecientes y, aunque el descubrimiento de una partícula compatible con el bosón de Higgs pueda estimular durante un tiempo breve el imaginario colectivo de los que administran el dinero, no cabe esperar muchas inversiones en algo que tiene de entrada pocas aplicaciones prácticas desde su punto de vista.
En las próximas décadas, salvo hallazgos no previstos en el modelo estándar que nos depare el LHC (más improbables si la partícula descubierta se confirma que, efectivamente, es el bosón de Higgs del modelo estándar), la física fundamental estará centrada en comprender la materia oscura (partículas fundamentales que interactúan con la de materia ordinaria aparentemente sólo a través de la gravedad) y en encontrar ondas gravitacionales (lo que permitiría unir la gravedad, explicada actualmente por la torre de marfil que es la teoría general de la relatividad, con la física cuántica que explica el resto de la física). Para conseguir ambos fines bastarían en principio instrumentos relativamente baratos comparados con un megaacelerador de partículas lineal, por ejemplo.
La otra gran incógnita de la física es la energía oscura, eso que hace que el universo se expanda aceleradamente. A diferencia de las dos anteriores, su resolución requiere de una revolución teórica previa más que de nuevos datos. Y esto entra de lleno en el dominio de los cisnes negros. Puede que ahora, mientras lees esto, un parado esté garabateando, en un parque de Málaga, la que podría ser la solución a este problema.
La revolución nanobiomática.
Para el año 2050, parece bastante probable que sepamos, más allá de la certeza estadística, que la vida es abundante en el universo. El estudio de los planetas extrasolares con nuevos telescopios espaciales parece que es algo que tiene la financiación poco menos que garantizada: la pregunta de si estamos solos en el universo es fácilmente entendible por los administradores y también interesante para ellos.
Un aspecto relacionado es el origen de la vida en la Tierra. La respuesta puede que venga del mejor conocimiento del funcionamiento celular y la identificación de sus partes más primitivas, y de la experimentación, es decir, de la creación de organismos vivos en el laboratorio a partir de moléculas químicas sencillas.
Pero los descubrimientos en biología están entrando en una fase exponencial que nosotros atribuimos a cuatro motivos principales:
-
La capacidad desarrollada recientemente de secuenciar el ADN rápidamente y en cantidades enormes.
-
Las mejoras en microscopia, en el sentido más amplio, desde sistemas de tinción a fotografías a nivel atómico, que permiten una mejor comprensión de los procesos celulares.
-
Las técnicas para el estudio específico del encéfalo y su funcionamiento, probablemente el objeto de estudio científico más interesante del universo.
-
La asunción generalizada de que la investigación biológica tiene que tener una perspectiva evolutiva.
Cabe esperar que en próximo par de décadas la caracterización genética de todas las especies esté completa. Alrededor del año 2030, dependiendo de la financiación, la mayor parte de la vida conocida habrá sido caracterizada, incluyendo la microbiológica marina o la subterránea profunda (de existir). En el proceso es posible que nos encontremos grandes sorpresas (asumimos que con más fundamento que la vida basada en arsénico).
Lo anterior, completar el álbum de cromos de la vida terrestre, es fascinante e intelectualmente atractivo. Pero esta base de datos genéticos gigantesca y el conocimiento biológico derivado de ella, abriría la puerta a la explotación industrial, lo mismo que ocurrió con la química en el XIX. En esto trabajan ya activamente personas como Craig Venter, ya sea por la vía de crear de vida sintética de diseño, ya por la creación de nuevos organismos transgénicos o directamente por el uso de nuevas especies.
Pero, sin duda, el punto de inflexión lo marcará la combinación de la biología con la nanociencia y la informática: la nanobiomática.
Digámoslo claramente, y citando a un sabio malagueño: la nanotecnología ha tenido un arranque de caballo andaluz y un parón de burro manchego. Durante los últimos veinte años se ha hablado mucho de nanotecnología pero, a fin de cuentas, salvo algunas estructuras que quedan muy espectaculares en fotografía y la alteración de las propiedades de algunos materiales, ya sea por la incorporación de otros o por técnicas de encapsulación, poco más se ha conseguido. Estamos a años-luz de esos ejércitos colaborativos de micromáquinas que prometían los visionarios de los años noventa. Pero esto cambiará cuando se conozca mejor el comportamiento de las células.
Las proteínas, el ARN o el ADN son moléculas grandes y tienen exactamente el tamaño típico de los objetos con los que opera la nanociencia: mayor que el de la química tradicional, pero aún suficientemente pequeños como para que la influencia de las interacciones supramoleculares electrostáticas sea crítica impidiendo que la ingeniería mecánica clásica pueda lidiar con ellas. De hecho, fueron estas interacciones las que arruinaron las predicciones de los visionarios: los engranajes y levas de las micromáquinas se veían alterados por las fuerzas de van der Waals y otros efectos mal comprendidos.
Pero, hete aquí que los sistemas vivos, obviamente, funcionan. Una vez que se analicen apropiadamente aparecerá todo un abanico de aplicaciones tecnológicas: ya sean organismos altamente modificados, o sistemas completamente artificiales que simplemente toman sus fundamentos de la biología, como los robots de Karel Capek, el inventor del término en 1921.
Pero unos robots así requerirían también la intersección de la biología, además de con la nanotecnología, con la informática y la inteligencia artificial, lo que hemos dado en llamar nanobiomática. La unión de una mejor compresión del funcionamiento del cerebro con una capacidad de computación artificial mucho más sofisticada. Las nuevas técnicas para el estudio del cerebro pondrán de manifiesto cómo se organiza el cerebro a nivel celular (conectoma). Los ordenadores, más rápidos y potentes, permitirán modelar como software esa nueva información. Así sabremos cómo funciona el cerebro de verdad, lo que permitirá la construcción de cerebros artificiales que trabajarán con los mismos principios, pero mucho más potentes y sin errores. Cerebros artificiales nanobiomáticos que puede que funcionen conscientemente.
Curiosamente, según la teoría de Taleb, nadie podrá hacer una fortuna apostando a nada de lo anterior: lo previsible no es novedoso realmente. Y es que el futuro lo conformarán los cisnes negros.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El futuro de hace 10 años se ha escrito en Cuaderno de Cultura Científica.
La urgencia de los neuroderechos humanos
Txetxu Ausín, Aníbal Monasterio Astobiza, Belén Liedo, Daniel López Castro, Manuel Aparicio Payá, Mario Toboso Martín y Ricardo Morte Ferrer
 Shutterstock / JLStock
Shutterstock / JLStock
Imagine que está pensando en hacer un regalo a Marta. Ella siempre le ha ayudado cuando más lo ha necesitado y ahora quiere mostrar gratitud. Estaba pensando en regalar a su amiga una nueva chaqueta de color amarillo, como le gustan a ella. Nada más terminar de visualizar en su cabeza el tipo de chaqueta que le puede gustar, el móvil le manda una notificación: “He encontrado varias opciones para comprar una chaqueta amarilla. Diríjase a…”.
Esto puede parecer ciencia ficción, pero es una de las posibles aplicaciones de la neurotecnología en un futuro no muy lejano. Con ciertas reservas, podemos pensar que la neurotecnología comprende dispositivos tecnológicos, artefactos o máquinas que pueden de algún modo “leer nuestra mente”.
Controlando la mente
En síntesis, la neurotecnología es el conjunto de tecnologías que permiten visualizar, manipular, registrar, medir y obtener información del cerebro y del sistema nervioso con el objetivo de controlar, reparar o mejorar sus funciones.
La neurotecnología utiliza distintas técnicas para registrar o estimular el cerebro. Estas técnicas se pueden dividir principalmente entre aquellas que requieren un contacto directo con el cerebro y el sistema nervioso (invasivas) y aquellas que no necesitan un contacto directo (no-invasivas).
Otra división útil para clasificar las neurotecnologías es entre aquellas técnicas que se dedican a registrar y medir la actividad del cerebro y del sistema nervioso (como la EEG o la resonancia magnética funcional) y técnicas que pueden estimularlos (como la implantación de electrodos).
Por supuesto, estas no son las únicas formas de clasificar las distintas técnicas dentro de la neurotecnología. Tampoco es una lista exhaustiva de las técnicas existentes o que pueden desarrollarse. Sin embargo, constituyen una cartografía útil para orientarse en un campo en constante evolución.
Revolución 4.0
Para crear técnicas de neurotecnología confluyen disciplinas como la neurociencia –el estudio del cerebro–, la ingeniería –la aplicación de la ciencia y tecnología para resolver problemas–; y la inteligencia artificial (IA) –la ciencia que estudia y crea sistemas artificiales inteligentes–. Forman parte de la llamada Cuarta Revolución industrial o Revolución 4.0, que supone la convergencia de tecnologías digitales, físicas y biológicas que evolucionan a gran velocidad.
Estas tecnologías reciben el nombre NBIC (nano-bio-info-cogno): nanotecnologías, biotecnologías, tecnologías de la información y ciencias cognitivas (IA, ciencia de datos, robótica, interfaces cerebro-máquina, biología sintética, nanotecnología).
Dada la interdisciplinariedad y la complejidad de su objeto de estudio (el cerebro y el sistema nervioso), la neurotecnología no escapa al “principio de Skolnikoff”. Según este principio, una tecnología puede ser utilizada para cualquier otro propósito que no había sido previsto originalmente en su diseño. Así, las implicaciones de las neurotecnologías van más allá de lo técnico para plantear interrogantes de corte ético, político y social.
Imagine que el dispositivo de neurotecnología que detecta la información relevante directamente desde su actividad neuronal ya no se utiliza solo para ayudarle a encontrar el regalo que busca, sino para extraer otro tipo de datos relevantes de su mente. Imagine que distintas técnicas de neurotecnología se utilizan incluso para controlar e intervenir en su pensamiento o comportamiento.
Esta posibilidad puede no parecer tan lejana de escenarios que ya conocemos dentro de nuestros teléfonos móviles o de determinadas técnicas de marketing. Pero la barrera que se franquearía en el caso de las neurotecnologías es, sin embargo, capital: se trata de la integridad de la propia mente.
 Shutterstock / Jirsak
Shutterstock / JirsakDefender los neuroderechos
Ante la relevancia de preservar esta integridad, se postulan los llamados neuroderechos: derechos humanos específicamente referidos al uso y aplicaciones de las neurotecnologías. Estos nuevos derechos son entendidos como una evolución de los derechos humanos aplicada al auge de las tecnologías que pueden ser consideradas disruptivas para la integridad mental y psicológica de las personas.
Se han propuesto tanto desde la filosofía y el derecho (Marcelo Ienca & Roberto Andorno, Towards new human rights in the age of neuroscience and neurotechnology) como desde la neurociencia (Rafael Yuste, director del proyecto BRAIN).
Entre estos neuroderechos, uno de los que más continuidad guarda con las preocupaciones generales acerca de la inteligencia artificial y la llamada internet de las cosas (IoT) es la privacidad. La creciente datificación y mercantilización de las informaciones personales de los individuos corre el riesgo de atentar contra la privacidad y la intimidad, y esta posibilidad se multiplica en el caso de las neurotecnologías.
Más allá de la privacidad, el llamado derecho a la libertad cognitiva se sitúa en continuidad con el derecho humano a la libertad y libre desarrollo de la conciencia, evitando posibles usos coercitivos de ciertas herramientas neurotecnológicas.
Asimismo, también es relevante el derecho a la integridad mental, de tal manera que se preserve a los usuarios de posibles injerencias que puedan modificar su estado neuronal.
Por último, se destaca el derecho a la continuidad psicológica, referida a la capacidad de las personas de mantener la continuidad de su identidad y personalidad de forma libre.
Por el momento, Chile parece ser el primer país del mundo que va a incorporar los neuroderechos en su proyecto de reforma constitucional en curso.
Disrupción social, brecha de desigualdad y ética
Las neurotecnologías forman parte, como hemos dicho, de las tecnologías emergentes que combinan una evolución técnica acelerada y discontinua con un potencial de disrupción social importante. Más aún, el acceso o no a esas tecnologías puede provocar una nueva brecha de desigualdad e injusticia.
La incertidumbre acerca de los escenarios futuros reclama que la atención a los aspectos éticos y sociales acompañe al desarrollo tecnológico. Como otras tecnologías potencialmente disruptivas, las posibilidades de contribución al bienestar de la sociedad son amplias, pero también los riesgos ante los que prevenirnos.
Sería conveniente evitar un futuro en el que elegir un regalo para su amiga Marta abra escenarios de incertidumbre en su control sobre su propio estado cerebral. Los neuroderechos son una protección que puede contribuir a ello.
Sobre los autores: Txetxu Ausín, científico titular, Grupo de Ética Aplicada, Instituto de Filosofía, Centro de Ciencias Humanas y Sociales (CCHS – CSIC); Aníbal Monasterio Astobiza, investigador posdoctoral en ciencias cognitivas y éticas aplicadas, Universidad de Granada; Belén Liedo, investigadora predoctoral en ética y filosofía, Centro de Ciencias Humanas y Sociales (CCHS – CSIC); Daniel López Castro, investigador predoctoral, Grupo de Ética Aplicada, Instituto de Filosofía, Centro de Ciencias Humanas y Sociales (CCHS – CSIC); Manuel Aparicio Payá, profesor asociado del Departamento de Filosofía, Universidad de Murcia; Mario Toboso Martín, científico titular, Instituto de Filosofía (IFS-CSIC) y Ricardo Morte Ferrer, investigador predoctoral en filosofía, Universidad de Granada. Estos autores constituyen la “Mente Colmena” del Instituto de Filosofía del CSIC, un grupo interdisciplinar que trabaja sobre ética, ciencia y sociedad.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La urgencia de los neuroderechos humanos se ha escrito en Cuaderno de Cultura Científica.
Supervivientes
 Fundulus heteroclitus fotografiado en la bahía de Chesapeake (costa este de los Estados Unidos). Foto: Brian Gratwicke / Wikimnedia Commons
Fundulus heteroclitus fotografiado en la bahía de Chesapeake (costa este de los Estados Unidos). Foto: Brian Gratwicke / Wikimnedia CommonsLa ciudad de Paterson, Nueva Jersey, alumbró el desarrollo industrial de los Estados Unidos tras su independencia. El río Passaic, a cuya orilla se fundó, aportó el agua utilizada por la industria, que era muy contaminante ya desde sus inicios: la tercera parte de su caudal ha llegado a ser utilizada con fines industriales durante algunos periodos. En sus orillas se instalaron fundiciones, fábricas de pintura, de sustancias químicas, empresas farmacéuticas y curtiderías, entre otras. Utilizaban ácido sulfúrico, arsénico, acetato de plomo, cromo, nitrato de mercurio y, más recientemente, bifenilos policlorados, los famosos PCBs, con propósitos variados.
La planta de la empresa Diamond Alkali en Newark empezó produciendo fertilizantes a partir de huesos de animales; en 1940 pasó a fabricar DDT, un insecticida hoy prohibido en todo el mundo; más tarde produjo herbicidas, el más conocido el defoliante Agente Naranja, del que manufacturó 2,6 millones de litros. La planta se hizo famosa por sus vertidos a gran escala de DDT, ácido sulfúrico y herbicidas al río Passaic. Entre los residuos resultantes de su producción estaban las dioxinas, unas sustancias de muy alta toxicidad. La fábrica fue descrita por el senador estadounidense Cory Booker, como la mayor escena criminal de Nueva Jersey.
Aguas abajo, en Arthur Kill, un estrecho intermareal situado tras la bahía de Newark, entre Nueva Jersey y State Island (Nueva York) por donde el río Passaic discurre hasta el Atlántico, reposan los restos de centenares de barcos. En las bodegas y depósitos de muchos de ellos sigue habiendo sustancias tóxicas para la mayor parte de la fauna de aquellas costas.
Sin embargo, también hay animales capaces de tolerar los efectos de la contaminación causada por las sustancias dañinas que se acumularon allí durante los años de máxima actividad industrial en la cuenca del Passaic. Abundan gusanos poliquetos, almejas y tunicados, animales que se alimentan de partículas orgánicas del sedimento, por lo que están impregnadas de los contaminantes vertidos. También hay cangrejos azules o jaibas. Cada uno de ellos contiene suficiente cantidad de dioxinas como para poder causar cáncer a quien se lo coma.
Otro animal que convive con la contaminación es Fundulus heteroclitus, un pez que tolera condiciones ambientales en general difíciles. Es capaz de vivir y progresar en agua dulce y salada, y está adaptado a un amplio rango de temperaturas. Cuando llega el invierno y baja mucho la temperatura, se entierra en el fango y permanece allí hasta que las condiciones mejoran. La NASA ha enviado peces de esta especie al espacio, para saber si podían nadar en ausencia de gravedad. Nadaron. Es más, llegaron a liberar sus gametos. Los ejemplares de esta especie que viven en lugares muy contaminados, como la Bahía de Newark toleran concentraciones de contaminantes muchísimo más altas que las que toleran la mayoría del resto de peces. Y en el caso de Fundulus, esa capacidad, que es de base genética, se ha adquirido en unas pocas décadas. Han experimentado lo que los biólogos denominamos “evolución rápida”.
Ninguna especie ha transformado nuestro planeta de forma tan profunda y radical como lo ha hecho la nuestra. No solo hemos aplanado montañas, alterado el curso de los ríos, rellenado valles y hondonadas, redibujado la línea de la costa o reconfigurado el paisaje. Hemos transformado plantas y animales para poder alimentar con ellos a miles de millones de personas. Y hemos provocado verdaderas catástrofes ecológicas, alterando de forma radical o destruyendo, incluso, ecosistemas completos. Sorprendentemente, sin embargo, hay especies que han conseguido resistir el efecto de la acción humana, adaptarse a las condiciones deletéreas y medrar allí donde pocos lo consiguen. Son verdaderos supervivientes.
Fuente: Cal Flyn (2021): Islands of Abandonment-Life in the Post-human Landscape. William Collins.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Supervivientes se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Helena González-Burón – Lectura incómoda
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

La incomodidad de una lectura depende de la persona que la ha de leer y de sus circunstancias. Sin embargo, hay lecturas que son objetivamente incómodas, como las secuencias de nucleótidos del ADN. ¿Cómo se puede extraer información útil de una hilera larguísima de cuatro letras que se repiten de forma aparentemente aleatoria? Helena González-Burón quien, aparte de ser directora y cofundadora de Big Van Ciencia, tiene un doctorado en genética, te lo explica muy clarito.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Helena González-Burón – Lectura incómoda se ha escrito en Cuaderno de Cultura Científica.
Memoria y envejecimiento: los efectos beneficiosos del ejercicio físico son tremendamente volátiles
 Fuente: pasja1000 / Pixabay
Fuente: pasja1000 / PixabayCon el fin de fomentar un envejecimiento cerebral sano durante la tercera edad, suele recomendarse introducir diversas modificaciones en nuestro estilo de vida, tales como llevar una dieta más sana, potenciar las actividades cognitivas rutinarias y, especialmente, dedicar más tiempo al ejercicio físico. Más allá del proverbio latino ‘mens sana in corpore sano’, el fundamento de esa recomendación se basa en observaciones epidemiológicas que sostienen que la actividad física se asocia con menor incidencia de la enfermedad de Alzheimer y otras demencias, estimándose que el sedentarismo podría ser el origen de más de cuatro millones de casos de demencia anualmente.
“Diversos ensayos clínicos en los que se ha incluido ejercicio físico moderado como terapia han demostrado un efecto positivo tanto en la cognición como en el grosor cortical”, confirma Alfredo Ramos-Miguel, investigador del Departamento de Farmacología de la Universidad del País Vasco/Euskal Herriko Unibertsitatea.
Los estudios preclínicos en modelos animales han sugerido que el ejercicio físico podría potenciar las habilidades cognitivas mediante un aumento de la sinaptogénesis, es decir, la generación de nuevas conexiones neuronales. Sin embargo, como indica el investigador, “la dificultad para realizar estudios moleculares en cerebro humano limita las posibilidades de hallar los mecanismos biológicos que median los efectos beneficiosos del ejercicio físico sobre la salud mental y cognitiva durante el envejecimiento”.
Para establecer las bases anatómico-patológicas y moleculares del declive cognitivo y psicomotor, el Proyecto Memoria y Envejecimiento (MAP, por sus siglas en inglés) del Rush Alzheimer’s Disease Center, en Chicago EE UU, lidera desde 1997 un estudio longitudinal y prospectivo con voluntarios que se prestan a realizar periódicamente evaluaciones cognitivas y psicomotrices, y a ceder sus órganos tras su defunción. El diseño de ese estudio permite correlacionar directamente los hábitos cotidianos y estados de salud con alteraciones estructurales y funcionales ocurridos en los cerebros de los participantes.
En la última publicación de ese proyecto, se presentan resultados en 404 individuos cuya actividad física fue monitorizada con actímetros ubicados en relojes o pulseras, durante una media de 3.5 años ante-mortem. Tras su defunción, se recogieron muestras de hasta doce áreas cerebrales esenciales para las habilidades cognitivas y psicomotrices, en las que se realizaron análisis cuantitativos y funcionales de ocho proteínas sinápticas, así como una evaluación histopatológica completa, que examina diez neuropatologías asociadas al envejecimiento.
Los resultados obtenidos confirmaron que mayores tasas de actividad física diaria se asocian, de manera global, con un enriquecimiento en la cantidad y funcionalidad de todas las proteínas sinápticas analizadas. Esa asociación se observó acentuada en regiones cerebrales relacionadas con el control motor, tales como el núcleo caudado y putamen. Asimismo, la relación entre ejercicio físico y densidad sináptica era independiente tanto de la carga neuropatológica hallada en las mismas áreas cerebrales como de la presencia de patologías que afectan a las habilidades motoras, indicando que la actividad física puede ser beneficiosa para cualquier persona de avanzada edad con independencia de su estado de salud.
Por otra parte, analizados longitudinalmente, datos de actigrafía indicaron que los efectos beneficiosos del ejercicio físico son tremendamente volátiles, pues aquellos participantes con elevada rutina física durante etapas tempranas y que descontinuaron ese hábito en los últimos dos años de vida, presentaban densidades sinápticas similares a las observadas en participantes más sedentarios.
En definitiva, “este estudio pone de manifiesto, por primera vez en humanos, que ejercitarse físicamente, incluso en edades avanzadas, contribuye bien a promover procesos de sinaptogénesis o bien a incrementar la resiliencia sináptica frente a los efectos deletéreos de las lesiones neuropatológicas”, afirma Ramos-Miguel.
Referencia:
Casaletto K., Ramos-Miguel A., VandeBunte A., Memel M., Buchman A., Bennett D., Honer W. Late-life physical activity relates to brain tissue synaptic integrity markers in older adults (2021) Alzheimer ‘s Dement. doi: 10.1002/alz.12530
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Memoria y envejecimiento: los efectos beneficiosos del ejercicio físico son tremendamente volátiles se ha escrito en Cuaderno de Cultura Científica.
¿Por qué le dicen Pliniana cuando deberían llamarla Vesubiana?
 Tipos de erupciones volcánicas: islándica = fisural; hawaiiana = efusiva; estromboliana, vulcaniana, peleana y pliniana = explosivas (por orden creciente de nivel de explosividad). Fuente: Encyclopædia Britannica (2011).
Tipos de erupciones volcánicas: islándica = fisural; hawaiiana = efusiva; estromboliana, vulcaniana, peleana y pliniana = explosivas (por orden creciente de nivel de explosividad). Fuente: Encyclopædia Britannica (2011).En los últimos meses, la actividad volcánica de nuestro planeta ha copado portadas y noticias, convirtiéndose en trending topic en las redes sociales de medio mundo. Gracias a esta repercusión mediática, todos hemos aprendido que existen distintos tipos de erupciones volcánicas, desde las más efusivas, en las que un magma de composición básica (menos de un 50% de SiO2), con elevada temperatura y baja viscosidad da lugar a la salida de una lava muy fluida que recorre grandes distancias, hasta las más explosivas, donde un magma de composición ácida (más de un 50% de SiO2), de menor temperatura, muy viscoso y con un elevado contenido en gases provoca la expulsión violenta de piroclastos (fragmentos de magma desgasificado enfriados rápidamente y que adquieren diferentes tamaños) y la acumulación de una lava también muy viscosa que puede taponar el cráter eruptivo.
Y el nombre de estos tipos de erupciones son bastante poéticos y evocadores, de esos que no dejan lugar a dudas sobre su origen. Podemos encontrarnos con una erupción de tipo hawaiano, esas erupciones efusivas que son típicas de los volcanes que han dado origen a las islas del archipiélago de Hawái. O con una erupción de tipo estromboliano, donde se alternan periodos explosivos con momentos de cierta calma volcánica y cuyo nombre proviene de las erupciones características del volcán siciliano Estrómboli, inmortalizado por Julio Verne en su novela “Viaje al centro de la Tierra”. Incluso, podemos toparnos con una erupción de tipo vulcaniano, llamadas así en honor a las erupciones mucho más explosivas y que generan una gran columna eruptiva que se producen en la isla también siciliana de Vulcano.
Pero hay un tipo de erupción con un nombre más particular y cuyo origen es bastante curioso. Seguro que, si os hablo de erupciones de tipo vesubiano, no habéis oído hablar de ellas en ningún momento. Pero si os digo erupción de tipo pliniano, os suena un poco más.
Una erupción pliniana, o de tipo pliniano, es una erupción muy explosiva, en la que se produce la expulsión de una enorme columna de gases y piroclastos que puede ascender varias decenas de kilómetros en altura y donde los materiales rocosos caen como si fuese una continua lluvia ardiente. Pero llega un momento en el que esta columna colapsa y toda esa mezcla de gases y piroclastos acaba discurriendo a gran velocidad por la ladera del volcán como una enorme ola ardiente (decenas a centenares de grados centígrados) que lo arrasa todo a su paso. Pero, ¿de dónde procede su nombre? Pues para eso, tenemos que remontarnos a hace casi dos mil años.
 Ilustración de Gaius Plinius Secundus conocido como Plinio el Viejo incluida en la obra de Cesare Cantù Grande Illustrazione del Lombardo Veneto ossia storia delle città, dei borghi etc., Vol. III (1859, Milán). Fuente: Wikimedia Commons.
Ilustración de Gaius Plinius Secundus conocido como Plinio el Viejo incluida en la obra de Cesare Cantù Grande Illustrazione del Lombardo Veneto ossia storia delle città, dei borghi etc., Vol. III (1859, Milán). Fuente: Wikimedia Commons.Corría el año 79 de nuestra era, según algunas fuentes históricas era finales de agosto, según otras, finales de octubre, pero fuera como fuese, ese año el monte Vesubio, situado en la Campania italiana, decidió entrar en erupción. Justo en la orilla de enfrente del Golfo de Nápoles, un tío y su sobrino observaron las primeras nubes piroclásticas salir del volcán y alzarse con esplendor sobre un cielo despejado de comienzos de la tarde. Ambos no solo compartían parentesco, sino también nombre, con un pequeño mote para diferenciar uno del otro. El mayor, militar, naturalista y erudito, creador de la primera enciclopedia de la que se tiene conocimiento y a la que tituló “Historia Natural”, era Plinio, llamado el Viejo. El sobrino, futuro senador romano, era Plinio, apodado el Joven.
Plinio el Viejo, animado tanto por su curiosidad científica como por su espíritu militar para prestar auxilio a varios amigos cuyas villas se encontraban cerca de la ciudad de Pompeya, en las laderas del Vesubio, decidió montar una pequeña flotilla de barcos y cruzar el Golfo de Nápoles de inmediato, lanzándose a la boca del volcán. Antes de soltar amarras, preguntó a su sobrino, Plinio el Joven, si quería acompañarle en su periplo. El muchacho declinó la oferta, prefería quedarse en la otra orilla y ocuparse de proteger a sus parientes y pertenencias. Y esta decisión fue vital para la historia.
 El último día de Pompeya, obra del pintor ruso Karl Briulov realizada entre 1830 y 1833. Fuente: Wikimedia Commons.
El último día de Pompeya, obra del pintor ruso Karl Briulov realizada entre 1830 y 1833. Fuente: Wikimedia Commons.Plinio el Viejo murió a los pies del Vesubio durante la erupción que arrasó con las villas de Pompeya y Herculano. Y la historia de su muerte fue relatada por carta por su sobrino, Plinio el Joven, al historiador romano Tácito años más tarde, acompañada de una descripción muy detallada de todas las fases eruptivas del volcán. En aquella época, Plinio el Joven defendía convencido que la muerte de su tío se debió al efecto nocivo de los gases volcánico, que acabaron asfixiándole. Actualmente, médicos y científicos de diversa índole creen que Plinio el Viejo murió debido a un ataque al corazón que sufrió en el camino en barco a través de la Bahía de Nápoles y que el volcán no tuvo nada que ver, simplemente cubrió su cuerpo ya inerte con una fina capa de cenizas a forma de manto mortuorio.
Pero, independientemente de la causa real de su muerte, Plinio el Viejo quedó para siempre unido a la historia de la erupción del Vesubio. Hasta tal punto que su nombre se emplea para describir este tipo de erupciones volcánicas a modo de homenaje geológico. Y sí, el término erupción tipo vesubiana es totalmente correcto y utilizado en la literatura científica, pero como los geólogos también somos un pelín poéticos, siempre preferiremos llamarlas plinianas.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿Por qué le dicen Pliniana cuando deberían llamarla Vesubiana? se ha escrito en Cuaderno de Cultura Científica.
Kazimierz Kuratowski, el talento y el compromiso de un matemático de Varsovia
Él era un profesor de primer año, por así decirlo, y yo era un estudiante de primer año. Desde la primera clase me encantó la claridad, lógica y brillantez de su exposición, y el material que presentaba. […] Pronto pude responder algunas de las cuestiones más difíciles en el curso de teoría de conjuntos, y comencé a plantear otros problemas. Desde el principio aprecié la paciencia y la generosidad de Kuratowski al pasar tanto tiempo con un novato.
Stanislaw Ulam, MacTutor
 Kazimierz Kuratowski (1959). Fuente: Wikimedia Commons.
Kazimierz Kuratowski (1959). Fuente: Wikimedia Commons.
Kazimierz Kuratowski nació el 2 de febrero de 1896 en Varsovia, ciudad que formaba parte en aquel momento del Zarato de Polonia, controlado por el Imperio ruso. Era hijo de Marek Kuratow, un abogado, y Róża Karzewska.
Tras completar la escuela secundaria, en 1913 se matriculó en un curso de ingeniería en la Universidad de Glasgow (Escocia), en parte porque estaba prohibida la enseñanza en polaco y no deseaba estudiar en ruso. El estallido de la Primera Guerra Mundial le permitió completar solo un año de formación. En 1915 tuvo lugar la Gran retirada rusa; en septiembre de ese año prácticamente toda Polonia estaba bajo el control del Imperio alemán y del Imperio austrohúngaro. La Universidad de Varsovia volvió a abrirse con el polaco como idioma de enseñanza; Kuratowski reinició allí su educación universitaria ese mismo año, pero cambió la ingeniería por las matemáticas.
Obtuvo su doctorado en 1921, supervisado por los matemáticos Zygmunt Janiszewski (1888-1920) y Stefan Mazurkiewicz (1888-1945). Su memoria de tesis, que resolvía algunos problemas de teoría de conjuntos planteados por el matemático Charles-Jean de La Vallée Poussin (1866-1962), constaba de dos partes. La primera se centraba en una construcción axiomática de la topología a través de los axiomas de clausura, y la segunda parte se dedicaba a continuos irreducibles entre dos puntos.
En 1923, Kuratowski fue nombrado profesor adjunto de matemáticas en la Universidad de Varsovia. Cuatro años más tarde fue contratado como profesor titular de matemáticas en el Politécnico de Leópolis, ejerciendo como director del departamento de Matemáticas hasta 1933.
Kuratowski tuvo la oportunidad de trabajar con algunos de los miembros de la Escuela de Matemáticas de Leópolis (como Stefan Banach (1892-1945) y Stanislaw Ulam (1909-1984)) y del círculo de matemáticos que acudía al Café Escocés. Pero siempre mantuvo estrechos vínculos con su ciudad natal, y regresó a la Universidad de Varsovia en 1934. Aunque no aportó ningún problema al conocido como libro escocés (que comenzó a elaborarse en 1935), colaboró estrechamente con Banach en la resolución de algunos problemas en la teoría de la medida.
 Algunos de los miembros de la Escuela de Matemáticas de Leópolis (1930). Fuente: Wikimedia Commons.
Algunos de los miembros de la Escuela de Matemáticas de Leópolis (1930). Fuente: Wikimedia Commons.
Durante la Segunda Guerra Mundial, al estar prohibida la educación superior para la población polaca durante la ocupación alemana, Kuratowski impartió clases en la universidad clandestina de Varsovia.
La importancia de la educación clandestina consistía, entre otras cosas, en mantener el espíritu de resistencia, así como el optimismo y la confianza en el futuro, tan necesarios en las condiciones de la ocupación. Las condiciones de vida de un científico en ese momento eran verdaderamente trágicas. Más dolorosas fueron las pérdidas humanas.
Kazimierz Kuratowski, MacTutor
Tras la Segunda Guerra Mundial, Kuratowski participó activamente en la reconstrucción de la vida científica en Polonia. En 1945 se convirtió en miembro de la Academia Polaca de Aprendizaje, desde 1949 fue elegido vicepresidente de la Sociedad Científica de Varsovia y, en 1952, se convirtió en miembro de la Academia de Ciencias de Polonia, de la que fue vicepresidente entre 1957 y 1968.
La investigación de Kuratowski se centró fundamentalmente en estructuras topológicas y métricas; como ya hemos comentado, estableció los axiomas de clausura. Los resultados más relevantes obtenidos tras la guerra son los que se relacionan la topología y la teoría de funciones analíticas. Junto a Ulam (a quien dirigió la tesis doctoral durante su estancia en Leópolis), introdujo el concepto de cuasi-homeomorfismo que abrió un nuevo campo en los estudios topológicos.
Junto a Alfred Tarski (1901-1983) y Wacław Sierpiński (1882-1969) proporcionó la mayor parte de la teoría sobre los espacios polacos. Bronisław Knaster (1893-1980) y Kuratowski aportaron un completo estudio a la teoría de componentes conexas.
Kuratowski demostró el lema de Kuratowski-Zorn en 1922, trece años antes que Max August Zorn (1906-1993), a quien se le da el único crédito en muchos textos.
Algunas de sus otras muchas contribuciones a las matemáticas incluyen la introducción del algoritmo de Tarski-Kuratowski en lógica matemática o la caracterización de los grafos planares: el llamado teorema de Kuratowski.
Recordemos que un grafo está definido por un conjunto de vértices y otro de aristas uniendo algunos de estos vértices. Y se denomina plano cuando puede dibujarse en el plano sin que ninguna arista se cruce. Los ejemplos más sencillos de grafos no planos son los llamados K5 y K3,3.
 Grafos K5 y K3,3. Wikimedia Commons.
Grafos K5 y K3,3. Wikimedia Commons.
En 1930, Kuratowski demostró este bello teorema que caracteriza la ‘planitud’ de cualquier grafo:
Un grafo es plano si y solo si no contiene ningún subgrafo homeomorfo a K5 o K3,3.
Kuratowski publicó alrededor de 170 trabajos entre artículos, monografías y libros traducidos a varios idiomas, como su Introducción a la teoría de conjuntos y la topología.
Falleció el 18 de junio de 1980 en la ciudad que le vio nacer y en la que realizó la mayor parte de sus aportaciones en matemáticas.
El profesor Kuratowski destaca no solo como una gran figura en la investigación matemática, sino también por su habilidad, tan rara entre los científicos originales, para organizar y dirigir escuelas de investigación y educación matemática.
Stanislaw Ulam, MacTutor
Referencias
-
O’Connor, John J.; Robertson, Edmund F., Kazimierz Kuratowski, MacTutor History of Mathematics archive, University of St Andrews
-
Kazimierz Kuratowski, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Kazimierz Kuratowski, el talento y el compromiso de un matemático de Varsovia se ha escrito en Cuaderno de Cultura Científica.
La asombrosa variedad genética de las neuronas humanas
 Neuronas de la corteza cerebral observadas con la técnica brainbow. Imagen: Tamily Weissman / Harvard University
Neuronas de la corteza cerebral observadas con la técnica brainbow. Imagen: Tamily Weissman / Harvard UniversityLos análisis genómicos de neuronas humanas individuales, tanto extraídas post mortem como obtenidas en cultivo, ponen de manifiesto que existe en ellas una considerable variación en el número de copias del ADN. Es probable que estas diferencias genéticas afecten a las funciones de las células encefálicas y que podrían, por tanto, tener influencia en nuestra personalidad, inteligencia o en la susceptibilidad a desarrollar enfermedades neurológicas.
En las neuronas existen una serie de cambios genéticos conocidos: la aneuploidía es el cambio en el número de cromosomas; en las retrotransposiciones una secuencia de ADN se mueve a otra parte del genoma mediante transcripción a ARN; y, finalmente, la expresión de enzimas que alteran el ADN. Todas estas fuentes de diversidad genética son frecuentes en el encéfalo.
Durante mucho tiempo ha existido la idea de que, dada la enorme variedad de tipos de células en el encéfalo, deberían existir mecanismos genéticos que generaran esta diversidad. Uno de los mecanismos genéticos potentes que podrían contribuir a esta variedad celular, aparte de los anteriores, es la variación en el número de copias (VNC). Una VNC es una modificación estructural del ADN, en la que una parte significativa del mismo desaparece o aparece duplicada tras una copia en determinados cromosomas. No hay que confundir las VNC con los polimorfismos de un sólo nucleótido, que afectan a un solo gen y que son los cambios más estudiados para ver la influencia genética en determinado proceso.
Para determinar la variabilidad genómica como consecuencia de la VNC es necesario una tecnología que permita analizar célula a célula pues, de lo contrario, con las técnicas de secuenciación habituales lo que se obtiene es un promedio de un gran número de células presentes en el tejido analizado y este promedio tenderá, en general, a acercarse a una sola copia conforme sea mayor el número de células consideradas.
McConnell y sus colegas consiguieron secuenciar células individuales gracias a una técnica desarrollada en el Laboratorio Cold Spring Harbour (EE.UU.). En concreto analizaron 110 neuronas individuales extraídas de tres personas fallecidas. Y el resultado es sorprendente: el 41% de las células contienen una o más VNC, la mayoría borrados o duplicaciones.
Por otra parte, el análisis de neuronas derivadas en cultivos a partir de células madre pluripotentes inducidas (CMPI) reveló la existencia de un número de VNC similar: de 40 células secuenciadas, 13 presentaban cambios únicos en sus genomas.
Un aspecto interesante es que las células progenitoras neuronales derivadas de estas mismas líneas de CMPI no tenían tanta diversidad. Esto sugeriría, primero, que la variación genética de las neuronas tiene lugar sólo en las etapas posteriores de diferenciación y, segundo, que la variación se desarrolla en un corto espacio de tiempo (las neuronas necesitan siete semanas para diferenciarse de sus progenitores). También podría concluirse que la variación detectada en las neuronas tomadas post mortem no sería un efecto del envejecimiento (en principio, la copia repetida aumentaría la probabilidad de un fallo en una copia).
Por tanto, si los cambios genéticos tienen lugar pronto, resulta que nos acompañan durante la mayor parte de nuestra vida y, por consiguiente, la probabilidad de que afecten a la configuración y funcionamiento de nuestro encéfalo aumentaría, con lo que ello implica para el comportamiento, la inteligencia o las enfermedades neuropsiquiátricas. ¿Cuánto? Eso tendrá que esperar, entre otras cosas, a nuevos avances tecnológicos que permitan estudiar VNC y expresión genética en la misma célula individual.
Referencia:
McConnell M.J., Lindberg M.R., Brennand K.J., Piper J.C., Voet T., Cowing-Zitron C., Shumilina S., Lasken R.S., Vermeesch J.R. & Hall I.M. & (2013) Mosaic Copy Number Variation in Human Neurons Science doi: 10.1126/science.1243472
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 7 de noviembre de 2013.
El artículo La asombrosa variedad genética de las neuronas humanas se ha escrito en Cuaderno de Cultura Científica.

