El aguacate, un fruto de otros tiempos
La sombra y la competencia por los nutrientes y el agua podrían malograr las semillas si caen junto a la madre, por lo que las plantas tienen diferentes estrategias para dispersar a sus retoños tras la reproducción. Algunas se valen del viento, otras del agua, otras se adhieren al pelo de animales… El aguacate lo resuelve envolviendo la semilla en un apetitoso fruto para grandes herbívoros.
El aguacate procede de Centroamérica. Se desarrolló durante el Pleistoceno, en ecosistemas habitados por grandes herbívoros, como mamuts, perezosos gigantes y caballos americanos, entre otros. El tamaño del fruto estaba diseñado para esos enormes animales, capaces de ingerirlo entero y transportar el hueso en sus aparatos digestivos, depositándolo a kilómetros, bien abonado con sus excrementos.
En este caso de coevolución, varias especies se beneficiaban mutuamente: unas con un alimento nutritivo y la otra, ampliando su distribución. El problema es que las especies que evolucionan paralelamente dependen en cierto modo unas de otras. La desaparición de una especie puede tener consecuencias para las otras.
Al final del Pleistoceno, hace aproximadamente 13.000 años, los grandes mamíferos americanos se extinguieron, poco tiempo después de la llegada de los primeros humanos al continente. Hay más ejemplos en la historia de extinciones tras la colonización de un territorio virgen, posiblemente como consecuencia de las actividades humanas.
El aguacate se quedó sin diseminadores naturales,a partir de entonces, ya que los herbívoros actuales no pueden comer el fruto entero. Por eso, algunos autores lo consideran un anacronismo evolutivo, es decir, una especie adaptada a las condiciones de otra época. No ha pasado tiempo suficiente para que la evolución seleccione aguacates de menor tamaño, menos costosos energéticamente de producir para el árbol. 13.000 años son apenas 50 generaciones del árbol.
Se desconoce cómo este árbol pudo sobrevivir, con sus anacrónicos frutos, hasta el posterior desarrollo de la agricultura, que le ha garantizado la supervivencia. Ha conseguido dispersarse por todo el planeta y evolucionar rápidamente a las diferentes variedades actuales.
 Imagen: El aguacate es un árbol originario de Centroamérica. Se desarrolló durante el Pleistoceno, cuando grandes herbívoros comían sus frutos y diseminaban las semillas. El aguacate sobrevivió a la extinción de esos grandes mamíferos, pero sigue adaptado a un ecosistema que ya no existe. (Ilustración: María José Calvo Díaz)
Imagen: El aguacate es un árbol originario de Centroamérica. Se desarrolló durante el Pleistoceno, cuando grandes herbívoros comían sus frutos y diseminaban las semillas. El aguacate sobrevivió a la extinción de esos grandes mamíferos, pero sigue adaptado a un ecosistema que ya no existe. (Ilustración: María José Calvo Díaz)El aguacate es un fruto del pasado, sobrevivió a la extinción de los grandes mamíferos americanos, con algunos de los cuales había coevolucionado. Su caso nos habla de un pasado remoto en el que vivían otros animales, de la fragilidad de los ecosistemas y de la dependencia de las especies entre sí. Pero en lo que respecta al aguacate, puede decirse que su historia tiene un final feliz.
Referencias consultadas:
Bronaugh, Whit (2010). The trees that miss the mammoths. American Forests, 7, 38-43.
Galindo-Tovar, M.E., Arzate Fernández, A.M. (2010). Consideraciones sobre el origen y promera dispersión del aguacate (Persea americana, Lauraceae). Cuadernos de Biodiversidad, 33, 11-15. DOI: 10.14198/cdbio.2010.33.02
Autora: María José Calvo Díaz (IG: @maria_josecalvo) es licenciada en biología, profesora de biología en educación secundaria e ilustradora científica. Alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2019/20
Artículo original: El aguacate debería haberse extinguido, pero él no lo sabe todavía. Rocío Pérez Benavente, Cuaderno de Cultura Científica, 1 de diciembre de 2016.
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo El aguacate, un fruto de otros tiempos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El aguacate debería haberse extinguido, pero él no lo sabe todavía
- Metamorfosis criogénica de la rana del bosque
- En el mar, allí donde todo comienza
Amargo protector
 Foto: Alex Guillaume / Unsplash
Foto: Alex Guillaume / UnsplashDecimos que hay cinco sabores básicos, aunque quizás haya alguno más. Para cada uno de esos sabores se han identificado uno o varios receptores. El sabor dulce, del que se conocen dos sensores, nos gusta desde que nacemos, porque nos informa de alimentos de alto contenido energético. Se incluyen los azúcares naturales, pero también, en menor medida, los que resultan de la digestión parcial en la boca de moléculas como el almidón del pan o las patatas, por ejemplo, o el glucógeno, de los mejillones en temporada. Y la leche con que nos amamantan.
El umami es el sabor del glutamato y de algunas moléculas similares. Abunda en productos como la carne, algunos pescados, champiñones, algunos quesos y tomates, así como salsas fermentadas, como la de soja, el miso o salsas de pescado, como el garum. También la leche materna tiene un intenso sabor umami y esa es otra razón por la que nacemos con una fuerte inclinación hacia ella.
El sabor salado es más complicado, porque nos gusta la comida con sal, pero solo hasta un punto; si se pasa, desagrada. Eso ocurre porque necesitamos mantener la concentración de sodio en el plasma dentro de un intervalo relativamente estrecho de concentraciones. En la recepción del sabor salado intervienen dos poblaciones de células diferentes, unas responden a bajas concentraciones de sal y están conectadas a regiones encefálicas que evocan placer; y otras responden a altas concentraciones, y están vinculadas a regiones que evocan aversión. Se conoce el sensor de la concentración alta, se llama ENaC, pero se desconoce el de la baja.
El sabor ácido suele ser aversivo, sobre todo si es intenso, porque es un indicador de fermentación, como en la leche agria, y por lo tanto de comida que se encuentra en malas condiciones. También es característico de alimentos difíciles de digerir, como la fruta sin madurar. Los recién nacidos rechazan el sabor ácido sin necesidad de aprendizaje. Solo hay un sensor de sabor ácido porque la sustancia que lo estimula es única, el protón.
Así pues, estos sabores solo necesitan uno o dos receptores para ser caracterizados. Por eso es tan llamativo que haya 25 receptores de sabores amargos. Algunos responden a una amplia variedad de sustancias, y otros a una sola. La mayor parte de las que percibimos como amargas proceden de plantas, y la función de muchas de ellas, como la cafeína -del café- o los isocianatos -del brócoli-, es defender a la planta de infecciones bacterianas o fúngicas, o de depredadores, insectos principalmente. Otros compuestos amargos son producidos por bacterias. Así pues, el sabor amargo es un indicador o bien de toxinas en la planta o de una infección bacteriana y, por lo tanto, provoca el rechazo de la comida en cuestión. Los recién nacidos rechazan las sustancias amargas con un gesto facial de asco muy expresivo, sacando la lengua. Es innato.
Hay miles de sustancias, sin relación estructural entre ellas, susceptibles de provocar sabor amargo. Veamos dos ejemplos. El receptor T2R38 está capacitado para detectar sustancias amargas provenientes de bacterias, así como de glucosinolatos, característicos de plantas crucíferas, como el brócoli y las coles de Bruselas. Y el T2R1 es uno de los que detecta isohumulonas, las sustancias que dan a la flor del lúpulo y, por ende, a la cerveza, su sabor amargo. Hay una enseñanza en todo esto: nos interesa detectar las innumerables sustancias peligrosas que pululan por ahí. Pero el gusto por el brócoli o por la cerveza obedecen a otra lógica, cultural en gran medida, porque el gusto se educa si se le da tiempo y ocasión.
Fuente: David Linden (2020): Unique: The New Science of Human Individuality. Basic Books.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Amargo protector se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ciencia que deberías saber antes de comprar tu protector solar (1)
- La ciencia que deberías saber antes de comprar tu protector solar (3)
- La ciencia que deberías saber antes de comprar tu protector solar (y 4)
Javier Pedreira – Naukas 19: Artemisa y la primera mujer en la Luna
 Foto: SpaceX / Unsplash
Foto: SpaceX / UnsplashLa misión Apolo fue la que puso a los primeros seres humanos en la superficie de otro astro, la Luna, hace más de 50 años. Artemisa es el nombre que ha elegido la NASA para la misión que la devolverá a la Luna y más allá. Javier Pedreira «Wicho» hizo en esta charla de 2019 un repaso a las posibilidades de que esta misión tenga éxito en breve y encontraba algunas dificultades. Es especialmente interesante verla teniendo presente lo que hemos aprendido y vivido en estos casi dos años.
Javier Pedreira es el responsable de informática de los Museos Científicos Coruñeses y uno de los creadores de Microsiervos, uno de los blogs sobre ciencia y tecnología más leídos en castellano. Aero y espaciotrastornado confeso y sin remedio.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Javier Pedreira – Naukas 19: Artemisa y la primera mujer en la Luna se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- 1969: el año en el que llegamos a la Luna e inventamos Internet
- Naukas Pro 2017: Javier Burgos y el alzhéimer
- Carlos Briones – Naukas Bilbao 2019: Luna
La larga nube de agua de Arsia Mons
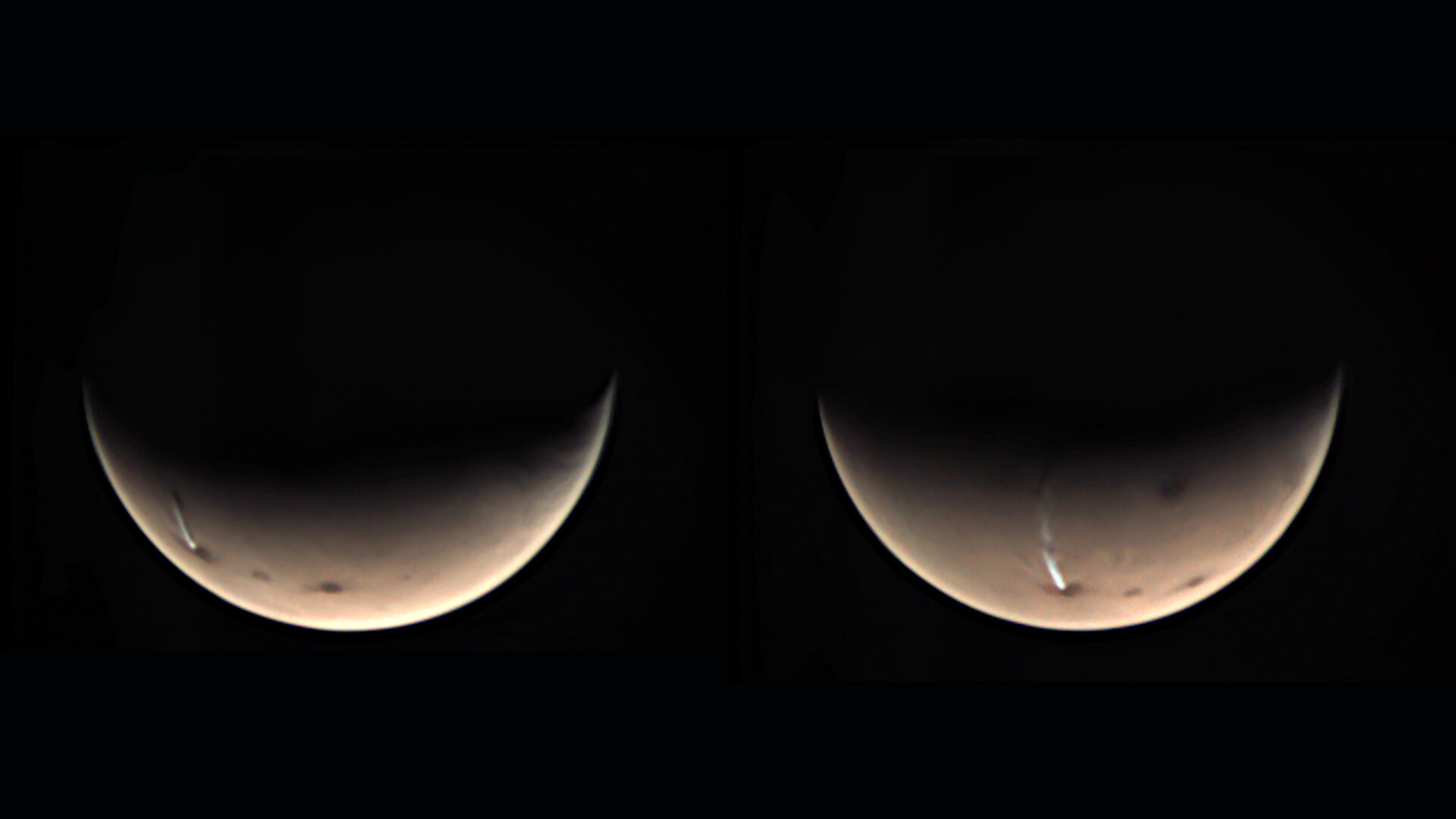 Foto: ESA/GCP/UPV-EHU
Foto: ESA/GCP/UPV-EHUCuando la primavera llega al sur de Marte, una inmensa nube de hielo de agua emerge cerca del volcán Arsia Mons, de 20 km de altura. En su máxima extensión, la nube mide unos 1.800 km de largo y 150 km de ancho. La nube se forma cuando el volcán actúa como un obstáculo para el viento, forzando a que el aire ascienda por sus laderas, y haciendo que la humedad que porta condense al enfriarse. Se crea así lo que lo que se conoce como una nube orográfica.
La peculiaridad de esta nube orográfica es que, una vez formada, a una altura de 45 km, el viento la arrastra, haciendo que se expanda rápidamente a una velocidad de unos 600 km/h; así, en sólo 2 o 3 horas, nos encontramos ante la nube orográfica más grande jamás vista en Marte.
La nube experimenta un rápido ciclo diario que se repite cada mañana durante varios meses. Comienza creciendo antes del amanecer, se expande rápidamente, y luego deja de expandirse, se separa de su ubicación inicial y acaba por evaporarse a última hora de la mañana, a medida que aumentan la temperatura de la atmósfera con la salida del Sol.
Ese es el ciclo diario de la nube que han descrito los investigadores del Grupo de Ciencias Planetarias de la UPV/EHU, como parte de un equipo internacional, combinando las imágenes tomadas por varias cámaras, entre las que destacan las nuevas observaciones realizadas con una pequeña cámara a bordo de la sonda Mars Express de la ESA, una longeva misión para la exploración de Marte en órbita desde 2003.
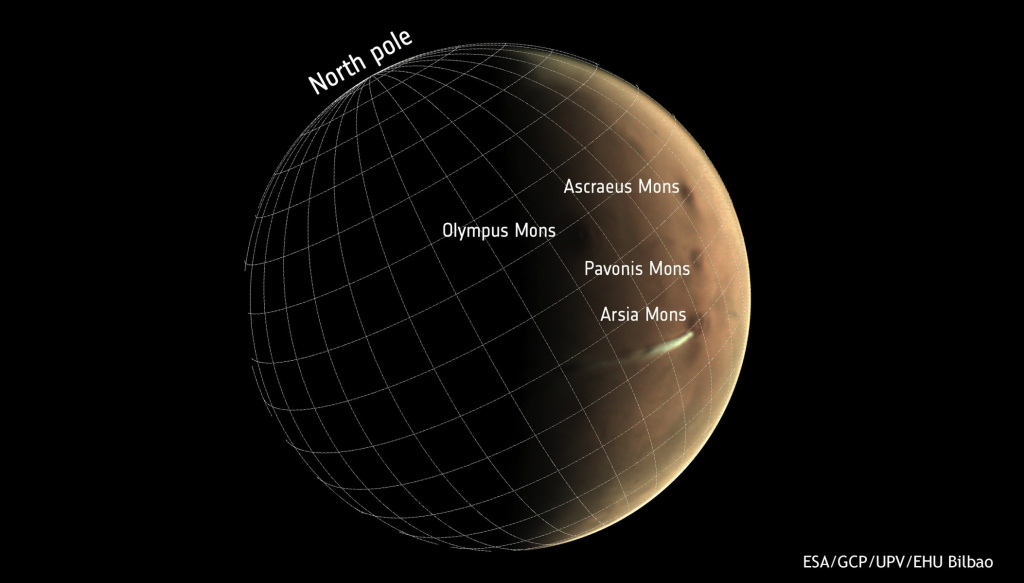
La nube resulta difícil de observar en su totalidad debido a los rápidos cambios en la dinámica de la atmósfera marciana y a las limitaciones en la órbita de muchas naves. “Para superar estos obstáculos, utilizamos una de las herramientas de Mars Express: la Cámara de Seguimiento Visual (VMC)”, señala Jorge Hernández Bernal, investigador predoctoral del Grupo de Ciencias Planetarias y autor principal del estudio.
Este instrumento, apodado la “cámara web” de Marte, presenta una resolución similar a la de una cámara web estándar de 2003; sin embargo, este trabajo ha demostrado un uso muy interesante, y que no estaba previsto, de la VMC, debido a que estos últimos años la cámara no estaba siendo utilizada para la investigación científica. “Aunque tiene una resolución espacial baja, presenta un gran campo de visión, algo esencial para disponer de una mayor perspectiva a distintas horas del día, y es estupenda para seguir la evolución de un determinado fenómeno a lo largo de un periodo de tiempo prolongado y a pequeños intervalos. Así, hemos podido estudiar toda la nube en numerosos ciclos de vida”, añade el investigador.

El equipo de investigación ha combinado las observaciones de la cámara VMC con las de otros dos instrumentos de Mars Express y de otras naves, e incluso han empleado observaciones realizadas en los años setenta. Las cámaras de alta resolución de Mars Express tienen campos de visión estrechos y las observaciones siempre se planifican con antelación. Así, los fenómenos meteorológicos —que suelen ser imprevisibles— normalmente se detectan por casualidad. No obstante, una vez que los investigadores comenzaron a comprender el ciclo vital y los patrones anuales de esta nube alargada, pudieron guiar al equipo de estas otras cámaras de alta resolución al lugar y la hora apropiados para capturarla mientras surgía.
“Muchos orbitadores marcianos no pueden siquiera observar esta parte de la superficie del planeta hasta primera hora de la tarde, debido a las propiedades de sus órbitas, por lo que esta es la primera exploración detallada de este interesante fenómeno, algo posible no solo gracias a la diversidad de instrumentos de Mars Express, sino también a su órbita”, explica Agustín Sánchez Lavega, catedrático de la UPV/EHU, coautor del estudio y responsable científico de la VMC. “Aunque en la Tierra se observan con frecuencia nubes orográficas, no alcanzan esta enorme longitud ni ofrecen una dinámica tan cambiante. Comprender esta nube nos brinda una excelente oportunidad para intentar replicar su formación con modelos que mejorarán nuestros conocimientos sobre los sistemas climáticos tanto de Marte como de la Tierra”, concluye.
Referencia:
J. Hernández‐ Bernal, A. Sánchez‐ Lavega, T. del Río‐ Gaztelurrutia, E. Ravanis, A. Cardesín ‐Moinelo, K. Connour, D. Tirsch, I. Ordóñez ‐Etxeberria, B. Gondet, S. Wood, D. Titov, N. M. Schneider, R. Hueso, R. Jaumann, E. Hauber (2021) An Extremely Elongated Cloud Over Arsia Mons Volcano on Mars: I. Life Cycle Journal of Geophysical Research doi: 10.1029/2020JE006517
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La larga nube de agua de Arsia Mons se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Tormentas convectivas de agua muy energéticas en Júpiter
- La importancia del agua en un biomarcador contra el cáncer
- Métodos no destructivos para analizar muestras marcianas
La estufa interior
 Ilustración: María Lezana
Ilustración: María LezanaMuchos mamíferos tienen una pequeña estufa en su interior. No es una estufa muy potente pero, en su modestia, cumple una función muy importante, pues les proporciona calor cuando necesitan compensar el que pierden. La estufita en cuestión es la llamada grasa parda o grasa marrón. Y es característica de los mamíferos que hibernan y también de los bebés humanos.
La razón por la que los animales homeotermos somos capaces de mantener constante nuestra temperatura corporal es que el metabolismo produce una gran cantidad de calor. Haciendo variar esa producción de calor y, en la medida de lo posible, controlando y modulando la cantidad que disipamos, ajustamos las ganancias y las pérdidas de manera que la temperatura no experimente apenas variaciones. Lo que es imprescindible es que exista una fuente de calor interna; sin ella la regulación térmica no sería posible. Normalmente, es el conjunto de la actividad metabólica la responsable de esa producción de calor, pero algunos homeotermos disponen de grasa parda, un tejido cuyo cometido específico consiste, precisamente, en producir calor.
La grasa parda y la grasa blanca son los dos tipos de tejido graso con que cuentan los mamíferos. Son muy diferentes. La blanca puede desempeñar diferentes funciones, dependiendo de su composición y su localización, pero tratándose de un compuesto con un alto contenido energético, su cometido principal es el de actuar como reserva energética. La parda, por el contrario, tiene una única función, la de producir calor. En las células que la forman hay lípidos, por supuesto, pero junto a los lípidos hay mitocondrias, muchas mitocondrias, y hay además una alta densidad de capilares sanguíneos. Que en los adipocitos (células llenas de lípidos) que conforman la grasa parda haya muchas mitocondrias y abundantes vasos sanguíneos quiere decir que se trata de un tejido metabólicamente muy activo. Lo curioso es que esa alta actividad metabólica no se traduce en trabajo, ni biológico ni mecánico, ni de ningún otro tipo. Desde ese punto de vista, se trata de un tejido “inútil”. Pero produce calor.
Como es bien sabido, el objeto y la consecuencia principal del catabolismo de sustratos energéticos es producir trifosfato de adenosina (ATP). Como sus enlaces fosfato contienen mucha energía química, puede desempeñarse un buen número de actividades (absorción de nutrientes, transporte de iones, síntesis de proteínas, contracción del músculo, y otras) haciendo uso de dicha energía. Sin embargo, en la grasa parda no se produce ATP como consecuencia del catabolismo de los lípidos que contiene; en las células de este tejido el catabolismo de los sustratos y la vía de producción de ATP se hallan desacopladas. Eso ocurre debido a la acción de una proteína desacoplante (UCP1, por uncoupling protein), también denominada termogenina.
Se las llama proteínas desacoplantes porque desvinculan (o desacoplan) el flujo de protones desde el espacio intermembranal de las mitocondrias hacia la matriz mitocondrial, de la producción de ATP a cargo de la correspondiente sintetasa. Veamos esto con algún detalle.
En la mayoría de las células con metabolismo aerobio, las mitocondrias utilizan oxígeno para completar el catabolismo de sustratos energéticos, de manera que la energía contenida en estos se convierte en energía química en forma de ATP, a la vez que se producen, además, CO2 y H2O. En bioquímica y fisiología decimos que el oxígeno es el aceptor final de electrones en la cadena respiratoria mitocondrial. En la secuencia que conduce a ese final hay un paso muy importante: la energía que procede de los sustratos se utiliza para acumular protones (H+) en el espacio entre las membranas interior y exterior de la mitocondria. Se genera así una diferencia de concentración de protones muy grande entre ese espacio intermembranal y el interior (la matriz) mitocondrial. En las células aerobias “normales”, esos protones retornan a la matriz mitocondrial a través de la sintetasa de ATP (la enzima que cataliza la síntesis de ATP y que es, además, un canal de protones), que utiliza el movimiento de aquellos a favor de gradiente electroquímico como fuente de energía para sintetizar ATP a partir de ADP. Decimos, por ello, que la síntesis de ATP está acoplada al flujo de protones.
En las células que contienen termogeninas, estas conducen a los protones a su través (también son canales de protones) para retornar a la matriz, pero su movimiento a favor de gradiente electroquímico no está acoplado a ningún otro proceso que utilice la energía que se libera, sino que se disipa en forma de calor. Lo que en una mitocondria normal es una transformación de la energía inherente al gradiente electroquímico de protones, se convierte en una transformación en la que el resultado es otra forma de energía: calor.
La grasa parda cumple una función esencial en los mamíferos que hibernan, puesto que es la fuente de calor que permite reiniciar la actividad en los fugaces despertares que experimentan durante la hibernación. También al final de ese periodo, cuando retoman la actividad normal.
Los mamíferos recién nacidos, gracias a la grasa parda, compensan, en parte, la dificultad que tienen para calentarse como lo hacemos los adultos y la gran propensión a perder calor que experimentan por el hecho de ser tan pequeños. De hecho, el calor producido por el catabolismo de los lípidos es imprescindible para compensar las pérdidas de calor que sufren y mantener así el balance térmico estable. En los bebés recién nacidos la grasa parda puede representar un 5% de la masa corporal. Al ser de tamaño tan pequeño tienen una superficie corporal muy grande con relación a su volumen (o masa), por lo que, comparativamente, pierden mucho más calor que los individuos grandes. Tienen, por otro lado, una cabeza de gran tamaño (también en relación con su masa) y, además, la cabeza es la parte del cuerpo por donde más calor se pierde. Por si todo esto no fuera suficiente, debido al limitado desarrollo del tejido muscular, no son capaces de tiritar ni de realizar ningún otro tipo de contracción muscular efectiva. Así pues, los bebes tienen muy buenas razones para disponer de un tejido específico que produzca calor.
Luego, al crecer, adquieren la capacidad de tiritar y de contraer la musculatura general con eficiencia, y junto con eso, van perdiendo la grasa parda. O al menos, eso es lo que se pensaba antes. Porque resulta que hace unos años se descubrió que algunas personas adultas no la pierden por completo. Se desconoce la razón por la que unos la pierden y otros no, pero los investigadores que se han ocupado de esta cuestión han hecho una interesante observación: quienes no la han perdido están más delgados que los demás. Lo más probable es que gracias al metabolismo que alimentan esos lípidos, una parte de la energía absorbida se disipe en forma de calor, razón por la que no se deposita en los tejidos.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La estufa interior se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El organismo humano es una estufa de unos pocos vatios
- Grasa parda
- El tamaño relativo de los órganos animales
Propuesta de actividad: crear un regalo multiplicativo
Cuando hace casi dos años presenté mi libro Los secretos de la multiplicación, de los babilonios a los ordenadores (Caratara, 2019), de la colección Miradas Matemáticas (ICMAT, FESPM), en la Biblioteca de Bidebarrieta (Bilbao), se me ocurrió que sería bonito hacer un regalo personal a aquellas personas que vinieran a la presentación del libro. Esta idea me vino a la cabeza recordando la presentación de la novela negra De entre el humo (Destino, 2019), en la que su autor, el cocinero y escritor donostiarra Xabier Gutierrez (podéis visitar su página web Xabier Gutierrez cocinero), nos regaló una pequeña pistola de chocolate a quienes asistimos a la misma.
 Portada del libro Los secretos de la multiplicación, de los babilonios a los ordenadores (Caratara, 2019), de la colección Miradas Matemáticas (ICMAT, FESPM)
Portada del libro Los secretos de la multiplicación, de los babilonios a los ordenadores (Caratara, 2019), de la colección Miradas Matemáticas (ICMAT, FESPM)
La idea estaba ahí, me gustaba, pero tenía un pequeño problema. ¿Qué podía regalar yo relacionado con mi libro Los secretos de la multiplicación? La respuesta evidente era que podía regalar “una multiplicación”. De hecho, existen diferentes algoritmos desarrollados a lo largo de la historia de la humanidad para esta operación aritmética, aunque nosotros prácticamente solo conozcamos la que nos enseñaron en la escuela, de los que precisamente hablaba yo en este libro. Desde el método natural en el origen prehistórico de los números y la aritmética, métodos de multiplicar con las manos, la forma de multiplicar de los sumerios con los “cálculos” de arcilla o la multiplicación de los chinos para los números representados con varillas, hasta una multitud de métodos inventados por indios, árabes y europeos para nuestro sistema de numeración posicional moderno, pasando por la forma de multiplicar de los babilonios, con su sistema numeración posicional en base 60, la multiplicación egipcia, o el método de multiplicar de los campesinos rusos.
El problema estaba en qué significaba exactamente regalarles una multiplicación. Dándole vueltas a esta idea se me ocurrió una respuesta muy personal, les regalaría una multiplicación especial cuyo resultado fuese la fecha de cumpleaños de la persona en cuestión. Esta es la actividad que os propongo en esta entrada, crear un regalo matemático, personal y artístico.
 Tarjeta de regalo muy personal con una multiplicación por rombo
Tarjeta de regalo muy personal con una multiplicación por rombo
La primera parte de la actividad consiste en coger la fecha de nacimiento de la persona a la que le vayamos a regalar la tarjeta, o cualquier otra fecha especial. Por ejemplo, consideremos el 18 de febrero de 1968. Lo siguiente es convertir la fecha elegida en un número. En nuestro caso, 18.021.968, aunque también podría ser 19.680.218 u otras opciones. Después se calcula la descomposición en factores primos de ese número (existen calculadoras online de factores primos):
18.021.968 = 24 x 223 x 5.051.
Después hay que expresar, utilizando esa factorización, el número como producto de dos números de unos cuatro dígitos. Por ejemplo, en nuestro caso,
18.021.968 = 3.568 x 5.051.
Lo siguiente es elegir un método de multiplicación. Un algoritmo que sea interesante y con cierta belleza mejor. Aunque hay muchas opciones yo elegí fundamentalmente dos métodos, la multiplicación árabe o de celosía (sobre la que podéis leer en el artículo Los huesos de Napier, la multiplicación árabe y tú o más extensamente mi libro Los secretos de la multiplicación) y la multiplicación por rombo, que es uno de los métodos que aparece en la obra Summa de arithmetica (1494), del matemático italiano Luca Pacioli (aprox. 1445-1517).

La multiplicación por rombo está relacionada con el siguiente diagrama, que recoge conjuntamente los productos de las cifras del multiplicador con las cifras del multiplicando, diagrama que también está relacionado con el algoritmo moderno que utilizamos para la multiplicación, pero considerados estos productos parciales en otro orden y escritos de una forma particular que describiremos a continuación.
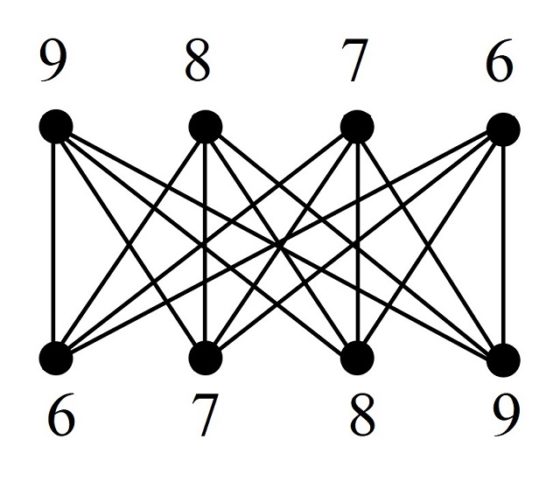 Multiplicación por rombo de los números 9.876 y 6.789
Multiplicación por rombo de los números 9.876 y 6.789
Expliquemos este algoritmo. Si se quiere realizar la multiplicación 9.876 x 6.789, primero se escriben los dos números, uno encima del otro, y se traza una línea debajo de ellos, como en el algoritmo moderno. A continuación, en cada fila, debajo de la línea trazada, se escriben los productos parciales de las cifras en función de la inclinación de los segmentos que unen las cifras en el diagrama conjunto (véase la imagen de arriba). En el ejemplo de la multiplicación por rombo que acompaña a este texto, se muestran, en orden, los diagramas de las siete filas que componen el método de multiplicación por rombo.
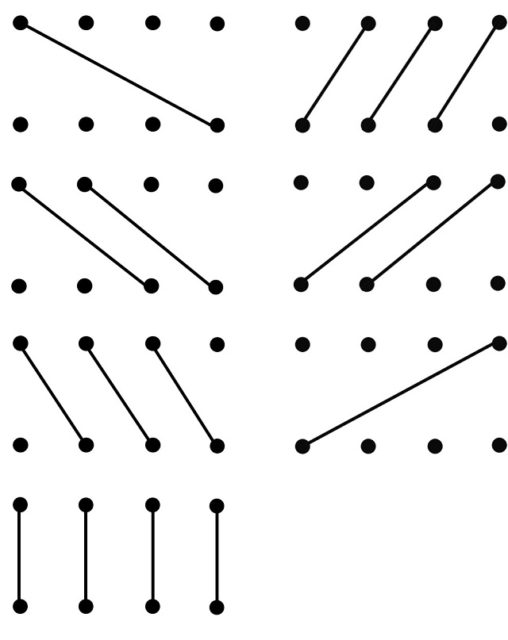

Podéis comprobar este método para la multiplicación asociada a la fecha 18/02/1968, 3.568 x 5.051.
La última parte de la actividad consiste en el desarrollo artístico de la multiplicación. En mi caso, elegí un bonito papel y dibujé con un rotulador especial la multiplicación sobre el papel. Estas multiplicaciones son las que repartí a las personas que asistieron a la presentación de mi libro. Fue un hermoso regalo. Algunas de esas personas incluso enmarcaron la tarjeta con la multiplicación. Seguro que a vosotras se os ocurren desarrollos más artísticos aún. Os animo a que los desarrolléis.
 Tarjeta multiplicativa realizada para la Semana de la Ciencia / Zientzia Astea de la UPV/EHU, con la multiplicación por rombo
Tarjeta multiplicativa realizada para la Semana de la Ciencia / Zientzia Astea de la UPV/EHU, con la multiplicación por rombo
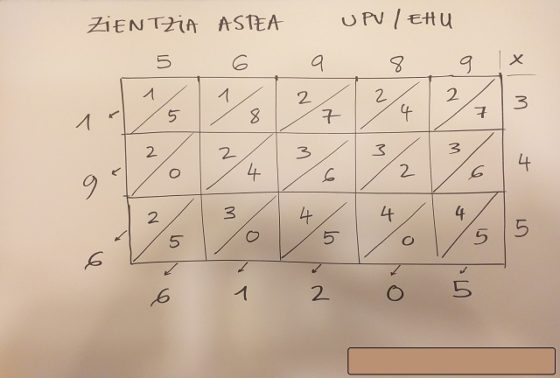 Tarjeta multiplicativa realizada para la Semana de la Ciencia / Zientzia Astea de la UPV/EHU, con la multiplicación por celosía
Tarjeta multiplicativa realizada para la Semana de la Ciencia / Zientzia Astea de la UPV/EHU, con la multiplicación por celosíaSobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Propuesta de actividad: crear un regalo multiplicativo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La hoja de papel con cuatro caras, una propuesta de taller
- Un regalo digno de un matemático
- Multiplicar con las manos
Actúa localmente: bacteriófagos contra la resistencia bacteriana
 Foto: Enrique López Garre / Pixabay
Foto: Enrique López Garre / PixabayEn su nota descriptiva actualizada a 31 de julio de 2020 la Organización Mundial de la Salud afirma la resistencia a los antibióticos es hoy una de las mayores amenazas para la salud mundial, la seguridad alimentaria y el desarrollo. Cada vez es mayor el número de infecciones —por ejemplo, neumonía, tuberculosis, gonorrea y salmonelosis— cuyo tratamiento se vuelve más difícil debido a la pérdida de eficacia de los antibióticos.
Los antibióticos son medicamentos utilizados para prevenir y tratar las infecciones bacterianas. La resistencia a los antibióticos se produce cuando las bacterias mutan en respuesta al uso de estos fármacos. Son las bacterias, por tanto, y no los seres humanos ni los animales, las que se vuelven resistentes a los antibióticos. Estas bacterias farmacorresistentes pueden causar infecciones en el ser humano y en los animales y esas infecciones son más difíciles de tratar que las no resistentes.
La resistencia a los antibióticos hace que se incrementen los costos médicos, que se prolonguen las estancias hospitalarias y que aumente la mortalidad.
Es necesario que se cambie urgentemente la forma de prescribir y utilizar los antibióticos. Aunque se desarrollen nuevos medicamentos, si no se modifican los comportamientos actuales, la resistencia a los antibióticos seguirá representando una grave amenaza. Los cambios de comportamiento también deben incluir medidas destinadas a reducir la propagación de las infecciones, a través de la vacunación, el lavado de las manos, la seguridad de las relaciones sexuales y una buena higiene alimentaria.
La resistencia a los antibióticos está aumentando en todo el mundo a niveles peligrosos. Día tras día están apareciendo y propagándose en todo el planeta nuevos mecanismos de resistencia que ponen en peligro nuestra capacidad para tratar las enfermedades infecciosas comunes. Un creciente número de infecciones, como la neumonía, la tuberculosis, la septicemia, la gonorrea o las enfermedades de transmisión alimentaria, son cada vez más difíciles —y a veces imposibles— de tratar, a medida que los antibióticos van perdiendo eficacia.
Allí donde los antibióticos se pueden adquirir sin receta médica para uso humano o veterinario, la aparición y propagación de la farmacorresistencia empeora. En los países que carecen de directrices terapéuticas normalizadas, el personal sanitario y veterinario tiene tendencia a prescribirlos —y la población general a consumirlos— en exceso.
Si no se toman medidas urgentes, el mundo está abocado a una era post-antibióticos en la que muchas infecciones comunes y lesiones menores volverán a ser potencialmente mortales. Veamos un caso concreto de problema y del tipo de medidas que pueden adoptarse.
La campilobacteriosis, que en su mayor parte se produce por el consumo de carne de pollo contaminada con la bacteria Campylobacter, es la intoxicación alimentaria más frecuente en Europa, con 220.682 casos reportados en 2019 y un coste asociado de 2.400 millones de euros al año.
Las medidas de control actual en las granjas se basan principalmente en el uso de antibióticos lo que contribuye a la diseminación de cepas de Campylobacter. ¿Habría otra forma de combatir a esta bacteria que no fuese con antibióticos?
En el mercado existen ya algunos productos basados en fagos, organismos que infectan y destruyen ciertas bacterias diana, como en el caso de los patógenos alimentarios Listeria monocytogenes, Escherichia coli o Salmonella. Sin embargo, aún no existen productos específicos frente a Campylobacter.
AZTI lidera el proyecto C-SNIPER (sniper es francotirador en inglés) está desarrollando un producto que llenará ese hueco. A través de una estrategia de mitigación que utiliza los fagos, esta iniciativa reduciría la presencia de Campylobacter en la granja, en el matadero o en instalaciones de procesado de aves de corral. Además, esta herramienta contra Campylobacter podría ser integrada fácilmente en los protocolos de higiene ya establecidos en la producción y el procesado.
Se trata de una alternativa a los antibióticos que, por ser altamente específica frente a un único género de bacterias (Campylobacter), resulta inocua tanto para plantas, como para los animales, humanos incluidos, como para el resto del microbiota natural circundante. Además, esta solución facilitaría el control de la diseminación de este patógeno sin afectar a la apariencia y calidad del producto final.
A pesar de la especificidad de los fagos, el proyecto C-SNIPER analiza explícita y experimentalmente el impacto general de la solución sobre el crecimiento, la salud y el bienestar animal. Así, se están llevando a cabo estudios para descartar la aparición de desequilibrios en la flora intestinal de las aves y el posible desarrollo de resistencias a los bacteriófagos tras el tratamiento. De esta manera, mediante la aportación de nuevas evidencias científicas, el proyecto contribuirá a facilitar la regulación sobre el empleo de bacteriófagos, ya que, si bien varios países como EE. UU., Canadá o Suiza, han aprobado la utilización de bacteriófagos en alimentos, en la Unión Europea no hay regulación específica por el momento.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Actúa localmente: bacteriófagos contra la resistencia bacteriana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una nueva vía para la lucha contra la resistencia a los antibióticos
- Concurso: diseña el primer símbolo que represente la resistencia a los antibióticos
- Actúa localmente: huesos a partir de ARN modificado e impresoras 3D
La grandeza de las ballenas, un misterio sin resolver
Las ballenas son una de las criaturas más grandes que ha habitado sobre la Tierra a lo largo de la historia. Existen varias hipótesis que tratan de explicar por qué se hicieron tan grandes. Sin embargo, la ciencia aún no ha dado con la respuesta definitiva.
En 2010, Graham Slater, biólogo e investigador de la Universidad de Chicago, propuso que hace 30 millones de años los cetáceos se dividieron en grupos de distintos tamaños y que se han mantenido así desde entonces.
Sin embargo, 7 años más tarde, el paleobiólogo Nicholas Pyenson, el biólogo Jeremy Goldbogen y el propio Graham Slater publicaron un estudio que indicaba que las ballenas no aumentaron de tamaño hasta hace aproximadamente 4,5 millones de años, durante el Plio-Pleistoceno. Este aumento coincidió con el inicio de una glaciación y se estableció un régimen estacional de afloramientos. El afloramiento, o ascenso de masas profundas de agua ricas en nutrientes, causaba la proliferación del plancton y las ballenas que se alimentaban por filtración se volvieron más eficientes que otros competidores.
 Imagen: Las principales hipótesis para explicar por qué son tan grandes las ballenas. (Ilustración: Alain Sorazu Agirre)
Imagen: Las principales hipótesis para explicar por qué son tan grandes las ballenas. (Ilustración: Alain Sorazu Agirre)La mayoría de las hipótesis que tratan de explicar el tamaño descomunal de las ballenas ven el agua como medio liberador. En el agua, estos animales no tienen que soportar su propio peso y cuerpos más grandes les permiten cubrir mayores territorios en busca de alimento. Otra hipótesis propone que el aumento del tamaño fue una respuesta evolutiva de defensa contra depredadores.
William Gearty, investigador de la Universidad de Stanford, propuso una nueva hipótesis en el año 2018. En el agua la pérdida de calor corporal es mayor que en la tierra y la forma más eficiente de disminuir esta pérdida es aumentar de tamaño. Sin embargo, organismos más grandes necesitan más alimentos. Según Gearty, la masa de los mamíferos marinos está limitada por debajo por la necesidad de mantenerse caliente y por arriba por la disponibilidad de alimento. Gearty calculó que los distintos grupos de mamíferos marinos alcanzaron de forma independiente una masa media óptima de 500 kg. Las ballenas, gracias a su capacidad de filtrar agua con sus barbas, son mucho más eficientes que otros mamíferos marinos y lograron superar el umbral de los 500 kg hasta convertirse en los gigantes que hoy conocemos.
Aunque aún sigue sin estar claro el por qué del gran tamaño de las ballenas, estas investigaciones nos acercan un poco más a la resolución del misterio que albergan estos grandes animales.
Referencias consultadas:
Gearty, W., McClain, C. R., Payne, J. L. (2018). Energetic tradeoffs control the size distribution of aquatic mammals. PNAS, 115 (16), 4194-4199. DOI: https://doi.org/10.1073/pnas.1712629115
Slater, Graham J., Price, Samantha A., Santini, Francesco y Alfaro, Michael E. (2010). Diversity versus disparity and the radiation of modern cetaceans. Proceedings of the Royal Society B, 277 (1697), 3097–3104. DOI: https://doi.org/10.1098/rspb.2010.0408
Slater, Graham J., Goldbogen, Jeremy A. y Pyenson, Nicholas D. (2017). Independent evolution of baleen whale gigantism linked to Plio-Pleistocene ocean dynamics. Proceedings of the Royal Society B, 284, 28420170546. DOI: http://dx.doi.org/10.1098/rspb.2017.0546)
Autor: Alain Sorazu Agirre, alumno del Postgrado de Ilustración Científica de la UPV/EHU – curso 2019/20
Artículo original: ¿Por qué son tan grandes las ballenas? Rocío Pérez Benavente, Cuaderno de Cultura Científica, 4 de marzo de 2019.
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo La grandeza de las ballenas, un misterio sin resolver se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Por qué son tan grandes las ballenas?
- El pueblo que hablaba con las ballenas, ¿podría enseñarnos su idioma a los demás?
- Eran nuestras ballenas
Una respuesta a los múltiples errores de Juan Manuel De Prada en «Evolución»
Juan Gefaell
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsEl pasado 31 de mayo, en su sección de Firmas del semanario XL-Semanal, el escritor y crítico literario Juan Manuel De Prada publicó un artículo sobre la evolución y la biología evolutiva en general titulado Evolución, negando la realidad del hecho evolutivo y defendiendo una cosmovisión creacionista. Dicho artículo está plagado de errores y argumentos fallidos. Probablemente debido a ello, el artículo de De Prada ha generado gran revuelo no solo entre el público general, sino dentro de la propia comunidad científica de biólogos evolutivos. A día de hoy ya han sido publicadas algunas respuestas a dicho artículo. Sin embargo, aunque valiosas, considero que estas respuestas pecan de dos defectos. En primer lugar, en algunos casos emplean un tono excesivamente beligerante, lo cual hace que los argumentos y las evidencias presentados queden sepultados bajo una ristra descalificaciones y argumentos ad hominem completamente innecesarios. Entiendo que, cuando los debates son apasionados, es difícil mantener un tono correcto y respetuoso. No obstante, comparto con el filósofo John Locke que, para el prevalecimiento de la verdad “(…) no hay mejor camino que el empleo de fuertes argumentos y buenas razones, unidos a la suavidad de la cortesía y de las buenas maneras.” (1988, p. 22) En segundo lugar, considero que las anteriores respuestas al artículo de Juan Manuel De Prada no son todo lo eficaces que debieran ser porque obvian que algunos de los argumentos que esboza este escritor son de naturaleza filosófica o histórica. Por ese motivo, no tener en cuenta estas disciplinas hace que se yerre en el diagnóstico de la situación y se dejen pasar errores de bulto cometidos por De Prada.
En lo que sigue, he tratado de articular una respuesta punto por punto al artículo de Juan Manuel De Prada que subsane los defectos de las respuestas realizadas con anterioridad. Antes de pasar a ella me gustaría, no obstante, aclarar cuál ha sido mi motivación al haber escrito esta respuesta. Considero que el artículo de Juan Manuel De Prada no debe ser considerado una mera excentricidad. A mi juicio, dicho artículo constituye un nuevo caso flagrante de lo que el sociólogo Diego Gambetta ha denominado “machismo discursivo”, esto es, un estilo argumentativo que conjuga un tono taxativo y dogmático junto con un completo desconocimiento de la materia sobre la que se opina. Un estilo argumentativo que, tal y como ha puesto de relieve Ignacio Sánchez-Cuenca en La desfachatez intelectual (2016), sería la tónica habitual de buena parte de los tertulianos e intelectuales públicos españoles. Dicha clase de estilo argumentativo es objetable en la medida en que dificulta la discusión racional acerca de las cuestiones relacionadas con la vida pública y, en consecuencia, pone piedras en las ruedas de la democracia. No obstante, es posible argumentar que el artículo de Juan Manuel De Prada es, si cabe, más reprochable, en la medida en que el objeto del mismo es una de las teorías científicas más consolidadas de la ciencia moderna.
La teoría de la evolución tiene una historia tan plagada de éxitos explicativos como de reacciones adversas por parte de ciertos colectivos religiosos. No en vano, en la que hasta ahora constituye la principal potencia científica mundial, los Estados Unidos de América, las cuestiones relacionadas con la enseñanza de esta teoría científica han acabado en los tribunales en más de una ocasión. A pesar de que múltiples autores e instituciones han enfatizado que el supuesto conflicto entre la teoría evolutiva y la religión es en realidad un falso conflicto, ciertas facciones del protestantismo dogmático han tratado de realizar una cruzada contra la biología evolutiva que no tiene parangón en la historia de la ciencia moderna. Si bien hasta ahora la biología evolutiva ha salido indemne de todos los embates jurídicos y sociales a los que ha sido sometida, no debemos suponer que lo mismo vaya a suceder necesariamente en el futuro.
El florecimiento de la ciencia, como el de la democracia, requiere un compromiso cívico y cultural con los ideales de la racionalidad, la ponderación, el respeto a la evidencia y el gusto por los matices (Koertge 2005). En una democracia madura, la ciencia ha de ser tomada en serio por los ciudadanos, que no han de tolerar la proliferación de los diversos negacionismos científicos, y que han de cortar de raíz cualquier cuestionamiento de la evidencia científica fundamentada por motivos exclusivamente ideológicos. Ahora bien, a la hora de confrontar dichos negacionismos, es preciso tratar de entender los motivos y las sutilezas conceptuales que en ocasiones están detrás de los mismos, para, de ese modo, no convertir la defensa de la ciencia y la racionalidad en un mero ejercicio de cientificismo. Es por estos motivos por los cuales he decidido tratar de articular esta respuesta. Vayamos con ella.
 Foto: Samuel Scrimshaw / Unsplash
Foto: Samuel Scrimshaw / UnsplashEl contenido del artículo de Juan Manuel De Prada, punto por punto
He considerado que, dada la cantidad de errores e imprecisiones empíricas y conceptuales en las que incurre Juan Manuel De Prada, la mejor forma de dar respuesta a su artículo es analizarlo punto por punto. Así pues, con esta afirmación comienza De Prada:
“El evolucionismo postula que todos los seres vivos, vegetales y animales –incluido el hombre– se habrían originado a partir de una, o unas pocas, formas vivientes originales, por transformaciones sucesivas, lentas y graduales, en el curso de millones de años, gracias a modificaciones producidas al azar y a la acción de la selección natural.”
Este fragmento contiene un error filosófico de bulto: el empleo del término “evolucionismo” para referirse a la teoría de la evolución. Si bien en ocasiones los biólogos evolutivos utilizan “evolucionismo” en un sentido laxo, incluyendo bajo el mismo la teoría de la evolución o incluso a la biología evolutiva como disciplina, lo cierto es que “evolucionismo” y “teoría evolutiva” no son la misma cosa. El evolucionismo, aunque implica a la teoría de la evolución, es más que esta, como bien sabe Juan Manuel De Prada. Normalmente, se entiende por evolucionismo una filosofía de la naturaleza que, apoyándose en una interpretación particular de la teoría de la evolución, defiende la idea de que no existen entidades o procesos sobrenaturales de ningún tipo, sino únicamente entidades y procesos estrictamente naturales. En otras palabras: el evolucionismo es la suma de la teoría de la evolución junto con lo que los filósofos denominan el naturalismo metafísico. Así pues, de acuerdo con los partidarios del evolucionismo, la teoría de la evolución proporcionaría razones para dudar de la existencia de Dios, así como de cualquier otro ente sobrenatural.
A Juan Manuel De Prada habría que decirle que, si bien el evolucionismo entendido de este modo es una tesis filosófica respetable, no todos los biólogos evolutivos se adscriben automáticamente al evolucionismo, aunque por supuesto no duden de la veracidad de la teoría evolutiva. Así pues, muchos de ellos compatibilizan la aceptación de la teoría evolutiva con alguna otra cosmovisión filosófica, incluidas algunas de corte teísta (p. e. Miller 2007). Lo único que todos los biólogos evolutivos comparten por el mero hecho de ser científicos es lo que en la literatura filosófica se conoce como “naturalismo metodológico” (McDonald y Tro 2009), es decir, la convicción de que al hacer ciencia solo debe apelarse a entidades y procesos naturales como explicación de los fenómenos. Las creencias religiosas deben dejarse a un lado a la hora de hacer ciencia.
Juan Manuel De Prada sabe que el evolucionismo no es lo mismo que la teoría de la evolución, tal y como deja claro al final de su artículo. Sin embargo, trata de confundir deliberadamente el primero con la segunda, incurriendo en una maniobra habitual entre la mayoría de creacionistas y, lamentablemente, entre algunos biólogos evolutivos de gran proyección mediática (estoy pensando en Richard Dawkins; p. e., Dawkins 1995): la confusión deliberada o inconsciente de una teoría científica con una tesis filosófica. No son lo mismo, y no debe hacer pasarse a la teoría de la evolución por una doctrina filosófica. La teoría evolutiva es una teoría científica. Punto. Criticar el “evolucionismo” o incluso el ateísmo no debe pasar por criticar a la teoría de la evolución. Tal y como señala Jacques Monod en un pasaje al comienzo de su clásico El azar y la necesidad (1986), del que se hace eco el filósofo Elliott Sober (2011): “(…) hay que evitar toda confusión entre las ideas sugeridas por la ciencia y la ciencia misma.” (p. 12) Si se quiere criticar la teoría de la evolución, debe hacerse en el plano estrictamente científico, cosa que está condenada al fracaso. Si se quiere criticar el evolucionismo, debe hacerse en el plano filosófico, dejando a un lado la teoría de la evolución, que no es responsable directa de las afirmaciones realizadas por los partidarios del “evolucionismo”.
Continua De Prada afirmando lo siguiente:
“En la actualidad, incluso, la hipótesis evolucionista pretende también explicar la ‘biogénesis’, es decir, el origen espontáneo de la vida a partir de la materia inanimada. Así se podría explicar la evolución, como si dijéramos, desde el átomo hasta el hombre.”
En este caso, habría que responderle al autor que esta afirmación es imprecisa. Tal y como está formulada, da a entender que la teoría de la evolución pretende explicar todos y cada uno de los pasos que se establecieron hasta dar lugar al surgimiento de los primeros seres vivos. Esto no es cierto. Lo único que establece la teoría evolutiva es que una vez surgieron entidades con capacidad autorreplicadora y susceptibles de mostrar variabilidad heredable, entonces el mecanismo de la selección natural pudo comenzar a operar, dando lugar a evolución. En ciertos casos, estas entidades autorreplicadoras podrían no haber sido ser seres vivos propiamente dichos, si no más bien biomoléculas con capacidad autorreplicadora. Esto es lo que defiende, a grandes rasgos, la hipótesis del mundo ARN: tras el surgimiento de dichas biomoléculas con capacidad autorreplicadora (similares a las actuales ribozimas), el mecanismo de la selección natural habría podido ponerse en marcha, dando lugar eventualmente, a través de procesos de variación heredable y selección, a las primeras células (Novo 2016). Ahora bien, cómo se formaron en primer lugar dichas biomoléculas con capacidad autorreplicadora no es algo que pretenda explicar la teoría de la evolución, sino que queda en manos de los bioquímicos proporcionar tal explicación. Así pues, la frase tal y como es formulada por Juan Manuel De Prada es confusa y lleva a malentendidos acerca del alcance explicativo de la teoría evolutiva: esta no pretende explicar la evolución desde “el átomo hasta el hombre”, sino, en todo caso, desde las primeras biomoléculas autorreplicadoras hasta los organismos actuales.
A continuación, afirma:
“La tesis de Darwin incluye dos proposiciones distintas: por un lado, la ascendencia común de los seres vivos, el famoso ‘árbol de la vida’; por otro, la transformación de unas especies en otras, mediante un proceso evolutivo de selección natural que implica la supervivencia de los mejor dotados. Pero si todos los seres vivos procedieran de un origen común, lo normal sería que existiesen infinitas formas de transición entre ellos, un abanico de seres en transformación que conectara las distintas especies, mediante multitud de formas intermedias. Pero lo que contemplamos en la naturaleza son, por el contrario, especies perfectamente conformadas. Darwin aseguraba que esos seres intermedios en constante transformación no han sobrevivido, pues eran «poco aptos para la lucha por la supervivencia». Pero estaba seguro de que los avances paleográficos nos depararían multitud de fósiles que demostrarían la existencia de seres intermedios que conectasen los invertebrados con los peces, los peces con los anfibios, los anfibios con los vertebrados completamente terrestres… Sin embargo, tales seres intermedios no se han hallado. Se han encontrado, por supuesto, fósiles de especies ya extintas que, al igual que el ornitorrinco o el pez saltarín del fango, poseen órganos perfectamente desarrollados y funciones propias de diversas especies animales, pero no formas intermedias con órganos semidesarrollados que no sean completamente funcionales.”
En este párrafo, Juan Manuel de Prada defiende que el registro fósil no revela la existencia de fósiles de transición, dado que estos fósiles deberían mostrar órganos semidesarrollados que no serían completamente funcionales. Antes de comenzar a responder a esta afirmación, errónea de todo punto, es preciso aclarar que Juan Manuel de Prada está mezclando aquí dos cuestiones diferentes: el hecho de la evolución con la teoría de la evolución. Tal y como ha sido señalado en numerosas ocasiones (véase, por ejemplo, Gould (1994), una cosa es el hecho de la evolución, esto es, la constatación de que la vida ha ido cambiando de forma más o menos paulatina a lo largo de la historia geológica, y otra es la teoría de la evolución, que reúne el conjunto de mecanismos que pretenden dar cuenta de dicho cambio, entre los que destaca la selección natural. Parece que lo que aquí está impugnando Juan Manuel de Prada es el hecho de la evolución, dejando intacta la teoría de la evolución. Se trata de una distinción necesaria de cara a evitar futuras confusiones.
Pues bien, una vez constatado esto, se puede proseguir con la réplica a la afirmación de Juan Manuel de Prada acerca de la inexistencia de los fósiles de transición. Esta afirmación es simple y llanamente falsa. Para mostrar por qué, lo primero que debemos hacer es aclarar qué se entiende en la literatura científica moderna por “fósil de transición”. Según Herron & Freeman (2014), un fósil de transición es aquel que muestra rasgos comunes a un grupo de organismos ancestral y a su grupo taxonómico descendiente. Partiendo de esta definición, lo cierto es que el registro fósil está repleto de fósiles de transición. Simplemente por ceñirnos a los casos que De Prada cita, en la actualidad están descritos fósiles de transición entre invertebrados y peces (candidatos a esto son los organismos del Cámbrico Pikaia o Haikouichthys; Morris y Caron 2012, Shu et al. 2003), entre peces y anfibios (Tiktaalik, del Devónico; Daeschler et al. 2006) y entre anfibios y vertebrados completamente terrestres (Casineria, del Carbonífero; Paton et al. 1999). Así pues, es totalmente falso que no existan fósiles de transición si nos atenemos a la definición empleada en su día a día por los biólogos evolutivos.
Teniendo en cuenta lo improbable de la fosilización (solo un porcentaje ínfimo de organismos terminan fosilizados), el hecho de haber encontrados tantos fósiles de transición es una prueba indudable a favor del hecho de la evolución. En cualquier caso, a diferencia de lo que piensa Juan Manuel De Prada, la existencia de fósiles de transición no es un requisito indispensable para aceptar la evolución. Hay linajes de organismos, como por ejemplo el de los platelmintos, en los cuales no existen fósiles (Dawkins 2009). Sin embargo, nadie duda de que los platelmintos han evolucionado al igual que otros linajes de organismos. El motivo es que el resto de pruebas del hecho de la evolución (la biogeografía, la anatomía comparada, la genética, los órganos vestigiales, etc.) son suficientemente abrumadoras de por sí como para hacer innecesarios los fósiles. En este sentido, los fósiles son un añadido extra al conjunto de pruebas de la evolución.
Hay un segundo elemento que es preciso señalar con respecto a la duda de Juan Manuel De Prada acerca de los fósiles de transición. Probablemente, ante la anterior respuesta, él replicaría que no es suficiente para persuadirle, pues este autor entiende que los fósiles de transición necesariamente han de mostrar órganos semidesarrollados no funcionales. Por ese motivo, los animales que hemos presentado como fósiles de transición, dado que eran animales plenamente funcionales, no cuentan como tales. Esta es una versión simplificada del argumento de la funcionalidad de la “media ala” de George J. Mivart, que fue formulado originalmente en tiempos de Darwin (Bowler 2003). Hay múltiples formas de responder a este argumento. Una de ellas consiste en señalar que el hecho de que un órgano esté “semidesarrollado” para una función (desde el punto de vista de la actualidad) no significa que no sea plenamente funcional para llevar a cabo otras funciones. En ese sentido, un órgano semidesarrollado para caminar en tierra puede ser plenamente funcional para nadar, y por ello ser perfectamente útil para un animal que solo realice pequeñas incursiones en tierra firme y pase la mayor parte del tiempo en el agua. Siempre y cuando se mantengan ambas funciones, un animal como este podría evolucionar gradualmente unas patas plenamente funcionales a partir de unas aletas plenamente funcionales. Esto es lo que se conoce en biología evolutiva como “exaptación” (Gould & Vrba 1982). En la exaptación, un órgano que surgió con una determinada función puede evolucionar para pasar a tener otra función diferente. En la actualidad, la exaptación sirve para dar cuenta del origen de múltiples órganos, tales como, por ejemplo, la vejiga natatoria de los peces (Farmer 1997). Otro caso representativo en este sentido es el de las alas: existe evidencia experimental obtenida con crías de aves actuales de que las protoalas o alas “semidesarrolladas” podrían haber tenido un papel funcional en la evolución incipiente de las alas antes de que estas se empleasen para el vuelo. Así, parece que las protoalas o alas “semidesarrolladas” permiten trepar más eficazmente a los árboles y, gracias a ello, ayudan a escapar mejor de los depredadores (Dial et al. 2006). En consecuencia, el argumento de De Prada acerca de los órganos “semidesarrollados” falla también en este punto: cuando se busca, se encuentra evidencia a favor de la utilidad de estos hipotéticos órganos no plenamente funcionales.
Acto seguido, Juan Manuel De Prada señala:
“Viendo que los fósiles no brindaban apoyo suficiente a sus teorías, el evolucionismo recurrió al estudio de las semejanzas moleculares entre los seres vivos. Pero el estudio de las secuencias de aminoácidos de la globina de diversas especies no permite establecer taxativamente una ‘secuencia evolutiva’ que las relacione.”
Dejando a un lado el hecho de que el autor vuelve a confundir el hecho de la evolución con la teoría de la evolución, y que vuelve a utilizar el rótulo “evolucionista” de forma inadecuada, aquí De Prada comete un doble error. El primero de ellos revela un completo desconocimiento de la disciplina de la filogenia molecular, pues asume que la única forma de estudiar el parentesco molecular de las especies es comparar la secuencia de aminoácidos de la hemoglobina de diversas especies. Dicha técnica fue la empleada originalmente por, entre otros, Emile Zuckerkandl y Linus Pauling en los años 60 del siglo pasado para estudiar el parentesco molecular (Zuckerkandl & Pauling 1965). Sin embargo, en la actualidad hay técnicas mucho más fiables y sofisticadas de determinación de las relaciones filogenéticas entre especies, como aquellas que comparan las secuencias del ARN de la subunidad pequeña de los ribosomas (Ajawatanawong 2017). Estas técnicas han puesto de manifiesto de forma indudable y reiterada el parentesco taxonómico entre todas las especies del planeta. De hecho, gracias a ellas tenemos un conocimiento bastante exacto de lo que Francisco J. Ayala (1985) denomina “el camino de la evolución”, es decir, la secuencia de episodios históricos que han dado lugar a la diversidad de especies vivientes de la actualidad. Por este motivo, convendría que Juan Manuel De Prada actualizase sus fuentes antes de opinar de forma tan taxativa.
Sin embargo, el segundo error, de carácter histórico, es, si cabe, de mucha mayor envergadura. De Prada parece sugerir que, debido a que los fósiles no constituían una prueba suficientemente robusta para la teoría de la evolución, entonces los seguidores de Darwin cambiaron de estrategia y comenzaron a estudiar los genes para ver si encontraban apoyo en estos. Sin embargo, esta tesis no cuenta con el más mínimo aval histórico. De forma muy resumida, la historia de la biología evolutiva desde Darwin hasta el surgimiento de la biología molecular es la siguiente: gracias El origen de las especies, publicado originalmente en 1859, Darwin consiguió persuadir a la comunidad de biólogos y naturalistas de su época del hecho evolutivo. Sin embargo, no hizo lo propio con su teoría de la selección natural. En consecuencia, tras la muerte de Darwin en 1882 comenzaron a surgir múltiples escuelas de pensamiento evolutivo que, aunque aceptaban el hecho de la evolución, proponían distintas teorías para dar cuenta del mismo (Bowler 1983, 2003). Entre dichas escuelas se encontraba una conformada casi exclusivamente por paleontólogos, la escuela ortogenetista, que defendía que la evolución procedía por medio de un impulso interno de los organismos a evolucionar en direcciones determinadas aun a costa de sacrificar la adaptabilidad de las especies. Otra de estas escuelas estaba conformada, a su vez, por genetistas, y recibía el nombre de “mutacionismo”. Los mutacionistas, inspirados por la naturaleza cualitativa del cambio hereditario postulada por el primer mendelismo, pensaban que la evolución se producía de forma súbita por medio de cambios de gran envergadura en el material genético. Tanto los ortogenetistas como los mutacionistas, coetáneos en el tiempo, desconfiaban de la teoría darwiniana de la selección natural. Sin embargo, ambos aceptaban sin ambages el hecho de la evolución, que trataban de explicar con ahínco. Con el paso del tiempo, las tesis de los mutacionistas y los ortogenetistas fueron siendo abandonadas paulatinamente por falta de apoyo empírico. Así, los estudios de genética llevados a cabo en el laboratorio de Thomas H. Morgan revelaron que la mayor parte de cambios genéticos son de pequeña magnitud, y que los grandes saltos mutacionales constituyen una rara excepción. Por su parte, los estudios de George G. Simpson sobre las tendencias y patrones revelados por el registro fósil mostraron a las claras que las supuestas tendencias ortogénicas postuladas por la escuela homónima no tenían lugar en el registro fósil (Bowler 2003).
Tras las contribuciones realizadas en la década de 1920 por J. B. S. Haldane, Robert Fisher y Sewall Wright, que consiguieron compatibilizar la genética mendeliana con la teoría de la selección natural, un conjunto de científicos provenientes de las distintas ramas de la biología y la historia natural, capitaneados por el genetista Theodosius Dobzhansky (cristiano, por cierto; Collins 2006), consiguieron aunar en un gran marco teórico evolutivo las aportaciones de la genética de poblaciones, la taxonomía, la botánica y la paleontología. A dicho marco teórico se le denominó la Síntesis Evolutiva Moderna. La Síntesis Evolutiva Moderna, construida sobre una base darwinista, supuso la estocada final a las escuelas que surgieron en el campo de los estudios evolutivos tras la muerte de Darwin, incluidas el mutacionismo y la ortogénesis. Esta teoría no solo consiguió persuadir al conjunto de la comunidad científica del hecho de la evolución (algo que ya había hecho Darwin), sino que además consiguió fundamentar sobre una base más sólida la teoría de la selección natural darwiniana. Una vez constituida la Síntesis Evolutiva Moderna, el surgimiento paralelo de la biología molecular aportó todavía más pruebas y argumentos a favor tanto del hecho como la teoría de la evolución, revelando la estructura molecular de las mutaciones o diseñando la técnica del reloj molecular para el cálculo de filogenias.
En el anterior relato histórico no hay ningún atisbo de la tesis de Juan Manuel De Prada: es completamente falso que los biólogos evolutivos se desviasen desde la paleontología hasta la genética para obtener las pruebas a favor de la evolución que los fósiles no revelaban. Ambos trabajaron paralelamente hasta su integración bajo la Síntesis Evolutiva Moderna bajo la premisa de que la evolución es un hecho. Tanto los paleontólogos como los genetistas estaban convencidos desde la publicación de El origen de las especies de la realidad del hecho evolutivo. No necesitaban encontrar más pruebas de las que Darwin aportó. Es más, tanto los paleontólogos como los genetistas quedaron convencidos no solo del hecho de la evolución, sino también de la teoría de la selección natural, una vez la Síntesis Evolutiva Moderna mostró que la paleontología era compatible con la genética de poblaciones y con la selección natural. Así pues, de nuevo, Juan Manuel De Prada comete un error de bulto, esta vez de naturaleza histórica.
El escritor prosigue así su artículo:
“Y tampoco las mutaciones genéticas confirman plenamente las tesis evolucionistas, pues toda mutación azarosa tiende por lo común a deteriorar el código genético, no a mejorarlo. Las mutaciones ‘favorables’, en el estricto sentido de la palabra, sólo se dan una entre un millón; y no deben confundirse con la variabilidad genética que tiene todo organismo, que hace que en determinadas circunstancias se expresen genes que ya estaban presentes –aunque reprimidos– porque su funcionamiento no era necesario.”
La frase con la que se inicia este párrafo revela un profundo desconocimiento de los fundamentos más básicos de la genética contemporánea, lo cual ya debería hacernos dudar de todo lo que dice Juan Manuel De Prada a continuación. En efecto, De Prada señala que las mutaciones azarosas tienden a deteriorar el “código genético”. Esta afirmación carece de sentido, pues el código genético es la correspondencia entre tripletes de nucleótidos y aminoácidos proteinogénicos, y dicho código no puede ser “deteriorado” en ningún sentido científicamente válido.
Si nos atenemos al principio de la caridad en filosofía y teoría de la argumentación (Blackburn 1994), según el cual debemos interpretar las palabras de nuestro interlocutor de la forma más racional posible, obviando los posibles malentendidos que contenga e intentando entender lo que dice, supongo que el verdadero mensaje de Juan Manuel es que la mayoría de mutaciones son deletéreas. Esta afirmación es cierta. Sin embargo, esto no cuestiona ni el hecho ni la teoría de la evolución, tal y como parece sugerir De Prada por el contexto en el que se enmarca su afirmación. Hay al menos dos motivos para ello: el primero es que la cantidad de pruebas a favor del hecho evolutivo sigue siendo abrumadora independientemente de cuál sea la naturaleza de las mutaciones; y el segundo es que, aunque la mayoría de mutaciones sean deletéreas, el hecho de que la selección fije aquellas de naturaleza beneficiosa, aunque sean una minoría, hace posible el cambio acumulativo adaptativo en el genoma de los organismos. Por tanto, de nuevo el argumento de De Prada falla.
La siguiente frase del artículo es la que sigue:
“Las mutaciones sólo pueden alterar algo que ya existe, no pueden crear nuevos genes ni aumentar la información genética.”
Esta afirmación es, de nuevo, falsa, y se soluciona con un mínimo de conocimiento sobre biología evolutiva. Parece que Juan Manuel De Prada asume que las mutaciones se restringen a lo que en genética se conoce como mutaciones puntuales, que afectan a un solo nucleótido del genoma. Sin embargo, además de las mutaciones puntuales, existen otras de mayor envergadura que implican a genes enteros, regiones del genoma, cromosomas o, incluso al genoma entero. Entre estas mutaciones se encuentran las conocidas como duplicaciones, en las cuales un fragmento determinado del genoma (o un cromosoma, o el genoma entero) se duplica. Las duplicaciones, que aumentan la información genética de un genoma, parecen haber sido un elemento bastante frecuente en la evolución de los distintos linajes de organismos. Por ejemplo, la evolución de los vertebrados parece haber sido posible por una duplicación completa del complejo de genes Hox, que regulan el proceso de desarrollo en todos los eumetazoos (Carroll et al. 2004). Una vez más, De Prada debía haberse informado debidamente antes de hacer afirmaciones como esta.
Una de las últimas afirmaciones del artículo de Juan Manuel De Prada es el siguiente:
“Pero aun en el caso de que se hayan dado mutaciones ‘favorables’, estas no bastan para producir una nueva especie; para ello, son precisas ‘transmutaciones’ del organismo que sólo pueden lograrse en laboratorio. O sea… mediante la intervención de una inteligencia que las provoque y encauce.
Y es que el organismo de un ser vivo es un conjunto infinitamente complejo de estructuras integradas e interrelacionadas entre sí que funcionan como un todo, con vistas a un fin; y que, por lo tanto, no puede cambiar por partes. Por consiguiente, para que un cambio significativo en una estructura o en una función sea viable, tiene que cambiar simultáneamente todo el organismo; y, para que esto ocurra, tendría que cambiar toda la información hereditaria, de forma simultánea y sin un solo error. Es decir, debería ocurrir una mutación gigantesca, un reordenamiento radical de todo el genoma, dirigido y especificado hasta en los más mínimos detalles. Lo cual constituye un verdadero milagro… que es precisamente lo que el evolucionismo trata de negar.”
En estos pasajes, Juan Manuel De Prada sugiere que la evolución no es posible por medio de mutaciones favorables en determinados puntos del genoma debido a que los organismos son totalidades integradas que no pueden cambiar por partes. Una mutación en una región requeriría cambios en otras regiones del organismo. Vayamos por partes. Estoy de acuerdo con la afirmación de que los organismos son totalidades integradas. Sin embargo, de esto no se deduce necesariamente que no sean susceptibles de evolución por partes.
El motivo de esto es que, aunque sea correcto pensar que los organismos son totalidades integradas dirigidas a fines (p. e. Walsh 2015), esto no quita que dichas totalidades están compuestas por módulos funcionales relativamente autónomos (Gilbert & Epel 2009). Este es uno de los hallazgos más fascinantes de la “evo-devo” o biología evolutiva del desarrollo, uno de los últimos avances dentro de la disciplina de la biología evolutiva. Estos módulos permiten la evolución de determinadas partes del organismo de una forma relativamente independiente a la del resto de módulos. Ahora bien, es cierto que, para mantener la integridad funcional, los organismos deben poseer mecanismos de autoensamblaje que garanticen la coherencia morfológica de sus distintas partes. Esto se consigue, entre otras formas, por medio de lo que se denomina “acomodación fenotípica”. La acomodación fenotípica se refiere al proceso por el cual, tras una mutación genética en un sistema, el resto de sistemas se reacomodan a dicha mutación mediante plasticidad fenotípica u otros mecanismos de autoorganización, de forma que no es necesario que en dichos sistemas se produzcan nuevas mutaciones para dar lugar a organismos integrados y coherentes (West-Eberhard 2003; Sterelny 2009). La acomodación fenotípica es un fenómeno que los biólogos evolutivos contemporáneos reconocen sin ningún tipo de problemas, y que ayuda a explicar por qué los cambios evolutivos no necesariamente implican grandes mutaciones, algo que desde Thomas H. Morgan se sabe que es la excepción y no la regla. Así pues, de nuevo Juan Manuel De Prada yerra en su análisis.
Por último, De Prada finaliza:
“Pecaríamos de ingenuidad si pensásemos que el evolucionismo es tan sólo una hipótesis científica. El evolucionismo es, sobre todo, un postulado filosófico materialista cuyo objetivo último es negar no la narración literal de los primeros capítulos del Génesis (algo que ya San Agustín nos advirtió que no debía hacerse), sino la intervención divina en la creación de la vida. La Evolución, con mayúscula, se convierte así en la responsable única de toda la historia del universo, una fuerza ciega y mecánica que estaría cambiando constantemente el mundo y dirigiéndolo hacia algo diferente y mejor. He aquí la idea que subyace detrás de las bellas historias de dinosaurios mutantes que tanto nos encandilan.”
En este último párrafo, Juan Manuel De Prada vuelve a incurrir en el error de confundir la teoría de la evolución, una teoría científica, con el evolucionismo, que tal y como él mismo afirma, es un postulado o tesis filosófica. Tal y como señalé en la primera parte de esta respuesta, se puede criticar el evolucionismo sin por ello tratar de atacar la teoría evolutiva, que, por sí sola, no implica necesariamente el evolucionismo. La crítica del evolucionismo o naturalismo metafísico (que De Prada denomina “materialismo”) debe realizarse sobre bases filosóficas, no criticando los principales hallazgos y teorías de una de las disciplinas más consolidadas de la ciencia moderna, la biología evolutiva. Dicha estrategia, además de estar condenada al fracaso desde un punto de vista teórico, es contraproducente desde un punto de vista social, ya que da alas a los movimientos anti-ciencia en un momento de pandemia mundial.
La evolución es un hecho. La teoría de la evolución explica satisfactoriamente ese hecho. Parece que lo que verdaderamente preocupa a Juan Manuel De Prada es la asociación que algunos pensadores hacen entre el ateísmo y teoría de la evolución. Sin embargo, tal y como han demostrado múltiples biólogos y filósofos (por ejemplo, Ruse 2004; Collins 2006; Miller 2007; Sober 2011), es posible creer en Dios, incluido el Dios de los cristianos, y no albergar dudas acerca de la biología evolutiva. La crítica del evolucionismo no pasa por criticar ni el hecho ni la teoría de la evolución. Afirmar creacionismo para defender la creencia en Dios no es una postura respetable intelectualmente y, además, es perniciosa por fomentar la desconfianza en la ciencia motivada por razones ideológicas. Los intelectuales públicos como Juan Manuel De Prada deberían cuidarse más de opinar a la ligera sobre temas técnicos, dada su gran influencia para el gran público. Pongamos fin al machismo discursivo. No demos alas al negacionismo científico. Fomentemos una cultura intelectual más informada y responsable.
Referencias:
Ajawatanawong P (2017) Molecular phylogenetics: Concepts for a newcomer. Advances in Biochemical Engineering/Biotechnology, 160:185-196
Ayala FJ (1985) The theory of evolution: recent successes and challenges. En: McMullin E (ed) Evolution and creation. University of Notre Dame Press, Notre Dame, pp 59-90.
Blackburn S (1994) The Oxford dictionary of philosophy. Oxford University Press, Oxford
Bowler PJ (1983) The eclipse of darwinism: anti-darwinian evolutionary theories in the decades around 1900. Johns Hopkins University Press, Baltimore
Bowler PJ (2003) Evolution: the history of an idea, 3rd edn. University of California Press, Berkeley
Carroll SB, Grenier JK, Weatherbee SD (2009) From DNA to diversity: Molecular genetics and the evolution of animal design. Wiley-Blackwell, Hoboken (NJ)
Collins FS (2006) The language of God: A scientist presents evidence for belief. Free Press, New York
Daeschler EB, Shubin NH, Jenkins FA Jr (2006) A Devonian tetrapod-like fish and the evolution of the tetrapod body plan. Nature, 440: 757-763
Dawkins R (1995) River out of Eden: A Darwinian view of life. Basic Books, New York
Dawkins R (2009) The greatest show on Earth: The evidence for evolution. Free Press, New York
Dial KP, Randall RJ, Dial TR (2006) What use is half wing in the ecology and evolution of birds? BioScience, 56(5): 437-445
Farmer C (1997) Did lung and the intracardiac shunt evolve to oxygenate the heart in vertebrates? Paleobiology, 23(3): 358-372
Gilbert SF & Epel D (2009) Ecological developmental biology. Sinauer, Sunderland (MA)
Gould SJ (1994) Evolution as fact and theory. En: Hen’s Teeth and Horse’s Toes. W. W. Norton, New York, pp. 253-262
Gould SJ, Vrba ES (1982) Exaptation- a missing term in the science of form. Paleobiology, 8(1): 4-15
Herron JC, Freeman S (2014) Evolutionary analysis, 5th edn. Pearson, New York
Koertge N (ed) (2005) Scientific values and civic virtues. Oxford University Press, Oxford
Locke J (1988) Carta sobre la tolerancia. Tecnos, Madrid
McDonald P, Tro NJ (2009) In defense of methodological naturalism. Christian Scholar’s Review, XXXVIII (2): 201-229
Miller KR (2007) Finding Darwin’s God: A scientist’s search for common ground between God and evolution. Harper Collins, New York
Monod J (1986) El azar y la necesidad. Orbis, Barcelona
Morris SC, Caron JB (2012) Pikaia gracilens Walcott, a stem-group chordate from the Middle Cambrian of British Columbia. Biological Reviews, 87(2): 480-512
Novo FJ (2016) Origen de la vida. En: Diccionario Interdisciplinar Austral. Editado por Vanney CE, Silva I, Franck JF. Recuperado de: http://dia.austral.edu.ar/index.php?title=Origen_de_la_vida
Paton RL, Smithson TR, Clack JA (1999) An amniote-like skeleton from the Early Carboniferous of Scotland. Nature, 398 (6727): 508-513
Ruse M (2004) Can a Darwinian be a Christian? Cambridge University Press, Cambridge
Sánchez-Cuenca I (2016) La desfachatez intelectual: Escritores e intelectuales ante la política. Madrid: Catarata
Shu DG, Morris SC, Han J, Zhang ZF, Yasui K, Janvier P, Chen L, Zhan XL, Liu JN, Li Y, Liu HQ (2003) Head and backbone of the Early Cambrian vertebrate Haikouichthys. Nature, 421(6922): 526-529
Sober E (2011) Why Methodological Naturalism? En: Aulette G, LeClerc M, Martinez R (eds), Biological Evolution: Facts and Theories. Gregorian Biblical Press: 359-378.
Sterelny, K. (2009) Novelty, Plasticity and Niche Construction: The Influence of Phenotypic Variation on Evolution. In: Barberousse, A., Morange, M., & Pradeu, T. (eds.) Mapping the Future of Biology: Evolving Concepts and Theories (pp. 93-110). Dordrecht: Springer.
Walsh DM (2015) Organisms, agency, and evolution. Cambridge University Press, Cambridge
West-Eberhard MJ (2003) Developmental plasticity and evolution. Oxford University Press, Oxford
Zuckerkandl E, Pauling L (1965) Evolutionary Divergence and Convergence in Proteins. En: Bryson V, Vogel HJ (eds.) Evolving Genes and Proteins. Academy Press, New York
Sobre el autor: Juan Gefaell se graduó en psicología en la Universidad Pontificia de Salamanca y en biología en la Universidad de Vigo; tras cursar un máster en lógica, historia y filosofía de la ciencia en la UNED, en la actualidad realiza su doctorado en biología evolutiva en el departamento de Bioquímica, Genética e Inmunología de la Facultad de Biología de la Universidad de Vigo.
El artículo Una respuesta a los múltiples errores de Juan Manuel De Prada en «Evolución» se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Juan Manuel Bermúdez-García – Naukas Pro 2019: Sólidos como refrigerantes
- El Universo en un día: Cultura y evolución humana, por Juan Ignacio Pérez
- «Chimpancé + Jilguero = ¿Humano? Sobre la evolución de la facultad del lenguaje» por Juan Uriagereka
Conchi Lillo – Naukas 19: Como nunca lo has sentido

Algunos animales poseen sentidos que nosotros no tenemos y que, por ello precisamente, nos parecen superpoderes. Conchi Lillo hace un repaso de algunos de los más llamativos y de su funcionamiento.
Conchi Lillo dirige el grupo de investigación ‘Trastornos degenerativos del sistema visual’ en el Instituto de Neurociencias de Castilla y León (INCYL) de la Universidad de Salamanca. Lillo es licenciada en biología por la Universidad de Salamanca (1996) y doctora en neurociencias por la misma Universidad (2001). Investigó en The Scripps Research Institute en La Jolla, California (EE.UU.) entre 2002 y 2006. En julio de 2006 se reincorporó a la Universidad de Salamanca, donde desde el año 2011 es profesora titular del área de biología celular en la Facultad de Biología.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Conchi Lillo – Naukas 19: Como nunca lo has sentido se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Percepción del arte a través de la neurobiología, la psicología y la crítica del arte
- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
- #Naukas16 ¿Perdemos el sentido cuando perdemos los sentidos?
Cannabinoides, una especificidad subcelular de control comportamental
 Fuente: UPV/EHU
Fuente: UPV/EHUEn todo el mundo están aumentando los usos recreativos y terapéuticos de los compuestos cannabinoides. Sin embargo, sus importantes efectos secundarios, como deterioros cognitivos o disfunciones motoras, entre otros, han provocado un intenso debate tanto sobre la seguridad de su consumo recreativo como sobre la explotación medicinal de estos principios activos para, por ejemplo, controlar la sensibilidad al dolor en entornos clínicos.
Comprender los mecanismos de los efectos terapéuticos y adversos inducidos por cannabinoides es, por tanto, vital para el uso más seguro de estos compuestos. Así, es conocido que el principal componente psicoactivo de la planta cannabis sativa (marihuana) es el delta-9 tetrahidrocanabinol o THC, que, en el cerebro, actúa principalmente activando a los receptores cannabinoides de tipo-1 (CB1). También se sabe que la activación farmacológica del receptor CB1 afecta el control motor en animales de experimentación y que, en seres humanos, la principal causa de accidentes de tráfico relacionados con el consumo de cannabis son los efectos de tipo cataléptico.
Sin embargo, por un lado, el receptor CB1 se encuentra ampliamente distribuido en todo el cerebro y en diferentes compartimentos celulares y, por otro, los procesos moleculares y celulares específicos subyacentes son poco conocidos. Sobre ambos campos arroja luz este estudio.
Así, desvela que si la activación de los receptores CB1 inducida por cannabinoides se produce en la mitocondria se provocan efectos catalépticos; mientras que si se estimulan los receptores CB1 de la membrana plasmática se reduce la sensibilidad al dolor. Y en ambos casos el proceso tiene lugar a través de la regulación de vías moleculares específicas en el circuito cerebral formado por el núcleo estriado y la sustancia nigra (circuito estriatonigral).
Por tanto, estos resultados no solo desvelan nuevos mecanismos celulares responsables de la acción de los cannabinoides, sino que representan un nuevo marco conceptual en neurociencias. “Antiguamente se creía que la forma del cráneo determinaba los rasgos de personalidad, después se estableció que diferentes estructuras cerebrales se encargaban de funciones específicas; recientemente el enfoque se ha volcado al estudio de circuitos neuronales como los responsables del comportamiento. En este estudio damos un paso más allá, mostrando que una proteína (en este caso el receptor CB1) en distintos sitios celulares (mitocondria frente a membrana plasmática) dentro de un mismo circuito cerebral (circuito estriatonigral) modula distintos comportamientos. Es decir, hemos descubierto una especificidad subcelular de control comportamental”, afirma el primer autor del estudio Edgar Soria-Gómez.
Referencia:
Edgar Soria-Gomez, Antonio C. Pagano Zottola, Yamuna Mariani, Tifany Desprez, Massimo Barresi, Itziar Bonilla-del Río, Carolina Muguruza, Morgane Le Bon-Jego, Francisca Julio-Kalajzić, Robyn Flynn, Geoffrey Terral, Ignacio Fernández-Moncada, Laurie M. Robin, José F. Oliveira da Cruz, Simone Corinti, Yasmine Ould Amer, Julia Goncalves, Marjorie Varilh, Astrid Cannich, Bastien Redon, Zhe Zhao, Thierry Lesté-Lasserre, Peggy Vincent, Tarson Tolentino-Cortes,Arnau Busquets-García, Nagore Puente, Jaideep S. Bains, Etienne Hebert-Chatelain, Gabriel Barreda-Gómez, Francis Chaouloff, Alexander W. Lohman, Luis F. Callado, Pedro Grandes, Jerome Baufreton, Giovanni Marsicano, Luigi Bellocchio (2021) Subcellular specificity of cannabinoid effects in striatonigral circuits Neuron DOI: 10.1016/j.neuron.2021.03.007
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Cannabinoides, una especificidad subcelular de control comportamental se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo los olores nos incitan a comer
- Un nexo cannabinoide entre mitocondrias y memoria
- Por qué los antipsicóticos atípicos causan deterioro cognitivo
La partitura del cuco
El canto de los pájaros ha fascinado a músicos, escritores y científicos desde la Antigüedad. En el siglo I a.C., el poeta y filósofo Lucrecio atribuyó el origen de la música a estas criaturas emplumadas. Según creía, las melodías de los humanos no eran más que una imitación1:
A través de todos los bosques escucharon el encantador ruido
del canto de los pájaros, y trataron de reconstruir su voz
e imitarla. Así los pájaros instruyeron al hombre
y le enseñaron canciones antes de que su arte apareciera.
Lamentablemente, y a pesar de la belleza de este mito, el origen de la musicalidad humana es bien distinto y probablemente tiene más que ver con nuestro propio lenguaje. Pero no cabe duda de que el canto de las aves ha inspirado a los compositores de todas las épocas. En sus pentagramas, nos han dejado breves retratos de sus competidores alados, sonografías que nos hablan del paisaje sonoro del pasado.
De entre todas las aves, el cuco y el ruiseñor parecen haber recibido una atención especial dentro del repertorio de la música occidental. La popularidad del cuco, en concreto, probablemente se deba a la sencillez de su canto, tan característico y fácil de recordar. Está formado por solo dos notas, que dibujan un mismo patrón descendente y repetitivo. El mismo nombre de “cuco”, es claramente onomatopéyico y tiene su origen en este dibujo melódico. También en latín, Cuculus, recuerda esta sonoridad, mientras que Canorus (el nombre de especie del cuco común) deriva del verbo canō «cantar».
Además de en su nombre, la escueta partitura del cuco está escrita en sus genes. Difícilmente podrían aprenderla de sus padres, de hecho, ya que los cucos son una especie parasitaria. Tras aparearse, dejan sus huevos cuidadosamente camuflados en el nido de otra ave, de alguna otra especie. Cuando el cuco nace, se deshace de sus hermanos y los pobres padres adoptivos se pasan el resto de la temporada alimentando a ese polluelo gordo y acaparador, que nadie sabe muy bien a quién habrá salido.
 Un carricero alimentando una cría de cuco. Fuente: Wikimedia Commons.
Un carricero alimentando una cría de cuco. Fuente: Wikimedia Commons.Como contamos en su día (también, esta semana, en el canal de Jaime Altozano), las aves cantoras tienen oído absoluto, y el cuco no es una excepción. Cada cuco repite su canto siempre con las mismas notas de un día para otro, de manera que su melodía se convierte en una seña de identidad2. Sin embargo, los tonos y su duración pueden variar ligeramente para cada cuco, en función también de su subespecie, la región donde habita3 y la especie a la que parasita4. El rango de la nota más grave (el segundo cú), en la actualidad y según se ha podido observar en una población de cucos de Budapest, suele situarse entre los 500 Hz y los 600 Hz5 (entre un si y un re, aproximadamente).
Esta variabilidad se puede rastrear también en los recuerdos de tinta de la música occidental. Probablemente, el primer cuco inmortalizado sobre la rejilla de las cinco líneas se encuentra en una partitura de 1226 atribuida a John of Fornsete, Sumer Is Icumen In, cuya notación se corresponde con las notas fa – re (o probablemente mi ♭ – do, de acuerdo con la afinación actual).
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsOtro ejemplo especialmente bonito aparece en Musurgia Universalis (cuyo título se podría traducir como “El arte musical universal”). Este tratado de 1650 retrata a distintas aves acompañadas por sus respectivas partituras. Entre ellas, el cuco entona repetidamente las notas do – la, (un rango particularmente grave).
 Fuente: Institut Für Musikwissenschaft
Fuente: Institut Für MusikwissenschaftLa lista es interminable, en cualquier caso. En 1624, Frescobaldi escribe un Capricho inspirado en este canto (re – si). Medio siglo más tarde, otro organista llamado Kasper Kerl utiliza las mismas notas en su Capricio Kuku. Poco después, Bernardo Pasquini le dedica una toccata (mi – do#) y ya en el siglo XVIII, Louis Claude Daquin se hizo especialmente celebre gracias a “Le Coucou” (sol-mi).
Vivaldi, Handel, Haydn… son solo algunos de los otros nombres que le dedicaron sus propias corcheas a esta ave cantora. Pero el ejemplo más célebre, sin duda, se lo debemos a Ludwig van Beethoven. Al final de su sinfonía Pastoral, la orquesta se detiene para dejar el volar el canto alegre de una flauta. Mientras ella trina, le responde el clarinete: cu-cú (re – si ♭). Su sonido es el de un cuco grave, con un timbre redondo de viento madera. Pero me pregunto si sus referentes plumíferos lo reconocerían, si un día sonase en medio del bosque, al menos como una buena imitación.
Referencias:
1Mansfield, Orlando A. “The Cuckoo and Nightingale in Music.” The Musical Quarterly, vol. 7, no. 2, 1921, pp. 261-277.
2Zsebok, Sándor, et al. “Individually distinctive vocalization in Common Cuckoos (Cuculus canorus).” Journal of Ornithology, vol. 158, 2017, pp. 213–222.
3Wei, Chentao, et al. “Geographic variation in the calls of the Common Cuckoo (Cuculus canorus): isolation by distance and divergence among subspecies.” Journal of Ornithology, vol. 156, 2015, pp. 533–542.
4Jung, Won-Ju, et al. “‘‘cu-coo’’: Can You Recognize My Stepparents? – A Study of Host-Specific Male Call Divergence in the Common Cuckoo.” PLOS ONE, vol. 9, no. 3, 2014. PLOS ONE, https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0090468.
5Esta es la frecuencia medida en una población de cucos de Budapest, por Zsebok, Sándor, et al. “Individually distinctive vocalization in Common Cuckoos (Cuculus canorus).” Journal of Ornithology, vol. 158, 2017, pp. 213–222.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo La partitura del cuco se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Del Tíbet a Debussy en una partitura
- ¿En qué se parecen un trombón y un elefante?
- El oído absoluto de los animales
Lluvia, hoy no te siento
Lluvia, hoy no te siento.
Hoy no eres nada
más que agua vertical.
Apenas si te escucho
golpear el pavimento
y llamar con tu clave
sobre mi ventanal
Lluvia, hoy no eres nada
para mi desaliento
nocturno y abismal.
Cuando era niña hallaba
en tu canción un cuento,
y ya en mi adolescencia
me diste un madrigal.
Ahora, lluvia, tengo
tanta tristeza adentro,
que no me dices nada,
solo te oigo golpear.
Lluvia, Matilde Alba Swan
Hoy planteamos un juego para ejercitar un poco la lógica. Fue propuesto por el matemático Howard C. Saar y apareció publicado en el Recreational Mathematics Magazine en octubre de 1962.
Reto meteoro-lógico
«Anteayer, Matilde, la mujer del tiempo, decidió dar su predicción meteorológica de una manera poco habitual, apelando a las capacidades lógicas de sus oyentes:
El tiempo de hoy es diferente al de ayer. Si el tiempo de mañana es el mismo que el de ayer, entonces pasado mañana hará el mismo tiempo que anteayer. Pero si el tiempo de mañana es el mismo que el de hoy, entonces pasado mañana hará el mismo tiempo que ayer.
Hoy llueve y llovió anteayer. ¿Podrías decir que tiempo hizo ayer?».
Solución
Por favor, piensa un poco antes de leer el razonamiento y la respuesta.

Reescribimos los datos fijando fechas, para que sea más sencillo el razonamiento. Además, cuando hablamos del tiempo, estamos pensando en lluvia o sol.
Hoy es 9 de junio, así que la predicción meteorológica de Matilde es de fecha 7 de junio. Y lo que dice es:
-
El tiempo del 7 de junio es distinto que el del 6 de junio.
-
Si el tiempo del 8 de junio (Matilde habla de “su mañana”) es el mismo que el del 6 de junio, entonces el tiempo del 9 de junio y el del 5 de junio serán iguales.
-
Pero, si el tiempo del 8 de junio es el mismo que el del 7 de junio, entonces el tiempo del 9 de junio y el del 6 de junio serán iguales.
Como dato adicional (ya no habla Matilde, la mujer del tiempo), se nos informa que:
-
Hoy, 9 de junio, llueve y llovió el 7 de junio.
La pregunta es: ¿qué tiempo hizo el 8 de junio?
Hay dos respuestas posibles, o bien 8 de junio hizo sol o bien llovió. Razonemos ambas posibilidades.
Supongamos que el 8 de junio llovió. Por 4), llovió el 7, el 8 y el 9 de junio. Aplicando 1), el 6 de junio hizo sol. No tiene sentido aplicar la condición 2). Pero si puede aplicarse 3), ya que el 7 y el 8 de junio llovió. Así, se deduce que el tiempo del 6 y del 9 de junio debería ser el mismo. ¡Pero esto no es verdad! Como hemos llegado a una contradicción, necesariamente el 8 de junio debió de lucir el sol.
De cualquier manera, quizás Matilde ha planteado mal su adivinanza… No hay que fiarse de todo lo que nos dicen. Así que vamos a comprobar si, efectivamente, con las condiciones planteadas por la meteoróloga, el 8 de junio no llovió. Las conclusiones de 1) y 4) son las mismas de antes. Ahora no podemos aplicar 3) ya que el día 7 llovió, mientras que el día 8 hizo sol. Pero podemos aplicar 2), que afirma que (ya que los días 6 y 8 de junio lució el sol), el 5 y el 9 de mayo tuvieron el mismo tiempo. Así, nos enteramos, de paso, que el 5 de junio también llovió. No hay contradicción alguna, así que, efectivamente, el 8 de junio hizo sol…
Por cierto, el título no es engañoso, porque hoy 9 de junio llueve, y el poema habla de sensaciones: «Lluvia, hoy no te siento. / Hoy no eres nada / más que agua vertical».
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Lluvia, hoy no te siento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas13 Lo siento Planck, pero no me lo creo
- Plattner y la cuarta dimensión
- El teorema de los cuatro colores (1): una historia que comienza en 1852
Actua localmente: inteligencia artificial en procesos para la industria 4.0

Una famosa introducción a algunas producciones de Disney cantaba que “el mundo es cascada de colores” y eso, que queda muy mono en una pantalla, es inexacto. Vivimos en un mundo que es una cascada de datos de la que nuestros encéfalos intentan obtener información relevante, no siempre con éxito.
La consciencia de que los datos son un activo económico toma cuerpo en empresas como Facebook, que se dedican a recabar datos de multitud de usuarios, organizarlos y clasificarlos, y servirlos en bandeja de plata a los anunciantes que buscan determinado público para sus productos.
La cantidad de datos que se generan a diario en el mundo es abrumadora. Y obtener información de ellos es cualquier cosa menos fácil, tanto por la capacidad que se requiere para manejar esa cantidad de datos como por el diseño e implementación de unos algoritmos que sean capaces de extraer información útil. Por eso Facebook gana dinero.
Pero no todo van a ser redes sociales. Actualmente se están desarrollando de forma masiva productos y servicios en los ámbitos del internet de las cosas, la robótica, el desarrollo de gemelos digitales [1]*, la fabricación aditiva (impresión 3D), la realidad aumentada y muchos otros. Todos tienen en común una cosa: datos, más datos y analítica de datos. Consideremos que una fábrica que sea algo más que un taller genera teras de datos por día.
El tratamiento inteligente de los datos está revolucionando la fabricación de cosas: es parte de lo que se llama la industria 4.0. Lo que se suele llamar Big Data, sería conveniente llamarlo mejor Huge Data, debido a la enorme cantidad de ellos que pueden recogerse y procesarse. Decíamos antes que cualquier fábrica emite teras de datos por día. Nos enfrentamos a unas cantidades de datos tan grandes, que es muy difícil procesarlos con un fin útil. Como si esto fuese poca dificultad nos encontramos con la granularidad del origen de los datos: diferentes procesos industriales obedecen a diferentes ciclos temporales, incluso muchos de ellos pueden no ser deterministas, lo cual implica la redefinición de las series temporales [2].
En una industria 4.0, además, hay que pensar en diferentes niveles de procesamiento de datos:
- A nivel de dispositivo/máquina/etapa. Los datos los proporcionan sensores y actuadores que interaccionan físicamente con el proceso. Esto va más allá de la internet de las cosas y requiere de desarrollos específicos que en algunos casos pueden requerir conexión con la nube (más abajo hablamos de ella). Tiene hasta nombre, edge computing, porque es la interfase entre el mundo físico y el digital.
- A nivel de línea de producción (conjunto de dispositivos/máquinas/etapas coordinadas que producen una cosa concreta). Las diferentes fases de una fabricación se comunican unas con otras creando la oportunidad de optimizar el proceso industrial. De nuevo tenemos nombre específico, fog computing, computación en la niebla que, como es sabido, es una nube pegada al terreno.
- A nivel de fábrica/empresa. Todas las líneas de producción deben coordinarse con los distintos departamentos de la empresa (compras, ventas, administración, personal, calidad, seguridad e higiene) generando multitud de interacciones cruzadas y más oportunidades de optimización. Aquí es donde entra el cloud computing [3], la computación en la nube, donde grandes cantidades de datos se extraen de diferentes fuentes y se procesan todas ellas en un servidor dedicado. Estas operaciones generalmente se enfocan hacia el direccionamiento de la empresa y de la producción.
¿Qué hacemos con todos estos datos? Buscamos en ellos la información que nos ayude a fines muy diversos como: fabricar mejor, vender mejor, optimizar la calidad y aumentar con todo ello el beneficio de la empresa [4]. Se recurre para ello a las ciencias de los datos, para ayudar a encontrar correlaciones, patrones y pautas en los datos.
Un ejemplo de vanguardia de edge computing. La fusión de lecho de polvo es la tecnología preferida para la fabricación de objetos metálicos de precisión y con geometrías complejas. Existen distintos procesos en función de la fuente de calor empleada (haz láser o de electrones) y del grado de fusión del material (sinterizado o fusión). El proceso más extendido para la fabricación de piezas metálicas es la denominada fusión selectiva por láser (Selective Laser Melting o SLM). Se pueden procesar mediante SLM materiales como aceros inoxidables, aceros de herramienta, aleaciones de titanio, aleaciones de base níquel y aleaciones de aluminio, entre otros.
Una cooperativa como Lortek usa para SLM una máquina que trabaja con 4 láseres simultáneamente. Monitorizar los datos en tiempo real es ya un ejercicio de emisión de gran cantidad de datos (big bata streaming), análisis de los mismos (data analytics) e inteligencia artificial con la idea de fabricar sin defectos. Respecto a esta última hay que decir que Lortek usa deep learning (aprendizaje profundo) desarrollando algoritmos de descubrimiento de conocimiento que aprenden desde cero. Estos algoritmos son capaces de detectar estados de estrés en el proceso, predecir la probabilidad de cometer fallos bajo ciertas condiciones, y hasta aconsejar cómo evitarlas.
Y esto solo en una máquina…
Notas:
[1] Un gemelo digital es una réplica virtual de un producto, servicio o sistema real que permite adelantarse a posibles problemas y experimentar sin correr riesgos antes de lanzar nuevas funcionalidades.
[2] Una serie temporal es una sucesión de datos medidos en determinados momentos y ordenados cronológicamente.
[3] El peatón común (un mamífero bípedo que vive conectado a intenet) piensa que Amazon gana dinero con sus grandes almacenes online. Gana, sí, pero muy poco, apenas un 2 % de margen. El gran negocio de Amazon es el cloud computing.
[4] Combiene recordar que las empresas se crean para obtener beneficios. Si no hay beneficios desaparecen y, con ellas, el empleo y los impuestos que pagan tanto la propia empresa como sus trabajadores. La persona informada se alegra de que las empresas tengan beneficios.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Actua localmente: inteligencia artificial en procesos para la industria 4.0 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Actúa localmente: robots inteligentes autoadaptativos para la producción industrial
- Actúa localmente: blockchain para la cadena de suministros
- Actúa localmente: el dron espía del cambio climático
Miltos, un pigmento muy preciado, pero no por su color
El ocre rojo de óxido de hierro, también conocido como miltos, fue uno de los minerales de uso clínico más populares de la literatura médico-científica de la antigüedad grecoromana. Sin embargo, también tenía usos decorativos, era útil en la agricultura, en el mantenimiento de barcos, o se empleaba como cosmético. Curiosamente, según donde se extrajese se le daba un uso u otro.
Un grupo de investigadores de distintas universidades de Reino Unido y Grecia decidieron colaborar para estudiar este mineral. Para ello extrajeron muestras de cinco enclaves de Grecia, destacados en los textos de la época, cuatro provenientes de la isla de Kea y una de la isla de Lemnos.
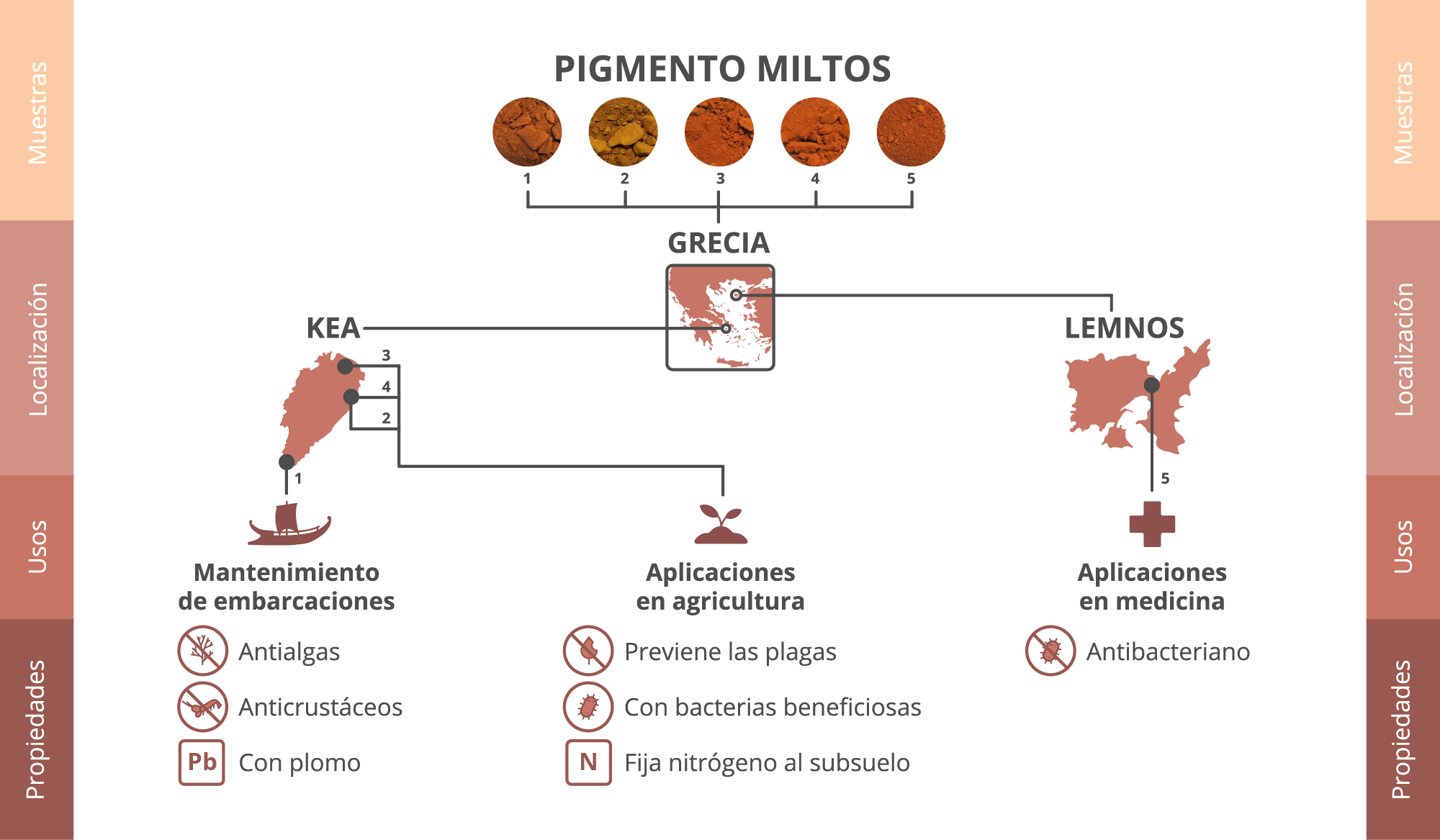 Imagen: Localizaciones populares de miltos en la antigüedad clásica, usos y propiedades. Ilustración: María Candamil López
Imagen: Localizaciones populares de miltos en la antigüedad clásica, usos y propiedades. Ilustración: María Candamil LópezEl análisis geoquímico, microbiológico y mineral determinó que no había una fórmula única de ocre rojo. La variación de la composición química favorecía el desarrollo de microbiotas diferentes y la combinación de ambos factores, determinaba sus propiedades. Esto explicaba por qué la localización determinaba el uso.
El miltos de Kea obtenido en Petroussa contenía plomo. El plomo es tóxico, por lo que la pintura para barcos fabricada con ese ocre impedía que las algas y los invertebrados pudieran adherirse al casco de la embarcación y dificultar la navegación. Sin embargo, si se extraía de otras zonas de la isla, tenía bacterias fijadoras del nitrógeno del subsuelo. Al diluirlo en soluciones acuosas se convertía en un gran fertilizante, mientras que aplicándolo en polvo sobre las raíces de los árboles prevenía la aparición de enfermedades. En cambio, el miltos de Lemnos era el mejor para uso médico, ya que la alunita, el óxido de titanio y una ausencia total de metales tóxicos, le otorgaban propiedades antibacterianas.
El miltos no era apreciado solo por ser un efectivo pigmento rojo. De hecho, los griegos ya habían descubierto su versatilidad de forma empírica, pero gracias a estos recientes estudios conocemos los motivos.
Referencias consultadas:Photos-Jones, E., Knapp, C. W., Vernieri, D., Christidis, G. E., Elgy, C., Valsami-Jones, E., Gounaki, I., Andriopoulo, N. C. (2018). Greco-Roman mineral (litho)therapeutics and their relationship to their microbiome: The case of the red pigment miltos. Journal of Archaelogical Science, 22, 179-192. DOI: https://doi.org/10.1016/j.jasrep.2018.07.017
Autora: María Candamil López, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2019/20
Artículo original: El ocre rojo de la antigüedad y los porqués de sus propiedades. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 20 de enero de 2019.
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo Miltos, un pigmento muy preciado, pero no por su color se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El ocre rojo de la antigüedad y los porqués de sus propiedades
- ¿Es posible el arte sin ciencia?
- ¿Azúcar moreno o azúcar milagro?
Trampas de CO2 más baratas
 Foto: Patrick Hendry / Unsplash
Foto: Patrick Hendry / UnsplashHasta ahora, al pensar en las medidas más eficaces para combatir el calentamiento del planeta, se ha puesto especial énfasis en la limitación de la emisión de gases con efecto invernadero, CO2 especialmente, por ser el que más se emite a la atmósfera. Ese efecto consiste en la retención, por esos gases, de radiaciones infrarrojas en el interior de la atmósfera, del mismo modo a como lo hacen los vidrios de un invernadero. Como consecuencia, la temperatura de la atmósfera aumenta.
La combustión de materiales orgánicos fósiles para obtener energía es la fuente principal de producción de los gases en cuestión, por lo que no es de extrañar que se promueva la limitación de las emisiones como forma de evitar o mitigar el calentamiento. Para ello es necesario limitar el consumo de energía, por un lado, y recurrir cada vez en mayor medida a fuentes de energía inagotables (hidráulica, eólica, solar u otras) o, cuando menos, que no conlleven la emisión de esos gases. Sin embargo, eso no es nada fácil. Por un lado, quemar carbón y otros combustibles fósiles sigue siendo la forma más barata de obtener energía. La nuclear cuenta con muy mala prensa en los países occidentales. Los métodos alternativos son caros y su uso no ha crecido lo suficiente como para que sean una solución a corto plazo.
Por esas razones también se trabaja en el diseño de métodos que permitan retirar de la atmósfera parte del CO2 presente en ella. De esa forma, combinando limitaciones a la emisión con su retirada, podría conseguirse estabilizar la concentración atmosférica del gas y evitar que siga intensificándose el efecto. Podría, incluso, llegar a revertirse la tendencia y disminuir su concentración.
El problema es que los métodos para retirar CO2 son muy caros. La tecnología que se utiliza en la actualidad se sirve de aminas disueltas en agua. Las aminas son derivados del amoniaco (NH3) en el que uno, dos o los tres átomos de hidrógeno han sido sustituidos por un radical. Una de las formas de atrapar CO2 consiste en rociar los gases emitidos con una disolución acuosa de aminas. La disolución cargada con el CO2 se procesa de manera tal que puede recuperarse aquella a la vez que el gas es retirado y almacenado. El método es caro porque requiere llevar la disolución de aminas a ebullición y su posterior condensación para volverla a utilizar. Requiere mucho gasto de energía.
Recientemente, sin embargo, se ha ensayado un procedimiento que permite reducir los costes en cerca de un 20%. No utiliza agua, sino un disolvente orgánico pobre en agua basado en la amina 2-EEMPA (N-(2-etoxietil)-3-morfolinopropan-1-amina). La ventaja de este método es que, una vez el CO2 ha quedado atrapado por la amina, no es necesario llevar el disolvente a ebullición para recuperarlo y, tras retirar el gas, volver a ser utilizado. Basta con calentarlo. Y eso reduce el coste de forma significativa.
Se ha investigado mucho para hallar procedimientos para capturar el CO2 contenido en las emisiones gaseosas industriales y utilizarlo o almacenarlo después. En 2020 se capturaron 40 millones de toneladas (en adelante, M t) de CO2 procedente de emisiones industriales. Se calcula que las 30 instalaciones de captura ya proyectadas en el mundo permitirán retirar hasta 140 M t anuales. Pero las emisiones globales ascienden a 35000 M t en la actualidad. Por lo tanto, para acercar la captura al volumen de emisiones, es necesario multiplicar el esfuerzo actual y, para ello, va a ser necesario reducir los costes prácticamente a la mitad, de los actuales 50€ a 25€ por tonelada.
Referencias:
Robert F. Sevice (2021) New generation of carbon dioxide traps could make carbon capture practical Science News
Richard Zheng et al. (2021) A single-component water-lean post-combustion CO2 capture solvent with exceptionally low operational heat and total costs of capture – comprehensive experimental and theoretical evaluation Energy & Environmental Science doi: 10.1039/D0EE02585B
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Trampas de CO2 más baratas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ley del gas ideal y la tercera ley de la termodinámica
- África arde más de lo que se pensaba
- Carnot y los comienzos de la termodinámica (2)
Aitziber López-Cortajarena – P4K 2019: Ingeniería de proteinas: nuevas terapias y biomateriales
 Imagen: National Cancer Institute / Unsplash
Imagen: National Cancer Institute / UnsplashAitziber López-Cortajarena dirije el Laboratorio Cortajarena del CIC biomaGUNE especializado en nanotecnología biomolecular. Dicho así puede sonar entre raro y directamente de ciencia ficción. Pero cuando Aitziber nos cuenta en cómo pretenden construir biomateriales y nanoestructuras funcionales prediseñadas partiendo de como se ensamblan proteínas simples, la cosa pasa a oscilar entre la psicodelia y la más pura fascinación. Las posibilidades y aplicaciones de esta tecnología son increíbles.
Aitziber López-Cortajarena se doctoró en bioquímica por la Universidad del País Vasco en 2002. Fue becaria postdoctoral y, posteriormente, investigadora asociada en el Departamento de Biofísica Molecular y Bioquímica de la Universidad de Yale (New Haven, Connecticut, Estados Unidos) hasta 2010, cuando estableció su propio grupo de investigación en la Fundación IMDEA Nanociencia de Madrid. Desde 2016 es profesora de investigación Ikerbasque en Cic biomaGUNE.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Aitziber López-Cortajarena – P4K 2019: Ingeniería de proteinas: nuevas terapias y biomateriales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ana María Zubiaga – Naukas Pro 2019: La difícil búsqueda de terapias contra el cáncer
- Ignacio López Goñi – Naukas P4K 2019: La sopa amarilla de la dinastía Ming
- Virginia Arechavala – Naukas Pro 2019: Buscando terapias para enfermedades poco frecuentes
25 años del escándalo Sokal: la culpa de todo la tienen los posmodernos
Urko Gorriñobeaskoa y Ekai Txapartegi
 Imagen: Shutterstock / paseven
Imagen: Shutterstock / paseven
“El objetivo de este libro es hacer una contribución limitada pero original a la crítica del ‘Zeitgeist’ ciertamente obscuro que hemos llamado ‘posmodernismo’”.
Con esta firme declaración, Alan Sokal y Jean Bricmont inauguraban el primer epígrafe de su polémica obra de 1996, Imposturas intelectuales. En ella, los autores acusan a los editores y académicos posmodernos de falta de rigor, de dejarse llevar por sus sesgos ideológicos y de mala praxis académica. Cabe preguntarse, ¿es realmente el posmodernismo un enemigo natural de las ciencias? ¿Esta clase de imposturas son exclusivas de los estudios posmodernos y de las humanidades? Analizar algunas de las polémicas académicas más sonadas de los últimos años puede arrojar algo de luz a estas preguntas.
Echemos un vistazo al suceso con el que empezó todo: el escándalo Sokal. Fue en 1996 cuando Social Text, revista académica centrada en estudios culturales, publicó el artículo Transgressing the Boundaries: Towards a Transformative Hermeneutics of Quantum Gravity, de Alan Sokal. Este artículo había sido redactado por su autor a modo de broma y engaño.
Plagado de sinsentidos, el artículo fue aceptado por la revista posmoderna, y confirmó así las sospechas de Sokal: estas publicaciones aceptarían cualquier cosa que sonase bien y estuviese dentro de su línea ideológica. Poco después de su salida al público, Sokal admitió que se trataba de un engaño y reveló sus motivos.
Las respuestas al escándalo y al libro de Sokal no tardaron en llegar. Jacques Derrida escribió que la lectura de Sokal y Bricmont en el libro era exageradamente simplista. Según el autor francés, Sokal hizo un hombre de paja del posmodernismo y sus argumentos no se sostenían.
Baudouin Jurdant, filósofo de la ciencia francés, reunió a un grupo de científicos de distintas ramas para comprobar el rigor de las acusaciones de Sokal y Bricmont. Estos científicos eran, además, especialistas en los autores citados en Imposturas intelectuales. En conjunto, escribieron un artículo mostrando que Sokal y Bricmont no conocían con la profundidad suficiente las ideas que trataban de criticar. Por otra parte, científicos como Richard Dawkins y filósofos como Thomas Nagel alabaron el trabajo de Sokal y Bricmont, y coincidieron en que muchas revistas de humanidades se dejaban influenciar por sus sesgos políticos.
Este no es el único bulo intelectual que ha avergonzado a la academia en las últimas décadas. En 2018, James Lindsay, Peter Boghossian y Helen Pluckrose dieron a conocer un engaño similar que habían estado urdiendo. Los tres autores escribieron una veintena de artículos de corte posmoderno plagados de sinsentidos y tesis insostenibles, pero que empleaban de manera correcta la terminología habitual de estos campos.
De todos sus artículos, aproximadamente un tercio fueron publicados o aceptados; otro tercio fue rechazado y los restantes seguían pendientes de revisión en el momento en el que se destapó la mentira. Igual que en el caso Sokal, este escándalo desencadenó tanto elogios como críticas por parte de los académicos.
Las ciencias ‘de verdad’ también pican
Quienes alaban los resultados de ambos bulos tienden a leer estos episodios como parte de una polémica mayor: el problema de las dos culturas. Aparentemente, engaños de este estilo solo podrían darse en disciplinas relacionadas con los estudios sociales y culturales, en revistas de humanidades posmodernas donde el rigor brilla por su ausencia. Al contrario, quienes investigan y publican acerca de ciencias de verdad, como la física o la biología, jamás se dejarían embaucar por una treta tan simple.
Sin embargo, la historia reciente nos enseña que esto no es necesariamente cierto.
Alrededor del año 2002 distintos medios comenzaron a hacerse eco de una controversia similar que amenazó, en este caso, al campo de la cosmología. Los protagonistas de esta polémica fueron los hermanos Igor y Grichka Bogdanov, dos divulgadores científicos que trabajaban para la televisión francesa. Al parecer, varias dudas acerca de su legitimidad como físicos llevaron a los hermanos a perseguir sendos títulos de doctorado en la Universidad de Borgoña. Tras un periodo extraordinariamente largo, consiguieron graduarse bajo la condición de que publicasen algunos artículos en revistas de su campo.
Una vez las tesis y artículos de los Bogdanov fueron abiertas al público, diversos especialistas comenzaron a analizarlas. Muchos autores apreciaron que sus trabajos eran más bien pobres, que sus tesis no tenían sentido y que podrían encontrarse ante un escándalo à la Sokal, pero a la inversa. Sin ir más lejos, John Baez, reputado matemático estadounidense, afirmó que su trabajo “es una mezcolanza de frases aparentemente plausibles que contienen las palabras técnicas correctas en el orden aproximadamente correcto. Pero no hay lógica ni cohesión en lo que escriben.” Curiosamente, el diagnóstico es muy similar a aquel que hiciera Sokal de las revistas posmodernas de humanidades.
Pero esto no acaba aquí. En 2005 tres estudiantes del MIT gastaron una broma pesada a una escena académica que consideraban plagada de intereses económicos. Para Jeremy Stribling, Dan Aguayo y Max Krohn, muchos congresos científicos se organizaban con el objetivo principal de aprovecharse económicamente de los investigadores jóvenes ansiosos por hacer currículum. Es por ello por lo que los tres jóvenes desarrollaron un programa informático de IA que generaba artículos académicos automáticamente mezclando frases y tecnicismos aleatorios de otros trabajos. La polémica estalló cuando uno de esos artículos fue aceptado en una conferencia de informática ese mismo año.
Dada la abundancia y diversidad de casos de bulos académicos en los últimos años, creo que podemos sugerir que esta clase de imposturas no se deben exclusivamente a los sesgos de los editores. Casos como el de los Bogdanov y los chicos del MIT parecen indicar que esta clase de engaños son fenómenos poliédricos y que atienden a una variedad de motivos. Tal vez algunos editores de revistas posmodernas den demasiada manga ancha a artículos pobres solo porque suenan bien. Pero esto no debe enmascarar el hecho de que la realidad académica actual está repleta de fallos, métodos de revisión deficientes e intereses extraacadémicos. Además, tal y como muestran algunos de los ejemplos comentados, esta clase de intereses y deficiencias también se dan en las ciencias de verdad.
En un mundo donde publicar es cada vez más necesario para labrarse una carrera, y donde la labor editorial y la organización de conferencias pueden llegar a ser negocios muy lucrativos, ¿cómo no va a primar la cantidad sobre la calidad?![]()
Sobre los autores: Urko Gorriñobeaskoa es doctorando en historia y filosofía de la ciencia y Ekai Txapartegi, profesor de filosofía, ambos en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo 25 años del escándalo Sokal: la culpa de todo la tienen los posmodernos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un cómic de hace dos mil años a todo color
- Todo lo que se puede medir en un río
- ¿Por qué los átomos tienen el tamaño que tienen?
Toman agua por la piel
 Hyla versicolor. Ilustración: María Lezana
Hyla versicolor. Ilustración: María LezanaRanas y sapos pueden respirar a través de la piel. En determinadas épocas del año la piel es, de hecho, su principal órgano respiratorio. Pero no son gases lo único que intercambian con el medio externo por esa vía. También incorporan agua.
La mayoría de los anfibios terrestres no beben agua. La necesitan, por supuesto, pero la absorben a través de la piel, gracias a su gran permeabilidad. Eso tiene sus contrapartidas, ya que, de la misma forma que la adquieren, también la pueden perder. Por eso han desarrollado estrategias especiales para almacenarla. El medio interno o la misma vejiga, incluso, pueden funcionar como depósitos, de manera que pueden reutilizar el agua en ellos contenida en caso de riesgo de deshidratación.
Algunas ranas y sapos tienen una zona – la pélvica- especializada para facilitar la incorporación de agua. Es una zona comprendida entre la pelvis y el abdomen, la situada entre las inserciones de las extremidades posteriores al tronco. De hecho, los anfibios terrestres, cuando necesitan hidratarse, no tienen por qué sumergirse en una masa de agua; les basta con colocarse, sentados, sobre un sustrato húmedo o mojado, o aplastar la zona pélvica contra ese sustrato. El epitelio de esa zona está lleno de capilares sanguíneos, por lo que puede llegar a absorberse un volumen importante de agua. La cantidad que una rana puede absorber de ese modo en un día es equivalente al triple de su masa corporal.
La fuerza que impulsa la absorción de agua es un gradiente osmótico. El agua que se absorbe está muy diluida, casi no tiene sales. La sangre del sapo es de mayor concentración osmótica que el agua; tiene muchas más sales disueltas. Por esa razón, el agua del exterior tiene una fuerte tendencia a penetrar a través de la piel que, al fin y al cabo, es una membrana semipermeable, ya que permite el paso de agua a su través, pero no el de las sales. Eso sí, la sangre ha de circular rápidamente para que pueda ser absorbida el agua. Veamos esto con algún detenimiento.
Cuando penetra el agua y se mezcla con la sangre, ésta se diluye, puesto que la misma cantidad de solutos pasa a estar disuelta en un volumen mayor de agua, de plasma, en este caso. Por lo tanto, la fuerza que impulsa la absorción disminuye, y disminuirá en mayor medida cuanto más lenta sea la renovación de la sangre. Por esa razón, la sangre ha de circular con rapidez, porque si lo hiciese lentamente, la concentración de sales disueltas bajaría demasiado poco. Circulando rápidamente, la diferencia de concentración osmótica entre el interior y el exterior disminuye muy poco, por lo que la fuerza de absorción prácticamente se mantiene constante. En virtud de ese mecanismo, el flujo sanguíneo es proporcional a las necesidades hídricas. Esto es, cuando la deshidratación es baja, la sangre circula lentamente por la zona pélvica, pero la velocidad se eleva cuando el sapo tiene necesidad de agua.
Las hormonas que intervienen en la regulación de la economía del agua y los electrolitos en los vertebrados juegan un papel importante en este proceso. El péptido angiotensina II provoca que aumente la tendencia del sapo a sentarse y la hormona antidiurética (ADH) eleva la permeabilidad del epitelio de la zona pélvica. Por ello, el volumen de agua absorbido puede aumentar mucho como consecuencia de la acción de esas dos hormonas.
No quiero terminar la descripción de este fenómeno sin hacer notar el hecho de que la angiotensina II forma parte del sistema renina-angiotensina que interviene en la regulación de la actividad de la aldosterona en mamíferos y que la hormona antidiurética actúa en el epitelio de los tubos colectores de las nefronas aumentando, precisamente, su permeabilidad al agua. Como vimos aquí, esos sistemas hormonales promueven el ahorro y la recuperación de agua, esto es, lo mismo que promueven en las ranas y sapos que “beben” por su piel abdominal.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Toman agua por la piel se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los intercambios de agua y sales en los tetrápodos acuáticos
- La distribución del agua animal y el curioso caso del potasio
- Los animales que respiran en agua
36 días de tipos (de números)
En esta entrada del Cuaderno de Cultura Científica me gustaría hablaros de un proyecto interesante y hermoso que descubrí en la cuenta de Instagram de Calpurnio (creador de El bueno de Cuttlas) el pasado mes de abril. Se trata del proyecto 36 Days of Type (36 días de tipos).
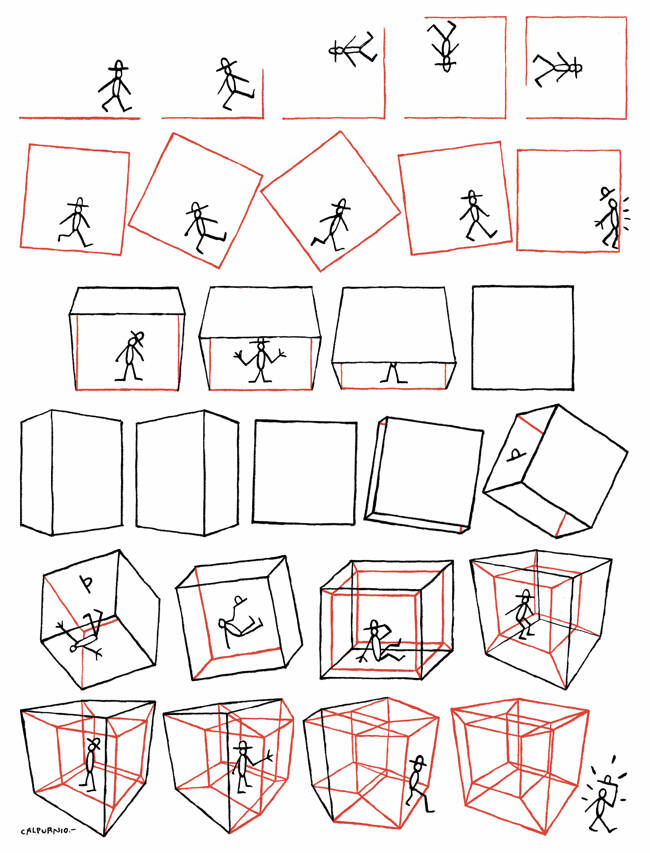 El bueno de Cuttlas en la cuarta dimensión, de Calpurnio, publicado el 29 de marzo de 2021 en Valencia Plaza
El bueno de Cuttlas en la cuarta dimensión, de Calpurnio, publicado el 29 de marzo de 2021 en Valencia Plaza
Este es un proyecto creado en 2014 por la diseñadora gráfica Nina Sans y el diseñador gráfico Rafa Goicoechea, del estudio de diseño gráfico treintayseis, de Barcelona. Como cuentan sus creadores en la página web del proyecto 36 Days of Type, ellos decidieron desafiarse a sí mismos creando algo nuevo cada día, nuevos diseños personales en torno a la tipografía y el diseño gráfico. Entonces decidieron invitar a más personas a sumarse a este desafío. Para ello crearon el proyecto 36 Days of Type: “Una celebración de 36 días de la tipografía y la creatividad, animando a diseñadores, artistas visuales y creativos de todos los campos en un acto global y simultáneo de creatividad alrededor de la tipografía y la forma de las letras (y números)”.

¿En qué consistía el proyecto 36 Days of Type? El objetivo del mismo era animar a diseñadores, ilustradores y artistas gráficos a crear nuevos diseños, o interpretaciones personales, de las letras del alfabeto y los números (cifras básicas) del alfabeto latino, durante 36 días consecutivos. Cada día estaría dedicado a una letra del alfabeto o a un número, siguiendo un calendario prefijado (como el que aparece en la siguiente imagen, correspondiente a la edición de 2021). Los participantes en el proyecto debían de subir su diseño de la letra o número correspondiente a ese día en Instagram, etiquetando la imagen convenientemente, según las instrucciones indicadas en la página del proyecto.
 Calendario de la edición de 2021 del proyecto 36 Days of Type
Calendario de la edición de 2021 del proyecto 36 Days of Type
Cada día, durante los treinta y seis que duraba el reto gráfico, la organización del proyecto seleccionaba algunos de los diseños presentados y los publicaba en su página oficial de Instagram (36daysoftype), así como en Facebook y Twitter. Además, a lo largo del año se irán publicando el resto de diseños que se han presentado al proyecto, para mostrar el trabajo de los artistas gráficos involucrados.
 Diseños de Calpurnio de algunas de las letras, una D geométrica, una G áurea, una H imposible o una K poliédrica
Diseños de Calpurnio de algunas de las letras, una D geométrica, una G áurea, una H imposible o una K poliédrica
En la cuenta de Instagram del proyecto 36 Days of Type podéis encontrar los hermosos e interesantes diseños seleccionados cada día, de letras y números. Aunque en esta entrada del Cuaderno de Cultura Científica os mostraré algunos de los diseños de números que fueron seleccionados por la organización. Iremos día a día o, mejor dicho, cifra a cifra.
La parte numérica del proyecto se inició el día 1 de mayo, con el número 0. El primer diseño que he seleccionado es del diseñador brasileño Daniel Escudeiro (aquí podéis ver parte de su trabajo, en la página del diseñador en Behance: Daniel Escudeiro).
 Diseño del número 0 realizado por el diseñador Daniel Escudeiro
Diseño del número 0 realizado por el diseñador Daniel Escudeiro
El siguiente diseño del número 0, que es un delicado diseño hecho a mano, es de la letrista finlandesa Monika Fällman.
 Diseño a mano del número 0 realizado por la finlandesa Monika Fällman
Diseño a mano del número 0 realizado por la finlandesa Monika Fällman
El primer diseño que os muestro del número 1 es un diseño geométrico del artista valenciano Tormius, Adrià Tormo (aquí podéis ver parte de su trabajo, en la página del artista, Tormius).
 Diseño geométrico del número 1 realizado por el valenciano Tormius
Diseño geométrico del número 1 realizado por el valenciano Tormius
El siguiente diseño del número 1 lleva el título Gender Equality 1+1=1 (Igualdad de género, 1+1=1), de la artista francesa Katell (página en Etsy, Quatelle [https://www.etsy.com/fr/shop/QUATELLE]).
 Diseño del número 1, Gender Equality 1+1=1, realizado por la artista francesa Katell
Diseño del número 1, Gender Equality 1+1=1, realizado por la artista francesa Katell
Siguiendo la cuenta creciente de los números, ahora nos toca el número 2. El primer diseño que vamos a mostrar corresponde a la agencia creativa estadounidense Swoon Studios (cuya página web es Swoon Studios).
 Diseño del número 2 de Swoon Studios
Diseño del número 2 de Swoon Studios
El segundo diseño del número 2 es un diseño plumífero de la artista finlandesa Jenni Pasanen (podéis acceder a sus diferentes páginas en esta dirección Jenni Pasanen).
 Diseño del número 2 de la artista finlandesa Jenni Pasanen
Diseño del número 2 de la artista finlandesa Jenni Pasanen
Podéis ver más diseños de este número, y de los demás números, en las diferentes cuentas del proyecto, por ejemplo, en Facebook, de donde estamos seleccionando los diseños, sus imágenes, para esta entrada del Cuaderno de Cultura Científica.
Para el número 3 os traigo un diseño muy festivo, esta creación de la diseñadora gráfica Jessie Noble (podéis ver algunos trabajos de esta artista en la página de Dribbble).
 Diseño del número 3 de la artista Jessie Noble
Diseño del número 3 de la artista Jessie Noble
La siguiente propuesta es de la diseñadora y letrista rusa Olemie (cuya página es Olemie).
 Diseño del número 3 de la artista rusa Olemie
Diseño del número 3 de la artista rusa Olemie
El juego “cuatro en raya” es la idea generadora del interesante diseño seleccionado para el número 4, del artista gráfico y creador de videos estadounidense Dylan Blau (podéis disfrutar de sus trabajos en la página del artista Dylan Blau).
 Diseño del número 4 del artista estadounidense Dylan Blau
Diseño del número 4 del artista estadounidense Dylan Blau
Y la artista gráfica, afincada en Beirut, Nancy Kouta (cuya página web es Nancy Kuota) propuso la siguiente imagen.
 Diseño del número 4 de la artista Nancy Kouta
Diseño del número 4 de la artista Nancy Kouta
Entre los hermosos diseños del número 5, hemos elegido este de la diseñadora colombiana Lagabrie, Gabriela Parra.
 Diseño del número 5 de la artista colombiana Lagabrie, Gabriela Parra
Diseño del número 5 de la artista colombiana Lagabrie, Gabriela Parra
Y otro hermoso diseño de la artista gráfica y letrista chilena Flor Flay (Florencia Study), algunos de cuyos trabajos podéis apreciar en su página web Florencia Study.
 Diseño del número 5 de la artista chilena Flor Flay
Diseño del número 5 de la artista chilena Flor Flay
Seguimos con el número 6. Como para otros números, y letras, hay diseños que son animaciones. Podéis visitar las diferentes cuentas del proyecto 36 Days of Type para ver estos diseños también, algunos son impresionantes. El primer diseño que he seleccionado para el número 6 es de la artista británica Amber Maxwell, que, aunque es una imagen animada, mostramos aquí el inicio del diseño.
 Diseño del número 6 realizado por la artista británica Amber Maxwell
Diseño del número 6 realizado por la artista británica Amber Maxwell
Y la segunda elección para el número 6 es este diseño del artista afincado en Estados Unidos Zsolt M, Zsolt van den Már (aquí tenéis su página en Dribble, Zsolt).
 Diseño del número 6 del artista Zsolt M
Diseño del número 6 del artista Zsolt M
Seguimos avanzando en los números y ya llegamos al número 7 (sobre este número podéis leer la entrada del Cuaderno de Cultura Científica dedicada al mismo: Siete, un número muy popular). El primer diseño que traemos a esta entrada, de entre los seleccionados por el proyecto, es de la artista gráfica y letrista suiza Océane Haenni (cuya página en Behance es Océane Haenni). Es un diseño para las personas amantes de los gatos.
 Diseño del número 7 de la artista suiza Océane Haenni
Diseño del número 7 de la artista suiza Océane Haenni
El segundo diseño del número 7 es de la diseñadora gráfica india Seema Surana (podéis disfrutar de más trabajos suyos en la página de Behance de Seema Surana).
 Diseño del número 7 de la artista india Seema Surana
Diseño del número 7 de la artista india Seema Surana
El diseñador afincado en Berlín, Christian Pietrzok, que en Instagram tiene la cuenta A letter a day donde publica desde 2017 cuando empezó el reto de publicar un nuevo diseño de una letra, o un número, cada día de ese año, nos propone el siguiente diseño para el número 8.
 Diseño del número 8 de Christian Pietrzok
Diseño del número 8 de Christian Pietrzok
El segundo diseño que os traemos del número 8 es del diseñador gráfico danés Aggerhomes (Martin Aggerholm), cuya página web es Aggerhomes.
 Diseño del número 8 del diseñador gráfico suizo Aggerhomes
Diseño del número 8 del diseñador gráfico suizo Aggerhomes
El último número del proyecto con el que finalizaba la octava edición del proyecto 36 Days os Type, fue el número 9 (al que también dediqué una entrada con el título El número nueve en una noche de verano). El diseñador gráfico de Barcelona, Loor Nicolas (del que podéis disfrutar de más trabajos en su página de Behance, Loor Nicolas), propuso un diseño de ficción.
 Diseño del número 9 del diseñador gráfico de Barcelona Loor Nicolas
Diseño del número 9 del diseñador gráfico de Barcelona Loor Nicolas
Y terminamos con una propuesta muy africana de la diseñadora británica Ella Smith, a través de su cuenta Ella Create.
 Diseño del número 9 de la diseñadora gráfica británica Ella Smith
Diseño del número 9 de la diseñadora gráfica británica Ella Smith
Espero que hayáis disfrutado de este pequeño paseo por algunos diseños de los números, de las diez cifras básicas, de nuestro sistema de numeración, del 0 al 9, dentro del proyecto 36 Days of Type. Podéis admirar, como ya hemos comentado, los demás diseños en Instagram. Facebook o Twitter.
Me gustaría terminar con una propuesta personal muy sencilla. Está basada en la hipótesis fantástica sobre el origen de la grafía de los números del astrólogo árabe Aben Ragel (siglo X-XI), que mostré en mi entrada Teorías fantásticas del origen de la grafía de las cifras y en los colores del artista neerlandés Piet Mondrian (1872-1944). El diseño de las diez cifras básicas sería el siguiente.










¿Se os ocurre a vosotras algún otro diseño para los números? Podéis animaros con los vuestros.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo 36 días de tipos (de números) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los números apocalípticos
- Los números que proporcionan alegría
- El secreto de los números que no querían ser simétricos

