¿Por qué nos gusta el azúcar?
Josu Lopez-Gazpio
El azúcar que consumimos cada día tiene un gran poder adictivo. Los efectos que produce en el organismo pueden compararse a los que produce el alcohol. Así lo afirma el equipo científico de la Universidad de California que firmó el artículo The toxic truth about sugar -la verdad tóxica sobre el azúcar-. En su opinión, el consumo crónico y continuado tanto de azúcar como de alcohol pueden generar diversas afecciones: hipertensión, enfermedades de hígado y de corazón, obesidad, pancreatitis, etc. La ciudadanía, en general, tiene bastante claro que el azúcar no es bueno -aunque no se tenga muy claro cuáles son las consecuencias concretas-, pero, en tal caso, ¿por qué no eliminamos el azúcar de nuestra dieta?, ¿por qué nos atraen tanto las tartas, los helados, los dulces, los bollos, etc., y no tanto los alimentos como el brócoli, las espinacas o la berza? Lo más probable es que exista una razón evolutiva en la base de esta inclinación que tenemos por el dulce.
 Nuestra predilección por el azúcar puede tener una razón evolutiva. (Fotografía: congerdesign – imagen de dominio público. Fuente: pixabay.com)
Nuestra predilección por el azúcar puede tener una razón evolutiva. (Fotografía: congerdesign – imagen de dominio público. Fuente: pixabay.com)Las declaraciones publicadas por los investigadores Robert Lustig, Laura Schmidt y Claire Brindis en 2012 en la revista Nature crearon una gran polémica y, a día de hoy, el debate sigue abierto. Afirmaron que el azúcar y el alcohol pueden tener unas consecuencias parecidas en la salud y que es necesario tomar medidas para reducir su consumo. El debate está servido. Según algunas personas, lo realmente perjudicial no es el azúcar en sí, sino la obesidad. Otras fuentes afirman que sí, que el azúcar es prácticamente un veneno. Antes del debate surgido a raíz del artículo de 2012, la comunidad científica ya estaba más o menos de acuerdo en que el azúcar no es bueno para la salud. Pero lo cierto es que el dulce nos resulta más atractivo que otros alimentos con mayor cantidad de nutrientes. Si es tan perjudicial -no son más que calorías-, ¿por qué nos gusta tanto?
La ciencia ha intentado dar respuesta a esta cuestión en numerosas ocasiones. Basándose en los fenómenos estudiados, el primer factor destacable es el siguiente: a muchas personas adultas les gusta el azúcar, pero entre los niños y las niñas es aún más llamativo; prácticamente a todos les gustan los dulces.
Las investigaciones han corroborado que esto es así, y que, además, la preferencia de las niñas y niños por los alimentos dulces es desde que nacen. Se ha llegado a la conclusión de que a los recien nacidos también les gusta el dulce y, por otro lado, es un patrón que se repite en la mayoría de las culturas y lugares del mundo. En el caso de la infancia, además, no hay límite de nivel de azúcar. Si bien entre las personas adultas, por ejemplo, se ha comprobado que las bebidas dulces, por encima de ciertos niveles de azúcar ya no son tan apetecibles, en el caso de los niños y las niñas, se ha observado que no hay límite. A pesar de disolver todo el azúcar posible en una bebida -superado el nivel de saturación de la disolución-, les sigue gustando.
Si bien es verdad que, en cierta medida, el azúcar es necesario; como fuente energética tiene muchas calorías. Si esa energía es necesaria, el azúcar la ofrece. El problema es que el aporte calórico es muy grande. En el caso de los niños y las niñas, la explicación puede estar en el crecimiento de los huesos. Los huesos que están en crecimiento segregan unas hormonas, las cuales pueden influir en el metabolismo. Además, se sabe que otras hormonas metabólicas, como la leptina o la insulina, han demostrado actuar en las áreas cerebrales que controlan los antojos y apetitos, e incluso directamente se unen a lengua, donde inciden en la preferencia por los gustos dulces.
Pero, ¿cuál es la verdadera razón para esa preferencia por el azúcar? Tal y como hemos señalado al inicio, debemos remitirnos a motivos evolutivos. En las primeras etapas de la evolución humana, los seres humanos que consumían mayor cantidad de calorías eran los que vivían por más tiempo; por lo tanto, era más probable para ellos transmitir sus genes a sus sucesores. Es posible que los humanos que se alimentaban de fruta tuvieran una vida más larga que los que se alimentaban de verduras, ya que las primeras tienen más calorías que las segundas. Las frutas tienen una mayor cantidad de azúcares, por eso son más dulces que las verduras y otro tipo de alimentos. A fuerza de la evolución, la selección natural y el tiempo, poco a poco, se normalizó la preferencia por los alimentos dulces. La progresiva priorización de los alimentos dulces se convirtió en una ventaja evolutiva.
Aunque la preferencia por lo dulce parece ser una característica que está adherida en los genes, hoy nuestra vida no tiene nada que ver con la de aquellos primeros seres humanos. No tenemos las mismas necesidades energéticas y obtener calorías no es ningún problema. En el día a día, extraemos el azúcar de la fruta para añadirlo de forma concentrada a otros alimentos. Sin embargo, abusamos del azúcar, no porque comamos demasiada fruta -que tiene más nutrientes-, sino porque ingerimos alimentos que son puro azúcar y aportan una gran cantidad de calorías.
Sin lugar a dudas, debemos afrontar el problema de la ingesta excesiva de azúcar para reducir los niveles de obesidad -sobre todo la obesidad infantil- y el primer paso es el tratar de conocer la química y la biología que hay detrás de esta «predilección» por el azúcar.
Fuentes:
- Ramirez, I. (1990). Why do sugars taste good? Neurosci Biobehav Rev., 14(2), 125-134. DOI: 10.1016/s0149-7634(05)80213-1
- Pepino, Yanina M., Mennella, Julie A. (2005). Sucrose-induced analgesia is related to sweet preferences in children but not adults. Pain, 119(1-3), 210-218. DOI: 10.1016/j.pain.2005.09.029
- Coldwell, S. E., Oswald, T. K., & Reed, D. R. (2009). A marker of growth differs between adolescents with high vs. low sugar preference. Physiology & behavior, 96(4-5), 574–580. DOI: https://doi.org/10.1016/j.physbeh.2008.12.010
- Ventura, Alison K., Mennella, Julie A. (2011). Innate and learned preferences for sweet taste during childhood. Current Opinion in Clinical Nutrition and Metabolic Care, 14(4 ), 379-384. DOI: 10.1097/MCO.0b013e328346df65
- Lustig, R.; Schmidt, L. & Brindis, C. (2012). The toxic truth about sugar. Nature, 482, 27–29. DOI: https://doi.org/10.1038/482027a
Más información:
- McGee, Harold (2017). La cocina y los alimentos: Enciclopedia de la ciencia y la cultura de la comida, Madrid, España: Penguin Random House Grupo Editorial.
- Stierwalt, Sabrina (6 de febrero de 2020). Why Does Sugar Taste So Good? Scientific American. Consultado el 13 de junio de 2020.
Sobre el autor: Josu Lopez-Gazpio (@Josu_lg) es doctor en Química, profesor y divulgador científico.
Este artículo se publicó originalmente en euskara el 24 de junio de 2020 en el blog Zientzia Kaiera. Artículo original.
El artículo ¿Por qué nos gusta el azúcar? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Azúcar moreno o azúcar milagro?
- Azúcar moreno, ¿mejor que el azúcar blanco?
- El azúcar oculto en los alimentos
La superioridad ilusoria y otros vicios mentales
 Imagen: Elias Sch / Pixabay
Imagen: Elias Sch / PixabayCasi nadie piensa de sí mismo que es un idiota. Es más, no todos piensan de un idiota que, efectivamente, lo es; porque quizás tenga familiares y amistades que, muy probablemente, no tendrán tan mal concepto de su pariente o amigo.
Parte de la dificultad para objetivar estas cosas, así como para ponernos de acuerdo acerca de lo limitadas que son las personas que conocemos o que es uno mismo, se debe a que el pensamiento se ve muy afectado por vicios sistemáticos a los que denominamos sesgos. Son vicios que nos ayudan a vivir y, algunos al menos, se hallan firmemente instalados en nuestra mente porque ayudaron a nuestros antepasados a dejar descendencia, razón por la que esos rasgos se han perpetuado. Otros quizás son subproductos inevitables de la forma en que funciona la mente. Es bueno, no obstante, ser consciente de su existencia y tratar de identificarlos en nosotros mismos. Solo así podremos aliviar sus efectos aunque nunca podamos librarnos del todo de ellos. Veamos algún ejemplo.
Tendemos a percibir los sesgos en los juicios de los demás, mientras que no los percibimos en nosotros mismos. Se denomina a este efecto prejuicio del punto ciego, y tiene su origen en una motivación, denominada automejora, que hace que tengamos una imagen favorable de nosotros mismos. Resulta, por supuesto, muy útil, porque nos ayuda a superar obstáculos o a crecernos en la adversidad. La contrapartida es que hace muy difícil que mejoremos, menos aún si son otros los que nos señalan que no lo estamos haciendo bien.
Otro sesgo muy común es el del status quo, que consiste en la preferencia por que las cosas no cambien y el sentimiento de que cualquier cambio conllevará un empeoramiento. Esta tendencia nos impulsa, por ejemplo, a mantener costumbres, fijar el sentido del voto en unas elecciones, o no cambiar la marca de nuestro refresco favorito.
De otra naturaleza es la falacia del jugador (del apostador), que consiste en atribuir una menor probabilidad a que ocurran cosas que han ocurrido de forma muy frecuente en el periodo anterior o lo contrario. Esta falacia tiene su origen en la creencia de que sucesos aleatorios pasados condicionan los futuros. No es más probable que salga cara en la siguiente ocasión que lancemos una moneda al aire por el hecho de que hayan salido seis cruces de manera consecutiva. Pero tendemos a pensar que sí.
Si tuviera que destacar un sesgo por encima de todos los demás, al menos en lo que se refiere a sus implicaciones sociales, me quedaría con el efecto Dunning-Kruger. Es muy simple, aunque de consecuencias impresionantes. El efecto, también denominado de superioridad ilusoria, consiste en la tendencia de las personas menos dotadas intelectualmente a pensar lo contrario de sí mismas. Esto es, en general, los más incapaces tienden a pensar que lo son menos que los demás; se creen muy listos, de hecho. La razón para que piensen así es que es su misma incapacidad lo que les impide darse cuenta de ella. Viven en un mundo intelectualmente satisfactorio, sabiéndose, de forma completamente ilusoria, que son más listos que los demás.
Ese efecto tiene su reverso: es relativamente frecuente que los más dotados intelectualmente sufran el denominado síndrome del impostor. Consiste en creerse inferiores a aquellos con quienes se suelen encontrar e, incluso, no ser merecedores de su compañía.
Pocos sesgos pueden tener un efecto tan devastador como el Dunning-Kruger: piense, si no, en todos esos legos que creen saber más de virus y pandemias que quienes han dedicado su vida profesional a estudiarlos.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La superioridad ilusoria y otros vicios mentales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La osteopontina evita la aparición precoz de la enfermedad de hígado graso no alcohólica por envejecimiento
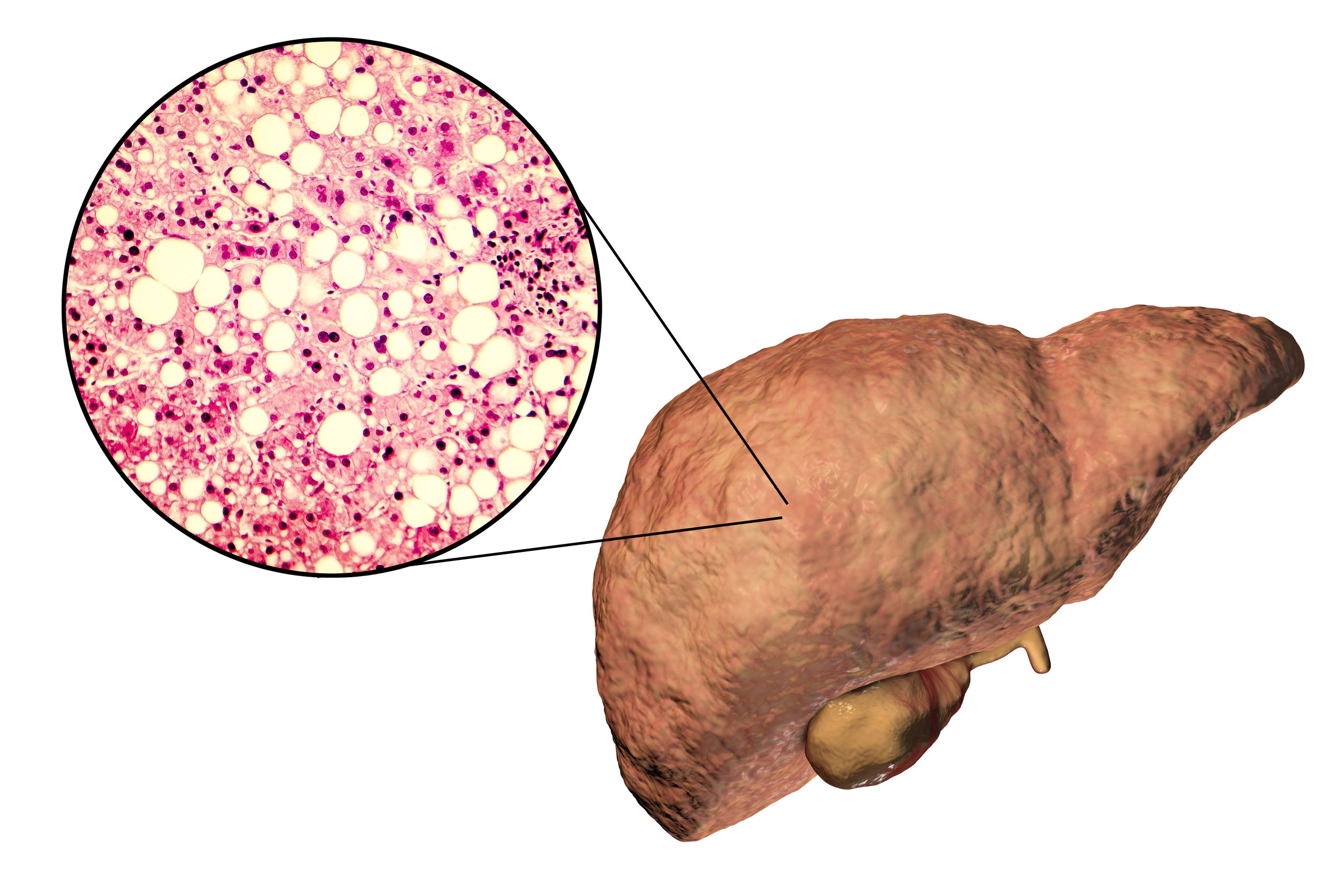 Hígado graso no alcohólico. Imagen: Kateryna Kon / 123RF
Hígado graso no alcohólico. Imagen: Kateryna Kon / 123RFEn un trabajo reciente el grupo de investigación Lipids & Liver de la UPV/EHU muestra que, al contrario de lo que se esperaba, durante el envejecimiento es necesario mantener los niveles fisiológicos hepáticos de la osteopontina, una proteína multifuncional relacionada con varias enfermedades graves, para prevenir la progresión de la enfermedad de hígado graso no alcohólica relacionada con la edad.
La enfermedad hepática metabólica grasa también conocida como enfermedad de hígado graso no alcohólica es una de las causas más comunes de enfermedad hepática en los países occidentales e incluye un espectro de trastornos. Está fuertemente asociada a enfermedades metabólicas como la obesidad o la diabetes mellitus tipo 2. Durante el envejecimiento se produce un aumento en la acumulación de lípidos dentro del hígado que puede comprometer su función normal. El grupo de investigación de la UPV/EHU Lipids & Liver, del Departamento de Fisiología de la Facultad de Medicina y Enfermería, investiga “la enfermedad de hígado graso no alcohólica y enfermedades metabólicas asociadas. En este trabajo nuestro objetivo fue encontrar qué mecanismos pueden estar implicados en el desarrollo de esta enfermedad hepática a lo largo del envejecimiento, para poder tratar o retrasar su aparición”, explica la doctora Patricia Aspichueta, responsable del grupo de investigación.
Se trata de una enfermedad de progresión lenta: “En algunos pacientes no evoluciona, se queda en la primera fase de acumulación de grasa, simplemente en hepatoesteatosis; en otros pacientes puede tardar incluso 20 años en progresar desde una hepatoesteatosis hasta que aparece esteatohepatitis, asociada o no a fibrosis; sin embargo, hay pacientes en los que evoluciona más rápido con la edad”, explica Aspichueta. Por eso es muy importante saber “qué mecanismos están implicados en hacer que el hígado sea más vulnerable a determinados inputs, fomentando el desarrollo y/o progresión de la enfermedad”.
Una de las proteínas relacionadas con el envejecimiento celular es la osteopontina, una proteína multifuncional que se encuentra en muchos tejidos y que, como muestran estudios anteriores desarrollados por Lipids & Liver, modula el metabolismo en el hígado y “que se ha asociado a procesos de enfermedades muy negativas como el cáncer y la cirrosis hepática”, explica Aspichueta. En un trabajo que ha sido parte de la tesis doctoral de la investigadora Beatriz Gómez Santos, “curiosamente encontramos, en contra de lo esperado, que la osteopontina es protectora, es decir, que se necesita para evitar una aparición prematura de esta enfermedad durante el envejecimiento —añade—. Hemos visto que si se inhibe o silencia la osteopontina, como se propone en ciertos contextos (para evitar fibrosis hepáticas, etc.), esa aparición de grasa es precoz y la enfermedad aparece antes. Por tanto, durante el envejecimiento, es fundamental mantener esta proteína en niveles fisiológicos en el hígado”.
El estudio de enfermedades metabólicas es complejo, porque los cambios metabólicos que se generan son muy dinámicos y ocurren de manera coordinada entre varios tejidos. Además, se estudian los cambios producidos en las moléculas a lo largo de su metabolización: “Utilizamos, entre otras, moléculas marcadas radiactivamente y hacemos un seguimiento al camino que siguen, dónde se incorporan, etc.”. Las investigadoras afirman que “este hallazgo es fundamental porque hemos aprendido muchísimo del proceso de envejecimiento”.
Actualmente, Gómez Santos está estudiando “la vulnerabilidad hepática que hombres y mujeres desarrollan a lo largo de la edad para padecer la enfermedad hepática”. Estamos analizando en paralelo en hombres y mujeres los procesos metabólicos relacionados con el desarrollo y progresión de la enfermedad hepática”. La evidencia de distintos estudios sugiere que la incidencia de la enfermedad de hígado graso no alcohólica es mayor en hombres que en mujeres. Además, en mujeres la incidencia parece ser menor en premenopáusicas. Se trata de un complejo estudio con diferentes variables con un único objetivo: “Al final lo que queremos conseguir es un envejecimiento saludable. Queremos evitar que la enfermedad metabólica aparezca, o si ya ha aparecido que evolucione de manera rápida”.
Referencia:
Beatriz Gómez-Santos, Diego Saenz de Urturi, Maitane Nuñez-García, Francisco Gonzalez-Romero, Xabier Buque, Igor Aurrekoetxea, Virginia Gutiérrez de Juan, Maria J. Gonzalez-Rellan, Carmelo García-Monzón, Águeda González-Rodríguez, Lorena Mosteiro, Gaizka Errazti, Patricia Mifsut, Sonia Gaztambide, Luis Castaño, Cesar Martin, Rubén Nogueiras, María L. Martinez-Chantar, Wing-Kin Syn, Patricia Aspichueta (2020) Liver osteopontin is required to prevent the progression of age-related nonalcoholic fatty liver disease Aging Cell DOI: 10.1111/acel.13183
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La osteopontina evita la aparición precoz de la enfermedad de hígado graso no alcohólica por envejecimiento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Avances contra la enfermedad de hígado graso no alcohólica
- La enfermedad del hígado graso no alcohólico, una gran desconocida
- Una infección vírica puede activar la aparición de diabetes tipo I
Un sonido para hablar con los dioses
“–Mi amigo soplaba con esto.
Ralph comprendió al fin y lanzó el aire desde el diafragma. Aquello empezó a sonar al instante. Una nota estridente y profunda estalló bajo las palmeras, penetró por todos los resquicios de la selva y retumbó en el granito rosado de la montaña. De las copas de los árboles salieron nubéculas de pájaros y algo chilló y corrió entre la maleza. Ralph apartó la concha de sus labios. – ¡Qué bárbaro!
Su propia voz pareció un murmullo tras la áspera nota de la caracola.“
En El señor de las moscas, la famosa novela de William Golding, un avión se estrella en medio del Pacífico y convierte a una treintena de adolescentes en los únicos habitantes de una isla desierta1. Poco después del accidente, dos de ellos se encuentran caminando por una playa. A lo lejos, entre las algas, avistan un objeto de color cremoso, ¡una caracola! Aunque al principio Ralph no sabe cómo usarla, su poderoso sonido le acaba convirtiendo en el jefe de una peculiar tribu. Primero, el instrumento sirve para congregar a los demás supervivientes de la isla. Una vez reunidos, la caracola se utiliza para articular una especie de democracia asamblearia donde quienquiera que la sostenga tiene la palabra y debe recibir la atención silenciosa del resto. El instrumento se convierte así en un símbolo de la razón, la convivencia y el orden, y Ralph, como su descubridor, es elegido líder de todo el grupo.
Resulta tentador intentar imaginar al primer ser humano que hace decenas de miles de años hizo vibrar sus labios contra una concha vacía y descubrió esa misma sensación de poder que Golding ejemplifica en su novela. El instrumento debió de otorgarle la capacidad de alcanzar distancias nunca antes imaginadas, una verdadera voz sobrehumana. No sabemos si sus compañeros le harían jefe de su cueva o qué pero, como mínimo, esa tarde tendría algo interesante que contar. Tampoco podemos conocer con precisión cuándo pudo suceder esto. A fin de cuentas, para hacer sonar una caracola basta con ir a la playa y encontrarse una con la punta un poco rota. Claramente, este tipo de objetos antecede por mucho a cualquier cultura humana. Es su uso con fines sonoros lo que los convierte en un instrumento musical. Pero los soplidos no dejan restos arqueológicos. Es necesario rastrearlos a partir de otras huellas más indirectas.
 Fuente: Wikimedia Commons.
Fuente: Wikimedia Commons.Se considera que uno de los ejemplos más tempranos de concha musical procede la región del Mediterráneo y data del periodo Magdaleniense a finales del Paleolítico superior. Se trata de un ejemplar de Charonia lampas semi fosilizado descubierto en 1931 en una cueva de los Pirineos23. Tiene aproximadamente unos 20.000 años de antigüedad. Se piensa que fue eso, un instrumento, porque además de encontrarse entre otros objetos y pinturas humanas, la cueva de Marsoulas está a 250 kilómetros de la costa más cercana. Y las caracolas no vuelan, claro. Alguien debió de llevarla consigo hasta allí, a pesar del esfuerzo que esto pudiera suponer. Esto nos hace pensar que se trataba de un objeto valioso. Existen, además, otras evidencias de su uso. La punta estaba rota y el desgaste general sugiere que la concha pasó de mano en mano de forma continuada. Sin embargo, es posible también que se usase para beber o con algún otro fin ritual. Por desgracia, de nuevo, los soplidos se los lleva el viento y tampoco se han encontrado más ejemplos de la misma época que ayuden a dirimir la cuestión.
 Conchas talladas o shankhas, siglos XI-XII, India. La de la izquierda está tallada con una imagen de los dioses Lakshmi y Vishnu. Fuente: Wikimedia Commons
Conchas talladas o shankhas, siglos XI-XII, India. La de la izquierda está tallada con una imagen de los dioses Lakshmi y Vishnu. Fuente: Wikimedia CommonsExisten bastantes más caracolas del periodo Neolítico que sugieren que el instrumento debió de tener un uso continuado. Sorprende todavía más que sea común en culturas de casi todo el mundo. Se han encontrado ejemplos procedentes de Europa, India, China, Japón, el Tíbet, Oceanía y las Américas, con la curiosa excepción de África del norte4. En todos los casos, la potencia sonora del instrumento parece determinar sus usos culturales, bien por su capacidad para comunicarse a través de grandes distancias (como corno de guerra, por ejemplo), bien con fines espirituales y religiosos. Aunque bien se podría argumentar que ambos usos responden al mismo objetivo. A fin de cuentas, qué mayor distancia que la que se necesita atravesar para comunicarse con los dioses. Ese mismo sonido, de un origen tan humilde, ha hechizado a humanos de todo el mundo desde la prehistoria. Y probablemente, por un mismo motivo: a todos les sorprendió lo mismo que su propia voz pareciese “un murmullo tras la áspera nota de la caracola”.
Notas y referencias:
1Aparte del libro, recomiendo también, esta lectura en The Guardian: The real Lord of the Flies: what happened when six boys were shipwrecked for 15 months
2JT Russell, 1932. Report on archeological research in the foothills of the Pyrenees (with eight plates). Smithsonian Miscellaneous Collections.
3Bégouën Comte, JT Russell, 1933: La Campagne de Fouilles de 1931 à Marsoulas, Tarté et Roquecourbère Mission Franco-Américaine de Recherches Préhistoriques.
4“The Conch Horn. Shell Trumpets of the World from prehistory to today”. Jeremy Montagu.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Un sonido para hablar con los dioses se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Más FUN WITH MATHS, diversión con matemáticas
Hace un año, con el inicio del período de las vacaciones estivales de los centros educativos, publicamos en el Cuaderno de Cultura Científica la entrada FUN WITH MATHS, diversión con matemáticas, en la que se explicaban algunos sencillos trucos de magia relacionados con las matemáticas. En esta entrada recuperamos esta idea y mostramos otros dos trucos de magia matemática con los números.
 Rompecabezas inventado por Sam Loyd (1841-1911) Get off the Earth / Borrado de la faz de la Tierra (1896). La Tierra es un disco que gira sobre su centro de forma que en la primera posición –esta imagen–, con la flecha apuntando hacia NE, se ven 13 guerreros chinos. Imagen de este rompecabezas antiguo de George Glazer Gallery
Rompecabezas inventado por Sam Loyd (1841-1911) Get off the Earth / Borrado de la faz de la Tierra (1896). La Tierra es un disco que gira sobre su centro de forma que en la primera posición –esta imagen–, con la flecha apuntando hacia NE, se ven 13 guerreros chinos. Imagen de este rompecabezas antiguo de George Glazer Gallery
 En la segunda posición, con la flecha hacia NW, ha desaparecido un guerrero chino y solo hay 12. Imagen de este rompecabezas antiguo de George Glazer Gallery
En la segunda posición, con la flecha hacia NW, ha desaparecido un guerrero chino y solo hay 12. Imagen de este rompecabezas antiguo de George Glazer GalleryVayamos con el primer truco. Es un sencillo truco en el que se pide a una persona del público que piense en un número de cuatro dígitos, que finalmente vamos a recuperar tras algunas operaciones aritméticas. Una parte muy importante de los trucos de magia es la presentación de los mismos, así como todo el teatro que se realiza en su puesta en escena. Por ejemplo, este truco se puede presentar de la siguiente forma.
La persona que realiza el truco dispone de una pizarra o una hoja de papel grande sobre la que realizará el truco. Para empezar, le pide a alguien del público que piense un número de cuatro dígitos y que lo diga en alto, para que todo el mundo lo escuche. La persona que realiza el truco, con cierta teatralidad, le dirá que ha elegido un número muy especial, con propiedades mágicas. A continuación, se explican cuáles son esas propiedades mágicas.
El mago, o la maga, escribirá en la pizarra, en grande, el número que ha elegido la persona voluntaria del público. Pensemos que ese número es 7.483.
Después, siempre con la mayor teatralidad posible, escribirá en la pizarra el primer dígito, desde la izquierda, del número: en nuestro ejemplo, 7.
Debajo de este, y con el objetivo de realizar una suma, escribirá el número formado por los dos primeros dígitos, desde la izquierda: en el ejemplo, 74.
Más abajo aún escribirá el número formado por los tres primeros dígitos: 748. Y sumará esos tres números. Para el número elegido el resultado es 7 + 74 + 748 = 829.
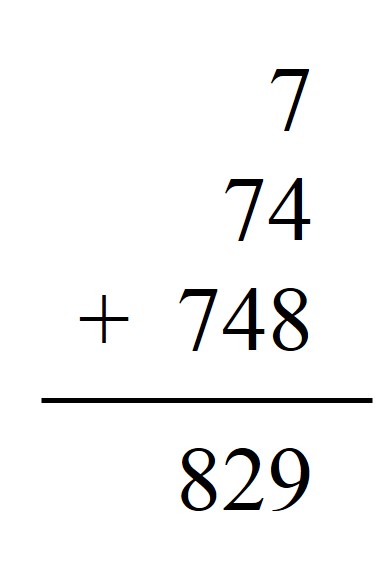
El siguiente paso es multiplicar en la pizarra el resultado de la operación anterior por 9. En el ejemplo elegido quedará 829 x 9 = 7.461.
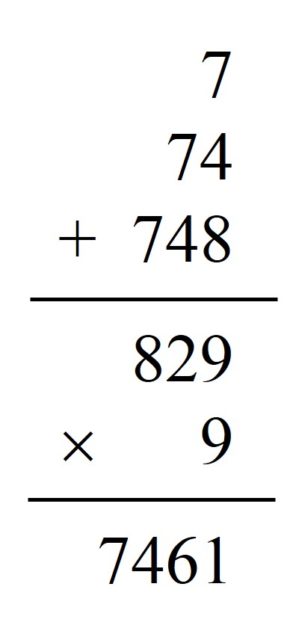
Finalmente, hay que sumar a ese resultado la suma de los dígitos del número elegido por la persona voluntaria, que en nuestro ejemplo es 7 + 4 + 8 + 3 = 22, y sorpresa, sorpresa, el resultado es efectivamente el número mágico en cuestión, 7.461 + 22 = 7.483.
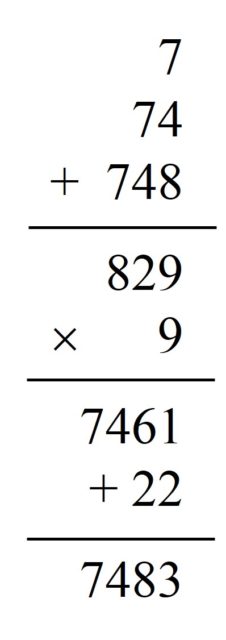
Se puede comprobar fácilmente que este truco funciona siempre. Dado un número de cuatro dígitos abcd, la operación mostrada en el truco, que es (a + ab + abc) x 9 + (a + b + c + d) da como resultado abcd.
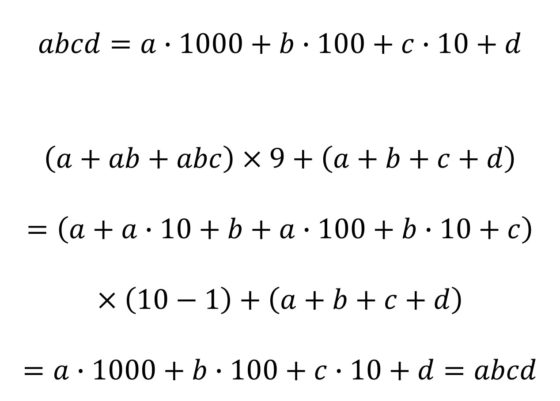
Si se realiza con detalle la operación anterior podemos darnos cuenta de por qué funciona el truco y, además, de que funcionará con un número con cualquier cantidad de dígitos.
Es un truco que no se puede hacer dos veces seguidas, al menos presentado así, ya que el público descubriría que todos los números son especiales. Lo mejor es hacerlo una vez y luego hacer otro sencillo truco, por ejemplo, el truco de la calculadora que expliqué en el video de la sección Una de mates, de la Cátedra de Cultura Científica, y que fue emitido en el programa de humor y ciencia de televisión, dirigido por José A. Pérez Ledo, Orbita Laika (segunda temporada) de La2, de Televisión Española: Una de mates, magia matemática.
 Otro rompecabezas del tipo de desapariciones, como el anterior, es el rompecabezas del huevo mágico, que fue utilizado como tarjeta anuncio en 1880, por la Wemple & Company de Nueva York. Si se corta por las líneas de puntos y se recolocan los cuatro trozos se puede formar un rectángulo con 6, 7, 8, 10, 11 o 12 huevos. Imagen de Redbubble
Otro rompecabezas del tipo de desapariciones, como el anterior, es el rompecabezas del huevo mágico, que fue utilizado como tarjeta anuncio en 1880, por la Wemple & Company de Nueva York. Si se corta por las líneas de puntos y se recolocan los cuatro trozos se puede formar un rectángulo con 6, 7, 8, 10, 11 o 12 huevos. Imagen de Redbubble
El segundo truco es un truco de cálculo mental que se puede presentar como una competición entre la mente del mago y la calculadora. Para realizar el truco se necesita una pizarra, o una hoja de papel, grande que puedan ver todas las personas del público, y una calculadora de las básicas.

Se explica que va a ser una competición entre la mente del mago y la calculadora, por lo que se necesita una persona voluntaria para que realice las operaciones en la calculadora, intentando hacerlo rápido y ganar al cálculo mental. Además, se le dará papel y lápiz por si necesita apuntar algo. Se le pide a otra persona del público que piense, y diga en alto, un número de cuatro dígitos (llamémosle en la explicación A), que se escribirá en la pizarra como se muestra más adelante en la imagen.
Para el cálculo que se va a realizar se necesita un segundo número, también de cuatro dígitos, para multiplicar por el primero, pero si solo fuese eso sería muy simple y efectivamente fácil que ganara la calculadora, por lo que vamos a complicar un poco la operación aritmética. ¿Cómo? Otra persona del público dará ese segundo número de cuatro dígitos (llamémosle B para la explicación) y la persona que realiza el truco un tercer número de cuatro dígitos (denotémoslo C). La competición consiste en multiplicar el primer número (A) por cada uno de los otros dos (A x B y A x C) y sumar el resultado (A x B + A x C). Para explicarlo mejor al público y realizar el truco se pinta el siguiente diagrama en la pizarra, suponiendo que el primer número A ofrecido por el público sea 7.354.
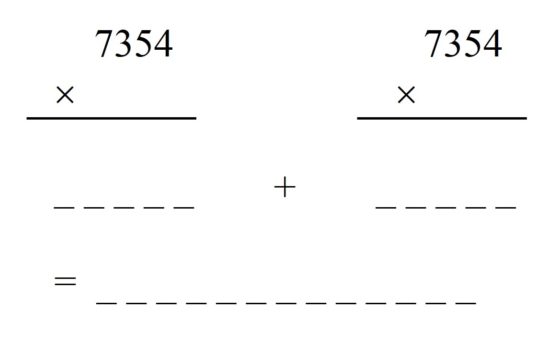
Debajo del 7.354, a la izquierda, se escribirá el segundo número proporcionado por quienes están presentes en el espectáculo de magia matemática, mientras que debajo del 7.354, a la derecha, se escribirá el número que aporta la maga matemática. Y en ese momento empieza la competición. Repetimos, se trata de ver quién consigue antes el resultado de multiplicar ese primer número 7.354 por cada uno de los dos anteriores y sumar esos resultados parciales.
Expliquemos con un ejemplo el desarrollo del truco de magia matemática. Supongamos que la segunda persona del público sugiere el número 4.067, entonces la persona que hace el truco deberá aportar el tercer número, que debe parecer que es uno cualquiera que se le ocurre en ese momento, pero que realmente cada uno de sus dígitos es el complementario respecto a 9 del dígito correspondiente del segundo número. Por lo tanto, en el ejemplo, como el segundo número es 4.067, el número que aportará el mago será 5.932 (4 + 5 = 9, 0 + 9 = 9, 6 + 3 = 9 y 7 + 2 = 9).
Es decir, con estos números concretos la competición consiste en realizar las multiplicaciones del primer número por cada uno de los otros dos, 7.354 x 4.067 y 7.354 x 5.932, y sumar los resultados de las mismas, es decir, (7.354 x 4.067) + (7.354 x 5.932).
El mago, que realiza el cálculo mental, escribirá rápidamente la solución en la parte de debajo de la pizarra, que es 73.532.646 (más adelante explicaremos de dónde ha sacado el mago ese número). La persona de la calculadora y el público se quedarán sorprendidos de la rapidez del mago, ya que habrá sido imposible realizar la operación con la calculadora en tan corto plazo de tiempo. Entonces, con ayuda de quien tiene la calculadora, se escribirán en la pizarra los pasos intermedios y el resultado final, como se muestra en la siguiente imagen, para comprobar que el número escrito es el correcto.

Expliquemos cómo ha conseguido el mago ese número y por qué sabe que es la solución buscada. Los cuatro primeros dígitos consisten en el primer número proporcionado por el público menos 1, es decir, 7354 – 1 = 7353. Mientras que los cuatro siguientes dígitos son los complementos respecto a 9 de cada uno de los dígitos de este, esto es, 2646. Juntando todo, y poniendo los puntos correspondientes, 73.532.646.
El motivo es el siguiente. Si llamamos a los tres números proporcionados A, B y C como se indicaba más arriba, el resultado que se busca es:
![]()
Pero por la propiedad distributiva, eso es lo mismo que:
![]()
Aquí está la clave del truco de magia. Como la persona que realiza el truco puede elegir C esto le permite controlar el valor de B + C y simplificar la operación aritmética. Veamos un ejemplo sencillo. Si se elige C de forma que B + C = 10.000, entonces A x (B + C) es el primer número elegido seguido de cuatro ceros, en nuestro ejemplo, 73.540.000. Pero de esta forma las personas presentes se darían cuenta de cómo has realizado el truco. Es decir, hay que esconder el truco y que parezca realmente una operación aritmética complicada.
Por este motivo se elige C para que B + C = 9.999, es decir, los complementos dígito a dígito respecto de 9 del número B. Y la operación se transforma en A x 9.999, que como es A x (10.000 – 1), el resultado es el número A menos 1 seguido de su complemento dígito a dígito respecto de nueve. En el ejemplo, 7353 y 2646, que puesto junto y poniendo los puntos de los miles (esto esconde un poco de donde viene el número, por lo que es aconsejable poner los puntos) es 73.532.646.
Bueno, pues ya conocéis otro par de trucos de magia para amenizar las reuniones familiares o con amigos. Espero que os hayan gustado.
 El rompecabezas Sailing Under False Colors/Navegando bajo falsos colores apareció en el libro Cyclopedia of 5000 Puzzles, Tricks, and Conundrums (1914) de Sam Loyd y consistía en cortar la bandera estadounidense en dos partes de forma que al recolocarla la nueva imagen de la bandera tuviese 13 barras en lugar de las 15 normales. Imagen de la versión online de la Cyclopedia of 5000 puzzles
El rompecabezas Sailing Under False Colors/Navegando bajo falsos colores apareció en el libro Cyclopedia of 5000 Puzzles, Tricks, and Conundrums (1914) de Sam Loyd y consistía en cortar la bandera estadounidense en dos partes de forma que al recolocarla la nueva imagen de la bandera tuviese 13 barras en lugar de las 15 normales. Imagen de la versión online de la Cyclopedia of 5000 puzzles Solución del rompecabezas Sailing Under False Colors/Navegando bajo falsos colores. Imagen de la versión online de la Cyclopedia of 5000 puzzles
Solución del rompecabezas Sailing Under False Colors/Navegando bajo falsos colores. Imagen de la versión online de la Cyclopedia of 5000 puzzles
Bibliografía
1.- Peter McOwan, Matt Parker, The manual of Mathematical Magic.
2.- Pedro Alegría, El rincón matemático (DivulgaMAT)
3.- Pedro Alegría, MAGIA por principios, Publidisa, 2008.
4.- Fernando Blasco, Matemagia, Temas de Hoy, 2007.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Más FUN WITH MATHS, diversión con matemáticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- FUN WITH MATHS, diversión con matemáticas
- Abril comienza con matemáticas y bromas
- Un kilogramo de novelas y matemáticas
La radiactividad no es una reacción química
 Foto: Oleksandra Bardash / Unsplash
Foto: Oleksandra Bardash / UnsplashLa emisión de partículas alfa y beta planteaba cuestiones muy difícilmente compatibles con las ideas existentes sobre la materia y su estructura. El rápido desarrollo de la química en el siglo XIX había hecho que la hipótesis atómico-molecular de la materia fuera extremadamente convincente [1]. Según la versión decimonónica de este modelo un elemento puro consta de átomos idénticos, que son indivisibles e inmutables.
Pero si un átomo radiactivo emite un fragmento tan sustancial como una partícula alfa, que resultaba ser un átomo de helio ionizado, ¿puede el átomo radiactivo permanecer inmutable? Eso no parecía plausible. Todo lo contrario, parecía que ocurría una transformación en la que el átomo radiactivo se transformaba en un átomo de un elemento químico diferente.
Si un átomo emite una partícula alfa, una parte significativa de su masa (cuatro unidades de masa atómica) se irá con la partícula. ¿Qué pasa con los átomos que emiten partículas beta? La partícula beta, que resultó ser un electrón, es mucho menos masiva que la partícula alfa. Sin embargo, su masa no es cero; por lo que un átomo radiactivo también debe sufrir algún cambio cuando emite una partícula beta.
De nuevo había que concluir que los átomos radiactivos pueden, de hecho, dividirse en dos partes de masa marcadamente desigual, una conclusión contraria al antiguo concepto básico de que el átomo es indivisible.
Otra cuestión fundamental surgió en relación con la energía asociada a los rayos emitidos por las sustancias radiactivas. Ya en 1903, Rutherford y Frederick Soddy, por un lado, y Pierre Curie y Albert Laborde, por otro, notaron que una muestra de radio se mantenía a una temperatura más alta que su entorno simplemente absorbiendo parte de la energía de las partículas alfa emitidas por los átomos de la muestra. Curie y Laborde encontraron que 1 g de radio puede producir alrededor de 0,1 kcal de energía térmica por hora. Una muestra de radio, de hecho, puede seguir liberando energía año tras año durante mucho mucho tiempo. [2]
La liberación continua de tal cantidad de energía no puede explicarse tratando la radioactividad como una reacción química ordinaria, que era la única transformación de la materia conocida en la época. Estaba claro que la radiactividad no implicaba cambios químicos en el sentido habitual [3]. La energía era emitida por muestras de elementos puros [4] y la emisión de energía de los compuestos que contienen elementos radiactivos no dependía del tipo de molécula en la que estaba presente el elemento radiactivo.
El origen de la producción de energía térmica había que buscarlo en algunos cambios profundos dentro de los átomos de elementos radiactivos, más que en reacciones químicas entre átomos. Esto era una idea revolucionaria y se necesitaba una hipótesis igualmente atrevida para explicarla. De nuevo Rutherford estaría implicado en la generación del modelo que terminaría siendo universalmente aceptado.
Notas:
[1] La hipótesis atómica dejó de ser tal para convertirse en uno de los pilares incontrovertibles de nuestro conocimiento del universo cuando Einstein formuló el modelo del movimiento browniano basándose en ella en 1905 y Perrin lo confirmó experimentalmente en 1908. Hay que enfatizar que el que los átomos existan no implica que no puedan tener estructura, a ver si una etimología nos va a nublar la razón.
[2] Tanto es así que una parte sustancial del calor interno de la Tierra proviene de procesos radiactivos.
[3] Los cambios químicos se producen en la relación de unos átomos con otros.
[4] Entre los átomos de un elemento puro puede haber reacciones químicas, ya que se forman unos enlaces y no otros, lo que hace que existan distintas estructuras del elemento que se llaman alotropos. Por ejemplo, el diamante, el grafito y el grafeno son alotropos del carbono, con propiedades muy diferentes. Las transformaciones de un alotropo en otro ni son ni espontáneas (los diamantes no se convierten en minas de lápices y las minas de lápices en diamantes de forma espontánea), ni pueden emitir energía continua durante mucho tiempo ni mucho menos a los niveles en los que lo hace la radiactividad.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La radiactividad no es una reacción química se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ratonera de Rutherford y Royds
- La ley del gas ideal a partir del modelo cinético
- La carga de las partículas radiactivas
El modelo SIR, un enfoque matemático de la propagación de infecciones
Javier Duoandikoetxea
En este periodo atípico que vivimos a menudo se subraya el valor y el papel que juega la ciencia. En este contexto, también las matemáticas hacen su aportación. Entre otras cosas, ponen a nuestra disposición herramientas que nos permiten prever la evolución de las epidemias. Pronto cumplirán su primer centenario los primeros modelos matemáticos propuestos para tal fin.
Los modelos matemáticos
Los modelos matemáticos se sirven de herramientas matemáticas para estudiar un fenómeno de la vida real de manera abstracta y simplificada. Para ello se expresan mediante una formulación matemática las relaciones entre las magnitudes que intervienen en el fenómeno. El uso y el éxito de los modelos matemáticos varía de unas ciencias a otras. Es obvio que la física está muy matematizada, pero en las ciencias de la vida, por ejemplo, la presencia de las matemáticas no ha sido tan notoria. Hay quien piensa que todo lo relacionado con la vida es demasiado complejo para ajustarse a los modelos simples y abstractos de las matemáticas. Parece que uno de los retos de la matemática aplicada en el siglo XXI será precisamente la ampliación del uso de la matemática en las ciencias de la vida.
En cualquier caso, las primeras propuestas para la aplicación de modelos matemáticos en biología vienen de lejos, si bien en los últimos tiempos es cuando se han producido importantes avances en este terreno. Así, los modelos aplicados a las enfermedades infecciosas no son nuevos, como atestigua el que trataremos aquí, presentado en un artículo que William Ogilvy Kermack y Anderson Gray McKendrick publicaron en 1927 —esto es, hace casi cien años— con el título A Contribution to the Mathematical Theory of Epidemics.
 Imagen 1: el bioquímico O. Kermack y el epidemiólogo McKendrick. (Fuentes: Royal Society y Universidad de Aberdeen, respectivamente).
Imagen 1: el bioquímico O. Kermack y el epidemiólogo McKendrick. (Fuentes: Royal Society y Universidad de Aberdeen, respectivamente).El modelo SIR
Los miembros de una población se clasifican en tres grupos: susceptibles (S=susceptible), infectados (I=infected) y recuperados (R=recovered). Cada miembro de la población pertenece únicamente a uno de los tres grupos en un momento dado. Sin embargo, se puede pasar de un grupo a otro, aunque solo en una dirección, como se muestra en el siguiente esquema:

Por tanto, un miembro susceptible se puede contagiar (pasar de S a I) y uno contagiado se puede recuperar (pasar de I a R) o puede morir. En este modelo se supone que la recuperación proporciona inmunidad y no se regresa al grupo S.
Las personas que fallecen por la enfermedad se incluyen también en el grupo R, con lo que la población total se mantiene constante. Como se habrá notado, el modelo introduce una simplificación, pues no tiene en cuenta ni los nacimientos ni las muertes por otros motivos. Existen modelos más complejos que también contemplan esos casos.
Ecuaciones
Sea t la variable que indica el tiempo y S(t), I(t) y R(t) el número de personas que hay en cada grupo en un momento t determinado. Por las razones expuestas, su suma es una constante. Sea N el tamaño de la población, es decir, S(t) + I(t) + R(t) = N, para todo t. Para plantear las ecuaciones, es necesario formular la velocidad de cambio de esas tres funciones. La expresión matemática de la velocidad es una derivada.
He aquí las ecuaciones del modelo SIR:
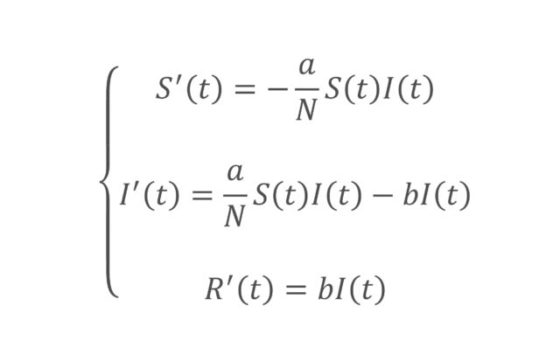
El contacto entre personas susceptibles e infectadas causará el contagio de algunos miembros de S. Dado que el riesgo de contagio depende de los contactos entre miembros de los grupos S e I, la hipótesis del modelo SIR es que sus encuentros son proporcionales al producto de S por I. Además existe un factor llamado tasa de transmisión que debe multiplicarse por dicho producto para calcular la velocidad de cambio del grupo susceptible. Expresamos esa tasa como a/N. El término figura en la ecuación porque expresa la velocidad con que se pasa de S a I. Dado que en el proceso el n.º de susceptibles disminuye y el de personas infectadas aumenta, es negativo para S’ y positivo, en cambio, para I’.
Por otra parte, quienes se curen o fallezcan pasarán de I a R. Para calcular cuántas personas lo hacen tenemos la tasa de recuperación, que ha de multiplicarse por el número de personas infectadas. Por eso aparece el término en las ecuaciones; es negativo para I’, porque reduce el n.º de personas infectadas y positivo para R’, porque hacer aumentar el n.º de recuperadas.
Para resolver las ecuaciones es necesario disponer de los datos iniciales, es decir, el n.º de miembros de cada grupo en el momento en que t=0. Se puede suponer que al principio I(0) = 1 (paciente cero), pero cabe la posibilidad de que fuera superior a uno. Además, tendremos que S(0) > 0 , pues para que haya contagio es necesario que haya susceptibles.
Soluciones de la ecuación
No se puede calcular la solución exacta de las ecuaciones, pero esto no es un problema, pues se pueden obtener soluciones aproximadas por ordenador. En cualquier caso, aun sin resolver el sistema de ecuaciones, las herramientas matemáticas nos permiten determinar algunas propiedades cualitativas de las soluciones.
Así, se observa que el comportamiento de las soluciones depende del número a/b. Se trata del número R0, la tasa básica de reproducción, en este caso. Si R0 > 1, la infección comenzará a extenderse, y si R0 < 1, esto no ocurrirá. De todas formas, si bien ese valor básico tiene incidencia al principio, posteriormente es mejor usar la tasa de reproducción efectiva o aS(t)/Nb. Como al principio S(0) y N son prácticamente iguales, cuando t=0 es casi igual a R0, pero después va reduciéndose a la vez que S.
Plantear ecuaciones formales es fácil, lo problemático es asignar unos valores adecuados a los parámetros a y b. El segundo se puede decidir observando el tiempo que se tarda en recuperarse de la enfermedad. Sin embargo, es más difícil asignar un valor a a. Si partimos de cero, ese valor es desconocido, por lo que es necesario observar el ritmo de contagios del principio. A veces se emplean datos de otros territorios o periodos, pero estos pueden proporcionar información errónea. Además, este modelo simplificado mantiene a y b constantes a lo largo del tiempo, pero en la práctica se pueden adoptar medidas para cambiar estos valores.
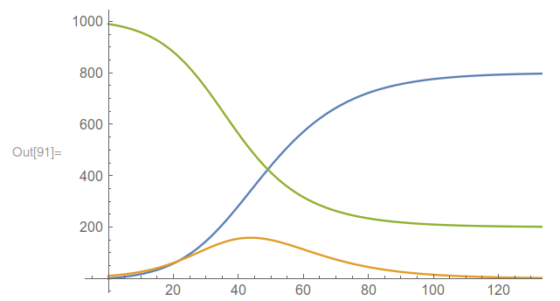 Imagen 2: una ejemplo posible del modelo SIR: S =verde -población susceptible-, I = anaranjado -población infectada-, R = azul -población recuperada-. (Fuente: Wikipedia)
Imagen 2: una ejemplo posible del modelo SIR: S =verde -población susceptible-, I = anaranjado -población infectada-, R = azul -población recuperada-. (Fuente: Wikipedia)Sea como fuere, una de las conclusiones de las ecuaciones es que el valor I(t) tiende a 0 según avanza el tiempo, es decir, se reduce el n.º de personas infectadas. De hecho, el análisis de las ecuaciones indica que debe darse un valor umbral para que la infección se propague. Si el n.º de susceptibles es inferior a ese valor, la infección no se propaga, es decir, dejará de haber personas infectadas, aunque siga habiendo susceptibles. Viendo los datos reales no se percibe la existencia de este umbral, por lo que el modelo matemático fue esencial para llegar a esa conclusión.
Por otro lado, la función I(t) llega a un valor máximo y luego comienza a descender, sin incrementarse de nuevo. Es decir, tiene un único pico. Esta es otra de las propiedades que revela el modelo matemático. No obstante, hay que recordar que el modelo es muy simple y a veces la realidad puede ser distinta.
Intervención pública
El modelo muestra que se puede frenar la propagación de la infección incidiendo en la tasa de reproducción efectiva. En el caso de los virus, se pueden emprender las siguientes acciones:
- Acortar el tiempo de la enfermedad con medicamentos.
- Reducir los contactos entre personas susceptibles e infectadas mediante medidas de aislamiento.
- Reducir la probabilidad de transmisión mediante el lavado frecuente de manos y el uso de mascarillas.
- Reducir el valor inicial S(0) mediante vacunas.
Nos suenan, ¿verdad? Las lectoras y lectores pueden pensar que estos consejos se formularon en el contexto de la Covid-19. Pues no, los he copiado de un artículo de divulgación de 2013 y se referían a la gripe. Tiene presente la evolución de las soluciones de las ecuaciones matemáticas, ya que reducir a y S(t) y aumentar b son formas de minorar la tasa de reproducción efectiva.
Efecto de las vacunas
Una de las recomendaciones anteriores era la vacunación, medida que reduce el número inicial de susceptibles y convierte la tasa de reproducción efectiva en a(1-p)/b , donde p es la fracción vacunada de la población total, teniéndose en cuenta también la efectividad de la vacuna. Por ejemplo, si el 70 % de la población está vacunado y la vacuna tiene una efectividad del 90 %, tendremos que p=0,63. Como normalmente no se puede vacunar a toda la población, y además la efectividad no suele ser del 100 %, tenemos que p < 1.
Por lo tanto, dependiendo de los valores de los parámetros a y b, se puede calcular qué proporción de la población se debe vacunar para evitar (o frenar considerablemente) la propagación de la infección. El objetivo es que el número de susceptibles se mantenga desde el principio por debajo del valor umbral mencionado más arriba. Cuando esto se consigue, se dice que se ha logrado la inmunidad comunitaria. La inmunidad comunitaria protege también a quienes no se han vacunado, incluidas, por supuesto, las personas contrarias a las vacunas. Sin embargo, si una parte significativa de la población se opone a las vacunas, se pierde la oportunidad de lograr la inmunidad comunitaria desde el principio.
Otros modelos
Como dijo el estadístico británico George Box, «todos los modelos se equivocan, pero algunos son útiles». Los modelos simplifican mucho la realidad, por lo que siempre habrá diferencia entre lo que prevén las matemáticas y lo que ocurre realmente. No obstante, lo más importante es la utilidad de la que hablaba Box. Algunos trabajos han demostrado que el modelo SIR, en su simplicidad, se ajusta bien a algunas epidemias. En cualquier caso, este ajuste puede ser más fácil a posteriori, una vez que se controlan mejor los parámetros de las ecuaciones.
Sea como fuere, el SIR no es el único modelo, y a veces se recurre a versiones más desarrolladas del mismo. De entre las que no incluyen grupos nuevos, se pueden mencionar las siguientes:
- El que tiene en cuenta la dinámica vital: los nacimientos se incluyen en el grupo S; en todos los grupos se dan fallecimientos por causas distintas a la infección.
- Modelo SIS: no hay inmunidad. Las personas infectadas que se recuperan pasan de nuevo al grupo S.
- Modelo SIRS: la inmunidad es temporal. Del grupo R se pasa de nuevo al S, pero no inmediatamente.
En otros modelos se añaden uno o más grupos nuevos, como, por ejemplo:
- E (exposed): personas en fase de incubación. Están infectadas, pero aún no transmiten la enfermedad.
- M (maternally derived immunity): las criaturas recién nacidas tienen inmunidad temporal, gracias a los anticuerpos de la madre.
- D (deceased): personas fallecidas por la infección. Estas salen del grupo R, donde quedan quienes sobreviven a la enfermedad.
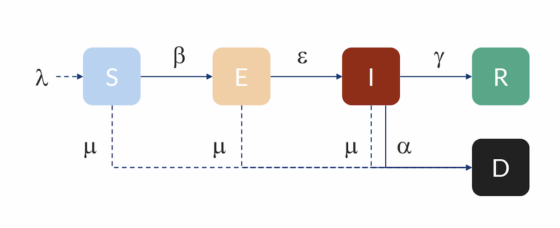 Imagen 3: esquema de un modelo SEIRD. (Fuente: Comsol)
Imagen 3: esquema de un modelo SEIRD. (Fuente: Comsol)Tendiendo esto en cuenta, se han propuesto modelos como SEIR, SEIS, MSIR, SIRD, SEIRD, MSEIR, MSEIRS, etc., cuyas denominaciones reflejan claramente los grupos que incluyen y la forma en que se pasa de un grupo a otro. En estos casos harán falta más ecuaciones y parámetros.
Para saber más:
En la red se puede encontrar abundante información sobre el tema. Estas son algunas de las fuentes que se pueden consultar:
- Ridenhour, Benjamin, Kowalik, Jessica M. y Shay, David K. (2018). El número reproductivo básico (R0): consideraciones para su aplicación en la salud pública. American Journal of Public Health, 108(S6), S455_S465. DOI: https://doi.org/10.2105/AJPH.2013.301704s
- Weiss, Howard (2013). The SIR model and the Foundations of Public Health. Materials matemàtics, 2013(0), 1-17.
- Hethcote, Herbert W. (2000). The mathematics of infectious diseases. SIAM Review, 42(4), 599-653.
- Artículo sobre la Covid-19: Ed Fontes, Modeling the Spread of COVID-19 with COMSOL Multiphysics, COMSOL blog, 07-04-2020.
- Artículo de la Wikipedia en inglés: Compartmental models in epidemiology.
Sobre el autor: Javier Duoandikoetxea es catedrático de Análisis Matemático en la UPV/EHU.
Este artículo se publicó originalmente en euskara el 16 de junio de 2020 en el blog Zientzia Kaiera. Artículo original.
El artículo El modelo SIR, un enfoque matemático de la propagación de infecciones se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El modelo cuántico de Rabi, un sencillo modelo para dominarlos a todos
- Roberto Frucht, matemático en tránsito
- Ilustraciones artísticas de un matemático
Bañadores y dopaje tecnológico
Leire Sangroniz y Ainara Sangroniz
El desarrollo de la ciencia y la tecnología nos ha dado la oportunidad de obtener más y mejores materiales deportivos, y, por lo tanto, el rendimiento de los y las deportistas ha aumentado. Pero, ¿dónde está el límite? Cuando un equipamiento concreto ofrece a las personas deportistas ciertas ventaja sobre sus adversarios, hablamos de dopaje tecnológico. El dopaje tecnológico se ha dado en varios deportes: ciclismo, tenis, atletismo, y también en el golf. Pero puede que el ejemplo más destacable sea el de la natación. En la pasada década surgió una gran polémica en los Juegos Olímpicos, en torno a los bañadores.
 Imagen 1: el nadador sueco Arne Borg en 1927 con el bañador Racerback de la casa Speedo. (Fotografía: V&A / Museum of Applied Arts and Sciences)
Imagen 1: el nadador sueco Arne Borg en 1927 con el bañador Racerback de la casa Speedo. (Fotografía: V&A / Museum of Applied Arts and Sciences)A principios del siglo XX no se tenía en cuenta la velocidad de los nadadores a la hora de diseñar los trajes de baño. Eran unas camisetas y pantalones de lana que se mojaban enseguida y cogían mucho peso. Pero en aquella época era impensable diseñar algo más ligero.
El primer cambio importante ocurrió en 1927, cuando la casa Speedo comercializó el bañador Racerback; fue toda una revolución, ya que el bañador se ajustaba mucho al cuerpo. La espalda y los hombros quedaban al descubierto para facilitar el movimiento, y en vez de lana, se utilizó seda. Este bañador fue muy innovador, sin embargo, en muchas playas se prohibió su uso. Los siguientes años, el desarrollo de la tela sintética, es decir, la tela realizada con polímeros permitió realizar bañadores más ligeros, entre ellos los de nylon (poliamida), en la década de los 50, o los de elastano (copolímero de poliurea poliéster), en los 70. Estos materiales eran bastante nuevos en aquella época, ya que fueron creados a principios y a mediados del siglo XX, respectivamente, por la casa DuPont. Durante los años siguientes la tendencia fue la misma: telas de polímero y bañadores más pequeños, ligeros y ajustados.
La empresa Speedo continuó con sus avances y en el año 2000 desarrolló el bañador Fastskin. Tenía marcas en forma de V en la superficie, para reducir la resistencia al agua, y muchos deportistas lo usaron en los juegos de Sydney. Después, desarrollaron el bañador LZR Razer; con ese bañador quedó claro el impacto que tiene la tecnología en el rendimiento de los deportistas, sobre todo en natación. En los Juegos Olímpicos de Beijing (2008) se batieron 25 marcas mundiales de natación. Detrás de esos resultados había algo más que la buena forma física de los deportistas: El bañador LZR Racer de Speedo. El 98 % de las personas nadadoras que ganaron una medalla llevaban ese bañador.
El traje en cuestión mejoraba el rendimiento de los nadadores y nadadoras, comprimiendo sus músculos y obteniendo un aspecto más hidrodinámico. Además, cubría el cuerpo desde las pantorrillas hasta las muñecas y atrapaba las burbujas de aire entre el cuerpo y el bañador, aumentando la flotabilidad.
Cabe destacar que el traje estaba realizado en poliuretano, material hidrofóbico, y eso tiene una ventaja: repele el agua. De todas formas, el bañador no podría hacerse solamente de poliuretano, ya que se rompía facilmente. Siendo así, se le añadió otro polímero, una poliamida especialmente tratada, para aumentar la hidrofobicidad y no absorber agua. Asimismo, las piezas estaban unidas mediante ultrasonidos, para evitar las costuras y reducir la resistencia.
 Imagen 2: la nadadora Nađa Higl en el Campeonato Europeo de Natación de 2010 con el bañador «Super-body Jaked J01» de la casa Jaked. (Fuente: Wikipedia)
Imagen 2: la nadadora Nađa Higl en el Campeonato Europeo de Natación de 2010 con el bañador «Super-body Jaked J01» de la casa Jaked. (Fuente: Wikipedia)Según los estudios realizados, el éxito de este traje de baño residía en su flotabilidad; de hecho, las pequeñas burbujas de aire que se alojaban entre la piel y el bañador mejoraban la flotabilidad. Como la resistencia al aire es más pequeña que la resistencia al agua, cualquier pequeño detalle puede influir mucho en la velocidad.
El resto de marcas también realizaron avances; Arena, por ejemplo, consiguió desarrollar un bañador enteramente realizado en poliuretano. Siendo así, el bañador de Speedo quedó desfasado, ya que el bañador de poliuretano de Arena tenía una menor resistencia al agua, puesto que era completamente impermeable e hidrofóbico. En 2009, en el XIII Campeonato Mundial de Natación, casi todos los nadadores y nadadoras llevaron el bañador de Arena y este uso hizo que la Federación Internacional de Natación (FINA) se encontrara con un problema. Las marcas mundiales se superaban fácilmente y esto hizo que algunos deportistas y parte del público se incomodaran y cuestionaran los resultados, perdiendo su valor.
Se empezó a hablar de dopaje tecnológico, ya que los logros fueron gracias a un desarrollo tecnológico importante, no solo al esfuerzo de los y las nadadoras. Así que la Federación Internacional de Natación decidió prohibir este tipo de bañadores a partir de 2009. Desde ese momento solamente se permitirían los tejidos permeables; es decir, trajes que no formaran burbujas de aire. Además, se limitaron las dimensiones de los trajes. En el caso de los hombres, podrían abarcar solamente desde la cintura hasta la rodilla; en el caso de las mujeres, no podrían cubrir más allá de los hombros, ni por debajo de las rodillas.
Probablemente, en el futuro, a medida que la ciencia y la tecnología avancen volverá a hacerse evidente la delgada línea existente entre la mejora de los equipamientos deportivos y el dopaje tecnológico.
Fuentes:
- Morrison, Jim (2012). How Speedo Created a Record-Breaking Swimsuit. Scientific American.
- Blanco, J.F., Hunt-Hurst, P. K., Doerin, M.D. y Vaughan-Lee, H. (2016). Clothing and Fashion: American Fashion from Head to Toe. ABC-CLIO, Santa Barbara, California.
- Roberst, Jacob (2017). Winning Skin. Science History Institute.
- Trinidad Morales, A., Tamayo Fajardo, J. A. y González-García, H. (2019). High-Speed Swimsuits and Their Historical Development in Competitice Swimming. Frontiers in Psychology, 10, 2639. DOI: 10.3389/fpsyg.2019.02639
- Nasa Spinoff. Space Age Swimsuit Reduces Drag, Breaks Records. 2020ko uztailaren 2an kontsultatua.
Sobre las autoras: Leire Sangroniz y Ainara Sangroniz son doctoras en Química e investigadores del Departamento de Ciencia y Tecnología de Polímeros de la Facultad de Química de la UPV/EHU y del Instituto Polymat.
Este artículo se publicó originalmente en euskara el 14 de julio de 2020 en el blog Zientzia Kaiera. Artículo original.
El artículo Bañadores y dopaje tecnológico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Materiales inteligentes y multifuncionales para impulsar el desarrollo tecnológico
- Zientziateka: Rendimiento deportivo, ayudas ergogénicas y dopaje
- Cómo conseguir que la superhidrofobia dure
Encontrando valor en los neumáticos usados
 Foto: Darren Nunis / Unsplash
Foto: Darren Nunis / UnsplashLos neumáticos usados suponen un grave peligro medioambiental por los daños que puede ocasionar su almacenamiento en el entorno. Su generación aumenta año tras año en los países desarrollados, por lo que su gestión eficiente es del mayor interés, en el marco de normativas cada vez más restrictivas. Encontrar valor en ellos es un factor clave.
“La pirólisis es una alternativa de gran interés para revalorizar la materia de los neumáticos con el objetivo de obtener combustibles alternativos y productos petroquímicos de alto valor añadido. En este contexto, la pirólisis es la degradación del caucho de la rueda mediante el calor en ausencia de oxígeno. Los productos y su rendimiento dependen de las condiciones a las que se lleva a cabo a cabo la pirólisis”, señala Miriam Arabiourrutia Gallastegui, profesora del grupo PROCAT-VARES (Procesos Catalíticos-Valorización de Residuos) de la UPV/EHU.
En una revisión reciente el grupo de investigación analiza las ventajas más importantes en la valorización de neumáticos usados mediante la pirólisis catalítica. “El principal interés de la valorización de los residuos de neumáticos por pirólisis se basa en el potencial de los productos obtenidos: gas, líquido y un sólido conocido como char. El rendimiento y composición de todos ellos dependen de las condiciones de la pirólisis”, comenta Arabiourrutia.
“El principal producto obtenido en la pirólisis catalítica es el líquido. Este líquido es fundamentalmente el que tiene mayor interés porque se puede utilizar como combustible si se incorporara, por ejemplo, en una refinería. Este líquido tiene una composición compleja incluyendo compuestos de diferente naturaleza (aromáticos, parafinas, olefinas y naftenos) y compuestos de azufre que limitan su uso directo como combustible. Por ello, el interés de la pirólisis catalítica está usualmente relacionada con la mejora de las propiedades o rendimiento de esta fracción. Así, de la pirólisis catalítica se ha puesto gran interés en la producción de compuestos aromáticos (benceno, tolueno…) porque tienen aplicaciones comerciales”, explica la investigadora de la UPV/EHU.
“Los gases de pirólisis también pueden ser usados como combustible para obtener energía. Finalmente, el char es el sólido que se queda sin degradar y está compuesto fundamentalmente del negro de humo que contiene el neumático; el negro de humo es el compuesto que aporta las propiedades antiabrasivas al neumático. Se está estudiando la posible activación del char para utilizarlo como carbón activo —quizás se podría reutilizar como negro de humo en la fabricación del neumático—“, añade Arabiourrutia.
En el proceso que investiga el grupo de la UPV/EHU la pirólisis catalítica tiene unas condiciones muy específicas: «el tiempo de residencia de los gases que se generan en el reactor es corto y esto promueve una serie de reacciones que hacen, por ejemplo, que se obtenga un alto rendimiento de la fracción líquida. Además, hemos visto que gracias a este proceso se obtiene sobre todo el producto líquido que puede ser utilizado en las refinerías para obtener combustible”, subraya Miriam Arabiourrutia Gallastegui.
Según indica la investigadora, “gracias a todos estos trabajos vamos modificando y mejorando el proceso de pirólisis para intentar conseguir una distribución de productos con una composición más adecuada de cara a su potencial aplicación como combustible o materia prima para obtener compuestos de interés”.
Referencia:
Miriam Arabiourrutia, Gartzen Lopez, Maite Artetxe, Jon Alvarez, Javier Bilbao, Martin Olazar Waste tyre valorization by catalytic pyrolysis – A review (2020) Renewable and Sustainable Energy Reviews doi: 10.1016/j.rser.2020.109932
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Encontrando valor en los neumáticos usados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Encontrando exoplanetas tapando las estrellas
- Un hidrogel de almidón/grafeno, conductor y antibacteriano, para implantes neurológicos
- Bioóleo a partir de residuos cítricos
La pandemia de plástico
Desde el Ártico a la Antártida, desde la superficie del mar al sedimento del fondo de los océanos, en todos los ambientes marinos que los científicos han explorado aparece el plástico. Y, por supuesto, también en el suelo y en las aguas dulces, incluso en la atmósfera. Persiste durante años, siglos, milenios afirman algunos expertos, mata animales y plantas, contamina el entorno y ensucia y satura cualquier hábitat. Comenzó a fabricarse en la década de los treinta del siglo pasado y en los cincuenta llegó la producción en masa.
 Foto: Erik Mclean / Unsplash
Foto: Erik Mclean / UnsplashComo ejemplo sirve la publicación de 2018 del grupo de Thomas Maes, del Centro para el Ambiente, Pesquerías y Ciencia de la Acuicultura de Lowestoft, en Inglaterra, sobre la presencia de plástico en el fondo del mar, en el entorno de Gran Bretaña e incluyendo el Mar del Norte. De 1992 a 2017, el 63% de los puntos de muestreo tienen, por lo menos, algún objeto o fragmento de plástico. Hay algunos plásticos, como pueden ser las bolsas de plástico, que han disminuido hasta en un 30% desde 2010. No tengo datos sobre si la pandemia COVID-19 ha cambiado estas cifras.
En 2015, la producción global de plásticos era de 380 millones de toneladas, muy lejos de los 2 millones de toneladas de 1950. El total del plástico producido entre 1950 y 2015 era de casi 8000 millones de toneladas, y la mitad, unos 4000 millones, se fabricaron entre 2002 y 2015, en solo 13 años. Solo China, en 2015, produjo el 28% del total. Para 2010 eran 275 millones de toneladas de plástico las que se vertían en 192 países y, de esa basura, entre 4.8 y 12.7 millones de toneladas terminaban en el mar. De estas cifras, Roland Geyer y su grupo, de la Universidad de California en Santa Barbara, afirman que, en 2017, 4900 millones han terminado en la basura, el 79%, y solo 600 millones, el 10%, se han reciclado.
Muchos de los plásticos vertidos miden menos de 5 milímetros y son llamados microplásticos. Esta fue la palabra del año 2018 para la Fundéu BBVA. Incluso se pueden degradar y fragmentar hasta nanoplásticos con un tamaño de 1 a 100 nanómetros (millonésima parte de un milímetro). Con modelos de ordenador se ha calculado que, en los océanos, hay entre 15 y 51 billones de nanopartículas de plástico. Incluso ahora se ha encontrado plástico en muestras de agua del Mar del Norte recogidas en los años sesenta. En conclusión, la contaminación con plásticos comenzó en el momento en que se empezó a fabricar y utilizar en masa.
La isla Henderson, en el sur del Pacífico Central, es parte del territorio británico de las islas Pitcairn. Mide 9.6 kilómetros de longitud por 5.1 kilómetros de anchura. En total son 37.3 kilómetros cuadrados de superficie. Está a 115 kilómetros al noroeste de la isla Pitcairn, la principal del grupo. La isla Henderson está deshabitada y se encuentra a unos 5000 kilómetros de grandes extensiones de tierra, con sus grandes poblaciones y gran desarrollo social e industrial.
No existen fuentes locales de contaminación y, por tanto, toda la basura de la isla Henderson viene del exterior. En 2015, Jennifer Lavers y Alexander Bond, de la Universidad de Tasmania y de la Real Sociedad para la Protección de las Aves, en Inglaterra, visitaron la isla, entre mayo y agosto, y cuantificaron la basura de plásticos de su costa.
Recogieron muestras tanto en las playas como en los fondos cercanos a ellas. En las playas encontraron de 20 a 670 fragmentos de plástico por metro cuadrado, y en los fondos, de 53 a 4500 fragmentos por metro cuadrado. El 65% son microplásticos. Calcularon, a partir de estos datos, que el número de fragmentos de plástico en la isla, visibles o enterrados, era de casi 38 millones, con un peso de más de 17 toneladas. Cada día llegan a la isla entre 17 y 268 nuevos fragmentos de plástico.
Los autores suponen que el plástico llega a la isla llevado por las corrientes oceánicas que provocan el Gran Giro de Plásticos del Pacífico Sur pues la isla se encuentra en la parte oriental de ese Giro. Como ejemplo sirve que la mayor parte de los restos relacionados con la pesca, sobre todo fragmentos de redes y boyas, vienen de empresas de China, Japón y Chile. Más al norte, en Hawai, se estima que 80000 toneladas de plásticos llegan cada año, y el 54% viene de Norteamérica y Asia.
El plástico está en los océanos, los científicos no saben cómo retirarlo y, mucho menos, los micro- y nanoplásticos. Se depositan en los sedimentos del fondo y, allí, cimentarán con otros materiales y, en el futuro, esa capa de sedimentos con plásticos será nuestro legado al futuro, el legado del Antropoceno.
Ya se han encontrado rocas sedimentarias entre cuyos componentes hay fragmentos de plástico. Lo han descrito Patricia Corcoran y su grupo, de la Universidad de Ontario Occidental en Canadá, con muestras recogidas en la Playa Kamilo, en las Islas Hawai. Son rocas con fragmentos de plástico y cementadas con arena de la playa. Los autores las llaman plastiaglomerados. También describen como, en algunos casos, las rocas con plástico se forman en el suelo, debajo de los abundantes fuegos de campamento y barbacoas que se hacen en la playa.
Solo para recordarlo, hay que mencionar que, en nuestras costas, el grupo de Nikole Arrieta, de la UPV/EHU de Leioa, ha encontrado rocas formadas con la cementación de escorias procedentes de vertidos, con gabarras, de los altos hornos. Otro signo de actividad humana para el futuro, de nuevo el legado del Antropoceno.
Un lugar donde ya se han integrado los plásticos es el hielo del Ártico. El grupo de Andrés Cózar, de la Universidad de Cádiz, ha detectado una fuerte corriente oceánica hacia el norte desde el Atlántico y por el este y el oeste de Groenlandia. Esta corriente lleva plásticos desde el Giro del Atlántico Norte hacia el Ártico. También está ocurriendo que, con el calentamiento global y la fusión de parte de los hielos del Ártico, se están liberando fragmentos de plástico que estaban en el hielo desde hace tiempo. El equipo de Rachel Obbard, del Colegio Darmouth, en Estados Unidos, ha encontrado grandes cantidades de plástico en el Ártico, algunos fabricados hace bastantes años, y, quizá, estaban congelados en el hielo.
Como decía, estas capas de sedimentos con plásticos son un marcador de la actividad humana, de la era geológica Antropoceno, reivindicada por un numeroso grupo de investigadores de todo el mundo en la revisión liderada por Jan Zalasiewicz, de la Universidad de Leicester, en Inglaterra. Entre los que participan en esta revisión está Alejandro Cearreta, de la UPV/EHU de Leioa. La Era Antropoceno se define como la época geológica en que la actividad humana tiene un impacto geológico sobre los ecosistemas y la geología del planeta.
En la revisión, describen como, desde el siglo pasado, los plásticos aparecen en todos los hábitats. Son muy evidentes en sedimentos terrestres y, más recientemente, en los depósitos sedimentarios marinos. La cantidad de plástico se ha doblado varias veces en las últimas décadas. Son los llamados tecnofósiles y son, por supuesto, marcadores del Antropoceno.
Y pueden llegar lejos como muestra el estudio de J.A. Gil Delgado y su grupo, de la Universidad de Valencia, en cuatro lagos de Castilla-La Mancha en las provincias de Cuenca, Ciudad Real y Toledo. Analizan las heces de tres especies de aves acuáticas: focha común (Fulica atra), ánade real o azulón (Anas platyrhynchos) y tarro blanco (Tadorna tadorna). Toman 89 muestras y el 48% tienen restos de plástico, y la mayoría de ese plástico procede del entorno cercano y es de uso en agricultura.
Es interesante destacar que, a pesar de la presencia de plástico en todos los hábitats, según Kinga Kik y sus colegas, de la Universidad de Lodz, en Polonia, y en una revisión publicada este año 2020, no hay estudios de los efectos de estos compuestos, en este caso del poliestireno, sobre el organismo humano.
 Foto: Yifan Zhang / Unsplash
Foto: Yifan Zhang / UnsplashPodemos volver a los océanos, a las profundidades de los océanos, allí donde el grupo de M.L. Taylor, de la Universidad de Oxford, ha encontrado microplásticos en el sistema digestivo de seis especies de cnidarios (medusas, …), equinodermos (erizos de mar, …) y artrópodos (langostas, …). Y son muestras tomadas por un robot a profundidades entre 300 y 1700 metros de profundidad en el Atlántico, el Mediterráneo, el Índico y el Pacífico.
Los plásticos son esenciales en nuestra sociedad pero, también, y ya lo hemos comentado varias veces, suponen un grave y enorme riesgo de contaminación, sobre todo en los ecosistemas marinos con enormes islas de plástico flotantes con tamaño continental. Sin embargo, esta alarma ambiental provocada por la acumulación de plásticos de difícil y larga degradación ha empujado a científicos e instituciones a buscar procesos y métodos que los degraden. Son difíciles de degradar en entornos naturales por su estructura complicada, gran tamaño de molécula y su naturaleza hidrofóbica. Evitan el agua que, por otra parte, es el medio en el que mejor se encuentran los seres vivos que los podrían degradar. Como escriben Harry Austin y sus colegas, de la Universidad de Portsmouth, en Inglaterra, ya se han encontrado bacterias que producen enzimas que metabolizan plásticos y los utilizan como fuente de alimento y energía.
Este grupo trabaja con la bacteria Ideonella sakaiensis, que es capaz de crecer en el plástico tereftalato de polietileno o PET, en sus siglas en inglés, que es muy utilizado en botellas, ropa, envases o alfombras. Esta bacteria sintetiza y libera al medio una enzima, la PETasa, que degrada el ftalato y lo separa en componentes más pequeños y, se supone, inocuos. La historia de esta bacteria, Ideonella, comenzó en el Japón, donde fue aislada por el grupo de S. Yoshida, de la Universidad Keio de Yokohama. La encontraron en un medio muy contaminado, con basura y botellas de plástico, de PET, medio sumergidas en agua. Y en una de esas botellas aislaron y caracterizaron a la Ideonella. También determinaron la enzima PETasa y otra enzima, la METasa, que actuaba sobre los productos de descomposición del ftalato y producía ácido tereftálico y etilenglicol, compuestos menos contaminantes que el ftalato original.
Pero antes del hallazgo de Yoshida, en 2010, ya se habían publicado algunos estudios de la degradación de plásticos por bacterias. Por ejemplo, Naima Atiq y sus colegas, de la Universidad de Islamabad, en Pakistán, encontraron cuatro cepas de bacterias que degradaban poliestireno, el plástico que se conoce como expandido y que se utiliza en envases por su excelente comportamiento en aislar el contenido de cambios de temperatura.
Atiq y su grupo colocaban poliestireno con muestras de suelo del jardín de su universidad. Encontraron bacterias que crecían sobre el plástico y lo degradaban y utilizaban como fuente de energía. Eran bacterias de los géneros Microbacterium, Paenibacillus, Bacillus y Pseudomonas. Fue una investigación con escasa difusión, de un país de Asia y publicado en una revista africana y, por ello, hasta años más recientes no se ha conocido.
No solo bacterias, también se han encontrado hongos adheridos a la superficie de plásticos durante su degradación. El grupo de Urooj Zafar, de la Universidad de Manchester, los ha encontrado enterrando placas del plástico poliuretano en restos orgánicos durante el proceso de compostaje. Varias especies de hongos se asocian al poliuretano en el tiempo que se necesita para conseguir el compost. Las más numerosas son especies del género Aspergillus. Cuando termina el compostaje, las comunidades de hongo sobre el plástico no son las mismas que las que aparecen en el compost y, por ello, parece que se han seleccionado las que más eficazmente utilizan el plástico como alimento y energía.
Una de las especies del hongo Aspergillus, también aislada en Islamabad, en Pakistán, es el Aspergillus tubingensis, y el grupo de Sehroon Khan, de la Academia China de Ciencia de Kunming, ha demostrado que degrada poliuretano. Lo hace en dos meses en el laboratorio y, también, cuando el plástico es enterrado.
Además de bacterias y hongos, una tercera línea de investigación sobre organismo que degradan plásticos estudia las larvas de insectos. Así, S.S. Yang y sus colegas, de la Universidad de Stanford, trabajaron con larva del coleóptero Tenebrio molitor, conocida como el gusano de la harina. Se alimenta con poliestireno. En 12 a 15 horas ingiere el plástico, y a las 2-3 semanas ha utilizado el 65% de la cantidad que se le ha proporcionado. Si, a la vez, se le dan restos de vegetales, la degradación del plástico se dobla. Cuando se ha dejado que estas larvas alimentadas con poliestireno lleguen a adultos y se reproduzcan, la siguiente generación sigue alimentándose con plástico. Sin embargo, un reciente estudio del grupo de Konrad Matyja, de la Universidad de Wroclaw, en Polonia, muestra que las larvas de Tenebrio alimentadas con poliestireno rara vez completan su ciclo vital y no llegan a adultos. El alimento que se les proporciona con el plástico no es suficiente y necesitan un complemento nutricional de avena.
Los autores sugieren que la degradación del poliestireno no la hace directamente el gusano de la harina sino algún microorganismo que vive en su tubo digestivo. En otra publicación, este grupo ha identificado una de las bacterias del tubo digestivo que degrada el poliestireno. Pertenece al género Exiguobacterium.
En la misma línea, Paolo Bombelli y su equipo, de la Universidad de Cambridge, han trabajado con la polilla de la cera, larva del lepidóptero Galleria mellonella, que se alimenta de la cera de las colmenas. Colocan láminas de polietileno en contacto directo con las polillas y, en 40 minutos, aparecen orificios en el plástico. Son, de media, 2.2 orificios por larva y por hora. Si se ponen más de 100 polillas en contacto con una bolsa de polietileno, del tipo de las usadas para recoger y transportar la compra, en 12 horas disminuye su peso en 92 miligramos o, si se quiere, en unas 14 horas su peso cae un 13%.
De nuevo los autores sugieren que el proceso de desintegración del polietileno lo hace algún microorganismo del tubo digestivo de la polilla.
En 2017, Wilkes y Aristilde, de la Universidad Cornell de Ithaca, en Estados Unidos, publicaron una revisión sobre las bacterias de un solo género, Pseudomonas, con capacidad de degradar plásticos. Hay citadas 17 especies y cepas de este género que pueden degradar hasta nueve tipos de plástico con diferentes grados de eficacia.
Otra revisión reciente sobre microorganismos que degradan plástico, en concreto poliestireno, Ba Thanh Ho y sus colegas, de la Universidad Nong Lam de la Ciudad Ho Chi Minh, en Vietnam, enumeran 33 especies y variedades, y tres de ellas vienen del tubo digestivo de larvas de insectos. Los autores plantean que se debe investigar cómo aumentar la velocidad del proceso de degradación del poliestireno. Y, también, la conservación de las infraestructuras que llevan este plástico.
Para terminar con una revisión reciente, de este año 2020, Sunil Ghatge y su grupo, desde Gwangjin, en Corea, mencionan 31 especies de bacterias y nueve de hongos que biodegradan el polietileno.
Referencias:
Arrieta, N. et al. 2017. Characterization of ferruginous cements related with weathering of slag in a template anthropogenic beachrock. Science of the Total Environment 581-582: 49-65.
Atiq, N. et al. 2010. Isolation and identification of polystyrene biodegrading bacteria from soil. African Journal of Microbiology Research 4: 1537-1541.
Austin, H.P. et al. 2018. Characterization and engineering of a plastic-degrading aromatic polyesterase. Proceedings of the National Academy of Sciences USA doi: 10.1073/pnas.1718804115
Bombelli, P. et al. 2017. Polyethylene biodegradation by caterpillars of the wax moth Galleria mellonella. Current Biology 27: R292-R293.
Corcoran, P.L. et al. 2014. An anthropogenic marker horizon in the future rock record. GSA Today doi: 10.1130/GSAT-G198A.1
Cózar, A. et al. 2017. The Artic Ocean as a dead end for floating plastics in the North Atlantic branch of the Termohaline Circulation. Science Advances 3: e1600582
Cressey, D. 2016. The plastic ocean. Nature 536: 263-265.
Geyer, R. et al. 2017. Production, use, and fate of all plastics ever made. Science Advances 3: e1700782.
Ghatge, S. et al. 2020. Biodegradation of polyethylene: a bierf review. Applied Biological Chemistry 63: 27.
Gil-Delgado, J.A. et al. 2017. Presence of plastic particles in waterbirds faeces collected in Spanish lakes. Environmental Pollution 220: 732-736.
Ho, B.T. et al. 2018. An overview on biodegradation of polystyrene and modified polystyrene: the microbial approach. Critical Reviews in Biotechnology 38: 308-320.
Jambeck, J.R. et al. 2015. Plastic waste from land into the ocean. Science 347: 768-771.
Khan, S. et al. 2017. Biodegradation of polyester polyurethane by Aspergillus tubingiensis. Environmental Pollution doi: 10.1016/j.envpol.2017.03.012
Kik, K. et al. 2020. Polystyrene nanoparticles: Sorces, occurrence in the environment, distribution in tissues, accumulation and toxicity to various organisms. Environmental Pollution 262: 114297.
Lavers, J.L. & A.L. Bond. 2017. Exceptional and rapid accumulation of anthropogenic debris in one of the world’s most remote and pristine islands. Proceedings of the National Academy of Sciences USA doi: 10.1073/pnas.1619818114
Maes, T. et al. 2018. Below the Surface: Twenty-five years of seafloor litter monitoring in coastal seas of Northwest Europe (1992-2017). Science of the Total Environment 630: 790-798.
Matyja, K. et al. 2020. Effects of polystyrene diet on Tenebrio molitor larval growth, development and survival: Dynamic Energy Budget (DEB) model analyses. Environmental Pollution 264: 114740.
Obbard, R.W. et al. 2014. Global warming releases microplastics legacy frozen in Artic Sea ice. Earth’s Future 2: 315-320.
Taylor, M.L. et al. 2016. Plastic microfibre ingestión by deep-sea organisms. Scientific Reports 6: 33997
Wilkes, R.A. & L. Aristilde. 2017. Degradation and metabolism of synthetic plastics and associated products by Pseudomonas sp.: capabilities and challenges. Journal of Applied Microbiology 123-582-593.
Yang, S.S. et al. 2018. Biodegradation of plystyrene wastes in yellow mealworms (larvae of Tenebrio molitor Linnaeus): Factors affecting biodegradation rates and the ability of polystyrene-fed larvae to complete their life cycle. Chemosphere 191: 979-989.
Yang, Y. et al. 2015. Biodegradation and mineralization of polystyrene plastic-eating mealworms. Part 2. Role of gut microorganisms. Environmental Science and Technology 49: 12087-12093.
Yoshida, S. et al. 2016. A bacterium that degrades and assimilates poly(ethylene terephthalate). Science 351: 1196-1199.
Zafar, U. et al. 2014. Biodegradation of polyester polymethane during commercial composting and analysis of associated fungal communities. Bioresource Technology 158: 374-377.
Zalasiewicz, J. et al. 2016. The geological cycle of plastics and their use as a stratigraphic indicator of the Anthropocene. Anthropocene 13: 4-17.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo La pandemia de plástico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Adiós a las microesferas de plástico en los cosméticos
- ¿Y si la bolsa de plástico fuese más sostenible que las de papel o algodón?
- Una fibra óptica de plástico actúa como concentrador solar luminiscence
Tareas de un matemático loco
 Sello conmemorando el centenario del nacimiento de Antón Chejov. Imagen: Wikimedia Commons.
Sello conmemorando el centenario del nacimiento de Antón Chejov. Imagen: Wikimedia Commons.Antón Chéjov publicó Tareas de un matemático loco en 1882 bajo el seudónimo de “Antosha Chejonté”. Se trata de una hilarante parodia del quehacer matemático a través de ocho absurdas cuestiones planteadas por un matemático “loco” y que se reproducen debajo (ver [1]):
-
Me perseguían 30 perros, de los cuales 7 eran blancos, 8 grises y los restantes negros. Se pregunta: ¿en qué pierna me mordieron los perros, en la derecha o en la izquierda?
-
Autolimioi nació en el 223, y murió tras vivir 84 años. Una mitad de la vida la pasó en viajes, un tercio lo gastó en placeres. ¿Cuánto vale una libra de clavos y estuvo acaso casado Autolimio?
-
En el año nuevo, de la mascarada del teatro Bolshói fueron sacados 200 hombres por pelea. Si los que peleaban eran doscientos pues, ¿cuántos eran los injuriosos, los borrachos, los levemente borrachos y los que deseaban, pero no hallaban ocasión de pelear?
-
¿Qué se obtiene tras la suma de esas cifras?
-
Se compraron 20 cajas de té. En cada caja había 5 pudsii, cada pud tenía 40 libras. De los caballos que cargaban el té, dos se cayeron en el camino, uno de los cocheros se enfermó y 18 libras se derramaron. La libra tiene 96 zolotniksiii de té. Se pregunta, ¿qué diferencia hay entre el pepino en salmuera y la perplejidad?
-
La lengua inglesa tiene 137 856 738 palabras, la francesa 0,7 más. Los ingleses se juntaron con los franceses y unieron ambas lenguas en una. Se pregunta, ¿qué vale el tercer papagayo y cuánto tiempo se necesitó para subyugar a esos pueblos?
-
El miércoles 17 de junio de 1881, a las 3 de la madrugada, debió salir el tren de la estación A por la vía férrea, para llegar a la estación B a las 11 de la noche pero, antes de la misma partida del tren, se recibió la orden de que el tren llegara a la estación В a las 7 de la noche. ¿Quién ama más prolongado, el hombre o la mujer?
-
Mi suegra tiene 75 años y mi esposa 42. ¿Qué hora es?
Informó Antosha Chejonté
Si alguien conoce la respuesta a alguna de estas cuestiones, ¿sería tan amable de compartirla? Gracias.
 Schioti, ábaco ruso. Imagen: Wikimedia Commons.
Schioti, ábaco ruso. Imagen: Wikimedia Commons.Pasemos a unas matemáticas un poco más serias. Dos años más tarde Chéjov publicó El repetidor. Estamos en Rusia, a finales del siglo XIX. Egor Ziberov, un estudiante de séptimo curso, da clases particulares a Petia, un niño de 12 años. El padre del pequeño asiste a la clase; Egor pretende lucirse para pedir un aumento de sueldo. Tras el latín, llega la clase de matemáticas (ver [1]):
— Pasemos ahora a la aritmética. Coja la pizarra. ¿Qué problema toca?
Petia escupe sobre la pizarra, y la borra después con la manga. El profesor coge el libro de problemas y dicta:
— Un comerciante compró ciento treinta y ocho varas de paño negro y azul por valor de quinientos cuarenta rublos. Se pregunta: ¿Cuántas varas compró del uno y del otro si el azul costaba a cinco rublos la vara y el negro a tres? ¡Repita usted el problema!
Petia lo repite; y comienza inmediatamente, sin decir palabra, a dividir quinientos cuarenta entre ciento treinta y ocho.
— ¿Para qué divide usted? ¡Espere!… Bueno, sí…, siga. ¿Hay residuo? No tiene que haberlo. Traiga, yo lo dividiré. Ziberov lo divide y obtiene de resultado tres con residuo, lo que se apresura a borrar.
«Es extraño —piensa, tirándose del cabello y enrojeciendo—. ¿Cómo es este problema?… ¡Hum!… Debe de ser de ecuación indeterminada y no de aritmética —el profesor consulta las soluciones y halla setenta y cinco y sesenta y tres —. ¡Hum! ¡Qué extraño!… Quizá haya que sumar cinco y tres y luego dividir quinientos cuarenta entre ocho. ¿Será eso?… No, tampoco es eso».
— ¡Bueno!… ¡Haga el favor de resolverlo de una vez! —dice Petia.
— Pero ¿por qué lo piensas tanto? ¡El problema es sencillísimo! —dice Udodov a Petia— ¡Qué bobo eres, hijito! ¡Resuélvaselo usted por esta vez, Egor Alekseich!
Egor Alekseich coge el pizarrín y se dispone a resolverlo. Tartamudea. Enrojece. Palidece.
— El caso es que este problema es de álgebra —dice —. Podría resolverse con X y con Y. Y también sin esto… ¿Ve?… Yo aquí divido… ¿Comprende?… Ahora esto hay que restarlo… ¿Comprende?…, o si no… Lo mejor será que me lo traiga usted resuelto mañana… ¡Piénselo bien!
Petia sonríe maliciosamente; Udodov sonríe también. Ambos comprenden la turbación del profesor. El estudiante de séptimo se azara todavía más, se levanta y empieza a pasear por la habitación.
— Puede resolverse sin acudir al álgebra —dice Udodov. Y tendiendo la mano hacia el schiotiiv añade con un suspiro—: Mire. Es así…
Hechos los cálculos sobre el schioti, obtiene sin dificultad los setenta y cinco y sesenta y tres precisados.
— Esto está hecho a nuestra manera…, no científica.
El profesor se siente terriblemente incómodo. Con el corazón sin latidos, mira el reloj y comprueba que para el fin de la lección falta todavía hora y cuarto. ¡Toda una eternidad!
Efectivamente, el problema es sencillo. Si X e Y designan, respectivamente, la cantidad de varas de paño negro y la de azul, basta con plantear un sistema de dos ecuaciones con dos incógnitas (X+Y=138 y 3X+5Y=540), resultando X=75 e Y=63. Pero Petia no debe hacerlo de esta manera, ya aún no ha aprendido a resolver sistemas de ecuaciones. Así, debe hallar la solución usando métodos elementales. Puede hacerlo suponiendo que, si toda la tela hubiese sido azul, las 138 varas de tela habrían costado 5×138=690 rublos, es decir 150 rublos (690-540=150) más del importe real. Basta con notar que la diferencia de precios entre una vara de tela azul y una de negra es de 2 rublos. Así, dividiendo 150 entre 2, deducimos que debe de haber 75 varas de tela negra y por lo tanto el resto, 63 (138-75=63), debe ser de azul. Simple aritmética.
Incluso un “matemático loco”, en algunas ocasiones, es incapaz de resolver un problema sencillo sin recurrir a artificios. Udodov, con su ábaco, encuentra la solución al problema “a su manera…, no científica” ante el avergonzado Egor que, probablemente, se quede sin su aumento de sueldo…
Referencias
[1] Antón Chéjov, Cuentos completos (1880-1885), Edición de Paul Viejo, Titivillus, 2013
[2] Yakov Perelman, El Abaco Antiguo y sus Descendientes en Aritmética recreativa, 1954
Notas:
i Autolimio es un nombre inventado por Chéjov.
ii El pud es una unidad de masa equivalente 40 libras rusas, unos 16,38 kilogramos.
iii El zolotnik es una antigua unidad de masa rusa equivalente a unos 4,26 gramos.
iv Ábaco ruso.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Tareas de un matemático loco se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El problema matemático de las cartas extraviadas
- Ilustraciones artísticas de un matemático
- Un convite matemático ‘de altura’
La ratonera de Rutherford y Royds
 Foto: Daniel Park / Unsplash
Foto: Daniel Park / UnsplashSe descubrió por primera vez que el helio existía en el Sol mediante el análisis espectroscópico de la radiación solar. Más tarde, se descubrió que se puede encontrar gas helio en la Tierra dentro de algunos minerales radiactivos. Además, William Ramsey y Frederick Soddy, que trabajaban en el Laboratorio Cavendish de Cambridge, habían descubierto, en 1903, que el helio se desprende de un compuesto radiactivo, el bromuro de radio. Esto llevó a Rutherford, también en Cambridge, a plantear la hipótesis de que la partícula alfa es un átomo de helio doblemente ionizado (He2+), es decir, un átomo de helio menos sus dos electrones, o, como diríamos ahora, el núcleo de un átomo de helio.
En una serie de experimentos realizados entre 1906 y 1909 Rutherford logró demostrar la veracidad de su hipótesis de varias formas diferentes. El último y más convincente de estos experimentos se realizó en 1909, como los demás en colaboración con Thomas Royds, al construir lo que James Jeans llamó más tarde «una especie de ratonera para partículas».
El experimento hacía uso del elemento radiactivo radón (Rn). Pierre Curie y Andre Debierne habían descubierto el radón en 1901. Previamente, habían encontrado que el radio emite un gas radiactivo. Una pequeña cantidad de este mostraba que el gas era un emisor de partículas alfa. Demostraron que el gas era un elemento nuevo, al que llamaron «emanación de radio», más tarde llamado «radón». Luego, Ramsey y Soddy descubrieron que cuando el radón se almacena en un recipiente cerrado el helio siempre termina apareciendo en el recipiente.
 La ratonera de Rutherford y Royds. Imagen: Cassidy Physics Library
La ratonera de Rutherford y Royds. Imagen: Cassidy Physics LibraryRutherford y Royds pusieron una pequeña cantidad de radón en un tubo de vidrio con una pared de solo 0,01 mm de espesor. Esta pared era lo suficientemente delgada como para que las partículas alfa pudieran atravesarla, pero el radón no pudiese hacerlo. La ampolla formada por este tubo con radón sellado la colocaron dentro en un tubo de vidrio exterior de paredes gruesas que tenía una sección de descarga eléctrica en la parte superior (véase figura). Extrajeron el aire del tubo exterior (a) y dejaron reposar el aparato durante aproximadamente una semana. Durante este tiempo, las partículas alfa del radón atravesaban las delgadas paredes de la ampolla pero no las del tubo exterior (b). Pasada la semana se encontró que se había acumulado un gas en el espacio en el que previamente se había evacuado el aire.
A continuación Rutherford y Royds bombearon mercurio en la parte inferior del aparato para comprimir la pequeña cantidad de gas producida y confinarlo en el tubo de descarga (c). Cuando aplicaron una diferencia de potencial a los electrodos del tubo se produjo una descarga eléctrica en el gas. El examen de la luz resultante con un espectroscopio mostraba que las líneas espectrales eran las características del elemento helio. [1][2]
De este resultado se podía concluir con seguridad que el gas helio que se acumulaba en el tubo de vidrio exterior se formaba a partir de las partículas que habían pasado al tubo exterior y habían recogido algunos electrones para formar átomos de helio. Las partículas alfa eran por tanto núcleos de helio.
El resultado de Rutherford y Royds también apuntaba otra cosa importante: por lo visto, un átomo de un elemento (radón) puede emitir espontáneamente un fragmento (una partícula alfa) que es el ¡núcleo de otro elemento (helio)! Esta era una idea sorprendente, pero solo el comienzo de cosas aún más sorprendentes que estaban por descubrir.
Notas:
[1] En un experimento de control paralelo, se colocó gas helio en el tubo interior de pared delgada y se comprobó que no se filtraba a través de la pared del tubo interior.
[2] Este, en opinión de un servidor, es uno de los experimentos intelectualmente más elegantes de todos los tiempos.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La ratonera de Rutherford y Royds se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El modelo atómico de Rutherford
- La carga de las partículas radiactivas
- Rutherford: la radiactividad y el descubrimiento del núcleo atómico, por El zombi de Schrödinger
Lecciones de una señal SOS sobre la meteorología espacial
Juanma Gallego
Los comienzos del siglo XX fueron tiempos épicos. En nuestro planeta existían lugares y entornos aún inexplorados y la expediciones para descubrir aquellos sitios únicos se sucedían. En aquella época habían comenzado a darse los primeros pasos de la aviación y las comunicaciones inalámbricas se encontraban en una situación similar. En los momentos en los que todos estos hitos convergían, ocurrían historias muy curiosas. Una de esas historias fue la de la expedición del dirigible Italia al Polo Norte.
El 25 de mayo de 1928 Italia regresaba a su base después de sobrevolar el Polo Norte cuando naufragó a unos 400 km al noreste de las Islas Svalbard (oceáno Ártico). Los supervivientes intentaron sin éxito enviar mensajes de socorro a través de un transmisor de radio portátil de alta frecuencia (HF), para establecer un enlace de radio con el barco de la marina italiana Città di Milano, anclado en archipiélago Svalbard.
Un equipo formado por miembros del Istituto Nazionale di Geofisica e Vulcanologia de Italia (INGV) y del Rutherford Appleton Laboratory del Reino Unido (RAL), ha analizado desde la perspectiva de la meteorología espacial lo ocurrido en la emisión de dichas señales de SOS. Los resultados indican que las condiciones meteorológicas espaciales de la época influyeron significativamente en el envío del SOS. Los investigadores han señalado que se puede aprender mucho de este tipo de sucesos y esperan que pueda servir de ayuda para que no ocurra algo parecido en la exploración espacial.
 Imagen 1: la expedición del dirigible Italia tenía la esperanza de ser la segunda aeronave en llegar al Polo Norte. Lo consiguió, pero en el viaje de regreso las cosas se complicaron. (Foto: Bundesarchiv, Bild 102-05738 / Georg Pahl – bajo licencia CC-BY-SA 3.0. Fuente: Wikipedia)
Imagen 1: la expedición del dirigible Italia tenía la esperanza de ser la segunda aeronave en llegar al Polo Norte. Lo consiguió, pero en el viaje de regreso las cosas se complicaron. (Foto: Bundesarchiv, Bild 102-05738 / Georg Pahl – bajo licencia CC-BY-SA 3.0. Fuente: Wikipedia)El 15 de abril de 1928, el dirigible Italia despegó de Milán con la esperanza de ser la segunda aeronave en llegar al Polo Norte (dos años antes lo había conseguido el dirigible Norge). El 24 de mayo la expedición consiguió su objetivo. Exultantes de alegría, estuvieron a punto de bajar de la nave para pisar la nieve, pero no lo hicieron porque tenían encima una tormenta polar de aspecto preocupante. El regreso, sin embargo, se convirtió en una pesadilla. El Italia se desplomó y los fuertes vientos se llevaron el dirigible. 17 miembros de la expedición perdieron la vida de forma dramática.
Los nueve miembros de la tripulación que iban en la cesta principal tuvieron mejor suerte y, aunque muchos de ellos estaban heridos, lograron sobrevivir sobre una placa de hielo, a unos 400 kilómetros de las islas Svalbard. Algunos instrumentos no sufrieron daños en el accidente, podían utilizarse, y entre ellos había un radiotelégrafo. Tenían forma de salvarse, o eso parecía.
Sin embargo, a veces el destino resulta muy caprichoso. Emitirieron mensajes pidiendo ayuda. A pesar de intentarlo una y otra vez en diferentes frecuencias, sus mensajes no recibían respuesta. Aquello no tenía sentido. Ellos escuchaban la radio: eran capaces de escuchar una emisora de radio de Roma, a 4.000 kilómetros de distancia, y también los mensajes enviados por el barco Città di Milano. Este barco era una nave de apoyo a la expedición, pero en él no recibían los mensajes de petición de ayuda de los expedicionarios. Ante ese supuesto silencio, el mundo dio por desaparecidos a todos los exploradores.
Diez días después, cuando todo parecía perdido, un radioaficionado ruso recibió una señal SOS de los supervivientes. Las labores de rescate no fueron nada fáciles y tuvieron que permanecer semanas sobre una placa de hielo a la deriva. Pero esa es otra historia.
Un artículo publicado en la revista Space Weather ha intentado aclarar lo sucedió en aquella expedición. Y, sí, tal y como se puede deducir del nombre de la revista, el tiempo espacial tuvo mucho que ver en el asunto. Los expertos que han analizado la cuestión aseguran que los náufragos estuvieron expuestos a un vacío radiofónico o zona silenciosa, una región donde no se puede recibir una transmisión por radio. En esta región, no se puede captar ninguna señal porque, debido a las condiciones de la ionosfera local, las ondas de radio no se reflejan sino que penetran en la ionosfera. La ubicación exacta de este vacío puede variar según las condiciones de la ionosfera y los investigadores creen que fue eso lo que ocurrió en 1928.
Debemos tener en cuenta que las comunicaciones por radio utilizan la ionosfera ‑situada a una altitud de entre 50 y 1.000 kilómetros‑ para propagarse a grandes distancias. Básicamente, las ondas de radio se reflejan en esa capa y, de rebote, vuelven a reflejarse en el suelo, lo que hace posible la transmisión. Pero cerca de los polos, esa capa, que normalmente es bastante estable, se vuelve más inestable.
 Imagen 2: la zona silenciosa es una región donde no se puede recibir una transmisión de radio; es la región entre el punto donde termina la cobertura de la onda baja (triángulo azul) y el primer punto donde se puede recibir la señal, después de ser refractado de vuelta a la superficie de la Tierra por la ionosfera. (Imagen: Zolesi, B. et al. / Space Weather)
Imagen 2: la zona silenciosa es una región donde no se puede recibir una transmisión de radio; es la región entre el punto donde termina la cobertura de la onda baja (triángulo azul) y el primer punto donde se puede recibir la señal, después de ser refractado de vuelta a la superficie de la Tierra por la ionosfera. (Imagen: Zolesi, B. et al. / Space Weather)Los autores del estudio creen que en aquellas fechas confluyeron varios fenómenos asociados a las tormentas solares. Aunque hoy sabemos que ocurren este tipo de fenómenos, en la época del Italia desconocían que las tormentas solares afectaban a las emisiones de radio. Sabían que el clima en las inmediaciones del Polo Norte era extremo, pero no podían ni imaginar que en esa zona hubiera que tener en cuenta algo llamado meteorología espacial.
La radio portátil de la que disponían los náufragos emitía en frecuencias de 9,1 a 9,4 megahercios, pero en las Svalbardas se daba el fenómeno del vacío radiofónico mencionado anteriormente para ese tramo de frecuencias, y era en esa zona donde se encontraba el barco de apoyo. Por otro lado, una tormenta solar empeoró la situación, aumentando la absorción de las ondas de radio. Por eso, los autores creen que al menos en los primeros días disminuyó mucho el rango de frecuencias utilizables.
Para reconstruir la situación de la ionosfera en esos días se han utilizado datos históricos recogidos en varios observatorios: el observatorio Abinger del Reino Unido (hoy en día conocido como Hartland), el de Lerwick, y el Observatorio Real de Bélgica.
En declaraciones a la revista OSE de la Unión Geofísica Americana, Ljiljana Cander, física y coautora del estudio, ha destacado que «esta es una lección de historia que podría reproducirse durante otras exploraciones como viajes lunares o interplanetarios, por lo que se deben tener en cuenta aún más los posibles problemas de comunicación debido a las adversas condiciones climáticas espaciales».
Los investigadores han destacado que el estudio de sucesos del pasado puede ser una fuente de información útil y muy valiosa en el campo de la meteorología espacial, una disciplina todavía relativamente joven. En este sentido, hay que recordar, por ejemplo, lo importante que resulta analizar el evento Carrington, la mayor tormenta solar conocida desde que existen registros históricos fiables.
Referencias bibliográficas:
Zolesi, B., Pezzopane, M., Bianchi, C., Meloni, A., Cander, L. R., & Tozzi, R. (2020). The shipwreck of the airship “Dirigibile Italia” in the 1928 polar venture: A retrospective analysis of the ionospheric and geomagnetic conditions. Space Weather, 18 (7), e2020SW002459. DOI: https://doi.org/ 10.1029/2020SW002459
Sobre el autor: Juanma Gallego (@juanmagallego) es periodista científico.
Este artículo se publicó originalmente en euskara el 17 de julio de 2020 en el blog Zientzia Kaiera. Artículo original.
El artículo Lecciones de una señal SOS sobre la meteorología espacial se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los riesgos de la exploración espacial
- El cielo sobre nuestras cabezas
- Dudas sobre las vacunas: problemas y soluciones
Genuinamente humano
 Foto: Cristian Newman / Unsplash
Foto: Cristian Newman / UnsplashAlgunos rasgos humanos son peculiares. La forma en que habitualmente practicamos el sexo, por ejemplo, y algunas de sus características son propias de nuestra especie. Si la comparamos con otros primates y, más en concreto, con los otros miembros de la familia Hominidae -orangutanes, gorilas, chimpancés y bonobos- que son nuestros parientes más cercanos, uno de los rasgos que nos diferencia –o, mejor dicho, que diferencia a las hembras humanas de las de esas especies- es que las de la nuestra son sexualmente receptivas de manera permanente y ocultan la ovulación.
Las hembras de los demás primates son receptivas cuando se encuentran, desde el punto de vista fisiológico, en situación de concebir, tras la ovulación. En esas circunstancias los machos están muy interesados en copular, porque es cuando el apareamiento puede desembocar en una gestación y el nacimiento de un nuevo individuo. Pero las mujeres están receptivas siempre, tanto en la fase del ciclo en que puede ser fecundado un óvulo, como fuera de esa fase, de donde se deriva que en nuestra especie la práctica del sexo cumple funciones distintas de la reproductiva.
Otro rasgo humano es que somos, generalmente, monógamos sociales. Esto es, en nuestra especie se forman parejas relativamente estables. Monógamos sociales, sí, pero monógamos sexuales, no tanto. La monogamia sexual es aquella en que la práctica del sexo está restringida al ámbito de la pareja. Es muy habitual que la monogamia social no venga acompañada por la sexual, lo que quiere decir que uno o ambos miembros de la pareja (estable) busca (y a veces consigue) copular con otro individuo. Es cierto que hay algunas sociedades poligínicas, en las que un único varón tiene varias parejas reproductivas femeninas, y también que hay sociedades –pocas- poliándricas, en las que una única mujer tiene varias parejas masculinas. Pero esas condiciones no son las más frecuentes.
La monogamia social es un rasgo distintivo de nuestra especie porque nuestros parientes más cercanos no la practican. En orangutanes y gorilas hay una fuerte competencia para erigirse en el macho alfa, que es el que copula con las hembras de su territorio (orangután) o grupo (gorila). Y los chimpancés y bonobos son promiscuos; no forman parejas estables. Ninguno de ellos, como puede comprobarse, circunscribe la práctica del sexo a la pareja porque, para empezar, en ninguno de ellos existen tales parejas.
Otra diferencia notable entre nuestra especie y los demás homínidos es que nosotros nos escondemos para practicar el sexo. Nos parece lo normal, pero lo cierto es que es una rareza. Orangutanes, gorilas, chimpancés y bonobos no se esconden, sino que copulan a la vista de los demás miembros del grupo. La práctica del sexo en privado no es un rasgo cultural en nuestra especie. Salvo alguna extraña forma de práctica sexual de carácter ritual u orgías normalmente aderezadas por el consumo de alguna droga, no hay grupos humanos en los que se practique sexo a la vista de los demás. No depende del código moral del grupo; es un rasgo universal.
Todo esto quizás se deba a lo costosa que es la crianza de la prole en nuestra especie. Lo es tanto, que es necesaria la aportación de los dos miembros de la pareja, lo que favorece la existencia de un vínculo fuerte entre ambos. A ello obedecería el carácter monógamo de la relación. La ocultación del celo y la receptividad sexual permanente de las hembras cumpliría, en ese contexto, la función de reforzar el vínculo. Y la práctica del sexo en privado probablemente contribuye también, a través de una mayor intimidad en la relación, al mismo fin.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Genuinamente humano se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los números del sistema circulatorio humano
- ¿Cuántas células hay en el cuerpo humano?
- El gran encéfalo humano es un “encéfalo social”
Películas magnetoactivas de fibroína de seda para la generación de tejido óseo
Investigadores de la UPV/EHU, BCMaterials y de la Universidade do Minho (Portugal) han demostrado que la combinación de andamios biocompatibles formados por componentes de la seda y la estimulación de las células mediante magnetismo es un método válido para la generación de tejido óseo. “El objetivo último de esta línea de investigación sería poder generar tejidos que luego podrían ser implantados para curar enfermedades relacionadas con los huesos”, comenta José Luis Vilas Vilela, director del Departamento de Química Física de la UPV/EHU y uno de los autores de este estudio.
 Sección transversal de un fémur
Sección transversal de un fémurEl nuevo material está formado por un andamio, o matriz, cuya base es uno de los principales componentes de la seda, la fibroína, un material biocompatible, al que se han incorporado nanopartículas magnéticas. El objetivo de añadir las nanopartículas es convertir este material en “magnetoactivo”, de forma que responda al aplicarle un campo magnético y pueda transmitir estímulos mecánicos y eléctricos a las células. Está comprobado que el hecho de introducir estímulos, tanto eléctricos, magnéticos, mecánicos o de otra naturaleza, favorece el crecimiento y diferenciación celular, ya que de alguna manera se simula el microambiente celular y se imitan los estímulos que se dan en el medio en el que las células desarrollan su función.
El presente estudio, realizado in vitro, ha probado dos metodologías para obtener la matriz de fibrina: en una se han creado films y en la otra han elaborado una especie de tejido, entrelazando las fibras. ”Se trata de dos metodologías bastante buenas para confeccionar estos andamiajes que simulan la matriz extracelular, el soporte donde las células pueden adherirse para crecer —detalla el investigador—. Las nanopartículas magnetoactivas forman también parte de la estructura, ya que están incorporadas en la fibrina. Así, cuando aplicamos un campo magnético provocamos una respuesta de estas nanopartículas, que vibran y de esta forma deforman la estructura, la estiran, transmitiendo ese esfuerzo mecánico a las células”.
Los resultados muestran que “ambos tipos de matriz favorecen el crecimiento celular, siendo el de tipo film la que mejor funciona, las células crecen mejor, pero sobre todo hemos comprobado por primera vez que el estímulo magnético tiene un efecto positivo en el crecimiento celular”.
Esto ha supuesto un paso adelante en la línea de investigación que tiene este grupo de investigación en la búsqueda de materiales y métodos adecuados para la fabricación de tejidos. “Sabemos que nuestro objetivo es a largo plazo, y ahora estamos dando los pasos iniciales. Estamos desarrollando varios tipos de materiales, estímulos y procesos, para llegar a tener vías de obtener la regeneración de diferentes tejidos. La idea sería, además, partir de células madre de los propios pacientes, y ser capaces de diferenciarlas hacia el tipo de célula con la queremos formar el tejido, ya sea óseo, muscular, cardíaco o el que se necesitara. Ese sería el objetivo final, en el que ya estamos dando pasos significativos”, opina.
Para llegar a ese objetivo final, este grupo de investigación debe ir superando diferentes retos. Los más próximos deberían ser, según Vilas Lilela, “combinar diferentes estímulos e introducir alguna variación a los ya aplicados, como la dirección en la que se aplica la deformación de la estructura utilizada. También tenemos que estudiar la viabilidad y la funcionalidad de las células, la forma en la que se alimentan las células y se extraen los residuos generados por estas. Son muchos los factores en los que hay que avanzar, pero lo conseguido nos da pie a seguir”.
Referencia:
A. Reizabal, R. Brito-Pereira, M. M. Fernandes, N. Castro, V. Correia, C. Ribeiro, C. M. Costa, L. Perez, J. L. Vilas, S. Lanceros-Méndez (2020) Silk fibroin magnetoactive nanocomposite films and membranes for dynamic bone tissue engineering strategies Materialia doi: 10.1016/j.mtla.2020.100709
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Películas magnetoactivas de fibroína de seda para la generación de tejido óseo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Magnetosomas para el tratamiento del cáncer
- Cómo ver todas las células en tejido cerebral vivo
- Polímeros biocompatibles para integrar dispositivos electrónicos en nuestro cuerpo
El letargo del ratón
 Ilustración: María Lezana
Ilustración: María LezanaCasi todo el mundo sabe que los osos, en otoño, entran en letargo y permanecen así hasta el final del invierno. Llamamos hibernación a ese estado aunque, en realidad, no es tal, sino una condición de reducción térmica y metabólica que se le asemeja. Hibernan los mamíferos de menor tamaño, como marmotas, ardillas o murciélagos. La hibernación es un estado que permite ahorrar en una estación en la que la temperatura ambiental es muy baja, de manera que, para mantener la corporal en niveles fisiológicos normales, haría falta gastar mucha energía. Además, el alimento escasea, por lo que quizás ni siquiera sería posible conseguir esa energía.
Lo que seguramente es menos conocido es que hay otras formas de letargo. El ratón Mus musculus es ese pequeño roedor que convive con nosotros desde hace milenios. Es un animal muy activo. Por eso, y también por su pequeño tamaño, su tasa metabólica es muy alta y, en consecuencia, sus necesidades energéticas, muy grandes.
Esas necesidades son, muy probablemente, la razón por la que en numerosas ocasiones el ratón entra en letargo. Pero curiosamente, que entre o no en ese estado, depende de las circunstancias. Por ejemplo, lo hace si se queda sin alimento o si la temperatura ambiental es muy baja. En cualquiera de esos dos casos, -ayuno o frío-, el ratón corre el riesgo de incurrir en un balance energético negativo. Si está en ayunas, el ratón no adquiere energía y el letargo es un modo excelente de ahorrarla. Y si la temperatura ambiental baja en exceso, ha de gastar demasiada energía para producir el calor necesario que compensase las pérdidas.
Así pues, la mejor vía para mantener el balance energético en esas condiciones, consiste en reducir la temperatura corporal. Esa reducción reporta dos beneficios. Por un lado, disminuye la diferencia térmica con el exterior, de manera que la pérdida de calor se atenúa mucho, porque la transferencia hacia el entorno es directamente proporcional a la diferencia térmica entre el organismo y el entorno. Y por el otro, esa reducción de la temperatura corporal conlleva, por razones puramente cinéticas, un descenso de la tasa metabólica, y gracias a ese descenso el balance energético no se deteriora demasiado.
Y hay una tercera circunstancia bajo la que puede ocurrir que el ratón entre en letargo. Si para conseguir el alimento debe realizar un gasto energético excesivo, también adoptará ese estado. La intensidad de la hipotermia (magnitud del descenso de su temperatura corporal) y la duración del tiempo durante el que los ratones permanecen en letargo dependen también de eso. Si el esfuerzo que han debido hacer para obtener el alimento es muy alto, la reducción térmica corporal será más intensa y el letargo se prolongará durante más tiempo que si ese esfuerzo ha sido menor. Todo depende de la magnitud del balance energético.
Es una característica curiosa, pero tiene sentido. Es curiosa, porque incluso los ratones alimentados ad libitum pueden entrar en letargo si para conseguir esa muy abundante comida se tienen que esforzar demasiado. Y tiene sentido porque en términos de balance energético, incluso bajo condiciones de alimentación abundante pueden comprometer su ganancia de energía.
El comportamiento metabólico de Mus musculus muestra gran flexibilidad. Pone de manifiesto que el letargo es una buena herramienta para mantener el balance energético. Y si bien hace años se consideraba como algo excepcional y muy restringido en el mundo animal, cada vez son más las especies de las que sabemos que lo adoptan de manera habitual.
Volviendo a nuestros ratones, un equipo de la Facultad de Medicina de la Universidad de Harvard (EEUU), ha dado a conocer los resultados de una investigación en la que han identificado un conjunto de neuronas implicadas en la entrada y salida del letargo. Son neuronas que muestran una actividad elevada cuando se produce la reducción de actividad muscular, metabólica y térmica. Son neuronas hipotalámicas, en concreto del área preóptica medial y lateral. Estimulando esas neuronas, los investigadores han conseguido inducir el estado de letargo, incluso en condiciones fisiológicas que no hubiesen propiciado esa transición. El hipotálamo es la estructura nerviosa que, entre otras funciones, controla la temperatura corporal en homeotermos, por lo que es lógico que el control de la entrada y salida en letargo se encuentre radicado en ella. Además, es responsable, mediante sus conexiones con la hipófisis, de la coordinación de gran parte del sistema endocrino, por lo que ejerce un control amplio sobre las funciones vegetativas, en general, y el metabolismo en particular.
Fuentes:
Hrvatin, S, Sun, S, Wilcox, O F et al. (2020): Neurons that regulate mouse torpor. Nature 583, 115–121.
Schubert, K A, Boerema, A S, et al. (2009): Daily torpor in mice: high foraging costs trigger energy-saving hypothermia. Biology Letters 6: 132–135.
Nota:
Esta anotación está basada en El ratón y su letargo cotidiano, publicada en Zoo Logik.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El letargo del ratón se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Soluciones sencillas a problemas complejos: criptografía y secuencias binarias
Estaba estos días buscando información sobre criptografía, cuando fui a parar a un libro que podemos considerar ya todo un clásico de divulgación de las matemáticas, publicado un poco antes del año 2.000 –que recordemos que fue el Año Mundial de las Matemáticas– y que lleva muchos años en mi biblioteca, Las matemáticas en la vida cotidiana, de la editorial Addison-Wesley, junto con la Universidad Autónoma de Madrid (en su edición en castellano). Allí encontré un ejemplo bonito de cómo en ocasiones los problemas difíciles, como puede ser la seguridad en las comunicaciones, pueden tener soluciones sencillas. La entrada de hoy quiero dedicarla a mostrar este curioso ejemplo.
 Portada del libro Las matemáticas en la vida cotidiana, Addison-Wesley/Universidad Autónoma de Madrid, 1999
Portada del libro Las matemáticas en la vida cotidiana, Addison-Wesley/Universidad Autónoma de Madrid, 1999En la actual era de la información vivimos rodeados de tecnología digital, desde los ordenadores, las tabletas o los Smartphones, hasta toda la comunicación a través de internet, pasando por la imagen y sonido digitales, la televisión digital o las casas inteligentes. Una de las características de la tecnología digital es que toda la información está en formato “digital”, es decir, codificada en forma de números. Y estos números están representados en la base binaria (véase Una de mates: números binarios), es decir, como secuencias de unos (1) y ceros (0).
A continuación, vamos a explicar un ejemplo en el que las secuencias binarias y la suma digito a dígito de secuencias binarias han permitido a plataformas de televisión por cable, como HBO, Showtime o Canal Disney –por citar las que se mencionan en el libro Las matemáticas en la vida cotidiana–, evitar el acceso a su contenido audiovisual a quienes no han estado abonados a las mismas.
En 1984, cuando el canal de televisión HBO empezó a codificar su señal, los usuarios accedían a la misma –en forma de ondas electromagnéticas– a través de una antena parabólica, aunque hoy en día toda la información nos llega a través de la fibra óptica u otros medios.
 Logo de la plataforma HBO
Logo de la plataforma HBOTres elementos eran necesarios para evitar el acceso pirata a la señal de televisión por cable. Por una parte, una contraseña mensual del canal de televisión –que se enviaba junto con la señal–, una clave para cada usuario y una operación, que explicaremos a continuación, para asegurar que ese usuario era realmente un abonado de la plataforma.
Tanto la contraseña mensual del canal de televisión, como la clave de usuario eran secuencias binarias, en aquellos años de longitud 56, aunque en esta entrada, para simplificar la explicación, utilizaremos solo secuencias de 8 dígitos, es decir, de longitud 8. Por ejemplo, 10101110 es una secuencia binaria de longitud 8.
Ya sabemos que la información –contraseña mensual y clave de usuario– va a estar dada en forma de secuencias binarias, en esta explicación consideradas de longitud 8, por lo que estamos en condiciones de explicar la operación de suma que se utilizaba para asegurar que el usuario era realmente un abonado de la plataforma. Esta suma no es una suma normal de números binarios, sino que es una suma dígito a dígito. Dadas dos secuencias binarias de la misma longitud, se suman los dígitos de las mismas posiciones, teniendo en cuenta que 0 + 0 = 0, 1 + 0 = 0 + 1 = 1 y 1 + 1 = 0, para obtener una nueva secuencia binaria de la misma cantidad de dígitos. Veamos algunos ejemplos:
 Ejemplos de sumas, dígito a dígito, de secuencias binarias de longitud 8
Ejemplos de sumas, dígito a dígito, de secuencias binarias de longitud 8
Una propiedad importante de esta suma dígito a dígito es que la suma de dos secuencias binarias es 00000000 si, y sólo si, las dos secuencias binarias son la misma. Por ejemplo, esto es lo que ocurre en la última suma de los ejemplos que hemos mostrado, 10001110 + 10001110 = 00000000.
Veamos en qué consistía la solución al problema de que se piratease la señal de televisión de HBO, y otros canales de televisión por cable. Como ya hemos comentado, cada mes el canal de televisión cambiaba la contraseña p. Consideremos, por ejemplo, que un mes la contraseña era p = 11001011.
Por otra parte, cada uno de los abonados del canal disponía de su propia clave. Como cada abonado disponía de una clave distinta, existían tantas claves como abonados, c1, c2, …, ck (donde k = número de abonados de ese mes). Imaginemos que mi clave de usuario de HBO fuese c = 01110101.
Ese mes el canal de televisión transmitía, con la señal de televisión, la contraseña mensual p y las secuencias binarias p + c1, p + c2, …, p + ck. En cada una de las “cajas de descodificación” de los abonados, cada una de las cuales disponía de la correspondiente clave de ese usuario ci, se calculaban las sumas
ci +(p + c1), ci +(p + c2), …, ci +(p + ck).
El microprocesador de la caja de descodificación, después de realizar estas sumas, las comparaba con la contraseña p y si alguna de ellas coincidía con ella se trataba de un abonado y se descodificaba la señal. Observemos que se va a producir esa coincidencia cuando se suma ci con (p + ci), ya que, por la propiedad anterior, ci + ci = 00000000, de donde, ci +(p + ci) = p.
En nuestro ejemplo, la contraseña mensual es p = 11001011 y mi clave de abonado c = 01110101, entre las secuencias binarias que transmite el canal estará p + c = 10111110, que al sumarse en mi descodificador con mi clave c + (p + c) = 11001011, que efectivamente coincide con p, puesto que soy un abonado real del canal de televisión por cable.
Por último, tengamos en cuenta que las secuencias binarias reales son de longitud, al menos, 56, luego la cantidad de posibles claves que existen son 256, más de 72 mil millones, en concreto: 72.057.594.037.927.936. Por lo tanto, piratear una clave no es algo tan sencillo como intentar ir probando diferentes secuencias binarias de 56 dígitos.
 La ceramista estadounidense Laura C. Hewitt crea cerámicas con números binarios, con tipografías de máquinas de escribir, como este hermoso plato. La imagen pertenece a su tienda de Etsy
La ceramista estadounidense Laura C. Hewitt crea cerámicas con números binarios, con tipografías de máquinas de escribir, como este hermoso plato. La imagen pertenece a su tienda de EtsyEn el libro Contemporary abstract algebra se explica que esta misma sencilla idea puede ser utilizada para proteger las transacciones a través de internet.
Supongamos que alguien quiere comprar mi libro Los secretos de la multiplicación, de los babilonios a los ordenadores (Los libros de la Catarata, 2019) en alguna de las librerías o tiendas online que existen. Para ello, cuando estamos realizando la compra, nos piden nuestra tarjeta de crédito. Pero, por supuesto, no queremos que ningún hacker pueda interceptar nuestro número de la tarjeta de crédito durante la transacción. Para ello el número de la tarjeta de crédito, escrito como una secuencia binaria, tendrá que ser enviado a la tienda online de una forma segura.
Cuando estamos rellenando la orden de compra en la tienda on-line, esta envía a nuestro ordenador, tableta o Smartphone una clave c en forma se secuencia binaria de unos y ceros con tantos dígitos como los que tiene la secuencia binaria p del número de la tarjeta de crédito. Entonces, cuando añadimos nuestra tarjeta de crédito a la orden de compra, las dos secuencias binarias – de la clave enviada por la tienda y de la tarjeta que introducimos– se suman c + p, mediante la suma dígito a dígito de secuencias binarias. El resultado de esa suma es lo que se envía, a través de internet, a la tienda de comercio en línea, de forma que cualquier hacker no accede al número de la tarjeta p, sino a la suma c + p, con lo que no consigue robar nuestra información. Una vez que esa información llega a la tienda de internet, para conocer cuál es el número de nuestra tarjeta de crédito no tienen nada más que sumar de nuevo la clave c, ya que c + (c + p) = p.
 ¡Están lloviendo números binarios!, ilustración realizada por KHJ y vendida en camisetas, sudaderas, tazas y pegatinas en su página de Teepublic
¡Están lloviendo números binarios!, ilustración realizada por KHJ y vendida en camisetas, sudaderas, tazas y pegatinas en su página de TeepublicVeamos un ejemplo concreto, pero para no complicarlo utilizaremos otra vez secuencias binarias de longitud 8. Supongamos que el número de nuestra tarjeta de crédito codificada como una secuencia binaria es p = 10011011, que la clave que nos manda la tienda online es c = 01111101, entonces nuestro ordenador envía a la tienda de internet la información c + p = 01111101 + 10011011 = 11100110. Si algún hacker accede a esa información no puede conocer cuál es la secuencia binaria de nuestra tarjeta de crédito, pero al llegar la información de nuevo a la tienda, se suma la clave c + (c + p) = 01111101 + 11100110 = 10011011, obteniendo así nuestra tarjeta de crédito p = 10011011, para efectuar la compra.
Para terminar, me gustaría agradecer a Paco Roca y a la editorial Astiberri que nos permitieran leer durante el periodo del confinamiento por el coronavirus (marzo-abril 2020), de forma gratuita, el magnífico libro de Paco Roca, publicado en Astiberri, Memorias de un hombre en pijama (2011).
En este libro tenemos además dos momentos matemáticos. El primero cuando el hombre en pijama, el Paco Roca de la ficción, está pensando en qué profesiones le habría gustado tener si no hubiese dedicado su vida a “dibujar y contar historias”. En la segunda viñeta leemos que piensa “Recuerdo que quería ser un gran científico. Un matemático famoso que resolvería la conjetura de Poincaré”, como podemos ver en la siguiente imagen.

Mientras que el segundo es el final del mismo. El Paco Roca de ficción, el hombre en pijama, decide dejar de enviar más entregas de Memorias de un hombre en pijama al periódico en el que salían estas (esta historieta fue publicada por primera vez, por entregas, en el periódico Las provincias, en 2010). La idea para la última entrega se le ocurrió en una fiesta en la que bebió mucho, por lo que la apuntó en su móvil, ya que no tenía a mano su libreta, para no olvidarse. Pero cuando va a mirar cuál es esa idea que había apuntado…

Bibliografía
1.- VV. AA. (director del proyecto Solomon Garfunkel), Las matemáticas en la vida cotidiana, Addison-Wesley/Universidad Autónoma de Madrid, 1999.
2.- Joseph A. Gallian, Contemporary abstract algebra, Brooks/Cole, 2012 (octava edición).
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Soluciones sencillas a problemas complejos: criptografía y secuencias binarias se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Dudas sobre las vacunas: problemas y soluciones
- Buscando las soluciones del cubo de Anda
- Las dos culturas de las matemáticas: construir teorías o resolver problemas
La masa de las partículas radiactivas

Foto: Chris Beck / Pexels
Los experimentos con campos magnéticos también permiten determinar la masa de las partículas radiactivas.
La desviación de una partícula cargada cuando atraviesa campos eléctricos y magnéticos depende tanto de su carga como de su masa. Por lo tanto, la relación de carga (q) a masa (mq) para partículas beta se puede calcular a partir de las desviaciones medidas en campos magnéticos de intensidad conocida. Becquerel, investigando partículas beta en 1900, utilizó un procedimiento que era esencialmente el mismo que el utilizado por J.J. Thomson en 1897 para obtener un valor fiable para la relación de carga a masa para las partículas en los rayos catódicos.
Para esas fechas el hecho de que se hubiera encontrado un valor único constante de e / meyahabía establecido cuantitativamente la existencia del electrón [1]. Haciendo que rayos beta atravesasen campos eléctricos y magnéticos, Becquerel pudo calcular la velocidad de las partículas. Obtuvo un valor de q / mq para partículas beta que estaba muy cerca del encontrado por Thomson para el electrón. Esto permitió deducir que las partículas de los rayos beta son electrones. [2]
La naturaleza de la radiación alfa fue más difícil de establecer. Era necesario utilizar un campo magnético muy fuerte para producir desviaciones medibles de los rayos alfa. El valor de q / mq encontrado para las partículas alfa (4.8 · 107 C / kg) era aproximadamente 4000 veces menor que q / mq para las partículas beta. La razón del pequeño valor q / mq podría ser tanto un valor pequeño de q como un valor grande de m. Otros indicios disponibles en ese momento apuntaban a que la magnitud de la carga q de una partícula alfa probablemente no era menor que la de una partícula beta. Por lo tanto, se concluyó que la masa mq tendría que ser mucho mayor para la partícula alfa que para la partícula beta.
El valor de q / mq encontrado para las partículas alfa es solo la mitad que el q / mq conocido para un ion molecular de hidrógeno. Por tanto, el valor podría explicarse razonablemente si la partícula alfa fuera como una molécula de hidrógeno menos un electrón (H2+), o si fuera un átomo de helio (cuya masa se sabía que era aproximadamente cuatro veces mayor que la de un átomo de hidrógeno) sin sus dos electrones (He2+). So podían incluso contemplar otras posibilidades. Sin embargo, la identificación correcta resultó ser la de los núcleos de helio y tiene una masa de aproximadamente cuatro unidades de masa atómica. La prueba final merece su propio artículo.
Notas:
[1] Aquí e es la carga del electrón, y me su masa.
[2] De aquí no se deduce que existan electrones en el núcleo atómico. Los electrones que forma la radiación beta se crean durante la emisión.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La masa de las partículas radiactivas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La carga de las partículas radiactivas
- Las partículas de los rayos catódicos
- Trayectorias de las partículas cargadas en un campo magnético
No vas a hacer nada contra la emergencia climática si no ves la casa en llamas
Lucas Sánchez
Con la pandemia de COVID-19 estamos sufriendo las consecuencias de una falta de reacción global y es muy probable que también las suframos por el cambio climático. Ambas crisis nos ponen ante un espejo en el que no quedamos reflejados como seres tan racionales: entender es secundario, la experiencia es clave.
 “Quiero que actúen como si la casa estuviera en llamas”, dijo Greta Thunberg recurriendo a la metáfora porque no somos capaces de percibir la emergencia climática. / Wearbeard, SINC
“Quiero que actúen como si la casa estuviera en llamas”, dijo Greta Thunberg recurriendo a la metáfora porque no somos capaces de percibir la emergencia climática. / Wearbeard, SINCSucede en la primera escena del cuarto capítulo de la serie Chernobyl. En ella, una anciana ordeña una vaca en su cabaña, cerca de la central, días después del inicio del desastre nuclear. Un soldado, a las puertas de su establo, le pide que le acompañe. La mujer se niega y le responde con un discurso sobre las decenas de años que ha sobrevivido en una zona donde ha sufrido guerras y perdido familiares, que termina con: “¿Después de todo lo que he visto, me estás diciendo que me vaya por algo que no puedo ver en absoluto?”.
La pregunta hoy duele porque estamos viendo lo que ocurre por no actuar ante cosas que no podemos ver, pero de las que se nos ha avisado. Con la pandemia por el nuevo coronavirus estamos sufriendo las consecuencias de nuestra falta de reacción y es muy probable que las suframos más adelante por culpa de la crisis climática.
La escena de Chernobyl me hizo recordar un discurso que Greta Thunberg dio delante del Consejo Social, en Bruselas, el 16 de abril de 2019. Greta arrancó con “Quiero que entren en pánico porque la casa está en llamas”. Su objetivo lo verbalizó algo mejor segundos más tarde: “Quiero que actúen como si la casa estuviera en llamas”. Y si tuvo que recurrir a la metáfora es porque muy poca gente lo ve y menos gente todavía actúa. Estamos tranquilos con la emergencia climática y también lo estábamos como testigos en la distancia de la epidemia. ¿Qué falla en nosotros?
En el 50 aniversario del primer Día de la Tierra, tenemos claro que nuestro mundo se está calentando. Lo sabemos porque podemos verlo en gráficas consensuadas por toda la comunidad científica. Eso, lamentablemente, no significa que vayamos a hacer algo.
El problema es que ver esos datos no es ver el cambio climático. Para hacer algo, ese dato debe cuadrar con la experiencia personal, con nuestra propia evidencia. Nos es más fácil ver la casa en llamas cuando realmente vemos la casa en llamas. También nos ha sido más fácil ver el virus cuando hemos sido testigos del sufrimiento de nuestros enfermos. El cambio climático y esta pandemia nos ponen delante de un espejo en el que los humanos no quedamos reflejados como seres tan racionales: entender es secundario, la experiencia es clave.
80 años para un consenso social
En 2013 los investigadores Szafran, Williams y Roth publicaron un estudio en el que calculaban cuánto tiempo haría falta para que todo el mundo pudiera vivir en sus propias carnes el fenómeno del calentamiento global. Si necesitamos experimentar tres veranos más calurosos que la media para convencernos, solo en EE UU y teniendo en cuenta sus previsiones climáticas, ya podemos esperar al menos 86 años en tener un buen consenso social. 82 si necesitamos 3 años más lluviosos que la media.
Igual que no podíamos esperar a tener el virus en España para asustarnos, ya sabemos que no podemos esperar 80 años sin hacer nada, ya que implicaría vivir en 2100 con 5 grados de media más, un escenario casi apocalíptico.
Pero si digo 80 años pongo problemas encima de la mesa. No somos animales que lidien bien con las distancias temporales y espaciales, y el cambio climático siempre lo hemos sentido lejos y en el futuro. Aunque el planeta se esté calentando rápidamente, no lo hace tan rápido como necesitamos para sentirlo como una amenaza.
Ojalá después de masticar un filete fuéramos testigos de una pequeña ola de calor, una subida de 5 grados en casa. Esa distancia causa-efecto tan corta nos permitiría experimentar el nexo entre ambos procesos y caminaríamos mucho más rápido hacia una de las soluciones: hay que dejar de comer tantos filetes.
Somos malos calculadores de riesgos
Antes de que el cambio climático fuera ni siquiera algo de lo que hablar, los expertos en economía Daniel Kahneman y Amos Tversky hicieron varios experimentos para entender cómo lidiamos con el riesgo y la toma de decisiones, y vieron que la percepción del riesgo de los humanos es horrorosa.
Tenemos grandes dificultades para juzgar la frecuencia y la magnitud de los eventos, ya que nos fiamos más de lo último que ha sucedido, porque es lo que mejor recordamos. A este proceso lo bautizaron como sesgo de disponibilidad.
De su mano también aprendimos que tenemos una aversión a las pérdidas en el corto plazo e indiferencia en el largo plazo. Si le añadimos cierto grado de incertidumbre, el efecto se agrava. Tampoco es algo nuevo: el alcohol puede generar cirrosis ya de mayor. El tabaco quizás cáncer de pulmón. Ese “puede” y ese “quizás”, esa cirrosis y ese cáncer, se parecen mucho a la enfermedad que afecta a nuestro planeta.
Por eso nos negamos a saciar nuestras ganas de filete de hoy a cambio de un ahorro energético o económico en el futuro. Por eso y porque se juntan con otros sesgos, como el sesgo optimista: tendemos a pensar que corremos menos riesgos que otras personas. Vamos a tener más suerte que los dinosaurios, extinguirse se extinguen otros. Esto no es China. Nuestro sistema sanitario es mejor que el de Italia.
Ahora que la epidemia ya está aquí hay mucha gente enfadada. Ahora. Las semanas previas circulaban memes y chistes que se burlaban de lo que podría venir.
Pero, ¿habéis visto a alguien enfadarse muchísimo por culpa del cambio climático? No digo enfadarse por que el cambio climático se esté produciendo y ya veamos sus efectos, o por la inacción de otros. Me refiero a enfadarse visceralmente hasta que te salta la vena del cuello y rompes a llorar contra el Señor Cambio Climático. Yo, nunca. Y eso es porque no existe el Señor Cambio Climático. No lleva un uniforme, no mata a niños, no sigue un patrón predecible.
Tememos lo que podemos imaginar
El enemigo, para nuestro cerebro, siempre ha sido una persona, animal o microorganismo repugnante que actuaba de forma abrupta e inmoral sobre los nuestros. Al salvaje Señor Cambio Climático sí le tendría miedo la viejecita de la granja de Chernobyl, pero, ¿cómo tememos algo abstracto, invisible, que actúa muy lentamente y que no es inmoral? Es difícil, muy difícil.
Pero supongamos que lo conseguimos. Que logramos poner a un grupo de personas delante de una casa en llamas, la ven en llamas y la sienten en llamas. Tocaría entonces empezar a apagar el fuego. Pues resulta que, aunque nos queme el fulgor de las llamas en la cara y escuchemos el crepitar del fuego, nos giraremos y esperaremos a ver qué hacen los demás.
Si alguien coge un cubo de agua, nos pondremos manos a la obra. Si nadie se mueve, nos quedaremos embobados mirando el incendio. Esta reacción tiene que ver con la cooperación condicional y el efecto espectador. Si somos los únicos que presenciamos un incidente, actuamos. Si lo sabe todo un colectivo, esperamos al consenso social.
Incluso cuando vemos y actuamos, ni siquiera hacemos todo lo que podemos. La mayoría sufrimos el sesgo de acción única. Parece que realizar determinadas acciones nos impide hacer otras igual de positivas y complementarias. Por ejemplo, usar bombillas de bajo consumo, reciclar o usar bolsas de tela ya nos hace sentir que hacemos algo significativo.
En ocasiones es incluso peor, porque compensamos nuestras actitudes sostenibles con otras que pueden incluso emitir más carbono. Como las personas que queman las calorías de media caña de cerveza corriendo y ese día se toman dos en vez de una, ¡que han salido a correr!
Límites a la preocupación
Finalmente, aunque hayamos vivido la casa en llamas, tenemos una capacidad muy limitada para preocuparnos. Crisis financieras en distintos países muestran que la preocupación por estos fenómenos hizo que el porcentaje de individuos preocupados por el cambio climático disminuyera.
Los científicos le llaman el banco finito de preocupación. Una crisis, la pérdida del empleo, la enfermedad de nuestros familiares… no podemos preocuparnos por muchas cosas graves a la vez. De hecho, es complicado publicar una columna como esta en días en los que hay una pandemia y las UCI están llenas de gente luchando por sobrevivir.
En condiciones normales la inacción climática nos lleva a una culpa casi inevitable, y eso que no nos imaginamos la situación completa. Dentro de la metafórica casa en llamas, la nevera no tendría apenas comida. Del grifo solo saldría agua a determinadas horas. Se desplazaría por corrimientos de tierras y se inundaría tres veces al año. No se podría dormir del calor y habría que elegir entre mosquiteras o malaria. Y esa casa existe ya. Las fechas 2050 o 2100 son horizontes prácticos para ayudarnos a imaginar escenarios más duros que están por venir.
Si empezamos a ver el fuego, la inundación, la sequía y las olas de frío y calor como cambio climático, este dejará de ser abstracto para ser concreto, abrupto e impactante. Vivible y sufrible. Este pequeño cambio de paradigma es un esfuerzo comunicativo y todo apunta a que los resultados merecerían la pena. Pero, además, podemos ver el cambio climático como un problema de salud pública o de refugiados.
Entrenamiento y leyes
Quizá tengamos que crear redes para recordarnos unos a otros que debemos mantenerlo presente, de la misma forma que salimos a aplaudir a las 8 de la tarde. A fin de cuentas, hay que entrenar la anticipación sobre las buenas conductas y evitar resignarte a reincidir en actitudes poco ecológicas.
También podríamos intentarnos vacunar frente a sesgos de disponibilidad y hacer campañas como las de Naciones Unidas en Davos, que enseñó mediante realidad virtual cómo era la guerra de Siria a líderes mundiales. ¿Necesitamos ver casas en llamas?, veamos casas en llamas. ¿Crisis de refugiados climáticos? Veamos crisis de refugiados climáticos. Lo importante es que el cerebro practique, que nos nutramos de experiencias, aunque sean virtuales.
Acabemos con el sesgo espectador con nuevas leyes a medida para la crisis climática. Porque las leyes nos obligan a sincronizarnos en acciones que racionalmente nos parecen positivas, pero no ocurrirán de forma espontánea. No nos habríamos quedado encerrados en casa durante semanas sin un estado de alarma.
El soldado de Chernobyl, al no convencer a la anciana, dispara y mata a su vaca para obligarla a hacerle caso. El problema es que no tenemos un soldado en nuestra cabeza que dispare a nuestros sesgos; es más probable que solo tengamos una pequeña activista que nos repita ese “How dare you?” frunciendo el ceño cada vez que cogemos un chuletón forrado de plástico en el supermercado. Pero la pobre ocupa un espacio muy pequeño de la mente de un animal que no ve llamas por ninguna parte y al que bien le apetece un filete.
Sobre el autor: Lucas Sánchez es director de la agencia de comunicación científica Scienceseed, a cargo del Departamento de Comunicación y Creatividad. Antes, durante diez años, investigador en inmunología y virología en el Centro Nacional de Biotecnología y en la Yale University School of Medicine.
Este artículo se publicó originalmente el 22 de abril de 2020 en SINC con motivo del 50 aniversario del Día de la Tierra. Artículo original.
El artículo No vas a hacer nada contra la emergencia climática si no ves la casa en llamas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lo prudente es hablar de emergencia climática
- Lo verdaderamente divertido es hacer Ciencia
- Crisis, emergencia, apocalipsis
Gustave le Bon y la equivalencia masa-energía
Si preguntamos a cualquier persona con una mediana formación científica sobre quién fue el primero en proponer la equivalencia entre masa y energía, nos respondería inmediatamente y sin vacilación que Albert Einstein. Puede que incluso nos diese la fecha (1905) y hasta la expresión matemática, E = m·c2. Sin embargo, puede que no sea tan evidente. Y es que Gustave le Bon tuvo una magnífica intuición poco antes.
 Gustave le Bon. Fuente: Wikimedia Commons
Gustave le Bon. Fuente: Wikimedia CommonsGustave le Bon nació en 1841 en Nogent-le-Rotrou (Francia) y se doctoró en medicina en 1866 en la Universidad de París. En la actualidad se le conoce por sus trabajos en psicología de grupos y en sociología (hay quien le considera uno de los fundadores de esta disciplina), pero también escribió sobre astronomía, física y cosmología. Según le Bon el universo material habría aparecido a partir del éter primordial e imponderable y terminaría regresando a este estado, en una serie de ciclos sin fin. Como parte de este concepto incluía la equivalencia de materia y energía.
En 1896 le Bon anunció que había descubierto lo que llamó “luz negra”, un nuevo tipo de radiación invisible que él creía que estaba relacionada posiblemente con los rayos X y los rayos catódicos pero que era distinta a éstos. Sus afirmaciones atrajeron la atención de los físicos, fundamentalmente franceses, muchos de los cuales le dieron su apoyo en el descubrimiento así como a sus ideas sobre la materia, la radiación y el éter. Aunque al final la existencia de la “luz negra” fue descartada (no se pudieron reproducir sus resultados en condiciones controladas) durante un tiempo permitió que le Bon fuese una figura importante en la vida intelectual y científica francesa. En 1903 fue incluso nominado para el Nobel de física.
Entre sus amigos y admiradores se encontraban científicos de primer nivel, incluyendo el químico Henri Ferdinand-Frédéric Moissan, el astrónomo Henri Alexandre Deslandres y los matemáticos Charles Émile Picard y Jules Henri Poincaré. Pero lo que nos interesa ahora es que en sus escritos sobre la “luz negra” estaba la primera descripción cualitativa de la equivalencia entre materia y energía.
Le Bon expuso sus ideas más elaboradamente en “La evolución de la materia” (texto completo en francés, en inglés), un libro publicado, mire usted, en 1905. En él concluía que toda la materia es inestable y está degenerando, emitiendo constantemente radiación en forma de rayos X, radioactividad y “luz negra”. Las características de la materia serían epifenómenos que aparecerían durante el proceso de transformación en éter, informe e imponderable, del que había surgido. Según le Bon, la energía y la materia eran dos aspectos de la misma realidad, diferentes etapas en el gran proceso evolutivo que en un futuro lejano llevaría al universo a un estado puramente etéreo.
Su principal argumento para la continua degradación de la materia en éter era la radioactividad, que él consideraba que era algo que toda la materia exhibía en mayor o menor grado. Pero le Bon, llevaba esta idea a sus últimas consecuencias. Si todos los elementos emiten radiación por la radiactividad, todos terminarían desapareciendo, por tanto la materia, en última instancia, no se explicaría en términos materiales sino etéreos. Paradójicamente, el estudio de la materia llevaba al inmaterialismo, algo muy bien recibido por determinados círculos intelectuales del fin de siglo francés.
Le Bon tomó su versión de la evolución cósmica de la hipótesis nebular de Laplace, pero la revistió con el lenguaje de la entonces popularísima física del éter. Y, sin embargo, el éter no era para le Bon el último estadio final, ya que sugería que este fin del universo sería seguido de un renacimiento y posterior evolución, y que este proceso cíclico continuaría eternamente.
Probablemente lo más interesante de su argumento es que afirmaba que todos los átomos contenían enormes cantidades de energía que se iría liberando conforme los átomos se desintegrasen, y que esta energía “intra-atómica”, como él la llamaba, era la fuente del calor solar y de todas las otras fuerzas del universo. Incluso empleaba cálculos (elementales) de energía cinética (T = mv2/2) para encontrar órdenes de magnitud de esas energías. Cuando Einstein se hizo famoso por su demostración de que la masa y la energía eran equivalentes según E = m·c2 , le Bon reclamó parte del mérito para él. En 1922 escribió cartas a Einstein informándole de lo que él consideraba su prioridad en el descubrimiento de la reciprocidad de la masa y la energía. Ni que decir tiene que para esta época sus ideas estaban completamente desfasadas.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto se publicó originalmente el 13 de octubre de 2013 y reeditado el 16 de mayo de 2018 en el blog personal del autor.
El artículo Gustave le Bon y la equivalencia masa-energía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
