Los vampiros
“Vampiro. 1. Espectro o cadáver que, según cree el vulgo en algunos países, va por las noches a chupar poco a poco la sangre de los vivos hasta matarlos.
2. Murciélago hematófago de América del Sur.”
Diccionario de la Lengua.
“Si hay una historia bien documentada en el mundo, es la de los vampiros. No falta nada: interrogatorios, certificaciones de notables, de cirujanos, de sacerdotes de la parroquia, de magistrados. La prueba judicial es una de las más completas. Y con todo eso, ¿quién cree en los vampiros? ¿Estaremos todos condenados por no haber creído?
Jean-Jacques Rousseau, Carta a Christopher de Beaumont, 1762.
“Los vampiros les causan a menudo grandes sufrimientos, mordiéndoles en la cruz, no tanto a causa de la pérdida de sangre que resulta de la mordedura, como a causa de la inflamación que luego produce el roce de la silla. Sé que en Inglaterra han puesto en duda últimamente la veracidad de este hecho; por tanto, es una buena suerte el haber estado yo presente un día en que se cogió a uno de esos vampiros (Desmodus d’Orbigny, Wat.), en el mismo dorso de un caballo. Vivaqueábamos muy tarde una noche cerca de Coquinho, en Chile, cuando mi criado, advirtiendo que un caballo de los nuestros estaba muy agitado, fue a ver qué ocurría; creyendo distinguir algo encima del lomo del caballo, acercó con rapidez una mano y cogió un vampiro. A la mañana siguiente, la hinchazón y los coágulos de sangre permitían ver dónde había sido mordido el caballo; tres días después hicimos uso de éste, sin que pareciera resentirse ya de la mordedura.”
Charles Darwin, Viaje de un naturalista alrededor del mundo, 1839.
Contaba Anthony Masters en su libro sobre vampiros, publicado en 1974, que hay dos tipos de vampiro, el mítico y el real, y ambos, según cuenta, pueden matar y son asesinos. El mítico, cuenta la leyenda, mata personas por miles, incluso solo por el terror que provoca. En su tiempo, y quizá ahora, era juzgado, condenado y ejecutado por asesino psicópata o, si no era así, simplemente era linchado. El vampiro real ataca para alimentarse y se le tiene por cruel y estremecedor.
 Foto: Clément Falize / Unsplash
Foto: Clément Falize / UnsplashLa mitología del vampiro, de ese vampiro mítico, no el real, aparece en muchas culturas y religiones de todo el mundo, tal como detalla Anthony Masters. La definición de vampiro y de vampirismo varía según el origen de la leyenda. En la mitología, los vampiros son seres no muertos, inmortales por tanto, y misteriosos y nocturnos. Ocupan la frontera, que atraviesan si les apetece, entre el mundo de los vivos y el de los muertos. El grupo de K. Gubb, del Hospital Box-Hill de Melbourne, en Australia, escribe que los vampiros son criaturas poderosas que provocan miedo, intrigan y fascinan, y dominan a otras personas. Se hicieron famosos y conocidos con los escritos de John Polidori y Bram Stoker en el siglo XIX.
En la revisión sobre vampirismo, que publicaron en 2013, Lennon da Costa Santos y sus colegas, de la Universidad Federal de Minas Gerais, en Brasil, proponen que se cree en la existencia de los vampiros cuando, en alguna persona, se observan síntomas de algunas enfermedades que recuerdan la descripción del aspecto de los vampiros de las leyendas. Mencionan la porfiria, que provoca un semblante anémico con una palidez exagerada. Es una enfermedad causada por un defecto metabólico que impide la síntesis de la hemoglobina de la sangre y, como efectos, hay anemia y palidez. La síntesis de la hemoglobina se detiene un paso anterior, cuando se produce la porfirina, molécula que precede a la hemoglobina, que, por tanto, se acumula en los tejidos del paciente, sobre todo en la zona subcutánea, los huesos y los dientes.
Además, la porfirina reacciona a la luz y produce radicales de oxígeno que, al sol, pueden provocar heridas en la piel. De ello la leyenda sobre la aversión al sol de los vampiros que, incluso, los puede destruir, y su obligada vida nocturna. La porfirina, en casos graves, llega a deformar el rostro, retrae los labios y muestra la dentadura que, así, parece más grande de lo habitual. Son los afilados colmillos del vampiro. Los enfermos de porfiria desarrollan conductas antisociales, agresividad y aislamiento, incluso desórdenes mentales. Para la imaginación popular, son seres malditos o demonios encarnados.
 Vampiro (1895) de Edvard Munch
Vampiro (1895) de Edvard MunchLos autores aluden al Doctor Juan Gómez Alonso que, en su tesis, defendida en 1992, y en publicaciones posteriores, relaciona el vampirismo popular con la rabia y menciona la coincidencia de una epidemia de esta enfermedad en Hungría, a principios del siglo XVIII, con la difusión de leyendas sobre vampiros en áreas montañosas y remotas de los Cárpatos. Gómez Alonso comenta que el vampirismo, según el mito, se transmite por mordedura, como muchas enfermedades transmitidas por animales y, entre ellas, la rabia. Además, el vampiro se puede transformar a voluntad en lobo, perro o murciélago, animales todos ellos que pueden contagiar de la rabia.
Es una enfermedad que altera la conducta, provoca más agresividad, y actúa en áreas cerebrales del sistema límbico, como el hipotálamo o la amígdala, encargadas de sentimientos y emociones. Lleva a conductas nocturnas, como la leyenda dice de los vampiros. Hay otros síntomas de la rabia que recuerdan a los relatos de vampiros: espasmos musculares, gruñidos, hidrofobia, fotofobia o, incluso, evitar la propia imagen en el espejo.
En conclusión, para Gómez Alonso, las epidemias de rabia del siglo XVIII pudieron ampliar y difundir los mitos sobre vampiros, ya existentes, en Europa centra y oriental.
Una tercera enfermedad a la que se atribuye la leyenda sobre los vampiros es la pelagra, provocada por la deficiencia en vitamina B3 o niacina que, en el siglo XVIII, en la época de la difusión de las leyendas sobre vampiros, se atribuye a la extensión del cultivo del maíz, que llegó a Europa desde América y, poco a poco, por su fácil cultivo y rendimiento, se convirtió en la base de la alimentación de las clases más pobres. La falta de vitamina B3 en el maíz provocó la deficiencia en esta vitamina en quienes lo tenían como el alimento más consumido.
Según la hipótesis de Jeffrey Hampl y William Hampl III, de las universidades de Massachusetts y de Rhode Island, la pelagra provoca dermatitis y demencia, con insomnio e irritabilidad, y, además, hipersensibilidad a la luz que les provoca alteraciones en la piel y quemaduras. Se inflaman los labios y los dientes parecen más grandes. Todos ellos son síntomas que también describen a los vampiros.
En psiquiatría, el vampirismo clínico se define como una creencia en fantasmas chupadores de sangre o que intentan conseguir sangre pues les produce un profundo placer sexual. Otros autores, según Gubb, consideran que el vampirismo clínico es el acto concreto de beber sangre de la víctima, una conducta poco común que se asocia con la esquizofrenia. Y hay expertos que asocian el vampirismo con actos agresivos o sexuales con cadáveres o con moribundos. Incluso se han descrito pacientes con autovampirismo cuando el sujeto bebe su propia sangre.
Uno de los vampiros más famosos del último siglo fue Peter Kürten, conocido como el Vampiro de Dusseldorf, nacido en 1893, asesinó, según la sentencia que le condenó, a nueve personas, con más intentos frustrados y más de ochenta agresiones sexuales. Murió guillotinado en 1931, a los 48 años, y la leyenda cuenta que preguntó, poco antes de la ejecución, si, una vez cortada la cabeza, oiría, aunque fueran unos segundos, la sangre saliendo de su cuerpo. En el juicio relató su pasión por beber la sangre de sus víctimas, en un síndrome llamado hematodipsia.
A pesar de la popularidad del vampirismo, las publicaciones científicas sobre este síndrome son escasas, sobre todo a partir de 1940, lo que indica la escasa investigación sobre ello. El grupo de Gubb llega a esta conclusión después de comentar trabajos publicados en Sudáfrica, Francia, Suiza y Estados Unidos hasta 2006.
 Un vampiro común (Desmodus rotundus) alimentándose de un cerdo (animales disecados expuestos en el Museo de Historia Natural de Viena). Foto: Sandstein /Wikimedia Commons
Un vampiro común (Desmodus rotundus) alimentándose de un cerdo (animales disecados expuestos en el Museo de Historia Natural de Viena). Foto: Sandstein /Wikimedia CommonsDespués de repasar el mito vamos a conocer la realidad del vampiro. Son murciélagos con una dieta exclusivamente de sangre. Son los únicos mamíferos con alimentación hematófaga o, si se quiere, sanguívora aunque sea una palabra que no está en el Diccionario. Solo hay tres especies de murciélagos con dieta de sangre: el vampiro común, Desmodus rotundus, que ya conocía Darwin; el vampiro de piernas peludas, o Dyphylla ecaudata, y el vampiro de alas blancas o Diaemus youngi, que solo gusta de la sangre de aves. Las tres especies se encuentran en Centro y Sudamérica, desde México hasta Chile y Argentina.
Las tres especies pertenecen a la misma familia aunque a distintos géneros, y se supone que han tenido un antepasado común. En esa familia hay murciélagos con dietas muy variadas como, por ejemplo, se alimentan con néctar, polen, insectos, frutas, pescado y carne. Y, como sabemos, solo tres especies tienen dieta de sangre, unos 10 mililitros al día. Al morder, segregan un anticoagulante que es una proteína muy apropiadamente llamada draculina. Horas después de la mordedura, la herida sigue sangrando con suavidad. Por cierto, rara vez muerden a una persona y, si lo hacen, es en las extremidades, los dedos o la nariz.
Es una dieta poco habitual y supone adaptaciones para que sea funcional y eficaz: mucho líquido y, por tanto, un potente sistema renal para eliminarlo, y una gran vejiga para almacenar la orina; riesgo, si no se controla y elimina el exceso de hierro, de provocar síntomas de toxicidad; además, es una dieta con exceso de proteínas y pocos carbohidratos y vitaminas; fuertes caninos para morder; sistema sensorial para detectar, por medio de infrarrojos, las zonas calientes de la piel de la víctima como las áreas con más cercanía del sistema circulatorio y de la sangre y allí, morder,…
El estudio del genoma del vampiro común, Desmodus rotundus, del grupo de Lisardia Zepeda, de la Universidad de Copenhague, ha localizado algunas de las adaptaciones a la dieta de sangre. Tienen vías de síntesis de vitamina B, que es muy escasa en la sangre y necesitan elaborarla. Hay proteínas en el intestino del vampiro que, con agua y dióxido de carbono, abundantes en la sangre, sintetizan hidratos de carbono. El exceso de hierro en la sangre se controla por genes que dirigen su eliminación. Las proteínas de la sangre se metabolizan y los productos resultantes se eliminan por el sistema renal en la orina.
Estos autores también han localizado los genes que dirigen la detección de radiación infrarroja, es decir, de calor, para encontrar en la piel las zonas con más circulación de sangre y, así, elegir el lugar para morder.
Estas adaptaciones, según el estudio publicado por el grupo de Fidel Botero Castro, de la Universidad de Montpellier, sobre el ADN de las mitocondrias, revelan que se habían seleccionado hace unos 4 millones de años, con una relativa rapidez para lo que duran estos procesos.
Referencias:
Botero Castro, F. et al. 2018. In cold blood: Compositional bias and positive selection drive the high evolutionary rate of vampire bats mitocondrial genomes. Genome Biology and Evolution 10: 2218-2239.
Gómez, J.A. 1998. Rabies: a posible explanation for vampire legend. Neurology 51: 856-859.
Gubb, K. et al. 2006. Clinical vampirism: a review and illustrative case report. South African Psychiatry 9: 163-168.
Hampl, J.S. & W.S. Hampl III. 1997. Pellagra and the origin of a myth: evidence from European literatura and folklore. Journal of the Royal Society of Medicine 90: 636-639.
Masters, A. 1974. Historia natural de los vampiros. Ed. Bruguera. Barcelona. 318 pp.
Santos, L.C.S. et al. Medical explanations for the myth of vampirism. Revista Medica de Minas Gerais 23: 510-514.
Velasco, E. 2018. Descubren cómo los vampiros pasaron a alimentarse solo de sangre. La Vanguardia 20 enero.
Wikipedia. 2018. Vampire bat. 29 October.
Wikipedia. 2020. Peter Kürten. September 4.
Zepeda Mendoza, M.L. et al. 2018. Hologenomic adaptations underlying the evolution of sanguivory in the common vampire bat. Nature Ecology & Evolution doi: 10.1038/s41559-018-0476-8
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Los vampiros se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:César Tomé López – Naukas P4K 2019: ¿Eureka?¿En serio?

Aunque un experimento te lo cuente cualquier libro de texto no quiere decir que como te lo cuentan sea correcto. Por eso es tan importante reproducir los experimentos. El caso de Arquímedes y la corona ilustra el argumento. Da la charla César Tomé López, editor de este Cuaderno de Cultura Científica, de Mapping Ignorance y responsable de proyección internacional de Euskampus Fundazioa.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo César Tomé López – Naukas P4K 2019: ¿Eureka?¿En serio? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- José Miguel Viñas – Naukas P4K 2019: De nubes las pinacotecas están llenas
- Joaquín Sevilla – Naukas P4K 2019: Lo que esconden unos champiñones al ajillo
- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
El cannabis rompe el equilibrio metabólico entre neuronas y astrocitos alterando el comportamiento social
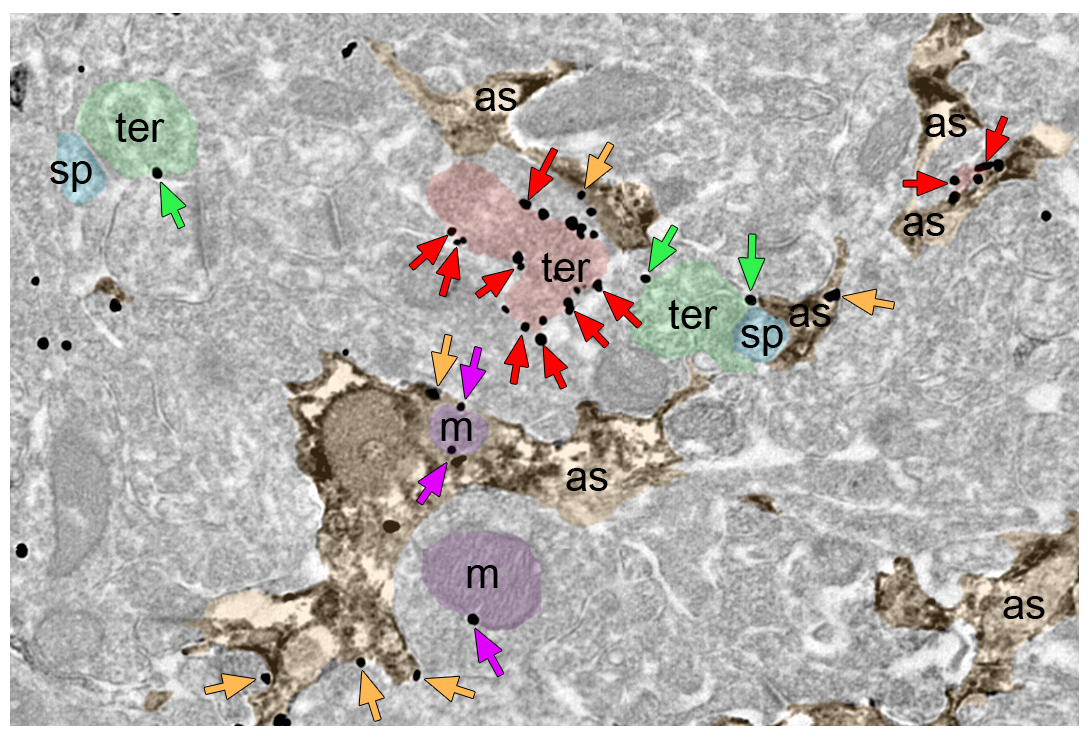
El sistema nervioso está formado por neuronas y células gliales. De estas últimas, las más abundantes son los astrocitos, que, entre otras muchas funciones, se encargan de captar la glucosa del torrente sanguíneo para proporcionar energía y permitir la actividad neuronal necesaria, y así asegurar que las funciones cognitivas se ejecuten de una manera correcta. Los receptores cannabinoides tipo 1 (CB1), que modulan la comunicación entre los astrocitos y las neuronas, constituyen la principal diana del componente psicoactivo del cannabis, llamado delta-9-tetrahidrocannabinol (THC).
¿Qué pasa cuando el THC actúa sobre los astrocitos? La investigación, en la que ha participado el grupo del doctor Pedro Grandes del Departamento de Neurociencias de la Facultad de Medicina y Enfermería de la UPV/EHU, concluye que la activación de los receptores de cannabinoides CB1 en las mitocondrias (orgánulos celulares encargados de la producción de energía) de los astrocitos de ratón impide el metabolismo de la glucosa y la producción de lactato en el cerebro, lo cual altera la función neuronal, causando un deterioro de las conductas de interacción social.
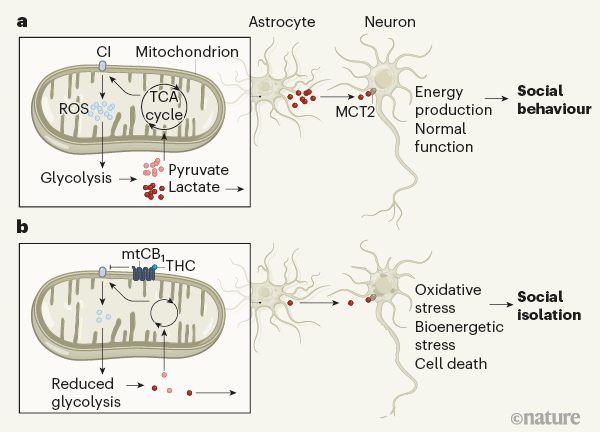
Según el Dr. Grandes, “la activación de estos receptores conduce a que los astrocitos generen una menor cantidad de especies reactivas de oxígeno, lo que afecta negativamente a la producción glucolítica de lactato causando un estrés neuronal y una falta de interacción social. La importancia de esta investigación radica no sólo en la identificación de este déficit que puede revertirse mediante la manipulación genética y farmacológica de estos cambios moleculares y bioquímicos causados por el tratamiento cannabinoide, sino también por lo que aporta al conocimiento de las alteraciones causadas por el cannabis en el cerebro”.
La colaboración del grupo de investigación del Dr. Pedro Grandes con el equipo del Dr. Giovanni Marsicano, de la Universidad de Burdeos, resultó fundamental hace unos años para demostrar por primera vez la presencia de receptores CB1 en las mitocondrias de las neuronas, cuya activación reduce la actividad mitocondrial causando pérdida de memoria. Los resultados de estos estudios se publicaron en el año 2012 en Nature Neuroscience y en 2016 en Nature. Sin embargo, “quedaba pendiente conocer cuál era la función de los receptores CB1 localizados en mitocondrias de astrocitos, de ahí la relevancia de este nuevo hallazgo, que además supone una continuidad en la línea de investigación y cooperación transfronteriza”, explica el doctor Grandes. Este descubrimiento se ha publicado en Nature.
Referencias:
Jimenez-Blasco D, Busquets-Garcia A, Hebert-Chatelain E, Serrat R, Vicente-Gutierrez C, Ioannidou C, Gómez-Sotres P, Lopez-Fabuel I, Resch-Beusher M, Resel E, Arnouil D, Saraswat D, Varilh M, Cannich A, Julio-Kalajzic F, Bonilla-Del Río I, Almeida A, Puente N, Achicallende S, Lopez-Rodriguez ML, Jollé C, Déglon N, Pellerin L, Josephine C, Bonvento G, Panatier A, Lutz B, Piazza PV, Guzmán M, Bellocchio L, Bouzier-Sore AK, Grandes P, Bolaños JP, Marsicano G. (2020) Glucose metabolism links astroglial mitochondria to cannabinoid effects Nature doi: 10.1038/s41586-020-2470-y
Magistretti, P.J. (2020) How lactate links cannabis to social behaviour Nature (News & Views) 583, 526-527 doi: 10.1038/d41586-020-01975-5
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El cannabis rompe el equilibrio metabólico entre neuronas y astrocitos alterando el comportamiento social se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El límite entre la vida y la muerte en las neuronas
- Un nexo cannabinoide entre mitocondrias y memoria
- El citoesqueleto de las neuronas y el alzhéimer
Mayas y aztecas en la orquesta
 Concha trompeta de Chipícuaro. Arte tolteca (años 300-900). Fuente: Smithsonian Institution
Concha trompeta de Chipícuaro. Arte tolteca (años 300-900). Fuente: Smithsonian Institution
Las caracolas han fascinado a los humanos desde siempre. Sus formas intrincadas, sus hermosos colores y patrones, el misterio de su cámara interior capturan la imaginación. Pero además de estas cualidades visuales, tienen un encanto adicional. Gracias a su potente sonido, las caracolas se han utilizado desde la antigüedad en culturas de todo el mundo para atravesar las distancias y el corazón de los dioses. En Nueva Guinea, aún existen llamadas estándar que dan la voz alarma, anuncian una caza exitosa u otros eventos importantes. Sus poderes sobrenaturales fueron conocidos asimismo en Europa. En Bohemia Occidental, se hacía sonar una caracola para ahuyentar a las tormentas. En la India, el shankha es una pieza esencial del budismo y el hinduismo. Constituye un recipiente ritual, así como un instrumento para ocasiones solemnes y ceremonias religiosas. En la mitología hindú, es un emblema sagrado del dios Vishnu. Los monjes tibetanos aún hoy la hacen sonar para convocar a los devotos. Como los niños náufragos de la novela de Golding, los fieles acuden a su llamada limpia y penetrante a través de la distancia.
 Quetzalcoatl con la coraza del viento al cuello. Fuente: Wikimedia Commons.
Quetzalcoatl con la coraza del viento al cuello. Fuente: Wikimedia Commons.De entre todas estas culturas, la caracola jugó un papel ritual especialmente importante en las sociedades precolombinas de América central y América del sur. Su uso está particularmente bien documentado en la mayoría de las áreas culturales de mesoamérica y en la zona de México occidental, donde se vinculaba a eventos sociales y ceremonias religiosas. Muchos de sus restos se han encontrado en sitios funerarios, indiando su papel como ofrendas1 en diversos ritos de paso. Normalmente, estaban ricamente decoradas, con todo tipo de relieves y pinturas. Cumplían asimismo un papel importante en la guerra, como instrumento de llamada. En algunas sociedades, se asociaban a los rituales y la parafernalia de los chamanes, que ejercían como líderes tanto espirituales y guerreros. De manera más general, la caracola se asociaba como símbolo a Quetzalcoatl, la serpiente emplumada, el dios azteca del viento, el aire y el aprendizaje que siempre llevaba alrededor del cuello la «coraza de viento» o ehecailacocozcatl. Este talismán con forma espiral se fabricaba, precisamente, a paritr de la sección transversal de una caracola y fue usado como collar por gobernantes y sacerdotes.
Una ilustración en el Códice Magliabecchiano muestra a un caracolista (en la cultura azteca eran conocidos como quiquizoani)con su mano introducida dentro de su instrumento (quiquiztli). Podría parecer una forma casual de sujetarlo pero no es el caso. Una de las limitaciones de la concha, es que, a priori, no puede producir más de una nota. Su tono viene dado por su longitud y a priori, este parámetro no es algo que se pueda cambiar. Sin embargo, los caracolistas como Steve Turre, son capaces de afinar varios sonidos introduciendo la mano en el extremo abierto de la caracola. Al hacerlo, el espacio disponible en su interior se vuelve más pequeño, las ondas sonoras se acortan y el resultado es un sonido sensiblemente más agudo que el original. El efecto es el mismo que cuando alguien vierte agua dentro una botella para cambiar su tono: la mano haría la función del líquido, en este caso. Hoy en día, los intérpretes de trompa utilizan esta misma técnica de afinación “manual” para afinar ciertas notas. Este instrumento de viento metal hermosamente acaracolado, tiene de hecho un origen muy similar al de la concha. Las versiones primitivas de la trompa consistían sencillamente en cuernos de animales encontrados (en inglés su nombre todavía es horn, de hecho), que fueron ganando complejidad hasta adquirir su actual forma metálica. Sin embargo, el recurso de afinar con la mano no fue explotado en Europa hasta el siglo XVIII. La ilustración del Códice Magliabecchiano sugiere que ya era utilizado por los intérpretes de conchas aztecas al menos desde dos siglos antes.
 Códice Magliabecchiano, XIII, 11, 3. Xochipilli, “noble flor”, dios del sol naciente, las flores y la alegría, es llevado en una litera adornada con mazorcas. Códice Magliabechiano, f. 35r. Reprografía: Marco Antonio Pacheco / Raíces. Fuente: Wikimedia Commons
Códice Magliabecchiano, XIII, 11, 3. Xochipilli, “noble flor”, dios del sol naciente, las flores y la alegría, es llevado en una litera adornada con mazorcas. Códice Magliabechiano, f. 35r. Reprografía: Marco Antonio Pacheco / Raíces. Fuente: Wikimedia Commons
Curiosamente, la vinculación de las conchas con las culturas de centroamérica ha traído de vuelta este instrumento al mundo de las orquestas. Muchos compositores contemporáneos, especialmente en ese lindísimo país llamado México, han utilizado su característico sonido para evocar los ecos del pasado de su nación. Recuerdo la primera vez que yo escuché el penetrante tono de una caracola, brillante, tenso y doloroso, llenando la sala Nezahualcóyotl de la Ciudad de México. Sonaba el último movimiento La Noche de los Mayas (20’30’’) de Silvestre Revueltas y el público había hecho suyo aquel concierto. Fue un momento emocionante.
Referencia:
1Novella, Robert. (1991). Shell Trumpets from Western Mexico. Papers from the Institute of Archaeology. 2. 42. 10.5334/pia.16.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Mayas y aztecas en la orquesta se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Un juego con un premio colosal
Se propone un juego entre cuatro personas (Ana, Blas, Carmen y David) con un “colosal” ipremio para aquella que gane: las obras completas de Paul Erdős.

Las reglas del juego son las siguientes: cada participante recibe dos dados con las caras numeradas de una manera que no es la habitual. El primer dado tiene marcadas en sus caras los números 2, 7, 7, 12, 12 y 17, y el segundo las cifras 3, 8, 8, 13, 13, y 18. Los dados son equilibrados, es decir, cada cara tiene la misma probabilidad de salir, que es de 1/6.
En privado, sin nadie observando, cada participante tira 20 veces ambos dados. Anota el resultado de la suma de las cantidades alcanzadas en cada tirada y adiciona los veinte resultados obtenidos. Gana la persona cuya puntuación final sea mayor.
Sin embargo, quizás por los nervios o quizás por torpeza, puede suceder que las sumas no sean correctas. Incluso puede ocurrir que alguno de los participantes, pensando que así tendrá más posibilidades de vencer en el juego, mienta en su resultado. La posibilidad engañar existe, ya que nadie les está vigilando.
Por todo ello se dispone de un juez imparcial, Ernesto, preparado para descalificar a cualquier participante si, con un 90 % de certeza, cree que ese jugador o jugadora ha fallado al sumar o, abiertamente, ha mentido.
Después de explicar estas reglas, los participantes se encierran para proceder a lanzar sus dados… y sumar (¿quizás inventar?). Tras finalizar sus tiradas, declaran lo siguiente:
-
Ana confirma que ha sacado 385 puntos,
-
Blas dice que ha obtenido 840 puntos,
-
Carmen afirma que sus tiradas suman 700 puntos y
-
David anuncia que ha conseguido 423 puntos.
Pocos minutos después, Ernesto, el juez, declara: “Sin ninguna duda, Ana es la ganadora”.
¿Sabrías explicar la razón?
Antes de argumentar, vamos a reflexionar sobre las sumas que se pueden obtener.
-
Observar que los números del primer dado son todos congruentes con 2 módulo 5, es decir, las cifras 2, 7, 12 y 17, al dividirlas por 5, dan como resto 2. Del mismo modo, los números del segundo dado son todos congruentes con 3 módulo 5, es decir, las cifras 3, 8, 13 y 18, al dividirlas por 5 dan como resto 3. Así, al sumar las cantidades obtenidas en una tirada (las procedentes de los dos dados), la cantidad resultante es siempre un múltiplo de 5, por lo que la suma final también debe serlo.
-
La menor suma que puede obtenerse en una tirada es 5 (2+3) y la mayor 35 (17+18). Así, el resultado final de las sumas tras las 20 tiradas oscila entre 100 (5×20) y 700 (35×20).
Tras estas sencillas observaciones, Ernesto ha podido descalificar directamente a David (la suma que da este jugador no es un múltiplo de 5) y a Blas (es imposible obtener 840 puntos sumando los resultados de las 20 tiradas) que, o bien se han equivocado al sumar o bien han querido hacer trampa.
Carmen afirma que sus tiradas han sumado 700, lo que significa que, en cada una de las 20 tiradas, ha obtenido la máxima puntuación, que es de 35… y desde luego es posible que eso haya sucedido. Pero, ¿cuál es la probabilidad de que suceda? La probabilidad de que salga 35 en una tirada es de 1/62=1/36 (se debe obtener 17 en el primer dado y 18 en el segundo). Por lo tanto, la probabilidad de que salga 35 en las veinte tiradas es de 1/640 (cada tirada es un suceso independiente). Y este número es del orden de 1,34×10-31, una cantidad realmente pequeña. Claro que es posible que Carmen haya sacado un montante de 700 por azar, pero es muy poco probable. Así que Ernesto, con el 90 % de certeza, puede descalificar a Carmen.
¿Lo que dice Ana es creíble? Desde luego 385 es un múltiplo de 5. El resultado más probable es el de 400 (20×20=400). ¿Por qué? Porque puede obtenerse una suma de 20 en una tirada de diez maneras distintas: 2+18 (un modo), 7+13 (cuatro formas), 12+18 (cuatro maneras) y 17+3 (un modo). El resto de las sumas posibles son: 5 (2+3), 10 (2+8, 7+3; de cuatro modos), 15 (2+13, 7+8; 12+3, de ocho maneras), 25 (7+18, 12+13; 17+8; de ocho maneras), 30 (12+18, 17+13; de cuatro modos) y 35 (17+18; de una manera).
Por otro lado, la suma de 385 es posible de obtener (por ejemplo, con 17 tiradas sumando 20 y otras tres sumando 15. O con 10 tiradas de 25, 7 de 15 y 3 de 10, etc.). Así que lo que dice Ana es creíble y, habiendo sido excluidos Blas, Carmen y David, ¡ella es la ganadora!
Notas:
Este problema se ha extraído de ¿Puedes resolver el acertijo del rey tramposo? de Dan Katz en TED-ed.
iPaul Erdös (1913-1996) fue uno de los más prolíficos matemáticos en cuanto a publicaciones científicas: unos 1.500 artículos con más de 500 coautores. Por ello podemos calificar sus obras completas como un premio “colosal”.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Un juego con un premio colosal se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El juego del Sim
- Un juego de mesa para entender la irreversibilidad
- Matemáticas en el juego de cartas SET (1)
La impureza, por definición, de las muestras radiactivas
 Foto: ActionVance on Unsplash
Foto: ActionVance on UnsplashConviene quizás en este punto de nuestra exploración del núcleo atómico pararnos un momento a considerar qué significa desde el punto de vista práctico que tengamos una muestra de un determinado material radiactivo puro. La muestra, sin actuar sobre ella y aislada, no será pura si pasa el tiempo suficiente. Esto es algo fundamental que hace que un material radiactivo sea algo completamente diferente de una sustancia o un elemento no radiactivos. Para ilustrar esta idea recomendamos leer Las series de desintegración radiactiva y tener presente la tabla que presentábamos en esa anotación:
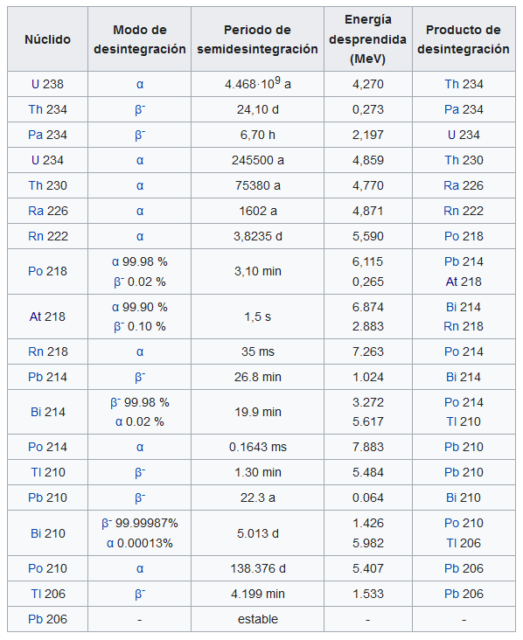
Fijémonos, por ejemplo, en la porción de la serie uranio-radio que empieza con el polonio-218. Se puede recoger polonio-218 exponiendo un trozo de material ordinario, como una lámina delgada de aluminio, a gas radón. Algunos de los átomos de radón se desintegran en átomos de polonio-218, que luego se adhieren a la superficie de la lámina. Ya tenemos nuestra muestra pura. Ahora la dejamos aislada y no hacemos nada. ¿Qué ocurre? Lo ilustra la siguiente gráfica:
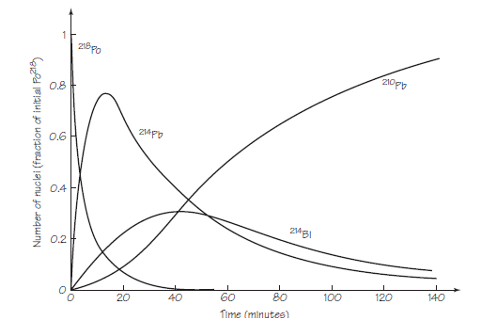
El polonio-218 (218Po) se desintegra en plomo-214 (214Pb), que se desintegra en bismuto-214 (214Bi), que se desintegra en polonio-214 (214Po), luego plomo-210 (210Pb), luego bismuto-210 (210Bi), etc. Si la muestra original contenía 1,000,000 átomos de 218Po cuando la recogimos, después de 20 min contendrá alrededor de 10,000 átomos de 218Po, alrededor de 660,0000 átomos de 214Pb, alrededor de 240,000 átomos de 214Bi y alrededor de 90,000 átomos de 210Pb. El número de átomos de 214Po es insignificante porque la mayoría de los 214Po se habrá transformado en 210Pb en una pequeña fracción de segundo.
Análogamente, una muestra de radio puro recién obtenida (226Ra) también cambiaría en composición de una manera compleja, pero mucho más lentamente. Con tiempo suficiente, consistiría en una mezcla de algo de 226Ra restante, más radón-222, polonio-218, plomo-214 y el resto de los miembros de la cadena hasta el «radio G» estable (plomo-206). De manera similar, una muestra de uranio puro puede contener, después de un tiempo, otros 14 elementos de los cuales 13 (todos menos la última parte estable) contribuyen a la emisión radiactiva, cada uno a su manera.
En todos estos casos, el resultado es una mezcla compleja de elementos. Pero, fijémonos, que desde el punto de vista de las emisiones radiactivas también se ha producido un cambio fundamental: Tras comenzar como un emisor alfa puro, la muestra original termina emitiendo toda clase de partículas, alfa, beta y rayos gamma, aparentemente de forma continua y simultánea.
Vemos pues que la separación de los diferentes miembros de una cadena radiactiva entre sí es algo muy difícil, especialmente si algunos miembros de la cadena se desintegran rápidamente. Uno de los métodos empleados con éxito dependía de la hábil purificación química de una sustancia radiactiva en concreto, como habían hecho los Curie con el radio y el polonio. La enorme complejidad y el ingenio del trabajo experimental necesarios para aislar y determinar las propiedades de cada uno de los elementos de una serie radiactiva son dignos de admiración.
Supongamos ahora que hemos obtenido una muestra de la que se han eliminado todos los átomos radiactivos excepto los de radio-226. La muestra comienza a emitir gas radón inmediatamente. Este último puede extraerse y examinarse sus propiedades antes de que se contamine seriamente por la desintegración de muchos de sus átomos en polonio-218. Si conseguimos hacer esto, encontraremos que el radón se desintegra (a través de varias transformaciones) en plomo mucho más rápidamente que el radio se desintegra en radón. Pero, ¿cómo medimos la velocidad de desintegración y por qué existen velocidades diferentes?
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La impureza, por definición, de las muestras radiactivas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La transformación radiactiva
- La carga de las partículas radiactivas
- Las series de desintegración radiactiva
Las huellas dactilares, el FBI y la teoría de Fourier modernizada
Javier Duoandikoetxea
Las huellas dactilares nos identifican, por eso los detectives las buscan en el lugar donde se ha producido un delito. No resulta sorprendente, por tanto, saber que hay colecciones gigantescas de huellas dactilares en los archivos policiales.
 Imagen 1: Ventana de vidrio simulando huellas dactilares. (Fotografía: Eveline de Bruin – Licencia Pixabay. Fuente: pixabay.com)
Imagen 1: Ventana de vidrio simulando huellas dactilares. (Fotografía: Eveline de Bruin – Licencia Pixabay. Fuente: pixabay.com)El FBI comenzó a tomar huellas dactilares en 1924 mediante el uso de fichas de cartón, en las que los dedos mojados en tinta dejaban su marca. En 1993, ya tenía almacenadas más de 25 millones de fichas. Para entonces, el uso de los ordenadores ya había comenzado a extenderse y estaba claro que los archivos digitales reportarían grandes ventajas, tanto para guardar huellas dactilares como para realizar búsquedas, por lo que se procedió a la digitalización.
Es importante asegurar con la mayor precisión posible a quién pertenece una huella dactilar. Por eso, para digitalizar los archivos se eligió una imagen de 500 puntos por pulgada, a escala de colores grises de 8 bytes. Esto generaba un fichero de 10 MB de cada ficha, de modo que la digitalización de todo el archivo requería soportes con gran espacio. Además, hace 25 años la capacidad de almacenamiento de los dispositivos era muy inferior a la actual. Entonces, ¿qué hacer? La clave estaba en la compresión.
Recordemos que comprimir es reducir el tamaño del fichero y que, para que eso resulte útil, hay que hacerlo sin perder información importante. El sistema de compresión JPEG, habitual para las fotografías, se lanzó en 1992 y fue el elegido por los expertos del FBI para llevar a cabo el proceso de digitalización. A pesar de ello, no quedaron satisfechos con los resultados, ya que la imagen resultante no les parecía adecuada. ¿Por qué?
En la mayoría de los casos, al pasar de un píxel a otro el cambio de color que se produce es pequeño, que es lo que aprovecha el sistema JPEG. Por eso, en las zonas de los bordes el resultado no es tan bueno, ya que se pueden producir cambios de color importantes en los píxeles de alrededor. Se puede decir, en cierta medida, que en las imágenes de las huellas dactilares lo único que tiene importancia son los bordes (rayas).
Para resolver el problema, investigadores de varias universidades y agencias gubernamentales de Estados Unidos colaboraron en la búsqueda de un buen algoritmo adaptado a la compresión de imágenes de huellas dactilares.
Intervalo matemático
En 1984, el matemático francés Yves Meyer trabajaba como profesor en la Universidad de París-Orsay cuando un compañero físico le enseñó un artículo, pensando que sería de su interés. Los autores eran Jean Morlet y Alex Grossmann, ingeniero geofísico de la empresa Elf Aquitaine el primero y físico de la Universidad de Marsella el segundo.
 Imagen 2: Alex Grossmann (1930-2019) y Jean Morlet (1931-2007), en 1991. (Fuente: Centre de Physique Théorique, Universidad de Marsella)
Imagen 2: Alex Grossmann (1930-2019) y Jean Morlet (1931-2007), en 1991. (Fuente: Centre de Physique Théorique, Universidad de Marsella)El artículo proponía una nueva vía de detección de gas y petróleo. Para detectar el petróleo y las bolsas de gas subterráneas, se emite una onda y, mediante el análisis de la señal que regresa tras atravesar varias capas, se obtiene información sobre la composición interna. Morlet presentó una nueva técnica para hacerlo y trabajó el campo matemático con Grossmann, pero no tuvo mucho éxito en la empresa y, según dicen, únicamente consiguió una jubilación anticipada. Sin embargo, la fama le llegó del mundo de la ciencia.
Yves Meyer se quedó sorprendido por lo que vio en el artículo: en él se encontró con fórmulas conocidas, de un campo que dominaba perfectamente, y consideró que podía ser un camino fructífero entablar relación con los autores. Según cuenta él mismo, tomó el tren para Marsella en busca de Grossmann. En pocos años, Meyer y sus colegas y discípulos convirtieron aquellos torpes pasos iniciales en una teoría matemática.
Los componentes básicos para desarrollar una función en la teoría clásica de Fourier son las funciones trigonométricas. En la nueva teoría, estos componentes básicos cambian y se utilizan dilataciones y traslaciones de una función madre. Eso sí, esa madre necesita propiedades adecuadas para ser de utilidad. De todas formas, hay muchas opciones y se puede decidir la más apropiada en función del uso, lo cual ya es, en sí mismo, una ventaja en las aplicaciones.
Morlet le puso un nombre francés al nuevo objeto: ondelette. Posteriormente, cuando el término llegó al inglés, se convirtió en wavelet, que es la denominación con la que ha recorrido el mundo científico. Aunque muchos usuarios utilizan el préstamo tal cual (wavelet), existen términos adaptados a cada idioma: ondícula (esp.), ondeta (cat.), onduleta (port.), por ejemplo.
 Imagen 3: Stéphane Mallat, Yves Meyer, Ingrid Daubechies y Emmanuel Candès han tenido una gran importancia en el desarrollo de la teoría de las wavelets y sus aplicaciones. (Fotografía: S. Jaffard – La lettre d’infos du CMLA, junio de 2017)
Imagen 3: Stéphane Mallat, Yves Meyer, Ingrid Daubechies y Emmanuel Candès han tenido una gran importancia en el desarrollo de la teoría de las wavelets y sus aplicaciones. (Fotografía: S. Jaffard – La lettre d’infos du CMLA, junio de 2017)El análisis tradicional de Fourier no detecta bien los grandes cambios de una función que se producen en un intervalo reducido, porque las funciones trigonométricas que utiliza como componentes no están localizadas. Las ondículas, en cambio, se localizan y se adaptan mejor para estudiar cambios drásticos de funciones. Además, conviene elegir la ondícula madre adecuada según el uso que le vayamos a dar. Esto puede tener un coste matemático mayor y, si es para aplicarlo, quizás también un coste económico, pero hará mejor el trabajo que queremos o necesitamos.
Sistemas de compresión WSQ y JPEG2000
La teoría de las ondículas, a diferencia de la teoría de las series de Fourier que le precedió, ha abordado al mismo tiempo el campo puramente matemático y las aplicaciones. Se comenzó a utilizar inmediatamente para el procesamiento de las señales y las técnicas habituales se adaptaron al nuevo campo. El salto de aquellos primeros pasos al mundo real no se hizo esperar. Es más, las aplicaciones han alimentado la propia teoría matemática, lanzando nuevos problemas.
El sistema de compresión WSQ (Wavelet Scalar Quantization) para las necesidades del FBI se inventó con ayuda de ondículas. Además, lo pusieron a disposición de todo el mundo, libre. Este sistema usa matemáticamente una pareja de wavelets madre, una para la descomposición y la segunda para la reconstrucción de la imagen. Básicamente, siempre se hace lo mismo para la compresión: proporcionar la información que queremos guardar mediante una receta de componentes básicos (en este caso, wavelets) y hacer 0 los coeficientes de componentes de menor relevancia. Así, en la información que se va a almacenar se obtienen muchos ceros; se han ideado medios para guardar de forma breve esas listas de ceros.
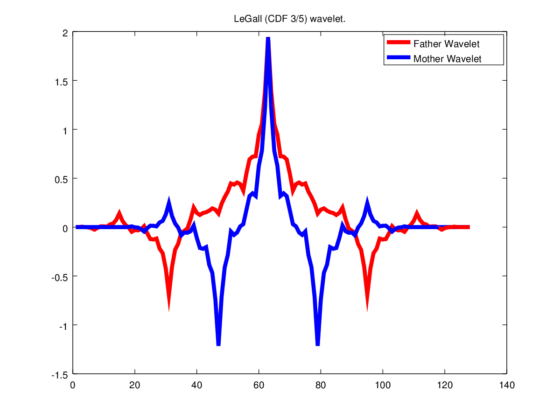 Imagen 4: para la compresión WSQ se utiliza una ondícula descubierta por la matemática Ingrid Daubechies.
Imagen 4: para la compresión WSQ se utiliza una ondícula descubierta por la matemática Ingrid Daubechies.Sin embargo, el uso de las ondículas para la compresión no quedó ahí. El mismo grupo que inventó el JPEG para las fotografías, creó otro estándar a través de wavelets: JPEG2000. Este modelo también se utiliza en la compresión de huellas dactilares cuando se toman imágenes de 1000 puntos por pulgada, pero no solo para eso: JPEG2000 se utiliza tanto en el cine digital, como en las imágenes que toman los satélites o en el protocolo DICOM de imágenes médicas.
Fourier moderno vs. Fourier clásico
El análisis de Fourier se enmarcó en el campo de las matemáticas teóricas a lo largo del siglo XIX y principios del XX. Sin embargo, posteriormente, se descubrieron multitud de campos en los que podía aplicarse en el mundo real, y con el aumento de la capacidad de cálculo de los ordenadores, se ampliaron aún más las posibilidades: señales, sonidos, imágenes médicas, espectrometría, cristalografía, telecomunicaciones, astronomía, visión artificial, reconocimiento de voz, etc.
La teoría de las ondículas, el nuevo campo que hemos visto crear y desarrollar, ha dado un nuevo impulso a estas aplicaciones. En el caso mencionado, el de las huellas dactilares, ofrece mejores resultados que la vía clásica, pero cabe preguntarse ¿merecerá la pena utilizar siempre las wavelets en lugar de las funciones trigonométricas? No, decidiremos en función de lo que queramos hacer. Por ejemplo, en nuestras cámaras fotográficas utilizamos JPEG porque no merece la pena recurrir a otro sistema de compresión para hacer fotos normales. La nueva teoría complementa la anterior, no la sustituye.
En 2017 el matemático Yves Meyer fue galardonado con el mayor premio que existe actualmente en matemáticas, el Premio Abel, «por su trabajo fundamental en el desarrollo de la teoría matemática de las ondículas«. Y en 2020 Yves Meyer, Ingrid Daubechies, Terence Tao y Emmanuel Candès han sido premiados con el Premio Princesa de Asturias de Investigación Científica y Técnica 2020, «por sus contribuciones pioneras y trascendentales a las teorías y técnicas matemáticas para el procesamiento de datos, que han ampliado extraordinariamente la capacidad de observación de nuestros sentidos y son base y soporte de la moderna era digital».
Para saber más:
En la red se puede encontrar más información sobre el tema. Estas son algunas de las fuentes que se pueden consultar:
- C. M. Brislawn, C.M. (1995). Fingerprints go digital. Notices of the American Matematical Society, 42 (11), 1278-1283.
- Web Mathouriste: Après Fourier, c’est encore du Fourier! (Hay abundante información sobre el análisis de Fourier, histórica en particular, en varias páginas del sitio web.)
- Web The Abel Przie: The Abel Prize Laureate 2017 – Yves Meyer.
Sobre el autor: Javier Duoandikoetxea es catedrático jubilado de Análisis Matemático en la UPV/EHU.
Este artículo se publicó originalmente en euskara el 19 de junio de 2019 en el blog Zientzia Kaiera. Artículo original.
El artículo Las huellas dactilares, el FBI y la teoría de Fourier modernizada se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una teoría cinética para los sistemas financieros
- Elogio de la teoría
- Pál Turán: teoría de grafos y fábricas de ladrillos
Zorros (auto)domesticados
 Foto: UW Urban Canid Project
Foto: UW Urban Canid ProjectDimitri Beliáyev fue un genetista que vivió y trabajó en una época y un país en los que la genética mendeliana era considerada una falsa ciencia. El lugar era Rusia y la época, el periodo durante el que Iósif Stalin regía los destinos de la Unión Soviética, las décadas centrales del siglo XX. Algunos genetistas pagaron su adhesión a la ciencia con duras penas de prisión, y alguno incluso con la muerte. Beliáyev, sin embargo, consiguió mantener su posición en el Departamento de Reproducción de Animales Peleteros gracias a que hacía pasar sus estudios como investigaciones de fisiología. En 1948, no obstante, fue cesado como director del Departamento. Tras la muerte de Stalin en 1953 las cosas mejoraron para los genetistas, y en 1958 empezó a trabajar en la División Siberiana de la Academia de Ciencias de la URSS, de cuyo Instituto de Citología y Genética fue nombrado director en 1963, cargo que ocupó hasta su muerte en 1985.
En el instituto desarrolló, junto con Lyudmila Trut, uno de los experimentos de más largo alcance en la historia de la biología, tanto por su duración (sigue en marcha), como por su contenido. Criaron zorros plateados (Vulpes vulpes) en cautividad, y de cada generación seleccionaban a los más mansos. En la décima generación un 18% de la progenie eran mansos, y en la vigésima ese porcentaje había llegado al 33%. Así, mediante un programa de reproducción selectiva de los más mansos consiguieron zorros plateados domesticados.
Lo más interesante del experimento de Beliáyev y Trut es que verificaron en los zorros domesticados la aparición de un conjunto de rasgos al que se denomina síndrome o fenotipo de domesticación. Es algo que se había observado en otras especies y que había sido descrito por el mismo Darwin. Los rasgos anatómicos propios del síndrome, aunque no aparezcan los mismos en todas las especies domesticadas, son los siguientes: orejas flácidas, pigmentación irregular (a veces en forma de motas), cara (u hocico) corto, molares más pequeños, cráneo más redondeado y pequeño, y cuerpo de menor tamaño. En la edad adulta retienen rasgos juveniles (fenómeno denominado neotenia) y son más fértiles. Además, tienen un umbral de reacción a los estímulos externos más alto y se asustan menos por la presencia de ejemplares de otras especies.
El síndrome de domesticación parece ser debido a déficits leves en el número de células de la cresta neural, una estructura característica del desarrollo embrionario de los vertebrados. Y, al parecer, ese déficit podría tener su origen en cambios de carácter epigenético en genes implicados en el desarrollo temprano de esa estructura embrionaria.
Durante prácticamente todo el último siglo, los zorros comunes han ido penetrando en grandes ciudades, no solo de Europa Continental, sino también de Gran Bretaña y Australia. En las últimas décadas su número se ha multiplicado y lo ha hecho gracias, principalmente, a los zorros urbanos. Se han adaptado a utilizar los residuos que, de una u otra forma, abandonan los seres humanos, y han perdido el miedo a acercárseles. Los raposos parecen haber iniciado una relación de comensalismo con las personas similar a la que, muy probablemente, condujo a la domesticación de los perros y, quizás, otras especies también. Seguramente por eso no tienen miedo a acercarse a los seres humanos. Y, tal y como hemos sabido este mismo año, han experimentado algunos cambios anatómicos compatibles con el síndrome de domesticación.
Si ese proceso está, efectivamente, en marcha, los zorros estarían experimentando su propia autodomesticación. No debería extrañarnos: al fin y al cabo, como los zorros, también los seres humanos nos hemos domesticado a nosotros mismos.
Fuentes:
Anastasiadi D., Piferrer F. (2019): Epimutations in developmental genes underlie the onset of domestication in farmed European sea bass. Molecular Biology and Evolution DOI: 10.1093/molbev/msz153
Dugatin L. A., Trut L. (2017): How to Tame a Fox (and Build a Dog) The University of Chicago Press.
Parsons K. J. et al (2020): Skull morphology diverges between urban and rural populations of red foxes mirroring patterns of domestication and macroevolution. Proceedings of the Royal Society B. 28720200763
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Zorros (auto)domesticados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Joaquín Sevilla – Naukas P4K 2019: Lo que esconden unos champiñones al ajillo
 Fuente: Cocinatis
Fuente: CocinatisLas leyes científicas se cumplen en todas partes y en todo momento, por eso son leyes. Esto incluye el cocinar unos champiñones al ajillo. Nos lo explica Joaquín Sevilla, doctor en físicas, profesor de tecnología electrónica y director de área de Cultura y Divulgación en la Universidad Pública de Navarra (UPNA).
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Joaquín Sevilla – Naukas P4K 2019: Lo que esconden unos champiñones al ajillo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
- José Miguel Viñas – Naukas P4K 2019: De nubes las pinacotecas están llenas
- Naukas Bilbao 2017 – Joaquín Sevilla: Los instrumentos del capitán Fitzroy
Cómo garantizar la seguridad del suministro eléctrico en España sin nucleares ni carbón
Investigadores de la UPV/EHU y el BC3 han proyectado la evolución que tendrán la demanda y la generación eléctrica en España en las próximas décadas; se considera un futuro sin energía nuclear ni proveniente del carbón, y con mayor peso de fuentes renovables. Han simulado la seguridad de suministro en ese escenario y proponen que, entre otras medidas, las centrales hidroeléctricas podrían ayudar a mitigar el riesgo de falta de suministro que pudiera darse.
 Embalses de La Serena y Orellana (parte superior derecha) en Badajoz (España)
Embalses de La Serena y Orellana (parte superior derecha) en Badajoz (España)Los investigadores del Instituto de Economía Pública de la UPV/EHU y el BC3, el Centro Vasco contra el Cambio Climático, llevan varios años colaborando en el estudio y proyección de lo que se conoce como seguridad del suministro eléctrico en España. El país es una “isla eléctrica”, debido a su escasa interconexión con los países vecinos, característica clave para hacer una proyección de la demanda y la capacidad de generación y suministro que tendrá España en las próximas décadas. Esto les ha permitido modelar el nivel de seguridad del suministro, y evaluar cómo cambiará esa seguridad en función de las fuentes de electricidad que se vayan impulsando o abandonando.
Partiendo de valores conocidos de consumo y generación eléctrica, el grupo de investigadores ha desarrollado un modelo mediante el que han podido proyectar la evolución de estas dos variables en los años 2020, 2030, 2040 y 2050. “Otros autores han realizado proyecciones del consumo eléctrico, y apuntan a que este consumo irá creciendo década a década, algo más de un 1 % cada año. En cuanto a las fuentes de electricidad, en los próximos 10 años las proyecciones indican que la electricidad proveniente del carbón y la nuclear sufrirán un recorte considerable, y ya en 2040 estas dos tecnologías dejarán de operar”, comenta José Manuel Chamorro Gómez, investigador del Instituto de Economía Pública de la UPV/EHU. La capacidad de generación que se perderá se compensará con un aumento de energías renovables. Es más, “la capacidad del total de centrales renovables que se pondrán en marcha será mayor que la ya instalada de generación no renovable, pero todo parece indicar que la seguridad de suministro se verá afectada”, añade el investigador.
La naturaleza propia de las fuentes renovables de electricidad introduce en el sistema incertidumbre, intermitencia e incapacidad de gestión, lo que eleva el riesgo de que una fracción de la demanda de electricidad se quede sin cubrir por las fuentes disponibles, haciendo el suministro menos seguro. “Ahora mismo el sistema existente no garantiza el 100 % del suministro en cualquier escenario, pero en nuestros modelos hemos visto que la fracción potencialmente no cubierta será mucho mayor en el futuro, y esa falta de suministro se dará con una frecuencia mayor”, detalla el investigador.
Los investigadores han estudiado en detalle las posibilidades que ofrece una fuente de energía renovable que se presta a una gestión más flexible: la hidráulica. “Las centrales hidroeléctricas pueden ser moduladas por las personas responsables de su gestión, y pueden regular el flujo de agua hacia la turbina en todo momento, algo que sin duda aliviaría en parte el riesgo de falta de suministro. Es más, aquellas centrales hidroeléctricas con turbinas reversibles desempeñan una doble función: además de aumentar la generación eléctrica en los momentos de mayor demanda, cuando esta es baja pueden utilizar la turbina para bombear agua hacia la parte superior de la presa (consumiendo energía), y así acumular agua que poder utilizar para generar electricidad nuevamente cuando vuelva a aumentar la demanda. Según hemos comprobado, esto aliviaría hasta cierto punto el riesgo de no poder responder a la demanda de electricidad en los momentos en los que esta crece”, argumenta.
No obstante, los autores también mencionan los aspectos medioambientales que deben ser tenidos en cuenta a la hora de plantear y planificar el uso y gestión de las centrales hidroeléctricas: “Desde el punto de vista de generación eléctrica, el agua constituye un recurso, pero, claro, este recurso está en un contexto. El impacto que las centrales y las presas tienen en las cuencas de los ríos es innegable. Por tanto, las administraciones o los agentes que están por encima de quien opera las centrales son quienes tienen que marcar las reglas de juego, y estas reglas tienen que ser claras, en cuanto a caudales ecológicos, frecuencias de descarga y demás parámetros”, opina Chamorro.
Además del recurso de las centrales hidroeléctricas, el investigador enumera otra serie de medidas que se podrían tomar para atender plenamente a la demanda, y así garantizar la seguridad de suministro: “Por un lado, hay mucha investigación en temas de almacenamiento de electricidad. Si consigues un sistema de almacenamiento, donde, digamos, acumulas la electricidad que ha generado el viento en un tramo horario con escasa demanda, tendrás forma de utilizarla cuando sí sea necesaria. O impulsar a los consumidores a hacer uso de sus electrodomésticos en las franjas horarias en las que el precio de la electricidad es más bajo. O incluso los coches eléctricos podrían abastecer en un momento dado de electricidad a la red, para complementar el suministro. Se está avanzando en diferentes aspectos para alcanzar un sistema donde los picos de demanda estén lo más cubiertos posible”, concluye.
Referencia:
Luis M. Abadie, José M. Chamorro, Sébastien Huclin, Dirk-Jan van de Ven (2020) On flexible hydropower and security of supply: Spain beyond 2020 Energy doi: 10.1016/j.energy.2020.117869
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Cómo garantizar la seguridad del suministro eléctrico en España sin nucleares ni carbón se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Generada en plataformas eólicas marinas, desembarcada como hidrógeno
- Desmantelando metódicamente instalaciones nucleares
- La gestión de la salud y seguridad en el trabajo de las mujeres
La mielitis transversa: el embotellamiento inflamatorio de la médula espinal
Diego Clemente
 Funete: Wikimedia Commons
Funete: Wikimedia CommonsLa empresa farmacéutica AstraZeneca ha pausado el ensayo clínico de la vacuna contra la COVID-19 que desarrolla junto a la Universidad de Oxford debido a un evento adverso serio aparecido en uno de los participantes. Aunque no se ha confirmado la naturaleza clínica de tal evento, el New York Times ha revelado que podría tratarse de mielitis transversa. ¿Qué es esta enfermedad?
La palabra mielitis ya nos indica que es una enfermedad neurológica, en la que se inflama la médula espinal. Por otro lado, transversa indica que afecta de manera completa –es decir, bilateral, tanto al área derecha como a la izquierda– a un segmento concreto de la médula.
Al igual que en la esclerosis múltiple, esta inflamación suele conllevar desmilienización. En otras palabras, se elimina la capa lipídica que envuelve los axones de las neuronas lo que, en consecuencia, produce fallos en el impulso nervioso. En la esclerosis múltiple este proceso no suele ser completo ni afectar a un único segmento de la médula, y también se ve afectada la mielina del cerebro.
La mielina es una adquisición evolutiva del sistema nervioso central que sirve para que el impulso nervioso se transmita a una alta velocidad sin necesidad de tener un axón muy grueso. Esto permite tener muchos axones más finos en un pequeño espacio. Gracias a ella podemos sentir y enviar órdenes a los músculos u órganos en milésimas de segundo, algo muy útil ante un peligro inminente o cuando tenemos que hacer varias cosas a la vez. A veces, la velocidad es un factor importante para poder sobrevivir o para destacar sobre otros individuos.
En el caso de la mielitis transversa, la desmielinización del segmento concreto de la médula puede tener una causa sospechada o no. Aunque se han descrito casos de esta enfermedad tras procesos de vacunación, un buen número de los casos de mielitis transversa son posteriores a una infección viral, o a una invasión bacteriana.
En ese caso, podría ser el propio invasor quien ataque a la mielina y ser el disparador de la desmielinización. Pero también puede ser la consecuencia del ataque inmunitario al microorganismo invasor, con lo que sería la propia respuesta del sistema inmune la causante de la desmielinización. En este caso, hablaríamos de un fenómeno de autoinmunidad.
¿Qué quiere decir esto? Pues que nuestras propias defensas atacan a nuestro organismo, sin conocerse muchas veces la causa concreta que les impulsa a hacerlo. En la mielitis transversa, no está claro aún si es una o ambas razones la que la causan. También puede estar asociada a otras patologías autoinmunes o incluso a determinados tumores. Pero hay que destacar que, en la mayoría de los casos, la mielitis transversa no tiene una causa sospechada, denominándose en ese caso como idiopática. Finalmente, hay que apuntar que también se ha descrito algún caso de mielitis transversa asociada a la COVID-19.
Otro aspecto a tener en cuenta en esta mielitis viene dado por el apellido de la enfermedad: transversa. No en todas las mielitis transversas se afecta el mismo segmento de la médula. Este aspecto es crucial para saber el grado de afectación de la persona con esta enfermedad.
¿Qué pasa cuando se ve afectado por completo un segmento de la médula espinal?
La médula espinal tiene muchas neuronas en su interior, las motoneuronas, que mandan órdenes a los músculos. También reciben muchos axones de neuronas sensitivas alojadas en los ganglios espinales y cuya información sensorial de músculos u otros órganos hace una primera parada en la propia médula espinal sobre las denominadas interneuronas quienes, a su vez, se comunican con las motoneuronas. De hecho, ambas señales, la de envío de órdenes y la de recepción de sensaciones, se integran y ordenan en la médula espinal.
Dependiendo del nervio espinal del que vengan o hacia donde vayan, el ordenamiento y procesamiento de esta información se hace a un nivel u otro de la médula espinal. Por ello, de manera general podemos decir que los segmentos cervicales participan en integración de información de cuello y músculos de la respiración, los torácicos del torso y parte de los brazos, los lumbares, las caderas y piernas, y los sacros, la ingle, los dedos de los pies y parte de las piernas.
Pero no pensemos en la médula espinal como un conjunto de anillas colocadas una encima de otra que no se comunican entre sí, sino que hay comunicación entre unos segmentos y otros, también a través de axones, también con mielina.
Para más complicación, la médula espinal es una gran autovía de paso de información desde todas las partes del cuerpo al cerebro y desde este a la médula y después a los órganos y músculos de nuestro cuerpo. Los carriles de la autovía son los axones de las neuronas, los vehículos los impulsos nerviosos, y la mielina sirve para que señales del cerebro lleguen a la punta del pie y viceversa muy rápidamente.
Por ello, cuando todo un segmento de la médula espinal se ve afectado por la mielitis transversa, no solo se afectan los músculos u órganos a los que envía y de los que reciben información las neuronas de esa parte concreta, sino que se ve afectada la intercomunicación entre segmentos, sobre todo con los segmentos por debajo de este y, algo muy importante, se ve muy afectada la movilidad en la gran autovía de impulsos nerviosos hacia o procedentes del cerebro.
Por esta razón, si la afectación medular es en los niveles más cercanos al cuello, el embotellamiento nervioso será mucho mayor y afectará a todos los segmentos inferiores al mismo, mientras que si es en la zona sacra se verán afectados menos segmentos de la médula y los síntomas serán menores. Normalmente, en la mielitis transversa se suele ver afectada la zona torácica, la de la parte alta de la espalda.
Síntomas y pronóstico variable
De ahí que los síntomas de la mielitis transversa varíen entre personas, aunque de manera más habitual son dolor, modificaciones en la sensibilidad y percepción de sensaciones aberrantes como hormigueos, parálisis de las extremidades (brazos o piernas dependiendo del segmento afectado), que pueden llegar incluso a ser causantes de una paraplejia y, en muchas ocasiones, afectación de la vejiga y de los intestinos, lo que afecta de manera importante a la vida diaria de las personas.
Al contrario que en la esclerosis múltiple, en la mielitis transversa se suele dar un único episodio sintomático del que la persona se puede recuperar completa o parcialmente, o de la que, lamentablemente, no puede recuperarse. Aproximadamente se calcula en un tercio cada una de las tres posibilidades.
Hoy en día no existe tratamiento curativo para la mielitis transversa, aunque normalmente se aplican corticoides al paciente para reducir la inflamación de la misma.
En la actualidad se investiga en conocer la causa de esta patología y en buscar terapias que ayuden a regenerar lo dañado por la inflamación. De lo que no hay duda, y de eso sabemos y mucho en el Hospital Nacional de Parapléjicos, es de que los pacientes cuya médula espinal está afectada se ven muy beneficiados por una buena rehabilitación, adecuada y específica a las partes del cuerpo que sean coordinadas por el segmento desmielinizado, pero también por los posteriores, así como por la comunicación con el cerebro. De ahí que sea tan importante la existencia de centros como el nuestro, donde, además de los músculos, se rehabilita la mente, la sexualidad, y se ayuda a afrontar la nueva vida de cada persona.
Sobre el autor: Diego Clemente es Investigador Principal del Laboratorio de Neuroinmuno-Reparación del Hospital Nacional de Parapléjicos
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La mielitis transversa: el embotellamiento inflamatorio de la médula espinal se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sistemas nerviosos: la médula espinal
- Estar obeso se parece mucho (demasiado) a envejecer
- Los supermicrobios amenazan con ser más letales que el cáncer
Arte Moebius (I)
A lo largo de algunas entradas de la sección Matemoción del Cuaderno de Cultura Científica hemos mostrado ejemplos de cómo las matemáticas han sido, y son, tanto una fuente de inspiración para el arte –en especial para el arte contemporáneo–, como una herramienta en el proceso creativo del artista. Algunos ejemplos para el caso de las artes plásticas pueden encontrarse en las siguientes entradas:
– Cuadrados latinos, matemáticas y arte abstracto
– Hipercubo, visualizando la cuarta dimensión
– Bernar Venet, la estética de las matemáticas
– El teorema de Pitágoras en el arte
– El poema de los números primos
– La geometría poética del cubo
– El arte contemporáneo que mira al tangram
E incluimos más entradas en la misma línea en la bibliografía de esta. Aunque estos son solamente una pequeña cantidad de ejemplos de la profunda e interesante interacción entre las matemáticas y las artes plásticas.
 Triángulo de Morley (1969), de Crockett Johnson. Imagen de la página web de The National Museum of American History
Triángulo de Morley (1969), de Crockett Johnson. Imagen de la página web de The National Museum of American History
En la presente entrada vamos a centrar nuestra atención en uno de los objetos más interesantes e inspiradores de la geometría y la topología, la banda de Moebius. No es la primera vez que se habla de este objeto geométrico en relación al arte en el Cuaderno de Cultura Científica, ya que se han dedicado algunas entradas a su presencia en la novela gráfica (De menú para hoy dos novelas gráficas negras con salsa matemática y Guía matemática para el cómic Promethea), en la poesía (Poesía retorcida sobre banda de Mobius) o en la literatura (Cuatro leyes consumadas siguiendo una banda de Mobius). Y para conocer más ejemplos se puede consultar el artículo de Marta Macho, Listing, Möbius y su banda o el libro de Clifford Pickover, The Möbius strip (2006). Aunque en la serie de entradas que iniciamos aquí, vamos a mostrar una pequeña colección de ejemplos de su presencia en las artes plásticas, y en especial, en la escultura.
La banda de Moebius es una superficie “topológica” (véase la entrada La topología modifica la trayectoria de los peces) que fue descubierta, de forma independiente, por los matemáticos alemanes Johann Benedict Listing (1808-1882) y August Ferdinand Moebius (1790-1868). Es decir, es un objeto matemático, pero que también podemos observar y entender en nuestra vida cotidiana.
 Grabado del matemático alemán August Ferdinand Moebius, realizado por Adolf Neumann alrededor de 1850. Imagen de Wikimedia Commons
Grabado del matemático alemán August Ferdinand Moebius, realizado por Adolf Neumann alrededor de 1850. Imagen de Wikimedia Commons
Las superficies que vemos a nuestro alrededor, como una hoja de papel, un canutillo de cartón o una pelota, tienen dos caras, sin embargo, aunque pueda parecer sorprendente existen superficies que solamente poseen una única cara, como la cinta de Moebius.
Para construir esta superficie, la banda de Moebius, de una forma sencilla y cotidiana solamente se necesita una tira de papel y cinta adhesiva. Por ejemplo, puede cogerse una hoja de papel DIN A4 y cortar a lo largo una tira de unos 2 o 3 centímetros de anchura. Si juntamos los extremos de la tira de papel y los pegamos con la cinta adhesiva, se obtiene una banda normal, con dos caras, la interior y la exterior, que podríamos pintarlas de dos colores distintos. Pero además tiene dos bordes, “el de arriba y el de abajo”.

Pero, si cogemos una nueva tira de papel y antes de juntar los extremos, como hemos hecho antes, giramos uno de ellos media vuelta y después los pegamos, la superficie que se obtiene es una banda retorcida, la superficie de Moebius.
Podemos intentar comprobar experimentalmente cuántas caras tiene esta nueva superficie, para lo cual se va a utilizar un rotulador. Se empieza pintando la tira de papel retorcida en un punto dado y se continúa pintando en una cierta dirección hasta llegar al punto por el que habíamos empezado. Y descubriremos que está pintada toda la banda, luego solo tiene una cara, ya que para pintarla entera solo se utiliza un color.

Pero hay más sorpresas, si ahora tomamos otro rotulador y vamos recorriendo el borde de la banda de Moebius, veremos que cuando regresemos al punto inicial habremos recorrido todo el borde, es decir, ¡la banda de Moebius tiene un único borde!
Esta superficie tiene insólitas propiedades. Veamos una de ellas en el siguiente experimento que podéis realizar en casa. La cuestión que nos planteamos en este experimento es la siguiente: ¿Qué ocurre si cortamos la cinta de una sola cara por la mitad (con un corte longitudinal)?
Si cortásemos longitudinalmente una banda normal y corriente por la mitad, lo que se obtienen son dos bandas normales de igual longitud, pero más estrechas que la original. Mientras que si se realiza un corte longitudinal a una banda de Moebius lo que ocurre es que se tiene una única banda retorcida de doble de longitud que la banda de Moebius original.

Aunque la cuestión ahora es qué tipo de superficie es la que se ha generado, si será como una cita de Moebius o como una banda normal. O, dicho de otra manera, nos preguntamos cuántas caras tiene. Si utilizásemos de nuevo el rotulador podríamos observar que tiene dos caras y dos bordes, luego no es una banda del tipo de la de Moebius, sino una “banda normal retorcida” (es decir, si partimos de una tira de papel, se ha dado una vuelta entera a la tira antes de pegar los extremos).
Todas estas primeras cuestiones pueden verse en el en el video de la sección Una de mates, del programa de humor y ciencia de televisión, dirigido por José A. Pérez Ledo, Orbita Laika (primera temporada) de La2, de Televisión Española: La banda de Moebius.
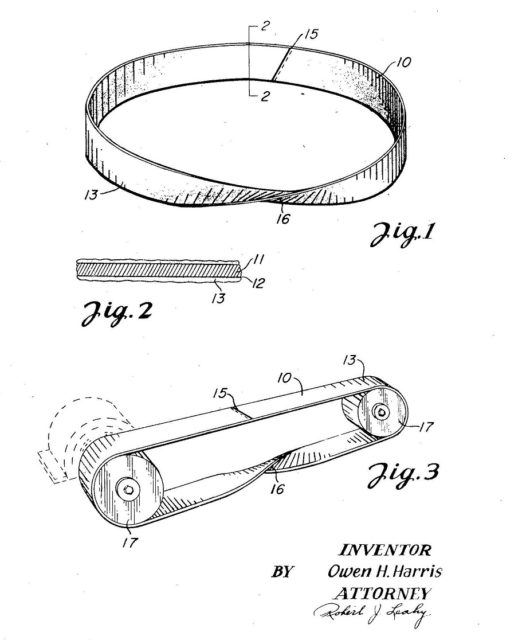 Imagen de la patente US2.479.929, del inventor Owen H. Harris, de una correa abrasiva que, en lugar de tener la forma de una banda normal, tiene la forma de una banda de Moebius, para duplicar la zona de abrasión
Imagen de la patente US2.479.929, del inventor Owen H. Harris, de una correa abrasiva que, en lugar de tener la forma de una banda normal, tiene la forma de una banda de Moebius, para duplicar la zona de abrasión
Las extraordinarias propiedades de la superficie de Moebius, que solo tenga una cara y un borde, han cautivado no solo a personas del mundo de la ciencia y las matemáticas, sino también del arte. Por ejemplo, el director de cine, actor y escritor norteamericano Woody Allen, en su cuento El sol no sale para todos del libro Pura Anarquía (2007), escribía:
Deseoso de captar su atención, me había propuesto levantar en dos tiempos una barra equivalente en peso a un par de Steinways cuando de pronto mi columna vertebral adoptó la forma de una banda de Möbius, y buena parte de mi cartílago se separó audiblemente.
En particular, esta superficie ha cautivado a muchas personas del ámbito de las artes plásticas, con una especial incidencia en el mundo de la escultura, como veremos en esta serie de entradas.
Sin ninguna duda, el artista que más se relaciona con la banda de Moebius es el artista suizo Max Bill (1908-1994), uno de los máximos representantes del denominado arte concreto y miembro del grupo Abstracción-Creación (véase El teorema de Pitágoras en el arte para ver otras obras de Max Bill relacionadas con las matemáticas).
Como cuenta mi compañera y amiga Marta Macho en el artículo Listing, Mobius y su banda, en 1935 Max Bill estaba trabajando “en distintas posibilidades estéticas para una escultura colgante, cuando creó un objeto de una sola cara al que llamó Unendliche Schleife (cinta sin fin), sin ser consciente de que tales superficies se conocían desde hacía un siglo. Se comenta que sintió tal frustración al saber que él no había sido el inventor de esta forma, que pasó una larga temporada sin trabajar sobre ella”.
En cualquier caso, Max Bill diseñó y realizó hermosas esculturas con esta superficie sin fin y gracias a él fue ampliamente conocida en el mundo del arte. Veamos dos de estas esculturas de Max Bill.
 Cinta sin fin (1953, original de 1935), de Max Bill. Museo de Arte de Baltimore
Cinta sin fin (1953, original de 1935), de Max Bill. Museo de Arte de Baltimore
 Giro sin fin (1953-1956), de Max Bill. Museo de Amberes
Giro sin fin (1953-1956), de Max Bill. Museo de Amberes
Tanto la obra artística de Max Bill, como su filosofía del arte, han tenido una gran influencia en el arte contemporáneo.
Uno de los artistas vascos contemporáneos por el que siento una gran admiración y en el que se puede apreciar una clara influenciada de la obra de Max Bill, de hecho, también se ha interesado por la banda de Moebius, es el artista navarro José Ramón Anda. Como comentamos en la entrada La geometría poética del cubo, dentro del arte de José Ramón Anda, una de las figuras fundamentales de la escultura vasca contemporánea, conviven dos grandes corrientes artísticas como son la abstracción geométrica, con una fuerte influencia del arte concreto, y la escultura orgánica, en la cual la naturaleza y sus formas, en particular, la madera, como material e inspiración, reivindican su importancia.
En sus primeros años, el escultor navarro realizó dos esculturas con cintas sin fin, realizadas en madera de roble, Dos cintas sin fin (1975, roble) y Cintas macladas triangulares (1975, roble).
 Dos cintas sin fin (1975), de José Ramón Anda, realizada en madera de roble. Imagen de la página web de José Ramón Anda
Dos cintas sin fin (1975), de José Ramón Anda, realizada en madera de roble. Imagen de la página web de José Ramón Anda
En la magnífica exposición la exposición LANTEGI, José Ramón Anda, que tuvo lugar en la sala Kubo Kutxa de Donostia-San Sebastián, desde el 23 de mayo al 25 de agosto de 2019, pudimos observar una nueva escultura con una banda de Moebius.

Otro artista influenciado por el trabajo escultórico de Max Bill fue el artista británico John Robinson (1935-2007). En la década de los años 70, tras haber estado trabajando en escultura figurativa, empezó a realizar esculturas simbólicas abstractas con inspiración matemática. Entre los temas matemáticos con los que trabaja están los anillos de Borromeo (véase su definición en la Wikipedia), la teoría de nudos (puede leerse sobre nudos en las entradas La artista Anni Albers, The Walking Dead y la teoría de nudos y Del nudo gordiano al nudo de los enamorados por territorio matemático), los nudos tóricos (recordemos que en matemáticas un “toro” es la superficie que tiene la forma de un flotador), los fractales (véase Fractus, arte y matemáticas) o la banda de Moebius. Pueden verse muchas de sus obras simbólicas abstractas en la página del artista en la Fundación Bradshaw.
Una de sus obras simbólicas más emblemáticas es Inmortalidad (1982), que es una banda de Moebius con forma de nudo de trébol, realizada en bronce.
 Inmortalidad (1990), de John Robinson, realizada en bronce y acero. Propiedad del departamento de matemáticas de la Universidad de Bangor (Gales). Imagen de ArtUK
Inmortalidad (1990), de John Robinson, realizada en bronce y acero. Propiedad del departamento de matemáticas de la Universidad de Bangor (Gales). Imagen de ArtUK
Otra serie de sugerentes y hermosas esculturas con la idea de la superficie de una sola cara es la formada por obras como Seres dependientes (1980, bronce pulido y patinado) o Eternidad (1980, bronce pulido). Si pensamos en la obra Seres dependientes, podemos entender su estructura de dos formas distintas. La primera sería pensar en una banda de Moebius, como la que hemos construido con una tira de papel, pero en lugar de tener un grosor de 0,1 milímetros –que es más o menos el grosor de una hoja de papel–, que tenga un grosor del mismo ancho del papel, de unos 2 o 3 centímetros. Ahora el borde se convierte en otra banda de Moebius, de forma que la escultura posee dos cintas sin fin “entrelazadas”. Como decía el propio escultor, en relación a Seres dependientes (escultura del Centre de Recerca Matemàtica, de Barcelona): “el hombre y la mujer entrelazados para formar un solo Ser”.
 Seres dependientes (1980), de John Robinson, realizada en bronce pulido y patinado, perteneciente al Centre de Recerca Matemàtica, de Barcelona)
Seres dependientes (1980), de John Robinson, realizada en bronce pulido y patinado, perteneciente al Centre de Recerca Matemàtica, de Barcelona)
Pero esta escultura la podemos entender también de otra forma. Si nos fijamos, la sección de la escultura es más o menos un cuadrado, luego puede entenderse la figura geométrica de estas esculturas como considerar un prisma cuadrado largo y flexible, retorcerlo media vuelta y unir los extremos.
Por otra parte, la escultura Eternidad (1980), que realizó después de Seres dependientes (1980), está realizada con una sección triangular, en lugar de cuadrada. Es decir, sería como considerar un prisma triangular largo y flexible, retorcerlo un tercio de vuelta –120 grados– para que vaya lado con lado y unir los extremos. De esta forma se genera una única superficie de tipo Moebius, de una sola cara.
 Eternidad (1980), de John Robinson, realizada en bronce pulido. La escultura está en la plaza Pietre de Camberra, Australia
Eternidad (1980), de John Robinson, realizada en bronce pulido. La escultura está en la plaza Pietre de Camberra, Australia
 Detalle de la realización de la escultura Eternidad (1980), de John Robinson, utilizando 100 triángulos equiláteros
Detalle de la realización de la escultura Eternidad (1980), de John Robinson, utilizando 100 triángulos equiláteros
En la página del artista en la Fundación Bradshaw se pueden encontrar gifs de estas y otras esculturas de John Robinson.
La siguiente serie de esculturas de cintas si fin la descubrí por casualidad. Estaba viendo la película de intriga estadounidense Un pequeño favor (2018), dirigida por Paul Feig, el creador de la serie Freaks and Geeks (1999), e interpretada por Anna Kendrick y Blake Lively. En una de las escenas aparece una escultura en la entrada de una casa, como se ve en la siguiente imagen, y rápidamente me puse a averiguar de quien era esa escultura. Su autor es el artista británico Jeremy Guy, en cuya página web pueden verse muchas de sus esculturas.
 Escena de la película Un pequeño favor (2018), dirigida por Paul Feig, en la que se ve la escultura Mobius H3, del escultor inglés Jeremy Guy. Imagen de la página web del escultor
Escena de la película Un pequeño favor (2018), dirigida por Paul Feig, en la que se ve la escultura Mobius H3, del escultor inglés Jeremy Guy. Imagen de la página web del escultor
Dentro de esa serie de obras está por ejemplo Mobius H12, realizada en granito negro, que el artista inglés realizó para el centro comercial Ion Orchard de Singapur.
 Mobius H12, del escultor inglés Jeremy Guy. Imagen de la página web del escultor
Mobius H12, del escultor inglés Jeremy Guy. Imagen de la página web del escultor
Muchas otras obras del artista Jeremy Guy utilizan esta superficie de una sola cara, aunque muchas de ellas utilizando una idea similar, aunque más plástica, a la construcción de la escultura Seres dependientes de John Robinson, como la escultura Overtura o la serie Zephyr, todas ellas realizadas en granito negro.
 Overtura, del escultor inglés Jeremy Guy, que aparece en la imagen junto a su obra. Imagen de la página web del escultor
Overtura, del escultor inglés Jeremy Guy, que aparece en la imagen junto a su obra. Imagen de la página web del escultor
Mientras preparaba esta entrada, he descubierto una obra muy singular, se trata del mosaico Banda de Moebius, que se encuentra en el edificio del Central Economic Mathematical Institute de la Academia Rusa de Ciencias, en Moscú, y que se conoce con el nombre “Casa con oreja”.
 Escultura Banda de Moebius, de los artistas Vladimir Vasiltsov y Eleonora Zharenova, en el edificio del Central Economic Mathematical Institute (CEMI) de la Academia Rusa de Ciencias, de Moscú, realizado por el arquitecto Leonid Pavlov en 1978. Imagen de GreyScape
Escultura Banda de Moebius, de los artistas Vladimir Vasiltsov y Eleonora Zharenova, en el edificio del Central Economic Mathematical Institute (CEMI) de la Academia Rusa de Ciencias, de Moscú, realizado por el arquitecto Leonid Pavlov en 1978. Imagen de GreyScape
Otra escultura que se encuentra en la capital rusa y que toma como estructura la banda de Moebius es la escultura pública Banda de Möbius (1972), del escultor ruso Andrey Zakhidovich Nalich. La escultura es una superficie de Moebius, pero no es una superficie lisa, sino que toma la forma del cuerpo de una mujer. Además, en su base está escrito “Diferentes puntos de vista sobre un tema”.
 Banda de Möbius (1972), del escultor ruso Andrey Zakhidovich Nalich, situada cerca del cine Horizon en Komsomolsky Prospekt, Moscú. Imagen de Another City
Banda de Möbius (1972), del escultor ruso Andrey Zakhidovich Nalich, situada cerca del cine Horizon en Komsomolsky Prospekt, Moscú. Imagen de Another City
Una tercera escultura en Moscú es El árbol de la vida (1956-1998) del escultor ruso-americano Ernst Neizvestny (1925-2016), realizado con varias copias de cintas de Moebius, cuyo conjunto tiene la forma de un corazón humano. La escultura, que se gún su autor, es “una celebración del alma humana y el conocimiento”, está compuesto de cientos de imágenes de “personajes” históricos, como Adán y Eva, Jesús, Buda o Yuri Gagarin.
 El árbol de la vida (1956-1998), del escultor ruso-americano Ernst Neizvestny, que se encuentra en el centro comercial Bragation de Moscú. Imagen de Other Moscow-LiveJournal
El árbol de la vida (1956-1998), del escultor ruso-americano Ernst Neizvestny, que se encuentra en el centro comercial Bragation de Moscú. Imagen de Other Moscow-LiveJournal
La artista multidisciplinaria japonesa Mariko Mori también ha utilizado la superficie de Moebius para la realización de diseños y esculturas. Por ejemplo, diseñó una banda de Moebius para el escenario de la representación de la opera Madame Butterfly de Puccini.
 Enorme banda de Moebius sobre el escenario del Teatro La Fenice en Venecia, para la representación de la opera Madame Butterfly de Puccini. Imagen de Factum Arte
Enorme banda de Moebius sobre el escenario del Teatro La Fenice en Venecia, para la representación de la opera Madame Butterfly de Puccini. Imagen de Factum Arte
Así mismo ha realizado esculturas basadas en las formas de Moebius, como algunas de las obras de la exposición Cyclicscape (Sean Kelly Gallery, 2015).
 Tres obras de la artista japonesa Mariko Mori, pertenecientes a la exposición Cyclicscape (Sean Kelly Gallery, 2015), basadas en la banda de Moebius. Imagen de la Sean Kelly Gallery
Tres obras de la artista japonesa Mariko Mori, pertenecientes a la exposición Cyclicscape (Sean Kelly Gallery, 2015), basadas en la banda de Moebius. Imagen de la Sean Kelly Gallery
 Ekpyrotic String II (2014), de la artista japonesa Mariko Mori, perteneciente a la exposición Cyclicscape (Sean Kelly Gallery, 2015), basada en la banda de Moebius. Imagen de la Sean Kelly Gallery
Ekpyrotic String II (2014), de la artista japonesa Mariko Mori, perteneciente a la exposición Cyclicscape (Sean Kelly Gallery, 2015), basada en la banda de Moebius. Imagen de la Sean Kelly Gallery
Para terminar una curiosa escultura, realizada con pequeños coches de juguete, Circunvalación de Moebius (2012), del artista estadounidense Chambliss Giobbi, cuya estructura es la misma que la de la obra Seres dependientes de John Robinson, es decir, un prisma cuadrado rotado media vuelta y pegado por los extremos generando una doble banda de Moebius.
 Circunvalación de Moebius (2012), del artista estadounidense Chambliss Giobbi. Imagen de la página web de Chambliss Giobbi
Circunvalación de Moebius (2012), del artista estadounidense Chambliss Giobbi. Imagen de la página web de Chambliss Giobbi
Bibliografía
1.- Raúl Ibáñez, Cultura pitagórica: arte, Cuaderno de Cultura Científica, 2013.
2.- Raúl Ibáñez, El cubo soma: diseño, arte y matemáticas, Cuaderno de Cultura Científica, 2014.
3.- Raúl Ibáñez, Hipercubo, visualizando la cuarta dimensión (y 2), Cuaderno de Cultura Científica, 2015.
4.- Raúl Ibáñez, Catenarias en las artes plásticas, Cuaderno de Cultura Científica, 2016.
5.- Raúl Ibáñez, Artistas que miran a las matemáticas, Cuaderno de Cultura Científica, 2017.
6.- Raúl Ibáñez, Variaciones artísticas del teorema de Napoleón, Cuaderno de Cultura Científica, 2018.
7.- Raúl Ibáñez, El poema de los números primos (2), Cuaderno de Cultura Científica, 2019.
8.- Raúl Ibáñez, Los ritmos primos de Anthony Hill, Cuaderno de Cultura Científica, 2019.
9.- Raúl Ibáñez, La geometría poética del cubo (2), Cuaderno de Cultura Científica, 2019.
10.- Raúl Ibáñez, Fractus, arte y matemáticas, Cuaderno de Cultura Científica, 2020.
11.- Raúl Ibáñez, La cuarta dimensión, ¿es nuestro universo la sombra de otro?, RBA libros, 2011.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Arte Moebius (I) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de Pitágoras en el arte
- Arte y geometría del triángulo rectángulo: Broken Lights
- El arte contemporáneo que mira al Tangram
Las series de desintegración radiactiva
 Foto: Franck V. / Unsplash
Foto: Franck V. / UnsplashLos estudios pormenorizados de la desintegración del radio y sus derivados llevaron al descubrimiento que la transformación radiactiva terminaba en un producto final estable que se identificó por su comportamiento químico como plomo. Algunos de los eslabones de la cadena que comienza con el radio emiten partículas alfa y otros emiten partículas beta. Algunos rayos gamma se emiten durante la serie de desintegración, pero los rayos gamma nunca aparecen solos; se emiten solo junto con una partícula alfa o una partícula beta.
Rutherford y Soddy sugirieron que, dado que el radio siempre se encuentra en los minerales de uranio, como la pecblenda, que los Curie habían analizado, el propio radio podía ser miembro de una serie que comenzase con el uranio como antepasado de todos los miembros. La investigación mostró que este es realmente el caso. Cada átomo de uranio puede dar lugar con el tiempo a átomos hijos sucesivos, siendo el radio la sexta generación y el plomo estable la decimonovena.
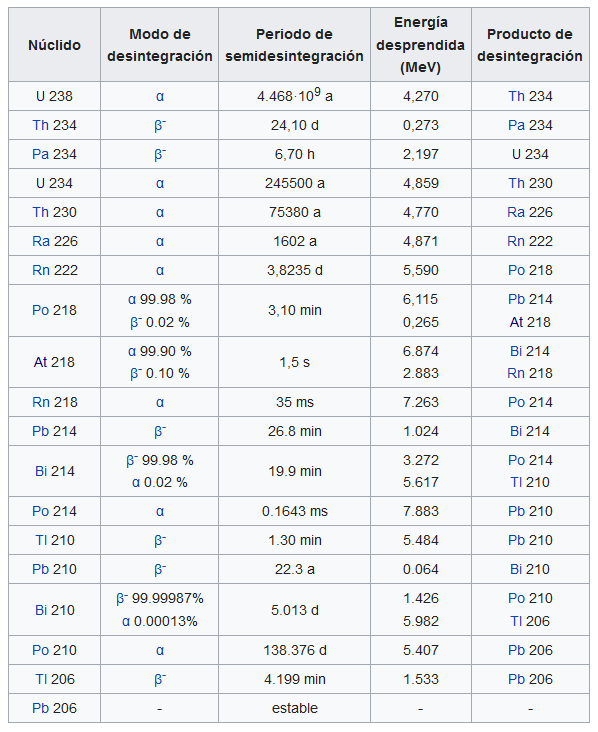 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsLa tabla muestra todos los miembros de la llamada serie uranio-radio [1]. El número que sigue al nombre de un elemento, como en el uranio-238, indica la masa atómica en unidades de masa atómica. Si nos fijamos veremos que hay variedades más pesadas y ligeras del elemento, como uranio-238 y uranio-235, polonio-218, 214 y 210 [2]. Se han encontrado otras dos series radiactivas naturales; una comienza con el torio-232 y la otra con el uranio-235.
Cada miembro de la serie difiere física y químicamente de su padre inmediato (colocado encima) o de su hijo (colocado debajo); por tanto, en teoría debería ser posible separar los diferentes miembros en cualquier muestra radiactiva. Esto no es que sea imposible de hacer, pero el problema de la separación se dificulta mucho por el hecho de que las diferentes especies radiactivas se desintegran a diferentes velocidades, algunas muy lentamente, otras rápidamente, otras a velocidades intermedias. Estas velocidades y su significado merecen un artículo específico, pero el hecho de que las velocidades difieran da lugar a efectos importantes que será lo próximo que veamos.
Notas:
[1] Aún es necesario introducir algunos conceptos para entender todos los datos de la tabla. Eso se hace un poco más adelante en esta serie. De momento nos basta tomar los nombres en la lista como correspondientes a cosas distintas desde el punto de vista físico/químico.
[2] Hay un artículo específico dedicado al concepto de isótopo en esta serie.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las series de desintegración radiactiva se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La transformación radiactiva
- La distribución de velocidades moleculares de Maxwell
- No solo el uranio emite rayos
Historias genéticas de un fósil viviente
Koldo Garcia Etxebarria
Pronto llegará el otoño y muchos árboles se despojarán de sus hojas. Entre esos árboles desnudos que encontraremos a nuestro alrededor, hay uno que es bastante especial: el ginkgo (Gingko biloba). Decimos que este árbol es especial porque es un fósil viviente. Aunque este término no es científico, así se dan a conocer las especies actuales que se asemejan a aquellas que se pueden encontrar en el registro fósil. Estas especies no tienen parientes vivos, es decir, son especies aisladas, testigos de un mundo pasado que parecen haber quedado congeladas en la evolución. Esta circunstancia convierte el estudio genético del ginkgo en un análisis de gran valor.
El ginkgo no ha sufrido cambios significativos en su aspecto durante los últimos 200 millones de años y ha sobrevivido a las glaciaciones en los parajes de China. El encanto que posee este árbol ha propiciado que en los últimos años se haya extendido por todo el mundo de la mano del ser humano, que lo ha usado como adorno. A pesar de que este árbol ha sido objeto de numerosas investigaciones, un nuevo trabajo ha tratado de aclarar algunos aspectos aún desconocidos: dónde se refugió, cómo se enfrentó al cambio climático en el Pleistoceno, cuál fue el papel del ser humano en su dispersión y qué factores han influido en su supervivencia.
Para la realización de este trabajo, se han secuenciado los genomas de 545 ginkgos de 51 lugares. Principalmente se han estudiado ejemplares de China, pero también se han analizado árboles de Corea, Japón, Europa y América. Hay que tener en cuenta que el genoma del ginkgo contiene más de diez mil millones de «letras» de ADN, es decir, es tres veces más largo que el genoma humano. Por lo tanto, la cantidad de datos que se han extraído es enorme, y analizarlos supone un trabajo sustancioso.
 Gingko con colores otoñales en una pequeña aldea china. (Fotografía: Kohji Asakawa – Licencia Pixabay. Fuente: pixabay.com)
Gingko con colores otoñales en una pequeña aldea china. (Fotografía: Kohji Asakawa – Licencia Pixabay. Fuente: pixabay.com)Para analizar el origen de los ginkgos actuales se emplearon varios métodos, obteniendo el mismo resultado: que en su origen había cuatro grandes poblaciones y que tres regiones funcionaron como refugios. Estas cuatro poblaciones originarias estaban situadas en el este, sur, suroeste y norte de China respectivamente (esta última ubicación era el punto de unión de las otras tres). Los autores del trabajo proponen que la población del norte de China se originó hace unos 140.000 años, al mezclarse las poblaciones del sur y del suroeste. A partir de este resultado se han definido tres zonas de protección: los ya conocidos del suroeste y el este, más un nueva zona al sur. De hecho, estas tres zonas de protección son lugares con una gran biodiversidad que actúan como zonas de protección de gran cantidad de plantas.
En cuanto al tamaño de las poblaciones, el ginkgo ha experimentado varios ciclos de expansión y reducción que tuvieron lugar en las glaciaciones del Pleistoceno. A partir de los datos genéticos y las simulaciones, sabemos que las mayores poblaciones existieron hace 15 millones de años, 1,05 millones de años y 0,5 millones de años; mientras que las menores, hace 4 millones de años, 0,1 millones de años y 0,06 millones de años. En los últimos 2 millones de años, la disminución de las poblaciones ha estado relacionada con los climas fríos.
En cuanto a los ginkgos que se encuentran fuera de China, analizando su origen genético se puede concluir que son descendientes de poblaciones del este de China. En primer lugar, los ginkgos fueron llevados a Japón y Corea, que son similares a los del este de China, y más tarde a Europa y América. Los árboles que hay en Europa son parientes de los ginkgos del este de China; y los que hay en América se asemejan a los ginkgos del este de China, Japón, Corea y Europa. Por ello, los investigadores creen que gracias al influjo humano los ginkgos se han trasladado varias veces desde el este de China a América.
 Hojas de ginkgo. (Fotografía: Marzena P.– Licencia Pixabay. Fuente: pixabay.com)
Hojas de ginkgo. (Fotografía: Marzena P.– Licencia Pixabay. Fuente: pixabay.com)El estudio de los factores que influían en esta dispersión concluyó que siete variables climáticas afectaban a dicha distribución, entre otras, destacaban la estacionalidad de la temperatura, la de la lluvia o la cantidad de precipitaciones en el mes más seco. Además, el peso de estas variables fue diferente en los ginkgos del este y del suroeste de China, quizá debido a las preferencias de hábitat de cada grupo.
Para analizar la evolución de los ginkgos se seleccionaron 58 árboles del grupo oriental y 38 del suroeste. Se buscaron señales de la selección natural en los genomas de estos árboles y se constató que en cada grupo las regiones genómicas con indicios de selección habían sido diferentes. Analizando los genes localizados en estas regiones, concluyeron que estos genes tenían la función de combatir el estrés abiótico y biótico; que eran concretamente genes relacionados con las defensas para combatir insectos y hongos y genes para responder a la deshidratación, las bajas temperaturas y el exceso de sal. De hecho, ya se sabía que los ginkgos eran resistentes al estrés, especialmente frente a herbívoros y patógenos.
En resumen, el estudio del genoma de los ginkgos ha permitido obtener nuevos datos específicos sobre su dispersión y, a la vez, sobre su historia evolutiva. Esto nos aporta información sobre la evolución de las especies, ya que no es habitual recopilar tantos datos génicos sobre una especie aislada. A lo largo de los siglos, el ginkgo ha sido fuente de inspiración para el mundo de las artes, ha tenido presencia en la medicina y ha cautivado a los seres humanos. Hoy sigue seduciéndonos, incluso en el campo de la genética.
Referencia bibliográfica:
Zhao, Y., Fan, G., Yin, P. et al., (2019). Resequencing 545 ginkgo genomes across the world reveals the evolutionary history of the living fossil. Nature Communications, 10(1), 4201. DOI: https://doi.org/10.1038/s41467-019-12133-5.
Sobre el autor: Koldo Garcia Etxebarria (@koldotxu) es doctor en Genética, investigador en Biodonostia-Instituto de Investigación Biosanitaria y divulgador científico.
Este artículo se publicó originalmente en euskara el 26 de noviembre de 2019 en el blog Zientzia Kaiera. Artículo original.
El artículo Historias genéticas de un fósil viviente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Historias de la malaria: Las drogas sintéticas
- Historias de la malaria: El parásito
- Historias de la Malaria: La vacuna
Ingredientes para la receta: El bacalao
“Pusieronle la mesa a la puerta de la venta, por el fresco, y trújole el huésped una porción del mal remojado y peor cocido bacalao y un pan tan negro y mugriento como sus armas”.
Miguel de Cervantes, El Quijote, 1605.
“… pues no sería buen bilbaíno si no hiciera en cualquier ocasión los honores debidos a un buen plato de bacalao con aquella salsa de bermellón y a una azumbre de chacolí de Somorrostro”.
Benito Pérez Galdós, Luchana, 1899.
Hace unos años escribía Juan Carlos Capel, gran gastrónomo y experto en pescado, que, “atendiendo a su origen y número de anécdotas, recetas y bibliografía documental, el bacalao es, sin lugar a dudas, el pescado más enciclopédico de la gastronomía española”. Cierto es, y cuesta más decidir que no contar que buscar algo para decir, por lo menos por ahora. Allá voy, a ver que sale.
 Gadus morhua. Fuente: Wikimedia Commons
Gadus morhua. Fuente: Wikimedia CommonsEl bacalao atlántico, o Gadus morhua, se encuentra en el Atlántico norte, de Canadá y Estados Unidos, pasando por Groenlandia e Islandia, hasta el norte de Noruega y Rusia. Por el sur llega al Mar del Norte y el Canal de La Mancha.
Hacia el año 1000, el vikingo Leif Ericson llegó a Norteamérica, a Vineland, el País de las Viñas, a la tierra que ahora llamamos Terranova. Quizá ya pescaban bacalao. Ericson y sus compañeros se mantuvieron cerca de la costa, donde el bacalao es abundante y fácil de capturar. Los vikingos, en Escandinavia e Islandia, ya pescaban bacalao, por lo menos, desde finales del siglo VIII. Sin embargo, los vikingos de Groenlandia casi no probaron el pescado según los escasos restos encontrados en sus vertederos. Se ha propuesto que fueron los primeros en secar bacalao, quizá primero en Terranova y, después, en Islandia. Los vascos desarrollaron, al final de la Edad Media, un próspero comercio que enriqueció los puertos de Vizcaya, Guipúzcoa y Lapurdi, según publicó Anton Erkoreka, de la UPV/EHU, en 2004. El mismo autor plantea que la estructura de los barcos vikingos, eficaces y seguros, cambió la construcción naval en el Golfo de Vizcaya. Esos barcos permitieron, como hacían los vikingos, atravesar el océano y practicar la captura y comercio del bacalao.
Para pescar y preparar el bacalao, en las primeras pesquerías en Terranova, José María Merino nos cuenta el método que se seguía entonces.
“Hay numerosos puertos en Terranova y Bacaillos donde los navíos anclan por tres meses. Al amanecer los marineros van a la campaña del salazón, a una, dos o tres leguas a tomar su carga. Para la una o las dos de la tarde han llenado cada cual su chalupa y vuelven al puerto donde hay un enorme muelle, especie de hórreo de madera construido al borde del mar … Allí hay una gran mesa sobre la que se acomoda el pescado descargado. Después de salarlo se lleva a secar sobre las rocas expuestas al viento o sobre el cascajo que el mar ha amontonado. A las seis horas se les da vuelta y así muchas veces. Después se recogen y apilan; y de nuevo lo mismo a los ocho días de estar al aire libre. Al fin, ya seco se les prensa.”
El bacalao, según una publicación de 1943 del Instituto Español de Oceanografía, que transcribe Mª Teresa Tolosa, era preparado según llegaba al barco. Nos puede servir de ejemplo de cómo se elaboraba para el transporte y la comercialización. La autora indica que:
“los ejemplares se descabezaban, se arrojaban sobre la mesa del siguiente compartimiento. La mesa estaba dividida en 2 partes por medio de un listón, y en la segunda operaban dos tronchadores de pie sobre banquillos, enfrentados cara a cara, el primero con el cuchillo abre el pescado a lo largo de la línea media del vientre, se desviscera echando el hígado y las huevas en cestos a sus pies; el pescado limpio se echa en cestos que colmados pesan unos 65 kilogramos, y se arrastran por medio de ganchos hasta la escotilla de la bodega a la que se arrojan los pescados por medio de una lona de deslizamiento. En la bodega el maestro salador y ayudantes reciben el pescado sobre una capa de sal. El pescado se apila en capas alternas con sal. Las pilas tienen un metro de altura por 1,20 de anchura y se extienden de banda a banda. Cada pila pesa unas siete toneladas. Se utilizaba en proporción el 75% de sal en relación al pescado. Que se reduce por desecación en una tercera parte al descargar en la factoría”.
La grasa dificulta la salazón del pescado. La sal tarda en penetrar la grasa y, además, con el tiempo de secar al aire puede tomar sabor a rancio. El bacalao tiene poca grasa y, por tanto, se puede secar al aire y, después, salar en un proceso sencillo y eficaz.
Volvamos atrás en el tiempo a pesar de que la detección de restos de peces en los yacimientos arqueológicos no es fácil. Son pequeños y delicados sus huesos y, además, durante mucho tiempo los métodos de estudio no eran adecuados y no se buscaban en los trabajos de arqueozoología. En el estudio de Lucy Cramp y su grupo, de la Universidad de Bristol, sobre restos de comida encontrados en cerámica de yacimientos del noroeste de Europa, se han encontrado restos de lípidos de origen marino fechados hace 6000-7000 años y, todavía en más cantidad, entre los siglos IX y XIV, durante el auge de las incursiones de los vikingos. Sin embargo, los autores no pueden concretar si entre los restos hay alguno de bacalao.
En la costa de los Países Bajos, Alemania y Dinamarca, los restos más abundantes corresponden a gádidos, entre los que se encuentra el bacalao. No abundan en los fechados en la Edad del Hierro, hace unos 5000 años, pero se recogen en los datados hace unos 2500 años y aumentan en la dieta en la Edad Media, hacia los 400 años de nuestra era y siglos posteriores. Los autores, Witzke Prummel y Dirk Heinrich, de las universidades de Groningen, en Holanda, y de Kiel, en Alemania, suponen que existía entonces un gran comercio de estas especies de gádidos, entre ellas el bacalao.
De sus hallazgos deducen que desde los siglos V al VII, hay comercio de bacalao en Suecia. Y, en yacimientos de la época romana en las zonas estudiadas, hay restos de pescado salado.
En la revisión de Inge Enghoff, de la Universidad de Copenhague, hay restos de bacalao desde los VIII y IX en Dinamarca, desde el siglo VIII en Alemania y Países Bajos, y en Bélgica desde el siglo XII al XIII. Hay más abundancia en el siglo XVI y, también, aparecen esos restos en yacimientos del Reino Unido. En Haithabu, en Alemania, cerca de la frontera actual con Dinamarca, el grupo de Bastiaan Star, de la Universidad de Oslo, encontró restos de bacalao, fechados entre los siglos IX y XI, que, con análisis de ADN, situaron su origen en el norte de Noruega. De nuevo los viajes de los vikingos.
En los Países Bajos y en restos del siglo XVI, hay marcas de cortes en el esqueleto que indican que era bacalao seco y, para algunos expertos, no son capturas del Mar del Norte sino que vienen de pesquerías más lejanas, más al norte. A menudo se encuentran ejemplares de dos tamaños: pequeños, de pesquerías locales; y grandes, sin cabeza, importados del norte de Europa y secos y salados. Para los restos del siglo XVII ya se ha podido establecer el origen de ese bacalao seco en las islas Spitzbergen, muy al norte, en el Océano Ártico. Este tráfico de bacalao desde el norte llegó a las 6000 toneladas anuales en la Edad Media.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsPor esos años, hacia 1400, algunos pescadores europeos adoptaron los métodos de conservación en sal desarrollados por los vascos. Se ha propuesto que los vascos pescaban bacalao y lo salaban desde el siglo X. El bacalao seco, salado y duro como la madera, se podía transportar por tierra a cualquier lugar del interior de Europa o, más en concreto, al litoral más urbanizado del sur del Mar del Norte. Así, en Europa, el bacalao se convirtió en parte importante de la dieta. Ayudó a su éxito en la dieta la Iglesia Católica con los días y fiestas en los que obligaba a la vigilia, a no comer carne.
Es difícil establecer cuando llegó el bacalao a la dieta de los habitantes de la Península Ibérica. Incluso L. Benavides escribe que lo trajeron los fenicios. José María Merino cuenta como, en un tratado fechado en 1354 entre los reyes de Inglaterra y Castilla, se permitía a los castellanos, entre ellos a los vascos, preparar y salar pescados en las costas inglesas. Ya se conocía el bacalao en Castilla e, incluso, era cuestión de negociación entre reyes. Y en 1519, según José Carlos Capel, la palabra “bacalao” aparece escrita por vez primera en castellano. Servía, de forma genérica, para varias especies de pescado marino conservadas en sal.
Cinco siglos después que los vikingos, en 1497, llegó a Terranova John Cabot, navegante genovés al servicio de Enrique VII de Inglaterra. Se sorprendieron de la abundancia de bacalao y, parece ser, que lo pescaban simplemente hundiendo en el mar grandes cestas que recogían llenas de peces.
Pocos años después, o quizá antes, llegaron vascos y portugueses que, además, utilizaban sal para conservar el bacalao. Cuando en 1535 llegó a Terranova y al San Lorenzo en su segundo viaje a la zona, Jacques Cartier, enviado por el Rey Francisco I de Francia, encontró numerosos barcos pescando bacalao. Era vascos, españoles, portugueses y bretones. En 1548, Francisco I envió una flota con 150 veleros a pescar bacalao. Llevaban las capturas a tierra, preparaban el pescado y lo colgaban a secar en los fríos vientos del Ártico.
La época dorada de la pesca de bacalao por los vascos duró de 1560 a 1600. El primer barco de nuestro entorno más cercano del que existe prueba documental de ir a la pesca del bacalao en Terranova, según el estudio de Thierry Du Pasquier, es el “Catherine d’Uturbie”, Su capitán, Adam de la Gaberie, se comprometió el 22 de marzo de 1530, antes de su partida, a vender a dos comerciantes de Burdeos, “cuatro millares y medio de bacalao seco”. Más adelante, en noviembre de 1603, el “Santiago” llegó a Bilbao, después de la campaña de Terranova, con ballena y bacalao.
Las pruebas históricas indican que desde entonces, siglos XV y XVI, el bacalao se ha comercializado en muchos países europeos. En el Mar Báltico, las primeras evidencias de consumo de bacalao que conocemos son del siglo XIII, con pescado de Noruega. O en Islandia, con aumento de la demanda de bacalao por mercaderes alemanes e ingleses en el siglo XIII, hasta el siglo XVI en que disminuyeron las capturas y las ventas. Y el bacalao de Terranova aparece en los yacimientos arqueológicos a partir del siglo XVI, después de las exploraciones de Cabot. Algunos autores mencionan las 200000 toneladas anuales de pesca de bacalao fresco en Terranova en el siglo XVI.
La primera parte de El Quijote se publicó en 1605. En su primera salida, el Caballero llegó a la venta de Puerto Lápice (que todavía existe), y allí tuvo bacalao par a comer. Era viernes y en cuaresma y, por tanto, había que guardar la vigilia. Repito la cita del principio de este texto:
“Pusieronle la mesa a la puerta de la venta, por el fresco, y trújole el huésped una porción del mal remojado y peor cocido bacalao y un pan tan negro y mugriento como sus armas”.
Una receta como para probar es el atascaburras manchego, aunque la receta actual lleva patatas que, a principios del siglo XVII, estaban recién llegadas de los Andes y todavía no eran de uso popular. Este es el atascaburras que mencionaba, según Lorenzo Díaz en su recetario del Quijote.
“Se cuecen las patatas con el bacalao desalado. En un mortero se pican ajos, y se van echando las patatas cocidas una a una y se machaca todo junto. Se desmenuza el bacalao y se añade al mortero y se sigue machacando, y a la vez, se añade, poco a poco, aceite crudo. Así se consigue un puré consistente. Se adorna con rodajas de huevo duro y nueces. A la mesa.”
El comercio de bacalao llegó a muchos países y se han encontrado restos, por ejemplo, en el Caribe cerca de los alojamientos de finales del siglo XVIII para esclavos africanos. Es un ejemplo temprano de globalización.
Durante el siglo XVIII y, sobre todo, en el XIX, Bilbao fue el gran mercado de bacalao para el norte de la península. En esos años, en 1758, Juan Altamiras publicó su “Nuevo arte de la cocina española” con alguna receta de bacalao salado. Son pocas, una docena. Es plato del pueblo, nada elegante e, incluso es un pescado de “poca sustancia”.
Para el bacalao salado de Terranova fue España el mejor mercado durante la primera mitad del siglo XIX, entre 1815, al terminar las guerras napoleónicas, y 1840. Hacia 1870, el comercio con España declina, y a finales de siglo, es muy escaso. Los mayores competidores son Noruega y Francia.
 Bacalao al pil pil. Fuente: Wikimedia Commons
Bacalao al pil pil. Fuente: Wikimedia CommonsEn el siglo XIX, en 1836 y durante la primera guerra carlista, Bilbao fue sitiada por las tropas de Zumalacárregui. Y en Bilbao, se cuenta que, durante el sitio, para comer había, sobre todo, bacalao. Es más, la tradición afirma que entonces se inventó el bacalao al pil pil. Benito Pérez Galdós, para sus Episodios Nacionales escribió Luchana, libro en el que narra el sitio de Bilbao. Menciona un plato extraordinario con bacalao en salsa bermellón o, más habitual, en salsa roja. Es el bacalao a la vizcaína, con una salsa de color rojo conseguida con la carne de los típicos pimientos choriceros. De una receta de Karlos Arguiñano, en la que añade patatas que voy a quitar, se dice cómo hacer este bacalao y, por favor, sin salsa de tomate.
“Cocer el bacalao, desalado, en caldo de pescado con carne de pimientos choriceros. Algo así como cuatro minutos por cada lado, y a servir. Hay quienes a todo esto le añaden cebolla pochada en aceite y manteca de cerdo o tocino de un buen jamón. Y también cortezas de pan seco mojadas y desmenuzadas. Lo que les apetezca.”
El libro Luchana se publicó en 1899, y cuatro años antes, en 1895, Sabino Arana pasó la Navidad en la cárcel de Larrínaga, en Bilbao. Sus seguidores le llevaron su cena de Navidad que, como debía ser, incluía bacalao a la vizcaína, ese bacalao en salsa bermellón que cita Pérez Galdós.
En la tercera guerra carlista, en el sitio de Bilbao, comenzó la leyenda del bacalao al pil pil. Un almacenista de salazones de Bilbao apellidado Gurtubay hizo un pedido de bacalao, unos 30 o 40 fardos que, por error de quien sea, se convirtieron en 30040 fardos. Comenzó el sitio y, en Bilbao, se comía, sobre todo, bacalao. Y hay quien asegura que entonces se inventó el bacalao al pil pil. Por cierto, la bibliografía sobre este tema es confusa: fue la primera o la tercera guerra carlista, la que cuenta Benito Pérez Galdós; y se debate sobre si Gurtubay era José María o Simón., etc. Quizá todo sea leyenda. Por otra parte, no hay acuerdo entre expertos como, por ejemplo, José Mª Busca Isusi, si el bacalao al pil pil y el bacalao ligado son la misma o diferentes recetas para cocinar este pescado.
Al otro lado del Atlántico, en la costa este de Estados Unidos, Rudyard Kipling sitúa su novela Capitanes valientes, publicada en 1897. Relata la pesca del bacalao cuando era abundante y se pescaba con relativa facilidad desde chalupas que partían del barco pesquero y volvían a él para limpiarlo, prepararlo y almacenarlo en la bodega. Es la técnica de pesca utilizada hasta 1950 y desde muy antiguo, como antes explicaba José María Merino.
La primera cena del novato protagonista de la historia es ”un plato de fritura de lenguas y vejigas de bacalao, pedazos de carne de cerdo y patatas fritas; una hogaza de pan caliente y una taza de café negro y fuerte”. En Terranova hay un plato típico para la cena familiar. Se cocina así:
“Se cuece en agua bacalao desalado y patatas cortadas trozos pequeños durante media hora. Después se fríen los trozos de bacalao hasta que estén dorados. Se dora cebolla picada con el cerdo mientras se fríe. Unir el bacalao y las patatas con el cerdo y la cebolla frita. Algo de pimienta negra y a la mesa.”
A principios del siglo XX, entre 1900 y la primera Guerra Mundial, el comercio del bacalao en España creció y casi se triplicó. También el precio subió y, según Daniel Vickers, por el aumento de la población debido a la revolución industrial y a la globalización del comercio mundial y al descenso de capturas del bacalao por la sobreexplotación.
 Recetas de bacalao PYSBE (1936). Fuente: IberLibro
Recetas de bacalao PYSBE (1936). Fuente: IberLibroEn 1926 se fundó la empresa Pesquerías y Secaderos de Bacalao de España, conocida por sus siglas PYSBE. Organizó el negocio el armador francés Louis Legasse, conocido por sus intereses en la pesca desde St. Pierre et Miquelon, islas francesas en el Atlántico noroeste, en Terranova. En España, el gobierno ayudó a la prosperidad del negocio al imponer, en 1922, un arancel al bacalao importado.
La empresa, cuya sede estaba en Pasajes y que consiguió que este puerto fuera el primer puerto bacaladero del país y uno de los primeros de Europa, emitió 4000 acciones, a 500 pesetas cada una, que adquirieron banqueros, empresarios, aristócratas adinerados e, incluso, el rey Alfonso XIII. A finales de los veinte botó los seis primeros pesqueros, y sus campañas consiguieron que el porcentaje de bacalao nacional consumido en el país pasara del 2%, en 1927, al 15%, en 1934.
Después de la guerra civil, PYSBE amplió su actividad y construyó un muelle y factoría en El Ferrol, y depósitos frigoríficos en Málaga y Sevilla. También tuvo agencias en Gales, Inglaterra, Noruega, Islandia, Canadá, Terranova, Azores y St. Pierre et Miquelon.
La empresa desapareció en los setenta cuando la sobreexplotación del recurso comenzaba a notarse y los países más cercanos, como Canadá o Islandia, ampliaron su zona económica exclusiva y limitaron la actividad pesquera en sus caladeros. No supo reaccionar a los cambios en la pesca y en el tratamiento del pescado como, por ejemplo, el desarrollo de la congelación. En 1973 comenzó la liquidación de la empresa y, en 1974, presentaron el expediente de crisis.
Las capturas de bacalao de Terranova en los siglos XIX y XX eran de 100000 toneladas anuales en 1800, llegaron a 300000 en 1900 y cayeron a 50000 entre 1970 y 2000. Era el mayor stock del planeta. Durante años y años soportó la extracción de entre 200000 y 400000 toneladas anuales. Y, por fin, entre 1985 y 1995, colapsó y prácticamente desapareció. Ahora, George Rose y Sherrylynn Rowe, de la Universidad Memorial de Terranova en St. John’s, nos dan la buena noticia de que la población del bacalao del norte está creciendo a partir de los pocos ejemplares que quedaron después del colapso.
Los autores calculan la población de bacalao a partir de escuchas con el sonar, tomadas desde 1999 a 2015, en el Corridor Bonavista, al nordeste de Terranova, zona de migración del bacalao para la puesta. Los ecogramas demuestran la presencia de bacalao hasta 1992. Después desaparece y vuelve de nuevo en los ecogramas de marzo de 2008 y, con mayor presencia, en los meses de mayo de 2014 y 2015.
La biomasa calculada, en el Corridor Bonavista, es de algo más de un millón de toneladas en 1990, entre 1000 y 5000 toneladas entre 1995 y 2005, y un aumento hasta 240000 toneladas en 2014. El aumento de la población entre 2005 y 2014 es exponencial, con un aumento lento al principio, con unos miles de toneladas anuales, y mucho más rápido al final, hasta esas 240000 toneladas de 2014.
Con datos de capturas por arrastre entre 1978 y 2013, Eric Pedersen y su equipo, de la Universidad McGill de Montreal, llegan a parecidas conclusiones. Dan a la biomasa de bacalao de 1981 el valor de 100, cae hasta 5 en 1995 y sube a 17 en 2013 en un lento proceso de recuperación.
En la actualidad, inicios del siglo XXI, hay países con flotas especializadas en la pesca del bacalao: Islandia, Noruega, Dinamarca, Reino Unido, Rusia y otros. Fue en 2017 cuando la FAO clasificó al bacalao entre las diez especies más pescadas del planeta.
Portugal es el país que más bacalao consume, unas 80000 toneladas anuales a principios de este siglo. Le sigue España con 35000 toneladas. Brasil llegó a las 40000 toneladas en 1998. Italia consume 20000 toneladas anuales y Francia 10000 toneladas, sobre todo por los portugueses que residen en el país.
En el siglo XXI comenzó, en Noruega, la investigación para desarrollar y promover la acuicultura del bacalao. El programa nacional de cría de bacalao se inició en 2002. Pronto la producción llegó a las 19000 toneladas anuales en el momento de su máximo desarrollo. Pero, con la crisis de 2008, la producción se detuvo y todo terminó en 2014.
En 2019, reiniciaron los estudios y los ensayos y se consiguió que se recuperara la producción y la mejora de los métodos y técnicas de cultivo. Los huevos son difíciles de manejar pero, cuando el juvenil nace y pesa 1-2 gramos es un pequeño bacalao capaz de alimentarse por su cuenta. Los ejemplares se conservan hasta que maduran sexualmente y, después, se colocan en jaulas en el mar. A los 21 meses pesan alrededor de tres kilos y se comercializan.
Referencias:
Barrett, J.H. 2018. An environmental (pre)history of European fishing: past and future archaeological contributions to sustainable fisheries. Journal of Fish Biology 94: 1033-1044.
Barrett, J.H. et al. 2011. Interpreting the expansion of sea fishing in medieval Europe using stable isotope analysis of archaeological cod bones. Journal of Archaeological Science doi: 10.1016/j.jas.2011.02.017
Benavides-Barajas, L. 1995. Nueva clásica cocina andalusí. Ed. Dulcinea. Granada. 328 pp.
Bjorndal, T. et al. 2017. Cod-nations: Trade of a expanding commodity. Conference Paper June. 11 pp.
Capel, J.C. 1997. Manual del pescado. R & B Ed. Bilbao. 366 pp.
Collier, K. 2011. 19th century salt fish markets, 1810-1914. Newfoundland and Labrador Heritage Web Site.
Cramp, L.-J.E. et al. 2014. Immediate replacement of fishing with dairying by the earliest farmers of the norteast Atlantic archipelagos. Proceedings of the Royal Society B 281: 20132372
Díaz, L. 1993. La cocina del Quijote. Servicio de Publicaciones de la Junta de Comunidades de Castilla-La Mancha. 270 pp. + 111 pp.
Du Pasquier, T. 2000. Les baleiniers basques. Ed. S.P.M. Paris. 452 pp.
Edvardsson, R. et al. 2019. Change in Atlantic cod migrations and adaptability of early land-based fishers to severe climate variation in the North Atlantic. Quaternary Research doi: 10.1017/qua.2018.147
Enghoff, I.B. 2000. Fishing in Southern North Sea región from the 1st to the 16th century AD: Evidence from fish bones. Archaeofauna 9: 59-132.
Erkoreka, A. 2004. Los vikingos en Vasconia. En “Los vikingos en la Península Ibérica”, p. 9-40. Fundación Reina Isabel de Dinamarca. Madrid.
García-Orellán, R. & J. Beobide Arburua. 2009. Hombres de Terranova. La pesca del bacalao (1926-2004). Stella Maris. Santurce. 389 pp.
Hayward, V. 2017. Nuevo arte de la cocina española, de Juan Altamiras. Círculo de Lectores. Barcelona. 493 pp.
Klippel, W.E. 2001. Sugar monoculture, bovid skeletal part frequencies, and stable carbon isotopes: Interpreting enslaved African diet at Brimstone Hill, St. Kitts, West Indies. Journal of Archaeological Science 28: 1191-1198.
Kurlansky, M. 1999. El bacalao. Biografía del pez que cambió el mundo. Ed. Península. Barcelona. 267 pp.
Kurlansky, M. 2003. Sal. Historia de la única piedra comestible. Ed. Península. Barcelona. 508 pp.
Macías, O. 2002. La cultura culinaria de Bilbao a finales del siglo XIX. XV Congreso de Estudios Vasco, Ciencia y cultura y redes telemáticas, Donostia, Eusko Ikaskuntza, p. 259-265.
Merino, J.M. 1991. La pesca desde la Prehistoria hasta nuestros días (La pesca en el País Vasco). Servicio Central de Publicaciones del Gobierno Vasco. Vitoria-Gasteiz. 494 pp.
Orton, D.C. et al. 2011. Stable isotope evidence for Late Medieval (14th-15th C). Origins of the Eastern Baltic cod (Gadus morhua) fishery. PLOS One 6: e27568.
Pedersen, E.J. et al. 2017. Signatures of the collapse and incipient recovery of an overexploited marine ecosystem. Royal Society Open Science 4: 170215.
Prummel, W. & D. Heinrich. 2005. Archaeological evidence of former occurence and changes in fishes, amphibians, birds, mammals and mollusc in Wadden Sea area. Helgoland Marine Research 59: 55-70.
Rose, G.A. & S. Rowe. 2015. Northern cod comeback. Canadian Journal of Fisheries and Aquatic Sciences DOI: 10.1139/cjfas-2015-0346
Star, B. et al. 2017. Ancient DNA reveals the Arctic origin of Viking Age cod from Haithabu, Germany. Proceedings of the National Academy of Sciences USA 114: 9152-9157.
Tolosa Bernárdez, M.T. 2000. La pesca del bacalao en el siglo XX: el caso de la Compañía P.Y.S.B.E. Itsas Memoria Revista de Estudios Marítimos del País Vasco 3: 363-382.
Vázquez, A. 2009. La pesca española del bacalao en Terranova. Foro dos Recursos Mariños e da Acuicultura das Rías Galegas 11: 123-140.
Vega Pérez de Arlucea, A. 2019. El bacalao según la PYSBE. El País 29 marzo.
Vickers, D. 1996. The price of fish: A price index for cod. Acadiensis 25: 92-194.
Vié, B. 2001. La morue entre sel et mer. Jean-Paul Rocher Ed. Paris. 222 pp.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Ingredientes para la receta: El bacalao se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ingredientes para la receta: El arroz
- Ingredientes para la receta: El maíz
- Ingredientes para la receta: El conejo
José Miguel Viñas – Naukas P4K 2019: De nubes las pinacotecas están llenas
 Las lanzas o La rendición de Breda de Diego Rodríguez de Silva y Velázquez. Hacia 1635. Óleo sobre lienzo, 307,3 x 371,5 cm. Fuente: Museo del Prado
Las lanzas o La rendición de Breda de Diego Rodríguez de Silva y Velázquez. Hacia 1635. Óleo sobre lienzo, 307,3 x 371,5 cm. Fuente: Museo del PradoA lo largo de los siglos los pintores recogieron en sus paisajes rasgos característicos del tiempo atmosférico para cada época y lugar. Esas nubes, vistas con ojos de meteorólogo nos revelan qué cambios ha habido desde que se pintaron algunos cuadros. José Miguel Viñas, físico del aire y comunicador científico, meteorólogo en Meteored, en el portal www.tiempo.com, y consultor de la Organización Meteorológica Mundial, nos presta sus ojos en esta conferencia.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo José Miguel Viñas – Naukas P4K 2019: De nubes las pinacotecas están llenas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos
- Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
¿Sirve de algo la ‘pastilla del colesterol’?
Saioa Gómez Zorita & Maria Puy Portillo
 Foto: Michal Jarmoluk / Pixabay
Foto: Michal Jarmoluk / PixabayEl colesterol es una molécula imprescindible para la vida del ser humano, puesto que cumple funciones vitales. Por ejemplo, es un precursor de la síntesis de hormonas sexuales y de ácidos biliares, y forma parte de múltiples estructuras del cuerpo.
Esta molécula puede tener dos orígenes:
- Exógeno: ingerido a partir de la dieta y absorbido en el intestino delgado. En contra de lo que se creía, se ha demostrado que no afecta mucho a los niveles de colesterol en sangre.
- Endógeno: sintetizado por el organismo, en el hígado. Depende de diversos factores genéticos y dietéticos. Los azúcares simples y la grasa saturada incrementan la síntesis endógena de colesterol.
Las concentraciones de colesterol excesivamente elevadas –o demasiado bajas– puede desencadenar problemas en la salud. La hipercolesterolemia se asocia a un mayor riesgo de enfermedades cardiovasculares, la principal causa de mortalidad en nuestra sociedad.
Es importante distinguir entre dos tipos de colesterol. El LDL, conocido como “malo”, no debería sobrepasar cierto límite puesto que aumenta el riesgo de enfermedades cardiovasculares. El HDL, conocido como “bueno”, es deseable que sea elevado, ya que protege de las enfermedades cardiovasculares.
En la actualidad hay diversos métodos para determinar el riesgo cardiovascular, lo que permite estimar el riesgo de muerte por esta causa. Esto es de gran utilidad en personas asintomáticas y, además, de bajo coste.
Los principales métodos empleados para predecir el riesgo de muerte por un evento cardiovascular a los 10 años se basan en las tablas REGICOR y SCORE. Las primeras tienen en cuenta si el paciente es fumador, diabético, la edad, los valores de presión arterial, colesterol total, colesterol HDL y colesterol LDL. Las segundas tienen en cuenta sexo, edad, presión arterial, concentraciones plasmáticas de colesterol y si el sujeto fuma o no.
En pacientes no diabéticos ambas tablas aportan resultados muy similares. Teniendo en cuenta el resultado de este análisis y la presencia de otras patologías, se determina si el paciente debe recibir o no tratamiento farmacológico, siempre que la dieta y la actividad física no sean suficientes o hayan fracasado.
¿Qué pacientes pueden tomar estatinas?
El tratamiento farmacológico para disminuir el colesterol total y LDL y, por tanto, el riesgo cardiovascular, son las estatinas.
Los pacientes que podrían beneficiarse de su uso son los siguientes.
Individuos cuyos niveles de colesterol LDL sobrepasan los 240 mg/dL y pacientes con valores superiores a 190 mg/dL con dislipemia familiar o hipertensión arterial grave.
Así mismo, el objetivo es alcanzar valores de colesterol LDL menores de 70 mg/dL en pacientes con enfermedad cardiovascular establecida como las cardiopatías isquémicas, con diabetes mellitus tipo I y lesión de un órgano diana, diabetes mellitus tipo II con factores de riesgo cardiovascular asociados o lesión de un órgano diana, con enfermedad renal crónica avanzada, y pacientes con niveles de SCORE ≥ 10 %.
Finalmente, el objetivo de valores de colesterol LDL inferiores a 100 mg/dL se establece en pacientes con diabetes mellitus tipo I y II sin lesiones de ningún órgano diana ni factores de riesgo cardiovascular asociados, pacientes con enfermedad renal crónica moderada y pacientes con unos valores de SCORE entre un 5 y un 10 %.
En caso de que los valores SCORE estén entre un 1 y un 5 %, el objetivo terapéutico son niveles de colesterol LDL inferiores a 115 mg/dL. Esto es más necesario cuanto mayor sea el valor de SCORE.
 Figura 1. Regulación de los niveles de colesterol en sangre.
Figura 1. Regulación de los niveles de colesterol en sangre.
Las estatinas inhiben un enzima que participa en la síntesis hepática de colesterol, la hidroximetilglutaril coenzima A reductasa (HMG-CoA reductasa). En otras palabras, disminuyen su formación (Figura 1).
Como consecuencia, se necesitará utilizar una parte del colesterol sanguíneo y el colesterol LDL disminuirá entre un 15 y un 50 %.
Además, se ha observado que los triglicéridos séricos disminuyen ligeramente y aumenta el colesterol HDL. Las estatinas disponibles hoy en día son las siguientes: atorvastatina, fluvastatina, lovastatina, pitavastatina, pravastatina, rosuvastatina y simvastatina.
Efectos secundarios
En general se trata de fármacos seguros y bien tolerados, pero algunos pacientes sufren efectos secundarios como dolor muscular.
También pueden aparecer otros efectos no deseados como alteraciones cognitivas y dolor de cabeza. Estos son más frecuentes en personas que toman otros medicamentos simultáneamente (corticoides, antirretrovirales, opioides), en mujeres, en personas mayores de 65 años y en personas con otras patologías.
Por tanto, es necesario tener en cuenta la relación riesgo-beneficio del tratamiento en cada persona. Los principales efectos adversos con dosis terapéuticas habitualmente utilizadas se producen a nivel gastrointestinal y son náuseas, vómitos y dispepsia (dolor o molestias en la zona alta del abdomen).
El debate sobre el tratamiento hipolipemiante con estatinas surgió principalmente cuando se asoció su utilización con un incremento del riesgo de padecer cáncer. No obstante, es importante señalar que muchos de los resultados provienen de estudios llevados a cabo en animales y que, por el contrario, los ensayos clínicos realizados hasta el momento no muestran un cambio en la incidencia de esta patología
Es bien conocido que las estatinas aumentan algunos enzimas relacionados con el daño hepático (transaminasas). No obstante, la aparición de este efecto negativo está estrechamente relacionado con la dosis empleada y además muy raramente esta situación progresa a insuficiencia hepática.
Por otro lado, es cierto que estos fármacos aumentan el riesgo de padecer diabetes, pero en ocasiones se trata de un riesgo asumible. Finalmente, algunos estudios han mostrado un incremento de peso corporal en estos pacientes. Sin embargo este hecho puede estar relacionado con los hábitos de alimentación y de actividad física de cada individuo. Estas personas, al observar una disminución en su nivel de colesterol, se relajan.
Alternativas a las estatinas
En caso de que las estatinas no sean suficiente o no puedan administrarse, se puede recurrir a otros tratamientos combinados o no con las estatinas como los secuestradores de ácidos biliares.
Estos, al obligar al hígado a sintetizar nuevos ácidos biliares, producen una disminución del colesterol plasmático. No obstante, presentan el problema de que no suelen ser bien tolerados y pueden incrementar los triglicéridos séricos. También pueden utilizarse los fibratos, que disminuyen el colesterol total, LDL y triglicéridos en sangre, mientras que aumentan los niveles de HDL.
A modo de conclusión cabe señalar que, para mantener unos niveles adecuados de colesterol y de riesgo cardiovascular bajo, es importante seguir unos hábitos dietéticos adecuados, realizar actividad física de forma regular y no fumar.
En caso de que fuera necesario y el profesional sanitario así lo considerara, se debe seguir el tratamiento farmacológico indicado y notificar cualquier efecto adverso que se padezca.
Además es importante recordar que, como todos los medicamentos, las estatinas no están exentas de riesgos. Los efectos secundarios no deseados dependen de diversos factores y algunos de los que hemos oído hablar en diversos medios de comunicación y redes sociales en los últimos años no están demostrados o totalmente justificados. Finalmente, en caso de duda consulte a su médico o farmacéutico.![]()
Sobre las autoras: Saioa Gómez Zorita es investigadora y Maria Puy Portillo catedrática de nutrición en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Sirve de algo la ‘pastilla del colesterol’? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Sirven para algo los enjuagues con clorhexidina?
- Aunque tengas colesterol, podrás desayunar huevos
- El amor es algo bonito que acaba mal
La reinvención de la ciencia
Antonio Lafuente
 Foto: Chris Montgomery / Unsplash
Foto: Chris Montgomery / UnsplashLa COVID-19 traerá cambios profundos en nuestro modo de vida. Quienes todavía tienen esperanza de que las cosas vuelvan a su sitio, esperan la vacuna como una especie de santo grial. Las zoonosis, las PCR, la hidroxicloroquina, la inmunidad de grupo, las células T, la variante G614 son parte del nuevo lenguaje de nuestra vida diaria.
Son conceptos nacidos en el laboratorio pero que han desbordado sus fronteras e ingresado en el lenguaje común. Nuestras existencias ordinarias dependen de lo que suceda en esos espacios extraordinarios, donde se está experimentando con más de 140 vacunas potencialmente eficaces. Vivimos una especie de laboratorización de la vida. Si en la anterior crisis vivíamos pendientes del Fondo Monetario Internacional y sus hombres de negro, ahora nuestra atención es para la OMS y gentes con bata blanca.
Los laboratorios son las nuevas fábricas de lo social y, sin embargo, no salen en la televisión, que no distingue entre un empresario y un investigador. Las imágenes se parecen mucho: bustos parlantes rotulados como virólogos, bioquímicos o epidemiólogos. Nunca están en el banco de experimentación. Se muestran como oficinistas o expertos, gentes que entienden, pero que no es seguro que nos entiendan. Sus pantallas son parte del atrezo y emiten en bucle ese icono inolvidable del coronavirus, pleno de colorines y de enigmas. ¿No es increíble que una cosa tan bonita pueda ser tan destructiva?
Hay una espectacularización de la pandemia. Todavía no sabemos si es un decorado o es parte sustancial y estratégica de lo que sucede. Pronto lo sabremos. De momento parece indiscutible el logro de un consenso amplio que, por mor de líderes como Trump o Bolsonaro, no es global: necesitamos la ciencia.
Los científicos parecen los nuevos atletas epocales. Y es justo reconocer que se están esforzando en no decepcionarnos. Quieren mostrarse como personas sabias y cercanas, cultas y cómplices. Han renunciado masivamente a la torre de marfil. Han salido de la zona de confort que representaba imaginarse como redactores de papers y cosechadores de citas.
Están trabajando duro y han logrado que, casi milagrosamente, de repente, desaparezcan todas las trabas burocráticas y administrativas que les impedían movilizarse de urgencia, emprender con alto riesgo, obtener recursos en plazos récord, desbordar las barreras disciplinarias, aparcar los conflictos corporativos, sortear las carencias institucionales, reinventar los modos de comunicar, ensanchar la transversalidad de sus redes, asumir las ventajas de la ciencia abierta, reclamar las bondades del sistema público, gozar del respeto de la ciudadanía, sentir el apoyo de los media, vivir el paraíso de la abundancia y, en fin, asumir su condición de nuevos lideres culturales.
La lucha contra la COVID-19 obliga a reinventar la ciencia. La ciencia no es sólo eso que ocurre entre pipetas, lentes y bits. ¡Claro que hacen falta muchos instrumentos! Pero cuanto mejores sean los equipamientos, más robustas son también las dependencias invisibles que se ocupan de que todo funcione.
En esto, a la ciencia le pasa como a la salud que, además de doctoras, necesita enfermeras, celadoras, cocineras, limpiadoras y recepcionistas. Recordemos un par de obviedades. La ciencia es una práctica social que involucra grandes inversiones, costosas infraestructuras, sofisticadas relaciones internacionales, ingentes contrataciones, múltiples edificios, numerosas leyes, gobernanzas diversas y, desde luego, la gestión de expectativas, presupuestos, nombramientos, premios y carreras individuales. En la ciencia hay científicos, congresos, revistas y laboratorios, con sus instrumentos, reactivos y computadores. Sin duda son parte fundamental de la coreografía que estamos describiendo. Son la parte más visible, pero están acompañados por una corte gigantesca de actores que sería injusto no mencionar, o seguir invisibilizando.
Hay gestores, técnicos, ayudantes, administrativos, becarios y estudiantes, además de un sinfín de roles imprescindibles que van desde los editores y divulgadores a los decanos, rectores y ministros. Hay máquinas, presupuestos, convocatorias, dictámenes, prioridades, comisiones, laboratorios, redes, libros blancos y planes estratégicos. Todos y todas forman eso que llamamos ciencia. Todos y todas son necesarios y su organización es fruto de una inteligencia colectiva y persistente. Nada es porque sí y todo ha necesitado de un gigantesco trabajo invisible y secular. Y aún no hemos acabado con nuestro listado de actores necesarios.
Cometeríamos un grave error si dejáramos de mencionar a los empresarios, los donantes, los inversores, los emprendedores y los concernidos, colectivos que se expresan mediante fundaciones, think tank, organizaciones gremiales o sindicales, asociaciones profesionales, movimientos sociales, agrupaciones ciudadanas o comunidades de afectados.
No vamos a aburrirles nombrando más actores, que los hay. Lo que tratamos de decir es que hace falta una enorme inteligencia organizacional para que toda esta maquinaria funcione armoniosamente.
Para disponer de una vacuna hay que movilizar muchos mundos. Los mejores científicos no lograrán nada si los consume la burocracia, la desidia o la competición. Tampoco llegarán muy lejos si no sienten que le acompañamos en sus esfuerzos, circunstancia que les exige un mayor esfuerzo de comunicación y escucha. En estos días les hemos visto explicarse con generosidad, sin delegar en otros, como era costumbre, la tarea de conectar con su entorno. Una novedad que, unida a las otras ya mencionadas, alumbra una diferente intelección de cómo articular un nuevo pacto social por la ciencia.
No necesitábamos la COVID-19 para aprender esto, como tampoco la pandemia nos ha descubierto la importancia de la digitalización. Hay consenso en afirmar que los procesos que ya estaban en marcha se han acelerado de forma irreversible.
¿Será verdad que la administración de la ciencia, que se atiene a las mismas leyes que las otras actividades públicas, ha modernizado en dos meses sus prácticas más que en los casi 50 años de democracia? ¿Cómo es que cosas que eran imposibles hace 5 meses son ya ordinarias? El ejemplo de la ciencia deberíamos analizarlo con mucho cuidado porque tal vez hayamos descubierto otros bienes que no sean los buscados, la vacuna, pero que en el futuro también podrían tener un impacto espectacular sobre nuestras vidas.
Recapitulemos. La proclamación del estado de alarma ha provocado la movilización urgente de (casi) todos los recursos científicos del país, especialmente de los vinculados al estado. En el CSIC, en particular, todos hemos sentido esa vibración y la llamada. De repente éramos necesarios y no un lujo más o menos prescindible. De pronto, los investigadores se volcaron sobre sus bancos de experimentación y redes de validación, porque aparecieron los dineros y se diluyeron los obstáculos. Las cosas que antes se hacían en meses comenzaron a suceder en horas.
Es increíble, pero cierto. Aunque nada era nuevo, todo parece distinto. Y, sin duda, es mejor. La ciencia española ha mostrado una musculatura, probado que estaba en forma y que aguardaba una oportunidad.
Lo que ha pasado se explica pronto: quien ha querido ha tenido la oportunidad de dejar aparcado lo que estaba haciendo e involucrarse en esta ciencia de guerra que nos convocó a una victoria sin cuartel que reclamaba todas las inteligencias disponibles. A cambio, se les ha bañado en un mar de (nueva) modernidad: financiación rápida, desburocratización feroz, mediación eficiente y desjerarquización responsable.
En cinco meses hemos cambiado de cultura, de siglo y de mundo. Hemos transitado desde la cultura del paper y de la excelencia a la cultura del compromiso y la competencia. Los científicos han dado un paso al frente y se han mostrado como una compañía responsable que quería hacerse cargo de los problemas de sus conciudadanos. Se han esforzado en mostrarse cercanos, solidarios y comprometidos, olvidando la tentación de aparecer elitistas, regañones y arrogantes. Quizás una semiótica visual propia habría ayudado en entender mejor su novedad: esa voluntad expresa de mostrarse parte de la solución a diferencia de lo que ocurre con los expertos que, con frecuencia, parecen una parte del problema.
En cinco meses han descubierto que la burocracia excesiva es un reducto de privilegios que asfixia la capacidad de asumir riesgos e innovar. Toda esa trama de comités, jurados, comisiones,… debe ser revisada: consume mucho tiempo, mucho dinero y mucha energía. Sus beneficios tampoco están claros, porque no han logrado en décadas acabar con la endogamia, el corporativismo, las oposiciones y otras truculencias casposas y decimonónicas.
En cinco meses se ha movido más información por las listas de correo de la que en décadas ha circulado por registros de autentificación, planes estratégicos y boletines informativos. La información era creada, distribuida y organizada por los propios interesados, sin un plan director ni un jefe de protocolo. Hubo un tránsito desde una visión patrimonialista de la institución a otra que me atrevería a llamar democrática, abierta y confiada. Es como si de repente se abrazaran unas coreografías más paritarias que verticales, más colaborativas que competitivas y más solidarias que profesionistas.
Los científicos nos hemos beneficiado de la presunción de inocencia. No hemos sido tratados como tramposillos de medio pelo, ni como tontarras que se creen unos listillos. Se nos han dado los medios para hacer nuestro trabajo. Y nos hemos dejado la piel. No lo hemos hecho por la institución. Lo hicimos por nuestros vecinos, amigos y familiares. Y queremos seguir haciéndolo. Veremos.
Sobre el autor: Antonio Lafuente es investigador en el Instituto de Historia, Centro de Ciencias Humanas y Sociales (CCHS – CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La reinvención de la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lo verdaderamente divertido es hacer Ciencia
- Ciencia para todos a través del cine y la literatura de ciencia ficción
- La ciencia mola (o debería)
Raíz de 2 no es racional: 65 ejercicios de estilo

En Rationnel mon Q. 65 exercices de stylei (Hermann, 2010) de Ludmila Duchêne y Agnès Leblanc, las autoras demuestran de 65 maneras que √2 –y algunos más, como √3, √11 ó √42– no es un número racional.
La editorial presenta el libro de la siguiente manera:
La raíz cuadrada de 2, es 1,414 y pico… ¡Y qué pico! Granos de arena que impiden escribir la raíz de 2 como una fracción. En otras palabras, esta raíz no está en Q. Así es la historia, una verdad matemática conocida e incluso demostrada desde hace tiempo, a veces injustamente olvidada.
Esta es la historia que inspira a las dos autoras cómplices que son Ludmila Duchêne y Agnès Leblanc sesenta y cinco «ejercicios de estilo» a la manera de Raymond Queneauii, pastiches mezclando ciencia, literatura e incluso cine. Con la participación excepcional, para hablar de Q y de raíces cuadradas, de Abel, Bourbaki, Lewis Caroll, Pâquerette Dugras, Euclides, Fellini, Goldbach, Hitchcock, Idéfix, Monsieur Jourdain, Kafka, François Le Lionnais, Mersenne, el pequeño Nicolás, Ohm, Perec, Queneau, Racine, Stokes, Tales, Ulises, Anton Voyl, Witten, X, Yang, Zazie, y otros…
Las autoras presentan aquí textos que demuestran la irracionalidad de √2 (y algunos otros). Es un número, √2 es un número cuyo cuadrado es igual a 2. Ese número debe existir: es, según el teorema de Pitágoras, la longitud de la diagonal de un cuadrado cuyo lado es de longitud 1. Lo que queremos demostrar es que este número no se puede escribir como una fracción p/q, donde p y q son números enteros. ¿Por qué estos textos? Por amor, amor por las matemáticas y amor por la literatura.
Las autoras hacen constantes guiños a textos y a contraintes –trabas, restricciones en la escritura– del grupo OuLiPo. Se refieren, por ejemplo, a algunos de los denominados plagiarios por anticipación –escritores que han trabajado sujetos a contrainte de manera más o menos consciente antes de la fundación de OuLiPo–. También utilizan en sus ejercicios de estilo trabas oulipianas –contraintes– como el anagrama, el lipograma, la traba del prisionero, la quenina de orden 5, la quenina de orden 7 –que, por cierto, no existe–, el monovocalismo, el S+7, la bella ausente o la homofonía.
Las autoras también aluden a obras de otros autores, como Esperando a Godotde Samuel Beckett, Mersonne de m’aime de Nicole-Lise Bernheim y Mireille Cardot, Al otro lado del espejo de Lewis Carroll, Bouvard y Pécuchet de Gustave Flaubert, W o recuerdo de la infancia de Georges Perec, Me acuerdo de Georges Perec o Lisístratade Aristófanes.
En attendant Giii
– Qu’est-ce qu’on fait maintenant ?
– En attendant.
– En attendant.
Silence
– Si on faisait nos exercices ?
– Nos enchaînements.
– Logiquement.
– Avec application.
– Circonvolutions.
– Application.
– Pour nous réchauffer.
– Pour nous calmer.
– Allons-y.
Ils ne bougent pas.
Incluso se hacen referencias al cine –por ejemplo, a Con la muerte en los talones de Alfred Hitchcock o Barry Lyndonde Stanley Kubrick– y a la pintura de René Magritte y su La traición de las imágenes–Esto no es una pipa–.
Ceci n’est pas une preuveiv
Je pourrais supposer que √2 est rationnel et l’écrire comme une fraction, mais je ne le ferai, pas plus que je ne mentionnerai le caractère factoriel de l’anneau Z, il suffirait alors, je le sais bien, d’évaluer la valuation 2-adique des termes en cause pour conclure, mais non, nous n’avons ni le temps, ni la place.
Para personas que se dedican a las matemáticas o aquellas que no lo hagan, el libro permite divertirse y ‘demostrar’ la irracionalidad de ciertos números de formas un tanto singulares.
Si entendéis francés, esta presentación de Arno Caravel para Universcience contiene alguno de estos 65 ejercicios de estilo:
Notas:
iEl título, leído en alto, suena parecido a “Rationnel mon cul”, que significa –en versión un ‘poco vulgar’– “Racional, ¡venga ya!”.
ii Se refiere al libro Ejercicios de estilo (Cátedra, 1989) de Raymond Queneau.
iiiEsperando a G
– ¿Qué hacemos ahora?
– Mientras esperamos.
– Mientras esperamos.
Silencio
– ¿Y si hiciéramos nuestros ejercicios?
– Nuestros encadenamientos.
– Lógicamente.
– Con aplicación.
– Circunvolución.
– Aplicación.
– Para entrar en calor.
– Para calmarnos.
– Vamos.
No se mueven.
ivEsto no es prueba
Podría suponer que √2 es racional y escribirlo como una fracción, pero no lo haré; ni mencionaré el carácter factorial del anillo Z; bastaría entonces, lo sé, evaluar la valoración 2-ádica de los términos en cuestión para concluir, pero no, no tenemos ni el tiempo ni el espacio.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Raíz de 2 no es racional: 65 ejercicios de estilo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La transformación radiactiva
 Foto: davisco / Unsplash
Foto: davisco / UnsplashRutherford y Soddy propusieron un modelo muy audaz de la transformación radiactiva para explicar la naturaleza de estos cambios. Sugirieron que cuando un átomo radiactivo emite una partícula alfa o beta, en realidad lo que ocurre es que se rompe en dos partes: la partícula alfa o beta que se emite y una parte sobrante con la mayor parte de la masa que es física y químicamente diferente del átomo “progenitor”.
Había mucha pruebas que apoyaban esta última parte del modelo. Por ejemplo, se sabía que se formaba gas radón a partir del radio. Cuando se determinó la masa atómica del radón, resultó ser más pequeña que la del radio en solo cuatro unidades de masa atómica, la masa de una partícula alfa.
La idea de transformación radiactiva se puede representar mediante una «ecuación» similar a la que se utiliza para representar reacciones químicas. Por ejemplo, usando los símbolos Ra y Rn para representar átomos de radio y radón, y He para representar una partícula alfa después de que ha recogido dos electrones para formar un átomo de helio, la transformación del radio en radón se puede expresar como
Ra → Rn + He.
El proceso se puede describir como la transformación, también llamada “desintegración”, o “transmutación”, del radio en radón, con la emisión de una partícula alfa.
Muchos procesos de desintegración, además del ejemplo recién citado, habían sido encontrados y estudiados por los Curie, por Rutherford y sus compañeros de trabajo, y por otros, y estos procesos encajaban fácilmente en el modelo propuesto por Rutherford y Soddy [1]. Por ejemplo, el radón también es radiactivo, emite otra partícula alfa y, por lo tanto, se transmuta en un átomo de un elemento que en ese momento se llamó «radio A». Más tarde se demostró que el radio A era polonio (Po):
Rn → Po + He.
El polonio también es un sólido radiactivo. De hecho, los átomos de radio “progenitores” originales experimentan una serie o cadena de transformaciones en una generación tras otra de nuevos elementos radioactivos “hijos”, que termina con un elemento hijo que no es radiactivo o, en otras palabras, estable. Estas series radiactivas son tan importantes que las veremos con más detalle.
Notas:
[1] Es reseñable que tanto Rutherford (1908) como Soddy (1921) recibieran su premio Nobel en química, no en física. También es cierto que Rutherford habría merecido un segundo premio Nobel en física, porque la mayor parte del trabajo por el que es famoso lo hizo después de su premio Nobel; recordemos que su modelo nuclear del átomo es de 1911.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La transformación radiactiva se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ratonera de Rutherford y Royds
- La radiactividad no es una reacción química
- Rayos alfa, beta y gamma

