¿Cómo mejorar la comunicación entre las matemáticas y las ciencias de la vida?
Pablo Rodríguez Sánchez
A modo de preámbulo
Durante el periodo 2015-2019, trabajé como matemático para un departamento de biología. Mi tarea era llevar a cabo una investigación que acabaría convirtiéndose en mi tesis doctoral. Este texto es una adaptación y traducción al castellano de parte del último capítulo de dicha tesis. La tesis completa, “Cycles and interactions. A mathematician among biologists”, está disponible aquí.
Esta simbiosis entre biólogos y matemáticos, aunque pueda parecer exótica a primera vista, tiene una larga historia. El matemático Leonardo Pisano, más conocido como Fibonacci, creó su famosa secuencia (), muy popular entre los matemáticos aficionados, para describir un problema de cría de conejos. Esto sucedía en una fecha tan temprana como 1202.
El conocimiento matemático ha evolucionado mucho desde el siglo XIII. El corazón de las herramientas matemáticas utilizadas por los biólogos modernos, esto es, el cálculo infinitesimal, fue desarrollado en el siglo XVII por Isaac Newton y Gottfried Leibniz, con el propósito de resolver problemas mecánicos. El gran matemático Leonhard Euler y el economista y demógrafo Thomas R. Malthus, dos de los pioneros en el uso de las ecuaciones diferenciales para arrojar luz sobre problemas biológicos, ya habían publicado sus obras de dinámica de poblaciones antes de que el siglo XIX viera la luz.
La colaboración interdisciplinar entre matemáticas y ciencias de la vida goza, a día de hoy, de una excelente salud. Algunos de los nombres más influyentes de la ecología de los siglos XX y XXI tienen formación en matemáticas (como Robert MacArthur, Simon Levin o Alan Hastings) o física (como Robert May).
El acceso cada vez más fácil y barato a los supercomputadores, sumado a la necesidad cada vez mayor de añadir técnicas como la programación y el análisis de datos a los currículos investigadores, anuncian un futuro en el que las habilidades técnicas necesarias en un laboratorio biológico difieren cada vez menos de las que uno encontraría en un departamento de físicos o matemáticos aplicados. Cabe esperar, pues, que esta simbiosis entre matemáticos y biólogos se mantenga sólida, e incluso se vuelva más estrecha, en el futuro cercano.
El presente texto ofrece algunos consejos para biólogos y matemáticos (entendidos aquí como profesionales con afinidad por las matemáticas, incluyendo por ejemplo a físicos e ingenieros) interesados en explorar “el otro lado”. Contiene la clase de consejos que me hubieran venido bien en 2015, cuando me sumergí en el mundo de la biología con esa suicida candidez tan habitual en los físicos novatos como el que yo era entonces.
Las matemáticas se perciben a menudo como un tema árido y difícil, tanto por los profesionales de la ciencia como por el público general. Por otro lado, independientemente de si nos gustan o no, las matemáticas se utilizan en prácticamente cualquier rama del conocimiento humano, y nunca faltan en los proyectos multidisciplinares.
Disciplinas diferentes llevan asociadas no sólo un conjunto de conocimientos de base distintos, sino también una cultura académica diferente. Cuando uno cruza las fronteras entre disciplinas académicas, aprender los nuevos datos y protocolos requiere ni más ni menos que tiempo y estudio, pero aceptar y adaptarse a una cultura diferente puede ser mucho más difícil y no se aprende en los libros.
Como sucede con cualquier cultura, los matemáticos y los biólogos difieren ligeramente en lenguaje, valores, normas e intereses. Como suele suceder en la comunicación intercultural, es muy fácil caer en malentendidos, y cada subgrupo posee mitos y prejuicios respecto al otro.
 Foto: Michael Dziedzic / UnsplashConsejos para biólogos trabajando con matemáticos
Foto: Michael Dziedzic / UnsplashConsejos para biólogos trabajando con matemáticos
Invierte en matemáticas aplicadas
Cuando hablamos de matemáticas aplicadas no nos referimos necesariamente a matemáticas sencillas. El adjetivo “aplicadas” o “puras”, acompañando a la palabra “matemáticas”, nos habla del objeto que queremos estudiar, pero no nos dice nada sobre su dificultad. De hecho, el arsenal matemático necesario será tan complejo como lo sea su objeto de estudio.
Veamos un ejemplo. Puede ser frustrante darse cuenta de que es necesario familiarizarse con los tensores de segundo orden (una herramienta matemática particularmente complicada) si uno quiere estudiar mecánica de fluidos. Los matemáticos no utilizan esta herramienta por perversidad ni para torturar a los recién llegados, sino porque los tensores son la herramienta más sencilla posible para estudiar un fenómeno complejo que no podemos esquivar si queremos estudiar fluidos: la deformación.
La dificultad nos la da el fenómeno que estemos estudiando, no la herramienta que usemos.
Las ecuaciones y el rigor no son instrumentos de tortura
Según la célebre frase del prefacio de “Breve historia del tiempo”, de Stephen Hawking, por cada ecuación impresa en un libro la audiencia potencial se divide entre dos.
Nos gusten o no, las ecuaciones y el lenguaje matemático son a menudo la mejor manera de comunicar y compartir información compleja de una manera práctica y compacta. Es una buena idea invertir algo de tiempo en aprender a leerlas. Los análisis detallados y rigurosos, por otra parte, a menudo hacen falta para dar con detalles difíciles de abordar desde la intuición.
Es importante saber también que la misma ecuación puede ser escrita de diferentes maneras, siendo todas ellas correctas. Eso sí, algunas serán más claras que otras. Un uso consistente de mayúsculas o minúsculas (por ejemplo, mayúsculas para variables de estado, minúsculas para parámetros), subíndices y superíndices, la definición de funciones auxiliares, una alineación lógica de ecuaciones relacionadas y otras reglas sencillas pueden incrementar enormemente la legibilidad de una publicación.
La clave del modelado es la simplificación
La simplificación es el corazón del modelado matemático. Y no es fácil. En la fase de diseño de un modelo matemático de un sistema biológico la comunicación es clave. Quizá a algunos les sorprenda saber que, a la mayoría de matemáticos, la forma de hablar de los biólogos a menudo les resulta abrumadora. Los biólogos tienden a proporcionar demasiada información.
Al tratar con matemáticos es aconsejable centrarse más en las ideas que en los detalles. Es fácil minusvalorar la dificultad de la biología. Como regla general, los detalles experimentales pueden omitirse: un matemático simplemente dará por sentado que los resultados experimentales son correctos.
Otra idea recomendable es tratar de resumir el proceso de investigación en términos de entradas, procesos y salidas. Esto es muy práctico no sólo para mejorar la comunicación interdisciplinar, sino también para diseñar experimentos o incluso para estructurar un texto.
 Foto: Markus Spiske / UnsplashConsejos para matemáticos trabajando con biólogos
Foto: Markus Spiske / UnsplashConsejos para matemáticos trabajando con biólogos
Haz las paces con la incertidumbre
Debido a la complejidad del objeto de estudio, es un error esperar la misma precisión de un modelo biológico que de un modelo físico. Olvida todo lo que aprendiste en la escuela de matemáticas, física o ingeniería. Los tiempos dorados en los que descartabas cualquier resultado con un inferior a han pasado. Ahora trabajas con sistemas biológicos y, por lo tanto, complejos. Los modelos funcionan lo mejor posible, ni más ni menos. Además, estos modelos rara vez permiten ser formulados de manera elegante o resueltos de forma analítica.
Explica tus motivaciones
Cuando estés explicando un método matemático, jamás comiences introduciendo una idea de forma genérica. En su lugar, comienza siempre por explicar la utilidad de lo que va a venir a continuación, a ser posible usando ejemplos concretos. Tu audiencia perderá rápidamente la motivación si no les convences rápido de que lo que vas a explicar les servirá de algo.
Una experiencia particularmente elocuente me sucedió explicando el producto matricial a un grupo de biólogos. Es un tema especialmente aburrido que normalmente se presenta como una regla que hay que memorizar. En su lugar, decidí abordarlo de una forma diferente: primero, provoqué que los estudiantes comprendieran la necesidad de utilizar una notación compacta para uno de sus problemas prácticos. Hice esto pidiéndoles que escribieran, línea a línea, varios modelos de competición de especies de plancton con cada vez mayor número de especies. Posteriormente, les mostré cómo las aparentemente arbitrarias reglas del producto matricial resuelven precisamente esta necesidad.
Al presentarlo de esta manera, los estudiantes entendieron que la herramienta matemática tratada en la clase resolvía un problema que ya tenían, en lugar de crear uno nuevo (el de tener que aprenderla). Además, las explicaciones acerca de por qué la regla es como es ayudó a fijar sus conocimientos.
Las demostraciones asustan
Quizá pienses que las demostraciones no deberían asustar a nadie, pero el hecho es que lo hacen. Una demostración es una suerte de viaje, un viaje desde un conjunto de ideas de partida hasta una conclusión, y es importante que tus colaboradores disfruten del camino.
A menudo, las demostraciones pueden ser sustituidas usando un enfoque gráfico o intuitivo. Algunos detalles podrían caerse por el camino, pero normalmente la simplificación vale la pena. Podrían, pero no tienen por qué: piensa que los Elementos de Euclides, probablemente el libro de matemáticas más influyente de la historia, contiene principalmente demostraciones geométricas y, por tanto, visuales.
En caso de que una demostración sea realmente necesaria, es importante esforzarse en explicar la notación y todos los pasos. La forma más rápida de frustrar a la audiencia es usando la palabra trivial, que debe ser evitada a toda costa. Cuando se escriba para una revista científica no especializada en matemáticas, es buena idea relegar las demostraciones al apéndice y simplemente mencionarlas en el cuerpo. Del mismo modo que los matemáticos no pondrán en duda los métodos experimentales de los biólogos, los biólogos rara vez pondrán en duda la corrección de las demostraciones.
Usa la visualización todo lo posible
Aprovéchate del sistema de adquisición de información más avanzado de la naturaleza: la visión. Ilustra tus ideas con gráficas, o incluso con películas o animaciones cuando sea posible. Si son buenas, pueden incluso reemplazar a una ecuación.
 Foto: Jacinto Román / UnsplashConsejo para ambos
Foto: Jacinto Román / UnsplashConsejo para ambos
Comunica tu ciencia
Si te parece que la comunicación entre disciplinas es complicada, intenta comunicar tu disciplina a un público general. No solamente te darás cuenta de que es aún más difícil, sino que además mejorará sustancialmente tus habilidades comunicativas.
A día de hoy existen multitud de posibilidades, desde blogs a eventos, en los que poner en práctica esta habilidad. La práctica de la comunicación científica nos obliga a familiarizarnos de una manera muy profunda el contenido a comunicar. Nos fuerza a eliminar lo superfluo, identificar qué partes son complicadas para la audiencia y por qué, además de adelantarnos a sus preguntas y dudas. Hacer comunicación científica requiere, en una palabra, comprender.
Sobre el autor: Pablo Rodríguez Sánchez es doctor en matemáticas aplicadas e ingeniero de software de investigación en el Netherlands eScience Center (Amsterdam, Países Bajos)
El artículo ¿Cómo mejorar la comunicación entre las matemáticas y las ciencias de la vida? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El problema de Josefo o cómo las matemáticas pueden salvarte la vida
- Las matemáticas como herramienta (IV): De la grandeur a las matemáticas puras
- El límite entre la vida y la muerte en las neuronas
Los animales entienden la muerte más de lo que se pensaba
Antonio José Osuna Mascaró y Susana Monsó
 Unsplash/Tandem X Visuals
Unsplash/Tandem X Visuals
Dorothy había tenido una vida durísima, una que no desearíamos a nadie. Mataron a su madre cuando ella era muy joven, y a ella se la llevaron para venderla a un parque de atracciones en Camerún. Pasó 25 años de su vida entre cadenas, burlas, alcohol y tabaco. Finalmente fue rescatada y llevada al centro de rescate Sanaga-Yong, y allí pudo hacer las paces con el mundo. Por fin ocho años de calma, se había acabado el sufrimiento. Estos años le sirvieron para reconstruirse, entablar fuertes amistades y acabar por convertirse en una figura respetada y amada por su nueva comunidad de chimpancés.
Dorothy, una chimpancé que se aproximaba a los 50 años de edad, murió de un paro cardiaco el 23 de Septiembre de 2008, pero falleció entre sus seres queridos. Monica Szczupider, una voluntaria del centro de rescate, inmortalizó aquel momento con una fotografía que en 2009 daría la vuelta al mundo gracias a National Geographic.
Los chimpancés de aquella comunidad se amontonaban tras una verja de metal, cada uno de ellos protagonista de una historia terrible con final agridulce. Contemplaban emocionados, manos sobre los hombros de sus compañeros, cómo los cuidadores del centro se llevaban para siempre el cuerpo sin vida de Dorothy.
El éxito de aquella fotografía era quizás predecible. Era muy fácil conectar con la escena. Un individuo querido y respetado era retirado para siempre, ante la impotencia de una sociedad que observaba con las emociones a flor de piel.
Cuidado con el antropocentrismo
El estudio de las reacciones de otras especies ante la muerte es una especialidad a la que llamamos “tanatología comparada”, y tiene una historia muy reciente. Desde las detalladas y conmovedoras descripciones de Jane Goodall, hasta rocambolescas propuestas experimentales actuales con las que se pretenden estudiar las reacciones de los animales ante situaciones extrañas e inesperadas, como altavoces que emiten la voz de elefantes muertos y cabezas animatrónicas.
La tanatología comparada es un campo muy centrado en los primates, y lo es por varios motivos que pueden resumirse en uno: nosotros somos primates.
La muerte tiene una importancia enorme para nosotros y, si vamos a estudiar la forma en la que otras especies reaccionan ante ella, es esperable que nos centremos en aquellas que están lo más cerca posible. Esto obedece a cierta parsimonia evolutiva, pero también a un sesgo que empapa profundamente nuestro pensamiento: el antropocentrismo, una suerte de egocentrismo extendido a todo lo que nos recuerda a nosotros.
En nuestro reciente artículo defendemos que existen dos formas de antropocentrismo que se han interpuesto en el desarrollo de la tanatología comparada. Nos hemos estado equivocando por el efecto distorsionador de dos prismas a través de los cuales observamos el mundo natural: un antropocentrismo intelectual y otro emocional.
La muerte es de una importancia máxima para cada uno de nosotros. El dolor que acompaña la pérdida de un ser querido solo es comparable al terror que despierta el silencio absoluto que nos espera a todos. El miedo resultante ha dado lugar a toda clase de creencias para sofocarlo, con las que nos sentimos fuertemente identificados. Algo tan cargado de emociones, tan humano, es fácilmente sobreestimable. La tanatología comparada no ha quedado exenta de este sesgo.
Tendemos a intelectualizar en exceso la muerte. Ese es probablemente el motivo por el que muchos autores consideran este concepto como algo inalcanzable para otras especies: o la entienden como nosotros, o no lo hacen en absoluto.
A esto se une la forma en la que la muerte encaja en nuestra peculiar cultura WEIRD (acrónimo anglosajón para sociedades occidentales, educadas, industrializadas, ricas y democráticas), en la que los muertos son personas que se desvanecen de nuestra vida y nuestros planes. Esto ha llevado a propuestas teóricas absolutamente faltas de perspectiva.
Algunos de los requerimientos teóricos que se han propuesto como necesarios para entender la muerte son altísimos. Desorbitados. Por ejemplo, la necesidad de una teoría de la mente (la capacidad de crear modelos mentales que representan la mente de otros individuos) o de un concepto de ausencia. Pero la muerte en la naturaleza es mucho más sencilla y mucho más común de lo que es para nosotros. En nuestro mundo urbanita corremos el riesgo de olvidar que los muertos son esencialmente cuerpos rotos sin arreglo.
Esto es algo que Susana Monsó defendió al proponer el concepto mínimo de la muerte. Si liberamos nuestra elaboradísima concepción de la muerte de toda la carga innecesaria, nos queda lo esencial para entenderla: cuerpos que dejan de comportarse como solían y pierden sus funciones para siempre. Entender esto no requiere de mentes privilegiadas, y probablemente muchas especies puedan alcanzarlo, aunque haya diferencias en su manera de concebirla.
Como ya hemos comentado, la muerte no solo es importante para los humanos, también suele ser una tragedia. Si cometemos el error de esperar que otras especies reaccionen como nosotros ante ella, caemos en un antropocentrismo emocional. Este es uno de los motivos por los cuales la tanatología comparada se ha centrado tanto en los primates, pues nos recuerdan a nosotros no solo en el aspecto físico e intelectual, sino también en sus relaciones.
Las reacciones ante la muerte pueden ser muy distintas a la pena o al duelo (aunque hay buenas evidencias de ambos en la naturaleza). El concepto de la muerte es compatible con una infinidad de reacciones emocionales, y el duelo es solo una de ellas.
Pensemos en los depredadores y su relación con la muerte. Imaginemos el leopardo que, tras años abatiendo antílopes, ha aprendido a distinguir el momento exacto en que, tras aplicar el mordisco letal, su presa pierde las funciones vitales. En los cadáveres no solo se desvanecen para siempre las funciones típicas de la vida, también aparecen otras nuevas. Un cadáver es diferente a todos los sentidos. Esto favorece el aprendizaje en animales a los que les puede ir la vida en ello.
No siempre es fácil ser un depredador (los leones solo tienen un 26 % de probabilidades de atrapar a una gacela), y sabemos que el éxito o el fracaso dependen en gran medida de ese aprendizaje. Por ello, los depredadores prestan especial atención a cualquier pista que las presas les puedan proporcionar. Esta atención no solo es evidencia de la capacidad de atender a la funcionalidad, también puede ser el origen de lo que podría ser una evidencia ignorada de la existencia del concepto de la muerte en los depredadores.
¡Hazte el muerto!
Entre los biólogos evolutivos se suele repetir la sugestiva idea de que los machos de pavo real están moldeados por la mente de las hembras. Las preferencias de las hembras han dado forma, con el paso de las generaciones, a las ostentosas colas de los machos. Conociendo la forma y el comportamiento de los machos podemos conocer la mente de esas hembras de pavo real.
Con los depredadores y algunas de sus presas podríamos tener un caso similar.
Nos estamos refiriendo a un fenómeno relativamente extendido en el reino animal: la llamada “tanatosis”. Muchos animales, cuando se ven en peligro, pueden quedar completamente paralizados (desde arañas a tiburones, pasando por gallinas y seres humanos). Esto, en ocasiones, les salva la vida.
En algunos casos, como ocurre con la muerte, no solo desaparece el movimiento, también se añaden funciones nuevas, propias de los cadáveres. Es esa similitud con la muerte a la que la tanatosis debe su nombre. En algunas especies, el mimetismo con la muerte es absolutamente fantástico: adoptan una expresión facial propia de un cadáver y bajan su temperatura corporal. Algunas incluso expulsan sangre por la boca.
Las especies mejor adaptadas a la tanatosis no tienen nada que envidiar al mimetismo de un insecto con forma de hoja y, como dicho insecto, no tienen por qué tener conocimiento alguno de estar imitando algo. Las formas más elaboradas se desencadenan probablemente de forma automática.
La importancia de la tanatosis surge cuando nos preguntamos por la evolución de la misma, pues es la mente de los depredadores la que ha dado forma a dicha imitación de la muerte. Como la cola del pavo real, esta estrategia defensiva nos abre una ventana a la mente de los depredadores, su capacidad para entender la muerte y lo que esperan de ella.
La tanatología comparada es una rama muy reciente de la ciencia, y probablemente nos guarde aún muchas sorpresas. El verdadero interés científico en esta rama de la ciencia comenzó en 2010, justo después de la publicación de aquella fotografía en la que los chimpancés del centro de rescate Sanaga-Yong se despedían de Dorothy.
Aquella fotografía supuso un revulsivo enorme para la sociedad y para la comunidad científica. Tenía todo lo necesario para encajar con nuestro antropocentrismo intelectual y emocional. Ahora es momento de que la tanatología comparada se libere de esas limitaciones y explore por sí misma un mundo mucho más rico y complejo de lo que cualquiera habría esperado. La muerte es común en la naturaleza, y el concepto de la muerte también parece serlo.
Sobre los autores: Antonio José Osuna Mascaró, es doctor en paleontología y biología evolutiva por la Universidad de Granada y actualmente está realizando otro doctorado en cognición comparada en la University of Veterinary Medicine, Vienna; Susana Monsó es investigadora postdoctoral en ética animal y filosofía de la mente animal en la University of Veterinary Medicine, Vienna
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Los animales entienden la muerte más de lo que se pensaba se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Almudena M. Castro – Naukas P4K 2019: Música, guerra y paz
 Imagen de Ute Friesen en Pixabay
Imagen de Ute Friesen en PixabayDar palmadas al ritmo de la música es tan difícil que computacionalmente hemos sido incapaces de reproducirlo. Es una cuestión de reconocer patrones regulares de tiempo.
Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y colaboradora del Cuaderno de Cultura Científica.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Almudena M. Castro – Naukas P4K 2019: Música, guerra y paz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- César Tomé López – Naukas P4K 2019: ¿Eureka?¿En serio?
- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
- Joaquín Sevilla – Naukas P4K 2019: Lo que esconden unos champiñones al ajillo
Un catálogo de estructuras magnéticas topológicas
El sistema de periodos original ordenaba los elementos químicos por sus propiedades químicas. Esta clasificación en su día condujo a Dmitri Ivanóvich Mendeléyev a la predicción – y al posterior descubrimiento – de nuevos elementos. Análogamente, los sólidos cristalinos no magnéticos se han podido clasificar recientemente mediante una “tabla periódica topológica” basada en una nueva teoría llamada Química Cuántica Topológica (TQC, por sus siglas en inglés) e indicadores de simetría. A partir de esta clasificación se han identificado decenas de miles de materiales no magnéticos potencialmente topológicos, lo que ha llevado ya al descubrimiento de un número considerable de aislantes topológicos.
 Foto: Gustavo Candido da Silva / Unsplash
Foto: Gustavo Candido da Silva / UnsplashSin embargo, a diferencia de los materiales no magnéticos, hasta ahora los compuestos magnéticos no podían clasificarse aplicando una metodología similar, principalmente por la inexistencia de una química cuántica topológica para los materiales magnéticos. En su lugar, las investigaciones sobre materiales magnéticos topológicos se venían realizando caso por caso, motivadas por posibles aplicaciones como conversores termoeléctricos eficaces, componentes de dispositivos microelectrónicos energéticamente eficientes que podrían constituir el núcleo de los ordenadores cuánticos, o soportes de almacenamiento magnético mejorados.
Aunque los primeros estudios teóricos de los materiales topológicos y sus propiedades a principios de la década de 1980 se concibieron en sistemas magnéticos (esfuerzos que fueron premiados con el Premio Nobel de Física en 2016), paradójicamente los avances en los últimos 40 años en el descubrimiento de materiales topológicos se han producido en gran medida en aislantes y semimetales topológicos no magnéticos.
La relativa ausencia de candidatos a materiales magnéticos topológicos puede atribuirse a dos causas principales. Por una parte a las complicadas simetrías de los cristales magnéticos: las estructuras no magnéticas se clasifican en 230 grupos espaciales, los materiales magnéticos en 1.421. Por otra a las dificultades teóricas y experimentales que conlleva la simulación y medición de los imanes cuánticos; así, mientras que en las bases de datos existentes se pueden buscar cientos de miles de compuestos cristalinos, en las mayores de materiales magnéticos solo hay unos cientos de estructuras magnéticas medidas experimentalmente. “Además de esto, en todos los sistemas magnéticos también debemos tener en cuenta otras interacciones, que son mucho más difíciles de simular. Esto hace que la tarea de predecir materiales topológicos magnéticos sea significativamente más complicada, incluso aunque los números fueran más favorables”, afirma B. Andrei Bernevig, profesor de física de la Universidad de Princeton.
El trabajo del grupo de Bernevig, publicado en la revista Nature, ha dado un gran paso hacia el descubrimiento de materiales magnéticos con propiedades electrónicas topológicas no triviales.
Previamente, en 2017, este mismo equipo desarrolló un completo y novedoso enfoque para entender la estructura de bandas en materiales no magnéticos. “En esta teoría, llamada TQC, vinculamos las características topológicas de un material con su química subyacente. Esto convirtió la búsqueda de materiales topológicos no magnéticos en una tarea que podía ser automatizada de manera efectiva”, señala Luis Elcoro, profesor de la Facultad de Ciencia y Tecnología de la UPV/EHU y coautor de ambos estudios. La TQC representa un marco universal para predecir y caracterizar todas las posibles estructuras de bandas en materiales cristalinos. La TQC se aplicó a 35.000 compuestos no magnéticos conocidos experimentalmente y condujo al descubrimiento de 15.000 nuevos materiales topológicos.
“En los últimos dos años hemos identificado miles de materiales topológicos, mientras que en las últimas dos décadas sólo se habían identificado unos pocos cientos de ellos. Antes de la aplicación de estas novedosas herramientas, la búsqueda de nuevos materiales con estas sorprendentes propiedades era como buscar una aguja en un pajar al anochecer. Ahora, la búsqueda de materiales topológicos no magnéticos es casi un ejercicio rutinario” dice Maia G. Vergniory, investigadora asociada Ikerbasque en el DIPC, y coautora también de ambos estudios.
Para reproducir el éxito logrado con los materiales no magnéticos los investigadores se enfrentaban a dos obstáculos principales: por un lado, la maquinaria teórica que hay que dilucidar para analizar estructura de bandas de un material magnético determinado es muy compleja. Y, por otro, el número de materiales magnéticos cuya estructura magnética se conoce con detalle de forma fiable es bastante pequeño. “Mientras que teníamos 200.000 compuestos no magnéticos para analizar, la mayor base de datos de estructuras magnéticas medidas experimentalmente tiene aproximadamente 1.000 registros”, aclara el profesor Elcoro.
“Afortunadamente, contábamos con el minucioso trabajo de las personas que están detrás de la base de datos de estructuras magnéticas del Bilbao Crystallographic Server, lo que nos permitió introducir los parámetros iniciales correctos en nuestros modelos teóricos”, dice Yuanfeng Xu, investigador postdoctoral del Instituto Max Planck de Halle, y primer autor del estudio. La información magnética está alojada en el Bilbao Crystallographic Server (www.cryst.ehu.es), que ha sido en parte desarrollado por el profesor Elcoro.
Tras una selección de los mejores candidatos potenciales, el equipo analizó 549 estructuras magnéticas aplicando primero simulaciones a partir de primeros principios que no usan parámetros iniciales empíricos para obtener las simetrías magnéticas de las funciones de onda electrónicas, y luego, construyendo una extensión magnética de la TQC para determinar qué estructuras magnéticas albergaban una topología de banda electrónica no trivial.
Como resultado en el estudio se predice la existencia de 130 materiales magnéticos topológicos. Asimismo, han encontrado que la proporción de materiales magnéticos topológicos (130 de 549) en la naturaleza parece ser similar a la proporción en los compuestos no magnéticos.
Los autores se muestran optimistas con los resultados, ya que, a pesar del reducido número absoluto de compuestos magnéticos en comparación con los miles de materiales no magnéticos estudiados hasta la fecha, han encontrado una mayor diversidad de características fascinantes que los hacen muy interesantes para diseñar futuros experimentos. “Ahora que hemos predicho nuevos materiales magnéticos topológicos, el siguiente paso es verificar experimentalmente sus propiedades topológicas”, dice G. Vergniory.
Los investigadores también han creado una base de datos en línea para acceder libremente a los resultados del presente estudio: www.topologicalquantumchemistry.fr/magnetic. Utilizando diferentes herramientas de búsqueda, los usuarios pueden explorar las propiedades topológicas de las más de 500 estructuras magnéticas analizadas. “Hemos sentado las bases de un catálogo de estructuras magnéticas topológicas”, afirma Elcoro. Es de esperar que la estandarización del uso de la simetría magnética en entornos experimentales y teóricos, acompañada de la adopción generalizada de las herramientas desarrolladas en este trabajo, conduzca en los próximos años a una gran explosión de descubrimientos en materiales magnéticos.
Referencia:
Yuanfeng Xu, Luis Elcoro, Zhida Song, Benjamin J. Wieder, M. G. Vergniory, Nicolas Regnault, Yulin Chen, Claudia Felser, and B. Andrei Bernevig (2020) High-throughput calculations of magnetic topological materials Nature doi:10.1038/s41586-020-2837-0
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un catálogo de estructuras magnéticas topológicas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La teoría de bandas de los sólidos se hace topológica
- Nanopartículas magnéticas contra células tumorales
- Aislantes topológicos en sólidos amorfos
Fanfarria

La autora hace sonar una Charonia tritonis, que ocupa el lugar central de Fanfare. Fuente: Sound the Trumpets (and a Conch)! / The MET
En el Museo Metropolitano de Arte de Nueva York (el MET) puede visitarse una preciosa instalación titulada Fanfarria. En ella, una humilde caracola se sitúa en el centro de una explosión imaginaria que da lugar a todos los instrumentos de viento metal de la historia. La caracola es el punto de partida. A su alrededor las formas y materiales divergen, se tuercen, se ramifican… pero todas tienen un origen común. El título de la instalación hace referencia a una forma musical, de corta duración y sonoridad rimbombante, que solía utilizarse para anunciar la llegada de alguna personalidad importante. Las fanfarrias eran interpretadas por trompetas u otros instrumentos de viento metal, con el acompañamiento ocasional de la percusión. Su nombre procede del mozárabe farfar y comparte su raíz, probablemente, con la palabra fanfarrón. Desde entonces, el timbre del viento metal y las trompetas en particular se han asociado a la realeza y al poder, a las marchas militares, la pompa y la circunstancia. El motivo último de esta asociación se encuentra probablemente en una de sus propiedades acústicas más destacadas. Al igual que las caracolas, los demás instrumentos de viento metal destacan por su gran potencia sonora, lo que los hace ideales para comunicar señales en el campo de batalla.
En el ámbito musical, esa gran sonoridad ha marcado también el uso de estos instrumentos. Existen incluso chistes al respecto. Según una cita atribuida a Richard Strauss (o alternativamente, a Richard Wagner), un buen director de orquesta no debe “nunca mirar a los trombones: solo los alienta”. El trombón es, de hecho, el instrumento con mayor potencia sonora dentro de la orquesta, con picos que alcanzan los 115 decibelios. Un sonido así puede dañar el oído en 30 segundos de exposición: es más intenso que el de una sierra eléctrica o el de una sirena de ambulancia. La cita de Strauss, por otra parte, es ligeramente apócrifa. Pero solo ligeramente. Se trata de una exageración basada en la cuarta de sus “10 reglas de oro para el joven director de orquesta”. Allí Strauss recomienda: “no mirar nunca de manera alentadora al viento metal, salvo con un leve vistazo para dar alguna indicación importante”. Por otra parte, tampoco parece que Strauss dirigiese “miradas alentadoras” a ningún miembro de la orquesta en absoluto.
 Richard Strauss dirigiendo.
Richard Strauss dirigiendo.Debido a su potencia y brillo, el timbre de estos instrumentos, especialmente cuando tocan en una dinámica forte, se ha calificado a menudo también como “metálico” o, en inglés, “brassy”. Sin embargo, esta sonoridad no tiene nada que ver con el material con que están hechos. Resulta paradójico que siempre se utilicen nombres de materiales para calificar a los instrumentos de viento ¡justo los instrumentos en los que el material tiene menos relevancia! Varios estudios123 muestran que el característico sonido brassy se debe en realidad a la amplitud de las ondas sonoras, que provoca efectos no lineales en la propagación del sonido dentro del tubo. Dichos efectos dan lugar a ondas de choque (una variación de la presión que se mueve más rápido que el propio sonido en ese medio) y hacen que la energía sonora se concentre en frecuencias más agudas, donde nuestro oído es más sensible. Cuanto más largo es el tubo, más probable es que se produzca este fenómeno, lo cual explica por qué el trombón, con sus casi tres metros de longitud, es especialmente “brassy”.
El resultado es una sonoridad brillante y áspera, algo estridente incluso. Gracias a ella, los instrumentos de viento metal tienden a sobresalir por encima de los demás en la orquesta. No se trata solo de decibelios: su timbre “metálico” también ayuda a ello. Probablemente por eso, el mismo Richard Strauss que evitaba dirigirles la mirada a los trombones también recomienda a los jóvenes directores: “si crees que los instrumentos de viento metal no están sonando lo suficiente, haz que bajen el volumen un grado o dos más”.
Referencias:
1Beauchamp, J. (1980) ‘‘Analysis of simultaneous mouthpiece and output waveforms,’ Audio Engineering Society preprint No. 1626.
2Hirschberg, A., Gilbert, J., Msallam, R., Wijnands, A.P.J. (1996). “Shock waves in trombones,“ J. Acoust. Soc. Am. 99, 1754-1758.
3Rendón, Pablo & Orduña-Bustamante, Felipe & Narezo Guzman, Daniela & Pérez-López, Antonio & Sorrentini, Jacques. (2010). Nonlinear progressive waves in a slide trombone resonator. The Journal of the Acoustical Society of America. 127. 1096-103. 10.1121/1.3277221.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Fanfarria se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Una mirada topológica al conjunto de Cantor
No es la primera vez que aludo a Georg Cantor (1845-1918) en este Cuaderno de Cultura Científica. Su figura y su obra matemática me fascinan. He tenido la suerte de tener muy presentes sus matemáticas en mi investigación y mi docencia. Probablemente Cantor fue una de esas pocas personas que es capaz de “pensar” las cosas de otra manera. Esa mirada distinta, genial y osada, provocó grandes cambios en la manera de entender y abordar las matemáticas.
 Georg Cantor. Fuente: Wikimedia Commons.
Georg Cantor. Fuente: Wikimedia Commons.
Uno de los más bellos ejemplos que nos ha proporcionado es el conocido como conjunto de Cantor.
En realidad –al menos como registro publicado conocido– fue el matemático Henry J. Stephen Smith quien introdujo este tipo de conjunto en 1874, en el artículo On the Integration of Discontinuous Functions(Proc. London Math. Soc. 1 (6): 140-153): tras una exposición sobre la integración de funciones discontinuas, presentaba un método para construir conjuntos densos en ninguna parte:
Sea m un número entero mayor que 2. Se divide el intervalo [0,1] en m partes iguales y se suprime el último segmento de cualquier división posterior. Se dividen cada uno de los m-1 segmentos restantes en m partes iguales y se eliminan los últimos segmentos de cualquier división posterior. Si esta operación se continúa ad infinitum, se obtiene una cantidad infinita de puntos de división P en el intervalo [0,1]. Estos puntos forman un conjunto denso en ninguna parte…
Aunque no se dice explícitamente en el enunciado, los intervalos eliminados son abiertos, con lo que el conjunto resultante P es cerrado. En el momento actual, el conjunto descrito por Smith se llamaría conjunto de Cantor generalizado.
Entre 1879 y 1884, Cantor escribió una serie de cinco artículos que contienen, entre otros, el primer tratamiento sistemático de la topología de la recta real. En el quinto artículo de esta serie, Cantor discute las particiones de un conjunto en dos componentes que llama reducible y perfecta, y define lo que es un conjunto
perfecto. Muestra que un conjunto perfecto no es necesariamente denso, y en un pie de página introduce su famoso conjunto ternario, el conjunto de los puntos que pueden expresarse de la forma (*):
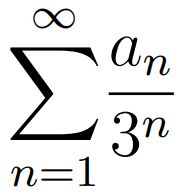
donde an=0 ó 2.
Cantor prueba que este conjunto es infinito, perfecto y que no es denso en ningún intervalo (es totalmente disconexo, es decir, sus componentes conexas son sus puntos).
Puede darse una construcción geométrica alternativa (pueden verse los detalles en [3]) y fácil de entender. Se toma el intervalo [0,1], se divide en tres partes iguales de longitud 1/3 y se elimina el intervalo abierto central (1/3,2/3). Con los dos intervalos cerrados restantes se repite la misma operación: cada uno de los intervalos [0,1/3] y [2/3,1] se divide en tres intervalos de la misma amplitud (en este caso 1/9) y se eliminan los intervalos centrales (1/9,2/9) y (7/9,8/9). Quedan entonces cuatro intervalos cerrados: [0,1/9], [2/9,1/3], [2/3,7/9] y [8/9,1], con los que se repetirá el mismo proceso, y así de manera indefinida. El conjunto resultante es el conjunto ternario de Cantor. Es fácil probar que los puntos del ternario de Cantor son precisamente los elementos del intervalo [0,1] que se pueden expresar de la forma (*) con an=0,2.
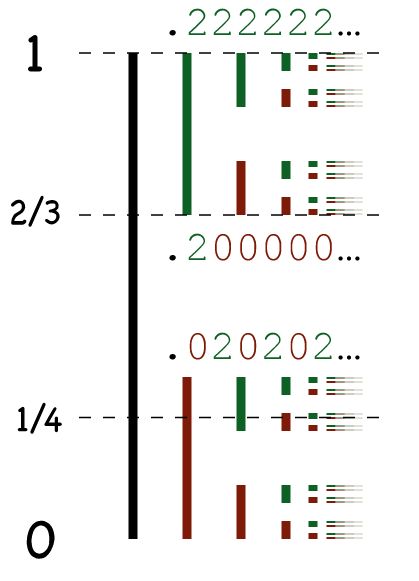 De izquierda a derecha, sucesivos pasos de la construcción geométrica del conjunto de Cantor. Fuente: Wikimedia Commons
De izquierda a derecha, sucesivos pasos de la construcción geométrica del conjunto de Cantor. Fuente: Wikimedia CommonsDe hecho, los elementos del primer intervalo abierto eliminado en la construcción, (1/3,2/3), son los que tienen en la expresión (*) el coeficiente a1=1. Los puntos de los intervalos abiertos eliminados en el segundo paso de la construcción –(1/9,2/9) y (7/9,8/9)– tienen el coeficiente a2=1 en la suma (*). De hecho, los puntos de (1/9,2/9) tienen como primeros coeficientes en (*) a1=0 y a2=1; y los de (7/9,8/9) a1=2 y a2=1. En el paso n de esta iteración, los intervalos abiertos eliminados corresponden a los puntos con an=1 en la expresión (*). Por eso, al final del proceso de construcción, los puntos que quedan, los del ternario de Cantor, son los que se escriben según la expresión (*) con coeficientes an=0 ó 2.
La suma de las longitudes de los intervalos abiertos eliminados en este proceso es 1, dicho de otra manera, el conjunto de Cantor es de medida 0. Es uno de los primeros ejemplos de conjunto de medida nula que se dan en un curso de Análisis. Pero para mí, como topóloga, la propiedad más importante del conjunto de Cantor es que es un modelo topológico de cierto tipo de espacios métricos, los expresados en el siguiente teorema (ver [4]):
Todo espacio métrico totalmente disconexo, perfecto y compacto es homeomorfo al conjunto ternario de Cantor.
Un hermoso ejemplo de conjunto que cumple las propiedades del anterior teorema es el collar de Antoine, del que hablamos en este blog: es un conjunto topológicamente equivalente al conjunto de Cantor, que parte de una construcción sobre un sólido de dimensión tres.
Se puede realizar la misma construcción que la del ternario de Cantor eliminando de [0,1] un intervalo abierto (por ejemplo, el central) de longitud 1/4. De los dos intervalos cerrados restantes se elimina el intervalo abierto central de longitud 1/16, y así sucesivamente. Al final del proceso, la suma de las longitudes de los intervalos abiertos eliminados es 1/2. Es decir, el conjunto restante –que es homeomorfo al conjunto de Cantor, según el teorema anterior– mide 1/2. Es una manera de comprobar que la medida no es una propiedad topológica.
El conjunto ternario de Cantor tiene otras muchas propiedades sorprendentes… pero esa es otra historia.
Referencias:
[1] La biografía Georg Cantor: his Mathematics and Phylosophy of the infinite(1990), escrita por Joseph Warren Dauben, es probablemente una de las mejores maneras de aprender sobre la vida del matemático.
[2] Recomiendo también la bellísima biografía novelada Villa del hommes (2007) de Denis Guedj, en la que se reconoce a Georg Cantor en la figura del viejo matemático Hans Singer, recluido en un manicomio.
[3] Marta Macho Stadler, Curiosidades sobre el conjunto de Cantor, Un Paseo por la Geometría 1999/2000 (2001) 97-116
[4] Stephen Willard, General Topology, Addison Wesley, 1970
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Una mirada topológica al conjunto de Cantor se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cuando las palabras no son suficientes: conjunto vacío
- Una visión topológica de la Odisea
- Fractus, arte y matemáticas
Historia del cura rompecristales
El descubrimiento de la estructura cristalina fue un paso de gigante en el descubrimiento de lo diminuto. René Just Haüy fue uno de los padres de la cristalografía como ciencia y el descubridor de que los cristales pueden romperse en estructuras geométricas elementales.
Tenemos que aclarar, porque hemos recibido algún comentario en este sentido, que los mineralogistas distinguen dos formas de romper: fracturar y exfoliar. En el vídeo no hacemos esa distinción y usamos romper de forma genérica. Tampoco Haüy iba usando el martillo a la ligera. ¿Por qué esto es importante? Porque, por ejemplo, la pirita se exfolia en cubos (como se menciona en el vídeo) pero se fractura irregularmente (lo que en jerga se llama fractura concoidea).
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia del cura rompecristales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cristalografía (6): El cura rompecristales
- El frustrante viaje de un átomo de carbono, mención especial del jurado «On zientzia»
- Historia de Uri Geller
Efectos y aplicaciones de la radiactividad
 Foto: National Cancer Institute / Unsplash
Foto: National Cancer Institute / UnsplashDe los efectos de la radiactividad en los tejidos vivos ya los hemos mencionado al hablar de las partículas radiactivas. Efectivamente, la radiactividad tiene consecuencias dañinas pero también aplicaciones muy útiles.
De entre los efectos dañinos tenemos, por ejemplo, que la «lluvia» de polvo radiactivo de las pruebas de armas nucleares tanto en la atmósfera como subterráneas durante la década de 1950 fue tan dañina para todos los seres vivos, humanos incluidos, que llevó a que se firmase un tratado internacional para detener tales pruebas [1]. Pero, ¿cómo afecta la lluvia radiactiva en concreto?
Por ejemplo, el estroncio-90 es un isótopo radiactivo que se produce en las reacciones de fisión que pueden llegar a las capas altas de la atmósfera superior por explosiones nucleares no subterráneas. El elemento estroncio está justo debajo del calcio en la tabla periódica. Cuando el estroncio-90 termina cayendo al suelo, las vacas lo ingieren cuando pastan y puede reemplazar al calcio en la formación de la leche, ingresando así en la cadena alimentaria donde puede dañar los órganos internos, no solo de la vaca y su cría, sino también de los humanos que beban esa leche.
Estos procesos de daño por radiación a los organismos biológicos son objeto de considerable investigación en la actualidad. Paradójicamente, algunos de los resultados obtenidos tienen importantes aplicaciones en la agricultura, la medicina y otras áreas. Un área importante de investigación, con muchas ramificaciones, es descubrir cómo la radiación produce cambios genéticos. Ahora sabemos que muchos de los procesos químicos clave en las células están organizados por cadenas simples de moléculas, incluido el ADN. Parece obvio, por tanto, que una sola partícula radiactiva con la energía suficiente puede, al romper un enlace químico en dicha cadena, causar un efecto permanente y quizás un cambio desastroso en la célula.
El metabolismo de plantas y animales se puede estudiar con la ayuda de cantidades extremadamente pequeñas de nucleidos radiactivos llamados trazadores isotópicos. Un isótopo radiactivo, por ejemplo, 14C, actúa químicamente (y por lo tanto fisiológicamente) como un isótopo estable (12C). Así, podemos seguir un trazador radiactivo con detectores y descubrir el comportamiento de una especie químico determinada a medida que pasa por varios procesos metabólicos. De esta forma se puede estudiar, por ejemplo, el papel de los micronutrientes [2].
De forma análoga, los experimentos agrícolas con fertilizantes que contienen isótopos radiactivos han demostrado en qué punto del crecimiento de una planta es esencial el fertilizante. En química, los isótopos radiactivos ayudan en la determinación de los detalles de las reacciones químicas y de la estructura de moléculas complejas, como proteínas, vitaminas y enzimas.
Quizás los usos más directamente relacionados con nuestro bienestar de los radioisótopos se han encontrado en la investigación, el diagnóstico y la terapia médicos. Por ejemplo, los trazadores pueden ayudar a determinar la tasa de flujo de sangre a través del corazón y las extremidades, ayudando así en el diagnóstico de condiciones anormales. Las dosis intensas de radiación pueden causar daños graves a todas las células vivas, pero las células enfermas suelen dañarse más fácilmente que las células normales. Por tanto, la radiación se puede utilizar para tratar algunas enfermedades, por ejemplo, para destruir tumores cancerosos. Algunas partes del cuerpo toman preferentemente elementos concretos. Por ejemplo, la glándula tiroides absorbe el yodo fácilmente. Se pueden administrar radioisótopos especialmente preparados de tales elementos a los pacientes de ciertas enfermedades, suministrando así la radiación deseada directamente en el sitio de la enfermedad.
Este método se ha utilizado, además de en el tratamiento del cáncer de la glándula tiroides, en enfermedades de la sangre y tumores cerebrales y en el diagnóstico de enfermedades de la tiroides, el hígado o los riñones. Se ha llego a tal nivel de especificidad que para destruir una neoplasia maligna en la próstata, se pueden insertar en ella «semillas» que contienen materiales radiactivos.
Aún nos queda por mencionar un uso importante de los elementos radiactivos, como relojes. Pero eso amerita su propio artículo.
Notas:
[1] Lamentablemente, que se firme un tratado no quiere decir que todos los países lo respeten.
[2] Elementos esenciales, en cantidades extremadamente pequeñas, para el bienestar de plantas y animales.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Efectos y aplicaciones de la radiactividad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La radiactividad no es una reacción química
- La naturaleza estadística del periodo de semidesintegración
- Periodo de semidesintegración
Cora Ratto: en búsqueda de armonía
Alberto Mercado Saucedo
Además de una de las primeras matemáticas formadas en Argentina fue también protagonista de emblemáticas luchas, tanto por los derechos de la mujer como en defensa de la democracia en el mundo. Su trayectoria como matemática fue dramáticamente interrumpida en varias ocasiones por rupturas políticas de su país, que finalmente ocasionaron que falleciera en el exilio en 1981.
 Ilustración de Constanza Rojas-Molina. Todos los derechos reservados; cesión en exclusiva para su publicación en el Cuaderno de Cultura Científica.
Ilustración de Constanza Rojas-Molina. Todos los derechos reservados; cesión en exclusiva para su publicación en el Cuaderno de Cultura Científica.Corina Eloisa Ratto, a quien se le suele recordar como Cora Ratto de Sadosky, nació en 1912 en la capital argentina, ingresó a la Universidad de Buenos Aires a estudiar matemáticas en los años treinta, una época de explosivo crecimiento de la disciplina, sobre todo gracias al impulso de Julio Rey Pastor, español llegado al país en 1917 por un proyecto para impulsar el desarrollo de las matemáticas. Cora tenía muchos otros intereses y durante sus estudios universitarios participó en la dirigencia de la Federación Universitaria Argentina, máxima organización de estudiantes universitarios del país. Se involucró, cada vez en mayor medida, en causas políticas y humanitarias en favor de víctimas de la discriminación racial del nazismo
Se casó en 1937 con Manuel Sadosky, su compañero de estudios y de luchas políticas, al tiempo que ambos terminaban sus carreras universitarias. Manuel realizó enseguida un doctorado en la UBA, se graduó en 1940 con una tesis sobre métodos de resolución aproximada de ecuaciones diferenciales y habría de convertirse en un reconocido científico; en particular es recordado por haber gestionado la adquisición de Clementina, la primera computadora en Argentina y por haber creado la carrera de ciencias computacionales. En resumen, es considerado el padre de la computación en el país. Pero este artículo es sobre Cora y no sobre Manuel, así que regresamos a ella: no es difícil imaginar que también se le ocurre realizar un doctorado, teniendo en cuenta la consolidación de la investigación en matemáticas que se alcanza en Buenos Aires en la época. El liderazgo de Rey Pastor rinde frutos, y se doctora un buen número de estudiantes, sobre todo bajo su dirección. En 1936 se funda la UMA, Unión Matemática Argentina, la primera organización de su tipo en Latinoamérica. Al trabajo de Rey Pastor se suma la llegada de Luis A. Santaló y Beppo Levi en 1939, y el Seminario de Matemáticas de Buenos Aires alcanza importante actividad científica. El crecimiento de la disciplina en el país es promisorio.
No podemos estar seguros si la idea de proseguir con sus estudios cruza por la mente de Cora en esos años, pero lo cierto que otras responsabilidades están por llegar. En 1940, el mismo año que Manuel se doctora, nace la hija de la pareja. Además, con el estallido de la Segunda Guerra Mundial, Cora se convierte en protagonista de una singular lucha por los derechos de las mujeres y por la defensa de los valores democráticos. Se convierte en Secretaria General de la Junta de la Victoria, organización política que agrupa mujeres de muy diversos ámbitos y cuyo principal objetivo es el de apoyar a los países invadidos en el enfrentamiento mundial. Su principal referencia es la ayuda organizada a favor de los republicanos españoles en la guerra civil, en la cual Cora estuvo directamente involucrada como representante de organizaciones estudiantiles de la UBA. La experiencia política de la Junta es inédita en Latinoamérica y en el mundo, y se puede considerar como antecedente de la aprobación del derecho de las mujeres al voto en Argentina ocurrido en 1947, momento que representa un punto de inflexión en la vida de Cora.
Ese año, al tiempo que termina la actividad de la Junta de la Victoria y comienza el primer gobierno de Juan Domingo Perón en Argentina, Manuel obtiene una beca para hacer investigación en Francia. Todo esto significa un hito en la vida de la familia, que se instala en París, donde Cora inicia un doctorado dirigido por Maurice Frechet, reconocido matemático que contribuyó a desarrollar las bases del análisis funcional, y que por cierto es el autor del conocido concepto de espacio métrico, generalización de la noción de distancia que sirve para estudiar conjuntos abstractos. Cora interrumpe su tesis debido a otra mudanza de la familia, esta vez a Italia, donde Manuel realiza una estadía de investigación posdoctoral. La familia regresa a la Argentina a finales de los años cuarenta, tiempos muy complicados políticamente, lo que en particular implica que no pueden acceder a ningún trabajo en la universidad.
Las condiciones del país cambian en 1955, la Universidad de Buenos Aires gana la autonomía y tanto Cora como Manuel obtienen trabajos como académicos en la Escuela de Ciencias. Sigue una década de fecunda actividad académica, la época dorada de la ciencia argentina, según testimonios de científicos que fueron testigo de ello. Cora obtiene el doctorado en 1959 con una tesis en análisis armónico dirigida por Mischa Cotlar, quien siendo muy joven había inmigrado de su Ucrania natal a Uruguay y luego a Argentina, donde estudió matemáticas de manera autodidacta e hizo investigación sin ningún cargo formal hasta que obtuvo un doctorado en la Universidad de Chicago en 1953, tras lo cual regresó a Argentina y realizó una importante carrera científica y formó a gran cantidad de estudiantes, entre ellos a Cora.
Durante esta época de gran armonía, Cora Sadosky, la hija de Cora y Manuel, ingresa a la universidad a estudiar matemáticas, toma clases en la UBA con Pedro Alberto Calderón y Antoni Zygmund, reconocidos investigadores en análisis armónico. Termina la licenciatura en 1960, un año después que su madre se graduara del doctorado. Viaja a realizar estudios de posgrado en Chicago, donde realiza una tesis, también en análisis armónico, bajo la dirección de Calderón. Cora Sadosky -fallecida en 2010- se convertiría en una referente en el área y también sería recordada por su permanente lucha por la visibilidad de las mujeres en las matemáticas.
El análisis armónico, área en la que madre e hija se especializan, toma su nombre del término armonía, introducido en la Grecia clásica para referirse a notas musicales que al sonar juntas lo hacen en concordancia, suenan bonito cuando se superponen; los armónicos son sonidos que se quieren. Podemos pensar que eso es justamente lo que ocurre en un hecho matemático fundamental en el área: Joseph Fourier, matemático francés nacido en 1768, demostró que cualquier onda periódica puede descomponerse en ondas simples superpuestas, cada una de frecuencia igual a un múltiplo de una frecuencia fija. Son ondas básicas que funcionan como los armónicos de la descomposición de los sonidos, en cuya superposición puede intervenir un número infinito de frecuencias y que se conocen como series de Fourier, típicamente formadas por funciones sinusoidales. Pues bien, en el análisis armónico se estudia la representación de funciones por medio de estas series, y se generalizan sus propiedades gracias a las relaciones con diversos conceptos matemáticos como los espacios de Hilbert y la teoría de grupos, lo que proporciona un poderoso marco abstracto que permite obtener resultados profundos e interesantes. La conocida teoría de wavelets es un interesante ejemplo: se trata de un perfeccionamiento de las series de Fourier cuyo desarrollo comenzó en los años 80’s con el trabajo del ingeniero francés Jean Morlet en prospección sísmica y que fue sistematizado matemáticamente por su compatriota Yves Meyer. Las aplicaciones de esta teoría van desde el método de compresión del conocido formato JPG-2000 hasta la detección de ondas gravitacionales realizada por el observatorio norteamericano LIGO, entre muchas otras.
Regresamos a Buenos Aires y la década dorada, años de ferviente trabajo de Cora, durante los cuales dicta cursos, organiza seminarios avanzados y gestiona la publicación de varias monografías de investigación. Escribe, en coautoría con Misha Cotlar, el libro Introducción al Álgebra, de rigurosidad inédita para textos en español de la época. Sin duda que Cora tuvo una gran influencia en su medio académico, sobre todo en la formación de muchos estudiantes que se convertirían años después en investigadores, sobre todo en análisis armónico. El 1958 se crea el CONICET, organización clave para el desarrollo científico de Argentina, y nace la Editorial Universitaria de Buenos Aires, emblemático proyecto del mundo de los libros en español.
Este fructífero periodo para la ciencia argentina culmina en 1966 con un golpe de estado en el país, que tiene una patética representación en la infame noche de los bastones largos: la universidad es brutalmente intervenida por agentes de la dictadura militar, muchos profesores son golpeados y literalmente echados a la calle; termina el gobierno tripartito en la institución. La ciencia argentina sufre una gran pérdida: cientos de personas que dedican su vida a la investigación se ven obligadas a dejar la universidad o incluso a salir del país.
Cora y Manuel resisten y se quedan en Buenos Aires, donde Manuel se dedica a negocios relacionados con la tecnología. Durante los años siguientes, Cora escribe y publica diversos artículos, sobre todo de contenido político, traduce del francés textos de matemáticas y filosofía y crea la publicación periódica Columna 10, con el objetivo de crear conciencia pública sobre la tragedia de la guerra en Vietnam. La situación política empeora y la familia sufre amenazas directas de grupos fascistas como la Alianza Anticomunista Argentina, conocida como AAA, por lo que Manuel y Cora se ven obligados a dejar el país en 1974. De vuelta de un congreso, no toman el vuelo en conexión que los regresaría a Buenos Aires, y se instalan en Caracas, Venezuela. Un tiempo después se trasladan a Barcelona, donde finalmente Cora fallece en 1981.
Desde 1996 se instaura en Vietnam el premio Cora Ratto, dedicado a mujeres con buen desempeño en las olimpiadas de matemáticas.
Cora vivió en un mundo que le exigió múltiples esfuerzos de distintos tipos y que la enfrentó a diversos obstáculos; a pesar de ello mantuvo una apasionada lucha, tanto en la academia como en la organización política, contra las injusticias de las que fue testigo, por lo cual es recordada como un gran ejemplo inspirador.
Referencias:
Cotlar, Mischa; Ratto de Sadosky, Cora. Introducción al Álgebra. Nociones de álgebra lineal. Editorial Universitaria de Buenos Aires, Buenos Aires 1966.
Bettye Anne Case (Editor), Anne M. Leggett (Editor). Complexities: Women in Mathematics.
Sandra McGee Deutsch. Argentine Women Against Fascism: The Junta de la Victoria, 1941 – 1947. Politics, Religion & Ideology Vol. 13, No. 2, 221–236, June 2012.
Remembering Cora Sadosky, a tribute in the Newsletter of the Association for Women in Mathematics, Vol. 41, No. 2 (March-April 2011), 5-14.
De los wavelets a las ondas gravitacionales: las matemáticas detrás de acontecimientos científicos del 2017. Alberto Mercado. El mostrador, 30 diciembre, 2017.
Sobre el autor: Alberto Mercado Saucedo es profesor de matemáticas en la Universidad Técnica Federico Santa María (Valparaíso, Chile)
Sobre la ilustradora: Constanza Rojas Molina es profesora del departamento de matemáticas de la CY Cergy Paris Université (Cergy-Pontoise, Francia)
El artículo Cora Ratto: en búsqueda de armonía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lo que la búsqueda de inteligencia extraterrestre nos enseña para entender la pandemia
- La búsqueda de la verdad
- Roberto Frucht, matemático en tránsito
¿Los organismos móviles más antiguos?
 Imagen: CDC / Unsplash
Imagen: CDC / UnsplashUn equipo internacional liderado por Frederic Delarue, un científico de la Universidad Sorbona, de París, afirma haber descubierto restos fósiles de 3400 millones de años (en adelante m.a.) de microorganismos capaces de desplazarse de forma activa, mediante el concurso de una especie de cola semejante a un látigo.
Los primeros indicios de vida de que disponemos son unas rocas de unos 3800 m.a. de antigüedad que contienen un grafito en el que la proporción de los isótopos de carbono refleja cierta actividad biológica en su formación. Es posible, incluso, que formas primordiales de vida aparecieran antes, quizás hace 4000 m.a., 500 m.a. después de la formación del planeta y en una época en la que sufría aún el impacto frecuente de asteroides. No obstante, los fósiles de organismos unicelulares más antiguos de que se tiene noticia datan de unos 3500 m.a. atrás.
Los microfósiles con supuestas estructuras motrices han sido hallados en la Formación del Lago Strelley, en el Oeste de Australia. Se habrían formado a partir de microorganismos con forma de hoja, y de una longitud de entre 30 y 84 µm y la mitad de anchura. Para confirmar que no se trataba de restos puramente inorgánicos, los paleontólogos han demostrado la existencia en los microfósiles de fósforo y nitrógeno, elementos característicos de los seres vivos. De los quinientos hallados, cuatro presentan una especie de bastón en uno de los extremos de la célula, y es a esa estructura a la que los investigadores atribuyen la condición de apéndice motriz, aunque sospechan que se trata de estructuras incompletas. La ausencia del apéndice en la mayoría de los restos, o la de fragmentos del mismo en los cuatro hallados, se debería a su pérdida durante el largo tiempo transcurrido desde su formación. Muchos microorganismos actuales, para desplazarse, hacen uso de estructuras similares, tales como flagelos -cuya rotación los impulsa en medio líquido- u otras.
Los investigadores han dado a conocer su hallazgo en un documento publicado en bioRxiv, un repositorio de acceso libre para el campo de biociencias, y está pendiente de examen por otros especialistas antes de su publicación en una revista. Por tanto, no ha pasado aún el filtro que han de superar los informes científicos para su aceptación formal como productos de investigación genuinos. Además, algunos expertos han manifestado dudas acerca de la interpretación de los hallazgos, por lo que han de tomarse con cautela.
Los autores de la investigación defienden, como es lógico, su validez, así como la interpretación que de ellos hacen. Y frente a quienes ponen en duda que las estructuras observadas pudiesen tener funciones motoras, sostienen que hay razones fundadas para su aparición temprana en la historia de la vida. Al fin y al cabo, la capacidad de movimiento proporciona acceso rápido a la comida, por lo que seguramente hubo un fuerte incentivo –presiones selectivas en la jerga biológica- para que apareciesen estructuras motrices. La razón por la que no se habían observado hasta ahora o se han hallado en tan pequeña proporción habría sido su gran fragilidad.
La historia de la vida y, sobre todo, la historia de sus orígenes está llena de incógnitas. De algunos hitos fundamentales no disponemos de pruebas concluyentes. La propuesta de Delarue y colaboradores puede acabar siendo aceptada por la comunidad científica o puede que sea refutada. Así funciona la ciencia, a partir de especulaciones basadas en indicios o pruebas a veces confusas o de difícil interpretación. El tiempo, no obstante, gracias a pruebas adicionales, acaba decantando el conocimiento que consideramos verdadero. Cada vez más, y cada vez mejor; pero nunca completo.
Fuente: F. Delarue et al (2020): Evidence for motility in 3.4 Gyr-old organic-walled microfossils?
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo ¿Los organismos móviles más antiguos? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Gemma del Caño – Naukas P4K 2019: ¡Que si quiere bolsa!
 Foto: Maria Lin Kim / Unsplash
Foto: Maria Lin Kim / UnsplashTras el uso de una bolsa en la que poder transportar nuestra compra del supermercado hay todo un mundo de química, industria, salud y legislación da igual el material de que esté hecha. Gemma del Caño, farmacéutica especialista en I+D+i y seguridad alimentarias en la industria, nos revela algunos de los intríngulis de ese mundo.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Gemma del Caño – Naukas P4K 2019: ¡Que si quiere bolsa! se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
- Gemma Del Caño y Marián García – Naukas Bilbao 2018: Sandwich mixto en tres actos
- César Tomé López – Naukas P4K 2019: ¿Eureka?¿En serio?
Mascarilla y COVID-19: ¿dilema del prisionero o juego de coordinación?
Annick Laruelle
 Grafiti en una calle de Varsovia (Polonia). Foto: Adam Nieścioruk / Unsplash
Grafiti en una calle de Varsovia (Polonia). Foto: Adam Nieścioruk / UnsplashEn seis meses la mascarilla se ha vuelto un objeto cotidiano en todo el mundo. Los gobiernos de China, Hong Kong o Taiwán fueron los primeros en recomendar su uso. Desde junio de 2020 la posición de Organización Mundial de la Salud es que los gobiernos deberían alentar al público a que use la mascarilla en situaciones específicas (como el transporte público). La decisión acerca de recomendar o hacer obligatorio el uso de mascarilla varía según los países.
Si el uso de la mascarilla no es obligatorio, los individuos se enfrentan a la decisión de ponérsela o no. Las preferencias individuales pueden depender de las circunstancias, de las personas con quienes uno se encuentra… y de lo que deciden los demás individuos.
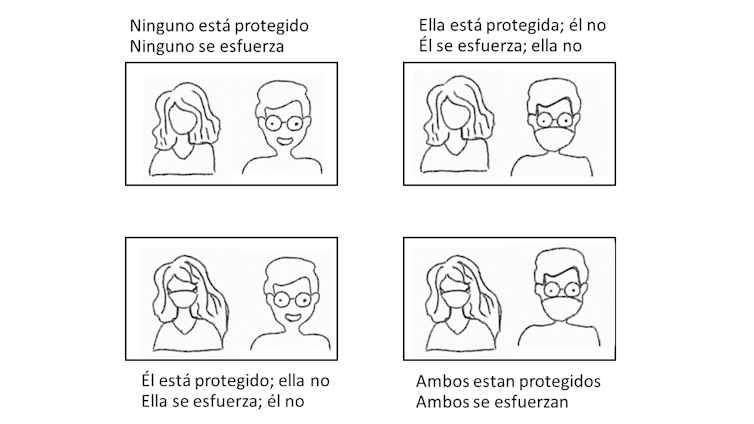
Se puede analizar la situación con la teoría de juegos: cada persona tiene que decidir si llevar la mascarilla o no. El resultado final depende de lo que han decidido todos. En un encuentro con otra persona, cada uno tiene dos acciones posibles y evalúa cuatro resultados.
 Los cuatro resultados en un encuentro entre dos personas.
Los cuatro resultados en un encuentro entre dos personas.La teoría de juegos no realiza ningún juicio ético o moral sobre las preferencias de los individuos. Solamente intenta determinar las decisiones de equilibrio en función de ellas. En el equilibrio, ningún individuo se arrepiente de la decisión que ha tomado: el resultado es estable.
La situación puede dar lugar al conocido “dilema del prisionero”. Si llevar la mascarilla constituye más una protección para los demás que para los que la llevan y llevarla conlleva un cierto esfuerzo, la mejor opción para una persona que se preocupa exclusivamente de su bienestar individual es no llevar la mascarilla y que el otro la lleve.
La segunda mejor opción es que los dos lleven la mascarilla; la tercera opción que ninguno la lleve y la cuarta llevar la mascarilla y que el otro no la lleve. Una persona con estas preferencias es un free-rider, en el sentido de que intenta aprovecharse de los esfuerzos de los demás y no llevar la mascarilla – aunque no le gustaría que los demás hagan lo mismo.
 Dilema del prisionero.
Dilema del prisionero.En un encuentro entre dos free-riders, si ambos no llevan la mascarilla ninguno de los dos se arrepiente de su decisión. Es la tercera mejor opción para cada uno, pero cambiar de decisión significaría ser el único de los dos en llevar la mascarilla, la peor opción de todas para un free-rider. Es el único equilibrio. En cambio, si ambos llevan la mascarilla, cada uno se arrepiente de su decisión: preferiría quitársela si el otro la lleva. Que ambos lleven la mascarilla no es un equilibrio, aunque es la segunda mejor opción para cada uno.
¿Se puede justificar el uso obligatorio?
El dilema del prisionero tiene esta característica paradójica: un resultado mejor que el resultado del equilibrio no se puede alcanzar de manera descentralizada. En una sociedad de free-riders se puede justificar el uso obligatorio de la mascarilla.
En la práctica es (afortunadamente) poco probable que todos los individuos de un grupo social sean free-riders con respecto a la mascarilla. Un experimento realizado en Alemania con unos 925 participantes sugiere que el uso de la mascarilla está visto como un contrato social: los participantes perciben de manera positiva a los que llevan la mascarilla. Tienden a recompensar a los que la llevan y castigar a los que no la llevan. Este comportamiento se podría justificar por preferencias para la reciprocidad: si la otra persona lleva la mascarilla uno prefiere llevarla y prefiere no llevarla si el otro no la lleva.
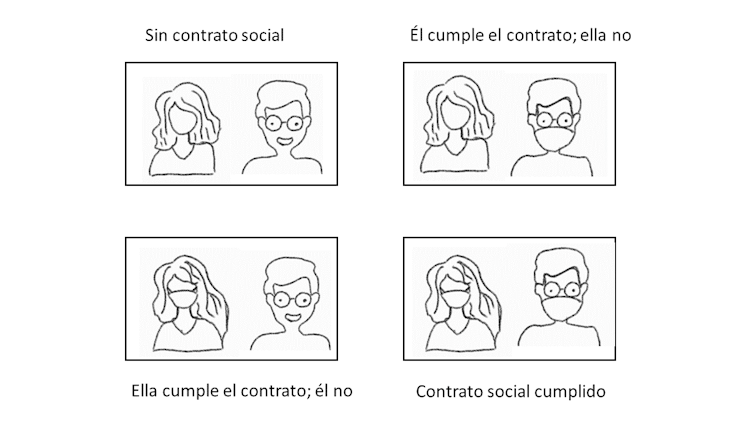 Juego de coordinación.
Juego de coordinación.En este caso la situación corresponde a un juego de coordinación con dos equilibrios. En un equilibrio ambos llevan la mascarilla o ambos no la llevan.
La teoría de juegos no puede predecir cuál de los equilibrios puede emerger. Las circunstancias (espacio cerrado o no; con distancia o no) podrían ayudar a las personas a coordinarse en un equilibrio o el otro.
El uso obligatorio de la mascarilla se justifica en sociedades de free-riders: resuelve el dilema social.
A cambio, si el uso de la mascarilla es un contrato social, el uso de la mascarilla por parte de todos es un equilibrio posible.
Dilemas sociales
Las medidas para luchar contra la pandemia generan dilemas sociales. El uso de la mascarilla es una de ellas, como lo son también el confinamiento o la vacuna.
En este ultimo caso, dado que los beneficios son bienes públicos, los individuos “free riders” tienen el incentivo de no contribuir y beneficiarse de los esfuerzos de los demás. Con respecto a la futura vacuna contra la COVID-19, el epidemiólogo de la Organización Mundial de la Salud advirtió en agosto que los países tomarían la decisión de hacerla obligatoria o no.
La encuesta del CIS realizada a principios de octubre (pregunta 6) revela que el 43,8% de los encuestados no están dispuestos a vacunarse.
Sobre la autora: Annick Laruelle es profesora Ikerbasque de Fundamentos del Análisis Económico en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Mascarilla y COVID-19: ¿dilema del prisionero o juego de coordinación? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Relación entre genoma y las formas graves de COVID-19
- El dilema de la hepatitis C
- Un extraño juego de dados
Los invasores: Invasiones biológicas
“Los invasores. Seres extraños de un planeta que se extingue. Destino: la Tierra. Propósito: adueñarse de ella.”
En los créditos de la serie de televisión “Los invasores”. 1967-1968.
“Hoy en día vivimos en un mundo muy explosivo, y aunque no sepamos dónde o cuándo será el próximo estallido, esperamos encontrar formas de detenerlo o, en cualquier caso, de mitigar su fuerza”.
Charles Elton, La ecología de las invasiones de animales y plantas, 1958.
“En el fondo, bajo los rayos perpendiculares del sol, brillaba un pequeño lago, que el aburrimiento de un inglés pobló de ciprínidos con escamas de oro o de plata.”
Julio Verne. En el lago del volcán Caldeira en la isla Fayal de las Azores. Agencia Thompson y Cía, 1907. Allí siguen los ciprínidos (Filipe Ribeiro y su grupo, Universidade de Lisboa).
La introducción de agentes de control biológico en una nueva región es un ejemplo de los efectos peligrosos de las especies invasoras. Así, Diana Kimberling, de la Universidad Estatal de Oregon, revisa los efectos de 87 especies de insectos introducidas en Estados Unidos entre 1900 y 1981. De ellas, 57 no funcionaron como control biológico de la especie a vigilar. Y 24 actúan sobre especies diferentes al blanco original.
Hay 18 especies típicas de mamíferos terrestres que viven en entornos húmedos en Francia, y siete de ellas son introducidas. La mayor parte son ejemplares escapados de granjas de cría para comercializar su piel, como ha ocurrido con el visón y el castor americanos.
En 1869 se inauguró el Canal de Suez. En el sistema de canales que lo forman hay un lago con baja salinidad que funciona como barrera para el paso de especies entre los mares Rojo y Mediterráneo, pero para el 2000, más de 250 especies habían llegado al Mediterráneo.
Cuando la isla de Krakatoa estalló en 1883, las cenizas del volcán destruyeron toda la vida de la isla. Pero, 50 años más tarde era recolonizada por especies llegadas de islas cercanas, al menos a 40 kilómetros de distancia. En 1933, medio siglo después de la destrucción, se encontraron en Krakatoa 720 especies de insectos y 30 de aves. También había reptiles y mamíferos.
El número de especies de peces introducidas en Estados Unidos fue de 67 entre 1850 y 1900, de 140 entre 1901 y 1950, y de 488 entre 1951 y 1996.
Las especies invasoras en la Bahía de San Francisco fueron, de media, una por año entre 1851 y 1960, y de más de tres por año entre 1961 y 1995.
Entre 2000 y 2008, una media de 196 especies no nativas se estableció en Europa cada año. En 2009, los insectos no nativos eran cerca de 1300, pero diez años después, en 2019, alcanzaban las 2500 especies. Uno de los caminos de entrada es el tráfico marítimo de contenedores. Entre febrero y agosto de 1996, se inspeccionaron 1174 contenedores y se encontraron más de 7400 especies de insectos. En Nueva Zelanda, y en 2001 y 2002, se inspeccionaron 11200 contenedores. El 4.1% de los contenedores con carga y el 3.6% de los contenedores vacíos llevaban insectos.
Según EASIN, European Alien Species Information Network, a 21 de octubre de 2019, en Europa hay censadas 14165 especies no nativas.
 Conejo silvestre en Australia. Fuente: Wikimedia Commons
Conejo silvestre en Australia. Fuente: Wikimedia CommonsLas invasiones biológicas son una de las consecuencias más serias de la actividad de la especie humana. La globalización de la biota del planeta está transformando las floras y faunas regionales y locales. Anthony Ricciardi comentó que, en 2008, la especie humana movía unas 7000 especies cada día. Es lo que algunos autores denominan neozoismo: introducir especies no nativas y homogeneizar faunas y floras. Desde la más pequeña y remota isla hasta el continente más extenso, la introducción intencionada o accidental de nuevas especies está alterando la composición y el entorno de las especies allí establecidas. Los problemas potenciales asociados con la introducción de especies no indígenas se conocen desde hace tiempo. Este es el aviso de peligro que un grupo de investigadores de trece países, liderado por Petr Pysek, de la Academia Checa de Ciencias, publicó hace unos meses, y en el que participó Montserrat Vilá, de la Estación Biológica de Doñana.
En general, las especies extrañas se perciben como problemas ambientales potenciales. Por supuesto, la especie invasora con más éxito es Homo sapiens, la especie humana, que ha llegado a todo el planeta y, con ella, han viajado muchas otras que ahora llamamos invasoras.
Para ilustrar la peligrosidad de las especies invasoras nos sirve el estudio reciente de Xuan Liu y su equipo, de la Academia China de Ciencias, sobre la presencia de especies invasoras cerca de áreas protegidas. Han revisado 894 especies invasoras terrestres en casi 200000 áreas protegidas de todo el planeta. Encuentran que hay especies invasoras en menos del 10% de las áreas protegidas pero hay al menos una en el entorno. El 84% de las áreas protegidas tienen especies invasoras a menos de 10 kilómetros, y el 99% a menos de 100 kilómetros.
Algunos ejemplos de esas especies invasoras cercanas son la paloma doméstica, el faisán, el gorrión común, el conejo, el visón americano, el ratón doméstico, la rata, la abeja africana o el mosquito de la fiebre amarilla.
El hombre siempre ha mantenido relaciones privilegiadas con un buen número de especies animales y vegetales. Muchos ejemplos lo demuestran: las representaciones en las pinturas rupestres, los bestiarios de la Edad Media o, más cercano a nosotros y en otro registro, las movilizaciones mundiales para salvar a las focas o las ballenas de la extinción. La domesticación de animales y plantas para la ganadería y la agricultura constituyen un ejemplo evidente de esas relaciones.
Pero la armonía no ha sido siempre, ni mucho menos, la regla de conducta entre humanos y fauna y flora en la medida en que, en primer lugar, la relación ha sido trófica, es decir, por su utilidad para comer, vestir, etc. En la época histórica, está documentada la desaparición de especies porque competían, de una u otra manera, con la especie humana o con sus especies animales y vegetales acompañantes.
Es James Carlton, del Colegio Williams de Mystic, en Estados Unidos, el que plantea los procesos de cambio que puede ser la causa del movimiento de especies a nuevos entornos. Menciona transformaciones en la región de origen, la aparición de nuevas regiones con especies disponibles para moverse, cambios en la región de recepción que atraigan especies de otras zonas, combinaciones de estos factores que supongan la apertura de nuevas ventanas a la invasión, y la presencia de vectores que ayuden a la invasión en cualquiera de sus fases como, por ejemplo, las actividades de la especie humana.
Pueden provocar importantes modificaciones en la estructura y funcionamiento de los ecosistemas, llegando a la extinción de especies nativas. Los mecanismos más habituales son la competición, la depredación, el parasitismo y las alteraciones en la cadena trófica o en ciclos de nutrientes. Son menos frecuentes los cambios en el propio hábitat. Sin embargo, Mark Davis, del Colegio Macalester, de St. Paul, en Estados Unidos, comenta que la extinción rara vez ocurre por una competición directa con la especie invasora, más bien es por cambios en el entorno o en otras especies relacionadas de alguna manera con la especie que desaparece.
 Presa realizada por castores oriundos de Amética del Norte en Tierra del Fuego. Fuente: Wikimedia Commons
Presa realizada por castores oriundos de Amética del Norte en Tierra del Fuego. Fuente: Wikimedia CommonsPero el grupo de Gyan Sharma, de la Universidad Hindu Baranas, en la India, afirma que más del 40% de las especies en riesgo de extinción lo están por la acción de especies invasoras. El 20% o más de las especies de plantas son, de media, no nativas en algunas áreas continentales y el 50% en algunas islas. Calculan que el 10% de las 260000 especies de plantas vasculares que conocemos tiene el potencial de convertirse en invasoras.
Cada una de las especies invasoras es un capítulo más en la larga historia de transgresiones ecológicas que provoca la especie humana. Poner y quitar especies, llevarlas y traerlas, depara siempre consecuencias casi siempre imprevisibles y, a veces, no beneficiosas. Aunque, no hay que olvidarlo, no todas las plantas invasoras son peligrosas. La introducción en un determinado entorno de especies no nativas puede suponer tanto un desastre ecológico como algún beneficio. De esas especies invasoras se alimenta la especie humana pues suministran el 70% de la dieta con solo nueve cultivos: trigo, maíz, arroz, patata, cebada, mandioca, soja, caña de azúcar y avena. Todas ellas han sido transportadas por la especie humana a todo el planeta y se cultivan lejos de su lugar de origen. O, también, el 85% de las plantaciones forestales industriales son especies de tres géneros: Eucalyptus, Pinus y Tectona (teca). En resumen, las especies no nativas tienen un papel integral en la economía y en los cultivos de todas las regiones.
Hay un grupo de ecólogos expertos en invasiones, liderados por Mark Davis, que proponen que no hay que diferenciar entre especies en un hábitat según su origen, nativas o invasoras, sino por su impacto en el entorno, por su integración y por su contribución a la biodiversidad del área a la que llegan. Debe aplicarse un enfoque dinámico y pragmático a la conservación y gestión de las especies. Hasta ahora, lo prioritario ha sido la preservación de la biodiversidad original y a su restauración ecológica. Para Davis y su grupo, estos objetivos se han convertido, más bien, en metáforas militares de lucha contra invasores. En conclusión, hay que centrarse en las funciones de las especies más que en su origen. Por todo ello, Martin Schlaepfer, de la Universidad de Ginebra, propone que las especies introducidas e invasoras deben incluirse en los índice de biodiversidad y sostenibilidad del hábitat en el que se encuentran.
 Lantana, oriunda de América, invadiendo un campo de cítricos en Israel. Fuente: Wikimedia Commons
Lantana, oriunda de América, invadiendo un campo de cítricos en Israel. Fuente: Wikimedia CommonsUno de los objetivos más actuales de la investigación sobre especies invasoras con éxito es el análisis de sus propiedades biológicas y ecológicas en la búsqueda de características generales que permitan identificarlas. No conocemos un carácter morfológico, fisiológico o ecológico sencillo que podamos relacionar con la capacidad invasora de una especie o de un grupo de especies. Sin embargo, debemos precisar los conceptos y la terminología utilizados en la biología de las invasiones. En una revisión publicada en 2006, Jannike Falk-Petersen y su grupo, de la Universidad de Tromso, en Noruega, recopilan nada menos que 145 definiciones que se utilizan en este tema, y concluyen que no encuentran una definición concreta, sencilla y rápida cuando se investigan especies invasoras. Piden algo así: una especie invasora es un organismo extranjero (alien) que se ha establecido en un área nueva y está expandiendo su rango de distribución.
La teoría ecológica no está suficientemente desarrollada para tratar el problema de las invasiones biológicas, escribe Kristin Shrader-Frechette, de la Universidad de Notre Dame, en Estados Unidos. En primer lugar, no hay concepto y definición claros y precisos de especie invasora y, por tanto, los expertos pueden utilizar el mismo término para distintos conceptos o, por el contrario, el mismo concepto para diferentes procesos. Esta confusión no permite comparaciones, debates y generalizaciones teóricas. En segundo lugar, las teorías más utilizadas tienen poca o ninguna capacidad predictiva y no permiten asegurar si una especie puede promover o dañar la diversidad del hábitat invadido. Y, en tercer lugar, las teorías no predicen si una especie puede vivir en el nuevo hábitat o fracasará en el intento.
Las etapas de la invasión, según Alfredo Vilches y sus colegas, de la Universidad Nacional de La Plata, en Argentina, son, en primer lugar, el transporte de la especie al nuevo entorno, con el resultado de muerte, captura o introducción. Después está el establecimiento o naturalización que, también, puede fallar. En tercer lugar, hay un aumento de la población y su dispersión. Y, después, llega la percepción de la presencia de la nueva especie por la especie humana y se estudia el impacto creado, bajo o alto.
Desde la UPV/EHU, Ana Rallo y Loreto García-Arberas propusieron las siguientes definiciones para aclarar los problemas en conceptos y terminología tan habituales en los estudios de la biología de las invasiones. He añadido algunas aportaciones de Petr Pysek, de la Universidad Agrícola de Praga, y del grupo de expertos liderado por David Richardson, de la Universidad de Ciudad del Cabo.
.- Especie nativa o autóctona: la que se encuentra en su área habitual de distribución.
.- Especie exótica o alóctona o no nativa: fuera del área de distribución habitual, por acción directa o indirecta de la especie humana.
.- Especie exótica o alóctona o no nativa con potencial invasor: que podría convertirse en invasora, sobre todo si ya lo ha conseguido en otras regiones.
.- Especie exótica o alóctona o no nativa invasora: establecida en un hábitat diferente al suyo natural y que puede ser un peligro para la biodiversidad local, y se reproducen en cantidad, a veces, a distancia de los progenitores y con capacidad para extenderse.
.- Especie exótica o alóctona o no nativa aclimatada o casual: en un hábitat diferente al suyo pero sin reproducción establecida, aunque lo haga ocasionalmente.
.- Especie exótica o alóctona o no nativa establecida: con poblaciones reproductoras durante varios ciclos vitales y sin intervención humana.
Por otra parte, Brandon Larson propone un lenguaje más neutro, no tan hiperbólico y catastrofista como el que se usa habitualmente. Sin embargo, este lenguaje más neutro presenta dos inconvenientes. En primer lugar, separa los resultados científicos de los debates sociales entre los ciudadanos interesados. Y, en segundo lugar, no es consistente con los valores conservacionistas evidentes y mayoritarios que animan a muchos científicos a investigar las invasiones biológicas.
En los últimos años, las investigaciones se han centrado en los procesos y patrones de las invasiones. Es importante conocer las causas del éxito invasor de una especie. En 1994, Sarah Reichard publicó una propuesta, en diez apartados, como observaciones preliminares, no todas probadas y, según la autora, alguna puede ser falsa. Anthony Ricciardi y Joseph Rasmussen, de las universidades Laval y McGill de Canadá, plantean características parecidas para especies invasoras del medio acuático.
En general, una especie invasora se caracteriza por:
1.- Tiene una distribución amplia y abundante en su hábitat nativo; es generalista, y con facilidad para ser trasladada e introducida, especialmente de manera accidental.
2.- Gran variabilidad genética, con más posibilidades a nuevas condiciones del entorno.
3.- Existe una correspondencia estrecha en cuanto a las condiciones climáticas entre su hábitat nativo y el invadido; ha evolucionado en determinadas condiciones y no es fácil que prospere en otras radicalmente diferentes.
4.- Generalista en su dieta o tolerante a diferentes condiciones del entorno, y más adaptables a condiciones no habituales del hábitat invadido.
5.- Tienen éxito invasor porque huyendo evitan a los depredadores del hábitat original, lo que supone más individuos en la reproducción. Así, Lorne Wolfe de la Universidad del Sur de Georgia, menciona la planta Silene latifolia, que invadió Norteamérica a principios del siglo XIX y que ha calculado que tiene 17 veces más probabilidades de ser dañada por alguna especie enemiga en su hábitat original de Europa que en Norteamérica.
6.- Se asocian con la especie humana para su dispersión, para conseguir más alimentos o aprovechar la degradación del hábitat a invadir por la actividad humana. Muchas especies introducidas tienen éxito en la invasión porque los ambientes modificados por la actividad humana permiten su instalación. Y, además, la especie humana puede ayudar con un número alto de individuos o con repetidos episodios de transporte.
7.- Tienen mecanismos de dispersión muy efectivos para formar poblaciones viables lejos de la población de origen.
8.- Con fases juveniles cortas, alcanzan la madurez sexual con rapidez.
9.- Pueden colonizar a partir de uno o de muy pocos individuos con, por ejemplo, una hembra fertilizada o por partenogénesis.
10.- Tienen una tasa reproductora alta y pueden construir poblaciones con rapidez y, así, la invasión progresa rápida y potente. Incluso, como menciona Petr Pysek, de la Academia de Ciencias de la República Checa, una característica importante es la posibilidad de la reproducción clonal, como ocurre con el alga Caulerpa en el Mediterráneo.
Algunas de las plagas más conocidas y extendidas por el planeta se deben a especies introducidas. Es un asunto en debate cuántas de las especies pueden ser invasoras y cuántas llegarán a provocar una plaga. Es la famosa regla del 10%. Mark Williamson apoya esta regla. De 10 especies nuevas que llegan a un área geográfica concreta, solo una aparece en el entorno natural; una de cada 10 introducidas se establece y una de cada 10 de las establecidas se convierte en un peligro, en una plaga. Hay datos que no coinciden con este 10% como, por ejemplo, los que publicó Max Wade, de la Universidad de Loughborough, en Inglaterra. De los árboles introducidos en el centro de Alemania en la década de los noventa, unas 3150 especies, el 10% aumenta su área de distribución y se expande, el 2% se establece, y el 1% acaba formando parte de la vegetación habitual de la región. Aquí los porcentajes siguen la regla de 10:2:1. No es el 10% sin más.
Fue David Lodge, de la Universidad de Notre Dame, en Estados Unidos, quien propuso, en la década de los noventa, una nueva línea de investigación para la búsqueda de las características de los hábitats susceptibles de ser invadidos. Incluye, en parte, la propuesta de Sarah Reichard de 1994. Como una primera aproximación enumera que el clima sea parecido al de la región de origen de la especie invasora, que, en la región nueva, haya una diversidad baja y escasa presencia de depredadores y, además, que sea un hábitat perturbado, con recursos escasos o alterados. Si el nivel de recursos es estable, hay menos probabilidad de que se convierta en un hábitat invadido. A todo ello, añaden Luis Espínola y Horacio Ferreira, de las universidades Estatal de Maringá y de Sao Paulo, el aislamiento geográfico e histórico de la región invadida.
 Kudzu, una planta trepadora oriunda de Asia Oriental, creciendo sobre los árboles en Atlanta (Georgia, Estados Unidos). Fuente: Wikimedia Commons
Kudzu, una planta trepadora oriunda de Asia Oriental, creciendo sobre los árboles en Atlanta (Georgia, Estados Unidos). Fuente: Wikimedia CommonsEn conclusión, y como John Ewel y otros veinte expertos de todo el planeta escribían en 1999, hay varios temas de investigación sobre especies invasoras sobre los que existe un amplio consenso. No hay que olvidar que, aunque a la ciencia se le piden bases científicas detalladas y certezas de los efectos que provocan las especies invasoras, siempre es adecuado partir del principio de precaución al tomar decisiones.
Según Ewel, las especies invasoras tienen un gran potencial para dar grandes beneficios económicos y ecológicos a la sociedad; además, continuará la introducción de especies aunque se debe vigilar su impacto que tendrá una distribución desigual; la actividad humana facilita el movimiento de especies y también su establecimiento; puede pasar mucho tiempo entre la introducción de una especie y su expansión; una vez establecida es casi imposible de erradicar; una especie invasora que se ha establecido con éxito en un determinado hábitat predice su potencial invasivo en otros hábitats.
Para las invasiones biológicas también hay mitos, y Stephen Gollasch, de GoConsult de Hamburgo, y James Carlton, del Colegio Williams de Williamstown, en Estados Unidos, nos comentan algunos.
El primero se puede resumir en la optimista afirmación de “todas las especies que podrían haberse introducido ya están aquí” y, por tanto, no hay peligro de que lleguen más. No es así y, cuando se dé la combinación adecuada de factores, sobre todo el número suficiente de individuos de la especie invasora para conseguir una población viable puede llegar la nueva invasión.
Otro mito es preguntarnos “por qué necesitamos estar atentos ahora”, ya lo haremos cuando llegue la invasión. Hay que estar atentos porque llegará, con la globalización otras especies pueden ser invasoras y hay que responder de inmediato.
El tercer mito que mencionan Gollasch y Carlton es que “las invasiones son parte de la naturaleza y sucederán de todos modos; lo único es que ahora se acelera el proceso”. No es cierto, no es fácil que una especie llegue de manera natural, por ejemplo, del Pacífico a Europa occidental. Pero lo puede conseguir, y con rapidez, por la intervención de la especie humana. Nos sirven de ejemplo los ciclos de vida del zooplancton, demasiado cortos como para poder atravesar un océano, pero la intervención humana puede acelerar la velocidad del viaje y, transportada en el agua de lastre de los barcos, llegar viables a otro continente.
El siguiente mito afirma que “los humanos no deben interferir con la distribución de las especies como fenómeno natural que es”. Sin embargo, la actividad humana ha adquirido tal importancia que sobrepasa con mucho un fenómeno natural.
Y, para terminar, “solo el 10% de las invasiones tiene un impacto significativo”. Es la típica regla del 10% que, cuando se entra en el debate, no tiene ninguna evidencia clara. A menudo, el impacto más visible de una especie invasora es evidente cuando la población ha aumentado de manera notable, incluso tiempo después de su introducción. Soplo hay que recordar, en nuestro entorno, del plumero de la Pampa.
La dispersión de especies por la actividad humana no es simplemente una cuestión de aceleración de un proceso normal que siempre ha ocurrido o que ocurrirá antes o después. Los movimientos naturales de especies suceden por corredores predecibles: márgenes continentales, corrientes oceánicas o caminos que se abren y cierran en una escala temporal geológica. Por el contrario, los movimientos de especies mediados por la especie humana a menudo suponen procesos impredecibles e instantáneos independientes de barreras en el espacio o en el tiempo. No existe un flujo natural de especies entre, por ejemplo, los estuarios templados del sur de Australia y los de Europa occidental. Sin embargo, por el transporte de especies de interés comercial, o por accidente, una especie puede ser transportada entre Australia y Europa en cuestión de días e, incluso, de horas.
Referencias:
Carlton, J.T. 1996. Pattern , process, and prediction in marine invasion ecology. Biological Conservation 78: 97-106.
Carlton, J.T. 1999. Molluscan invasions in marine and estuarine communities. Malacologia 41: 439-454.
Davis, M.A. et al. 2000. Fluctuating resources in plant communities: a general theory of invasibility. Journal of Ecology 88: 528-534.
Davis, M.A. 2003. Biotic globalization: Does competition from introduced species threaten biodiversity? BioScience 53: 481-489.
Davis, M. et al. 2011. Don’t judge species on their origins. Nature 474: 153-154.
Espínola, L.A. & H. Ferreira Júlio Junior. 2007. Espécies invasora: Conceitos, modelos e atributos. Interciencia 32: 580-585.
Ewel, J.J. et al. 1999. Deliberate introductions of species: research needs. BioScience 49: 619-630.
Falk-Petersen, J. et al. 2006. On the numerous concepts in invasión biology. Biological Invasions DOI: 10.1007/s10530-005-0710-6
Gollasch, S. & J. Carlton. 2004. To whom it may concern “Invasion on myths” – GoConsult. 2004-06-09, 2.
Kimberling, D.N. 2004. Lessons from history: predicting successes and risks of intentional introductions for arthropod biological control. Biological Invasions 6: 301-318.
Kinzelbach, R. 1995. Neozoans in European waters – Exemplifying the worlwide process of invasion and species mixing. Experientia 51: 526-538.
Kolar, C.S. & D.M. Lodge. 2001. Progress in invasion biology: predicting invaders. Trends in Ecology & Evolution 16: 199-204.
Larson, B.M.M. 2007. An alien approach to invasive species: objectivity and society in invasion biology. Biological Invasions 9: 947-956.
Levine, J.M. & C.M. D’Antonio. 1999. Elton revisited: a review of evidence linking diversity and invasibility. Oikos 87: 15-26.
Liu, X. et al. 2020. Animal invaders threaten protected areas worldwide. Nature Communications 11: 2892.
Lodge, D.M. 1993. Biological invasions: Lessons for Ecology. Trends in Ecology & Evolution 8: 133-137.
Marchioro, M. et al. 2020. Light traps in shipping containers: A new tool for the early detection of insect alien species. Journal of Economic Entomology doi: 10.1093/jee/toaa098.
Maurin, H. 1997. L’homme et les mamifères de France métropolitaine: Évolution historique et introductions d’espèces dans les milieux humides et aquatiques. Bulletin Français de la Pêche et de la Pisciculture 344/345: 117-132.
Mooney, H.A. & E.E. Cleland. 2002. The evolutionary impact of invasive species. Proceedings of the National Academy of Sciences USA 98: 5446-5451.
Morton, B. 1997. The aquatic nuisance species problema: A global perspective and review. En “Zebra mussel and aquatic nuisance species”, p. 1-54. Ed. Por F.M. D’Itri. Ann Arbor Press Inc. Chelsea, Michigan.
Pysek, P. 1995. On the terminology used in plant invasion studies. En “Plant invasions – General aspects and special problems”, p. 71-81. Ed. por P. Pysek et al. SPB Academic Publ. Amsterdam.
Pysek, P. 1997. Clonality and plant invasions: Can a trait make a difference? En “The ecology and evolution of clonal plants”, p. 405-427. Ed. Por H. de Kroon & J. van Groenendael. Backhuys Publ. Leiden.
Pysek, P. 1998. Is there a taxonomic pattern to plant invasions? Oikos 82: 282-294.
Pysek, P. et al. 2020. Scientists’ warning on invasive alien species. Biological Review doi: 101111/brv.12627
Rallo, A. & L. García-Arberas. 2012. Fauna exótica invasora en Bizkaia. Diputación Foral de Bizkaia. Bilbao. 330 pp.
Reichard, S. 1994. What makes a species a successful invades? En “Biological invasion as a global change”, p. 63-64. Ed. Por S.J. Hassol & J. Katzeberger. ASPEN Global Change Institute. Aspen, Colorado.
Reise, K. et al. 2006. Are aliens threatening European aquatic coastal ecosystems? Helgoland Marine Research 60: 77-83.
Ribeiro, F. et al. 2009. Non-native fish in the fresh waters of Portugal, Azores and Madeira Islands: a growing threat to aquatic biodiversity. Fisheries Management and Ecology 16: 255-264.
Ricciardi, A. & J.B. Rasmussen. 1998. Predicting the identity and impact of future biological invaders: a priority for auqtic resource management. Canadian Journal of Fisheries and Aquatic Sciences 55: 1759-1765.
Richardson, D.M. et al. 2000. Naturalization and invasion of alien plants: concepts and definitions. Diversity and Distributions 6: 93-107.
Schlaepfer, M.A. 2018. Do non-native species contribute to biodiversity? PLOS Biology 16: e2005568.
Sharma, G.P. et al. 2005. Plant invasions: Emerging trends and future implications. Current Science 88: 726-734.
Shrader-Frechette, K. 2001. Non-indigenous species and ecological explanation. Biology and Philosophy 16: 507-519.
Vilches, A. et al. 2010. Introducción a las invasiones biológicas. Boletín Biológica 17: 14-19.
Wade, M. 1997. Predicting plant invasions: making a start. En “Plant invasions: Studies from North America and Europe”, p. 1-18. Ed. por J.H. Brock et al. Backhuiys Publ. Leiden, Holanda.
Williamson, M. & A. Fitter. 1996. The varying success of invaders. Ecology 77: 1661-1666.
Wolfe, L.M. 2002. Why alien inveders succeed: Support for the Escape-from-Enemy Hypothesis. American Naturalist 160: 705-711.
Zimmer, C. 2008. Una especie exótica puede ayudar, no asfixiar, a la diversidad. New York Times 25 septiembre.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Los invasores: Invasiones biológicas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La cooperación no favorece a los invasores rápidos
- Los invasores
- Catástrofe Ultravioleta #18 INVASORES
Rompecabezas matemáticos con números
El sudoku es sin lugar a dudas uno de los rompecabezas más populares de los últimos tiempos, que ha tenido además un desarrollo vertiginoso. Todo el mundo lo relaciona con las matemáticas porque hay que colocar números en sus casillas, aunque su relación con esta ciencia es más profunda.
Desde que se diera a conocer internacionalmente el verano de 2005, el sudoku se ha convertido en todo un fenómeno de masas. Tenemos sudokus en los periódicos, revistas de sudokus, libros de sudokus, sudokus en todos los dispositivos electrónicos existentes (móviles, tabletas, ordenadores, etc), juegos de sudokus en las tiendas de juguetes, programas de ordenador para crear sudokus, colecciones por entregas relacionadas con el sudoku en los estancos, sudokus infantiles y una enorme cantidad de variantes del original.
 Sudoku 3 9×9-63 Typesetting F (2014), del artista esloveno Jaka Bonča (conocido también como Rototype). Imagen de la página web de Jaka Bonča
Sudoku 3 9×9-63 Typesetting F (2014), del artista esloveno Jaka Bonča (conocido también como Rototype). Imagen de la página web de Jaka BončaAunque seguramente las personas que estén leyendo esta entrada del Cuaderno de Cultura Científica ya conocerán perfectamente qué es un sudoku, empezaremos recordando las reglas de este pasatiempo matemático. El sudoku normal consiste en una cuadrícula de 9 x 9 celdas, dividida en 9 regiones de 3 x 3 celdas, y hay que rellenar las 81 celdas con las cifras del 1 al 9 (partiendo de una situación inicial en la que algunos números ya están colocados en algunas de las celdas), de manera que no se puede repetir ninguna cifra en una misma fila, columna o región. El sudoku está relacionado con los cuadrados latinos (véase la entrada Cuadrados latinos, matemáticas y arte abstracto o el libro Del ajedrez a los grafos, la seriedad matemática de los juegos) estudiados por el matemático Leonard Euler (1707-1783), aunque el juego moderno fue creado en la década de 1970 por el arquitecto jubilado y diseñador de pasatiempos Howard Garns (1905-1989) y publicado bajo en nombre number place en la revista Dell Pencil Puzzles & Word Games.
Maki Kaji, presidente de la editorial Nikoli, especializada en juegos y pasatiempos, en particular, rompecabezas lógicos, lo exportó a Japón y empezó a publicarlo en 1984 en su revista Monthly Nikolist bajo el nombre Suji wa dokushin ni kagiru (los números deben estar solos), que se abrevió a Su Doku. Su expansión por el resto del mundo vino de la mano del juez retirado neozelandés, residente en Hong Kong, Wayne Gould, quien desarrolló un programa de ordenador para crear rápidamente sudokus. En 2004 empezaron a publicarse sudokus en periódicos británicos, como The Times y The Guardian, y acabó convirtiéndose, desde 2005, en un rompecabezas muy popular que aparecía en la mayoría de los periódicos del mundo.
 Un típico sudoku, en el que aparecen algunos números, pero las demás casillas están vacías y hay que rellenarlas siguiendo las reglas del rompecabezas. Imagen de Wikimedia Commons
Un típico sudoku, en el que aparecen algunos números, pero las demás casillas están vacías y hay que rellenarlas siguiendo las reglas del rompecabezas. Imagen de Wikimedia Commons
 Solución del sudoku anterior. Imagen de Wikimedia Commons
Solución del sudoku anterior. Imagen de Wikimedia Commons
La relación del sudoku con las matemáticas no es que se utilicen números, ya que se podrían utilizar letras, colores o cualesquiera otros símbolos, sino que es de tipo combinatorio, está basada en la relación entre las diferentes posiciones de los símbolos (números) en las filas, columnas y regiones. Si observamos la solución de un sudoku, como la anterior imagen, se trata de un tipo particular de cuadrado latino (recordemos que un cuadrado latino de orden n es un retículo cuadrado de tamaño n x n en el que cada entrada es un número del 1 al n, de tal forma que cada número de {1, …, n} aparece una vez, y sólo una vez, en cada fila y cada columna) de tamaño 9 x 9, en el que se verifica también que los números del 1 al 9 aparecen solo una vez en cada una de las nueve regiones 3 x 3.
 Cuadro del pintor suizo Richard Paul Lohse, que bajo el título “Komplementäre Gruppen durch sechs horizontale systematische Farbreihen” -Grupos complementarios formados por seis series sistemáticas horizontales de color- (1950 y 1976), recoge un cuadrado latino de orden 6 cuyos símbolos son los colores
Cuadro del pintor suizo Richard Paul Lohse, que bajo el título “Komplementäre Gruppen durch sechs horizontale systematische Farbreihen” -Grupos complementarios formados por seis series sistemáticas horizontales de color- (1950 y 1976), recoge un cuadrado latino de orden 6 cuyos símbolos son los colores
Existen diferentes cuestiones matemáticas implicadas en este rompecabezas, como cuántas estructuras de solución, es decir, cuadrados latinos de orden 9 que cumplen la regla de las regiones diferentes, hay (que resultan ser 6.670.903.752.021.072.936.960, aunque si tenemos en cuenta las simetrías, estas se reducen a 5.472.730.538 soluciones de sudokus distintas); dado un cuadrado latino de orden 9 que es solución de sudoku, cuántos rompecabezas sudokus distintos se pueden generar a partir del mismo (es decir, eliminando los números de las casillas hasta dejar una pequeña cantidad inicial que es el punto inicial del juego, las pistas) y cuál es la cantidad mínima de números iniciales (pistas) que se necesitan para que el sudoku esté bien definido, esto es, que exista una solución única (que resultan ser 17 pistas), entre otras.
Sin embargo, mi intención en esta entrada de la sección Matemoción del Cuaderno de Cultura Científica no es hablar de las matemáticas de los sudokus (puede verse, por ejemplo, el artículo Sudokus y modelización, de María Merino), sino presentar otros rompecabezas matemáticos similares a este, en el sentido de que se colocan números sobre una estructura reticular.
En el año 2010, Jai Gomer, de Kobayaashi Studios, desarrolló una serie de rompecabezas numéricos, llamados sujiko y suko, herederos de los sudokus, pero que ya implican algo de aritmética –en concreto la suma– en sus reglas. Estos aparecieron primero en los periódicos ingleses como The Times y The Telegraph, y posteriormente en periódicos de todo el mundo, como, por ejemplo, El País.
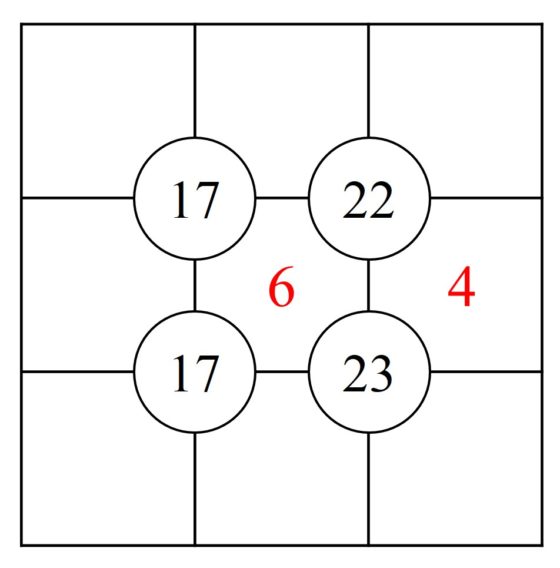
El tablero del sujiko es una cuadrícula 3 x 3, con cuatro espacios circulares colocados en las cuatro intersecciones de las líneas horizontales y verticales de la cuadrícula, en los cuales hay escritos cuatros números (por ejemplo, 17, 22, 17, 23, en la imagen anterior). El objetivo del pasatiempo es colocar los números del 1 al 9 en las celdas –aunque puede haber ya alguno colocado, como pista (en el sujiko anterior 6 y 4)– de forma que la suma de los números que estén en los recuadros alrededor de cada círculo es exactamente el número escrito en el mismo.
Este rompecabezas de resuelve de forma lógica, como el sudoku, pero teniendo en cuenta su regla, que la suma de los números de las celdas alrededor de un círculo es el valor del mismo. Veamos cómo resolver el sujiko anterior, que es de los sencillos.
Los números de las dos casillas de arriba a la derecha deberán sumar 12, ya que 6 y 4 están también alrededor del 22 y su suma es 6 + 4 = 10. Como en esas casillas no pueden estar 6 y 4, que ya están colocados, las dos opciones son 9 y 3, o 7 y 5, sin determinar aún cual va en cada una de las dos casillas. Si realizamos el mismo razonamiento para las dos celdas de abajo a la derecha, que deberán sumar 13, la única posibilidad es 8 y 5. Como aquí estaría el número 5, en las dos celdas de arriba tendrían que ser los números 9 y 3.
Veamos el orden arriba. En la casilla central de la fila de arriba va el 3 o el 9, si fuese el 9 tendríamos que alrededor de la casilla del 17 ya se sumaría 9 + 6 = 15, luego las otras dos casillas deberían sumar 2, lo cual es imposible, puesto que la suma más baja posible sería 1 + 2 = 3. En conclusión, en la primera fila, el número 3 iría en la casilla central y el 9 en la derecha.
Antes de seguir, pensemos en que tres números nos faltan de utilizar para las celdas de la columna de la izquierda. Serían 1, 2 y 7. Entonces, alrededor del 17 de arriba tenemos 3 + 6 = 9, más la suma de los números de las dos celdas, que deberá ser 8, luego los números de esas dos celdas son 1 y 7. Si seguimos este razonamiento un poco más, obtendremos la solución definitiva, que aparece en la imagen de abajo.
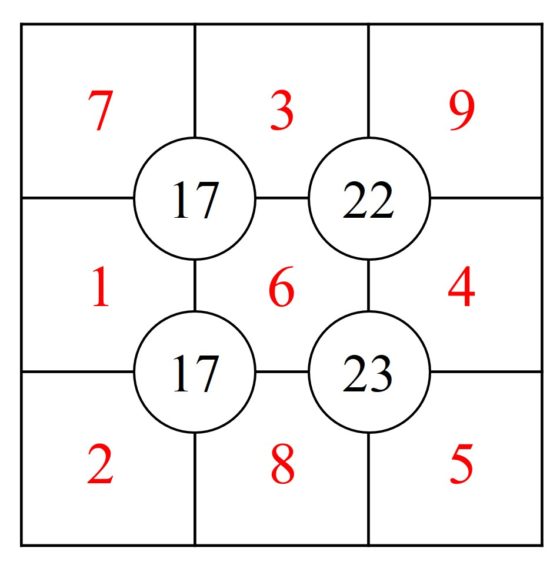
Podemos presentar este problema de la siguiente forma. La información del mismo está dada en el siguiente esquema, donde en las celdas tenemos las variables del juego y en los círculos los datos del mismo.
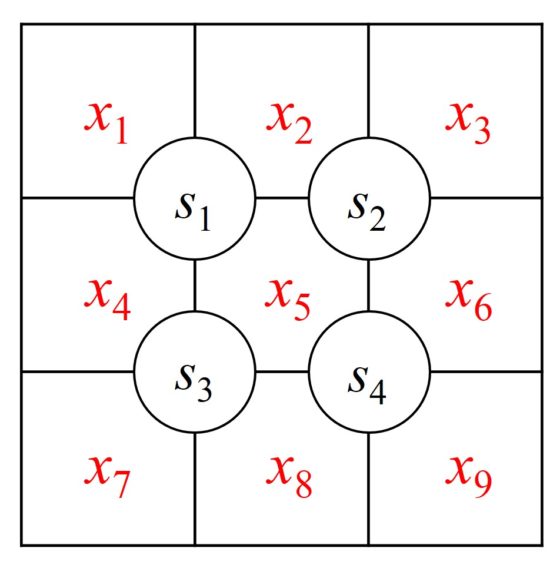
Luego la solución del sujiko es la solución de un sistema de cuatro ecuaciones y nueve incógnitas, aunque con las siguientes restricciones, las variables solo toman valores entre los números 1, 2, 3, 4, 5, 6, 7, 8, 9 y cada variable toma un valor distinto a las otras.
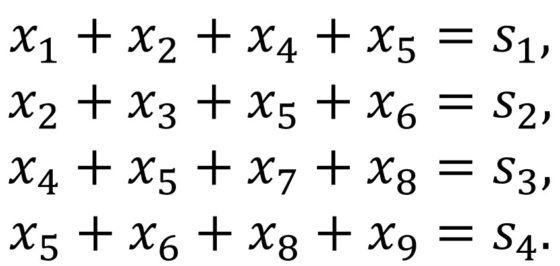
Aunque la diversión del sujiko está en obtener la solución de forma lógica, se puede utilizar también el planteamiento algebraico como ejemplo para estudiantes que estén trabajando el álgebra lineal de la resolución de los sistemas de ecuaciones lineales.
Os dejo con dos sujikos, de niveles medio y alto, que he sacado de la página Sudokasana, donde se denominan Minisum puzzles. Aunque también podéis encontrar sujikos en la página de pasatiempos del periódico The Times.
Por otra parte, el rompecabezas suko es como el sujiko, pero al que se le añade una nueva condición relacionada con regiones del retículo 3 x 3. La condición es que la suma de los números de las casillas de un mismo color suman la cantidad indicada en el pasatiempo, como aparece en la siguiente imagen (suko que hemos tomado de la página de pasatiempos de The Times).
Desde el punto de vista algebraico, en el suko añadimos tres ecuaciones lineales más, luego tenemos un sistema de siete ecuaciones lineales con nueve incógnitas, y la solución del rompecabezas es la solución del sistema de ecuaciones.
Otro rompecabezas relacionado con el sudoku, o más bien con los cuadrados latinos, pero que añade aritmética –aunque ahora las cuatro operaciones aritméticas, no solo la suma– a sus reglas es el KenKen.
El rompecabezas KenKen, también conocido con los nombres KenDoku, MathDoku o CalcuDoku, fue inventado por el profesor de matemáticas japonés Tetsuya Miyamoto como una herramienta para ejercitar el cerebro. Su nombre se deriva del vocablo japonés Ken que significa inteligencia o ingenio.
En 2007 el inventor de juguetes Robert Fuhrer, propietario de la empresa de juguetes Nextoy, descubrió en Japón varios libros con este pasatiempo y su interés por el mismo haría que el rompecabezas lógico acabara en las páginas del periódico británico The Times y después en muchos otros periódicos de todo el mundo.
Las reglas del KenKen son las siguientes. Se parte de una cuadrícula n x n sobre la que hay que colocar los números de 1 a n de forma que en cada fila y cada columna estén todos los n números y no se repita ninguno (luego será un cuadrado latino de orden n), pero además la retícula está dividida en una serie de regiones, en cada una de las cuales aparecen una operación aritmética (suma, resta, multiplicación o división) y un número, que será el resultado de aplicar la operación aritmética indicada a los números de las celdas de esa región.
En el siguiente ejemplo de rompecabezas KenKen tenemos una cuadrícula 4 x 4, luego hay que escribir los números 1, 2, 3 y 4 en las celdas de la misma, de forma que se constituya un cuadrado latino –en cada fila y cada columna aparece cada uno de los cuatro números una y solo una vez– y se cumplan las condiciones aritméticas de las regiones –por ejemplo, en la región de arriba a la izquierda la división de los dos números es 2, o en la región de la derecha la resta de los dos números es también 2–.
La solución de este KenKen viene dada en la siguiente imagen.
En la página KenKen, puzzles that make you smarter se pueden encontrar rompecabezas con cuadrículas desde 3 x 3 hasta 9 x 9, de diferentes niveles de dificultad. Os dejamos con uno para que os divirtáis de tamaño 6 x 6 y dificultad media.
Otro de los juegos de la editorial Nikoli, famosa internacionalmente por el Sudoku, es el Hitori, término que en japonés significa “solitario”. Este pasatiempo consiste en una retícula con números en todas sus celdas y la acción del mismo consiste en eliminar una serie de números, o pintar de negro las celdas correspondientes, de forma que se cumplan las siguientes reglas:
i) en cada fila y cada columna no se repite ningún número;
ii) las celdas tachadas o negras no pueden ser adyacentes (pueden tocarse esquina con esquina, pero no lado con lado);
iii) el resto de las celdas con números tienen que estar conectadas, vertical u horizontalmente, entre sí, es decir, no pueden quedar celdas aisladas.
Veamos en qué consiste el juego mediante un ejemplo concreto de tamaño 5 x 5.
La solución aparece en la siguiente imagen. Como podemos observar, se cumplen las tres condiciones de este rompecabezas lógico. En cada fila y cada columna de la solución no se repite ningún número, por ejemplo, en la primera fila había dos celdas con el número 3, luego se ha tenido que tachar una. Las celdas tachadas solo se tocan por los vértices o no se tocan. Y no hay celdas aisladas de las demás.

En la página Hitori Conquest [www.hitoriconquest.com/] pueden encontrarse más rompecabezas Hitori de tamaños 5 x 5, 8 x 8 y 12 x 12, como el que dejamos a continuación para aquellas personas que queráis pasar un buen rato resolviéndolo.
Vamos a concluir esta entrada del Cuaderno de Cultura Científica con otro de los rompecabezas lógicos popularizado por la editorial japonesa Nikoli, el conocido como Numberlink (que podríamos traducir como “conecta los números”). Este juego tiene su origen en la matemática recreativa clásica, ya que una versión del mismo fue propuesta por el matemático recreativo estadounidense Sam Loyd (1841-1911) en 1897 y también por el matemático recreativo inglés Henry Dudeney (1857-1930), en su libro Amusements in Mathematics (1917), el problema 252, que vemos en la siguiente imagen.

El rompecabezas consiste en una retícula en la que aparecen parejas de números (aunque también podrían ser letras, colores u otros símbolos), dos unos, dos doses, dos tres, etcétera. El jugador tiene que conectar cada número con su igual mediante una línea que pasa de una celda a otra, horizontal o verticalmente, de tal forma que las líneas no se pueden cruzar entre sí, ni volver hacia atrás a celdas ya recorridas y no debe de quedar ninguna celda sin ser recorrida por alguna línea (aunque hay algunos diseñadores de juegos que se saltan esta regla).
Veamos un sencillo ejemplo y su solución.
Os dejamos propuesto un rompecabezas lógico conecta los números, sacado de la página Puzzle’s Baron Numberlinks, para vuestro disfrute.
Para todos los rompecabezas lógicos presentados en esta entrada existen aplicaciones para móviles que os podéis bajar y jugar en cualquier momento. Yo mientras escribía esta entrada me he bajado algunas a mi móvil para poder jugar tranquilamente.
 2x Sudoku I (2006), de la artista polaca Eliza Kopec. Imagen de la página Affordable Art Fair
2x Sudoku I (2006), de la artista polaca Eliza Kopec. Imagen de la página Affordable Art FairBibliografía
1.- Raúl Ibáñez, Sudoku, Las matemáticas en la publicidad, DivulgaMAT, 2011.
2.- María Merino, Sudokus y modelización, Un paseo por la Geometría 2009/2010, UPV/EHU, 2010.
3.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, colección El mundo es matemático, RBA, 2015.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Rompecabezas matemáticos con números se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Locura instantánea, un rompecabezas con cubos de colores
- Números errores de impresión
- Quipu y yupana, instrumentos matemáticos incas (II)
Historia de Uri Geller
Hay personas que son capaces de hacer cosas extraordinarias. Entre ellas, por ejemplo, se encuentran las y los deportistas de élite, que son capaces de realizar proezas imposibles para el resto de los mortales. Pero también nos encontramos con otras que realizan cosas, en apariencia, imposibles y que se escapan a nuestra compresión.
Una de ellas es Uri Geller. Un ilusionista que se hizo famoso hace unas cuantas décadas porque doblaba las cucharas con el supuesto poder de su mente. Sí, Uri acudió a distintos programas de televisión haciendo su número de las cucharas. Pero… ¿tenía realmente poderes mentales para hacer tal cosa?
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia de Uri Geller se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Historia de la quinina
- La historia del bolígrafo más famoso del mundo
- Ciencia y Misterio, la webserie
Las reglas de desplazamiento radiactivo
 Foto: Sebastian Yepes / Unsplash
Foto: Sebastian Yepes / UnsplashEl concepto de isótopo fue un avance muy significativo en la comprensión de la radiactividad. Pero aun estaban sobre la mesa dos cuestiones fundamentales, a saber, ¿cómo se producen los cambios en la naturaleza química cuando un átomo sufre una desintegración radiactiva? y ¿qué determina si el número atómico Z aumenta o disminuye en una transformación radiactiva dada?
En 1913, Soddy en Inglaterra y Kazimierz Fajans [1] en Alemania respondieron estas preguntas de forma independiente. Ambos propusieron dos reglas que sistematizaban todas las observaciones relevantes de la radiactividad natural. Se llaman reglas (hay quien las llama leyes) de Fajans-Soddy, reglas de transformación de la radiactividad o reglas de desplazamiento radiactivo.
Para 1913 el modelo nuclear del átomo de Rutherford estaba generalmente aceptado. Usando este modelo se podía considerar que un átomo radiactivo tiene un núcleo inestable que emite una partícula alfa o una partícula beta (a veces con emisión de un rayo gamma). Cada núcleo tiene una carga positiva dada por Ze, donde Z es el número atómico y e es la magnitud de la carga de un electrón. El núcleo está rodeado por Z electrones que hacen que el átomo en su conjunto sea eléctricamente neutro y determinan el comportamiento químico del átomo.
Por otra parte, sabemos que una partícula alfa tiene una masa atómica de aproximadamente cuatro unidades y una carga positiva de dos unidades, +2e. Una partícula beta tiene una carga negativa de una unidad, -e, y muy poca masa en comparación con una partícula alfa.
Con esta información en mente, las reglas de transformación radiactiva [2] dicen lo siguiente:
1. Cuando un núcleo emite una partícula alfa, la masa del átomo disminuye en cuatro unidades de masa atómica y el número atómico Z del núcleo disminuye en dos unidades; el átomo resultante pertenece a un elemento dos espacios hacia atrás en la tabla periódica.
2. Cuando un núcleo emite una partícula beta, la masa del átomo cambia muy poco, pero el número atómico Z aumenta en una unidad; el átomo resultante pertenece a un elemento un espacio hacia delante en la tabla periódica.
3. Cuando solo se emite un rayo gamma, no hay cambio en el número correspondiente a la masa atómica, ni en el número atómico.
 La tabla de la serie radiactiva que venimos usando como ejemplo muestra cómo se aplican estas reglas de desintegración radiactiva a esa serie, al menos en lo que respecta al número atómico.
La tabla de la serie radiactiva que venimos usando como ejemplo muestra cómo se aplican estas reglas de desintegración radiactiva a esa serie, al menos en lo que respecta al número atómico.
Estas reglas, usando ahora el modelo del átomo de Rutherford-Bohr-Sommerfeld, ayudan a explicar por qué se produce un cambio en la naturaleza química como resultado de la emisión de una partícula alfa o beta. La emisión de una partícula alfa requiere dos cargas positivas del núcleo y cuatro unidades de masa atómica del átomo. Un ejemplo es el siguiente:
21884Po → 21482Pb + α
El nuevo átomo resultante (82Pb) con su núcleo menos positivo puede contener en sus capas externas dos electrones menos que antes, por lo que los dos electrones en exceso se pierden. El comportamiento químico de los átomos está controlado por el número de electrones; por lo tanto, el nuevo átomo actúa químicamente como un átomo de un elemento con un número atómico dos unidades menor que el del átomo original.
Por otro lado, en el caso de la emisión beta, el núcleo, y con él todo el átomo, adquiere una carga positiva. Un ejemplo es el siguiente:
23490Th → 23491Pa + β
El número de electrones que el átomo puede contener alrededor del núcleo ha aumentado en uno. Después de que ha recogido un electrón extra para volverse neutral nuevamente, el átomo actúa químicamente como un átomo con un número atómico una unidad mayor que el del átomo antes de que ocurriera el cambio radiactivo.
Usando estas reglas de transformación, Soddy y Fajans pudieron determinar el lugar en la tabla periódica para cada una de las sustancias (o nucleidos) en la serie radiactiva; no era necesaria ninguna revisión de la tabla periódica existente. Ahora se sabe que muchos de los elementos entre Z = 82 (plomo) y Z = 92 (uranio) contienen varios isótopos cada uno. Estos resultados se podían deducir de la hipótesis de la existencia de isótopos, pero también se buscaron, y se obtuvieron, pruebas directas e independientes en 1914.
Notas:
[1] Unos de esos científicos olvidados de la primera mitad del siglo XX , a los que el Nobel pasó rozando y que lo hubieran merecido. Hoy sus descubrimientos están en libros de texto de física y química, muchas veces de forma anónima.
[2] A estas alturas de la serie, la lectora atenta posiblemente encontrará las reglas dignas de Pero Grullo, pero en 1913 fueron un gran avance.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las reglas de desplazamiento radiactivo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:¿Se pueden ver los átomos?
Javier Fernández Panadero
Hay preguntas muy fáciles de hacer y no tan fáciles de contestar… pero vamos a intentarlo.
Repuesta simple: ¿Ves este plátano? ¿Sí? Pues está hecho de átomos. Conclusión: ves los átomos.
¿Seguro? No sé vosotros, pero mis ojos no ven “plátanos”. Mi retina es sensible a la luz, no a la fruta.
Eso significa que, cuando hablo de que veo algo, en realidad, lo que estoy haciendo es detectar luz que proviene de aquello que digo ver. Bien porque ese objeto la emita o bien porque la refleje o disperse.
En el caso del plátano, una parte de la luz incidente se absorbe y otra parte se refleja, pero no de forma igual para todos los colores. Las frecuencias próximas al “amarillo” resultan reflejadas en mayor cuantía. De esta forma, la luz reflejada llega a mi retina y así percibo la forma, “su” color, si la piel es suave o rugosa y otras características que son capaces de alterar de alguna manera la radiación incidente, para que la reflejada “transporte” información sobre ellas.
Bien, ¿es eso, entonces, VER?
Este… no.
VER es un proceso que quizá comience en el ojo, pero que sin duda termina en el cerebro.
Contestadme a esta pregunta: ¿Qué es esto?
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsSi habéis dicho “Un cubo”, estáis hablando de algo más allá de lo que ven los ojos. Un cubo es una figura tridimensional, pero esto que ves es un dibujo PLANO. Son unas líneas sobre un plano que te “hacen pensar” en un objeto tridimensional, es lo que llamamos perspectiva. De hecho, si os concentráis podéis conseguir ver el “cubo” de dos formas distintas, según escojáis en vuestra mente si son los vértices inferiores los que están “delante” o son los superiores.
Por lo tanto, el acto de VER se completa cuando la mente modeliza el patrón de puntos e interpreta un modelo de lo que está percibiendo.
A veces “viendo” cosas que no existen, por ejemplo “completando” la imagen percibida, como en este caso, donde el triángulo blanco, que todos “vemos”, no existe.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsMirad esta otra.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsEn este caso, nuestra mente interpreta que las “vías” son paralelas, y están alejándose, por lo que esa barra amarilla que hay “a lo lejos” debe de ser más grande que la que está “delante”. Pero todo eso son interpretaciones de nuestro cerebro para adecuar la percepción en el modelo del mundo que nos hemos ido construyendo… y esto supera con creces la información que está contenida en la imagen, de hecho, nos puede llevar a conclusiones erróneas sobre ella, como en este caso.
Bien, pero volvamos a la pregunta inicial.
Asumiendo todas estas limitaciones sobre el acto de VER, ¿podemos ver los átomos, Javi?
No, son muy pequeños, tus ojos no llegan a tanto. Si pensamos en la parte óptica de tu ojo: el cristalino, la pupila, los humores, la resolución de la retina… No, no llegas a resolver algo tan pequeño.
Muy bien -protestas, pero, ¿qué me dices de esto?
https://culturacientifica.com/app/uploads/2020/10/Espermatozoides.ogvSon espermatozoides, muy pequeños como para verlos al ojo desnudo, pero visibles a través de métodos ópticos, interponiendo lentes de suficiente potencia como para ampliarlos hasta que pueda percibirlos usando los ojos.
Por lo tanto, usando “lupas gordas” podemos “ver con los ojos” cosas muy pequeñas. ¿Podríamos, entonces, poner una enorme lente y ver los átomos?
No. Son demasiado pequeños. Pero, tenme paciencia, de verdad que quiero contestar a tu duda inicial. Mira la siguiente imagen y contéstame a una pregunta.
 Fuente: Wikimedia Commons
Esto es lo que llamamos una imagen térmica. Nuestros ojos no pueden ver la radiación infrarroja, pero esta cámara sí es capaz de detectarla y “crear” una imagen en una pantalla.
Fuente: Wikimedia Commons
Esto es lo que llamamos una imagen térmica. Nuestros ojos no pueden ver la radiación infrarroja, pero esta cámara sí es capaz de detectarla y “crear” una imagen en una pantalla.
Podéis hacer un experimento sobre esto con la cámara de vuestro teléfono móvil y un mando a distancia. Mirad la “bombillita” del mando a distancia. Cuando pulsáis un botón no se ve nada… porque la emisión es infrarroja. Ahora, miradla a través de la cámara de vuestro móvil y pulsad algún botón del mando. A través del móvil veréis que emite un parpadeo, un código con la orden que está mandando el mando. Según tu teléfono lo veréis de un color ligeramente diferente, por ejemplo violeta o blanco (funciona en casi todos los modelos de teléfono). Pero si miráis directamente al mando veréis… que no veis nada. Aquí puedes ver un vídeo con esta demostración de mi libro Experimentos para entender el mundo. La ciencia para todos.
Tengo una pregunta para ti. Ese color violeta que veo a través de la cámara, ¿es violeta? Quiero decir: ¿Es el color violeta de la luz visible que veo normalmente? No, ¿verdad? Si esa “bombillita” emitiese luz violeta, de la de “verdad”, la podría ver sin necesidad de la cámara. Ese color se lo “inventa” la cámara del móvil, ha convertido esa radiación infrarroja en luz visible con el color que le ha parecido. A eso lo llamamos falso color.
Volvamos a la foto del gato. Ese gato no tiene partes naranja, blancas o moradas. Eso son códigos de colores que elige el sistema de imagen térmica para representar distintas temperaturas. De hecho, tenéis la correspondencia entre color y temperatura a la derecha de la imagen. Como os podréis imaginar, esas escalas pueden modificarse, según lo que queramos medir.
Y ahora te pregunto yo, a la vista de esta imagen, ¿dirías que estamos VIENDO la temperatura?
Hay quien contestaría que no, que solo podemos hablar de VER si estamos usando sistemas ópticos y el ojo. Para ellos, aquí termina su viaje. No podemos ver los átomos.
Pero si eres más flexible en tu definición y te permites llamar VER a esto que hemos hecho con la temperatura, digamos a cambiar tu retina por un sistema de sensores y tu mente por un procesador que lo convierta en una imagen, te diré que sí, que podemos ver los átomos.
Para ello vamos a necesitar un sistema que sea capaz de medir a escala suficientemente pequeña, para luego componer, crear, inventarse una imagen a partir de esos datos, una representación. Lo mismo que hicimos con el gato y el mapa de falso color de temperaturas. Es importante que recuerdes que esa imagen coloreada del gato no existe, no es “real”, está construida a partir de datos.
Pero además con el átomo tenemos otro problema… un átomo no es “sólido”. Se parece más a una pequeña partícula (el núcleo) rodeada de un enjambre de electrones que, debido a su movimiento dan la impresión de formar una pequeña “bola”, pero no es algo macizo.
Así que de nuevo tenemos un problema. ¿Qué es lo que vamos a intentar “ver” del átomo? Pues vamos a intentar “percibir” ese enjambre de electrones, que, aunque sólo sea uno, se mueve por una región tan amplia y a tanta velocidad que da la impresión de una distribución de carga negativa esférica alrededor de ese núcleo, de una “nube”.
Un aparato capaz de esto es el microscopio de efecto túnel. Y este es un esquema de su funcionamiento:
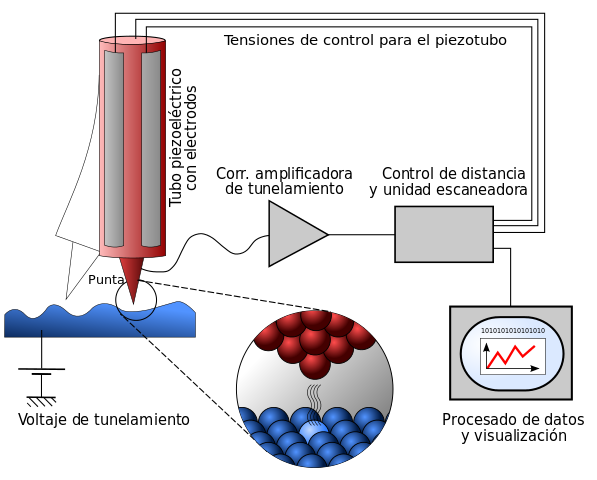 Fuente: Wikimedia CommonsLas “bolitas” rojas representan los átomos finales de la punta que escanea el material y las azules, los de la muestra del material que queremos medir.
Fuente: Wikimedia CommonsLas “bolitas” rojas representan los átomos finales de la punta que escanea el material y las azules, los de la muestra del material que queremos medir.
Se dispone un voltaje suficientemente pequeño para que, según la física clásica, no se establezca una corriente entre la punta y el material… pero por una curiosa propiedad cuántica, sí se producirá una corriente. Y esa corriente tiene una relación muy estrecha con la anchura de la separación entre punta y material. De esta forma, midiendo la corriente, podemos estimar esa distancia.
Como habrás notado, esto se diferencia mucho de lo que solemos llamar “ver”.
Si vamos moviendo la punta por toda la superficie del material y vamos calculando las distancias… podríamos DIBUJAR un “mapa” de ese material, ponerlo en una pantalla y… verlo.
Efectivamente, aquí tenéis:
 Fuente: Wikimedia Commons
Y, efectivamente, esto es oro… y esas bolitas, los átomos de oro.
Fuente: Wikimedia Commons
Y, efectivamente, esto es oro… y esas bolitas, los átomos de oro.
Bueno, en realidad, son las “cortezas”, las nubes electrónicas de esos átomos, interaccionando con la punta del microscopio de efecto túnel.
Bueno, en realidad, son las medidas de distancias, calculadas a partir de las medidas de corriente eléctrica que hemos obtenido al ir paseando la punta del microscopio por la muestra de oro.
Bueno, en realidad, es la representación gráfica de esas distancias, (que han PINTADO de amarillo para que te parezca más oro, qué tramposos), en una foto, hecha pixel a pixel.
Así que, por fin, hemos llegado al final del camino y voy a contestar a la pregunta con que empezamos…
Los átomos son tan pequeños que no podemos verlos con nuestros ojos desnudos.
Los átomos son tan pequeños que no podemos verlos con sistemas ópticos.
Los átomos ni siquiera tienen un “cuerpo macizo” que pudiéramos ver, así que nos conformamos con poder “sentir” su corteza electrónica.
Así que lo que hacemos es usar unos aparatos que midan con más precisión que nuestros sentidos y poner todos esos datos en forma de una imagen.
Para mí, eso es VER. Medir y organizar datos para poder hacerme un modelo del mundo.
Por lo tanto, yo veo los átomos.
¿Qué opinas tú? ¿Crees que acabas de ver átomos?
Sobre el autor: Javier Fernández Panadero es físico y profesor de secundaria además de un prolífico autor de libros de divulgación científica.
El artículo ¿Se pueden ver los átomos? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Entrelazamiento cuántico entre dos nubes de átomos ultrafríos
- ¿Por qué los átomos tienen el tamaño que tienen?
- De cómo se formaron los átomos de mi mano
De la química al tratado internacional o de por qué la ciencia cambia cosas
Mikel Mancisidor
Hace unos días el Comité Nobel anunció que este año las premiadas en su modalidad de Química serían la francesa Emmanuelle Charpentier y a la estadounidense Jennifer A. Doudna “por el desarrollo de un método para la edición del genoma”. Ese mismo día, el azar a veces tiene estas cosas, moría quien había ganado ese mismo premio 25 años antes: el mexicano Mario Molina.
 José Mario Molina Pasquel y Henríquez (1943-2020). Fuente: nobelprize.org Foto: © University of California, San Diego / Donna Coveney / MIT
José Mario Molina Pasquel y Henríquez (1943-2020). Fuente: nobelprize.org Foto: © University of California, San Diego / Donna Coveney / MIT
Molina obtuvo el Nobel de Química en 1995 por su participación en el descubrimiento del agujero de la capa de ozono y por sus trabajos sobre los compuestos de cloro como causante de ese agujero. Gracias a su trabajo (y el de otros, claro está, que la ciencia acostumbra a ser una empresa colectiva) la comunidad internacional pudo conocer el problema, se hizo consciente de su gravedad y de la necesidad de combatirlo. A raíz de ello se adoptó el Convenio de Viena para la protección de la capa de ozono (1985) y posteriormente su Protocolo de Montreal (1989), que prohibió la producción y emisión de los CFC causantes de ese deterioro. Este Protocolo incluía compromisos concretos y diferenciados por parte de los países y fechas concretas para su cumplimiento. Se incluyeron medios técnicos, jurídicos y financieros. Los estados y los agentes industriales y comerciales cumplieron. Como resultado de todo ello, la emisión de esos productos se eliminó en unos años, permitiendo que su concentración se vaya poco a poco reduciendo. El Convenio y su Protocolo han sido un éxito: la situación está ya revirtiendo y se espera que en 35 años la capa de ozono se haya recuperado prácticamente por completo.
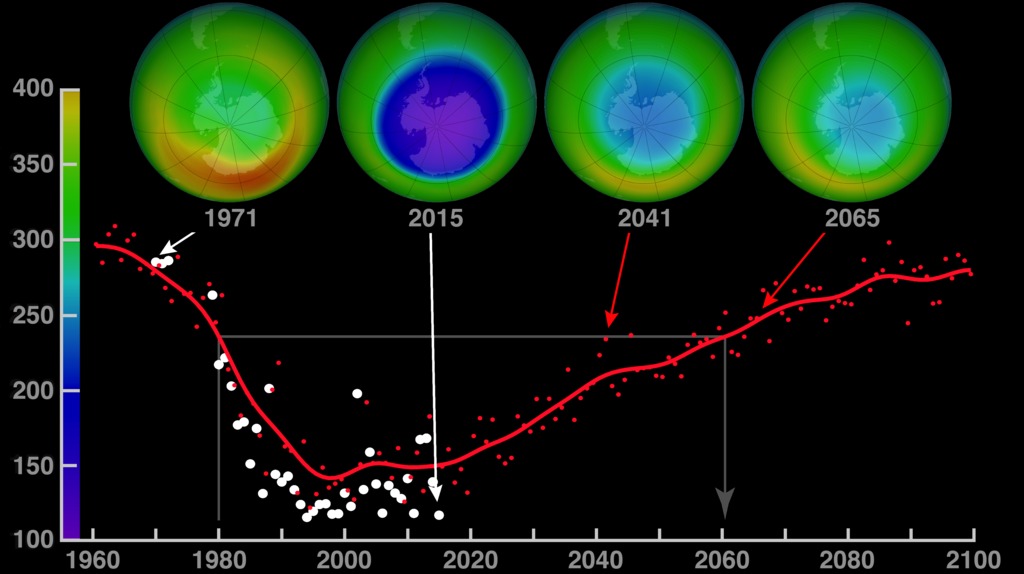 Evolución del agujero antártico de la capa de ozono desde 1960 y proyección a 2100. Fuente: NASA
Evolución del agujero antártico de la capa de ozono desde 1960 y proyección a 2100. Fuente: NASANo sé si ustedes lo han observado, pero de vez en cuando uno lee o escucha a comentaristas que emplean este caso de éxito para defender exactamente lo contrario de lo que a mi juicio podría enseñarnos. Hace no mucho, por poner un ejemplo entre tantos, un medio online de los más importantes del país publicaba un artículo de uno de sus colaboradores que decía: “el cambio climático está de moda. Yo, que he vivido la moda del agujero en la capa de ozono (¿alguien sabe qué pasó con el agujero y, mayormente, con el ozono?), debo reconocer que duermo muy tranquilo por las noches mientras el planeta se dirige hacia su destrucción total. Lo siento: duermo por las noches arrullado por mil problemas personales y ninguno es el cambio climático. En cierta medida, les envidio. Envidio que ustedes tengan tiempo de salvar un planeta mientras yo apenas puedo salvar mi matrimonio.”
Como gracieta tampoco es tan original, de hecho no es la primera vez que oigo o leo que esto del cambio climático es una distracción de ociosos y diletantes como lo fue, al aparecer, la moda de la emergencia del agujero de la capa de ozono que, según parece, surgió de la nada, alarmó gratuitamente un par de temporadas (coincidiendo con la no menos alarmante moda de las hombreras) y por arte de magia desapareció de la agenda sin dejar rastro. En algo estoy de acuerdo: debemos recordar el caso del agujero de la capa de ozono. Pero yo leo aquí justo lo contrario que quienes creen que son modas que vienen y se van. «¿Alguien sabe qué pasó con el agujero y con el ozono?», se pregunta el articulista como queriendo dar a entender que nadie lo sabe. Pero sí se puede saber: basta con interesarse un poco y dedicarle unos minutos de atención en fuentes rigurosas.
No estamos ante una graciosa historia de una moda tonta que vino y se fue. Estamos ante un problema que muy justificadamente alarmó y que la comunidad internacional fue capaz de revertir reaccionando con conocimiento científico, implicación social y voluntad política. Este es un buen ejemplo para otros problemas, especialmente para el cambio climático y de alguna forma también para la pandemia de la COVID-19. Estos retos, como aquel, solo se pueden afrontar sumando conocimiento científico riguroso, responsabilidad ciudadana y buena dirección política.
Los problemas citados son diferentes, sin duda. El problema de los CFC se pudo atajar de una forma tan eficaz, entre otras cosas, porque se trataba de un problema bien definido, sobre el que había alternativas técnicas maduras que eran económicamente asumibles y no presentaban dificultades políticas insalvables. Pero no por ello fue un problema menor, ni fácil, ni una experiencia que podamos despreciar o de la que podamos darnos el lujo de no querer aprender.
Cierto que el problema del cambio climático es más complejo técnica y científicamente, con alternativas más difíciles, mucho más caras, con implicaciones endiabladas. No quiero decir por tanto que la forma de afrontar el problema del Cambio Climático pueda seguir los mismos pasos o al mismo ritmo que el problema de la capa de ozono, pero sí que, tanto en un caso como en otro, nada podrá hacerse si no es en alianza entre la ciencia, la sociedad, la economía y la política.
Mario Molina lo dijo recientemente en una de sus últimas entrevistas: «La capa de ozono es un ejemplo importantísimo de un problema global que se pudo resolver con éxito». Y lo dijo mucho antes, con enorme visión, en su discurso de recepción del Nobel en 1995:
“[…] este problema global nos ha mostrado que diferentes sectores de la sociedad pueden trabajar juntos – la comunidad científica, la industria, las organizaciones medioambientales, los representantes gubernamentales y los gestores públicos- para llegar a acuerdos internacionales: el protocolo de Montreal ha establecido un importante precedente para la solución de problemas medioambientales globales”.
Hemos tenido estas últimas semanas polémicas, no siempre constructivas, sobre la relación entre la ciencia y la política. Molina también habló en su momento de estas cosas: «los científicos pueden plantear los problemas con base en la evidencia disponible, pero su solución no es responsabilidad de los científicos, es de toda la sociedad».
¿Puede usted imaginar mensajes más actuales, más ambiciosos, más inspiradores? Mis respetos a un gran científico que con su trabajo y su visión nos ha legado un mundo mejor.
La buena noticia para terminar este escrito es que en nuestra sociedad hay cada vez más molinas trabajando en diferentes problemas: ¡cuidemos nuestra ciencia y a nuestros científicos si queremos un mundo mejor! Y es que hoy más nunca #SinCienciaNoHayFuturo.
Sobre el autor: Mikel Mancisidor (@MMancisidor1970) es miembro del Comité de Derechos Económicos, Sociales y Culturales de la ONU y Adjunct Professor of International Human Rights Law, Washington College of Law, American University (Washington D. C.)
El artículo De la química al tratado internacional o de por qué la ciencia cambia cosas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La química analítica como base para el estudio de las prácticas pastoriles prehistóricas
- Un camaleón plasmónico que cambia de color en función del entorno
- De la materia a la vida: ¿Química? ¡Química!, por Jean-Marie Lehn
Javier Armentia – Naukas P4K 2019: La vie en rose (ciencia y sociedad de un color muy suyo)
 Imagen: Stephane YAICH / Unsplash
Imagen: Stephane YAICH / UnsplashJavier Armentia, director del Planetario de Pamplona y conocido divulgador, nos ofrece una charla sobre el color más heteropatriarcal que imaginarse pueda.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Javier Armentia – Naukas P4K 2019: La vie en rose (ciencia y sociedad de un color muy suyo) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Pro 2017: Javier Burgos y el alzhéimer
- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
- Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
La posverdad es más peligrosa que la mentira
Agustín Arrieta Urtizberea
 Foto: Ryoji Iwata / Unsplash
Foto: Ryoji Iwata / UnsplashDe la posverdad se habla tanto que, en el año 2016, “posverdad” fue nombrada palabra del año por los diccionarios Oxford. ¿Pero a qué fenómeno se refiere esa palabra? En un principio, cabría decir que en tiempos de posverdad se ha dejado atrás la verdad, como en la posmodernidad se pretendía superar la modernidad. ¿En qué consiste eso de dejar atrás la verdad?
Tiempos de posverdad, tiempos de engaño
Son varios los fenómenos que circundan o acompañan a la posverdad. Mentira, ignorancia, charlatanería, desinformación, fake news, populismo, redes sociales, propaganda, negacionismo… Son fenómenos heterogéneos que suscitan la idea de engaño masivo.
Pero lo que mejor caracteriza a la posverdad es la falta de respeto por la verdad o el desprecio hacia la misma. Esta característica no hay que identificarla con la mentira. La mentira y el desprecio a la verdad son diferentes formas de engaño. El mentiroso sabe cuál es la verdad, juega la partida de la verdad, pero la oculta intencionadamente. Sin embargo, la posverdad va más allá (o más acá). Ignora el juego de la verdad, se desentiende: la verdad es ignorada, obviada.
El charlatán como origen
Quiero mencionar a dos autores que hurgaron en el fenómeno de la posverdad, si bien la palabra todavía no estaba en circulación. El más cercano en el tiempo es Harry G. Frankfurt. En el año 2005, en un breve texto titulado On Bullshit, Frankfurt analiza el fenómeno de la charlatanería y contrapone dicho fenómeno con la mentira. Sobre esta contraposición se debate actualmente con gran intensidad, por ejemplo, en el ámbito de la pragmática.
Este filósofo estadounidense está preocupado por una figura que en ese momento, con los cambios sorprendentes en el universo de la comunicación, se está expandiendo sin cesar en distintos foros: el charlatán. El charlatán menosprecia la verdad, ignorándola, pasando por encima de ella. Habla sin cesar, produce discursos. Su actitud no es la del mentiroso.
Sin embargo, subraya Frankfurt, hay algo perturbador en su figura. Y es que históricamente se ha sido menos tolerante con el mentiroso que con otra formas de engaño. El mentiroso siempre ha sido perseguido y castigado (“¡No darás falso testimonio ni mentirás!”, rezaba el mandamiento católico). El charlatán, a lo sumo, ha sido objeto de mofa. Frankfurt, en cambio, ve una terrible amenaza en esta última figura: es el comienzo de la posverdad, aun antes de que se creara un nombre para este fenómeno.
La verdad y la política: Hannah Arendt
Con anterioridad (finales de los 60, principios de los 70 del siglo XX), Hannah Arendt también habla de este fenómeno. Arendt realiza un análisis muy interesante acerca de las relaciones intrínsecas entre la política y la mentira, y vislumbra novedades en dicha relación.
Comprueba que las mentiras de su época (entre otros casos, se ocupa de los famosos Papeles del Pentágono) ya no son sobre cuestiones secretas sino sobre cuestiones de sobra conocidas. Comprueba que la política sigue estrategias propias de la publicidad. Señala ese menosprecio hacia la verdad que nos está dejando sin la brújula requerida para poder caminar y avanzar en nuestras vidas con una orientación mínima.
Estas estrategias publicitarias de los poderes públicos abren las puertas a nuevos totalitarismos (Arendt es una gran conocedora y analista de los totalitarismos de Hitler y Stalin). Se trata, pues, de una auténtica amenaza. Considera que el fenómeno del menosprecio está afectando a lo que denomina “repositorios de la verdad” (reservas de la verdad): el sistema judicial, la universidad y el sistema educativo en general; la ciencia (que, en sus palabras, ha sido posible gracias a un ansia de objetividad) y finalmente el periodismo (que ella ejerció, por ejemplo, en el caso Adolph Eichmann).
La posverdad no es de derechas o de izquierdas
Hay un gran debate sobre los orígenes, las raíces y la evolución de esta actitud de menosprecio. Numerosos autores (véase McIntyre 2018, cap. 6) han argumentado que dicha actitud ha ido trasladándose de vertiente ideológica: de ser propia de un pensamiento político de izquierdas (crítico con el carácter absoluto de la verdad o del conocimiento o de la ciencia), a vincularse con la derecha (Trump es el gran modelo).
Sin embargo, por interesante que sea este debate desde un punto de vista histórico, político y conceptual, lo realmente problemático es que la posverdad está empapando todo lo que nos rodea, desde lo más cercano a lo más remoto. No es una cuestión de izquierdas y derechas.
Menosprecio de la verdad
Lo novedoso no es que se mienta o se engañe acerca de esto o de aquello. Lo novedoso es que la verdad misma se menosprecia. Es inquietante ver a la ignorancia manifestándose arrogantemente frente a la estupefacción del que investiga. Piénsese en las protestas negacionistas relacionadas con la pandemia, o en el negacionismo con respecto al evolucionismo o al cambio climático, o en las concepciones ligadas a los movimientos antivacunas.
Lo novedoso es que los conceptos sobre los que giran “necesariamente” determinadas actividades humanas son menospreciados. Por ejemplo, no se trata ya de debatir sobre si un artículo o trabajo periodístico es más o menos objetivo (debate interesante, difícil e irrenunciable, según mi parecer), sino que con el eslogan “la objetividad no existe” se paraliza dicha reflexión, se abre la puerta a otra concepción de la actividad “periodística”. ¿Dónde queda el periodismo representado en la excelente película “Spotlight”? Retomando las palabras de Arendt y aplicándolas en otro contexto, negar “el ansia por la objetividad” es abrir la veda a otro “periodismo”.
Por supuesto, reflexiones y preocupaciones análogas pueden aplicarse a otros ámbitos. En tiempos de COVID e incertidumbre, ¿qué no hemos oído acerca de la ciencia? ¿Qué idea de la ciencia transmite el negacionismo?
La importancia de los repositorios de la verdad
Hemos subido un escalón en la vía del engaño. Se menosprecia la verdad misma y toda una serie de conceptos (denominados “conceptos epistémicos”) que son satélites de aquella: la objetividad, la consistencia, la imparcialidad, la sinceridad, contrastar las creencias (hipótesis o teorías), el respeto a las evidencias, la precisión, el reconocimiento de la falibilidad y la búsqueda de la minimización de errores, la autocorrección…
En la actualidad hay más medios que nunca para el despliegue masivo de un ambiente de posverdad. Entre otros elementos, las nuevas tecnologías y las redes sociales proporcionan un hábitat adecuado para su desarrollo.
¿Qué hacer? Recordando a Arendt, protejamos los repositorios de la verdad. ¿Cómo? Siendo fieles a los valores arriba mencionados, por lo menos en las actividades humanas donde esos valores son requeridos. Por supuesto, esa fidelidad está acompañada de numerosos obstáculos y fracasos. La posverdad ignora todo ello, juega (o pretende jugar) en otro terreno.
Sobre el autor: Agustín Arrieta Urtizberea, Profesor de Filosofía en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Lea el original.
El artículo La posverdad es más peligrosa que la mentira se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
