La pitón ajusta el tamaño del corazón a su dieta
Las serpientes pitón practican la estrategia depredadora conocida como “siéntate y espera”. Se trata de permanecer inmóvil y esperar a que una presa se ponga al alcance de sus mandíbulas, algo que sucede muy de tarde en tarde. Esta estrategia requiere que en los largos periodos de ayuno se reduzca drásticamente el metabolismo, y que las presas sean suficientemente grandes para compensar esos periodos.
 Figura 1. Pitón de Birmania (Python bivittatus). Foto: NPSPhoto, R. Cammauf, dominio público
Figura 1. Pitón de Birmania (Python bivittatus). Foto: NPSPhoto, R. Cammauf, dominio públicoLa pitón de Birmania (Python bivittatus) es una serpiente que alcanza los cuatro metros de longitud (Figura 1). Es capaz de permanecer durante meses sin alimentarse, pero cuando captura una presa y comienza a digerirla, su metabolismo se multiplica por diez. En 2005 se descubrió que en las 48 horas posteriores a la ingesta se producía un aumento del 40% en el tamaño del corazón. El crecimiento no se producía por proliferación de las células musculares cardiacas (los cardiomiocitos), sino por un incremento en la síntesis de proteínas, sobre todo las del aparato contráctil, lo que llevaba a un aumento del tamaño de los cardiomiocitos. Se trataba, por tanto, del proceso conocido como hipertrofia cardiaca.
Una vez terminada la digestión, al cabo de 7-10 días, el metabolismo de la pitón vuelve a reducirse al mínimo y el corazón disminuye de tamaño hasta regresar a su volumen inicial. Este rápido proceso de aumento y disminución del tamaño cardiaco en cuestión de días resultaba excepcional, no se había observado nada parecido en otros animales.
En los humanos, una hipertrofia cardiaca reversible puede inducirse por el ejercicio prolongado y también ocurre de forma natural durante el embarazo, pero se trata de fenómenos mucho más lentos. También existe hipertrofia y remodelación cardiaca en respuesta a situaciones patológicas (infarto, hipertensión), pero suele ser irreversible. Por ello, el fenómeno observado en las pitones de Birmania cobraba un potencial interés clínico.
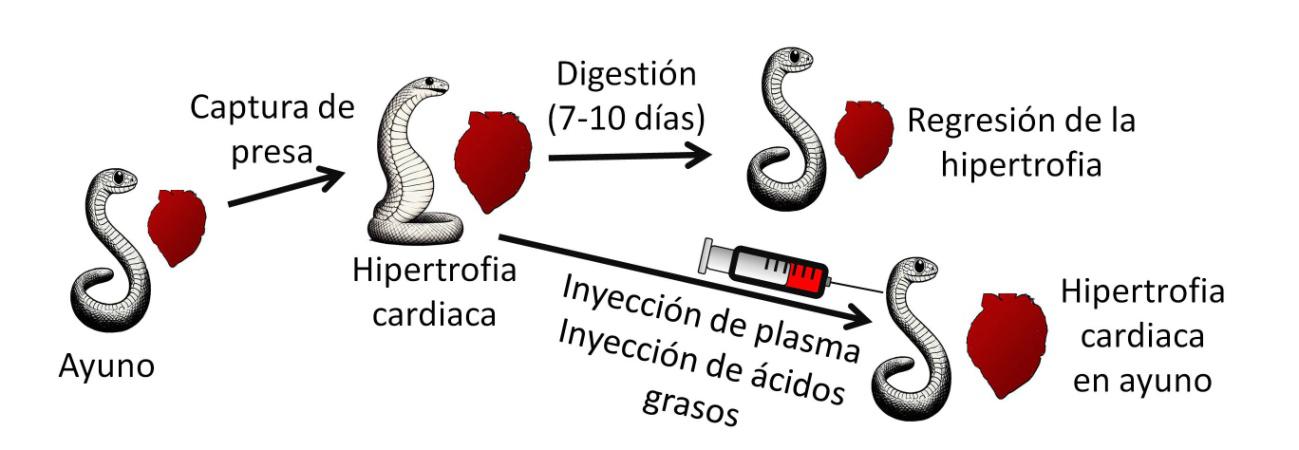 Figura 2. La captura de una presa provoca un rápido crecimiento del corazón (hipertrofia) que responde al fuerte aumento del metabolismo. Finalizada la digestión, el corazón regresa a su tamaño normal en el plazo de 7-10 días tras la ingesta. La hipertrofia cardiaca puede ser inducida en pitones en ayunas mediante la inyección de plasma de pitón recién alimentada o de una combinación de ácidos grasos (mirístico, palmítico y palmitoleico).
Figura 2. La captura de una presa provoca un rápido crecimiento del corazón (hipertrofia) que responde al fuerte aumento del metabolismo. Finalizada la digestión, el corazón regresa a su tamaño normal en el plazo de 7-10 días tras la ingesta. La hipertrofia cardiaca puede ser inducida en pitones en ayunas mediante la inyección de plasma de pitón recién alimentada o de una combinación de ácidos grasos (mirístico, palmítico y palmitoleico).Un equipo de investigación de la Universidad de Colorado (EE.UU.) descubrió en 2011 que la hipertrofia cardiaca era inducida por factores circulantes en la sangre de la pitón. Después de analizar los compuestos del plasma tras la ingesta de alimento, se seleccionaron como candidatos algunos ácidos grasos (mirístico, palmítico, palmitoleico). Bastaba la inyección de estos tres ácidos grasos en la sangre de la pitón para inducir un aumento del tamaño del corazón similar al provocado por la ingesta de una presa (Figura 2). Se observó incluso un aumento en la masa del ventrículo izquierdo de ratones tras la inyección de estos ácidos grasos.
Aclarado este punto, el grupo de investigación se aplicó al estudio de la rápida disminución del tamaño del corazón al volver a la fase de ayuno. Sus resultados acaban de ser publicados en la revista PNAS. Registrando cambios en la expresión génica durante la fase regresiva, se observó la activación de un conjunto de genes regulados por el factor de transcripción FoxO1. Como ya hemos comentado anteriormente en esta serie de artículos, los factores de transcripción se unen al ADN activando o reprimiendo a otros genes.
FoxO1 es bien conocido por su papel en múltiples procesos fisiológicos, como la regulación de la adipogénesis, los niveles de glucosa, el ciclo celular o la respuesta inmune. Más recientemente se ha descrito un papel importante de los factores FoxO en el proceso llamado autofagia, consistente en la degradación controlada de proteínas, orgánulos y otros elementos celulares. La autofagia es necesaria cuando la célula tiene que adaptarse al ayuno, o cuando debe reciclar orgánulos y proteínas deteriorados o que se han vuelto innecesarios. Se trata de un proceso conocido desde hace relativamente poco tiempo. De hecho, el Premio Nobel 2016 en Medicina y Fisiología fue otorgado al japonés Yoshinori Ohsumi por sus estudios pioneros sobre la autofagia.
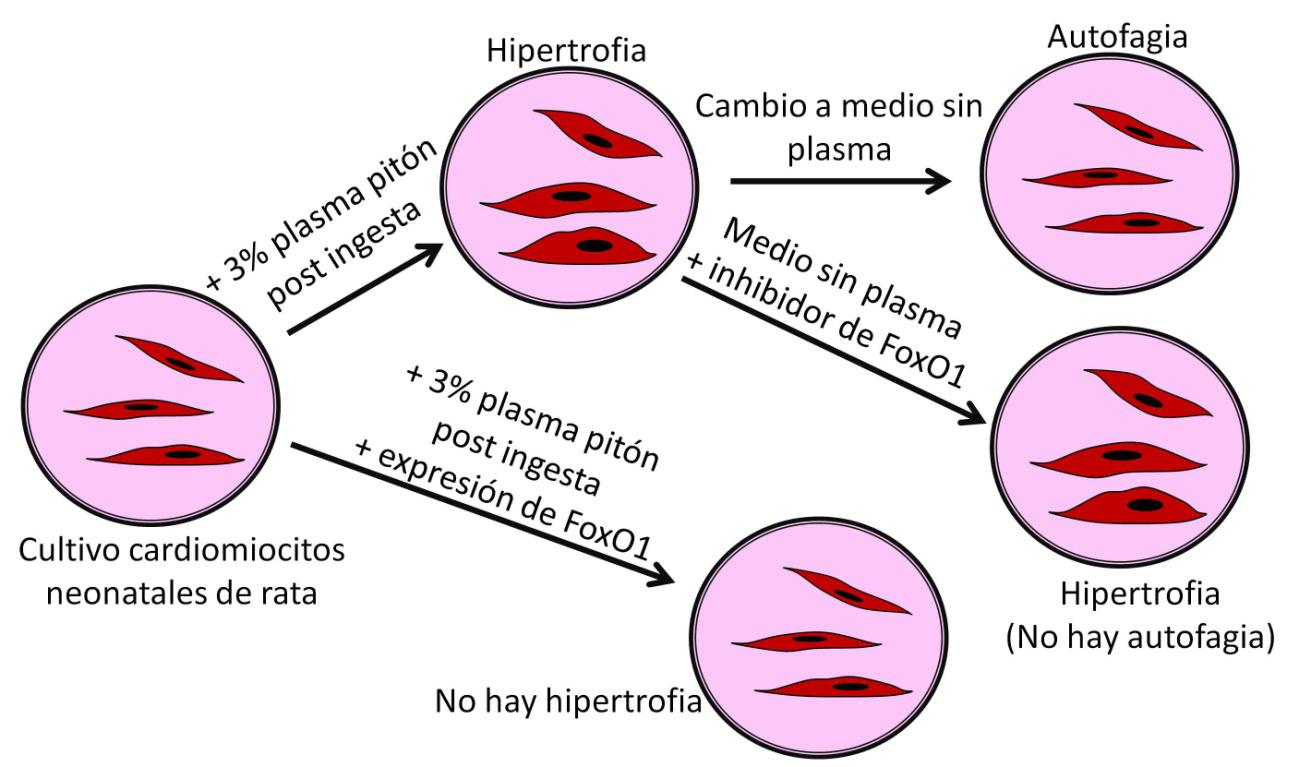 Figura 3. La adición de plasma de pitón recién alimentada al medio de cultivo provoca la hipertrofia de cardiomiocitos de rata recién nacida. Estos cardiomiocitos revierten a su tamaño normal después de un cambio a medio de cultivo sin plasma, debido a un proceso de autofagia (degradación de proteínas y otros componentes celulares). Si este medio contiene un inhibidor farmacológico del factor FoxO1, se evita el proceso de autofagia y los cardiomiocitos mantienen su gran tamaño. Por el contrario, si se fuerza la expresión de FoxO1 mediante vectores adenovirales, se bloquea la hipertrofia en presencia de plasma de pitón
Figura 3. La adición de plasma de pitón recién alimentada al medio de cultivo provoca la hipertrofia de cardiomiocitos de rata recién nacida. Estos cardiomiocitos revierten a su tamaño normal después de un cambio a medio de cultivo sin plasma, debido a un proceso de autofagia (degradación de proteínas y otros componentes celulares). Si este medio contiene un inhibidor farmacológico del factor FoxO1, se evita el proceso de autofagia y los cardiomiocitos mantienen su gran tamaño. Por el contrario, si se fuerza la expresión de FoxO1 mediante vectores adenovirales, se bloquea la hipertrofia en presencia de plasma de pitónEn el caso de la serpiente pitón, el papel de FoxO1 en los cardiomiocitos consistía en desencadenar un proceso de autofagia. A partir del sexto día tras la ingesta, FoxO1 activa la degradación de proteínas y otros elementos celulares en los cardiomiocitos, provocando una drástica reducción de tamaño. Para demostrarlo, se utilizó un modelo de cardiomiocitos neonatales de rata cultivados con un 3% de plasma de pitón recién alimentada (Figura 3). El equipo confirmó que aumentaban de tamaño 24 h después del tratamiento, y regresaban a su tamaño normal 48 h tras el cambio a un medio de cultivo normal. Pero cuando se desactivó FoxO1 en los cardiomiocitos hipertrofiados mediante un inhibidor farmacológico, estos mantuvieron su gran tamaño en condiciones de ayuno. Por otro lado, cardiomiocitos en los que se forzó la expresión de FoxO1 mediante adenovirus no se hipertrofiaron a pesar de ser cultivados con plasma de pitón recién alimentada.
En conclusión, tanto los mecanismos de activación de la hipertrofia cardiaca como los implicados en la rápida reducción del corazón han quedado desvelados en la pitón de Birmania. Será muy importante saber si este nuevo conocimiento ayudará a comprender mejor la inducción y la reversión de la hipertrofia cardiaca humana en condiciones normales (embarazo, ejercicio) o patológicas.
Referencias
Andersen, J.B., Rourke, B.C., Caiozzo, V.J. et al. (2005) Postprandial cardiac hypertrophy in pythons. Nature. doi: 10.1038/434037a.
Martin, T.G., Hunt, D.R., Langer, S.J. et al. (2024) Regression of postprandial cardiac hypertrophy in burmese pythons is mediated by FoxO1. Proc Natl Acad Sci U S A. doi: 10.1073/pnas.2408719121.
Riquelme, C.A., Magida, J.A., Harrison, B.C. et al. (2011) Fatty acids identified in the Burmese python promote beneficial cardiac growth. Science. doi: 10.1126/science.1210558.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo La pitón ajusta el tamaño del corazón a su dieta se ha escrito en Cuaderno de Cultura Científica.
Por qué hoy el Titanic no se habría hundido
 El Titanic durante su construcción. Foto:Robert John Welch (1859-1936) / Wikimedia Commons
El Titanic durante su construcción. Foto:Robert John Welch (1859-1936) / Wikimedia Commons
La falta de un conocimiento adecuado en ciencia e ingeniería de materiales, así como priorizar otros intereses, ha contribuido a algunos de los mayores desastres tecnológicos de la historia. Son ejemplos icónicos la tragedia del transbordador espacial Challenger; los dramáticos accidentes del Havilland Comet, el Columbia y los buques Pendleton y Fort Mercer, además de la caída del puente Hasselt Road en Bélgica. Sin olvidarnos del desastre del Titanic.
Todas estas catástrofes se habrían evitado con los avances en materiales que conocemos hoy.
La fragilidad del acero del TitanicEl 1 de septiembre de 1985, Robert Ballard encontró el Titanic a 3 700 m en el fondo del océano Atlántico. El barco se había dividido en dos secciones principales, separadas por unos 600 m. La colisión había creado aberturas en el casco por un total de 1 115 m².
Durante una expedición a los restos del naufragio en el Atlántico Norte el 15 de agosto de 1996, los investigadores trajeron acero del casco del barco para realizar análisis metalúrgicos. El minucioso análisis desveló que el acero tenía una alta temperatura de transición dúctil-frágil, lo que le hacía inadecuado para el servicio a bajas temperaturas. En el momento de la colisión, la temperatura del agua era –2° C.
Hoy, la calidad de estos aceros se ha multiplicado exponencialmente.
El error se mantuvo en los Liberty shipsDurante la Segunda Guerra Mundial, Estados Unidos construyó más de 6 000 buques Liberty ships para apoyar a Gran Bretaña. Una de las peculiaridades en su fabricación fue que la planchas de acero del casco estaban soldadas y no unidas por remaches. Cuando tres de estos buques se partieron literalmente por la mitad, la razón pareció estar clara en un primer momento y se responsabilizó a la soldadura de las planchas. Sin embargo, la verdadera causa estaba relacionada con la fragilidad del acero a bajas temperaturas.
 En 1943 el petrolero SS Schenectady estaba amarrado en el muelle de prueba de Swan Island. El casco se agrietó casi por la mitad.
En 1943 el petrolero SS Schenectady estaba amarrado en el muelle de prueba de Swan Island. El casco se agrietó casi por la mitad.Wikimedia commons
Estos buques, junto con el SS Schenectady y los Pendleton y Fort Mercer, soportaron temperaturas próximas a -2⁰ C , como las que sufrió el Titanic al hundirse en el Atlántico Norte en 1912
A esas temperaturas, el acero utilizado en los cascos se volvía frágil, rompiéndose con facilidad. La clave del problema radica en la temperatura que determina cuándo un material pasa de ser dúctil a frágil (DBTT). Este cambio de comportamiento no se descubrió hasta años después y ha supuesto un reto para la investigación metalúrgica en la última mitad de siglo.
Los avances en metalurgia del siglo XX han permitido modificar la composición del acero para que no ocurra una transición tan brusca y poder reducir este riesgo. Hoy en día sabemos que la relación entre los elementos que forman el acero es clave para optimizar su comportamiento, y también que esto influye en su sensibilidad a las bajas temperaturas y su susceptibilidad a la formación de grietas.
Con algunos cambios en la composición del acero, muchos desastres se habrían evitado. Y no solo el hundimiento de barcos.
Challenger: el efecto de la temperaturaLa tragedia del Challenger en 1986 fue uno de los desastres más impactantes del siglo XX. Este vuelo de la NASA tenía una relevancia especial, ya que a bordo iba Christa McAuliffe, una profesora seleccionada para el programa Teachers in Space, promovido por el gobierno de Ronald Reagan.
Se esperaba que el lanzamiento reavivara el interés en los viajes espaciales, mostrando su creciente seguridad. Sin embargo, 73 segundos después del despegue el Challenger se desintegró a 14,6 kilómetros de altura, causando la muerte de los siete tripulantes.
La investigación reveló que el accidente fue causado por un fallo en las juntas tóricas de los propulsores de combustible sólido. Estas juntas, fabricadas con fluoroelastómeros (FKM), tenían pérdida de elasticidad a bajas temperaturas.
La mañana del lanzamiento, la temperatura era de -3⁰ C, lo que impidió que las juntas se sellaran adecuadamente. Esto permitió la fuga de gases calientes que provocaron la ruptura del propulsor derecho, desatando el desastre.
En 1986 ya sabía que las juntas tóricas eran vulnerables a bajas temperaturas, y varios expertos sugirieron posponer el despegue. Pero la presión por el éxito de la misión prevaleció, ignorando las advertencias sobre el comportamiento del material en condiciones adversas.
Havilland Comet y la fatiga del metalEl Havilland DH.106 Comet fue el primer avión comercial a reacción y marcó un hito en la aviación cuando comenzó a operar en 1949. Propulsado por turbinas, volaba a mayor altitud y con menos turbulencias, lo que mejoraba la comodidad para los pasajeros. Su diseño aerodinámico, con alas en flecha y motores empotrados, lo hacía más eficiente.
Sin embargo, entre 1953 y 1954 el Comet sufrió una serie de accidentes, incluido el vuelo G-ALYV, que se desintegró sobre Calcuta.
Inicialmente, se pensó que las causas eran climáticas. Pero la investigación reveló un problema en el diseño estructural del avión: las ventanas cuadradas.
 Detalle de las ventanas del Havilland DH Comet que provocaban la ruptura del avión.
Detalle de las ventanas del Havilland DH Comet que provocaban la ruptura del avión.Wikimedia commons, CC BY
Estas ventanas actuaban como concentradores de tensiones, lo que generaba grietas debido a los ciclos de presión durante los vuelos. Con cada ciclo, las fisuras aumentaban hasta provocar una descompresión explosiva, causando la desintegración del avión.
Este descubrimiento resultó clave para la industria de la aviación, que adoptó las ventanas ovaladas que ahora vemos en los aviones para evitar la concentración de tensiones y reducir el riesgo de fatiga del metal.
Trasbordador espacial Columbia: la corrosiónEl 1 de febrero de 2003, el transbordador espacial Columbia se desintegró durante su reingreso a la atmósfera, causando la muerte de sus siete tripulantes.
El desastre se debió a un daño en el ala izquierda, causado por una pieza de espuma aislante que se desprendió durante el lanzamiento, afectando las planchas de protección térmica. Este daño expuso la estructura interna del transbordador a los gases calientes de la atmósfera, lo que debilitó la nave y causó su desintegración.
Uno de los factores fue la corrosión de los materiales metálicos, que se agrava en el espacio debido a la exposición al oxígeno elemental altamente reactivo en las capas superiores de la atmósfera. Desde entonces, las inspecciones de seguridad han prestado mayor atención a la corrosión de los materiales, que ya no se pasa por alto, lo que evita futuros accidentes.
La apuesta por la ciencia e ingeniería de materialesLos desastres mencionados resaltan la importancia de la ciencia e ingeniería de materiales en la seguridad y el éxito de las tecnologías modernas.
Entender cómo se comportan los materiales en diferentes condiciones es fundamental para prevenir fallos catastróficos. Figuras como Elon Musk han destacado la importancia de esta disciplina, alentando a estudiar carreras en ciencia e ingeniería, cruciales para el desarrollo de la industria espacial y otros campos. Y, como hemos visto, para evitar terribles accidentes en la historia futura.![]()
Sobre la autora: Paula Alvaredo Olmos, Profesora Titular en Ciencia e Ingeniería de Materiales, Universidad Carlos III
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Por qué hoy el Titanic no se habría hundido se ha escrito en Cuaderno de Cultura Científica.
Naukas Pro 2024: Corrientes oceánicas y submarinos amarillos

Los últimos avances en el ámbito de las energías renovables marinas o la proliferación de los microplásticos fueron algunos de los temas que componen la última edición de NAUKAS PRO. Una cita en la que el personal investigador se sube al escenario del Euskalduna Bilbao para hablar de las investigaciones más destacadas del momento en un ámbito concreto.
En esta ocasión el personal investigador de la Universidad del País Vasco, de la Estación Marina de Plentzia (PiE-UPV/EHU), AZTI, Tecnalia o el CSIC acercaron las últimas investigaciones relacionadas en el ámbito marítimo.
La conferencia Corrientes oceánicas y submarinos amarillos corre a cargo de Anna Rubio Company, investigadora del Centro de Investigación Marina y Alimentaria AZTI.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Pro 2024: Corrientes oceánicas y submarinos amarillos se ha escrito en Cuaderno de Cultura Científica.
Desimetrización enantioselectiva de ciclobutanos
Los sistemas vivos están basados en biomoléculas que son asimétricas. El Grupo de Investigación en Catálisis metálica y Organocatálisis liderado por el catedrático de la Universidad del País Vasco José Luis Vicario ha conseguido, en colaboración con la Universidad Rovira i Virgili, “sintetizar moléculas con una asimetría esquiva utilizando una novedosa metodología que abre una nueva vía a un tipo de estructuras moleculares nunca conseguidas hasta el momento, que potencialmente podrían utilizarse como fármacos, entre otras cosas”.
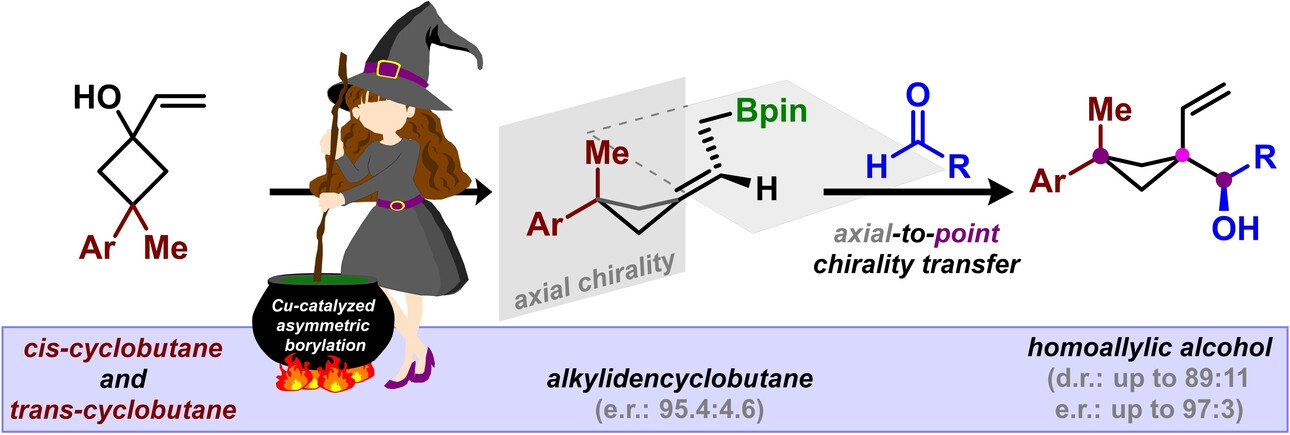
El grupo de la Facultad de Ciencia y Tecnología de la UPV/EHU, que trabaja en síntesis asimétrica de moléculas orgánicas de pequeño tamaño, ha conseguido “sintetizar moléculas cíclicas intrínsecamente asimétricas empleando catálisis. Hemos desarrollado una metodología eficaz y directa, utilizando pequeñas cantidades de un catalizador derivado del cobre, un metal abundante y no nocivo”, señala el Catedrático de Química Orgánica de la UPV/EHU.
La gran mayoría de moléculas orgánicas (basadas en una estructura de carbono) no son planas, tienen geometría tridimensional. Dependiendo de la manera en que los átomos se ordenan dentro de cada molécula se pueden obtener resultados. En algunos casos una molécula y su imagen especular (es decir, dos moléculas simétricas que guardan la misma relación que la que tiene un objeto con su imagen en un espejo) pueden tener propiedades totalmente diferentes.
Utilicemos el símil de las manos para explicarlo: nuestras manos son las imágenes especulares una de la otra; se puede decir que son idénticas. Sin embargo, cuando se dispone una mano sobre la otra (no en disposición de juntar las palmas, sino superponiendo una mano a la otra), la posición de los dedos no es la misma. Ocurre lo mismo con algunas moléculas, la organización de los átomos no coincide. Cada una de las imágenes especulares de una molécula que no son superponibles se llama enantiómero.
Simétricas pero con propiedades muy diferentes“En la naturaleza y en farmacología existen muchísimos ejemplos en los que los dos enantiómeros tienen propiedades dispares. Es el caso de la talidomida (un fármaco administrado como sedante y calmante de las náuseas durante los tres primeros meses de embarazo, que provocó miles de casos de malformaciones congénitas), uno de los enantiómeros tiene propiedades analgésicas y el otro produce malformaciones —explica el doctor de la UPV/EHU Efraim Reyes, uno de los autores principales del trabajo—. Eso ocurre porque las dianas terapéuticas no interaccionan de la misma manera con un enantiómero u otro. Por tanto, es fundamental controlar la síntesis de este tipo de moléculas, para conseguir únicamente uno de los dos enantiómeros”.
La investigadora predoctoral Josebe Hurtado ha sido capaz de construir selectivamente una de las dos moléculas enantioméricas de un grupo de ciclobutanos (moléculas cíclicas que contienen esencialmente átomos de carbono e hidrógeno), “mediante la desimetrización; es decir, rompiendo la simetría planar y convirtiéndolas en bloques sintéticos elementales de moléculas más complejas”, explica su director de tesis Efraim Reyes.
Este logro responde a un gran reto actual y un área de investigación de interés creciente. “Hemos conseguido sintetizar moléculas con una asimetría axial (sustentada en un eje), que no tiene precedente en la naturaleza y que abre una puerta al estudio de un nuevo tipo de moléculas, que pueden servir también para desarrollar nuevas vías terapéuticas”, añade Vicario. Además, a través de un estricto control de las reacciones “hemos roto la simetría planar para convertirla en asimetría axial y a continuación en asimetría puntual (sustentada en un punto)”, explica el profesor catedrático de la UPV/EHU. Esto demuestra “que existe una posibilidad real de que las biomoléculas con asimetría puedan tener también un origen común”.
La desimetrización espontánea, origen de la vidaEste hallazgo recuerda a una de las teorías relacionadas con el origen de la vida, que se basa en que mediante una desimetrización espontánea de la simetría se formaron las moléculas que dieron lugar a la vida. “Una de las teorías del origen de la vida, muy aceptada, dice que originalmente solo había moléculas simétricas y que por un proceso de desimetrización espontánea surgieron moléculas asimétricas, que son evidentemente el origen de la vida, porque todo nuestro organismo y los sistemas vivos están basados en biomoléculas que son asimétricas y solo contienen uno de los dos enantiómeros”, concluye Reyes.
Referencia:
Josebe Hurtado, Nerea Iragorri, Efraim Reyes, Jose L. Vicario, Elena Fernández (2024) Cu-Catalyzed Enantioselective Borylative Desymmetrization of 1-Vinyl Cyclobutanols and Axial-to-Point Chirality Transfer in a Diastereoconvergent/Stereoretentive Allylation Scenery Angewandte Chemie International Edition doi: 10.1002/anie.202411232
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Desimetrización enantioselectiva de ciclobutanos se ha escrito en Cuaderno de Cultura Científica.
Amianto, una historia de terror
Basta pronunciar la palabra amianto, o asbesto, para que a muchos —y, sobre todo, a los propietarios de las casas de los programas de reformas— se nos pongan los pelos de punta. Utilizada desde la Antigüedad en numerosos ámbitos, las propiedades de esta fibra mineral son ampliamente conocidas desde entonces, algunas muy útiles, de ahí su popularidad, y otras muy dañinas. Aun así, no fue hasta 2005 cuando la Unión Europea prohibió completamente su uso —algunos países miembros ya lo habían empezado a eliminar mucho antes—. Pero ¿qué es exactamente el amianto?, ¿para qué se ha utilizado a lo largo de la historia?, ¿por qué es tan peligroso? Para empezar, hasta que se empezaron a estudiar sus nocivos efectos sobre la salud, fue el material del futuro, un compuesto milagroso a prueba de todo… y con aplicaciones para casi todo.
 Fibras de amianto (tremolita, en este caso) sobre un mineral de muscovita. Créditos: Dominio Público/Aram Dulyan
Fibras de amianto (tremolita, en este caso) sobre un mineral de muscovita. Créditos: Dominio Público/Aram Dulyan
El amianto es un grupo de seis minerales fibrosos de origen metamórfico compuestos de silicatos —los de mayor abundancia en la naturaleza—: grunerita (o amosita, para la variante fibrosa), crisotilo, riebeckita (crocidolita), tremolita, bisolita (actinolita) y antofilita. La combinación de este origen mineral y que se presente en forma de fibras largas, flexibles y resistentes es lo que le otorga tanto sus propiedades como su versatilidad. Estamos ante un material ignífugo, con excelentes propiedades aislantes tanto eléctricas como térmicas, una gran durabilidad, resistencia química y mecánica, y, sobre todo, abundante y barato. Su ligereza y que se presente en forma de fibras posibilita, además, manipularlo con facilidad, pero también es lo que lo convierte en un peligro para la salud.
 Microfibras de amianto (amosita), vistas a través de un microscopio electrónico de barrido. El pequeño tamaño que pueden alcanzar hace que puedan inhalarse sin detectarse. Una vez alojadas en los pulmones, el cuerpo tiene mucha dificultad para eliminarlas. Créditos: CC BY-SA 3.0/Ravaka
Microfibras de amianto (amosita), vistas a través de un microscopio electrónico de barrido. El pequeño tamaño que pueden alcanzar hace que puedan inhalarse sin detectarse. Una vez alojadas en los pulmones, el cuerpo tiene mucha dificultad para eliminarlas. Créditos: CC BY-SA 3.0/Ravaka
La inhalación de fibras microscópicas de amianto, que pueden encontrarse flotando en el ambiente en cualquier entorno en el que se esté trabajando con él, puede provocar graves patologías. Estas se quedan alojadas en los pulmones durante largo tiempo, dada la dificultad del cuerpo para eliminarlas, lo que, a largo plazo, acaba produciendo inflamación y daño celular. Aparecen así enfermedades como la asbestosis, que causa fibrosis pulmonar, o ciertos tipos de cáncer como el de pulmón y el mesotelioma, que afecta a la pleura o el peritoneo.
Que las personas que trabajaban con amianto enfermaban se sabe desde casi los orígenes de su uso. Existen testimonios incluso de Plinio el Viejo, que ya habló del padecimiento pulmonar de los esclavos que manipulaban habitualmente amianto, y en 1899, se documentó clínicamente en Londres el primer caso de fibrosis pulmonar de una trabajadora del amianto de 33 años por inhalación de estas fibras. Las primeras regulaciones del trabajo con amianto, dada su alta peligrosidad, se remontan a los años treinta, por eso sorprende que no haya sido hasta hace relativamente poco cuando por fin se han tomado medidas. Y no solo eso: la locura comercial y la mayor expansión de la industria del amianto se produjo, incluso sabiendo esta información, durante la década de los años cuarenta, con su pico durante los cincuenta y los sesenta.
A lo largo de la historia de la ciencia ha sido habitual que, ante la llegada de un nuevo descubrimiento o adelanto tecnológico, este se haya visto como una especie de santo grial o piedra filosofal que iba a solucionar todos nuestros problemas. Sucedió con la electricidad, con la radiactividad —recordemos todos aquellos productos de uso cotidiano que llevaban radio, como pastas de dientes—, e incluso puede que esté sucediendo ahora con la inteligencia artificial. El amianto no se quedó atrás, pero con la diferencia de que, en su momento de mayor auge, como hemos comentado, sí se conocían los riesgos que su uso implicaba.
La mayoría de aplicaciones del amianto son de sobra conocidas. En la construcción se ha usado como aislamiento, revestimiento, para aumentar la durabilidad y resistencia de los suelos… En la industria automotriz, era un material habitual en pastillas de freno y embragues, pero las aplicaciones más espeluznantes fueron, probablemente, en el ámbito textil, para la confección de ropa ignífuga. Se utilizó incluso en electrodomésticos, sobre todo en aquellos que generan calor, como calentadores, hornos y secadores. Lo que tal vez muchos no sepan es que, durante mucho tiempo, se promovió muchísimo su uso en objetos mucho más cotidianos. Y, para muestra, este documento de 1942:
Cortinas, fundas, manteles… también mantas, guantes de cocina, bolsas, cuerdas… incluso el tejido para confeccionarlos uno mismo se anunciaba como maravilloso. Todos estos productos se vendían con total, demasiada, normalidad. Por ejemplo, para los fanáticos de la Navidad que ya estén pensando en la decoración de su árboles y belenes existía incluso nieve artificial hecha de amianto.
 Nieve decorativa de amianto y mica. Créditos: Flickr/Asbestorama fuck you
Nieve decorativa de amianto y mica. Créditos: Flickr/Asbestorama fuck you
Parece que del mismo tipo que la que le cayó a Dorothy, el Espantapájaros y el León de camino a Oz.
 La nieve artificial que se usó en El mago de Oz en 1939 eran fibras de amianto. Créditos: Metro Goldwyn Mayer
La nieve artificial que se usó en El mago de Oz en 1939 eran fibras de amianto. Créditos: Metro Goldwyn Mayer
Solo cabe hacerse una pregunta cuando la historia nos pone en situaciones similares: ¿cuál es nuestra prioridad? ¿El beneficio económico o el beneficio humano? El uso de amianto, a diferencia de lo que sucedió con el radio y sus efectos, no se promovió desde la ignorancia.
Bibliografía
The Mesothelioma Center. (s. f.). History of asbestos. Asbestos.com. https://www.asbestos.com/asbestos/history/
Asbestorama. Perfil de Flickr. https://www.flickr.com/photos/asbestos_pix/asbestos
Rare Historial Photos (s. f.). Vintage photos show how asbestos products were once marketed, 1930s-1970s. Rare Historial Photos. https://rarehistoricalphotos.com/asbestos-vintage-advertisements/
Tweedale, G. (2000). Magic mineral to killer dust. Oxford University Press.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Amianto, una historia de terror se ha escrito en Cuaderno de Cultura Científica.
Fibonacci está en todas partes (y III)
Esta es la última jornada de un paseo por algunos lugares de lo más curiosos e inesperados, en los que aparecen los números de Fibonacci. Durante la primera jornada, recogida en la entrada del Cuaderno de Cultura Científica titulada Fibonacci en todas partes (I), visitamos espacios destacados como el árbol genealógico de un zángano (abeja macho), los paseos de una abeja por un panal de dos filas de celdas o los embaldosados con fichas de dominó, mientras que para la segunda jornada, Fibonacci en todas partes (II), reservamos la visita a lugares de interés como la óptica de la luz, unas escaleras que se suben, o se bajan, de una en una o de dos en dos, y las sumas de números con unos y doses.
 Girasole (en italiano), acrílico sobre lienzo, 60 x 70 cm, del artista suizo Eugen Jost. Obra perteneciente a la exposición Everything is numberPintando un edificio de apartamentos
Girasole (en italiano), acrílico sobre lienzo, 60 x 70 cm, del artista suizo Eugen Jost. Obra perteneciente a la exposición Everything is numberPintando un edificio de apartamentos
Con el problema de pintar un edificio de apartamentos con dos colores distintos iniciamos la tercera jornada de este paseo. El enunciado de este clásico problema dice así.
Problema: Si un edificio de apartamentos de n plantas va a ser pintado de azul y amarillo, de manera que cada planta esté pintada de un color y no haya dos plantas adyacentes pintadas ambas de amarillo, ¿de cuántas formas es posible hacerlo?
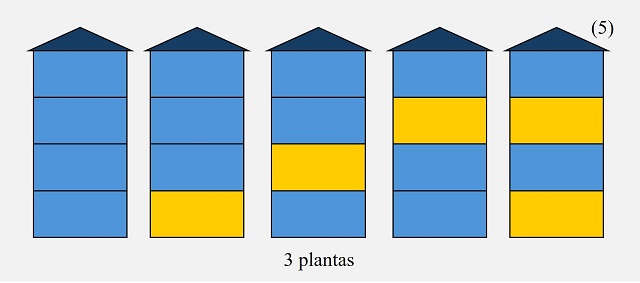
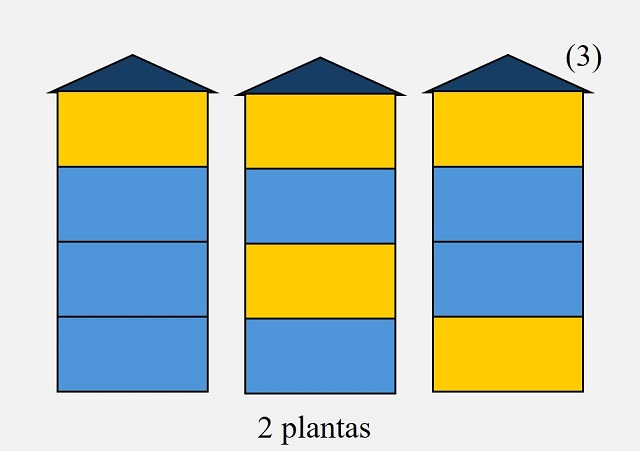
Para resolver este problema, podemos empezar de forma experimental, viendo qué ocurre para los edificios con un número pequeño de plantas. Para un edificio de apartamentos con una sola planta, existen solo dos opciones (2), pintar esa única planta de azul o de amarillo. Para dos plantas, hay tres opciones (3), pintar las dos plantas de azul, ambas de amarillo no es posible, o pintar cada planta de un color, lo cual se puede hacer de dos formas distintas, como se observa en la siguiente imagen. Mientras que para un edificio de tres plantas pueden pintarse todas de azul, puede pintarse una de amarillo, que puede ser la primera, la segunda o la tercera planta, o pueden pintarse dos plantas de amarillo, que por la condición de que no haya plantas amarillas contiguas, solo puede hacerse de una manera, en las plantas de los extremos, en total cinco formas distintas (5).
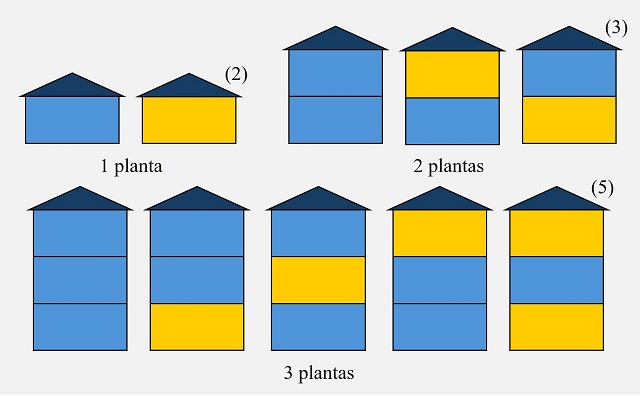 Maneras de pintar un edificio de apartamentos de una, dos o tres plantas de azul y amarillo, si el color amarillo no lo pueden compartir plantas contiguas
Maneras de pintar un edificio de apartamentos de una, dos o tres plantas de azul y amarillo, si el color amarillo no lo pueden compartir plantas contiguas
Si ahora consideramos un edificio de cuatro plantas, puede pintarse todo de azul, con una planta amarilla y hay cuatro plantas, o con dos plantas amarillas, que puede hacerse de tres formas diferentes sin que coincidan de amarillo plantas adyacentes, pero no es posible que tres o cuatro plantas estén pintadas de amarillo. En total, hay ocho (8) maneras de pintar el edificio de apartamentos.
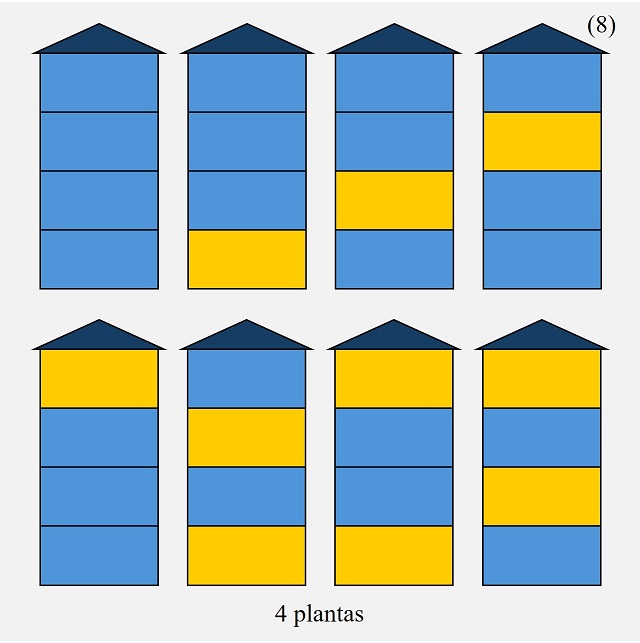 Formas de pintar un edificio de apartamentos de cuatro plantas de azul y amarillo, si el color amarillo no lo pueden compartir plantas contiguas
Formas de pintar un edificio de apartamentos de cuatro plantas de azul y amarillo, si el color amarillo no lo pueden compartir plantas contiguas
Como observamos los números que nos salen son 2, 3, 5 y 8, que son números de la sucesión de Fibonacci. Veamos que es la sucesión de Fibonacci, empezando en 2 y 3, viendo que satisface la condición recursiva, que la cantidad de maneras de pintar un edificio de n plantas se puede obtener a partir de las de n – 1 y n – 2 plantas. Para ello, observemos qué ocurre con el caso de n = 4 (cuatro plantas).
Si tomamos los edificios de 3 plantas (n – 1, en general) y consideramos una planta más, por encima de las otras, pintada de azul, generaremos algunos de los casos posibles para un edificio de 4 plantas (n, en general), tantos como las formas de pintar un edificio de 3 plantas (n – 1 plantas en general), que son 5 maneras distintas. Observemos que no podemos pintar de amarillo en todos los casos puesto que en algunos la última planta está pintada de amarillo, por lo que coincidirían dos plantas amarillas, mientras que los casos en los que la última planta es azul, aunque sí podríamos pintar la siguiente de amarillo, ese caso va a estar considerado en los casos que se derivan del edificio de n – 2 plantas (2 plantas en nuestro ejemplo), que veremos a continuación. Recíprocamente, si tomamos las maneras de pintar un edificio de 4 plantas (n, en general) en las cuales su última planta es azul, son todas las de 3 plantas (n – 1), a las que le añadimos una última planta azul.
 Las distintas maneras de pintar un edificio de 4 plantas, en las cuales su última planta es azul, son todas las posibles para 3 plantas, a las que le añadimos una última planta azul
Las distintas maneras de pintar un edificio de 4 plantas, en las cuales su última planta es azul, son todas las posibles para 3 plantas, a las que le añadimos una última planta azul
Si tomamos los edificios de 2 plantas (n – 2, en general) y consideramos dos plantas más, por encima de las otras, pintadas de amarillo y azul (de arriba a abajo), generaremos algunos de los casos posibles para un edificio de 4 plantas (n, en general), tantos como las formas de pintar un edificio de 2 plantas (n – 2 plantas en general), que son 3 maneras distintas. Observemos que no podríamos pedir pintar esas dos plantas superiores de azul y amarillo, ya que podrían coincidir dos plantas adyacentes amarillas, además los casos en los que sí se pueda, ya que la última planta de las anteriores es azul, ya está considerado en el caso anterior. Más aún, así cubrimos todos los casos de un edificio de 4 plantas (n, en general) en las cuales su última planta es amarilla.
 Las distintas maneras de pintar un edificio de 4 plantas, en las cuales su última planta es amarilla, son todas las posibles para 2 plantas, a las que le añadimos dos plantas más, por encima de las otras, pintadas de amarillo y azul (de arriba a abajo)
Las distintas maneras de pintar un edificio de 4 plantas, en las cuales su última planta es amarilla, son todas las posibles para 2 plantas, a las que le añadimos dos plantas más, por encima de las otras, pintadas de amarillo y azul (de arriba a abajo)
En consecuencia, hemos demostrado que se cumple la misma propiedad recursiva que para la sucesión de Fibonacci, Fn = Fn – 1 + Fn – 2. Por lo tanto, el número de formas distintas de pintar un edificio de apartamentos de n plantas, pintado de azul y amarillo, de manera que cada planta esté pintada de un color y no haya dos plantas adyacentes pintadas ambas de amarillo, es Fn + 2.
Palabras de n-bitsEmpecemos por lo elemental. Una palabra de n-bits es una cadena de n bits, donde un bit –acrónimo de bi[nary digi]t / dígito binario– es la unidad mínima de información y se corresponde con un dígito del sistema de numeración binario, 0 ó 1. Así, 1001001 sería una palabra de 7-bits o 1010101110110 una palabra de 13-bits.
Si lo pensamos un momento, resulta que la cuestión anterior de pintar de dos colores (azul y amarillo) un edificio de n plantas es equivalente al siguiente resultado.
Teorema: El número de palabras de n-bits que no contengan dos 1s consecutivos es igual a Fn + 2.
Veamos en la siguiente tabla, las palabras de n-bits para longitudes n pequeñas.
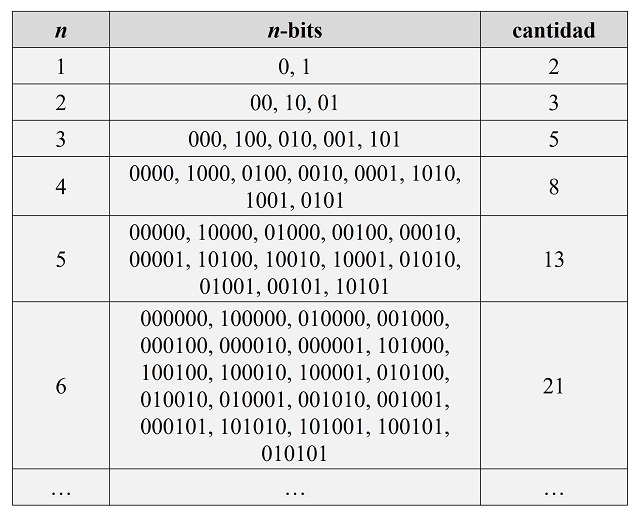 Número de palabras de n-bits que no contengan dos 1s consecutivos
Número de palabras de n-bits que no contengan dos 1s consecutivosLa demostración del teorema anterior es la misma que la de las maneras de pintar un edificio. Si se consideran las palabras de n-bits, las que terminan en 1 (por la derecha) son las palabras de (n – 1)-bits a las que se les añade un 1 por la derecha, mientras que las palabras que terminan en 0 son las palabras de (n – 2)-bits a las que se les añade 10 por la derecha.
Lanzar una monedaLlegados a este punto del paseo, nos podemos plantear una visita extra a un lugar que es un problema de probabilidad.
Problema: Si lanzamos una moneda n veces (sea n la cantidad que queramos), ¿cuál es la probabilidad de que no haya dos lanzamientos adyacentes que sean ambos cara?
Empecemos recordando que la probabilidad de que un evento ocurra se calcula dividiendo “el número de casos favorables” entre “el número de casos posibles” (pueden leerse las entradas relacionadas con la probabilidad, La probabilidad en el banquillo de los acusados o El cuento de la ruleta rusa ). Así, dada una determinada familia con dos “hijos”, si nos preguntamos cuál es la probabilidad de que los dos sean chicas, tendríamos que calcular primero el espacio muestral, es decir, el espacio de todos los casos posibles. En esta ocasión, habrá cuatro posibles casos (chica, chica), (chica, chico), (chico, chica) y (chico, chico), donde el orden en el par expresa el orden cronológico de nacimiento. Como solo uno de los cuatro es favorable, son dos chicas, la probabilidad de que los dos “hijos” sean chicas es 1/4 = 0,25, es decir, una probabilidad del 25%.
 Escena de la película No es país para viejos (2007), dirigida por Joel Coen y Ethan Coen, e interpretada por Tommy Lee Jones, Javier Bardem y Josh Brolin, entre otros, en la cual el personaje interpretado por Javier Bardem, un asesino a sueldo, decide si deja vivir al dependiente de una gasolinera lanzando una moneda al aire
Escena de la película No es país para viejos (2007), dirigida por Joel Coen y Ethan Coen, e interpretada por Tommy Lee Jones, Javier Bardem y Josh Brolin, entre otros, en la cual el personaje interpretado por Javier Bardem, un asesino a sueldo, decide si deja vivir al dependiente de una gasolinera lanzando una moneda al airePara analizar nuestro problema, si lanzamos una moneda al aire puede salir cara (que vamos expresarlo, para simplificar, pero también para disponer de una notación simple, con un 1) o puede salir cruz (que lo expresaremos con un 0). De esta manera, si lanzamos una moneda n veces, la representación de un posible resultado es un n-bit. Por ejemplo, si hablamos de lanzar la moneda 5 veces, entonces 10011 representa la posibilidad de que salga cara / cruz / cruz / cara / cara, mientras que 00101 sería cruz / cruz / cara / cruz / cara.
Por lo tanto, ya estamos en condiciones de calcular la probabilidad de que, si lanzamos una moneda n veces, no haya dos lanzamientos adyacentes que sean ambos cara. En primer lugar, calculemos el número de casos posibles. Estos son, teniendo en cuenta la descripción anterior de los posibles lanzamientos, todas las palabras de n-bits, que son 2n, ya que cada vez que lanzamos la moneda hay dos posibilidades, cara (1) o cruz (0), en un total de n lanzamientos. Y ahora toca calcular el número de los casos posibles, que, por la descripción anterior, son las palabras de n-bits para las que no hay dos 1s consecutivos, que ya hemos calculado y que es igual al número de Fibonacci Fn + 2.
Por lo tanto, la probabilidad de que, si lanzamos una moneda n veces, no haya dos lanzamientos adyacentes que sean ambos cara, es igual a:
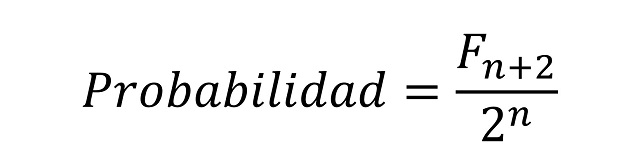
Por ejemplo, si lanzamos una moneda 5 veces, la probabilidad de que no haya dos lanzamientos consecutivos que sean cara es 13 / 32 = 0,40625, es decir, un 40,625 por ciento. Si vamos realizando cada vez más lanzamientos, nos podemos plantear si esa probabilidad aumenta o disminuye. Si lo pensamos un poco, intuitivamente es bastante claro que esa probabilidad irá disminuyendo, ya que con más lanzamientos será más fácil que salgan dos caras seguidas. Veamos qué pasa con las primeras cantidades de lanzamientos.
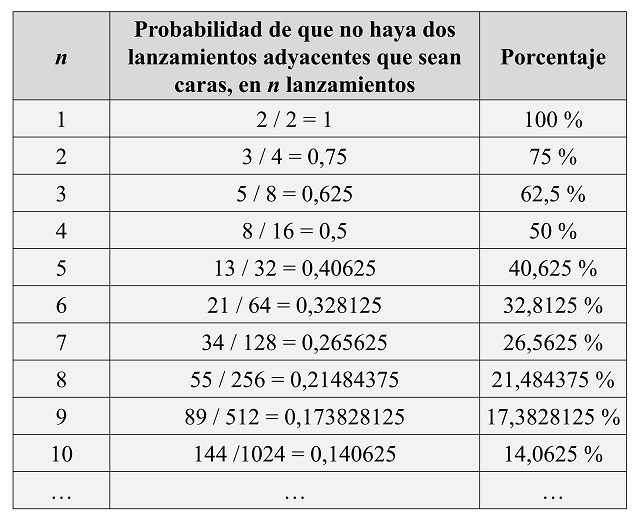
Efectivamente, la probabilidad va disminuyendo, como intuíamos. Esto se debe, matemáticamente, a que la sucesión de las potencias de 2 crece más rápido que la sucesión de los números de Fibonacci.
Subconjuntos alternadosVamos a terminar este paseo con un problema propuesto por el matemático francés Olry Terquem (1782-1862), del que ya hablamos en la entrada La circunferencia de los nueve puntos.
Un subconjunto del conjunto {1, 2, 3, …, n – 1, n} se dice que es alternado si sus elementos, cuando se colocan en orden creciente, siguen el patrón impar, par, impar, par, etcétera. Por ejemplo, los conjuntos {4}, {3, 6} o {1, 2, 5, 6} son subconjuntos alternados de {1, 2, 3, 4, 5, 6}, mientras que {2, 4, 5} o {1, 2, 3, 5} no lo son. El problema que se planteó Terquem fue calcular el número de subconjuntos alternados del conjunto {1, 2, 3, …, n – 1, n}. Veamos qué ocurre para los primeros casos.
 Cantidad de subconjuntos alternados del conjunto {1, 2, 3, …, n}, para n = 1, 2, 3, 4, 5, 6
Cantidad de subconjuntos alternados del conjunto {1, 2, 3, …, n}, para n = 1, 2, 3, 4, 5, 6Por lo tanto, el número de subconjuntos alternados del conjunto {1, 2, 3, …, n – 1. n} es igual al número de Fibonacci Fn + 2.
Podemos llegar a la sucesión de Fibonacci de muchas otras maneras, pero esas os las dejo para quienes os animéis a indagar sobre este tema.
 Coyote Breath / Aliento de coyote (2016), monotipo de la artista estadounidense Holli Marmon
Coyote Breath / Aliento de coyote (2016), monotipo de la artista estadounidense Holli MarmonBibliografía
1.- Alfred S. Posamentier, Ingmar Lehmann, The Fabulous Fibonacci Numbers, Prometheus Books, 2007.
2.- Thomas Koshy, Fibonacci and Lucas Numbers with Applications, John Wiley & Sons, 2001.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Fibonacci está en todas partes (y III) se ha escrito en Cuaderno de Cultura Científica.
Un magnetómetro de tamaño atómico
Si colocas unos cuantos átomos de hierro en fila sus espines magnéticos pueden organizarse en un patrón antiferromagnético alterno. O, mejor dicho, patrones. Debido a su naturaleza cuántica los átomos se encuentran en una superposición de dos estados antiferromagnéticos. Normalmente, la fila de átomos oscila rápidamente entre los dos estados. Pero un equipo de investigadores acaba de demostrar que es posible llevar una cadena corta de átomos de hierro a un punto diabólico, con el efecto de alargar espectacularmente el tiempo que la cadena pasa en un estado u otro. Este efecto podría ser la base sobre la que fabricar un magnetómetro de tamaño atómico.
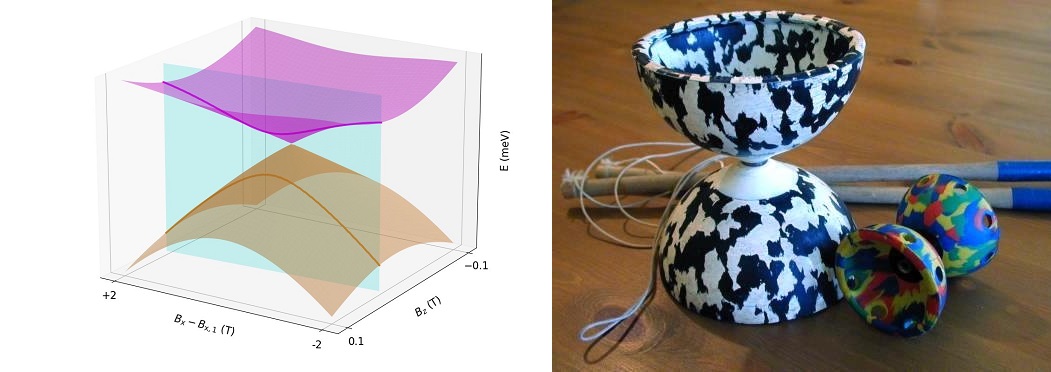 A la izquierda diábolo, figura geométrica (véase el texto). Fuente: Elbertse et al. (2024). A la derecha, diábolos, juguetes. Fuente: StoatBringer / Wikimedia Commons
A la izquierda diábolo, figura geométrica (véase el texto). Fuente: Elbertse et al. (2024). A la derecha, diábolos, juguetes. Fuente: StoatBringer / Wikimedia CommonsEl punto diabólico recibe su nombre del diábolo, un yoyó chino cuyas dos mitades cónicas opuestas se unen en un cuello estrecho. Si se representa gráficamente la energía de una cadena de espín antiferromagnética frente a la fuerza del campo magnético aplicado se obtiene una forma similar: un cono que apunta hacia arriba es el estado fundamental, mientras que el cono que apunta hacia abajo es el primer estado excitado. En su unión (el punto diabólico), los dos estados están degenerados.
 Elbertse et al. (2024)
Elbertse et al. (2024)Para crear su punto diabólico los investigadores colocaron cinco átomos de hierro sobre una superficie de nitruro de cobre a baja temperatura y en un vacío ultraalto. Encontraron que un campo magnético aplicado en paralelo a la superficie tenía el valor justo para crear unos estados fundamental y excitado casi degenerados.
Midiendo el giro del átomo central con un microscopio de efecto túnel los investigadores descubrieron que, en el punto diabólico, el patrón antiferromagnético cambiaba de dirección aproximadamente cada 10 segundos. Al variar el campo paralelo y aplicar un campo perpendicular adicional puediron crear un mapa de las condiciones alejadas del punto diabólico. A la distancia más grande, el tiempo de cambio de dirección se redujo en 3 órdenes de magnitud.
Los investigadores afirman que la sensibilidad del tiempo de cambio de dirección al campo magnético local podría aprovecharse para construir un magnetómetro de tamaño atómico.
Referencias:
R. J. G. Elbertse, D. Borodin, J. Oh, T. Ahn, J. Hwang, J. C. Rietveld, A. J. Heinrich, F. Delgado, S. Otte, and Y. Bae (2024) Long-Lived Magnetization in an Atomic Spin Chain Tuned to a Diabolic Point Phys. Rev. Lett. doi: 10.1103/PhysRevLett.133.166703
C. Tomé López (2017) Defeating spin decoherence Mapping Ignorance ISSN 2529-8992
C. Day (2024) Diabolical Nanomagnets Physics 17, s118
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un magnetómetro de tamaño atómico se ha escrito en Cuaderno de Cultura Científica.
¿Procede la Luna de un intercambio de parejas planetario?
La Tierra, nuestro planeta, tiene un único satélite natural. Esta obviedad, que a veces queda en un segundo plano por la llegada de pequeños “satélites” temporales, es algo más que una mera curiosidad. Si echamos un vistazo a los planetas interiores -Mercurio, Venus, la Tierra y Marte- dos de ellos carecen de satélites y Marte tiene dos cuya diferencia de tamaños con el planeta es de alrededor de 2,5 órdenes de magnitud menores, tan pequeños en comparación con el planeta que no fueron descubiertos hasta la segunda mitad del siglo XIX.
Sin embargo, si nos fijamos en los planetas exteriores -Júpiter, Saturno, Urano y Neptuno- estos cuentan con un extraordinario rebaño de satélites, lo que nos lleva a hacernos la siguiente pregunta, ¿Por qué los gigantes gaseosos y de hielo tienen tantos satélites, pero no pasa lo mismo con los planetas terrestres? ¿Es más difícil la formación de satélites alrededor de planetas pequeños? ¿O quizás, si se forman, van perdiéndose a lo largo del tiempo a causa de distintos procesos?
Existen tres grandes mecanismos que dan origen a los satélites: acreción, captura y grandes impactos. En el caso de la acreción, los satélites se forman a partir del material que queda “sobrante” tras la formación de un planeta. Es parecido a como los planetas se forman alrededor de las estrellas, solo que en este caso ocurre alrededor de un planeta. Muy probablemente este fue el proceso dominante en los gigantes gaseosos y de hielo de nuestro Sistema Solar.
 Figura 1. Tritón, el satélite de Neptuno, observado en 1989 por la Voyager 2. Imagen cortesía de NASA/JPL/USGS.
Figura 1. Tritón, el satélite de Neptuno, observado en 1989 por la Voyager 2. Imagen cortesía de NASA/JPL/USGS.El mecanismo de captura de un satélite ocurre cuando un objeto, a veces un asteroide -en sensu lato– o un sistema binario es atrapado por el campo gravitatorio de un planeta, como podría ser el caso de Tritón, el satélite de Neptuno o incluso los dos satélites de Marte, Fobos y Deimos.
También se pueden formar satélites a partir de grandes impactos, cuando dos cuerpos colisionan y se expulsa una gran cantidad de materia a la órbita de uno de estos. Lentamente todos esos materiales pueden ir coalesciendo formando uno o varios satélites. Esta es la teoría dominante desde hace décadas sobre la formación de nuestra Luna.
Pero un nuevo estudio publicado por Williams et al. (2024) en The Planetary Science Journal propone una nueva alternativa: La captura por intercambio binario, un proceso por el cual un planeta puede capturar uno de los cuerpos de un sistema binario, parejas de objetos que orbitan uno alrededor del otro.
Los sistemas binarios son un fenómeno común en el universo: Parejas de objetos que están unidos gravitatoriamente el uno al otro. Los vemos en la población de asteroides, e incluso en el cinturón de Kuiper donde, por ejemplo, el sistema formado por Plutón y Caronte podría ser considerado como binario ya que el centro de gravedad del sistema no cae dentro de Plutón.
Pero, ¿qué novedad propone realmente este artículo? El mecanismo de captura por intercambio binario sugiere que si tuviésemos un encuentro cercano con un sistema binario -valga la redundancia-, las interacciones gravitatorias entre los tres cuerpos podrían romper el vínculo de los que forman el sistema binario pudiendo uno de ellos entrar en órbita alrededor del otro planeta.
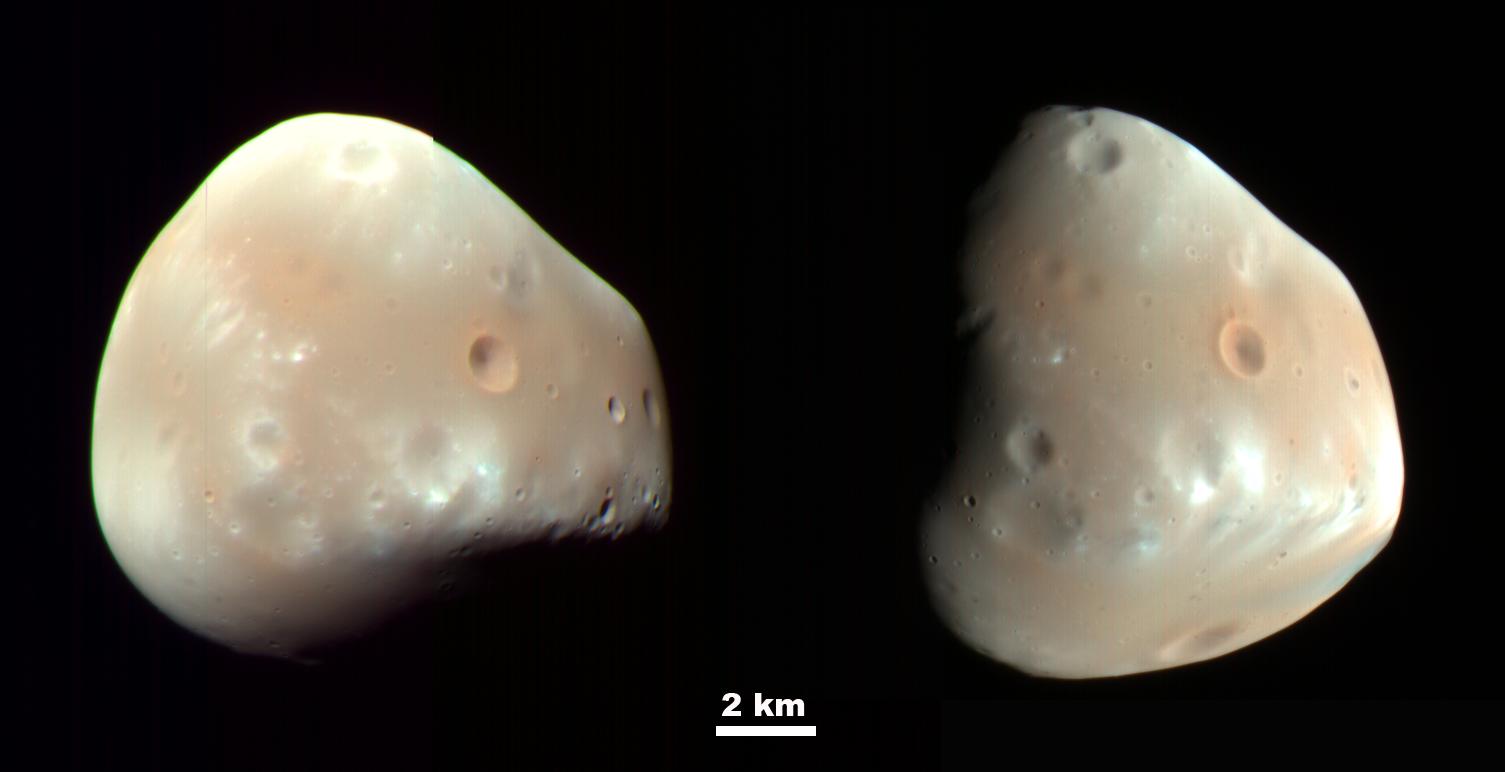 Figura 2. Imagen de Deimos, uno de los dos satélites de Marte. ¿Se formó en el entorno del planeta rojo o es un asteroide capturado? Imagen cortesía de NASA/JPL-Caltech/University of Arizona.
Figura 2. Imagen de Deimos, uno de los dos satélites de Marte. ¿Se formó en el entorno del planeta rojo o es un asteroide capturado? Imagen cortesía de NASA/JPL-Caltech/University of Arizona.Para llegar a esta conclusión, los científicos han realizado una serie de simulaciones en las cuales ocurren distintos encuentros entre un planeta del tamaño de la Tierra y distintos sistemas binarios con el objetivo de observar si estos encuentros son capaces por sí solos de dejar un satélite del tamaño de nuestra Luna alrededor de un planeta como la Tierra.
Los resultados hablan por sí solos, ya que satélites de entre 0.01 y 0.1 veces la masa de la Tierra (es decir, de la masa de la Luna y más pequeños) podrían ser capturados por un planeta como el nuestro bajo unas condiciones adecuadas. De hecho, un encuentro lento y más directo entre el sistema binario y el planeta incrementaría las posibilidades del intercambio.
Pero a esta teoría le surge un problema: La órbita del nuevo satélite tiene que ser estable para mantenerse durante miles de millones de años y no acabar colisionando con el planeta. Y en el caso de nuestra Luna, también es importante explicar cómo puede haber conseguido tener una órbita tan circular, ya que la órbita resultante de la captura sería muy excéntrica.
Las interacciones gravitatorias y en especial las fuerzas de marea -las mismas que provocan las mareas en nuestros océanos- podrían hacer que este satélite capturado adquiriese una órbita cada vez más circular y volviéndola estable durante miles de millones de años.
 Figura 3. ¿Cómo se formó nuestra Luna? ¿Fue a través de un gran impacto o por un intercambio binario? Imagen cortesía de NASA/JPL/USGS.
Figura 3. ¿Cómo se formó nuestra Luna? ¿Fue a través de un gran impacto o por un intercambio binario? Imagen cortesía de NASA/JPL/USGS.Obviamente hay muchos puntos que solucionar en esta teoría: para capturar un satélite de esta manera tuvo que existir un sistema binario en las proximidades de la Tierra y encontrarnos con una geometría y velocidad muy concretas. Pero independientemente de nuestro caso, Tritón, el satélite de Neptuno, podría ser uno de esos satélites capturados mediante este proceso.
Todavía quedan muchas páginas por escribir sobre la formación de nuestra Luna y de todos los satélites del Sistema Solar, así que este nuevo mecanismo añade un nuevo proceso que complementa a las otras teorías sobre como se forman los satélites de los planetas y al mismo tiempo arroja algo de luz a como podrían haber sido esas primeras etapas caóticas de la formación de nuestro sistema planetario.
¿Vendrá esta nueva teoría para quedarse o nos servirá para explicar el origen de otros satélites de nuestro Sistema Solar y más allá? El tiempo lo dirá, pero sin duda, nos ayudará a comprender mejor la dinámica de nuestro Sistema Solar, especialmente en sus primeras etapas tras la formación planetaria.
Referencias:
Williams, Darren M, and Michael E Zugger (2024) Forming Massive Terrestrial Satellites through Binary-Exchange Capture. The Planetary Science Journal, vol. 5, no. 9, 1 Sept. 2024, pp. 208–208, doi: 10.3847/psj/ad5a9a
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Procede la Luna de un intercambio de parejas planetario? se ha escrito en Cuaderno de Cultura Científica.
El muelle de la Tierra
Edward Page Mitchell (1852-1927) fue un periodista norteamericano especialmente reconocido por los relatos de ciencia ficción que publicó en el diario The Sun de Nueva York, del que llegó a ser editor jefe hasta su jubilación en 1926. En 1973 se publicó una antología de 30 de sus primeras narraciones (1874-1886) bajo el título “The crystal man” [1], que correspondía con uno de sus más sugerentes relatos sobre la invisibilidad y que fue publicado en 1881, 16 años antes de que la famosa novela de H. G. Wells viera la luz.
Diez historias de Mitchell fueron traducidas y publicadas en castellano [2], en las que -además del hombre invisible- se tratan cuestiones como el viaje en el tiempo, el cerebro artificial (superior a la máquina analítica de Babbage) o la teleportación. De estos diez excelentes relatos de ciencia ficción, mi favorito no tiene que ver con las posibles tecnologías cuánticas o la infame IA, que tan a menudo se citan hoy día incorrectamente. Se trata del Taquipompo.
El TaquipompoUna pareja enamorada pide permiso para casarse, pero el obstáculo principal se encuentra en que el novio demuestre su verdadero merecimiento para entrar en una familia matemática insigne. Sin entrar en más detalles del relato, cuya lectura recomiendo efusivamente, mostraremos a continuación algunas resoluciones matemáticas y físicas del artilugio protagonista.
Para transportar objetos rápidamente debemos usar tierra, mar o aire, y además gastar mucha energía. De forma mucho más eficiente, mucho más rápida y sin gasto de energía usamos el Taquipompo. ¿Cómo funciona el Taquipompo en la Tierra?
Para hacer cálculos, a los físicos nos gusta establecer hipótesis simplificadoras, como la famosa vaca esférica en el vacío. En este caso supondremos que podemos hacer un agujero desde Auckland (Nueva Zelanda) a Ronda (España). Como son ciudades antípodas una de la otra y suponemos que nuestro planeta es una esfera, el túnel pasa por el centro de la Tierra. Supondremos además que la densidad de la Tierra es constante y que el agujero lo vaciamos de aire. Esto es el Taquipompo, como lo ilustramos en la Figura 1.
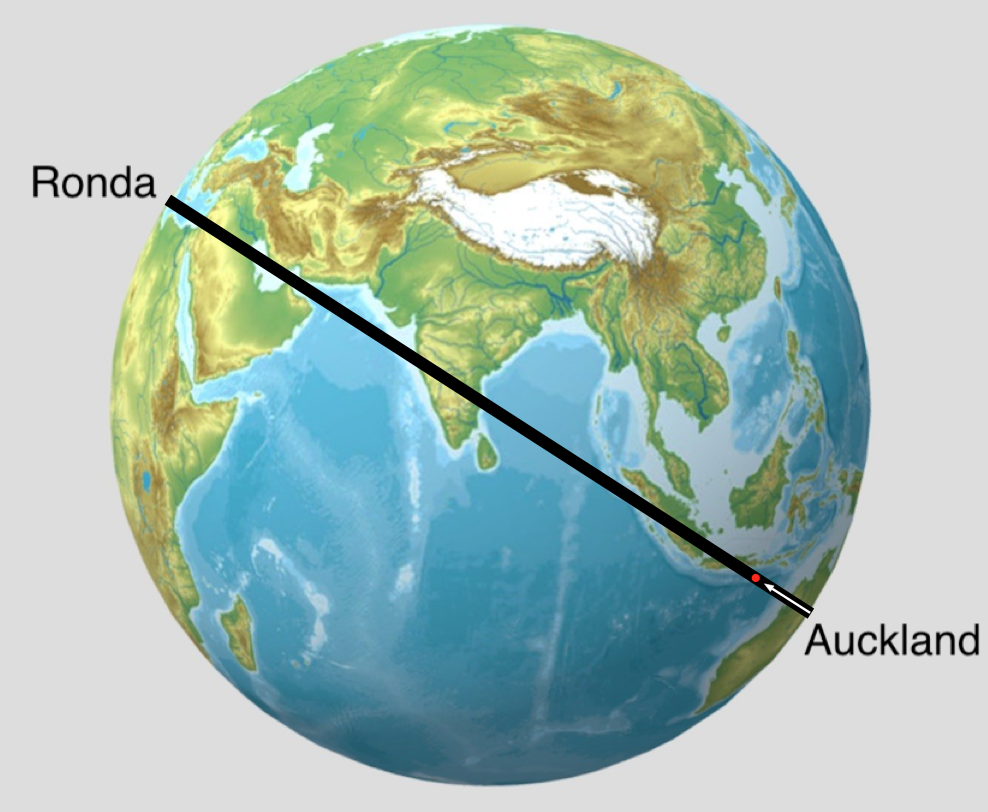 Figura 1. Transporte rápido de mercancías entre antípodas. Fuente: Sketchfab globo-terráqueo-mapa-físico modificado CC Commons
Figura 1. Transporte rápido de mercancías entre antípodas. Fuente: Sketchfab globo-terráqueo-mapa-físico modificado CC CommonsCómo funciona
Tenemos que hacer un envío urgente desde Auckland a Ronda así que directamente tiramos el paquete por el agujero. La ley de gravitación universal nos dice que hacia el exterior del planeta su fuerza gravitatoria es inversamente proporcional al cuadrado de la distancia, pero ¿qué pasa por dentro del túnel mientras cae la pieza que hemos enviado? Los cálculos no son difíciles, pero tampoco son triviales, porque la aceleración no es constante sino dependiente de la distancia del objeto al centro de la Tierra.
Si utilizamos la Ley de Gauss aplicada al campo gravitatorio, y calculamos el volumen de la esfera cuyo radio es la distancia del objeto al centro de la Tierra, podemos demostrar que la aceleración (y la fuerza sobre dicho objeto) desciende linealmente con la distancia al centro de la Tierra. De esta manera resulta muy sencillo calcular la constante de proporcionalidad de la fuerza sobre el cuerpo que hemos enviado por el Taquipompo, que depende de la densidad del planeta y de la constante de gravitación universal.
En la Figura 2 ilustramos la fuerza gravitatoria que la Tierra ejerce sobre el objeto, sea por dentro del túnel como en el espacio exterior. El cambio radical se produce en la superficie del planeta. Dentro del Taquipompo esta fuerza proporcional a la distancia es idéntica a la Ley de Hooke para los muelles, lo cual nos indica que la Tierra se comporta como un resorte.
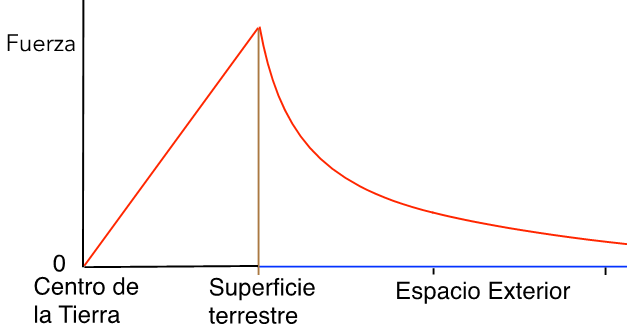 Figura 2. Fuerza de atracción de la Tierra sobre el objeto, en función de su posición respecto del centro del planeta
Figura 2. Fuerza de atracción de la Tierra sobre el objeto, en función de su posición respecto del centro del planeta
Nos encantan a los físicos los osciladores armónicos, que aparecen en los vaivenes de los muelles, en los instrumentos musicales o en todo tipo de ondas, con las que queremos explicar todo el Universo. En el humilde caso del Taquipompo lo que esto nos dice es que el paquete urgente que mandábamos de Auckland a Ronda caerá al centro de la Tierra con aceleración linealmente descendente, superará el punto medio a máxima velocidad, y simétricamente llegará a Ronda. Si no recogemos el paquete en Ronda, éste volverá a caer y llegará de vuelta a Auckland; y tanto la ida como la vuelta sin gastar energía.
Cifras del Taquipompo en el planeta Tierra¿Cuánto tarda el transporte desde una localidad a la otra? Un sencillo cálculo integral -usando la constante de gravitación universal G (6,67 10-11 N m2/kg2) y la densidad de la Tierra (5520 kg/m3)- nos permite deducir que al Taquipompo le bastan 2530 segundos para colocar el envío en su destino (es decir: poco más de 42 minutos), y da igual que el paquete sea pesado o ligero.
En términos del movimiento armónico simple este tiempo es la mitad del período de oscilación, luego el período de este movimiento armónico son T=5060 segundos (viaje de ida y vuelta). La frecuencia en Hercios (Hz) de esta oscilación es el inverso del período.
El Taquipompo es mucho más rápido que cualquier otro medio de transporte de los que disponemos hoy día. Si calculamos el pico de velocidad que adquiere el artilugio en el centro de la Tierra, éste resulta ser 7910 m/s para cualquier paquete que enviemos, y no gastamos combustible ni electricidad. Esperamos que este logro fuera de suficiente entidad como para que la feliz pareja del relato de Edward P. Mitchell demostrara su merecimiento.
Referencias
[1] Sam Moskowitz (Ed.) (1973) The Crystal Man: Stories by Edward Page Mitchell. Doubleday Science Fiction ISBN: 978-0385031394
[2] Edward Page Mitchell (2015) El espectroscopio del alma. Orciny Press ISBN: 978-8494318115
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo El muelle de la Tierra se ha escrito en Cuaderno de Cultura Científica.
Naukas Pro 2024: Deduciendo paleoclimas a partir de sedimentos marinos

Los últimos avances en el ámbito de las energías renovables marinas o la proliferación de los microplásticos fueron algunos de los temas que componen la última edición de NAUKAS PRO. Una cita en la que el personal investigador se sube al escenario del Euskalduna Bilbao para hablar de las investigaciones más destacadas del momento en un ámbito concreto.
En esta ocasión el personal investigador de la Universidad del País Vasco, de la Estación Marina de Plentzia (PiE-UPV/EHU), AZTI, Tecnalia o el CSIC acercaron las últimas investigaciones relacionadas en el ámbito marítimo.
La conferencia Deduciendo paleoclimas a partir de sedimentos marinos corre a cargo de Aitor Payros Agirre, investigador del Departamento de Geología de la UPV/EHU
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Pro 2024: Deduciendo paleoclimas a partir de sedimentos marinos se ha escrito en Cuaderno de Cultura Científica.
Un algoritmo para aumentar la resolución de los mapas de áreas quemadas
Utilizando datos de dos satélites que recogen imágenes ópticas y de otros cuatro satélites que miden las altas temperaturas causadas por los incendios, un equipo de investigadoras propone un algoritmo para obtener la cartografía global de las áreas quemadas con una mayor resolución.
 Fuente: Bastarrika et al (2024)
Fuente: Bastarrika et al (2024)La obtención de información precisa y actualizada de las zonas afectadas por el fuego es fundamental para comprender mejor la calidad del aire, los ciclos biogeoquímicos o el clima, así como para contribuir a la gestión de los incendios. Hace unas décadas, la cartografía o mapeo de las áreas quemadas se realizaba a partir del estudio de las zonas rurales pero, desde el lanzamiento de satélites para la observación de la Tierra, la teledetección se ha convirtido en una opción más práctica para localizar las zonas quemadas, ya que los satélites facilitan la medición de la cobertura de los incendios, tanto a escala regional como mundial.
El problema de las zonas cartografiadas mediante satélites se encuentra en la resolución. De hecho, hasta ahora la resolución de las observaciones globales ha sido mala. “El error de omisión en los productos actuales es muy grande: muchas zonas que están realmente quemadas no se identifican como tales”, señala Aitor Bastarrika, investigador de la UPV/EHU. “Los sistemas actuales utilizan un tamaño de píxel de entre 250 y 500 metros, por lo que no detectan incendios que no alcancen los 250 metros. Y en algunos ecosistemas son muy frecuentes los incendios de esas dimensiones”.
El estudio liderado por Aitor Bastarrika ha desarrollado un algoritmo para lograr una mayor resolución, utilizando datos de seis satélites diferentes. Por un lado, han aprovechado las imágenes captadas por los dos satélites ópticos de la constelación Sentinel-2: ofrecen una buena resolución espacial, de 10-20 metros, pero con una baja frecuencia temporal, ya que solo se obtienen imágenes de un lugar determinado cada 5 días. Por otro lado, se han aprovechado los productos MODIS (derivados de los satélites Terra y Aqua) y VIIRS (derivados de los satélites Suomi NPP y NOAA-20) que detectan incendios activos: detectan estos puntos de alta temperatura con una resolución espacial baja de 375-1000 metros, pero con una frecuencia alta, ya que recogen datos todos los días.
Un algoritmo probado en cientos de áreasEl algoritmo desarrollado por el equipo de Bastarrika utiliza los datos de los dos productos para la detección de incendios activos y con ellos entrena un sistema de imágenes ópticas de cara a desarrollar un sistema de clasificación. Posteriormente proporciona predicciones sobre lo que se ha quemado y lo que no. “Además, estas previsiones se han probado en 576 áreas de todo el mundo, es decir, el algoritmo se ha analizado en todos los ecosistemas en los que las zonas quemadas son significativas”, explica Bastarrika.
El algoritmo desarrollado por el equipo de Bastarrika no es el único, hay otras propuestas similares. Sin embargo, la aportación de los investigadores de la UPV/EHU es especialmente importante porque el algoritmo está preparado para ser aplicado a escala global y para obtener resultados con una resolución media. “Ya existen algoritmos para cartografiar zonas concretas con una resolución media, pero nuestra propuesta sirve para cartografiar áreas quemadas de todo el mundo, lo hace con una resolución aceptable y está lista para ser utilizada”.
De cara al futuro, el objetivo es crear nuevos productos con este algoritmo desarrollado. “Así como hasta ahora están preparados para usar sistemas de baja resolución, a partir de ahora el objetivo es crear productos que ofrezcan resultados con un nivel de resolución medio. Pasar de baja a media resolución supondría una gran contribución a la hora de identificar algunos ecosistemas y de estudiar el clima”, ha afirmado Bastarrika.
Referencia:
Aitor Bastarrika, Armando Rodriguez-Montellano, Ekhi Roteta, Stijn Hantson, Magí Franquesa, Leyre Torre, Jon Gonzalez-Ibarzabal, Karmele Artano, Pilar Martinez-Blanco, Amaia Mesanza, Jesús A. Anaya, Emilio Chuvieco (2024) An automatic procedure for mapping burned areas globally using Sentinel-2 and VIIRS/MODIS active fires in Google Earth Engine ISPRS Journal of Photogrammetry and Remote Sensing doi: 10.1016/j.isprsjprs.2024.08.019
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un algoritmo para aumentar la resolución de los mapas de áreas quemadas se ha escrito en Cuaderno de Cultura Científica.
¿Por qué la llaman piedra si quieren decir roca?
La banda italiana de heavy metal Wind Rose acaba de lanzar un nuevo disco que incluye una canción titulada “Rock and Stone” (roca y piedra), sumándose así a la apasionante discusión sobre qué término es el correcto, si son o no sinónimos o cuándo hay que usar una palabra o la otra. Por suerte (o desgracia, ya veremos), la Real Academia Española (RAE) de la Lengua ha acudido en nuestro rescate, añadiendo unas definiciones precisas para piedra y roca que pueden (o no) aclararnos todas estas dudas. Veamos lo que nos dicen.
 Habrá quien las llame piedras, pero son rocas. Foto: Sean Stratton / Unsplash
Habrá quien las llame piedras, pero son rocas. Foto: Sean Stratton / UnsplashLa RAE tiene varias acepciones para la palabra piedra, pero si nos fijamos en la primera, a priori la más importante, definen este término como “sustancia mineral, más o menos dura y compacta”. Por su parte, la primera definición de roca es “piedra, o vena de ella, muy dura y sólida”. Vamos, que parece que lo que diferencia ambos conceptos es la dureza que presentan: si es muy dura, se trata de una roca, mientras que si es más blandita, sería una piedra. Y aquí es donde se nos erizan los pelos de la nuca a todas las personas profesionales de la Geología.
La dureza es una propiedad de los minerales que se refiere a su resistencia mecánica a sufrir una fractura o alteración permanente en la superficie al aplicarles un objeto u otro mineral. Aunque la más conocida es la de Mohs, existen diversas escalas que ordenan los minerales de acuerdo a su dureza, y en ninguna de ellas encontramos una división en dos grandes grupos que nos diga “de aquí hasta aquí son piedras y a partir de aquí son rocas”. Entonces, ¿de dónde se ha sacado la RAE que el criterio diferenciador entre ambos conceptos es la dureza? Pues de una malinterpretación de una vulgarización geológica.
Me explico. Como en cualquier otra ciencia, en Geología nos encanta hacer clasificaciones de absolutamente todo y ponerle nombres a cuál más complicado a cada uno de los subgrupos definidos. Y una de estas clasificaciones se fundamenta en el tamaño de grano del sedimento, es decir, en el diámetro de las partículas que son erosionadas, transportadas y depositadas en la superficie terrestre, antes de su enterramiento y litificación. Así se ha definido la escala granulométrica de Udden-Wentworth, que incluye tres grandes grupos: lodo, que alberga las partículas con diámetros inferiores a 0,063 mm; arena, que se refiere a los materiales con diámetros comprendidos entre 0,063 mm y 2 mm; y grava, para sedimentos de diámetros superiores a 2 mm. Estos son los nombres oficiales, los que encontraréis en los libros de texto y en las publicaciones científicas de índole geológica. Pero, ¿sabéis cómo los nombramos en privado las y los geólogos? Barro, arena y piedras.
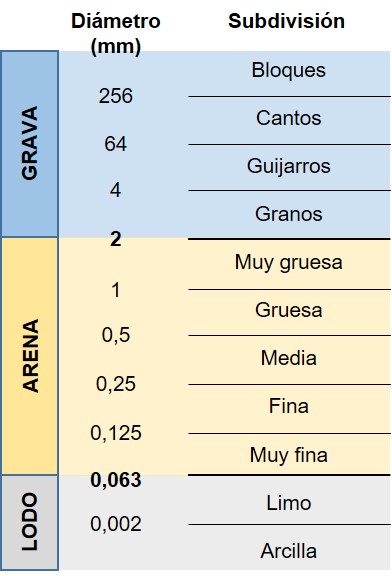 Escala granulométrica de Udden-Wentworth donde se detallan los tres grandes grupos de sedimentos, con los valores límites del diámetro de las partículas y los subgrupos que podemos encontrar en cada uno de ellos. Imagen modificada de Setiawan, B., Antonie, S. y Adhiperdana, B. (2019). Grain-size characteristics of Aceh’s coastal deposits. IOP Conference Series: Materials Science and Engineering. 523.
Escala granulométrica de Udden-Wentworth donde se detallan los tres grandes grupos de sedimentos, con los valores límites del diámetro de las partículas y los subgrupos que podemos encontrar en cada uno de ellos. Imagen modificada de Setiawan, B., Antonie, S. y Adhiperdana, B. (2019). Grain-size characteristics of Aceh’s coastal deposits. IOP Conference Series: Materials Science and Engineering. 523.Aquí es donde encontramos la palabra que buscábamos, en una denominación informal que hace referencia a pequeños fragmentos de roca, generalmente de menos de 20 o 30 cm de diámetro, que podemos coger con la mano y meterlos en la mochila cuando estamos en el campo. Pero esta definición de piedra es el secreto mejor guardado de las personas que nos dedicamos a la Geología, jamás diremos en público que usamos estos términos para referirnos a los materiales sedimentarios. Por eso la RAE ha errado en su definición, ya que no tenían toda la información: el tamaño de grano no tiene nada que ver con la dureza de los materiales.
Piedra es roca alteradaPero no todo va a estar mal en el diccionario de la lengua española. Si prestamos atención a la cuarta y última acepción del término roca, veremos que dice “material sólido de origen natural formado por una asociación de minerales o por uno solo, que constituye una parte importante de la corteza terrestre”. Esa definición es casi perfecta, parece directamente sacada de un manual de Geología. ¿Y en el caso de piedra? Pues en la segunda entrada pone “trozo de piedra que se usa en la construcción”, mientras que la tercera alude a “piedra labrada con alguna inscripción o figura”, entendiendo en ambas el término piedra como esa “sustancia mineral, más o menos dura y compacta”. De nuevo, ambas entradas dan en el clavo. Porque la verdadera diferencia entre los conceptos roca y piedra, mundialmente aceptada en el ámbito geológico y que debería permear en la sociedad en general, es que una roca es un material sólido natural, mientras que una piedra es una roca que ha sido alterada de alguna manera por el ser humano (cortada, pulida, tallada, etc.). De esta manera, cuando vamos a una cantera encontraremos un afloramiento de rocas que van a ser explotadas y, en cuanto cortamos un nivel para sacar unas losas con las que trabajar, tendremos en nuestras manos unas piedras ornamentales.
 A) Afloramiento de roca caliza, material sólido natural. B) Ejemplo de piedra caliza, una roca transformada por el ser humano como elemento decorativo.
A) Afloramiento de roca caliza, material sólido natural. B) Ejemplo de piedra caliza, una roca transformada por el ser humano como elemento decorativo.Así que, aunque las personas profesionales de la Geología nos enfademos con el resto del mundo cuando usa la palabra piedra, no podemos decir nada si se están refiriendo a la encimera de la cocina, a la baldosa de la acera o a una punta de flecha encontrada en una excavación arqueológica. Pero seguiremos corrigiendo a la gente si llama piedra a un guijarro que se encuentre en el margen del cauce de un río, porque eso, aunque sea pequeña, es una roca, ya que es un material natural que no ha sufrido ninguna manufactura humana. Y permitidme un último consejo, no os quedéis solo con la primera entrada de la definición de una palabra cuando la busquéis en el diccionario, porque ya hemos visto que, a veces, son las últimas las que te dan la descripción correcta.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿Por qué la llaman piedra si quieren decir roca? se ha escrito en Cuaderno de Cultura Científica.
Las matemáticas del “Día del mol”
Hoy, como cada 23 de octubre, se celebra el Día del mol. Es una celebración informal que festejan las personas vinculadas a la química de manera profesional o amateur.
 Imagen del #MoleDay 2014. Fuente: Andy Brunning/Compound Interest.
Imagen del #MoleDay 2014. Fuente: Andy Brunning/Compound Interest.
No se celebra durante todo el día; se hace solo entre las 6:02 de la mañana y las 6:02 de la tarde de cada 23 de octubre. Estas horas y esta fecha –escritas a la manera anglosajona– quedarían representadas por
6:02 10/23
una expresión que recuerda a la forma decimal del número de Avogadro con tres cifras significativas: 6,02 x 1023.
El mol como unidad de medidaEl mol es la unidad con que se mide la cantidad de sustancia; es una de las siete magnitudes físicas fundamentales del Sistema Internacional de Unidades (SI). Se adoptó como unidad de medida el 4 de octubre de 1971.
La decisión se tomó en la 14e Conférence Générale des Poids et Mesures (CGPM), el órgano de decisión de la Oficina Internacional de Pesas y Medidas, que se encarga de tomar decisiones en materia de metrología y, en particular, en lo que afecta al SI.
 Fuente: Comptes Rendus des Séances de la quatorzième CGPM (Paris, 4-8 octobre 1971), pág. 78.
Fuente: Comptes Rendus des Séances de la quatorzième CGPM (Paris, 4-8 octobre 1971), pág. 78.
En la imagen anterior, extraída del informe de la CGPM de 1971, se puede leer:
La Decimocuarta Conferencia General de Pesos y Medidas,
TENIENDO EN CUENTA las opiniones de la Unión Internacional de Física Pura y Aplicada, de la Unión Internacional de Química Pura y Aplicada y de la Organización Internacional de Normalización sobre la necesidad definir una unidad de cantidad de materia,
DECIDE
-
El mol es la cantidad de sustancia de un sistema conteniendo tantas entidades elementales como átomos hay en 0,012 kilogramos de carbono 12; su símbolo es «mol».
-
Cuando se emplea el mol, las entidades elementales deben especificarse y pueden ser átomos, moléculas, iones, electrones, otras partículas o agrupaciones especificadas de tales partículas.
-
El mol es una unidad de base del Sistema Internacional de Unidades.
La constante de Avogadro es el número de entidades elementales –normalmente átomos o moléculas– en un mol de una sustancia cualquiera. Su nombre* se debe al físico y químico Amedeo Avogadro (1776-1856), quien formuló la ley de Avogadro en 1812: “Volúmenes iguales de gases distintos bajo las mismas condiciones de presión y temperatura contienen el mismo número de partículas”.
Así, un mol de cualquier sustancia contiene exactamente ese número de átomos o moléculas. Por supuesto, dependiendo de la masa de los átomos o moléculas, la masa total de un mol de una sustancia puede variar: un mol de agua pesa un poco más de 18 gramos, mientras que un mol de sal común, el cloruro de sodio, pesa 58,4 gramos.
El Día del molEl Día del mol comenzó a gestarse a partir de la publicación de un artículo escrito en 1985 por Margaret Christoph, profesora de ciencias de Delaware. En él mencionaba que celebraba un día de química con su alumnado cada mes de octubre. Inspirado por este escrito, el 15 de mayo de 1991, el profesor de química de enseñanza secundaria Maurice Oehler fundó la National Mole Day Foundation (NMDF). Y el Día del mol empezó a celebrarse desde ese año para despertar el interés por la química:
La gente lo suficientemente loca como para celebrar el Día del mol tiene que ser maravillosa. No estoy seguro de lo que le depara el futuro a la fundación, pero sí sé que es viable y que seguirá entusiasmando a los niños con la química. Mi objetivo es que al menos todos los profesores de química se enteren y celebren de alguna manera el Día del mol cada año. Tenemos un largo camino por recorrer, pero lo estamos logrando.
En inglés “mol” es «mole”, pero “mole” es también “topo”, ese enigmático mamífero subterráneo. Por ese doble sentido, la NMDF tiene un topo como “mascota”. Un mol es una cantidad realmente grande:
Un topo oriental (Scalopus aquaticus) pesa alrededor de 75 gramos, lo que significa que un mol de topos pesa
(6,022 × 1023) × 75 g ≈ 4,52 × 1022 kg.
Eso es un poco más de la mitad de la masa de nuestra luna.
Los mamíferos están compuestos principalmente de agua. Un kilogramo de agua ocupa un litro de volumen, por lo que si los moles de topos pesan 4,52×1022 kilogramos, ocupan aproximadamente 4,52×1022 litros de volumen. Es posible que notes que ignoramos los espacios entre los topos. En un momento, verás por qué.
La raíz cúbica de 4,52×1022litros es 3562 kilómetros, lo que significa que estamos hablando de una esfera con un radio de 2210 kilómetros, o un cubo de 2213 millas por cada lado. (Es una coincidencia muy interesante que nunca había notado antes: una milla cúbica equivale casi exactamente a 4/3π kilómetros cúbicos, por lo que una esfera con un radio de X kilómetros tiene el mismo volumen que un cubo de X millas por cada lado).
Si estos moles de topos fueran liberados sobre la superficie de la Tierra, la llenarían hasta alcanzar 80 kilómetros de altura, casi hasta el (antiguo) borde del espacio […]
Cada año, este especial día tiene un tema protagonista, elegido con mucho sentido del humor e involucrando algún juego de palabras. En 2024 el tema elegido es “EncantMole” e invita a explorar los aspectos mágicos de los topos, los moles y el “encantador” mundo de los átomos y las moléculas. ¡A celebrarlo!
 Cartel oficial del Día del mol. Fuente: NMDF.
Cartel oficial del Día del mol. Fuente: NMDF.
Referencias
- Margaret Christoph. Mole day. The Science Teacher 52 (7) (1985) 47–48
- Mole Day
- Andy Brunning, Mole Day – What is a mole in chemistry?, Compound Interest,23 octubre 2014
- A mole of moles, xkcd
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
* Nota del Editor: Su nombre, que no su cálculo ni su definición. Véase a este respecto Las constantes de Planck y el caballo blanco de Santiago, últimos párrafos.
El artículo Las matemáticas del “Día del mol” se ha escrito en Cuaderno de Cultura Científica.
Un siglo para un gran avance en un problema matemático que parece simple
Una nueva prueba sobre los números primos ilumina la sutil relación entre la suma y la multiplicación, y aumenta la esperanza de avances en la famosa conjetura abc.

Una mañana del pasado noviembre, el matemático Héctor Pastén finalmente resolvió el problema que lo había perseguido durante más de una década utilizando un truco de productividad archiconocido: la procrastinación.
Tenía que ponerse a redactar un examen final para su clase de teoría de números en la Pontificia Universidad Católica de Chile en Santiago. Para evitarlo, se puso a pensar, por enésima vez, en una de sus secuencias favoritas: 2, 5, 10, 17, 26 y así sucesivamente, la lista de todos los números de la forma n2 + 1 (donde n es un número entero).
Los matemáticos han utilizado esta secuencia durante más de un siglo para investigar la complicada relación entre la suma y la multiplicación, una tensión que se encuentra en el corazón de la teoría de números. Los problemas fundamentales sobre la multiplicación (por ejemplo, sobre cómo se factorizan los números en primos) de repente se vuelven mucho más profundos y desafiantes tan pronto como la suma entra en escena. Una de las cuestiones abiertas más grandes de las matemáticas, por ejemplo, pregunta si todo número par mayor que 2 es la suma de dos primos; otra pregunta si hay infinitos pares de primos que difieren solo en 2, como 11 y 13.
La sucesión n2 + 1 ofrece un buen punto de partida para investigar la relación entre la suma y la multiplicación, porque combina uno de los tipos más simples de multiplicación (elevar un número al cuadrado) con uno de los tipos más simples de adición (sumar 1). Eso no significa que la sucesión en sí sea simple. Los matemáticos aún no pueden responder a preguntas elementales sobre ella, como por ejemplo si contiene infinitos números primos. “No hace falta mucho para llegar al límite de nuestro conocimiento”, afirma Andrew Granville de la Universidad de Montreal. Cuando los matemáticos logran desplazar este límite, aunque sea un poco, las técnicas que desarrollan a menudo arrojan luz sobre cuestiones mucho más amplias sobre la suma y la multiplicación.
Pastén intentaba demostrar que los números de la secuencia siempre deben tener al menos un factor primo que sea bastante grande. La mañana en que debería haber estado preparando el examen final, finalmente lo logró, al descubrir cómo incorporar información sobre los factores primos de n2 + 1 en la estructura de una ecuación llamada curva elíptica.
Ese día, durante el almuerzo, le describió la prueba a su esposa, la matemática Natalia García-Fritz. Dada la sorprendente solidez de su resultado, ella “me dijo que probablemente debería comprobarlo muchas veces”, cuenta Pastén. “Esa tarde lo hice y los teoremas seguían ahí”.
 Héctor Pastén pasó más de una década intentando resolver un problema matemático en la intersección de la suma y la multiplicación. Finalmente lo logró cuando decidió posponer la redacción de un examen final para uno de sus cursos. Foto: Natalia García-Fritz
Héctor Pastén pasó más de una década intentando resolver un problema matemático en la intersección de la suma y la multiplicación. Finalmente lo logró cuando decidió posponer la redacción de un examen final para uno de sus cursos. Foto: Natalia García-FritzHabía un solo inconveniente: Pastén no tenía ningún examen que poner a sus alumnos. Les pidió que escribieran un ensayo sobre el tema que quisieran. “El resultado fue un trabajo de muy alta calidad”, dice.
Pastén envió su prueba a Inventiones Mathematicae, una de las revistas más importantes de matemáticas, donde fue aceptada en poco más de un mes, un abrir y cerrar de ojos según los estándares de publicación habituales en el campo. “Es un avance encantador en algo que no ha experimentado mucho progreso durante prácticamente 100 años”, comenta Cameron Stewart de la Universidad de Waterloo. Los matemáticos esperan que también se traduzca en avances en secuencias numéricas relacionadas.
La técnica de Pastén también le permitió avanzar en ciertos casos de la conjetura abc, otra cuestión que trata de la interacción entre la suma y la multiplicación, y uno de los problemas sin resolver más famosos —y controvertidos— de las matemáticas. “Las ideas nuevas (y correctas) en esta área han sido escasas”, escribe Granville en un correo electrónico. “La originalidad y la promesa de sus métodos merecen mucha atención”.
Primos grandesSi una secuencia de números se hace cada vez más grande, eso no garantiza que sus factores primos más grandes hagan lo mismo. Tomemos la secuencia n2: los números 1, 4, 9, 16, etc. Es fácil encontrar números en esta secuencia cuyos factores primos sean pequeños. Por ejemplo, cualquier potencia de 2 en esta lista (4, 16, 64, 256, 1024…) tiene solo un factor primo: 2.
Pero cuando se añade 1 a esta secuencia, “se destruye por completo toda la información que se tenía” sobre los factores primos, afirma Pastén. “Los primos se comportan de una manera muy loca”.
En 1898, Carl Størmer demostró que, a diferencia de la sucesión n2, los factores primos más grandes números en la sucesión n2+ 1 se acercan al infinito a medida que n crece. Este hallazgo demostró que “algo interesante está sucediendo, algo inusual”, explica Stewart.
 A mediados de la década de 1930, los matemáticos Kurt Mahler (arriba) y Sarvadaman Chowla demostraron de forma independiente que había un límite en la velocidad a la que podía crecer el mayor factor primo de una secuencia de números. El nuevo trabajo marca la primera mejora importante de su resultado. Fotos: MFO; cortesía de Shelby White y Leon Levy Archives Center
A mediados de la década de 1930, los matemáticos Kurt Mahler (arriba) y Sarvadaman Chowla demostraron de forma independiente que había un límite en la velocidad a la que podía crecer el mayor factor primo de una secuencia de números. El nuevo trabajo marca la primera mejora importante de su resultado. Fotos: MFO; cortesía de Shelby White y Leon Levy Archives CenterPero Størmer no pudo determinar con qué rapidez crecen los factores primos más grandes de n2 + 1, un siguiente paso natural en la caracterización del comportamiento de la secuencia.
Si empiezas a calcular números de la secuencia, la mayoría de ellos parecen tener al menos un factor primo muy grande. Pero, ocasionalmente, hay una caída enorme. Por ejemplo, un número de la secuencia, 586.034.187.508.450, tiene un factor primo de 67.749.617.053. Pero el factor primo más grande del siguiente número de la secuencia, 586.034.235.924.737, es solo 89. Son estas excepciones las que hacen que el problema sea difícil.
A mediados de la década de 1930, Sarvadaman Chowla y Kurt Mahler demostraron de forma independiente que, para cualquier valor de n, el mayor factor primo de n2+ 1 siempre debe ser al menos tan grande como log(log n). Pero log(log n) crece increíblemente despacio (si lo graficamos, parece plano a simple vista). Los matemáticos sospechaban que el mayor factor primo de n2 + 1 en realidad crece mucho más rápido, pero no podían demostrarlo.
En 2001, Stewart y Kunrui Yu, de la Universidad de Ciencia y Tecnología de Hong Kong, desarrollaron un nuevo enfoque para estudiar los factores primos en secuencias, utilizando un área de las matemáticas llamada teoría de la trascendencia. Dos años después, Julien Haristoy descubrió cómo aplicar su método a la secuencia n2 + 1 , logrando una pequeña mejora respecto del resultado de Chowla y Mahler.
Pero desde entonces, el tema había quedado en un punto muerto. “Hacía tiempo que necesitabamos un nuevo ingrediente”, apunta Granville.
Exponentes pequeñosPastén lleva más de una década cultivando ese nuevo ingrediente. En 2012, cuando era estudiante de posgrado en la Queen’s University de Kingston (Ontario), su director, Ram Murty, le sugirió que se centrara en problemas que exploraran la interacción entre la suma y la multiplicación.
Una de las herramientas más potentes de los teóricos de números para estudiar esta interacción es codificar los números en un tipo de ecuación llamada curva elíptica. Por ejemplo, los números pueden aparecer como soluciones de la ecuación o en un cálculo relacionado llamado discriminante. Con la codificación adecuada, los matemáticos pueden aprovechar la rica estructura de las curvas elípticas y hacer uso de objetos matemáticos asociados conocidos como formas modulares. “Siempre que se pueden incorporar esas formas modulares, para las que existe toda una maravillosa teoría, se obtiene mucha información”, explica Marc Hindry de la Universidad Paris Cité.
Con el paso de los años, Pastén desarrolló una nueva teoría que incluía formas modulares y entidades relacionadas, llamadas curvas de Shimura, que le permitieron abordar muchas de las preguntas que Murty le había planteado. “Pero no pude hacer ningún progreso en el problema n2+ 1, absolutamente nada”, cuenta. “Esto me molestó durante muchos años”.
En la mañana de noviembre en la que Pastén se suponía que tenía que estar redactando el examen, el problema n2+ 1 representaba una vía de escape en más de un sentido. A principios de ese año, su padre había muerto y Pastén se encontró recurriendo a las matemáticas en busca de consuelo. “Me resultaron muy útiles para eso”, explica. “Las matemáticas no se tratan solo de demostrar teoremas; tal vez se traten de una forma de interactuar con la realidad”.
Obtener el control directo sobre los factores primos de la secuencia n2+ 1 parecía demasiado difícil, por lo que Pastén había puesto hace tiempo su mira en un ataque más indirecto: obtener el control sobre los exponentes en la factorización en primos. Si estás factorizando un número grande, puede consistir en primos pequeños elevados a exponentes grandes, o primos grandes elevados a exponentes pequeños. Pero no puede consistir en primos pequeños elevados a exponentes pequeños: eso no daría un número lo suficientemente grande. Por lo tanto, si puedes demostrar que los exponentes son pequeños, entonces al menos uno de los primos debe ser grande, exactamente lo que Pastén quería demostrar.
Mientras Pastén observaba en su pizarra algunos cálculos del día anterior, de repente se dio cuenta de que podría controlar los exponentes en la factorización prima de n2+ 1 creando el tipo correcto de curva elíptica. Después de algunos experimentos, encontró una: la ecuación y2 = x3 + 3x + 2n, cuyo discriminante es n2+ 1 multiplicado por un factor de −108.
Al aplicar su teoría de las curvas de Shimura a esta curva elíptica en particular, pudo demostrar que el producto de los exponentes de n2+ 1 debe ser bastante pequeño. Esto no significaba necesariamente que todos los exponentes debían ser pequeños, pero le dio suficiente control sobre ellos para poder aplicar el antiguo método de Stewart y Yu de la teoría de la trascendencia. Al utilizar las dos técnicas juntas, pudo demostrar que el mayor factor primo de n2+ 1 debe ser al menos aproximadamente (log(log n))2, el cuadrado de la estimación que Chowla y Mahler descubrieron en la década de 1930. La nueva tasa de crecimiento de Pastén es mucho más alta que el récord anterior, aunque los matemáticos sospechan que la tasa de crecimiento real es aún mayor.
Aun así, “es una mejora notable”, afirma Hindry.
Pastén también pudo usar sus técnicas para mejorar las estimaciones para ciertos casos de la conjetura abc, que dice que si tres números enteros a, b y c (que no comparten factores primos) satisfacen la ecuación a + b = c, entonces el producto de sus factores primos debe ser grande comparado con c. La conjetura, una de las más importantes en la teoría de números, ha estado en el centro de una controversia durante una década: el matemático Shinichi Mochizuki afirma haberla demostrado, pero la mayoría de la comunidad matemática no está de acuerdo. El trabajo de Pastén representa un enfoque completamente diferente del problema. Si bien su resultado está lejos de ser una prueba de la conjetura completa, según algunas medidas representa el primer progreso significativo en décadas. «Siento que la conjetura abc es un tema muy estancado», comenta Granville.
Después de que Chowla y Mahler propusieran su límite hace 90 años, los matemáticos establecieron gradualmente el mismo límite para una familia infinita de secuencias relacionadas, como n2 + 3 o n5 + 2. Es probable que los investigadores intenten hacer lo mismo con el nuevo límite de Pastén, mientras exploran también las ramificaciones de su método para otros problemas en la interfaz de la adición y la multiplicación. “La novedad del ataque” hace que esta sea una perspectiva emocionante, afirma Barry Mazur de la Universidad de Harvard.
Es difícil predecir qué surgirá de estas exploraciones. “Ese es el problema de la originalidad”, comenta Granville. Pero “definitivamente obtuvo algo muy bueno”.
El artículo Un siglo para un gran avance en un problema matemático que parece simple se ha escrito en Cuaderno de Cultura Científica.
Innovación evolutiva en peces tríglidos: Apéndices locomotores, táctiles y ¡olfativos!
Los rubios (familia Triglidae) son peces marinos con un significado especial para mí. Fueron mi primer tema de investigación, y dediqué mi tesina de licenciatura a una de sus especies, el armado (Peristedion). La característica más llamativa de los tríglidos es la presencia de tres “patitas” a cada lado del cuerpo, derivadas de radios de las aletas pectorales. Con estos apéndices caminan sobre el fondo marino, como vemos en el vídeo de abajo. Dos recientes artículos publicados en Current Biology por investigadores de las universidades de Harvard y Stanford han revelado el sorprendente sistema de formación de estos apéndices locomotores y cómo algunas especies han desarrollado en ellos un nuevo órgano sensorial.
El primer artículo describe la forma en que tres radios pectorales se independizan del resto durante el desarrollo larvario para formar los apéndices locomotores en la especie Prionotus carolinus (Figura 1). Al comparar la expresión de genes en la parte dorsal y en la parte ventral de la aleta, se observó que el gen tbx3a se expresaba exclusivamente en los radios precursores de los apéndices, pero no en el resto (Figura 2).
 Figura 1. Prionotus carolinus. Las puntas de flecha muestran los apéndices locomotores. De Herbert et al., artículo citado en referencias, con licencia CC-BY
Figura 1. Prionotus carolinus. Las puntas de flecha muestran los apéndices locomotores. De Herbert et al., artículo citado en referencias, con licencia CC-BYTBX3, el gen humano correspondiente al tbx3a, codifica un factor de transcripción, es decir, una proteína que se une al ADN y activa o reprime la expresión de otros genes. De esta forma, TBX3 participa en el desarrollo de muchos órganos, entre ellos el corazón, extremidades, mamas y genitales. Las mutaciones de TBX3 producen el síndrome ulnar-mamario, caracterizado por varias malformaciones, entre ellas defectos en el cúbito (ulna) y la parte posterior de la mano (Figura 2). Esta es, anatómicamente, la zona de nuestro brazo que corresponde a la región en la que se desarrollan los apéndices de los tríglidos.
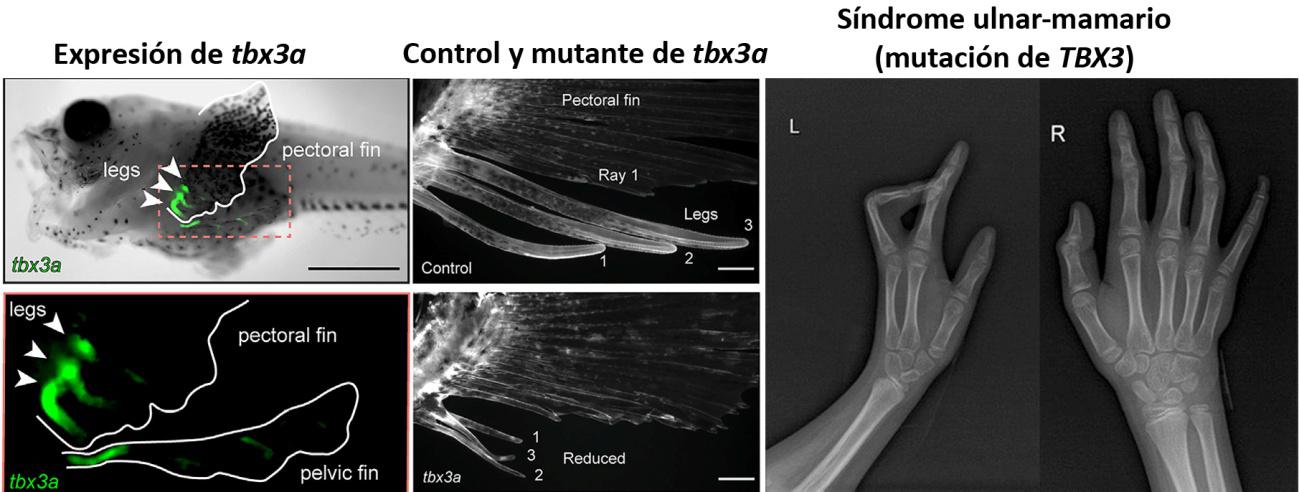 Figura 2. A la izquierda se muestra la expresión del gen tbx3a en larvas de Prionotus. La expresión se produce en los precursores de los tres apéndices locomotores. En el centro vemos el resultado de la mutación de tbx3a. En lugar de formarse los apéndices (control, arriba) aparecen tres pequeños radios libres (mutante, abajo). A la derecha, síndrome ulnar-mamario humano causado por mutaciones en TBX3. El brazo izquierdo es el afectado, con ausencia de cúbito y dedos anular y meñique. Esa parte de la mano corresponde anatómicamente con la región inferior de la aleta de Prionotus, y durante su desarrollo expresa TBX3. De Herbert et al., artículo citado en referencias, con licencia CC-BY. La radiografía es de Zhang et al., Front. Pediatr. 11, 2023, doi: 10.3389/fped.2023.1052931, con licencia CC-BY
Figura 2. A la izquierda se muestra la expresión del gen tbx3a en larvas de Prionotus. La expresión se produce en los precursores de los tres apéndices locomotores. En el centro vemos el resultado de la mutación de tbx3a. En lugar de formarse los apéndices (control, arriba) aparecen tres pequeños radios libres (mutante, abajo). A la derecha, síndrome ulnar-mamario humano causado por mutaciones en TBX3. El brazo izquierdo es el afectado, con ausencia de cúbito y dedos anular y meñique. Esa parte de la mano corresponde anatómicamente con la región inferior de la aleta de Prionotus, y durante su desarrollo expresa TBX3. De Herbert et al., artículo citado en referencias, con licencia CC-BY. La radiografía es de Zhang et al., Front. Pediatr. 11, 2023, doi: 10.3389/fped.2023.1052931, con licencia CC-BYEl siguiente experimento consistió en mutar tbx3a en la larva de Prionotus utilizando tecnología CRISPR-CAS9. Los peces mutantes no desarrollaron los apéndices y, en su lugar, formaron tres radios libres, similares a los de las aletas (Figura 2). En conclusión, el gen tbx3a y su correspondiente gen TBX3 humano participan en la organización de la parte posterior del miembro pectoral, tanto si se trata de formar apéndices locomotores como dedos.
Esta coincidencia no debe sorprendernos. Los animales somos el resultado de un programa de desarrollo regulado genéticamente. Podemos concebir los genes que controlan dicho programa como herramientas que se emplean en el proceso de construcción del embrión. El resultado final (un pez o un humano) va a depender de cómo y cuándo se empleen las herramientas a lo largo del proceso, pero dichas herramientas (genes como Tbx3a/TBX3) van a ser las mismas.
El segundo artículo sobre Prionotus carolinus resulta aún más sorprendente. Los investigadores observaron la capacidad de este pez para localizar presas enterradas en el sedimento. Sus apéndices, densamente inervados, eran capaces de detectar pequeños movimientos. Pero cuando sustituyeron las presas por cápsulas con extracto de mejillón, incluso con extractos conteniendo solo pequeñas moléculas orgánicas, los peces siguieron encontrándolas. Parecía evidente que los peces eran capaces de “olfatear” de alguna manera a sus presas independientemente del sentido del tacto. Los terminales nerviosos libres de los apéndices funcionan como mecanorreceptores y explican la sensación táctil, pero nunca constituyen receptores de sustancias químicas. La quimiorrecepción debía producirse por otra vía.
Se comprobó que otras especies cercanas, como Prionotus evolans, no eran capaces de encontrar presas enterradas. Los apéndices de P. carolinus mostraban una especie de papilas que no existían en P. evolans. Cuando se comparó la expresión diferencial de genes en la zona de las papilas, destacó un gen, t1r3, que se activaba en el epitelio de las papilas. T1r3 codifica una proteína de membrana que se asocia con otras proteínas similares para constituir receptores gustativos. Las mismas células epiteliales de P. carolinus expresan a bajos niveles el gen t1r2 con lo que pueden constituir estos receptores. Curiosamente, un dímero T1R3/T1R2 se encuentra en las papilas de nuestra lengua, y constituye un receptor del sabor dulce.
Este resultado es sorprendente. Células del epitelio que recubre las papilas de P. carolinus expresan las proteínas necesarias y suficientes para convertirse en células quimiosensibles utilizando el mismo mecanismo que nosotros tenemos en la lengua. Esta innovación evolutiva solo se ha registrado en dos especies de tríglidos estrechamente emparentadas (P. carolinus y P. sciturus), por lo que debe haberse producido hace relativamente poco tiempo, antes de que el linaje de estas dos especies se separara del resto.
 Figura 3. Innovaciones evolutivas en los tríglidos. En una fase inicial de su evolución se desarrollaron apéndices locomotores bajo el control del gen tbx3a. En el linaje de Prionotus carolinus y P. sciturus se han desarrollado además papilas que actúan como receptores táctiles gracias a su densa inervación. La expresión de t1r3 en el epitelio de las papilas también hace posible la quimiorrecepción. De esta forma, ambas especies pueden localizar presas enterradas en el sedimento y han ampliado su nicho ecológico.
Figura 3. Innovaciones evolutivas en los tríglidos. En una fase inicial de su evolución se desarrollaron apéndices locomotores bajo el control del gen tbx3a. En el linaje de Prionotus carolinus y P. sciturus se han desarrollado además papilas que actúan como receptores táctiles gracias a su densa inervación. La expresión de t1r3 en el epitelio de las papilas también hace posible la quimiorrecepción. De esta forma, ambas especies pueden localizar presas enterradas en el sedimento y han ampliado su nicho ecológico.En resumen, la secuencia evolutiva debió ser la siguiente (Figura 3): Tbx3a se expresa en la parte posterior de la aleta pectoral, y controla el desarrollo de tres radios especializados para formar apéndices locomotores. En algunas especies estos apéndices recibieron una intensa innervación aumentando su capacidad mecanorreceptora (táctil). Y en una tercera etapa, que ha ocurrido recientemente, las células que cubren sus papilas han adquirido capacidad quimiorreceptora (olfativa) mediante la expresión de las mismas proteínas que nosotros utilizamos en nuestra lengua para el sentido del gusto.
Referencias
Allard, C.A.H., Herbert, A.L., Krueger, S.P. et al. (2024) Evolution of novel sensory organs in fish with legs. Curr Biol. doi: 10.1016/j.cub.2024.08.014.
Herbert, A.L., Allard, C.A.H., McCoy, M.J. et al. (2024) Ancient developmental genes underlie evolutionary novelties in walking fish. Curr Biol. doi: 10.1016/j.cub.2024.08.042.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Innovación evolutiva en peces tríglidos: Apéndices locomotores, táctiles y ¡olfativos! se ha escrito en Cuaderno de Cultura Científica.
El fageoma: un reino oculto en su intestino
Las entrañas humanas están repletas de virus que infectan a las bacterias. ¿Qué están tramando?
 Fagos atacando una célula bacteriana. Fuente: Graham Beards / Wikimedia Commons
Fagos atacando una célula bacteriana. Fuente: Graham Beards / Wikimedia Commons
Probablemente haya oído hablar del microbioma —las hordas de bacterias y otras diminutas formas de vida que viven en nuestros intestinos—. Pues bien, resulta que esas bacterias tienen virus que existen dentro y alrededor de ellas —con importantes consecuencias tanto para ellas como para nosotros—.
Les presento al fageoma.
En el interior del aparato digestivo humano hay miles de millones, quizá incluso billones, de estos virus, conocidos como bacteriófagos (“comedores de bacterias” en griego) o solo “fagos” para sus amigos. La ciencia del fageoma (también conocido como fagoma) se ha disparado recientemente, afirma Breck Duerkop, bacteriólogo de la Facultad de Medicina Anschutz de la Universidad de Colorado, y los investigadores se esfuerzan por comprender su enorme diversidad. Los investigadores sospechan que, si los médicos pudieran aprovechar o dirigir los fagos adecuados, podrían mejorar la salud humana.
“Habrá fagos buenos y fagos malos”, afirma Paul Bollyky, médico especialista en enfermedades infecciosas e investigador en la Escuela de Medicina de Stanford. Pero por ahora, aún no está claro cuántos fagos ocupan el intestino —quizás uno por cada célula bacteriana, o incluso menos—. También hay bacterias que contienen genes de fago, pero no producen virus de forma activa; las bacterias solo viven sus vidas con ADN de fago en sus genomas.
Y hay muchos fagos que aún no han sido identificados; los científicos los llaman la “materia oscura” del fageoma. Una parte importante de la investigación actual sobre fagos consiste en identificar estos virus y sus bacterias hospedadoras. La base de datos de fagos intestinales contiene más de 140.000 fagos, pero seguramente se trata de una subestimación. “Su variedad es simplemente extraordinaria”, afirma Colin Hill, microbiólogo de la Universidad de Cork en Irlanda.
Los científicos encuentran los fagos examinando secuencias genéticas extraídas de muestras fecales humanas. Ahí es donde los investigadores encontraron el grupo de fagos intestinales más común, llamado CrAss-fago. (Salga de dudas: su nombre viene del inglés, CrAssphage, Cross-Assembly phage, nombre que se debe a la técnica de “ensamblaje cruzado” que extrajo sus genes de la mezcolanza genética). En un estudio reciente, Hill y sus colegas detallaron la forma de bombilla de los CrAss-fago, con un cuerpo de 20 lados y un tallo para inyectar ADN en las bacterias huésped.
No está claro si los CrAss-fago influyen en la salud humana, pero dado que infectan a uno de los grupos más comunes de bacterias intestinales, Bacteroides, a Hill no le sorprendería que lo hicieran. Otros grupos comunes, que también infectan a Bacteroides, son el Gubaphage (fago de bacteroidales intestinales) y el LoVEphage (muchos elementos genéticos virales).
Los fageoma varían mucho de una persona a otra. También cambian en función de la edad, el sexo, la dieta y el estilo de vida, como describen Hill y sus colegas en el Annual Review of Microbiology 2023.
Aunque los fagos infectan a las bacterias y a veces las matan, la relación es más complicada que eso. “Solíamos pensar que los fagos y las bacterias se pelean”, dice Hill, “pero ahora sabemos que en realidad están bailando; son socios”.
Los fagos pueden beneficiar a las bacterias aportándoles nuevos genes. Cuando una partícula de fago se está ensamblando dentro de una bacteria infectada, a veces puede introducir genes bacterianos en su cubierta proteínica junto con su propio material genético. Más tarde, inyecta esos genes en un nuevo huésped, y esos genes transferidos accidentalmente podrían ser útiles, dice Duerkop. Podrían proporcionar resistencia a los antibióticos o la capacidad de digerir una nueva sustancia.
Los fagos mantienen en forma a las poblaciones bacterianas al picarles constantemente los talones, afirma Hill. Las bacterias Bacteroides pueden presentar hasta una docena de tipos de cubiertas azucaradas en su superficie exterior. Los distintos recubrimientos tienen diferentes ventajas: evadir el sistema inmunitario, por ejemplo, u ocupar un rincón diferente del aparato digestivo. Pero cuando hay CrAss-fagos alrededor, dice Hill, los Bacteroides deben cambiar constantemente de cubierta para eludir a los fagos que reconocen una cubierta u otra. El resultado: en un momento dado, hay Bacteroides con diferentes tipos de cubierta, lo que permite a la población en su conjunto ocupar una variedad de nichos o hacer frente a nuevos retos.
Los fagos también evitan que las poblaciones bacterianas se descontrolen. El intestino es un ecosistema, como el bosque, y los fagos son depredadores de bacterias, como los lobos son depredadores de ciervos. El intestino necesita a los fagos como el bosque a los lobos. Cuando esas relaciones depredador-presa se alteran, pueden producirse enfermedades. Los investigadores han observado cambios en el fageoma del síndrome inflamatorio intestinal (SII), la enfermedad del intestino irritable y el cáncer colorrectal; por ejemplo, el ecosistema vírico de una persona con SII suele ser poco diverso.
Las personas intentan reequilibrar el microbioma intestinal con dietas o, en casos médicos extremos, trasplantes fecales. El estudio de los fagos podría proporcionar un enfoque más afinado, afirma Hill. Por ejemplo, los científicos buscan fagos que puedan utilizarse terapéuticamente para infectar las bacterias que causan las úlceras.
Dé gracias a los billones de fagos que gestionan su ecosistema intestinal. Sin ellos, sugiere Hill, unos pocos tipos de bacterias podrían dominar rápidamente, lo que podría impedirle digerir algunos alimentos y provocarle gases e hinchazón.
El salvaje y maravilloso fageoma es una pareja de baile tanto para las bacterias, como para los humanos.
Sobre la autora: Amber Dance es colaboradora de Knowable magazine
Artículo traducido por Debbie Ponchner
Una versión de este artículo apareció en Knowable Magazine el 26 de septiembre de 2024
El artículo El fageoma: un reino oculto en su intestino se ha escrito en Cuaderno de Cultura Científica.
¿Y si la Luna no existiese?
Si la Luna no existiese las alteraciones en la rotación del planeta Tierra lo harían incompatible con la vida humana.
Los vídeos ‘¿Y sí…?´ se plantean cuestiones ficticias pero que nos permiten aprender mucho sobre el mundo en el que vivimos. Se han emitido en el programa de divulgación científica de Televisión Española Órbita Laika, y producido en colaboración con la Cátedra de Cultura Científica de la Universidad del País Vasco.
Ficha técnica: Idea: José Antonio Pérez Ledo
Producción ejecutiva: Blanca Baena
Dirección: Aitor Gutierrez
Guion: Manuel Martinez March
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Locución: José Antonio Pérez Ledo
El artículo ¿Y si la Luna no existiese? se ha escrito en Cuaderno de Cultura Científica.
El injustificado pánico hacia el pan
 Foto: Kate Remmer / Unsplash
Foto: Kate Remmer / UnsplashEl pan parece responsable poco menos que de todos los males del mundo. Por lo menos así lo hacen ver ciertos contenidos de internet que aseguran difundir consejos de alimentación. Ante eso, es como si estuviéramos atrapados en la trama de la novela Miedo y asco en Las Vegas, de Hunter S. Thompson, en la que las percepciones se distorsionan y las exageraciones toman el control de la realidad divisada.El pan ha sido un alimento básico desde hace más de 10 000 años. Últimamente se le endilga la causa de la hipertensión y la diabetes, cuando estas condiciones crónicas son multifactoriales. De hecho, el consumo de ciertos tipos de pan está asociado con una reducción del riesgo de enfermedades cardiovasculares.
El pan es fuente de carbohidratos complejos, fibra dietética, vitaminas y minerales. La fibra es esencial para el funcionamiento digestivo y la prevención de enfermedades como el cáncer colorrectal y la obesidad. El consumo diario recomendado de alrededor de 25 gramos de fibra puede ser cubierto con la ingesta de pan.
Los carbohidratos complejos proporcionan energía útil para el organismo y el vilipendio hacia ellos se da por la confusión entre los carbohidratos simples y los complejos:
- Los carbohidratos simples pueden causar aumentos repentinos en los niveles de azúcar en la sangre.
- Los carbohidratos complejos tienen un efecto moderado y sostenido sobre la glucosa en sangre, lo cual puede ayudar a prevenir la resistencia a la insulina y, en última instancia, la diabetes tipo 2.
La glucosa es la fuente principal de energía del cuerpo. Lo relevante no es su presencia en los alimentos, sino la rapidez con la que se absorbe en el torrente sanguíneo. El índice glucémico de ciertos tipos de pan es menor comparado con otros alimentos ricos en azúcares simples. Además, la presencia de fibra ralentiza tanto la digestión como la absorción de glucosa.
¿Qué pasa con el gluten y los aceites vegetales?El gluten, un complejo proteico que se encuentra en el trigo y otros cereales, ha tenido su cuota de demonización en algunos círculos. Sin embargo, las enfermedades relacionadas con el gluten, como la enfermedad celíaca y la sensibilidad al gluten, afectan a una pequeña parte de la población (menos del 1 % para la enfermedad celíaca; entre el 1 y el 6 % para la sensibilidad no celíaca).
Eso implica que para la gran mayoría de personas, más del 90 %, el gluten no supone ningún daño. El daño lo puede generar consumir sin necesidad muchos productos sin gluten que, paradójicamente, están más procesados y contienen menos nutrientes y menos fibra que los elaborados con gluten.
También se han criticado los aceites vegetales y la margarina usados en las formulaciones de pan. Las grasas con ácidos grasos trans, presentes en las margarinas clásicas y los aceites hidrogenados, están asociadas con un mayor riesgo de enfermedad cardíaca. Sin embargo, las margarinas modernas han reducido su contenido y algunas están formuladas con aceites vegetales ricos en ácidos grasos insaturados.
Los aceites vegetales no hidrogenados (como el aceite de oliva y el de canola) son conocidos por sus beneficios para la salud cardiovascular. El aceite de oliva, en particular, es una piedra angular de la dieta mediterránea, la cual tiene al pan como una de sus guarniciones emblemáticas, siendo esta reconocida mundialmente por su impacto positivo en la longevidad y la salud en general.
¿Es el pan un ultraprocesado?El consumo excesivo de alimentos ultraprocesados y dietas ricas en azúcares añadidos y grasas (particularmente aquellas con ácidos grasos saturados) contribuye al riesgo de enfermedades crónicas. El pan, no obstante, no cae necesariamente en esta categorización.
La inclusión de granos enteros en las formulaciones de pan se relaciona con una reducción del riesgo de diabetes tipo 2, obesidad y enfermedades cardíacas. El pan puede contener compuestos con acción antioxidante y compuestos antiinflamatorios que pueden reducir el daño celular y la inflamación sistémica.
El consumo de granos enteros, como los que se encuentran en el pan integral, se asocia con una reducción significativa del riesgo de mortalidad por cualquier causa, incluidas las enfermedades cardiovasculares y cáncer.
El pan puede formar parte de una dieta sanaTodos estos estudios enfatizan la importancia de considerar la calidad del pan y su inclusión dentro de un patrón de alimentación saludable en lugar de realizar afirmaciones categóricas sobre su peligrosidad.
El pan no es inherentemente dañino. Las afirmaciones extremas sobre su consumo pasan por alto su complejidad. Como parte de una dieta balanceada con alimentos frescos, granos enteros, frutas, verduras y grasas saludables, el pan puede ser el complemento que proporciona energía y nutrientes esenciales.
Otorgarle a un solo alimento la responsabilidad principal de varios problemas de salud desvía la atención de los factores de riesgo reales, como el consumo excesivo de alimentos ultraprocesados y el sedentarismo. El consumo moderado de pan, de hecho, puede ayudarnos a tener una percepción de la realidad no distorsionada en un cuerpo sano y satisfecho por períodos prolongados.![]()
Sobre el autor: Fabián Patricio Cuenca Mayorga, Research fellow, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El injustificado pánico hacia el pan se ha escrito en Cuaderno de Cultura Científica.
Termodinámica, redes neuronales y psicohistoria
El pasado 8 de octubre se anunció que el Premio Nobel de Física de este año sería para John J. Hopfield y Geoffrey E. Hinton por sus trabajos en redes neuronales y aprendizaje automático. Para muchos, esto supuso un triple salto mortal del comité de la Academia de Ciencias sueca en un intento por premiar una disciplina, las matemáticas, que no tiene categoría propia; sin embargo, en este caso la física juega un papel más importante del que parece o, al menos, algunos de los modelos matemáticos que rigen determinados fenómenos.
 El Premio Nobel de Física de 2024 ha sido para John J. Hopfield y Geoffrey E. Hinton.
El Premio Nobel de Física de 2024 ha sido para John J. Hopfield y Geoffrey E. Hinton.
Aunque esto es algo en lo que no siempre se enfatiza demasiado en las asignaturas de Física ―lo que puede llevar a cualquier estudiante a tener un cacao de ecuaciones importante en la cabeza―, fenómenos similares utilizan ecuaciones similares. Esto es: una ecuación de ondas es una ecuación de ondas en mecánica, electromagnetismo o física cuántica, lo que cambia de un ámbito a otro son los «ajustes» que le hacemos. Esto lo explicaba muy bien Richard Feynman en sus populares Lectures poniendo el ejemplo de un oscilador amortiguado mecánico ―un muelle con una masa unida a uno de sus extremos, con rozamiento― y un oscilador eléctrico ―un circuito RLC, con una resistencia, una bobina de inducción y un condensador―: la ecuación que describe ambos sistemas es la misma y, por tanto, se comportan igual.
Física estadística para neuronasPensemos en el potencial de esto a la hora de entender el mundo que nos rodea, en varios sentidos. Puede suceder que, por cualquier motivo, no tengamos acceso a determinados datos, recursos… para hacer un experimento, pero sí su análogo. Podemos hacer una sustitución y extrapolar los resultados de uno al otro. Pero también podríamos, una vez descubierta cierta propiedad o comportamiento de un sistema físico, tratar de reproducirlo en otro ámbito. Eso es más o menos lo que hicieron Hopfield y Hinton: ambos aplicaron modelos matemáticos extraídos de la física estadística a su trabajo con redes neuronales.
La física estadística estudia las propiedades de sistemas compuestos por una gran cantidad de partículas. Es una aproximación necesaria en muchos casos ante la imposibilidad de realizar los cálculos componente a componente cuando hay demasiadas y se empezó a utilizar, sobre todo, en el ámbito de la termodinámica y el comportamiento de los gases, para explicar fenómenos como la temperatura o la presión a partir del comportamiento de los átomos o moléculas que los componen. Pero no tiene por qué estar limitada a esto: una red neuronal artificial puede describirse también como un sistema de este tipo. Y tanto Hopfield como Hinton se basaron en la mecánica estadística para desarrollar sus modelos de aprendizaje automático. El primero, en el modelo de Ising del ferromagnetismo; el segundo, en la distribución de Boltzmann.
Hopfield y el modelo de Ising para el ferromagnetismoEl modelo de Ising explica el comportamiento de los materiales ferromagnéticos.1 A grandes rasgos, explica qué es lo que pasa a nivel atómico para que algunos materiales, como el hierro, presenten propiedades magnéticas bajo determinadas condiciones ―normalmente la presencia de un campo magnético externo―. Pero hay un detalle aún más interesante: cuando «desmagnetizamos» un material de este tipo ―retirando el campo magnético externo, por ejemplo―, suele quedar un campo residual. Se podría considerar que tiene una «memoria» de su historia pasada. Ese «residuo» queda almacenado en la configuración de energía de la red de átomos del material, y es el principio que utiliza la red de Hopfield para aprender patrones.
 El hierro es el material ferromagnético más popular. En presencia de un campo magnético externo, los campos magnéticos individuales de los átomos que lo forman se agrupan en «dominios» magnéticos y se van alineando, confiriéndole las propiedades macroscópicas que todos conocemos cuando están todos ordenados. Créditos: CC BY-SA 3.0/Tomihahndorfy
El hierro es el material ferromagnético más popular. En presencia de un campo magnético externo, los campos magnéticos individuales de los átomos que lo forman se agrupan en «dominios» magnéticos y se van alineando, confiriéndole las propiedades macroscópicas que todos conocemos cuando están todos ordenados. Créditos: CC BY-SA 3.0/Tomihahndorfy
Cambiemos las configuraciones de los espines atómicos ―solo pueden encontrarse en dos estados― del modelo de Ising, que es de donde emergen las propiedades magnéticas del material, por estados de neuronas artificiales, encendido/apagado, y las interacciones entre los espines por pesos sinápticos ―que miden la probabilidad de que una neurona esté activada―, y tendremos una red de Hopfield. ¿Cómo aprende? Reforzando los pesos sinápticos que lleven a configuraciones de baja energía o, en otras palabras, que lleven hacia los patrones de memoria que buscamos.
Hinton y la distribución de BoltzmannCon las máquinas de Bolztmann de Geoffrey E. Hinton sucede algo similar. Son una extensión de las redes de Hopfield basadas en la distribución de Bolztmann. Por supuesto, el físico austriaco no estaba pensando en inteligencia artificial, sino en cómo interaccionan los átomos en un gas para explicar sus propiedades macroscópicas Una visión que, por otro lado, lo llevó a desarrollar una descripción matemática de la entropía de un sistema y a establecer la dirección preferente de los procesos termodinámicos hacia estados en los que esta es mayor.
 En la lápida de Ludwig Bolztmann, en Viena, está grabada su ecuación estadística para la entropía de un gas ideal. Créditos: CC BY-SA 3.0/Daderot
En la lápida de Ludwig Bolztmann, en Viena, está grabada su ecuación estadística para la entropía de un gas ideal. Créditos: CC BY-SA 3.0/Daderot
La distribución de Boltzmann mide la probabilidad de encontrar un sistema termodinámico ―en equilibrio térmico― en un determinado estado macroscópico en función de los microestados de los átomos o moléculas que lo componen. De nuevo, y como en el modelo de Ising, el punto clave aquí es que un sistema que obedezca esta ecuación tenderá siempre a buscar estados de menor energía, ya que son los que tienen más probabilidad de darse. Y, de nuevo, podemos aplicarlo a ámbitos muy diversos. Eso fue lo que hizo Hinton. Cambiemos moléculas e interacciones por neuronas y pesos sinápticos.
Con esta perspectiva, en la que ni siquiera se ha mencionado ante qué tipos de redes neuronales nos encontramos, ni hemos hablado de algoritmos ni informática, ya podemos volver a preguntarnos si la física está relacionada o no con el Premio Nobel de este año.
Tengamos en cuenta algo más, ¿no intenta la inteligencia artificial simular el comportamiento humano? ¿Y no forman parte los seres humanos de un universo regido por determinadas leyes? No parece tan descabellado inspirarnos, por tanto, en modelos que ya conocemos, ¿no?
…y la psicohistoriaEn el caso concreto de la distribución de Boltzmann, sus aplicaciones a otros ámbitos están por todas partes. Se utiliza en química, en biología, en economía, en sistemas complejos… se utilizó hasta en ciencia ficción. La psicohistoria de Isaac Asimov no es más que el estudio del comportamiento de una sociedad a partir de los comportamientos individuales de sus ciudadanos siguiendo el modelo estadístico de Boltzmann: normalmente tendemos a buscar estados estables, de baja energía, aunque también es posible que un elemento disruptivo como el Mulo u otro tipo de inestabilidades económicas, culturales, etc., rompan el equilibrio. Lo que cabría plantearse ahora es que si las máquinas de Boltzmann de Hinton y la psicohistoria de Asimov siguen el mismo principio, ¿es posible entonces que Hari Seldon fuera el entrenador de una red neuronal galáctica?
Bibliografía
Ackley, D. H.; Hinton, G. E. y Sejnowski, T. J. (1985). A learning algorithm for bolztmann machines. Cognitive Science,9(1), 147-169.
Baños, G. (2024). El sueño de la inteligencia artificial. Shackleton Books.
Feynman, R. (2010 [1963]). The Feynman Lectures on Physics. Volume I: Mainly mechanis, radiation and heat. The New Millenium Edition. Basic Books.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational habilities. Proc. Natl. Acad. Sci. USA, 79.
The Royal Swedish Academy of Sciences (2024). The Nobel Prize in Physics 2024. https://www.nobelprize.org/prizes/physics/2024/summary
Nota:
1 Más precisamente, aquellos que en los que, ante la presencia de un campo magnético, los momentos magnéticos microscópicos de los átomos o partículas que lo componen se alinean en la misma dirección.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Termodinámica, redes neuronales y psicohistoria se ha escrito en Cuaderno de Cultura Científica.
Fibonacci está en todas partes (II)
En la anterior entrada del Cuaderno de Cultura Científica titulada Fibonacci en todas partes (I) iniciamos un paseo por algunos lugares de lo más curiosos e inesperados, en los que aparecen los números de Fibonacci, como en el árbol genealógico de un zángano (abeja macho), en los paseos de una abeja por un panal de dos filas de celdas o en los embaldosados con fichas de dominó.
Por ejemplo, en relación con los embaldosados con fichas de dominó, mostramos que la cantidad de embaldosados rectangulares posibles de 2 filas y n columnas (es decir, una cuadrícula rectangular de tamaño n x 2), para n = 1, 2, 3, etc, con fichas de dominó (teniendo en cuenta que una ficha de dominó puede ir en horizontal, 1 x 2, o en vertical, 2 x 1), era igual a la sucesión de Fibonacci 1, 2, 3, 5, 8, … (en la siguiente imagen se muestran los 5 embaldosados rectangulares posibles de tamaño 5 x 2).
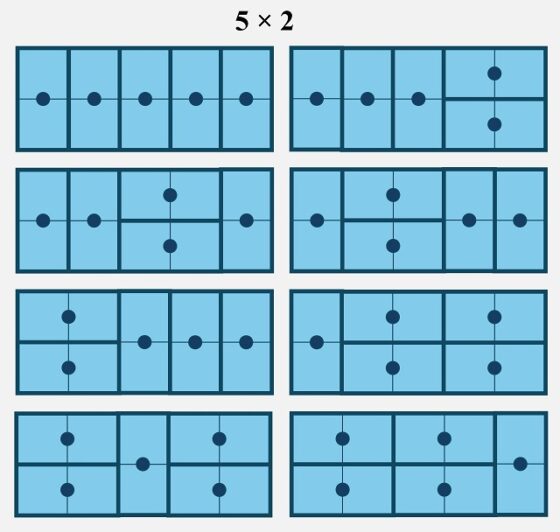
En esta entrada vamos a continuar este interesante paseo por nuevos y curiosos ejemplos.
La óptica de los rayos de luzEn el primer número, del primer volumen, de la revista Fibonacci Quarterly, del año 1963, los matemáticos austriaco-canadiense Leo Moser (1921-1970) y canadiense Max Wyman (1916-1991) propusieron el siguiente problema.
Problema: Los rayos de luz caen sobre una pila de dos placas de vidrio paralelas, un rayo pasa sin reflejarse, dos rayos (uno de cada interfaz interna opuesta al rayo) se reflejarán una vez, pero de formas diferentes, tres se reflejarán dos veces, pero de formas diferentes. Demuéstrese que el número de trayectorias distintas, que se reflejan exactamente n veces, es el número de Fibonacci Fn + 2.
Antes de nada, expliquemos el problema. En el mismo se consideran dos placas de cristal, cada una con dos superficies de reflexión. Denominamos cara 1 a la superficie de reflexión de la izquierda de la primera placa y cara 2 a la de la derecha, mientras que las caras 3 y 4 se corresponden con la segunda placa.
En el problema se considera un rayo de luz atravesando las placas desde uno de sus laterales, por ejemplo, desde la izquierda. Además, se estima que puesto que hay cuatro superficies de reflexión, el rayo de luz puede reflejarse interiormente de cuatro formas distintas, antes de volver a salir de nuevo, o por el lado contrario o por el mismo lado. Así, si no hay ninguna reflexión, el rayo de luz sale directamente por el otro lado, el lateral derecho (véase la siguiente imagen). Si se produce solo una reflexión, esta será en la cara 2 o en la cara 4, para después salir el rayo por el mismo lado por el que entró, el lateral izquierdo (véase la siguiente imagen). Mientras que, si se producen dos reflexiones, si la primera es en la cara 2, la segunda tendrá que ser en la cara 1, y luego la luz saldría por la derecha; mientras que, si la primera reflexión es en la cara 4, la segunda puede ser en las caras 1 o 3 (véase la siguiente imagen).
Por lo tanto, como dice el enunciado del problema, el número de trayectorias distintas si no hay reflexión es 1, si hay una reflexión es 2, mientras que si hay dos reflexiones es 3. Podemos seguir con las siguientes reflexiones, por ejemplo, para tres reflexiones, que aparece en la siguiente imagen, hay 5 trayectorias posibles.
Y para cuatro reflexiones, son 8 trayectorias posibles.
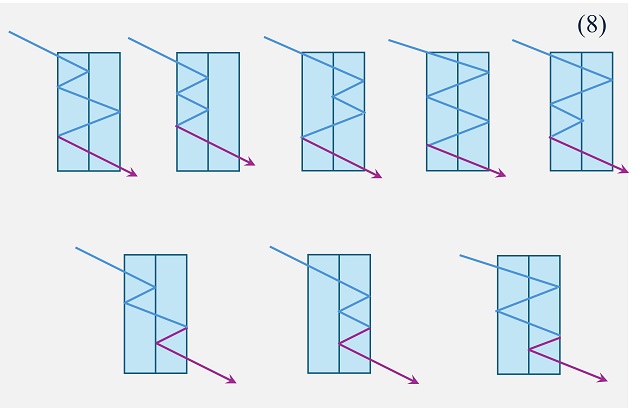
De esta manera, vamos observando paso a paso que la solución es efectivamente la sucesión de los números de Fibonacci, pero demostremos que realmente el número de trayectorias es Fn + 2, para n reflexiones. Para ello, basta demostrar que se cumple la propiedad recursiva de la sucesión de Fibonacci, que la cantidad de trayectorias para n reflexiones es igual a la suma de la cantidad de trayectorias para n – 1 y para n – 2 reflexiones.
La imagen anterior nos da la idea, ya que hemos añadido en morado cómo se pasa de los patrones de trayectorias anteriores, para n – 1 y n – 2 reflexiones (en nuestro ejemplo, 3 y 4) a los de n reflexiones. A partir de las trayectorias para n – 1 reflexiones, cuyo rayo de luz sale por el lado contrario que para n trayectorias, se añade una última reflexión para cada una de las trayectorias en la cara final que cruza después las dos placas; mientras que para n – 2 trayectorias, cuyo rayo sale por el mismo lado que para n trayectorias, se añaden dos reflexiones para cada una de las trayectorias, una en la cara final y otra en el medio (no puede ser en la cara del otro lateral, ya que esa estaría contada dentro del anterior caso), con lo cual el rayo regresa a la misma dirección de salida.
Subiendo o bajando escalerasImaginaos una escalera que tenéis que subir, o quizás bajar. Lo normal es que la subáis de un escalón en un escalón, pero también cabe la posibilidad de que la subáis de dos en dos si tenéis prisa o si estáis jugando, al menos yo jugaba a cosas así cuando era un niño. La cuestión es que también la podéis subir intercalando las dos maneras, de una en una y de dos en dos. El problema que nos vamos a plantear a continuación tiene que ver con las diferentes formas de subir, o bajar, una escalera.
 Fotograma de la película estadounidense El show de Truman (1998), de Peter Weir, interpretada por Jim Carrey, Laura Linney y Ed Harris
Fotograma de la película estadounidense El show de Truman (1998), de Peter Weir, interpretada por Jim Carrey, Laura Linney y Ed HarrisProblema: Demostrar que el número de diferentes formas de subir la escalera con n peldaños, de manera que puedes subir uno o dos peldaños en casa paso, es el número de Fibonacci Fn + 1.
El matemático Leo Moser propuso un problema similar a este en el mismo número de la revista Fibonacci Quarterly, del año 1963, mencionado arriba. El problema dice así.
Problema: Demostrar que, teniendo en cuenta el orden, el número de diferentes formas de pagar n dólares, utilizando únicamente billetes de 1 y 2 dólares, es igual al número de Fibonacci Fn + 1.
Sumas con unos y dosesSi lo pensamos un poco, los dos problemas anteriores, nos están pidiendo que veamos las formas de obtener un número natural n como suma ordenada de unos y doses, lo que en la literatura matemática se denomina “composiciones de n con 1s y 2s”. Veamos los primeros casos, en los que observaremos claramente que aparece la sucesión de Fibonacci.

La demostración es muy sencilla, basta observar que las composiciones de n con 1s y 2s pueden obtenerse a partir de las composiciones de n – 1 y n – 2 con 1s y 2s, de la siguiente manera. Las composiciones de n con 1s y 2s que terminan en 2 (como la composición de 6 siguiente 1 + 2 + 1 + 2) son una composición de n – 2 a la que se le suma, por la derecha (ya que el orden es importante), 2 (en nuestro ejemplo 1 + 2 + 1 + 2, tenemos que se obtiene sumando 2, a la derecha, a la composición de 4, 1 + 2 + 1). Mientras que las composiciones de n con 1s y 2s que terminan en 1 (como la composición de 6 siguiente 2 + 2 + 1 + 1) son una composición de n – 1 a la que se le suma, por la derecha, 1 (en nuestro ejemplo, 2 + 2 + 1 + 2 se obtiene sumando 1, a la derecha, a la composición de 5, 2 + 2 + 1). En la siguiente imagen se muestra el caso de las composiciones de 6 con 1s y 2s, utilizando colores para separarlo (azul composiciones de 5 y verde composiciones de 4).

Por lo tanto, podríamos escribirlo en forma de teorema.
Teorema: El número de composiciones de un número natural n con 1s y 2s, es decir, el número de maneras de obtener n como suma ordenada de 1s y 2s, es igual a Fn + 1.
Si buscamos el origen de este resultado, algunas fuentes mencionan el artículo Compositions with ones and twos, de los matemáticos indio-estadounidense Krishnaswami Alladi (1955) y estadounidense Verner Emil Hoggatt Jr. (1921-1980), publicado en la revista Fibonacci Quarterly en 1975, en el que se estudian este tipo de composiciones. Sin embargo, este resultado ya era conocido con mucha anterioridad. Por ejemplo, en la segunda mitad del siglo xix matemáticos como el británico Arthur Cayley (1821-1895) estudiaron las composiciones en general, es decir, las descomposiciones de un número natural como sumas ordenadas de números. Pero podemos remontarnos más atrás en el tiempo ya que, como se explica en la entrada El origen poético de los números de Fibonacci, este resultado, relacionado con los poemas en sanscrito de la India, ya era conocido varios siglos antes, al menos en el siglo xii, pero probablemente mucho antes aún.
Si se analiza detenidamente el ejemplo de los embaldosados con fichas de dominó puede observarse que realmente es una versión de este resultado matemático. E incluso el ejemplo de la óptica de los rayos de luz, también puede traducirse de esta manera.
Fibonacci y Cayley se dan la manoComo ya se ha mencionado más arriba, el matemático británico Arthur Cayley (de quien puede leerse la biografía Cayley, el origen del álgebra moderna) estudió las composiciones de números, en particular, obtuvo otro resultado relacionado con los números de Fibonacci.
 Fotografía del matemático británico Arthur Cayley, anterior a 1883, realizada por el fotógrafo británico Herbert R. Beraud (1845–1896)
Fotografía del matemático británico Arthur Cayley, anterior a 1883, realizada por el fotógrafo británico Herbert R. Beraud (1845–1896)
En su artículo Teoremas sobre trigonometría y matemáticas (Messenger of Mathematics, 1876), Cayley demostró que el número de composiciones de un número n (formas de expresar n como suma ordenada de números naturales), con números estrictamente mayores que 1, es igual al número de Fibonacci Fn – 1. Veamos los primeros casos.
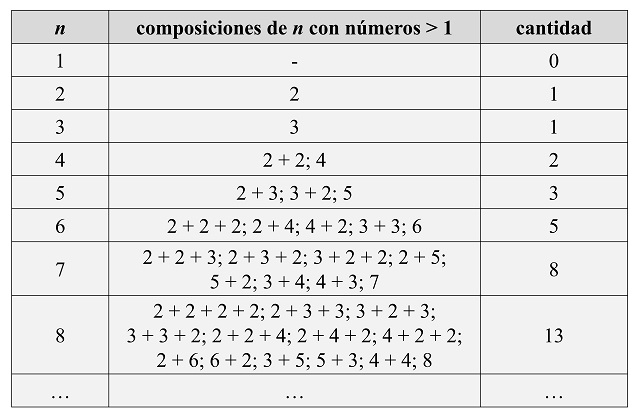
Y aún nos queda una tercera etapa de este paseo para una siguiente entrada del Cuaderno de Cultura Científica, en la que hablaremos de pintar apartamentos de dos colores, de algunos números binarios o de subconjuntos de puntos, entre otras cuestiones.
 Secuencia de Fibonacci F72 (2016), de los artistas estadounidenses Chris Klapper y Patrick Gallagher. Imagen de la página web de Chris Klapper
Secuencia de Fibonacci F72 (2016), de los artistas estadounidenses Chris Klapper y Patrick Gallagher. Imagen de la página web de Chris KlapperBibliografía
1.- Alfred S. Posamentier, Ingmar Lehmann, The Fabulous Fibonacci Numbers, Prometheus Books, 2007.
2.- Thomas Koshy, Fibonacci and Lucas Numbers with Applications, John Wiley & Sons, 2001.
3.- Martin Gardner, Circo matemático, Alianza editorial, 1988.
4.- Raúl Ibáñez, Cayley, el origen del álgebra moderna, Genios de las Matemáticas, RBA, 2017.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Fibonacci está en todas partes (II) se ha escrito en Cuaderno de Cultura Científica.

