Una nueva (e inesperada) función de los sacos aéreos
Desde el punto de vista energético el vuelo de las aves es prodigioso. Los músculos de las aves, y de forma especial los pectorales, requieren un ingente aporte de energía para cumplir su función. El esfuerzo muscular y el mantenimiento de una temperatura constante hacen que las aves consuman una gran cantidad de alimento, generalmente entre el 10 y el 20% de su masa corporal cada día. El caso extremo es el de los colibríes, los animales endotérmicos con mayor tasa metabólica, que pueden consumir diariamente hasta cinco veces su masa corporal.
El alimento no es el único condicionante del metabolismo aviar. Ese alimento debe ser oxidado para producir energía, por lo que el sistema respiratorio debe suministrar oxígeno en grandes cantidades. Esta es la razón por la que el sistema respiratorio de las aves es completamente diferente al de cualquier otro grupo de vertebrados, incluyendo a los mamíferos. Y un componente esencial de este particular sistema son los sacos aéreos.
Los sacos aéreos son divertículos de los pulmones que se distribuyen por el cuerpo del animal. Un grupo se localiza en la parte anterior del tronco y otro en la región posterior del tórax y en el abdomen. Se les atribuyen funciones tales como regular la temperatura interna, reducir la fricción entre los músculos o disminuir la densidad corporal. Pero su función principal está relacionada con el sofisticado sistema de ventilación pulmonar de las aves.
Los pulmones de las aves no se hinchan y deshinchan como los nuestros. Esto no sería suficientemente eficaz, ya que en los pulmones de los mamíferos el contenido en oxígeno se va empobreciendo tras la inspiración, al ir pasando a la sangre. Al final del ciclo el aire enrarecido es exhalado y se renueva en la siguiente inspiración.
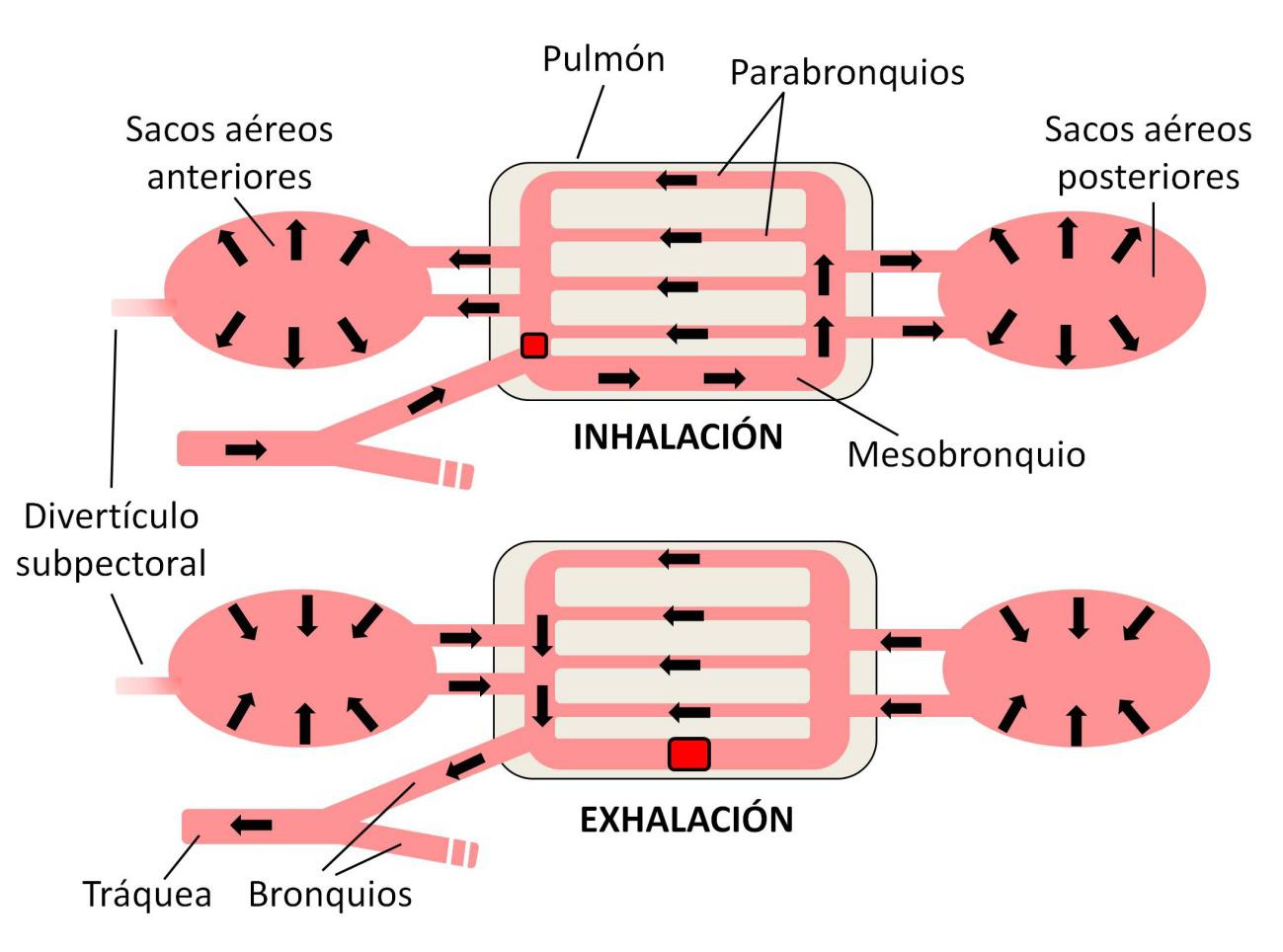 Figura 1. Ciclo de ventilación pulmonar en las aves. Durante la inhalación, el aire llena los sacos aéreos posteriores y circula por los parabronquios. El aire empobrecido en oxígeno se acumula en los sacos aéreos anteriores. En la exhalación, la contracción de los sacos aéreos posteriores mantiene una corriente de aire fresco a través de los parabronquios, mientras que se expulsa el aire de los sacos anteriores. Un sistema de válvulas (en rojo) regula los flujos. Se muestra la posición del divertículo subpectoral
Figura 1. Ciclo de ventilación pulmonar en las aves. Durante la inhalación, el aire llena los sacos aéreos posteriores y circula por los parabronquios. El aire empobrecido en oxígeno se acumula en los sacos aéreos anteriores. En la exhalación, la contracción de los sacos aéreos posteriores mantiene una corriente de aire fresco a través de los parabronquios, mientras que se expulsa el aire de los sacos anteriores. Un sistema de válvulas (en rojo) regula los flujos. Se muestra la posición del divertículo subpectoralLos pulmones de las aves (Figura 1) están formados por una compleja red de tubos finos y muy vascularizados llamados parabronquios. Por estos parabronquios circula una corriente continua de aire fresco, lo que mantiene siempre altos los niveles de oxígeno para su captación por la sangre. Los sacos aéreos posteriores, funcionando como el fuelle de la gaita gallega, almacenan el aire de entrada y lo dirigen hacia los parabronquios durante la espiración. El aire empobrecido en oxígeno se almacena en los sacos anteriores hasta su expulsión. Así, aunque el ave inspire y espire de forma cíclica, el flujo de aire en los parabronquios es continuo, unidireccional y rico en oxígeno.
El llenado y vaciado rítmico de los sacos aéreos se logra por acción de los músculos torácicos y abdominales. Es decir, la acción muscular contribuye a la ventilación pulmonar, de una forma análoga a lo que hace nuestro diafragma. Por eso ha resultado tan sorprendente el descubrimiento de que, a la inversa, los sacos aéreos tienen una función importante en la mecánica del vuelo, en concreto del vuelo planeado.
 Figura 2. El alimoche (Neophron percnopterus) es un ave planeadora que utiliza el mecanismo de los divertículos subpectorales para reducir el esfuerzo de sus músculos pectorales. Fuente: lifegyptianvulture.it
Figura 2. El alimoche (Neophron percnopterus) es un ave planeadora que utiliza el mecanismo de los divertículos subpectorales para reducir el esfuerzo de sus músculos pectorales. Fuente: lifegyptianvulture.itLas aves planeadoras mantienen las alas desplegadas para generar su sustentación (Figura 2). Sus músculos pectorales tienen que trabajar menos que los encargados de batir las alas, pero así y todo deben realizar un esfuerzo sustancial para mantener el despliegue de las alas. Curiosamente, las aves planeadoras generalmente tienen unos pequeños divertículos de los sacos aéreos anteriores, localizados bajo los músculos pectorales y de función hasta ahora desconocida. Se denominan divertículos subpectorales, y no aparecen en aves con vuelo batido.
Un reciente artículo publicado en Nature ha mostrado que este divertículo apareció al menos siete veces de forma independiente en la evolución de las aves, siempre coincidiendo con el desarrollo del vuelo planeado. Tienen divertículos subpectorales las gaviotas, grullas, albatros, cormoranes, pelícanos, águilas y otras rapaces planeadoras. La propuesta de los autores de este estudio es que el inflado del divertículo subpectoral disminuye el esfuerzo necesario para mantener el despliegue de las alas durante el vuelo planeado.
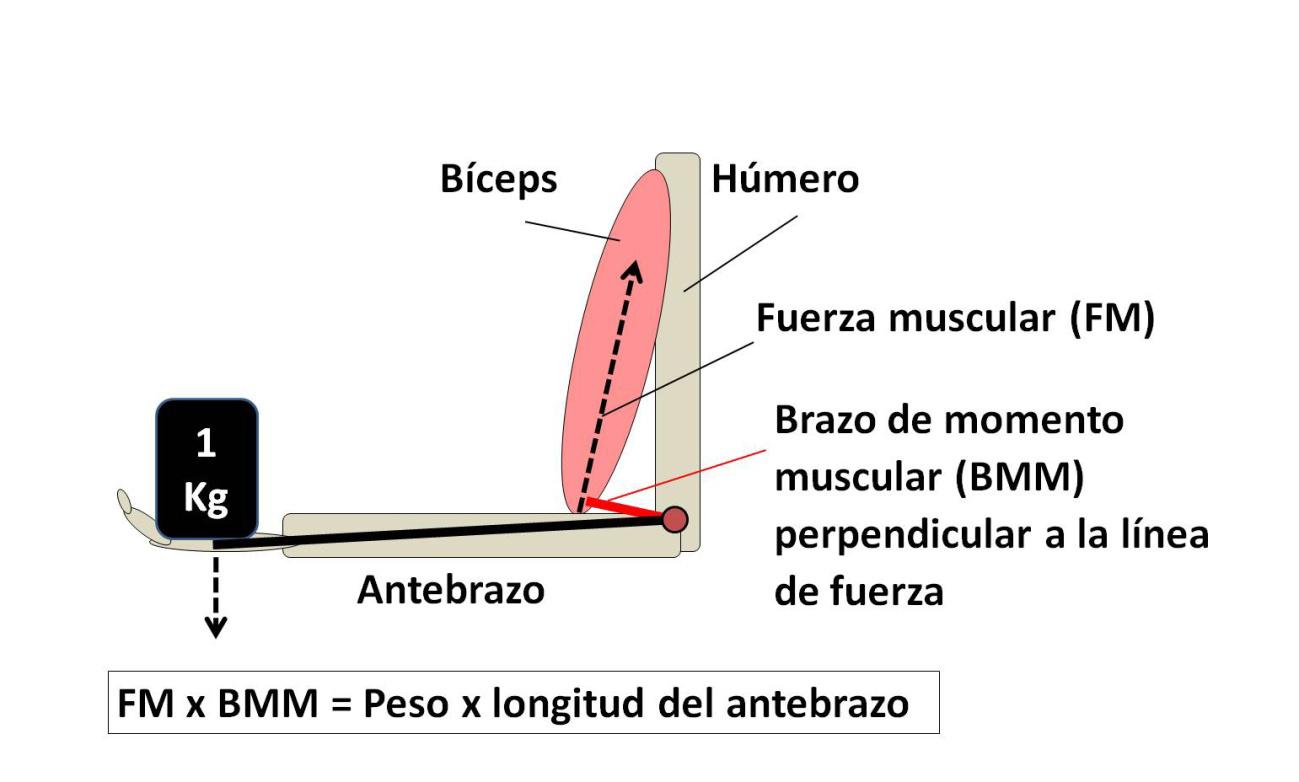 Figura 3. Cuando sostenemos un peso con el brazo en ángulo recto a una distancia determinada del codo, dicha distancia multiplicada por el peso debe ser igual a la fuerza ejercida por el bíceps multiplicada por el brazo de momento muscular
Figura 3. Cuando sostenemos un peso con el brazo en ángulo recto a una distancia determinada del codo, dicha distancia multiplicada por el peso debe ser igual a la fuerza ejercida por el bíceps multiplicada por el brazo de momento muscularPara comprender esto tenemos que explicar el concepto de brazo de momento, la distancia perpendicular entre la línea de acción de una fuerza y un eje de rotación. La figura 3 ilustra esta idea. Si ponemos el brazo en ángulo recto y sostenemos un peso, la fuerza que tenemos que hacer será tanto mayor cuando más cerca del codo esté el eje del bíceps y viceversa. Esta distancia perpendicular entre línea de fuerza muscular y articulación del codo es el brazo de momento muscular.
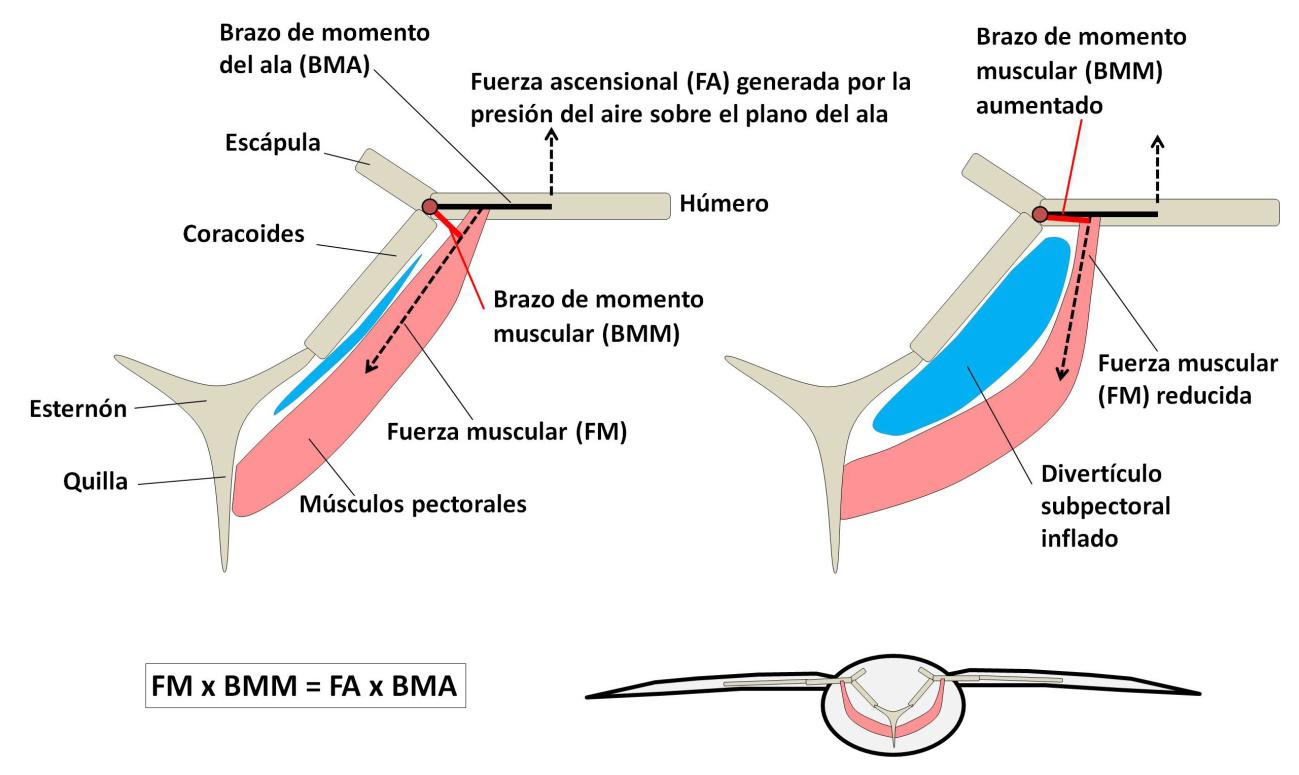 Figura 4. La disminución del esfuerzo necesario para mantener el ala desplegada en las aves planeadoras se produce por el inflado del divertículo subpectoral, que cambia el ángulo de inserción de los músculos pectorales sobre el húmero. De esta forma, aumenta el brazo de momento muscular
Figura 4. La disminución del esfuerzo necesario para mantener el ala desplegada en las aves planeadoras se produce por el inflado del divertículo subpectoral, que cambia el ángulo de inserción de los músculos pectorales sobre el húmero. De esta forma, aumenta el brazo de momento muscularLa figura 4 ayudará a entender la insospechada función de los divertículos subpectorales. Los músculos pectorales se insertan en el húmero y en el esternón, pasando por encima de otros huesos de la cintura pectoral (coracoides y clavícula). Para mantener el planeo, la fuerza desplegada por los músculos debe compensar la fuerza ascensional generada por la presión del aire sobre las alas. Para ser más preciso, el brazo de momento muscular de los pectorales (BMM) multiplicado por la fuerza muscular (FM) debe igualar al brazo de momento del ala (BMA) multiplicado por la fuerza ascensional (FA):
BMM x FM = BMA x FA
La clave está en que el inflado del divertículo subpectoral aumenta el brazo de momento muscular, y disminuye proporcionalmente el esfuerzo muscular necesario para equilibrar la fuerza ascensional. Se trata de una nueva e inesperada función de los sacos aéreos, una innovación adquirida al menos por siete linajes de aves de forma concomitante al desarrollo del vuelo planeado. Y otro fascinante ejemplo de bricolaje evolutivo.
Referencias:
Schachner, E.R., Moore, A.J., Martinez, A. et al. (2024) The respiratory system influences flight mechanics in soaring birds. Nature. doi:10.1038/s41586-024-07485-y
Tobalske BW. (2024) Air sacs reduce energy costs for soaring birds. Nature. doi: 10.1038/d41586-024-01508-4.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Una nueva (e inesperada) función de los sacos aéreos se ha escrito en Cuaderno de Cultura Científica.
Algo repentino acabó con el mamut lanudo
Un análisis genómico demuestra que la población de estos grandes mamíferos en la isla de Wrangel, en Rusia, fue relativamente estable hasta su repentina desaparición hace tan solo 4000 años. Este descubrimiento refuta la teoría de que se extinguieron por razones genéticas.
 Colmillo de mamut lanudo (Mammuthus primigenius) en la isla rusa de Wrangel. Foto: Love Dalén
Colmillo de mamut lanudo (Mammuthus primigenius) en la isla rusa de Wrangel. Foto: Love DalénLa última población de mamut lanudo (Mammuthus primigenius) quedó aislada en la isla de Wrangel (Rusia), frente a la costa de Siberia, hace unos 10.000 años, cuando el nivel del mar subió y separó la montañosa isla del continente.
Un nuevo análisis genómico revela que los mamuts aislados, que vivieron en la isla durante los 6.000 años siguientes, se originaron a partir de un máximo de 8 individuos, pero crecieron hasta 200-300 ejemplares en 20 generaciones.
Según el estudio, publicado en la revista Cell, los genomas de los mamuts de la isla de Wrangel mostraban signos de endogamia y baja diversidad genética, pero no hasta el punto de poder explicar su definitiva y misteriosa extinción.
«Ahora podemos rechazar con confianza la idea de que la población era simplemente demasiado pequeña y que estaban condenados a extinguirse por razones genéticas», afirma la autora principal Love Dalén, genetista evolutiva del Centro de Paleogenética (iniciativa conjunta del Museo Sueco de Historia Natural y la Universidad de Estocolmo).
«Esto significa que probablemente fue algún suceso aleatorio el que acabó con ellos, y si ese suceso no hubiera ocurrido, entonces seguiríamos teniendo mamuts hoy en día», afirma.
Enseñanzas para la conservaciónAdemás de arrojar luz sobre la dinámica de población del mamut lanudo, este análisis de los mamuts de la isla rusa podría ayudar a fundamentar las estrategias de conservación de animales actuales en peligro de extinción.
«Los mamuts son un sistema excelente para comprender la actual crisis de biodiversidad y lo que ocurre desde el punto de vista genético cuando una especie sufre un cuello de botella poblacional, porque reflejan el destino de muchas poblaciones actuales», afirma la primera autora, Marianne Dehasque, del Centro de Paleogenética.
Para comprender las consecuencias genómicas del cuello de botella de la isla de Wrangel en la población de mamuts, el equipo analizó los genomas de 21 mamuts lanudos: 14 de la isla de Wrangel y 7 de la población continental anterior al cuello de botella. En total, las muestras abarcaban los últimos 50.000 años de existencia del mamut lanudo, lo que permitía comprender cómo había cambiado la diversidad genética de los mamuts a lo largo del tiempo.
La comparación de los genomas de los mamuts de la isla con los de sus antepasados del continente fue lo que reveló los signos de endogamia y baja diversidad genética en los primeros. Además, mostraban una diversidad reducida en el complejo mayor de histocompatibilidad, un grupo de genes conocidos por desempeñar un papel fundamental en la respuesta inmunitaria de los vertebrados.
 Foto de la réplica de mamut en el Royal British Columbia Museum. Foto: Geoff Peters / Wikimedia CommonsUn tamaño de la población estable
Foto de la réplica de mamut en el Royal British Columbia Museum. Foto: Geoff Peters / Wikimedia CommonsUn tamaño de la población estable
Los investigadores demostraron que la diversidad genética de la población siguió disminuyendo durante los 6.000 años que los mamuts habitaron la isla de Wrangel, aunque a un ritmo muy lento, lo que indica que el tamaño de la población se mantuvo estable hasta el final.
Y aunque la población de mamuts de la isla fue acumulando mutaciones moderadamente dañinas a lo largo de sus 6.000 años de permanencia, los investigadores demostraron que la población iba purgando lentamente las mutaciones más dañinas.
«Si un individuo tiene una mutación extremadamente dañina, básicamente no es viable, así que esas mutaciones desaparecieron gradualmente de la población con el tiempo, pero por otro lado, vemos que los mamuts fueron acumulando mutaciones medianamente dañinas casi hasta que se extinguieron», dice Dehasque.
«Es importante que los programas de conservación actuales tengan en cuenta que no basta con que la población vuelva a tener un tamaño decente –subraya–, y también hay que vigilarla genéticamente y de forma activa, porque estos efectos genómicos pueden durar más de 6.000 años».
Los últimos años del mamutAunque los genomas de mamut analizados en este estudio abarcan un amplio periodo de tiempo, no incluyen los últimos 300 años de existencia de la especie. Sin embargo, los investigadores han desenterrado fósiles del periodo final del mamut y planean llevar a cabo la secuenciación genómica en el futuro.
«No sabemos por qué se extinguieron después de haber estado más o menos bien durante 6.000 años, pero creemos que fue algo repentino», afirma Dalén, que concluye: «Yo diría que aún hay esperanzas de averiguar por qué se extinguieron, pero no hay promesas».
Una versión anterior de este artículo se ha publicado originalmente en SINC
El artículo Algo repentino acabó con el mamut lanudo se ha escrito en Cuaderno de Cultura Científica.
Cambios cerebrales durante el embarazo y la maternidad

Los cambios del cerebro durante el embarazo y la maternidad, cómo el estrés ha pasado de ser un mecanismo de supervivencia a un eventual elemento de riesgo para nuestra salud o cuál ha sido el papel que ha jugado el suicidio en la evolución del ser humano fueron algunos de los temas que se tratarán en la VI Jornada Nacional sobre Evolución y Neurociencias.
La jornada tuvo lugar el Bizkaia Aretoa de la UPV/EHU los pasados 25 y 26 de abril y estuvo dirigida por Eva Garnica y Pablo Malo, de la Red de Salud Mental de Bizkaia, institución que organizó la jornada junto a la Cátedra de Cultura Científica de la UPV/EHU.
El encuentro, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolutivo y divulgar de un modo accesible para todos los públicos.
Los cambios fisiológicos y neuronales asociados al embarazo y crianza de los hijos transforman a la persona. Susana Carmona nos explica cómo afectan al cerebro de las madres en Cambios cerebrales durante el embarazo y la maternidad.
Susana Carmona Cañabate, psicóloga clínica y doctora en neurociencias, es investigadora principal del Grupo de Neuroimagen del Hospital General Universitario Gregorio Marañón (Madrid).
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Cambios cerebrales durante el embarazo y la maternidad se ha escrito en Cuaderno de Cultura Científica.
La IA podría convertir la ciencia en algo incomprensible
Hace unos días un artículo preaceptado en la revista Nature nos hablaba de las maravillas del modelo de inteligencia artificial (IA) AlphaFold 3, que superaban en mucho a su versión anterior. Se trata de un sistema capaz de predecir la estructura de proteínas, ácidos nucleicos y moléculas pequeñas cuyo potencial para la medicina de precisión y la creación de medicamentos es enorme. Además, el uso de modelos –tanto predictivos como generativos– de IA para diagnóstico está produciendo resultados asombrosos.
Casi al mismo tiempo, se nos informaba en los medios del proyecto de creación en la Unión Europea de un centro de investigación en IA dedicado especialmente al desarrollo de sistemas útiles para la investigación científica.
Todo esto no ha hecho más que comenzar. Las consecuencias que la extensión del uso de modelos predictivos tendría para la ciencia desde el punto de vista epistemológico y metodológico es un asunto sobre el que hay un creciente interés.
 Esta imagen fue creada por Twistedpoly como parte del proyecto Visualizando la IA de Google DeepMind. Foto: Google DeepMind / Unsplash
Esta imagen fue creada por Twistedpoly como parte del proyecto Visualizando la IA de Google DeepMind. Foto: Google DeepMind / UnsplashEn otro artículo publicado este año en Nature se señalan tres ilusiones a las que puede conducir una aplicación acrítica de la IA en la investigación científica:
- La ilusión de profundidad explicativa. Consistiría en hacer creer a los científicos que entienden más sobre un conjunto de fenómenos porque han sido predichos con exactitud por un modelo de IA.
- La ilusión de amplitud exploratoria. Consistiría en creer que lo que puede ser modelizado por la IA agota la realidad que ha de ser explorada.
- La ilusión de objetividad. Consistiría en creer que las herramientas de la IA eliminan cualquier elemento de subjetividad y representa a todos los puntos de vista relevantes.
Son tres peligros que habrá que esquivar. La pérdida de importancia de la comprensión profunda de los fenómenos en la ciencia es un riesgo. La ciencia ha buscado la explicación y la predicción. Cabe la posibilidad de que el enorme éxito predictivo conseguido a través de sistemas de IA –que se comportan como cajas negras, puesto que son incapaces de justificar sus resultados–, relegue a un segundo plano la capacidad explicativa.
Como resultado, perdería peso la elaboración teórica en la ciencia y la búsqueda de las causas.
Estos modelos predictivos pueden ser muy útiles en la práctica, puesto que son capaces establecer correlaciones precisas que nos avisen con bastante seguridad de cuándo puede suceder algo –cuándo está aumentando la incidencia de una enfermedad–, pero el precio a pagar podría ser la imposibilidad de desentrañar lo que ocurre para encontrar una explicación causal.
Es cierto que no todos los sistemas de IA que se emplean en investigación funcionan como cajas negras. También es cierto que las correlaciones halladas por los modelos predictivos podrían ayudar a encontrar, mediante investigaciones ulteriores, relaciones causales imprevistas, conexiones nuevas e incluso fenómenos no conocidos o no conceptualizados hasta entonces.
Sin embargo, el empleo cada vez más extendido de sistemas de IA que presentan lo que se ha denominado opacidad epistémica puede conducir a la merma en la comprensión de la realidad que nos procura la capacidad explicativa de hipótesis, modelos y teorías.
“Calla y calcula”Se suele decir que la interpretación de Copenhague de la mecánica cuántica se resume en el mandato “calla y calcula”. Es una exageración, claro está, que buscaba que los físicos no se entretuvieran demasiado con las cuestiones de fundamento, ampliamente filosóficas, y se centraran en el éxito predictivo de la teoría. Cabría la posibilidad de que muchos científicos tomaran esa boutade como un mandato inevitable de la ciencia sometida a los designios de la IA.
Esta actitud podría tener consecuencias negativas en ciencias sociales y biomédicas, en las que se basan políticas públicas, y las decisiones que se tomen pueden afectar a la vida de las personas a causa, por ejemplo, de sesgos no detectados. Estas ciencias tratan sobre sistemas complejos en los que con frecuencia una pequeña variación en las condiciones iniciales puede llevar a resultados completamente diferentes.
¿Cómo decirle a un paciente que un modelo predictivo ha dado como resultado una alta probabilidad de padecer una enfermedad mortal de la que no muestra ningún síntoma, pero sin que haya posibilidad de darle ninguna explicación acerca de cómo el sistema ha llegado a tal conclusión? ¿Bastará con señalarle que el sistema es altamente fiable porque su éxito predictivo está bien constatado? ¿Debería un médico actuar de alguna manera o prescribir un tratamiento sin tener una garantía epistémica adicional que justifique su intervención?
Un resultado interesante a este respecto es que algunos estudios recientes han mostrado que las personas son favorables a priorizar la exactitud en las predicciones de los sistemas de IA frente a la explicabilidad de los resultados si tienen que elegir entre ambas cosas.
De esa elección entre explicación y predicción podrían decir mucho todas las ciencias basadas en modelos matemáticos, como la economía o la biología evolutiva. Pero, hasta ahora, incluso en esas ciencias los modelos cuantitativos buscaban establecer en la medida de lo posible relaciones causales, cosa que no es objetivo central de los modelos predictivos de IA, que solo buscan el acierto.
Sin embargo, la tentación de usar estos modelos predictivos es fuerte, puesto que los gestores de políticas públicas reclaman con frecuencia a los científicos sociales respuestas claras para los problemas acuciantes. Aquí se trata en el fondo de obtener respuestas fiables a problemas complejos, aún a costa de no entender bien por qué esa debe ser la respuesta correcta. Hay quienes abogan por una integración de ambos tipos de modelos, los centrados en la explicación causal y los centrados en la predicción. Está por ver cómo lograr tal cosa.
¿Hacia una ciencia ininteligible?El uso generalizado de estos modelos en la ciencia afectaría también a la idea de que el progreso científico se basa en la elaboración de hipótesis revisables que van siendo sustituidas por mejores hipótesis. En ese proceso, como ya señaló el filósofo de la ciencia Larry Laudan, una ganancia explicativa puede compensar una cierta pérdida predictiva.
No menos perturbadora sería la tendencia a creer que lo no tratable mediante modelos de IA deja de tener interés para la propia ciencia. En último extremo, podría conducir incluso a una ciencia en buena medida ininteligible para los humanos, en el sentido de que tendrán resultados conseguidos mediante modelos no interpretables. Este cambio nos obligaría a replantearnos no ya solo qué noción de verdad es la que aceptaremos sino, incluso, si no tendríamos que abandonar el concepto como tal, contentándonos con la mera utilidad de una creencia.
No parece que el ser humano esté, de momento, capacitado para este cambio.
Todo esto son buenas razones para no poner todo el peso de la investigación en los modelos predictivos, por beneficiosos que puedan ser. Estos modelos han de ser completados con el uso de modelos explicativos y con la búsqueda de hipótesis explicativas contrastables. Una contrastación para la que los modelos predictivos pueden cumplir una importante función.
Otra cosa sería que finalmente pudiera lograrse abrir de algún modo esas cajas negras, quizás mediante otros sistemas de IA que no fueran a su vez ellos mismos cajas negras, o bien que pudiera alcanzarse en el futuro una IA transparente, en la que los algoritmos fueran capaces de dar cuenta cabal de sus resultados de un modo inteligible para los seres humanos. Es un objetivo en el que se trabaja con creciente atención por parte de la inteligencia artificial explicable (XAI), pero el camino es aún incierto. Ojalá seamos capaces de hallarlo pronto.![]()
Sobre los autores: Antonio Diéguez Lucena, Catedrático de Lógica y Filosofía de la Ciencia, Universidad de Málaga e Iñigo De Miguel Beriain, Investigador distinguido, Facultad de Derecho, Ikerbasque Research Professor, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La IA podría convertir la ciencia en algo incomprensible se ha escrito en Cuaderno de Cultura Científica.
El software humano del Proyecto Manhattan
A día de hoy, impresiona bastante darse cuenta de que algunos de los hitos científicos y tecnológicos más relevantes de la historia reciente se consiguieron con una capacidad computacional limitada por la cantidad de cerebros humanos que hubiera disponibles para trabajar en un problema. Pero el caso es que, en algunos centros de investigación, esos cerebros estaban casi mejor organizados que cualquier máquina de la que pudieran disponer. Ese fue el caso, alrededor de 1943, de las instalaciones de computación de Los Alamos durante el Proyecto Manhattan.
Lo importante de toda esta cuestión, y sin entrar ahora a detallar cómo se gestó o las circunstancias científicas, políticas y bélicas que llevaron hasta la determinación de financiar la creación de la primera bomba atómica, es que en los años cuarenta del siglo XX, los cálculos necesarios para diseñar un artefacto semejante no eran, ni mucho menos, triviales. Sobre todo en lo que concernía al diseño del mecanismo y el cálculo de la hidrodinámica de implosión de la bomba de plutonio ―el tipo que la que se probó en el test Trinity―, lo que suponía, entre otras cosas, determinar cuánta energía liberaría el artefacto. La imposibilidad, sobre todo al principio, de hacer pruebas implicaba que había que trabajar con modelos matemáticos que conllevaban la resolución de ecuaciones diferenciales en derivadas parciales no lineales, algo, para cualquiera que no esté familiarizado con ellas, bastante arduo sin un ordenador.
En aquel momento, sobre todo antes de la Segunda Guerra Mundial, se contaba, principalmente, con tres tipos de dispositivos de cálculo: calculadoras electromecánicas de escritorio; máquinas tabuladoras de tarjetas perforadas, y analizadores diferenciales ―un tipo de computador analógico como el que Vannevar Bush construyó en el MIT―. En el Proyecto Manhattan se utilizaron, sobre todo, los dos primeros. El analizador diferencial se destinó durante la guerra sobre todo a la elaboración de tablas de artillería.
A principios de 1943, Stanley P. Frankel y Edred Nelson llegarían a Los Alamos para encargarse de organizar todo el trabajo de matemáticas teórico. Ya habían adquirido experiencia de ese tipo en el Laboratorio Lawrence de Berkeley haciendo cálculos relacionados con la separación de isótopos de uranio y la estimación de la masa crítica necesaria para mantener una reacción en cadena. En Nuevo México se encargarían, en un principio, de los cálculos relacionados con la bomba de uranio, de tipo balístico, para más tarde, hacia 1944 y tras la insistencia de John von Neumann en un cambio de enfoque, pasar a encargarse de los relacionados con la bomba de uranio y su mecanismo de implosión.
Para ello, lo primero que hicieron fue encargar ciertas unidades de calculadoras de escritorio Marchant, Fridens y algunas Monroe, y las distribuyeron entre las «computadoras humanas» que se encargarían del proceso y que solían ser mujeres. Más adelante empezaron a valorar la posibilidad de utilizar máquinas tabuladoras y en marzo de 1944 llegó el refuerzo de las IBM 601, entre otras.
 En Los Alamos, computadoras humanas, normalmente mujeres, realizaban a mano los cálculos necesarios para el desarrollo de la bomba atómica con calculadoras electromecánicas Marchant similares a la que aparece en la foto. Fuente: CC0 1.0/Daderot
En Los Alamos, computadoras humanas, normalmente mujeres, realizaban a mano los cálculos necesarios para el desarrollo de la bomba atómica con calculadoras electromecánicas Marchant similares a la que aparece en la foto. Fuente: CC0 1.0/Daderot
 La IBM 601 era una máquina tabuladora capaz de multiplicar ―aunque no dividir― dos números que se introducían en ella utilizando tarjetas perforadas. Se llegaron a instalar cuatro de ellas en Los Alamos para finales de 1944, además de otros modelos similares de IBM con otras aplicaciones. El sistema se componía de ocho máquinas en total. Fuente: CC BY-SA 3.0/Sandstein
La IBM 601 era una máquina tabuladora capaz de multiplicar ―aunque no dividir― dos números que se introducían en ella utilizando tarjetas perforadas. Se llegaron a instalar cuatro de ellas en Los Alamos para finales de 1944, además de otros modelos similares de IBM con otras aplicaciones. El sistema se componía de ocho máquinas en total. Fuente: CC BY-SA 3.0/SandsteinAquí merece la pena hacer un inciso. Es de sobra conocido que, en los inicios de la historia de la computación, quienes se encargaban principalmente de las labores de programación de los primeros computadores eran ellas. En el caso del Proyecto Manhattan, quienes lo hacían eran, en un gran porcentaje, las esposas de los científicos que trabajaban allí. Así, podemos encontrar nombres como Mary Frankel, que llegó a supervisar uno de los grupos de cálculo, o Mici Teller, cuyos apellidos de casadas no deberían resultar desconocidos. También son reseñables los trabajos que Klara Dan von Neumman llevó a cabo allí tras la guerra con el ENIAC. Se estima que hubo más de trescientas mujeres allí ocupando puestos técnicos en el Proyecto Manhattan. En el caso de Los Alamos, el lugar era, además, una ciudad en miniatura donde se mudaron familias enteras, y se incentivó activamente el trabajo de estas mujeres, muchas de ellas amas de casa, otorgándoles ciertas ayudas, normalmente relacionadas con el cuidado del hogar y de los hijos.
 Mary Frankel (X214) y Mici Teller (X169) fueron dos de las numerosas mujeres calculadoras que trabajaban en Los Alamos. Fuente: Los Alamos National Laboratory
Mary Frankel (X214) y Mici Teller (X169) fueron dos de las numerosas mujeres calculadoras que trabajaban en Los Alamos. Fuente: Los Alamos National Laboratory
No obstante, lo que más llama la atención del el equipo de computación de Frankel y Nelson no eran ni las mujeres calculadoras ni las máquinas que utilizaban en sí, sino la organización. Cuando empezaron a valorar el uso de máquinas tabuladoras para realizar los cálculos, idearon un sistema para agilizarlos creando una especie de «programa» o diagrama de flujo que dividía el proceso de resolución de una ecuación en pasos sencillos. Hasta que contaron con las IBM no pudieron probarlo directamente, así que hicieron una especie de simulacro utilizando el equipo de mujeres calculadoras. El proceso era bastante intuitivo. Con su Marchant encima de la mesa, cada una efectuaba uno de los pasos: unas hacían multiplicaciones, otras divisiones, otras raíces cuadradas… siempre lo mismo, y pasaban su resultado a la siguiente mesa en una tarjeta para que otra compañera continuara con su parte del cálculo. El sistema funcionó increíblemente bien, muchísimo mejor y más eficientemente que si una sola persona resolvía la ecuación completa paso a paso.
En medio de todo aquello se encontraba un jovencísimo físico de veintiséis años que en el futuro casi pasaría más a la historia por tocar los bongos que por ganar un premio Nobel: Richard Feynman. Era uno de los que se encargaba de reparar las calculadoras Marchant cuando se rompían ―no había tiempo de enviarlas al fabricante y esperar a que las devolviera―, y conocía muy bien el funcionamiento de todo aquello. Cuando llegaron las primeras IBM, en abril de 1944, también ayudó a Frankel y Nelson a montarlas ―el secretismo extremo alrededor de todo lo relacionado con el Proyecto Manhattan complicó, en un primer momento, que ningún empleado de IBM consiguiera autorización para ir a Los Alamos para hacerlo―. Y en cuanto todo estuvo listo, obviamente, Feynman tuvo una de sus peculiares ideas: poner a competir a las mujeres calculadoras y a las máquinas tabuladoras realizando el mismo trabajo: ¿quién tardaría menos en resolver un problema? A día de hoy, diríamos que cualquier ordenador, pero entonces ganaron las mujeres. La única desventaja que mostraron, utilizando el mismo proceso de cálculo, era que, obviamente y a diferencia de las IBM, la fatiga acababa haciendo mella en ellas.
Aquel «programa» humano, unido al uso de las máquinas tabuladoras ya operativas, supuso un aumento de rendimiento espectacular porque, además, vieron que de esta manera no tenían que limitarse a realizar un solo cálculo por vez, sino que podían llegar a efectuar hasta dos o tres en paralelo. Utilizando tarjetas de colores, en cada puesto se realizaba el mismo paso siempre, pero para diferentes asuntos, cada uno identificado con un color.
Es curioso, además, como aquellas máquinas tan básicas hicieron perder la cabeza a Stanley Frankel, que se puso a utilizarlas para cualquier cosa menos para lo que las habían comprado y a probar qué serían capaces de hacer ―como el geek que se compra un PC nuevo con las últimas especificaciones del mercado―. Feynman acabaría sustituyéndolo en su puesto, y demostró ser un gran organizador. El equipo que trabajaba con las máquinas tabuladoras, ahora formado principalmente por chavales jóvenes sacados del instituto con algún conocimiento técnico o de ingeniería, ni siquiera sabía para qué eran todos aquellos cálculos. Feynman consiguió permiso para contárselo y, de nuevo, la productividad se disparó: los chicos empezaron a buscar maneras de mejorar y agilizar los procesos trabajando día y noche. Se pasó de resolver tres problemas en nueve meses, antes de las tabuladoras y de aquel software humano, a nueve problemas en tres meses.
Es increíble, que con tan solo lápiz, papel y talento, los científicos sacaran todo ese partido a aquellas máquinas rudimentarias y se las apañaran para desentrañar uno de los secretos más intrincados del átomo.
 La única imagen a color de la explosión de Trinity con buena exposición, tomada por Jack Aeby. Fuente: Wikimedia Commons
La única imagen a color de la explosión de Trinity con buena exposición, tomada por Jack Aeby. Fuente: Wikimedia Commons
Bibliografía
Archer, B. J. (2021). The Los Alamos computing facility during the Manhattan Project. Nuclear technology, 204, pp. S190-S203. doi: 10.1080/00295450.2021.1940060
Feynman, R. P. (2018 [1987]). ¿Está usted de broma, Sr. Feynman? Aventuras de un curioso personaje. Alianza Editorial.
Howes, R. y Herzenberg, C. L. (1999). Their day in the sun. Women of the Manhattan Project labor and social change. Temple University Press.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo El software humano del Proyecto Manhattan se ha escrito en Cuaderno de Cultura Científica.
El teorema de Morley
La geometría euclidiana y, en particular, la geometría plana, está repleta de hermosos y sorprendentes teoremas, que suelen venir acompañados de diagramas con mucho encanto, como el teorema de Napoleón (véase la entrada Variaciones artísticas del teorema de Napoleón), el teorema de van Aubel (véase la entrada Una pequeña joya geométrica: el teorema de van Aubel), el teorema de Viviani (cuya demostración sin palabras podéis admirar en la entrada Teoremas geométricos sin palabras: Viviani), el teorema de la circunferencia de Conway (un moderno resultado geométrico del que podéis leer en la entrada Teoremas geométricos sin palabras: Conway), el teorema de Marion (véase la entrada El teorema de Marion (Walter)), el teorema de la bandera británica (véase la entrada El teorema de la ikurriña), o el mismísimo teorema de Pitágoras (véase la entrada Pitágoras sin palabras), entre muchos otros.
 Línea polar de un punto y un círculo (Apolonio), del dibujante e ilustrador infantil estadounidense Crockett Johnson (1906-1975). Imagen de la página web de The National Museum of American History
Línea polar de un punto y un círculo (Apolonio), del dibujante e ilustrador infantil estadounidense Crockett Johnson (1906-1975). Imagen de la página web de The National Museum of American HistoryExisten muchos otros fascinantes teoremas geométricos del plano. En esta entrada del Cuaderno de Cultura Científica vamos a hablar de uno especialmente interesante y atractivo, que ha cautivado a muchas personas, en particular, del ámbito de las matemáticas, a lo largo del siglo XX (no es un teorema antiguo). Durante este tiempo se han desarrollado una cantidad importante de diferentes demostraciones, muchas de ellas de la mano de grandes matemáticos, como el matemático francés, que recibió la Medalla Fields en 1982, Alain Connes (1947), el matemático húngaro Béla Bollobás (1943), el matemático, físico y científico de la computación Edsger W. Dijkstra (1930-2002), el prolífico e imaginativo matemático británico John H. Conway (1937-2020), creador del autómata celular denominado el juego de la vida, o el matemático y físico matemático británico Roger Penrose (1931), que recibió el Premio Nobel de Física en 2020, entre muchos otros. Es el teorema de Morley, que debe su nombre al matemático británico, que vivió gran parte de su vida en Estados Unidos, Frank Morley (1860-1937), relacionado con las trisectrices de un triángulo cualquiera.
El teorema de las trisectrices de MorleyAntes de nada, enunciemos la versión simple del teorema de Morley, que es un resultado geométrico de una especial sencillez en su enunciado, pero de una gran profundidad en su significado.
Teorema de Morley (1899): Los puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera, son los vértices de un triángulo equilátero.
Expliquémoslo brevemente. Partimos de un triángulo ABC cualquiera, como el que vemos en la siguiente imagen.
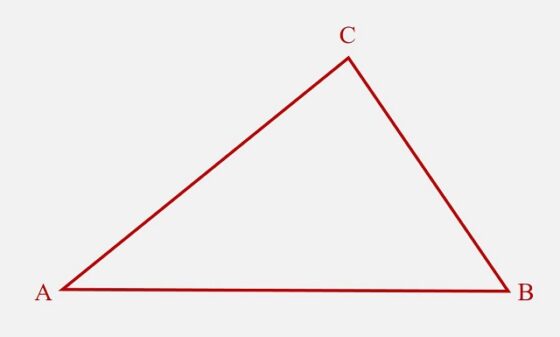 Triángulo ABC
Triángulo ABC
A continuación, en cada uno de los tres ángulos del triángulo ABC se trazan las trisectrices, es decir, las dos rectas que dividen al ángulo en tres ángulos iguales, como se muestra en la siguiente imagen.
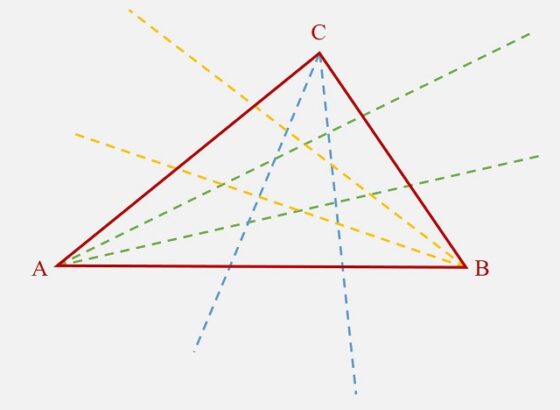 Los tres pares de trisectrices, líneas rectas, de los ángulos del triángulo ABC
Los tres pares de trisectrices, líneas rectas, de los ángulos del triángulo ABC
Alguien, al leer que estamos tomando las trisectrices de un ángulo, podría pensar que esto no es posible. La confusión puede venir del hecho de que hay tres problemas clásicos de la matemática griega, la cuadratura del círculo, la trisección de un ángulo y la duplicación de un cubo, que no tienen solución, pero solo si esta solución se intenta construir “con regla y compás”, que son los instrumentos clásicos de la matemática griega (véase, por ejemplo, el artículo Los tres problemas clásicos, de Santiago Fernánez, o el libro Historia de las matemáticas, de Carl B. Boyer).
A continuación, se toman los tres puntos que son la intersección de las trisectrices adyacentes de los ángulos del triángulo ABC, que en la imagen hemos denominado E, F y G.
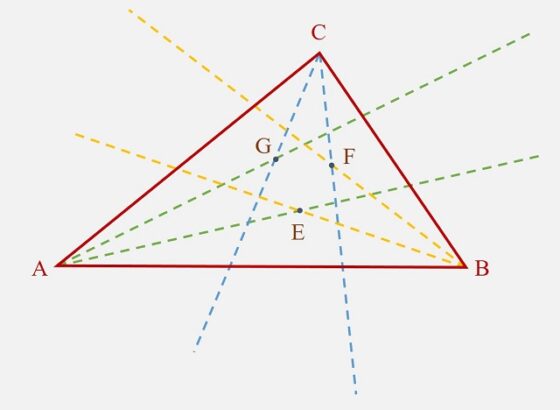 Los puntos E, F y G son las intersecciones de las trisectrices adyacentes de los ángulos del triángulo ABC
Los puntos E, F y G son las intersecciones de las trisectrices adyacentes de los ángulos del triángulo ABC
Entonces, el teorema de Morley establece que el triángulo EFG, cuyos vértices son los puntos de intersección de las trisectrices adyacentes de los ángulos del triángulo ABC, es un triangulo equilátero, es decir, con los tres lados iguales (así como sus ángulos, de 60 grados). A este triángulo equilátero se le llama “triángulo de Morley”.
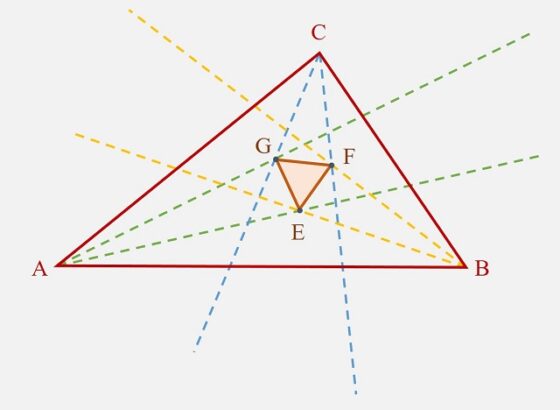 El triángulo EFG es equilátero
El triángulo EFG es equilátero
Si en lugar de tomar las trisectrices de los ángulos interiores del triángulo, se toman las trisectrices de los ángulos exteriores, se forma otro triángulo equilátero. Antes de mostrar este resultado, recordemos cuales son los ángulos exteriores de un triángulo.
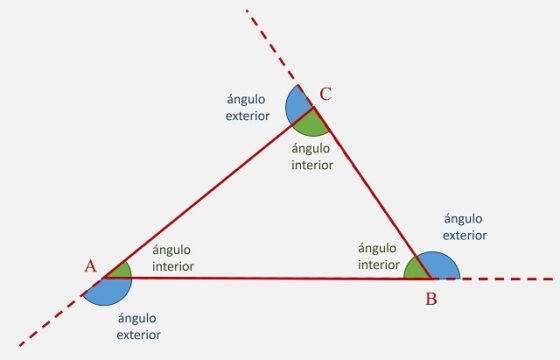 Ángulos interiores y exteriores de un triángulo ABC
Ángulos interiores y exteriores de un triángulo ABC
Por lo tanto, también sería cierto el teorema de Morley para ángulos exteriores, es decir, que los puntos de intersección de las trisectrices adyacentes de los ángulos exteriores de un triángulo cualquiera, son los vértices de un triángulo equilátero.
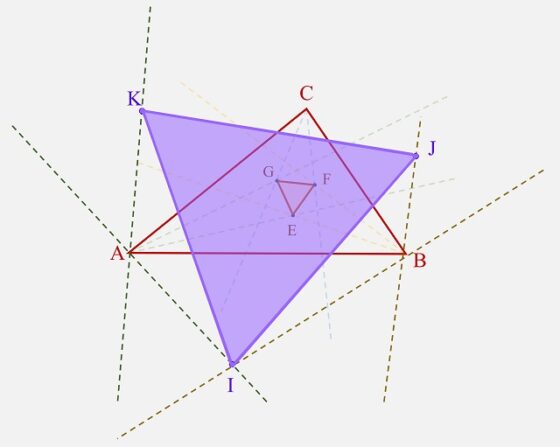 Teorema de Morley para las trisectrices de los ángulos exteriores, es decir, el triángulo IJK es equilátero
Teorema de Morley para las trisectrices de los ángulos exteriores, es decir, el triángulo IJK es equiláteroLa historia del teorema de Morley
Como se comentaba al principio de esta entrada del Cuaderno de Cultura Científica, el teorema de Morley debe su normbre al matemático británico, afincado en Estados Unidos, Frank Morley (1860-1937).
Aunque de origen británico, Frank Morley, graduado en el King’s College de la Universidad de Cambridge en 1884, emigró a Estados Unidos en 1887, donde fue contratado en el Haverford College, en centro cuáquero de Pensilvania. Como se puede leer en el obituario de la American Mathematical Society, Frank Morley, In memoriam, en 1889 se casó con la británica Lilian Janet Bird y tuvieron tres hijos, el periodista y escritor Christopher Morley, autor de novelas como La librería ambulante, La librería encantada o Kathleen, que pueden leerse en las ediciones en castellano de la editorial Periférica, el periodista, ganador del Premio Pulitzer, Felix Morley, y el matemático Frank Vigor Morley, que publicaría con su padre el libro Inversive Geometry.
Tras su periodo en el Haverford College, en 1900 se trasladó a la Universidad Johns Hopkins, en Baltimore (Maryland), donde dirigió el departamento de matemáticas hasta que se jubiló en 1928, siendo además editor de su prestigiosa revista, American Journal of Mathematics, de 1900 a 1920. Fue miembro de la New York Mathematical Society (fundada en 1888) y su sucesora la American Mathematical Society, donde ocupó varios cargos, entre ellos su presidencia. Entre sus publicaciones destacan los libros A Treatise on the Theory of Functions (Macmillan, 1893) y Introduction to the Theory of Analytic Functions (Macmillan, 1898).
 Retrato del matemático británico-estadounidense Frank Morley, realizado por el artista y fotógrafo Alfred Hugh Fisher (1867-1945)
Retrato del matemático británico-estadounidense Frank Morley, realizado por el artista y fotógrafo Alfred Hugh Fisher (1867-1945)En 1900, Frank Morley publicó su excepcional artículo On the Metric Geometry of the Plane n-line, en el primer número de la revista Transactions of the American Mathematical Society, en el que desmuestra varios resultados sobre el comportamiento de las n-líneas en el plano. Aunque en este artículo, como era normal en esa época, no se estructuraba en la forma actual de teorema/demostración. Inmerso dentro del contenido de este brillante artículo estaba enuciado el conocido como “teorema de Morley” (los puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera, son los vértices de un triángulo equilátero), más aún su teoría consideraba 18 casos de triángulos equiláteros “de Morley”. Uno de los casos cuando se consideran las trisectrices de los ángulos interiores (el primero de los casos analizados en esta entrada, el teorema de Morley en su versión simple y clásica), otro de los casos cuando se consideran las trisectrices de los ángulos exteriores (el otro triángulo equilátero de Morley, más grande, visto arriba) y los casos, no mencionados aún, de cuando se mezclan las trisectrices de dos angulos exteriores y uno interior (un ejemplo con los tres triángulos equiláteros exteriores que aparecen ahora se muestra en la siguiente imagen), siendo los demás casos más complejos.
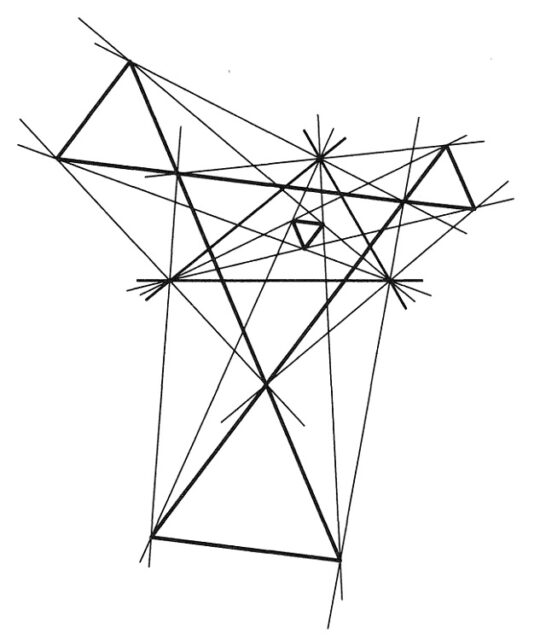 Cinco, de los dieciocho, triángulos equiláteros de Morley, construidos mediante las trisectrices de los ángulos de un triángulo cualquiera. Imagen del libro The Penguin Dictionary of Curious and Interesting Geometry, de David Wells
Cinco, de los dieciocho, triángulos equiláteros de Morley, construidos mediante las trisectrices de los ángulos de un triángulo cualquiera. Imagen del libro The Penguin Dictionary of Curious and Interesting Geometry, de David WellsEl geómetra Frank Morley era completamente consciente de este resultado, el conocido como teorema de Morley, en su versión simple, y con los 18 triángulos equiláteros en su versión completa, que era parte de una teoría más global, sin embargo, no publicó el enunciado del teorema de forma explícita y separada, ni ofreció una demostración del mismo. Aunque sí lo menciónó en sus comunicaciones privadas, en particular, sus cartas a sus amigos, como las que escribió en 1904 al matemático británico Herbert William Richmond (1863-1948) y al físico y matemático británico Sir Edmund Taylor Whittaker (1873-1956).
La primera vez que se publica el teorema de Morley es en forma de problema, presentado por E. J. Ebden, en la revista británica The Educational Times (revista que se publicó entre 1847 y 1923, cuando se convirtió en la revista Education Today), como el problema 16381 (que se muestra en la siguiente imagen), en 1908; así como, el mismo año, presentado por T. Delahaye y H. Lez, en la revista belga Mathesis (que se publicó entre los años 1881 y 1915), como problema 1655.
 Problema 16381, presentado por E. J. Ebden, en The Educational Times (1908)
Problema 16381, presentado por E. J. Ebden, en The Educational Times (1908)La primera solución al problema 16381 de The Educational Times fue dada por M. Satyanarayana ese mismo año, en julio, mientras que el problema había sido publicado en febrero. En la siguiente imagen vemos la solución mencionada. Mientras que los mismos T. Delahaye y H. Lez, publicaron la solcuión al problema 1655 en la revista belga Mathesis.
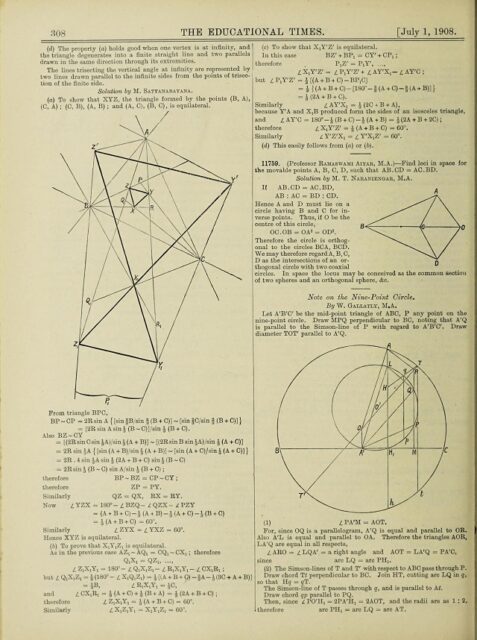 Solución al problema 16381, en The Educational Times (1908) , dada por M. Satyanarayana
Solución al problema 16381, en The Educational Times (1908) , dada por M. SatyanarayanaLa siguiente demostración conocida es la del matemático indio Mandyam T. Naraniengar (1871-1940), que sería presidente de la Indian Mathematical Society (1930-1932), así como editor de la revista Journal of the Indian Mathematical Society (1909-1927), publicada en Mathematical Questions and Solutions, from The Educational Times, en 1909.
Por otra parte, la solución completa del teorema de Morley, considerando los casos de los 18 triángulos equilateros, fue publicada en 1913, en el artículo The six trisectors of each of the angles of a triangle, de la revista Proceedings of the Edinburgh Mathematical Society, por los matemáticos F. Glanville Taylor y W. L. Marr, que lo reconocían como un resultado de Frank Morley.
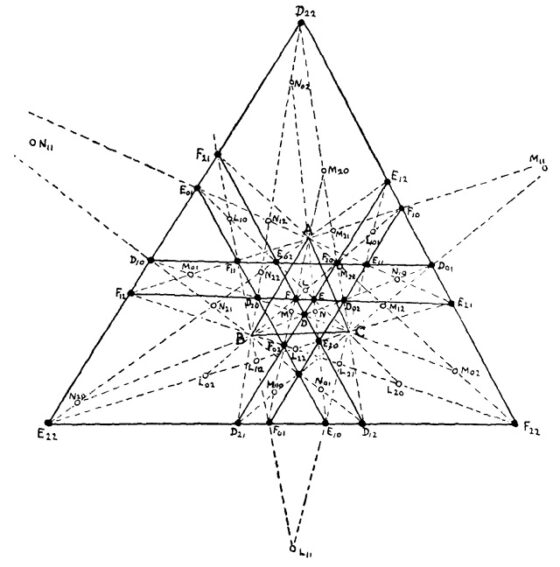 Esquema general del teorema de Morley, con los 18 triángulos equiláteros asociados, que aparece en el artículo de los matemáticos F. Glanville Taylor y W. L. Marr
Esquema general del teorema de Morley, con los 18 triángulos equiláteros asociados, que aparece en el artículo de los matemáticos F. Glanville Taylor y W. L. Marr
Desde entonces, se han publicado muchas demostraciones del teorema de Morley.
Una demostración del teorema de MorleyExisten muchas demostraciones diferentes del teorema de las trisectrices de Morley, también conocido como el teorema del milagro de Morley, pruebas geométricas, trigonométricas o algebraicas, algunas bastante técnicas, otras de ideas más sencillas y algunas de una gran belleza, como la demostración del matemático británico John H. Conway. En la página Cut the knot [https://www.cut-the-knot.org/], del matemático Alexander Bogomolny, podéis encontrar veintisiete pruebas diferentes, más otras tres que no son válidas.
Vamos a terminar esta entrada con una pequeña idea de la demostración clásica de Naraniengar del teorema de Morley. Recordemos que queremos demostrar que “los puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera, son los vértices de un triángulo equilátero”.
En primer lugar, Naraniengar demuestra el siguiente lema técnico.
Lema: Si cuatro puntos Y’, Z, Y, Z’ satisfacen las condiciones
i) Y’Z = ZY = YZ’
ii) ángulo(YZY’) = ángulo (Z’YZ) = 180º – 2 (alpha) > 60º,
entonces los cuatro puntos Y’, Z, Y, Z’ están en una misma circunferencia. Además, si un punto A, en el lado contrario al punto Y respecto a la recta Y’Z’, está colocado tal que ángulo(Y’AZ’) = 3 (alpha), entonces el quinto punto A también está en la misma circunferencia.
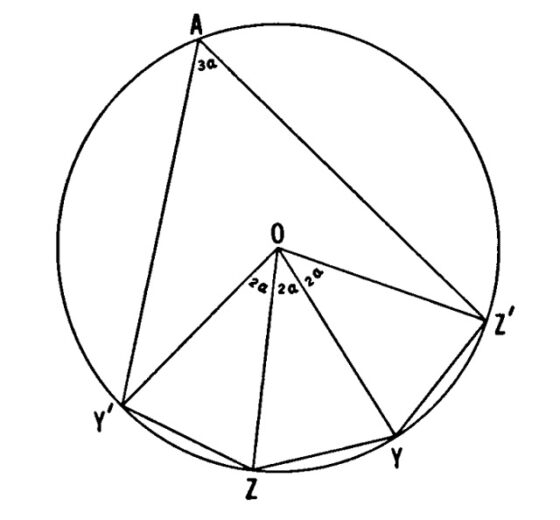 Ilustración del lema técnico de la demostración de Naraniengar
Ilustración del lema técnico de la demostración de Naraniengar
En segundo lugar, dado un triángulo cualquiera ABC, con ángulos internos iguales a 3 (beta), en B, y a 3 (gama), en C, como en la siguiente imagen, se consideran los dos pares de trisectrices de los ángulos en B y C, y sus intersecciones en los puntos U y X.
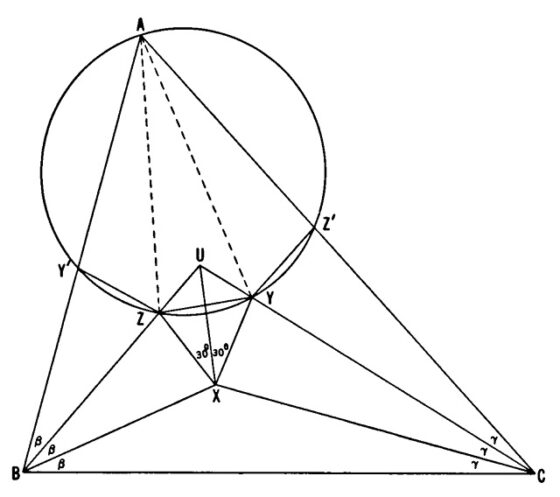
Si ahora tomamos el triángulo BCU, entonces los ángulos en B y C son bisecados por las rectas BX y CX, por lo tanto X es el incentro del triángulo BCU (recordemos que el incentro es el punto en el que se cortan las tres bisectrices de sus ángulos internos). En consecuencia, la recta UX biseca el ángulo en U.
Ahora se construyen los puntos Y y Z que están en los segmentos CU y BU, tales que los segmentos XY y XZ forman un ángulo de 30 grados con el segmento XU en lados opuestos, como en la imagen. Lo que nos lleva a que los triángulos UXY y UXZ son semejantes, los segmentos XY y XZ son iguales, y el ángulo en X es de 60 grados. Por lo tanto, el triángulo XYZ es un triángulo equilátero.
La última parte de la demostración de Naraniengar consiste en demostrar que Z e Y son precisamente las otras dos intersecciones de las trisectrices de A con las trisectrices de B y C adyacentes, de esta manera el triángulo central descrito por el teorema de Morley sería XYZ, que ya sabemos que es equilátero. Para ello se utilizará el lema técnico. Lo primero que hacemos es definir los puntos Y’ y Z’ de la siguiente forma. Sobre el segmento BA consideramos el punto Y’ tal que BY’ = BX, mientras que sobre el segmento CA consideramos el punto Z’ tal que CZ’ = CX. Entonces, por semejanza de triángulos, se observa fácilmente que
Y’Z = ZX = ZY = YX = YZ’.
Por otra parte, comparándo los ángulos alrededor de Z y alrededor de Y, se puede observar que los ángulos implicados ángulo(YZY’) y ángulo (Z’YZ) son iguales y de la forma 180º – 2 (alpha) > 60º.
Finalmente, aplicando el lema técnico. Entonces, como las cuerdas Y’Z, ZY y YZ’ son iguales, también lo son los tres ángulos que determinan en A, luego las líneas AZ y AY son trisectrices del ángulo en A. De esta forma, se concluye que los puntos X, Y, Z son las intersecciones de las trisectrices adyacentes de los ángulos del triángulo ABC que forman un triángulo, como ya se ha probado al principio, equilátero. Y queda demostrado el teorema de Morley.
 Morley Triangle (1969), del dibujante e ilustrador infantil estadounidense Crockett Johnson. Imagen de la página web de The National Museum of American History.
Morley Triangle (1969), del dibujante e ilustrador infantil estadounidense Crockett Johnson. Imagen de la página web de The National Museum of American History.En una próxima entrada disfrutaremos de la hermosa demostración del teorema de Morley propuesta por el matemático británico John H. Conway.
Bibliografía
1.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.
2.- Martin Gardner, Nuevos pasatiempos matemáticos, Alianza editorial, 2018.
3.- H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, Mathematical Association of America, 1967.
4.- C. O. Oakley, J. C. Baker, The Morley Trisector Theorem, American Mathematical Monthly 85, pp. 737-745, 1978.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El teorema de Morley se ha escrito en Cuaderno de Cultura Científica.
Un solo campo explica la inflación observada
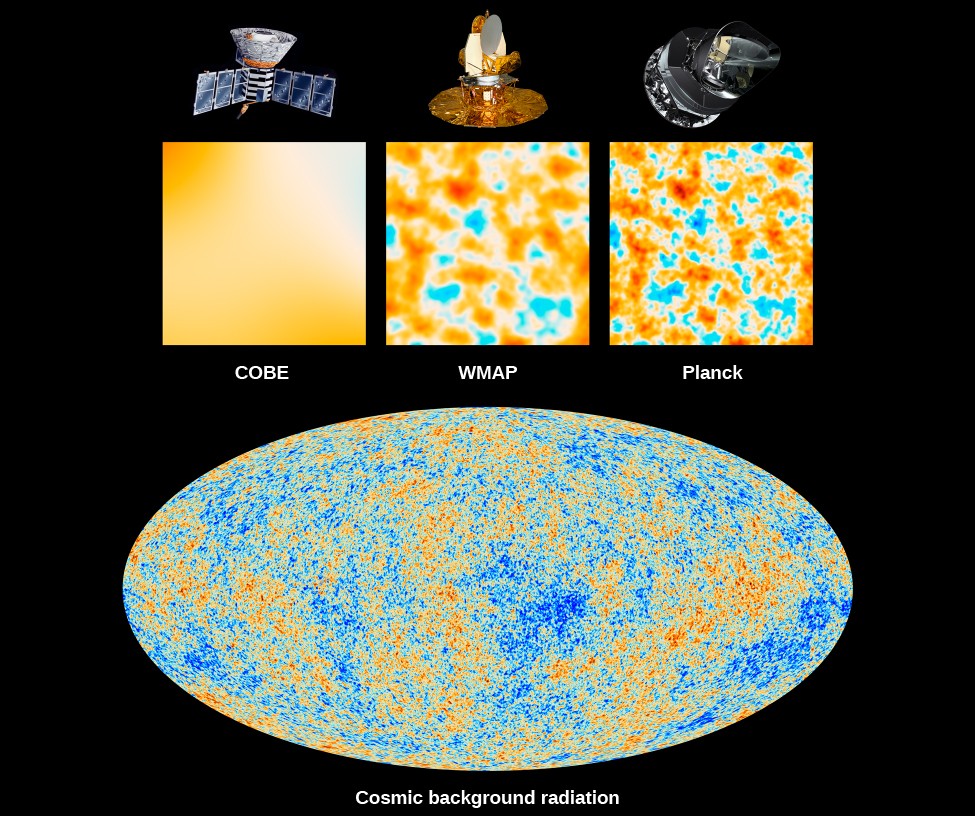 Arriba: Ilustración de los satélites CBE, WMAP y Planck, con una imagen muestra resolución de cada experimento. Abajo: mapa de la radiación del Fondo de Microondas obtenida con Planck. Fuente: Astronomy/OpenStax CNX.
Arriba: Ilustración de los satélites CBE, WMAP y Planck, con una imagen muestra resolución de cada experimento. Abajo: mapa de la radiación del Fondo de Microondas obtenida con Planck. Fuente: Astronomy/OpenStax CNX.La inflación cósmica, la teórica expansión exponencial del espacio en el Universo temprano, ofrece soluciones a importantes enigmas cosmológicos. Explica por qué el Universo parece perfectamente plano: la expansión estira cualquier curvatura hasta el punto de ser imperceptible. También explica cómo las fluctuaciones del vacío cuántico podrían convertirse en semillas de la estructura del Universo.
La mayoría de los modelos de física más allá del modelo estándar implican muchos campos cuánticos nuevos, lo que sugiere que la inflación podría haber sido impulsada por múltiples campos. Sin embargo, las observaciones de la radiación del fondo de microondas cósmico favorecen la existencia de un solo campo “inflatón”. Entonces, ¿son los modelos multicampo incompatibles con las observaciones?
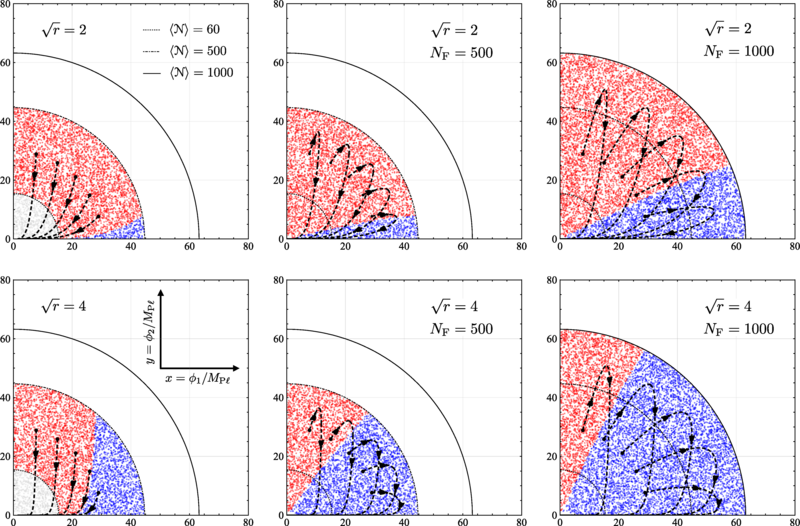
Ahora, Koki Tokeshi, de la Universidad de Tokio (Japón), y Vincent Vennin, de la Universidad de la Sorbona (Francia), proponen una explicación para la aparición de un único campo que domina la inflación. Los investigadores consideran un modelo de inflación que involucra dos campos inflatón cuyas fluctuaciones cuánticas hacen que su dinámica sea estocástica. En cualquier porción microscópica del espacio los campos evolucionan estocásticamente hasta que termina la inflación.
Utilizando una prueba existente, el dúo calcula que, en esa zona, esta evolución puede hacer que el campo más ligero (el asociado a un “parámetro de masa” más pequeño) domine sobre el otro. Por lo tanto, la inflación en esa zona podría aproximarse bien mediante una teoría con un solo campo.
Pero, ¿qué tan comunes son las zonas del Universo susceptibles de una evolución como esta? Tokeshi y Vennin muestran que las zonas con condiciones iniciales adecuadas corresponden a regiones espacio-temporales que sufren más inflación y, por tanto, acaban teniendo mayores volúmenes.
Como resultado, la inflación con dos campos puede parecer inflación de un solo campo porque estas regiones terminan constituyendo la mayor parte del volumen del Universo. Los investigadores dicen que esperan que se obtengan resultados similares en el caso de más de dos campos.
Referencias:
K. Tokeshi and V. Vennin (2024) Why does inflation look single field to us? Phys. Rev. Lett. doi: 10.1103/PhysRevLett.132.251001
C. M. Peterson and M. Tegmark, (2011) Testing two-field inflation Phys. Rev. D doi: 10.1103/PhysRevD.83.023522
R. Garisto (2024) One Field to Rule Them All Physics 17, s78
El artículo Un solo campo explica la inflación observada se ha escrito en Cuaderno de Cultura Científica.
¿Cuánta sal tiene el océano de Plutón?
Ochenta y cinco años pasaron entre el descubrimiento de Plutón -allá por 1930- y la primera visita por parte de una sonda espacial en julio de 2015, cuando la sonda New Horizons nos permitió ver de cerca por primera vez la superficie del hoy planeta enano y que, a priori, debido a su pequeño tamaño y la aparente ausencia de fuentes de energía que pudiese ayudarle a mantener cierto grado de actividad, pensábamos que podría tratarse de un cuerpo frío y anodino.
Nada más lejos de la realidad: lo que pudimos ver fue un mundo complejo y activo con llanuras y glaciares de nitrógeno, montañas de hielo de agua y una tenue atmósfera. Precisamente en la mayor de sus llanuras, Sputnik Planitia, los científicos encontraron una serie de patrones poligonales que parecían indicar un mecanismo convectivo dentro del hielo que lo obligara a fluir, pero no solo eso, sino que la presencia de la propia llanura podría apuntar a la existencia de un océano de agua líquida bajo la superficie.
 Imagen de Plutón. Obsérvese la gran diversidad presente en su superficie, con lugares llanos, montañosos y zonas totalmente desnudas de cráteres. Fuente: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.
Imagen de Plutón. Obsérvese la gran diversidad presente en su superficie, con lugares llanos, montañosos y zonas totalmente desnudas de cráteres. Fuente: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.¿Cómo es posible que a esa distancia del Sol y un cuerpo tan pequeño como Plutón haya sido capaz de mantener un océano subterráneo? En primer lugar, en su núcleo rocoso todavía podrían existir elementos radioactivos que durante su desintegración fuesen capaces de generar un calor que mantenga una temperatura adecuada para que el agua pueda mantenerse en estado líquido.
Por otro, la presencia de sales dentro del propio océano serviría como un anticongelante, bajando todavía más la temperatura necesaria para congelar el agua, de un modo similar a cuando, en invierno, usamos la sal para ayudar a eliminar el hielo de nuestras carreteras.
Pero hay un detalle más: Sputnik Plantia podría ser una de las grandes cuencas de impacto de nuestro Sistema Solar, como la de Hellas en Marte o la de Caloris en Mercurio y su posición y características se pueden explicar mejor si existe un océano por debajo de esta, como explican Nimmo et al. (2016), ya que la anomalía gravitatoria positiva que se ha detectado en esta zona estaría provocada por el ascenso de aguas frías y densas del océano hacia la superficie.
 En esta imagen oblicua de la superficie de Plutón podemos ver perfectamente las montañas formadas principalmente por bloques de hielo de agua y Sputnik Planitia, extendiéndose más allá del horizonte. Fuente: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.
En esta imagen oblicua de la superficie de Plutón podemos ver perfectamente las montañas formadas principalmente por bloques de hielo de agua y Sputnik Planitia, extendiéndose más allá del horizonte. Fuente: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.Si, además, le sumamos el efecto del depósito de nitrógeno sobre la llanura, provocado por la congelación de este gas desde la atmósfera cuando las temperaturas son muy bajas, la anomalía gravitatoria también se puede comprender mejor. La anomalía gravitatoria detectada tampoco se podría explicar solo con el depósito de nitrógeno, ya que se necesitaría una capa de más de 40 kilómetros de espesor para explicar las observaciones.
Uno de los requisitos de los que hablábamos para mantener el agua líquida es que el océano sea salado, pero, ¿cuánta sal necesita para mantenerlo en este estado? Un nuevo estudio publicado por McGovern et al. (2024) ha analizado la respuesta del océano ante la carga que le supone la corteza superior (recordemos, de hielo) y cuál sería la deformación que debemos esperar en la superficie ante el peso del hielo de nitrógeno.
Obviamente no hay una respuesta única a esta pregunta, ya que el resultado es diferente según el espesor de la propia corteza de hielo, la profundidad de Sputnik Planitia y, en último lugar, por la densidad del océano subterráneo. Por ello, los científicos han tenido que crear una serie de escenarios diferentes variando los parámetros. Por ejemplo, para la salinidad han escogido valores en los que la densidad del agua varía entre los 1000 y los 1400 kg/m3. O lo que es lo mismo, de agua pura a agua muy salina.
Uno de los hallazgos más interesantes de estos modelos es que si se incrementa la salinidad del océano, algo que haría las aguas más densas, las estructuras geológicas que se observan en la superficie no se ajustarían tan bien a los modelos, pero si la densidad de agua del océano está por debajo 1100 kg/m3. Este detalle implica una salinidad muy modesta, hay un mejor ajuste entre el modelo y la deformación observada en la superficie.
 La atmósfera de Plutón destaca en esta imagen por crear un “brillo” provocado por la dispersión de la luz del Sol y que rodea el planeta. fuente: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.
La atmósfera de Plutón destaca en esta imagen por crear un “brillo” provocado por la dispersión de la luz del Sol y que rodea el planeta. fuente: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.Un océano menos salino sería más estable a lo largo del tiempo y provocaría una menor deformación en la corteza de hielo, al mismo tiempo generando menos deformación en la superficie, algo que explica por qué la superficie de Sputnik Planitia es tan suave a nivel topográfico.
Por otro lado, una salinidad moderada tiene muchas implicaciones astrobiológicas ya que, si se confirma este dato, el océano de Plutón sería un lugar mucho más hospitalario para la vida que si fuese extremadamente salado por lo que este estudio deja de manifiesto que, al menos en este aspecto, el océano de Plutón podría ser un ambiente potencialmente habitable.
Probablemente tardaremos todavía muchas décadas en volver a ver una misión que surque los cielos de Plutón y nos pueda decir si estos modelos están en lo cierto pero, sea cual sea la respuesta, estoy seguro que este planeta enano no dejará de sorprendernos.
Referencias:
Nimmo, F., D. P. Hamilton, W. B. McKinnon, P. M. Schenk, R. P. Binzel, C. J. Bierson, R. A. Beyer, et al. (2016) Reorientation of Sputnik Planitia Implies a Subsurface Ocean on Pluto Nature 540, no. 7631 (2016): 94–96. doi: 10.1038/nature20148.
Kimura, Jun, and Shunichi Kamata (2020) Stability of the Subsurface Ocean of Pluto Planetary and Space Science doi: 10.1016/j.pss.2019.104828
McGovern, P. J., and A. L. Nguyen (2024) The Role of Pluto’s Ocean’s Salinity in Supporting Nitrogen Ice Loads within the Sputnik Planitia Basin Icarus doi: 10.1016/j.icarus.2024.115968.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario, divulgador científico y autor de la sección Planeta B.
El artículo ¿Cuánta sal tiene el océano de Plutón? se ha escrito en Cuaderno de Cultura Científica.
El queso, entre los genes y la cultura
Todos los mamíferos nos alimentamos de leche al nacer. La leche es un alimento complejo y muy nutritivo, que contiene proteínas, grasas, hidratos de carbono, vitaminas A y B, y minerales como calcio y fósforo: casi todo lo que necesitamos para vivir. Los primeros indicios de consumo de leche animal por parte de la humanidad se remontan al primer Neolítico. Por ejemplo, en yacimientos arqueológicos de hace casi 9.000 años, cerca del mar de Mármara en la actual Turquía, se encontraron grasas lácteas en antiguos fragmentos de cerámica [1].
La capacidad humana para digerir la leche de otros animales se desarrolló recientemente, y con probabilidad según los estudios genéticos, en los últimos 10.000 años. Un puñado de mutaciones permitió a buena parte de las personas adultas persistir la producción de la enzima lactasa, capaz de descomponer el azúcar de la leche, la lactosa. No toda la población mundial tiene extendidas las mismas mutaciones respecto a la persistencia de la lactasa.
La transformación de la leche -y muy en particular la producción de queso- constituyó un acontecimiento cultural fundamental para la historia de la humanidad. Ello no sólo permitía conservar los productos lácteos de manera no perecedera, sino que también hacía de la leche un alimento mucho más digerible y aprovechable para las primeras poblaciones agricultoras-ganaderas del Neolítico, con o sin beneficiosas mutaciones genéticas [2]. Es muy llamativo que esto es un ejemplo de coevolución genética-cultural a escalas temporales diferentes, pero beneficiosas simultáneamente para la supervivencia humana y su desarrollo. La fabricación del queso no es, por tanto, una actividad humana menor, sino de primera importancia.
 Queso tipo Idiazábal confeccionado por el autor. Foto: Victor Etxebarria
Queso tipo Idiazábal confeccionado por el autor. Foto: Victor EtxebarriaHoy día la industria láctea produce múltiples tipos de leche que podemos ver en las estanterías de los supermercados. No todas las leches son leches, ya que se someten a procesos industriales más o menos beneficiosos para obtener bebidas lácteas. Hace unas décadas el único proceso que se efectuaba era la pasteurización de la leche, o el hervido en casa de la leche cruda adquirida directamente a las granjas o ganaderías. Esto es importante para consumir leche con seguridad, ya que es la forma más sencilla y eficaz de matar posibles microorganismos patógenos que se pueden desarrollar en la leche.
La fabricación de gran cantidad de queso en la industria láctea requiere recoger leche de distintas ganaderías y tienen que pasteurizarla porque no pueden garantizar su higiene y calidad global. De esta manera, el queso que se produce en la industria no es de calidad superior.
Las granjas dedicadas al pastoreo elaboran quesos con leche cruda, ordeñando su propio rebaño para producir algunos de los mejores quesos del mundo. La proximidad de las casas rurales a la propia fuente les permite controlar la calidad de la leche y la producción del queso. A diferencia de otros productores, no mezclan la leche de una vaca enferma tratada con antibióticos con la leche utilizada para hacer queso, mantienen escrupulosa limpieza, la salud individual de los miembros de su cabaña, así como la cadena de frío de la leche.
La leche cruda no es peligrosa para la fabricación de queso, si se mantiene su higiene y frescura. El queso elaborado con leche cruda es muy superior a la versión pasteurizada por la complejidad de su composición inicial y las características, texturas y sabores que puede proporcionar. En cualquier caso, el ganado sano y la leche fresca, limpia y de calidad (pasteurizada o no pasteurizada) es el factor más importante de todos en el proceso de elaboración del queso. Este proceso consiste a grandes rasgos en fermentar, cuajar, salar y curar, lo cual elimina las posibles bacterias patógenas. Además, y de forma inversa, la idea de que la leche pasteurizada ya no puede contaminarse no es cierta [3].
La fabricación de queso implica en primer lugar la fermentación por medio de bacterias presentes en la leche cruda, que transforman la lactosa en ácido láctico. Esta acidificación de la leche facilita su conversión en queso por medio de enzimas proteasas que actúan sobre las proteínas de la leche y precipitan en una cuajada de proteínas y grasa. La fermentación bacteriana continúa consumiendo la lactosa hasta que la eliminación del suero sobrante y el salado de los cuajos detienen la acidificación. Este queso puede colocarse en un molde y curarlo durante unos meses, desarrollando su textura, aromas y sabores, principalmente mediante las enzimas de la leche cruda que catalizan la ruptura de las moléculas grasas (lipolisis) y proteicas (proteólisis), liberando ácidos grasos de cadena corta y aminoácidos libres. Estos componentes volátiles generan el olor del queso, sus sabores y transforman su estructura molecular.
Este proceso resulta en un nutritivo manjar. La ley alimentaria en la mayor parte de los países permite la venta de quesos fabricados a partir de leche cruda, si se han curado durante al menos 60 días, proceso que elimina posibles patógenos. La pasteurización de la leche para quesería calienta la leche al menos a 72ºC durante 30 segundos. Esto mata la mayor parte de las bacterias (patógenas o no) e inutiliza todas sus enzimas. El queso puede fabricarse, pero la materia prima no es óptima. La ordinaria pasteurización UHT (150ºC durante 2 segundos) permite conservar los principales nutrientes de la leche muchos meses en un envase tipo tetrabrik, pero hace inviable fabricar queso.
Existen muchos tipos de quesos en el mundo. Solamente en Francia al parecer existen unas 1000 variedades. La mayor parte de los quesos pueden alimentar a todo tipo de personas, incluidas las intolerantes a la lactosa. En cierto sentido, el queso es un alimento pre-digerido por los fermentos y por el curado. La reducción drástica de la lactosa y el segmentado de las moléculas grasas y proteicas, lo hacen muy fácil de asimilar, muy nutritivo y exquisito. Si a usted no le gusta mucho el queso, es muy probable que no ha buscado bien, porque los sabores, aromas, texturas y sutilezas que existen son casi infinitas. Algunas joyas son quesos artesanos producidos por pequeñas explotaciones ganaderas en todo el mundo. Como casi siempre, es mejor apostar por la calidad que por la cantidad, y la ciencia y la tecnología del queso forma parte de la cultura universal.
Referencias
[1] Evershed, R., Payne, S., Sherratt, A. et al. (2008) Earliest date for milk use in the Near East and southeastern Europe linked to cattle herding. Nature 455, pp 528–531 https://doi.org/10.1038/nature07180
[2] Salque, M., Bogucki, P., Pyzel, J. et al. (2013) Earliest evidence for cheese making in the sixth millennium BC in northern Europe. Nature 493, pp 522–525. https://doi.org/10.1038/nature11698
[3] Montel, M.C., Buchin, S., Mallet, A., Delbes-Paus, C., Vuitton, D.A., Nathalie Desmasures, N. and Berthier, F. (2014) Traditional cheeses: Rich and diverse microbiota with associated benefits. International Journal of Food Microbiology vol. 177, pp.: 136–154. https://doi.org/10.1016/j.ijfoodmicro.2014.02.019
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo El queso, entre los genes y la cultura se ha escrito en Cuaderno de Cultura Científica.
La inversión de las élites en la prehistoria

Los cambios del cerebro durante el embarazo y la maternidad, cómo el estrés ha pasado de ser un mecanismo de supervivencia a un eventual elemento de riesgo para nuestra salud o cuál ha sido el papel que ha jugado el suicidio en la evolución del ser humano fueron algunos de los temas que se tratarán en la VI Jornada Nacional sobre Evolución y Neurociencias.
La jornada tuvo lugar el Bizkaia Aretoa de la UPV/EHU los pasados 25 y 26 de abril y estuvo dirigida por Eva Garnica y Pablo Malo, de la Red de Salud Mental de Bizkaia, institución que organizó la jornada junto a la Cátedra de Cultura Científica de la UPV/EHU.
El encuentro, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolutivo y divulgar de un modo accesible para todos los públicos.
El aburrimiento ha acompañado al ser humano desde que es ser humano. En La inversión de las élites en la prehistoria Josefa Ros Velasco nos cuenta el papel del aburrimiento en la prehistoria de la mano de las tesis de Hans Blumenberg de que se trataría de una presión selectiva.
Josefa Ros Velasco es investigadora especializada en el aburrimiento. Se doctoró en filosofía por la Universidad Complutense de Madrid y ha sido investigadora postdoctoral en distintas instituciones, entre ellas la Universidad de Harvard. Ha editado de varios libros especializados sobre el aburrimiento y el suicidio, y es la autora de «La enfermedad del aburrimiento» (Alianza Editorial).
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo La inversión de las élites en la prehistoria se ha escrito en Cuaderno de Cultura Científica.
El origen de la Gran Mancha Roja
Investigadores de la Universidad del País Vasco, de la Universitat Politècnica de Catalunya – BarcelonaTech (UPC) y del Barcelona Supercomputing Center– Centro Nacional de Supercomputación (CNS-BSC) ha analizado las observaciones históricas de la Gran Mancha Roja de Júpiter desde el siglo XVII y ha desarrollado a partir de ellas modelos numéricos para explicar la longevidad y naturaleza de este impresionante fenómeno meteorológico en la atmósfera del planeta gigante gaseoso.
 Imagen obtenida por la Voyager 1 de la Gran Mancha Roja de Júpiter en 1979. Fuente: NASA / Caltech/JPL
Imagen obtenida por la Voyager 1 de la Gran Mancha Roja de Júpiter en 1979. Fuente: NASA / Caltech/JPLLa Gran Mancha Roja de Júpiter (conocida como GRS por sus siglas en inglés, Great Red Spot), es probablemente la estructura atmosférica más conocida, un icono popular entre los objetos del Sistema Solar. Su gran tamaño (actualmente tiene el diámetro de la Tierra) y el contraste de su color rojizo frente a las nubes pálidas del planeta, hace que sea un objeto fácilmente visible incluso con pequeños telescopios. La Mancha Roja de Júpiter es un enorme remolino anticiclónico por cuya periferia los vientos circulan a 450 km/h. Es el vórtice más grande y longevo de todos los existentes en las atmósferas de los planetas del Sistema Solar, pero su edad es objeto de debate y el mecanismo que dio origen a su formación, permanece oculto.
 Cambios en la Gran Mancha Roja de Júpiter en los últimos 134 años. Izquierda: Imagen obtenida el 14 de octubre de 1890 por el Observatorio Lick (EE.UU.). Fuente: BDIP-Observatoire de Paris. Derecha: Imagen obtenida por el Telescopio Espacial Hubble el 5 de enero de 2024. Fuente: HST / NASA / ESA /OPAL Program
Cambios en la Gran Mancha Roja de Júpiter en los últimos 134 años. Izquierda: Imagen obtenida el 14 de octubre de 1890 por el Observatorio Lick (EE.UU.). Fuente: BDIP-Observatoire de Paris. Derecha: Imagen obtenida por el Telescopio Espacial Hubble el 5 de enero de 2024. Fuente: HST / NASA / ESA /OPAL ProgramLas elucubraciones sobre el origen de la GRS se remontan a las primeras observaciones telescópicas del astrónomo Giovanni Domenico Cassini, quien en 1665 descubrió un óvalo oscuro en la misma latitud que la GRS y lo bautizó como “Mancha Permanente” (PS de sus siglas en inglés), ya que fue observada por él y por otros astrónomos hasta 1713. Posteriormente se perdió su rastro durante 118 años y no es hasta 1831 y en años posteriores cuando S. Schwabe observa de nuevo una estructura clara, de forma aproximadamente ovalada y en la misma latitud que la GRS, que puede considerarse como la primera observación de la GRS actual, quizás de una GRS naciente. Desde entonces, la GRS se ha venido observando regularmente con telescopios y por las diferentes misiones espaciales que han visitado el planeta, hasta nuestros días.
En el estudio llevado a cabo los autores han analizado, por una parte, la evolución del tamaño a lo largo del tiempo, su estructura y los movimientos de ambas formaciones meteorológicas, la antigua PS y la GRS; para ello han acudido a fuentes históricas que se remontan a mediados del siglo XVII, poco después de la invención del telescopio. “De las medidas de tamaños y movimientos deducimos que es altamente improbable que la actual GRS fuese la PS observada por G. D. Cassini. Probablemente la PS desapareció en algún momento entre mediados de los siglos XVIII y XIX, en cuyo caso podemos decir que la Mancha Roja tiene al menos, por ahora, una longevidad de más de 190 años” explica Agustín Sánchez Lavega, catedrático de física de la UPV/EHU que ha liderado esta investigación. La Mancha Roja, que en 1879 tenía un tamaño de 39.000 km en su eje más largo ha ido contrayéndose a la vez que se ha redondeado, hasta alcanzar actualmente unos 14.000 km.
Por otra parte, desde la década de los años 70, diferentes misiones espaciales han estudiado de cerca este fenómeno meteorológico. Recientemente, “diferentes instrumentos a bordo de la misión Juno en órbita alrededor de Júpiter han mostrado que la GRS es poco profunda y delgada cuando se compara con su tamaño horizontal, pues verticalmente se extiende unos 500 km”, explica Sánchez Lavega.
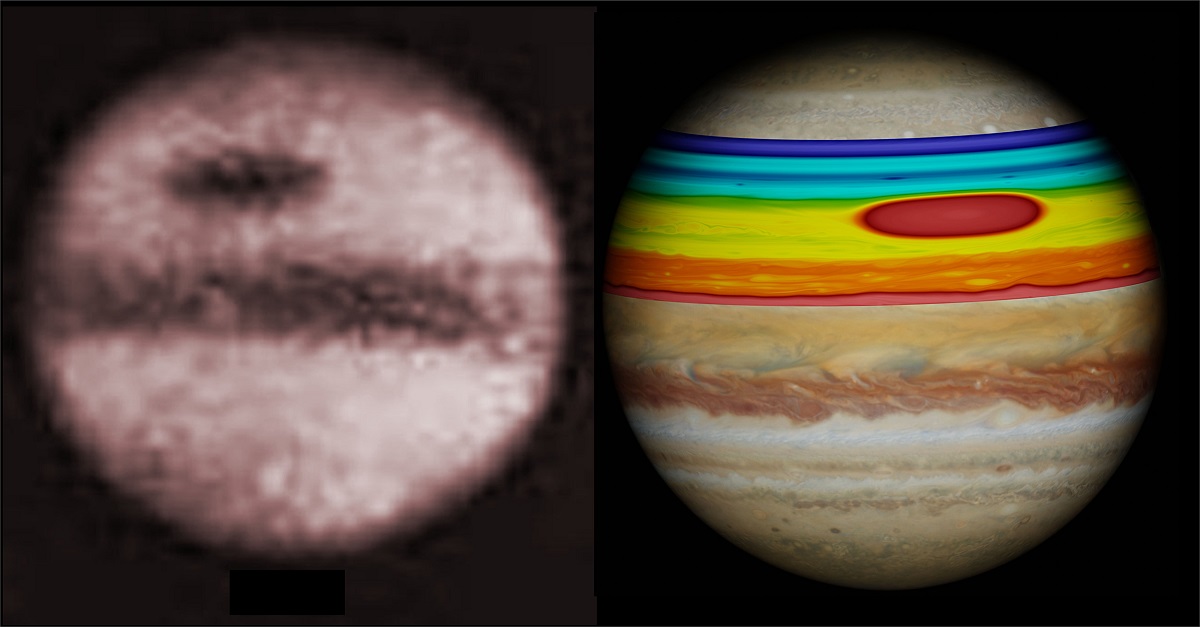 Izquierda: Primera fotografía de la Gran Mancha Roja obtenida por A.A. Common desde Ealing (Reino Unido) el 3 de septiembre de 1879. Derecha: Superposición de una simulación numérica de la mancha de aquel año sobre una imagen reciente obtenida por el Telescopio Espacial Hubble. Fuente: UPV/EHU – UPC.
Izquierda: Primera fotografía de la Gran Mancha Roja obtenida por A.A. Common desde Ealing (Reino Unido) el 3 de septiembre de 1879. Derecha: Superposición de una simulación numérica de la mancha de aquel año sobre una imagen reciente obtenida por el Telescopio Espacial Hubble. Fuente: UPV/EHU – UPC.Con el fin de averiguar cómo pudo formarse este inmenso torbellino, los equipos de la UPV/EHU y de la UPC han realizado simulaciones numéricas en superordenadores españoles como el MareNostrum IV del BSC, integrado en la Red Española de Supercomputación (RES), mediante dos tipos de modelos complementarios del comportamiento de vórtices delgados en la atmósfera de Júpiter. En el planeta gigante, dominan intensas corrientes de vientos que fluyen a lo largo de los paralelos alternando en su dirección con la latitud. Al norte de la GRS, los vientos soplan hacia el Oeste con velocidades de 180 km/hr mientras que por el sur, lo hacen en sentido contrario, hacia el Este, con velocidades de 150 km/hr. Esto genera una enorme cizalla de norte a sur en la velocidad del viento, que es un ingrediente básico para que crezca el vórtice en su seno.
En la investigación han explorado diferentes mecanismos para explicar la génesis de la GRS, entre ellos la erupción de una gigantesca supertormenta, semejante a las que muy rara vez se observan en el planeta gemelo Saturno, o bien la fusión de múltiples vórtices más pequeños engendrados por la cizalla del viento. Los resultados indican que, si bien en ambos casos se forma un anticiclón, este difiere en su forma y propiedades dinámicas de los de la actual GRS. “Además pensamos que de haberse producido uno de tales inusuales fenómenos, seguramente él o sus consecuencias en la atmósfera, hubieran sido observadas y reportadas por los astrónomos de la época”, señala Sánchez Lavega.
En un tercer grupo de experimentos numéricos, el equipo de investigación ha explorado la generación de la GRS a partir de una conocida inestabilidad en los vientos que, en opinión de los investigadores, es capaz de engendrar una célula alargada que los encierra y atrapa. Dicha célula sería una proto-GRS, una Mancha Roja naciente, cuyo posterior encogimiento daría lugar a la GRS compacta y rápidamente rotante que se observa a finales del siglo XIX. La formación de grandes células alargadas ya se ha observado en la génesis de otros vórtices importantes en Júpiter. “En nuestras simulaciones, gracias al uso de superordenadores, hemos encontrado que las células alargadas son estables cuando rotan por su periferia con la velocidad de los vientos de Júpiter, tal y como se esperaría cuando se forman por dicha inestabilidad” declara Enrique García-Melendo, investigador del Departamento de Física de la UPC. Utilizando dos tipos diferentes de modelos numéricos, uno en la UPV/EHU y el otro en la UPC, los investigadores concluyen que si la velocidad de rotación de la proto-GRS es menor que la de los vientos circundantes, esta se fragmenta, haciendo imposible la formación de un vórtice estable. Y, si es muy alta, sus propiedades difieren de las de la actual GRS.
Las futuras investigaciones estarán encaminadas a intentar reproducir el encogimiento de la GRS en el tiempo para conocer con más detalle los mecanismos físicos que subyacen a su sostenimiento en el tiempo. A la vez que intentarán pronosticar si la GRS se desintegrará y desaparecerá al alcanzar un tamaño límite, como pudo pasarle a la PS de Cassini, o bien si se estabilizará en un tamaño límite en el cual pueda perdurar durante muchos más años.
Referencia:
A. Sánchez-Lavega, E. García-Melendo, J. Legarreta, A. Miró, M. Soria, K. Ahrens-Velásquez (2024) The origin of Jupiter’s Great Red Spot Geophysical Research Letters doi: 10.1029/2024GL108993
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El origen de la Gran Mancha Roja se ha escrito en Cuaderno de Cultura Científica.
Modelado del paisaje: la cirugía plástica de nuestro planeta
Uno de los aspectos geológicos más llamativos de la Tierra, que nos genera bienestar al verlo y, a la vez, deja volar nuestra imaginación, dando lugar a múltiples mitos y leyendas, es el paisaje. Esas formas de la parte externa y superficial del planeta cinceladas con paciencia por múltiples procesos que nunca se detienen, provocando que cambien su morfología sin cesar. De ahí que la disciplina geológica que los estudia se llame geodinámica externa. Sí, hoy os voy a hablar de los procesos geológicos externos, culpables de la formación de los paisajes que nos rodean.
Estos procesos geomorfológicos forman parte del denominado ciclo de las rocas, un ciclo sin fin de formación, destrucción y transformación de los tres tipos de rocas que encontramos en nuestro planeta: sedimentarias, metamórficas e ígneas. Y, más concretamente, son los protagonistas, por no llamarlos culpables, de la fase inicial de formación de las rocas sedimentarias.
Como ya sabéis, en Geología nos encanta clasificarlo y agruparlo absolutamente todo, y los procesos geológicos externos no son una excepción. Así que os los voy a presentar siguiendo el orden en el que suceden en la naturaleza.
 A) Esquema del proceso de meteorización física conocido como gelifracción o crioclastia que culmina con la rotura de las rocas. Fuente: British Geological Survey B) Bloque de roca granítica de Escocia fracturado por efecto de la gelifracción. Fuente: Velela / Wikimedia Commons
A) Esquema del proceso de meteorización física conocido como gelifracción o crioclastia que culmina con la rotura de las rocas. Fuente: British Geological Survey B) Bloque de roca granítica de Escocia fracturado por efecto de la gelifracción. Fuente: Velela / Wikimedia CommonsEl primero de ellos es la meteorización, que se define como la rotura de las rocas en fragmentos cada vez más pequeños y que se quedan en el mismo sitio en el que se han producido. Esta meteorización puede ser de tres tipos: en primer lugar tenemos la mecánica, que se produce por procesos físicos que afectan a las rocas, tales como cambios en la temperatura, la acción del viento o el efecto del agua, ya sea dulce, salada, en estado líquido o congelada. Un ejemplo muy curioso es la gelifracción o crioclastia, que se produce en zonas con importantes cambios de temperatura entre el día y la noche, de tal manera que el agua de lluvia se infiltra en las fracturas de la roca, al congelarse por la noche el hielo actúa como una cuña que expande las fracturas, provocando que, al fundirse durante día, el agua pueda penetrar a más profundidad en el material, se vuelva a congelar por la noche y así sucesivamente hasta que fractura por completo la roca. El segundo tipo es la meteorización química, que se debe a los cambios en la composición química de los minerales que conforman las rocas al reaccionar con el agua de lluvia, que es ligeramente ácida al llevar disuelto dióxido de carbono, o con los gases atmosféricos. Y en tercer lugar encontramos la meteorización biológica, que es aquella producida por los animales, incluidos los seres humanos, al pasar por encima de las rocas o cuando construyen sus madrigueras, y por las plantas al penetrar las raíces en el terreno.
El siguiente proceso que nos encontramos es la erosión. En realidad, es muy similar a la meteorización, pero con una pequeña diferencia, aquí las partículas fracturadas de las rocas, a las que llamamos sedimentos, son desplazadas de su lugar de origen. La erosión de las rocas se produce por la acción de diversos procesos o agentes erosivos (valga la redundancia), que pueden actuar juntos o por separado. En primer lugar tenemos la gravedad, que provoca el hundimiento, caída o desplazamiento de los materiales que estén dispuestos de manera inestable sobre el terreno. En segundo lugar encontramos el viento, que, sobre todo si lleva incorporados granos de arena o pequeños cristales de sal procedentes del agua marina en áreas litorales, golpea las rocas como si fuese un martillo pilón hasta romperlas. Y, por último, vuelve a aparecer el agua, ya sea en forma de lluvia cayendo sobre la superficie del terreno, de oleaje desbocado arrasando los acantilados y las costas, de glaciares de montaña excavando valles en forma de U a su paso o de ríos encajando su cauce y generando valles con forma de V.
Enlazando con la erosión pasamos al siguiente proceso, el transporte geológico. Y no, aquí no se incluye llevar rocas desde una cantera en un camión. Me refiero al transporte de los sedimentos por medios naturales, principalmente por el viento y el agua, como lenguas glaciares, arroyos y ríos o corrientes marinas. De acuerdo al tamaño, morfología y densidad de las partículas, así como a la energía del agente que provoca el desplazamiento, los sedimentos pueden recorrer grandes distancias durante su transporte, quedando muy alejados de su área fuente.
El último proceso geológico externo es la sedimentación, que se refiere al depósito de los materiales transportados por el viento o el agua (voy a repetirlo de nuevo, ya sea en ríos, arroyos, hielo o corrientes marinas) en las cuencas sedimentarias, que no son más que zonas deprimidas del terreno tales como lagos o el fondo marino. Estos sedimentos se van acumulando unos sobre otros hasta acabar enterrándose, comenzando así la siguiente fase de formación de las rocas sedimentarias. Pero eso es otra historia.
 Panorámica del paisaje de Bárdenas Reales de Navarra, donde se producen algunos de los procesos geomorfológicos externos aquí descritos: meteorización física, química y biológica; erosión por gravedad, por el viento y por el agua de lluvia y de arroyos; transporte por el agua de avenidas y arroyos; y depósito de los sedimentos al pie de las laderas y en el fondo de los cañones.
Panorámica del paisaje de Bárdenas Reales de Navarra, donde se producen algunos de los procesos geomorfológicos externos aquí descritos: meteorización física, química y biológica; erosión por gravedad, por el viento y por el agua de lluvia y de arroyos; transporte por el agua de avenidas y arroyos; y depósito de los sedimentos al pie de las laderas y en el fondo de los cañones.Como os decía al principio, estos procesos no dejan de actuar sobre los materiales que se encuentran en la superficie de nuestro planeta. Y su acción no solo modifica la forma del paisaje natural que tenemos a nuestro alrededor, también afecta a nuestras construcciones e infraestructuras. Los monumentos sufren la meteorización y erosión implacable de los agentes meteorológicos, las vías de comunicación se deben enfrentar a posibles movimientos del terreno o los muelles, puertos y diques están a la merced de la fuerza de las corrientes litorales. No podemos enfrentarnos a la naturaleza y no debemos menospreciar el poder de los agentes modeladores del terreno, lo que tenemos que hacer es estudiarlos, comprenderlos y adaptarnos a ellos. Además de disfrutar de las morfologías que nos rodean en cada momento, porque puede que mañana hayan cambiado.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Modelado del paisaje: la cirugía plástica de nuestro planeta se ha escrito en Cuaderno de Cultura Científica.
Alice Bache Gould, la matemática e historiadora estadounidense con una calle en Simancas
Alice Bache Gould se graduó en matemáticas e inicio una tesis doctoral en geometría que no consiguió terminar. La mayor parte de su vida la dedicó a la historia. Fue precisamente esa ocupación la que la llevó a Simancas (Valladolid) donde descubrió numerosos detalles sobre los viajes de Colón.
 Alice Bache Gould. Fuente: Archivo Digital Nacional de Puerto Rico.
Alice Bache Gould. Fuente: Archivo Digital Nacional de Puerto Rico.Una infancia entre Estados Unidos y Argentina
Alice Bache Gould nació el 5 de enero de 1868 en Cambridge, Massachussets (Estados Unidos). Era la tercera de los cinco hijo e hijas de Mary Apthorp Quincy y Benjamin Apthorp Gould.
Su padre había estudiado matemáticas y astronomía en la Universidad de Harvard. Gracias a la fortuna privada y al apoyo de su esposa Mary pudo llevar adelante su trabajo astronómico. Estaba interesado en observar el cielo del sur por lo que en 1865 se puso en contacto con el gobierno de Argentina para presentarles su plan para establecer un observatorio en Córdoba. Aunque ese proyecto no llegó a buen término por falta de financiación, cuatro años más tarde fue invitado por el entonces presidente de Argentina, Domingo Faustino Sarmiento, para fundar el Observatorio Nacional de Argentina en Córdoba. En mayo de 1870, la familia Gould emprendió el viaje hacia Argentina. A finales de 1871, tras la inauguración oficial del observatorio en Córdoba, Alice fue enviada de nuevo a Massachussets para vivir al cuidado de sus tías maternas.
La educación primaria de Alice tuvo lugar entre Estados Unidos y Argentina; en este último país aprendió la historia, la cultura y la lengua del país. Su educación secundaria se desarrolló en parte en Estados Unidos y en parte en Inglaterra.
La madre de Alice falleció en Boston en 1883, durante una estancia en la que Benjamin Apthorp Gould estaba organizando el estudio de las placas fotográficas que había tomado en el Observatorio de Córdoba. El astrónomo regresó a Córdoba, dejando a Alice y a sus dos hijos pequeños en un internado en Boston (en febrero de 1874 las dos hermanas mayores de Alice fallecieron en un accidente mientras nadaban en un río en Río Primero, Córdoba).
Los estudios de matemáticas y una tesis inacabadaEn 1885, Alice regresó a Estados Unidos y, poco después, ingresó en la Society for the Collegiate Instruction of Women (más tarde pasó a llamarse Radcliffe College), una institución creada para que las mujeres, que no podían estudiar en la Universidad de Harvard, pudieran recibir formación. Allí estudió matemáticas, y un año más tarde ingresó en el Bryn Mawr College, una universidad privada que ofrecía formación de posgrado a mujeres. Alice se graduó con una licenciatura en matemáticas y física en 1889.
Entre 1890 y 1893, estudió matemáticas en el Instituto Tecnológico de Massachusetts y en Inglaterra, en el Newnham College de Cambridge. Aunque este centro permitía a las mujeres asistir a las clases, no recibían ningún título.
Alice enseñó matemáticas en Carleton College en Northfield (Minnesota) durante el curso académico 1893/1894 y dejó la docencia al obtener una beca para estudios de posgrado en matemáticas en la Universidad de Chicago. Allí, en 1894, comenzó sus estudios tutorizada por Eliakim Moore. Gould comenzó a preparar su trabajo de doctorado en geometría con un trabajo de Henri Brocard como punto de partida. Sus avances eran lentos debido a sus problemas de salud.
Benjamin Apthorp Gould falleció en 1896 y Alice dedicó gran parte de sus esfuerzos a crear una beca en la Academia Nacional de Ciencias en honor de su padre y destinada a personas trabajando en astronomía de precisión. Ella misma donó veinte mil dólares a esa institución para conseguir su objetivo.
En 1900, mientras avanzaba lentamente con su tesis (que nunca consiguió finalizar), comenzó a escribir una biografía del naturalista estadounidense Louis Agassiz. Se publicó en 1901 y obtuvo muy buenas reseñas.
Entusiasmada con la historia de la colonizaciónEn 1903, tras sufrir una fuerte gripe, Gould decidió viajar a Puerto Rico y pasar allí un tiempo recuperándose de su afección pulmonar. Finalmente, permaneció durante siete años. Allí se interesó por la historia de la colonización de la isla y comenzó sus investigaciones. También colaboró en la mejora del sistema educativo creando el «Fondo de Maestros de Puerto Rico» que recaudó dinero para fundar una escuela de enfermería.
Tras regresar a Boston, en 1911, emprendió un viaje a Roma con una amiga. Ésta enfermó durante el trayecto y cuando el barco atracó en Gibraltar rumbo a Italia, ambas mujeres decidieron quedarse. Alice encontró allí la oportunidad de continuar sus investigaciones sobre la colonización de las Indias Occidentales y visitó el Archivo General de Indias de Sevilla. Aunque su amiga regresó a Estados Unidos tras recuperarse, Gould se quedó en España y se centró en explorar el recorrido de los viajes de Cristóbal Colón e indagar sobre las personas que le acompañaban.
En 1914, cuando estalló la Primera Guerra Mundial, Gould estaba en España estudiando documentos en el Archivo General de Simancas. Cuando Estados Unidos entró en la guerra en abril de 1917, Alice ofreció sus servicios a la Embajada de su país en Madrid. Debido a la preocupación de su familia, regresó a Boston en marzo de 1918. Para apoyar el esfuerzo bélico, aceptó un puesto en la Universidad de Chicago en el que enseñó matemáticas en un curso de navegación para personal de la Marina.
Gould regresó a España en 1925 y retomó sus investigaciones sobre los viajes de Colón. Durante la guerra civil española volvió a su país y después regresó a España para vivir en Simancas, donde, entre otros, fundó una escuela para niñas y niños sin recursos.
Alice trabajaba en un libro sobre Colón cuando falleció repentinamente en julio de 1953. Aunque no llegó a publicar sus investigaciones, en 1984 salió a la luz el documento Nueva lista documentada de los tripulantes de Colón en 1492 que elaboró tras estudiar los registros del Archivo General de Simancas. Alice buscaba documentos con cualquier información sobre los viajes de Colón, en particular sobre quienes formaban parte de su tripulación. Entre otros, ratificó la presencia judía en los viajes de descubrimiento, como Luis de Torres, el intérprete de Colón, o Rodrigo Sánchez de Segovia. Identificó a 87 de los 90 tripulantes, demostrando que solo cuatro de ellos tenían problemas con la justicia, desmintiendo la versión aceptada hasta entonces que aseguraba que la mayor parte de la tripulación estaba formada por criminales. Se le atribuye, además, haber salvado documentos que de otro modo habrían sido ignorados e incluso destruidos.
 Portada de “Nueva lista documentada de los tripulantes de Colón en 1492”. Fuente: Bibliotheca Sefarad.
Portada de “Nueva lista documentada de los tripulantes de Colón en 1492”. Fuente: Bibliotheca Sefarad.
Entre otros reconocimientos, Gould fue elegida miembro correspondiente de la Real Academia Española de la Historia en 1942, y obtuvo la Orden de Isabel la Católica en 1952.
Tras su repentina muerte (por un derrame cerebral el día 25 de julio de 1953) en el jardín del castillo de Simancas, cerca de los archivos, se colocó en la entrada del edificio una placa en su honor:
A miss Alice B. Gould, ilustre investigadora norteamericana y gran amiga de España. Trabajó en este archivo durante cuarenta años y murió a su entrada el día 25 de julio de 1953.
En Simancas, una calle lleva su nombre.
Referencias
- Alice Bache Gould, MacTutor History of Mathematics Archive, St Andrews University
- Edgardo Ronal Minniti Morgan (2011) Alice Bache Gould. La convergencia de la astronomía, la historia, la matemática y el espionaje, Historia de la astronomía
- Deborah Kent, Alice Bache Gould: mathematician in search of war work, 1918, BSHM Bulletin: Journal of the British Society for the History of Mathematics Volume 27, Issue 1, 2012
- Alice Bache Gould, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Alice Bache Gould, la matemática e historiadora estadounidense con una calle en Simancas se ha escrito en Cuaderno de Cultura Científica.
La mayor parte de la vida en la Tierra está aletargada
Muchos microbios y células están en un sueño profundo, esperando el momento adecuado para activarse. Los biólogos han descubierto una proteína muy extendida que detiene abruptamente la actividad de una célula y la vuelve a activar con la misma rapidez.
Un artículo de Dan Samorodnitsky. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Cuando las cosas se ponen difíciles, muchos microbios quedan inactivos. Una nueva investigación ha descubierto una proteína ubicua que detiene la producción de proteínas de una célula en un instante. Fuente: Nico Roper/ Quanta Magazine
Cuando las cosas se ponen difíciles, muchos microbios quedan inactivos. Una nueva investigación ha descubierto una proteína ubicua que detiene la producción de proteínas de una célula en un instante. Fuente: Nico Roper/ Quanta MagazineSe ha informado recientemente del descubrimiento de una proteína natural, llamada Balon, que puede detener por completo la producción celular de nuevas proteínas. Balon se ha encontrado en bacterias que hibernan en el permafrost ártico, pero también parece ser que es producida por muchos otros organismos y podría ser un mecanismo de letargo pasado por alto en todo el árbol de la vida.
Para la mayoría de las formas de vida, la capacidad de aislarse es una parte fundamental de mantenerse con vida. Las condiciones duras como la falta de alimentos o el clima frío pueden aparecer de la nada. En esta situación desesperada, en lugar de desplomarse y morir, muchos organismos han dominado el arte del letargo. Ralentizan su actividad y metabolismo. Luego, cuando vuelven tiempos mejores, se reaniman.
Permanecer en un estado latente es en realidad la norma para la mayoría de la vida en la Tierra: según algunas estimaciones, el 60% de todas las células microbianas están hibernando en un momento dado. Incluso en organismos cuyo cuerpo entero no está inactivo, como la mayoría de los mamíferos, algunas poblaciones celulares dentro de ellos descansan y esperan el mejor momento para activarse.
«Vivimos en un planeta aletargado», afirma Sergey Melnikov, biólogo molecular evolutivo de la Universidad de Newcastle. «La vida se trata principalmente de estar dormido».
Pero, ¿cómo logran las células esta hazaña? A lo largo de los años, los investigadores han descubierto una serie de «factores de hibernación», proteínas que las células utilizan para inducir y mantener un estado latente. Cuando una célula detecta algún tipo de condición adversa, como hambre o frío, produce un conjunto de factores de hibernación para detener su metabolismo.
Algunos factores de hibernación desmantelan la maquinaria celular; otros impiden que los genes se expresen. Los más importantes, sin embargo, desactivan el ribosoma, la máquina celular para construir nuevas proteínas. La producción de proteínas representa más del 50% del uso de energía en una célula bacteriana en crecimiento. Estos factores de hibernación arrojan arena en los engranajes del ribosoma, impidiéndole sintetizar nuevas proteínas y ahorrando así energía para las necesidades básicas de supervivencia.
A principios de este año, en una publicación en Nature, un equipo de investigadores ha informado del descubrimiento de un nuevo factor de hibernación, al que han llamado Balon. La proteína es sorprendentemente común: una búsqueda de su secuencia genética descubrió su presencia en el 20% de todos los genomas bacterianos catalogados. Y funciona de una manera que los biólogos moleculares nunca antes habían visto.
Anteriormente, todos los factores de hibernación conocidos que alteraban los ribosomas funcionaban pasivamente: esperaban a que un ribosoma terminara de construir una proteína y luego le impedían iniciar una nueva. Balon, sin embargo, tira del freno de mano. Se introduce en cada ribosoma de la célula, incluso interrumpiendo los ribosomas activos en mitad de su trabajo. Antes de Balon, los factores de hibernación sólo se habían observado en ribosomas vacíos.
«El artículo Balon es sorprendentemente detallado», comenta el biólogo evolutivo Jay Lennon, que estudia la latencia microbiana en la Universidad de Indiana y que no ha participado en el nuevo estudio. «Ampliará nuestra visión de cómo funciona el letargo».
 Karla Helena-Bueno descubrió un factor de hibernación común cuando accidentalmente dejó una bacteria del Ártico en el hielo durante demasiado tiempo. «Traté de buscar en un rincón poco estudiado de la naturaleza y encontré algo», cuenta. Fuente: Karla Helena-Bueno
Karla Helena-Bueno descubrió un factor de hibernación común cuando accidentalmente dejó una bacteria del Ártico en el hielo durante demasiado tiempo. «Traté de buscar en un rincón poco estudiado de la naturaleza y encontré algo», cuenta. Fuente: Karla Helena-BuenoMelnikov y su estudiante de posgrado Karla Helena-Bueno descubrieron Balon en Psychrobacter urativorans, una bacteria adaptada al frío nativa de los suelos helados y recolectada del permafrost ártico. (Según Melnikov, la bacteria se encontró por primera vez infectando un paquete de salchichas congeladas en la década de 1970 y luego fue redescubierta por el famoso geneticista Craig Venter en un viaje al Ártico). Estudian P. urativorans y otros microbios inusuales para caracterizar la diversidad de herramientas de construcción de proteínas utilizadas en todo el espectro de la vida y para comprender cómo los ribosomas pueden adaptarse a ambientes extremos.
Debido a que el letargo puede ser desencadenado por una variedad de condiciones, incluyendo el hambre y la sequía, los científicos llevan a cabo esta investigación con un objetivo práctico en mente: «Probablemente podamos usar este conocimiento para diseñar organismos que puedan tolerar climas más cálidos», apunta Melnikov. “y por lo tanto resistir el cambio climático”.
Presentamos: BalonHelena-Bueno descubrió Balon por pura casualidad. Estaba intentando convencer a P. urativorans para que creciera felizmente en el laboratorio. En lugar de eso, hizo lo contrario. Dejó el cultivo en una cubeta de hielo durante demasiado tiempo y logró aplicarle un golpe de frío. Para cuando recordó que estaba allí, las bacterias adaptadas al frío ya estaban en letargo.
No queriendo desperdiciar el cultivo, los investigadores persiguieron de todos modos sus intereses originales. Helena-Bueno extrajo los ribosomas de las bacterias afectadas por el frío y los sometió a crio-EM. Abreviatura de microscopía electrónica criogénica, crio-EM es una técnica para visualizar estructuras biológicas minúsculas en alta resolución. Helena-Bueno vio una proteína atascada en el sitio A del ribosoma paralizado, la «puerta» por donde se entregan los aminoácidos para la construcción de nuevas proteínas.
Helena-Bueno y Melnikov no reconocieron la proteína. De hecho, nunca antes se había descrito. Tenía similitud con otra proteína bacteriana, una que es importante para desmontar y reciclar partes ribosomales, llamada Pelota en referencia al término en español. De ahí que llamaran a la nueva proteína Balon, por el homónimo español a “pelota”, “balón”.
La capacidad de Balon para detener la actividad del ribosoma es una adaptación crítica para un microbio bajo estrés, comenta Mee-Ngan Frances Yap, microbióloga de la Universidad Northwestern que no ha participado en el trabajo. «Cuando las bacterias crecen activamente, producen muchos ribosomas y ARN», continúa. «Cuando se encuentran con estrés, una especie podría necesitar detener la traducción» del ARN en nuevas proteínas para comenzar a conservar energía para un período de hibernación potencialmente largo.
Llamativamente, el mecanismo de Balon es un proceso reversible. A diferencia de otros factores de hibernación, se puede insertar para detener el crecimiento y luego expulsarlo rápidamente como una cinta de casete. Permite que una célula entre rápidamente en estado de letargo en caso de emergencia y que resucite con la misma rapidez para readaptarse a condiciones más favorables.
Balon puede hacer esto porque se adhiere a los ribosomas de una manera única. Cada factor de hibernación ribosómica descubierto previamente bloquea físicamente el sitio A del ribosoma, por lo que cualquier proceso de producción de proteínas que esté en progreso debe completarse antes de que el factor pueda unirse para desactivar el ribosoma. Balon, por otro lado, se une cerca del canal, pero no a través de él, lo que le permite ir y venir independientemente de lo que esté haciendo el ribosoma.

A pesar de la novedad mecánica de Balon, es una proteína extremadamente común. Una vez identificada, Helena-Bueno y Melnikov encontraron parientes genéticos de Balon en más del 20% de todos los genomas bacterianos catalogados en bases de datos públicas. Con la ayuda de Mariia Rybak, bióloga molecular de la Rama Médica de la Universidad de Texas, caracterizaron dos de estas proteínas bacterianas alternativas: una del patógeno humano Mycobacterium tuberculosis, que causa la tuberculosis, y otra de Thermus thermophilus, que vive en el último lugar en el que econtrarías a P. urativorans, en las ultracalientes fuentes hidrotermales submarinas. Ambas proteínas también se unen al sitio A del ribosoma, lo que sugiere que al menos algunos de estos parientes genéticos actúan de manera similar a Balon en otras especies bacterianas.
Balon está notablemente ausente en Escherichia coli y Staphylococcus aureus, las dos bacterias más comúnmente estudiadas y los modelos más utilizados para el letargo celular. Al centrarse sólo en unos pocos organismos de laboratorio, los científicos habían pasado por alto una táctica de hibernación generalizada, afirma Helena-Bueno. «Traté de buscar en un rincón poco estudiado de la naturaleza y encontré algo».
Todo el mundo hibernaCada célula necesita la capacidad de permanecer aletargada y esperar su momento. Melnikov explica que el modelo de laboratorio de la bacteria E. coli tiene cinco modos diferentes de hibernación, cada uno de los cuales por sí solo es suficiente para permitir que el microbio sobreviva a una crisis.
«La mayoría de los microbios se están muriendo de hambre», comenta Ashley Shade, microbióloga de la Universidad de Lyon que no ha participado en el nuevo estudio. “Existen en un estado de necesidad. No se están duplicando. No están viviendo su mejor vida”.
Pero el letargo también es necesario fuera de los períodos de hambruna. Incluso en organismos, como la mayoría de los mamíferos, cuyo cuerpo entero no queda completamente inactivo, las poblaciones celulares individuales deben esperar el mejor momento para activarse. Los ovocitos humanos permanecen inactivos durante décadas esperando ser fertilizados. Las células madre humanas nacen en la médula ósea y luego permanecen inactivas, esperando que el cuerpo las llame para crecer y diferenciarse. Los fibroblastos del tejido nervioso, los linfocitos del sistema inmunitario y los hepatocitos del hígado entran en fases latentes, inactivos y sin división y se reactivan más tarde.
«Esto no es algo exclusivo de bacterias o arqueas», afirma Lennon. “Cada organismo del árbol de la vida tiene una forma de lograr esta estrategia. Pueden pausar su metabolismo”.
Los osos hibernan. Los virus del herpes se lisogenizan. Los gusanos tienen una etapa dauer. Los insectos entran en diapausa. Los anfibios estivan. Los pájaros entran en torpor. Todas estas son palabras para exactamente lo mismo: un estado de letargo que los organismos pueden revertir cuando las condiciones son favorables.
«Antes de la invención de la hibernación, la única forma de vivir era seguir creciendo sin interrupciones», dice Melnikov. “Poner la vida en pausa es un lujo”.
También es un tipo de seguro a nivel poblacional. Algunas células persiguen el estado de letargo detectando cambios ambientales y respondiendo en consecuencia. Sin embargo, muchas bacterias utilizan una estrategia estocástica. «En entornos que fluctúan aleatoriamente, si a veces no entras en estado de letargo, existe la posibilidad de que toda la población se extinga» a través de encuentros aleatorios con desastres, explica Lennon. Incluso en los cultivos de E. coli más sanos, felices y de más rápido crecimiento, entre el 5% y el 10% de las células permanecerán inactivas en cualquier caso. Son los supervivientes designados que vivirán si algo les sucede a sus primos más activos y vulnerables.
En ese sentido, el letargo es una estrategia de supervivencia ante catástrofes globales. Por eso Helena-Bueno estudia la hibernación. Le interesa saber qué especies podrían permanecer estables a pesar del cambio climático, cuáles podrían recuperarse y qué procesos celulares, como la hibernación asistida por Balon, podrían ayudar.
Más fundamentalmente, Melnikov y Helena-Bueno esperan que el descubrimiento de Balon y su ubicuidad ayude a las personas a replantear lo que es importante en la vida. Todos nos quedamos inactivos con frecuencia y muchos de nosotros lo disfrutamos bastante. «Pasamos un tercio de nuestra vida durmiendo, pero no hablamos de ello en absoluto», comenta Melnikov. En lugar de quejarnos de lo que nos perdemos cuando dormimos, tal vez podamos experimentarlo como un proceso que nos conecta con toda la vida en la Tierra, incluidos los microbios que duermen en las profundidades del permafrost del Ártico.
El artículo original, Most Life on Earth is Dormant, After Pulling an ‘Emergency Brake’, se publicó el 5 de junio de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo La mayor parte de la vida en la Tierra está aletargada se ha escrito en Cuaderno de Cultura Científica.
Los hongos carnívoros “olfatean” a sus presas
Estoy seguro de que este título ha sorprendido a los lectores. Primero, por el concepto de “hongo carnívoro” bastante opuesto a lo que conocemos sobre estos seres. Segundo, porque atribuimos un cierto sentido del olfato a organismos carentes de sistema nervioso. Lo explicamos a continuación.
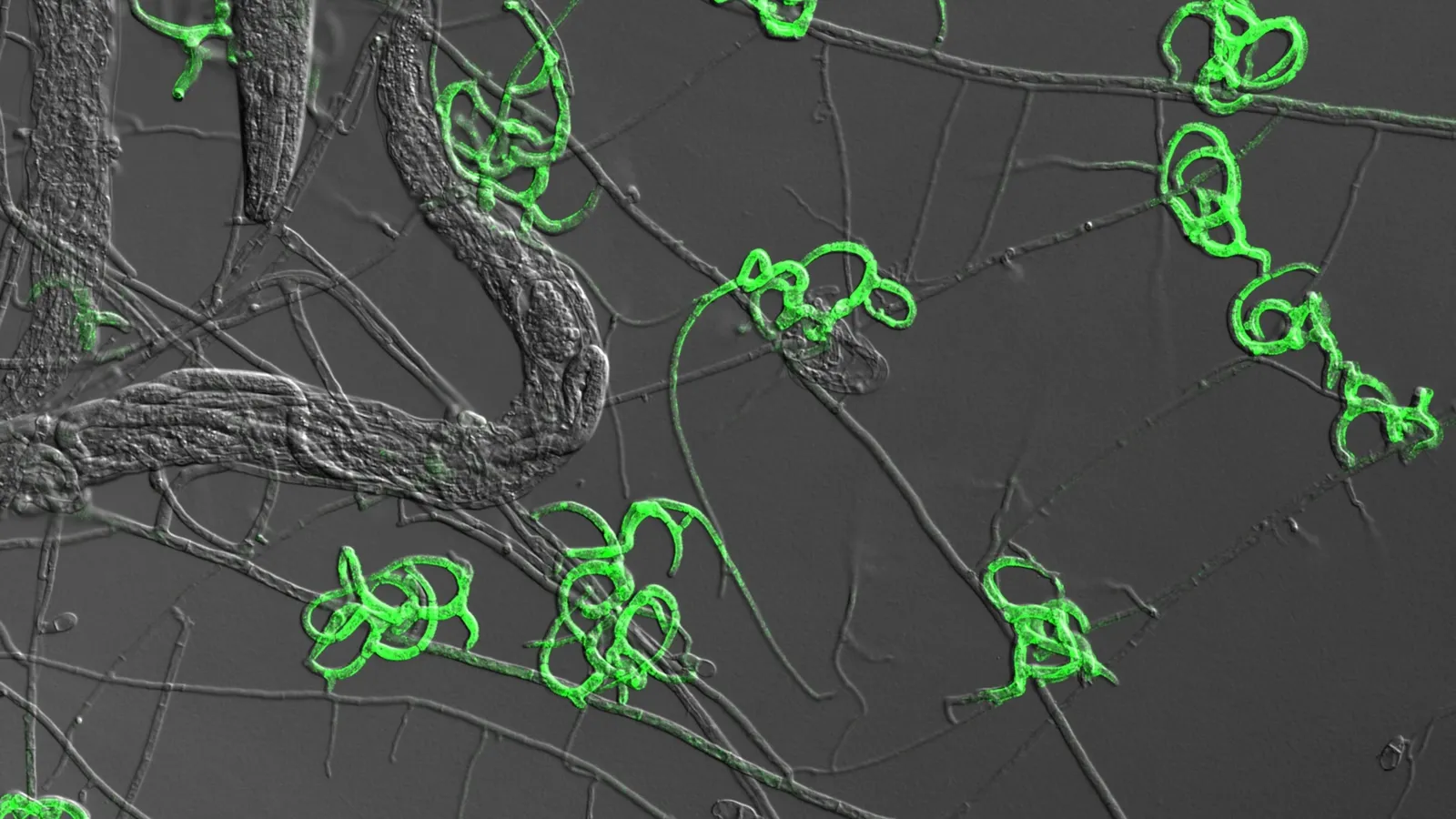 En verde, las células producidas por el hongo hambriento ayudan a atraer y atrapar gusanos nematodos. Las líneas grises en forma de hilo son micelio, las hebras conectivas que forman un solo hongo.
En verde, las células producidas por el hongo hambriento ayudan a atraer y atrapar gusanos nematodos. Las líneas grises en forma de hilo son micelio, las hebras conectivas que forman un solo hongo.Foto: Yen-Ping Hsueh
Los hongos y los animales compartimos algunas características importantes. Somos pluricelulares y heterótrofos. Esto quiere decir que estamos formados por multitud de células organizadas que obtienen su energía a partir de la oxidación de materia orgánica. Esto nos distingue de seres autótrofos como las plantas, que son capaces de utilizar energía de fuentes no orgánicas como la luz.
Hongos y animales también somos diferentes en ambos aspectos. La pluricelularidad se alcanza en los animales a través de un desarrollo embrionario. Esto no sucede en los hongos, cuyo micelio crece a partir de esporas, sin formar tejidos ni órganos. Por otro lado, la alimentación de los hongos es fundamentalmente pasiva, por crecimiento del micelio sobre una fuente de materia orgánica. Los animales (salvo esponjas y placozoos) desarrollamos un sistema nervioso que nos permite desplegar un comportamiento proactivo de detección y obtención del alimento.
La capacidad evolutiva de los seres vivos produce innovaciones insólitas que rompen estos esquemas simples. Hay un grupo de hongos, conocidos genéricamente como NTF (nematode trapping fungi), que en condiciones de inanición y presencia de nematodos son capaces de desarrollar rápidamente unos filamentos adhesivos que atrapan al gusano, causan su muerte y les proporcionan alimento.
Los mecanismos que regulan este sorprendente comportamiento están siendo revelados por una serie de estudios sobre el NTF Arthrobotrys oligospora, liderados por la investigadora taiwanesa Yen-Ping Hsueh. Este hongo ya era conocido por su capacidad de producir compuestos químicos que actuaban como cebo para atraer a los nematodos, simulando el olor de fuentes de alimento o incluso feromonas para la atracción sexual.
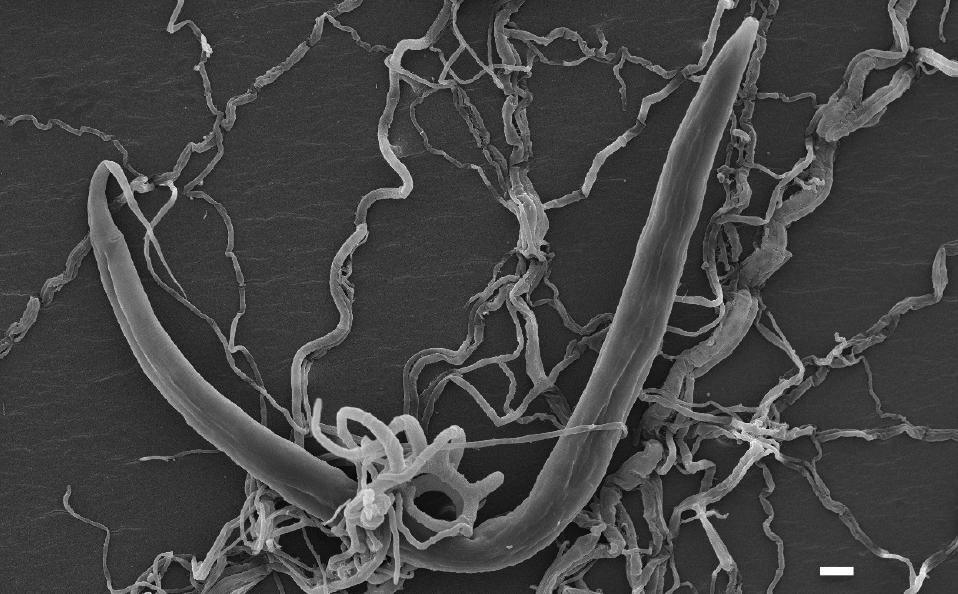 Figura 1. El nematodo C. elegans atrapado por el hongo A. oligospora. Escala=10 μm. Fuente: Hsueh et al. (2017) eLife 2017;6:e20023
Figura 1. El nematodo C. elegans atrapado por el hongo A. oligospora. Escala=10 μm. Fuente: Hsueh et al. (2017) eLife 2017;6:e20023Más recientemente, el grupo de Yen-Ping Hsueh mostró que la presencia del nematodo Caenorhabditis elegans provocaba en el hongo la activación de un gran número de genes. Esta respuesta inducía cambios morfológicos, sobre todo el crecimiento rápido de los filamentos de las trampas (Figura 1). Al mismo tiempo se expresaban proteínas adhesivas para dificultar la huida del gusano, y finalmente se secretaban enzimas, en concreto metaloproteasas, que digerían al infortunado C. elegans haciendo posible su absorción por el hongo. El proceso se puede ver en este espectacular vídeo del laboratorio de la Dra. Hsueh1.
¿Cómo se regula a nivel molecular la rápida respuesta de A. oligospora a la presencia del nematodo? El equipo taiwanés identificó la vía AMPc-PKA como la activadora de este proceso. El adenosín monofosfato cíclico (AMPc) es un “segundo mensajero”. Cuando una célula recibe una señal externa a través de un receptor es habitual que se desencadene una cascada de reacciones en el interior que culmine en una respuesta fisiológica, por ejemplo, la expresión de determinados genes. Este proceso se conoce como “transducción de señales” y en él intervienen muchas veces segundos mensajeros, es decir, pequeñas moléculas como el AMPc o iones como el calcio (Ca2+). En concreto el AMPc activa la proteína kinasa A (PKA), activadora a su vez de otras proteínas que regulan la respuesta celular.
Yen-Ping Hsueh y sus colaboradores mostraron que la inactivación de esta vía de señalización hacía que los hongos fueran indiferentes a la cercanía de sus presas potenciales. Pero todavía quedaba una cuestión por resolver, ¿cómo detecta un hongo sin sistema nervioso la presencia de C. elegans?
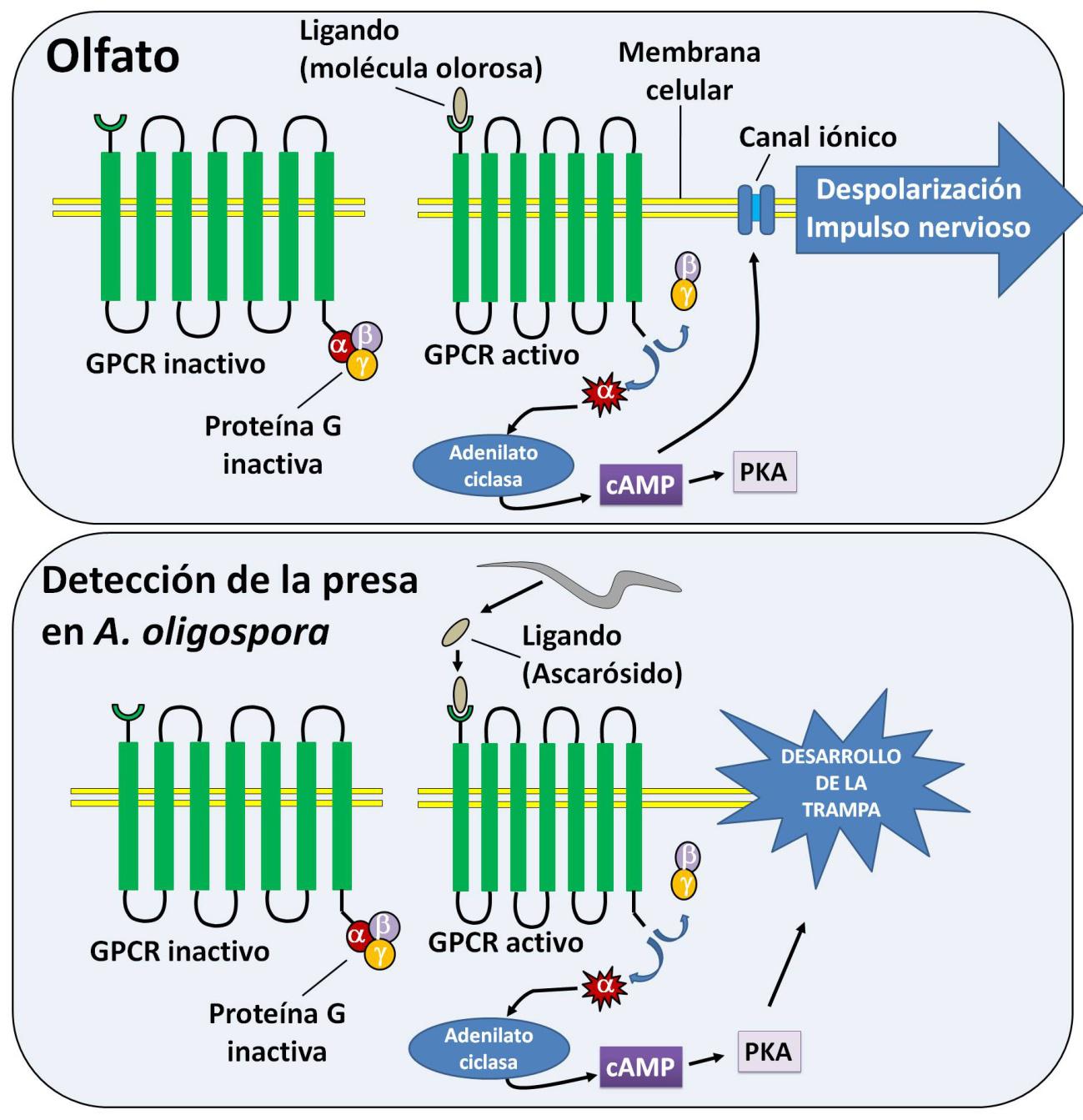 Figura 2. Nuestra sensación olfativa se genera cuando un receptor GPCR del epitelio olfativo capta un ligando (molécula olorosa) y cambia su configuración. Esto provoca la disociación y activación de la proteína G cuya subunidad α activa la enzima sintetizadora de AMPc. Esta molécula provoca la apertura de canales iónicos, la despolarización de la membrana celular y la generación del impulso nervioso. En el caso del hongo A. oligospora el ligando de las GPCRs es un ascarósido segregado por el nematodo. La elevación de los niveles de AMPc activa la proteína kinasa A y se dispara el mecanismo de desarrollo de la trampa
Figura 2. Nuestra sensación olfativa se genera cuando un receptor GPCR del epitelio olfativo capta un ligando (molécula olorosa) y cambia su configuración. Esto provoca la disociación y activación de la proteína G cuya subunidad α activa la enzima sintetizadora de AMPc. Esta molécula provoca la apertura de canales iónicos, la despolarización de la membrana celular y la generación del impulso nervioso. En el caso del hongo A. oligospora el ligando de las GPCRs es un ascarósido segregado por el nematodo. La elevación de los niveles de AMPc activa la proteína kinasa A y se dispara el mecanismo de desarrollo de la trampa
En cierto sentido A. oligospora “huele” al nematodo. Evidentemente no existen órganos olfativos en los hongos, pero el mecanismo que utilizan es sorprendentemente parecido al que usamos nosotros para percibir los olores (Figura 2).
Nuestro sentido del olfato se basa en receptores acoplados a proteína G (GPCRs, por G protein-coupled receptors). Se trata de proteínas cuya cadena atraviesa siete veces la membrana celular. Cuando su porción extracelular detecta las señales adecuadas (hormonas, péptidos, diverso tipo de moléculas…) cambia la configuración del receptor disociando la proteína G unida a su dominio intracelular, lo que desencadena la transducción de la señal.
Estos receptores son importantísimos en la detección de señales. Para hacernos una idea, los humanos tenemos más de 800 GPCRs que intervienen en multitud de procesos sensoriales y de respuesta a hormonas o neurotransmisores. Por esto son la principal diana de los fármacos que utilizamos.
En un reciente artículo, el equipo de Yen-Ping Hsueh acaba de identificar dos familias de GPCRs usadas por A. oligospora para detectar la presencia de nematodos. Una de estas familias detecta ascarósidos, pequeños glicolípidos que secretan continuamente los nematodos a modo de feromonas. La segunda familia detecta otras moléculas segregadas por los nematodos y que todavía no han sido identificadas. En ambos casos la activación de las proteínas G dispara la vía AMPc-PKA y pone en marcha el programa de construcción de las trampas.
En resumen, los hongos NTF no “huelen” al nematodo en un sentido estricto de la palabra, pero el paralelismo entre el uso de GPCRs para la detección de presas y el funcionamiento de nuestro olfato es extraordinariamente llamativo.
Referencias:
Chen SA, Lin HC, Hsueh YP. (2022) The cAMP-PKA pathway regulates prey sensing and trap morphogenesis in the nematode-trapping fungus Arthrobotrys oligospora. G3 (Bethesda). doi: 10.1093/g3journal/jkac217.
Hsueh YP, Gronquist MR, Schwarz EM, Nath RD, Lee CH, Gharib S, Schroeder FC, Sternberg PW. (2017) Nematophagous fungus Arthrobotrys oligospora mimics olfactory cues of sex and food to lure its nematode prey. Elife. doi: 10.7554/eLife.20023.
Kuo CY, Tay RJ, Lin HC, Juan SC, Vidal-Diez de Ulzurrun G, Chang YC, Hoki J, Schroeder FC, Hsueh YP. (2024) The nematode-trapping fungus Arthrobotrys oligospora detects prey pheromones via G protein-coupled receptors. Nat Microbiol. doi: 10.1038/s41564-024-01679-w.
Lin HC, de Ulzurrun GV, Chen SA, Yang CT, Tay RJ, Iizuka T, Huang TY, Kuo CY, Gonçalves AP, Lin SY, Chang YC, Stajich JE, Schwarz EM, Hsueh YP. (2023) Key processes required for the different stages of fungal carnivory by a nematode-trapping fungus. PLoS Biol. doi: 10.1371/journal.pbio.3002400.
Nota:
1 En la primera parte. En una segunda parte se muestra la estrategia de otro hongo carnívoro, Pleurotus ostreatus, que produce una toxina volátil que paraliza al nematodo.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Los hongos carnívoros “olfatean” a sus presas se ha escrito en Cuaderno de Cultura Científica.
Las mentiras visuales de la IA
Federico Kukso
A medida que se expande la inteligencia artificial en cada rincón de nuestras vidas, un cliché se consolida: el de representar visualmente estos sistemas como robots humanoides blancos, cerebros destellantes o con referencias a la ciencia ficción. Un grupo cada vez mayor de especialistas se opone a esta iconografía cargada de sesgos históricos sobre género, etnia y religión que genera expectativas poco realistas y enmascara los efectos sociales de estas tecnologías.
 Las imágenes mediáticas que representan la IA como robots humanoides blancos y sensibles enmascaran la responsabilidad de los humanos que realmente desarrollan esta tecnología. Foto: Jezael Melgoza / Unsplash
Las imágenes mediáticas que representan la IA como robots humanoides blancos y sensibles enmascaran la responsabilidad de los humanos que realmente desarrollan esta tecnología. Foto: Jezael Melgoza / UnsplashEl 25 de abril de 2018, la Comisión Europea publicó un documento que marcó el inicio de su camino hacia la primera ley regulatoria de la inteligencia artificial del mundo. En él, se detallaban las recomendaciones presentadas por un grupo de expertos, se enumeraban los pasos a seguir y se proponían directrices éticas para una IA confiable. Sin llamar mucho la atención, una atractiva imagen acompañaba al texto: una mano humana y una mano robótica –brillante y metálica– se extendían delante de un fondo azul y gris, casi tocándose con las yemas de los dedos.
Inspirada en La creación de Adán de Miguel Ángel, fresco que desde el siglo XVI adorna el techo de la Capilla Sixtina en el Vaticano, esta composición que presenta a la IA como una fuerza creativa divina o como una chispa, una conexión entre lo humano y lo divino, se ha convertido en uno de los pósteres oficiales de la inteligencia artificial.
 Imágenes que recrean ‘La creación de Adán’ de Miguel Ángel son usadas con frecuencia para ilustrar la IA, como hizo la Comisión Europea en 2018. Fuente: Michelangelo / Comisión Europea
Imágenes que recrean ‘La creación de Adán’ de Miguel Ángel son usadas con frecuencia para ilustrar la IA, como hizo la Comisión Europea en 2018. Fuente: Michelangelo / Comisión EuropeaSe la ve una y otra vez en sitios de noticias y revistas, en publicidades, en portadas de libros, en comunicados de empresas, en afiches de cursos y conferencias, a la par de retratos pintorescos de robots humanoides siempre blancos, cerebros azules brillantes, placas de circuitos, código binario y trilladas referencias a personajes de ciencia ficción como Terminator.
Conforman la iconografía actual de la IA, su traducción visual, cada vez más criticada por especialistas que advierten sobre sus peligros y las suposiciones estereotipadas y potencialmente discriminatorias que arrastran sobre género, etnia y religión.
“Estas imágenes tergiversan completamente las realidades de la IA”, advierte a SINC la investigadora en ética Tania Duarte, fundadora de We and AI, una organización sin fines de lucro del Reino Unido que busca mejorar la alfabetización en inteligencia artificial para la inclusión social e impulsar el pensamiento crítico. “Refuerzan mitos sobre la IA –subraya–, ideas falsas sobre la infalibilidad, la sensibilidad y el misticismo religioso que envuelve a estas tecnologías y no ayudan al público a desarrollar una comprensión de lo que está en juego”.
El poder de la imagenComo hace tiempo explicó la escritora Susan Sontag, las imágenes son elementos poderosos. Enmarcan nuestra percepción del mundo, confirman, refuerzan o disipan estereotipos. Influyen en la forma en que la sociedad piensa y comprende temas que retratan. En el caso de la IA, ciertas ilustraciones exageran las capacidades de estos sistemas informáticos cada vez más ubicuos.
Otras, en cambio, siembran miedo, aumentan la desconfianza pública, enmascaran la responsabilidad de los humanos y perpetúan un entendimiento demasiado limitado y temeroso de la IA pero también misterioso, al no mostrar su contexto real, ni sus procesos y ni sus aplicaciones o limitaciones. Y desvían el debate sobre las consecuencias potencialmente significativas para la investigación, la financiación, la regulación y la recepción de estos sistemas cada vez más ubicuos.
Para combatir estos clichés y distorsiones, Duarte y un equipo de más de cien ingenieros, artistas, sociólogos y especialistas en ética impulsan un programa conocido como Better Images of AI.
Con el apoyo del Alan Turing Institute, el Centro Leverhulme para el Futuro de la Inteligencia y del departamento de investigación y desarrollo de la BBC, exponen cómo estas representaciones dominantes refuerzan conceptos erróneos y limitan la comprensión pública del uso y funcionamiento de los sistemas de IA.
“Necesitamos imágenes que retraten de manera más realista la tecnología y las personas detrás de ella y que señalen sus fortalezas, debilidades, contextos y aplicaciones”, indican sus promotores, que ofrecen un repositorio gratuito de mejores imágenes de IA y una guía de consejos para un uso responsable.
 Una de las imágenes del colectivo ‘Better Images of AI’. Fuente: Alan Warburton / BBC / Better Images of AIImperios visuales
Una de las imágenes del colectivo ‘Better Images of AI’. Fuente: Alan Warburton / BBC / Better Images of AIImperios visuales
Una parte importante de las fotografías e ilustraciones que se emplean en publicidades, marketing corporativo, diseño de sitios web y también en sitios de noticias provienen de “fábricas de imágenes”: el negocio de las fotografías de archivo o de stock, una industria global de miles de millones de dólares, dominada por un puñado de corporaciones transnacionales –Getty Images, Corbis, Alamy, Shutterstock, Adobe Stock, Science Photo Library (SPL), entre otras–, con una fuerza poderosa en la cultura visual contemporánea.
Como indican los investigadores Gaudenz Urs Metzger y Tina Braun de la Escuela Superior de las Artes de Zúrich (Suiza) en un estudio publicado en el Journal of Death and Dying, estas imágenes influyen en cómo se imagina un tema, así como en lo que se puede decir y no decir en una sociedad.
A medida que las empresas periodísticas invierten cada vez menos en fotógrafos y diseñadores de infografías, las imágenes de stock expanden su presencia.
Por lo general, se trata de montajes, gráficos o ilustraciones genéricas, con un estilo realista, aunque más simbólico que documental, que buscan atraer la atención del lector al representar visualmente temas complejos como las tijeras moleculares de la técnica CRISPR de edición genética, el mundo subatómico, el interior del cuerpo humano, la computación cuántica, el blockchain (cadena de bloques) o la computación en la nube.
En el caso de la IA, el robot humanoide blanco ha sido elevado en el último tiempo al rol de embajador visual de estas tecnologías complejas por directa influencia de la cultura popular. Como registró el AI Narratives Project de la Royal Society de Londres, existe una fuerte tendencia a concebir las máquinas inteligentes con forma humana.
Una IA con formas hipersexualizadas“Cuando las personas imaginan a otros seres inteligentes, estas imaginaciones tienden a tomar forma humanoide”, destaca el documento principal de esta iniciativa. “Una consecuencia de este antropomorfismo es que los sistemas de IA son con frecuencia representados con género: sus formas físicas a menudo no son andróginas, sino que tienen las características sexuales secundarias estereotipadas de hombres o mujeres. De hecho, a menudo están hipersexualizados: tienen cuerpos masculinos exageradamente musculosos y tendencias agresivas, como Terminator, o formas femeninas convencionalmente hermosas como Ava en la película Ex Machina”.
La IA y sus ramas, como el aprendizaje automático, no son temas sencillos de explicar ni de ilustrar. Pero imaginar estas tecnologías como androides es problemático: desinforma, plantea expectativas demasiado altas, sugiere que su fin último es el de reemplazar a los humanos y dificulta que se consideren sus beneficios reales. Además, cuanto más humanos se ven estas representaciones, más étnicamente blancas son sus características.
De ahí que Stephen Cave y Kanta Dihal, investigadores de la Universidad de Cambridge (Reino Unido), señalen en su ensayo The Whiteness of AI que la representación de la IA sufre de un problema racial. “Imaginar máquinas que sean inteligentes, profesionales o poderosas es imaginar máquinas blancas porque el marco racial blanco atribuye estos atributos predominantemente a la blancura”, dicen los también autores de Imagining AI: How the World Sees Intelligent Machines.
“En las sociedades europeas y norteamericanas, la blancura está normalizada hasta tal punto que la vuelve en gran medida invisible. Al centrar la blancura como el color predeterminado del futuro, estas imágenes contribuyen a imaginar un futuro tecnológico que excluye a las personas de color de la misma manera que lo hacen las grandes empresas tecnológicas en la actualidad”, apuntan.
Clichés visuales y confusión sobre la IALos clichés visuales son varios: placas de circuitos, código binario descendente, brillantes cerebros situados en un espacio oscuro y vacío, aislados de las necesidades de un cuerpo, es decir, una clara alusión a la inteligencia, si bien gran parte de la IA y el aprendizaje automático que se utilizan hoy en día están muy alejados de la inteligencia humana. “Las personas que no entienden qué es la IA no pueden defender las formas en que la tecnología debería o no impactar a la sociedad”, señala Duarte.
 Cerebros brillantes y robots blancos conforman la iconografía actual de la IA. Fuentes: Wiley / Routledge / Apress
Cerebros brillantes y robots blancos conforman la iconografía actual de la IA. Fuentes: Wiley / Routledge / ApressAdemás de la prevalencia de robots blancos, el color favorito de las empresas de tecnología para representar sus sistemas es el azul, usualmente asociado con inteligencia, confianza, seriedad, eficiencia pero también con masculinidad, como destaca la historiadora Alexandra Grieser en Blue Brains: Aesthetic Ideologies and the Formation of Knowledge Between Religion and Science.
“Existe una gran brecha entre la realidad de la IA y la percepción que tiene el público general, que es alimentada por representaciones en los medios y películas que a menudo presentan la IA como robots autónomos con capacidades casi humanas”, indica la desarrolladora de software mexicana Yadira Sánchez, asesora de Better Images of AI.
“Esta distorsión es preocupante porque impide que el público comprenda y participe efectivamente en debates cruciales sobre cómo la IA está remodelando áreas esenciales como la atención médica, la agricultura y la vigilancia estatal. Además –añade–, estas imágenes inexactas crean pensamientos futuristas muy optimistas o muy pesimistas sobre la IA y esto es peligroso porque generan expectativas y miedos en la sociedad”.
Otras imágenes para minimizar la confusiónPara minimizar la confusión, sostienen los investigadores de Better Images of AI, es importante utilizar imágenes que representen honestamente la realidad de la IA, como los recursos naturales y materiales que se consumen en su desarrollo. Por ejemplo, la extracción de litio en América Latina, o el agua y los ríos que se usan para mantener centros de datos en funcionamiento.
“Deberíamos mostrar cómo la IA se integra y afecta nuestros entornos naturales y sociales”, agrega Sánchez, “y cómo su infraestructura impacta directamente en el ecosistema y la vida cotidiana de las personas”.
“La enfermedad de la fotografía de stock de la IA ha alcanzado el estado epidémico”, señaló hace unos años el investigador Adam Geitgey, especialista en aprendizaje automático y reconocimiento facial. Aunque la IA no es la única rama científica que sufre estas tergiversaciones visuales. Más bien, todas las disciplinas, en algún grado u otro, las padecen cuando son representadas en periódicos, avisos publicitarios, campañas públicas o en webs de instituciones.
“Los medios optan por la solución más sencilla: utilizar imágenes que la gente reconozca y asocie rápidamente con la ciencia”, apunta la socióloga portuguesa Ana Delicado, quien estudió las representaciones visuales de la ciencia durante la pandemia de la covid-19 en sitios web de instituciones políticas y medios de comunicación en Portugal y España.
“Las imágenes de stock siempre se basan en estereotipos. Son productos comerciales: su objetivo es vender, no reflexionar sobre los temas que venden. Las imágenes estereotipadas en los medios de comunicación contribuyen a perpetuar representaciones estereotipadas en la opinión pública”, recalca.
En su análisis, publicado en la revista Frontiers in Communication, esta investigadora del Instituto de Ciencias Sociales da Universidad de Lisboa registró el abuso de ilustraciones del coronavirus SARS-CoV-2 con sus púas y pintado de rojo, haciéndolo parecer más amenazador.
También detectó una gran lista de elementos visuales que aluden a la actividad científica: hélices de ADN, células, moléculas, radiografías, equipos de laboratorio como microscopios, tubos, placas de Petri y pipetas, a menudo sostenidos por manos incorpóreas enguantadas, así como la presencia de personas con batas blancas, gafas protectoras y mascarillas, pero sin diversidad étnica, lo que refleja la subrepresentación de las minorías en la comunidad científica.
“La elección de imágenes para ilustrar la ciencia de la covid-19 tiende a reproducir nociones estereotipadas de la investigación científica como una actividad centrada en el laboratorio”, indica Delicado.
Nuevos generadores del imágenesAhora, con el auge de los sistemas de IA generadores de imágenes, como Stable Diffusion, Midjourney y DALL·E, se teme que empeoren las distorsiones sobre la realidad de la IA y la actividad científica en general. Como ya han demostrado algunas investigaciones, estas herramientas que producen imágenes a partir de indicaciones de texto suelen dar resultados racistas y sexistas.
Es decir, reproducen y amplifican sesgos raciales y de género, pues son entrenadas con imágenes utilizadas por medios de comunicación, organizaciones mundiales de salud y bases de datos de internet. “Estas imágenes son utilizadas sin crítica, sin reflexión”, advierte la socióloga portuguesa, “y la IA va a seguir perpetuando los estereotipos sobre la ciencia y las tecnologías”.
Una versión de este artículo fue publicada originalmente en SINC el 3 de mayo de 2024.
El artículo Las mentiras visuales de la IA se ha escrito en Cuaderno de Cultura Científica.
El protagonismo de los cuidados en la evolución humana

Los cambios del cerebro durante el embarazo y la maternidad, cómo el estrés ha pasado de ser un mecanismo de supervivencia a un eventual elemento de riesgo para nuestra salud o cuál ha sido el papel que ha jugado el suicidio en la evolución del ser humano fueron algunos de los temas que se tratarán en la VI Jornada Nacional sobre Evolución y Neurociencias.
La jornada tuvo lugar el Bizkaia Aretoa de la UPV/EHU los pasados 25 y 26 de abril y estuvo dirigida por Eva Garnica y Pablo Malo, de la Red de Salud Mental de Bizkaia, institución que organizó la jornada junto a la Cátedra de Cultura Científica de la UPV/EHU.
El encuentro, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolutivo y divulgar de un modo accesible para todos los públicos.
¿Cuándo comenzamos a cuidarnos entre los humanos? ¿Cómo se encuadra este comportamiento en nuestra evolución? Los orígenes de los cuidados están estrechamente vinculados al desarrollo de comportamientos que consideramos emblemáticamente humanos: en particular, nuestra disposición a cooperar por un bien mayor y nuestras habilidades de organización social. Explorar cuándo y por qué surgió este rasgo es un reto apasionante, y debe hacernos reflexionar sobre el impacto que su estudio debe producir, y produce, en la ciencia y en la sociedad actual. Estos son los temas que trata la conferencia El protagonismo de los cuidados en la evolución humana. La imparte Roberto Sáez, Doctor en Antropología, Máster en Ingeniería Industrial y divulgador científico, experto en Evolución Humana y en la Bioarqueología del Cuidado. Sáez es el autor del blog Nutcracker man.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo El protagonismo de los cuidados en la evolución humana se ha escrito en Cuaderno de Cultura Científica.
Uso y abuso de la pregabalina
 Envase de Lyrica (pregabalina) comercializado en Finlandia. Fuente: Acdx / Wikimedia Commons
Envase de Lyrica (pregabalina) comercializado en Finlandia. Fuente: Acdx / Wikimedia CommonsEl pasado mes de marzo, una noticia llegada desde Reino Unido generó cierta alarma respecto a la seguridad de la pregabalina, medicamento utilizado frecuentemente para el tratamiento del dolor crónico y la ansiedad. Una investigación del periódico británico The Sunday Times relacionaba el consumo de este fármaco con la muerte de 3 400 personas en los últimos años y describía los problemas de abuso y adicción que puede generar.
Dada la gravedad de la crisis sociosanitaria que sufre EE. UU. por la adicción a los opioides, los problemas de seguridad que puede plantear el uso de medicamentos como la pregabalina constituye un tema de especial interés.
Usos no contemplados en la ficha técnicaLa pregabalina es un medicamento con una estructura química similar a la del neurotransmisor GABA (ácido gamma-amino-butírico), sustancia que regula de forma inhibitoria la actividad del cerebro. Junto con la gabapentina, forma un grupo de medicamentos denominado gabapentinoides.
En España, el primer medicamento con pregabalina lo lanzó al mercado el laboratorio farmacéutico Pfizer, con el nombre comercial Lyrica. Inicialmente, fue aprobado para tratar la epilepsia y el dolor neuropático, y después se autorizó para tratar el trastorno de ansiedad generalizada.
Con el tiempo, el uso de Lyrica se amplió para tratar otras patologías que no contaban con la autorización sanitaria, como el dolor crónico, el dolor lumbar, la prevención del dolor postoperatorio, la fibromialgia y la profilaxis de la migraña. Esta aplicación se conoce como off-label o fuera de ficha técnica. En ocasiones, dichos usos pueden estar médicamente justificados si no existen alternativas terapéuticas autorizadas, y en todo caso se encuentran regulados por ley.
Lo que está prohibido es publicitarlo, y esto condenó a Pfizer a pagos de multas millonarias. Es conveniente recordar que el uso off-label de los medicamentos puede constituir un problema de seguridad, incrementar los costes del tratamiento o, directamente, resultar ineficaz, ya que se ha demostrado que su beneficio terapéutico es insuficiente.
Sin embargo, distintos estudios concluyen que más de la mitad de las recetas de gabapentinoides se realizan para indicaciones no autorizadas; mayoritariamente para tratar distintos tipos de dolor, a pesar de que los estudios científicos no recomiendan su uso.
Un consumo disparadoHoy en día, disponemos de 168 medicamentos que contienen pregabalina, incluidos los llamados genéricos. Los datos de consumo se pueden consultar en la página web de la Agencia Española de Medicamentos y Productos Sanitarios (AEMPS), concretamente en el informe sobre la utilización de analgésicos no opioides.
Esta información se expresa en DHD, es decir, en la dosis diaria definida (DDD) por cada 1 000 habitantes y día. Así sabemos que en los últimos 10 años el consumo de pregabalina se ha incrementado un 66 %, puesto que entre 2012 y 2022 el DHD pasó de 3,56 a 5,92. Este último dato significa que cada día un promedio de 5,92 personas de cada 1 000 recibe una DDD de pregabalina. Actualmente, se encuentra en el tercer puesto de fármacos analgésicos no opioides con mayor consumo en España, por detrás del paracetamol y el metamizol.
¿Es seguro tomar pregabalina?La pregabalina, como todos los medicamentos, no está libre de producir efectos adversos, es decir, efectos que no deseamos pero que en muchos casos no se pueden evitar. Por suerte, los más frecuentes, que aparecen en al menos una de cada 10 personas, son leves. Entre ellos destacan los mareos, la somnolencia y el dolor de cabeza.
También pueden manifestarse otros con menor frecuencia. Todos ellos pueden ser consultados en la ficha técnica en la página web del centro de información de la AEMPS, de acceso abierto, o en el prospecto del medicamento. Es importante señalar que los efectos adversos son más frecuentes cuando la pregabalina se toma en dosis altas y de forma crónica. Y en cualquier caso, este tipo de uso no ha demostrado aliviar mejor del dolor.
Entre los efectos más graves encontramos el riesgo de reducir la respiración, debido a que actúan sobre la zona del cerebro que controla esa función. Es importante tener esto en cuenta si el paciente ya está tomando otros medicamentos que tienen el mismo efecto, ya que su combinación en dosis altas podría llegar a paralizar la respiración y causar la muerte.
Estos otros medicamentos depresores son los analgésicos opioides (como la morfina), que utilizamos para aliviar dolores fuertes, y las benzodiazepinas (como el orfidal), que tomamos para dormir o calmar los nervios. Diversos estudios indican que el 60 % de los pacientes que usa gabapentinoides toma también los otros depresores. Una combinación fatal podría estar detrás del incremento de muertes asociadas al uso de pregabalina que describía el The Sunday Times.
Ese mismo efecto depresor de la pregabalina, pero ejercido sobre el sistema límbico del cerebro, produce una sensación de euforia y bienestar que puede conducir a comportamientos de abuso y dependencia. El concepto de dependencia se refiere a la necesidad de seguir tomando una sustancia para experimentar sus efectos deseados o aliviar el malestar que causa no consumirla (síndrome de abstinencia).
Si no se ingiere el medicamento, aparecen síntomas que provocan malestar y empujan a seguir tomándolo, a pesar de los posibles efectos negativos; es lo que coloquialmente llamamos “estar enganchado”. Son especialmente vulnerables aquellas personas que han sufrido con anterioridad problemas de adicción.
Siempre bajo supervisión médicaLos riesgos asociados al abuso de pregabalina pueden minimizarse con un seguimiento adecuado de la pauta médica, valorando periódicamente la necesidad de mantener o retirar el tratamiento según criterios de eficacia, tolerabilidad, efectos adversos y adherencia. Si la valoración recomienda suspender el tratamiento, se realizará de forma gradual y con supervisión médica.
En todo caso, la pregabalina está autorizada para tratar el dolor neuropático –que se produce por el daño de un nervio–, la epilepsia y la ansiedad porque los estudios indican que los beneficios del tratamiento superan los riesgos. En este contexto, la evaluación de la relación riesgo-beneficio del tratamiento con pregabalina corresponde a los profesionales médicos y cuentan con el apoyo de la AEMPS.
Finalmente, no podemos olvidar el papel de la ciudadanía en la gestión activa de su salud: es fundamental seguir las indicaciones médicas y comunicar si sufrimos efectos adversos y si notamos que el tratamiento no está funcionando. Transmitir toda esta información en las visitas a la consulta es clave para que el médico o la médica evalúe correctamente la utilidad del tratamiento y su seguridad.![]()
Sobre las autoras: María Torrecilla Sesma y Cristina Bruzos Cidón son Profesoras de Farmacología en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Uso y abuso de la pregabalina se ha escrito en Cuaderno de Cultura Científica.
Un coloso de la informática
El 18 de enero de 1944, llegó a Bletchley Park un camión con una carga muy especial: una máquina de cálculo que pesaba una tonelada, medía 2,13 x 5,18 x 3,35 metros, estaba construida con alrededor de 1600 válvulas termoiónicas y era capaz de operar a una velocidad de 5000 caracteres por segundo. La llamaron Colossus, se considera la primera computadora electrónica, programable y digital de la historia… y estuvo a punto de no existir.
Durante la Segunda Guerra Mundial, Bletchley Park fue uno de los centros neurálgicos de los servicios de inteligencia británicos. Bajo el nombre en clave de Ultra, allí se descifraban todas las comunicaciones que Inglaterra interceptaba al Ejército y la diplomacia de la Alemania nazi y pasó a la historia, sobre todo, por el duelo que tuvo lugar allí entre el matemático inglés Alan Turing y la supuestamente impenetrable Enigma naval de la Kriegsmarine que utilizaban los U-Boote del Atlántico.
 Máquina enigma de cuatro rotores expuesta en Bletchley Park. Funete: Tim Gage / CC BY-SA 2.0
Máquina enigma de cuatro rotores expuesta en Bletchley Park. Funete: Tim Gage / CC BY-SA 2.0
En 1941, casi a la par que la Enigma naval quedaba al descubierto tras un arduo trabajo por parte del barracón 8 que dirigía Turing, las estaciones de escucha británicas comenzaron a interceptar una nueva clase de mensajes indescifrables que no se estaban retransmitiendo en morse, como los de Enigma, sino en el código internacional del teletipo. Alemania había puesto en escena una nueva máquina de cifrado automática y mucho más sofisticada que Enigma para las comunicaciones diplomáticas: la Lorenz SZ, a la que apodaron Tunny.
En este caso, fue el coronel John Tiltman quien consiguió descifrar un mensaje de Tunny por primera vez a finales de aquel mismo año. Con el trabajo de este, el matemático Bill Tutte dedujo cómo debía de ser el funcionamiento de la máquina. Por último, Alan Turing ideó un método algorítmico, la «turingería» ―de «Turing» e «ingeniería»― que permitió acotar sustancialmente las posibles configuraciones de los doce rotores de los que constaba el disposivo y… entonces se marchó a Estados Unidos.
 Máquina de cifrado Lorenz SZ40, sin la carcasa, en el US National Cryptologic Museum. En ella se pueden apreciar los doce rotores. Fuente: Mark Pellegrini / CC BY-SA 2.5
Máquina de cifrado Lorenz SZ40, sin la carcasa, en el US National Cryptologic Museum. En ella se pueden apreciar los doce rotores. Fuente: Mark Pellegrini / CC BY-SA 2.5
Fue Bill Tutte el que continuó trabajando en nuevos métodos de descifrado de Tunny, pero, a medida que Alemania aumentó la extensión aquella red de comunicaciones, que los aliados bautizaron como Fish, y mejoró la seguridad, los cálculos empezaron a volverse inabarcables: se iba a necesitar algún tipo de dispositivo electromecánico para realizarlos, al igual que se habían necesitado las Bombe para poder romper Enigma.
El primer intento de mecanizar el descifrado de Tunny vino de la mano de Max Newman y sus «Heath Robinson» unos cacharros llamados así en honor a William Heath Robinson, un ilustrador que solía hacer dibujos de inventos bizarros dada la lentitud, imprecisión y tendencia al sobrecalentamiento que tenían. Pero un ingeniero eléctrico de Bletchley Park, al que, en un principio, habían reclutado como ayudante de Alan Turing, tenía en mente desde hacía algún tipo una idea de máquina mucho más rápida, precisa y eficiente.
 Réplica de una de las Heath Robinson de Max Newman en el National Museum of Computing, de Bletchley Park. Fuente: TedColes / CC BY-SA 4.0
Réplica de una de las Heath Robinson de Max Newman en el National Museum of Computing, de Bletchley Park. Fuente: TedColes / CC BY-SA 4.0
Tommy Flowers había nacido en una familia humilde en uno de los distritos más pobres de Londres, Poplar, muy cerca de Whitechapel, y ya desde muy pequeño le había llamado la atención la ingeniería. Estuvo durante un tiempo como aprendiz en el Arsenal Real de Londres hasta que encontró trabajo en el departamento de ingeniería de Correos mientras se sacaba el título en la escuela nocturna. Allí conoció y empezó a investigar las posibilidades que ofrecía un nuevo componente electrónico que podía realizar tareas de interruptor a una velocidad mucho más alta de la habitual: la válvula termoiónica o de vacío.
 Tommy Flowers. Fuentes: Dominio público
Tommy Flowers. Fuentes: Dominio público
Aunque ya se estaban utilizando en algunos dispositivos ―y las Heath Robinson eran uno de ellos, aunque solo parcialmente―, el uso de las válvulas de vacío aún era bastante limitado. Tommy Flowers fue el primero al que se le ocurrió que podían utilizarse en un número mucho mayor para fabricar máquinas de computación completamente electrónicas. Pero, como sucede casi siempre que alguien presenta una idea demasiado disruptiva, en Bletchley Park aquello les pareció una locura.
Sin el apoyo que necesitaba, pero convencido de que un computador completamente electrónico era posible, pese a las dificultades de diseño que presentaba, Flowers reunió a cincuenta científicos, ingenieros y técnicos del laboratorio de la oficina de Correos de Dollis Hill donde trabajaba y se pusieron manos a la obra, trabajando doce horas al día, seis días y medio a la semana para crear, en un tiempo récord de diez meses, el primer computador electrónico: Colossus. Cuando se presentaron con él en Bletchley Park y, más aun, cuando lo pusieron en funcionamiento, el personal no daba crédito a lo que tenía delante.
El primer prototipo de Colossus que llegó a Bletchley funcionaba muy bien, pero no lo todo lo rápido que se necesitaba, así que Tommy Flowers y su equipo se pusieron de nuevo a trabajar contrarreloj en una versión mejorada que el Gobierno quería tener lista, como muy tarde, para el 1 de junio: aquella iba a ser la fecha inicial en la que iba a tener lugar el Día-D y se necesitaba que la máquina estuviera ya operativa. Colossus Mark II, con 2400 válvulas y una velocidad de 25 000 caracteres por segundo, lo estuvo y, de hecho, el 5 de junio se descifró con ella un mensaje de Adolf Hitler dirigido al mariscal Erwin Rommel en el que los aliados pudieron confirmar que la maniobras de los servicios secretos para desviar la atención del Führer lejos de las playas de Normandía había funcionado. Al día siguiente, el Ejército aliado tomó la costa francesa y comenzó la ofensiva por la liberación de Europa occidental. Mientras tanto, una Colossus tras otra iba llegando a Bletchley Park a medida que las fuerzas aliadas penetraban en el continente. Veinticuatro horas al día, siete días la semana, un ejército de WRENs ―mujeres pertenecientes al Women’s Royal Naval Service― averiguaba sin descanso la configuración diaria de la las máquinas Tunny y dejaba al descubierto las comunicaciones enemigas.
 Colossus Mark II en Bletchley Park, operada por las WRENs (Women’s Royal Naval Service) Dorothy Du Boisson y Elsie Booker en 1943.
Colossus Mark II en Bletchley Park, operada por las WRENs (Women’s Royal Naval Service) Dorothy Du Boisson y Elsie Booker en 1943.
A menudo se ha tratado de establecer el impacto que todo el trabajo de criptoanálisis de Bletchley Park tuvo sobre el desarrollo de la guerra. Hay quienes dicen que ayudó a acortar el conflicto en unos dos o tres años, por ello, resulta bastante inquietante pensar que Colossus fue posible gracias a una serie de serendipias que podrían, perfectamente, no haber tenido lugar.
A finales de agosto de 1939, y con las tensiones en Europa a punto de hacer estallar todo, algún superior no muy centrado envió a Tommy Flowers a Berlín en viaje de trabajo. Tan pronto como este puso el pie en la capital alemana, la Embajada británica lo llamó para advertirle de que abandonara el país lo antes posible. Flowers consiguió cruzar a Holanda apenas unas horas antes de que se cerraran las fronteras de Alemania, evitando así, seguramente, acabar como prisionero del régimen nazi. También fue providencial que luego la oficina de Correos lo enviara a él, y no a otro, a ayudar a Alan Turing con Enigma y las Bombe, porque cuando alguien iba a consultarle al matemático cualquier tema de ingeniería o problema con los equipos, Alan simplemente respondía: «Flowers»… Lo que llevó a este hasta Newman, luego hasta Tunny, luego hasta Colossus y, finalmente, a marcar ―casualidades que pasan― el primer gran hito de la historia de la computación.
Referencias:
Copeland, B. Jack, et. al. (2006). Colossus. The secrets of Bletchley Park’s codebreaking computers. Oxford University Press.
Copeland, B. Jack (2021 [2013]). Alan Turing. El pionero de la era de la información. Turner.
Para saber más:
Marian Rejewski, el matemático que «rompió» la Máquina Enigma
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Un coloso de la informática se ha escrito en Cuaderno de Cultura Científica.
El infinito en un segmento (3)
A finales del siglo XIX, el matemático ruso-alemán Georg Cantor (1845-1918) conmocionó al mundo de las matemáticas, rompiendo las creencias existentes sobre el concepto de infinito. Entre los revolucionarios resultados que demostró están que existe más de un infinito o que la cantidad de puntos de un segmento es la misma que la cantidad de puntos de un cuadrado. A esta revolución matemática hemos dedicado, en el Cuaderno de Cultura Científica, la miniserie titulada El infinito en un segmento.
 Página de la novela gráfica Logicomix, de Apostolos Doxiadis y Christos H. Papadimitiou, Bloomsbury, 2009. En la viñeta se muestra una noticia con motivo del Congreso Internacional de Matemáticos de 1900, con una caricatura de dos matemáticos enfrentados, el francés Henri Poincaré, con su frase “¡Le acuso Señor Cantor! ¡La teoría de conjuntos es una enfermedad de la que hay que curar a las matemáticas!”, y el alemán David Hilbert, con su frase “Nadie nos expulsará del paraíso que Herr Cantor ha creado para nosotros”
Página de la novela gráfica Logicomix, de Apostolos Doxiadis y Christos H. Papadimitiou, Bloomsbury, 2009. En la viñeta se muestra una noticia con motivo del Congreso Internacional de Matemáticos de 1900, con una caricatura de dos matemáticos enfrentados, el francés Henri Poincaré, con su frase “¡Le acuso Señor Cantor! ¡La teoría de conjuntos es una enfermedad de la que hay que curar a las matemáticas!”, y el alemán David Hilbert, con su frase “Nadie nos expulsará del paraíso que Herr Cantor ha creado para nosotros”
La primera entrega de esta miniserie, El infinito en un segmento (1), se centró en cómo resolvió el matemático ruso-alemán el problema de comparar dos conjuntos con infinitos elementos. La respuesta es sencilla y está en la base del origen del concepto de número. Dos conjuntos tienen la misma cantidad de elementos cuando se puede establecer una “correspondencia uno-a-uno” entre los elementos de los dos conjuntos. De esta forma, llegamos a la paradoja de que para un conjunto infinito existen subconjuntos propios del mismo que tienen la misma cantidad de elementos que el propio conjunto. Por ejemplo, el conjunto de los números pares tiene la misma cantidad de elementos que el conjunto de los números naturales (que está formado por los números pares y los números impares).
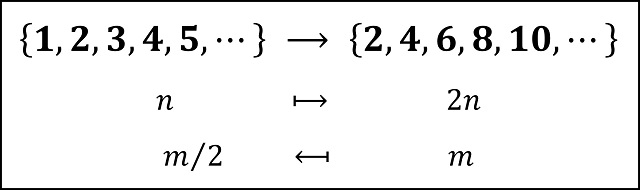 Existe una correspondencia uno-a-uno entre el conjunto de los números pares y el conjunto de los números naturales
Existe una correspondencia uno-a-uno entre el conjunto de los números pares y el conjunto de los números naturales
De hecho, Georg Cantor tomó esta paradoja del ininfito como definición de “conjunto infinito”, es decir, un conjunto es infinito si existe un subconjunto propio suyo que tiene la misma cantidad de elementos que el conjunto.
En esta primera entrega de la serie se demostró también que los conjuntos de los números enteros y de los números racionales son conjuntos numerables, es decir, tienen la misma cantidad de elementos que el conjunto de los números naturales.
En la segunda entrega de esta miniserie, El infinito en un segmento (2), se mostró que el conjunto de los números reales (de forma explícita, en la demostración se consideró el intervalo (0,1), es decir, los números reales entre 0 y 1) no es numerable, no se puede poner en correspondencia uno-a-uno con los números naturales. Por lo tanto, existe más de un infinito, al menos, el infinito de los números naturales (cuyo cardinal se denomina aleph-zero) y el infinito de los números reales (cuyo cardinal se denomina cardinal del continuo, c).
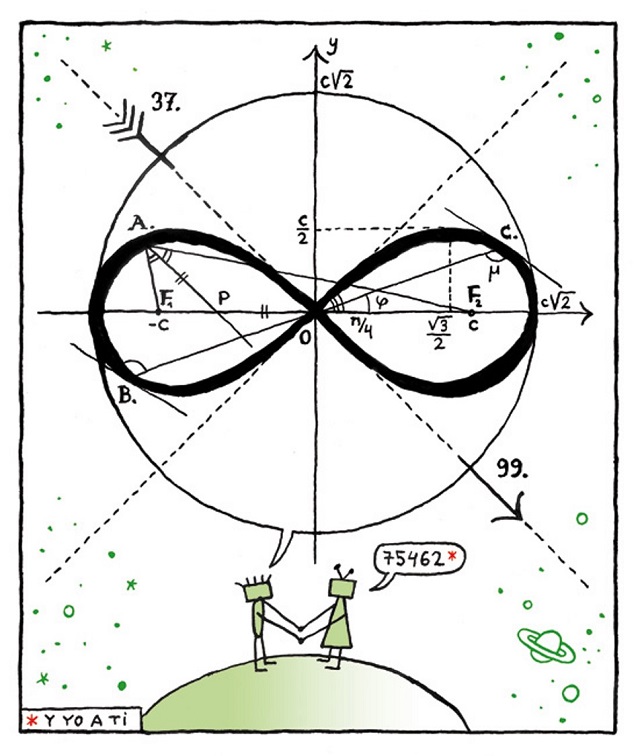 El bueno de Cuttlas (4MOR, 37 & 99), de Calpurnio, publicado en 20 MinutosEl infinito en un cuadrado
El bueno de Cuttlas (4MOR, 37 & 99), de Calpurnio, publicado en 20 MinutosEl infinito en un cuadrado
Como se comentó al final de la segunda entrada de esta miniserie, una vez demostrado que el cardinal del continuo c (el infinito de los números reales) es mayor que aleph-zero (el infinito de los números naturales), Georg Cantor se planteó si el plano (de dimensión 2) tiene una mayor cantidad de puntos que la recta (de dimensión 1), es decir, si el infinito del plano es mayor que el infinito del continuo. Simplificando la cuestión.
Problema: ¿Hay la misma cantidad de puntos en el segmento unidad [0,1] que en el cuadrado unidad [0,1] x [0,1]?

Para abordar el anterior problema, primero recordemos un par de cuestiones básicas. La primera es que los números reales del intervalo [0,1], es decir, mayores que 0 y menores que 1, se escriben en forma decimal como
donde, si todos los dígitos son 0 se obtendría el número cero (0), y si todos los decimales son 9 se obtendría el número uno (1), ya que, como se comentó en la anterior entrada, el número 1 se puede representar de dos formas distintas 1,00000000… (infinitos ceros) y 0,99999999… (infinitos nueves). Por ejemplo, el número pi menos 3, que es un número real del intervalo (0,1) se expresa como 0,1415926535…
La segunda cuestión básica es que todo elemento del plano real se puede identificar con sus coordenadas cartesianas, es decir, con un par (x, y), donde x e y son números reales, como se muestra en la siguiente imagen (aunque en ella solamente se han utilizado puntos cuyas coordenadas x e y son números enteros).
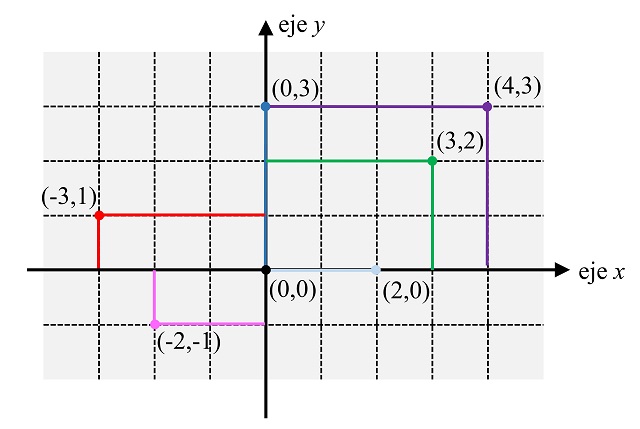
De manera, que los elementos del cuadrado [0,1] x [0,1], serán los puntos del plano (x, y), donde x e y son números reales del intervalo [0,1]. Es decir, son de la forma
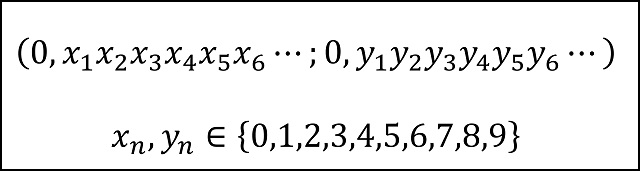 (Nota: hemos utilizado el punto y coma “;” para separar las coordenadas, en lugar de la tradicional coma “,”, con la intención de que quede más clara la separación entre las dos coordenadas)
(Nota: hemos utilizado el punto y coma “;” para separar las coordenadas, en lugar de la tradicional coma “,”, con la intención de que quede más clara la separación entre las dos coordenadas)
Ahora, una cuestión técnica. Antes de entrar en la construcción de la buscada correspondencia uno-a-uno entre el segmento y el cuadrado, vamos a tener en cuenta lo siguiente, de cara a dicha construcción. Como se puede demostrar (aunque no quiero meterme ahora en esta cuestión para no complicar más esta entrada) que los segmentos [0,1], es decir, los números reales mayores o iguales que 0 y menores o iguales que 1; (0,1], es decir, los números reales mayores que 0 y menores o iguales que 1; y (0,1), es decir, los números reales mayores que 0 y menores que 1, tienen la misma cantidad de elementos (existen correspondencias uno-a-uno entre ellos), es equivalente demostrar que existe una correspondencia uno-a-uno entre el segmento [0,1] y el cuadrado [0,1] x [0,1], que entre el segmento (0,1] y el cuadrado (0,1] x (0,1] o que entre el segmento (0,1) y el cuadrado (0,1) x (0,1). Por motivos técnicos, nosotros vamos a centrarnos en construir una correspondencia uno-a-uno entre el segmento (0,1] y el cuadrado (0,1] x (0,1], es decir, los puntos (x, y) tales que sus coordenadas x e y pertenecen a (0, 1].
Por lo tanto, ya estamos en condiciones de mostrar la construcción de Georg Cantor de la correspondencia uno-a-uno entre los elementos del segmento (0,1] y los elementos del cuadrado (0,1] x (0,1], que prueba que ambos conjuntos tienen la misma cantidad de elementos. La idea básica es asignar a cada elemento A del intervalo (0,1], es decir, un número real con su expresión decimal (por ejemplo, 0,1234567891011…), un elemento (B, C) del cuadrado (0,1] x (0,1] tal que los decimales de la primera coordenada B son los decimales en las posiciones impares de A y los decimales de la segunda coordenada C son los decimales en posiciones pares de A, como se muestra en la imagen.
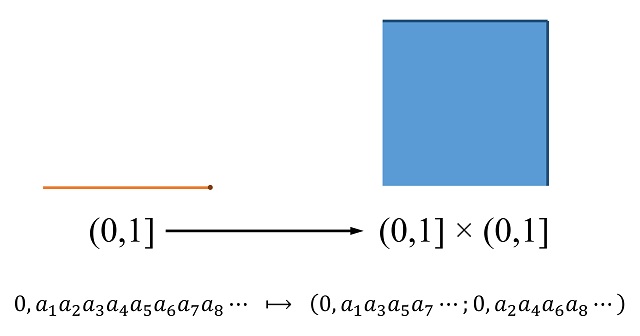
Y cuya aplicación inversa, es decir, que envía los elementos del cuadrado (0,1] x (0,1] en elementos del segmento (0,1], está definida mediante la construcción inversa, juntando los decimales de ambas coordenadas e intercalándolos en posiciones impares y pares.
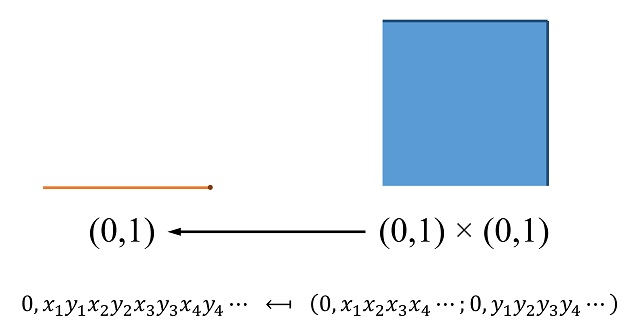
Por ejemplo, la imagen de la conocida “constante de Champernowne”, que es el número real, entre 0 y 1, cuyos decimales son los números naturales ordenados de izquierda a derecha, es decir,
0,123456789101112131415161718192021…
es el punto del cuadrado (0,1] x (0,1] cuyas coordenadas son
(0,135790123456789012…; 0,24681111111111222…).
Por otra parte, si tomamos el punto del cuadrado (0,1] x (0,1] dado por las coordenadas (x, x), donde x es la raíz de 2 menos 1, es decir, el punto
(0, 41421356237309…; 0, 41421356237309…),
su imagen, mediante la aplicación inversa, es el elemento del segmento (0,1] dado por la siguiente expresión
0, 4411442211335566223377330099…
Resolviendo algunas cuestiones técnicasLa idea de Cantor es ingeniosa, sin embargo, el hecho de que haya números reales, en concreto, los números racionales con un número finito de decimales (incluido en caso en el que no hay decimales, es decir, los números enteros) que tienen dos representaciones genera algunos problemas en la anterior aplicación, que hay que resolver.
Problema 1. Como decíamos, hay números que tienen dos representaciones decimales, por ejemplo, el número racional 11/20 se puede representar como 0,55 (o si lo preferimos 0,55000000…) y 0,54999999… Esto es un problema, ya que ese número racional tendría dos posibles imágenes mediante la anterior construcción
(0,500000…; 0,500000…) y (0,599999…; 0,499999…).
Por lo tanto, lo que hizo Cantor fue quedarse con una única representación de las dos, la que tiene infinitos nueves, en este caso, 0,54999999… De esta forma, solo existe, a priori, una imagen en (0,1] x (0,1] de cada número real de (0,1], que, en el ejemplo anterior, es (0,599999…; 0,499999…).
Problema 2. Pero al elegir una única representación de las dos se genera un problema añadido, ya que puede haber números reales de (0,1] cuya imagen contenga una expresión de las primeras y ya no sea válida, como 118/275 = 0,429090909…, cuya imagen sería, por la construcción de Cantor, el punto del cuadrado (0,49999…; 0,20000…), que ya no es un punto válido puesto que para el número 0,2 se ha elegido la representación 0,199999… Notemos que si se admitiesen aquí las dos representaciones se tendría que dos números reales distintos 0,429090909… y 0,4199999999… tendrían la misma imagen (0,49999…; 0,20000…) = (0,49999…; 0,19999…), es decir, la correspondencia no sería uno-a-uno.
Este nuevo problema lo resuelve Cantor de una forma ingeniosa. En la aplicación del segmento (0,1] en el cuadrado (0,1] x (0,1], en lugar de separar dígitos en posiciones pares e impares (y en la aplicación inversa intercalar los dígitos de las dos coordenadas del punto), lo que propone es separar (respectivamente, intercalar) grupos de dígitos, de manera que los ceros consecutivos dentro de la representación decimal se “pegan” al siguiente dígito no nulo. Por ejemplo, los grupos de dígitos de 118/275 = 0,429090909… serían
4 / 2 / 9 / 09 / 09 / 09 …
Por lo tanto, su imagen mediante la aplicación de Cantor sería ahora
(0,49090909…; 0,2090909…).
De hecho, el punto (0,49090909…; 0,2090909…) sería el único punto de (0,1] x (0,1] cuya imagen es 118/275 = 0,429090909…
Veamos otro ejemplo. El número real 0,01002000300004000005… tendría los siguientes grupos de dígitos
01 / 002 / 0003 / 00004 / 000005 …
por lo que su imagen sería el punto del cuadrado de coordenadas (0,010003000005…; 0,002000040000006…). Y ese punto del cuadrado es el único cuya imagen inversa es el número real 0,01002000300004000005…
Por supuesto, los números que no tienen ceros entre sus decimales funcionan como antes. Así, 1/2 = 0,4999999… tiene como imagen (0,4999999…, 0,9999999) y este punto es el único cuya imagen inversa es 1/2 = 0,4999999…
En conclusión, Cantor demostró que existen tantos puntos en el intervalo (0,1], como en el cuadrado (0,1] x (0,1].
 Retrato del matemático ruso-alemán Georg Cantor, de alrededor de 1910. Imagen obtenida de “Library of Congress, courtesy AIP Emilio Segrè Visual Archives”
Retrato del matemático ruso-alemán Georg Cantor, de alrededor de 1910. Imagen obtenida de “Library of Congress, courtesy AIP Emilio Segrè Visual Archives”Bibliografía
1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – FESPM, 2021.
2.- David Foster Wallace, Todo y más, Breve historia del infinito, RBA, 2013.
3.- J. Stillwell, The Real Numbers: An Introduction to Set Theory and Analysis, Undergraduate Texts in Mathematics, Springer, 2013.
4.- Eli Maor, To infinity and Beyond, A Cultural History of Infinity, Birkhauser, 1987.
5.- José A. Prado-Bassas, Historia del infinito (el apasionante relato de uno de los conceptos más profundos y enigmáticos de las matemáticas), Pinolia, 2023.
6.- Erich Kamke, Theory of Sets, Dover, 1950.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El infinito en un segmento (3) se ha escrito en Cuaderno de Cultura Científica.

