Cristalografía (3): Goniómetros y óxidos dulces

Alrededor de 1780, Arnould Carangeot, recibió un encargo de su jefe, Jean Baptiste Romé de l’Isle: tenía que hacer copias en arcilla de su colección de cristales. La tarea no era fácil en absoluto y más teniendo en cuenta lo puntilloso que podía llegar a ser de l’Isle. Pero eso no era problema para el metódico y meticuloso Carangeot. Éste se dio cuenta de que si quería reproducir fielmente los cristales era crítico que respetase los ángulos entre sus caras y que, para ello necesitaba medirlos con precisión suficiente. El compás resultaba útil para los cristales más grandes, no así para los más pequeños. Ni corto ni perezoso, Carangeot diseñó un aparato que le permitiese medir los ángulos: había nacido el goniómetro de contacto.

Fue usando este goniómetro que de l’Isle reunió datos suficientes para poder afirmar en 1783 que la primera ley de la cristalografía de Steensen era válida para todos los cristales, no sólo los de cuarzo y hematita.
Habida cuenta de la íntima relación entre estructura cristalina y composición química, no es de extrañar que el uso del goniómetro llevase poco tiempo después de su construcción a descubrimientos químicos.

Cuando René Just Haüy decidió realizar una serie de mediciones en un conjunto de cristales etiquetados como “sulfato de barita”, le sorprendió el hecho de que las muestras provenientes de Sicilia tuviesen diferentes ángulos interfaciales que las que venían de Derbyshire en Inglaterra. La diferencia era sólo de un par de grados, pero era lo suficiente como para convencer a Haüy de que debían tener una composición distinta. El encargado de comprobar esta conjetura fue Jean Baptiste Vauquelin que demostró que las muestras sicilianas eran en realidad sulfato de estroncio.

Haüy también se dio cuenta de que los ángulos del berilo y la esmeralda eran idénticos y aventuró que la esmeralda debía ser una versión verde del berilo. De nuevo pidió a Vauquelin que realizara los análisis pertinentes, que tuvieron como resultado, aplicando la misma tecnología electroquímica de contacto que había usado Hooke con los cristales de la urea (la lengua), una sustancia igualmente dulce en ambos casos. A esta sustancia es a la que terminó llamando “berilia” (el primer nombre fue “glucinia”, por su dulzor) y demostró en 1798 que se trataba del óxido de un nuevo elemento. Finalmente el berilio elemental fue obtenido a partir del cloruro por Friedrich Wöhler e independientemente por Antoine Bussy, ambos en 1828.
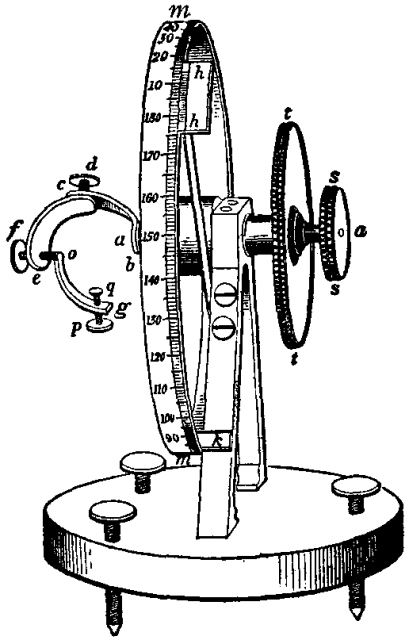
El goniómetro de contacto se convirtió así en una herramienta habitual para los cristalógrafos, y eso a pesar de ser, no obstante su utilidad, una artilugio bastante grosero, válido sólo para mediciones con una precisión no mayor de 15′ de cristales, en general, grandes. Por eso no es de extrañar que se inventase un dispositivo más preciso poco después. Así, en 1809 William Hyde Wollaston describió el goniómetro de reflexión, u óptico, que mide los ángulos entre las normales a los planos de las caras de los cristales. Este goniómetro permitía medir ángulos con gran precisión en cristales mucho más pequeños, incluidos aquellos que, preparados en el laboratorio, no excedían de un par de milimetros.

Durante la primera mitad el siglo XIX el goniómetro óptico fue refinándose cada vez más: se le añadió un anteojo para centrar el cristal, y posteriormente otro para observar las reflexiones, lo que facilitó mucho las mediciones, un colimador para conseguir un haz de luz paralelo y, finalmente, una fuente de luz artificial. Se construyeron goniómetros de diseños y geometrías muy diferentes, como el de Eilhard Mitscherlich o el de Jacques Babinet, que llegaron a aumentar la precisión a 30”.
En 1874 William Hallowes Miller dio un primer paso hacia el goniómetro de dos circulos montando un goniómetro Wollaston sobre otro. Pero no sería hasta 1890 que Evgraf Stepánovich Fiodorov desarrollase el goniómetro óptico de dos círculos, que facilitaría mucho tanto la precisión como la realización de la medida.

El goniómetro de dos círculos se mantuvo como un instrumento cristalográfico estándar, con mejoras menores, durante el siglo posterior. Sólo comenzó a ser reemplazado por la aparición de difractómetros automatizados controlados por ordenador en los años 70 del siglo XX.
Referencias generales sobre historia de la cristalografía:
[1] Wikipedia (enlazada en el texto)
[3] Molčanov K. & Stilinović V. (2013). Chemical Crystallography before X-ray Diffraction., Angewandte Chemie (International ed. in English), PMID: 24065378
[4] Lalena J.N. (2006). From quartz to quasicrystals: probing nature’s geometric patterns in crystalline substances, Crystallography Reviews, 12 (2) 125-180. DOI:10.1080/08893110600838528
[5] Kubbinga H. (2012). Crystallography from Haüy to Laue: controversies on the molecular and atomistic nature of solids, Zeitschrift für Kristallographie, 227 (1) 1-26. DOI: 10.1524/zkri.2012.1459
[6] Schwarzenbach D. (2012). The success story of crystallography, Zeitschrift für Kristallographie, 227 (1) 52-62. DOI: 10.1524/zkri.2012.1453
Este texto es una revisión del publicado en Experientia docet el 28 de noviembre de 2013
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cristalografía (3): Goniómetros y óxidos dulces se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cristalografía (2): Las rocas con lengua y la orina de Hooke
- Cristalografía (1): Protociencia, del “Homo erectus” a Linneo
- Los triángulos de luz y el sintético a priori
¿Por qué si nunca hemos vivido mejor que ahora el mundo nos parece cada vez peor?

Las tasas de mortalidad, las de pobreza, las de analfabetismo, las de desnutrición, las de violencia… Si bien el mundo en el que vivimos no es ni mucho menos perfecto, es difícilmente discutible que el progreso existe y cada vez es un mundo mejor. Entonces, ¿por qué hay tanto pesimista que sigue viéndolo todo negro allí donde cada vez hay más grises y blancos?
Según un estudio realizado por investigadores del Departamento de Psicología de la Universidad de Harvard, el motivo es un fenómeno llamado “cambio de concepto inducido por la prevalencia” y que viene a decir que cuando la prevalencia de un problema se reduce, los seres humanos tendemos a redefinirlo, de forma que cuanto menor es un problema, más amplia es la idea conceptual que tenemos de él. Eso nos impide ver que lo hemos resuelto, o lo cerca que estamos de hacerlo.
Lo que antes era violeta, ahora nos parece azul
La investigación se ha publicado hace poco en la revista Science, y en ella los autores describen los experimentos realizados para llegar a esa conclusión. Cogieron a un grupo de voluntarios no daltónicos y les enseñaron varias imágenes formadas por puntos de distintos colores, en distintos tonos de azul y violeta. Se les pidió que determinasen si cada uno de los puntos era azul o no.
Vídeo elaborado por Science explicando la investigación
Durante las primeras pruebas, en las que el número de puntos se dividía aproximadamente al 50% entre azules y violetas, esas fueron las respuestas que dieron los participantes. Pero progresivamente el número de puntos azules se iba reduciendo en cada imagen, y a medida que eso pasaba, iba cambiando la interpretación que los voluntarios hacían de los colores. Hacia el final, interpretaban como azules los mismos puntos que antes habían considerado violetas, es decir, que su concepto del color azul se había ampliado lo suficiente como para incluir en él tonos que antes habían quedado excluidos por considerarlos de otro color.
Descubrieron que esto ocurría incluso cuando se les advertía previamente de la posibilidad de caer en este comportamiento, e incluso cuando se les incentivaba con una recompensa económica para evitar que ocurriese. Los resultados mostraron que a pesar de ello, seguían alterando lo que consideraban en principio el color azul para incluir puntos previamente descartados.
Más caras amenazantes, más estudios problemáticos
Los científicos incluyeron otros experimentos para comprobar si esto ocurre también con otros conceptos que no sean colores, y resulta que sí: preguntados por la cualidad amenazante de una serie de caras, al reducirse la prevalencia de las previamente consideradas amenazantes se ampliaba ese concepto lo suficiente como para incluir otras previamente descartadas.
En un experimento más práctico, se pidió a los participantes que actuasen como miembros de un comité ético de un organismo de investigación y evaluasen una serie de propuestas de estudio que variaban desde muy éticas a muy poco éticas. “Con el tiempo, fuimos reduciendo la prevalencia de estudios poco éticos y, cuando lo hicimos, los participantes comenzaron a identificar como problemáticos estudios que antes les habían parecido inocuos”, ha explicado Daniel Gilbert, director del estudio.

Fuente: Pixabay
De la obsesión con la corrección a la sensibilidad ante problemas sutiles
Son unos hallazgos muy interesantes que pueden explicar en parte ese pesimismo vital del que hablábamos al principio según el cual seguimos considerando el mundo un lugar oscuro y peligroso a pesar de serlo ahora mucho menos de lo que ha sido siempre. También es interesante porque nos da una idea no solo sobre los problemas, sino como pensamos en ellos.
Para algunos, es una explicación de la obsesión por la corrección política que muchos critican, ya que refleja el mecanismo por el cual, cuando un problema como la discriminación se va resolviendo y reduciendo, ampliamos su definición para seguir encontrando comportamientos discriminatorios con los que anteriormente no parecíamos tener ningún problema.
En el lado contrario, podemos argumentar que es una explicación a como a medida que una sociedad progresa se vuelve más sensible a los matices, y reconsidera e identifica problemas que antes pasaban desapercibidos.
En cualquier caso, nos sirve para saber que resolver un problema complejo no es fácil porque la propia definición del problema puede cambiar en nuestra cabeza, y ser consciente de ello o incluso tener incentivos concretos para evitar que ocurra no parece ser suficiente para evitarlo.
Referencias
Prevalence-induced concept change in human judgment – Science
Are these dots purple or blue? Your answer might not be as reliable as you think – Science
‘Prevalence induced concept change’ causes people to re-define problems as they are reduced, study says – MedicalXpress
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo ¿Por qué si nunca hemos vivido mejor que ahora el mundo nos parece cada vez peor? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cinco motivos por los que sin jirafas el mundo sería un lugar peor
- Puedes presumir de tener la mejor piel del mundo.
- Cada vez más vida, cada vez más pronto
Fútbol es fútbol

Treinta y tres cámaras de vídeo se utilizan en cada partido del campeonato del Mundo de balompié que se disputa en Rusia para, si es el caso, advertir al árbitro de los errores graves que cometa. Y aunque no es fácil determinar cuando un error conduce a un resultado diferente del que se hubiese producido de haber actuado el árbitro correctamente, se pretende evitar así que ciertos errores decidan de forma injusta el desenlace de un encuentro. Analizando jugadas de encuentros oficiales en los que ya se ha utilizado el sistema, se ha estimado que en un 9% de los partidos el videoarbitraje permite rectificar decisiones que podían haber modificado el resultado, y la precisión global de las decisiones se eleva del 93% al 98,8%.
La historia del fútbol está bien nutrida de faltas en el área no pitadas, fueras de juego inexistentes, tarjetas polémicas o goles fantasma. En un partido que acabó siendo legendario se llegó, incluso, a invocar la mano de Dios. Las jugadas en las que los futbolistas incurren en la falta conocida como “fuera de juego” son especialmente controvertidas, porque los jueces de línea tienden a pitar falta en una medida significativamente mayor de la que deberían. Se comete falta de fuera de juego cuando un jugador que ataca se encuentra más próximo a la línea de gol que el segundo último jugador del equipo que defiende en el momento en el que el compañero de equipo que conduce el balón se lo lanza. Es un galimatías, sí, pero los aficionados al fútbol saben perfectamente en qué consiste.
La razón por la que los linieres tienden a pitar esa falta de forma desproporcionada no es que le tengan especial afición a frustrar las ansias de los atacantes por meter gol. Lo que les ocurre es que les afecta un sesgo de percepción denominado “efecto flash-lag”. En virtud de ese efecto, un objeto en movimiento se percibe más alejado del observador de lo que realmente está cuando, a la vez, se observa otro hecho relevante. En la jugada del fuera de juego el “objeto en movimiento” es el jugador atacante y el “otro hecho relevante” es el lanzamiento del balón hacia su posición por parte de su compañero. O sea, el juez de línea ve de hecho al jugador atacante en posición de fuera de juego.
El efecto flash-lag se puede corregir si a los jueces de línea se les adiestra utilizando imágenes de jugadas en las que compañeros suyos o ellos mismos se han visto afectados por ese sesgo de percepción. Aprenden a corregirlo de manera consciente. En el campeonato del Mundo de 2002 celebrado en Japón, una de cada cuatro faltas de fuera de juego pitadas lo fueron de forma errónea. Cuatro años después, en Alemania, tras recibir los linieres formación específica, el porcentaje de fallos de ese tipo se redujo a la mitad.
El citado no es el único sesgo en que incurren los árbitros. Se sabe que el griterío en las gradas eleva la probabilidad de que se piten faltas contra el equipo visitante. Las exclamaciones de dolor aumentan la probabilidad de que el causante de la falta sea expulsado. Y es muy improbable que un árbitro pite dos penaltis en contra de un mismo equipo. Mediante el uso del vídeo se pretende corregir algunos de esos errores o sesgos. Pero hay aficionados que no lo ven claro; opinan que los errores arbitrales forman parte esencial del espectáculo y que, sin ellos, el fútbol quizás pierda parte de su atractivo. Y es que, como sentenciase Bujadin Boskov, “fútbol es fútbol”.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 1 de julio de 2018
El artículo Fútbol es fútbol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los beneficios de las prendas de compresión para los jugadores de fútbol
- La condición física de los árbitros de fútbol
- La ciencia del balón de fútbol
Zientziateka: Santiago Pérez Hoyos – Explorando el espacio a través de la literatura de ciencia ficción

La convergencia entre las diferentes áreas de estudio ha supuesto desde siempre una herramienta maravillosa para reflejar de una forma global y fidedigna la realidad de cada tiempo. En este sentido, la conexión entre la naturaleza, la literatura y la ciencia es, quizás, una de las formas más fabulosas que tiene el ser humano para diseñar una ventana desde donde poder contemplar y enseñar el mundo desde múltiples y complementarias perspectivas.
La unión de estas tres áreas de conocimiento fue la temática principal del ciclo de conferencias “Naturaleza, Literatura y Ciencia” que albergó Azkuna Zentroa entre el 10 y el 19 de abril pasados.
El astrofísico e investigador del grupo de Ciencias Planetarias de la UPV/EHU Santiago Pérez Hoyos explica en “Explorando el espacio a través de la literatura de ciencia ficción” cómo se ha explorado el espacio en la literatura, en particular a través de las nóvelas de ciencia ficción que se escribieron desde comienzos del XIX. Mediante el análisis de algunos ejemplos, el astrofísico hablará de la difícil relación que ha existido siempre entre licencias narrativas y rigor científico, pero también de cómo la literatura de ciencia ficción ha contribuido a enriquecer el ideario de la humanidad sobre el espacio.
Explorando el espacio a través de la literatura de ciencia ficciónEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Zientziateka: Santiago Pérez Hoyos – Explorando el espacio a través de la literatura de ciencia ficción se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia para todos a través del cine y la literatura de ciencia ficción
- A través del espejo: la literatura mira a las científicas, por Marta Macho
- Las dos culturas: ciencia ficción en la universidad
Bioóleo a partir de residuos cítricos

Residuos cítricos secos. Foto: Egoi Markaida. UPV/EHU.
La sustitución paulatina del uso de combustibles fósiles precisa del estudio de diferentes estrategias de obtención de biocombustibles, y el hecho de darle salida a grandes volúmenes de residuos generados por la actividad humana, le confiere un valor añadido. Un estudio llevado a cabo en el grupo de investigación Catalytic Processes & Waste Valorization de la UPV/EHU, en el que han participado universidades brasileñas e iraníes, ha puesto de manifiesto que los restos cítricos son una fuente de energía renovable abundante, barata y asequible.
La investigación surgió de una petición de la Universidad Federal de São Carlos, debido a que en Brasil, en 2011, por ejemplo, se produjeron cerca de 9,3 millones de toneladas de residuo en la elaboración de zumos. En la UPV/EHU han obtenido bioóleo mediante la pirólisis rápida de este residuo en un reactor cónico de lecho en surtidor. Los residuos cítricos son secados y troceados antes de ser suministrados al reactor, y una vez pirolizados a 500 ˚C , se obtiene una proporción de bioóleo del 70-75 %.
“Hemos conseguido dar salida a los residuos que se acumulan en las plantas de elaboración de zumos. Si se consiguiera secar y pirolizar estos residuos en la propia planta, el bioóleo producido se podría utilizar en las calderas para obtener calor para la empresa. Teniendo en cuenta que generan miles de toneladas de residuos, el excedente del bioóleo que no se consumiera se podría enviar a refinerías, para la obtención de un combustible más noble”, afirma el doctor Martin Olazar, responsable de la investigación. Una empresa brasileña “se ha mostrado dispuesta a poner en marcha un pequeño proyecto piloto”. Están a la espera de la resolución de un proyecto de cooperación europeo más amplio para el desarrollo de Brasil.
“Debido a la dificultad que presentaba tratar los cítricos separadamente, comenzamos a tratarlos mezclados con arena. Utilizando arena gruesa se necesitaban bombas muy potentes en el reactor, y eso suponía un gran gasto, por lo que empezamos a utilizar arena fina, pero esta se escapaba con el aire y el gas. Tuvimos que colocar un dispositivo para confinar el aire en la parte superior, confinamos el surtidor, y hemos visto que esto conlleva grandes ventajas. Tanto que lo hemos patentado”, explica el catedrático Olazar.

Martin Olazar con una muestra de bioóleo obtenido de restos de cítricos. Foto: Egoi Markaida. UPV/EHU.
En la UPV/EHU han desarrollado prototipos de este nuevo sistema, pero para ver qué sucedería a escalas mayores, los investigadores iraníes han llevado a cabo modelos de simulación del sistema de confinamiento: “Hemos visto qué comportamiento mostraría el sistema de confinamiento con diferentes dimensiones y en diferentes posiciones. Los modelos desarrollados son muy buenos para predecir lo que sucedería en niveles mayores”.
En otra línea de investigación trabajan en buscar salida al excedente de bioóleo que se produce. “Lo que sucede es que en las refinerías lo tienen todo dispuesto para trabajar con petróleo y son reacios al cambio. En otros países han obligado a las refinerías a aceptar este tipo de bioóleos, y aquí también se debería hacer algo similar”, comenta Olazar. Asimismo, en otra línea de investigación del grupo se está estudiando la producción de hidrógeno, en lugar de bioóleo, a partir de residuos cítricos, mediante un proceso de dos etapas.
Referencias:
Patente. Altzibar, H., Pablos, A., Olazar, M., Aguado., R., Bilbao, J., Vicente, J., Varona, E.: Confinador de fuente para contactores de lecho en surtidor y contactor de lecho en surtidor. Referencia: P201730388. Propietaria: UPV/EHU. Empresa explotadora: Novattia S.L.
Jon Alvarez, Bahar Hooshdaran, Maria Cortazar, Maider Amutio, Gartzen Lopez, Fabio B. Freire, Masoud Haghshenasfard, Seyyed Hossein Hosseini, Martin Olazar (2018) Valorization of citrus wastes by fast pyrolysis in a conical spouted bed reactor Fuel doi: 10.1016/j.fuel.2018.03.028
Aitor Arregi, Maider Amutio, Gartzen Lopez, Javier Bilbao, Martin Olazar (2018) Evaluation of thermochemical routes for hydrogen production from biomass: A review Energy Conversion and Management doi: 10.1016/j.enconman.2018.03.089
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Bioóleo a partir de residuos cítricos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo obtener hidrógeno a partir de una placa de circuitos impresos
- Andamios con aplicaciones biomédicas a partir subproductos alimentarios ricos en quitina
- La variedad de residuos madereros y la riqueza ecológica de los hayedos
La ciencia que deberías saber antes de comprar tu protector solar (1)
Ilustración de Tamara Feijoo.
Cuando llega el verano y renovamos los protectores solares surgen dudas. Las redes son un hervidero de información y desinformación. Además, cada año tenemos una mayor oferta y variedad: protección específica para niños, para para pieles con manchas, diferentes factores de protección, diferentes texturas y acabados, resistentes al agua, brumas, geles…
También nos preocupamos por cosas que antes no conocíamos: ¿Son mejores unos filtros solares que otros? ¿Necesito protegerme de los UVA, los UVB y los infrarrojos, o no? ¿Tendré problemas con la vitamina D si abuso del protector? ¿Tengo que usar protección solar los días nublados? ¿La ropa me protege del sol? ¿Cómo se mide el SPF y cómo sé cuál debería usar? ¿Puedo reutilizar la crema que me sobró del verano pasado? ¿Funciona igual una bruma que una crema? ¿Hay filtros solares que producen más impacto medioambiental que otros? ¿Puedo usar una crema solar en lugar de mi hidratante de día? ¿Son seguros los filtros micro y nano?
A continuación, la primera parte de una serie de artículos en los que analizaremos la evidencia científica de la que disponemos sobre todas estas cuestiones, y resolveremos las dudas más frecuentes sobre protección solar.
1. ¿Son mejores unos filtros que otros?
Los protectores solares funcionan gracias a una serie de ingredientes llamados filtros. Los hay de dos tipos: filtros físicos y filtros químicos.
Los filtros físicos, también llamados filtros minerales, habitualmente son óxido de titanio y óxido de zinc. Estos compuestos actúan como espejos que reflejan la radiación ultravioleta. Funcionan porque son sustancias fluorescentes.
La fluorescencia es un fenómeno por el cual la radiación ultravioleta es absorbida y reemitida como radiación de menor energía, inocua para la piel. La principal ventaja es que protegen de los rayos UVA y UVB. La desventaja es son de un intenso color blanco, y por ello son los responsables de que algunas cremas solares dejen un antiestético rastro blanco en la piel. Otra desventaja es que son sustancias deshidratantes.
Los filtros químicos, también llamados filtros orgánicos, son moléculas orgánicas basadas en el carbono, denominadas grupos cromóforos.
Los filtros orgánicos actúan por absorción de la radiación solar ultravioleta. Captan la energía incidente y la reemiten nuevamente como radiación térmica, inocua para la piel. En función de la radiación absorbida se distingue entre los filtros UVB, UVA y de amplio espectro. Todos ellos requieren del orden de treinta minutos para ejercer esta acción, por lo que deben aplicarse con la debida antelación antes de la exposición solar.
La principal ventaja de los filtros químicos es que son muy cosméticos. No dejan rastro blanco en la piel y pueden estar presentes en fórmulas hidratantes. La desventaja es que algunos de ellos pueden degradarse por acción de la luz, es decir, se gastan, cosa que no ocurre con los físicos. Una sustancias fluorescente es siempre fluorescente, no va perdiendo esa propiedad. Eso implica que los tiempos de reaplicación de los productos con filtros químicos se reducen. Normalmente estos filtros van asociados a otras sustancias llamadas fotoestabilizadores, que evitan que esto ocurra. El fotoestabilizador más común es el octocrileno. Éste impide que el filtro químico se degrade y llegue a penetrar en la piel, evitando así posibles intolerancias.
También existen filtros químicos como los Mexoryl que son estables a la luz por sí mismos, no penetran en la piel y que, precisamente, se utilizan para formular productos destinados para pieles sensibles y para niños. Es un mito eso de que los productos solares específicos para pieles sensibles solo lleven filtros físicos, ya que también pueden y deben llevar filtros químicos.
En la actualidad, un gran número de protectores solares están formulados con ambos tipos de filtros, físicos y químicos, para así aprovechar las ventajas de ambos. No hay por qué elegir.
2. ¿De qué radiación solar tengo que protegerme?
La radiación solar que llega a la Tierra se divide en tres tipos: la de mayor energía es la radiación ultravioleta (UV), a continuación está la radiación visible (la única que podemos observar como colores) y la de menor energía es la radiación infrarroja (IR), que es la responsable del calor. La energía que llega al nivel del mar es aproximadamente un 49% radiación infrarroja, un 42% luz visible y un 9% radiación ultravioleta.
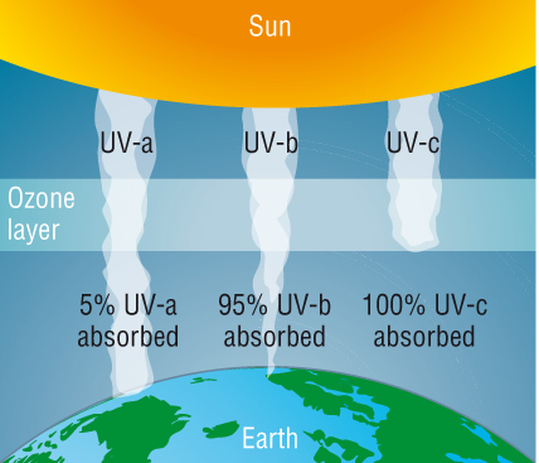
La radiación ultravioleta emitida por el sol se puede dividir en UVA, UVB y UVC, de menor a mayor energía, pero como la atmósfera terrestre absorbe gran parte de esta radiación, el 99% de los rayos ultravioletas que llegan a la superficie de la Tierra son del tipo UVA y el 1% son UVB. La radiación UV-C, que sería la más peligrosa para la salud, no llega a la Tierra porque es absorbida al 100% por el oxígeno y el ozono de la atmósfera, y por lo tanto no produce daño.

La radiación solar más energética, la ultravioleta, es capaz de ionizar átomos (de arrancarles electrones), de excitar electrones (de que los electrones pasen a niveles energéticos superiores a su estado fundamental) y de romper moléculas en unidades más pequeñas formando los temidos radicales libres, responsables del envejecimiento prematuro y promotores del cáncer.
La radiación visible no es capaz de hacer nada de esto porque no tiene la energía suficiente y, por tanto, la infrarroja, que tiene todavía menos energía, tampoco puede producir daños en la piel. Por esta razón debemos protegernos y preocuparnos exclusivamente por la radiación UVA y UVB.
Para saber si un protector solar nos protege tanto del UVA como del UVB, debemos fijarnos en los símbolos que figuran en el envase. Si aparece la palabra UVA rodeada por un círculo significa que ese producto nos protege tanto del UVB como del UVA.
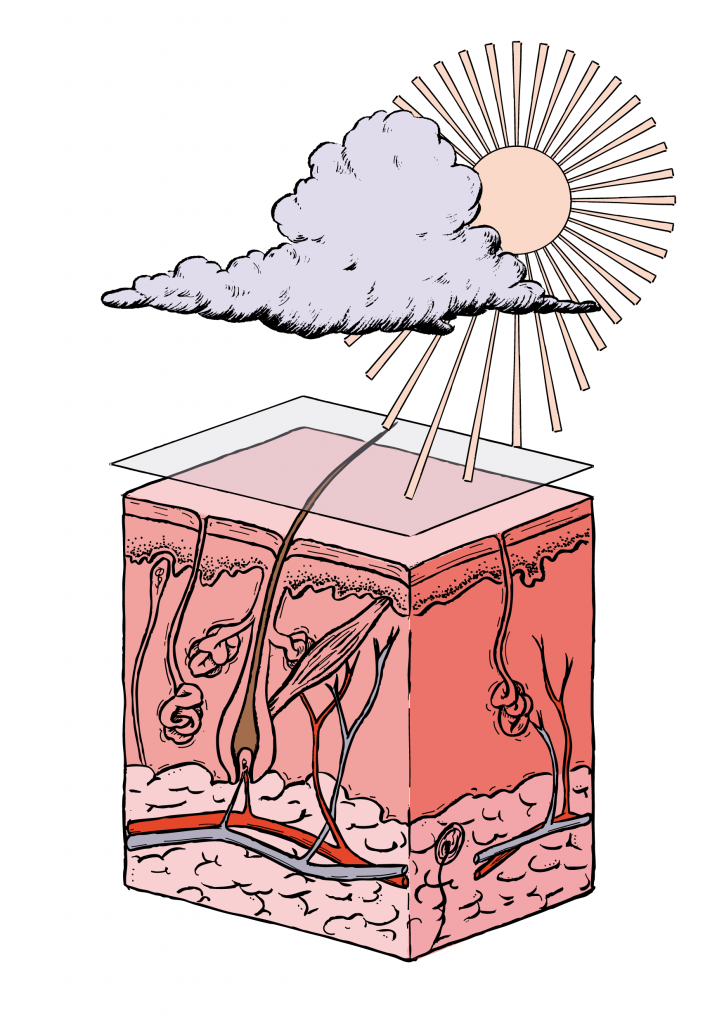
3. ¿Cómo afecta la radiación UVA y UVB a mi piel?
La capa más externa de la piel es la epidermis. Por debajo está la dermis y la hipodermis. Los rayos UVB, más energéticos, penetran poco en la piel, pero son los que provocan las quemaduras, el eritema, el enrojecimiento y aumentan el riesgo de cáncer, por lo que son los más peligrosos. Las radiaciones UVB operan sobre las células productoras de melanina, consiguiendo que se active la producción de melanina. Son responsables del mantenimiento del color bronceado de la piel a largo plazo.
Los rayos UVA penetran hasta la dermis. Son capaces de deteriorar la elastina y el colágeno de la piel, proteínas responsables de la textura, elasticidad y firmeza. Entre sus efectos negativos figura ser el máximo responsable del fotoenvejecimiento de la piel: de la elastosis (degeneración de fibras elásticas de la piel) y de la queratosis (engrosamiento de la epidermis o capa superior de la piel).
La radiación UVA actúa oxidando la melanina, la sustancia responsable del color de la piel, lo que provoca un bronceado directo que se caracteriza por desaparecer rápidamente. Así es como funcionan las cabinas de bronceado, por radiación UVA que oxida la melanina. Es decir, la radiación UVA oxida la melanina y la UVB hace que se produzca más melanina. Ambas cosas suceden en los melanocitos de la piel.
Hay que tener en cuenta que, tanto la producción de más melanina como su oxidación, son procesos acelerados por los UVB y los UVA. La piel reacciona de esta manera como mecanismo de defensa. El bronceado nunca es sinónimo de salud, sino de una piel que se ha tenido que defender de una agresión.
Tanto los UVA como los UVB son lo suficientemente energéticos como para romper los enlaces de las moléculas y generar fragmentos muy reactivos llamados radicales libres. Los radicales son tan reactivos que consiguen alterar las moléculas de ADN. Esto se traduce en que la radiación UV es mutagénica, modifica el ADN, y por tanto es potencialmente cancerígena.
Otros problemas cutáneos, como la rosácea, algunos tipos de dermatitis y el acné, se agravan a causa de la exposición a la radiación ultravioleta. Por este motivo es importantísimo protegerse de la radiación ultravioleta, tanto la UVA como la UVB.
4. ¿Son seguros los filtros micro y nano?
Los filtros físicos tienen el inconveniente de ser muy blancos. Para que resulten más cosméticos hemos conseguido reducir tanto el tamaño de partícula que el temido rastro blanco se ha convertido en cosa del pasado. Estos filtros pueden ser micro o nanoparticulados, de modo que apenas dejan residuo en la piel, sobre todo los nano, que son los más pequeños y resultan casi invisibles. Los encontramos en la lista de ingredientes fácilmente porque van precedidos del prefijo micro y nano.
Ni penetran más allá de la dermis, ni producen alergias, así que son totalmente seguros. Recordemos que la seguridad de un cosmético y de sus ingredientes está avalada por las mismas autoridades que regulan los medicamentos. Tanto es así que estos filtros nanoparticulados los encontramos en productos destinados para niños, para pieles sensibles, sensibilizadas por dermatitis, alergias y eritemas.
5. ¿Ponerse demasiada protección solar puede afectar a los niveles de vitamina D?
Tal y como he explicado en este vídeo, la vitamina D es esencial. La necesitamos para fijar el calcio a nuestros huesos. La obtenemos por dos vías: una es la alimentación (leche, huevos, pescado, setas…) y por acción de la radiación ultravioleta. La radiación ultravioleta favorece la formación de vitamina D como parte de la ruta metabólica del colesterol.
Salvo casos excepcionales, como personas afectadas por osteoporosis, los niveles de vitamina D de la población son buenos, así que no necesitamos suplementarnos ni exponernos a sol más de lo debido. Ya nos exponemos al sol sin protección muchas veces sin darnos cuenta, bien porque confiamos erróneamente en que la ropa nos protege, bien porque utilizamos menos protector del que deberíamos, no lo reponemos con la frecuencia adecuada, o no usamos ninguna protección los días nublados o los días que no vamos a la playa.
También hay que tener en cuenta que los filtros solares no actúan como pantallas frente a la radiación. Es decir, por muy alto que sea el SPF, no implica que la protección sea del 100%. Siempre hay cierto porcentaje de radiación ultravioleta que llega a nuestra piel. Este porcentaje es suficiente para nuestro metabolismo. Así que usando protección solar, obtenemos igualmente vitamina D, y así lo hacemos de forma segura, sin riesgo para nuestra salud.
Es tu turno
En los próximos artículos iremos resolviendo las cuestiones planteadas en la introducción. Si tienes alguna duda más, puedes hacérnosla llegar a través de los comentarios o directamente a través de las redes sociales utilizando la etiqueta #cienciaprotectorsolar y la incluiremos en las próximas entradas.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo La ciencia que deberías saber antes de comprar tu protector solar (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Así es la mejor crema antiedad según la ciencia
- Saber y saber que se sabe
- Estimada OCU: recuerda que NO se pueden utilizar las cremas solares del año pasado
Buscando lagunas de números no primos
En la mítica novela Contacto (1985), del astrónomo y divulgador científico estadounidense Carl Sagan (1934-1996), que sería posteriormente llevada al cine en 1997 por el director Robert Zemeckis, famoso por películas como Regreso al futuro (1985) o Forrest Gump (1994), los extraterrestres envían un mensaje, en forma de impulsos de radio, que consiste en una lista de números primos.
“… lo que estamos recibiendo semeja una larga secuencia de números primos, números enteros solo divisibles por sí mismos y por uno. Como ningún proceso astrofísico genera números primos, me atrevería a suponer que, de acuerdo con todos los criterios que conocemos, esto tiene visos de ser auténtico. […]
– El hecho de que yo sea asesor presidencial sobre temas científicos no significa nada –dijo él–, puesto que mi campo es la biología. Por eso le pido que me explique todo muy despacio. Entiendo que, si la fuente emisora se halla a veintiséis años luz, el mensaje debió de haber sido enviado hace veintiséis años. Digamos que, en la década de los sesenta, unos hombrecitos de aspecto extraño y orejas puntiagudas quisieron hacernos saber cuán aficionados eran a los números primos. Sin embargo, los números primos no son difíciles, o sea que ellos no estarían haciendo alarde de nada. Esto más bien se parece a un curso de recuperación de matemáticas. Quizá deberíamos sentirnos ofendidos.
–No –repuso ella con una sonrisa–. Piénselo de este modo. Todo esto no es más que una señal para atraer nuestra atención. Habitualmente recibimos impulsos insólitos provenientes de cuásares, púlsares y galaxias. Sin embargo, los números primos son muy específicos, muy artificiales. Por ejemplo, ningún número par es también primo. Nos cuesta creer que alguna galaxia en explosión o plasma radiante pueda emitir un conjunto de señales matemáticas como estas. Los números primos tienen como objeto despertar nuestra curiosidad.
–Pero ¿para qué? –preguntó él, desconcertado.
–No lo sé, pero en estas cuestiones es preciso armarse de paciencia. A lo mejor, dentro de un tiempo dejan de enviarnos números primos y los reemplazan por otra cosa, algo más significativo, el mensje verdadero. No nos queda más remedio que seguir escuchando.
Esa era la parte más difícil de explicar al periodismo: que las señales no tenían ningún sentido. Eran solo los primeros centenares de números primos, en orden, para comenzar otra vez desde el principio. 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31…
El 9 no era número primo, sostenía Ellie, porque era divisible por 3 (además de por 9 y 1, desde luego). El 10 tampoco lo era, porque era divisible por 5 y por 2 (además de por 10 y 1). El 11 sí era número primo, ya que solo era divisible por 1 y por sí mismo. Sin embargo, ¿por qué optaban por transmitir dichos números? Pensó en un idiot savant, una de esas personas deficientes en destrezas comunes, verbales o sociales, pero también capaces de realizar complicadísimas operaciones matemáticas tales como calcular al momento en qué día de la semana va a caer el 1 de junio del año 6977. No lo hacen para nada, sino solo porque les gusta, porque son capaces de hacerlo…”

Escena de película “Contact”, dirigida por Robert Zemeckis en 1994, en la que aparecen los protagonistas Judie Foster, en el papel de la cientifica Ellie Arroway, y Matthew McConaughey, como el filósofo cristiano Palmer Joss
Los números primos son muy importantes desde el punto de vista matemático, y juegan un papel fundamental en todas las áreas de las matemáticas, en particular, en la aritmética y la teoría de números. Esto seguramente se deba a que los números primos son los ladrillos con los que se contruye todo el edificio de los números naturales, como nos dice el teorema fundamental de la aritmética, es decir, todo número natural se puede expresar como producto de números primos, de forma única. Además, los números primos tienen importantes aplicaciones para nuestra sociedad, siendo la más conocida el sistema de codificación RSA, dentro de la criptografía, que se basa precisamente en la factorización de los números naturales como producto de números primos.
Pero no es ni la importancia de los números primos, fuera y dentro de las matemáticas, ni las aplicaciones de los mismos, el objetivo de esta entrada del Cuaderno de Cultura Científica, sino el problema de la distribución de los números primos dentro de los números naturales, o más bien, la distribución de los no primos.
Aunque empecemos por el principio. Los números primos son aquellos números naturales que solamente se pueden dividir por 1 y por ellos mismos. Así, por ejemplo, el número 25 no es primo ya que se puede dividir por 5 (además de por 1 y 25), o tampoco el 27 (divisible por 3 y 9), mientras que el número 19 sí es primo, ya que solamente es divisible por el 1 y él mismo, al igual que lo son los números 2, 3, 5, 7, 11 y 13, entre otros. A los números que no son primos, se les llama números compuestos. El número 1 no se considera primo, ya que en ese caso la factorización de los números naturales (teorema fundamental de la aritmética) no sería única, siempre se puede multiplicar por 1, pero tampoco se considera compuesto.

Humor gráfico del humorista chileno Alberto Montt sobre número primos. Viñeta aparecida el 29/04/10 en Dosis Diarias.
Si empezamos por los primeros números primos… el primero es el 2. Y es obvio que todos los múltiplos de 2 no van a ser números primos, puesto que son divisibles por 2, es decir, podemos quitar a todos los números pares de la lista de candidatos a números primos. Siguiendo el orden natural dentro de los números, nos encontramos con el siguiente número primo, el 3, y podemos quitar todos los múltiplos de 3 de la lista de candidatos a números primos. El siguiente número que no hemos eliminado y, por lo tanto, es primo, es el 5, luego podemos tachar a todos los múltiplos de 5 de la lista de números primos, y así continuamos con los múltiplos de 7, 11, 13, 17, 19, etc… Este es el conocido como método de la criba Eratóstenes (matemático griego del siglo III a.c.) para obtener los números primos, mediante la eliminación de los múltiplos de los primos que se van obteniendo.
En la siguiente imagen, hemos incluido la criba de Eratóstenes, pero solo con números impares (ya hemos eliminado los múltiplos de 2, los pares), para números más pequeños que 361 = 192. Hemos dibujado las líneas de los múltiplos de 3, 5, 7, 11, 13 y 17, con las cuales ya hemos eliminado todos los números compuestos menores que 361. Los números que quedan son todos los números primos menores que 361.
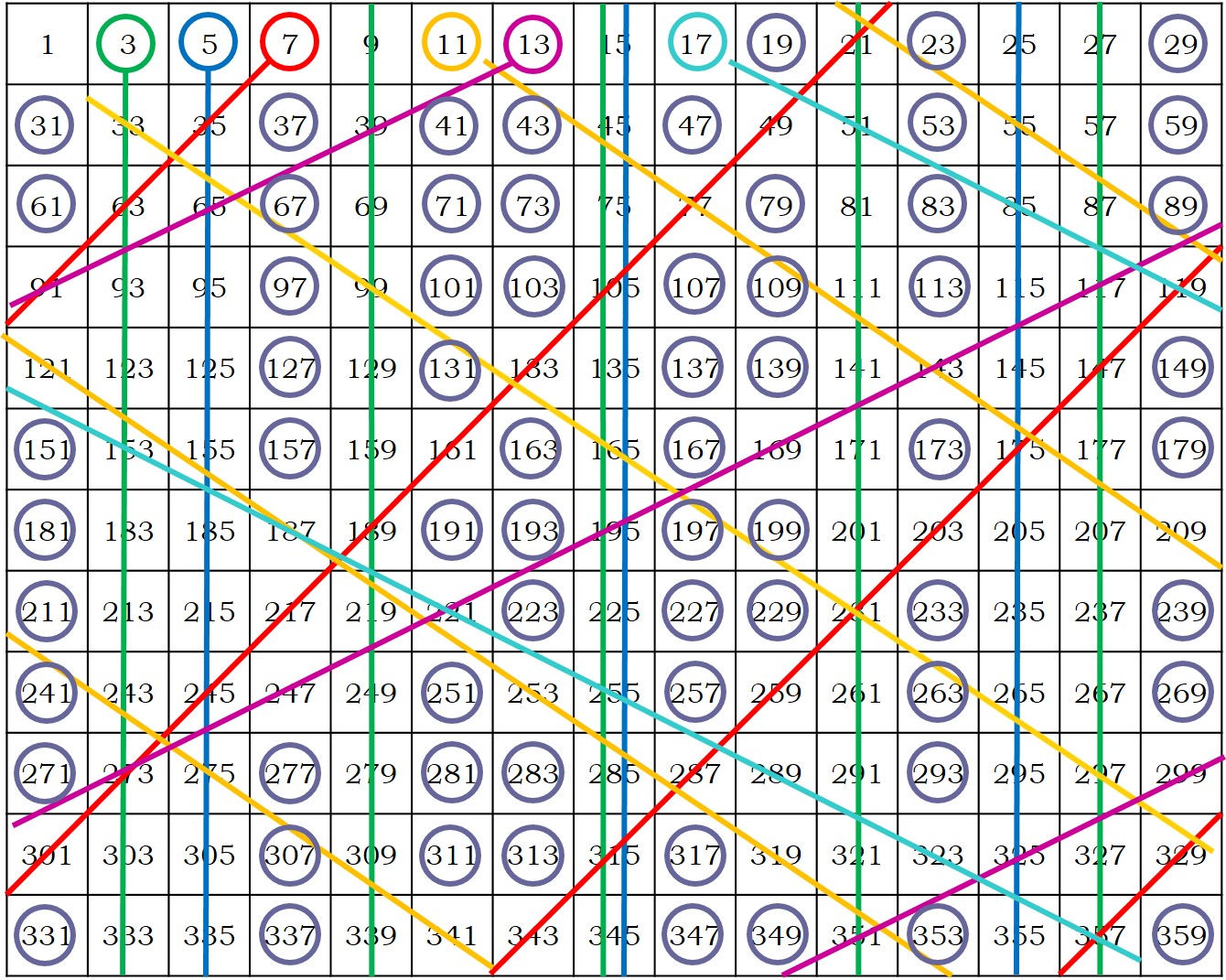
Criba de Eratóstenes de números impares menores que 361
La Criba de Eratóstenes nos permite ir obteniendo los números primos desde el 2 en adelante, pero es un método lento para obtener números primos, aunque con paciencia y muchos, muchos cálculos pueden obtenerse tablas de primos. La primera tabla amplia de números primos fue obtenida en 1606 por el matemático italiano Pietro Cataldi (1548 – 1626), que mostraba los números primos menores que 800. Así, se fueron obteniendo tablas cada vez más largas. Los primos menores que 1.020.000 fueron obtenidos en 1811 por el matemático húngaro Ladislaus Chernac (1742-1816) y hasta 100.330.200 se llegó hacia 1863, por el matemático nacido en la ciudad del imperio austriaco Lenberg (ahora ciudad ucraniana de Lviv) Jakob Philipp Kulik (1793-1863). Kulik estuvo 20 años preparando su tabla, que ocupó 8 volúmenes manuscritos con un total de 4.212 páginas. Al morir Kulik, que había dedicado su vida a la obtención de tablas matemáticas, se dijo de él: “ha dejado de calcular y de vivir”. Este tipo de tablas de números primos incluía también las descomposiciones en factores primos de los números compuestos. Todo esto antes de la era de los ordenadores.
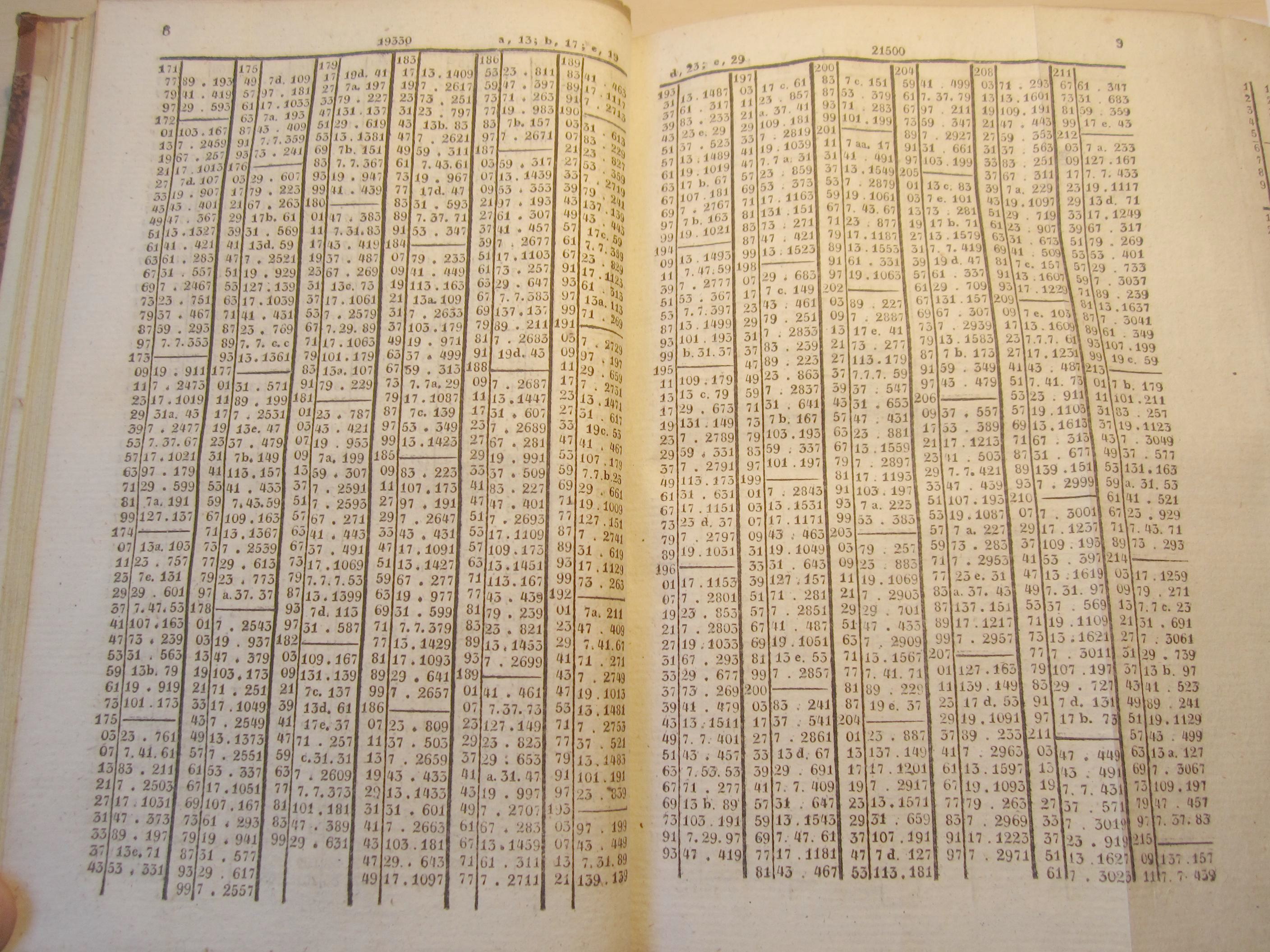
Página de la primera tabla que publicó J. P. Kulik en 1824, con la descomposición en factores, distintos de 2, 3 y 5, de los números hasta el número 21.500. Por ejemplo, arriba a la izquierda, podemos observar que el número 17177 se descompone como 89 x 193 y el siguiente 17179, como 41 x 419
Sin embargo, el método descrito por Eratóstenes no nos permite saber si un cierto número alto, por ejemplo, 28.295.303, es primo o no, salvo que se tenga ya la tabla que alcance a ese número. Para saberlo tendríamos que ver si se puede dividir por todos los números primos menores que él, lo cual es complicado como ya menciona el gran matemático alemán Carl Friedrich Gauss (1777-1855) en su obra Disquisitiones Arithmeticae (1801). Por cierto, el número 28.295.303 es compuesto y se puede dividir por 269, 293 y 359.
“El problema de distinguir los números primos de los compuestos y de descomponer estos últimos en sus factores primos se sabe que es uno de los más importantes y útiles de la aritmética. Ha ocupado el trabajo y la sabiduría de los geómetras antiguos y modernos hasta tal extremo que sería superfluo tratar el problema en toda su extensión… Es más, la propia dignidad de la ciencia parece requerir que se explore todo medio posible para la solución de un problema tan elegante y tan famoso.”
[Disquisitiones Arithmeticae, 1801, Carl F. Gauss]
Con el método de la Criba de Eratóstenes podemos ir obteniendo primos “lentamente” y con muchos cálculos. Son los números que quedan al ir eliminando los múltiplos de los primos que vamos obteniendo. Así, se puede ir consiguiendo cada vez más números primos, por lo que la primera cuestión evidente que nos podemos plantear es si llegará algún momento en que nos quedemos sin números primos, es decir, ¿hay una cantidad finita o infinita de números primos?
Los griegos ya conocían la respuesta a esta pregunta. A pesar de lo que afirma uno de los personajes de la novela La conjetura de Perelman (Ediciones B, 2011), del escritor murciano Juan Soto Ivars, la matemática Ludmila, madre en la novela de Grigory Perelman, “Se han hecho listas de números primos con ese método de comprobación, pero no se sabe si más allá siguen existiendo. No sabemos si son infinitos porque no sabemos cómo se generan”, existe una cantidad infinita de números primos.
La demostración aparece recogida en la gran obra Los Elementos del matemático griego Euclides (aprox. 325-265 a.c.). En concreto, la Proposición 20, del Libro IX, de Los Elementos, dice así “Los números primos son más que cualquier cantidad propuesta de números primos”.

Caricatura del matemático griego Euclides, perteneciente a la exposición El rostro humano de las matemáticas, de la Real Sociedad Matemática Española, y realizada por Gerardo Basabe de Viñaspre
El argumento de Euclides es el siguiente. Si existiese una cantidad finita de números primos, p1, p2, …, pn, se puede construir un número más grande que los números p1, p2, …, pn-1 y pn, pero que no es divisible por ninguno de ellos, a saber, el número p1x p2x … x pn + 1, en consecuencia, o es primo o es divisible por un primo que no es ninguno de los anteriores. Por lo tanto, existen infinitos números primos.
Por ejemplo, si consideramos los cinco primeros primos números primos 2, 3, 5, 7 y 11, podemos construir el número
2 x 3 x 5 x 7 x 11 + 1 = 2.311,
que no se puede dividir por ninguno de los números primos 2, 3, 5, 7 o 11. De hecho, 2.311 es otro número primo. O si tomamos los seis primeros números primos
2 x 3 x 5 x 7 x 11 x 13 + 1 = 30.031,
se obtiene un número que no se puede dividir por ninguno de esos seis números primos, pero como no es primo, se tiene que poder factorizar mediante números primos mayores que 13, como así es, 30.031 = 59 x 509, ambos dos nuevos primos.
Volvamos a la idea de la Criba de Eratóstenes. Cuantos más números primos se van obteniendo, mayor cantidad de números compuestos se pueden generar como multiplicación de los mismos y sus potencias, que son los que vamos descartando en este método de obtención de los números primos. Por lo tanto, aunque sabemos que existen infinitos números primos, da la impresión de que cada vez hay menos, ya que generamos muchísimos números compuestos, ¿será esto cierto o se irá manteniendo más o menos constante la cantidad de primos que van apareciendo dentro de los números naturales?
Miremos los listados de números primos. Si miramos la Criba de Eratóstenes anterior, observaremos que entre los 100 primeros números hay 25 primos, es decir, 1 de cada 4 números es primo. Sin embargo, si miramos entre los 1.000 primeros números, resulta que hay 168 que son primos, 1 de cada 6 números. Un porcentaje menor. Y así, como podemos ver en la siguiente tabla, según vamos ampliando la cantidad de números considerados, existe un menor porcentaje de números primos. Luego según vamos avanzando en la recta de números naturales, los números primos van siendo cada vez más infrecuentes, y los números compuestos van ocupando más el espacio dentro de los números naturales.
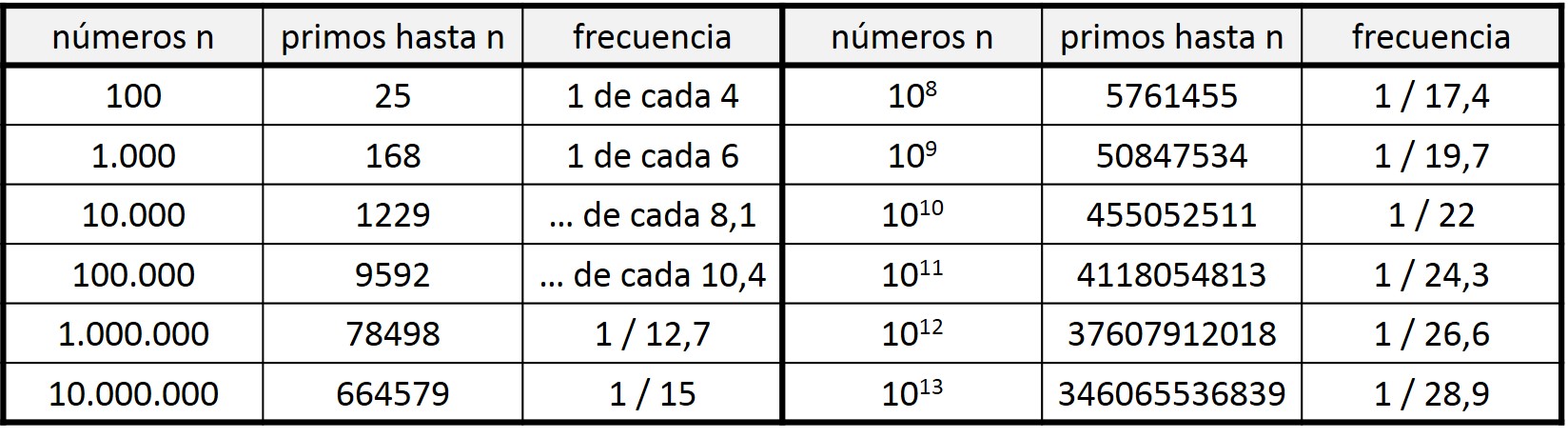
Tabla con la cantidad de números primos y frecuencia de los mismos para cantidades de números que son potencias de 10
El problema de la distribución de los números primos dentro de la recta de los números naturales es un problema importante de la teoría de números, relacionado con uno de los siete problemas del milenio “la hipótesis de Riemann”, del que ya hablaremos en el Cuaderno de Cultura Científica en otra ocasión. En esta entrada queremos hacer una pequeña reflexión sobre el problema dual, la distribución de los números compuestos.
Si volvemos a mirar la imagen de la Criba de Eratóstenes anterior observamos que al principio hay muchos números primos y la distancia entre ellos no es muy grande. Los primos 2 y 3 están pegados. Entre los primos 3 y 5, 5 y 7, 11 y 13, o 17 y 19, solamente hay un número par (de hecho, los números primos que están tan cerca, que solo les separa un número par, se llaman números primos gemelos). Entre los primos 7 y 11, 13 y 17, o 19 y 23, hay un hueco de tres números compuestos. Poco más adelante encontramos un hueco de cinco números no primos, entre el 23 y el 29, y un hueco de siete lo encontramos entre los números 89 y 97. El hueco más grande de números compuestos entre los menores de 361, que son los que aparecen en esa tabla, lo encontramos entre los números 113 y 127, que es una laguna sin números primos de 13 números compuestos. Al igual que entre los números 317 y 331.
Como hemos comentado anteriormente, cada vez hay menos números primos y más números compuestos, por lo que nos podemos plantear si existen lagunas de números compuestos tan grandes como queramos, que tengan, al menos, 100, 1.000, 1.000.000 o cualquier otra cantidad de números compuestos.
Si miramos en la literatura matemática descubriremos que el primer hueco con más de 100 números compuestos se produce a partir del número primo 370.261. De hecho, hay 111 números compuestos entre ese primo y el siguiente. Esta laguna fue encontrada por el matemático inglés James Whitbread Lee Glaisher (1848-1928) en 1877.

La primera laguna de más de 1.000 números compuestos nos la encontramos a partir del número primo 1.693.182.318.746.371. Entre este número primo y el siguiente existen 1.131 números compuestos consecutivos. Esta laguna fue obtenida por el matemático sueco Bertil Nyman en 1999.

Pero, ¿existen lagunas de números compuestos, entre dos números primos, tan grandes como queramos? La respuesta es afirmativa.
A continuación, vamos a mostrar una sencilla técnica para obtener este tipo de lagunas, para la cual necesitamos utilizar el factorial de un número. Recordemos que el factorial de un número n, que se denota n!, se define como el producto de todos los números naturales desde 1 hasta n,
n! = 1 x 2 x 3 x … x (n – 1) x n.
Aquí podéis ver un pequeño video, de la sección Una de mates del programa Órbita Laika (año 2015) de La 2, con una explicación sobre el significado del factorial de un número.
Ahora, vamos a construir lagunas de números compuestos, entre números primos, de tamaños tan grandes como deseemos. Pero vayamos poco a poco. Imaginemos que queremos encontrar dos números primos entre los cuales haya, por lo menos, 4 números compuestos consecutivos. Entonces consideramos los números
5! + 2 = 122, 5! + 3 = 123, 5! + 4 = 124, 5! + 5 = 125,
que resulta que no son números primos, ya que, por ejemplo, 5! + 2, es divisible por 2, puesto que 5! + 2 = 1 x 2 x 3 x 4 x 5 + 2 = 2 x (1 x 3 x 4 x 5 + 1), sacando el 2 como factor común. De igual forma, 5! + 3 es divisible entre 3, 5! + 4 entre 4 y 5! + 5 entre 5, luego no son primos. En consecuencia, entre el primo anterior a 122 y el siguiente a 125 se genera una laguna con, al menos, 4 números primos. Aunque, de hecho, es la laguna que hemos comentado anteriormente, entre 113 y 127, que tiene 13 números compuestos consecutivos entre ambos.
Si se desea construir una laguna de, al menos, 7 números no primos consecutivos, utilizando esta técnica, se considera el factorial de 8, que da lugar a los siguientes 7 números compuestos no consecutivos:
8! + 2, 8! + 3, 8! + 4, 8! + 5, 8! + 6, 8! + 7 y 8! + 8.
Si tenemos en cuenta que 8! = 40.320, entonces los números compuestos anteriores son 40.322, 40.323, 40.324, 40.325, 40.326, 40.327 y 40.328.
En general, si buscamos una laguna con al menos n números compuestos consecutivos, debemos de considerar el factorial de (n + 1), con el que podemos generar los n números compuestos siguientes
(n + 1)! + 2, (n + 1)! + 3, …, (n + 1)! + (n + 1).
Esta técnica es válida para cualquier número n. Luego el punto fuerte de este resultado es que nos asegura la existencia de lagunas de números compuestos tan grandes como queramos, aunque como ponen de manifiesto los ejemplos anteriores, esas lagunas pueden no ser óptimas en los siguientes sentidos.
La laguna de números no primos consecutivos puede ser más grande que el n del que partimos, como en el primer ejemplo, para el cual n = 4, luego aseguramos una laguna de, al menos, 4 elementos, pero realmente la laguna llega a tener 13 elementos. La otra cuestión es que para generar una laguna de, al menos, 8 números compuestos nos vamos al número 40.322 y los siguientes, aunque realmente una laguna con al menos 8 números no primos la encontramos ya entre los primeros números naturales, ya que como hemos comentado antes, entre los números primos 113 y 127, hay 13 números que no son primos. La cosa es más grave aún para números mayores, por ejemplo, 1000 (que tampoco es que sea excesivamente grande), ya que 1001! es un número enorme, con 2.571 dígitos, en contraste con la laguna de, al menos, 1000 números compuestos consecutivos vista anteriormente.

Chiste sobre números primos del artista gráfico Sydney Harris, que se ha dedicado al humor gráfico relacionado con la ciencia desde 1955
Bibliografía
1.- Clifford A. Pickover, La maravilla de los números, Ma Non Troppo, 2002.
2.- John Conway, Richard K. Guy, The book of numbers, Springer-Verlag, 1996.
3.- Enrique Gracián, Los números primos, un largo camino al infinito, El mundo es matemático, RBA, 2010.
4.- Wikipedia: Prime Number Theorem
5.- Eric W. Weisstein, Prime Gaps, fromMathWorld-A Wolfram Web Resource.
6.- Thomas R. Nicely, First occurrence prime gaps
7.- Página web del humorist gráfico Sydney Harris
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Buscando lagunas de números no primos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una conjetura sobre ciertos números en el ‘sistema Shadok’
- El origen poético de los números de Fibonacci
- El gran cuatro, o los números siguen estando locos
Cristalografía (2): Las rocas con lengua y la orina de Hooke
Los libros modernos de cristalografía suelen comenzar con una versión simplificada del concepto puramente matemático (de teoría de grupos y geometría) de retículo: una malla o celda unidad que es capaz de ocupar todo el espacio sin dejar huecos ni superponerse (esta es la definición de teselación en tres dimensiones). Sin embargo, los libros de texto de mediados del siglo XX y anteriores que tienen un enfoque más macroscópico de la cristalografía, suelen reflejar más pronto que tarde la que se llama Primera Ley de la Cristalografía, a saber, “los ángulos entre dos caras correspondientes de un cristal de cualquier especie química son constantes y característicos de la especie”. Esta ley fue la primera afirmación científica de la cristalografía y, aunque hoy nos pueda parecer una obviedad digna de Pero Grullo, se necesitaron nada menos que dos milenios de observaciones cristalográficas para establecerla.
Efectivamente, las observaciones del aspecto de los cristales de cualquier sustancia afirmaban que su forma no era constante, por lo que era de esperar que los ángulos entre sus caras tampoco lo fuesen. Bien entrado el siglo XVI Conrad Gessner escribía en De rerum fossilium, lapidum et gemmarium (1564) que “un cristal difiere de otro en sus ángulos y, por consiguiente, en su figura”. Se necesitó un observador de la naturaleza excepcional para ver más allá de la apariencia, Niels Steensen.

Steensen (más conocido por la versión latina de su nombre, Nicolaus Steno), fue hijo de un orfebre de Copenhague pero, en vez de continuar con el negocio familiar, decidió estudiar medicina (puede que motivado por la epidemia que mató a 200 compañeros de escuela de Steensen entre 1654 y 1655) y terminó realizando descubrimientos anatómicos importantes. Con todo, algo debió de quedarle de vocación paterna porque durante sus estudios médicos siguió coleccionando fósiles, piedras preciosas y minerales en general. En 1661 dejó su Dinamarca natal y, tras pasar un tiempo en los países bajos y Francia, terminó asentándose en Italia en 1666.
El mismo año de su llegada se capturó un enorme tiburón hembra cerca de Livorno y Steensen tuvo la oportunidad de diseccionar la cabeza del animal. Se dio cuenta de que los dientes del tiburón se parecían mucho a ciertos objetos que aparecían dentro de rocas, conocidos en esa época como glossopetrae (lenguas de roca o, mejor, rocas con lengua). Steensen llegó a la conclusión de que las glossopetrae no eran otra cosa que dientes de tiburón petrificados.
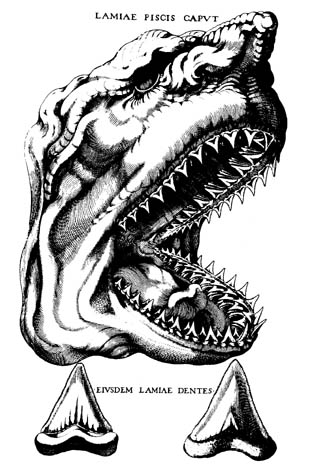
Este hallazgo le llevó a a considerar la cuestión de qué forma podía terminar un objeto sólido (como el diente de un tiburón) dentro de otro sólido (una roca). En lo que se refiere a cristales Steensen se concentró exclusivamente en el cuarzo y la hematita. A pesar de lo limitado de su enfoque, sus conclusiones tuvieron un enorme impacto.

Steensen afirmó que los cristales crecen por la acumulación de nuevas capas de partículas diminutas, capas cuya existencia queda probada por la existencia de finas estrías en los cristales. Por lo tanto, los cristales no tenían esa forma desde el comienzo de los tiempos, sino que crecían y que lo seguían haciendo en el presente. Pero la afirmación más importante que hizo Steensen fue, sin duda, la que, publicada en su De solido intra solidum naturaliter contento dissertationis prodromus (1669) decía que, si bien el número y tamaño de los lados pueden variar de un cristal a otro, los ángulos entre los lados correspondientes son siempre los mismos:
In plano axis laterum et numerum et longitudinem varie mutari, non mutatis angulis
Esta fue también la última gran contribución de Steensen a la ciencia. Steensen, nacido luterano, se había convertido al catolicismo en 1667. Después estudió teología y fue ordenado sacerdote en 1675. En 1677 ya era obispo y desde 1680 obispo auxiliar de Münster (norte de Alemania), en plena batalla contrarreformista. Murió en “olor de santidad” en 1686. Fue beatificado en 1988 por Juan Pablo II.

Volviendo a la primera ley de la cristalografía, uno esperaría que una afirmación de ese calado y para nada evidente estuviese basada en el estudio sistemático y la medición precisa y meticulosa de una gran cantidad de cristales. Pues no está tan claro. Steensen no menciona para nada que midiese cristal alguno. O bien Steensen tenía algún aparato para medir ángulos y no consideró necesario mencionarlo o simplemente llegó a esta conclusión por pura observación y especulación filosófica.
Quien se tomó el trabajo de realizar una comprobación experimental concienzuda de la ley de constancia de los ángulos fue Jean-Baptiste L.Romé de l’Isle, que recogió sus conclusiones en su obra en tres volúmenes Cristallographie, de 1783, más de cien años después de la publicación de Steensen.

Con todo, cuatro años antes de la publicación del De solido de Steensen ya se había informado de la medición de un ángulo en un cristal. En 1665, en su obra maestra Micrographia, Robert Hooke describía numerosas observaciones realizadas con el microscopio junto con otras tantas bastante más macroscópicas. Entre ellas estaban las figuras de hielo que aparecían en los charcos de orina:
Donde quiera que hubiese un centro, las ramificaciones a partir de él, […], no eran nunca menos, o más, de seis, que habitualmente se unían, o se encontraban la una a la otra muy cerca en el mismo punto o centro; aunque muchas veces no exactamente; y estaban inclinadas a cada una de las otras por un ángulo, de muy cerca de sesenta grados, digo, muy cerca, porque, aunque me apliqué a medirlos lo más precisamente de lo que fui capaz, con los compases más grandes que tenía, no pude encontrar ninguna variación apreciable de esa medida, aunque como la figura parecía componer un ángulo sólido, tenía que ser necesariamente algo menos.
Podríamos pensar que esta observación de que el ángulo era menor de 60º era errónea, pero ello sería injusto con la meticulosidad de Hooke. Efectivamente, Hooke se había dado cuenta de que el centro de las figuras está siempre un poco elevado sobre la superficie (debido a que el hielo se expande al formarse), lo que le llevó a la conclusión de que el ángulo entre las “ramas”, que en una proyección bidimensional sería exactamente 60º, como mostraban sus compases, tenía que ser ligeramente menor.
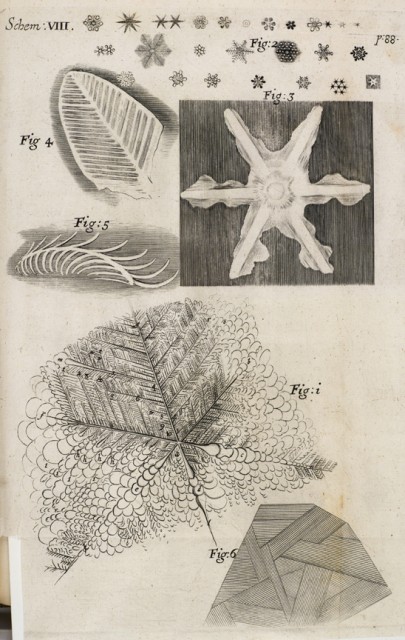
Hooke también llegó a la conclusión de que esos cristales que se formaban en los charcos de orina podría ser probablemente agua. Para ello utilizó un método electroquímico de contacto puramente cualitativo: su lengua.
Probando varias piezas claras de este hielo no pude encontrar ningún sabor urinario en ellas, sino que aquellas pocas que probé tenían un sabor tan insípido como el agua.
El método de Hooke para medir ángulos en los cristales usando un compás es aplicable si el cristal que se estudia es plano y, sobre todo, grande. Sin embargo, la mayoría de los cristales son cuerpos tridimensionales y no como los cristales estudiados por Hooke, “por encima de un pie de longitud”. Era pues necesario diseñar un instrumento para medir los ángulos de los cristales. Esta necesidad, a pesar de todo, no se hizo evidente hasta un siglo después.
Referencias generales sobre historia de la cristalografía:
[1] Wikipedia (enlazada en el texto)
[3] Molčanov K. & Stilinović V. (2013). Chemical Crystallography before X-ray Diffraction., Angewandte Chemie (International ed. in English), PMID: 24065378
[4] Lalena J.N. (2006). From quartz to quasicrystals: probing nature’s geometric patterns in crystalline substances, Crystallography Reviews, 12 (2) 125-180. DOI:10.1080/08893110600838528
[5] Kubbinga H. (2012). Crystallography from Haüy to Laue: controversies on the molecular and atomistic nature of solids, Zeitschrift für Kristallographie, 227 (1) 1-26. DOI: 10.1524/zkri.2012.1459
[6] Schwarzenbach D. (2012). The success story of crystallography, Zeitschrift für Kristallographie, 227 (1) 52-62. DOI: 10.1524/zkri.2012.1453
Este texto es una revisión del publicado en Experientia docet el 21 de noviembre de 2013
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cristalografía (2): Las rocas con lengua y la orina de Hooke se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cristalografía (1): Protociencia, del “Homo erectus” a Linneo
- Clasificación y origen, los dos problemas de la mineralogía
- Montañeros, espeleólogos y mineros
Túbulos excretores: protonefridios y metanefridios
Hay tres grandes tipos de órganos excretores: protonefridios, metanefridios y túbulos de Malpigio. Dejaremos estos últimos para otra ocasión y nos centraremos en los dos primeros.
Protonefridios
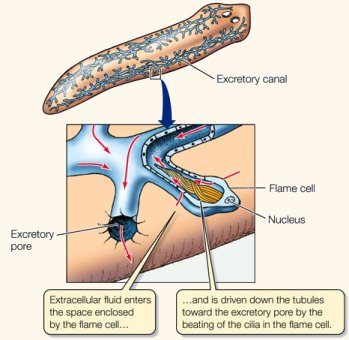
Los protonefridios forman la orina por filtración, principalmente, a partir del líquido intersticial o del líquido de alguna cavidad corporal, como el pseudoceloma o el celoma. Es propio de animales en los que no hay una cavidad interna o, si la hay, el líquido que contiene no se encuentra a la suficiente presión como para permitir por sí misma que se produzca la orina primaria. Por esa razón, el gradiente de presión necesario para generar la orina se produce gracias a que en el extremo ciego de los túbulos se concentran células flamígeras dotadas de penachos de cilios que, al batir, impulsan el fluido que se encuentra en la luz del tubo dando así lugar a una presión hidrostática negativa. Es esa presión negativa la responsable de generar el gradiente necesario. Alternativamente, en vez de células flamígeras, puede haber solenocitos, que son células de tamaño grande con un único flagelo que cumple la misma función. El agua pasa de un lado del epitelio nefridial al otro a través de perforaciones en las células próximas al extremo ciego del túbulo, y junto con el agua también pasan sustancias de pequeño tamaño.
El conducto que sigue a la zona proximal puede modificar la composición y concentración de la orina mediante reabsorción de sales, agua u otras sustancias, o mediante la secreción de solutos que deban ser eliminados. El movimiento del líquido en el interior del tubo por efecto del movimiento ciliar o flagelar es el que finalmente impulsa a la orina hacia el exterior por el nefridioporo.
Los protonefridios son propios de platelmintos, nemertinos, rotíferos y de larvas de anélidos, moluscos, algunos peces y algunos anfibios. Muy probablemente surgieron en animales de agua dulce en los que cumplían la función de expulsar el agua sobrante que entraba en abundancia en los organismos a favor de gradiente osmótico y, más adelante, de forma secundaria, empezaron a desempeñar funciones de regulación osmótica e iónica más completas.
Metanefridios
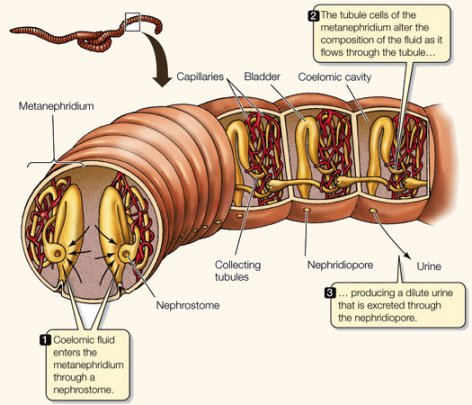
Los metanefridios son sistemas excretores propios de animales en los que hay dos o más compartimentos líquidos internos (celoma o cavidad derivada y sistema circulatorio, como mínimo). Son túbulos que comienzan con una cápsula de filtración asociada al sistema circulatorio o con una estructura similar a un embudo ciliado, abierto por su parte ancha a la cavidad celómica. En el primer caso la filtración se produce, lógicamente, a nivel de la cápsula, y en el segundo en áreas en las que el sistema circulatorio y la cavidad celómica se hallan en contacto. El gradiente de presión hidrostática no se genera en este caso desde el interior del tubo, sino que tiene su origen en la cavidad corporal de la que procede el medio interno que atraviesa el filtro debido a que se halla a una presión suficientemente alta.
Como en los protonefridios, también aquí puede sufrir la orina modificaciones en su concentración y composición mediante los procesos ya citados de secreción activa o de reabsorción. El túbulo puede presentar diversas morfologías, con plegamientos y otras disposiciones como expansiones vesiculares, y que, finalmente, se abren al exterior.
Muchos invertebrados, como anélidos, artrópodos (no insectos) y moluscos cuentan con metanefridios.
En los vertebrados los túbulos renales (metanefridiales) se llaman nefronas, y son estructuras que sufren importantes variaciones a lo largo de su desarrollo. La primera estructura se denomina pronefros, y solo es funcional en larvas de peces y de anfibios, y en peces bruja y lampreas; o sea, en estadios ontogenéticos muy tempranos o en especies muy primitivas. En peces y anfibios adultos el pronefros degenera, excepto su componente tubular, que se convierte en el mesonefros, que es el riñón de peces y anfibios adultos. En amniotas el mesonefros es el riñón embrionario, y el metanefros, que procede del anterior y es bastante más complejo, es el riñón de los adultos.
Los metanefridios han evolucionado en más de una ocasión de manera independiente. Han aparecido en moluscos adultos, anélidos, algunos artrópodos, como los crustáceos, y en vertebrados. En algunas ocasiones un único túbulo forma el órgano renal, como en la denominada glándula antenal de crustáceos. Y en otros grupos, como en vertebrados, numerosos metanefridios se ensamblan en tejido conjuntivo para formar un órgano mayor, al que llamamos riñón.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Túbulos excretores: protonefridios y metanefridios se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Así forman la orina los animales
- La regulación osmótica e iónica en los teleósteos marinos
- La regulación osmótica de los animales de agua dulce
Sobre el origen del uso de herramientas en aves
“Hugin y Munin
vuelan todos los días
alrededor del mundo
temo menos por Hugin
de que no regrese,
aún más temo por Munin”
Edda poética – Grímnismál, estrofa 20
Huggin (el pensamiento) y Munin (la memoria), dos cuervos que volaban al amanecer para recorrer el mundo recogiendo información; en la tarde regresaban para posarse en los hombros de Odín. Dos aves que, literalmente, formaban parte de esta deidad, motivo por el cual Odín esperaba impacientemente todos los días su regreso.
El cuerpo extendido de Odín, también llamado el dios-cuervo, ahora tiene una nueva extensión igualmente mágica; las herramientas que estas y otras aves son capaces de utilizar.

Hugin y Munin, modificada de “Ravens under the desert heat” / 500px – Antonio J. Osuna Mascaró (Tay)
Los seres humanos somos animales muy especiales, y parte de nuestra original forma de interactuar con el mundo se la debemos al uso de herramientas. Sin duda, nuestra relación con las herramientas fue el motivo por el que, por mucho tiempo, se consideró su uso como una exclusiva de nuestra especie, algo que requería habilidades cognitivas muy avanzadas y muy lejos del alcance para otras formas de vida.
Han pasado varias décadas desde que Jane Goodall descubriese la silueta de David Greybeard pescando termitas en aquel Gombe (Tanzania) de 1960. Greybeard, que era su chimpancé favorito, representaba un pequeño ejemplo de la riqueza cultural que ahora conocemos en esa especie, no solo en Gombe, sino en muchas otras regiones de África. Desde entonces la idea de que no somos los únicos animales que usan herramientas comenzó a extenderse en la sociedad, y aunque hoy en día aún seguimos desvelando detalles de aquel primer descubrimiento, en este tiempo ya hemos aprendido muchísimo.
Recientemente se han descubierto muchas otras especies que usan herramientas, desde otros primates hasta aves, peces o insectos. Pero también sabemos que hacer uso de herramientas no depende de habilidades cognitivas excepcionales, de hecho, usarlas no nos dice casi nada acerca de la inteligencia de una especie animal. Hay avispas que entran en esta categoría (las avispas excavadoras de los géneros Amnophila y Sphex), pero su comportamiento es absolutamente instintivo, rígido, ciego a posibles variables. Lo que nos aporta información acerca de la inteligencia de un animal no es el hecho de que usen herramientas sino cómo las usan.
Si hay un grupo animal que está poniendo patas arriba todo lo que creíamos conocer acerca del comportamiento, es el de las aves. Carentes de las manos que nos permiten a los primates manipular el entorno con sumo cuidado, el uso de herramientas entre las aves es excepcionalmente raro. Solo dos especies de córvidos y una de paseriformes (el pinzón carpintero, uno de los “pinzones de Darwin”) las usan de forma habitual. Es bien conocido el caso de los cuervos de Nueva Caledonia, y cómo el equipo de Oxford de Alex Kacelnik descubrió en 2002 con Betty y Abel algo que dejó al mundo asombrado.
Ya se conocía el uso de herramientas en esta especie desde 1972, cuando Ronald Orenstein, un investigador de la Universidad de Michigan, paseando por los bosques de Nueva Caledonia, se quedó boquiabierto al ver un cuervo usar una ramita para extraer un alimento (sin éxito alguno, por cierto). Pero fue en Oxford cuando Betty (una hembra nacida en libertad), y Abel (rescatado después de 10 años en un circo) protagonizaron una anécdota que se recordará por muchos años. Debían extraer un pequeño cesto con comida del interior de un cilindro, y para ello contaban con unos alambres rectos (opción incorrecta) y uno en forma de gancho (opción correcta). Cuando Abel voló con el único alambre con forma de gancho, a Betty solo le quedó una opción: agarró un alambre recto, voló hasta una pared donde había un pequeño hueco, y allí introdujo el alambre y lo dobló. Esto rompió los esquemas de la comunidad científica. En un solo movimiento Betty había demostrado ser capaz de diseñar una solución a un problema y de ponerla en práctica, fabricó su propia herramienta (de un material que no se parecía en nada a los que encontraría en la naturaleza). El entusiasmo científico se extendió rápidamente, los cuervos de Nueva Caledonia, alejados de nosotros 300 millones de años por la evolución, representaban una forma de inteligencia inusual en la naturaleza.
Betty doblando un alambre para sacar el cesto del interior de un cilindro. Este es uno de los vídeos originales publicados en 2002.
Han pasado casi dos décadas desde aquellas primeras observaciones y ahora debemos actualizar lo que sabemos. Desde 2016 existen evidencias de que aquel comportamiento de Betty no era tan sorprendente como parecía en aquel momento, aquella no fue una acción excepcional, sino algo que esta especie hace de forma habitual en su isla. Descubrieron que los cuervos de Nueva Caledonia sí doblan ramitas en el bosque, y las ramitas dobladas les son mucho más efectivas que las rectas a la hora de conseguir alimento. Los críticos decían que Betty se había comportado como un “robot”, solo había puesto en práctica aquello que su especie hace de forma sistemática en la naturaleza.
Esto fue un chasco sin duda, pero el entusiasmo despertado en 2002 con Betty había dado lugar a gran cantidad de experimentos que nos permiten ir mucho más allá. Tenemos muy claro que los cuervos de Nueva Caledonia sí son extremadamente inteligentes, pero el uso de herramientas parece ser solo una más de sus capacidades.
En 2009 investigadores de Cambridge demostraron que los grajos, que no usan herramientas en la naturaleza, son capaces de resolver de forma espontánea las pruebas más importantes superadas por los cuervos de Nueva Caledonia, incluyendo aquel mismo reto del alambre. Aunque ahora sepamos que la selección natural ha favorecido el uso de herramientas en algunas especies, y ha parcialmente “robotizado” este comportamiento, el uso creativo de herramientas depende de habilidades cognitivas que son comunes probablemente a todos los córvidos. De hecho, existen evidencias de que la visión y la forma del pico podrían ser los únicos factores limitantes para que algunas especies puedan usarlas o no.
Recientemente se ha descubierto que otra especie, los cuervos alalā de Hawai, también usan herramientas, y su pico parece resultado de adaptaciones específicas relacionadas con ello. Probablemente las habilidades cognitivas de los cuervos alalā tampoco sean muy distintas de las de otras especies de córvidos, al fin y al cabo, los córvidos, junto con los loros, son las aves más inteligentes que existen. Esto es algo que se ha corroborado recientemente, al descubrir que la densidad neuronal de las aves es muy superior a la nuestra (algo que explicaría por qué las palomas son superiores a nosotros en “multitasking”). Es especialmente interesante el caso de cuervos y loros donde además la proporción de neuronas dedicadas a comportamiento flexible/inteligente (similar a nuestra corteza) es muy superior a la nuestra. Sus encéfalos son mucho más pequeños que los de los primates, pero aprovechan mucho mejor el espacio.
Pese a los cientos de millones de años que separan a los primates de las aves, hemos descubierto que compartimos muchas de las habilidades cognitivas de las que nos sentimos más orgullosos (incluyendo incluso la llamada teoría de la mente, la capacidad de inferir los estados mentales de otros). Nuestro antepasado común con las aves (poco más que un pequeño lagarto) vivió antes de que los dinosaurios existiesen (los primeros dinosauros vivieron hace unos 230 millones de años), y con una altísima probabilidad no poseía estas habilidades. Es por ello deducible que las características que compartimos con las aves y que no esperamos encontrar en un reptil, se han desarrollado independientemente en su evolución y en la nuestra.
Esta convergencia es tan interesante como inesperada, pero eclipsa parcialmente otra que ya he tratado de forma indirecta. Cuervos y loros son los dos grupos de aves con las habilidades cognitivas más sorprendentes, y entre ellos hay cerca de 82 millones de años de distancia evolutiva. Esto es más fácil de poner en perspectiva comparándolo con los cerca de 94 millones de años que nos separan a nosotros de un cachalote, o de un lobo. Una distancia inmensa que hace que cuervos y loros sean protagonistas de otra interesantísima convergencia a estudiar.
Y, ¿qué hay del uso de herramientas en loros? Ninguna especie parece usarlas de forma habitual, pero sabemos que algunos loros sí tienen el potencial para usarlas.
Fue en 2012 cuando Fígaro, una cacatúa de las Tanimbar de un centro de investigación de Viena, sorprendió a la comunidad científica. El “Goffin Lab”, dónde se alojan estas cacatúas en Viena, es una pequeña casita donde estas aves tienen varias estancias, una de ellas exterior separada del bosque por una valla metálica. Fígaro estaba jugando con una piedra pequeña, cuando se le cayó fuera de la reja. Como no podía alcanzarla, Fígaro arrancó un trozo de madera de la pared, y lo utilizó para tratar de recuperar la piedra (sin éxito, por cierto). Esta observación supuso el pistoletazo de salida para muchos experimentos para revelar la capacidad de estos animales de fabricar y usar herramientas en la resolución de problemas. Se desvelaron con ellos unas capacidades cognitivas totalmente inesperadas.
Goffin Lab de Alice Auersperg (Viena, Austria). Una cacatúa nos demuestra cómo es capaz de: fabricar y usar herramientas, fabricar una misma herramienta con distintos materiales, modificar la forma, seleccionar y descartar herramientas, así como también una enorme destreza con el pico/lengua y curiosidad por destruir mi cámara.
Estas cacatúas jamás habían sido vistas usando herramientas en la naturaleza, pero resultaron ser capaces de mucho más: aprendían a usarlas por observación (aprendieron unas de otras), eran capaces de diseñar utensilios adecuados a cada problema, de modificar la forma, de crear una misma herramienta con distintos materiales, o incluso de guardarlas para usos posteriores. En 2017, un año después de que se descubriese que el comportamiento de Betty con los alambres era algo natural, y quizás menos inteligente de lo inicialmente pensado, las cacatúas del “Goffin Lab”, demostraron ser capaces de doblar y desdoblar alambres para fabricar herramientas en función de la necesidad.
Algunas especies de loros son capaces de usar herramientas al nivel de los mismísimos cuervos de Nueva Caledonia. Aunque destacan especialmente las cacatúas de las Tanimbar y los keas, esto podría ser algo común entre los loros. Salvando las distancias, recordemos el caso de los bonobos, animales que comparten muchísimas características con los chimpancés, capaces de usar herramientas a nivel casi humano (habilidades que han sido comparadas a la primera industria lítica de nuestra evolución: Oldowan), pero que apenas las usan en la naturaleza y nunca para conseguir alimento.
Es ahora cuando hemos descubierto la primera cacatúa usando herramientas en libertad, al menos ahí es a donde apunta nuestro análisis. Un solo individuo, de una población invasora en Singapur (Las islas Tanimbar se encuentran a unos 3000km de allí), usando ramitas y hojas, a modo de cuña, para abrir un enorme agujero en un coco y poder alimentarse de su interior. En más de 2000 observaciones de campo en Tanimbar, nunca se había observado uso de herramientas en estas cacatúas, lo cual sugiere fuertemente que ésta podría ser una innovación de un solo individuo.
El artículo es de acceso gratuito y lo podéis encontrar en este enlace.

Esta podría ser la primera observación de una cacatúa de las Tanimbar usando herramientas en libertad.
En 2012 Fígaro había descubierto las herramientas por sí mismo en Viena, y ahora otro individuo (al que no hemos puesto nombre), esta vez en libertad, parecía encontrarse en un punto similar; habíamos encontrado un innovador, un descubridor de herramientas.
Las cacatúas de las Tanimbar parecen estar a punto de desarrollar uso de herramientas de forma habitual a nivel de especie, tienen todas las habilidades que necesitan para usarlas de forma cultural. Es muy difícil encontrar la manifestación de un comportamiento en una especie antes de que dicho comportamiento se haga habitual entre la población, pero este parece ser un caso.
Las cacatúas de las Tanimbar, como los bonobos o los cuervos, poseen las habilidades cognitivas necesarias para el uso de herramientas. Quizás los requerimientos cognitivos necesarios para usar herramientas podrían alcanzarse desde distintos caminos a lo largo de la evolución. Puede que los animales generalistas, exploradores y por qué no decirlo, inteligentes, tengan mayor facilidad para entender la relación causa-efecto, las relaciones físicas entre los objetos, y quizás esa flexibilidad comportamental les haga más fácil extender los límites de su cuerpo mediante el uso de objetos. Pero, entre ser capaz de hacer algo y hacerlo hay una gran distancia. Es difícil que la selección natural pueda perfeccionar un comportamiento que solo es posible en potencia. ¿Qué se nos escapa?
Los lugares donde se encuentran estas aves tienen mucho en común. Las Tanimbar, Nueva Caledonia, Hawai y las Galápagos son todas islas tropicales remotas. Quizás entre los factores desencadenantes necesarios se encuentren: la falta de alimentos fáciles de obtener (sin pinchos, sin cáscara, sin encontrarse ocultos), la ausencia de depredadores (que favorece el juego, la tranquilidad y el tiempo necesario para experimentar), y la ausencia de competidores más especializados. En otros lugares estos nichos ecológicos están ocupados por especialistas; los pájaros carpinteros en Eurasia, América y África, el aye-aye en Madagascar y el falangero listado en Australia, por ejemplo.
Usar o no herramientas parece ser una cuestión ecológica, alcanzable por animales de habilidades cognitivas muy distantes (desde las avispas hasta nosotros), y una vez alcanzada, la selección natural acabaría favoreciendo su uso, modificando la forma del cuerpo, la percepción (ambas se evidencian en los cuervos), o la propia motivación a usarlas (como parece que ocurre entre chimpancés y bonobos). El juego, la exploración, el aprendizaje social, son características comportamentales de aves que las necesitan para sobrevivir y que se las pueden permitir.
En este planeta parece ser que usar herramientas no es indicativo de ser inteligente, pero ser inteligente sí puede ser indicativo del uso de herramientas.
Algunas referencias:
Birds have primate-like numbers of neurons in the forebrain. (2016) Olkowicz S, Kocourek M, Lučan RK, Porteš M, Fitch WT, Herculano-Houzel S, Němec P. Birds Proc Natl Acad Sci U S A. 113(26):7255-60. doi: 10.1073/pnas.1517131113
Can hook-bending be let off the hook? Bending/unbending of pliant tools by cockatoos. (2017) Laumer, I. B., Bugnyar, T., Reber, S. A., & Auersperg, A. M. I. Proceedings of the Royal Society B: Biological Sciences, 284(1862), 20171026. http://doi.org/10.1098/rspb.2017.1026
Cognition without cortex. (2016) Güntürkün, O. & Bugnyar, T. Trends Cogn Sci 20(4):291-303 DOI: http://dx.doi.org/10.1016/j.tics.2016.02.001
Extreme binocular vision and a straight bill facilitate tool use in New Caledonian crows. (2012) Troscianko J, von Bayern AM, Chappell J, Rutz C, Martin GR. Nat Commun. 3:1110. doi: 10.1038/ncomms2111
Functional morphology and integration of corvid skulls – a 3D geometric morphometric approach. (2009) Kulemeyer C, Asbahr K, Gunz P, Frahnert S, Bairlein F. Front Zool. 6:2.
Goffin’s cockatoos make the same tool type from different materials. (2016) Auersperg AM, Borasinski S, Laumer I, Kacelnik A. Biol Lett. (11). pii:20160689
Insightful problem solving and creative tool modification by captive nontool-using rooks. (2009) Bird CD, Emery NJ. Proc Natl Acad Sci U S A. 106(25):10370-5. doi:10.1073/pnas.0901008106.
Intelligence in Corvids and Apes: A Case of Convergent Evolution? (2009) Seed A, Emery N, Clayton N Ethology. 115(5):401–420 DOI:10.1111/j.1439-0310.2009.01644.x
On the brink to tool use? Object combinations during foraging in a feral Goffin’s cockatoo (Cacatua goffiniana) may result in rewarding tool innovations. (2018) Osuna-Mascaró & Auersperg. ABC 2018, 5(2):229–234 DOI: 10.26451/abc.05.02.05.2018
Rooks use stones to raise the water level to reach a floating worm. (2009) Bird CD, Emery NJ. Curr Biol. 19(16):1410-4. doi:10.1016/j.cub.2009.07.033
Shaping of hooks in New Caledonian crows. (2002) Weir AA, Chappell J, Kacelnik A. Science. 297(5583):981
Spontaneous innovation in tool manufacture and use in a Goffin’s cockatoo. (2012) Auersperg AM, Szabo B, von Bayern AM, Kacelnik A. Curr Biol. 22(21):R903-4. doi:10.1016/j.cub.2012.09.002
The mentality of crows: convergent evolution of intelligence in corvids and apes. (2004) Emery NJ, Clayton NS. Science. 306(5703):1903-7. DOI: 10.1126/science.1098410
Tool Use in Digger Wasps (Hymenoptera: Sphecinae) (1985) Psyche A Journal of Entomology 92(2-3) DOI: 10.1155/1985/73184
Tool-use by the New Caledonian crow (Corvus moneduloides). (1972) Orenstein RI. Auk 89, 674–676
Este post ha sido realizado por Antonio J. Osuna Mascaró (@Biotay) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Sobre el origen del uso de herramientas en aves se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las herramientas de edición genética CRISPR y los ratones avatar
- Las aves de Prometeo
- Sobre la predisposición genética a padecer enfermedades (II)
Zientziateka: Déborah García Bello – Elementos a vuelapluma

La convergencia entre las diferentes áreas de estudio ha supuesto desde siempre una herramienta maravillosa para reflejar de una forma global y fidedigna la realidad de cada tiempo. En este sentido, la conexión entre la naturaleza, la literatura y la ciencia es, quizás, una de las formas más fabulosas que tiene el ser humano para diseñar una ventana desde donde poder contemplar y enseñar el mundo desde múltiples y complementarias perspectivas.
La unión de estas tres áreas de conocimiento fue la temática principal del ciclo de conferencias “Naturaleza, Literatura y Ciencia” que albergó Azkuna Zentroa entre el 10 y el 19 de abril pasados.
En “Elementos a vuelapluma” García Bello analiza el papel protagonista que juegan la química y sus fenómenos en la literatura. La ponente invita a los asistentes a sumergirse en libros y canciones en los que la química se ha colado a vuelapluma, convirtiéndose en un poderoso elemento literario.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Zientziateka: Déborah García Bello – Elementos a vuelapluma se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Déborah García Bello: Saboer
- Zientziateka: Raúl Ibáñez – El teorema de la rosa
- Mestizajes: La ciencia en “La educación de Henri Adams”, por José Manuel Sánchez Ron
Ruido en el aprendizaje de idiomas

¿Quién no ha intentado mantener una conversación en una lengua extranjera en un bar ruidoso y se ha dado cuenta de que no comprende casi nada? Gran número de estudiantes de idiomas extranjeros han experimentado la dificultad de entender ese idioma fuera de las aulas. En la vida real, las conversaciones se suelen desarrollar en ambientes bulliciosos como bares y restaurantes, estaciones de tren o calles con tráfico, con muchas fuentes de ruido y hablantes simultáneos. En esos escenarios, a las personas que no dominan completamente un idioma les cuesta mucho más entender la lengua extranjera que su lengua materna. Esto se debe a que cuando los niños y las niñas aprenden su lengua materna lo hacen con gran variedad de hablantes y en circunstancias y ambientes muy diversos, en muchas ocasiones con ruido y otras perturbaciones, que es lo habitual en el mundo real. Con lo cual desarrollan estrategias que les permiten comprender su idioma en dichas situaciones.
Esta circunstancia llevó a plantearse al grupo de investigación de la UPV/EHU, formado por Maria Luisa García Lecumberri y Martin Cooke, que incluir ruido de fondo en el entrenamiento de sonidos extranjeros podría ser beneficioso para la comprensión de la lengua extranjera. No obstante, también cabía la posibilidad de que, dada la dificultad añadida, introducir ruido en el entrenamiento pudiera resultar contraproducente.
Sin embargo, en su estudio, despejan las dudas y demuestran que enseñar los sonidos de un idioma con ruido de fondo, por un lado, no es en absoluto perjudicial, ya que se aprenden de igual manera que en un ambiente silencioso. Y por otro lado, se logra entender mejor ese idioma en situaciones y lugares en los que hay ruido, en los que, en definitiva, transcurre el día a día de cualquier persona.
En la investigación participaron 88 personas bilingües hablantes de euskera y castellano. Sometieron a un entrenamiento en consonantes del inglés a dos grupos de personas unas con y otras sin ruido de fondo durante 10 sesiones. A lo largo de cinco semanas trabajaron con 200 ejemplos de cada consonante inglesa, más de 4.800 ítems en total. Se les comparó con dos grupos de control expuestos a vocales con y sin ruido y con un grupo de nativos ingleses.
«Los resultados demuestran que el entrenamiento con ruido es eficaz y no perjudicial. Es más, los estudiantes entrenados con ruido fueron ligeramente superiores al identificar consonantes que los entrenados en entornos silenciosos», señala Maria Luisa García Lecumberri.
Lo más notorio del estudio es lo beneficioso que resulta el entrenamiento para entender el idioma extranjero en la vida real. «Antes del mismo las personas no nativas cometían errores en casi la mitad de las consonantes presentadas en ambiente ruidoso mientras que después de entrenarles con ruido de fondo los errores se redujeron a niveles casi nativos, aproximadamente 3 errores de cada 10 consonantes». Asimismo, a la hora de percibir las consonantes en ambientes silenciosos, las personas entrenadas con ruido obtuvieron puntuaciones muy similares a las de los entrenados sin ruido y muy cercanas a las de los nativos.
«Nuestro estudio demuestra la importancia de reproducir las condiciones naturales cuando se aprende una lengua extranjera, incluyendo variedad de hablantes y ambientes con ruidos de diverso tipo, a diferencia de la enseñanza en condiciones de laboratorio asépticas», resume Martin Cooke. El siguiente paso es averiguar cómo funciona este aprendizaje en ruido. Una de las hipótesis que baraja el grupo de investigación es que la escucha de los sonidos con ruido estimula a los oyentes a centrarse, de entre los múltiples rasgos de cada sonido, en los más robustos a las perturbaciones.
Referencia:
Martin Cooke & Maria Luisa Garcia Lecumberri (2018) Effects of exposure to noise during perceptual training of non-native language sounds Journal of the Acoustical Society of America DOI: 10.1121/1.5035080
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Ruido en el aprendizaje de idiomas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El aprendizaje del inglés es mejor si se usa para aprender otra cosa
- La enseñanza multilingüe de las lenguas
- Cómo cargar el móvil a partir del ruido magnético ambiente
El robado prestigio de la ciencia

El Instituto Nacional de la Salud estadounidense acaba de cancelar un gran proyecto de investigación, una de esas cooperaciones público/privadas que a los políticos les encantan. Se trata del llamado MACH15 que pretendía determinar mediante un estudio a largo plazo si la ingesta de moderadas cantidades de alcohol puede ser beneficiosa para la salud, y que iba a ser financiado por contribuciones de hasta 100 millones de dólares de la industria de las bebidas alcohólicas. Tras denuncias en la prensa sobre comportamientos sospechosos y la apertura de dos investigaciones internas el INS ha decidido que el modo como se ha solicitado el dinero y se proponía repartirlo era incompatibles con sus normas internas de conflicto de intereses y habrían descalificado cualquier resultado. MACH15 ha sido así cancelado, y para bien.
No es el único caso de excesiva proximidad entre intereses económicos e investigaciones científicas; las redes están llenas de airadas acusaciones sobre estudios financiados por empresas privadas que demasiado a menudo tienden a respaldar conclusiones que favorecen a quienes los pagan. Las universidades e instituciones de investigación han incorporado a sus normas internas reglas para evitar este tipo de problemas, y de vez en cuando ocurre un caso como el del MACH15 y un estudio se cancela. Y así es como debe ser: no es de recibo que el conocimiento de la Humanidad se retuerza en favor de los intereses económicos de algunos, de modo que es necesario poner cortapisas a este tipo de comportamientos. Como por ejemplo la financiación pública de la investigación, que sortea el problema de raíz.
Pero no hablamos de las necesarias precauciones que hay que instalar para evitar el sesgo de los resultados científicos en favor del dinero, sino del innegable y continuo empeño tanto de empresas como de actores interesados (como las pseudociencias) por investirse del mando de la ciencia sea como sea. Los vendedores de toda laya anhelan disponer del respaldo de datos, batas blancas, laboratorios y gráficos coloreados para los anuncios de sus productos. Están dispuestos a llegar a cualquier tipo de arreglo, más o menos legal, más o menos ético, con tal de darle una buena capa de investigación científica a lo que venden. Sean los datos reales o no. Y esto nos dice algo importante: la ciencia tiene prestigio real, un prestigio ganado a pulso y por buenas razones en la sociedad.
Un prestigio que intentan robar quienes financian estudios para que respalden sus productos, o quienes llenan sus anuncios de batas bancas y coloridos líquidos en tubos y matraces.
La ciencia vende porque la gente cree en la ciencia, incluso cuando no la entiende; porque los avances basados en la investigación han mejorado de forma espectacular la vida de las personas y la gente lo sabe. Si los intereses económicos son capaces de llegar a extremos como gastar dinero en fabricar datos a medida que les favorezcan es porque saben que la apariencia de ciencia le dará respaldo a sus productos y beneficios a sus cuentas. Lo que hacen es apropiarse del prestigio ajeno, duramente ganado, para engordar sus propias arcas; un engaño y un robo. El prestigio, empero, es real, y merecido, y hay que defenderlo de los abusos.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo El robado prestigio de la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Los 880 cuadrados mágicos de orden 4 de Frénicle
Bernard Frénicle de Bessy (¿1605?-1675) fue un matemático francés, uno de los miembros fundadores (en el área de geometría) de la Académie royale des sciences, creada en 1666, durante el reinado de Luis XIV,bajo el patrocinio de su primer ministro Jean-Baptiste Colbert.

El ministro Jean-Baptiste Colbert presentando a los miembros fundadores de la “Académie royale des sciences” a Luis XIV. Siendo Bernard Frénicle de Bessy uno de los fundadores será probablemente una de las personas situadas a la izquierda del lienzo. El cuadro (¿1675-1680?) es de Henri Testelin. Fuente: Wikimedia Commons.
Frénicle se interesó por la astronomía y la mecánica, pero es sobre todo conocido por sus trabajos en teoría de números y combinatoria.
Como recordaba Raúl Ibáñez en Las matemáticas del taxi, el famoso número de Hardy-Ramanujan –el menor número natural que puede expresarse como la suma de dos cubos positivos y de dos formas diferentes– fue introducido por Frénicle en 1657.
Frénicle describió los cuadrados mágicos (serie de números enteros situados en una matriz de tal forma que la suma de los números por columnas, filas y diagonales principales sea la misma) de orden 4 en Des quarrez ou tables magiques, publicado a título póstumo en 1693. Allí describió los 880 cuadrados mágicos “esencialmente diferentes” (obvió los obtenidos al permutar o se trasponer filas o columnas en esa larga lista) de orden 4.
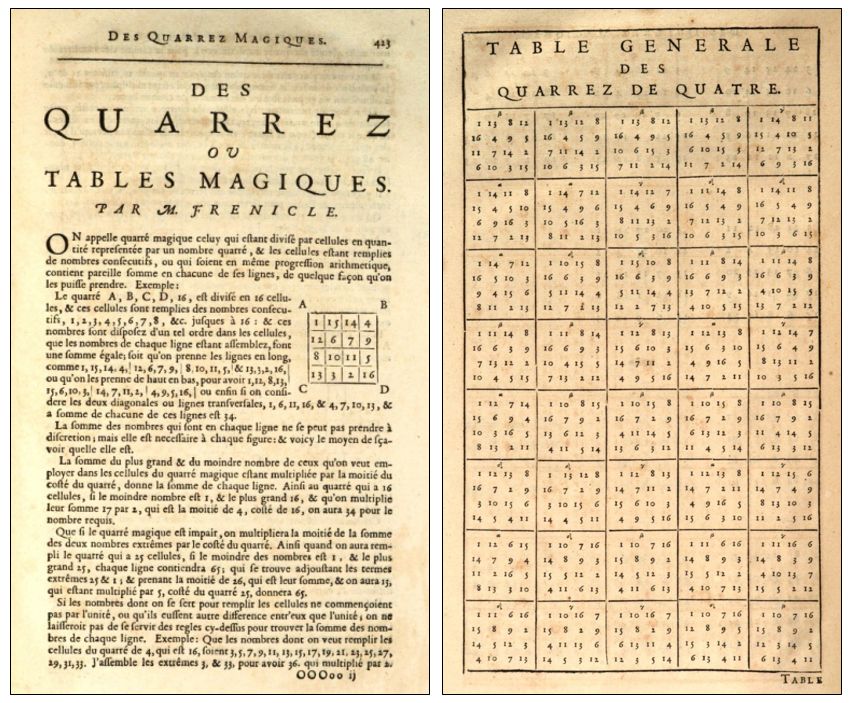
Primera página de “Des quarrez ou tables magiques” y primera página de “Table générale des quarrez de quatre”. Extraídas de “Divers ouvrages de mathematique et de physique” (páginas 423 y 484). Fuente: Google Books.
Los cuadrados mágicos de orden 4 descritos por Frénicle –formados por números que van desde el 1 al 16– poseen una curiosa propiedad: si a cada número de cada casilla del cuadrado se le resta 1, obtenemos un cuadrado mágico con números que van del 0 al 15. En este nuevo cuadrado, cada una de las filas y columnas tiene una suma de nim igual a 0. ¿Y qué es la suma de nim? Lo explicaremos con un ejemplo. Debajo aparece un cuadrado de Frénicle (con números del 0 al 15) y junto a él la matriz de esos números escritos en base 2.

Sumar los dígitos de las filas de la matriz en base 2 ‘a la nim’, supone decidir que 1+1=0 y no se tiene en cuenta ‘la llevada’. Así, tenemos:
0000 + 0101 + 1010 + 1111 = 0000,
1110 + 1011 + 0100 + 0001 = 0000,
1101 + 1000 + 0111 + 0010 = 0000, y
0011 + 0110 + 1001 + 1100 = 0000.
Del mismo modo, si se suman ‘a la nim’ las columnas, queda:
0000 + 1110 + 1101+ 0011 = 0000,
0101 + 1011 + 1000 + 0110 = 0000,
1010 + 0100 + 0111 + 1001 = 0000, y
1111 + 0001 + 0010 + 1100 = 0000.
¡Curiosa propiedad!
Por cierto, lleva el nombre de este matemático la forma estándar de Frénicle de un cuadrado mágico. Recordemos que un cuadrado mágico está en forma estándar de Frénicle si cumplen las dos condiciones siguientes:
- el elemento situado en la posición (1,1) –la esquina superior izquierda– es el menor de los cuatro elementos de ángulo, y
- el elemento situado en la posición (1,2) –a la derecha de la esquina superior izquierda– es menor que el elemento situado en la posición (2,1) –bajo la esquina superior izquierda–.
Esta forma estándar se ideó ya que, como hemos comentado arriba, un cuadrado mágico es “esencialmente el mismo” si se permutan o se trasponen sus filas o columnas. Existen ocho cuadrados mágicos que comparten una misma forma estándar. Por ejemplo, los ocho que aparecen debajo, siendo el último el que está en forma estándar de Frénicle.

Ocho cuadrados «esencialmente iguales».
Visto en The Nimm0 Property, Futility Closet, 14 junio 2018
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Los 880 cuadrados mágicos de orden 4 de Frénicle se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Habibi y los cuadrados mágicos II
- The grid (Habibi y los cuadrados mágicos: un estrambote)
- Habibi y los cuadrados mágicos III
Cristalografía (1): Protociencia, del “Homo erectus” a Linneo

De pocas ciencias puede afirmarse que tienen un origen anterior incluso a la propia especie humana. Y es que la fascinación que ejercen los cristales llevó a antecesores del Homo sapiens a recogerlos, conservarlos y usarlos como herramientas. Este es el caso de los cristales de cuarzo encontrados entre huesos de Homo erectus pekinensis de entre 250.000 y 700.000 años de antigüedad y herramientas de piedra excavados en la cueva de Zhoukoudian (China). Es llamativo, sin embargo, que algunos de estos cristales no muestran signos de haber sido usados y podrían haber tenido alguna otra función, posiblemente decorativa o ceremonial. Lo mismo ocurre con los seis cristales de cuarzo no utilitarios encontrados en Singi Talav (cerca de Didwana, en el desierto de Thar, Rajastán, India) encontrados en una capa arqueológica ocupada por Homo erectus hace entre 150.000 y 300.000 años.
Es comprensible que la belleza de algunos especímenes minerales cristalinos atrajesen la atención de nuestros antepasados y, por esta sola razón, fuesen recogidos como objetos preciosos. De aquí a que adquieran valor más allá del utilitario había un paso; hay constancia de uso ornamental por los antiguos sumerios, egipcios, chinos y mayas. El siguiente, paso, el mágico/religioso fue casi contemporáneo y se ve reflejado incluso en los libros sagrados. Efectivamente, sólo el Antiguo Testamento, por ejemplo, recoge 23 minerales de uso ornamental/litúrgico:
Lo guarnecerás de piedras preciosas, dispuestas en cuatro hileras: en la primera habrá un jaspe rojo, un topacio y una esmeralda; en la segunda, un rubí, un zafiro y un diamante; en la tercera, un ágata, una cornalina y una amatista; y en la cuarta, un crisólito, un lapislázuli y un jaspe verde. Todas ellas estarán engarzadas en oro. Éxodo, 28: 17-20 (se repite en Éxodo, 39: 10-13)
Estabas en Edén, el Jardín de Dios, recubierto de piedras preciosas de todas las especies: sardo, malaquita y diamante, crisólito, ónix y jaspe, zafiro, topacio y esmeralda. Llevabas adornos labrados en oro y encajes preparados para ti el día en que fuiste creado. Ezequiel, 28:13
[..] porque Jerusalén será reconstruida, y también su Templo por todos los siglos! ¡Feliz de mí, si queda alguien de mi descendencia para ver tu gloria y celebrar al Rey del cielo! Las puertas de Jerusalén serán hechas de zafiro y esmeralda, y todos sus muros, de piedras preciosas; las torres de Jerusalén serán construidas de oro, y sus baluartes, de oro puro. Las calles de Jerusalén serán pavimentadas de rubíes y de piedras de Ofir; Tobías, 13:17

La palabra cristal viene del griego clásico κρύσταλλος (crústallos), que denominaba tanto a los témpanos de hielo como al cristal de roca (cuarzo) y, por extensión a cualquier sólido transparente, y ésta de κρύος (crúos), escarcha. Los griegos creían que el cristal de roca era hielo muy congelado, algo que debería parecerle absurdo a cualquiera que lo tocase y se diese cuenta de que no estaba frío. Pero el conocimiento antiguo era poco experimental y esta creencia se mantuvo durante toda la Edad Antigua, la Edad Media y el Renacimiento. La prueba que se daba era que se decía que existían pequeñas gotitas de agua dentro de los trozos de cristal de roca. Esta invención era un lugar tan común, que hasta los poetas como Claudius Claudianus le dedicaban sentidos epigramas.
Otro ejemplo de las consecuencias de la repetición y comentario de textos anteriores y la falta de interés por el experimento entre filósofos y escolásticos es que Caius Plinius Secundus (conocido como Plinio el Viejo), del que hablaremos algo más en un momento, afirmaba que existían montañas de imanes en las que una persona que llevase botas con clavos de hierro se quedaba atascada y, también otras, de imanes invertidos que repelían el hierro y donde una persona con esas botas no podía pisar. Además menciona que un imán pierde sus propiedades si se le frota con ajo. Este “hecho” se creyó a pies juntillas hasta finales del siglo XVI, más de 1.500 años después de Plinio, cuando a William Gilbert se le ocurrió hacer el experimento e informar de ello en De magnete, magneticisque corporibus, et de magno magnete tellure (Sobre los imanes, los cuerpos magnéticos y el gran imán terrestre) en 1600.
No es de extrañar, pues, que los conceptos de cristal y mineral fuesen bastante vagos antes de 1.500 y que las fuentes que los mencionan sean muy escasas. Notaremos algunas de las importantes.

En la obra maestra de Titus Lucrecius Carus, De rerum natura (publicada en el siglo I a.e.c.), presenta los principios del atomismo yaparecen listados algunos sólidos ordenados según su dureza: diamante, cuarzo (corindón), hierro, bronce y, lo que es más interesante, liga sus propiedades a su composición atómica.
Lucrecio también propuso, en el libro II de De rerum natura aunque fuese muy esquemáticamente, un mecanismo para el crecimiento de los cristales, aunque no los mencionase explícitamente: los cuerpos crecen cuando muchos átomos se adhieren a ellos y se reducen cuando los átomos se separan de ellos.
Cuál es el movimiento con que engendran y a los cuerpos destruyen los principios de la materia, y cuál es el impulso y cuál la rapidez que hace que vuelen por el espacio inmenso sin descanso. Porque seguramente la materia no es una masa inmóvil, pues que vemos disminuirse un cuerpo, y de continuo manando, se consumen a la larga y el tiempo nos los roba de la vista; se conserva sin pérdidas la suma: empobreciendo un cuerpo, los principios van a enriquecer otro, y envejecen los unos para que otros reflorezcan; ni en un sitio se paran; de este modo el universo se renueva siempre […] Traducción de José Marchena
Plinio, a pesar de lo que decíamos más arriba, ofreció algunos atisbos de proto-cristalografía y proto-mineralogía en su obra más importante Naturalis historia (publicada poco antes del año 77 e.c.). Plinio aparece fascinado por las caras perfectamente planas y lisas del cuarzo y describe cuatro piedras preciosas cuyos cristales se encuentran habitualmente en la naturaleza: el cuarzo (crystallus), la piedra-arcoiris (iris, lo más seguro cuarzo con impurezas), el diamante (adamas) y el berilo (smaragdus, del griego σμάραγδος , “gema verde”; la esmeralda, un berilo verde, deriva su nombre de aquí). Los cristales se describen como “hexagonales” (sexangula figura) y “hexaédricos” (sexangulus laterbius) pero no existe nombre ni concepto de cristal.

Otra referencia interesante de Plinio está en la descripción de las ventanas e invernaderos de las casas ricas de Roma, cubiertas por cristales de lapis specularis, una forma deshidratada del sulfato de calcio (yeso), debido a su transparencia (estrictamente hablando es translúcido), tamaño (hasta un metro) y planaridad.
La información mineralógica contenida en la Naturalis historia de Plinio fue preservada y mejorada algo en libro XVI “de piedras y metales” de las Etimologiae (publicadas alrededor de 630) de Isidoro de Sevilla. Y también se encuentra recogida en el Lapidario (publicado alrededor de 1250), tratado fundamentalmente astrológico mandado escribir por Alfonso X de Castilla. Y poco más hasta mediados del siglo XVI.

Efectivamente, las mayores contribuciones a la cristalografía desde Plinio aparecen casi simultáneamente en términos históricos: nos referimos a la De la pirotechnia de Vannoccio Biringuccio de 1540 y a De re metallica de Georg Pawer (más conocido por su nombre latinizado Georgius Agricola), publicada en 1556.
Biringuccio aporta descripciones precisas de muchos cristales en De la pirotechnia, además de constatar la habitual fascinación con su perfección. Así los cristales de alumbre son “gruesos cuadrados con bellas esquinas que parecen grandes diamantes”, y los de pirita son “pequeños cubos […] tan bien cuadrados que ningún dibujante podría dibujar sus esquinas con mayor precisión o mejor con cualquier tipo de instrumento”. También da detalles de cómo la cristalización puede usarse para la purificación de menas minerales, como el vitriolo verde (FeSO4·nH2O) y el alumbre.
Sin embargo, incluso este inteligente observador de la naturaleza y amante de la tecnología, que critica a los “alquimistas” y otros “filósofos” que escriben a partir de libros en vez de la experiencia, no puede sustraerse a la tentación al hablar de las piedras preciosas, a las que atribuye propiedades fantásticas. Entre estas propiedades está que el rubí neutraliza los venenos y purifica “el aire corrompido por un vapor pestilente”, que los diamantes se vuelven quebradizos si se manchan con sangre de cabrito o que las esmeraldas se encuentran en los nidos de los grifos y previenen la epilepsia, pero que “se rompen en muchos lugares si se lleva durante el coito”.
De forma análoga, Agricola, cuyo texto, por lo demás muy cuidadoso en las cuestiones técnicas, e influyente hasta bien entrado el siglo XVII, mantiene muchas de las viejas creencias heredadas, como la capacidad del ajo de desmagnetizar la magnetita.
Aunque pueda extrañar a alguno, está breve exposición de la cristalografía como protociencia no quedaría completa si no mencionásemos al que es considerado, por lo demás, un científico de pleno derecho, uno de los padres de la biología, Carl Nilsson Linnæus. Al leer lo que sigue consideremos que Linneo fue contemporáneo (finales del XVIII), nada menos, que de Jean-Baptiste Romé de l’Isle, uno de los padres de la cristalografía moderna.
Linneo, al igual que hizo con las plantas y los animales, dividió los minerales en su obra maestra, Systema naturae, en clases, órdenes, familias y géneros, y a cada mineral le dio dos nombres, análogamente a lo que hoy llamamos comúnmente nombre científico (taxones) de plantas y animales. En este sistema existían tres clases de minerales: Petrae (rocas), Minerae (menas) y Fossilia (excavados). La mayoría de los materiales macrocristalinos los clasificó como Minerae, y éstos los dividió en Salia (sales, la mayoría de cristales transparentes), Sulphura (azufres, incluyendo el ámbar, los aceites y los sulfuros) y Mercuralia (mercúricos, los metales). La clasificación de Linneo no tenía en cuenta ni la composición química ni las reglas cristalográficas ya conocidas en la época. Además Linneo aún reflejaba en su obra la idea de John Duns Scotus de que los cristales están vivos ya que, al igual que las plantas, crecen a partir de una semilla, y mueren cuando se disuelven o funden.
De hecho, Systema naturae podría considerarse una pura curiosidad histórica protocristalográfica más, si no fuese por un hecho fortuito. Fue el libro que despertó el interés por la mineralogía en René Just Haüy; y de los resultados de ese interés hablaremos extensamente en su momento.
Referencias generales sobre historia de la cristalografía:
[1] Wikipedia (enlazada en el texto)
[3] Molčanov K. & Stilinović V. (2013). Chemical Crystallography before X-ray Diffraction., Angewandte Chemie (International ed. in English), PMID: 24065378
[4] Lalena J.N. (2006). From quartz to quasicrystals: probing nature’s geometric patterns in crystalline substances, Crystallography Reviews, 12 (2) 125-180. DOI: 10.1080/08893110600838528
[5] Kubbinga H. (2012). Crystallography from Haüy to Laue: controversies on the molecular and atomistic nature of solids, Zeitschrift für Kristallographie, 227 (1) 1-26. DOI: 10.1524/zkri.2012.1459
[6] Schwarzenbach D. (2012). The success story of crystallography, Zeitschrift für Kristallographie, 227 (1) 52-62. DOI: 10.1524/zkri.2012.1453
Este texto es una revisión del publicado en Experientia docet el 15 de noviembre de 2013
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cristalografía (1): Protociencia, del “Homo erectus” a Linneo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Esa pesadilla científica llamada mineralogía
- Clasificación y origen, los dos problemas de la mineralogía
- Montañeros, espeleólogos y mineros
El arte de abrir cráneos: neurocirugía y trepanaciones durante el imperio inca
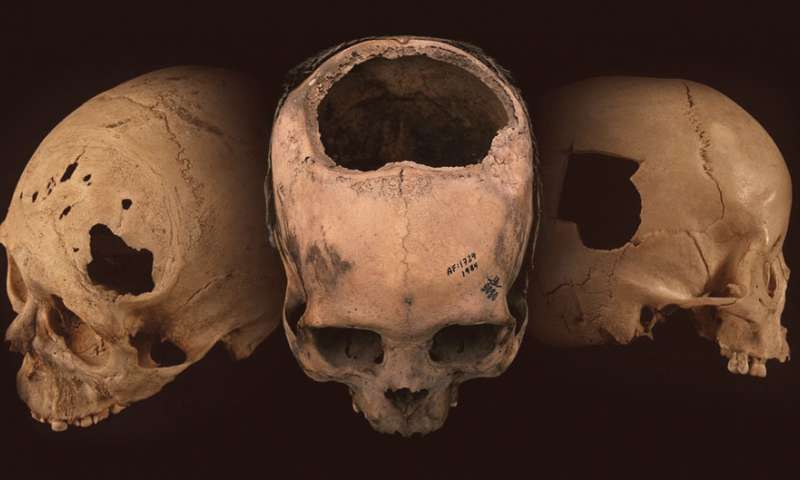
Tres cráneos trepanados. Fuente: Universidad de Miami
De todas las operaciones quirúrgicas que esperamos no necesitar a lo largo de nuestra vida, la de que nos abran el cráneo para acceder a nuestro cerebro es probablemente una de las primeras de la lista. La mera idea de una trepanación, un término que en sí mismo ya suena medieval, resulta extremadamente intimidante.
Y eso que los avances en neurocirugía han hecho esta intervención mucho más sutil, delicada y segura de lo que ha sido nunca antes. Porque el ser humano lleva cientos de años llevando a cabo este tipo de operaciones, especialmente en el Perú precolombino donde se han encontrado más cráneos trepanados que en ningún otro lugar del mundo.
Muchos fallecieron durante el proceso, o poco después como resultado de éste, pero muchos otros no. Incluidos más de 100 súbditos del imperio inca. Un estudio reciente, publicado en la revista World Neurosurgery y del que se hace eco Science, ha analizado durante tres décadas más de 800 cráneos de la época y ha revelado que la tasa de éxito de estos neurocirujanos de la antigüedad era bastante más alto de lo que podríamos esperar: un 80% de los pacientes sobrevivía. Si lo comparamos con la época de la guerra civil americana, 400 años después, en la que solo tenían éxito el 50% de las operaciones, la cifra resulta aun más sorprendente.
Para curar heridas y para mitigar dolores
Gracias a los restos encontrados por todo el mundo, sabemos que la trepanación surgió como una técnica para aliviar heridas y lesiones en la cabeza: era una forma de limpiar esas heridas y de aliviar la presión en el cerebro, que en seguida empieza a hincharse y a acumular líquido. Pero esa no debía ser su única función, ya que algunos cráneos trepanados no muestran señales de lesiones. Por eso sabemos que también debía usarse para tratar otros problemas de salud que no dejan señal en los huesos, como dolores de cabeza o enfermedades mentales.
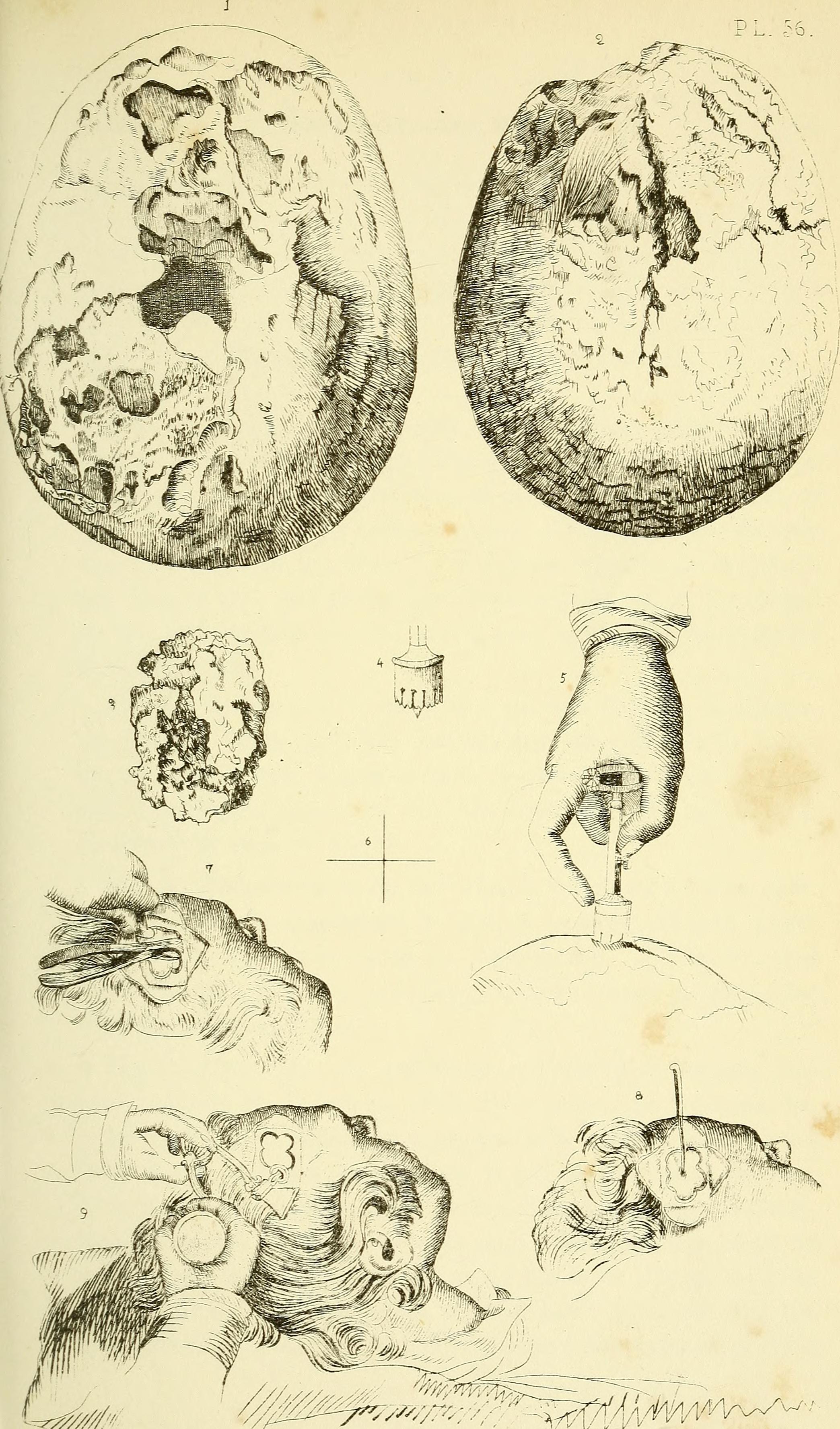
Lámina ilustrativa de una trepanación. Richard Upton Piper & Henry Jacob Bigelow, “Anaesthetic agents, their mode of exhibition, and physiological effects”. Fuente: Wikipedia Commons
En este último estudio, un estudio multidisciplinar de neurólogos y bioarqueólogos estadounidenses ha analizado cráneos trepanados localizados en distintas zonas de Perú y datados en distintas fechas, incluido un grupo de 160 hallados en los alrededores de Cuzco, capital del imperio inca, de entre finales del siglo XV y mediados del XVI.
Si en torno al agujero realizado durante la operación no se había formado nuevo tejido óseo, los investigadores sabían que el paciente había fallecido durante la operación o poco después, pero si podían observar hueso nuevo, más suave que el antiguo, podían deducir que había sobrevivido meses e incluso años tras la trepanación.
Sobrevivían hasta 8 de cada 10 pacientes
Los resultados sorprendieron a los científicos: en el grupo de cráneos más antiguos la tasa de supervivencia era del 40%, y en otro apenas superaba el 50%, pero en el grupo de huesos del imperio inca, las tasas aumentaban hasta el 83%.
Al mismo tiempo que una mejora en el número de supervivientes tras esta operación, los cráneos desvelaban una mejora en las técnicas de trepanación: agujeros más pequeños, cada vez menos taladros o cortes y más ranuras o raspados, es decir, intentos más delicados de acceder al interior del hueso sin dañar el cerebro y sus membranas protectoras que demuestran la habilidad y conocimientos de estos neurocirujanos precolombinos.
Más éxito que en etapas posteriores
Los autores también compararon estos datos con los resultados de neurocirugías en otras épocas históricas, como la guerra civil americana, ocurrida cuatro siglos más tarde, en la que también se practicaban técnicas similares. Durante la contienda, los cirujanos trataban algunas heridas en la cabeza agujereando el hueso y tratando de no dañar las membranas cerebrales. Según los registros de la época, entre el 46 y el 56% de los pacientes de estas cirugías morían en el proceso o poco después, mucho más que entre el 17 y el 25% que lo hacían los incas.

Set de trepanaciones de en torno a 1850. Fuente: Medical Antiques
Hay que tener en cuenta que las heridas de una y otra época eran muy diferentes (piedras y armas blancas frente a balas y ballonetas), también lo eran el tipo de operaciones que se realizaban: en medio de una contienda bélica moderna, las heridas se trataban con rapidez, junto al campo de batalla y en condiciones precarias, sin comprender y por tanto sin poder evitar los procesos de infección de las heridas.
A día de hoy, las trepanaciones son operaciones más o menos comunes con una tasa de supervivencia mucho más alta que en cualquier otra época histórica, e igual que hicieron los antiguos incas, los neurocirujanos siguen estudiando y mejorando las técnicas para ayudar lo mejor posible a sus pacientes.
Referencias:
Trepanation Procedures/Outcomes: Comparison of Prehistoric Peru with Other Ancient, Medieval, and American Civil War Cranial Surgery – World Neurosurgery
South America’s Inca civilization was better at skull surgery than Civil War doctors – Science
La sofisticada cirugía cerebral de los incas – El Mundo
Healing following cranial trauma – Journal of forensic science
Wounded by bayonet, ball, and bacteria: medicine and neurosurgery in the American Civil War – Neurosurgery
Holes in the head – Phys.org
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo El arte de abrir cráneos: neurocirugía y trepanaciones durante el imperio inca se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La neurocirugía con el paciente despierto
- La secuencia de estructuras intermedias durante la división de la membrana celular
- Reconstruyendo la evolución del entorno durante 35.000 años
El duelo de los pecaríes

Un día de enero de 2017 Dante de Kork vio un grupo de pecaríes de collar en la parte trasera de su casa, en Arizona, EEUU. Uno de ellos parecía enfermo. Al día siguiente una hembra de pecarí yacía muerta en el lugar en que se encontraba el grupo el día anterior; otros individuos merodeaban a su alrededor. Al tercer día Dante se acercó al sitio al que su madre había llevado el cadáver de la pecarí, algo más lejos, e instaló una cámara de vídeo con un sensor de movimiento acoplado. Cada vez que se acercase algún animal y fuese detectado por el sensor, la cámara grabaría la escena. Dante mantuvo la cámara grabando durante las dos semanas siguientes, y con algunas de las imágenes que obtuvo y sus observaciones directas confeccionó un poster que presentó en la feria regional de ciencia que se celebró unos días después.
Las imágenes ofrecieron escenas antes nunca vistas. Los miembros del grupo de pecaríes visitaron con frecuencia a la hembra muerta, de uno en uno o en parejas. Se le quedaban mirando, lo olían, acariciaban su cuerpo con el hocico, lo mordisqueaban, intentaban levantarlo introduciendo el hocico entre el cuerpo y el suelo y empujando hacia arriba; y en ocasiones se acurrucaban a su lado y dormían allí. Llegaron incluso a defender con éxito el cadáver de la pecarí frente al ataque de un grupo de coyotes que querían comérselo. Algunas actitudes reflejadas en las imágenes sugerían tristeza, denotaban pena; parecía que los otros miembros del grupo llorasen incluso.
Quiso la casualidad que la copresidenta del Grupo Especializado en Pecaríes de la Unión Internacional para la Conservación de la Naturaleza, Mariana Altrichter, viera el poster. Mariana y Dante se encontraron y de aquella conversación surgió la idea de publicar un artículo en la revista científica Ethology, dando cuenta de tan extraordinarias observaciones. Dante de Kork tenía, a la sazón, 8 años; el artículo fue publicado el pasado mes de diciembre y él figura como primer autor.
Los pecaríes son mamíferos sociales que suelen vivir en grupos de tamaños variables dependiendo de la especie. Parecen jabalíes, con los que guardan un cierto parentesco; ambos pertenecen al orden Artiodactyla, en el que también se encuadran cetáceos, jirafas y bóvidos, entre otros. El comportamiento observado por el joven de Kork no había sido visto antes en esta ni en especies próximas; fue una sorpresa para los especialistas. Se sabía que los elefantes reaccionan a la muerte de sus congéneres; les afecta, incluso, la visión de otro elefante muerto o de sus restos óseos. Hay chimpancés que se sientan junto al cadáver de un miembro de su mismo grupo que acaba de morir, y las hembras pueden llevar de un sitio a otro el cadáver de una de sus crías durante semanas. Han sido vistos delfines del género Tursiop alzando a una cría muerta hasta la superficie del agua como si quisieran ayudarla a respirar. Pero de los pecaríes no se sabía nada similar.
Una fría mañana de hace unos años, en un prado asturiano, vi a un pastor que arrastraba un cordero exangüe. Lo había matado, al parecer, una gineta. Lo acompañaba, un poco adelantado, un pequeño rebaño con algunas ovejas, un carnero y unos cuantos corderos. Una oveja, a la altura del pastor, no se separaba del cadáver del cordero. Y no dejaba de balar. Balaba y miraba al pastor, como si le interpelase, como pidiéndole una explicación o como si pudiese devolver la vida a su cría recién nacida. La mirada de la oveja mostraba una tristeza infinita.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 8 de abril de 2018
El artículo El duelo de los pecaríes se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Zientziateka: Raúl Ibáñez – El teorema de la rosa

La convergencia entre las diferentes áreas de estudio ha supuesto desde siempre una herramienta maravillosa para reflejar de una forma global y fidedigna la realidad de cada tiempo. En este sentido, la conexión entre la naturaleza, la literatura y la ciencia es, quizás, una de las formas más fabulosas que tiene el ser humano para diseñar una ventana desde donde poder contemplar y enseñar el mundo desde múltiples y complementarias perspectivas.
La unión de estas tres áreas de conocimiento fue la temática principal del ciclo de conferencias “Naturaleza, Literatura y Ciencia” que albergó Azkuna Zentroa entre el 10 y el 19 de abril pasados.
En “El teorema de la Rosa”, Raúl Ibáñez habla de la importancia de las matemáticas como herramienta fundamental para el estudio de la naturaleza y la comprensión de su belleza. El objetivo de esta charla es adentrar al público, a través de la mirada crítica y creativa de la literatura actual, en las matemáticas de la naturaleza. Para ello, Ibáñez acercará al auditorio algunos sencillos e interesantes ejemplos, como la sucesión de Fibonacci, la razón áurea, la teoría de los nudos o los fractales.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Zientziateka: Raúl Ibáñez – El teorema de la rosa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- “La cultura científica o la misteriosa identidad del señor Gauss” por Raúl Ibáñez
- Naukas Bilbao 2017 – Raúl Gay: Todo sobre mi órtesis
- La magia del teorema de Zeckendorf
La caracterización de la cuarcita arqueológica
La comunidad científica conoce bastante bien el sílex, que es en la Región Cantábrica Oriental la piedra más empleada por las sociedades paleolíticas, pero casi no se conoce nada desde un punto de vista geo-arqueológico sobre la materia principal en el resto de la Región Cantábrica y la Península, la cuarcita. Un equipo de investigadores de la UPV/EHU ha establecido la primera metodología para la comprensión y caracterización de las cuarcitas en contextos arqueológicos, lo que permitirá entender la economía articulada en torno a esta piedra por parte de las sociedades prehistóricas que habitaron la Región Cantábrica durante el Paleolítico.

Bifaz lanceolado de cuarcita marrón encontrado en Chañe y que actualmente se conserva en el Museo de Segovia.
En el trabajo se establece una sistemática para poder indicar en el futuro cuál es la fuente de aprovisionamiento de cuarcitas por parte de los grupos prehistóricos (en aquellas regiones en las que hay muy poco sílex). “A medida que esta metodología se extienda, conoceremos las características de cada afloramiento de esa materia prima y podremos completar el mapa “económico” del Paleolítico (en este momento, casi vacío, excepto en el País Vasco y Cataluña) con las restantes regiones peninsulares”, comenta Alejandro Prieto, coautor del estudio. Así, la presencia de una cuarcita característica de un afloramiento en un valle distante cientos de kilómetros, por ejemplo, revelaría ese desplazamiento por parte de los grupos humanos que la portaban. Multiplicando el número de observaciones, se podrán mapear los movimientos de las poblaciones prehistóricas entre los afloramientos de materia prima y los yacimientos en que quedaban esos restos trabajados, tras su amortización.
Como se ha comentado, en el ámbito geográfico en el que se circunscribe el trabajo, la Cornisa Cantábrica, la cuarcita es la segunda materia prima lítica en cantidad. La importancia en el registro arqueológico es aún mayor en las zonas centrales y occidentales de la región cantábrica, así como en momentos antiguos del Paleolítico, concretamente en el Paleolítico Inferior y Medio. Por tanto, la caracterización de ese material abre una nueva ventana al conocimiento de las sociedades paleolíticas, a partir del entendimiento de los mecanismos de aprovisionamiento, transformación y utilización de uno de los recursos más importantes de ese periodo.
Para entender y caracterizar la cuarcita arqueológica, se han seleccionado 17 muestras de los materiales de los yacimientos de El Habario y El Arteu. Las dos colecciones de industria lítica están caracterizadas como Musterienses, claramente asociado al Paleolítico Medio (150.000-40.000 BP) y talladas por poblaciones neandertales. Los dos yacimientos están situados en el occidente de la actual provincia de Cantabria, en una zona de alta variabilidad geológica. El primero se encuentra en una zona amesetada en las estribaciones nororientales de los Picos de Europa y está adyacente a unos pequeños conglomerados con cantos de cuarcita. El segundo está situado en el Desfiladero de la Hermida, en una zona con una orografía más escarpada, rodeado de estratos de caliza, y está relativamente cercano al río Deva.
La metodología utilizada se ha basado en la aplicación de la petrografía, el análisis digital de imagen, y en la fluorescencia de rayos X. Esas tres técnicas han permitido caracterizar las texturas de las láminas delgadas y los granos de cuarzo que conforman la cuarcita; conocer los tamaños, las formas y la orientación de los granos de cuarzo; conocer los minerales que componen junto con el cuarzo esas cuarcitas; y caracterizar la composición geoquímica de las cuarcitas. “Los resultados de este trabajo nos han permitido entender los procesos genéticos, de creación y formativos, de las cuarcitas y detectar diferentes ambientes formativos. Estos van desde los puramente sedimentarios (acumulación de granos de cuarzo) a otros claramente metamórficos (creación de nuevos granos de cuarzo a través de la recristalización), pasando por una gradación de mecanismos diagenéticos y de deformación más avanzados”, explica el investigador.
La comprensión de esos procesos, así como su contextualización, ha permitido establecer seis tipos de cuarcitas, que han sido utilizados para entender parcialmente el registro de ambos yacimientos y comprobar complejos mecanismos de adquisición y gestión de la cuarcita. Así, la adquisición dual (en conglomerados y depósitos fluviales) de recursos líticos permite observar mecanismos de movilidad y utilización de medios diversos (media montaña y fondos de valle), que sugieren pautas de movimientos interanuales que aún hoy perduran en ámbitos rurales y ganaderos. Se ha corroborado la movilidad de poblaciones neandertales y el transporte de herramientas, así como la utilización de multitud de tipos cuarcíticos por parte de los Neandertales. Por otra parte, la captación y utilización preferente de tipos cuarcíticos altamente deformados o metamórficos, debido a las aptitudes favorables para la talla y el uso, lleva a pensar en pautas de comportamiento “modernas” y “complejas” de las poblaciones neandertales.
Referencia:
Alejandro Prieto, Iñaki Yusta y Álavaro Arrizabalaga (2018) Defining and Characterizing Archaeological Quartzite: Sedimentary and Metamorphic Processes in the Lithic Assemblages of El Habario and El Arteu (Cantabrian Mountains, Northern Spain) Archaeometry doi: 10.1111/arcm.12397
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La caracterización de la cuarcita arqueológica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los espacios del arte parietal
- La complejidad de la mente neandertal
- Flores en su tumba, hace 16.000 años
Querido Paracelso: el veneno no solo reside en la dosis
“Todas las sustancias son venenos, no existe ninguna que no lo sea. La dosis diferencia un veneno de un remedio”. Esta frase, pronunciada por el alquimista, médico y astrólogo suizo Theophrastus Philippus Aureolus Bombastus von Hohenheim, mas conocido por Paracelso, es usada constantemente por muchos divulgadores científicos para explicar que la toxicidad de un compuestos químico, proceda de una planta natural o se sintetice químicamente en el laboratorio, depende de la cantidad en la que se ingiera y no de su origen. Si consumimos una cantidad de un compuesto químico por debajo de determinada dosis los efectos sobre nuestra salud pueden no existir o incluso ser positivos. Sin embargo, si la ingesta supera dicho umbral las consecuencias pueden llegar a ser nefastas.

Theophrastus Phillippus Aureolus Bombastus von Hohenheim, Paracelso.
Pero esto no es siempre es cierto. Un compuesto puede tener propiedades negativas si es consumido en bajas cantidades y, al subir su concentración, puede ser que los efectos sean muy positivos. También puede ocurrir lo contrario. ¿Por qué? Porque en muchas ocasiones al aumentar la concentración de un compuesto cambia su estructura físico-química hasta el punto de que un mismo compuesto, a concentraciones diferentes, puede comportarse como dos totalmente distintos con propiedades opuestas. Veamos un ejemplo.
Durante muchos años la industria alimentaria ha tenido total impunidad para publicitar auténticos disparates en el etiquetado de los alimentos funcionales con el propósito de llamar la atención del consumidor. Eslóganes publicitarios tales como ‘Favorece el desarrollo del sistema inmune’, ‘Baja la tensión arterial’, ‘Mejora la salud intestinal’ o ‘Reduce la osteoporosis’, sirvieron para enganchar al consumidor a pesar de que pocas de estos reclamos publicitarios estaban basadas en estudios rigurosos. La ausencia de una legislación internacional que abarcara todos y cada uno de los aspectos concernientes a los alimentos funcionales permitía que ‘todo valiera’ en el etiquetado de estos productos. Para intentar poner fin a tanto descontrol, se elaboró el ‘Reglamento (CE) 1924/2006 relativo a las declaraciones nutricionales y de propiedades saludables en los alimentos’.
Desde que entró en vigor la nueva reglamentación europea, cuando una empresa quiere que se apruebe una alegación saludable para poder usarla en la publicidad de su producto debe enviar una documentación muy exhaustiva a la Autoridad Europea de Seguridad Alimentaria (EFSA). Concretamente se piden los siguientes tipos de estudios:
1.- Estudios de intervención en humanos: ensayos controlados aleatorizados, no aleatorizados, no controlados, etc.
2.- Estudios observacionales en humanos: cohortes, casos-control y transversales.
3.- Estudios sobre seres humanos dedicados a los mecanismos que pueden originar el efecto declarado del alimento, incluidos los estudios sobre la biodisponibilidad.

EFSA, Autoridad Europea de Seguridad Alimentaria
Los datos obtenidos de estudios no realizados en seres humanos deben incluir:
- Datos sobre animales, incluidos los estudios acerca de aspectos relativos a la absorción, la distribución, el metabolismo o la excreción del alimento, estudios sobre el mecanismo y otros estudios.
- Datos ‘ex vivo’ o ‘in vitro’, basados en muestras biológicas humanas o animales vinculados con los mecanismos que pueden originar el efecto declarado del alimento, y otros tipos de estudios no realizados en seres humanos.
Pues bien, una vez analizados todos esos datos la EFSA emite un informe basándose en tres aspectos principales de la solicitud:
A) Que el alimento (o el ingrediente alimenticio) esté bien caracterizado.
B) Comprobar que la propiedad saludable que se le quiere atribuir está claramente definida y, además, ejerce un efecto beneficioso sobre la salud.
C) Verificar que existe una correlación entre la ingesta del alimento (o ingrediente alimenticio) y tal alegación saludable.
Como he contado en muchas ocasiones la inmensa mayoría de las solicitudes presentadas por las empresas a la EFSA han sido rechazadas por el máximo organismo internacional en materia de alimentación. Un porcentaje elevadísimo de estos rechazos son debidos a que el apartado C anteriormente citado (verificar que existe una correlación entre la ingesta del alimento y una alegación saludable) no está suficientemente demostrado. Son necesarios muchos más estudios en humanos que corroboren que existe dicha correlación. Sin embargo, hay casos donde el apartado A tampoco está suficiente claro y hacen falta más investigaciones que sirvan para caracterizar el ingrediente alimenticio en cuestión.
Un ejemplo que abarca ambos casos es el de la molécula protagonista del post de hoy: el ácido linoleico conjugado. Por una parte hacen falta más estudios en humanos que demuestren los efectos sobre la salud del consumo de este compuesto y, por otra, hay que caracterizarlo mucho mejor. ¿En qué me baso para dar esta opinión? En los informes oficiales de la EFSA y en una reciente investigación publicada por el grupo de investigación de “Bioquímica y Biotecnología enzimática” de la Universidad de Murcia al que pertenezco y que no solo ayuda a caracterizar físico-químicamente el ácido linoleico conjugado sino que apoya la tesis con la que empecé este post sobre las excepciones a la teoría de Paracelso. Les cuento.
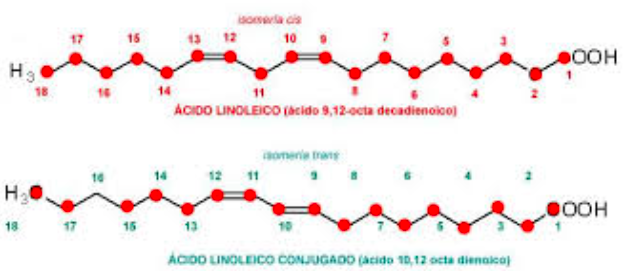
Ácido Linoleico conjugado
Por el nombre de “ácido linoleico conjugado” se conoce no a uno, sino a una familia de por lo menos 28 isómeros del ácido linoleico encontrados principalmente en la carne y productos lácteos provenientes de rumiantes. Desde el punto de vista estructural la gran diferencia entre el ácido linoleico conjugado y el ácido linoleico tradicional es que mientras el primero de ellos presenta dos dobles enlaces conjugados (alternados por un único enlace simple), en el ácido linoleico tradicional los dobles enlaces no están conjugados tal y como podemos observar en la anterior figura.
En los últimos años son muchas las propiedades beneficiosas que se le han atribuido a varios miembros de la familia de los ácidos linoleico conjugados. Por ello forman parte de famosísimos suplementos nutricionales y alimentos funcionales. Sin embargo, a día de hoy la EFSA no ha aprobado ni una sola de las health claims (alegaciones saludables) solicitadas por diferentes empresas del sector alimentario para el ácido linoleico conjugado. Aunque hay estudios prometedores no hay evidencias científicas sólidas que relacionen la ingesta de este compuesto con la reducción del peso corporal, el incremento de la masa muscular, la protección del ADN frente al daño oxidativo…
Pero los resultados encontrados por nuestro grupo pueden ayudar a que el ácido linoleico conjugado pase los difíciles exámenes de la EFSA. Empleando técnicas de fluorescencia y química computacional hemos demostrado que uno de los isómeros del ácido linoleico conjugado, el ácido ruménico, adopta una estructura físico-química diferente dependiendo de la concentración a la que se encuentre en el medio de reacción… y eso puede cambiar totalmente sus propiedades.
El ácido ruménico cuando se encuentra a baja concentración se presenta en forma de unidades individuales llamadas monómeros. Los monómeros se encuentran aislados unos de otros sin formar ningún tipo de asociación entre ellos. Sin embargo, si aumentamos la concentración del ácido ruménico en el medio de reacción llega un momento en el que los monómeros se agregan dando lugar a grandes estructuras de tipo micelar en forma de pelota.
MICELA
Las micelas de ácido ruménico son agregados esféricos donde las moléculas se orientan para favorecer al máximo las interacciones hidrofóbicas e hidrofílicas. Así, las cadenas del ácido graso están orientadas hacia el interior y los grupos polares hacia la superficie. Estas estructuras tienen propiedades totalmente diferentes a las de los monómeros aislados y el valor exacto de concentración de ácido graso al cual éste pasa súbitamente de forma monomérica a forma micelar se denomina concentración micelar crítica.
¿Y se puede calcular el valor exacto de la concentración micelar crítica del ácido ruménico en el cuál el ácido ruménico cambia de estructura y, por tanto, sus propiedades son diferentes? Sí.
Para ello utilizamos una sonda fluorescente llamada difenilhexatrieno que, al adicionarse al medio de reacción, se incorpora a la estructura del ácido ruménico. Esta sonda es incapaz de emitir fluorescencia en un entorno polar. Por ello, mientras el ácido graso con la sonda acoplada se encuentran en forma monomérica no hay emisión de fluorescencia. Sin embargo, en el momento en el que sobrepasamos la concentración micelar crítica el ácido ruménico se agrega formando la micela, la sonda fluorescente se incorpora a la micela que es más apolar que el medio que la rodea y aumenta súbitamente la fluorescencia de la disolución.
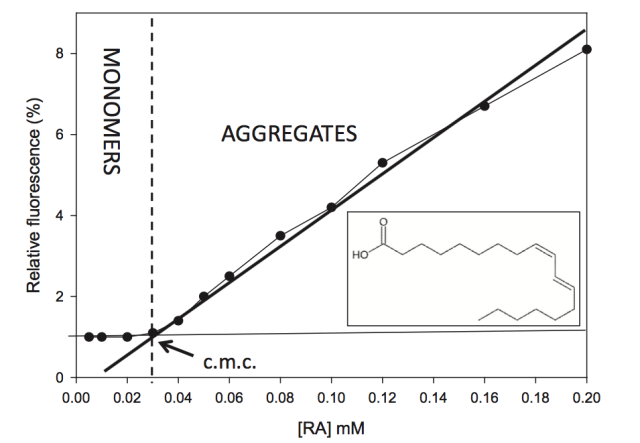
Determinación de la CMC del Ácido Ruménico. Insertada se puede ver su estructura.
En la anterior imagen les muestro una gráfica donde se puede observar claramente un punto de intersección entre la región pre-micelar y post-micelar que define la concentración micelar crítica. En la gráfica se aprecia el súbito incremento de la fluorescencia que se produce cuando la concentración de ácido ruménico es 0.3 milimolar. Justo a ese valor se produce el paso de monómeros a micela.
Y ahora llega la gran pregunta. Todo lo expuesto…¿sirve para algo? La importancia de lo que hoy les he contado es altísima.
Por una parte conocer las razones de la aparición de las micelas de ácido ruménico y de la existencia de un equilibrio monómero/micela de tipo dinámico es clave para entender las funciones de ese ácido graso. Varios estudios han demostrado como las propiedades nutricionales, espectroscópicas, fisiológicas y funcionales de un mismo compuesto no solamente son diferentes, sino que pueden llegar a ser opuestas dependiendo si se encuentra en estado monomérico o micelar. En el caso del ácido linoleico conjugado hay estudios en la literatura científica que muestran como sus efectos sobre la salud son totalmente dependientes de la concentración a la que sea ingerido. Los resultados publicados por el grupo de investigación “Bioquímica y Biotecnología enzimática” podrían ser la explicación a dichos estudios.
Por otra parte la puesta a punto de un método fluorimétrico rápido, fiable y preciso para determinar el punto exacto de formación de las micelas (la concentración micelar crítica) es fundamental si queremos alterar el equilibrio monómero/micela, desplazándolo hacia la zona que más nos convenga. Sabiendo el valor exacto de la concentración micelar crítica del ácido ruménico podremos elaborar alimentos funcionales y fármacos más efectivos.

Figura 6 Ejemplo de producto enriquecido con Ácido Linoleico Coonjugado
Dejo para el final lo más importante. Lo que hoy les he contado respalda una idea que llevo defendiendo durante años. Es absurdo hablar de las propiedades beneficiosas o perjudiciales de una molécula (incluidas su efectividad o su toxicidad) sin especificar no solo a qué concentración se encuentra sino también cuál es el pH o la temperatura del medio de reacción. De hecho el ácido linoleico conjugado, incluso a una misma concentración, presenta propiedades muy distintas si se encuentra en una disolución básica o alcalina, ya que su estructura también cambia con el pH.
“Pequeños cambios en los parámetros físico-químicos de una molécula o del medio de reacción en el que se encuentre pueden cambiar totalmente su estructura, convirtiéndola en otra molécula totalmente diferente que puede matarnos…o salvarnos la vida”.
Querido Paracelso: el veneno no solo reside en la dosis, la estructura es aun más importante.
Este post ha sido realizado por José M. López Nicolás (@ScientiaJMLN) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.
Bibliografia: Physicochemical, thermal and computational study of the encapsulation of rumenic acid by natural and modified cyclodextrins. Adrián Matencio, Carlos Javier García Hernández-Gil, Francisco García-Carmona, José Manuel López-Nicolás. Food Chemistry 216 (2017) 289–295. doi: 10.1016/j.foodchem.2016.08.023
El artículo Querido Paracelso: el veneno no solo reside en la dosis se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Bill Haast y el veneno de las serpientes más peligrosas del mundo
- Homeopatía y dosis
- La pantalla de tu móvil solo tiene tres colores

