No es una percepción
De acuerdo con las conclusiones de un estudio recién publicado por el Pew Research Center [1], el lugar de trabajo de las mujeres que desempeñan profesiones relacionadas con ciencia, tecnología, ingeniería o matemáticas (agrupadas bajo el acrónimo STEM) es un entorno diferente, en ocasiones más hostil, que el de sus compañeros masculinos. Perciben con más frecuencia discriminación y acoso sexual [2], y piensan que el ser mujer representa más una desventaja que una ventaja para el éxito de sus carreras.
Entre todas las que trabajan en estas áreas, la probabilidad de que declaren haber sido tratadas peor es mayor en tres grupos de mujeres: las que trabajan en entornos en los que la mayoría de compañeros son hombres, las que trabajan en tareas relacionadas con ordenadores y las que tienen estudios de posgrado.
El estudio aporta información adicional acerca de la distribución de hombres y mujeres en las 74 ocupaciones clasificadas dentro de la categoría STEM, con un desequilibrio a favor de las mujeres en el campo de la salud (75% mujeres) y a favor de los hombres en física (39% mujeres), informática y ordenadores (25%) e ingeniería (14%). Hay un cierto equilibrio en matemáticas (47%) y ciencias de la vida (48%); en conjunto, el 50% de los puestos de trabajo está ocupado por mujeres. Estos y los anteriores datos corresponden a los Estados Unidos aunque lo más probable es que sus principales conclusiones sean válidas para el conjunto de países occidentales.
Si nos limitamos al mundo de la investigación y la academia, las investigadoras representan el 32 % del total en los países occidentales (Europa Occidental y Norteamérica), aunque en España ese porcentaje llega al 39 %. En nuestro entorno el porcentaje de mujeres en los estudios de grado y entre quienes completan el doctorado es algo superior al de hombres, y en algunos casos, como ocurre en la UPV/EHU, acceden al doctorado más mujeres (58%) que hombres (42%) en disciplinas STEM. Sin embargo, tal y como han mostrado diversos estudios, conforme se asciende en el escalafón y, sobre todo, en los niveles de máxima responsabilidad, autoridad y reconocimiento, las proporciones de mujeres se desploman hasta valores de entre el 10% y el 25%, dependiendo de la instancia y sector de que se trate. Los informes al respecto del CSIC, MICINN y Comisión Europea (She Figures 2015) aportan abundante y pormenorizada información.

Las tendencias que apuntan esos informes tienen su reflejo más depurado en la proporción de mujeres a las que se conceden los máximos galardones en sus respectivas disciplinas y, muy en especial, a las que se ha concedido el premio Nobel. Desde su creación, solo el 3% de estos premios ha sido otorgado a mujeres. Suele argumentarse, para justificar ese bajo porcentaje, que refleja la presencia de las mujeres en el mundo de la investigación científica desde que existen esos galardones. Es indudable que cuanto menos son los miembros de un colectivo a segmento de la población que desempeñan una actividad, menos son quienes alcanzan los niveles más altos. Pero si nos fijamos en la última década, se han concedido a mujeres el 6,5 % de los galardones. Y si bien es cierto que los méritos que se reconocen pueden datar de décadas atrás, es más que dudoso que las mujeres solo hayan representado el 6,5 % de quienes se dedicaron a la ciencia al más alto nivel durante el último cuarto del siglo XX. Y de haber sido así, tal desequilibrio sería, en buena medida, consecuencia de otros desequilibrios relacionados con las diferentes oportunidades de hombres y mujeres para acceder a los recursos y las posiciones que facultan para desempeñar una carrera científica al más alto nivel [3].
Los límites a la presencia de las mujeres en las posiciones de más alto rango en las carreras científica y profesional son, de suyo, injustos y tienen, además, dos consecuencias perniciosas. Por un lado, privan al sistema científico y a la sociedad en general de la aportación de las mujeres más capacitadas al bien común. Y por la otra, contribuyen a alimentar los estereotipos que muestran a las profesiones científicas y tecnológicas como inadecuadas o impropias de las mujeres, con las consecuencias amplificadoras que tales estereotipos tienen (el círculo vicioso).
La Universidad del País Vasco está comprometida con el objetivo de una sociedad en la que hombres y mujeres tengan los mismos derechos y gocen de las mismas oportunidades. La Cátedra de Cultura Científica de la UPV/EHU comparte ese compromiso y se ha propuesto, en la medida de sus modestas posibilidades, contribuir a cambiar ese estado de cosas. Por esa razón publica desde el 8 de mayo de 2014 Mujeres con ciencia.
Pero hoy, 11 de Febrero, no hemos querido quedar al margen de la celebración internacional, promovida por Naciones Unidas del Día Internacional de la Mujer y la Niña en la Ciencia. Con ese propósito hemos producido “No es una percepción“, el vídeo que acompaña este texto. Quiere ser un gesto de denuncia y, en consecuencia, una llamada a la acción y, sobre todo, al trabajo. Por eso, para la Cátedra de Cultura Científica de la UPV/EHU mañana, como ayer, también será día de la mujer y la niña en la ciencia.
“No es una percepción” es una producción dirigida por Jose A. Pérez Ledo y grabada en la Universidad del País Vasco gracias a la colaboración de cinco científicas e investigadoras de la propia universidad:
- Itziar Alkorta, bioquímica.
- Arantza Aranburu, geóloga.
- Gotzone Barandika, química.
- Txelo Ruiz, ingeniera informática.
- Ana Zubiaga, genetista.
Notas:
[1] Pew Research Center es un prestigioso think tank estadounidense especializado en el estudio de tendencias sociales y demográficas.
[2] Aunque los resultados del trabajo se publicaron el pasado 9 de enero, el trabajo de campo se realizó en el verano de 2017, antes de que se produjese la ola de denuncias por acoso sexual contra personajes masculinos prominentes de diferentes sectores profesionales.
[3] El caso de Jennifer y John es un ejemplo ilustrativo de los desequilibrios mencionados.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
El artículo No es una percepción se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
- Hoy es el día de la mujer y la niña en la ciencia, todos lo son
- La percepción del propio peso es peor en las chicas que en los chicos
Naukas Bilbao 2017 – Raúl Gay: Todo sobre mi órtesis
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Raúl Gay habla de discapacidad desde una perspectiva muy diferente a la habitual: llamando a las cosas por su nombre. Posiblemente, una de las charlas más memorables de esta edición de Naukas Bilbao.
Raúl Gay: Todo sobre mi órtesisEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Raúl Gay: Todo sobre mi órtesis se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- Naukas Bilbao 2017 – Mónica Lalanda: Una muerte de cómic
- Naukas Bilbao 2017 – Diana González: Identidad digital y robots
Traducción automática neuronal sin supervisión

La mayoría de los sistemas de aprendizaje automático requieren supervisión humana, y la traducción automática no es una excepción: el ordenador utiliza millones de traducciones hechas por personas para extraer patrones y, de esta forma, aprender a traducir cualquier texto. Este método funciona bien con pares de idiomas como el inglés y el francés, pues existen muchas traducciones entre ambos. Sin embargo, no es tan efectivo para la gran mayoría de pares de idiomas con recursos limitados, como es el caso del alemán-ruso o el euskera-inglés, por ejemplo.
En este contexto, Mikel Artetxe, Eneko Agirre y Gorka Labaka, investigadores del grupo IXA de la Facultad de Informática de la UPV/EHU, han desarrollado un método de traducción automática basado en el aprendizaje sin supervisión, es decir, sin necesidad de diccionarios o traducciones humanas.
“Imagina que le das a una persona una gran cantidad de libros escritos en chino y otros tantos, distintos, en árabe, con el objetivo de que aprenda a traducir del chino al árabe. A priori parece una tarea imposible para un ser humano. Pero nosotros hemos demostrado que un ordenador es capaz de hacerlo”, afirma Mikel Artetxe, que está realizando su tesis doctoral sobre el procesamiento del lenguaje natural y el aprendizaje automático.
Este nuevo método que proponen los investigadores de la UPV/EHU supone un gran avance en el campo de la traducción automática, ya que abre una nueva línea de trabajo que muestra que las redes neuronales, algoritmos informáticos que se inspiran en el cerebro humano, pueden aprender a traducir sin necesidad de traducciones preexistentes.
Se da la casualidad que otro estudio, desarrollado por un equipo de investigadores de Facebook y la Universidad de la Sorbona de París, ha propuesto un método similar. “Es sorprendente -subraya Artetxe- que nuestros métodos sean tan parecidos. Pero al mismo tiempo es positivo, pues significa que esta nueva aproximación va por el buen camino”.
Los dos estudios, de los que se ha hecho eco la revista científica Science en su sección digital de noticias, fueron publicados en el repositorio virtual arXiv con un día de diferencia, y serán presentados en uno de los congresos más relevantes del área, el sexto encuentro internacional sobre el aprendizaje de representaciones (International Conference on Learning Representations – ICLR), que se celebrará en el mes de abril en Vancouver, Canadá.
En los únicos resultados comparables entre ambos estudios, el método del grupo IXA de la UPV/EHU obtuvo resultados ligeramente superiores, con una puntuación BLEU del 15% entre el francés y el inglés. A modo de comparativa, la máxima puntuación la obtienen métodos supervisados como Google Translate con cerca del 40%, si bien una persona supera el 50%. “Estamos en los inicios -aclara Mikel Artetxe- por lo que no sabemos hasta dónde puede llegar esta nueva línea de investigación”.
Referencia:
Mikel Artetxe, Gorka Labaka, Eneko Agirre, Kyunghyun Cho (2017) Unsupervised Neural Machine Translation arXiv:1710.11041
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Traducción automática neuronal sin supervisión se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Buscando la traducción automática perfecta
- Chatbots de traducción automática profunda
- La hiperactividad neuronal impide que las microglías realicen su trabajo
Nacido para ser autista

Mary Temple Grandin
En los años sesenta, Leo Kanner (uno de los dos primeros descubridores del autismo) defendía su teoría de las “madres nevera/refrigerador”. En ella argumentaba que el autismo de los hijos era consecuencia de la falta de contacto materno adecuado: afirmaba que estas madres de hijos autistas eran distantes, poco afectivas con sus hijos y llegó incluso a decir que esas mujeres se habían “descongelado” lo justo para dar a luz a un hijo. Según Kanner, si una mujer tenía un hijo autista era porque ella había hecho algo mal. Esta idea falsa que directamente culpabilizaba a las madres tuvo un importante calado e incluso hoy en día es posible encontrar personas que argumentan que el origen de los trastornos del espectro autista (TDA) se deben a la educación, traumas, etc. Lo cual significa que hay gente que cree que los TDA son algo adquirido. Mientras que el enfoque opuesto es pensar que los TDA son trastornos del desarrollo: es decir, que su origen está en alteraciones internas producidas durante el propio desarrollo del individuo.
Antes de ver cuál de estos dos planteamientos es el correcto, creo que es importante aclarar qué es exactamente el autismo. Lo primero que debemos saber es que no existe “el autismo” sino los trastornos del espectro autista (TDA), dentro de los cuales hay una gran diversidad. Esto ya se ve en los dos primeros estudios donde se documentan estos trastornos: el trabajo de Leo Kanner (1943) describe niños que mayoritariamente tienen muchas dificultades para hablar y discapacidad intelectual, mientras que en el estudio de Hans Asperger (1944) los niños tienen un uso preciso del lenguaje y no presentan discapacidad intelectual. Hablo de niños porque los TDA afectan principalmente a varones en una proporción que va desde 4 a 1, hasta 8 niños por cada niña según el tipo de TDA. Independientemente del género, algunas de las características principales de los trastornos del espectro autista son problemas en el uso del lenguaje o habilidades sociales. Además, junto con el propio trastorno los pacientes suelen padecer algún tipo de discapacidad intelectual en más de la mitad de los casos o epilepsia (alrededor del 30% de los casos); entre otros problemas.
La primera pista sobre el origen de estos trastornos la tenemos en el incremento de los casos en las últimas décadas, que ahora se sitúa en cerca del 1% de la población y es un porcentaje superior al documentado con anterioridad. Esta subida se debe principalmente a tres motivos: el primero es una mejora de las técnicas diagnósticas que permiten detectar más casos, el segundo es un cambio en lo que entendemos por TDA hacia una definición clínica más amplia que recoge casos que antes no se consideraban TDA, y el tercer motivo es un incremento de la edad a la que las parejas conciben hijos. Aquí está la pista. Muchos estudios están documentando que cuanto más mayores son los progenitores a la hora de concebir un hijo (y en muchos de ellos se señala que es especialmente importante la edad del padre), más probable es que su descendencia tenga un TDA. ¿Por qué? Porque conforme envejecemos nuestra capacidad de generar células reproductoras es peor y los genes que trasmitimos a través de ellas contienen más fallos. Esto indica que los problemas genéticos tienen un papel importante en el desarrollo del TDA, y eso es algo que también se ve si uno estudia árboles genealógicos o trabajos donde se ha documentado casos de gemelos. En ellos se ha visto que si uno de ellos desarrolla un TDA, en el 60-90% de los casos el otro hermano también desarrollará un TDA.
Que la genética tenga un factor decisivo en la aparición de TDA no es suficiente para definirlo como un trastorno que se produce durante el desarrollo del organismo: para ello es esencial ver cuándo aparece el TDA. Los seres humanos nacemos extremadamente poco desarrollados, siendo además el cerebro el tejido más inmaduro y tarda unas dos décadas en acabar de formarse. Trastornos neurológicos que se manifiesten dentro de este espacio de tiempo pueden deberse en parte a anomalías del desarrollo, y cuanto más pronto aparezcan pues es más probable que el desarrollo nervioso esté implicado en su aparición. En el caso de los TDA, los diagnósticos tempranos se sitúan entorno a los dos/tres años de edad. Lo cual ya es muy temprano pero es que además, en estudios con bebés de seis meses ha sido posible analizar el funcionamiento de sus redes neuronales a los seis, doce y veinticuatro meses; encontrándose que aquellos pequeños que a los veinticuatro meses eran diagnosticados con un TDA, a los seis meses ya presentaban alteraciones en el funcionamiento de sus redes neuronales. Y además, se ha hallado una correlación entre la severidad de estas anomalías a los seis meses y la gravedad de los síntomas a los veinticuatro meses.
En resumen, todo esto nos dice que los TDA son intrínsecos a la propia formación del sistema nervioso del paciente y por lo tanto es parte de ellos mismos. No es algo que se adquiera después de nacer sino que se manifiesta después de nacer. Se nace siendo autista. Esto es importante por dos aspectos: en primer lugar para no culpar al entorno, la familia, el calendario de las vacunas infantiles, etc. de los casos que aparezcan. Y en segundo lugar es vital para el tratamiento: actualmente la única posibilidad para intentar mitigar los síntomas del TDA es diagnosticar y tratar a los pacientes cuanto antes, porque los procesos del desarrollo son mayoritariamente irreversibles pero durante las fases iniciales a veces hay un cierto margen para dirigirlos parcialmente en otra dirección.
Este post ha sido realizado por Pablo Barrecheguren (@pjbarrecheguren) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias:
- Constantino, J. N., & Marrus, N. (2017). The Early Origins of Autism. Child and Adolescent Psychiatric Clinics of North America, 26(3), 555–570.
- John D. Lewis*, Alan C. Evans, John R. Pruett Jr, Kelly N. Botteron, Robert C. McKinstry, Lonnie Zwaigenbaum, Annette Estes, Louis Collins, Penelope Kostopoulos, Guido Gerig, Stephen Dager, Sarah Paterson, Robert T. Schultz, Martin Styner, Heather Hazlett, and Joseph Piven, for the IBIS network. (2017). The emergence of network inefficiencies in infants with autism spectrum disorder. Biol Psychiatry. 2017 August 01; 82(3): 176–185.
- Principles of Neural Science, Fifth Edition (2012). Editorial McGraw-Hill Education.
- Swaab D. We are our brains (2014). Penguin Books.
El artículo Nacido para ser autista se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El universo recién nacido
- Luminoterapia para el cambio de estación
- ¿Cuántos animales se usan en España para experimentación?
Autismo y educación: problemas y pautas en el aula

¿Cómo se tratan algunos de los trastornos cognitivos más frecuentes en las aulas? ¿Son efectivos los programas y herramientas del sistema educativo actual? ¿Carecen de eficacia algunas de las prácticas educativas más populares?
Estas son algunas de las cuestiones que se debatieron en la jornada “Las pruebas de la educación”, que se celebró el pasado 2 de febrero de 2018 en el Bizkaia Aretoa de Bilbao. El evento, en su segunda edición, estuvo organizado por la Cátedra de Cultura Científica de la UPV/EHU y el Consejo Escolar de Euskadi, con la colaboración de la Fundación Española para la Ciencia y la Tecnología (FECYT).
Las ponencias de los expertos que expusieron múltiples cuestiones relacionadas con la educación, basándose siempre en las pruebas científicas existentes. Los especialistas hicieron especial hincapié en destacar cuál es la mejor evidencia disponible a día de hoy con el objetivo de abordar las diferentes realidades que coexisten en las aulas y en el sistema educativo en general.
“Las pruebas de la educación” forma parte de una serie de eventos organizados por la Cátedra de Cultura Científica de la UPV/EHU para abordar cuestiones del día a día como la educación o el arte desde diversos ámbitos de la actividad científica. La dirección del seminario corre a cargo de la doctora en psicología Marta Ferrero.
En “Autismo y educación: Problemas y pautas en el aula”, José Ramón Alonso, neurobiólogo y catedrático de biología celular en la Universidad de Salamanca, nos acerca al concepto del autismo, sus posibles causas y los tratamientos más empleados, con el objetivo de identificar las pautas concretas que pueden ayudar a maestros y profesores a tratar en el aula este trastorno cognitivo.
José Ramón Alonso: ''Autismo y educación: Problemas y pautas en el aula''Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Autismo y educación: problemas y pautas en el aula se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las ideas erróneas sobre educación entre el profesorado: prevalencia, causas y soluciones
- La ciencia perdida: los curiosos casos de los protocolos de TDAH y de leer.es
- Del mito al hecho: hemisferios, gimnasia cerebral y estilos de aprendizaje
Si hacer fármacos fuese como jugar a Lego, la pieza más guay se llamaría carbino

Muchos de los fármacos que conocemos son compuestos muy complejos. Esto quiere decir que están formados por muchos átomos unidos entre sí de una manera concreta. Hacer que estos átomos se unan de una forma y no de otra es una tarea complicada. Al estudio de estos procesos de ensamblaje de átomos se le llama «síntesis química».
Los átomos no se comportan como piezas de Lego. No siempre podemos ensamblarlos y desensamblarlos a nuestro antojo, ya que unos átomos tienen más afinidad por unos que por otros, tienen tendencia a colocarse en unas posiciones y no en otras, a girarse, etc. Por eso es tan importante diseñar una buena ruta de síntesis, en la que cada átomo acabe ocupando la posición deseada.
Uno de los átomos más famosos de los fármacos es el carbono. El carbono está presente en casi todos los fármacos que conocemos. Es capaz de unirse a otros átomos de forma muy diferente. El carbono es como una pieza de Lego con cuatro posiciones de ensamblaje. Desgraciadamente es muy difícil conseguir una pieza solitaria de este carbono. En la naturaleza siempre está unido a más piezas y, en el caso de tener alguna posición libre (formando lo que denominamos radicales libres) son muy inestables y enseguida encuentran a quién unirse.
Esto ha sido un quebradero de cabeza para los químicos que trabajan en síntesis. Al menos hasta ahora. Recientemente, un grupo de investigadores del Instituto Catalán de Investigación Química (ICIQ), liderado por el joven químico Marcos García Suero, acaba de encontrar un método revolucionario que permite conseguir la ansiada pieza solitaria de carbono. Esta pieza sólo tiene una de sus posiciones ocupadas por hidrógeno, el resto están listas para ensamblarse a los átomos que deseemos. Esta pieza se denomina carbino.

El carbino fue una de las primeras moléculas halladas en el espacio interestelar. Los astrofísicos lo detectaron en los años 30 del siglo pasado. Estos carbinos se detectan en eventos astonómicos muy energéticos y violentos, como en la formación de estrellas. Duran muy poco como carbinos porque tienen esa tendencia a unirse rápidamente a otros átomos. Esto es lo que los hace tan escurridizos.
Lo que han hecho los investigadores del ICIQ es sintetizar un equivalente de los carbinos. Este equivalente se llama radical diazometilo. Si seguimos con la analogía de las piezas de Lego, el radical diazometilo sería como una pieza de carbino con sus posiciones ocupadas por piezas de quita y pon, fáciles de intercambiar por piezas definitivas.
Tanto el hallazgo de este carbino equivalente, como la forma de sintetizarlo, ha llevado a estos investigadores a publicar su descubrimiento en la prestigiosa revista científica Nature. Su artículo lleva por título «Generación de carbinos equivalentes por medio de catálisis fotorredox». Para obtener carbino en el laboratorio no se pueden emular los violentos eventos astronómicos. Lo que han hecho estos investigadores es darle un empujón a la reacción de obtención de estos carbinos ayudándose de catalizadores. Los catalizadores que utilizaron son unos compuestos con rutenio sensibles a la luz, de ahí el prefijo foto de catálisis fotorredox. El catalizador, al recibir un fotón de luz LED, da el pistoletazo de salida para que se forme el carbino. Los procesos de fotocatálisis son, de hecho, una de las líneas de investigación más importantes del ICIQ.
Estos investigadores han probado la eficacia del carbino para modificar a antojo algunos medicamentos ya existentes. Así, han modificado con éxito el principio activo del ibuprofeno, del antidepresivo duloxetina, del antitumoral taxol, y del fingolimod, el primer tratamiento oral que existe para la esclerosis múltiple.
Este carbino no solo se podrá usar para mejorar los fármacos que ya conocemos, sino que podrá ayudar a acelerar el diseño y desarrollo de nuevos medicamentos. Si la química del desarrollo de fármacos fuese como jugar a Lego, la pieza más guay se llamaría carbino.
Agradezco a Fernando Gomollón Bel su ayuda con este artículo.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Si hacer fármacos fuese como jugar a Lego, la pieza más guay se llamaría carbino se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo mecanizar una pieza de cobre usando bacterias
- Otra pieza en el puzle de la fotosíntesis
- Cómo hacer más eficiente un mini aerogenerador
Óxido de vanadio (IV), un material para una revolución de ciencia ficción

Nanoestrellas de óxido de vanadio (IV)
Primero vino el interruptor. Luego el transistor. Ahora otra innovación puede revolucionar la forma en que controlamos el flujo de electrones a través de un circuito: el óxido de vanadio (IV), de fórmula VO2. Una característica clave de este compuesto es que se comporta como un aislante a temperatura ambiente, pero como un conductor a temperaturas superiores a 68 °C. Este comportamiento, también conocido como transición de aislante de metal, podría ser muy útil para una variedad de aplicaciones nuevas y emocionantes.
Los científicos conocen desde hace mucho tiempo las propiedades electrónicas del VO2, pero no han podido explicarlas hasta ahora. Resulta que su estructura atómica cambia de fase a medida que aumenta la temperatura, pasando de una estructura cristalina a temperatura ambiente a una metálica, a temperaturas superiores a 68 ° C.
Lo verdaderamente interesante es que esta transición ocurre en menos de un nanosegundo, algo que lo hace muy útil para aplicaciones electrónicas. No solo eso, además de a la temperatura, resulta que el VO2 también es sensible a otros factores que podrían hacer que cambie de fase, como la inyección de energía eléctrica, determinadas iluminaciones, o la aplicación de un pulso de radiación de terahercios (en el límite entre microondas e infrarrojo). Todo ello implica que el consumo energético del interruptor es minúsculo.
Contrariamente a lo que podamos suponer, 68ºC es una temperatura de transición demasiado baja para la electrónica de los dispositivos actuales, donde los circuitos funcionan sin problemas a unos 100 ºC. Una solución a este problema la propusieron investigadores de la Escuela Politécnica Federal de Lausana (Suiza) en julio de 2017 que consistía en añadir germanio a una lamina de VO2. Simplemnete con esto la transición pasaba a ocurrir a 100 ºC.

Un chip basado en dióxido de vanadio (IV) fabricado en la Escuela Politécnica Federal de Lausana. Imagen: EPFL / Jamani Caillet
Solucionado este problema, investigadores del mismo grupo suizo, que incluye a la ingeniera española Montserrat Fernández-Bolaños, han sido capaces de fabricar por primera vez filtros de frecuencia modulables ultracompactos. Esta tecnología hace uso de las características de interruptor por cambio de fase del VO2 y es especialmente eficaz en un rango de frecuencias que es crucial para las comunicaciones espaciales, la llamada banda Ka. Esta banda es la que se emplea, por ejemplo, para la descarga de datos científicos del telescopio espacial Kepler y es la que se usará en telescopio espacial James Webb. Los filtros pueden programarse para modular entre los 28,2 y los 35 GHz.
Estos primeros resultados es muy posible que estimulen la investigación de las aplicaciones del VO2 en dispositivos electrónicos de potencia ultrabaja. Además de las comunicaciones espaciales que mencionábamos, otras posibilidades podrían ser la computación neuromórfica (computación basada en circuitos analógicos que simulan estructuras neurobiológicas) y los radares de alta frecuencia para automóviles autónomos.
Referencia:
E. A. Casu , A. A. Müller, M. Fernández-Bolaños et al (2018) Vanadium Oxide bandstop tunable filter for Ka frequency bands based on a novel reconfigurable spiral shape defected ground plane CPW IEEE Access doi: 10.1109/ACCESS.2018.2795463
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Óxido de vanadio (IV), un material para una revolución de ciencia ficción se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Siligrafeno, ¿el material para la revolución optoelectrónica?
- Un equipo de alta fidelidad de ciencia ficción
- Ciencia para todos a través del cine y la literatura de ciencia ficción
Las vacas de Narayana, la versión hindú de los conejos de Fibonacci
En octubre de 2002, el compositor minimalista norteamericano Tom Johnson visitó la Universidad del País Vasco/Euskal Herriko Unibertsitatea. Durante dicha visita Tom Johnson ofreció dos interesantes seminarios sobre su forma de componer utilizando las matemáticas y se organizaron algunos conciertos. Una de las composiciones musicales que tuve el placer de escuchar entonces fue Las vacas de Narayana (1989), interpretada por los miembros del grupo Kuraia Ensemble (Asociación de Música Contemporánea del País Vasco), Andrea Cazzaniga (violín), Rafael Climent (clarinete) e Iñigo Ibaibarriaga (saxofón).

El compositor minimalista norteamericano Tom Johnson preparando el instrumento para ejecutar la obra “Galileo” (2001), que estrenó en la Facultad de BBAA de la UPV/EHU en 2002
Para componer la obra Las vacas de Narayama, Tom Johnson se basó en el problema homónimo propuesto por el matemático indio Narayana Pandita (1340-1400) en su tratado de aritmética Ganita Kaumudi (1356). Una de las cuestiones estudiadas por Narayana Pandita en esta obra fueron las sucesiones que él llamó “aditivas”, entre las que se encuentra la que nosotros conocemos como sucesión de Fibonacci.
El problema de las vacas de Narayana dice lo siguiente:
Si las vacas tienen una cría cada año, y cada ternera, después de los tres años que necesita para convertirse en una vaca madura, tiene una cría a principio de cada año, ¿cuántas vacas habrá después de 20 años a partir de una primera ternera?

El proyecto artístico “CowParade” es un proyecto internacional que se ha desarrollado en muchas ciudades del mundo, entre ellas Bilbao, Barcelona o Madrid. La vaca “cowculus” fue exhibida en Kansas city (EE.UU.)
Si empezamos con una ternera recién nacida, a principios de año, durante los tres primeros años solamente tendremos una (1) vaca, esa primera ternera. El cuarto año empezará realmente a crecer la población bovina, con la vaca inicial y su primera ternera, luego dos (2) vacas en total. Habrá una ternera más al principio de cada uno de los dos siguientes años, luego tres (3) el quinto año y cuatro (4) el sexto. Al inicio del séptimo, la primera ternera nacida de la vaca original ya puede tener también terneras, por lo que ese año habrá dos vacas adultas y cuatro terneras, en total, seis (6) vacas. El siguiente año una nueva ternera pasa a la madurez y tres vacas tienen una ternera cada una, luego en total hay tres vacas maduras y seis terneras, luego nueve (9) vacas. Al inicio del noveno año, habrá trece (13) vacas, cuatro adultas y nueve terneras. En el siguiente gráfico hemos representado la evolución de vacas en esos nueve primeros años.
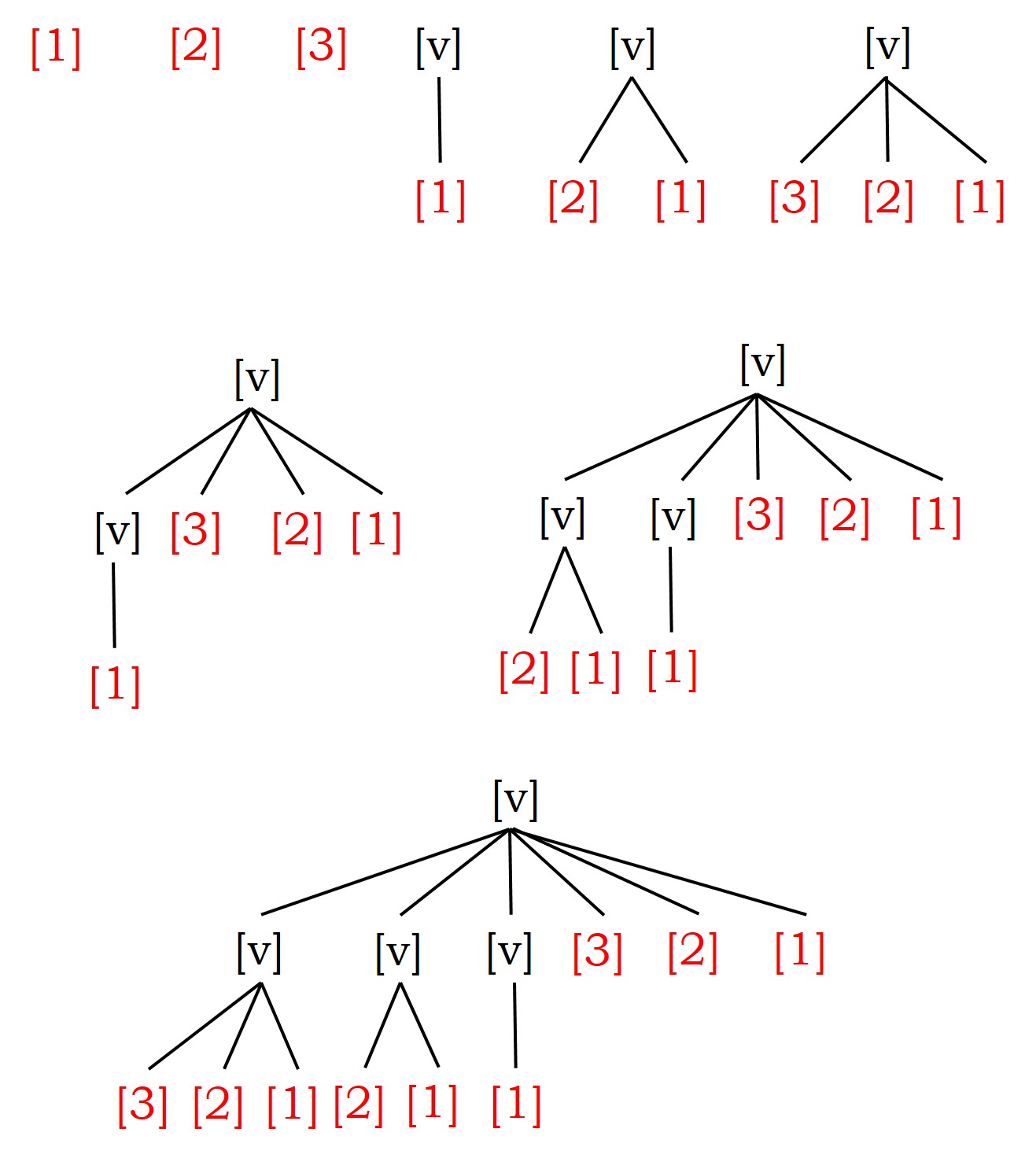
Gráfico del problema de las vacas de Narayana en los nueve primeros años
Pero continuemos… ¿cuántas vacas habrá el décimo año? Estarán las que ya estaban el año anterior, es decir, trece (13) vacas, más las terneras de las vacas que ese año pueden tener crías, que son exactamente las vacas que había hace tres años, seis (6) vacas, en total, diecinueve (13 + 6 = 19) vacas. Como se ve en el siguiente gráfico, seis son vacas maduras y trece son terneras, pero también podemos numerarlas por generaciones, la vaca original es la primera generación, hay siete vacas de la segunda generación, diez de la tercera y una de la cuarta.
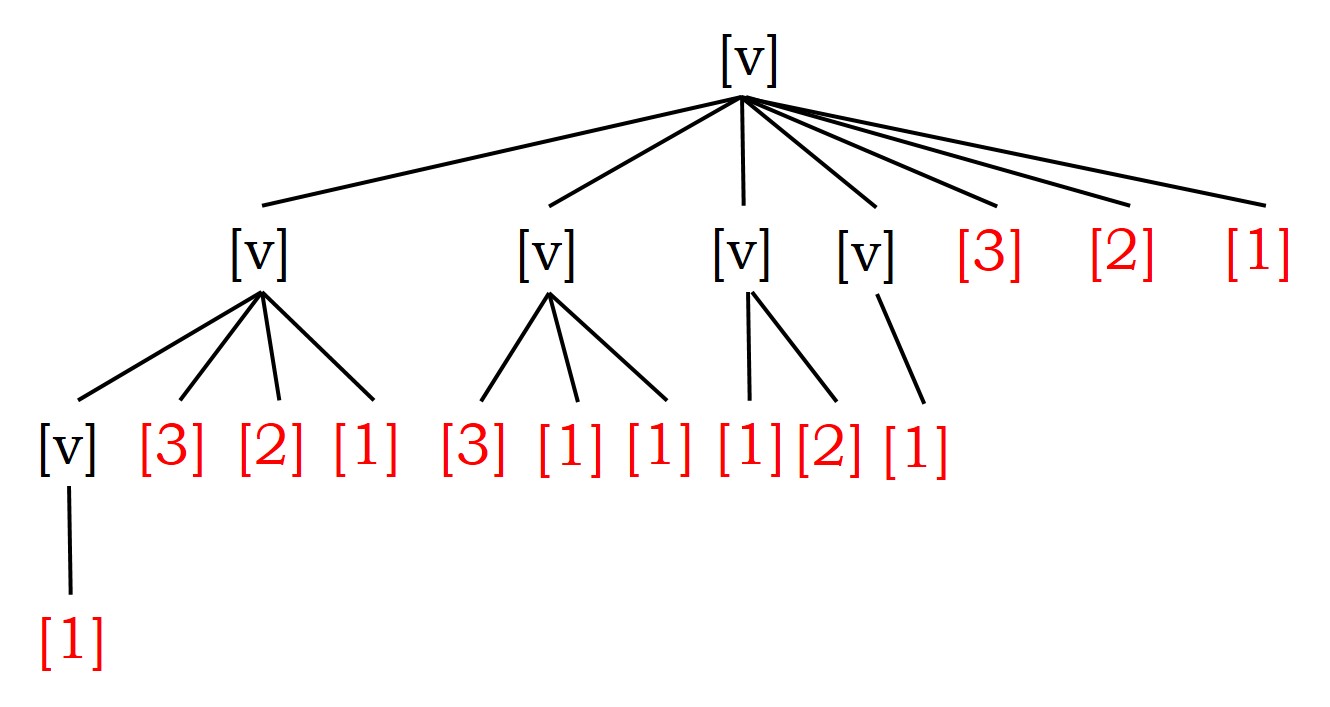
Gráfico del problema de las vacas de Narayana en el décimo año
El razonamiento que hemos realizado para obtener el número de vacas al inicio del décimo año es, de hecho, general y realmente nos da una fórmula recursiva para resolver el problema de las vacas de Narayana. Si se denota por v(n) el número de vacas que habrá en el año n, entonces
v(n) = v(n – 1) + v(n – 3),
siendo además, v(1) = v(2) = v(3) = 1.
Por lo tanto, se pueden obtener fácilmente los primeros veinte números de la sucesión de vacas de Narayana,
1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60, 88, 129, 189, 277, 406, 595, 872, …
Luego, después de veinte años, es decir, al inicio del año veintiuno, habrá 406 + 872 =1.278 vacas.
Incluso, podemos hacer una tabla de la sucesión de vacas de Narayana, viendo las vacas que hay de cada generación.
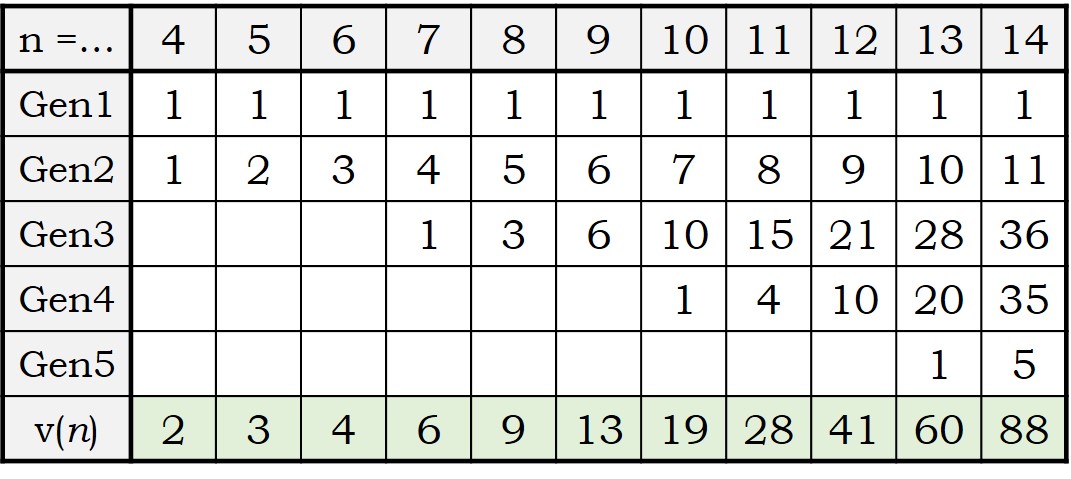
Observando esta tabla con los primeros años ya podemos extraer algunas curiosas conclusiones. Por ejemplo, el número de vacas de la segunda generación son los números naturales, puesto que son las vacas que van naciendo de la vaca original, y cada año tiene una nueva ternera, luego cada año una más, 1, 2, 3, 4, 5, …
En la tercera generación se obtienen los números triangulares, ya que son las sumas de los primeros números naturales, puesto que son las vacas descendientes de las de la generación anterior. Por ejemplo, en el décimo año hemos visto que el número de vacas de la segunda generación eran 1 + 2 + 3 + 4 = 10. Recordemos que los números triangulares T(n), que se llaman así puesto que son los que se obtienen al colocar piedras o discos circulares formando un triángulo equilátero (como se ve en la imagen siguiente), son aquellos que son la suma de los primeros números naturales, T(n) = 1 + 2 + 3 + … + (n – 1) + n.
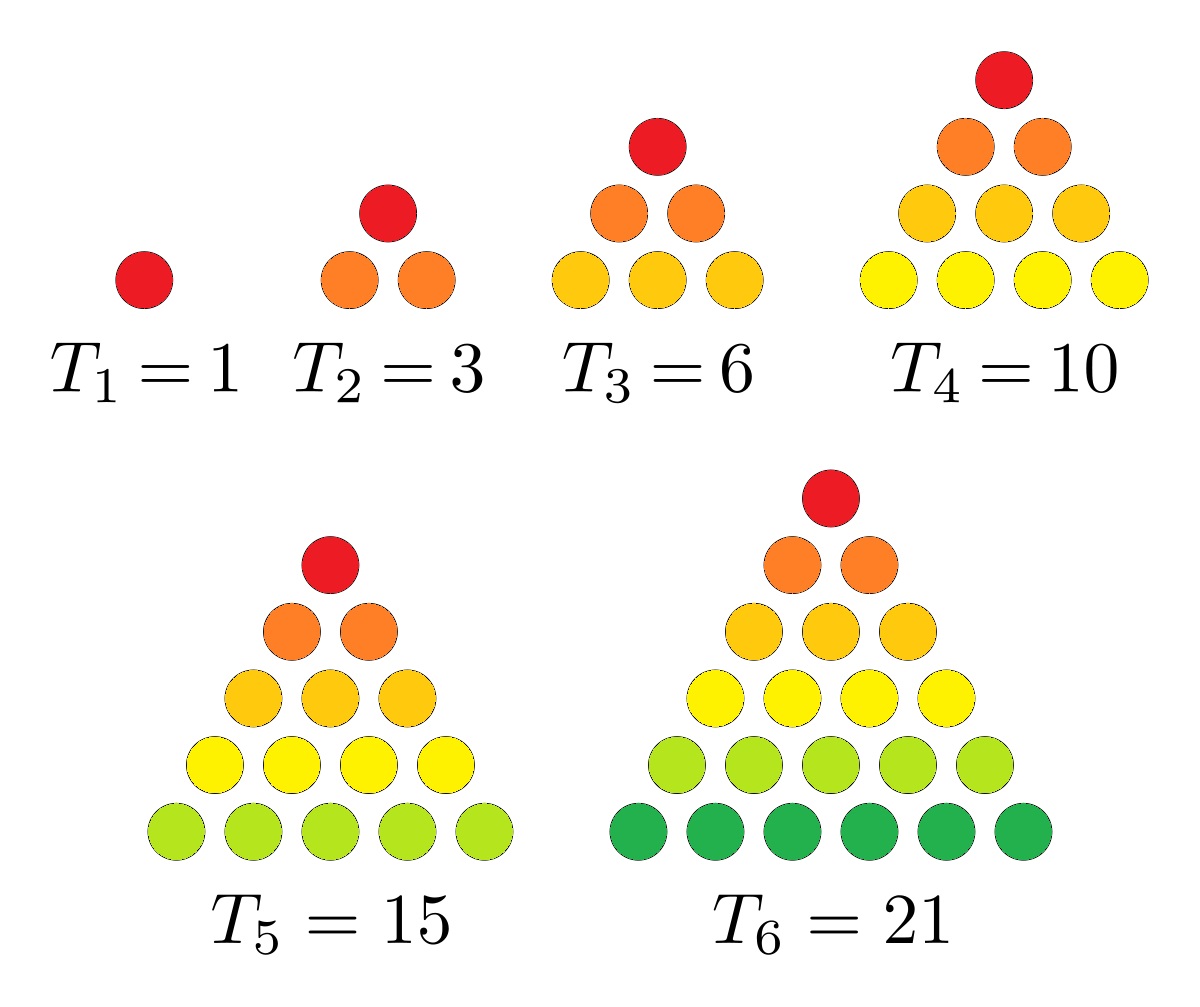
: Los números triangulares son aquellos que son la suma de los primeros números naturales, 1, 1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10, 1 + 2 + 3 + 4 + 5 = 15, 1 + 2 + 3 + 4 + 5 + 6 = 21,…
Por el mismo motivo, las vacas de la cuarta generación serán los llamados números tetraédricos, 1, 4, 10, 20, 35, … ya que serán las sumas de los primeros números triangulares, los que aparecen en la tercera generación. Recordemos que los números tetraédricos son el número de bolas que hay en una pirámide triangular (como la de la imagen), es decir, un tetraedro, y que es igual a la suma de los primeros números triangulares, TT(n) = T(1) + T(2) + … + T(n).

Los números tetraédricos son aquellos que son la suma de los primeros números triangulares, 1, 1 + 3 = 4, 1 + 3 + 6 = 10, 1 + 3 + 6 + 10 = 20, 1 + 3 + 6 + 10 + 15 = 35, … Imagen de cults3d.com
Dejemos por un momento la sucesión de las vacas de Narayana y volvamos a la composición musical basada en este problema. Pero antes presentemos brevemente a su autor, el compositor Tom Johnson.

El compositor norteamericano Tom Johnson
Tom Johnson (Greeley, Colorado, EE.UU.), es un compositor minimalista y teórico de la música estadounidense. Se graduó en la Universidad de Yale, donde obtuvo además su grado avanzado en música. Fue alumno del compositor Morton Feldman (1926-1987), uno de los artífices, junto con John Cage (1912-1992), de la música aleatoria.
Es un compositor minimalista, ya que trabaja con formas simples, escalas limitadas y de manera general, con material reducido. Y dentro del minimalismo destaca por el uso de las matemáticas en el proceso creativo. Fórmulas matemáticas, trigonometría, simetrías, teselaciones, combinatoria, sucesiones de números enteros, teoría de números o fractales, son algunas de las teorías matemáticas que utiliza en sus composiciones.
Tom Johnson ha escrito de su música: “quiero encontrar la música, no componerla”, o como decía su maestro Morton Feldman “Deja a la música hacer lo que quiere hacer”. Mientras John Cage, o Morton Feldman, realizan esta búsqueda mediante el azar, Tom Johnson lo hace mediante las matemáticas.
Entre sus obras encontramos óperas como Riemannoper (1988), Trigonometría (1997) o la más famosa La ópera de las cuatro notas (1972), que fue representada en España en 2015 por Vania Produccions bajo la dirección de Paco Mir (que muchos conoceréis por ser uno de los miembros del trío Tricicle) o composiciones musicales muy creativas e interesantes, como Nueve campanas (1973), Simetrías (1981), Melodías Racionales (1982), Melodías infinitas (1986), Música para 88 (1988), Las vacas de Narayana (1889), Galileo (2001), Mosaicos (2002), o Ritmos de Vermont (2008), entre muchas otras.
Ha escrito libros como la colección de artículos de crítica musical The voice of the new music (Apollohuis, 1989), Self-similar Melodies (Editions 75, 1996) o Looking at numbers (Birkhauser, 2014).
En la composición musical Las vacas de Narayana, Tom Johnson realiza en esta obra una demostración musical del problema matemático. Para ello, divide la pieza en diferentes partes, cada una de las cuales se corresponde con un año del problema de las vacas, y en cada una de esas piezas hay tantas notas como el número de vacas que hay ese año, siendo una nota larga para cada vaca madura y una nota corta para cada ternera.
Aunque antes de seguir hablando de esta composición, lo que debemos hacer es escucharla. Esta pieza está incluida en el álbum Kentzy plays Johnson (2004), con el saxofonista Daniel Kientzy y en el álbum Cows, Chords and Combinations (2011), del grupo Ensemble Klang. Os traemos aquí dos conciertos que están en youtube. Uno es un concierto en Toronto en 2010, organizado por Continuum Contemporary Music.
mientras que el otro es un concierto en 2014, en el Switchboard Music Festival
Como hemos podido observar los conciertos empiezan en el cuarto año, cuando la vaca original tiene su primera ternera. Además, Tom Johnson distribuye las notas largas y cortas, que se corresponden con vacas maduras y terneras en la composición, siguiendo unas estructuras de árbol similares a los que hemos incluido más arriba para los diez primeros años del problema, y leyendo las vacas que hay, de arriba hacia abajo y de derecha a izquierda en esos diagramas de tipo árbol.
Por ejemplo, si escuchamos (o leemos la partitura, cuya primera página hemos incluido más abajo) la sucesión de notas que se corresponde con el quinto año del concierto (el octavo en el problema entero de las vacas de Narayana, o también en la partitura escrita) y miramos al diagrama de árbol de ese año, observaremos que las notas serán
larga – corta – corta – corta – larga – corta – larga – corta – corta

Primera página de la partitura de “Las vacas de Narayana” (1989), de Tom Johnson
Cuando se escucha la obra de Tom Johnson, los primeros años de la composición musical sirven para entender el problema de las vacas de Narayana y la forma en la que el compositor asocia las notas musicales con las vacas maduras y crías, mientras que según van pasando los años vamos percibiendo la estructura, que surge a partir del problema matemático, de la composición musical.
Regresemos de nuevo a las matemáticas de la sucesión numérica de las vacas de Narayana. Es un hecho muy conocido, tanto en la literatura matemática, como por las personas interesadas en la sucesión de Fibonacci (véase alguno de los libros titulados La proporción áurea, de Mario Livio o Fernando Corbalán), que si se toma el cociente entre dos miembros consecutivos de la sucesión de Fibonacci F(n + 1) / F(n), esta sucesión de cocientes, converge (al ir aumentando n) a la proporción áurea, phi = 1,6180339…
1/1 = 1; 2/1 = 2; 3/2 = 1,5; 5/3 = 1,666…; 8/5 = 1,6; 13/8 = 1,625; 21/13 = 1,615…; 34/21 = 1,619…; 55/33 = 1,617…; etc…
¿Ocurrirá algo similar si tomamos la sucesión de los cocientes de números consecutivos de la sucesión de las vacas de Narayana? La respuesta es afirmativa, como vamos a ver a continuación.
Empezamos en la fórmula recursiva de la sucesión de vacas de Narayana
v(n + 1) = v(n) + v(n – 2),
a la que le dividimos por v(n) y además, en el último sumando, multiplicamos y dividimos por v(n – 1), para obtener la expresión
v(n + 1) / v(n) = 1 + v(n – 2) / v(n – 1) × v(n – 1) / v(n).
Si llamamos κ al límite, cuando n tiene de infinito, del cociente v(n + 1) / v(n), la anterior expresión nos dice que κ satisface la ecuación de tercer grado κ 3 – κ 2 – 1 = 0, que podemos llamar la ecuación de Narayana. Esta ecuación tiene tres soluciones, dos de ellas imaginarias, y la solución real que buscamos es (calculada con WolframAlfa)

Aproximadamente, κ = 1,46557123187676802665673… que podríamos llamar la proporción de Narayana.

Kodhai. Vaca rescatada del Santuario Dakshin Vrindavan, de la artista Charlotte Gerrard
Vamos a terminar esta entrada del Cuaderno de Cultura Científica mostrando algunas caracterizaciones interesantes de la sucesión de vacas de Narayana.
A. Número de embaldosados con triominós rectos de rectángulos 3 × (n – 1).
Consideremos un rectángulo de tamaño 3 × (n – 1), como el que aparece en la imagen de abajo (ese en particular es de tamaño 3 × 5), entonces el número v(n) de la sucesión de vacas de Narayana para el año n, es igual a la cantidad de embaldosados posibles con triominós rectos, fichas de tamaño 1 × 3, también llamados I-triominós (véase la entrada Embaldosados con L-triominós (un ejemplo de demostración por inducción) [https://culturacientifica.com/2014/07/16/embaldosando-con-l-triominos-un-ejemplo-de-demostracion-por-induccion/]), es decir, el número de diferentes maneras que hay de colocar triominós rectos en el rectángulo 3 × (n – 1).
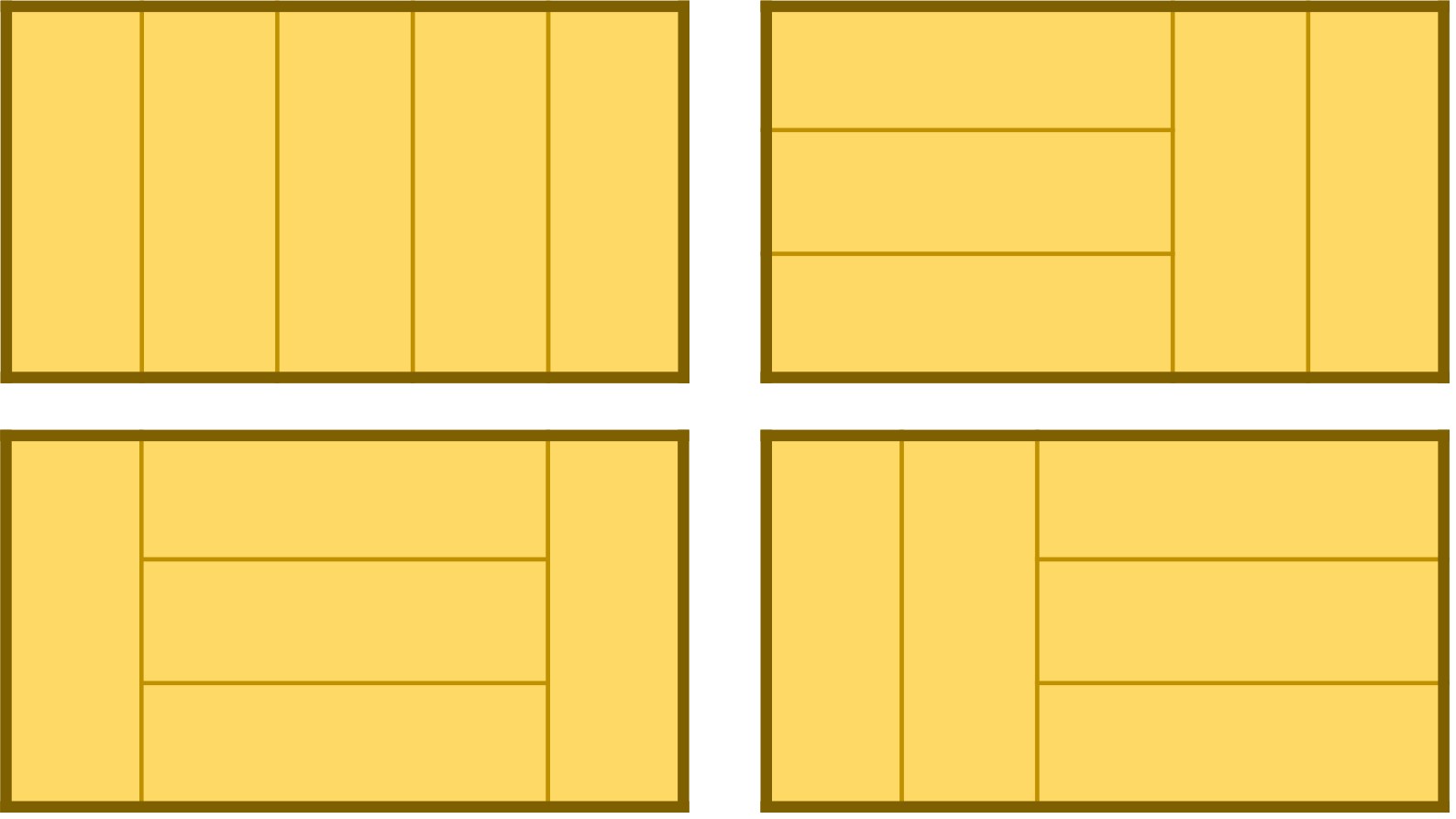
El número de vacas del sexto año, v(6), es 4, al igual que el número de embaldosados con triominós rectos del rectángulo 3 × 5
Esta caracterización es una versión geométrica del siguiente resultado de la Teoría de números relacionado con las particiones de los números.
B. Número de composiciones del número n – 1, con el 1 y el 3.
Recordemos primero dos conceptos básicos de la Teoría de números, como son las particiones y las composiciones. Una partición de un número entero positivo es una forma de expresarlo como suma de números enteros positivos, donde el orden no es relevante. Por ejemplo, el número 3 puede expresarse como suma de tres formas distintas {1 + 1 + 1, 2 + 1, 3}, mientras que existen cinco particiones del número 4 {1 + 1 + 1 + 1, 2 + 1 + 1, 2 + 2, 3 + 1, 4}. Si se denota por p(n) el número de particiones de n, entonces p(3) = 3 y p(4) = 5.
Si en las particiones se tuviera en cuenta el orden, se obtendrían las composiciones, o particiones ordenadas, que se denotan c(n). Así, las particiones ordenadas de 4 son: {1 + 1 + 1 + 1, 2 + 1 + 1, 1 + 2+ 1, 1 + 1 + 2, 2 + 2, 3 + 1, 1 + 3, 4}. Luego, c(4) = 8, mientras que p(4) = 5.
La sucesión de números de Narayama, al igual que la de Fibonacci (véase, por ejemplo, el libro Cayley, el origen del álgebra moderna), se puede relacionar con ciertos tipos de composiciones de números. En particular, la anterior caracterización geométrica es equivalente a que el número v(n) de la sucesión de vacas de Narayana para el año n, es igual al número de composiciones del número n – 1 con únicamente los números 1 y 3. Así, como las composiciones, con 1 y 3, de 6 son {1+1+1+1+1+1, 1+1+1+3, 1+1+3+1, 1+3+1+1, 3+1+1+1, 3+3}, entonces v(7) = 6.
C. Número de formas de colocar n – 2 alfombras tatami en una habitación de tamaño 2 × (n – 2), sin que los vértices de 4 alfombras coincidan.
Recordemos que las alfombras tatami de las casas tradicionales japonesas tienen una relación de tamaño de 1 × 2.

Una distribución de alfombras tatami en una habitación de tamaño 2 × 7

Una distribución no válida de alfombras tatami, ya que los vértices de cuatro alfombras coinciden, en una habitación de tamaño 2 × 7
Existen 13 formas de cubrir una habitación de tamaño 2 × 7 con alfombras tatami, sin que coincidan las esquinas de cuatro de ellas, que es exactamente el número v(9). De hecho, esas 13 maneras pueden describirse de la forma 1111111, 111112, 111121, 111211, 112111, 121111, 211111, 11212, 12112, 21112, 12121, 21121, 21211.
Si lo pensamos un momento, la descripción con 1 y 2 de colocar las alfombras tatami (1 para las verticales, 2 para las horizontales) nos está diciendo realmente que podemos describir el número de la sucesión de vacas de Narayana v(n) como las composiciones de n – 2 con tan solo los números 1 y 2, pero sin que haya dos 2 juntos.
D. Número de composiciones del número n – 2, con el 1 y el 2, sin que haya dos 2 juntos.
Como despedida de esta entrada otra pieza del compositor minimalista norteamericano Tom Johnson, la primera de sus melodías racionales, en mi opinión una hermosa pieza, interpretada por el Gruppo di Musica Contemporanea Steffani, en el Conservatorio Steffani, de Castelfranco Veneto (Italia), en 2009.

Portada del disco Rational Melodies/Bedtime stories, de Tom Johnson, con Roger Heaton al clarinete. El diseño de la portada es la obra de Esther Ferrer, “Project Drawing With Prime Number Series, Spiraling Out From 19.000.041”
Bibliografía
1.- Página web de Editions 75
2.- Tom Johnson, Kientzy plays Johnson (álbum), 2004.
3.- Jean-Paul Allouche, Tom Johnson, Narayana’s Cows and Delayed Morphisms, Cahiers du GREYC Troisiemes Journées d’Informatique Musicale (JIM 96) 4, p. 2-7, 1996.
4.- Parmanand Singh, The so-called Fibonacci Numbers in Ancient and Medieval India, Historia Mathematica 12, p. 229-244, 1985.
5.- Krishnamurthy Kirthi, Subhash Kak, The Narayana Universal Code, ArXiv, 2016.
6.- Tom Johnson, Self-Similar Melodies, Editions 75, 1996.
7.- Tom Johnson, Looking at numbers, Birkhäuser, 2014.
8.- Fernando Corbalán, La proporción áurea, El lenguaje matemático de la belleza, RBA, 2010.
9.- Mario Livio, La proporción áurea, La historia de phi, el número más sorprendente del mundo, Ariel, 2006.
10.- Página web de la artista Charlotte Gerrard
11.- N. J. A. Sloane, La sucesión de vacas de Narayana, A000930 [https://oeis.org/A000930], Enciclopedia on-line de sucesiones de números enteros.
12.- Raúl Ibáñez, Cayley, el origen del álgebra moderna, colección Genios de las matemáticas, RBA, 2017.
13.- Frank Ruskey, Jennifer Woodcock, Counting Fixed-Height Tatami Tilings, The Electronic Journal of Combinatorics 16, 2009.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Las vacas de Narayana, la versión hindú de los conejos de Fibonacci se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un rebaño de vacas pastando como sistema complejo
- Los números (y los inversos) de Fibonacci
- #Naukas14 ¿Por qué explota una granja de vacas?
Sistemas respiratorios: almacenamiento y transferencia de oxígeno
En diferentes especies animales y bajo diversas circunstancias, la transferencia de oxígeno desde el medio externo hasta su destino final en las mitocondrias se produce a través de dos pigmentos respiratorios diferentes. En tales casos, los pigmentos suelen mostrar diferente afinidad por el oxígeno y esa diferencia constituye un elemento clave de su funcionamiento. Repasaremos aquí algunos de esos sistemas pigmentarios sin ánimo de exhaustividad.
Sangre fetal y sangre materna
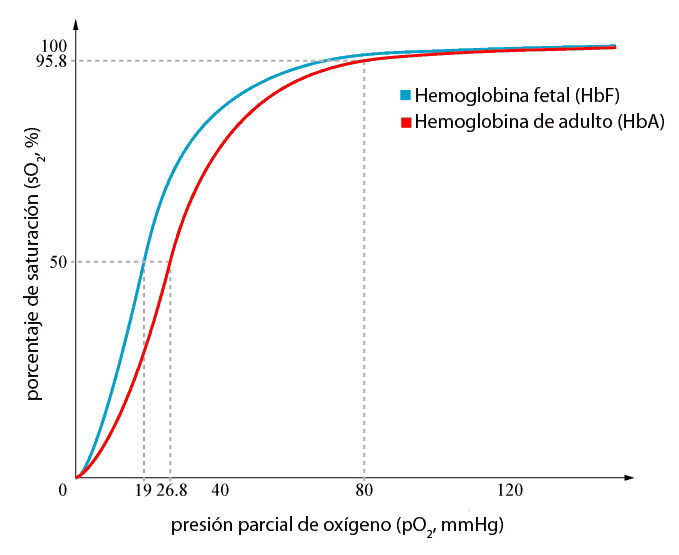
Cuando se comparan las curvas de disociación de la sangre fetal y la sangre materna en mamíferos placentarios, se observa que la curva de la sangre fetal se halla desplazada hacia la izquierda en relación con la de la sangre materna. Quiere decir que la sangre fetal tiene una mayor afinidad por el oxígeno que la materna o, lo que es lo mismo, que para una tensión parcial de oxígeno dada, la fetal se encuentra saturada en un porcentaje mayor que la sangre materna.
Esa diferencia en la afinidad obedece a dos razones. Por un lado, la hemoglobina fetal es algo diferente de la hemoglobina de los adultos, y esa diferencia determina una mayor afinidad. Y además, la concentración de fosfatos orgánicos en los eritrocitos de la sangre fetal es menor que en los de sangre de adultos, por lo que en estos el efecto de esas sustancias moduladoras es mayor. Tras el nacimiento, la hemoglobina fetal es sustituida de forma gradual por hemoglobina de adultos y en los eritrocitos tiende a elevarse la concentración de los fosfatos orgánicos.
La diferente afinidad de las dos hemoglobinas tiene una utilidad evidente para el feto, puesto que de otro modo, la transferencia de oxígeno de la sangre materna a la sangre fetal en la placenta se vería limitada en cierto grado. Y debe tenerse en cuenta que el feto, por su pequeño tamaño y por estar formado por tejidos en pleno desarrollo, tienen una alta demanda de oxígeno.
Función de las mioglobinas
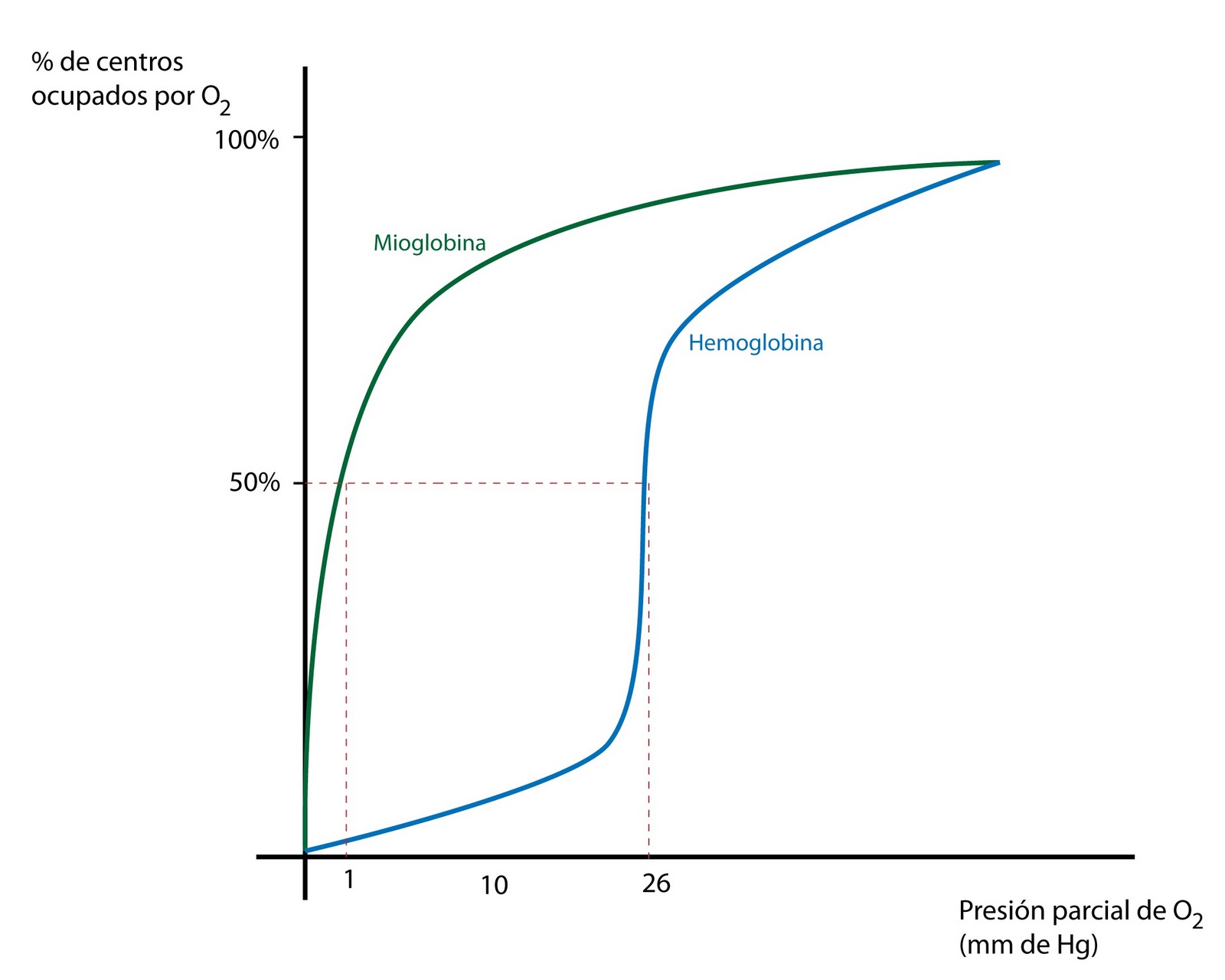
Las mioglobinas son pigmentos musculares muy similares a las hemoglobinas sanguíneas. La diferencia es que son de pequeño tamaño puesto que están formadas por una única cadena de aminoácidos. La mioglobina tiene mayor afinidad por el oxígeno que la hemoglobina.
Gracias a esa diferencia de afinidad capta el O2 sanguíneo y facilita su difusión a las mitocondrias musculares. Se ha comprobado experimentalmente la importancia de esta función con ratones a los que se les privó de la posibilidad de sintetizar mioglobina; aunque los ratones pudieron desarrollar una vida normal, hubieron de compensar la falta de mioglobina elevando de forma significativa la densidad de capilares sanguíneos en los músculos. De otra forma no habrían podido suministrar a los músculos el oxígeno necesario para mantener niveles adecuados de metabolismo aerobio.
La mioglobina sirve, además, de almacén de oxígeno. En especies que respiran con normalidad en medios con suficiente disponibilidad de oxígeno, ese almacén garantiza el suministro de O2 a las mitocondrias durante los breves periodos de tiempo (segundos o fracciones de segundo) que, tras iniciarse una actividad muscular intensa, el sistema cardiovascular necesita para hacer llegar a los músculos el oxígeno necesario. Y también cuando los capilares se ocluyen transitoriamente por efecto de las contracciones musculares. La función de almacén es mucho más importante en las especies –como los mamíferos marinos- que dejan de respirar durante periodos de tiempo relativamente prolongados al sumergirse para ir en busca de alimento. De estas especies, no obstante, nos ocuparemos con más detalle en otra ocasión.
La mioglobina no solo se encuentra en la musculatura de vertebrados. El músculo radular del molusco Cryptochiton también tiene mioglobina, y lo llamativo de este caso es que su pigmento vascular no es hemoglobina, sino hemocianina. Es muy probable que este no sea el único caso en que esto ocurre.
Pigmento vascular y pigmento celómico

Se conocen varios sistemas pigmentarios en invertebrados aunque, quizás, el mejor conocido es el del sipuncúlido Dendrostomum. Este sipuncúlido tiene hemeritrina, tanto en su sangre como en el fluido celómico. Los tentáculos rodean la boca y se encuentran bien irrigados de sangre; el gusano vive dentro de la arena y los tentáculos se proyectan hacia el exterior –hacia la masa de agua circundante- y cumplen una función respiratoria. La hemeritrina celómica de Dendrostomum tiene una mayor afinidad por el oxígeno que la sanguínea, lo que quiere decir que el oxígeno captado por la sangre de los tentáculos es transferido con facilidad al fluido celómico. Y del fluido celómico pasa a las células.
———————————————–
Como se ha podido ver aquí, existen en el mundo animal diversas disposiciones anatómicas y funcionales en las que es necesario el concurso de más de un pigmento para que el O2 pueda ser transferido desde el exterior hasta su destino final (feto, músculos, u otros tejidos) y en todas esas disposiciones el juego de afinidades es clave para que tal transferencia pueda cursar con suficiencia y normalidad. En algunos casos, además, uno de los pigmentos cumple funciones de almacenamiento de oxígeno, lo que constituye una garantía de provisión constante ante la existencia de fluctuaciones de diferente intensidad y duración en el suministro al animal (su órgano respiratorio) o a los músculos.
Fuentes:
John D. Jones (1972): Comparative physiology of respiration. Edward Arnold, Edinburgh
Knut Schmidt-Nielsen (1997): Animal Physiology. Adaptation and Environment. Cambridge University Press; Cambridge
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Sistemas respiratorios: almacenamiento y transferencia de oxígeno se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sistemas respiratorios: los pigmentos respiratorios
- Sistemas respiratorios: pigmentos de alta afinidad
- Sistemas respiratorios: pigmentos de baja afinidad
Equivalencia entre masa y energía

El USS Enterprise en 1964 durante la operación “Sea Orbit” en la que dio la vuelta al mundo en 65 días sin repostar, demostrando la capacidad de la tecnología basada en la equivalencia entre masa y energía.
Después de que Einstein completara su artículo sobre la teoría especial de la relatividad en 1905 descubrió una consecuencia más de los postulados de la relatividad que presentó, como una idea de último momento, en un artículo de solo tres páginas posterior ese mismo año. Desde el punto de vista del efecto de la física en la historia mundial, resultó ser el más significativo de todos sus hallazgos: la quivalencia entre masa y energía.
Sabemos que cuando se realiza trabajo sobre un objeto, como golpear una pelota de tenis con una raqueta, el objeto adquiere energía. En la teoría de la relatividad, el aumento de la velocidad y, por lo tanto, el aumento de la energía cinética de una pelota de tenis o de cualquier otro objeto, da como resultado un aumento de la masa (o inercia), aunque en el día a día suele ser solo un aumento infinitesimal.
Al examinar esta relación entre velocidad relativa y masa efectiva con más detenimiento Einstein descubrió que cualquier aumento en la energía de un objeto debería producir un aumento de la masa medida; este incremento de energía daría igual si se hace acelerando el objeto, o calentándolo, o cargándolo con electricidad, o simplemente realizando trabajo elevándolo en el campo gravitacional de la Tierra. En resumen, Einstein descubrió que un cambio en la energía es equivalente a un cambio en la masa.
No solo eso. Descubrió además que la equivalencia funciona en ambos sentidos: un aumento o disminución de la energía en un sistema aumenta o disminuye correspondientemente su masa, y un aumento o disminución de la masa corresponde a un aumento o disminución de la energía. En otras palabras, la masa en sí misma es una medida de una cantidad equivalente de energía.
Dicho de otra manera, un cambio (recordemos que los cambio se expresan con la letra griega delta mayúscula, Δ) en la cantidad de energía, E, de un objeto es directamente proporcional a un cambio en su masa, m. Lo que Einstein hizo en su articulito de tres páginas es demostrar que esa constante de proporcionalidad es el cuadrado de la velocidad de la luz en el vacío, c2. En símbolos, ΔE = Δm·c2, o de forma más genérica, E = m·c2, probablemente la ecuación más famosa de todos los tiempos.
Significa que un cambio de masa observado es equivalente a un cambio de energía, y viceversa. Pero también significa que la propia masa de un objeto, incluso si no cambia, es equivalente a una enorme cantidad de energía, ya que la constante de proporcionalidad, c2, el cuadrado de la velocidad de la luz en el vacío, es un número enorme.
Por ejemplo, la energía contenida en un solo gramo de materia es de E = 0,001 kg · (299792485 m/s)2 = 8,988·1013 kg·m2/s2≈ 9·1013 J. Esta enorme cantidad de energía es aproximadamente la misma que libera la explosión de 20 toneladas de TNT.
La transformación de masa en energía es Es la fuente de las energías liberadas por las sustancias radiactivas, por nuestro Sol y otras estrellas, por las armas nucleares y por los reactores nucleares que producen energía eléctrica.
No solo masa y energía son “equivalentes”, podemos afirmar que la masa es energía. Esto es exactamente lo que concluyó Einstein en 1905: “La masa de un cuerpo es una medida de su contenido energético”. Nada impide que consideremos la masa como “energía congelada”, congelada en el momento en que el Universo se enfrió poco después del Big Bang y la energía se agrupó formando “bolas” de materia, las partículas elementales de las que se compone la materia ordinaria.
Por lo tanto, cualquier energía adicional que se añada a una masa aumentará su masa aún más. Por ejemplo, a medida que aceleramos los protones en el laboratorio a casi la velocidad de la luz, su masa aumenta de acuerdo con la fórmula relativista para mm. Este aumento también se puede interpretar como un aumento en el contenido de energía de los protones.
Estas dos deducciones diferentes de la teoría de la relatividad -aumento de masa y equivalencia de masa de energía- son consistentes entre sí. Esta equivalencia tiene un significado muy importante. Primero, dos grandes leyes de conservación se convierten en dos formas alternativas de una sola ley. En cualquier sistema cuya masa total se conserve, la energía total también se conserva. En segundo lugar, surge la idea de que parte de la energía en reposo podría transformarse en una forma de energía más familiar. Dado que el equivalente energético de la masa es tan grande, una reducción muy pequeña en la masa en reposo liberaría una enorme cantidad de energía, por ejemplo, energía cinética o energía electromagnética.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Equivalencia entre masa y energía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La relatividad de la masa
- Se intuye la conservación de la energía (1)
- Se establece el principio de conservación de la energía
Inteligencia y ateísmo

Los británicos R. Lynn y J. Harvey, y el danés H. Nyborg, se preguntaron si la idea que Richard Dawkins expresa en The God Delusion de que no es inteligente creer en la existencia de Dios es o no correcta. Y la respuesta a esa pregunta la publicaron en abril de 2008 en la edición digital (en 2009 en papel) de la revista Intelligence en un artículo titulado Average intelligence predicts atheism rates across 137 nations. El estudio da cuenta de la existencia de una correlación negativa significativa entre la inteligencia (expresada mediante el índice “g” de inteligencia general) y el grado de religiosidad de la población de diferentes países.
Los autores, en su introducción, revisaron los trabajos anteriores sobre este mismo tema, e indicaron que las evidencias de la existencia de una relación negativa entre inteligencia y fe religiosa proceden de cuatro fuentes diferentes: 1) Existencia de correlación negativa entre las dos variables; como ejemplo, en un estudio realizado con más de 14.000 norteamericanos jóvenes el IQ varió de la siguiente forma: no religiosos = 103’09; algo religiosos = 99’34; bastante religiosos = 98’28; muy religiosos = 97’14. 2) Menores porcentajes de personas con creencias religiosas entre las personas más inteligentes que en el conjunto de la población. 3) Disminución de las creencias religiosas de niños y adolescentes conforme crecen y desarrollan sus habilidades cognitivas. 4) Disminución de la creencia religiosa durante el siglo XX conforme aumentaba la inteligencia de la población.
Los resultados del estudio se resumen en que la correlación entre el nivel de inteligencia general “g” y la variable “incredulidad religiosa” (religious disbelief) era de 0’60 para un conjunto de 137 países. Si se analizaban por separado los segmentos superior e inferior en que puede dividirse el conjunto de datos (para comprobar si la relación es consistente en todo el rango) se obtenían correlaciones positivas en ambos, aunque esa correlación era alta en el tramo superior y baja en el inferior. O sea, la máxima variación se producía entre los países con mayor nivel de inteligencia y mayor “incredulidad religiosa”.
Un último elemento de interés de ese trabajo es que los autores atribuían las diferencias observadas a factores de naturaleza genética e indicaban que la religiosidad (o creencias religiosas) es altamente heredable (heredabilidad de 0’4-0’5)1.
Los resultados comentados en los párrafos anteriores no constituyen ninguna excepción, sino que se han visto confirmados en diferentes ocasiones y en contextos muy diferentes. Por otro lado, se ha comprobado también que la religiosidad influye en el estilo cognitivo. De acuerdo con la denominada “hipótesis del procesamiento dual”, la cognición tiene una componente intuitiva (rápida) y otra componente lógica (lenta). Y recientemente se han obtenido pruebas experimentales que demuestran un vínculo entre religiosidad y estilo cognitivo. Por ello, se ha sugerido que el efecto de la religiosidad sobre la inteligencia se sustenta en sesgos cognitivo-comportamentales que dan lugar a dificultades al detectar situaciones en las que la intuición y la lógica entran en conflicto. En otras palabras, los individuos religiosos tienden a hacer uso de la componente lógica de la cognición en menor medida que los no religiosos y detectan peor contradicciones entre el razonamiento y la intuición. Y por esa razón obtendrían peores resultados en los test psicométricos.
Richard E. Daws y Adam Hampshire, del Imperial College de Londres, han publicado hace unas semanas en la revista Frontiers of Psycology las conclusiones de un trabajo en el que han sometido a contraste empírico la hipótesis recogida en el párrafo anterior; y sus resultados parecen avalarla.
Su investigación confirma que, en promedio, las personas no religiosas realizan mejor las tareas cognitivas que las religiosas. La magnitud del efecto es pequeña pero significativa, y es acorde con una diferencia de 2-4 puntos en el cociente de inteligencia (CI), tal y como habían puesto de manifiesto estudios psicométricos anteriores a gran escala. La comparación entre ateos y creyentes más dogmáticos llega a arrojar una diferencia de 6.45 puntos en el CI.
Según los autores del estudio, el sesgo cognitivo-comportamental antes descrito sería el causante del efecto de la religiosidad sobre los resultados de los test de inteligencia y no obedecería, por lo tanto, a una menor inteligencia por sí misma. Esa conclusión se ve reforzada por el hecho de que el efecto de la religiosidad se relaciona de forma significativa con los componentes de los test relativos al razonamiento y apenas tiene relación con la memoria de trabajo. Los fallos de razonamiento surgirían cuando los procesos intuitivos rápidos no son contrarrestados por los procesos lógicos lentos. Las diferencias en la calidad del razonamiento serían, por lo tanto, relativas a la capacidad y estilo cognitivo de los individuos, no a su inteligencia.
En conclusión, de acuerdo con el trabajo reseñado, la religiosidad estaría asociada con un peor desempeño en las tareas que provocan un conflicto cognitivo. Ese efecto puede reflejar sesgos cognitivos-comportamentales aprendidos que propician una toma de decisiones basada en mayor medida en intuiciones; y no sería consecuencia de una menor capacidad para entender reglas lógicas complejas o para mantener información en la memoria de trabajo.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
Nota:
1 Se entiende por heredebailidad el porcentaje de la variabilidad observada en un rasgo dado que es atribuible a la herencia genética.
El artículo Inteligencia y ateísmo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Pro 2017: Julián Estévez y la inteligencia computacional
- La búsqueda de la inteligencia artificial, en la próxima zientziateka
- Máquinas inteligentes (II): Inteligencia artificial y robótica
El síndrome de Frankenstein (o de Frankenfood )
La novela Frankenstein o El moderno Prometeo, de Mary W. Shelley, se publicó en Londres el 1 de enero de 2018. Celebremos, a nuestra manera, el 200 aniversario de un evento que es crucial en la relación de la ciencia con la sociedad en nuestro tiempo.

“Tu eres mi creador, pero yo soy tu dueño: ¡obedece!”
Mary W. Shelley, Frankenstein o El moderno Prometeo, 1818.
Una definición del síndrome de Frankenstein aparece en Wikipedia: es el temor de que los descubrimientos de la ciencia se vuelvan contra la especie humana y la dañen o, incluso, la destruyan. Es, en último término, el temor patológico hacia las creaciones humanas. Así, en nuestro tiempo, nos asustan las vacunas, los móviles, la electricidad, las ondas electromagnéticas, las centrales nucleares o, como veremos, las plantas transgénicas.
Entre los descubrimientos más recientes que tanto temor provocan están las organismos modificados genéticamente (GMO, del inglés Genetically Modified Organism), llamados, con propiedad y acierto, Frankenfoods. Es un término que se puede juzgar peyorativo, y que se aplica, sobre todo, a las plantas y animales modificados genéticamente en el laboratorio. El término apareció por primera vez el 16 de junio de 1992, en el New York Times, en una carta al director, firmada por Paul Lewis, profesor de inglés del Colegio Boston, y enviada en respuesta a un artículo de Edmund Andrews, publicado el 13 de junio, que presentaba la patente del primer alimento modificado genéticamente, en este caso, un tomate. Era una patente de la empresa DNA Plant Technology Corporation que, en el grupo dirigido por Pamela Dunsmuir, había insertado en el tomate los genes que dirigían la síntesis de péptidos anticongelantes en el lenguado de invierno. Este pez, de nombre científico Pseudopleuronectes americanus, resiste el frío en su área de distribución de la costa este de Estados Unidos, en el Atlántico Norte. Así se conseguía un tomate resistente al frío, tanto en el campo como luego en el almacenamiento y transporte refrigerados. A este tomate le llamaron Flav Savr.
Consiguieron la patente en 1992, la noticia apareció en el New York Times en junio y provocó la respuesta de Paul Lewis que, en su carta al director, decía:
“Desde que el barón de Mary Shelley liberó de su laboratorio a su creación que mejoraría la especie humana, los científicos no han parado de traer a la vida novedades parecidas. Si ellos quieren vendernos Frankenfoods, quizá es el momento de convocar a los campesinos, prender las antorchas y asaltar el castillo.”

La realidad es que, en estos momentos, el 75% de los alimentos procesados que se consumen en Estados Unidos tienen alguno o varios de las ocho GMO que se comercializan en la actualidad: maíz, soja, alfalfa, remolacha azucarera, colza, algodón, papaya y calabacín.
Precisamente ahora, en las últimas semanas, el salmón gigante transgénico se ha puesto a la venta en Canadá. La empresa que lo comercializa ha declarado que ya ha vendido unas cuatro toneladas y media en filetes. En Estados Unidos también tienen permiso para comercializar este salmón desde 2015, pero todavía no ha llegado al mercado.
Era inevitable que a este salmón se le llamara Frankenfish, y es la primera especie animal GMO que llegará, y ha llegado en Canadá, a nuestra cocina y nuestra mesa.
Y, de nuevo recientemente, Sánchez y Parrott, de la Asociación Gremial ChileBio CropLife, de Santiago de Chile, y de la Universidad de Georgia, respectivamente, han publicado un meta-análisis sobre los trabajos que tratan de los riesgos de las GMO.
Un 5% de los estudios publicados sobre riesgos de plantas transgénicas concluyen que representan algún peligro. En total, son 35 artículos de un total de casi 700. Es curioso que, de esos 35 trabajos, el 43% venga de Italia o el 17% de Egipto y, en cambio, solo uno trate de investigaciones hechas en Estados Unidos, aunque la publicación venga de Australia.
Son investigaciones puntuales con GMO concretas, aunque, cuando llegan a los medios y al público, lo que es típico y habitual, el riesgo para una sola especie se amplia a todos los cultivos de transgénicos.
En general, los estudios vienen de pocos laboratorios y se publican en revistas no muy importantes. Además, presentan problemas metodológicos que invalidan sus conclusiones. Después de 20 años de cultivos comerciales de GMO, los autores del meta-análisis destacan que todavía no se ha publicado ningún trabajo que demuestre efectos peligrosos para la salud humana.
Termino, por ahora, sobre este asunto con la recomendación de repasar el blog de José Miguel Mulet y, ya que parece que hay tantas publicaciones interesantes en los últimos meses sobre las GMO, y lean la entrada titulada “AntiOGM, si no tienes argumentos: invéntalos”.
Vamos a profundizar en la acción de los medios en relación con el síndrome de Frankenstein. Son importantes para difundir la ciencia entre los ciudadanos y crear una cultura científica que ayude a tomar decisiones. En Estados Unidos, Mary Nucci y Robert Kubey, de la Universidad Estatal de Nueva Jersey, han repasado las noticias sobre las GMO en las tres cadenas nacionales de televisión más vistas: ABC, CBS y NBC.
Ya sabemos que la televisión es un medio esencial para difundir noticias con rapidez y a grandes audiencias. Sin embargo, el tratamiento de las GMO en estas tres cadenas es menor y más ligero que en la prensa escrita. Solo se le concede más tiempo en momentos puntuales de crisis. En general, el público sabe poco de las GMO, lo que no impide que, en muchos casos, tenga fuertes convicciones a favor o en contra.
Además, no hay que olvidar que, como escribe José Miguel Mulet, los periodistas aplican un exagerado principio de equidistancia en asuntos, como el de las GMO, que van desde un consenso científico extendido a declaraciones de falsedad manifiesta. Aunque también es cierto que, por lo menos en Estados Unidos, lo que llega de los científicos profesionales al público no influye mucho cuando se forman una opinión, basada más en creencias que en evidencias.
El mismo grupo, liderado por Mary Nucci, también analiza las noticias sobre GMO en la prensa escrita entre 1992 y 2002. Después de repasar cientos de referencias en periódicos y revistas de tirada nacional en Estados Unidos, destacan que el enfoque es muy variado así como el número de noticias, con picos en 1999 y 2000.
Sin embargo, el resultado final es confuso, los debates son continuos, las exageraciones abundan y, en último término, el ciudadano no sabe si las GMO suponen un riesgo o no. Así, un 31% de los consumidores no pueden nombrar un caso concreto sobre los riesgos de las GMO y, algunos, como mucho, recuerdan que es “algo relacionado con el maíz”. En el estudio de Kami Silk y sus colegas, de la Universidad Estatal de Michigan, encuestan a 958 ciudadanos, con 482 mujeres, con edades de 18 a 73 años, y edad media de 29.5 años. El grupo mayor, con 357 voluntarios, no tiene muchos conocimientos sobre las GMO y, también, su respuesta es emocional y tibia. Están a la espera de más información para tomar una decisión. En el otro extremo, otro grupo, con 50 voluntarios, son anti-GMO y las consideran peligrosas, sobre todo porque son parte de nuestros alimentos y las ingerimos. Es más, la mayoría de los encuestados no es consciente de que ya come GMO. Recordar que, en Estados Unidos, el 75% de los alimentos llevan algún GMO. Incluso algunos, quizá muchos, se asustan pues tienen asumido que con los GMO ingerimos “genes”, lo que, creen, es imposible cuando comemos los alimentos de siempre.
El término Frankenfood entró rápidamente en el debate sobre las GMO, siempre con una base psicológica importante en el síndrome de Frankenstein. Evoca profundas respuestas emocionales, como las provocaba la criatura de la novela de Shelley y, sobre todo, la película dirigida por James Whale en 1931. Frankenfood aparece con la incertidumbre que crea la continua polémica sobre las GMO. Es una metáfora que nos ayuda a comprender lo que para muchos supone el peligro de las GMO. Y refleja el miedo que la ciencia y la tecnología provocan en muchas personas y, todavía más, si se considera que la ciencia sobrepasa lo que algunos consideran sus límites. Ese límite es, como en la novela y se repite con las GMO, crear vida.
Además, es un debate que no es fácil simplificar pues, como tantos otros desacuerdos en nuestra complicada sociedad actual, incluye ciencia, política, ideología, salud humana y ambiental, patentes, economía, grandes multinacionales y la opinión pública de una cultura globalizada. Solo con mencionar Frankenfood ya sentimos creencias, emociones e ideología.
Referencias:
Andrews, E.L. 1992. Patents: Keeping ice out of flood that’s frozen. New York Times June 13.
Glass-O’Shea, B. 2011. The history and future of genetically modified crops: Frankenfoods, superweeds, and the developing world. Journal of Food Law and Policy 7: 1-33.
Hightower, R. et al. 1991. Extression of antifreeze proteins in transgenic plants. Plant Molecular Biology 17: 1013-1021.
Maximen, A. 2012. Politics holds back animal engineers. Nature 490: 318-319.
Mazanek, C. 2016. Frankenfoods: Conceptualizing the Anti-GMO argument in the Anthropocene. News Errand’s: The Undergraduate Journal of American Studies 3: 1-12.
McInnery, C. et al. 2004. The flow of scientific knowledge from lab to the lay public. The case of genetically modified food. Science Communication 26: 1-31.
Nucci, M.L. & R. Kubey. 2007. “We begin tonight with fruits and vegetables”. Genetically modified food on the evening news 1980-2003. Science Communication 29: 147-176.
Sánchez, M.A. & W.A. Parrott. 2017. Characterization of scientific studies usually cited as evidence of adverse effects of GM food/feed. Plant Biotechnology Journal DOI: 10.1111/pbi.12798
Shelley, M.W. 2001 (1818). Frankenstein o El moderno Prometeo. Cátedra. Madrid. 356 pp.
Silk, K. et al. 2005. Gene cuisine or Frankenfood? The theory of reasoned action as an audience segmentation strategy for messages about genetically modified foods. Journal of Health Communication 10: 751-767.
Van Ennennaam, A.L. & W.M. Muir. 2011. Transgenic salmon: a final leap to the grocery shelf? Nature Biotechnology 29: 706-710.
Wikipedia. 2016, Síndrome de Frankenstein. 16 febrero.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo El síndrome de <i>Frankenstein</i> (o de <i>Frankenfood</i> ) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los 2 casos del síndrome de Hikikomori en España
- El caso de Rin Tin Tin y sus amigos
- Una herramienta para evaluar el síndrome premenstrual
Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – María José Calderón y Belén Valenzuela: Esta física es la leche
- Naukas Bilbao 2017 – Daniel Marín: Algo se muere en el alma cuando una sonda se va
- Naukas Bilbao 2017 – Mónica Lalanda: Una muerte de cómic
Cómo criopreservar células madre
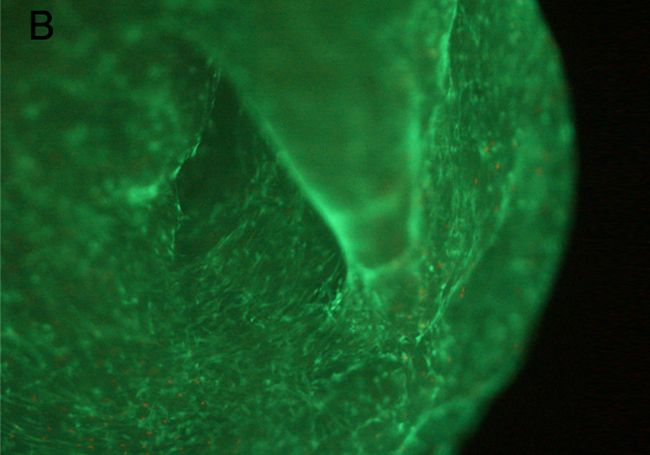
Foto del biosistema con la tinción calceína-etidio tras la congelación (células vivas teñidas de verde y muertas de rojo).
Las células madre mesenquimales son células adultas y pluripotentes con morfología fibroblastoide y capacidad de diferenciarse a diversos linajes celulares como condrocitos, osteocitos y adipocitos entre otros. Su uso para el tratamiento de enfermedades de diverso carácter se está incrementando de manera considerable en la última década.
Una de las aplicaciones en las que se están utilizando (todavía en ensayos clínicos) es el tratamiento de la osteoartritis, la cual se caracteriza por una degeneración paulatina del cartílago articular y el tejido circundante. Las últimas investigaciones parecen mostrar que estas células son capaces de regenerar el tejido dañado y cambiar la comunicación circundante del tejido inflamado, pudiendo reducir el dolor causado por esa enfermedad. En el caso de tratar tejidos cartilaginosos, diversas investigaciones han descrito que las células madre derivadas del líquido sinovial poseen características superiores a las extraídas de otros tejidos.
La Unidad de Cirugía Artroscópica (UCA) ubicada en el Hospital Vithas San José de Vitoria-Gasteiz, dirigida por Mikel Sánchez, ha elaborado un andamio o matriz que ha mostrado unas propiedades muy favorables para el cultivo y crecimiento de esas células. La matriz se elabora a partir de plasma rico en plaquetas, líquido sinovial y células madre mesenquimales derivadas del líquido sinovial de un mismo paciente.
La formación de este biosistema es simple y tiene la ventaja de que no necesita del aislamiento celular del líquido sinovial, lo que incrementaría el coste y el tiempo de producción del mismo. Los pacientes con osteoartritis necesitan tratamiento más de una vez durante la enfermedad y se ha demostrado que esas células, con el incremento de la edad del paciente, pierden algunas de sus propiedades beneficiosas. Por ello, la preservación de ese biosistema con las células madre mesenquimales después de su primera extracción podría tener un gran potencial terapéutico para el tratamiento de la osteoartritis en un mismo paciente en el futuro.
Es en ese ámbito donde el grupo NanoBioCel de la Facultad de Farmacia de la UPV/EHU, dirigida por el catedrático José Luis Pedraz, participa. La preservación de diversas células en biomateriales es una nueva línea de investigación impulsada en ese grupo y ha propiciado su colaboración con la UCA para poder preservar ese biosistema para su futuro uso.
Existen diferentes métodos para la preservación de células en biomateriales, pero en NanoBioCel se han especializado en la criopreservación lenta, donde las muestras han de ser tratadas previamente y son congeladas siguiendo un perfil de congelación concreto, permitiendo recuperar su función y características tras su descongelación. El trabajo conjunto de los dos grupos ha propiciado que este innovador estudio para la preservación de una de las terapias celulares más investigadas haya sido posible.
En el trabajo, se han utilizado muestras de diferentes pacientes para realizar la matriz viva y ha sido realizado en pequeña escala. En primer lugar, se demostró que la matriz optimizada por la UCA era la adecuada para la preservación de las células madre mesenquimales.
En una segunda parte del trabajo, se quiso determinar la composición óptima de esa solución y, combinando diferentes moléculas, se obtuvieron diferentes soluciones con notables efectos protectores durante la congelación.
Por último, para poder estar seguros de cuál era la mejor combinación para preservar el biosistema, se realizaron ensayos más específicos para determinar la funcionalidad de las células que se encargarían de reparar los tejidos, confirmando que sus características no se perdían durante su almacenamiento a bajas temperaturas.
Todo apunta, pues, a que con ese biosistema es posible preservar las características beneficiosas de las células y de la matriz en la que se encuentran. Este trabajo abre una nueva puerta para la preservación de las células madre mesenquimales reduciendo tanto el coste como la complejidad de los procesos, dos de los obstáculos que suelen frenar el paso al uso clínico.
Referencia:
Haritz Gurruchaga at al (2017) Cryopreservation of Human Mesenchymal Stem Cells in an Allogeneic Bioscaffold based on Platelet Rich Plasma and Synovial Fluid Scientific Reports doi: 10.1038/s41598-017-16134-6
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Cómo criopreservar células madre se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Microcápsulas biomiméticas de células madre
- Naukas Pro 2017: Manuel Collado y las células madre
- Ciencia express: Qué son las células madre
Del zumo de naranja a la selva, un ejemplo de reciclaje extremo
Cuando en 2013 Timothy Treuer, investigador del Departamento de Ecología y Biología Evolutiva de la Universidad de Princeton, buscaba una zona en la que un colega le había mencionado que realizaron un experimento 15 años antes, tuvo que volver a pasar una segunda vez para dar con ella. Fue incapaz de ver a la primera la señal de más de dos metros con brillantes letras amarillas que señalaba la zona. Estaba casi oculta por la vegetación. ¿Qué pasó hace dos décadas en ese lugar?
En 1997 un matrimonio de investigadores de la Universidad de Pensilvania, Daniel Janzen y Winnie Hallwachs, se encontraban trabajando como consultores para el Área de Conservación de Guanacaste en Costa Rica que por aquel momento buscaba ser reconocida por la UNESCO. Esta pareja de ecólogos tuvieron una brillante idea: proponer a la empresa de zumos Del Oro que, a cambio de que estos donaran parte de sus terrenos forestales a la futura zona protegida, les dejarían depositar gratuitamente sus restos de materia orgánica en una zona del parque degradada por la sobreexplotación ganadera. Un win-win en toda regla.

Restos de naranjas en Guanacaste. Fuente: Universidad de Princeton
Más de 1000 camiones depositaron 12.000 toneladas de pieles y pulpa de naranja en una zona delimitada de tres hectáreas. La idea era realizar un seguimiento anual de este aporte de materia orgánica pero una empresa rival, TicoFruit, pleiteó contra el acuerdo. El juez consideró que Del Oro estaba contaminando un parque nacional y lo revocó. El área cubierta de restos de naranja cayó en el olvido hasta que en el verano de 2013, cuando Treuer discutía líneas de investigación con Janzen, este mencionó la historia y le dijo que esa zona nunca había sido estudiada a fondo más que para identificar especies por parte de los taxónomos del parque.
Treuer decidió acercarse a echar un vistazo en un viaje que tenía que realizar a Costa Rica y ver si de verdad valía la pena estudiar ese lugar. Lo que se encontró al llegar fue una frondosa vegetación de árboles y lianas que lo cubrían todo, nada que ver con el otro lado de la carretera que constituía la zona control del experimento. Supo inmediatamente que tenía que volver a estudiarlo para cuantificar lo que estaban viendo sus ojos y determinar si realmente el muro verde que tenía delante se debía a los desperdicios depositados allí lustros antes.

El resultado de 12.000 toneladas de restos de naranjas y 16 años de lluvias tropicales. Fuente: Universidad de Princeton
El estudio de biodiversidad y suelo fue realizado recogiendo muestras y analizando las especies tres metros alrededor de transectos de 100 metros que se replicaron en el área de control. Las muestras de suelos fueron combinadas con otras realizadas y analizadas en el año 2000 por una de las co-autoras de la investigación, la Dr. Laura Shanks, cuyos resultados nunca fueron publicados.
Las conclusiones fueron espectaculares. La biodiversidad era tres veces mayor en la zona fertilizada respecto a la zona control y la diferencia de biomasa superficial era del 176 %. El suelo contenía mas riqueza en nutrientes, tanto macro como micro, y las fotografías mostraban que el dosel de copas de arboles era significativamente superior.
Estos datos abren una vía de colaboración entre las industrias alimentarias de la zona que no saben que hacer con sus residuos orgánicos (las opciones son pagar por su incineración o enterramiento) y las áreas de conservación natural dentro de lo que se llama economía circular o de residuo cero.
Al fin y al cabo la mayoría de los problemas ambientales están producidos por industrias que fabrican lo que la gente necesita y es necesaria una mayor colaboración entre estos entes y los gestores de la conservación para que los restos de estas compañías puedan convertirse algo aprovechable.
Estos casos de economía circular exitosa no solo son un win-win para los agentes implicados sino para el resto de la sociedad.
Este post ha sido realizado por Txema Campillo (@Txemacg) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias:
Treuer, T. L. H, et al. (2017), Low-cost agricultural waste accelerates tropical forest regeneration. Restor Ecol. doi:10.1111/rec.12565
Orange is the new green: How orange peels revived a Costa Rican forest. Servicio de noticias de la Universidad de Princeton.
El artículo Del zumo de naranja a la selva, un ejemplo de reciclaje extremo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Tesoros que oculta el reciclaje
- Antes de que el león se hiciese con el trono de rey de la selva
- Las cartas de Darwin: ¡La geología por encima de todo!
Programar no es “divertido”, es técnica y éticamente complejo
Walter Vannini

Michael/Flickr
La programación [1] de ordenadores es pan comido. O eso es lo que los gurús de las habilidades digitales del mundo nos quieren hacer creer. Desde la promesa de la entidad sin ánimo de lucro Code.org de que “¡Cualquiera puede aprender!” hasta el comentario del director ejecutivo de Apple, Tim Cook, de que escribir código es “divertido e interactivo”, el arte y la ciencia de hacer software ahora son tan accesibles como el alfabeto.
Desafortunadamente, este mundo ideal no tiene relación con la realidad. Para empezar, el perfil de la mente de una programadora [2] es bastante raro. Además de ser altamente analíticas y creativas, las desarrolladoras de software necesitan una concentración casi sobrehumana para administrar la complejidad de sus tareas. La atención maníaca al detalle es imprescindible; las chapuzas están verboten [3]. Alcanzar este nivel de concentración requiere un estado mental llamado estar “in the flow” [4], una relación casi simbiótica entre la humana y la máquina que mejora el rendimiento y la motivación.
Programar no es el único trabajo que exige una intensa concentración. Pero nunca escucharás a nadie decir que la neurocirugía es “divertida”, o que la ingeniería estructural es “fácil”. Cuando se trata de la programación, ¿por qué los encargados de diseñar las políticas y los tecnólogos pretenden lo contrario? Por un lado, ayuda a atraer gente al campo en un momento en el que el software (en palabras del capitalista de riesgo Marc Andreessen) está “devorando al mundo”, por lo que, al aumentar la reserva de trabajadores, se mantiene la industria funcionando y los salarios bajo control. Otra razón es que la misma palabra “programación” suena rutinaria y repetitiva, como si hubiera algún tipo de clave que las desarrolladoras apliquen de memoria para resolver cualquier problema. No ayuda que Hollywood haya descrito al ‘programador’ como un pirata informático socialmente cuestionado, que teclea primero y piensa después, inevitablemente blanco y masculino, con el poder de frustrar a los nazis o introducirse en la CIA.
Insistir en el glamur y la diversión de programar es la forma incorrecta de familiarizar a las niñas con la informática. Insulta su inteligencia y planta la noción perniciosa en sus cabezas de que no necesitas disciplina para progresar. Como sabe cualquier persona con una exposición mínima a crear software, tras un minuto de teclear hay una hora de estudio.
Es mejor admitir que programar es complicado, técnica y éticamente. Los ordenadores, por el momento, solo pueden ejecutar órdenes, en diversos grados de sofisticación. De modo que depende de la desarrolladora ser clara: la máquina hace lo que tú dices, no lo que quieres decir. Cada vez se confían más ‘decisiones’ al software, incluidas las de vida o muerte: piensa en automóviles que conducen por sí mismos; o en armas semi-autónomas; o en Facebook y Google haciendo inferencias sobre tu estado civil, psicológico o físico, antes de venderlo al mejor postor. Sin embargo, rara vez interesa a las empresas y a los gobiernos alentarnos a investigar qué ocurre tras estos procesos.
Todas estas situaciones se construyen sobre cimientos exquisitamente técnicos. Pero no podemos reaccionar ante ellas respondiendo preguntas exclusivamente técnicas. La programación no es un detalle que pueda dejarse a las “técnicas” bajo el falso pretexto de que sus elecciones serán “científicamente neutrales”. Las sociedades son demasiado complejas: lo algorítmico es político. La automatización ya ha asestado un golpe a la seguridad laboral de los trabajadores poco cualificados en fábricas y almacenes de todo el mundo. Las oficinistas son las siguientes en la fila. Los gigantes digitales de hoy funcionan con una fracción de las empleadas de los gigantes industriales de ayer, así que la ironía de alentar a más personas a trabajar como programadores es que ellas mismas se están movilizando lentamente para quedarse sin trabajos.
En un mundo cada vez más intrincado y conectado, donde el software desempeña un papel cada vez más importante en la vida cotidiana, es irresponsable hablar de programar como una actividad liviana. El software no es simplemente líneas de código, ni es simplemente técnico. En unos pocos años, entender de programación será una parte indispensable de la ciudadanía activa. La idea de que programar ofrece un camino sin problemas para el progreso social y la mejora personal funciona en beneficio de la creciente tecno-plutocracia que se está aislando tras su propia tecnología.
Sobre el autor: Walter Vannini es consultor e investigador digital y reside en Milán (Italia).
Texto traducido y adaptado por César Tomé López a partir del original publicado por Aeon el 23 de septiembre de 2016 bajo una licencia Creative Commons (CC BY-ND 4.0).
Notas del traductor:
[1] Traducimos “coding” como “programar”, pensando que es mejor y más simple que “codificar” o “escribir código”.
[2] Todas las palabras que hacen referencias de género este texto se traducen en femenino ya que, en definitiva, se refieren a persona o personas. Así, por ejemplo, “programadora” se refiere a “persona programadora”. Solo existe una excepción obligada por el contexto.
[3] “Prohibidas”. En alemán en el original.
[4] Literalmente, “en el flujo”.
![]()
El artículo Programar no es “divertido”, es técnica y éticamente complejo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un rebaño de vacas pastando como sistema complejo
- Lo verdaderamente divertido es hacer Ciencia
- Ni lo más importante ni lo más divertido
Pseudociencia y arrogancia

Vivimos en tiempos de magia y hechicería en los que mucha gente cree que el universo, de una u otra forma, tiene voluntad y querencia y atiende a las necesidades y los ruegos de los humanos. Abundan las teorías mágicas sobre vibraciones, cristales, memoria del agua o la capacidad de curar cualquier enfermedad mediante plantas; millones de personas sinceramente creen que llevando un determinado tipo de mineral o tomando agua azucarada según un retorcido y complejo ritual mejorará su salud, su vida, o su suerte. En un mundo en el que la tecnología lleva a cabo prodigios y la ciencia ha avanzado hasta lo inimaginable en la comprensión del cosmos un significativo porcentaje de la población escoge rechazar estos avances y explicaciones para refugiarse en lo místico, lo desconocido y lo ignoto prefiriendo creer que las reglas del Universo son optativas y están sujetas de alguna manera a nuestra voluntad.
Los defensores de las pseudociencias a menudo usan como explicación de sus creencias el rechazo a la arrogancia de la ciencia, la tecnología y la sociedad a la que pertenecen. En su discurso el conocimiento de la medicina, la ingeniería o la física son insuficientes para explicar por completo el cosmos, pero aun así se arrogan ser la única explicación. En las justificaciones de la efectividad de una pseudoterapia o en la explicación de complejas conspiraciones como los chemtrails siempre hay un elemento de desconfianza y rechazo a lo que se presenta como una aplastante maquinaria tecnocientífica asociada a mecanismos sociales y políticos opresivos. Para sus partidarios las teorías alternativas que subyacen bajo terapias ancestrales o naturales o bajo prácticas pseudomágicas como el uso de cristales, colores o Flores de Bach son teorías de la liberación: un modo de resistirse a la aplastante conformidad de la sociedad, un sustrato teórico para la oposición y la revolución contra una sociedad tiránica que rechaza al disidente y aplasta las alternativas. En su mente los defensores de la magia forman parte de la resistencia contra la opresión.
Y sin embargo cuando se analizan sus argumentos en realidad lo que subyace es justo lo contrario: una especie de retorcida sensación de superioridad moral sobre los ‘pobres creyentes’ que aceptan las explicaciones de la ciencia. Los antivacunas se consideran víctimas de la perversa industria farmacéutica, y no les falta razón cuando denuncian la existencia de abusos en ciertas compañías y circunstancias. Pero cuando rechazan vacunar a sus hijos porque temen efectos secundarios graves su actitud es de superioridad: yo conozco algo que tú no sabes, y por tanto estoy más capacitado que tú para tomar decisiones. Lo mismo ocurre con los defensores de la sensibilidad química múltiple, la alergia a las ondas electromagnéticas, los chemtrails o la homeopatía: una buena parte de sus razonamientos destilan la superioridad del que desconfía de la ‘versión oficial’, una especie de ‘cuñadismo científico’ que desprecia la explicación estándar porque él mismo está por encima y sabe más.
En muchas ocasiones esta arrogancia está acompañada de una actitud francamente aprovechada que consiste en usar las ventajas de la explicación ‘oficial’ pero sin asumir los costes. Un ejemplo está en los antivacunas, cuyos hijos están protegidos por la inmunidad grupal proporcionada por los hijos de los demás que sí están vacunados y que según la ideología ‘anti’ corren por tanto con los riesgos. A menudo los tratamientos homeopáticos que acompañan a una terapia ‘convencional’ son los únicos que sus defensores recuerdan cuando se produce una curación, que achacan al agua azucarada olvidando convenientemente el medicamento alopático.
Los creyentes en las explicaciones alternativas no son por tanto oprimidos miembros de la resistencia que luchan contra la aplastante persecución de una maquinaria implacable, sino convencidos de su propia virtud que piensan estar en un plano superior de conocimiento y consciencia. No se trata de denunciar la arrogancia ajena sino de ejercer la propia, convencidos de que su conocimiento es superior al de los demás y de que su razón está por encima de la ajena. Buena es la crítica, el escepticismo y la desconfianza; nadie tiene por qué aceptar religiosamente explicaciones o conocimientos., Pero mucho ojo cuando esa sana desconfianza se convierte en celo proselitista y arrogante, porque nada ciega más a las personas que la fe en su propia superioridad: una trampa en la que resulta demasiado fácil caer.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo Pseudociencia y arrogancia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El metanol es clave para entender cómo se forman las estrellas
Si a la pregunta de cómo nacen las estrellas masivas alguien dijese que una forma de averiguarlo sería estudiando el metanol, ese alcohol que puede conseguir que te quedes ciego si tomas una bebida alcohólica destilada de aquella manera, diríamos probablemente que no coordina demasiado bien. Salvo que supiésemos del último resultado de Boy Lankhaar, de la Universidad Tecnológica Chalmers (Suecia) y sus colaboradores, claro.
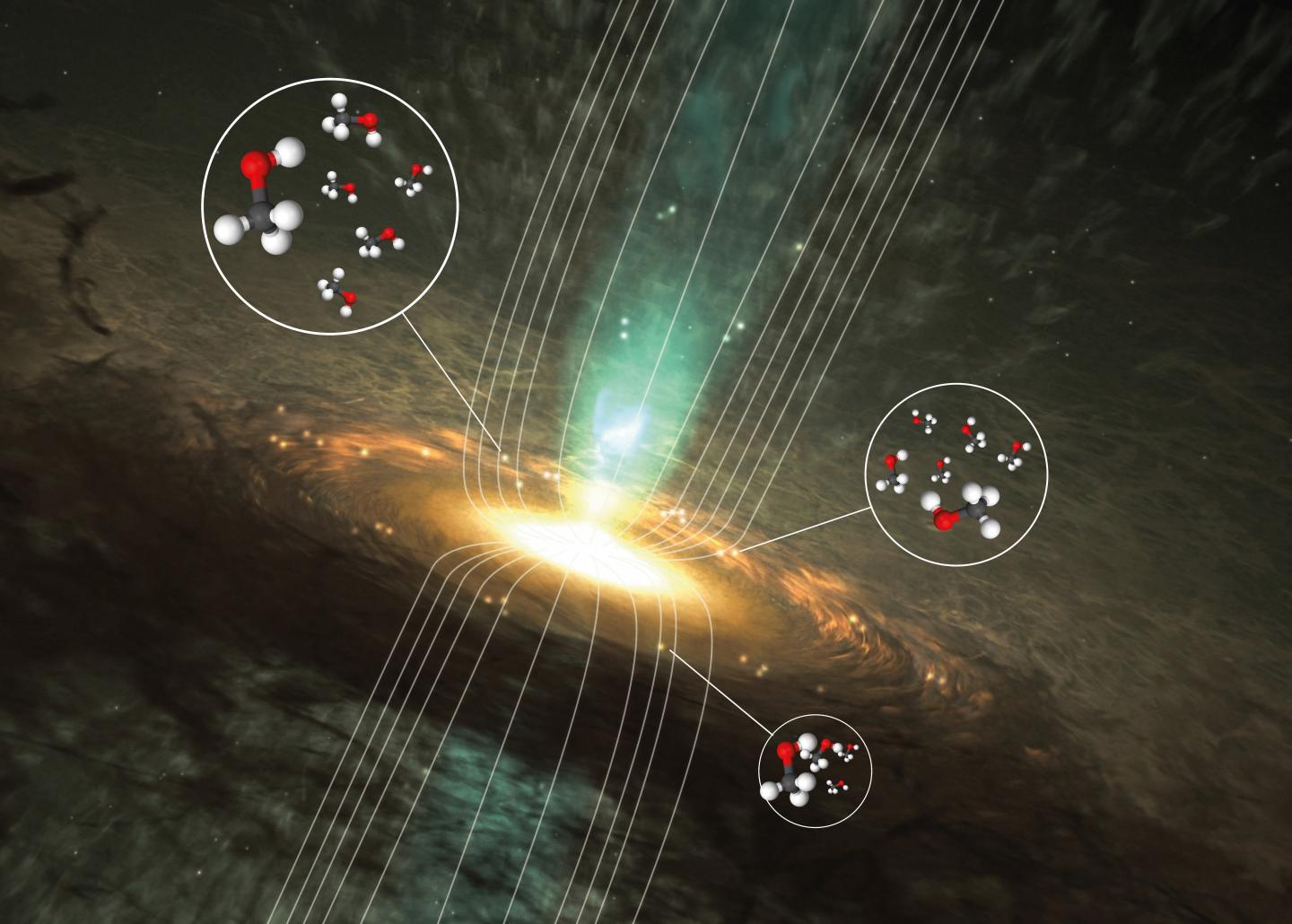
Imagen: Wolfgang Steffen/Boy Lankhaar et al. (2018)
Durante el último medio siglo se han descubierto muchas moléculas en el espacio. Utilizando radiotelescopios los astrónomos han podido, con la ayuda de estas moléculas, investigar lo que sucede en las oscuras y densas nubes donde nacen nuevas estrellas y planetas.
Los científicos pueden medir la temperatura, la presión y los movimientos del gas cuando estudian la firma (las señales características) de las moléculas en los datos que detectan. Pero especialmente donde nacen las estrellas más masivas hay otra variable importante que es más difícil de medir: los campos magnéticos.
El uso de mediciones de metanol (CH3OH) en el espacio para investigar los campos magnéticos se sugirió hace muchas décadas. En el gas denso que rodea a muchas estrellas recién nacidas, las moléculas de metanol brillan intensamente como láseres de microondas, los llamados máseres, naturales. Las señales que podemos medir de los máseres de metanol son fuertes y emitidas a frecuencias muy específicas. Debido a su ocurrencia en las partes más densas de las regiones de formación de estrellas, los máseres son la principal fuente de mediciones de fuerza y morfología del campo magnético alrededor de estrellas en formación.
Los primeros intentos de medir las propiedades magnéticas del metanol en condiciones de laboratorio, algo necesario para poder interpretar las señales espaciales, no han tenido todo el éxito esperado. Por ello Lankhaar y sus colegas decidieron construir un modelo químico teórico, a partir de primeros principios, asegurándose de que fuera consistente tanto con la teoría anterior como con las mediciones de laboratorio disponibles.
Este modelo arrojan unos nuevos resultados, que incluyen la compleja estructura hiperfina debida a la rotación interna de la molécula, que abren nuevas posibilidades para comprender los campos magnéticos en el universo a base de estudiar las señales del metanol en las regiones en las que se están formando estrellas.
Estos resultados también muestran cómo la química teórica puede ayudar a resolver los problemas en astroquímica. Se requieren cálculos teóricos sumamente detallados para poner de manifiesto en qué señales se traduce la complejidad molecular, y necesitamos esta traducción para interpretar las medidas muy precisas que hacemos con los mejores radiotelescopios actuales. Es en cierto modo paradójico que se necesiten expertos en la muy planetaria ciencia química en sus aspectos más teóricos para conseguir nuevos descubrimientos futuros sobre la formación de las estrellas.
Referencia:
Boy Lankhaar et al (2018) Characterization of methanol as a magnetic field tracer in star-forming regions Nature Astronomy doi: 10.1038/s41550-017-0341-8
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo El metanol es clave para entender cómo se forman las estrellas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Hay más estrellas masivas de lo que se creía y lo que eso implica para la historia del universo
- Cómo diseñar un sistema para comunicarse con el otro lado de la galaxia
- Un juego de mesa para entender la irreversibilidad
El Organum Mathematicum: una enciclopedia portátil
Athanasius Kircher (1602-1680) fue uno de los científicos más importantes de la época barroca. Él y sus cinco hermanas y hermanos ingresaron en diversas órdenes religiosas, ya que la familia era demasiado pobre para costearles los estudios. Él fue ordenado sacerdote jesuita en 1628, en cuyas instituciones se formó en humanidades, ciencias naturales y matemáticas, lenguas clásicas y filosofía, entre otras.
Estudió e investigó en campos tan diversos como la vulcanología, el chino, el magnetismo o una posible escritura universal. Tenía reputación como experto en resolver jeroglíficos, en parte por su conocimiento de la lengua copta. Tal era su fama que el alquimista Georgius Barschius, uno de los primeros propietarios del famoso Manuscrito Voynich, le escribió en varias ocasiones para que intentara descifrarlo, aunque no tuvo ningún éxito.
A lo largo de su obra describió diferentes artilugios e inventó varias máquinas, con éxito diverso. El Organum Mathematicum fue precisamente uno de sus inventos: fue descrito completamente en el monumental y póstumo Organum Mathematicum : Libris IX Explicatum (1668) escrito por Gaspar Schott (1608-1666), ayudante del jesuita.
Era un dispositivo diseñado para ayudar a realizar cálculos matemáticos y de otro tipo. Se inspiró en otros instrumentos como el ábaco de Napier, algunos almanaques y su propia Arca Musarithmica. –dispositivo inventado por el jesuita para componer música eclesiástica: a través de simples técnicas combinatorias era capaz de producir millones de piezas de música polifónica en cuatro partes–.

El Organum Mathematicum de Athanasius Kircher ilustrado en el libro Organum Mathematicum de Gaspar Schott (1668). Imagen: Wikimedia Commons.
El Organum Mathematicum era una especie de caja, un cofre de madera divido en nueve o más compartimentos, cada uno de los cuales contenía unas varillas de madera –Kircher las llamaba tariffa– que ayudaban a realizar diferentes cálculos de matemáticas y otras ciencias o artes.
Como hemos comentado, cada compartimento estaba dedicado a un tema: aritmética, geometría, fortificaciones, cronología, orografía, astronomía, astrología, esteganografía y música. Y, a su vez, cada uno de ellos contenía unas veinticuatro varillas de madera –coloreadas en su parte superior y en forma triangular– con definiciones e información sobre el tema correspondiente.
Las varillas aritméticas eran capaces de realizar la multiplicación de números de varios dígitos y divisiones; las geométricas ayudaban a determinar alturas; las de fortificaciones apoyaban el diseño de planos de baluartes; las varillas de la sección de cronología podían usarse para determinar las fechas de festividades eclesiásticas como la Pascua; las correspondientes al compartimento de orografía contenían la información necesaria para construir relojes de sol; las de la sección de astronomía proporcionaban, para cada día del año, información sobre la duración del día y la noche, los horarios de salida y puesta del sol y la duración de los crepúsculos matutino y vespertino –todo ello basado en mediciones tomadas a 48 grados de latitud (Viena) –; las de astrología contenían tablas describiendo los movimientos de los planetas, la constelación Draco y también daba interpretaciones astrológicas de los doces signos del zodiaco; las de esteganografía se usaban para encriptar y descifrar textos –usando un cifrado de transposición cíclica basado en una palabra clave–; finalmente, en el compartimento de música, las varillas ayudaban a personas sin formación a componer música eclesiástica, de la misma manera que en su Arca Musarithmica –contenían conjuntos de frases que podían combinarse aleatoriamente para componer versos acordes a la música y produciendo millones de himnos. En las referencias 4, 5 y 6 se dan ejemplos de composiciones musicales usando esta máquina–.
Para usar el Organum Mathematicum se tomaban los listones correspondientes al tema elegido, y se reordenaban para efectuar la operación requerida. Por ejemplo, en el de aritmética, para multiplicar 74 por 8, se elegía la varilla negra del compartimiento de aritmética y se colocaba junto a los listones numerados 7 y 4. La octava línea de la varilla de punta negra devolvía el producto deseado.

Organum Mathematicum en el Museo Galileo en Florencia (Italia). Imagen ´compuesta a partir de dos extraídas de Wikimedia Commons.
El Organum Mathematicum servía para componer música de manera automática, para efectuar operaciones… era una pequeña enciclopedia portátil, un sistema global de organización del conocimiento, un ancestro de nuestros modernos ordenadores.
Más información:
-
Organum Mathematicum, Museo virtual Galileo
-
The Organum Mathematicum: A 17th Century Computer, Neatorama, 2015
-
Jim Bumgardner, Kircher’s Mechanical Composer: A Software Implementation, Crazy Dad
-
Organum Mathematicum, Crazy Dad, 2006
-
Christophe Robert, A. Kircher : Organum Mathematicum – Mode d’emploi, MusicAlgo, 2017
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo El <i>Organum Mathematicum</i>: una enciclopedia portátil se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un espectrómetro Raman portátil mide el punto óptimo de maduración del tomate
- #Naukas14 La música de las esferas
- El joven Arquímedes
Sistemas respiratorios: moduladores de la afinidad de los pigmentos
Las características básicas del pigmento respiratorio de un mismo individuo pueden experimentar importantes variaciones como consecuencia de la acción de varios agentes moduladores. La más importante de esas modulaciones es la conocida como efecto Bohr, pero no es la única.
El efecto Bohr

El efecto Bohr se llama así por Christian Bohr, padre de los Bohr más famosos, Niels (físico) y Harald (matemático) Bohr .
El efecto Bohr lo experimentan algunos pigmentos respiratorios y consiste en una reducción de la afinidad por efecto de la concentración de CO2 o de H+ en la sangre. En términos gráficos se puede decir que la elevación de la concentración de protones y de CO2 sanguíneos provoca un desplazamiento de la curva de disociación del pigmento hacia la derecha. El efecto fue dado a conocer en 1904 por un trío encabezado por Christian Bohr del que formaba parte August Krogh, quien posteriormente recibiría el premio Nobel de Fisiología por otros hallazgos muy relevantes en fisiología respiratoria.
Hoy sabemos que el CO2 ejerce un efecto doble sobre la afinidad del pigmento. Hay por un lado un efecto directo, ya que se puede combinar con el pigmento y funcionar como modulador alostérico. Y por otro lado, al disolverse en el plasma sanguíneo una parte del CO2 reacciona con el agua para dar iones bicarbonato, iones carbonato y protones. Y esos protones, al combinarse con el pigmento, actúan también como moduladores alostéricos. En ambos casos aumenta la dificultad para que el pigmento y el O2 se unan, o lo que es lo mismo, se reduce su afinidad. Por otra parte, la concentración de protones en la sangre se puede elevar no sólo al aumentar la de CO2 sino también por otras causas. En los vertebrados, cuando la musculatura esquelética realiza un ejercicio físico intenso no es raro que se produzca lactato, que pasa a la sangre para ser reciclado posteriormente en el hígado; pues bien, ese ácido láctico es también una fuente de protones que puede, a su vez, reducir la afinidad de la hemoglobina.
El efecto Bohr amplía la descarga de oxígeno del pigmento y se cree que esa es la razón por la que se ha seleccionado en ciertas especies. Para entender de dónde viene la ventaja que reporta hay que pensar que la sangre, al salir del órgano respiratorio, va cargada de oxígeno, contiene muy poco CO2 y su pH es relativamente alto. Al llegar a los tejidos el oxígeno pasa de los capilares a las células y, a la vez, el CO2 sale de estas y pasa a la sangre. CO2 y protones se combinan con la hemoglobina y la afinidad de esta por el O2 disminuye. Como consecuencia, se facilita la liberación de más oxígeno, por lo que su transferencia a las células resulta favorecida.

En una ballena jorobada (“Megaptera novaeangliae”), uno de los animales más grandes del planeta, el efecto Bohr tiene una magnitud similar a la que tiene en el conejillo de indias.
El efecto Bohr no se produce en todos los pigmentos y su magnitud es muy variable, seguramente porque las circunstancias de cada especie son también distintas. En mamíferos, el tamaño del animal, por ejemplo, influye: cuanto más pequeño es el animal y, por lo tanto, mayor es su tasa metabólica, el efecto es de mayor intensidad. Tortugas, lagartos y serpientes experimentan un efecto Bohr de menor magnitud que los mamíferos, pero en los cocodrilos es muy intenso. Se cree que ese intenso efecto ayuda a los cocodrilos a ahogar a sus presas bajo el agua: al atraparlas y sumergirlas ha de dejar de respirar, por lo que su única fuente de O2 es la sangre; y su liberación hacia las células se ve favorecida por tal efecto.
El efecto Root
Algunas especies de peces, teleósteos principalmente, tienen más de un tipo de hemoglobina en su sangre; se denominan isoformas. Unas son muy sensibles a la concentración de CO2 y a la de protones, y las otras no. La peculiaridad de las sensibles consiste en que experimentan una pérdida de su capacidad para combinarse con el O2 no solo porque disminuya su afinidad, sino porque se reduce de forma importante su capacidad de oxígeno o capacidad de carga. A ese fenómeno se le denomina efecto Root, por el nombre de su descubridor1.
Gracias al efecto Root las especies que lo experimentan elevan la tensión parcial de oxígeno en el entorno de dos órganos, la vejiga natatoria y los ojos. La acidificación de la sangre en esos entornos provoca que una parte importante del oxígeno pase a estar en forma disuelta. Aumenta así la tO2 en ese entorno y, como consecuencia de ello, el O2 disuelto pasa al interior de la vejiga o de los globos oculares. De ese modo pueden aumentar el contenido gaseoso de la vejiga natatoria y actuar sobre la flotabilidad. Y en lo relativo a los globos oculares, la retina de algunos peces necesita altas tensiones parciales de oxígeno para funcionar correctamente.
Las isoformas insensibles, por su parte, son una especie de seguro anti-asfixia: sin ellas podría ocurrir que un exceso de CO2 y H+ en sangre por efecto de una actividad física muy intensa provocase una pérdida de la capacidad del pigmento para captar O2 del exterior tal que llegase incluso a asfixiarse.
Moduladores orgánicos
La afinidad de la hemoglobina de muchos vertebrados varía en función de la concentración de ciertas sustancias orgánicas fosfatadas. En mamíferos (seres humanos, caballos, perros, o ratas) se trata del 2,3-bifosfoglicerato (2,3-DPG), en aves es el inositol pentafosfato (IIP) y en peces es el adenosina trifosfato (ATP) (predominante en salmónidos, tiburones y rayas) y el guanosina trifosfato (GTP) (predominante en anguilas, carpas y carpas doradas). Esas sustancias se encuentran en el interior de los eritrocitos, puesto que son productos de su metabolismo, y se combinan de forma reversible con el pigmento reduciendo su afinidad. La reducción de la afinidad no se limita, como ocurría con la provocada por la acidificación y el CO2 propios del efecto Bohr, a la sangre que se encuentra en los tejidos, sino que es un efecto permanente, ya que se encuentran en el interior de los glóbulos rojos en todo momento.
Al parecer, la concentración de los moduladores orgánicos citados aumenta en el interior de los eritrocitos en respuesta a condiciones de hipoxia (ya sea de origen ambiental o por razones patológicas), lo que facilita la descarga de O2 a los tejidos; sin embargo, también dificulta su captación desde el órgano respiratorio, aunque el balance neto de estos efectos favorece el suministro de oxígeno a los tejidos en esas condiciones.
Temperatura
La elevación de la temperatura provoca un desplazamiento de la curva de disociación del pigmento hacia la derecha y, por lo tanto, un descenso de su afinidad por el O2. Quiere esto decir que a igualdad de tO2, el pigmento contiene menos oxígeno a altas que a bajas temperaturas. Por lo tanto, un aumento de temperatura facilita la descarga de O2 del pigmento. Las consecuencias prácticas de este efecto térmico son evidentes; los aumentos de temperatura -incluso los que ocurren localmente en tejidos especialmente activos de animales homeotermos- están asociados a una mayor actividad metabólica, de manera que al facilitarse la descarga por efecto térmico, se favorece el suministro de oxígeno a las células que más lo necesitan o cuando lo necesitan en mayor medida.
Fuentes:
Richard W. Hill, Gordon A. Wyse & Margaret Anderson (2004): Animal Physiology. Sinauer Associates, Sunderland
Knut Schmidt-Nielsen (1997): Animal Physiology. Adaptation and Environment. Cambridge University Press; Cambridge
Lauralee Sherwood, Hillar Klandorf & Paul H. Yancey (2005): Animal Physiology: from genes to organisms. Brooks/Cole, Belmont.
Nota:
1 Según algunos autores el efecto Root no es sino un fuerte efecto Bohr.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Sistemas respiratorios: moduladores de la afinidad de los pigmentos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sistemas respiratorios: pigmentos de alta afinidad
- Sistemas respiratorios: pigmentos de baja afinidad
- Sistemas respiratorios: los pigmentos respiratorios

