El origen genético de la familia de lenguas indoeuropeas
Un estudio, en el que ha participado Iñigo Olalde, investigador Ramón y Cajal e Ikerbasque Research Fellow en el grupo BIOMICs de la Universidad del País Vasco, ha analizado el ADN antiguo de 435 individuos de sitios arqueológicos en toda Eurasia entre 6.400 y 2.000 a. C. Este trabajo proporciona nuevos datos que nos acercan a la respuesta a una pregunta de 200 años de antigüedad: ¿Dónde se encuentra el origen de la familia de lenguas indoeuropeas? Según se demuestra en la investigación, una población del Cáucaso y el Bajo Volga, recientemente reconocida, puede conectarse con todas las poblaciones de habla indoeuropea.
Las lenguas indoeuropeas, que suman más de 400 e incluyen grupos importantes como el germánico, el romance, el eslavo, el indoiraní y el celta, son habladas por casi la mitad de la población mundial actual. Originadas de la lengua protoindoeuropea, los historiadores y lingüistas han estado investigando sus orígenes y difusión desde el siglo XIX, ya que todavía existe una brecha de conocimiento en ese campo.
 Tumba de la cultura Yamnaya. Fuente: Wikimedia Commons
Tumba de la cultura Yamnaya. Fuente: Wikimedia CommonsEstudios genéticos anteriores habían demostrado que la cultura Yamnaya (3.300-2.600 a. C.), de las estepas póntico-caspias al norte de los mares Negro y Caspio, se expandió tanto a Europa como a Asia central a partir de aproximadamente 3.100 a. C., lo que explica la aparición de ‘ascendencia esteparia’ en las poblaciones humanas en toda Eurasia entre 3.100 y 1.500 a. C. Esas migraciones desde las estepas tuvieron el mayor efecto sobre los genomas humanos europeos que cualquier otro evento demográfico en los últimos 5.000 años y son ampliamente consideradas como el probable vector de la difusión de las lenguas indoeuropeas.
La única rama de las lenguas indoeuropeas que no había mostrado ninguna ascendencia esteparia anteriormente era la anatolia, incluido el hitita, probablemente la rama más antigua en separarse, preservando de manera única arcaísmos lingüísticos que se perdieron en todas las demás ramas de dichas lenguas. Estudios anteriores no habían encontrado ascendencia esteparia entre los hititas porque, según sostiene el nuevo artículo, las lenguas anatolias descendían de una lengua hablada por un grupo que no había sido descrito adecuadamente, una población eneolítica fechada entre 4.500 y 3.500 a. C. en las estepas entre las montañas del Cáucaso Norte y el bajo Volga. Cuando se utiliza como fuente la genética de esa población del Cáucaso-Bajo Volga recientemente reconocida, al menos cinco individuos en Anatolia fechados antes o durante la era hitita muestran ascendencia con esa zona.
El nuevo estudio muestra que la población Yamnaya obtuvo aproximadamente el 80 % de su ascendencia del grupo Cáucaso-Bajo Volga, que también proporcionó al menos una décima parte de la ascendencia de los habitantes de Anatolia central de la Edad del Bronce, hablantes de hitita. Por lo tanto, el grupo Cáucaso-Bajo Volga puede conectarse con todas las poblaciones de habla indoanatolia y es el mejor candidato como origen de la población que hablaba indoanatolia, el antepasado tanto del hitita como de todas las lenguas indoeuropeas posteriores, en el Cáucaso Norte y la región del Bajo Volga entre 4.400 a. C. y 4.000 a. C.
Referencia:
Lazaridis, I., Patterson, N., Anthony, D. et al. (2025) The genetic origin of the Indo-Europeans. Nature doi: 10.1038/s41586-024-08531-5
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El origen genético de la familia de lenguas indoeuropeas se ha escrito en Cuaderno de Cultura Científica.
Teatro y Geología, un buen tándem para visibilizar pioneras
Febrero es el mes en el que todas las científicas intentamos visibilizar nuestro trabajo dentro de la celebración del «11F, Día Internacional de la Mujer y la Niña en la Ciencia» buscando cumplir con el mismo objetivo: generar vocaciones entre las niñas y las chicas más jóvenes para que se planteen su futuro como científicas, normalizando la presencia femenina en carreras históricamente tan masculinizadas como la Geología.
La manera más generalizada para conseguir este objetivo es que las científicas visitemos los centros educativos para realizar charlas, conferencias y presentaciones ante el alumnado contando los problemas a los que se enfrentaron las pioneras de nuestras disciplinas, comparando sus vicisitudes con las barreras que tuvimos, y aún tenemos, que superar nosotras en nuestra carrera.
Esta fórmula, eficaz gracias a la cercanía que fomenta entre las niñas y las profesionales, puede convertirse en contraproducente. Al final, las jóvenes reciben la visita de muchas científicas de disciplinas diferentes, contando vivencias muy diversas en un corto periodo de tiempo, lo que les impide procesar toda la información y recordar con detalle todo lo que les hemos contado. Así que, para no ser una anécdota más entre recuerdos infantiles, debemos buscar una manera de destacar y llamar la atención de nuestro público objetivo.
 Póster promocional de Mi Primer Geolodía Granada 2025, celebrado en Diezma el sábado 22 de febrero.
Póster promocional de Mi Primer Geolodía Granada 2025, celebrado en Diezma el sábado 22 de febrero.Así es como nació «Mary Anning visita Mi Primer Geolodía Granada». Ya os hablé el año pasado de «Mi Primer Geolodía«, una iniciativa de la comisión Mujeres y Geología de la Sociedad Geológica de España que consiste en talleres interactivos, charlas, excursiones y actividades lúdicas para que las niñas y niños conozcan la Geología de manera amena y divertida. Pues dentro de las actividades programadas en Granada se encuentra una pequeña obra de teatro sobre la vida y los descubrimientos de Mary Anning, una de las pioneras de la Paleontología.
 Foto de grupo tras una de las representaciones de la obra «Mary Anning visita Mi Primer Geolodía Granada» realizada en el hall del ayuntamiento de Diezma. De izquierda a derecha: Josefina Sánchez (Mary Anning adulta), Lucía Moreno (Mary Anning niña), Ana Ruiz (presidenta de la Sociedad Geológica de España y coordinadora de Mi Primer Geolodía Granada), Emilia Troncoso (alcaldesa de Diezma) y Blanca Martínez (paleontóloga actual).
Foto de grupo tras una de las representaciones de la obra «Mary Anning visita Mi Primer Geolodía Granada» realizada en el hall del ayuntamiento de Diezma. De izquierda a derecha: Josefina Sánchez (Mary Anning adulta), Lucía Moreno (Mary Anning niña), Ana Ruiz (presidenta de la Sociedad Geológica de España y coordinadora de Mi Primer Geolodía Granada), Emilia Troncoso (alcaldesa de Diezma) y Blanca Martínez (paleontóloga actual).En esta obra, Mary Anning, nacida hace 226 años en Lyme Regis, Inglaterra (si queréis conocerla mejor, podéis hacerlo aquí o aquí), viaja en el tiempo y en el espacio hasta la Granada de hoy en día para visitar los talleres de Mi Primer Geolodía, que este año se han realizado en Diezma, descubriendo cómo ha avanzado el conocimiento geológico en estos dos siglos. Aquí se encuentra con una paleontóloga que la reconoce y empiezan a entablar una conversación. De esta forma, Mary hace un pequeño repaso de su vida, recordando que desde niña tuvo que ganarse la vida recolectando y vendiendo fósiles a los grandes naturalistas de la época, que pusieron en duda sus descubrimientos paleontológicos por el simple hecho de ser una mujer sin estudios. Pero la paleontóloga actual no pierde la oportunidad de poner en relieve sus hallazgos científicos, realizando explicaciones sobre algunos de los descubrimientos de Mary, como el ictiosaurio o el plesiosaurio, hasta el punto de que, hoy en día, se la reconoce como la madre de la Paleontología gracias a los avances que propiciaron en esta ciencia sus estudios sobre diversos grupos fósiles, como los ammonites. Incluso, se menciona que los descubrimientos de Mary plantearon las bases de la teoría de la evolución de las especies de Darwin (con la intercesión de Lyell, en realidad).
Como os podéis imaginar, la obra de teatro tiene un mensaje muy potente, resaltando no solo cómo ha cambiado el conocimiento geológico en los últimos doscientos años, si no también poniendo en evidencia las barreras que tuvieron que superar las mujeres que nos precedieron, remarcando que, por desgracia, algunos de estos problemas aún siguen vigentes. Pero lo hace en un tono distendido y cómico para alcanzar al público infantil, al que también se le ofrecen explicaciones científicas muy rigurosas en un lenguaje sencillo adaptado a sus edades. Así, en los ojos infantiles que observan la representación se dibujan destellos de curiosidad y admiración, mientras que en muchos ojos adultos asoman lágrimas sinceras.
Y esta metodología docente, funciona. En otros talleres de Mi Primer Geolodía, se volvía a nombrar a Mary Anning. Cuando las monitoras preguntaban a las niñas y niños si la conocían, quienes habían visto la obra de teatro siempre daban la misma respuesta: «Claro, es la madre de la Paleontología y descubrió el ictiosaurio». La primera fase de nuestro trabajo ya está hecha, hemos sembrado la semilla de la curiosidad en las nuevas generaciones, ahora solo nos falta seguir regándola los próximos años, dando a conocer a otras pioneras geólogas y visibilizando el trabajo de las actuales, mientras les descubrimos más curiosidades geológicas con las que puedan entender los paisajes que les rodea. ¿Hemos creado vocaciones científicas entre las niñas? Quizás nunca lo sepamos. Pero seguro que jamás se olvidarán de esas geólogas que hicieron una obra de teatro sobre la madre de la Paleontología en su pueblo.
Agradecimientos:
La obra de teatro «Mary Anning visita Mi Primer Geolodía Granada» ha salido de las prodigiosas mentes de Ana Constán y Ana Ruiz Constán (madre e hija, porque de casta le viene al galgo), que han escrito el guion, elaborado el vestuario de las protagonistas y preparado la puesta en escena. Además, no habría sido posible representarla sin el trabajo y dedicación de Lucía Moreno, nuestra Mary Anning niña, joven artista aficionada al teatro y la interpretación, y de Josefina «Fini» Sánchez, que cambió su acento cordobés por uno puramente británico para meterse en su papel de Mary Anning adulta. Y no quiero olvidarme de María Druet, nuestra roca en la primera representación, y de Manuela Chamizo y Raquel Martín, las reporteras gráficas que se emocionaron al ver la actuación. ¡Qué aburrida sería mi vida sin vosotras, chicas!
La representación de la obra de teatro «Mary Anning visita Mi Primer Geolodía Granada» se retransmitió en directo por la cuenta oficial de Instagram de la Sociedad Geológica de España. Puede verse aquí.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Teatro y Geología, un buen tándem para visibilizar pioneras se ha escrito en Cuaderno de Cultura Científica.
Marília Chaves Peixoto, especialista en sistemas dinámicos
Además del incuestionable valor de las investigaciones que desarrolló, Marília Peixoto rompió con valentía un discurso virulento y arraigado que desalentaba a las mujeres a dedicarse a determinadas áreas del conocimiento y a determinadas actividades laborales, discurso normalmente basado en la idea de la existencia de una relación inequívoca entre los atributos biológicos de género, en la que lo femenino se limita al ejercicio de las funciones domésticas y a un número muy reducido de profesiones, generalmente de menor prestigio social y remuneración. Al convertirse en una profesional de referencia en un área considerada, hasta entonces, como exclusivamente masculina, la matemática Marília Peixoto abre un precedente de dignidad para todas las mujeres brasileñas, que aún permanecen en la lucha por la igualdad en el campo de los estudios formales y del trabajo.
Las anteriores palabras son de la política y profesora universitaria brasileña Dorinha Seabra Rezende quien, en 2020, presentó una resolución para dar el nombre de Marília Chaves Peixoto al Pleno 13 del Anexo II de la Cámara de Diputados de su país.
 Marília Chaves Peixoto. Fuente: Wikimedia Commons.
Marília Chaves Peixoto. Fuente: Wikimedia Commons.Deseando estudiar matemáticas
Marília Chaves nació el 24 de febrero de 1921 en Sant’Ana do Livramento, ciudad situada al sudoeste de Río Grande del Sur, en Brasil. Era la mayor de los tres hijos (Lúcia nació en 1924 y Livio en 1926) de Tullio de Saboia Chaves (profesor de la Facultad de Medicina Quirúrgica de Río de Janeiro) y Zillah da Costa Magalhães.
Gracias al apoyo de sus padres, pudo asistir a un colegio de Santana do Livramento, donde las chicas no podían estudiar de manera oficial. Como estudiante privada, pudo hacer los exámenes con los chicos.
Posteriormente pasó al menos un año en el Colégio Andrews, fundado por Isabella Robinson Andrews en 1918. En este centro se ofrecía una educación laica a niñas y niños, algo inusual en esa época en Brasil. Esta institución tenía entonces unos 1500 estudiantes de todos los niveles; los preparaban, tanto a niñas como a niños, para ingresar a las escuelas de Medicina, Derecho e Ingeniería.
Marília deseaba estudiar matemáticas y se preparaba para ingresar en la Escuela Nacional de Ingeniería de la Universidad de Brasil en Río de Janeiro: en 1939 obtuvo el tercer lugar entre los 73 estudiantes que consiguieron inscribirse. Las mujeres que lograron un puesto no llegaban al 7 % del total; no era muy común contar con alumnas en las escuelas de ingeniería de esa época.
Compartió aula con Maurício Matos Peixoto y Leopoldo Nachbin; los tres siguieron cursos de matemáticas avanzadas ya que su intención no era seguir una carrera de ingeniería. En 1943, Marília Chaves se graduó en ingeniería civil.
El 6 de septiembre de 1946, Marília y Maurício Matos Peixoto se casaron en Río de Janeiro. El matrimonio tuvo dos hijos, Marta (1949) y Ricardo (1953).
Impartiendo docencia e investigando en sistemas dinámicosMarília presentó su tesis en 1949; fue aceptada para un doctorado en matemáticas, convirtiendo a Chaves Peixoto en la primera mujer brasileña en obtener un doctorado en esta materia. Y gracias a ello obtuvo la Cátedra de la Escuela Nacional de Ingeniería, donde enseñó cálculo diferencial e integral.
El 1 de julio de 1951 fue elegida miembro asociada de la Academia Brasileña de Ciencias, convirtiéndose en la primera mujer brasileña en ser elegida miembro de esta institución. Antes que ella, Marie Curie había sido elegida miembro asociada extranjera de esta Academia en 1926.
En 1955 publicó el manual Cálculo vetorial dirigido a estudiantes de ingeniería. Tres años después de la muerte de Marília, el libro fue reeditado con un prefacio de Maurício Peixoto en el que escribía, entre otros comentarios:
Claro, metódico, objetivo y bien elaborado, es un buen reflejo de sus cualidades didácticas y su ejemplar dedicación a la docencia.
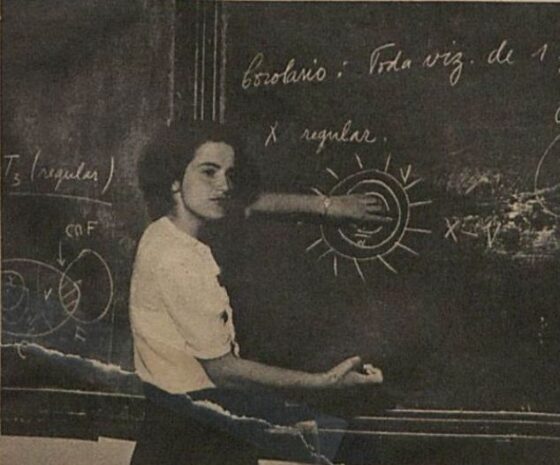 Marília Peixoto impartiendo docencia, 1952. Fuente: XIII SNHM.
Marília Peixoto impartiendo docencia, 1952. Fuente: XIII SNHM.
Marília y su marido trabajaron juntos en la estabilidad estructural de los sistemas dinámicos; ella realizó una contribución sustancial para demostrar el teorema de Peixoto que proporciona la caracterización de sistemas estructuralmente estables en variedades bidimensionales. En 1959, Marília y Maurício Peixoto publicaron el artículo conjunto Structural Stability in the plane with enlarged boundary conditions. Este fue uno de los tres artículos (los otros dos fueron publicados por Maurício en solitario) sobre esta materia que ayudaron a enunciar el hoy conocido como el teorema de Peixoto en un artículo publicado en 1962. El matemático señalaba:
Me gustaría señalar que este trabajo sobre estabilidad estructural se llevó a cabo básicamente en varios artículos que se mencionan a continuación, uno de los cuales fue en colaboración con mi primera esposa Marília, quien no vivió para ver el final de esta aventura. Sin embargo, su influencia fue grande en aquellos días dorados, decisivos y ya lejanos, en el otoño de 1957 en Princeton.
Honores póstumos
Marília Chaves Peixoto falleció el 5 de enero de 1961 debido a problemas cardiacos. Ese mismo año la especialista en educación matemática Maria Laura Mozinho impartió una conferencia en la Academia Brasileña de Ciencias en la que dijo:
Al ver a aquella muchacha tranquila, de ojos muy grandes y expresivos, fue necesario que alguien nos susurrara que era una destacada profesora de Cálculo y Mecánica de la Escuela Nacional de Ingeniería, enérgica y, a la vez, generosa, además de tener una inteligencia aguda que se volcaba a la investigación matemática.
Una calle en su ciudad natal de Sant’Ana do Livramento se llama Rua Marília Chaves Peixoto.
Maurício Peixoto ayudó a fundar en 1971 la Escuela Municipal Marília Chaves Peixoto en la región de Controes de Petrópolis, una región rural donde el padre de Marília tenía una finca que cedió para fundar este centro de enseñanza. Fue una iniciativa muy aplaudida, ya que muchos de los residentes locales eran analfabetos y la escuela más cercana estaba a unos 10 kilómetros de distancia. Durante casi 40 años, más de trescientos estudiantes asistieron a la escuela primaria. En 1969, Maurício Peixoto recibió el Prêmio Moinho Santista de la Fundación Bunge por el teorema que lleva su nombre y que tanto debía a Marília. Peixoto utilizó el dinero del premio para financiar esta escuela.
Referencias
- John J. O’Connor and Edmund F. Robertson, Marília de Magalhães Chaves Peixoto, MacTutor History of Mathematics archive, University of St Andrews
- Circe Mary Silva da Silva, Marília Chaves Peixoto. Uma matemática brasileira à sombra, XIII SNHM, 150-170, agosto 2019
- Marília Chaves Peixoto, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Marília Chaves Peixoto, especialista en sistemas dinámicos se ha escrito en Cuaderno de Cultura Científica.
Cómo Hans Bethe se topó con las teorías cuánticas perfectas
Los cálculos cuánticos son estimaciones sofisticadas, pero en 1931 Hans Bethe intuyó con precisión cómo se comportaría una cadena de partículas, una intuición que tuvo enormes consecuencias.
Un artículo de Matt von Hippel. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Hans Bethe fue pionero en un método que, cuando las estrellas se alinean, permite a los físicos comprender perfectamente el comportamiento colectivo de cualquier número de partículas cuánticas. Ilustración: Señor Salme para Quanta Magazine
Hans Bethe fue pionero en un método que, cuando las estrellas se alinean, permite a los físicos comprender perfectamente el comportamiento colectivo de cualquier número de partículas cuánticas. Ilustración: Señor Salme para Quanta MagazineEn 1928, los físicos cuánticos parecían estar a punto de desentrañar los secretos finales de la materia. El investigador alemán Walter Gordon había aplicado la emergente teoría de la mecánica cuántica al átomo de hidrógeno, el átomo más simple del universo, y había descubierto exactamente cómo se comportaba. Parecía seguro que el dominio de todos los átomos vendría detrás.
No fue así. Cuando las partículas cuánticas se influyen entre sí, sus posibilidades se entrelazan de tal manera que superan la capacidad de los físicos para predecir su futuro. En la búsqueda de respuestas precisas, el electrón solitario del átomo de hidrógeno marcó el inicio y el final del camino; incluso los dos electrones del átomo de helio condenaron al fracaso a planteamientos tan exactos como el de Gordon. Es una limitación con la que los físicos todavía lidian hoy. Casi todas las predicciones cuánticas son un poco aproximadas.
Sin embargo, tres años después del triunfo de Gordon, su compatriota Hans Bethe había encontrado una sorprendente manera de resolver este problema. El ansatz de Bethe, que en alemán significa “punto de partida”, resultó ser capaz de captar perfectamente el comportamiento de cualquier cantidad de partículas cuánticas, desde un solo electrón hasta los innumerables electrones de una capa de hielo. Sin embargo, este extraordinario poder tiene sus propias limitaciones, que llevaría décadas comprender.
El ansatz de Bethe ha cautivado a generaciones de investigadores. Richard Feynman, el legendario físico teórico, lo estaba estudiando cuando murió en la década de 1980. Hoy en día, son pocas las áreas de la física que no se han visto afectadas por la casi centenaria idea de Bethe.
“Su importancia ha seguido creciendo hasta el día de hoy”, explica Charlotte Kristjansen, profesora del Instituto Niels Bohr de Copenhague.
Imanes en una cadenaA principios de la década de 1930, Bethe intentaba utilizar la mecánica cuántica para comprender cómo se magnetiza el hierro. Pero un trozo de metal tiene muchas más partículas que un átomo de hidrógeno, por lo que no había forma de utilizar herramientas cuánticas estándar para comprender exactamente el imán. Necesitaba una forma de abordar un sistema cuántico mucho más complicado.
Bethe empleó un modelo simplificado de imán, conocido como cadena de espín: una única línea de átomos, cada uno apuntando hacia arriba o hacia abajo como su propio imán diminuto. Si todos los polos norte apuntaran hacia arriba, por ejemplo, la cadena se magnetizaría. Su reto era calcular la energía necesaria para hacer girar los átomos hasta esa posición. En principio, para ello era necesario llevar un registro de cada átomo, una tarea hercúlea que parecía necesitar aproximaciones, atajos que simplifican el cálculo pero introducen imprecisiones.
La cadena de espín se basó en el trabajo pionero de Felix Bloch de 1930. Bloch había dejado de lado los átomos individuales y sus numerosas interacciones y, en cambio, se centró en el movimiento colectivo que surgía de esas interacciones.
En una cadena de espín, ese movimiento son ondas como las que se ven en los estadios. Si se da la vuelta a un átomo, éste dará la vuelta a sus vecinos, que a su vez darán la vuelta a sus vecinos, y así sucesivamente. Estas ondas siguen siendo extremadamente complicadas: cuando dos ondas recorren el mismo tramo de partículas, cualquier partícula puede dar la vuelta a cualquier otra partícula, lo que da lugar a un caos. La teoría de Bloch prohibía este desorden. Supuso que cada átomo sólo podía dar la vuelta a su vecino inmediato. Luego supuso que, como consecuencia, las ondas resultantes siempre colisionarían suavemente, atravesándose unas a otras con una perturbación mínima. La suposición mantenía las cosas lo suficientemente ordenadas como para poder manejarlas.
 Hans Bethe, un físico famoso por su meticulosidad, se basó en el trabajo de Bloch para desarrollar una forma de capturar a la perfección el comportamiento de ciertos sistemas cuánticos complejos. Foto: Los Alamos National Laboratory.
Hans Bethe, un físico famoso por su meticulosidad, se basó en el trabajo de Bloch para desarrollar una forma de capturar a la perfección el comportamiento de ciertos sistemas cuánticos complejos. Foto: Los Alamos National Laboratory.
Su intuición casi resolvió el problema, pero pasó por alto un detalle matemático clave. “Si hubiera sido menos perezoso con las arcotangentes o los logaritmos, llamaríamos a esto el ansatz de Bloch”, asevera Jean-Sébastien Caux, profesor de la Universidad de Ámsterdam.
Bethe se dio cuenta de que había una segunda posibilidad para que dos ondas pudieran coexistir: podían atraerse entre sí de forma que viajarían juntas. Con esto, Bethe captó todo lo que la cadena de espín podía hacer. Teniendo en cuenta estos dos movimientos colectivos (choques suaves y viajes en pares), pudo calcular la energía exacta para cada posible disposición de la cadena.
Bethe había dado con una teoría cuántica perfecta, que funcionaba para cualquier número de partículas. Sin embargo, nunca la utilizó para explicar los imanes del mundo real. Funcionaba para cadenas, pero no para bloques de átomos, como él había imaginado. En cambio, demostraría su valor de otras maneras.
Las raíces de la perfección cuánticaCuando Hitler ascendió al poder en los años siguientes, Bethe huyó de Alemania y llegó a los Estados Unidos, donde trabajó como líder del Proyecto Manhattan. Después de la guerra, continuó estudiando física, pero nunca regresó a su ansatz.
Serían otros los que descubrirían hasta qué punto podía funcionar el ansatz de Bethe. Funcionó para cadenas de espín con defectos e incluso para cadenas de partículas que se influyen entre sí de forma no magnética. Sin embargo, curiosamente, siguió fallando con los bloques de átomos del mundo real que originalmente habían motivado a Bethe. No fue hasta la década de 1960, cuando los teóricos lo aplicaron a delgadas láminas de hielo (otro sistema de innumerables partículas cuánticas), que descubrieron por qué.
Los investigadores, al enfriar el hielo a temperaturas inauditas, descubrieron un misterio: si el hielo perdía todo su calor, esperaban que sus moléculas se asentaran formando un cristal perfecto y único. En cambio, encontraron un extraño desorden, como si las moléculas pudieran acabar en diferentes disposiciones que variaban sutilmente de un experimento a otro.
Los teóricos se dieron cuenta de que las capas congeladas también contenían ondas que viajaban a lo largo de una línea. Cada capa formaba efectivamente un cristal perfecto de moléculas de H2O repetidas. Pero cada molécula podía adoptar una de seis configuraciones diferentes, como un píxel que puede ser rojo, verde, azul, amarillo, naranja o violeta. Cada vez que los experimentadores enfriaban el hielo, obtenían una imagen multicolor diferente. Pero había un método en la locura. Los teóricos descompusieron la imagen, comenzando por la parte superior, tomándola línea por línea. Trataron cada cadena de píxeles como un fotograma de una película. Y cuando reprodujeron la película, vieron ondas. Un píxel verde podía ondular la línea hacia la derecha, para dar un ejemplo demasiado simplista. Y cuando estas ondas chocaban, lo hacían suavemente, manteniendo su forma, exactamente como en la cadena de espín de Bethe.
De modo que con el ansatz de Bethe, los físicos podían calcular con precisión las probabilidades de medir esos patrones en un experimento. Era otra teoría cuántica perfecta.

Felix Bloch worked out much of the physics that would ultimately become known as the Bethe ansatz. Foto: Dominio público
Esta suavidad y esta geometría eran la base del poder del ansatz de Bethe, como argumentó el físico australiano Rodney Baxter a principios de los años 1970. Muchos sistemas conservan el momento y la energía, incluso durante colisiones violentas. Pero en las capas de hielo, la suavidad de las colisiones preservaba muchas más cantidades. El momento y la energía eran solo las primeras de una lista interminable de leyes de conservación, cada una basada en la anterior. Basándose en estas leyes, Baxter explicó qué problemas podía resolver el ansatz de Bethe. Si un sistema contenía ondas que chocaban suavemente en alguna cadena, ya sea momento a momento o línea a línea, la multitud de leyes de conservación lo domaría.
En estos casos, “se tiene una historia completa de la A a la Z. Se empieza desde lo microscópico y se deriva absolutamente todo”, explica Caux.
El último enigma de FeynmanCon esta comprensión más profunda, los físicos continuaron utilizando el ansatz de Bethe de nuevas maneras. Después de su muerte, una fotografía de la pizarra de Feynman capturó las palabras: “Lo que no puedo crear, no lo entiendo”, junto con una lista rotulada “para aprender”, que comienza con el ansatz de Bethe.
En sus últimos meses, Feynman había hablado de un “ambicioso sueño” de utilizar el ansatz de Bethe para comprender las colisiones entre partículas de alta energía, que los físicos predecían mediante aproximaciones complicadas. Señaló que dos protones a menudo pasan a toda velocidad uno al lado del otro como si fueran coches en carriles opuestos de una autopista. En lugar de hacer contacto directo, intercambian partículas de vida corta. Este intercambio los acerca o los aleja, pero no afecta significativamente a su alta velocidad. Los cambios importantes se producen momento a momento a lo largo de una línea, como en una cadena de espín.
El cáncer se llevó a Feynman antes de que pudiera desarrollar la idea. Pero otros acabaron uniendo las piezas del rompecabezas. Cuando Ludvig Faddeev, físico ruso y maestro del ansatz de Bethe, dio una charla en la Universidad de Stony Brook en 1994, escribió en la pizarra una fórmula extraída de uno de sus artículos anteriores. En ella se describía un sistema concreto cuyo comportamiento podía calcularse utilizando el ansatz de Bethe. Gregory Korchemsky, un físico de partículas que se encontraba entre el público, la reconoció inmediatamente de otro contexto. Los premios Nobel David Gross y Frank Wilczek habían utilizado la misma fórmula en la década de 1970 para describir las partículas energéticas que “abrían” un protón.
Trabajando juntos, Faddeev y Korchemsky descubrieron que, efectivamente, el ansatz de Bethe se aplicaba a las colisiones de partículas de alta energía, haciendo realidad el sueño de Feynman. Lo que Gross y Wilczek habían aproximado, ellos lo calcularon con exactitud. El ansatz de Bethe ha encontrado más usos desde entonces, como en modelos de juguete perfectos de la gravedad cuántica.
En un mundo de muchas partículas, los efectos de todo sobre todo lo demás a menudo superan a los teóricos. Sin embargo, la suposición de Bethe proporcionó a los físicos una forma de comprender por completo ciertos sistemas cuánticos. Durante el siglo siguiente, los físicos destilaron su idea en una receta que, cuando las estrellas se alinean, les permite predecir con precisión lo que de otro modo sería incognoscible. Y se han maravillado de cómo esas estrellas a veces se alinean, lo que permite predicciones perfectas sobre el hielo, los protones, los agujeros negros y más.
Los métodos de ansatz Bethe Ansatz aparecen en muchos lugares, comenta Pedro Vieira, profesor del Instituto Perimeter de Física Teórica en Waterloo, Canadá. “Parece que la naturaleza aprecia las cosas bellas”.
El artículo original, How Hans Bethe Stumbled Upon Perfect Quantum Theories, se publicó el 12 de febrero de 2025 en Quanta Magazine.
Traducido por César Tomé López
El artículo Cómo Hans Bethe se topó con las teorías cuánticas perfectas se ha escrito en Cuaderno de Cultura Científica.
Las gambas mantis: ataque ultrarrápido y escudo fonónico
Las galeras (Squilla mantis) son unos crustáceos estomatópodos que se capturan en grandes cantidades en nuestras costas. A pesar de su excelente sabor son poco apreciadas por su aspecto. Sus patas adaptadas para atrapar presas recuerdan a las de las mantis religiosas (Figura 1).
 Figura 1. A la izquierda vemos la galera de nuestras costas (Squilla mantis), mostrando sus patas adaptadas para atrapar presas. Foto: Dominio público. A la derecha, la gamba mantis (Odontodactylus scyllarus) con sus patas convertidas en mazas. Foto: Silke Baron, CC BY 2.0
Figura 1. A la izquierda vemos la galera de nuestras costas (Squilla mantis), mostrando sus patas adaptadas para atrapar presas. Foto: Dominio público. A la derecha, la gamba mantis (Odontodactylus scyllarus) con sus patas convertidas en mazas. Foto: Silke Baron, CC BY 2.0Unos estomatópodos tropicales, los gonodactiloideos, conocidos como gambas mantis, han modificado estos apéndices para convertirlos en auténticas mazas con las que golpear a sus presas (Figura 1). Las propiedades de esta adaptación son impresionantes. El apéndice se pliega por acción muscular almacenando energía mecánica en una especie de resorte, algo parecido a lo que ocurre con una ballesta. Cuando se libera el resorte, el apéndice se dispara hacia delante para golpear el objetivo. La maza adquiere una velocidad de 30 metros por segundo en menos de tres milisegundos (Figura 2). La aceleración es similar a la de una bala de pequeño calibre, y podemos comprobar sus efectos en los siguientes vídeos.
Aquí vemos en acción a la gamba mantis pavo real (Odontodactylus scyllarus) rompiendo la concha de un cangrejo ermitaño. Se describe también el sorprendente sistema visual de estos animales, equipado con doce tipos de fotorreceptores capaces de detectar luz polarizada y ver en el espectro ultravioleta El mecanismo de golpeo de la gamba mantis también le sirve como defensa. Aquí vemos como es capaz de derrotar a un pulpo mucho mayor que ellaSe trata de uno de los ataques más fulminantes registrados en el reino animal. Los más sólidos caparazones de artrópodos o conchas de moluscos terminan rompiéndose tras uno o varios golpes. Se ha descrito incluso como el cristal de un acuario se rompió a consecuencia de estos impactos.
Utilizando sensores muy precisos se observó que la presa recibe dos golpes en cada ataque. El primero de ellos tiene una fuerza de 400-1500 newtons. Para hacernos una idea, esta es la fuerza del puñetazo de un boxeador profesional. Menos de medio milisegundo después, la presa es golpeada de nuevo por una fuerza de unos 500 newtons.
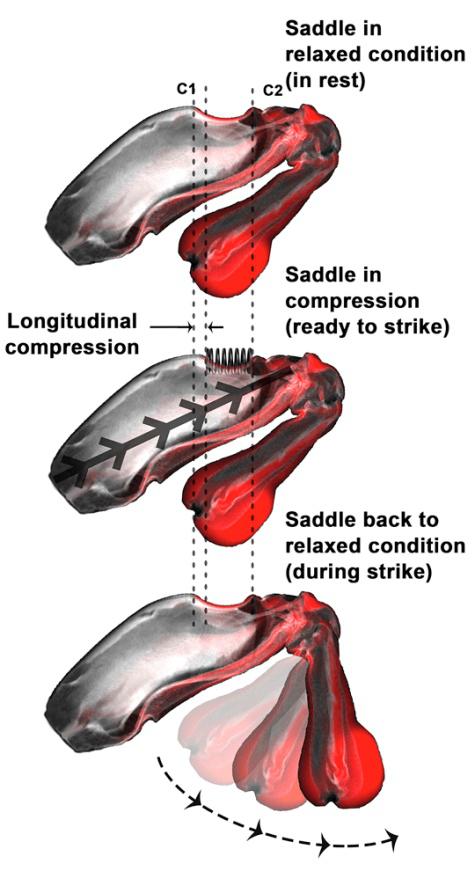 Figura 2. Mecanismo de golpeo de las gambas mantis. La energía de la contracción muscular es almacenada en un resorte en forma de silla de montar. Su liberación provoca el lanzamiento de la maza hacia delante, alcanzando una velocidad de 30 m/s en menos de 3 milisegundos. De Tadayon M et al. (2018), iScience. CC-BY-NC-ND
Figura 2. Mecanismo de golpeo de las gambas mantis. La energía de la contracción muscular es almacenada en un resorte en forma de silla de montar. Su liberación provoca el lanzamiento de la maza hacia delante, alcanzando una velocidad de 30 m/s en menos de 3 milisegundos. De Tadayon M et al. (2018), iScience. CC-BY-NC-NDLa explicación de este doble golpe resultó asombrosa. El desplazamiento del fluido por el rapidísimo movimiento del apéndice provoca una burbuja de cavitación, formada por vapor de agua. La burbuja implosiona en nanosegundos, alcanzando temperaturas de miles de grados, emitiendo luz y sonido y provocando ondas de choque1. Estas ondas, de altísima frecuencia, son las que causan el segundo impacto sobre el objetivo.
Se estima que una gamba mantis es capaz de propinar 50 000 golpes en el intervalo entre mudas del caparazón. La pregunta es inevitable: ¿cómo es posible que sus apéndices sean capaces de quebrar los materiales más duros y no resulten dañados por tantos golpes?
Esta cuestión acaba de ser respondida en un estudio publicado en Science por investigadores de la universidad Northwestern, especializados en ingeniería de biomateriales. Empleando técnicas muy precisas de análisis, el equipo comprobó que las mazas de la gamba mantis están organizadas en dos capas. La zona de impacto está formada por una delgada capa (70 μm) de hidroxiapatito (el durísimo material inorgánico de nuestros huesos y dientes) y por otra capa (0,5 mm) de fibras mineralizadas de quitina en forma de espiga. Por debajo encontramos una capa de haces de fibras dispuestas de una forma helicoidal periódica. Se trata de una estructura Bouligand (Figura 3). Según los autores del estudio, estas estructuras constituirían un “escudo fonónico”, algo que debemos explicar más despacio.
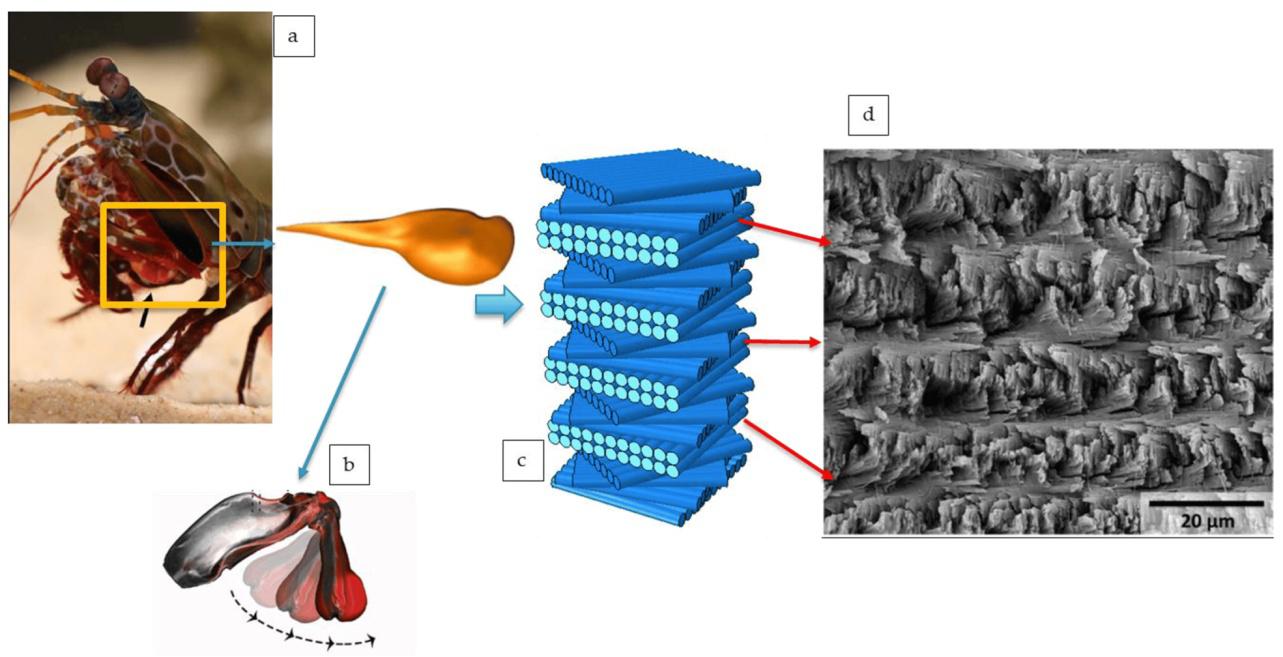 Figura 3. En el centro se muestra cómo se organizan las fibras en la capa periódica de la maza formando una estructura Bouligand. A la derecha vemos una imagen de esta capa a microscopía electrónica de barrido. De Malekinejad, H. et al. (2024) J. Compos. Sci. CC BY 4.0
Figura 3. En el centro se muestra cómo se organizan las fibras en la capa periódica de la maza formando una estructura Bouligand. A la derecha vemos una imagen de esta capa a microscopía electrónica de barrido. De Malekinejad, H. et al. (2024) J. Compos. Sci. CC BY 4.0Los cristales fotónicos son nanoestructuras ópticas diseñadas para afectar el movimiento de los fotones a causa de los diferentes índices de refracción de sus capas, que se repiten periódicamente. Esto causa interferencias destructivas para determinadas longitudes de onda (colores) que no pueden propagarse por el material. De forma análoga, un material fonónico se comportaría ante ondas sonoras como un cristal fotónico ante la luz. Es decir, determinadas frecuencias de sonido quedarían atenuadas o anuladas al atravesar la estructura2.
Los resultados publicados en Science muestran que la estructura Bouligand periódica de la maza de la gamba mantis dispersa y atenúa por un mecanismo fonónico las ondas de alta frecuencia producidas por la cavitación. Estas ondas son especialmente perjudiciales para la integridad de la maza.
Los resultados pueden tener aplicación industrial, por ejemplo en el diseño de materiales destinados a recibir impactos violentos. No resulta sorprendente que entre los organismos que financian esta investigación se encuentren las oficinas de investigación de la Marina y las Fuerzas Aéreas de los EE.UU. En cualquier caso, este es un excelente ejemplo de cómo soluciones estructurales desarrolladas por los seres vivos en el transcurso de su evolución pueden ser aplicadas en la ingeniería.
Referencias
Alderete, N.A., Sandeep, S., Raetz, S. et al. (2025). Does the mantis shrimp pack a phononic shield? Science doi: 10.1126/science.adq7100
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
Notas:
1 No son los únicos animales capaces de generar estas burbujas de plasma. Sus parientes, las gambas pistola, también las producen al atacar a sus presas, en esta ocasión con chorros de agua a alta presión
2 Los interesados no deben perderse el excelente artículo de mi amigo Francis Villatoro sobre el tema. Allí se cuenta que la escultura “Órgano” de Eusebio Sempere (Fundación Juan March, Madrid) se comporta como un objeto fonónico, aunque no se había pretendido que tuviera esta propiedad
El artículo Las gambas mantis: ataque ultrarrápido y escudo fonónico se ha escrito en Cuaderno de Cultura Científica.
Quipu, la superestructura más grande del universo conocido
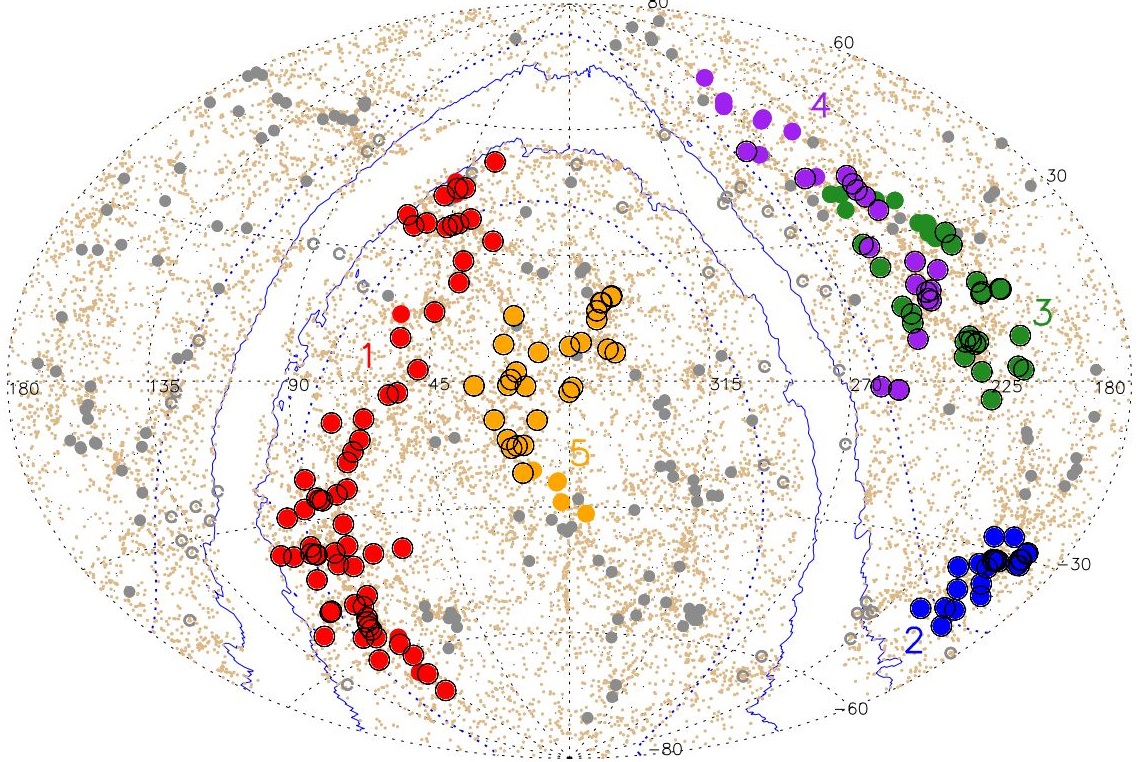 La imagen muestra las superestructuras descubiertas en el estudio. En rojo aparece Quipu, la mayor que se ha encontrado en el universo local. El resto son: Shapley (azul), Serpens-Corona Borealis (verde), Hercules (violeta) y Sculptor-Pegasus (beige). Fuente: Boehringer et al. (2025) arXiv
La imagen muestra las superestructuras descubiertas en el estudio. En rojo aparece Quipu, la mayor que se ha encontrado en el universo local. El resto son: Shapley (azul), Serpens-Corona Borealis (verde), Hercules (violeta) y Sculptor-Pegasus (beige). Fuente: Boehringer et al. (2025) arXivPara la mente humana resulta muy difícil entender las colosales dimensiones del universo. En nuestra evolución hemos ajustado el mundo a la utilidad del día a día y somos capaces de asimilar de manera natural las escalas de metros, kilómetros, minutos o años, pero terminamos desconcertados por los modelos que incluyen distancias astronómicas fuera de nuestro rango de experiencia cotidiana. Los tamaños, masas, distancias y velocidades que operan en esa escala cósmica se escapan a nuestra intuición y lo único que podemos hacer para acercarnos a su entendimiento es utilizar analogía, metáforas y comparaciones.
Por ejemplo, se suele decir que las naves más rápidas construidas por el hombre tardarían miles de años simplemente para llegar a la estrella más cercana. La Voyager 1, lanzada en septiembre de 1977, realizó varias maniobras de asistencia gravitatoria que la aceleraron a una velocidad de escape de 61,000 km/h (unos 17 km/s) en relación con el Sol y, sin embargo, tras casi medio siglo de viaje, apenas ha salido de nuestro sistema solar. Manteniendo esas cifras tardaría más de 70.000 años en llegar hasta Próxima Centauri, situada a poco más de cuatro años luz de nosotros. Si usáramos como referencia la sonda Solar Parker Probe, que se mueve alrededor del Sol a unos 340.000 km/h, el viaje hasta nuestra vecina estelar se alargaría casi 6.600 años. Si intentamos imaginar ahora cómo sería cruzar la Vía Láctea, nuestra humilde y relativamente pequeña galaxia de unos 100.000 años luz de diámetro, nos encontramos que la Solar Parker Probe tardaría más de 150 millones de años y nuestra mente comienza a perderse…
En nuestra vida cotidiana podemos entender, e incluso visualizar mentalmente, cuánto pesan cuarenta kilos, cuánto miden veinte centímetros o cómo sería un trayecto de ochenta kilómetros. Tenemos experiencias que nos ayudan a interiorizar esas medidas, pero ese apoyo desaparece cuando se trata de entender la masa de Eta Carinae o la distancia que nos separa del exoplaneta Kepler-22b. En ningún momento de nuestra existencia hemos necesitado entender medidas como el año luz, la unidad astronómica o el parsec para poder sobrevivir y, de esta manera, no es de extrañar que nuestro cerebro requiera de un esfuerzo adicional para aproximarse a algo parecido a la comprensión. Por ello, va a resultar difícil entender el reciente artículo, publicado en el repositorio científico ArXiv, en el que un equipo de astrónomos anuncia el descubrimiento de «la mayor superestructura del universo», un monstruo gigantesco, una estructura cósmica de dimensiones difíciles de concebir, un verdadero titán al que han llamado «Quipu».
 Un quipu inca de la colección del »Museo Arqueológico Rafael Larco Herrera de Lima», Perú Fuente: Claus Ableiter / Wikimedia Commons
Un quipu inca de la colección del »Museo Arqueológico Rafael Larco Herrera de Lima», Perú Fuente: Claus Ableiter / Wikimedia CommonsAntes de la llegada de los europeos al Nuevo Mundo, las civilizaciones andinas no contaban con un sistema de escritura convencional, es decir un sistema en el que se representan sonidos o palabras individuales mediante símbolos gráficos, como ocurre con los alfabetos. En su lugar desarrollaron otras técnicas, bastante ingeniosas, que les permitían representar la realidad matemática utilizando diferentes cuerdas y nudos (quipus) o diseños geométricos plasmados en tejidos, cerámicas y otros objetos artísticos (topacus).
Los quipus eran un sofisticado sistema de cuerdas que los incas utilizaron para almacenar información numérica como registros contables, censos o datos administrativos. Podían ser muy simples, apenas un par de cuerdas y algunos nudos, o convertirse en verdaderas marañas de colores representativos con cientos o incluso miles de cuerdas y nudos. Inspirados por esta idea del Quipu, los autores del artículo científico han bautizado con su nombre a «la estructura cósmica más grande descubierta hasta la fecha». Una pincelada de poesía histórica, una metáfora artística (otra más) para ayudarnos a visualizar mejor uno de los titánicos andamios de nuestro universo local.
Una de las características más destacadas del universo es que es muy uniforme a gran escala. Cuando en 1965 los físicos estadounidenses Arno Penzias y Robert Wilson detectaron por primera vez la radiación de fondo cósmico de microondas (CMB) se dieron cuenta de que esa radiación electromagnética presentaba las mismas propiedades por todos lados y en todas direcciones. Las diferentes imágenes del CMB representan la radiación emitida tan solo 380.000 años después del Big Bang, cuando el universo se volvió transparente a la radiación y, a grandes rasgos, son mapas de temperaturas donde las diferencias son mínimas. Era un universo muy caliente, a unos 2500 grados centígrados, pero las fluctuaciones de temperatura y densidad apenas representaban diferencias del orden de una parte en cien mil. Y aún así, no deberíamos infravalorar esas diminutas variaciones (anisotropías) porque terminaron convirtiéndose en las semillas de las futuras estructuras del universo, de las galaxias y de los cúmulos de galaxias.
Al igual que las cuerdas de los quipus incas, la estructura descrita en el estudio contiene largos filamentos que se extienden, aproximadamente, 1300 millones de años luz, unas dimensiones que la convierten en el objeto más grande el universo local, superando a récords anteriores como el supercúmulo Laniākea, en el que se encuentra la Tierra. Está formada por cúmulos de galaxias y cúmulos de cúmulos de galaxias con una masa estimada, asombrosa y difícil de comprender, de unos «200 cuatrillones de masas solares».
 Supercúmulo Shapley con más de 8.000 galaxias y 1.000 cúmulos de galaxias. Fuente: ESA /Planck Collaboration
Supercúmulo Shapley con más de 8.000 galaxias y 1.000 cúmulos de galaxias. Fuente: ESA /Planck CollaborationEl estudio también describe otras superestructuras cósmicas entre ellas el supercúmulo Shapley, que ya se conocía anteriormente y que poseía el récord como «la estructura cósmica más grande del universo local» pero que, ahora, palidece ante la grandeza de otras estructuras descubiertas como Serpens-Corona Borealis, Hercules o Sculptor-Pegasus. Todas ellas se encuentran a una distancia aproximada de entre 425 y 815 millones de años luz de la Tierra, pero Quipu destaca sobre el resto con una longitud que superaría 13.000 veces el diámetro de nuestra Vía Láctea. En conjunto, estas cinco superestructuras contienen el 45% de los cúmulos de galaxias, el 30% de las galaxias y el 25% de la materia del universo observable y, en total, constituyen el 13% del volumen del universo conocido.
Contamos con diferentes modelos cosmológicos que predicen estas grandes estructuras pero detectarlas no es un trabajo sencillo. Necesitamos datos de la distribución de la materia del universo en diferentes longitudes de onda, un buen número de datos recogidos por nuestros instrumentos ópticos terrestres, telescopios espaciales, sondas y observatorios que midan las «variaciones en el fondo cósmico de microondas, las distorsiones causadas por lentes gravitacionales a gran escala o la influencia de movimientos de transmisión a gran escala en las mediciones de la constante de Hubble».
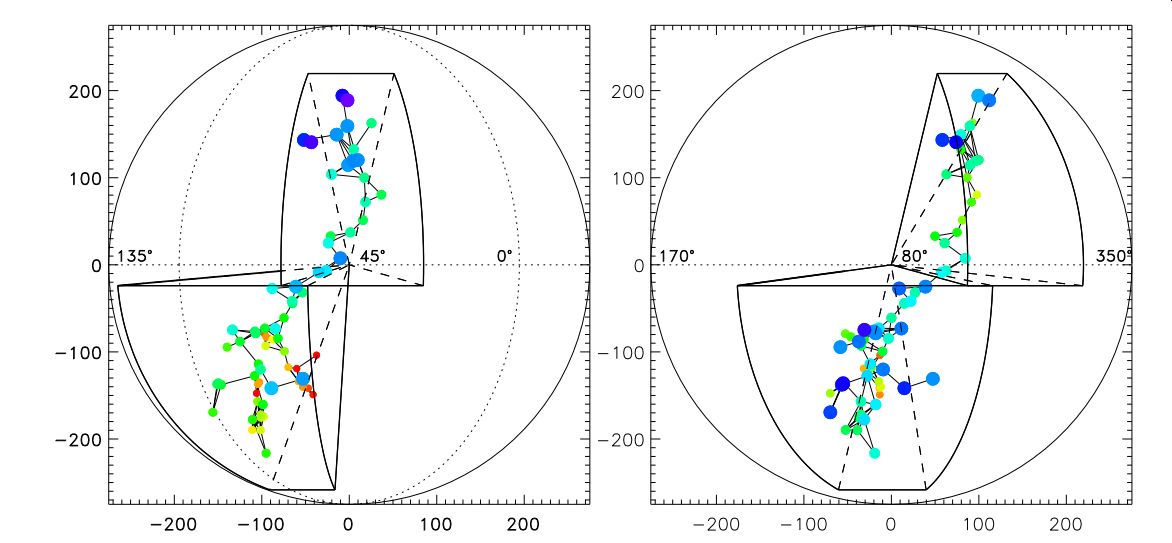 Representación tridimensional de la Superestructura de Quipu. Los puntos son miembros del cúmulo con tamaños y colores que indican la distancia a un observador externo, azul para el cúmulo más cercano y rojo para el más distante. Fuente: Boehringer et al. (2025) arXiv
Representación tridimensional de la Superestructura de Quipu. Los puntos son miembros del cúmulo con tamaños y colores que indican la distancia a un observador externo, azul para el cúmulo más cercano y rojo para el más distante. Fuente: Boehringer et al. (2025) arXivSe trata de un artículo importante, que ya ha sido aceptado para su publicación en breve en la revista Astronomy and Astrophysics y que nos deja pistas palpables para entender el funcionamiento del universo a gran escala. Estas grandes acumulaciones de materia tienen un gran impacto en el entorno general, en las velocidades y trayectorias de miles de galaxias e incluso «afecta las mediciones de la expansión general del universo: donde reinan las superestructuras, la expansión local de las galaxias puede distorsionar la medición de la expansión general del universo, conocida como la constante de Hubble». Finalmente, la atracción gravitatoria de tanta materia también puede causar una curvatura de la luz (efecto de lente gravitacional) que puede distorsionar las imágenes del cielo distante.
Futuros estudios de estas superestructuras afectan tanto al presente como al futuro del universo. Son estructuras temporales, como casi todo en nuestro cosmos, y la expansión del espacio-tiempo las irán desintegrando, dividiendo y dispersando en diferentes unidades más pequeñas pero, por ahora y según los propios autores, «representan entidades físicas con propiedades características y entornos cósmicos especiales que merecen una atención especial».
Referencias y más información:
Boehringer, Hans, et al. (2025)Unveiling the largest structures in the nearby Universe: Discovery of the Quipu superstructure arXiv doi: 10.48550/arXiv.2501.19236.
Stephanie Pappas (2025) Astronomers discover ‘Quipu’, the single largest structure in the known universo Live Science (2025)
Sobre el autor: Javier «Irreductible» Peláez (Puertollano, 1974) es escritor y comunicador científico. Autor de 500 años de frío. La gran aventura del Ártico (Crítica, 2019) y Planeta Océano (Crítica 2022). Es uno de los fundadores de la plataforma Naukas.com, editor de ciencia en Yahoo España y Latinoamérica. Es guionista científico en los programas de televisión «El Cazador de Cerebros» y «Órbita Laika» de RTVE. Durante más de una década ha escrito en diferentes medios de comunicación (El País, El Español, National Geographic, Voz Populi). Es autor de los podcasts Catástrofe Ultravioleta y La Aldea Irreductible, y ha colaborado en diferentes proyectos radiofónicos y televisivos (Radio Nacional de España, Radio Televisión Canaria). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Quipu, la superestructura más grande del universo conocido se ha escrito en Cuaderno de Cultura Científica.
¿Y si la Tierra dejase de rotar?
Si la Tierra dejase de rotar de forma abrupta, de entrada tendríamos un grave problema con la inercia.
Los vídeos ‘¿Y sí…?´ se plantean cuestiones ficticias pero que nos permiten aprender mucho sobre el mundo en el que vivimos. Se han emitido en el programa de divulgación científica de Televisión Española Órbita Laika, y producido en colaboración con la Cátedra de Cultura Científica de la Universidad del País Vasco.
Ficha técnica: Idea: José Antonio Pérez Ledo
Producción ejecutiva: Blanca Baena
Dirección: Aitor Gutierrez
Guion: Manuel Martinez March
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Locución: José Antonio Pérez Ledo
El artículo ¿Y si la Tierra dejase de rotar? se ha escrito en Cuaderno de Cultura Científica.
Los cerebros de aves, reptiles y mamíferos han seguido trayectorias evolutivas diferentes
Dos estudios publicados en el último número de la revista Science, liderados por el Dr. Fernando García-Moreno, investigador Ikerbasque en el centro de investigación Achucarro Basque Center for Neuroscience (ACHUCARRO) y en la Universidad del País Vasco (UPV/EHU), y colaboradores, han revelado que aves, reptiles y mamíferos han desarrollado circuitos cerebrales complejos de forma independiente, a pesar de compartir un ancestro común. Estos hallazgos desafían la visión tradicional de la evolución del cerebro y demuestran que, aunque existen funciones cerebrales comparables entre estos grupos, los mecanismos de formación embrionaria y tipos celulares han seguido trayectorias evolutivas diferentes.
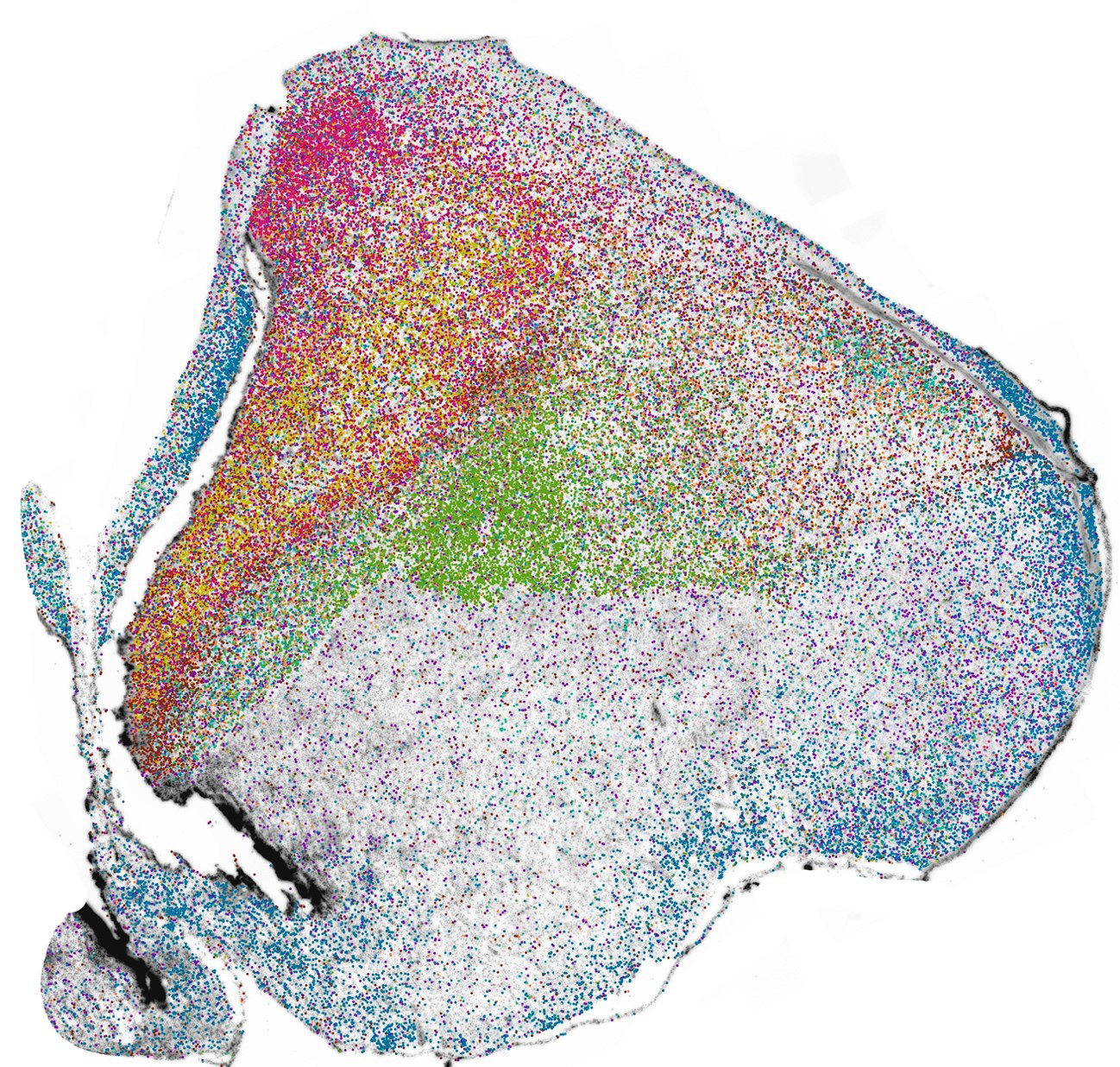 Distribución de neuronas en el cerebro del pollo. Fuente: Fernando García-Moreno
Distribución de neuronas en el cerebro del pollo. Fuente: Fernando García-MorenoEl palio es la región del cerebro donde se forma la neocorteza en mamíferos, esa región del cerebro responsable de funciones cognitivas y complejas y que más diferencia a los humanos del resto de especies. El palio ha sido tradicionalmente considerado una estructura comparable entre mamíferos, aves y reptiles, variando tan sólo en niveles de complejidad. Se asumía que esta región albergaba tipos neuronales similares, con circuitos equivalentes para el procesamiento sensorial y cognitivo. Estudios previos habían identificado la presencia de neuronas excitatorias e inhibitorias compartidas, así como patrones generales de conectividad que sugerían una evolución similar en estas especies de vertebrados. Sin embargo, los nuevos estudios han revelado que, aunque las funciones generales del palio sean equivalentes entre estos grupos, los mecanismos de desarrollo y la identidad molecular de sus neuronas han divergido sustancialmente a lo largo de la evolución.
Circuitos durante el desarrollo embrionarioEl primer estudio, desarrollado por Eneritz Rueda-Alaña y Fernando García Moreno en ACHUCARRO y apoyados por un equipo multidisciplinar de colaboradores de los centros vascos CICbioGUNE y BCAM, el madrileño CNIC, la Universidad de Murcia, Krembil (Canadá) y la Universidad de Estocolmo, muestra que aunque aves y mamíferos han desarrollado circuitos con funciones similares, la forma en que estos circuitos se generan durante el desarrollo embrionario es radicalmente diferente. “Sus neuronas nacen en lugares y momentos del desarrollo diferentes para cada especie” explica el Dr. García Moreno, director del laboratorio de desarrollo y evolución cerebral, “indicando que no son neuronas comparables derivadas de un ancestro común”. Mediante análisis de transcriptómica espacial y modelado matemático, los investigadores encontraron que las neuronas responsables del procesamiento sensorial en aves y mamíferos se conforman empleando grupos de genes diferentes. “Las herramientas genéticas que utilizan para cimentar su identidad celular varía de unas especies a otras, cada una muestra tipos celulares nuevos y únicos”. Todo ello indica que estas estructuras y circuitos no son homólogos, sino el resultado de evolución convergente, es decir, “han llegado a generar estos circuitos neuronales esenciales mediante caminos evolutivos diferentes”.
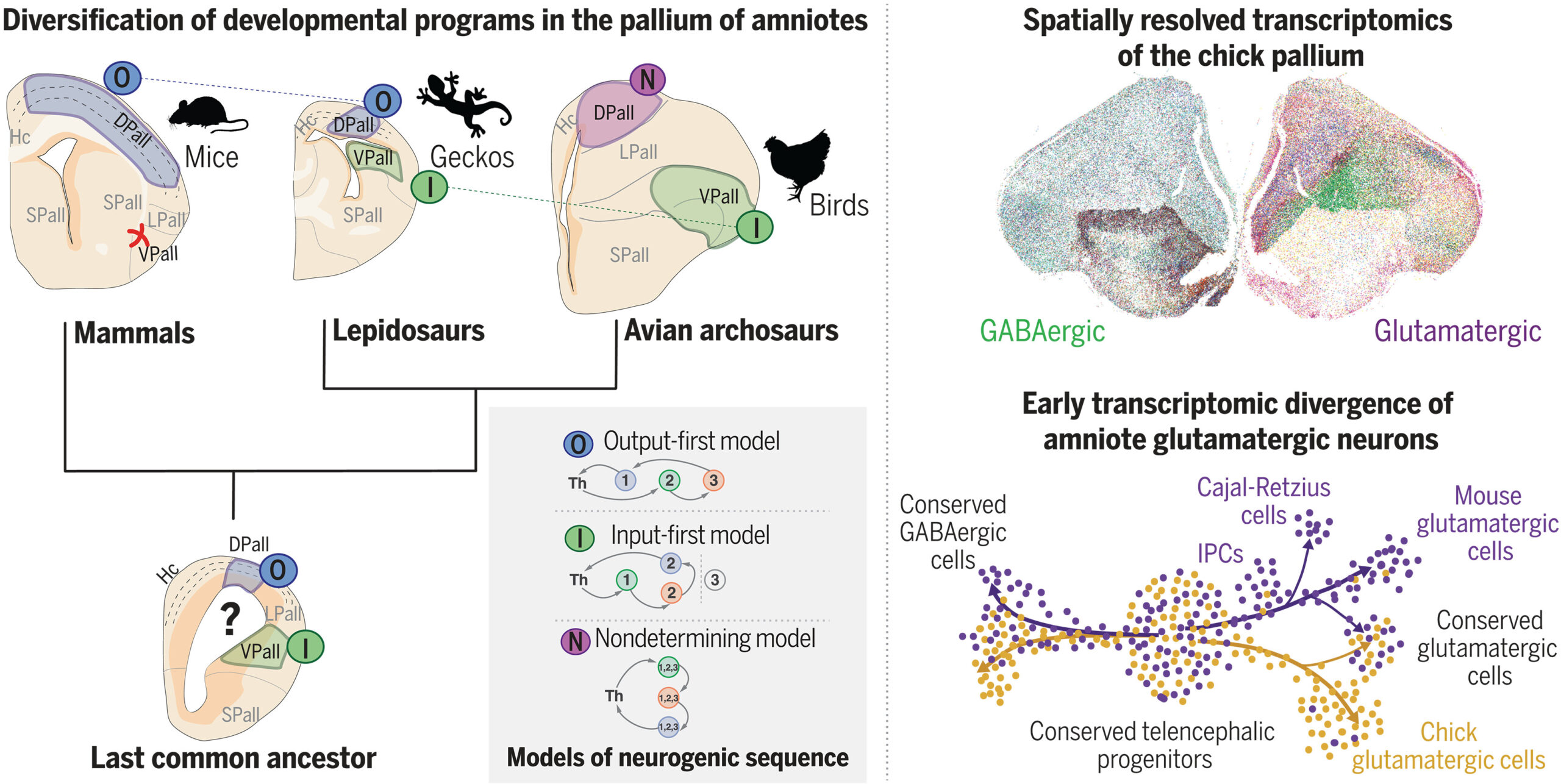 Fuente: Eneritz Rueda-Alaña et al. (2025)Atlas de tipos celulares
Fuente: Eneritz Rueda-Alaña et al. (2025)Atlas de tipos celulares
El segundo estudio, abunda en estas diferencias. Llevado a cabo en la Universidad de Heidelberg (Alemania) y co-dirigido por Bastienne Zaremba, Henrik Kaessmann y Fernando García Moreno, proporciona un atlas detallado de los tipos celulares en el cerebro de las aves y lo compara con el de mamíferos y reptiles. “Hemos podido describir los cientos de genes que emplea cada tipo de neurona en estos cerebros, célula a célula, para compararlos con herramientas de bioinformática”. Los resultados muestran que las aves han conservado la mayoría de las neuronas inhibitorias presentes en otros vertebrados, desde hace cientos de millones de años. Sin embargo, sus neuronas excitatorias encargadas de la transmisión de la información en el palio, han evolucionado de manera única. Tan sólo se identificaron algunos tipos celulares en el cerebro aviar con perfiles genéticos similares a otras presentes en mamíferos, como el claustro y el hipocampo, lo que sugiere que algunas neuronas son muy antiguas y compartidas. “Sin embargo, la mayoría de las neuronas excitatorias han evolucionado de modos nuevos y diferentes en cada especie” detalla el Dr. García-Moreno.
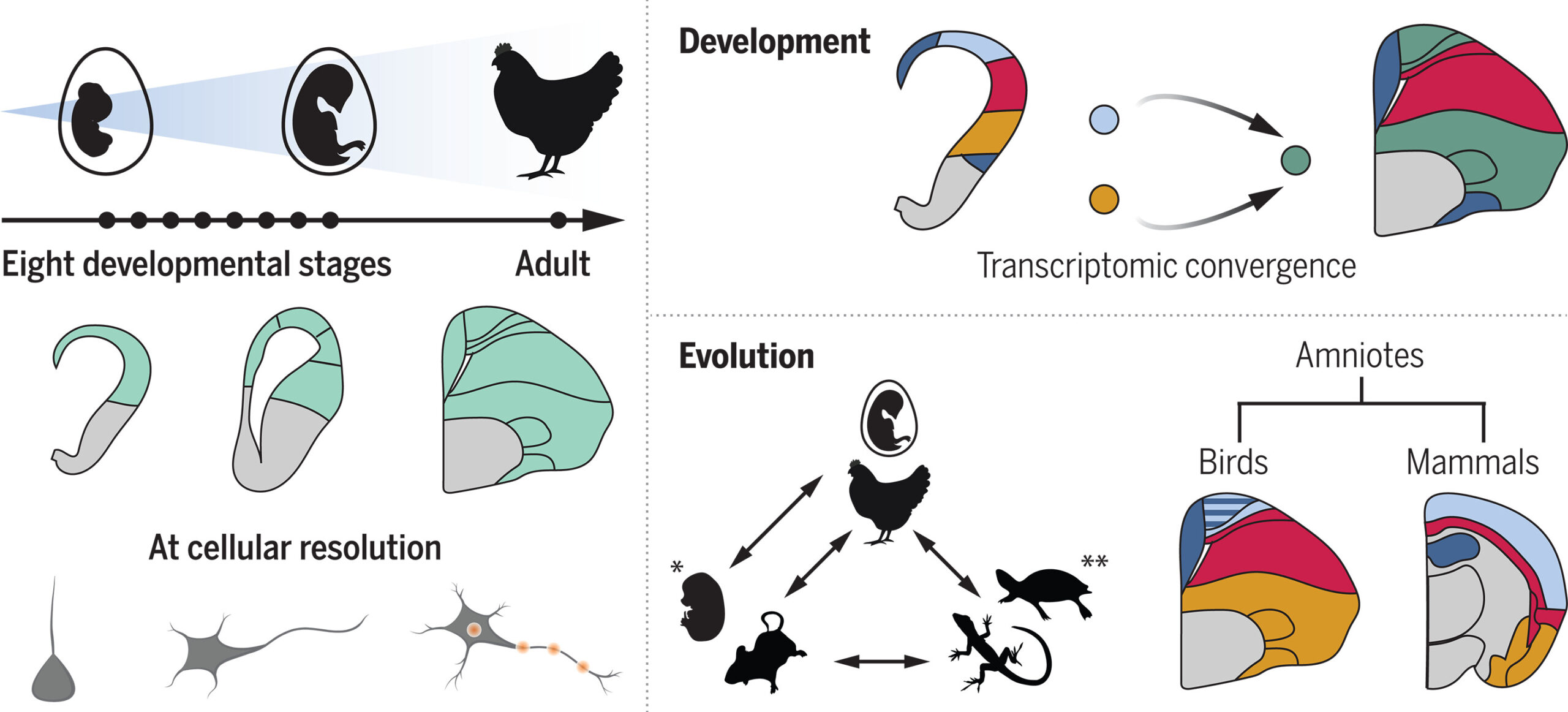 Fuente: Bastienne Zaremba et al. (2025)
Fuente: Bastienne Zaremba et al. (2025)Los estudios, publicados en Science, utilizaron técnicas avanzadas de transcriptómica espacial, neurobiología del desarrollo, análisis de células individuales y modelado matemático para trazar la evolución de los circuitos cerebrales en aves, mamíferos y reptiles.
Reescribiendo la historia evolutiva del cerebro“Nuestros estudios demuestran que la evolución ha encontrado múltiples soluciones para construir cerebros complejos”, explica el Dr. García-Moreno. “Las aves han desarrollado circuitos neuronales sofisticados a través de mecanismos propios, sin seguir el mismo camino que los mamíferos. Esto cambia la forma en que entendemos la evolución del cerebro.”
Estos hallazgos subrayan la flexibilidad evolutiva del desarrollo cerebral, mostrando que funciones cognitivas avanzadas pueden emerger a través de vías celulares y genéticas muy diferentes.
“Nuestro cerebro nos hace humanos, pero también nos une al resto de especies animales a través de una historia evolutiva compartida” explica el Dr. García Moreno. El descubrimiento de que aves y mamíferos han desarrollado circuitos neuronales de forma independiente tiene importantes implicaciones para la neurociencia comparada. Comprender los diferentes programas genéticos que dan lugar a tipos neuronales específicos podría abrir nuevas vías para la investigación en neurodesarrollo. El Dr. García Moreno apuesta por este tipo de investigación básica, “sólo entendiendo cómo se forma el cerebro, tanto en su desarrollo embrionario como en su historia evolutiva, podremos alcanzar a comprender cómo funciona”.
Referencias:
Rueda-Alaña E, Senovilla-Ganzo R, Grillo M, Vázquez E, Marco-Salas S, Gallego-Flores T, Ftara A, Escobar L, Benguría A, Quintas A, Dopazo A, Rábano M, dM Vivanco M, Aransay AM, Garrigos D, Toval A, Ferrán JL, Nilsson M, Encinas JM, De Pitta M, García-Moreno F (2025) Evolutionary convergence of sensory circuits in the pallium of amniotes Science doi: 10.1126/science.adp3411
Zaremba B, Fallahshahroudi A, Schneider C, Schmidt J, Sarropoulos I, Leushkin E, Berki B, Van Poucke E, Jensen P, Senovilla-Ganzo R, Hervas-Sotomayor F, Trost N, Lamanna F, Sepp M, García-Moreno F, Kaessmann H (2025) Developmental origins and evolution of pallial cell types and structures in birds Science doi: 10.1126/science.adp5182
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Los cerebros de aves, reptiles y mamíferos han seguido trayectorias evolutivas diferentes se ha escrito en Cuaderno de Cultura Científica.
Impresión funcional: revolucionando la integración de capacidades electrónicas
En el segmento de la electrónica de consumo, se estima que las ventas alcanzarán los 1000 billones de dólares. A esta cifra se suman los mercados de aplicaciones que integran funcionalidades electrónicas, como sensores, calefactores o antenas.
El sector ha encontrado nuevas vías de crecimiento gracias a las oportunidades y necesidades que ofrece la conectividad generalizada y el Internet of Things. Existe una demanda real de incorporar funcionalidades electrónicas en nuevos productos; no obstante, las tecnologías convencionales enfrentan limitaciones intrínsecas en los procesos y materiales comúnmente utilizados.
El desafío consiste en integrar estas funcionalidades en lugares donde antes no era posible hacerlo de manera eficiente. La solución podría residir en la impresión funcional.

Durante muchos años, la electrónica convencional ha sido la base de la innovación tecnológica. Utilizando circuitos impresos rígidos (PCBs), esta tecnología ha posibilitado desarrollar de una amplia gama de dispositivos electrónicos, desde computadoras personales hasta equipos médicos.
-
La solidez y durabilidad de las PCBs rígidas las convierten en la opción perfecta para aplicaciones en las que la estabilidad del circuito es fundamental.
-
La estandarización en su fabricación permite la producción en masa, lo que a su vez disminuye los costes y los tiempos de producción.
La rigidez de estas PCBs conlleva sin embargo limitaciones importantes.
-
Su falta de flexibilidad restringe su uso en aplicaciones que necesitan doblarse o estirarse, como ropa inteligente o dispositivos portátiles.
-
También, su tamaño y forma inalterables pueden representar un desafío en el diseño de productos, ya sean más compactos y ergonómicos o más voluminosos y de geometría compleja.
Estas limitaciones nos llevan a cuestionarnos: ¿cómo podemos sortear estos retos y qué opciones existen para la electrónica convencional?
Una integración completaLa impresión funcional se presenta como una posible solución a las restricciones de la electrónica tradicional, siendo una tecnología emergente con el potencial de transformar el diseño y la producción de dispositivos electrónicos. Gracias a los progresos en las técnicas de impresión, que abarcan desde la consolidada serigrafía hasta los diversos métodos digitales de jetting, ahora es factible aplicar materiales funcionales sobre sustratos flexibles o incluso directamente sobre el producto final.
 Impresión funcional sobre una pieza mecanizada. Fuente: TECNALIA
Impresión funcional sobre una pieza mecanizada. Fuente: TECNALIAGracias a esta tecnología, es posible desarrollar circuitos que se ajustan de manera óptima a las formas y movimientos del entorno donde se implementan, lo que abre un sinfín de oportunidades para diseñar productos innovadores y hechos a medida.
Además de resolver los problemas relacionados con las dimensiones y la rigidez, la impresión funcional permite fabricar componentes electrónicos como sensores, calefactores, antenas y circuitos de iluminación. Esta tecnología incluso tiene el potencial de sustituir el cableado tradicional, resultando en dispositivos más ligeros y con un uso del espacio más eficiente.
Estamos presenciando el comienzo de una nueva etapa en la electrónica debido a esta tecnología, donde la adaptabilidad y la personalización son esenciales para cumplir con las exigencias de un mercado en continuo cambio y con expectativas cada vez mayores.
Procesos sosteniblesConsiderando la sostenibilidad, la impresión funcional supone un progreso notable. Como tecnología aditiva, permite aplicar materiales solo en las áreas necesarias, disminuyendo así el desperdicio y el uso de recursos. A diferencia de los métodos tradicionales, que suelen ser sustractivos y eliminan material para dar forma al producto final. La posibilidad de emplear tintas y sustratos biodegradables o reciclables, alineándose con las crecientes demandas de responsabilidad ambiental en la producción industrial, mejora significativamente el perfil ecológico de esta tecnología.
Respecto al proceso, la digitalización de ciertas técnicas de impresión funcional ofrece una mayor versatilidad y dinamismo en los procesos de trabajo. El paso de los diseños desde la fase conceptual hasta la producción se realiza de manera más ágil y eficiente, permitiendo ajustes en tiempo real sin requerir cambios en herramientas físicas o moldes. Esto promueve la experimentación y la personalización, permitiendo a los fabricantes adaptarse ágilmente a las tendencias del mercado y a las demandas específicas de los clientes
Sin embargo, es en el campo de la innovación de producto donde la impresión funcional destaca verdaderamente, permitiendo aplicaciones disruptivas que antes eran inimaginables. La integración de componentes electrónicos en casi cualquier superficie y forma permite desarrollar productos inteligentes y conectados en una variedad de sectores, incluyendo el aeroespacial, la medicina y la arquitectura.
Nos encontramos en el inicio de una nueva etapa donde la funcionalidad y la forma se combinan, elevando la innovación a un nivel totalmente diferente.
El compromiso de TECNALIAEn TECNALIA creemos firmemente que estas tecnologías tendrán un impacto significativo en el corto y mediano plazo. Por ello, hemos decidido implementar una estrategia de especialización que se apoya en el conocimiento acumulado de la organización y en las sinergias entre nuestros diversos grupos de investigación.
En consecuencia, estamos creando soluciones transversales que abarcan todos los sectores y se centran en las siguientes técnicas de impresión funcional:
-
Implementamos funcionalidades directamente en superficies finales, sin importar su geometría o material. Para ello, desarrollamos los procesos necesarios utilizando nuestra base de datos de materiales y un laboratorio avanzado que dispone de las principales tecnologías de impresión, así como un equipamiento único para impresión e hibridación en superficies 3D.
-
Incorporación de funcionalidades impresas en materiales compuestos. Hemos desarrollado y patentado un proceso que permite la impresión e hibridación de componentes electrónicos en las capas del material, facilitando su posterior procesamiento con diversas tecnologías de fabricación de composites.
-
Fabricación aditiva de dispositivos electrónicos. Estamos investigando las oportunidades de incorporar funcionalidades impresas durante la fabricación aditiva de polímeros. Esto es posible gracias a un equipo singular multicabezal único que permite la impresión simultánea de estructuras poliméricas 3D y la integración de printed electronics.
-
Integración de alimentación y comunicaciones inalámbricas. Entendemos que la conectividad es uno de los desafíos a resolver en la impresión funcional. En TECNALIA, optamos por reemplazar, en ciertos casos, los conectores físicos por antenas impresas que permiten la captación y transmisión de energía y datos.
La impresión funcional ha dejado de ser una promesa y se ha establecido como un complemento muy valioso con respecto a la electrónica convencional, ofreciendo múltiples aplicaciones en diversos sectores. Desde la automoción hasta el sector aeroespacial, incluyendo la salud, el packaging y la construcción, la integración de funcionalidades electrónicas impresas está permitiendo a las empresas añadir valor a sus productos. Como resultado, las empresas ven un aumento significativo en su competitividad.
En TECNALIA, apoyamos a las empresas en este recorrido, ofreciendo nuestra extensa experiencia en impresión funcional, así como en otras tecnologías necesarias para cada caso de uso específico.
Sobre el autor: Ibai Santamaría es ingeniero industrial y el el responsable de la plataforma de impresión funcional de TECNALIA
Sobre TECNALIA: El mayor centro de investigación aplicada y desarrollo tecnológico de España, un referente en Europa y miembro de Basque Research and Technology Alliance (BRTA).

Basque Research & Technology Alliance (BRTA) es un consorcio que se anticipa a los retos socioeconómicos futuros globales y de Euskadi y que responde a los mismos mediante la investigación y el desarrollo tecnológico, proyectándose internacionalmente. Los centros de BRTA colaboran en la generación de conocimiento y su transferencia a la sociedad e industria vascas para que sean más innovadoras y competitivas. BRTA es una alianza de 17 centros tecnológicos y centros de investigación cooperativa y cuenta con el apoyo del Gobierno Vasco, SPRI y las Diputaciones Forales de Araba, Bizkaia y Gipuzkoa.
El artículo Impresión funcional: revolucionando la integración de capacidades electrónicas se ha escrito en Cuaderno de Cultura Científica.
Ariel, un mundo de cañones
Durante cientos de años los satélites de Urano -los primeros, Titania y Oberón fueron descubiertos a finales del siglo XVIII- han sido unos enigmáticos habitantes de las afueras de nuestro sistema solar debido a la enorme distancia a nuestro planeta, dificultando mucho su descubrimiento y estudio. Y solo una sonda, la Voyager 2, visitó fugazmente el sistema de Urano en 1986, resolviendo algunas dudas, pero suscitando muchas otras preguntas. Algunas de estas cuestiones están relacionadas con sus satélites, muy interesantes a nivel geológico y astrobiológico. Dentro de estos, uno destaca y no precisamente por su tamaño: Ariel.
Apenas tiene un tercio del tamaño de nuestra Luna, pero su superficie cubierta de sistemas de fracturas y de cañones ha despertado el interés de los científicos desde que la Voyager tomó las únicas imágenes “de cerca” de las que disponemos. ¿Podría Ariel tener un océano subterráneo y, además, una “tectónica de placas” sobre hielo?
 Ariel visto desde la Voyager 2 el 24 de enero de 1986. Se aprecia perfectamente su tortuosa superficie cubierta de cráteres y de grandes sistemas de valles. Cortesía de NASA/JPL.
Ariel visto desde la Voyager 2 el 24 de enero de 1986. Se aprecia perfectamente su tortuosa superficie cubierta de cráteres y de grandes sistemas de valles. Cortesía de NASA/JPL.Si miramos con detenimiento la superficie de Ariel salta a la vista que está dominada por una gran red de cañones o, en términos más apropiados para la geología planetaria, chasmata. No son pequeños valles, sino grandes sistemas de valles con altísimos acantilados que muestran que Ariel ha sufrido importantes procesos geológicos -algunos de rejuvenecimiento- de su superficie en un periodo reciente.
Un nuevo estudio publicado en The Planetary Science Journal por Beddingfield et al. (2025) pone precisamente el ojo en estos cañones, pero no en todos, sino en los que contienen un tipo específico conocido como “medial grooves” y que podríamos traducir al castellano como “canales medianeros”. Estas formas del relieve son unos valles mucho más estrechos que existen en el interior de otros valles, a veces recorriéndolos de manera paralela.
Los investigadores sugieren que estos canales no tienen nada de casual, sino que tienen un enorme significado dentro del contexto geodinámico del satélite. Para ellos representan la prueba de lo que en nuestro planeta conocemos como centros de expansión, los lugares donde dos o más placas tectónicas se separan pudiendo dar lugar a un océano entre ellas. De hecho, hoy en día en la Tierra la mayoría de estos centros de expansión son las dorsales oceánicas, recorriendo el fondo de los océanos como una inmensa cordillera que nos recuerda que, a ambos lados de esa división, antaño estuvimos unidos.
 Una perspectiva de Ariel más de cerca. A esta resolución los cráteres son mucho más evidentes, especialmente algunos de ellos, cubiertos por un manto blanco. ¿Quizás material expulsado por el propio impacto o surgido del interior de Ariel a partir de sus fisuras? Imagen cortesía de NASA/JPL.
Una perspectiva de Ariel más de cerca. A esta resolución los cráteres son mucho más evidentes, especialmente algunos de ellos, cubiertos por un manto blanco. ¿Quizás material expulsado por el propio impacto o surgido del interior de Ariel a partir de sus fisuras? Imagen cortesía de NASA/JPL.Pero Ariel no es un cuerpo rocoso como nuestro planeta, y su corteza que está compuesta principalmente por hielo. Entonces, ¿cómo podría darse un proceso similar en materiales totalmente distintos? La respuesta está, precisamente, en las propiedades mecánicas del hielo a muy baja temperatura y la posible existencia de un océano subterráneo.
De hecho, los científicos proponen que estas medial grooves son directamente la expresión de una tectónica sobre hielo donde, en vez de ascender el magma desde las profundidades, lo que asciende es una forma de hielo más plástico -y a una mayor temperatura- o incluso un lodo rico en agua desde el interior, sirviendo como una especie de cuña que empuja y sirve para agrandar los sistemas de valles y crear nueva corteza, igual que en nuestro planeta ocurre en las dorsales oceánicas.
Hay un detalle sobre los valles que no quería que pasase desapercibido: Si comparamos el fondo de estos frente al resto de la superficie de Ariel, nos daremos cuenta que, el número de cráteres que hay en su interior, es mucho menor que el que hay en otras zonas del planeta, lo que nos indica que es una superficie más joven y esto nos trae una consecuencia de gran importancia a nivel astrobiológico: Que este pequeño satélite está o ha estado activo geológicamente en un pasado muy reciente.
 En esta imagen podemos apreciar algunos de los grandes sistemas de valles que pueblan Ariel. Si nos fijamos, estos valles tienen un fondo plano, con cráteres pequeños, frente al elevado relieve del terreno más antiguo, cubierto de cráteres más grandes. En el centro de la imagen, donde la sombra de la noche se transforma en día aparece un valle muy estrecho que surca el interior del valle más ancho y plano. Pues bien, esa sería una de las “medial grooves” del artículo que comentamos hoy. Imagen cortesía de NASA/JPL.
En esta imagen podemos apreciar algunos de los grandes sistemas de valles que pueblan Ariel. Si nos fijamos, estos valles tienen un fondo plano, con cráteres pequeños, frente al elevado relieve del terreno más antiguo, cubierto de cráteres más grandes. En el centro de la imagen, donde la sombra de la noche se transforma en día aparece un valle muy estrecho que surca el interior del valle más ancho y plano. Pues bien, esa sería una de las “medial grooves” del artículo que comentamos hoy. Imagen cortesía de NASA/JPL.Pero hay más… ¿y si estos centros de expansión pudiesen estar relacionados con un océano subterráneo que de algún modo sirviese como correa de transmisión de la energía interna de Ariel hacia el exterior, pero también de materia? Las últimas observaciones realizadas tanto con telescopios terrestres como con el JWST han mostrado que su superficie está cubierta por hielo de monóxido y dióxido de carbono. Estos dos compuestos son volátiles y, de manera natural, se sublimarían rápidamente y escaparían al espacio bajo las condiciones de temperatura de Ariel salvo que haya algún mecanismo que vaya “rellenando” -o mejor dicho- volviendo a cubrir su superficie de estos compuestos. Y, además, también hay evidencias de compuestos relacionados con el amoniaco en su superficie.
El amoniaco es un ingrediente -si me permiten el término culinario- fundamental para la supervivencia de los océanos subterráneos, ya que es un poderoso anticongelante, consiguiendo que el punto de congelación del agua baje de una manera significativa. Incluso una pequeña cantidad de amoniaco disuelta en el agua podría permitir que existiese un océano de agua líquida en las profundidades de Ariel a escala de tiempo geológica.
Y aquí es donde vuelven a entrar estas medial grooves en el juego, ya que podrían ser la autopista que llevara estos compuestos volátiles hacia la superficie, como una especie de conducto que comunica el exterior de Ariel con un océano subterráneo o con una capa parcialmente líquida: Lo que viene siendo un volcán en toda regla, bueno, en este caso criovolcán, permitiendo la expulsión del CO, el CO2, el amoniaco y otros materiales desde el interior a la superficie a través de estas fisuras. Por cierto, un mecanismo ya nada exótico y que hemos podido observar en funcionamiento en satélites como Encélado.
Las consecuencias de este estudio son claras y contundentes: los mundos océano podrían ser todavía más comunes de lo que imaginamos y, por lo tanto, nuestro sistema solar un lugar con más objetivos interesantes desde el punto de vista de la astrobiología. Eso sí, la ventana de habitabilidad de estos cuerpos probablemente dependa en su mayoría de las interacciones gravitatorias con su planeta y otros satélites, condiciones que pueden cambiar, haciendo que pierda la fuente de energía que mantenga su océano en estado líquido. Así que si todavía existe este océano, somos unos afortunados por haber llegado en el momento exacto.
Pero, desgraciadamente, todavía nos queda mucho para confirmar estudios como este. Las imágenes de la Voyager 2 tienen una resolución limitada y apenas cubrieron el 35% de la superficie de Ariel, así que para poder comprobar si efectivamente estamos ante un mundo con una tectónica sobre hielo y un océano subterráneo necesitaremos volver a Urano con misiones modernas y más sofisticadas que puedan aportarnos todos esos detalles que nos faltan por conocer de este apasionante sistema.
Referencias:
Beddingfield, C. B., Cartwright, R. J., Jozwiak, L. M., Nordheim, T. A., & Patterson, G. W. (2025). Ariel’s medial grooves: Spreading centers on a candidate ocean world. The Planetary Science Journal doi: 10.3847/psj/ad9d3f
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Ariel, un mundo de cañones se ha escrito en Cuaderno de Cultura Científica.
Primeras evidencias de presencia humana en Europa hace 2 millones de años
 Restos fósiles de animales con marcas de corte datadas en 1,95 Millones de años, descubiertos en Grăunceanu . Fuente: Curran, Sabrina C., et al. (2025)
Restos fósiles de animales con marcas de corte datadas en 1,95 Millones de años, descubiertos en Grăunceanu . Fuente: Curran, Sabrina C., et al. (2025)Hace algo más de medio siglo, durante la década de los sesenta, un equipo de paleontólogos y antropólogos realizó un interesante hallazgo cerca de la pequeña localidad de Grăunceanu, Rumania. Junto al valle del río Olteţ, centenares de huesos de animales prehistóricos, acumulados en un solo yacimiento, resurgían de la tierra ante el asombro de los investigadores. El inexorable paso del tiempo y la paciente acción fluvial habían arrastrado, sedimento tras sedimento, capa tras capa, una impresionante cantidad de restos fósiles, concentrándolos en un rincón de apenas 90 m2. Una amplia diversidad de huesos que el agua fue arrastrando durante milenios y que los investigadores de la época describieron como «mamuts, varias especies de bóvidos y cérvidos, jirafas, équidos, rinoceróntidos, múltiples especies de carnívoros, roedores (castor, puercoespín), avestruces, una gran especie de mono terrestre (Paradolichopithecus) y el representante más temprano de los pangolines en Europa». La colección llegó a alcanzar miles de restos que se guardaron en dos instituciones, el Instituto de Espeleología «Emil Racoviţă» y el Museo de Oltenia… y allí se quedaron durante décadas, guardados en cajas y volviendo a cubrirse de polvo en algún almacén olvidado.
Un nuevo examenSesenta años más tarde, un equipo internacional de investigadores recordó aquel antiguo yacimiento de Grăunceanu y se propuso revisar los restos guardados con la mirada que proporcionan las avanzadas tecnologías actuales. Los huesos aún estaban en sus cajas pero la documentación que los identificaba y clasificaba no aparecía por ningún lado. «Desafortunadamente, casi todos los registros de la excavación y datos de procedencia de los restos se han perdido», explica Sabrina C. Curran, investigadora principal.
Comienza entonces una exhaustiva labor de reidentificación, que se extendió durante cuatro veranos (años 2019 al 2022), y en la que se utilizaron modernas técnicas de datación mediante uranio-plomo (U-Pb) de alta precisión así como análisis de isótopos estables de oxígeno y carbono de alta resolución. El resultado de estas campañas fue alentador y descubrió que algunos de estos restos se remontaban dos millones de años en el pasado. «Nuestro equipo ha identificado e inventariado un total 5527 restos, incluyendo materiales de Grăunceanu (4983) y localidades más pequeñas como Fântâna lui Mitilan (139) y La Pietriș (116)». Una rica biodiversidad que, según las reconstrucciones paleoecológicas, se desarrolló en un entorno de pastizales abiertos, con bosques, ríos y lagos, comparable a un hábitat de bosque-estepa.
Presencia de homínidosEn ocasiones, el conocimiento científico no llega gracias a un nuevo y flamante descubrimiento sino al cuidadoso análisis o revisión de uno antiguo, y es aquí donde llegan las novedades más fascinantes. Los resultados de esta moderna revisión de los restos hallados en Grăunceanu se han publicado hace unos días en Nature Communications y nos sorprenden con las evidencias más antiguas de presencia humana (homininos) en Europa que se remontan a hace unos dos millones de años. Es un salto considerable si tenemos en cuenta que, hasta ahora, las pistas más antiguas que teníamos del género homo en Europa pertenecían al célebre yacimiento de Dmanisi (Georgia) donde se descubrieron restos de homínidos que datan de hace 1,8 millones de años.
«No hay que olvidar que la presencia de homínidos en el yacimiento de Dmanisi se basa directamente en restos humanos mientras que el nuevo estudio está basado en pruebas indirectas», nos explica Roberto Sáez, Doctor en Antropología y divulgador científico, experto en evolución humana.
Este es un hecho que los propios investigadores reconocen al afirmar que «aunque no hemos identificado restos de homínidos ni industria lítica in situ en Grăunceanu […] en este trabajo presentamos evidencia de la presencia de homínidos en Eurasia hace al menos 1,95 millones de años en forma de huesos con marcas de corte, respaldados por estimaciones de edad de uranio-plomo (U-Pb) de alta precisión».
 Restos fósiles de animales con marcas de corte datadas en 1,95 Millones de años, descubiertos en Grăunceanu. Fuente: Curran, Sabrina C., et al. (2025)
Restos fósiles de animales con marcas de corte datadas en 1,95 Millones de años, descubiertos en Grăunceanu. Fuente: Curran, Sabrina C., et al. (2025)El equipo analizó un total de 4746 especímenes a la búsqueda de modificaciones de la superficie ósea para descartar en primer lugar «cualquier marca abiótica (por ejemplo, matriz adherida, alisado, picaduras en la superficie ósea, erosión/disolución, agrietamiento/división de sedimentos, exfoliación/descamación) o bióticas no antropogénicas (modificación de carnívoros u homínidos, pisoteo, grabado de raíces/rizomorfos fúngicos, roedores, actividad de insectos, digestión, marcas de preparadores)». Para ello utilizaron herramientas ópticas de aumento con especial atención a las marcas líneas, «definidas como cualquier marca al menos el doble de larga que ancha». Cuando identificaron las marcas de interés, los investigadores siguieron los criterios cualitativos y protocolos de atribución ya establecidos en la literatura científica para registrar la trayectoria, orientación, morfología, número de marcas visibles, simetría, etc.
Según los resultados publicados se han encontrado un total de veinte especímenes que exhiben marcas de corte de interés de las cuales, siete muestran marcas de corte de alta confianza, doce muestran marcas de corte probables y un espécimen presenta ambos tipos de marcas, lo que lleva a los autores a «argumentar a favor de una presencia de homínidos en Europa hace al menos dos millones de años».
Qué homínidosLos yacimientos más antiguos (anteriores a 2 millones de años) fuera de África se agrupan en Oriente Medio, Rusia occidental alrededor de los mares Negro y Caspio, Asia central y China. Estos yacimientos incluyen una mezcla de localidades en la que se han encontrado líticos y/o una pequeña cantidad de huesos con marcas de corte. Aunque existen yacimientos donde se han descubierto posibles restos de homínidos de esa antigüedad (como los seis dientes descubiertos en Longgudong), los expertos aún albergan dudas sobre ellos y el consenso científico es que el yacimiento con restos humanos confirmados más antiguos fuera de Europa sigue siendo Dmanisi.
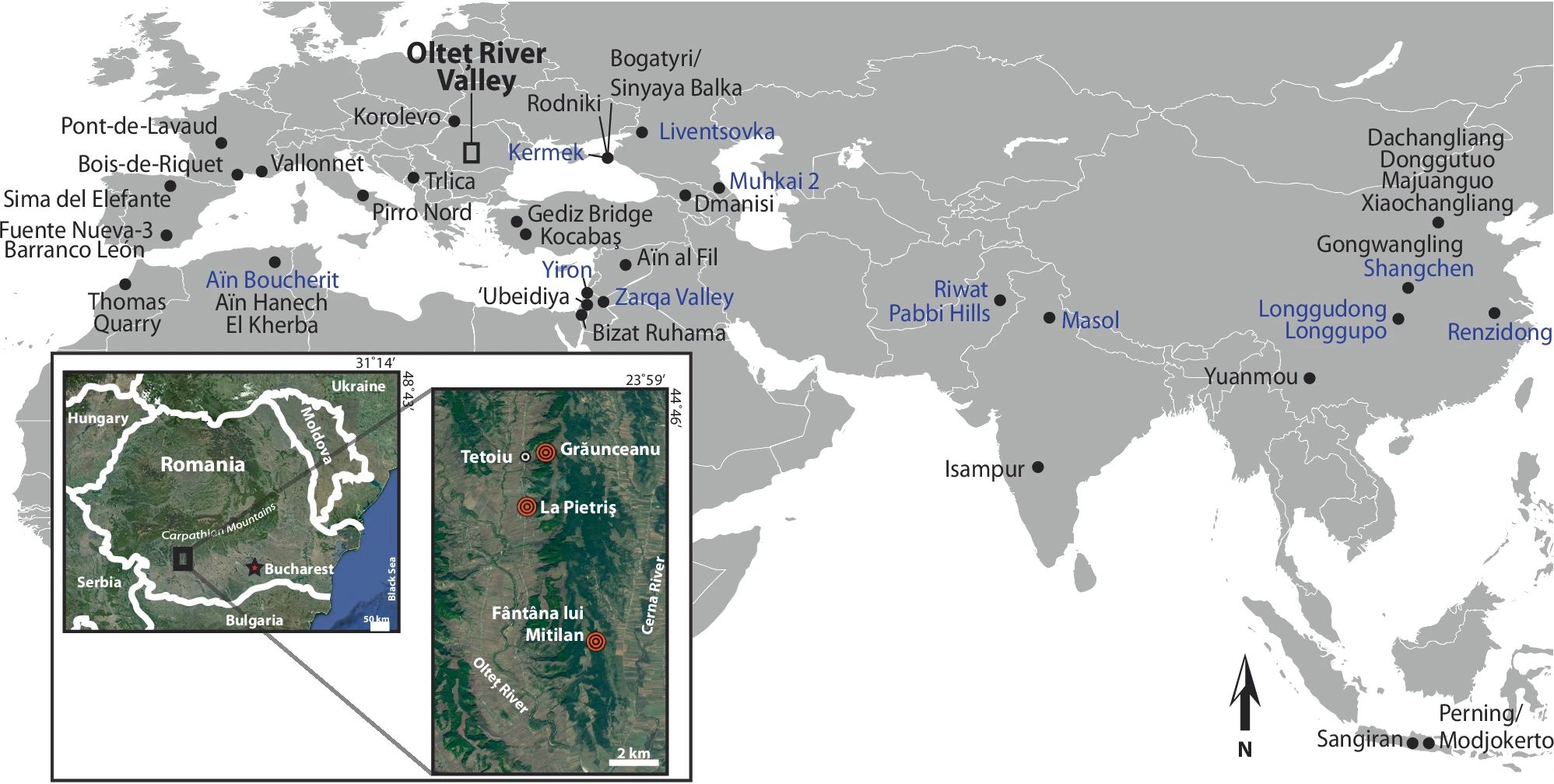 Los yacimientos en letra en azul poseen una antigüedad superior a dos millones de años. El recuadro inferior izquierdo muestra las ubicaciones de los yacimientos analizados en este estudio. Fuente: Curran, Sabrina C., et al. (2025)
Los yacimientos en letra en azul poseen una antigüedad superior a dos millones de años. El recuadro inferior izquierdo muestra las ubicaciones de los yacimientos analizados en este estudio. Fuente: Curran, Sabrina C., et al. (2025)El estudio publicado evita deliberadamente entrar en el espinoso tema de qué especie de homínido pudo realizar esas marcas en los animales de Grăunceanu. «Este es un período en el que múltiples especies de homínidos coexistieron en sitios en el este y sur de África». La afinidad taxonómica de casi todos los fósiles de homínidos descubiertos hasta ahora sigue en pleno debate y abarca diferentes grupos homo, como el erectus o el ergaster.
No es el único hueco que nos queda por rellenar, aún nos faltan muchas piezas para completar el puzle de esas primeras migraciones, pero los hallazgos y estudios publicados en las últimas décadas nos animan a afirmar que, hace aproximadamente unos dos millones y medio de años, se inició la primera gran oleada de diferentes especies de homínidos desde África hacia Eurasia. «La interpretación actual es que no fue migración única sino muchas, intermitentes, que alcanzaron lugares tan lejanos como el norte de China», aclara Sáez. Contábamos con pistas indirectas, como industria lítica o marcas de cortes con herramientas, que indican presencia de homínidos por toda Asia y con una datación de hasta 2,1 millones de años, pero hasta ahora no habíamos encontrado pruebas en Europa con esa antigüedad. El estudio publicado en Nature Communications abre por fin esta puerta.
Referencias y más información:
Curran, Sabrina C., et al. (2025) Hominin Presence in Eurasia by at Least 1.95 Million Years Ago Nature Communications doi: 10.1038/s41467-025-56154-9.
Roberto Sáez «Homininos en Europa hace dos millones de años» Nutcrackerman.com
Sobre el autor: Javier «Irreductible» Peláez (Puertollano, 1974) es escritor y comunicador científico. Autor de 500 años de frío. La gran aventura del Ártico (Crítica, 2019) y Planeta Océano (Crítica 2022). Es uno de los fundadores de la plataforma Naukas.com, editor de ciencia en Yahoo España y Latinoamérica. Es guionista científico en los programas de televisión «El Cazador de Cerebros» y «Órbita Laika» de RTVE. Durante más de una década ha escrito en diferentes medios de comunicación (El País, El Español, National Geographic, Voz Populi). Es autor de los podcasts Catástrofe Ultravioleta y La Aldea Irreductible, y ha colaborado en diferentes proyectos radiofónicos y televisivos (Radio Nacional de España, Radio Televisión Canaria). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Primeras evidencias de presencia humana en Europa hace 2 millones de años se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2024: Neurodiversidad
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

José Ramón Alonso es catedrático de la Universidad de Salamanca, y está especializado en neurociencia. Lleva años investigado y escribiendo sobre neurodiversidad, eso que comúnmente llamamos trastornos del espectro autista, o hiperactividad o lo que sea. José Ramón nos explica que igual que la biodiversidad de especies es una riqueza, también lo es la biodiversidad dentro de nuestra especie.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: Neurodiversidad se ha escrito en Cuaderno de Cultura Científica.
La importancia de la diversidad estructural de los bosques frente al cambio climático
Un nuevo estudio apunta a que la heterogeneidad en los tamaños de los árboles de un bosque influye en cómo el cambio climático afecta a su crecimiento. Así, los bosques con árboles de tamaños más homogéneos son más vulnerables a las alteraciones climáticas.
 Bosque de hayas trasmocho. Foto: Julen Astigarraga
Bosque de hayas trasmocho. Foto: Julen AstigarragaLa investigación, que ha sido liderada por la Universidad de Alcalá y la Universidad del País Vasco (UPV/EHU), se centra en el análisis de datos de crecimiento anual de hayas en el límite sur de su distribución, utilizando técnicas dendrocronológicas.
Desde la década de 1970, la sincronía en el crecimiento de los árboles ha aumentado debido a la mayor frecuencia de eventos climáticos extremos.
“Hemos observado cómo los impactos antropogénicos directos sobre los bosques, a través de los cambios en el uso del suelo, y los impactos indirectos, a través del cambio climático, determinan la sincronía en el crecimiento, siendo los bosques con individuos jóvenes los más vulnerables frente al cambio climático”, indica Julen Astigarraga, autor principal del estudio.
El trabajo resalta la importancia de mantener bosques estructuralmente diversos para mitigar los efectos del cambio climático. “En general, las estructuras más diversas se encuentran en bosques maduros. Sin embargo, esos bosques son muy escasos en todo el continente europeo, pero a su vez, son extremadamente valiosos para mitigar los impactos del cambio climático, como demuestra este estudio”, comenta Paloma Ruiz-Benito, investigadora de la Universidad de Alcalá.
De manera sorprendente, el trabajo ahora publicado ha evidenciado que los bosques de hayas trasmochos, un ecosistema cultural y ecológico caracterizado por bosques abiertos con brotes abundantes en el tronco principal y muy comunes en Gipuzkoa, la zona de estudio, muestran una notable resiliencia frente al cambio climático.
«Incrementar la diversidad estructural de los bosques, además de reducir la sincronía en el crecimiento de los árboles, puede ayudar a disminuir la mortalidad de los mismos, potenciar el secuestro de carbono y fomentar la biodiversidad al aumentar la disponibilidad de hábitats», añade Asier Herrero, investigador de la Universidad del País Vasco.
El estudio ha sido posible gracias a la colaboración de diversos investigadores de toda la península, así como a los guardas forestales y habitantes de Oñati (Gipuzkoa), quienes han mostrado un gran interés y apoyo en el proceso de recolección de datos. «Es impresionante la generosidad que hemos recibido de la comunidad local durante todo este trabajo, y esperamos que los resultados de este estudio contribuyan a adaptar los hayedos frente al cambio climático, no solo en Oñati, sino también en todo el continente europeo», concluye Astigarraga.
Referencia:
Astigarraga J., Calatayud J., Ruiz-Benito P., Madrigal-González J., Tijerín-Triviño J., Zavala MA., Andivia E., Herrero A. (2025) Forest structural diversity modulates tree growth synchrony in response to climate change Forest Ecology and Management doi: 10.1016/j.foreco.2025.122505
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La importancia de la diversidad estructural de los bosques frente al cambio climático se ha escrito en Cuaderno de Cultura Científica.
El verdadero Brexit geológico
Si nos subimos a un barco pesquero en el Mar del Norte y echamos una red de arrastre frente a las costas de los Países Bajos, uno de los botines marinos más comunes que podemos sacar a flote no son merluzas o bacalaos, sino restos fósiles de mamut, rinoceronte lanudo y león de las cavernas. Y su presencia nos está contando una increíble historia de mundos sumergidos al más puro estilo de las leyendas de la Atlántida.
Para comenzar nuestra aventura, debemos viajar a hace unos 20.000 años. En este periodo temporal nos encontramos dentro de lo que se conoce como el Último Máximo Glacial, es decir, el momento más frío y de mayor avance de los casquetes y mantos de hielo continentales de la última glaciación en el hemisferio norte. Esta acumulación de hielo se produjo por el secuestro en tierra firme del agua marina evaporada, ya que cuando caía en forma de precipitación en el continente, inmediatamente se congelaba, sin tener la posibilidad de regresar al océano como agua superficial. Lo cual produjo lo inevitable, un descenso del nivel marino, que llegó a encontrarse unos 120 m por debajo de la actualidad en aquel momento.
 Restos fósiles de mamut encontrados en las redes de pesca de un barco danés mientras fondeaba en el Mar del Norte. Fuente: North Sea Fossils
Restos fósiles de mamut encontrados en las redes de pesca de un barco danés mientras fondeaba en el Mar del Norte. Fuente: North Sea FossilsEn estas condiciones de nivel del mar bajo, el aspecto del océano Atlántico europeo no se parecía en nada al actual. Lo que hoy en día conocemos como archipiélago británico estaba unido a la Europa continental por un brazo de tierra que se extendía desde el norte de Dinamarca hasta el norte de Francia, conformando una enorme península que se conoce como Doggerland.
Durante unos 10.000 años, Doggerland soportó el continuo ascenso del nivel del mar producido por el regreso del agua de fusión de los glaciares continentales al océano tras el final del último periodo glacial, permaneciendo como un ambiente litoral en el que se desarrollaron amplios estuarios y marismas. Lugares por los que se producía un continuo tránsito de fauna entre las actuales Europa continental y las islas británicas, que incluía mamuts, rinocerontes, ciervos y, por supuesto, seres humanos. De hecho, estudios de arqueología submarina realizados en el Mar del Norte han localizado algunos asentamientos mesolíticos donde las poblaciones humanas se ponían las botas con esa estupenda caza conformada por enormes vertebrados.
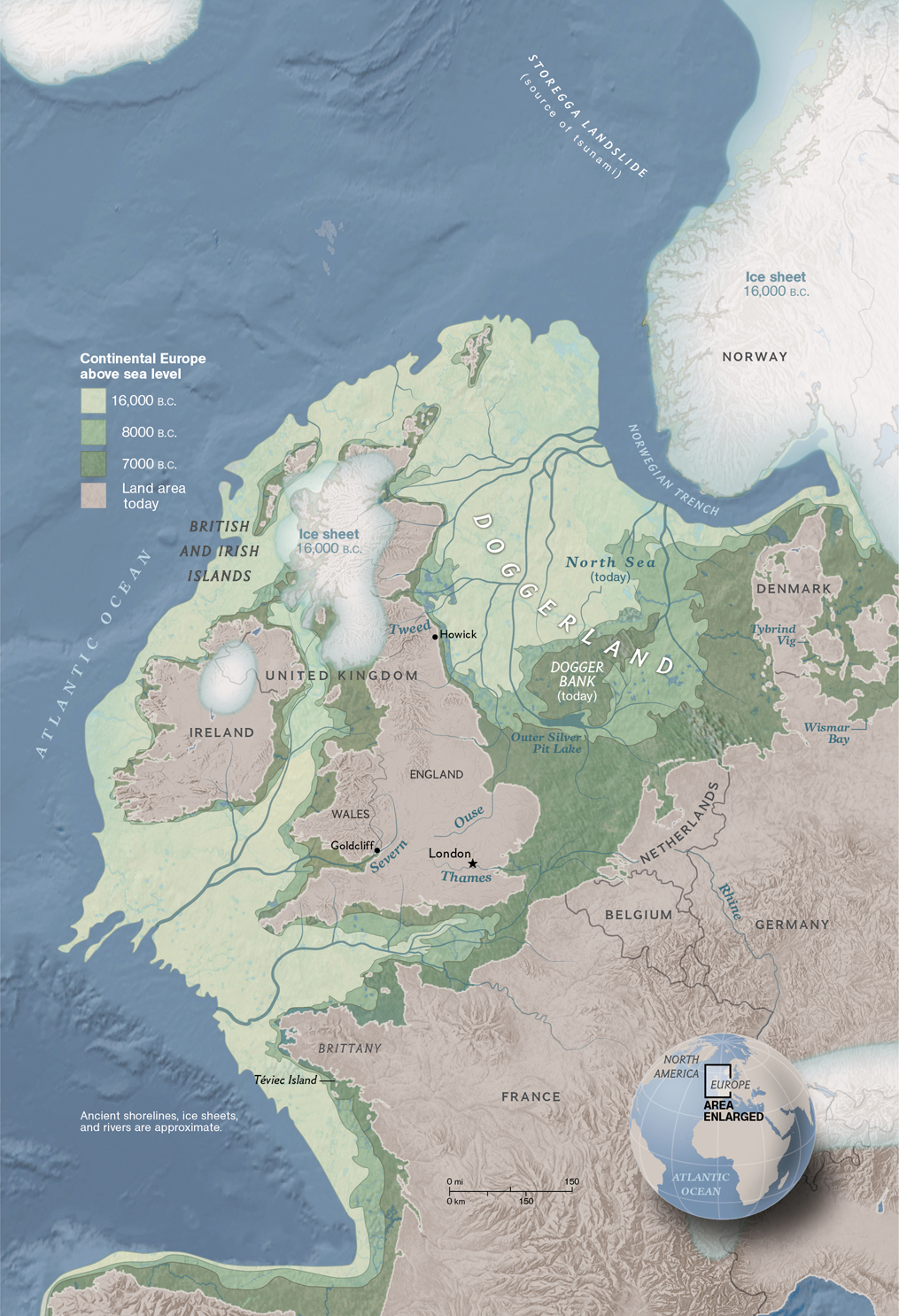 Reconstrucción del puente de tierra conocido como Doggerland que unía el archipiélago británico con la Europa continental a finales de la última glaciación. Mapa de William E. McNulty y Jerome N. Cookson / National Geographic Magazine
Reconstrucción del puente de tierra conocido como Doggerland que unía el archipiélago británico con la Europa continental a finales de la última glaciación. Mapa de William E. McNulty y Jerome N. Cookson / National Geographic MagazinePosiblemente, el imparable aumento del nivel marino durante el actual periodo cálido del Holoceno habría acabado anegando Doggerland, dejando así aislado el archipiélago británico. Pero, al igual que el famoso Brexit político, la separación geológica de las islas británicas de Europa fue un evento catastrófico.
Hace unos 8.200 años, se produjo lo que se conoce como deslizamiento de Storegga (palabra de origen noruego que significa “gran borde”), un gran desprendimiento de sedimentos, que se calcula que pudieron tener el volumen de la actual isla de Islandia, desde la plataforma continental de Noruega hacia el fondo oceánico del Mar de Noruega. Aún no se tiene muy claro el desencadenante de este deslizamiento, discutiendo si el culpable fue un terremoto submarino que afectó al margen continental noruego o si se produjo por una inestabilidad de los sedimentos al fundirse el manto de hielo que los mantenía unidos, pero lo que sí se conoce es lo que provocó en todo lo que había a su alrededor. En cuanto ese volumen de sedimentos se desprendió hacia el fondo marino, desplazó millones de toneladas de agua oceánica y generó un enorme tsunami con olas que superaron los 10m de altura, arrasando todo el litoral noruego y penetrando hacia el sur a través del actual Mar del Norte. Aquí, el agua inundó toda el área estuarina de Doggerland, devastando los asentamientos mesolíticos que pillaba a su paso y aniquilando a miles de personas.
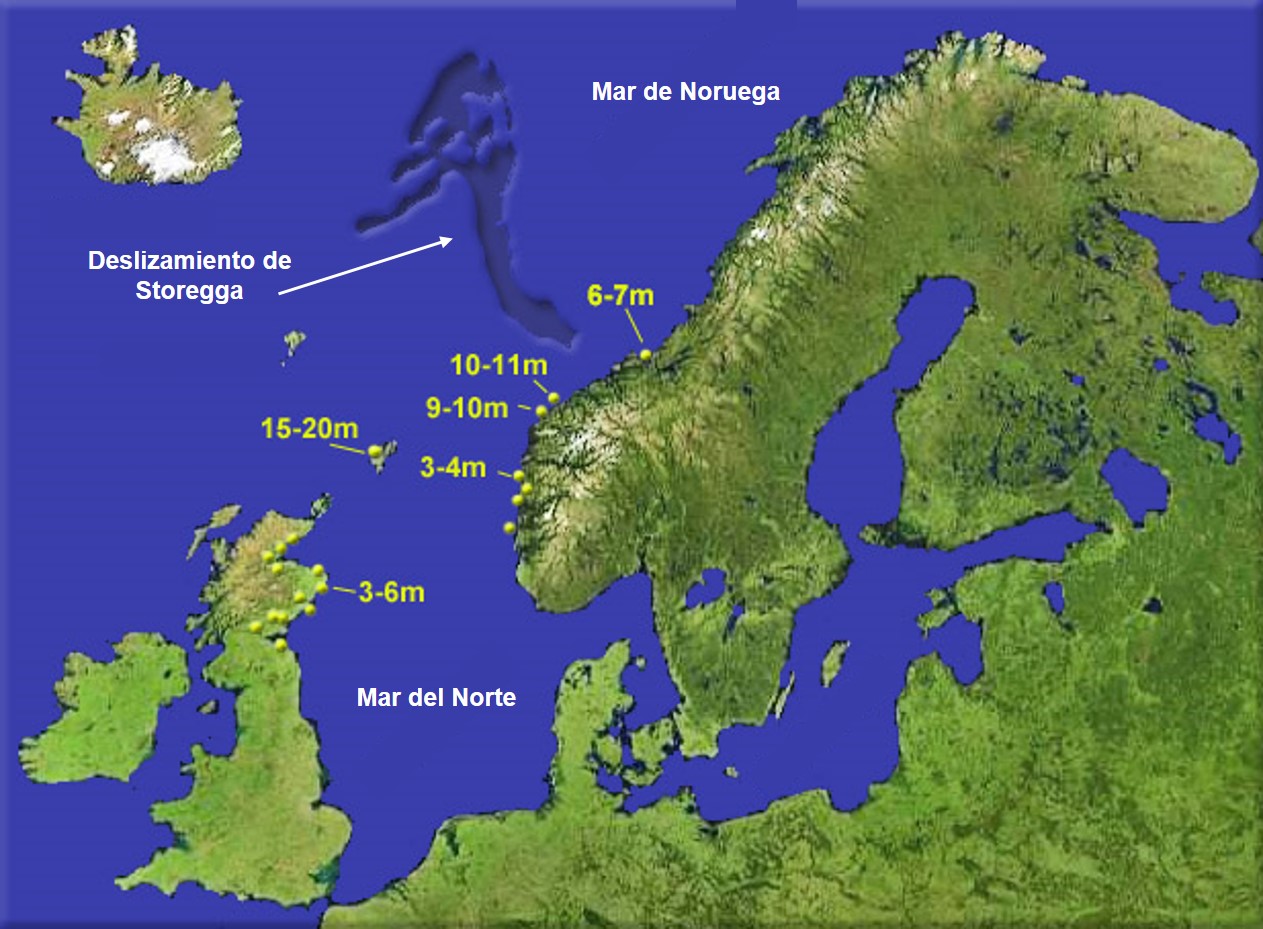 Localización del depósito submarino de sedimentos provocado por el deslizamiento de Storegga ocurrido hace unos 8.200 años en el Mar de Noruega. En amarillo se indican las alturas estimadas de las olas fruto del tunami producido. Imagen modificada de Lamiot / Wikimedia Commons
Localización del depósito submarino de sedimentos provocado por el deslizamiento de Storegga ocurrido hace unos 8.200 años en el Mar de Noruega. En amarillo se indican las alturas estimadas de las olas fruto del tunami producido. Imagen modificada de Lamiot / Wikimedia CommonsCuando el tsunami terminó y el agua se calmó, el brazo de tierra de Doggerland había desaparecido y el Canal de la Mancha se convirtió en una barrera que separó las islas británicas de la Europa continental. Esto detuvo no solo el paso de las grandes faunas litorales de un lado a otro, sino también el intercambio cultural entre las tribus mesolíticas británicas y las europeas, provocando una evolución social diferente en ambos márgenes. Vamos, que el verdadero Brexit se produjo hace unos 8.200 años.
Como siempre os digo, la Geología es una ciencia apasionante que nos permite comprender cómo ha evolucionado nuestra sociedad a lo largo del tiempo. Una historia que comenzó encontrando restos fósiles de mamuts y rinocerontes en el fondo marino frente al litoral de Países Bajos, me ha permitido hablaros de cambio climático, variaciones del nivel marino, asentamientos humanos de hace miles de años y la salida original (y geológica) del Reino Unido (y de Irlanda) de la Unión Europea. Espero haberos sorprendido con ella.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo El verdadero Brexit geológico se ha escrito en Cuaderno de Cultura Científica.
Alice Roth, la inventora del “queso suizo” (matemático)
Ningún matemático debe permitirse olvidar que las matemáticas, más que cualquier otro arte o ciencia, son un asunto de jóvenes. […] Consideremos, por ejemplo, la trayectoria de un hombre que ciertamente fue uno de los tres matemáticos más grandes del mundo. Newton dejó las matemáticas a los 50 años, habiendo perdido su entusiasmo por ellas bastante antes. Sin duda alguna, se dio perfecta cuenta a los cuarenta años de que sus grandes días creativos pertenecían ya al pasado. […] Galois murió a los 21, Abel a los 27, Ramanujan a los 33 y Riemann a los 40. Ha habido matemáticos que han llevado a cabo una obra maestra bastante más tarde; la magna obra de Gauss sobre la geometría diferencial se publicó cuando tenía 50 años (aunque había tenido las ideas fundamentales 10 años antes). No conozco un ejemplo de un avance matemático de importancia desarrollado por una persona que haya superado los 50. Si una persona madura pierde su interés y abandona las matemáticas, es probable que la pérdida no sea demasiado importante ni para las matemáticas ni para él.
G. H. Hardy, Apología de un matemático,1940
En esta cita, Hardy no nombra a ninguna mujer entre esos “relevantes” matemáticos que brillaron en su juventud. Alice Roth fue una joven matemática brillante, pero lo fue aún más a partir de su jubilación.
Alice Roth nació el 6 de febrero de 1905 en Berna, Suiza. Era la segunda hija (entre sus hermanos Conrad y Walter) de Conrad Roth y Marie Landolt, una familia acomodada.
Tras sus estudios de secundaria, tenía claro que quería estudiar matemáticas. Su madre no tenía nada en contra de esta elección, pero quería que su hija aprendiera antes los conceptos básicos de gestión del hogar. Y, obediente, así lo hizo.
 Alice Roth. Fuente: Agnes Scott College.
Alice Roth. Fuente: Agnes Scott College.Una estudiante brillante, una tesis premiada y el olvido
En otoño de 1925, Alice ingresó en la Eidgenössische Technische Hochschule (ETH) en Zúrich, una universidad con alumnado ampliamente masculino. En los cuatro años posteriores su principal campo de estudio fueron las matemáticas, con la física como primera especialidad y la astronomía como segunda. Y logró unos resultados extraordinarios. En 1930 obtuvo su tesis de maestría dirigida por el matemático George Pólya (1887-1985).
Mientras impartía docencia de matemáticas y física en una escuela para niñas, comenzó a trabajar en su tesis doctoral, de nuevo con Pólya como tutor. En 1938 defendió su tesis (Approximationseigenschaften und Strahlengrenzwerte meromorpher und ganzer Funktionen), codirigida por Heinz Hopf (1894-1971), y que fue reconocida como excelente.
La tesis de Roth era de tanta calidad que recibió un premio monetario y la Medalla de Plata en la ETH, siendo la primera mujer en obtener este reconocimiento.
A pesar de su éxito en la ETH, con Pólya trabajando desde 1940 la Universidad de Stanford (Estados Unidos), Alice se apartó de la investigación. Comenzó a trabajar como docente en una escuela privada, ocupación mal remunerada y con una gran carga docente, pero que ella realizaba con dedicación y con un gran aprecio por parte de su alumnado. Sus estudiantes mencionaban su gran capacidad docente y los esfuerzos que realizaba al explicar los conceptos y resultados de muchas maneras diferentes.
Roth fue muy amiga de Marie Boehlen (1911-1999), una abogada bernesa, activista por los derechos familiares y sufragista. La propia Alice fue una firme defensora del derecho al voto de las mujeres. A menudo expresaba su frustración frente a un sistema que la obligaba a pagar impuestos, pero no le permitía tener voz en la gobernanza. Las mujeres suizas recibieron el derecho al voto en 1971, el año en el que Alice Roth se jubiló.
Tras la jubilación, un nuevo comienzo en matemáticasPoco antes de jubilarse, Roth anunció a sus allegados su deseo que volver a la investigación en matemáticas. Se trataba de una tarea complicada tras un parón de tantos años.
La cita de Hardy que abre este escrito nos podría hacer pensar que, con más de sesenta años, Alice Roth no iba a poder aportar matemáticas demasiado valiosas. Sin embargo, durante los treinta años que Roth había permanecido enseñando, el área de investigación en el que ella había trabajado en sus comienzos y que tan bien conocía se había puesto de moda.
Paul Gauthier, un joven matemático de la Universidad de Montreal, leyó la primera publicación de Alice tras su jubilación, y comenzaron a colaborar científicamente. A sus 70 años, Alice realizaría su primer “viaje matemático” fuera de Suiza, invitada por Gauthier, para impartir una conferencia.
Uno de los principales resultados de la tesis de Roth de 1938 fue el llamado conjunto del queso suizo, un ejemplo de un conjunto compacto en el que no todas las funciones continuas pueden aproximarse uniformemente mediante funciones racionales. Este resultado fue olvidado y redescubierto, independientemente, en 1952 por Sergey Mergelyan; el crédito correspondiente fue restablecido en 1969.
En Suiza, como en otros lugares, las mujeres matemáticas son escasas… La tesis de Alice Roth recibió una medalla de la ETH y apareció poco después de su finalización en una revista matemática suiza… Un año después estalló la guerra, el mundo tenía otras preocupaciones al margen de las matemáticas y el trabajo de Alice Roth simplemente cayó en el olvido. Tan completamente olvidado que alrededor de 1950 un matemático ruso redescubrió resultados similares sin tener la menor idea de que una joven matemática suiza había publicado las mismas ideas más de una década antes que él. Sin embargo, su prioridad fue reconocida.
Peter Wilker (antiguo alumno de Alice Roth), obituario en el periódico Der Bund, 29 julio 1977
En 1976, le diagnosticaron a Alice un cáncer. Fue hospitalizada en 1977, aunque continuó con su investigación matemática, ayudada por Wilker en la traducción y redacción de su último trabajo sobre teoría de la aproximación, área en la que realizó importantes contribuciones.
Falleció el 22 de julio de 1977.
El trabajo pasado y futuro de Roth tuvo una fuerte y duradera influencia en los matemáticos que trabajaban en esta área [teoría de aproximación racional]. Su queso suizo ha sido modificado (a toda una variedad de quesos)… El lema de fusión de Roth, que apareció en su artículo de 1976… influyó en una nueva generación de matemáticos en todo el mundo.
Ulrich Daepp, Paul Gauthier, Pamela Gorkin y Gerald Schmieder, 2005
Referencias
-
Larry Riddle, Alice Roth, Biographies of Women Mathematicians, Agnes Scott College
-
Ulrich Daepp, Paul Gauthier, Pamela Gorkin, and Gerald Schmieder. Alice in Switzerland: The Life and Mathematics of Alice Roth, Mathematics Intelligencer 27 (1) (2005), 41-54
-
Alice Roth, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Alice Roth, la inventora del “queso suizo” (matemático) se ha escrito en Cuaderno de Cultura Científica.
Cómo el teorema de Noether revolucionó la física
Emmy Noether demostró que las leyes físicas fundamentales son solo una consecuencia de simetrías simples. Un siglo después, sus ideas siguen dando forma a la física.
Un artículo de Shalma Wegsman. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
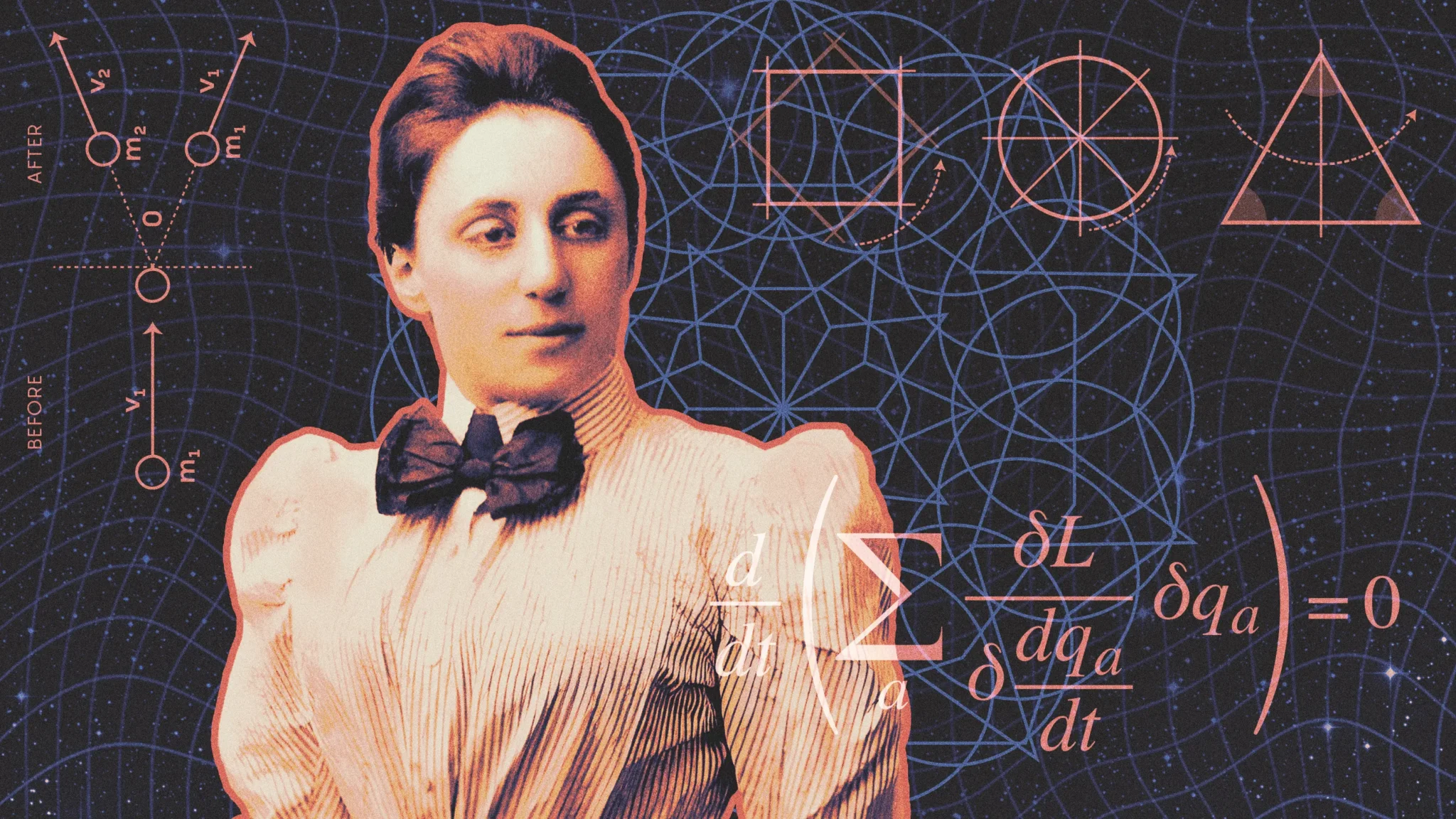 Ilustración: Kristina Armitage / Quanta Magazine
Ilustración: Kristina Armitage / Quanta MagazineEn el otoño de 1915, los cimientos de la física empezaron a resquebrajarse. La nueva teoría de la gravedad de Einstein parecía implicar que debería ser posible crear y destruir energía, un resultado que amenazaba con trastocar dos siglos de pensamiento en la física.
La teoría de Einstein, llamada relatividad general, transformó radicalmente el significado del espacio y el tiempo. En lugar de ser telones de fondo fijos de los acontecimientos del universo, el espacio y el tiempo eran ahora personajes por derecho propio, capaces de curvarse, expandirse y contraerse en presencia de materia y energía.
Un problema con este espacio-tiempo cambiante es que, a medida que se estira y se encoge, la densidad de la energía en su interior cambia. Como consecuencia, la ley clásica de conservación de la energía que describía toda la física no encajaba en este marco. David Hilbert, uno de los matemáticos más destacados de la época, identificó rápidamente este problema y se propuso, junto con su colega Felix Klein, tratar de resolver este aparente fallo de la relatividad. Cuando no pudieron resolverlo, Hilbert le pasó el problema a su asistente, Emmy Noether, de 33 años.
Noether era asistente solo de nombre. Ya era una matemática formidable cuando, a principios de 1915, Hilbert y Klein la invitaron a unirse a ellos en la Universidad de Gotinga. Pero otros miembros de la facultad se opusieron a contratar a una mujer, y a Noether se le impidió unirse a la facultad. A pesar de todo, pasaría los siguientes tres años presionando la falla que separa la física de las matemáticas, lo que finalmente desencadenó un terremoto que sacudiría los cimientos de la física fundamental.
En 1918, Noether publicó los resultados de sus investigaciones en dos teoremas fundamentales. Uno explicaba las leyes de conservación en pequeñas regiones del espacio, una proeza matemática que más tarde resultaría importante para comprender las simetrías de la teoría cuántica de campos. El otro, ahora conocido simplemente como el teorema de Noether, dice que detrás de cada ley de conservación se esconde una simetría más profunda.
En términos matemáticos, una simetría es algo que le puedes hacer a un sistema sin que cambie. Consideremos el acto de rotación. Si comenzamos con un triángulo equilátero, veremos que podemos rotarlo en múltiplos de 120 grados sin que cambia su apariencia. Si comenzamos con un círculo, podemos rotarlo cualquier ángulo. Estas acciones sin consecuencias revelan las simetrías subyacentes de estas formas.
Pero las simetrías van más allá de la forma. Imagina que haces un experimento, luego te mueves 10 metros hacia la izquierda y lo vuelves a hacer. Los resultados del experimento no cambian, porque las leyes de la física no cambian de un lugar a otro. Esto se llama simetría de traslación.
Ahora espera unos días y repite el experimento. Los resultados no cambian, porque las leyes de la física no cambian con el paso del tiempo. Esto se llama simetría de traslación temporal.
Noether comenzó con simetrías como estas y exploró sus consecuencias matemáticas. Trabajó con la física establecida utilizando una descripción matemática común de un sistema físico, llamada lagrangiano.
 Como la mayoría de los académicos judíos en Alemania, Emmy Noether fue despedida tras la llegada al poder de los nazis. Más adelante, ese mismo año se fue al Bryn Mawr College en los EE. UU. y murió después de una cirugía de cáncer en 1935. Tenía 53 años. Fuente: Archivos del Bryn Mawr College
Como la mayoría de los académicos judíos en Alemania, Emmy Noether fue despedida tras la llegada al poder de los nazis. Más adelante, ese mismo año se fue al Bryn Mawr College en los EE. UU. y murió después de una cirugía de cáncer en 1935. Tenía 53 años. Fuente: Archivos del Bryn Mawr CollegeEn este punto, la intuición de Noether trascendió los símbolos en la página. Sobre el papel, las simetrías no parecen tener ningún impacto en la física del sistema, ya que no afectan al lagrangiano. Pero Noether se dio cuenta de que las simetrías deben ser importantes desde el punto de vista matemático, ya que limitan como puede comportarse un sistema. Trató de determinar cuál debería ser esta restricción y, de las matemáticas del lagrangiano, surgió una cantidad que no puede cambiar. Esa cantidad corresponde a la propiedad física que se conserva. El impacto de la simetría había estado oculto bajo las ecuaciones todo el tiempo, fuera de la vista.
En el caso de la simetría de traslación, el momento total del sistema nunca debería cambiar. En el caso de la simetría de traslación temporal, la energía total de un sistema se conserva. Noether descubrió que las leyes de conservación no son axiomas fundamentales del universo, sino que surgen de simetrías más profundas.
Las consecuencias conceptuales son difíciles de exagerar. Los físicos de principios del siglo XX se sorprendieron al darse cuenta de que un sistema que rompe la simetría de traslación temporal puede romper con ella la conservación de la energía. Ahora sabemos que nuestro propio universo hace esto. El cosmos se está expandiendo a un ritmo acelerado, estirando la luz sobrante del universo primitivo. El proceso reduce la energía de la luz a medida que pasa el tiempo.
“Antes del teorema de Noether, el principio de conservación de la energía estaba envuelto en misterio”, escribió el físico y matemático Feza Gürsey en 1983. “… La formulación matemática simple y profunda de Noether hizo mucho por desmitificar la física”.
El teorema de Noether también ha influido en el mundo cuántico. En la década de 1970, desempeñó un papel importante en la construcción del Modelo Estándar de la física de partículas. Las simetrías de los campos cuánticos dictan leyes que restringen el comportamiento de las partículas fundamentales. Por ejemplo, una simetría en el campo electromagnético obliga a las partículas a conservar su carga.
El poder del teorema de Noether ha inspirado a los físicos a buscar la simetría para descubrir nueva física. Más de un siglo después, las ideas de Noether siguen influyendo en la forma de pensar de los físicos.
“Hay mucho que todavía nos queda por aprender si reflexionamos sobre el teorema de Noether”, afirma el físico matemático John Baez. “Tiene capas y capas de profundidad”.
El artículo original, How Noether’s Theorem Revolutionized Physics, se publicó el 7 de febrero de 2025 en Quanta Magazine.
Traducido por César Tomé López
El artículo Cómo el teorema de Noether revolucionó la física se ha escrito en Cuaderno de Cultura Científica.
Berberechos equipados con fibra óptica
Las plantas y otros organismos fotosintéticos fijan el CO2 y elaboran carbohidratos. Los animales no podemos hacer la fotosíntesis y aprovechar directamente la energía de la luz solar. No obstante, algunos animales establecen relaciones de simbiosis con organismos unicelulares fotosintéticos. Estos organismos reciben el nombre de zooxantelas y generalmente son dinoflagelados del género Symbiodinium, aunque pueden ser algas de diferentes tipos.
Las zooxantelas obtienen protección y elementos inorgánicos de su hospedador, y a cambio le proporcionan moléculas orgánicas. El caso más conocido de esta fotosimbiosis es el de los corales arrecifales. De hecho, el gravísimo problema conocido como blanqueo del coral se debe a la expulsión de las zooxantelas a causa de cambios medioambientales que provocan estrés en los corales.
Además de los corales, otros casos de fotosimbiosis se registran en esponjas, medusas o moluscos. Un caso excepcional es el gasterópodo Elysia chlorotica, la babosa esmeralda. Su color verde se debe a que se alimenta de algas, pero almacena los cloroplastos en divertículos digestivos en los que se sigue produciendo la fotosíntesis.
 Figura 1. El cárdido Tridacna crocea expone su manto a través de la abertura entre las valvas. Los intensos colores se deben a la simbiosis con zooxantelas fotosintéticas y a los iridóforos, células que reflejan la luz ultravioleta. De David Witherall y Sarah Davies, CC BY 3.0
Figura 1. El cárdido Tridacna crocea expone su manto a través de la abertura entre las valvas. Los intensos colores se deben a la simbiosis con zooxantelas fotosintéticas y a los iridóforos, células que reflejan la luz ultravioleta. De David Witherall y Sarah Davies, CC BY 3.0Varios grupos de moluscos lamelibranquios o bivalvos también aparecen asociados con zooxantelas, pero solo en dos de ellos se puede hablar de simbiosis obligada, sin la cual la supervivencia del molusco está comprometida. Los dos casos pertenecen a la familia de los cárdidos. Aquí encontramos a las famosas tridacnas, las almejas gigantes, que pueden alcanzar más de un metro de longitud y 300 Kg de peso (Figura 1). Se calcula que entre el 75% y el 90% de su nutrición deriva de la fotosíntesis. El segundo grupo de bivalvos con zooxantelas incluye a los berberechos de la subfamilia Fraginae, que tienen la característica forma de corazón que da nombre a los cárdidos (Figura 2).
 Figura 2. Dos ejemplares del berberecho Corculum cardissa. Abajo los vemos iluminados desde el interior, lo que permite apreciar las ventanas que dejan pasar la luz. De McCoy et al. (2024). CC BY-NC-ND 4.0
Figura 2. Dos ejemplares del berberecho Corculum cardissa. Abajo los vemos iluminados desde el interior, lo que permite apreciar las ventanas que dejan pasar la luz. De McCoy et al. (2024). CC BY-NC-ND 4.0En ambos casos las zooxantelas se ingieren durante el crecimiento de larvas y juveniles, y se almacenan en complejos divertículos del tubo digestivo. El problema es que estas zooxantelas necesitan exposición a la luz solar, y esto no es sencillo en un animal con valvas calcáreas. Las grandes tridacnas solucionan esto manteniendo sus valvas abiertas, incluso exponiendo su manto fuera de ellas (Figura 1). Sin embargo, los pequeños berberechos se mantienen cerrados y reciben la luz a través de sus conchas. ¿Cómo es posible?
Un estudio de las universidades de Chicago y Stanford, liderado por la Dra. Dakota McCoy, ha revelado las sorprendentes adaptaciones de Corculum cardissa para llevar la luz solar a sus zooxantelas. Este pequeño berberecho (3-4 cm) permanece semienterrado en la arena, exponiendo una zona aplanada de sus valvas al exterior. En esa zona existen una serie de pequeñas ventanas de forma variable que permiten el paso de la luz (Figura 2). Podría pensarse que se trata de zonas adelgazadas de la concha, pero no es así. De hecho, estas ventanas pueden ser más gruesas que las áreas opacas de la valva. ¿Cómo permiten el paso de la luz?
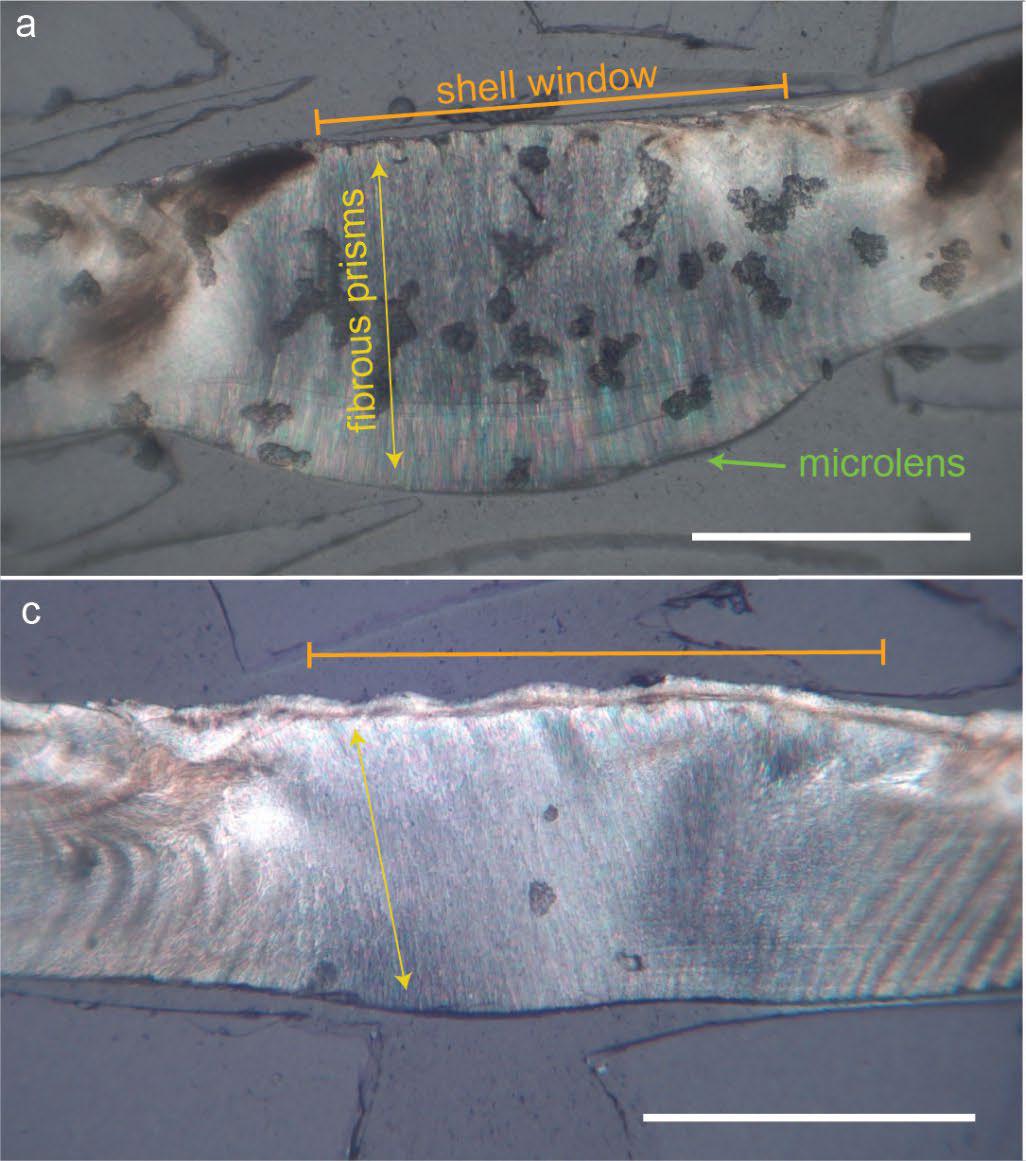 Figura 3. Sección de la concha de C. cardissa a nivel de las ventanas. La figura superior muestra una microlente asociada a la ventana. Obsérvese la presencia de finísimos prismas de aragonito que actúan como fibras ópticas. Escala= 0,5 mm. De McCoy et al. (2024). CC BY-NC-ND 4.0
Figura 3. Sección de la concha de C. cardissa a nivel de las ventanas. La figura superior muestra una microlente asociada a la ventana. Obsérvese la presencia de finísimos prismas de aragonito que actúan como fibras ópticas. Escala= 0,5 mm. De McCoy et al. (2024). CC BY-NC-ND 4.0El estudio de McCoy y sus colaboradores ha mostrado que las ventanas están formadas por haces de finísimos cristales de aragonito (una forma cristalina del carbonato cálcico) de un micrómetro de diámetro, que funcionan como auténticas fibras ópticas (Figura 3). No se trata de que estos cristales sean transparentes y dejen pasar la luz, sino que la conducen a lo largo del cristal con mínimas pérdidas. De hecho, si se superpone el haz de fibras sobre una imagen, la imagen aparece proyectada en la superficie contraria.
La transmisión de la luz a través de las fibras de aragonito está optimizada para ser mucho mayor en las longitudes de onda largas (luz naranja y roja) y mucho menor en las cortas (radiación ultravioleta, perjudicial para las zooxantelas) (Figura 4). La luz roja produce una mayor eficiencia fotosintética a diferencia de la luz verde, que es reflejada. Precisamente por esto las plantas son verdes.
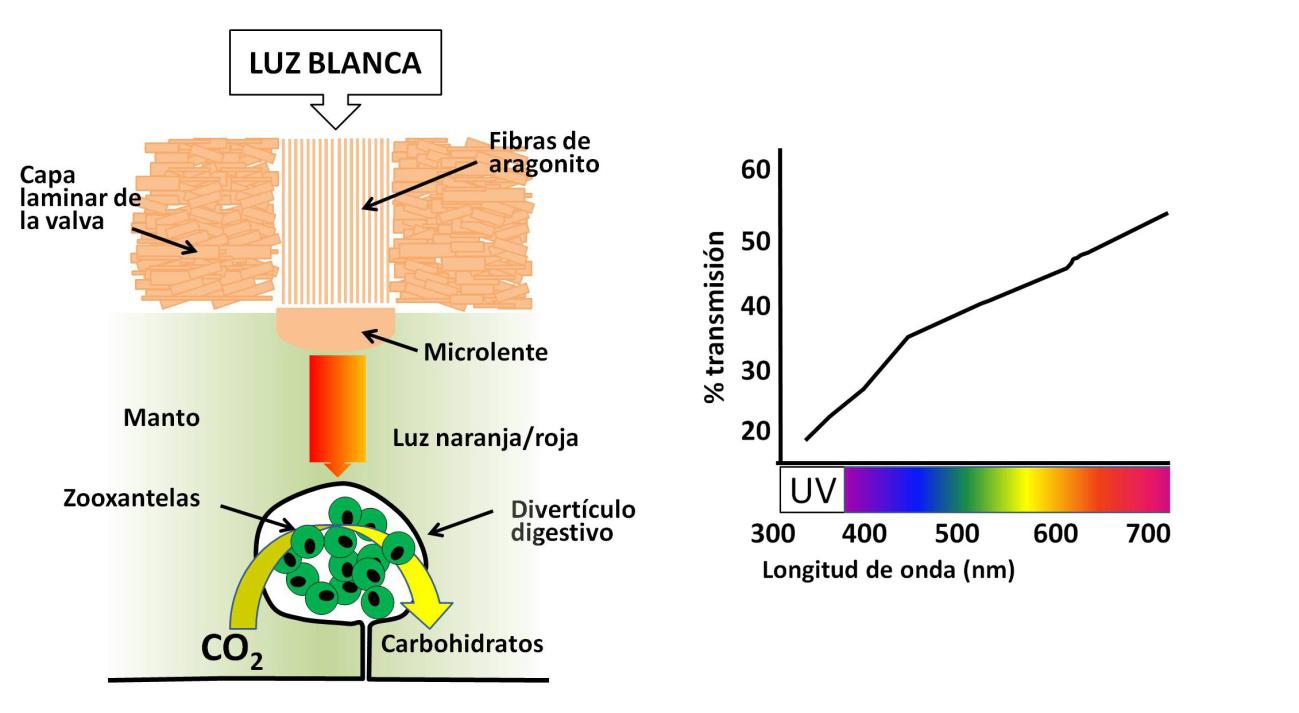 Figura 4. Esquema de la transmisión de luz por las fibras de aragonito. La microlente condensa la luz en un haz que penetra en el manto hasta alcanzar las zooxantelas, albergadas en divertículos del sistema digestivo. A la derecha vemos cómo la máxima transmisión de luz se produce en las mayores longitudes de onda (naranja/rojo), más adecuadas para la fotosíntesis (11-62%, con una media del 31%). Los rayos ultravioletas, perjudiciales, son filtrados (5-28%, con una media del 14%)
Figura 4. Esquema de la transmisión de luz por las fibras de aragonito. La microlente condensa la luz en un haz que penetra en el manto hasta alcanzar las zooxantelas, albergadas en divertículos del sistema digestivo. A la derecha vemos cómo la máxima transmisión de luz se produce en las mayores longitudes de onda (naranja/rojo), más adecuadas para la fotosíntesis (11-62%, con una media del 31%). Los rayos ultravioletas, perjudiciales, son filtrados (5-28%, con una media del 14%)Las ventanas ocupan aproximadamente la mitad de la superficie de la concha expuesta a la luz. El resto está formado por cristales de aragonito en forma de láminas entrecruzadas, lo que da mayor solidez a la concha que la disposición en fibras. Existe, por tanto, un compromiso entre resistencia mecánica y transmisión de luz. En una parte de las ventanas, bajo el haz de fibras ópticas, hay un abultamiento que funciona como lente, concentrando la luz en un haz de 1 mm de diámetro y permitiendo una mayor penetración en los tejidos blandos (Figura 4).
Los parámetros del haz de fibras han mostrado que son el sistema óptimo para la transmisión de luz, tanto en lo que se refiere a su orientación (perpendicular a la superficie), su diámetro (1 m) e incluso el eje óptico elegido. El aragonito es un mineral ópticamente anisótropo. Esto significa que su índice de refracción es diferente en los tres ejes espaciales. Las fibras de aragonito están orientadas de acuerdo con el eje de mayor índice de refracción, orientación que coincide con la máxima eficiencia óptica. Cualquier otra disposición, según las simulaciones hechas con ordenador, resulta en una menor transmisión de luz.
Según los autores del artículo, este constituye el primer caso de haces de fibras ópticas encontradas en un ser vivo. Solo algunas espículas de esponjas tienen propiedades ópticas similares, aunque es dudoso que tengan utilidad relacionada con la transmisión de la luz. Por otro lado, solo se conoce otro caso de lentes aplicadas a la fotosíntesis: ciertas células epidérmicas de plantas angiospermas. En conclusión, las adaptaciones de Corculum cardissa para suministrar luz a sus fotosimbiontes son realmente extraordinarias.
Referencias
McCoy, D.E., Burns, D.H., Klopfer, E. et al. (2024). Heart cockle shells transmit sunlight to photosymbiotic algae using bundled fiber optic cables and condensing lenses. Nat Commun. doi: 10.1038/s41467-024-53110-x
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Berberechos equipados con fibra óptica se ha escrito en Cuaderno de Cultura Científica.
La IA que sueña con ovejas eléctricas
 Foto: Possessed Photography / Unsplash
Foto: Possessed Photography / Unsplash
Soñar con ovejas eléctricas significa, hasta hoy, tener un cerebro humano. De ahí el inmortal título de la novela ciberpunk de Philip K. Dick. ¿Sueñan los androides con ovejas eléctricas? ¿Esta más cerca de producirse una inteligencia artificial genérica parecida a la humana, la llamada singularidad? Este es el camino.
Hoy, año 2025A pesar de enormes avances, los transistores, que son la base de la inteligencia artificial no son a día de hoy, ni actúan, como neuronas, y una computadora no calcula como un cerebro humano piensa. Una inteligencia artificial genérica parecida a la humana no va a producirse mañana. Pero… ¿estamos en el camino?
Existen enfoques, como la computación neuromórfica (el nombre no puede ser más explícito) que persiguen imitar el funcionamiento de nuestro cerebro. Para ello utilizan elementos inspirados en las neuronas y sus conexiones sinápticas, que son de naturaleza eléctrica, y buscan la misma eficiencia energética de un cerebro humano.
¿En qué punto estamos? ¿Nos encontramos más cerca de convivir con inteligencias que imiten la nuestra? Para poder responder a esto, habría que aclarar qué significa imitar nuestra inteligencia.
Imitar un cerebro humanoLa palabra “imitar” nos lleva rápidamente al “juego de la imitación” de Alan Turing y su famoso test.
A la hora de comparar la inteligencia artificial y la natural, el enfoque puede ser “filosófico” o “funcional”. El de Turing se parecería más a este último: como dijo alguien, la cuestión de si una máquina puede pensar no es más interesante que la de si un submarino puede nadar.
Para Turing, si una máquina podía engañar a un humano haciéndole creer que estaba hablando con otra persona humana, mostraría un comportamiento inteligente. Muchos no estarían de acuerdo con el bueno de Alan.
Pasar el test de Turing podría ser una condición necesaria pero no suficiente para darle el cum laude en inteligencia a una máquina. Para esos muchos, echar mano de ingeniosos trucos algorítmicos es de alguna manera degradar la pregunta central que está en juego y que hoy en día no tiene una respuesta clara: ¿qué es el pensamiento? ¿Qué tiene que ver con la autoconciencia?
Pensar con metáforasNosotros, los humanos, a partir de los datos que nos llegan de los sentidos y que describen la realidad circundante, derivamos nueva información. A partir de ellos podemos generar conocimiento asociativo que nos ayuda a actuar, reaccionar o incluso anticipar el curso de los acontecimientos.
Este conocimiento asociativo puede trascender la realidad misma, a veces solo por el simple capricho o placer de hacerlo. Esta asociación conceptual abstracta puede conducir, por ejemplo, a metáforas o poesía.
Pero, aparentemente, todo ello se reduce a una elaborada estrategia de supervivencia que ha servido bien a nuestra autoconservación. Por eso llevamos sapiens en nuestro apellido. Dijo Einstein: “el mejor resultado de la inteligencia no es el conocimiento sino la imaginación”. La IA, hasta la fecha, no razona ni imagina.
El teorema de los monos infinitosLos motores de IA parecen operar principalmente como máquinas de optimización de objetivos que aprovechan una vasta base de datos de conocimiento preexistente. ChatGPT materializa en tiempo récord el teorema de los infinitos monos, que establece que infinitos monos presionando al azar las teclas de máquinas de escribir durante una cantidad infinita de tiempo acabarán escribiendo las obras completas de William Shakespeare en algún momento.
Sin embargo, una IA recién nacida, sin acceso a bases de datos, ¿sería capaz de operar únicamente sobre la base de información fresca y puntual de sensores?
¿Soñaría una IA con ovejas eléctricas?
Esto nos lleva de nuevo a la cuestión de la conciencia artificial y a la probabilidad de que surja de forma espontánea.
La profetizada singularidadEl científico informático Ray Kurzweil acuñó el término de singularidad para tal suceso. El advenimiento de tal superinteligencia puede ser considerado como potencialmente benigno o tan desafortunado, o maligno, que los humanos vamos a salir necesariamente malparados, ya sea involuntariamente (como en 2001, una odisea del espacio) o voluntariamente (como en la serie de películas de Terminator).
La singularidad ha recuperado protagonismo a raíz de herramientas similares a ChapGPT, como la disruptiva DeepSeek, su rápida evolución y aparente creatividad. Han surgido varias voces, como la de Noam Chomsky, que dudan de su verdadera naturaleza inteligente.
En este debate entra el veterano libro La nueva mente del emperador, de Roger Penrose, que sostiene que nuestro cerebro no es algorítmico y no puede ser replicado por mera, aunque poderosa, computación. También afirmaba que el funcionamiento de nuestro cerebro se basa en cierta medida en la mecánica cuántica.
El nacimiento de HalHAL nació en la ficción en 2001, una película de 1968. El levantamiento de Skynet, el nombre de la inteligencia artificial que lidera al ejército de las máquinas en la saga Terminator, tuvo lugar en 1997, imaginado por un film estrenado en 1984. Son fechas ya bien caducadas. La IA parecía una más de las promesas futuristas aquejadas por la paradoja de Zenón, como los coches voladores o la fusión nuclear. Sin embargo, el mundo de la computación está viviendo tiempos y perspectivas interesantes y la IA que necesitamos para navegar el avance exponencial de la tecnología está provocando un debate encendido sobre las implicaciones sociales de la inteligencia no humana.
El mencionado Ray Kurzweil, directivo de Google y “profeta” tecnológico, predijo en 2005 que habría una máquina inteligente sobrehumana en 2045, con una etapa intermedia consistente en una inteligencia similar a la humana en 2029. Esto lo tenemos casi en la punta de nuestros dedos temporales.
Si la singularidad se produjera, el nacimiento de esa IA genérica intermedia, llamémosla infantil y recemos por una adolescencia corta, plantearía un dilema ético interesante. ¿Qué hueco le hacemos?
Si la singularidad ocurreSi la singularidad ocurre, podemos pensar en leyes como las de los Grandes Simios, que en algunas jurisdicciones les confieren la condición de personas, considerándolos seres y no cosas. Estas leyes se apoyan sobre la base de cierta habilidad lingüística, autocontrol, autoconciencia y la capacidad de proyectarse a sí mismos en el futuro.
También podemos inspirarnos en el capítulo de los Derechos del Niño que establece que se les debe facilitar los medios para su desarrollo material y espiritual; proveerles de las condiciones que les permitan ganarse la vida protegiéndolos de la explotación, y educarlos en la idea de que sus talentos deben dedicarse al servicio de sus semejantes.
Alcanzar ese estado de convivencia con inteligencias artificiales y hacerlo con éxito sería un pequeño paso para la humanidad, pero un gran salto para toda vida inteligente, ya sea basada en el carbono como en el silicio.![]()
Sobre el autor: Luis Antonio Fonseca Chácharo, Profesor de Investigación en microelectrónica, Instituto de Microelectrónica de Barcelona (IMB-CNM-CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La IA que sueña con ovejas eléctricas se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2024: El cubata de Brunelleschi
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

Miguel Ángel Cajigal, conocido en las redes sociales como «El barroquista», nos explica en esta charla como se solucionó el problema de la construcción de la cúpula de la catedral de Florencia, algo que sus promotores se comprometieron a que fuese la más grande jamás construida, a pesar de que nadie había hecho nada parecido hasta el momento. Una historia de arte, tecnología y chulería.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: El cubata de Brunelleschi se ha escrito en Cuaderno de Cultura Científica.
Descifrando el código de los materiales

¿Alguna vez os habéis preguntado por qué el cobre conduce la corriente eléctrica y el vidrio no? ¿Por qué el diamante es tan duro y el grafito de los lápices tan blando, aunque ambos estén compuestos de carbono? La respuesta no se encuentra a simple vista.
Pensemos en el ADN. El orden específico de las bases nitrogenadas del ADN codifica las peculiaridades de cada ser vivo. Nuestro código genético determina, por ejemplo, el color de nuestros ojos. De manera similar, cada material posee una distribución interna de sus electrones característica, conocida como “bandas de energía”, que dicta su comportamiento y condiciona propiedades tan importantes como su capacidad para conducir corriente o para imantarse, su reactividad química, o como veremos a continuación, su color.
 Así como nuestro código genético define nuestras características, las propiedades de un material vienen dadas por su propio código: la estructura de bandas electrónica. Fuente: Composición a partir de imágenes de Wikimedia Commons
Así como nuestro código genético define nuestras características, las propiedades de un material vienen dadas por su propio código: la estructura de bandas electrónica. Fuente: Composición a partir de imágenes de Wikimedia Commons
Imaginemos un material como una enorme escalera, donde cada peldaño corresponde a niveles de energía de sus electrones. Aquí es crucial el papel de la física cuántica. Sabemos que los electrones pertenecen a la clase de partículas conocidas como fermiones. El físico Wolfgang Pauli formuló para ellos el “principio de exclusión”, según el cual dos fermiones pertenecientes a un mismo sistema no pueden encontrarse en el mismo estado. Por otro lado, también necesitamos algo de física clásica. Los electrones poseen carga electrostática, por lo que están sujetos a la ley de Coulomb, que establece que las cargas de signo opuesto se atraen y las de igual signo se repelen. Los electrones, por tener carga negativa, son atraídos por los núcleos de los átomos, de carga positiva, a la vez que son repelidos por los demás electrones presentes en el material. Al hacer balance de todas estas normas, el resultado que obtenemos es que los electrones no pueden estar en cualquier nivel de energía del material: algunos niveles están prohibidos.
 La distribución de las energías de los electrones de un material se puede interpretar como una escalera en la que algunos peldaños están prohibidos y en otros se puede almacenar un número dado de electrones.
La distribución de las energías de los electrones de un material se puede interpretar como una escalera en la que algunos peldaños están prohibidos y en otros se puede almacenar un número dado de electrones.Así, la estructura de bandas electrónicas de cada material es su «ADN» o seña de identidad, formada por una combinación específica de niveles de energía permitidos y prohibidos, que condicionará sus principales propiedades. Por ejemplo, esta combinación específica determina si un material conduce bien la electricidad, como los conductores, si no deja fluir la corriente eléctrica, como en los aislantes…o incluso si la conduce sin resistencia ni pérdida de energía, el caso de los superconductores.
La aplicación de las leyes de la mecánica cuántica nos permite ir más allá y predecir cómo responderá un material ante la aplicación de un estímulo externo, como puede ser una presión mecánica, un campo magnético, o algo tan común como la luz. En semiconductores y aislantes, al absorber luz de una determinada longitud de onda, los electrones son “excitados”, lo que significa que pueden saltar a peldaños vacíos de mayor energía. Este tipo de proceso determina el color con el que vemos el material. Asimismo, se puede dar el proceso contrario de “desexcitación» de electrones, mediante el cual el material emite luz de una determinada longitud de onda en función de los peldaños descendidos. La tecnología LED, presente en muchos de los dispositivos que usamos diariamente, aprovecha este fenómeno de emisión de luz.
 Las propiedades conductoras de un material están definidas por su estructura de bandas. Así, los metales se emplean en transporte de corriente y los semiconductores en chips y LEDs. Se puede hacer levitar a un superconductor, gracias a su especial propiedad de expeler los campos magnéticos. Fuente: Composición a partir de imágenes de Wikimedia Commons
Las propiedades conductoras de un material están definidas por su estructura de bandas. Así, los metales se emplean en transporte de corriente y los semiconductores en chips y LEDs. Se puede hacer levitar a un superconductor, gracias a su especial propiedad de expeler los campos magnéticos. Fuente: Composición a partir de imágenes de Wikimedia Commons
En un laboratorio podemos medir experimentalmente la estructura de bandas de los materiales a partir de la observación del resultado de excitar los electrones con distintas fuentes de luz, en particular de rayos-X y luz ultravioleta (UV). Pero si queremos ser realmente precisos al realizar nuestra “radiografía del material», debemos emplear la intensa luz procedente de radiación sincrotrón, que solo se encuentra disponible en instalaciones especiales. Entre ellas destaca el sincrotrón ALBA, situado en la provincia de Barcelona.
 Cámara de ultra-alto vacío, situada en el Centro de Física de Materiales (CFM-MPC) CSIC-UPV/EHU en Donostia-San Sebastián, donde se combinan distintas técnicas experimentales, como la microscopia túnel y la espectroscopia fotoelectrónica para el estudio experimental de la estructura atómica y electrónica de superficies. Fuente: UPV/EHU
Cámara de ultra-alto vacío, situada en el Centro de Física de Materiales (CFM-MPC) CSIC-UPV/EHU en Donostia-San Sebastián, donde se combinan distintas técnicas experimentales, como la microscopia túnel y la espectroscopia fotoelectrónica para el estudio experimental de la estructura atómica y electrónica de superficies. Fuente: UPV/EHU Vista aérea de las instalaciones del sincotrón ALBA, situado en Cerdanyola del Vallès (Barcelona). Fuente: Consorcio para la Construcción, Equipamiento y Explotación del Laboratorio de Luz Sincrotrón (CELLS)
Vista aérea de las instalaciones del sincotrón ALBA, situado en Cerdanyola del Vallès (Barcelona). Fuente: Consorcio para la Construcción, Equipamiento y Explotación del Laboratorio de Luz Sincrotrón (CELLS)También podemos calcular la estructura de bandas empleando software de simulación basado en las llamadas teorías “ab initio”. Estas simulaciones reproducen el comportamiento de los electrones del material a partir de una serie de ecuaciones matemáticas formuladas a partir los dos fundamentos físicos descritos anteriormente: la mecánica cuántica y la ley de Coulomb. Se trata de cálculos tan complejos, que a veces requieren el uso de supercomputadores.
Finalmente, los físicos experimentales y teóricos colaboramos estrechamente para combinar nuestros hallazgos y así descodificar la estructura de bandas del material. Gracias a estas investigaciones, podemos diseñar y fabricar materiales con las propiedades específicas que deseemos.
Sobre las autoras: Maider Ormaza y Maria Blanco, profesoras investigadoras de la Facultad de Química de la Universidad del País Vasco/Euskal Herriko Unibersitatea

La Facultad de Química de la UPV/EHU cumple este año 50 años. Con motivo de este aniversario se han organizado un gran número de actividades festivas, de orientación del alumnado de secundaria, investigación, transferencia y divulgación. Entre estas últimas podemos encontrar “12 meses – 12 temas”, conjunto de actividades que pretende mostrar a la sociedad las temáticas desarrolladas en la Facultad. Entre estas actividades podemos encontrar el ciclo de charlas “50 años difundiendo la química”, en Ernest Lluch Kulturetxea, así como vídeos de divulgación, entrevistas en radio y artículos en los blogs de divulgación de la Cátedra de Cultura Científica. Durante todo el año contaremos con invitados especiales, como los cuatro Centros de Investigación nacidos de la Facultad (CIDETEC, CFM, DIPC y POLYMAT), así como los Premios Nobel Albert Fert y Jean Marie Lehn. Se puede consultar el conjunto de actividades programadas en la página web de nuestro 50 Aniversario.
El artículo Descifrando el código de los materiales se ha escrito en Cuaderno de Cultura Científica.

