Naukas Bilbao 2022: La fina línea

Es posible que, en alguna ocasión, un sentimiento homicida te haya invadido ante según qué plantemientos de tu profesor de matemáticas. Sentimiento este que podría verse correspondido desde el momento en que para algún matemático el asesinato es la única salida lógica a determinadas cuestiones. Este matemático ingresó en un manicomio, pero su fama empezó ahí, precisamente. Juan Antonio Prado nos cuenta su historia.
Juan Antonio Prado Bassas es profesor titular del departamento de Análisis Matemático y vicedecano de Innovación Docente y Divulgación Científica de la Facultad de Matemáticas de la Universidad de Sevilla.
Si no ve correctamente el vídeo, use este enlace.
Más sobre el tema:
André Bloch: el asesinato como una cuestión de lógica matemática
Matemáticos y sin embargo criminales
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2022: La fina línea se ha escrito en Cuaderno de Cultura Científica.
El impacto de la violencia en la incertidumbre de vida
La duración de la vida en países con altas tasas de violencia es menos predecible y la esperanza de vida de los jóvenes puede ser hasta 14 años más corta en comparación con los países pacíficos, según un nuevo estudio realizado por un equipo internacional, liderado por la Universidad de Oxford y en el que ha participado el investigador Ikerbasque en la UPV/EHU, Tim Riffe.
 Foto: Tengyart / Unsplash
Foto: Tengyart / UnsplashSegún la investigación, las muertes violentas son responsables en una alta proporción del diferente nivel de incertidumbre de vida entre los países violentos y los pacíficos. La incertidumbre de vida hace referencia a la dispersión en las edades de mortalidad; cuanto mayor es la dispersión, mayor incertidumbre. El impacto de la violencia en la mortalidad va más allá de acortar vidas, ya que cuando, debido a la violencia se pierden vidas de forma continuada, las personas supervivientes tienen mayor incertidumbre sobre quién será la siguiente víctima. En palabras de los autores de la investigación lo más sorprendente de este estudio ha sido constatar que la incertidumbre sobre la vida tiene una mayor asociación con la violencia que la esperanza de vida, de ahí su importancia para analizar los cambios en los patrones de mortalidad
Utilizando los datos de mortalidad de 162 países y el Índice de Paz Interna entre 2008 y 2017, el estudio muestra que los países más violentos también son aquellos con mayor incertidumbre de vida. En el caso de Oriente Medio son las muertes relacionadas con el conflicto a edades tempranas las que más contribuyen a la percepción de incertidumbre elevada. Asimismo, en América Latina se observa un patrón similar resultado de los homicidios y de la violencia interpersonal. En el otro extremo nos encontramos que la incertidumbre de vida fue «notablemente baja» entre 2008 y 2017, en la mayoría de los países del norte y sur de Europa.
En los países de ingresos altos la reducción de la mortalidad temprana por cáncer ha influido en reducir la incertidumbre de vida. Sin embargo, en las sociedades más violentas, la incertidumbre de vida es incluso experimentada por aquellos que no están directamente involucrados en la violencia. El informe recoge que “Los ciclos de pobreza, inseguridad y violencia magnifican los patrones estructurales preexistentes de desventaja para las mujeres. En algunos países de América Latina, los asesinatos a mujeres han aumentado en las últimas décadas y la exposición a entornos violentos tiene consecuencias sociales y de salud, en particular para niños y mujeres”. Según los autores del estudio «Si bien los hombres son las principales víctimas directas de la violencia, las mujeres tienen más probabilidades de experimentar sus consecuencias en contextos violentos»
Según el informe la esperanza de vida más baja suele estar asociada con una mayor incertidumbre de vida. Además, vivir en una sociedad violenta crea vulnerabilidad e incertidumbre y eso, a su vez, puede conducir a un comportamiento más violento. Los países con altos niveles de violencia tienen una esperanza de vida más baja que los más pacíficos. Se estima una brecha de alrededor de 14 años en la esperanza de vida entre los países menos y más violentos. Así, en países como El Salvador, Honduras, Guatemala o Colombia la brecha en la esperanza de vida con los países de altos ingresos se explica principalmente por el alto nivel de mortalidad debido a los homicidios.
Según el investigador Ikerbasque de la UPV/EHU, Tim Riffe, autor del estudio, es importante mostrar en un sentido amplio los efectos que la violencia tiene para la salud de la población, de modo que pueda considerarse un problema de salud pública y, por lo tanto, pueda ser susceptible de programas de prevención. La violencia como causa de muerte resulta, en principio, más fácil de prevenir que otras grandes causas, como puede ser el cáncer, y los beneficios de hacerlo son tanto inmediatos como duraderos. De hecho, existen muchos ejemplos de sociedades que transitaron de una situación de elevada violencia a otra de paz prolongada.
El estudio está basado en el uso masivo de datos y se fundamenta, en parte, en estimaciones de mortalidad modeladas por el proyecto Global Burden of Disease. Muchas de las poblaciones incluidas no tienen información demográfica directa sobre la mortalidad, debido a que, en gran parte del mundo, los sistemas de registro vital, que permiten desarrollar una investigación como esta de forma directa, están aún por desarrollar o requieren de mejoras significativas.
Referencia:
José Manuel Aburto, Vanessa di Lego, Tim Riffe, Ridhi Kashyap, Alyson van Raalte, and Orsola Torrisi (2023) A global assessment of the impact of violence on lifetime uncertainty Science Advances doi: 10.1126/sciadv.add9038
Para saber más:
Serie Preparados para matar
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El impacto de la violencia en la incertidumbre de vida se ha escrito en Cuaderno de Cultura Científica.
Geóloga, ¿una especie en peligro de extinción?
Geóloga
El sábado once de febrero se celebró el Día Internacional de la Mujer y la Niña en la ciencia. Este evento pretende visibilizar el papel femenino en las disciplinas científicas y técnicas, buscando crear referentes entre las más jóvenes, de tal manera que puedan plantearse su futuro como profesionales en este ámbito, incluidas las Ciencias de la Tierra.
De manera general, la Geología siempre se ha considerado como una ciencia muy masculinizada. En la sociedad, tanto en el pasado como en la actualidad, nunca se ha visto como “muy femenino” una profesión que implica ir al campo a llenarse de barro, dar martillazos a rocas y cargar en la espalda con una mochila llena de muestras durante largos paseos en mitad del monte. Como mucho, se normalizaba más la presencia de mujeres en el laboratorio, procesando esas muestras de roca, apretando botoncitos en máquinas y dejándose la vista ante un microscopio contando minerales y fósiles microscópicos. De hecho, generalmente nuestro papel era el de “secretarias” que pasaban a limpio las sesudas divagaciones y complejos esquemas realizados por los compañeros varones. Pero sin darnos la opción de pensar en hipótesis demasiado complejas para nuestro limitado conocimiento científico. Y sin que se nos pasase por la cabeza la remota posibilidad de redactar, ni siquiera firmar, publicaciones científicas resultantes de esas investigaciones.
Pero esta imagen dista mucho de la realidad. Hace más de doscientos años que las mujeres han ido realizando importantísimos descubrimientos que han permitido avanzar en el conocimiento de la historia de nuestro planeta, sentando las bases de la Geología tal y como la conocemos en la actualidad, aunque su nombre se haya cubierto con el polvo del paso del tiempo. Por eso, uno de los deberes de aquellas que, muchas veces sin saberlo, seguimos sus pasos es coger nuestro martillo geológico y retirar esas capas de roca que cubren su legado hasta desvelar sus nombres y trabajos al mundo.
 Portada del libro “GEAS, Mujeres que estudian la Tierra” en su versión en castellano.
Portada del libro “GEAS, Mujeres que estudian la Tierra” en su versión en castellano.Con este objetivo nació la Comisión Mujeres y Geología en el seno de la Sociedad Geológica de España. Y una de sus últimas actividades ha sido la colaboración en la publicación del libro “GEAS, Mujeres que estudian la Tierra”. Escrito por Rosa Mateos y Ana Ruiz Constán, geólogas del Instituto Geológico y Minero de España (IGME-CSIC) y bellamente ilustrado por Nívola Uyá, recoge las biografías de doce pioneras de las Ciencias de la Tierra que han cambiado el mundo de la Geología en los dos últimos siglos. Sin hacer muchos spoilers, descubriremos como antes de que Charles Lyell animase a otro Charles, Darwin, a lanzar su teoría de la evolución, una joven medio analfabeta inglesa había descubierto cómo cambiaban las especies fósiles con el tiempo, dándole a Lyell las pruebas que necesitaba para sustentar sus hipótesis. O cómo una geofísica danesa descubrió que el núcleo interno es sólido mientras que el núcleo externo es líquido, algo básico para que se forme el campo magnético terrestre y se sustente la vida en nuestro planeta. Incluso, conoceremos a la geóloga marina que, dibujando los mapas de los fondos marinos, dio con la clave de la tectónica de placas, a pesar de que se burlasen de sus descubrimientos sus propios compañeros de laboratorio. Este libro, traducido a más de diez idiomas, también se ha convertido en una exposición itinerante solicitada por varios museos, instituciones y centros educativos, para trasladar su legado a todos los rincones posibles.
 Paneles que componen la exposición itinerante de “GEAS, Mujeres que estudian la Tierra” colocados en el Parque de las Ciencias de Granada, donde permanecerán todo el mes de febrero.
Paneles que componen la exposición itinerante de “GEAS, Mujeres que estudian la Tierra” colocados en el Parque de las Ciencias de Granada, donde permanecerán todo el mes de febrero.Pero el trabajo de la Comisión Mujeres y Geología no termina aquí. Dos cosas que tenemos muy claras es que no debemos caer en el error de transmitir a las futuras generaciones que para ser geóloga debes ser brillante y hacer un descubrimiento que cambie los pilares de la ciencia, ni tampoco que esta visibilización de nuestro trabajo deba realizarse únicamente un día al año. Por este motivo pusimos en marcha la iniciativa Geocharlas, que consisten en charlas, conferencias, talleres y paseos geológicos ofertados de manera totalmente gratuita a centros educativos, museos, instituciones y asociaciones de diversa índole durante todo el año. Así, las geólogas pertenecientes a la Comisión nos desplazamos a los centros demandantes para hablar de nuestro trabajo y nuestra disciplina científica a un público muy diverso, principalmente estudiantes de niveles preuniversitarios, para aumentar su conocimiento en Ciencias de la Tierra y crear referentes cercanos para las más jóvenes: nosotras mismas.
 Taller didáctico ofertado como una Geocharla ante alumnado de educación primaria.
Taller didáctico ofertado como una Geocharla ante alumnado de educación primaria.Crear vocaciones científicas es una tarea ardua y muy noble, pero al igual que cuando siembras una semilla hay que regarla y cuidarla continuamente para que se desarrolle la planta, también debemos mantener y potenciar el interés por la Geología en las jóvenes. Con este propósito surgió una de las últimas iniciativas que hemos desarrollado en la Comisión, el “Programa de Mentorización Geólogas en Red” (GERMEN). Se trata de un programa en el que geólogas experimentadas de diferentes disciplinas, ámbitos de conocimiento y puestos laborales, no solo relacionados con la investigación, actuamos como mentoras de jóvenes que inician su camino como profesionales de las Ciencias de la Tierra y buscan una mano amiga para que las guíe y aconseje. Realmente, hemos creado una red de apoyo en la que todas podemos ayudarnos mutuamente a mejorar en nuestra profesión.
 Reunión de bienvenida de las mentoras y mentorizadas de la última edición del “Programa de Mentorización Geólogas en Red”.
Reunión de bienvenida de las mentoras y mentorizadas de la última edición del “Programa de Mentorización Geólogas en Red”.Todas estas actividades no serían posibles si no remásemos todas en la misma dirección, compartiendo objetivos comunes que nos dan la capacidad de aumentar nuestros esfuerzos y dedicación. Salvo que las geólogas queramos acabar extinguiéndonos en unas pocas décadas.
Si queréis conocer con más detalle las actividades que realizamos en la Comisión Mujeres y Geología, solicitarnos alguna Geocharla o uniros a nuestra lista de distribución de información, no dejéis de visitar nuestra página web. Estaremos encantadas de atenderos.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Geóloga, ¿una especie en peligro de extinción? se ha escrito en Cuaderno de Cultura Científica.
Sophie Bryant, matemática y educadora irlandesa
Sophie Bryant fue la primera mujer de Gran Bretaña e Irlanda que obtuvo un doctorado en cualquier disciplina: ocurrió en 1884. También fue la primera mujer que publicó un artículo científico en las actas de la London Mathematical Society: sucedió en 1885. Y, además, fue la primera mujer irlandesa que publicó un libro de texto de matemáticas: ocurrió en 1897, era el primero de varios tomos sobre la geometría de Euclides.
 Sophie Bryant. Fuente: Wikimedia Commons.
Sophie Bryant. Fuente: Wikimedia Commons.
Sophie Willock nació el 15 de febrero de 1850 en Dublín (Irlanda). Era la tercera de los seis hijos de Sophie Morris y el reverendo William Alexander Willock, miembro del Trinity College de Dublín donde enseñaba matemáticas. Fue educada en su casa por su padre y por institutrices privadas. Estas últimas eran francesas o alemanas y, gracias a ellas, Sophie consiguió hablar con fluidez ambas lenguas.
En 1863 William Alexander Willock fue nombrado titular de la Cátedra de Geometría de la Universidad de Londres y la familia se mudó a esta ciudad. Sophie pudo ingresar en 1866 en el Bedford College gracias a la concesión de una beca Arnott para ciencias. Al año siguiente se presentó al examen local de Cambridge que acababa de abrirse a mujeres; sus buenos resultados en matemáticas la colocaron en la primera clase.
En 1869 se casó con un cirujano, William Hicks Bryant, diez años mayor que Sophie. El médico enfermó y falleció un año más tarde. Sophie Bryant comenzó a trabajar entonces como maestra en una escuela para mujeres en Highgate, cerca de Londres. Pero no abandonó sus propios estudios.
La influencia de Frances Mary BussSophie conoció a la educadora Frances Mary Buss (1827-1894) en 1867, cuando se presentó al examen local de Cambridge para mujeres. Buss, que había fundado en 1850 la North London Collegiate School, animó a Bryant a continuar con su educación tras la muerte de su marido.
En 1875, la invitó a formar parte del personal del colegio para niñas que dirigía, trabajando como profesora de matemáticas. En realidad, Sophie no poseía ningún título universitario, ya que las mujeres no podían obtenerlos en ese momento. Finalmente, en 1878, la Universidad de Londres abrió sus puertas a las mujeres; Buss volvió a animar a Bryant a continuar con sus estudios. Aunque Sophie debió salvar previamente algunas carencias en su formación; su educación en casa no había incluido el aprendizaje del latín, y esa materia era necesaria para ser admitida en la universidad. Así que tuvo que recurrir de nuevo a clases particulares para aprender esa lengua y completar también sus conocimientos en alguna otra materia como la biología. En 1881 consiguió un grado con honores de primera clase en ciencias mentales y morales (filosofía) y honores de segunda clase en matemáticas. Tres años más tarde consiguió un doctorado sobre filosofía mental y moral, convirtiéndose en la primera mujer en Inglaterra en obtener este título.
 Frances Mary Buss y Sophie Bryant. Fuente : Wikimedia Commons.
Frances Mary Buss y Sophie Bryant. Fuente : Wikimedia Commons.
En 1882, Bryant fue admitida como miembro de la London Mathematical Society; fue la tercera mujer en entrar en esa sociedad científica tras la geómetra algebraica Charlotte Angas Scott (1858-1931) y la lógica Christine Ladd-Franklin (1847-1930), que ingresaron en 1881.
Bryant fue la primera mujer en publicar un artículo en la revista Proceedings of the London Mathematical Society. Fue en 1884; el trabajo se titulaba On the Ideal Geometrical Form of Natural Cell-Structure. En él investigaba la forma hexagonal de los panales de abejas. Su enfoque era lógico y descriptivo, no era demasiado matemático para los estándares actuales, aunque su manera de proceder era una práctica común en la época. En su artículo, Bryant explicaba cómo la forma de los panales podría deberse a la actividad natural de las abejas, a su intuición usando el método de prueba y error. Argumentaba que era necesario que cada abeja excavara su propia celda, aproximadamente al mismo ritmo que las demás, y concluía que los semidodecaedros rómbicos alargados eran la forma natural de las celdas de los panales de abeja.
En 1895 Frances Mary Buss falleció y Bryant la sucedió como directora de la North London Collegiate School, ocupando este cargo hasta que se jubiló en 1918. Durante esos años escribió sobre temas de educación y de educación matemática.
Pionera en la educación de las mujeres, nacionalista irlandesa y feministaEntre otras muchas actividades, Sophie Bryant jugó un papel decisivo en la creación del Cambridge Training College for Women, ahora llamado Hughes Hall.
Fue miembro de la London Ethical Society, una de las primeras comunidades humanistas que defendía una vida moral al margen de la religión. Además, apoyó abiertamente el sufragio femenino, aunque defendió su aplazamiento hasta que las mujeres tuvieran una mejor educación.
Interesada en la política irlandesa y entusiasta nacionalista, Bryant escribió varios libros sobre la historia de Irlanda y la antigua ley irlandesa.
Falleció practicando senderismo en los Alpes: su cadáver fue descubierto el 28 de agosto de 1922, tras permanecer dos semanas desaparecida. Algunas noticias apuntaban a un asalto para robar sus pertenencias.
Referencias
-
Sophie Willock Bryant, MacTutor History of Mathematics Archive, St Andrews University
-
Patricia Rothman, ‘So work the honey bees… building roofs of gold’. The Story of Sophie Bryant, The London Mathematical Society Newsletter 311 (2003) 22-24
-
Patricia Rothman, A biography of Sophie Bryant, Chalkdust Magazine,18 octubre 2017
-
Peter Berresford Ellis, Sophie Bryant (part 1) y Sophie Bryant (part 2), Irish Democrat
-
Sophie Bryant, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Sophie Bryant, matemática y educadora irlandesa se ha escrito en Cuaderno de Cultura Científica.
Un simulador hidrodinámico de superradiación
Los fluidos permiten crear sistemas a escala de laboratorio que simulan objetos muy diversos, desde átomos a agujeros negros. Los experimentos con estos fluidos ofrecen información valiosa sobre procesos que pueden ser muy difíciles de estudiar directamente. El último ejemplo de este uso de los fluidos lo proporciona un equipo de investigación del Instituto Tecnológico de Massachusetts que ha demostrado que un análogo de este tipo puede mostrar un comportamiento que recuerda a la superradiación.

En óptica cuántica, la superradiación es un fenómeno que ocurre cuando un grupo de N emisores, átomos excitados, por ejemplo, interactúa con una luz monocromática, como la de un láser. Si la longitud de onda de la luz es mucho mayor que la separación entre los emisores, entonces los emisores interactúan con la luz de manera colectiva y coherente. Esto hace que el grupo emita luz como un pulso de alta intensidad, proporcional a N2. Este es un resultado sorprendente, drásticamente diferente al caso de una longitud de onda menor que la separación, en el que la intensidad de la luz emitida es proporcional a N.
La superradiación no solo ocurre a nivel atómico. En 1969 Roger Penrose describió un proceso por el que se puede extraer la energía rotacional de un agujero negro. Un objeto cercano al horizonte de sucesos del agujero negro se divide en dos partículas. Una, con energía negativa, cae al agujero negro, haciendo que la velocidad de rotación de este disminuya. La otra, con energía positiva, escapa. El resultado neto es que se ha extraído energía a costa de la energía rotacional del agujero negro.
La superradiación en teoría general de la relatividad sería el equivalente al proceso Penrose pero con ondas. Así, en las ondas electromagnéticas o gravitacionales que se acercan a un agujero negro que rota es posible que, para algunas frecuencias, parte de la onda, con energía negativa, sea absorbida por el agujero negro, con el resultado de que la parte de la onda no absorbida tenga mayor energía e intensidad que la onda incidente.
La superradiación como fenómeno colectivo de emisión de luz tiene tanto interés fundamental como práctico. Se le pueden encontrar aplicaciones en varios campos, incluida la criptografía y la información cuántica.
https://culturacientifica.com/app/uploads/2023/02/video1.mp4El equipo ha conseguido ahora un comportamiento similar al de la superradiación en un baño líquido con vibración vertical que contenía dos pozos circulares. Un aumento en la fuerza vibratoria hizo que la superficie líquida inicialmente plana se desestabilizara en un patrón de ondas. Un aumento adicional en la fuerza resultó en la ruptura de estas ondas y la emisión de gotas de los dos pozos. El equipo descubrió que la tasa de emisión era más alta que la de dos pozos aislados y oscilaba a medida que variaba la distancia entre los pozos. Por lo tanto, este efecto hidrodinámico captura las características clave de la superradiación en los sistemas ópticos. Este simulador físico podría proporcionar una plataforma para explorar versiones hidrodinámicas de otros fenómenos superradiativos de emisión de partículas.
Referencias:
V. Frumkin et al. (2023) Superradiant droplet emission from parametrically excited cavities Phys. Rev. Lett. doi: 10.1103/PhysRevLett.130.064002.
Ryan Wilkinson (2023) A Hydrodynamic Version of Superradiance Physics 16, s16
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un simulador hidrodinámico de superradiación se ha escrito en Cuaderno de Cultura Científica.
¿Por qué, a veces, la somnolencia después de comer?
 Imagen: Piyapong Saydaung / Pixabay
Imagen: Piyapong Saydaung / PixabayUn día, como otro cualquiera, te enfrentas a la jornada con la voluntad e ilusión de que sea especialmente productivo y así terminar una buena cantidad de tareas pendientes porque tú lo vales. Pasan las horas y vas sacando faena adelante, lo que te motiva aún más. Llega la hora de comer y te decides a ingerir un menú contundente porque, al fin y al cabo, te lo has ganado y tienes un apetito voraz. Y ahí se termina la racha productiva. Cuando pasan entre 30 y 60 minutos tras la generosa comida te invade un aplastante sopor y la concentración y la motivación que te embargaban desaparecen de forma fulminante. Bienvenido a la somnolencia postprandial.
La somnolencia postprandial o, como dicen los anglosajones, el «coma alimentario», es un fenómeno muy frecuente que no solo ocurre en los seres humanos, sino que también está documentado en múltiples especies animales, desde gatos, perros y ratones hasta moscas de la fruta y gusanos. Este estado, que suele durar entre una y dos horas, se caracteriza por la presencia de sueño, cansancio, pesadez y de estar «bajo de energías», además de dificultad para concentrarse. Estudios en humanos han observado cambios en la actividad cerebral, registrada mediante electroencefalografía, durante esta fase.
A pesar de ser algo tan cotidiano, lo cierto es que no está claro qué mecanismos provocan este estado de sopor tras las comidas. Para la medicina, esta reacción fisiológica no deja de ser una curiosidad y, por ello, son relativamente pocos los estudios que se han centrado en ella. No se trata de algo excepcional, ocurre algo similar con el hipo y el bostezo, cuyas causas también se desconocen y existen múltiples hipótesis al respecto.
Entre lo poco que sabemos sobre la somnolencia postprandial hay algunos hechos que sí están bastante claros: su aparición y magnitud depende de numerosas variables como la cantidad de comida ingerida y las característica de esta. Además, cada persona tiene una susceptibilidad diferente a «sufrir» este estado.
Por otro lado, no es cierto que una posible causa para esta somnolencia sea un flujo sanguíneo menor al cerebro por un incremento de la irrigación en el aparato digestivo. Aunque esta idea siga persistiendo en la actualidad, lo cierto es que el aporte sanguíneo al cerebro está regulado de forma precisa en todo momento y no se observan cambios significativos en este tras la ingestión de comidas. En su lugar, lo que ocurre es que hay un ligero descenso del flujo sanguíneo de los músculos esqueléticos, para que llegue más sangre al aparato digestivo en sus tiempos de mayor actividad.
Las hipótesis sobre las posibles causas detrás de la somnolencia postprandial son variadas, pero su validación científica en humanos ha sido entre escasa y nula, por lo que, a día de hoy, no es posible saber su origen. Las explicaciones que más respaldo tienen en la actualidad son las siguientes:
- El sueño y la sensación de baja energía serían unos de los muchos efectos del sistema nervioso parasimpático y la inhibición del simpático tras la ingesta de alimentos. Estos sistemas autónomos se encargan de controlar multitud de procesos involuntarios: respiración, circulación sanguínea, digestión de alimentos, función sexual, excreción de desechos, estado de alerta… El parasimpático, activado a través del nervio vago tras las comidas, causaría sueño, además de todos sus efectos bien conocidos: potenciar los movimientos intestinales (peristaltismo intestinal), relajar las válvulas gastrointestinales (esfínteres), estimular la salivación y la liberación de diversas moléculas implicadas en la digestión y absorción de nutrientes (insulina, gastrina, lipasas (enzimas que metaboliza grasas) secretina…), entre otras tareas.
- La liberación de una o varias hormonas/neurotransmisores después de comer (melatonina, adenosina, serotonina u otras) provocaría sueño al modular la actividad de ciertas regiones cerebrales como el hipotálamo, que está involucrado en la regulación de los ciclos de vigilia y sueño. La liberación de estas moléculas se produciría como consecuencia del incremento de glucosa en sangre tras la ingestión de alimentos. Las hormonas causarían la inhibición de unas neuronas específicas del hipotálamo llamadas orexigénicas (que provocan ganas de comer), lo que llevaría a una diminución del estado de alerta y a experimentar sueño.
Quizás ambos mecanismos podrían estar participando en la somnolencia postprandial de forma coordinada, junto con la posible influencia de los ritmos circadianos que llevan a un aumento de la melatonina (una hormona que estimula el sueño) y de la temperatura corporal justo en las horas posteriores a la comida. La participación conjunta de todos estos mecanismos no sería ninguna sorpresa si se considera la gran interconexión funcional que existe entre los diferentes elementos que componen el sistema nervioso. La inducción del sueño sería una forma de priorizar la función digestiva, frente a otros procesos o actividades del organismo.
En cualquier caso, sea cual sea el mecanismo que provoca el sopor tras las comidas, se recomienda no darse grandes comilonas y evitar el consumo de alcohol para reducir el riesgo de que aparezca. Varias investigaciones en personas han observado que la somnolencia postprandial surge con más frecuencia entre aquellos que comen más. Por otro lado, salir a dar un paseo tras la comida estimula el sistema nervioso simpático, lo que podría reducir los efectos soporíferos de la comida. Claro que si nos queremos rendir a los efectos de la somnolencia postprandial, una buena siesta (de entre 20 y 30 minutos) puede ser también una excelente opción para descansar y retomar el día con fuerzas renovadas.
Para saber más:
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo ¿Por qué, a veces, la somnolencia después de comer? se ha escrito en Cuaderno de Cultura Científica.
Media, mediana y moda
 Foto: Pop & Zebra / Unsplash
Foto: Pop & Zebra / UnsplashSegún los datos del estudio de estructura salarial que realiza el Instituto Nacional de Estadística (INE) en España, de media el salario en 2020 era de 25 165 € (en bruto, considerando los salarios a tiempo completo). Si eso implicara que la mayoría de los trabajadores a tiempo completo cobran esa cantidad, podríamos estar razonablemente satisfechos.
Lamentablemente, no es esa la realidad. El dato de 25 165 euros es la media. Pero si analizamos el salario mediano, es decir, aquel que se sitúa justo en la mitad del conjunto ordenado de salarios, fue de 20 920 €, sensiblemente más bajo.
Es más, el salario más frecuente (el salario modal o la moda de los salarios, otro valor estadístico) fue de 18 490 €. Es decir, lo más habitual es cobrar casi un tercio menos que el salario medio. ¡Hay casi 7 000 € de diferencia entre el salario más frecuente y el salario medio!
Media, mediana o moda, ¿cuál es mejor?Cuando analizamos unos datos, ya sean de empleo, de salud o de consumo energético, deberíamos elegir el valor estadístico que mejor los represente. Pero para hacerlo es importante comprender conceptualmente el significado de cada una de las tres medidas de centralización que acabamos de utilizar: la media, la mediana y la moda.
- La media es el valor que resultaría de repartir equitativamente el total observado entre los individuos de la muestra.
- La mediana es el valor que divide la secuencia ordenada de observaciones en dos partes iguales.
- La moda es el valor más frecuente.
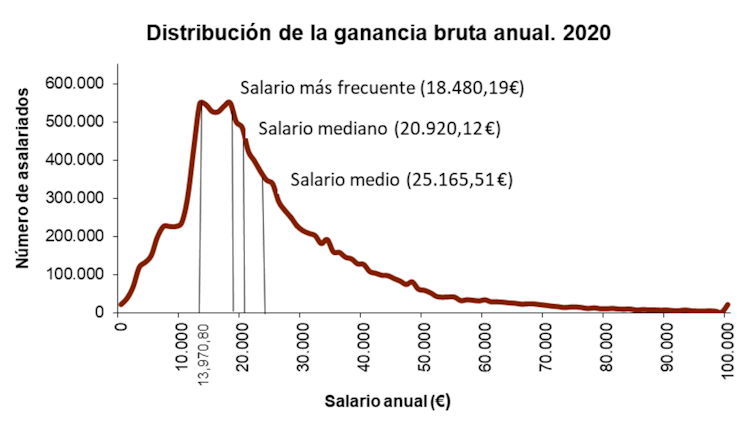 Salario medio, salario más frecuente y salario mediano en España en el año 2020.
Salario medio, salario más frecuente y salario mediano en España en el año 2020.INE, Author provided
Además, conviene tener presente que para interpretar un conjunto de datos no solo cuenta su tendencia central: también hay que conocer su distribución. ¿Se parecen mucho los valores entre sí? ¿O hay valores muy distintos del valor central? Aquí es donde entran en juego otro tipo de medidas, las de dispersión, que nos informan de la lejanía o cercanía de los datos entre ellos y con respecto a alguna de las medidas centrales.
Cuando los valores extremos distorsionan los datosExplicar por qué hay casi 7 000 € de diferencia entre el salario más frecuente y el salario medio es sencillo si hacemos un paralelismo con otra variable más sencilla de interpretar, como es el número de mascotas por familia.
Imaginemos que se estudia el número de mascotas en el hogar entre el personal de una oficina. La muestra nos ofrece 3 personas sin mascotas, 3 personas que tienen 1 mascota y otras 3 personas con 2 mascotas. En ese caso, dado que hay 9 observaciones, la mediana es la que ocupa la 5ª posición en la secuencia ordenada de valores:
0, 0, 0, 1, >1
Es decir que la mediana es 1, porque nos deja 4 valores por debajo y otros tantos por encima, lo cual parece un valor bastante central. Coincide con la media, que resulta ser: (0+0+0+1+1+1+2+2+2)/9 = 1
Pero imaginemos que cambiamos a uno de los trabajadores con 2 mascotas por otro que tenga 20 mascotas. Es un numero elevado, sí, pero podemos pensar en que tiene, por ejemplo, peces. En ese caso, la media pasa a ser 3: (0+0+0+1+1+1+2+2+20)/9 = 3
La presencia de ese único valor anómalo (20 mascotas) ha triplicado la media. Ya no parece razonable pensar que el empleado típico tiene 3 mascotas, a la vista de la distribución. Sin embargo, ¿qué ha pasado con la mediana? Pues, con independencia de que el mayor valor haya pasado de ser 2 a ser 20, el valor 1 sigue ocupando la posición 5ª: 0, 0, 0, 1, 1, 1, 2, 2, 20
Por lo tanto, la mediana no ha cambiado por la presencia de ese valor anómalo.
Con ese ejemplo comprobamos la sensibilidad de la media a la presencia de valores anómalos o extremos (los llamados outliers en estadística), así como la mayor robustez de la mediana ante esa situación. Por este motivo, la media puede no ser una buena medida de tendencia central cuando en la muestra hay valores mucho mayores o mucho menores que el resto.
Cuando buscamos el valor central de distribuciones fuertemente asimétricas tiene más sentido tomar de referencia la mediana, como en los ejemplos anteriores del salario y el número de mascotas, y en general para variables socioeconómicas.
La mediana también suele ser una medida más fiel a la realidad central de unos datos cuando se estudia la supervivencia a una enfermedad o la respuesta a un medicamento, ya que puede haber individuos con respuestas muy anómalas (en estos casos, una supervivencia extraordinariamente longeva o una reacción muy adversa al medicamento).
Otras veces, la moda, a pesar de ser una medida que en muchas ocasiones no es muy informativa, tiene un valor fácilmente interpretable cuando entendemos el centro como la medida típica. El ejemplo inicial del salario nos podría servir: ¿cuál es el salario bruto más habitual en España? La respuesta sería la moda (18 490 €).
La media está sobrevaloradaSocialmente se le otorga excesivo valor a la media, algo que está relacionado con el denominado espejismo de proporcionalidad (ilusion of linearity, en inglés). Es decir, la tendencia a creer que lo proporcional es lo habitual, incluso lo justo.
Esta idea se refuerza desde la etapa escolar, cuando todas las calificaciones numéricas se obtienen calculando la nota media: socialmente se asume como la nota más “justa” o al menos la más indiscutible. Aunque no tiene por qué ser así. Pensemos en el carné de conducir: se repite el examen hasta que se supera, no se hace la media de los dos primeros intentos fallidos con el tercero exitoso. Ni desde luego se hace la media de las primeras clases en las que nos sentamos en el coche de la autoescuela con el día que aprobamos el carné.
Sin embargo, asumimos normal que tres controles realizados durante un trimestre hagan media con uno realizado al final. Y asumimos como indiscutible que si una estudiante obtiene en sucesivos exámenes 2, 9, 9 y 9, su nota media sea un 7,25. Si considerásemos la mediana como calificación más justa, obtendría un 9.
Exijamos gráficas para entender los datosLo que parece indiscutible es que, cuando únicamente proporcionamos la información de una medida central (ya sea moda, mediana o media), corremos el riesgo de que quien reciba la información construya una imagen mental que sitúe muchos, la mayoría o casi todos los valores de la variable en torno a ese valor central. Asimilando, por ejemplo, que “la mayoría de las personas en España tienen un salario bruto anual alrededor de 25 000 €”, cosa absolutamente falsa.
No solo es necesario saber dónde está el centro de los datos, también cuánto se separan los valores entre sí y respecto a la medida central (la dispersión) y de qué forma se disponen (más o menos simétrica, más o menos plana, etc.).
Por este motivo, resulta fundamental la visualización de los datos para hacerse una idea más aproximada a la realidad. En definitiva: desconfíen y pidan más información cuando les hablen solo de una media.![]()
Sobre el autor: Luis José Rodríguez Muniz, Catedrático del departamento de Estadística e Investigación Operativa y Didáctica de la Matemática, Universidad de Oviedo
Este artículo fue publicado originalmente en The Conversation. Artículo original.
Para saber más:
El artículo Media, mediana y moda se ha escrito en Cuaderno de Cultura Científica.
Género, identidad y estereotipos en la comunicación de la ciencia y la tecnología
Conforme van creciendo, niños y niñas adquieren una comprensión cada vez más sofisticada del entorno social que les rodea y, a la vez, desarrollan un sentido de su propia identidad, especialmente en relación con las características que los unen y los diferencian de los demás. Tanto la comprensión de la realidad social como el desarrollo de su identidad están muy condicionadas por la pertenencia a un grupo.

Algunas de las características del grupo al que se pertenece derivan de o, directamente, son estereotipos sin bases objetivas. Por otro lado, dado que la creencia en estereotipos puede condicionar las expectativas acerca de lo que se puede hacer y lo que no, el sentido de pertenencia a un grupo y la identidad que confiere este condicionan esas expectativas en muchos casos. Los estereotipos, de ese modo, dan forma a las autopercepciones académicas, incluidas las creencias en la capacidad propia para cursar ciertos estudios y desempeñar ciertas profesiones, y las relativas al sentido de pertenencia al grupo de quienes optan por ciertos estudios o de quienes no lo hacen.
Es importante, por tanto, entender dónde y de qué forma surgen los estereotipos citados y cómo se transmiten. Que sean adquiridos por chicos y chicas en el entorno familiar no quiere decir que surjan de forma espontánea. No son consecuencia de una revelación ni inspiración sobrenatural. Las familias no viven en un vacío social. Los estereotipos tienen carácter cultural y, para empezar, pueden surgir en el seno de la comunidad científica, por la forma en que se generan nuevas nociones y cómo, después, se difunden hacia otras esferas. Y se transmiten a través del entorno familiar, los grupos de amigos y amigas, la escuela, y los medios de comunicación. Estos reproducen los esquemas vigentes en la sociedad a través de la información que difunden, el tratamiento que hacen de la perspectiva de género o la representación e imágenes que emiten y proponen. Esta reproducción transmite los estereotipos y consolida determinadas formas de actuar acordes con aquellos.
Además de la génesis y transmisión de los estereotipos, es importante conocer de qué forma, mediante qué mecanismos se difunden. Hay multitud de señales sutiles cuya transmisión contribuye a configurar las identidades a que me he referido antes. Por ejemplo, el lenguaje, más allá de su carácter incluyente o excluyente –que es en lo que más nos fijamos o en lo único en que reparamos–, contiene claves que dan forma a la identidad y la dotan de atributos (supuestos) con consecuencias de largo alcance. Y las imágenes tampoco son neutras. Lenguaje verbal y lenguaje visual son las dos herramientas de comunicación mediante las que, de forma sutil, se pueden transmitir preconcepciones y modelos estereotipados. Lo dicho no es importante solo para quienes se dedican a la comunicación de forma profesional, el personal investigador muchas veces no es consciente de que tan importante o más que el valor denotativo de lo que se afirma o niega, pueden serlo sus connotaciones. Todo ello influye de forma determinante en lo que se transmite y, por lo tanto, en los valores que se difunden y promueven.
El pasado día 9 de febrero, y en el marco de los actos para conmemorar el Día Internacional de la Mujer y la Niña en la Ciencia, la Cátedra de Cultura Científica de la UPV/EHU celebró una jornada bajo el título Género y Comunicación de la Ciencia. Hasta ahora, hemos celebrado esa efeméride difundiendo vídeos mediante los que hemos intentado llamar la atención y concienciar acerca de las desigualdades entre chicos y chicas en el acceso a ciertos estudios científico-tecnológicos y en el progreso en la carrera científica por parte de hombres y mujeres.
Después de los cinco vídeos difundidos durante el lustro anterior, hemos decidido dar un salto y buscar la forma de llevar a la práctica acciones que contribuyan de forma efectiva a combatir esas desigualdades. Ese ha sido el objetivo de la jornada, aportar datos, valorar la situación y proponer remedios en el terreno de la comunicación científica. Parte de los estereotipos que dibujan diferentes predisposiciones, actitudes y aptitudes en chicos y chicas para con la ciencia, las matemáticas y la tecnología tiene su origen en la forma en que esos contenidos se generan en la comunidad científica y se transmiten a la sociedad a través de los medios de comunicación. Estos y la comunicación en sí pueden consolidar los esquemas de género predominantes en la sociedad o pueden inducir al cambio. El cambio exige prescindir de estereotipos y roles consolidados que no se compadecen con la realidad, y comunicar el conocimiento e información de manera que su transmisión sea coherente con la idea de la igualdad esencial de hombres y mujeres en su relación – como estudiantes o como profesionales– con la ciencia y la tecnología. Por eso hemos pensado que merecía la pena indagar acerca de todo ello y tratar de llegar a conclusiones prácticas. Hemos querido pasar del binomio reflexión y denuncia, a otro binomio diferente: reflexión y acción.
No quiero terminar sin recordar, como cada 11 de febrero, que para la Cátedra de Cultura Científica de la UPV/EHU todos los del año son Día Internacional de la Mujer y la Niña en la Ciencia, como muestra el hecho de que Mujeres con Ciencia publique un artículo todos los días del año.
Referencias:- Angulo, E. (2020). El estereotipo de las mujeres en la ciencia. Mujeres con Ciencia.
- García-Jimenez, L., Torrado-Morales, S., eta Díaz Tomás, J.M. (2022). El rol de la mujer en la ciencia y la docencia en comunicación: análisis a partir de los programas universitarios en España. Revista de comunicación, 21 (2), 91-112. DOI: https://doi.org/10.26441/RC21.2-2022-A5
- Gómez-Escalonilla, Gloria eta Izquierdo-Iranzo, Patricia (2021). Género y comunicacón en revistas y congresos científicos. Comunicación y género, 5 (1), 1-11. DOI: https://doi.org/10.5209/cgen.77148
- Master, A. (2021). Gender Stereotypes Influence Children´s STEM Motivation. Child Dev Perspect, 15, 203-210. DOI: https://doi.org/10.1111/cdep.12424
- Master, A., Cheryan, S., eta Meltzoff, A. N. (2016). Computing whether she belongs: Stereotypes undermine girls’ interest and sense of belonging in computer science. Journal of Educational Psychology, 108, 424– 437. DOI: https://doi.org/10.1037/edu0000061
- Master, A., eta Meltzoff, A. N. (2020). Cultural stereotypes and sense of belonging contribute to gender gaps in STEM. International Journal of Gender, Science, and Technology, 12, 152– 198.
- Master, A., Meltzoff, A. N. eta Cheryan, S. (2021). Gender stereotypes about interests start early and cause gender disparities in computer science and engineering. Proceedings of the National Academy of Sciences, 118 (48), e2100030118. DOI: https://doi.org/10.1073/pnas.2100030118
- Napp, C., Breda, T. (2022). The stereotype that girls lack talent: A worldwide investigation. Science Advances 8 (10). DOI: 10.1126/sciadv.abm3689
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
Más sobre el 11 de febrero- Juan Ignacio Pérez, Hoy es el día de la mujer y la niña en la ciencia, todos lo son, 11 febrero 2017.
- Juan Ignacio Pérez, No es una percepción, 11 febrero 2018.
- Juan Ignacio Pérez, Mi hija quiere ser ingeniera, 11 febrero 2019.
- Juan Ignacio Pérez, Motivos para un día internacional, 11 de febrero 2020.
- Juan Ignacio Pérez, La historia de June Almeida, 11 de febrero de 2021.
- Juan Ignacio Pérez, Regla de modestia, 11 de febrero de 2022.
El artículo Género, identidad y estereotipos en la comunicación de la ciencia y la tecnología se ha escrito en Cuaderno de Cultura Científica.
Los límites de los test de ADN para la predicción de enfermedades
 Chis Hemsworth fotografiado durante la promoción de Thor: Ragnarok. Foto: Mark Metcalfe/Getty Images for Disney
Chis Hemsworth fotografiado durante la promoción de Thor: Ragnarok. Foto: Mark Metcalfe/Getty Images for DisneyHace poco, el actor que encarna a Thor en las películas de la Marvel, Chris Hemsworth, se sometió a un test de ADN que supuestamente le informó de sus altas probabilidades de sufrir alzhéimer.
Dicho así, podríamos pensar que estamos ante una predicción devastadora, una espada de Damocles sobre la cabeza del pobre Chris, condenado sin remisión a padecer en el futuro una grave enfermedad que no sabemos prevenir y para la que hoy en día no existe cura.
La realidad es un poco distinta. Es cierto que las personas que como Chris poseen dos copias de la variante e4 en el gen APOE pueden tener hasta 15 veces más riesgo de desarrollar la dolencia neurogenerativa. Pero resulta imposible saber con certeza si acabará padeciéndola.
Esto es así porque se trata de una enfermedad compleja. En la susceptibilidad contribuyen muchas otras regiones del genoma, junto con factores ambientales y de estilo de vida que pueden modificar ese riesgo. La genética aporta solamente una parte de las probabilidades. Como intentaremos explicar, todavía queda mucho por conocer para poder hacer una predicción fiable en esta y otras afecciones complejas.
¿Hay pruebas genéticas 100 % fiables?Desde la Antigüedad sabemos que los rasgos físicos y las enfermedades se agrupan en las familias. Los genes que heredamos de nuestros progenitores, junto con el ambiente compartido del hogar influyen en prácticamente cualquier dolencia, como el alzhéimer, pero también el cáncer o incluso infecciones graves.
Desde que en 1983 se asociara por primera vez un marcador genético con la enfermedad de Huntington, hoy en día se conoce el gen responsable de miles de patologías hereditarias para las que existe una relación directa entre una mutación en un gen y la enfermedad, en virtud de lo establecido por las leyes de Mendel.
Son enfermedades poco frecuentes, pero existen pruebas genéticas específicas para casi todas ellas, y se realizan en enfermos y familiares de forma rutinaria en muchas especialidades médicas. También se conocen formas raras de alzhéimer de inicio temprano (entre los 30 y 60 años), causadas directamente por mutaciones en los genes APP, PSEN1 o PSEN2.
A pesar de la certeza de los test de ADN de estas dolencias inusuales, estos siempre deben acompañarse de asesoramiento clínico experto. Se deben contextualizar explicando previamente la naturaleza de la prueba y las consecuencias médicas, familiares, psicológicas e incluso socioeconómicas de un resultado positivo.
¿Qué peso tiene la genética en las enfermedades más comunes?En las últimas dos décadas se ha investigado mucho sobre la contribución del componente genético a enfermedades más frecuentes pero más complejas, como las formas comunes de alzhéimer o los trastornos cardiovasculares, la diabetes, la artritis y la esquizofrenia.
En ellas, la agrupación familiar es más difusa y también participan factores ambientales y de estilo de vida. No existe una mutación directa que pueda causar estas patologías. Se trata de una mayor o menor susceptibilidad genética debida a variantes del genoma comunes en la población: los llamados polimorfismos genéticos.
Estudios de esta variabilidad genética común en numerosos pacientes y controles han identificado cientos de miles de polimorfismos que se asocian con el riesgo de desarrollar más de 5 000 enfermedades o rasgos complejos. La importancia de la genética está clara en todos ellos, pero la aportación de cada polimorfismo al riesgo individual es muy pequeña.
Además, en la gran mayoría de los casos, los mecanismos por los que estas variantes aumentan la predisposición a padecer una patología son desconocidos. A esto se añade el desconocimiento de los factores ambientales que la desencadenan al incidir sobre el riesgo genético. Por eso, los expertos desaconsejan la utilización clínica rutinaria de este conocimiento.
Entonces, ¿sirven de algo los test de ADN?A día de hoy, los test de ADN en el caso de una enfermedad compleja como el alzhéimer no tienen utilidad para confirmar un diagnóstico, ni mucho menos para predecir lo que sucederá en el futuro. Probablemente nunca exista una prueba genética infalible para este tipo de dolencias.
No obstante, conocer los factores genéticos de estas patologías tiene un enorme valor. En un contexto de investigación, es posible calcular una puntuación de riesgo genético de padecer la enfermedad para cada participante del estudio. Posteriormente, vigilar a los individuos agrupados en función de su mayor o menor riesgo nos ayudará a asociar los polimorfismos con cambios tempranos que preceden a la dolencia.
Estos cambios podrán utilizarse como marcadores para realizar un diagnóstico más certero, e incluso nos ayudarán a encontrar formas de retrasarlos o revertirlos antes de que aparezcan los síntomas más graves. Seremos capaces de diseñar mejores ensayos clínicos para nuevos fármacos, así como programas de asesoramiento y seguimiento más precisos y eficientes para cada grupo de riesgo.
La predisposición genética de Chris Hemsworth de desarrollar alzhéimer no se puede cambiar. Sus probabilidades de acabar padeciéndolo sí pueden hacerlo, porque dependen de lo que avancemos en el conocimiento de esta enfermedad compleja antes de que cumpla los 65 años.![]()
Sobre el autor: Jose Ramón Bilbao Catalá es profesor agregado de Genética Médica, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Para saber más:
Sobre la predisposición genética a padecer enfermedades
Las bases genéticas de las enfermedades digestivas
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Los límites de los test de ADN para la predicción de enfermedades se ha escrito en Cuaderno de Cultura Científica.
Isótopos y variabilidad climática
 Foto: Aarom Ore / Unsplash
Foto: Aarom Ore / UnsplashNos han enseñado desde chicos, que los elementos químicos existen, conforman toda la materia que conocemos, que podemos ver, tocar y la que no. Nos han dicho que el oxígeno es fundamental para la vida como la conocemos hoy, que es un elemento que podemos ver en la tabla periódica, que no tiene olor ni color, que tiene 8 electrones, 8 neutrones y 8 protones; y que así es como existe en la naturaleza. Sin embargo, eso no es del todo cierto, ya que muchos elementos químicos tienen una “contraparte” (o varias), como si tuvieran un gemelo con el que comparten prácticamente el 100 % de sus características, pero no llegan al ser del todo iguales (p ej. los gemelos humanos pueden llegar a variar ligeramente en talla, color de piel, peso). En el caso de los elementos químicos, es eso último exactamente lo que diferencia ambas “contrapartes”, que comparten las mismas características, pero tienen una diferencia, su masa.
Sin embargo, este “peso” no se suele expresar en gramos o kilogramos, más bien se calcula según el número de protones y de neutrones que tiene cada átomo (los componentes del núcleo). Para continuar con el oxígeno, que, si sumamos el número de neutrones y de protones obtenemos el número 16, siendo este al que llamaremos de ahora en adelante como “oxígeno dieciséis”. Este oxígeno dieciséis tiene su gemelo, el “oxígeno dieciocho” (sí, como los androides 16 y 18 de Dragon Ball), con 8 protones y 10 neutrones, siendo el dieciocho el más pesado de los dos. Lo sorprendente es que ambos tipos de oxígeno existen en la naturaleza y así ocurre con varios elementos en la naturaleza, a los que se denominan isótopo: del griego isos = igual, y topos = lugar; debido a que su número atómico es el mismo (igual lugar en la tabla periódica), pero tienen un peso atómico diferente (diferente número de neutrones).
Ahora, se preguntarán, si es que existe, ¿por qué nunca he oído hablar de él? Bueno, la respuesta a la pregunta es: así como la probabilidad de encontrar gemelos entre los humanos es baja, la de encontrar isótopos más pesados es baja y, sin embargo, están presentes en la naturaleza. Así, se suele nombrar únicamente al oxígeno dieciséis, ya que es la forma en la que se encuentra el 99,75 % del oxígeno, mientras que el oxígeno dieciocho únicamente corresponde al 0,20 %. Así, si se quiere ser más específico, por cada 100 átomos de oxígeno en la naturaleza, menos del 1 % corresponderá al oxígeno dieciocho. Muy poco ¿verdad? Bueno, esta proporción puede cambiar, pero ¿cómo?
Todos los procesos químicos y físicos que existen en la naturaleza y que participen los elementos químicos (todos) son como un filtro, en el que se tiene inicialmente una cantidad de oxígeno dieciséis y oxígeno dieciocho; pero en el filtro, de acuerdo con sus características va a retener una cantidad mayor o menor de uno de los isótopos, por lo tanto, después que el oxígeno pase por un proceso (filtro), se obtendrán cantidades diferentes a las originales. A esto, se le denomina fraccionamiento.
Así, los científicos han estudiado cómo los procesos físicos y químicos afectan de forma diferente este fraccionamiento. Un ejemplo para ilustrar esto es cómo la lluvia y la evaporación del agua, funcionan como filtro para que ocurra el fraccionamiento del oxígeno presente en el agua: el isótopo más ligero se va a evaporar más fácilmente, quedando el isótopo más pesado en el agua líquida, ¡sólo por el hecho de ser más pesado! Fascinante ¿no?
Debido a esta relación y, si es posible conocer cómo varía la proporción de los isótopos, entonces ¿es posible inferir qué procesos ocurrieron para que se diera X valor isotópico a partir del valor de fraccionamiento que ocurre en los isótopos? La respuesta es: ¡sí! Estudiando cómo varía el comportamiento de los isótopos y cuáles son los factores físicos y químicos que modulan su variación, es posible hacer inferencias de qué ocurrió en casi cualquier instante del tiempo y el espacio.
Pero ¿cómo? El fraccionamiento del oxígeno presenta variaciones a lo largo del ciclo del agua y varía en asociación con la temperatura. Cuando hay mucha evaporación, el oxígeno dieciséis al ser más liviano, se liberará del agua líquida de forma más rápida; así, el agua en las nubes que recién se forman, se encuentran con una mayor proporción del isótopo más ligero que las condiciones
originales. Por otro lado, al perder el oxigeno dieciséis el agua de donde provino el agua evaporada quedará con mayor proporción de oxígeno dieciocho. ¡Y sí! Estas proporciones son medibles, lo que hace una herramienta muy útil para evaluar eventos en los que hubo variaciones de temperatura, lluvias, cambios en las concentraciones de gases como el dióxido de carbono y ¡cambios en el clima del planeta!
Sin embargo, antes de continuar en cómo pueden ayudarnos los isótopos a entender el clima del planeta es necesario dejar claro qué es el clima y otros conceptos subyacentes que se asocian hoy en día con el concepto de “clima”, ya que suelen usarse de forma unilateral, dejando la impresión de que todo lo asociado al concepto de “clima” hace referencia a lo mismo. Para ilustrarlo con un ejemplo: se escucha personas, incluso reconocidos investigadores en un tema no ajeno al estudio del clima, pero sí uno en el que no son expertos, así como a personas ajenas a las precisiones de los conceptos, que los efectos de eventos de El Niño–Oscilación del Sur (ENOS) en la temperatura, lluvias y otros procesos en todo el planeta, son un resultado del cambio climático. Y, no lo son. Ya que, si bien puede llegar a ser cierto, no es del todo preciso. De igual forma, se escucha a muchos decir: “no existe un cambio en el clima, porque si hubiese un cambio en el clima, por qué seguimos teniendo invierno y verano como siempre los hemos tenido”.
¿Por qué? Si vamos a la definición más general (pero realmente precisa) del concepto “clima” se refiere a las condiciones de un determinado lugar por un periodo prolongado de tiempo. Para el sistema climático de la tierra, de acuerdo a la Organización Meteorológica Mundial (OMM), son condiciones que perduran a lo largo de por lo menos cientos y miles de años, conservando un rango de valores determinado para variables como concentraciones de gases, temperatura, precipitaciones, etc. Por otro lado, si bien estos rangos se mantienen estables a escalas espaciotemporales importantes, ello no implica que no varíen. Las variaciones en dicho sistema pueden ir desde a escalas de días, en las que la temperatura (por ejemplo) pueden variar y tener máximos posterior a la máxima radiación solar recibida por la tierra (~12 horas) y mínimas cuando no incide radiación en una región localizada de la tierra; a variaciones generadas por otros eventos de escalas pequeñas como tormentas y ciclones tropicales (que son elementos que se encuentran de forma “natural” en el sistema de la tierra), que son estudiados por la meteorología (Figura 1).
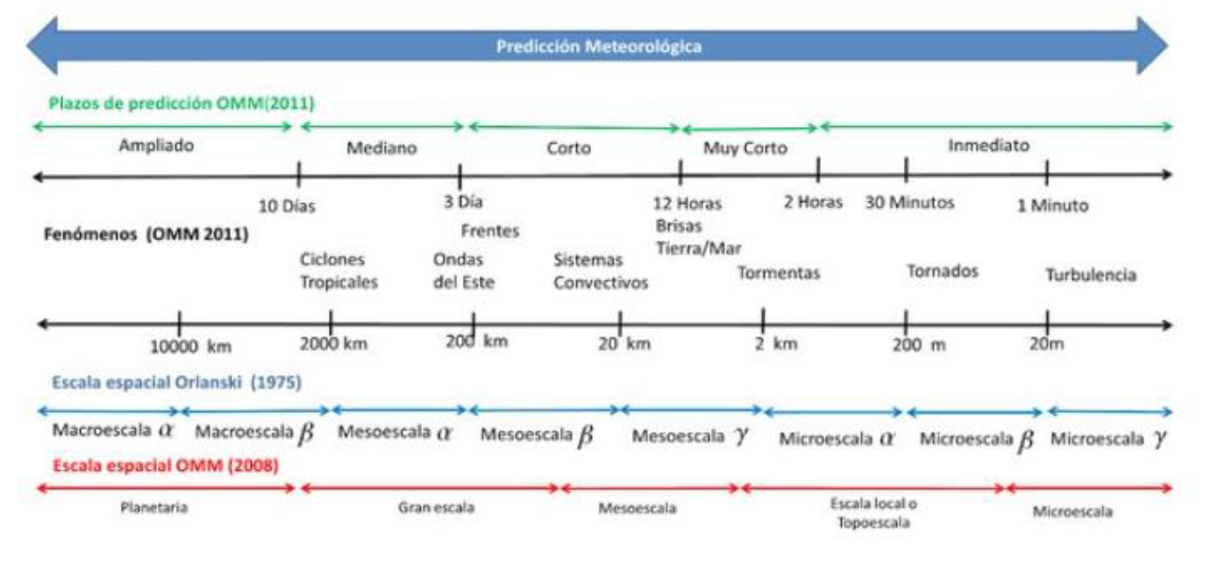 Figura 1. Escalas de variación y predicción meteorológica. Fuente: Díaz G., Diana C.. (2017). Modelado y Simulación de Sistemas Climáticos: Desde la escala global hasta los microclimas.
Figura 1. Escalas de variación y predicción meteorológica. Fuente: Díaz G., Diana C.. (2017). Modelado y Simulación de Sistemas Climáticos: Desde la escala global hasta los microclimas. Por otro lado, existen otros eventos de variabilidad climática que también corresponden a una variación natural del sistema, que suele darse a manera de oscilaciones. Dentro de estas escalas, se encuentran las estaciones como las conocemos, que son variaciones que se dan a lo largo del año. Así mismo, más allá de un año, existen eventos (una vez más, naturales), que generan cambios en las variables como la precipitación y la temperatura; dentro de estos se encuentra el anteriormente mencionado ENOS que genera variaciones en el sistema climático a escala interanual, cada 2–7 años aproximadamente. Así mismo, por mencionar otro evento de variabilidad climática se encuentra la Oscilación Decadal del Pacífico, que, así como las otras, genera fluctuaciones de variables atmosféricas, pero esta vez a escalas superiores a los 10 años (Figura 2).
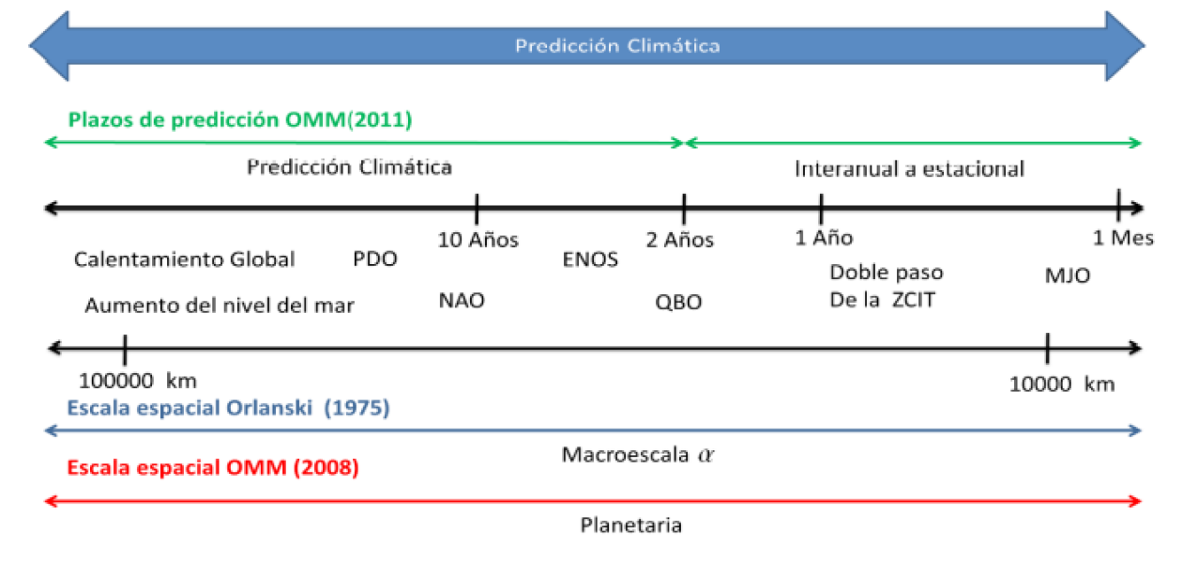 Figura 2. Escalas de variabilidad y predicción climática. Fuente: Díaz G., Diana C.. (2017). Modelado y Simulación de Sistemas Climáticos: Desde la escala global hasta los microclimas.
Figura 2. Escalas de variabilidad y predicción climática. Fuente: Díaz G., Diana C.. (2017). Modelado y Simulación de Sistemas Climáticos: Desde la escala global hasta los microclimas.
Volviendo a los isótopos, son una herramienta que por sus características nos permite evidenciar cambios en las condiciones a diferentes escalas espaciotemporales. Un ejemplo de esto es el estudio de los valores de oxígeno dieciséis en las matrices de crecimiento de los corales en estudio reciente[1], en donde resaltan que para la isla de Borneo, una región en dónde se ven reflejados los efectos de eventos ENOS en la proporción de isótopos estables en el esqueleto calcáreos con una importante relación con estos valores y los de variables oceánicas y atmosféricas incluyendo la salinidad, temperatura superficial del mar, precipitaciones y descarga de ríos. Demostrando no sólo que el registro de los isótopos permite, al correlacionar efectivamente los valores isotópicos de los variables océano–atmosféricas, sino que existen cambios en los procesos que influyen en el fraccionamiento en matrices de organismos vivos que pueden contener registros de cientos de años.
Y así como el estudio anterior logró correlacionar dichas variables con una matriz de un organismo vivo, es posible hacer un análisis de isótopos con fósiles, obteniendo información no solo de las últimas décadas o centenios, sino de miles de años. Es el caso de otro estudio [2] en el que, haciendo análisis de fósiles de una especie de molusco de Perú, con el fin de observar un registro histórico de un evento de variabilidad interanual (el ENOS) durante el Holoceno. Buscando responder la pregunta si anteriormente hubo una variabilidad espacial del ENOS como la reportada en las últimas décadas, donde se han descrito en el que el cambio en la temperatura en el Pacífico tropical asociado a estos eventos se puede encontrar centrado en el Pacífico Oriental (PO) o en el Pacífico Central (PC) en dónde se señala, debido a la variación de los isótopos de oxígeno que antes de los 8000 años antes y después de los 4000 años, los eventos del ENOS se encontraron dominados por eventos del PO, mientras que una baja variabilidad de isotópica entre los 6700 a 7500 años señalan una posible dominancia de eventos PC, los cuáles se han demostrado tienen diferentes efectos a nivel oceánico y atmosférico, así como diferentes patrones de teleconexión, pudiendo afectar de forma diferente el sistema climático del planeta en el tiempo reciente, dando luz no sólo a cambios generados a nivel temporal, sino demostrando que es una herramienta muy útil para determinar cambios a nivel espacial de eventos de variabilidad climática como el ENOS.
Así, debido a la influencia de factores atmosféricos y oceánicos en los procesos físicos, químicos y biológicos, con un par de ejemplos nos permiten conocer cómo los isótopos son una herramienta muy útil para conocer cómo ha variado el clima del planeta, no solo en escalas de tiempo superiores, sino cómo han variado eventos de variabilidad climática que tienen efecto a nivel intra e interanual en el sistema climático a lo largo de la historia de la tierra y así mismo, poder inferir sobre el futuro de dicho sistema y cómo podría afectar a los ecosistemas y a la humanidad
en los próximos años.
Referencias:
[1] Krawczyk, H., Zinke, J., Browne, N. et al. (2020) Corals reveal ENSO-driven synchrony of climate impacts on both terrestrial and marine ecosystems in northern Borneo. Sci Rep 10, 3678 (2020). doi: 10.1038/s41598-020-60525-1
[2] Matthieu Carré at al. (2014) Holocene history of ENSO variance and asymmetry in the eastern tropical Pacific Science doi: 10.1126/science.1252220
Para saber más:
Testigos del pasado
He visto la Tierra cambiar
Las lapas como indicador paleoclimático de alta resolución
Sobre el autor: Gabriel Gutiérrez es biológo marino por la Universidad Jorge Tadeo Lozano (Colombia) y está especializado en oceanografía
El artículo Isótopos y variabilidad climática se ha escrito en Cuaderno de Cultura Científica.
La espiral de Baravelle
En junio de 2021 la galería virtual CHDF, creada por Sylvain Clot, publicó en su cuenta de Instagram la siguiente imagen, en la cual aparecía una obra de la artista concreta suiza Suzanne Daetwyler (1948).
 Pintura de la artista concreta suiza Suzanne Daetwyler, publicada en la cuenta de Instagram de la galería virtual CHDF/Sylvain Clot
Pintura de la artista concreta suiza Suzanne Daetwyler, publicada en la cuenta de Instagram de la galería virtual CHDF/Sylvain ClotEn esta pintura aparece representado un objeto geométrico que se conoce con el nombre de espiral de Baravelle. Sobre ella vamos a hablar en esta entrada del Cuaderno de Cultura Científica.
Primero, veamos cómo se construye la espiral de Baravelle que aparece en la obra de Suzanne Daetwyler. Se parte de un cuadrado. Después se unen los puntos medios de sus lados consecutivos mediante segmentos rectos, dibujándose así un nuevo cuadrado dentro del anterior, luego más pequeño, pero girado y que forma un rombo. De esta manera el cuadrado original queda dividido en cuatro triángulos isósceles apoyados en los vértices de ese cuadrado y el cuadrado más pequeño, con forma de rombo, que se acaba de crear. A continuación, con el nuevo cuadrado (el rombo de lados iguales) se realiza la misma operación, que da lugar a un nuevo cuadrado más pequeño dentro del anterior, pero en la misma posición que el inicial, junto a cuatro triángulos isósceles apoyados en los vértices del rombo. Y se puede continuar con este procedimiento geométrico tantas veces como se desee, hasta el infinito, obteniéndose una familia encajonada de cuadrados, como en la siguiente imagen, en la que hemos realizado seis veces la anterior construcción.
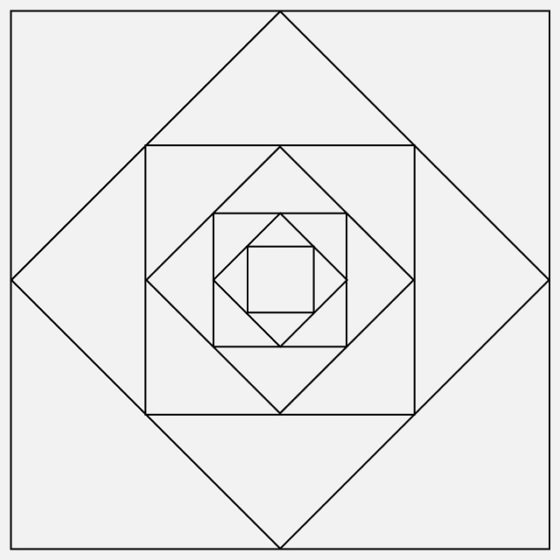
Para obtener la espiral (o espirales) de Baravelle se pintan del mismo color ciertos triángulos isósceles. En concreto, se parte de uno de los triángulos isósceles del cuadrado inicial, los más grandes, y se pinta del mismo color un triángulo isósceles de cada uno de los pasos, es decir, de cada tamaño, pero siempre en una posición girada 45 grados respecto al anterior, para crear la sensación de espiral. Al realizar la construcción geométrica anterior de forma infinita se obtendría la espiral de Baravelle (ideal), aunque normalmente se representa solo una serie finita de pasos. En la siguiente imagen se muestra la espiral de Baravelle pintada en escala de grises (realizada con seis pasos).
 Espiral (o espirales) de Baravelle, pintadas en escala de grises
Espiral (o espirales) de Baravelle, pintadas en escala de grises
El diagrama anterior puede ser considerado una demostración visual (de esas demostraciones sin palabras de las que hemos hablado en más de una ocasión, como en las entradas Pitágoras sin palabras, Matemáticas para ver y tocar, Más matemáticas para ver y tocar, Teoremas geométricos sin palabras: Viviani, Teoremas geométricos sin palabras: Conway, Teoremas geométricos sin palabras: Herón o Teoremas geométricos sin palabras: Snover) de la suma de una serie infinita. En concreto, si nos fijamos en la espiral formada por los triángulos negros y consideramos que el cuadrado inicial tiene área igual a 1, entonces el triángulo isósceles negro más grande tiene un área de 1/8, ya que podemos dividir la superficie del cuadrado más grande en 8 copias de ese triángulo (las cuatro copias de las esquinas, más las cuatro copias en las que se puede dividir el rombo, que junto a los cuatro triángulos anteriores ocupan el cuadrado grande), el segundo (en tamaño) triángulo isósceles negro tiene un área de 1/16, ya que necesitamos 8 triángulos isósceles para llenar el rombo, que es la mitad del cuadrado original (o equivalentemente, necesitamos 16 triángulos isósceles de este segundo tamaño para cubrir el cuadrado grande), el tercer triángulo isósceles negro tiene un área de 1/32, y así podemos continuar hasta el infinito. Como así queda cubierta la cuarta parte del cuadrado grande (la espiral negra) se deduce la serie infinita siguiente:
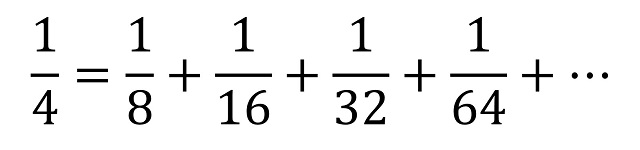
Equivalentemente, si pensamos en las cuatro espirales, que cubren todo el cuadrado original de área 1, tenemos la serie:
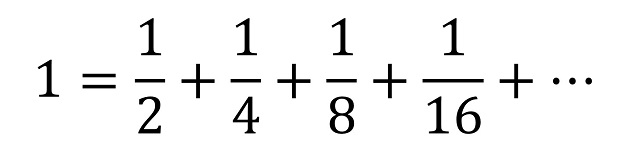
Otro artista que ha hecho uso de la anterior construcción geométrica en sus obras de arte ha sido el constructivista alemán Kunibert Fritz (1937). Desde la década de 1960 este artista ha trabajado con la construcción geométrica asociada a la llamada espiral de Baravelle, pero dando color a los triángulos de diferentes formas y creando diferentes estructuras asociadas. En la siguiente imagen se muestra una vista de la exposición Kunibert Fritz: Unidad en la dualidad en el Museo Vasarely de Budapest (17/09/2022-19/03/2023), en la cual se ven tres de estas obras.
Pero volvamos a la espiral de Baravelle. Esta familia de espirales puede ser definida para cualquier polígono regular, como el triángulo equilátero, el cuadrado, el pentágono, el hexágono, así hasta cualquier número de lados.
 Imagen de la exposición Kunibert Fritz: Unidad en la dualidad en el Museo Vasarely de Budapest (17/09/2022-19/03/2023). Más información en la página del museo: Museo Vasarely de Budapest
Imagen de la exposición Kunibert Fritz: Unidad en la dualidad en el Museo Vasarely de Budapest (17/09/2022-19/03/2023). Más información en la página del museo: Museo Vasarely de BudapestEn la siguiente imagen vemos el resultado de la construcción geométrica para el triángulo equilátero, tras realizar cinco pasos en la construcción.
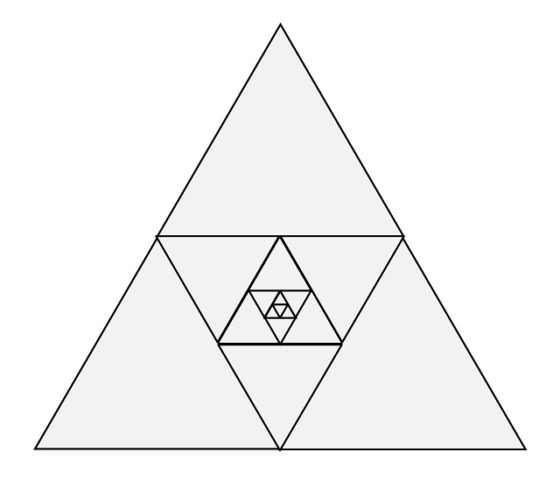
Si ahora pintamos las espirales de Baravelle (en este caso utilizamos tres colores, verde, azul y rojo, y los bordes de cada triángulo pintados del color del triángulo), queda la siguiente imagen, de una cierta belleza.
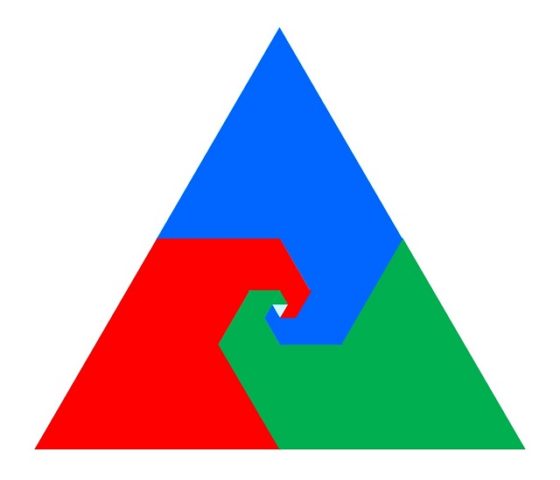
Al igual que en el caso de la espiral empezando en un cuadrado, ahora la imagen anterior puede ser considerada una demostración visual para la siguiente serie infinita.
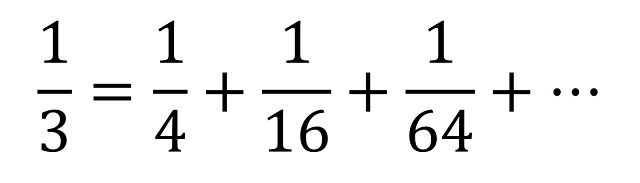
Y podemos continuar con la construcción para el pentágono, es decir, el polígono de cinco lados. En la siguiente imagen se muestra la espiral (o espirales) de Baravelle para el pentágono, después de catorce pasos.
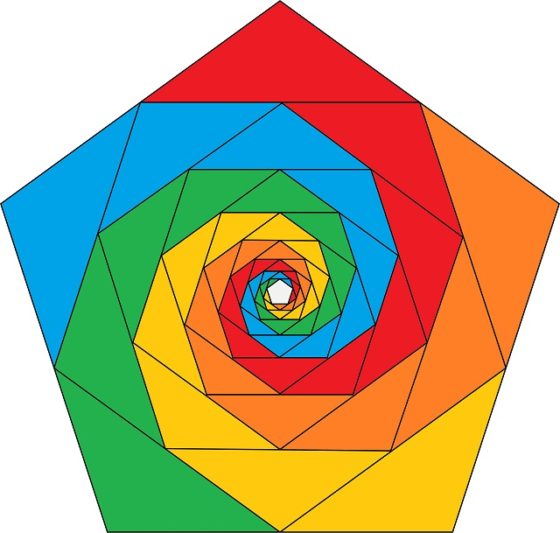
Por otra parte, a partir de la espiral de Baravelle del triángulo, el cuadrado o el hexágono se pueden hacer diseños planos más sofisticados, puesto que, con el triángulo, el cuadrado y el hexágono se puede embaldosar el plano.
Por ejemplo, con el triángulo podemos construir diseños como el siguiente:

O este otro:
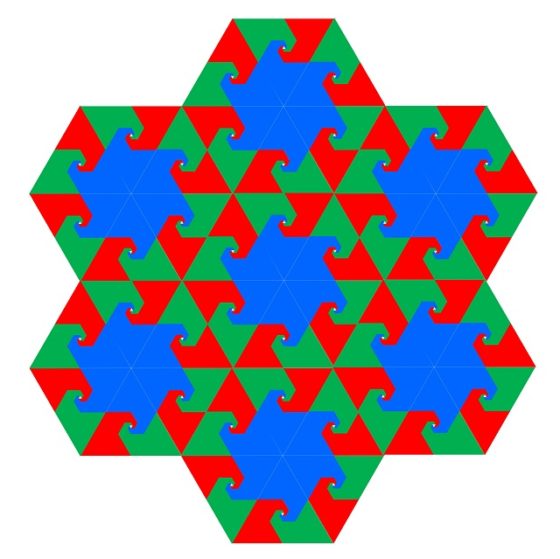
Con cuadrados he realizado este diseño, inspirado en una idea que encontré en internet.

Empezábamos esta entrada con un ejemplo de la aparición de la espiral de Baravelle en las artes plásticas, pero un campo de las artes en las que nos las encontramos también es el arte textil, en concreto en la realización de quilts.
 Ejemplo de diseño de quilt sobre un hexágono, realizado por RaNae Merrill. Imagen de la página web RaNae Merrill Quilt Design
Ejemplo de diseño de quilt sobre un hexágono, realizado por RaNae Merrill. Imagen de la página web RaNae Merrill Quilt Design Indiana Puzzle mathematical quilt / Quilt de un rompecabezas matemático de Indiana (2000), realizado por la matemática, educadora y artista Elaine Krajenke Ellison y perteneciente a la colección del Science Museum Group. Imagen de la página de Science Museum Group
Indiana Puzzle mathematical quilt / Quilt de un rompecabezas matemático de Indiana (2000), realizado por la matemática, educadora y artista Elaine Krajenke Ellison y perteneciente a la colección del Science Museum Group. Imagen de la página de Science Museum GroupBuscando información sobre el origen del nombre de esta artística espiral, me he topado con el pedagogo, matemático, físico y astrónomo suizo Hermann von Baravalle (1898-1973) que enseñó matemáticas dentro de la HfG – Hochschule für Gestaltung, conocida como la Escuela de Ulm, que fue una escuela universitaria de diseño en Ulm (Alemania) fundada por el artista, diseñador gráfico y tipógrafo suizo Max Bill (1908-1994), la escritora alemana Inge Aicher-Scholl (1917-1998) y el diseñador gráfico y tipógrafo alemán Otl Aicher (1922-1991). Dentro de las matemáticas enseñadas por Baravalle en la HfG, así como en algunos de sus libros, nos encontramos muchos tipos de espirales, en particular, las que hemos mostrado en esta entrada del Cuaderno de Cultura Científica. Por ejemplo, en su libro Geometrie als Sprache der Formen / La geometría como lenguaje de las formas (1963) aparecen estas espirales construidas para el cuadrado, hexágono y el octógono.
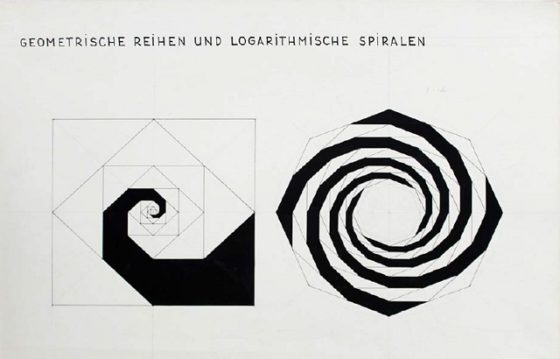 Imagen perteneciente al libro La geometría como lenguaje de las formas (1963) de Hermann von Baravalle
Imagen perteneciente al libro La geometría como lenguaje de las formas (1963) de Hermann von Baravalle Imagen perteneciente al libro La geometría como lenguaje de las formas (1963) de Hermann von Baravalle
Imagen perteneciente al libro La geometría como lenguaje de las formas (1963) de Hermann von BaravalleAunque no he encontrado una referencia directa a que el nombre de la espiral de Baravelle provenga de este matemático y pedagogo, aunque su apellido es Baravalle y no Baravelle, es bastante probable que así sea.
Me gustaría terminar con otra imagen del libro La geometría como lenguaje de las formas de Baravalle, en la cual vemos que la anterior construcción geométrica puede realizarse también tomando, no los puntos medios de los lados, sino otros puntos de los lados, por ejemplo, los que están a una distancia igual a un tercio de un vértice y dos tercios del otro.
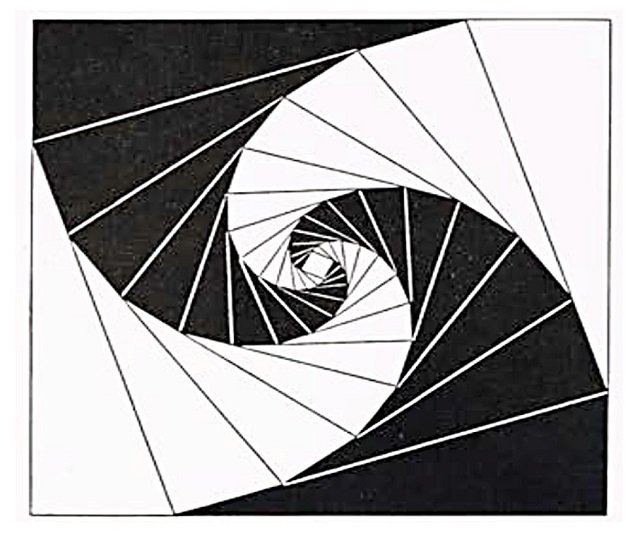 Imagen perteneciente al libro La geometría como lenguaje de las formas (1963) de Hermann von Baravalle
Imagen perteneciente al libro La geometría como lenguaje de las formas (1963) de Hermann von BaravalleSobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La espiral de Baravelle se ha escrito en Cuaderno de Cultura Científica.
Gotas autopropulsadas
 Foto: SpaceX / Unsplash
Foto: SpaceX / UnsplashLa nucleación de hielo en las gotas que se están congelando puede aumentar repentinamente la velocidad de estas por un mecanismo a reacción similar al de un cohete.
Un equipo de investigadores estaban observando cómo se congelaban espontáneamente gotas de agua superenfriada en movimiento cuando notaron algo inesperado: las gotas desaparecían de pronto de forma consistente. Inicialmente pensaron que las gotas perdidas se habían hecho añicos al congelarse. Pero, comprobándolo con más detenimiento, encontraron que las gotas congeladas seguían estando ahí, simplemente se habían salido de foco.
El equipo ha desarrollado un modelo cuantitativo para describir este comportamiento, atribuyéndolo a un mecanismo de propulsión similar al de un cohete e inducido por el proceso de congelación. Este modelo pordría servir de base para diseñar sistemas autopropulsados que tomen su energía de transiciones de fase.
Estos resultados vienen a sumarse a una creciente bibliografía sobre gotas autopropulsadas. Los mecanismos causantes del movimiento varían enormemente, pero todos tienen en común que implican el concepto de ruptura de la simetría.
Para las gotas congeladas esta ruptura de simetría surge cuando la nucleación del hielo comienza alejada del centro. Cuando el hielo se nuclea, el cambio en la estructura libera calor latente, lo que hace que la tasa de evaporación local aumente repentinamente y, si la nucleación está descentrada, esta evaporación potenciada se produce de manera desigual sobre la superficie de la gota. Como un cohete que expulsa gases generados por una reacción química, esta evaporación asimétrica aumenta el momento de la gota, y el modelo del equipo predice velocidades máximas de casi 1 m/s.
Este mecanismo de propulsión tiene una característica única que podría hacerlo atractivo para futuras aplicaciones: a diferencia de la mayoría de las partículas autopropulsadas no requiere ni superficies ni fluido circundante (los experimentos se realizaron en el vacío).
Referencia:
C. A. Stan et al. (2023) Rocket drops: The self-propulsion of supercooled freezing drops Phys. Rev. Fluids doi: 10.1103/PhysRevFluids.8.L021601
Para saber más:
Nanomotores autopropulsados que reparan microcircuitos
Un nanosubmarino, autoensamblado, autoorientable y autodestruible
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Gotas autopropulsadas se ha escrito en Cuaderno de Cultura Científica.
¿Cuanto duran los asteroides?
Seguro que más de una vez has escuchado la archiconocida frase de “un diamante es para siempre”. Y aunque ese “para siempre” sea relativo, lo cierto es que -a grandes rasgos- son capaces de durar mucho más que nosotros y nuestros compromisos, a menos que los hagamos sufrir hasta transformarlos en grafito.
Bromas aparte, ¿alguna vez te has preguntado cuánto dura un asteroide? A menudo hablamos de los asteroides como esos fragmentos sobrantes de la formación de nuestro Sistema Solar, aquellos que no acabaron formando parte de cuerpos de tamaño planetario, pero, ¿quiere decir eso que sea exclusivamente así?
Lo cierto es que hoy sabemos que el cinturón de asteroides es un lugar mucho más dinámico y cambiante de lo que podríamos pensar, y que esa procesión de asteroides girando al unísono alrededor de nuestro Sol a veces se ve alterada por las colisiones con otros cuerpos, que pueden dar como resultado la destrucción de los cuerpos implicados, la formación de familias de asteroides e incluso la creación de otros nuevos.
 Imagen de Itokawa, un asteroide visitado por la Hayabusa 1 y de las que trajo a nuestro planeta unas muestras en junio de 2010. Imagen cortesía de JAXA.
Imagen de Itokawa, un asteroide visitado por la Hayabusa 1 y de las que trajo a nuestro planeta unas muestras en junio de 2010. Imagen cortesía de JAXA.Hace dos semanas hablábamos del posible origen de Dimorfos, el satélite de Dídimos al que se dirigió la misión DART, pero poco nos centramos en este último, y asteroide más grande del sistema, y es por eso que hoy quería aprovechar para hablar de la categoría a la que pertenece Dídimos y la importancia de comprender mejor este tipo de asteroides para protegernos ante futuros impactos.
Es posible que lo haya repetido en más de una ocasión a lo largo de estas entradas de Planeta B, pero cuando le preguntamos a alguien que describa en voz alta un asteroide, suele sugerir que es algo parecido a una roca gigantesca que vaga por el espacio. Y es que, hasta no hace muchas décadas, esa era la imagen más común que teníamos de los asteroides… no solo a nivel cinematográfico sino también a nivel científico.
A finales de la década de los 70 y principios de los 80 se empezó a definir una nueva categoría de asteroides, aquellos que no estaban formados un bloque de roca monolítico, sino que más bien estaban formados por innumerables rocas y polvo que viajan juntos por efecto de la gravedad y a los que conocemos como “rubble pile” o “pila de escombros”, aunque la existencia de este tipo de asteroides no se demostraría hasta finales del siglo XX y principios del XXI, cuando las distintas misiones espaciales tuvieron la oportunidad de ver de cerca estos cuerpos.
Estos asteroides son muy particulares, ya que tienen una densidad muy baja debido a su gran porosidad, puesto que las rocas que lo componen no están unidas en el sentido literal -como si estuviesen soldadas o formando parte de un bloque-, sino que más bien estos asteroides son como un gran saco que lleva en su interior rocas y el polvo. La tela del saco sería, por lo tanto, la gravedad.
 El asteroide P/2010 A2 muestra en esta imagen del Telescopio Espacial Hubble una gran cola, dándole la apariencia de un cometa. Algunos científicos opinan que esto se debe a una colisión entre dos asteroides, liberando una gran cantidad de material que libera este polvo que forma la cola. Imagen cortesía de NASA, ESA y D. Jewitt (UCLA).
El asteroide P/2010 A2 muestra en esta imagen del Telescopio Espacial Hubble una gran cola, dándole la apariencia de un cometa. Algunos científicos opinan que esto se debe a una colisión entre dos asteroides, liberando una gran cantidad de material que libera este polvo que forma la cola. Imagen cortesía de NASA, ESA y D. Jewitt (UCLA).Y las rocas, por supuesto, no encajan a la perfección, como si de un puzle se tratase, dejando huecos entre estas, y que conforma esa porosidad a la que hacíamos mención en el párrafo anterior. El proceso más habitual que da lugar al nacimiento de estos asteroides es la violenta colisión entre distintos cuerpos, que fragmenta los asteroides, y parte de cuyos restos acaban coalesciendo y formando un tercer (o más) cuerpos por efecto de la gravedad.
Se pensaba que este tipo de asteroides eran relativamente raros -a menudo es difícil saber de lejos si un asteroide entra dentro de esta categoría o no desde la distancia- pero hoy se sabe que es muy probable que sean bastante numerosos entre la población de asteroides que miden entre varios centenares de metros y los diez kilómetros.
Hecha la introducción, ¿a qué venía el título de este artículo? Pues resulta que un nuevo estudio publicado a partir de los datos que nos han aportado las muestras del asteroide 25143 Itokawa recogidas por la misión Hayabusa 1 demuestran que los asteroides de tipo “pila de escombros” podrían tener una vida promedio 10 veces más larga, e incluso más, que un cuerpo monolítico.
 Una imagen del asteroide Bennu, visitado por la misión OSIRIS-REx. La forma de algunos asteroides de este tipo que han sido visitados nos recuerda vagamente a la forma de un diamante. Imagen cortesía de NASA/Goddard/University of Arizona.
Una imagen del asteroide Bennu, visitado por la misión OSIRIS-REx. La forma de algunos asteroides de este tipo que han sido visitados nos recuerda vagamente a la forma de un diamante. Imagen cortesía de NASA/Goddard/University of Arizona.Los científicos estiman que los asteroides monolíticos del orden del tamaño de alrededor de un kilómetro de diámetro pueden tener unas vidas de unos cientos de millones de años antes de ser destruidos por colisiones entre asteroides, pero parece que los asteroides de tipo “rubble pile” son capaces de aguantar mucho más debido a su propia naturaleza, que los transforma en una especie de sacos de boxeo interplanetarios capaces de absorber gran parte de los impactos sin destruirse por completo.
Este hecho pone de manifiesto que un gran número de los asteroides que observamos en el Sistema Solar podrían ser de este tipo y, por lo tanto, debemos tenerlo en cuenta de cara a buscar estrategias de defensa apropiadas. Sabemos gracias a la DART que con un impactador cinético podríamos desviarlos si los detectamos con tiempo suficiente, pero si no fuese este el caso, tendríamos que buscar alternativas que no fuesen dirigidas a destruir el asteroide, sino a desviarlo, ya que su destrucción sería muy difícil y podríamos provocar un problema mayor.
 En esta imagen de Bennu tomada por la OSIRIS-Rex desde unos cinco kilómetros de distancia podemos ver perfectamente su superficie, formada por un “montón” de rocas sueltas. Imagen cortesía de NASA/Goddard/University of Arizona.
En esta imagen de Bennu tomada por la OSIRIS-Rex desde unos cinco kilómetros de distancia podemos ver perfectamente su superficie, formada por un “montón” de rocas sueltas. Imagen cortesía de NASA/Goddard/University of Arizona.Para poder llegar a esta conclusión, los científicos han estudiado los minerales de los granos de material traídos de Itokawa, buscando en estos señales de impactos pasados y poniéndoles fecha gracias a las técnicas de datación radiométrica -en este caso la datación Argon/Argón- pudiendo reconstruir desde su origen, probablemente hace unos 4200 millones de años cuando se formó, hasta otros impactos ocurridos hace también 4200, 2300 y probablemente 1300 y 500 millones de años y lo suficientemente importantes como para dejar su señal en los minerales que forman parte de Itokawa.
Eso sí, aunque estos impactos no lograron destruirlo, si cambiaron su forma y lo hicieron un poco más pequeño debido al material eyectado durante las colisiones y que pudo escapar de su gravedad, por lo que el asteroide ha seguido evolucionando a lo largo del tiempo tanto en forma como en masa. Y así será, probablemente, hasta que choque con algún cuerpo mayor, o hasta que los sucesivos impactos acaben dejándolo progresivamente más “delgado”, haciéndolo desaparecer.
Este estudio pone de manifiesto que quizás el número de asteroides de este tipo, los “rubble pile” sean más numerosos de lo que pensábamos con anterioridad y este mismo hecho nos tiene que hacer reflexionar sobre las técnicas de protección planetaria a usar en caso de ser necesarias, ya que las posibilidades de que aquellos asteroides que puedan cruzarse con nosotros sean de este tipo parecen ser más altas de lo que pensábamos.
Referencias:
Jourdan, F. et al. (2023) Rubble pile asteroids are forever Proceedings of the National Academy of Sciences doi: 10.1073/pnas.2214353120.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Cuanto duran los asteroides? se ha escrito en Cuaderno de Cultura Científica.
La piel es un órgano
 Foto: Nsey Benajah / Unsplash
Foto: Nsey Benajah / UnsplashLa piel es la frontera. Aísla el organismo del mundo exterior. De esa manera facilita que ciertas características internas –estado de hidratación, concentración de sales y temperatura, fundamentalmente– apenas varíen. La piel nos defiende; es la primera barrera que se opone a la entrada de patógenos en nuestro interior. Al contar con buen número y variedad de receptores sensoriales –de presión, dolor, temperatura–, es también fuente importante de información externa. Y tiene encomendadas algunas tareas más.
Representa del orden del 10% de la masa corporal, por lo que es el órgano más pesado. Su grosor varía desde los 0,5 a los 4 o 5 mm. Es también, con una superficie de 1,8 m2, el más extenso que tenemos. Aunque esa no es la mayor área superficial que un órgano humano expone al medio externo; la superficie interna de los alveolos pulmonares es enorme: cada pulmón tiene una superficie alveolar agregada de 70 m2, la de un apartamento grande o un piso pequeño.
En contraste con la gran mayoría de especies de mamíferos y con todos los primates, la piel humana está, casi en su totalidad, desprovista de pelaje. No se puede decir que carezca de vello, porque en realidad, tiene una densidad equivalente a la de los simios antropoides, como chimpancés o gorilas, pero nuestro pelo corporal es mucho más fino y más corto, hasta el punto de que muchos individuos parecen carecer de él. Las excepciones son el de la cabeza, que probablemente nos protege de golpes, calor y quemaduras solares, y el de axilas y pubis, cuyas funciones están seguramente relacionadas con la señalización de la madurez sexual.
Además de la aparente ausencia de vello, la otra característica distintiva de la piel humana es la capacidad para producir sudor. Tenemos dos tipos de glándulas sudoríparas, ecrinas y apocrinas. Estas segundas se limitan, principalmente, a las axilas, las areolas, el área perineal, las orejas y los párpados. No se abren directamente a la superficie de la epidermis, sino que lo hacen al canal de los folículos pilosos. Empiezan a producir sudor tras la pubertad y su actividad es máxima en momentos de estrés o de excitación sexual. Las glándulas sudoríparas ecrinas se distribuyen por gran parte del cuerpo y son responsables de secretar el sudor acuoso y salobre que se produce de forma más abundante, normalmente en respuesta a una temperatura corporal demasiado alta.
Tenemos entre 2 y 4 millones de glándulas sudoríparas ecrinas, tanto en la piel desnuda (palmas de las manos y plantas de los pies), como en la vellosa. En las palmas de las manos y las plantas de los pies hay entre 250 y 550 glándulas/cm2. La densidad propia de las zonas vellosas es 2 a 5 veces menor, pero como abarcan una superficie muy superior, pueden producir grandes volúmenes de sudor. En reposo y sin que nos demos cuenta, eliminamos 500 ml de sudor al día; la llamamos sudoración insensible. La máxima de un adulto puede consistir en una producción de 2 a 4 litros –aunque algunas fuentes reducen esas cifras a un intervalo de 0,7 a 1,5 litros por hora–, o de 10 a 14 litros por día, pero es menor en los niños antes de la pubertad.
La humanidad “civilizada” le ha declarado la guerra al sudor. Dedicamos muchos recursos a eliminarlo. Pero casi nada en un organismo es ocioso. Olores corporales al margen –que también han cumplido su función–, la evaporación de un gramo de sudor extrae de nuestro cuerpo cerca de 600 calorías. Recuerde esto en medio de una ola de calor.
Para saber más:
Puedes presumir de tener la mejor piel del mundo
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La piel es un órgano se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: Vida y muerte

El periodo azul de Picasso, en el que este color inunda sus obras, de una profunda melancolía, habría comenzado por un lamentable hecho, chapucero en parte, de lo que hoy conocemos como violencia de género. Oskar Gonzalez nos cuenta los detalles de una de las obras de esta etapa de la producción picassiana, en la que los rayos X revelan que el pintor reciclaba sus lienzos. Obra visible y obra reciclada explican el título de la charla.
Oskar Gonzalez «kimikArte» es químico, y profesor de las Facultades de Ciencia y Tecnología y Bellas Artes de la UPV/EHU.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2022: Vida y muerte se ha escrito en Cuaderno de Cultura Científica.
Modelos neuronales para la transformación de las tecnologías lingüísticas
neuronales
 Foto: Ali Shah Lakhani / Unsplash
Foto: Ali Shah Lakhani / UnsplashLa producción científica y el desarrollo tecnológico en general no han tenido tan en cuenta el castellano, y mucho menos el euskera, como el inglés, por lo que hasta el momento no ha habido grandes oportunidades de transformar el sector de las tecnologías lingüísticas y de la inteligencia artificial mediante el desarrollo del procesamiento del lenguaje natural y sus servicios asociados.
Para mejorar la situación del euskera y del castellano en esta materia, el personal investigador del centro HiTZ de la Universidad del País Vasco – UPV/EHU, Orai NLP y Vicomtech ha trabajado en el proyecto Deeptext, liderado por el centro HiTZ. Su objetivo ha sido crear una nueva generación de herramientas de inteligencia artificial basada en modelos lingüísticos neuronales que transformen las tecnologías lingüísticas de la industria. El resultado han sido modelos para el euskera y el castellano (en el caso del euskera han sido los primeros), así como modelos plurilingües (que engloban el euskera, el castellano, el francés y el inglés).
“El procesamiento del lenguaje natural tiene como objetivo que las máquinas sean capaces de comprender y crear nuestro lenguaje para tener la capacidad de realizar ciertas tareas”, según los investigadores del consorcio. Las técnicas utilizadas hasta ahora para este fin han quedado obsoletas y ahora se utilizan sistemas basados en modelos lingüísticos neuronales. En los últimos años se está produciendo un cambio de paradigma totalmente disruptivo en el procesamiento del lenguaje natural: “Se entrenan modelos lingüísticos neuronales genéricos utilizando corpus de texto gigantes para que tengan un conocimiento general del lenguaje y luego se adecuan para que sean capaces de realizar una determinada tarea (hacer búsquedas, clasificar temas de textos, detectar sentimientos en textos, hacer resúmenes automáticos, etc.)”, explican.
Las lenguas de escasos recursos tienen problemas a la hora de formar corpus tan grandes, pero en este proyecto se ha completado el mayor corpus para el euskera: un corpus de 350 millones de palabras. Así, utilizando este corpus y el corpuseuscrawl (de 288 millones de palabras y creado por IXA Taldea), han creado los primeros modelos lingüísticos neuronales para el euskera, utilizando el nuevo paradigma, y los han entrenado para realizar diferentes tareas para su implantación en nuevos sistemas.
Los modelos lingüísticos neuronales plurilingües se utilizan para establecer herramientas para lenguas de escasos recursos. Según explica el personal investigador: “Hay alrededor de 7.000 lenguas en el mundo, la mayoría de las cuales son lenguas de escasos recursos. Debido a su escaso corpus y material digital, tienen dificultades a la hora crear ejemplos de entrenamiento. El euskera se podría incluir también en este grupo. En estos casos, la utilización de modelos lingüísticos plurilingües es una alternativa eficaz (son capaces de comprender textos de diferentes lenguas e incluso de lenguas de escasos recursos). Esta base se entrena con ejemplos de una lengua grande, como el inglés, y luego se prueba con datos en euskera para ver qué resultados da”. El personal investigador admite que esta técnica, denominada transfer learning, no proporciona resultados «óptimos», “pero sí resultados muy interesantes para, por ejemplo, realizar búsquedas por pregunta-respuesta”.
No solo para el euskeraAdemás, se ha creado un entorno de evaluación para medir la capacidad de comprensión lingüística de los modelos lingüísticos neuronales, imprescindible para llevar a cabo investigaciones en este campo. “Este entorno de evaluación engloba una serie de tareas lingüísticas (detección de nombres propios, detección de sentimientos, clasificación temática, resolución de correferencias, respuesta a preguntas…). Hemos creado el entorno para evaluar el euskera y el castellano”, explican. El personal investigador otorga especial importancia al apartado de evaluación del euskera (BasqueGLUE), que es el primero para este idioma.
En su opinión, “hemos dado un paso imprescindible en el desarrollo de las tecnologías lingüísticas de Euskal Herria. En estos dos años hemos investigado la base tecnológica necesaria para el avance de las tecnologías lingüísticas para el euskera, el castellano, el inglés y otras lenguas de escasos recursos. Hoy en día, los modelos lingüísticos neuronales son necesarios para desarrollar productos de tecnologías lingüísticas y obtener los mejores resultados. Hasta ahora no se había creado un modelo así para el euskera. Se ha estudiado el uso de modelos lingüísticos neuronales y se han adecuado para realizar tareas concretas, y se ha aprendido la transferencia entre lenguas y entre dominios (literatura, medicina).
Es evidente la importancia de contar con capacidades científico-tecnológicas independientes para mejorar la competitividad de la industria vasca y el desarrollo de tecnologías clave. Para ello es urgente continuar la investigación fundamental, idear técnicas innovadoras basadas en modelos neuronales y experimentar con ellas. El personal investigador está con muchas ganas de seguir en este camino y espera que tenga su reflejo en las políticas públicas y los fondos para el impulso de proyectos de I+D.
El proyecto ha sido liderado por Aitor Soroa, de IXA Taldea (centro HiTZ) y ha contado con la participación de personal investigador de Orai NLP Teknologiak y del centro tecnológico Vicomtech. Ha contado con una subvención del programa Elkartek del Gobierno Vasco. Aquí pueden encontrarse todos los recursos generados por el proyecto.
Para saber más:
Gradualismo o saltacionismo… en evolución lingüística
Respuestas a preguntas en lenguaje natural, el nuevo paradigma de los buscadores basados en inteligencia artificial
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Modelos neuronales para la transformación de las tecnologías lingüísticas se ha escrito en Cuaderno de Cultura Científica.
Y minerales que curan
sal
Hay un dicho muy famoso que me encanta, porque tiene un gran componente geológico, y que suelo aplicarme en esta vida cada vez que algo me sale rematadamente mal o, por el contrario, tengo una suerte tremenda: “dar una de cal y otra de arena”.
Pues esto es lo que he hecho en mis dos últimos artículos con los minerales. Mientras que en el anterior me centraba en aquellos que, de una manera u otra, pueden ser perjudiciales para nuestra salud, en esta ocasión voy a hablaros de algunos minerales que son más que beneficiosos para el ser humano. Pero voy a intentar no coger un camino fácil y poneros algunos ejemplos que, espero, os resulten llamativos.
 Removilización de las salmueras en las eras de desecación para favorecer la precipitación de la sal mineral en Salinas de Añana (Álava). Fuente: Fundación Valle Salado de Añana
Removilización de las salmueras en las eras de desecación para favorecer la precipitación de la sal mineral en Salinas de Añana (Álava). Fuente: Fundación Valle Salado de AñanaUna de las maneras con las que me gusta sorprender y captar la atención del público más joven en actividades de divulgación es decirles que yo, todos los días, como minerales. Y eso que no soy una comerrocas del mundo de Fantasía de La Historia Interminable. Tras dejar que se lo piensen un poco, les respondo que, aparte de exagerar un pelín, esta afirmación se debe a que le echo sal a las comidas. Esa sal de mesa no es más que cloruro sódico (NaCl), un compuesto que se encuentra disuelto en algunas aguas y que, al precipitar, lo hace en forma de un mineral denominado halita. Para obtener esta sal de mesa tenemos dos opciones: o dejamos evaporar agua salada, que no tiene por qué ser exclusivamente agua marina, hasta que precipitan los cristales de halita, o explotamos depósitos minerales salinos formados por la evaporación natural de agua salada hace millones de años y que han quedado enterrados por materiales más modernos. Y no es necesario traer esta sal desde el Mar Muerto o el Himalaya, porque tenemos zonas de desecación de agua salada bien cerquita, como en Salinas de Añana (Álava), o explotaciones de depósitos formados hace millones de años, como en Poza de la Sal (Burgos) o Cabezón de la Sal (Cantabria).
Siguiendo con la comida, cada vez es más frecuente encontrar alimentos enriquecidos en calcio, tales como leche o galletas. Pues ese elemento se extrae, principalmente, de minerales como la calcita o el aragonito, que están formados por carbonato cálcico (CaCO3). Pero esto no quiere decir que se machaque el mineral hasta hacerlo polvo y se añada directamente a la leche, es necesario hacer un tratamiento químico para asegurar que es un producto comestible que no entraña ningún problema de salud para las personas.
Aquí no termina la relación entre la calcita y la comida. Si tenemos algún problema para hacer la digestión, generalmente nos tomamos un antiácido. Pues uno de los principales componentes de este medicamento es el carbonato de calcio. Y si bien es cierto que hace siglos directamente molían los cristales de calcita y tomaban el polvo para aliviar los problemas y las úlceras estomacales, hoy en día los antiácidos que podemos adquirir en las farmacias están debidamente testados y procesados.
Después de comer, lo recomendable es lavarse los dientes empleando una pasta dentífrica para evitar las caries y enfermedades bucales, y aquí también aparecen los minerales. Al cepillarse los dientes, lo que limpia nuestra dentadura no es la espuma que genera el dentífrico, sino unas pequeñas partículas minerales que hacen de abrasivo y retiran los restos de comida que se han quedado adheridas al esmalte dental. Para ello los minerales más utilizados son la caolinita, un tipo de arcilla con fórmula química Al2Si2O5(OH)4, y la calcita, así como la diatomita, que es una roca formada por la acumulación de diatomeas, unas algas acuáticas que construyen un caparazón silíceo (SiO2).
 Zona de entrada de una antigua explotación minera de glauberita en el valle del Jarama (Madrid), en el Lugar de Interés Geológico (LIG) “Escarpes salinos y yacimientos de sulfato sódico del Jarama”. Fuente: Instituto Geológico y Minero de España (IGME-CSIC)
Zona de entrada de una antigua explotación minera de glauberita en el valle del Jarama (Madrid), en el Lugar de Interés Geológico (LIG) “Escarpes salinos y yacimientos de sulfato sódico del Jarama”. Fuente: Instituto Geológico y Minero de España (IGME-CSIC)Un ejemplo muy curioso es el del sulfato sódico (Na2SO4). Este compuesto se utiliza para la síntesis de enzimas para la elaboración de vino. También se emplea en farmacia como excipiente de ciertos medicamentos, como el Paracetamol, lo cual viene muy bien tener a mano cuando te pasas tomando vino. Y es uno de los componentes principales del detergente en polvo, que es básico para poder limpiar las manchas de vino del mantel o la ropa. Pues el sulfato sódico se obtiene, principalmente, de tres minerales, la thenardita y la mirabilita, ambos de fórmula química Na2SO4, y la glauberita, formado por sulfato sódico y cálcico (Na2SO4·Ca2SO4). Y hay que destacar que España es actualmente el único país de la Unión Europea con explotaciones de menas de estos minerales, con minas en las provincias de Burgos, Madrid y Toledo.
Ya que he entrado en el mundo de la limpieza, algo básico para asegurarnos una buena salud es fregar a conciencia el menaje de cocina después de las comidas, por lo que no puede faltar en la fregadera un buen estropajo. Seguro que os habéis fijado en que tienen diferentes colores según su dureza, siendo el verde y el azul los más comunes. Pues esta dureza depende de los minerales que se incluyan en la composición de los estropajos, entrelazados en las fibras sintéticas que los forman: los más suaves incluyen partículas de calcita, mientras que los más duros tienen fragmentos de cuarzo(SiO2).
 Cristales de talco de la mina San Andrés (Puebla de Lillo, León) de diferentes tonalidades: 1- talco blanco, 2- talco rosado y verdoso, 3- talco negro, del Lugar de Interés Geológico (LIG) “Yacimiento de talco y pirita de Puebla de Lillo”. Fuente: Instituto Geológico y Minero de España (IGME-CSIC)
Cristales de talco de la mina San Andrés (Puebla de Lillo, León) de diferentes tonalidades: 1- talco blanco, 2- talco rosado y verdoso, 3- talco negro, del Lugar de Interés Geológico (LIG) “Yacimiento de talco y pirita de Puebla de Lillo”. Fuente: Instituto Geológico y Minero de España (IGME-CSIC)Para terminar, me voy a pasar al ámbito de la higiene personal. Y el principal ejemplo que nos viene a la cabeza de mineral utilizado para este cometido es el talco (Mg3Si4O10(OH)2). Pero hay que tener cuidado con él, ya que debe superar un estricto control de calidad para poder ser utilizado como producto cosmético, porque puede estar acompañado de otros minerales del grupo de los asbestos o de materia orgánica que podrían llegar a ser tóxicos para el ser humano. Otro ejemplo bastante conocido es el de los desodorantes o antitranspirantes conformados por la denominada “piedra de alumbre”. Alumbre es el nombre que recibe un sulfato generalmente de aluminio y, en el caso de los desodorantes, el más empleado es el alumbre de potasio, que se obtiene de un mineral llamado calinita (Kal(SO4)2·12H2O).
Y mejor me paro aquí, porque podría seguir poniendo cientos de ejemplos como estos, pero creo que ya os habéis hecho una idea de la importancia de los minerales en nuestra salud. Aunque no quiero terminar sin recordar una obviedad: los minerales no son ni buenos ni malos, todo depende de su composición química y del uso que les demos los seres humanos.
Para saber más:
Serie Introducción histórica a la mineralogía
Ingredientes para la receta: La sal común
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Y minerales que curan se ha escrito en Cuaderno de Cultura Científica.
Usando la lógica para averiguar quién es quién
Cinco personas residen en un mismo edificio de viviendas; se llaman (por orden alfabético) Ignacio, Uxune, Víctor, Ziortza y Zuri. Cada una de estas personas trabaja en oficios (y solo en uno de ellos) relacionados con el diseño, la docencia, la electricidad, la floristería y la panadería. Además, Uxune, Ignacio, Zuri, Ziortza y Víctor tienen cada uno de ellos una afición favorita para sus ratos de ocio: la gimnasia, las matemáticas, el ocultismo, el teatro y el violín.
Uxune y Ziortza son nombres de mujer e Ignacio y Víctor de hombre. Pero el nombre de Zuri se puede usar tanto para chicas como para chicos.
 Composición realizada con imágenes extraídas de Wikimedia Commons
Composición realizada con imágenes extraídas de Wikimedia CommonsTe proponemos un juego para averiguar a qué se dedican y con qué se entretienen Ignacio, Uxune, Víctor, Ziortza y Zuri. Usando la lógica y las ocho pistas que se dan a continuación, ¿eres capaz de encontrar la solución?
Las ocho pistas
1) Uxune, que trabaja de pie, tiene muy mal oído musical por lo que nunca ha querido aprender a tocar un instrumento.
2) El florista no está nada interesado en el mundo espíritus.
3) Ignacio no tiene ninguna capacidad para el dibujo, pero le gusta salir a escena a actuar… le encanta que le aplaudan.
4) El docente no es el comediante… el único escenario que utiliza es el de la tarima del aula en la que imparte sus clases.
5) Zuri, que vive en el mismo piso que la electricista, invoca de vez en cuando a los espíritus; “se eleva” al más allá sin necesidad de levadura que, de hecho, no emplea en ningún momento del día.
6) A la electricista le encanta resolver retos matemáticos cuando tiene un rato libre.
7) Víctor y Zuri no soportan a las personas menores de 25 años. Por ello eligieron trabajos que evitaban encontrarse con alguna de ellas.
8) Ziortza trabaja en algunas ocasiones al aire libre.
Con estas ocho pistas, seguro que eres capaz de relacionar a cada persona con su profesión y su pasatiempo favoritos. Debajo incluimos la solución razonada por si acaso necesitas un poco de ayuda.
Razonando a partir de las pistas
Por 1), Uxune no puede ser diseñadora (entendemos que para realizar proyectos es necesario sentarse) y no puede tocar el violín (bueno, podría, pero no parece que le guste ni que lo pueda hacer bien).
En 2) se habla de “el florista”, así que ni Uxune ni Ziortza pueden tener esta profesión; en el caso de Zuri no podemos concluir nada.
Según 3), Ignacio no se gana la vida como diseñador (entendemos que para dedicarse a esta profesión hay que saber dibujar) y sus aficiones tienen que ser el violín o el teatro; es decir, no hace ni gimnasia, ni matemáticas, ni se dedica al ocultismo en sus ratos libres.
En 4) se habla del docente, así que Uxune y Ziortza no se dedican a la enseñanza. Desconocemos, de nuevo, si este comentario puede aplicarse a Zuri.
Por 5), la persona que se dedica a la electricidad (que no es Zuri) es una mujer; de aquí deducimos que ni Ignacio ni Víctor se dedican a esta profesión. Zuri no tiene como profesión la panadería (puesto que no usa levadura nunca) y su afición es el ocultismo.
Volviendo a 2), Zuri no puede ser florista, ya que a Zuri le gustan los espíritus y el florista no está nada interesado por ellos.
Por 7); Víctor y Zuri no son docentes, así que el docente (que es un hombre) tiene que ser Ignacio. Como el florista es un hombre (por 2), y como hemos visto no es Zuri, e Ignacio es docente, se deduce que debe ser Víctor.
Como el docente es Ignacio, volviendo a 4), Ignacio no es el aficionado al teatro, así que es el que toca el violín en sus ratos de ocio (por 3) habíamos descartado el resto de las aficiones).
Según 8), Ziortza debe ser la electricista (ya sabemos que no es ni docente ni se dedica al mundo de las flores), porque el trabajo de diseño y la preparación del pan se realizan dentro de edificios. Como Uxune no puede ser electricista, ni arquitecta por 1), ni florista por 2), ni docente por 4), es la panadera. De aquí se deduce que Zuri se dedica al diseño (ya que las demás profesiones ya se habían descartado para él o ella).
En 6) se dice que la electricista le “da a las matemáticas” en su tiempo de ocio. Así que es Ziortza la que se dedica al noble arte de los números para divertirse en sus ratos libres.
Víctor es entonces el comediante (que es un hombre por 4) y no es ni Ignacio ni Zuri, así que Uxune debe ser la que se dedica a la gimnasia.
La solución al juego
Terminamos ordenando las conclusiones obtenidas.
Ignacio es un docente que toca en sus ratos libres el violín.
Uxune es panadera y en su tiempo de ocio se dedica a hacer gimnasia.
Víctor es florista y se dedica al teatro cuando el oficio de las plantas le deja un rato libre.
Ziortza es electricista y se divierte (como nos pasa a muchas personas) resolviendo retos matemáticos.
Y, finalmente, Zuri (que seguimos sin saber si es una mujer o un hombre) trabaja en el mundo del diseño y el ocultismo es su gran afición.
Referencia
Extraído y adaptado de: Georges Perec, Jeux intéressants, Zulma, 2008.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Usando la lógica para averiguar quién es quién se ha escrito en Cuaderno de Cultura Científica.
Cómo ascienden las burbujas en el agua, y no es en línea recta
El movimiento de las burbujas de gas, sea este aire o dióxido de carbono, en el agua juega un papel central en una amplia gama de fenómenos naturales. La cerveza, los vinos espumosos, los refrescos carbonatados, los gases en la sangre de un buceador o las burbujas que salen de su boquilla, por no mencionar muchos procesos químicos industriales, dependen, de una forma u otra de cómo ascienden las burbujas en el agua. De hecho, es un fenómeno muy estudiado, tanto experimental como teóricamente, pero no del todo resuelto.
 Foto: Jakob Boman / Unsplash
Foto: Jakob Boman / UnsplashSin embargo, a pesar de estos esfuerzos, y disponiendo hoy día de una enorme potencia computacional, no ha sido posible reconciliar los experimentos con simulaciones numéricas de las ecuaciones hidrodinámicas completas para una burbuja de aire deformable en el agua. Esto es especialmente cierto para la observación, documentada ya por Leonardo da Vinci, de que las burbujas de aire suficientemente grandes no ascienden en línea recta, sino que realizan un movimiento periódico.
 Esbozo de Leonardo da Vinci en el manuscrito conocido como Códice Leicester, donde se ilustra el movimiento en espiral de una burbuja ascendente.
Esbozo de Leonardo da Vinci en el manuscrito conocido como Códice Leicester, donde se ilustra el movimiento en espiral de una burbuja ascendente.De hecho, una burbuja de aire ascendente presenta grandes desafíos numéricos y teóricos. En primer lugar, la pequeña viscosidad del agua implica la aparición de finas capas límite, que deben resolverse con precisión para capturar la interacción entre la flotabilidad y la disipación, que establece la velocidad de ascenso. En segundo lugar, la capacidad del fluido exterior para deslizarse sobre la superficie de la burbuja sin fricción (el efecto del gas concreto puede despreciarse) significa que los efectos viscosos surgen solo debido a la curvatura de la línea de flujo, cuyo sutil efecto debe capturarse con precisión. En tercer lugar, y lo más importante, la burbuja se deforma en respuesta a las fuerzas ejercidas por el fluido y, a su vez, la forma de la burbuja cambia el carácter del flujo.
Todos estos factores, que cualitativamente se pueden describir con tanta facilidad, hasta ahora se habían resistido a ser incluidos en un modelo matemático que respondiese a los resultados experimentales. Un reciente trabajo de Miguel Ángel Herrada (Universidad de Sevilla) en colaboración con Jens Eggers (Universidad de Bristol) parece haber encontrado una solución.
Los autores han desarrollado una técnica de discretización numérica para caracterizar con precisión la interfaz aire-agua de la burbuja, lo que permite simular su movimiento y estudiar su estabilidad. Sus simulaciones concuerdan bien con mediciones de alta precisión del movimiento inestable de las burbujas e indican que estas se desvían de la trayectoria recta en el agua si su radio esférico supera los 0,926 milímetros, un resultado que solo se desvía un 2% de los valores experimentales obtenidos con agua ultrapura en los años noventa, cuando se estudió de forma sistemática el fenómeno.
Los investigadores proponen un mecanismo para la inestabilidad de la trayectoria de la burbuja en el que una inclinación periódica de esta cambia la curvatura, lo que afecta a la velocidad de ascenso y provoca un bamboleo en su trayectoria, inclinando hacia arriba el lado de la burbuja cuya curvatura ha crecido. A continuación, a medida que el fluido se mueve más deprisa y su presión desciende alrededor de la superficie de alta curvatura, el desequilibrio de presión devuelve la burbuja a su posición original, reiniciando el ciclo periódico.
Este comportamiento es intermedio entre el de un sólido y el de burbujas pequeñas de gas que, en ambos casos, se pueden considerar indeformables a efectos prácticos.
Referencia:
Miguel A. Herrada and Jens G. Eggers (2023) Path instability of an air bubble rising in water PNAS doi: 10.1073/pnas.2216830120
Para saber más:
El frío de las burbujas
Bañadores y dopaje tecnológico
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cómo ascienden las burbujas en el agua, y no es en línea recta se ha escrito en Cuaderno de Cultura Científica.
Investigación contra el cáncer: ¿Qué hemos conseguido y qué queda por hacer?
 Foto: National Cancer Institute / Unsplash
Foto: National Cancer Institute / Unsplash
La reciente muerte de la influencer Elena Huelva, que mostró su día a día con cáncer en las redes sociales a millones de personas, ha vuelto a abrir el debate sobre la falta de inversión en la investigación del cáncer. El fallecimiento de Huelva por un sarcoma de Ewing (un tumor óseo de mal pronóstico una vez que se ha extendido), con tan solo 20 años, causa tristeza e impotencia. ¿Podría la ciencia médica haber salvado su vida y la de otros pacientes si dedicásemos más fondos a ella? Es imposible responder a esta pregunta con rigor. Lo que sí sabemos con seguridad es que conforme más se investiga sobre el cáncer, mejor conocemos los mecanismos implicados, más efectivos son los tratamientos y mayor es la probabilidad de curación de los pacientes.
Si echamos un vistazo a la evolución de la supervivencia de las personas afectadas por diferentes tipos de cáncer, podemos observar que se ha dado una notable mejora en las últimas décadas. Las muertes por cáncer estandarizadas por edad han caído un 15 % desde 1990 hasta 2019 en el mundo. En los países más ricos esta cifra es aún mayor. Por ejemplo, en Estados Unidos y Alemania el porcentaje es de un 20 % y en España un 18 %.
Además, las supervivencias a cinco años de los pacientes han aumentado de forma clara para todos los tipos de cáncer. Esta supervivencia se ha duplicado en 40 años (siendo del 55 % en hombres y del 61 % en mujeres). Destaca la supervivencia frente a tumores de próstata y de mama, ya que casi todos ellos se curan en la actualidad (supervivencia a cinco años superior al 90 % en ambos casos).
Ahora contamos con más opciones que nunca en la detección precoz y el tratamiento contra cáncer. En los últimos años, la inmunoterapia ha irrumpido en la clínica con unos resultados espectaculares en el tratamiento de tumores sanguíneos (leucemias y linfomas) que habrían provocado una muerte segura tiempo atrás.
Sin embargo, la investigación de tratamientos contra el cáncer se enfrenta a numerosos retos. En primer lugar, aunque nos refiramos al «cáncer» como una única dolencia, en realidad es el conjunto de más de 200 enfermedades diferentes con un punto en común: la proliferación descontrolada de células tumorales en el organismo. Cada tipo o subtipo de cáncer puede ser radicalmente diferente del otro en cuanto a velocidad de proliferación, sensibilidad a ciertos tratamientos, probabilidad de supervivencia del paciente…. Esto complica el desarrollo de nuevas terapias, pues, con mucha frecuencia, lo que puede servir para un tipo de tumor puede ser inútil para el otro.
Otro gran desafío en el establecimiento de nuevos tratamientos es la toxicidad. Las células tumorales son las propias células del paciente que han sufrido una serie de mutaciones. Atacar a estas sin provocar graves daños a las células sanas es uno de los principales obstáculos en las terapias antitumorales. Por otro lado, existen ciertos tipos de tumores, como el cáncer de páncreas, cuyo pronóstico sigue siendo muy sombrío por una suma de factores: es un tumor muy agresivo, que crece muy rápido, y cuando da la cara ya se encuentra en una fase bastante avanzada.
Si consideramos la inversión total en investigación científica en el mundo, el área del cáncer es una de las más privilegiadas. Se destinan miles de millones de euros cada año en investigar el cáncer, con importantes sumas de dinero tanto desde el ámbito público como del privado. Las grandes farmacéuticas tienen gran interés económico en este campo y desembolsan grandes cifras en la investigación, ya que es una enfermedad muy frecuente, con tratamientos de larga duración, que pueden llegar a ser muy rentables.
Aun así, a pesar de los grandes esfuerzos y recursos destinados en la investigación del cáncer, este es la segunda causa de muerte en el mundo tras las enfermedades cardiovasculares. En 2019, 10 millones de personas murieron por cáncer, lo que implica que aproximadamente uno de cada seis fallecimientos se debe a esta dolencia. El envejecimiento progresivo de muchas poblaciones y el aumento de la población mundial llevan, irremediablemente, a un aumento de los casos de cáncer. Aunque queda mucho por hacer, no hay que olvidar todo lo conseguido: muchas personas habrían muerto de forma prematura por cáncer si no fuera por todo lo que se ha avanzado.
Para saber más:
Sin atajos frente al cáncer
¿De dónde viene el cáncer y por qué no ha desaparecido con la evolución?
La senescencia celular: el gran desafío para entender y tratar el cáncer
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo Investigación contra el cáncer: ¿Qué hemos conseguido y qué queda por hacer? se ha escrito en Cuaderno de Cultura Científica.

