A tomar el sol
 Foto: Mincho Kavaldzhiev / Unsplash
Foto: Mincho Kavaldzhiev / UnsplashEn las últimas décadas los expertos han recomendado evitar las exposiciones excesivas al sol pues son la principal causa de daños en la piel y, sobre todo, de la aparición de melanoma, un cáncer extendido y muy peligroso. La revisión, publicada en 2017, por Natalie Matthew y sus colegas, de la Universidad de Providence, en Estados Unidos, informa de que la incidencia del melanoma en todo el planeta ha crecido con rapidez en los últimos 50 años.
La tasa es mayor en personas de piel blanca y en zonas cercanas a los trópicos y al ecuador. Nuestra especie apareció en los trópicos del centro de África, un área geográfica con mucho sol. Homo necesita sol para el metabolismo de la vitamina D en la piel. Sin embargo, la exposición al sol es peligrosa por los rayos ultravioleta que tiene y, para evitarlos, apareció la melanina, el pigmento que oscurece la piel y evita los ultravioleta. Pero, cuando nuestra especie salió de África hacia el norte, hacia Eurasia, colonizó zonas con menos incidencia solar y, por tanto, menos producción de vitamina D en la piel. Se aclaró la piel y se seleccionó piel blanca, con poca melanina, que dejaba pasar la luz solar y permitía la síntesis de vitamina D. Pero, con el tiempo, los originarios de Eurasia se extendieron por todo el planeta, y, con su piel blanca, muchos volvieron a los trópicos, con demasiado sol para este tipo de piel con escasa melanina protectora. El exceso de sol, con su componente ultravioleta, produce daños en la piel y, en último término, la aparición del melanoma.
En conclusión, la relación de la piel de nuestra especie con el sol es complicada: buena para la vitamina D y dañina por el exceso con desarrollo de cáncer. Hasta ahora se ha intentado evitar el melanoma y, para conseguirlo, los protocolos de exposición al sol piden evitar el exceso y el uso de protectores solares.
Para explicar brevemente los efectos sobre la salud de la deficiencia en vitamina D, nos sirve la revisión publicada por Michael Holick, de la Universidad de Boston, el año pasado. Enumera, como consecuencia de la falta de vitamina D, a enfermedades agudas y crónicas como la caries en niños, osteoporosis, psoriasis, enfermedades autoinmunes, enfermedades cardiovasculares, algunos tipos de cáncer, diabetes tipo 2 y desordenes neurológicos.
Hay que tener mucho cuidado con el sol y, para tomarlo, no hacerlo a las horas centrales del día, cubierta la cabeza, con ropa adecuada y gafas de sol y, siempre, con protector solar, a ser posible con un factor superior a 30.
Pero, hemos visto que la vitamina D es esencial para muchas funciones del organismo y se sintetiza en la piel por la acción de los rayos ultravioleta solares. Eleni Linos y su equipo, de la Universidad de Stanford, aseguran que tanta protección frente al sol puede afectar a los niveles de vitamina D en el organismo. Esta deficiencia vitamínica, como hemos visto, aumenta el riesgo de varias enfermedades y en ello interviene el uso de los protectores solares.
Los protectores solares, en experimentos de laboratorio y en experimentos controlados, reducen los niveles de vitamina D. Ahora Eleni Linos pretende relacionar los niveles de vitamina D con el uso de protectores solares en la población en general y en situaciones de vida normal. A partir de una encuesta nacional sobre salud en Estados Unidos, con datos tomados de 2003 a 2006 a 5920 personas, consigue, por una parte, conocer el uso de protectores solares y, por otra, el nivel de vitamina D en sangre de los voluntarios (en realidad, del precursor 25-hidroxi-vitamina D que pasa a vitamina D en el riñón).
Al analizar los resultados, los autores encuentran que más de la mitad de los encuestados se protegen del sol de alguna manera, aunque el método varía según la raza, sobre todo en relación con los protectores solares: más de la mitad de los blancos (56%) los utilizan con frecuencia mientras que sólo lo hace un tercio de los hispanos (31%) y algo menos de la sexta parte de los negros (14%). Estar a la sombra, en cambio, es más frecuente en hispanos (37%) y negros (43%) que en blancos (25%). En cuanto al nivel de vitamina D en sangre, más del 70% de los que tienen deficiencia se protegen del sol a la sombra o usan la ropa adecuada (sobre todo las camisas de manga larga).
Las conclusiones son curiosas: la deficiencia en vitamina D la provoca la sombra y las mangas largas, no así los protectores solares que, según los investigadores, se utilizan poco o en poca cantidad y, por tanto, no protegen adecuadamente del sol y, de rebote, no provocan niveles bajos de vitamina D.
Hay que añadir que el grupo de Pelle Lindqvist, del Instituto Karolinska de Estocolmo, ha encontrado una relación entre evitar la exposición al sol y la tasa de mortalidad. Ha revisado datos de 29518 mujeres entre 1990 y la actualidad y que tenían de 25 a 64 años cuando se inició el estudio. Para este estudio, tomar poco el sol es, durante el verano, no tomarlo nunca, y tomarlo mucho es, en verano, hacerlo más de 30 veces.
Hasta 2011, fecha de la revisión de datos, habían muerto 2545 voluntarias. El número de fallecimientos es mayor cuanto menos se toma el sol. No hay que olvidar que los datos son de Suecia, un país al norte y con escasez de sol. Cuando se compara la mortalidad entre las que evitan el sol y las que lo toman, la tasa de mortalidad se dobla entre las que lo evitan. Para los autores, la causa está en la deficiencia en vitamina D, con las consecuencias para la salud que antes he mencionado. Conciliar el riesgo de melanoma con la deficiencia en vitamina D necesita un estudio más detallado y preciso para elaborar un protocolo adecuado.
El mismo grupo de Estocolmo estableció poco después que tomar el sol baja la tasa de mortalidad por enfermedades cardiovasculares y por otras enfermedades excepto cáncer. Calculan, por el contrario, que evitar el sol disminuye la esperanza de vida entre 0.6 y 2.1 años. Debido a la mayor esperanza de vida y a que evitan algunas enfermedades, las mujeres que toman el sol padecen cáncer años más tarde.
En conclusión, la radiación solar ultravioleta es esencial para la síntesis de vitamina D pero, a la vez, crece el riesgo de cáncer de piel, del peligroso melanoma. Sin embargo, cuando se ha buscado una relación entre el nivel de vitamina D con el riesgo de melanoma, no s eha encontrado. El estudio de Upekha Liyanage y su grupo, del Instituto de Investigación Médica Berghofer de Brisbane, en Australia, con datos de 36077 voluntarios, concluye que los niveles de vitamina D no se pueden asociar como causa y efecto con el riesgo de melanoma.
 Foto: Dimitris Vetsikas / Pixabay
Foto: Dimitris Vetsikas / PixabayQueda por mencionar un inesperado daño colateral en esta conducta de evitar el sol: la contaminación marina provocada por los protectores solares. Fue un grupo de las islas Baleares el primero en detectarlo en Mallorca.
El riesgo asociado a la exposición al sol ha llevado, en los últimos 80 años y según cuentan Antonio Tovar y sus colegas del Instituto Mediterráneo de Estudios Avanzados de Esporles, en Mallorca, a la invención, desarrollo y producción masiva de protectores solares. En consecuencia, también ha llegado su entrada masiva en el ambiente marino costero.
Su composición es compleja, con sustancias que filtran los rayos ultravioleta, algunas orgánicas como los aminobenzoatos, las benzofenonas, los derivados del alcanfor y muchos más, y otras inorgánicas como los óxidos de titanio o de zinc. Todas ellas reflejan y dispersan la radiación ultravioleta e impiden que llegue a la piel. Hay unos 45 compuestos de este tipo cuya producción está regulada en diferentes países.
Además de estas sustancias que actúan como filtros de ultravioleta, una crema solar lleva conservantes, colorantes, agentes que forman geles sobre la piel, controladores de viscosidad, fragancias, etcétera. Y todos ellos acaban, antes o después, en el ambiente, sobre todo en el mar.
El grupo de Antonio Tovar ha medido la presencia de alguno de estos compuestos en cinco puntos de tres zonas de costa de la isla de Mallorca con gran ocupación (entre 3 y 5 personas por metro de costa), en agosto y septiembre de 2011, temporada alta de turismo.
El análisis de las muestras de agua demuestra que los cuatro productos medidos están en el medio. Hay una benzofenona entre 53.6 y 577.5 nanogramos (millonésima parte del miligramo) por litro; un derivado del alcanfor entre 51.4 y 113.4 nanogramos por litro; óxido de titanio entre 6.9 y 37.6 microgramos (millonésima parte del gramo) por litro; y óxido de zinc entre 1.0 y 3.3 microgramos por litro. Estas concentraciones varían entre puntos de muestreo y, también a lo largo del día con el máximo entre las 14.00 y las 18.00 horas.
Para conseguir una primera aproximación de la posible influencia de estos compuestos en el medio marino, los ensayan sobre el crecimiento de un alga diatomea habitual en la zona, la Chaetoceras gracilis, y en ensayos cortos de 72 horas, en lo que se denomina toxicidad aguda. Con todos los compuestos hay una caída del crecimiento de la diatomea aunque las concentraciones necesarias son mucho más altas, a nivel de miligramos por litro, es decir, un millón de veces más altas que las encontradas en las playas. Pero no hay que olvidar que el periodo de exposición en el experimento era muy corto, solo 72 horas, y a más largo plazo, semanas, meses o años, incluso con concentraciones más bajas, no conocemos los efectos que provocan y los componentes de los protectores solares podrían ser peligrosos.
Referencias:
Holick, M.F. 2017. The vitamin D deficiency pandemic: Approaches for diagnosis, treatment and prevention. Reviews in Endocrine and Metabolic Disorders 18: 153-165.
Lindqvist, P.G. et al. 2014. Avoidance of sun exposure as a risk factor for all-cause mortality: results from the Melanoma in Southern Sweden cohort. Journal of Internal Medicine doi: 10.1111/joim.12251
Lindqvist, P.G. et al. 2016. Avoidance of sun exposure as a risk factor for major causes of death: a competing risk analysis of the Melanoma in Southern Sweden cohort. Journal of Internal Medicine doi: 10.1111/joim.12496
Linos, E. et al. 2012. Sun protective behaviors and vitamina D levels in the US population: NHANES 2003-2006. Cancer Causes Control 23: 133-140.
Liyanage, U.E. et al. 2020. Is there a causal relationship between vitamin D and melanoma risk? A Mendelian randomization study. British Journal of Dermatology 182: 97-103.
Matthews, N.H. et al. 2017. Epidemiology of melanoima. En “Cutaneous melanoma: ethology and therapy”, p. 3-22. Ed. por W.H. Ward & J.M. Farma. Codon Publ. Brisbane, Australia.
Tovar-Sánchez, A. et al. 2013. Sunscreen products as emerging pollutants to coastal waters. PLOS ONE 8: e6545
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo A tomar el sol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las mutaciones que aclaran la piel
- Biomarcadores para la detección precoz del melanoma
- Cómo nos ayuda la ciencia a tomar decisiones correctas
Eragin genetiko txikia hezkuntza errendimenduan

Irudia: Geneen eragina hezkuntza errendimenduan aztertu duten ikertzaileen arabera, besteak beste, hezkuntza-lorpenaren eta errendimendu kognitiboaren gaineko ondorio genetikoak behin eta berriz aldatzen dira ingurumen-testuinguruen bidez. (Argazkia: Aline Ponce – domeinu publikoko irudia. Iturria: Pixabay.com)
Egun, bestelakoak dira gauzak. Izan ere, DNAren –ondorengoei oinordetzan utzitako informazioa kodetzen duen makromolekula– katea osatzen duten molekulen ordena zehatza ezagutzea ahalbidetzen duten teknikek garapen ikusgarria izan dute, eta izugarri merkatu dira. Horrela, norbanako batzuetatik beste batzuetara dauden ezberdintasunak zehatz-mehatz azter daitezke, eta aldaera genetikoak bereizi. Eta, orobat, norbanako askorentzat egin daiteke. Zenbait kasutan, aukera dago gene bat zein prozesutan dagoen zehazki jakiteko, baina gehienetan ez.
Duela hilabete batzuk, lagin handi bateko banakoen konfigurazio genetikoaren eta haiek beraiek lortutako hezkuntza mailaren arteko lotura aztertzeko analisiaren emaitzak argitaratu dira. Milioi bat eta ehun mila pertsonak baino gehiagok osatzen zuten lagina. Ikertzaileek 1.271 aldaera –nukleotido bakarreko polimorfismoak, hizkuntza teknikoan– antzeman zituzten; horiek, oro har, hezkuntza mailarekiko lotura adierazgarria erakutsi zuten, hezkuntza sisteman egondako urte kopuruan islatzen den legez.
Hezkuntza jardunari loturiko aldakortasunaren zati handi batek eragina du, batetik, garun garapenaren prozesuetako geneetan eta, bestetik, lotura sinaptiko izenekoen bidez neuronen artean ezarritako komunikazioan. Lotura horiek bide ematen dute ondoko neuronei informazioa transmititzeko, eta molekulen esku hartzearen bitartez gertatzen da, mezulariena egiten baitute.
Agidanez, herrialde batzuetatik besteetara aldatzen da aldaera genetikoen eragina. Hala ere, ikertzaileek ezin izan dute eraginon zergatia zehaztu, baina litekeena da herrialdeetako hezkuntza sistemen arteko aldeekin zerikusia izatea, haietako bakoitzean sustatutako gaitasunei edo trebetasunei dagokienez. Baliteke konfigurazio batzuk arazoak ebazteko egokiagoak izatea, eta beste batzuk, berriz, oroimenezko ikaskuntzarako, besteak beste.
Lotura genetiko globala ez da oso esanguratsua: hezkuntza jardunaren aldakortasunaren % 11 eta % 13 bitartean dago lotuta aldakortasun genetikoarekin. Hots, ingurumen faktoreek, hala nola familiaren ezaugarriek, gurasoen hezkuntza mailak eta eskola inguruneari lotutako faktoreek, askoz ere eragin handiagoa dute. Horrez gain, mota horretako karaktereetan, konfigurazio genetikoak, ezaugarri jakin batzuk zehaztu baino gehiago, horiek garatzeko aurretiko jarrera transmititzen du; horrenbestez, tarte zabala dago ingurumen eraginari lotutako aldeak sortzeko.
Ez da garrantzi txikiko ondorioa kontuan hartzen badugu hezkuntza jardunak helmen handiko eragin garrantzitsuak dituela; esaterako, ongizate ekonomikoa, osasun egoera helduaroan edota bizi itxaropena.
Iturri bibliografikoa:
Lee, J.J., Wedow, R., Okbay, A. et al. (2018). Gene discovery and polygenic prediction from a genome-wide association study of educational attainment in 1.1 million individuals. Nature Genetics, 50: 1112-1121. DOI: https://doi.org/10.1038/s41588-018-0147-3
———————————————————————————-
Egileaz: Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
———————————————————————————
The post Eragin genetiko txikia hezkuntza errendimenduan appeared first on Zientzia Kaiera.
La hipótesis de la abuela
 Foto: djmboxsterman / Pixabay
Foto: djmboxsterman / PixabayLa menopausia es, desde una perspectiva evolutiva y en apariencia, una anomalía. De hecho, es un fenómeno muy poco frecuente en el mundo animal. En casi todas las especies las hembras se mantienen fértiles a lo largo de toda su vida. Nuestra especie forma parte de un pequeño grupo de mamíferos en los que la capacidad reproductiva se deteriora de forma acelerada con relación al declive orgánico general. El grupo lo forman, además de la especie humana, el calderón tropical, la beluga, el narval y la orca, todos ellos cetáceos odontocetos. Las hembras de esas especies pueden vivir décadas después de cesar de ovular y, por lo tanto, de poder procrear.
El biólogo norteamericano George C Williams propuso en 1957 que la menopausia podría ser, en realidad, una adaptación. Pensó que desde el punto de vista evolutivo, podría resultar más conveniente para las mujeres dedicar sus esfuerzos a apoyar a sus descendientes que tener ellas una progenie mayor. Conforme envejecemos aumenta la probabilidad de morir, por lo que si una mujer tiene descendencia a una edad avanzada, no sería improbable que sus últimos hijos no pudieran sobrevivir al morir ella. En tal caso, el esfuerzo que esa mujer hubiese dedicado a esos últimos hijos habría resultado baldío, pues sus genes no habrían podido replicarse y ser transmitidos a las siguientes generaciones a través de esos últimos descendientes. Por otro lado, que en una población haya individuos que no se reproducen carece de sentido desde un punto de vista evolutivo, pues esos individuos consumen unos recursos que podrían utilizar otros en beneficio de su propia progenie.
Por estas razones, Williams propuso que las mujeres de mayor edad contribuyen de una forma más efectiva a transmitir sus genes a las generaciones posteriores dedicando sus esfuerzos a los descendientes que ya forman parte del grupo, o sea, a sus nietos y nietas, en vez de hacerlo a los hijos e hijas que a una edad avanzada pudiera llegar a tener ellas mismas.
La “hipótesis de la abuela”, como se conoce en la actualidad la propuesta de Williams, cuenta con respaldo empírico en nuestra especie. Tanto en grupos de cazadores-recolectores, como en sociedades preindustriales se ha comprobado que las abuelas que no se reproducen aumentan la probabilidad de supervivencia de sus nietos. En otras palabras, su presencia en el grupo facilita que sus genes –los que han llegado hasta los nietos- perduren tras su propia muerte o, dicho en lenguaje darwinista, mejore su propia adecuación o éxito evolutivo (fitness) a través del cuidado que presta a sus nietos.
Hay especies, como el elefante asiático y posiblemente también los africanos, de las que sabemos que las abuelas mejoran la supervivencia de los nietos, aunque en este caso las abuelas se siguen reproduciendo. Pero aparte de la especie humana, en ningún otro animal se contaba con pruebas fehacientes en favor de la “hipótesis de la abuela”. Hasta hace unas semanas, pues se acaba de publicar un estudio con orcas –también llamadas, impropiamente, ballenas asesinas- que documenta el efecto positivo de abuelas que no se reproducen en la supervivencia de sus nietos. El estudio recién publicado no solo confirma ese efecto, también muestra que las abuelas que siguen procreando no prestan un apoyo similar al que brindan las orcas menopaúsicas.
La importancia que ese periodo posmenopáusico tan extenso tiene en seres humanos y en orcas habría impulsado, según los especialistas, un aumento en la longevidad de las dos especies, pues la mayor supervivencia de los nietos durante los años de vida añadidos habría compensado con creces, en términos evolutivos, el cese de la procreación.
Fuente: S. Nattrass et al (2019): Postreproductive killer whale grandmothers improve the survival of their grandoffspring. PNAS.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La hipótesis de la abuela se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Asteon zientzia begi-bistan #299

SARS-CoV-2 birusa detektatzeko CRISPR-en oinarritutako diagnostiko azkarreko tresna azkar bat proposatu dute; emaitza 45 minutu inguruan ematen du, RT-PCR proben antzeko zehaztasunarekin. Elhuyar aldizkariak azaldu du COVID-19 gaitza duten 36 pazienteren eta bestelako arnas gaixotasunak dituzten 42ren laginak hartu dituztela. Kasu positiboetan, %95eko zehaztasuna lortu zuten, eta negatiboetan, berriz, %100ekoa.
COVID-19 gaitza detektatzeko testez hitz egiten ari gara egunero baina Berrian Ana Galarragak esaten digun moduan, hauek mugak aurkezten dituzte. Smriti Mallapaty ikertzaileak Nature aldizkarian dio testen ahalmenari balio handiegia eman zaiola, eta txikiegia haien mugei. Zeintzuk dira, hortaz, muga hauek? Halere, ez dugu ahaztu behar testak ezinbesteko tresnak direla jakiteko zenbat hedatu den eta nori eragin dion pandemiak.
Testez gain, maskarak izan dira gizartearen kezka nagusia. Zer dakigu bere erabilerari buruz? Horiek erabiltzea beharrezkoa al da? Zenbat mota daude? Denok eskuragarri izango ditugu? Berrian honen ingurukoak.
Eta ildo honi jarraiki, artikulu honetan maskara motak eta horiek egiteko erabiltzen diren materialez mintzatu dira. Oro har, bi maskara mota daude: kirurgikoak eta babes-maskarak. Horiez gain, baina, beste batzuk aipatzen dira: maskara higienikoak eta etxean egindakoak. Ez galdu horiei buruzko azalpen argigarriak!
Denok gaude konfinamendu hau noiz bukatuko den zain. Bada Osasunaren Mundu Erakundeak (OMEk) bere irizpideak argitaratu ditu transmisio komunitarioko agertoki iraunkor batetik transmisio txikiko agertoki batera igarotzeko. Artikulu honen bidez, Miren Basarasek bildu dizkigu irizpide horiek. Ez galdu!
Miren Basarasek artikulu honetan galdera bat planteatzen digu: benetan prestatu gara eta neurriak aldez aurretik hartu dira pandemia hipotetiko horri aurre egiteko? Hain justu, iazko irailean OMEk eta Munduko Bankuko aditu-talde batek txosten bat kaleratu zuten eta bertan ohartarazi zuten osasun larrialdi global baten arriskuaz. Oro har, bertan azaltzen zen ez dagoela nahikoa egiturarik hurrengo pandemia hilgarriari aurre egiteko.
Noiz arte iraungo du urruntze sozialak? Ez dakigu neurri honek zenbat iraungo duen baina badirudi luzarorako joango dela. Halaxe dio Harvard institutuko ikertzaile batzuek lan batean: aurreikusten dute 2022 arte derrigorrezkoa izango dela koronabirus berri honen transmisioa gainditu ahal izateko. Berrian informazio guztia.
Bizi dugun pandemiak ondorio psikologikoak utziko dituela esan dute adituek. OMEk ere ohartarazi du “leku guztietan artatu beharko dela jendearen buru osasuna: lanean, eskoletan, gizarte zentroetan…”. Pandemiak ekar ditzakeen ondorio psikologikoak hondamendi eta gerretakoekin parekatu ditu gainera. Testu honetan, Maite Elizondo psikologoaren eta Iñaki Markez eta Blanca Morera psikiatren hausnarketak aurkituko dituzue.
SARS-CoV-2 birusa eta tabakoaren artean harremana dago Pitié Salpêtrière Parisko ospitalean egindako ikerketa baten arabera. Hipotesi moduan argitaratu dute: tabakoa erretzea aldagai babeslea da COVID-19aren aurrean. Ikertzaileen ustez, giltza nikotina izan daiteke. Izan ere, SARS-COV-2 birusak erasotzen dituen zelula askok nikotinaren errezeptoreak dituzte. Berrian irakur daiteke.
Jose Antonio Lozano BCAM Matematika Aplikatuen Euskal Zentroko zuzendaria elkarrizketatu dute Berrian. Antza lantalde berezi bat sortu dute eta UPV/EHUrekin eta Ikerbasquerekin elkarlanean ari dira Eusko Jaurlaritzakoek erabakiak informazio gehiagorekin hartu ahal ditzaten. Haren esanetan, bi lan dituzte: “Alde batetik, epe motzera begira aurreikusten saiatzea, ea zenbat jende ospitaleratu beharko den eta zenbatek egon beharko duten zainketa intentsiboetako unitateetan [ZIU]; bestetik, luzera begira, eredu makroago bat edukitzea, ikusteko gaitzak nola eboluzionatuko duen eta gobernuaren neurriek nola eragiten duten kutsatuen kopurua”.
Munduan zehar egin diren hainbat ikerketak ondorioztatu dute COVID-19ak kutsadura gehien duten hirietan duela eraginik latzena. Berriako testu honetan, egin diren azterlanen emaitzak irakurtzeko parada izango duzue. Adibidez, Harvardeko Unibertsitateko T.H.Chan Osasun Publikoko Sailak egindako ikerketa baten arabera, PM 2,5 partikulen kutsadura gehien duten Ameriketako Estatu Batuetako hirietan ari da koronabirusa jende gehien hiltzen. Europan egindako azterlanak ere ondorio berdinera iritsi dira. Ez galdu!
GenetikaAzken hilabete hauetan birusak bilakatu dira gure bizitzaren erdigune. Egoera honi jarraiki, Koldo Garcia genetikariak birusei buruz dugun iritzi negatibo hori zokoratu du eta gugan bizi diren birusak izan ditu mintzagai honetan. Hasteko, biroma osatzen duten birusak hiru talde handitan sailka daitezkeela aipatu -erretrobirus endogenoak, zelula eukariotoen birusak eta bakteriofagoak-, eta horiei buruz hitz egin digu. Aukera polita duzue ikusteko gugan bizi diren birus batzuk garrantzitsuak direla, adibidez, gure mikrobiota osasuntsu mantentzeko.
Pandemia honek ekarri dituen gaiak eta arloak askotarikoak izan dira. Horien artean, eta animaliei dagokienez, pangolinak eta saguzarrak aipatu dira. Koldo Garciak bi animalia hauek hizpide hartuta, euren genetikaz mintzatu zaigu, beste ertz batetik, alegia, ikuspegi osoa izan dezagun.
Zer da zitokinen ekaitza? Immune-sistemaren gehiegizko erreakzio bat da. Garciak azaltzen digunez, bertan zelula txuriek kontrolik gabe ekoizten dituzte zitokinak deitzen diren molekulak. Eta prozesu horretan zein genek hartzen du parte? Erantzuna, artikulu honetan.
COVID-19 pandemiak behartu gaitu historian jazotako beste pandemia eta epidemia ugari gogoratzera. Garciak testu interesgarri batzuen bitartez, HIESa, Ebola eta Kolera aurkeztu dizkigu. Aukera paregabea duzue historian atzera egiteko! Ez galdu!
MedikuntzaEuropako bost estatutan –Espainian, Frantzian, Alemanian, Italian eta Erresuma Batuan– egindako inkesta batek gurasoek txertoekiko duten jarrera aztertu dute. Emaitzen arabera, Espainiako gurasoak dira txertoekiko konfiantza handiena dutenak (%94). Tartean, Alemania (%88), Italia (%87) eta Erresuma Batuko (%86) gurasoak daude eta azkenik, Frantziako gurasoak (%73). Elhuyar aldizkarian topatuko dituzue xehetasun gehiago.
EboluzioaGizakiok hitz egiteko behar ditugun bide neuronalak uste zena baino lehenago garatu zituzten primateek. Orain arte uste zen duela 5 milioi urte sortu zela konexio hori baina orain badirudi duela 25 milioi urte sortu zela ikerketa batek aditzera eman duenez. Ikertzaileentzat harrigarria izan da aurkikuntza hori. Elhuyar aldizkarian xehetasunak.
Orain dela gutxi egindako azterlan batek duela 5.500 eta 3.000 urte artean Europan bizi ziren gizabanakoen genomak eta egungo europarrenak konparatu ditu. Bertan, oinarri genetikoan aldaketa gehien eta gutxien izan duten funtzioak identifikatu dira. Halaber, funtzio hauetan parte hartzen duten aldaera genetikoak hartu dira kontuan. Testu honetan funtzioetako batzuk azaltzen dira adibide gisa, gure giza espeziaren bilakaera ikusteko.
Emakumeak zientzianTina Negus zoologoak (Erresuma Batua, 1941) hamabost urte zituenean teoria zoro bat proposatu zuen: organismo konplexuen bizitza frogatzen zuen Charnia masoni fosil bat aurkitu zuen baina fosil hori bizia oraindik existitzen ez zen garaikoa zela gaineratu zuen, hau da, Kanbriarraurreko arokoa zela esan zuen (beranduago egiaztatu zen Ediacararra garaian izandako bizimodua zela). Baina ez zen hemen bukatu istorioa. Izan ere, urte batzuk beranduago, fosil hori jada ez zegoela jabetu zen. Nork hartu zuen Negusek aurkitutako fosila? Emakume zientzialari honen ingurukoak artikuluan.
AstrofisikaOrain arte ikusitako supernobarik argitsuenaren berri eman dute; SN2016aps izenekoa argitsuena, energetikoena eta masiboena da, aurkitzaileen arabera. Testuan azaltzen diguten moduan, supernoba batek egiten duen eztanda halako hamar izan da oraingoa eta jatorrizko izarraren tamaina gure Eguzkiarena halako 50-100 izan dela uste dute.
–——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
———————————————————————————-
Egileaz: Uxue Razkin (@UxueRazkin) kazetaria da.
———————————————————————————-
The post Asteon zientzia begi-bistan #299 appeared first on Zientzia Kaiera.
Herramientas de luz: de la ciencia ficción a las películas moleculares

Desde su descubrimiento en 1960, los rayos láser han servido de inspiración de películas y series de ciencia ficción. Gracias a desarrollos posteriores algunas de estas fantasías se han hecho realidad. De hecho, ha sido posible crear potentes herramientas de luz de aplicación en ámbitos tan diversos como la biología, la medicina, la industria, las telecomunicaciones o la investigación básica en general.
La conferencia titulada “Herramientas de luz: de la ciencia ficción a las películas moleculares” describe algunas de estas aplicaciones de los rayos láser y abordará las nuevas perspectivas que existen con las fuentes láser de gran intensidad concentrada en pulsos de tiempos muy cortos. Estas fuentes láser permiten filmar los procesos moleculares o incluso adentrarse en el mundo de los electrones, ámbitos antes inexplorables para la ciencia.
Nerea Zabala es la ponente de esta charla del ciclo Bidebarrieta Científica, iniciativa impulsada por la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta. La conferencia ttuvo lugar el pasado 26 de febrero de 2020 en la Biblioteca Bidebarrieta de Bilbao.
Nerea Zabala, doctora en Física, es investigadora asociada en el Centro de Física de Materiales (centro mixto CSIC-UPV/EHU) y en el Donostia International Physics Center (DIPC), y profesora en la Facultad de Ciencia y Tecnología de la UPV/EHU. Actualmente su investigación se centra en el estudio del comportamiento de la luz en la nanoescala.
Edición realizada por César ToméLópez
El artículo Herramientas de luz: de la ciencia ficción a las películas moleculares se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #NaukasKids14 Física y ciencia ficción
- Un equipo de alta fidelidad de ciencia ficción
- Ciencia, arte y cultura callejera: física y música
Ezjakintasunaren kartografia #304

Zelako bizitza, halako mikrobioma erleen kasuan. Mikrobioma egokia izateko aukerak haien biziraupenerako lagungarri izan daitekeenez, mikrobioma zelan sortzen den jakitea da lehenengo pausua. Lila Westreichek hauxe ikertzen du Bees seeking bacteria: How bees find their microbiome
Garuna aldatzen al du telefono mugikorraren erabilerak? Horixe, baietz. Marrazten edo irakurtzen ikasteak bezala. Erabilera adikzio bihurtzen denean zelan aldatzen den da gakoa. Rosa García-Verdugoren Brain structure differences associated with smartphone addiction
Grafeno nanotirei talde funtzionalak akoplatuta materialaren banda elektronikoekin gauza izugarriak egin daitezkeela frogatu dute DIPCn: Engineering hybrid graphene nanoribbons with active electronic properties
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #304 appeared first on Zientzia Kaiera.
Lo que la búsqueda de inteligencia extraterrestre nos enseña para entender la pandemia
 Unsplash/Donald Giannatti, CC BY-SA
Unsplash/Donald Giannatti, CC BY-SAComprender el significado de los números cuando se refieren a cantidades muy grandes o muy pequeñas es complicado. Esto es algo que experimentamos ahora mismo con la pandemia del COVID-19. La combinación de unos números muy grandes (la población total susceptible de ser contagiada) junto con unas probabilidades ínfimas (las asociadas al contagio individual y a la aparición de determinados síntomas graves) da como resultado unas cantidades de muy difícil interpretación. Sobre todo si ignoramos la disponibilidad de servicios hospitalarios. Así, las diferencias entre el riesgo individual y el comunitario se entremezclan y en ocasiones se oscila entre el excesivo alarmismo y el optimismo injustificado.
Para ilustrar esta situación en un contexto más amable, podemos utilizar la fórmula presentada en 1961 por el radioastrónomo Frank Drake para dar una base cuantitativa al proyecto SETI (Search for ExtraTerrestrial Intelligence) en la segunda mitad del siglo XX. SETI suponía un intento científico para determinar la probabilidad de establecer contacto con civilizaciones extraterrestres en nuestra galaxia, algo que muchos verán como mera ciencia-ficción pero que podemos abordar con un espíritu analítico.
¿Cómo podríamos determinar el número de eventos de un determinado suceso tan improbable como la comunicación con una sociedad tecnológica extraterrestre? La estrategia consiste en separar los factores que deben concatenarse para lograr un positivo. Asumiremos que todos estos sucesos son independientes y que, por lo tanto, podemos determinar la probabilidad de que se den simultáneamente con una sencilla multiplicación. Añadiendo factores podemos llegar a una estimación razonable sobre la probabilidad del evento final: aquel en el que todos los sucesos se combinan perfectamente.
Esta tarea abarca un buen número de disciplinas que van desde las ciencias experimentales hasta especulaciones de muy discutible fundamento, pasando por áreas del conocimiento más difícilmente mensurables como la historia y las ciencias sociales.
Podríamos comenzar tomando como primeros factores la fracción de estrellas en la galaxia que presentan planetas en su entorno y la cantidad de estos que tienen la composición adecuada y están en la zona de habitabilidad. Estas son cuestiones que las últimas misiones espaciales como Kepler, Gaia y TESS nos permiten cuantificar. Pisamos tierra firme o, al menos, un suelo más firme de lo que Drake pudo hacer en su momento.
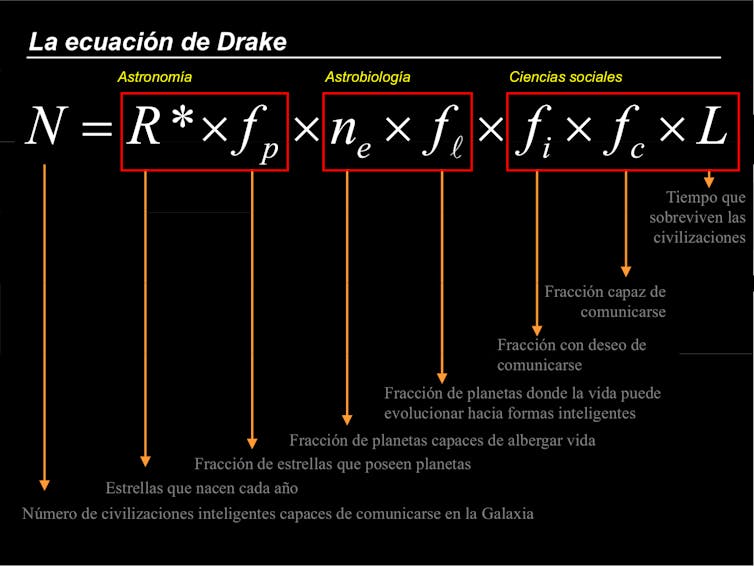 Ecuación de Drake.
Ecuación de Drake.¿Cómo cuantificamos la probabilidad de que surja vida en un planeta que aparentemente reúne las condiciones adecuadas? ¿En cuántos de ellos se ha desarrollado la vida inteligente en forma de civilizaciones? Hasta la fecha, aunque Marte o Venus reunieran condiciones habitables en el pasado, solo conocemos un caso positivo: la Tierra. Ninguno de los más de 4 000 planetas extrasolares conocidos ha demostrado de momento sustentar una biosfera como la nuestra.
A partir de aquí la cuestión se complica. Necesitaríamos cuantificar la evolución de las sociedades hacia la tecnología y el deseo de comunicarse con el resto del universo. También influirá el tiempo durante el cual sean capaces de hacerlo: un siglo, mil años o, como sugirió Drake, hasta 10 000 años. Los datos experimentales para establecer estas cantidades son muy escasos y se basan en la historia humana y en la dinámica de las sociedades que solo comenzamos a comprender de una forma cuantitativa.
En el momento en que Frank Drake asignó valores a todos los términos se encontró con un resultado extraordinario: hasta diez civilizaciones deberían ser detectables mediante SETI. Pero, si así fuera, ¿dónde se encuentran? Esta es la llamada Paradoja de Fermi, opuesta al optimismo de Drake. Encontrar las razones de este inquietante silencio, como se le ha llamado, es también una buena manera de explorar nuestro futuro inmediato y tratar de adivinar los riesgos que como civilización nos pueden esperar a la vuelta de la esquina cósmica.
Otros autores discreparon con los números de Drake desde el primer instante, obteniendo valores mucho más bajos que manifestaban la improbabilidad de lograr el contacto gracias al proyecto SETI. Pequeñas variaciones en los términos que se multiplican en esa larga cadena resultaban en cambios notables del resultado final y, peor aún, las incertidumbres se propagaban exponencialmente en el resultado.
De la ecuación de Drake podemos aprender que los eventos individuales pueden ser realmente infrecuentes o improbables pero, aplicados a una población lo suficientemente grande, su aparición es inevitable. Además, cuando los eventos dependen de una larga cadena de condiciones cuyas probabilidades no podemos estimar con total certeza, nuestra capacidad de predecir los eventos futuros se enturbia. La diferencia con la epidemiología es que, en esta, buscamos que los eventos sucedan en el menor número posible y, para ello, podemos actuar sobre algunos de los factores involucrados.
Desde un punto de vista sanitario, la probabilidad de un evento único, como que enfermemos con síntomas graves, puede ser muy baja, casi despreciable. Aplicada sin embargo sobre el conjunto de la población, terminará sucediendo. Y lo hará más de una vez. Los factores que influyen incluyen la biología, fisiología y la sociología, con una transversalidad similar a la de la astrobiología.
La buena noticia es que cambiar esto se encuentra en nuestra manos: alterando unos pocos factores podemos reducir el número a una cantidad, si no nula, al menos manejable. En ello estamos.![]()
Sobre el autor: Santiago Pérez Hoyos es investigador doctor permanente en astronomía y astrofísica en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original
El artículo Lo que la búsqueda de inteligencia extraterrestre nos enseña para entender la pandemia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La búsqueda de la inteligencia artificial
- Un juego de mesa para entender la irreversibilidad
- La búsqueda de la inteligencia artificial, en la próxima zientziateka
Orain arte ikusitako supernobarik argitsuenaren berri eman dute
Pertsona baten garrantziaren eta aberastasunaren arabera izan ohi da ere haren hileta. Goi mailako agintariak hiltzen direnean, Estatu hiletak ere egoten dira. Hildakoa etxerik gabeko txiroa bada, berriz, hobi komuna izango du betikotasunerako aterpe bakarra. Dena dela, hildako guztiak, berdin-berdin bilakatuko dira hauts. Bizitzaren etengabeko joan-etorrian, euren atomoak birziklatuko dira. Azken uneetan, milaka lagunen azken agurraz lagunduta ala udal funtzionario baten begiradapean, errefusaren biltegira ez baizik unibertsoaren ontzi marroira joango gara guztiak. Kontsolamendu eskasa.
Izarren artean ere antzeko zerbait gertatzen da. Duten tamaina zein den, horren arabera izango da horien heriotza. Dakigula, ez dago giza hiletak bereizten dituen sailkapenik —tira, egon, egongo dira, antropologo baten doktoretza tesiren batean bederen—, baina izarren azken uneak oso ondo sailkatuta daude. Ez da arraroa, unibertsoan izaten diren objektu itzel asko izarren heriotzan abiatzen direlako; funtsean, izarretako hilotzak dira: izar nano zuriak, neutroi izarrak, eta zulo beltzak.

1. irudia: SN2016aps supernobaren irudikapena. Hain distiratsua izan da ezen zenbait hilabetez haren galaxia ezkutatu baitu. Eztandak galaxia horren berri eman du gainera, aurretik ez baitzen ezagutzen (Irudia: M. Weiss)
Aurrean aipatu bezala, izarraren tamaina da haren bizitzaren eta heriotzaren gakoak. Hau ulertzeko, kontuan izan behar da funtsean izarrak etengabeko borroka baten barruan lortzen den orekaren ondorio direla. Batetik, izarraren barruan sortzen diren erreakzio nuklearrek eragindako presioa dago. Bestetik, izarraren beraren grabitatea. Hortaz, udako gau izartsu bat malabaristez beteriko paisaia kosmikoa da.
Eguzkiaren antzeko tamaina duten izarrek nano zuri gisa emango dituzte azken milioika urteak, supernoba bihurtu gabe. Hori posible da izarraren elektroiek izarraren kolapsoari eusten diotelako. Lehenago aurreko fase batetik igaroko dira (erraldoi gorri gisa), baina, amaieran, oso pixkanaka, hoztuko dira. Nano zuriek Lurraren antzeko tamaina dute, baina Eguzkiaren adinako masa mantentzen dute. Hortaz, dentsitate izugarri handia dute.
Baina Eguzkia baino tamaina handiagoa duten izarren kasuan datoz ikuskizunik handienak. Horietan, behin hidrogenoa, helioa eta taula periodikoan dauden burdinara arteko elementu guztiak fusionatu direnean, grabitatea hain da handia ezen elektroiek ezin baitiote eutsi grabitateari, eta izarra bertan behera amiltzen da, kolapso izugarri handi batean. Hor sortzen dira supernobak, izugarrizko eztanda baten moduan. Hemen ere, tamaina da gako. Eztandaren ondoren, neutroi izarra sortzen da, grabitateari eutsi ezin izan dioten elektroi horiek protoiekin batu direlako, neutroiak sortuz. Txundigarriak dira neutroi izarrak: 20 kilometro inguruko diametro batean dentsitate izugarria dute, eta oso azkar biratzen dira. Izar horietako batzuk gainera, erradiazio isuriak botatzen dituzten pulsar izan daitezke, edo, urriagoak diren magnetar ere izan daitezke, sinestezina dirudien eremu magnetikoa sortzen dutenak.
Jatorrizko izarra oso masiboa den kasuetan (Eguzkiaren masa halako 20-30), gainera, zulo beltzak sortzen dira. Horiek ezagunagoak dira kalean, eta arras jakina da ere haien ezaugarririk nabarmenena: hain da handia dentsitatea ezen argia ere ezin baitaiteke askatu bertatik.
Honaino objektu bitxi hauen sailkapen orokor bat. Astrofisikariek sailkapen zehatzagoak dituzte, noski, eta ohiko sailkapenetatik aldentzen diren fenomenoak ere gertatzen dira. Horren adibide da orain aurkeztu duten eztanda baten kasua. SN2016aps izendatu duten supernobak orain arteko marka guztiak gainditu ditu: argitsuena, energetikoena eta masiboena da, aurkitzaileen arabera.
2016an aurkitu zuten, aurrenekoz, Pan-STARRS teleskopioaren bitartez. Bi urtez egin dute fenomenoaren jarraipena, supernobatik askatzen zen energiaren bilakaera aztertzen. Orain, emaitzak ezagutarazteko moduan egon dira. Nature Astronomy aldizkarian eman dute ikasitakoaren berri.
Zalantza barik, zenbaki superlatiboez beteriko fenomenoa da aztertu dutena: egin dituzten kalkuluen arabera, ohiko supernoba batek egiten duen eztanda halako hamar izan da oraingoa, eta jatorrizko izarraren tamaina (edo izarren tamaina, aurrerago ikusiko dugunez) gure Eguzkiarena halako 50-100 izan dela uste dute.
“Orain arte ikusi dugun beste edozein supernoba baino argitsuagoa izan da; baina, horrez gain, baditu beste zenbait propietate eta ezaugarri, eta unibertsoan gertatzen diren beste izarretako eztanden aldean, bitxia da”, adierazi du prentsa ohar batean Edo Berger astrofisikariak. Ikusitakoak atakan jarri ditu ikertzaileak, eta behaketak interpretatzeko azalpen berriak bilatu behar izan dituzte.
Lehen zantzu arraroa iraupenarena izan da. Eztanda atzeman eta hilabete batzuetara ohartzen hasi ziren zerbait berezia zela, argia oso pixkanaka desagertzen ari zelako. Hasieran hain distira handia izanda, eta hain motel desagertuta, ezinbestean horrek esan nahi zuen izugarrizko eztanda izan behar zuela. Haren galaxiaren distiraren gainetik gailendu zen supernoba.

2. irudia: irudia: Pan-STARRS teleskopioaren bitartez ikusi zuten aurrenekoz supernoba, baina jarraipena egiteko beste hainbat teleskopio baliatu dituzte; tartean, Hubble espazio teleskopioa. (Argazkia: Forest Starr / Kim Starr CC BY 2.0)
Galaxiaren ezkutatze hori ez da arraroa: supernoba gehienen kasuan gertatzen da hori, baina, modu berean, estaltze horrek denbora gutxi irauten du: egun batzuk, edo, askoz jota, aste batzuk igarotzen dira supernobaren distira amaitu eta teleskopioetan berriro galaxia ikusten den arte. SN2016aps supernobaren kasuan, berriz, hainbat hilabetez mantendu da galaxiaren distiraren gainetik. Are gehiago, supernoba hau detektatu aurretik, 3.600 milioi argi urte ingurura dagoen galaxia hori ez zen ezagutzen.
Beste ezaugarri bitxi bat hidrogenoari dagokio. Ikertzaileek azaldu dutenez, masa asko duten izarrek hidrogeno gehiena galtzen dute supernoba bihurtu baino lehen. Baina oraingo honetan hidrogeno asko ikusi dute espektroan. Kontraesan hau modu batean edo bestean azaldu ahal izateko, proposatu dute bi izar masiboen arteko talka baten ondorioa izan dela, izar txikiagoak gai direlako hidrogenoa denbora gehiago mantentzeko. Era horretan, bederen, kontuak ateratzen zaizkie.
Fenomenoaren indarra azaltzeko, beste faktore sartu dute prozesuan. Eztanda egin baino lehen, izar masiboek gas mantu erraldoi bat askatzen dute. Bada, une egokian eztanda eginez gero, supernobaren eztandak gas geruza horren kontra joko du, eta horrek eztandaren tamaina handituko du, energia kopuru izugarri handia askatuz. Orain hori gertatu dela uste dute.
Funtsean, horrela geratu zaie azalpena: galaxia urrun batean, duela 3.600 milioi urte inguru, bi izar masibok bat egin zuten, izar ikaragarri handia osatuz, eta bikotea hil baino lehen gas geruza erraldoi bat askatu zuen, gainera. Berez ikaragarri handia zen supernobaren eztandak geruza horrekin talka egitean… tira, Hollywooden ere ikusten ez den leherketa hiper erraldoia sortu zen. Argiaren abiadura dela eta, noski, gu orain konturatu gara horretaz.
Zientzialariek uste dute horrelako izar erraldoiak ohikoak izan zirela unibertsoaren hasierako uneetan. Aurreratu dutenez, hemendik urte batzuetara, James Webb espazio teleskopioari esker aukera egongo da unibertsoan sortu ziren lehen izarrak ikusteko, eta horregatik espero dute antzeko supernoba gehiago detektatu ahal izango direla.
Edo Berger ikertzailearen esanetan, “orain badakigu hain eztanda energetikoak egon daitezkeela naturan”. Teleskopio berriei esker —bereziki, aipatutako James Web bera zein eraikuntzan den Txileko Vera C. Rubin behatokia—, posible izango da denboran are atzerago joatea eta unibertsoaren lehenengo izarren heriotzen garaira iristea.
Erreferentzia bibliografikoa:
Nicholl, M., Blanchard, P.K., Berger, E. et al. (2020). An extremely energetic supernova from a very massive star in a dense medium. Nature Astronomy. DOI: https://doi.org/10.1038/s41550-020-1066-7.
———————————————————————————-
Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.
———————————————————————————-
The post Orain arte ikusitako supernobarik argitsuenaren berri eman dute appeared first on Zientzia Kaiera.
¿Por qué suena triste el modo menor?
Hace cuatro milenios, en Mesopotamia, los sumerios ya utilizaban un sistema musical de siete notas y siete modos para componer sus canciones. Este sistema fue heredado por los griegos que se lo contagiaron al resto de Europa y, desde entonces hasta ahora, —pasando por la larga Edad Media— distintos modos han ido ganando y perdiendo popularidad, según la época. En la actualidad, solemos utilizar preferentemente dos de esos antiguos modos que hemos rebautizado como Modo Mayor y modo menor.
Quizás este desenlace no sea más que un accidente fortuito de la historia. No sabemos si en algún universo paralelo, el reguetón se escribe en el modo frigio y la salsa suena mucho más a mixolidio. Pero, de acuerdo con la hipótesis del profesor David Huron, una vez reducidas las alternativas a dos, su asociación emocional era inevitable: es posible que el modo menor sea, en gran medida un accidente cultural y su asociación con la tristeza deba ser aprendida. Pero esto no significa que sea una asociación arbitraria.
La idea de Huron es que el modo menor suena triste porque suena más triste que el Modo Mayor1. Este, en cambio, saca a relucir su alegría cuando se pone en contraste con su oscuro hermano menor. La clave de esta comparación vuelve a encontrarse en las características de la prosodia humana y cómo esta se ve afectada por nuestras emociones. Pero, para entenderlo, debemos volver a sacar al humano triste de paseo.
Un humano triste, recordemos, es un humano al que le han quitado las pilas. Por eso (y porque tensar las cuerdas vocales también requiere su esfuerzo, aunque no lo parezca), es común que hable bajito, sin cambiar mucho el tono de voz, balbuceando a menudo. Particularmente: es típico que el humano triste produzca sonidos más graves de los que son habituales en él.
Sin embargo, para identificar este cambio en su tono de voz no nos basta con atender a su frecuencia, sin más. Si fuese así, los hombres —que, por lo general, tienen la voz hasta una octava más grave que las mujeres— sonarían siempre tristes, deprimidos, no serían capaces de expresar alegría. Esto, evidentemente, no sucede y el motivo es que, para identificar una voz triste, lo que hacemos es establecer una comparación: entre el tono de esa misma voz en su estado neutro y su tono cuando la invade la tristeza.
Del mismo modo, cuando escuchamos música, realizamos sin darnos cuenta una comparación parecida: entre los tonos que predominan en esa canción y los tonos que se utilizan habitualmente en el resto de nuestra música. O, también, entre los tonos que estamos escuchando en ese momento y los tonos que predominan en el resto de la canción. Y aquí es donde la correspondencia entre los modos Mayor y menor se vuelve relevante, porque si colocamos estas escalas en paralelo, nota a nota, lo que observamos es que el modo menor es una versión oscurecida del Modo Mayor: un modo al que se le han agravado ciertas notas y acortado ciertos intervalos2.
Si bien el uso del modo menor en nuestra tradición musical es, por sí mismo, un accidente cultural, esta especie de tristeza por agravio comparativo parece ser mucho más universal. En 2007, Parag Chordia y Alex Rae quisieron ponerla a prueba utilizando, esta vez, fragmentos musicales procedentes de la India. A través de internet recibieron 22000 respuestas de 500 participantes encargados de clasificar emocionalmente pequeños fragmentos de ragas (los modos melódicos utilizados en la música clásica india). El compendio de todas ellas desvelaba un mismo patrón: los fragmentos con tonos comparativamente más graves e intervalos más pequeños, eran percibidos como más tristes3.
Este es quizás el motivo por el que resulta sorprendente escuchar canciones ya conocidas… a las que alguien ha cambiado el modo (Youtube está lleno de ejemplos). Nuestro recuerdo de la canción original fija un estándar sobre el que inevitablemente superponemos la versión alterada y el contraste saca a relucir la tristeza (o la alegría) percibida
No obstante, mi uso preferido de este contraste se da cuando algún compositor lo establece dentro de una misma canción. Como en esta preciosa canción de El Kanka que, de repente, se quita la ironía y cambia sorpresivamente al modo mayor para hablar de un pasado aparentemente más feliz (se escucha el cambio sobre la misma melodía, en 1’08’’, por ejemplo).
También, me viene a la mente el Lago de los Cisnes de Tchaikovsky. Cuando, en la última escena, después de todo el drama, después de que el tema se haya repetido 500 veces en modo menor, con los protagonistas ya bien muertos y suicidados… el hechizo de los cisnes se rompe y, de repente, escuchamos el mismo tema (2’55’’) ¡pero esta vez triunfante, en Modo Mayor! Parece mentira que pueda tratarse de la misma melodía, cambiando apenas unas pocas notas.
Notas:
1David Huron (2008) A Comparison of Average Pitch Height and Interval Size in Major- and Minor-key Themes: Evidence Consistent with Affect-related Pitch Prosody. Empirical Musicology Review
2El lector que tenga conocimientos musicales quizás se plantee que, al agravar ciertas notas algunos intervalos se harán necesariamente más grandes debido a la estructura cíclica de las escalas. David Huron analizó esta cuestión partiendo de casi 10.000 piezas instrumentales en modo Mayor y menor. Debido a la frecuencia de aparición desigual de los posibles intervalos, el efecto global de cambiar estas notas daba lugar a melodías con intervalos más reducidos en el modo menor.
3Parag Chordia y Alex Rae. “Understanding Emotion in Raag: An Empirical Study of Listener Responses”. Computer Music Modeling and Retrieval. Sense of Sounds, 2008.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo ¿Por qué suena triste el modo menor? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Tina Negus: “Norbaitek nire fosila hartu du!”

1. irudia: Tina Negus gaztetan. (Argazkia: Trowelblazers)
Txikitatik liluratu zuen fosilen ikerketak. Haren bizilekutik gertu (Grantham), harrobi huts bat zegoen eta han jolastea laket zitzaion; bertan, amoniteen eta belemniteen fosil ugari zeuden. Liburutegi publikoan igarotzen zituen ordu mordoxka; bertako liburuetan, fosilei buruzko azalpenak irakurtzen zituen eta, gainera, geologia, biologia eta paleontologia arloei buruzko liburu mardulak ikastea atsegin zuen.
Hamabost urte zituela, bere abentura zientifikoan pauso bat emateko xedez, Charnwoodeko basora joatea otu zitzaion; horretarako, gurasoei laguntzeko eskatu zien. Liburutegian irakurritako liburu batean baso zehatz hori aipatzen zela ikusi, eta bere kabuz egiaztatu nahi izan zuen lerro horietan deskribatzen zena. Negusek eskuz kopiatu zituen arakatu nahi zituen bazterrak; jarraian, egindako mapa hori poltsikoan sartu eta ahabiak biltzeko aitzakiaz, bideari ekin zion. Txango hartan, iratze baten hosto moduko fosil bat topatu zuen; erdiko nerbiorik gabeko fronde bat, alde bietan lumen antzeko folioloek osatzen zuten irudia, hain zuzen ere. Une hartan zur eta lur gelditu zen, izan ere, irakurritako liburuen arabera, fosil hori ez zen existitzen. Hura zen ezustekoa hura. Negus, aldiz, ziur zegoen begien aitzinean zuenaz.
Lapurreta batAurkikuntza egin ostean, Negus zalantza izpirik ez zuela joan zen bere geologia irakaslearengana; ez zen erraza izango hura limurtzea baina sikiera saiatu behar zuen. Irakasleak Negusen azalpenak aditu eta berehala, modu oso zorrotzean ihardetsi zion: “Ez dago fosilik Kanbriarraurreko arroketan”. Alabaina, Negusek ez zuen amore eman eta hurrengo egunean bere aitonari bi orri eta arkatz bat eskatu zizkion iratze baten hosto moduko hori marraz zedin, irudi hori buruan atxikitzea ezinezkotzat jo izan balu bezala. Horren ondotik, figura hori poltsikoan zuela, museora joan zen, bertako bildumako piezaren batekin antzekotasunen bat ote zuen egiaztatzeko. Horretaz gain, aurretik hainbestetan irakurri zituen liburuak errepasatu zituen liburutegian, xehetasunen batek ihes egin ote zion jakiteko. Ez zuen ezertxo ere aurkitu eta horregatik erabaki zuen momentuz fosilaren afera alboratzea eta marrazturikoa karpeta batean gordetzea.
Handik urtebetera, 1957an, berriro ere jakin-minak animatu zuen zuhaizti hartara itzultzea. Leku berera iritsi zenean, ordea, fosila jada ez zegoela jabetu zen. Are gehiago, antza norbaitek fosil hori erauzi egin zuen! Negus harrituta eta etsita itzuli zen etxera; bere aurkikuntza lapurtu ziotelakoan zegoen.

2. irudia: Charnia masoni fosila. (Argazkia: Smith609 – CC BY 2.5 lizentziapean. Iturria: Wikimedia Commons)
Urteek aurrera egin zuten, eta Negus, 1961ean, Zoologian graduatu zen Readingo Unibertsitatean. Bi urtez, ur gezatako muskuiluen ekologia aztertzen jardun zuen baina, egia esan, fosil hura burutik kendu ezinean zebilen. Horregatik, bere garaian egindako marrazkiak eskatu zizkien gurasoei eta aipatutako unibertsitateko geologia departamentuan aurkeztu zituen. Bertan azaldu ziotenez, duela gutxi argitaratu berria zen Leicester Unibertsitateko Trevor Ford doktorearen lan bat honako izenburuarekin: “Charnwoodeko basoaren Kanbriarraurreko fosilak“.
Abentura berak batutaHistoriak gainazalean dagoena errazago ikusarazten digu sarri; haatik, gure dimentsiotik ihes egiten duen abenturarik ere bada: Roger Mason gaztearena, alegia. Inork ez zuen bere garaian jakin, ezta Negusek ere, baina Masonek ere ikertu zuen fosil hori, Negusek Charnwoodeko basoan aurkitu zuena, hain zuzen ere (Rogerren abizenak eman zion izena fosilari). Negusek ez bezala, Masonek lagun eta ezagun ugari zituen inguruan, Ford doktorea kasu. Behin aurkikuntza eginda, harekin harremanetan jarri, eta Fordek, bere ikertzaile taldearekin batera, erauzi egin zuen fosila. Honetaz gain, beste fosil batzuk ere aurkitu zituen, Charniodiscus concentricus deiturikoa, esaterako.
Inork ez du auzitan jartzen Negus eta Mason izan zirela istorio honetako benetako protagonistak: haiek, nork bere aldetik, Ediacararreko biota aurkitu zuten. Aurkikuntza honen ondoren, Negusek bere istorioa kontatu zuen 1997an argitaratu zuen liburu batean: The Fossil. Bere abenturari buruzko poema bat ere idatzi zuen, hemen irakur daitekeena. Era berean, bere antologia poetikoa 2012an argitaratutako On the other side lanean bilduta dago. Poeta izateaz gain, argazkilaritzan eta margolaritzan aritu zen.
Aurrerago, fosil honen istorio osoa ezagutzeko asmoz, Fordekin eta Masonekin harremanetan jarri zen Negus. Gainera, Fordek zein Masonek Charnia masoniren aurkikuntzaren 50. urteurrena ospatzeko hitzaldi batera gonbidatu zuten Negus, aurkikuntza horretan hark parte hartu izana ukaezina baitzen. Charnia masoni fosilak ez daroa bere izenik, baina behintzat jendeak gogoan tinko eutsiko dio Negusen historiari.
Iturriak:
- La pizarra de Yuri, Tina en el bosque de Charnia, la vida que no podía existir.
- Tina Negus, An account of the discovery of Charnia.
- University of Reading, Graduate scientist given inaugural fossil research award in honour of unsung hero.
———————————————————————–
Egileaz: Uxue Razkin (@UxueRazkin) kazetaria da.
———————————————————————–
The post Tina Negus: “Norbaitek nire fosila hartu du!” appeared first on Zientzia Kaiera.
La hoja de papel con cuatro caras, una propuesta de taller
Hace unos cuantos días, pensando en la situación de confinamiento en la que nos encontramos en estos momentos, me pareció que sería una buena idea preparar una actividad sencilla para enviar a la gente y que pudieran realizarla en su casa. Mi idea era que fuese una actividad para personas de cualquier edad, desde pequeños (acompañados si es necesario) hasta mayores. Entonces, me decidí por un taller que hago desde hace algunos años, aunque relacionado con otras cuestiones, y que me gusta mucho. Consiste en construir un objeto matemático sencillo y sorprendente, una hoja de papel con cuatro caras.
Este objeto matemático, cuyas instrucciones de construcción os voy a explicar en esta entrada del Cuaderno de Cultura Científica, pertenece a la familia de objetos llamados flexágonos y que fue descubierta por el matemático inglés Arthur Stone, de quien ya hemos hablado en relación con el problema de la cuadratura del cuadrado en 1939. Aunque estos objetos fueron dados a conocer y popularizados por el gran divulgador de las matemáticas Martin Gardner (1914-2010) en su columna Juegos matemáticos de la revista Scientific American. En concreto, el objeto matemático que vamos a construir en esta entrada es un tetraflexágono, es decir, un flexágono con cuatro lados (cuadrado o rectángulo), además, como va a poder mostrar cuatro caras, se denomina un tetratetraflexágono.
 Portadas de los dos primeros libros de Martin Gardner en los que se recogen los artículos de su columna Juegos matemáticos en la revista Scientific American. En el primero aparece su artículo Hexaflexagons y en el segundo Tetraflexagons
Portadas de los dos primeros libros de Martin Gardner en los que se recogen los artículos de su columna Juegos matemáticos en la revista Scientific American. En el primero aparece su artículo Hexaflexagons y en el segundo Tetraflexagons
Pero vayamos directamente a nuestro objeto matemático, esa hoja de papel de cuatro caras, el tetratetraflexágono, y a su construcción: materiales e instrucciones.
Material básico para el taller: una hoja de papel normal, por ejemplo, din A4, un lápiz y una regla.
Instrucciones para construir el tetratetraflexágono, la hoja de papel con cuatro caras:
Punto 1. Tomamos la hoja de papel, que colocamos con el lado largo en horizontal, y lo vamos a dividir –por delante y por detrás- en cuatro columnas y tres filas, utilizando líneas trazadas con un lápiz. Generando de esta forma 4 x 3 = 12 casillas rectangulares en cada lado.
Punto 2. En cada una de las casillas vamos a pintar, centrado, un número. En las 12 casillas de la parte frontal pintamos los números 4, 4, 3, 2 (en la primera fila, la de arriba), luego 2, 3, 4, 4 (en la segunda fila, en medio) y 4, 4, 3, 2 (en la tercera). Ahora en las casillas de la parte trasera pintamos los números 1, 1, 2 y 3 (arriba), 3, 2, 1, 1 (en medio), 1, 1, 2, 3 (abajo). Ojo, aquí quien lo desee puede echarle imaginación y pintar unos números chulos.
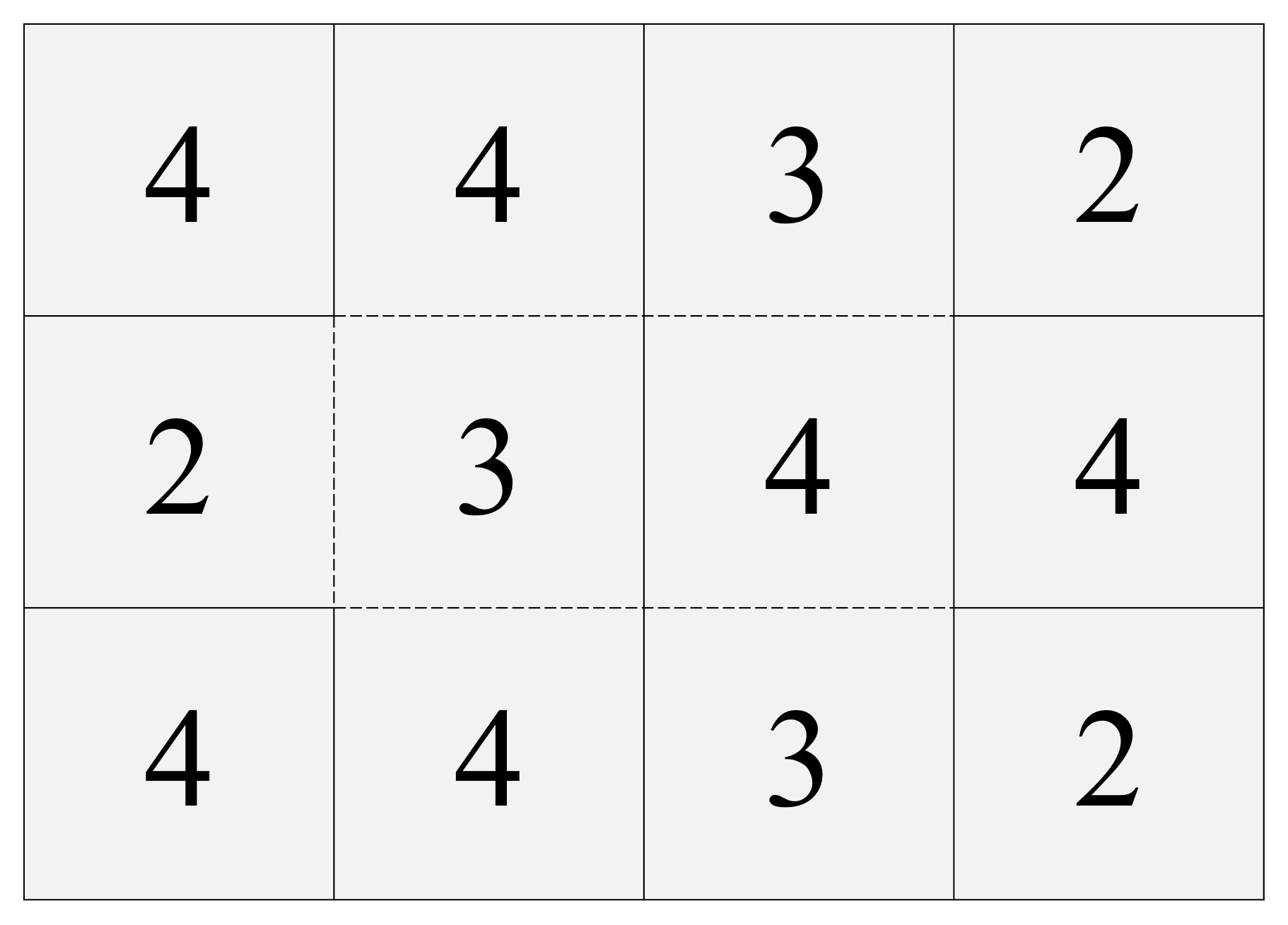 Números de las doce casillas de la parte frontal del folio original
Números de las doce casillas de la parte frontal del folio original
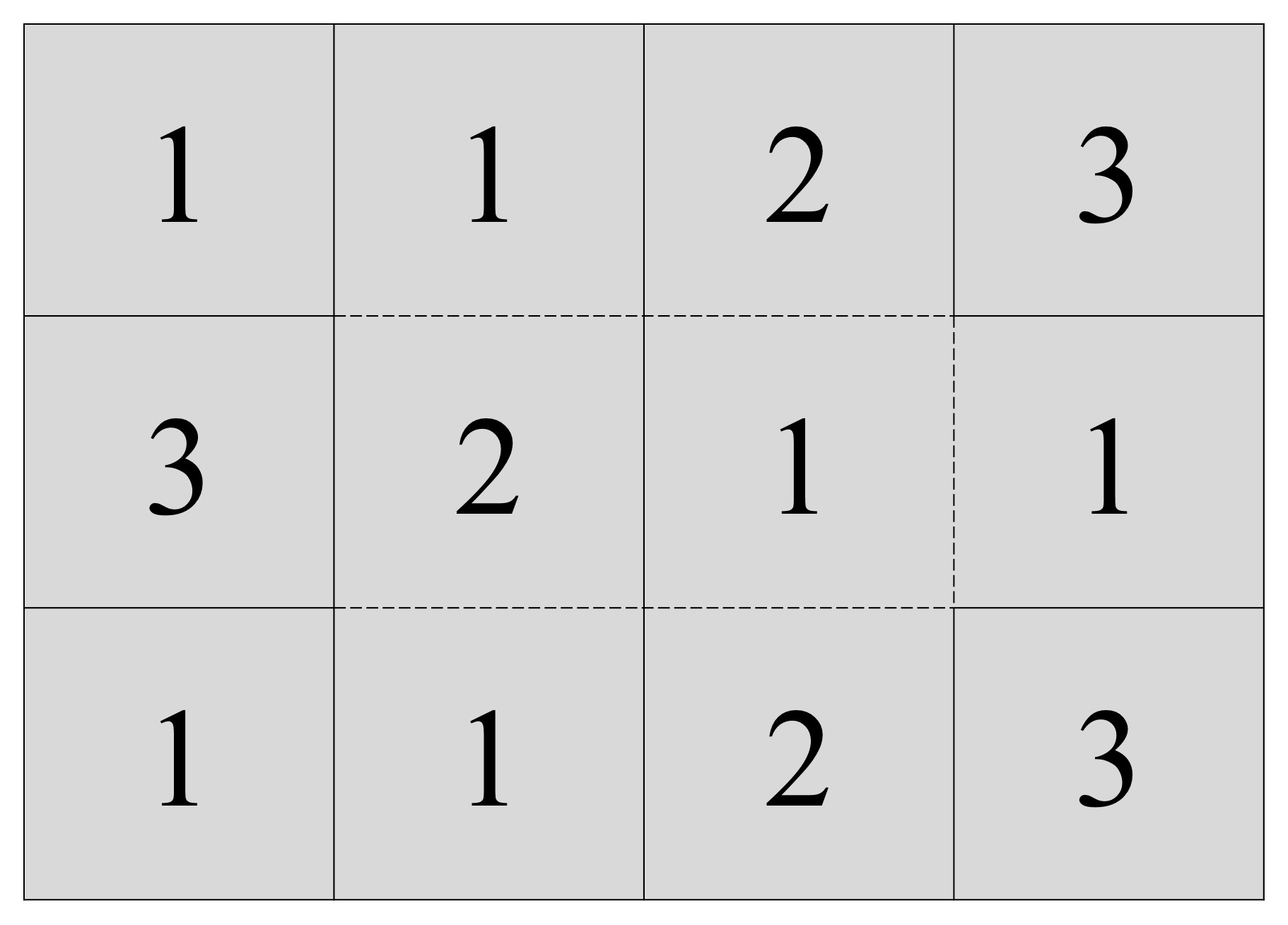 Números de las doce casillas de la parte trasera del folio original
Números de las doce casillas de la parte trasera del folio original
Punto 3. Ahora tenemos que realizar un pequeño corte con unas tijeras, por lo tanto, hay que tener cuidado. Si la actividad la realizan niños y niñas pequeños necesitarán la ayuda, o supervisión, de una persona mayor. Antes de realizar el corte, doblad por las líneas rectas que habéis pintado a lápiz, os ayudará a realizar el corte y además es necesario para la parte final.
Pero vayamos con el corte. Si consideramos la hoja de papel con la parte frontal, la primera, la que tiene solo doses, treses y cuatros, entonces vamos a cortar el papel para separar las dos casillas del centro –con los números 3 y 4- del resto, pero por todos los lados, salvo uno, el derecho –donde se unen los dos cuatros (véase la siguiente imagen).
Es decir, cortaremos los lados de arriba de las casillas centrales, 3 y 4, el lado izquierdo de la casilla del 3 y los lados de debajo de esas dos casillas centrales. De esta forma, estas dos casillas, 3 y 4, que están unidad entre sí, solo están unidas al resto por el lado derecho, el lado entre los dos cuatros.
Punto 4. A continuación, vamos a realizar unos cuantos dobleces para generar nuestra nueva hoja de papel, que tendrá 2 x 3 = 6 casillas.
Primero, doblamos esa parte central, de dos casillas, hacia la derecha, de forma que va a quedar un 2 hacia arriba, donde estaba el 4, y el 1 que lo acompaña quedará por debajo de la hoja.
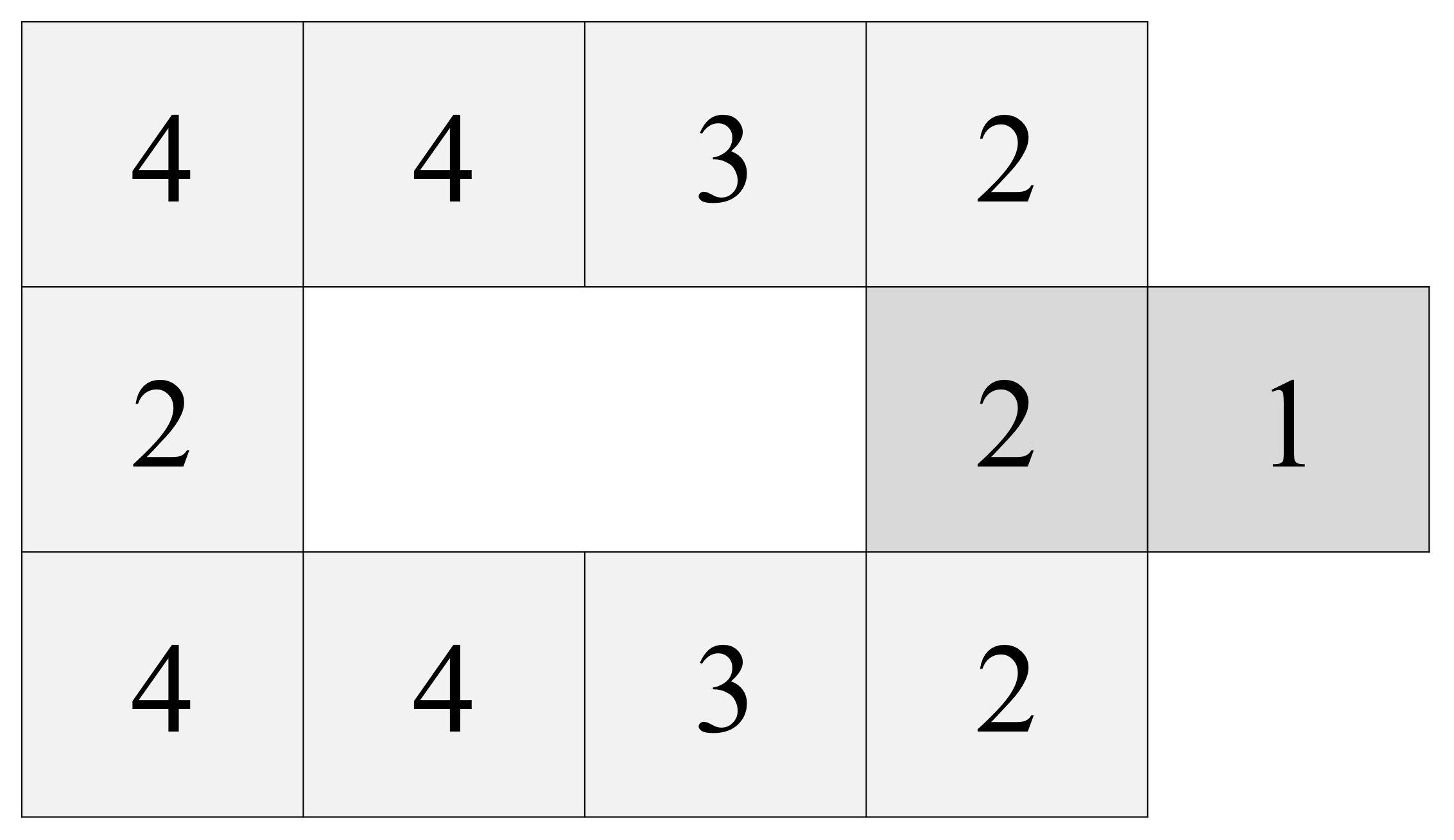
Después, doblamos la columna 4, 2, 4 hacia la derecha, una vez, y después toda la nueva columna (sobre la que ahora vemos los números 3, 1, 3) de nuevo hacia la derecha.
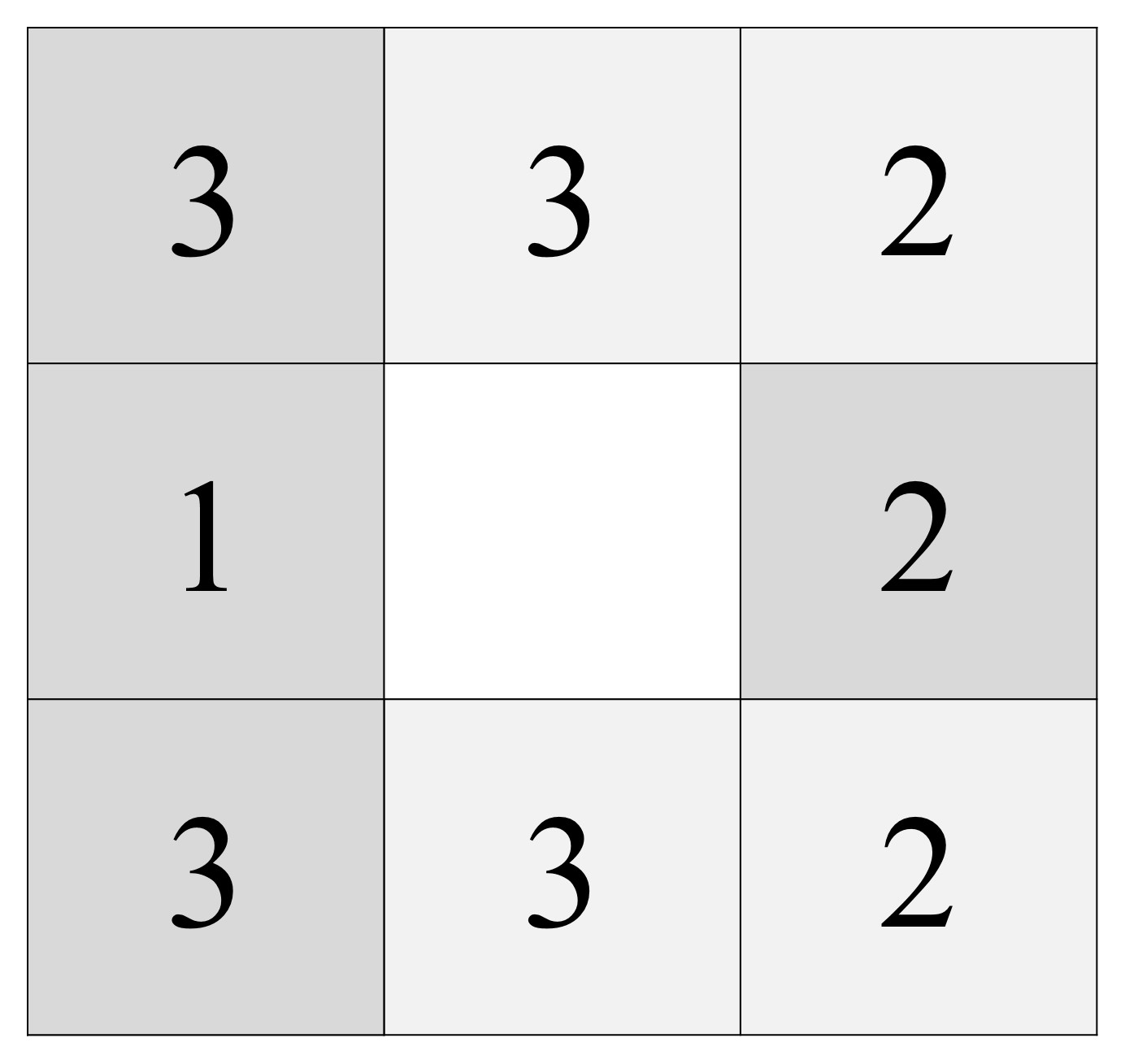
Nos quedará una hoja de papel con 2 x 3 = 6 casillas, con un 2 en todas las casillas, como muestra la siguiente imagen.
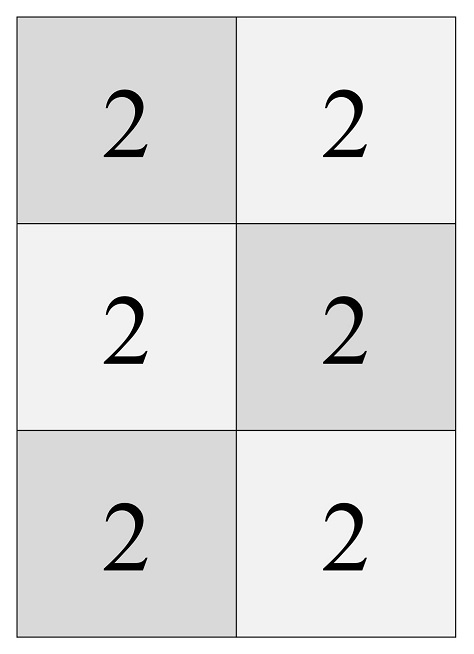
Punto 5. Si le dais la vuelta a la nueva hoja de 6 casillas, tendréis una hoja de papel con un 1 en todas las casillas (la imagen de abajo). Estamos entonces en el último paso. Hay que poner un poco de celo uniendo los dos unos de la fila del centro, el de la izquierda con el de la derecha.
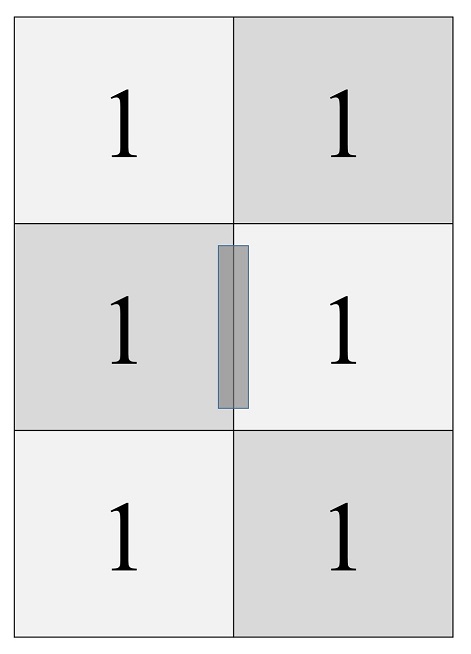
Y ya tenéis la “nueva” hoja de papel con cuatro caras. Veámoslo. En la que tenemos delante solo hay unos (1), le damos la vuelta y solo hay doses (2), luego dos caras. Ahora, con los doses mirando hacia nosotros, doblaremos la hoja por la mitad vertical, llevando las dos mitades hacia atrás, y cuando lleguemos a juntar las dos partes veremos que se nos abre la hoja por el medio, la ayudamos a abrirse con nuestros dedos y veremos que la hoja que tenemos delante tiene todo treses (3).

Si volvemos a doblar la hoja por la mitad vertical, hacia atrás, descubriremos una nueva cara con todo cuatros (4). Es decir, tenemos una hoja de papel con cuatro caras, un tetratetraflexágono. Solo un consejo, antes de mostrárselo a las demás personas practicad el paso de una cara a otra.
La parte básica del taller es la que acabamos de describir arriba, pero a partir de ahí cada cual puede echarle imaginación y hacer el flexágono lo más artístico o curioso que considere oportuno. Por ejemplo, Cristina Barcala, una apasionada de la divulgación científica y lectora del Cuaderno de Cultura Científica, nos mandaba su propia versión, de tamaño mini (la siguiente imagen).

Aunque si os ha gustado esta actividad sobre la realización de un tetraflexágono, podemos abordar la realización de los otros dos tetraflexágonos que aparecen en el artículo Tetraflexagons, del libro de Martin Gardner The 2nd Scientific American Book of Mathematical Puzzles and Diversions (1961), uno de tres caras –tritetraflexágono- y otro de seis caras –hexatetraflexágono-.
Empecemos con el tritetraflexágono. Para realizarlo hay que construir con una hoja de papel una “tira de papel” de dos filas, como la que aparece en la siguiente imagen, trazar las seis casillas de cada cara y dibujar los números 1, 2 y 3 en las casillas, de la parte frontal y trasera, como aparece en la imagen.
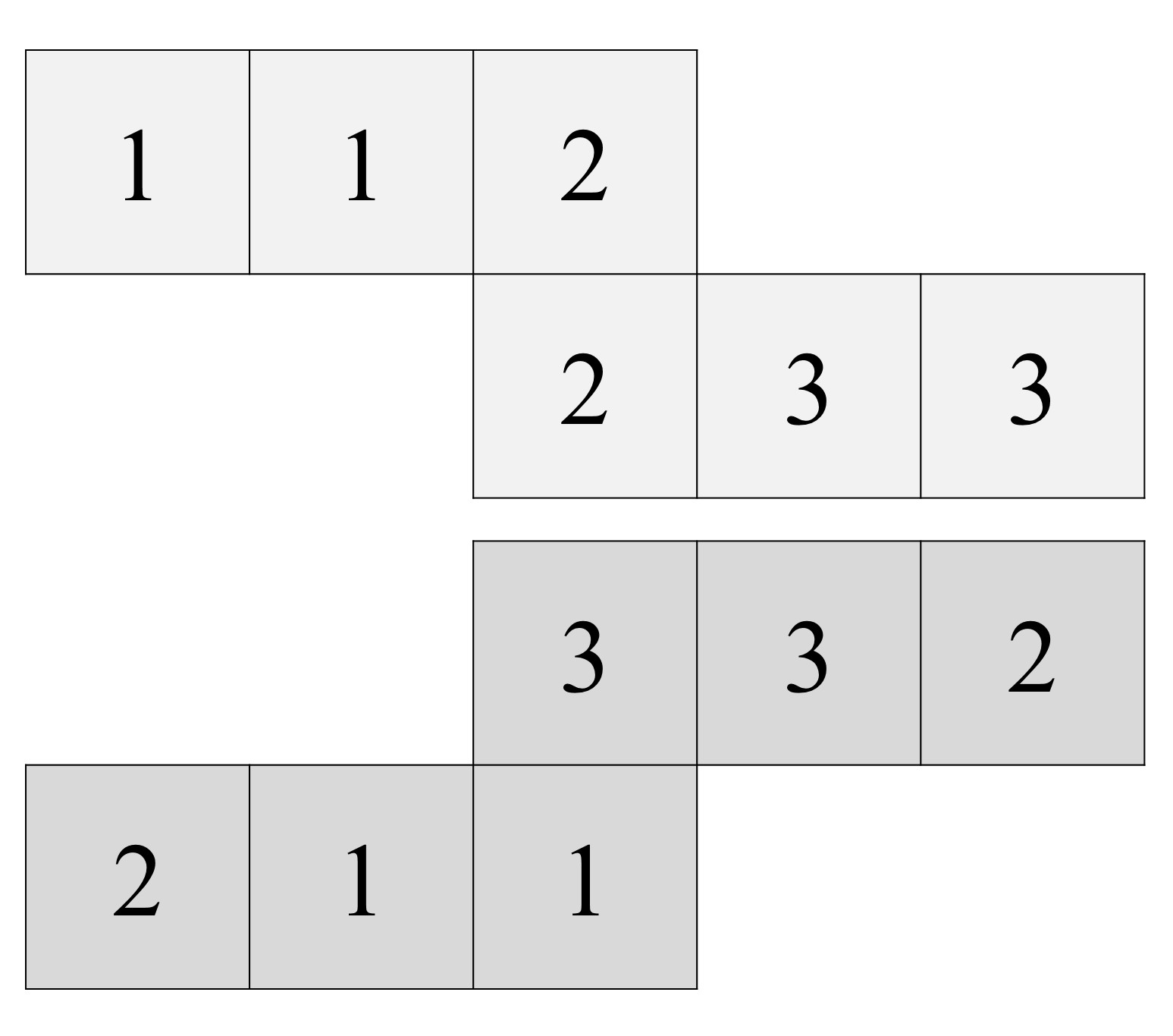
Después doblamos hacia atrás las dos casillas de la izquierda, las que tienen los unos, quedando nuestra tira de papel como se ve en la imagen.
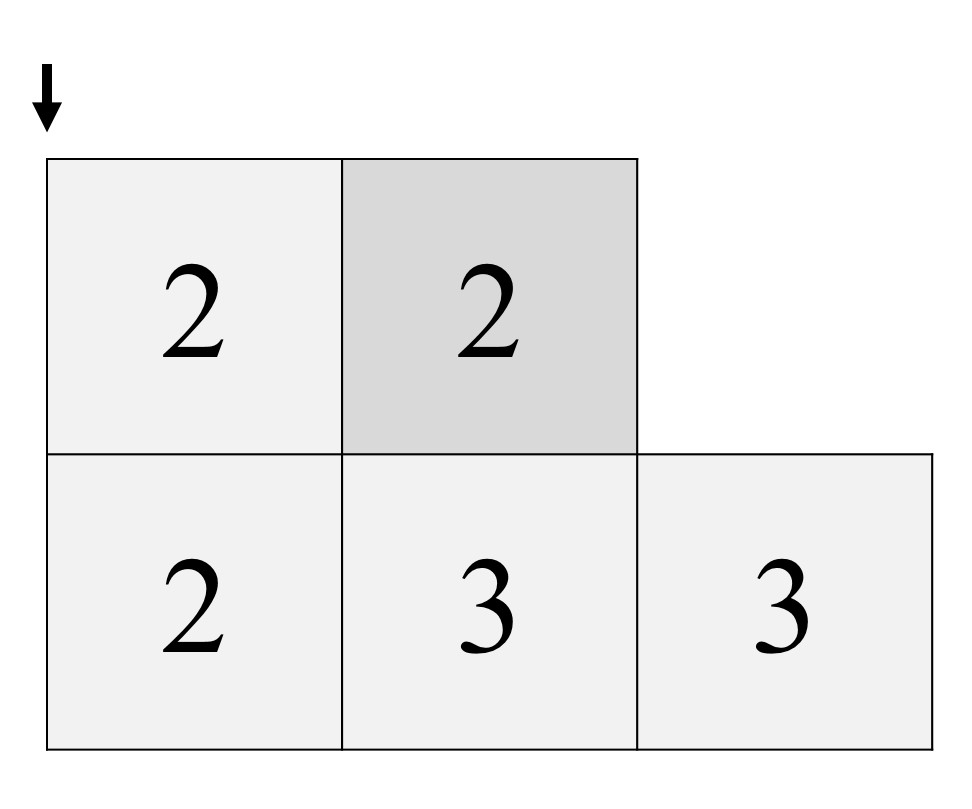
Y doblamos, ahora hacia delante, la casilla de la derecha, la que tiene el tres, quedando así todas las casillas con doses frente a nosotros.
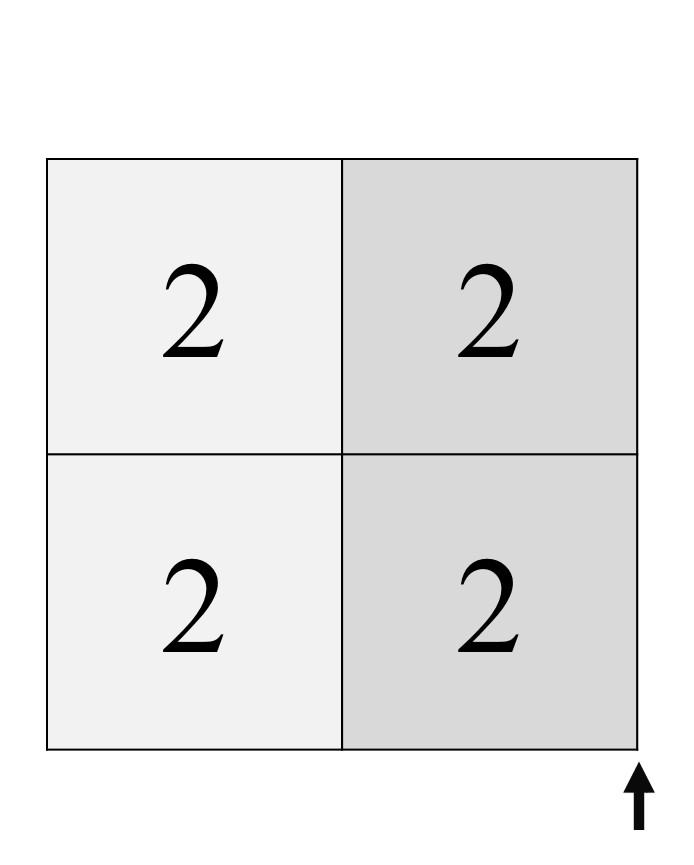
Para finalizar, solo hay que colocar un pequeño trozo de celo entre las dos casillas de la derecha, como se muestra en la imagen.
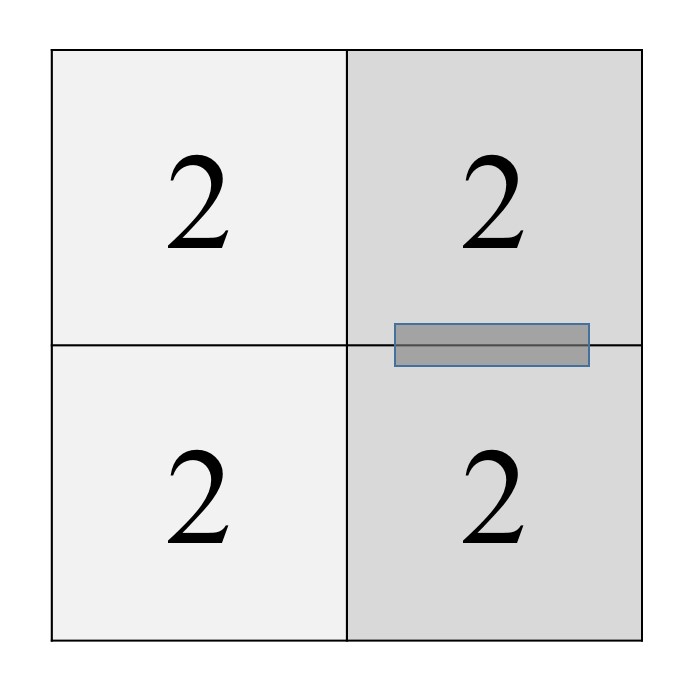
De esta forma, hemos construido el tritetraflexágono, que tiene tres caras, podemos mostrar en cada una de esas caras, todos unos, doses o treses.
Por último, vamos a terminar con los esquemas para realizar el hexatetraflexágono. Para este flexágono, partimos de una hoja cuadrada, dividida en 16 casillas –cuatro filas y cuatro columnas- en cada cara, a la que le hemos cortado las cuatro casillas del centro. Luego solo le quedan las 12 casillas del exterior. Esta vez vamos a utilizar seis colores (aunque mantenemos los números para seguir las instrucciones de la construcción) para pintar cada casilla, de la parte frontal y trasera, como aparece en las siguientes imágenes.
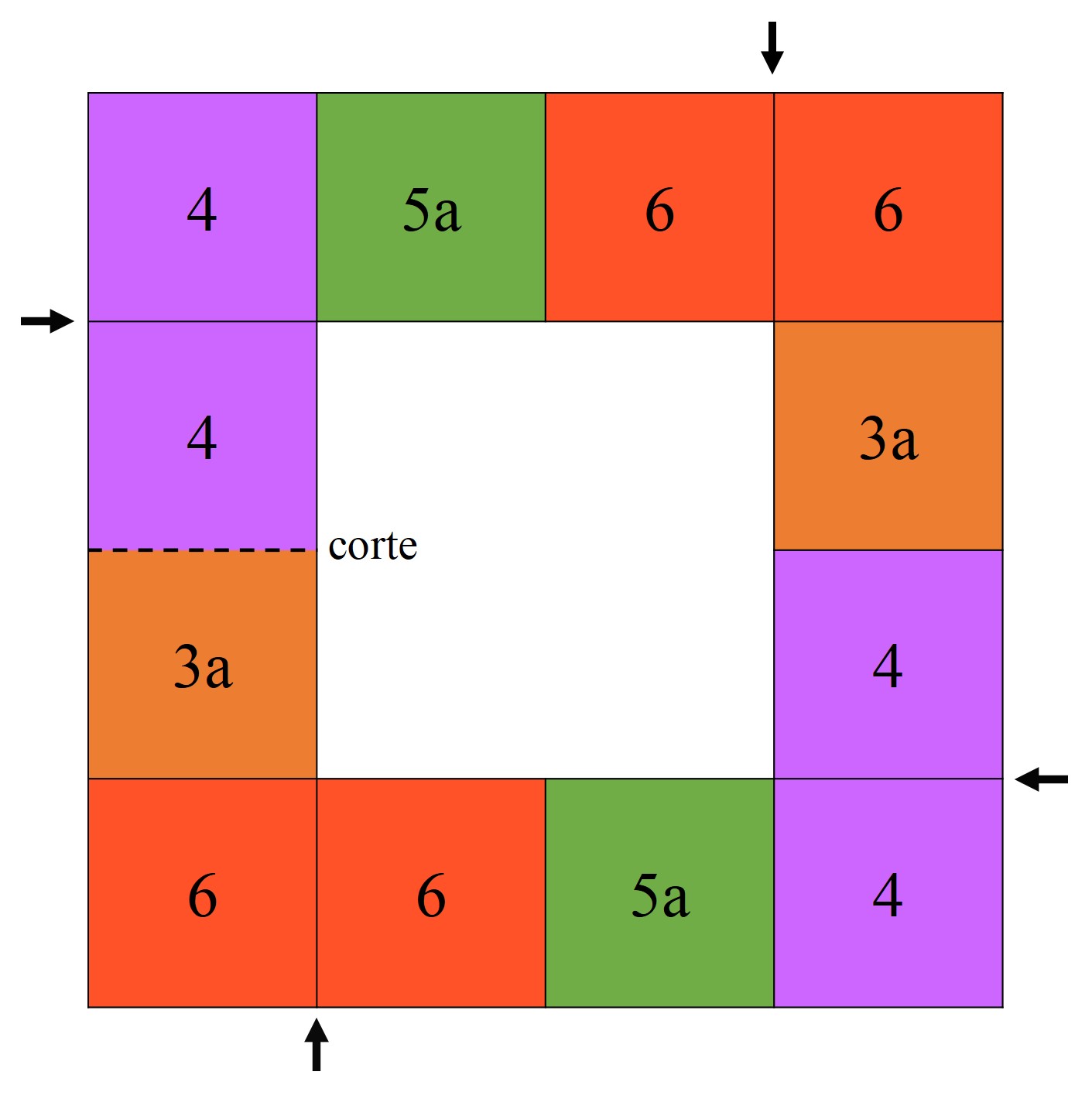
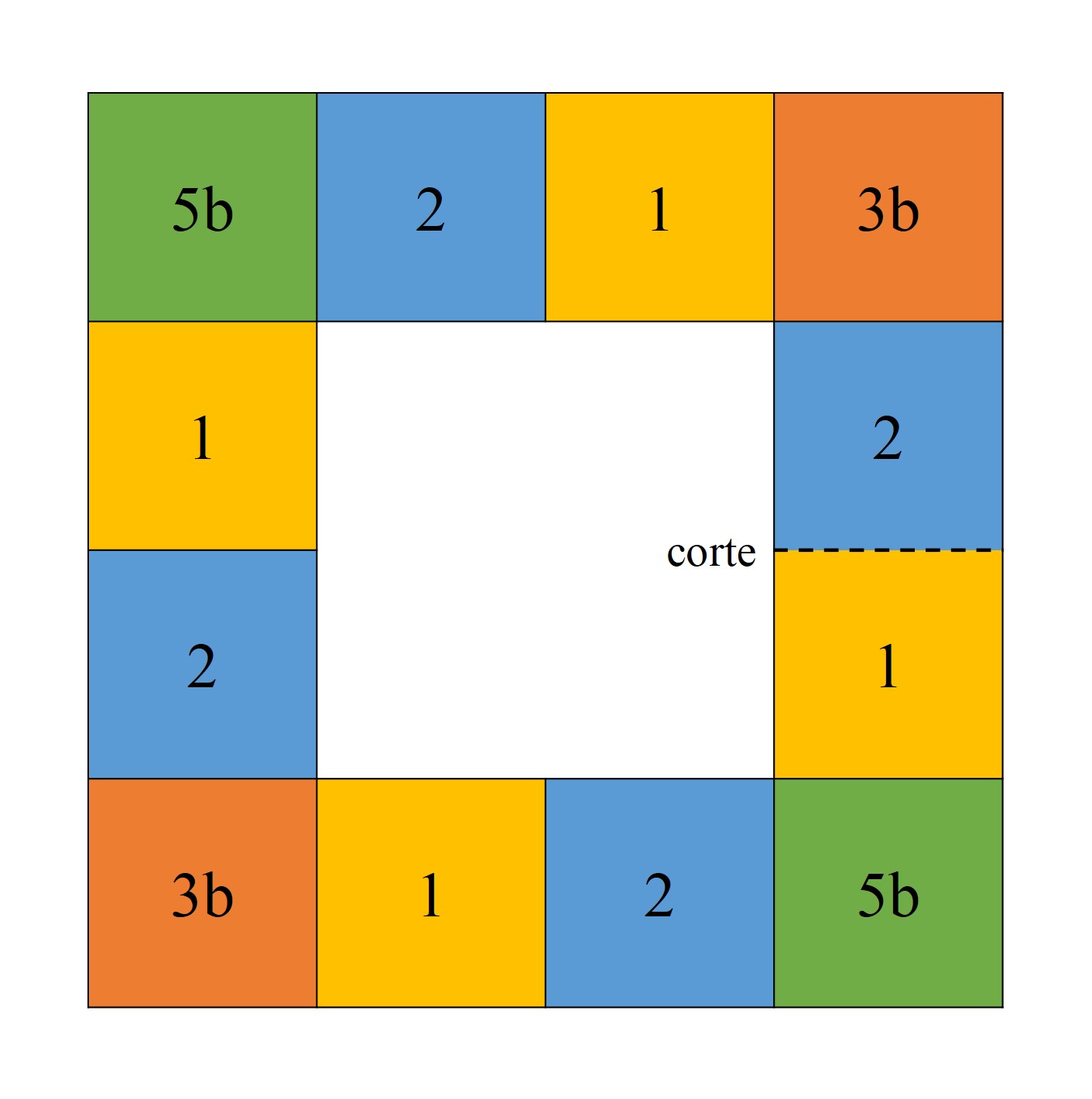
Las dos casillas de la derecha (en la primera imagen) se separan con un pequeño corte horizontal. Entonces, vamos doblando por donde indican las flechas, empezando por la flecha de abajo y en el sentido de las agujas del reloj, de forma que lo que nos queda al terminar es la siguiente imagen.

De nuevo, doblamos por donde indican las flechas, hasta que quede como la siguiente imagen. Para terminar, solamente hay que añadir un trozo de celo para unir, por arriba, la casilla superior izquierda de delante, con la que tiene atrás.

Y ya tendríamos nuestro hexatetraflexágono.
Bibliografía
1.- Martin Gardner, The 2nd Scientific American Book of Mathematical Puzzles and Diversions, University of Chicago Press, 1987 (publicado originalmente en 1961).
2.- Robert Ghattas, Bricológica, Treinta objetos matemáticos para construir con las manos, RIALP, 2011.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La hoja de papel con cuatro caras, una propuesta de taller se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema?
- El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba
- Cuatro leyes consumadas siguiendo una banda de Möbius
Maskarak, diruditen baino konplexuagoak

1. irudia: Azken egunetan maskarak gehien bilatzen diren produktuak bihurtu dira. Hainbat motakoak ikusi ditugu jantzita baina badakigu zertarako den bakoitza eta zerez eginak dauden? (Argazkia: Willfried Wende – domeinu publikoko irudia. Iturria: Pixabay.com)
Aipatu bezala, bi maskara mota bereizten dira haien funtzioaren arabera: maskara kirurgikoak maskara daraman pertsonak ingurunea kutsatzea ekiditen du. Babes-maskarak, berriz, maskara daraman pertsona babesten du ingurunetik.
Mundu mailan dagoen maskara gabezia dela eta, garrantzitsuena gaixoak eta osasun-langileak dagokien maskarekin hornitzea da. Agintarien gomendioak hurrengoak dira: birusa daukaten gaixoek maskara kirurgikoak erabiltzea gainontzeko pertsonak ez kutsatzeko, eta, osasun-langileek, berriz, babes-maskarak erabiltzea.
Aipatu beharra dago, maskarak eraginkorrak izan daitezen, higienea zaindu behar dela. Oso garrantzitsua da maskara jarri aurretik eskuak ondo garbitzea eta erabili bitartean maskara ez ukitzea. Maskarak hezetasuna hartzen badu aldatu egin behar da, eraginkortasuna galtzen baitu. Erabili eta gero kontuz kendu behar da, aurrealdea ukitu gabe, eta, ondoren, berriz ere eskuak garbitu behar dira. Urrats hauek jarraitzea ezinbestekoa da kutsadura saihesteko.
Maskara kirurgikoaMota honetako maskara daraman pertsonak ez ditu mikroorganismoak kanporatzen; zeren eta, maskarak, arnasterakoan kanporatzen ditugun listu tantak edo aerosolak harrapatzen baititu. Kontuan izan behar da koronabirusaren tamaina 0.1 mikrometrokoa dela, baina orain arte egin diren ikerketen arabera, koronabirusa listu tanten bitartez garraiatzen da eta tanta horiek zenbait mikrometroko tamaina izan dezakete. Beraz, maskara hauek gai dira listu tantak harrapatzeko.

2. irudia: Maskara kirurgikoak ehundu gabeko ehun bi dituzte. Ehundu gabeko ehuna prozedura mekaniko, termiko edo kimikoen bidez lotutako ehun-mota bat da. Ehun honetan sare bat lortzen da baina zuntzak hari bihurtu gabe. Ehun-material horiek ez dira zirpiltzen eta hori dela eta, errendimendu handiko jantziak eta osagarriak egiteko erabiltzen dira. (Argazkia: Vesna Harni – domeinu publikoko irudia. Iturria: pixabay.com)
Oro har, erabili eta botatzekoak diren maskara kirurgikoak 3 geruzaz daude osatuta.
- Lehenengo geruza, erabiltzailearen aurpegiarekin kontaktuan dagoena, ehundu gabeko ehunez egina dago eta hezetasuna xurgatzen du.
- Bigarren geruza iragazki bat da eta mikrobioen eta zenbait kutsatzaileren aurrean hesi gisa jokatzen du. Geruza hau polipropilenozkoa da eta teknika berezi baten bidez lortzen da (melt blown).
- Hirugarren geruza edo kanpoko geruza ehundu gabeko ehuna da eta, haren kasuan, likidoekiko iragazgaitza da.
Aipatu behar da, kasu guztietan polipropilenoa erabiltzen bada ere, kanpoko eta barneko geruzen egiturak desberdinak direla eta, ondorioz, ezaugarriak ere desberdinak dituztela. Aipaturiko polipropilenoa plastiko edo polimero mota bat da, propileno gas molekulak beren artean erreakzionatuz lortzen dena. Material honek abantaila ugari ditu: merkea da, erraz moldatu daiteke nahi den forma emanez, ezaugarri mekaniko egokiak ditu eta piezak zein zuntzak egiteko erabil daiteke.
Hain zuzen ere, ehun ez ehundua egiteko gehien erabiltzen den materiala da polipropilenoa. Ehun hau egiteko teknologia oso garatua dago eta kostu baxuan ekoiztu ahal da. Izango dituen erabileren arabera ehunak ezaugarri batzuk izan beharko ditu eta horretarako hurrengo parametroak aldatu daitezke: zuntzaren diametroa (mikrometroetatik nanometroetara bitartean), zuntz-dentsitatea azalera unitateko (zuntz kopurua azalera unitateko) edota zuntzen orientazioa.
Babes-maskarakBabes-maskarek pertsona inguruneko kutsaduratik babesten dute. Maskarak askotariko partikula eta kutsatzaileak iragazi behar ditu, baina arnasarekiko erresistentzia txikia azaldu behar du. Garrantzitsua da maskara aurpegira ondo doitzea hutsunerik ez gelditzeko; erosoa izan behar du gainera, eta narritadurarik eragin ez.

3. irudia: Babes-maskarak eraginkortasun handiko maskarak bezala ere ezagutzen dira. Erabiltzailea babesten dute, inguruneko partikula eta aerosol likidoak iragazten ditu erabiltzaileak ez ditzan arnastu. (Argazkia: Ri Butov –domeinu publikoko irudia. Iturria: Pixabay.com)
Babes-maskarak 4 geruzaz daude osatuta:
- Lehengo geruza, azalarekin kontaktuan dagoena, kotoizkoa edo beste ehun batekoa izan daiteke eta azalaren narritadura ekidin behar du.
- Bigarren geruza elektrostatikoki kargatuta dago. Hori oso eraginkorra da mikrometro bat baino txikiagoak diren partikulak harrapatzeko.
- Hirugarren geruzak iragazki gisa jokatzen du partikulak harrapatuz.
- Laugarren geruza edo kanpoko geruza. Geruza honek arnasarekiko erresistentzia txikia dauka.
Ohikoa da horrelako maskarek balbula bat izatea; balbula hori soilik arnasa botatzean irekitzen da eta maskararen barruan dagoen airea hoztea errazten du. Oso lagungarria da ingurune bero eta hezeetan ibili behar bada.
Geruza hauek airean dauden partikulak geldiarazten dituzte hiru mekanismo desberdin erabiliz: inpaktu inertzialaren bidez harrapatuta gelditzen dira aerosol partikula handiak, haien tamaina 1 mikrometro baino handiagoa denez gero. Partikula txikiagoak, berriz, difusio bidez iragazten dira; hau da, geruza osatzen duten zuntzek bide malkartsu bat osatzen dute eta partikula txiki hauek bertan harrapatuta gelditzen dira. Azkenik, partikula handi zein txikiak harrapatzeko beste teknika eraginkor bat erakarpen elektrostatikoa da. Zuntzei tratamendu egokia ezarriz karga jakin bat izango dute eta aurkako karga duten partikulak erakarriko dituzte; bertan itsatsita geldituko dira orduan.
Maskaren iragazpen-ahalmenaren arabera hiru motatako babes-maskarak bereizten ditu Europako Normalizazio Batzordeak (CEN):
- FFP1 (gutxienez 0.3 mikrometroko diametroa duten partikulen %80 iragazten du),
- FFP2 (partikulen %94),
- FFP3 (partikulen %99).
Estatu Batuetan arautegia beste era batekoa da; han erabilienak N95 maskarak dira eta gutxienez partikulen %95 iragazten dute.
Maskara higienikoak eta etxean egindakoakGoian azaldutako bi maskara motez gain azken asteetan maskara higienikoak eta etxean egindakoak ere aipatu dira. Maskara higienikoek zenbait arau bete behar dituzte eta hauek ekoizteko material jakin batzuk bakarrik erabil daitezke. Etxeko maskaren kasuan berriz, herritarrak etxean aurki ditzaketen materialak erabiltzen ari dira. Oraingoz, Osasunaren Mundu Erakundeak (OME) ez du etxean egindako maskarak erabiltzearen aldeko edo kontrako gomendiorik eman. Bi maskara mota hauen inguruan ikerketa gutxi egin da; ikerketa batzuen arabera, etxean egindako maskarek maskara kirurgikoek baino eraginkortasun txikiagoa daukate.
Beraz, nahiz eta denak maskarak izan, bakoitzak bere ezaugarriak ditu, erabilitako material eta geruza desberdinen arabera. Material horiek erabakitzen dute maskararen funtzioa, hots, pertsonak daraman maskara ingurunea ez kutsatzeko ote den (maskara kirurgikoak) ala pertsona inguruneko kutsaduratik babesteko (babes-maskarak). Hala ere, maskara erabili edo ez, adituek gomendatzen dute urruntze soziala mantentzea eta eskuak sarritan garbitzea.
Iturriak:
- Davies, A.; Thompson, K. A.; Giri, K.; Kafatos, G.; Walker, J.; Bennett, A. (2013). Testing the Efficacy of Homemade Masks: Would They Protect in an Influenza Pandemic? Disaster Medicine and Public Health Preparedness, 7 (4), 413-418. DOI: 10.1017/dmp.2013.43.
- Institute of Medicine (2006). Reusability of Facemasks During an Influenza Pandemic: Facing the Flu. Washington, DC: The National Academies Press. DOI: https://doi.org/10.17226/11637.
- Borealisgroup.com: To shield against pollution and viruses – take cover with protective face masks – made possible with plastics.
- European Committe for Standardization: Respiratory protective devices – Filtering half masks to protect against particles – Requirements, testing, marking.
- European Centre for Disease Prevention and Control – ECDC: Using face masks in the community – Reducing COVID-19 transmission from potentially asymptomatic or pre-symptomatic people through the use of face masks. Data: 2020-04-08.
- Iruin, Juan José – El blog del búho: Mascarillas, polímeros y tejidos no tejidos.
- Osakidetza: Mascarillas- GuiaSL23c.
- Sistema Español de Notificación en Seguridad en Anestesia y Reanimación – Sensar: Uso adecuado de mascarillas quirúrgicas.
- World Health Organization: Advice on the use of masks in the context of COVID-19: Interim guidance. Data: 2020-04-06.
- 3M.com: Worker Health & Safety.
———————————————————————————-
Egileez: Leire Sangroniz eta Ainara Sangroniz Kimikan doktoreak dira eta UPV/EHUko Kimika Fakultatearen, Polimeroen Zientzia eta Teknologia Saileko ikertzaileak Polymat Institutuan.
———————————————————————————-
The post Maskarak, diruditen baino konplexuagoak appeared first on Zientzia Kaiera.
La teoría de bandas explica la conducción eléctrica
 Foto de Josep Castells / Unsplash
Foto de Josep Castells / UnsplashLa idea básica tras las bandas de Bloch en un sólido es que se crean al unirse los estados cuánticos de los átomos individuales. Bloch y otros ampliaron y refinaron la teoría de bandas de los sólidos durante la década de 1930, hasta el punto de que explica muy bien el comportamiento de conducción eléctrica de los distintos materiales.
Cuando los átomos se unen en un cristal, cada uno de los estados cuánticos individuales de los átomos se une con los estados correspondientes en otros átomos (idénticos) en el cristal para formar las diversas bandas de energía dentro del material. De hecho, si hay un total de N átomos idénticos en el material, entonces hay N estados cuánticos dentro de cada banda. Los electrones en los átomos llenan los estados disponibles dentro de cada banda. Así, si hay N estados en una sola banda, puede haber hasta 2N electrones en cada banda [1].
La física interesante ocurre en la parte superior de las bandas llenas. Cuando se aplica un campo eléctrico externo (voltaje) al material, un electrón puede responder al campo solo si puede moverse a un estado cuántico ligeramente más alto, ya que tendría un poco más de energía al ser afectado por el campo. Esto será posible solo si hay algunos estados libres cercanos a los que el electrón pueda saltar. Este es el caso de los materiales conductores, como el cobre y la plata, ya que sus electrones se llenan en los estados disponibles de modo que la banda más alta está llena solo parcialmente. Los electrones en esta banda, que se llama banda de conducción, son libres de ser conducidos (en realidad, propagados como ondas) por el material, ya que hay estados cuánticos vacíos cercanos en su banda de energía. Pero los electrones en las bandas inferiores llenas no pueden moverse, ya que no hay estados libres cerca.
Por otro lado, si las bandas se llenan de manera que se ocupa exactamente el límite superior de una banda, entonces los electrones no pueden responder a un campo eléctrico, ya que hay una brecha de energía [2] que les impide llegar a un estado cuántico en el que pueden moverse libremente [3]. Un material con estas características es lo que conocemos como aislante. [4]
Finalmente, si estamos ante un caso como el de los aislantes pero la brecha de energía con la banda de conducción no es demasiado grande, puede resultar que la energía térmica sea suficiente como para que algunos electrones salten a ella. Este es el caso de los semiconductores.
Notas:
[1] De acuerdo con una regla en la mecánica cuántica solo dos electrones pueden ocupar un estado de energía cuántica de un solo átomo. El principio de exclusión de Pauli establece que no pueden existir dos partículas en un sistema, electrones en un átomo o quarks en un hadrón, que tengan un conjunto de números cuánticos idéntico. Aplica solo a las partículas llamadas fermiones, no a los hadrones. Los electrones son en todo iguales e indiscernibles salvo porque unos tiene una “cosa” llamada espín con un valor y otros con otro valor. Por eso solo puede haber dos electrones en un estado cuántico de energía: en ese estado todos los números cuánticos son iguales salvo el espín, si hubiese un tercer electrón se violaría el principio de exclusión. Aunque parece un principio inventado para que cuadren los datos, se justifica por el teorema de la estadística del espín de la teoría cuántica de campos relativista.
[2] Una «banda prohibida» por la naturaleza cuántica de las bandas.
[3] Normalmente. Si el voltaje es enorme algunos electrones podrán desplazarse, porque adquirirán energía suficiente como para saltar de la banda de valencia a la banda de conducción. Véase [3]
[4] Un ejemplo es el diamante, en el que el estado cuántico lleno más alto también llena una banda de energía. Esta banda se llama banda de valencia, ya que está ocupada por los electrones de valencia externos de los átomos. La brecha de energía a la siguiente banda, que está vacía, es de aproximadamente 6 eV, por lo que los electrones en el diamante normalmente no pueden alcanzar la banda de conducción y, por lo tanto, el diamante es un buen aislante. En los conductores la banda de conducción se solapa con la llamada banda de valencia, por lo que no hay brecha de energía.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La teoría de bandas explica la conducción eléctrica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las bandas de Bloch
- La teoría de bandas de los sólidos se hace topológica
- El modelo de Bohr explica las regularidades en el espectro del hidrógeno
Gugan bizi diren birusak
Genoma izena ematen zaio gene-osagaien multzoari; proteoma deitzen zaio proteinen multzoari; metaboloma, metabolitoen multzoari. Horrela izendatzen da maila omiko bakoitza. Era horretan, mikroorganismoen multzoari mikrobioma deitzen zaio eta, mikrobiomaren barruan, biroma izenez ezagutzen da birusen multzoa. Biroma osatzen duten birusak hiru talde handitan sailka daitezke: erretrobirus endogenoak, zelula eukariotoen birusak eta bakteriofagoak.
Erretrobirus endogenoak hainbat animaliaren genoman aurkitzen diren birusen arrastoak dira. Giza genomaren kasuan, % 8 birus horien sekuentziak dira, antzina gure arbasoek pairatutako infekzioen isla. Berez, erretrobirus endogenoak ez daude aktibo gure espeziean; hau da, ez dute bere burua kopiatzeko gaitasunik. Hala ere, hainbat gaixotasunekin lotura dutela ikusi da. Esate baterako, aktibo daudela ikusi da minbizi mota batzuetan, esklerosi anizkoitzean eta artritis erreumatoidean. Horrez gain, sekuentzia fosil hauek baliagarriak dira funtzio berriak eskuratzeko ere, berrerabili egiten baitira haien sekuentziak. Adibidez, plazenta osatzeko ezinbestekoa den gene batek birus hauen sekuentzia batean du jatorria. Giza genomaren parte direnez, erraza da haiei buruzko gene-informazioa lortzea eta, hortaz haiek identifikatzea ez da lan zaila.

1. irudia: Gure genometan badira birus fosilak, antzinako infekzioen aztarna direnak (Argazkia: Laurent Arroues – Pixabay lizentziapean. Iturria: pixabay.com)
Zelula eukariotoen birusak dira birus hitza irakurtzen dugunean burura etortzen zaizkigun birusak, gaixotasunekin lotura duten birusak, hain zuzen ere. Gizakion zelulak infektatzeko gai diren birusez gain, multzo horretan biltzen dira gurekin bizi diren protozooak eta onddoak infektatzeko gai diren birusak ere. Gaixotasunekin lotzen ditugun arren, horietako hainbat birusek ez dute zertan sintomarik sortu; edo latente gera daitezke. Horren adibiderik argiena herpesaren birusa da, giza populazioaren % 65 inguruk birus hori baitu. Zelula eukariotoen birusen identifikazioa neketsua izan ohi zen sekuentziazio masiboen aurretik. Orain, teknika horiei esker, birusen gene-materiala errazago eskura eta azter daiteke, ez baita beharrezkoa birusak laborategi batean haztea aztertu ahal izateko. Hala, lortu da birusen andui berriak identifikatzea eta ikusi da presente daudela giza gorputzeko hainbat organotan. Horri esker, ondorioztatu da aurretik birusen parte-hartzea ezezaguna zuten hainbat gaixotasunetan parte hartzen dutela; edo gaixotasun berean birus talde edo andui ezberdinek parte hartzen dutela.
2. irudia: Zelula eukariotoak infektatzen dituzten birusak dira gehien ezagutzen ditugunak (Argazkia: PIRO4D – Pixabay lizentziapean. Iturria: pixabay.com)
Bakteriofagoak dira bakterioak infektatzeko gai diren birusak, askotan fago deiturara laburtzen direnak. Birus horiek gero eta interes gehiago izaten ari dira mikrobiotan —adibidez, hesteko floran— duten eraginagatik. Dirudienez, dietak baldintzatzen ditu hesteko mikrobiotan agertzen diren fagoak; eta fagoen banaketa gorputzeko atal bakoitzean espezifikoa bada ere, handia da indibiduoen arteko aldakortasuna. Fagoek, gainera, gure bakterioak infektatzeaz gain, bakterio horien arteko gene-elkartrukea errazten dute. Horrela, bakterioek gene-funtzio berriak lor ditzakete. Zelula eukariotoen birusekin gertatzen den bezala, sekuentziazio masiboei esker posible da fagoak identifikatzea.

3. irudia: Bakterioak infektatzen dituzten birusek gure mikrobiota moldatzen dute (Argazkia: Baroco Ferison – Pixabay lizentziapean. Iturria: pixabay.com)
Hala ere, sekuentziazio masiboei esker zelula eukariotoen eta prokariotoen birusak identifikatzea erraztu bada ere, oraindik erronka handiak daude biroma bere osotasunean behar bezala karakterizatu ahal izateko. Alde batetik, birusak DNAz edo RNAz osotuta egon daitezke eta ezberdina da mota bakoitzetik gene-informazioa eskuratzeko prozedura. Horrek lagin bakoitzetik lor daitekeen gene-informazioa mugatzen du. Beste alde batetik, behin birusen sekuentziak lortu direnean, ezagutzen diren birusen sekuentziekin konparatzen dira sekuentzia horiek identifikatzeko. Hortaz, jada ezaguna denak identifikazioa mugatzen du, eta birusen sekuentzia batzuk sailkatu gabe edo talde oso orokorretan sailkatuta gera daitezke. Bi faktore hauen ondorioz, galdu egiten da biroma behar bezala aztertzeko bereizmena.
Biroma ezagutzea beharrezkoa da hainbat gaixotasunetan duten funtzioagatik. Agerikoa da infekzioak sortzen dituzten birusak hainbat gaixotasunen eragile direla. Baina birusek beste gaixotasun batzuetan hain agerikoa ez den funtzioa ere izan dezakete. Hala, ikertu da biromak zein eragin duen diabetesean, hesteetako hanturazko gaixotasunean edo minbizi mota batzuetan. Gaixotasun horietan, aldaketak detektatu dira biromaren osaketan eta, hortaz, haren ikerketan sakontzea beharrezkoa dela dirudi.
Gugan bizi diren birusak gero eta gehiago ezagutzen baditugu ere, oraindik lan asko dugu aurretik. Batzuek gaixotasunak sor ditzakete, bai, baina beste batzuk gure mikrobiotaren parte diren heinean, garrantzitsuak ere badira gure mikrobiota osasuntsu mantentzeko. Gainera birusek moldatzen dituzte bai gure genoma bai gugan bizi diren bakterioen genomak. Oro har, birusei buruz ikuspuntu negatiboa badugu ere, ezin da ukatu eboluzio-eragile garrantzitsuak direla.
Erreferentzia bibliografikoa:
Santiago-Rodriguez, T. M., et al. (2019). Human Virome and Disease: High-Throughput Sequencing for Virus Discovery, Identification of Phage-Bacteria Dysbiosis and Development of Therapeutic Approaches with Emphasis on the Human Gut. Viruses, 11 (7), 656. DOI: 10.3390/v11070656.
—————————————————–
Egileaz: Koldo Garcia (@koldotxu) Biodonostia OIIko ikertzailea da. Biologian lizentziatua eta genetikan doktorea da eta Edonola gunean genetika eta genomika jorratzen ditu.
—————————————————–
The post Gugan bizi diren birusak appeared first on Zientzia Kaiera.
Los males de la ciencia tienen remedio
 Foto: Vlad Tchompalov / Unsplash
Foto: Vlad Tchompalov / UnsplashEn las anotaciones precedentes nos hemos dedicado a repasar los que a nuestro juicio son los males de la ciencia actual. La serie empezó por una presentación de la empresa científica, el marco institucional y económico en el que se desarrolla, y el entramado de las publicaciones científicas como producto principal. Seguimos analizando los valores de la ciencia tal y como los formuló Merton a mediados del siglo pasado. Y a continuación abordamos el repaso de una serie de males que pueden considerarse propios, específicos de la empresa científica. Las últimas anotaciones han tratado de las resbaladizas relaciones entre investigación científica y ética en diferentes planos.
La relación de “males” o “patologías” no ha pretendido ser exhaustiva. Algunas de las malas prácticas presentadas aquí lo son porque vulneran las normas de Robert K Merton, incumplen el ethos de la ciencia en los términos en que él lo definió y que, implícitamente, asumimos gran parte de los científicos. Otras tienen más que ver con aspectos nucleares de la práctica científica o con el sistema de publicaciones o de financiación de la investigación. Son, por lo tanto, diferentes y seguramente los remedios que requieran también lo sean. Pero sospechamos que una gran parte de los problemas se atenuaría si universidades y centros de investigación modificasen el sistema de incentivos que utilizan para reconocer y premiar el trabajo de su personal científico. La cantidad debería perder importancia como criterio, para ir valorando cada vez más la calidad del trabajo y la trascendencia o relevancia de las investigaciones. No se trata de acudir a indicadores de las publicaciones tal y como se utilizan hoy o, al menos, no solo a esos indicadores (basados en métricas de impacto y similares), sino de recurrir a la valoración experta del nivel y alcance del trabajo realizado.
Tenemos por último, todos esos ámbitos en los que el desarrollo de la ciencia se enfrenta a dilemas de naturaleza ética. No se trata de dilemas específicos de la ciencia, o dilemas cuya resolución deba recaer exclusivamente sobre el mundo científico. Son, en su gran mayoría, dilemas sociales. La ciencia es, si acaso, el instrumento, pero es en el ámbito social y político donde se han de resolver. Si se han de exprimir al máximo las posibilidades que nos brinda la biotecnología, o si debemos permanecer pasivos ante la previsible robotización de la sociedad, son cuestiones que no corresponde dirimir a los científicos. Quienes hacen la investigación científica deberán aportar su criterio experto, y tanto la sociedad como los responsables deberían tomar buena nota y tener en cuenta el dictamen experto, pero en última instancia, las decisiones son de carácter social y político. Nos interesa remarcar esta diferencia, porque los males que hemos considerado intrínsecos a la ciencia lo son porque de no neutralizarlos, está en juego el propio funcionamiento del sistema científico, y en ese terreno, los miembros de ese sistema tenemos mucho que decir y que hacer. Precisamente por esa razón, no nos parece saludable que los científicos se desentiendan de las implicaciones sociales de su trabajo. Creemos que tenemos una especial responsabilidad al respecto, precisamente porque somos quienes mejor podemos calibrar el alcance de nuestro trabajo más allá de cómo quede recogido en las publicaciones científicas.
La ciencia sufre de esos y de otros males; son males serios y de graves consecuencias. Las que afectan, con carácter general, al desarrollo del conocimiento son evidentes. Pero esas no son las únicas. También hay consecuencias prácticas de gran trascendencia. En los Estados Unidos se estima que la investigación preclínica no reproducible tiene un coste anual de 28 mil millones de dólares y, por supuesto, retrasa el desarrollo de tratamientos que salvan vidas humanas y mejoran la calidad de vida. Es de suponer que en el resto de potencias científicas las cosas estarán, en su correspondiente proporción, más o menos igual.
Hay investigadores que son reticentes a abordar de forma abierta estas cuestiones, porque temen que pueden conducir a un debilitamiento de la empresa científica porque la sociedad deje de confiar en los científicos. Creo que se trata precisamente de lo contrario. La opacidad sería contraproducente. Una herida que se cierra sin haberla limpiado debidamente, se cierra en falso porque cultiva la infección en su interior y antes o después, aflorará. La vía más eficaz para sanar los males pasa por conocerlos y buscar las medidas para combatirlos. No hay que ser tan ingenuo como para pensar que muchos de los problemas aquí expuestos tienen una solución definitiva. Ningún problema complejo suele tener soluciones definitivas y, desde luego, nunca son soluciones simples. De lo que se trata es de conseguir un funcionamiento de la empresa científica razonablemente mejor que el actual, más sano, con mejores resultados, más eficiente, y que se base más en la realización de interesantes trabajos que en la producción de ingentes cantidades de artículos.
Pero a la vez que han de preocuparnos los males, también debemos congratularnos de que sea la misma comunidad científica la que está tratando de aportar soluciones. Porque han sido científicos profesionales quienes han investigado y dado a conocer las patologías que aquejan a la práctica científica. Han sido científicos profesionales y organizaciones científicas las que han propuesto medidas para afrontar los problemas y resolverlos. Y algunas revistas científicas están adoptando medidas para incentivar la transparencia y la reproducibilidad de los resultados. Esas son las buenas noticias.
Fuentes:
Agin, D (2007): Ciencia basura. Starbooks, Barcelona.
Briggle, A (2012): Scientific Responsability and Misconduct, in Encyclopedia of Applied Ethics, Vol 4, pp.: 41-48, 2nd edition, Academic Press, London
Ferris, Timothy (2010): The Science of Liberty, Harper Collins, Nueva York
Fischer, B A, Zigmond, M J (2012): Scientific Publishing, in Encyclopedia of Applied Ethics, Vol 4, pp.: 32-40, 2nd edition, Academic Press, London
Häyry, M (2012): Genetic Engineering of Human Beings, in Encyclopedia of Applied Ethics, Vol II, pp.: 437-444, 2nd edition, Academic Press, London
Holm, S, Stokes E (2012): Precautionary Principle, in Encyclopedia of Applied Ethics, Vol III, pp.: 569-575, 2nd edition, Academic Press, London
Johnson, J (2012): Ethical Experiments, in Encyclopedia of Applied Ethics, Vol 2, pp.: 149-156, 2nd edition, Academic Press, London
Johnson, S (2012): Nanotechnology, in Encyclopedia of Applied Ethics, Vol III, pp.: 183-185, 2nd edition, Academic Press, London
López Nicolás, J M (2016): Vamos a contar mentiras. Cálamo, Madrid.
Menéndez Viso, A (2005): Las ciencias y el origen de los valores. Siglo XXI.
Merton, R K (1942): “Science and Technology in a Democratic Order” Journal of Legal and Political Sociology 1: 115-126. [Traducción al español como “La estructura normativa de la ciencia” en el volumen II de “La Sociología de la Ciencia” Alianza Editorial 1977, traducción de The Sociology of Science – Theoretical and Empirical Investigations, 1973]
Neri, D (2012): Eugenics, in Encyclopedia of Applied Ethics, Vol 1, pp.: 189-199, 2nd edition, Academic Press, London
Oreskes, N y Conway, E N (2018): Mercaderes de la duda. Cómo un puñado de científicos oscurecieron la verdad sobre cuestiones que van desde el humo del tabaco al calentamiento global. Capitán Swing, Madrid.
Resnik, D B (2012): Developing World Bioethics, in Encyclopedia of Applied Ethics, Vol 1, pp.: 771-778, 2nd edition, Academic Press, London
Solbakk J H, Vidal, S M (2012): Research Ethics, Clinical, in Encyclopedia of Applied Ethics, Vol 3, pp.: 775-785, 2nd edition, Academic Press, London
Spier, R E (2012): Science and Engineering Ethics, Overview, in Encyclopedia of Applied Ethics, Vol 4, pp.: 14-31, 2nd edition, Academic Press, London
Di Trocchio, F (1993): “Las mentiras de la ciencia” Alianza Editorial.
Ziman, J (2000): Real Science: What It Is and What It Means. Cambridge University Press.
Zuk, M (2013): Paleofantasy: What Evolution Really Tells Us about Sex, Diet, and How We Live. Norton & Co, New York.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Los males de la ciencia tienen remedio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- No todo vale al servicio de la ciencia
- Dilemas éticos en la frontera de la ciencia
- No todas las personas tienen las mismas oportunidades de dedicarse a la actividad científica
Zibilizazioak giza espeziea aldatu du
Orain dela gutxiko ikerketa batean, duela 5.500 eta 3.000 urte artean Europan bizi ziren gizabanakoen genomak eta egungo europarrenak konparatu dira. Ikerketa horretan, oinarri genetikoan aldaketa (mutazio) gehien eta gutxien izan duten funtzioak identifikatu dira, alegia, aldaera gehien eta gutxien ekarri dutenak. Gehitu egin dira honako funtzio hauetan parte hartzen duten aldaera genetikoak: karbohidratoen metabolismoan, desintoxikazio mekanismoetan, mintz bidezko substantzien eroapenean, immunitate defentsarako sisteman, zelulen seinaleztapenean, ariketa fisikoan eta usaimenean. Eta murriztu, berriz, obuluen sorkuntzarekin –beraz, emakumeen ugalketa fisiologiarekin– eta epe luzeko potentziazioa deritzon mekanismo neurologikoan. Ikus ditzagun, adibide modura, funtzioetako batzuk euren testuinguruan.

Irudia: Gizakiak naturatik bereizten dituen ingurune artifizialak sortzen aritu dira eta ingurune berri horiek erantzun berriak sortzen dituzte. (Argazkia: Pixabay.com – domeinu publikoko irudia)
Karbohidratoen metabolismoari loturiko aldaerak genetikoki aberatsagoak izatea, ziur aski, nekazaritzaren eta abeltzaintzaren hedapenari zor zaio. Zerealen ekoizpenak dietan karbohidratoen proportzioa handitzea ekarri zuen, eta abeltzaintzak, berriz, helduek esnea kontsumitzea, laktosa (funtsean, azukre mota bat) digeritzeko gaitasunari bide eman zion mutazioari esker.
Antzera gertatu da immunitate sistemaren funtzionamenduan eragina duten aldaerekin. Biztanle dentsitate handiak eta, batik bat, animaliak etxekotzeak baldintza egokiak sortu zituen parasito patogenoak ugaritzeko. Ez da harritzekoa, beraz, nekazari eta abeltzain herriek ehiztari-biltzaileek ez zituzten gaitasunak eskuratzea, edo funtzionamenduaren alderdi batzuk indartzea, baldintza horiek zirela medio.
Epe luzeko potentziazioaren mekanismoak biziagotu egiten du neuronen arteko seinale transmisioa, eta hori lotuta egon daiteke ikasteko gaitasunarekin eta oroimenarekin. Mekanismo horretan oinarri genetikoaren aldaerak gutxitu izanaren kausa ikaskuntzaren eta kultura transmisioaren garrantzi gero eta handiagoa izan daiteke, herriguneak sortzearen eta zibilizazio esaten diogun horren agerpenaren ondorioz. Dena dela, ez dakigu lotura hori nolakoa den.
Lehen –eta orain ere bada horrela pentsatzen duenik– uste zen zibilizazioak, bere erosotasunekin eta egurats gorriak giza organismoan izan ditzakeen ondorioak arintzeko duen gaitasunarekin, giza leinuaren bilakaera geldiarazi duela eta, historiaurreko hautespen presioak desagertuta, gero eta izaki akastunagoak bihurtu garela, gaitasun gutxien dutenak gehiago bizi direlako eta, gainera, ondorengoak izan ditzaketelako. Gauzak ez direla horrela, ordea, askoz ere konplexuagoak baizik, ohi den bezala. Izan ere, hautespen presioak ez dira desagertu, aldatu baino. Eta horiek aldatuta, gure zerizana ere bai.
Erreferentzia bibliografikoa:
Chekalin, Evgeny, et al. (2019). Changes in Biological Pathways During 6,000 Years of Civilization in Europe. Molecular Biology and Evolution, 36 (1), 127–140. DOI: https://doi.org/10.1093/molbev/msy201.
———————————————————————————-
Egileaz: Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
———————————————————————————
The post Zibilizazioak giza espeziea aldatu du appeared first on Zientzia Kaiera.
Van Eyck al descubierto

Antes de convertirse en el año de la pandemia 2020 iba a servir para homenajear a dos de los pintores más importantes de todos los tiempos: Jan van Eyck y Rafael Sanzio. Hagamos de este espacio un refugio y disfrutemos del arte de estos dos genios durante las próximas entregas. Por deferencia, comenzaremos por el que nació primero. De este modo nos sumamos al tributo que se le estaba rindiendo a van Eyck en Gante, donde se guarda una de sus más emblemática obras: La adoración del cordero Místico. La ciudad belga lucía sus mejores galas y bajo el lema “OMG! Van Eyck was here” había preparado una serie de eventos, incluyendo una exposición de pinturas del artista flamenco como nunca antes se había visto. Afortunadamente las nuevas tecnologías nos permiten disfrutar de estas obras sin tener que salir de casa.
Los “primitivos” flamencos
Jan van Eyck y su hermano mayor Hubert fueron, junto a Robert Campin, los primeros de un grupo que ha pasado a la historia del arte con el nombre de los primitivos flamencos. Tomemos ese adjetivo en el sentido de que fueron unos pioneros y no en referencia a un estilo poco desarrollado. ¿Os atreveríais a decir eso de alguien que hace las virguerías que os muestro en la Imagen 1? En la primera mitad del s. XV estos pintores fueron dejando atrás el estilo gótico internacional entonces imperante, en pos de una nueva forma de entender la pintura. Pese a que se trata de un momento crucial de la historia del arte, se ha visto un tanto eclipsado por el coetáneo Renacimiento italiano. A favor de los maestros flamencos hemos de decir que en ciertos aspectos técnicos igualaban o superaban a los italianos, aunque sus nombres no sean tan conocidos como el de Donatello o el de Leonardo, por poner dos ejemplos.
 Imagen 1. Virgen del Canónigo Van der Paele (122×158 cm) y detalles. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 1. Virgen del Canónigo Van der Paele (122×158 cm) y detalles. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.El florecimiento de este estilo en la región de los Países Bajos no fue por casualidad. A principios del s. XV urbes como Brujas o Gante habían prosperado gracias al comercio y a la artesanía. Por lo tanto, a la nobleza y al clero se le sumaba una incipiente burguesía con ganas de demostrar su estatus social. En ese entorno destacó Jan van Eyck, quien tras trabajar en diferentes ciudades se instaló en 1425 en la corte de Felipe el Bueno, duque de Borgoña, la gran potencia de la zona en aquel momento. Desde esa fecha hasta su muerte en 1441 realizó las obras que le han colocado en el Olimpo de la pintura. Si algo destaca en van Eyck, más allá de su brillante técnica, es su capacidad de innovación: fue todo un pionero. Su contribución más importante fue la pintura al óleo. Aunque no inventó esta técnica como se afirma en ciertas partes, la perfeccionó y ayudó a popularizarla. Hasta entonces la pintura al temple era la más habitual, pero la posibilidad de aglutinar los pigmentos con aceites abrió nuevas posibilidades, sobre todo gracias a las veladuras, capas de pintura semitransparentes que permiten dar matices y crear juegos de luces.
Pero van Eyck fue mucho más que el adalid de la pintura al óleo. También tuvo la capacidad de incorporar el paisaje a sus obras, otorgándoles sensación de profundidad en una suerte de perspectiva atmosférica previa a Leonardo (Figura 2A). Trataba los detalles con una meticulosidad absoluta, posiblemente debido a su pasado como pintor de miniaturas (Figura 2B), y sus óleos recogen hasta el más mínimo pliegue y ornamento de las sofisticadas lanas flamencas o las alfombras orientales. No había ilusión óptica que se escapase a sus afilados pinceles. Una buena muestra es el Díptico de la Anunciación del Museo Thyssen en el que el Arcángel y la Virgen parecen esculturas que se escapan de la hornacina (Figura 2C). Otra, el espejo de El matrimonio Arnolfini, con permiso de Velázquez, el más famoso de la historia del arte (Figura 2D).
 Imagen 2. A) Virgen del Canciller Rolin (66×62 cm) y B) detalle C) Díptico de la Anunciación (aprox. 39 x 24 cm cada imagen) D) Espejo de El matrimonio Arnolfini. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 2. A) Virgen del Canciller Rolin (66×62 cm) y B) detalle C) Díptico de la Anunciación (aprox. 39 x 24 cm cada imagen) D) Espejo de El matrimonio Arnolfini. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
A estas alturas espero haberles convencido (si no lo estaban ya) de la importancia que ha tenido van Eyck en la historia del arte. No cabe duda de que su obra merecía ser estudiada empleando los mejores instrumentos a nuestro alcance. Bienvenidos al proyecto VERONA.
El Proyecto VERONA: Van Eyck Research in OpeN Access
La producción artística de Jan van Eyck fue muy reducida, por lo menos teniendo en cuenta las pinturas que se conservan. Hasta tal punto que sólo existen nueve cuadros que lleven su firma. A lo largo del s. XX los historiadores del arte estudiaron con detalle estas obras y, con menor o mayor polémica, llegaron a atribuir una veintena de obras al genio flamenco. Aun sumando las miniaturas del Libro de Horas de Turín-Milán que se le atribuyen a él y a su hermano Hubert, es un legado escaso. Hemos de tener en cuenta que aquellos estudios estilísticos se hicieron en base a unos recursos técnicos limitados, por lo que se antojaba necesario realizar nuevos análisis adaptándose a los tiempos que corren. Así se podría entender mejor el proceso creativo de van Eyck y revisar su creación artística. De eso se encargaron los expertos del Instituto Real del Patrimonio Cultural de Bélgica (KIK-IRPA) quienes, mediante tecnología puntera y siguiendo un protocolo estandarizado, analizaron la obra de Jan van Eyck y la pusieron a disposición no sólo de los expertos, sino del público en general.
En 2014 cargaron una furgoneta con los instrumentos necesarios y viajaron por toda Europa para documentar las pinturas atribuidas a van Eyck que se hallan desperdigadas por diferentes museos (también hay alguna obra en Estados Unidos). En un trayecto de 12 000 kilómetros recogieron 16 298 imágenes para un total de 1 499 gigas de información. Casi nada. Aquí les tenéis estudiando el Díptico de la Anunciación del Museo Thyssen-Bornemisza, por si les queréis ver con las manos en la masa.
 Imagen 3. La instrumentación con la que viajó el equipo del KIK-IRPA. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 3. La instrumentación con la que viajó el equipo del KIK-IRPA. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
El primer paso del proceso consistía en tomar una fotografía de alta resolución, asegurándose de que se usaban siempre las mismas condiciones para todas las obras. Para ello emplearon una cámara Hasselblad H4D-200MS con un sensor de 50 megapíxeles que, obviamente, no sujetaban a pulso. Se colocaba en un soporte mecánico que se podía desplazar por raíles, lo que permitía realizar macrofotografías (15×20 cm o 7.5×10 cm) que luego se montaban digitalmente para ofrecer imágenes en las que podemos apreciar hasta el más pequeño de los detalles (Imagen 4). Además de tomar las fotografías con iluminación normal, las tomaron con luz rasante y bajo luz ultravioleta, algo que ofrece información complementaria como ya vimos en su momento.
 Imagen 4. Realización de una macrofotografía sobre el Tríptico de Dresden y una ampliación de San Francisco Recibiendo las Agallas a escala milimétrica en la que podemos observar el craquelado de la pintura. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 4. Realización de una macrofotografía sobre el Tríptico de Dresden y una ampliación de San Francisco Recibiendo las Agallas a escala milimétrica en la que podemos observar el craquelado de la pintura. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
La cámara Hasselblad también estaba equipada para trabajar en el infrarrojo, de modo que se pudiese estudiar el dibujo subyacente de las pinturas. En cualquier caso, para lograr imágenes con una mayor capacidad de penetración se empleó un instrumento de reflectografía infrarroja que permitía trabajar entre los 900 y los 1700 nm. Recordemos que a esas longitudes de onda muchos de los pigmentos no absorben prácticamente energía, mientras que el carbono, tradicionalmente empleado en el dibujo preparatorio, sí lo hace. Gracias a esta técnica se puede conocer mejor el modus operandi de un pintor y ver los cambios realizados a lo largo del proceso de creación. Precisamente uno de los casos paradigmáticos del empleo de la luz infrarroja es El Matrimonio Arnolfini, en cuyo reflectograma se pueden observar los numerosos cambios realizados por van Eyck. Pero quedémonos aquí con un ejemplo que he encontrado trasteando en la web del proyecto VERONA: ¿No os parece que tanto el Niño como la Madre en La Virgen del Canciller Rolin iban a tener los brazos en otra posición?
 Imagen 5. Reflectografía infrarroja del Niño de La Virgen del Canciller Rolin en la que se aprecia el cambio de composición respecto al resultado final. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 5. Reflectografía infrarroja del Niño de La Virgen del Canciller Rolin en la que se aprecia el cambio de composición respecto al resultado final. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Siguiendo con la idea de penetrar en la pintura, no se podía dejar de lado el uso de la radiografía. Como la materia absorbe los rayos X en función de los átomos que la componen y la densidad del material, podemos lograr información valiosísima sobre el uso de pigmentos y el estado de la obra. El equipo belga realizó las radiografías mediante instrumentos de rayos X portátiles empleando películas para radiografías (30 x 40 cm) que luego montaron digitalmente. Aquí hemos de decir que el protocolo no está tan estandarizado y que en muchos casos emplearon radiografías realizadas con anterioridad, algo perfectamente comprensible teniendo en cuenta que se trata de una técnica más compleja que las anteriores. Para que os hagáis una idea del tipo de información que se obtiene, os traigo como ejemplo el retrato de Margaret, la mujer del artista (otra de las cosas en las que van Eyck fue un innovador, ya que no era nada habitual este tipo de retratos). Si observáis la Imagen 6, veréis que el tocado ofrece un color claro en la radiografía. Es muy posible que el pintor emplease albayalde, un pigmento blanco que tiene plomo y que por lo tanto absorbe los rayos X.
 Imagen 6. Radiografía de El Retrato de Margaret van Eyck (41×34 cm). Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 6. Radiografía de El Retrato de Margaret van Eyck (41×34 cm). Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Acabemos este recorrido por los estudios técnicos subrayando que, en algunas de las obras, también se han aplicado análisis más específicos sobre pigmentos gracias al uso de la fluorescencia de rayos X. De momento no están disponibles en la página web del proyecto, pero crucemos los dedos para que pronto lo estén. Lo que sí que podemos hacer en dicha web es juguetear con las macrofotografías (Imagen 7), las imágenes en infrarrojo y las radiografías de más de veinte obras obtenidas con la misma escala en una iniciativa que ojalá sólo sea la primera de muchas.
 Imagen 7. Apariencia de la página web del proyecto Verona al comparar cuatro macrofotografías de diferentes vírgenes pintadas por van Eyck. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 7. Apariencia de la página web del proyecto Verona al comparar cuatro macrofotografías de diferentes vírgenes pintadas por van Eyck. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
La firma
No quería finalizar el artículo sin llamar la atención sobre un aspecto de las pinturas que suele pasar desapercibido: el marco. En las macrofotografías de algunas de las obras podemos observar los marcos originales que todavía se conservan. Ahí es donde en varias ocasiones el artista flamenco dejó su firma, junto al lema AΛΣ IXH XAN (Als Ich Kan). Esta frase vendría a significar “como (mejor) puedo”, toda una fórmula de humildad, aunque también se ha interpretado como un juego de palabras para decir “como van Eyck (sólo) pudo”, lo que tendría un significado bastante diferente. En cualquier caso, no cabe duda de que van Eyck pudo. Vaya si pudo.
 Imagen 8. Marco original de La Virgen de la Fuente con la firma de Jan van Eyck y el lema “AΛΣ IXH XAN” parcialmente visible. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 8. Marco original de La Virgen de la Fuente con la firma de Jan van Eyck y el lema “AΛΣ IXH XAN” parcialmente visible. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo Van Eyck al descubierto se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: Cobre
- Descubierto el proceso por el que las bacterias fabrican nanoimanes
- Festín burlesco, una visita al alma del museo
Asteon zientzia begi-bistan #298

Koronabirus berriak eragin duen osasun krisi honetan, adituek testak egitearen garrantziaz hitz egin dute. Baina zeintzuk dira test horiek? Zer detektatzen dute? Zein da proba hauen fidagarritasuna? Horien inguruan mintzatu da Iosu Razquin Biologian doktorea. Kontuan izan behar dugu, oro har, bi multzo handitan banatzen direla: birusa zuzenean detektatzen duten teknikak eta modu ez-zuzenean egiten dutenak. Aukera paregabea duzue testen inguruko xehetasunak artikulu honetan irakurtzeko!
Azalpen honi jarraiki, Berriak ere argitaratu du gida bat testak hobeto ezagutzeko.
SARS-CoV-2 birusaren jatorria saguzarretan egon daitekeela zabaldu da. Egoera honen aurrean, Joxerra Aihartza zoologo eta UPV/EHUko Zientzia eta Teknologia Fakultateko irakasleak esan du Berrian birusa genetikoki aztertu dela, eta, “orain arte topatu diren birusekin konparatu ostean, antzekoena saguzarretan topatutako birus bat omen da”. Halere, gaineratzen du gakoa ez dela birusa nondik etorri den jakitea, baizik eta nola egokitu den birus hori gizakioi ere kalte egiteko.
Hainbat hipotesi ezagutu ditugu birusaren jatorriaren inguruan. Batzuek diote laborategi batean sortu zela, baina ikertzaile batzuek jada jakinarazi dute hori gezurra dela. Eta laborategi batean ez bada sortu, non izan da? Honako hiru teoria hauek ezagutzen dira oraingoz: lehenengoa, hautespen naturala gordeleku animalia batean gertatu izana; bigarrena, hautespen naturala gizakietan gertatzea, eta hirugarrena, hautespen hori animalietatik gizakira salto horretan izatea. Berrian informazioa.
Holandako Osasun Publikoaren eta Ingurumenaren Institutu Nazionalean egindako ikerketa batek ezagutzera eman du SARS-CoV-2 koronabirusa hondakin-uretan detektatu izan dela. Ikerketa horretan esan dute gainera hondakin-uren monitorizazioa estrategia egokia dela biztanlerian birusaren infekziorik dagoen detektatzeko. Espainian ere hondakin-urak izan dituzte jomugan: Valentziako ikertzaile talde batek test bat garatu du hondakin-uretan SARS-CoV-2a dagoen atzemateko. Berrian honen ingurukoak.
Osasunaren Mundu Erakundeak (OME) nazioarteko lankidetza-ekimen bat abiatu du COVID-19ren aurkako txerto baten garapena bizkortzeko. Erakundeak adierazi du pandemia hau kontrolatzeko beharrezkoa dela txerto bat lortzea. Egitasmo honetan zientzialariak, medikuak, finantzatzaileak eta ekoizleak daude. Elhuyar aldizkarian aurkituko dituzue xehetasunak.
COVID-19ren aurkako borrokan funtsezkoak diren diziplina batzuei buruz hitz egin digu Juan Ignacio Pérez Iglesiasek, hala nola birologia, genetika molekularra –honi esker ezagutzen dugu SARS-CoV-2 birusak gizaki batengana egindako lehen jauzitik aurrera zein leinutan dibertsifikatu den-, epidemiologia, biologia eta immunologia. Osasun krisi honetan beharrezkoak diren arlo horien garrantzia nabarmentzen du.
Birusak zeharo baldintzatu du natur zientzien ikerketen jarduera. Batzuen kasuan, ohiko lan-erritmoan eragin du krisialdi honek, beste batzuek ez dute aldaketa asko nabari. Artikulu honetan, hainbat zentrotako ikertzaileen azalpenak aurkituko dituzue, izan ere, batzuek baldintza berrietara egokitu behar izan dute, proiektuak eten… Aurreikuspenak ere egin dituzte. Ez galdu Berriako informazioa!
Konfinamenduaren eragina aztertu du Massachusettseko Teknologia Institutuak esperimentu baten bitartez. Emaitzei dagokienez, erresonantzia magnetiko bidezko irudiak bat zetozen boluntarioek adierazten zuten gose eta bakardade subjektiboekin. Baina egun bizi dugun konfinamendu-agindua ez da esperimentu boluntario bat. Honen harira, Nafarroako Unibertsitate Publikoko ikertzaileek egiaztatu dute konfinamenduak larriagotu egin duela lehendik ere bakarrik zeuden adinekoen sentimendua. Berriako artikulu honetan aurkituko dituzue datu gehiago.
BiologiaBirusei buruzko hirugarren artikulu honetan, Josu Lopez-Gazpiok gure organismoak birusei aurre egiteko martxan jartzen dituen mekanismoei buruz jardun du. Birusaren erasoa gelditzeko, immunitate-sistema dugu. Gai da birusaren mintzetako proteinak ezagutzeko eta horiek arrotzak direla ikusteko. Horren aurrean, immunitate-sistemak antigorputzak sortzen ditu.
Zer da RNA? Zertarako balio du? Ainara Castellanos Rubiok, RNA hitza inoiz baino gehiagotan aipatu den garai honetan, horri buruzko artikulua idatzi du Berrian. Tartean, azkenaldian egiten ari diren ikerketa bi azaldu dizkigu, RNAren gaitasun miresgarriak ezagutzeko.
Emakumeak zientzianElda Emma Anderson fisikariak Manhattan Proiektuan parte hartu zuen, eta laborategian lehen uranio-235 lagin hutsa prestatzea lortu zuen. Halere, Hiroshima eta Nagasaki hirien gaineko bonba atomikoa jaurti zutenean, Andersonek erabaki zuen abiatu zituen ikerketak bertan behera utziko zituela. Horren ondotik, fisikaren esparruan gaiak lantzen jarraitu zuen baina beste bide bat hartu zuen: erradiazioak gizakien osasunean dituen ondorioetan jarri zuen arreta. Emakume honen ingurukoak artikuluan.
GenetikaBeldurraren genetikaren inguruan jardun du Koldo Garciak honetan. COMT genea eta SLC6A4 geneak aipatzen ditu. Lehenengoak neurotrasmisoreen maila kontrolatzen ditu, neutrotrasmisoreak deseginda. Bigarrenak, serotoninaren garraiatzailea da eta jakina denez, serotoninak beldurra modulatzen du. Garciak azaltzen digunez, egoera baten aurrean sentitzen dugun beldurra eta antsietatea ezberdin erantzungo dugu gene horren zein aldaera dugun arabera.
COVID-19a dela eta, gure osasun-informazioa eta kokalekua jasotzen duten mugikorren APPak instalatzeko eskatu dute erakundeek, eta horri jarraiki, Garciak gene-datuen erabileraren inguruan mintzatu da, zehazki, gene-datuen erabilera irekiak komunitate Indigenetan nola eragiten duen. Izan ere, horiek esperientzia negatiboak izan dituzte gene-datuen kudeaketan eta horregatik, hainbat gako eman dezakete gene-datuen gobernantza hobetzeko.
Genomak zer diren definitzen ausartuko zinatekete? Ez larritu, Garciak beharrezkoak direna azalpenak eman dizkigu honetan. Genoma dugun gene-materiala da. Hori argi izan behar dugu. Testuan azaltzen duenaren arabera, espezie bakoitzeko erreferentziazko genoma bat dugu, espezie bakoitzaren gene-longitudea eta gene-latitudea ezartzen duena. Baina, genomak aldakorrak dira, indibiduo bakoitzak ezberdintasun gehiago ala gutxiago dituela bere genoman, erreferentziazko genoma horrekin alderatuta. Ez galdu artikulu interesgarri honetan eman dizkigun gakoak!
Munduko Osasun Erakundeak Gaixotasunen Nazioarteko Sailkapena (ICD, ingelesez) garatu zuen; bertan, gaixotasun, sintoma edo beste edozein gorabeherak kode bat du. Sailkapen hori aldatzen joan da eta berriki publikatu duten bertsioan aldaketa nabarmenak daude. Kode hauen inguruko xehetasunak eman dizkigu Garciak.
ArkeologiaAbri du Maras (Frantzia) Paleolitoko aztarnategi batean neandertalek landare-zuntzez egindako objekturik zaharrena izan daitekeena aurkitu dute: soka-zati bat da, 6 cm-koa, eta 41.000-52.000 urte dituela kalkulatu dute. Orain arte zaharrena zena Ohalo II aztarnategian (Israel) aurkitu zuten. Azken honek 19.000 urte inguru ditu. Honi buruzko xehetasunak Elhuyar aldizkarian aurkituko dituzue.
AstrofisikaZulo beltz baten zorrotada inoizko zehaztasun handienarekin behatu du EHT (Event Horizon Telescope) lankidetzak, Elhuyar aldizkariak azaldu digunez. Duela urtebete, zulo beltz baten irudia erakutsi zuten eta orain bost mila milioi argi-urtera dagoen galaxia batean ikusi dute zorrotada, 3C 279 quasarrean.
IngurumenaIkerketa batean ontzien argiztapenak Artikoko gauean duen eragina aztertu dute inguruan dauden arrainen kopuruari erreparatuta. Delawereko Unibertsitateko (AEB) ikertzaile Jonathan Cohenen esanetan: Itsaso ilun batean pizturiko Gabonetako zuhaitza ematen dute. Bi egoera desberdinetan egin dituzte neurketak: argiak itzalita eta argiak piztuta. Ondorioztatu dute argiak eragina baduela.
–——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
———————————————————————————-
Egileaz: Uxue Razkin (@UxueRazkin) kazetaria da.
———————————————————————————-
The post Asteon zientzia begi-bistan #298 appeared first on Zientzia Kaiera.
Ezjakintasunaren kartografia #304
Adikizioek oso eragin kaltegarriak izan ditzakete. Eta horietako bati oso esposizio handia du gizarteak. Droga gogorren antzera jokatzen du azukreak. Rosa García-Verdugoren Sweet addiction
Mielina deituriko kapa lipidikoaz daude estalita neuronak. Espektro autistaren eta kapa honen kalitatearen arteko harremana egotea baliteke. José Ramón Alonsoren Myelin and autism
Argiarekin elkarreragiten duten materialen erantzuna modulatzea etorkizuneko nanofotonikaren pausu garrantzitsua izango da. DIPCren ekarpena: On-demand spectral response of phonon polaritons in van der Waals materials
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #304 appeared first on Zientzia Kaiera.
Por qué los biobots no son un problema ético (de momento)
 Un organismo 3D diseñado por un algoritmo evolutivo y construido a partir de células vivas.
Un organismo 3D diseñado por un algoritmo evolutivo y construido a partir de células vivas.Douglas Blackiston, CC BY-SA
El pasado 13 de enero se publicó un avance científico que tiene todas las papeletas para convertirse en un hito en la historia de la investigación biotecnológica. Un equipo de cuatro investigadores estadounidenses ha creado un sistema orgánico funcional novedoso, una forma de vida diferente a todas las que existían, algo que jamás se había conseguido antes.
El proceso para llegar a este resultado fue extremadamente arduo. Para empezar, hubo que utilizar un algoritmo evolutivo complejo alojado en un superordenador. Este mecanismo fue el que determinó qué tipo de material biológico – y con qué estructura – habría de emplearse para lograr el objetivo perseguido. A partir de los resultados proporcionados por esa herramienta, se decidió utilizar células procedentes de la piel y el corazón de embriones de ranas africanas, que se moldearon de la forma diseñada por la inteligencia artificial.
La entidad resultante fue una estructura biológica de un milímetro de anchura que se comportaba de manera coordinada en circunstancias hasta ahora esquivas a la acción humana. De hecho, pueden trabajar conjuntamente y sobrevivir incluso semanas sin necesidad de alimento.
Sus posibles aplicaciones incluyen gestionar la contaminación radioactiva, recolectar microplásticos en los océanos e incluso inocular un medicamento en un tumor. Además, estas entidades tienen la ventaja de ser biodegradables, por lo que, en principio, desaparecerían sin dejar rastro una vez cumplido su cometido.
¿Xenobots o biobots?
Nos encontramos ante un descubrimiento de primer orden, que abre las puertas de un mundo desconocido y lleno de promesas, pero tan novedoso que también encierra múltiples interrogantes. Para empezar, ni siquiera está claro cómo tendríamos que denominar a estas criaturas.
En las primeras informaciones facilitadas se ha propuesto el nombre de “Xenobots”, que combina su origen (la denominación científica de las ranas africanas es Xenopus laevis) con el tipo de entidad de la que se trata -– “bots” o robots –.
A mi juicio esta terminología resulta un tanto equívoca, porque la palabra “xeno” significa en griego “extranjero” o “extraño”. Me parece poco afortunado introducir este concepto, que normalmente asociamos a pensamientos negativos, en una nueva tecnología.
Tiene más sentido elegir la denominación de “biobots”, que une a la idea de robotsla de bios, un prefijo que muestra ostensiblemente su carácter de materia viva. Una característica, por cierto, esencial en este caso, ya que es la que dota a las nuevas criaturas tanto de gran plasticidad como de una capacidad a la que suelen ser ajenas las estructuras sintéticas: la de regenerarse a sí mismas en caso de sufrir daño.
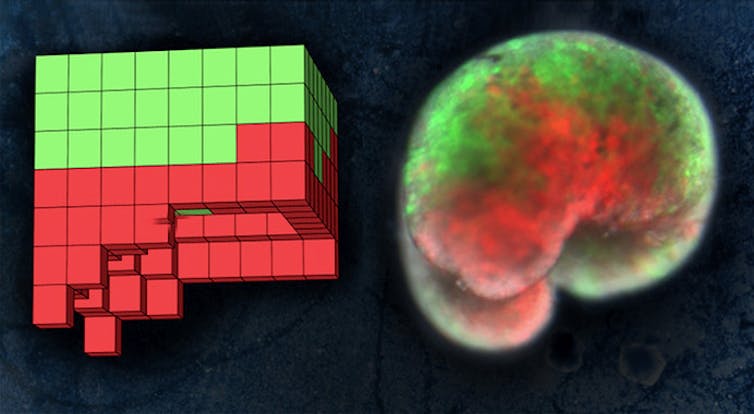 A la izquierda, el plano anatómico de un organismo diseñado por ordenador. A la derecha, el organismo vivo, construido a partir de piel de rana (verde) y células del músculo cardíaco (rojo).
A la izquierda, el plano anatómico de un organismo diseñado por ordenador. A la derecha, el organismo vivo, construido a partir de piel de rana (verde) y células del músculo cardíaco (rojo).Sam Kriegman (UVM), CC BY
Los miedos mitológicos no son razonables
Las cuestiones que se entrelazan con la ética requieren un análisis más profundo. Es fácil presuponer que habrá voces que clamen contra los biobots, ya sea porque nos exponen a escalofriantes peligros aún por determinar o porque su creación atenta por sí misma contra la naturaleza.
La fortaleza de estos argumentos proviene de que conectan muy bien con el imaginario colectivo. Al fin y al cabo, tanto la mitología antigua como la ciencia ficción contemporánea se han encargado de infundirnos un considerable temor a todo lo que parece poco natural. Lo han hecho a través de ejemplos de consecuencias que trae la ambición humana cuando se aúpa a un papel hacedor que no le corresponde.
Contamos con visiones muy pesimistas de lo que la biotecnología puede desencadenar sobre la especie humana. Los ejemplos van desde el mito de quimera, que hizo que los romanos exigiesen forma humana a los recién nacidos para considerarlos personas, hasta relatos como los de La isla del doctor Moreau y películas como GATTACA. Hay toda una herencia de miedo a lo artificial, a lo hecho por el ser humano, entre la que es difícil abrir camino a lo razonable.
La realidad se encuentra, al menos en lo que se refiere a los biobots, muy lejos de parecerse a esos escenarios dantescos.
A diferencia de lo que ocurre con otras tecnologías como la edición genética, las quimeras humano-animales y los organoides, en este caso estamos muy lejos de utilizar material humano, al menos de momento.
Aunque algún día llegáramos al punto de usar células embrionarias humanas para constituir estas estructuras vivas seguiríamos sin poder hablar de seres dotados de valor moral (dignidad). Esta frontera solo se avistará si empezamos a introducir estructuras neuronales en estos biobots.
Este escenario está muy lejos, si es que es viable algún día. Por tanto, solo aquellos que defienden la necesidad de valorar todas y cada una de las formas de vida – una línea de pensamiento minoritaria – podrían preocuparse por la aparición de estas nuevas entidades.
¿Sufren los biobots?
Ahora bien, ¿no debería preocuparnos un cambio tan radical en la estructura de la vida, aunque no afecte al material biológico humano? A mi juicio es obvio que no, aunque entiendo la raíz última de estas inquietudes.
Nuestra visión de la naturaleza tiende a idealizarla. Hablamos de la madre naturaleza y su sabiduría innata, algo panteístico. El sistema que nos rodea no posee atributos como la bondad y la inteligencia. Ciertamente, el mundo físico tiene un orden (variable) y unas normas, una forma de organización. No hay nada, sin embargo, que certifique que ese orden sea el óptimo para nosotros. De hecho, llevamos milenios pensando lo contrario, de ahí las alternaciones de la naturaleza que ha provocado el desarrollo de la medicina, la agricultura y el transporte
Introducir otras, como la creación de biobots,no debería resultar inquietante por sí misma. Otra cosa será inferir si la mera existencia como biobot causa sufrimiento a la criatura creada artificialmente. Este es el punto en el que nos hallamos en el caso de los organoides cerebrales, pero cuesta pensar que las dudas sean extrapolables a entidades que carecen de un centro de interpretación de señales nerviosas.
Si en el futuro nos encontramos ante una situación más compleja, será el momento de retomar esta discusión. Por ahora parece superflua.
Sin riesgos (de momento)
Esto no significa que debamos permitir cualquier uso de esta tecnología. La liberación de organismos de este tipo en un entorno no controlado podría entrañar graves riesgos para el ecosistema.
Tampoco parece posible autorizar, en un futuro próximo, experimentos que impliquen su introducción en el cuerpo de seres vivos, sean o no humanos, por razones de seguridad.
Para evitar estos excesos se encuentra ya en vigor toda una normativa que nos protege de usos poco razonables de tecnologías experimentales. Toda una pléyade de organismos, desde las agencias de seguridad hasta los comités de ética de la investigación, se encargan de vetar iniciativas de dudosa utilidad o elevado riesgo. Al menos, mientras no se hayan recorrido todos los pasos que ha de transitar cualquier tecnología nueva antes de su aplicación práctica.
El derecho también tendrá que estudiar qué estatuto proporciona a estos biobots, o si será necesario desarrollar alguna norma concreta que regule su uso, y seguro que su respuesta será más que satisfactoria.
Mientras tanto, quienes han de aplicar las normas tendrán que intentar hallar en su articulado unas guías generales con las que establecer pautas de acción concretas en este momento preciso. Dudo muchísimo que la aparición de formas de vida como estas suponga un desafío a este respecto.
Cabe pensar que este avance tecnológico merece una mirada esperanzada, aunque sea todavía muy pronto para calibrar su impacto en la práctica. No parece que un uso ordenado de esta tecnología plantee problemas éticos o jurídicos preocupantes. Habrá, en todo caso, que estar muy atentos a sus futuros desarrollos. Ellos nos confirmarán (o no) este primer diagnóstico.![]()
Sobre el autor: Iñigo De Miguel Beriain es Ikerbasque Research Professor e investigador distinguido de la Facultad de Derecho, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Por qué los biobots no son un problema ético (de momento) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Pozos de conocimiento: el problema de la profundidad
- El comportamiento corpuscular de la luz: momento lineal del fotón
- Estroncio en la leche

