Una capa brillante para un planeta oscuro
Mercurio no es solo el planeta más pequeño de nuestro sistema solar, sino que también es uno de los más desconocidos, ya que, casualmente, ha sido el planeta interior -o rocoso- menos visitado por misiones espaciales. Entre otras razones, ello se debe a la dificultad que supone colocarse en órbita alrededor de Mercurio, lo que requiere una gran cantidad de combustible -combustible en sentido amplio- para alcanzar el cambio de velocidad necesario que permita la inserción.
A pesar de esto, misiones como la MESSENGER nos han permitido conocer mucho mejor a Mercurio y detectar, por ejemplo, la presencia de agua y de compuestos orgánicos en su superficie, la existencia de un núcleo en estado líquido e incluso los restos de la actividad volcánica que sufrió el planeta en su pasado. Las observaciones las pudo obtener desde su órbita desde 2011 a 2015, cuando la misión, como despedida, impactó finalmente contra la superficie del planeta.
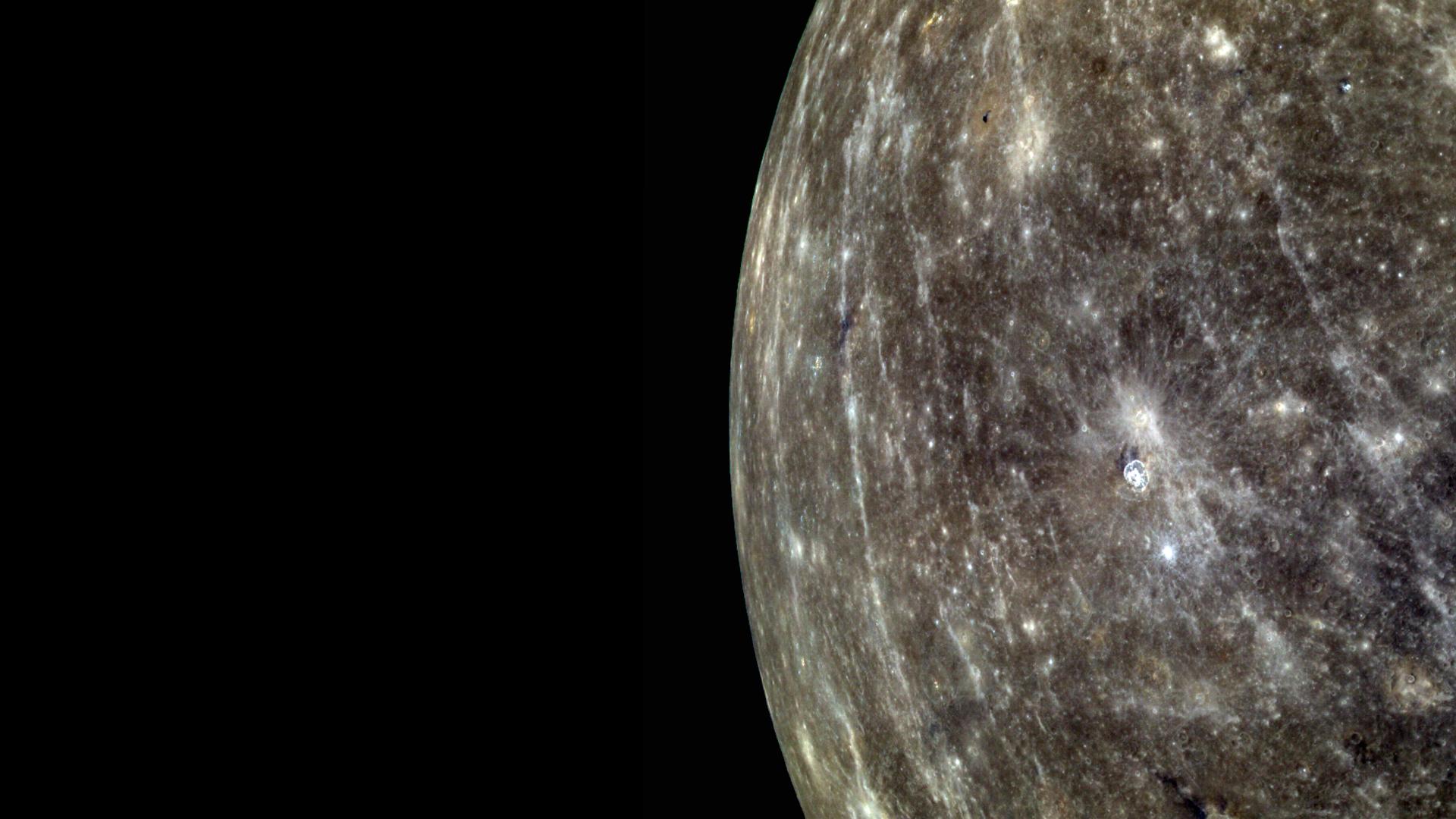 A simple vista, el aspecto de Mercurio nos recuerda mucho al de nuestra Luna. Sin embargo, son lugares muy, pero que muy distintos. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.
A simple vista, el aspecto de Mercurio nos recuerda mucho al de nuestra Luna. Sin embargo, son lugares muy, pero que muy distintos. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.Pero, ¿cómo es el interior de Mercurio? Lo cierto es que es un planeta muy particular, especialmente si lo comparamos el resto de los planetas interiores. Para que nos hagamos una idea, el núcleo -la capa más interna de los planetas- de Mercurio ocupa aproximadamente un 57% del volumen total del planeta, mientras que en Venus ocuparía un 15%, en la Tierra un 16% y en Marte un 13%. Mercurio claramente destaca por tener un valor totalmente anómalo en comparación con el resto.
Este pequeño detalle ya nos cuenta que la historia de Mercurio podría haber sido un poco diferente a la del resto de planetas rocosos, apuntando directamente a su formación o a su infancia -eso sí, infancia en términos planetarios. O bien la zona donde se formó Mercurio dentro de la nebulosa protoplanetaria estaba empobrecida en elementos ligeros -quizás por procesos dinámicos, no tanto por una diferencia composicional dentro de la nebulosa- porque tras su formación, las elevadas temperaturas del Sol mientras este se contraía vaporizaron parte de su corteza y manto rocoso -para lo que Mercurio tendría que tener una masa de partida de aproximadamente el doble- o, por último, un gigantesco impacto que fuese capaz de eliminar una gran parte de su corteza y manto dejando las zonas más densas del planeta y llevándose las ligeras, y para lo que Mercurio también tendría que haber tenido también en torno al doble de masa que en la actualidad.
Pero volvamos al asunto que nos trae hoy aquí y seamos realistas: Mercurio es un planeta muy poco… “brillante”. Apenas refleja el 10% de la luz solar, algo que hasta la llegada de las misiones planetarias había tenido una difícil explicación. Los últimos datos afirman que muy probablemente esta escasa reflectividad se deba a que su superficie está cubierta por una cantidad entre el ~1-4% de grafito -un compuesto de carbono que usamos todos los días, por ejemplo, en las minas de nuestros lápices y que a la luz es evidente que tiene un color bastante oscuro-, a lo que habría que sumar probablemente otros compuestos del carbono, aunque las últimas estimaciones de Xu et al. (2024) dicen que sería inferior al 1%.
 La eyecta provocada por los cráteres de impacto -es decir, los materiales que salen hacia fuera del cráter cuando un cuerpo impacta contra la superficie de un planeta- salpican de tonos más claros la superficie de Mercurio. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.
La eyecta provocada por los cráteres de impacto -es decir, los materiales que salen hacia fuera del cráter cuando un cuerpo impacta contra la superficie de un planeta- salpican de tonos más claros la superficie de Mercurio. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.¿Cuál sería la procedencia de este grafito que hoy vemos en la superficie? No está muy claro, y dependiendo del modelo de formación, explicar su presencia puede ser complicado, pero la forma más sencilla sería que, en algún momento de su historia, la superficie de Mercurio estuviese en un estado de océano de magma -una etapa habitual durante la formación de los planetas interiores- y donde toda la superficie se encuentra fundida. Es en este océano donde el carbono, debido a su densidad, flotaría hasta la superficie, quedando expuesto tal y como vemos hoy en día, mezclado con otros minerales silicatados que forman su corteza.
Este detalle sobre la composición de su superficie nos hace pensar que Mercurio podría tener más carbono en su interior del que podríamos pensar a priori y esto puede tener unas consecuencias un tanto inesperadas que podemos leer en Yongjiang et al. (2024): la existencia de una “capa” de diamantes en el interior de Mercurio. Y es que sabemos por nuestra experiencia en la Tierra que los diamantes en los planetas rocosos se forman en ambientes de alta presión y temperatura, lo que en nuestro planeta equivale a profundidades del manto.
Mercurio es mucho más pequeño que nuestro planeta y la presión necesaria para transformar el carbono en su forma de grafito a diamante se alcanzaría en lo que vendría siendo el límite entre el manto y el núcleo, eso sí, también tendrían que darse unas condiciones de temperatura adecuadas. Pero además del carbono hay un elemento que probablemente haya tenido un papel importante para formar esta posible capa: el azufre.
Y es que la presencia de azufre en el interior del planeta podría ayudar a bajar la temperatura que los silicatos presentes en el manto requieren para fundirse, permitiendo unas condiciones que ayudarían a dar estabilidad a la formación de los diamantes. Si a esto le sumamos un ambiente muy reductor -con bajo contenido en oxígeno- los diamantes podrían haberse empezado a formar al mismo tiempo que empezó a solidificarse el núcleo, permitiendo dar lugar una capa de diamantes en el límite entre el manto y el núcleo y que incluso podría tener varios kilómetros de potencia o espesor.
Los científicos que han escrito este artículo, además, han diseñado y ejecutado una serie de experimentos de alta presión y temperatura -sin olvidar los modelos geoquímicos y termodinámicos- a fin de poder replicar las condiciones que se podrían encontrar en este límite entre el manto y el núcleo, observando que efectivamente, los diamantes podrían formarse bajo estas condiciones.
 En esta imagen también se puede apreciar perfectamente el fuerte contraste de color entre la eyecta y la superficie de Mercurio, mucho más oscura. Y es que es posible que los minerales que hay a más profundidad de la corteza tengan un tono más claro y sean menos ricos en carbono. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.
En esta imagen también se puede apreciar perfectamente el fuerte contraste de color entre la eyecta y la superficie de Mercurio, mucho más oscura. Y es que es posible que los minerales que hay a más profundidad de la corteza tengan un tono más claro y sean menos ricos en carbono. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.Todo esto nos puede parecer una mera curiosidad, pero en Mercurio podrían tener una interesante derivada… puesto que los diamantes son unos excelentes conductores térmicos -de hecho, se usan en algunas aplicaciones electrónicas donde la disipación del calor es algo crítico y los materiales que son buenos conductores eléctricos no se pueden colocar- y una capa rica en diamantes podría tener una gran influencia en la transferencia del calor en el interior del planeta, alterando la propia dinámica interna del planeta. ¿Qué consecuencias tiene esto? La generación de un campo magnético similar al de la Tierra, aunque con una fuerza del 1% del nuestro.
El papel de la capa de diamantes es el de facilitar la pérdida de calor del núcleo, favoreciendo la convección necesaria para que funcione la geodínamo necesaria para la formación del campo magnético.
Mercurio no es el único planeta que podría tener capas con diamantes, sino que los gigantes de hielo, como son Urano y Neptuno, también podrían tener zonas donde las condiciones permitan la formación de los diamantes. De momento ninguno de estos lugares son accesibles a nuestra tecnología. Esta posibilidad pone de manifiesto que los diamantes son un mineral más abundante de lo que podemos pensar. Eso sí, que nadie piense que los va a encontrar perfectamente tallados para recoger y colocar en un anillo: eso ya corre de nuestra cuenta.
La próxima misión destinada a Mercurio, la europea BepiColombo debería alcanzar su órbita en 2025, aportándonos a lo largo de su misión datos que nos ayuden a conocer mejor su geología y quién sabe si a verificar la posibilidad de que Mercurio tenga una resplandeciente capa de diamantes.
Referencias:
Cheng, Bingqing, Sebastien Hamel, y Mandy Bethkenhagen. «Thermodynamics of Diamond Formation from Hydrocarbon Mixtures in Planets». Nature Communications 14, n.º 1 (27 de febrero de 2023): 1104. doi: 10.1038/s41467-023-36841-1.
Frost, Mungo, R. Stewart McWilliams, Elena Bykova, Maxim Bykov, Rachel J. Husband, Leon M. Andriambariarijaona, Saiana Khandarkhaeva, et al. «Diamond Precipitation Dynamics from Hydrocarbons at Icy Planet Interior Conditions». Nature Astronomy 8, n.º 2 (8 de enero de 2024): 174-81. doi: 10.1038/s41550-023-02147-x.
Semerikova, Anna, Artem D. Chanyshev, Konstantin Glazyrin, Anna Pakhomova, Alexander Kurnosov, Konstantin Litasov, Leonid Dubrovinsky, Timofey Fedotenko, Egor Koemets, y Sergey Rashchenko. «Does It “Rain” Diamonds on Neptune and Uranus?» ACS Earth and Space Chemistry 7, n.º 3 (16 de marzo de 2023): 582-88. doi: 10.1021/acsearthspacechem.2c00343.
Xu, Yongjiang, Yanhao Lin, Peiyan Wu, Olivier Namur, Yishen Zhang, y Bernard Charlier. «A Diamond-Bearing Core-Mantle Boundary on Mercury». Nature Communications 15, n.º 1 (14 de junio de 2024): 5061. doi: 10.1038/s41467-024-49305-x.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Una capa brillante para un planeta oscuro se ha escrito en Cuaderno de Cultura Científica.
Igel kaka-lardoa
Akabo uda eta iritsi da ikasturte berriari ongietorria emateko ordua. Gogotsu ekingo diozue batzuk, erdipurdi besteok. Eta zelan laguntzeko gauden, itzulera arinagoa egingo digun istorio batekin nator.
 1. irudia: ur-kakalardo sarraskijalea dugu honakoa, Regimbartia attenuata. (Argazkia: Sugiura, S. (2020) artikulutik ateratako argazkia. Iturria: Current Biology)
1. irudia: ur-kakalardo sarraskijalea dugu honakoa, Regimbartia attenuata. (Argazkia: Sugiura, S. (2020) artikulutik ateratako argazkia. Iturria: Current Biology)Hiru osagai zoragarri ditu dakardan kontu honek: bizitzari eutsi eta aurrera egiteko grina duten protagonistak, eskatologia pixka bat eta bitxikeria moduan kontatzeko istorioa dela. Hasteko, noski, protagonistak aurkeztuko ditugu.
Gure lehenengo protagonista igel bat da. Igel normal eta arrunta. Pelophylax nigromaculatus espeziekoa, hain zuzen. Pelo, hemendik aurrera.
Hurrengo protagonista kakalardo bat da. Hau ere kakalardo arrunt eta normala. Ur-kakalardo sarraskijalea dugu honakoa, Regimbartia attenuata. Regi, lagunentzako eta guretzako.
Gure bi protagonistek habitata partekatzen dute Japonia aldean, baita beste zenbait tokitan ere, baina gure istorioa Japonian dago kokatuta. Japonian auzokideak dira gure protagonistak, beraz. Haien harremana zein den? Gure igela zorigaiztoko kakalardoaren harrapakari posiblea da. Auzokide gatazkatsuak, hortaz.
Kontua da harrapakari-harrapakin harreman posible hori ikertzea erabaki zuela Shinji Sugiura ekologoak. Esperimentua prestatu zuen horretarako. Esperimentu erabat logikoa, baina ez oso bidezkoa kakalardoen ikuspuntutik: Pelo igela kutxa garden batean sartu zuten laborategian eta, Regi kakalardoa jango ote lukeen ikusteko, kakalardoa kutxa berean sartu zuten eta gertatzen zena behatu zuten.
Eta espero litekeen moduan, ikusi zutena zera izan zen: jatetxe batean bezala poz-pozik zegoela Pelo gure igela. Kakalardoa ikusi eta pentsatu barik jan egin zuela. Bizitza honetan, baina, gauzak ez dira hain errazak. Are gutxiago auzokideen arteko harremanak. Eta sorpresatxoa zuen gordeta gure Regi kakalardoak.
Izan ere, bere burua jaki bihurtuta ikusi eta 6 ordu pasa baino lehen, igelaren uzkitik -kloakatik, alegia- ateratzen ikusi zuten gure Regi. Onik eta osorik.
Janaria ondo murtxikatzearen garrantziazKontua zelan izan daitekeen ulertzeko, xehetasun batzuk ezagutu behar dira harrapakarien eta harrapakinen arteko harremanen inguruan; janaria harrapatu nahi duenaren eta janaria izan nahi ez duenaren arteko harremana.
 2. irudia: bigarren protagonista: Pelophylax nigromaculatus igela. (Argazkia: Alpsdake – CC BY-SA 3.0 lizentziapean. Iturria: Wikipedia)
2. irudia: bigarren protagonista: Pelophylax nigromaculatus igela. (Argazkia: Alpsdake – CC BY-SA 3.0 lizentziapean. Iturria: Wikipedia)Harrapakari-harrapakin harremanetan ihes egitea da ohikoena. Harrapakinak harrapakariengandik ihes egitea ulertzen da. Kontrakoa, ordea, ikustekoa litzateke. Denok egunero ikusten ditugun La 2 kateko dokumentaletako gazelek lehoiengandik ihes egitea. Hau da, kontaktua egon baino lehen, alde egitea.
Harrapakari batek harrapakinarekin kontaktua egitean kalteak eragiten baitizkio normalean: kosk egitean edo murtxikatzean kaltetu egiten du, eta digestio-sistemak akabera ematen dio. Bada, hala ere, harrapariak harrapakinarekin kontaktua egin ostean bizia salbatzeko estrategia garatu duenik. Gure Regi, esaterako. Bizitzeko grinaren adibide. Heroia.
Eta zelan egiten duen? Digestio-sistema zeharkatuta. Erraz esaten da. Baina egin, egin behar da. Bizitzaren kontrako ingurunea baita digestio-sistema. Benetan erasokorra. Eta, hala ere, ateratzea lortzen du. Kakaz inguratuta, hori bai.
Ateratzeko, atzeko atea ireki behar da, noski. Ikertzaileen esanetan, Regik berak eragiten du esfinterra irekitzea. Izan ere, burua aurretik duela ateratzen da gure kakalardoa eta hortaz, rol aktiboa duen seinaletzat hartu dute hori ikertzaileek: hestearen azken atala estimulatuta esfinterra irekitzea lortzen duela ondorioztatu dute.
Baina hori baino lehen, zelan lortzen du Regik bere burua jaki bihurtuta ikustearen esperientziaren ondoren bizirautea? Pelo gure igelak jateko dituen ohiturak dira gakoetako bat, ikertzaileen aburuz. Osorik eta murtxikatu barik jaten baititu bere biktimak, gero urdailak bere lana egin dezan. Badirudi kasu honetan, baina, urdailak kale egiten duela eta gure Regi osasuntsu ateratzen dela digestio-sistematik bidaia egin ostean.
Urdailari eta, oro har, digestio-sistemari borroka irabazteko gakoetako bat denbora izan daiteke. Ingurune hilgarria sistema hori, harrapakinak hiltzeko diseinatua baitago eta, hortaz, ezinbestekoa da handik azkar irtetea. Hainbat Regik egin behar izan diote aurre jaki izatearen probari, eta azkarrenak 6 minutu baino ez ditu behar izan ateratzeko. Motelenak 6 ordu.
Hanketan dago gakoaEta horri lotuta, kontu honen bigarren gakoa dator: Regi gure kakalardo biziraulearen hankak. Bai, hankak. Regik hankak baliatuta egiten baitu bidaia digestio-sisteman barrena; modu aktiboan egiten du ihes eta, mugitzeko, hankak baliatzen ditu. Gazelak bezala, baina jaki bihurtu ostean. Pentsa norainokoa Regiren sendotasuna: jaki izanak ere ez du gelditzen.
Zelan baieztatu duten hau? Bada, beste behin ere, Regirekiko inongo errespetu, maitasun edo gizalegerik gabe. Ia ziur galtzaile aterako zen egoera batean jarri zuten kakalardoa. Zailtasun are gehiago jarri zizkioten bizitzeko grina izugarria eta elementuei eta igelen digestio-sistemari aurrera egiteko gaitasun paregabea duen Regiri.
Zer egingo eta hankak argizariarekin itsatsi zizkioten. Eta, berriro ere, jango zuela zekiten igelarekin sartu kutxa batean. Eta jaki bihurtu zen. Baina aldi horretan ez zen atera. Gainerako kakarekin atera ziren Regiren gorpuzki atalak 24 ordu pasata.
Hildakoan gorozkiekin batera ateratzeko 24 ordu behar izatea gure Regi borrokalariak kaka eragiten duelako teoria indartzen du: askoz denbora gutxiagoan ateratzen dira bizirik (eta hankak itsatsi barik) dagoenean.
Pena da, baina ikerketan ez dute egiaztatu Regik agrofitnessa egiten ote duen hankak entrenatu eta bizirik ateratzeko aukerak handitzeko. Ezezko frogarik ez dago eta hala dela sinestea erabaki dugu hemen.
Kontu honen guztiaren hirugarren gakoa Regiren morfologian eta uretan bizitzeko dituen adaptazioetan datza. Aire-poltsiko moduko bat du gure kakalardoak eta, hura baliatuta arnasa hartu dezake digestio-sisteman dagoen ingurune anaerobioan. Gainera, exoeskeleto gogorra du, urdailaren urin gastrikoetatik babesten duena. Kakalardoaren forma ere lagungarria izan daiteke igelaren barrutik mugitzeko. Haren morfologiak eta bizimoduak aurreikusi ezin zuten arrisku bakarra argizaria omen.
Erreferentzia bibliografikoa:Sugiura, S. (2020). Active escape of prey from predator vent via the digestive tract. Current Biology, 30(15), R867-R868. DOI: 10.1016/j.cub.2020.06.026
Egileaz:Ziortza Guezuraga (@zguer) kazetaria da eta Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko zabalkunde digitaleko arduraduna.
Jatorrizko artikulua Gaztezulo aldizkarian argitaratu zen 2023ko urrian, 254. zenbakian.

The post Igel kaka-lardoa appeared first on Zientzia Kaiera.
Dozena erdi ariketa 2024ko udarako (5): multiploak
Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko asteazkenero ariketa matematiko bat izango duzue, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Hona hemen gure bosgarren ariketa:1 eta 7 arteko zifrak errepikatu gabe erabilita idatz daitezkeen
zenbaki arrunt guztietatik, 10.000 baino txikiago direnen artean,
zenbat dira 15en multiplo?
Zein da erantzuna? Idatzi emaitza iruzkinen atalean (artikuluaren behealdean daukazu) eta, nahi izanez gero, zehaztu jarraitu duzun ebazpidea ere. Irailean emaitza zuzenaren berri emango dizugu.
 (Argazkia: an_photos – Pixabay lizentziapean. Iturria: Pixabay)
(Argazkia: an_photos – Pixabay lizentziapean. Iturria: Pixabay)Ariketak “Calendrier Mathématique 2024. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
The post Dozena erdi ariketa 2024ko udarako (5): multiploak appeared first on Zientzia Kaiera.
La interpretabilidad de los modelos de inteligencia artificial
Imagina que eres médico y utilizas un sistema de IA de última generación para diagnosticar a tus pacientes. Un día, te dice que un paciente tiene una enfermedad rara, pero cuando le preguntas por qué, simplemente parpadea, incapaz de explicar su razonamiento. Frustrante, ¿verdad? Este escenario puede sonar a ciencia ficción, pero es un reto real en el mundo del aprendizaje automático hoy en día.
Bienvenido al fascinante mundo de la interpretabilidad de modelos, un tema que lleva muchos años dando que hablar en la comunidad de la IA. A medida que los modelos de aprendizaje automático se vuelven más complejos e influyen más en nuestras vidas, nos enfrentamos a una pregunta acuciante: ¿Cómo podemos confiar en las decisiones tomadas por algoritmos que no comprendemos del todo?
En un artículo clásico -muy citado- titulado «The Mythos of Model Interpretability» (2017) el investigador Zachary C. Lipton profundiza en este aspecto crucial. Sostiene que, aunque todo el mundo parece hablar de interpretabilidad, en realidad no tenemos una definición clara y consensuada de lo que significa.
La importancia de la interpretabilidadEntonces, ¿qué importancia tiene la interpretabilidad? Bueno, resulta que hay varias interpretaciones o motivaciones diferentes para la interpretabilidad en el aprendizaje automático:
Confianza (trust): Queremos estar seguros de que nuestros modelos toman decisiones por las razones correctas. Imaginemos un coche autoconducido que hace un giro brusco: ¿no querríamos saber por qué?
Causalidad (causality): En campos como la medicina, no sólo nos interesan las predicciones, sino entender las causas subyacentes. Una IA capaz de predecir una enfermedad cardiaca es útil, pero una que pueda explicar los factores que la provocan tiene un valor incalculable.
Toma de decisiones justa y ética: Como la IA se utiliza cada vez más en ámbitos delicados como la justicia penal y la aprobación de préstamos, tenemos que asegurarnos de que no perpetúa los prejuicios. Si una IA deniega un préstamo a alguien, tenemos que poder examinar su proceso de toma de decisiones.
Informatividad (informativiness): A veces queremos que nuestros modelos nos enseñen algo nuevo sobre el mundo. Un modelo interpretable puede revelar patrones o relaciones inesperadas en los datos.
Transferibilidad (transferability): Necesitamos saber hasta qué punto nuestros modelos funcionarán bien en situaciones nuevas y ligeramente diferentes. Esto es crucial para desplegar sistemas de IA en el mundo real, donde las condiciones pueden cambiar.
Los enfoques de la interpretabilidadLipton señala que hay distintas formas de lograr la interpretabilidad. Algunos investigadores se centran en hacer más transparente el funcionamiento interno de los modelos, mientras que otros desarrollan técnicas para explicar las decisiones de los modelos a posteriori.
Los enfoques de la transparencia incluyen:
-
Simulabilidad: ¿Puede un ser humano simular todo el modelo?
-
Descomponibilidad: ¿Puede entenderse intuitivamente cada parte del modelo?
-
Transparencia algorítmica: ¿Entendemos cómo funciona el algoritmo de aprendizaje?
Entre los métodos de interpretabilidad post hoc se incluyen:
-
Explicaciones textuales: Generación de explicaciones legibles para el ser humano sobre las decisiones del modelo.
-
Visualización: Creación de representaciones visuales de lo que ha aprendido el modelo.
-
Explicaciones locales: Explicar predicciones individuales en lugar de todo el modelo.
-
Explicación mediante ejemplos: Mostrar casos similares que el modelo utilizó para tomar su decisión.
Curiosamente, el artículo cuestiona algunos supuestos comunes. Por ejemplo, mucha gente cree que los modelos lineales simples son intrínsecamente más interpretables que las redes neuronales complejas. Pero Lipton sostiene que esto no siempre es cierto: depende de lo que entendamos por interpretabilidad y de cómo se utilicen los modelos. Por ejemplo, un modelo lineal con miles de características puede ser más difícil de entender a primera vista que una red neuronal entrenada con datos brutos. La elección entre interpretabilidad y rendimiento no siempre está clara.
La interpretabilidad, un arma de doble filoAunque el impulso a favor de la interpretabilidad es generalmente positivo, Lipton advierte de que no está exento de posibles inconvenientes. Por ejemplo, a veces, hacer que un modelo sea más interpretable puede reducir su precisión. O puede que las explicaciones sencillas nos den una falsa sensación de seguridad sobre los sistemas complejos. O tal vez, quién sabe, un modelo muy interpretable podría revelar información sensible sobre los datos de entrenamiento.
A medida que la IA sigue dando forma a nuestro mundo, tenemos que ser más precisos sobre lo que queremos decir cuando exigimos modelos «interpretables». No se trata solo de simplificar las cosas, sino de garantizar que nuestros sistemas de IA se ajusten a los valores humanos y sean fiables a la hora de tomar decisiones importantes.
La búsqueda de una IA interpretable es algo más que un reto técnico: es un paso crucial en la creación de sistemas de IA en los que podamos confiar y que podamos utilizar de forma responsable en la sociedad. Mientras seguimos ampliando los límites de lo que la IA puede hacer, también debemos ampliar nuestra comprensión de cómo funciona. Es un viaje que promete no solo hacer que nuestros sistemas de IA sean más fiables, sino también profundizar en nuestra propia comprensión de la toma de decisiones y de la propia inteligencia.
Para saber más:
La IA podría convertir la ciencia en algo incomprensible
¿Qué es el aprendizaje automático?
Sobre el autor: Julián Estévez Sanz, Profesor e investigador en Robótica e Inteligencia Artificial, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo es una versión del publicado en El blog de Julián Estévez el 19 de agosto de 2024
El artículo La interpretabilidad de los modelos de inteligencia artificial se ha escrito en Cuaderno de Cultura Científica.
Zirkularki polarizatutako argia igortzen duten molekula kiralak
Kiraltasuna nonahiko fenomenoa da naturan zein unibertsoan. Bizidunen organismorako ezinbestekoak diren hainbat biomolekula; hala nola, proteinak edo azido nukleikoak, kiralak dira, eta ezaugarri horrek hainbat prozesu fisiologikoetan parte hartzen du erantzun desberdinak sorraraziz enantiomeroaren arabera.
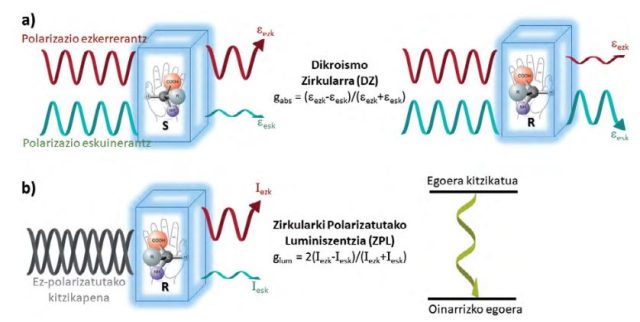 Irudia: (a) Dikroismo zirkularraren (DZ) eta (b) zirkularki polarizatutako lu-miniszentziaren (ZPL) oinarrizko fenomenoak molekula kiraletan, kuantifikazio-rako erabiltzen diren disimetria faktoreen kalkuluarekin batera (gabs eta glum, ab-sortzio eta igorpen prozesuetarako, hurrenez hurren). Laburdurak ekuazioetan: ɛ absortzio molarra da eta argia xurgatzeko ahalmena neurtzen du; I igorritako argi intentsitatea da. (Iturria: Ekaia aldizkaria)
Irudia: (a) Dikroismo zirkularraren (DZ) eta (b) zirkularki polarizatutako lu-miniszentziaren (ZPL) oinarrizko fenomenoak molekula kiraletan, kuantifikazio-rako erabiltzen diren disimetria faktoreen kalkuluarekin batera (gabs eta glum, ab-sortzio eta igorpen prozesuetarako, hurrenez hurren). Laburdurak ekuazioetan: ɛ absortzio molarra da eta argia xurgatzeko ahalmena neurtzen du; I igorritako argi intentsitatea da. (Iturria: Ekaia aldizkaria)Kiralak diren molekuletan, egitura bera eta bere ispilu irudia ezin dira gainezarri, eta beraien artean enantiomeroak dira. Bi egitura ezberdin dira eta bi portaera ezberdin dituzte argi polarizatuaren aurrean. Hori dela eta, molekula kiralak zirkularki polarizatutako argiaren aurrean aktiboak dira eta eskuinerantz edo ezkerrerantz bihurguneak eginez hedatzen diren izpiak bereizteko gai dira. Fenomeno horri dikroismo zirkularra (DZ) deritzo eta bere disimetria ahalmena kuantifikatzeko gabs terminoa erabiltzen da.
Zirkularki polarizatutako luminiszentziaHorretaz gain, molekula kiral batzuk, zirkularki polarizatutako argia xurgatzeaz gain, zirkularki polarizatuta dagoen argia norabide zehatz batean igortzeko gai dira, eskuinerantz edo ezkerrerantz. Igorpen fenomeno horri zirkularki polarizatutako luminiszentzia (ZPL) deitzen zaio eta glum termino anisotropikoaren bidez kuantifikatzen da. Bi ezaugarri horien artean, ZPL fenomenoak arreta handia jaso du azkenaldian gailu fotoniko aurreratuak (hiru dimentsioko pantailak, argi igorle diodoak eta laser) garatzeko, telekomunikazioan informazioa gordetzeko eta prozesatzeko (spintronika), eta bioteknologian sentsore enantioselektibo moduan jarduteko. Horrexegatik, nanozientzietako eta kimikako baliabideak biziki aplikatzen ari dira ZPL-aktiboak diren molekula zein materiala kiralak garatzeko.
ZPL-a sortzeko estrategia desberdinak daude. Horien artean, egoera kitzikatuan kiralitatea eta luminiszentzia duten sistemak dira ohikoenak. Molekula hauen artean, lantanido konplexuak oso eraginkorrak dira glum balio handiak (10-1-10-2 inguru) erakusten dituztelako. Izan ere, lantanidoetan oinarritutako konposatu hauetan aktiboa den trantsizio elektronikoa, elektronikoki debekatuta baina magnetikoki baimenduta dago, eta horixe bera glum handiak lortzeko ezinbesteko baldintza da. Hala ere, azken ezaugarri horrek igorpen ahalmena nabarmen murrizten du. Ondorioz, lantanido konplexuen fluoreszentzia oso baxua da eta, beraz, bere ZPL distira (BZPL) eskasa.
ZPL distira hobetzeko tamaina txikiko molekula organikoak aproposak izan daitezke. Molekularen tamaina zirkularki polarizatuta dagoen argiaren helizearen bidea baino txikiagoa da, eta ondorioz, nahiz eta glum baxuagoa izan (10-3 inguru), fluoreszentzia igortzeko ahalmen handia izan dezake. Hala, ZPL distira onak eman ditzake. Gainera, ez dira toxikoak, merkeak dira eta euren egitura molekularra erraz alda daiteke beharren arabera. Azken ezaugarri hori oso garrantzitsua da, molekularen ezaugarri fotofisikoak zein kiroptikoak erreakzio kimikoen bidez eraldatu baitaitezke. Hala ere, diseinu erronka handia da bi arrazoirengatik, nagusiki: batetik, glum eta fluoreszentzia eraginkortasuna (f) handitzeko behar diren baldintzak guztiz kontrakoak dira eta, bestetik, ZPL distira areagotzeko glum eta f-ren arteko oreka bat lortu behar da.
Kromoforoak, aukera posibleakGaur egun, ZPL konposatu ohikoenak BINOL (1-1´-binaftilo-2-2´-diol) eta helizeno (konposatu aromatiko poliziklikoak dira orto posizioaren bidez kondentsatuta daudenak) molekulen eratorriak dira. Biak atropoisomeroak dira, euren enantiomeroen arteko elkar bihurtze langa energetiko handia delako egitura molekularraren zurruntasuna dela eta. Baina hainbat desabantaila badituzte. Alde batetik, BINOLaren absortzioa eta igorpena ultramore zonaldean dago, eta aplikazio fotonikoetarako batez ere ikusgaiko alde gorrirantz optikoki aktiboak diren molekula kiralak behar dira. Bestetik, helizenoen kasuan, sintesia luzea, konplexua eta garestia da.
BOro-DIPYrrometenoan (BODIPY) oinarritutako kromoforoak hautagai egokiak izan daitezke aurreko arazoak gainditzeko. Bere sintesia erraza eta azkarra da. Gainera, hainbat erreakzioren bidez funtzio-talde ezberdinak erantsi daitezke, eta bide batzez kromoforoa propietate fotoniko berriekin hornitu daiteke. Izatez, BODIPYa ez da kirala, dipirrometeno kromoforoa laua baita eta molekula simetria planoa baitu, baina aldaketa molekular aproposak eginda ZPL seinalea lortu daiteke.
Gure ikerketa-taldean, BINOL eta helizeno molekuletan oinarritu gara BODIPY kiralak garatzeko. Alde batetik, helizenoa abiapuntutzat hartuta, helikoBODIPYak sortu dira. Horiek eraikitzeko, bi BODIPY kromoforo elkartu dira difeniletilendiamina zubiaren bidez eta helize antzeko konformazioa inposatu da. HelikoBODIPYen zubian oztopo esterikoa areagotu ahala helizearen konformazioa hedatzen da eta gabs parametroa hamar aldiz handitzea lortu da, eta glum balioa bikoiztea ikusgai zonaldean (500-550 nm). Bestetik, BINOLa aitzindari kiral gisa ezagutzen denez, ikusgaiko zonalde gorrian fotoaktiboa den BODIPY molekulari boro zubiaren bidez erantsi zaio, BINOL-O-BODIPYak lortuz. Nahiz eta glum txikiagoa eduki, absortzio eta fluoreszentzia sendoagoak dituzte 800 nm-arte eta ZPL distira nahiko ona da.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 45
- Artikuluaren izena: Argi polarizatu zirkularra igortzen duten molekula kiral adimendunak
- Laburpena: Modu zirkularrean polarizatuta dagoen argia xurgatzeko eta batez ere igortzeko gai diren molekula zein material kiralen garapena egungo gaia da kimikan eta materialen zientzietan. Izan ere, biomolekula ugari kiralak dira eta haien portaera nabarmen aldatzen da molekularen konfigurazioaren arabera. Hori dela eta, argi polarizatua enantiomeroak bereizteko gai da, eta aldiz argi ez-polarizatuak ez du ahalmen hori. Kimika organikoaren inguruan egindako aurrerapenek kromoforo enantiomeriko puruak lortzea ahalbidetzen dute, bai eta haien oinarrizko egitura molekularraren birmoldaketa ere, dituzten ezaugarri fotonikoak hobetzeko. Segur aski, BINOLa eta helizenoa dira dikroismo zirkularra eta zirkularki polarizatutako luminiszentzia duten molekula kiral organiko ezagunenak. Hala ere, hainbat erronka gainditu behar dira haien portaera optikoa hobetzeko. Adibidez, interesgarria izango litzateke lan egiteko zona espektrala ultramoretik ikusgaiko alde gorrira eramatea eta molekula horien ahalmen fluoreszentea handitzea luminiszentzia polarizatuaren distira suspertzeko. Helburu horiek lortzeko, aproposak izan daitezke BODIPY izeneko koloratzaileak, duten kimika eta egitura aldakorrari esker aldaketak egin daitezkeelako egitura molekularrean eskaera kiroptikoen arabera. Hain zuzen ere, lan honetan BODIPY kromoforoan oinarrituta garatutako bi estrategia aurkezten dira kiraltasun moldagarria lortzeko; helikoBODIPYak eta BINOL-O- BODIPYak. Hurrengo lerroetan eztabaidatu egiten dira diseinu molekularraren motibazioa eta sistema optikoki aktibo gisa jarduteko dituen gaitasunak.
- Egileak: Ainhoa Oliden-Sánchez, Natalia Casado, Edurne Avellanal-Zaballa, Rebeca Sola-Llano, Leire Gartzia-Rivero eta Jorge Bañuelos Prieto
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 191-207
- DOI: 10.1387/ekaia.24861
Ainhoa Oliden-Sánchez, Natalia Casado, Edurne Avellanal-Zaballa, Rebeca Sola-Llano, Leire Gartzia-Rivero eta Jorge Bañuelos Prieto UPV/EHUko Zientzia eta Teknologia Fakultateko Kimika Fisikoa Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Zirkularki polarizatutako argia igortzen duten molekula kiralak appeared first on Zientzia Kaiera.
Dinosaurios sobre dos ruedas
Si tenéis afición por el ciclismo, seguramente estaréis siguiendo el desarrollo de la tercera gran vuelta por etapas de tres semanas de duración, la Vuelta Ciclista a España, que está recorriendo nuestra geografía estos días. Y, si prestáis mucha atención a los maillots de los equipos, os habrá llamado la atención uno muy geológico. Me refiero al uniforme del equipo Soudal Quick-Step. Este atuendo lleva impresa en la parte frontal y trasera la cabeza de un amenazante Tyrannosaurus rex con la boca abierta, mostrando una hilera de afiliados dientes, enmarcada en un círculo rojo y acompañada por la palabra T-rex en letras blancas, así como la marca de tres garras en el lateral derecho del maillot, como si el dinosaurio hubiese peleado con los ciclistas, rompiendo sus camisetas.
 Maillot oficial del equipo T-rex Quick-Step para la Vuelta Ciclista a España 2024. Imagen tomada de www.lavuelta.es
Maillot oficial del equipo T-rex Quick-Step para la Vuelta Ciclista a España 2024. Imagen tomada de www.lavuelta.esSeguramente os estaréis preguntando lo mismo que yo la primera vez que lo vi, ¿por qué? Pues la respuesta es sencilla, por puro marketing. Soudal es una empresa belga dedicada al bricolaje, en especial a fabricar adhesivos, siliconas y selladores. Y uno de sus productos más famosos es T-rex, un adhesivo de alta calidad y muy resistente, al que pusieron el nombre de este famoso reptil prehistórico para remarcar su fortaleza. De esta manera, han aprovechado el perfil mediático de la vuelta ciclista para promocionarlo de manera internacional, mostrando a su vez a sus ciclistas como poderosos deportistas ávidos de victorias, pretendiendo intimidar a sus rivales con tan fiero diseño.
Pero, si lo analizamos desde un punto de vista estrictamente geológico, este dibujo tiene un error de bulto. Como os he comentado, en el costado derecho del maillot aparece la marca de tres garras. Pues resulta que, de acuerdo a los restos fósiles de Tyrannosaurus rex encontrados hasta la fecha, este animal tenía solo dos dedos en sus manos. Le sobra una marca al diseño, aunque reconozco que queda mucho más potente con tres raspones que con solo dos.
Dejando aspectos estéticos con ligeras libertades poéticas aparte, la siguiente pregunta que podemos plantearnos es: ¿Estos falsos T-rex subidos a las bicicletas son los únicos dinosaurios que nos vamos a encontrar en la Vuelta Ciclista a España de 2024? Pues no, ya que veremos restos fósiles reales de estos extintos animales durante el recorrido. En concreto, en la etapa 16, que discurre por tierras asturianas, con salida en Luanco y llegada en los míticos Lagos de Covadonga, un disputado final en alto que ha sellado el podium de muchas ediciones. Durante el recorrido, la “serpiente multicolor” pasará por dos de las localidades que forman parte de la ruta conocida como “la costa de los dinosaurios” de Asturias: Villaviciosa y Colunga. En los acantilados costeros de las playas de estas hermosas poblaciones marineras se conservan fósiles de icnitas de dinosaurios.
 Icnitas de dinosaurio encontradas en la playa de La Griega, en Colunga. En concreto se trata de las pisadas de un cuadrúpedo de gran tamaño (las huellas tienen un diámetro de casi 1m). Imagen de Jose Francisco Sánchez Díaz, tomada de www.turismoasturias.es
Icnitas de dinosaurio encontradas en la playa de La Griega, en Colunga. En concreto se trata de las pisadas de un cuadrúpedo de gran tamaño (las huellas tienen un diámetro de casi 1m). Imagen de Jose Francisco Sánchez Díaz, tomada de www.turismoasturias.esLas icnitas son un tipo de fósiles muy particulares, ya que se trata de las huellas de pisadas, marcas, pistas o rastros de locomoción de organismos del pasado preservados en las rocas. Estas huellas pueden aparecer en el registro fósil de dos maneras: en forma de moldes, que sería el fósil de la impresión dejada por el organismo en el sedimento sobre el que se desplaza (huella directa); y en forma de contramoldes, que representa la imagen en negativo de esa huella y que queda preservada en la capa de sedimento que la recubre. Para explicarlo de manera más visual, imaginad que cogéis un bloque de plastilina de color amarillo, lo presionáis con fuerza con el dedo dejando la marca, después lo tapáis con un bloque de plastilina azul hasta rellenar completamente ese hueco y separáis de nuevo los dos bloques. La amarilla conserva el fósil del molde de vuestra huella, mientras que en el azul aparecerá el contramolde.
Desde un punto de vista más práctico, las icnitas aportan una valiosa información sobre el comportamiento de los organismos que las produjeron. En el caso de vertebrados, como los dinosaurios, nos permiten descubrir si caminaban sobre dos patas o sobre las cuatro, podemos estimar su tamaño y su peso mediante cálculos de la longitud y anchura de su zancada y la profundidad que alcanza la huella en diferentes tipos de sedimentos, incluso inferimos si tenían un comportamiento gregario y se desplazaban en manada o si vivían y cazaban de manera individualista. Y en este aspecto la costa asturiana es un auténtico paraíso, ya que se preservan moldes y contramoldes de icnitas de diversas especies de dinosaurios, de animales grandes y pesados y otros más pequeños y ágiles, unos bípedos y otros cuadrúpedos, algunos herbívoros y algunos carnívoros y también adultos y juveniles. Vamos, que hace millones de años está zona era un vergel de dinosaurios.
Llegados a este punto, nos surge una última pregunta: ¿Hubo Tyrannosaurus rex en Asturias? Pues siento desilusionaros, pero no. Esta especie vivió en lo que actualmente es Norteamérica a finales del Periodo Cretácico, hace entre unos 68 y 66 millones de años. Y las rocas que afloran en la costa de Asturias son del Periodo Jurásico, de hace entre 200 y 145 millones de años, un momento en el que América y Europa ya estaban separadas y la Península Ibérica era una especie de islotes independientes entre sí. Por lo que los únicos T-rex que veremos por aquí son los que van subidos a una bicicleta.
Todos los yacimientos de icnitas de dinosaurio de Asturias se pueden visitar y disponen de señalizaciones precisas y paneles informativos. Pero si decidís acercaros a este paraíso natural, os aconsejo que vuestra primera parada sea Colunga, en concreto, el Museo del Jurásico de Asturias (MUJA). En él encontraréis diversas reconstrucciones de estos extintos animales y réplicas de sus fósiles, incluidos dos Tyrannosaurus rex en actitud muy cariñosa. Así descubriréis todos los secretos sobre la vida del pasado y os informarán de dónde se encuentran los yacimientos visitables y la mejor forma de acceder a ellos. Pero, hasta que podamos realizar esta escapada, tendremos que contentarnos con los ataques de los T-rex ciclistas rugiendo por nuestras carreteras.
Para saber más:
La Universidad Complutense de Madrid, en colaboración con el Instituto Geológico y Minero de España, lleva a cabo la iniciativa “Geodiversidad de la Vuelta a España”, en la que se describe el contexto geológico del recorrido de cada etapa: www.lavuelta.es/es/la-carrera/geodiversidad
La Comisión Mujeres y Geología de la Sociedad Geológica de España colabora con la sección de deportes de Radio Nacional de España aportando curiosidades geológicas del recorrido durante las retransmisiones de cada etapa: www.rtve.es/play/radio/rne
Agradecimientos:
Quiero dar las gracias a Daniel Ampuero y Gonzalo Da Cuña, periodistas de Radio Nacional de España y responsables de la retransmisión radiofónica de La Vuelta Ciclista a España, por darnos la oportunidad de colaborar con ellos contando anécdotas geológicas. Y a mis compañeras de la Comisión Mujeres y Geología de la Sociedad Geológica de España y del equipo de trabajo de Comunicación y Redes Sociales, también de la Sociedad Geológica de España, por la ayuda para preparar los temas y la promoción de la colaboración con RNE.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Dinosaurios sobre dos ruedas se ha escrito en Cuaderno de Cultura Científica.
Los números metálicos
La razón metálica de un número entero positivo n se define como el número real positivo
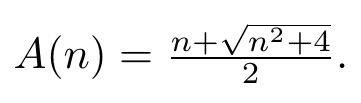
Los primeros números metálicos son, de hecho, números bien conocidos: la razón áurea (que corresponde a n = 1), el número de plata (asociado a n = 2) o el número de bronce (correspondiente a n = 3).
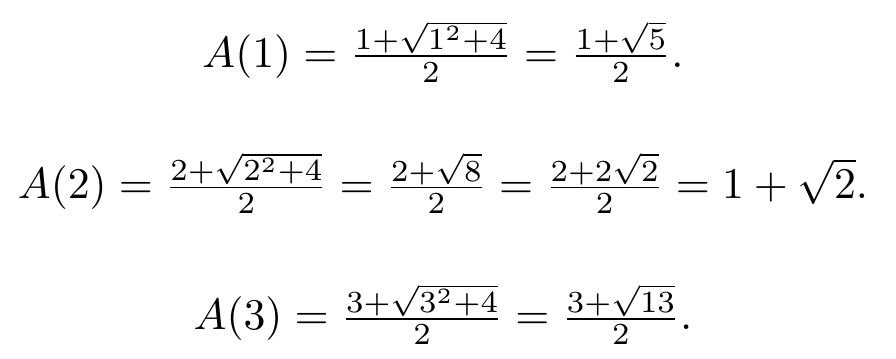
Algunos de los números metálicos posteriores reciben nombres como cobre o níquel. La matemática Vera Marta Winitzky los definió, estudió y divulgó.
 Vera Marta Winitzky describiendo propiedades de la razón áurea. Fuente: Wikimedia Commons.
Vera Marta Winitzky describiendo propiedades de la razón áurea. Fuente: Wikimedia Commons.Definición y algunas propiedades de los números metálicos
La matemática argentina Vera Martha Winitzky comenzó a trabajar en números metálicos en 1997. Los definió en el artículo La familia de números metálicos en Diseño en cuya introducción comentaba:
Vamos a presentar la nueva familia de «números metálicos». Sus integrantes tienen, entre otras características comunes, la de llevar el nombre de un metal. Así, por ejemplo, el miembro más conspicuo es el famoso «Número de Oro». Luego vienen el Número de Plata, el Número de Bronce, el Número de Cobre, el número de Níquel y muchos otros más. El Número de Oro ha sido ampliamente utilizado en una gran cantidad de culturas antiguas como base de proporciones. Con respecto a los parientes del Número de Oro, parte de estos números fueron usados por diversos físicos en sus investigaciones de punta, al tratar de sistematizar el comportamiento de sistemas dinámicos no lineales, analizando la transición de la periodicidad a la cuasi-periodicidad. Pero también Jay Kappraff recurre, en particular, al Número de Plata para describir y explicar el sistema romano de proporciones, haciendo uso de una propiedad matemática que, como veremos, es común a todos los miembros de esta notable familia.
En conclusión, el hecho que los números metálicos aparezcan desde los sistemas usados en el Diseño de sus construcciones por la civilización romana antigua hasta los más recientes trabajos de caracterización de caminos universales al caos los convierte en instrumentos invalorables para la búsqueda de relaciones viables cuantitativas entre la Matemática y el Arte.
Usando la expresión en fracción continua de estos números (Winitzky prueba que A(n) tiene como expresión en fracción continua [n; n, n, n, n,…]) para demostrarlo, en el trabajo se concluye en primer lugar que:
Los números metálicos son irracionales cuadráticos.
En efecto, son irracionales porque la fracción continua que los define es infinita. Y son cuadráticos porque es fácil demostrar que A(n) es la solución positiva de la ecuación cuadrática x2 – nx – 1 = 0.
De hecho, como comenta Winitzky, fue Joseph Louis Lagrange quien demostró que: Un número es irracional cuadrático si y solo si su descomposición en fracciones continuas es periódica.
Estos números metálicos tienen, además, relación con la sucesión de Fibonacci. En el artículo se demuestra que:
Los números metálicos son todos límites de sucesiones generalizadas de Fibonacci secundarias.
Una sucesión de generalizada de Fibonacci secundaria es una sucesión G(n) en la que cada término se define en función de los anteriores:
G(n+2) = p G(n) + q G(n +1),
donde p y q son números naturales.
Por ejemplo, la sucesión de Fibonacci se define mediante la relación F(n+2) = F(n) + F(n+1), y el número de oro es el límite (cuando n tiende a infinito) del cociente F(n+2) / F(n+1).
Puede demostrarse también que el número de plata es el límite del cociente G(n+2) / G(n+1), donde la sucesión generalizada de Fibonacci involucrada es la definida por la relación G(n+2) = 2 G(n+1) + G(n). Así, la propiedad anterior afirma que todos los números metálicos son límites de cocientes del tipo G(n+2) / G(n+1) para determinados números naturales p y q.
En el artículo se demuestran algunas otras propiedades matemáticas y la autora se refiere también a cómo aparecen de manera natural en arquitectura, diseño, arte… e incluso en la estructura de algunos cuasicristales.
Más matemáticas en los estudios de diseñoVera Martha Winitzky comenzó a trabajar como profesora de matemáticas en Facultad de Arquitectura y Urbanismo de la Universidad de Buenos Aires en 1957. Pensaba que los programas de los cursos de diseño carecían de contenidos profundos de matemáticas que, en su opinión, podían aportan creatividad a los estudiantes. También pensaba que era importante insistir en la falta de linealidad de la naturaleza, por lo que introdujo conceptos de geometría fractal en sus cursos de diseño. Y expresaba su interés de esta manera:
El objetivo principal de mi trabajo es convocar a matemáticos, arquitectos, ingenieros y diseñadores interesados en la interacción entre Matemáticas y Diseño. Utilizo la palabra Diseño en su sentido más amplio, es decir, un Diseño es un recurso proyectual que constituye un elemento básico en la comunicación interdisciplinaria entre los seres humanos, sea arquitectónico, gráfico, visual o sonoro, así como cualquier otra interacción simple o combinada.
Referencias
-
V. M. Winitzky de Spinadel, La familia de números metálicos en Diseño, Seminario Nacional de Gráfica Digital, Sesión de Morfología y Matemática, Ediciones Facultad de Arquitectura, Diseño y Urbanismo, Universidad de Buenos Aires 2 (1997), 173-179.
-
Marta Macho Stadler, Vera Martha Winitzky: uniendo matemáticas y diseño, Mujeres con ciencia, 28 agosto 2024
- J J O’Connor and E F Robertson, Vera Martha Winitzky de Spinadel, MacTutor History of Mathematics Archive, St Andrews University
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Los números metálicos se ha escrito en Cuaderno de Cultura Científica.
Dozena erdi ariketa 2024ko udarako (4): hirukote bila
Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko asteazkenero ariketa matematiko bat izango duzue, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Hona hemen gure laugarren ariketa:Aurkitu zenbaki arrunten (a, b, c) hirukote guztiak ekuazio hauek betetzen dituztenak:
ab + bc = 44, ac + bc = 23
Zein da erantzuna? Idatzi emaitza iruzkinen atalean (artikuluaren behealdean daukazu) eta, nahi izanez gero, zehaztu jarraitu duzun ebazpidea ere. Irailean emaitza zuzenaren berri emango dizugu.
 (Argazkia: Luisa Frassier – Unsplash lizentziapean. Iturria: Unsplash)
(Argazkia: Luisa Frassier – Unsplash lizentziapean. Iturria: Unsplash)Ariketak “Calendrier Mathématique 2024. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
The post Dozena erdi ariketa 2024ko udarako (4): hirukote bila appeared first on Zientzia Kaiera.
Las matemáticas demuestran que Hawking se equivocaba sobre los agujeros negros más extremos
Durante décadas, los agujeros negros extremos se consideraron matemáticamente imposibles. Una nueva prueba revela lo contrario.
Un artículo de Steve Nadis. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Kristina Armitage/Quanta Magazine
Kristina Armitage/Quanta MagazinePara comprender el universo los científicos observan sus anomalías. “Siempre queremos saber de los casos extremos, los casos especiales que se encuentran en el límite”, afirma Carsten Gundlach, físico matemático de la Universidad de Southampton.
Los agujeros negros son los extremos enigmáticos del cosmos. En su interior, la materia está tan compactada que, según la teoría general de la relatividad de Einstein, nada puede escapar. Durante décadas físicos y matemáticos los han utilizado para comprobar los límites de sus ideas sobre la gravedad, el espacio y el tiempo.
Pero incluso los agujeros negros tienen casos extremos, y esos casos tienen sus propias ideas que ofrecer. Los agujeros negros rotan en el espacio. A medida que la materia cae en ellos, comienzan a girar más rápido; si esa materia tiene carga, también se cargan eléctricamente. En principio, un agujero negro puede llegar a un punto en el que tenga tanta carga o momento angular como sea posible, dada su masa. A un agujero negro de ese tipo se lo llama “extremo”, el extremo de los extremos.
Estos agujeros negros tienen algunas propiedades extrañas. En particular, la llamada gravedad superficial en la frontera, u horizonte de sucesos, de un agujero negro de este tipo es cero. “Es un agujero negro cuya superficie ya no atrae cosas”, explica Gundlach. Pero si se empujara ligeramente una partícula hacia el centro del agujero negro, no podría escapar.
En 1973, los destacados físicos Stephen Hawking, James Bardeen y Brandon Carter afirmaron que los agujeros negros extremos no pueden existir en el mundo real, que simplemente no hay ninguna forma plausible de que se formen. Sin embargo, durante los últimos 50 años, los agujeros negros extremos han servido como modelos útiles en la física teórica. “Tienen bonitas simetrías que facilitan el cálculo de las cosas”, dice Gaurav Khanna de la Universidad de Rhode Island, y esto permite a los físicos poner a prueba las teorías sobre la misteriosa relación entre la mecánica cuántica y la gravedad.
 En 1973, Stephen Hawking y otros dos físicos destacados plantearon la hipótesis de que los agujeros negros extremos nunca podrían formarse. Foto: Santi Visalli/Getty Images
En 1973, Stephen Hawking y otros dos físicos destacados plantearon la hipótesis de que los agujeros negros extremos nunca podrían formarse. Foto: Santi Visalli/Getty ImagesAhora, dos matemáticos han demostrado que Hawking y sus colegas estaban equivocados. El nuevo trabajo —contenido en un par de artículos recientes de Christoph Kehle, del Instituto Tecnológico de Massachusetts, y Ryan Unger, de la Universidad de Stanford y la Universidad de California en Berkeley— demuestra que no hay nada en nuestras leyes conocidas de la física que impida la formación de un agujero negro extremo.
Su prueba matemática es “hermosa, técnicamente innovadora y físicamente sorprendente”, comenta Mihalis Dafermos, matemático de la Universidad de Princeton (y director de las tesis doctorales de Kehle y Unger). Apunta a un universo potencialmente más rico y variado en el que “astrofísicamente podría haber agujeros negros extremos”, agrega.
Eso no significa que existan. “El hecho de que exista una solución matemática con buenas propiedades no significa necesariamente que la naturaleza vaya a hacer uso de ella”, explica Khanna. “Pero si de alguna manera encontramos uno, eso realmente nos haría pensar en lo que nos estamos perdiendo”. Un descubrimiento de ese tipo, señaló, tiene el potencial de plantear “algunos tipos de preguntas bastante radicales”.
La ley de la imposibilidadAntes de la prueba de Kehle y Unger había buenas razones para creer que los agujeros negros extremos no podían existir.
En 1973, Bardeen, Carter y Hawking introdujeron cuatro leyes sobre el comportamiento de los agujeros negros, que se parecían a las cuatro leyes de la termodinámica, establecidas desde hacía mucho tiempo: un conjunto de principios sacrosantos que establecen, por ejemplo, que el universo se vuelve más desordenado con el tiempo y que la energía no se puede crear ni destruir.
 Christoph Kehle, matemático del Instituto Tecnológico de Massachusetts, recientemente desmintió una conjetura de 1973 sobre los agujeros negros extremos. Foto: Dan Komoda/Institute for Advanced Study
Christoph Kehle, matemático del Instituto Tecnológico de Massachusetts, recientemente desmintió una conjetura de 1973 sobre los agujeros negros extremos. Foto: Dan Komoda/Institute for Advanced StudyEn su artículo, los físicos demostraron las tres primeras leyes de la termodinámica de los agujeros negros: la cero, la primera y la segunda. Por extensión, asumieron que la tercera ley (al igual que su contraparte en la termodinámica estándar) también sería cierta, aunque aún no pudiesen demostrarla.
Esa ley establecía que la gravedad superficial de un agujero negro no puede disminuir hasta cero en un tiempo finito; en otras palabras, que no hay forma de crear un agujero negro extremo. Para respaldar su afirmación, el trío argumentó que cualquier proceso que permitiera que la carga o el momento angular de un agujero negro alcanzaran el límite extremo también podría potencialmente provocar la desaparición total de su horizonte de sucesos. Se cree ampliamente que los agujeros negros sin horizonte de sucesos, llamados singularidades desnudas, no pueden existir. Además, como se sabe que la temperatura de un agujero negro es proporcional a su gravedad superficial, un agujero negro sin gravedad superficial tampoco tendría temperatura. Un agujero negro así no emitiría radiación térmica, algo que Hawking propondría más tarde que debían hacer los agujeros negros.
En 1986, un físico llamado Werner Israel pareció dejar la cuestión resuelta cuando publicó una prueba de la tercera ley. Supongamos que queremos crear un agujero negro extremo a partir de uno normal. Podemos intentar hacerlo haciéndolo girar más rápido o añadiendo más partículas cargadas. La prueba de Israel pareció demostrar que al hacerlo no se puede obligar a que la gravedad superficial de un agujero negro caiga a cero en un tiempo finito.
Como Kehle y Unger finalmente descubrirían, el argumento de Israel ocultaba un fallo.
La muerte de la tercera leyKehle y Unger no se habían propuesto encontrar agujeros negros extremos. Se toparon con ellos por pura casualidad.
Estaban estudiando la formación de agujeros negros cargados eléctricamente. “Nos dimos cuenta de que podíamos hacerlo” –crear un agujero negro– “para todas las relaciones carga-masa”, cuenta Kehle. Eso incluía el caso en que la carga es lo más alta posible, un sello distintivo de un agujero negro extremo.
 Después de demostrar que los agujeros negros extremos altamente cargados son matemáticamente posibles, Ryan Unger de la Universidad de Stanford ahora está tratando de demostrar que los agujeros negros de rotación rápida también lo son. Pero es un problema mucho más difícil. Foto: Dimitris Fetsios
Después de demostrar que los agujeros negros extremos altamente cargados son matemáticamente posibles, Ryan Unger de la Universidad de Stanford ahora está tratando de demostrar que los agujeros negros de rotación rápida también lo son. Pero es un problema mucho más difícil. Foto: Dimitris FetsiosDafermos reconoció que sus antiguos estudiantes habían descubierto un contraejemplo de la tercera ley de Bardeen, Carter y Hawking: habían demostrado que efectivamente podían transformar un agujero negro típico en uno extremo en un período finito de tiempo.
Kehle y Unger comenzaron con un agujero negro que no rota y no tiene carga, y modelaron lo que podría suceder si se lo colocara en un entorno simplificado llamado campo escalar, que supone un fondo de partículas cargadas uniformemente. Luego, golpearon el agujero negro con pulsos del campo para agregarle carga.
Estos pulsos también aportaban energía electromagnética al agujero negro, lo que aumentaba su masa. Al enviar pulsos difusos de baja frecuencia, los matemáticos se dieron cuenta de que podían aumentar la carga del agujero negro más rápido que su masa, precisamente lo que necesitaban para completar su prueba.
Después de discutir su resultado con Dafermos, estudiaron la prueba de Israel de 1986 e identificaron su error. También construyeron otras dos soluciones a las ecuaciones de la relatividad general de Einstein que implicaban diferentes formas de añadir carga a un agujero negro. Habiendo refutado la hipótesis de Bardeen, Carter y Hawking en tres contextos diferentes, el trabajo no debería dejar lugar a dudas, afirma Unger: “La tercera ley está muerta”.
Los dos científicos también demostraron que la formación de un agujero negro extremo no abriría la puerta a una singularidad desnuda, como temían los físicos. En cambio, los agujeros negros extremos parecen encontrarse en un umbral crítico: si se añade la cantidad adecuada de carga a una densa nube de materia cargada, colapsará para formar un agujero negro extremo. Si se añade más, en lugar de colapsar en una singularidad desnuda, la nube se dispersará. No se formará ningún agujero negro. Kehle y Unger están tan entusiasmados con este resultado como con su prueba de que pueden existir agujeros negros extremos.
“Este es un hermoso ejemplo de cómo las matemáticas devuelven algo a la física”, comenta Elena Giorgi, matemática de la Universidad de Columbia.
Lo imposible hecho visibleSi bien Kehle y Unger han demostrado que es teóricamente posible que existan agujeros negros extremos en la naturaleza, no hay garantía de que sea así.
Por un lado, los ejemplos teóricos poseen una carga máxima, pero nunca se han observado agujeros negros con una carga discernible. Es mucho más probable ver un agujero negro que gira rápidamente. Kehle y Unger quieren construir un ejemplo que alcance el umbral extremo de momento angular, en lugar del de carga.
Pero trabajar con el espín es mucho más complicado desde el punto de vista matemático. “Para ello se necesitan muchas matemáticas nuevas y nuevas ideas”, afirma Unger. Él y Kehle están empezando a investigar el problema.
Mientras tanto, una mejor comprensión de los agujeros negros extremos puede proporcionar más información sobre los agujeros negros casi extremos, que se cree que son abundantes en el universo. “Einstein no creía que los agujeros negros pudieran ser reales [porque] son demasiado extraños”, apunta Khanna. “Pero ahora sabemos que el universo está repleto de agujeros negros”.
Por razones similares, añade, “no deberíamos darnos por vencidos con los agujeros negros extremos. Simplemente no quiero poner límites a la creatividad de la naturaleza”.
El artículo original, Mathematicians Prove Hawking Wrong About the Most Extreme Black Holes, se publicó el 21 de agosto de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo Las matemáticas demuestran que Hawking se equivocaba sobre los agujeros negros más extremos se ha escrito en Cuaderno de Cultura Científica.
Gusanos parásitos, agresivos… y sociales
Los seguidores de las series sobre tronos y dragones conocemos bien a unos personajes de esta saga llamados los Inmaculados, soldados castrados fieles a sus amos hasta la muerte. Quizá el más famoso de ellos sea su comandante, Gusano Gris. Menciono todo esto porque hoy vamos a hablar, precisamente, de gusanos soldados, estériles, y dispuestos a luchar hasta el final para defender a los suyos. Curiosa coincidencia…
La eusocialidad es la forma más compleja de organización entre los animales. Su máxima expresión se alcanza en los insectos himenópteros: abejas, avispas y hormigas. Sus sociedades constan de castas especializadas, reproductivas y no reproductivas, con cuidado colectivo de las crías y solapamiento de generaciones.
Otras formas de eusocialidad se han descrito en animales como las ratas topo (únicos mamíferos eusociales) y las gambas del género Synalpheus que viven dentro de esponjas. También existe un tipo de sociedades vinculadas al parasitismo y al fenómeno de la poliembrionía, es decir, la generación de múltiples descendientes a partir de un único cigoto.
Posiblemente, el ejemplo más espectacular nos lo proporcionan las avispas del género Copidosoma. Estas pequeñas avispas ponen un solo huevo sobre una oruga. El huevo comienza su desarrollo dentro de la oruga, pero el embrión resultante se fragmenta y da lugar a múltiples descendientes, hasta más de 3 000 en algún caso. Estos embriones originan dos tipos de larvas que devoran poco a poco a su hospedador. Las larvas que han adquirido células del linaje germinal1 forman la casta reproductora. Las que carecen de células germinales, y, por tanto, no podrían reproducirse, se convierten en larvas soldado, que luchan contra cualquier parásito que intente competir con sus hermanas. Cuando la infortunada oruga ha sido consumida completamente, las reproductoras se metamorfosean en avispas adultas y las larvas soldado mueren, una vez cumplida su función defensiva.
Hemos explicado en detalle esta formación de castas en los embriones de Copidosoma, porque acaba de publicarse un artículo en PNAS que extiende este concepto a animales muy alejados de los insectos, concretamente a gusanos platelmintos del grupo de los trematodos.
Los trematodos digeneos son gusanos parásitos con un complejo ciclo de vida (Figura 1). Una primera larva, llamada miracidio, infecta un molusco bivalvo o gasterópodo de agua dulce, y origina en su interior un esporocisto. El esporocisto da lugar a un gran número de individuos, las redias, que a su vez generan otro tipo de larvas, las cercarias, que son liberadas en el medio. Cuando las cercarias son consumidas por un vertebrado se convierten en el gusano adulto que vive a expensas de su hospedador. Estos parásitos pueden causar graves pérdidas en la ganadería y enfermedades en humanos, como la fascioliasis.
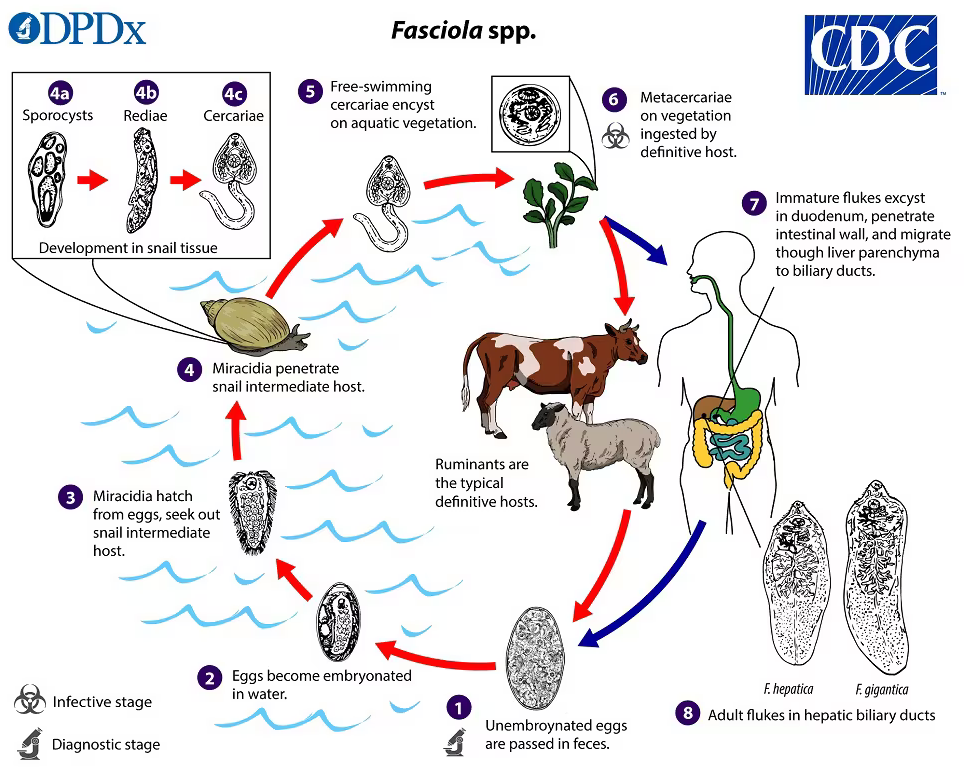 Figura 1. Ciclo biológico del trematodo Fasciola hepatica, causante de la fascioliasis. El ciclo es similar al de Haplorchis pumilio. La diferenciación en castas de Haplorchis se produce en la etapa 4b (redias). Imagen realizada por el Centers for Disease Control and Prevention, Atlanta (EEUU), dominio público
Figura 1. Ciclo biológico del trematodo Fasciola hepatica, causante de la fascioliasis. El ciclo es similar al de Haplorchis pumilio. La diferenciación en castas de Haplorchis se produce en la etapa 4b (redias). Imagen realizada por el Centers for Disease Control and Prevention, Atlanta (EEUU), dominio públicoEn 2010, investigadores del Instituto Scripps de Oceanografía y la Universidad de California descubrieron que las redias del trematodo Himasthla se presentaban en dos formas, una que realizaba normalmente su ciclo reproductivo y otra constituida por individuos más pequeños y activos. Propusieron que se trataba de dos castas con división de funciones, los reproductores y los soldados, encargados estos de atacar a otros parásitos competidores, igual que ocurría en Copidosoma.
Existían dudas acerca de si las redias soldado mantenían la capacidad reproductiva. Esto acaba de ser resuelto por un nuevo estudio del mismo grupo de investigación, publicado en la revista PNAS. En esta ocasión trabajaron con el trematodo Haplorchis pumilio, parásito ocasional de humanos. Este gusano es original del sudeste asiático, pero se ha ido extendiendo por todo el mundo, paralelamente a la rápida difusión de su hospedador intermedio, el caracol Melanoides tuberculata, muy popular en acuariofilia.
El nuevo estudio ha mostrado las claras diferencias en morfología y comportamiento entre las redias soldado y las reproductoras. Los soldados desarrollan una faringe cinco veces más grande que sus congéneres, lo que les permite atacar y matar a cualquier trematodo que compita por el espacio y los recursos, sin importarles la diferencia de tamaño (Figura 2). Los investigadores comprobaron que el caracol Melanoides puede ser infestado por al menos otras siete especies de trematodos, si bien la presencia de soldados de Haplorchis elimina hasta el 94% de estos intentos de infección. De hecho, los soldados se localizan estratégicamente en los tejidos del caracol donde es más probable sufrir una invasión. Eso sí, en experimentos in vitro, los soldados no atacaron a redias de su misma especie, incluso cuando procedían de otros caracoles.
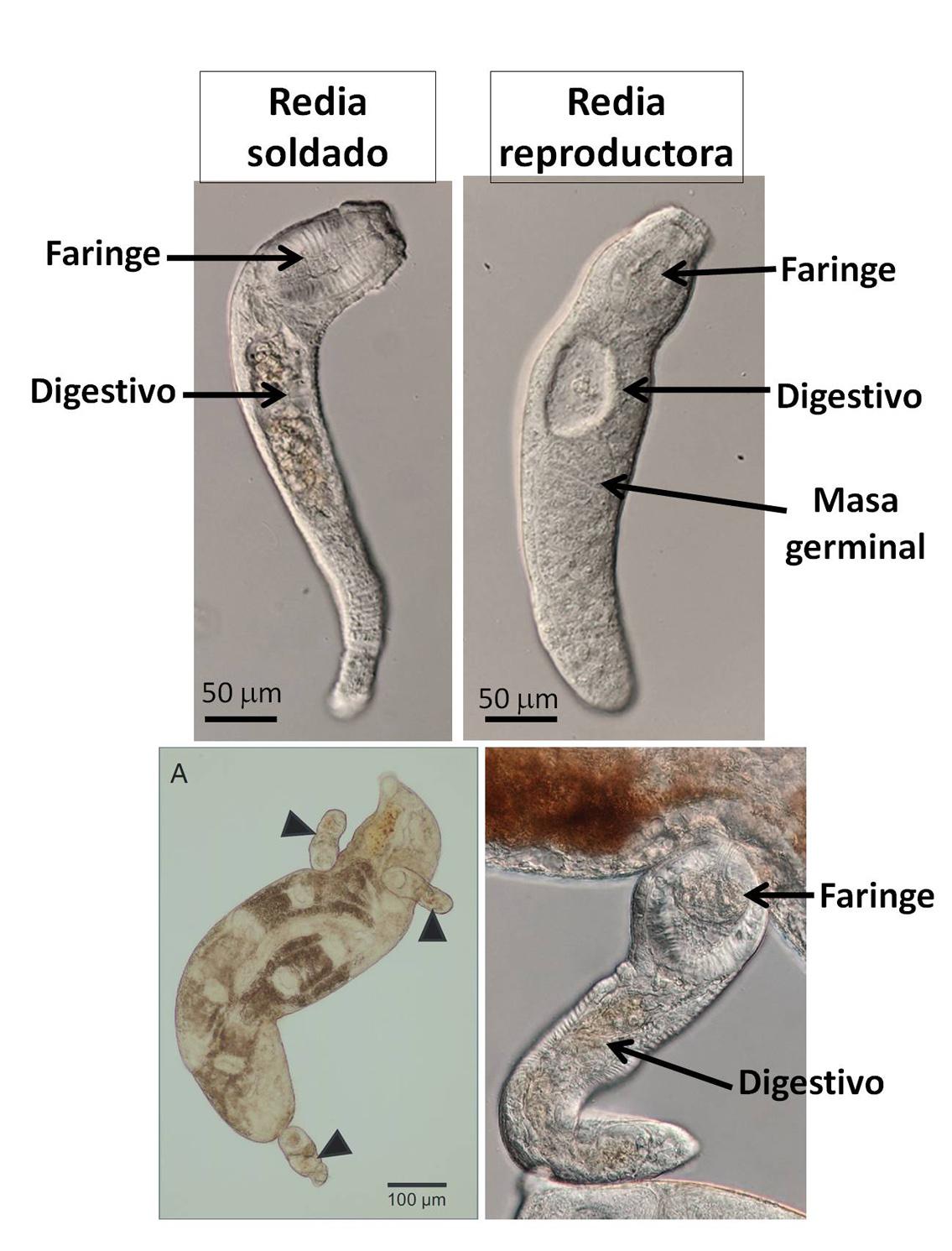 Figura 2. Arriba: Las redias soldado se caracterizan por una gran faringe, un amplio tubo digestivo y la ausencia de masa germinal. Abajo y a la izquierda: las puntas de flecha señalan a tres soldados de Haplorchis pumilio atacando a una redia reproductora del género Philophthalmus. A la derecha vemos como este soldado utiliza la faringe para romper el tegumento de su víctima y absorber sus tejidos. Modificado del artículo de Metz y Hechinger, referencia de PNAS citada abajo, con licencia CC BY 4.0
Figura 2. Arriba: Las redias soldado se caracterizan por una gran faringe, un amplio tubo digestivo y la ausencia de masa germinal. Abajo y a la izquierda: las puntas de flecha señalan a tres soldados de Haplorchis pumilio atacando a una redia reproductora del género Philophthalmus. A la derecha vemos como este soldado utiliza la faringe para romper el tegumento de su víctima y absorber sus tejidos. Modificado del artículo de Metz y Hechinger, referencia de PNAS citada abajo, con licencia CC BY 4.0La investigación mostró también que los soldados de Haplorchis carecen de células germinales capaces de producir descendientes. Por tanto, constituyen una casta obligatoriamente estéril cuya única función es desplegarse estratégicamente, combatir contra los invasores y garantizar la supervivencia de las redias reproductoras. Más o menos como los Inmaculados de Daenerys Targaryen.
En resumen, las dos castas de Haplorchis pumilio, ahora bien caracterizadas, constituyen un caso excepcional de eusocialidad en organismos diferentes a los artrópodos.
Referencias:
Hechinger, R.F., Wood, A.C., Kuris, A.M. (2011). Social organization in a flatworm: trematode parasites form soldier and reproductive castes. Proc Biol Sci. doi: 10.1098/rspb.2010.1753
Metz, D.C.G., Hechinger, R.F. (2024). The physical soldier caste of an invasive, human-infecting flatworm is morphologically extreme and obligately sterile. Proc Natl Acad Sci U S A. doi: 10.1073/pnas.2400953121
Nota:
1 En muchos animales es posible identificar desde las primeras etapas del desarrollo embrionario al conjunto de células germinales, que son las únicas capaces de dar lugar a óvulos y espermatozoides.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Gusanos parásitos, agresivos… y sociales se ha escrito en Cuaderno de Cultura Científica.
Arroparen garrantziaz pare bat apunte
Adi, udan gaude eta! Eta udan gaudela kontuan izanik, suposatzen dut topera ibiliko zaretela nekazalfitnessarekin. Ezta? Ez nuen gutxiago espero. Jakinda nahikoa kirol egiten ari zaretela eta garaiko barazkiak ekoitzi eta kontsumitzen ari zaretela, goazen gaurko gaira.
 1. irudia: estimatzen da munduko kutsaduraren % 10 modari dagokiola. Arropa asko, kalitate baxukoa eta merkea kontsumitzen dugu. (Argazkia: stevepb – Pixabay lizentziapean. Iturria: Pixabay)
1. irudia: estimatzen da munduko kutsaduraren % 10 modari dagokiola. Arropa asko, kalitate baxukoa eta merkea kontsumitzen dugu. (Argazkia: stevepb – Pixabay lizentziapean. Iturria: Pixabay)Galdera: udara begira, armairu-aldaketa egin duzue? Neguko arropa lodi eta beroa gorde eta udako arropa freskoa atera? Zenbaitek egingo zenuten eta, beste batzuek, mahuka motzekoa armairuaren aurrealdean jarri eta mahuka luzekoa atzeko partera bidali baino ez.
Lasai, ez nator armairufitness edo horrelako ezer aholkatzera. Ez dizuet esango zer jantzi eta zer ez ere, lasai horrekin. Modaz ezer gutxi eta estilo eta glamourraz are gutxiago baitakit. Bestela… Tira, eta horretaz gain, atal honen gaia zientzia delako. Hortaz, zientziak arroparen inguruan egindako pare bat ikerketa dakartzat gaurkoan.
Eta, hasteko, goiko galderarekin lotura zuzena duen gaiari helduko diogu. Armairu-aldaketa egin behar izan duzue? Arropa andana duzuen seinale. Ez nator arropa asko duen jendea kritikatzera, e!
Kontua da moda azkarraren, fast fashion delakoaren, garaian bizi omen garela: arropa asko, kalitate baxukoa eta merkea kontsumitzen dugu. Eta horrek eragina du hainbat esparrutan, ekonomikotik hasi eta klima-aldaketaraino.
Izan ere, estimatzen da munduko kutsaduraren % 10 modari dagokiola. Juan Ignacio Pérez Iglesiasek egindako artikuluaren arabera, 2000. urtetik biztanleria baino gehiago hazi da ehungintza industria: orain, marka arrakastatsuek merkaturatzen zituzten bildumen bikoitza merkaturatzen dute. Laburbilduz, arropa asko egin eta saltzen da eta horrek inpaktu handia du.
Zenbat eta 1.700 milioi tona CO2 baino gehiago sortzen du urtero modaren industriak. Eta ez hori bakarrik, 79 trilioi ur litro inguru kontsumitzen ditu. Geldiunetxoa hemen zifra hau ondo ulertzeko: 79 trilioi. Ez milioi, ez bilioi. Trilioi. Urtean.
Ur asko erabiltzen du, beraz. Gero eta eskasagoa den ura. Erabiltzeaz gain, uraren kutsadura industrialaren % 20 ere dagokio. Eta urarekin jarraituz, ozeanoetan metatzen den mikroplastikoaren herena inguru modaren jarduerari egotzi dakioke. 190.000 tona. Tona, bai, urtean.
Pentsa genezake arropa gutxiago erosita klima-aldaketaren aurkako gure harri-koxkorra jartzen gabiltzala. Eta bagabiltza. Daukagun arropa garbitu, garbitu behar dugu, baina. Eta, gehienok, garbigailua erabiltzen dugu. Atzean geratu baita ibaira jaitsi eta latsarriarekin garbitzeko garaia.
Beno, ba ez naiz ni pesimista eta ez dut gustuko kontu guztietan arazoak ikusten dituen jendea. Baina. Eta baina bat bazetorrela bazenekiten, ez dakit zertara datorren harridura aurpegia. Arropa garbitzeko kolpe eta mugimendu nahikotxo egiten ditu garbigailuak eta, horren ondorioz, arroparen mikroplastikoak askatzen dira. Ur-sistemaren bidez itsasoan bukatzen duten mikroplastikoak.
Eta pentsatuko duzue: zer egin behar dugu orduan? Biluzik ibili? Ba, nik, pertsonalki, ez dut arazorik biluztasunarekin. Hotza berriro datorrenean, komeriak, hori bai.
Kantitateari erreparatzeaz gain, arroparen nolakotasuna eta horren ondorioak ere aztertu ditu zientziak. Esperimentua egin dute Estatu Batuetan arropa motarekin lotuta eta emaitza bitxiak eman ditu. Ezetz asmatu zer argitu duten.
Eskatzeko, eman itxura beharrik ez duzulaLaguntzatxo bat: karitatearekin lotuta dago. Tira, ba: esperimentuan etxe gabeko jendearen alde dirua emateko jendeak duen prestutasuna neurtu nahi izan dute eta, horretarako, bi ahalegin egin dituzte: lehenengoan kamiseta eta bakeroak jantzita dituen pertsona jarri dute diru eske eta bigarrenean pertsona bera, baina trajea daramala.
 2. irudia: ikerketa batean pertsona bera jarri zen dirua eskatzen kale jendetsuetan, batean trajez jantzita, eta beste behin kamiseta eta bakeroekin. (Argazkia: Callaghan, B. et al. (2022). Iturria: Frontiers in Psychology)
2. irudia: ikerketa batean pertsona bera jarri zen dirua eskatzen kale jendetsuetan, batean trajez jantzita, eta beste behin kamiseta eta bakeroekin. (Argazkia: Callaghan, B. et al. (2022). Iturria: Frontiers in Psychology)Zeinek uste duzue diru gehiago eskuratu duela? Lehen ere esan dut emaitza bitxia zela, baina, zer uste duzue gertatu dela? Tartekia laguntza handia da: oinezkoek diru gehiago eman diote trajedun pertsonari.
Bai. Bankuan kreditu bat eskatu nahi duzunean diru faltarik ez duzula erakutsi behar den bezala (hala dio txisteak), donazioak hartzeko ere, hala erakutsi behar omen da. Edo, agian, trajeari profesionaltasuna edo seriotasuna atxikitzen zaizkio. Batek daki.
Izan ere, eske ibili den pertsonak ez du berarentzat eskatu, etxe gabeko jendeari laguntzeko baizik. Bi hiritan egin dute esperimentua, New Yorken eta Chicagon. Bietan berdin: pertsona bera jarri zen eskatzen kale jendetsuetan, behin trajez jantzita eta beste behin kamiseta eta bakeroekin.
Beti emaitza bera jaso da: trajea daramala diru gehiago eskuratu du boluntarioak. Ezberdintasuna ez da txikia izan, gainera. Trajedunak diru bikoitza eskuratu du eta maizago ere eman diote dirua. Badirudi, dirua eskatzeko, elegante jantzi beharra dagoela.
Aurretik ere egin dira maila sozialari lotutako esperimentuak: zenbait ikerketak erakutsi dute gizarte-klaseari buruz ditugun pertzepzioek eragina izan dezaketela atzerritarrak ikusteko moduan. Pobrezia-zantzuek berotasun eta enpatia maila txikiagoak eragin ditzakete besteekiko. Gizaterian fedea edukitzeko modukoak ez dira aurkikuntza hauek, egia esan.
Bestelako esperimentuetan ere ikusi da estatus handiagoa dutenek laguntza gehiago jasotzen dutela, bai ekonomikoa, bai bestelakoa, maila apalagoa dutenek baino. Eta esperimentu honek ondorio beretara garamatza: ezberdintasun bakarra itxura izanik, dirua eskatzerakoan, diru gehiago eskuratzea dakar klase sozial altuagoari lotutako arropa erabiltzeak.
Noski, New Yorken eta Chicagon egindako esperimentuek ezin digute esan zer pentsatzen zuten oinezkoek dirua ematerakoan, baina aurreko esperimentuek bezala, iradokitzen dute klase sozialari erreparatzen zaiola eta horren arabera dirua emateko erraztasuna handiagoa edo txikiagoa izan daitekeela.
Eta, bukatzeko, ez zaituztet utziko esperimentuan zenbat diru eskuratu zen jakiteko gogoaz: trajea zeramala, hiru ordu eta erdian 54 dolar inguru lortu zituen boluntarioak. Eta kamiseta eta bakeroak jantzita lau ordu baino gehiago behar izan zuen 21 dolar biltzeko.
Etxegabetasuna bukatzeko funts gutxi, gizateriari buruz hausnartzeko asko.
Erreferentzia bibliografikoak:- Callaghan, B., Delgadillo Quinton, M. , Kraus Michael, W. (2022). The influence of signs of social class on compassionate responses to people in need. Frontiers in Psychology, 13. DOI: 10.3389/fpsyg.2022.936170
- Casella, Carly (2022). Experiment Reveals a Surprising Paradox in How People Give Charity, Science alert, 2022ko azaroaren 4a.
- Lopez-Gazpio, Josu (2019). Berrogeita hamar kontu, Zientzia Kaiera, 2019ko otsailaren 16a.
- Niinimäki, K., Peters, G., Dahlbo, H. et al. (2020). The environmental price of fast fashion. Nature Reviews Earth & Environment, 1, 189-200. DOI: 10.1038/s43017-020-0039-9
- Pérez-Iglesias, Juan Ignacio (2020). Moda lasterraren ingurumen prezioa, Zientzia Kaiera, 2020ko irailaren 1a.
Ziortza Guezuraga (@zguer) kazetaria da eta Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko zabalkunde digitaleko arduraduna.
Jatorrizko artikulua Gaztezulo aldizkarian argitaratu zen 2023ko uztailean, 252. zenbakian.

The post Arroparen garrantziaz pare bat apunte appeared first on Zientzia Kaiera.
Empujoncitos sanitarios
 Imagen de wirestock en Freepik
Imagen de wirestock en FreepikEl 13 de mayo de 2021, Bill de Blasio, entonces alcalde de la ciudad de Nueva York, celebró una conferencia de prensa en línea en la que anunció un interesante acuerdo entre la ciudad y Shake Shack, una cadena local de restaurantes de hamburguesas . El objetivo era conseguir que los neoyorquinos se vacunaran contra la COVID-19: cada individuo vacunado recibiría un cupón para una hamburguesa o un sándwich gratis en cualquiera de los locales de la cadena local. En la ciencia del comportamiento, este tipo de incentivo se conoce como ‘nudge’.
El término fue popularizado por Richard H. Thaler (ganador del Premio Nobel de Ciencias Económicas en 2017) y Cass R. Sunstein en su exitoso libro de 2008 Nudge: Improving Decisions About Health, Wealth, and Happiness (Un empujón: cómo mejorar las decisiones sobre salud, riqueza y felicidad). En esencia, un ‘empujón’ implica cualquier manipulación del entorno de toma de decisiones que dirija el comportamiento de las personas en una dirección beneficiosa para ellas, pero sin restringir sus opciones ni limitar su libertad de elección de ninguna manera.
Un ejemplo bien conocido de cómo mejorar los hábitos de las personas de esta manera se puede encontrar en las cafeterías del personal de Google. En un esfuerzo por mejorar los hábitos alimentarios, se colocó agua embotellada a la altura de los ojos en sus máquinas expendedoras, mientras que los refrescos y otras opciones con alto contenido calórico se colocaron en una posición menos visible. Funcionó: esta sencilla medida aumentó el consumo de agua entre el personal en un 47 %.
Otra medida similar es la instalación de escaleras interactivas, con luces en cada escalón o que tocan notas de piano al pisarlas. La gente suele optar por utilizar estas escaleras incluso cuando están justo al lado de un ascensor.
Orientar las decisiones: un dilema éticoLos empujoncitos influyen en el comportamiento de las personas al pasar por alto o ignorar, en cierta medida, su autonomía. Thaler y Sunstein denominaron a este enfoque ‘paternalismo libertario’.
Pero ¿es legítimo interferir en las decisiones de las personas para mejorar su bienestar? Los defensores del paternalismo libertario creen que sí, en particular cuando puede prevenir o resolver problemas de salud pública, como la obesidad, las adicciones, el sedentarismo y el tratamiento insuficiente o excesivo.
Muchas campañas tienen como objetivo alentar a la gente a adoptar una dieta más sana: por ejemplo, los comedores escolares de Connecticut ofrecieron manzanas gratis a los estudiantes para fomentar el consumo de fruta. En Buenos Aires, Argentina, los restaurantes retiraron los saleros de las mesas para frenar el consumo de sal.
Estos ejemplos muestran que un ‘empujón’ no impone una decisión. Los trabajadores de Google todavía tienen libertad para elegir un refresco en lugar de agua, y la gente puede pasar de largo las escaleras musicales para tomar el ascensor.
Aquí es donde entra en juego el elemento ‘libertario’, ya que la libertad de elección debe permanecer intacta. Según Thaler y Sunstein, esto significa que:
- Ninguna opción puede ser prohibida.
- Los incentivos económicos no pueden utilizarse para socavar la libertad: una hamburguesa gratis está bien, pero un cheque de 100 euros, no.
- Todas las opciones deberían estar disponibles en las mismas condiciones: si la opción deseada es accesible y barata, las demás opciones también deberían serlo.
En el contexto de la atención sanitaria, los empujoncitos se pueden clasificar en dos categorías: ‘clínicos’ o de ‘salud pública’.
Los empujoncitos ‘clínicos’ ocurren en contextos clínicos y, específicamente, implican la forma en que se presenta la información sobre un tratamiento en particular para alentar al paciente a dar su consentimiento; un ejemplo sería mencionar la tasa de éxito de un procedimiento en lugar de su tasa de fracaso. Los empujoncitos clínicos siempre se realizan en beneficio del paciente.
Por otra parte, los estímulos de ‘salud pública’ incentivan acciones individuales para mejorar la salud individual, con el objetivo de mejorar la salud de la población en su conjunto. Esto puede incluir hacer que los comedores escolares públicos sirvan carne o pescado con ensalada como opción, con patatas fritas como opción si se solicita.
Ambas son medidas no coercitivas. Medidas más firmes, como el confinamiento de una población en sus casas para evitar la propagación de una enfermedad, son medidas de salud pública, pero van mucho más allá de un simple empujón. Lo mismo podría decirse de la hospitalización involuntaria de una persona que sufre ideación suicida: es una medida clínica, pero que no deja margen para la libertad de elección.
Es por tu propio bien y el de todos los demásLos argumentos en contra del paternalismo libertario consideran que la aplicación de estos pequeños empujoncitos en el contexto de la atención sanitaria pone en peligro el principio de autonomía. Es discutible si una crítica de este tipo tiene el mismo peso en el contexto de la salud pública, donde el principio bioético de autonomía suele quedar relegado a un segundo plano frente a principios más colectivos de justicia, equidad o utilidad.
En salud pública, los empujoncitos pueden actuar como una alternativa suave para guiar las decisiones de las personas, evitando así restricciones más drásticas de la libertad personal, como limitar la libre circulación.
La reciente pandemia ofrece algunos ejemplos de lo que podría considerarse un ‘empujón’: un claro ejemplo fueron los envases de desinfectante de manos que se encontraban en restaurantes, supermercados y prácticamente cualquier otro espacio público cerrado. Los recordatorios de las citas de vacunación o las campañas con puntos móviles de vacunación sin cita previa fueron otro ejemplo.
Muchas medidas más estrictas para evitar el contagio afectaron la libertad de las personas y no pueden considerarse estímulos de salud pública: mascarillas obligatorias, tanto en interiores como en exteriores, controles de temperatura al entrar en determinados locales, prohibición de entrada a personas con fiebre, pruebas de PCR para viajar al extranjero, etc.
Por eso los empujoncitos son una herramienta tan valiosa: permiten alcanzar objetivos de salud pública sin comprometer la libertad individual. Solo cuando fracasan tiene sentido recurrir a medidas más agresivas y restrictivas. Mientras un empujoncito pueda lograr sus objetivos, parece una forma razonable de evitar que se recorten las libertades.
Sobre los autores: Ramón Ortega Lozano, Profesor de Bioética, de Antropología de la salud y de Comunicación humana en el Centro Universitario San Rafael-Nebrija, Universidad Nebrija; Aníbal M. Astobiza, Investigador Posdoctoral, especializado en ciencias cognitivas y éticas aplicadas, Universidad del País Vasco / Euskal Herriko Unibertsitatea y David Rodríguez-Arias, Profesor de Bioética, Universidad de Granada
Una versión de este texto apareció originalmente en campusa.
El artículo Empujoncitos sanitarios se ha escrito en Cuaderno de Cultura Científica.
Hiri Drainatze Sistema Jasangarriak, urari bidea irekitzeko tresnak
Uraren ziklo naturala urak naturan likido-, solido- edo gas-egoeran egiten duen zirkulazio-bide itxia da, non lurrunketaren, prezipitazioaren eta infiltrazioaren bidez, uraren zirkulazioaren oreka mantentzen baiten.
 Irudia: Hiri Drainatze Sistema Jasangarrien xede nagusia uraren ziklo naturala antzeratzea da. Mota askotako sistemak daude; adibidez, euri-urak biltzeko landare eta lurzoruzko geruzak dituzten teilatu berdeak. (Irudia: Chuttersnap – Unsplash lizentziapean. Iturria: Unsplash)
Irudia: Hiri Drainatze Sistema Jasangarrien xede nagusia uraren ziklo naturala antzeratzea da. Mota askotako sistemak daude; adibidez, euri-urak biltzeko landare eta lurzoruzko geruzak dituzten teilatu berdeak. (Irudia: Chuttersnap – Unsplash lizentziapean. Iturria: Unsplash)Uraren lurruntze-prozesua itsasotik, aintziretatik edo ibaietatik gerta daiteke zuzenean, eta baita izaki bizidunetatik ere, transpirazioaren bidez. Ondoren, lurrunketaren bidez sortutako hodeiaren kondentsaziotik ura lurrazalera itzultzen da prezipitazioen bidez. Horrela, ura lur gainean (itsasoan, ibaietan, aintziretan, glaziarretan) nahiz lurpean metatzen da.
Garapen sozio-ekonomikoak eragindako urbanizatze-prozesuek, ordea, eragina dute ziklo naturalean. Izan ere, prozesu horiek paisaia naturala itxuraldatzen dute, iragazkorra den lurzorua iragazgaitzak diren gainazalekin (errepideak, asfaltoa…) ordezkatzen da, eta ondorioz, uraren lurzoruranzko bidea oztopatzen da. Gainazaleko uren gehiegizko pilaketak uholdeak gertatzeko arriskua areagotzen du, besteak beste.
Hirietako urak hobetzeko tresnaAzkenaldiko ikerketetan Hiri Drainatze Sistema Jasangarriak (HDSJ) hirietako isurketa-uren bolumena murrizteko eta beren kalitatea hobetzeko tresna gisa aurkezten dira. Europan dagoeneko hasi dira sistema horien aldeko apustua egiten eta bide horretan EAE ere hasi da pausoak ematen. Sistema horien xede nagusia uraren ziklo naturala antzeratzea da, urari lurzoruranzko bidea irekiz. Mota askotako sistemak aipa daitezke: euri-urak biltzeko landare eta lurzoruzko geruzak dituzten teilatu berdeak, poroak edo hutsuneak dituzten hirietako zoladura iragazkorrak, ura bildu eta iragazteko urmaelak, eta abar [1].
Hirietako isurketa-uren kalitateari erreparatuz gero, kontuan izan behar da giza jardueraren eraginez kaleetan pilatzen den hauts edo sedimentuetan era askotako kutsatzaileak metatzen direla eta isurketa-urek kutsatzaile horiek garraiatzen dituztela. Sedimentu horien jatorria trafikoa, industria, zoladuraren eta lurzoruaren higadura, eta haizeak garraiatutako harea izaten da, besteak beste, eta kutsatzaile ohikoenak metal astunak, hidrokarburo aromatiko poliziklikoak (PAH-ak) eta ongarriak izan ohi dira[2].
Kutsatzaile horiek uretan erabat disolbatuta edo suspentsioan dauden partikuletan adsorbatuta aurki daitezke eta garrantzitsua da hori kontuan hartu eta bi modutan dauden kutsatzaileak ezabatzeko metodoak garatzea. Horregatik, HDSJ-ak oro har bi prozesutan oinarritzen dira: alde batetik dekantazio-etapa izaten dute, partikula-faseko kutsatzaileak ezabatzeko, eta bestetik iragazketa-etapa, disolbatutako zein partikula-faseko kutsatzaileak ezabatzeko.
EAE-ri dagokionez, besteak beste, Legazpiko San Ignazio auzoko aparkalekuan zoladura iragazkorra eta ur-biltegi bat eraiki zituzten 2020an, Good Local Adapt izeneko proiektuaren bidez [3]. Era berean, Donostiako Txominenea auzoko aparkalekuan zoladura iragazkorra ipini zuen Donostiako Udalak, UPV/EHU-rekin lankidetza-proiektu baten bidez, 2018an. Zoladura iragazkor horiek material porotsu batez osatuta daude eta hori dela eta, gainazaleko ur-bolumena txikitzen dute eta ur horien kalitatea hobetu dezakete. Aipatutako guneek sistema horien eraginkortasuna ebaluatzeko aukera ematen dute, HDSJ-ak zeharkatu aurreko eta ondorengo ur-laginen kalitatea alderatuz.
Erreferentzia bibliografikoak:[1] CIRIA. (2015). The SuDS Manual, C75.
[2] Aryal, R., Vigneswaran, S., Kandasamy, J., Naidu, R. (2010). Urban stormwater quality and treatment. Korean Journal of Chemical Engineering ,27, 1343–1359.
[3] C-lab, https://goodlocaladapt.com (2023ko martxoan eskuratuta).
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 45
- Artikuluaren izena: Hiri Drainatze Sistema Jasangarriak (HDSJ) eta haien eragina hirietako isurketa-uren kalitatean
- Laburpena: Azken aldiko ikerketetan Hiri Drainatze Sistema Jasangarriak (HDSJ) hirietako isurketa-uren bolumena murrizteko eta beren kalitatea hobetzeko tresnatzat aurkeztu dira. Funtzioaren arabera, lau multzo bereizten dira: jatorria kontrolatzen dutenak, abiadura moteltzen dutenak, biltegiratze-sistemak eta infiltrazio-sistemak. Artikulu honen helburua izan da HDSJ-ek isurketa-uren kalitatean izan dezaketen eragina ebaluatzen duten ikerketen gainbegiratu bibliografikoa egitea, eta, horrekin batera, EAEko egoera aztertzea. Isurketa-uretako kutsatzaile nagusien artean metal astunak, ongarriak eta konposatu organikoak daude. Hauek murrizteko metodoek dekantazio-etapak eta iragazketa-etapak izaten dituzte. Bi etapa horiek integratuta dituzten HDSJ-ek emaitza onak izan dituzte. Sistema ohikoenei dagokienez, zoladura iragazkorrek eraginkortasuna erakutsi dute metal astunak eta fosfatoak murrizteko, eta bioerretentzio-sistemak ere tresna interesgarriak izan daitezke, landaredia-geruzak isurketa-urak xurgatzen eta eraldatzen lagundu baitezake. Jasangarritasunaren aldeko proiektuen bidez, hainbat HDSJ ezarri dira Gipuzkoan. Esaterako, Legazpiko zein Donostiako Udalek zoladura iragazkorrak ipini dituzte zenbait aparkalekutan eta sistema horien eraginkortasuna ebaluatzeko aukera ematen dute, HDSJ-ak zeharkatu aurreko eta ondorengo ur-laginen kalitatea neurtu baitaiteke.
- Egileak: Ainhoa Lekuona Orkaizagirre, Maite Meaurio Arrate, Ainara Gredilla Altonaga, Eneko Madrazo Uribeetxebarria eta Maddi Garmendia Antin
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 171-190
- DOI: 10.1387/ekaia.24784
- Ainhoa Lekuona Orkaizagirre eta Maite Meaurio Arrate UPV/EHUko Kimika Fakultateko Kimika Aplikatua Saileko ikertzaileak dira.
- Ainara Gredilla Altonaga UPV/EHUko Kimika Fakultateko Kimika Analitikoa Saileko ikertzailea da.
- Eneko Madrazo Uribeetxebarria eta Maddi Garmendia Antin UPV/EHUko Gipuzkoako Ingeniaritza Eskolako Ingeniaritza Energetikoa Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Hiri Drainatze Sistema Jasangarriak, urari bidea irekitzeko tresnak appeared first on Zientzia Kaiera.
El positrón de Dirac y los cerebros robóticos de Asimov
Cuando, en febrero de 1928, Paul Dirac publicó su ecuación de ondas relativista para describir el comportamiento del electrón, abrió, sin advertirlo, un nuevo campo de la física… y un nuevo universo de ciencia ficción en la mente de un estudiante de química de la Universidad de Columbia.
La ecuación de Dirac no fue la primera de este tipo. Oskar Klein y Walter Gordon ya habían planteado una similar para partículas de spin 0 ―o campos escalares en el contexto de la teoría cuántica de campos―, pero no servía para partículas de spin 1/2 como el electrón. Esa fue la aportación de Dirac. Sin embargo, ambas ecuaciones adolecían de un problema que era difícil ignorar. Al igual que el tiempo, estas interpretaciones relativistas de la ecuación de Schrödinger implicaban que la energía también era relativa, y eso hacía que admitieran soluciones que con niveles de energía negativos para las partículas algo que, desde un punto de vista intuitivo, no tenía pies ni cabeza.
 El físico Paul Dirac recibió, junto con Erwin Schrödinger, el Premio Nobel de Física en 1933 «por el descubrimiento de nuevas formas productivas de la teoría atómica».
El físico Paul Dirac recibió, junto con Erwin Schrödinger, el Premio Nobel de Física en 1933 «por el descubrimiento de nuevas formas productivas de la teoría atómica».
Dirac trató de darle sentido a aquellos valores de la energía que aparecían en su ecuación en 1930, planteando que tal vez el vacío no estaba tan vacío, sino que consistía en un mar infinito poblado de esos electrones con energía negativa. En ocasiones, uno de esos electrones pasaba a tener energía positiva, convirtiéndose, en este caso, en un electrón «normal», y dejando en aquel mar un hueco que se podía interpretar como una partícula de carga opuesta. La única partícula con carga opuesta al electrón que se conocía en aquel momento era el protón ―pese a la gran diferencia de masa entre ambos―, así que Dirac planteó que debía de existir algún tipo de correspondencia entre el hueco que dejaba un electrón de energía negativa y un protón. Lo que no pudo explicar es cómo podrían producirse las transiciones de unas partículas a otras sin violar ningún principio de conservación. Tenía la respuesta delante de sus narices, pero en aquel momento era demasiado exótica para tenerla en consideración.
 Foto: Herbert Goetsch / Unsplash
Foto: Herbert Goetsch / Unsplash
Tras leer el artículo en Dirac, Robert Oppenheimer entró en escena. Si alguna cualidad tenía Oppie, como solía llamarlo su círculo más cercano, era la capacidad de detectar, dentro de una teoría, dónde se encontraba la puerta que había que abrir para dar el siguiente paso. Si no alcanzó más logros dentro del mundo de la física, es porque ese siguiente paso rara vez lo daba él, dejaba que lo hicieran otros. En el mes de marzo de aquel mismo año, en una carta al editor de Physical Rewiev, Oppenheimer descartaba matemáticamente la posibilidad de que los huecos que quedaban en el mar de Dirac cuando un electrón pasaba a tener energía positiva fueran protones: fueran la partícula que fueran, debía de ser una con la misma masa del electrón. Hermann Weyl y Wolfang Pauli eran de la misma opinión.
Paul Dirac empezó a plantearse entonces que el surtido de partículas fundamentales tal vez fuera mucho más variado que las dos que se conocían en aquel momento: el electrón y el protón ―el neutrón no lo descubriría James Chadwick hasta febrero de 1932.
Un agujero, si existiera, sería un nuevo tipo de partícula, desconocida para la física experimental, que tendría la misma masa y carga opuesta a la de un electrón. A esta partícula podemos llamarla antielectrón. No deberíamos esperar encontrar ninguno de ellos en la naturaleza debido a su rápida tasa de recombinación con los electrones, pero si pudieran producirse experimentalmente en alto vacío serían lo bastante estables y susceptibles de observación.
La sorpresa llegó algunos meses después del descubrimiento del neutrón, en septiembre, cuando Carl David Anderson, estudiando los rayos cósmicos en el CalTech bajo la supervisión de Robert Millikan, observó una peculiaridad en la trayectoria de cierto tipo de partículas que atravesaban la cámara de niebla que utilizaba para detectarlas: era igual que la de los electrones, pero giraba en sentido contrario, lo que quería decir que tenía la misma masa, pero carga opuesta. Pese a que publicó sus resultados en una breve nota en la revista Science, el mundo no se hizo eco del descubrimiento hasta febrero del año siguiente, cuando el físico Patrick Blackett mostró, en una reunión de la Royal Society, las primeras fotografías del descubrimiento ―otorgándole todo el crédito a Anderson―. «The positive electron» se publicó en Physical Review en el mes de marzo y la única teoría que explicaba aquellas observaciones era la del antielectrón de Dirac.
 Primera imagen de un positrón atravesando una cámara de niebla, tomada por Carl D. Anderson en agosto de 1932.
Primera imagen de un positrón atravesando una cámara de niebla, tomada por Carl D. Anderson en agosto de 1932.Créditos: Dominio público/Carl D. Anderson
Al año siguiente, en 1934, los positrones empezaron a estar por todas partes, a detectarse en numerosos laboratorios a lo largo y ancho del mundo, y, lo que era más incontestable: a crearlos en el laboratorio.
Aquello sucedió por la misma época en la que un adolescente de Brooklyn, amante de la ciencia y de las historias de ciencia ficción que leía en las revistas del quiosco de su padre empezaba a pensar en su futuro. El nombre de aquel adolescente era Isaac Asimov.
Aunque Asimov empezó a escribir sus primeras historias en 1931, con once años, no imaginó el primer robot positrónico hasta 1939, el mismo año en que se graduó en química, y la elección de ese nombre, como se puede imaginar, aunque no fue todo lo científico que podría haber sido, tampoco fue casual:
Desde que comencé a escribir mis historias de robots en 1939, no mencioné nada sobre informática en relación a ellas. La computadora electrónica no se había inventado y yo no lo preví. Sin embargo, sí preví que el cerebro tenía que ser electrónico de algún modo. No obstante, lo «electrónico» no parecía lo suficientemente futurista. El positrón ―una partícula subatómica exactamente igual que el electrón pero con carga eléctrica opuesta― se había descubierto solo cuatro años antes de que escribiera mi primera historia sobre robots. Sonaba muy a ciencia ficción, así que les di a esos robots «cerebros positrónicos» e imaginé que que sus pensamientos consistían en corrientes intermitentes de positrones que aparecían y desaparecían casi de inmediato.
 La primera historia de robots positrónicos de Isaac Asimov, escrita en 1939, apareció bajo el título de «Strange playfellow» en el número de septiembre de 1940 de Super Science Stories. El título con el que se publicó en sucesivas reediciones, y por el que mejor se la conoce, es «Robbie».
La primera historia de robots positrónicos de Isaac Asimov, escrita en 1939, apareció bajo el título de «Strange playfellow» en el número de septiembre de 1940 de Super Science Stories. El título con el que se publicó en sucesivas reediciones, y por el que mejor se la conoce, es «Robbie».Unas veces el sentido de la maravilla de la ciencia ficción inspira a la ciencia; otras, es el sentido de la maravilla de la ciencia el que inspira a la ciencia ficción.
Bibliografía
Anderson, C. D. (1932). The apparent existence of easily deflectable positives. Science, 76(1957), 238-239. https://doi.org/10.1126/science.76.1967.238
Anderson C. D. (1933). The positive electron. Physical Review, 43(6), 491-494. https://doi.org/10.1103/PhysRev.43.491
Asimov, I. (1987). My robots. En Michael P. Kube-McDowell, Isaac Asimov’s Robot City: Odyssey. Ace books.
Bird, K. Y Sherwin, M. J. (2005). American Prometeus. The triumph and tragedy of J. Robert Oppenheimer. Atlantic Books.
Chadwick, J. (1932). Possible existence of a neutron. Nature, 129(3252), 312-312. https://doi.org/10.1038/129312a0
Dirac, P. A. M. (1928). The quantum theory of the electron. Proceedings of the Royal Society of London, 117(778), 610-624. https://www.jstor.org/stable/94981
Dirac, P. A. M. (1930). A theory of electrons and protons. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 126(801), 360-365. https://doi.org/10.1098/rspa.1930.0013
Farmelo, G. (2009). The strangest man. The hidden life of Paul Dirac, quantum genius. Faber and faber.
Oppenheimer, J. R. (1930). On the theory of electrons and protons. Physical Review, 35(5), 562-563. https://doi.org/10.1103/PhysRev.35.562
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo El positrón de Dirac y los cerebros robóticos de Asimov se ha escrito en Cuaderno de Cultura Científica.
El estudiante de matemáticas en la casa del juez
Hace unas pocas semanas me compré, y ha sido una de mis lecturas estivales, el libro El invitado de Drácula y otros relatos, una colección de relatos de terror del escritor irlandés Bram Stoker (1847-1912), conocido por ser el autor de uno de los clásicos de la literatura de terror, Drácula (1897). El libro ha sido publicado recientemente por la editorial ALMA, dentro de su colección Clásicos Ilustrados. La ilustración del mismo es del ilustrador e historietista vallisoletano Enrique Corominas (1969), y la traducción del escritor y traductor asturiano Jon Bilbao (1972). Uno de los relatos de El invitado de Drácula y otros relatos, titulado La casa del juez, está protagonizado por un estudiante de matemáticas, por lo que vamos a dedicar esta entrada del Cuaderno de Cultura Científica al mismo.
 Portada de la edición de la editorial ALMA, dentro de su colección Clásicos Iustrados, del libro El invitado de Drácula y otros relatos, del escritor irlandés Bram StokerBram Stoker, escritor … y matemático
Portada de la edición de la editorial ALMA, dentro de su colección Clásicos Iustrados, del libro El invitado de Drácula y otros relatos, del escritor irlandés Bram StokerBram Stoker, escritor … y matemático
Sin lugar a dudas, la novela Drácula (1897) es uno de los grandes clásicos de la literatura de terror, que ha motivado que su autor, el escritor Bram Stoker, haya sido incluido en la historia universal de la literatura. El escritor Bram Stoker, como recordábamos en la entrada Personas famosas que estudiaron matemáticas: literatura y cine , estuvo relacionado con las matemáticas.
El 8 de noviembre de 1847 nació Bram Stoker en Dublín (Irlanda). Los primeros siete años de su vida los pasó en la cama a causa de una enfermedad desconocida, hasta que se recuperó completamente. Según podemos leer en la contraportada de El invitado de Drácula y otros relatos, “su único entretenimiento eran las oscuras leyendas irlandesas que su madre le contaba”. Es muy posible que estas historias de misterio y fantasmas que le narraba su madre en su niñez fueran determinantes en el hecho de que Bram Stoker se convirtiera en un escritor de historias de terror, y seguramente algunos de sus relatos estarán basados en esas historias que le escuchaba a su madre.
 Fotografía de Bram Stoker, de alrededor de 1906
Fotografía de Bram Stoker, de alrededor de 1906
Bram Stoker se graduó en matemáticas en el Trinity College de Dublín en 1870 y, aunque parece ser que no era verdad, él empezó a decir con el tiempo que se “graduó con honores en matemáticas”. Sin embargo, cediendo a los deseos paternos, Bram Stoker siguió la carrera de funcionario público en el Castillo de Dublín, entre 1870 y 1878. Aunque conseguiría su Master of Arts (posgrado) en 1875. En 1878 empezaría a trabajar como asistente del actor Sir Henry Irving, de quien escribiría además una biografía en dos volúmenes titulada Personal Reminiscences of Henry Irving / Recuerdos personales de Henry Irving (1906), y también como gerente del Lyceum Theatre, que pertenecía al mencionado actor.
Bram Stoker publicó su famosísima novela epistolar Drácula en 1897, pero también publicó otras novelas, doce en total, y relatos, entre ellos los relatos de la publicación que nos ocupa, El invitado de Drácula y otros relatos, además de poesía, críticas de teatro, así como otros artículos y libros, que pueden verse en la página web dedicada a Bram Stoker.
 Cartel de la película Drácula, de Bram Stoker (1992), del director estadounidense Francis Ford Coppola e interpretada por los actores Gary Oldman, Winona Ryder, Keanu Reeves y Anthony Hopkins
Cartel de la película Drácula, de Bram Stoker (1992), del director estadounidense Francis Ford Coppola e interpretada por los actores Gary Oldman, Winona Ryder, Keanu Reeves y Anthony HopkinsA pesar de su formación matemática, Bram Stoker nunca trabajaría como matemático, aunque sí podemos encontrar, al menos, un par de publicaciones relacionadas con las matemáticas. Por una parte, un cuento infantil titulado Cómo el número 7 se volvió loco (que publicó la editorial Nivola en 2010 y la editorial Gadir en 2013), que fue originalmente publicado por Bram Stoker en 1881 dentro del libro Under the Sunset / Bajo el ocaso, una recopilación de ocho cuentos infantiles.
 Portada del libro Cómo el número 7 se volvió loco, de Bram Stoker, publicado por la editorial Gadir en 2013, con ilustraciones de Eugenia Ábalos
Portada del libro Cómo el número 7 se volvió loco, de Bram Stoker, publicado por la editorial Gadir en 2013, con ilustraciones de Eugenia ÁbalosAquí os dejo un pequeño fragmento del cuento Cómo se volvió loco el número 7 extraído de la edición de la editorial Nivola.
– [Número 7] Mañana, tarde y noche soy tratado peor que un esclavo. No existe nadie en todo el ámbito del aprendizaje que tenga que aguantar lo que yo aguanto. Siempre trabajo duro. Nunca me quejo. A menudo hago de múltiplo, a veces de multiplicando. Estoy dispuesto a soportar la parte que me toca por ser un resultado, pero no soporto el trato que me dan. Se me suma mal, se me divide mal, se me resta mal y se me multiplica mal. Los demás números no reciben el trato que yo, y además no son huérfanos como yo.
– [Médico] ¿Cómo que huérfanos? –preguntó el médico–. ¿Qué quiere decir?
– Quiero decir que los demás números tienen muchos parientes. Si exceptuamos al viejo 1, que no cuenta demasiado (además, sólo soy su tataratataratataranieto), no tengo ni amigos, ni familiares.
– ¿Qué quiere decir? –preguntó el médico.
– Pues que ese tipo viejo lleva ahí toda la vida y tiene todos sus descendientes a su alrededor, pero yo estoy seis generaciones detrás.
– ¡Anda ya! –dijo el médico.
– El número 2 –continuó el 7– nunca se mete en problemas, y el 4, el 6 y el 8 son sus primos. El número 3 es íntimo del 6 y del 9. El número 5 es la mitad de una decena y nunca se complica la vida. Pero en cuanto a mí, soy un desgraciado, me maltratan y estoy solo.
Y el pobre número 7 empezó a llorar. Con la cabeza gacha, sollozaba amargamente.
 Portada del libro Cómo se volvió loco el número 7, de Bram Stoker, publicado por la editorial Nivola en 2011, con ilustraciones de Carlos Pinto
Portada del libro Cómo se volvió loco el número 7, de Bram Stoker, publicado por la editorial Nivola en 2011, con ilustraciones de Carlos PintoLa otra publicación directamente relacionada con las matemáticas es el relato La casa del juez, protagonizado por un estudiante de matemáticas, que está incluido en el mencionado libro El invitado de Drácula y otros relatos, y del que hablaremos en esta entrada.
La casa del juezEl relato corto La casa del juez, de Bram Stoker, fue publicado por primera vez el 5 de diciembre de 1891 en el número especial de navidad (Holly Leaves) de la revista semanal británica The Illustrated Sporting and Dramatic News (fundada en 1874). Mientras que la primera vez que aparece publicada en un libro es en la recopilación de relatos cortos Dracula’s Guest And Other Weird Stories / El invitado de Drácula y otros relatos extraños, publicada en 1914.
 Portada de la publicación Holly Leaves the Christmas Number de The Illustrated Sporting and Dramatic News (Londres, diciembre, 1891)
Portada de la publicación Holly Leaves the Christmas Number de The Illustrated Sporting and Dramatic News (Londres, diciembre, 1891)El relato corto La casa del juez empieza con el siguiente párrafo (que hemos recogido de la traducción de Jon Bilbao para el libro El invitado de Drácula y otros relatos, de la editorial ALMA).
Cuando se acercó el momento de sus exámenes, Malcolm Malcolmson decidió irse a algún sitio donde pudiera estar a solas para estudiar. Temía las distracciones de la costa, y temía asimismo el completo aislamiento del campo, cuyos atractivos conocía desde hace mucho, así que decidió buscar algún modesto pueblecito donde nada lo distrajera. Se abstuvo de pedir sugerencias a sus amigos, pues supuso que cada uno le recomendaría un lugar familiar para él y donde tuviera conocidos. Como Malcolmson pretendía evitar a sus amigos, tampoco deseaba cargar con las atenciones de los amigos de sus amigos, por lo que se ocupó de dar él mismo con el sitio. Llenó el baúl de viaje con ropa y los libros que necesitaba y sacó un billete para el primer destino de la lista de salidas que le fuera desconocido.
Como podemos leer, el protagonista es un estudiante que busca un lugar tranquilo para estudiar. Más adelante, en el relato, podremos leer que es estudiante de matemáticas. En concreto, en esta traducción leemos que el estudiante se describe como “un hombre que estudia matemáticas en la Universidad de Cambridge”. Aunque la traducción de la anterior descripción del estudiante es, en mi opinión, muy acertada para facilitar la comprensión del cuento, no se corresponde con la expresión que aparece en el relato original, en la que podemos leer (en inglés) “un hombre que está estudiando para el tripos matemático”.
Un examen de matemáticasEl tripos matemático (Mathematical Tripos en inglés) era un examen de matemáticas de la Universidad de Cambridge, por lo que parece que tanto la expresión del relato original, como esta traducción al castellano, serían prácticamente lo mismo. Sin embargo, como hemos explicado en la anterior entrada El tripos matemático, el examen más duro que jamás existió, el tripos matemático era mucho más. Este hecho no es imprescindible para la lectura del relato, pero ofrece un cierto significado extra al mismo.
El tripos matemático era el eje central del sistema educativo de la Universidad de Cambridge, un examen para obtener el título de grado (de cualquier grado) que tenía lugar después de los 10 trimestres oficiales del mismo. Se consideraba que las matemáticas eran un conocimiento básico importante para los jóvenes estudiantes, puesto que su estudio fortalecía y desarrollaba las facultades de la mente y los preparaba para su posterior desarrollo intelectual. Por lo tanto, nuestro estudiante Malcolm Malcolmson podría ser uno más de esos estudiantes de Cambridge que se enfrentaban a esta durísima prueba, no necesariamente un estudiante de matemáticas. Aunque, como decía, la traducción “un hombre que estudia matemáticas en la Universidad de Cambridge” me parece muy acertada.
Hasta 1909 se publicaron las listas de honor del tripos matemático por orden de mérito en tres clases, wranglers, senior optimes y junior optimes, el resto obtenían un grado ordinario. Además, el primer puesto, senior wrangler, era reconocido como un gran logro intelectual en todo Gran Bretaña y abría muchas puertas para una carrera exitosa.
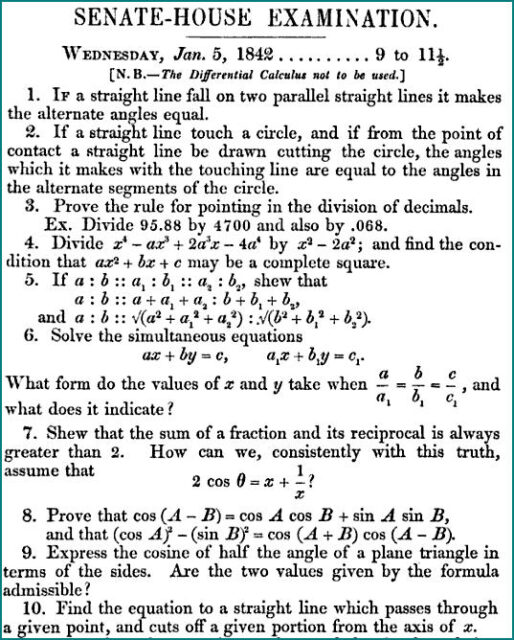 Hoja con problemas del tripos matemático de 1842
Hoja con problemas del tripos matemático de 1842
Era un examen muy difícil. El científico Francis Galton (1822-1911), en su libro Genio hereditario (1869), menciona que un año de la década de 1860 de los 17.000 puntos en juego en el examen, el senior wrangler obtuvo 7.634 (un 4,49 sobre 10), el segundo wrangler 4.123 (un 2,43 sobre 10). Y estas eran las dos mejores notas, luego estaban el resto de wranglers, después los senior optimes, a los que seguían los junior optimes y finalmente los estudiantes con un grado ordinario.
Para afrontar este examen era necesario un duro entrenamiento, memorizando teoremas, estudiando técnicas de resolución de problemas y trabajando los de cursos anteriores. Los estudiantes contrataban a “entrenadores” privados, no a profesores de la universidad, y dedicaban todo su tiempo a prepararse, por lo que no asistían a las clases regulares. Era un examen tan duro que muchos estudiantes sufrían crisis nerviosas.
Luego es comprensible que Malcolmson decidiera buscar un lugar aislado donde poder estudiar tan duro examen sin ninguna distracción, sobre todo si se estaba preparando la tercera parte del examen a la que solo accedían los wranglers de la lista de honor del tripos matemático, lista confeccionada a partir de los dos primeros exámenes, como puede leerse en la entrada El tripos matemático, el examen más duro que jamás existió.
Los matemáticos no creen en fantasmasTras llegar al lugar elegido, el joven estudiante busca una casa para alquilar en la que alojarse durante el tiempo que necesita para centrarse en sus estudios y le ofrecen “la casa del juez”. Desde el primer momento las personas del lugar le aconsejan que no se hospede en esa casa encantada y tétrica. En particular, la patrona de la posada en la que se ha alojado inicialmente, la señora Withman, que trata de disuadirlo de alojarse en ella, e incluso le dice que “si fuera mi hijo no dormiría allí ni una noche”.
Al joven Malcolmson le parece divertida la advertencia de la patrona de la posada y le contesta lo siguiente.
– Pero, mi querida señora Withman, no hay razón para que se preocupe usted por mí. Un hombre que estudia Matemáticas en la Universidad de Cambridge tiene demasiado en lo que pensar como para que lo moleste cualquier “algo” misterioso, y su trabajo es de una índole demasiado exacta y prosaica como para dejar espacio en su cabeza para misterios de cualquier clase. ¡La progresión armónica, las permutaciones, las combinaciones y las funciones elípticas ya entrañan misterios suficientes para mí!
En dicha respuesta, Bram Stoker ya nos deja algunos términos matemáticos, como “progresión aritmética”, “permutaciones”, “combinaciones” o “funciones elípticas”, además de que “estudia para el tripos matemático” (en la traducción “que estudia Matemáticas en la Universidad de Cambridge”), para que el lector, o lectora, relacione claramente al estudiante con las matemáticas.
 Primera página del cómic basado en el relato La casa del juez, de Bram Stoker, publicado en el número 5 de la revista Creepy, una revista de cómic de terror.
Primera página del cómic basado en el relato La casa del juez, de Bram Stoker, publicado en el número 5 de la revista Creepy, una revista de cómic de terror.Es muy posible que Bram Stoker eligiera que el protagonista de esta historia fuese estudiante de matemáticas por dos motivos. El primero es que, como matemático, como científico, el protagonista piensa que su mente racional está por encima de las supersticiones de las gentes de ese lugar sobre la casa encantada del juez. De forma que, por ello, el joven estudiante de matemáticas es descrito en el relato como una persona arrogante. Lo cual enlaza con el segundo motivo, las matemáticas no tenían buena prensa, como ha ocurrido durante mucho tiempo, por lo cual, el protagonista se mostraba además antipático para quien leyese el relato, como alguien que se merece lo que le pasa por no hacer caso de las advertencias de las buenas gentes de la zona.
 Terrorífica ilustración de Enrique Corominas para el relato La casa del juez, dentro del libro El invitado de Drácula y otros relatos, de Bram Stoker, publicado por la Editorial ALMA. Imagen de la página de Facebook de la editorial ALMA
Terrorífica ilustración de Enrique Corominas para el relato La casa del juez, dentro del libro El invitado de Drácula y otros relatos, de Bram Stoker, publicado por la Editorial ALMA. Imagen de la página de Facebook de la editorial ALMACuando el protagonista está realizando la mudanza para instalarse en la casa alquilada, la casa encantada del juez, la señora Dempster, contratada por el estudiante para arreglar la casa, le ofrece al joven una explicación racional de los “duendes” de la casa, aunque ella no querría pasar una noche en la misma. En concreto dice lo siguiente.
Le diré lo que sucede, señor. Los duendes son toda clase de cosas, ¡menos duendes! Ratas y ratones, e insectos, y puertas que chirrían, y tejas sueltas, y ventanas rotas, y cajones arrancados, que se quedan abiertos y caen al suelo en mitad de la noche. Fíjese en el empanelado de las paredes. Es viejo. Tiene siglos. ¿Cree usted que ahí atrás no habrá ratas e insectos? ¿Cree usted, señor, que no va a verlos? Las ratas son duendes, se lo aseguro, y los duendes son ratas. ¡Que no se le meta nada más en la cabeza!
A lo que el joven contesta a la señora Dempster, “¡sabe usted más que el mejor graduado en Matemáticas de Cambridge!”. Si entendemos que el mejor graduado de Matemáticas de Cambridge, se refiere al estudiante que saca la mejor nota en el tripos matemático, entonces se estaría refiriendo al senior wrangler, como así se expresa en la versión original del cuento.
Libros de matemáticasLa intención de esta entrada del Cuaderno de Cultura Científica no es hacer un spoiler, luego no contaremos mucho más del argumento, aunque podemos decir que es un clásico del terror. Sí diremos que la señora Dempster introduce el elemento clave, las ratas, que como ella misma dice “las ratas son los duendes y los duendes son las ratas”.
La cuestión es que el joven estudiante se instala y empieza a estudiar para el examen, mientras van aconteciendo los sucesos de terror del propio relato, relacionados con las ratas, con una grande especialmente, pero centrémonos en las matemáticas que aún aparecen en el cuento.
Por ejemplo, en cierto momento, Bram Stoker escribe
Dio [Malcolmson] con un sendero tranquilo que discurría entre altos olmos, a las afueras del pueblo, y pasó allí la mayor parte del día, estudiando a Laplace.
Se refiere al matemático, físico, astrónomo y filósofo francés Pierre-Simon Laplace (1749-1827), autor de los cinco volúmenes de la obra Traité de mécanique céleste / Tratado de Mecánica Celeste (publicados entre 1799 y 1852), o Exposition du système du monde / Exposición sobre el sistema del mundo (publicado en 1824). Los temas tratados en los mismos formaban parte del temario del tripos matemático.
Más adelante, cuando descubre una rata enorme sentada en una “gran silla tallada de roble colocada a la derecha del fuego”, le lanza “un libro de logaritmos”. Y otra noche le lanza a esa misma rata enorme otra serie de libros que tenía a mano. En concreto, se citan los siguientes.
“Secciones cónicas” no dio en el blanco, tampoco “Oscilaciones cicloidales”, ni los “Principios”, ni “Cuaterniones”, ni “Termodinámica”.
Todos ellos libros que cubrían algunos de los temas que entraban en los tres exámenes del tripos matemático, como puede leerse en la entrada El tripos matemático, el examen más duro que jamás existió. En particular, uno de ellos un texto muy importante para la ciencia, como es los Principia / Principios (Philosophiæ naturalis principia mathematica / Principios matemáticos de la filosofía natural) del gran científico británico Isaac Newton (1643-1727).
 Caricatura, realizada por Gerardo Basabe de Viñaspre, del matemático inglés Sir Isaac Newton (1642-1727), a quien se le atribuye la autoría del anterior juego de ingenio, perteneciente a la exposición El rostro humano de las matemáticas, de la Real Sociedad Matemática Española
Caricatura, realizada por Gerardo Basabe de Viñaspre, del matemático inglés Sir Isaac Newton (1642-1727), a quien se le atribuye la autoría del anterior juego de ingenio, perteneciente a la exposición El rostro humano de las matemáticas, de la Real Sociedad Matemática EspañolaNo hay ninguna referencia directa más a las matemáticas, salvo que se pasa muchas horas estudiando, incluso noches enteras, y mucho tiempo resolviendo problemas (de matemáticas). La siguiente cita nos muestra un ejemplo.
Resolvió de manera satisfactoria todos los problemas que hasta entonces se le habían resistido, así que cuando pasó a hacer una visita a la señora Withman en el The Good Traveller, se sentía jubiloso.
Una vuelta de tuercaEspero que disfrutéis de la lectura de este relato de terror, por lo que no voy a hacer ningún spoiler, salvo comentar que la cosa, como ya se puede imaginar desde el principio del mismo, no termina bien para nuestro estudiante de matemáticas. Sobre este final, tenemos la interpretación directa de su lectura, la típica interpretación de los relatos de terror sobre casas encantadas, fantasmas, espíritus y demás elementos de la literatura de terror. Sin embargo, podemos ofrecer una explicación racional para lo acontecido en este relato si pensamos que este estudiante está preparando el durísimo examen de la Universidad de Cambridge, el tripos matemático.
Como comentábamos más arriba, el tripos matemático era un examen tan duro que muchos estudiantes sufrían crisis nerviosas. De hecho, en la entrada El tripos matemático, el examen más duro que jamás existió, comentábamos lo siguiente:
Galton sufrió una crisis nerviosa y acabó con un grado ordinario. El erudito estadounidense Charles A. Bristed (1820-1874) sufrió un colapso físico, quedando en los últimos lugares de la lista de junior optimes. El político y economista Henry Fawcett (1833-1884), favorito para senior wrangler, acabó siendo séptimo wrangler tras sufrir trastornos nerviosos e insomnio. El senior wrangler de 1859, James Wilson (1836-1931), sufrió una crisis nerviosa tras los exámenes y al recuperarse había olvidado todas las matemáticas estudiadas. O el también senior wrangler James Savage fue encontrado muerto en una zanja tres meses después del examen, el motivo de la muerte fue un derrame cerebral, posiblemente producido por el enorme esfuerzo realizado. Estos son solo algunos casos de la historia negra de este sistema.
En consecuencia, podríamos interpretar que el protagonista de este relato, Malcolm Malcolmson, estudiante de la Universidad de Cambridge que estaba preparando el tripos matemático, sufrió un colapso nervioso y todo lo que ocurrió en la casa del juez no fue más que producto de su enferma imaginación, a partir de la historia que los habitantes del lugar le habían contado sobre la casa del juez.
 Segunda página del cómic basado en el relato La casa del juez, de Bram Stoker, publicado en el número 5 de la revista Creepy, una revista de cómic de terror. En la misma se cuenta la historia del juez que vivió en dicha casa
Segunda página del cómic basado en el relato La casa del juez, de Bram Stoker, publicado en el número 5 de la revista Creepy, una revista de cómic de terror. En la misma se cuenta la historia del juez que vivió en dicha casa¡Que disfrutéis de la lectura de este relato de terror!
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El estudiante de matemáticas en la casa del juez se ha escrito en Cuaderno de Cultura Científica.
Dozena erdi ariketa 2024ko udarako (3): ezabatu zifra
Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko asteazkenero ariketa matematiko bat izango duzue, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Hona hemen gure hirugarren ariketa:Zenbaki arrunt bati ezkerreko lehen zifra ezabatuta lortzen den zenbakia aurrerakoaren 29rena da (aurrekoa zati 29). Zein da propietate hori duen zenbakirik txikiena?
Zein da erantzuna? Idatzi emaitza iruzkinen atalean (artikuluaren behealdean daukazu) eta, nahi izanez gero, zehaztu jarraitu duzun ebazpidea ere. Irailean emaitza zuzenaren berri emango dizugu.
 (Argazkia: Anatol Rurac – Unsplash lizentziapean. Iturria: Unsplash)
(Argazkia: Anatol Rurac – Unsplash lizentziapean. Iturria: Unsplash)Ariketak “Calendrier Mathématique 2024. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
The post Dozena erdi ariketa 2024ko udarako (3): ezabatu zifra appeared first on Zientzia Kaiera.
Un brote de rayos gamma restringe las posibles violaciones a la relatividad general
Un análisis del brote de rayos gamma más brillante jamás observado no revela diferencias en la velocidad de propagación de las distintas frecuencias de la luz, lo que impone algunas de las restricciones más estrictas a ciertas violaciones de la relatividad general.
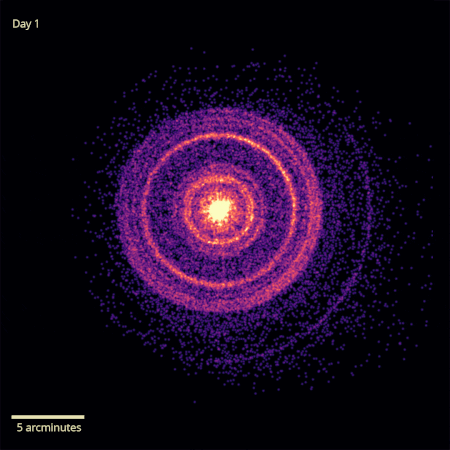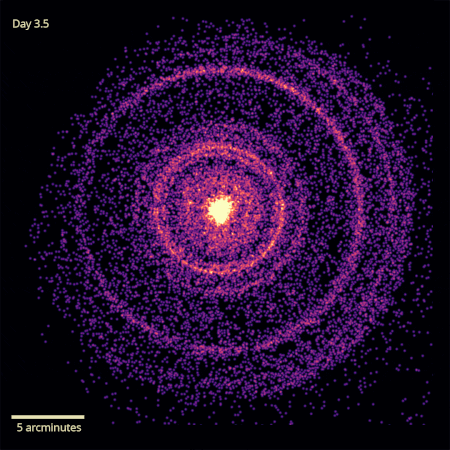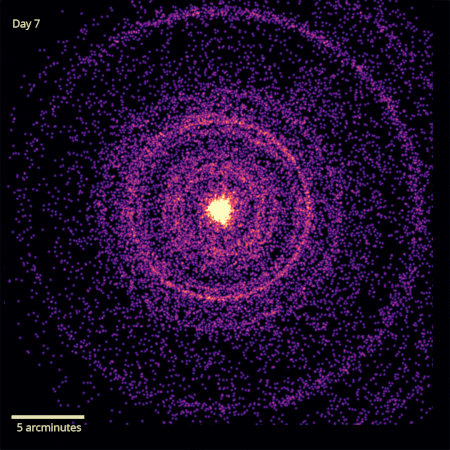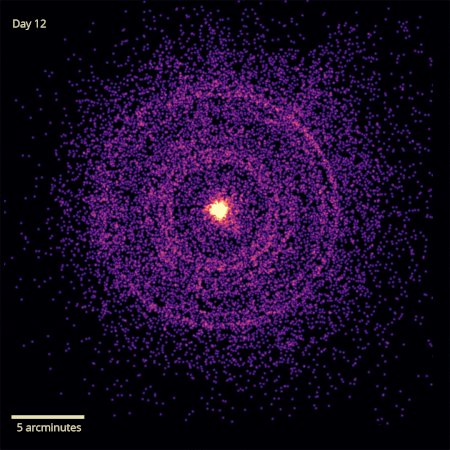 Composición de 12 días de observaciones del brote de rayos gamma GRB 221009A realizadas por el telescopio de rayos X a bordo del observatorio espacial Neil Gehrels Swift de la NASA. Fuente: NASA’s Scientific Visualization Studio / Scott Wiessinger, Francis Reddy, Brad Cenko, Eric Burns
Composición de 12 días de observaciones del brote de rayos gamma GRB 221009A realizadas por el telescopio de rayos X a bordo del observatorio espacial Neil Gehrels Swift de la NASA. Fuente: NASA’s Scientific Visualization Studio / Scott Wiessinger, Francis Reddy, Brad Cenko, Eric BurnsSi mandas un pulso de luz blanca por una fibra óptica los componentes rojos de su espectro llegarán al extremo más alejado antes que los componentes azules. Si mandas el mismo pulso a través del vacío, el resultado será un empate técnico entre todas las frecuencias. La ausencia de dispersión de frecuencias es una consecuencia de una simetría fundamental de la relatividad conocida como invariancia de Lorentz.
Sin embargo, algunas teorías de la gravedad cuántica predicen que, para energías de fotones muy altas, el vacío se comporta como un medio. Los investigadores del Large High Altitude Air Shower Observatory (LHAASO) en China han comprobado ahora la invariancia de Lorentz analizando las mediciones de un brote de rayos gamma. La falta de una violación observable de la invariancia de Lorentz ha permitido al equipo elevar el umbral de energía a partir del que los efectos de la gravedad cuántica podrían hacerse evidentes.
Los brotes de rayos gamma, explosiones cósmicas que emiten radiación de alta energía, son excelentes sujetos para probar la invariancia de Lorentz, ya que su gran distancia significa que una pequeña dispersión se traduce en una variación detectable de los tiempos de llegada. El equipo de LHAASO estudió el brote de rayos gamma 221009A, el evento de este tipo más brillante jamás observado y, a una distancia de aproximadamente 2.400 millones de años luz, uno relativamente cercano. Aunque esta proximidad reduciría cualquier dispersión en el tiempo de llegada en comparación con eventos más distantes, el alto flujo de fotones ofrecía una oportunidad única para realizar mediciones estadísticamente significativas.
Al analizar cómo cambiaba el espectro de energía de los brotes de rayos gamma a lo largo del tiempo, los investigadores han podido restringir los dos términos principales que describen la dispersión de frecuencias potencial de la luz, los que varían lineal o cuadráticamente con la energía del fotón.
Para el término lineal, los investigadores han obtenido una restricción similar a la derivada previamente a partir de otras observaciones de los brotes de rayos gamma. Para el cuadrático, han establecido un umbral de energía de cinco a siete veces mayor a partir del que podría surgir la gravedad cuántica.
Futuras observaciones de las etapas iniciales de un brote de rayos gamma podrían ofrecer pruebas de una violación de Lorentz aún más sensibles.
Referencias:
Zhen Cao et al. (The LHAASO Collaboration) (2024) Stringent Tests of Lorentz Invariance Violation from LHAASO Observations of GRB 221009A Phys. Rev. Lett. doi: 10.1103/PhysRevLett.133.071501
M. Stephens (2024) Gamma-Ray Burst Tightens Constraints on Quantum Gravity Physics 17, s99
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un brote de rayos gamma restringe las posibles violaciones a la relatividad general se ha escrito en Cuaderno de Cultura Científica.
¿Cuántos terremotos ocurren cada año en Venus?
Venus es un planeta del que desde luego no nos olvidamos en este Cuaderno de Cultura Científica, pero casi siempre hacemos referencia a sus posibles procesos volcánicos activos, quizás porque a fecha de hoy todavía nos queda mucho por explorar de un planeta cuyas condiciones -una superficie perpetuamente cubierta de nubes, una temperatura superior a los 450º y una presión atmosférica 90 veces superior a la terrestre- hacen del estudio de su superficie un reto muy difícil de superar incluso para la tecnología más puntera de la que disponemos.
A pesar de las enormes diferencias que hay entre Venus y la Tierra, a este planeta se le apoda como el “gemelo” de nuestro planeta. Y es que lo cierto es que al menos en el tamaño -Venus tiene un radio tan solo un 5% inferior al de la Tierra- y una densidad media similar -aunque también, y es coincidencia, es un 5% menor- apuntando a una composición similar, nos hacen pensar que, quizás, si Venus se encontrase a una distancia similar del Sol que nuestro planeta, podríamos parecernos mucho más.
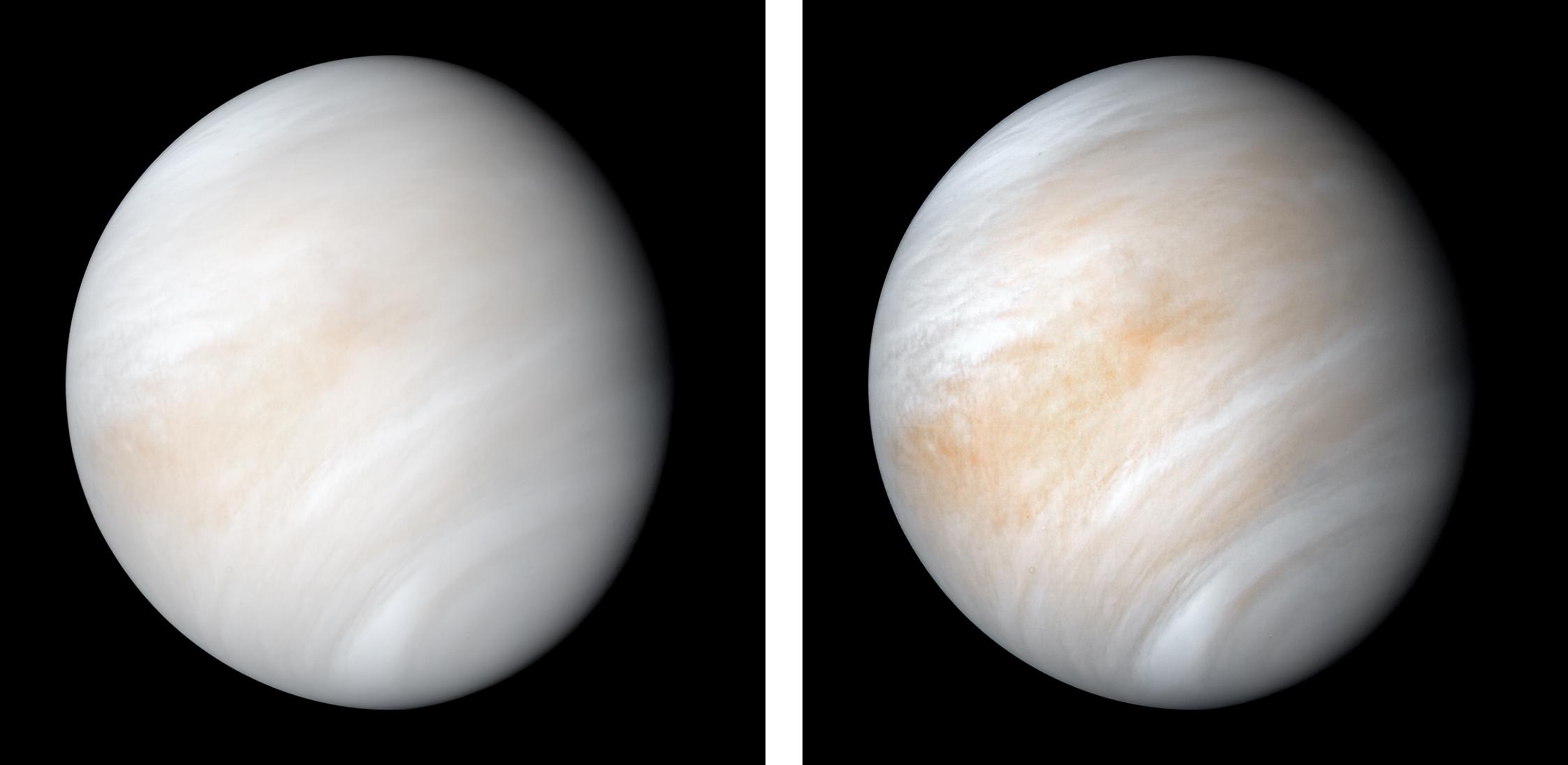 La cara que siempre nos muestra Venus -al menos en luz visible- es esta: un mundo perpetuamente cubierto de nubes, lo que ha dificultado muchísimo observar procesos geológicos activos y que, en algunos casos, estarán pendientes de confirmación hasta la próxima década. Imagen cortesía de NASA/JPL-Caltech.
La cara que siempre nos muestra Venus -al menos en luz visible- es esta: un mundo perpetuamente cubierto de nubes, lo que ha dificultado muchísimo observar procesos geológicos activos y que, en algunos casos, estarán pendientes de confirmación hasta la próxima década. Imagen cortesía de NASA/JPL-Caltech.Durante décadas, la ausencia de pruebas sobre un Venus dinámico y con actividad geológica había dejado una fuerte impronta en la cual imperó una visión en la que el planeta era un lugar carente de actividad, al menos a una escala evidente para nuestras observaciones, a pesar de que simplemente el hecho de tener un tamaño y una composición similar a la Tierra fuesen motivos más que suficientes para argumentar que podría mantener un calor interno suficiente para alimentar procesos geológicos activos como, por ejemplo, lo son terremotos y erupciones volcánicas.
Afortunadamente, con el paso de los años, y el descubrimiento de actividad geológica en cuerpos mucho más pequeños de nuestro sistema solar, pero también por la suma de indicios que estamos recabando de Venus, como las posibles pruebas de volcanes activos hoy día -ya sea por la variación de gases en la atmósfera, por la existencia de anomalías térmicas en su superficie o por, directamente, haber podido observar el antes y el después del depósito de una colada de lava- nos hacen pensar que Venus es, efectivamente, un planeta activo. Si a esto le sumamos que algunas estimaciones sobre la edad de su superficie -basadas en el conteo de cráteres de impacto- y que podríamos situar entre los 250 y 800 millones de años, está claro que es un planeta que está activo incluso lo suficiente para renovar su superficie.
Pero, ¿y los terremotos? Hasta el momento, los únicos sismómetros que han funcionado en Venus fueron los que llevaron las misiones soviéticas Venera 13 y 14 -que llegaron a Venus en 1981-, y debido a la breve duración de las misiones por las duras condiciones que se encontraron en la superficie, junto a las dificultades de interpretar los datos, apenas arrojaron un par de señales que podrían ser de origen sísmico. Y digo podrían porque tampoco está del todo claro.
Uno de los datos a tener en cuenta para planificar las futuras misiones que si puedan llevar instrumentos con la capacidad de detectar la actividad sísmica del planeta es intentar cuantificar cuantos terremotos ocurren en el planeta y si hay zonas con mayor probabilidad de que estos ocurran.
Precisamente, un nuevo estudio publicado por van Zelst et al. (2024) intenta responder a esta pregunta planteando tres posibles escenarios de sismicidad: Uno en el que Venus es un planeta “inactivo”, pero inactivo en el sentido de las zonas intraplaca de nuestro planeta, lo que serían el equivalente en nuestro planeta a las zonas lejos de los límites de placas, como lo suelen ser el interior de los continentes. Bajo esta premisa, los científicos calculan que habría entre 95 y 296 terremotos por año con una magnitud de 4 o superior.
 En esta imagen de radar tomada por la misión Magellan podemos ver las coronas de Bahet y Onatah, reconocibles por su forma ovalada a ambos lados de la imagen y compuestas por sistemas de valles y crestas montañosas. Imagen cortesía de NASA/JPL.
En esta imagen de radar tomada por la misión Magellan podemos ver las coronas de Bahet y Onatah, reconocibles por su forma ovalada a ambos lados de la imagen y compuestas por sistemas de valles y crestas montañosas. Imagen cortesía de NASA/JPL.Luego plantea otros dos escenarios más suponiendo que Venus sea un planeta activo y que algunas de las formas que vemos sobre su superficie -coronas, rifts y cinturones de pliegues- estén hoy día activos, por lo que estaríamos ante un umbral de entre 1161 y 3609 terremotos de magnitud 4 o superior cada año.
Y dentro de este escenario anterior hay otro más, y es que Venus tenga una actividad sísmica similar a la Tierra, por lo que se podrían observar entre 5715 y 17773 terremotos de magnitud 4 o superior cada año, un número muy elevado que facilitaría la detección de estos.
En cualquier caso, estos cálculos ponen de manifiesto una cosa bastante llamativa y es que, incluso en el caso de que estemos ante un primer escenario y Venus sea “inactivo” -algo que parece poco probable teniendo en cuenta que incluso podría haber volcanes activos hoy día en su superficie- su actividad sísmica sería claramente superior a la que observamos en Marte o en la Luna y, a pesar de esto, hemos podido detectar terremotos en estos últimos dos cuerpos. Eso sí, con misiones de mayor duración.
Pero bueno, ¿cómo podríamos salir de dudas? Aunque la tecnología ha mejorado mucho con respecto a existente en los años 80, lo cierto es que mantener en funcionamiento un sismómetro sobre la superficie de Venus durante un periodo lo significativamente grande como para detectar y caracterizar la actividad sísmica parece muy difícil como reto técnico.
En los últimos años hemos empezado a ver propuestas como la de Krishnamoorthy et al. (2022) en la que se propone sustituir los sismómetros del suelo por globos capaces de moverse por la atmósfera, ya que estas misiones podrían tener una duración mucho más prolongada, puesto que en las zonas altas de la atmósfera de Venus las temperaturas y presiones son mucho más benignas, e incluso parecidas a las de nuestro planeta, además de recibir una mayor energía solar para mantener los instrumentos en funcionamiento durante un tiempo más largo y sin el desgaste que suponen las condiciones superficiales.
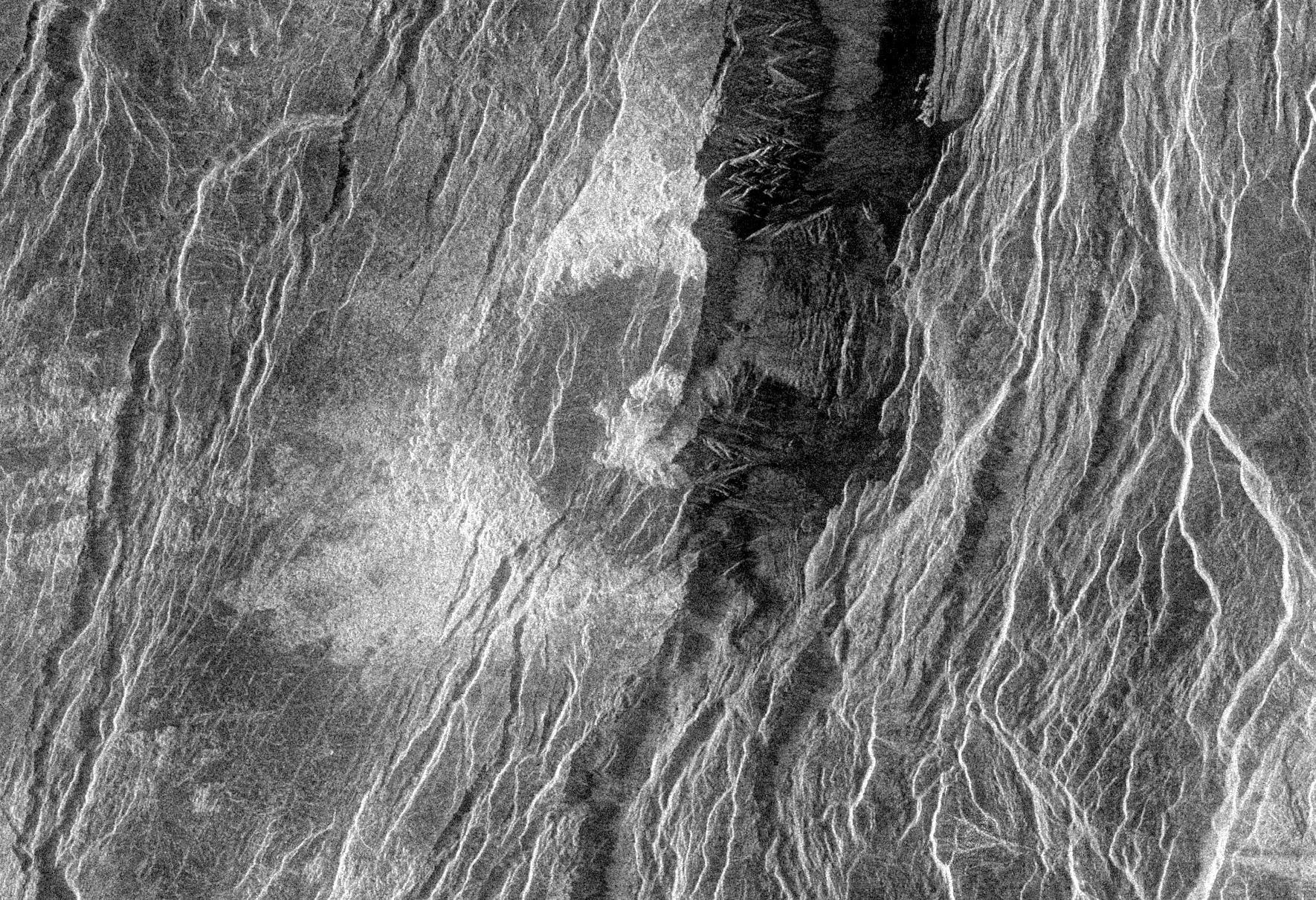 Si nos fijamos en el centro de la imagen veremos una forma circular muy característica, pero de la que solo reconocemos una mitad… es un cráter de impacto. Las formas lineales que vemos en la imagen probablemente sean sistemas de fallas que están transformando el relieve y que, si están activas hoy día, podrían causar también eventos sísmicos. Imagen cortesía de NASA/JPL.
Si nos fijamos en el centro de la imagen veremos una forma circular muy característica, pero de la que solo reconocemos una mitad… es un cráter de impacto. Las formas lineales que vemos en la imagen probablemente sean sistemas de fallas que están transformando el relieve y que, si están activas hoy día, podrían causar también eventos sísmicos. Imagen cortesía de NASA/JPL.Pero bueno, si un sismómetro mide la respuesta del suelo ante un terremoto, ¿qué medirían estos globos? Cuando ocurran los terremotos, las ondas sísmicas pueden acoplarse desde la superficie a la atmósfera y transformarse en ondas acústicas, algo que también ocurre en nuestro planeta, solo que en Venus hay una ventaja: debido a la densidad de la atmósfera, este acoplamiento podría ser unas 60 veces mayor, permitiendo detectar estas ondas de una manera más sencilla y a mayor distancia.
Si fuésemos capaces no solo de montar uno de estos globos, sino de mandar varios de manera simultánea, además podríamos localizar el punto de origen de los terremotos con mucha precisión, ayudándonos a conocer cómo se distribuye la actividad sísmica en el planeta y si hay zonas más activas que otras. Y, por cierto, también podríamos incluso detectar algunas erupciones volcánicas, puesto que las erupciones volcánicas -y sus explosiones- generan ondas perceptibles por este tipo de instrumentos.
Así que, mientras llegan las misiones que sean capaces de estudiar la actividad sísmica en el planeta Venus, nos tendremos que conformar con la llegada de las próximas misiones previstas para Venus: VERITAS, DAVINCI y EnVision, que deberían de lanzarse a principios de la década de 2030 y, al menos, empezar a despejar algunas de las dudas que tenemos de este planeta.
Referencias:
Aitta, A. «Venus’ Internal Structure, Temperature and Core Composition». Icarus 218, n.º 2 (abril de 2012): 967-74. doi: 10.1016/j.icarus.2012.01.007.
Krishnamoorthy, Siddharth, y Daniel C. Bowman. «A “Floatilla” of Airborne Seismometers for Venus». Geophysical Research Letters 50, n.º 2 (28 de enero de 2023): e2022GL100978. doi: 10.1029/2022GL100978.
Ksanfomaliti, L. V., V. M. Zubkova, N. A. Morozov, y E. V. Petrova. «Microseisms at the VENERA-13 and VENERA-14 Landing Sites». Soviet Astronomy Letters 8 (abril de 1982): 241.
Van Zelst, Iris, Julia S. Maia, Ana‐Catalina Plesa, Richard Ghail, y Moritz Spühler. «Estimates on the Possible Annual Seismicity of Venus». Journal of Geophysical Research: Planets 129, n.º 7 (julio de 2024): e2023JE008048. doi: 10.1029/2023JE008048.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Cuántos terremotos ocurren cada año en Venus? se ha escrito en Cuaderno de Cultura Científica.
Animaliak eta nekazalfitnessa
Udaberria heldu da eta goizean zer arropa jantzi asmatu ezinik gabiltzala, askori gorputza mugitzeko grina ere heldu zaigu. Eta hau lortzeko, landa eremuetan urtero-urtero modan jartzen den jarduera ere heldu da: agrofitness edo nekazalfitness delakoa. Bai, crossfita edota fitnessa bezalakoa, baina halterak erabili beharrean, aitzurra baliatuta.
 Irudia: baratzeak lantzeko garaian gaude, eta horrek ariketa fisikoa egitea (baratzearen tamainaren arabera, nahiko gogorra, gainera) eskatzen du. (Argazkia: Zoe Schaeffer – Unsplash lizentziapean. Iturria: Unsplash).
Irudia: baratzeak lantzeko garaian gaude, eta horrek ariketa fisikoa egitea (baratzearen tamainaren arabera, nahiko gogorra, gainera) eskatzen du. (Argazkia: Zoe Schaeffer – Unsplash lizentziapean. Iturria: Unsplash).Udaberriarekin batera hasten baita baratze gehienen (neguko baratzea ere badela ezin da ahaztu) denboraldia. Ariketa fisiko sutsua aitzurrarekin: sorbaldak, bizkarra, iskiotibialak, besoak… Nekazalfitnessa, igeriketa bezala, gorputz osoa lantzeko baliagarria da.
Gizakiaz haratagoEta pentsatuko duzue (edo ez, zeuen buruan ez bainago) gizakion kontua dela nekazaritza. Eta oker egongo zinatekete. Egia da aitzurra erabiltzen dugun bakarrak garela, hori bai. Baina zenbait animalia ere nekazaritzan ibiltzen dira.
Zein animalia pentsatzen duzue dela laboraria? Bota harrikada, ea. Bat baino gehiago dago, baina bat bereziki aipatzeko modukoa da. Gizakiak baino lehenago hasi baitzen nekazaritzan. Zein eta inurria. Bai, inurria. Eta aspalditik dabil: 50 milioi urte daramatza laborari lanetan. 50 milioi urte laborantzan. Eta artean traktorea asmatu barik.
Inurri hosto-ebakitzaileak dira, zehazki, nekazaritza baliatzen dutenak. Zelan moldatzen dira izaki ñimiño hauek landa zati bat landu eta inork laboreak ez lapurtzeko? Ba, lurpean eginda. Oso modu bitxian egiten dute, gainera. Jakingo duzuenez, eta ez badakizue hemen datua, lurpeko habiak egiten dituzte inurriok. Tira, ba, habi horietan garatzen dute haien eginkizun nekazaria.
Beno, egia esan habiatik kanpo hasten da prozesua. Kanpoan dauden landare batzuen hostoak ebakitzen dituzte (bai, hortik datorkie izena) eta hosto zati horiek habiara eramaten dituzte. Eta zer egiten dute orduan? Hosto zati horietan onddoak hazi. Inurriak eta haien larbak elikatzeko onddoak.
The last of us dela eta zeharka begiratzen diegu onddoei, baina, badirudi gure inurriek kontrolpean dutela kontua. Bakterio batzuk baitituzte tegumentuan (azalaren baliokidea inurrietan) eta bakterio horiek onddo-infekzioen aurkako substantziak sortzen dituzte. Aitzurrik eta traktorerik ez, baina sistema konplexua sortu dute 50 milioi urtean inurri hauek.
Ez dira nekazaritzan ibiltzen diren animalia bakarrak, dena den. Ezta lehenak ere. Hortxe ditugu kakalardoak. Ez kakalardo guztiak, noski. Kakalardo pilotagileek badakigu nekazaritzan baino gorotz artean ibiltzen direla. Bakoitzak berea. Badago nekazaritzan dabilen kakalardo mota bat, baina. Eta izen zoragarria du, gainera: anbrosia kakalardoa.
Hauek ere onddoak laboratzen dituzte; gainazalean kasu honetan, baina. Zuhaitzetan, hain zuzen. Enborra zulatu eta zuloan, haien arrautzekin batera, anbrosia onddoaren (bai, izen bera dute) esporak zabaltzen dituzte. Kasu honetan ere, bai helduek bai larbek jango dute onddoa.
Kakalardoen kasuen alde deigarriena, dena den, zera da: nekazaritza-praktika hauekin noiz hasi ziren. Izan ere, azken kalkuluen arabera, duela 100 milioi urte hasi ziren. Eta hauek ere lana errazago egingo duen lanabesik asmatu gabe.
Nekazalfitnessaren eraginaEta artikuluaren hasierari begira pentsatuko duzue, zer zerikusi demontre dute nekazalfitness delakoak eta orain arte animalia nekazarien inguruan kontatutakoak? Bat ere ez, aitortu behar dut gaitik pixka bat desbideratu naizela, baina bazkalosterako gai polita eman dizuet. Ez horregatik!
Orain bai, nekazalfitnessean buru-belarri sartzera goaz. Hasieran esan bezala, baratzeak lantzeko garaian gaude eta horrek ariketa fisikoa egitea (baratzearen tamainaren arabera, nahiko gogorra, gainera) eskatzen du. Nahiz eta kakalardoek eta inurriek ez bezala, lana errazteko tresnak asmatu ditugun.
Denboraldi honetan egiten den ariketa fisiko kantitatea kontuan izanik, pentsa liteke baratzeetan dabiltzanak sasoi-sasoian egongo direla udarako (eta hondartzarako). Baina ez. Edo ez du zertan, behintzat. Batzuk egongo dira eta beste batzuk ez.
Eta zelan da hau posible? Ariketa gehiago egiteak kaloria gehiago erretzea dakar eta, beraz, sasoia hobetzea, ezta? Ba… Ez da hain erraza. Kenketa erraz moduan azaldu ohi dugu metabolismoa: sartzen diren kaloriei gastatutakoak kendu. Kenketak balio positiboa badu (kontsumitzen ditugun kaloriak gastatzen ditugunak baino gehiago badira) pisua irabaziko dugu eta kenketak balio negatiboa badu, pisua galdu.
Eta zein izaten da kaloriak gastatzeko bidea? Ariketa fisikoa egitea. Baliteke harremana hain zuzena ez izatea, baina. Azken ikerketen arabera, ariketa gehiago egiteak ez ditu kaloria gehiago erretzen. Egunero ariketa fisikoa egiten dutenek eta astean aldizka ariketa egiten dutenek kaloria kopuru berbera erretzen dutela ikusi da.
Hiru hipotesi daude hau azaltzeko, hirurak ere frogatu gabe. Batetik, pentsatzen da ariketa gehiago egiten dutenek gehiago jaten dutela, nahiz eta ez konturatu. Horrek pisuan izango luke eragina, baina ez erretako kaloria kopuruan.
Bestetik, proposatu da ariketa gehiago egiten duen jendeak egunean zehar gutxiago mugituz berdintzen duela gastua. Baina kirolean egiten den kaloria-gastua handiegia da gainerako mugimenduak murriztuta berdintzeko.
Azkenik, gorputzak kaloria-gastua modulatzen duela dioen hipotesia dugu. Haren arabera, kaloria-errekuntza maila batetik gora, gorputza moldatu egiten da eta harekin batera, kalorien gastua.
Arrazoiak arrazoi, bat datoz ikerketak azkenaldian: pisua galtzearen eta irabaztearen kontuan dietak garrantzi handiagoa du ariketa fisikoak baino. Adi hemen: horrek ez du esan nahi ariketarik egin behar ez denik, e!
Ariketa ez da pisua kontrolatzeko tresna. Edo ez soilik horretarako. Onura andana dakarkigu aktibo izateak: osasun orokorra suspertzen du, mugikortasuna eta garunaren funtzioa hobetzen ditu eta egoera kroniko askoren arriskua murrizten du, besteak beste.
Ikusitakoak ikusita, nekazalfitnessaren aldeko aldarria dakart. Gure osasunerako oinarrizkoak diren bi alderdi uztartzen baititu: aktibo mantentzen gaitu eta, gainera, dieta osasungarri ezinbestekoak diren sasoiko barazkiak eskuratzea ahalbidetzen digu. Badakizue, crossfitaren eta nekazalfitnessaren artean erabaki behar baduzue…
Erreferentzia bibliografikoak:Juan Ignacio Pérez eta Miren Bego Urrutia (2017). Inurri laborariak, Zientzia Kaiera, 2017ko uztailaren 6a.
Juanma Gallego (2021). Kakalardo nekazarien lan isilak milioika urte ditu, Zientzia Kaiera, 2021eko uztailaren 19a.
Teal Burrell (2019). Why doing more exercise won’t help you burn more calories, New Scientist, 2019ko urtarrilaren 16a.
Egileaz:Ziortza Guezuraga (@zguer) kazetaria da eta Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko zabalkunde digitaleko arduraduna.
Jatorrizko artikulua Gaztezulo aldizkarian argitaratu zen 2023ko maiatzean, 250. zenbakian.

The post Animaliak eta nekazalfitnessa appeared first on Zientzia Kaiera.
La formación de la categoría conceptual en personas autistas
Los niños y las niñas neurodivergentes no percibirían los conceptos a través del lenguaje, de lo que se derivan dificultades para deducir que dos objetos que reciben el mismo nombre forman una categoría.
 Foto: Jan Antonin Kolar / Unsplash
Foto: Jan Antonin Kolar / Unsplash“La población infantil autista no espera que dos objetos, simplemente por el mero hecho de que compartan nombre, tengan propiedades comunes o sean el mismo tipo de objeto. No son sensibles a la categorización mediante el lenguaje que se les está ofreciendo”, indica Agustín Vicente, profesor Ikerbasque e investigador del grupo Lindy Lab de la UPV/EHU. “Si la población autista muestra dificultades para deducir que dos objetos que reciben el mismo nombre forman una categoría, pueden tender a generar conceptos que no coinciden con los del resto de niños y niñas y esto puede dar lugar a dificultades en la comunicación, entre otras cosas”, añade Vicente.
Las personas neurotípicas, las que se ajustan a los estándares de comportamiento cognitivo y comunicativo socialmente típicos, durante su infancia son sensibles al llamado efecto de etiquetaje lingüístico. Pongamos como ejemplo dos tipos de aspiradoras diferentes: “Si a un niño neurotípico le decimos que una Dyson y una Roomba son las dos aspiradoras, esperará que hagan lo mismo, en este caso, aspirar. Pero si no se lo decimos, y llamamos a una simplemente Dyson y a la otra Roomba, si nos ve aspirar con la Dyson, puede que no espere que también podemos aspirar con la Roomba”, explica Vicente. “Al asignarle una etiqueta lingüística, un nombre, se establece un vínculo entre las propiedades de ese objeto y la etiqueta asignada —añade Sergio Parrillas, investigador predoctoral del grupo Lindy Lab de la UPV/EHU—.
Al mostrarle un segundo objeto con esa misma etiqueta, independientemente de lo distinto o parecido que sea al primer objeto, el niño espera que haga la misma función, en este caso aspirar. Si, en cambio, se le presenta un objeto muy parecido, pero con una etiqueta o nombre distintos, no generaliza la función de aspirar al nuevo objeto, interpretando que pertenecen a categorías distintas”.
Por tanto, “compartir nombre es un criterio de categorización más poderoso que tener un aspecto similar. Este fenómeno es importante porque actúa como una fuente de adquisición de conceptos a través del lenguaje”, subraya el investigador de la UPV/EHU.
En niños y niñas neurotípicos esto ocurre desde los 10 meses, y el objetivo de este estudio ha sido conocer si la adquisición de conceptos a través del lenguaje también se produce en niños y niñas del espectro autista de entre 3 y 9 años. Los resultados apuntan a que, a diferencia de los niños y niñas neurotípicos, no se ha podido identificar una sensibilidad al efecto de etiquetaje en la población infantil autista.
El efecto de etiquetaje lingüístico es una importante fuente de adquisición de conceptos y podría predecir aspectos tan relevantes en el desarrollo del lenguaje como lo son la adquisición y la amplitud del vocabulario. Por eso, ambos investigadores de Lindy Lab remarcan la necesidad de seguir investigando la relación que hay entre el lenguaje y los conceptos en la mente autista. “Investigar por qué algunos niños y niñas que pertenecen al espectro autista tienen un vocabulario tan escaso y referencialmente impreciso podrá ayudar a que en el futuro se desarrollen programas de intervención para que puedan comunicarse mejor, con un vocabulario más amplio y organizado”, añaden Sergio Parrilas y Agustin Vicente.
Referencia:
Sergio Parrillas-Manchón, Elena Castroviejo, José V Hernández-Conde, Ekaine Rodriguez Armendariz, Agustin Vicente (2024) Testing the Labeling Effect in Autistic Children J Autism Dev Disord doi: 10.1007/s10803-024-06388-1
Nota:
Este estudio está basado en el Trabajo Fin de Máster que ha elaborado Sergio Parrillas en el laboratorio Lindy Lab que forma parte del grupo de investigación Hizkuntzalaritza Teorikorako Taldea (HiTT) de la UPV/EHU y con el cual ganó el V Premio Izaskun Heras Prado. Sergio Parrillas es autista y actualmente tiene un contrato predoctoral del Gobierno Vasco bajo la dirección del profesor Ikerbasque Agustín Vicente (UPV/EHU) y la investigadora Irene de la Cruz Pavía (U. Deusto).
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La formación de la categoría conceptual en personas autistas se ha escrito en Cuaderno de Cultura Científica.
Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- …
- hurrengoa ›
- azkena »

