La isla Pitcairn y el motín de la ‘Bounty’
Bounty = Generosidad
 HMS Bounty II, réplica de 1960 del HMS Bounty original, en una imagen de 2010. Este barco se hundió frente a las costas de Carolina del Norte en 2012 a consecuencia del huracán Sandy.
HMS Bounty II, réplica de 1960 del HMS Bounty original, en una imagen de 2010. Este barco se hundió frente a las costas de Carolina del Norte en 2012 a consecuencia del huracán Sandy.El 26 de octubre de 1788, el barco Bounty de Su Majestad llegó a Tahití. El capitán era el Teniente de la Armada Real William Bligh, experimentado y capaz de terminar con éxito las misiones que le encomendaban. Era de los mandos que había acompañado a James Cook en su tercera expedición. La Bounty había partido del puerto de Spithead, en Inglaterra, frente a Southampton, el 23 de diciembre de 1787. Tenía 215 toneladas, construido en 1784, con 28 metros de largo y 7.6 metros de ancho. La tripulación la componían 46 hombres. Era un barco de carga que compró la Armada Real para el viaje a Tahití en una expedición, promovida por la Royal Society, con el objetivo de recoger plantones del árbol del pan en Tahití y llevarlos al Caribe para replantarlos, iniciar su cultivo y cosechar un alimento barato para los miles de esclavos que se traían de África a las plantaciones de las Antillas. Contaré esta historia con la ayuda del extraordinario relato periodístico, titulado “Los amotinados de la Bounty”, que Julio Verne publicó en 1879.
El árbol del pan, de nombre científico Artocarpus altilis, procede de antepasados del mismo género de Filipinas y las islas Molucas, al sur de Filipinas y que, ahora, pertenecen a Indonesia. Su origen está en el oeste del Pacífico. Las migraciones humanas, de oeste a este, por las islas del Pacífico, llevaron el árbol del pan a Oceanía y evolucionaron, por cultivo y selección, en la especie, Artocarpus altilis, que conocemos ahora. A partir del siglo XVII, los navegantes europeos lo llevaron a todas las zonas tropicales del planeta y, especialmente, a las Antillas.
 Hojas y fruto del árbol del pan. Foto: Wikimedia Commons
Hojas y fruto del árbol del pan. Foto: Wikimedia CommonsSeis meses permaneció la Bounty en la isla de Matavai, en el grupo de Tahití, mientras recolectaban los plantones del árbol del pan. Allí, la tripulación encontró amigos y parejas entre los tahitianos. Cargaron 1015 ejemplares del árbol del pan hasta llenar la bodega.
Cuando Bligh ordenó partir para llevar la carga al Caribe, la tripulación no quería hacerlo, estaban a gusto en Tahití. Pero partieron, y el 28 de abril de 1789, con la Bounty en el mar, camino al Caribe, estalló el motín a bordo. Fletcher Christian, segundo de a bordo, junto a 18 miembros de la tripulación, se amotinó contra el capitán Bligh. Abandonaron al capitán y a los que no se amotinaron en una barca y, después de 47 días de viaje y 6500 kilómetros, llegaron a Timor, fueron rescatados y regresaron a Inglaterra.
 Isla Pitcairn. Foto: Wikimedia Commons
Isla Pitcairn. Foto: Wikimedia CommonsLos amotinados eran 29 que, bajo el mando de Fletcher Christian, partieron en la Bounty y regresaron a Tahiti. Pronto empezaron los problemas entre los amotinados. Unos querían quedarse en Tahití y otros huir y esconderse en alguna isla del Pacífico. Christian, con nueve amotinados, seis tahitianos y 13 tahitianas más una niña, cargaron el barco con plantas y animales necesarios para instalarse en otra isla y marcharon de noche de Tahití. Los tahitianos fueron invitados a una fiesta en el barco que zarpó durante la noche, y los amotinados los raptaron. Su intención era llegar a la isla Pitcairn y refugiarse en ella.
Al llegar a la isla, el 15 de enero de 1790, quemaron el barco para borrar su rastro y que no les encontrase la vengativa y justiciera Armada Real. Todavía se ven los restos de la Bounty en la costa de la isla y los isleños celebran cada 23 de enero el aniversario quemando una maqueta de pequeño tamaño del barco.
 Bounty Bay, en la isla Pitcairn, a donde llegó la Bounty y fue quemada.
Bounty Bay, en la isla Pitcairn, a donde llegó la Bounty y fue quemada.Para 1794 quedaban cuatro de los amotinados. Habían continuado las peleas entre ellos, sobre todo por las mujeres de Tahití que les acompañaban. Incluso Christian fue acuchillado por un tahitiano en una pelea. Fueron años de alcohol, violaciones y asesinatos, y para 1800 solo quedaban dos amotinados, Young y Adams, y el primero murió de una ataque de asma. En la isla sobrevivió Adams como único hombre, con seis mujeres tahitianas y unos veinte niños que llevaban los apellidos de los amotinados. Todavía los utilizan los habitantes actuales de la Isla Pitcairn que descienden de aquellos marineros amotinados .
John Adams recuperó una Biblia de los libros que iban en la Bounty, volvió a la religión y a las buenas costumbres, llegó la paz, la isla prosperó y la población creció. Unos años más tarde, la Armada Real los encontró.
Era 1814, décadas después del motín, cuando dos barcos de guerra ingleses, el Briton y el Tagus, a las órdenes del capitán Thomas Staines, navegando por el centro del Pacífico Sur, encontraron una pequeña isla volcánica, con 9.6 kilómetros de circunferencia, unos 4 kilómetros de longitud, 4.35 kilómetros cuadrados de superficie y un cono volcánico que, en su punto más alto, alcanzaba los 300 metros. La había descrito años atrás el explorador Philip Cateret, que había descubierto la isla el 3 de julio de 1767. Fue bautizada como Pitcairn en recuerdo de uno de los marineros que primero habían desembarcado en ella. Era una isla montañosa, pequeña, volcánica y con unas costas escarpadas, casi sin playas ni puertos accesibles. Ahora es el último Territorio Británico de Ultramar en el Pacífico. Por cierto, había una copia de los diarios de viaje de Cateret en la Bounty y sirvió de guía a Fletcher Christian para encontrar la isla y refugiarse en ella.
El Briton y el Tagus fueron recibidos por una pequeña embarcación con dos hombres que se presentaron como descendientes de los amotinados de la Bounty. Para 1856 los descendientes de los amotinados eran 196 y el gobierno británico consideró que la isla no tenía suficientes recursos para mantenerlos y los trasladó a la isla Norfolk, más cercana a Nueva Zelanda y Australia y a unos 6000 kilómetros al oeste de la isla Pitcairn. Quedó deshabitada pero, un par de años más tarde, 16 de los trasladados regresaron y, en otros cinco años, lo hicieron 27 más. En la actualidad, en la isla Norfolk hay 1600 residentes permanentes y, según el censo de 2006, la mitad descienden de los amotinados que no volvieron a Pitcairn.
Los que quedaron en Norfolk, años después, en 2015, sirvieron a Miles Benton y su grupo, de la Universidad Tecnológica de Queensland, en Australia, para estudiar su ADN. Lo analizaron en las mitocondrias, heredado por vía materna, y en el cromosoma Y del núcleo, que solo se encuentra en los hombres.
 Habitantes de la isla Pitcairn en 1916
Habitantes de la isla Pitcairn en 1916Los resultados confirman lo que había supuesto Miles Benton, según la historia que conocía de los habitantes de la isla Pitcairn: el ADN mitocondrial es de linaje polinésico, de las únicas mujeres que llegaron a la isla, las tahitianas que secuestraron Fletcher Christian y sus hombres; y el cromosoma Y tiene su origen en Europa ya que viene de los marineros europeos amotinados en la Bounty. Dos siglos después y once generaciones más tarde, el ADN confirma el origen genético de los descendientes de la Bounty. Más de siglo y medio después, en los primeros años del siglo XXI, en la isla Pitcairn, en 2014, quedan 56 habitantes.
El motín de la Bounty y los hechos y aventuras que le siguieron son populares y han aparecido, según Maria Amoamo, de la Universidad de Otago, en Nueva Zelanda, en unos 1200 libros, más de 3200 artículos en periódicos y revistas, en documentales e, incluso y lo que más difusión le ha dado, en tres superproducciones de Hollywood con mucho presupuesto y grande estrellas como protagonistas. Es Maria Amoamo la mayor especialista sobre la población actual de la isla Pitcairn. Vivió en la isla entre 2008 y 2013, más o menos dos años y medio, acompañando a su marido, médico de profesión y contratado por el gobierno británico para cubrir el servicio sanitario en la isla. Durante su estancia, Maria Amoamo contactó con la población, aprendió de su modo de vida y tomó numerosas notas y fotografías de las actividades cotidianas en la isla. Con ello completó su proyecto postdoctoral en la Universidad de Otago.
El futuro de la isla y de sus habitantes se basa, en la actualidad, en el turismo y en los cruceros que llegan para visitarla. Para atraer visitantes tiene su historia, tan conocida y propagada, sobre todo por Hollywood, una historia que crea morbo y lleva a los turistas a Pitcairn a conocer a sus habitantes, descendientes de los amotinados de la Bounty, y, también, tiene la naturaleza, aun poco conocida y todavía menos publicitada. Como ejemplo sirve el estudio de Alan Friedlander y su grupo, de la Sociedad Geográfica Nacional de Estados Unidos, en las cuatro islas del grupo Pitcairn: Ducie, Henderson, Oeno y Pitcairn. Han recogido animales y algas en 97 lugares de las costas de estas islas entre 5 y 30 metros de profundidad, y han explorado con cámaras de video 21 puntos entre 78 y 1585 metros.
Los resultados son espectaculares, con nuevas citas de especies conocidas de otras zonas del Pacífico y algunas especies nuevas todavía sin describir. Los autores proponen que, por su gran biodiversidad y la rareza de las especies encontradas, deben protegerse las costas de la todas las islas del grupo.
Pero ya en 1995, T.G. Benton, de la Universidad de Cambridge, comparó la basura de las playas de las islas Ducie y Oeno, del grupo Pitcairn y deshabitadas, con la basura de la playa Inch Straud, en el sudoeste de Irlanda. Y, sorprendentemente, no encontró mucha diferencia. En el Pacífico hay botellas de cristal y de plástico, y boyas de pesca, y en Irlanda abundan los envoltorios de chucherías y las bolsas de plástico. Como ejemplo, de las 130 botellas de vidrio encontradas en las playas de la isla Ducie, 41 venían de Japón, 11 de Escocia y 9 de Gran Bretaña, y la mayoría eran de whisky.
 Basura en Pitcairn. Fuente: newshub.co.nz
Basura en Pitcairn. Fuente: newshub.co.nzY 20 años más tarde, como veíamos hace unas semanas, es evidente que la contaminación en nuestro planeta ya es un problema global, sin límites geográficos, y llega a lugares tan apartados como estas solitarias islas del centro del Pacífico. Fueron Jennifer Lavers y Alexander Bond, quienes visitaron la isla Henderson del grupo Pitcairn, deshabitada y conocida como un paraíso para las aves. Pero, cuantificaron los plásticos de sus playas y se encontraron que era uno de los lugares con más plásticos de todos los mares del planeta. En las playas, había de 20 a 670 fragmentos de plástico por metro cuadrado, y en los fondos frente a la costa, el número era de 53 a 4500 fragmentos por metro cuadrado.
Cada día llegan a la isla, arrastrados por las corrientes oceánicas, entre 17 y 268 nuevos fragmentos. Y, no hay que olvidar, que es una isla deshabitada, es decir, todo el plástico viene del exterior y, además, de lugares muy lejanos, algunos a miles de kilómetros. Los autores detectan que los restos de plástico relacionados con la pesca llegan desde China. Japón y Chile.
Para terminar, años más tarde del famoso motín, el entonces Vicealmirante William Bligh, al mando del Assisstance, partió de nuevo hacia el Pacífico para llevar el árbol del pan a las Antillas, y lo consiguió. En la actualidad, el árbol del pan es un alimento barato y popular en el Caribe.
Referencias:
Amoamo, M. 2016. Pitcairn Island: Heritage of Bounty descendants. Australian Folklore 31: 155-171.
Amoamo, M. 2016. Pitcairn and the Bounty story. En “Tourist Pacific Cultures”, p. 73-87. Ed. por K. Alexeyeff & J. Taylor. ANU Press. Canberra, Australia.
Amoamo, M. 2017. Re-imaging Pitcairn Island. Shima 11: 80-101.
Benton, M.C. et al. 2015. “Mutiny on the Bounty”: the genetic history of Norfolk Island reveals extreme gender biased admixture. Investigative Genetics DOI: 10.1186/s13323-015-0028-9
Benton, T.G. 1995. From castaways to throwaways: marine litter in the Pitcairn Islands. Biological Journal of the Linnean Society 56: 415-422.
Bligh, W. 2015 (1838). El motín de la Bounty (Diarios del capitán Bligh). ePub r1.3. Titivillus. 13.04.15.
Diamond, J. 2006. Colapso. Random House Mondadori. Barcelona. 457 pp.
Friedlander, A.M. et al. 2014. The real Bounty: Marine diversity in the Pitcairn Islands. PLOS ONE 9: e100142
Gibbs, M. & D. Roe. 2016. Do you bring your gods with you or Do you find them there waiting? Reconsidering the 1790 Polynesian colonization of Pitcairn Island. Australian Folklore 31: 173-191.
González, D. 2011. Pitcairn, la isla de la endogamia. Blog Fronteras. 17 octubre.
Lavers, J.L. & A.L. Bond. 2017. Exceptional and rapid accumulation of anthropogenic debris in the one of the world’s most remote and pristine islands. Proceedings of the National Academy of Sciences USA DOI: 10.1073/pnas1619818114
Verne, J. 2006 (1879). Los amotinados de la Bounty. Biblioteca Virtual Universal. Ed. del Cardo. 14 pp.
Wikipedia. 2017. Pitcairn Island. 5 December.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo La isla Pitcairn y el motín de la ‘Bounty’ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Particiones: Hardy y Ramanujan
Una partición de un número entero positivo n es una forma de descomponerlo como suma de enteros positivos. El orden de los sumandos no es relevante, por lo que normalmente se escriben de mayor al menor. Por ejemplo, las particiones del número 4 son:
4 = 2+1+1 = 3+1 = 2+2 = 1+1+1+1.
Estas particiones se suelen visualizar a través de diagramas, como los diagramas de Ferrers, que deben su nombre al matemático Norman Macleod Ferrers.
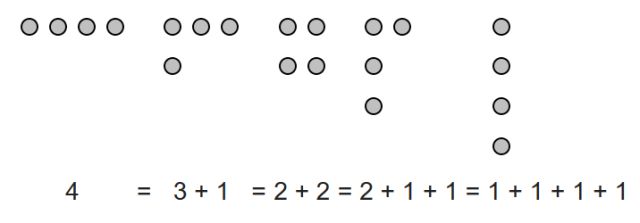 Diagrama de Ferrers del número 4. Imagen: Wikimedia Commons.
Diagrama de Ferrers del número 4. Imagen: Wikimedia Commons.
La teoría de particiones de números se utiliza en el estudio de polinomios simétricos, del grupo simétrico y en teoría de representación de grupos, entre otros.
La función de partición >p>(n) indica el número de posibles particiones del entero n; por ejemplo, p(4)=5. El valor de p(n) crece muy rápidamente al aumentar n. Por ejemplo, p(100)=190.569.292 y p(1000)=24.061.467.864.032.622.473.692.149.727.991.
 Godfrey Harold Hardy y Srinivasa Ramanujan. Imágenes: Wikimedia Commons.
Godfrey Harold Hardy y Srinivasa Ramanujan. Imágenes: Wikimedia Commons.
Matemáticos de la talla de Godfrey Harold Hardy (1877-1947) y Srinivasa Ramanujan (1887-1920) trabajaron en el tema de las particiones de números, obteniendo algunas expresiones asintóticas para la función partición. Y Partition es precisamente el título de una obra de teatro del dramaturgo Ira Hauptman con los dos geniales matemáticos antes citados como protagonistas.
El título Partition se refiere tanto a la teoría matemática de las particiones de números como a las particiones –en el sentido de antagonismo– de temperamento, de cultura y de método matemático que distanciaron a los dos personajes.
La obra comienza en 1918, con una escena en Scotland Yard, donde un oficial de policía interroga a Ramanujan. El joven matemático ha intentado suicidarse tirándose a las vías del tren; ha bebido sin darse cuenta Ovaltine que contiene rastros de productos animales y, por lo tanto, piensa que ‘está contaminado’. Hardy consigue que no le encarcelen declarando ante la policía que Ramanujan es miembro de la Royal Society.
La siguiente escena tiene lugar cinco años antes. Hardy y Alfred Billington –un colega ¿ficticio? de Hardy de la Universidad de Cambridge– discuten sobre una carta que el matemático británico acaba de recibir. Es de Ramanujan, un joven autodidacta indio que, junto a la misiva, le ha enviado algunos cuadernos que contienen extraordinarias fórmulas matemáticas. Intrigado por los brillantes resultados de Ramanujan, Hardy decide invitarle a Cambridge para conocer los detalles de su método de trabajo.
Ramanujan, un simple empleado de correos perteneciente a una de las castas más bajas de la India y sin formación universitaria, acepta la invitación y viaja a Inglaterra desde Madrás.
 Cartel de una de las representaciones de Partition. Imagen: University of California, Berkeley.
Cartel de una de las representaciones de Partition. Imagen: University of California, Berkeley.
Nada más conocerse, Hardy y Ramanujan perciben el abismo que los separa. El británico es ateo, seguro de sí mismo, independiente, fiel a la lógica racional y tenaz defensor del método deductivo. Por el contrario, el joven indio es religioso, tímido, leal a su intuición y mantiene que sus resultados matemáticos le son concedidos por la diosa Namagiri durante el sueño.
Hardy intenta inculcar a Ramanujan el rigor científico basado en las demostraciones; quiere hacer del él un ‘matemático completo’. Pero el genio indio no consigue entender lo que el profesor quiere explicarle; Ramanujan sabe que sus fórmulas son ciertas porque Namagiri se las dicta en sueños. Hardy intenta convencer al joven matemático de la necesidad de demostrar sus resultados para ratificarlos. Pero Ramanujan está convencido de que las matemáticas se descubren, en contra de la opinión del profesor que asegura que se deducen.
En Partition, Hardy propone a Ramanujan abordar la solución del Último Teorema de Fermat –es pura ficción, nunca trabajaron en este tema–. El joven se obsesiona con este problema y pide ayuda a Namagiri, quien conversa con el espectro de Pierre Fermat para complacer a su protegido. Fermat confiesa a la diosa que no recuerda la demostración de su teorema; de hecho reconoce que ni siquiera es consciente de haber escrito alguna vez una prueba…
La guerra estalla en Europa. Hardy deja en un segundo plano las matemáticas para dedicarse a la política. Ramanujan, desvalido, se obsesiona con el problema de Fermat y acaba enfermando. Al poco tiempo, ya en su país, muere afectado de una tuberculosis.
La obra finaliza con un emotivo discurso de Hardy ante los miembros de la London Mathematical Society sobre la figura de su admirado, y ya desaparecido, Ramanujan.
Por cierto, casi al final de la obra, Hardy visita a Ramanujan en el hospital y se alude al famoso número de Hardy-Ramanujan: el profesor comenta al joven que ha llegado al sanatorio en el taxi número 1729; inmediatamente Ramanujan advierte que 1729 es el menor entero positivo que puede expresarse como una suma de dos cubos de dos maneras diferentes (1729=103+93=123+13).
Referencias
-
Ira Hauptman, Partition, Libreto de la obra (puede adquirirse en Playscripts Inc.)
-
Kenneth A. Ribet,Theater Review: a Play by Ira Hauptman, Notices AMS Vol 50, núm. 11, 1407-1408, diciembre 2003.
-
Marta Macho Stadler, Partición, de Ira Hauptman, DivulgaMAT, 2007
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Particiones: Hardy y Ramanujan se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema del pollo picante (o sobre particiones convexas equitativas)
- Pál Turán: teoría de grafos y fábricas de ladrillos
- Uno, dos, muchos
Los espectros de absorción de los gases
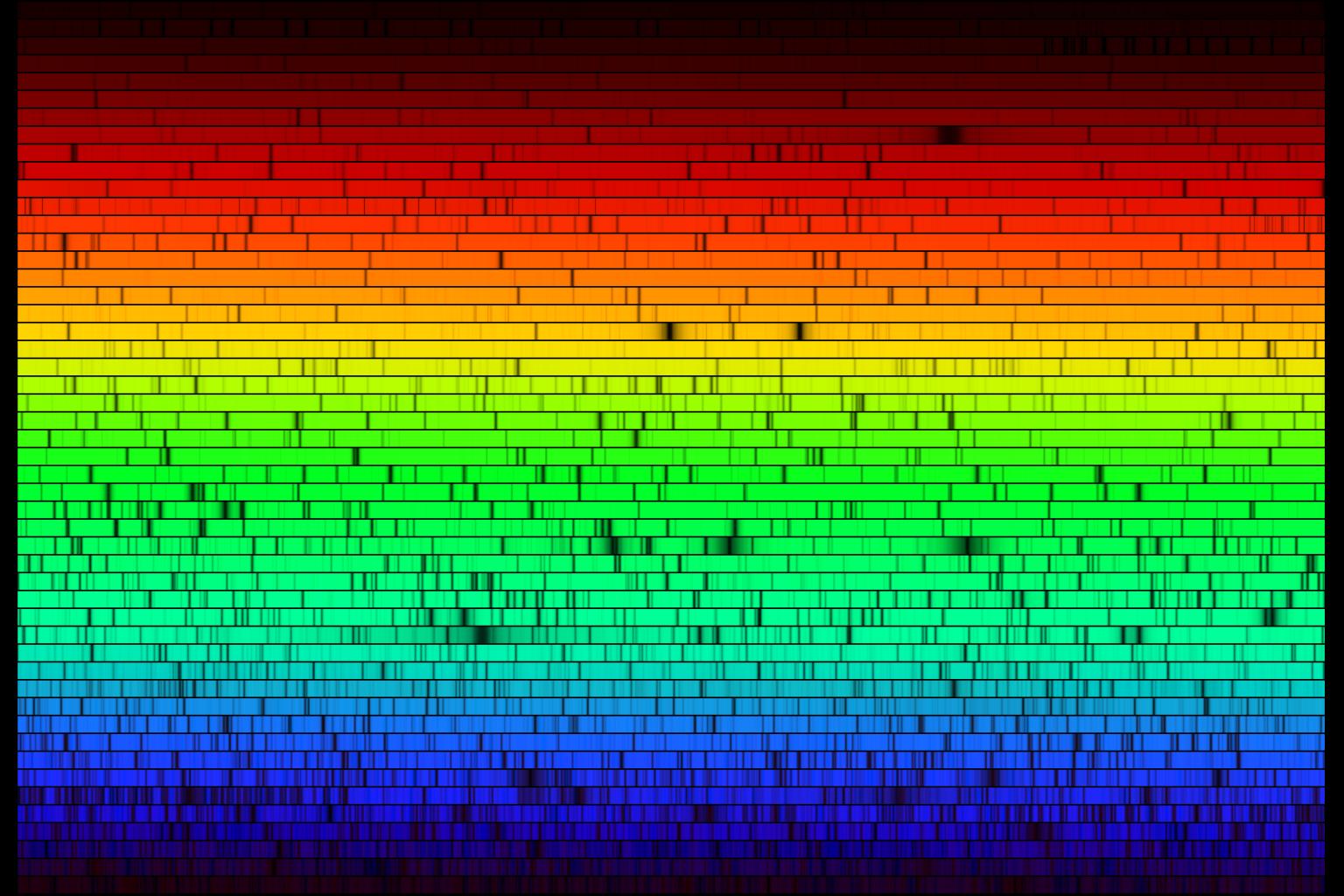 Los muchos cientos de líneas de absorción del espectro solar. Fuente: NOAO
Los muchos cientos de líneas de absorción del espectro solar. Fuente: NOAOEn 1802, William Wollaston vio en el espectro de la luz solar algo que antes se había pasado por alto. Wollaston notó un conjunto de siete líneas [1] oscuras, muy definidas, espaciadas irregularmente, a lo largo del espectro solar continuo. No entendía por qué estaban allí y no investigó más.
Una docena de años después, Joseph von Fraunhofer, utilizando mejores instrumentos, detectó muchos cientos de esas líneas oscuras. A las líneas oscuras más prominentes, von Fraunhofer asignó las letras A, B, C, etc. Estas líneas oscuras se pueden ver fácilmente en el espectro del Sol incluso con espectroscopios modernos bastante simples. Las letras A, B, C,. . . todavía se usan para identificarlas. En los espectros de varias estrellas brillantes von Fraunhofer también encontró líneas oscuras similares. Muchas, pero no todas, de estas líneas estaban en las mismas posiciones que las del espectro solar. Todos estos espectros se conocen como espectros de líneas oscuras o espectros de absorción. [2]
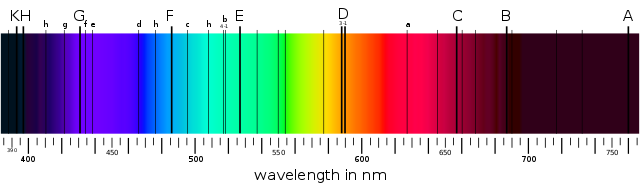 Espectro solar en el que se aprecian las líneas principales de von Fraunhofer. Fuente: Wikimedia Commons
Espectro solar en el que se aprecian las líneas principales de von Fraunhofer. Fuente: Wikimedia CommonsEn 1859, Kirchhoff hizo algunas observaciones clave que condujeron a una mejor comprensión tanto de los espectros de los gases, tanto de los de absorción como los de emisión. Ya se sabía que las dos líneas amarillas prominentes en el espectro de emisión del vapor de sodio calentado tenían las mismas longitudes de onda que dos líneas oscuras prominentes vecinas en el espectro solar [3]. También se sabía que la luz emitida por un sólido forma un espectro perfectamente continuo que no muestra líneas oscuras. Esta luz, que contiene todos los colores, es una luz blanca. Kirchhoff hizo algunos experimentos con ella. La luz blanca primero pasó a través de un vapor de sodio a temperatura baja y el resultado por un prisma. El espectro producido mostró el patrón de arco iris esperado, pero tenía dos líneas oscuras prominentes en el mismo lugar en el espectro que las líneas D del espectro del Sol. Por lo tanto, era razonable concluir que la luz del Sol también estaba pasando a través de una masa de gas de sodio. Esta fue la primera prueba de la composición química de la envoltura de gas alrededor del Sol.
El experimento de Kirchhoff se repitió con varios otros gases relativamente fríos, colocados entre un sólido brillante y el prisma. Cada gas produce su propio conjunto característico de líneas oscuras. Evidentemente, cada gas absorbe de alguna manera la luz de ciertas longitudes de onda de la luz que pasa. Además, Kirchhoff mostró que la longitud de onda de cada línea de absorción coincide con la longitud de onda de una línea brillante en el espectro de emisión del mismo gas [4]. La conclusión es que un gas puede absorber solo la luz de esas longitudes de onda que, cuando se excita, puede emitir.
Cada una de las diversas líneas de von Fraunhofer en los espectros del Sol y otras estrellas se ha identificado en el laboratorio como correspondiente a la acción de algún gas. De esta manera, se ha determinado toda la composición química de la región exterior del Sol y otras estrellas. Esto es realmente impresionante desde varios puntos de vista. Primero, es sorprendente que la comunidad científica pueda conocer la composición química de objetos a distancias inimaginables, algo que hasta ese momento, casi por definición, se creía imposible. Es aún más sorprendente que los sustancias químicas fuera de la Tierra resulten ser las mismas que las de la Tierra [5][6]. Finalmente, este resultado lleva a una conclusión sorprendente: los procesos físicos que causan la absorción de luz en el átomo deben ser los mismos en las estrellas y en la Tierra. [7]
Notas:
[1] Ya explicamos aquí (nota 3) por qué son líneas.
[2] Un momento. ¿Espectros de absorción en algo que emite luz? ¿Eso como va a ser? Ello se debe a que las estrellas tienen capas y parte de la luz emitida por las interiores es absorbida por la más externa. Brutamente, las líneas de los espectros de absorción de las estrellas nos dicen qué composición tiene esta capa externa, como explicamos a continuación.
[3] A estas líneas oscuras del espectro solar von Fraunhofer les había asignado la letra D.
[4] Ojo. La recíproca no es cierta, esto es, no todas las líneas de emisión están representadas en el espectro de absorción. Pronto veremos por qué.
[5] Newton asume que esto es así pero sin pruebas, con todo lo que ello supone.
[6] Esto es así porque el espectro más complejo de una estrella puede reproducirse empleando los elementos químicos disponibles en un laboratorio terrícola.
[7] Galileo y Newton asumieron que la física terrestre y la celeste obedecen las mismas leyes. Se había comprobado a nivel macroscópico; he aquí la prueba a nivel microscópico.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Los espectros de absorción de los gases se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los espectros de emisión de los gases
- Computación cognitiva de espectros infrarrojos
- Absorción del alimento
No era tan fácil: wifi y cáncer
 La radiación cancerígena no es la wifi, sino la ultravioleta del Sol. Foto: Bernard Hermant / Unsplash
La radiación cancerígena no es la wifi, sino la ultravioleta del Sol. Foto: Bernard Hermant / UnsplashNos habréis oído miles de veces decir que las radiaciones electromagnéticas de baja frecuencia, como las ondas de radio, las que se usan para telefonía o la WIFI no son cancerígenas porque no son ionizantes. Lo decimos y lo repetimos mil veces, luchando contra los que propagan el miedo (algunos interesadamente) a las antenas, los cables de alta tensión, etc. En ocasiones se nos escapa un tono áspero, impaciente, como si se tratara de un asunto evidente o sencillo de entender. Pero no lo es, ni mucho menos.
Ser una radiación ionizante quiere decir que al interaccionar con la materia será capaz de “arrancar” electrones a esos átomos, produciendo cambios. Por ejemplo, en la molécula de ADN podrían inducir mutaciones que llevasen a transformar células en cancerosas, o si se tratase de embriones podrían crear malformaciones o hacerlos inviables.
Vayamos por partes.
Los saltos electrónicos
Ya sabéis que los electrones se sitúan en los átomos en niveles de energía discretos, separados, que pueden tener sólo ciertos valores y no otros. Ejemplo inventado: en el átomo de nosécuantitos los niveles de energía serán 1, 3, 7, 12 (todos los números a partir de aquí son inventados para que se pueda seguir mejor la explicación). De esta forma un electrón que esté en el nivel de energía 3 necesita cuatro unidades de energía para pasar al nivel siguiente. Si no recibe esa energía, no podrá subir de nivel.
Los cuantos
Con la llegada de la física cuántica descubrimos que la energía se transmitía en “paquetes”, en cuantos, y que esos paquetes dependían de la frecuencia de la radiación (en la luz visible sería el color, menos frecuencia para el rojo y más para el azul, con valores intermedios en todo el arcoiris). De esta forma los paquetes de luz roja, por ejemplo, podrían tener una energía de una unidad, en cambio los de luz azul de dos unidades. La luz se compone de esos cuantos, de esos paquetitos, cuando tenemos más intensidad de luz es porque mandamos más paquetes, no que esos paquetes tengan más energía cada uno, os recuerdo que la energía de cada paquete solo depende de la frecuencia de la luz.
La luz y la materia
¿Qué pasa cuando la luz llega a la materia? Pues que los electrones pueden absorber esos cuantos de luz, esos fotones, y ascender de nivel. Si volvemos al ejemplo que pusimos, tenemos un electrón en el nivel de energía correspondiente a 3 unidades y, para saltar al nivel de 7 unidades, necesita de 4 unidades de energía. Si iluminamos con luz roja (dijimos que cada fotón tenía una unidad) no será suficiente la absorción de un fotón para saltar de nivel, así que el salto no se produce. Esa luz no se absorberá, el electrón no puede ir “guardándose” fotones). Si iluminamos con luz azul tampoco (dijimos que cada fotón azul tenía dos unidades). Así que será necesario iluminar con una luz de una frecuencia suficientemente alta para que esos fotones tengan la energía suficiente para hacer que el electrón cambie de estado. Quizá ocurra con luz ultravioleta, rayos X, etc.
Sería como si le diéramos pequeñas escaleras a alguien que tiene que escalar un muro, pero de insuficiente altura. Por más escaleras pequeñas que le demos (y que no puede empalmar) será imposible que suba el muro. De la misma manera, por más intensa que sea la luz roja con que iluminemos (por más numerosos que sean los paquetes) será imposible que el electrón cambie de nivel energético.
El efecto fotoeléctrico
Este fenómeno se observó en el llamado efecto fotoeléctrico: al iluminar una sustancia se producía una corriente eléctrica (se “arrancaban” electrones), pero si la frecuencia bajaba de cierto valor (frecuencia de corte) dejaba de producirse la corriente. Esto llamaba mucho la atención, porque se entendía que si la energía de a luz que iluminaba era suficientemente alta el efecto debía producirse. Tuvo que ser con la llegada de la teoría de los cuantos que se diera la explicación correcta al fenómeno, y tuvo que ser Einstein el que resolviera el entuerto, quien posteriormente recibiría el premio Nobel por esta contribución (y no por la Teoría de la Relatividad, como a veces se cree).
No era tan fácil
Como veis, no era tan fácil eso de que las radiaciones de baja frecuencia no son ionizantes. Hemos tenido que tirar de la teoría cuántica y del amigo Einstein para tener una explicación científicamente satisfactoria del asunto. Esto es algo que no habría que perder de vista cuando contamos con aspereza a profanos que las radiaciones de baja frecuencia no son ionizantes.
Demostraciones que quizá no demuestran lo suficiente
Un amigo me contaba un día que para ilustrar esto le gusta un experimento que es bastante curioso. Si iluminas un cartel de esos de “Extintor”, “Salida”, con una luz de baja frecuencia, por ejemplo un puntero láser rojo, no dejan casi “huella brillante”, pero si lo iluminas con luz azul, una vez que apagas la luz, queda como una “pintura de luz” por donde pasaste. Señal de que, a pesar de la intensidad total de la luz, hay paquetitos de más energía y paquetitos de menos energía. Si queréis hacerlo, probadlo primero, porque no funciona con todos los tipos de carteles.
El problema es que mi amigo decía que con la luz de baja frecuencia “casi” no quedaba rastro… y este “casi” es un problema. La frecuencia de corte es un corte abrupto, no hay efecto a partir de ahí. Si hubiera un efecto pequeño, este podría ser apreciable si aumentásemos la intensidad de la luz, si algunos paquetitos consiguen funcionar, podríamos mandar muchos y montar un buen lío… Pero se supone que lo que queríamos ilustrar es que en frecuencias bajas NO hay efecto.
Medidas epidemiológicas
Aunque no sería necesario buscar el efecto de algo que no tiene sentido con los conocimientos asentados, no cuesta mucho (más que personal, tiempo y dinero) llevarlo a cabo, y como hay gente interesada y preocupada por esto, pues se ha hecho. Las conclusiones mirando todos los estudios y teniendo en cuenta que se hayan hecho de forma adecuada (sin problemas metodológicos, p.ej.) es que no hay tal efecto de un aumento de cáncer en personas sometidas a intensidades comunes de radiaciones de baja frecuencia. Si lo hubiera, nos habría tocado buscar si era una correlación espúrea, si necesitábamos modificar nuestras fórmulas… pero no es así.
Así que ni el conocimiento sobre radiación, ni los estudios en población muestran que estar en un edificio donde hay wifi, o usar teléfonos móviles, vaya a aumentar tus probabilidades de tener cáncer.
No, no era tan fácil
¿Era evidente? ¿Era fácil? ¿Tenéis conocimientos de cierta profundidad sobre electromagnetismo y cuántica, interacción radiación-materia? Bueno, incluso si así fuera, ¿hemos de tratar con altivez a quien no los tiene? Yo diría que no.
Sigamos informando, expliquemos (aquí tenéis una manera de cómo hacerlo), luchemos contra los que se aprovechan del miedo de los poco informados… pero, repito, no es un asunto tan fácil.
Si te preocupa el cáncer…
Dejadme que aproveche para recordar que, en cambio, el consumo de alcohol y tabaco, o la excesiva exposición a la radiación UV (y otras radiaciones ionizantes, de mayor frecuencia, como los rayos X) sí son cancerígenos comprobados y bastante “eficientes”. Esto es algo que sabemos tanto por los estudios en laboratorios, como por los epidemiológicos. De manera que si queréis reducir vuestras probabilidades de tener cáncer, ya tenéis algunas cosas que podéis hacer.
Sobre el autor: Javier Fernández Panadero es físico y profesor de secundaria además de escritor de libros de divulgación.
El artículo No era tan fácil: wifi y cáncer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sin atajos frente al cáncer
- Hacia la decisión compartida en los programas de cribado de cáncer de mama
- Microbiota y cáncer
Evolución [Para creyentes y otros escépticos]
Ignacio López-Goñi, lector
No todas las religiones, ni todos los cristianos, abominan de la evolución
Todavía hoy en día siempre que se trata el tema de la evolución, muchos creyentes muestran cierta reticencia a asumir el hecho de la evolución de la vida y del ser humano con todas sus consecuencias. Piensan que hay ciertos momentos de la historia del cosmos que la evolución supuestamente no puede explicar, y recurren a esos “huecos” para “meter” la acción de Dios en el mundo. Para algunos Dios no es más que un gran mago capaz de sacar cualquier truco de su chistera, ocupado en insuflar vida, o “almas”, en ciertos momentos de la historia natural, o en arreglar algo que se le había ido de las manos. Ese es el Dios del creacionismo o de eso que se llama diseño inteligente, un Dios que sólo puede actuar como lo haría un ingeniero: diseñando, construyendo y ensamblando piezas. Pero creación y creacionismo no son lo mismo. El creacionismo, popular e incluso beligerante en el mundo anglosajón entre los movimientos cristianos protestantes, mantiene una interpretación literal de los relatos bíblicos, que es claramente contraria con la evidencia científica. En el extremo opuesto se sitúa el pensamiento materialista, para el que la evolución del cosmos es suficiente para explicar el origen del mundo que nos rodea, sin necesidad de un Dios que le dé sentido. Pero, ¿pueden ser compatibles ambas posturas, afirmar que la vida ha surgido como consecuencia de mecanismos puramente naturales y la existencia de un Dios creador?
 Evolución [Para creyentes y otros escépticos]. Javier Novo. 2019. ISBN: 978-84-321-5053-1
Evolución [Para creyentes y otros escépticos]. Javier Novo. 2019. ISBN: 978-84-321-5053-1Javier Novo, es Catedrático de Genética en la Universidad de Navarra y trabaja en la evolución de las secuencias genéticas que controlan el desarrollo del cerebro humano, y acaba de publicar un libro titulado “Evolución para creyentes y otros escépticos”. En él explica de manera muy asequible para un público general cómo funciona la evolución, y argumenta que esa cadena de casualidades que ocurren en la evolución del cosmos se puede ajustar muy bien con la idea de un Dios que da sentido a todo, y no de un Dios artesano, como tantos cristianos e incluso escépticos piensan.
La evolución no es progresar sino explorar
En los primeros capítulos, Novo explica con multitud de ejemplos sencillos y de forma muy didáctica, cómo funciona realmente la evolución, que resumo aquí esquemáticamente en ocho puntos:
1. Evolución no significa que todos los individuos de una especie deban estar constantemente transformándose para alcanzar el “siguiente” estado evolutivo, transformarse de golpe en otra especie. Es mucho mejor hablar de “poblaciones” de individuos que de especies. La evolución ocurre dentro de una gran población, cuando un pequeño número de individuos sufren algún cambio que les permite adaptarse mejor a las condiciones ambientales en las que viven. Se seleccionan las variaciones que ya estaban presentes en la población antes de que se diese ninguna necesidad de poseerlas, antes de que fuesen útiles. La selección natural no “crea” nada, simplemente escoge entre las variantes existentes.
2. La selección natural explica muy bien cambios sencillos. Pero es un error pensar que la evolución siempre funciona de manera gradual, a base de pequeñitos cambios que gradualmente van llevando una población de seres vivos hacia su óptimo, siempre adaptándose mejor y mejor; y que es precisamente la acumulación sucesiva de muchos de estos cambios infinitesimales lo que explica los grandes cambios macroevolutivos (la conversión de un ala en brazo o de un mono a un ser humano).
3. La evolución no es una línea única, no es un gran tronco lineal en el que las especies se van sucediendo una tras otra, hasta llegar a la penúltima y por fin al ser humano. En un árbol en el que las especies que existen en la actualidad son los brotes más externos, un árbol lleno de nudos y ramillas que se han quedado en el camino y nunca han llegado a formar parte de la copa.
4. La selección natural no lo es todo. No es correcto presentar la evolución como un lento e imparable proceso de optimización que siempre alcanza la solución mejor. A veces existen situaciones de aislamiento más o menos brusco que hace que las poblaciones sigan derroteros diferentes. Estos cambios bruscos son tanto más drásticos cuanto menor es el número de individuos que han quedado aislados. Este fenómeno (deriva genética) ha sido más la regla que la excepción en la historia de la Tierra. La colonización del planeta se ha hecho a base de ocupar nuevos nichos, en un proceso repleto además por varias extinciones masivas. Colonización y extinción constituyen dos poderosas fuerzas evolutivas.

5. La evolución a veces es “sucia” y un tanto chapucera. La deriva genética no solo introduce cierta impredictibilidad, sino que explica la existencia de diseños “malos”: en la naturaleza abundan las estructuras que analizadas en detalle responden a un diseño bastante deficiente. La evolución no conoce otra forma de arriesgar que generando lo inesperado; y lo inesperado a menudo es lo no perfecto. Lo verdaderamente sorprendente es que esas imperfecciones constituyan la base para lograr auténticos avances, nuevos modos de sobrevivir y prosperar en las innumerables oportunidades que ofrece nuestro planeta.
6. La evolución no es un proceso uniforme, gradual, que se produce a una velocidad constante (habitualmente lenta), siempre en la misma dirección. No, la evolución puede dar saltos. A veces, un cambio ecológico sencillo puede provocar una transición evolutiva notable. Fue lo que ocurrió en la denominada explosión del Cámbrico, un breve lapso de tiempo (cuarenta millones de años) en los que se originaron la mayor parte de los planes corporales de los animales.
7. Evolución y desarrollo embrionario tienen mucho que ver. Los genes implicados en el control del desarrollo embrionario son esencialmente los mismos en la mayoría de los seres vivos. Muchos cambios que parecen grandes saltos evolutivos pueden explicarse por un recableado o reconfiguración de determinadas redes genéticas que controlan el desarrollo embrionario, son pequeñas modificaciones en esa maraña de conexiones genéticas que pueden tener como resultado trayectorias evolutivas separadas. Se pueden modificar así estructuras biológicas enteras a partir de cambios relativamente sencillos. No hace falta una mutación para cambiar el brazo, seguida de otra para la mano, otra después para cada dedo … No, cuando cambia la red genética que controla el desarrollo del miembro superior, todo el miembro se reconfigurará; pequeños cambios en los sistemas genéticos que determinan la forma de la cabeza ayudarán a entender cómo puede crecer el cráneo y cambiar la cara a la vez. Cuando hablamos de redes complejas como éstas, cambios ligeros en el input pueden dar como resultado modificaciones relativamente drásticas y difíciles de predecir.
8. La evolución a veces retrocede. En realidad simplemente selecciona de entre lo que tiene a su disposición, que a su vez es el resultado de selecciones anteriores. Por eso, evolucionar no es progresar, sino explorar. Muchas veces genes que ya estaban en organismos más sencillos haciendo determinadas cosas, son después “reutilizados” para nuevas funciones en otros organismo más adelante. La evolución se comporta como un amante del bricolaje que toma cosas viejas, ya usadas, y las combina de modos nuevos (la idea es del Premio Nobel François Jacob). Por eso, a veces, la evolución “crea” estructuras que parecen mal diseñadas, no son las “mejores” pero son lo suficientemente buenas como para permitir que la vida siga adelante en ese nicho ecológico concreto. La evolución nunca construye un órgano partiendo de cero, no planifica el funcionamiento del sistema circulatorio como lo haría un experto en hidráulica, no conecta las neuronas como lo haría un ingeniero electrónico. Al contrario, está limitada por las imperfecciones y los fallos del pasado, y con esas herramientas tiene que salir adelante. El resultado final de esa exploración a tientas es el famoso árbol de la vida: unas ramas se habrán quedado secas a mitad de camino, de los nudos interiores han salido otras que hoy forman la copa.
El “problema” de la mente y el ser humano
Hasta aquí la lectura del libro de Novo nos habrá permitido entender un poco mejor cómo funciona la evolución, con la intención de prepararnos para la pregunta esencial: el origen del ser humano. Novo comienza a abordar este tema hablando de la evolución de la mente, ese conjunto de fenómenos cognitivos y emocionales que da lugar a una experiencia subjetiva, a ese “yo” que vive en primera persona sensaciones sublimes que resulta tan difícil explicar con palabras.
En el fondo, el tema de la evolución humana se reduce al problema de la aparición de la mente humana, esa dimensión espiritual que algunos designan con la palabra “alma”. ¿Cómo han aparecido todos esos fenómenos que describimos como mente humana? ¿Ha sido un proceso puramente natural? ¿Ha intervenido Dios de algún modo? Esta es, sin duda alguna, la principal piedra de tropiezo para el creyente que se enfrenta con el hecho evolutivo. La enseñanza católica en este punto es algo difusa, pero suele resumirse con la afirmación de que Dios ha “infundido el alma”, ha insuflado el aliento de vida mediante el cual los seres humanos adquieren esa dimensión espiritual.
Con demasiada frecuencia se ha acudido a la “solución” un tanto ingenua de decir que “la evolución crea el cuerpo y Dios crea el alma”. Pero no podemos pensar que nuestra mente, espíritu, consciencia o alma es una cosa, una especie de “nubecilla”, una sustancia separada que hizo su aparición súbitamente sobre la superficie de la tierra con la aparición de los primeros seres humanos. Hoy en día, es innegable que los sustratos neurológicos sobre los que se asienta la consciencia están presentes en el reino animal y por tanto tienen una historia muy antigua. Lo cual tiene mucho sentido si recordamos que la evolución es exploración, búsqueda incansable de nuevas soluciones. En este contexto, no tiene nada de extraño que todas las habilidades cognitivas necesarias para la vida social, la cooperación, la empatía, la equidad, la planificación, el viaje mental, la fabricación de herramientas o la comunicación simbólica hayan sido “probadas” o “intentadas” repetidas veces a lo largo de la historia evolutiva.
Determinar con certeza quienes fueron los primeros humanos quizá sea imposible. Así, explorando a tientas, el hombre llegó al mundo sin hacer ruido, silenciosamente. Teilhard de Chardin fue el primero en utilizar el término hominización para este largo proceso, y tuvo también la magnífica intuición de compararlo con la infancia. Hablamos a menudo del uso de razón que alcanzan los niños en torno a los seis o siete años. Parece que antes de esa edad aún no son totalmente racionales, y por eso no les exigimos responsabilidades; pero llega un momento en su vida en que adquieren esa racionalidad y comienzan a construir su propia historia. De modo que un niño, se hace mayor y se convierte en un ser capaz de tomar decisiones libres. Algo ha cambiado en esa mente, en los procesos cognitivos que la sustentan, pero el cambio ha ido fraguándose durante años y ha llegado silenciosamente.
De modo semejante, los últimos dos millones de años de evolución humana han sido esa infancia que preparaba el momento de nuestra irrupción final en la historia del cosmos. Es inútil buscar un instante preciso, y es muy probable que nunca lleguemos a saber los detalles exactos de lo que sucedió. La pregunta de quién fue realmente el primer humano resulta irrelevante, como irrelevante es intentar precisar el momento en el que un niño pierde la inocencia y se hace mayor; porque cuando tenemos la seguridad de que el cambio se ha producido, ya es tarde. Cuando vemos los rastros de un comportamiento adulto en nuestro deambular evolutivo, ya han transcurrido miles de años de infancia.
Dios y evolución
Notables escépticos como el premio Nobel de Física Steven Weinberg aluden al hecho de que la ciencia muestra la ausencia de propósito o sentido en las leyes que gobiernan el universo: “cuanto más estudiamos el universo, menos sentido encontramos”. En efecto, el conocimiento de los mecanismos evolutivos nunca nos dirá nada acerca del sentido o significado que tienen; se trata de una cuestión totalmente ajena a la propia metodología científica, ¿por qué debería la ciencia encontrar sentido? Sencillamente, no es el objeto de la ciencia experimental encontrar el sentido, propósito o significado que puedan tener los procesos naturales.
Resulta absurdo pensar que Dios se ha dedicado a ensamblar unas moléculas orgánicas para formar la primera célula, o a toquitear un circuito neuronal en el cerebro de un homínido para que pudiera ponerse a hablar. Dios no es un gran ingeniero ataviado con el ropaje blanco de Gandalf. Por eso, resulta inútil buscar las “huellas” de su actuar en determinados cambios físicos o biológicos que la ciencia no puede todavía explicar adecuadamente. A Dios no se le encuentra en los lugares oscuros a los que no ha llegado aún la luz de la explicación científica; de hecho, probablemente esos sean los peores sitios donde buscarle. Si Dios es verdaderamente real, está dando sentido, significado y propósito a todo lo que ha sido, es y será. La fe en la creación no nos dice cuál es el sentido del mundo, sino simplemente que el mundo tiene sentido.

Llegados a este punto, Novo utiliza el ejemplo del tapiz para explicar el papel de Dios en el mundo. Cuando observamos por detrás uno de esos magníficos tapices antiguos que cuelgan de palacios reales, lo que vemos es un montón de pequeños nudos. Los hilos que componen el tapiz han sido trenzados y anudados con gran habilidad; pero si miramos esta parte -el lado malo- no vemos escena alguna. Es más, para alguien que no haya visto nunca el otro lado del tapiz, o que no haya visto jamás un tapiz, resultará muy difícil aceptar que realmente hay una escena por el otro lado, que todos esos nudos tienen en realidad algún sentido, que no están ahí sin más, al azar. Para aceptar eso hay que dar un salto en el vacío, hay que hacer un acto de fe.
El gran descubrimiento de la ciencia es, precisamente, que esos hilos tienen la increíble propiedad de que se atan solos, por sí mismos. La evolución biológica, a tientas, con un explorar errático, mediante fuerzas puramente naturales (selección natural, deriva genética, ecología, re-estructuración de programas de desarrollo embrionario, …) ha conseguido dar paso a un tipo de cognición, una mente, capaz de generar un sistema no-genético, no-biológico, de rápido progreso cultural: el ser humano. Si los nudos realmente se atan por sí mismos, entonces quizás no haya nadie al otro lado; es más, quizás ni siquiera haya escena alguna que contemplar.
Sin embargo, es perfectamente posible sostener que las cuerdas del tapiz son realmente autónomas en su modo de operar y tener al mismo tiempo la convicción de que al otro lado está apareciendo una escena cada vez más fantástica. Diferenciar bien estos dos planos es crucial. Pensar que Dios existe porque ha anudado directamente alguno de esos nudos, por bien hecho que esté, supone que también ha causado los otros nudos contrahechos y feos que dan a este lado del tapiz la apariencia de un gran océano de sinsentido.
Llegados a este punto, cada uno debe decidir si esto significa que al otro lado del tapiz hay algo que dé sentido a todo esto. Es el punto en que el creyente ha de soltar el último asidero y dar el salto definitivo de fe. El escéptico se contentará con contemplar este lado e intentar darle algún significado, tarea ardua y necesariamente infructuosa. Lo importante es que a esa decisión se llega por caminos diversos, pero no tiene nada que ver con la ciencia; y mucho menos con la evolución.
Ficha:
Autor: Javier Novo
Título: Evolución [Para creyentes y otros escépticos]
Año: 2019
Editorial: Rialp
Sobre el autor de la reseña: Ignacio López-Goñi (@microbioblog) es biólogo y catedrático de Microbiología en la Universidad de Navarra.
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
El artículo Evolución [Para creyentes y otros escépticos] se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Coloquios escépticos: ¿hijos de dios?, con Francisco Mora
- Los primeros pasos de la evolución darwiniana y sesgos cognitivos y evolución (Día de Darwin 2018)
- Escépticos y dogmáticos
Ciencia de datos y fútbol: predicción del riesgo de lesiones en el deporte profesional

El fútbol es el deporte alrededor del cual orbitan, además de los miles de fieles seguidores, sectores como la hostelería, el periodismo, la publicidad o la moda. Pero, ¿hay lugar para la ciencia?
Aunque resulte difícil imaginar la relación que pueda existir entre disciplinas científicas como la física, las matemáticas o la antropología y el fútbol, cada vez son más las ocasiones en las que, sorprendentemente, la ciencia puede explicar muchos de los acontecimientos que suceden en un campo de fútbol e incidir en aspectos como la mejora del rendimiento de los jugadores y, en consecuencia, de los resultados.
La relación entre estas dos disciplinas fue el hilo conductor de un ciclo de conferencias organizado por la Cátedra de Cultura Científica con el apoyo de la Diputación Foral de Bizkaia y la colaboración de Fundación Española para la Ciencia y la Tecnología (FECYT) – Ministerio de Ciencia, Innovación y Universidades”, que tuvo lugar en el Bizkaia Aretoa de la UPV/EHU de Bilbao los meses de octubre y noviembre de 2018. Enmarcado en el ciclo de conferencias “Zientziateka”, que contó con cinco conferencias impartidas por especialistas de diversos campos en las que se ilustró la conexión que existe entre diferentes disciplinas científicas y el fútbol.
Dae-Jin Lee, doctor en Ingeniería Matemática e investigador del Centro Vasco de Matemática Aplicada (BCAM), presenta en esta charla el campo emergente de la bioestadística deportiva y su relevancia para la prevención de lesiones en el deporte profesional. A lo largo de ella aborda la ciencia detrás de la prevención de lesiones deportivas (principalmente en el fútbol de élite) basada en la analítica avanzada de datos. El objetivo final del ponente es dar valor a la necesidad de perfiles multidisciplinares que incorporen la bioestadística, las matemáticas, la computación, la epidemiología y la salud pública en el deporte profesional.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Ciencia de datos y fútbol: predicción del riesgo de lesiones en el deporte profesional se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Fútbol, periódicos y estadísticas
- La trama vasco-rusa que eliminó a España del Mundial 2018
- Ciencia y valores en la sociedad del riesgo
50 años modificando genes (en animales)
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Transgénesis en mamíferos
En un artículo previo hemos tratado el tema de la tecnología del DNA recombinante (rDNA) y la transgénesis en bacterias. Continuando con esta temática, en este artículo nos centramos en la transgénesis en animales y, especialmente, en la transgénesis en mamíferos.
Un animal transgénico es aquél al que se le ha transferido un DNA exógeno (en muchas ocasiones de otra especie), el cual ha quedado integrado en el genoma de sus células germinales. Las células germinales son las que dan lugar a óvulos o espermatozoides, por lo que un animal transgénico puede transmitir el DNA exógeno a sus descendientes, a través de la reproducción sexual.
Inicialmente, los mamíferos transgénicos se crearon inyectando directamente un DNA exógeno en el núcleo de un óvulo fertilizado in vitro y manteniendo en cultivo el embrión resultante durante las primeras divisiones celulares, hasta implantarlo en una madre subrogada (Figura 1). Los primeros mamíferos transgénicos se produjeron en 1981, cuando científicos de la Universidad de Ohio introdujeron en ratones el gen de la hemoglobina de conejo.
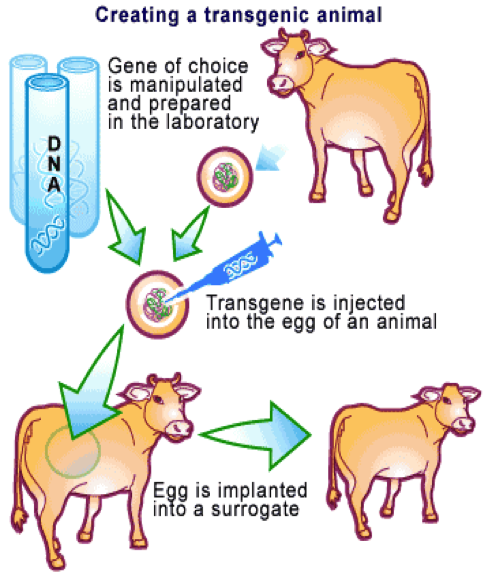 Figura 1. Creación de un animal transgénico inyectando el transgén en un óvulo e implantando el embrión en una madre subrogada. Fuente: Helmutkae / The Science Creative Quarterly.
Figura 1. Creación de un animal transgénico inyectando el transgén en un óvulo e implantando el embrión en una madre subrogada. Fuente: Helmutkae / The Science Creative Quarterly.
A partir de ese momento comenzaron a mejorarse las técnicas de fertilización in vitro y de inyección de genes en embriones de diferentes especies, para incrementar la eficacia de la generación de animales transgénicos.
Los motivos para crear este tipo de animales son diversos. En ocasiones se trata de conseguir aplicaciones de interés biomédico, como producir en la leche una molécula de utilidad terapéutica (anticuerpos monoclonales, interleukina-2, eritropoyetina, hormona de crecimiento humana, son algunos ejemplos de proteínas así obtenidas). Para este tipo de aplicación se suelen generar cabras, conejos, ovejas o vacas transgénicos. Otras aplicaciones están relacionadas con el uso de animales como donantes de tejidos u órganos; en este caso, los cerdos suelen ser la especie de elección y la transgenia pretende mejorar la compatibilidad del xenotransplante. También algunos animales se generan por interés comercial de la industria alimentaria, que busca generar animales resistentes a enfermedades, con una tasa de crecimiento más elevada, o con propiedades nutricionales modificadas y acordes a los intereses del mercado.
Además, existe un gran interés en la generación de animales transgénicos en el ámbito científico, donde se emplean para avanzar en el conocimiento molecular de las enfermedades, en la función de los genes o en el efecto de mutaciones concretas. Los modelos de animales transgénicos para enfermedades humanas están permitiendo no solo descubrir los aspectos moleculares responsables de las patologías, sino también disponer de herramientas para investigar la progresión de una enfermedad, o para evaluar estrategias terapéuticas de forma previa a su aplicación en humanos, entre otras aplicaciones. Sin ninguna duda, la especie preferida para este tipo de estudios es el ratón, debido a su bajo coste de mantenimiento, a su reducido período de gestación, a la relativamente estrecha relación evolutiva que existe entre su genoma y el genoma humano, y a la disponibilidad de cepas de ratones genéticamente puras con las que iniciar el procedimiento. Además, como se detalla a continuación, las tecnologías para la generación de organismos transgénicos están particularmente bien desarrolladas para la introducción de modificaciones genéticas en el ratón. Todo ello ha conducido a que el uso de ratones transgénicos sea una herramienta ampliamente utilizada en el ámbito de la investigación biomédica.
Transgénesis dirigida en ratones
A pesar de sus numerosas aplicaciones, la transgénesis mediante inyección nuclear descrita en la sección anterior presenta el inconveniente de que la integración de los transgenes exógenos en el genoma hospedante se realiza de manera aleatoria, lo cual puede generar efectos variables no deseados. En ratones, este inconveniente se solventó en 1988, cuando se consiguió generar un ratón mediante una metodología compleja que se ha denominado transgénesis dirigida porque permite introducir los transgenes en lugares específicos del genoma hospedante. El desarrollo de esta tecnología llevó a sus creadores, los Dres. Capecchi, Smithies y Evans a obtener el premio Nobel en 2007.
Para llevar a cabo la transgénesis dirigida se utilizan células madre embrionarias (ES, del inglés embryonic stem), un tipo de células que pueden mantenerse indefinidamente in vitro en un estado no diferenciado pero que, cuando se inyectan en un embrión, contribuyen a la formación de todos los tejidos del ratón en desarrollo. Las células ES en cultivo, se someten a un tipo de modificación genética, denominada recombinación homóloga, mediante la cual el transgén de interés se integra en un punto concreto de su genoma. A pesar de que la recombinación homóloga es poco eficaz, las células ES en las que el proceso ha sucedido correctamente pueden seleccionarse e incrementar su número mediante su cultivo in vitro (Figura 2A).
Posteriormente, las células ES seleccionadas que contienen el transgén correctamente insertado, se inyectan en un embrión de ratón en etapa muy temprana de su desarrollo (blastocisto), dando lugar a un ratón quimérico que contiene células no modificadas y células ES modificadas genéticamente. Si este ratón quimérico porta la modificación genética en su línea germinal (óvulos o espermatozoides) la podrá transmitir a su descendencia, generándose así, en la siguiente generación, ratones con todas sus células modificadas. (Figura 2B).
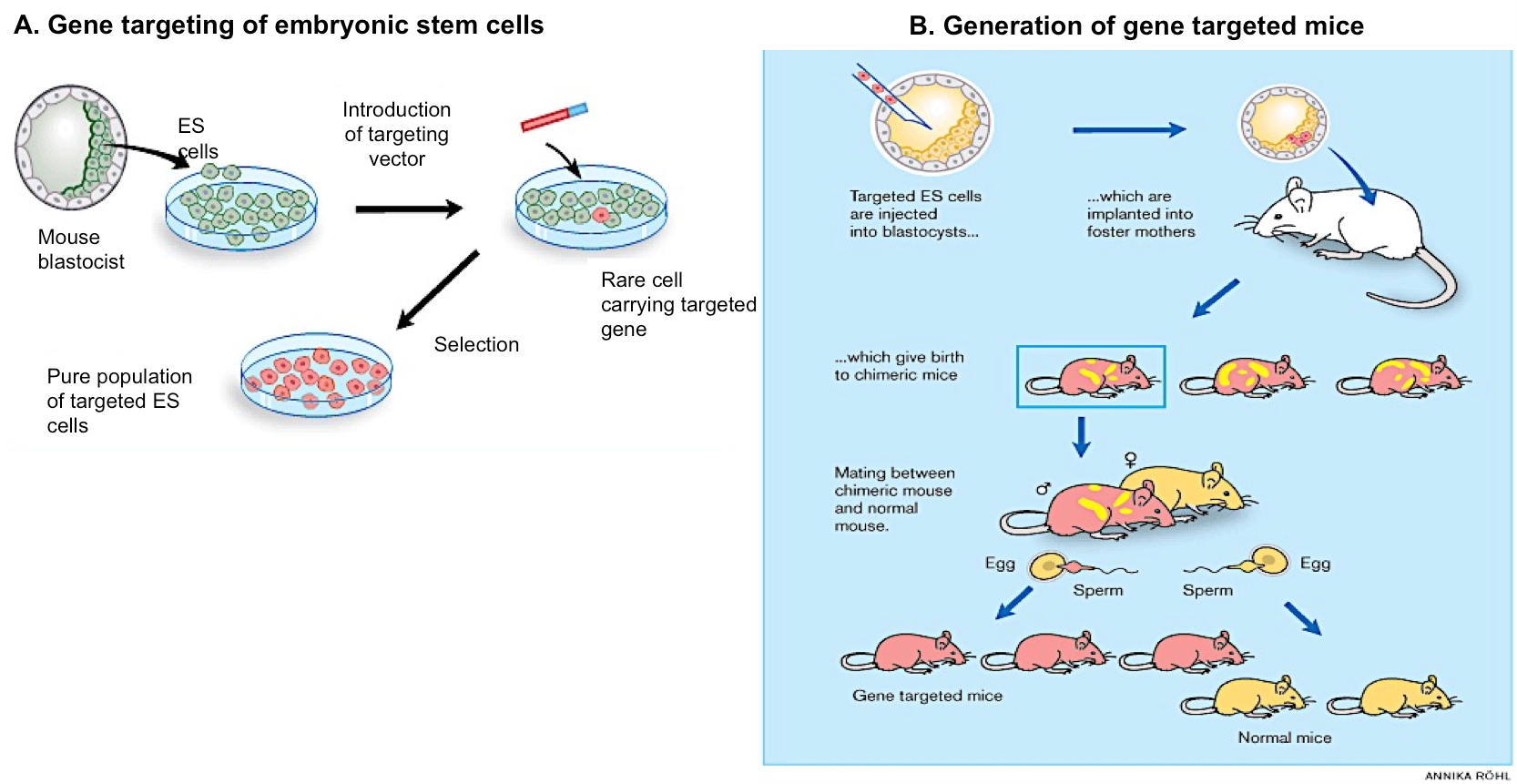 Figura 2. Obtención de un ratón transgénico mediante transgénesis dirigida. A) El transgén se introduce en el genoma de células madre por recombinación homóloga. Las células madre modificadas genéticamente se seleccionan in vitro. B) Inyección de las células madre modificadas genéticamente en blastocistos e implantación del embrión en una madre subrogada. Algunos ratones quimera cuando nacen portan el transgén en la línea germinal. Fuente: nobelprize.org
Figura 2. Obtención de un ratón transgénico mediante transgénesis dirigida. A) El transgén se introduce en el genoma de células madre por recombinación homóloga. Las células madre modificadas genéticamente se seleccionan in vitro. B) Inyección de las células madre modificadas genéticamente en blastocistos e implantación del embrión en una madre subrogada. Algunos ratones quimera cuando nacen portan el transgén en la línea germinal. Fuente: nobelprize.org
Esta tecnología se utiliza frecuentemente para producir mutantes nulos, también llamados «knockouts» (KO), es decir, ratones que presentan un gen anulado y que no producen una determinada proteína. El objetivo de esta estrategia es identificar la función de un gen, observando el efecto que se obtiene cuando se elimina. Nuestro grupo de investigación ha venido participando activamente en la generación y caracterización de ratones knockout para genes implicados en el control del ciclo celular (genes E2f1 y E2f2). Los resultados de estas investigaciones han permitido demostrar que los genes E2f desempeñan un papel esencial en la homeostasis del animal, al prevenir el desarrollo tumoral (E2f1), la autoinmunidad (E2f2) o la degeneración glandular (E2f1 y E2f2).
Actualmente, no existe una cifra exacta del número de ratones modificados genéticamente que se han generado hasta la fecha, aunque a buen seguro se trata de varios miles. La mayoría de ellos están siendo empleados como modelos de estudio para un mejor conocimiento de la fisiología y patología humanas y para analizar el efecto molecular de alteraciones que han sido descritas como responsables de numerosas enfermedades humanas
Edición de genes mediante CRISPR
En el año 2012, las investigadoras Jennifer Doudna y Emmanuelle Charpentier comunicaron el desarrollo de una poderosa y nueva metodología, llamada edición génica (o genómica), basada en conocimientos básicos previos, aportados fundamentalmente por el investigador español Francisco Martínez Mojica, sobre un sistema de defensa que poseen la mayoría de las bacterias y de las arqueas denominado CRISPR (del inglés, clustered, regularly interspersed palindromic repeats).
La metodología CRISPR, que permite modificar genes de manera más precisa y rápida que la mayoría de los métodos anteriores, incluye el uso de varias moléculas que deben ser administradas a las células que se quieren editar, así como la intervención de los sistemas de reparación que existen en las propias células.
El proceso consiste básicamente en utilizar una proteína que corta el DNA, denominada Cas9, y un RNA guía, complementario a la región del genoma que se quiere modificar (Figura 3). Con estos elementos, se consigue cortar el genoma de las células en los lugares deseados. La reparación de la rotura por parte de las propias células genera con frecuencia deleciones o inserciones de 1-2 nucleótidos que conducen a la inactivación del gen en el que se ha producido esa rotura. Por otra parte, si junto con la enzima Cas9 y el RNA guía se aportan moléculas de DNA con secuencias diseñadas específicamente para un objetivo determinado (por ejemplo, la introducción de una mutación puntual), se puede conseguir la sustitución de la secuencia original por la secuencia diseñada.
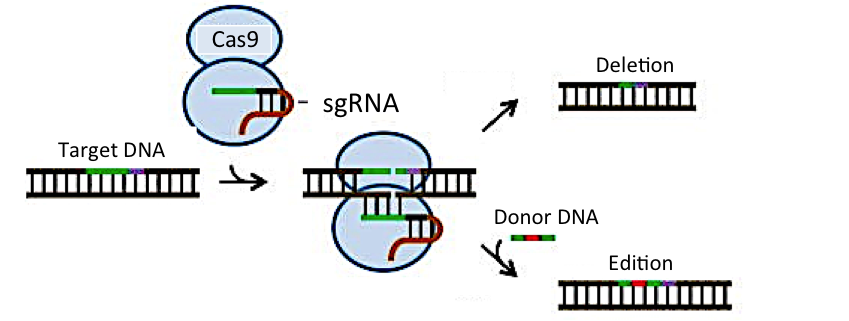 Figura 3. Modificación genética mediante CRISPR. La molécula de RNA guía (sgRNA) conduce a la proteína Cas9 a un lugar concreto del genoma. Cas9 genera un corte en la molécula de DNA endógena que, durante su reparación, puede generar deleciones o modificaciones genéticas. Fuente: Modificado de Doudna & Charpentier. Science, 346:1258096 (2014)
Figura 3. Modificación genética mediante CRISPR. La molécula de RNA guía (sgRNA) conduce a la proteína Cas9 a un lugar concreto del genoma. Cas9 genera un corte en la molécula de DNA endógena que, durante su reparación, puede generar deleciones o modificaciones genéticas. Fuente: Modificado de Doudna & Charpentier. Science, 346:1258096 (2014)
La técnica CRISPR está suponiendo una verdadera revolución: en el año 2018, solo seis años después de la primera publicación, ya eran más de 17.000 los artículos publicados. Los motivos de esta rápida expansión en el uso de esta tecnología tienen que ver con que constituye un método directo, rápido y tremendamente eficiente para generar animales transgénicos: se trata de una técnica mucho más precisa que todas las utilizadas hasta ahora (aunque no lo es al 100%), más eficaz (un porcentaje elevado de las células tratadas pueden ser editadas), más rápida y más barata. Todo ello ha contribuido a “democratizar” su uso y a que una gran proporción de los laboratorios que trabajan en Biología Molecular la utilicen para sus investigaciones, tanto a nivel celular como para la generación de animales modelo, entre otras aplicaciones. Nuestro equipo de investigación también se ha sumado al uso de esta tecnología, habiendo generado ya varias líneas celulares que portan mutaciones específicas en los genes E2F para su empleo en estudios del ciclo celular y cáncer.
Además, la técnica CRISPR tienen ventajas adicionales, por ejemplo, permite modificar varios genes simultáneamente. El investigador Rudolph Jaenisch fue el primero en mostrar el poder de CRISPR para generar knockouts de ratón. En un artículo de 2013 su equipo publicaba la generación de un ratón al que le habían anulado cinco genes simultáneamente, mediante el empleo de esta técnica. Y lo que es aún más importante, demostraron que podían hacerlo sin necesidad de utilizar las células ES, eliminando directa y simultáneamente los cinco genes en zigotos unicelulares o en óvulos fertilizados de ratón. Se estima que diseñar un ratón mediante CRISPR es un 30% más barato que con células ES, lo que hace que su costo promedio actual sea de alrededor de 10.000€.
A pesar de su enorme utilidad, la técnica de CRISPR no está exenta de potenciales problemas, que incluyen la modificación accidental de regiones no específicas del genoma o la aparición de reacciones inmunológicas. Actualmente se está trabajando de forma muy activa para solventar estos inconvenientes, a fin de que la técnica CRISPR sea más precisa, segura y barata para la generación de animales transgénicos y para otras aplicaciones experimentales, pero sobre todo, para que su aplicación a los seres humanos pueda realizarse con las mayores garantías posibles. El siguiente artículo de esta serie trata, justamente, sobre la utilización de la tecnología del rDNA y de CRISPR en humanos.
¿Plantea problemas éticos la transgénesis?
La transgénesis en animales, y especialmente en mamíferos, tiene importantes implicaciones éticas relacionadas fundamentalmente con el bienestar de los animales transgénicos que se generan. Esta cuestión es especialmente importante cuando se busca conseguir un animal modelo para una patología humana que conlleva severos problemas de salud también para el animal. Por ejemplo, investigadores de la Academia China de Ciencias en Shanghai han obtenido recientemente 5 macacos transgénicos a partir de un ejemplar editado mediante CRISPR, para portar una versión alterada de un gen implicado en la regulación del ciclo circadiano (los ritmos biológicos asociados a los cambios de luz y de temperatura). En humanos, los trastornos del ciclo circadiano se asocian a alteraciones del sueño, depresión, diabetes mellitus, cáncer y enfermedades neurodegenerativas como Alzheimer. Los macacos obtenidos tras la modificación y posterior clonación, presentan alteraciones del sueño, ansiedad, depresión y conductas similares a la esquizofrenia. Como modelo para el estudio de este trastorno, estos monos pueden resultar muy útiles, pero es evidente que su bienestar se encuentra comprometido.
Parece claro que, a medida que la tecnología avance, las posibilidades para generar nuevas aplicaciones que afecten al bienestar de los animales también van a aumentar, así que urge adoptar medidas consensuadas por la sociedad, que permitan la toma de decisiones éticas sobre qué aplicaciones son asumibles y cuáles no.
Sobre los autores: Ana I. Aguirre, José Antonio Rodríguez y Ana M. Zubiaga son profesores del departamento de Genética, Antropología Física y Fisiología Animal de la Facultad de Ciencia y Tecnología, e investigadores del grupo de investigación consolidado del Gobierno Vasco Biología Molecular del Cáncer.
El artículo 50 años modificando genes (en animales) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- 50 años modificando genes (en bacterias)
- 50 años de secretos: la era de la criptografía moderna
- Animales eurihalinos
El mural de la cantera: arquitectura, ciencia y arte contra el calentamiento global
 Los espíritus de la cantera, de Francisca Ros Nicolás (2008)
Los espíritus de la cantera, de Francisca Ros Nicolás (2008)El sonido de la porcelana es más agudo que el del yeso. La porcelana también es más fría. A simple vista el yeso, tratado con la debida pulcritud, puede confundirse con porcelana. El tacto revela que la porcelana es cristalina y que el yeso es amorfo. La porcelana rompe en fragmentos dentados, el yeso se desmenuza. Si uno de estos materiales se encuentra en la ficha técnica de una escultura, inmediatamente recreamos su sonido y su temperatura.
Las propiedades físicas de los materiales se emplean en el arte como cualidades estéticas. Es un discurso plástico que a menudo resulta difícil de expresar de otra manera. En gran medida es un uso sinestético de los materiales en el que la percepción de unos sentidos es resuelta por otros: la temperatura de un color, el tacto de un sonido.
En ocasiones, las cualidades estéticas de los materiales de las que se sirven los artistas revelan unas propiedades físicas que resultan útiles. Así, un material cálido efectivamente interacciona con la radiación de forma diferente que un material frío. Este conocimiento es muy valioso para la arquitectura, por ejemplo. Y si hablamos de materiales y temperatura, esto también resulta de gran utilidad científica para un tema de importancia capital: el calentamiento global.
Si mezclamos todos los conocimientos sobre materiales que nos brinda el arte, la arquitectura, el diseño, la química, podemos enfrentarnos a ciertos problemas medioambientales y estéticos de hoy en día. Una suerte de Bauhaus que desdibuja las fronteras entre conocimientos que nunca debieron parcelarse.
 Mural da canteira de Leopoldo Nóvoa (1989) fotografiado por Xurxo Lobato
Mural da canteira de Leopoldo Nóvoa (1989) fotografiado por Xurxo Lobato
La obra Mural da canteira, del artista gallego Leopoldo Nóvoa, tapiza uno de los muros del Parque de Santa Margarita de A Coruña desde 1989. Se trata de un mural de 700 m2 construido con materiales de obra desechados. Puede recordar a una casa deconstruida, como una suerte de ruina moderna aplastada contra un muro. También puede enmarcarse en el arte povera por el uso de materiales pobres y recuperados.
En esta obra se entremezclan materiales blancos —cerámica refractaria y cuarzo—, grises —cemento y vigas de hormigón—, cenizas —antracita, pizarra y carbón de coque— y ocres —ladrillo calcinado, tuberías cerámicas—. El mural está completamente expuesto hacia el Este en una de las vías principales de A Coruña, lo que permite que la luz solar incida sobre estos materiales desde el amanecer hasta el mediodía. Uno de los códigos que emplea el artista es precisamente ese, el aspecto cambiante del mural según cómo incide la luz.
El mural originalmente iba a ocupar más del doble de lo que finalmente ha ocupado. Diferentes avatares políticos impidieron la total ejecución de la obra. Para más inri, la construcción de una pasarela de entrada al parque, además de ensombrecer parte del mural a ciertas horas del día y por tanto alterar dramáticamente la incidencia de la luz, también supuso la destrucción de parte del mural. En 2015, tres años después del fallecimiento del artista, el arquitecto Pablo Gallego se encargó de la restauración del mural y la parcial recuperación de las zonas destruidas.
Los materiales del Mural da canteira juegan con el relieve original del muro. Crean el espejismo de oquedades y depresiones semiesféricas, como las del centro del mural. De todos modos, el muro no fue tratado por Nóvoa como si fuese un lienzo maltrecho, sino que lo atravesó con vigas para enfatizar la tridimensionalidad de la obra. Podemos interpretar que esas vigas perforan y se adentran en la materia o, por el contrario, interpretar que brotan de ella.
 Mural da canteira (detalle) de Leopoldo Nóvoa (1989) fotografiado por Xurxo Lobato
Mural da canteira (detalle) de Leopoldo Nóvoa (1989) fotografiado por Xurxo LobatoTambién hay partes del muro que dejan al descubierto la cantera original. De esta forma, Nóvoa evidencia la permeabilidad entre la superficie y el fondo, otorgando protagonismo localizado a la propia naturaleza, en bruto, con sus texturas y rugosidades propias. Para Nóvoa el concepto rugosidad, propio del tacto, es tratado como un concepto visual y sonoro.
Para el escritor Paco Yáñez, la Avenida de Arteixo desde la que se puede contemplar el mural, «conforma una holgada butaca urbana en la que el pintor pasó horas y horas observando el crecimiento de su mural, percibiendo la incidencia de la luz, los juegos de sombras sobre los volúmenes y la textura de los materiales para conocer las calidades de su rugosidad».
La rugosidad del mural de Nóvoa se va revelando según cómo la luz incide sobre él. El conocimiento de los materiales que lo componen nos da una idea de su temperatura. Algo que podemos percibir gracias al sentido de la vista, a través de la lente de la radiación visible, también podemos observarla a través de la lente de la radiación térmica.
De igual manera que una cámara óptica puede captar los distintos colores de esta obra de arte, una cámara térmica puede captar el calor (la radiación infrarroja) que emiten los distintos materiales empleados debido a la irradiación de la luz sobre ellos, presentándonos un patrón térmico de temperaturas diferentes.
Bajo la misma iluminación estos materiales se van a calentar en mayor o menor medida y van a alcanzar distintas temperaturas en función de su naturaleza. Por ejemplo, los materiales con colores más claros como el cuarzo o la cerámica blanca absorberán menos luz y, por tanto, se calentarán menos que los materiales más oscuros como la pizarra o la antracita. Además, la superficie pulida del cuarzo permite reflejar mayor cantidad de luz, calentándose aún menos que la cerámica blanca. Por otro lado, también es importante tener en cuenta factores como el calor específico (cantidad de energía necesaria para incrementar la temperatura del material) y la conductividad térmica (capacidad de conducir o transferir el calor). De este modo, cuanto mayor sea el calor específico de un material y menor sea su conductividad térmica, este mantendrá su calor y temperatura durante mayor tiempo. Mientras que un material con bajo calor específico y alta conductividad térmica, en seguida transferirá el calor al aire que lo rodea, bajando más rápidamente su temperatura.
 Imágenes ópticas (1,3) y térmicas (2,4) del Mural da Canteira de Leopoldo Nóvoa en A Coruña. En las imágenes ópticas se pueden apreciar los diferentes colores, texturas y relieves de los materiales de obra empleados. Mientras que en las imágenes térmicas se pueden apreciar las distintas temperaturas que alcanza los diferentes materiales expuestos a la misma iluminación solar; diferencias debidas a factores como la distinta absorción y reflexión de luz, así como al calor específico y conductividad térmica de dichos materiales. Aquí los colores amarillos representan las zonas más calientes y los colores violáceos representan las zonas más frías, observándose una diferencia de temperatura de hasta 10 oC. Fuente: fotografías y termografías tomadas por Juan Manuel Bermúdez García para su canal de divulgación Thermogramer en Facebook, Twitter e Instagram.
Imágenes ópticas (1,3) y térmicas (2,4) del Mural da Canteira de Leopoldo Nóvoa en A Coruña. En las imágenes ópticas se pueden apreciar los diferentes colores, texturas y relieves de los materiales de obra empleados. Mientras que en las imágenes térmicas se pueden apreciar las distintas temperaturas que alcanza los diferentes materiales expuestos a la misma iluminación solar; diferencias debidas a factores como la distinta absorción y reflexión de luz, así como al calor específico y conductividad térmica de dichos materiales. Aquí los colores amarillos representan las zonas más calientes y los colores violáceos representan las zonas más frías, observándose una diferencia de temperatura de hasta 10 oC. Fuente: fotografías y termografías tomadas por Juan Manuel Bermúdez García para su canal de divulgación Thermogramer en Facebook, Twitter e Instagram.
Estos patrones térmicos no solo nos revelan una dimensión oculta de la obra de Nóvoa que nos permite apreciarla desde un nuevo espectro de luz; sino que también nos recuerda que podemos controlar el calor y la temperatura de las edificaciones mediante una selección eficiente de sus materiales de construcción, lo que nos brinda herramientas arquitectónicas para combatir el calentamiento global.
En los últimos años, prestigiosos centros de investigación, como Berkeley Lab (California), han demostrado que la selección de materiales de construcción “blancos” resulta muy eficaz para contrarrestar el calentamiento. Estos materiales, como si de un espejo se tratase, maximizan la reflexión de la luz solar, minimizando la absorción de calor y redirigiendo dicha radiación de vuelta al espacio exterior. Aunque puede parecer una idea vaga, la eficiencia de este método de construcción sostenible ya ha sido demostrada en vehículos de transporte, tejados y fachadas de edificios, así como en pavimentos de carretera. Por ejemplo, el uso de pavimentos “blancos”, también denominados “fríos”, disminuye la absorción de luz solar de un 95 % a un 50 %, mostrando diferencias de temperatura de hasta 17 oC con respecto a los pavimentos tradicionales.
 Imagen óptica y térmica de una calzada con tramos oscuros y claros. La imagen térmica muestra una diferencia de 17 oC entre el tramo oscuro y el claro. Fuente: Imagen tomada por Larry Scofield, American Concrete Pavement Association.
Imagen óptica y térmica de una calzada con tramos oscuros y claros. La imagen térmica muestra una diferencia de 17 oC entre el tramo oscuro y el claro. Fuente: Imagen tomada por Larry Scofield, American Concrete Pavement Association.
En Montevideo, Uruguay, hay otra obra de Leopoldo Nóvoa, Mural del Cerro, en la que el artista ya investigaba sobre el mismo campo de problemas que en la de A Coruña. Sobre esa obra dijo algo que bien podría aplicarse al Mural da canteira: «Desde los albores del día hasta la puesta del sol, el muro va cambiando abruptamente de apariencia, la luz le arranca nuevos destellos, las sombras no dejan de crear movimientos…».
El Mural da canteira de Nóvoa, intelectualmente nunca ha sido un muro. Coincidiendo con su construcción en A Coruña en 1989 con el derribo del muro más emblemático de nuestro tiempo: el muro de Berlín; el mural de Nóvoa establece puentes entre la arquitectura y el arte. La ruina de unos se emplea como materia prima de otros.
Las apreciaciones estéticas de los materiales, como su sonido o su temperatura, fueron recogidas inicialmente por esa pulsión funcional de la escuela de arquitectura de la Bauhaus. Y estas fueron traducidas a propiedades físicas a través de la ciencia de materiales. Hoy en día sabemos, sabemos porque hemos medido, que en esas propiedades estéticas y funcionales de los materiales de construcción, reside uno de los frentes desde los que lidiar con el calentamiento global.
La reflexión de nuestros días sobre el Mural da canteira, revisitado bajo una luz para la que no fue concebido, nos recuerda que las fricciones entre las fronteras del saber revelan excelsas formas de conocimiento.
Sobre los autores: Déborah García Bello es química y divulgadora científica y Juan Manuel Bermúdez García (@thermogramer) es investigador postdoctoral en la Universidad de A Coruña y en la Universidad de Cambridge (UK).
Nota de los autores: Agradecemos a Enric Stern-Taulats de la Universidad de Cambridge y a Lorena Alonso Marañón de la Queen Mary University of London la ayuda que nos han brindado para escribir este artículo.
El artículo El mural de la cantera: arquitectura, ciencia y arte contra el calentamiento global se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El calentamiento global y el aceite de oliva
- La ciencia contra lo obvio
- Arte & Ciencia: Analogías entre el arte y la ciencia como formas de conocimiento
Buscando las soluciones del cubo de Anda
Algunas de las actividades que suelen definir mi periodo de vacaciones estivales, aunque realmente formen parte de mi vida durante todo el año, son la lectura de novelas, la visita a exposiciones de arte y disfrutar de la resolución de algunos juegos de ingenio, acompañado todo ello de largos paseos.
Este mes de agosto he empezado a tope con la lectura de novelas, una de las pasiones que comparto con el matemático inglés Arthur Cayley (1821-1895), uno de los matemáticos a los que admiro y cuya biografía tuve el placer de escribir hace un par de años, Cayley, el origen del álgebra moderna (RBA, 2017). He terminado la novela que tenía entre manos, Los lobos de Praga, de Benjamin Black (Alfaguara, 2019), he disfrutado de las últimas aventuras del particular detective Touré, No digas nada (Erein, 2019), de Jon Arretxe, he devorado una de las sorpresas que me ha deparado el verano, Rialto 11 (Libros del Asteroide, 2019), de Belén Rubiano, que me recomendó Javier Cámara, de la Librería Cámara en Bilbao, y ahora estoy con uno de los muchos libros que tengo pendientes, La playa de los ahogados (Siruela, 2009), de Domingo Villar.
Con las exposiciones voy un poco retrasado este año. He visitado de nuevo la maravillosa exposición LANTEGI, José Ramón Anda en la sala Kubo Kutxa de Donostia-San Sebastián, así como dos de las exposiciones del Museo Guggenheim (Bilbao), la impactante exposición Lucio Fontana. En el umbral y la interesante videoinstalación Este espectáculo innombrable – This nameless spectacle (2011), de Jesper Just. Espero que mis siguientes visitas sean la exposición Calder Stories, en el Centro Botín (Santander) y el Museo Wurth en La Rioja.
 Cartel de la exposición LANTEGI, José Ramón Anda en la sala Kubo Kutxa de Donostia-San Sebastián, del 24 de mayo al 25 de agosto. Imagen de Kubo Kutxa
Cartel de la exposición LANTEGI, José Ramón Anda en la sala Kubo Kutxa de Donostia-San Sebastián, del 24 de mayo al 25 de agosto. Imagen de Kubo KutxaRespecto a los juegos, siempre tengo alguno a mano, que mis amigos Iñaki y Zuriñe, de la Juguetería Pinocchio (Bilbao), me recomiendan. Y este año no ha sido una excepción. Sin embargo, con motivo de la anterior entrada que había escrito para el Cuaderno de Cultura Científica, titulada La geometría poética del cubo (2), la segunda parte de la serie sobre la investigación artística de la figura geométrica del cubo realizada por el escultor navarro José Ramón Anda, yo había realizado un par de reproducciones, con las piezas del material LiveCube, de su escultura Zazpiak bat [Las siete, una] (1976). Como ya expliqué en dicha entrada, la obra Zazpiak bat está formada por una descomposición del cubo en siete policubos, por lo que podemos considerar que esta escultura propone además al espectador un “juego geométrico”.
 Las siete piezas, policubos, que componen la escultura de José Ramón Anda, Zazpiak bat [Las siete, una] (1976), realizadas con las piezas del material Live CubeEl juego geométrico básico del “cubo de Anda”, Zazpiak bat, consiste en rehacer el cubo 3 x 3 x 3, a partir de las siete piezas que lo componen. Aunque el “juego” artístico y geométrico va más allá, ya que se trata de utilizar las siete piezas para realizar diferentes formas a partir de las mismas, al igual que en la obra Descomposición del cubo (1973), que analizamos en la entrada La geometría poética del cubo, aunque ahora con más posibilidades, fruto del mayor número de piezas de la obra.
Las siete piezas, policubos, que componen la escultura de José Ramón Anda, Zazpiak bat [Las siete, una] (1976), realizadas con las piezas del material Live CubeEl juego geométrico básico del “cubo de Anda”, Zazpiak bat, consiste en rehacer el cubo 3 x 3 x 3, a partir de las siete piezas que lo componen. Aunque el “juego” artístico y geométrico va más allá, ya que se trata de utilizar las siete piezas para realizar diferentes formas a partir de las mismas, al igual que en la obra Descomposición del cubo (1973), que analizamos en la entrada La geometría poética del cubo, aunque ahora con más posibilidades, fruto del mayor número de piezas de la obra.
Desde el momento que realicé la reproducción de Zazpiak bat, me entretenía deshaciendo el cubo y volviéndolo a montar. Era tanto un momento de relax, mientras estaba liado con algún tema del trabajo, como una pequeña diversión mientras estaba tranquilamente en casa. La cuestión es que, con el inicio de las vacaciones estivales, empecé a dedicarle tiempo a buscar diferentes soluciones al cubo de Anda. Y entonces decidí realizar una búsqueda un poco más sistemática y ordenada de las diferentes maneras de colocar las siete piezas para formar el cubo.
 Una de las soluciones del cubo de Anda, Zazpiak bat
Una de las soluciones del cubo de Anda, Zazpiak batPor lo tanto, el reto planteado era buscar cuántas soluciones distintas existían al cubo de Anda, Zazpiak bat, es decir, de cuántas formas distintas (salvo rotaciones del cubo, esto es, si una solución es una rotación de otra, entonces son la misma solución, o dicho de otra forma, si tenemos una solución y la rotamos, sigue siendo la misma solución) se pueden colocar las siete piezas para conformar el cubo 3 x 3 x 3.
Problema: ¿Cuántas soluciones distintas existen del cubo de Anda, Zazpiak bat?
Después de un pequeño análisis de las diferentes posibilidades, que explicaremos más adelante, obtuve la siguiente solución.
Solución del problema: Existen más de cien soluciones distintas, de hecho, 131, del cubo de Anda.
Aunque, quizás debería ser un poco más cauto y decir que “existen, al menos, 131 soluciones distintas del cubo de Anda”, ya que quizás se me haya pasado alguna en mi análisis.
Para obtener las distintas soluciones del cubo de Anda, procedí de forma similar a como lo habían hecho los matemáticos ingleses John H. Conway y Richard K. Guy para resolver el cubo soma, como expliqué en la entrada El cubo soma: diseño, arte y matemáticas.
Vayamos por partes. Primero, las piezas que componen Zazpiak bat. Como ya hemos mencionado son siete policubos (esto es, figuras geométricas tridimensionales que se forman al unir dos o más cubos por alguna de sus caras), formadas por 1, 2, 4, 4, 5, 5 y 6 cubos pequeños, pero todas ellas piezas distintas entre sí, como puede verse en la imagen de arriba. Para realizar el análisis, nombré cada pieza con una letra: 1) a la pieza blanca en la imagen anterior, con 6 cubos pequeños, la llamé P, ya que era como una U con una punta; 2) a la pieza azul, con 5 cubos pequeños, la llamé, por motivos obvios, U; 3) a la pieza amarilla, con 5 cubos pequeños, la llamé R, ya que estaba retorcida; 4) a la pieza roja, con 4 cubos, la llamé E, ya que era como una esquina; 5) a la pieza verde, con 4 cubos, la llamé L; 6) a la pieza bicolor, rojo y azul, de dos cubitos, la llamé D, por el número dos; 7) y llamé I, la unidad, a la pieza con un único cubo pequeño, negra en la imagen.
Después clasifiqué, como se había hecho con el cubo soma, los diferentes tipos de cubos pequeños dentro del cubo 3 x 3 x 3, que era el objeto que había que formar con las siete piezas, en función de su posición en el mismo. El cubo grande 3 x 3 x 3 tiene 27 cubos pequeños, de los cuales 8 son cubos vértice (para los que hemos utilizado cubos rojos en la siguiente imagen), 12 cubos lado (verdes en la imagen), 6 cubos cara (en blanco) y un cubo central (que no se ve en la imagen, ya que está en el interior).
 El cubo 3 x 3 x 3, que está formado por 27 cubos pequeños, tiene 8 cubos vértice (rojos), 12 cubos lado (verdes), 6 cubos cara (blancos) y 1 cubo central
El cubo 3 x 3 x 3, que está formado por 27 cubos pequeños, tiene 8 cubos vértice (rojos), 12 cubos lado (verdes), 6 cubos cara (blancos) y 1 cubo centralA raíz de esta clasificación de las posiciones de los cubos pequeños, nos podemos plantear la siguiente cuestión, que nos ayudará en la futura búsqueda de las soluciones, que es: ¿cuántos vértices puede ocupar cada una de las siete piezas? La respuesta está en el siguiente cuadro.
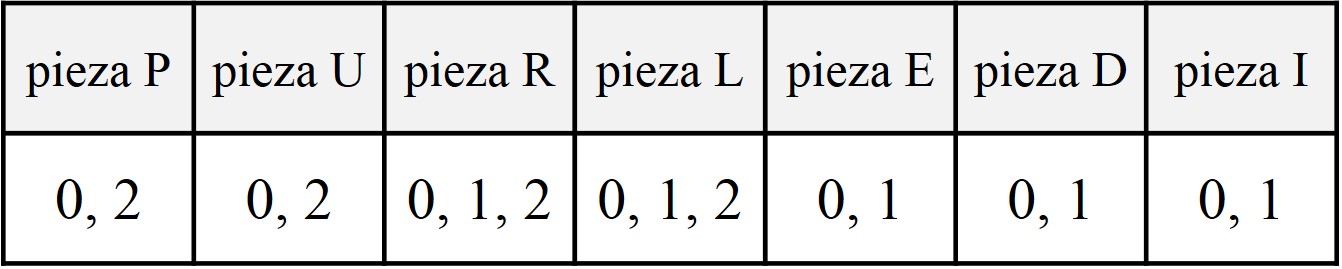 Número de vértices que puede ocupar cada una de las siete piezas del cubo Zazpiak bat
Número de vértices que puede ocupar cada una de las siete piezas del cubo Zazpiak batPor lo tanto, a la hora de buscar las soluciones del cubo de Anda nos podíamos apoyar en la anterior información, ya que hay que buscar las diferentes combinaciones de las piezas que sumen 8 vértices. Por ejemplo, utilizando las cuatro piezas P, U, R y L, cada una tocando dos vértices, ya tenemos los 8 vértices del cubo. De hecho, la solución mostrada más arriba es una solución de este tipo, con las cuatro piezas P, U, R y L ocupando los 8 vértices.
La siguiente información relevante en la búsqueda de las soluciones de este puzle geométrico fue la siguiente. Si tomamos el cubo 3 x 3 x 3 y lo coloreamos, en blanco y negro, de forma ajedrezada, como se muestra en la siguiente imagen, habrá 14 cubos pequeños blancos (los 8 cubos vértice y los 6 cubos cara) y 13 cubos pequeños negros (los 12 cubos lado y el cubo central).
 Cubo 3 x 3 x 3 coloreado, en blanco y negro, de forma ajedrezada
Cubo 3 x 3 x 3 coloreado, en blanco y negro, de forma ajedrezadaEntonces, nos podemos plantear cuántos cubos blancos y negros, de la anterior coloración del cubo grande, puede tener cada una de las siete piezas, una vez que las hemos montado para formar el cubo grande 3 x 3 x 3. La respuesta está en el siguiente cuadro.
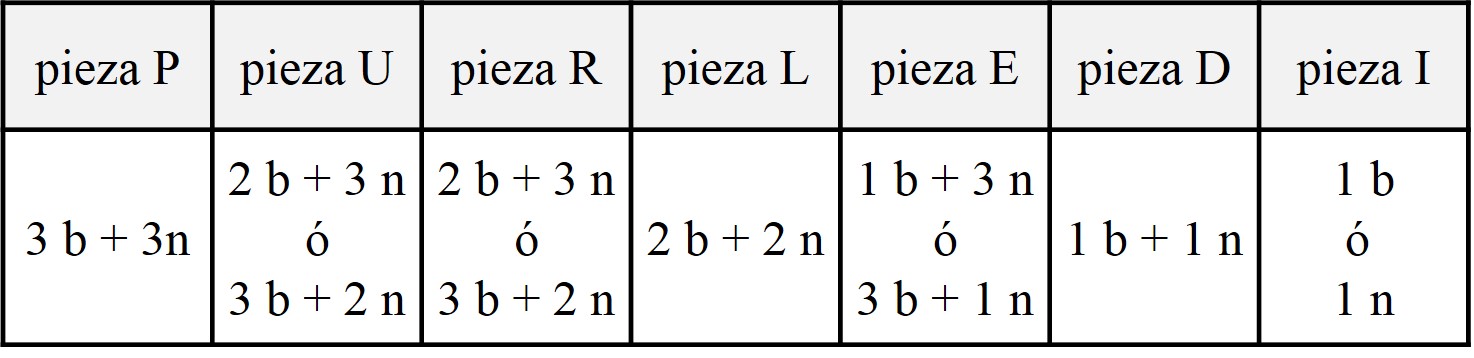 Número de cubos pequeños blancos y negros que puede ocupar cada una de las siete piezas del puzle geométrico
Número de cubos pequeños blancos y negros que puede ocupar cada una de las siete piezas del puzle geométricoComo vemos, el número máximo de cubos pequeños blancos que se puede ocupar con las siete piezas es 16 (= 3 + 3 + 3 + 2 + 3 + 1 + 1), por lo que, teniendo en cuenta que el cubo grande tiene 14 cubos blancos, solamente se pueden ahorrar 2 cubos blancos entre las siete piezas. Por ejemplo, si la pieza E está colocada en una posición, en el cubo grande, tal que contiene 1 cubo blanco y 3 negros, en la bicoloración ajedrezada, lo cual ocurriría por ejemplo si estuviese colocada en una esquina, entonces todas las demás piezas deberán tener su máximo de cubos blancos, para poder sumar 14.
Ya tenemos toda la información necesaria para abordar el análisis de las soluciones del cubo de José Ramón Anda. Para realizar una búsqueda ordenada de las soluciones podemos ir analizando las diferentes formas de ocupar los 8 vértices con las siete piezas: 1) P + U + R + L; 2) P + U + R + E + D; 3) P + U + R + E + I; 4) P + U + R + D + I; etcétera, y ver cuántas soluciones hay en cada una de estas categorías.
Aunque esto fue lo que hice en un principio, luego reduje el número de categorías considerando otro punto de vista. Estas son las categorías que he considerado para mi análisis:
A) P + U + R + L = 8 vértices;
B) la pieza L no tiene ninguno de los 8 cubos vértices (así, esta categoría incluye las combinaciones siguientes de las piezas que sí tocarían los 8 vértices: P + U + R + E + D, P + U + R + E + I, P + U + R + D + I, P + U + R + E + D + I, donde en esta última la pieza R solo tocaría un vértice);
C) la pieza R no tiene ninguno de los 8 cubos vértices;
D) la pieza U no tiene ninguno de los 8 cubos vértices;
E) la pieza P no tiene ninguno de los 8 cubos vértices.
F) P + U + R (1 vértice) + L + otra, es decir, la pieza R tiene un solo vértice del cubo, las piezas P, U y L tienen dos vértices, y el último vértice corresponde a una de las piezas E, D o I.
A continuación, expliquemos los resultados de cada categoría.
Categoría A: P + U + R + L = 8 vértices.
Antes de empezar a buscar las soluciones de esta categoría, podemos sacar algunas conclusiones en relación a los cubos pequeños que tocarían las siete piezas en las soluciones de esta categoría, al tener en cuenta las piezas que tocan los vértices, que son blancos. Podemos resumirlo en la siguiente expresión, donde cada sumando nos indica los cubos blancos de cada pieza y con los corchetes indicamos cuando hay dos posibilidades, cuales son estas.

La primera conclusión que sacamos es que en el quinto sumando, relativo a la pieza E, no puede tomar el valor 1, ya que entonces es imposible sumar 14, luego la pieza E no puede tener un cubo blanco y tres negros, en particular, no podrá ser una esquina del cubo.
Otra conclusión es que, para sumar 14, si en el segundo sumando fuese un 3 (es decir, la pieza U tiene tres cubos blancos, luego son los cuernos de la U los que tocan dos esquinas), entonces el séptimo sumando sería un 0 (luego la pieza I sería un cubo negro). Y al revés, si el segundo sumatorio fuese un 2 (la pieza U tendría 2 blancos y las esquinas de la U serían dos vértices del cubo), el séptimo sería un 1 (la pieza I sería blanca).
La importancia de estas dos informaciones está en que nos permiten eliminar algunas de las posibilidades, posiciones de las piezas, que nos aparecen en el análisis de las soluciones de esta categoría.
Pero vayamos con el resumen de los resultados de esta categoría. Las soluciones del cubo de Anda para las cuales las piezas P (blanca), U (azul), R (amarilla) y L (verde), cada una de ellas tiene dos de los vértices del cubo 3 x 3 x 3, son:
18 soluciones, en 16 de las cuales la pieza unidad I ocupa un cubo cara y en 2 de ellas ocupa un cubo lado.
Veamos dos de estas soluciones. La primera con la pieza I en una posición de cubo cara, luego se corresponde con un cubo blanco. En consecuencia, la pieza U con dos cubos blancos, los vértices, y tres cubos negros.

Y la segunda solución con la pieza I en una posición de cubo lado, luego de color negro en la bicoloración ajedrezada en blanco y negro. Y, en consecuencia, la pieza U con tres cubos blancos, dos de ellos los vértices, y dos negros.

Categoría B: la pieza L no tiene ninguno de los 8 cubos vértices.
Como la pieza L no tiene ninguno de los 8 cubos vértices, entonces tiene que estar colocada en alguno de los tres planos del cubo que pasan por el cubo centro.
Por otra parte, como la pieza P tiene que tocar necesariamente dos vértices, la he tomado como referencia para ordenar la colocación de la pieza L en esos seis planos.
En resumen, el número de soluciones del cubo de Anda en esta categoría es
23 soluciones, en 8 de las cuales la pieza unidad I ocupa un cubo cara, en 4 de ellas un cubo lado y en 11 un cubo vértice.
Las soluciones en las que el cubo I ocupa posiciones de caras o lados, se corresponden con el hecho de que las piezas que tocan los vértices son P, U, R, E y D, como en la siguiente (cuya pieza I está en la cara de abajo).

Mientras que las 11 soluciones en las que la pieza I ocupa un vértice, se corresponden con el hecho de que las piezas que tocan los vértices son P, U, R, E e I, como la siguiente.

Sin embargo, no hay soluciones en las que los vértices sean para las piezas P, U, R, D e I, o P, U, R, E, D e I (en esta última, R con un solo vértice).
Y al igual que en la categoría anterior, no existen soluciones en las cuales E sea una esquina, de hecho, 1 cubo blanco y tres negros. Aunque en este caso, si pudiesen dar los números (en la suma total de cubos blancos) en el último de los casos anteriores, es decir, P, U, R, E, D e I (en esta última, R con un solo vértice), siendo 3 + 3 + 3 + 2 + 1 + 1 +1 = 14, la suma de la cantidad de cubos blancos de cada pieza en este caso.
Categoría C: la pieza R no tiene ninguno de los 8 cubos vértices.
Para empezar, si buscamos soluciones del cubo de Anda en las cuales la pieza R no tiene ninguno de los vértices del cubo, entonces en esas soluciones el eje de la pieza R (los tres cubos pequeños colocados en línea de la pieza) solo puede coincidir con uno de los tres ejes del cubo, es decir, un conjunto de tres cubos pequeños colocados uno a continuación del otro, en línea, y cuyo cubo central es el centro del cubo. En tal caso, para las soluciones en las cuales la pieza R esté colocada en uno de los ejes del cubo, la pieza R tendrá 3 cubos negros y 2 cubos blancos.
En conclusión, las posibilidades de suma de los cubos blancos de cada pieza, en esta categoría, se resumen en la misma expresión de antes:
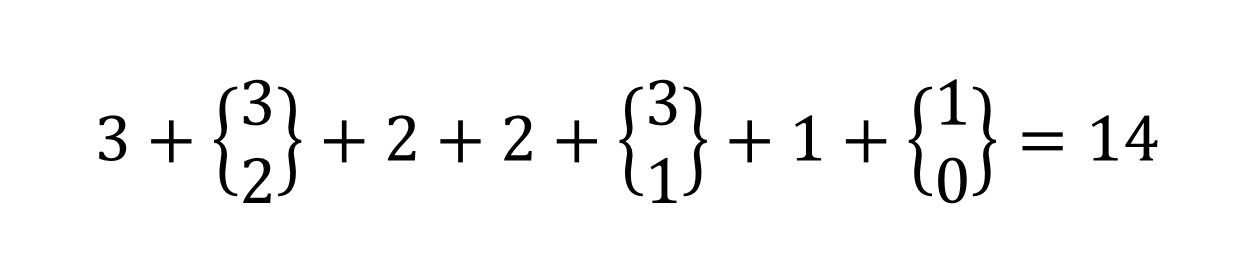
Y, por tanto, las consecuencias son las mismas. En particular, no existen soluciones en las que la pieza E sea una esquina, de hecho, que tenga un cubo blanco y tres negros.
El número de soluciones del cubo Zazpiak bat en esta categoría es
23 soluciones, en 9 de las cuales la pieza unidad I ocupa un cubo cara, en 2 de ellas un cubo lado y en 12 un cubo vértice.
En la imagen siguiente vemos indicadas tres soluciones de esta categoría. La pieza R está en el eje vertical y alrededor tiene las piezas P, U y E. Además, hay tres formas de colocar las piezas L, D e I, obteniendo tres soluciones, dos de ellas con la pieza I en una posición de cara y la otra en un vértice.

Categoría D: la pieza U no tiene ninguno de los 8 cubos vértices.
El hecho de que la pieza U no tenga ninguno de los 8 vértices del cubo, nos dice que necesariamente estará colocada en uno de los tres planos que pasan por el centro.
De nuevo, en el análisis he utilizado la pieza P como auxiliar, para ayudarme en la búsqueda de soluciones. En esta categoría hay
16 soluciones, con 5 caras, 2 lados y 9 vértices.
A continuación, mostramos una de estas soluciones, en las cuales la pieza U (azul) no tiene ningún vértice del cubo y está en uno de los planos que pasan por el centro del mismo. En ella la pieza I está en una posición de cubo lado.

Y una vez más, para ninguna de las posiciones la pieza E es esquina, ni ocupa tres cubos negros y uno blanco.
Categoría E: la pieza P no tiene ninguno de los 8 cubos vértices.
Una vez más, como la pieza P no toca ninguno de los vértices del cubo, entonces la parte principal de la misma, con forma de U, estará en alguno de los tres planos del cubo que pasan por el centro.
Existen
26 soluciones, en esta categoría, en dos de ellas la pieza I está en el centro del cubo, en 9 en un cubo cara, en 1 en un lado y en 14 en un vértice. En ninguna de ellas la pieza E ocupa tres posiciones de cubos negros y uno blanco, luego tampoco es esquina.
La solución de esta categoría que aparece en la siguiente imagen tiene la pieza I (negra) en el centro del cubo.

Categoría F: P + U + R (1 vértice) + L + otra (E, D o I) = 8 vértices.
Esta categoría contiene
25 soluciones, de las cuales, una es una solución en la que la pieza unitaria I está en el centro, dos son soluciones con la pieza I en una cara, 21 tienen a la pieza I en un lado y 1 en el vértice.
En esta categoría nos encontramos las dos únicas soluciones en las cuales la pieza E tiene un cubo en una posición blanca y tres en posiciones negras, aunque no es una esquina. Una de esas dos soluciones es la siguiente.

En resumen, el número de soluciones del cubo de Anda, Zazpiak bat [Las siete, una], es (al menos) 18 + 23 + 23 + 16 + 26 + 25, es decir,
131 soluciones distintas.
 Escultura Sin título (2014-2016), de José Ramón Anda, realizada en madera de roble, con un tamaño de 61 x 120 x 10 cm, en la exposición LANTEGI, José Ramón Anda en la sala Kubo Kutxa de Donostia-San Sebastián. Fotografía de Raúl Ibáñez
Escultura Sin título (2014-2016), de José Ramón Anda, realizada en madera de roble, con un tamaño de 61 x 120 x 10 cm, en la exposición LANTEGI, José Ramón Anda en la sala Kubo Kutxa de Donostia-San Sebastián. Fotografía de Raúl IbáñezSobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Buscando las soluciones del cubo de Anda se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El cubo soma: diseño, arte y matemáticas
- La geometría poética del cubo (2)
- La geometría poética del cubo
Los espectros de emisión de los gases
 Foto: Enrique López Garre / Pixabay
Foto: Enrique López Garre / PixabayUna de las primeras pistas verdaderamente importantes que llevaron a desentrañar la estructura atómica implicaba el estudio de la emisión y absorción de luz por los átomos de diferentes elementos. Los físicos sabían por la teoría de Maxwell que la luz es emitida y absorbida solo por cargas aceleradas. Esto sugería que el átomo podría contener cargas en movimiento. Podía esperarse por tanto que los patrones y las regularidades en las propiedades de la luz emitida proporcionasen indicios sobre la naturaleza precisa de los movimientos de estas cargas. Los resultados de este estudio fueron tan importantes para desentrañar la estructura atómica que necesitaremos revisar su desarrollo aquí con cierto detalle [1]. Empezamos con los espectros de emisión.
Se sabía desde hacía mucho tiempo que se emite luz por gases o vapores cuando se excitan en una de las siguientes formas:
(1) calentando el gas a una temperatura alta, como cuando una sustancia volátil se pone en una llama;
(2) por una descarga eléctrica a través del gas en el espacio entre los terminales de un arco eléctrico; o
(3) por una corriente eléctrica continua en un gas a baja presión, como en los letreros de neón.
El físico Thomas Melvill realizó los primeros experimentos sobre la luz emitida por varios gases excitados en 1752 [2]. Puso una sustancia tras otra en una llama, «después de haber colocado un cartón con un agujero circular entre mi ojo y la llama […], examiné la constitución de estas diferentes luces con un prisma ”. Melvill descubrió que el espectro de luz visible de un gas caliente de un solo elemento era diferente del conocido espectro arcoiris de un sólido o líquido calientes. El espectro de Melvill no era un continuo ininterrumpido de colores del violeta al rojo. Por el contrario, consistía en trozos aislados, cada uno con el color de esa parte del espectro continuo en el que se localizaba. Había espacios oscuros o, dicho de otra forma, faltaban colores entre los trozos.
Más tarde, se generalizó el uso de una ranura estrecha a través de la cual se dejaba pasar la luz. Los trozos de color de Melvill se convirtieron en líneas [3]. Estos espectros muestran que la luz emitida por un gas es una mezcla de solo unos pocos colores definidos o, en general, de subconjuntos de longitudes de onda muy restringidos. Estos tipos de espectros se denominan espectros de emisión y su estudio se conoce como espectroscopia.
 Espectro de emisión del hidrógeno. Imagen: Wikimedia Commons
Espectro de emisión del hidrógeno. Imagen: Wikimedia CommonsMelvill también señaló que los colores y las ubicaciones de las líneas [3] eran diferentes cuando se ponían diferentes sustancias en la llama. Por ejemplo, con la sal de mesa común en la llama, el color dominante era «amarillo brillante» (ahora se sabe que es característico del elemento sodio). De hecho, el espectro de emisión es muy diferente para cada gas químicamente disitnto porque cada elemento químico emite su propio conjunto característico de longitudes de onda. [4]
 Espectro de emisión en la región visible del vapor de hierro. Imagen: Wikimedia Commons
Espectro de emisión en la región visible del vapor de hierro. Imagen: Wikimedia CommonsAlgunos gases tienen espectros de emisión relativamente simples. Así, la parte más prominente del espectro visible del vapor de sodio es un par de líneas amarillas brillantes. Esta es la razón por la cual, por ejemplo, la llama en una estufa de gas se vuelve amarilla cuando la sopa, o cualquier líquido que contenga sal, cae sobre ella al hervir. Algunos gases o vapores tienen espectros muy complejos. El vapor de hierro, por ejemplo, tiene unas 6000 líneas brillantes solo en el rango visible.
En 1823, el astrónomo John Herschel sugirió que cada gas podría identificarse por su espectro de emisión característico. A principios de la década de 1860, el físico Gustav R. Kirchhoff y el químico Robert W. Bunsen habían descubierto conjuntamente dos elementos nuevos (rubidio y cesio) al observar líneas de emisión no reportadas previamente en el espectro del vapor de un agua mineral. Este fue el primero de una serie de descubrimientos basados en espectros de emisión. Con él comenzó el desarrollo de una técnica para el análisis químico rápido de pequeñas cantidades de materiales mediante espectroscopía.
Notas:
[1] Para ello, a lo largo de entradas sucesivas seá necesario que aparezcan algunas ecuaciones matemáticas. Como siempre en nuestras series serán muy simples y solo utilizarán poco más que las cuatro reglas de la aritmética más elemental. Merecerá la pena el esfuerzo extra.
[2] No, no es una errata. A mediados del siglo XVIII, exactamente el mismo año en el que Benjamin Franklin llevaba a cabo en una colonia británica llamada Pennsylvania un experimento con cometas, llaves y rayos.
[3] Estas líneas brillantes son, de hecho, imágenes a color de la ranura. Cuando se habla de líneas del espectro estamos asumiendo que hay una rajita en alguna cosa opaca por la que se deja pasar la luz. Dicho de otra forma, las líneas espectrales son líneas porque los instrumentos usan ranuras, no porque se emitan como líneas.
[4] Al mirar una fuente gaseosa sin la ayuda de un prisma o una rejilla, nuestro encéfalo combina los colores separados. Percibe la mezcla como rojiza para el neón, azul pálido para el nitrógeno, amarillo para el vapor de sodio (aun el de muchas de las farolas de muchas ciudades españolas), y así sucesivamente.
[5] La «prueba de llama» suele ser hoy día una práctica de laboratorio muy simple en los primeros cursos de introdución a la química.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Los espectros de emisión de los gases se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Computación cognitiva de espectros infrarrojos
- El hidrógeno en el Universo (I): La emisión del hidrógeno neutro a 21 cm.
- Patrón de interferencia en ondas periódicas
Los dragones de Komodo son unos comodones venenosos
 Foto: Pixabay
Foto: PixabaySon tan hipnóticos como peligrosos. Bautizados con el nombre de un animal legendario como el dragón, los dragones de Komodo tienen poco que envidiar a sus equivalentes de cuento: son grandes, fuertes y tienen la habilidad de cazar presas mucho más grandes que ellos con un solo mordisco.
Esta semana sabemos un poco más sobre cómo los dragones de cómodo han llegado a ser como son gracias a que se ha publicado por primera vez una secuenciación de su genoma en la revista Nature Ecology & Evolution, algo muy útil si tenemos en cuenta algunas de sus peculiares habilidades y características, como un potente sentido del olfato para ser reptiles o un metabolismo inusualmente rápido que les permite extraer energía de la comida durante un tiempo más prolongado de lo habitual en otros reptiles
Para entender y descodificar ese genoma, los autores del estudio han dedicado 8 años a recopilar datos y secuenciar genomas de cuatro dragones que viven en cuatro zoológicos diferentes y los compararon con otros 15 reptiles de la familia Varanidae, a la que pertenecen los dragones de Komodo, tres aves y cuatro mamíferos.
Para celebrar este hito, que permitirá conocer mejor a estos imponentes animales, así como favorecer su preservación y la de sus hábitats, aquí van algunas cosas que hemos ido aprendiendo sobre ellos.
1. Un veneno que hace que la presa se desangre
Los dragones de Komodo son capaces de matar presas bastante más grandes y fuertes que ellos con un solo mordisco. A menudo aprovechan el factor sorpresa para pegar la dentellada y luego se retiran a una distancia prudencial hasta que el desdichado bicho muere desangrado. Juega a su favor el potente veneno que se encuentra en su saliva.
Durante mucho tiempo se pensó que la presencia de bacterias en su boca causaba una rápida sepsis (infección de la sangre) que era lo que acababa con sus presas, pero ahora parece claro que ese no es el único efecto de su mordida: su saliva contiene también compuestos que impiden la coagulación de la sangre y causan hipertensión, de forma que el animal mordido se desangra rápidamente y muere al poco rato.
2. Pero que a ellos mismos no les afecta
Las peleas entre dragones de Komodo pueden ser temibles, pero este reciente trabado de decodificación de su propio genoma ha ayudado también a entender cómo su cuerpo es inmune al veneno de las mordidas de otros individuos de su misma especie.
En concreto, los investigadores han hallado una serie de genes que codifican proteínas que intervienen en los procesos de hemostasis, el conjunto de mecanismos que tiene un cuerpo para detener las hemorragias y retener la sangre dentro del organismo. El trabajo de los científicos permite entender como la presión evolutiva ha favorecido esos genes en los dragones de Komodo de forma que lo que les sirve para cazar o defenderse de otras especies no les haga matarse entre ellos con tanta facilidad.
3. Un veneno convertido en tratamiento
No es raro que médicos y científicos busquen en los venenos de la naturaleza remedios para los males humanos, y la saliva del dragón de Komodo no es una excepción. Después de todo, los problemas de coagulación son una enfermedad que afecta seriamente a la vida de las personas que la padecen, ¿no podrían las propiedades de esta sustancia intervenir en su tratamiento.
En 2017, científicos de la Universidad de Queensland, en Australia, publicaban en la revista Toxins una investigación en la que analizaban la composición del veneno de varios tipos de lagartos, entre ellos del dragón de Komodo, para tratar de aislar y aprovechar sus compuestos anticoagulantes en el tratamiento de enfermedades relacionadas con la trombosis y otros problemas cardiovasculares.
 Foto: Wikimedia Commons
Foto: Wikimedia Commons4. Los dragones de Komodo son bastante comodones
Pido perdón por el terrible juego de palabras, no me he podido resistir. Pero tiene algo de cierto: resulta que los dragones de Komodo podían haberse expandido más allá de sus hábitats actuales, pero por alguna razón simplemente prefirieron no hacerlo. Esa era la principal conclusión de una investigación publicada en la revista Proceedings of the Royan Society B el año pasado.
Para estudiar este asunto, los investigadores desplazaron 7 dragones adultos a cierta distancia de su territorio: algunos a unos 25 kilómetros dentro de la misma isla mientras que otros fueron transportados a islas vecinas a menos de medio kilómetro de distancia. En menos de cuatro meses los lagartos desplazados por tierra habían vuelto a su territorio mientras que los que estaban en otra isla, mucho más cerca y a pesar de ser perfectamente capaces de nadar esa distancia, ni siquiera lo intentaron.
Esta reticencia a moverse tiene sus inconvenientes, pero también sus ventajas. Por un lado, les hace vulnerables a problemas de escasez de alimentos y a terminar debilitándose a causa de la consanguineidad a la hora de reproducirse. Por otro, arriesgarse a explorar islas desconocidas puede suponer un riesgo demasiado alto si en ella no hay alimento suficiente o no consiguen aparearse con ningún otro individuo en esa nueva isla. Por eso quizá volver por tierra a casa puede ser una opción atractiva aunque la distancia sea relativamente grande, pero cruzar las aguas, por breves que sean, no merezca la pena.
Referencias:
Enter the Dragon: The Dynamic and Multifunctional Evolution of Anguimorpha Lizard Venoms – Toxins
Genome of the Komodo dragon reveals adaptations in the cardiovascular and chemosensory systems of monitor lizards – Nature Ecology and Evolution
Exploring mechanisms and origins of reduced dispersal in island Komodo dragons – Proceedings of the Royal Society B
Sangre de Dragón – Cuaderno de Cultura Científica
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Los dragones de Komodo son unos comodones venenosos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sangre de dragón
- El organismo humano es una estufa de unos pocos vatios
- Rediles para ganado de unos 5.000 años de antigüedad en Álava
Sociedades miniatura experimentales
 Imagen: Gordon Johnson / Pixabay
Imagen: Gordon Johnson / PixabayEn 2015 Amazon desarrolló un software para contratar a miles de personas para hacer pequeñas tareas para mejorar su web. Más tarde alquiló ese mismo software a otras empresas para que pudiesen hacer lo propio. Desde entonces, más de medio millón de personas han sido contratadas para trabajar en el sistema. Ese software y otros similares han resultado ser muy útiles también para hacer experimentos en campos en los que no había sido posible antes. El laboratorio dirigido por el sociólogo (y también médico) Nicholas Christakis, de la Universidad de Yale, es uno de los que ha recurrido a esos servicios para hacer experimentos sociales a gran escala. Mediante un programa desarrollado en su laboratorio han creado sociedades en miniatura cuyos integrantes son trabajadores del servicio de Amazon. Los investigadores relacionan a unos individuos con otros dentro de esas minisociedades, y manipulan variables tales como la estructura de las interacciones o su naturaleza.
En un primer experimento, a 785 personas distribuidas en 4 minisociedades se les asignaron entre una y seis relaciones sociales, de manera que cada participante tenía un esquema diferente de conexiones. En el experimento pretendían emular las condiciones para la producción de bienes públicos. Para ello, a los participantes se les daba una cantidad de dinero; y podían quedarse con todo o entregar una parte a las personas con las que estaban conectados. En este segundo caso los experimentadores entregaban al receptor una cantidad igual a la donada, de manera que este obtenía el doble. Al ejecutar rondas sucesivas del “juego”, se generaban condiciones que propiciaban reciprocidad. Esto es, cuando alguien no donaba, lo normal es que en la siguiente ronda los otros tampoco le diesen nada a esa persona. Podía ocurrir, por ello, que al cabo de varias rondas todo un grupo llegase a dejar de hacer donaciones, o lo contrario. Cuando a los participantes no se les permitía cambiar sus relaciones, lo normal es que cesase la cooperación. Pero si se les dejaba una cierta capacidad para elegir a sus “amigos”, se acababan configurando grupos formados por colaboradores, marginando a quienes no lo hacían.
En otro experimento con 1.529 personas distribuidas en 90 grupos, estudiaron cómo cambiaba el grado de cooperación en función del grado de fluidez social. Y observaron que la cooperación era mínima en las sociedades con una estructura rígida, porque en ellas no se puede evitar interactuar con individuos egoístas; pero una vez alcanzado un nivel máximo de cooperación, los grados más altos de fluidez tampoco son beneficiosos; al parecer, un cambio demasiado frecuente en las relaciones interpersonales desincentiva la cooperación.
En un tercer experimento con 1.163 individuos distribuidos en 48 sociedades, midieron la medida en qué el beneficio debía exceder al coste de la cooperación para que esta fuese posible. Hallaron que, como norma, la relación coste beneficio debía ser superior al número de relaciones de cada individuo. En otras palabras, cuantos más individuos interactúan mayor ha de ser el beneficio relativo, seguramente porque al aumentar el número de personas implicadas, también aumenta la dificultad de la cooperación. Y por último, comprobaron también que las desigualdades económicas entre los participantes no influían en el grado de cooperación, salvo que tales desigualdades fuesen visibles.
Aunque se trata de experimentos y, por lo tanto, no reflejan con total fidelidad las condiciones de la vida social real, los resultados de estos “juegos” ayudan a entender lo que ocurre en situaciones reales. Hay quien critica estos experimentos porque simplifican mucho el funcionamiento de las sociedades. Es cierto; tan cierto como que los experimentos en ciencias naturales también simplifican mucho los sistemas naturales.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Sociedades miniatura experimentales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Matemáticas experimentales
- Comprobaciones experimentales de la relatividad general (1)
- Comprobaciones experimentales de la relatividad general (y 2)
Fútbol, periódicos y estadísticas

El fútbol es el deporte alrededor del cual orbitan, además de los miles de fieles seguidores, sectores como la hostelería, el periodismo, la publicidad o la moda. Pero, ¿hay lugar para la ciencia?
Aunque resulte difícil imaginar la relación que pueda existir entre disciplinas científicas como la física, las matemáticas o la antropología y el fútbol, cada vez son más las ocasiones en las que, sorprendentemente, la ciencia puede explicar muchos de los acontecimientos que suceden en un campo de fútbol e incidir en aspectos como la mejora del rendimiento de los jugadores y, en consecuencia, de los resultados.
La relación entre estas dos disciplinas fue el hilo conductor de un ciclo de conferencias organizado por la Cátedra de Cultura Científica con el apoyo de la Diputación Foral de Bizkaia y la colaboración de Fundación Española para la Ciencia y la Tecnología (FECYT) – Ministerio de Ciencia, Innovación y Universidades”, que tuvo lugar en el Bizkaia Aretoa de la UPV/EHU de Bilbao los meses de octubre y noviembre de 2018. Enmarcado en el ciclo de conferencias “Zientziateka”, que contó con cinco conferencias impartidas por especialistas de diversos campos en las que se ilustró la conexión que existe entre diferentes disciplinas científicas y el fútbol.
Kiko Llaneras es doctor en Sistemas de Automática Industrial y consultor de visualización y ciencia de datos y habla en esta interesantísima charla, tomando como eje su experiencia personal en el diario El País escribiendo sobre fútbol y estadística, sobre si es apropiado o no hablar de predicciones y probabilidades sujetas al azar en los periódicos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Fútbol, periódicos y estadísticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La trama vasco-rusa que eliminó a España del Mundial 2018
- Fórmulas matemáticas y números: cómo ayuda la economía al fútbol
- Ciencia, arte y cultura callejera: física y música
50 años modificando genes (en bacterias)
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Desde la expansión de la agricultura y la ganadería, que se inició en el neolítico, los humanos hemos intentado modificar la información genética de animales y plantas, en nuestro propio interés. Así lo atestiguan algunos bajorrelieves de 850 años AC, donde se aprecian dioses asirios polinizando artificialmente palmeras datileras. Hasta hace poco menos de 50 años, estas modificaciones solo podían realizarse de forma indirecta, mediante cruzamientos entre organismos de la misma especie, o de especies muy relacionadas, y la selección de aquellos descendientes que presentan los caracteres de interés (por ejemplo, un mayor tamaño, frutos más dulces, animales más dóciles, …), para realizar con ellos nuevos cruces y así, progresivamente, ir modificando la composición genética de las poblaciones, de acuerdo a nuestros intereses.
Sin embargo, en las últimas 5 décadas, se han desarrollado herramientas moleculares que permiten realizar modificaciones genéticas de manera directa. Varios grupos de investigación de la Facultad de Ciencia y Tecnología de la UPV/EHU hemos seguido muy de cerca estos avances y hemos participado activamente en algunas de sus aplicaciones. En este artículo y en los dos que le sucederán, presentamos brevemente algunos de los desarrollos más importantes en este ámbito, destacando sus aplicaciones en el campo biomédico y mencionando algunos de los debates científicos y sociales que su uso propició o que sigue generando hoy día.
El término «ingeniería genética» se acuñó a principios de los años 40 del siglo pasado. Curiosamente, los avances científicos que la hicieron posible no sucedieron hasta unos cuantos años más tarde, primero con el descubrimiento de la estructura del DNA, por Franklin,Watson y Crick en1953, y luego con el descubrimiento de la tecnología del DNA recombinante, por Cohen y Boyer en 1973 (Figura 1). La tecnología del DNA recombinante implica la unión de fragmentos de DNA, procedentes de una misma especie o de especies diferentes, para crear moléculas de DNA “híbridas” que pueden posteriormente introducirse en una célula hospedante.
 Figura 1. A) Diagrama de la doble hélice de DNA propuesto por James Watson y Francis Crick en 1953 a partir de imágenes de rayos X obtenidas por Rosalind Franklin. Fuente: Watson, J. D. et. al., Molecular Structure of Nucleic Acids. Nature, 171: 737-738. B) La introducción del DNA recombinante (rDNA) híbrido (plásmido recombinante) en una bacteria permite que el DNA recombinante se replique naturalmente en la bacteria (clonación génica). Fuente: Wikimedia Commons
Figura 1. A) Diagrama de la doble hélice de DNA propuesto por James Watson y Francis Crick en 1953 a partir de imágenes de rayos X obtenidas por Rosalind Franklin. Fuente: Watson, J. D. et. al., Molecular Structure of Nucleic Acids. Nature, 171: 737-738. B) La introducción del DNA recombinante (rDNA) híbrido (plásmido recombinante) en una bacteria permite que el DNA recombinante se replique naturalmente en la bacteria (clonación génica). Fuente: Wikimedia Commons
En los primeros años de la tecnología del DNA recombinante, su uso generó mucha suspicacia y preocupación, por tratarse de una manipulación de la esencia misma de la vida (recordemos que el DNA se consideró la “molécula de la vida”). Se temía que estos genes híbridos llevaran consigo capacidades incontrolables para dañar a los seres humanos. Tal es así que en 1974 los propios científicos se auto-impusieron una moratoria en sus investigaciones hasta que se celebró una reunión internacional (la Conferencia de Asilomar en 1975) para debatir si la experimentación con DNA recombinante planteaba algún peligro plausible para la salud pública. En esta reunión unos 150 científicos discutieron durante días sobre los riesgos potenciales de la nueva tecnología y sobre su regulación, y elaboraron directrices voluntarias para garantizar la seguridad de la tecnología del DNA recombinante (Figura 2). Acordaron, por ejemplo, que fuera una bacteria específica (E. coli cepa K12) la utilizada en experimentos de DNA recombinante. Se trata de una cepa no patógena, genéticamente modificada para que no pueda colonizar el tracto digestivo humano ni sobrevivir fuera del laboratorio y, tras más de 40 años trabajando con ella, podemos decir que estas medidas fueron totalmente efectivas.
Los participantes en la Conferencia de Asilomar también se esforzaron por llevar la ciencia al dominio público. Según los organizadores Paul Berg y Maxine Singer, la conferencia “marcó el comienzo de una era excepcional, tanto para la ciencia como para la discusión pública de las políticas científicas”, y cumplió el importante propósito de poner fin a muchos temores sociales con respecto a los usos responsables de las metodologías del DNA recombinante.
 Figura 2. Izquierda: Algunos participantes de la Conferencia de Asilomar (Febrero, 1975). Fuente: DeWitt Stetten, Jr., Museum of Medical Research. Derecha: Debate en la Conferencia de Asilomar. De izquierda a derecha: Maxine Singer, Norton Zinder, Sydney Brenner y Paul Berg. Fuente: United States National Library of Medicine
Figura 2. Izquierda: Algunos participantes de la Conferencia de Asilomar (Febrero, 1975). Fuente: DeWitt Stetten, Jr., Museum of Medical Research. Derecha: Debate en la Conferencia de Asilomar. De izquierda a derecha: Maxine Singer, Norton Zinder, Sydney Brenner y Paul Berg. Fuente: United States National Library of MedicineLas pautas establecidas en la conferencia, permitieron realizar experimentos con la tecnología del DNA recombinante de una manera más regulada y con un conocimiento más profundo del proceso, e hicieron posible que, en pocos años, esta tecnología fuera considerada ya madura. En 1980, la Corte Suprema de EEUU dictaminó que los microorganismos genéticamente modificados podían ser patentados. Esto generó un entorno favorable en el ámbito industrial y académico para aprovechar la nueva capacidad científica de reorganizar la información genética creando nuevos tipos de moléculas de DNA en un tubo de ensayo.
Una de las aplicaciones de la ingeniería genética que mayor desarrollo ha experimentado es la transgénesis o creación de organismos transgénicos. La transgénesis consiste en introducir un determinado gen (denominado transgén) en un organismo de otra especie. Dado que el código genético es universal para todos los seres vivos, el organismo transgénico resultante puede expresar el gen ajeno.
La transgénesis puede usarse, por ejemplo, para producir en bacterias proteínas humanas de valor terapéutico. Para ello, el gen humano de interés debe ser insertado primeramente en un vector (típicamente una molécula circular de DNA llamada plásmido) mediante la tecnología de DNA recombinante. El plásmido recombinante que porta el gen humano, se transfiere a las bacterias, las cuales lo copian en cada división celular y lo utilizan para producir la proteína de interés. De este modo es posible obtener en muy poco tiempo un número enorme de copias del gen, y, también una gran cantidad de la proteína expresada por ese gen.
La insulina, una hormona pancreática que regula los niveles de azúcar en la sangre, fue la primera proteína humana producida en bacterias mediante técnicas de ingeniería genética (1978). Hasta ese momento, las personas diabéticas que no producían niveles adecuados de insulina debían ser tratadas con insulina aislada de cerdos. Se calcula que la empresa fabricante Eli Lilly, solo en los EEUU, necesitaba cerca de 56 millones de animales por año para satisfacer la demanda de este producto. Además del coste de producción de la insulina porcina, había otros problemas relacionados con el riesgo de infecciones y con la aparición de reacciones inmunitarias de rechazo. Todo ello promovió el desarrollo de otras formas de obtención de la insulina para uso terapéutico como, por ejemplo, obtenerla a partir de la expresión en bacterias del gen humano de la insulina.
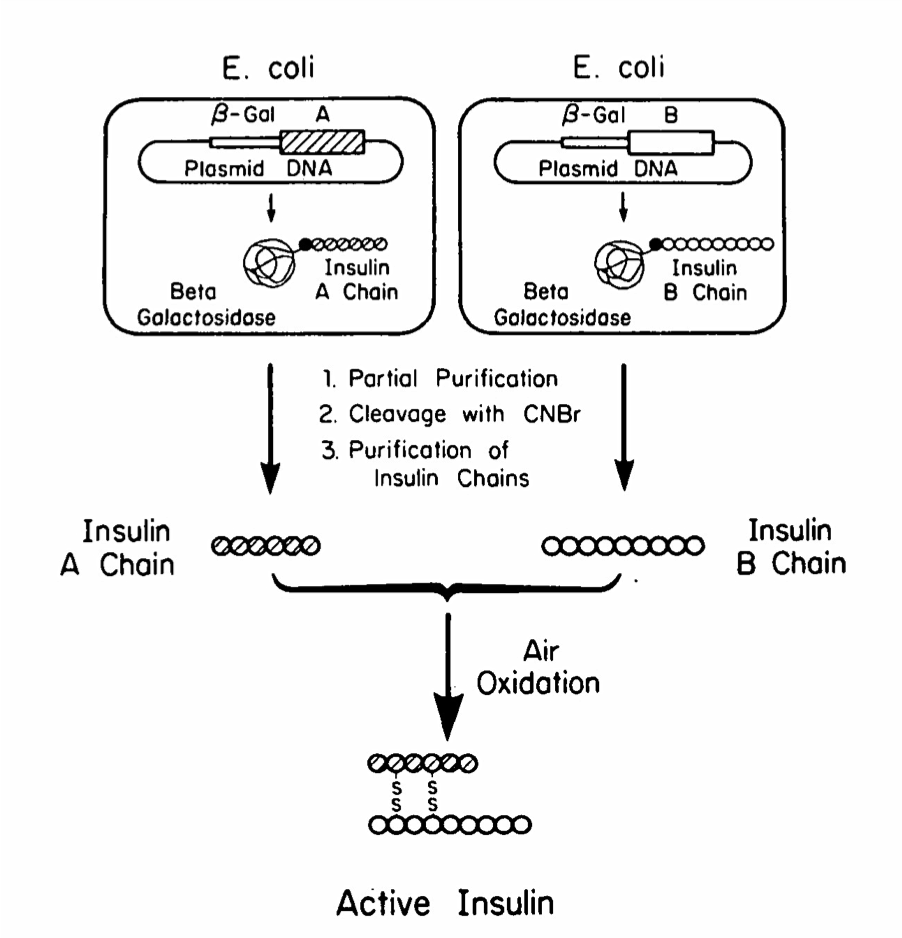 Figura 3. Descripción esquemática del procedimiento para la producción de insulina humana por bacterias. Se construyeron dos cepas de E. coli, cada una con capacidad para sintetizar la cadena A o B de la insulina in vivo. Las cadenas peptídicas de insulina se purificaron por separado, y se unieron in vitro. Fuente: Riggs AD & Itakura K. Synthetic DNA in Medicine. Am J Hum Genet 31:532-538 (1979)
Figura 3. Descripción esquemática del procedimiento para la producción de insulina humana por bacterias. Se construyeron dos cepas de E. coli, cada una con capacidad para sintetizar la cadena A o B de la insulina in vivo. Las cadenas peptídicas de insulina se purificaron por separado, y se unieron in vitro. Fuente: Riggs AD & Itakura K. Synthetic DNA in Medicine. Am J Hum Genet 31:532-538 (1979)
La insulina humana está formada por dos cadenas peptídicas, A y B, unidas entre sí por enlaces químicos llamados puentes disulfuro. Por ello, hubo que generar 2 moléculas de DNA recombinante (una para cada cadena). Cada una se transfirió a cultivos de bacterias independientes, se expresó y purificó cada cadena y, después, ambas se combinaron para formar la molécula de insulina completa, idéntica a la producida por el páncreas humano (Figura 3). Sin necesidad de depender de los animales, los investigadores podían ahora producir insulina recombinante en cantidades ilimitadas, libre de contaminantes y de agentes infecciosos animales. En 1982, la Insulina Humana Biosintética (BHI), desarrollada conjuntamente por Genentech y Eli Lilly se convirtió en el primer producto farmacéutico comercial sintetizado mediante tecnología del DNA recombinante, aprobado por la Administración de Alimentos y Medicamentos de los Estados Unidos (FDA). Actualmente, más del 95% de los usuarios de insulina a nivel mundial utilizan alguna forma de insulina recombinante.
Tras este éxito, rápidamente se aprobaron diversos medicamentos sintetizados en bacterias mediante la tecnología del DNA recombinante, incluidas la hormona de crecimiento humano (en 1985), la vacuna para la hepatitis B (en 1986), el interferón (un medicamento contra el cáncer, en 1986), o la glucocerebrosidasa, (un enzima para tratar la enfermedad de Gaucher, en 1991).
La producción y comercialización de proteínas de interés terapéutico liderada por la industria biotecnológica, no es la única aplicación de la tecnología del DNA recombinante en bacterias. Esta tecnología se utiliza de forma rutinaria en investigación experimental en la mayoría de los laboratorios de biología molecular del mundo, incluidos los de nuestra Facultad. De hecho, nuestros estudiantes de los Grados de Biociencias realizan prácticas experimentales durante su formación universitaria, en las que aprenden a utilizar estas metodologías en diferentes entornos formativos y como ejemplo de sus diversas aplicaciones.
La posibilidad de generar bacterias transgénicas inició una carrera que ha llevado al desarrollo de otros organismos transgénicos, incluyendo muchas especies de animales y plantas. En próximas reseñas trataremos algunas de ellas, como la generación, uso y aplicaciones de los animales mamíferos transgénicos generados para usos científicos y/o biomédicos, y la aplicación de la tecnología del DNA recombinante en terapia humana.
Sobre los autores: Ana I. Aguirre, José Antonio Rodríguez y Ana M. Zubiaga son profesores del departamento de Genética, Antropología Física y Fisiología Animal de la Facultad de Ciencia y Tecnología, e investigadores del grupo de investigación consolidado del Gobierno Vasco Biología Molecular del Cáncer.
El artículo 50 años modificando genes (en bacterias) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- 50 años de secretos: la era de la criptografía moderna
- Bacterias contra bacterias
- La historia de la insulina, 90 años salvando vidas
Los orígenes de la visualización de datos
Hoy en día, vivimos inmersos en gráficas, mapas e infografías de toda índole. En la era de la información, la visualización de datos se percibe como un lenguaje familiar que, además, gracias a las computadoras, resulta muy accesible. Pero no siempre fue ni tan obvio ni tan sencillo, sino que se lo debemos a unos pocos pioneros que, a base de papel y tinta, tuvieron la visión y la destreza de combinar arte y estadística para revolucionar nuestra manera de estudiar los datos.
Como resultado, las gráficas son una parte vital de la comunicación en ciencia y tecnología, además de otros muchos ámbitos como economía, educación y medios de comunicación. No es de extrañar pues que el nacimiento de las gráficas estadísticas coincidiese en el tiempo con esa nueva manera metódica de observar el mundo de los primeros científicos, también llamados filósofos naturales. Y tampoco es casualidad que los primeros gráficos se desarrollasen con el objetivo de analizar datos de tipo histórico y económico.
Hace poco más de 250 años, el filósofo natural y teólogo Joseph Priestley (1733-1804) publicaba en su obra A New Chart of History los primeros cronogramas que se conocen. Aparte de su buena reputación como científico gracias a sus escritos sobre electricidad, sus trabajos con gases (fue capaz de aislar el oxígeno e inventó la soda), Priestley era un gran pedagogo en materias muy diversas como la gramática o la historia, cuyo estudio era para él un imperativo moral. Y fue precisamente para sus clases de historia para las que diseñó un tipo de gráfica donde diferentes barras sobre una línea temporal representaban en contexto y permitían comparar diferentes períodos de tiempo, como vidas de personas o duraciones de imperios. Los cronogramas de Priestley causaron gran sensación, y su obra fue reeditada docenas de veces.
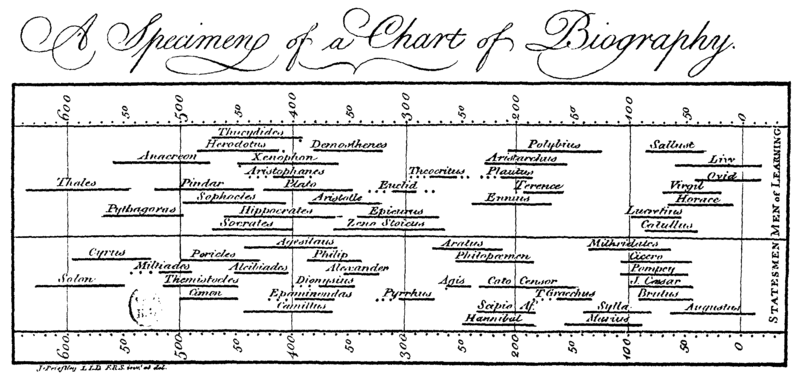 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsDos décadas después, inspirado por Priestley, William Playfair (1759-1823), ingeniero y economista político escocés, fue un precursor del uso de gráficos para explorar, entender y comunicar datos al inventar diversos tipos de diagramas. Concretamente en 1786 publicó su Commercial and Political Atlas, considerada la primera obra de importancia con gráficas estadísticas.
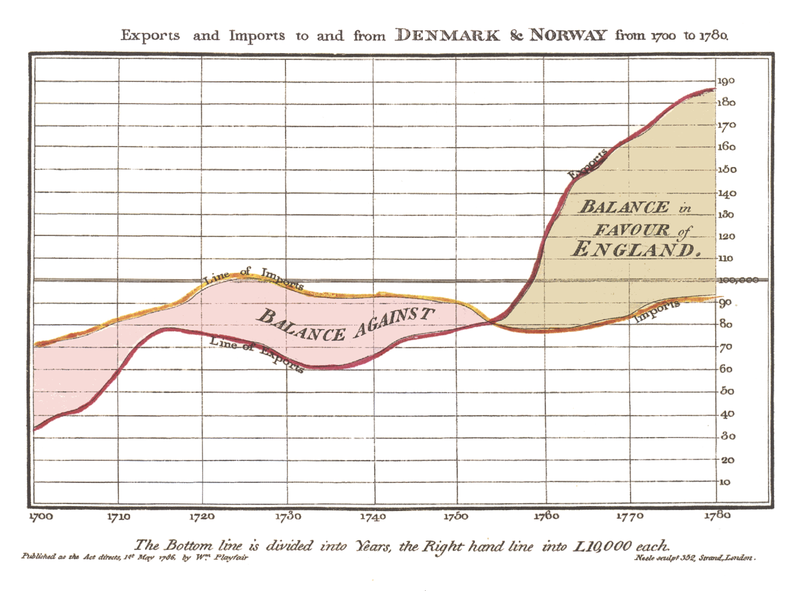 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsEn 43 maravillosas gráficas, Playfair utiliza líneas para representar la evolución a lo largo de los años de importaciones y exportaciones entre diversos países. Incidentalmente, la ausencia de datos históricos para Escocia, que le impedía reproducir ese mismo análisis, lo llevó a una segunda innovación: la gráfica de barras. Dado que disponía de datos para un único año, decidió disponer las exportaciones e importaciones en 17 pares de barras, uno por cada país con el que Escocia tenía relaciones económicas.
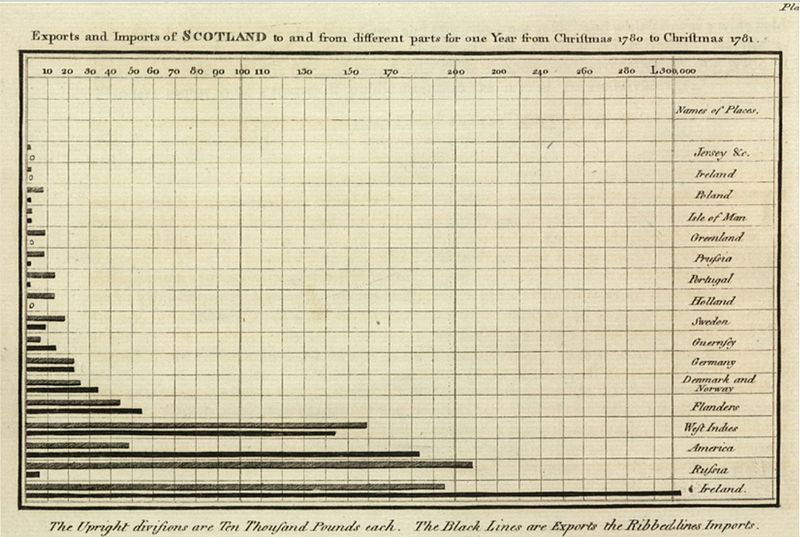 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsCuriosamente, esta es la primera gráfica que se conoce que no tiene una dimensión espacial (como un mapa) o temporal (como los cronogramas de Priestley). Por primera vez en la historia, se da solución gráfica a un problema de comparación pura de datos cuantitativos. Y por si fuera poco, además de considerarse el padre de las gráficas de líneas, áreas y barras, Playfair también tiene el dudoso honor de ser el inventor de la gráfica de tarta, en su obra Statistical Breviary de 1801.
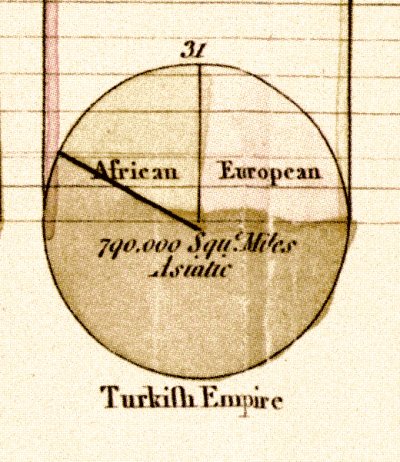 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsNo en vano, fue esta gráfica de tarta, diseñada para comparar proporciones de una manera compacta, la que inspiró a la siguiente protagonista: Florence Nightingale (1820-1910). Nightingale fue una enfermera, escritora y estadística británica, considerada la fundadora de la enfermería moderna y primera mujer en ser elegida miembro de la Royal Statistical Society en 1859. Fue un mito viviente de la Inglaterra victoriana por su importante labor durante la Guerra de Crimea (1853-1856). En el hospital militar en el que se encontraba destinada, se dedicó a llevar una contabilidad minuciosa de las causas de muerte de los soldados, y utilizó el denominado diagrama de la rosa para comunicar los resultados de su estudio.
 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsSe trata de un histograma circular que da cuenta de la estacionalidad de las diversas causas de muerte y de su impacto, destacando las muertes por enfermedades infecciosas. Gracias a esta visualización, logró convencer al parlamento británico de la necesidad de realizar una reforma drástica de las medidas de higiene en centros hospitalarios.
Por supuesto, no se puede hablar de historia de la visualización de datos sin mencionar hitos como el mapa del cólera de John Snow, el revolucionario mapa de flujo de Charles Joseph Minard sobre las pérdidas del ejército de Napoleón en la campaña de Rusia, los mapas de datos jerárquicos de Charles Louis de Fourcroy, o las primeras gráficas en 3D de Luigi Perozzo.
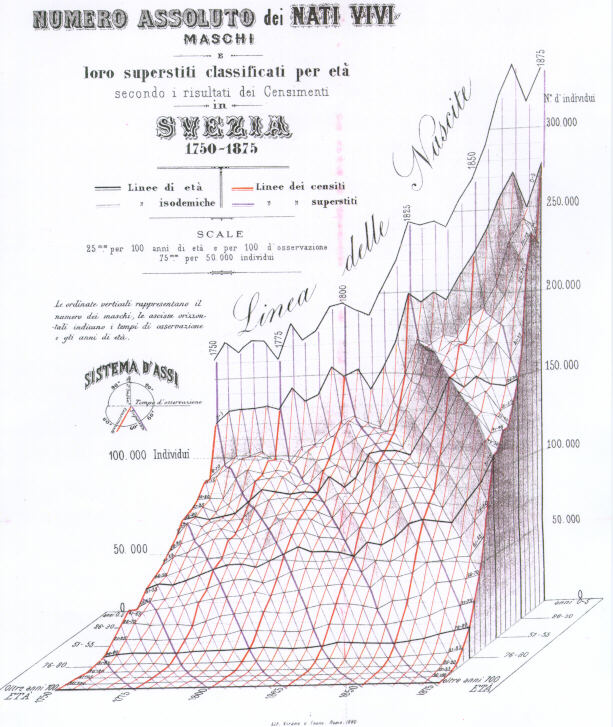 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsEstos y otros pioneros han hecho de las gráficas una parte fundamental del análisis estadístico de datos, y sus innovaciones siguen estando vigentes, además de servir de excelentes modelos de claridad en la representación.
Sobre el autor: Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute.
El artículo Los orígenes de la visualización de datos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Datos que entran por los ojos
- Gráficas para la ciencia y ciencia para las gráficas
- Doce reglas para una mala gráfica
El grafo de Marion (Gray)
Hace casi dos años hablamos en este Cuaderno de Cultura Científica del teorema de Marion (Walter), un bonito enunciado de geometría afín, nombrado en honor a la matemática Marion Walter –que justamente ayer cumplió 91 años–.
Hoy traemos un objeto matemático, el grafo de Marion. En este caso, la matemática que da nombre a este grafo es otra Marion, Marion Gray.
 Marion Gray. Imagen: © School of Mathematics, University of Edinburgh.
Marion Gray. Imagen: © School of Mathematics, University of Edinburgh.Marion Gray nació en Escocia en 1902. Se interesó fundamentalmente por las matemáticas y la física. Estudió en la Universidad de Edimburgo y, tras graduarse, trabajó durante dos años como estudiante de postgrado bajo la supervisión del conocido matemático Edmund Taylor Whittaker.
En 1924 viajó a los Estados Unidos para estudiar en el Bryn Mawr College (Pensilvania). Allí aprendió matemáticas con Anna Johnson Pell Wheeler, David Vernon Widder y Marguerite Lehr. Defendió su tesis doctoral –The theory of singular ordinary differential equations of the second order– en 1926 bajo la supervisión de Anna Johnson Pell Wheeler.
Regresó a Edimburgo, donde trabajó como profesora asistente durante un año. De allí se trasladó a Londres donde trabajó como profesora asistente de matemáticas en el Imperial College durante tres años.
En 1930 regresó a los Estados Unidos y fue contratada como ingeniera asistente en el Departamento de Desarrollo e Investigación de la American Telephone and Telegraph Company de Nueva York.
En 1932, buscando “redes completamente simétricas”, descubrió el grafo que lleva su nombre, un grafo cúbico con 54 vértices y 81 aristas.
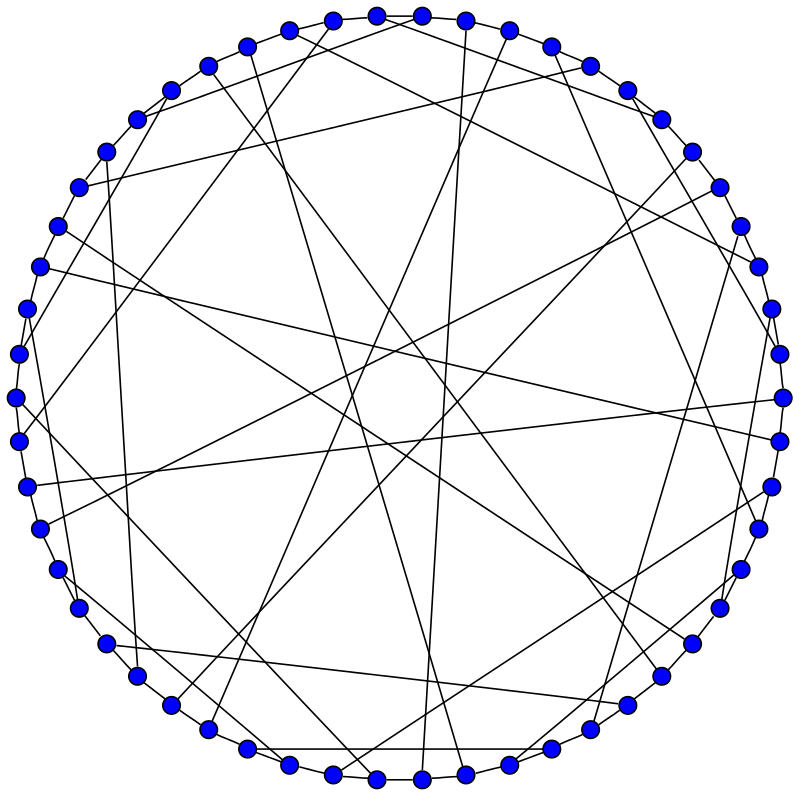 Grafo de Gray. Imagen: Wikimedia Commons.
Grafo de Gray. Imagen: Wikimedia Commons.
Aunque Marion no publicó nada sobre este grafo –pensaba que se trataba de un resultado teórico sin aplicaciones–, el matemático Izak Zurk Bouwer lo citó en su artículo An edge but not vertex transitive cubic graph [Canad. Math. Bull.11 (1968) 533-535], en el que lo describía –fundamentalmente sus propiedades de simetría– y comentaba en una nota a pie de página:
El grafo descrito en esta nota fue descubierto por la Dra. Marion C. Gray en 1932. El autor lo ha redescubierto de manera independiente y cree que aquí aparece publicado por primera vez.
En junio de 1969, Bouwer escribió a Gray para comentarle su aprecio por el hecho de que, en un momento en que la teoría de grafos era prácticamente inexistente, ella ya había encontrado este grafo con unas propiedades tan interesantes.
¿Y cuáles son esas propiedades tan interesantes? Además de las comentadas antes, el diámetro del grafo de Gray –la distancia maximal entre dos vértices– es 6, y la longitud de su ciclo más corto es 8. Es un grafo conexo, y para desconectarlo, es preciso eliminar como mínimo tres vértices o tres aristas.
Este grafo de Gray es además semi-simétrico –fue Bouwer quien lo probó en su artículo de 1968–, es decir, es arista-transitivo –existe un automorfismo del grafo que lleva cualquier arista en otra–, regular –todos los vértices tienen el mismo grado–, y no es vértice-transitivo –no existe ningún automorfismo del grafo que lleve cualquier vértice en otro–.
Además es el menor grafo cúbico semi-simétrico, como demostraron Aleksander Malnič, Dragan Marušič, Primož Potočnika y ChangqunWang en 2002 [An infinite family of cubic edge- but not vertex-transitive graphs, Discr. Math. 280, 133-148].
Por cierto, Marion se equivocó: este grafo –y otros similares– es fundamental en teoría de redes.
¿Y qué fue de nuestra protagonista? En 1934, se unió al personal técnico de los Bell Telephone Laboratories, donde pasó más trabajando de 30 años hasta su jubilación. Durante ese tiempo publicó varios artículos de investigación y realizó cientos de revisiones de trabajos de otros. También formó parte del comité que preparó el famoso Handbook of Mathematical Functions editado por Milton Abramowitz e Irene Stegun (1964).
Después de su jubilación, en 1967, Gray regresó a Edimburgo, donde falleció en 1979.
Referencias
-
Marion Cameron Gray, MacTutor History of Mathematics, University of St. Andrews
-
Judy Green and Jeanne Laduke, Supplementary material for pioneering women in American Mathematics: the pre-1940 Phd’s, pp. 218-220, AMS, 2009
-
Catherine Booth, Celebrating Scottish women of science: Marion Gray (1902–1979), Discover NLS 23 (2013) 20–21
-
Marta Macho Stadler, El grafo de Gray, de Marion Gray, ZTFNews, 16 septiembre 2014
-
Gray Graph, Wolfram MathWorld
-
Marion Cameron Gray, Wikipedia (consultado el 28 julio 2019)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo El grafo de Marion (Gray) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de Marion (Walter)
- Un grafo no planar bipartito completo… para un sexteto amoroso
- El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema?
El impacto científico, médico y comercial de los rayos X
 Foto: Owen Beard / Unsplash
Foto: Owen Beard / UnsplashEl descubrimiento de Röntgen de los rayos X entusiasmó a los científicos de todo el mundo. Sus experimentos se repitieron y ampliaron de inmediato en muchos laboratorios de Europa y América. Las revistas científicas durante el año 1896 estaban llenas de cartas y artículos que describían nuevos experimentos o confirmaban los resultados de experimentos anteriores. El paso de la electricidad a través de los gases había sido un tema popular de estudio para los físicos; esto hizo que la experimentación generalizada fuera mucho más fácil durante los años posteriores al descubrimiento de Röntgen, porque muchos laboratorios de física tenían tubos de rayos catódicos y, por lo tanto, podían producir rayos X fácilmente.
Su utilidad en medicina generó un enorme interés en los rayos X más allá de los laboratorios de física. En los 3 meses posteriores al descubrimiento de Röntgen, el uso de los rayos X se convirtió en habitual en las intervenciones quirúrgicas de un hospital de Viena. Un uso que se extendió rápidamente. Desde la época de Röntgen, los rayos X han revolucionado algunas fases de la práctica médica, especialmente el diagnóstico de algunas enfermedades y el tratamiento de algunas formas de cáncer (porque los rayos X también pueden destruir el tejido maligno).
Los rayos X también encontraron aplicación rápidamente en otros campos de la ciencia. Entre estas aplicaciones destaca el estudio de la estructura cristalina de los materiales, incluidos los biológicos, como el ADN; el «diagnóstico industrial», la búsqueda de posibles defectos en materiales y estructuras de ingeniería; o su uso en historia del arte y restauración, donde permiten ver qué hay detrás de la superficie ópticamente visible de pinturas y esculturas; y muchos otras.
La reacción pública al descubrimiento de los rayos X también fue sensacional. Muchas personas se apresuraron a irradiar sus cuerpos con los nuevos rayos, pensando que tenían propiedades milagrosas, mientras que otros se preocuparon por el deterioro moral si la modestia tan característica del XIX daba paso a la pervertida «visión de rayos X».
Del aparato utilizado en el descubrimiento original de Röntgen, surgieron dos vías de desarrollo para la tecnología médica. Una se concentró en el fluoroscopio, la otra en mejorar la radiografía; Thomas Edison fue crucial en ambas.
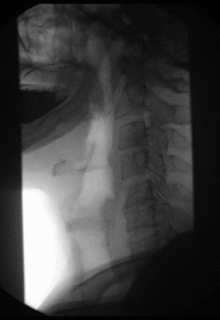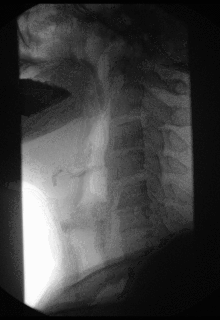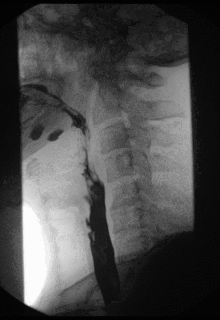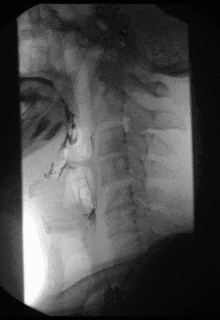 ¿Qué ves en esta imagen de fluoroscopio? [6]Fue la familiaridad de Edison con el tubo Crookes, en muchos aspectos similar muy similar a su bombilla de filamento de carbono de 1879 [1], lo que le permitió hacer una de las primeras mejoras en la tecnología de rayos X. Al construir un tubo con un vidrio más delgado, Edison descubrió que podían escapar más rayos X. Edison también dirigió la investigación que encontró que el tungstenato de calcio [2] podría producir una imagen más clara en la pantalla fluorescente que el platino-cianuro de bario utilizado anteriormente. Edison lo usó para la fabricación de un «fluoroscopio», un dispositivo que permitía a una persona mirar a través de una caja en una pantalla cubierta con tungstato de calcio, y ver una imagen en movimiento del interior del cuerpo de otra persona.
¿Qué ves en esta imagen de fluoroscopio? [6]Fue la familiaridad de Edison con el tubo Crookes, en muchos aspectos similar muy similar a su bombilla de filamento de carbono de 1879 [1], lo que le permitió hacer una de las primeras mejoras en la tecnología de rayos X. Al construir un tubo con un vidrio más delgado, Edison descubrió que podían escapar más rayos X. Edison también dirigió la investigación que encontró que el tungstenato de calcio [2] podría producir una imagen más clara en la pantalla fluorescente que el platino-cianuro de bario utilizado anteriormente. Edison lo usó para la fabricación de un «fluoroscopio», un dispositivo que permitía a una persona mirar a través de una caja en una pantalla cubierta con tungstato de calcio, y ver una imagen en movimiento del interior del cuerpo de otra persona.
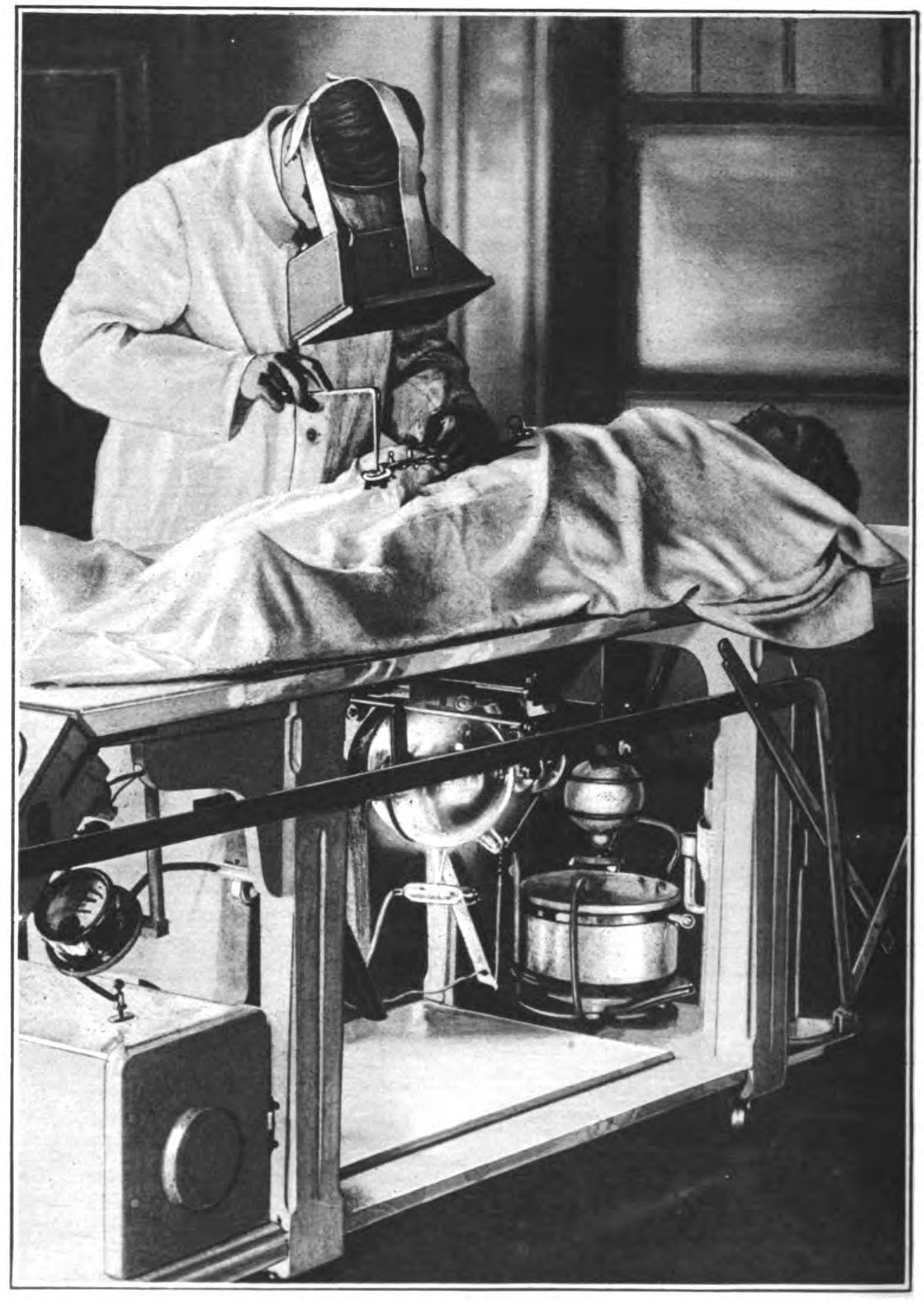 Operación quirúrgica empleando un fluoroscopio durante la Primera Guerra Mundial. Imagen: Wikimedia Commons
Operación quirúrgica empleando un fluoroscopio durante la Primera Guerra Mundial. Imagen: Wikimedia CommonsUn amigo de Edison, Michael Pupin [3], tomó esta mejora en la pantalla fluorescente y la combinó con una placa fotográfica, creando la radiografía, que reducía el tiempo de exposición del paciente de 1 hora a solo unos minutos, al tiempo que aumentaba la claridad de la imagen. Esto redujo en gran medida el peligro de daño a los tejidos. [4]
Uno de los aspectos más problemáticos de la tecnología de rayos X durante las dos primeras décadas fue la poca fiabilidad de los tubos de vidrio, que a menudo se agrietaban al calentarse. La alta incidencia de grietas se eliminó en 1913 cuando William Coolidge, mientras trabajaba para General Electric [5], inventó el tubo de rayos X de alto vacío, cátodo caliente y objetivo de tungsteno. Como parte de su investigación sobre filamentos de bombillas eléctricas, Coolidge descubrió que debido a que el tungsteno se vaporizaba menos que cualquier otro metal, podría reducir la acumulación de residuos de gas. Aplicando este conocimiento Coolidge reemplazó el platino con tungsteno en el tubo de rayos catódicos. Cuando estos «tubos Coolidge» salieron al mercado en 1913, arrasaron: podían producir duplicaciones más claras de imágenes anteriores, ajustarse con mucha más precisión y, debido a su mayor flexibilidad, podían organizarse para pasar instantáneamente de alta a baja penetración.
La Primera Guerra Mundial (1914-1918) consolidaría el uso generalizado de los rayos X en medicina y establecería la investigación sobre ellos como una prioridad médica, científica y comercial.
Notas:
[1] Con el señor Edison, cuyo mérito no discute nadie, siempre es necesario matizar cosas. Edison fue, ante todo, lo que hoy se llama un emprendedor, lo que de toda la vida ha sido un empresario. Eso no le desmerece en absoluto, pero sí es necesario tenerlo en cuenta para entender su forma de actuar, siempre con ánimo de lucro y en términos de competencia en un mercado limitado. Un equivalente más contemporáneo sería Steve Jobs, de Apple. Edison creaba, mejoraba lo que hacían otros y sobre todo, y por encima de todo, ponía en el mercado magistralmente productos revolucionarios. Todo lo anterior es para mencionar que la primera bombilla de filamento de carbono la creó Joseph Swan en febrero de 1879 (la de Edison es de octubre de ese año), quien también fue el primero en suministrarlas para un uso comercial, en concreto para iluminar el Hotel Savoy de Londres en 1881.
[2] También llamado wolframato de calcio en los ambientes. En esta casa seguimos las leyes de la termodinámica y la terminología IUPAC. El tungstenato de calcio es el mineral scheelita.
[3] Un personaje impresionante, a la altura del propio Edison, solo que con menos éxito comercial. Su vida fue tan rocambolesca y él la contó tan bien que su autobiografía ganó el premio Pulitzer en 1924.
[4] Daño que experimentaron en sus carnes los colaboradores y el propio Edison.
[5] Nombre original de la compañía Edison General Electric Company que quedó en General Electric tras la fusión en 1892 con Thomson-Houston Electric Company. Edison fundó 14 empresas. Véase Nota 1.
[6] En la imagen se ve una persona ingiriendo una papilla de bario.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El impacto científico, médico y comercial de los rayos X se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Ingredientes para la receta: El pimiento
“También hay mucho axí, ques su pimiento, della que más que pimienta, y toda la gente no come sin ella, que la halla muy sana; puedense cargar cincuenta carabelas cada año en aquella Española”.
Diario de Colón, 15 enero 1493.
“[El ají] comido con moderación ayuda al estómago para la digestión, pero si es demasiado, tiene muy ruines efectos: porque de suyo es muy cálido, humoso y penetrativo. Por donde el mucho uso de él en mozos es perjudicial a la salud, mayormente del alma, porque provoca sensualidad”.
José de Acosta, Historia natural y moral de las Indias, 1590.
“La cocina picante se puede considerar como el equivalente culinario de una actividad masoquista benigna como un salto en paracaídas, un baño caliente, una ducha helada o una película de terror”.
Bernd Nilius & Giovanni Appendino, 2013.
 Foto: RitaE / Pixabay
Foto: RitaE / PixabayEl pimiento pertenece al género Capsicum, de la familia de las solanáceas, con 40 especies aceptadas de las casi 200 descritas. De ellas, cinco especies se cultivan, y tal como revisan Charles Heiser y Barbara Pickersgill, de las universidades de Indiana, en USA, y de Reading, en Inglaterra, son: Capsicum annuum, C. baccatus, C. chinense, y C. frutescens.En estas especies cultivadas hay infinidad de variedades de cultivo, más de 3000 se ha calculado, sobre todo por el fruto, por su forma, color, picor, uso y procedencia. Así se citan el pimiento morrón, la ñora, la guindilla, el pimiento choricero, el del piquillo, el chile habanero y muchos más.
El género Capsicum tiene su origen en Centro y Sudamérica y crece desde el nivel del mar hasta más de 2000 metros de altura. Parece que se domesticó en varios lugares tanto en México como en Sudamérica. Bolivia podría ser uno de los Centros Vavilov de Capsicum pues allí se encuentran 27 especies. El otro centro estaría en el noreste y centro-este de México, y destaca la Península de Yucatán. Más en concreto, el origen de C. annuum y de C. frutescens estaría en México y Centroamérica y quizá se domesticó en el Amazonas, el C. chinense del norte de la Amazonia, y el C. pubescens y el C. baccatum en los Andes de Sudamérica, desde Colombia a Chile, y por el este a Brasil y norte de Argentina.
Hay restos arqueológicos de pimiento en México desde hace más de 7000-9000 años. Para entonces ya se consumía y, quizá, se cultivaba el pimiento. Del yacimiento del Valle de Tehuacán, en Puebla, se han recuperado semillas en coprolitos humanos y en vertederos de la época, aunque las más antiguas son más pequeñas que las actuales, y quizá es pimiento silvestre recolectado. En los mismos yacimientos se encontraron restos del mortero de basalto, que se sigue utilizando en la actualidad, para preparar salsa de chile.
Los restos de la cueva de Coxcatlán, de hace 7000-5500 años, llevan semillas como las actuales y, son, por tanto, chile domesticado. Y en Loma Torremole, en Cuantitlán, se han encontrado trojes para almacenar las semillas. Ya se cultivaba en extensión hace 5000-4250 años.
El grupo de Linda Perry, del Museo Nacional Smithsoniano de Historia Natural de Washington, ha identificado restos de pimientos, fechados hace 6000 años, en Lomo Alto, Ecuador, en el área de los Andes donde tiene su segundo centro de origen el pimiento. También han encontrado restos de pimiento, más recientes, en Panamá, Bahamas, Perú y Venezuela.
Cristóbal Colón trajo y entregó a los Reyes Católicos el pimiento, con plantas y semillas, a la vuelta de su primer viaje en 1493. En el Caribe encontró a los indios Arawak que cultivaban Capsicum. Lo habían traído desde el norte de Sudamérica en su migración, que había comenzado 1200 años antes y pasado por Trinidad y las Pequeñas Antillas donde, en la época de Colón, también se cultivaban especies de Capsicum. A la vez, otro grupo de especies de Capsicum llegó a las Antillas desde Centroamérica. Se llamaba chili, según el idioma de la tribu Nahuatln, denominación que todavía se utiliza en la actualidad.
Fue el 15 de enero de 1493 cuando Colón dejó, por primera vez, constancia escrita en sus diarios de la planta que, como los indios, llamó ají, término que todavía se conserva, y que sería nuestro pimiento. Colón escribió “que es su pimienta, que vale más que la pimienta”.
En México, cuando llegó Hernán Cortés, se pagaban impuestos en el imperio azteca con chiles, y los españoles siguieron cobrando impuestos igual. Bernal Díaz del Castillo, en su relato de la lucha con los aztecas, cuenta que, a su paso por Cholula camino de Tenochtitlán, los indígenas quería matarlos y “comer nuestras carnes” y “ya tenían aparejadas las ollas con sal y ají y tomates”. Añade que los aztecas comían las piernas y los brazos de los sacrificados con una salsa de chimole, hecha con chile, tomate, cebolla y sal. En quince años, los españoles que llegaron a América se hicieron a la dieta mexicana. El pimiento también aporta a la dieta minerales y las vitaminas A y C, y por ello se convirtió en una buena solución para el escorbuto en los largos viajes entre Europa y América.
El fraile dominico y cronista de Indias Bartolomé de las Casas escribió que “sin el chile, los mexicanos no creen que están comiendo”. Añade que “en todas las cosas que comían estas gentes, cocidas o asadas o crudas, echaban de la pimienta que llaman axí… la cual ya es en toda España conocida; tienese por especia sana, según acá dicen nuestros médicos…·. También Gonzalo Fernández de Oviedo en su Historia general y natural de las Indias, publicada en 1526, escribe que se utilizaban las hojas de pimiento en el caldo de la olla de carne y en salsas “tan buenas o mejor que el gusto del perexil”. Llegó el pimiento a España e Italia con tanto éxito que escribió que “en verdad, el axí es mejor con la carne e con el pescado, que la muy buena pimienta”.
 Foto: Jill Wellington / Pixabay
Foto: Jill Wellington / PixabayAunque también el pimiento presentaba problemas para algunos viajeros españoles en América. El misionero José de Acosta, a finales del siglo XVI, escribió que el chile era perjudicial para la salud en los mozos, y mayormente para la salud de su alma, pues provocaba sensualidad. Además, el chile era algo molesto pues quemaba “al entrar y al salir, también”.
Las primeras descripciones de los pimientos en Europa son de 1542. Aparecieron en De historia stirpium comentarii insignes, escrito por Leonhart Fuchs y publicado en Basilea. Describe algunas variedades de pimiento que considera vienen de la India.
Como ocurre con otras plantas que llegaron de América, su llegada a Europa provocó siglos después un debate ya conocido. El arqueobotánico sueco Hakon Hjelmqvist afirmó, en 1995, que en una excavación en Lund se había encontrado C. frutescens, variedad picante que incluye, por ejemplo, la guindilla. Proponía que había llegado desde Asia, aunque otras hipótesis plantean que ya lo conocían los romanos o que lo habían traído de América los vikingos en el siglo X.
Las variedades de México y Perú que encontraron los españoles se adaptaron bien al cultivo en las zonas templadas de Europa y el Oriente Medio. Medio siglo después de la llegada a Europa, ya se cultivaban en las costas de África y en la India, en el Asia de los monzones y el sudoeste de China, y en los Balcanes, Europa Central e Italia. En concreto, en Europa, los pimientos de citan en Italia en 1533, en Alemania, hemos visto que en 1542, en Inglaterra se cultivaba en 1548, y en Moravia, hoy en la República Checa, hay grandes sembrados en 1585, y, sin confirmar, se cultivaba en Hungría en 1526. Hay ejemplares en herbarios desde el principio del siglo XVII. Con un cultivo sencillo y semillas fáciles de almacenar, pronto se convirtió en un ingrediente barato de la dieta de pobres y ricos de medio planeta, y se sembraba en todas las huertas domésticas, cerca de la casa.
Como ejemplo de la rápida popularidad del pimiento y, también, de su uso culinario cotidiano son las guindillas que pintó Velázquez en dos de sus cuadros, fechados de 1618, y que se conocen como “Jesús en casa de Marta y María” y “La vieja friendo huevos”. En ambas obras, el entorno es humilde pues el pimiento era barato y fácil de cultivar. Seguro que ayudó a consolar muchas hambrunas. En los cuadros, Velázquez pinta guindillas, una en el primero y dos en el segundo. Según Jesús Moreno, estas guindillas son el primer producto alimentario americano que aparece en la pintura.
Quizá esta receta nos ilustre de la utilización del pimiento por todas las clases sociales, en este caso lo traemos de una sociedad gastronómica de Tolosa, tal como la recogió José Castillo, en 1973, de José Luis Pecina. Pero estoy seguro de que esta receta se aplicó del siglo XVIII en adelante siempre que fuera deseable y oportuno. El hambre manda mucho.
“Fritada de burro (astoa) joven: necesitamos carne de burro joven, cebolla, ajos, aceite, pimientos rojos, tomate y guindilla. Arrimar una sartén grande al fuego con aceite y ajos fileteados, cuando se empiecen a dorar añadir los pimientos cortados en tiritas, que se vayan cocinando lentamente y añadir tomate picadito sin pellejos. Todo junto que se vaya haciendo, y sacar la sartén fuera del fuego para usarlo más tarde.
Colocar en una cazuela aceite y cebolla picada, y arrimándola al fuego añadir el burro cortado en pedazos grandes y rehogarlos bien. Cuando casi estén tiernos añadir vino tinto, echar el tomate y pimientos que están en una sartén, más algo de guindilla. Todo junto que hierva lentamente hasta que esté tierno el burro. Seguidamente se pasa todo a una cazuela de barro y se hierve un poco arrimándola al fuego”.
Como especia, el pimiento tuvo su mayor difusión en Europa durante las guerras napoleónicas, cuando el bloqueo de los puertos continentales impidió la llegada de las especias de gran uso, la mayoría de origen asiático. Por ejemplo, como ingrediente picante se usaba la pimienta, importada de Asia. Por ello, cuando Colón encontró el Capsicum en sus viajes y vio que era una planta que picaba, la bautizó con el masculino de pimienta, o sea, pimiento.
Ahora se cultiva en toda Europa, Asia Central y Oriental, Turquía, India, China, Corea o Japón, como en toda América. En 2013, la producción mundial de pimientos fue de 346 millones de toneladas. El 47% procedía de China, y es la India el primer productor de pimientos secos con 1.4 millones de toneladas. En pimiento fresco, después de China están México, Turquía, Indonesia y España con un millón de toneladas. Se ha calculado, escribe Jean Andrews, que más de un cuarto de la población mundial se alimenta con pimientos o sus derivados cada día. Es la especie y condimento más utilizado en todo el mundo.
Para ilustrar la popularidad planetaria del pimiento podemos irnos a China y cocinar una receta de su cocina, tomada de el libro de Huang Su Huei, publicado en 1972.
“Col china con pimiento rojo seco y picante: Cortamos la col en trozos grandes, como de cinco centímetros, y los pimientos en tiras de unos dos centímetros. Freímos la col en aceite muy caliente hasta que se ablande. Más o menos, como un minuto. Sacamos la col y la secamos. Freímos los trozos de pimiento con unos granos de pimienta y raíz de jengibre picada. Añadimos la col y harina de maíz, salsa de hoja, vino de arroz (vale con vino blanco), aceite de sésamo (vale de oliva), azúcar y vinagre. Freír hasta que se caliente y servir”.
De Hungría viene la paprika que se obtiene al moler el típico pimiento húngaro seco. Ahora es España el primer exportador de pimiento en polvo, como pimentón o paprika, con el 60% del mercado mundial. La mayor producción de pimentón se da en Murcia, seguida de Extremadura y Valencia. Es un componente esencial de muchas recetas e indispensable, por ejemplo, en la cocina de Castilla La Vieja.
Los pimientos pican porque sintetizan y acumulan capsaicina, o (E)-N-(4-hidroxi-3-metoxibencil)-8-metil-6-nonenamida, un compuesto alcaloide sin color, ni sabor, ni olor, y lipofílico, o sea, que se disuelve en las grasas.. Su fórmula reducida es C18H27NO3. Es el compuesto que da el sabor típico picante a muchas variedades de pimiento. Su concentración varía en cada variedad y, dentro de ella, en cada planta, y va, en general, del 0.5% al 1%. La síntesis de capsaicina, según el estudio de Charles Stewart, Jr., y su grupo, de la Universidad Cornell de Ithaca, y en la especie C. chinense, la controla el gen Pun1, con su alelo recesivo pun12 en las variedades que no pican. Un 86% de la capsaicina se sintetiza en la placenta, o sea, en los soportes donde crecen las semillas y, por ello, donde más pica un pimiento es en esa zona.
Se ha propuesto que es un método de defensa seleccionado para evitar que los mamíferos ingieran el fruto. Las aves, que no son sensibles a la capsaicina, se alimentan de pimientos y, después, esparcen la semilla con las heces. Además, parece que las semillas se activan al pasar por el sistema digestivo de las aves y germinan mejor al caer a tierra.
El picor varía según las condiciones de cultivo, la edad del fruto y de la variedad de que se trate, es decir, de su genética. La falta de agua y el estrés en el cultivo aumentan el picor. Si después de recogido el fruto se le seca al aire pero a la sombra, el picor se conserva mejor.
En los mamíferos, la capsaicina activa las células sensoriales de la boca y otras zonas del digestivo que responden a aumentos de temperatura por encima de 43ºC. La información que envían estas células sensoriales al cerebro se traduce por una sensación de quemazón que avisa de que hay un peligro, de que el alimento que pasa por la boca es capaz de quemar. Además, la capsaicina estimula el apetito y la secreción de jugos gástricos y la movilidad del estómago y el intestino.
El pimiento más picante conocido es la variedad Carolina Reaper, con 2200000 unidades Scoville. También sirve como ejemplo que la capsaicina pura disuelta en 100000 partes de agua sigue provocando un fuerte picor persistente, como una quemadura en la lengua. Y, además, la capsaicina es ocho veces más picante que la piperina, el compuesto que causa el picor en la pimienta negra.
 Pimientos a laventa con indicación de la escala Scoville en Houston (Texas, EEUU). Foto: WhisperToMe / Wikimedia Commons.
Pimientos a laventa con indicación de la escala Scoville en Houston (Texas, EEUU). Foto: WhisperToMe / Wikimedia Commons.Cuantificar el picor es interesante para quien cultiva y comercializa estas plantas. Y a ello dedicó años de su vida Wilbur Lincoln Scoville y, de su trabajo vienen las unidades Scoville. Fue un químico estadounidense que nació en 1865 en Bridgeport, Connecticut, y murió en 1942. En 1912, cuando trabajaba para la farmaceútica Parke-Davis, desarrolló lo que se denomina Examen Organoléptico Scoville, con el que se cuantifican las unidades Scoville (en inglés SHU, Scoville Heat Units) que, a menudo, aparecen en las etiquetas de los alimentos picantes.
El Examen Organoléptico Scoville consiste en utilizar una solución concreta de extracto de la planta picante (un grano en 100 centímetros cúbicos de alcohol durante una noche) y diluirla en agua azucarada hasta que deja de picar para un comité formado, habitualmente, por cinco examinadores. El grado de dilución es la unidad Scoville para esa planta. Así, un pimiento que no pique tiene cero de unidad Scoville; por el contrario, los chiles más picantes tienen de unidad Scoville 300000, pues ese es el número de veces que hay que diluir su extracto para que deje de picar, o sea, que pica mucho. El inconveniente del método es que depende de la subjetividad de los examinadores (por eso son cinco); en la actualidad, ya se utilizan métodos cuantitativos de análisis químico en el laboratorio.
La capsaicina pura tiene de unidad Scoville 16000000; el piri piri, un C. frutescens que se desarrolló en el sureste de África, llega a 200000; la pimienta Cayena, que nos parece terrible, se queda en 50000 como mucho; el chile tabasco pica como la Cayena, entre 30000 y 60000; el jalapeño esté entre 2500 y 10000 unidades Scoville; la guindilla anda por los 1500; y el pimiento, si pica, puede llegar a 500.
La capsaicina del pimiento se une a un receptor de la membrana de la célula sensorial, cambia la permeabilidad de esa membrana y entra calcio a la célula lo que, a su vez, provoca la sinapsis con una o varias neuronas que transmiten la información al cerebro. La respuesta, frente al dolor, es la liberación de endorfinas que mitigan la sensación dolorosa y dan una sensación de bienestar y placer que, incluso, puede provocar adicción al picante, aunque hay autores, como Janet Long, que lo niega.
Los receptores que se unen a la capsaicina son los TRPV1 (Receptores de Potencial Transitorio Vanilloide 1) y que se encuentran, sobre todo en la boca y primera parte del sistema digestivo pero que, poco a poco van apareciendo en muchos otros tipos celulares. Se activa a más de 43ºC y con la capsaicina y, es curioso, hay otro termorreceptor, el VRL-1, análogo al TRPV1, que se activa a más de 52ºC pero no con la capsaicina.
Cuando el TRPV1 responde al picante entra calcio en su citoplasma pero, si el picante actúa durante un tiempo prolongado, se agota el calcio, y las células sensoriales dejan de funcionar. Así, el exceso de picante puede llevar a la insensibilidad hasta que se repone el calcio del entorno celular. La respuesta del cerebro es aumentar el ritmo cardíaco, la secreción de sudor y liberar endorfinas.
Una de las líneas de investigación más interesantes sobre estos receptores TRPV1 es su relación con células cancerosas. La revisión de Lea Weber, de la Universidad del Ruhr en Bochum, estudia la acción de la capsaicina en osteosarcoma, cáncer de colón de páncreas y de mama. En concreto, este grupo alemán estudia su acción sobre células cancerosas del cáncer de mama que, se ha encontrado que tienen los TRPV1 en su membrana celular.
Los resultados que encuentran son claros: la capsaicina inhibe el crecimiento de estas células en cultivo y provoca su muerte en tiempos que van de horas a días. Ensayan la capsaicina en nueve cultivos de células de cáncer de mama de diferentes pacientes. Los autores sugieren que la capsaicina funciona como un tóxico que activa los receptores TRPV1, provoca la entrada de calcio y la célula muere. Sería un buen objetivo terapéutico para estudiar la destrucción de células tumorales.
También la capsaicina está relacionada con el metabolismo de lípidos y, en último término, con la obesidad y el control del peso, tal como escriben Nilius y Appendino. La adición de pimento picante al desayuno inhibe la absorción de lípidos y proteínas. Parece ser que la capsaicina activa el catabolismo de lípidos y la termogénesis y, por tanto, en la utilización y metabolismo de las grasas. En general, concluyen los autores que la toma de capsaicina en la dieta activa los mecanismos metabólicos contra la obesidad.
Sin embargo, la relación entre el consumo de picante y sus beneficios para la salud no se ha demostrado de manera directa, sugerida por estudios epidemiológicos sin una demostración directa de causa y efecto. O, en algunos casos, son estudios solo con animales de laboratorio o con cultivos celulares o in vitro. Y siempre con escasa confirmación en ensayos clínicos.
El picante en los pimientos sigue siendo un enigma sin resolver por completo. Los humanos son la única especie animal que deliberada y sistemáticamente consume alimentos que pican, que queman, sin que conozcamos el significado biológico de esta conducta, ni el impacto evolutivo que supone para la especie, tal como explican Bernd Nilius y Giovanni Appendino, de las universidades de Lovaina y Novara respectivamente.
En una publicación reciente, Charles Spence, de la Universidad de Oxford, ha revisado algunas de las hipótesis que tratan de explicar esta curiosa preferencia de nuestra especie. En primer lugar, la ya mencionada hipótesis masoquista/búsqueda de emociones, con la liberación de endorfinas. Spence también menciona la hipótesis microbiana, que sugiere que el picante se añade a los alimentos porque elimina bacterias y protege de enfermedades trasmitidas por los alimentos. La siguiente hipótesis que explica Spence es la termorregulación/inducción de la salivación, con el aumento de la secreción de saliva y sudor que, a su vez, provoca la bajada de la temperatura corporal. Y la última hipótesis revisada por Spence es la que relaciona el picante con la salud, la dieta y, en general, con sus propiedades medicinales. Ya hemos repasado la influencia de la capsaicina en la destrucción de células tumorales y en el metabolismo de lípidos.
Como escriben Joshua Tewksbury y su grupo, de la Universidad de Washington en Seattle, la presencia o ausencia de picor es muy variable. En su estudio con 29 poblaciones salvajes de tres especies de Capsicum en el sudoeste de Bolivia, han muestreado el picor y su distribución geográfica.
En primer lugar, los individuos picantes y no picantes pueden convivir en la misma población. El porcentaje de individuos picantes crece con la altura. Por encima de 900 metros todos los individuos de todas las poblaciones, excepto dos, son picantes. Y de esas dos poblaciones en que hay no picantes, en una de ellas es la especie humana la responsable de la presencia de los individuos no picantes. El contenido de capsaicina sigue los mismos parámetros: a más altura, más capsaicina y, así, de 500 a 1000 metros, crece un 30%. Además, aumenta la síntesis de capsaicina con menos agua y más sol.
Tewksbury propone que la síntesis de capsaicina se basa en el coste y el beneficio que permiten a la planta, a cada individuo, sobrevivir y reproducirse. con éxito, quizá por el paso de las semillas y su activación en el sistema digestivo de aves.
La capsaicina tiene también usos fuera de la gastronomía Por ejemplo, en los sprays de pimienta que se usan como arma de defensa personal no letal. Es más antiguo de lo que pensamos pues, entre los aztecas, se castigaba a los niños con humo de una hoguera en la que se quemaban chiles picantes. Ese humo también se utilizaba como arma de guerra para rendir a combatientes cercados. Y la crema de capsaicina sirve para aliviar dolores musculares.
Como ejemplo de la utilización de la Escala Scoville para la fabricación de armas (quién lo iba a suponer) hay que mencionar que hace unos años se descubrió en la India uno de los chiles más picantes que se conoce: nada menos que 1000000. Es la variedad “Bhut Jolokia” de la especie Capsicum chinense. Lo han estudiado en detalle Paul Bosland y Jit Baral, de la Universidad del Estado de Nuevo Mexico en Las Cruces. De inmediato, los investigadores de la Organización de Investigación y Desarrollo para la Defensa de la India, en Nueva Delhi, se han interesado en el “superchili” con la intención de fabricar granadas similares a las de gas lacrimógeno para disolver manifestaciones. Incluso, en Estados Unidos, ya se ha presentado una patente para fabricar un spray de defensa personal. Seguro que no era esto lo que tenía en mente Wilbur Scoville cuando desarrolló su Examen Organoléptico.
Por cierto, unos consejos finales. Ante la sensación de picor no hay que beber agua pues la capsaicina, sustancia lipofílica que se disuelve en grasas y no en agua, no se eliminará. Es bueno masticar pan y, todavía mejor, el aceite y la leche entera. Lo más gustoso es mojar pan en aceite.
Para terminar, una receta sencilla y rápida que nos explica Rafael Castellanos en su “Cocina romántica”: es el arroz con pimientos.
“En una cazuela con un poco de aceite freímos cebolla picada; cuando este pochada añadimos el arroz, se revuelve un poco y se ponen los pimientos enteros, se llena con agua la cazuela, ponemos pimienta y azafrán y se cuece. Servir”.
Abad Alegría, F. 2001. Color rojizo en nuestra historia culinaria. El especiado con azafrán, y pimentón en las cocinas hispanas. Discurso de Ingreso en la Academia Aragonesa de Gastronomía. Zaragoza.
Referencias:
Andrews, J. 2000. Chilli peppers. En “The Cambridge world history of food, Vol 1”, p. 281-288. Ed. por K.E. Kiple & K.C. Ornelas. Cambridge University Press. Cambridge. 1120 pp.
Basu, S.K. & A.K. De. 2003. Capsicum: historical and botanical perspectives. En “Capsicum. The genus Capsicum”, p. 1-15. Ed. por A.K. De. Taylor & Francis. London and New York.
Bosland, P.W. & J.B. Baral. 2007. “Bhut Jolokia”-The world’s hottest known chile pepper is a putatuve naturally occurring interspecific hybrid. HortScience 42: 222-224.
Bryant, V. & G. William-Dean. 1975. The coprolites of man. Scientific American. January.
Callen, E.O. 1967. Analysis of the Tehuacan coprolites. En “Science in archaeology”. Ed. por Brothwells & E. Higgs. Thames& Hudson. London.
Castellano, R. 1995. La cocina romántica. R & B Ed. Donostia.
Castillo, J. 1973. Recetas de 200 cocineros de sociedades vascas. Ed. del Autor. San Sebastián.
Caterina, M.J. et al. 1997. The capsaicin receptor: a heat-activated ion cannel in the pain pathway. Nature 389: 816-824.
Chayapathy, N.P.B., G. Parvatam, V. Kumar & G.A. Ravishankar. 2006. Spray formulation for pungency enhancement in Capsicum. US Patent nº.: US2006/0073121 A1.
Heiser, C.B. & B. Pickersgill. 1969. Names for the cultivated Capsicum species (Solanaceae). Taxon 18: 277-283.
Huang Su Huei. 1972. Chinese cuisine-Wei-Chuan cooking book. School of the Home Economics. Taipei, Taiwan. 181 pp.
Long-Solís, J. 1998. Capsicum y cultura. La historia del chilli. Fondo de Cultura Económica. México.
Long-Tavell, J. 2011. El Capsicum a través de la historia mexicana. En “El chile, protagonista de la Independencia y la Revolución”, p. 7-19. Ed. por K. Richterich. Fundación Herdez. México.
López Riquelme, G.O. 2003. Chili, la especia del Nuevo Mundo. Ciencias 69 marzo: 66-75.
Mathur, R., R.S. Dangi, S.C. Dass & R.C. Malhotra. 2000. The hottest chilli variety in India. Current Science 79: 287-288.
Moreno Gómez, J. 2001. Los productos americanos en la pintura: El pimiento en el bodegón de Velázquez. Isla de Arriarán 18: 289-303.
Nilius, B. & G. Appendino. 2013. Spices: The savory and beneficial science of pungency. Reviews in Physiology, Biochemistry and Pharmacology doi: 10.1007/112_2013_11
Pérez Castañeda, L.M. et al. 2015. Avances y perspectivas sobre el estudio del origen y la diversidad genética de Capsicum spp. Ecosistemas y Recursos Agropecuarios 2: 117-128.
Perry, L. et al. 2007. Starch fossils and the domestication and dispersal of chili peppers (Capsicum spp. L) in the Americas. Science 315: 986-988.
Pickersgill, B. 1961. The domestication of chilli peppers. En “The domestication and exploitation of plants and animals”. Ed. por P.J. Ucko & G.W. Dimbley. Duckorth. London.
Pickersgill, B. 1971. Relationships beetwen weedy and cultivated forms in some species of chilli peppers (Genus Capsicum). Evolution 25: 683-691.
Proctor, V. 1968. Long distance dispersal of sedes by retention in digestive tract of birds. Science 160: 321-322.
Rozin, P. & P. Schiller. 1980. The nature and acquisition of a preference for chilli pepper by humans. Motivation Emotion 4: 77-101.
Scoville, W.L. 1912. Note on Capsicums. Journal of American Pharmaceutical Association 1: 453-454.
Spence, C. 2018. Why is piquant/spicy food so popular? International Journal of Gastronomy and Food Science 12: 16-21.
Stewart, Jr., C. et al. 2007. Genetic control of pungency in C. chinense via the Pun1. Journal of Experimental Botany 58: 979-991.
Suzuki, J.I. et al. 1957. Some observations on red pepper. Food Technology 11: 100-103.
Tewskbury, J.J. et al. 2006. Where did the chili get its spice? Biogeography of capsaicinoid production in ancestral wild chili species. Journal of Chemical Ecology 32: 547-564.
Tominaga, M. & D. Julius. 2000. Capsaicin receptor in the pain pathway. Japan Journal of Pharmacology 83: 20-24.
Weber, L.V. et al. 2016. Expression and functionality of TRPV1 in breast cancer cells. Breast Cancer – Targets and Therapy 8: 243-252.
Wikipedia. 2018. Capsicum. 4 noviembre.
Yang, F. & J. Zheng. 2017. Understand spiciness: mechanism of TRPV1 channel activation by capsaicin. Protein Cell 8: 169-177.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Ingredientes para la receta: El pimiento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ingredientes para la receta: El ajo
- Ingredientes para la receta: El conejo
- Ingredientes para la receta: El kiwi
La tabla periódica en el arte: Arsénico
No diga veneno, diga arsénico. Pocos elementos químicos imponen tanto respeto como el arsénico. Lo usaron los Borgia para quitarse del medio a sus enemigos políticos y más de un noble para acceder a su herencia antes de tiempo. También ha servido para mandar al otro barrio a algún que otro marido y para dar de baja a todo tipo de personajes de novela negra. Pero si miramos más allá de su toxicidad, veremos que el arsénico es un elemento que ofrece un arcoíris de colores en forma de pigmentos.
 Imagen 1. Un recipiente de pintura verde etiquetado como veneno. Fuente: Wikimedia Commons.
Imagen 1. Un recipiente de pintura verde etiquetado como veneno. Fuente: Wikimedia Commons.
Cuando el verde puede matar
El sueco Carl Wilhem Scheele ocupa un lugar de honor en el Olimpo de la química. Y eso que uno de sus más grandes descubrimientos no ha servido para granjearle muy buena fama. En 1775 sintetizó un pigmento de un agradable color verde más duradero que los carbonatos de cobre ampliamente utilizados hasta esa fecha. El proceso para lograrlo no era excesivamente complicado: calentar una disolución de carbonato de sodio en la que poco a poco se disolvía óxido de arsénico, añadir sulfato de cobre, recoger el precipitado que se formaba y calentarlo. Así se obtenía el verde de Scheele (principalmente CuHAsO3), un sólido que cambiaba de tonalidad según la proporción de cobre y arsénico.
Sin embargo, había un problema: la elevada toxicidad del arsénico. Según nos cuenta la historiadora Victoria Finley, el propio Scheele estaba al tanto del problema y en 1777 escribió a un colega preocupado porque pensaba que se debía alertar del peligro a los consumidores. Como con las cajetillas de tabaco, vamos. Sea como fuere, el producto salió al mercado al año siguiente y tuvo un éxito arrollador.
 Imagen 2. Un grabado del s. XIX que hace referencia a la toxicidad del arsénico. Fuente: Wellcome Images.
Imagen 2. Un grabado del s. XIX que hace referencia a la toxicidad del arsénico. Fuente: Wellcome Images.
El éxito fue todavía mayor cuando, con el cambio de siglo, apareció un compuesto similar más estable (3 Cu(AsO2)2·Cu(CH3COO)2). En su preparación se empleaba ácido acético, pero la fórmula se mantuvo en secreto hasta que fue descubierta por un joven Justus von Liebig. Liebig y Scheele, dos grandes químicos unidos por el verde y por el arsénico. El pigmento tuvo muchos nombres: verde esmeralda, verde de París, verde Veronés, etc. Pero que sus evocadores nombres no nos dejen engañar. Si, además de usarse en pintura, sirve de raticida por algo será.
Estos nuevos pigmentos verdes no solo entusiasmaron a los prerrafaelitas y los impresionistas, sino que triunfaron como tinte para los vestidos de señora, para dar color a libros, velas y jabones y, especialmente, para colorear el empapelado de las casas. Ni en la más macabra trama urdida por Agatha Christie hubiera habido tanto arsénico. Ya en 1857 un doctor de Birmingham advertía en la prestigiosa The Lancet sobre los peligros del papel teñido de verde: “En una ocasión un niño chupó unas tiras de papel y apenas escapó con vida”.
Pero, ¿era necesario chupar el papel para envenenarse? En absoluto. Existen otras dos teorías para explicar el envenenamiento por el “empapelado asesino”. La primera apunta a que pequeñas partículas de pintura se descascarillaban y podían entrar en el sistema respiratorio como si fuesen motas de polvo. La segunda resulta mucho más interesante desde el punto de vista científico. En condiciones de humedad pueden aparecer ciertos mohos en la pared. Estos mohos, en su afán por sobrevivir a las altas cantidades de arsénico, lo metabolizan y forman compuestos orgánicos volátiles. De la pared al aire y del aire a los pulmones.
Podríamos recrearnos en el uso del arsénico como veneno y hablar de una de sus (supuestas) víctimas más ilustres: Napoleón. Por poético que resulte y por mucho que se repita, es muy poco probable que fuese este elemento quien asesinó Emperador. Dicho esto, hablemos de un tema más agradable: la pintura. Lo cierto es que se conocen pocas obras que contienen verde de Scheele. Básicamente porque la aparición al de poco tiempo del verde esmeralda le comió la tostada. Aun así, no podemos pasar por alto al más ilustre pintor de acuarelas de todos los tiempos: Joseph Mallord William Turner. Paradójicamente, la obra en la que se ha encontrado este pigmento es un óleo.
 Imagen 3. Guildford desde la orilla del rio Wey (25×20 cm), de Turner (1805). Fuente: TATE.
Imagen 3. Guildford desde la orilla del rio Wey (25×20 cm), de Turner (1805). Fuente: TATE.
El verde esmeralda fue uno de los verdes más importantes del s. XIX como demuestra la lista de ilustres pintores que lo usó: Manet, Monet, Pisarro, Gauguin, etc. Pero si alguien destaca sobre todos los demás, ese es van Gogh. Entre 1888 y 1889 el pintor holandés mantuvo una producción frenética en Arles. Allí realizó varios retratos a la familia Roulin, cuyos miembros posaron sin descanso mientras el artista daba espesas pinceladas de verde esmeralda. ¡Qué pensarían Joseph, Augustine, Armand, Camille y Marcelle si les hubiesen dicho que sus rostros iban a colgarse en los museos más importantes del mundo!
 Imagen 4. Retrato del cartero Joseph Roulin (81×65 cm) y Madame Roulin meciendo la cuna (93×74 cm), de Vincent van Gogh (1888 y 1889). Fuente: Wikimedia Commons.
Imagen 4. Retrato del cartero Joseph Roulin (81×65 cm) y Madame Roulin meciendo la cuna (93×74 cm), de Vincent van Gogh (1888 y 1889). Fuente: Wikimedia Commons.El amarillo del rey
La palabra arsénico deriva de arsenikon que en griego significa viril o macho. No parece una etimología muy apropiada hasta que no se indaga un poco más. El vocablo griego proviene a su vez del persa zarnik donde encontramos la raíz que significa oro. Esto ya empieza a cobrar sentido. Ese es el nombre que se le daba un mineral compuesto por azufre y arsénico que tiene color dorado. Hoy en día lo llamamos oropimente (As2S3), del latin auripigmentum. De hecho, los alquimistas estaban convencidos de que contenía oro y trataron por todos los medios de extraer del mineral el más preciado de los metales. Obviamente, lo único que lograron fue algún que otro envenenamiento.
 Imagen 5. Oropimente en forma mineral (dorado) junto con rejalgar (anaranjado). Fuente: James St. John
Imagen 5. Oropimente en forma mineral (dorado) junto con rejalgar (anaranjado). Fuente: James St. JohnEl oropimente tiene un color amarillo brillante que ha hecho que se emplee como pigmento desde los tiempos del Imperio Nuevo de Egipto (s. XVI a.e.c.). En cualquier caso, tampoco ha sido el amarillo más popular, quizás porque se ennegrece en contacto con muchos otros pigmentos o porque es muy venenoso. Si Scheele se preocupaba por la toxicidad de su verde en el s. XVII, Estrabón ya hablaba de los peligros del arsénico en época de Augusto. En su Geografía cuenta cómo hace 2000 años los condenados a trabajar en las minas de Asia Menor morían por culpa de la sandáraca. Hoy sabemos que se refería al oropimente o al rejalgar, del que nos ocuparemos más adelante. En la Edad Media también eran muy conscientes de que el oropimente debía ser tratado con respeto. Ya lo advertía Cennino Cennini en su indispensable Libro del Arte “Amarillo es un color que se denomina oropimente. Dicho color es artificial y hecho de alquimia; es realmente venenoso, y de una bella tonalidad amarilla que recuerda al oro”.
Este pasaje nos transporta inevitablemente a la manufactura del pigmento dorado. Pese a que se puede obtener de forma natural del mineral homónimo, desde época medieval se produce artificialmente. La mejor receta nos la dejó el químico y farmacéutico Robert Dossie en el s. XVIII. En ella explica cómo el arsénico en polvo debe mezclarse con flores de azufre en proporción de veinte a uno. Luego se calienta la mezcla para lograr la sublimación (pasar de sólido a gas) y se recoge el oropimente. Al parecer el pigmento logrado de forma sintética se conocía como amarillo del rey y era de mayor pureza. Recuerden, lo natural no tiene por qué ser mejor.
Aunque hemos dicho que este pigmento no ha sido excesivamente empleado a lo largo de la historia (occidental), hay unas cuantas obras de gran relevancia que podemos destacar. Para reflejar la variedad de técnicas y soportes en las que se ha empleado mencionaremos el singular libro de Kells en el Trinity Collegue (s. IX), el altar de Esquius en el Museo Nacional de Arte de Cataluña (s. XII) o las pinturas de la cúpula de la mezquita Al-Aqsa de Jerusalén (s.XIV).
 Imagen 6. El oropimente está presente en el Libro de Kells (Trinity College), el Altar de Esquius (Museu Nacional d’Arte de Catalunya) y las pinturas de la cúpula de la Mezquita Al-Aqsa en Jerusalén (Wikimedia Commons).
Imagen 6. El oropimente está presente en el Libro de Kells (Trinity College), el Altar de Esquius (Museu Nacional d’Arte de Catalunya) y las pinturas de la cúpula de la Mezquita Al-Aqsa en Jerusalén (Wikimedia Commons).
Pero quedémonos con un óleo barroco que muestra cómo las obras de arte están vivas y cambian con el tiempo. Jan Davidsz. de Heem pintó una guirnalda con frutas y flores en la segunda mitad del s. XVII que hoy podemos disfrutar en el Rijksmuseum de Amsterdam. Bajo la granada que muestra su apetitoso contenido cuelga un cítrico con un aspecto poco atractivo. Los análisis químicos nos han permitido saber que posiblemente el fruto fuese de un color mucho más vivo y brillante, no en vano estaba pintado con oropimente. Pero este pigmento se puede degradar a óxidos de arsénico y desvanecerse. Al analizar las diferentes capas de la pintura se observó que los óxidos habían penetrado hacia el interior del cuadro y habían reaccionado con el plomo de otros pigmentos. Todo ello dio como resultado una especie de limón que ha madurado en exceso.
 Imagen 7. Guirnalda con frutas y flores (74×60 cm), de Jan Davidsz. de Heem (ca. 1665). Fuente: Rijksmuseum
Imagen 7. Guirnalda con frutas y flores (74×60 cm), de Jan Davidsz. de Heem (ca. 1665). Fuente: RijksmuseumEl polvo de la cueva
El oropimente tiene un primo de color naranja y composición química similar conocido como rejalgar (As4S4, As2S2 o AsS). Con dicho nombre sólo puede tener origen árabe: ráhǧ alḡár “polvo de la mina”. No en vano, al igual que el oropimente, es un mineral natural que, como decíamos antes, los romanos llamaban sandáraca. Posiblemente por el parecido, esta palabra se usa hoy para una resina de color rojizo en un caprichoso cruce etimológico entre dos materiales artísticos.
 Imagen 8. El rejalgar en forma mineral (arriba) y la resina sandáraca (abajo). Fuentes: Wikimedia Commons.
Imagen 8. El rejalgar en forma mineral (arriba) y la resina sandáraca (abajo). Fuentes: Wikimedia Commons.El rejalgar ha tenido un papel menos importante que el oropimente en la Historia del Arte, así que podemos decir que es el primo pobre. Incluso hay quien lo llamaba oropimente quemado, como si no tuviese entidad para tener su propio nombre. Eso no quiere decir que no haya tenido su momento de gloria. En China se usaba con frecuencia y en Persia e India, por ejemplo, se empleó en la elaboración de manuscritos. De hecho, en la medicina oriental tuvo un importante rol en medicina. Será por aquello de que lo que no te mata te hace más fuerte.
Dado que oropimente y rejalgar están inevitablemente unidos, pondremos el broche final a este artículo con una obra maestra en el que ambos pigmentos conviven en armonía. Se trata del retrato de Vincenzo Morosini realizado por Tintoretto, uno de los grandes exponentes de la escuela veneciana. Aquella en la que el color lo dominó todo. Y para colores los del arsénico, que además de los pigmentos verdes, amarillos y naranjas que acabamos de ver, está presente en el azul esmalte y en el violeta de cobalto.
 Imagen 9. Retrato de Vincenzo Morosini (85×52 cm), de Tintoretto (1580). En la banda del personaje se ha detectado oropimente y rejalgar. Fuente: National Gallery.
Imagen 9. Retrato de Vincenzo Morosini (85×52 cm), de Tintoretto (1580). En la banda del personaje se ha detectado oropimente y rejalgar. Fuente: National Gallery.
Para saber más:
E. West FitzHugh. Artist’s Pigments: A Handbook of Their History and Characteristics. (Volume 3). National Gallery of Art (1998).
N. Eastaugh, V. Walsh, T. Chaplin y R. Siddall. Pigment Compendium: A Dictionary and Optical Microscopy of Historic Pigments. Routledge, Londres (2008).
V. Finlay. Colores. Editorial Océano, Barcelona (2004).
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo La tabla periódica en el arte: Arsénico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: Cobre
- La tabla periódica en el arte: Cobalto
- La tabla periódica en el arte: ¿Qué átomos hay en una obra?
La trama vasco-rusa que eliminó a España del Mundial 2018

El fútbol es el deporte alrededor del cual orbitan, además de los miles de fieles seguidores, sectores como la hostelería, el periodismo, la publicidad o la moda. Pero, ¿hay lugar para la ciencia?
Aunque resulte difícil imaginar la relación que pueda existir entre disciplinas científicas como la física, las matemáticas o la antropología y el fútbol, cada vez son más las ocasiones en las que, sorprendentemente, la ciencia puede explicar muchos de los acontecimientos que suceden en un campo de fútbol e incidir en aspectos como la mejora del rendimiento de los jugadores y, en consecuencia, de los resultados.
La relación entre estas dos disciplinas fue el hilo conductor de un ciclo de conferencias organizado por la Cátedra de Cultura Científica con el apoyo de la Diputación Foral de Bizkaia y la colaboración de Fundación Española para la Ciencia y la Tecnología (FECYT) – Ministerio de Ciencia, Innovación y Universidades”, que tuvo lugar en el Bizkaia Aretoa de la UPV/EHU de Bilbao los meses de octubre y noviembre de 2018. Enmarcado en el ciclo de conferencias “Zientziateka”, que contó con cinco conferencias impartidas por especialistas de diversos campos en las que se ilustró la conexión que existe entre diferentes disciplinas científicas y el fútbol.
José Manuel López Nicolás, doctor en Ciencias Químicas y catedrático de Bioquímica y Biología Molecular en la Universidad de Murcia, explica en esta conferencia inaugural la importancia que tiene la multidisciplinariedad científica en el fútbol moderno. Para ello analiza las claves que llevaron a la selección española a la eliminación del último mundial, siguiendo un sorprende hilo conductor que vinculará a científicos, entrenadores y futbolistas de diferentes épocas y nacionalidades.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo La trama vasco-rusa que eliminó a España del Mundial 2018 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Redescubriendo el primer arte vasco: nuevos hallazgos, nuevas investigaciones
- Las pruebas de la educación 2018: El coloquio
- Ciencia, arte y cultura callejera: física y música

