La civilización ha transformado la especie humana
 Foto: Thomas Tucker / Unsplash
Foto: Thomas Tucker / Unsplash
La selección natural opera a través del éxito reproductor de los individuos. Los rasgos hereditarios de quienes dejan más descendencia son los que, andando el tiempo, serán más abundantes. Y las razones para ello no son en absoluto evidentes. Las transformaciones que se produjeron tras la adopción de la agricultura y la ganadería, entre las que cabe incluir el cambio de la alimentación y la vida en núcleos estables de población de tamaño creciente, por ejemplo, ha tenido efectos evolutivos en nuestra especie. O sea, la frecuencia de determinadas variantes genéticas en las poblaciones humanas ha aumentado, mientras que la de otras ha disminuido. Por otro lado, ciertas funciones biológicas se han enriquecido genéticamente -en la población hay más variantes implicadas en ellas-, mientras que otras se han empobrecido.
En una investigación reciente se han comparado los genomas de individuos que vivieron en Europa hace entre 5.500 y 3.000 años con los de europeos actuales. En el estudio han identificado las funciones cuyo sustrato genético ha sufrido más cambios (mutaciones), dando lugar, por lo tanto, a más variantes, y también aquellos en los que ha ocurrido lo contrario. Ha aumentado el número de variantes genéticas implicadas en el metabolismo de carbohidratos, los mecanismos de desintoxicación, el transporte de sustancias a través de membranas, el sistema de defensa inmunitaria, la señalización celular, la actividad física y la percepción olfativa. Y han disminuido las relacionadas con la generación de óvulos -y por lo tanto, en ese aspecto, con la fisiología reproductiva femenina-, y con un mecanismo neurológico denominado potenciación a largo plazo. Veamos, a modo de ejemplo, algunas de estas funciones en su contexto.
Que se hayan enriquecido genéticamente las relacionadas con el metabolismo de carbohidratos tiene que ver, seguramente, con la expansión de la agricultura y la ganadería. La producción de cereales provocó un aumento de la proporción de carbohidratos en la dieta y la ganadería propició el consumo de leche por adultos, gracias a la mutación que les permite retener la capacidad para digerir lactosa, que es un azúcar, al fin y al cabo.
Algo similar ha ocurrido con las variantes implicadas en el funcionamiento del sistema inmunitario. Las altas densidades de población y, en especial, la convivencia próxima con animales domésticos generó condiciones propicias para la proliferación de parásitos patógenos. No es de extrañar, pues, que el sistema inmunitario de los pueblos agricultores y ganaderos haya adquirido capacidades de las que carecía el de cazadores-recolectores, o haya reforzado ciertos aspectos de su funcionamiento como consecuencia de esas condiciones.
La potenciación a largo plazo es un mecanismo que intensifica la transmisión de señales entre neuronas, por lo que está implicado en el aprendizaje y la memoria. Que ese mecanismo haya experimentado una reducción de variantes en su sustrato genético quizás esté relacionado con la importancia creciente del aprendizaje y la transmisión cultural a partir del asentamiento en poblaciones y la emergencia de lo que conocemos como civilización. Aunque ignoramos cómo es esa relación.
Antes se pensaba –y todavía hay quien lo cree- que la civilización, con sus comodidades y su capacidad para amortiguar los efectos de la intemperie sobre nuestro organismo, ha detenido la evolución del linaje humano e, incluso, que al desaparecer las presiones selectivas que actuaron en la prehistoria, nos hemos ido convirtiendo en seres cada vez más defectuosos, pues los menos aptos cada vez sobreviven en mayor medida; y pueden además dejar descendencia. Pero las cosas no son así, sino, como suele ocurrir, más complejas. Porque las presiones selectivas no desaparecen; cambian. Y con ellas, también nuestra naturaleza se transforma.
Fuente: Evgeny Chekalin et al (2019): Changes in Biological Pathways During 6,000 Years of Civilization in Europe. Molecular Biology and Evolution, Vol 36 (1): 127–140
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La civilización ha transformado la especie humana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Apocalipsis alienígena: ¿puede alguna civilización sobrevivir a un cambio climático?
- Una proteína humana para potabilizar agua
- Activa Tu Neurona – Evolución Humana
Palo seco

Deborah García Bello, las tipografías y pi. A palo seco.
Quizás sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que existen en el mundo, estudiada por el ser humano desde hace más de 4.000 años. La fascinación que ha suscitado durante siglos es tal que el popular número cuenta con su propio día en el calendario, así el mes de marzo se celebra el Día de Pi en todo el planeta.
Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien lanzó en 1988 la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés) y además, la celebración coincide con la fecha del nacimiento de Albert Einstein. En 2009, el congreso de EEUU declaró oficialmente el 14 de marzo como el Día Nacional de Pi.
Actualmente, el Día de Pi es una celebración mundialmente conocida que sobrepasa el ámbito de las matemáticas. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
Este 2019 nos unimos de nuevo al festejo con el evento BCAM–NAUKAS, que se desarrolló a lo largo del 13 de marzo en el Bizkaia Aretoa de UPV/EHU. BCAM-NAUKAS contó durante la mañana con talleres matemáticos para estudiantes de primaria y secundaria y durante la tarde con una serie de conferencias cortas dirigidas al público en general.
Este evento es una iniciativa del Basque Center for Applied Mathematics -BCAM, enmarcada en la celebración de su décimo aniversario, y de la Cátedra de Cultura Científica de la Universidad el País Vasco.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Palo seco se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- E-pi-logo (después de esto, mi carrera ha muerto)
- El efecto Talbot: tejiendo alfombras con luz
- Sigue al conejo blanco
Dietas de adelgazamiento
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Todos hemos oído hablar de ellas. La del Dr. X, la del Dr. Y, la del pomelo, la del pepino… La lista sería interminable. Todas garantizan una rápida pérdida de peso sin ningún sacrificio. Por supuesto, el que haya tantas “dietas milagro” tiene una explicación sencilla: son todas falsas.
 Foto: Jan Sedivy / Unsplash
Foto: Jan Sedivy / Unsplash
¿Por qué fallan? Hay dos motivos por los cuales las “dietas milagro” no funcionan nunca. Uno es que, muchas veces, las dietas no tienen ningún fundamento racional: es como si quisiéramos curarnos el dolor de muelas subiendo en el ascensor tres veces al tercer piso, en jueves. El segundo es que, otras tantas veces, aun cuando a largo plazo pudieran funcionar, son tan poco apetecibles que nadie es capaz de mantenerlas por mucho tiempo.
El negocio del sobrepeso. El abandono de las dietas estrafalarias me lleva a otro tema muy relacionado: el negocio (fraudulento) del adelgazamiento. Vivimos en una sociedad en la que uno puede ser cualquier cosa… menos gordo. La publicidad, dirigida sobre todo a adolescentes, se encarga de recordárselo a todas horas. Se forma así un círculo diabólico en el que: (a) con razón o sin ella, uno se ve gordo, (b) comienza una dieta que no la soportaría Robinson Crusoe aunque no tuviera otra comida en su isla, (c) la abandona, por razones obvias, y (d) se culpabiliza por su “falta de voluntad”. Hemos pasado de tener un supuesto sobrepeso a tener una bonita combinación de sobrepeso y falta de autoestima: gran éxito. Pero, claro está, ésta es la base, más bien el círculo vicioso, en el que se apoya el mercado multimillonario derivado de supuestas obesidades y muy humanas debilidades.
¿Es malo estar gordo? Desgraciadamente, el negocio fraudulento del adelgazamiento tiene bastante razón en una cosa: la obesidad es una enfermedad, y es un agente que causa o empeora otras enfermedades. Ahora bien, todo es cuestión de grados, no es lo mismo un sobrepeso ligero que una obesidad mórbida, y cuál sea nuestro problema concreto lo podemos averiguar fácilmente midiéndonos en casa y pesándonos en una farmacia. Y el principal problema de la obesidad no es que nos vaya a quedar mal el traje de baño en la playa.
¿Por qué hay tantos gordos? Los biólogos suelen decir que en biología nada se entiende si no es a la luz de la teoría de la evolución. La obesidad no es una excepción. Desde que la vida existe sobre la tierra (unos 4.000 millones de años) el alimento ha sido la principal limitación para el crecimiento de las especies. En otras palabras, de toda la vida, lo normal ha sido pasar hambre. Sólo hace unas pocas generaciones (¿100 años?) en una región privilegiada del planeta, el llamado primer mundo, se da el fenómeno inaudito de una población que, en el caso de los humanos, tiene asegurada una comida caliente tres veces al día. Hasta ahora, se comía cuando había, que eran pocas veces. En esas condiciones sobrevivían los que, por azar, llevaban los genes que les permitían almacenar energía en forma de grasa cuando comían. Hoy, la inmensa mayoría de los miembros de nuestra sociedad actual son herederos de aquéllos supervivientes, y mantienen intactos sus genes almacenadores de grasa. Ésta es la sencilla verdad, no hay que darle más vueltas al asunto y, sobre todo, no hay que culpabilizarse.
Cambiar de vida. Si, primero, objetivamente necesitamos adelgazar, y, segundo, queremos hacerlo, no nos basta con seguir una u otra dieta. Nuestra tarea es mucho más difícil: tenemos que luchar contra nuestros genes. Tenemos que corregir una deriva de millones y millones de años de evolución. ¿Es imposible? No, pero hay que acertar con la dieta. Para los antiguos griegos, la dieta no era sólo un régimen de comidas, sino todo un sistema de vida. Eso es lo que tenemos que hacer para adelgazar, seguir la dieta adecuada, y no solo la de comidas. Y así, no esperaremos adelgazar en un mes, ni en tres. Todo esto es un proceso a largo plazo. Un objetivo razonable es perder un kilo al mes. Al cabo de un año, serán doce kilos, que no está mal.
Adelgazamiento y termodinámica. La termodinámica es una parte importante de la física, pero la verdad es que se puede entender bastante bien si uno se la imagina como una especie de contabilidad, solo que, en vez de ser una contabilidad de euros, es una contabilidad de calorías. Para entender esta analogía, hay que imaginar nuestro cuerpo como una libreta de ahorros, solo que la cuenta no está en euros, sino en calorías. Y, cosa rara, queremos tener cada vez más euros, pero cada vez menos calorías. Salvando esto, el mecanismo es el mismo. Para tener muchos euros, debemos ingresar mucho, y/o sacar poco. Para tener pocas calorías, debemos sacar muchas, y/o meter pocas. Es igual que metamos cien euros por la mañana o por la noche. En billetes de veinte, o de diez. Es igual que los saquemos en día par o impar. A fin de mes, el estado de nuestra cuenta dependerá de la suma de los ingresos menos la suma de los gastos. Y de nada más. En física, esto se llama el “primer principio de la termodinámica”, y es una ley que no conoce excepción alguna. Así pues, olvídese el lector de desayunar mucho o poco, comer más que cenar o viceversa, una comida o cinco, etc. Solo cuenta el saldo de la libreta a fin de mes.
La dieta. No digo “una dieta”, ni “las dietas”, digo “la dieta”. Con pequeños ajustes, como es natural, pero “la dieta”. Y, ¿en qué consiste esa dieta tan universal? Pues, en comer menos. Bastante menos, e incluso mucho menos. Ojo: aquí no se engaña a nadie, ya hemos dicho que para adelgazar (permanentemente, aquí no estamos hablando de la Operación Bikini), hay que CAMBIAR DE VIDA. Y lo esencial en esa nueva vida es comer significativamente menos. Por poner una cifra, variable según los casos, un 40% menos. No menos de unas cosas, o de otras, sino menos de todo. Bueno, dirá el lector, también podré seguir empapuzándome si de una vez me pongo a hacer ejercicio. Pues, no señor. No tenemos hueco aquí para explicar los detalles, o más bien para hacer las cuentas de la termodinámica del ejercicio, pero algo así como una hora diaria de ejercicio moderado (que es el objetivo realista cuando es para toda la vida) no va a aumentar significativamente el número de calorías que salen de la hucha. Paradójicamente, los buenos dietistas saben que el ejercicio es esencial en el adelgazamiento, pero no tanto por la energía que consume sino por los efectos relajantes sobre el organismo, que compensan el stress de la restricción calórica. En fin, por si no quedaba claro, comer menos y hacer más ejercicio. No queda otra.
A mí no me funciona. Pues algo falla con Vd., y ese algo no es el primer principio de la termodinámica. A ver si lo hemos entendido. Si Vd. come menos (no un poco menos) y hace ejercicio (nada del otro jueves), va a adelgazar. Y si no adelgaza, tendrá que comer aún menos. Tenga la completa seguridad de que su sobrepeso, no digamos obesidad, se debe exclusivamente a que come mucho más de lo que necesita.
Por supuesto que el procedimiento es costoso. Pero piense en dos cosas. La primera, es el ÚNICO modo de adelgazar. Y la segunda, mucho antes de lo que se piensa, quizá en unas pocas semanas, Vd. se habrá habituado a su nueva vida, y no le costará nada mantenerla. Y al cabo de seis meses, o de un año, comprobará que el esfuerzo ha valido la pena. ¡ÁNIMO!
Pues Fulanito come como una lima, y no engorda. La vida es injusta, a veces. El pobre Fulanito carece de los genes de almacenamiento de grasas. Si se embarcan Fulanito y Vd., y su balsa se extravía en el océano, y se pasan dos meses a la deriva, lo probable es que sólo sobreviva uno de los dos, y, créame, salvo antropofagia, el superviviente no será Fulanito, sino Vd., y sin sus lorcitas.
Sobre el autor: Félix M. Goñi es catedrático en el Departamento de Bioquímica y Biología Molecular de la Facultad de Ciencia y Tecnología de la UPV/EHU.
El artículo Dietas de adelgazamiento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La adherencia, clave en el seguimiento de las dietas
- Las dietas detox ni desintoxican ni adelgazan
- 50 años de secretos: la era de la criptografía moderna
Cómo nos ayuda la ciencia a tomar decisiones correctas
![]()
Jose Luis Arroyo Barrigüete y Francisco Borrás Palá
 Unsplash, CC BY-SA
Unsplash, CC BY-SAImaginemos que, tras diez años trabajando en una empresa, otra compañía nos llama y nos hace una oferta de trabajo. Esta tiene ventajas respecto a nuestras condiciones actuales pero, como en toda decisión, hay riesgos asociados a la incertidumbre. ¿Me llevaré bien con los compañeros? ¿Tendré una buena relación con mi nuevo jefe? ¿Encajaré en la cultura corporativa de esta compañía?
Ahora supongamos que alguien nos dijera cuál es la probabilidad que tenemos de equivocarnos. Por ejemplo que, en caso de aceptar la oferta, tenemos una probabilidad del 0,7 % de estar tomando la decisión incorrecta. Dicho de otra forma: tenemos un 99,3 % de probabilidad de tomar la decisión adecuada. En estadística, a esto lo llamamos p-valor.
En ciencia es muy frecuente utilizar el contraste de hipótesis. La idea es partir de una hipótesis nula (H₀), que no es sino el statu quo, la situación actual. En nuestro ejemplo, permanecer en la empresa en la que estamos. Frente a ella se contrasta la hipótesis alternativa (H₁), es decir, una idea contraria a la anterior. En nuestro caso, cambiar de trabajo.
Si encontramos una fuerte evidencia empírica en contra de la hipótesis nula, decimos que la rechazamos y, por tanto, aceptamos la alternativa. Siguiendo con nuestro ejemplo, esta evidencia sería lo que yo pudiera llegar a saber, después de investigarlo, sobre las mejores condiciones de trabajo que nos ofrecen.
Pero, ¿qué significa “fuerte evidencia empírica”? Para responder a esa pregunta, tenemos un concepto muy útil llamado p-valor. Este es la probabilidad que tenemos de equivocarnos si rechazamos la hipótesis nula con la información (evidencia empírica) de la que disponemos.
Cuanto más pequeño sea el p-valor, más improbable es que nos estemos equivocando al rechazar la hipótesis nula. Dicho de otro modo, más probable es que estemos acertando. En nuestro ejemplo, cuanto más pequeño sea el p-valor, más probable es que cambiar de trabajo sea una decisión adecuada.
Entonces, ¿qué p-valor necesitaría yo para cambiar de trabajo? ¿Cuánto riesgo estaría dispuesto a asumir? ¿Un 10 %? ¿Quizá un 5 %? ¿O se sentiría más cómodo con un 1 %? Estos son, de hecho, valores típicos usados en ciencia. Usaremos uno u otro en función del riesgo que estemos dispuestos a asumir.
Estos porcentajes son valores subjetivos que dependen del individuo que toma la decisión y de las consecuencias de la misma. En cambio, el p-valor es un dato objetivo que calculan todos los programas informáticos de estadística a partir de los datos de una muestra. Aparece de forma mágica como un resultado, aunque detrás hay un proceso de cálculo.
Si el p-valor se encuentra por debajo del nivel de riesgo, rechazaremos H₁. De hecho, los ordenadores habitualmente facilitan todavía más la decisión poniendo un asterisco al lado del p-valor si es menor que el 10 %, dos si es menor que el 5 % y tres si es menor que el 1 %.
En nuestro ejemplo de la oferta de trabajo, con un p-valor del 0,7 % los tres asteriscos nos dejarían bastante tranquilos respecto a aceptar la propuesta, salvo que seamos de esas personas que no se arriesgan nunca.
En el año 2314…
Ana sale de casa con sus gafas cuantrónicas de realidad aumentada, y tras llegar a la oficina en su aerodeportivo, se plantea si tomar un segundo café antes de entrar, o bien subir directamente a su despacho para comenzar la jornada. Sus gafas captan el pensamiento, y tras apenas unos microsegundos de cálculo, proyectan en el visor tridimensional el siguiente mensaje:
H₀ : subir directamente al despacho, como es habitual.
H₁ : tomar un segundo café.
P-valor: 0.841
Ana, sorprendida por un p-valor tan alto, decide subir directamente y olvidar la idea del café, pero se pregunta a qué se deberá tal cifra. Solo mientras asciende hasta la planta 159 en el ascensor gravítico cae en la cuenta de que, apenas en media hora, tiene una importante reunión que debe preparar. De haber tomado ese café, probablemente no habría tenido el tiempo suficiente para hacerlo. Esa es la información de que disponían sus gafas cuantrónicas, que no se olvidan de nada.
 Shutterstock
ShutterstockTras una intensa jornada, Ana recibe una holo-llamada de Bernardo, que la invita a cenar esta noche. Ana, tras haber terminado una relación previa hace varios meses, tiene dudas sobre si está interesada en la proposición. Las gafas, captando sus pensamientos, proyectan un nuevo mensaje:
H₀ : cenar sola en casa, como es habitual.
H₁ : aceptar la proposición de Bernardo y cenar con él.
P-valor: 0.053
Por segunda vez en el día, Ana queda sorprendida por la información que le proporcionan sus gafas. ¿A qué se debe un p-valor tan bajo? ¿Tan seguro está su micro-ordenador de que debe aceptar la propuesta de Bernardo? ¿Solo una probabilidad del 5,3 % de equivocarse si la acepta? Ana reflexiona unos segundos y recuerda que las gafas han sido capaces de buscar todo el rastro que ha ido dejando Bernardo en las redes sociales en un instante, muchísimo menos tiempo que el que hubiera empleado ella. Entonces le responde…
Volviendo al presente
¿Qué sucedería si dispusiésemos de las gafas cuantrónicas de Ana? Ante cualquier pequeña decisión, estas procesarían toda la información disponible y nos facilitarían de inmediato la probabilidad de equivocarnos. No cabe duda de que, por una parte, nos equivocaríamos mucho menos. Por otra, ¡la vida sería mucho más aburrida!
Como, afortunadamente, aún estamos muy lejos de que tales gafas existan, de momento el p-valor queda restringido a la experimentación científica, donde nos dará una idea de cuán probable es que estemos equivocados. En el resto de casos, deberemos seguir utilizando un análisis DAFO.
La próxima vez que lea algún estudio en el que se menciona el p-valor, ya sabe a qué se refieren los autores: al riesgo que tienen de equivocarse en sus afirmaciones con la evidencia empírica de los datos de una muestra. Como la muestra es solo una parte de la población, es una información imperfecta. Por ello el p-valor no podrá ser nunca 100 % o 0 %, que supondría una seguridad absoluta a la hora decidir.![]()
Sobre los autores: Jose Luis Arroyo Barrigüete y Francisco Borrás Palá son profesores de métodos cuantitativos en ICADE – Universidad Pontificia Comillas
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Cómo nos ayuda la ciencia a tomar decisiones correctas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Fórmulas matemáticas y números: cómo ayuda la economía al fútbol
- Cómo hacer ciencia en un periódico: la experiencia de ‘Público’
- Cómo descubrimos tres libros venenosos en la biblioteca de nuestra universidad
La eterna promesa del ‘blockchain’
Este año se cumple una década de la aparición del famoso paper que planteó el sistema Bitcoin, dando así pistoletazo de salida a la proliferación del “dinero electrónico”. Esta y otras criptomonedas se sustentan en una tecnología denominada blockchain que, de acuerdo con muchos analistas, está llamada a ser una revolución en el ámbito de la llamada Industria 4.0. Pero ¿qué es el blockchain y qué capacidad transformadora tiene?
 Foto: Hitesh Choudhary / Unsplash
Foto: Hitesh Choudhary / Unsplash
El blockchain surge en 2009 como solución a un problema clásico de sistemas de moneda virtual descentralizados: el problema del doble gasto. Las divisas tradicionales funcionan porque hay una entidad central que se encarga de su buen funcionamiento, y por ende donde el sistema económico y financiero deposita la confianza (e.g., el Banco Central Europeo). Con la adopción de Internet y los sistemas distribuidos, surge un interés en el desarrollo de divisas digitales que no dependan de un mediador de confianza, pero todos los planteamientos chocan frontalmente con el problema del doble gasto: que una misma moneda (en el sentido de “unidad básica” de la divisa) pueda ser falsificada y gastada más de una vez. Hasta 2009, cuando el creador del Bitcoin (bajo el pseudónimo Satoshi Nakamoto) propone una solución basada en un triple enfoque: todas las transacciones se comparten públicamente; las transacciones válidas se determinan por un sistema de prueba de trabajo (proof of work); y se incentiva económicamente la contribución a este sistema (por los llamados mineros).
Estos tres pilares se integran en la tecnología blockchain, que no es más que la unión de dos técnicas bien conocidas y desarrolladas: los árboles Merkle y la criptografía (en forma de firma digital de clave pública y funciones hash). El árbol Merkle es una estructura de datos ideada y patentada en 1979 por Ralph Merkle, diseñada para concatenar información de forma que un nodo dado permite verificar de forma segura y eficiente toda la información que cuelga de él. Tiene muchas aplicaciones, como en el intercambio de archivos en redes P2P o en software de control de versiones como Git. Blockchain es básicamente una cadena de bloques (tipo Merkle, pero, en principio, sin ramificaciones) a la que se añade la firma digital para verificar los participantes en las transacciones.
Bitcoin funciona como una red distribuida de forma que las transacciones se propagan por todos los nodos de la red. Estas transacciones se validan y, en un primer momento, se encuentran sin confirmar. Los mineros recolectan transacciones y tratan de añadirlas en forma de nuevo bloque al blockchain en un proceso que requiere gran capacidad de computación. El incentivo principal por conseguirlo es una fracción de Bitcoin (proporcional a la dificultad en términos de cómputo, que es variable, en ese momento), que no es otra cosa que crear dinero de la nada (de ahí lo de minero…), aunque también se puede llevar un impuesto sobre las transacciones que agrega el bloque. Por supuesto, puede suceder que varios bloques diferentes sean añadidos al blockchain más o menos simultáneamente por diferentes mineros. Lo que sucede es que, al no haber una autoridad central, la propia red “decide” qué rama es la válida, y es simplemente la que la mayoría acepta y sigue utilizando para poner nuevos bloques con transacciones. Los bloques de las ramas que no se continúan quedan huérfanos y dejan de tener validez.
Como consecuencia, este sistema ha dado lugar a una carrera “armamentística” para acumular capacidad de cómputo hasta un límite en el que el gasto energético para minar un bloque es mayor en muchas partes del mundo que el rédito que se obtiene. El Bitcoin, la gran promesa de las monedas libres, ha sido básicamente absorbido por el mercado y se ha convertido en un instrumento financiero más de especulación (recordemos la gran burbuja de finales de 2017), y es susceptible de quedar controlado por las grandes granjas de minado que se han establecido en países donde la energía es barata. El llamado “ataque del 51%” es una sombra que planea sobre este tipo de divisas, y que se hace más fácil a medida que la capacidad para minar se centraliza.
En definitiva, el Bitcoin (y demás criptodivisas) no ha triunfado ni triunfará en los términos que sus proponentes imaginaban. Los problemas no son meramente técnicos, sino fundamentales a la tecnología: es un sistema donde las transacciones son costosas, irreversibles y lentas; es un sistema que solo merece la pena para personas que operan fuera de la ley, o bien, como decíamos, como producto de especulación. Una criptomoneda puede ser 1) descentralizada, 2) barata, 3) segura; y solo podemos elegir dos. Para evitar la necesidad de una autoridad central, se necesitan mecanismos que son computacionalmente costosos de falsificar; para que sea segura, el coste económico del minado tiene que ser alto para que se desincentiven los ataques al sistema. Cualquier intento de arreglar un aspecto compromete el resto.
What are some industries where #blockchain would be useful?
✔️ #voting#CyberSecurity #HealthIT #education #Insurtech #Retail #SupplyChain #WEFLIVE pic.twitter.com/aEtz1J23Q2
— Michael Fisher (@Fisher85M) January 22, 2018
A partir del surgimiento de las criptomonedas, se ha propuesto a lo largo de esta década una infinidad de aplicaciones del blockchain, donde es usado como contenedor genérico de otros tipos de dato, en lugar de transacciones monetarias. Aquí, cabe destacar que poner información en un blockchain simplemente asegura que no se puede cambiar sin mucho esfuerzo y dinero, pero no dice nada de la validez de esa información. A pesar de ello, año tras año, hemos venido asistiendo a un desfile interminable de analistas y gurús de toda índole donde se nos promete que el blockchain es la nueva revolución en todo tipo de campos, pero esa revolución sigue sin llegar, ni siquiera en su aplicación original. En efecto, ¿cómo podría una base de datos lenta y costosa transformar nuestra industria?
Sobre el autor: Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute.
El artículo La eterna promesa del ‘blockchain’ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Sumas y sucesiones alícuotas
Elige un número entero positivo n. Encuentra los números positivos que lo dividen (es decir, el resto de la división es cero). Súmalos y resta a la cantidad obtenida el entero de partida n. A esa cantidad, s(n), se le llama suma alícuota de n. Por ejemplo, n=10, es divisible por 1, 2, 5 y 10. Así que s(10)=8.
 Imagen: Pixabay
Imagen: Pixabay
Esta suma sirve para caracterizar ciertas clases notables de números. Por ejemplo,
-
1 es el único número cuya suma alícuota es 0.
-
Un número n es primo si y solo si s(n)=1.
-
Un número n es perfecto si coincide con su suma alícuota, es decir, s(n)=n. Por ejemplo, 6 es un número perfecto (sus divisores son 1, 2, 3 y 6).
-
Un número n es deficiente si es mayor que su suma alícuota, es decir, s(n)<n. El 1 es el primer número deficiente. Y, obviamente, todos los números primos son también deficientes.
-
Un número n es abundante si es menor que su suma alícuota, es decir, s(n)>n. El primer número abundante es el 12 ya que s(12)=16. Los números abundantes son los que no son ni perfectos ni deficientes.
-
Un número n es quasiperfecto si s(n)=n+1. Aun no se ha encontrado ninguno de estos números…
-
Un número n es casi perfecto si s(n)=n-1. Los únicos números casi perfectos conocidos (de momento) son las potencias de 2.
-
Un número n se llama intocable si no existe ningún entero m de modo que s(m)=n. Abu Mansur al-Baghdadi demostró que 2 y 5 son intocables. Paul Erdős demostró que existen infinitos números intocables. Y aún se desconoce si 5 es el único número intocable impar.
¿Y qué sucede si se calcula la suma alícuota manera iterada? Es decir, ¿qué se obtiene al computar s(n), s2(n), s3(n),… y así sucesivamente? A {s(n), s2(n), s3(n),…} se le llama sucesión alícuota de n.
Por ejemplo, la sucesión alícuota de 10 es {10, 8, 7, 1} ya que:
- 10 es divisible por 1, 2, 5 y 10, con lo que s(10)=8.
- 8 es divisible por 1, 2, 4 y 8, con lo que s(8)=s2(10)=7.
- 7 es divisible por 1 y 7, con lo que s(7)=s3(10)=1.
- 1 es divisible solo por 1, con lo que a partir de este punto ya no puede repetirse el proceso.
Solo existen cuatro posibilidades para la sucesión alícuota de un número entero (a priori, porque se desconoce si existen ejemplos de todas ellas):
-
que sea finita y termine en 1 (en este caso, el anteúltimo número de la sucesión es un primo). Un ejemplo es n=10;
-
que sea finita y termine en un número perfecto. Un ejemplo es n=6, para el que sk(6)=6 para todo entero positivo k;
-
que sea finita y termine en un par de números amigos (como 220 y 284) o en un ciclo (como el caso de los números sociables);
- que sea infinita.
Para n=276 no se sabe si su sucesión alícuota es finita o infinita. De momento se ha calculado hasta el término 469 de la sucesión:
s469(276)=149 384 846 598 254 844 243 905 695 992 651 412 919 855 640.
¿Volverá a descender esa cantidad para algún sk(276) con k mayor que 469? Se desconoce en este momento. Pero podría suceder porque, por ejemplo, para n=138, existe un k en el que se alcanza un “pico”, sk(138)= 179 931 895 322, y la sucesión empieza a descender a partir de ese momento hasta llegar a un 1.
Aunque esto parece un mero juego, existen muchas conjeturas alrededor de sumas y sucesiones alícuotas que mantienen a muchas personas ocupadas y ¡haciendo matemáticas serias!
Referencias
- Aliquot sequences, Futility Closet, 12 junio 2019
- Jean Luc Garambois, Aliquot sequences
- Wolfgang.Creyaufmueller, Aliquot sequences,
- Juan Luis Varona, Aliquot sequences
- Aliquot sequences, OEIS
-
Richard K. Guy and J. L. Selfridge, What Drives an Aliquot Sequence ?, Maths of Computation 29 (1975) 101-110
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Sumas y sucesiones alícuotas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Construye tu propia calculadora de sumas y restas
- La magia de los números (el teorema de Moessner)
- La magia del teorema de Zeckendorf
El desconcertante efecto fotoeléctrico
 El Museo Guggenheim de Bilbao está recubierto por planchas de titanio, un metal. «El gran árbol y el ojo» la escultura de bolas es de acero. ¿Emiten fotoelectrones? Fuente: Jon del Rivero / Unsplash
El Museo Guggenheim de Bilbao está recubierto por planchas de titanio, un metal. «El gran árbol y el ojo» la escultura de bolas es de acero. ¿Emiten fotoelectrones? Fuente: Jon del Rivero / Unsplash
En 1887, Heinrich Hertz estaba comprobando la teoría de las ondas electromagnéticas de Maxwell. Se dio cuenta de que una superficie metálica puede emitir cargas eléctricas cuando incide sobre ella una luz de longitud de onda muy corta. Debido a que intervienen la luz y la electricidad este fenómeno pasó a conocerse como efecto fotoeléctrico.
Cuando las cargas eléctricas producidas de esta manera se hacía pasar a través de campos eléctricos y magnéticos, sus trayectorias se veían afectadas de la misma manera que las de los rayos catódicos. Por el mismo razonamiento empleado con ellos se dedujo que las cargas eléctricas emitidas por el efecto fotoeléctrico consisten en partículas cargadas negativamente. En 1898, J.J. Thomson midió el valor de la relación q / m para estas partículas. Utilizando el mismo método que había usado para las partículas de los rayos catódicos Thomson obtuvo el mismo valor para las partículas fotoeléctricas que para las partículas de los rayos catódicos.
Estos experimentos (y otros) demostraron que las partículas fotoeléctricas tenían las mismas propiedades que los electrones. De hecho, los físicos ahora consideran que estas partículas son electrones, aunque a menudo se les llama fotoelectrones, para indicar su origen. Trabajos posteriores demostraron que todas las sustancias (sólidos, líquidos y gases) exhiben el efecto fotoeléctrico en condiciones apropiadas. Para comprender bien en qué consiste y sus implicaciones nos será más conveniente centrarnos en el efecto en las superficies metálicas.
Quizás convenga señalar ahora que el efecto fotoeléctrico tuvo un lugar muy importante en el desarrollo de la física atómica básicamente porque el efecto no se puede explicar en términos de física clásica. Fue necesario introducir nuevas ideas para dar cuenta de los resultados experimentales. En concreto, la introducción del concepto revolucionario de cuanto inició una nueva rama de la física llamada teoría cuántica. Esta teoría y el concepto físico de cuanto surgen, en buena medida, debido a la explicación proporcionada para el efecto fotoeléctrico [1].
Veamos que es lo que se observó. La información básica para estudiar el efecto fotoeléctrico proviene de dos tipos de medidas:
1. Mediciones de la corriente fotoeléctrica (el número de fotoelectrones emitido por unidad de tiempo); y
2. Mediciones de las energías cinéticas de los fotoelectrones emitidos.
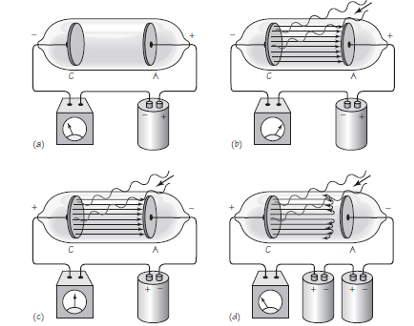 Figura 1. Fuente: Cassidy Physics Library
Figura 1. Fuente: Cassidy Physics Library
La corriente fotoeléctrica se puede estudiar con un aparato como el que se muestra en la Figura 1 (a). Dos placas de metal, C y A, están selladas dentro de un tubo de cuarzo [2] en el que se ha hecho el vacío. Las dos placas están conectadas a una fuente de diferencia de potencial (por ejemplo, una batería de alto voltaje). En el circuito también hay un amperímetro, que mide la corriente eléctrica. Mientras la luz incide en la placa C, como en Figura 1 (b), se emiten electrones con un rango de energías cinéticas (velocidades). Si el potencial de la placa A es positivo en relación con la placa C, estos fotoelectrones emitidos se acelerarán hacia la placa A [3]. La corriente eléctrica resultante la indica el amperímetro. .
Los primeros resultados del experimento son: cuanto más fuerte (o más intenso) sea el haz de luz de un color (frecuencia) dado, mayor será la corriente fotoeléctrica. Cualquier metal utilizado como placa C muestra un efecto fotoeléctrico, pero solo si la luz tiene una frecuencia mayor que un cierto valor. Este valor de la frecuencia se denomina frecuencia umbral para ese metal. Diferentes metales tienen diferentes frecuencias umbral. Pero si la luz incidente tiene una frecuencia inferior a la umbral, no se emiten fotoelectrones, ¡sin importar lo grande que sea la intensidad de la luz o cuánto tiempo permanezca encendida! Este es el primer conjunto de descubrimientos sorprendentes.
Las energías cinéticas de los electrones se pueden medir en una versión ligeramente modificada del aparato, que vemos en la Figura 1(c). La batería se invierte, de modo que la placa A ahora tiende a repeler los fotoelectrones. El voltaje puede cambiarse de cero a un valor lo suficientemente grande para evitar que los electrones alcancen la placa A, como se indica en la Figura 1(d).
Cuando el voltaje entre las placas es cero, el medidor indicará una corriente [3]. Esta lectura muestra que los fotoelectrones, que emergen con energía cinética de la superficie metálica, pueden alcanzar la placa A. A medida que aumenta el voltaje de repulsión, la corriente fotoeléctrica disminuye. Finalmente, se alcanza un cierto voltaje en el que incluso los electrones más rápidos se repelen y, por lo tanto, la corriente se vuelve cero, como se indica en en la Figura 1(d). Este voltaje, llamado voltaje de parada, es una medida de la energía cinética máxima de los fotoelectrones emitidos (Ecmax). Si llamamos Vp para al voltaje de parada, entonces la energía cinética máxima viene dada por la relación Ecmáx = e ·Vp , donde e es la magnitud de la carga del electrón. Se encontró que la energía cinética máxima medida de los electrones emitidos era proporcional a la frecuencia de la luz incidente.
En nuestro camino hacia poder explicar la tabla periódica y la estructura de los átomos, continuaremos discutiendo estos resultados, cómo la física clásica no puede explicarlos y qué solución propuso Einstein.
Nota:
[1] El concepto de cuanto fue introducido por Planck a finales de 1899. Pero en ese momento era poco más que un artificio matemático. El verdadero uso útil del mismo se lo dio Einstein en 1905 para explicar el efecto fotoeléctrico. Ya llegaremos a eso.
[2] El cuarzo es transparente a la luz ultravioleta, así como a la luz visible, no como el vidrio común a base de sílice, que es opaco en mayor o menor medida a la ultravioleta.
[3] Por la naturaleza del fenómeno existe una probabilidad no nula de que algunos electrones emitidos lleguen a la placa A, incluso si no es positiva en relación con C.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El desconcertante efecto fotoeléctrico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La estructura 3D de la cota de malla invierte el efecto Hall
- Una nueva cosmoquímica por descubrir gracias al efecto túnel cuántico
- El sistema de la difusión social de la ciencia: Efecto de las actividades de difusión científica
Anisakis
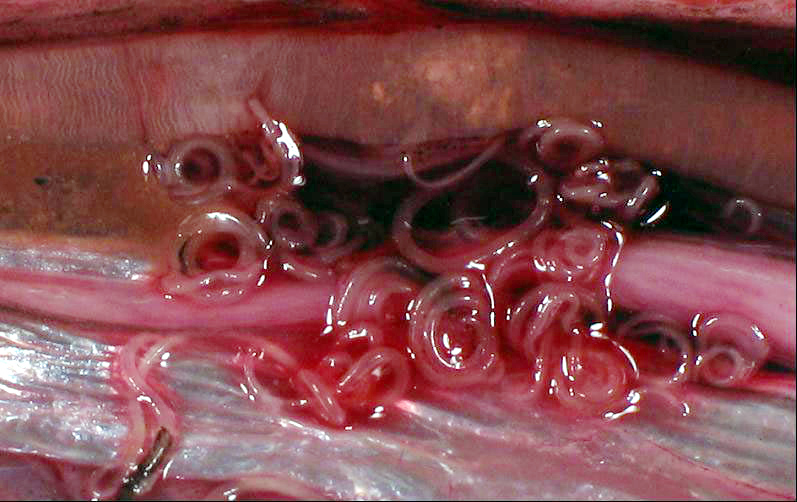 Larvas de anisakis en el interior de un arenque. Imagen: Wikimedia Commons
Larvas de anisakis en el interior de un arenque. Imagen: Wikimedia Commons
Los nematodos parásitos de animales marinos pueden hospedarse en nuestra especie y provocar la enfermedad llamada anisakidosis son las especies Anisakis simplex y Pseudoterranova decipiens, antes conocida como Phocaneura decipiens, tal como revisan Natasha Hochberg y Davidson Hamer, de la Universidad de Boston. La especie Anisakis simplex fue descrita en 1845 por el zoólogo francés Félix Dujardin, como parásito de tiburones, en su monumental obra Histoire naturelle des helminthes ou Vers intestinaux. Anisakidosis es la enfermedad resultado de la infección accidental con las fases larvarias de varios nematodos que se encuentran en peces o cefalópodos marinos y que se ingieren crudos o poco cocinados. Según la reunión de expertos celebrada en 1988, la anisakidosis es la enfermedad provocada por parásitos de la familia Anisakidae, y anisakiosis es la enfermedad provocada por parásitos del género Anisakis. Los nematodos se conocen vulgarmente como gusanos redondos o gusanos cilíndricos debido a la forma redondeada de su cuerpo en un corte transversal. Son organismos esencialmente acuáticos, aunque aparecen también en ambientes terrestres. Existen especies de vida libre, marinas, en el suelo, y especies parásitas de plantas y animales, incluyendo el hombre. Son agentes causales de enfermedades de transmisión por alimentos y provocan enfermedades como la triquinosis, la filariasis y, entre otras más, la anisakidosis. El número de especies que parasitan directamente al hombre son un grupo muy pequeño en comparación al número total de especies de nematodos.
El primer caso de anisakidosis documentado en la bibliografía científica fue conocido en 1876 con un niño vomitando un gusano, pero la primera descripción completa llegó en 1960, cuando Van Thiel, del Instituto de Medicina Tropical de Leiden, en Holanda, identificó al parásito como un nematodo cuya fase larvaria se localizó en el arenque, el bacalao, la merluza y la caballa, y el adulto en el tiburón y la raya. El paciente de Van Thiel lo había ingerido de arenque. También menciona en su artículo otros diez casos, con parecidos síntomas y diagnosticados entre 1955 y 1959.
El primer caso de infección con anisakis en España lo publicó el equipo de Juan José Arenal, en 1991, en el Hospital Pío Del Río Hortega de Valladolid, en un varón de 41 años en el que no se pudo establecer cómo se contagió con el nematodo.
Las infecciones con anisakis provocan síntomas en el tracto digestivo, con dolores abdominales, incluso hay algún caso de apendicitis aguda, y, además, reacciones alérgicas. En personas sensibles a estos nematodos, pueden darse solo reacciones alérgicas sin molestias digestivas. En España, se han descrito reacciones alérgicas a anisakis en merluza, anchoa, bacalao, atún, sardina, sepia, caballa y gallo. Más en concreto, en Vitoria-Gasteiz, se han encontrado reacciones alérgicas después de consumir merluza cocinada o anchoas cocinadas o crudas, y el equipo de Luis Fernández Corres ha diagnosticado 100 casos de reacción alérgica, una cifra que destaca en la literatura médica sobre este parásito.
De los, más o menos, 20000 casos de anisakidosis que se detectan cada año en todo el mundo, más del 90% ocurren en el Japón, sobre todo en hombres y en las zonas costeras. El 10% restante se diagnosticó sobre todo en Europa y, en concreto, en Holanda, Reino Unido, Alemania, Italia, Francia y España; y también en Asia, en Corea; en Norteamérica, en Estados Unidos y Canadá; en los países del Pacífico en Sudamérica; y en Nueva Zelanda. En resumen, en todos los continentes y todos los océanos.
El aumento de casos en el reciente medio siglo, más en concreto en los últimos veinte años y según la revisión, publicada en 2008, de Audicana y Kennedy, del Hospital Santiago de Vitoria-Gasteiz y la Universidad de Glasgow, respectivamente, se debe a que es una enfermedad mal diagnosticada, con falta de información incluso en los ambientes médicos y con buenos métodos de detección recientes. Y, también, por la moda gastronómica de los últimos años de consumir pescado crudo o poco cocinado según la tendencia culinaria creciente de no cocinarlo en exceso. O, si se quiere, de no cocinarlo adecuadamente. Es indudable que, a causa de la moda de la dieta mediterránea, ha crecido la demanda de pescado por los consumidores. También se ha propuesto un aumento reciente de la presencia de estos parásitos en las especies de pescado que se comercializan.
En una revisión sobre parasitosis con anisakis en España, publicada en 2018, Zaida Herrador y su grupo, del Instituto de Salud Carlos III de Madrid, revisan los datos de hospitalización desde 1977 a 2015, con un total de 2471 ingresos con síntomas y diagnóstico de anisakidosis. Ya en 2017 y con datos de 2013, Miguel Bao había colocado en cabeza de número de casos a Cantabria seguida del País Vasco.
El grupo de Zaida Herrador detecta un aumento constante de casos en los 19 años revisados y, además, con dos picos muy altos en 2002 y 2014. La media es de 2.93 casos por millón de habitantes, con la tasa más alta en Madrid, con 9.17 casos por millón, seguida de Castilla-León y La Rioja. En el País Vasco, la tasa es de 4.62 casos por millón de habitantes. Los autores proponen que el número de enfermos no diagnosticados por año en España está entre 10000 y 20000.
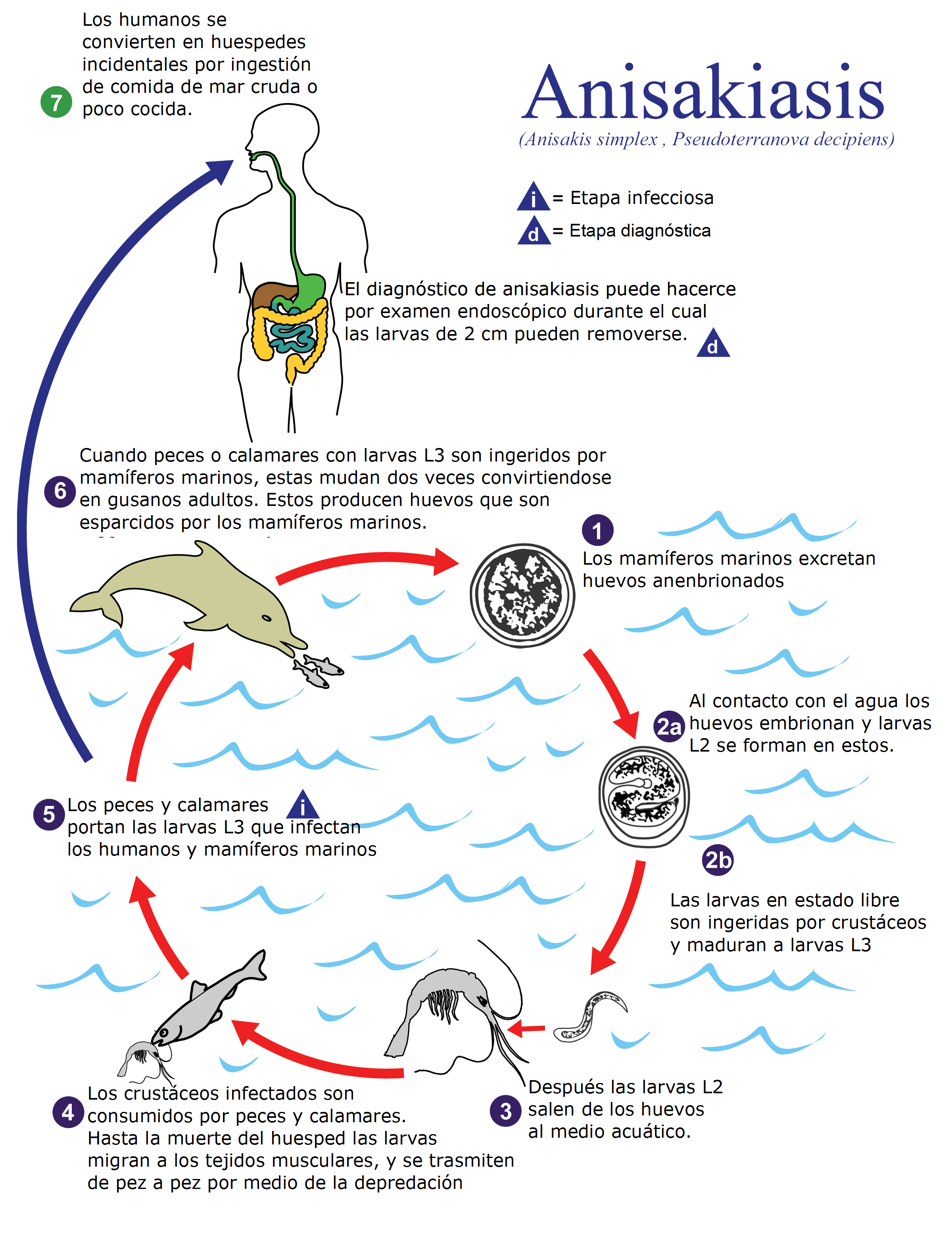 Se conoce como anisakidosis a la infección por cualquier miembro de la familia Anisakidae y anisakiasis a la infección por algún gusano en concreto del género Anisakis. Imagen: Wikimedia Commons
Se conoce como anisakidosis a la infección por cualquier miembro de la familia Anisakidae y anisakiasis a la infección por algún gusano en concreto del género Anisakis. Imagen: Wikimedia Commons
El contagio depende de la cultura de cada país respecto a la alimentación con pescado. En el Japón son el sushi y el sashimi la mayor fuente de pescado crudo, aunque los cocineros profesionales detectan la infección con anisakis con rapidez. Pero hay peces y cefalópodos que se consumen por particulares en sus domicilios y que también pueden estar infectados. En Estados Unidos es el salmón, en Holanda el arenque salado o ahumado, en Sudamérica es el ceviche y en España, los boquerones.
Las especies marinas portadoras de anisakis y especies cercanas de nematodos están en todos los mares del planeta. Como ejemplo para comenzar a entender el problema sanitario que suponen estos parásitos, nos sirve que, en un mercado de venta de pescado del Japón, el 98% de la caballa o el 94% del bacalao lleva anisakis. En un mercado en España, en Granada, el 39.4% de la caballa lleva anisakis. Parecidas cifras se han encontrado en Escocia, Italia, Francia o Estados Unidos. Más en concreto, en España se han encontrado larvas de anisakis en más de 35 especies de pescado de consumo habitual. En merluza hay anisakis en el 88% de los ejemplares; en bacaladilla, hasta el 85%; en jurel, hasta el 60%, en anchoa es el 5.6%, y en sardina hasta el 9%. Hay variantes curiosas cuya causa no se conoce y, así, según Adroher y sus colegas, de la Universidad de Granada, en 1990 el 49.5% de las caballas del Cantábrico tenían anisakis, el 36% de las del Atlántico y solo el 6.3% de las caballas del Mediterráneo.
 Boquerones crudos en vinagre. Imagen: Wikimedia Commons
Boquerones crudos en vinagre. Imagen: Wikimedia Commons
La mejor protección contra la anisakidosis es la educación del público sobre el peligro de consumir pescado crudo o poco cocinado o si proviene de pescado salado o ahumado. Sin embargo, tal como escribe Ignacio Ferre, de la Universidad Cardenal Herrera-CEU de Valencia, es difícil cambiar las costumbres alimentarias de países con culturas de consumir pescado crudo, tal como ocurre, por ejemplo, con el Japón, el Perú y el ceviche o España con los boquerones. Hay que aplicar, en lo posible, las medidas de prevención que se pueda ya que, en muchos lugares, el combustible para cocinar o el congelador son lujos inalcanzables por ser países en desarrollo.
Y, también, hay que aplicar los métodos de destrucción de las larvas en el pescado. Mueren si pasan por temperaturas superiores a 60ºC durante más de un minuto, y mejor llegar a entre 5 y 10 minutos. El pescado ahumado necesita que el proceso tenga una temperatura alta, y el pescado en salazón debe alcanzar una concentración muy alta de sal durante un tiempo largo. Con el microondas se debe cocinar a 74ºC o más a potencia máxima más de dos minutos. Para el pescado que se quiere consumir crudo, se debe congelar a -20ºC como poco durante 24 horas y, mejor, de dos a tres días y hasta siete días.
En general, preparar pescado con sal, secado, marinado, con vinagre o ahumado hasta 40ºC, esteriliza otros patógenos pero no lo consigue con el anisakis. Así, el grupo de Pilar Puente, de la Universidad Complutense, detectó que la presencia de anisakis es mayor en los consumidores habituales de pescado crudo o poco cocido que en los que antes lo congelan y después lo cocinan.
La relación entre aumento de casos de anisakis y nuevas modas culinarias se puede ilustrar con lo que menciona Oscar Caballero en su historia cultural del mar. En 1965 y en París, se empezaron a servir en los restaurantes filetes de salmón salteados solo 15 segundos por cada lado. O también se empieza a conocer el carpaccio de lubina, es decir, la lubina cruda. Caballero escribe que “el pescado crudo entra de rondón en el restaurante un cuarto de siglo antes de que irrumpan sashimis y luego ceviches”. Fue hacia 1970 cuando el restaurante L’Arête, en Montparnasse, comenzó a servir su primer pescado “rosé à l’arête”, con la carne rosada contra la espina. Es el pescado casi crudo, es la nouvelle cuisine, la cocina que se impondrá en todo el mundo.
En España y a principios de los ochenta, José Carlos Capel reivindicaba los asados “en rosa”, que venían de Francia, con la carne poco hecha y la espina del pescado sonrosada, “una técnica que pretende respetar las cualidades gastronómicas de los alimentos, evidenciando al mismo tiempo su verdadera calidad, Una moda que se nos antoja definitiva, porque representa el único método válido para conservar en toda su pureza los impagables sabores del mar”. Es evidente que la nouvelle cuisine ignora una de las más importantes funciones del fuego para nuestra especie: esterilizar los alimentos durante el cocinado y eliminar parásitos y, entre ellos, el anisakis y otros nematodos en el pescado.
Y, para terminar, unos ejemplos de estos cambios culinarios. En 1930 y en el restaurante Amparo cocinaban la merluza durante media hora. En 1973, en la Sociedad Beztartxo de Villarreal de Urretxua lo hacían en 45 minutos. Pero en 1976, Ana María Calera recomienda quince minutos, y Arguiñano en 1996 recomienda 10-12 minutos, pero Arzak lo pone en 6 minutos, y en 2018 y en Internet, la compañía de alimentación Pescanova recomienda cuatro minutos. En 90 años hemos pasado de media hora a 4 minutos.
Referencias:
Adroher, F.J. et al. 1996. Larval anisakids (Nematoda: Ascardoidea) in horse mackerel (Trachurus trachurus) from the fish market in Granada (Spain). Parasitology Research 82: 253-256.
Arenal Vera, J.J. et al. 1991. Anisakiasis como causa de apendicitis aguda y cuadro reumatológico: primer caso en la literatura médica. Revista Española de Enfermedades Digestivas 79: 355-358.
Audicana, M.T. & M.W. Kennedy. 2008. Anisakis simplex: from obscure infections worm to inducer of immune hypersensitivity. Clinical Microbiology Reviews 21: 360-379.
Bao, M. et al. 2017. Assessing the risk of an emerging zoonosis of worldwide concern: anisakiasis. Scientific Reports 7: 43699.
Caballero, O. 2018. Océanos, peces, platos. Una historia cultural del mar. Arpa y Alfil Eds. Barcelona. 379 pp.
Capel, J.C. 1997. Manual del pescado. R & B Eds. Bilbao. 366 pp.
del Pozo, M.D. et al. 1997. Anisakis simplex, a relevant ethologic factor in acute urticaria. Allergy 52: 576-579.
Ferre, I. 2001. Anisakiosis y otras zoonosis parasitarias transmitidas por consumo de pescado. AquaTIC 14: 20 pp.
Herrador, Z. et al. 2018. Epidemiological scenario of anisakidosis in Spain base don associated hospitalizations: The tip of the iceberg. Clinical Infectious Diseases doi: 10.1093/cid/ciy853
Hochberg, N.S. & D.H. Hamer. 2010. Anisakidosis: Perils of the deep. Clinical Infectious Diseases 51: 806-812.
Nawa, Y. et al. 2000. Sushi delights and parasites: The risk of fish borne and food borne parasitic zoonoses in Asia. Clinical Infectious Diseases 41: 1297-1303.
Puente, P. et al. 2008. Anisakis simplex: The high prevalence in Madrid (Spain) and its relation with fish consumption. Experimental Parasitology 118: 271-274.
Terán-Ángel, G. & J. Rojas. 2012. Anisakidosis, inflamación e hipersensibilidad. Avances en Biomedicina 1: 30-37.
Van Thiel, P.H. et al. 1960. A nematode parasitic to herring, causing acute abdominal syndromes in man. Tropical and Geographical Medicine 12: 97-111.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Anisakis se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El caso de los enfermos de Minamata
- El petróleo, los desastres y la prensa
- El caso de la mujer barbuda
La tabla periódica en el arte: Cobalto
El cobalto no es un elemento químico tan conocido como el oro, el hierro o el cobre. Sin embargo, desde una posición más humilde ha jugado un papel fundamental en la Historia del Arte. En muchísimas ocasiones lo ha hecho desde el más absoluto de los anonimatos, ya que artistas y artesanos lo emplearon sin conocer su existencia hasta que Georg Brandt lo aisló en 1735. El elemento tomó el nombre de los kobolds, seres mitológicos a los que se acusaba de reemplazar los preciados minerales de los mineros sajones por otros que aparentemente no tenían ningún valor. De esos minerales sin valor es de donde Brandt había extraído el cobalto.
Ladrillos de colores: el vidriado.
Pese a que los egipcios fueron pioneros en el uso del cobalto, empezaremos nuestro viaje en Babilonia. Más concretamente en la puerta de Isthar, ese acceso monumental que ordenó construir Nabucodonosor II en el s. VI a.e.c. para impresionar e intimidar a cuantos entrasen a la vía procesional de la ciudad. Dragones, toros y leones dorados nos aguardan sobre un fondo de un color azul intenso. Si nos acercásemos a la puerta, veríamos que ese azul es irregular. En la pared destacan rectángulos de diferentes tonalidades que podrían ser píxeles de una pantalla de televisión. Esas formas rectangulares no son otra cosa que ladrillos, sólo que en lugar de presentar el color anodino de la cerámica cocida fueron coloreados mediante la técnica del vidriado. El vidriado consiste en aplicar sobre la cerámica una pasta que en el proceso de cocción se funde y adquiere aspecto cristalino. Podemos decir que vidriar una cerámica es como vestir a una persona: cuestión de estética y funcionalidad. No sólo se aumenta la belleza de la pieza, sino que se reduce la porosidad del objeto, haciendo que sirva para albergar líquidos.
 Imagen 1. Puerta de Ishtar. Museo de Pérgamo (Berlín). Fuente: flickr / youngrobv
Imagen 1. Puerta de Ishtar. Museo de Pérgamo (Berlín). Fuente: flickr / youngrobv
La receta de la pasta empleada en el proceso de vidriado es simple: una fuente de sílice (arena), un fundente para reducir el punto de fusión de la mezcla y alúmina para controlar la viscosidad. A esa receta básica se le pueden añadir otros ingredientes, ya sea para lograr un aspecto opaco o para darle color. Y es en este último punto donde entra en juego nuestro protagonista, ya que el óxido de cobalto se caracteriza por otorgar color azul al vidriado.
Lo cierto es que no hace falta viajar tantos siglos en el tiempo para disfrutar del color que ofrece el cobalto. La loza de Delft, esa cerámica blanca y azul que abarrota las tiendas de suvenires holandesas, adquiere su bicromía gracias al óxido de estaño (opacificante blanco) y al óxido de cobalto (azul).
 Imagen 2. Cerámica de Delft en el interior de la Tienda Tártara del castillo de Groussay.
Imagen 2. Cerámica de Delft en el interior de la Tienda Tártara del castillo de Groussay.
Bleu de Chartres: cuando la luz se convierte en azul
El azul es un color esquivo. La naturaleza nos regala pocas substancias de este color, lo que ha conducido al ser humano a una lucha sin cuartel para poder plasmarlo en obras de arte. Una de esas batallas se venció en la Francia del s. XII, cuna de un nuevo estilo artístico y nuestra próxima parada en este viaje por la historia del cobalto.
En Sant-Denis el abad Suger supervisa la construcción de un templo que sentará las bases de un nuevo estilo arquitectónico y cuya protagonista absoluta será la luz: el gótico. Los techos de los edificios se elevarán hasta el cielo y gracias a los avances técnicos se abrirán ventanales enormes que, cubiertos con vitrales de colores, permitirán crear una atmósfera mística. El uso de vitrales ya se documenta en Bizancio en el s. VII, pero es en el gótico donde alcanzó su máximo esplendor. Sin embargo, los artesanos tenían dificultades enormes para obtener vidrios azules. Tanto es así que los que tenían el conocimiento para lograr este color mantenían un secreto que se transmitía de generación en generación. Guardaban con celo absoluto una substancia procedente de minas desconocidas que, añadida durante la elaboración del vidrio, proporcionaba el ansiado azul. Se trataba, obviamente, de óxidos de cobalto. El azul de las vidrieras se hizo tan célebre que adquirió nombre propio. Lo tomó de la catedral gótica donde este arte alcanzó su cenit: Chartres.
 Imagen 3. La Virgen Azul de Chartres (ca. 1180). Fuente: flickr / Walwyn
Imagen 3. La Virgen Azul de Chartres (ca. 1180). Fuente: flickr / Walwyn
Pese a la falta de conocimientos, aquella gente con su metodología de prueba y error estaba realizando algo que bien podría ser investigación puntera de nuestro siglo: el uso de nanopartículas. Efectivamente, el azul de Chartres debe su color a la interacción de partículas de escala nanométrica con la luz. Como la longitud de onda de la luz y la de las partículas de cobalto son similares, suceden ciertos fenómenos físicos que explican la aparición del color azul.
Esmalte: de los vitrales a la paleta
Al oír la palabra esmalte es muy posible que te venga a la cabeza un producto cosmético empleado como pintauñas. Pero en este caso nos referimos a la pasta de vidrio coloreado que se aplica a una superficie metálica o de vidrio. Eso sí, también tiene fines decorativos. Triturando el esmalte coloreado con óxidos de cobalto podemos lograr un pigmento muy empleado a lo largo de la historia: el azul esmalte. En resumidas cuentas, este pigmento no es otra cosa que vidrio azul pulverizado. El polvo se puede juntar con un aglutinante (óleo, tempera, etc.) para formar una pintura que resulta más pálida cuanto más pequeños sean los cristalitos.
Como sucede con el azul de Chartres el origen del azul esmalte está sumido en el misterio. Tendríamos que viajar hasta la Bohemia de 1540 para ver como Christopher Schurer lograba el pigmento empleando minerales de cobalto extraídos en las cercanas minas sajonas. El método consistiría en obtener una substancia llamada zaffre o zaffer mediante un proceso de combustión en el que se eliminaba el arsénico. Esa substancia se podría añadir al vidrio para otorgarle color azul, igual que sucedía con el polvo que unos siglos antes los artesanos medievales pasaban de padres a hijos para teñir las vidrieras. Eso es por lo menos la historia que cuentan los textos del s. XVII, aunque hoy en día sabemos que tanto en Europa como en China el azul esmalte se había empleado antes de 1540.
 Imagen 4. La Venus del Espejo (122 x 177 cm), de Velázquez (1647-51) fue pintada con azul esmalte. Fuente: National Gallery.
Imagen 4. La Venus del Espejo (122 x 177 cm), de Velázquez (1647-51) fue pintada con azul esmalte. Fuente: National Gallery.
Más azules, más cobalto
El azul esmalte tuvo su época de gloria, pero poco a poco fue perdiendo protagonismo por la aparición de otros pigmentos azules de mayor calidad, entre ellos dos con cobalto: el azul cobalto y el cerúleo. Volvemos a Francia y avanzamos hasta el s. XIX, sin duda el mejor siglo para los amantes del azul. Recordemos que además de estos dos pigmentos se logró sintetizar el azul ultramar.
Hacia 1803 el químico francés Louis Jacques Thénard publicaba sus estudios sobre un nuevo pigmento que inmediatamente se lanzó al mercado: el azul cobalto (CoO-Al2O3). Más de 200 años después el compuesto se sigue comercializando, en ocasiones con el nombre de azul de Thénard en honor a su descubridor. No sabemos qué le haría más ilusión al bueno de Louis Jacques, que su apellido haya bautizado a un pigmento o que esté grabado en la Torre Eiffel junto al de otros 71 grandes científicos. Precisamente el país donde más triunfó este nuevo pigmento fue en la propia Francia. Recordemos que en la segunda mitad del s. XIX los impresionistas acaparaban el panorama artístico y el azul cobalto fue uno de sus favoritos.
El otro azul con cobalto protagonista de ese siglo es el azul cerúleo, un estannato de cobalto (CoO · n SnO2). Su éxito no fue tan inmediato como el de nuestro anterior protagonista y tuvieron que pasar varias décadas desde que un tal Höpfner lo sintetizase hasta que George Rowney lo comercializase en Inglaterra en 1860. Su compañía, ahora como Daler-Rowney, sigue vendiendo el azul cerúleo tantos años después. El origen etimológico de este pigmento es bastante obvio y proviene de la palabra latina caeruleus que, a su vez, deriva de caelum (cielo). No en vano, ha sido muy empleado desde que irrumpió en el mercado para pintar la bóveda celeste.
Más allá del azul
Hasta el momento el azul ha monopolizado nuestra atención. Pero la química ofrece un amplio abanico de combinaciones y ha querido que el cobalto se asocie con otras moléculas para completar una especie de parchís al que suman el amarillo, el verde y el violeta.
 Imagen 5. Los diferentes colores que ofrece el cobalto. Fuente: Twitter
Imagen 5. Los diferentes colores que ofrece el cobalto. Fuente: Twitter
Dentro de este abanico de colores, el pigmento más destacable es el violeta de cobalto, la sal que se forma con fosfato (Co3(PO4)2) o arseniato (Co3(AsO4)2). Cuando se descubrió en el s. XIX los pintores lo codiciaron por ser uno de los escasísimos pigmentos de color morado que existían en el mercado; color que de lo contrario tenían que lograr mezclando rojos y azules. Desafortunadamente era muy caro, por lo que su uso no se extendió demasiado. Lo que es seguro es que Monet consiguió hacerse con él para pintar el óleo Irises de la National Gallery. Teniendo en cuenta que en sus últimos años de vida realizó una serie de más de 200 obras con nenúfares y flores, podemos suponer que disponía de buenas reservas de violeta de cobalto. Aunque para obsesión con el cobalto la de Frank T. Edelmann, profesor en la Universidad Otto-von-Guericke de Magdeburg que dispone de una colección que haría las delicias de cualquier departamento de Química Inorgánica.
 Imagen 6. La biblioteca de complejos de cobalto de Frank T. Edelmann. Fuente: Twitter. Usada con permiso del autor.
Imagen 6. La biblioteca de complejos de cobalto de Frank T. Edelmann. Fuente: Twitter. Usada con permiso del autor.
También en el s. XIX se sintetizó por primera vez la aureolina o amarillo de cobalto (K3[Co(NO2)6]), si bien su éxito fue efímero y pronto el amarillo de cadmio lo relegó a un papel muy secundario. En una época mucho más reciente apareció el titanato de cobalto (Co2TiO4), un pigmento verde que se obtiene de la calcinación de los óxidos de cobalto y titanio y que sólo se ha documentado en obras vanguardistas como Near the Lagoon de Jasper Johns (2002).
Para saber más
A. Roy et al. “Renoir’s ‘Umbrellas’ Unfurled Again” National Gallery Technical Bulletin (33) 2012.
M.F. Ashby et al. “Nanomaterials, Nanotechnologies and Design: An Introduction for Engineers and Architects” Ed. Butterworth-Heinemann (2009).
J.M. Mimoso. “Origin, early history and technology of the blue pigment in azulejos” International Conference Glazed Ceramics in Cultural Heritage
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo La tabla periódica en el arte: Cobalto se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: ¿Qué átomos hay en una obra?
- La tabla periódica en el arte: Cobre
- La tabla periódica en el arte: Mercurio
E-pi-logo (después de esto, mi carrera ha muerto)

Aniceto Murillo Mas es catedrático en el departamento de álgebra, geometría y topología de la Universidad de Málaga. Excelente comunicador, nos deja en esta conferencia-monólogo una muestra de su arte…matemático.
Quizás sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que existen en el mundo, estudiada por el ser humano desde hace más de 4.000 años. La fascinación que ha suscitado durante siglos es tal que el popular número cuenta con su propio día en el calendario, así el mes de marzo se celebra el Día de Pi en todo el planeta.
Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien lanzó en 1988 la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés) y además, la celebración coincide con la fecha del nacimiento de Albert Einstein. En 2009, el congreso de EEUU declaró oficialmente el 14 de marzo como el Día Nacional de Pi.
Actualmente, el Día de Pi es una celebración mundialmente conocida que sobrepasa el ámbito de las matemáticas. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
Este 2019 nos unimos de nuevo al festejo con el evento BCAM–NAUKAS, que se desarrolló a lo largo del 13 de marzo en el Bizkaia Aretoa de UPV/EHU. BCAM-NAUKAS contó durante la mañana con talleres matemáticos para estudiantes de primaria y secundaria y durante la tarde con una serie de conferencias cortas dirigidas al público en general.
Este evento es una iniciativa del Basque Center for Applied Mathematics -BCAM, enmarcada en la celebración de su décimo aniversario, y de la Cátedra de Cultura Científica de la Universidad el País Vasco.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo E-pi-logo (después de esto, mi carrera ha muerto) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El efecto Talbot: tejiendo alfombras con luz
- Sigue al conejo blanco
- Diagnóstico de enfermedades: una cuestión de probabilidades
¿Existe algún fármaco que nos haga más inteligentes?
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

En la serie Sin límites (Fox, 2016) creada a partir de la película homónima, el protagonista (Brian Finch) es un músico mediocre que ha perdido su talento y que su vida no parece conducir a ninguna parte. Siente que, de hecho, no es capaz de expresar adecuadamente sus habilidades y todo su potencial mental. Todo esto cambia cuando toma una pastilla transparente y completamente ilegal (la NZT), que lo hace más inteligente. Bajo la influencia de la pastilla, sus habilidades de procesamiento mental se vuelven más eficaces y rápidas e incluso recuerda hechos y eventos que creía perdidos en su memoria. Este nuevo talento lo lleva a trabajar para el FBI y resolver complejos crímenes que otros detectives no habían podido descifrar.
¿Es esta fantasía, que la mayoría de nosotros compartimos, ser más inteligente y mejorar el potencial de nuestro cerebro, posible?
En los últimos años ha habido un tremendo progreso en la comprensión de los mecanismos responsables del aprendizaje, la memoria y otros componentes de la cognición humana. Comenzamos, ahora, a comprender los procesos cognitivos a nivel celular, molecular y sináptico (sinapsis = conexiones entre las células nerviosas). Los modernos métodos de análisis de imagen permiten identificar en tiempo real los circuitos que participan en diferentes tipos de memoria y aprendizaje, tanto en animales como en personas. Además, con técnicas de modificación genéticas sofisticadas, hoy en día es posible crear memorias artificiales en ratones mediante la manipulación de circuitos cerebrales específicos y de células nerviosas en el cerebro.
 Póster de la película «Sin Límites». Fuente: © 2011 Relativity Media Ltd. All Rights Reserved. Reproducido bajo los términos de fair use de la United States copyright law
Póster de la película «Sin Límites». Fuente: © 2011 Relativity Media Ltd. All Rights Reserved. Reproducido bajo los términos de fair use de la United States copyright law
¿Qué es la mejora cognitiva?
Antes de describir algunos de los compuestos utilizados para mejorar las capacidades mentales, explicaremos qué es la mejora cognitiva. Sería esta una mejora en nuestra capacidad para procesar datos, aprender cosas nuevas, llegar a conclusiones correctas, recordar detalles del pasado y usarlos de la manera correcta en el presente. Hay intentos de alcanzar estos resultados mediante el uso de compuestos químicos (drogas o medicamentos), dispositivos y manipulaciones genéticas. Este artículo lo dedicaremos a los posibles compuestos químicos capaces de mejorar la memoria.
¿Cómo se forman los recuerdos?
Para saber cómo mejorar la memoria, primero debemos entender cómo se crean los recuerdos. En las células cerebrales y las sinapsis de las células nerviosas, millones de procesos bioquímicos ocurren de maneras sucesivas o paralelas. Sabemos que algunos de estos procesos, amplificados o debilitados por diferentes estímulos y experiencias, contribuyen a la creación de recuerdos, pero estamos muy lejos de estar familiarizados con todo el proceso. Sin embargo, ya existe un conocimiento considerable de varias docenas de moléculas clave que se consideran críticas para la creación o retención de memorias. Estas moléculas se han encontrado utilizando métodos sofisticados, que incluyen ingeniería genética, registro eléctrico de células nerviosas, imágenes de alta resolución y el uso de virus modificados genéticamente.
Una forma importante de desarrollar fármacos para el mejoramiento cognitivo es comprender por qué algunos ratones transgénicos muestran capacidades cognitivas deficientes y otros muestran capacidades cognitivas mejoradas en relación con los ratones normales. Resulta que la mayoría de los «súper-ratones» expresan diferentes niveles de proteínas que de alguna manera están relacionadas con la función de las sinapsis. En otras palabras, la capacidad de mejorar la transmisión de información entre una neurona y otra es probablemente crítica para el buen aprendizaje y la memoria.
Cuando se identifica una molécula o ruta bioquímica que tiene un impacto significativo en el aprendizaje o la memoria, se intenta transformar ese conocimiento en un medicamento que mejorará la función cognitiva al modificar la actividad de esta molécula crítica o de la ruta bioquímica.
 Imagen promocional de la serie de televisión Limitless (Sin límites). Fuente: © 2015 CBS Television Studios, Inc. All Rights Reserved. Reproducida bajo los términos de fair use de la United States copyright law
Imagen promocional de la serie de televisión Limitless (Sin límites). Fuente: © 2015 CBS Television Studios, Inc. All Rights Reserved. Reproducida bajo los términos de fair use de la United States copyright law
FGL – para mejorar el aprendizaje y la memoria
FGL es un ejemplo clásico de desarrollo de un fármaco que mejora el aprendizaje y la memoria. La proteína NCAM se conoce desde hace décadas como una proteína cuya función en los procesos de aprendizaje y memoria es crucial para la comunicación celular, entre otras cosas, a través de la activación de un receptor llamado FGFR. Investigadores en Dinamarca asilaron la parte de NCAM que se une al receptor de FGFR y sintetizaron un análogo artificial que se denomino FGL.
Sorprendentemente, tras inyectar FGL en ratas mejoró su aprendizaje y memoria durante más de dos semanas. Es importante señalar que estas ratas no tenían deficiencias cognitivos antes del tratamiento , lo que indica que incluso cuando el cerebro funciona perfectamente, se puede mejorar su rendimiento.
En nuestro grupo de investigación y usando métodos de biología molecular y registros eléctricos de las células nerviosas, hemos podido descubrir por qué FGL mejora la capacidad cognitiva. Cuando se une al receptor FGFR, activa un complejo sistema de procesos bioquímicos en las células nerviosas y el resultado final es el fortalecimiento de las sinapsis entre las células nerviosas. (Enlace a la investigación completa sobre el tema). Este refuerzo aumenta la eficiencia de la transferencia de información entre las células nerviosas, lo que mejora el aprendizaje y la memoria. El FGL aún se encuentra en periodo de desarrollo. Los resultados de los ensayos clínicos son prometedores, pero aún faltan muchos años de trabajo para disponer de un potenciador cognitivo seguro y eficaz.
PDZ-PTEN – mecanismo de bypass del alzhéimer
PDZ-PTEN es una sustancia que hemos desarrollado después de varios años de investigando el porqué de la perdida de memoria en los pacientes de alzhéimer. Estos pacientes acumulan una proteína tóxica en el cerebro llamada beta amiloide. Esta proteína inicialmente interrumpe la comunicación entre las neuronas para finalmente causar su muerte. Durante mucho tiempo no se conocía exactamente cómo la beta amiloide interrumpe esta comunicación. Nuestras investigaciones descubrieron que la interrupción de la comunicación entre las células nerviosas se debe, al menos en parte, a la inserción de una proteína llamada PTEN en las sinapsis en respuesta al beta amiloide. El resultado final es el debilitamiento de las sinapsis y la interrupción de la transmisión de información de una neurona a otra.
Para contrarrestar este fenómeno, desarrollamos un compuesto que evita esta asociación entre PTEN y otros componentes sinápticos. Cuando inyectamos este compuesto en ratones transgénicos «modelos de alzhéimer», resultó que, aunque sus cerebros estaban llenos de beta amiloide, su capacidad cognitiva era similar a la de los ratones sanos. (Y aquí hay un enlace al estudio completo). De esta manera, logramos evitar el pernicioso efecto de la beta amiloide. Este compuesto se está desarrollando actualmente como medicamento para la enfermedad de Alzheimer. Esperamos que un futuro no muy lejano, nuestra investigación se transforme en una terapia real para el tratamiento de esta enfermedad
En la actualidad y conscientes del problema que supone para nuestra sociedad, muchos grupos de investigación y empresas farmacéuticas se han volcado a la investigación de nuevas terapias para el tratamiento del alzhéimer. Desgraciadamente la vacuna contra el amiloide beta o los medicamentos que reducen su cantidad en el cerebro no han de mostrado ser muy eficaces y su seguridad para el uso humano está en entredicho. A pesar de estos esfuerzo, creemos que en el futuro la enfermedad de Alzheimer se tratará no solo con un medicamento, sino con una combinación de varios, como ya se está realizando en el tratamiento del cáncer. Una posible combinación serían medicamentos que prevén la muerte de las células nerviosas, junto con los medicamentos que causan nuevas sinapsis y medicamentos que previenen el fallo sináptico.
¿Cuál es el peligro de usar potenciadores cognitivos?
Más allá de los efectos secundarios que pueden acompañar el uso de cualquier medicamento, las mejoras cognitivas pueden tener efectos secundarios únicos y desconocidos. Teóricamente, el potenciador cognitivo puede mejorar los recuerdos deseables, como el temario para un examen, pero existe el peligro de que también aumente los recuerdos sin importancia y que nuestro cerebro se inunde de recuerdos que no necesitamos, causándonos una gran confusión y posiblemente una disfunción mental.
Peor aún, un potenciador cognitivo puede amplificar los recuerdos traumáticos que de otro modo y en un cerebro normal estarían suprimidos. Aumentar recuerdos dolorosos puede ser devastador para algunas personas. La conclusión obvia es no apresurarse a probar los potenciadores cognitivos, incluso si los ensayos clínicos han tenido éxito. Por más atractivo que pueda ser el uso de estos compuestos, su empleo debería restringirse a personas con un problema real de memoria, por ejemplo, pacientes con Alzheimer y no por personas con un funcionamiento cognitivo normal.
¿Es ético usar potenciadores cognitivos?
En la actualidad asistimos a un amplio debate sobre las posibles consecuencias derivadas del uso de potenciadores cognitivos. Por ejemplo, ¿Debería exigirse la supervisión legal de tales materiales? ¿Un estudiante que consuma potenciador cognitivo engaña realmente? ¿Qué pasa con aquellos que no pueden permitirse comprar estos compuestos? ¿Habrá presión, por ejemplo, en pilotos, soldados, médicos e incluso en trabajadores de oficina para que tomen estos fármacos para mejorar su eficiencia en el trabajo? Aunque en los medicamentos utilizados hoy en día, su eficacia como potenciadores cognitivos es cuestionable, no es imposible que pronto nos encontremos con medicamentos mas efectivos y todas estas cuestiones éticas se pondrán a prueba en la realidad.
Desde 2013, la Unión Europea ha gastado más de 3 millones de euros en esfuerzos para elaborar códigos de empleo para el futuro uso de los fármacos capaces de mejorar los procesos cognitivos, pero cada país debe formular posiciones que tengan en cuenta las ventajas y desventajas de vigilar los potenciadores cognitivos.
Conclusión:: La mejora cognitiva se puede lograr a través de varias tecnologías y conlleva la promesa (o amenaza) de cambiar nuestras vidas por completo. Estamos avanzando en pasos gigantes hacia un tiempo nuevo, sorprendente, desafiante, pero al mismo tiempo aterrador, en el que no estaremos satisfechos con las capacidades mentales que la naturaleza nos ha dado, pero intentaremos con todas nuestras fuerzas romper los límites de la capacidad humana. ¿Esto nos hará más felices? El tiempo lo dirá.
Sobre los autores: La profesora Ikerbasque Shira Knafo y Miguel Morales son neurocientificos en el Instituto Biofisika (UPV/EHU-CSIC) y colaboran con el departamento de Bioquimica y Biología Molecular de la Facultdad de Ciencia y Tecnología de la UPV/EHU.
El artículo ¿Existe algún fármaco que nos haga más inteligentes? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un nuevo fármaco revierte el déficit cognitivo asociado a esquizofrenia
- Máquinas inteligentes (I): Del molino de viento al test de Turing
- Máquinas inteligentes (y III): Deep blue, HAL 9000 y más allá
Piensa bien y acertarás: los casos de Pfizer e Isdin

En el periodo de una semana los grandes medios de comunicación difundieron informaciones falsas en contra de dos importantes laboratorios farmacéuticos: Isdin y Pfizer. Isdin fue acusado de comercializar un producto de protección solar pediátrica con un SPF menor al indicado. Pfizer fue acusado de ocultar pruebas que indicaban que uno de sus fármacos previene el alzhéimer.
Cuesta encontrar alguna razón coherente por la que estos laboratorios tendrían interés en engañar con un factor de protección solar o en ocultar ni más ni menos que un fármaco contra el alzhéimer. Sin embargo, estas informaciones falsas fueron reproducidas en los principales medios de comunicación en televisión, radio, prensa y redes sociales. Ante informaciones tan descabelladas como estas, deberían saltar todas las alarmas de que estamos ante fake news. Sí, estamos ante fake news, pero muchos lo pasaron por alto.
Ni Isdin, ni ningún otro laboratorio, mienten acerca del factor de protección solar
Ningún producto cosmético puede salir al mercado indicando un factor de protección solar si antes no ha sido validado por las autoridades sanitarias.
Cualquier producto cosmético en el que se indique un factor de protección solar (SPF), sea de la magnitud que sea, ha tenido que certificarlo ante las autoridades sanitarias mediante ensayos clínicos tipificados. En el caso de España, el resultado de estos ensayos clínicos ha de ser validado por la Agencia Española del Medicamento y el Producto Sanitario (AEMPS). Una vez validados los resultados del ensayo clínico, el laboratorio puede incluir en indicativo del SPF correspondiente en su producto. Estos ensayos se hacen producto por producto, individualmente y en el producto acabado.
Para certificar el SPF se hace un ensayo in vivo, el generalmente tipificado bajo la norma ISO 24444:2010 (equivalente al International Sun Protection Factor Test Method o método COLIPA). En este ensayo se cubre una zona de piel con el producto a evaluar a razón de 2 mg/cm2. Se mide por cuánto se multiplica el tiempo de exposición a la radiación UV hasta la aparición de enrojecimiento o eritema con y sin el producto aplicado. La principal radiación responsable de las quemaduras (eritemas) es la UVB, por eso el SPF es realmente una medida de protección contra la radiación UVB. Así, un SPF 30 significa que se multiplica al menos por 30 el tiempo al que la piel puede estar expuesta al sol sin sufrir quemaduras. Un SPF 50+, que actualmente es el mayor factor de protección solar, indica que la protección ante las quemaduras dura por encima de 50 veces más que la piel sin protección. Los productos pediátricos suelen tener SPF 50+.
La validación por parte de la AEMPS y el coste del ensayo clínico, que no es precisamente barato, es el mismo para cualquier SPF.
Para certificar la protección frente a la radiación UVA, el llamado UVA-PF, se hace un ensayo diferente, generalmente el tipificado bajo la norma ISO 24443:2012 (equivalente in vitro al PDD, Persistent Pigment Darkening). El PDD se calcula por medio del cociente entre la dosis mínima de UVA necesaria para inducir un oscurecimiento pigmentario persistente de la piel protegida por un producto de protección solar y la dosis mínima de UVA necesaria para inducir el oscurecimiento mínimo de la misma piel sin proteger. Si el cociente entre el SPF y el UVA-PF es de 1/3 o inferior, el fabricante podrá incluir el indicativo de protección solar frente al UVA. Este indicativo no es numérico, sino el del UVA rodeado con un círculo.
La última semana de mayo de 2019, la Organización de Consumidores y Usuarios (OCU), una organización privada cuyo objetivo es defender los derechos del consumidor, envió una nota de prensa a los medios de comunicación indicando que habían hecho un estudio con 17 productos de protección solar pediátrica, de los cuales dos de ellos no llegaban al SPF indicado. El de los laboratorios Isdin fue el peor parado: según la OCU, uno de sus productos con SPF 50+ solo llegaba a SPF 15. La nota de prensa fue reproducida en los principales medios de comunicación, acaparando la atención durante días.
Isdin hizo públicos los estudios y resultados que certifican que ese producto cumple con el SPF y con el UVA-PF indicados, que en su día fueron facilitados a la AEMPS. La OCU no hizo públicos sus estudios, alegando que no podían desvelar la identidad de su laboratorio. Este dato ya debería ser suficiente para que los medios de comunicación decidiesen no publicar la nota de prensa. En cambio, la nota se publicó sin que nadie antes pudiese comprobar que ese estudio existía o que era veraz.
Si un cosmético es defectuoso, causa algún tipo de alergia o reacción adversa, tenemos la sospecha de que no protege del sol como debería, no tiene buen aspecto u olor… debemos notificarlo. Debemos notificarlo directamente en la AEMPS a través de su servicio de cosmetovigilancia, o podemos notificarlo a personal sanitario, a los distribuidores del producto o en la farmacia. Las farmacias tienen la obligación de notificar cualquier incidencia tanto al laboratorio como a la AEMPS. A partir de ese momento se pondrá en marcha un proceso de análisis del producto para detectar si se trata de una alerta real, de una alerta concreta o bien de una alerta extensible a un lote de productos defectuosos. Si se tratase de una alerta real, se procedería a la retirada inmediata del producto en todos los puntos de venta.
Si un cosmético es defectuoso o tenemos la sospecha de que así lo sea, hay que notificarlo primero y en exclusiva a las autoridades sanitarias, en este caso la AEMPS. Lo que no hay que hacer es enviar una nota de prensa a los medios de comunicación antes de que la AEMPS verifique si estamos ante un producto defectuoso, ni siquiera antes de que la AEMPS decida cuál es la mejor forma de proceder: enviar una circular a los puntos de venta, crear una alerta para que la difundan los medios de comunicación, retirada inmediata del producto, etc. Lo que ha hecho la OCU es precisamente lo que no hay que hacer. Se han saltado el procedimiento y han creado una alerta sin supervisión de la AEMPS. Para más inri, todo esto este disparate fue promovido y agitado por los medios de comunicación.
Pfizer no ocultó un medicamento contra el alzhéimer
El 4 de junio The Washington Post publicaba que el laboratorio farmacéutico Pfizer tenía pistas de que su fármaco superventas podía prevenir el alzhéimer y que las ocultó al mundo. En pocas horas la prensa española reproducía el artículo acompañado de titulares desinformadores y demagógicos. Aunque el cuerpo de la mayor parte de estos artículos era una reproducción del original, algunos medios argüían sobre las posibles razones que llevarían a Pfizer a ocultar tremendo descubrimiento: que si la patente estaba a punto de expirar y no sería rentable, que es más rentable la enfermedad que la cura… Razones absolutamente delirantes. Obviando las cuestiones éticas, descubrir un fármaco que cura o previene el alzhéimer es, a todas luces, muy rentable.
El principio activo del medicamento Enbrel de Pfizer es etanercerp. El etanercerp es una proteína quimérica que inhibe la acción de la TNF-α, una molécula que produce el organismo que promueve los procesos inflamatorios. Esta molécula se lleva comercializando desde 1998 para el tratamiento de la artritis reumatoide por una compañía que desde 2009 pertenece a Pfizer.
Desde hace años sabemos que uno de los síntomas del Alzhéimer es la inflamación, pero desconocemos cuál es el papel de la inflamación en esta enfermedad, y si su supresión palía sus síntomas o si frena su progresión. Esta es una de las líneas de investigación. Es por ello que los antiinflamatorios, entre ellos el etanercerp y otra veintena de moléculas biosimilares a esta, se hayan estudiado como posibles fármacos contra el alzhéimer.
En 2006 se publicó un estudio piloto que evaluó el uso de etanercerp contra el alzhéimer. Aunque los resultados eran altamente preliminares, sí parecían prometedores. Más adelante se descubrió que estos antiinflamatorios curaban el alzhéimer en animales (al menos una réplica de la enfermedad) pero desgraciadamente no funcionaba así con humanos.
En 2015 se hizo el primer ensayo clínico doble ciego, aleatorizado y controlado con placebos, para evaluar el etanercerp contra el alzhéimer. Este estudio fue financiado por Pfizer. Los resultados de eficacia fueron decepcionantes, no distinguibles del placebo. La conclusión del estudio es que el etanercerp no cura ni previene el alzhéimer.
El periodista que escribió para The Washington Post relataba que había llegado a sus manos un power point en el que figuraban datos cruzados de compañías de seguros. Según estos datos, había una menor incidencia de alzhéimer entre personas con artritis reumatoide tratadas con etanercept, que entre personas con artritis reumatoide sin tratar. Se acusó a Pfizer de ocultar esta información. Pero ni siquiera estos datos se ocultaron: en 2016 ya se había publicado un estudio en el que se cruzaban datos de pacientes con artritis reumatoide tratados con etanercept relacionándolos con la incidencia de alzhéimer.
No sabemos si hay una relación causa-efecto, ya que correlación no implica causalidad. La realidad es que, de confirmarse esa relación causa-efecto, solo sería aplicable a personas que padecen artritis reumatoide y con carácter preventivo. No sería ni efectivo ni conveniente para personas sin esta enfermedad. La razón es que los efectos adversos del etanercerp sobre el sistema inmune hacen que sea impensable administrar este fármaco como tratamiento preventivo del alzhéimer. No se puede tratar a personas sanas con inmunosupresores como el etanercerp durante largos periodos de tiempo.
Pfizer declaró ante los medios de comunicación que rechazó continuar esa línea de investigación por razones estrictamente científicas. De hecho, la evidencia científica de la que disponemos nos indica que, desgraciadamente, etanercerp no sirve para prevenir el alzhéimer.
Algunos medios de comunicación acusaron a Pfizer de ocultar datos por razones económicas, en vista de que la patente sobre etanercerp estaba a punto de caducar. Aunque ya hemos visto que no han ocultado ningún dato relevante, tampoco es cierto que la patente estuviese a punto de caducar. La patente de este antiinflamatorio caducó en 2015, así que etanercerp ni siquiera es una molécula propiedad de Pfizer. Sin embargo, en EEUU la patente seguirá en vigor hasta 2028, ya que es propiedad de otra compañía, Amgen, que consiguió una prórroga. De todos modos, si Pfizer o Amgen descubriesen un nuevo uso clínico de la molécula, la patente podría extenderse hasta 20 años más, tiempo más que suficiente como para rentabilizar un descubrimiento de tal envergadura.

Consecuencias de estas fake news
No es la primera vez que los medios de comunicación, la OCU y otras empresas ponen en duda la efectividad y seguridad de los productos cosméticos. Y no es la primera vez que tienen que desdecirse. Ya ocurrió con las cremas solares, con las BB cream, con las hidratantes… Tras analizar estos productos, con metodologías puestas en cuestión por asociaciones como Stanpa, la compañía publica un ranking. Ranking al que solo se puede acceder previo pago de la cuota de socio. Casualmente la “compra maestra” de esos rankings siempre es la de un cosmético de marca blanca, de la misma marca blanca. Aun así, no podemos acusar a la OCU de mantener una relación comercial interesada con la distribuidora de esa marca blanca porque no hay pruebas de ello.
Una de las consecuencias es que el producto de marca blanca bate récord de ventas y se agota en unos días. Otra de las consecuencias es que la OCU recibe muchas visitas y atención por parte de todos los medios de comunicación. Es una gran estrategia de propaganda.
Toda aquella información que corrobora un prejuicio (en este caso en contra de los laboratorios cosméticos) y que nos dice lo que queremos oír (que es tan bueno el cosmético más barato como el más caro) es una garantía de éxito mediático. La realidad es que los productos cosméticos son seguros, funcionan y que, salvo contadas excepciones, cuestan lo que valen. Pero la verdad no genera tantos clics.
El caso reciente de la acusación pública de la OCU hacia los laboratorios Isdin es todavía más intolerable. Poner en cuestión la eficacia de los productos de protección solar tiene unas implicaciones sanitarias fatales. Según la Asociación Española Contra el Cáncer, actualmente tenemos unas muy buenas cifras de concienciación sobre protección solar. Estas cifras peligran cada vez que los medios de comunicación ponen en duda la eficacia de los productos de protección solar. Que los medios de comunicación compartan notas de prensa como las de la OCU, sin tan siquiera ponerse en contacto con expertos, con el laboratorio, con la AEMPS, sin solicitar los estudios que corroboran las acusaciones, es de una enorme irresponsabilidad.
Hay que considerar también las pérdidas económicas. Por un lado para las farmacias y parafarmacias, que es donde se comercializan los productos de Isdin. Por otro lado, Isdin es un laboratorio cosmético muy focalizado en los productos de protección solar. Precisamente esta oleada de desprestigio mediático llega en el momento clave de la campaña de solares. Por poner un ejemplo, el salario de los delegados comerciales de estos laboratorios está sujeto a objetivos, con lo que el descenso en las ventas y las devoluciones repercute directamente en el salario de estos trabajadores. Un descenso en ventas en España, donde este laboratorio es especialmente fuerte, repercutirá en los salarios y puestos de trabajo de muchos profesionales, entre ellos un gran número de científicos. Han ido a dar donde duele y cuando más duele, caiga quien caiga.
La OCU ha manifestado que los estudios sobre protectores solares que han hecho ya están en manos de la AEMPS. Hasta la fecha la AEMPS no ha iniciado ningún procedimiento de retirada de productos. Lo más probable es que los estudios de la OCU no estuviesen bien hechos, como ya ha ocurrido con anterioridad. También podría suceder que hubiese un producto o lote de productos defectuosos. Sea como fuere, esta no es la forma responsable de proceder, ni por parte de la OCU ni por parte de los medios de comunicación.
Con respecto a Pfizer, parece que de momento no ha habido consecuencias económicas reseñables. Las acciones de la compañía no se han visto afectadas por el incidente. La principal consecuencia de todo esto es la imagen desgastada de los laboratorios farmacéuticos, y con ello, de la investigación científica. De un caso anecdótico se ha hecho un juicio generalizado hacia un sector entero.
Con respecto a los medios de comunicación, muchos o no trabajan o trabajan mal. Y quienes leen y comparten lo que estos publican, tienen muy dañado su detector de desinformación.
La noticia de que Pfizer ocultó la cura del alzhéimer es tan rocambolesca como los delirios de los charlatanes que afirman que se ha encontrado la cura del VIH y que se oculta, o la cura del cáncer. Tan inverosímil como que las farmacéuticas son las que crean las enfermedades y otras conspiraciones de similar calibre.
Esta clase de noticias deberían hacer saltar todas las alarmas de detección de fake news. Ante la duda es recomendable preguntarse quién se beneficia. Desde luego no hay beneficio posible para Isdin. Comercializar protectores solares infantiles con menos SPF del indicado no beneficia a nadie, y menos al laboratorio. Si Pfizer hubiese descubierto una cura para el alzhéimer, ocultarlo sería la opción menos rentable. Sobre todo sabiendo lo rentable que sería para el laboratorio que una de sus moléculas sirviese para tal fin. Los únicos beneficiarios posibles son las empresas cuyos ingresos dependen del clic. De ahí el título de este artículo: piensa bien y acertarás. Antes de creer que los laboratorios farmacéuticos son el demonio, al menos parémonos a pensar si hacer el mal les beneficiaría de algún modo. De lo contrario, a cuento de qué iban a engañar. Es una sandez de tal magnitud, que dejar escrito este párrafo me parece una forma de insulto.
Las fake news no solo circulan a través de estrafalarias páginas y grupos de las redes sociales, ni por whatsapp. Las fake news más peligrosas son las que llegan a los grandes medios de comunicación.
La excusa de los medios de comunicación es la precariedad. Por eso se reproducen noticias publicadas en The Washington Post aunque el titular sea fehacientemente demagógico. Por eso se comparten notas de prensa de la OCU aunque no aporten como fuente ni el estudio al que se refieren. Todo esto aderezado con un titular jugoso que garantice un buen número de clics. Mejor pan para hoy.
Ofrecer información de calidad sobre estos temas de índole científica requiere tiempo y, sobre todo, requiere conocimientos de partida. Si eso no se respeta, va a ser imposible salir de esta crisis informativa y reconquistar la confianza.
Solo aquellos que ofrecen información de calidad tienen porvenir. Para los demás, hoy pan y mañana suerte.
Para más información:
La ciencia del protector solar. Deborah García Bello. Fronteras, Cuaderno de Cultura Científica. Junio-agosto de 2018.
No, Pfizer no ha ocultado al mundo un fármaco que cura o previene el alzhéimer (I) y (II). Javier Yanes. Ciencias mixtas, 20 Minutos. 6 y 7 de junio de 2019.
Nota de la autora:
Deliberadamente en este artículo no se han incluido enlaces a las fake news publicadas acerca de Isdin o Pfizer a fin de no contribuir más a su difusión.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Piensa bien y acertarás: los casos de Pfizer e Isdin se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ciencia perdida: los curiosos casos de los protocolos de TDAH y de leer.es
- Los nórdicos no siempre hacen las cosas bien, o sí
- Casos de corrupción
La geometría poética del cubo
La sala Kubo Kutxa de Donostia-San Sebastián acoge estos días, desde el 23 de mayo al 25 de agosto de 2019, la exposición LANTEGI, José Ramón Anda, una exposición retrospectiva del escultor navarro José Ramón Anda (Bakaiku, Navarra, 1949), una de las figuras fundamentales de la escultura vasca contemporánea.
El título de la exposición, “lantegi”, es decir, taller en euskera (aunque el término también está relacionado con la gestión de la madera de los árboles en una comunidad, como puede leerse en el catálogo de la exposición), destaca un elemento fundamental para el escultor de Bakaiku, su taller, el lugar en el cual se crea la magia del arte, el espacio en el que José Ramón Anda piensa y trabaja, donde construye sus pequeñas maquetas de arcilla (buztina, en euskera), algunas de las cuales luego se harán mayores realizadas en madera, o en otros materiales, como hierro, bronce, aluminio, hormigón o piedra.
Las personas que tengan el privilegio de visitar su taller en Bakaiku podrán disfrutar de la belleza y originalidad de sus maquetas de buztina, materialización de muchas de las ideas geométrico-escultóricas del artista, y que, aunque nunca se hagan mayores, son hermosas obras de arte por sí mismas.
 Fotografía de las maquetas de arcilla/buztina en el taller del escultor navarro José Ramón Anda. Imagen de la página web del artista
Fotografía de las maquetas de arcilla/buztina en el taller del escultor navarro José Ramón Anda. Imagen de la página web del artista
Empecemos esta entrada del Cuaderno de Cultura Científica con algunas pinceladas sobre el artista y su obra.
– José Ramón Anda procede de una familia de tallistas y ebanistas, lo cual explica su profundo conocimiento de la madera, su respeto hacia ella y la delicadeza con la que la trabaja. Este es el material fundamental con el que realiza su trabajo el escultor de Bakaiku. Normalmente madera de los montes de Urbasa y Aralar, en Navarra, como roble, nogal, boj, castaño, tejo, cerezo o plátano.
– Estudió en la Escuela Superior de Bellas Artes de San Fernando (Madrid), entre los años 1970 y 1974. Después obtuvo una beca para completar su formación en la Academia Española de Bellas Artes de Roma, donde conectó con destacados artistas italianos contemporáneos, como Giacomo Manzú, Marino Marini y Arturo Martini, y una beca del Ministerio de Cultura, para la promoción de las Artes Plásticas y la Investigación de nuevas formas expresivas. Además, durante algún tiempo fue profesor de la Escuela de Bellas Artes de la Universidad del País Vasco.
– Entre las referencias artísticas de José Ramón Anda podemos citar como fundamental al artista suizo Max Bill (1908 – 1994), uno de los máximos exponentes del arte concreto, o al escultor rumano Constantin Brancusi (1876 – 1957). Así como a los escultores vascos Jorge Oteiza (1908 – 2003) y Eduardo Chillida (1924 – 2002), máximos representantes de la Escuela Vasca de Escultura, en la que podemos enmarcar también al escultor navarro.
– Dentro de su arte conviven dos grandes corrientes artísticas como son la abstracción geométrica, con una fuerte influencia del arte concreto (recordemos que este movimiento propone que el arte debe ser creado enteramente en la mente humana, sin referencias externas, no debe inspirarse en la naturaleza, la sensualidad o el sentimentalismo, utilizando las matemáticas –en particular, elementos geométricos básicos como el cuadrado, el círculo y el triángulo– como herramienta creativa), y la escultura orgánica, en la cual la naturaleza y sus formas, en particular, la madera, como material e inspiración, reivindican su importancia.
 Escultura Ikutu/Tocar (2007 – 2012), realizada cn madera de roble, tejo, boj y nogal, del artista José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez
Escultura Ikutu/Tocar (2007 – 2012), realizada cn madera de roble, tejo, boj y nogal, del artista José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez
Siento una profunda admiración por la obra escultórica de José Ramón Anda, quizás por mi doble condición de persona interesada por el arte contemporáneo y matemático, lo cual me ha animado a compartir en esta entrada del Cuaderno de Cultura Científica, que espero se convierta en una serie, mi visión personal de su trabajo artístico.
Muchas son las referencias geométricas y matemáticas que nos encontramos en la obra del escultor navarro, aunque en esta entrada vamos a centrarnos en la figura geométrica del cubo. Este, aparentemente, sencillo objeto, símbolo de las tres dimensiones del espacio, ha sido fundamental, pero sobre todo una rica herramienta de creación artística, en el arte de José Ramón Anda. Empezó a trabajar con el mismo en los últimos años de su formación, cuando empezaba a dar sus primeros pasos en la abstracción geométrica, y continúa trabajando en la actualidad. A lo largo de todo este tiempo, este genial escultor ha investigado, desde diferentes perspectivas, la estructura geométrica que subyace a la figura del cubo, en particular, distintas descomposiciones del mismo, así como sus posibilidades plásticas.
De este análisis del cubo surgen obras muy dispares, como Descomposición del cubo (1973), Nahi eta ezin [Querer y no poder] (1975), Zazpiak bat [Las siete, una] (1976), Preso jaioa [Nacido preso] (1978), Homenaje a Juan de Antxieta (1979 – 1986), Haizean [Al viento] (1978 – 2002) Pilotara [A la pelota] (1980), Basaldeko ateak [Las puertas del bosque] (2011 – 2017), o Acotar el vacío I, II y III (2019), entre otras, así como una gran cantidad de potentes maquetas de buztina.
 Escultura Nahi eta ezin [Querer y no poder] (1975), de José Ramón Anda, en posición cerrada, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez
Escultura Nahi eta ezin [Querer y no poder] (1975), de José Ramón Anda, en posición cerrada, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez Escultura Nahi eta ezin [Querer y no poder] (1975), de José Ramón Anda, en posición abierta en la que se ve una esfera en su interior, en la exposición LANTEGI, José Ramón Anda, en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl IbáñezDos de las primeras descomposiciones del cubo en las que trabajó el artista, en el año 1973, son las siguientes. Para entenderlas bien, debemos de pensar en el cubo como formado por 27 cubos pequeños, es decir, cada lado del cubo está formado por 3 de estos cubos (siendo el cubo grande una estructura 3 x 3 x 3), como ocurre, por ejemplo, en el cubo de Rubik, y podemos pensar que las piezas de la descomposición están formadas por la unión de algunos de estos cubos pequeños (este tipo de piezas se conocen en matemáticas como “policubos”).
Escultura Nahi eta ezin [Querer y no poder] (1975), de José Ramón Anda, en posición abierta en la que se ve una esfera en su interior, en la exposición LANTEGI, José Ramón Anda, en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl IbáñezDos de las primeras descomposiciones del cubo en las que trabajó el artista, en el año 1973, son las siguientes. Para entenderlas bien, debemos de pensar en el cubo como formado por 27 cubos pequeños, es decir, cada lado del cubo está formado por 3 de estos cubos (siendo el cubo grande una estructura 3 x 3 x 3), como ocurre, por ejemplo, en el cubo de Rubik, y podemos pensar que las piezas de la descomposición están formadas por la unión de algunos de estos cubos pequeños (este tipo de piezas se conocen en matemáticas como “policubos”).
Estas dos descomposiciones del cubo cuentan con tres piezas cada una, dos exteriores e iguales entre sí (simétricas), con 7 cubos pequeños cada una, y una interior, comprendida entre las dos anteriores, con 27 – 14 = 13 cubos pequeños. En ambos casos, los dos elementos exteriores están formados por tres lados del cubo, representando las tres dimensiones del espacio, y colocados en posición simétrica respecto al centro.
En una de las descomposiciones (véanse las imágenes siguientes) cada una de las piezas externas son tres lados que convergen en un mismo vértice, que nos recuerda la típica imagen de los ejes x, y, z, que confluyen en el origen, en el espacio de coordenadas cartesianas tridimensional. Y cada una de las dos piezas está apoyada en vértices opuestos, de forma que no se tocan entre sí.

 Primera maqueta de arcilla de una descomposición del cubo en tres piezas, dos exteriores y una interior, realizada por José Ramón Anda, en el año 1973, y que forma parte de las maquetas del taller del artista. Fotografías de Raúl Ibáñez
Primera maqueta de arcilla de una descomposición del cubo en tres piezas, dos exteriores y una interior, realizada por José Ramón Anda, en el año 1973, y que forma parte de las maquetas del taller del artista. Fotografías de Raúl Ibáñez
En la otra descomposición del cubo, los dos elementos exteriores están formados también por tres lados cada uno, pero son elementos “continuos”, sin puntos “múltiples”.

 Segunda maqueta de arcilla de una descomposición del cubo en tres piezas, dos exteriores y una interior, realizada por José Ramón Anda, en el año 1973, y que forma parte de las maquetas del taller del artista. Fotografías de Raúl Ibáñez
Segunda maqueta de arcilla de una descomposición del cubo en tres piezas, dos exteriores y una interior, realizada por José Ramón Anda, en el año 1973, y que forma parte de las maquetas del taller del artista. Fotografías de Raúl Ibáñez
Las dos descomposiciones gozan de una cierta simetría, aunque quizás encierra una mayor simetría la primera de ellas. Por ejemplo, si nos fijamos en la pieza central (en la imagen de abajo he reproducido ese elemento central con piezas cúbicas del material LiveCube y lo he colocado tumbado respecto a la primera imagen en la que se mostraba) tiene una simetría rotacional de 120 grados respecto a un eje que pasa por el centro y es perpendicular a la mesa en la que se apoya, es decir, si la giramos un tercio de vuelta sobre la mesa en la que se apoya, la pieza se queda colocada de la misma forma (aparentemente, en la misma posición), además de una simetría rotacional de 180 grados, respecto a un eje perpendicular al anterior (eje izquierda-derecha en la imagen), es decir, si damos la vuelta a la pieza de la imagen queda, de nuevo, la misma forma (aparentemente, en la misma posición).
 Pieza central de la primera descomposición del cubo, que posee dos tipos de simetrías rotacionales, de 120 grados y de 180 grados
Pieza central de la primera descomposición del cubo, que posee dos tipos de simetrías rotacionales, de 120 grados y de 180 grados
Mientras que el elemento central de la segunda descomposición (de nuevo, lo he realizado con las piezas del LiveCube) si lo tumbásemos podríamos ver que tiene dos simetrías rotacionales similares a las anteriores, pero ahora ambas de 180 grados (media vuelta). Aunque quizás lo más peculiar estéticamente es que esta pieza está formada por dos partes con direcciones perpendiculares (en la imagen la parte de arriba está dispuesta en dirección izquierda-derecha, mientras que la de abajo, lo está en la dirección adelante-atrás), es decir, está como retorcida.
 Pieza central de la segunda descomposición
Pieza central de la segunda descomposición
Jose Ramón Anda se percató de que esta segunda descomposición le brindaba una mayor riqueza plástica y realizó la obra Descomposición del cubo (1973), de un tamaño de 19 x 18 x 18 centímetros. Esta escultura tiene algunas peculiaridades importantes, que han seguido formando parte de su filosofía artística. La primera peculiaridad de esta obra de arte, que comparten muchas de las obras de este escultor vasco, es que se puede, y se debe, tocar, no es solamente una escultura estática para ser admirada. Pero, de hecho, no solo se puede tocar, como ocurre con muchas otras esculturas (por ejemplo, más arriba hemos mostrado una obra que lleva por nombre Ikutu/Tocar, invitando a las personas a que la toquen para poder captar la esencia de esa escultura), sino que se pueden mover los tres elementos que la componen, invitando al público a que los disponga de la manera, o maneras, que le parezcan estéticamente más bellas o sugerentes. Es decir, la escultura se transforma en una obra dinámica, en un “juego” artístico que requiere que el público no sea meramente un espectador, sino que tome una actitud activa ante la creación artística.
 Escultura Descomposición del cubo (1973), realizada en madera de roble, del artista navarro José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez
Escultura Descomposición del cubo (1973), realizada en madera de roble, del artista navarro José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez
La obra está formada por tres elementos geométricos que interaccionan entre sí, pero José Ramón Anda no elige una relación estética fija entre ellas para crear una obra impactante y única, sino que crea una obra que es al mismo tiempo todas las variaciones posibles, tanto las que se le han podido ocurrir a él mismo, como las que se les han ido ocurriendo a todas las personas que han interaccionado con la misma, e incluso, las que están por venir, que existen solo en potencia.
Precisamente, en la exposición LANTEGI, José Ramón Anda, en la Sala Kubo Kutxa, en la que está expuesta esta genial obra de arte, se incluye una serie de fotografías, del fotógrafo Juantxo Egaña, con una serie de posiciones de las tres piezas de la escultura de una enorme potencia estética, de una gran belleza. La escultura del artista de Bakaiku son todas ellas, y muchas más.
 Fotografía del interior de la cubierta del catálogo de la exposición LANTEGI, José Ramón Anda (Sala Kubo Kutxa, 2019), que incluye 30 fotografías, de Juantxo Egaña, con otras tantas variaciones de la escultura Descomposición del cubo (1973), de José Ramón Anda
Fotografía del interior de la cubierta del catálogo de la exposición LANTEGI, José Ramón Anda (Sala Kubo Kutxa, 2019), que incluye 30 fotografías, de Juantxo Egaña, con otras tantas variaciones de la escultura Descomposición del cubo (1973), de José Ramón Anda
El recorrido artístico de esta descomposición del cubo no termina con esta escultura, sino que José Ramón Anda, consciente de las posibilidades plásticas que esta le brinda, sigue trabajando con la misma.
Los tres elementos de la descomposición son piezas “rectas”, con ángulos de noventa grados, ángulos rectos. El artista suaviza esos ángulos creando piezas más suaves y redondeadas, lo que confiere a la descomposición un mayor dinamismo. Después de alguna pieza intermedia, realiza una escultura muy potente, Homenaje a Juan de Antxieta (1979 – 1986), con una versión en bronce de 1979, de un tamaño de 33 x 33 x 33 centímetros, y una versión en piedra caliza de Lastur, de un tamaño aproximado de 2 x 2 x 2 metros, que se instala en 1986 en el Parque de Irubide (Pamplona).
 Escultura Homenaje a Juan de Antxieta (1979), realizada en bronce, de José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez
Escultura Homenaje a Juan de Antxieta (1979), realizada en bronce, de José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez
La siguiente serie de obras que surgen de esta peculiar descomposición del cubo tienen como protagonista a la pieza central tras la eliminación de los ángulos, que la convierten en una pieza curva retorcida. José Ramón Anda continúa trabajando con esa pieza central redondeada, seguramente con el objetivo de extraer la esencia de la forma de la misma, y decide “adelgazarla” transformándola en una superficie, que resulta ser lo que, en la parte de las matemáticas conocida como “geometría diferencial de superficies”, se conoce como una superficie de curvatura (de Gauss) negativa, y como consecuencia, una superficie llamada de doble curvatura. Esa superficie nos recuerda, por esa propiedad geométrica de la curvatura, a otra de curvatura negativa muy importante en Arquitectura (por ejemplo, en la obra del arquitecto catalán Antoni Gaudí (1852 – 1926)), el paraboloide hiperbólico, aunque sean superficies diferentes.
 Superficie de un paraboloide hiperbólico, realizada con el programa Python por Nicoguaro para Wikimedia Commons
Superficie de un paraboloide hiperbólico, realizada con el programa Python por Nicoguaro para Wikimedia Commons
Expliquemos de forma visual qué significa que la superficie sea de curvatura (de Gauss) negativa. Significa que para cada punto de la superficie (aunque se observa muy bien en el punto central, tanto en la imagen anterior del paraboloide hiperbólico, como en las siguientes esculturas generadas por la superficie que se obtiene de la pieza central de la descomposición del cubo), si se toma el plano tangente a la superficie en dicho punto (en el centro del paraboloide hiperbólico de la imagen es el plano horizontal), parte de la superficie queda a un lado de la misma y parte al otro. Más aún, existe una dirección (en el punto) en la que la superficie es cóncava y otra, perpendicular a la anterior, en la que es convexa. Es decir, que en cada punto parte de la superficie se dobla en un sentido (en la imagen del paraboloide hiperbólico, si estamos en el centro, en una dirección la superficie se curva hacia arriba, sería cóncava), mientras que otra parte, perpendicular a la anterior, se dobla en el sentido opuesto (en el centro del paraboloide sería la parte que se curva hacia abajo, convexa).
En una superficie de curvatura (de Gauss) positiva, como es la esfera, no ocurre lo anterior, sino todo lo contrario. En cada punto de la esfera, esta queda situada por entero a un lado de su plano tangente. Es decir, esta siempre se dobla, se curva, en el mismo sentido, siempre “alejándose” (convexa), si se mira desde fuera, o siempre “acercándose” (cóncava), si se mira desde dentro.
Por otra parte, para explicar esta serie de obras necesitamos tener en cuenta dos aspectos más. El primero es la importancia de la cultura vasca para el artista de Bakaiku y su interés por el juego de la pelota mano, o pelota vasca, en el cual el objeto central del juego es la pelota, es decir, un objeto esférico, lo cual nos enlaza con la segunda cuestión que quería mencionar, a la figura geométrica del cubo se le añade ahora la de la esfera. Para generar esta serie de obras el escultor introduce mentalmente la superficie obtenida a partir de la pieza central en una esfera imaginaria y se queda solo con lo que está dentro, es decir, el borde de la superficie es una curva dentro de la superficie esférica.
Esta es la forma que José Ramón Anda utiliza en las siguientes esculturas, Airean (omenaldia pilotara) [Al aire (homenaje a la pelota)] (1978 – 2000), realizada en aluminio, Pilotara [A la pelota] (1980), realizada en madera de boj, y la escultura pública Haizean [Al viento] (1978 – 2002), realizada en acero y aluminio, que se encuentra instalada en la plaza del Trinkete, en Tolosa (Gipuzkoa).
 Escultura Pilotara [A la pelota] (1980), realizada en madera de boj, del escultor navarro José Ramón Anda. Imagen perteneciente al catálogo de la exposición José Ramón Anda. Causa formal y materia – Kausa formala eta materia, que tuvo lugar en el Museo Oteiza, en 2017
Escultura Pilotara [A la pelota] (1980), realizada en madera de boj, del escultor navarro José Ramón Anda. Imagen perteneciente al catálogo de la exposición José Ramón Anda. Causa formal y materia – Kausa formala eta materia, que tuvo lugar en el Museo Oteiza, en 2017 Escultura pública Haizean [Al viento] (1978 – 2002), realizada en acero y aluminio, instalada en la plaza del Trinkete, en Tolosa. Imagen de la página web del artistaLos nombres de estas esculturas, Airean [Al aire] o Haizean [Al viento] describen otra peculiaridad de estas obras, que son esculturas móviles, es decir, que se mueven con el aire o el viento, dando vueltas alrededor de su eje vertical. Más aún, cuando la superficie de Anda gira media vuelta, con el viento, está generando toda la esfera. Es decir, que si viésemos juntas todas las posiciones de la superficie en ese giro veríamos realmente la esfera.
Escultura pública Haizean [Al viento] (1978 – 2002), realizada en acero y aluminio, instalada en la plaza del Trinkete, en Tolosa. Imagen de la página web del artistaLos nombres de estas esculturas, Airean [Al aire] o Haizean [Al viento] describen otra peculiaridad de estas obras, que son esculturas móviles, es decir, que se mueven con el aire o el viento, dando vueltas alrededor de su eje vertical. Más aún, cuando la superficie de Anda gira media vuelta, con el viento, está generando toda la esfera. Es decir, que si viésemos juntas todas las posiciones de la superficie en ese giro veríamos realmente la esfera.
Pero existe otra serie de esculturas más recientes que tienen como idea generadora la descomposición del cubo analizada en esta entrada. José Ramón Anda regresa a la idea matriz, a la descomposición del cubo originaria, pero fija ahora su atención en los laterales de las piezas de la descomposición, trabajando a partir de algunos de ellos para crear obras tan impactantes y singulares como las siguientes.
 Esculturas Basaldeko ateak [Las puertas del bosque] (2011 – 2017), del artista José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez
Esculturas Basaldeko ateak [Las puertas del bosque] (2011 – 2017), del artista José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez Escultura Acotar el vacío III [Hutsa mugatzea III] (2019), del artista José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez
Escultura Acotar el vacío III [Hutsa mugatzea III] (2019), del artista José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Raúl Ibáñez Conjunto de obras Acotar el vacío I, II y III [Hutsa mugatzea I, II eta III] (2019), del artista José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Juantxu EgañaLa otra descomposición del cubo vista en esta entrada también formó parte de una escultura, en concreto Pesadilla de mili (1979), en la cual permanecen las dos piezas exteriores, mientras que la pieza interior es sustituida por una masa informe que representaría el cerebro de la persona que ha ido a la mili. Esta escultura se basa en la maqueta de arcilla que se muestra a continuación.
Conjunto de obras Acotar el vacío I, II y III [Hutsa mugatzea I, II eta III] (2019), del artista José Ramón Anda, en la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián. Fotografía de Juantxu EgañaLa otra descomposición del cubo vista en esta entrada también formó parte de una escultura, en concreto Pesadilla de mili (1979), en la cual permanecen las dos piezas exteriores, mientras que la pieza interior es sustituida por una masa informe que representaría el cerebro de la persona que ha ido a la mili. Esta escultura se basa en la maqueta de arcilla que se muestra a continuación.
 Maqueta de buztina, base de la obra Pesadilla de mili (1979), de José Ramón Anda
Maqueta de buztina, base de la obra Pesadilla de mili (1979), de José Ramón Anda
En mi siguiente colaboración en la sección Matemoción del Cuaderno de Cultura Científica continuaremos analizando las diferentes investigaciones plásticas de José Ramón Anda sobre la geometría del cubo, así como las esculturas, o maquetas de buztina, que ha realizado a partir de las mimas.
 Fotografía de Juanjo Egaña con algunas de las esculturas de la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián, entre las que destacan, en el centro, dos versiones de Ikusmira [Perspectiva]No me gustaría terminar esta entrada sin expresar mi más profundo y sincero agradecimiento a José Ramón Anda, por las interesantes conversaciones que hemos mantenido, desde que nos conocimos hace unos años, sobre su obra artística y la relación de la misma con la geometría y las matemáticas, así como por permitirme utilizar las imágenes de sus bellas e impactantes esculturas en esta publicación.
Fotografía de Juanjo Egaña con algunas de las esculturas de la exposición LANTEGI, José Ramón Anda (2019), en la Sala Kubo Kutxa, de Donostia/San Sebastián, entre las que destacan, en el centro, dos versiones de Ikusmira [Perspectiva]No me gustaría terminar esta entrada sin expresar mi más profundo y sincero agradecimiento a José Ramón Anda, por las interesantes conversaciones que hemos mantenido, desde que nos conocimos hace unos años, sobre su obra artística y la relación de la misma con la geometría y las matemáticas, así como por permitirme utilizar las imágenes de sus bellas e impactantes esculturas en esta publicación.
Bibliografía
1.- Jose Ramón Anda (escultor), Javier Balda (comisario), Lantegi, José Ramón Anda (catálogo), Sala Kubo Kutxa (Donostia-San Sebastián), 23 de mayo – 25 de agosto de 2019, Kutxa Fundazioa, 2019.
2.- Página web de la Sala Kubo Kutxa
3.- Página web del artista José Ramón Anda
4.- Jose Ramón Anda (escultor), Javier Balda (comisario), José Ramón Anda. Causa formal y materia – Kausa formala eta materia, Museo Oteiza (Alzuza, Navarra), 21 de junio – 1 de octubre de 2017, Fundación Museo Oteiza, 2017.
5.- Jose Ramón Anda (escultor), Javier Balda (comisario), José Ramón Anda, Denboraren aurkako formak, Formas contra el tiempo, Museo de Bellas Artes de Bilbao, 7 de mayo – 9 de septiembre de 2012, Museo de Bellas Artes de Bilbao, 2012.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La geometría poética del cubo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El cubo soma: diseño, arte y matemáticas
- La geometría de los ‘cristaloides’, según Léopold Hugo
- La botella de Klein: geometría ‘palindrómica’
El modelo atómico de Thomson

¿Cómo es el átomo? A principios del siglo XX se disponía de suficiente información química y física para que muchos físicos pudieran diseñar modelos de átomos. Se sabía que las partículas negativas con propiedades idénticas (electrones) se podían obtener de muchas sustancias diferentes y de diferentes maneras. Esto sugería que los electrones son componentes de todos los átomos.
Pero los electrones están cargados negativamente mientras que las muestras de un elemento son eléctricamente neutras. Por lo tanto, los átomos que constituyen tales muestras también serán probablemente eléctricamente neutros. Si es así, y en los átomos hay electrones con carga negativa, esto indicaría que en un átomo es necesaria la presencia de una cantidad igual de carga positiva.
Mencionamos al hablar de los electrones como las partículas de los rayos catódicos que los átomos de hidrógeno tienen unas 1800 veces más masa que los electrones, que tienen una masa de 9,109·10-31 kg. De aquí se sigue que los electrones constituyen una parte muy pequeña de la masa total de un átomo.
Así pues, cualquier modelo de átomo que se proponga debía tener en cuenta la siguiente información:
- un átomo eléctricamente neutro debe contener la misma cantida de cargas positivas y negativas:
- la carga negativa está asociada con solo una pequeña parte de la masa total del átomo, y la aportan los electrones
Adicionalmente cualquier modelo atómico tenía que ser capaz de responder a dos preguntas básicas:
- ¿Cuántos electrones hay en un átomo? [1]
- ¿Cuál es la disposición de los electrones y la carga positiva en el átomo?
Durante los primeros 10 años del siglo XX se propusieron varios modelos atómicos, pero ninguno fue satisfactorio. Hasta 1911, el modelo más popular para el átomo fue el propuesto por J.J. Thomson en 1904. Thomson sugirió que un átomo consistía en una esfera de electricidad positiva en la que se distribuía una cantidad igual de carga negativa en forma de pequeños electrones. A partir de los estudios electroquímicos a lo largo del XIX y por los realizados con radiación X [2], la cantidad de carga positiva en cada átomo se supuso que era igual al número atómico del átomo Z (un número entero) multiplicado por la magnitud de la carga del electrón e, es decir, la carga positiva de un átomo es igual a Z·e. Para cumplir con la condición de que el átomo sea eléctricamente neutro debe haber un número igual de electrones cargados negativamente.
Con estas suposiciones, el átomo de Thomson era como un «pudín de pasas» de electricidad positiva, con los electrones negativos esparcidos en él como ciruelas o pasas. Así, el hidrógeno (Z=1) consistía en un electrón, carga -1e, incrustado en una esfera de carga positiva +1e. El helio (Z=2) consistía en dos electrones incrustados en una esfera de carga positiva +2e, y así sucesivamente.
 Modelo de pudin de pasas para los seis primeros elementos. Fuente: Cassidy Physics Library
Modelo de pudin de pasas para los seis primeros elementos. Fuente: Cassidy Physics Library
Thomson asume en este modelo que «la masa del pudin» positiva actúa sobre los electrones negativos, manteniéndolos en el átomo solo por fuerzas eléctricas [3] y que el radio de los átomos tendría que ser de un orden de magnitud de 10-10 m, basándose para ello en información de la teoría cinética de los gases [4] y otras consideraciones.
Sin embargo, Thomson no podía explicar cómo se mantenía unida «la masa del pudin» positiva, ya que lo que se sabía de electricidad indicaba que debería desmoronarse debido a la repulsión eléctrica. Tampoco podía explicar las propiedades químicas ni el sistema de periodos.
Se requería mucha más información experimental y un nuevo concepto radical, el concepto de cuanto de energía, para construir un modelo del átomo mucho más satisfactorio. Este concepto se introdujo mediante el uso de los resultados obtenidos al estudiar un conjunto de problemas completamente diferente, la radiación térmica y el enigma del efecto fotoeléctrico, de eso se encargarían Max Planck y Albert Einstein [5].
Notas:
[1] Démonos cuenta que a principios del siglo XX la respuesta a esta pregunta no era en absoluto evidente. Menos cuando aun había gente que negaba la existencia de los átomos. Recordemos que hasta 1908 no se demostró más allá de toda duda razonable su existencia, como vimos aquí.
[2] Volveremos sobre esto más adelante en la serie.
[3] Hoy sabemos que en un átomo actúan fuerzas adicionales además de las eléctricas.
[4] Véase a este respecto El tamaño de las moléculas
[5] No nos olvidaremos de Rutherford. Baste mencionar ahora que el modelo atómico de Rutherford no es más que un caso particular del de Thomson.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El modelo atómico de Thomson se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- 1913-2013: del modelo atómico de Bohr al Higgs
- Del modelo estándar
- La ley del gas ideal a partir del modelo cinético
Lo que Venus, el gemelo infernal de la Tierra, podría enseñarnos sobre lo que hace a un planeta habitable
 Comparación de Venus con la Tierra. Fuente: Wikimedia Commons
Comparación de Venus con la Tierra. Fuente: Wikimedia Commons
Empiezo pidiendo perdón por haber insultado así a Venus, llamándole infernal, algo inmerecido para un planeta que ya tuvo que sufrir a Mecano. Pero Venus tendrá que reconocer que no nos lo pone fácil para adjetivarle con amabilidad: 400 grados de temperatura, una presión atmosférica capaz de aplastar cualquier cosa y nubes de ácido sulfúrico pululando de aquí para allá. Como para darse un paseíto por allí una tranquila mañana de primavera.
Pero no siempre fue así. Venus fue una vez un planeta muy similar a la Tierra y algunos investigadores sugieren que durante tres mil millones de años, Venus fue un planeta cubierto por grandes océanos capaces de albergar vida. Eso lo convertiría en el primer planeta habitable del sistema solar, un punto con las mismas probabilidades que la Tierra de desarrollar formas de vida. Algunas de sus similitudes aún persisten hoy: ambas se parecen en tamaño, densidad y composición química. Otras como los océanos y la atmósfera habitable, no tanto…
El caso es que algo ocurrió y cambió Venus de un lugar no quizá parecido a la tierra a una suerte de su Mr. Hyde, y por eso, cuenta Nature en un detallado reportaje, equipos de científicos de distintas agencias espaciales de todo el mundo quieren saber qué fue. Esto, además de profundizar en el conocimiento sobre nuestro planeta vecino y con él sobre nuestro sistema solar, puede servirnos para determinar en cuáles de los cientos de planetas rocosos que seguimos descubriendo más allá del sistema solar puede haber vida.
Las agencias espaciales ponen los ojos en Venus
 Venus en color a partir de imágenes de la sonda Mariner 10. Fuente: Wikimedia Commons
Venus en color a partir de imágenes de la sonda Mariner 10. Fuente: Wikimedia Commons
India es la primera que va a probar suerte. La Organización India de Investigación Espacial lanzará su sonda en 2023 que pasará varios meses orbitando alrededor de Venus. Estados Unidos podría seguirla de cerca; varios grupos de científicos propondrán misiones a Venus a la NASA con la idea de partir en 2025. La Agencia Espacial Europea está considerando enviar su propio orbiter en 2032, y la agencia espacial rusa Roscosmos trabaja ya en colaboración con la NASA para enviar una ambiciosa misión entre 2026 y 2033 que incluiría una sonda para orbitar, otra para aterrizar que envíe mediciones a corto plazo y una estación de investigación que permanecería sobre Venus más tiempo.
Todo son pretendientes para Venus… ahora. Esto no siempre ha sido así: Venus ha sido durante décadas la gran olvidada frente a Marte. En los últimos 65 años, la NASA ha enviado 11 sondas a orbitar en torno al planeta rojo y 8 misiones que han aterrizado. En comparación, solo 2 naves han sido enviadas a orbitar alrededor de Venus, y la última fue en 1994. No ha sido en cualquier caso una falta de interés científico lo que ha detenido a la agencia espacial estadounidense, ya que sus equipos de investigación han propuesto cerca de 30 misiones a Venus en todos esos años, pero ninguna ha sido aprobada.
Las tornas han cambiado, y mientras tanto muchos de esos equipos científicos y técnicos han desarrollado los métodos y la tecnología para estudiar y sobrevivir en un entorno tan destructivo.
Venus fue nuestro primer destino… con poco éxito
 Venus captado por el telescopio Hubble el 24 de enero de 1995. Fuente: Wikimedia Commons
Venus captado por el telescopio Hubble el 24 de enero de 1995. Fuente: Wikimedia Commons
Probablemente esa desafección de las agencias por Venus comenzó en los inicios de la exploración espacial. Porque en aquellas primeras etapas sí que pusieron los ojos allí: Venus fue el escenario de la primera prueba interplanetaria (EEUU en 1962), el primer planeta en el que se estrelló una misión (la URSS en 1965) y el primer planeta extraterrestre en el que una misión aterrizó con éxito (también la URSS en 1966). Pero ya en aquellos años las observaciones que pudieron hacerse revelaron que Venus era un planeta asfixiante y tórrido: era difícil imaginarlo como un lugar en el que la raza humana fuese a establecer colonias, y tampoco un sitio donde la búsqueda de formas de vida resultase muy prometedora. Era difícil incluso estudiar sus condiciones con detalle.
Sin embargo, está claro que tenemos que volver allí. Algunas teorías, como decíamos, apuntan a que Venus pudo ser el primer lugar habitable del sistema solar pero, en algún momento, algo fue mal, muy mal, y toda esa habitabilidad se fue al garete. Quizá no haga tanto tiempo de aquello, quizá fue hace apenas 700 millones de años. Saber qué y cuándo ocurrió puede ayudarnos a entender mejor qué hace de la Tierra un lugar especial donde la vida apareció y se ha desarrollado, en principio el único lugar con estas características que conocemos hasta ahora.
Es una pregunta aun más importante ahora que la cuenta de planetas rocosos que orbitan en torno a estrellas en las llamadas zonas de habitabilidad (lo suficientemente cerca pero lo suficientemente lejos como para que la temperatura de la atmósfera permita la presencia de agua líquida) más allá de nuestro sistema solar no para de aumentar. Muchos de esos exoplanetas podrían ser muy similares a Venus. Cuanto más sepamos de nuestro extraño vecino, más sabremos sobre esos mundos lejanos.
Aparatos que sobrevivan (y funcionen)
 Superficie de Venus obtenida por la sonda Magallanes. Fuente: Wikimedia Commons
Superficie de Venus obtenida por la sonda Magallanes. Fuente: Wikimedia Commons
Algo que es un desafío tecnológico considerable. Muchos de los equipos que quieren ir allí a echar un vistazo no se conformarían con orbitar alrededor de Venus: quieren un módulo aterrizando en su superficie, algo que no se ha conseguido en 35 años. Y de aquellos que lo hicieron con éxito tampoco se pudo extraer mucho más, ya que la presión en la superficie es demoledora. La misión que más tiempo sobrevivió lo hizo durante poco más de 2 horas, 127 minutos en total.
Desde entonces ha pasado mucho tiempo y la tecnología y el conocimiento han avanzado considerablemente, así que los equipos que están proponiendo las nuevas misiones creen que sus dispositivos podrán aguantar allí varios meses. Una de las alternativas propuestas por científicos de la NASA sugiere que en vez de blindar el equipamiento con escudos gruesos y resistentes para que absorban el calor y le hagan frente a base de equipos de refrigeración, los sensores se construyan a base de electrónica sencilla hecha con carburo de silicio, un híbrido de silicio y carbono utilizado habitualmente para fabricar diamantes falsos que podría aguantar las duras condiciones del entorno venusiano.
Utilizando esos materiales, testados en cámaras que reproducen las condiciones de ese entorno, han diseñado una estación de prueba, del tamaño de una tostadora y que será capaz de medir la temperatura, la presión, la dirección y velocidad del viento, la cantidad de radiación solar en la superficie y la presencia de determinadas sustancias químicas en la zona más baja de la atmósfera durante varios meses. El resultado debería estar listo a mediados de la década de 2020 y que ofrecerá a otros países si quieren utilizarlo en sus propias misiones.
De una forma u otra, parece que Venus va a ser un lugar concurrido en los próximos 10 o 20 años, rectificando así un olvido histórico y abriendo, si lo conseguimos, un nuevo mundo a explorar con mucha información interesante. Quien sabe si, finalmente (disculpadme un último chascarrillo ochentero), no terminaremos yendo a Venus en un barco…
Referencias:
Venus is Earth’s evil twin — and space agencies can no longer resist its pull – Nature
Was Venus the First Habitable World of our Solar System? – Arxiv.org, Cornell University
Shukrayaan-1 – Wikipedia
Rusia y EEUU completan el diseño de su misión al infierno de Venus – Europa Press
Medio siglo desde el primer aterrizaje en un planeta extraterrestre – El País
Long-Lived In-Situ Solar System Explorer (LLISSE) – NASA
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Lo que Venus, el gemelo infernal de la Tierra, podría enseñarnos sobre lo que hace a un planeta habitable se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El pueblo que hablaba con las ballenas, ¿podría enseñarnos su idioma a los demás?
- Matemáticas del Planeta Tierra (MPE2013), en Bilbao
- Planeta X, en busca del inquilino invisible del sistema solar
Obesidad y delgadez también se heredan
 Imagen: Pixabay
Imagen: Pixabay
Ganar o perder peso es, simplificando algo las cosas, el resultado de un balance entre adquisición y gasto de energía. El organismo adquiere la que asimila a partir del alimento ingerido. Y debido a las actividades que desarrolla también gasta energía, la pierde en forma de calor disipado. Las actividades son muy variadas: unas son las necesarias para el normal funcionamiento de los sistemas orgánicos (actividades cardiacas, renales, nerviosas, etc.), entre las que se incluye el mantenimiento de la temperatura corporal; otras están ligadas a la renovación y reparación de células y tejidos; están, por otro lado, las responsables de la síntesis de nuevas estructuras; y por último, también las musculares implicadas en el ejercicio físico. Cuando la adquisición de energía supera al gasto, el organismo gana masa. Y lo contrario ocurre si el gasto es mayor que la asimilación de energía.
Dicho de esa forma las cosas parecen muy sencillas. Aunque en estos asuntos nada es tan sencillo como pueda parecer, la adquisición de energía es un término relativamente simple; hay dos factores principales a considerar, la cantidad de comida y su composición, que afecta a su contenido energético y a la facilidad o dificultad para digerirla y asimilarla. El gasto de energía tiene más complicaciones, porque influyen diversos factores.
Teniendo en cuenta cuáles son los determinantes de los elementos de adquisición y gasto energético, a nadie sorprende que el sobrepeso y la obesidad hayan alcanzado una gran prevalencia en las sociedades actuales. Hay mucha comida y, además, en general tenemos predilección por alimentos suculentos, de alto contenido energético y fácil absorción. Eso en lo que a la adquisición de energía se refiere. Y en lo relativo al gasto, tenemos una notable tendencia al sedentarismo y la inactividad física y, además, vivimos en entornos de gran confort térmico: difícilmente nos encontramos en condiciones que obliguen al organismo a gastar mucha energía para mantener estable la temperatura corporal. Lo dicho: las cosas parecen muy sencillas. Y sin embargo, no lo son tanto.
Todos conocemos personas que, aunque sean delgadas, no se privan a la hora de comer. Quienes tenemos tendencia a engordar los contemplamos con envidia, conscientes de lo duro que resulta limitarse ante una buena mesa, no picar entre horas o sufrir corriendo por las calles, o en el gimnasio pedaleando de manera desaforada encima de una bicicleta estática. Lo contrario también nos resulta conocido, personas que parecen no comer gran cosa y que, sin embargo, tienen excesivo peso.
¿Por qué ingiriendo similares cantidades de alimento y manteniendo parecidos niveles de actividad física unos estamos más gordos y otros más flacos? ¿A qué obedecen esas “incongruencias” metabólicas? Algunas pueden ser debidas a factores no tomados en consideración. Pero otro elemento importante a tener en cuenta es el factor genético y su incidencia sobre el metabolismo.
Han comparado el genoma de 1600 personas muy delgadas, 2000 muy obesas y 10400 de peso normal, y han confirmado algo que ya se sabía: la obesidad es una condición heredable en un grado no muy alto pero importante: el 32%, para ser precisos. La delgadez también lo es, aunque en una medida ligeramente inferior, un 28%. Esos porcentajes indican la proporción de la variabilidad del rasgo estudiado –obesidad o delgadez- en la población que es debida a factores hereditarios. Además, han identificado un conjunto de variantes genéticas ligadas a una condición, algunas de las cuales ya se conocían, y otras vinculadas con la opuesta. Por lo tanto, obesidad y delgadez, en parte al menos, también se heredan, aunque esto, a algunos, no nos sirva de mucho consuelo.
Fuente: Fernando Riveros-McKay et al (2019): Genetic architecture of human thinness compared to severe obesity PLOS Genetics 15(1): e1007603
——————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Obesidad y delgadez también se heredan se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El pteroestilbeno como posible tratamiento de la obesidad
- Gripe, obesidad y cáncer. Medicina de frontera.
- El organismo humano es una estufa de unos pocos vatios
¿Se podría clonar a una persona?
¿Te imaginas que hubiera una copia genética exacta a ti? Eso sí, esa copia exacta sería en términos de ADN nuclear. Todo esto quizá sea factible en el año 2100 o tal vez no. Hoy solo sabemos que es teóricamente factible. Ya que, más allá de las evidentes cuestiones éticas, todavía hay procesos biológicos que no controlamos.
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de cienciaÓrbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Se podría clonar a una persona? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Podría un humano vivir en el mar?
- ¿Qué tienen en común Einstein y una zanahoria?
- ¿Qué pasa en tu cuerpo cuando te enamoras?
De robots geólogos y rayos X
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Cuando se habla de geología se suele poner en perspectiva la escala temporal. Hablar del tiempo en términos geológicos supone hablar en millones de años. Por lo tanto, hablar de un periodo de tiempo de 50 años apenas significa un suspiro en la historia de nuestro planeta. Irrisorio a escala geológica, pero enorme a escala del/la geólogo/a. Concretamente el último medio siglo ha sido una vorágine de logros científicos y para muestra solo hemos de mirar aquello que tengamos sobre la mesa, en nuestro bolsillo o, mismamente, el instrumento a través del cual estemos leyendo este artículo.
Hace 50 años Neil Amstrong y Buzz Aldrin ponían los pies en la luna en lo que probablemente sea el mayor símbolo del progreso de nuestra especie en el último siglo. Lo que menos gente sabe es que uno de los objetivos de la tripulación del Apolo 11 era recoger muestras del suelo lunar. Una suerte de geólogos espaciales que se trajeron de vuelta a la tierra 22 kg de muestras que después fueron analizadas mediante difracción de rayos X.
Y es aquí donde llegamos al meollo de la cuestión, al entrar en la relación entre la exploración del terreno (terrestre o lunar) como una de las labores fundamentales del/la geólogo/a y la difracción de rayos X como una técnica ya rutinaria en la geología, transversal a casi todas las ciencias y herramienta fundamental para el progreso de nuestra especie. No sólo en los últimos 50 años, sino en los últimos 120. Para entender su importancia y trascendencia es imperativo retroceder a finales del siglo XIX, a la Universidad de Würzburg, Alemania.
Wilhelm Conrad Röntgen era catedrático de física de aquella universidad y su investigación se centraba en el poder de penetración de los rayos catódicos. El 8 de noviembre de 1895, cuando se encontraba experimentando el poder de penetración de los rayos catódicos, observó que una placa de cartón cubierta de cristales de platino-cianuro de bario, emitía una fluorescencia. Ésta desaparecía cuando desconectaba la corriente. La tarde de ese viernes llamo a su esposa Anna a la que pidió que pusiera la mano ante aquella placa de cartón. Anna tuvo que estar quieta 15 minutos y después contempló una imagen de su mano, pero en esta podía ver a través de su piel, sus huesos. Se dice que la reacción de su Anna fue una mezcla de fascinación y temor al ver aquella imagen, la primera radiografía de la historia.
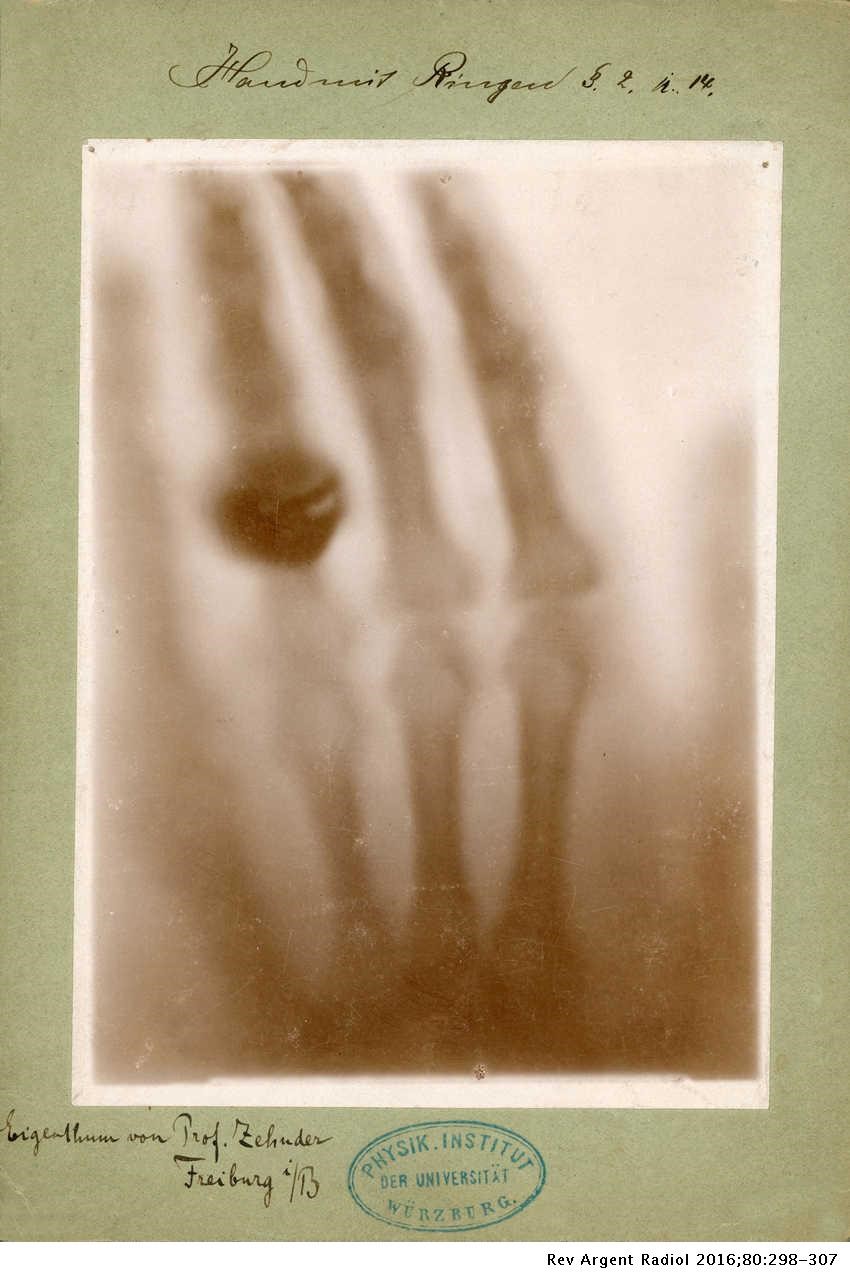 Figura 1. Primera radiografía de la historia de la mano de Anna Bertha Röntgen [1]
Figura 1. Primera radiografía de la historia de la mano de Anna Bertha Röntgen [1]
Röntgen corrió a publicar sus hallazgos un mes más tarde en la Sociedad de Física y Medicina en Würzburg. En aquella publicación contaba que una radiación desconocida se emitía desde el tubo y seria la causante de esa fluorescencia en la placa de platino-cianuro de bario. Nombró a la radiación con la letra de las incógnitas matemáticas, por no saber exactamente lo que era. Este fue el descubrimiento de los rayos X, un tipo de “luz” distinta, un tipo de radiación electromagnética con una longitud de onda similar al tamaño de los átomos y el inicio de una revolución científica en toda regla que le valió el premio Nobel de física a Röntgen en 1901. El primer premio Nobel de física de la historia.
Los años posteriores fueron todo un vergel en cuanto al uso e investigación de los rayos X destacando el nombre de 3 personas que culminan el trabajo que comenzó Röntgen.
El primero de ellos fue Max Von Laue, que estudió el fenómeno de la difracción de los rayos x que se producía al incidir con la materia cristalina. Laue irradiaba sobre cristales obteniendo unos patrones de difracción en los que se apreciaba una simetría concreta que estaba relacionada con la disposición de átomos y moléculas que los componían. Esto supuso el premio Nobel de física en 1914 y el motivo del siguiente Nobel de física en 1915 para William Henry Bragg y William Lawrence Bragg, por definir matemáticamente el fenómeno de la difracción de los rayos X y resolver la primera estructura cristalina: el mineral de la halita.
 Figura 2. Patrón de difracción de Laue [2]
Figura 2. Patrón de difracción de Laue [2]
Hasta ese momento no se tenía constancia de cuál era la organización de átomos, iones y moléculas que componían la materia, por lo que estas contribuciones nos abrieron una ventana para “ver” con otro tipo de “luz” los materiales a otro nivel. Metafóricamente, podríamos decir Röntgen encendió esa luz, Laue la enfocó hacia la materia y los Bragg miraron en su interior. Y este grupo de célebres científicos de principios de siglo XX, con sus logros, nos lanzaron un poderoso mensaje: si podemos cristalizar algo, utilizando la difracción de los rayos X, podremos saber cómo se disponen los átomos, iones y moléculas que lo componen, y por tanto estudiar y comprender sus propiedades y saber cómo aplicarlas.
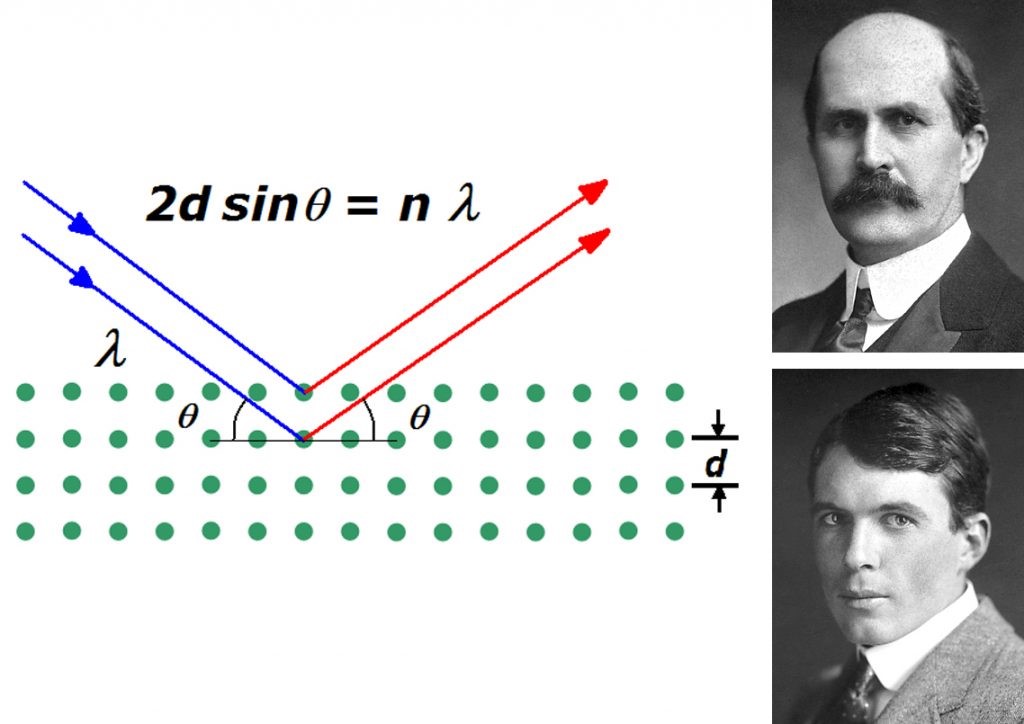 Figura 3. Ley de Bragg (izqda). W. Henry Bragg (arriba) y W. Lawrence Bragg (abajo).
Figura 3. Ley de Bragg (izqda). W. Henry Bragg (arriba) y W. Lawrence Bragg (abajo).
Era el inicio de una nueva disciplina: La cristalografía de rayos X. Una de las áreas del conocimiento más transversales a todas las ciencias y más prolíficas en cuanto a generación del conocimiento. 29 premios Nobel y casi 50 personas laureadas dan buena cuenta de ello. Ha supuesto, supone y supondrá una herramienta fundamental para el progreso de nuestra especie que ha procurado avances como la comprensión del enlace químico, los cristales líquidos, nuevos materiales como el fullereno, los cuasicristales o la resolución de la estructura del ADN así como la de multitud de proteínas y hormonas responsables de enfermedades o de procesos biológicos vitales.
Todos estos frutos de incuestionable trascendencia en nuestro progreso gracias a una disciplina que nace del estudio de los minerales y que está lejos del imaginario popular de revolución científica, como lo pudiera ser la llegada a la luna. 50 años más tarde exploramos otro planeta gracias a la cristalografía de rayos X, pues los Rover que enviamos a Marte llevan incorporados equipos de difracción de rayos X que analizan el suelo marciano. Es decir, robots geólogos hasta que podamos enviar a geólogos/as de carne y hueso a hacer su tradicional trabajo de campo. Un símbolo del alcance de la cristalografía.
A dónde nos llevará esta disciplina es algo aventurado de adivinar, pues como decía Niels Bohr “hacer predicciones es muy difícil, especialmente cuando se trata del futuro”. Sin embargo, es casi una certeza que la cristalografía nos acompañará en nuestros próximos descubrimientos. No habrá que esperar periodos de tiempo geológico para que vuelva a sorprendernos.
Para saber más:
[1] U. Busch (2016) “Wilhelm Conrad Roentgen. El descubrimiento de los rayos x y la creación de una nueva profesión médica” Rev Argent Radiol. 80(4), 298-307. DOI: 10.1016/j.rard.2016.08.003
[2] CSIC (2019), Cristalografía
Sobre el autor: Eder Amayuelas se doctoró en la Facultad de Ciencia y Tecnología de la UPV/EHU y actualmente es investigador en el CNRS (Francia).
El artículo De robots geólogos y rayos X se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Rayos X y gamma
- La luz se propaga en línea recta pero los rayos de luz no existen
- Las partículas de los rayos catódicos
Los primeros humanos alcanzaron el Mediterráneo mucho antes de lo que pensábamos
![]()
Mathieu Duval y Mohamed Sahnouni
 Excavación arqueológica en Ain Boucherit, Argelia.
Excavación arqueológica en Ain Boucherit, Argelia.Mathieu Duval, Author provided
Mathieu Duval, Griffith University y Mohamed Sahnouni, Centro Nacional de Investigación sobre la Evolución Humana (CENIEH)
¿Cuándo llegaron los primeros humanos a las costas del Mediterráneo? Una nueva publicación en la revista Science muestra con evidencias arqueológicas su presencia en el norte de África hace al menos 2,4 millones de años. Es decir, 600.000 años antes de lo que se pensaba.
Estos resultados están extraídos del yacimiento arqueológico de Ain Boucherit, situado en el noreste de Argelia. Gracias a ellos tenemos nueva información en una ventana temporal que incluye los primeros individuos del género Homo.
Estos descubrimientos son el resultado de excavaciones e intensas investigaciones realizadas desde el año 1992 dentro del marco del proyecto Ain Hanech.
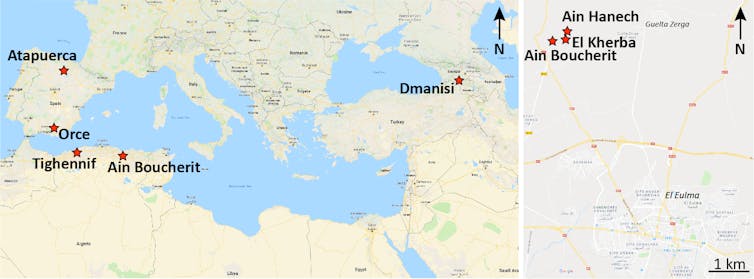 Ubicación de Ain Boucherit y otros sitios prehistóricos mencionados en el texto. A la derecha, ampliación de las cercanías de la ciudad de El Eulma.
Ubicación de Ain Boucherit y otros sitios prehistóricos mencionados en el texto. A la derecha, ampliación de las cercanías de la ciudad de El Eulma.Mathieu Duval; Mapas modificados de Google map
Ubicada en el norte de la ciudad de El Eulma, la zona de estudio ya era conocida por el descubrimiento previo de herramientas líticas (= de piedra) y de huesos fósiles con marcas de cortes, datados de hace unos 1,8 millones de años (yacimientos de Ain Hanech y El Kherba en el mapa de arriba). Hasta ahora habían sido los hallazgos más antiguos del norte de África.
En 2006 y en 2009 se encontraron nuevas herramientas líticas en Ain Boucherit. Distribuidas en dos niveles arqueológicos, ambos localizados estratigráficamente por debajo de los hallazgos anteriores, dichas herramientas indicaban entonces una presencia humana en la zona aún más antigua.
Los nuevos descubrimientos arqueológicos
Las excavaciones en los niveles arqueológicos inferior (AB-Lw) y superior (AB-Up) sacaron a la luz más de 250 herramientas de piedra y casi 600 restos fósiles.
Se identificaron distintas especies animales, entre las que se incluyen elefantes, caballos, rinocerontes, hipopótamos, antílopes, cerdos, hienas y cocodrilos. Todos estos animales viven hoy en día en una sabana abierta con abastecimiento permanente de agua, lo que sugiere que en el pasado existían unas condiciones similares.
Las herramientas de piedra descubiertas están compuestas principalmente por cantos tallados (chopping tools en ingles) y otros elementos de corte de bordes afilados que se utilizaban para trocear los cadáveres de los animales. Estas herramientas están hechas de piedra caliza y sílex, recolectados cerca, en antiguos arroyos.
La fabricación de estos útiles es típica de la tecnología Olduvayense, procedente de las zonas del este de África, y datados entre 2,6 y 1,9 millones de años. Sin embargo, el yacimiento de Ain Boucherit tiene la peculiaridad de presentar también otras herramientas de forma esferoidal, cuya función sigue siendo desconocida.
 Dos ejemplos de herramientas de piedra de Ain Boucherit: un núcleo lítico Olduvayense (izquierda) del que se sacaron las lascas afiladas que se pueden usar para cercenar los huesos (derecha).
Dos ejemplos de herramientas de piedra de Ain Boucherit: un núcleo lítico Olduvayense (izquierda) del que se sacaron las lascas afiladas que se pueden usar para cercenar los huesos (derecha).Mohamed Sahnouni
Algunos de los huesos muestran marcas que no parecen ser de origen natural, sino más bien el resultado de una acción intencionada. Se identificaron dos tipos: marcas producidas por lascas afiladas (como muestra la imagen situada debajo), lo que sugiere que el animal fue despellejado, desollado y eviscerado; y marcas provocadas por un percutor, lo que sugiere actividades de extracción de médula ósea.
Estos descubrimientos demuestran que hace 2,4 millones de años los primeros humanos podían comer la carne y el tuétano extraídos de los animales. La teoría es respaldada por otros estudios llevados a cabo en otros yacimientos contemporáneos del África del este.
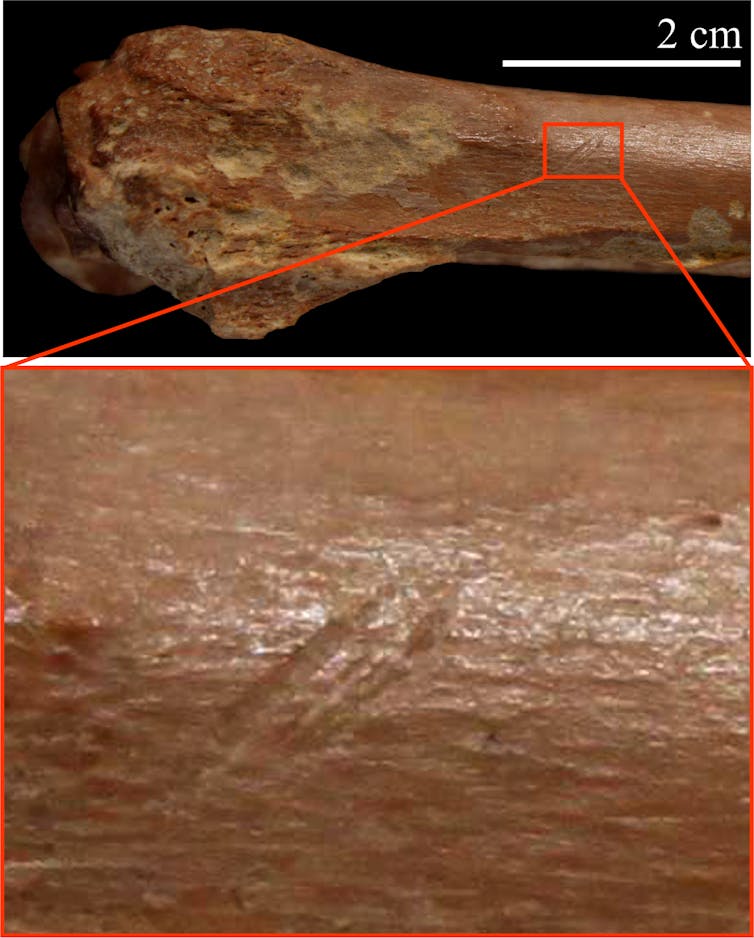 Un pequeño hueso bóvido con marcas de corte producidas por herramientas de piedra.
Un pequeño hueso bóvido con marcas de corte producidas por herramientas de piedra.Isabel Caceres
¿Cómo datamos las herramientas?
Establecer la antigüedad del yacimiento supuso todo un desafío. No podíamos aplicar las técnicas empleadas tradicionalmente en África del Este debido a la ausencia de depósitos volcánicos.
Entonces, datamos las herramientas de piedra de manera indirecta, es decir, analizando el sedimento en el cual se encontraron y estudiando los fósiles extraídos de la excavación. Para resumir, empleamos una combinación de cuatro métodos distintos: la estratigrafía, el paleomagnetismo, la resonancia de espín electrónico (mas conocida por su acrónimo en ingles ESR) y la biocronología.
- La estratigrafía es un campo de la geología que permite dividir los depósitos geológicos en diferentes niveles o capas. Este tipo de trabajo proporciona una primera información cronológica, ya que los depósitos situados por encima de otros siempre tienen una datación mas reciente.
- El análisis paleomagnético de los depósitos nos permitió identificar una sucesión de intervalos de polaridad normal (como en la actualidad) y de polaridad inversa. El paleomagnetismo es un método basado en el estudio de las inversiones del campo magnético a lo largo del tiempo, y tiene muchas aplicaciones en arqueología, como en Atapuerca por ejemplo.
Para poder identificar con mas precisión estos intervalos de polaridad normal e inversa, usamos la ESR y la biocronología.
- La ESR es una técnica basada en la evaluación de los efectos de la radiactividad a lo largo del tiempo. Permite determinar cuándo un grano de cuarzo dejó de ver la luz del sol y quedó enterrado.
- En cambio, la biocronología se basa en la identificación de los animales fósiles presentes en un yacimiento para deducir una cronología relativa (es decir, determinar si un yacimiento es mas antiguo o mas reciente que otro datado de manera independiente).
Gracias a estos métodos, pudimos identificar un intervalo de polaridad normal llamado Olduvai. Este intervalo es muy conocido y está datado entre 1,95 y 1,78 millones de años.
Como el nivel arqueológico superior está posicionado dentro de este intervalo Olduvai, sabemos entonces que tiene una datación dentro del rango de 1,95-1,78 millones de años mencionado antes. Además, como el arqueológico inferior está localizado por debajo de este intervalo Olduvai, sabemos entonces que tiene una fecha mas antigua que 1,95 millones de años.
Finalmente, observando la distancia de los niveles arqueológicos superior e inferior con respecto al inicio y el final de Olduvai, podemos refinar esta primera estimación cronológica y aventurarnos a proponer dataciones de unos 1,9 y 2,4 millones de años, respectivamente.
La importancia del descubrimiento
Este nuevo descubrimiento nos fuerza a actualizar nuestro conocimiento acerca de la creación y la difusión de la tecnología Olduvayense, tanto en África como fuera del continente. El hallazgo, al ser anterior a lo que se pensaba (600.000 años antes), acorta la diferencia temporal entre las más antiguas evidencias encontradas en el extremo oriental de África (2,6 millones de años) y los primeros habitantes humanos del Mediterráneo.
Esto indica que la expansión del Olduvayense desde el este de África fue rápida (al menos, más de lo que se suponía), aunque es también posible que el comienzo de la elaboración de estos utensilios tuviera lugar al mismo tiempo en el norte y en el este del continente.
Como consecuencia, parece que los primeros poblamientos en el margen sur del mar Mediterráneo son mucho más antiguos que los del norte. En el sur de Europa, la evidencia más antigua (Atapuerca y Orce, en España) no supera los 1,4 millones de años, mientras que los fósiles de homínidos encontrados en Dmanisi (Georgia), a las puertas de Europa, datan de hace 1,8 millones de años.
El arqueólogo del CENIEH Mohamed Sahnouni, coautor del artículo, explica los hallazgos.¿Quién fabricó estas herramientas?
Ya que no se encontraron fósiles de homínidos en Ain Boucherit, solo podemos especular acerca de quiénes fueron los fabricantes de estas piezas de piedra Olduvayenses.
El registro de fósiles homínidos en el norte de África es casi insignificante, tanto que no se ha encontrado ninguno de la antigüedad de las evidencias descubiertas en Ain Boucherit.
Los fósiles más antiguos encontrados en Argelia datan de hace aproximadamente 700.000 años y fueron encontrados en Tighennif (anteriormente conocido como Ternifine, consultar el mapa de arriba).
Si bien su nomenclatura ha cambiado a lo largo del tiempo (al principio recibieron el nombre de Atlanthropus mauritanicus, ahora son llamados Homo erectus u Homo heidelbergensis, dependiendo del autor), estos fósiles son realmente jóvenes en comparación con lo descubierto en Ain Boucherit, por lo que no se puede establecer conexión alguna entre los dos yacimientos.
Todos los restos fósiles de los primeros homínidos encontrados en el área del Mediterráneo, así como las herramientas de piedra Olduvayenses, son un millón de años más jóvenes que los restos de Ain Boucherit. En Europa Occidental, las evidencias más antiguas son las de parte de una mandíbula encontrada en la Sima del Elefante, en Atapuerca, y el diente de leche hallado en Barranco León, en el municipio de Orce (Granada). Estos descubrimientos datan de hace 1,2 y 1,4 millones de años, respectivamente.
Por lo tanto, los favoritos en cuanto a antigüedad se encuentran en África Oriental, a pesar de la distancia que separa a la región del norte del continente. Varios homínidos son más o menos coetáneos de los restos encontrados en Ain Boucherit (lo cual se explica muy bien aquí en inglés), incluyendo los australopitecinos y diferentes miembros del género Homo, como el Homo habilis, el Homo rudolfensis o el espécimen de Homo indefinido de Ledi-Geraru (Etiopía).
Dicho esto, no podemos obviar la posibilidad de que las herramientas encontradas en Ain Boucherit procedan de otra especie de homínidos, perteneciente o no al género Homo, que aún no haya sido descubierta.
Esperamos que las excavaciones que llevemos a cabo en el yacimiento argelino nos brinden la oportunidad de identificar a estos fabricantes de herramientas de piedra.![]()
Sobre los autores: Mathieu Duval es ARC Future Fellow en la Griffith University (Australia) y Mohamed Sahnouni, arqueólogo y profesor del Centro Nacional de Investigación sobre la Evolución Humana (CENIEH)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Los primeros humanos alcanzaron el Mediterráneo mucho antes de lo que pensábamos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Tres historias italianas: vacunas, homeopatía, niños y derechos humanos
- Antes de que el león se hiciese con el trono de rey de la selva
- Los efectos climáticos de un calentamiento sin precedentes en el Mediterráneo
No sabéis cantar cumpleaños feliz
Todos los años me sucede lo mismo. Pasan 365 días y al volver al mismo punto de la órbita donde se dio mi nacimiento, mis seres queridos se reúnen… para torturarme.
 Foto: Pixabay
Foto: Pixabay
Sí, hablo de la canción de Cumpleaños Feliz y hoy vengo a denunciar un hecho cierto, doloroso y universal: la gente no sabe cantarlo.
No habrá sido por falta de tiempo como para aprender. El tema de cumpleaños feliz fue compuesto a finales del siglo XIX por las hermanas Patty y Mildred Hill. Patty era directora de una guardería en Kentucky y Mildred era pianista y compositora. “Good Morning to All” (el título original de la melodía) nació como una canción pedagógica que los niños entonaban al llegar a clase. Fue publicada en 1893 en un libro de canciones infantiles. Su asociación a la letra del Happy Birthday apareció más tarde y fue publicada por primera vez en 1912 (aunque probablemente existiese con anterioridad).
A partir de ese momento, comienza todo un culebrón de jueces, abogados y sellos discográficos en torno a la propiedad intelectual de la canción… que ya lo quisiera Juego de Tronos. Como resultado os resumo: casi seguro, todos le debemos pasta a Warner/Chappell. O, al menos, todos los que en alguna ocasión hemos cantado el cumpleaños feliz en público, antes del 1 de enero de 20171 en Europa. En Estados Unidos la canción entró a formar parte del dominio público por la vía judicial apenas un año antes. Hasta ese momento, Warner Chappell había estado ganando alrededor de 2 millones de dólares al año por los derechos de copyright.
Con sus ciento y pocos años, “Happy Birthday to You” se ha convertido en la canción más reconocida en lengua inglesa. Ha sido traducida a 18 idiomas, incluyendo el árabe, hebreo, chino y, claro, español. Se podría argumentar que es una de las canciones más populares del mundo… y uno se esperaría que después de tantos años cumplidos, tantas velas sopladas y tanta repetición, la gente hubiese aprendido a afinarla.
PERO NO. Y francamente… tampoco me extraña.
Una de las grandes paradojas del cumpleaños feliz es que, para tratarse de un tema popular, es francamente complicado de cantar.
Pensemos, por contraste, en otras canciones típicas del repertorio popular: los villancicos. Aunque no es algo estricto, casi todos siguen algunos patrones melódicos muy básicos (sobre en los estribillos) que los convierten en canciones especialmente fáciles de cantar. Algunas de estas “normas” podrían resumirse así:
Normas no escritas (bueno, ahora sí) para escribir un villancico.
1- El estribillo debe poder cantarlo hasta Joaquín Sabina de resaca.
2- Las estrofas pueden tener un poquito más de fantasía. Solo un poquito. Se supone que las canta un solista.
Para que el estribillo sea especialmente fácil de cantar:
3- La melodía debe avanzar por grados conjuntos (es decir, notas seguidas: después de do, puede ir re o si).
4- Si hay saltos, que sean de 3ª (saltándose una nota). Nunca más grandes que una 5ª
5- Si verdad tiene que haber saltos, que no sea a mitad de frase, para que la gente respire.
6- Todo el estribillo debe estar contenido en un rango de notas más bien pequeño. Intenta que no supere una 8ª (el rango de una escala musical, de do a do).

Son normas no escritas porque, de alguna manera, ha sido el propio tiempo el que las ha seleccionado. Los temas se hacían populares si el pueblo los cantaba. Y el pueblo no suele tener un entrenamiento vocal especialmente sofisticado. Cantar por grados conjuntos, notas cercanas entre sí, es más fácil porque implica hacer menos cambios bruscos con las cuerdas vocales. Restringir el rango vocal hace más fácil que mucha gente pueda llegar a todas las notas. Y eso sin contar los contextos festivos (y etílicos) donde se suelen entonar estas canciones. Más vale poner las cosas muy fáciles… pocas notas, ritmos sencillos, mucha repetición. Estamos aquí para pasarlo bien.
La paradoja es que cumpleaños feliz no es un tema de “origen” popular (sus compositoras tienen nombres y apellidos) y no ha sido pulido todavía por el tiempo. Por eso, nos encontramos con una melodía que, de hecho, incumple bastantes de las normas básicas de sencillez vocal.

Para empezar, y de manera especialmente sangrante: fijaos en los saltos de la melodía. Desde el compás 1, cumpleaños feliz empieza ya fuerte con ¡un salto de 4ª! La cosa sólo empeora en el compás 3, arriesgando un poco más hasta la 5ª. Pero el desastre absoluto llega en el compás 5, ¡con un salto de 8ª, ni más ni menos! Y encima, a mitad de frase. Qué digo, a mitad de palabra. Cada vez que veo acercarse ese “te deséamos”… me estremezco.
Por si el salto no fuese lo bastante complicado, resulta que la melodía comienza en la nota más grave de todo su rango. En realidad, cumpleaños no es especialmente exigente en cuanto a rango vocal, es decir: su nota más aguda y más grave no están demasiado alejadas, no necesitas ser Bobby McFerrin para afinarlas. Normalmente, se considera que una persona sin entrenamiento vocal puede abarcar hasta dos octavas (puede cantar de do a do, un par de veces seguidas). Cumpleaños sólo requiere una octava, que no es mucho. El problema es que la gente empieza a cantar muy animada “cumpleaños” en el registro que le resulta más cómodo (o, probablemente, un pelín más agudo, por la emoción del momento) y no se da cuenta de que va a tener que elevar el tono de su voz hasta una 8ª, apenas 4 compases más tarde. El resultado es… desgañite, desafine, gallinas descontroladas… dolor, mucho dolor.
Por si todo esto fuera poco, la manera en que cantamos cumpleaños cae, directamente, en la polirritmia. Fijaos: toda la canción está en un compás ternario, es decir: podríais cantarla bailando un vals, por ejemplo. Sin embargo, al llegar al “te deséamos todos”, de repente, todo el mundo hace una pausa. Es como si, por sorpresa, el vals tuviese un paso de más, no escrito pero cantado por todos que lo desencaja todo un poco. Después de ese momento, la coordinación se vuelve especialmente complicada.
Y luego está… el tema de la letra. Quizás por tratarse de palabras encajadas sobre la melodía a posteriori, casi con calzador, ningún acento musical cae donde debería. La sílaba más aguda de las dos primeras repeticiones coincide sobre “fe” (cumpleaños feliz), aunque tiene un pase ya que “liz” tiene el apoyo de la parte fuerte del compás. El desastre, de nuevo, lo encontramos en “te deséamos”: porque tanto la nota aguda de la melodía como la parte fuerte del compás coinciden sobre “sé”, pero ese verbo no es esdrújulo y aún así, lo he escrito tres veces con tilde en este artículo sin que probablemente llamara tu atención.
¿Y entonces? Qué podemos hacer. Para mi desdicha, este problema no tiene fácil solución… yo desde aquí invoco al pueblo para que vaya limando esta melodía y, con el paso de los años, la convierta en algo realmente fácil de cantar. Hasta que ese momento llegue, aquí os presento mi versión de cumpleaños más feliz. Ojalá os convenza y dejéis de desafinar… ¡malditos!
Nota:
1Según Wikipedia: ”Warner/Chappell claimed copyright for every use in film, television, radio, anywhere open to the public, and for any group where a substantial number of those in attendance are not family or friends of whoever is performing the song”.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo No sabéis cantar cumpleaños feliz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
