¿Podría un humano vivir en el mar?
Los bajau laut viven en torno a las costas de Filipinas, Indonesia, Malasia y Brunéi y son mundialmente conocidos como «los nómadas del mar». Esta denominación es debida a que el pueblo bajau vive literalmente en el mar desde hace, como mínimo, 1.000 años. Pero, ¿cómo es eso de que viven en el mar?
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Podría un humano vivir en el mar? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué tienen en común Einstein y una zanahoria?
- ¿Hemos intentando contactar con extraterrestres?
- ¿Qué pasa en tu cuerpo cuando te enamoras?
El pico petrolero
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

 Fotografía: Pixabay
Fotografía: Pixabay
¿Qué es el pico del petróleo (peak oil)?
El pico (o cénit) petrolero es el momento de máxima tasa de extracción del petróleo. Es un momento teórico a partir del cual se espera que la cantidad de petróleo disponible decline de manera irreversible. El concepto de pico del petróleo se atribuye a Marion King Hubbert (1903-1989) geólogo y geofísico estadounidense, quien en 1956 lo presentó por primera vez de manera formal (Figura 1). Este concepto se basa en extrapolar la historia conocida de yacimientos en explotación o que han sido explotados al total mundial. Los yacimientos de petróleo alcanzan muy rápido su pico de producción, para pasar después a una meseta, en la que la producción se mantiene más o menos constante, seguida de un largo declive. De hecho, la mayor parte del petróleo de un yacimiento se extrae en esta última fase.
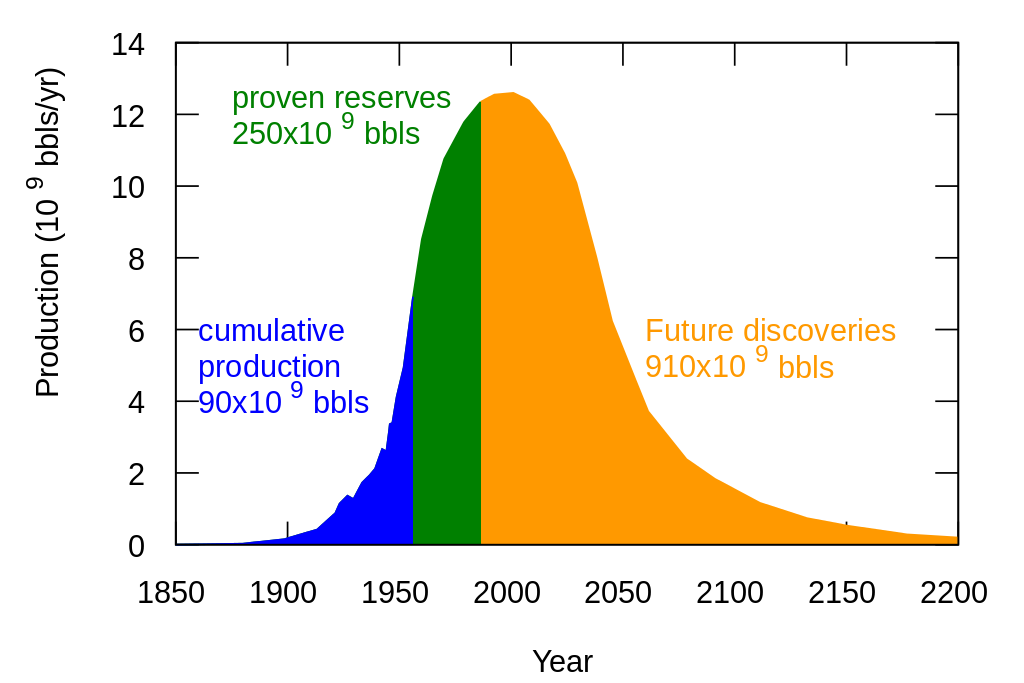 Figura 1. Propuesta M. King Hubbert de 1956 en la que se muestra la producción acumulada (en azul), así como una proyección hacia el futuro en base a las reservas probadas (en verde) y descubrimientos futuros. Este geólogo proponía el pico del petróleo en el año 2000 con una producción máxima de alrededor de la mitad que se produjo en 2016 (29.400 millones de barriles al año). Esta predicción fue realizada casi una década antes de que se produjera el máximo de descubrimientos de petróleo, en la década de los 60 (Figura 2). Licencia Creative Commons.
Figura 1. Propuesta M. King Hubbert de 1956 en la que se muestra la producción acumulada (en azul), así como una proyección hacia el futuro en base a las reservas probadas (en verde) y descubrimientos futuros. Este geólogo proponía el pico del petróleo en el año 2000 con una producción máxima de alrededor de la mitad que se produjo en 2016 (29.400 millones de barriles al año). Esta predicción fue realizada casi una década antes de que se produjera el máximo de descubrimientos de petróleo, en la década de los 60 (Figura 2). Licencia Creative Commons.
¿Qué es la tasa de retorno energético (TRE)?
El TRE se calcula dividiendo la cantidad de energía total que es capaz de producir una fuente de energía y la cantidad de energía que es necesaria “invertir” para explotar esta fuente. Un TRE alto indica una fuente de energía “rentable” (en términos energéticos), un TRE de 1 indica la cantidad de energía “invertida” y producida es la misma, por lo cual no aportaría energía extra al sistema, mientras que un TRE menor de uno indicaría que se trata de un sumidero energético, una fuente que aporta menos energía neta que la que es necesario invertir.
Si aplicamos el concepto de TRE a los yacimientos de petróleo vemos que cada yacimiento tiene un TRE distinto, y que, en promedio, el TRE de los yacimientos descubiertos ha ido disminuyendo a lo largo del tiempo. Los yacimientos con un petróleo de más calidad y cercanos a la superficie y, por tanto, más fácilmente explotables, fueron los primeros en explotarse. Posteriormente se han ido explotando yacimientos de más difícil acceso, y que, por lo tanto, tienen menores TREs. En el cómputo global, por tanto, a partir del cénit de extracción no sólo hay cada vez menos petróleo, sino que además se explotan yacimientos con cada vez menor TRE.
¿Hemos llegado al pico del petróleo?
Ésta es una pregunta complicada, por varios motivos. Por un lado, porque certificar con seguridad el pico petrolero solo puede hacerse una vez éste ha pasado y actualmente sólo podemos intentar estimar el mismo en base a las tendencias en la producción y descubrimiento de yacimientos. Por otro lado, lo que habitualmente llamamos petróleo en realidad engloba varias categorías de hidrocarburos líquidos: petróleo crudo convencional, crudo extra-pesado, arenas bituminosas, petróleo ligero de roca, etc, cuyo cénit de producción debería calcularse por separado. Aunque el número de descubrimientos se mantiene estable desde finales del s. XX, después de haber tenido su máximo en la década de los 60 del pasado siglo (Figura 2), el TRE de estos yacimientos es menor. Esto no debe sorprendernos, ya que se trata de un recurso finito, no-renovable, y es razonable pensar que los yacimientos más grandes y más ricos fueron los primeros en ser descubiertos. Algunas estimaciones indican que es probable que estemos viviendo actualmente el pico del petróleo crudo convencional.
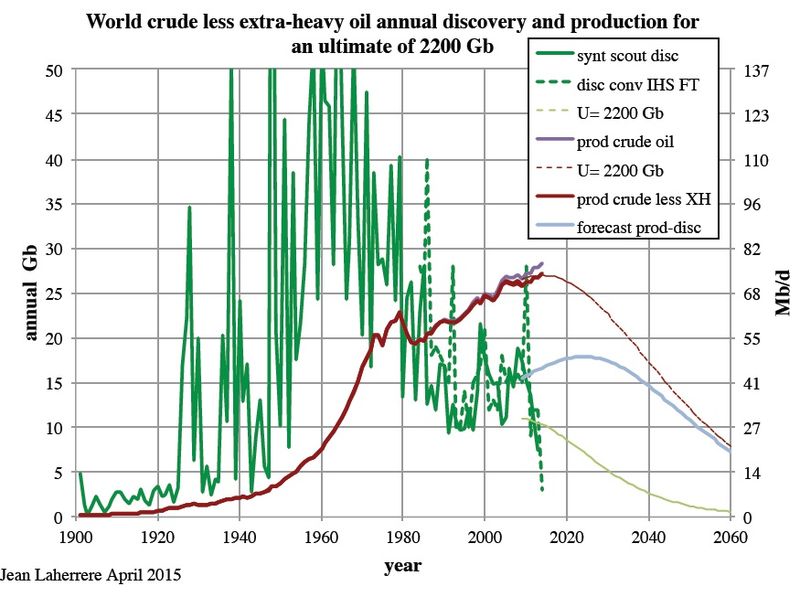 Figura 2. Descubrimiento de petróleo (en verde) junto con la producción (en rojo). En esta gráfica se puede ver que el máximo de descubrimientos se realizó en la década de los 60. La producción creció muy rápidamente a partir del fin de la segunda guerra mundial para alcanzar un primer máximo en 1979, con un crecimiento posterior más lento. Fuente: Figura por Jean Laherrere (Creative Commons).
Figura 2. Descubrimiento de petróleo (en verde) junto con la producción (en rojo). En esta gráfica se puede ver que el máximo de descubrimientos se realizó en la década de los 60. La producción creció muy rápidamente a partir del fin de la segunda guerra mundial para alcanzar un primer máximo en 1979, con un crecimiento posterior más lento. Fuente: Figura por Jean Laherrere (Creative Commons).
¿Cuáles son las implicaciones del pico petrolero?
La primera, implícita en la propia definición del pico petrolero es la disminución progresiva del petróleo y de la energía que puede ser extraída del mismo. La Agencia Internacional de la Energía (AIE; o IEA en sus siglas en inglés) publica cada año un informe sobre la situación energética internacional (World Energy Outlook; WEO), tratando distintos apartados, entre ellos el petróleo. El último informe indica una previsión de crecimiento de la demanda mundial de petróleo debido al creciente transporte por carretera, aviación y de las petroquímicas, que se cifra en más de 10 millones de barriles diarios para 2025. Por otro lado, la AIE realiza una predicción de la producción del petróleo y prevé que para el año 2025 faltarán al menos 13 millones de barriles de petróleo para satisfacer las demandas. En base a los datos publicados por la AIE, Antonio Turiel, científico titular del CSIC, ha calculado la energía neta que de manera realista ofrece el petróleo actualmente y que ofrecerá en el futuro. Esos cálculos indican una disminución de más del 50% en los próximos 25 años, pasando de 69 millones de barriles equivalentes diarios a 33 millones en el año 2040 (Figura 3).
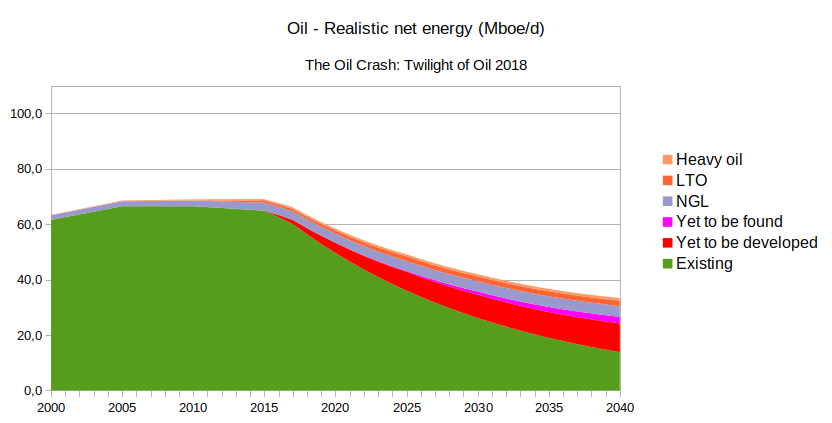 Figura 3. Estimación de la energía neta a partir del petróleo hasta el año 2040. Se ha usado la predicción de producción proporcionada por la Agencia Internacional de la Energía, aplicándole la tasa de retorno energético. Gráfica realizada por Antonio Turiel.
Figura 3. Estimación de la energía neta a partir del petróleo hasta el año 2040. Se ha usado la predicción de producción proporcionada por la Agencia Internacional de la Energía, aplicándole la tasa de retorno energético. Gráfica realizada por Antonio Turiel.
El cénit de producción es un concepto que se puede aplicar a todo recurso no renovable. De hecho, además del cénit de producción del petróleo también se habla de otros cénits de recursos energéticos como el carbón, el uranio o el gas natural, algunos de los cuales (los combustibles fósiles) podrían estar también próximos en el tiempo ( menos de 20 años). En definitiva, la perspectiva de una disminución de la energía neta disponible es real.
Los intentos de mejora de la eficiencia energética podrían ayudar a la disminución de la energía por persona. Por desgracia, parece probado que la mejora de la eficiencia en la que se usa un recurso debido al desarrollo tecnológico, más que disminuir el consumo de dicho recurso, hace más probable un aumento en el consumo del mismo (paradoja de Jevons). Por otro lado, la sustitución del petróleo y otros combustibles fósiles por otras fuentes de energía, no es un asunto sencillo, ya que hay ciertos sectores (p.ej., transporte aéreo, transporte pesado por mar y carretera) cuya electrificación no es viable. Además, estos intentos de sustitución necesitarían en su desarrollo ingentes cantidades de energía y/o de materias primas raras y escasas.
Existe una correlación entre la economía real y la cantidad de energía disponible, y el petróleo está muy imbricado en todos los sectores económicos. Por ello, la disminución de la cantidad disponible de petróleo y otros combustibles fósiles, y por ende, de la energía disponible, tiene implicaciones a muchos niveles en el sistema económico mundial. Además, el control de recursos energéticos y minerales son los condicionantes principales de las agendas geoestratégicas de las grandes potencias.
El cénit de la producción de petróleo, al igual que el cénit de producción de otros combustibles fósiles, son parte y consecuencia del cambio global; es decir, del conjunto de cambios que tiene un origen antropogénico y que están teniendo repercusiones a escala geológica. Las consecuencias de las actividades humanas, incluyendo el cambio climático y la pérdida masiva de biodiversidad, son los grandes desafíos a los que se debería estar enfrentando nuestra especie actualmente.
Para saber más:
Miller Richard, G., Sorrell Steven, R., 2014. The future of oil supply. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 372, 20130179.
A. Turiel (2019).
M. Mediavialla et al. (2019).
G. Tverberg (2019).
Sobre el autor: Asier Gómez es investigador Ramón y Cajal en el Departamento de Estratigrafía y Paleontología de la Facultad de Ciencia y Tecnología de la UPV/EHU.
El artículo El pico petrolero se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Energía oscura
- Espectrometría de masas: de un isótopo de neón a elefantes que vuelan
- Proteómica: cuando las proteínas y la espectrometría de masas van de la mano
El progreso nos salvará del ecologismo
 Clausura (2014) de Santiago Talavera. Acuarela, tinta, lápiz de color y collage sobre papel. 180 x 152 cm
Clausura (2014) de Santiago Talavera. Acuarela, tinta, lápiz de color y collage sobre papel. 180 x 152 cm
El ecologismo surgió en la década de 1960 como consecuencia de, primero, el conocimiento científico resultado de la ecología, las ciencias de la Tierra, la meteorología, la zoología, la botánica, etc. Y, segundo, de la romantización de la naturaleza. Esto tiene como origen la definición presocrática de la naturaleza, es decir, que la naturaleza es la totalidad de las cosas a excepción del hombre y de las cosas del hombre.
En esencia, el ecologismo podría entenderse como una forma de progreso, ya que su prioridad es la salud del planeta. El planeta es nuestra casa, así que su mantenimiento es, a fin de cuentas, una garantía de evolución y bienestar humanos. Sin embargo, el movimiento ecologista tradicional se desmarca del progreso, precisamente por cómo define la naturaleza. Tanto es así, que para el ecologismo el progreso es una suerte de reiterados pecados contra la naturaleza. Así es el movimiento ecologista gestado en la década de 1970, esa ideología verde de activistas como Al Gore, el papa Francisco o Greenpeace.
El ecologismo verde o ecologismo tradicional anhela una naturaleza prístina. Como si esa naturaleza hubiese sido mancillada por la humanidad. Es una visión infantilizada de la naturaleza. Esta idealización tiene sus consecuencias, en primer lugar intelectuales, que son las más graves, y en segundo lugar prácticas, que afectan a la economía, la política, la ciencia y la tecnología, entre otras.
Algunas de las consecuencias intelectuales del ecologismo tradicional son el pesimismo y el nihilismo. El ecologismo es un movimiento apocalíptico: agotamiento de recursos, superpoblación, pobreza, enfermedad… Y, como la mayoría de movimientos apocalípticos, es misántropo. Culpa a la humanidad de la inevitable catástrofe, definiendo así a la humanidad como el cristianismo se refiere al pecado. Y no solo culpa a la humanidad, sino que solicita su retirada. Con frecuencia aluden a la humanidad como al cáncer de la naturaleza, y como tal, hay que combatir la enfermedad siguiendo una estrategia radical. La fantasía última es un planeta despoblado. Por lo de pronto pretenden el retroceso de las actividades humanas: la desindustrialización y el rechazo al progreso, a la ciencia y a la tecnología. Esto lo vemos en el ecologismo que rechaza la ingeniería genética, la síntesis química, la radiación wifi o la energía nuclear. Un movimiento que nació en parte como consecuencia del conocimiento científico, ahora lo contradice.
El ecologismo tradicional incurre en una serie de errores precisamente por tratarse de un movimiento anticientífico, o contrailustrado, como quiera llamarse. Por ejemplo, la idealización de las reservas naturales. Este es un fenómeno curioso, ya que las llamadas reservas naturales no son santuarios naturales, sino producto de la civilización. Son espacios protegidos y controlados. Lo mismo ocurre con la llamada agricultura ecológica. Agricultura ecológica es un oxímoron. La agricultura, por definición, contradice a la ecología tradicional. La agricultura es una de las prácticas humanas que produce un mayor impacto medioambiental y supone un desequilibrio dirigido de los ecosistemas. No hay más que ver la parcelación del paisaje. Destrozamos el suelo, lo allanamos, lo inundamos y lo plagamos de monocultivos. Cultivos que, por cierto, son engendros genéticos que ni siquiera sobrevivirían sin el cuidado permanente que hacemos de ellos.
La llamada agricultura ecológica genera más impacto que la llamada agricultura tradicional precisamente porque la agricultura ecológica rechaza el progreso científico y tecnológico. Necesita más terreno para producir la misma cantidad de alimento, tiene menor rendimiento, con lo cual es menos sostenible. Por ejemplo, la agricultura ecológica no contempla los cultivos hidropónicos, que ni siquiera necesitan suelo. Ni el uso de transgénicos, aunque ello suponga dejar de emplear pesticidas. Es como si la agricultura ecológica respondiese a una idealización nostálgica de lo que fue la agricultura hasta un momento concreto, congelado en el tiempo de forma arbitraria. Esa es la idea, aunque en la práctica ni siquiera es así de romántica. Los cultivos ecológicos a menudo se encuentran bajo invernadero y apenas se diferencian de la agricultura tradicional que simplemente se ha quedado anclada unas décadas atrás.
El ecologismo tradicional se está convirtiendo en un movimiento meramente cosmético. Resulta muy ilustrativa la preocupación y el malestar que nos provoca encontrarnos con pequeños trozos de plástico en la playa, en contraposición con la indiferencia que nos producen los cantos de vidrio, cemento o ladrillo. Por si hay dudas, el impacto medioambiental de los materiales cerámicos es mayor que el de los plásticos. Otro ejemplo. Nos parece idílica y consecuente la vida en el campo, las casas antiguas con paredes de piedra. Efectivamente tienen un valor estético y arquitectónico, pero no ecológico. La vida en las ciudades, en edificios, además de dejar más espacio al campo, si se quiere, para las anheladas reservas naturales, necesita menos recursos para el desplazamiento, construcción y calefacción. El techo de uno es el suelo del otro. Otro ejemplo. Las cascadas artificiales de la energía hidráulica, los paneles solares de la energía fotovoltaica, los molinos de la energía eólica que abarcan inmensas extensiones de terreno. No los contemplamos como las perturbaciones del paisaje que de hecho son, sino como parte de la lucha contra el calentamiento global. Hemos aprendido a contemplar esas monstruosidades como ecologismo. Sin embargo, una central nuclear, que es más sostenible, genera mucha más energía a partir de menos recursos, con un menor impacto medioambiental, la apreciamos como lo contrario al ecologismo. Efectivamente el ecologismo es un movimiento cosmético.
Por estas razones, otro tipo de ecologismo es posible. El ecologismo ilustrado. Se trata de un ecologismo que permanece ligado al conocimiento científico y, por tanto, entiende que los problemas medioambientales a los que nos enfrentamos sí tienen solución y esta vendrá de la mano del progreso. No es un movimiento apocalíptico, sino optimista y realista. No define a la naturaleza al estilo presocrático, sino que la humanidad entra dentro de la definición de la naturaleza que se pretende preservar. Por tanto, el bienestar humano es crucial.
Las soluciones que propone el ecologismo ilustrado a los problemas medioambientales pasan por el uso de todo el conocimiento científico y tecnológico que hemos generado hasta ahora. De la ingeniería genética a la física nuclear.
Escapar de la pobreza requiere energía y alimentos en abundancia. Escapar de la pobreza intelectual requiere ilustración. Escapar de la pobreza requiere progreso.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo El progreso nos salvará del ecologismo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sin ciencia no hay progreso
- #Naukas14: La fragilidad del progreso
- El falso pan integral tiene los días contados
El poema de los números primos
El Centro Internacional de Cultura Contemporánea TABAKALERA, de Donostia/San Sebastián nos ha regalado estos días una maravillosa exposición de la artista donostiarra Esther Ferrer, comisariada por Laurence Rassel y Mar Villaespesa. Bajo el título Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… (del 5 de abril al 26 de mayo de 2019), la exposición recoge, en cuatro espacios conectados de Tabakalera, cuatro grupos de obras emblemáticas de la artista Esther Ferrer: proyectos espaciales, una visión general de las performances más significativas de su carrera (con realizaciones de las performances cada viernes), obras de la serie Poema de los números primos, y cuadros de la obra Pi.
 Cartel de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… (del 5 de abril al 26 de mayo de 2019), en el Centro Internacional de Cultura Contemporánea TABAKALERA, de Donostia/San Sebastián. Imagen de Tabakalera
Cartel de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… (del 5 de abril al 26 de mayo de 2019), en el Centro Internacional de Cultura Contemporánea TABAKALERA, de Donostia/San Sebastián. Imagen de Tabakalera
 Vista parcial del suelo de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera, mostrándonos un “mar de números primos” generado por la artista Esther Ferrer, para esta obra de la serie Poema de los números primos diseñada expresamente para la exposición. Fotografía: Raúl Ibáñez
Vista parcial del suelo de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera, mostrándonos un “mar de números primos” generado por la artista Esther Ferrer, para esta obra de la serie Poema de los números primos diseñada expresamente para la exposición. Fotografía: Raúl Ibáñez
Los números primos constituyen un elemento fundamental en la obra artística de Esther Ferrer, que ella ha utilizado desde las décadas de los años 1970 y 1980, a través de diferentes estructuras espaciales planas, como la conocida espiral de Ulam.
La propia artista, con motivo de su exposición en Artium en 2011, explica el origen de su trabajo con representaciones espaciales de los números primos:
“Tras algunos años, en la década de los 70, realizando proyectos con estructuras geométricas definidas únicamente en función de mis propios criterios, sentí la necesidad de pensar otras en las cuales mis preferencias estéticas jugaran un papel secundario. Estructuras libres que pudieran evolucionar por sí mismas, según su lógica interna…
Durante algún tiempo no conseguí un resultado que me satisficiera hasta que una noche soñé con los números primos, así empecé la serie, EL POEMA DE LOS NÚMEROS PRIMOS.”
Además, el título de la serie juega con la similitud de las palabras poema y teorema (recordemos que un teorema es una verdad matemática demostrable), “poema = teorema – ter + p”, así mismo este título nos habla de la poesía que está detrás de los números, en particular, de los números primos.
 Maqueta de un proyecto de números primos hexagonales, de la serie Poema de los números primos (1989), de la artista Esther Ferrer. Edición especial producida por ARTIUM, Centro-Museo Vasco de Arte Contemporáneo, en 2011
Maqueta de un proyecto de números primos hexagonales, de la serie Poema de los números primos (1989), de la artista Esther Ferrer. Edición especial producida por ARTIUM, Centro-Museo Vasco de Arte Contemporáneo, en 2011
Pero vayamos con los objetos matemáticos utilizados por la artista donostiarra, los números primos, la espiral de Ulam y otras estructuras geométricas planas formadas por números.
Aunque seguramente todas las personas que estáis leyendo esta entrada del Cuaderno de Cultura Científica conocéis el concepto de número primo, siempre es conveniente empezar por el principio. Los números primos son aquellos números que solamente se pueden dividir por 1 y por ellos mismos. Así, por ejemplo, el número 25 no es un número primo ya que se puede dividir por 5, además de por 1 y 25, o tampoco el 33, divisible por 3 y 11, mientras que el número 17 sí es primo, ya que solamente es divisible por el 1 y el mismo, al igual que los números 2, 3, 5, 7, 11, 13 o 19.
El teorema fundamental de la aritmética, que ya aparece en el libro Los Elementos, de Euclides de Alejandría (aprox. 325 -265 a.n.e.), y que nos dice que todo número puede expresarse, de forma única, como producto de números primos, por ejemplo, el número 924 es igual al producto de 2 x 2 x 3 x 7 x 11, pone de manifiesto la importancia de esta familia de números. Además, este resultado es el motivo por el cual el número 1 no se considera un número primo, puesto que en ese caso no se daría la unicidad.
En la Antigua Grecia ya conocían también un método para obtener números primos, conocido como la criba de Eratóstenes. Este método aparece descrito en el texto Introducción a la Aritmética, del filósofo y matemático Nicómaco de Gerasa (aprox. 60 – 120 n.e.), quien atribuye su autoría al sabio polifacético griego Eratóstenes de Cirene (276-194 a.n.e.), aquel que también estimó de forma muy certera el diámetro de la esfera terrestre (véase El tamaño sí importa, que se lo pregunten a Colón (o de la geometría griega para medir el diámetro de la Tierra)).
El método de la criba de Eratóstenes consiste en lo siguiente. Consideremos todos los números naturales hasta uno dado, por ejemplo, tomemos uno bajo para ilustrar el concepto, el 25. En primer lugar, escribimos todos los números hasta ese número:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 y 25.
El 1 no es primo, luego lo tachamos, es decir, lo eliminamos como número primo. Después tenemos el 2, que sí es primo, lo marcamos (nosotros lo hemos puesto en negrita) y tachamos todos los múltiplos de 2, los números pares, que no serán números primos, puesto que los podemos dividir por 2.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 y 25.
El siguiente número que aparece es el 3, que es primo, lo marcamos y tachamos todos los múltiplos de 3, puesto que no son primos.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 y 25.
El siguiente número que aparece es el 5, que, puesto que no está tachado (esto nos expresa que no es divisible por ningún número anterior), es un número primo, luego lo marcamos y tachamos sus múltiplos, los que aún no estén tachados.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 y 25.
El siguiente número no tachado es el 7, luego es un número primo, y debemos de tachar sus múltiplos, así hasta recorrer toda la lista hasta el número final, en este caso el 25. En este sencillo caso nos quedaría:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 y 25.
Luego, los números primos menores que 25 son 2, 3, 5, 7, 11, 13, 17, 19 y 23.
Este es un método sencillo que nos permite ir obteniendo números primos hasta un número dado, aunque es un método con muchas limitaciones, ya que no permite conocer si un número en concreto, por ejemplo, el número 76.243, es primo o no, para saberlo la criba debe de llegar hasta ese número (en este caso, sí es primo), ni generar números primos, ni conocer sencillas propiedades de estos números, como, por ejemplo, si existen infinitos números primos.
Puesto que nuestros elementos de escritura, como una hoja de papel, son rectangulares, y además una línea continua de números se nos extendería mucho, lo normal es representar los números, hasta el número considerado, en un rectángulo de números, como el que aparece abajo y aplicar sobre el mismo el método de la criba de Eratóstenes.
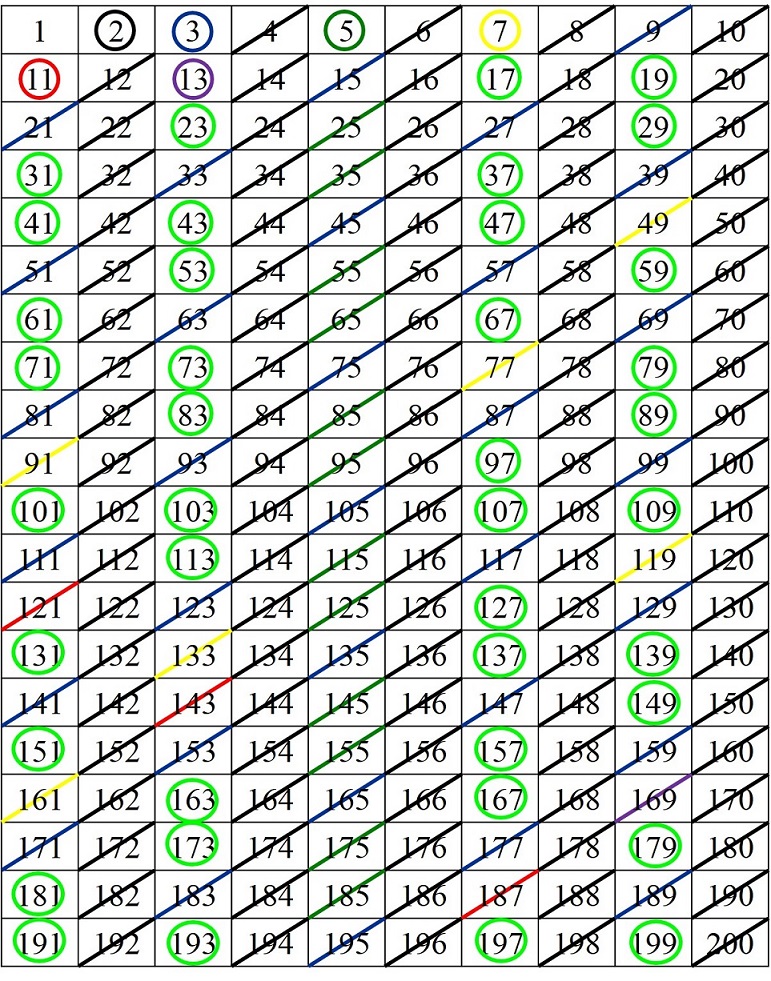
Así, los números primos hasta el 200 son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199.
La criba de Eratóstenes, expresada de esta forma, ya es una estructura geométrica plana, rectangular, que nos puede permitir buscar información de la estructura de la familia de números primos, como patrones visuales que puedan producirse a partir de los cuales obtener dicha información. Por ejemplo, aunque esto es evidente sin necesidad de la criba de Eratóstenes, podemos observar que todos los primos están en cuatro columnas, que se corresponden a los números que terminan en 1, 3, 7 y 9. Y nos permite ver que hay muchas parejas de números primos gemelos, que son aquellos números primos que están lo más cerca posible, es decir, con tan solo un número par entre ellos, como las parejas 11 y 13, 17 y 19, 41 y 43, 59 y 61, 71 y 73, 101 y 103, 107 y 109, 137 y 139, 149 y 151, 179 y 181, 191 y 193, 197 y 199, que se corresponden con las terminaciones (1, 3), (7, 9) o (9, 1). Estas parejas de números primos gemelos también han interesado a la artista Esther Ferrer.
Antes de continuar con la espiral de Ulam, remarquemos dos hechos muy importantes relacionados con los números primos, que juegan un papel central en la serie Poema de los números primos de la artista donostiarra y de los que ya hablamos en la entrada del Cuaderno de Cultura Científica Buscando lagunas de números primos, que existen infinitos números primos y que cada vez existen menos números primos en la recta de los números naturales, es decir, la densidad de números primos según vamos avanzando en los números naturales es cada vez menor.
“Un día soñé que nadaba en un mar de números y después del sueño todos los que se me venían a la cabeza eran primos. Así fue como empecé a trabajar en la serie Poema de los números primos, y a plantearme la cuestión del infinito, que trabajé más tarde recurriendo a Pi, sin duda un número infinito.”
(Conversación entre Esther Ferrer, Laurence Rassel y Mar Villaespesa en Esther Ferrer, todas las variaciones son válidas, incluida esta, 2017)
 Poema de los números primos (2016), de Esther Ferrer, dibujo para suelo, realizado en tita sobre papel cuadriculado, 104,5 cm x 83,5 cm, del Archivo de Esther Ferrer. Imagen del catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta, del Museo Nacional Centro de Arte Reina Sofía
Poema de los números primos (2016), de Esther Ferrer, dibujo para suelo, realizado en tita sobre papel cuadriculado, 104,5 cm x 83,5 cm, del Archivo de Esther Ferrer. Imagen del catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta, del Museo Nacional Centro de Arte Reina Sofía
La anterior obra tiene como base una criba de Eratóstenes rectangular de 76 columnas, es decir, la primera fila son los números del 1 al 76, y 99 columnas, luego nos determina los números primos hasta el número 7.524 (76 x 99). Esther Ferrer construye esta criba de Eratóstenes en la que se producen cuatro columnas vacías de números primos (la de la derecha, debajo del cero, es un añadido para dar simetría a la estructura), correspondientes a las columnas debajo del 19, 38, 57 y 76, múltiplos de 19.
Esther Ferrer genera, a través de su mirada personal, una determinada estructura espacial que subyace a la distribución real de los números primos dentro de la recta de los números naturales, que es una realidad del universo de los números, pero que observamos a través de la mirada creativa de la artista. Esta hermosa obra ha sido realizada en el suelo del Palacio de Velázquez, en el Parque del Retiro de Madrid, para la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta (2017). Además, al realizarla a un tamaño grande, dispuesta en el suelo y sobre la que pasear, cautiva a las personas que pasean sobre ella y realza aún más el impacto de la estructura de los números primos.
 Realización de la obra Poema de los números primos (2016), de Esther Ferrer, en el suelo del Palacio de Velázquez, para la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta (2017). Imagen de ZAS Madrid
Realización de la obra Poema de los números primos (2016), de Esther Ferrer, en el suelo del Palacio de Velázquez, para la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta (2017). Imagen de ZAS Madrid
Martin Gardner en su artículo The remarkable lore of the prime numbers cuenta que el matemático polaco Stanislaw Ulam (1909 – 1984), quien participó en el proyecto Manhattan y desarrollo junto con el matemático húngaro John Von Newmann (1903 – 1957) el método de Montecarlo, estaba escuchando una conferencia en el Laboratorio Científico de Los Álamos, que el propio Ulam describió como “un artículo largo y muy aburrido”, y empezó a hacer garabatos en una hoja, en concreto, empezó a escribir los números en espiral, empezando en el 1 y en el sentido contrario a las agujas del reloj, e hizo un círculo alrededor de los números primos. Entonces se dio cuenta de que los números primos se concentraban en líneas rectas, especialmente en diagonales, así mismo, había algunas diagonales, como las formadas solo por números pares, en las que no había ningún número primo.
En Los Álamos disponían del ordenador MANIAC II, que tenía guardados en su memoria los primeros 90 millones de números primos, por lo que junto a Myron L. Stein y Mark B. Wells programaron el ordenador para que realizara una espiral de números, con los números naturales desde el 1 hasta el 65.000, en la que se marcaran solamente los números primos. La imagen que obtuvieron (que hemos incluido más abajo y que aparece en el artículo de Ulam, Stein y Wells, A visual display of some properties of the distribution of primes, 1964) confirmaba lo que había visto Ulam, que los números primos aparecen alineados en rectas horizontales, verticales y, sobre todo, diagonales.
A esta estructura geométrica plana en la que los números naturales son escritos en espiral, empezando en el 1 y en el sentido contrario a las agujas del reloj, destacando los números primos, es lo que se conoce como la espiral de Ulam (dos imágenes más abajo puede verse con más claridad).
 Espiral de números primos representada por Stanislaw Ulam, Myron Stein y Mark Wells, con el ordenador Maniac II de Los Álamos, en 1964, en la que se observa que los números primos están alineados en rectas diagonales, verticales y horizontales
Espiral de números primos representada por Stanislaw Ulam, Myron Stein y Mark Wells, con el ordenador Maniac II de Los Álamos, en 1964, en la que se observa que los números primos están alineados en rectas diagonales, verticales y horizontales
Detrás de esta observación de Stanislaw Ulam está el hecho de que los números de las líneas verticales, horizontales y diagonales se corresponden con los valores de los polinomios cuadráticos de la forma 4n2 + bn + c, como puede verse en la siguiente imagen. En función de los valores de b y c se generan diferentes líneas que tendrán más o menos números primos. Por ejemplo, si b y c son pares, solo se producen números pares y no habrá números primos en dichas líneas, salvo quizás el 2. El polinomio de la imagen siguiente, 4n2 + 8n + 3, es igual a (2n + 1)(2n + 3), luego no genera números primos, salvo el 3, para n = 0. Mientras que otras líneas, como la diagonal 4n2 + 26n + 41, sí genera números primos, como 41, 71, 109 o 271, y no primos, como 155 y 209. Dos polinomios cuadráticos que generan muchos números primos son 4n2 – 2n + 41, que a partir de un cierto valor de n genera la línea diagonal de puntos blancos en la parte de arriba de la imagen de Ulam, Stein y Wells (la imagen anterior), y 4n2 + 2n + 41, que es la línea de abajo.
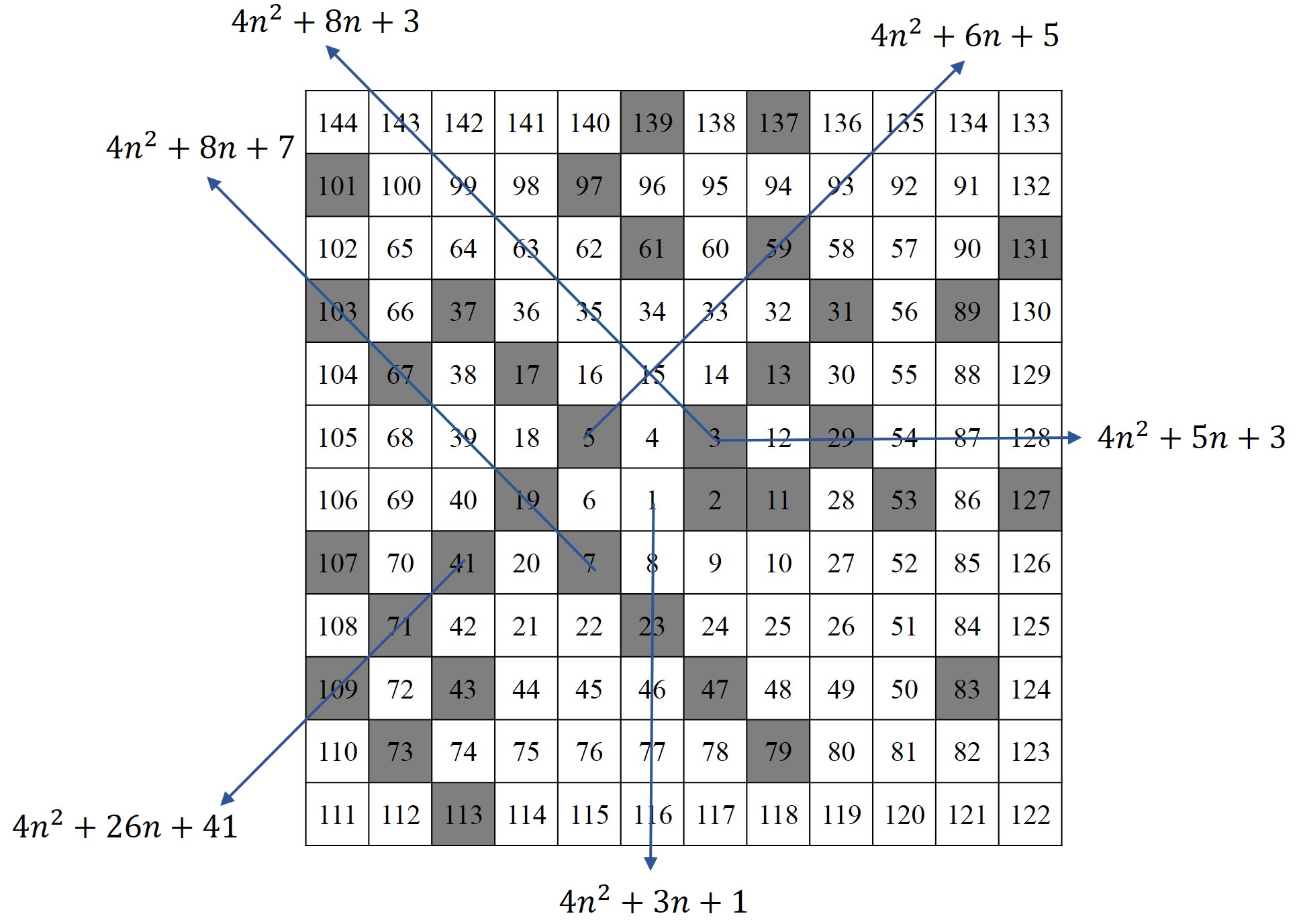 Espiral de Ulam, en una cuadrícula 12 x 12, y algunas líneas de números con los polinomios cuadráticos que las generan
Espiral de Ulam, en una cuadrícula 12 x 12, y algunas líneas de números con los polinomios cuadráticos que las generan
El siguiente dibujo de Esther Ferrer, de entre los años 1983 y 1985, nos da algunas claves de la forma en la que la artista trabaja con la espiral de Ulam. Para empezar el dibujo contiene la espiral de Ulam en una cuadrícula 16 x 16, luego con los números desde 1 hasta 256. Además, solo están escritos los números primos en la espiral y en las posiciones que corresponden a números compuestos, es decir, los números no primos, está dibujado un segmento diagonal “tachando” ese número, pero sin el número. En este dibujo, las diagonales tienen dos posiciones y dos colores posibles. El sentido de la diagonal y el color cambian cada vez que aparece un número primo, de forma que entre un primo y el siguiente, es decir, lo que conocemos como una laguna de números compuestos entre números primos (véase la entrada Buscando lagunas de números primos), las diagonales que aparecen tienen un mismo sentido y color. La confluencia de la construcción de la espiral de Ulam, junto con las diagonales inclinadas y de colores, confiere al conjunto de una estructura geométrica particular, casi laberíntica en este caso, que es el objetivo buscado por la artista.
 Dibujo de la serie Poema de los números primos (1983 – 1985), de Esther Ferrer, expuesto en la Galería Angels Barcelona, que reproduce la espiral de Ulam en una cuadrícula 16 x 16
Dibujo de la serie Poema de los números primos (1983 – 1985), de Esther Ferrer, expuesto en la Galería Angels Barcelona, que reproduce la espiral de Ulam en una cuadrícula 16 x 16
Stanislaw Ulam también realizó una espiral similar, pero empezando con el número 17, de forma que los números de una de las dos diagonales principales se correspondían con los valores, desde n = 0 hasta 15, del polinomio n2 + n + 17, eran números primos (17, 19, 23, 29, 37, …, 257), lo cual fallaba para el siguiente valor, n = 16, que es un número compuesto, 162 + 16 + 17 = 172. Este polinomio ya era conocido por el matemático suizo Leonhard Euler (1707 – 1783), como un polinomio que generaba muchos números primos.
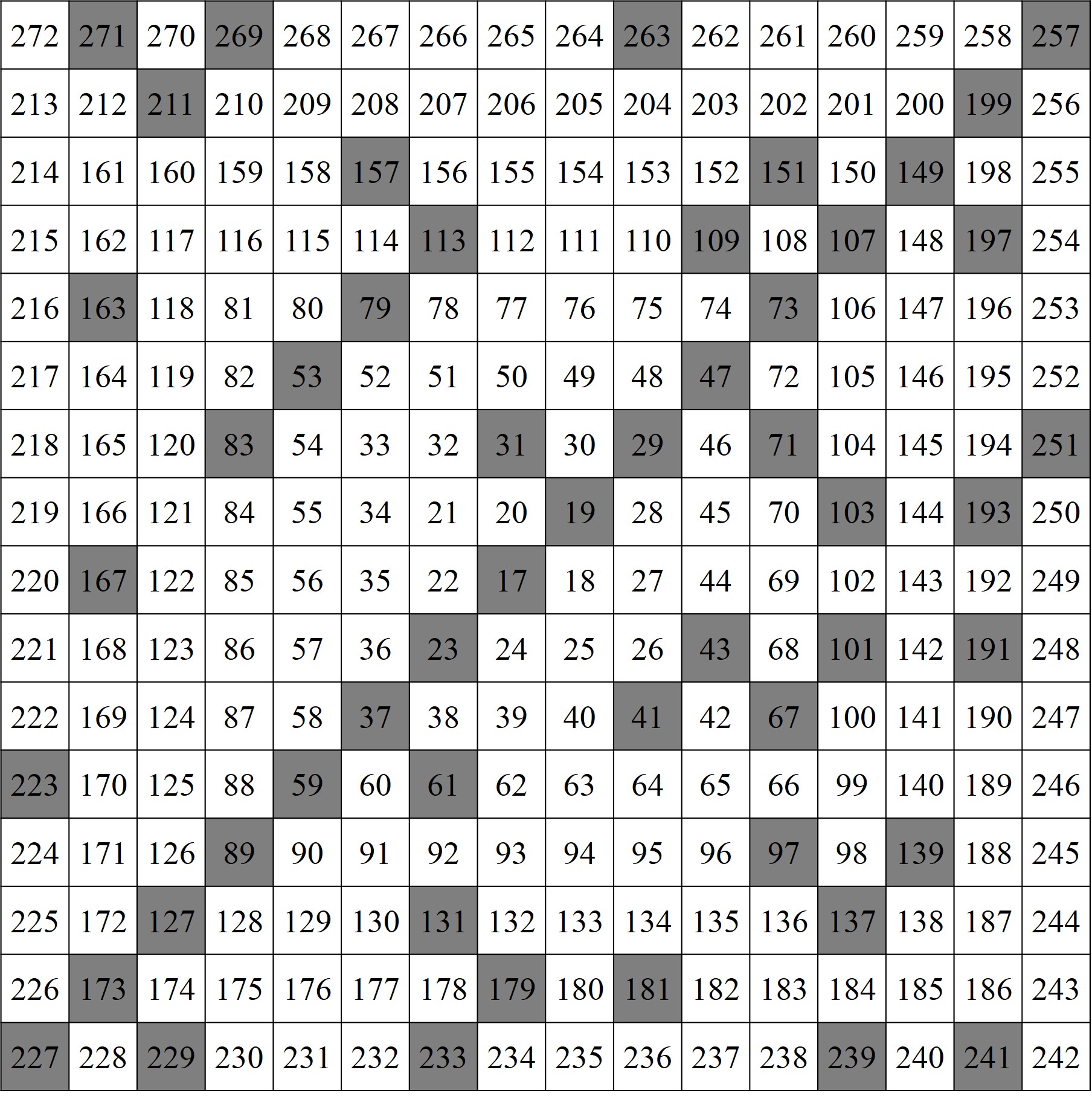 Espiral de Ulam empezando en el número 17, cuyos números de la diagonal son valores del polinomio n2 + n + 17, y son números primos para n = 0, …, 15, es decir, entre el 227 de abajo a la izquierda y el 257 de arriba a la derecha
Espiral de Ulam empezando en el número 17, cuyos números de la diagonal son valores del polinomio n2 + n + 17, y son números primos para n = 0, …, 15, es decir, entre el 227 de abajo a la izquierda y el 257 de arriba a la derecha
Un polinomio que genera muchos números primos y que también era conocido por el matemático Leonhard Euler (1772) es n2 + n + 41. Si se inicia la espiral de Ulam en el número 41, los números de la diagonal principal son valores de este polinomio generador de primos de Euler y para los valores entre n = 0 y n = 39, se genera un segmento continuo en esa diagonal de 40 números primos, que durante más de dos siglos fue el segmento más grande conocido de este tipo. Ulam, Stein y Wells encontraron que, para valores de n entre 0 y 10.000.000, el polinomio n2 + n + 41 genera un 47,5% de números primos, casi uno de cada dos (aunque en esta entrada no vamos a dedicarnos a este tema, en matemáticas se han continuado estudiando polinomios que generan muchos números primos). Los valores de este polinomio n2 + n + 41 son, en la espiral de Ulam empezando en 1, los valores del polinomio es 4m2 + 170m + 1847, haciendo el cambio n = 2m + 42.
La espiral de Ulam empezando en el número 41 alcanzó cierta notoriedad por esa diagonal principal con un segmento de 40 primos seguidos, con el 41 en el medio, 19 primos hacia abajo en la diagonal, hasta el número 1523, y 20 primos hacia arriba, hasta el número 1601.
 Dibujo de la serie Poema de los números primos (años 1970 – 1980), de Esther Ferrer, basado en la espiral de Ulam que empieza en el número 41, y con los 40 números primos en la diagonal principal. Imagen del catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta
Dibujo de la serie Poema de los números primos (años 1970 – 1980), de Esther Ferrer, basado en la espiral de Ulam que empieza en el número 41, y con los 40 números primos en la diagonal principal. Imagen del catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta
El anterior dibujo fue la base para la realización de una obra de la serie Poema de los números primos en el parque del Prado en Vitoria-Gasteiz, en 2003. Es una espiral de Ulam de 100 x 100 = 10.000 “números”, que empieza en el número 41 y cuyo último número primo es 10.039. Está realizada con baldosas de cerámica, de tamaño 20 x 20 cm cada una, en las que aparece una diagonal roja, una diagonal azul o un número primo. Luego el tamaño de la obra es de 20 x 20 metros.
 Instalación Poema de los números primos (2003), de la artista Esther Ferrer, en el parque del Prado (Vitoria-Gasteiz). Imagen de la web de ARTIUM
Instalación Poema de los números primos (2003), de la artista Esther Ferrer, en el parque del Prado (Vitoria-Gasteiz). Imagen de la web de ARTIUM
Esther Ferrer explica así el objetivo de elegir esa obra para el parque del Prado de Vitoria-Gasteiz:
“– es una obra que incita a la reflexión puesto que no corresponde exactamente a los cánones más o menos establecidos sobre lo que es o no es una obra de arte,
– es una obra dinámica, con posibilidades de interactividad libre y espontánea, sin normas,
– además de su belleza intrínseca, esta pieza aporta un elemento lúdico, puesto que los niños que frecuenten el parque jugarán sobre ella y quizás inventarán a partir de la misma sus propios juegos,
– podrán también empezar a comprender que las matemáticas no son forzosamente aburridas, y que con ellas puede hacerse incluso arte,
– por último, podrán aprender, iniciarse, sin prácticamente darse cuenta, en el universo de los números primos, esos números tan particulares, casi mágicos, conocidos desde la más remota antigüedad y que actualmente presentan una gran utilidad en diferentes campos, tanto científicos, como técnicos.”
 Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Imagen de la página de Esther Ferrer
Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Imagen de la página de Esther Ferrer
Como bien explica Esther Ferrer en su libro Maquetas y dibujos de instalaciones 1970/2011, para toda una serie de dibujos-maquetas de números primos, estos están “pensados para suelos, alfombras, murales por lo que pueden realizarse en materiales diversos (azulejo, lana, seda, hormigón,…). En los cuadrangulares o rectangulares se hace una cuadrícula y cada cuadrado es un número. Se marcan en esa enumeración los primos y luego se unen con hilos, o se dejan en blanco y el resto se colorea … según la variación elegida”.
 Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Imagen de la página de Esther Ferrer
Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Imagen de la página de Esther Ferrer
En este dibujo podemos observar de nuevo, que uno de los elementos importantes en la reflexión artística de Esther Ferrer son las lagunas de números primos, es decir, las zonas de números compuestos, no primos, entre dos números primos. Así, en esta obra, la artista ha coloreado los cuadrados de los números compuestos de los colores negro o rojo en función de la laguna a la que pertenezca el número natural. Por ejemplo, entre los números primos 257 y 263 (abajo en la espiral) aparecen, en la espiral, cuadrados de color rojo correspondientes a los números compuestos entre ellos, 258, 259, 260, 261 y 262, mientras que los cuadrados de la siguiente laguna, entre los números primos 263 y 269, están pintados de negro, 264, 265, 266, 267, 268.
Según vamos avanzando en los números naturales hay una menor cantidad de números primos, una menor densidad dentro de los números naturales, y las lagunas entre números primos son cada vez mayores, como se puede observan en el siguiente dibujo, en el que la artista Esther Ferrer construye una espiral de Ulam empezando en el número 1.344.326.696.347. Como en el dibujo-maqueta anterior, se trata de una cuadrícula 21 x 21, es decir, la correspondiente espiral en ambos casos está formada por 441 números, aunque en este segundo caso hay muchos menos números primos y las lagunas de números primos (los números compuestos entre dos números primos consecutivos) son mayores.
 Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Expuesto en la Galería Àngels Barcelona y en la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta, del Palacio Velázquez (2017). Imagen del catálogo
Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Expuesto en la Galería Àngels Barcelona y en la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta, del Palacio Velázquez (2017). Imagen del catálogo
A continuación, he repintado la estructura de la espiral de Ulam del anterior dibujo-maqueta, en colores azul y verde, para recuperar la espiral que subyace debajo de la obra, y para observar mejor las lagunas de números primos que existen.
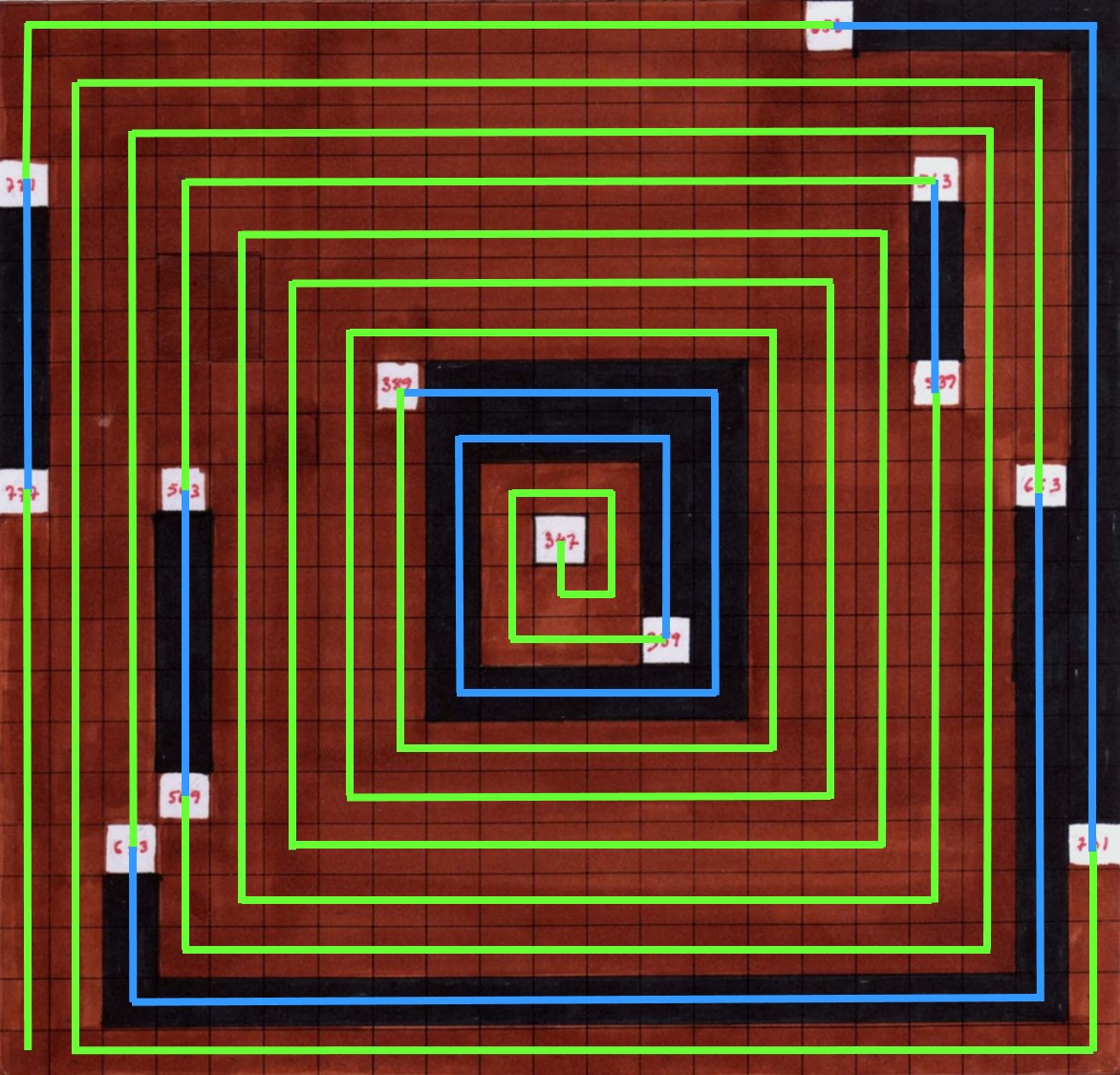
Dialogando con Laurence Rassel y Mar Villaespesa en Esther Ferrer, todas las variaciones son válidas, incluida esta (2017), la artista explica así su trabajo con la espiral de Ulam:
“… puedo trabajar los números primos a partir de la espiral de Ulam. Al utilizarla se crea una línea ininterrumpida durante cierta cantidad de números. Me gustó la idea de escribirlos en espiral, como una galaxia, los números primos tienen algo que ver con la estructura del universo; a medida que progresas en la serie hay menos números, el espacio entre ellos se agranda, me gusta ese vacío, es como si la serie se expandiera, como el universo.”
Existe toda una serie de obras de Esther Ferrer, pertenecientes a la serie Poema de los números primos, que tienen como punto de partida la espiral de Ulam, empezando en el número 41. A continuación, mostramos algunos ejemplos, que además nos muestran como la intervención creativa de la artista da lugar a diferentes resultados. La primera está realizada con hilos, alfileres de colores y tinta sobre lienzo, en la cual los colores están asociados con los números primos, de hecho, con la terminación en 1 (rojo), 3 (verde), 7 (azul) o 9 (amarillo) del número primo.
 Poema de los números primos (1980), de Esther Ferrer, realizada con hilos, alfileres y tinta sobre lienzo, de 122 x 120 cm. Obra expuesta en la Galería Àngels Barcelona.
Poema de los números primos (1980), de Esther Ferrer, realizada con hilos, alfileres y tinta sobre lienzo, de 122 x 120 cm. Obra expuesta en la Galería Àngels Barcelona.
 Detalle de la obra Poema de los números primos (1980), de Esther Ferrer, realizada con hilos, alfileres y rotulador sobre lienzo, de 122 x 120 cm. Obra expuesta en la Galería Àngels Barcelona
Detalle de la obra Poema de los números primos (1980), de Esther Ferrer, realizada con hilos, alfileres y rotulador sobre lienzo, de 122 x 120 cm. Obra expuesta en la Galería Àngels Barcelona
Las diferentes intervenciones artísticas de Esther Ferrer, sobre la misma base de la espiral de Ulam, generan diferentes patrones geométricos planos, como se pone de manifiesto con estas obras.
 Una de las tres partes de un tríptico de la serie Poema de los números primos (años 1980), de Esther Ferrer, realizada con rotulador e hilos sobre papel, de 68 x 67 cm
Una de las tres partes de un tríptico de la serie Poema de los números primos (años 1980), de Esther Ferrer, realizada con rotulador e hilos sobre papel, de 68 x 67 cm
En la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… de Tabakalera también nos encontramos obras que surgen del mismo punto que las anteriores, la espiral de Ulam empezando en el número 41, pero, una vez más, con sus propias características fruto de la acción de la artista.
 Obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera. Fotografía Raúl Ibáñez
Obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera. Fotografía Raúl Ibáñez
Y terminemos esta entrada, con unas palabras de la creadora donostiarra, con motivo de su exposición en Artium en 2011, en relación a su trabajo con los números primos:
“Lo primero que sorprende cuando se comienza a trabajar con la serie de los números primos es que – cualquiera que sea el sistema utilizado – el resultado es siempre equilibrado, hermoso, y lo segundo es que cuanto más grande es la obra, es decir, cuantos más números la forman, más interesante es la estructura, nunca simétrica, siempre en movimiento, por ello siempre he pensado en realizar obras monumentales como suelos, muros, tapicerías etc.
Al penetrar el universo de los números primos se tiene la sensación de que son la traducción, el reflejo, de un caos universal, magnífico, continuamente en evolución, que no se repite jamás, pero que, pese a ello, es siempre el mismo. Un caos en cuyo interior parece existir un orden, un orden extraño, curioso.”
 Obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera. La obra tiene como base la criba de Esratóstenes, donde la inclinación de las diagonales en los lugares de los números compuestos está dada en función de las lagunas de números primos, lo cual genera una curiosa estructura laberíntica. Fotografía de Raúl Ibáñez
Obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera. La obra tiene como base la criba de Esratóstenes, donde la inclinación de las diagonales en los lugares de los números compuestos está dada en función de las lagunas de números primos, lo cual genera una curiosa estructura laberíntica. Fotografía de Raúl Ibáñez
 Detalle de la anterior obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera
Detalle de la anterior obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera
Para concluir esta entrada, me gustaría expresar mi más sincero y profundo agradecimiento a Esther Ferrer por permitirme utilizar las imágenes de sus hermosas e interesantes obras en esta publicación, así como por las interesantes conversaciones que hemos mantenido sobre las matemáticas, y en particular, los números primos, en el conjunto de su obra artística.
Bibliografía
1.- Esther Ferrer, Maquetas y dibujos de instalaciones 1970/2011, Exit publicaciones, 2011.
2.- Rosa Olivares (comisaria), Esther Ferrer, Lau mugimenduan/En cuatro movimientos/In four movements, ARTIUM 08/10/2011 – 08/01/2012, Artium y Acción cultural española, 2011.
3.- Laurence Rassel y Mar Villaespesa (comisarias), Esther Ferrer, todas las variaciones son válidas, incluida esta, Palacio de Velázquez del Parque del Retiro 26/07/2017 – 25/02/2018, Museo Nacional Centro de Arte Reina Sofía, 2017.
4.- Martin Gardner, The remarkable lore of the prime numbers, Scientific American 210, n.3, 120 – 129, 1964.
5.- M. L. Stein, S. M. Ulam, M. B. Wells, A Visual Display of Some Properties of the Distribution of Primes, American Mathematical Monthly 71, p. 516 – 520, 1964.
6.- Paul Hoffman, El hombre que sólo amaba los números, la historia der Paul Erdös y la búsqueda de la verdad matemática, Granica, 2000.
7.- Wikipedia: Ulam spiral
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El poema de los números primos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Buscando lagunas de números no primos
- Una conjetura sobre ciertos números en el ‘sistema Shadok’
- El secreto de los números que no querían ser simétricos
Las redes 5G no afectan a la salud… pero podrían hacer que el hombre del tiempo acierte menos
 Imagen: EUMETSAT
Imagen: EUMETSAT
Igual que la radio en su momento, la televisión después, internet, el wifi o cualquier tecnología inalámbrica, hay gente a la que el 5G le pone nervioso. Esta evolución del 4G promete una forma más rápida y eficaz de transmitir la información y los datos que alimentan nuestros móviles y dispositivos, pero para muchos es una amenaza para la salud por el efecto que sus ondas podrían tener sobre los tejidos de nuestro cuerpo.
Lo cierto es que, igual que ocurre con el wifi, no hay evidencias de que el 5G cause ningún problema en realidad. Esta radiación no ionizante no tiene energía suficiente como para causar ningún efecto sobre nuestros tejidos, más allá de calentarnos levemente la oreja si nos pasamos mucho tiempo con el teléfono pegado a ella. Estudios epidemiológicos han tratado de encontrar una correlación entre la expansión de los teléfonos móviles, y después del wifi, y el número de cánceres y tumores. Si bien correlación no implica causalidad, podría ser la primera señal de que algo pasa. La búsqueda no ha tenido éxito.
Esto no ha impedido que mucha gente se oponga a la implementación de las redes 5G apelando al principio de precaución. En Bruselas, donde la legislación que limita las radiaciones es especialmente estricta, se estaba fraguando una excepción para permitir el desarrollo de un programa piloto de redes 5G que de otra forma sería imposible, pero el gobierno de la ciudad finalmente se ha echado atrás poniendo como motivo la precaución en el cuidado de la salud de sus ciudadanos.
Sí podría afectar a cómo estudiamos la meteorología
Otro grupo está empezando a alzar la voz respecto a los riesgos del 5G, estos parece que con una base un poco mas sólida para sus advertencias. Claro que aquí la salud no tiene nada que ver. Son los meteorólogos.
Según un artículo publicado recientemente en la revista Nature, advierten de que las redes 5G podrían interferir con las observaciones vía satélite que les permiten hacer su trabajo, observar la evolución del clima y hacer sus seguimientos de los fenómenos meteorológicos. En concreto, creen que esto les impedirá detectar y medir con precisión las masas de vapor de agua en la atmósfera. Temen que eso repercuta en peores predicciones meteorológicas en todo el mundo.
Por eso, en Estados Unidos la Administración Nacional para el Océano y la Atmósfera (NOAA) y la NASA están actualmente negociando con la Comisión Federal de Comunicaciones (FCC), que es la que controla las redes inalámbricas en este país. La NOAA y la NASA han pedido a la FCC que les ayude a proteger las frecuencias que se utilizan para las observaciones terrestres y atmosféricas para que el desarrollo de las redes 5G no interfieran con ellos. Pero la FCC sacó recientemente a subasta el primer paquete del espectro 5G sin tener en cuenta esas peticiones.
Un acuerdo global para que no haya interferencias
El debate no ha llegado aun a Europa, pero teniendo en cuenta el liderazgo en telecomunicaciones que ejerce Estados Unidos, sus decisiones seguro que influirán en cómo se trata el tema en otros países. En otoño de este año está previsto que se reúnan legisladores de todo el mundo en Egipto para llegar a acuerdos que permitan desarrollar esta tecnología a nivel global. Allí se debatirá qué frecuencias podrán utilizar estas empresas y cómo asegurar que la protección a las redes meteorológicas está garantizada.
Astrónomos y meteorólogos llevan mucho tiempo asegurándose de que compartir sus espectros de observación con otros usuarios no les causa problemas o interferencias en sus observaciones. Pero ahora, dicen, es la primera vez que ven amenazada su “joya de la corona”, esas frecuencias que consideran que deben ser solo suyas “y que debemos defender pase lo que pase”, explica en Nature Stephen English, meteorólogo del Centro para Predicciones Meteorológicas de Medio Alcance en Reading, Reino Unido.
Dentro de esa joya de la corona estaría la frecuencia de 23,8 GHz a la que el vapor de agua emite una débil señal. Algunos satélites, como el European MetOp, monitorizan constantemente la energía que emite la Tierra a través de esta frecuencia para medir la humedad que hay en la atmósfera justo bajo el satélite. La ventaja de esta medición es que se puede hacer con el cielo despejado o nublado de día o de noche. Los meteorólogos utilizan estos datos para alimentar los modelos que predicen cómo evolucionarán las tormentas y otros elementos climáticos en los días y horas siguientes.
¿Cómo lidiar con los vecinos ruidosos?
El problema con el 5G, dicen, es que una estación emitiendo en la misma frecuencia produciría una señal muy parecida a la de ese vapor de agua, lo cual impediría saber si es de origen natural o no. Incorporar esos datos dudosos haría los modelos mucho menos precisos. Es como tener un vecino ruidoso al otro lado de la pared: si pone la música muy alta, parte de su ruido te llegará a ti; si mantiene el volumen controlado, probablemente te libres del escándalo.
La NOAA y la NASA quieren que la FCC obligue a los vecinos a poner un aislamiento entre ellos y, si eso no es posible, a mantener el volumen a niveles que no les impidan trabajar. El problema es que los niveles que la FCC pide no les parecen suficientemente bajos como para no molestarles: -20 dBW, mientras que la Comisión Europea fija el máximo de ruido en -42 dBW y la Organización Meteorológica Mundial recomienda -55 dBW.
No está muy claro cuánto pueden empeorar las predicciones si las interferencias afectan a los 23,8 GHz y otras frecuencias necesarias para estas observaciones. Un informe de 2010 de las Academias Nacionales de Ciencias, Ingeniería y Medicina concluía que perder el acceso a la señal de los 23,8 GHz supondría eliminar un 30% de los datos útiles en las frecuencias de microondas, que contribuyen significativamente a las predicciones globales.
Referencias:
La tecnología 5G no tiene por qué preocuparte – Maldita Ciencia
Sí, Bruselas ha detenido la implantación de la tecnología 5G, pero no por “amenazar la salud de la humanidad” – Maldita Ciencia
Global 5G wireless networks threaten weather forecasts – Nature
Spectrum Management for Science in the 21st Century – National Academies of Sciences, Engineering and Medicine
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Las redes 5G no afectan a la salud… pero podrían hacer que el hombre del tiempo acierte menos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Menos felices y menos insatisfechos a medida que envejecemos
- Redes y arpones para cazar basura zombie en el espacio
- Hacia las redes 5G
La ley de proporciones definidas y la unidad de masa atómica
 Símbolos químicos de Dalton (1803). Fuente: Wikimedia Commons
Símbolos químicos de Dalton (1803). Fuente: Wikimedia Commons
Durante milenios la idea de que toda la materia está hecha de pequeños e indivisibles trozos llamados átomos ha rondado por la cabeza de los investigadores de la naturaleza. Sin embargo hubo que esperar al siglo XX para obtener una confirmación experimental sin ningún género de dudas. Durante el siglo XIX se habían logrado grandes avances al atribuir las leyes termodinámicas y algunas de las propiedades de la materia, especialmente de los gases, a la teoría cinético-molecular; fue a partir de esta teoría que Einstein en 1905 propuso un modelo del movimiento browniano que Jean Perrin confirmó experimentalmente en 1908, probando más allá de toda duda la existencia de los átomos.
Por otra parte, durante siglos se supo que existen diferentes tipos de los llamados “elementos” fundamentales en la naturaleza: oro, plata, cobre, sodio, etc. Eran los componentes más simples en los que se pueden dividir las sustancias por medios químicos. Finalmente, se encontró útil dar a los elementos símbolos especiales: se empezó usando grafías elaboradas de distinta especie hasta acabar, por motivos puramente operativos, con simples letras, por ejemplo, “C” para el carbono, “O” para el oxígeno, “H” para el hidrógeno, etc.
Para muchas personas, aunque nadie lo expresó tan explícitamente como John Dalton, estos diferentes elementos indicaban que la naturaleza también está formada por diferentes tipos de átomos, un tipo de átomo para cada elemento. Cada elemento no sería más que una colección de átomos idénticos e indestructibles químicamente, una idea que se confirmó en durante todo el desarrollo de la química durante el siglo XIX.
Cuando dos o más átomos se unen, forman una molécula. La molécula puede ser un elemento en sí mismo si ambos átomos son iguales, como en el oxígeno, O2, o puede ser un compuesto si los átomos son diferentes, como el agua, H2O. Dado que los átomos no son divisibles, la idea de unir dos átomos de hidrógeno a, digamos, átomo y medio de oxígeno en lugar de exactamente un átomo de oxígeno no tiene sentido [1].
La ley de las proporciones definidas establecida por Joseph Proust en 1794 es una consecuencia natural de la idea de que los elementos están formados por átomos idénticos e indestructibles. De hecho, Dalton postula su teoría atómica en 1808 en un intento de explicar esta ley (su primera propuesta atómica, mucho más simple, es de 1803). Cuando los elementos se combinan para formar compuestos siempre es necesaria la misma proporción de masas de los constituyentes para hacer un compuesto en concreto. Por ejemplo, 23,0 g de sodio siempre se combinan con 35,5 g de cloro para producir 58,5 g de cloruro sódico (NaCl, sal común). Si tenemos 25,0 g de sodio y 35,5 g de cloro, seguiremos obteniendo solo 58,5 g de sal, y sobrarán 2,0 g de sodio. Esta regla, la ley de proporciones definidas, se aplica a todos los compuestos [2][3].
De la ley de proporciones definidas se deduce que los átomos de los elementos que se combinan para formar compuestos como el NaCl no tienen la misma masa. Dado que solo 23,0 g de sodio se combinan con 35,5 g de cloro para formar 58,5 g de NaCl, los átomos de cloro deben tener más masa que los átomos de sodio. Así, si un átomo de sodio tiene 23,0 “unidades” de masa, entonces un átomo de cloro tendría 35,5 unidades de masa. Las unidades de masa pueden ser gramos, kilogramos, libras o lo que sea. Por conveniencia, se denominan unidades de masa atómica, para las cuales el símbolo estándar es u.[4]
Ahora sabemos que solo existen 94 [5] elementos diferentes que ocurren naturalmente en toda la naturaleza y, de hecho, en todo el Universo. Los átomos de cada elemento tienen una masa concreta expresada en unidades de masa atómica . Hoy en día, las unidades de masa atómica se miden en relación con un tipo, o isótopo [6], del carbono conocido como carbono-12 (12C), que se define como una masa atómica de 12,0000 u. Las masas atómicas de todos los demás elementos se dan en relación con el carbono-12. Por ejemplo, en relación con el carbono-12, el sodio natural tiene una masa atómica de 22,990 u, el hidrógeno tiene una masa atómica de 1,008 u, el oxígeno tiene una masa atómica de 15,999 u, el uranio tiene una masa de 238,029 u, y así todos los demás [7].
Algunos de estos elementos tienen propiedades similares: algunos son gases a temperatura ambiente; otros son metales sólidos. Existen diferencias en las densidades, los puntos de fusión y ebullición, la conductividad eléctrica, etc. Estas propiedades parecen seguir ciertas pautas. Para entender por qué son las que son y cómo varían iniciamos aquí un viaje al interior de los átomos. [8]
Notas:
[1] De la misma forma no tiene sentido diluir una sustancia por debajo de una concentración en la que haya menos de un átomo en la unidad de volumen considerado. Así de simple se demuestra que la homeopatía y sus diluciones cuasi infinitas es falsa. Dicho de otra forma: si los átomos existen, y existen, entonces la homeopatía es falsa. De aquí se sigue, primero, que cualquiera que quiera venderte o recomendarte homeopatía es o un ignorante o un estafador; segundo, que cualquier dinero empleado en demostrar una imposibilidad manifiesta es dinero tirado a la basura.
[2] La ley establece que para un compuesto dado las proporciones están definidas. Eso no quiere decir que dos elementos no puedan formar compuestos diferentes.
[3] Hoy sabemos que la ley de proporciones definidas no es estrictamente cierta. Si bien el argumento que exponemos es plenamente válido, la química de precisión actual sabe que existen proporciones variables en los compuestos debido a pequeñas impurezas (naturales o artificiales, como el dopado) y las características de las redes cristalinas.
[4] La unidad de masa atómica no forma parte del Sistema Internacional de unidades.
[5] Habrá lugares en los que leas 92. Depende de la antigüedad de la fuente.
[6] A lo largo del siglo XX se descubrió que todos los átomos de un elemento son iguales en sus características pero que pueden existir varios valores de la masa. Cada uno de los valores de masa corresponde a un isótopo. Ya llegaremos a esto más avanzada esta serie. Paso a paso.
[7] Aquí tienes la última tabla oficial publicada por la IUPAC (2013).
[8] Será un viaje largo pero muy entretenido, en el que, como siempre, solo emplearemos matemáticas elementales.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La ley de proporciones definidas y la unidad de masa atómica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La relatividad de la masa
- Equivalencia entre masa y energía
- La óptica se hace atómica: la lente más pequeña del mundo
El selenio, esencial y peligroso
 La Luna en el De Astronomia (Libri X) de Guido Bonatti (1550), representada por Selene
La Luna en el De Astronomia (Libri X) de Guido Bonatti (1550), representada por Selene
Ciertos elementos químicos, como el oxígeno o el hierro, por ejemplo, nos resultan familiares. Los nombres que los designan son de uso cotidiano. Pero lo normal es que de la mayoría no hayamos tenido noticia, salvo en las aulas. El selenio (Se), por ejemplo, es un gran desconocido. Quizás hemos visto su nombre en la formulación de alguna loción o champú, o hemos sabido de su uso en electrónica para hacer rectificadores de corriente en el pasado. Y poco más.
Fue descubierto en 1817 por el barón sueco Jakob Berzelius, considerado uno de los padres de la química moderna, y su colega y socio Joseph Gottlieg Gahn. Producían ácido sulfúrico en la fábrica de la que eran propietarios, y utilizaban para ello pirita procedente de la mina de Falun. La mina es muy conocida porque se comenzó a explotar alrededor del año 1000 y desde entonces ha proporcionado el 75% del cobre consumido en Europa hasta 1998, año en que se clausuró al dejar de ser rentable. Tres años después la UNESCO la declaró Patrimonio de la Humanidad.
El proceso de producción del sulfúrico dejaba lo que se denomina un precipitado (restos sólidos) de color rojo del que, al principio, Berzelius pensó que era un compuesto de arsénico. Pero su olor recordaba, más bien, a otro elemento, el telurio, que había sido descubierto en 1782 y con el que tiene cierta semejanza. Por esa razón, y porque al elemento descubierto 35 años antes se le nombró haciendo referencia al nombre latino de Tellus (Tierra), al nuevo elemento Berzelius lo denominó Selenium, por referencia a Selene, nombre griego de la diosa que personificaba a la Luna.
Según cuenta Daniel Torregrosa en su recomendable libro “Del mito al laboratorio”, Selene se enamoró del joven Endimión, un mortal de ilustre estirpe, pero mortal al fin y al cabo. Pidió por ello a Zeus que hiciese inmortal a su amado y Zeus, que tenía esas cosas, le concedió el deseo pero con la condición de que Endimión durmiese para siempre. Su estado de eterno durmiente no fue obstáculo, empero, para que Selene lo visitase cada noche y yaciese con él. Fruto del trajín llegó a concebir, al parecer, nada menos que cincuenta hijas. Sorprende que, siquiera por tal proeza, no fuese entronizada diosa de la fertilidad, honor que sin duda merecía. Quiere la casualidad, además, que haya una forma de infertilidad masculina, caracterizada por una movilidad espermática reducida, que se debe a la carencia de selenio.
El selenio es esencial para la vida. Aunque en concentraciones altas es muy dañino y puede ser letal, en concentraciones adecuadas (bajas) es necesario para el normal desarrollo de las funciones vitales. Por eso se suele incluir en complejos multivitamínicos y suplementos dietéticos.
Ese estrecho rango de concentraciones en que se requiere para un desarrollo óptimo de las funciones vitales tiene y ha tenido consecuencias curiosas e importantes. Por exceso de incorporación con la comida o el agua, el selenio ha sido causa de envenenamientos en animales y seres humanos. Hay lagos, ríos y bahías en los que se encuentra en concentraciones tóxicas a causa de la contaminación de origen industrial.
Pero su baja concentración en el medio es también perjudicial. Tres grandes extinciones de especies en la historia de la vida –las ocurridas al final de los periodos Ordovícico, Devónico y Triásico- han sido vinculadas con fuertes reducciones de la concentración de selenio en los océanos. Por el contrario, también se cree que favoreció la explosión del Cámbrico de hace quinientos millones de años, cuando surgió la mayoría de los grupos animales.
——————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El selenio, esencial y peligroso se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un cóctel peligroso
- “Conócete a ti mismo” no solo es un consejo estúpido, es realmente peligroso
- Sangre de dragón
¿Qué comes cuando comes comida basura?
Hay quien lo denomina “comida rápida” y quien lo llama “comida basura”. Llamemosle de una u otra manera, si la comemos dos veces por semana y mantenemos ese ritmo, en una década ganaremos entre 4 y 5 kg más que alguien que coma este tipo de comida solo una vez por semana.
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Qué comes cuando comes comida basura? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué pasa en tu cuerpo cuando te enamoras?
- ¿Qué pasa en tu cerebro cuando duermes?
- La comida en la basura
50 años de secretos: la era de la criptografía moderna
Tres personas que no se conocen, Ander, Blanca y Eva, se encuentran aisladas en una habitación. Blanca necesita saber la edad de Ander, que Eva no debe conocer bajo ningún concepto. ¿Hay alguna forma de que Ander pueda responder a Blanca sin revelar la información a Eva? Todo lo que cada uno diga o haga lo escucharán o verán los otros dos.
El sentido común dice que no: Blanca y Eva ven y oyen exactamente lo mismo, si en un momento dado una de ellas tiene información suficiente para deducir la edad de Ander, la otra la tendrá igualmente. Este problema, de haberse planteado hace cincuenta años, habría tenido seguramente la misma respuesta escéptica, sin embargo, en aquella época las cosas estaban cambiando.
Comenzaba una revolución, silenciosa para el ciudadano de a pie, cuyas consecuencias pocos podían prever. Se vivía el inicio de la revolución digital. Pesadas máquinas que llenaban habitaciones enteras eran capaces de efectuar cálculos y almacenar datos con una rapidez y un volumen desconocidos hasta entonces (que hoy nos haría sonreír) y poco a poco abandonaban los laboratorios de los centros de investigación para hacerse presentes en bancos y grandes industrias. Incluso con sus limitaciones, el manejo de grandes cantidades de datos trajo consigo nuevos retos a los que dar solución. Entre otros, establecer procedimientos para asegurar que la información se procesaba y transmitía libre de errores y protegerla de quien pudiera hacer uso malintencionado de ella.
No se puede decir que estos problemas fueran nuevos, pero sí lo era la escala de los potenciales afectados. En la era pre-digital la información que de verdad requería protección era relativamente poca, limitada esencialmente a ámbitos militares o de la burocracia gubernamental y en esos casos el coste que suponía mantener el nivel adecuado de seguridad era alto pero asumible.
La información es especialmente vulnerable mientras se transmite, antes o después de este momento su custodia no presenta grandes dificultades, pero ¿cómo puede protegerse mientras viaja a su destinatario por un canal que casi siempre escapa a nuestro control? La herramienta es el cifrado. En la era analógica, por llamar así a toda la historia de la humanidad salvo los aproximadamente últimos cincuenta años, la solución no dejaba de ser más o menos simple. Digamos que al espía o diplomático se le proveía de un “libro de claves” del que el receptor mantenía una copia.
En su versión más simple (pero también la más perfecta) un libro de claves no es más que una larguísima secuencia aleatoria de bits, es decir ceros y unos. Para cifrar un mensaje, que ya suponemos transcrito al lenguaje binario, el emisor suma simplemente los bits del mensaje, uno a uno, con los del libro empezando por el primero (emplea la suma binaria en la que 1+1=0). Así el mensaje cifrado resulta ser una cadena de bits tan aleatoria como la del libro y el enemigo que eventualmente capture el mensaje cifrado no tendrá absolutamente ninguna posibilidad de recuperar el mensaje original. Sin embargo, el receptor del mensaje, poseedor de una copia del libro de claves, no tiene ninguna dificultad puesto que si hace exactamente lo mismo que hizo el emisor descifrará el mensaje. Este es el esquema de la criptografia clásica, conocido y utilizado por la humanidad desde las civilizaciones más antiguas.
¿Pero por qué no sirve la criptografía clásica en el mundo digital? Pues porque exige algo que parece fácil a simple vista pero que en el mundo virtual es inviable por su coste: acordar cuál es el libro de claves. No es aceptable que cada vez que queramos comunicarnos con alguien, sea una persona de carne y hueso, una entidad bancaria, un comercio o una administración, estemos obligados a contactar previamente con ella, físicamente o mediante otro medio no digital, para establecer nuestra contraseña. Necesitamos hacerlo a través del mismo canal digital inseguro por el que se transmite toda la información. Estamos justamente enfrentados al problema de Ander, Blanca y Eva.
No está claro a quién atribuir la solución a este acertijo, sin la cual gran parte del mundo actual no podría funcionar. En 1976 los investigadores de la universidad de Stanford W. Diffie y M. Hellman publicaron un artículo que se considera el nacimiento oficial de la criptografía moderna, aunque, según parece, agencias de seguridad de algunos países ya habían desarrollado ideas similares poco antes. El fechar este suceso hace cincuenta años ha sido simplemente una pequeña licencia al hilo de la celebración del nacimiento de nuestra facultad.
Intentemos explicar en qué consiste eso de la criptografía moderna con un símil. Cifrar un mensaje no es más que meterlo en una caja que cerramos con un candado. En la criptografía clásica, como en la vida real, la “llave” que encripta y desencripta, esto es, la que cierra y abre el candado, es la misma, por eso no le sirve a Blanca, porque si le dice a Ander cómo tiene que encriptar, Eva, que está atenta, se da cuenta inmediatamente, no sólo de cómo encriptar, lo cual es inocuo, sino también, y esto es lo que queremos evitar a toda costa, de cómo desencriptar. Al dar la llave de cerrar a Ander, Blanca le está dando también la de abrir a Eva, puesto que es la misma (es decir, al dar la regla para encriptar a Ander le está dando sin querer la regla para desencriptar a Eva).
Lo que los descubridores (o inventores, cada cual que elija el término que considere más adecuado) de la criptografía moderna plantearon es que todo sería muy distinto si hubiera dos llaves diferentes, una para cerrar y otra para abrir. Entonces no habría ningún problema, Blanca podría dar con total tranquilidad una copia de la llave de cerrar a Ander (y también a Eva o a cualquiera) pero sólo ella retendría la llave de abrir. Así Eva vería pasar ante sus ojos la caja cerrada pero no podría hacer nada porque la llave que tiene sólo sirve para cerrar, es inútil para abrir.
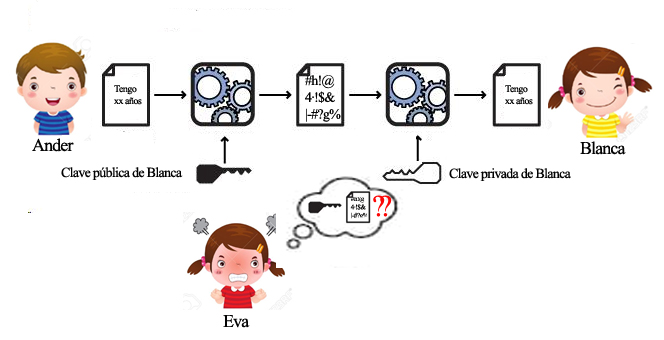 Fuente: elaboración propia a partir de Public Key Private Key Cryptography
Fuente: elaboración propia a partir de Public Key Private Key Cryptography
Lo anterior puede sonar convincente, pero sucede que las acciones de encriptar y desencriptar están inexorablemente ligadas, una no es más que el proceso inverso de la otra (como en el mundo real: cerramos girando la llave en un sentido y abrimos girándola en el sentido contrario). Sin embargo, es un hecho bastante común, al menos en el mundo matemático, que cuando dos procesos son inversos uno del otro, uno de ellos es mucho más costoso que su recíproco (así, es más difícil restar que sumar, dividir que multiplicar, extraer la raíz cuadrada que elevar al cuadrado… o recomponer los añicos de un jarrón chino que estrellarlo contra el suelo). Pero sucede que esto que nos protege de Eva, también afecta a Blanca, es decir para que nuestro esquema tenga sentido el proceso inverso (desencriptar) debe ser de una dificultad insuperable para Eva pero no para Blanca, que necesita saber cómo hacerlo para recuperar el mensaje original de Ander.
Las matemáticas están llenas de problemas difíciles, algunos con cientos o incluso miles de años de antigüedad, y que en ocasiones tienen enunciados arcanos sólo al alcance de iniciados. Afortunadamente éste no es el caso del que vamos a comentar ahora y que encaja en la tipología de los problemas inversos de los que hablábamos en el párrafo anterior. En la escuela todos aprendimos a multiplicar, primero los números de una cifra (un ejercicio de memorización) y luego los de dos o más. Ningún lector tendrá dificultad en realizar 17×71 o cualquier otra multiplicación que se quiera plantear, incluso aunque los factores tengan muchas más cifras. Es verdad que, si fueran dos números de, digamos, cien cifras, seguramente no tendríamos la paciencia suficiente para terminar (y, además, ¿qué interés puede haber en semejante operación?), sin embargo, con tiempo y motivación sería factible. Ni que decir tiene que un ordenador puede hacer este cálculo prácticamente al instante.
Lo interesante es ver qué pasa si lo intentamos al revés, es decir, si damos el resultado y el problema es encontrar dos números cuyo producto sea el indicado. Claro, si damos un número par es muy fácil. Pero ¿si damos 2021? (no hemos dado 2019 por razones obvias y tampoco 2017, por razones, quizá no tan obvias, que el lector sabrá adivinar). Pues no se me ocurre nada mejor que tantear: dividir entre 3, 5, 7, 11, 13, etc. (el lector reconocerá y entenderá por qué pruebo con estos números y no con 4, 6, 8, 9, 10, etc). Y sí, eventualmente encontramos que 2021=43×47. Pero, ¿y si en lugar de un número con 4 cifras damos uno con 100? La respuesta es que con un número bien elegido de 100 cifras hasta un potente ordenador tendría dificultades en encontrar su factorización, al menos en un tiempo razonable. Y si en lugar de 100 ponemos 200 ó 250 cifras podemos tener casi la certeza absoluta de que ni siquiera los grandes supercomputadores de las agencias de seguridad gubernamentales serían capaces de encontrar sus factores. Y que no piense el lector que el único método de factorización es la pura fuerza bruta de prueba y error como hemos podido dar a entender, pues en tal caso un número con sólo unas pocas decenas de cifras sería ya imposible de factorizar de esta manera. Se conocen algoritmos de factorización altamente sofisticados que utilizan matemáticas muy profundas, pero incluso estos algoritmos tienen limitaciones que, a día de hoy, hacen que podamos considerar imposible factorizar un número con 200 cifras.
Entonces ¿qué instrucciones da Blanca a Ander? Pues en primer lugar le proporciona dos números, digamos 2021 y 59; a continuación, le explica que calcule el resultado de elevar su edad a la potencia 59 y que cuando termine le diga el resultado. Hay un pequeño detalle: debe hacer las multiplicaciones de una manera un poco distinta a la habitual (y de hecho más simple): sólo debe considerar números de 0 a 2020, es decir debe tener en cuenta que a 2020 no le sigue 2021 sino ¡cero! y luego otra vez 1, etc. (por ejemplo, como 6561=3×2021+498, el número 6561 no es tal, sino 498). Con este procedimiento si la edad de Ander fuera 3 años (es sólo un ejemplo explicativo) calcularía
359 = ((((32)2)2)2)2×(((32)2)2)2×((32)2)2×32×3 = (65612)2×65612×6561×9×3
= (4982)2×4982×498×9×3 =…= 929.
Y éste sería el número que escucharíamos decir al pequeño (y superdotado) Ander. Sucede que Blanca sabe algo que, para dar verosimilitud a nuestra historia, suponemos nadie más conoce: la factorización 2021=43×47. Con los números 43, 47 y 59 y unas pocas matemáticas, que no tienen nada de secretas y se conocen bien desde hace más de 250 años, pero que por no abusar de la paciencia del lector no explicamos, Blanca calcula el número mágico 131, que es su clave secreta de descifrado. Y el milagro se produce: cuando Blanca eleva 929 a la potencia 131 y opera a la manera que antes hizo Ander, obtiene… ¡3! Eva, que sí conoce las matemáticas, pero no los factores 43 y 47, se ve incapaz de descubrir el número mágico 131 y por tanto se queda sin saber qué hacer con el número 929.
El sistema criptográfico que acabamos de explicar se llama RSA, es el primer sistema de clave pública que se descubrió y uno de los más utilizados desde entonces. La única diferencia es que obviamente no se emplean números como 43 y 47 sino números primos con 80 ó 100 cifras.
Así que finalmente Ander habla y dice: “Tengo 57 años”, a lo que Blanca responde, “Bonita edad. Además, es un número primo”.
Para saber más:
W. Diffie, M. E. Hellman (1976) “New Directions in Cryptography” IEE Transactions on Information Theory 22, no. 6, 644-654. Disponible como PDF aquí.
J. Sangroniz (2004) “Criptografía de clave pública: el sistema RSA” Sigma 25, 149-165. Disponible en como PDF aquí.
Sobre el autor: Josu Sangroniz es Profesor de Álgebra en el Departamento de Matemáticas de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo 50 años de secretos: la era de la criptografía moderna se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:¿Qué hay más allá de la orilla del mar?
![]()
 Shutterstock
Shutterstock
El relieve submarino es un gran desconocido. Aunque parezca extraño, en pleno siglo XXI conocemos mejor la topografía de algunos parajes marcianos que la de casi tres cuartas partes de nuestro propio planeta.
Desde la orilla no divisamos qué se esconde bajo el agua, ni tampoco podemos vaciar el mar para acceder al fondo. Por eso, el estudio de las profundidades marinas, denominado batimetría, se aborda de manera indirecta mediante el uso de ecosondas.
Estos aparatos emiten ondas acústicas hacia el fondo, cronometran cuánto tardan en regresar a la superficie y transforman el tiempo en valores de profundidad. Permiten obtener muchos datos batimétricos, pero son instrumentos complejos que requieren barcos capaces de realizar largas navegaciones.
El mar es vasto, inabarcable en ocasiones. A pesar de los esfuerzos de los últimos años, apenas hemos escudriñado un 5 % del total de los fondos oceánicos. Pero lo que hemos ido descubriendo revela que el relieve submarino dista de ser uniforme o aburrido. Es más, a menudo topamos con una asombrosa y accidentada topografía.
 Batimetría general de los océanos. La imagen está generada usando datos globales de baja resolución. Las zonas más profundas, en tonos azulados, se sitúan entre las dorsales medio-oceánicas (tonos amarillo-verdosos) y los márgenes continentales (tonos anaranjados).
Batimetría general de los océanos. La imagen está generada usando datos globales de baja resolución. Las zonas más profundas, en tonos azulados, se sitúan entre las dorsales medio-oceánicas (tonos amarillo-verdosos) y los márgenes continentales (tonos anaranjados).CC BY
Los principales rasgos del relieve submarino
En el fondo marino existen grandes cordilleras, extensas llanuras, profundas hondonadas y escarpados valles. Al igual que sus homólogos terrestres, estos relieves evolucionan en respuesta a una serie de procesos geológicos.
En el centro de casi todos los océanos encontramos las dorsales medio-oceánicas, que se alzan hasta 3.000 metros por encima de los fondos adyacentes. Estas elevaciones submarinas recorren una longitud total de 80.000 km y recubren cerca del 23 % de la superficie del planeta. Constituyen, de largo, la cadena montañosa más grande de la Tierra.
Entre las dorsales y las áreas continentales, a profundidades de entre 3 000 y 6 000 metros, se localizan las llanuras abisales. Estas extensas y monótonas regiones de centenares de km², destino final de muchos sedimentos oceánicos, son casi planas. Las más desarrolladas ocupan buena parte del suelo del océano Atlántico.
Los márgenes continentales son los fondos marinos adyacentes a los continentes y ocupan el 28 % del área cubierta por el mar. Por su proximidad, y por la importancia económica de muchos de los recursos que alberga, son la parte mejor conocida del relieve submarino.
Existen dos tipos principales de márgenes continentales. Los que presentan poca actividad sísmica se conocen como márgenes pasivos. Están formados por acumulaciones de sedimentos procedentes de la erosión de los continentes. Pueden extenderse centenares de kilómetros y se localizan, sobre todo, en las zonas costeras que bordean los océanos Índico y Atlántico.
Por su parte, los márgenes activos tienen mayor actividad sísmica. Presentan un desarrollo sedimentario menor y se localizan sobre todo en el océano Pacífico. Un rasgo distintivo es la presencia de un estrecho surco que se conoce con el nombre de fosa oceánica.
Las fosas oceánicas constituyen uno de los accidentes topográficos más espectaculares de la Tierra. Pueden tener miles de kilómetros de largo y son muy hondas. La fosa de la Marianas, situada al oeste de Filipinas, supera los 11.000 metros de profundidad. Es el lugar más profundo del planeta.
 Relieve en color del margen continental catalán y del continente adyacente, generado a partir de datos de alta resolución. Destaca el tamaño de los valles submarinos en relación con los valles fluviales. De sur a norte, los principales cañones de la zona son el de Valldepins (VA), del Foix (FO), del Besòs (BE), de Arenys (AR), de Blanes (BL), de Palamós (PA) y del Cap de Creus (CC).
Relieve en color del margen continental catalán y del continente adyacente, generado a partir de datos de alta resolución. Destaca el tamaño de los valles submarinos en relación con los valles fluviales. De sur a norte, los principales cañones de la zona son el de Valldepins (VA), del Foix (FO), del Besòs (BE), de Arenys (AR), de Blanes (BL), de Palamós (PA) y del Cap de Creus (CC).
Los valles submarinos
Entre los relieves más sobresalientes que salpican los fondos marinos destacan los valles submarinos. Estos se clasifican según el tipo, la intensidad y la duración de los procesos que los generan y mantienen activos.
Podemos encontrar desde surcos de origen glaciar en latitudes polares hasta canales profundos que serpentean el lecho marino en las cercanías de las grandes desembocaduras fluviales.
Los valles largos, sinuosos y encajados que cortan gran parte de los márgenes continentales se llaman cañones submarinos. Estos relieves erosivos actúan a modo de conductos: transfieren sedimentos, materia orgánica, desechos y contaminantes desde las zonas costeras hacia las partes profundas de las cuencas oceánicas.
Su distribución es global, con más de 5 800 cañones contabilizados. Sus tamaños son comparables a los de los grandes cañones terrestres. Pero algunos, situados en el mar de Bering entre Siberia y Alaska, son gigantescos y rebasan los 100 km de anchura, 400 km de longitud y 2 km de desnivel entre el borde y el fondo.
 Relieve 3D del cañón de Palamós, visto en detalle desde el sudeste. Este cañón se conoce también con el nombre de La Fonera.
Relieve 3D del cañón de Palamós, visto en detalle desde el sudeste. Este cañón se conoce también con el nombre de La Fonera.
Los cañones del margen continental catalán
No hay que ir tan lejos para tropezarnos con estos relieves. Gran parte del margen catalán está cortado por profundos y largos cañones cuyas dimensiones superan a las de cualquier valle terrestre cercano.
Un par de ellos llaman la atención.
El cañón de Blanes, cerca de la desembocadura del río Tordera, es el mayor y más complejo de todo el margen. Su trazado es sinuoso, sobre todo en los tramos inferiores, y supera los 150 km de longitud. En algunas tramos del curso superior la anchura sobrepasa los 20 km.
Más al norte, en la Costa Brava, el imponente cañón de Palamós inicia su andadura casi al tocar los acantilados litorales y se hunde hasta recorrer unos 110 km. En su curso superior presenta unas vertientes muy abruptas, una anchura de 16 km y un desnivel de más de 1 km.
Los cañones del margen catalán son también vías preferentes de transporte para el material que proviene del continente. Muchos estudios destacan el importante papel que desempeñan en la dinámica oceanográfica y en los procesos que controlan el funcionamiento de los ecosistemas marinos de la zona.
Así, la abundancia relativa de alimento que allí se encuentra y sus condiciones ambientales favorecen la proliferación de algunas especies marinas, algunas de ellas de gran interés pesquero. Esto los convierte en lugares muy ricos en biodiversidad.
¿Por qué estudiar el relieve submarino?
El conocimiento detallado del relieve submarino ayuda a mejorar la explotación de los recursos vivos marinos. Los mapas batimétricos también mejoran la seguridad de la navegación.
Otras aplicaciones incluyen temas de gestión litoral, como la protección de hábitats marinos y la regeneración de playas. También de ingeniería costera, como la instalación de infraestructuras y la construcción de puertos. Incluso para la localización de recursos como el petróleo y el gas.
Los reconocimientos batimétricos, por último, ayudan a los científicos a mejorar la interpretación de los estudios relacionados con el cambio climático, la evolución histórica de la línea de costa y la propagación e incidencia de los tsunamis.
Falta todavía mucho por reconocer, sobre todo en detalle. Tendremos que redoblar esfuerzos. Confío en que el próximo verano, tumbados de nuevo en la orilla del mar, recuerden y valoren que allí delante bajo el mar se extiende un paisaje especial que merece ser explorado.![]()
Sobre el autor: José Luis Casamor es profesor de Geología Marina en la Universitat de Barcelona
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Qué hay más allá de la orilla del mar? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Geología, ver más allá de lo que pisamos
- Más allá del mar de Yukawa
- Arrecifes fósiles, una paradoja geológica
Gráficas para la ciencia y ciencia para las gráficas
A menudo, las innovaciones en ciencia son, ante todo, herramientas que simplifican la manera de abordar un problema, transformaciones que lo hacen más aprehensible a través de nuestros sentidos (la vía que tenemos para incorporar nueva información a nuestros modelos mentales, al fin y al cabo). Pensemos, por ejemplo, en la importancia de la notación en matemáticas. Representar una derivada con un símbolo o con otro puede parecer una discusión vacía, una cuestión de forma al fin y al cabo. Pero es que la forma (en ciencia, así como en arte) posibilita la aparición de nuevos contenidos. Si no, como propone Pablo Rodríguez, probad a hacer multiplicaciones con lápiz y papel usando números romanos.
Del mismo modo, si John Snow hubiese intentado hacer su análisis de la epidemia del cólera usando sólo datos (víctimas y coordenadas, números desnudos), probablemente le hubiese costado mucho más llegar a la misma conclusión. O quizás nunca la hubiese alcanzado. Las gráficas se han convertido así en un recurso fundamental de la ciencia. Y, sin embargo, no siempre parecen recibir un servicio recíproco. En muchos casos, pensamos en este tipo de herramientas como una cuestión de “gusto” o de “intuición”: todo elemento gráfico puede configurarse según le dé al perpetrador (para eso se inventó la galería de horrores del Excel).

Nada más lejos de la realidad. No cualquier cosa vale, ni todos los recursos visuales son igualmente adecuados. Como en todo fenómeno observable, la efectividad de una gráfica también puede ser medida y comparada. Es posible hacer ciencia de las gráficas de datos, y esto fue lo que se propusieron William S. Cleveland y Robert McGill en los años 801:
Hoy en día, los gráficos son una parte vital del análisis de datos estadísticos y una parte vital de comunicación en ciencia y tecnología, negocios, educación y los medios de masas. Y aun así, el diseño de gráficos para el análisis y presentación de datos se hace en gran medida sin rigor científico.
Así, decidieron desarrollar y testar empíricamente unos principios básicos de la percepción gráfica. Para ello, formaron un modelo basado en tareas perceptivas elementales que realizamos cuando decodificamos información cuantitativa en gráficas, y las pusieron a prueba a través de experimentos.
El resultado es una teoría que permite predecir el rendimiento relativo de diferentes gráficas basándose en los elementos que la componen. De hecho, concluían que era necesario reemplazar muchos de los tipos de gráficas populares en aquel entonces (y que, desgraciadamente, todavía lo son; por ejemplo, la tristemente común gráfica de tarta).
Los elementos perceptivos que identifica la teoría de Cleveland y McGill, ordenados de mayor a menor exactitud perceptiva, son los siguientes:
- Posición en una escala común.
- Posición en escalas no alineadas.
- Longitud, dirección, ángulo.
- Área.
- Volumen, curvatura.
- Sombreado, saturación de color.
En otras palabras, las tareas que involucran elementos más simples —como los puntos, las líneas o las barras— son las que mejor funcionan perceptivamente, lo cual no resultará una sorpresa. Así, los diagramas de dispersión, las gráficas de evolución, de distribución y de comparación de magnitudes son las más efectivas para codificar un mensaje complejo. A medida que los recursos gráficos se van haciendo más complejos, aumentan las dificultades de lectura. La situación se vuelve dramática cuando se introducen elementos en 3D, que involucran profundidad y volumen. Porque, aunque somos relativamente buenos con la perspectiva, no olvidemos que las gráficas son generalmente imágenes planas, en 2D, donde la diversidad espacial que nos proporciona el hecho de tener dos ojos resulta totalmente inútil.
Estudios posteriores han refinado esta escala, añadiendo otros parámetros como tono de color y profundidad de campo. La escala, finalmente, queda como podéis ver aquí:
Como los propios autores originales admitían, obviamente estas tareas no son lo único que influye en la construcción de una buena gráfica, ni el único tipo de tareas que llevamos a cabo cuando leemos este tipo de representación visual. Pero sirve como base para priorizar unas tareas sobre otras y seleccionar el atributo más efectivo dependiendo de los datos que se vayan a representar.
Referencia:
1Graphical Perception: Theory, experimentation and application to the development of graphical methods.[PDF]
Sobre los autores: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica. Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute.
El artículo Gráficas para la ciencia y ciencia para las gráficas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas13 Malas gráficas
- El legado de Fisher y la crisis de la ciencia
- Ciencia Clip: un concurso de vídeos de ciencia para jóvenes estudiantes
La característica de Euler de una superficie: un invariante topológico
En la entrada Clasificando en topología: de lo local a lo global recordábamos un bellísimo teorema de clasificación:
Dada una superficie compacta (cerrada y acotada) y conexa (de una pieza), es topológicamente equivalente a una esfera, a una suma conexa de toros o a una suma conexa de planos proyectivos.
Una vez demostrado este teorema, surge una pregunta natural: ¿son estos tipos de superficies topológicamente diferentes? Es decir, ¿podría suceder que, para dos enteros positivos distintos m y n, la suma conexa de n toros fuera homeomorfa a la suma conexa de m toros? ¿Y podría ocurrir que, para dos enteros positivos m y n, la suma conexa de n toros fuera homeomorfa a la suma conexa de m planos proyectivos?
Para demostrar que esto no es posible se puede recurrir a un invariante numérico llamado la característica de Euler que tiene sus raíces en la conocida fórmula de Euler para poliedros que afirma que
Si P es un poliedro convexo con f caras, e aristas y v vértices, entonces v–e+f=2.
La fórmula de Euler para poliedros se puede generalizar a superficies compactas. Antes de comentar cómo, recordemos que cualquier superficie compacta y conexa puede obtenerse como el cociente de una región poligonal en el plano con un número par de aristas identificadas a pares. Cada superficie puede reconocerse a través de una presentación que se obtiene etiquetando con el mismo símbolo cada par de aristas identificadas y “leyendo” estas etiquetas en el orden en el que se presentan.
Por ejemplo, la esfera, el plano proyectivo, el toro y la botella de Klein son cocientes de cuadrados como se indica en la imagen de debajo. Cada flecha y cada letra indican las aristas que se identifican y la forma de realizar este “pegado”.
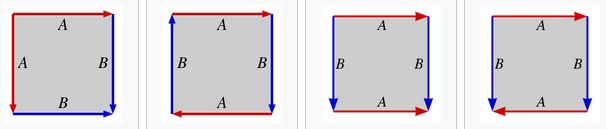 La esfera, el plano proyectivo, el toro y la botella de Klein. Imagen: Wikimedia Commons.
La esfera, el plano proyectivo, el toro y la botella de Klein. Imagen: Wikimedia Commons.
Cada una de las anteriores superficies tendría las presentaciones (empezando a “leer” desde la esquina superior izquierda):
-
la esfera: ABB-1A-1,
-
el plano proyectivo real: ABAB,
-
el toro: ABA-1B-1, y
-
la botella de Klein: ABAB-1
Una superficie no tiene una única presentación, depende de la manera de etiquetar. Pero dos presentaciones de la misma superficie son equivalentes en el sentido de que pueden transformarse la una en la otra por una serie de operaciones elementales. Los detalles pueden verse en [1], en las páginas 8 a 16.
Si S es una superficie con una presentación P dada, se define la característica de Euler de esa presentación como χ(P) = v–e+f, donde f es el número de caras, e el de aristas y v el de vértices de la presentación. Por ejemplo,
-
La esfera, con la presentación P=ABB-1A-1, tiene χ(P)=2–1+1=2 (tras las identificaciones, contamos 2 vértices, 1 arista y 1 cara).
-
El plano proyectivo real, con la presentación P=ABAB, tiene χ(P)=2–2+1=1 (tras las identificaciones, contamos 2 vértices, 2 aristas y 1 cara).
-
El toro, con la presentación P=ABA-1B-1, tiene χ(P)=1–2+1=0 (tras las identificaciones, contamos 1 vértice, 2 aristas y 1 cara).
-
La botella de Klein, con la presentación P=ABAB-1, tiene χ(P)=1–2+1=0 (tras las identificaciones, contamos 1 vértice, 2 aristas y 1 cara).
Se puede probar que χ(P) es un invariante de la superficie, es decir, no depende de la presentación dada para S; por ello se denota por χ(S) y se llama característica de Euler de la superficie. Además se demuestra que si S es homeomorfa a una esfera, entonces χ(S)=2, si es homeomorfa a la suma conexa de n toros es χ(S)=2−2n, y si es homeomorfa a la suma conexa de n planos proyectivos es χ(S)=2−n.
Con esto queda respondida la primera pregunta planteada al principio, ¿podría suceder que, para dos enteros positivos distintos m y n, la suma conexa de n toros fuera homeomorfa a la suma conexa de m toros? No, porque poseen distintas características de Euler.
¡Vaya! Pero la suma conexa de 2n planos proyectivos tiene la misma característica de Euler que la suma conexa de n toros. ¿Son ambas superficies homeomorfas? No, pueden distinguirse porque la primera superficie (suma conexa de 2n planos proyectivos) no es orientable, mientras que la segunda (suma conexa de n toros) si lo es. Y la orientabilidad es una propiedad topológica. Así que, para dos enteros positivos m y n, la suma conexa de n toros no puede ser homeomorfa a la suma conexa de m planos proyectivos…
Es decir, queda demostrado el siguiente teorema:
Si S1 y S2 son superficies compactas y conexas, son homeomorfas si y sólo si son ambas orientables o ambas no orientables y χ(S1)=χ(S2).
El anterior es un teorema topológico por excelencia. Se ha reducido el problema de clasificación de superficies compactas a la determinación de dos invariantes topológicos: la orientabilidad y la característica de Euler, ambos fácilmente calculables.
Nota 1: Los poliedros aludidos en la fórmula de Euler son homeomorfos a una esfera. Por eso su característica de Euler es 2.
Nota 2: El matemático Simon Antoine Jean L’Huillier (1750-1840) nació un 24 de abril. Generalizó la fórmula de Euler a poliedros con g asas: v–e+f=2-2g.
 Un poliedro con un asa. Imagen: Wikimedia Commons.
Un poliedro con un asa. Imagen: Wikimedia Commons.
Existe una relación entre la característica de Euler χ(S) de una superficie S y g(S), su número de asas. Si S es orientable, g(S)=1/2(2-χ(S)). Y si no lo es, entonces g(S)=2-χ(S). ¿Y qué son las asas de una superficie? Una esfera no posee asas, y la suma conexa de n toros o de n planos proyectivos posee n asas…
Referencia
[1] Marta Macho Stadler, Topología Algebraica, Apuntes Máster 2014-2015
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo La característica de Euler de una superficie: un invariante topológico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Clasificando en topología: de lo local a lo global
- Los ‘Leonhard Euler Facts’
- Visualizando la hiperesfera a través de la fibración de Hopf
Un medio sólido y rígido llena todo el espacio o la luz se transmite en el vacío
 Fuente: NASA, ESA & Jesús Maíz Apellániz (Instituto de Astrofísica de Andalucía) / Davide De Martin (ESA/Hubble)
Fuente: NASA, ESA & Jesús Maíz Apellániz (Instituto de Astrofísica de Andalucía) / Davide De Martin (ESA/Hubble)
Ya hemos mencionado que hay un factor parece faltar en el modelo de onda para la luz. En una de las primeras entregas de esta serie decíamos que las ondas son perturbaciones que se propagan por un medio y poníamos como ejemplos cuerdas o o masas de agua. ¿Cuál es entonces el medio para la propagación de las ondas de luz?
¿Es el aire el medio para las ondas de luz? Evidentemente no, porque la luz puede atravesar un espacio que no contiene aire, como ocurre con la luz que recibimos en la Tierra procedente del Sol y demás estrellas. Incluso antes de que se supiese que no existía aire entre el Sol y la Tierra, Robert Boyle ya había intentado el experimento de extraer casi todo el aire de un recipiente de vidrio, encontrando que los objetos dentro seguían siendo visibles lo que implicaba que la luz atrab¡vesaba el espacio en ausencia de aire.
Una onda es una perturbación, y es difícil pensar en una perturbación sin especificar qué se está perturbando. Así que era lo más lógico y natural era proponer que existía un medio específico para la propagación de las ondas de luz. Este medio hipotético se le llamó éter. La palabra “éter” originalmente fue el nombre para el quinto elemento de Aristóteles, el fluido transparente y puro que llenaba la esfera celestial y que más tarde se llamaría, en un alarde de originalidad, “quintaesencia”.
En los siglos XVII y XVIII, se pensaba que el éter era un fluido invisible de muy baja densidad. Este fluido podría penetrar toda la materia y llenar todo el espacio. De alguna manera podría estar asociado con el “effluvium” (fluido) que se empleaba para explicar las fuerzas eléctricas y magnéticas [1]. Pero ocurre que las ondas de luz deben ser transversales para explicar la polarización, y las ondas transversales generalmente se propagan solo en un medio sólido. Un líquido o un gas no pueden transmitir ondas transversales a ninguna distancia significativa por la misma razón que no puedes “retorcer” un líquido o un gas. Así que los físicos del siglo XIX asumieron que el éter debía ser un sólido.
Como vimos al tratar la propagación de las ondas, la velocidad de propagación aumenta con la rigidez del medio y disminuye con su densidad. La velocidad de propagación de la luz es muy alta en comparación con la de otros tipos de ondas, como el sonido. De aquí que se pensase que el éter tenía que ser un sólido muy rígido con una densidad muy baja.
Nos puede parecer absurdo afirmar que un medio rígido y sólido, el éter, llena todo el espacio. Después de todo un medio así debería provocar rozamiento, pero los planetas se mueven a través del espacio sin disminución detectable de velocidad. Y, por supuesto, tú no sientes resistencia cuando te mueves en un espacio que en el que la luz se transmite libremente.
Sin éter, la teoría ondulatoria de la luz, por lo demás tan sólida, parecía improbable. Pero el éter en sí tenía propiedades absurdas. Hasta principios de este siglo, este problema seguió sin resolverse, y estaba en el mismo punto en el que lo dejó Newton. Serían necesario un Maxwell [2], un Einstein [3] y unos cuantos experimentos ingeniosos para resolver el problema: la luz se transmite en el vacío.
Notas:
[1] A este respecto véase Imponderable: el primer modelo estándar de la física
[2] Las ecuaciones de Maxwell no necesitan de la hipótesis del éter, véanse La velocidad de las ondas electromagnéticas y la naturaleza de la luz o Maxwell y el éter
[3] Véase, por ejemplo, El principio de constancia de la velocidad de la luz
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un medio sólido y rígido llena todo el espacio o la luz se transmite en el vacío se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El intestino grueso
El intestino grueso de los vertebrados sigue al intestino delgado. Consta de tres partes principales: ciego, colon y recto (o cloaca). El ciego es una especie de bolsa que, como su propio nombre indica es ciego, o sea, es un fondo de saco. Recibe el quimo del íleo, la parte final del intestino delgado, aunque ciego e íleo se encuentran separados por la válvula ileocecal, que evita posibles retrocesos de los jugos intestinales. El íleo desemboca en un lateral del ciego y algo por debajo de ese punto se encuentra el apéndice, un tejido linfoide que no toma parte en la digestión, pero que contiene linfocitos.
El colon es la parte más extensa del intestino grueso y su estructura varía mucho de unas especies a otras en función de la dieta. Y dentro de los mamíferos también se da una gran variabilidad. En la especie humana se distinguen cuatro partes: el colon ascendente, el transverso, el descendente y el sigmoide.
En anfibios, reptiles (incluidas las aves) y algunos mamíferos, el intestino grueso finaliza en una cloaca en la que confluye con el sistema excretor y con el aparato reproductor. En los peces, sin embargo, los conductos de los tractos excretor y reproductivo salen al exterior de manera independiente del sistema digestivo. En reptiles (aves incluidas) unos pliegues o crestas delimitan la cloaca en tres áreas diferenciadas: coprodeo (anterior), a donde llegan las heces desde el intestino; urodeo (medio), que recibe la orina de los riñones a través de los uréteres y los materiales del oviducto; y el proctodeo (posterior), donde se almacenan las excretas. El proctodeo se abre al exterior a través de un ano muscular.
 Intestino grueso humano. Fuente: medlineplus.gov /A.D.A.M.
Intestino grueso humano. Fuente: medlineplus.gov /A.D.A.M.
Un colon humano recibe diariamente del orden de medio litro de quimo. Cuando llega procedente del intestino delgado, los nutrientes han sido digeridos y absorbidos prácticamente en su totalidad, por lo que contiene sobre todo residuos alimenticios indigeribles (como celulosa, por ejemplo), algunos componentes biliares que no se han absorbido y, sobre todo, agua y sales. Por esa razón, en el colon prosigue la absorción de agua, que tiene lugar gracias a la recuperación activa de sodio, que va acompañada por la correspondiente reabsorción (a favor de gradiente eléctrico) de cloro; el agua pasa a favor del gradiente osmótico generado por la reabsorción de ClNa.
El colon contiene una solución mucosa alcalina (HCO3– y PO43-) que tiene efecto tamponador. Esa solución protege la mucosa del intestino grueso del daño mecánico y químico que podría sufrir si careciese de ella. En caballos y cerdos basta con el HCO3– de origen pancreático para mantener tamponado el colon. La saliva de los rumiantes contiene cantidades importantes de PO43-, pero en los demás mamíferos el fosfato intestinal es de origen alimenticio. Los tampones neutralizan los ácidos producidos por la fermentación bacteriana (a la que nos referiremos en una anotación próxima), y el moco proporciona la lubrificación que facilita el paso de los contenidos intestinales y la expulsión final de las heces.
Las dimensiones y estructura de los sistemas digestivos y, en especial, del intestino grueso depende mucho de la dieta propia de cada especie. Los peces carnívoros, por ejemplo, tienen tractos digestivos cuya longitud es solo algo mayor que la longitud corporal; los herbívoros, sin embargo, pueden llegar a ser veinte veces más largos.
Los vertebrados carnívoros tienen tubos digestivos muy simples, y el colon suele ser corto y sin áreas diferenciadas. Apenas se diferencian el intestino delgado y el intestino grueso; no suelen tener ciego, y si lo tienen, es marginal. En estas especies la función principal (casi única) del intestino grueso es la absorción de sales y agua.
 Sistema digestivo del caballo. Fuente: ecuestre.es
Sistema digestivo del caballo. Fuente: ecuestre.es
En los omnívoros y, sobre todo, en los herbívoros, la estructura del intestino grueso tiende a ser más compleja; conejos y caballos son buenos ejemplos. El ciego de los herbívoros suele ser grande, en algunos casos mayor que el colon, incluso. Además, tanto el ciego como el colon suelen estar provistos de saculaciones (sacos laterales expandibles). No obstante, hay excepciones: ni canguros ni ovejas se caracterizan por tener colon y ciego de grandes dimensiones, ni por tener saculaciones.
Las saculaciones se forman cuando la capa exterior de músculo liso longitudinal no envuelve el intestino grueso por completo. En las especies cuyos intestinos gruesos presentan esas estructuras, hay bandas de musculatura lisa longitudinal denominadas taeniae coli (en singular taenia coli), que discurren todo a lo largo del ciego y el colon. La mayoría de los animales que las tienen cuentan con tres, aunque el caballo, por ejemplo, tiene cuatro. Son más cortas que lo que las capas muscular (circular) y mucosa subyacentes serían de no estar constreñidas en parte por las taeniae coli. La presencia de estas bandas musculares provoca, por ello, que se formen leves constricciones que, a su vez, delimitan los embolsamientos o saculaciones a los que denominamos haustras (haustra coli). Los haustras no son estructuras estáticas, sino que cambian de posición por efecto de las contracciones de la capa circular de musculatura lisa.
Las contracciones haustrales juegan un papel primordial en la motilidad del intestino grueso. Se inician debido a la actividad rítmica autónoma de las células musculares lisas del colon, y son similares a las contracciones que provocan la segmentación en el intestino delgado, solo que se producen con una frecuencia muy inferior. Se producen entre 9 y 12 contracciones de segmentación por minuto y, sin embargo, entre dos contracciones haustrales pasan del orden de 30 minutos. Como consecuencia de esa actividad contráctil, la localización de los sacos haustrales cambia, porque las zonas que se contraen y las que se relajan se van alternando. Esta motilidad no provoca desplazamiento unidireccional del contenido intestinal; su función es ir exponiéndolo gradualmente a la acción absortiva del epitelio. Y al no provocar su avance, permanece largo tiempo en el interior del intestino grueso, de manera que se prolonga el tiempo en que se produce la acción de las bacterias intestinales sobre los materiales de origen vegetal que no habían sido digeridos y absorbidos en el intestino delgado.
Además de la provocada por las contracciones haustrales, en el intestino grueso se producen otros dos tipos de motilidad. Por un lado están las contracciones peristálticas; son provocados por células marcapasos ubicadas en la zona media del colon y generan ondas lentas en las dos direcciones. Su efecto neto consiste en impulsar el contenido digestivo hacia el recto. La motilidad intestinal de las aves se basa, sobre todo, en contracciones peristálticas. Otras células marcapasos ubicadas en la región proximal del colon generan contracciones antiperistálticas, cuya principal función consiste en llenar el ciego. Son contracciones importantes en la mayoría de los herbívoros y en los cerdos, pues su acción de mezcla facilita la digestión bacteriana de la celulosa y la absorción de los ácidos grasos volátiles, producto de la fermentación.
Tras cada comida suele producirse un fuerte aumento de la motilidad del colon. Grandes segmentos se contraen de forma simultánea, desplazando el contenido intestinal entre un tercio y tres cuartas partes de su longitud en unos pocos segundos. Estos movimientos “en masa” (así se llaman), conducen el contenido del colon hacia la porción distal del intestino grueso, donde queda almacenado hasta su expulsión.
Cuando el alimento entra en el estómago, se producen los reflejos gastroileal y gastrocólico, en los que interviene la gastrina y nervios autónomos extrínsecos. El reflejo gastroileal provoca el vaciado del intestino delgado y el gastrocólico el desplazamiento del contenido del colon al recto. De esa forma se va haciendo hueco, primero en el intestino delgado y después en el ciego y el colon, a nuevos contenidos.
Cuando los movimientos en masa del colon llevan el material fecal al recto, la distensión a que da lugar estimula los receptores de estiramiento de la pared rectal, iniciando así el reflejo de defecación. Ese reflejo provoca la relajación del esfínter anal interno (musculatura lisa) y contracciones fuertes del colon sigmoide y del recto. El esfínter externo consiste en musculatura esquelética y, por lo tanto, controlada voluntariamente; por lo tanto, si se relaja ese esfínter también, se produce la defecación. No obstante, si el esfínter exterior permanece contraído de manera prolongada, las contracciones rectales cesan hasta que se produce la llegada de material fecal adicional por efecto de posteriores movimientos en masa, y se reinicia el reflejo de defecación.
Las heces está formadas por celulosa que no se ha digerido y otras sustancias que no se han podido absorber, como bilirrubina (o biliverdina), sales, agua y bacterias. Aunque en el colon tiene lugar una cierta absorción, su importancia cuantitativa es mínima comparada con la del intestino delgado. La superficie interna del intestino grueso es muy reducida por comparación con la del delgado, dada la ausencia en aquel de las estructuras que multiplican la superficie absortiva propias de este. Además, el colon de muchos vertebrados carece de mecanismos de transporte específicos para las sustancias que se absorben en el intestino delgado. La excepción es el colon de las aves, en el que se absorbe glucosa y aminoácidos mediante transporte secundario activo. De esa forma, los aminoácidos y la glucosa que no han sido recuperados de la orina por el riñón pueden ser reabsorbidos en el colon o ser utilizados por los microorganismos en los ciegos intestinales.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El intestino grueso se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Estructura y motilidad del intestino delgado
- El intestino no es nuestro segundo cerebro
- Soy esa bacteria que vive en tu intestino, mejor vídeo de divulgación “On zientzia”
La tabla periódica en el arte: Plomo
Una noche como otra cualquiera William Watts se agarró tal borrachera que se quedó dormido junto a la iglesia de Santa María de Redcliffe. Soñó que desde el campanario caía una lluvia de gotas esféricas de plomo, lo que le llevó a patentar un nuevo método para la elaboración de perdigones. Esa es por lo menos la leyenda urbana que circula por las calles de Bristol. El procedimiento consistía en pasar plomo fundido por una bandeja de zinc agujereada que se colocaba a varios metros del suelo. Fruto de la caída libre se iban formando bolas esféricas que poco a poco se enfriaban y se terminaban por solidificar al caer en un balde de agua. Para lograr esta gran elevación Watts empleó unas torres que hoy en día llevan su apellido (Imagen 1). Poco tiene que ver esta historia con el mundo del arte, pero nos sirve para conocer algunas de las propiedades más interesantes de este metal tan peculiar: se funde a una temperatura relativamente baja (a 327 °C) y se moldea con facilidad. Además, es bastante estable, abundante y barato, por lo que el ser humano le ha dado múltiples usos, entre ellos muchos relacionados con el arte
 Imagen 1. Vestigio de una torre de Watts en Bristol con la iglesia de Santa María de Redcliffe al fondo. Fuente: Martin Tester
Imagen 1. Vestigio de una torre de Watts en Bristol con la iglesia de Santa María de Redcliffe al fondo. Fuente: Martin Tester
Escultura a base de plomo
La facilidad con la que se funde el plomo ha permitido que se emplee para crear objetos metálicos mediante moldes, tal y como sucede con los clásicos soldaditos de plomo. Más allá de las técnicas en las que el plomo es fundido, la maleabilidad de este material facilita su uso escultórico mediante repujado, es decir, trabajando directamente sobre planchas del metal. Plinio ya contaba que este modo de trabajar el plomo era bien conocido en el Imperio Romano y así lo confirman los relieves que se han conservado. Mucho más reciente es el uso del denso metal por parte del aragonés Pablo Gargallo del que se conservan esculturas en el Museo de Arte Nacional de Catalunya y en el Reina Sofía (Imagen 2). Como sucede con las obras de Gargallo, las esculturas en plomo rara vez son de gran tamaño, puesto que su elevada densidad (11 kg/L) y maleabilidad pueden causar que se doblen por su propio peso. De hecho, la maleabilidad, que hemos citado como gran ventaja, puede jugar en contra de la conservación de las esculturas, ya que presentan poca resistencia a los golpes.
 Imagen 2. Mano con Pipa (25 x 16 x 14 cm) de Pablo Gargallo (1920). Fuente: Museo Nacional Centro de Arte Reina Sofía.
Imagen 2. Mano con Pipa (25 x 16 x 14 cm) de Pablo Gargallo (1920). Fuente: Museo Nacional Centro de Arte Reina Sofía.
El plomo: esqueleto de las vidrieras
Las bondades del plomo han llevado a que se le de usos tan dispares como la fabricación de cañerías o la elaboración de tipos móviles en las imprentas. En el mundo del arte, además de en escultura, se ha empleado en arquitectura. Quizás el ejemplo más espectacular era la aguja de Notre Dame que hasta hace poco arañaba el cielo parisino a más de 90 metros*. A pesar de la ligereza que transmitía su forma alargada, para su elaboración se emplearon 250 toneladas de denso plomo. Cabe destacar que, aunque esta catedral sea el paradigma del gótico, la aguja desaparecida era del s. XIX, ya que se había levantado durante la restauración de Eugène Viollet-le-Duc. En cualquier caso, si hay algo para lo que el plomo fue fundamental durante el gótico (el de verdad) es el arte de las vidrieras.
 Imagen 3. Notre-Dame de Paris. Fuente: Wikimedia Commons.
Imagen 3. Notre-Dame de Paris. Fuente: Wikimedia Commons.
Las vidrieras son conjuntos de piezas de vidrio coloreado que cubren ventanales y que normalmente asociamos a edificios religiosos. Su uso está documentado desde inicios de la Edad Media, pero fue durante el s. XIII cuando alcanzaron su máximo esplendor, especialmente en el periodo conocido como gótico radiante, en el que las iglesias se convirtieron en jaulas de cristal, siendo el mejor exponente otro edificio parisino: la Sainte Chapelle. Cuando pensamos en vidrieras, el protagonismo se lo concedemos al vidrio de colores, pero el plomo también es un componente indispensable. En varillas elaboradas con este metal se insertaban los vidrios siguiendo un patrón previamente establecido (como si de un puzle se tratase). Luego ambos se unían mediante una soldadura de estaño y así se lograba un efecto maravilloso que tiene uno de sus máximos exponentes en la catedral de León.
 Imagen 4. Vidrieras de la catedral de León. Fuente: Wikimedia Commons.
Imagen 4. Vidrieras de la catedral de León. Fuente: Wikimedia Commons.
Los pigmentos del plomo
Además de uso como metal, el plomo nos regala una gran variedad de compuestos químicos que pueden ser empleados como pigmentos en el arte de la pintura. Nos quedaremos con tres y reservaremos el resto para el momento en el que en esta sección nos ocupemos de los otros elementos químicos con los que se combina. Comenzaremos por el minio (Pb3O4), conocido para muchos de quienes leen estas líneas, ya que hasta hace unos años era muy habitual usarlo por sus propiedades antioxidantes. Así, los objetos metálicos que se hallaban a cielo abierto se recubrían con una capa de este compuesto antes de darles la capa definitiva de pintura. Este pigmento rojizo, al igual que el bermellón, se empleaba para decorar profusamente las letras iniciales de los manuscritos medievales. De ahí que este proceso de ilustración se denominase miniare, de donde pronto surgió miniatura, palabra que el léxico castellano tomó del italiano.
 Imagen 5. Códice miniado del s. XV. Fuente: Biblioteca Universidad de Sevilla
Imagen 5. Códice miniado del s. XV. Fuente: Biblioteca Universidad de Sevilla
Este pigmento se conocía en la Antigüedad Clásica y tal como explica Vitrubio se lograba calcinando otros compuestos con plomo. Sin embargo, hay que remontarse a la China de principios del s. V a.e.c. para encontrar el primer uso como material artístico. En ese mismo territorio el alquimista Ko Hung dejó un divertido testimonio: “El ignorante no cree que el minio y el blanco de plomo sean productos de transformación del plomo, al igual que puede no saber que el mulo es vástago de una yegua y un burro… Hay cosas que están tan claras como el cielo y aun así los hombres prefieren sentarse bajo un tonel volcado.” Esta cita es del s. IV, pero bien podría extrapolarse a nuestra época (y no precisamente aplicándose a conocimientos pictóricos).
Del rojo pasamos al blanco para hablar del pigmento con plomo más importante de la historia: el albayalde. Palabra eufónica donde las haya y que en árabe hispánico (Albayád) significaba blancura. Blanco es, en efecto, el color del carbonato básico de plomo que denominamos con tal nombre (2PbCO3·Pb(OH)2). Tampoco sería ninguna locura decir que se trata del pigmento más importante que ha existido, ya que no hay pintor que no tenga el blanco en la paleta para controlar la tonalidad del resto de colores. Como sucedía con el minio, el albayalde es un pigmento que se logra sintéticamente, aunque mediante un proceso ligeramente más desagradable, por lo menos según el método holandés. En este procedimiento se empleaban vasijas de barro especiales que disponían de dos compartimentos conectados. En el compartimento inferior se ponía vinagre y en el superior placas de plomo. Así el vapor de ácido acético entraba en contacto con el metal. Para que la reacción química tuviese lugar, las vasijas se cubrían con una fuente de calor y de dióxido de carbono (CO2): estiércol. Pasados unos meses, surgía una costra blanca sobre el plomo, que se retiraba, se limpiaba, se secaba y se molía. Las placas metálicas se volvían a meter en la vasija y se repetía el proceso hasta que se agotase el metal.
 Imagen 6. Placa de plomo antes y después del proceso holandés. Fuente: Imagen cedida por el Mauritshuis.
Imagen 6. Placa de plomo antes y después del proceso holandés. Fuente: Imagen cedida por el Mauritshuis.
Teniendo en cuenta la importancia del albayalde, lo podemos encontrar en un sinfín de obras elaboradas con diferentes técnicas, desde los temples al huevo de Botticelli a los retratos de El Fayum pintados con cera de abeja. Ahora bien, si en una técnica ha tenido especial relevancia, esa es la pintura al óleo en la que, como otros pigmentos con plomo, acelera el proceso de secado. Para muestra los cuasi escultóricos impastos de Rembrandt. Pero no todo es tan bonito. La toxicidad de este metal pesado puede causar una gran variedad de síntomas que incluyen enfermedades óseas o fallos en el sistema nervioso. La intoxicación por plomo también se conoce como saturnismo, ya que Saturno era el planeta con el que los alquimistas asociaron este elemento químico. Esta elección no es arbitraria y se debe a que era el planeta conocido con una órbita más lenta, algo que se podía vincular con la gran densidad del plomo. Resulta paradójico que en la mitología romana Saturno portase una guadaña, como advirtiendo del poder asesino del elemento que la divinidad representa. Pero más paradójico resulta todavía que los dos cuadros más célebres que tienen a este dios como protagonista fuesen realizados por Rubens y Goya, quienes pudieron sufrir intoxicación por plomo, especialmente el segundo, cuya sordera se considera una evidencia de saturnismo. Más allá de estos dos pintores, a muchos otros artistas se les ha considerado víctimas del plomo: Miguel Ángel, Caravaggio, van Gogh, Fortuny, Frida Kahlo… Eso sí, hacer un diagnóstico tantos años después no es sencillo y no siempre se cuenta con evidencias sólidas para hacer tales afirmaciones.
 Imagen 7. Saturno devorando a su hijo. A la izquierda la versión de Goya (ca. 1820), a la derecha la de Rubens (1636). Fuente: Wikimedia Commons.
Imagen 7. Saturno devorando a su hijo. A la izquierda la versión de Goya (ca. 1820), a la derecha la de Rubens (1636). Fuente: Wikimedia Commons.
Acabamos este recorrido por los pigmentos del plomo con uno que además contiene antimonio: el amarillo de Nápoles. En honor a la verdad, diremos que hoy en día no se comercializa por la toxicidad de estos elementos, pero el nombre ha sobrevivido para denominar a los sucedáneos que han ido apareciendo. También hemos de decir que el gentilicio de este amarillo es poco adecuado, ya que ni mucho menos es originario de la ciudad italiana, por lo que es más acertado el nombre de amarillo de antimonio o antimoniato de plomo (Pb2Sb2O7). Al parecer, dicha confusión se extendió entre los siglos XVIII y XIX porque pensaban que se extraía de minerales que abundaban en las faldas del Vesubio. Lo cierto es que el pigmento es muchísimo más antiguo, por lo menos 30 siglos más, y tiene el honor de ser el primer amarillo sintético de la historia. El mérito, como muchas otras veces, corresponde a los egipcios que ya lo sintetizaban durante la XVIII dinastía (hacia el s. XV a.e.c). En el país del Nilo empleaban este compuesto para colorear el vidrio al igual que lo hicieron en Mesopotamia unos siglos después. Las diferentes culturas que habitaron esa región lo utilizaron en procesos de esmaltado, como en el caso de la vía procesional de Babilonia. Un uso similar se le dio en Europa muchos siglos después donde se empleó para colorear la mayólica. Las primeras evidencias de su uso en pintura son muy posteriores, concretamente del primer tercio del s. XVII (Imagen 8), aunque vivió su máximo auge a lo largo de los dos siglos siguientes.
 Imagen 8. El primer uso del amarillo de Nápoles en Occidente se detectó en el Arresto de Cristo (151×205 cm) de Matthias Stom (ca. 1630). Fuente: Wikimedia Commons
Imagen 8. El primer uso del amarillo de Nápoles en Occidente se detectó en el Arresto de Cristo (151×205 cm) de Matthias Stom (ca. 1630). Fuente: Wikimedia Commons
Para saber más:
Julio Montes-Santiago “The lead-poisoned genius: Saturnism in famous artists across five centuries” Progress in Brain Research 203 (2013) 223-240.
Fernando Cortés Pizano “Estudio del plomo medieval en las vidrieras del monasterio de Pedralbes (Barcelona)” Materiales de construcción 259 (2000) 85-96.
Max Doerner “Los materiales de pintura y su empleo en el arte” Editorial Reverté, Barcelona (2005).
* Nota del autor: A la hora de redactar este texto el fuego no se había cebado con la catedral de Notre Dame. Todavía me resulta inconcebible que dos semanas después de escribir las líneas originales “La fléche” se derrumbase arrastrando con ella un pedacito de nuestra Historia. Sucesos como este nos deberían enseñar a valorar más nuestro Patrimonio y a cuidar de él si queremos que perdure.
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo La tabla periódica en el arte: Plomo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: ¿Qué átomos hay en una obra?
- La tabla periódica en el arte: Cobre
- Deconstruyendo la tabla periódica
¿Qué tienen en común Einstein y una zanahoria?
La próxima vez que te comas una ensalada quizás mastiques con más respeto.
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Qué tienen en común Einstein y una zanahoria? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué pasa en tu cuerpo cuando te enamoras?
- ¿Cuál es la postura más aerodinámica en ciclismo?
- ¿Qué pasa en tu cerebro cuando duermes?
Arrecifes fósiles, una paradoja geológica
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons
¿Qué es un arrecife? Si utilizamos nuestra memoria visual, la mayoría asociamos los arrecifes a mares tropicales de aguas cristalinas, rodeando islas de arena blanca y palmerales, y fondos tapizados por un universo de colores y maravillosas e inquietantes formas de vida submarina. Los cinéfilos, además, visualizarían barreras rocosas rodeando atolones e islas contra las que rompen olas y vientos huracanados, y que han engullido no pocos barcos e intrépidos aventureros. El término arrecife (reef, récif) tiene su raíz en “rif”, antiguo vocablo nórdico de uso marinero para designar las crestas rocosas que emergen del fondo marino y dificultan sobremanera la navegación. Estas sencillas concepciones ya resumen en gran medida la principal propiedad de los arrecifes: son estructuras “rocosas consistentes” que forman un “relieve” elevado sobre el fondo marino. Pero es necesario apuntar que no todo lo que en náutica se identifica como arrecife lo es desde un punto de vista científico; solo aquellos de naturaleza “calcárea” que demuestran haber crecido poco a poco por la acumulación de esqueletos y caparazones de invertebrados marinos que han crecido unos sobre otros de forma continuada encajarían en la definición científica estricta. En pocas palabras, los arrecifes actuales y fósiles son “edificios calcáreos bio-construidos”.
Los arrecifes tropicales actuales esencialmente se crean por la íntima asociación de colonias de corales escleráctinidos (Phylum Cnidaria) y algas calcáreas (Rhodophyta y Chlorophyta), a los que se asocian o acompañan diferentes invertebrados de caparazón o esqueleto calcáreo, tales como moluscos, equinodermos, esponjas, anélidos, briozoos, los poco conocidos foraminíferos (Protista) y toda una diversa comunidad de peces y otros vertebrados marinos. Por tanto, los arrecifes constituyen en sí mismos exuberantes y complejos ecosistemas que, además de sus singularidades tróficas, tienen la cualidad especial de “fijar” gran cantidad de carbonato cálcico, es decir, son “almacenes” naturales de Calcio y dióxido de Carbono, este último uno de nuestros temidos gases “invernadero”. Los arrecifes son y han sido siempre muy “dinámicos”: crecen a razones de varios milímetros/año y se expanden lateralmente por el apilamiento continuado de restos esqueletales calcáreos, ocasionalmente llegando a formar extensas barreras morfológicas. En la actualidad, estos “edificios bio-construidos” ocupan en conjunto más de 600.000 km2 de los fondos submarinos tropicales, una extensión nada desdeñable pero que no debe sorprendernos, ya que en algunos momentos del pasado geológico su extensión llegó a ser 10 veces más.
Durante los últimos 50 años y gracias al avance de las técnicas de inmersión, los investigadores han observado y analizado innumerables ejemplos de arrecifes de corales y algas a lo largo del Caribe, el Mar Rojo y los extensos océanos Índico y Pacífico, documentando su gran variedad en composición y morfología y, asimismo, desvelando su fragilidad ante procesos como la eutrofización, la acción de los rayos ultravioleta, la destrucción asociada al paso de huracanes o la proliferación súbita de especies invasivas. Son por esas señales uno de los principales “estandartes” utilizados por los investigadores del medio marino para intentar sensibilizar a la sociedad sobre el impacto generado por el cambio climático, la contaminación y la sobre-explotación de los mares tropicales.
No obstante, los arrecifes no son tan frágiles como parece, paradoja que se sustenta en un análisis riguroso de su evolución desde la perspectiva geológica. Bajo este enfoque debemos considerar no solo los arrecifes coralinos actuales, sino también todos los ejemplos de arrecifes fósiles que han documentados los geólogos en formaciones de rocas marinas de todos los continentes y edades geológicas. Así pronto percibiremos que los arrecifes, como ecosistemas generadores de edificios calcáreos, han estado presentes desde muy antiguo y que han evolucionado constantemente con el tiempo, durante múltiples fases de expansión, retracción y cambio marcado en sus características, siendo capaces de sobreponerse a numerosos acontecimientos climáticos y oceanográficos adversos, y a las crisis biológicas más dramáticas que han sacudido la vida sobre la Tierra (Figura 1). En algunas de tales etapas de estrés o crisis su adaptación simplemente se resolvió con una sustitución en el tipo principal de organismos constructores; en otros, en cambio, necesitaron de una completa “reinvención” del sistema y la cadena trófica que lo sustenta.
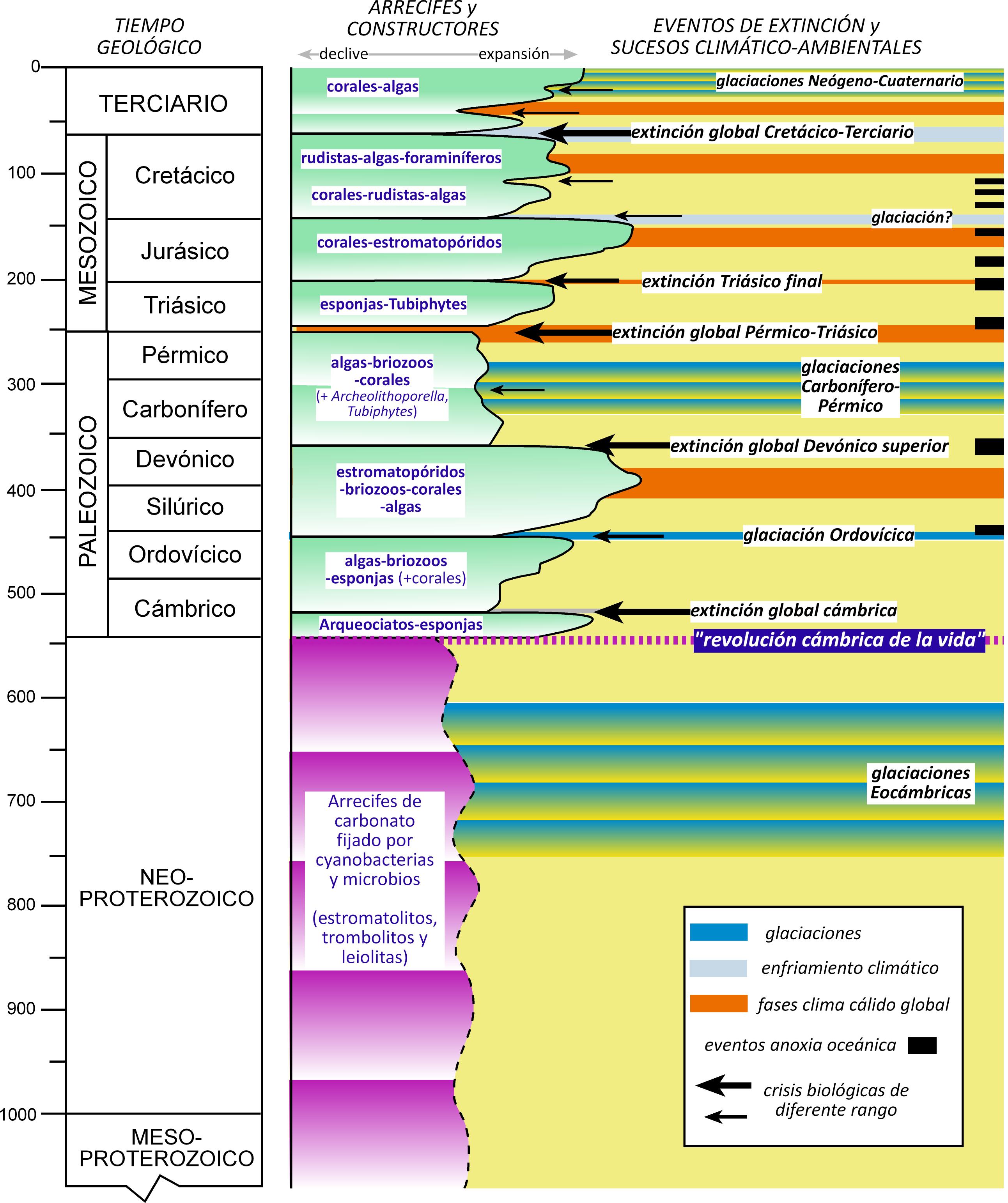 Figura 1. Principales tendencias evolutivas de los arrecifes desde el Proterozoico hasta la actualidad. Fuente: Juan Ignacio Baceta
Figura 1. Principales tendencias evolutivas de los arrecifes desde el Proterozoico hasta la actualidad. Fuente: Juan Ignacio Baceta
Las primeras construcciones arrecifales datan del Proterozoico medio y superior, entre 1600 y 540 Ma (millones de años), y se localizan en formaciones rocosas marinas de Canadá y Australia. Son edificios arrecifales bastante simples, básicamente compuestos por acumulaciones de estromatolitos, trombolitos y leiolitas, estructuras de morfología domal y organización interna laminada o masiva, construidos de forma “bio-inducida” por cianobacterias y calcimicrobios (procariotas y eucariotas fotosintéticos). Algunos de estos arrecifes proterozoicos alcanzaron cientos de metros de altura, formando verdades barreras próximas a la superficie del mar. Sin embargo, su naturaleza esencialmente microbiana hace que algunos investigadores no los consideren como “verdaderos” arrecifes.
La “revolución cámbrica” de la vida marina, hace unos 541 Ma, marcó la aparición y progresiva expansión de una ingente variedad de organismos pluricelulares y, entre ellos, de efectivos secretores de concha o esqueleto calcáreo y, por tanto, potenciales constructores de arrecifes. Durante el Cámbrico destacaron los arqueociatos, un grupo ancestral de esponjas (Porífera) que dominaron los océanos cálidos durante más de 25-30 Ma, para luego desaparecer de forma casi repentina. Los primeros metazoos constructores con cierta similitud a los actuales fueron los corales tabulados y rugosos, las algas calcáreas ancestrales, los estromatopóridos (Porífera), los crinoides (Echinodermata) y los primeros moluscos y braquiópodos. Todos estos grupos aparecieron durante el transito Cámbrico-Ordovícico (470 Ma) y se expandieron prodigiosamente durante el Silúrico y Devónico (442-372 Ma), periodos de condiciones climáticas globalmente cálidas. Los arrecifes de estas edades son muy numerosos y de enorme tamaño, habiéndose reconocido ejemplos en todos los continentes, desde Groenlandia y Norteamérica a Australia. A finales del Devónico una extinción biológica masiva de origen todavía controvertido provocó una retracción global, aunque arrecifes construidos por nuevos grupos de algas calcáreas y esponjas, y por organismos de afinidad biológica incierta (p.ej. algas filoides, Archeolithoporella, Palaeoaplysina, Tubiphytes) persistieron hasta el final del Paleozoico, sobrepasando varios ciclos de glaciación-deglaciación y cambio sustancial del nivel marino.
El tránsito del Paleozoico al Mesozoico, hace 252 Ma, estuvo marcado por la mayor extinción biológica que ha conocido nuestro planeta, el límite Pérmico-Triásico, atribuida a la confluencia de numerosas condiciones adversas (p.ej. pronunciado calentamiento y aridificación del clima, intenso volcanismo, impactos meteoríticos). Todo ello provocó una retracción drástica en los arrecifes, durante por lo menos 5-7 Ma. A pesar de ello, los arrecifes se recuperaron y expandieron de nuevo durante el Triásico, incorporando a los primeros representantes de los corales escleractínidos, los principales constructores de arrecifes en la actualidad. Estos prodigiosos cnidarios, parientes de las medusas, proliferaron durante el resto del Triásico y todo el Jurásico, junto a nuevas esponjas y moluscos, y las todavía importantes comunidades calcimicrobianas, con una importante retracción durante la crisis biológica del límite Triásico-Jurásico (200 Ma). Curiosamente, la mayor fase de expansión arrecifal del Mesozoico coincidió con el periodo de climas más cálidos de todo el Jurásico, al que sucedió una retracción notable durante el enfriamiento generalizado del tránsito al Cretácico. Durante el Cretácico (145-66 Ma), junto a los corales y algas calcáreas destacó un grupo singular de moluscos bivalvos, los rudistas, que de hecho alcanzaron la categoría de constructor principal durante el Cretácico superior, para luego desaparecer de forma brusca poco antes del límite Cretácico-Terciario (66 Ma). Los arrecifes de rudistas fueron muy extensos y se pueden reconocer desde el Himalaya a Oriente Próximo, a lo largo de todo el Mediterráneo y el dominio del Caribe, con algunos ejemplos espectaculares situados muy próximos a nosotros (Figura 2).
 Figura 2. Sierra de Aitzgorrigain (Itxina, Bizkaia). Frente preservado de la barrera arrecifal de 300 m construida por corales y rudistas (dcha.) en el Cretácico medio. Fuente: Juan Ignacio Baceta.
Figura 2. Sierra de Aitzgorrigain (Itxina, Bizkaia). Frente preservado de la barrera arrecifal de 300 m construida por corales y rudistas (dcha.) en el Cretácico medio. Fuente: Juan Ignacio Baceta.
El límite Cretácico-Terciario estuvo marcado por una fase de intenso volcanismo en la India, una sucesión de bruscos cambios climáticos y, finalmente, un impacto meteorítico descomunal en la península de Yucatán. En conjunto, todos ellos provocaron una nueva extinción biológica global, que en los continentes engulló a los últimos dinosaurios. Sorprendente, los organismos constructores de arrecifes se recuperaron de forma relativamente rápida tras la crisis, como lo atestiguan las extensas barreras arrecifales preservadas en el norte de África, los Alpes, los Cárpatos, y los Pirineos occidentales (Figura 3), formadas tan solo 2-4 millones de años tras la crisis global. En estos arrecifes, los corales y algas calcáreas ya se revelan como los principales constructores, aunque su evolución posterior hasta nuestros días estuvo jalonada de diferentes ciclos de expansión y retracción, en relación a fases de clima extremadamente cálido o de enfriamiento brusco, cambios marcados en el patrón de circulación oceánica y, finalmente, el progresivo tránsito a la Tierra refrigerada de las glaciaciones del Neógeno superior y Cuaternario.
 Figura 3. Sierra de los Alanos (Zuriza, Huesca). Espectacular alineación tipo barrera de los primeros arrecifes construidos por corales (dcha.) y algas calcáreas durante el Paleoceno, tras la crisis global del límite Cretácico-Terciario. Fuente: Juan Ignacio Baceta.
Figura 3. Sierra de los Alanos (Zuriza, Huesca). Espectacular alineación tipo barrera de los primeros arrecifes construidos por corales (dcha.) y algas calcáreas durante el Paleoceno, tras la crisis global del límite Cretácico-Terciario. Fuente: Juan Ignacio Baceta.
Como corolario, ¿qué conclusiones objetivas podemos sacar de la evolución de los arrecifes a lo largo de los tiempos geológicos?, ¿realmente son y han sido ecosistemas tan frágiles y vulnerables como revelan sus representantes actuales? Las respuestas no pueden ser sencillas. La idea de que los organismos constructores de arrecifes son sensibles a cambios ambientales es totalmente correcta, como lo demuestran su comportamiento actual y las innumerables fases y etapas de expansión y declive que han experimentado a lo largo de las edades geológicas. Sin embargo, la idea que comúnmente se argumenta en foros sociales y medios de comunicación de que los arrecifes van a desaparecer de nuestro planeta carece de rigor científico.
Si analizamos a los principales constructores de arrecifes actuales, los corales escleráctínidos, la evidencia geológica nos demuestra que estos organismos relativamente simples han tenido una extraordinaria capacidad adaptativa a cambios ambientales drásticos, ya que desde que aparecieron en el Triásico han sobrevivido a innumerables crisis, incluyendo eventos de extinción global, cambios climáticos pronunciados e incluso diferentes episodios de anoxia generalizada en los océanos (Fig. 1). A su vez, los corales de arrecifes actuales siguen demostrando tener un gran potencial de adaptación y especialización, ya que son capaces de proliferar en condiciones muy adversas e incluso de colonizar nuevos nichos marinos. Entre ellos destacan los mares de temperatura y salinidad más elevadas de lo normal (p.ej. en el Golfo Pérsico), las zonas litorales enturbiadas por el semi-continuo aporte de arcilla (litoral sureste de China) e, incluso, numerosos contextos relativamente profundos del Atlántico, el Caribe o el dominio indo-Pacífico, donde forman los denominados arrecifes coralinos “mesofóticos” y “afóticos”, creciendo a profundidades que oscilan entre los 50 a los 2000m. Estos arrecifes atípicos, en comparación a los arrecifes “eufóticos” que crecen próximos a la superficie del mar, eran poco conocidos hasta fechas recientes. Su estudio está evidenciando que asimismo se componen de comunidades coralinas complejas, adaptadas a baja o incluso nula visibilidad y, de forma llamativa, a fuertes fluctuaciones estacionales en la temperatura y los niveles de nutrientes. Por estas características, los arrecifes mesofóticos y afóticos parecen constituir el símil actual de lo que algunos especialistas denominan como “nichos refugio”, en los que las comunidades arrecifales pueden haber sobrevivido durante los diferentes periodos de crisis global reconocidos en el pasado, y ser el núcleo o punto de partida de las posteriores expansiones, una vez reestablecidas las condiciones ambientales favorables para ello.
En base a estas evidencias, no resulta demasiado aventurado afirmar que los arrecifes y sus protagonistas todavía van a estar bastante tiempo en nuestros océanos, aunque precisarán utilizar nuevos mecanismos de adaptación ante las condiciones ambientales adversas que potencialmente se avecinan. La pregunta clave a resolver es si la capacidad de adaptación de los corales y el resto de componentes arrecifales será suficiente ante la magnitud y velocidad de los cambios ambientales que ya están ocurriendo y previsiblemente ocurran, interrogante que constituye una de las piedras angulares de la investigación y las discusiones actuales entre los especialistas. A modo de reflexión, ante esta encrucijada ambiental, ¿estamos nosotros, la especie humana, tan preparados como creemos o desearíamos?
Para saber más
Aronson R.B. (Ed.) 2007. Geological Approaches to Coral Reef Ecology. Springer, 439p.
Kiessling W., Flügel E., Golonka, J. (Eds.) 2002. Phanerozoic Reef Patterns. SEPM Special Publications, 72. 775p.
Stanley G.D. (Ed.) 2001. The History and Sedimentology of Ancient Reef Systems. Kluver Academic, 458p.
Sobre el autor: Juan Ignacio Baceta es profesor en el Departamento de Estratigrafía y Paleontología de la Facultad de Ciencia y Tecnología de la UPV-EHU.
El artículo Arrecifes fósiles, una paradoja geológica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Geología, Antropoceno y cambio climático
- La FCT viaja a Marte
- Proteómica: cuando las proteínas y la espectrometría de masas van de la mano
La química del azul de Patinir
Patinir es considerado el primer paisajista flamenco. El azul de sus paisajes se concentra al fondo y va impregnando el cuadro hacia adelante, como una ola que avanza dejándolo todo perdido de color azul. Este efecto de avance lo consigue a través de planos paralelos escalonados. Al fondo el cielo, con la línea del horizonte bien alta, comparte azul con las montañas. Al fondo todo es azul.
 Joachim Patinir. El paso de la laguna Estigia.1520 – 1524. Óleo sobre tabla, 64 x 103 cm.
Joachim Patinir. El paso de la laguna Estigia.1520 – 1524. Óleo sobre tabla, 64 x 103 cm.
Yves Klein decía que «el azul es lo invisible haciéndose visible». El azul se ha utilizado en arte como concepto, especialmente para hacer notar lo inmaterial. Para pintar el paraíso y la oscuridad. El artista contemporáneo Anish Kapoor pintó un limbo azul oscurísimo que atrapa la luz en su Descenso al limbo. Los impresionistas renegaron del negro y pintaron las sombras de azul. El azul del Renacimiento es el azul de Patinir.
Se podría contar gran parte de la historia del arte a través del azul. Desde el azul egipcio, el ultramarino, el azul de cobalto, el cerúleo, el azul de manganeso, el de Berlín, el de París, el de Prusia, el de Milori, el de Bremen, hasta el azul de montaña, la azurita. Cada uno de ellos tiene un azul particular que puede describirse en gran medida gracias a la química de coordinación, como los azules que son azules por la presencia de metales de transición (cobalto, cobre, hierro, manganeso…). Algunos azules tienen matices de color que hay quien colocaría dentro de los violetas o los verdes. Algunos incluso mutan como consecuencia de la química y el tiempo. Hay artistas que han utilizado estas mutaciones o aparentes defectos de color en su beneficio. Entre ellos está el azul de Patinir, con frecuencia a caballo entre el color azul ultramarino y el turquesa.
El azul de Patinir es el azul de montaña, comúnmente llamado azurita. Hasta mediados del siglo XVIII fue el pigmento más utilizado en la pintura europea, y vino a sustituir el valioso azul ultramar auténtico, el que se extraía del lapislázuli y que provenía de Afganistán. La azurita, en cambio, se extraía de las montañas germanas, de ahí su nombre azul de montaña.
Hay constancia de que se conocía desde la antigüedad: los armenium y caeruleum que menciona Plinio eran seguramente tipos de azurita. Para diferenciarlos del ultramar se denominaban azzurrum ciramarinum o azzurro dell’Allemagna.
-
La química de la azurita en pintura
Químicamente la azurita es un carbonato básico de cobre, con un contenido en agua de cristalización variable (Cu3(CO3)2(OH)2). En los yacimientos se encuentra junto a la malaquita, con la que guarda una importante similitud química.
Se puede utilizar con medios acuosos como el temple o con gomas vegetales. Desprende un color azul luminoso. En comparación con el ultramarino tiende a verdoso con una leve tonalidad violácea.
En pinturas con medio aceitoso, como el óleo, capa a capa el resultado puede parecer casi negro. Añadiendo blanco es como se obtienen los azules más puros y cubrientes. Además, como la azurita es estable frente a los álcalis, se puede utilizar en medios oleosos mezclado con cal. El problema del óleo es que puede presentar rechazos de coloración y verdear, principalmente por formación de oleato de cobre.
-
Verdeado de la azurita
El tono aturquesado del azul de Patinir tiene que ver con la química de la azurita y su parcial transmutación en malaquita. Si el pigmento absorbe agua, parte de él acaba transformándose en malaquita (Cu2CO3(OH)2) que es de color verde. Esta es la razón por la que habitualmente las piedras que contienen azurita también presentan coloración verdosa de malaquita y viceversa.

Tanto la azurita como la malaquita pueden oxidarse y dar lugar a óxido de cobre o a sulfuro de cobre, en ambos casos de color negruzco. De ahí las zonas más oscuras de la piedra de la imagen anterior.
En cuanto el pigmento se mezcla con el aglutinante oleaginoso para formar la pintura al óleo, esta transmutación azurita-malaquita se queda congelada en el tiempo. Esa es la razón por la que las pinturas al óleo de azurita tienen tonos de color sutilmente diferentes, más verdes o azules.
El verdeado también puede deberse al propio amarilleamiento del aglutinante y, en mayor medida, al uso de barnices. A la hora de restaurar un cuadro hay que evaluar si el verdeado es propio del pigmento o es consecuencia de una alteración del medio. De hecho, es habitual que algunos pintores apliquen veladuras amarillas sobre la azurita para potenciar el verdeado. O que directamente mezclen pinturas como el amarillo de plomo con la azurita para conseguir pintura verde.
-
La azurita en la actualidad
La azurita tiene una composición química tan sencilla que ha sido fácil de obtener de forma sintética. A los carbonatos básicos de cobre producidos artificialmente se les conoce bajo el nombre de verditer. El grano que se comercializa es fino y regular, y resulta indistinguible de la azurita natural más débil de color. A pesar de que en el siglo XVIII ya existía el verditer, la batalla del azul la ganó el azul Berlín, un ferrocioanuro férrico mucho más estable y económico. Unos decenios más tarde se sumaron como sustitutos el azul ultramar artificial y el azul cobalto.
- El paso de la laguna Estigia
En 2013 hubo una exposición en el Museo del Prado llamada Historias naturales, un proyecto de Miguel Ángel Blanco. La exposición consistió en la instalación de alrededor de 150 piezas de historia natural, procedentes en su mayoría del Museo Nacional de Ciencias Naturales del CSIC –animales, plantas y minerales- junto a 25 obras de la colección del Museo, que entrañaban una estrecha relación con las mismas.

Una de las instalaciones que mejor definió el papel de Blanco dentro de las salas del Museo es su intervención en el emblemático cuadro de Joachim Patinir, El paso de la laguna Estigia. Delante de él colocó una gigantesca roca de azurita. Una roca a modo de prolongación de la laguna, o como resultado de su desecación, añadiendo un plano más a la obra original. La elección de la roca es coherente porque precisamente la azurita es el pigmento del azul que Patinir empleó en este cuadro.
El paso de la laguna Estigia está dividido verticalmente en tres zonas. En él se mezclan imágenes bíblicas junto a otras propias del mundo grecorromano. A la derecha está el Paraíso, con una zona de entrada angosta. En él prima el verde fresco y los azules. A la izquierda está el Infierno, con una entrada amplia y fácil, con verdes apagados, y al fondo negros y rojos que quedan fuera de la vista del navegante. En el centro Caronte lleva en su barca a un alma. Surcan la laguna turquesa en dirección al infierno.
-
De Patinir a Mejuto
El artista contemporáneo Vítor Mejuto ha traducido algunos de los cuadros más icónicos de la historia a un lenguaje geométrico. Uno de ellos es El paso de la laguna Estigia de Patinir. Mediante un proceso de síntesis, economía de formas y economía de color, Mejuto ha pintado el paso de la laguna Estigia empleando exclusivamente ocho planos de color sin transición entre ellos. De la misma forma que Mondrian eliminaba el velo que no le permitía ver la realidad en sus obras neoplásticas, Mejuto rescata lo grueso del cuadro de Patinir, como un ejercicio de optimización de la memoria.
 Vítor Mejuto. El paso de la laguna Estigia.2018. Acrílico sobre loneta resinada, 55 x 65 cm.
Vítor Mejuto. El paso de la laguna Estigia.2018. Acrílico sobre loneta resinada, 55 x 65 cm.
El azul de la laguna de Mejuto es el acrílico turquesa de Windsor & Newton. Este color se fabrica a partir del azul cobalto sintético o azul de Thénard, y químicamente es una espinela de óxido de cobalto (II) y óxido de aluminio (CoO·Al2O3), o aluminato de cobalto (II) (CoAl2O4). Es un pigmento de un azul intenso y puro que, combinado con óxido de cromo en la espinela, adquiere el color aturquesado final.
El uso del azul cobalto turquesa es la evolución lógica, desde un punto de vista técnico, de la renacentista azurita. Al igual que Patinir, Mejuto también empleó blanco en la mezcla para obtener el tono que encajaba. Patinir empleó blanco de plomo, actualmente en desuso por su toxicidad. Mejuto, blanco de zinc. También los blancos evolucionan en el arte cuanta más química sabemos sobre ellos.
Aunque el tema de El paso de la laguna Estigia es atemporal, tanto Patinir como Mejuto emplearon para pintarlo los azules de su tiempo.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo La química del azul de Patinir se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El Rubius hace un vídeo de química y la lía parda
- Los bimbaches de Punta Azul (El Hierro)
- Ensayo sobre el azul
El secreto de los números que no querían ser simétricos
Los números capicúas, o palíndromos, que son aquellos números tales que sus cifras leídas de izquierda a derecha y de derecha a izquierda son las mismas, son un tipo de números que, por la simetría que encierran, llaman la atención de la mayoría de las personas. De hecho, buscarlos, e incluso coleccionarlos, en las matrículas de los coches, los décimos de lotería, los billetes de medios de transporte, como autobús, tren o metro, los billetes de la moneda de cualquier país o cualquier otro lugar en el que aparezcan números de cuatro, o más dígitos, es algo bastante habitual. Más aún, muchas personas relacionan el hecho de encontrarse con un número capicúa, con la buena suerte.
 Billete de autobús Valencia-El Saler, con numeración capicúa, 13631. Imagen de la página web todocoleccion
Billete de autobús Valencia-El Saler, con numeración capicúa, 13631. Imagen de la página web todocoleccion
El concepto de número capicúa es muy sencillo y es muy fácil construir ejemplos de estos números. La forma más trivial es considerar un número con todos sus dígitos iguales, como 333.333.333, o se puede considerar una sucesión de cifras que luego se repiten en el sentido contrario, 12.433.421, aunque puede no repetirse el número central, 1.243.421. Así podemos crear todos los números palindrómicos que queramos: 232, 1.221, 55.555, 813.318, 1.756.571, etcétera. Claramente, existe una cantidad infinita de números capicúas, dado uno de estos números, siempre podemos generar uno más grande con solo añadir una misma cifra a la derecha y la izquierda del número, así dado el 121, podemos añadir el 7, obteniendo 71.217, si ahora añadimos el 3, se tiene 3.712.173, y este proceso es infinito.
 Antiguo billete de la Lotería Nacional, de abril de 1963, con un número capicúa, 28982. Imagen de la página Wallapop
Antiguo billete de la Lotería Nacional, de abril de 1963, con un número capicúa, 28982. Imagen de la página Wallapop
El concepto de palíndromo está fuertemente ligado a la representación posicional de los números, y además, depende de la base en la que se representan, en nuestro caso, es un sistema decimal, base 10. Por ejemplo, el número 2.002 es capicúa (en la base 10 en la que lo representamos de forma habitual), pero si se representa este mismo número en la base binaria, es decir, la base 2, con 0s y 1s, es decir, 11111010010, este ya no es capicúa. O si se representa el 2.002 en base octal, es decir, la base 8 (en la que utilizamos como cifras básicas 0, 1, 2, 3, 4, 5, 6 y 7), que se escribe como 3722, tampoco es capicúa.
Como sabemos, nuestro sistema de numeración posicional decimal viene la antigua India. Y precisamente, en la obra Ganatasarasamgraha – Compendio de la esencia de las matemáticas, del año 850, del matemático indio Mahaviracharya, se habla de un cierto número que “comienza por uno (y va aumentando de forma progresiva) hasta seis, para, a continuación, disminuir ordenadamente”, es decir, se refiere al número 123.45.654.321.
Esta familia de números capicúas, en la cual las cifras van subiendo, en una unidad, y luego bajando, tiene una propiedad curiosa, ya que puede obtenerse como el cuadrado de los números cuyos dígitos son solo unos:

Además, si cogemos cada uno de esos palíndromos, se verifica que la suma de las cifras del número es un número cuadrado.
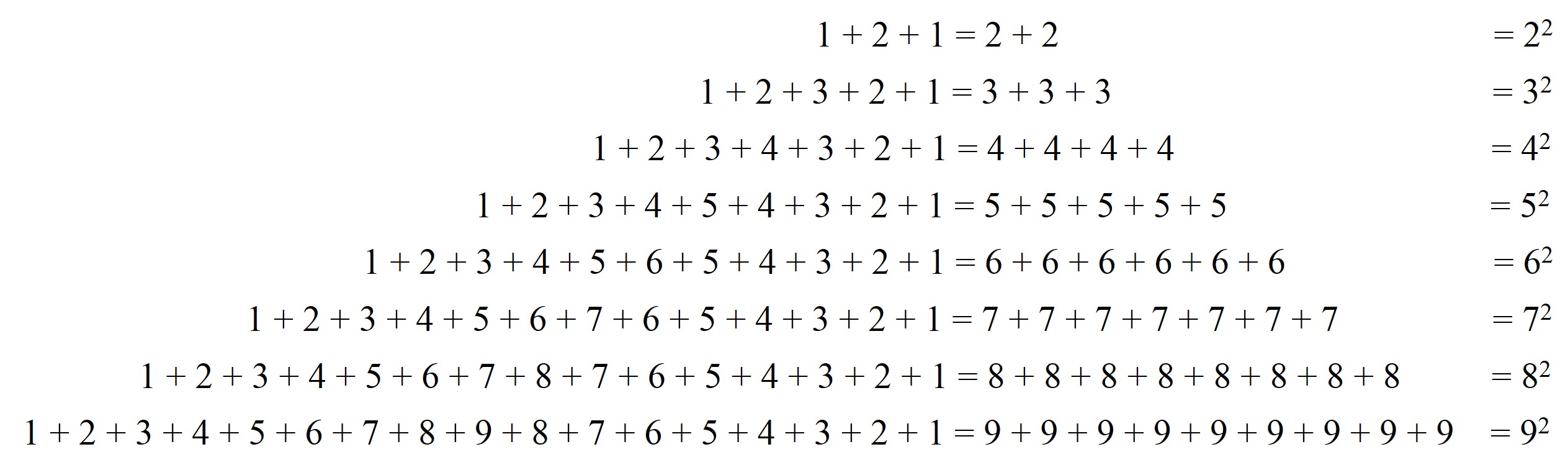
Más aún, estos particulares números capicúas, de la forma 12345654321, se pueden obtener también mediante una expresión simétrica bastante llamativa, aunque realmente solo es la combinación de las dos anteriores.
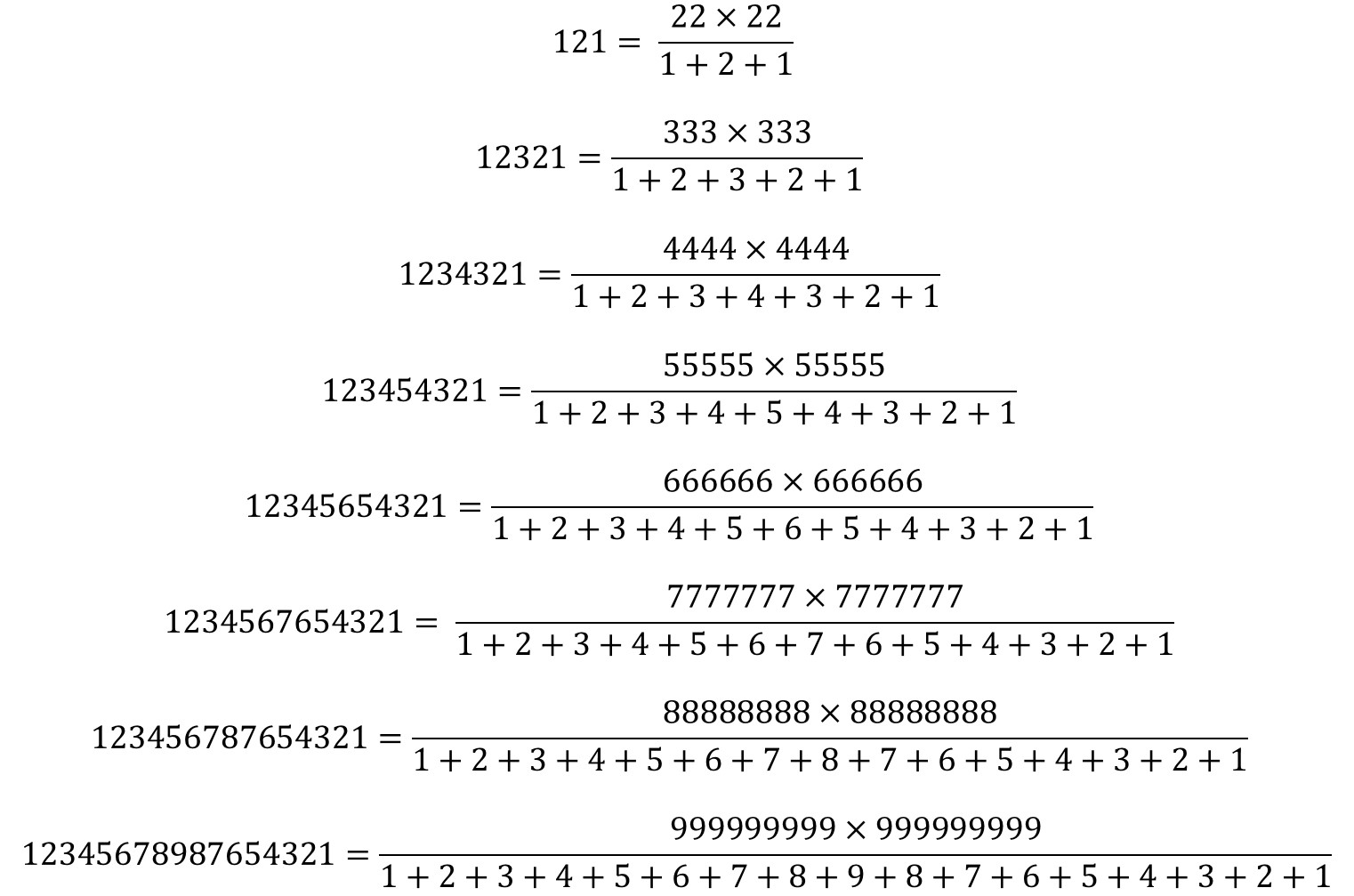
Pero vayamos con el objetivo central de esta entrada, una curiosa forma de obtener números capicúas. Tomemos un número cualquiera, por ejemplo, el 17 y sumémosle su simétrico, el 71, entonces se obtiene 17 + 71 = 55, que es palíndromo.
Probemos con otros números. Por ejemplo, el 75, entonces 75 + 57 = 132, que no es palíndromo, pero volvamos a realizar el mismo proceso con este resultado, 132 + 231 = 363, que ahora sí es capicúa, y lo hemos conseguido en dos pasos.
Veamos qué ocurre con algunos otros números. El 86, le sumamos su simétrico, 86 + 68 = 154, y como no es capicúa, seguimos el proceso, 154 + 451 = 605, una iteración más, 605 + 506 = 1111, de nuevo capicúa, en esta ocasión en tres pasos. Si empezamos en el número 87, después de cuatro pasos se obtiene el número 4.884, que es un número palindrómico. El número 88 ya es capicúa, es igual a su simétrico, luego no damos ningún paso con él. Si empezamos con el 89, necesitaremos 24 pasos hasta llegar a un número capicúa, el 8.813.200.023.188, como podéis comprobar.
Antes de continuar, podemos hacer una representación, con colores, de los 100 primeros números, distribuidos en una matriz cuadrada 10 x 10, de manera que el color esté relacionado con la cantidad de iteraciones que se necesitan para llegar a un palíndromo.
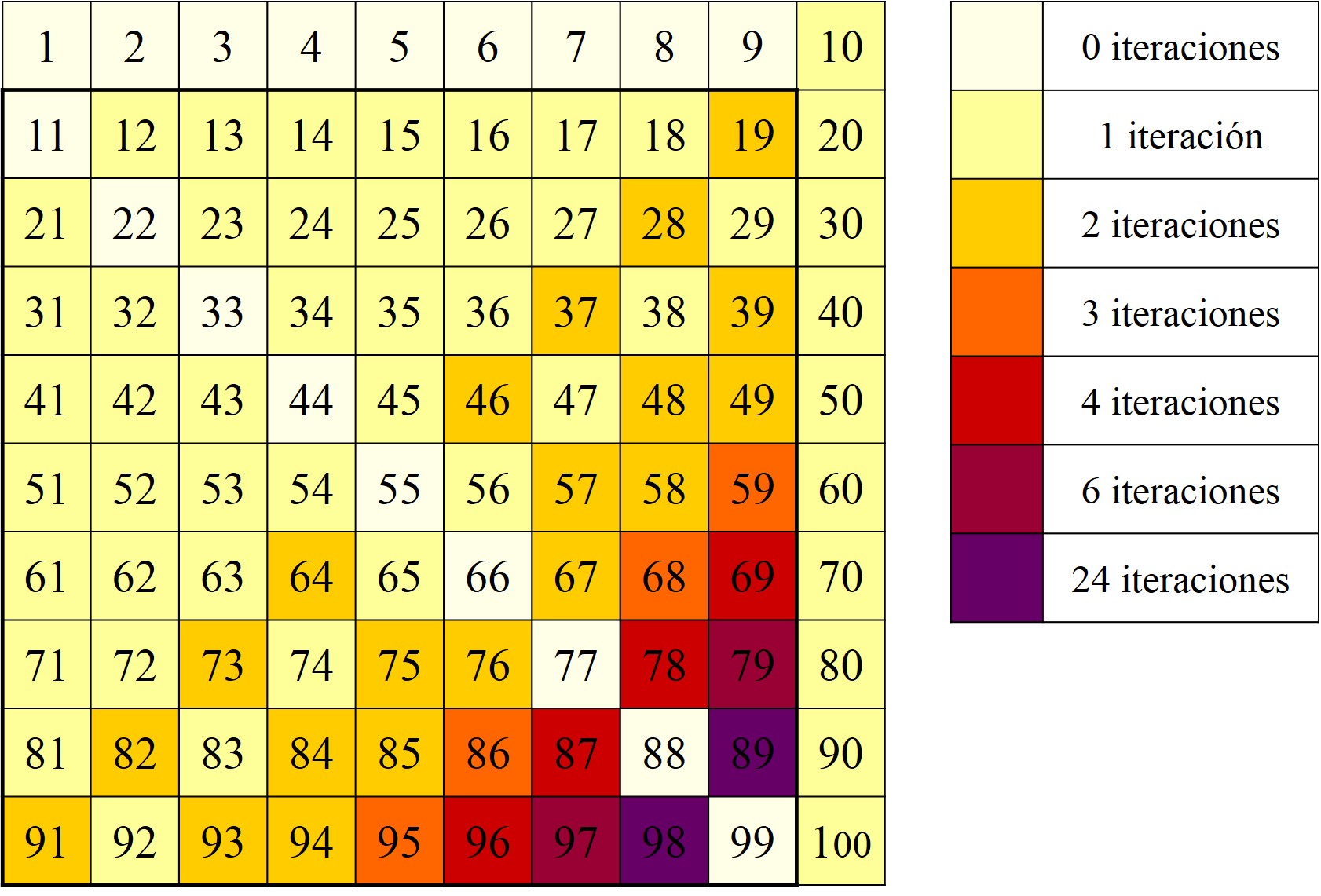
Como puede observarse, existe una cierta simetría alrededor del eje de los números de dos cifras formados por dos dígitos iguales, como 44 o 77, ya que los números a un lado y otro de este eje son los simétricos, como 67 y 76, que tienen igual comportamiento frente a este proceso.
La pregunta que se nos ocurre después de estos ejemplos, e incluso podemos intentarlo con algunos números más a ver qué ocurre, es:
Problema: ¿Se obtendrá siempre un número capicúa mediante este método iterativo, de sumar a un número su simétrico?
Este es un problema que aún está abierto, no se sabe si la respuesta es afirmativa o negativa. De hecho, el número 196, que no es un número muy grande, se desconoce si produce un número capicúa mediante este proceso iterativo. Veamos las primeras 26 iteraciones:

Desde la década de 1980, y haciendo uso de los ordenadores, se ha estado trabajando en realizar el mayor número de iteraciones posibles para ver si se alcanzaba un palíndromo, sin embargo, a día de hoy aún no se ha conseguido alcanzar un número con esta propiedad. En la actualidad, tenemos que Romain Dolbeau, con su programa “p196_mpi”, consiguió realizar en 2011 un billón de iteraciones, con las cuales alcanzó un número de más de 400 millones de dígitos, sin conseguir un número capicúa. Y en 2015 alcanzó un número con un billón de dígitos, sin conseguir el objetivo de llegar a un palíndromo. Por lo tanto, este es un problema abierto, aún se desconoce si empezando en el número 196, mediante el proceso iterativo “sumar el simétrico”, será posible obtener un número capicúa en algún momento, o si será este un proceso infinito, que nunca dará lugar a un palíndromo.
De hecho, se ha bautizado con el nombre de “números de Lychrel” (este nombre es un anagrama de Cheryl, el nombre de la novia, ahora mujer, de un matemático, Wade VanLandingham, que trabajaba en este tema), a aquellos números de los que se desconoce si generan un número palindrómico. Los primeros términos de la sucesión de estos números, etiquetada como A023108 en la Enciclopedia on-line de sucesiones de enteros de N. J. A. Sloane, son:
196, 295, 394, 493, 592, 689, 691, 788, 790, 879, 887, 978, 986, 1.495, 1.497, 1.585, 1.587, 1.675, 1.677, 1.765, 1.767, 1.855, 1.857, 1.945, 1.947, 1.997, …
Por otra parte, ya sabíamos que los números 887 y 1.675 también eran números de Lychrel, puesto que estaban en la sucesión de iteraciones del número 196. De hecho, se ha dividido a la familia de números de Lychrel en dos tipos de números, las “semillas”, que son los números más pequeños que generan un “hilo” de iteraciones, como el número 196, o los “familiares”, que son aquellos números que forman parte de un hilo generado por una “semilla”, como 887, 1.675 o 7.436, que están en el hilo del 196, o aquellos números que generan un mismo hilo que una semilla, como los números 295 (ya que, 295 + 592 = 887, que está en el hilo del 196, luego se genera este hilo a partir de 887), 394 (ya que, 394 + 493 = 887) o 689 (ya que, 689 + 986 = 1.675, que está en el hilo de 196). Dicho de otra forma, solamente hace falta estudiar las semillas, ya que los familiares tienen el mismo comportamiento que estas.
Solamente hay cuatro semillas menores que 10.000, que son 196, 879, 1.997 y 7.059, sin embargo, a partir de 10.000, ya hay muchas más semillas. Las siguientes son:
10.553, 10.563, 10.577, 10.583, 10.585, 10.638, 10.663, 10.668, 10.697, 10.715, 10.728, 10.735, 10.746, 10.748, 10.783, 10.785, 10.787, 10.788, 10.877, 10.883, 10.963, 10.965, 10.969, 10.977, 10.983, 10.985, 12.797, 12.898, etcétera.
 Billete de España de 500 pesetas, del año 1979, con la imagen de Rosalía de Castro, y con un número de serie capicúa, 2152512. Imagen de la página de Numismática Bilbao
Billete de España de 500 pesetas, del año 1979, con la imagen de Rosalía de Castro, y con un número de serie capicúa, 2152512. Imagen de la página de Numismática Bilbao
Volviendo a los números que sí generan un número capicúa mediante el proceso “sumar el simétrico”, hemos visto que el número 89 necesitaba de 24 iteraciones para alcanzar el palíndromo. Otra cuestión que nos podemos plantear es si, salvo en el caso de los números de Lychrel, se necesitan muchas iteraciones para llegar al capicúa. El mayor número de iteraciones para un número de 3 dígitos es 187, que necesita 23 pasos para alcanzar el palíndromo. Con 4 cifras es el 1.297, que necesita 21 iteraciones.
Aunque, a día de hoy, el mayor número de iteraciones necesarias para obtener un número palindrómico, mediante este proceso, es de 261, que convierten el número 1.186.060.307.891.929.990, con 19 dígitos, en un número capicúa de 119 dígitos. En el siguiente cuadro se recogen los records de iteraciones necesarias para números de entre 2 y 19 dígitos.
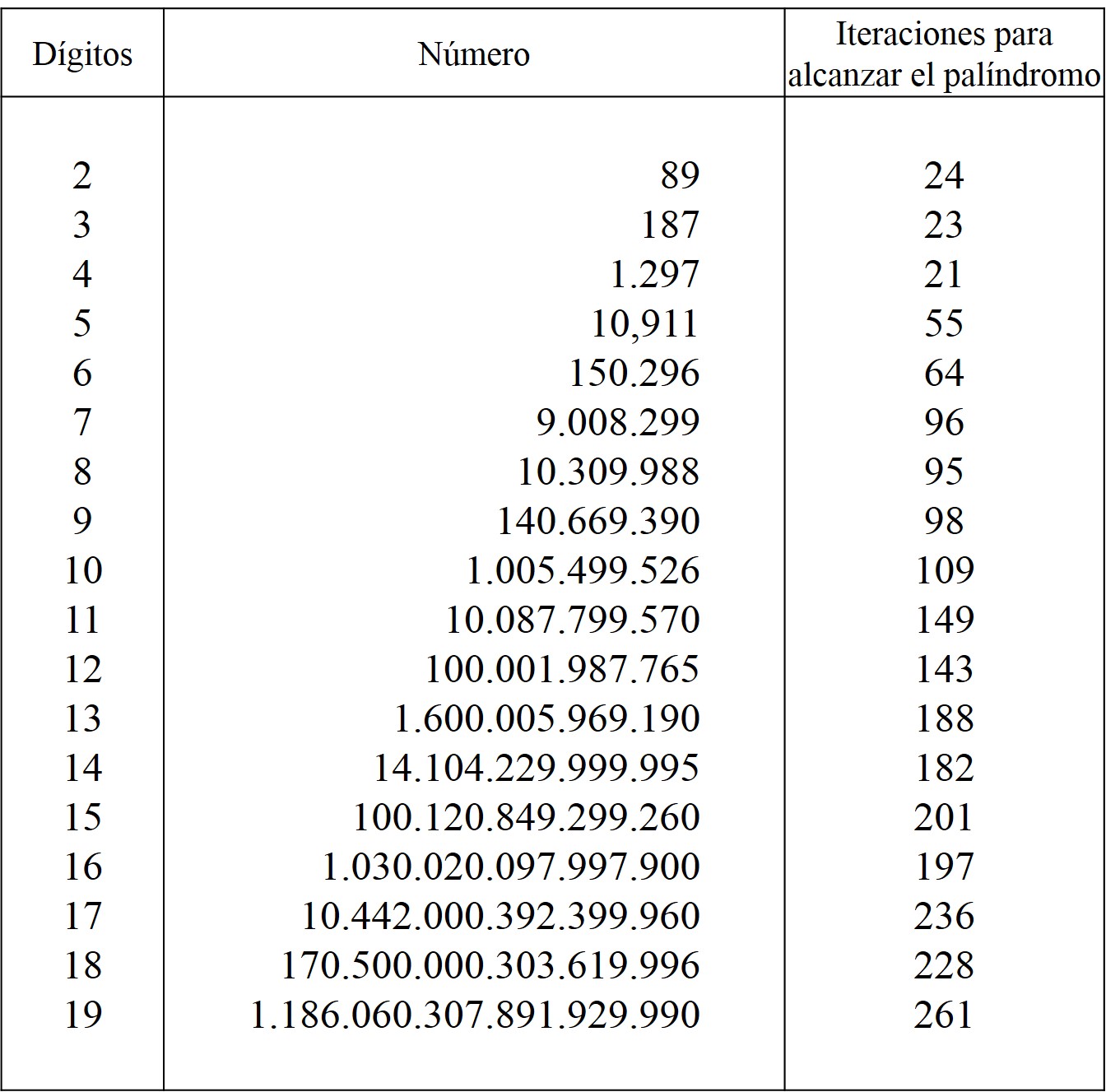
Para terminar, me gustaría hacer un breve comentario sobre algunas familias de números capicúa. En el mundo de las matemáticas nos encanta “jugar” y estudiar las diferentes propiedades matemáticas con las que nos encontremos, solo por el placer del conocimiento. Así, en el caso de los números palindrómicos, se estudian las familias de estos números que además satisfacen otras propiedades matemáticas, como ser números cuadrados, cúbicos o cualquier otra potencia, números triangulares y otros números poligonales, o números primos, así mismo se estudian diferentes objetos matemáticos formados con números capicúas, como las ternas pitagóricas o los cuadrados mágicos.
Veamos algunos ejemplos. Recordemos que los números triangulares son aquellos que se pueden representar con piedras como un triángulo equilátero y que coinciden con aquellos que son la suma de los primeros números naturales, como 1 + 2 + 3 = 6 ó 1 + 2+ 3 + 4 = 10 (véanse las entradas El asesinato de Pitágoras, historia y matemáticas (y II) o La magia de los números (el teorema de Moessner)). Y la fórmula general de los números triangulares es Tn = n x (n – 1) / 2.
¿Existirán números triangulares capicúas? Sí, por ejemplo, los primeros números triangulares capicúas son:
T1 = 1, T2 = 3, T3 = 6, T10 = 55, T11 = 66, T18 = 171, T34 = 595, T36 = 666, T77 = 3003, T109 = 5995, T132 = 8778, T173 = 15051, …
Por cierto, que el número de la bestia (véanse las entradas 666, el número de la Bestia (I) y 666, el número de la Bestia (II)) es un número triangular capicúa. Se conocen 147 números triangulares capicúas.
Un campo en el que se está trabajando mucho es en el estudio de los números capicúas primos, como los números 131 o 757. A continuación, os dejo el listado de los primeros palíndromos primos:
2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, 10.301, 10.501, …
 Obra Family vacation (2016), de la artista estadounidense Xylor Jane, en la que se observan dos columnas de 13 números, de 11 dígitos cada uno de ellos, que resultan ser números capicúas primos con 11 dígitos, que solo contienen 2 de las 10 cifras básicas, como 1.111.515.111 o 13.131.113.131. Imagen de la página web ART SY
Obra Family vacation (2016), de la artista estadounidense Xylor Jane, en la que se observan dos columnas de 13 números, de 11 dígitos cada uno de ellos, que resultan ser números capicúas primos con 11 dígitos, que solo contienen 2 de las 10 cifras básicas, como 1.111.515.111 o 13.131.113.131. Imagen de la página web ART SY
Vamos a terminar la entrada con tres cuadrados mágicos diabólicos (es decir, la suma de los elementos de las filas, de las columnas, de las diagonales principales, pero también de las diagonales no principales, que están partidas en dos partes), encajados, cada uno dentro del siguiente, formados con números capicúas, cuyas sumas mágicas son de nuevos números capicúas, 2.442 (en el central, de orden 4), 3.663 (en el de orden 6) y 4.884 (en el exterior de orden 8).
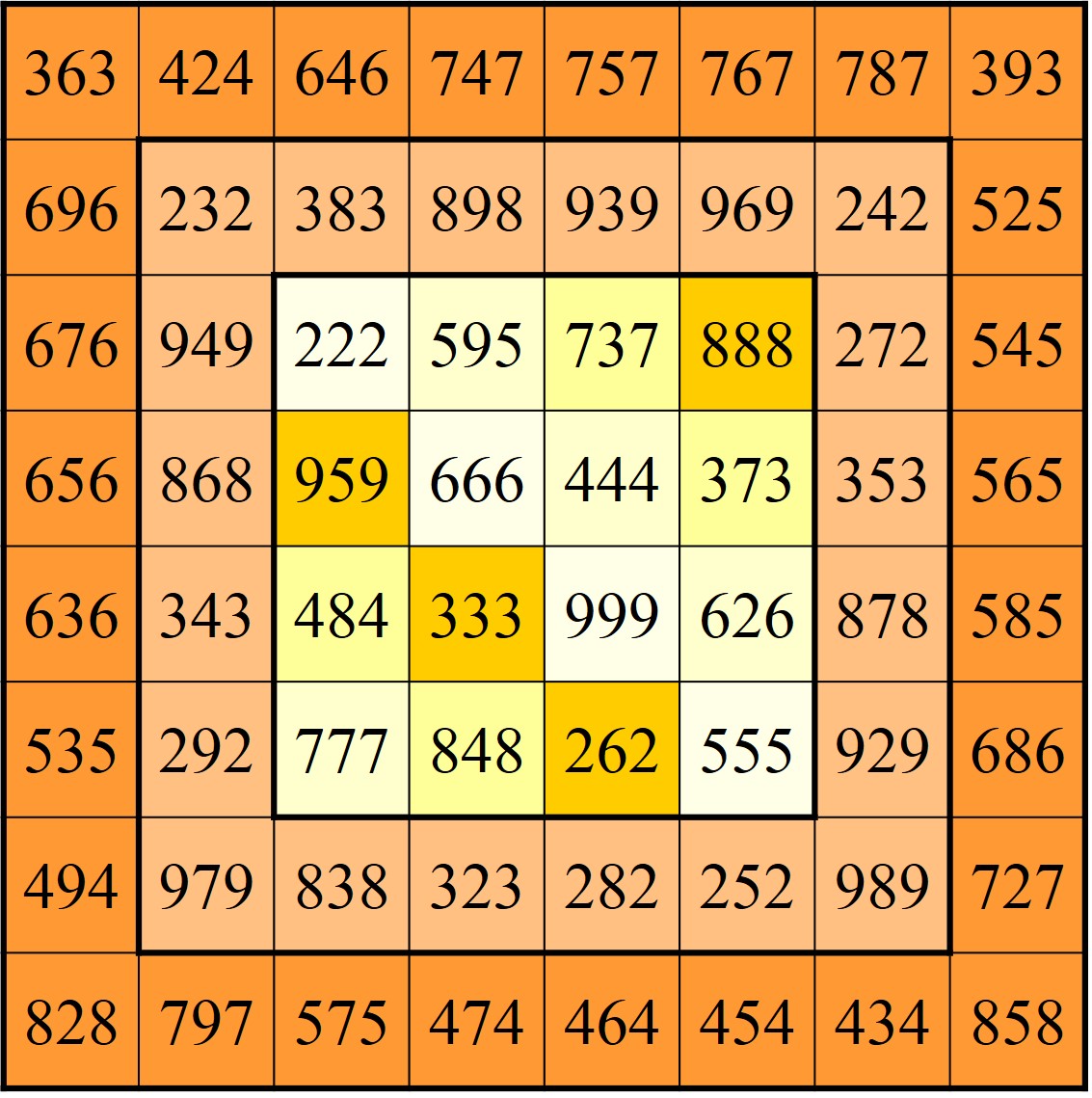 En el centro, un cuadrado mágico diabólico de orden 4 y suma mágica 2.442, formado por números capicúas. Se completa con un borde de números capicúas, dando lugar a un cuadrado mágico diabólico de orden 6 y suma mágica 3.663. Y se vuelve a completar con un borde de números capicúas, para dar lugar a un cuadrado mágico diabólico de orden 8 y suma mágica 4.884
En el centro, un cuadrado mágico diabólico de orden 4 y suma mágica 2.442, formado por números capicúas. Se completa con un borde de números capicúas, dando lugar a un cuadrado mágico diabólico de orden 6 y suma mágica 3.663. Y se vuelve a completar con un borde de números capicúas, para dar lugar a un cuadrado mágico diabólico de orden 8 y suma mágica 4.884
Bibliografía
1.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.
2.- Clifford A. Pickover, La maravilla de los números. Un viaje por los secretos de las matemáticas, sus desafíos y caprichos, Ma Non Troppo (ediciones Robinbook), 2002.
3.- Harvey Heinz, Palindromes
4.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A006960 (sucesión de números formados por la iteración “suma del simétrico” a partir del número 196)
5.- Romain Dolbeau, The p196_mpi page
6.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A023108 (números de Lychrel)
7.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A063048 (números de Lychrel semillas)
8.- Jason Doucette, World Records
9.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A003098 (números triangulares capicúas)
10.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A002385 (Números capicúas primos)
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El secreto de los números que no querían ser simétricos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una conjetura sobre ciertos números en el ‘sistema Shadok’
- El origen poético de los números de Fibonacci
- Los números enamorados
Polarizadores y el triunfo de la hipótesis ondulatoria
 Fuente: Polaroid / Safilo
Fuente: Polaroid / Safilo
Los estudios científicos sobre la polarización de la luz continuaron a lo largo del siglo XIX. Por ejemplo, la forma en que el espato de Islandia separa un haz de luz no polarizada en dos haces polarizados se muestra en la de abajo y es una representación que conceptualmente data originalmente de esa época. Sin embargo, las aplicaciones prácticas se vieron frustradas, principalmente porque las sustancias polarizadoras como el propio espato de Islandia eran escasas y muy frágiles.
 Fuente: Cassidy Physics Library
Fuente: Cassidy Physics Library
Uno de los mejores polarizadores era el cristal sintético herapatita, sulfato de yodo-quinina. Decimos sintético porque se descubrieron de forma accidental en 1852 cuando un estudiante añadió yodo a la orina de un perro al que habían suministrado quinina y observó que aparecían unos cristales verdosos. El responsable del laboratorio, William Bird Herapath, estudió los cristales al microscopio. Encontró que los cristales de herapatita en forma de aguja absorbían la luz que está polarizada en la dirección del eje largo del cristal y absorben muy poca de la luz polarizada en una dirección perpendicular al eje largo.
Los cristales de herapatita eran tan frágiles que parecía que no había forma de usarlos. Pero en 1928, Edwin H. Land, cuando aún era un estudiante de primer curso en la universidad, inventó una lámina de plástico que llamó “Polaroid”. Este primer polarizador era una película transparente de nitrocelulosa en la que había incrustado muchos pequeños cristales de herapatita de tal manera que, cuando se estiraba el plástico, los cristales en forma de aguja se alineaban en una dirección. Por lo tanto, todos interactuaban con la luz incidente de la misma manera.
Algunas de las propiedades de un material polarizador se pueden comprobar fácilmente. Por ejemplo, se pueden obtener dos superficies de polarización de las lentes de un par de gafas de sol polarizadas, o de las gafas “tridimensionales” usadas en los cines. Si sostenemos una de las lentes frente a una fuente de luz y miramos esta primera lente a través de la segunda, comprobamos que al girar la primera lente la intensidad de luz sube y baja alternativamente. Encontraremos que una rotación de 90º nos lleva de la intensidad másxima a la mínima.
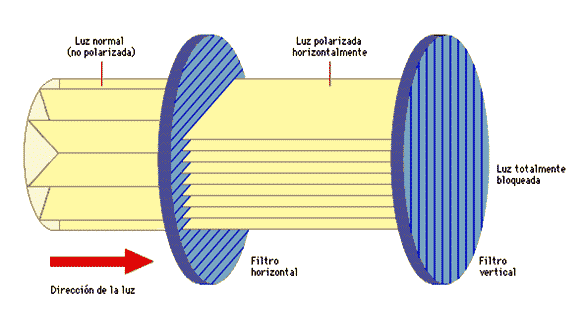 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons
¿Cómo se puede explicar este efecto? La luz que incide en la primera lente, o superficie de polarización, originalmente no está polarizada, es decir, es una mezcla de ondas polarizadas en diferentes direcciones, como ya vimos. La primera lente transmite solo las ondas que están polarizadas en una dirección y absorbe el resto. La onda transmitida que va hacia la segunda hoja ahora está polarizada en una dirección. Siempre que esta dirección coincida con la dirección de polarización de la segunda superficie, la onda no será absorbida por la segunda lente. Sin embargo, si la dirección es perpendicular a la dirección de polarización, la luz polarizada no pasará a través de la segunda lente, sino que será absorbida.
Como conclusión general de lo que hemos visto sobre las ondas de luz, vemos que los efectos de interferencia y difracción requerían un modelo de onda para la luz. Para explicar los fenómenos de polarización, el modelo de onda se tuvo que hacer más específico; la polarización podría explicarse solo si las ondas de luz son ondas transversales. En conjunto, este modelo para la luz explicaba muy satisfactoriamente todas las características de la luz consideradas hasta principios del siglo XX.
Pero, hay una nota disonante, ¿verdad? ¿En qué medio se transmiten las ondas de luz que vienen del Sol o de la Luna o de las estrellas?
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Polarizadores y el triunfo de la hipótesis ondulatoria se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
