Lo que Venus, el gemelo infernal de la Tierra, podría enseñarnos sobre lo que hace a un planeta habitable
 Comparación de Venus con la Tierra. Fuente: Wikimedia Commons
Comparación de Venus con la Tierra. Fuente: Wikimedia Commons
Empiezo pidiendo perdón por haber insultado así a Venus, llamándole infernal, algo inmerecido para un planeta que ya tuvo que sufrir a Mecano. Pero Venus tendrá que reconocer que no nos lo pone fácil para adjetivarle con amabilidad: 400 grados de temperatura, una presión atmosférica capaz de aplastar cualquier cosa y nubes de ácido sulfúrico pululando de aquí para allá. Como para darse un paseíto por allí una tranquila mañana de primavera.
Pero no siempre fue así. Venus fue una vez un planeta muy similar a la Tierra y algunos investigadores sugieren que durante tres mil millones de años, Venus fue un planeta cubierto por grandes océanos capaces de albergar vida. Eso lo convertiría en el primer planeta habitable del sistema solar, un punto con las mismas probabilidades que la Tierra de desarrollar formas de vida. Algunas de sus similitudes aún persisten hoy: ambas se parecen en tamaño, densidad y composición química. Otras como los océanos y la atmósfera habitable, no tanto…
El caso es que algo ocurrió y cambió Venus de un lugar no quizá parecido a la tierra a una suerte de su Mr. Hyde, y por eso, cuenta Nature en un detallado reportaje, equipos de científicos de distintas agencias espaciales de todo el mundo quieren saber qué fue. Esto, además de profundizar en el conocimiento sobre nuestro planeta vecino y con él sobre nuestro sistema solar, puede servirnos para determinar en cuáles de los cientos de planetas rocosos que seguimos descubriendo más allá del sistema solar puede haber vida.
Las agencias espaciales ponen los ojos en Venus
 Venus en color a partir de imágenes de la sonda Mariner 10. Fuente: Wikimedia Commons
Venus en color a partir de imágenes de la sonda Mariner 10. Fuente: Wikimedia Commons
India es la primera que va a probar suerte. La Organización India de Investigación Espacial lanzará su sonda en 2023 que pasará varios meses orbitando alrededor de Venus. Estados Unidos podría seguirla de cerca; varios grupos de científicos propondrán misiones a Venus a la NASA con la idea de partir en 2025. La Agencia Espacial Europea está considerando enviar su propio orbiter en 2032, y la agencia espacial rusa Roscosmos trabaja ya en colaboración con la NASA para enviar una ambiciosa misión entre 2026 y 2033 que incluiría una sonda para orbitar, otra para aterrizar que envíe mediciones a corto plazo y una estación de investigación que permanecería sobre Venus más tiempo.
Todo son pretendientes para Venus… ahora. Esto no siempre ha sido así: Venus ha sido durante décadas la gran olvidada frente a Marte. En los últimos 65 años, la NASA ha enviado 11 sondas a orbitar en torno al planeta rojo y 8 misiones que han aterrizado. En comparación, solo 2 naves han sido enviadas a orbitar alrededor de Venus, y la última fue en 1994. No ha sido en cualquier caso una falta de interés científico lo que ha detenido a la agencia espacial estadounidense, ya que sus equipos de investigación han propuesto cerca de 30 misiones a Venus en todos esos años, pero ninguna ha sido aprobada.
Las tornas han cambiado, y mientras tanto muchos de esos equipos científicos y técnicos han desarrollado los métodos y la tecnología para estudiar y sobrevivir en un entorno tan destructivo.
Venus fue nuestro primer destino… con poco éxito
 Venus captado por el telescopio Hubble el 24 de enero de 1995. Fuente: Wikimedia Commons
Venus captado por el telescopio Hubble el 24 de enero de 1995. Fuente: Wikimedia Commons
Probablemente esa desafección de las agencias por Venus comenzó en los inicios de la exploración espacial. Porque en aquellas primeras etapas sí que pusieron los ojos allí: Venus fue el escenario de la primera prueba interplanetaria (EEUU en 1962), el primer planeta en el que se estrelló una misión (la URSS en 1965) y el primer planeta extraterrestre en el que una misión aterrizó con éxito (también la URSS en 1966). Pero ya en aquellos años las observaciones que pudieron hacerse revelaron que Venus era un planeta asfixiante y tórrido: era difícil imaginarlo como un lugar en el que la raza humana fuese a establecer colonias, y tampoco un sitio donde la búsqueda de formas de vida resultase muy prometedora. Era difícil incluso estudiar sus condiciones con detalle.
Sin embargo, está claro que tenemos que volver allí. Algunas teorías, como decíamos, apuntan a que Venus pudo ser el primer lugar habitable del sistema solar pero, en algún momento, algo fue mal, muy mal, y toda esa habitabilidad se fue al garete. Quizá no haga tanto tiempo de aquello, quizá fue hace apenas 700 millones de años. Saber qué y cuándo ocurrió puede ayudarnos a entender mejor qué hace de la Tierra un lugar especial donde la vida apareció y se ha desarrollado, en principio el único lugar con estas características que conocemos hasta ahora.
Es una pregunta aun más importante ahora que la cuenta de planetas rocosos que orbitan en torno a estrellas en las llamadas zonas de habitabilidad (lo suficientemente cerca pero lo suficientemente lejos como para que la temperatura de la atmósfera permita la presencia de agua líquida) más allá de nuestro sistema solar no para de aumentar. Muchos de esos exoplanetas podrían ser muy similares a Venus. Cuanto más sepamos de nuestro extraño vecino, más sabremos sobre esos mundos lejanos.
Aparatos que sobrevivan (y funcionen)
 Superficie de Venus obtenida por la sonda Magallanes. Fuente: Wikimedia Commons
Superficie de Venus obtenida por la sonda Magallanes. Fuente: Wikimedia Commons
Algo que es un desafío tecnológico considerable. Muchos de los equipos que quieren ir allí a echar un vistazo no se conformarían con orbitar alrededor de Venus: quieren un módulo aterrizando en su superficie, algo que no se ha conseguido en 35 años. Y de aquellos que lo hicieron con éxito tampoco se pudo extraer mucho más, ya que la presión en la superficie es demoledora. La misión que más tiempo sobrevivió lo hizo durante poco más de 2 horas, 127 minutos en total.
Desde entonces ha pasado mucho tiempo y la tecnología y el conocimiento han avanzado considerablemente, así que los equipos que están proponiendo las nuevas misiones creen que sus dispositivos podrán aguantar allí varios meses. Una de las alternativas propuestas por científicos de la NASA sugiere que en vez de blindar el equipamiento con escudos gruesos y resistentes para que absorban el calor y le hagan frente a base de equipos de refrigeración, los sensores se construyan a base de electrónica sencilla hecha con carburo de silicio, un híbrido de silicio y carbono utilizado habitualmente para fabricar diamantes falsos que podría aguantar las duras condiciones del entorno venusiano.
Utilizando esos materiales, testados en cámaras que reproducen las condiciones de ese entorno, han diseñado una estación de prueba, del tamaño de una tostadora y que será capaz de medir la temperatura, la presión, la dirección y velocidad del viento, la cantidad de radiación solar en la superficie y la presencia de determinadas sustancias químicas en la zona más baja de la atmósfera durante varios meses. El resultado debería estar listo a mediados de la década de 2020 y que ofrecerá a otros países si quieren utilizarlo en sus propias misiones.
De una forma u otra, parece que Venus va a ser un lugar concurrido en los próximos 10 o 20 años, rectificando así un olvido histórico y abriendo, si lo conseguimos, un nuevo mundo a explorar con mucha información interesante. Quien sabe si, finalmente (disculpadme un último chascarrillo ochentero), no terminaremos yendo a Venus en un barco…
Referencias:
Venus is Earth’s evil twin — and space agencies can no longer resist its pull – Nature
Was Venus the First Habitable World of our Solar System? – Arxiv.org, Cornell University
Shukrayaan-1 – Wikipedia
Rusia y EEUU completan el diseño de su misión al infierno de Venus – Europa Press
Medio siglo desde el primer aterrizaje en un planeta extraterrestre – El País
Long-Lived In-Situ Solar System Explorer (LLISSE) – NASA
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Lo que Venus, el gemelo infernal de la Tierra, podría enseñarnos sobre lo que hace a un planeta habitable se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El pueblo que hablaba con las ballenas, ¿podría enseñarnos su idioma a los demás?
- Matemáticas del Planeta Tierra (MPE2013), en Bilbao
- Planeta X, en busca del inquilino invisible del sistema solar
Obesidad y delgadez también se heredan
 Imagen: Pixabay
Imagen: Pixabay
Ganar o perder peso es, simplificando algo las cosas, el resultado de un balance entre adquisición y gasto de energía. El organismo adquiere la que asimila a partir del alimento ingerido. Y debido a las actividades que desarrolla también gasta energía, la pierde en forma de calor disipado. Las actividades son muy variadas: unas son las necesarias para el normal funcionamiento de los sistemas orgánicos (actividades cardiacas, renales, nerviosas, etc.), entre las que se incluye el mantenimiento de la temperatura corporal; otras están ligadas a la renovación y reparación de células y tejidos; están, por otro lado, las responsables de la síntesis de nuevas estructuras; y por último, también las musculares implicadas en el ejercicio físico. Cuando la adquisición de energía supera al gasto, el organismo gana masa. Y lo contrario ocurre si el gasto es mayor que la asimilación de energía.
Dicho de esa forma las cosas parecen muy sencillas. Aunque en estos asuntos nada es tan sencillo como pueda parecer, la adquisición de energía es un término relativamente simple; hay dos factores principales a considerar, la cantidad de comida y su composición, que afecta a su contenido energético y a la facilidad o dificultad para digerirla y asimilarla. El gasto de energía tiene más complicaciones, porque influyen diversos factores.
Teniendo en cuenta cuáles son los determinantes de los elementos de adquisición y gasto energético, a nadie sorprende que el sobrepeso y la obesidad hayan alcanzado una gran prevalencia en las sociedades actuales. Hay mucha comida y, además, en general tenemos predilección por alimentos suculentos, de alto contenido energético y fácil absorción. Eso en lo que a la adquisición de energía se refiere. Y en lo relativo al gasto, tenemos una notable tendencia al sedentarismo y la inactividad física y, además, vivimos en entornos de gran confort térmico: difícilmente nos encontramos en condiciones que obliguen al organismo a gastar mucha energía para mantener estable la temperatura corporal. Lo dicho: las cosas parecen muy sencillas. Y sin embargo, no lo son tanto.
Todos conocemos personas que, aunque sean delgadas, no se privan a la hora de comer. Quienes tenemos tendencia a engordar los contemplamos con envidia, conscientes de lo duro que resulta limitarse ante una buena mesa, no picar entre horas o sufrir corriendo por las calles, o en el gimnasio pedaleando de manera desaforada encima de una bicicleta estática. Lo contrario también nos resulta conocido, personas que parecen no comer gran cosa y que, sin embargo, tienen excesivo peso.
¿Por qué ingiriendo similares cantidades de alimento y manteniendo parecidos niveles de actividad física unos estamos más gordos y otros más flacos? ¿A qué obedecen esas “incongruencias” metabólicas? Algunas pueden ser debidas a factores no tomados en consideración. Pero otro elemento importante a tener en cuenta es el factor genético y su incidencia sobre el metabolismo.
Han comparado el genoma de 1600 personas muy delgadas, 2000 muy obesas y 10400 de peso normal, y han confirmado algo que ya se sabía: la obesidad es una condición heredable en un grado no muy alto pero importante: el 32%, para ser precisos. La delgadez también lo es, aunque en una medida ligeramente inferior, un 28%. Esos porcentajes indican la proporción de la variabilidad del rasgo estudiado –obesidad o delgadez- en la población que es debida a factores hereditarios. Además, han identificado un conjunto de variantes genéticas ligadas a una condición, algunas de las cuales ya se conocían, y otras vinculadas con la opuesta. Por lo tanto, obesidad y delgadez, en parte al menos, también se heredan, aunque esto, a algunos, no nos sirva de mucho consuelo.
Fuente: Fernando Riveros-McKay et al (2019): Genetic architecture of human thinness compared to severe obesity PLOS Genetics 15(1): e1007603
——————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Obesidad y delgadez también se heredan se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El pteroestilbeno como posible tratamiento de la obesidad
- Gripe, obesidad y cáncer. Medicina de frontera.
- El organismo humano es una estufa de unos pocos vatios
¿Se podría clonar a una persona?
¿Te imaginas que hubiera una copia genética exacta a ti? Eso sí, esa copia exacta sería en términos de ADN nuclear. Todo esto quizá sea factible en el año 2100 o tal vez no. Hoy solo sabemos que es teóricamente factible. Ya que, más allá de las evidentes cuestiones éticas, todavía hay procesos biológicos que no controlamos.
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de cienciaÓrbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Se podría clonar a una persona? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Podría un humano vivir en el mar?
- ¿Qué tienen en común Einstein y una zanahoria?
- ¿Qué pasa en tu cuerpo cuando te enamoras?
De robots geólogos y rayos X
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Cuando se habla de geología se suele poner en perspectiva la escala temporal. Hablar del tiempo en términos geológicos supone hablar en millones de años. Por lo tanto, hablar de un periodo de tiempo de 50 años apenas significa un suspiro en la historia de nuestro planeta. Irrisorio a escala geológica, pero enorme a escala del/la geólogo/a. Concretamente el último medio siglo ha sido una vorágine de logros científicos y para muestra solo hemos de mirar aquello que tengamos sobre la mesa, en nuestro bolsillo o, mismamente, el instrumento a través del cual estemos leyendo este artículo.
Hace 50 años Neil Amstrong y Buzz Aldrin ponían los pies en la luna en lo que probablemente sea el mayor símbolo del progreso de nuestra especie en el último siglo. Lo que menos gente sabe es que uno de los objetivos de la tripulación del Apolo 11 era recoger muestras del suelo lunar. Una suerte de geólogos espaciales que se trajeron de vuelta a la tierra 22 kg de muestras que después fueron analizadas mediante difracción de rayos X.
Y es aquí donde llegamos al meollo de la cuestión, al entrar en la relación entre la exploración del terreno (terrestre o lunar) como una de las labores fundamentales del/la geólogo/a y la difracción de rayos X como una técnica ya rutinaria en la geología, transversal a casi todas las ciencias y herramienta fundamental para el progreso de nuestra especie. No sólo en los últimos 50 años, sino en los últimos 120. Para entender su importancia y trascendencia es imperativo retroceder a finales del siglo XIX, a la Universidad de Würzburg, Alemania.
Wilhelm Conrad Röntgen era catedrático de física de aquella universidad y su investigación se centraba en el poder de penetración de los rayos catódicos. El 8 de noviembre de 1895, cuando se encontraba experimentando el poder de penetración de los rayos catódicos, observó que una placa de cartón cubierta de cristales de platino-cianuro de bario, emitía una fluorescencia. Ésta desaparecía cuando desconectaba la corriente. La tarde de ese viernes llamo a su esposa Anna a la que pidió que pusiera la mano ante aquella placa de cartón. Anna tuvo que estar quieta 15 minutos y después contempló una imagen de su mano, pero en esta podía ver a través de su piel, sus huesos. Se dice que la reacción de su Anna fue una mezcla de fascinación y temor al ver aquella imagen, la primera radiografía de la historia.
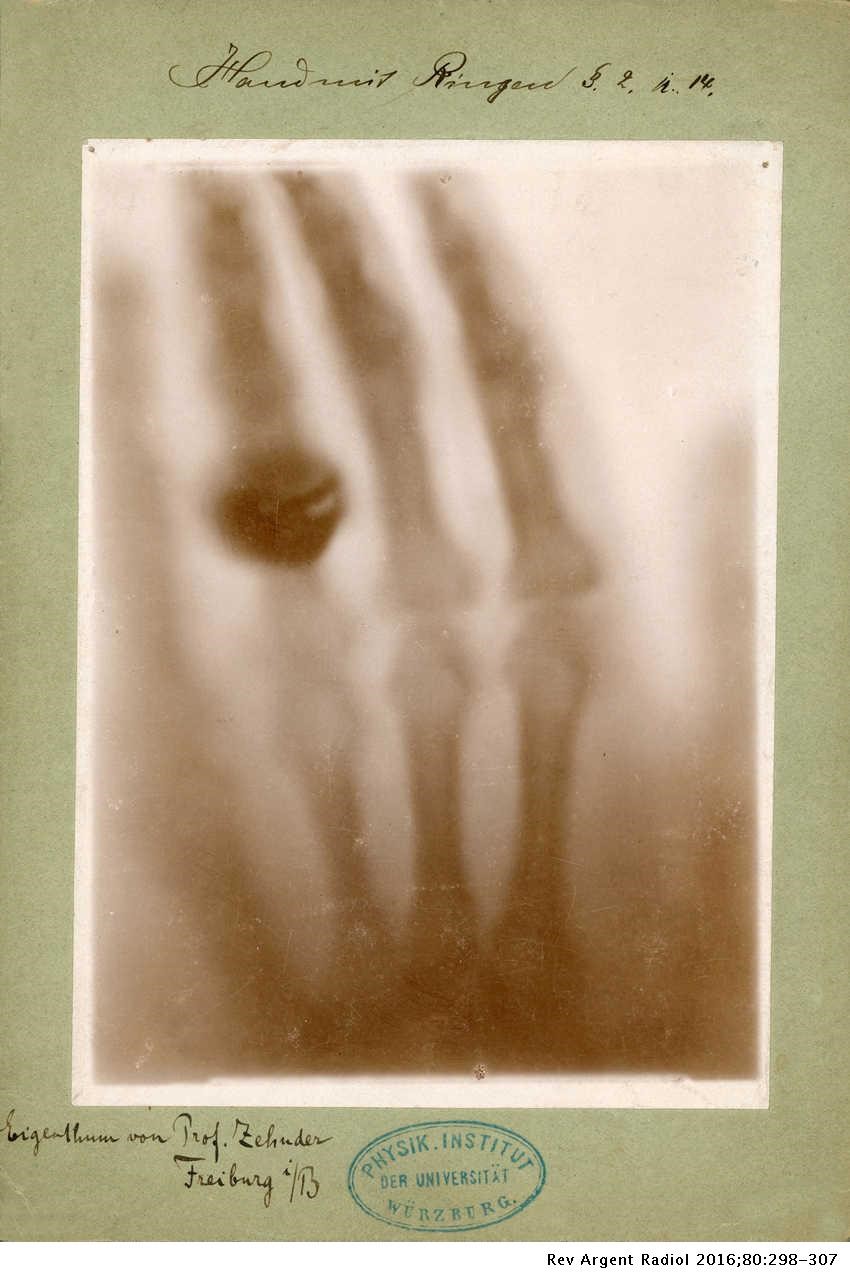 Figura 1. Primera radiografía de la historia de la mano de Anna Bertha Röntgen [1]
Figura 1. Primera radiografía de la historia de la mano de Anna Bertha Röntgen [1]
Röntgen corrió a publicar sus hallazgos un mes más tarde en la Sociedad de Física y Medicina en Würzburg. En aquella publicación contaba que una radiación desconocida se emitía desde el tubo y seria la causante de esa fluorescencia en la placa de platino-cianuro de bario. Nombró a la radiación con la letra de las incógnitas matemáticas, por no saber exactamente lo que era. Este fue el descubrimiento de los rayos X, un tipo de “luz” distinta, un tipo de radiación electromagnética con una longitud de onda similar al tamaño de los átomos y el inicio de una revolución científica en toda regla que le valió el premio Nobel de física a Röntgen en 1901. El primer premio Nobel de física de la historia.
Los años posteriores fueron todo un vergel en cuanto al uso e investigación de los rayos X destacando el nombre de 3 personas que culminan el trabajo que comenzó Röntgen.
El primero de ellos fue Max Von Laue, que estudió el fenómeno de la difracción de los rayos x que se producía al incidir con la materia cristalina. Laue irradiaba sobre cristales obteniendo unos patrones de difracción en los que se apreciaba una simetría concreta que estaba relacionada con la disposición de átomos y moléculas que los componían. Esto supuso el premio Nobel de física en 1914 y el motivo del siguiente Nobel de física en 1915 para William Henry Bragg y William Lawrence Bragg, por definir matemáticamente el fenómeno de la difracción de los rayos X y resolver la primera estructura cristalina: el mineral de la halita.
 Figura 2. Patrón de difracción de Laue [2]
Figura 2. Patrón de difracción de Laue [2]
Hasta ese momento no se tenía constancia de cuál era la organización de átomos, iones y moléculas que componían la materia, por lo que estas contribuciones nos abrieron una ventana para “ver” con otro tipo de “luz” los materiales a otro nivel. Metafóricamente, podríamos decir Röntgen encendió esa luz, Laue la enfocó hacia la materia y los Bragg miraron en su interior. Y este grupo de célebres científicos de principios de siglo XX, con sus logros, nos lanzaron un poderoso mensaje: si podemos cristalizar algo, utilizando la difracción de los rayos X, podremos saber cómo se disponen los átomos, iones y moléculas que lo componen, y por tanto estudiar y comprender sus propiedades y saber cómo aplicarlas.
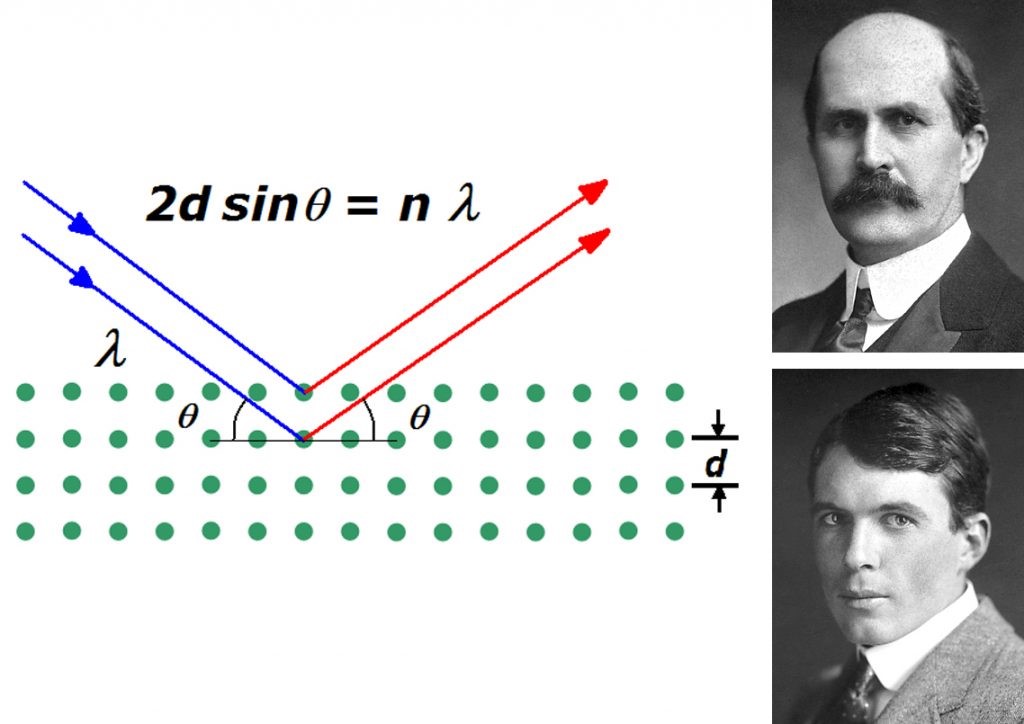 Figura 3. Ley de Bragg (izqda). W. Henry Bragg (arriba) y W. Lawrence Bragg (abajo).
Figura 3. Ley de Bragg (izqda). W. Henry Bragg (arriba) y W. Lawrence Bragg (abajo).
Era el inicio de una nueva disciplina: La cristalografía de rayos X. Una de las áreas del conocimiento más transversales a todas las ciencias y más prolíficas en cuanto a generación del conocimiento. 29 premios Nobel y casi 50 personas laureadas dan buena cuenta de ello. Ha supuesto, supone y supondrá una herramienta fundamental para el progreso de nuestra especie que ha procurado avances como la comprensión del enlace químico, los cristales líquidos, nuevos materiales como el fullereno, los cuasicristales o la resolución de la estructura del ADN así como la de multitud de proteínas y hormonas responsables de enfermedades o de procesos biológicos vitales.
Todos estos frutos de incuestionable trascendencia en nuestro progreso gracias a una disciplina que nace del estudio de los minerales y que está lejos del imaginario popular de revolución científica, como lo pudiera ser la llegada a la luna. 50 años más tarde exploramos otro planeta gracias a la cristalografía de rayos X, pues los Rover que enviamos a Marte llevan incorporados equipos de difracción de rayos X que analizan el suelo marciano. Es decir, robots geólogos hasta que podamos enviar a geólogos/as de carne y hueso a hacer su tradicional trabajo de campo. Un símbolo del alcance de la cristalografía.
A dónde nos llevará esta disciplina es algo aventurado de adivinar, pues como decía Niels Bohr “hacer predicciones es muy difícil, especialmente cuando se trata del futuro”. Sin embargo, es casi una certeza que la cristalografía nos acompañará en nuestros próximos descubrimientos. No habrá que esperar periodos de tiempo geológico para que vuelva a sorprendernos.
Para saber más:
[1] U. Busch (2016) “Wilhelm Conrad Roentgen. El descubrimiento de los rayos x y la creación de una nueva profesión médica” Rev Argent Radiol. 80(4), 298-307. DOI: 10.1016/j.rard.2016.08.003
[2] CSIC (2019), Cristalografía
Sobre el autor: Eder Amayuelas se doctoró en la Facultad de Ciencia y Tecnología de la UPV/EHU y actualmente es investigador en el CNRS (Francia).
El artículo De robots geólogos y rayos X se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Rayos X y gamma
- La luz se propaga en línea recta pero los rayos de luz no existen
- Las partículas de los rayos catódicos
Los primeros humanos alcanzaron el Mediterráneo mucho antes de lo que pensábamos
![]()
Mathieu Duval y Mohamed Sahnouni
 Excavación arqueológica en Ain Boucherit, Argelia.
Excavación arqueológica en Ain Boucherit, Argelia.Mathieu Duval, Author provided
Mathieu Duval, Griffith University y Mohamed Sahnouni, Centro Nacional de Investigación sobre la Evolución Humana (CENIEH)
¿Cuándo llegaron los primeros humanos a las costas del Mediterráneo? Una nueva publicación en la revista Science muestra con evidencias arqueológicas su presencia en el norte de África hace al menos 2,4 millones de años. Es decir, 600.000 años antes de lo que se pensaba.
Estos resultados están extraídos del yacimiento arqueológico de Ain Boucherit, situado en el noreste de Argelia. Gracias a ellos tenemos nueva información en una ventana temporal que incluye los primeros individuos del género Homo.
Estos descubrimientos son el resultado de excavaciones e intensas investigaciones realizadas desde el año 1992 dentro del marco del proyecto Ain Hanech.
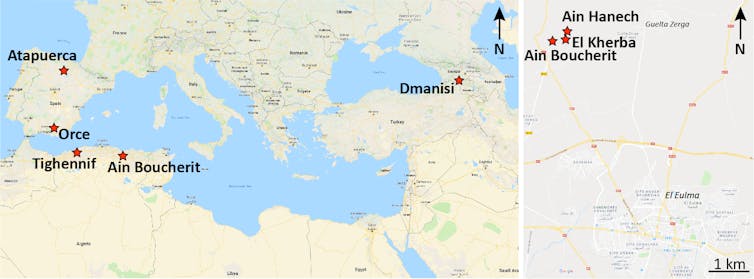 Ubicación de Ain Boucherit y otros sitios prehistóricos mencionados en el texto. A la derecha, ampliación de las cercanías de la ciudad de El Eulma.
Ubicación de Ain Boucherit y otros sitios prehistóricos mencionados en el texto. A la derecha, ampliación de las cercanías de la ciudad de El Eulma.Mathieu Duval; Mapas modificados de Google map
Ubicada en el norte de la ciudad de El Eulma, la zona de estudio ya era conocida por el descubrimiento previo de herramientas líticas (= de piedra) y de huesos fósiles con marcas de cortes, datados de hace unos 1,8 millones de años (yacimientos de Ain Hanech y El Kherba en el mapa de arriba). Hasta ahora habían sido los hallazgos más antiguos del norte de África.
En 2006 y en 2009 se encontraron nuevas herramientas líticas en Ain Boucherit. Distribuidas en dos niveles arqueológicos, ambos localizados estratigráficamente por debajo de los hallazgos anteriores, dichas herramientas indicaban entonces una presencia humana en la zona aún más antigua.
Los nuevos descubrimientos arqueológicos
Las excavaciones en los niveles arqueológicos inferior (AB-Lw) y superior (AB-Up) sacaron a la luz más de 250 herramientas de piedra y casi 600 restos fósiles.
Se identificaron distintas especies animales, entre las que se incluyen elefantes, caballos, rinocerontes, hipopótamos, antílopes, cerdos, hienas y cocodrilos. Todos estos animales viven hoy en día en una sabana abierta con abastecimiento permanente de agua, lo que sugiere que en el pasado existían unas condiciones similares.
Las herramientas de piedra descubiertas están compuestas principalmente por cantos tallados (chopping tools en ingles) y otros elementos de corte de bordes afilados que se utilizaban para trocear los cadáveres de los animales. Estas herramientas están hechas de piedra caliza y sílex, recolectados cerca, en antiguos arroyos.
La fabricación de estos útiles es típica de la tecnología Olduvayense, procedente de las zonas del este de África, y datados entre 2,6 y 1,9 millones de años. Sin embargo, el yacimiento de Ain Boucherit tiene la peculiaridad de presentar también otras herramientas de forma esferoidal, cuya función sigue siendo desconocida.
 Dos ejemplos de herramientas de piedra de Ain Boucherit: un núcleo lítico Olduvayense (izquierda) del que se sacaron las lascas afiladas que se pueden usar para cercenar los huesos (derecha).
Dos ejemplos de herramientas de piedra de Ain Boucherit: un núcleo lítico Olduvayense (izquierda) del que se sacaron las lascas afiladas que se pueden usar para cercenar los huesos (derecha).Mohamed Sahnouni
Algunos de los huesos muestran marcas que no parecen ser de origen natural, sino más bien el resultado de una acción intencionada. Se identificaron dos tipos: marcas producidas por lascas afiladas (como muestra la imagen situada debajo), lo que sugiere que el animal fue despellejado, desollado y eviscerado; y marcas provocadas por un percutor, lo que sugiere actividades de extracción de médula ósea.
Estos descubrimientos demuestran que hace 2,4 millones de años los primeros humanos podían comer la carne y el tuétano extraídos de los animales. La teoría es respaldada por otros estudios llevados a cabo en otros yacimientos contemporáneos del África del este.
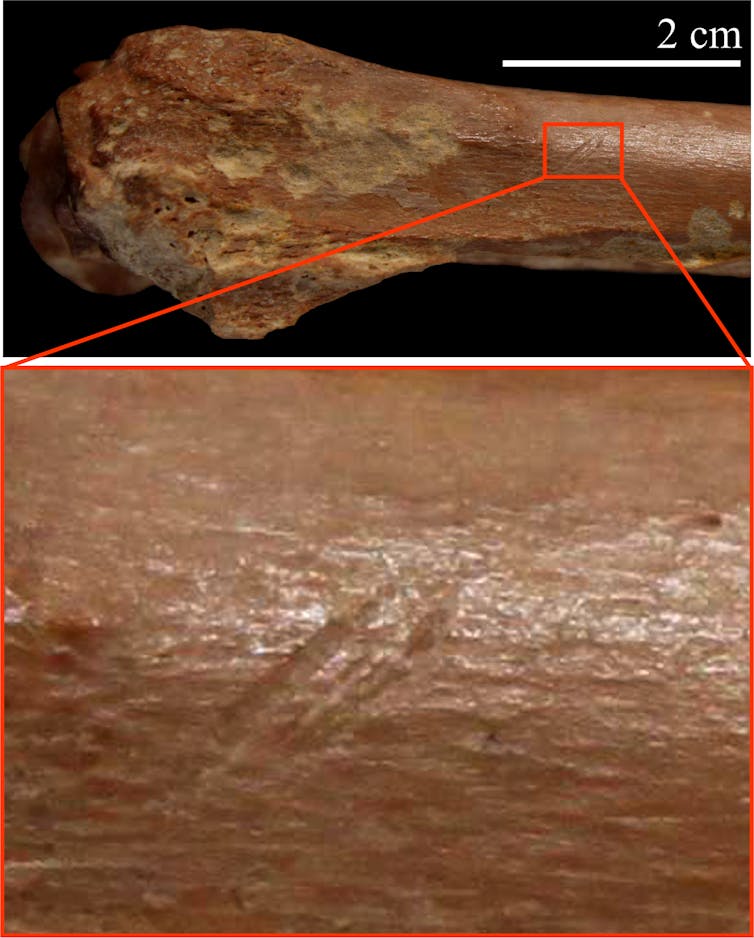 Un pequeño hueso bóvido con marcas de corte producidas por herramientas de piedra.
Un pequeño hueso bóvido con marcas de corte producidas por herramientas de piedra.Isabel Caceres
¿Cómo datamos las herramientas?
Establecer la antigüedad del yacimiento supuso todo un desafío. No podíamos aplicar las técnicas empleadas tradicionalmente en África del Este debido a la ausencia de depósitos volcánicos.
Entonces, datamos las herramientas de piedra de manera indirecta, es decir, analizando el sedimento en el cual se encontraron y estudiando los fósiles extraídos de la excavación. Para resumir, empleamos una combinación de cuatro métodos distintos: la estratigrafía, el paleomagnetismo, la resonancia de espín electrónico (mas conocida por su acrónimo en ingles ESR) y la biocronología.
- La estratigrafía es un campo de la geología que permite dividir los depósitos geológicos en diferentes niveles o capas. Este tipo de trabajo proporciona una primera información cronológica, ya que los depósitos situados por encima de otros siempre tienen una datación mas reciente.
- El análisis paleomagnético de los depósitos nos permitió identificar una sucesión de intervalos de polaridad normal (como en la actualidad) y de polaridad inversa. El paleomagnetismo es un método basado en el estudio de las inversiones del campo magnético a lo largo del tiempo, y tiene muchas aplicaciones en arqueología, como en Atapuerca por ejemplo.
Para poder identificar con mas precisión estos intervalos de polaridad normal e inversa, usamos la ESR y la biocronología.
- La ESR es una técnica basada en la evaluación de los efectos de la radiactividad a lo largo del tiempo. Permite determinar cuándo un grano de cuarzo dejó de ver la luz del sol y quedó enterrado.
- En cambio, la biocronología se basa en la identificación de los animales fósiles presentes en un yacimiento para deducir una cronología relativa (es decir, determinar si un yacimiento es mas antiguo o mas reciente que otro datado de manera independiente).
Gracias a estos métodos, pudimos identificar un intervalo de polaridad normal llamado Olduvai. Este intervalo es muy conocido y está datado entre 1,95 y 1,78 millones de años.
Como el nivel arqueológico superior está posicionado dentro de este intervalo Olduvai, sabemos entonces que tiene una datación dentro del rango de 1,95-1,78 millones de años mencionado antes. Además, como el arqueológico inferior está localizado por debajo de este intervalo Olduvai, sabemos entonces que tiene una fecha mas antigua que 1,95 millones de años.
Finalmente, observando la distancia de los niveles arqueológicos superior e inferior con respecto al inicio y el final de Olduvai, podemos refinar esta primera estimación cronológica y aventurarnos a proponer dataciones de unos 1,9 y 2,4 millones de años, respectivamente.
La importancia del descubrimiento
Este nuevo descubrimiento nos fuerza a actualizar nuestro conocimiento acerca de la creación y la difusión de la tecnología Olduvayense, tanto en África como fuera del continente. El hallazgo, al ser anterior a lo que se pensaba (600.000 años antes), acorta la diferencia temporal entre las más antiguas evidencias encontradas en el extremo oriental de África (2,6 millones de años) y los primeros habitantes humanos del Mediterráneo.
Esto indica que la expansión del Olduvayense desde el este de África fue rápida (al menos, más de lo que se suponía), aunque es también posible que el comienzo de la elaboración de estos utensilios tuviera lugar al mismo tiempo en el norte y en el este del continente.
Como consecuencia, parece que los primeros poblamientos en el margen sur del mar Mediterráneo son mucho más antiguos que los del norte. En el sur de Europa, la evidencia más antigua (Atapuerca y Orce, en España) no supera los 1,4 millones de años, mientras que los fósiles de homínidos encontrados en Dmanisi (Georgia), a las puertas de Europa, datan de hace 1,8 millones de años.
El arqueólogo del CENIEH Mohamed Sahnouni, coautor del artículo, explica los hallazgos.¿Quién fabricó estas herramientas?
Ya que no se encontraron fósiles de homínidos en Ain Boucherit, solo podemos especular acerca de quiénes fueron los fabricantes de estas piezas de piedra Olduvayenses.
El registro de fósiles homínidos en el norte de África es casi insignificante, tanto que no se ha encontrado ninguno de la antigüedad de las evidencias descubiertas en Ain Boucherit.
Los fósiles más antiguos encontrados en Argelia datan de hace aproximadamente 700.000 años y fueron encontrados en Tighennif (anteriormente conocido como Ternifine, consultar el mapa de arriba).
Si bien su nomenclatura ha cambiado a lo largo del tiempo (al principio recibieron el nombre de Atlanthropus mauritanicus, ahora son llamados Homo erectus u Homo heidelbergensis, dependiendo del autor), estos fósiles son realmente jóvenes en comparación con lo descubierto en Ain Boucherit, por lo que no se puede establecer conexión alguna entre los dos yacimientos.
Todos los restos fósiles de los primeros homínidos encontrados en el área del Mediterráneo, así como las herramientas de piedra Olduvayenses, son un millón de años más jóvenes que los restos de Ain Boucherit. En Europa Occidental, las evidencias más antiguas son las de parte de una mandíbula encontrada en la Sima del Elefante, en Atapuerca, y el diente de leche hallado en Barranco León, en el municipio de Orce (Granada). Estos descubrimientos datan de hace 1,2 y 1,4 millones de años, respectivamente.
Por lo tanto, los favoritos en cuanto a antigüedad se encuentran en África Oriental, a pesar de la distancia que separa a la región del norte del continente. Varios homínidos son más o menos coetáneos de los restos encontrados en Ain Boucherit (lo cual se explica muy bien aquí en inglés), incluyendo los australopitecinos y diferentes miembros del género Homo, como el Homo habilis, el Homo rudolfensis o el espécimen de Homo indefinido de Ledi-Geraru (Etiopía).
Dicho esto, no podemos obviar la posibilidad de que las herramientas encontradas en Ain Boucherit procedan de otra especie de homínidos, perteneciente o no al género Homo, que aún no haya sido descubierta.
Esperamos que las excavaciones que llevemos a cabo en el yacimiento argelino nos brinden la oportunidad de identificar a estos fabricantes de herramientas de piedra.![]()
Sobre los autores: Mathieu Duval es ARC Future Fellow en la Griffith University (Australia) y Mohamed Sahnouni, arqueólogo y profesor del Centro Nacional de Investigación sobre la Evolución Humana (CENIEH)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Los primeros humanos alcanzaron el Mediterráneo mucho antes de lo que pensábamos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Tres historias italianas: vacunas, homeopatía, niños y derechos humanos
- Antes de que el león se hiciese con el trono de rey de la selva
- Los efectos climáticos de un calentamiento sin precedentes en el Mediterráneo
No sabéis cantar cumpleaños feliz
Todos los años me sucede lo mismo. Pasan 365 días y al volver al mismo punto de la órbita donde se dio mi nacimiento, mis seres queridos se reúnen… para torturarme.
 Foto: Pixabay
Foto: Pixabay
Sí, hablo de la canción de Cumpleaños Feliz y hoy vengo a denunciar un hecho cierto, doloroso y universal: la gente no sabe cantarlo.
No habrá sido por falta de tiempo como para aprender. El tema de cumpleaños feliz fue compuesto a finales del siglo XIX por las hermanas Patty y Mildred Hill. Patty era directora de una guardería en Kentucky y Mildred era pianista y compositora. “Good Morning to All” (el título original de la melodía) nació como una canción pedagógica que los niños entonaban al llegar a clase. Fue publicada en 1893 en un libro de canciones infantiles. Su asociación a la letra del Happy Birthday apareció más tarde y fue publicada por primera vez en 1912 (aunque probablemente existiese con anterioridad).
A partir de ese momento, comienza todo un culebrón de jueces, abogados y sellos discográficos en torno a la propiedad intelectual de la canción… que ya lo quisiera Juego de Tronos. Como resultado os resumo: casi seguro, todos le debemos pasta a Warner/Chappell. O, al menos, todos los que en alguna ocasión hemos cantado el cumpleaños feliz en público, antes del 1 de enero de 20171 en Europa. En Estados Unidos la canción entró a formar parte del dominio público por la vía judicial apenas un año antes. Hasta ese momento, Warner Chappell había estado ganando alrededor de 2 millones de dólares al año por los derechos de copyright.
Con sus ciento y pocos años, “Happy Birthday to You” se ha convertido en la canción más reconocida en lengua inglesa. Ha sido traducida a 18 idiomas, incluyendo el árabe, hebreo, chino y, claro, español. Se podría argumentar que es una de las canciones más populares del mundo… y uno se esperaría que después de tantos años cumplidos, tantas velas sopladas y tanta repetición, la gente hubiese aprendido a afinarla.
PERO NO. Y francamente… tampoco me extraña.
Una de las grandes paradojas del cumpleaños feliz es que, para tratarse de un tema popular, es francamente complicado de cantar.
Pensemos, por contraste, en otras canciones típicas del repertorio popular: los villancicos. Aunque no es algo estricto, casi todos siguen algunos patrones melódicos muy básicos (sobre en los estribillos) que los convierten en canciones especialmente fáciles de cantar. Algunas de estas “normas” podrían resumirse así:
Normas no escritas (bueno, ahora sí) para escribir un villancico.
1- El estribillo debe poder cantarlo hasta Joaquín Sabina de resaca.
2- Las estrofas pueden tener un poquito más de fantasía. Solo un poquito. Se supone que las canta un solista.
Para que el estribillo sea especialmente fácil de cantar:
3- La melodía debe avanzar por grados conjuntos (es decir, notas seguidas: después de do, puede ir re o si).
4- Si hay saltos, que sean de 3ª (saltándose una nota). Nunca más grandes que una 5ª
5- Si verdad tiene que haber saltos, que no sea a mitad de frase, para que la gente respire.
6- Todo el estribillo debe estar contenido en un rango de notas más bien pequeño. Intenta que no supere una 8ª (el rango de una escala musical, de do a do).

Son normas no escritas porque, de alguna manera, ha sido el propio tiempo el que las ha seleccionado. Los temas se hacían populares si el pueblo los cantaba. Y el pueblo no suele tener un entrenamiento vocal especialmente sofisticado. Cantar por grados conjuntos, notas cercanas entre sí, es más fácil porque implica hacer menos cambios bruscos con las cuerdas vocales. Restringir el rango vocal hace más fácil que mucha gente pueda llegar a todas las notas. Y eso sin contar los contextos festivos (y etílicos) donde se suelen entonar estas canciones. Más vale poner las cosas muy fáciles… pocas notas, ritmos sencillos, mucha repetición. Estamos aquí para pasarlo bien.
La paradoja es que cumpleaños feliz no es un tema de “origen” popular (sus compositoras tienen nombres y apellidos) y no ha sido pulido todavía por el tiempo. Por eso, nos encontramos con una melodía que, de hecho, incumple bastantes de las normas básicas de sencillez vocal.

Para empezar, y de manera especialmente sangrante: fijaos en los saltos de la melodía. Desde el compás 1, cumpleaños feliz empieza ya fuerte con ¡un salto de 4ª! La cosa sólo empeora en el compás 3, arriesgando un poco más hasta la 5ª. Pero el desastre absoluto llega en el compás 5, ¡con un salto de 8ª, ni más ni menos! Y encima, a mitad de frase. Qué digo, a mitad de palabra. Cada vez que veo acercarse ese “te deséamos”… me estremezco.
Por si el salto no fuese lo bastante complicado, resulta que la melodía comienza en la nota más grave de todo su rango. En realidad, cumpleaños no es especialmente exigente en cuanto a rango vocal, es decir: su nota más aguda y más grave no están demasiado alejadas, no necesitas ser Bobby McFerrin para afinarlas. Normalmente, se considera que una persona sin entrenamiento vocal puede abarcar hasta dos octavas (puede cantar de do a do, un par de veces seguidas). Cumpleaños sólo requiere una octava, que no es mucho. El problema es que la gente empieza a cantar muy animada “cumpleaños” en el registro que le resulta más cómodo (o, probablemente, un pelín más agudo, por la emoción del momento) y no se da cuenta de que va a tener que elevar el tono de su voz hasta una 8ª, apenas 4 compases más tarde. El resultado es… desgañite, desafine, gallinas descontroladas… dolor, mucho dolor.
Por si todo esto fuera poco, la manera en que cantamos cumpleaños cae, directamente, en la polirritmia. Fijaos: toda la canción está en un compás ternario, es decir: podríais cantarla bailando un vals, por ejemplo. Sin embargo, al llegar al “te deséamos todos”, de repente, todo el mundo hace una pausa. Es como si, por sorpresa, el vals tuviese un paso de más, no escrito pero cantado por todos que lo desencaja todo un poco. Después de ese momento, la coordinación se vuelve especialmente complicada.
Y luego está… el tema de la letra. Quizás por tratarse de palabras encajadas sobre la melodía a posteriori, casi con calzador, ningún acento musical cae donde debería. La sílaba más aguda de las dos primeras repeticiones coincide sobre “fe” (cumpleaños feliz), aunque tiene un pase ya que “liz” tiene el apoyo de la parte fuerte del compás. El desastre, de nuevo, lo encontramos en “te deséamos”: porque tanto la nota aguda de la melodía como la parte fuerte del compás coinciden sobre “sé”, pero ese verbo no es esdrújulo y aún así, lo he escrito tres veces con tilde en este artículo sin que probablemente llamara tu atención.
¿Y entonces? Qué podemos hacer. Para mi desdicha, este problema no tiene fácil solución… yo desde aquí invoco al pueblo para que vaya limando esta melodía y, con el paso de los años, la convierta en algo realmente fácil de cantar. Hasta que ese momento llegue, aquí os presento mi versión de cumpleaños más feliz. Ojalá os convenza y dejéis de desafinar… ¡malditos!
Nota:
1Según Wikipedia: ”Warner/Chappell claimed copyright for every use in film, television, radio, anywhere open to the public, and for any group where a substantial number of those in attendance are not family or friends of whoever is performing the song”.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo No sabéis cantar cumpleaños feliz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Otto Spiegel, de la simetría a la teoría del caos
Otto. L’homme réécrit (Otto. El hombre reescrito, Éditions Delcourt, 2016) es una de las últimas novelas gráficas del guionista y dibujante Marc-Antoine Mathieu. Aunque ha sido traducida a otros idiomas, lamentablemente aun no se dispone de su versión en castellano. Esperemos que no tarde demasiado.
 Portada de Otto. L’homme réécrit.
Portada de Otto. L’homme réécrit.
Como muchas de las propuestas de Mathieu, Otto contiene numerosas referencias matemáticas. En este caso la simetría y la teoría del caos conducen la trama de la historia,… historia que comienza en el museo Guggenheim Bilbao, «el museo-espejo de Bilbao», según Mathieu.
Estamos en la parte trasera del museo. Una gran multitud espera la actuación de Otto Spiegeli, un artista de fama mundial que realiza performances jugando con los reflejos de su cuerpo sobre diferentes espejos. A la izquierda se alza la bella araña Maman de Louise Bourgeois y, a la derecha, una escultura en forma de banda de Möbius flota sobre uno de los estanques del museo.
 Parte trasera del Museo Guggenheim Bilbao. Imagen: Wikimedia Commons.
Parte trasera del Museo Guggenheim Bilbao. Imagen: Wikimedia Commons.
Otto observa su imagen sobre un gran espejo que manipula, gira y termina rompiendo al lanzarlo bruscamente sobre el suelo. Aunque el público le aplaude frenéticamente pensando que forma parte del espectáculo, Spiegel ha sentido durante un instante un profundo vacío que le ha inmovilizado. El artista decide dejar sus espectáculos durante una temporada.
Poco tiempo después, Otto se entera de que su madre y su padre han fallecido en un accidente de tráfico. Dejan como legado a su hijo su vieja casa y un gran baúl abandonado en el desván. El cofre contiene cuadernos, notas, dibujos, documentos fotográficos, audios y videos. Todos ellos son detalles de los siete primeros años de la vida del artista. Cada día, cada hora, cada instante de la existencia de Otto había sido examinado y registrado sin que él lo supiera.
Otto decide encerrarse para leer, ver y escuchar todos aquellos apuntes y grabaciones. Piensa que toda esa información puede ayudarle a encontrarse a sí mismo, a reescribirse. Y empieza su especial indagación comenzando por el día 365 de su séptimo año de vida, es decir, investiga en sentido inverso. Cada día registrado de su vida le lleva el mismo tiempo de estudio. A lo largo de los años de inspección del contenido del baúl, Otto recuerda hechos banales, detalles insignificantes, todo está grabado. Trozos de tela de pijamas, hojas de árbol, fotografías anodinas le ayudan a recordar su infancia. Otto percibe nuevas verdades, pierde ilusiones, se aísla cada vez más en este obsesivo proceso de reescribirse… con un final inesperado.
La teoría del caos es uno de los temas que surgen a medida que Otto avanza en la indagación sobre su propia identidad. Mathieu alude en el texto una cita del ingeniero químico Julio Ottino: «La característica común de todos los sistemas complejos es que muestran organización sin que se aplique realmente ningún principio externo de organización. Del mismo modo, la extrema complejidad de organización del cerebro humano no posee ninguna instancia superior, no hay ningún homúnculo que lleve las riendas»ii. A medida que Otto reescribe su historia, va construyendo una gran red de relaciones entre los hechos, los actos y los pensamientos que extrae de ese enorme baúl. Año tras año, el protagonista conecta todas esas informaciones parciales y termina tejiendo una forma singular que recuerda, así se dice en la novela, a un atractor extraño. Otto piensa que ese conjunto esconde la realidad de su ser, su síntesis, su verdad… Esta forma «… solo le pertenecía a él, solo a él. Un especialista en teoría del caos podría haber determinado su dimensión exacta: algo entre la tercera y la cuarta dimensión…»iii.
Notas:
iSpiegel significa ‘espejo’ en alemán. Observar, además, que el nombre Otto es un palíndromo, una palabra obtenida por simetría especular.
ii Traducción del texto (en francés) que aparece en la novela gráfica.
iii Traducción del texto (en francés) que aparece en la novela gráfica. Recordemos que un atractor es un conjunto de valores numéricos hacia los cuales tiende un sistema dinámico cuando evoluciona. En los sistemas caóticos, pequeñas perturbaciones pueden llevar a cambios inesperados. A pesar del aparente azar involucrado, la dinámica del sistema caótico es determinista y tiende hacia estas complejas formas, los atractores extraños, que tienen dimensión de Hausdorff no entera; son objetos fractales.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Otto Spiegel, de la simetría a la teoría del caos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La artista Anni Albers, The Walking Dead y la teoría de nudos
- Pál Turán: teoría de grafos y fábricas de ladrillos
- Arthur Cayley, la teoría de grafos y los isómeros químicos
La carga más pequeña
 Imagen: Pixabay
Imagen: Pixabay
Es un hecho conocido que un peine electrificado puede recoger una pequeña hoja de papel [1]. Obviamente, la fuerza eléctrica sobre el papel debe exceder la fuerza gravitacional ejercida sobre el papel por la Tierra. Esta observación tan simple indica sin embargo algo importante: que las fuerzas eléctricas generalmente son más fuertes que las fuerzas gravitacionales.
Usando el mismo principio, la fuerza gravitacional sobre un objeto microscópicamente pequeño [2] se puede equilibrar con la fuerza eléctrica ejercida sobre el mismo objeto cuando éste tiene una carga eléctrica neta distinta de cero, aunque solo sea la carga más pequeña posible. Esta carga más pequeña posible es la que posee el electrón, uno de los constituyentes básicos de todos los átomos.
Si nos fijamos el hecho de que la fuerza gravitacional sobre un objeto pequeño pueda ser equilibrada por la fuerza eléctrica puede ser la base de un método para medir la carga del electrón. De hecho este fue el método fue empleado por primera vez por Robert A. Millikan en 1909 [3].
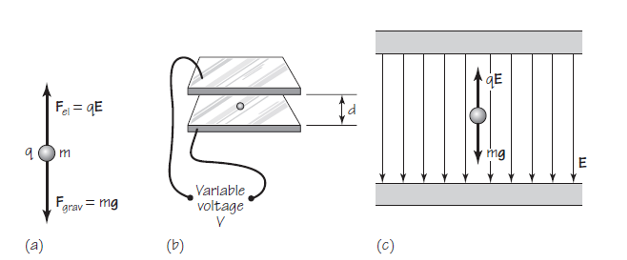 Esquema del experimento de Millikan. Fuente: Cassidy Physics Library
Esquema del experimento de Millikan. Fuente: Cassidy Physics Library
Supongamos que un pequeño cuerpo de masa m, por ejemplo, una pequeña gota de aceite, tiene una carga eléctrica neta negativa de magnitud q [4]. La gota de aceite cargada [5] se coloca en un campo eléctrico E [6] dirigido hacia abajo, con lo que se ejerce sobre ella una fuerza eléctrica hacia arriba Fel de magnitud qE. Por supuesto, también se ejerce sobre la gota una fuerza hacia abajo por la acción de la gravedad Fg de magnitud mg, donde g es la aceleración de la gravedad. La gotita de aceite se acelerará hacia arriba o hacia abajo dependiendo qué fuerza es mayor, si la fuerza eléctrica o la de la gravedad.
Al ajustar la magnitud de la intensidad del campo eléctrico E podemos conseguir que las dos fuerzas, elétrica y gravitatoria, sean exactamente iguales. ¿Qué sucede cuando las dos fuerzas que actúan sobre la caída están equilibradas? Recordemos que, por la primera ley de Newton del movimiento, para que un cuerpo cambie su estado de reposo o movimiento constante debe ejercerse sobre él una fuerza neta no nula. En este caso la resistencia del aire también tiene algo que decir, frenando la gota hasta que se pare. En el equilibrio de fuerzas la resultante neta es nula, por lo que la gota ni cae ni asciende, se queda suspendida en mitad del aire.
En esta situación se pueden realizar unos cálculos muy simples. Como Fel = Fg entonces qE = mg. De donde podemos calcular fácilmente la carga si conocemos E, m y g. Así, q = mg/E
De esta forma podemos encontrar en el laboratorio, como hizo Millikan, los distintos valores de carga que un pequeño objeto puede tener. Cuando hacemos esto, descubrimos un hecho notable: todas las posibles cargas libres mensurables en la naturaleza se componen de múltiplos enteros de una carga más pequeña [7]. Esta carga más pequeña posible es la magnitud de la carga en un electrón.
Al repetir el experimento muchas veces con una variedad de cargas muy pequeñas, podemos terminar encontrando un valor para laa carga en un electrón. Por convención, la carga de electrón está representada por el símbolo e.
En efecto, esto es lo que hizo Millikan. Obtuvo el valor de e = 1,6024·10-19 C [8] para la carga del electrón, y encontró que el signo de la carga en el electrón es negativo. Por lo tanto, cualquier carga q de un objeto se puede expresar como q = ne, donde n es el número total de cargas individuales, cada una de magnitud e. Por lo tanto, por ejemplo, en un culombio,1 C, hay exactamente 1/ 1,6024·10-19 electrones. Este valor concuerda con los resultados de muchos otros experimentos realizados desde entonces.
Ningún experimento ha puesto de manifiesto aun la existencia de una unidad de carga más pequeña que la del electrón en la materia ordinaria, de esa de la que están hechas las gotas de aceite.. Sin embargo, se ha descubierto que la mayoría de las que se creían partículas elementales como el protón y el neutrón están, de hecho, compuestas de entidades más pequeñas, conocidas como quarks, cada una de las cuales puede tener una carga de 2/3e o 1/3e. Pero los quarks no pueden existir de forma aislada, libre, por lo que la carga libre más pequeña que se puede observar en la materia ordinaria sigue siendo la carga del electrón, e.
Notas:
[1] Hablamos de ello extensamente aquí: Inducción electrostática.
[2] Microscópicamente pequeño y aun así todavía contiene varios miles de millones de átomos.
[3] Desde el punto de vista de la historia y la sociología de la ciencia este experimento es muy jugoso. La lectora interesada puede encontrar un magnífico resumen en G. Holton (1978) Subelectrons, Presuppositions, and the Millikan-Ehrenhaft Dispute Historical Studies in the Physical Sciences, 1978, vol 9, pp. 166–224. Se puede leer gratis en la página web.
[4] Millikan utilizó gotitas de aceite diminutas provenientes de un pulverizador. Las gotitas se cargan cuando se pulverizan de la misma manera que un peine se carga cuando se frota, por rozamiento. Se emplea aceite porque se evapora muy poco.
[5] El que lo está negativamente es una conclusión del experimento de Millikan, corraborando las observaciones realizadas con los rayos catódicos.
[6] Si necesitas repasar el concepto de campo eléctrico puedes leer Los conceptos de campo.
[7] También podríamos decir que la carga es una magnitud que está cuantizada y que el cuanto de carga es la carga del electrón. Podríamos, pero no lo diremos de esta forma exactamente por lo que decimos al final del texto. También al final explicamos por qué decimos libres.
[8] El último valor CODATA publicado (2014) refina esta cifra a −1,6021766208(98)·10−19 C. Para la inmensa mayoría de los cálculos 1,602· 10−19 C es más que suficiente.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La carga más pequeña se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ley de la fuerza eléctrica (2): la magnitud de carga y la ley de Coulomb
- La unidad de carga eléctrica
- Campo magnético y cargas en movimiento
Digestión simbiótica: otros vertebrados e invertebrados
 Silurus glanis. Fuente: Dieter Florian / Wikimedia Commons
Silurus glanis. Fuente: Dieter Florian / Wikimedia Commons
Además de la fermentación pregástrica propia de los rumiantes y de otros vertebrados con dispositivos similares, hay otras formas de digestión simbiótica en los metazoos. Al objeto de dar continuidad al tratamiento de esta materia en vertebrados, empezaremos por repasar los casos de fermentación en intestino medio y en intestino posterior en este grupo, para tratar después de forma sumaria algunos casos de simbiosis digestiva en diferentes invertebrados.
Fermentación posgástrica de vertebrados
Muchos peces herbívoros son considerados fermentadores de intestino medio porque una parte central del tracto digestivo cumple la función de cámara de fermentación. Tilapias, carpas y siluros presentan esa forma de digestión simbiótica.
En muchas aves de suelo la fermentación a cargo de microorganismos heterótrofos se produce en el ciego, en el colon o en ambos. Es el caso de gansos, urogallos, avestruces, y gallos y gallinas. Estas aves tienen grandes ciegos.
En mamíferos la fermentación posgástrica es especialmente importante en caballos, ballenas, elefantes, rinocerontes, cebras, didélfidos (marsupiales americanos), algunos roedores y koalas. Esa fermentación se suele producir en el ciego y colon, y aunque permite una primera digestión y absorción de proteínas y carbohidratos a cargo del propio sistema digestivo, pierde la posibilidad de utilizar las proteínas de alto valor producidas por las bacterias. Los microorganismos simbiontes del ciego y el colon sintetizan algunas vitaminas, y en especial, la vitamina K. Los microbios también producen algunos ácidos grasos volátiles.
Para poder mantener importantes masas de bacterias en el interior del intestino, estas deben poder disfrutar de un ambiente tamponado. En el caballo el íleo produce grandes volúmenes de soluciones tampón de bicarbonato y fosfato, que son transferidas al ciego, y juega un papel similar al de la glándula salivar de los rumiantes.
Los mamíferos con fermentación en el intestino posterior reutilizan el nitrógeno con menor eficiencia que los rumiantes. Pero eso no es así en el caso de las aves herbívoras antes citadas. En galliformes se ha observado que el ácido úrico y la urea que evacúan los uréteres a la cloaca fluyen hacia el colon y los ciegos de forma antiperistáltica. Los microbios descomponen esas sustancias a amonio, a partir del cual sintetizan aminoácidos. La mayor parte de esos aminoácidos los utilizan los microorganismos, pero otra parte es absorbida. También se absorbe parte del amonio, que es utilizado en el hígado para sintetizar aminoácidos. Esa capacidad para reciclar nitrógeno es muy valiosa, pues permite a las galliformes explotar hábitats de los que no pueden disfrutar otros animales.
Hay especies que recurren a otro procedimiento para beneficiarse de las ventajas que reporta la actividad intestinal microbiana de síntesis de vitaminas y proteínas: la coprofagia. Conejos, hámsteres y capibaras producen dos tipos de heces. Las heces blandas, que se producen durante la noche, son ingeridas, de manera que los productos de la digestión cecal pueden ser digeridos y absorbidos. Para expulsar esas heces la motilidad de la zona proximal del colon se inhibe, a la vez que se intensifica la de la zona distal próxima al ano. Las heces blandas de los conejos contienen un 50% de biomasa bacteriana y constituyen una valiosa fuente de vitamina B12. Las otras heces son oscuras y duras; no se ingieren.
En otras especies, la práctica de la coprofagia se limita a los individuos más jóvenes. Potros, y crías de elefantes, pandas, koalas e hipopótamos ingieren sus propias heces. De esa forma ayudan a establecer una población microbiana en el intestino grueso.
Simbiosis digestivas en invertebrados
 Coptotermes formosanus shiraki. Fuente: Scott Bauer / Wikimedia Commons
Coptotermes formosanus shiraki. Fuente: Scott Bauer / Wikimedia Commons
Un buen número de especies de diferentes grupos de invertebrados mantienen asociaciones de carácter simbiótico en su sistema digestivo con microorganismos heterótrofos. El ejemplo más conocido es el de las termitas, grupo en el que numerosísimas especies mantienen relaciones simbióticas con microorganismos gracias a las cuales son capaces de utilizar la celulosa y se alimentan de la madera. Las denominadas “termitas inferiores” mantienen en su intestino posterior comunidades de protistas flagelados y bacterias anaerobias que fermentan la celulosa y producen ácido acético que es después utilizado por el hospedador.
De un modo similar, muchas especies de escarabajos dependen de bacterias intestinales que fermentan la celulosa para producir ácidos grasos volátiles. Y no solo productos derivados directamente de la fermentación, como los citados ácidos grasos, sino que muchos microorganismos simbiontes también proporcionan vitaminas B y aminoácidos esenciales, y contribuyen a reciclar el nitrógeno.
La microbiota simbionte también cumple un papel fundamental en la síntesis de esteroles por los insectos, pues las especies de este grupo, al contrario que la mayor parte de los demás animales, no son capaces de sintetizar los precursores de esos compuestos y para ello necesitan del concurso de microorganismos simbiontes. Por último, los invertebrados ectoparásitos que se alimentan de sangre, como sanguijuelas, moscas tse-tsé, piojos y garrapatas necesitan bacterias simbiontes que les ayudan a digerirla.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Digestión simbiótica: otros vertebrados e invertebrados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Digestión simbiótica: los rumiantes
- Sistemas nerviosos: el sistema periférico de vertebrados
- La respiración de los invertebrados terrestres
¿Qué es el albinismo?
Lluis Montoliu, autor

En ocasiones, cuando no se dispone de tratamiento para una enfermedad o condición genética, el compartir toda la información disponible sobre el tema puede aportar el consuelo, la paz y la tranquilidad que necesitan los padres de un hijo, que acaba de ser diagnosticado con alguna de las llamadas enfermedades raras. Este es el punto de partida que me llevó, hace ya más de 20 años, a crear y mantener una página web sobre albinismo, la condición genética poco frecuente a la que he dedicado gran parte de mi vida profesional como genetista y biotecnólogo.
El albinismo es una condición genética relativamente compleja, causada por mutaciones en alguno de los 20 genes identificados, que todo el mundo cree conocer. Todos recordamos haber visto a personas de piel y cabellos blancos, con un déficit muy importante de melanina, el pigmento que tenemos en nuestras células pigmentarias de la piel, ojos y cabellos. Sin embargo, es la discapacidad visual severa que presentan estas personas lo que limita de forma importante su calidad de vida, no su falta de pigmentación, al menos en Europa y otras sociedades avanzadas. El déficit visual de las personas con albinismo es frecuentemente desconocido y fuente de muchos errores que tienden a minimizar el impacto del albinismo como una condición en la que uno debe esencialmente protegerse del sol para no quemarse la piel (lo cual es cierto) y poco más. En África, la falta de pigmentación y quemaduras consiguientes por el sol, determina la aparición de cáncer de piel que puede acabar causando la muerte de la persona con albinismo si no se trata el tumor adecuada y tempranamente, antes de que desarrolle metástasis.
A través de internet he conseguido llegar a muchas familias que han contactado conmigo buscando algo sencillo, pero que habitualmente no obtenían de los médicos que trataban a sus hijos: información. ¿Qué es esto del albinismo? ¿Por qué mi hijo es una persona con albinismo si ni mi pareja ni yo lo somos? ¿Por qué nos ha tocado a nosotros? ¿Qué consecuencias tendrá para su vida el albinismo? ¿Lo heredarán sus hijos? ¿Todas las personas con albinismo tienen los mismos problemas? ¿Qué puedo hacer para mejorar su calidad de vida? ¿Se cura el albinismo?… y un montón de preguntas más, todas ellas muy lógicas y razonables, que requieren respuestas adecuadas y entendibles. A través de las conversaciones con padres y madres de niños con albinismo, hablando también con personas adultas con albinismo, aprendiendo de su experiencia, de sus capacidades y limitaciones, consultando con otros colegas expertos en el tema (dermatólogos, oftalmólogos, genetistas…) la página web sobre albinismo en español fue convirtiéndose en una referencia para todas las familias interesadas en el tema.
Entre las personas que contactaron conmigo a través de la web quiero destacar a Carlos Catalá, padre de un niño (ahora ya un chico joven) con albinismo quien, desde Alicante, me contactó a principios del año 2005 para invitarme a impartir una charla en su ciudad ante un grupo de familias con niños con albinismo. Esa charla fue la primera de muchas por todo el país sobre este tema, acercando el albinismo a la gente interesada en esta condición genética, que puede ser muy aparente (por la falta de pigmentación) pero de la que solemos ignorar lo relevante (la severa discapacidad visual asociada).
Un año después de aquella primera reunión con familias con niños con albinismo fundamos ALBA, la asociación de ayuda a personas con albinismo. Con ellos he desarrollado un gran número de actividades (libros, vídeos, reuniones nacionales e internacionales, campañas de sensibilización, campañas de diagnóstico genético, etc…) y, tras la incorporación de nuestro laboratorio en el Centro Nacional de Biotecnología (CNB) del Consejo Superior de Investigaciones Científicas (CSIC) a finales de 2007 al Centro de Investigación Biomédica en Red de Enfermedades Raras (CIBERER) del Instituto de Salud Carlos III (ISCIII) hemos ido paulatinamente cerrando otras líneas de investigación hasta dedicarnos fundamentalmente a investigar sobre albinismo. Una decisión arriesgada profesionalmente, pero una decisión ante todo por responsabilidad social, de la que me siento muy orgulloso.
Casi desde el inicio de nuestra ya larga colaboración con ALBA nos propusimos preparar un libro que contuviera todas las preguntas y respuestas que cualquier padre o madre que acaba de tener un hijo con albinismo se plantea. Queríamos aprovechar la información que ya estaba disponible en nuestra página web sobre albinismo, y completarla con todo lo que habíamos aprendido del contacto habitual con muchas personas con albinismo, de todas las edades. Un verdadero privilegio al alcance de muy poca gente. Desde la sanidad pública o privada, simplemente por un puro efecto de la baja frecuencia de personas con albinismo en la sociedad (1 de cada 17.000, aproximadamente) es fácil que un médico no vea más de una o pocas personas con esta condición genética en toda su vida profesional. Sin embargo, nosotros, gracias a ALBA, tenemos contacto y hemos podido conocer a centenares de ellas. Y por ello hemos logrado obtener muchísima información que no está en los libros de texto. Por ejemplo, para poder correlacionar el efecto de una misma o distinta mutación en las personas con albinismo, una información especialmente relevante para intentar entender la etiología y los mecanismos moleculares subyacentes a esta condición genética. Si no comprendemos bien el albinismo y cómo se establece difícilmente podremos desarrollar tratamientos o terapias efectivas que consigan aliviar o, en el mejor de los casos, curar algunas o todas las anomalías asociadas a esta condición genética.
Ese libro con preguntas y respuestas sobre albinismo, destinado a padres y madres de niños con albinismo, y a cualquier persona con albinismo y a sus familiares y amigos, tantas veces planeado, finalmente vio la luz en septiembre de 2018. La edición del libro corrió a cargo de ALBA quien compartió con el CIBERER el coste de su publicación.
El libro “¿Qué es el albinismo?”, cuyo texto tuve la gran satisfacción de escribir, necesitaba ser ilustrado con imágenes que encajaran con las frases, fotografías especialmente cuidadas que aportaran información complementaria a las palabras. Desde el principio lo tuvimos claro. Este libro no podía publicarse sin la participación de Ana Yturralde, fotógrafa profesional freelance, que ya había colaborado con ALBA en proyectos anteriores, dotada de un talento especial para convertir sus fotografías en mensajes que hablan por sí solos, que transmiten un montón de datos y matices, de sensibilidad. Así fue como nació este libro sobre albinismo, con 150 páginas y casi un centenar de ilustraciones.
Toda persona interesada en este libro puede contactar con ALBA (contactar@albinismo.es) o directamente conmigo (montoliu@cnb.csic.es) para obtener un ejemplar gratuito.
Ficha:
Autor: LLuis Montoliu
Título: ¿Qué es el albinismo?
Año: 2018
Editorial: ALBA / Ciberer
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
El artículo ¿Qué es el albinismo? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Pro 2017: Lluis Montoliu y el albinismo
- #Naukas15 Mis queridos anillos…de luz sincrotón
- I, Mammal. The Story of What Makes Us Mammals
¿Cómo te está afectando el cambio climático?
Todos hemos notado que de un tiempo a esta parte tenemos olas de calor más duras, más largas y más húmedas. Es culpa del cambio climático. Esas olas afectan especialmente a las personas que trabajan al aire libre, a deportistas, niñas y niños, personas de edad avanzada y a quienes tienen patologías cardíacas. ¿Pero cuáles son los riesgos para la salud del calor extremo?
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de cienciaÓrbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Cómo te está afectando el cambio climático? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Cómo ven las galaxias los astrofísicos?
- ¿Cómo demonios funcionan las copas musicales?
- ¿Qué comes cuando comes comida basura?
La detección de ondas gravitacionales y la astronomía multimensajero
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Estamos viviendo estos últimos años el inicio de una nueva era en el conocimiento humano, en el conocimiento de nuestro entorno y el Universo. Estamos ante el surgimiento de una nueva astronomía, la astronomía de ondas gravitacionales y multimensajero.
Para llegar a comprender lo que está pasando (y lo que está por pasar), y hasta qué punto es excepcional este periodo en la historia, debemos entender qué son las ondas gravitacionales. Con ese objetivo empezamos con el concepto de «onda» y sus propiedades. Como nos explican en el colegio, las ondas son distorsiones (que llamamos oscilaciones) de un medio, que se propagan de un sitio a otro transportando energía. Dependiendo del medio las ondas reciben diversos nombres. Cuando el medio es un material se llaman ondas mecánicas. En particular, cuando el material es aire se llaman «sonido», en la superficie del mar se llaman «olas»… y en el colegio nos solían decir que la luz no necesita medio para propagarse, que se propaga en el vacío. Esto no es del todo cierto, puesto que ya sabemos que en lo que usualmente llamamos «vacío» siempre hay campo electromagnético, y que la luz son ondas electromagnéticas, distorsiones de ese campo.
Toda onda tiene asociadas una serie de propiedades que se miden, como la amplitud (proporcional a la energía), frecuencia (número de oscilaciones por segundo) y la velocidad de propagación. Es importante saber que la velocidad de la onda sólo depende del medio. En el caso de las ondas electromagnéticas la velocidad es la denominada «c», la velocidad de la luz, que es aproximadamente unos 300.000 km/s. La luz visible son ondas electromagnéticas en un rango determinado de frecuencias, y la variación dentro de ese rango produce los colores del arco iris. En la frecuencia más alta tenemos el violeta, y en la más baja, el rojo. De hecho, en este mundo moderno estamos muy habituados a usar todo tipo de ondas electromagnéticas: a frecuencias más bajas que la luz de color rojo tenemos los infrarrojos del mando a distancia, más abajo, radares, y las microondas de nuestros hornos, y en las frecuencias más bajas, las ondas de radio para los wifis y los móviles. En frecuencias más altas a la luz violeta se hallan primero los rayos X, y en las más altas, los rayos gamma.
En cuanto al segundo concepto, «gravitacional», debemos recordar qué es la fuerza de la gravedad. Ya en 1905 la relatividad especial surgió en parte del hecho empírico de que la medición del tiempo y el espacio depende del observador. Este hecho, que se traduce en que el tiempo y el espacio están ligados, lleva a la construcción de una estructura (en principio matemática) muy concreta, a la que llamamos espaciotiempo. Diez años más tarde el mismo Einstein propuso con su Relatividad General que la gravedad no era más que la deformación del espaciotiempo. Además, analizando las ecuaciones que rigen el espaciotiempo determinó la existencia de oscilaciones del propio espaciotiempo que se propagan a la misma velocidad que la luz y que transportan energía. Así predijo las ondas gravitacionales.
En los mismos trabajos también dedujo qué puede generar esas ondas, y consiguió alguna estimación de los rangos de energía asociados. En definitiva, cualquier masa acelerada produce ondas gravitacionales. El ejemplo paradigmático es el de dos masas que rotan una en torno a la otra: sistemas binarios de estrellas. Durante los años 70 se pudo calcular cómo son esas ondas, y con ello, la cantidad de energía que un sistema binario debería emitir en forma de ondas gravitacionales de manera muy precisa. Esta pérdida de energía del sistema binario se debería traducir en un acercamiento de las dos estrellas, y producir, a su vez, un giro más rápido.
Fue precisamente en 1974 cuando Hulse y Taylor pudieron observar un púlsar en un sistema binario. Un púlsar es una estrella de neutrones que gira muy rápido y actúa como un faro. El de Hulse y Taylor enfoca a la Tierra cada 59 milisegundos aproximadamente, pero analizando la señal de manera más fina observaron que el pulsar giraba en torno a una compañera con un periodo de 8 horas. Más aún, a lo largo de unos años pudieron apreciar que este periodo disminuía y que lo hacía al ritmo que el cálculo de ondas gravitacionales predecía! Hulse y Taylor recibieron el Premio Nobel en 1993 por este hallazgo. La predicción teórica de la disminución en el periodo acumulado sigue cuadrando con las observaciones hoy en día.
Desde los años 70 tenemos pues una evidencia indirecta muy clara de que las ondas gravitacionales existen, y la Relatividad General nos permite calcular la forma de la onda (el «sonido») que produce un sistema binario y la energía que transporta. El siguiente paso era obvio. Se quería detectar las ondas de manera directa. Para ello se debía construir un aparato que pudiese detectar oscilaciones en el espaciotiempo, oscilaciones que se sabía que debían ser muy, muy pequeñas. Un aguerrido grupo de científicos diseñaron y propusieron en los 70 la construcción de dos interferómetros gigantescos, uno a cada lado de los EEUU, y consiguieron que el gobierno americano se implicase (dinero) en su construcción. La construcción y sus mejoras se plantearon a largo plazo, y así fue como 40 años más tarde empezó a funcionar el LIGO (siglas en inglés de Observatorio de Ondas-gravitacionales por Interferómetro Laser) con una sensibilidad suficiente según indicaban las predicciones.
La base del funcionamiento de un interferómetro es la medición de la variación de la diferencia del tiempo que tarda la luz (laser) en recorrer dos caminos a lo largo de dos brazos. Si en un momento determinado la luz tarda lo mismo en recorrer esos dos brazos y más tarde eso cambia, entonces los caminos habrán variado (entre sí). Pero los aparatos están fijos, es el propio espacio lo que cambia. Esa es la variación del espaciotiempo que podemos medir, la oscilación de la longitud relativa entre los dos brazos. Esa oscilación produce una señal, como si de un sismógrafo se tratara.
Por otro lado, se necesitaba saber qué señal se esperaba observar por dos razones. Una, para poder filtrar la señal de la onda de entre el ruido provocado por cualquier vibración en la corteza terrestre. El filtrado es el proceso que hace nuestro cerebro habitualmente cuando somos capaces de identificar una canción entre un ruido a más volumen si la canción se conoce. La segunda razón es poder identificar lo que se observa.
Los cálculos realizados durante las décadas de los 70 y 80, que servían para estimar las ondas emitidas por sistemas binarios mientras rotan tranquilamente, no eran suficientes para deducir la forma precisa de las ondas que emanarían de la colisión última de las dos componentes del sistema binario. Los eventos que LIGO está preparado a «oir» deben ser suficientemente violentos. Hasta bien entrado el siglo XXI no se supo y pudo usar cálculo numérico en Relatividad General (en superordenadores) para predecir exactamente cómo son las ondas generadas por fusión de agujeros negros, fusión de estrellas de neutrones y supernovas. Por el año 2015 ya se disponía de una «discografía» de cientos de miles de señales predichas para diferentes parámetros de esas colisiones. Fue por aquel entonces, cuando en septiembre de 2015 el LIGO en versión avanzada se había vuelto a poner en marcha, cuando se produjo la primera detección de ondas gravitacionales. El análisis de la señal coincidía perfectamente con la señal predicha para la colisión de dos agujeros negros, de 36 y 29 masas solares respectivamente, a una distancia de 410 Megaparsecs. Muy lejos.
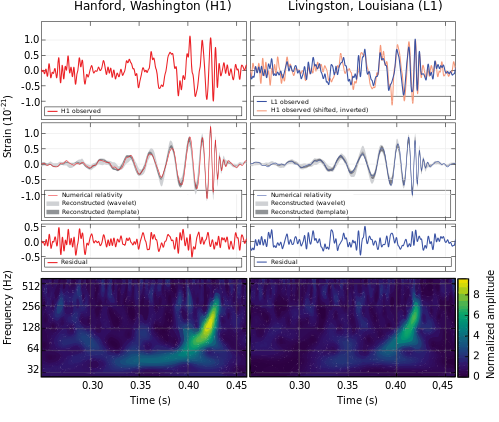 Figura 1. Primera detección de Ondas Gravitacionales en LIGO. Fuente: B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration) / Wikimedia Commons
Figura 1. Primera detección de Ondas Gravitacionales en LIGO. Fuente: B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration) / Wikimedia Commons
La señal de un choque de agujeros negros no se puede ver, solo se puede detectar por ondas gravitacionales. Esta detección es un hito de la humanidad. No sólo fue la primera detección de ondas gravitacionales, sino que fue la primera detección directa de un agujero negro (de hecho, dos!). Por esta detección recibieron el Premio Nobel en 2017, sólo dos años más tarde, los principales responsables del proyecto científico.
Por contra, una colisión de estrellas de neutrones, por ejemplo, debería dejar un rastro «visible» en forma de ondas electromagnéticas. Una analogía en este caso sería como «oír» una explosión, mirar en la dirección del sonido, y ver entonces unos fuegos artificiales. De hecho, sirviéndonos de la misma analogía, se podría determinar la diferencia de velocidades de las ondas de luz y las ondas gravitacionales, o si las velocidades son iguales, como se predecía. La comunidad estaba a la expectativa de ver si el Universo nos iba a regalar un evento con estrellas de neutrones para poder “ver” y “oír” a la vez.
Hablando de fuegos artificiales, ya desde los años 60 se venían observando explosiones de rayos gamma en el firmamento, sin saber la causa. La primera vez que se detectó una, en plena guerra fría, provocó un grave conflicto diplomático, ya que los EEUU pensaron que se trataba de pruebas nucleares soviéticas en el espacio. Desde entonces se intentaba hallar la causa de estos destellos. De entre las posibles explicaciones la más convincente era la colisión de estrellas de neutrones. Esta convicción no cuajó hasta que se pudieron realizar simulaciones numéricas de fusiones de estrellas de neutrones, usando la Relatividad General y la teoría de partículas elementales de que disponemos. Estas simulaciones, además de aportar una causa sólida a esas explosiones de rayos gamma, también predecían otro aspecto, que tiene que ver con la producción de elementos pesados, como por ejemplo el oro o el uranio. Ya en 2007 se había puesto en entredicho que la producción de los elementos más pesados de la tabla periódica proviniesen de explosiones supernova. Los cálculos de la época determinaban que la energía de esas explosiones no era suficiente, que hacía falta algo más violento. Fue durante 2016 y 2017 cuando esas simulaciones de fusiones de estrellas de neutrones aportaron una evidencia más sólida sobre la producción de esos elementos más pesados.
Todas estas predicciones se confirmaron en agosto de 2017. Para entonces ya se contaba con un tercer interferómetro, VIRGO, que está situado en Europa (norte de Italia). Al poder disponer de tres interferómetros podemos determinar con más precisión la dirección de la que proviene la onda. LIGO y VIRGO detectaron una señal de onda gravitacional que correspondía a la predicha para una fusión de dos estrellas de neutrones de 1,6 y 1,1 masas solares respectivamente, y a una distancia de unos 40 Megaparsecs. El satélite Fermi había detectado una explosión de rayos gamma justo a esa hora, de manera independiente. Esa información junto con la dirección que indicaban LIGO y VIRGO determinaban que la explosión se había producido en una región muy concreta del firmamento. Veinte minutos más tarde la mitad de los telescopios de la Tierra, y el Hubble en el espacio, apuntaban en esa dirección. Allí vieron los «fuegos artificiales» predichos por las simulaciones de fusiones de estrellas de neutrones: los rayos gamma, con una intensidad mayor que toda la luz de la galaxia (NGC4993) que albergaba las dos estrellas, seguidos horas y días después por rayos X, luz visible y ondas de radio. Esos días se pudo determinar la composición del material que la explosión había generado. La producción de elementos pesados era la predicha, que se corresponde, por cierto, a las abundancias de esos elementos en nuestro propio sistema solar. La portada del Financial Times en uno de aquellos días celebraba la producción de una cantidad de oro equivalente al peso de la Tierra.
 Figura 2. Detección de una fusión de estrellas de neutrones: ondas gravitacionales. Fuente: LIGO Scientific Collaboration and Virgo Collaboration. Creative Commons Attribution-Share Alike 4.0 International license.
Figura 2. Detección de una fusión de estrellas de neutrones: ondas gravitacionales. Fuente: LIGO Scientific Collaboration and Virgo Collaboration. Creative Commons Attribution-Share Alike 4.0 International license.
Esta observación ha servido, además, para comprobar que la velocidad de la luz y la de las ondas gravitacionales son la misma. La medición aporta una fiabilidad con un error de una parte en 10.000.000.000.000.000. Además de corroborar las predicciones de la Relatividad General, este dato nos ha permitido descartar toda una carpeta de teorías alternativas a la Relatividad General, que se habían planteado para resolver otro tipo de incógnitas cosmológicas.
 Figura 3. Detección de una fusión de estrellas de neutrones: explosión de rayos gamma. Fuente: Hubble Space Telescope, NASA and ESA/ Wikimedia Commons.
Figura 3. Detección de una fusión de estrellas de neutrones: explosión de rayos gamma. Fuente: Hubble Space Telescope, NASA and ESA/ Wikimedia Commons.
Estamos ante el nacimiento, por lo tanto, de la Astronomía de Ondas Gravitacionales y Multimensajero, combinando la información que aportan los dos tipos de ondas. En el futuro quizás podamos también añadir la esperada observación de neutrinos. Las posibilidades que la Astronomía Multimensajero puede llegar a ofrecer no se conocen aún, pero tienen visos de ser revolucionarias. La combinación de los datos aportados por la señal de la onda gravitacional junto a la electromagnética en esta detección de fusión de estrellas de neutrones ha provocado un avance en la comprensión de los procesos astrofísicos de muy alta energía comparable a décadas de investigación. Tenemos que tener en cuenta que hasta ahora habíamos observado el Universo usando algo que conocemos como seres biológicos: la luz. Primero a través de la vista, y desde principios del siglo XX, a través de detectores de luz en otras frecuencias, como son los rayos X, gamma… Pero lo que se ha conseguido ahora es un nuevo sentido, una nueva manera de observar el Universo. Algo que no sabíamos ni que existía hace apenas un siglo.
En nuestro departamento de la UPV/EHU trabajamos en la modelización de estrellas de neutrones y sistemas binarios, y en la emisión de ondas gravitacionales en el universo primordial. En un futuro no muy lejano se pondrá en órbita un interferómetro parecido a LIGO (llamado LISA) con la capacidad de observar ese tipo de ondas, lo que nos llevará a descubrir nueva física.
Sobre los autores: José Juan Blanco-Pillado, Jon Urrestilla y Raül Vera son investigadores en el Departamento de Física Teórica de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo La detección de ondas gravitacionales y la astronomía multimensajero se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La detección de ondas gravitacionales: el nacimiento de una nueva astronomía
- Cosmología de ondas gravitacionales en 29 órdenes de magnitud
- Ondas gravitacionales en la materia oscura
El ultraprocesado es malo hasta que yo lo hago

Si preguntamos si son más saludables los alimentos elaborados en casa o los elaborados por la industria, la mayoría responderá que son más saludables los alimentos caseros [1]. Incluso con alimentos ultraprocesados insanos, como galletas o bizcochos, también existe la creencia de que los elaborados en casa son más saludables que los que nos ofrece la industria.
La lectura que podemos hacer de estas creencias es que muchas personas creen que los alimentos preparados por la industria alimentaria se elaboran con ingredientes de peor calidad que los que uno mismo escogería, incluso sin ser experto en materia alimentaria. También indica que existe desconfianza sobre los procesos industriales que se emplean para preparar estos alimentos, o un exceso de confianza sobre las preparaciones caseras.
Otra lectura es que los alimentos insanos llegan a parecer menos insanos, o incluso saludables, si son caseros. Mientras que los alimentos industriales que podrían catalogarse como sanos, llegan a parecer menos saludables, o insanos, por el hecho de ser industriales.
-
¿Qué es un ultraprocesado?
El sistema actual más utilizado para clasificar los alimentos según su grado de procesamiento es el sistema NOVA [2]. Este sistema fue creado en 2010 por la Escuela de Salud Pública de la Universidad de Sao Paulo y es el sistema que aceptan autoridades como la OMS y la FAO [3].
La clasificación más reciente del sistema NOVA establece cuatro grupos:
El grupo 1 es el de alimentos sin procesar o mínimamente procesados (pasteurizado, congelado, tostado, desecado…). Aquí encontramos a los alimentos frescos como frutas, verduras, cereales, carnes, legumbres, huevos, leche y a algunos de sus derivados inmediatos, como la pasta, los zumos o los yogures sin azúcares añadidos.
En el grupo 2 encontramos comestibles que nos ayudan a cocinar y sazonar los alimentos del grupo 1 y que no es común comerlos de forma aislada. Por ejemplo la sal, el azúcar, los aceites y las mantequillas.
En el grupo 3 encontramos alimentos preparados con dos o tres ingredientes de los grupos 1 y 2. Pueden contener aditivos alimentarios que garanticen su seguridad y conservación. Por ejemplo, las legumbres en conserva, los pescados en conserva, las carnes en salazón, curados y ahumados, las frutas en almíbar, los frutos secos salados, el pan y los quesos. También se incluyen en este grupo las bebidas alcohólicas de baja graduación derivadas de la fermentación de los alimentos del grupo 1, como la cerveza, el vino y la sidra.
El grupo 4 es el denominado grupo de los ultraprocesados. Son alimentos que contienen más de 5 ingredientes. Aunque pueden contener ingredientes del primer grupo, sin procesar, la mayoría son ingredientes procesados. Entre ellos es frecuente encontrar ingredientes como almidón, lecitina, potenciadores del sabor o aromas que, aunque son sustancias que de forma natural componen alimentos del primer grupo, difícilmente podríamos encontrarlas de forma aislada en un supermercado. Son ultraprocesados las galletas, los bizcochos, los chocolates, los snacks, los refrescos, las varitas de pescado, los nuggets de pollo, etc.

- Consumo de alimentos utraprocesados y su relación con la salud.
Los autores del sistema NOVA aconsejan priorizar el consumo de alimentos del grupo 1. Es decir, una dieta saludable estará constituida principalmente por alimentos del grupo 1, con una cantidad reducida del grupo 2, y por un consumo eventual de alimentos del grupo 3. Los alimentos del grupo 4 no pueden formar parte de una dieta saludable.
Este consejo se fundamenta en el resultado de varios estudios científicos que relacionan el consumo de ultraprocesados con un mayor riesgo de mortalidad [4][5][6].
La Organización Mundial de la Salud define «salud» como un estado de completo bienestar físico, mental y social, y no solamente la ausencia de afecciones o enfermedades [7]. Cuando en dietética se habla de «dieta saludable» las recomendaciones quedan restringidas a la dieta exclusivamente. Desde el punto de vista dietético, ni una galleta ni una crema de chocolate, son saludables. Lo mismo ocurre con las bebidas alcohólicas, que no son saludables a ninguna dosis desde un punto de vista dietético, tampoco médico [8].
Sin embargo, si nos referimos a la salud de forma tan amplia como la que define la OMS, el consumo esporádico de alimentos ultraprocesados podría contemplarse dentro de la definición de salud. Aunque el placer no tiene por qué estar reñido con una dieta saludable, en algunos casos lo está: la copa de vino que los viernes te tomas con tus amigos, el chocolate que tomas de postre el domingo, el pastel típico de tu pueblo. Esos placeres proporcionan bienestar social y mental, sí son saludables aunque no formen parte de la definición de «dieta saludable».
Esta última aclaración parece obvia, pero es el núcleo de muchas discusiones entre lo que es saludable y lo que no. El origen de muchas discusiones está en la demarcación del problema, en qué se entiende por salud, en si se habla de «dieta saludable» o de la amplia y compleja definición de «salud».
 Fuente: rawpixel
Fuente: rawpixel
-
El ultraprocesado casero no es más sano que el industrial.
Una galleta es un ultraprocesado. Una crema de cacao también. Un bizcocho también. Incluidos los hechos en casa.
Es cierto que con los alimentos caseros somos nosotros los que escogemos los ingredientes y, por lo tanto, podemos hacer una elección más saludable. Por ejemplo, es más saludable la harina integral que la refinada y la fruta que el azúcar, y con eso podemos hacer un bizcocho más saludable que el bizcocho tradicional. También la industria puede hacerlo de este modo y de hecho lo hace.
Dentro de los ultraprocesados industriales también existen opciones mejores y peores. De la misma manera que dentro de los ultraprocesados caseros, también existen opciones mejores y peores. Unas galletas caseras hechas con 280 g de harina refinada, 100 g de azúcar, un huevo y 125 g de mantequilla, en poco o nada se diferencian de cualquier galleta industrial. El horno de nuestra casa no tiene unas propiedades mágicas que insuflan salud a los alimentos. Ni siquiera la fuerza de nuestro amor es capaz de convertir a unas galletas en un alimento propio de una dieta saludable.
Es más saludable un bizcocho sin azúcar hecho con dátiles —que difícilmente encontraremos como producto industrial— que un bizcocho tradicional. Esta afirmación es análoga a las siguientes: es más saludable un vaso de sidra que un cubata; es más saludable un zumo exprimido con su pulpa [9] que un refresco de naranja. Un error común es asumir que la sidra es saludable, que el zumo es saludable, o que el bizcocho de dátiles es saludable. Son opciones mejores, pero no son intrínsecamente saludables.
En algunos casos el alimento casero es menos saludable que su análogo industrial. Una parte importante de la salubridad de un alimento se refiere a la seguridad alimentaria, y en esto sale ganando por goleada la industria alimentaria. Por muy pulcros que seamos en nuestras cocinas, la mayoría no superaríamos los estrictos controles sanitarios que hay en la industria.
Otra parte se refiere a la optimización de procesos. En la industria se controlan las temperaturas y los tiempos con precisión. Se detectan y miden los subproductos indeseados que se pueden formar consecuencia del cocinado. Es algo que no podemos hacer en casa. Por ejemplo, las patatas fritas de bolsa, las industriales, son más saludables que las patatas fritas caseras [10] principalmente porque en la industria se controla y se minimiza la producción de acrilamida.
- Reflexiones finales
La creencia de que los alimentos caseros son más saludables que los industriales es una creencia errónea. Una de las consecuencias de esta creencia es que los alimentos ultraprocesados insanos, aquellos que no pueden formar parte de lo que entendemos como dieta saludable, se perciben como saludables solo por ser caseros. Un ultraprocesado insano seguirá siendo insano, tanto si se hace en casa como si se hace en la industria.
Esta creencia es el origen del uso de la denominación «casero» como reclamo, ya que es bien conocido que muchos lo interpretarán como sinónimo de «saludable». El flan casero no es saludable. Ni siquiera el de tu abuela que te quiere muchísimo.
Sobre esto puede hacerse una lectura más profunda. Creer que lo casero es más saludable implica que la imagen de la industria alimentaria está dañada. Tanto es así, que las primeras imágenes que vienen a la mente cuando se menciona a la industria alimentaria son las de la comida rápida o los utraprocesados. En primera instancia no vienen a la mente las legumbres en conserva, los yogures o la bolsa de canónigos. Y eso también es industria alimentaria.
Podemos quedarnos en la superficie, en la manida historia de héroes o villanos. Tu madre haciendo croquetas de madre en su casa, y Darth Vader haciendo croquetas del infierno en la industria. Como siempre, estas historias tienen sus aristas, generalmente con más enjundia que la historieta en sí, y su popularización tiene unas implicaciones sociológicas preocupantes. La divulgación nos permite hacer una transferencia de información, y un ciudadano informado será un ciudadano más libre. A veces es así. La divulgación no está exenta de populismos.
Esa imagen dañada de la industria alimentaria se ha convertido en una oportunidad de negocio, también para los oportunistas [12]. Aquellos cuya reflexión se limita a perseguir los errores de la industria alimentaria. Porque alimentando un prejuicio nos haremos más libres y tal. Aquellos que contando los terrones de azúcar de un tigretón te enseñan lo mala que es tu dieta y lo perversa que es la industria. Aquellos que popularizan dietas que se han llegado a convertir en ideologías en contra de todo un sector. Héroes de la obviedad que no son capaces de hacer un análisis más profundo de nada.
Fuentes:
[1] Encuesta realizada en Twitter con la participación de 1.072 votantes. El 85% opina que son más saludables los alimentos caseros.
¿Son más saludables los alimentos elaborados en casa o los elaborados por la industria?
A continuación os pongo una hilo-encuesta con alimentos concretos para que me digáis.
¡Gracias!
— Deborah García Bello (@deborahciencia) May 27, 2019
[2] Monteiro et al (2016) NOVA. The star shines bright World Nutrition Volume 7, Number 1-3, January-March
[3] FAO (2015) Guidelines on the collection of information on food processing through food consumption surveys
[4] Rico-Campà et al (2018) Ultra-Processed Food Consumption and All-Cause Mortality: The University of Navarra Follow-Up (SUN) Cohort Preprints with The Lancet
[5] Moubarac et al (2013). Consumption of ultra-processed foods and likely impact on human health. Evidence from Canada. Public Health Nutrition, 16(12), 2240-2248. doi: 10.1017/S1368980012005009
[6] Rauber, F. et al. (2015) Consumption of ultra-processed food products and its effects on children’s lipid profiles: A longitudinal study Nutrition, Metabolism and Cardiovascular Diseases , Volume 25 , Issue 1 , 116 – 122 doi: 10.1016/j.numecd.2014.08.001
[7] OMS (2019) Preguntas más frecuentes
[8] García Bello (2017) «Una copita de vino es buena para el corazón». Claro que sí, guapi Cuaderno de Cultura Científica
[9] Basulto (2017) El zumo de fruta no es “fruta”, ni siquiera si es casero El País
[11] García Bello (2015) Patatas fritas sin cáncer, gracias Dimetilsulfuro
[12] García Bello (2019) Humildemente, el mundo es mejor gracias a mí
Otras lecturas recomendadas:
Revenga (2018) Cómo distinguir los buenos procesados de los ultraprocesados insanos El comidista
Jiménez (2017) ¿Qué alimentos se consideran procesados y ultraprocesados? Lo que dice la ciencia para adelgazar
del Caño (2018) ¿Se nos está yendo REALmente la pinza con la FOOD? Farmagemma
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo El ultraprocesado es malo hasta que yo lo hago se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- No todo ha sido malo este año: la ciencia nos dejó algunas buenas noticias
- Del cerdo, hasta la hidroxiapatita
- El azúcar oculto en los alimentos
Multiplicar con las manos
Con motivo de mi charla “Las matemáticas en tus manos (una perspectiva cultural desde Bilbao La Vieja y San Francisco)”, dentro del ciclo Zientziaz Blai (¡empápate de ciencia!), que organiza la asociación Logos Elkartea en los barrios bilbaínos de San Francisco, Bilbao La Vieja y Zaballa, en la que hablaba de diferentes métodos de contar con los dedos de las manos, de los cuales ya he hablado en el Cuaderno de Cultura Científica en las entradas «Y tú, ¿cómo cuentas con los dedos? (1 y 2)» y Contar hasta un millón con los dedos de las manos, me preguntaron si existía algún método que generalizara la forma de memorizar la tabla del nueve con los dedos de las manos.
Recordemos que este método consiste en extender los diez dedos de nuestras dos manos, con las palmas mirando hacia nosotros, y bajar el dedo de la posición, empezando por la izquierda, que queremos multiplicar por 9 (recordemos que estamos hablando de la tabla de multiplicar por 9), así si queremos multiplicar 3 por 9 bajaremos el tercer dedo por la izquierda, es decir, el dedo corazón de la mano izquierda, de forma que las decenas del resultado es la cantidad de dedos que queda a la izquierda del dedo bajado y las unidades la cantidad que queda a la derecha, en nuestro caso, 2 y 7, que nos confirman que 3 x 9 = 27.
Mi respuesta fue que existía un sistema para multiplicar con los dedos de las manos, que no era exactamente lo mismo, pero que nos permitía realizar algunas multiplicaciones sencillas a partir de otras básicas, como multiplicar dos números entre el 6 y el 10, conociendo las pequeñas tablas de multiplicar de los cinco primeros números, desde 1 x 1 hasta 5 x 5. En esta entrada del Cuaderno de Cultura Científica explicaré este conocido método, que dejé sin explicación en mi charla.
Según he leído, esta práctica se utilizaba ampliamente en la Edad Media, y pudo tener su origen en la Antigua Roma. Su uso se ha mantenido hasta época reciente en diferentes lugares del mundo. Por ejemplo, por los campesinos franceses (de ahí el nombre de multiplicación de los campesinos franceses), rumanos o rusos, pero también en lugares más alejados, como Palestina o Siria. En Estados Unidos se la conoce como multiplicación cajún, cuyo nombre deriva de los cajunes, un grupo étnico de Luisiana, descendientes de franceses, formado por más de un millón de personas, con su propia lengua y cultura, y que utilizaban este sistema de multiplicación digital.
Este método permite realizar multiplicaciones de números comprendidos entre el 6 y el 10. Veamos un ejemplo, la multiplicación 7 x 9. En la mano izquierda se representa el primer número, bajando tantos dedos como indique el número, a partir de 5, en este caso, se bajan 2 dedos (5 + 2 = 7) y se quedan 3 levantados. En la mano derecha se representa el segundo, se bajan 4 dedos (5 + 4 = 9) y 1 queda levantado. Ahora, se suman los dedos bajados, 2 + 4, y se multiplica su resultado por diez, (2 + 4) x 10 = 60, y se le suma la multiplicación de los dedos levantados, 3 x 1. Así,
7 x 9 = (2 + 4) x 10 + 3 x 1 = 63.
La justificación matemática de este sistema de multiplicación con las manos es sencilla. Si llamamos a y b a los dedos bajados y c y d a los dedos que quedan levantados, entonces la multiplicación que se realiza de esta forma no es otra que (5 + a) x (5 + b) y el método que hemos utilizado para obtenerla viene dado por la expresión 10 x (a + b) + (c x d). Teniendo en cuenta que c = 5 – a y d = 5 – b, las dos expresiones matemáticas son la misma: 5 x 5 + 5 x a + 5 x b + a x b.
Veamos otro sencillo ejemplo, 6 x 8.
De forma similar, se pueden multiplicar números entre 11 y 15. Por ejemplo, para obtener el resultado de la multiplicación 12 x 12, en la mano izquierda se bajan 2 dedos (10 + 2 = 12) y en la derecha otros 2 dedos. Ahora, se suman los dedos bajados (2 + 2) y el resultado se multiplica por 15, se le suma la multiplicación de los dedos levantados (3 x 3) y finalmente se suma una cantidad fija, 75, obteniéndose el resultado
12 x 12 = (2 + 2) x 15 + (3 x 3) + 75 = 144.
Si se multiplica un número de cada zona, por ejemplo, 8 x 13, se puede reducir a dos multiplicaciones de las anteriores, 8 x 13 = (8 x 7) + (8 x 6).
En general, se pueden multiplicar números de zonas con cinco números más grandes y métodos similares a los descritos.
zona 6 – 10: 10 x (a + b) + (c x d)
zona 11 – 15: 15 x (a + b) + (c x d) + 75
zona 16 – 20: 20 x (a + b) + (c x d) + 200
zona 21 – 25: 25 x (a + b) + (c x d) + 375
zona 26 – 30: 30 x (a + b) + (c x d) + 600
en general,
zona (5 n + 1) – (5 n + 5): (5 n + 5) x (a + b) + (c x d) + 52 x (n2 – 1),
donde a y b son los dedos bajados y c y d los que quedan levantados, a partir del número anterior a la zona de cómputo.
 «Manos del apóstol» (1508), o manos que oran, de Alberto Durero (1471-1528). Imagen de Wikimedia Commons
«Manos del apóstol» (1508), o manos que oran, de Alberto Durero (1471-1528). Imagen de Wikimedia Commons
Bibliografía
1.- Georges Ifrah, Historia Universal de las cifras, Espasa, quinta edición, 2002.
2.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.
3.- Leon J. Richardson, Digital reckoning among the ancients, The American Mathematical Monthly, vol. 23, no. 1, pp. 7-13, 1916.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Multiplicar con las manos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Multiplicar no es difícil: de los egipcios a los campesinos rusos
- Contar hasta un millón con los dedos de las manos
- Y tú, ¿cómo cuentas con los dedos? (1)
Las partículas de los rayos catódicos
Decíamos que en 1897 J.J. Thomson, jefe del famoso Laboratorio Cavendish en la Universidad de Cambridge, realizó una serie de experimentos que convencieron a los físicos de que los rayos catódicos son partículas cargadas negativamente.
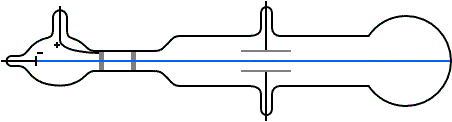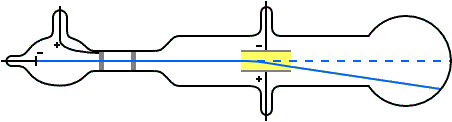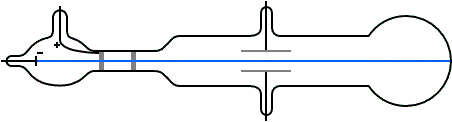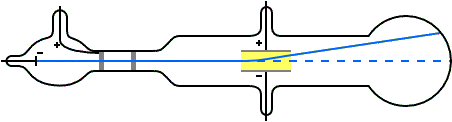 Esquema del tubo de Crookes que J.J. Thomson empleó en sus experimentos, en los que un campo eléctrico (en amarillo) modificaba la trayectoria de las partículas de los rayos catódicos. Fuente: Wikimedia Commons
Esquema del tubo de Crookes que J.J. Thomson empleó en sus experimentos, en los que un campo eléctrico (en amarillo) modificaba la trayectoria de las partículas de los rayos catódicos. Fuente: Wikimedia Commons
Para entonces era bien sabido que las trayectorias de las partículas cargadas se ven afectadas tanto por los campos magnéticos como por los eléctricos. Suponiendo que los rayos catódicos eran partículas cargadas negativamente, Thomson podía predecir qué sucedería cuando atravesasen estos campos. Por ejemplo, un campo eléctrico de la magnitud y dirección correctas debería equilibrar exactamente la desviación producida en un haz de rayos catódicos por un campo magnético. Thomson pudo comprobar que las predicciones eran correctas. De aquí, por tanto, pudo concluir que los rayos catódicos estaban hechos de partículas cargadas negativamente.
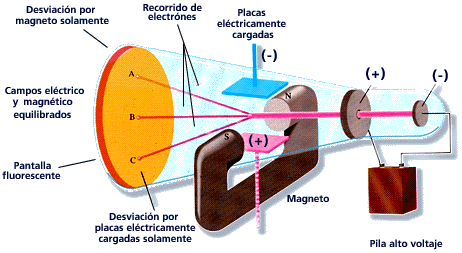 Experiemento de Thomson. Fuente: Pontificia Universidad Católica de Chile.
Experiemento de Thomson. Fuente: Pontificia Universidad Católica de Chile.
A partir de los datos experimentales podía calcular la relación entre la carga de una partícula y su masa. Esta relación la podemos representar como q / m, donde q es la carga y m es la masa de la partícula. Thomson descubrió que los rayos provenientes de cátodos hechos de diferentes materiales tenían el mismo valor de q / m: 1,76·1011 C / kg (culombios por kilo). Por lo tanto, estaba claro que los rayos catódicos debían estar hechos de algo que todos los materiales tienen en común.
El valor de q / m para las partículas de rayos catódicos resultó ser aproximadamente 1800 veces mayor que el valor de q / m para los átomos de hidrógeno cargados (iones), que se sabía que era 9,6 ·107 C / kg por experimentos de electrólisis química . De aquí se deducía que o la carga de las partículas de rayos catódicos es mucho mayor que la del ion de hidrógeno, o que la masa de las partículas de rayos catódicos es mucho menor que la masa del ion de hidrógeno.
Para decidir entre las dos posibilidades Thomson también midió la carga q en las partículas con carga negativa en los rayos catódicos con métodos distintos a la desviación por campos eléctricos y magnéticos. Sus experimentos no fueron muy precisos, pero fueron lo suficientemente buenos como para indicar que la magnitud de la carga negativa de una partícula de rayos catódicos era la misma o no muy diferente de la magnitud de la carga del ion hidrógeno positivo en la electrólisis. En vista del gran valor de q / m para las partículas de rayos catódicos, Thomson concluyó que la masa m de las partículas de rayos catódicos es mucho menor que la masa de iones de hidrógeno.
En resumen Thomson había descubierto que las partículas de rayos catódicos tienen tres propiedades importantes:
1. Los mismos tipos de partículas se emitiden por una amplia variedad de cátodos de diferentes materiales.
2. Eran mucho más pequeñas en masa que el átomo de hidrógeno, el átomo que tiene la masa más pequeña.
3. Tenían la misma magnitud de carga que la carga en el ion de hidrógeno.
A la vista de estos hechos Thomson no podía sino concluir que las partículas de rayos catódicos deben ser un componente hasta ahora no observado de toda la materia [1]. Dado que transporta carga eléctrica, la partícula de rayos catódicos se identificaría con un nombre inventado mucho antes, electrón. Tiene una carga negativa de -1,6·10-19 C. La magnitud [2] de la carga de electrones recibe el símbolo e, donde e =1,6·10-19 C.
El hallazgo de Thomson significó que el átomo no era el límite máximo para la subdivisión de la materia. Más bien, el electrón parecía ser parte de ciertos átomos, quizás incluso podría ser un componente básico de todos los átomos. [3]
Notas:
[1] Puedes deducir con estos datos que es parte de la materia, no parte de los átomos, ya que con el conocimiento de la época nada impedía que los electrones fuesen algo independiente de los átomos.
[2] La magnitud no incluye el signo.
[3]El electrón, cuya existencia Thomson probó por primera vez mediante un experimento cuantitativo, es una de las partículas fundamentales o «elementales» de las que está hecha toda la materia. ¿Pero cómo sabemos que es elemental y que es constituyente de todos los átomos?
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las partículas de los rayos catódicos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los fascinantes rayos catódicos
- El tubo de rayos catódicos, auge y caída de una pieza clave del siglo XX
- Del electrón (I)
Cómo entrenar a tu gato: cuatro experimentos para saber cuánto te quiere o si pasa de ti
 Imagen: Unsplash
Imagen: Unsplash
Creo firmemente que en algunas cuestiones la equidistancia está infravalorada. Obviamente no es el caso cuando hablamos de derechos humanos y la violación de los mismos, por ejemplo, pero sí en otras cuestiones, como si es mejor la tortilla de patata con cebolla o sin cebolla (por qué elegir entre dos cosas que están buenísimas si puedes disfrutar de ambas) o en si son mejores mascotas los perros o los gatos. Como alguien que ha tenido ambos, perros y gatos son alternativas diferentes pero igualmente amorosas. Desde aquí me declaro partidaria de ambos, sin elegir.
¿A qué este rollo, se preguntarán? Bien, pues a que, aunque perros y gatos son para mí mascotas perfectas, una pega habitual que se pone a los felinos es su absoluto pasotismo: su relación con su dueño suele ser, por norma general, más distante que las de los perros.
 Imagen: Pixabay
Imagen: Pixabay
Amor perruno, amor gatuno
Sí, sé que hay gatos cariñosos y entrañables, pero rara vez pueden alcanzar las muestras de cariño de las que un can sabe hacer gala: impetuosos recibimientos al llegar a casa cada tarde, como si hiciese una eternidad que no te ve; acudir inmediatamente a tu llamada con la cola en modo limpiaparabrisas de la alegría de ser llamado; aprender a seguir órdenes más o menos complejas solo por la recompensa de tu amor (y de alguna chuchería, claro…).
La mayoría de los dueños de un gato nunca recibirán esas respuestas. En su mayor parte, tampoco las esperan ni las quieren, ya que van acompañadas de una dependencia mucho mayor que su gato no impone: son capaces de pasar más horas solos, no se mueren de pena ante una ausencia más prolongada de lo normal y lo de los dos o tres paseos diarios no es una obligación impepinable. Claramente, la cosa tiene sus ventajas.
Pero eso no quiere decir que no pueda haber entre gato y dueño una relación especial, un entendimiento mutuo que forje entre ellos un vínculo similar al que ostentan los perros con sus amos. Los gatos son animales muy inteligentes y con una personalidad muy rica, capaces de percibir muchos detalles de su entorno y de las personas con las que viven y de reaccionar a esos detalles. Cuando quieren, claro.
Kristy Vitale es investigadora postdoctoral en la Universidad Estatal de Oregón y su trabajo se centra en estudiar la mente felina. En un artículo publicado recientemente en la web de Science cuenta que justo en mitad de su investigación adoptó a un gatito llamado Carl que se encontró en el arcén de la carretera un día cualquiera. El suyo fue un encuentro muy beneficioso para ambos en más de un sentido. No solo habían encontrado a un compañero de vida: Carl se iba a convertir en el objeto de una serie de experimentos para medir la inteligencia social de los gatos, ese campo de las habilidades cognitivas en el que solemos dar la ventaja sin dudar a los perros.
 Imagen: Pixabay
Imagen: Pixabay
Cuatro experimentos para hacer con tu gato
¿En qué consisten esos experimentos y qué es lo que sus resultados le dicen a los dueños de los gatetes puestos a prueba? Estos son algunos de ellos.
1. ¿Sabe tu gato cuál es su nombre? Para poner a prueba este punto, elige cuatro palabras que tengan la misma longitud y acentuación que su nombre, y pronúncialas seguidas dejando un intervalo de unos 15 segundos entre ellas. Pronuncia su nombre en quinto lugar, manteniendo el mismo tono y volumen. Si tu gato hace gradualmente menos caso a cada palabra pero reacciona cuando dices su nombre, ya sea girando la cabeza, enfocando las orejas o moviendo la cola, es probable que sea porque lo ha reconocido.
2. ¿Reconoce y reacciona a tus emociones? Coge a tu gato y entra con él en una habitación donde haya un objeto que no haya visto nunca pero pueda causarle nervios o miedo, como una aspiradora, por ejemplo. Suéltale (mejor con la puerta cerrada para que no se escape) y acércate a la aspiradora, tócala y habla en un tono calmado y amigable. Si al principio se aleja pero después de tu reconocimiento del objeto termina acercándose y olisqueándolo o tocándolo, es probable que se deba a que ha reconocido tus emociones y haya reaccionado ante ellas. Esto puede ser muy útil en situaciones de estrés para tu gatete, como por ejemplo cuando pases la dichosa aspiradora o en una visita al veterinario.
3. ¿Cómo de independiente es tu gato? Todos los dueños de gatos saben que no todos son igual de pasotas. Para medir la atención del tuyo, prueba a sentarte tranquilamente en la misma habitación que esté él pero sin hacerle caso, dedicando un par de minutos a leer o a mirar tu móvil. Después deja el libro y llámale. Si acude, acaríciale y háblale con cariño. Lo gatos más socializados se acercarán a su dueño en cuanto este les llame, mientras que los más independientes probablemente le recompensarán con una mirada o un giro de orejas, y gracias.
4. ¿Tu gato te quiere más a ti o a su comida? Coge unos cuantas chucherías, alguno de sus juguetes y colócalos por la habitación. Siéntate tú también en la misma habitación. Observa hacia donde se dirige tu felino. Repítelo en distintos momentos y situaciones para asegurarte que no le hayas pillado justo con hambre.
Son cuatro pruebas sencillas y básicas que pueden darte una idea del nivel de inteligencia social de tu gato. Pero incluso aunque obtengas resultados desmoralizantes en lo que al pasotismo de tu felino se refiere, eso no quiere decir que no sean capaces de cumplirlos. Los gatos domésticos, como especie, han evolucionado a lo largo de los siglos para comunicarse y entenderse con los humanos.
 Imagen: Unsplash
Imagen: Unsplash
Los gatos que miraban a las personas
En 2015, una investigación realizada por científicos italianos fue la primera que demostró que los gatos, igual que los perros, pueden modificar su comportamiento en base a las emociones de sus dueños humanos, algo que los dueños de gatos siempre han sospechado pero que estaba aun por probar. Lo hicieron con un experimento en el que se coloca un ventilador con cintas blancas y negras enganchadas a las aspas y se hace funcionar, el gato se queda cerca de su dueño, a veces detrás de él, y le mira entre asustado e intrigado, esperando una señal sobre si fiarse o no del ruidoso cacharro. Cuando su dueño se acerca calmadamente al ventilador y habla al gato amistosamente mientras lo toca, el gato es capaz de acercarse e incluso tumbarse junto a él.
Otro experimento< posterior fue un poco más allá y en ellos el dueño no se acerca o señala al objeto, simplemente lo mira. Según sus resultados, los gatos siguieron la mirada de sus dueños en un 70% de los casos, un porcentaje similar al de los perros.
La mayoría de los animales no suelen mirarse directamente a los ojos, y cuando lo hacen a menudo es una señal de hostilidad. Así que ver a los gatos utilizando una mirada directa de forma similar a como lo hacen los humanos, para compartir información e indicar órdenes, es muy sorprendente, y otra prueba de que los gatos han evolucionado de forma que son capaces de comunicarse de forma compleja con las personas.
De forma que si tu gato no responde a su nombre o no acude cuando le llamas, lo más probable es que no sea una cuestión de capacidad. Poder, puede hacerlo. Pero no quiere. Y ese también es uno de los atractivos de los gatos. Después de todo, ¿quién no tiene alguna habilidad especial pero pasa de enseñarla solo porque los demás se la piden?
Referencias:
Cats rival dogs on many tests of social smarts. But is anyone brave enough to study them? – Science
Social referencing and cat–human communication – Animal Cognition
Cats (Felis silvestris catus) read human gaze for referential information – Intelligence
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Cómo entrenar a tu gato: cuatro experimentos para saber cuánto te quiere o si pasa de ti se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Experimentos que te cambian la vida (para mal)
- ¿Quién quiere vivir para siempre?
- Un gato de Cheshire cuántico
Historia grabada en hielo
 Anverso y reverso de un penique acuñado en Melle alrededor del 660 e.c. Fuente: Loveluck et al (2018)
Anverso y reverso de un penique acuñado en Melle alrededor del 660 e.c. Fuente: Loveluck et al (2018)
El hielo que se ha acumulado durante centenares y miles de años guarda en su seno información valiosa sobre la historia natural y las condiciones ambientales del momento en que se depositó. Cualquiera de las grandes masas heladas del planeta es, de hecho, un fenomenal repositorio histórico. El problema estriba, claro está, en asignar esa información a cada periodo.
Pero hay técnicas que permiten hacer ese análisis con gran precisión. En un estudio realizado en el glaciar suizo Colle Gnifetti los investigadores han establecido la cronología de las capas de hielo que se habían ido depositando año tras año mediante conteo de muy alta resolución (utilizando láser). La estimación es muy precisa pues se pudo calibrar con referencias de fecha conocida, como el rastro químico que dejaron en el hielo ciertas erupciones volcánicas, por ejemplo.
Midieron también la concentración de plomo en las capas de hielo del siglo VII de nuestra era, para lo que utilizaron una técnica espectrométrica muy sofisticada. Los investigadores estaban interesados en las actividades de extracción y fundición de plata, y utilizaron como indicador el plomo que, procedente de la atmósfera, había quedado atrapado en el hielo. La plata se obtenía de galena (sulfuro de plomo), mineral en el que puede alcanzar una concentración en torno al 1%, y su minería y fundición provocaban la liberación a la atmósfera de importantes cantidades de plomo, parte del cual acababa en las sucesivas capas de hielo.
Además, modelaron matemáticamente la circulación atmosférica al objeto de aproximar la localización de las minas de las que procedía el plomo. Lo más probable es que fuesen las de Melle, en Francia, algo al norte del río Charente, al oeste del glaciar. Los datos obtenidos los combinaron con registros ambientales recogidos de la cata de hielo, además de información numismática, arqueológica y de fuentes escritas.
A lo largo del siglo VII se transformó el sistema monetario en el centro y noroeste de Europa. En la segunda mitad del siglo las monedas pasaron de ser de oro a ser de plata, y gracias a los datos extraídos del glaciar suizo esa transición está ahora mucho más clara. El cambio se produjo en dos fases. La primera, ya conocida, ocurrió hacia el año 640; en esa época el contenido en oro de las monedas se redujo en los reinos merovingios de un 92-94% a valores de entre el 30 y el 60%. La producción de la plata necesaria para la transformación dejó rastro en forma de plomo en el glaciar de Colle Gnifetti.
De acuerdo con los datos procedentes del hielo, la segunda fase se produjo alrededor de 660, cuando las monedas pasaron a estar acuñadas solo en plata. Antes se pensaba que ese cambio se había producido en 675-680, ya que la primera referencia escrita de las monedas de plata data de 682. Sin embargo, el plomo en el registro helado del glaciar indica que ocurrió unos veinte años antes.
Después de dos siglos de declive tras la caída del Imperio Romano, hacia 680 ya se habían consolidado importantes puertos marítimos en las dos orillas del Canal de la Mancha. Pues bien, la nueva cronología de la transformación del sistema monetario sugiere que el aumento del tráfico marítimo en el Canal y Mar del Norte, y la pujanza de los puertos de Lundenwic (Londres) y Quentovic pudieron haber sido impulsados, precisamente, por la mayor cantidad de monedas que empezó a circular veinte años antes. Una vez más, las fronteras entre las disciplinas se difuminan y permiten ahora iluminar uno de los periodos más oscuros de la historia de Occidente.
Fuente: Christopher P. Loveluck et al (2018): Alpine ice-core evidence for the transformation of the European monetary system, AD 640–670. Antiquity 92 (366): 1571-1585.
——————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Historia grabada en hielo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- En Groenlandia el hielo recupera el agua que pierde por sublimación
- Hielo cuadrado por doquier
- Cómo fabricar hielo extraterrestre y verlo molécula a molécula
¿Qué pasa cuando un avión pierde presión en la cabina?
Imagina que vas de viaje en un avión a 35.000 pies de altura, es decir, a 10.668 metros. El avión en el que viajas está diseñado para mantener la misma presión en cabina que la que hay a unos 8.000 pies de altura (2.438,4 metros). Pero, ¿sabes por qué? Porque si mantuviese la presión del suelo sometería a la estructura del avión a muchísimo esfuerzo y …, eso, no te gustaría demasiado.
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Qué pasa cuando un avión pierde presión en la cabina? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué pasa en tu cuerpo cuando te enamoras?
- ¿Qué pasa en tu cerebro cuando duermes?
- #Naukas16 ¿Por qué vuela un avión? (y el método científico)
El futuro del vehículo eléctrico
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Al hablar del vehículo eléctrico surgen siempre las siguientes preguntas. ¿Puede el vehículo eléctrico satisfacer las necesidades de la sociedad en un corto periodo de tiempo? ¿Cuáles son los retos a los que se enfrenta?
La necesidad de eliminar las emisiones de efecto invernadero, el alcance del trucaje de los motores diésel, el incremento del precio de los carburantes, las exigencias de las normativas anticontaminación cada vez más restrictivas y los avances tecnológicos han fortalecido el mercado del vehículo eléctrico en los últimos años. Las empresas del automóvil se están replanteando el futuro del diésel. Por el contrario, el número de vehículos eléctricos estimado en siete millones para el año 2020 aumentará significativamente en los años siguientes.
El transporte eléctrico se puede considerar como una de las revoluciones tecnológicas más importantes después de internet y del teléfono móvil. En los vehículos eléctricos que utilizan baterías para el almacenamiento de energía, los tres principales retos son: i) reducción de costes, ii) eliminar la dependencia de materiales críticos como el cobalto y iii) desarrollo de baterías seguras con tiempos de carga inferiores a 15 minutos.
En las baterías la energía eléctrica es almacenada mediante la conversión de energía química a través de reacciones redox entre los electrodos, ánodo y cátodo, (ver Figura 1). Las baterías más utilizadas son las de ion litio ya que presentan mayor densidad energética y ofrecen actualmente las mejores prestaciones.
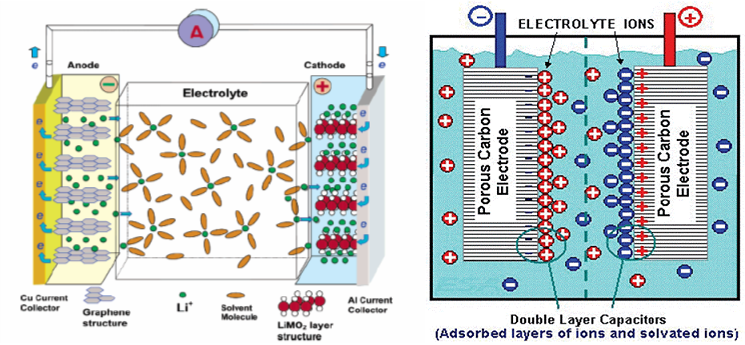 Figura 1. Bateria (izquierda) y supercondensador de doble capa (derecha). Fuente: US Department of Energy
Figura 1. Bateria (izquierda) y supercondensador de doble capa (derecha). Fuente: US Department of Energy
Sin embargo, la demanda de este metal se está incrementando significativamente y en 2025 será 11 veces mayor que la actual hasta alcanzar las 300.000 toneladas (un 33% del consumo total en la industria). Esto ha dado lugar a un aumento importante de los precios que en algunos mercados se han incrementado más de un 200 % en pocos meses. Los países productores son fundamentalmente Chile y Argentina y recientemente se han encontrado reservas en Bolivia y Afganistán países que, junto con el riesgo de suministro, pueden alterar significativamente el precio del litio en los mercados. Asimismo, otro de los componentes de estas baterías es el cobalto que representa hasta el 20 % del peso del cátodo. Este metal es toxico, escaso y caro siendo la Republica Democrática del Congo el único país productor lo cual condiciona significativamente su uso. Por tanto, es importante desarrollar una política o estrategia estándar en materia de reciclaje de baterías para disminuir el coste de los vehículos. Actualmente se está desarrollando una intensa actividad en la búsqueda de otro tipo de baterías alternativas a las de litio ion con mejores prestaciones y costes más reducidos.
Respecto a la seguridad de las baterías es importante recordar que los electrolitos son materiales orgánicos inflamables que pueden dar lugar a incendios de las propias baterías. En este sentido, las compañías automovilísticas están invirtiendo cantidades importantes para la búsqueda de baterías con todos sus componentes sólidos.
Hoy día hay una gran actividad en las compañías automovilísticas para desarrollar en sus factorías el coche eléctrico. Tesla ha puesto en el mercado varios modelos con diferentes precios. El modelo ultralujo S con un coste de 95.000 dólares con autonomía de más de 500 km y el nuevo Modelo 3 por 37.500 dólares (Figura 2). La empresa Volvo sacará al mercado a partir de 2019 todos sus vehículos (cinco modelos entre 2019-2021) con motor eléctrico. La empresa Volkswagen ha desarrollado el e-Golf 100 % eléctrico con una autonomía de 300 km con un tiempo de carga combinada de 30 minutos a un precio de 36.850 €. Nissan ha puesto en el mercado el Nissan Leaf 3.Zero con 270 km de autonomía siendo el coche más vendido en Europa en 2018 con un precio desde 32.000 €. Opel/Vauxhall del Grupo PSA tendrá una versión 100 % eléctrica adaptando en breve su línea de producción en Figueruelas (Zaragoza). Finalmente, comentar que la UE financiará un proyecto estratégico (Battery 2030) con 1 billón de euros en los próximos 10 años para garantizar la competitividad de Europa en la tecnología de baterías frente a los países asiáticos que gozan actualmente del predominio en esta tecnología.
 Figura 2. Coches eléctricos de Tesla enchufados a postes de carga. Fuente: Tesla
Figura 2. Coches eléctricos de Tesla enchufados a postes de carga. Fuente: Tesla
La escasez de puntos de carga (electrolineras) es hoy día uno de los principales desafíos a los que se enfrenta el vehículo eléctrico. La electrificación es urgente y necesaria. No obstante, para paliar en parte este tema los fabricantes de vehículos están creando su particular red de distribución nacional instalando en sus concesionarios postes de suministro rápido.
Cuando nos referimos al vehículo eléctrico no solo hablamos del coche eléctrico sino también vehículos de mayor tamaño tales como autobuses, camiones, tranvías, etc. En este sentido, estos vehículos utilizan en algunos casos supercondensadores como sistemas de almacenamiento de energía eléctrica la cual es almacenada físicamente en la interfase electrodo electrolito con altas densidades de potencia, con rápida autodescarga y largos ciclos de vida (ver Figura 1). En un símil deportista se podrían considerar a las baterías como corredores de maratón (energía) y a los supercondensadores como esprínteres o corredores de cien metros lisos (potencia). En la ciudad de Shanghái (China) toda la flota de autobuses utiliza supercondensadores como sistema de almacenamiento energético. La rápida respuesta de carga y descarga del orden de 20 ó 30 segundos es suficiente para permitir su recarga en las paradas mientras acceden los viajeros al vehículo. La empresa CAF utiliza sistemas basados en combinación hibrida de supercondesadores y baterías de ion litio en sus tranvías que permiten la circulación sin catenaria en diversas ciudades como las de Sevilla y Zaragoza. Almacenan la energía cinética liberada en la frenada para ser utilizada posteriormente mejorando así la eficiencia energética del vehículo (Figura 3).
 Figura 3. Tranvías de CAF. Fuente: CAF
Figura 3. Tranvías de CAF. Fuente: CAF
La empresa Mazda ha desarrollado el i-ELOOP (Intelligent Energy Loop) que recupera la energía cinética en el momento que el conductor levanta el pedal del acelerador y el vehículo comienza a desacelerar mejorando la economía de combustible en aproximadamente un 10 % en condiciones de conducción reales. La versión Euro VI del modelo Citaro de Mercedes Benz permite ahorrar entre un 3 y un 5 % de combustible, aproximadamente 1.000 litros por año o 2,6 toneladas de CO2 año en condiciones normales de uso.
Para el futuro del vehículo eléctrico la mejor opción puede ser la combinación de baterías y supercondensadores diseñados para altas densidades de energía, larga duración de los sistemas y bajo coste. Además, pueden permitir el uso de baterías de alta densidad energética con insuficiente potencia para ser utilizadas estas individualmente.
Otro tipo de vehículos eléctricos funcionan con pilas de combustible que son dispositivos de conversión directa de energía, capaz de transformar en energía eléctrica la energía química de un combustible que debe ser suministrado constantemente (ver figura 4). Se podría decir que en vez de recargar a través del enchufe como en el caso de las baterías lo hace mediante la reacción de hidrógeno comprimido, que se recarga a través de una manguera y se aloja en un tanque de almacenamiento, con oxígeno. Su principal ventaja es que esta recarga se lleva a cabo en un par de minutos permitiendo autonomías de 600-700 km y un recorrido de más de 250.000 km. Es, pues, un coche que se puede usar tanto en trayectos diarios como de larga distancia.
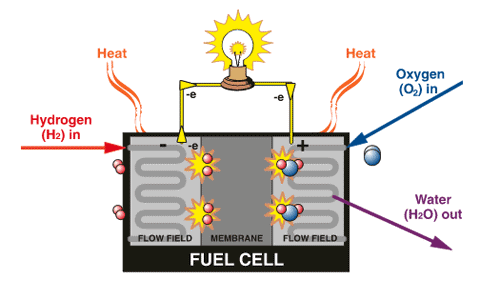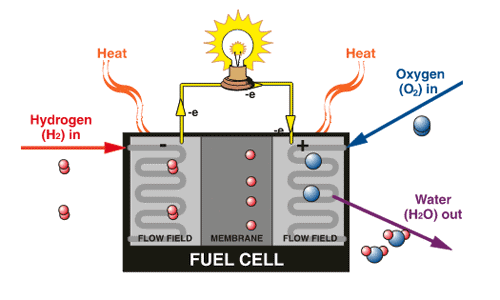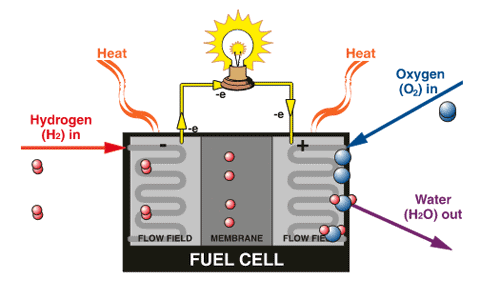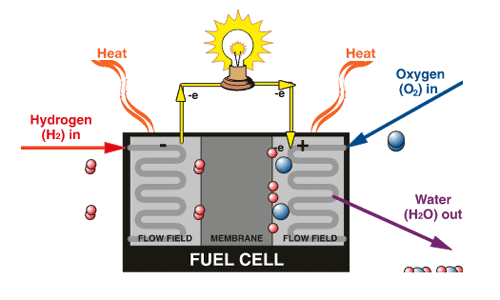 Figura 4. Pila de combustible. Fuente: ISMN-UCM
Figura 4. Pila de combustible. Fuente: ISMN-UCM
Existen distintos tipos de pilas de combustible, pero las generalmente utilizadas en el vehículo eléctrico son conocidas como pilas de combustible de membrana polimérica (PEM-FC) que utilizan como combustible hidrógeno. Estos dispositivos tienen densidades de energía cinco veces superior a las baterías de ion litio. Los principales inconvenientes de estos sistemas para su implantación en el mercado son el coste de los materiales, fundamentalmente los catalizadores, y la infraestructura integral de hidrógeno (producción, almacenamiento y transporte) así como la falta de hidrogeneras que podría suponer una inversión inicial de más de tres mil millones de euros, muy superior al coste de la infraestructura de carga para baterías. Ambas tecnologías no tienen por qué ser competidoras sino más bien complementarias. Las baterías son más adecuadas para rangos más cortos y vehículos más pequeños. Por el contrario, las pilas de combustible probablemente ofrecerán mejores prestaciones para vehículos grandes y de largo alcance.
Existen tres compañías de automóviles Hyundai, Toyota y Honda que ya disponen de vehículos de pilas de combustible fabricados en serie. Hyundai ha sido la primera compañía en matricular un coche en España de pilas de combustible (Figura 5a) con cero emisiones que funciona con hidrógeno y cuenta con una autonomía de 666 kilómetros siendo su tiempo de carga de solo cinco minutos. Esta compañía ha anunciado su plan ‘FCEV Vision 2030‘ que se desarrollará a largo plazo, reafirmando así su compromiso por acelerar el desarrollo de la sociedad del hidrógeno.
 Figura 5. De izquierda a derecha: Nexo (Hyundai), Toyota Mirai y Honda Clarity Fuel Cell. Fuentes: Hyundai, Toyota y Honda.
Figura 5. De izquierda a derecha: Nexo (Hyundai), Toyota Mirai y Honda Clarity Fuel Cell. Fuentes: Hyundai, Toyota y Honda.
Toyota ha sacado al mercado el modelo Mirai (que significa futuro en japonés) y consta de un motor eléctrico, dos depósitos de hidrogeno, una pila de combustible y una batería de níquel metal hidruro que tiene como misión almacenar los excedentes de energía producidos por la pila de combustible o por la energía generada en la frenada. Este vehículo tiene una autonomía homologada de 483 km y con un tiempo de recarga entre 3 y 5 minutos. Aún no se comercializa en España y tiene un precio superior a 70.000 €. La compañía Honda ha sacado el Honda Clarity Fuel Cell que es el primer coche de pila de combustible con cinco plazas y funciona con hidrogeno, se recarga en dos minutos y tiene una autonomía de 650 km. En el mercado japonés tiene un precio en torno a 57.000€ y no se comercializa aún en Europa. General Motors (GM) ha presentado el modelo Cadillac Provoq que combina la quinta generación de pila de combustible con autonomía de 483 km y con una batería de litio ion que puede almacenar hasta 9 kilovatios por hora de electricidad y proporcionar un pico máximo de 60 kilovatios. General Motors y Honda han acordado formar la primera empresa conjunta de fabricación de la industria del automóvil (Fuel Cell System Manufacturing) para producir en masa un sistema avanzado de pila de combustible de hidrógeno que se utilizará en los futuros automóviles de cada compañía.
Respecto a camiones con pilas de combustible se pueden mencionar el Class 8 de Toyota con 500 km de autonomía, el Maxity Electrique de Renault con una autonomía de 200 km y el nuevo camión eléctrico de Hyundai del que se desconoce actualmente el nombre y las especificaciones técnicas. Scania pondrá en funcionamiento su primer camión de basura de pila de combustible a finales de 2019, principios de 2020 para el tratamiento de residuos en las grandes ciudades.
La pregunta más inmediata que surge es ¿Será capaz de introducirse en el mercado el vehículo eléctrico de pilas de combustible en competición con el de baterías y/o supercondensadores?
Uno de los principales problemas para el desarrollo comercial de los vehículos de pilas de combustible es la falta de una red solida de estaciones de hidrogeno (Hidrogeneras). En Europa esta infraestructura es muy modesta y junto con su complejidad y elevado coste el progreso de incorporación de este tipo de vehículos en los próximos años será lento. No obstante, la Asociación del Hidrogeno de España considera que a pesar de que actualmente hay únicamente seis estaciones de servicio, que obtienen su combustible a través de electrolisis, en doce años habrá circulando más de 140.000 vehículos en este país.
Sobre el autor: Teófilo Rojo es catedrático en el Departamento de Química Inorgánica de la Facultad de Ciencia y Tecnología de la UPV/EHU.
El artículo El futuro del vehículo eléctrico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La parábola del coche eléctrico
- La diferencia de potencial eléctrico
- La ambulancia como vehículo de infecciones
Cómo descubrimos tres libros venenosos en la biblioteca de nuestra universidad
![]()
Jakob Povl Holck y Kaare Lund Rasmussen
 Raman Saurei / Shutterstock
Raman Saurei / ShutterstockAlgunas personas recordarán el libro mortífero de Aristóteles que constituye un elemento fundamental en la trama de El nombre de la rosa, la novela de Umberto Eco publicada en 1980. El ejemplar, envenenado por un monje benedictino loco, causa estragos en un monasterio italiano del siglo XIV, pues mata a todos aquellos que, al leerlo, se lamen la yema del dedo para pasar las páginas envenenadas. ¿Podría ocurrir algo así en la vida real? ¿Envenenamiento por un libro?
Los estudios que hemos llevado a cabo recientemente indican que es posible. Gracias a ellos, descubrimos en la colección de la biblioteca de la Universidad del Sur de Dinamarca tres libros raros sobre diversos temas históricos que contienen altas concentraciones de arsénico en la cubierta. Los libros datan de los siglos XVI y XVII.
Las propiedades tóxicas de estos volúmenes se detectaron al realizar varios análisis de fluorescencia de rayos X (micro-XRF). Esta tecnología permite conocer el espectro químico de un material mediante un análisis de la radiación “secundaria” característica que emite el material al ser sometido a un bombardeo de rayos X de alta energía. El uso de la tecnología micro-XRF está muy extendido en los ámbitos de la arqueología y el arte, por ejemplo, para investigar los elementos químicos de la cerámica y la pintura.
 Uno de los libros venenosos.
Uno de los libros venenosos.Imagen: SDU
Verde brillante
La razón por la que nos llevamos los tres libros raros al laboratorio de rayos X fue porque, previamente, la biblioteca había descubierto que para las tapas se habían usado fragmentos de manuscritos medievales, como, por ejemplo, copias de Derecho romano y Derecho canónico. Como sabemos por la abundante documentación disponible, los encuadernadores europeos de los siglos XVI y XVII reciclaban pergaminos más antiguos.
Así pues, intentamos averiguar cuáles eran los textos latinos utilizados, o al menos leer parte de su contenido. Sin embargo, nos encontramos con que resultaba difícil interpretar los textos latinos de las cubiertas de los tres volúmenes porque contenían una extensa capa de pintura verde que oscurecía las viejas letras manuscritas. De modo que los llevamos al laboratorio con la intención de observar a través de la capa de pintura con la tecnología micro XRF y centrarnos en los elementos químicos de la tinta que estaba debajo, por ejemplo, en el hierro y el calcio, esperando conseguir que las letras resultaran más legibles para los investigadores de la universidad.
Pero el análisis de fluorescencia de rayos X reveló que la capa de pigmento verde era arsénico. Este elemento químico es una de las sustancias más tóxicas del mundo, y la exposición puede causar diversos síntomas de envenenamiento, el desarrollo de cáncer e incluso la muerte.
 Accidentes provocados por el uso de arsénico verde, 1859.
Accidentes provocados por el uso de arsénico verde, 1859.© Wellcome Collection, CC BY-SA
El arsénico (As) es un metaloide que está presente en el entorno de forma natural. En la naturaleza, el arsénico normalmente se combina con otros elementos, como el carbono y el hidrógeno, y en este caso se conoce como arsénico orgánico. El arsénico inorgánico, que puede presentarse tanto en forma metálica pura como en compuestos, es una variante más nociva. Las propiedades tóxicas del arsénico no se debilitan con el tiempo.
En función del tipo y la duración de la exposición, pueden darse diversos síntomas de envenenamiento por arsénico, como irritación del estómago y el intestino, náuseas, diarrea, alteraciones de la piel e irritación de los pulmones.
 Verde París.
Verde París.Chris Goulet/Wikimedia Commons, CC BY-SA
Se cree que el pigmento verde portador de arsénico encontrado en las cubiertas de los libros puede ser verde de París, triarsenito acetato de cobre (II) o acetoarsenito de cobre (II) Cu(C₂H₃O₂)₂ ·3Cu(AsO₂)₂. También se conoce como “verde esmeralda”, por sus llamativos tonos verdes, parecidos a los de la popular piedra preciosa.
El pigmento de arsénico es un polvo cristalino fácil de elaborar y se ha utilizado profusamente con diversos fines, en especial en el siglo XIX. El tamaño de los granos de polvo influye en la tonalidad del color, como se aprecia en las pinturas al óleo y los barnices. Los granos de mayor tamaño producen un marcado color verde oscuro, mientras que los granos más pequeños generan un verde más claro. El pigmento se conoce especialmente por la intensidad de su color y por su resistencia a la decoloración.
Pigmento del pasado
La producción industrial del verde de París se inició en Europa a principios del siglo XIX. Los pintores impresionistas y posimpresionistas usaban diferentes versiones del pigmento para crear sus obras maestras de intensos colores, lo que implica que hoy en día muchas piezas de museo contienen veneno. En su apogeo, se pudo haber recubierto de verde de París toda clase de materiales, incluso tapas de libros y prendas de ropa, por razones estéticas. Lógicamente, el contacto continuo de la piel con esa sustancia conllevaba la aparición de síntomas de la exposición.
Sin embargo, hacia la segunda mitad del siglo XIX ya se conocían mejor los efectos tóxicos de la sustancia; la variante con arsénico dejó de usarse como pigmento y pasó a emplearse sobre todo como pesticida en tierras de cultivo. Se descubrieron otros pigmentos que sustituyeron el verde de París en la pintura, el sector textil y otros ámbitos, y a mediados del siglo XX también se descartó su uso en las tierras de cultivo.
 ‘The Arsenic Waltz’.
‘The Arsenic Waltz’.© Wellcome Collection, CC BY-SA
En el caso de nuestros libros, el pigmento no se usó con fines estéticos, sino que formaba una capa inferior de la cubierta. Una explicación posible de la aplicación –posiblemente en el siglo XIX– del verde de París en los libros antiguos es la intención de protegerlos contra insectos y parásitos.
En determinadas circunstancias, los compuestos de arsénico, como el arseniato y el arsenito, pueden transformarse en arsina (AsH₃) –un gas altamente tóxico con un característico olor a ajo– por acción de microorganismos. Se sabe que las terribles historias del papel pintado verde de la época victoriana que arrebataba la vida de los niños en sus dormitorios son reales.
Actualmente, la biblioteca conserva nuestros tres volúmenes venenosos en cajas de cartón separadas y con etiquetas de seguridad en un armario ventilado. También tenemos previsto digitalizarlos para reducir al mínimo la manipulación física. Uno nunca se imagina que un libro pueda contener una sustancia venenosa. Sin embargo, podría ocurrir.![]()
Sobre los autores: Jakob Povl Holck es bibliotecario investigador y Kaare Lund Rasmussen profesor titular de Física, Química y Farmacia en la Universidad del Sur de Dinamarca
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Cómo descubrimos tres libros venenosos en la biblioteca de nuestra universidad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¡Explora! Libros de divulgación científica para niños
- ¿Cómo llegó el darwinismo a España? 08. Los detractores – Gobierno y Universidad
- El problema de los tres caballeros y los tres criados

