Así es la química de una buena pizza

La pizza puede ser una comida rica y saludable. El secreto de ambas cosas está en una buena elección de ingredientes. La parte más complicada de encontrar son las bases de pizza precocinadas o masas extendidas elaboradas con 100% harina integral. Sin embargo, en poco más de media hora podemos hacer nosotros mismos una base para pizza excepcional. El secreto de una buena masa de pizza está en la química.
Necesitamos los siguientes ingredientes para 2-4 personas: 250 g de harina integral, 3 cucharadas soperas de aceite de oliva virgen extra, 25 g de levadura de pan, 125 ml de agua (medio vaso) y una cucharadita de sal.

-
¿Por qué es mejor usar harina integral?
Por sabor y por salud.
La harina puede ser refinada o integral. La diferencia entre una y otra es la parte del grano que se usa para su elaboración. En la harina refinada se utiliza sólo el endospermo del grano, mientras que la integral incluye el cereal completo.
Los cereales tienen tres partes: la cáscara del cereal es el salvado, donde está la mayor parte de la fibra; la parte central es el endospermo, compuesto mayoritariamente por almidón; y el núcleo es el germen, donde se concentra la fracción grasa del cereal. Por eso el sabor de las harinas integrales es más intenso y complejo que el de las refinadas.
Las harinas integrales contienen todas la vitaminas y nutrientes del cereal completo, siendo especialmente interesante para nuestra salud su alto contenido en fibra. La fibra favorece el tránsito intestinal y además hace que el pan sea más saciante. No es que el integral tenga menos calorías, de hecho tiene las mismas, pero al resultar más saciante necesitaremos comer menos cantidad.
La fibra hace que el pan integral tenga menor índice glucémico, es decir, hace que metabolicemos los carbohidratos lentamente y que no aumenten repentinamente los niveles de glucosa en sangre. Por el contrario, los panes blancos tienen alto índice glucémico, lo que significa que se metabolizan muy rápido dando elevados y repentinos picos de glucosa en sangre y, en consecuencia, picos de insulina. Este es el motivo por el que el pan blanco es poco saciante y por el que las personas con diabetes limitan su consumo.
Además de la tradicional harina de trigo, se puede obtener harina de distintos cereales ricos en almidón como la espelta, el centeno, la cebada, la avena, el maíz, e incluso de leguminosas como los garbanzos o las judías, o del arroz. La harina está formada básicamente por hidratos de carbono, y en menor proporción proteínas, dependiendo del tipo de harina. El hidrato de carbono de las harinas vegetales es el almidón.
Para elaborar pan y masas de pizza se suele utilizar la harina de trigo porque ésta contiene gluten, un conjunto de proteínas, esencialmente gliadina y glutenina, que le otorgan elasticidad y consistencia a la masa. Las harinas sin gluten como las de trigo sarraceno, maíz o garbanzo, son muy difíciles de manejar. Extenderlas en forma de base de pizza es una tarea muy compleja, precisamente porque no producen masas elásticas.
-
La química del amasado y del fermentado
Cuando hacemos la masa de una pizza tienen lugar varias reacciones químicas que serán las responsables de su textura, color y sabor.
Lo primero que hacemos es poner en un bol los 250 g de harina integral. A continuación desmenuzamos la levadura, añadimos la sal, el medio vaso de agua y las tres cucharadas de aceite de oliva virgen extra. Mezclamos inicialmente todos los ingredientes con ayuda de una cuchara, y a continuación amasamos a mano sobre una encimera durante 5-10 minutos. Después dejamos reposar la masa unos 30 minutos en el bol cubierto por un trapo.

Durante este proceso estarán ocurriendo una serie de reacciones químicas y bioquímicas que determinarán la textura y el sabor de la masa.
El protagonista del amasado es el gluten. La gliadina y la glutenina que componen el gluten se hidratan, captan el agua e interactúan entre sí dando lugar a la formación de un entramado reticular de gluten, que dota a la masa de elasticidad. El agua también hidrata el almidón, provoca la apertura de su estructura y la deja expuesta al ataque de las enzimas. Las enzimas también se activan al hidratarse, entre ellas las amilasas, que actúan rompiendo el almidón en hidratos de carbono simples.
La levadura (saccharomyces cerevisiae) la podemos comprar en el supermercado o en la panadería. La levadura se alimenta de los hidratos de carbono simples liberados y desprende dióxido de carbono y alcohol, responsables de la formación de burbujas. Para acelerar el proceso o crear más burbujas hay quien añade azúcar. La razón es que así la levadura tendrá más alimento con el que generar burbujas de dióxido de carbono. Aunque la textura puede mejorar en tiempo récord, nutricionalmente no es aconsejable añadir azúcar.
En el caso de no tener levadura, podemos hacer la masa con una cerveza, ya que la levadura de la cerveza es la misma que la del pan.
Hay que tener en cuenta que la sal inhibe el crecimiento de la levadura, así que añadir sal hace que el fermentado sea más lento, sin embargo, la fermentación lenta repercute positivamente en la textura final de la masa.
En el mercado tenemos otro tipo de productos que llamamos levaduras químicas que, aunque no son levaduras propiamente dichas, producen un efecto parecido sobre la masa. Se usan más en repostería para no tener que dejar fermentar la masa y poder hornearla inmediatamente. Estas levaduras químicas están compuestas esencialmente por bicarbonato sódico que en contacto con la masa y durante el horneado desprenden dióxido de carbono, responsable de las burbujas.
El aceite protege la masa de la pérdida progresiva de agua, lo que evita que se endurezca demasiado durante el horneado y una vez se enfríe.
Todas estas reacciones se producen durante el amasado y el reposo. Una vez transcurrido el tiempo de reposo, la masa habrá duplicado su volumen.

-
La química del horneado.
Una vez tenemos la masa fermentada, el siguiente paso será extenderla. Si la harina tiene gluten, este proceso será bastante sencillo porque la masa será muy elástica. Podemos extenderla con las manos o con ayuda de un rodillo.
Extendemos la masa sobre una bandeja de horno cubierta con papel de horno. Este papel es un papel vegetal sulfurizado. Se ha tratado químicamente con un baño de ácido sulfúrico -de ahí el nombre- para tapar los poros de la celulosa y hacerlo impermeable y antiadherente. Este proceso también lo hace resistente a las temperaturas que manejamos en los hornos domésticos.
Sobre la masa podemos añadir los ingredientes que nos apetezcan. En este caso he utilizado tomate triturado, orégano, queso mozzarella rallado, champiñones frescos, aceitunas negras, jamón cocido extra y pimientos rojos asados.

Metemos la pizza en el horno y la dejamos a 240oC con calor arriba y abajo entre 20 y 25 minutos.
La levadura de la masa muere como consecuencia de las altas temperaturas, y el alcohol se evapora. El almidón de la harina comienza a gelatinizar, es decir, a formar una estructura diferente a la original en la que es capaz de atrapar el agua de la masa. En este proceso también interviene el gluten, que se pega al almidón creando una red que evita que las burbujas se escapen de la masa. A medida que la temperatura aumenta y la pizza continúa en el horno, empieza a dorarse. Este cambio paulatino de color es debido a la reacción química más famosa de la cocina: la reacción de Maillard entre los hidratos de carbono y las proteínas.

Todas las formas de conocimiento guardan relación entre sí, en mayor o menor medida. Preparar una pizza tiene su fundamento químico detrás. Desde el punto de vista de la salud y desde el punto de vista gastronómico. Conocerlo nos permite disfrutar más de todo el proceso. Esto es así porque el conocimiento es una forma de placer.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Así es la química de una buena pizza se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Los números enamorados
El artista futurista italiano Giacomo Balla (1871-1958) pintó una obra titulada Los números enamorados en 1924, asociando una cualidad humana, como es el enamoramiento, a los números. También en el ámbito de las matemáticas nos gusta asociar a los números, en particular, a los números naturales, cualidades humanas. Existen números amigos, sociables, novios, narcisistas, felices, tristes, hambrientos, intocables, ambiciosos, afortunados, poderosos, malvados, odiosos, prácticos o raros, pero también, con otras denominaciones curiosas, como números vampiros, parásitos, perniciosos, apocalípticos, perfectos, poligonales, cíclicos, automorfos, sublimes, abundantes, escasos o intocables.
 Números enamorados (1924), del artista futurista italiano Giacomo Balla, MART, Museo d’arte moderna e contemponanea di Trento e Rovereto, Italia. Fotografía de MART
Números enamorados (1924), del artista futurista italiano Giacomo Balla, MART, Museo d’arte moderna e contemponanea di Trento e Rovereto, Italia. Fotografía de MARTAlgunas de estas familias de números deben su propiedad definitoria al comportamiento de sus divisores propios, es decir, entre los divisores no se considera al propio número. Son a estas familias de números naturales a las que vamos a dedicar la entrada de hoy de la sección Matemoción del Cuaderno de Cultura Científica.
Empecemos con unas familias de números con un origen muy antiguo. Un número se dice que es perfecto si es igual a la suma de sus divisores (propios), como ocurre con los números 6 = 1 + 2 + 3 y 28 = 1 + 2 + 4 + 7 + 14. Se los denominó perfectos porque en tiempos antiguos se dio a esta propiedad una interpretación divina. Por ejemplo, San Agustín relaciona el hecho de que Dios crease el mundo en 6 días, con la perfección de este número.
Los siguientes números perfectos, después de 6 y 28, conocidos ya desde la antigüedad, son
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 248
8.128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1.016 + 2.032 + 4.084
Se desconoce el origen exacto de los números perfectos, aunque ya eran conocidos por los matemáticos griegos. Euclides de Alejandría (aprox. 325 – 265 a.n.e.) los estudia en su obra Los Elementos, aunque antes los había estudiado Pitágoras (aprox. 570 – 495 a.n.e.), e incluso podrían haber sido conocidos por los egipcios.
Euclides demostró que para algunos números primos p, los números de la forma 2p–1 (2p – 1) son perfectos, por ejemplo, para p = 2, 3, 5, y 7, se obtienen los perfectos anteriores. Dos milenios después, el matemático suizo Leonhard Euler (1707 – 1783) demostraría que todos los números perfectos pares son de esta forma, con (2p – 1) un número primo.
El quinto número primo encontrado fue 33.550.336, para p = 13, que aparece en un manuscrito del siglo XV. El sexto y séptimo –para p = 17 y 19– fueron descubiertos por el matemático italiano Pietro Cataldi (1548 – 1626) en 1588, en concreto, 8.589.869.056 y 137.438.691.328. Y Euler, en 1772, descubrió el octavo, que es 230 (231 – 1) = 2.305.843.008.139.952.128.
Obtener números perfectos es una tarea muy difícil, luego podemos decir que “la perfección es difícil de conseguir”. Antes del siglo XX solo se conocían 9 números perfectos. El noveno fue obtenido, para p = 61, por el matemático ruso Iván Pervushin (1827 – 1900), en 1883. De hecho, en la fórmula de Euclides-Euler no basta con que p sea primo, ya que para p = 11, 211 – 1 = 2.047 = 23 x 89, no es primo, con lo cual 210 (211 – 1) no es perfecto.
Con la ayuda de los ordenadores ha sido posible calcular muchos más, pero no demasiados. Solo se conocen, hasta la fecha, 51 números perfectos. El último descubierto, en 2018, fue el correspondiente al primo p = 82.589.933.
Se desconoce si existe un número infinito o finito de números perfectos. Además, todos los números perfectos conocidos son pares, y no se sabe si existen impares. Lo que se ha conseguido demostrar es que de existir tendrían que cumplir una serie de propiedades, como tener al menos 9 divisores primos distintos o ser mayores que 101.500, entre muchas otras.
 Veintiocho (modelo para una escultura pública), 1992, del artista estadounidense Jonathan Borofsky. Imagen de su página web
Veintiocho (modelo para una escultura pública), 1992, del artista estadounidense Jonathan Borofsky. Imagen de su página webYa los griegos dividieron a los números naturales que no son perfectos en dos categorías, los abundantes y los deficientes. Los números que no son perfectos pueden ser abundantes, cuando el número es menor que la suma se los divisores, como el 12 deficientes en el caso contrario, como el 14 > 1 + 2 + 7 = 10 o todos los números primos, cuyo único divisor propio es el 1. Estos conceptos, como la perfección, formaron parte de la numerología griega.
El religioso, teólogo y matemático anglosajón Alcuino de York (735 – 804) relacionaba la “segunda creación” de Dios, el diluvio universal y el Arca de Noé, con el número 8, ya que la humanidad desciende de las 8 almas que se salvaron del diluvio refugiándose en el Arca de Noé. Por lo tanto, esta es una creación imperfecta, puesto que el número 8 es deficiente, 8 > 1 + 2 + 4.
Los números llamados abundantes no son, sin embargo, tan abundantes como su nombre indica. Existen 245 números abundantes menores que 1.000, aunque solo uno de ellos impar, el número 945 = 33 x 5 x 7, los demás son pares, y solo 3 números perfectos (por supuesto, pares), el resto son deficientes. Entre los primeros 50.000 números hay 37.602 deficientes, 4 perfectos y 12.394 abundantes. Entre estos 12.394 números abundantes, solo 114 son impares.
Así como lo bello y lo excelente es raro de encontrar y se cuenta pronto, pero lo feo y lo malo siempre es prolífico, así también los números abundantes y deficientes resultan ser muchos y en desorden, y su descubrimiento no obedece a sistema alguno. Pero los perfectos, son a un tiempo escasos en número y se hallan dispuestos en un orden apropiado.
Nicómaco de Gerasa (aprox. 60 – 120 n.e.), Introducción a la Aritmética
Imagen 3 (Pie de imagen: You know my name (look up the number), acrílico sobre papel, 63 x 90 cm, del artista suizo Eugen Jost. Entre las sucesiones de números que aparecen, están los primeros números perfectos. Imagen de Plus Magazine [https://plus.maths.org/content/postcard-italy])
Entre los números abundantes, es decir, aquellos que son menores que la suma de sus divisores, se considera que son números casi perfectos aquellos tales que la suma de sus divisores es uno menos que el número. Así, el 16 es un número casi perfecto ya que 1 + 2 + 4 + 8 = 15. De hecho, todas las potencias de 2 son casi perfectas:

Los únicos números casi perfectos que se conocen son las potencias de 2, y es un problema abierto demostrar que estos son los únicos que existen.
Otra familia de números relacionada con la perfección, son los números múltiplo-perfectos o multi-perfectos, aquellos tal que la suma de sus divisores (recordemos que todo el tiempo estamos refiriéndonos a los divisores propios) no es el número, sino un múltiplo del mismo. Por ejemplo, los divisores del número 120 = 23 x 3 x 5 son 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40 y 60, cuya suma es 240 = 2 x 120. Solo se conocen 6 números multi-perfectos cuya suma sea el doble del número, 120, 672, 523.776, 459.818.240, 1.476.304.896, 51.001.180.160, y todos son pares. O, se conocen 36 cuya suma es el triple, de nuevo todos pares, de los cuales el más pequeño es 30.240.
 Hardy’s Taxi, acrílico sobre lienzo, 60 x 60 cm, del artista suizo Eugen Jost. Obra perteneciente a la exposición Everything is number
Hardy’s Taxi, acrílico sobre lienzo, 60 x 60 cm, del artista suizo Eugen Jost. Obra perteneciente a la exposición Everything is numberMás aún, un número se dice que es ambicioso si puede llegar a ser perfecto de la siguiente forma. Dado el número se toma la suma de sus divisores, con este nuevo número se vuelve a considerar la suma de sus divisores, y se continúa así, de forma que el número es ambicioso si llega un momento que se alcanza un número perfecto, como en el caso del número 95, cuyos divisores suman 1 + 5 + 19 = 25, y los divisores de este suman 1 + 5 = 6, que es perfecto. Números no ambiciosos son el 24 o los números primos (cuyo único divisor es el 1).
Veamos que el 24 = 23 x 3 no es ambicioso. Sus divisores son 1, 2, 3, 4, 6, 8 y 12, cuya suma es 1 + 2 + 3 + 4 + 6 + 8 + 12 = 36. Ahora, los divisores de 36 = 22 x 32 son 1, 2, 3, 4, 6, 9, 12 y 18, cuya suma es 55. Ahora este número, 55 = 5 x 11, tiene solo tres divisores 1, 5 y 11, cuya suma es 17, que es primo, luego su único divisor es 1 y se estaciona la sucesión. En consecuencia, el 24 no es ambicioso. Solo se conocen 16 números ambiciosos, 25, 95, 119, 143, 417, 445, 565, 608, 650, 652, 675, 685, 783, 790, 909, 913, e incluso un número tan bajo como 276 se desconoce si es, o no, ambicioso (aunque seguramente no).
Y también relacionados con la perfección están los números sublimes, aquellos tales que tanto el número de sus divisores (incluido ahora el propio número), como la suma de los mismos son perfectos, como el 12, que tiene 6 divisores y su suma es 1 + 2 + 3 + 4 + 6 + 12 = 28, aunque solo se conoce otro número sublime más, que es el siguiente
6.086.555.670.238.378.989.670.371.734.243.169.622.657.830.773.351.885.970.528.324.860.512.791.691.264.
 Números amigos (2010), del artista británico Andrew Crane
Números amigos (2010), del artista británico Andrew CraneA continuación, vamos a introducir parejas de números con una fuerte conexión entre ellos, desde la perspectiva que estamos analizando en esta entrada. Empecemos por el número 284, que se puede escribir como la multiplicación de los números primos 71 y 2 de la siguiente forma 284 = 71 x 22. Por lo tanto, los divisores propios del 284 son 1, 2, 4, 71 y 142, cuya suma es
1 + 2 + 4 + 71 + 142 = 220.
Si ahora consideramos el número que nos ha salido, 220, y buscamos sus divisores, como 220 = 11 x 5 x 22, entonces estos son 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110, y la suma de ellos es
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284,
precisamente el primer número. Por este motivo, se dice que los números 220 y 284 son números amigos. Es decir, dos números son amigos si la suma de los divisores (propios) del primero es igual al segundo, y viceversa.
Este par de números amigos (220, 284) ya era conocido por los pitagóricos, quienes les atribuían propiedades místicas. En general, en la antigüedad se pensaba que estos números tenían poderes místicos, y eran utilizados en textos religiosos y de magia, en particular, en relación al amor y la amistad. Los astrónomos griegos los incorporaron en sus horóscopos, talismanes y amuletos.
“Las personas expertas en los talismanes afirman que los números amigos 220 y 284 ejercen una fuerte influencia para establecer una unión o una amistad muy fuerte entre dos personas”
Ibn Jaldún (1332-1406), Muqaddima (prolegómenos), 1377
Cuenta una leyenda que había un sultán aficionado a los puzzles, que al descubrir que tenía a un matemático como prisionero, decidió plantearle la siguiente cuestión. El sultán le dijo al matemático que le planteara un reto, un problema, y que estaría libre durante el tiempo que él necesitara para resolverlo, pero una vez resuelto por el sultán, el matemático sería ejecutado.
El matemático le explicó que los números 220 y 284 son números amigos, y le planteó que buscara otro par de números amigos. El sultán no lo consiguió y el matemático murió de viejo y siendo un hombre libre.
De hecho, calcular más pares de números amigos no es una tarea sencilla. Muchos matemáticos árabes estudiaron los números amigos, entre los siglos IX y XIV, como el iraquí Thabit ibn Qurra (826 – 901) quien dio una fórmula para obtener números amigos. En particular, se obtuvieron dos nuevos pares de números amigos
(17.296, 18.416) y (9.363.584, 9.437.056).
En el siglo XVII los grandes matemáticos franceses Pierre de Fermat (1601 – 1665) y René Descartes (1596 – 1650) redescubrieron la fórmula del matemático árabe, así como los dos anteriores pares de números amigos, que es ocasiones son atribuidos a ellos. Otro gran matemático ya mencionado, Leonhard Euler, extendió la fórmula de Qurra y obtuvo 64 nuevos pares de números amigos.
Curiosamente, a todos ellos se les pasó el siguiente par de números amigos más pequeño, después de (220, 284), el par (1.184, 1.210), descubierto por el adolescente Nicolo Paganini, de 16 años, en 1866.
La tarea siguió siendo compleja y hasta 1946 solo se consiguieron descubrir 390 pares de números amigos, hasta que llegó la era de los ordenadores, y su potencia de cálculo, que, junto a nuevos algoritmos, ha permitido calcular (según la wikipedia) hasta marzo de 2019 exactamente 1.223.386.359 parejas de números amigos. Sin embargo, a día de hoy no se sabe aún si existen infinitos pares de números amigos.
 Anillos hexagonales, con oro amarillo y oro rosa, con la pareja de números amigos 220 y 284, de la tienda londinense Comford Station, y la caja con la explicación de la pareja de números amigos
Anillos hexagonales, con oro amarillo y oro rosa, con la pareja de números amigos 220 y 284, de la tienda londinense Comford Station, y la caja con la explicación de la pareja de números amigosOtro nexo de unión entre números. Se dice que dos números son novios o casi-amigos si cada uno de ellos es igual a la suma de sus divisores menos 1, como el 48 = 1 + 3 + 5 + 15 + 25 – 1 y el 75 = 1 + 2 + 3 + 4 + 6 + 8 + 12 + 16 + 24 – 1. Las primeras parejas de números novios son (48, 75), (140, 195), (1.050, 1.925), (1.575, 1.648), (2.024, 2.295) y (5.775, 6.128). Los números de todas las parejas de novios conocidas tienen paridad opuesta, es decir, uno es par y el otro impar.
La propiedad de amistad puede generalizarse a un grupo de números, de forma que la suma de los divisores de cada uno es igual al siguiente, y la del último igual al primero, entonces se habla de números sociables. El grupo de números más pequeños que son sociables son 12.496, 14.288, 15.472, 14.536 y 14.264. Comprobémoslo:
1) 12.496 = 24 x 11 x 71, divisores: 1, 2, 4, 8, 11, 16, 22, 44, 71, 88, 142, 176, 284, 568, 781, 1.136, 1.562, 3.124 y 6.248, cuya suma es 14.288;
2) 14.288 = 24 x 19 x 47, divisores: 1, 2, 4, 8, 16, 19, 38, 47, 76, 94, 152, 188, 304, 376, 752, 893, 1.786, 3.572 y 7.144, cuya suma es 15.472;
3) 15.472 = 24 x 967, divisores: 1, 2, 4, 8, 16, 967, 1.934, 3.868 y 7.736, cuya suma es 14.536;
4) 14.536 = 23 x 23 x 79, divisores: 1, 2, 4, 8, 23, 46, 79, 92, 158, 184, 316, 632, 1.817, 3.634 y 7268, cuya suma es 14.264;
5) 14.264 = 23 x 1.783, divisores: 1, 2, 4, 8, 1.783, 3.566 y 7.132, cuya suma es 12.496.
Se conocen 5.410 grupos de números sociables (véase la lista de números sociables de David Moews), la mayoría formados por 4 números, aunque existe un grupo formado por 28 números.

También existen intocables dentro de la familia de los números naturales, son aquellos que no se pueden expresar como suma de los divisores de ningún número. El número 2 es intocable, el 3 no lo es (3 = 1 + 2, divisores del 4), el 4 tampoco (4 = 1 + 3, divisores del 9) y el 5 sí, ya que solo puede expresarse como 1 + 4, pero si el 4 es divisor del número, también lo es el 2 y la suma sería al menos 7. El siguiente intocable es el 52.
Los números intocables menores de 500 son:
2, 5, 52, 88, 96, 120, 124, 146, 162, 188, 206, 210, 216, 238, 246, 248, 262, 268, 276, 288, 290, 292, 304, 306, 322, 324, 326, 336, 342, 372, 406, 408, 426, 430, 448, 472, 474, 498.
El matemático húngaro Paul Erdös (1913-1996) demostró que existen infinitos números intocables.
“Dice Trece [la protagonista se refiere con números a los hombres que han pasado por su vida] que le ha hecho esos dos regalos –el libro [de Murakami] y lo del segundo cajón [un consolador]– para que se acuerde de él. Sin embargo, por la esencia oriental de uno y las dimensiones del otro, lo que Trece ha conseguido es que Pi, en lugar de acordarse de él, se acuerde de Dos. Por ambas razones.
Dos se ha convertido en una medida (de hecho, es un número intocable, pues no es la suma de los divisores de ningún número). No tiene tanta importancia como persona real en el presente […] sino como recuerdo y, sobre todo, como convención, como medida. Dos es la medida del sistema métrico sentimental”
Juan Pardo Vidal, La luz de la mesita de noche, Sloper, 2012
Por otra parte, un número se dice que es práctico si todos los números naturales más pequeños que él pueden ser expresados como suma de distintos divisores del número. Así, el número 12 es un número práctico ya que todos los números menores que él, desde el 1 al 11, pueden ser expresados como suma de algunos de los divisores de 12. Veámoslo: los divisores de 12 son 1, 2, 3, 4 y 6, luego 1 = 1, 2 = 2, 3 = 3, 4 = 4, 5 = 1 + 4, 6 = 2 + 4, 7 = 1 + 2 + 4, 8 = 2 + 6, 9 = 3 + 6, 10 = 4 + 6 y 11 = 1 + 4 + 6.
Los números prácticos menores que 100 son: 1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, 78, 80, 84, 88, 90 y 96.
El concepto fue definido en 1948 por el matemático indio A. K. Srinivasan, números que en su opinión eran interesantes de estudiar por su relación con las subdivisiones del dinero, los pesos y las medidas. Aunque estos números ya fueron utilizados por el matemático italiano Fibonacci (Leonardo de Pisa, 1170 – 1240), en su obra Liber Abaci (Libro del Ábaco, 1202), en relación a las fracciones egipcias (véase la entrada de Marta Macho, Sobre fracciones egipcias).
Claramente, todas las potencias de 2 son prácticas, ya que dado 2n, se puede expresar cualquier número entre 1 y 2n – 1 como suma de potencias de 2, menores que 2n, que son sus divisores. Es solamente una cuestión de divisibilidad y el fundamento del sistema binario. Se conocen muchas propiedades de los números prácticos, como que existen infinitos, el producto de dos números prácticos es un número práctico, los números perfectos pares, luego de la forma 2p–1 (2p – 1), son prácticos, o que, salvo el 1 y el 2, todos los números prácticos son divisibles por 4 o 6, entre otras.
 Instalación Forest of numbers – Bosque de números (2017), de la artista francesa Emmanuelle Moureaux. Imagen de su página web
Instalación Forest of numbers – Bosque de números (2017), de la artista francesa Emmanuelle Moureaux. Imagen de su página webY no podían faltar los números raros, o extraños, que son aquellos que son abundantes, es decir, la suma de los divisores es mayor que el número, pero no se puede obtener el número exacto quitando algunos de los divisores, es decir, como suma de un subconjunto de divisores propios. Por ejemplo, el 12 es abundante, pero como 12 = 2 + 4 + 6, no es raro, y el número raro más pequeño es 70 (cuyos divisores son 1, 2, 5, 7, 10, 14, 35).
Aunque se sabe que existen infinitos números raros, estos son relativamente escasos, por ejemplo, solamente hay 7 números raros menores que 10.000, que son 70, 836, 4.030, 5.830, 7.192, 7.912 y 9.272. Todos los números raros conocidos son pares y si existe alguno impar deberá ser, por lo menos, mayor que 1021.
Cerramos este repaso a algunas tribus numéricas con los números poderosos, que son aquellos tales que, si un número primo p es divisor suyo, también lo es su cuadrado p2, como el 36, cuyos divisores primos son 2 y 3, y sus cuadrados también son divisores de 36. Curiosamente, un número m es poderoso si, y sólo si, se puede expresar como m = a2b3, para algún par de números a y b. Claramente, si un número es de la forma a2b3 es poderoso (ya que los cuadrados de los primos de la descomposición en primos de a y b claramente dividen a a2b3), pero, además, todos los números poderosos son de esta forma. Veámoslo:

Por ejemplo, para el número m = 21.600 = 25 x 33 x 52, tendríamos que b = 2 x 3 = 6 y a = 2 x 5 = 10.
Existen algunos problemas interesantes sobre los números poderosos. Como se observa fácilmente, todo número impar es resta de dos cuadrados, luego de dos números poderosos, 2 k + 1 = (k + 1)2 – k2. Lo mismo ocurre con los múltiplos de 4, ya que 4 k + 4 = (k + 2)2 – k2.
Pero, ¿qué pasaba con los números pares no divisibles por 4, podían expresarse como resta de números poderosos? El matemático e ingeniero estadounidense Solomon W. Golomb (1932 – 2016), conocido por sus trabajos sobre juegos matemáticos, observó que algunos sí podían expresarse, como 2 = 33 – 52, 10 = 133 – 37 o 18 = 192 – 73 = 35 – 152, y conjeturó que el número 6 no podía expresarse como resta de números poderosos, así como infinitos otros números pares. El matemático polaco Władysław Narkiewicz demostró que el 6 no solo podía representarse de esta forma, 6 = 5473 – 4632, sino que existían infinitas formas de hacerlo. Más aún, en 1982, el matemático estadounidense Wayne L McDaniel extendió el resultado para todos los números pares, no divisibles por 4.
Por otra parte, Paul Erdös conjeturó, y fue demostrado por el matemático británico Roger Heath-Brown, que todo número natural suficientemente grande puede expresarse como suma de tres números poderosos.
 Instalación “SOHO” (2008), del artista japonés Tatsuo Miyajima. Imagen de su página web
Instalación “SOHO” (2008), del artista japonés Tatsuo Miyajima. Imagen de su página web Bibliografía
1.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.
2.- Clifford A. Pickover, La maravilla de los números. Un viaje por los secretos de las matemáticas, sus desafíos y caprichos, Ma Non Troppo (ediciones Robinbook), 2002.
3.- Lamberto García del Cid, Números notables. El 0, el 666 y otras bestias numéricas, El mundo es matemático, RBA, 2010.
4.- Howard H. Eves, Mathematical Circles, The Mathematical Association of America (MAA), 2003.
5.- Wikipedia: Perfect number
6.- David G. Kendall, The Scale of Perfection, Journal of Applied Probability, Vol. 19, Essays in Statistical Science, pp. 125-138, 1982.
7.- Eugen Jost, A postcard from Italy, Plus Magazine, 1999
8.- Wolfram Mathworld: Multiperfect number
9.- Wolfram Mathworld: Aspiring number
10.- Wikipedia: Amicable numbers
11.- Wikipedia: Betrothed or quasi amicable numbers
12.- Wikipedia: Untouchable number
13.- Wikipedia: Practical number
14.- Página web de la artista Emmanuelle Moureaux
15.- Wikipedia: Weird number
16.- Wikipedia: Powerful number
17.- Página web del artista japonés Tatsuo Miyajima
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los números enamorados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una conjetura sobre ciertos números en el ‘sistema Shadok’
- El origen poético de los números de Fibonacci
- Buscando lagunas de números no primos
Interferencia y difracción de la luz
 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsA principios del siglo XIX, cuando el prestigio de Newton era en gran medida el sostén de la hipótesis corpuscular de la luz, Thomas Young resucitó la hipótesis ondulatoria. En experimentos realizados entre 1802 y 1804 Young descubrió que la luz muestra el fenómeno de interferencia. La hipótesis corpuscular de la luz no puede explicar fácilmente los patrones de interferencia producidos por la luz. El famoso “experimento de doble rendija” de Young proporcionó la prueba convincente de que la luz tiene propiedades que solo se pueden explicar en términos de ondas.
El experimento de Young se puede realizar muy fácilmente. Consiste, básicamente, en dividir un solo haz de luz en dos haces para garantizar que estén en fase. Luego se permite que los haces resultantes de la división se superpongan, y los dos trenes de ondas interfieren, constructivamente en algunos lugares y destructivamente en otros. Para simplificar la interpretación del experimento, podemos suponer que se realiza con luz que tiene una única longitud de onda definida λ.
Young usó una pantalla negra con un pequeño agujero perforado para producir un haz de luz estrecho en una habitación a oscuras. En la trayectoria del haz colocó una segunda pantalla negra en la que había cortado dos rendijas estrechas, muy juntas. Tras esta pantalla colocó otra pantalla más, pero blanca. La luz que entraba por cada rendija se difractó y se extendió por el espacio más allá de la pantalla. La luz de cada rendija interfirió con la luz de la otra, y el patrón de interferencia se mostró en la pantalla blanca. Donde la interferencia era constructiva había una banda brillante en la pantalla. Donde la interferencia era destructiva, la pantalla permanecía oscura.
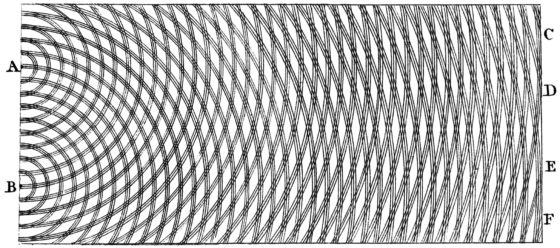 Reproducción del diagrama de Thomas Young (1807) para explicar el resultado del experimento de la doble rendija (situadas en A y B) que produce mínimos en C,D,E y F, tal y como aparece en T. Young (ed. G. Peacock), 1855, Miscellaneous Works of the late Thomas Young, London: J. Murray, vol. 1. Imagen: Wikimedia Commons
Reproducción del diagrama de Thomas Young (1807) para explicar el resultado del experimento de la doble rendija (situadas en A y B) que produce mínimos en C,D,E y F, tal y como aparece en T. Young (ed. G. Peacock), 1855, Miscellaneous Works of the late Thomas Young, London: J. Murray, vol. 1. Imagen: Wikimedia CommonsEs una medida del genio de Young el que pudiese encontrar, por experimento, valores numéricos para algo tan pequeño como la longitud de onda de la luz. Él lo expresó así:
From a comparison of various experiments, it appears that the breadth of the undulations constituting the extreme red light must be supposed to be, in air, about one 36 thousandth of an inch, and those of the extreme violet about one 60 thousandth.
A partir de una comparación de varios experimentos, parece que la amplitud de las ondulaciones que constituyen la luz roja extrema debe suponerse que sea, en el aire, aproximadamente una 36-milésima de pulgada. [7·10-7 m], y las del violeta extremo alrededor de una 60-milésima [4·10-7 m].
Al anunciar su resultado, Young hizo un especial esfuerzo por evitar las críticas de los seguidores de Newton, a quien se consideraba un partidario de la hipótesis corpuscular de la luz. Señaló que el propio Newton había hecho varias afirmaciones a favor de una teoría de la luz que tenía algunos aspectos de la hipótesis ondulatoria.
Sin embargo, Young no fue tomado en serio. No fue hasta 1818, cuando el físico francés Augustin-Jean Fresnel propuso su propia hipótesis ondulatoria de base matemática, que la investigación de Young comenzó a ser reconocida como merecía.
Fresnel también tuvo que enviar su trabajo para su aprobación a un grupo de físicos comprometidos con la hipótesis corpuscular de la luz. Uno de ellos, el matemático Simeón Poisson, trató de refutar la hipótesis ondulatoria de Fresnel. Si realmente describía el comportamiento de la luz, argumentaba Poisson, debería suceder algo muy peculiar cuando se coloca un pequeño disco macizo en un haz de luz. La difracción de algunas de las ondas de luz alrededor del borde del disco redondo debería conducir a una interferencia constructiva, produciendo un punto brillante en el centro de la sombra del disco en una pantalla blanca colocada detrás del disco. La hipótesis corpuscular de la luz no permitía ideas como la difracción y la interferencia constructiva. Además, nunca se había informado de la observación de un punto brillante; incluso la idea de un punto brillante en el centro de una sombra parecía absurda. Con estos razonamientos Poisson anunció que había refutado la hipótesis ondulatoria.
Sin embargo, Dominique-François Arago, presidente del comité de la Académie des sciences que entendía del asunto, era un empirist e inmediatamente dispuso que la prueba aparentemente ridícula de Poisson se probara mediante un experimento. ¡El resultado fue que apareció un punto brillante en el centro de la sombra!
 Sombra proyectada por un obstáculo de 5,8 mm de diámetro en una pantalla colocada a 183 cm detrás, cuando es iluminado por la luz del sol que pasa a través de un agujero colocado 153 cm por delante. Los colores tenues de las franjas muestran la dependencia de la longitud de onda del patrón de difracción. En el centro está el punto brillante de Poisson / Arago. Imagen: Wikimedia Commons
Sombra proyectada por un obstáculo de 5,8 mm de diámetro en una pantalla colocada a 183 cm detrás, cuando es iluminado por la luz del sol que pasa a través de un agujero colocado 153 cm por delante. Los colores tenues de las franjas muestran la dependencia de la longitud de onda del patrón de difracción. En el centro está el punto brillante de Poisson / Arago. Imagen: Wikimedia CommonsA partir de entonces, un número cada vez mayor de personas de ciencia valoró como importantísimos los resultados del experimento de Young de la doble rendija y el “punto brillante de Poisson”. Para 1850, con los experimentos de Foucault-Fizeau, la hipótesis ondulatoria de la luz era el consenso científico; los físicos ya habían comenzado a concentrarse en resolver las consecuencias matemáticas de este modelo y aplicarlo a las diferentes propiedades de la luz.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Interferencia y difracción de la luz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Patrón de interferencia en pulsos de ondas
- Patrón de interferencia en ondas periódicas
- Patrones de difracción
“Fuego, foca, foto…” ¿Podemos decir estas palabras gracias a la dieta de nuestros antepasados?
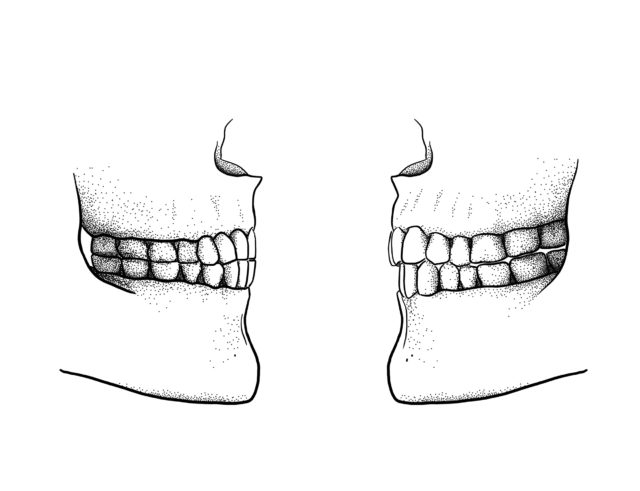 Alineación dental antes y después (derecha) de los cambios en la dieta. Imagen: Scott Moisik a partir de D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218
Alineación dental antes y después (derecha) de los cambios en la dieta. Imagen: Scott Moisik a partir de D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218 Fuego, foca, foto, fofo, fumar, fieltro, feminista… Es gustoso pronunciar el sonido de la efe, ¿verdad? Quizá por eso la palabra malsonante por excelencia en inglés sea “fuck” (disculpen el exabrupto), porque a los anglosajones se les da mejor que a nadie el convertir un sonido u onomatopeya en el centro de sus palabras (“crack” es más sonoro que “crujir”, aunque tampoco está mal, y “ring” es mejor que “llamar al timbre”, ahí sí que no hay discusión).
Pero volvamos al hilo, que me pierdo. Hablábamos del sonido de la efe, y la reflexión viene a cuento de un estudio recientemente publicado en la revista Science que sugiere que si somos capaces de pronunciarlo, así como otras consonantes labiodentales (en el castellano, solo le acompañaría la pronunciación tradicional de la uve, que solo se conserva en algunas regiones), es porque hace miles de años nuestros antepasados cambiaron su alimentación, eso cambió sus mandíbulas y con eso, los sonidos que eran capaces de pronunciar, abriendo la puerta a una variedad lingüística y comunicativa no disponible anteriormente.
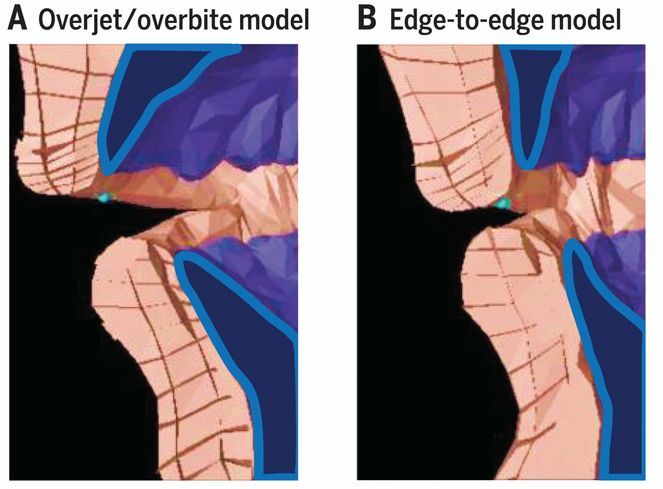 Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218
Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218Comida dura, mandíbulas potentes
Vamos por partes. El estudio ha sido realizado por Balthasar Bickel, Damián Blasi y Steven Moran, del laboratorio de Lingüística de la Universidad de Zúrich, en Suiza. Su intención era poner a prueba una idea propuesta por otro lingüista, el americano Charles Hockett en 1985. Hocket escribió entonces que las lenguas habladas por los cazadores-recolectores carecían de estas consonantes labiodentales y que, al menos en parte, su dieta podía ser responsable.
Según su teoría, consumir y masticar alimentos fibrosos y duros requería de una mayor fuerza en la mandíbula y suponía un mayor desgaste de los molares, y como tal, sus mandíbulas inferiores eran mayores y los molares ocupaban más espacio en ella, empujando las demás piezas dentales hacia delante y causando una alineación entre los dientes delanteros de la mandíbula inferior y la mandíbula superior.
Esto dificultaba, dijo Hockett entonces, que los dientes de arriba tocasen el labio inferior, contacto necesario para pronunciar la gustosa efe. Para hacerse una idea, pruebe a colocar hacia delante su mandíbula inferior hasta que dientes de arriba y abajo coincidan. ¿Verdad que le resulta una postura incómoda? Eso es por la llamada sobremordida, ese espacio que la mayoría tenemos entre los dientes superiores y los inferiores cuando cerramos la mandíbula. Al introducirse la agricultura y técnicas como el molido de los cereales, la fabricación de derivados lácteos y más formas de cocinado para la carne, la postura anterior habría sido menos necesaria y esta sobremordida habría ido haciéndose cada vez más común, hasta el día de hoy.
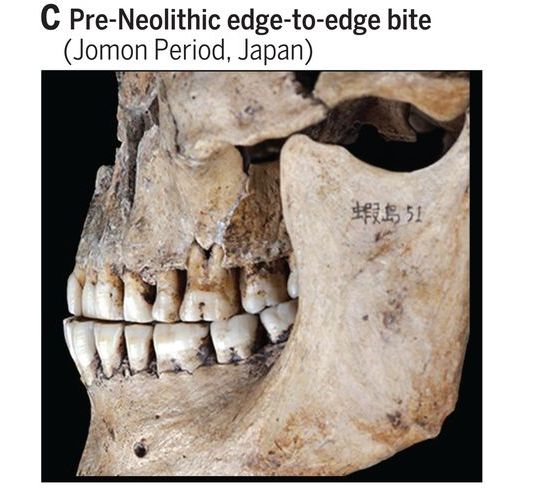 Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218
Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218Un 29% menos de energía para pronunciar la F
Blasi y compañía querían poner a prueba esta idea y, esperaban a priori, demostrar que Hockett se había equivocado.
Para empezar, los investigadores utilizaron un modelo informático para calcular que con una sobremordida, producir esas consonantes labiodentales cuesta un esfuerzo un 29% inferior. Después, analizaron las lenguas del mundo y descubrieron que en las civilizaciones de cazadores y recolectores hay un 75% menos de consonantes labiodentales que en las lenguas habladas en sociedades agrícolas. Por último, estudiaron las relaciones y evoluciones lingüísticas y determinaron que las consonantes labiodentales se difunden con rapidez, de forma que esos sonidos podrían haber pasado de ser raros a ser comunes en los 8.000 años que han pasado desde la adopción de la agricultura y otros métodos de manipulación de los alimentos.
Teniendo en cuenta estas averiguaciones. Bickel sugiere que a medida que la comida más blanda se fue haciendo más habitual, más adultos fueron desarrollando sobremordidas y fueron utilizando consonantes labiodentales de forma accidental, y que por ejemplo en la antigua India, el uso de esos sonidos pudo haber sido una señal de estatus al significar un acceso a una dieta más delicada y costosa. A día de hoy hay consonantes labiodentales en el 76% de los idiomas provenientes de lenguas indoeuropeas.
“Una de las conclusiones principales es que el panorama de sonidos que tenemos hoy en día está fundamentalmente afectado por la biología de nuestro aparato fonador. No es solamente una cuestión de evolución cultural”, explicaba Bickel en una rueda de prensa.
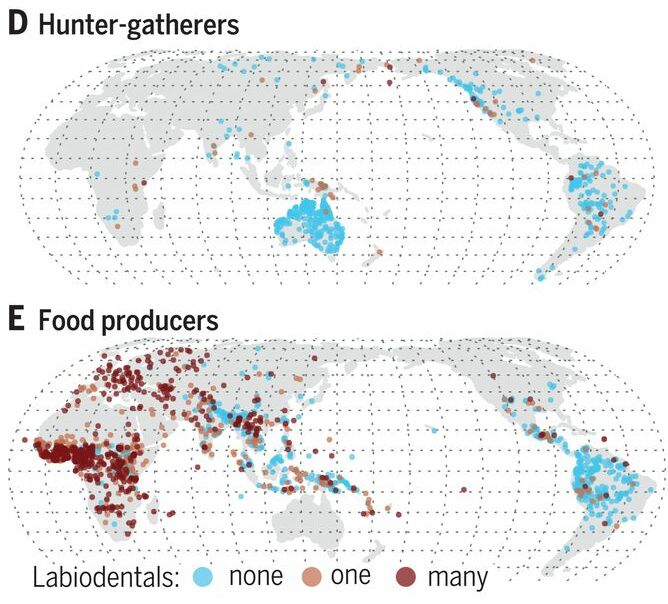 Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218
Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218Si ocurrió así, no ocurrió en todas partes
Aun así, no todo el mundo ve clara la relación que Bickel y su equipo proponen entre dieta, forma de la mandíbula y sonidos del idioma. Inevitablemente, su hipótesis está basada en algunas ideas difíciles de comprobar y también en algunas contradicciones. Por ejemplo, que en la Antigua China también se comenzó a cultivar y procesar arroz de forma que fuese más sencillo de masticar y comer y en las lenguas de esa región los sonidos labiodentales son mucho menos comunes que en las lenguas europeas.
Claro que los autores no defienden que la evolución hacia la sobremordida signifique necesariamente la aparición de las consonantes labiodentales, sino que “la probabilidad de producción de esos sonidos aumenta ligeramente con el tiempo, y eso significaría que es probable que algunas lenguas los adquieran, pero no todas”, explica otro de los autores, Steven Moran, en este artículo de Smithsonian Magazine.
“¿Dónde está la causalidad, que yo la vea?”
Algunos críticos, como el paleoantropólogo Rick Potts, no terminan de aceptar la conclusión del estudio: “En mi opinión, no dan suficientes razones para aceptar que la dieta fue el motivo por el que se hicieron más comunes estos sonidos, porque no tienen en cuenta en ningún momento los componentes anatómicos de producir estos sonidos”, explica en el artículo mencionado.
Potts explica que para hacer el sonido de la efe cuando no hay sobremordida simplemente hay que retraer un poco los músculos de los lados de la mandíbula, que la hacen retroceder ligeramente. “¿Cómo podría una dieta más dura y áspera limitar esa retracción? Esa es la base para hacer esos sonidos. El estudio no demuestra de ninguna forma que una mordida en la que los dientes coinciden impida o haga energéticamente más costoso pronunciar estos sonidos”, señala.
Así que en su opinión, el estudio señala algunas correlaciones que resultan interesantes pero no llega a demostrar una causalidad probable. Es, dice, como si una investigación descubriese que culturas que habiten en el ecuador tienen preferencia por el color rojo y también que esas personas tienen en sus ojos una densidad de receptores de color menor que las personas que habitan en el Ártico, por ejemplo, y concluyesen que la falta de receptores de color es lo que las hace preferir el color rojo.
“Pero ¿cómo íbamos con eso a descartar que fuese una cuestión cultural e histórica lo que hace que los habitantes de una cultura ecuatorial tiendan a elegir el rojo, y los habitantes de culturas del polo no lo hagan?”, argumenta, señalando que el estudio no ha tenido suficientemente en cuenta la acción de la historia, la cultura y la identidad de cada grupo y cada lengua a la hora de favorecer o no los sonidos labiodentales.
Referencias:
Human sound systems are shaped by post-Neolithic changes in bite configuration – Science
Ancient switch to soft food gave us an overbite—and the ability to pronounce ‘f’s and ‘v’s – Science
The Ability to Pronounce ‘F’ and ‘V’ Sounds Might Have Evolved Along With Diet – Smithsonian Magazine
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo “Fuego, foca, foto…” ¿Podemos decir estas palabras gracias a la dieta de nuestros antepasados? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué nos puede decir un elefante del cáncer en humanos?
- Los vegetales de la dieta neandertal
- Nuestros ancestros asesinos
Actos por el 50 aniversario de la Facultad de Ciencia y Tecnología de la UPV/EHU

50 años de ciencia viva
Los actos de conmemoración del 50 aniversario de la Facultad de Ciencia y Tecnología de la UPV/EHU comenzaron el 28 de enero de este año con la plantación de un tilo de hoja pequeña (Tila cordeta Mill.), que representa el Árbol de la Ciencia como símbolo de su unidad fundamental. El acto simbolizó la siembra de la semilla plantada en mayo de 1968, cuando se creó la Facultad de Ciencias de la Universidad de Bilbao, hoy en día Facultad de Ciencia y Tecnología.
Los primeros pasos de la Facultad de Ciencias en el curso 1968/69 se dieron junto al puente de Deusto, en “Botica Vieja, 1”. No fue hasta finales de 1971 cuando se trasladó a su emplazamiento actual en Leioa.
La Facultad de Ciencia y Tecnología ha sido una facultad viva en su oferta de titulaciones. Comenzó ofertando las cinco ramas clásicas de las Ciencias Naturales: Biología, Física, Geología, Matemáticas y Química. Entre los cursos 1994/95 y 2000/01, su oferta se amplía a las licenciaturas de segundo ciclo en Bioquímica, Ingeniería Electrónica, Ingeniería Química y Ciencias Ambientales, pasando a llamarse en el curso 2004/2005 Facultad de Ciencia y Tecnología. Hoy, oferta nueve grados, dos en la rama de Ingeniería (Ingeniería Electrónica e Ingeniería Química), y siete en la de Ciencias (Biología, Bioquímica y Biología Molecular, Biotecnología, Física, Geología, Matemáticas y Química). Se oferta también el doble grado en Física e Ingeniería Electrónica y tres dobles titulaciones internacionales de grado. Esta oferta hace de la Facultad de Ciencia y Tecnología uno de los referentes más importantes del País Vasco en la formación de profesionales capaces de jugar un papel crucial en los retos de nuestra sociedad, desde el desarrollo en nuevas tecnologías, el desarrollo sostenible, la conservación del medio ambiente o la investigación en biociencias.
Los inicios fueron precarios, como se podría esperar ante la difícil situación política de aquellos años. Hoy la facultad es un centro con gran experiencia en docencia, investigación y desarrollo tecnológico, como queda acreditado por las muy buenas posiciones en el ranking de Shanghái de distintas áreas de investigación que se desarrollan en nuestro centro.
La calidad de una facultad no se mide sólo por la excelencia del profesorado, sino también por la calidad de su alumnado: hoy cuenta con estudiantes de primer nivel. Las notas de acceso más elevadas para acceder a las titulaciones universitarias se encuentran en varias de las titulaciones de esta facultad. Un claro ejemplo es la nota de acceso superior a 13, sobre 14, para acceder al doble grado, la más alta de la UPV/EHU.
Tras 50 años de intenso trabajo, 17.500 personas han egresado en licenciatura, ingeniería o grado, y 2.000 se han doctorado. Estas cifras suponen una gran aportación de personal cualificado, profesionales que están trabajando en distintos ámbitos sociales, fundamentalmente en el tejido productivo, pero también en el institucional y el educativo, ocupando muchos de ellos puestos de responsabilidad.
Queremos compartir con la sociedad vasca el trabajo que la Facultad de Ciencia y Tecnología ha desarrollado a lo largo de medio siglo, mediante una investigación de excelencia y una formación rigurosa de profesionales en distintas áreas, mostrando así nuestro orgullo por haber colaborado en el crecimiento económico y social del País Vasco.
Biba Zientzia!, Ciencia Viva.
Todas las actividades programadas las encontrará aquí.
Las actividades programadas en el Bizkaia Aretoa de Bilbao durante los próximos 4 meses son:
Semana de la física
- 20 de marzo
18:30 Conferencia: A. Sanchez-Lavega: “¿Hay mas vida en el universo?
19:00 Mesa redonda: “Ciencia y Tecnología en el siglo XXI”
-Cristina Oyon (Responsable de Iniciativas Estratégicas del Grupo SPRI),
-Jose Maria Pitarke (Director General del CIC-Nanogune),
-Javier García-Abajo (Prof. Investigación CSIC y Research Prof. ICREA)
-Agustin Sanchez Lavega (Catedrático UPV/EHU)
Moderadora: Eva Caballero (Periodista de radio Euskadi)
- 21 de marzo
18:00 Conferencia: Roberto Emparan (Research Prof. ICREA y autor del libro de divulgación reciente “Iluminando el lado oscuro del Universo”): “Stephen Hawking: de los agujeros negros a la Teoría del Todo”
Semana de las matemáticas
- 25 de marzo
18:00 Mesa redonda: “Experiencias Matemáticas en empresa”
Dirigido a: Estudiantes de Bachillerato y de Matemáticas, Orientadores
- 2 de abril
19:00 Evento: Judith Rivas (UPV/EHU); Nagore de las Cuevas y Arkaitz Pascuas; Andoni Aresti Dantza Eskola y Mungiako Udal Dantza Eskola : “Pasos de baile a ritmo de matemáticas”
Dirigido a: Público general
Semana de la geología
- 1 de abril
18:00 Conferencia: Irantzu Guede, doctora de la UPV/EHU en Geología, en Mineralogía Petrología: “Geología en Mitos y Leyendas”.
- 2 de abril
18:00 Conferencia: Humberto Astibia, catedrático de la UPV/EHU: “Los fósiles, documentos de la historia de la Vida archivados en las rocas”.
16:00-20:00 Taller de Geología para familias. Aintzane Goffard (Geologa de la UPV/EHU, ayudante en Estratigrafía-Paleontología) e Irantzu Guede (Doctora de la UPV/EHU en Geología, Mineralogía-Petrología).
- 3 de abril
18:00 Conferencia: Blanca Martínez, doctora de la UPV/EHU en Geología, en Estratigrafía-Paleontología: “Geología y música”.
- 4 de abril
18:00 Conferencia: Ihintza Urain Alberdi, geóloga: “Geologia eta ingurugiroa: Geologoaren papera energia aldaketan eta Lurraren inguruko kultura berri baten aurrean”.
- 8 de abril
18:00 Conferencia: Jose María Tubía, catedrático de Geodinámica de la UPV/EHU: “Riesgo geológico de los tsunamis”.
Acto central
- 11 de abril
18:30 Conferencia: Prado Martín Moruno, 2017 L’Oreal-Unesco awarded Women for Science: “La energía oscura y el destino del Universo”.
Estreno de la obra de baile “GARGANTUA” (basada en el agujero negro GARGANTUA de la película “Interstellar”). Martxel Rodriguez, físico y bailarín profesional. Miembro de “KUKAI dantza taldea”.
Semana de la química
- 29 de abril
18:00 Conferencia: Oskar González. Profesor del Departamento de Química Analítica:“Artelanetan aurkitu diren gauzarik bitxienak”
- 30 de abril
18:00 Conferencia: Pascual Román, profesor emérito. Catedrático de Química Inorgánica: “El sesquicentenario de la tabla periódica de los elementos químicos”
- 2 de mayo
18:00 Conferencia: Jose Luis Vilas, director del Grupo de Química Macromolecular. Departamento de Química Física FCT-EHU: “Hidrogeles: imprimiendo salud”
Semana de la biociencia
- 6 de mayo
18:00 Mesa redonda: “Zientzia, jainkoaren esistentzia, zergatik du gizakiak sinisteko beharra”
Otros actos
- 27 de Junio
19:00 “ZTF/FCTren ekarpena Euskararen Normalizazioan” Conferenciantes: Pedro Miguel Etxenike, Jacinto Iturbe y Jesusmari Txurruka
Acto de clausura. 12 de julio
Bilbao Bizkaia AretoaSe comunicará
Sobre el autor: Fernando Plazaola Muguruza es el decano de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Actos por el 50 aniversario de la Facultad de Ciencia y Tecnología de la UPV/EHU se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
- Geología, ver más allá de lo que pisamos
- Geología: la clave para saber de dónde venimos y hacia dónde vamos
El cerebro humano tarda en madurar
 Imagen: Gordon Johnson / Pixabay
Imagen: Gordon Johnson / PixabayUna característica peculiar de los seres humanos es que, aunque nacemos con una cabeza de gran tamaño, tardamos en completar el crecimiento y desarrollo del encéfalo. A los dos años de edad alcanza el 85% de su volumen máximo, por lo que ha de seguir creciendo. Por otro lado, no todas sus áreas se desarrollan y maduran a la vez. La corteza cerebral, que es la parte más exterior, madura en último lugar. Y en ese proceso la proporción entre las denominadas materia gris y materia blanca cambia.
La materia gris corresponde a diferentes elementos: cuerpos neuronales y sus dendritas, que son prolongaciones ramificadas a través de las cuales una neurona recibe señales de otras; células de la glía, que dan soporte y protección a las anteriores; capilares sanguíneos, que proporcionan a neuronas y células gliales el oxígeno y los nutrientes que necesitan; y las conexiones entre neuronas, denominadas sinapsis. La materia gris se distribuye en la corteza del cerebro y del cerebelo, así como en numerosas estructuras de ubicación más profunda en el interior del encéfalo.
La materia blanca corresponde a los axones de las neuronas que se encuentran recubiertos por una sustancia lipídica denominada mielina. Un axón es una proyección de forma tubular que conducen señales nerviosas desde el cuerpo de una neurona hasta otras que pueden encontrarse a cierta distancia o hasta células musculares, principalmente. La vaina de mielina que recubre el axón lo aísla, y ayuda, de esa forma, a que los impulsos nerviosos se transmitan más rápida y eficazmente.
El volumen de materia gris de varias regiones de la corteza cerebral alcanza su máximo desarrollo alrededor de los 10 años de edad. Ese incremento refleja un aumento de las conexiones entre neuronas que se producen como consecuencia de la experiencia, el adiestramiento y el aprendizaje. Durante esos años, la actividad encefálica es tan intensa que llega a gastar un 60% de la energía que consume el organismo en reposo, y casi la mitad de las necesidades diarias totales de energía. Hay quienes atribuyen a ese gran consumo de energía el hecho de que el crecimiento del cuerpo durante la niñez sea lento y se prolongue en el tiempo.
A partir de los once o doce años las cosas cambian. El grosor de la materia gris de la corteza cerebral empieza a reducirse, y lo hace de forma sustancial durante la adolescencia. En algunas zonas esa reducción llega a ser del 17% hacia el final del proceso, unos 15 años después. Lo que ocurre, en parte, es que una cierta proporción de las conexiones sinápticas se “podan”, como se dice en la jerga neurocientífica. Esa poda elimina conexiones que no se usan o se usan poco y se mantienen las que más tráfico registran. A la vez aumenta la proporción de materia blanca. Eso es indicio de que los axones que conducen las señales se hacen más gruesos y que aumenta su grado de cobertura por la capa lipídica de mielina. El engrosamiento de los axones y el mayor grado de mielinización promueven una más rápida y eficaz transmisión de impulsos nerviosos y , por lo tanto, una comunicación más eficiente entre la corteza cerebral y el resto de áreas encefálicas. En definitiva: el cerebro funciona mejor.
La maduración de la corteza cerebral requiere tiempo y hace que la adolescencia sea un periodo difícil. Pero durante ese periodo la mente humana aprende a navegar en el complejo entorno social en que se desenvolverá en la edad adulta. La adolescencia puede entenderse así como el precio que paga por ese aprendizaje.
Nota:
Esta anotación es parte de una colección de tres artículos dedicados a la neuropsicología de la adolescencia. Los artículos son El desajuste adolescente, En busca de la identidad personal y este, El cerebro humano tarda en madurar.
——————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El cerebro humano tarda en madurar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sistemas nerviosos: el cerebro de vertebrados
- Daños estructurales por consumo de alcohol en el cerebro humano
- ¿Cuántas células hay en el cuerpo humano?
¿Hemos intentando contactar con extraterrestres?
¿Hemos intentando contactar con extraterrestres? Y si es así, ¿cómo y cuándo se ha hecho? ¿Quién lo ha hecho? Y sobre todo, ¿qué se les ha dicho en los mensajes que se han enviado? Todas las respuestas en minuto y medio.
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenarán en el programa de ciencia Órbita Laika (@orbitalaika_tve), a partir del próximo 18 de marzo todos los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Hemos intentando contactar con extraterrestres? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia express: los transgénicos
- Ciencia express: el carbono-14 y los rayos cósmicos
- Ciencia express: Cómo se formó la luna
Los biólogos de la UPV/EHU y la conservación de la naturaleza
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

 Toma de muestras de bivalvos en los manglares nicaragüenses. Foto: Ionan Marigomez / UPV/EHU
Toma de muestras de bivalvos en los manglares nicaragüenses. Foto: Ionan Marigomez / UPV/EHUA menudo se critica a la universidad por falta de conexión con la sociedad. Se afirma que la universidad enseña conocimientos arcanos y que la investigación apenas tiene implicaciones prácticas. Este punto de vista es compartido por bastantes universitarios, por lo que algo habrá detrás del mismo. Sin embargo, un poco de perspectiva histórica muestra que hay numerosas interacciones entre la universidad y la sociedad. A título de ejemplo, vamos a analizar cuál ha sido el impacto de la Sección de Biología en la conservación de la naturaleza.
La Sección de Biología comenzó su andadura muy modestamente en la por entonces denominada Facultad de Ciencias de la Universidad de Bilbao. Esta Sección carecía de catedráticos hasta 1975 y, de los tres profesores agregados de aquel momento, ninguno pertenecía a alguna de las áreas de la biología más naturalistas, es decir, la botánica, la zoología o la ecología. Tampoco llegaban fondos para apoyar proyectos de investigación en estos ámbitos. El bum llegó en la segunda mitad de los años 80, cuando se multiplicó el número de profesores, se potenció la formación de doctores y los grupos de investigación comenzaron a recibir financiación pública para el desarrollo de sus proyectos. Los años 90 vieron la aparición de cursos de postgrado tipo máster, como por ejemplo el de “Evaluación y Recuperación Ambiental”, y el afianzamiento de colaboraciones externas de los equipos de investigación. El siglo XXI ha supuesto la puesta de largo de la investigación en muchos de esos grupos, que participan en proyectos multinacionales de indudable repercusión sobre la conservación y el manejo de los recursos naturales, llegando a alcanzar niveles de excelencia y prestigio internacionales.
En estos años, la Facultad de Ciencia y Tecnología ha formado un gran número de personas en Biología, Ciencias Ambientales y otras disciplinas ligadas con la conservación de la naturaleza. Según las estadísticas oficiales, los egresados de la la FCT incluyen más de 3850 licenciados y más de 450 graduados en Biología, a lo que se suman centenares de estudiantes de master y 475 doctores. De ellos, muchos trabajan en ámbitos relacionados con la conservación de la naturaleza. Algunos lo hacen para la administración como técnicos de medio ambiente municipales, en consorcios y mancomunidades, en las diputaciones forales, departamentos del Gobierno Vasco, parques naturales, etc. Otros muchos trabajan en empresas relacionadas con la conservación de la naturaleza, como consultoras (por ejemplo, Anbiotek o Ekolur) o en centros de I+D+I como Neiker o Azti. Otros muchos se han dedicado a la enseñanza, tanto la reglada en institutos, ikastolas, colegios y universidades, como no reglada en aulas de naturaleza, CEIDAs, etc. Finalmente, muchos egresados colaboran en asociaciones y otras entidades en pro de la conservación de la naturaleza, como grupos ecologistas, asociaciones conservacionistas o entidades de estudio e interpretación del medio ambiente como la Sociedad de Ciencias Aranzadi. Aunque es imposible de cuantificar, podemos afirmar que esta masa de gente con una formación en biología y actitudes conservacionistas ha tenido mucho que ver con la transformación que se ha registrado en la forma de entender la relación de la especie humana con el medio ambiente en el País Vasco.
 Miembros de la FCT discutiendo un proyecto de restauración en el Parque Natural de Aiako Harria con técnicos de la Diputación Foral de Gipuzkoa, de Aguas del Añarbe de URA y de la Confederación Hidrográfica del Cantábrico. Fuente: Arturo Elosegi.
Miembros de la FCT discutiendo un proyecto de restauración en el Parque Natural de Aiako Harria con técnicos de la Diputación Foral de Gipuzkoa, de Aguas del Añarbe de URA y de la Confederación Hidrográfica del Cantábrico. Fuente: Arturo Elosegi.Por otro lado, algunos equipos de la FCT han sido muy activos en el inventariado y seguimiento de la biodiversidad de nuestro entorno. Por citar sólo algunos de ellos, el laboratorio de zoología abrió varias líneas de investigación sobre fauna fluvial y marina, sobre artrópodos del suelo o sobre moluscos terrestres. A esas líneas posteriormente se han incorporado otros grupos como el de murciélagos. Por su parte, el laboratorio de botánica abrió líneas de investigación sobre algas, musgos, plantas superiores y hongos, así como otra sobre geobotánica, que caracterizó y cartografió las principales comunidades vegetales de nuestro entorno. La información acumulada durante décadas ha sido esencial para caracterizar los lugares más biodiversos del País Vasco, para identificar sus principales factores de riesgo y, entre otras, para diseñar y optimizar la red Natura 2000.
Además de los inventarios de biodiversidad, algunos grupos han trabajado activamente en evaluar el estado de salud del medio ambiente, colaborando en poner las bases del sistema de información medioambiental del País Vasco. Por ejemplo, en los años 80, los entonces laboratorios de zoología y ecología se embarcaron en el primer gran estudio hidrobiológico de los ríos de Bizkaia, así como en la evaluación del estado medioambiental de la ría de Bilbao. El primer trabajo fue la semilla de la que derivó la red de seguimiento de los ríos del País Vasco, actualmente en manos de URA, la Agencia Vasca del Agua, mientras que el segundo comenzó una serie de estudios sobre la salud de nuestra costa. También hay que citar en este apartado al laboratorio de microbiología, que durante muchos años ha colaborado en la determinación de la calidad de las aguas de baño de la Comunidad Autónoma.
Otros grupos han centrado sus estudios en la detección y evaluación de los impactos que causa la actividad humana en la estructura y el funcionamiento de los ecosistemas. El grupo de ecología fluvial ha estudiado el impacto de las prácticas forestales, de la contaminación agrícola y urbana, de las detracciones de agua o del cambio climático en ríos vascos y de otras regiones. Lo que comenzó siendo el laboratorio de citología, por su parte, ha ido convirtiéndose en un grupo de investigación sobre ecotoxicología, que es hoy la base de la Estación Marina de Plentzia, mientras que el grupo de ecotoxicología animal y biodiversidad utiliza especies como centinelas del estado de salud de las aguas continentales. Otras líneas aplicadas han sido el estudio de suelos contaminados, que se ha abordado desde los laboratorios de zoología y fisiología vegetal, o los trabajos más agronómicos realizados en este último. Toda la información obtenida por estos grupos es utilizada por la Diputaciones Forales, por el Gobierno Vasco y por otras entidades en la planificación y gestión del territorio.
 Miembros de la FCT revisando trabajos de restauración ecológica en el río Araxes (Gipuzkoa), junto con técnicos de la Diputación Foral de Gipuzkoa, de las empresas Ekolur y Basoinsa, y un científico del IGB de Berlín. Fuente: Arturo Elosegi.
Miembros de la FCT revisando trabajos de restauración ecológica en el río Araxes (Gipuzkoa), junto con técnicos de la Diputación Foral de Gipuzkoa, de las empresas Ekolur y Basoinsa, y un científico del IGB de Berlín. Fuente: Arturo Elosegi.Más allá de la obtención de información, algunos grupos de la Sección han colaborado estrechamente con la administración en trabajos de gestión de poblaciones, comunidades o ecosistemas. Por ejemplo, el grupo de ecología y evolución del comportamiento ha trabajado en la gestión de mamíferos amenazados, como el visón, el desmán ibérico o los murciélagos, el de ecología y gestión del pastoreo en la gestión de la ganadería en pastos de montaña, el grupo de ecofisiología vegetal en la, entre otras, recuperación de suelos degradados o contaminados, y el de ecología fluvial en proyectos de restauración de ríos. Estos trabajos no se han limitado a evaluar el efecto de prácticas de conservación realizadas por la administración, sino que han implicado a la universidad en el diseño, ejecución y seguimiento de estas prácticas, muchas de las cuales han sido pioneras a nivel estatal.
Finalmente, no podemos olvidar el papel de asesoría realizado por muchos miembros de la Sección, en su participación en los patronatos de parques naturales o de la Reserva de la Biosfera de Urdaibai, o en Naturzaintza, el consejo asesor de conservación de la naturaleza del Gobierno Vasco. Además de estas colaboraciones, es habitual que miembros de la Sección participen en reuniones para definir estrategias y planes de la administración, como la Estrategia Española de Restauración de Ríos o la Estrategia Vasca de Biodiversidad.
La Sección de Biología continúa aportando conocimiento sobre los ecosistemas de nuestro entorno, lo cual facilita la gestión de nuestros recursos naturales. Si bien hasta hace bien poco esta aportación de conocimiento residía básicamente en las áreas más naturalistas referidas arriba, hoy en día las herramientas de la biología molecular son esenciales en el estudio de la biodiversidad, lo que aumenta el número de grupos que trabajan en este campo. Por todo ello, es de esperar que la Sección de Biología de la FCT siga teniendo un papel importante en la conservación de la naturaleza en el País Vasco y en el mundo en general.
Sobre los autores: Arturo Elosegi es profesor de ecología en el Departamento de Biología Vegetal y Ecología de la Facultad de Ciencia Tecnología de la UPV/EHU. Jesús Pozo se retiró recientemente del mismo departamento.
El artículo Los biólogos de la UPV/EHU y la conservación de la naturaleza se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una fórmula para dominarlos a todos: La conservación de la energía y la ley de la palanca
- De las leyes de conservación (I)
- Naturaleza, ciencia y cultura en el bicentenario de Henry David Thoreau
Aprendiendo de las máquinas
 Imagen: Pixabay
Imagen: PixabayLa segunda mitad del siglo XX vio nacer la computación y el sueño de la inteligencia artificial —“la ciencia de conseguir que las máquinas hagan cosas que requerirían inteligencia si las hiciesen humanos”, en palabras de Marvin Minsky—, que hoy en día está despertando un renovado interés gracias a la rama del aprendizaje automático. Se trata de un conjunto de técnicas que se benefician de los avances tecnológicos en materia de computación de las últimas dos décadas, y se caracterizan por su capacidad de engullir enormes cantidades de datos para enfrentarse a problemas de gran complejidad. Las aplicaciones son vastas, y ya forman parte de nuestro día a día: se utilizan para detección de fraude, navegación en vehículos autónomos, sistemas de recomendación (de productos, música…), diagnóstico médico, optimización de procesos, juegos… y un largo etcétera.
En todos estos casos, decimos que la máquina aprende. Y sabemos perfectamente cómo aprende (la lógica matemática y computacional subyacente), pero ¿qué aprende exactamente? Esta pregunta, aparentemente sencilla, nos persigue en todas sus aplicaciones. Por ejemplo, ¿qué lleva a AlphaZero a considerar ventajosos los movimientos que hace y que epatan por igual a aficionados y expertos ajedrecistas? Lo cierto es que no lo sabemos. La importancia de la cuestión puede parecer relativa en decisiones no críticas como la recomendación de una película, pero resulta esencial, e incluso abre derivadas éticas, cuando hablamos de cosas como conceder o no conceder un crédito, o la reacción de un coche autónomo ante un accidente.
En realidad, el tipo de problema al que se enfrentan las técnicas de aprendizaje automático es el mismo al que se viene enfrentando la ciencia, estadística mediante, desde su nacimiento: la inferencia de patrones, de generalizaciones, a partir de datos observacionales con el objetivo de obtener predicciones. En otras palabras, dada una entrada X, ¿qué modelo o función “f” genera la salida Y=f(X)? La gran diferencia se encuentra en que tradicionalmente nos hemos enfrentado a problemas para los cuales hay una teoría matemática previa que establece la estructura de “f”. La estadística clásica es la ciencia que estudia los diferentes tipos de modelos “f” y genera las técnicas para obtener y evaluar el mejor ajuste a partir de las observaciones (x, y). Por otro lado, las técnicas de aprendizaje automático de la nueva ciencia de datos son capaces de aprender la función “f” a partir de los datos sin ningún modelo previo, sin ningún conocimiento a priori del problema. La función “f” inferida se encuentra de alguna forma codificada tras el proceso de aprendizaje, pero nos es completamente desconocida y no hay forma de extraerla: es por eso que suelen llamarse “algoritmos de caja negra”.
Así pues, la estadística clásica define modelos matemáticos en los que las relaciones entre variables son explícitas y, por tanto, son directamente interpretables. Pensemos en una simple relación lineal: cuando crece X, crece Y; por tanto, obtenemos un valor grande de Y porque X es grande. En cambio, estos algoritmos de caja negra son capaces de capturar relaciones arbitrariamente complejas y predecir con gran precisión, pero su desventaja a día de hoy es que nos las ocultan, matemáticamente hablando: no somos capaces de interpretar qué propiedades de X influyen en Y.
Por tanto, uno de los grandes retos que la inteligencia artificial tiene por delante es el de intentar obtener conocimiento a partir de la estructura que las máquinas son capaces de extraer de grandes volúmenes de datos. Quizás se logre mediante una formalización matemática de las técnicas actuales, o quizás se desarrolle una nueva estadística ahora desconocida. Sea como sea, aprender de las máquinas puede ser uno de los principales hitos del presente siglo.
Sobre el autor: Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute
El artículo Aprendiendo de las máquinas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Máquinas inteligentes (y III): Deep blue, HAL 9000 y más allá
- Seminario Famelab: aprendiendo a hacer monólogos
- Máquinas inteligentes (II): Inteligencia artificial y robótica
Paradojas: contando peces, pesando patatas y… detectando agujeros
Tengo un acuario en casa. Contiene doscientos peces, de los cuales el 99% son rojos. Quiero conseguir que sólo el 98% de los peces de mi pecera sean colorados, eliminando sólo algunos de este color, pero sin tener que comprar más de otras tonalidades. ¿Cuántos peces rojos debo sacar del acuario?
 Imagen: Pixabay
Imagen: PixabaySeguro que son pocos los que debo extraer de mi pecera. Veamos: los peces rojos representan el 99%. Por lo tanto, el 1% no son colorados, es decir, solo hay dos peces que no son rojos en el acuario. Necesito extraer algunos peces rojos para conseguir que estos dos peces lleguen a ser el 2% de los peces del acuario. Así, si dos peces no colorados deben ser el 2% del total, una sencilla regla de tres dice que deben quedar en el acuario ¡solo 98 peces rojos! Es decir, deben sacarse 100 peces rojos para que el porcentaje de peces colorados pase del 99%al 98%. Sorprendente, ¿no?
¿Y qué hago ahora con los cien peces que me sobran? Decido cambiarlos a un colega por cien kilos de patatas. Es justo, ¿no? Un pez por un kilo de patatas… Y se me plantea un nuevo problema.
Tengo 100 kilos de patatas. El 99% de su peso corresponde al agua que contienen. Quiero deshidratarlas para conseguir que contengan solo un 98% de agua. Tras hacerlo, ¿cuánto pesan las patatas? ¡Si sólo pesan 50 kilos! ¿Por qué?
 Imagen: Wikimedia Commons.
Imagen: Wikimedia Commons.Veamos: si de esos 100 kilos, 99 kilos son de agua, 1 kilo corresponde a sólido seco. Vaya, parece que estoy teniendo un “déjà vu”… esto me recuerda mucho al caso de los peces rojos. Pero centrémonos, volvamos a los tubérculos. Si tras deshidratar las patatas la parte sólida pasa a ser del 2% del total –que sigue pesando 1 kilo, porque no se ve afectada por la deshidratación– de nuevo puedo hacer una sencilla regla de tres que me dice que debe de haber solo 49 kilos de agua. Así que, efectivamente, las patatas pasan a pesar 50 kilos. Bueno, así me costará menos transportarlas.
Creo que compraré algo de queso para elaborar alguna receta y acompañar a parte de esas patatas. Me gusta el Emmental porque tiene agujeros, y –como todo el mundo sabe– a las personas que nos dedicamos a la topología nos encanta contar agujeros. Para eso se inventó la teoría de homología, ¿no? Para eso, para contar agujeros de diferentes dimensiones y así distinguir espacios no homeomorfos.
Y me ha dado por pensar en los agujeros del queso, que parece que proceden de la fermentación producida por partículas microscópicas de heno presentes en la leche. A ver:
Cuanto más queso Emmental compre, más agujeros habrá. Pero, cuantos más agujeros haya, tendré menos queso. Es decir, cuanto más queso compre… ¡tendré menos queso!
 Imagen: Wikimedia Commons.
Imagen: Wikimedia Commons.¡No me lo puedo creer! Y todo esto por culpa de cien peces rojos…
Referencias
-
Marta Macho Stadler, La paradoja de los peces colorados, ZTFNews, 4 octubre 2013
-
Weisstein, Eric W., Potato Paradox, MathWorld
-
Paradoxe du fromage à trous, Wikipédia (consultado el 10 de marzo de 2019)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Paradojas: contando peces, pesando patatas y… detectando agujeros se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Patatas ‘perfectas’ con el método ‘Edge Hotel School’
- La topología modifica la trayectoria de los peces
- Los peces en el río
Reflexión y refracción de la luz
 Imagen: V Photography and Art (flickr)
Imagen: V Photography and Art (flickr)¿Qué ocurre cuando la luz que viaja por un medio (por ejemplo, el aire) alcanza el límite de otro medio (por ejemplo, el vidrio)? Las respuestas a esta pregunta dependen de si se utiliza el modelo de partícula o el de onda para la luz. ¿Qué implica cada uno y cuál es mejor? ¿Cómo explican el siguiente hecho experimental (Figura 1):
 Figura 1. Un haz de luz llega con un ángulo de 60º al límite entre dos medios; vemos que una parte es reflejada (también con un ángulo de 60º) y otra pasa al medio 2 con un cambio de dirección. Fuente: Wikimedia Commons
Figura 1. Un haz de luz llega con un ángulo de 60º al límite entre dos medios; vemos que una parte es reflejada (también con un ángulo de 60º) y otra pasa al medio 2 con un cambio de dirección. Fuente: Wikimedia CommonsEl modelo de onda ya lo hemos tratado aquí para la reflexión y aquí para la refracción. Recordemos las conclusiones principales aplicadas a la luz:
1. Un rayo de luz no es otra cosa que una línea perpendicular a las líneas de cresta de una onda. Un rayo representa la dirección en la que viaja un tren de ondas.
2. En la reflexión, el ángulo de incidencia(Θi) es igual al ángulo de reflexión (Θr), esto es, Θi = Θr
3. La refracción implica un cambio de la longitud de onda y velocidad de la onda a medida que pasa a otro medio. Cuando la velocidad disminuye, la longitud de onda disminuye y el rayo gira en una dirección hacia una línea perpendicular al límite entre los medios. Este giro hacia la perpendicular se observa, por ejemplo, cuando un rayo de luz pasa del aire al vidrio.
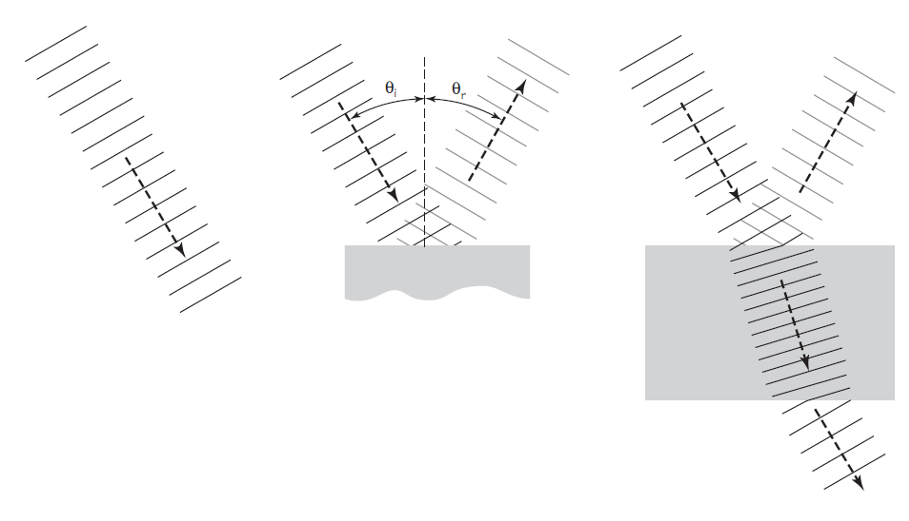 Figura 2. El modelo de ondas en acción. Fuente: Cassidy Physics Library
Figura 2. El modelo de ondas en acción. Fuente: Cassidy Physics Library ¿Cómo explicar las mismas observaciones mediante el modelo de partículas? Primero tenemos que considerar la naturaleza de la superficie del vidrio. Aunque aparentemente homogénea, estamos en realidad ante una superficie rugosa: un microscopio lo suficientemente potente mostraría que tiene multitud de colinas y valles. Si las partículas de luz fueran similares a pequeñas bolitas de materia, al golpear una superficie tan rugosa lo que cabría esperar es que se dispersasen en todas direcciones. Por tanto, no serían reflejadas ni refractadas. Por lo tanto, hay que refinar el modelo. Newton argumentó que en realidad debe haber “algún rasgo del cuerpo que esté disperso uniformemente sobre su superficie y por el cual este actúa sobre el rayo sin contacto inmediato (some feature of the body which is evenly diffused over its surface and by which it acts upon the ray without immediate contact).
Vamos a seguir la idea de Newton, a ver a donde nos lleva. De entrada, en el caso de la reflexión, la fuerza actuante tendría que ser una que repela las partículas de luz. Pero claro, por la misma regla de tres, es necesaria una una fuerza que atraiga a las partículas de luz en lugar de repelerlas para explicar la refracción. Esto parece que se complica para el modelo de partículas. O no. Veamos
Cuando una partícula de luz se acerca a un límite con otro medio, primero tendría que superar la fuerza repelente. Si lo consiguiera, entonces encontraría una fuerza atractiva en el medio que la atraería hacia el medio. Dado que la fuerza atractiva sería un vector perpendicular a la superficie del medio, tomando como referencia la dirección del movimiento de la partícula ese vector tendría un componente en la dirección del movimiento original de la partícula, lo que implica que la velocidad de la partícula tendría que aumentar. Otra consecuencia es que, si el rayo de partículas se moviera con un ángulo oblicuo al límite, cambiaría de dirección a medida que entrase en el medio, girando hacia la línea perpendicular al límite.
De acuerdo con el modelo de partículas*, por lo tanto, podríamos afirmar lo siguiente:
1. Un rayo representa la dirección en la que se mueven las partículas.
2. En la reflexión, los ángulos de incidencia y reflexión son iguales. Esta predicción se puede derivar aplicando la ley de conservación del momento a partículas repelidas por una fuerza.
3. La refracción implica un cambio de velocidad de las partículas a medida que entran en otro medio. En concreto, cuando actúa una fuerza atractiva, la velocidad aumenta y el rayo cambia de dirección al entrar en el medio.
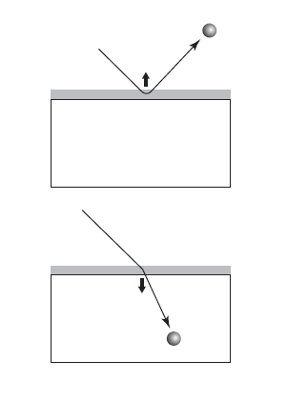 Figura 3. El modelo de partículas en acción. Fuente: Cassidy Physics Library
Figura 3. El modelo de partículas en acción. Fuente: Cassidy Physics Library Comparemos estas características del modelo de partículas con las características correspondientes del modelo de onda. La única diferencia está en la velocidad predicha para un rayo refractado. Observamos que un rayo se curva hacia la línea perpendicular cuando la luz pasa del aire al vidrio. El modelo de partículas predice que la luz tiene una velocidad mayor en el segundo medio. El modelo de ondas predice que la luz tiene una velocidad menor.
Podríamos pensar que no hay nada más fácil para averiguar qué modelo es el más correcto: diseñar un experimento para determinar qué predicción es correcta. Todo lo que uno tiene que hacer es medir la velocidad de la luz después de que haya entrado en el vidrio o en el agua y compararla con la velocidad de la luz en el aire. Pero no. A a finales del siglo XVII y principios del siglo XVIII, cuando Huygens argumentaba a favor del modelo de onda y Newton apoyaba el modelo de partículas, ningún experimento de este tipo era posible. La única forma disponible de medir la velocidad de la luz era la astronómica.
No sería hasta mediados del siglo XIX que Armand H.L. Fizeau y Jean B.L. Foucault conseguirían medir la velocidad de la luz en el agua. Los resultados concuerdan con las predicciones del modelo de onda: la velocidad de la luz es menor en el agua que en el aire.
Los experimentos de Foucault-Fizeau de 1850 se consideraron como el último clavo en el ataúd del modelo newtoniano de partículas para la luz, ya que, cuando se realizaron estos experimentos, buena parte de la comunidad científica ya había aceptado el modelo de onda por otras razones. Algunas de estas se derivaron del trabajo del científico inglés Thomas Young, y serán las que veamos a continuación.
Nota:
* Implícitamente en el argumento está la asunción sobre el límite del tamaño de las “partículas” de luz de Newton. Las partículas deben ser al menos tan pequeñas como las irregularidades en la superficie de un vidrio. Si fuesen mayores tendríamos el mismo efecto que una pelota de tenis rebotando en el rugoso suelo de hormigón, solo reflexión.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Reflexión y refracción de la luz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Un cartel para el día de pi
María Begoña Medel Bermejo

El alumnado del Grado en Creación y Diseño de la Facultad de Bellas Artes de la UPV/EHU comienza a adentrarse en el mundo del Diseño durante su tercer curso con una asignatura cuyo nombre es Diseño Gráfico.
Existe una discusión recurrente sobre la existencia o no de alguna diferencia entre el Arte y el Diseño. Desde esta asignatura, que imparto desde hace casi 30 años, suelo insistir en el hecho de que una de las características fundamentales, si no la más destacable, es la presencia de un cliente con una necesidad de comunicación. El cliente es el elemento que nos convierte en los profesionales intermediarios que resuelven un problema de comunicación, aplicando los conocimientos sobre el funcionamiento de la percepción humana en la creación de un conjunto único y original de imágenes y textos significantes que transmitirán el mensaje que se necesite.
Suele suceder que en el aula trabajamos con supuestos en los que el rol de cliente lo asume el docente o los propios alumnos, de manera rotativa. Pero, algunas veces tenemos la suerte de enfrentarnos a problemas reales para los que desarrollar soluciones de comunicación gráfica.
Durante este curso 2018-2019, de acuerdo con la Guía Docente de la asignatura Diseño Gráfico, el último proyecto que el alumnado debía desarrollar era un cartel.
Ya habíamos colaborado en otras ocasiones con otras facultades y entidades públicas en temas similares pero, nunca habíamos trabajado con la Facultad de Ciencia y Tecnología.
Tener como cliente a alguien cuyo día a día es tan diferente del nuestro era el mayor atractivo que encontré a esta posibilidad. La innovación, la creación nunca surge si trabajamos dentro de nuestra área de confort. Salir de lo común, de lo reiterativo, supone colocarse en ese lugar que resulta incómodo porque no lo conocemos, y mirar todo aquello que vamos descubriendo con ojos limpios.
Por todo lo dicho hasta ahora me puse en contacto con algunos profesores del área de Matemáticas para preguntarles si tenían algún tema en el que pudiéramos colaborar. La respuesta fue inmediata y muy positiva, necesitaban publicitar la jornada BCAM-Naukas en el día de Pi y era posible colaborar. Participar en un evento organizado por la Cátedra de Cultura Científica de la UPV/EHU, Naukas y BCAM (Basque Center for Applied Mathematics) ha sido un reto para el alumnado y la oportunidad de hacer algo que no quedara entre las paredes de la clase como un proyecto académico más, si no que consiguiera trascender y llegar al público colocando a ambas facultades y a la UPV/EHU en el punto de mira de nuestro cliente específico, el posible futuro alumnado.
Ya teníamos el tema para el proyecto de cartel de este curso.
En clase, cuando planteé el tema, hubo todo tipo de reacciones: desde el entusiasmo al temor ante lo desconocido. Pero, en general, fue bien acogido dado que la posibilidad de hacer algo real suele ser muy valorada por el alumnado.
Participaron 56 alumnas y alumnos de dos grupos, castellano y euskera, de tercer curso del grado en Creación y Diseño. Cada uno de ellos debía llevar a cabo una labor de recopilación de información sobre el tema que les permitiera llegar a concebir al menos tres conceptos totalmente diferentes que sirvieran para comunicar la celebración del día de Pi.
Cuando desarrollamos conceptos de comunicación gráfica trabajamos la creatividad desde diversos lugares para poder encontrar esa imagen que consiga atraer la atención del espectador estableciendo un vínculo emocional al conseguir descifrar el mensaje. Se trata de hacer sonreír a nuestro cerebro.
Creo que el resultado obtenido este curso permite constatar que el acercamiento al mundo de las matemáticas permite una multiplicidad de caminos. Como colofón de esta experiencia se han seleccionado dos carteles: el de Paula Castro como cartel de la jornada del 13 de marzo de 2019 y el de Jone Aldalur para comunicar la realización de talleres para escolares. Se trata de las dos primeras imágenes que aparecen a continuación junto con otros 10 carteles que fueron pre-seleccionados:
 Obra de Paula Castro. Éste ha sido el cartel seleccionado como imagen general del día de Pi. La relación y conexión entre la ciencia y la profundidad del cosmos se ha realizado mediante la utilización de la imagen icónica de la luna, que representa la circunferencia, y la estela de condensación que genera el cohete en referencia al diámetro.
Obra de Paula Castro. Éste ha sido el cartel seleccionado como imagen general del día de Pi. La relación y conexión entre la ciencia y la profundidad del cosmos se ha realizado mediante la utilización de la imagen icónica de la luna, que representa la circunferencia, y la estela de condensación que genera el cohete en referencia al diámetro. Obra de Jone Aldalur. Se utilizó la imagen para informar sobre los talleres del día de Pi. Las pelotas con números Pi dentro del frasco tienen colores llamativos para atrapar nuestra mirada y a su vez nos remiten a los juegos de azar en los que esos números pueden decidir nuestra suerte.
Obra de Jone Aldalur. Se utilizó la imagen para informar sobre los talleres del día de Pi. Las pelotas con números Pi dentro del frasco tienen colores llamativos para atrapar nuestra mirada y a su vez nos remiten a los juegos de azar en los que esos números pueden decidir nuestra suerte.  Obra de José Manuel García. Un contraluz crea un ambiente narrativo en el que el número Pi aparece sobre una colina desde la que surge un camino de estrellas hacia el cielo.
Obra de José Manuel García. Un contraluz crea un ambiente narrativo en el que el número Pi aparece sobre una colina desde la que surge un camino de estrellas hacia el cielo. Obra de David von Heeren. Gestos positivos realizados con las manos nos sirven para crear una pequeña adivinanza ayudados por los personajes del fondo, que nos proporcionan la pista necesaria para encontrar la clave.
Obra de David von Heeren. Gestos positivos realizados con las manos nos sirven para crear una pequeña adivinanza ayudados por los personajes del fondo, que nos proporcionan la pista necesaria para encontrar la clave. Obra de Jon Flores. A veces se ve más lo que no está que lo que está. Se trabaja con la elipsis repetida del elemento fundamental del cartel. Si no lo leemos en voz alta puede que no seamos capaces de descubrir el juego visual.
Obra de Jon Flores. A veces se ve más lo que no está que lo que está. Se trabaja con la elipsis repetida del elemento fundamental del cartel. Si no lo leemos en voz alta puede que no seamos capaces de descubrir el juego visual. Obra de Ainhoa Simpler. Como si fuera un juego solitario aparecen las cartas en grupos que remiten a las primeras cifras del número Pi y en cada una de ellas descubrimos la imagen de una matemática famosa.
Obra de Ainhoa Simpler. Como si fuera un juego solitario aparecen las cartas en grupos que remiten a las primeras cifras del número Pi y en cada una de ellas descubrimos la imagen de una matemática famosa. Obra de Maialen Sayans. El todo y sus partes. Los primeros números de la sucesión infinita de Pi colocados en visión frontal se convierten en un juego de transparencias que crean otra realidad.
Obra de Maialen Sayans. El todo y sus partes. Los primeros números de la sucesión infinita de Pi colocados en visión frontal se convierten en un juego de transparencias que crean otra realidad. Obra de Eva Muñoz. Hasta ahora muchos matemáticos han perdido el sueño investigando el número Pi y tomando café para mantenerse despiertos. La huella del café sobre la mesa es un guiño a la circunferencia y su diámetro.
Obra de Eva Muñoz. Hasta ahora muchos matemáticos han perdido el sueño investigando el número Pi y tomando café para mantenerse despiertos. La huella del café sobre la mesa es un guiño a la circunferencia y su diámetro. Obra de Mikel Larena. Juego de transparencias con la sucesión del número Pi.
Obra de Mikel Larena. Juego de transparencias con la sucesión del número Pi. Obra de Anne Fernandez. Un papel arrugado con forma esférica repleto de fórmulas matemáticas aparece en primer plano con un fondo realizado con una regla de círculos.
Obra de Anne Fernandez. Un papel arrugado con forma esférica repleto de fórmulas matemáticas aparece en primer plano con un fondo realizado con una regla de círculos. Obra de 11 Laiene Pagazaurtundua. Metáfora visual “el árbol de la ciencia”
Obra de 11 Laiene Pagazaurtundua. Metáfora visual “el árbol de la ciencia” Obra de Lukas Zelaia. Sustitución de un elemento arquitectónico por un Pi gigante que genera en el espectador nuevos puntos de vista y relaciones emocionales con la imagen mediante esta conexión inusual.
Obra de Lukas Zelaia. Sustitución de un elemento arquitectónico por un Pi gigante que genera en el espectador nuevos puntos de vista y relaciones emocionales con la imagen mediante esta conexión inusual.Todas ellas son imágenes muy diferentes que aportan acercamientos originales al concepto de PI desde el mundo del Diseño Gráfico.
Esperamos seguir colaborando en próximas ediciones siempre mejorando la presente y que sea de nuevo una experiencia enriquecedora para ambas facultades.
Sobre la autora: María Begoña Medel Bermejo es Doctora en Bellas Artes y profesora del Grado en Creación y Diseño BBAA/AAEE de la UPV /EHU
El artículo Un cartel para el día de pi se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una fórmula para dominarlos a todos: La conservación de la energía y la ley de la palanca
- Marcas de agua digitales, qué son y para qué sirven
- El consumo de alcohol para el corazón y las dificultades de divulgar ciencia
El hígado y la vesícula biliar
Además de las secreciones pancreáticas, el intestino delgado también recibe secreciones procedentes del sistema biliar, que está formado por el hígado y la vesícula biliar. Nos referimos, en concreto, a la bilis y, en particular, a las sales biliares. Es este el principal asunto que trataremos en esta anotación.
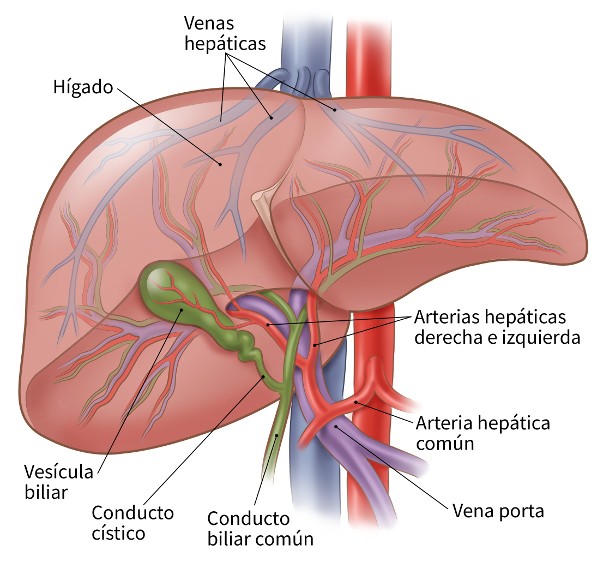 Higado y vesícula biliar humanos. Imagen: cancer.org
Higado y vesícula biliar humanos. Imagen: cancer.orgPero eso será algo más adelante, porque al hígado corresponden funciones adicionales de gran relevancia que queremos consignar aquí para dejar constancia de ellas. Para empezar, es el órgano que gobierna el metabolismo del conjunto del organismo; podría decirse que es el órgano metabólico maestro, su director. Se ocupa del procesamiento metabólico de proteínas, carbohidratos y lípidos, tras su absorción en el intestino, incluyendo también la gluconeogénesis (síntesis metabólica de glucosa a partir de precursores no glucídicos). Y almacena glucógeno y grasas, a la vez que otras sustancias de menor relevancia cuantitativa, como hierro, cobre y varias vitaminas.
El hígado también se ocupa de degradar productos residuales y hormonas, además de eliminar agentes tóxicos y sustancias, procedentes del exterior, sin utilidad biológica o potencialmente peligrosas (fármacos, por ejemplo). También sintetiza proteínas y lipoproteínas plasmáticas, entre las que se encuentran las que participan en la coagulación de la sangre y las que transportan fosfolípidos, colesterol y hormonas esteroideas y tiroideas.
A las tareas anteriores, hay que añadir que activa la vitamina D (tarea compartida con el riñón); elimina, mediante el concurso de sus macrófagos (células de Kupffer), bacterias y glóbulos rojos que ya han finalizado su vida útil; secreta las hormonas trombopoietina (estimula la producción de plaquetas), hepcidina (regula el metabolismo del hierro en mamíferos), IGF 1 o factor de crecimiento insulínico 1 (estimula el crecimiento); excreta el colesterol y la biliverdina y bilirrubina, que son productos derivados de la degradación de la hemoglobina; y en algunas especies de mamíferos (no en primates y conejillos de India) y de aves sintetiza ácido ascórbico (vitamina C).
Es de destacar que con la excepción de las células de Kupffer, todas las funciones aquí consignadas son realizadas por un mismo tipo celular, el hepatocito. Por lo tanto, no hay diferenciación de funciones con arreglo a tipos celulares (puesto que solo hay los dos citados), sino en virtud de los orgánulos en que se desarrolla cada una de ellas. En ellos radica la función y esta se diferencia de unos orgánulos a otros.
El hígado es un órgano muy irrigado, y el flujo sanguíneo en su interior está organizado de tal modo que cada hepatocito está en contacto con sangre venosa proveniente del tubo digestivo y sangre arterial procedente de la aorta. Los capilares procedentes del intestino se van agrupando hasta confluir en la vena porta hepática que penetra en el hígado donde se vuelve a ramificar en múltiples capilares, formando una red de (los denominados) sinusoides hepáticos. Esos sinusoides son los que permiten que la sangre procedente directamente del estómago e intestino delgado difunda a todas las células del hígado para que provean a estos de las sustancias absorbidas. La sangre sale del órgano con los productos elaborados o expulsados para su eliminación (como la urea, por ejemplo) y lo hace a través de la vena hepática, en la que confluyen los capilares que lo drenan. Además de la sangre procedente del digestivo, al hígado también le llega sangre arterial con oxígeno y otras sustancias procedentes del conjunto del organismo para su procesamiento en los hepatocitos.
El hígado se organiza en lóbulos, disposiciones hexagonales de tejido en torno a una vena central. A lo largo de los vértices exteriores de los lóbulos discurren una rama de la vena porta hepática, otra de la arteria hepática y un ducto biliar. De la vena y arteria citadas salen amplios sinusoides que se dirigen hacia la vena central. Las células de Kupffer tapizan los sinusoides, atrapan a cuantas bacterias y eritrocitos fuera de servicio se encuentran, y los eliminan. Los hepatocitos se disponen en placas de dos células cada una, de manera que todas se encuentran en contacto con los vasos sanguíneos, como hemos dicho antes. Las venas centrales de cada lóbulo convergen en la vena hepática que es la que sale del hígado y se une a la vena cava inferior.
El canalículo de la bilis discurre entre las dos células de cada placa, recibiendo secreción biliar de todas ellas. Los canalículos se dirigen hacia el exterior del lóbulo y transportan así la bilis hasta los ductos que se encuentran en los vértices de los hexágonos (lóbulos hepáticos); los ductos de cada lóbulo acaban agrupándose en el ducto hepático común, que es el que lleva la bilis al duodeno.
El hígado produce bilis de forma permanente, pero el acceso de la bilis al duodeno se encuentra controlado por el esfínter de Oddi, que solo permite su paso cuando hay quimo en el duodeno y puede, por lo tanto, ser utilizado. Cuando el esfínter se encuentra cerrado las sales biliares se acumulan en la vesícula biliar, que hace las veces de depósito. Con cada comida la bilis entra en el duodeno debido al vaciado de la vesícula y al aumento en la producción a cargo del hígado. Los seres humanos producimos entre 250 ml y 1 l de bilis cada día. El mensajero que desencadena la contracción de la vesícula y la relajación del esfínter de Oddi es la hormona CCK (la colecistoquinina que vimos en El páncreas) y que se libera por efecto de la presencia de grasa en el duodeno.
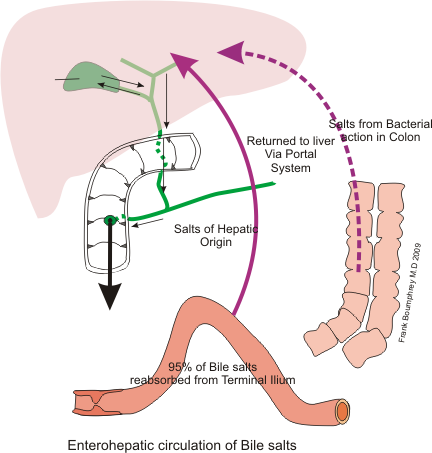 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsLa bilis contiene colesterol, lecitina, sales biliares, y bilirrubina y biliverdina, y estas sustancias se encuentran en una solución ligeramente básica, similar a la producida por las células de los ductos del páncreas. Las sales biliares son derivados del colesterol y participan en la digestión y absorción de las grasas debido a su acción detergente y a la formación de micelas. Tras su intervención la digestión de lípidos, son reabsorbidas mediante transporte activo en el íleon, la zona terminal del intestino delgado. De allí, a través del sistema porta, vuelven al hígado. Se calcula que en promedio, en cada comida unas mismas sales circulan dos veces por el duodeno e intestino delgado, y que cada día se pierden con las heces un 5% de las sales biliares. Su pérdida es repuesta por los hepatocitos de manera que el total se mantiene constante.
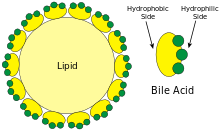 Emulsificación de los lípidos por las sales biliares. Imagen: Wikimedia Commons
Emulsificación de los lípidos por las sales biliares. Imagen: Wikimedia CommonsLas sales biliares intervienen en la digestión de las grasas favoreciendo su emulsificación. Convierten gotas grandes de lípidos en gotas de muy pequeño tamaño suspendidas en el quimo acuoso. De esa forma aumenta muchísimo la relación superficie/volumen y exponiendo una mayor superficie micelar a la acción de la lipasa pancreática, de manera que esta puede atacar las moléculas de triglicéridos. Sin la formación de emulsiones, la mayor parte de esos triglicéridos quedarían en el interior de las gotas grandes lejos del alcance enzimático.
Las sales biliares actúan como los jabones. Ambos son anfipáticos: contienen una porción hidrofóbica (un esteroide derivado del colesterol) y otra hidrofílica con carga negativa (una taurina o glicina) . Las sales se adsorben a la superficie de una gota de grasa, con una orientación acorde a su naturaleza; esto es, la porción liposoluble interactúa con la superficie de la gota lipídica, mientras que la porción cargada queda orientada hacia el exterior y disuelta en agua. Los movimientos intestinales ayudan a fragmentar esas gotas lipídicas y hacer que sean cada vez más pequeñas. En ausencia de sales biliares (detergente), las pequeñas gotas tenderían a caolescer, volviéndose a formar grandes gotas. Pero eso no ocurre porque las cargas negativas solubles en agua lo impiden; forman una especie de capa de cargas negativas que se repelen unas a otras, de manera que no llegan a entrar en contacto. Las gotas lipídicas pequeñas tienen un diámetro que varía entre 200 y 5000 nm.
Para la digestión de las grasas es esencial el concurso de la lipasa procedente del páncreas. La acción de esta enzima es efectiva porque el páncreas secreta la coenzima colipasa, también un péptido alifático, que ocupa el lugar de algunas sales biliares en la superficie de las gotas lipídicas y desde esa posición se une a la lipasa de manera que esta pueda hacer su trabajo. La enzima queda así enganchada a la superficie de las gotas, rodeada de sales biliares, pero de tal forma que puede actuar directamente sobre las moléculas lipídicas.
La absorción de lípidos en el intestino se produce gracias a la formación de micelas. Las micelas son estructuras de entre 3 y 10 nm de diámetro en las que intervienen, además de las sales biliares, el fosfolípido lecitina y el colesterol. La lecitina, como las sales biliares, es anfipática, de manera que se asocia con las sales formando agrupaciones cuya porción hidrofóbica se dispone en el interior, junto al colesterol, y la porción hidrofílica en el exterior. De esa forma, moléculas hidrofóbicas que resultan de la digestión de los lípidos (monoglicéridos, ácidos grasos libres y vitaminas liposolubles) son transportados en emulsión acuosa, gracias a la cubierta hidrofílica, hasta los enclaves del epitelio intestinal donde son absorbidos.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El hígado y la vesícula biliar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Avances contra la enfermedad de hígado graso no alcohólica
- Una ecuación para determinar la grasa en el hígado a partir de una resonancia
- Proteínas plasmáticas
La adaptación a los incendios forestales

Para empezar y como ejemplo nos sirve la Comunidad Autónoma del País Vasco. El 27 de diciembre de 2016 aprobó el Consejo del Gobierno Vasco el Plan Especial de Emergencias por Riesgo de Incendios Forestales. En el texto, en la página 9, aparece un cuadro con la superficie quemada en la Comunidad entre 1985 y 2012. El máximo está en el catastrófico 1989, en el mes de diciembre, con más de 27000 hectáreas de superficie arbolada. Fue una sequía en invierno, después de una larga sequía estival, y con fuertes vientos que dificultaban la extinción de los incendios.
El siguiente año en superficie quemada fue 1985, con casi 2600 hectáreas, seguido de 2002 con 700 hectáreas y 1995 con 600 hectáreas. En 2011 fueron 140 hectáreas y en 2012, último año con datos en este Plan, fueron 175 hectáreas. En España, y según datos del Ministerio de Medio Ambiente, los años recientes con más de 400000 hectáreas quemadas fueron 1985, 1989 y 1994.
Estos son los datos para la Comunidad y para España y no hay que olvidar que a nivel del planeta, más o menos el 3% de su superficie se quema cada año. Los incendios forestales aparecen cuando las plantas colonizan la tierra, en bosques de entre 350 y 400 millones de años de antigüedad. Hay restos de carbón de incendios tan antiguos como del Silúrico, hace unos 400 millones de años.
Cada fuego es una combinación particular de frecuencia, intensidad, tamaño, estación, tipo de propagación y extensión. Pero, también es evidente que los incendios influyen, además de todo lo que significan como suceso público, en nuestra percepción del entorno, en concreto, del paisaje. Francisco Lloret y sus colegas, de la Universitat Autònoma de Barcelona, han estudiado los cambios en el paisaje en el municipio de Tivissa, en Tarragona, entre 1956 y 1993.
 Tivissa. Imagen: Wikimedia Commons
Tivissa. Imagen: Wikimedia CommonsEs un municipio agrícola con zonas difíciles y poco productivas que se han abandonado en los últimos años, y se han cubierto de matorrales que han homogeneizado el paisaje. Además, ha disminuido la superficie de bosques. Los autores encuentran que los incendios son más probables en áreas homogéneas con árboles, y provocan que el paisaje posterior también sea homogéneo.
Concluyen que, en las zonas con actividad humana el paisaje es más heterogéneo, por ejemplo, con distintas actividades agrícolas y modelos de explotación de la tierra, y los incendios se controlan mejor quizá por ser heterogéneas, con diferentes plantaciones que, a su vez, tienen diferente capacidad de incendiarse. Y, además, los que se aprovechan de las actividades agrícolas procuran defenderlas del fuego y no provocar incendios.
En las zonas sin actividad agrícola, muy iguales, con árboles y arbustos, los incendios se extienden con más facilidad y provocan, después y en primer término, mayor diversidad.
Es evidente que, sea a más o a menos diversidad, los incendios influyen en el paisaje y en nuestra precepción del mismo.
 El incendio acercándose al complejo de Old Faithful en el Parque Nacional de Yellowstone (Estados Unidos) en 1988. Imagen: Wikimedia Commons
El incendio acercándose al complejo de Old Faithful en el Parque Nacional de Yellowstone (Estados Unidos) en 1988. Imagen: Wikimedia CommonsSin embargo, un paisaje quemado se puede recuperar, quizá no exactamente igual al que existía antes del fuego, y puede convertirse en un área ecológicamente saludable. Fue el año 1988, en una gran sequía que, al año siguiente, en 1989, provocaría los incendios en el País Vasco, cuando ocurrió el gran incendio en Estados Unidos, en el Parque Nacional de Yellowstone, en el que ardieron más de 600000 hectáreas, algo así como Gipuzkoa, Bizkaia y gran parte de Álava. Fue uno de los mayores incendios forestales en una zona templada que aparece en la historia escrita. Daniel Donato y su grupo, del Departamento de Recursos Naturales del Estado de Washington en Olympia, nos cuentan cómo está el parque 24 años después.
Las zonas centrales del bosque, más tupidas y con más árboles, se han regenerado con fuerza y no ha influido la severidad del incendio. Las zonas más secas, con menos árboles, se han recuperado peor, en más tiempo, y, sobre todo, lo hacían con más eficacia si cerca habían quedado parcelas pequeñas sin quemar que pueden funcionar como reserva de semillas.
 Una de las zonas de pino de Yellowstone que ardieron en 1988 tal y como se encontraba en 2006. El pino que sobrevivió (a la izquierda) es un Picea engelmannii, los jóvenes, Pinus contorta. Imagen: Wikimedia Commons
Una de las zonas de pino de Yellowstone que ardieron en 1988 tal y como se encontraba en 2006. El pino que sobrevivió (a la izquierda) es un Picea engelmannii, los jóvenes, Pinus contorta. Imagen: Wikimedia CommonsLa regeneración culminó, en general, a los 15 años del incendio aunque, en las mejores zonas, el crecimiento ha continuado. A los 24 años, en esas zonas de bosque más maduro, el reemplazamiento de los árboles anteriores al incendio está completo. En las áreas más secas y con menos bosque, ha quedado, en muchos lugares, una estepa herbácea que necesitará varias décadas o, incluso, teniendo en cuenta el calentamiento global, nunca volverá a ser bosque.
Los resultados sobre incendios en la Península Ibérica son parecidos, tanto en Galicia, según el grupo de Otilia Reyes, de la Universidad de Santiago de Compostela, como en Cataluña, según Santiago Martín y Lluis Coll, del Centro de Ciencias Forestales de Solsona.
Son dos paisajes diferentes en dos climas distintos, en el oeste y este de la Península. En ambos casos, los incendios fueron en bosques de pinos, con el pino marítimo (Pinus pinaster), en Serres, en la costa de A Coruña y en 2014, un año antes del estudio, y pino laricio (Pinus nigra) en el centro de Cataluña y en 1998, siete años anterior al estudio.
Los resultados son parecidos y, como en Yellowstone, cuanto más potente es el bosque original, mejor se recupera. Y, también, ayuda la presencia de pequeñas parcelas no quemadas como origen de semillas para repoblar. Solo en las zonas más secas aparecen áreas con arbustos o praderas. Para la recuperación de las zonas con buen bosque original no se necesita ninguna intervención.
Como nos cuentan William Bond y John Keeley, de las universidades de El Cabo, en Sudáfrica, y de California en Los Angeles, grandes áreas del mundo arden de manera regular y, por tanto, los ecosistemas se han incendiado durante cientos de millones de años. Hay evidencias de incendios de hace 420 millones de años, desde la aparición de las plantas terrestres. Así se ha construido el paisaje que conocemos y se mantienen la estructura y la función de esos ecosistemas, muy adaptados a los incendios periódicos. Por tanto, los incendios son una fuerza evolutiva de selección natural lo que implica que los bosques que ahora conocemos se han seleccionado y aguantan y se recuperan de los incendios porque así se han formado. Y el fuego estimula la regeneración con, por ejemplo, semillas que germinan estimuladas por el calor o por sustancias químicas emitidas por la madera quemada o, también, la floración acelerada por el fuego.
Después de revisar incendios y diversidad de plantas en todo el planeta, excepto la Antártida, y desde finales del siglo XX hasta inicios de XXI, Juli Pausas y Eloi Ribeiro, del CIDE-CSIC de Montcada, en Valencia, y del ISRIC de Wageningen, en Holanda, han recopilado casi 200 millones de citas. Sus resultados demuestran que la mayor diversidad de plantas se da con la mayor productividad y, también, con la actividad de incendios. Así, el fuego explica una proporción significativa de la diversidad de las plantas. En conclusión, el fuego aumenta la heterogeneidad del paisaje y crea nuevos nichos con oportunidades para una gran variedad de especies.
 Paisaje un año después de un incendio en un bosque de pinos. Imagen: Wikimedia Commons
Paisaje un año después de un incendio en un bosque de pinos. Imagen: Wikimedia CommonsLas plantas adaptadas al fuego han seleccionado determinadas características que les benefician en caso de incendio. En las áreas con clima mediterráneo, como la propia cuenca del Mediterráneo, California, región de El Cabo en Sudáfrica y Chile, el grupo de Philip Rundel, de la Universidad de California en Los Angeles, han revisado el número de especies vegetales adaptadas al fuego. En el Mediterráneo abundan las plantas que rebrotan después del incendio; tienen germinación estimulada por el fuego, sea por el calor, o por el humo; y florecen estimuladas por el fuego. Para estas especies, el fuego ha sido un estímulo importante para la diversificación y aparición de nuevas especies.
Como resumen final sirve la publicación de Juli Pausas y Jon Keeley, del Centro de Investigación sobre Desertificación del CSIC en Valencia y del Servicio Geológico de Estados Unidos respectivamente, cuando escriben que no solo el clima y el suelo explican la distribución de las especies animales y vegetales en el planeta, también interviene el fuego. Desde hace mucho tiempo, unos 400 millones de años, impulsando la aparición de especies nuevas adaptadas a los incendios periódicos. Sin embargo, nuestra especie ha cambiado la relación entre el fuego y los seres vivos. Primero, Homo utilizó el fuego para adaptar el entorno a sus necesidades. Pero, y en segundo lugar, lo hace con tal intensidad y extensión que cambió muchos ecosistemas y pone en peligro la sostenibilidad.
Referencias:
Archibald, S. et al. 2018. Biological and geophysical feedbacks with fire in the Earth system. Environmental Research Letters 13: 033003.
Bond, W.J. & Keeley, J.E. 2005. Fire as a global “herbivore”: the ecology and evolution of flammable ecosystems. Trends in Ecology and Evolution 20: 387-394.
Bowman, D.M.J.S. et al. 2009. Fire in the Earth system. Science 324: 481-484.
Donato, D.C. et al. 2016. Regeneration of montane forests 24 years after the 1988 Yellowstone fires: A fire-catalyzed shift in lower treelines? Ecosphere 7: e01410
Pausas, J.G. & Keeley, J.E. 2009. A burning story: The role of fire in the history of life. BioScience 59: 593-601.
Pausas, J.G. & Ribeiro. E. 2017. Fire and plant diversity at the global scale. Global Ecology and Biogeography DOI: 10.1111/geb.12596
Rundel, P.W. et al. 2018. Fire and plant diversification in Mediterranean-climate regions. Frontiers in Plant Science 9: 851.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo La adaptación a los incendios forestales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Incendios, los grafos de visibilidad y la conjetura de Collatz
- “El bien común como adaptación” por Antonio Lafuente
- Las aves de Prometeo
¿Existe el geoturismo?

Si cerrásemos los ojos para visualizar la imagen de un geólogo, probablemente imaginaríamos a una persona descubriendo fósiles y recopilando y coleccionando minerales. No obstante, esta disciplina académica cuenta con muchísimas más aplicaciones desconocidas para gran parte de la sociedad.
Con el objetivo de dar visibilidad a esos otros aspectos que también forman parte de este campo científico nacieron las jornadas divulgativas “Abre los ojos y mira lo que pisas: Geología para miopes, poetas y despistados”, que se celebraron los días 22 y 23 de noviembre de 2018 en el Bizkaia Aretoa de la UPV/EHU en Bilbao.
La iniciativa estuvo organizada por miembros de la Sección de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Ente Vasco de la Energía (EVE-EEE), el Departamento de Medio Ambiente, Planificación Territorial y Vivienda del Gobierno Vasco, el Geoparque mundial UNESCO de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.
Los invitados, expertos en campos como la arquitectura, el turismo o el cambio climático, se encargaron de mostrar el lado más práctico y aplicado de la geología, así como de visibilizar la importancia de esta ciencia en otros ámbitos de especialización.
Asier Hilario, director científico del Geoparque de la Costa Vasca, se encarga de ahondar en la geología como recurso. Algunos de los principales destinos turísticos del mundo son pura geología, tienen millones de visitantes y aunque muchos no lo sepan, hay algo de esa geología que les interesa. Desde su experiencia, expone las principales claves y oportunidades del geoturismo para crear destinos de turismo innovadores y sostenibles que fomenten el disfrute y conocimiento de las ciencias de la Tierra.
Edición realizada por César Tomé López
El artículo ¿Existe el geoturismo? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Geología, ver más allá de lo que pisamos
- Patrimonio geológico: la otra mitad del ambiente
- Geología: la clave para saber de dónde venimos y hacia dónde vamos
Proteómica: cuando las proteínas y la espectrometría de masas van de la mano
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebrará dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Durante las próximas semanas en el Cuaderno de Cultura Científica y en Zientzia Kaiera se publicarán regularmente artículos que narren algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas. Comenzamos con la serie “Espectrometría de masas”, técnica analítica que supone el ejemplo perfecto del incesante avance de la Ciencia y la Tecnología.

La espectrometría de masas (MS) es una técnica habitual entre los químicos desde hace ya 100 años, pero no fue hasta hace 3 décadas que se empezó a utilizar como técnica de análisis de proteínas. Para analizar un analito mediante espectrometría de masas (MS) es necesario ionizar dicho analito y pasarlo a fase gaseosa. Durante mucho tiempo, la posibilidad de ionizar macromoléculas como las proteínas o fragmentos de proteínas, es decir péptidos, y pasarlos a fase gaseosa se consideraba una tarea tan posible como hacer volar a un elefante. Sin embargo, el desarrollo y comercialización de dos métodos de ionización a los que se denominó ionización “suave”, demostraron que era posible analizar macromoléculas del tamaño de las proteínas, tanto en disolución como en estado seco cristalino; éstos métodos de ionización se conocen hoy día como ionización electrospray (ESI) y ionización por desorción láser asistida por matriz, (matrix assisted laser desorption ionization) (MALDI). En ESI, se aplica un alto voltaje a la solución que contiene el analito a su paso por una fina aguja perforada. A medida que se va evaporando la solución con las moléculas cargadas, se va reduciendo el tamaño de las gotas, hasta conseguir que pasen a estado gaseoso. Por su parte, en MALDI se dispara con láser a una placa de acero en la que se ha secado el analito junto con una matriz. La matriz absorbe la energía del láser que a su vez se transfiere a la muestra, haciendo que cambie a estado gaseoso.
Pero, ¿por qué las proteínas? ¿a qué viene ese interés por analizarlas? La razón es que las proteínas son las moléculas fundamentales de todos los seres vivos. Las proteínas son las encargadas de realizar diversas tareas en nuestras células; entre otras, catalizan reacciones químicas, transportan moléculas, mantienen la estructura celular y nos protegen frente a los patógenos. Nuestro cuerpo está formado por trillones de células, y cada una de ellas cuenta con miles de proteínas diferentes. De hecho, dependiendo del catálogo o conjunto de proteínas que contenga un tipo de célula, llevará a cabo unas u otras funciones y tendrá unas u otras características. Todas las células de un ser vivo contienen la misma información genética, es decir, el genoma de todas sus células es idéntico. La información necesaria para producir cada proteína está escrita en los genes. Dicho de otro modo, los genes son las recetas que se siguen para crear las proteínas, y dependiendo de las recetas que se utilicen en cada momento, se producirán unas proteínas u otras. Se denomina proteoma a la colección de proteínas de las que dispone una célula en un momento concreto. A diferencia del genoma, el proteoma celular varía continuamente; en respuesta a cualquier estímulo que llegue a las células, o cuando deben hacer frente a cualquier ataque, es decir, con el fin de adaptarse al entorno, las células producirán diferentes proteínas que trabajarán conjuntamente. Esto explica cómo, contando ambas con el mismo genoma, una oruga se convierta en mariposa (Imagen 1).
 Imagen 1. Papilio machaon oruga (a) y mariposa (b). Fuente: Wikimedia Commons.
Imagen 1. Papilio machaon oruga (a) y mariposa (b). Fuente: Wikimedia Commons.Las proteínas, al igual que nosotros, tienen sus propias «redes sociales». Cumplen sus funciones interaccionando entre ellas más que individualmente. A pesar de ello, estas interacciones suelen ser, en la mayoría de los casos, temporales. Se crean y se destruyen según las necesidades celulares. Habiendo millones de proteínas en la células, la red de interacciones intracelulares es tan compleja como la que puede haber entre todas las personas del planeta. El funcionamiento de esa red de proteínas condicionará la salud de la célula y, en consecuencia, la de todo el organismo. Por eso es tan importante estudiar las proteínas y sus interacciones, es decir, los proteomas, e intentar interpretarlos en su conjunto. En consecuencia, uno de los retos fundamentales de la biología actual es describir los proteomas cualitativamente y cuantitativamente. Dicho objetivo parece alcanzable y pocos dudan del liderazgo que ha tomado la proteómica en este camino.
La proteómica estudia los proteomas. Fue en 1975 cuando por primera vez se separaron miles de proteínas de la bacteria Escherichia coli mediante electroforesis bidimensional en gel (2DE). Sin embargo, la identificación de dichas proteínas, concretar cuáles eran exactamente, constituía otro reto diferente. Para abordarlo, fue necesario, tanto desarrollar técnicas de secuenciación parcial, léase degradación de Edman, como ajustar la propia técnica de espectrometría de masas (MS) al análisis de proteínas. La MS es, a día de hoy, el método que se utiliza habitualmente para identificar proteínas. Para poder interpretar los proteomas en su conjunto, además de identificar las proteínas, hay que cuantificarlas. Los primeros pasos para la cuantificación de proteínas se dieron mediante el análisis de imágenes de los geles de 2DE. Si bien sigue siendo una técnica adecuada para el análisis proteómico, hoy en día ocupa un segundo lugar, muy por detrás de la proteómica basada en la espectrometría de masas (MS-based proteomics). De hecho, actualmente, la MS es el método habitual para identificar y cuantificar las proteínas en muestras proteicas complejas. Se ha convertido pues en una técnica fundamental para interpretar la información codificada en el genoma.
Tal y como se ha mencionado anteriormente, las técnicas habituales utilizadas para ionizar y evaporar proteínas y péptidos son ESI y MALDI. La técnica MALDI-MS se utiliza para analizar mezclas de péptidos relativamente simples. En cambio, los sistemas ESI-MS acoplados a la cromatografía líquida (LC-MS), son los más adecuados para el análisis de muestras complejas. Siendo los proteomas, por definición, complejos, las técnicas de LC-MS han prevalecido en la proteómica. La precisión, sensibilidad y resolución de masas, junto con su velocidad, son las claves del éxito de las técnicas de LC-MS. Durante los últimos años, se ha podido identificar, cuantificar y caracterizar un enorme número de proteomas mediante diferentes procedimientos de LC-MS. Entre los logros conseguidos a nivel de proteómica, cabe destacar dos borradores del proteoma humano publicados en 2014, y el actual Proyecto Proteoma Humano (HPP) dirigido por la Organización Mundial del Proteoma Humano (HUPO)
Pero, ¿qué es lo que hacemos exactamente en un laboratorio de proteómica? Sea cual sea la muestra recibida (muestra obtenida de una biopsia, células animales o vegetales, bacterias, secreción biológica…), habitualmente se aplica el flujo de trabajo denominado proteómica bottom-up o proteómica ascendente, de abajo hacia arriba (Imagen 2). En primer lugar, se extraen las proteínas de la muestra. A continuación, se utiliza una enzima que digiere las proteínas, habitualmente la tripsina, para trocear las proteínas en trozos pequeños denominados péptidos. Los péptidos de la mezcla se separan en la cromatografía líquida de fase inversa acoplada a la ionización por electrospray. A medida que los péptidos eluyen de la columna, se van ionizando y pasan al espectrómetro de masas. Allí, los iones de los péptido se van separando y detectando en función de su relación masa-carga (m/z). Los péptidos más abundantes se aíslan del resto, y se fragmentan, dando lugar a espectros de fragmentación. Estos espectros son los que contienen la información que permite identificar y cuantificar los péptidos. Finalmente, los datos obtenidos por el espectrómetro de masas se analizan mediante herramientas informáticas específicas. De esta manera, es posible saber qué proteínas hay en la muestra analizada y en qué cantidad.
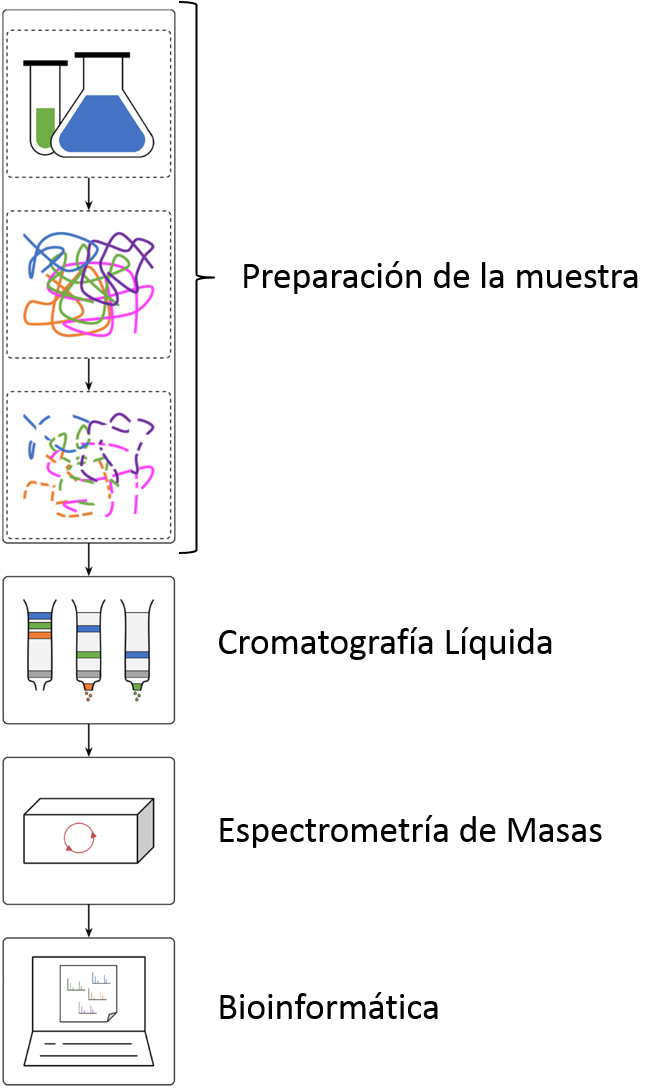 Imagen 2. Proteómica bottom-up Fuente: Autores.
Imagen 2. Proteómica bottom-up Fuente: Autores.Durante la última década, la proteómica basada en la MS se ha convertido en una de las principales herramientas analíticas para las biociencias. Ha permitido estudiar las proteínas desde diversas vertientes, y ha facilitado el camino para conocer sus estructuras, variaciones, cantidades, modificaciones postraduccionales e interacciones. Además, gracias a la proteómica nos encontramos más cerca de identificar las proteínas implicadas en el desarrollo de diversas enfermedades y los biomarcadores necesarios para el diagnóstico de las mismas. Durante los próximos años, se irán completando los catálogos proteicos de diferentes condiciones celulares. Junto a los resultados obtenidos a partir de la genómica, epigenómica, metabolómica y otras «ómicas» a gran escala, los descubrimientos obtenidos gracias a la proteómica contribuirán a la construcción de modelos celulares. De hecho, esa es la tendencia actual: trabajar desde un punto de vista multidisciplinar con el fin de construir modelos matemáticos y estadísticos que ayuden a aclarar la complejidad de los procesos biológicos; y es precisamente ahí donde la proteómica jugará un papel relevante.
Más información
- Fenn JB (2003) “Electrospray wings for molecular elephants (Nobel lecture)” Angew Chem Int Ed Engl. 42(33), 3871-94. DOI:10.1002/anie.200300605
- Fenn JB et al. (1989) “Electrospray ionization for mass spectrometry of large biomolecules” Science 246(4926), 64-71. DOI: 10.1126/science.2675315
- Tanaka K et al. (1988) “Protein and polymer analyses up to m/z 100 000 by laser ionization time-of-flight mass spectrometry” Rapid Communications in Mass Spectrometry 2(8), 151–153. DOI:10.1002/rcm.1290020802
- Karas M and Hillenkamp F (1988) “Laser desorption ionization of proteins with molecular masses exceeding 10,000 daltons” Anal Chem. 60(20), 2299-301. DOI: 10.1021/ac00171a028
- O’Farrell (1975) “High resolution two-dimensional electrophoresis of proteins” J Biol Chem 250(10), 4007-21.
- Kim MS et al. (2014) “A draft map of the human proteome” Nature 509(7502), 575-81. DOI: 10.1038/nature13302
- Wilhelm M et al. (2014) “Mass-spectrometry-based draft of the human proteome” Nature 509(7502), 582-7. DOI: 10.1038/nature13319
- HUPO: https://hupo.org/human-proteome-project
Sobre los autores: Miren Josu Omaetxebarria, Nerea Osinalde, Jesusmari Arizmendi y Jabi Beaskoetxea, miembros del departamento de Bioquímica y Biología Molecular, y Kerman Aloria, técnico de SGIker.
El artículo Proteómica: cuando las proteínas y la espectrometría de masas van de la mano se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cartografiando territorio inexplorado: imagen por espectrometría de masas
- Espectrometría de masas: de un isótopo de neón a elefantes que vuelan
- A new hero is born: La espectrometría de masas al servicio de la justicia
El orden es una fantasía
 Damian Ucieda Cortes. Demolition, Glasgow, Reino Unido, 2015
Damian Ucieda Cortes. Demolition, Glasgow, Reino Unido, 2015 Uno de los cometidos más sofisticados de las ciencias es mostrar el conocimiento de forma elegante. Pensemos en las fórmulas matemáticas que describen las leyes físicas. En los modelos de moléculas y cristales. En el enunciado de hipótesis. Con qué precisión del lenguaje y con qué precisión plástica describimos cómo es lo que nos rodea. Con qué elegancia.
Para muchos, entre los que me incluyo, el paradigma de todo esto es la Tabla Periódica de los Elementos.
A lo largo de la historia se han sucedido varios intentos de ordenar los elementos químicos. Una vez tuvimos la certeza de que algunas sustancias eran elementos químicos, es decir, que estaban formadas por un solo tipo de átomos; comenzamos a ordenarlos de acuerdo con sus propiedades: peso atómico, tipo y número de elementos con los que enlaza, estado natural… Teníamos la intuición y el deseo de que los elementos que lo conforman todo, el aire, la piel, la arena, todo, respondiesen a un orden mayor, como si este orden nos hubiese venido dado.
Hubo intentos bellísimos, como el del tornillo telúrico. Para ello se construyó una hélice de papel en la que estaban ordenados por pesos atómicos los elementos químicos conocidos, enrollada sobre un cilindro vertical, y al hacer coincidir elementos químicos similares sobre la misma generatriz se apreciaba que el resto de las generatrices surgidas también mostraban relación entre los elementos químicos unidos, lo que claramente indicaba una cierta periodicidad. Era tan bonito que era una pena que no fuese cierto. El tornillo telúrico no funcionaba con todos los elementos químicos, solo servía para los más ligeros.
Hubo otro intento especialmente refinado de ordenar los elementos químicos que tenía relación con la música. Qué fabulosa la relación entre la música y la química. Al ordenar los elementos de acuerdo con su peso atómico creciente -exceptuando el hidrógeno y los gases nobles, que todavía no se conocían- el que quedaba en octavo lugar tenía unas propiedades muy similares al primero. Se le llamó ley de las octavas. Era bonito ver tal relación entre la naturaleza de los elementos químicos y la escala de las notas musicales. Lamentablemente la ley de las octavas empezaba a fallar a partir del elemento calcio. Con lo bonita que era. Una lástima.
Cuando ya se conocían 63 elementos químicos -en la actualidad conocemos 118- se ordenaron en grupos de acuerdo con sus propiedades químicas. Y dentro del grupo, se organizaron por peso atómico creciente. Quien lo hizo por primera vez, hace 150 años, tuvo la osadía de corregir algunos pesos atómicos que hacían peligrar la estética de aquella tabla. Dejó huecos para elementos que, según él, se descubrirían en el futuro. Y es que la tabla, ante todo, tenía que ser bonita, porque la realidad es bonita y tiene que responder a algún orden. Qué locura si no. Pues la tabla de los elementos químicos también.
Aquella tabla fue el origen de la actual Tabla Periódica de los Elementos. Con el tiempo, efectivamente descubrimos más elementos químicos. Rellenamos los huecos, tal y como era de esperar. Y hasta descubrimos que aquel orden no respondía a pesos atómicos crecientes, o al menos no siempre, y de ahí los cambios propuestos. Aquel orden respondía al número de protones que cada elemento químico contiene en su núcleo. Lo llamamos número atómico, pero hace 150 años no se sabía nada de esto. Era bonito, era ordenado, era elegante. Tenía que ser verdad.
En las ciencias, y en cualquier otra forma de conocimiento, la belleza es criterio de verdad. Las leyes físicas que conseguimos expresar con fórmulas matemáticas, cuanto más bellas, más ciertas. Cuanto más y mejor comprimamos su verdad en estilosos caracteres del alfabeto griego, más ciertas. Nos brindan esa sensación tan placentera de tenerlo todo bajo control. Nos hacen creer que, si está ordenado, es que lo hemos entendido.
Las ciencias describen la realidad. Lo hacen a su manera, con su lenguaje propio. El de los números, las palabras, las ilustraciones. Esa descripción nos satisface cuando es lo suficientemente elegante. Podríamos tener un conjunto de 118 elementos químicos de los que conocer absolutamente todo, de forma individual, y no haberlos ordenado jamás. Y sabríamos lo mismo, pero nos daría la impresión de que, sin orden, los datos son solo datos. No hay conocimiento sin orden.
El orden es una fantasía. Esto puede interpretarse de dos formas de fácil convivencia. Es una fantasía porque es una ilusión. La realidad es un caos y somos nosotros con nuestras leyes y nuestras tablas los que creamos la ficción de orden. Es un deseo. Y es una fantasía porque es bonito. Porque así entendemos la belleza. Por eso el orden es un deseo de belleza autocumplido.
Los grandes hitos del conocimiento, entre ellos la Tabla Periódica de los Elementos, tienen algo en común: nos hablan de nosotros. Todos ellos revelan la pasta de la que estamos hechos.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo El orden es una fantasía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los cuantificadores se aprenden en el mismo orden, sea cual sea la lengua
- Los 880 cuadrados mágicos de orden 4 de Frénicle
- #Naukas15 Fantasía en la divulgación: una estrella para Cervantes
Personas famosas que estudiaron matemáticas: música y deporte
En mi anterior entrada de la sección Matemoción del Cuaderno de Cultura Científica estuvimos hablando de personas que han sido famosas en diferentes ámbitos de la sociedad y la cultura, en concreto, nos centramos en el mundo de la literatura y el cine, pero que se graduaron en matemáticas, e incluso realizaron un doctorado, Personas famosas que estudiaron matemáticas: literatura y cine. En esta entrada vamos a continuar mostrando ejemplos de otros dos ámbitos de la sociedad muy alejados el uno del otro, y a priori también del mundo de las matemáticas, como son la música y el deporte.
Efectivamente, dentro de la música también nos encontramos personas que sorprendentemente están relacionadas con las matemáticas. Uno de los más conocidos es el músico estadounidense Art Garfunkel, del famoso dúo musical Simon and Garfunkel, que fueron muy populares en la década de 1960. Algunas de sus canciones más conocidas son The sound of silence (el sonido del silencio), Mrs Robinson (Señora Robinson) o Bridge over troubled water (Puente sobre aguas turbulentas). Simon y Garfunkel empezaron a cantar juntos en 1955, bajo el nombre de Tom y Jerry (como los dibujos animados), pero fue en 1963 cuando inician el dúo Simon and Garfunkel, con el que estuvieron en activo hasta su separación en 1970, aunque se volverían a reunir para conciertos puntuales en varias ocasiones.
 Fotografía de Simon and Garfunkel en un concierto en Rotterdam (Holanda) en 1982, realizada por Rob Bogaerts, de la Agencia de Fotografía ANEFO. Imagen de Wikimedia Commons
Fotografía de Simon and Garfunkel en un concierto en Rotterdam (Holanda) en 1982, realizada por Rob Bogaerts, de la Agencia de Fotografía ANEFO. Imagen de Wikimedia CommonsArthur (Art) Garfunkel (Nueva York, 1941) estudió en la Universidad de Columbia. Se graduó en Historia del Arte y obtuvo el master en Matemáticas, en 1967. Empezó a realizar su tesis doctoral sobre enseñanza de las matemáticas, pero la música le desvió de ese camino. Tras la ruptura del dúo, en 1970, Garfunkel además de intentar iniciar su carrera en solitario en la música, estuvo dando clase de geometría en un instituto de secundaria en Connecticut durante dos años. Fue una pequeña laguna docente en su larga vida profesional, en la que compaginaría su trabajo como cantante, actor y poeta. En algunas entrevistas habla de ese corto período como docente de geometría, como un momento “extraño”, ya que había alcanzado un enorme éxito en el mundo de la música, con Simon and Garfunkel, y ahora enseñaba matemáticas en un instituto. Por ejemplo, comenta “Yo intentaba explicarles un problema de matemáticas y cuando les decía si tenían alguna pregunta, ellos me preguntaban cómo eran los Beatles”.
Pero vayamos a un cantante más actual, el músico inglés Jon Buckland¸ guitarrista y fundador del grupo Coldplay, conocido por álbumes como Parachutes (2000), A Rush of Blood to the Head (2002), X&Y (2005) o Viva la Vida or Death and all his Friends (2008).
Jon Buckland (Londres, 1977) estudió astronomía y matemáticas en el University College de Londres, allí conoció al otro miembro de la banda Chris Martin, quien estudiaba Cultura Antigua, se hicieron amigos y juntos montarían la banda Coldplay. Algunos títulos de la banda hacen referencia a las matemáticas, como Twisted Logic, Square One, Proof, Major Minus y 42.
 Jonny Buckland, en el concerto de Coldplay en el Fuji Rock Festival (2011), en Niigata (Japan). Fotografía de Christopher Johnson, en Wikimedia Commons, originalmente en Flickr
Jonny Buckland, en el concerto de Coldplay en el Fuji Rock Festival (2011), en Niigata (Japan). Fotografía de Christopher Johnson, en Wikimedia Commons, originalmente en FlickrOtro de los músicos muy conocidos relacionados con las matemáticas, aunque más con la astrofísica, es el músico británico Brian May, guitarrista y compositor de la banda de rock QUEEN. Algunas de las grandes canciones de esta mítica banda están firmadas por Brian May, como “Now I’m Here”, “We Will Rock You”, “Fat Bottomed Girls”, “Save Me”, “Flash”, “Hammer to Fall”, “Who Wants to Live Forever”, “I Want It All”, “The Show Must Go On”, “Headlong”, “Too Much Love Will Kill You” o “No-One but You (Only the Good Die Young)”.
 Brian May, junto a Freddy Mercury y John Deacon, en el concierto de New Heaven de noviembre de 1977. Fotografía de Carl Lender, en Wikimedia Commons, originalmente en Flickr
Brian May, junto a Freddy Mercury y John Deacon, en el concierto de New Heaven de noviembre de 1977. Fotografía de Carl Lender, en Wikimedia Commons, originalmente en FlickrBrian H. May (Londres, 1947) estudió matemáticas y física en el Imperial College de Londres, graduándose en física en 1968. Empezó su tesis doctoral en astrofísica en 1971 (realizó sus primeras observaciones del espacio, para su tesis, en el observatorio del Teide en Tenerife), pero la música se cruzó en su camino y abandonó su carrera científica. Aunque no de forma definitiva, ya que la retomaría treinta años más tarde, terminando su tesis doctoral en 2007.
Participó en varias ocasiones en el programa de televisión The Sky at Night, presentado por Sir Patrick Moore, con quien ha publicado un libro de astronomía en 2012, Bang! The complete history of the Universe.
Seguimos añadiendo personajes dentro del mundo de la música. El compositor minimalista estadounidense Philip Glass, quien ha compuesto más de 20 óperas, entre ellas La Bella y la Bestia (1994), Einstein on the Beach (1976), en la cual los números son muy importantes, solo se cantan en ella números y nombres de notas musicales, o sus óperas Galileo Galilei (2002) y Kepler (2009), un montón de bandas sonoras de películas, entre ellas Kundun (1997), de Martin Scorsese, El show de Truman (1998), de Peter Weir, Las horas (2002), de Stephen Daldry o El ilusionista (2006), de Neil Burger, así como muchos otros álbumes, por ejemplo, de composiciones para piano, entre otras. Su música se enmarca dentro del estilo de música New Age.
 Philip Glass, en cuatro momentos, durante un concierto en Aarhus (Dinamarca), en 2017. Fotografía de Hreinn Gudlaugsson, en Wikimedia Commons
Philip Glass, en cuatro momentos, durante un concierto en Aarhus (Dinamarca), en 2017. Fotografía de Hreinn Gudlaugsson, en Wikimedia CommonsCon 15 años, Philip Glass (Baltimore, Maryland, 1937) empezó a estudiar matemáticas y filosofía en la Universidad de Chicago, y se graduó a los 19 años. En una entrevista sobre la ópera Einstein on the Beach a Philip Glass, quien compuso la música y el texto, y a Robert Wilson, director y productor de la ópera, este contó que cuando se conocieron le preguntó a Philip Glass como componía y este le puso un ejemplo de una fórmula matemática. Y es que las matemáticas son importantes en la obra de Philip Glass, puesto que suele utilizar estructuras matemáticas para componer algunas de ellas.
La cantante estadounidense Barbara Hendricks, soprano lírica y también cantante de jazz, que en los últimos 20 años es también conocida por su activismo por los derechos humanos, se graduó en matemáticas y en química en la Universidad de Nebraska-Lincoln. Cuando en 2009 estuvo en Bilbao, en una entrevista afirmó lo siguiente:
“Las matemáticas sirven para todo en la vida, ya que te enseñan a razonar, a resolver problemas. Pero sobre todo me han dado disciplina para mí misma, una disciplina que no es para nada opresiva, sino que me facilita ser libre”.
 Fotografía, realizada por Anders Henrikson, de Barbara Hendricks en un concierto en Estocolmo (Suecia), en 2014. Imagen de Wikimedia Commons
Fotografía, realizada por Anders Henrikson, de Barbara Hendricks en un concierto en Estocolmo (Suecia), en 2014. Imagen de Wikimedia CommonsUna opinión diferente de las matemáticas tiene la cantante británica ESKA. Nacida en Londres (1971), pero cuya familia procedía de Zimbabue, Eska Mtungwazi estudió el grado de matemáticas en la prestigiosa London School of Economics. En esa época ya empezó a adentrarse en el mundo de la música, pero la presión por tener una carreara más convencional la llevó a empezar un master en matemáticas y estadística, después en enseñanza de las matemáticas, antes de empezar a trabajar como maestra de educación primaria.
Ella les da poca importancia a sus estudios de matemáticas. En una entrevista en la Revista Yorokobu afirma:
“La educación superior no tiene por qué ser ilustradora, esa educación sirve si ayuda a la persona a seguir interesada en aprender. Yo estoy agradecida a mis padres por haberme facilitado esa educación superior, eso lo llevo conmigo, pero, claro, ¿hasta qué punto tiene esto que ver con lo que estoy haciendo ahora?”.
 Portada del álbum ESKA (2015), de la cantante británica ESKA
Portada del álbum ESKA (2015), de la cantante británica ESKAEl compositor y letrista estadounidense Stephen Sondheim, conocido y premiado, en particular, por sus contribuciones al género del musical, aunque no posee un título en matemáticas, si está muy relacionado con esta ciencia. Stephen Sondheim ha recibido un Oscar de la Academia (por la canción Sooner or Later de la película Dick Tracy, interpretada por Madonna), 8 premios Tony de teatro (por musicales como A Funny Thing Happened on the Way to the Forum, Companies, Follies, A Little Night Music o Sweeney Todd, y uno a toda su carrera), 8 premios Grammy de la academia de la música, un Pulitzer (por el drama Sunday in the Park with George), y muchos premios más.
 Fotografía de Stephen Sondheim de alrededor de 1970 y cartel de la obra musical Sweeney Todd, el barbero diabólico de la calle Fleet, de la producción del National Youth Music Theatre, en el Teatro Rose de Kingston, Nueva York, en 2011. Imágenes de Wikimedia Commons
Fotografía de Stephen Sondheim de alrededor de 1970 y cartel de la obra musical Sweeney Todd, el barbero diabólico de la calle Fleet, de la producción del National Youth Music Theatre, en el Teatro Rose de Kingston, Nueva York, en 2011. Imágenes de Wikimedia CommonsLas matemáticas, así como los problemas y juegos de ingenio, fueron su primera pasión en su juventud, antes que la música, aunque ya tocaba el piano desde niño, y la literatura.
Stephen Sondheim empezó a estudiar el grado de matemáticas en el Williams College, de Williamson, Massachusetts, pero pronto empezó a interesarse solo por la música a raíz de un curso de música del primer cuatrimestre en el que se había matriculado y abandonó las matemáticas. En una entrevista sobre esos años afirma “Yo era matemático por naturaleza, y aún lo soy, pero sabía que no quería ser matemático”. Aunque en otra entrevista afirma en relación a las matemáticas, quizás por esa parte natural matemática que llevaba dentro, “me habría encantado trabajar en el teorema de Fermat”.
Y existen muchos más ejemplos, como el trompetista estadounidense de los años 1950, Clifford Brown, quien se graduó en matemáticas en el Delaware State College y en música en el Maryland State College; el músico canadiense Dan Snaith, cuyos nombres artísticos son Caribou, Manitoba o Daphni, realizó su tesis doctoral (cuyo título era Overconvergent Siegel Modular Symbols) sobre temas de álgebra, bajo la dirección del matemático Kevin Buzzard, en el Imperial College de Londres; el guitarra y vocalista del grupo de punk californiano Angry Samoans, Greg Turner, se graduó en matemáticas Claremont Graduate University e imparte clases de matemáticas en la New Mexico Highlands University; o el cantante y compositor, Phil Alvin, de la banda de rock and roll formada en 1978 en California, The Blasters, obtuvo su grado de master en matemáticas e inteligencia artificial en la California State University, en Long Beach, y después realizó su tesis doctoral en UCLA, donde también impartió clases de matemáticas. Incluso, hubo quien empezó, pero se quedó en el camino, como la cantante Carole King, que realizó solo un año de matemáticas.
 La cantante Carole King interpretando la canción “(You Make Me Feel Like) A Natural Woman” en el Madison Square Garden de Nueva York. Fotografía de Jonathan Schilling, en Wikimedia Commons
La cantante Carole King interpretando la canción “(You Make Me Feel Like) A Natural Woman” en el Madison Square Garden de Nueva York. Fotografía de Jonathan Schilling, en Wikimedia CommonsPara terminar con la música me gustaría añadir a la pionera de la música electrónica Delia Derbyshire. La música y compositora británica Ann Delia Derbyshire (1937-2001) obtuvo una beca para estudiar matemáticas en el Girton College de la Universidad de Cambridge, y finalmente se graduaría en matemáticas y música. Y salvo tres meses dando clases de matemáticas y música para el cónsul general británico en Ginebra, no volvería a tener relación con el mundo académico matemático.
Sin embargo, su relación con las matemáticas no termina ahí, ya que estas eran fundamentales para la composición de sus obras, como ella misma afirmaba en una de las pocas entrevistas que concedió. Por ejemplo, utilizó la sucesión de Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, 34, … para la creación de sus composiciones (para información sobre esta sucesión pueden leerse las entradas Póngame media docena de fibonaccis o El origen poético de la sucesión de Fibonacci, entre otras).
 La música y compositora Delia Derbyshire. Imagen de la página web Mujeres y música
La música y compositora Delia Derbyshire. Imagen de la página web Mujeres y músicaTambién nos encontramos en este grupo de personas relacionadas con las matemáticas a algunos deportistas.
Empecemos con un ejemplo curioso, ya que fue una persona conocida tanto dentro del fútbol, como de las matemáticas, es el danés Harald Bohr (1887-1951), hermano del premio Nobel de Física, Niels Bohr.
Harald Bohr estudió matemáticas en la Universidad de Copenhague, donde se licenció en 1909 y obtuvo su doctorado un año más tarde. Su área de trabajo fue el Análisis Matemático. Empezó estudiando, para su tesis doctoral, la conocida serie de Dirichlet, luego en colaboración con el matemático alemán Edmund Landau obtuvo el conocido como teorema de Bohr-Landau y fundó, junto con el matemático inglés G. H. Hardy, el campo de las funciones casi periódicas. Entre 1915 y 1930 fue profesor en Universidad Tecnológica de Dinamarca y después catedrático en la Universidad de Copenhague, durante 21 años, hasta su muerte.
 Fotografía de la asistencia al International Congress of Mathematicians de Zurich en 1932, entre la que se encuentra Harald Bohr (rodeado en azul). Imagen de Wikimedia Commons
Fotografía de la asistencia al International Congress of Mathematicians de Zurich en 1932, entre la que se encuentra Harald Bohr (rodeado en azul). Imagen de Wikimedia CommonsPero resulta que además de un buen matemático, fue un buen jugador de fútbol. En 1903, con dieciséis años, debutó en el club Akademisk Boldklub, del norte de Copenhague. En 1908 fue seleccionado para jugar con la selección danesa de fútbol en los Juegos Olímpicos de Londres, donde obtuvieron la medalla de plata. Volvería a jugar con la selección danesa en 1910 contra Inglaterra. Se convirtió en una celebridad como jugador de fútbol, hasta el punto de que cuando defendió su tesis doctoral dentro del público asistente a la misma había más fans de fútbol que personas del ámbito de las matemáticas.
 Fotografía del equipo danés de fútbol que compitió en los Juegos Olímpicos de Londres en 1908. El matemático Harald Bohr es el segundo, empezando por la izquierda, de la fila superior. Imagen de Wikimedia Commons
Fotografía del equipo danés de fútbol que compitió en los Juegos Olímpicos de Londres en 1908. El matemático Harald Bohr es el segundo, empezando por la izquierda, de la fila superior. Imagen de Wikimedia CommonsEl jugador inglés de fútbol Glen Johnson (Greenwich, Londres, 1984), quien jugó, entre los años 2002 y 2019, en seis clubs ingleses distintos, entre ellos el Chelsea y el Liverpool, y fue internacional en 54 partidos, entre ellos, los mundiales de Sudáfrica (2010) y Brasil (2014), empezó en 2012, en paralelo a su carrera en el fútbol, a estudiar el grado de matemáticas en la Open University, la universidad a distancia.
 Fotografía del jugador inglés Glen Johnson en 2011, cuando jugaba con el Liverpool. Imagen de Badudoy en Wikimedia Commons
Fotografía del jugador inglés Glen Johnson en 2011, cuando jugaba con el Liverpool. Imagen de Badudoy en Wikimedia CommonsEl exfutbolista camerunés, nacionalizado francés, Jean-Alain Boumsong (Douala, Camerún, 1979), que jugó en diferentes clubes europeos, como el francés Le Havre, el Glasgow Rangers escocés, el Newcastle United inglés, la Juventus de Turín, el Olympique de Lyon, y el Panathinaikos, así como en la selección francesa, se graduó en matemáticas por la Universidad de Le Havre.
Casi podríamos decir que también se graduó en matemáticas el mítico jugador de baloncesto de la NBA Michael Jordan (Nueva York, 1963), jugador de los Chicago Bulls, quizás el mejor jugador de baloncesto de la NBA de la historia, ya que empezó el grado de matemáticas, pero lo abandonó en su penúltimo año. Aunque sí terminó sus estudios de matemáticas el también jugador de baloncesto de la NBA David Robinson, apodado “el almirante”, que jugó durante 14 temporadas en los San Antonio Spurs. Al terminar del instituto, David Robinson ingresó en la Academia Naval de Estados Unidos, donde se graduó en matemáticas.
 Fotografía de uno de los míticos mates del jugador de Baloncesto de la NBA, de los Chicago Bulls, Michael Jordan
Fotografía de uno de los míticos mates del jugador de Baloncesto de la NBA, de los Chicago Bulls, Michael JordanUn jugador de baloncesto español que también es matemático es el alicantino Sergio Olmos (Elda, 1986). En un curso de verano Xpheres College, para profesionales del Baloncesto, Sergio Olmos se presentaba como “el matemático más alto del mundo” y es que este jugador de baloncesto, de 2,13 metros de altura, se graduó en matemáticas en la Universidad de Temple en Philadelphia, a donde se marchó con 17 años para continuar su carrera dentro del baloncesto. Después de los cuatro años jugando a baloncesto en la Universidad de Temple, y estudiando matemáticas, continuó su carrera de baloncesto en España, jugando en diferentes clubs, como el Valencia Basket, el Club Basquet Coruña o la Fundación Club Baloncesto Granada, en el que juega en la actualidad. Sin embargo, no abandonaría su carrera académica. Interesado por la estadística se graduó en Ciencias Económicas y Matemáticas en la británica Open University y realizó Máster de Bioestadística y Bioinformática de la Universitat de Barcelona. La empresa de bioestadística y estadística aplicada Biostatech, le incluye en su página web como uno de sus colaboradores. Y recientemente ha empezado a escribir un blog sobre matemáticas llamado Mínimos cuadrados.
 El jugador de Baloncesto Sergio Olmos, hacia el año 2016, jugando en el Club Basquet Coruña
El jugador de Baloncesto Sergio Olmos, hacia el año 2016, jugando en el Club Basquet CoruñaEl jugador de fútbol americano John Urschel que jugó en la NFL en los Baltimore Ravens, durante tres temporadas hasta que se retiró en 2017. Por otra parte, se graduó en matemáticas en la Universidad Estatal de Pensilvania (Penn State University) en 2012, y obtuvo el grado de master en 2013. En 2014 entró como profesor adjunto en esa misma universidad, donde continúa trabajando y en 2016 empezó a realizar su tesis doctoral en el MIT (Instituto Tecnológico de Massachusetts), sobre teoría de grafos espectral, álgebra lineal numérica y machine learning (aprendizaje automático).
Su primer artículo fue “Inestabilidades en el problema de los tres cuerpos de Sol-Jupiter-Asteroide” publicado en 2013 en la revista Celestial Mechanics and Dynamical Astronomy. Ha día de hoy, ya tiene 11 artículos publicados en revistas de investigación. Tiene número de Erdös 4. Recordemos que el número de Erdös es la distancia, en co-autoría de artículos de investigación matemática entre una persona que investiga en esta ciencia y el matemático húngaro Paul Erdös (1913-1996), así él mismo tiene número de Erdös 0, alguien que ha publicado un artículo con Erdös tiene número de Erdös 1, quien ha publicado con una persona con número de Erdös 1, tiene número de Erdös 2, y así se continúa (para más información El número de Erdös-Bacon-Sabbath).
 Fotografías de John Urschel, una como jugador de futbol americano en los Baltimore Ravens en 2015 (fotografía de Jeffrey Beall en Wikimedia Commons) y la otra frente a una pizarra en la Tufts University en 2018 (fotografía del propio John Urschel, en Wikimedia Commons)
Fotografías de John Urschel, una como jugador de futbol americano en los Baltimore Ravens en 2015 (fotografía de Jeffrey Beall en Wikimedia Commons) y la otra frente a una pizarra en la Tufts University en 2018 (fotografía del propio John Urschel, en Wikimedia Commons)Aunque no es el único jugador de fútbol americano con un grado en matemáticas. Por ejemplo, el jugador de los New York Giants y los Carolina Panthers, y en la actualidad entrenador de este último equipo, Chase Blackburn (Ohio, 1983), se graduó en matemáticas en la Universidad de Akron, en Ohio. O el jugador de las décadas de 1950 y 1960, Frank Ryan (Texas, 1936), que jugó en los equipos Los Ángeles Rams, Cleveland Browns o Washington Redskins, no solo es doctor en matemáticas por la Universidad de Rice (el título de su tesis doctoral es “A Characterization of the Set of Asymptotic Values of a Function Holomorphic in the Unit Disc”), sino que continuó su carrera como profesor e investigador en matemáticas, y tiene número de Erdös igual a 3.
Terminamos con otro deporte, como es el tenis. La tenista británica Virginia Wade, que ganó el torneo abierto de EEUU en 1968, el abierto de Australia en 1972 y el torneo de Wimbledon en 1977, estudió matemáticas y física en la Universidad de Sussex.
 Fotografía de Virginia Wade jugando al tenis. Imagen de la página web de la BBC
Fotografía de Virginia Wade jugando al tenis. Imagen de la página web de la BBC Estos no son todos los ejemplos que existen, pero es una buena muestra.
Bibliografía
1.- Entrada en la Wikipedia sobre Art Garfunkel
2.- Página web de Art Garfunkel
3.- Entrada en la Wikipedia sobre Jon Buckland
4.- Entrada en la Wikipedia sobre Brian May
5.- Página web de Philip Glass
6.- Entrada en la Wikipedia de Philip Glass
7.- Marta Macho, Barbara Hendricks y las matemáticas, Mujeres con ciencia, 2014.
8.- Página web de ESKA
9.- Entrada en la Wikipedia de Delia Derbyshire
10.- Página web de Delia Derbyshire
11.- Entrada en la Wikipedia de Harald Bohr
12.- Entrada en la Wikipedia de Glen Johnson
13.- Entrada en la Wikipedia de Jean-Alain Boumsong
14.- Entrada en la Wikipedia de Michael Jordan
15.- Entrada en la Wikipedia de John Urschel
16.- Entrada en la Wikipedia de Sergio Olmos
17.- Entrada en la Wikipedia de Virginia Wade
18.- David Richeson, Look who majored in mathematics, blog Division by zero, 2009.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Personas famosas que estudiaron matemáticas: música y deporte se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Personas famosas que estudiaron matemáticas: literatura y cine
- Con ‘n’, música ‘casi’ infinita
- Las dos culturas de las matemáticas: construir teorías o resolver problemas
La velocidad finita de la luz
 Ío con Júpiter de fondo. Fuente: NASA
Ío con Júpiter de fondo. Fuente: NASADado que podemos considerar que la luz viaja en línea recta, ¿podemos decir a qué velocidad lo hace? Galileo abordó este problema en sus Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze, publicado en 1638. Señaló que las experiencias cotidianas podrían llevarnos a concluir que la luz se propaga instantáneamente. Pero que estas experiencias, cuando se analizan más de cerca, solo muestran que la luz viaja mucho más rápido que el sonido. Por ejemplo, “cuando vemos disparar una pieza de artillería a gran distancia el destello llega a nuestros ojos sin que transcurra tiempo; pero el sonido llega al oído solo después de un intervalo perceptible”.
Pero, ¿cómo sabemos realmente si la luz se movió “sin que transcurra tiempo” a menos que tengamos alguna forma precisa de medir el lapso de tiempo? Galileo continúa describiendo un experimento mediante el cual dos personas que se encontrasen en colinas distantes y usando linternas podrían medir la velocidad de la luz. Concluyó que la velocidad de la luz era probablemente finita, no infinita. Galileo, sin embargo, no estima un valor definido concreto.
Las pruebas experimentales se relacionaron con éxito por primera vez con una velocidad finita para la luz por un astrónomo danés, Ole Rømer. Las observaciones detalladas de los satélites de Júpiter habían mostrado una irregularidad inexplicable en los tiempos registrados entre los eclipses sucesivos de los satélites por el planeta. Se esperaba que un eclipse del satélite Ío ocurriera exactamente 45 s después de las 5:25 de la mañana del 9 de noviembre de 1676 (calendario juliano). En septiembre de ese año, Rømer anunció a la Academia de Ciencias de París que el eclipse observado llegaría 10 minutos tarde. El 9 de noviembre, los astrónomos del Observatorio Real de París estudiaron cuidadosamente el eclipse. Aunque escépticos, informaron que el eclipse ocurrió tarde, tal como lo había previsto Rømer.
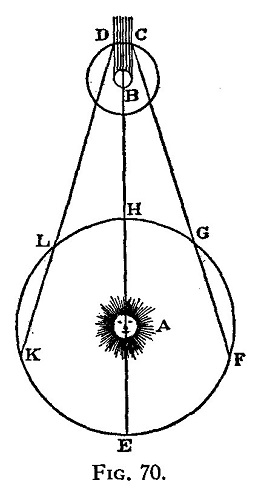 Ilustración empleada por Rømer en su informe Demonstration tovchant le mouvement de la lumiere trouvé par M. Römer de l’ Academie Royale des Sciences, fechado el 7 de diciembre de 1676. A: Sol; B: Júpiter; DC: Ío
Ilustración empleada por Rømer en su informe Demonstration tovchant le mouvement de la lumiere trouvé par M. Römer de l’ Academie Royale des Sciences, fechado el 7 de diciembre de 1676. A: Sol; B: Júpiter; DC: ÍoMás tarde, Rømer reveló la base teórica de su predicción a los desconcertados astrónomos en la Academia de Ciencias. Explicó que el tiempo originalmente esperado del eclipse se había calculado a partir de observaciones hechas cuando Júpiter estaba cerca de la Tierra. Pero ahora Júpiter se estaba más lejos. El retraso en el eclipse ocurrió simplemente porque la luz procedente de las inmediaciones de Júpiter, donde ocurría el eclipse, necesita un tiempo para llegar a la Tierra. Obviamente, este intervalo de tiempo debe ser mayor cuando la distancia relativa entre Júpiter y la Tierra en sus órbitas es mayor. De hecho, Rømer estimaba que la luz necesita alrededor de 22 minutos para cruzar la propia órbita de la Tierra alrededor del Sol.
Poco después, el físico holandés Christian Huygens utilizó los datos de Rømer para realizar el primer cálculo de la velocidad de la luz. Huygens combinó el valor de Rømer de 22 minutos para que la luz cruzara la órbita de la Tierra con su propia estimación del diámetro de la órbita de la Tierra. Huygens obtuvo un valor para la velocidad de la luz en el espacio que, en unidades modernas, es de aproximadamente 200.000 km/s. Esto es, aproximadamente dos tercios del valor actualmente aceptado. El error en el valor de Huygens se debió principalmente a que Rømer sobrestimó el intervalo de tiempo. Ahora sabemos que la luz solo necesita unos 16 minutos para cruzar la órbita de la Tierra.
La velocidad de la luz se ha medido de muchas maneras diferentes desde el siglo XVII. El desarrollo de dispositivos electrónicos en el siglo XX permitió mediciones muy precisas, haciendo de la velocidad de la luz una de las constantes físicas medidas con mayor precisión. Debido a la importancia del valor de la velocidad de la luz en las teorías físicas modernas*, en la actualidad su valor no se mide, sino que está definido a consecuencia de la definición de metro y es, exactamente, de 299,792,458 metros por segundo. La velocidad de la luz suele estar representada por el símbolo c.
Nota:
* Sobre esto puedes leer La velocidad de las ondas electromagnéticas y la naturaleza de la luz de la serie Electromagnetismo y El principio de constancia de la velocidad de la luz de la serie Teoría de la invariancia
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La velocidad finita de la luz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El principio de constancia de la velocidad de la luz
- La velocidad de las ondas electromagnéticas y la naturaleza de la luz
- La relatividad del tiempo (y 3)
¿Por qué son tan grandes las ballenas?
 Escultura metálica de “Bluebelle”, una ballena azul capturada en el Atlántico sur en 1912, expuesta en la ribera del Sena durante la Cumbre del Clima de París en 2015. Fuente: Bluebird Marine Systems
Escultura metálica de “Bluebelle”, una ballena azul capturada en el Atlántico sur en 1912, expuesta en la ribera del Sena durante la Cumbre del Clima de París en 2015. Fuente: Bluebird Marine SystemsComo miembro de una especie que habitualmente se cree el centro del universo, considero personalmente muy importante recibir de vez en cuando una bofetada de humildad ecológica. Una cosa que nunca falla, son las ballenas. Pensar en esos enormes mamíferos viviendo (o, bueno, sobreviviendo) en la inmensidad del océano siempre me recuerda lo insignificante que soy.
Y sin embargo, no tenía ni idea hasta hace poco de cómo las ballenas se hicieron tan grandes, ni por qué. Ni siquiera me lo había preguntado hasta que me topé con la respuesta. Por eso yo soy periodista científica, y no científica, supongo. No me hago las preguntas, pero me encanta contar las respuestas. Aquí voy con esta respuesta, por si ustedes tampoco la conocen.
¿Cuándo se hicieron enormes las ballenas?
No tenemos del todo claro cómo las ballenas se hicieron tan enormes, si les tengo que ser sincera, aunque es un debate abierto desde hace tiempo. En 2010, Graham Slater, biólogo evolucionista de la Universidad de Chicago, propuso una hipótesis según la cual los cetáceos (ballenas y delfines) se dividieron en grupos de distintos tamaños muy pronto en su evolución, hace aproximadamente 30 millones de años. En ese momento, los delfines quedaron como los más pequeños de la familia, las ballenas barbudas se convirtieron en gigantes y los zifios evolucionaron a un tamaño intermedio. Los tres grupos y sus descendientes se han mantenido más o menos estables en esos rangos de tiempo.
No todo el mundo está de acuerdo con esta teoría. Nicholas Pyenson, del Museo de Historia Natural perteneciente al Smithsonian, en Washington, decidió utilizar la enorme colección de fósiles del museo para aclarar las dudas. Tras determinar que el tamaño total de una ballena se puede inferir del tamaño de los huesos de su mandíbula, midió o obtuvo ese dato de los cráneos de 63 especies de ballena ya extinta, además de 13 especies actuales, y las fue colocando en una línea temporal que mostrase la evolución del árbol familiar de las ballenas.
Los datos obtenidos demostraban que las ballenas no aumentaron de tamaño tan pronto como Slater había sugerido en un principio, y también que no fue algo progresivo en el tiempo, sino que se habían vuelto moderadamente grandes y se habían mantenido así durante millones de años hasta hace unos 4,5 millones de años, según un estudio que publicaron después conjuntamente Pyenson, Slater y Jeremy Goldberg, de la Universidad de Stanford en Palo Alto.
En ese momento pasaron de relativamente grandes a gigantescas. La ballena azul que conocemos a día de hoy mide hasta 30 metros de largo, mientras que hace 4,5 millones de años las ballenas más grandes que existían medían solamente 10 metros.
¿Cómo fue posible?
Vale, ya sabemos cuándo. ¿Cómo pasó esto? Slater y compañía pasaron entonces a estudiar qué estaba ocurriendo en el mundo en aquel momento para que tuviese lugar este importante cambio de tamaño en las ballenas. Descubrieron que el estirón coincidió con el principio de la primera edad de hielo. En ese momento en que los glaciares se expandían, los deshielos de primavera y verano vertían enormes cantidades de nutrientes a las costas oceánicas que causaron una proliferación masiva del krill, los organismos microscópicos de los que se alimentan las ballenas.
Esto creó un nuevo patrón de alimentación: los deshielos estacionales creaban épocas de comida abundante separadas a lo largo del año, disponible para aquellos que pudiesen aprovecharla y con menos competencia debido a la desaparición de muchos otros peces y animales marinos.
Esto fue una ventaja para las ballenas: las ballenas que se alimentan cazando krill y filtrando el agua a través de sus barbas podían en este ambiente alimentarse de forma más eficiente que otros competidores. Y cuando mejor alimentadas, más grandes y rápidas eran para desplazarse de una zona de caza a otra.
¿Por qué ese tamaño gigantesco?
Quizá ahora sepamos un poco mejor, aunque todavía no de forma definitiva, cuándo y cómo las ballenas se hicieron descomunales, pero ¿por qué?
Tampoco aquí la respuesta está del todo clara. Algunos expertos postulan que pudo ser una respuesta evolutiva a los ataques de los megatiburones que poblaron los océanos hace millones de años. Pero la mayoría de las hipótesis se centran en el agua como un medio liberador: con la gravedad atenuada, los cuerpos de los mamíferos marinos, especialmente los de las ballenas, son capaces de manejar muchas más toneladas de peso. Además, es más fácil acceder a grandes territorios donde alimentarse y el menú es más variado.
Sin embargo, esta idea del océano como liberación también tiene sus detractores, y en 2018, William Gearty, de la Universidad de Stanford, propuso una explicación diferente: las ballenas y otros mamíferos marinos son tan grandes no por el alivio que el agua pone a sus limitaciones, sino porque impone otras nuevas.
A medida que entras en el agua, empiezas a perder un calor corporal que no estabas perdiendo sobre la tierra, y la forma más eficiente contrarrestar esa pérdida de temperatura es volverse más grande: a medida que crece cuerpo de un animal (de estos animales marinos concretamente cuyo cuerpo tiende a adoptar la forma de un globo), el volumen aumenta más rápido que su superficie, de forma que se genera más calor, pero se pierde menos en comparación. Claro que el volumen de un animal no puede aumentar infinitamente, ya que un cuerpo mayor también requiere más alimento, y hay un límite en la comida que un animal puede encontrar, atrapar y comer.
Según esta teoría, el tamaño de una especie se encuentra limitada por abajo por su necesidad de mantenerse caliente (demasiado pequeño y perderá demasiado calor) y por arriba por su necesidad de alimentarse (demasiado grande y no podrá comer lo suficiente). Y ese límite es mucho más estrecho en el mar que en la tierra, según el científico, que calculó que los mamíferos marinos (focas, cetáceos, manatíes…) han alcanzado de forma independiente una masa media óptima de unas 5 toneladas.
Las ballenas y las focas, en los extremos
Espera, ¿qué? ¿5 toneladas? Pero eso está muy, muy lejos de las 140 toneladas que puede pesar una ballena azul adulta, el animal más grande del mundo y con el que hemos abierto esta historia.
Sí, bueno, recordemos que se trata de una media. En el otro extremo estarían las focas, que pueden pesar, dependiendo de la especie, entre 100 y 250 kilos aproximadamente en su edad adulta. Diferencias evolutivas y de características podrían explicar como ambas especies han conseguido saltarse esos límites que propone Gearty, cada una por un lado. Las focas tienen una gruesa piel y pelo, y pasan mucho tiempo fuera del agua. Así podrían hacer frente a una pérdida de calor que en principio su pequeño tamaño facilita.
Y las ballenas azules y otras barbadas son los cazadores más eficaces del mundo y, si la explicación de Slater y sus colegas es cierta, supieron aprovechar una oportunidad que pocas especies coetáneas pudieron ver en un momento de rápidos cambios climáticos. Así han podido evolucionar y mantener esos cuerpos masivos allí donde los demás mamíferos marinos han conseguido ser grandes, pero no tanto. Gigantes de verdad, solo ellas.

Referencias:
Diversity versus disparity and the radiation of modern cetaceans – The Royal Society Publishing
Why whales grew to such monster sizes – Science
Energetic tradeoffs control the size distribution of aquatic mammals – Proceedings of the National Academy of Science
Why whales got so big – The Atlantic
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo ¿Por qué son tan grandes las ballenas? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El pueblo que hablaba con las ballenas, ¿podría enseñarnos su idioma a los demás?
- Cómo usar a las ballenas como detectores de radiación
- Eran nuestras ballenas

