Los riesgos dormidos: lo que usted debería saber

Si cerrásemos los ojos para visualizar la imagen de un geólogo, probablemente imaginaríamos a una persona descubriendo fósiles y recopilando y coleccionando minerales. No obstante, esta disciplina académica cuenta con muchísimas más aplicaciones desconocidas para gran parte de la sociedad.
Con el objetivo de dar visibilidad a esos otros aspectos que también forman parte de este campo científico nacieron las jornadas divulgativas “Abre los ojos y mira lo que pisas: Geología para miopes, poetas y despistados”, que se celebraron los días 22 y 23 de noviembre de 2018 en el Bizkaia Aretoa de la UPV/EHU en Bilbao.
La iniciativa estuvo organizada por miembros de la Sección de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Ente Vasco de la Energía (EVE-EEE), el Departamento de Medio Ambiente, Planificación Territorial y Vivienda del Gobierno Vasco, el Geoparque mundial UNESCO de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.
Los invitados, expertos en campos como la arquitectura, el turismo o el cambio climático, se encargaron de mostrar el lado más práctico y aplicado de la geología, así como de visibilizar la importancia de esta ciencia en otros ámbitos de especialización.
Virginia Ormaetxea de Harrilur Geotecnia y portavoz del Colegio de Geólogos de Euskadi (EGEO) expone dos de los riesgos geológicos que actualmente pueden afectarnos a cualquiera, cualquier día, debidos a la presión urbanística: los desprendimientos/deslizamientos de tierra y los riesgos asociados a las rocas ácido-sulfatadas.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Los riesgos dormidos: lo que usted debería saber se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Geología: la clave para saber de dónde venimos y hacia dónde vamos
- El (Paleo)Clima y ¿el frío que vendrá?
- #Naukas16 ¿Cómo saber si tu funeraria te estafa?
Espectrometría de masas: de un isótopo de neón a elefantes que vuelan
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebrará dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Durante las próximas semanas en el Cuaderno de Cultura Científica y en Zientzia Kaiera se publicarán regularmente artículos que narren algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas. Comenzamos con la serie “Espectrometría de masas”, técnica analítica que supone el ejemplo perfecto del incesante avance de la Ciencia y la Tecnología.

A principios del siglo XX J. J. Thomson estudiaba el cambio de trayectoria de los iones de ciertos gases sometidos a campos eléctricos y magnéticos. Estos experimentos derivaban del estudio de rayos catódicos que le habían valido el premio Nobel en 1906 y que habían esclarecido la naturaleza del electrón, entonces una partícula subatómica desconocida. Sir Thomson observó que los gases con carga positiva se podían separar en función de su relación masa/carga y que, conociendo el valor del campo eléctrico y magnético aplicado, podría determinar esta relación. En otras palabras, podía saber cuánto pesaban átomos o moléculas. Había nacido la espectrometría de masas.
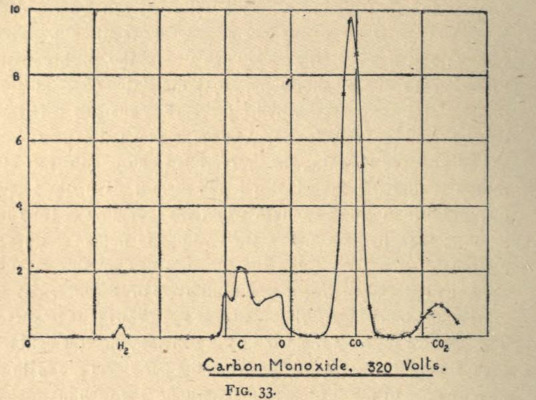 Imagen 1. Espectro del monóxido de carbono (CO), uno de los primeros espectros de masas de la historia. Extraído de Rays of positive electricty and their applications to chemical Analysis de J.J. Thomson (1921). Fuente: Archive.org
Imagen 1. Espectro del monóxido de carbono (CO), uno de los primeros espectros de masas de la historia. Extraído de Rays of positive electricty and their applications to chemical Analysis de J.J. Thomson (1921). Fuente: Archive.orgLa espectrometría de masas es hoy en día la técnica analítica más versátil y potente que disponemos. En campos como el análisis forense, el análisis de alimentos o el estudio de contaminantes nos permite determinar la concentración de compuestos a niveles extremadamente bajos. Además, también sirve para identificar nuevas moléculas, algo que resulta de gran ayuda en el desarrollo de fármacos. Por si esto fuera poco, en el ámbito de la Medicina y la Fisiología está propiciando grandes avances médicos, porque permite estudiar cómo se distribuyen ciertas moléculas en órganos vitales. A lo largo de los artículos que componen esta serie nos adentraremos en este fascinante abanico de aplicaciones. Pero antes, veamos cómo hemos podido llegar a este punto en apenas cien años.
Los primeros pasos
Viajemos hasta la Universidad de Cambridge, donde hemos dejado a Thomson trabajando con su protegido Francis William Aston. A él le debemos el siguiente gran hito en el campo que nos ocupa. En la Imagen 2 podéis observar el tipo de resultados que obtenían con aquellos primitivos espectrómetros de masas, entonces llamados espectrógrafos de parábola. En la placa fotográfica se pueden ver diferentes marcas ordenadas según las diferentes relaciones masa/carga. Aclararemos este concepto diciendo que no es otra cosa que la masa del átomo (o molécula) dividido entre el número de cargas. Por ejemplo, para el ion CO+ es 28 (la suma de la masa atómica* del carbono-12 y la del oxígeno-16 dividida entre uno), para el Hg+ es 200 y para el Hg2+ es 100 (dado que la masa atómica se divide entre dos por la doble carga). Como curiosidad añadiremos que a este parámetro se le asignó la unidad Th (Thomson) en honor al gran científico inglés, pero no ha sido reconocida internacionalmente y los resultados se presentan con el menos poético m/z.
 Imagen 2. Parábolas de diferentes iones capturados en una placa fotográfica. Modificado de Rays of positive electricty and their applications to chemical Analysis de J.J. Thomson (1921). Fuente: Archive.org
Imagen 2. Parábolas de diferentes iones capturados en una placa fotográfica. Modificado de Rays of positive electricty and their applications to chemical Analysis de J.J. Thomson (1921). Fuente: Archive.orgAston observó que junto a la señal que correspondía al ion de neón (20 m/z) aparecía otra pequeña señal (22 m/z) cuyo origen era desconocido. ¿Qué demonios hacía eso ahí? Como bueno científicos, realizaron varios experimentos y fueron descartando hipótesis: no se trataba de moléculas de CO2 con doble carga (44/2) ni de hidruro de neón (NeH2). La misteriosa señal aparecía siempre que se analizaba este gas noble y era nueve veces más pequeña. No había otra explicación: también era neón. En 1913 propusieron que el neón era una mezcla de dos tipos de átomos con diferente masa (20 y 22) en proporción 9 a 1. De ahí la diferencia de intensidad en las señales obtenidas. Y de ahí que el peso atómico logrado para este elemento mediante la medida de la densidad fuese 20,2 (el promedio de las masas teniendo en cuenta su abundancia). Aston había descubierto un nuevo isótopo, término que había acuñado hacía poco Frederick Soddy por sugerencia de Margarett Todd para describir los átomos con propiedades idénticas, pero de diferente masa. Hoy en día nos puede parecer un asunto trivial y cualquiera que tenga unas nociones mínimas de química sabrá que esto se debe al diferente número de neutrones. ¡Pero tened en cuenta que todavía no se había descubierto esa partícula subatómica!
Tras la Gran Guerra, Aston mejoró su instrumento y desarrolló los primeros “espectrógrafos de masas” (Imagen 3) que le permitieron descubrir 212 isótopos naturales. Como premio ganó el Nobel de Química en 1922 (Soddy lo había ganado el año anterior). En esta tierna infancia de la espectrometría de masas no nos podemos olvidar de Arthur Dempster que en la Universidad de Chicago diseñó los primeros espectrómetros de sector magnético en los que se basan muchos de los instrumentos actuales y con los que descubrió el uranio-235.
 Imagen 3. Réplica del tercer espectrómetro de masas desarrollado por Aston: Fuente: Jeff Dahl /Wikimedia Commons.
Imagen 3. Réplica del tercer espectrómetro de masas desarrollado por Aston: Fuente: Jeff Dahl /Wikimedia Commons.
Guerras, avances y difusión
Es, precisamente, el uranio-235 el protagonista de una de las primeras aplicaciones prácticas de la espectrometría de masas. Desgraciadamente. Durante el Proyecto Manhattan, el físico Alfred Nier revolucionó la espectrometría de masas con nuevos instrumentos de sector que permitieron aislar y conocer mejor el isótopo empleado en Little Boy. Pero sería injusto juzgar a Nier por la aplicación que se hizo de sus avances. Este científico fue un visionario que comprendió la importancia de la espectrometría de masas y extendió, en muchas ocasiones de forma altruista, sus usos a campos como la Biología (enriquecimiento de carbono-13) o la Geología (datación isotópica de la corteza terrestre).
Durante los años 40 y los años 50 se realizaron importantes mejoras y aparecieron instrumentos basados en nuevos principios para separar iones. Por su relevancia destacaremos los instrumentos de tiempo de vuelo (Time of Flight) propuestos por W.E. Stephens, en los que la separación se logra por la diferente velocidad a la que se mueven las moléculas al someterlas a un impulso (Imagen 4). Este es el sistema de separación más fácil de visualizar: cuanto más pesada sea la molécula más tiempo tardará en llegar al detector. El otro gran avance fue la creación de los instrumentos tipo cuadrupolo en los que los iones se pueden separar gracias al uso de cilindros que permiten realizar variaciones de corriente continua y radiofrecuencias. Prueba de su importancia es que Wolfgang Paul y Hans Georg Dehmelt obtuvieron el premio Nobel de Física en 1989 por el desarrollo de la trampa iónica, en la que extendieron estos principios en tres dimensiones.
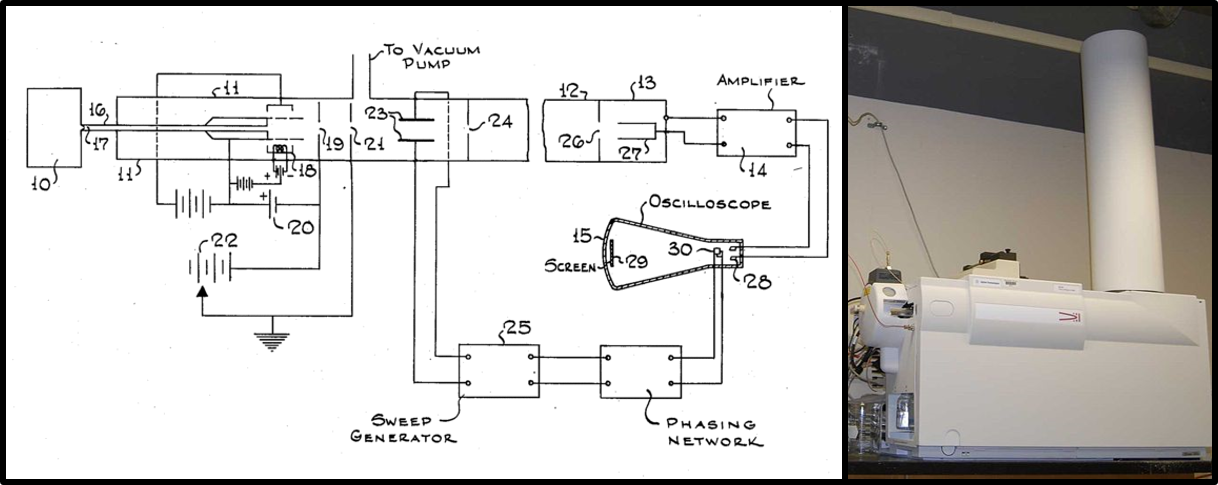 Imagen 4. Patente del espectrómetro tipo tiempo de vuelo de Stephens (1952) y un instrumento actual en el que se observa el “tubo de vuelo”. Fuente: Adaptado de Kkmurray/Wikimedia Commons.
Imagen 4. Patente del espectrómetro tipo tiempo de vuelo de Stephens (1952) y un instrumento actual en el que se observa el “tubo de vuelo”. Fuente: Adaptado de Kkmurray/Wikimedia Commons.Pero no avancemos tan rápido. Los primeros espectrómetros comerciales no recibieron una calurosa acogida. En gran medida por el desconocimiento de la técnica, la mayoría de las aplicaciones eran meramente cuantitativas, como por ejemplo el análisis de hidrocarburos en refinerías de petróleo. Es decir, se usaban para determinar la concentración de algún compuesto conocido en diferentes muestras (tengamos en cuenta que la señal del compuesto es proporcional a su concentración). De ese modo no se explotaba una de las grandes ventajas que ofrece la espectrometría de masas: la identificación de moléculas desconocidas. Conocer la masa molecular de un compuesto es un gran paso para esclarecer su identidad. Y se puede ir más allá. La molécula se puede fragmentar en el instrumento, por lo que también podemos conocer la masa de los fragmentos y elucidar la estructura original como si de un puzle se tratase. Hubo tres científicos que supieron ver esta gran ventaja: Fred McLafferty (conocido por su reordenamiento), Klaus Biemann y Carl Djerassi (aunque lo más fascinante es que Thomson ya había predicho su aplicabilidad para 1913). Gracias a ellos se extendió el uso de la espectrometría de masas en el campo de la química orgánica, aplicándose inicialmente al descubrimiento de alcaloides y esteroides (Djerassi fue uno de los padres de la píldora anticonceptiva). Así posibilitaron, en gran medida, que la espectrometría de masas se convirtiese, junto a la resonancia magnética nuclear, en la herramienta indispensable para conocer la estructura de nuevas moléculas.
El despegue definitivo
La espectrometría de masas empezaba a despuntar, pero todavía existía un enorme problema: ¿Cómo se convierten las moléculas en iones gaseosos? Hasta ahora nos hemos centrado en cómo medir la masa, dejando de lado este importante aspecto. Recordemos que esta técnica mide la relación masa/carga, así que si las moléculas no están ionizadas de poco nos puede servir. Los métodos empleados hasta finales de los 60 no eran aptos para moléculas no volátiles o provocaban la fragmentación total de la molécula causando la pérdida de información sobre la masa molecular. En esas condiciones la mayoría de biomoléculas no podían ser analizadas, especialmente las proteínas de gran tamaño. Hacía falta ir un paso más allá. Y entonces surgieron la Ionización por Electrospray (ESI) y la Ionización/Desorción Laser Asistida por Matriz (MALDI). Así se les puso alas a las “moléculas elefante” como dijo John B. Fenn en su conferencia por el premio Nobel de Química de 2002.
 Imagen 5. Dibujo inspirado por el título de la conferencia por el premio Nobel de John Fenn. Fuente: Realizado por Marianne Steinberg para la National Science Academy [PDF].Fenn compartió una parte del premio Nobel de 2002 con el japonés Koichi Tanaka por el “Desarrollo de métodos de ionización blandos para el análisis mediante espectrometría de masas de macromoléculas biológicas”. El primero fue galardonado por desarrollar la técnica ESI, aunque la invención se la debemos a Malcom Dole en 1968. El principio sobre el que se sustenta este modo de ionización es relativamente sencillo. El disolvente que contiene la muestra atraviesa un capilar al que se le aplica un voltaje para ionizar las moléculas (es decir, ponerles carga positiva o negativa). Al salir, el líquido formará un aerosol (de ahí lo de spray) con la ayuda de un gas de nebulización y, según se vaya evaporando el disolvente, las gotitas serán cada vez más pequeñas. Llega un punto en que las gotas reducen tanto su tamaño que la fuerza de repulsión entre las moléculas cargadas es superior a la tensión superficial y “explotan” (Imagen 6). De este modo se logran iones en forma gaseosa que pueden pasar al analizador de masas. Este tipo de ionización permite analizar multitud de moléculas, incluso con masas moleculares que superan los 100 000 Da. Además, tiene la gran ventaja de emplear disolventes líquidos, lo que hace que sea compatible con una de las técnicas de separación más comunes: la cromatografía líquida.
Imagen 5. Dibujo inspirado por el título de la conferencia por el premio Nobel de John Fenn. Fuente: Realizado por Marianne Steinberg para la National Science Academy [PDF].Fenn compartió una parte del premio Nobel de 2002 con el japonés Koichi Tanaka por el “Desarrollo de métodos de ionización blandos para el análisis mediante espectrometría de masas de macromoléculas biológicas”. El primero fue galardonado por desarrollar la técnica ESI, aunque la invención se la debemos a Malcom Dole en 1968. El principio sobre el que se sustenta este modo de ionización es relativamente sencillo. El disolvente que contiene la muestra atraviesa un capilar al que se le aplica un voltaje para ionizar las moléculas (es decir, ponerles carga positiva o negativa). Al salir, el líquido formará un aerosol (de ahí lo de spray) con la ayuda de un gas de nebulización y, según se vaya evaporando el disolvente, las gotitas serán cada vez más pequeñas. Llega un punto en que las gotas reducen tanto su tamaño que la fuerza de repulsión entre las moléculas cargadas es superior a la tensión superficial y “explotan” (Imagen 6). De este modo se logran iones en forma gaseosa que pueden pasar al analizador de masas. Este tipo de ionización permite analizar multitud de moléculas, incluso con masas moleculares que superan los 100 000 Da. Además, tiene la gran ventaja de emplear disolventes líquidos, lo que hace que sea compatible con una de las técnicas de separación más comunes: la cromatografía líquida.
Por su parte, Tanaka logró ionizar proteínas con un método radicalmente diferente: empleando un láser. Pese a que su mérito como pionero en el uso de la ionización laser es incuestionable, hubo cierta polémica cuando le otorgaron el Premio Nobel. Hay quien piensa que el galardón debería haber recaído en Hillenkamp y Karas, ya que la técnica que actualmente conocemos como MALDI (del inglés Matrix Assisted Laser Desportion/Ionization) fue desarrollada por ellos y difiere en ciertos aspectos de la propuesta por Tanaka. Dejando estos conflictos de lado, sólo queda decir que la técnica MALDI se basa en un sistema de ionización indirecta. A la muestra se le añade una matriz que se ioniza fácilmente con un láser y es esta matriz la que transfiere su carga a las moléculas. Este método de ionización es de un gran interés, especialmente porque permite hacer imágenes de superficies como puede ser un tejido animal.
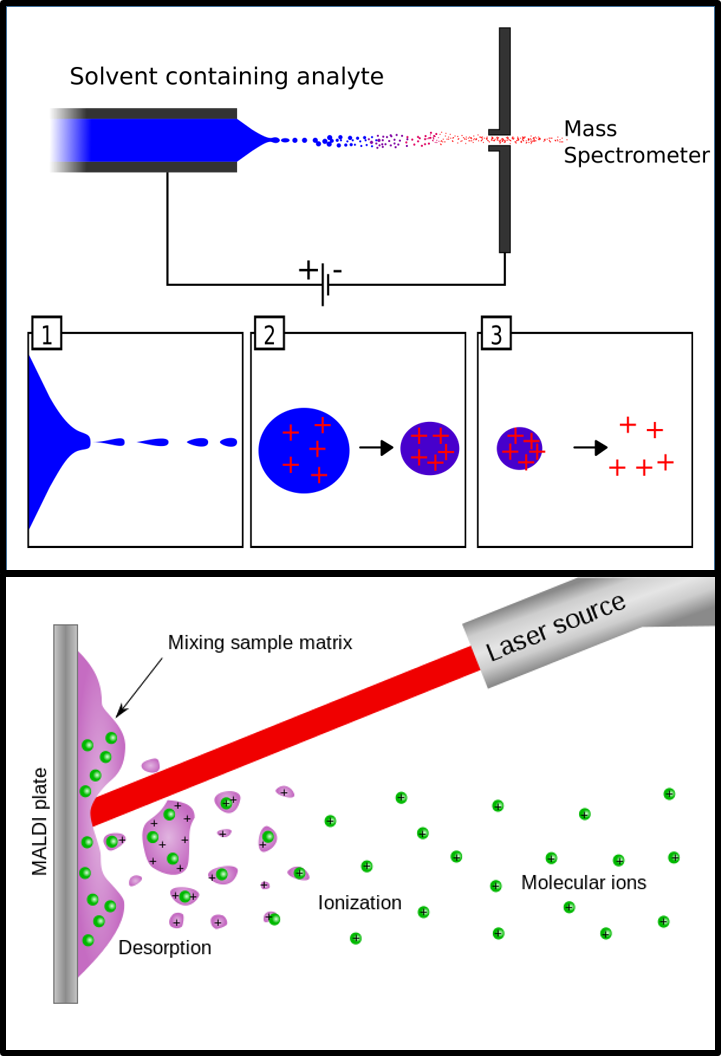 Imagen 6. Esquemas de ionización ESI (arriba) y MALDI (abajo). Fuente: Eva Mason y Mikayé
Imagen 6. Esquemas de ionización ESI (arriba) y MALDI (abajo). Fuente: Eva Mason y MikayéDurante el siglo XXI han continuado los avances en espectrometría de masas y los equipos de alta resolución (capaces de discernir entra moléculas con una relación masa/carga muy parecida) van ganado espacio. En este aspecto, puede que el mayor avance de los últimos años haya sido la aparición del Orbitrap, un espectrómetro de masas tipo trampa iónica con transformada de Fourier.
Pero del presente de la espectrometría de masas nos ocuparemos durante las próximas entregas de esta serie en la que iremos descubriendo diferentes casos en los que esta técnica ha sido de gran utilidad.
*N. del A. La forma de definir la masa atómica y el peso atómico ha variado a lo largo de los años. Diremos que la masa atómica es la masa de un isótopo específico y el peso atómico es el promedio de todos los isótopos de un elemento teniendo en cuenta su abundancia.
Para saber más:
Simon Maher et al. (2015) “Colloquium: 100 years of mass spectrometry: Perspectives and future trends” Reviews of Modern Physics, 87, 113-135.
Jennifer Griffiths et al. (2008) “A Brief History of Mass Spectrometry” Analytical Chemistry, 80, 5678-5683.
Stu Borman et al. (2003) “A Mass Spec Timeline” Today’s Chemist at Work, September, 47-49.
Sobre el autor: Oskar González es profesor en la Facultad de Ciencia y Tecnología y en la Facultad de Bellas Artes de la UPV/EHU.
El artículo Espectrometría de masas: de un isótopo de neón a elefantes que vuelan se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Así en la Tierra como en Marte: espectrógrafos y espectrómetros de masas
- Constantes durante al menos 12 mil millones de años
- En este núcleo sobra masa
La dieta saludable es cuestión de química

Mejor el pan y la pasta si son integrales. Mejor prescindir del azúcar. Mejor comer una fruta que beberse un zumo. Los cereales, las galletas y los cacaos de desayuno contienen mucho azúcar y harinas refinadas, por eso es mejor evitarlos. Más legumbres y menos pastas. Esto lo sabemos todos los que nos preocupamos por llevar una dieta saludable. La razón de todas estas decisiones tiene su origen en dos conceptos: el índice glucémico y la carga glucémica. Y todo esto puede explicarse de forma sencilla gracias a una rama de la química llamada bioquímica.
Tanto el índice glucémico como la carga glucémica tienen que ver con el contenido y tipo de hidratos de carbono que contienen los alimentos.
-
¿Qué son los hidratos de carbono y qué alimentos son ricos en ellos?
Hay una serie de alimentos que son ricos en hidratos de carbono, como por ejemplo el pan, la pasta, el arroz, en general todo aquello que se convierte en harinas o que se haga con harinas. También es un hidrato de carbono el azúcar y, en general, cualquier alimento dulce, desde pasteles a frutas son ricos en hidratos de carbono. De hecho, en bioquímica solemos denominar “azúcares” a todos los hidratos de carbono.
-
¿Cómo se metabolizan los hidratos de carbono?
Los hidratos de carbono de estos alimentos se acaban convirtiendo en moléculas más simples como la glucosa. La glucosa pasa a la sangre y las células la captan gracias a la insulina. La insulina es una hormona que se sintetiza en el páncreas y que actúa como llave de paso, permitiendo la entrada de la glucosa en las células.
Cuando comemos hidratos de carbono, lo primero que hace el organismo es almacenar la glucosa en forma de glucógeno, tanto en el músculo como en el hígado. Es una forma de almacenar energía. Pero una vez que estas reservas están llenas, el exceso de glucosa se transforma en grasa en los adipocitos.
-
¿Qué es el índice glucémico?
La índice glucémico (IG) nos dice con qué velocidad los hidratos de carbono se convierten en glucosa y pasan a la sangre. Los hay que lo hacen más rápido (alto IG) y más despacio (bajo IG).
Hay alimentos que van liberando poco a poco esa glucosa en la sangre, de modo que las células van gestionando sin problema esa glucosa que les llega progresivamente. Los alimentos que liberan su glucosa así, poco a poco, se denominan alimentos de bajo índice glucémico. En general son alimentos que contienen fibra, como los integrales, las frutas y las legumbres. Tampoco producen aumentos repentinos de insulina, sino que la insulina se libera también de forma progresiva. Estos alimentos tienen un IG por debajo de 55.
 Alimentos de bajo IG
Alimentos de bajo IGHay alimentos que, por el contrario, liberan la glucosa en sangre rápidamente, de modo que las células son incapaces de gestionar tanta glucosa en tan poco tiempo y se disparan los niveles de insulina. Los alimentos que liberan glucosa así, de golpe, son los alimentos de alto índice glucémico. Son alimentos hechos con harinas refinadas, que no contienen suficiente fibra y, sobre todo, alimentos con azúcar añadido y azúcar libre. Estos alimentos tienen un IG entre 70 y 100.
-
Otros factores que afectan al índice glucémico
Al procesar y cocinar los alimentos podemos cambiar la estructura y la disponibilidad de sus hidratos de carbono. Por ejemplo, las harinas refinadas no contienen la fibra original del cereal, por lo que sus hidratos de carbono están más disponibles. Por eso las harinas, panes y pastas refinadas tienen un IG más alto que sus respectivos integrales.
Al cocinar los alimentos también alteramos su IG. Por ejemplo, al cocer la pasta alteramos la estructura interna del almidón, con lo que se liberan más hidratos de carbono simples. Así, cuanto más cocida esté una pasta, mayor será su IG.
El IG también se ve afectado por el resto de los alimentos que ingerimos a la vez. Por ejemplo, las proteínas y las grasas hacen que los alimentos estén durante más tiempo en el estómago y lleguen más lentamente al intestino, de modo que pueden reducir su IG.
No todos los azúcares se absorben igual. Por ejemplo, la fructosa, que es el azúcar de la fruta, se absorbe más lentamente y se metaboliza en el hígado, así que el índice glucémico de casi todas las frutas suele ser bajo. Como excepción tenemos el melón, la sandía, los dátiles y las frutas deshidratadas como higos o pasas. Pero no hay que preocuparse por ellos porque, aunque su IG sea alto, habría que consumir una cantidad muy elevada de ellos, ya que no contienen tantos hidratos de carbono.
-
¿Qué es la carga glucémica?
El IG tiene sus limitaciones. Hay que tener en cuenta que los valores de IG se calculan para una cantidad de alimento tal que proporcione 50 gramos de hidratos de carbono disponibles biológicamente. En algunos alimentos esto se corresponde con una ración normal, pero en otros habría que consumir una ración extremadamente alta. Por ejemplo, la sandía es un alimento con alto IG, pero para que la sandía proporcione 50 g de hidratos de carbono tendríamos que comernos una sandía entera. De media, en 100 g de sandía hay solo 8 g de hidratos de carbono.
En cambio, en 100 g de pasta hay unos 80 de hidratos de carbono. Así, una ración de pasta, que tiene un IG medio, nos proporciona más hidratos de carbono que una porción del mismo peso de sandía. Para salvar esta limitación en el IG se emplea el término carga glucémica (CG), que tiene en cuenta tanto el IG del alimento como su contenido en hidratos de carbono.
La carga glucémica se calcula directamente a partir del IG, dividiéndolo por 100 y multiplicándolo por la cantidad de carbohidratos que aporta la ración de alimento. Así, la carga glucémica de la sandía es 4, y la de la pasta ronda el 70.

-
Consecuencias de consumir alimentos de alto índice glucémico y/o alta carga glucémica
El consumo de estos alimentos está relacionado con el sobrepeso, la obesidad, la diabetes tipo II y la percepción atrofiada del apetito.
El sobrepeso, la obesidad y sus enfermedades asociadas, como las cardiopatías [1], guardan cierta relación con el índice glucémico y la carga glucémica [2]. La razón principal estriba en el metabolismo de los hidratos de carbono. Parte de los hidratos de carbono de estos alimentos se transforman en grasas en lugar de almacenarse como glucógeno en el hígado y en el músculo, especialmente en personas que no hacen actividad física. Nuestras células no son capaces de gestionar tan rápido tanta cantidad de glucosa, con lo que los adipocitos terminan almacenando el exceso en forma de grasa. Así que, si sumamos la vida sedentaria a una dieta de alto índice y carga glucémica, estaremos aumentando el riesgo de padecer obesidad.
Los aumentos y descensos de insulina tan pronunciados que produce el consumo de estos alimentos está relacionado con una mayor incidencia de diabetes tipo II [3]. La diabetes tipo II es la resistencia a la insulina, es decir, que las células dejan de reconocer a la insulina y por tanto no permiten la entrada a la glucosa, con lo que ésta se queda en la sangre. De ahí expresiones del tipo “no tomo dulces porque me suben el azúcar”, ese azúcar es la glucosa en sangre incapaz de entrar en las células. La glucosa campando a sus anchas por nuestra sangre puede llegar a armar destrozos en nuestro organismo, dañando la retina, los riñones, las arterias o el corazón.
Las dietas con alimentos de bajo índice y carga glucémica, así como los alimentos ricos en fibra, son útiles para prevenir la diabetes tipo II [4].
Los alimentos de bajo índice y carga glucémica nos producen mayor saciedad. Cuando consumimos esta clase de alimentos, los niveles de glucosa en sangre se mantienen en el tiempo, y esto está relacionado con la percepción del apetito. Sin embargo, los alimentos de alto índice y carga glucémica producen aumentos repentinos de glucosa en sangre y su respectivo aumento en la secreción de insulina. Estos vaivenes en periodos cortos de tiempo rompen el equilibrio de saciedad/apetito provocando una falsa sensación de hambre al poco tiempo de haber comido.
Estas subidas y bajadas repentinas de glucosa e insulina repercuten en las hormonas que regulan el apetito, como la ghrelina y la leptina. En los casos en lo que ya hay sobrepeso y obesidad, el sistema hormonal que regula el apetito también pierde funcionalidad [5], con lo que seguir una dieta con alimentos de alto índice y carga glucémica, empeoran la situación y atrofian más si cabe la percepción de apetito.
-
Conclusión
Cuando decidimos consumir alimentos integrales, o dejamos de consumir azúcar, o alimentos con azúcar añadido, u optamos por comer fruta en lugar de beber zumo, lo hacemos por salud. Son decisiones que nos ayudan a prevenir la diabetes tipo II, la obesidad, el sobrepeso y nos ayudan a gestionar mejor el apetito. Todo esto puede entenderse desde un punto de vista metabólico, es decir, la química está detrás de las dietas saludables. Y dos de los conceptos clave para entender por qué esto es así son el índice glucémico y la carga glucémica de los alimentos.
Referencias:
[1] https://www.ncbi.nlm.nih.gov/pubmed/26480969
[2] https://www.ncbi.nlm.nih.gov/pubmed/23786819
[3] https://www.ncbi.nlm.nih.gov/pubmed/25547339
[4] https://www.ncbi.nlm.nih.gov/pubmed/12081851
[5] https://www.ncbi.nlm.nih.gov/pubmed/27376422
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo La dieta saludable es cuestión de química se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ni dieta equilibrada ni nutrientes. Es cosa de adherencia
- Vida saludable contra la diabetes
- Los vegetales de la dieta neandertal
Un dulce problema de Paul Erdös
En mi anterior entrada del Cuaderno de Cultura Científica, Las dos culturas de las matemáticas: construir teorías o resolver problemas, estuvimos hablando precisamente de eso, de lo que se conoce como las dos culturas de las matemáticas, construir teorías o resolver problemas.
Dentro del grupo de personas que hacen matemáticas “cuyo objetivo central es resolver problemas” se citaba al matemático húngaro Paul Erdös (1913-1996), considerado “el príncipe de los que resuelven problemas y el monarca absoluto de quienes saben proponer problemas”.
 Fotografía de Paul Erdös durante una conferencia en Trinity College (Universidad de Cambridge), en 1991, perteneciente al documental N is a number. A portrait of Paul Erdös (1993), del cineasta George P. Csicsery
Fotografía de Paul Erdös durante una conferencia en Trinity College (Universidad de Cambridge), en 1991, perteneciente al documental N is a number. A portrait of Paul Erdös (1993), del cineasta George P. CsicseryEste brillante y extravagante matemático, en la introducción del artículo Some of My Favourite Problems and Results (Algunos de mis problemas y resultados favoritos), escribe lo siguiente.
Los problemas han sido siempre una parte fundamental de mi vida matemática. Un problema bien elegido puede aislar una dificultad esencial en un área particular de las matemáticas, de forma que el mismo sirva de marca que hay que superar para que se produzca el progreso de esa área. Un problema de apariencia inocente a menudo no da ninguna pista de su verdadera naturaleza. Puede ser como un “malvavisco”, que sirve de delicioso bocado de cardenal proporcionando unos instantes de efímero placer. O puede ser como una “bellota”, que necesite agudos y profundos nuevos conocimientos a partir de los cuales pueda crecer un poderoso roble.
Leyendo estos días sobre algunos de los problemas que planteó y resolvió Paul Erdös, descubrí en el libro Mathematical Diamonds, del matemático canadiense Ross Honsberger (1929-2016), un curioso problema, con una sorprendente y hermosa demostración, que me ha parecido interesante comentaros en esta entrada del Cuaderno de Cultura Científica. Espero que disfrutéis de este problema “malvavisco”, tanto como yo disfruté cuando lo leí.
En la década de 1940, el matemático Paul Erdös estaba estudiando y planteando problemas relacionados con diferentes propiedades y estructuras de conjuntos de puntos del plano. Así, por ejemplo, en 1943 planteó en la revista American Mathematical Monthly el problema “Demostrar que, si un conjunto finito de puntos del plano no están todos sobre la misma recta, entonces existe una recta con exactamente dos de esos puntos”. Sin ser consciente de ello, Erdös reformuló el problema de la línea de Sylvester, que en su momento comentamos en la entrada El problema de la plantación de árboles en filas.
Pero vayamos al problema que nos interesa hoy. En el año 1945, Erdös planteó lo siguiente.
Problema (Paul Erdös): Si dado un conjunto infinito de puntos del plano, las distancias entre ellos son todas números enteros (podemos entender naturales), entonces todos los puntos están en una misma línea recta.
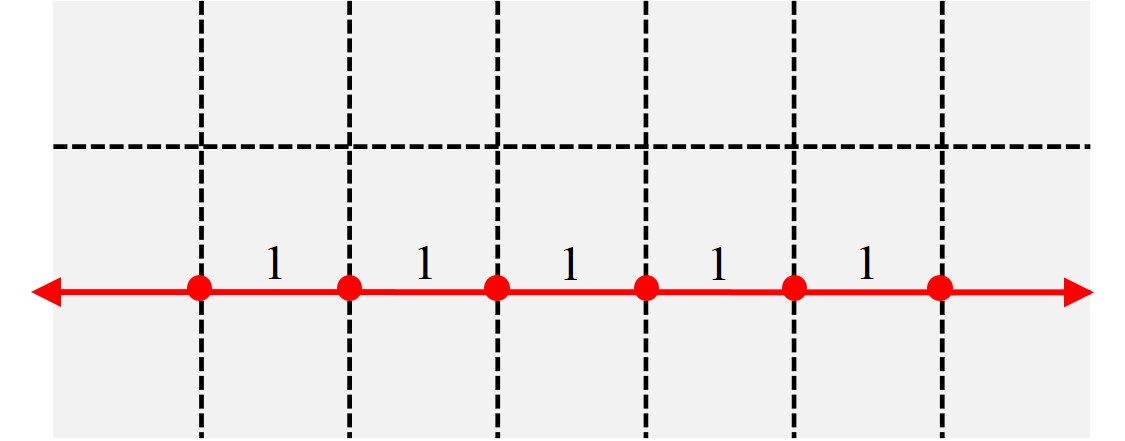
Claramente, si tomamos una recta cualquiera del plano podemos considerar una colección infinita de puntos tal que la distancia entre cualquier par de puntos sea un número natural, sin más que partir de un punto inicial e ir tomando hacia izquierda y derecha los puntos que están a una distancia unidad del inmediatamente anterior (como los puntos rojos que están sobre la recta roja del plano en la siguiente imagen). Lo sorprendente de la afirmación de Erdös en el enunciado del problema es que esa es la única forma de obtener una colección infinita de puntos tal que las distancias entre cualesquiera dos de ellos es siempre un número natural.
La demostración del problema es sencilla, sorprendente e ingeniosa, yo diría más, es una bella demostración. El argumento de la misma se centra en una curva de la familia de curvas cónicas, la hipérbola.
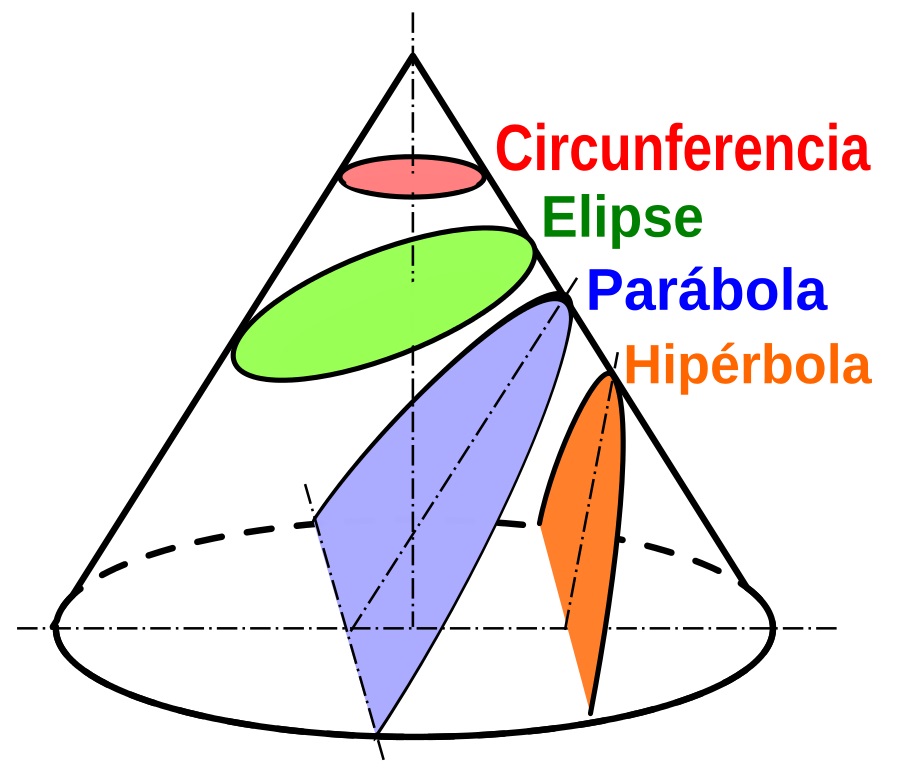 Las secciones cónicas son las curvas planas, que no son rectas, que se obtienen al intersecar un cono con un plano. Las curvas cónicas son la circunferencia, la elipse, la parábola y la hipérbola. Imagen: Wikimedia Commons
Las secciones cónicas son las curvas planas, que no son rectas, que se obtienen al intersecar un cono con un plano. Las curvas cónicas son la circunferencia, la elipse, la parábola y la hipérbola. Imagen: Wikimedia Commons El argumento de la demostración de Erdös es por “reducción al absurdo”. Supongamos que el resultado no fuese cierto, es decir, que existe un conjunto infinito de puntos del plano S, tal que la distancia entre cualesquiera dos de ellos es un número natural y que existen tres puntos A, B y C, del conjunto S, que no son colineales, no están en la misma recta. En ese caso, esos tres puntos determinan un triángulo del plano. Denotemos por a, b y c las longitudes de los lados del mismo, opuestas a los vértices A, B y C, respectivamente, que sabemos, por hipótesis, que son números naturales.
Ahora, consideremos otro punto cualquiera D del conjunto S (recordemos que este conjunto tiene infinitos puntos). Teniendo en cuenta que las distancias de D a los tres puntos A, B y C son también enteras, por estar todos en S, el matemático húngaro demostró que solamente puede haber un número finito de puntos del plano candidatos a ser D. En conclusión, S no puede ser infinito. Veámoslo.
El punto D no es uno de los vértices del triángulo, que son los puntos A, B y C, por lo que como mucho puede estar en una de las rectas que contienen a los lados del triángulo, AB, AC y BC. Es decir, podemos afirmar que existen (al menos) dos rectas, de las tres que contienen los vértices del triángulo, en los cuales no está el punto D. Supongamos que esas rectas, en las que no está el punto D, son las que contienen a los lados AC y BC.
Las distancias del punto D a los puntos B y C son números naturales, ya que los tres están en S, por lo tanto, la diferencia entre ellas |BD – CD| es también un número natural o cero. Como el punto D no está en la recta de BC, la desigualdad triangular (“la suma de las longitudes de dos lados cualesquiera de un triángulo es siempre mayor que la longitud del otro lado”) nos dice que |BD – CD| < BC = a.
Juntando todo lo anterior, tenemos que |BD – CD| = k, donde k es uno de los números enteros 0, 1, 2, …, a – 1. Por lo tanto, D es un punto que pertenece a la hipérbola con focos B y C, y tal que la diferencia de la distancia de sus puntos a los focos es k. Es decir, D está en una de las a hipérbolas que forman la familia de hipérbolas de focos B y C, y diferencias constantes k = 0, 1, 2, …, a – 1.
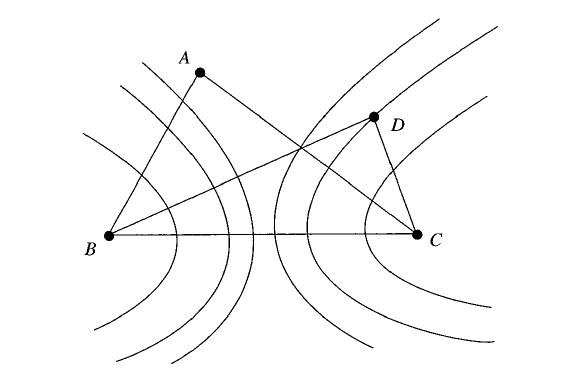 Representación intuitiva de algunas de las hipérbolas de la familia de hipérbolas con focos B y C y diferencia k un número entero entre 0 y a – 1. Imagen del libro Mathematical Diamonds, de Ross Honsberger
Representación intuitiva de algunas de las hipérbolas de la familia de hipérbolas con focos B y C y diferencia k un número entero entre 0 y a – 1. Imagen del libro Mathematical Diamonds, de Ross HonsbergerAntes de continuar, recordemos brevemente la propiedad métrica, que estamos mencionando, de las hipérbolas. En general, todas las curvas cónicas se pueden caracterizar mediante una propiedad métrica. Por ejemplo, la circunferencia está formada por los puntos del plano que equidistan, es decir, que están a la misma distancia, de un punto fijo, el centro de la misma.
En el caso de la hipérbola, existen dos puntos destacados, los focos (F1 y F2 en la siguiente imagen), y cada hipérbola está caracterizada por estar formada por los puntos P del plano tales que la diferencia de las distancias a los focos |PF1 – PF2| es una constante k, para cada hipérbola. Luego, dados dos focos F1 y F2, para cada constante k se obtiene una hipérbola como la de la siguiente imagen (con dos ramas). Para k = 0 se obtendría una hipérbola degenerada, que es la recta mediatriz del segmento F1F2, es decir, los puntos que están a la misma distancia de cada uno de los focos.
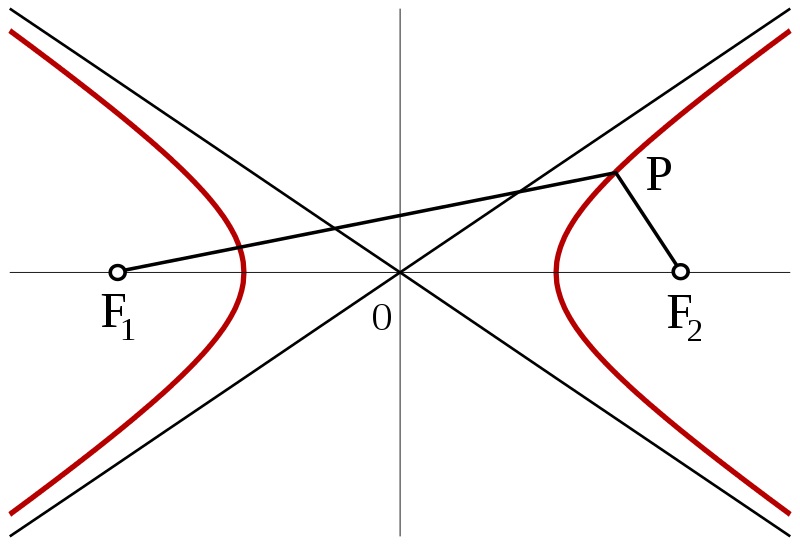 Dibujo de una hipérbola (en rojo) con focos F1 y F2. Imagen: Wikimedia Commons
Dibujo de una hipérbola (en rojo) con focos F1 y F2. Imagen: Wikimedia Commons Regresemos a la demostración. Hemos probado que como el punto D no está en la recta de BC, D está en alguna de las a (que es un número natural) hipérbolas que forman la familia de hipérbolas de focos B y C, y diferencias constantes k = 0, 1, 2, …, a – 1. De la misma forma, tendrá que ser cierto que, como el punto D no está en la recta que contiene a AC, D está en alguna de las b (que también es un número natural) hipérbolas que forman la familia de hipérbolas de focos A y C, y diferencias constantes m = 0, 1, 2, …, b – 1.
Como dos hipérbolas cualesquiera se intersecarán, como mucho, en 4 puntos distintos, entonces las a hipérbolas de la primera familia y las b hipérbolas de la segunda, se intersecarán a lo sumo en 4ab puntos del plano. Es decir, solo existe un número finito de posibles puntos del plano, (como mucho) 4ab, candidatos a ser D. Esto nos lleva a una contradicción con el hecho de que S es un conjunto infinito, y D es un punto del conjunto, también infinito, S – {A, B, C}, ya que hemos probado que solo hay un número finito de posibles puntos D. Por lo tanto, cualesquiera tres puntos A, B y C, de S, deberán estar alineados, luego los puntos de S están sobre la misma recta.
Q.E.D. (Quod erat demonstrandum)
 Página del texto original de la obra Ethica more geometrico demonstrata (Ética demostrada a la manera geomérica) del filósofo Spinoza (1632-1677), en la que vemos la abreviatura Q.E.D. al final de la demostración de la tercera proposición. Q.E.D. es una abreviatura de la expresión latina quod erat demonstrandum, que significa “lo que se quería demostrar” y se coloca al final de una demostración matemática para indicar el final de la misma
Página del texto original de la obra Ethica more geometrico demonstrata (Ética demostrada a la manera geomérica) del filósofo Spinoza (1632-1677), en la que vemos la abreviatura Q.E.D. al final de la demostración de la tercera proposición. Q.E.D. es una abreviatura de la expresión latina quod erat demonstrandum, que significa “lo que se quería demostrar” y se coloca al final de una demostración matemática para indicar el final de la mismaPero, como suele ocurrir en matemáticas, no nos paramos aquí. Una vez demostrado el problema de Erdös (Si dado un conjunto infinito de puntos del plano, las distancias entre ellos son todas números enteros, entonces todos los puntos están en una misma línea recta), podemos preguntarnos qué ocurre con un número finito de puntos. ¿Será posible disponer de un número finito n de puntos, para cualquier n, de forma que las distancias entre cualesquiera dos puntos sean números enteros y no estén todos en una recta?
Empecemos planteando el problema para tres puntos. Si consideramos tres vértices de un cuadrado de lado 1, estos no nos valdrán ya que mientras que los lados sí son distancias enteras, en concreto, 1, no lo es la diagonal, cuyo valor es la raíz de 2, sencillamente por el teorema de Pitágoras. Pero este resultado de la geometría clásica nos da una idea para construir un triángulo cuyos tres lados sí sean números enteros. Tomemos una terna pitagórica cualquiera (a, b, c), es decir, a2 + b2 = c2, y construyamos el triángulo rectángulo que tiene por lados esa terna. Por ejemplo, en el plano coordenado los puntos (0, a), (0, 0) y (b, 0). En la imagen siguiente hemos dibujado (en azul) el correspondiente a la terna (3, 4, 5).
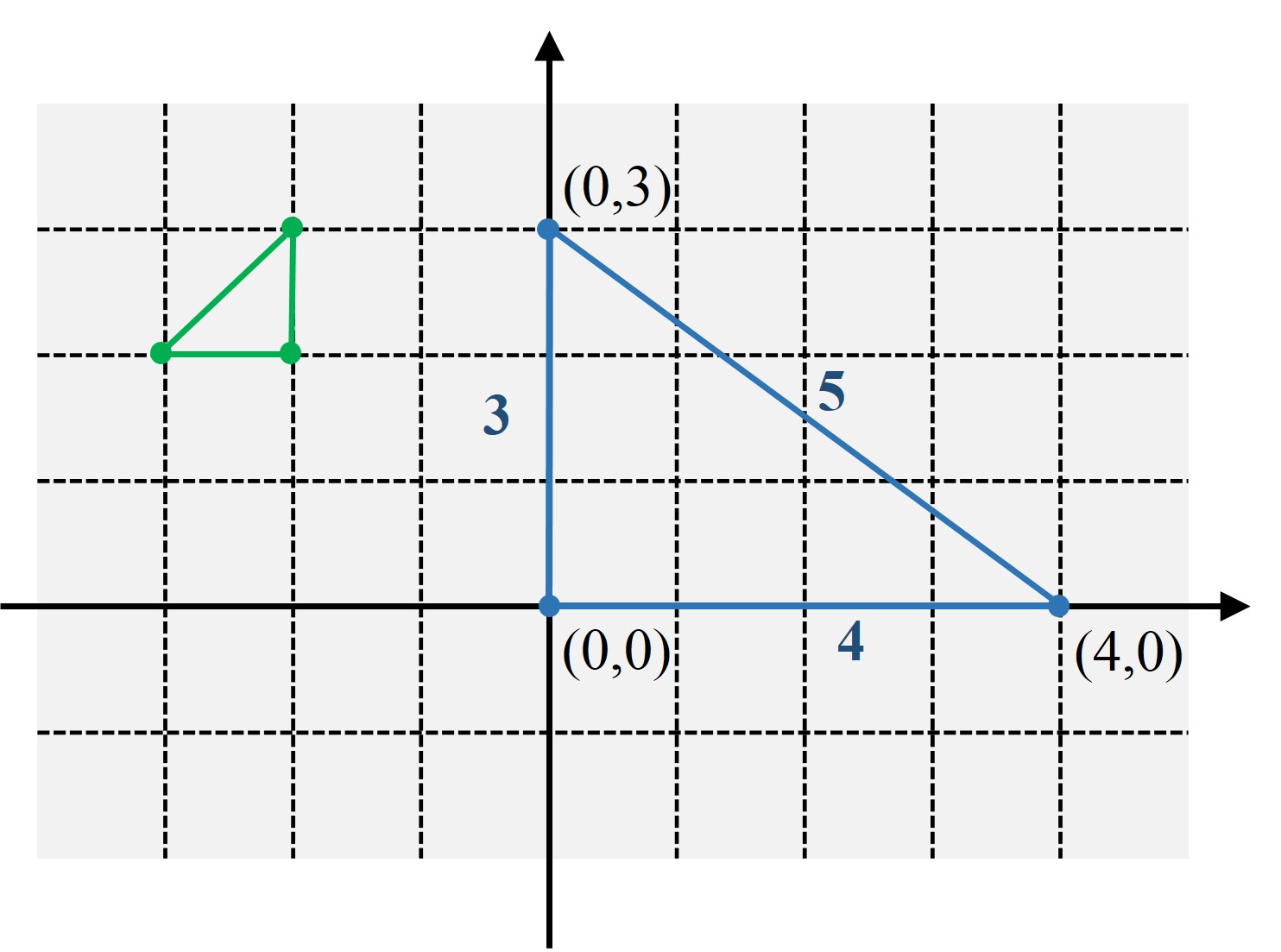
Precisamente, el matemático David Silverman, en 1963, utilizó las ternas pitagóricas irreducibles para demostrar que podía construirse un conjunto cualquiera de puntos del plano con distancias enteras entre ellos y que no fuesen colineales. Para empezar, recordemos que una terna pitagórica (a, b, c), es decir, a2 + b2 = c2, se dice que es irreducible si los tres números a, b y c no tienen, dos a dos, divisores comunes. Por ejemplo, la terna (3, 4, 5) es irreducible, pero no (6, 8, 10).
Sean m ternas pitagóricas irreducibles distintas, (ai, bi, ci), para i = 1, 2, …, m. Tomamos el producto P = a1 x a2 x … x am, David Silverman consideró los m + 1 puntos del plano coordenado siguientes:
(0, P) y ((bi / ai) P, 0), para i = 1, 2, …, m.
Como ai divide a P, cada uno de los puntos anteriores tienen coordenadas enteras, el primero está en el eje de ordenadas (eje y) y los demás en el eje de abscisas (eje x). Y, además, los puntos que están en el eje x distan entre ellos un número entero. Para concluir faltaría ver que la distancia entre el punto (0, P) y cualquiera de los otros ((bi / ai) P, 0) es entera. Esa distancia es
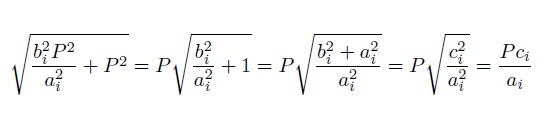
que claramente es entera, ya que ai divide a P.
Además, por ser los triples pitagóricos irreducibles cada punto ((bi / ai) P, 0) es distinto a los demás. Supongamos que existen i y j tales que ((bi / ai) P, 0) = ((bj / aj) P, 0), entonces bi / ai = bj / aj. Luego ai x bj = aj x bi. Como ai y bi no tienen divisores comunes, entonces ai divide a aj y como aj y bj no tienen divisores comunes, entonces aj divide a ai. En conclusión, ai = aj, y de forma equivalente se prueba que bi = bj, lo que implicaría que son el mismo triple pitagórico, lo cual no es cierto.
Por lo tanto, (0,0), (0, P) y ((bi / ai) P, 0), para i = 1, 2, …, m, son m + 2 puntos del plano, no colineales, y que distan entre ellos un número entero.
Efectivamente, el anterior es un ejemplo de un número finito de puntos no colineales que distan entre sí distancias enteras. Sin embargo, podríamos decir que dejan de ser colineales por la mínima ya que todos están en la misma recta, el eje x, salvo el punto (0, P).
En el libro Combinatorial Geometry in the plane, de Hugo Hadwiger y Hans Debrunner se obtiene un resultado más general. Se demuestra que, para cada n, existe un conjunto finito de n puntos del plano, de forma que las distancias entre cualesquiera dos puntos son números enteros y no solo no están todos en una misma recta, sino que, además, no hay tres puntos que sean colineales. Pero esa demostración la dejamos solo para las personas que estén interesadas en ir un poco más allá. Se puede leer en cualquiera de los libros mencionados, Mathematical Diamonds y Combinatorial Geometry in the plane.
 El gol de Pitágoras (década 1990), 22 x 45 x 7,5 cm, obra del artista colombiano Bernardo Salcedo (1939-2007). Imagen de la galería El Museo
El gol de Pitágoras (década 1990), 22 x 45 x 7,5 cm, obra del artista colombiano Bernardo Salcedo (1939-2007). Imagen de la galería El Museo Bibliografía
1.- William Timothy Gowers, Las dos culturas de las matemáticas, La GACETA de la RSME, vol. 7.2, pag. 371–386, 2004 (publicado originalmente como The Two Cultures of Mathematics, en Mathematics: Frontiers and Perspectives, V.I. Arnold, M. Atiyah, P. Lax y B. Mazur (eds.), AMS, 1999).
2.- Raúl Ibáñez, La cultura científica o la misteriosa identidad del señor Gauss, CIC-Network, n. 8, pag. 14-17, 2010. (versión online en el Cuaderno de Cultura Científica)
3.- Paul Erdös, Some of My Favourite Problems and Results, perteneciente al libro The Mathematics of Paul Erdös I, editado por Ronald L. Graham y Jaroslav Nesetril, Springer-Verlag, 1997.
4.- Ross Honsberger, Mathematical Diamonds, MAA, 2003.
5.- Hugo Hadwiger, Hans Debrunner, Combinatorial Geometry in the Plane, Dover, 1964.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Un dulce problema de Paul Erdös se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El problema de la plantación de árboles en filas (2)
- El problema de la plantación de árboles en filas
- El problema de Malfatti
Aplicaciones de la reflexión de ondas: el sonar
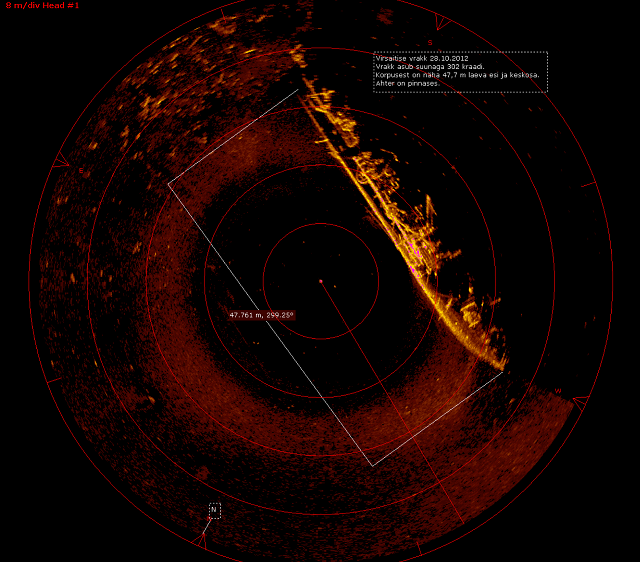 Imagen sonar del fondo marino en la que destaca con increíble detalle el pecio del dragaminas de la marina soviética T-297, hundido en aguas de la actual República de Estonia. Imagen: Wikimedia Commons
Imagen sonar del fondo marino en la que destaca con increíble detalle el pecio del dragaminas de la marina soviética T-297, hundido en aguas de la actual República de Estonia. Imagen: Wikimedia CommonsHemos visto que los principios básicos de la reflexión de ondas son muy sencillos. No solo eso, con el concepto de rayo son incluso fáciles de ilustrar. Vamos a usar este conocimiento para intentar entender la base de las tecnologías que empleamos diariamente, aunque no seamos conscientes de ello, y consolidarlo. Estas tecnologías se basan en el uso de reflectores de ondas. Podemos encontrar reflectores en los radares de tráfico o en los calefactores infrarrojos, por ejemplo.
Un poco de geometría elemental nos será muy útil. La Figura 1 (a) y (b) muestra cómo los rayos se reflejan en dos reflectores circulares. Recordemos que en estos esquemas solo se muestran algunos rayos incidentes y reflejados. (Las líneas de puntos son perpendiculares a la superficie de la barrera, para recordarlos que el ángulo incidente es igual al ángulo del rayo reflejado, Θi = Θr .) Los rayos reflejados desde el semicírculo (a) se alejan en todas direcciones. Sin embargo, los rayos reflejados desde un pequeño segmento del círculo (b) se acercan hasta casi juntarse en un solo punto. Los reflectores en forma de semicírculo no son muy útiles.
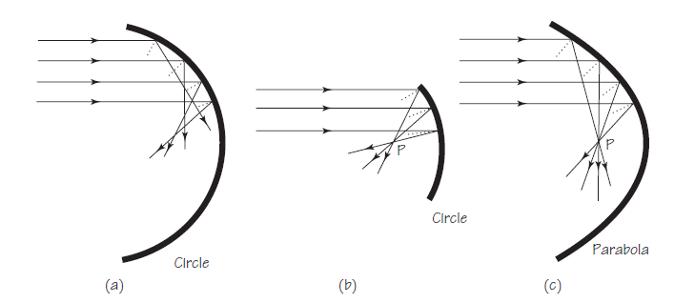 Figura 1. Fuente: Cassidy Physics Library
Figura 1. Fuente: Cassidy Physics LibraryUna barrera con la forma de una parábola (c) enfoca los rayos con bastante precisión en un punto, el foco de la parábola. En otras palabras, una superficie parabólica refleja ondas planas y las concentra en un punto. Un ejemplo impresionante es un radiotelescopio. Su enorme superficie parabólica refleja ondas de radio muy débiles del espacio exterior para enfocarlas en un detector. El mismo principio lo emplean las antenas parabólicas para la recepción de señales de satélites, para ver la televisión, por ejemplo.
 Radiotelescopio de Parkes (NSW, Australia), de 64 metros de tamaño, durante la puesta de Sol. La antena tiene forma parabólica y el detector está en su foco. Crédito: Ángel R. López-Sánchez (AAO/MQU).
Radiotelescopio de Parkes (NSW, Australia), de 64 metros de tamaño, durante la puesta de Sol. La antena tiene forma parabólica y el detector está en su foco. Crédito: Ángel R. López-Sánchez (AAO/MQU).Nada impide que las trayectorias de de los rayos indicadas en los diagramas se inviertan. Por ejemplo, si producimos ondas esféricas producidas en el foco las convertimos en ondas planas cuando se reflejan desde una superficie parabólica. La linterna y o el faro delantero de un coche son aplicaciones familiares de este principio. En estos casos una fuente de luz, ya sea una filamento incandescente, una bombilla halógena o un LED, colocados en el foco de un reflector parabólico producen rayos de luz casi paralelos.
En este punto es posible que sea necesario recordar que todas las afirmaciones que hemos hecho a lo largo de la serie se refieren a ondas mecánicas, auqnue estemos empleando la parte común con las ondas electromagnéticas en estos ejemplos.
Una aplicación con ondas sonoras es el sonar (del acrónimo inglés que se traduce como navegación y localización por sonido), empleado en la navegación y localización de objetos en el mar: desde barcos de pesca buscando bancos de peces, pasando por buques oceanográficos cartografiando el fondo marino o cazatesoros buscando barcos hundidos, a submarinos buscando su ruta o enemigos. Su desarrollo fue una cuestión de supervivencia durante la Primera Guerra Mundial, y para 1918 ya existían instrumento SONAR tanto activos (emiten sonido) como pasivos (solo “escuchan”). La Segunda Guerra Mundial llevó al desarrollo de su equivalente electromagnético, también como una cuestión de supervivencia para la bombardeada Inglaterra, el radar. Ambos sistemas se basan en dos principios básicos de la reflexión de ondas: el efecto eco y el desplazamiento Doppler.
El eco es un fenómeno muy familiar: grita tu nombre en una gran sala vacía y las paredes parecen gritarte a ti. Este tipo de eco es el resultado de la reflexión de las ondas de sonido en una superficie. Un pulso de ondas de sonido enviadas desde una antena se reflejará desde cualquier objeto que golpee, y parte de la onda volverá a donde se originó. El tiempo que transcurre entre la emisión del pulso y la recepción de la parte reflejada del pulso se puede usar para determinar la distancia entre el punto y la superficie reflectante. Esta es la descripción de un sonar activo.
![]()
El desplazamiento Doppler, también muy común en la vida diaria, ocurre cuando las ondas de cualquier tipo son emitidas o reflejadas por un cuerpo en movimiento. (Todo el mundo lo ha experimentado como el cambio en la frecuencia del ruido de un coche o el silbato de un tren mientras está en movimiento). Si las ondas enviadas desde un punto se reflejan en un cuerpo en movimiento, las ondas que regresan parecerán tener una mayor frecuencia si el objeto se mueve hacia el punto de emisión y una frecuencia más baja a medida que el objeto se aleja de él. Por lo tanto, la medición del desplazamiento Doppler de las ondas reflejadas se puede utilizar para determinar rápidamente la velocidad y la dirección de la superficie reflectante.
El sonar funciona muy bien en el agua y lo utilizan con gran éxito los submarinos para “ver” sin ver, tanto el entorno como a las amenazas. Pero el sonar no es práctico para su uso en el aire, porque en éste las ondas de sonido ordinarias no viajan lo suficientemente lejos, y su eco es demasiado débil para ser útil en detecciones precisas.
En este fragmento de “La caza del Octubre Rojo” vemos (y oímos) el uso del SONAR en todo su esplendor:
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Aplicaciones de la reflexión de ondas: el sonar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Reflexión de ondas: rayos
- Las ondas están por todas partes
- Patrón de interferencia en ondas periódicas
Estamos perdiendo el norte pero que no cunda el pánico porque lo vamos a recuperar
Hay pocas cosas inmutables en esta vida, e incluso aquellas que creemos que lo son a veces nos sorprenden mutando. El Polo Norte es una de ellas. Me refiero al polo norte magnético en esta ocasión, no al continente que llamamos Ártico o Polo Norte (de la deriva continental ya hablaremos otro día).
El caso es que el polo norte magnético, el punto hacia el que apuntan siempre nuestras brújulas y que utilizan los más sofisticados sistemas de posicionamiento como nuestros GPS y otros sistemas de satélites, ya no está donde estaba antes porque su posición está variando de forma constante y, sabemos ahora, más rápida de lo que los geólogos se esperaban.
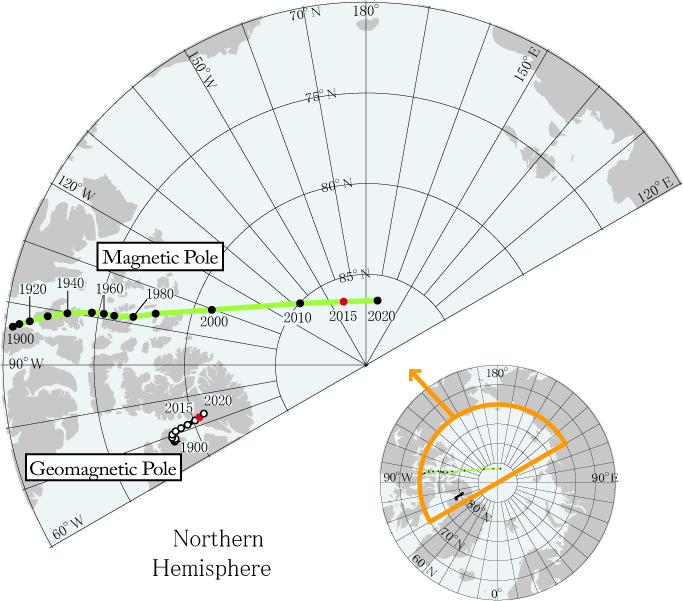 Variación de la posición del polo norte magnético en periodos de 5 años, la última en 2015, y proyección de su posición en 2020. Fuente: World Data Center for Geomagnetism/Universidad de Kyoto
Variación de la posición del polo norte magnético en periodos de 5 años, la última en 2015, y proyección de su posición en 2020. Fuente: World Data Center for Geomagnetism/Universidad de KyotoQue el polo norte magnético de la Tierra se está desplazando no es una novedad, lo ha hecho desde siempre y siempre lo hemos sabido. Si en torno a 1900 se encontraba en algún punto bajo Canadá, desde entonces ha ido alejándose de Norteamérica y acercándose a Siberia.
Un modelo que se desactualiza por momentos
Conscientes de esta situación y de la necesidad que la tecnología tiene hoy en día de tener el campo magnético terrestre perfectamente ubicado, geólogos de distintas instituciones científicas crearon y mantienen el llamado Modelo Magnético Mundial, una representación detallada de los campos magnéticos de la Tierra que sirve como estándar para el trabajo y las observaciones, entre otros, de la OTAN, la OMS o el Departamento de Defensa Estadounidense. Es de donde sacan la referencia también los sistemas de GPS que utilizan servicios como Google Maps.
Este modelo iba ser actualizado este mes de enero (aunque con el cerrojazo al gobierno estadounidense no está claro si finalmente podrá ser así) y eso no estaba previsto. Los equipos encargados de esta tarea están un poco desconcertados. Porque la última actualización se produjo en 2015 y debía ser suficiente hasta 2020, pero acaba de empezar 2019 y el desplazamiento del polo norte se ha acelerado tanto en los últimos meses que la diferencia entre el modelo y la realidad no para de aumentar. A principios de 2018 esa diferencia estaba a punto de superar los márgenes de error aceptables para los sistemas de navegación, así que el nuevo cambio no puede esperar más.
¿Por qué este acelerón inesperado en un proceso, el de la deriva del polo norte magnético, que si bien todavía no comprendemos perfectamente sí hemos sabido predecir hasta ahora? Hay varios motivos que lo explican.
El inesperado meneo de 2016
El primero es que en 2016, justo después de la última actualización del Modelo Magnético Mundial, cuando lo teníamos todo perfectamente colocadito para los próximos cinco años, al campo magnético de la Tierra le dio por hacer cosas raras de repente: se aceleró temporalmente bajo la zona norte de Sudamérica y la zona este del Pacífico. Este fenómeno, que no se había previsto, ya descolocó de partida el modelo recién actualizado, provocando que el cambio sí previsto ocurriese a mayor velocidad.
Por otro lado, el propio movimiento del polo magnético que, como decimos, fascina a los geólogos desde que se documentó por primera vez en 1831 pero todavía no lo comprendemos del todo. Sí sabemos que ha ido cogiendo velocidad en las últimas décadas: si hasta los 90 se movía unos 15 kilómetros al año, en ese momento aceleró y comenzó a moverse unos 55 kilómetros anuales. En el año 2001 entró oficialmente en el Océano Ártico, y lo está cruzando desde entonces, desde Canadá hacia Siberia.
Las consecuencias de este movimiento y del error existente respecto al modelo establecido son relativas. No es lo mismo el uso de una brújula para orientarse si salimos de excursión a la montaña en España, por ejemplo, que si somos una expedición en el Ártico. Allí no solo hay muchas menos referencias orientativas, sino que además por la geografía del lugar y su cercanía al Polo, el error se magnifica y puede convertirse en un riesgo para barcos y equipos que se desorienten en el lugar.
Por eso se decidió adelantar la siguiente actualización del modelo. Equipos del NOAA (National Oceanic and Atmosferic Administration) y del British Geological Survey, en Edimburgo, han actualizado el sistema con datos exhaustivos de los últimos tres años, incluido el impulso magnético inesperado de 2016 para corregir los errores actuales y mantener el modelo hasta su siguiente actualización que debería hacerse, si todo sigue según lo previsto, en 2020.
¿Por qué está pasando esto?
También intentan entender por qué el desplazamiento magnético se ha acelerado tanto en las últimas décadas y a qué se deben los acelerones ocasionales para poder preverlos y adelantarse a ellos.
Lo ocurrido en 2016 no tiene aun una explicación clara, pero hay varias hipótesis. Una de ellas es que estuviese provocado el movimiento en forma de olas de los metales y otros materiales en estado líquido que se encuentran en el núcleo terrestre y que pueden alterar el campo magnético de la superficie.
En cuanto al desplazamiento habitual pero cada vez más rápido del polo norte desde Canadá hacia Siberia, se cree que el motivo podría ser también el movimiento de materiales líquidos en el núcleo de la Tierra. En concreto, se ha detectado y medido una corriente de hierro líquido que circula a gran velocidad precisamente debajo de Canadá, y ese parece ser el motivo. La corriente, que mide 420 kilómetros de ancho, ha ido creciendo a un ritmo de 40 kilómetros al año entre los años 2000 y 2016, explicando así la aceleración que los científicos han observado.
Referencias:
Earth’s magnetic field is acting up and geologists don’t know why – Nature.com
World Magnetic Model – British Geological Survey
Geomagnetic acceleration and rapid hydromagnetic wave dynamics in advanced numerical simulations of the geodynamo – Geophysical Journal International
An accelerating high-latitude jet in Earth’s core – Nature Geoscience
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Estamos perdiendo el norte pero que no cunda el pánico porque lo vamos a recuperar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las tres conquistas del Polo Norte
- Geología: la clave para saber de dónde venimos y hacia dónde vamos
- El Antropoceno: ¿estamos en un nuevo tiempo geológico?
El ocre rojo de la antigüedad y los porqués de sus propiedades
 Diferentes muestras de miltos. La muestra ‘e’ es una pieza otomana del siglo XVI, la ‘b’ es una muestra control de óxido amarillo. Fuente: E. Photos-Jones et al (2018)
Diferentes muestras de miltos. La muestra ‘e’ es una pieza otomana del siglo XVI, la ‘b’ es una muestra control de óxido amarillo. Fuente: E. Photos-Jones et al (2018)A la variedad de ocre rojo a la que los griegos llamaban miltos se le atribuían en la antigüedad clásica propiedades notables, razón por la que era muy valorado. Se utilizaba como pigmento para el mantenimiento de embarcaciones, en agricultura, como cosmético, y en medicina. El miltos es una mezcla de goethita (forma mineral del oxihidróxido de hierro), hematita (forma mineral del óxido férrico) y calcita (forma mineral del carbonato cálcico), y está formado por partículas muy finas. El que se usaba en la época clásica procedía de enclaves muy concretos, como la isla de Kea, en las Cíclades; la isla de Lemnos, en el mar Egeo; y Sinope, Capadocia, aunque muy probablemente, su composición variaba dependiendo de su procedencia.
Además de su composición química y estructura, las propiedades de los minerales pueden depender de los microorganismos adheridos a su superficie. Cuanto más pequeño es un objeto, mayor es la superficie con relación al volumen. Dado el pequeñísimo tamaño de las partículas que lo conforman -entre 30 y 700 nm de diámetro-, un mineral como el miltos tiene, por unidad de masa, una gran superficie y sobre ella puede crecer una rica película microbiana. Por otro lado, la composición de la comunidad microbiana depende de las propiedades químicas del mineral y muy en especial de su contenido en ciertos metales que pueden resultar tóxicos. Por ello, también sus posibles efectos sobre otros seres vivos variarán en función de esos rasgos.
Partiendo de ese tipo de consideraciones, un grupo formado por arqueólogos, ingenieros y geólogos ha analizado muestras de miltos de diferentes orígenes, al objeto de identificar las características que confieren al mineral las propiedades que se le atribuían en el mundo clásico.
El alto contenido en plomo de alguna de las muestras explica, por ejemplo, que el ocre rojo procedente de Kea se destinara a los barcos. Aunque se había atribuido una función meramente decorativa a su uso, lo más probable es que su utilidad real se debiese a que, al ser aplicado sobre la superficie externa de los cascos de las embarcaciones, impedía que microorganismos, algas y ciertos invertebrados se les adhiriesen, dificultando así la navegación. El plomo, así como otros metales presentes en el miltos, es tóxico para muchos seres vivos y, por esa razón, en las muestras cuyo contenido en ese metal resultó ser alto, había poca diversidad de bacterias.
Se utilizaba, por otro lado, para prevenir enfermedades en las plantas cultivadas, debido a la acción biocida de algunos metales y sustancias orgánicas adheridas a la superficie. También fue de utilidad como fertilizante, función vinculada seguramente a la presencia en el ocre rojo de bacterias fijadoras de nitrógeno; la fijación de nitrógeno consiste en la conversión de un gas que es biológicamente inútil en sustancias nitrogenadas que pueden ser absorbidas por las plantas y utilizadas para su crecimiento. Se da la circunstancia de que el hierro del mineral es un componente importante de las enzimas y compuestos orgánicos implicados en esa fijación bacteriana. Por último, también cabe atribuir el efecto antibiótico del miltos de algunas procedencias a la presencia de ciertos metales minoritarios en la composición del mineral, así como a la proliferación en la superficie de las partículas de determinados microorganismos.
Hay referencias de miltos en tabletas micénicas de arcilla escritas en Lineal B hace unos 4000 años y autores clásicos como Teofastro, Dioscórides o Plinio se refirieron a él. Ahora hemos sabido que las propiedades que se le atribuían no eran milagrosas. Eso sí, ha habido que esperar miles de años para ello.
Fuente: E. Photos-Jones, C. W. Knapp, D. Vernieri, G. E. Christidis, C. Elgy, E. Valsami-Jones, I. Gounaki y N. C. Andriopoulo (2018): Greco-Roman mineral (litho)therapeutics and their relationship to their microbiome: The case of the red pigment miltos. Journal of Archaelogical Science: Reports 22: 179-192.
——————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 4 de noviembre de 2018.
El artículo El ocre rojo de la antigüedad y los porqués de sus propiedades se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Reduccionismo vs. emergencia (II): las propiedades emergentes
- Algunas observaciones someras relativas a las propiedades aerodinámicas de la suma
- Rediles para ganado de unos 5.000 años de antigüedad en Álava
Fitorremediación
Actualmente se tiene conocimiento de un total de quinientas especies vegetales denominadas hiperacumuladoras, que tienen la capacidad de acumular metales o metaloides. Estas plantas pueden ser usadas para descontaminar y limpiar entornos contaminados. A este uso se le denomina fitorremediación.
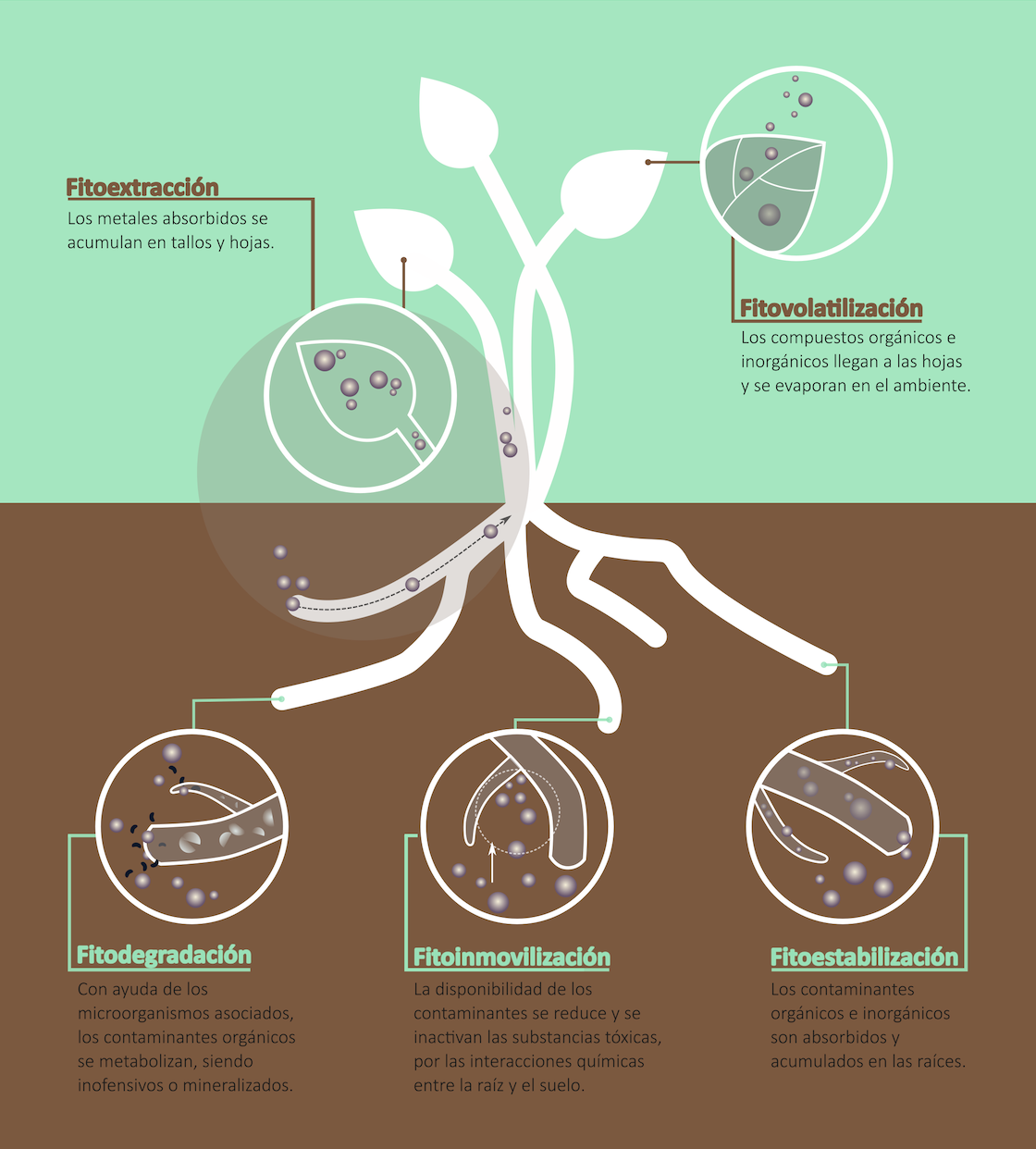 Imagen: Procesos de absorción, metabolización y degradación de compuestos que poseen las plantas. (Ilustración: Ruth Angélica Zambrano)
Imagen: Procesos de absorción, metabolización y degradación de compuestos que poseen las plantas. (Ilustración: Ruth Angélica Zambrano)Plantas, como la Tinorea niccolifera descubierta en Filipinas en 2014, tienen capacidades biológicas de absorber, acumular, metabolizar o estabilizar compuestos tóxicos perjudiciales para los organismos vivos. Esta característica biológica tan singular puede ser usada para hacer frente a problemas ambientales como descontaminar suelos con presencia de metales y substancias tóxicas.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Angélica Zambrano Cepra, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: Fitorremedios. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 7 de septiembre de 2014.
———————————-
El artículo Fitorremediación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un ornitisquio emplumado
- En el mar, allí donde todo comienza
- Metamorfosis criogénica de la rana del bosque
El (Paleo)Clima y ¿el frío que vendrá?

Si cerrásemos los ojos para visualizar la imagen de un geólogo, probablemente imaginaríamos a una persona descubriendo fósiles y recopilando y coleccionando minerales. No obstante, esta disciplina académica cuenta con muchísimas más aplicaciones desconocidas para gran parte de la sociedad.
Con el objetivo de dar visibilidad a esos otros aspectos que también forman parte de este campo científico nacieron las jornadas divulgativas “Abre los ojos y mira lo que pisas: Geología para miopes, poetas y despistados”, que se celebraron los días 22 y 23 de noviembre de 2018 en el Bizkaia Aretoa de la UPV/EHU en Bilbao.
La iniciativa estuvo organizada por miembros de la Sección de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Ente Vasco de la Energía (EVE-EEE), el Departamento de Medio Ambiente, Planificación Territorial y Vivienda del Gobierno Vasco, el Geoparque mundial UNESCO de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.
Los invitados, expertos en campos como la arquitectura, el turismo o el cambio climático, se encargaron de mostrar el lado más práctico y aplicado de la geología, así como de visibilizar la importancia de esta ciencia en otros ámbitos de especialización.
Eneko Iriarte, geólogo del Laboratorio de Evolución Humana de la Universidad de Burgos, analiza cómo la geología ayuda a desentrañar la evolución del clima a lo largo de la historia, descubriendo las causas de las enormes variaciones que han existido a lo largo del tiempo y cómo éstas han influido en los organismos presentes y pasados, incluidos los humanos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo El (Paleo)Clima y ¿el frío que vendrá? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Geología: la clave para saber de dónde venimos y hacia dónde vamos
- La imperfección de los modelos del clima, por Manuel Toharia
- Los ojos que explorarán la superficie de Marte (Mars2020)
Variantes genéticas exóticas, claves para nuestra salud
Son los individuos que viven en condiciones más extremas -inuit, tibetanos y otros- aquellos que tienen variantes genéticas más infrecuentes que les permiten afrontar situaciones muy duras. En esos genes, puede estar la clave de la solución a algunos de nuestros problemas de salud.
Por ejemplo, se ha identificado una mutación del gen PCKS9 en norteamericanos de origen africano, gracias al cual tienen niveles muy bajos de colesterol. Esta mutación ha permitido desarrollar fármacos anticolesterol que tienen como diana ese gen.
 Ilustración: Ana Madinabeitia
Ilustración: Ana MadinabeitiaHay, por lo tanto, todo un patrimonio genético por explorar que puede ser fundamental para resolver problemas de salud.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Ana Madinabeitia Olabarria (@AnaMadinabeitia), alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: Patrimonio genético. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 20 de marzo de 2016.
———————————-
El artículo Variantes genéticas exóticas, claves para nuestra salud se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Genética molecular para el rastreo de la caza furtiva
- Especies exóticas invasoras
- Frecuencia de variantes genéticas y alcoholismo
El citoesqueleto de las neuronas y el alzhéimer
José Martínez Hernández, investigador Ikerbasque del grupo Neuronal Ubiquitin Pathways del Departamento de Bioquímica y Biología Molecular de la Facultad de Ciencia y Tecnología de la UPV/EHU, ha participado en un estudio del Instituto de Neurociencias de Grenoble, en el que han descubierto la relación existente entre la presencia de péptidos beta-amiloide, conocidos por ser los componentes de las placas que se acumulan en el cerebro de las personas afectadas de alzhéimer, y la rápida pérdida de dinamismo del citoesqueleto de actina de las espinas dendríticas, las zonas de las neuronas encargada de recibir la información que viene de otras neuronas mediante sinapsis. Esta menor dinámica hace que la transmisión de la información no sea eficiente, lo que desemboca en la pérdida de las espinas y, por tanto, de la capacidad de formación de sinapsis de las neuronas.
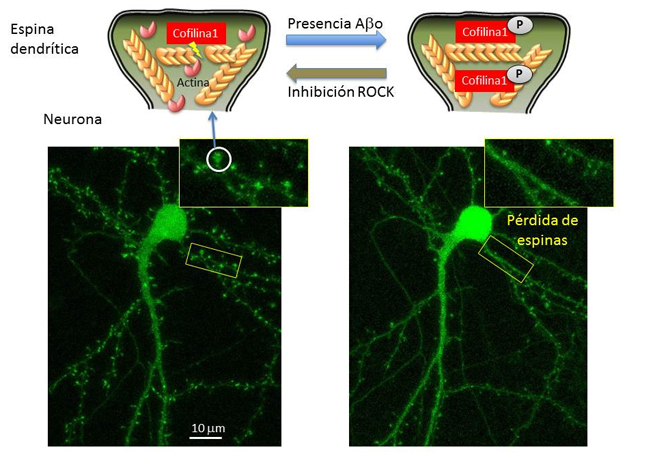 Pérdida de dinámica y posterior deterioro de las espinas dendríticas en las fases iniciales del alzhéimer. Detalles en el texto. Imagen: José Martínez Hernández / UPV/EHU.
Pérdida de dinámica y posterior deterioro de las espinas dendríticas en las fases iniciales del alzhéimer. Detalles en el texto. Imagen: José Martínez Hernández / UPV/EHU.El citoesqueleto es un entramado tridimensional de proteínas que provee de soporte interno a las células, organiza sus estructuras e interviene procesos como el transporte o el tráfico intracelular. Uno de los componentes del citoesqueleto son los filamentos de actina, que, tal como describe el doctor Martínez, “están ancladas pero en continuo movimiento, como si fueran una escalera mecánica; una proteína, llamada cofilina 1, se encarga de cortar los filamentos, y separar las unidades de actina, lo que mantiene activa esa dinámica”.
Sin embargo, en el caso de que la cofilina 1 sea fosforilada, es decir, se le añada un átomo de fósforo, esta proteína pasa a un estado inactivo, y deja de ejercer su función, lo que, a su vez impide que se lleve a cabo correctamente la actividad neuronal. “En nuestro estudio analizamos muestras de cerebros humanos con alzhéimer así como modelos animales de esta enfermedad, y en ellos vimos que la forma inactiva de la cofilina 1 aparecen en cantidades mayores que en neuronas sanas”.
En cultivos de neuronas vieron que la exposición a péptidos de beta-amiloide, el principal componente de las placas o depósitos que se acumulan en el cerebro de las personas con alzhéimer, provoca el aumento de la cofilina 1 fosforilada, y por tanto, provoca que se estabilicen demasiado los filamentos de actina, que pierdan dinamismo y altere el funcionamiento de las espinas dendríticas. “A largo plazo, además, los péptidos beta-amiloide hacen que haya menos espinas; al dejar de ser funcionales, se van perdiendo a lo largo del tiempo”, subraya el investigador
Una de las vías de fosforilación de la cofilina 1 es la ROCK, una quinasa, un tipo de enzima que modifica otras moléculas mediante fosforilación, a veces activándolas y otras desactivándolas. En el estudio quisieron ver si un medicamento que se utiliza en la práctica clínica, el Fasudil, cuya función es inhibir la acción de la enzima ROCK, revertía el efecto observado en los filamentos de actina, y “vimos que sí. No hemos propuesto un mecanismo de acción, pero hemos comprobado que la inhibición de esa vía de fosforilación de la cofilina 1 hace que la exposición a péptidos beta-amiloide no provoque la inactivación de la proteína, y el consecuente efecto en el citoesqueleto de las espinas dendríticas”, detalla Martínez.
“Nuestros resultados apoyan la idea que el daño provocado por los péptidos beta-amiloides a nivel de las espinas dendríticas en las primeras fases de la enfermedad puede prevenirse con la modulación de ROCK y la cofilina1, y que, por tanto, es necesaria la investigación en medicamentos que detengan esta fosforilación de manera específica de la cof1 en neuronas, para elaborar futuros tratamientos médicos contra el mal de Alzheimer”, concluye el doctor Martínez.
Referencia:
Travis Rush, Jose Martinez-Hernandez, Marc Dollmeyer, Marie Lise Frandemiche, Eve Borel, Sylvie Boisseau, Muriel Jacquier-Sarlin, Alain Buisson (2018) Synaptotoxicity in Alzheimer’s disease involved a dysregulation of actin cytoskeleton dynamics through cofilin 1 phosphorylation The Jounal of Neuroscience (2018) doi: 10.1523/JNEUROSCI.1409-18.2018
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El citoesqueleto de las neuronas y el alzhéimer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Implante de factores de crecimiento en nanoesferas para el tratamiento de alzhéimer y párkinson
- Háblame y te digo si tienes alzhéimer
- No dormir mata… neuronas
Bacterias contra bacterias
Un efecto secundario del tratamiento contra el cáncer es que debilita la microbiota (flora intestinal). Esta alteración puede aumentar el riesgo del paciente a padecer infecciones.
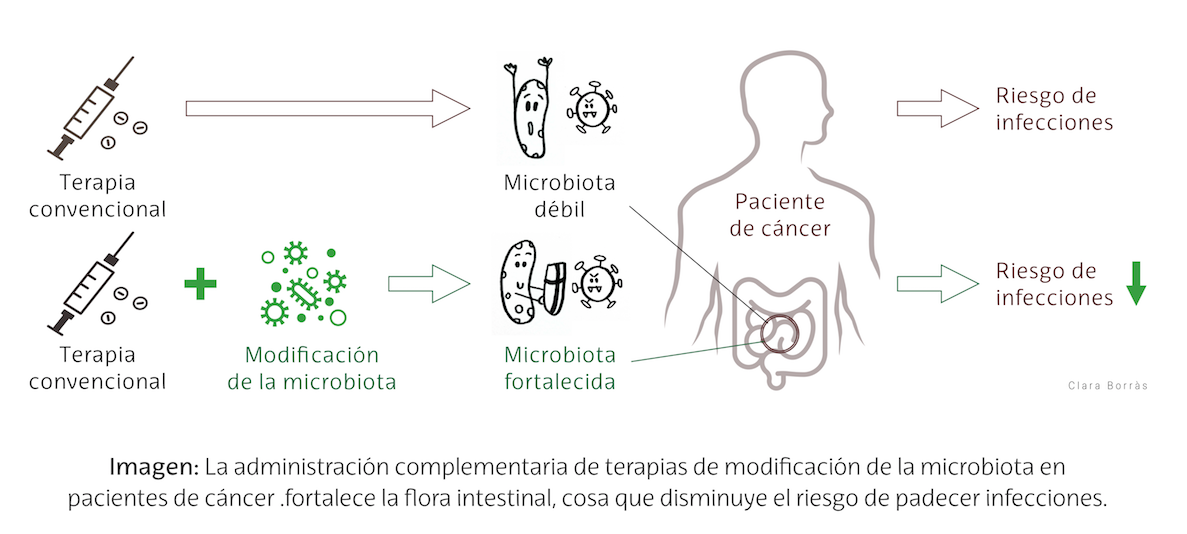 Ilustración: Clara Borrás
Ilustración: Clara BorrásLas estrategias terapéuticas que modifican y fortalecen la microbiota promueven una flora intestinal variada que protege de las bacterias infecciosas. Esto puede mejorar la calidad de vida del paciente con cáncer. En un futuro próximo, los datos de nuestro genoma, metabolismo, sistema inmune o microbioma se tendrán probablemente en cuenta a la hora de planear los tratamientos médicos personalizados o “a la carta”.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Clara Borrás Erodes, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: Microbiota y cáncer. Ignacio López-Goñi, Cuaderno de Cultura Científica, 10 de noviembre de 2017.
———————————-
El artículo Bacterias contra bacterias se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Metamorfosis criogénica de la rana del bosque
- En el mar, allí donde todo comienza
- Un ornitisquio emplumado
Las reglas de una buena melodía
Mah-nà mah-nà
Hay tonadillas tan conocidas que es imposible empezar escucharlas sin esperar ansiosamente su continuación.
Tu tu rururu.
Pero lo curioso de las expectativas musicales es que operan aunque sea la primera vez que escuchamos una determinada canción. En ese caso, las expectativas se basan en todo lo que sabemos (sin saberlo) de la música gracias a haber escuchado muchas otras canciones antes. De nuevo: con cada escucha hemos ido construyendo un modelo, un sentido de lo que es musical, que aplicamos a cada nueva escucha intentando siempre adivinar cuál es la nota que vendrá. Y, por supuesto, no manejamos un único modelo. Existen expectativas armónicas, rítmicas, tímbricas… que pueden ser generales o ajustarse a un determinado estilo musical.
Pero, por ahora, ciñámonos a las expectativas melódicas. En el post anterior comentamos algunas de los métodos que utiliza la psicología para medirlas. Ahora cabe preguntarse: ¿cuáles son esas expectativas?, ¿son verdaderamente descriptivas?, es decir: ¿se ajustan realmente a las melodías que solemos escuchar?
La buena noticia es que tenemos un montón de datos para averiguarlo. Basta tomar unas cuantas partituras (o unos cuantos miles) y empezar a buscar patrones. Estas son algunas de las cosas que la estadística nos cuenta sobre las melodías.
Grados conjuntos.
Piensa en tu canción preferida; en la primera estrofa, específicamente. No necesito ser adivina para saber que el cantante entona varias sílabas sobre la misma nota. Tiene truco, pensarás: la estrofa suele ser la parte menos lucida de la canción, la más monótona desde el punto de vista melódico. Pero incluso si jugamos con el estribillo, lo más probable es que todos los intervalos melódicos sean muy pequeños (de un tono normalmente) y que haya sólo un par de saltos, si acaso, un poco mayores.
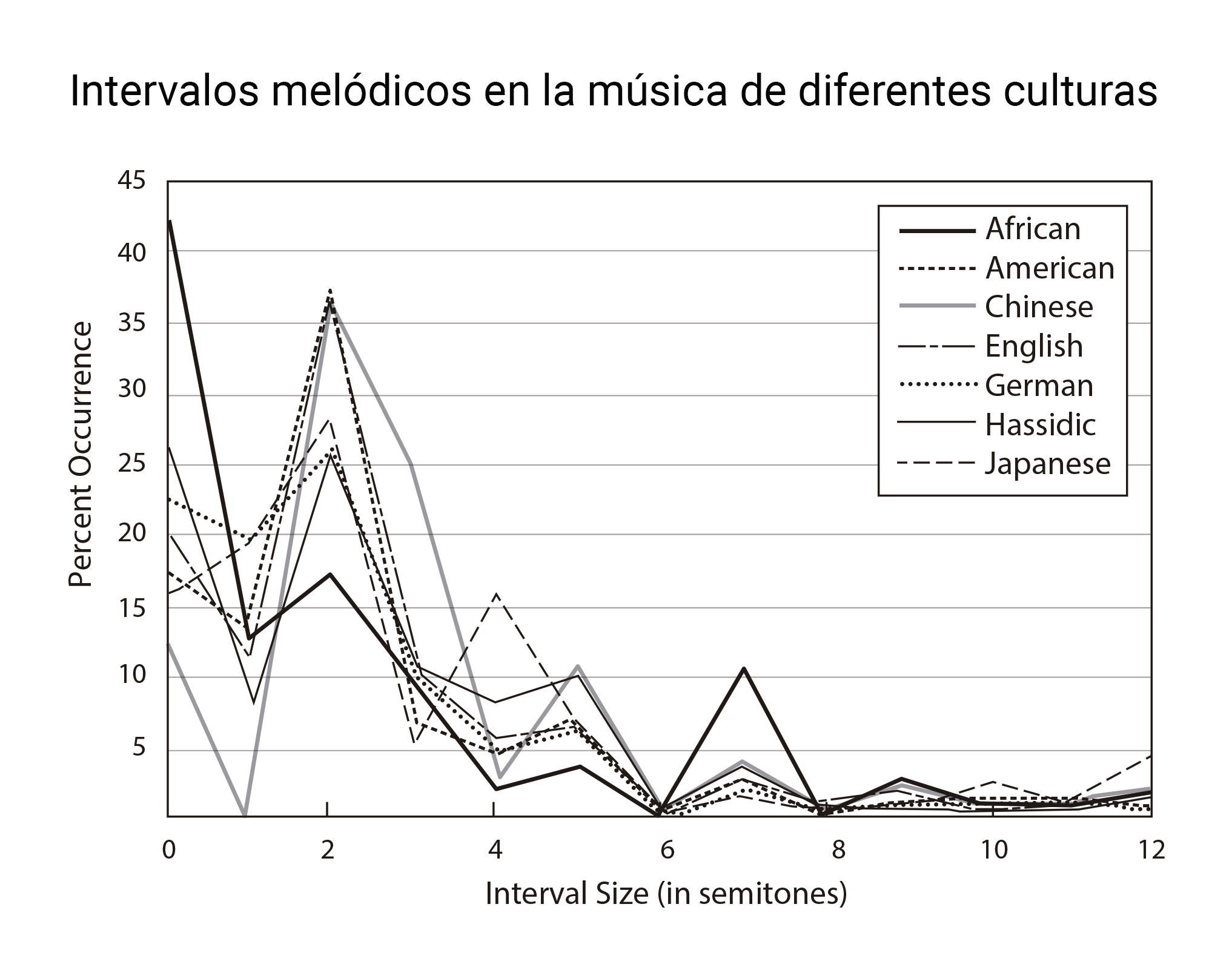
No es magia: es estadística. Las melodías más comunes se construyen, principalmente, por grados conjuntos. Y no se trata de un rasgo exclusivo de nuestra cultura. Podéis observarlo en la gráfica anterior1: a lo largo y ancho del planeta, los intervalos pequeños tienden a predominar, quizás debido a la dificultad que entraña cantar con precisión intervalos más amplios2. Asimismo, en 1978, Diana Deutsch mostró que las expectativas de los oyentes reflejan este patrón general3. Existen, eso sí, llamativas excepciones, como los yoiks escandinavos o el canto tirolés.
Pasos descendentes:
Las melodías más comunes tienden a utilizar intervalos pequeños pero todavía podemos decir más: en caso de producirse algún salto, lo más probable es que este sea ascendente (es decir: de sonidos graves hacia sonidos más agudos). David Huron comprobó que esta es, también, una característica a nivel universal de la música con muy contadas excepciones: las melodías saltan hacia el agudo y descienden por pequeños pasos hacia sonidos más graves.
Lo interesante es que este mismo dibujo es común al habla. Desde el punto de vista de la entonación, cada vez que hablamos tendemos a elevar la frecuencia de nuestra voz muy rápidamente al principio de cada frase y después vamos descenciendo poco a poco hacia sonidos más graves. De nuevo, existen excepciones: la entonación de las preguntas, ascendente al final, es una de ellas. Pero, en general, podemos decir que la voz hablada tiende a descender lentamente; probablemente debido a que la presión ejercida por el aire procedente de los pulmones disminuye a medida que este se agota. En realidad, cantar requiere un control mayor del flujo de aire, por lo que no parece probable que las líneas descendentes de las melodías se deban a esta misma causa fisiológica. Más bien: parece ser un préstamo directo procedente de la prosodia del lenguaje.
Inercia:
Los pasos descendentes tienden a ir seguidos por más pasos descendentes. No sucede así con los intervalos ascendentes que pueden cambiar de sentido con igual probabilidad. Sin embargo las expectativas de los oyentes, en este caso, no se corresponden perfectamente con la estadística: tendemos a esperar inercia en ambos sentidos. Quizás este modelo sea lo bastante descriptivo con un menor coste “computacional”, por así decirlo, pero el motivo no termina de estar claro.
Regresión melódica:
Imagina que vas por la calle y te cruzas con un tipo de dos metros. Lo más probable es que la siguiente persona que te cruces sea más baja. No es una relación causal, evidentemente; una persona alta no causa la aparición de personas más bajitas. Pero los valores extremos de una distribución normal son, simplemente, menos probables. Esto es lo que se conoce como regresión a la media.
Como las alturas humanas, los tonos de una melodía muestran una tendencia central: esto es, dentro de un espacio acotado de sonidos (la tesitura de la melodía), las notas más probables son aquellas que no son ni muy graves, ni muy agudas; sino que están situadas hacia el centro del rango sonoro. Por tanto, cada vez que alcanzamos una nota extrema, lo más probable es que la siguiente nota esté más cerca de la media.
Nuestras expectativas, nuevamente, reflejan este hecho musical. Aunque no de forma perfectamente fiel… en este caso, cada vez que se produce un salto melódico, los oyentes esperan que la siguiente nota se mueva en dirección contraria al salto. Y suelen acertar, puesto que los saltos melódicos tienden a acercar la melodía a los extremos de su tesitura. Como en el caso de la inercia, el modelo parece simplificar la realidad del fenómeno que quiere anticipar. Dado que, habitualmente, sus predicciones resultan ser correctas, es lo bastante bueno.
A fin de cuentas, ese es el único propósito de las expectativas; no se trata de alcanzar un conocimiento exacto de la música, basta con acertar. Y de hecho, lo consiguen: las melodías que escuchamos encajan con lo que esperamos de ellas, con aquello que nos resulta más musical. Y ahora cabe preguntarse: ¿qué fue antes, el huevo o la gallina?, ¿nuestras expectativas describen la música que nos rodea, o nos rodea música que se ajusta a nuestras expectativas?, ¿cuánto espacio queda para innovar?
Referencias:
David Huron (2008) Sweet anticipation: music and the psychology of expectation. The MIT Press.
Notas:
1 David Huron. “Tone and Voice: A Derivation of the Rules of Voice-Leading from Perceptual Principles”. Music Perception: An Interdisciplinary Journal, Vol. 19 No. 1. 2001.
2 La gráfica muestra dos picos especialmente prominentes: en 0 semitonos (una nota repetida) y en dos semitonos (un tono de distancia o grados conjuntos). En cambio, existe un mínimo peculiar sobre el número 6: este es el tamaño del tritono, un intervalo especialmente disonante y difícil de cantar (hasta el punto de ser conocido como “Diábolus in música”)
3 Deutsch, D. (1978). Delayed pitch comparisons and the principle of proximity. Perception & Psychophysics 23: 227–230.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Las reglas de una buena melodía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- «Una copita de vino es buena para el corazón». Claro que sí, guapi.
- Las partituras de Babel
- BertsoBot, el robot versolari
La adherencia, clave en el seguimiento de las dietas
La inquietud de la sociedad actual por lucir una buena imagen y sentirse sano, anima a los medios de comunicación y a la comunidad científica a la búsqueda de la dieta ideal. Este empeño parece solo quedarse en la utilización de la calculadora para cuantificar calorías, que según qué dietas (algunas de ellas verdaderos best sellers) estarán relacionadas con determinados grupos de alimentos y sus correspondientes nutrientes.
Lo que se está viendo en distintas investigaciones es que, además de la proporción de los diferentes alimentos a consumir en su justa medida, hay que tener en cuenta la continuidad de los hábitos dietéticos en el tiempo, la realización de actividad física y las creencias personales, a veces infundadas, respecto al consumo de ciertos alimentos.
 Ilustración: Héctor Márquez
Ilustración: Héctor MárquezLa adherencia personal por seguir estas pautas dietéticas, sin abandonar a las primeras de cambio, debe llegar a ser la base de la dieta equilibrada ideal de cada uno.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autor: Héctor Márquez Ortega, alumno del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: Ni dieta equilibrada ni nutrientes. Es cosa de adherencia. Aitor Sánchez García, Cuaderno de Cultura Científica, 6 de noviembre de 2015.
———————————-
El artículo La adherencia, clave en el seguimiento de las dietas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El ciclo de una infección
- En el mar, allí donde todo comienza
- Metamorfosis criogénica de la rana del bosque
Cuando las palabras no son suficientes: conjunto vacío
El reflejo se hace infinito. Y el infinito es un conjunto eternamente vacío.
Verónica Gerber Bicecci, Conjunto Vacío (página 181)
El conjunto vacío –no es uno, es EL– es el único conjunto que no posee elementos. El matemático francés André Weil (1906-1998), uno de los miembros del grupo Bourbaki, propuso denotarlo con el símbolo Ø. Se inspiró en esta letra vocal usada por los alfabetos danés y noruego y que, parece, también se utilizaba en el antiguo euskera. En la teoría de conjuntos de Zermelo la existencia del conjunto vacío es un axioma.
El título de esta anotación hace referencia a la novela Conjunto vacío (Pepitas de calabaza, 2017) de Verónica Gerber Bicecci, que se define a sí misma como una «artista visual que escribe».

La editorial Pepitas de calabaza presenta la novela de esta manera:
Conjunto vacío, primera novela de Verónica Gerber Bicecci, es una historia construida con una dura e infinita belleza; un relato en el que la escritura va de la saturación al vacío, y en el que la prosa experimenta un viaje que parte de la normalidad y se mueve hacia la extrañeza. Estamos ante un libro tremendamente original en su manera de contar, en el que se utilizan tanto recursos narrativos (párrafos cada vez más cortos, capítulos cada vez más sintéticos) como lingüísticos (escrituras ilegibles, disgrafías, lenguajes infantiles, idiomas inventados) o gráficos (los diagramas de Venn que se utilizan en la teoría de conjuntos) con el fin de completar una historia que conquista al lector desde la primera línea. Conjunto vacío narra la desaparición de la madre del personaje principal, y su historia reconstruye la generación de hijos del exilio, la relación entre imagen y palabra, el desdoblamiento y el juego de espejos que produce el silencio y lo «no dicho».
Conjunto Vacío cuenta la historia de una artista gráfica, Verónica, hija de exiliados argentinos en México. Tras ser abandonada por su pareja, la protagonista regresa a la casa familiar. Allí rememora la época en la que su madre desapareció. Abandonó a Verónica y a su hermano Alejandro: el niño y la niña la buscaban, sin conseguir encontrarla. Ahora, ya mayor, de regreso a casa –el búnker–, el fantasma de la madre sigue rondando. Verónica la escucha, habla con ella, pero no la ve. Sigue fingiendo, como de pequeña, que la madre sigue habitando la casa familiar.
Verónica encuentra un trabajo archivando las pertenencias de la recién fallecida escritora –también exiliada argentina– Marisa Chubut: se trata de un encargo de su hijo Alonso. Tras una breve relación amorosa con la protagonista, Alonso también desaparece de su vida.
Los diferentes abandonos –el desamor, la orfandad, el desamparo, el exilio, el desarraigo– producen un formidable vacío en la vida de Verónica. Solo es capaz de contar su historia jugando a que las palabras desaparezcan poco a poco: el texto contiene mensajes en clave, misivas escritas del revés o diagramas de Venn que ayudan a la narradora a expresar aquellas situaciones que no consigue reflejar con vocablos.
Cada personaje se identifica con una letra (ella es Y –de yo–, M es su madre, A es su hermano, etc.). Cada encuentro, cada abandono, cada relación con uno u otro personaje se expresa a través de estos diagramas de Venn y otras imágenes geométricas. En el video de debajo pueden verse algunos ejemplos.
En la época de la dictadura argentina, la que provocó el exilio de la familia de la protagonista a México, la enseñanza de la teoría de conjuntos se prohibió en las escuelas por ‘subversiva’. Entiendo que como acto de rebelión, Verónica cuenta su historia con la teoría de conjuntos como herramienta destacada.
A través de ellos se puede ver el mundo «desde arriba», por eso me gustan los diagramas de Venn. […] Sabemos, por ejemplo, que un jitomate pertenece al conjunto de jitomates (JI) y no al de cebollas (C) ni al de chiles (CH) ni al de cilantro (CI). ¿Dónde está la amenaza en un razonamiento como este?
Verónica Gerber Bicecci, Conjunto Vacío, página 84onjunto vacío es una bella narración en la que los vacíos cotidianos pasan a expresarse mediante imágenes, por medio de metáforas matemáticas, a través de teoría de conjuntos. Porque cuando las palabras no permiten expresar los sentimientos o mostrar las complejas relaciones humanas, quizás las imágenes puedan sustituirlas. Como la propia autora indica, por medio de diagramas ‘se puede ver el mundo «desde arriba»’.
Referencias:
Marta Macho Stadler, Conjunto vacío de Verónica Gerber Bicecci, DivulgaMAT, enero 2018
Conjunto vacío, página web de Verónica Gerber Bicecci
Carlos Pardo, Estrategias del ermitaño. ‘Conjunto vacío’ es reconocida como una de las novelas más imaginativas de la literatura latinoamericana reciente, Babelia, 26 julio 2017
Vivian Murcia G., Verónica Gerber Bicecci, la mujer del ‘Conjunto Vacío’, Ibe.tv, 8 marzo 2018
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Cuando las palabras no son suficientes: conjunto vacío se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La influencia de los genes en la felicidad
¿Qué nos hace realmente felices? ¿Las circunstancias de nuestra vida o cómo las percibimos? Investigadores de la Universidad de Essex (UK) han demostrado que nuestra actitud ante las circunstancias de la vida tiene un componente genético.
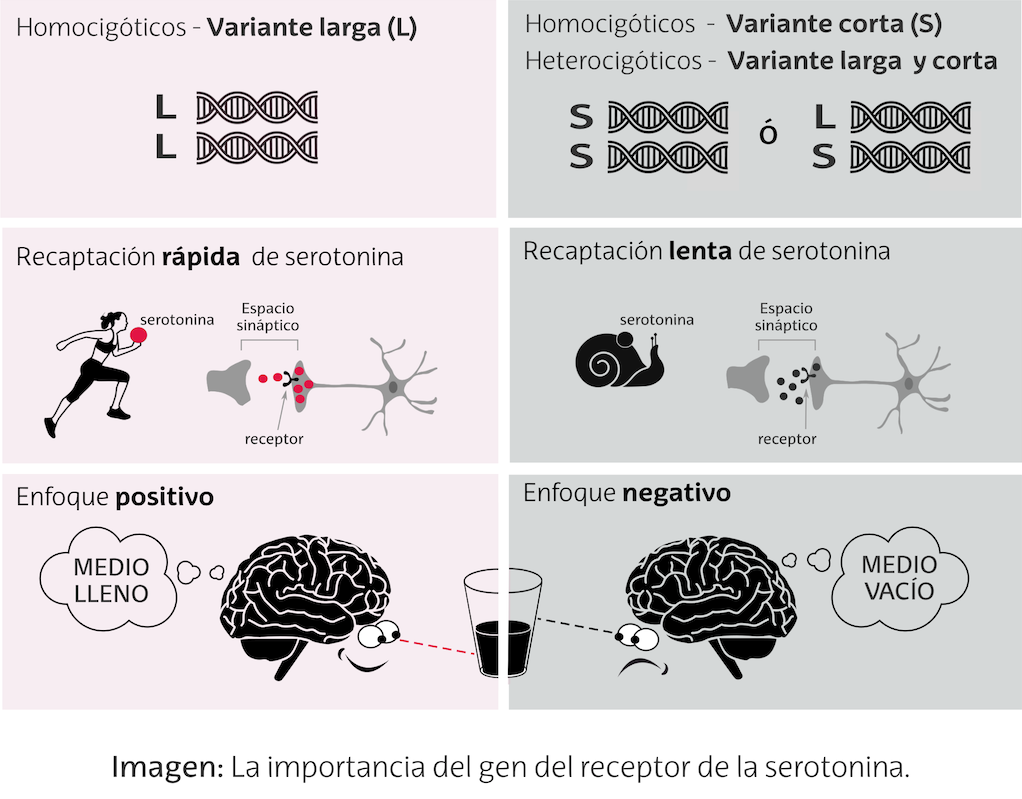 Ilustración: Inmaculada Martín
Ilustración: Inmaculada MartínSegún el trabajo de la investigadora Elaine Fox y sus compañeros, la tendencia a fijar nuestra atención en eventos desfavorables o a ignorarlos, en aras de lo positivo, está relacionada con diferencias en la longitud de la región promotora del gen del transportador de la serotonina (5-HTTLPR). Este gen determina la velocidad de recaptación de la serotonina hacia la neurona pre-sináptica. Así, en individuos homocigóticos para la variante larga (LL), la recaptación es más rápida dando lugar a un foco de atención centrado en los aspectos positivos. Mientras que la presencia de la región corta (SS o SL), da lugar a una recaptación lenta y a la ausencia del patrón de atención selectiva hacia los eventos favorables.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Inmaculada Martín Berenjeno, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: Un alelo para las gafas de color de rosa. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 7 de agosto de 2017.
———————————-
El artículo La influencia de los genes en la felicidad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Genética molecular para el rastreo de la caza furtiva
- En el mar, allí donde todo comienza
- Metamorfosis criogénica de la rana del bosque
Reflexión de ondas: rayos
 Fuente: Nearshore wave modeling / The COMET Program
Fuente: Nearshore wave modeling / The COMET ProgramHemos visto que las ondas pueden pasar una a través de otra y sortear obstáculos en sus trayectorias. Las ondas también se reflejan, al menos en cierta medida, cada vez que llegan a cualquier límite del medio en el que viajan. Los ecos son ejemplos familiares de la reflexión de las ondas sonoras. Todas las ondas comparten la capacidad de reflejarse, algo que tiene muchos usos, como veremos en la próxima entrega. Nuevamente, el principio de superposición será el que nos ayude a comprender qué sucede cuando hay reflexión.
Supongamos que uno de los extremos de una cuerda está muy bien atado a un gancho firmemente sujeto a una pared [1]. Desde el otro extremo enviamos un pulso por la cuerda hacia el gancho. Como el gancho no puede moverse, la fuerza ejercida por la onda de la cuerda no puede hacer ningún trabajo en el gancho [2]. Por lo tanto, la energía transportada en la onda no puede abandonar la cuerda en este extremo fijo. ¿Qué hace la onda entonces? Rebota, se refleja, con la misma energía [3].
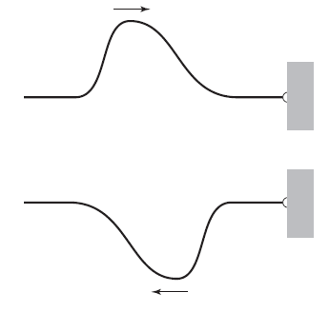 Figura 1. Imagen: Cassidy Physics Library
Figura 1. Imagen: Cassidy Physics Library¿Qué aspecto tiene la onda después de reflejarse? El sorprendente resultado es que la onda parece ponerse del revés en la reflexión. Imaginemos que la onda viene de izquierda a derecha, como en la Figura 1, y se encuentra con el gancho fijo. El efecto de la onda es intentar levantar (subir) el gancho. Según la tercera ley de Newton, el gancho debe ejercer una fuerza sobre la cuerda en la dirección opuesta mientras se lleva a cabo la reflexión. Los detalles de cómo varía esta fuerza en el tiempo son algo complicados y no los trataremos aquí, pero el efecto neto es que se envía de vuelta por la cuerda una onda invertida de la misma forma.
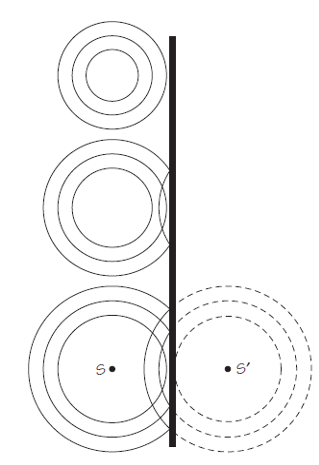 Figura 2. Imagen: Cassidy Physics Library
Figura 2. Imagen: Cassidy Physics LibraryFijémonos ahora en los tres diagramas de la Figura 2. Muestran los resultados de la reflexión de ondas en la superficie del agua en una pared recta. Puedes verificar si los diagramas son precisos al intentar reproducir el efecto en un lavabo o en una bañera. Espera hasta que el agua esté quieta, luego sumerge brevemente la punta del dedo o deja caer una gota en la masa de agua. En el diagrama de arriba, la cresta más exterior de la onda está cerca de la pared situada a la derecha. Los siguientes dos diagramas muestran las posiciones de las crestas después de que primero una y después dos se hayan reflejado.
Fijémonos en las curvas discontinuas en el último diagrama. Muestran que la onda reflejada parece originarse desde un punto S‘ que está tan lejos detrás de la pared como S está delante de ella. La fuente imaginaria en el punto S’ se llama imagen de la fuente S.
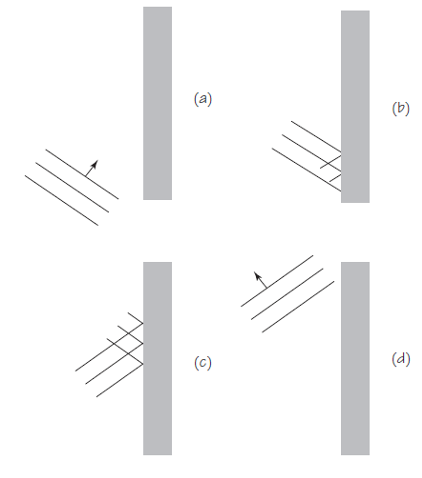 Figura 3. Imagen: Cassidy Physics Library
Figura 3. Imagen: Cassidy Physics LibraryHemos visto primero la reflexión de las ondas circulares, porque eso es lo que generalmente tenemos costumbre de ver cuando vemos ondas en la superficie del agua. Pero, en general, es más fácil usar un principio general para explicar la reflexión observando un frente de onda recto, reflejado desde una barrera también recta. Veamos los diagramas de la Figura 3 que indican lo que sucede cuando las crestas de las ondas se reflejan desde la barrera recta.
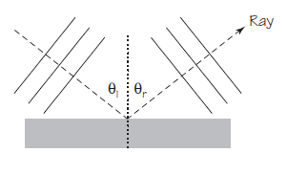 Figura 4. Imagen: Cassidy Physics Library
Figura 4. Imagen: Cassidy Physics LibraryParece que describir el comportamiento de los frentes de onda reflejados va a ser algo complicado. Sin embargo, es mucho más fácil si dibujamos perpendiculares a los frentes de onda. A esas líneas las vamos a llamar rayos, e indican la dirección de propagación de la onda. En la Figura 4 se han dibujado rayos para un conjunto de crestas onduladas justo antes de la reflexión y justo después de la reflexión desde una barrera. El rayo para las crestas incidentes forma un ángulo Θi con la pared. El rayo para las crestas reflejadas forma un ángulo Θr. El ángulo de reflexión Θr es igual al ángulo de incidencia Θi ; es decir, Θi = Θr.
Esto es un hecho experimental, que puedes verificar fácilmente.
Notas:
[1] Para ser rigurosos hemos de señalar que la pared tiene una masa enorme, está construida sólidamente y que no va a verse afectada en absoluto por lo que haga la cuerda.
[2] Que no puede hacer ningun trabajo significa que no puede desplazarlo (trabajo en física es fuerza por el desplazamiento que provoca), por estar anclado firmemente a una pared de las características de [1].
[3] Idealmente. Para que fuera exactamente así pared, gancho, sujeción al gancho y cuerda tendrían que ser ideales.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Reflexión de ondas: rayos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cuando las ondas se encuentran
- Ondas estacionarias
- Física de las ondas estacionarias: frecuencia fundamental y sobretonos
Mensajería electroquímica
El encéfalo es quien gobierna el organismo a través de una red de mensajería electroquímica encargada de recibir y gestionar toda la información.
 Imagen 1: El encéfalo humano. (Ilustración: Irene Manrique)
Imagen 1: El encéfalo humano. (Ilustración: Irene Manrique)En esta red se encuentran las neuronas, que junto con los sensores del encéfalo, coordinan las funciones vitales de nuestro cuerpo. Las neuronas realizan 5.000 conexiones entre ellas.
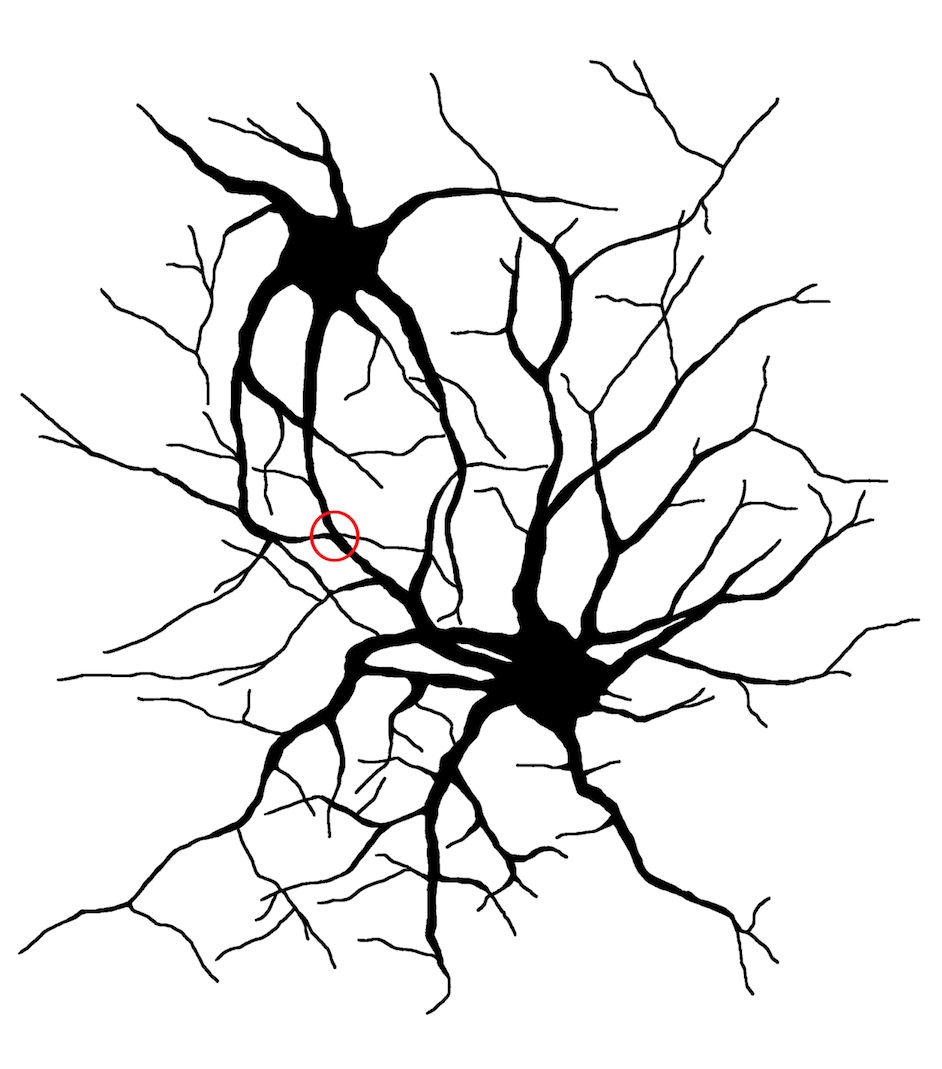 Imagen 2: Neuronas y conexiones sinápticas (círculo rojo). (Ilustración: Irene Manrique)
Imagen 2: Neuronas y conexiones sinápticas (círculo rojo). (Ilustración: Irene Manrique)Las neuronas trabajan en un millón de conexiones por segundo. En ellas se recibe la información en forma de presión, radiaciones electromagnéticas y sustancias químicas.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Inmaculada Manrique González, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: El encéfalo humano. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 14 de agosto de 2017.
———————————-
El artículo Mensajería electroquímica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Metamorfosis criogénica de la rana del bosque
- En el mar, allí donde todo comienza
- Especies exóticas invasoras
Digestión estomacal (I): el papel de las glándulas gástricas
La digestión estomacal cursa mediante la actuación de jugos gástricos sobre el quimo. Los produce el propio estómago, aunque la tasa a que se secretan depende de la alimentación. En los animales ectotermos que carecen de mecanismos de compensación térmica, una bajada de temperatura puede producir una disminución o, incluso, cese de la actividad alimenticia; en ese caso, también la secreción de jugos digestivos se reduce o se llega a detener. Y si se trata de animales cuya fuente de alimento es impredecible, pueden pasar largos periodos de tiempo sin alimentarse y sin actividad digestiva alguna: es lo que ocurre, por ejemplo, con ciertos reptiles como algunas serpientes, que capturan una presa cada mucho tiempo. En el extremo opuesto están los rumiantes, que digieren el alimento de forma permanente.
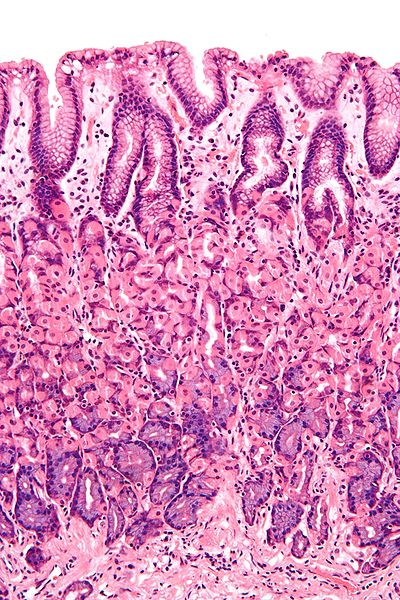 Micrografía de la mucosa gástrica. Imagen: Wikimedia Commons
Micrografía de la mucosa gástrica. Imagen: Wikimedia CommonsLa secreción de jugos en el estómago de mamíferos corre a cargo de células especializadas de su pared, la llamada mucosa gástrica. Se diferencian en ella dos grandes áreas, la mucosa oxíntica, que recubre el cuerpo y el fundus, y el área de glándulas pilóricas, que recubre el antro. La mucosa presenta múltiples pliegues, en cuyo interior se hallan las criptas gástricas, que son invaginaciones profundas del epitelio estomacal; las criptas configuran conductos y aperturas por los que las glándulas gástricas, que se encuentran en su base, evacúan sus productos a la luz estomacal.
Las glándulas gástricas están formadas por células secretoras de diferente tipo, unas son exocrinas y otras, endocrinas o paracrinas, aunque hay una diferencia importante entre los tipos de células secretoras de las glándulas de la mucosa oxíntica y las del área de glándulas pilóricas. A estas células y sus productos de secreción nos referiremos más adelante.
En el proventrículo de las aves hay dos tipos de glándulas, unas secretan moco y otras, HCl y pepsinógeno; ambas sustancias se producen en la misma célula, la llamada célula principal o célula oxinocopéptica.
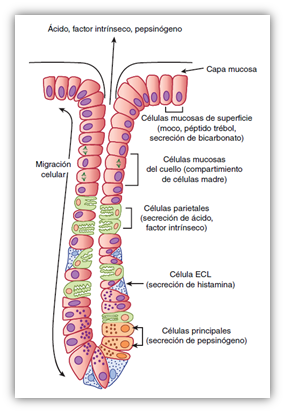 Estructura de una glándula gástrica del fondo y el cuerpo del estómago humano. Imagen: Adaptada de Barrett KE, Gastrointestinal Physiology. New York: Lange Medical Books/McGraw-Hill, Medical Pub. Division, 2006. Fuente.
Estructura de una glándula gástrica del fondo y el cuerpo del estómago humano. Imagen: Adaptada de Barrett KE, Gastrointestinal Physiology. New York: Lange Medical Books/McGraw-Hill, Medical Pub. Division, 2006. Fuente.En el estómago de mamíferos hay tres tipos de células secretoras exocrinas en las paredes de las criptas de la mucosa oxíntica:
(1) Las células mucosas recubren las criptas gástricas y la entrada a las glándulas; secretan un moco ligero de consistencia acuosa.
(2) Las células principales y las parietales recubren las zonas más profundas de las glándulas gástricas; las más numerosas son células principales y secretan pepsinógeno y lipasa gástrica.
(3) Las células parietales (u oxínticas) secretan ácido clorhídrico y el denominado factor gástrico intrínseco, una glucoproteína esencial para la posterior absorción de la vitamina B12 más tarde en el intestino.
Además, hay algunas células troncales que se dividen rápidamente para dar lugar a los diferentes tipos celulares del epitelio. Hay que tener en cuenta que se trata de un tejido muy activo y que la mucosa gástrica se renueva en su totalidad en pocos días: tan solo tres en el estómago humano.
Todas las secreciones exocrinas citadas se evacúan a la luz estomacal y son denominadas de forma conjunta jugos gástricos.
Las células parietales secretan HCl a la luz de las criptas, de donde es evacuado al interior del estómago. Los protones se producen en el interior de las propias células parietales, a partir de la escisión de moléculas agua. El OH– se combina con CO2 para dar ión bicarbonato mediante una reacción catalizada por la anhidrasa carbónica. Una ATPasa de H+/K+ bombea los protones (H+) al exterior de la célula (a la luz de la cripta). Esa bomba también introduce K+ en la célula, pero este difunde al exterior a continuación a través de los correspondientes canales. El transporte de H+ se realiza contra un gradiente de concentración enorme: en la cripta los protones pueden estar hasta tres o cuatro millones de veces más concentrados que el citoplasma de la célula parietal. Eso quiere decir que se necesita una cantidad de energía muy grande para salvar ese gradiente, lo que explica la abundancia de mitocondrias en las células parietales.
El cloruro procede del plasma, y su transporte está relacionado con la formación del bicarbonato (HCO3–) antes referida. Un antiporter de Cl–/HCO3– (en la membrana basolateral de las células parietales) traslada el bicarbonato al plasma a favor de su gradiente electroquímico y el Cl– desde el plasma al interior celular (en contra de gradiente de concentración). El ión cloruro se acumula así en el citoplasma y como está más concentrado aquí que en la luz estomacal y, además, la cara interna de la membrana es negativa, sale de la célula a favor de su gradiente electroquímico.
El ácido clorhídrico así formado en la luz del estómago cumple varias funciones importantes: (1) activa el pepsinógeno, convirtiéndolo en la enzima pepsina, a la vez que produce el grado de acidez óptimo para su actuación; (2) ayuda a la rotura del tejido conjuntivo y fibras musculares; (3) desnaturaliza las proteínas del alimento eliminando así su estructura terciaria y haciendo los enlaces peptídicos más accesibles a la acción digestiva; y (4) elimina la mayor parte de los microorganismos que han sobrevivido a la acción de la lisozima salivar (aunque no todos).
No todos los animales tienen digestión ácida estomacal. Los insectos, por ejemplo, no la realizan y tampoco tienen pepsinógeno. Los peces globo no tienen estómago y tampoco expresan el gen en ningún otro enclave digestivo (¡aunque sí en la piel!). Pero todos los vertebrados con estómago, salvo los ciclóstomos, tienen actividad péptica. El pepsinógeno, que se encuentra en vesículas secretoras de las células principales, es liberado al ducto de las criptas gástricas cuando se necesita. Una vez en la luz estomacal, debido al pH ácido, se convierte en pepsina y esta, a su vez, prosigue la activación de más unidades de pepsinógeno. La pepsina actúa sobre ciertos enlaces entre aminoácidos en el interior de las cadenas proteicas para rendir péptidos de menores dimensiones.
La digestión estomacal comprende, en realidad, tres actividades digestivas diferentes. En su tránsito por el fundus, las contracciones de la musculatura lisa que provocan las ondas peristálticas son todavía débiles. Por ello, en esa zona, el quimo es una sustancia semisólida de cierta consistencia y solo la zona exterior se encuentra expuesta a la acción de los jugos gástricos. En el interior de la masa semisólida sigue actuando la amilasa salivar. Más adelante, sin embargo, las contracciones peristálticas son más fuertes, hay más mezcla, el quimo pierde consistencia y los jugos gástricos tienen acceso a la mayor parte de las partículas en que se ha convertido el alimento. En esa fase cesa la digestión estomacal del almidón y el glucógeno y es cuando sobre todo el quimo actúan el HCl, la pepsina y la lipasa gástrica1.
Llegados a este punto conviene tener presente que los productos vertidos al interior del estómago son, potencialmente, muy lesivos para la pared gástrica, sobre todo el ácido clorhídrico, pero también las enzimas proteolíticas. Por esa razón, la pared necesita protección. El epitelio estomacal, entre las criptas, está formado por unas células que secretan un moco viscoso, de pH alcalino, que recubre todo el epitelio y sirve para protegerlo de la acción del ácido. Además de moco, esas células también secretan bicarbonato, que queda embebido en el propio moco y que neutraliza el ácido de su entorno. Además, la membrana celular de las células epiteliales es impermeable a los protones, por lo que estos no pueden penetrar en su interior ni causar daño, y esas células se encuentran unidas entre sí por uniones estrechas (zonulae occludentes), lo que impide o dificulta mucho que el ácido penetre entre ellas hacia la submucosa. Por último, hay que recordar que las células de la mucosa estomacal se renuevan muy rápidamente.
Nota:
1 Se estima que el 30% de la digestión de lípidos en la especie humana se debe a esa actividad.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Digestión estomacal (I): el papel de las glándulas gástricas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La motilidad estomacal
- Los tipos celulares humanos y su origen embrionario
- El estómago (u órgano equivalente)
Genética molecular para el rastreo de la caza furtiva
La genética molecular ha servido para desarrollar una herramienta que puede ser útil en los intentos de rastrear las diferentes partidas de colmillos de marfil que confisca la Interpol entre Asia y África.
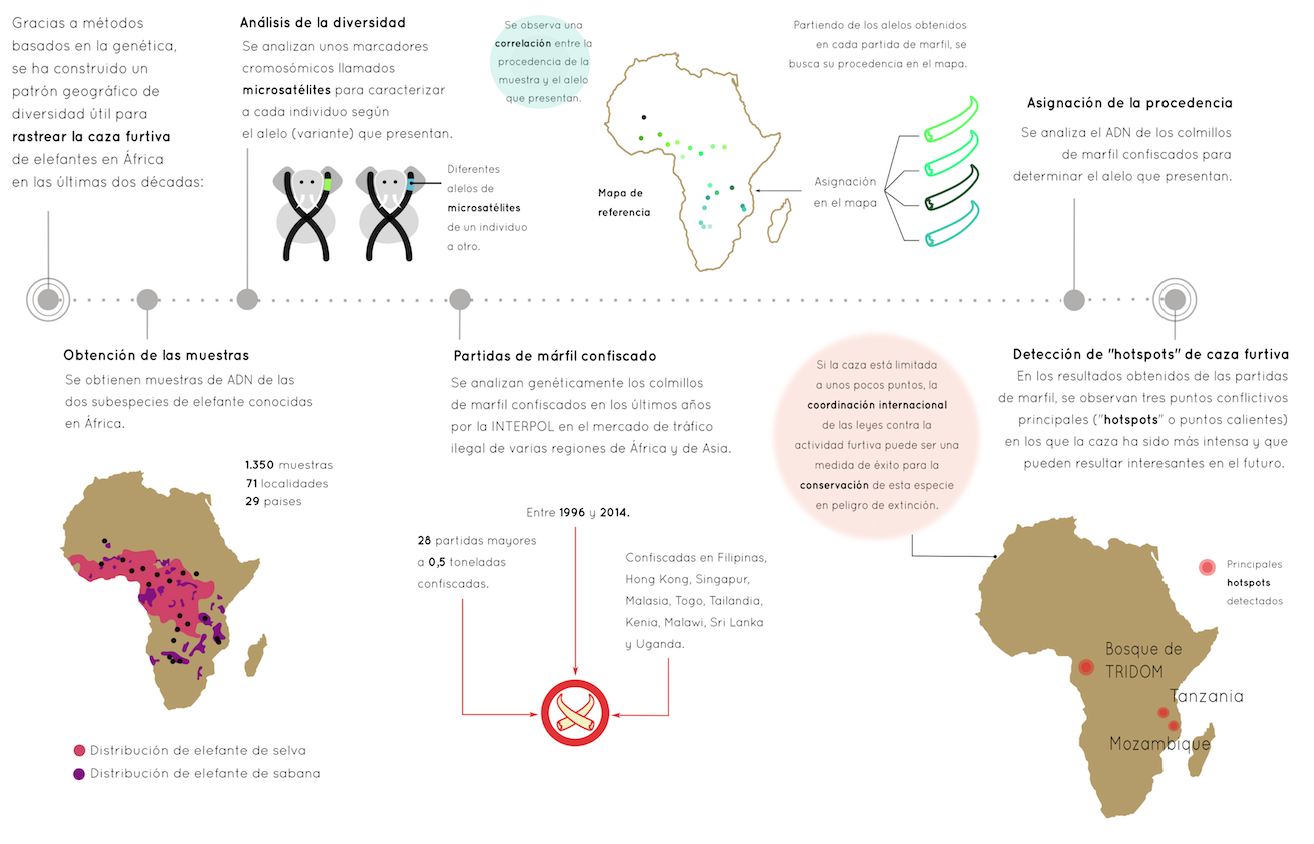 Imagen: Proceso detallado del estudio que ha determinado las zonas donde se desarrolla la caza furtiva de marfil. (Ilustración: Enara San Sebastian)
Imagen: Proceso detallado del estudio que ha determinado las zonas donde se desarrolla la caza furtiva de marfil. (Ilustración: Enara San Sebastian)En un estudio publicado en la revista Science Advances y llevado a cabo en la Universidad de Washington, con la colaboración de la entidad internacional, se ha concluido que la caza furtiva de marfil de las dos últimas décadas puede limitarse a tres zonas del continente africano: sudeste de Tanzania, el territorio contiguo al norte de Mozambique y la zona denomina TRIDOM (Trinational Dja-Odzala-Minkebe).
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Enara San Sebastian Casas (@enara_ssc), alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: Contra el furtivismo, genética molecular. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 4 de octubre de 2015.
———————————-
El artículo Genética molecular para el rastreo de la caza furtiva se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Contra el furtivismo, genética molecular
- En el mar, allí donde todo comienza
- Metamorfosis criogénica de la rana del bosque

