Características básicas de los riñones de vertebrados

Riñones de cordero.
Los riñones consisten en una batería de túbulos excretores llamados nefronas, que son sus unidades básicas. La pared de la nefrona está formada por una única capa de células epiteliales. Cada nefrona comienza por la denominada “cápsula de Bowman”, que es una invaginación del extremo ciego del túbulo de forma semiesférica. En el interior de la semiesfera se dispone un paquete de capilares sanguíneos denominado glomérulo, de manera que ambos epitelios, el capilar y el tubular, se encuentran en íntimo contacto. La estructura formada por la cápsula de Bowman y el glomérulo es lo que se conoce como corpúsculo renal y en su interior la disposición de los elementos que lo forman es tal, que constituyen una estructura de ultrafiltración.
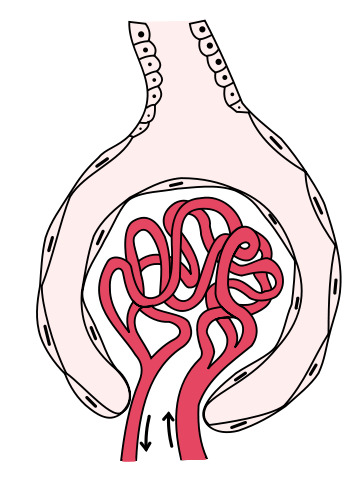
Corpúsculo renal con el glomérulo en rojo y la cápsula del Bowman en blanco.
La pared celular de la cápsula de Bowman está formada por células especializadas denominadas podocitos. Estas células tienen unas proyecciones hacia los podocitos adyacentes, creando una maraña de proyecciones entre las que queda un sistema de rendijas, que está considerado el principal elemento que participa en la filtración. Las sustancias disueltas de pequeño tamaño, como iones inorgánicos, glucosa, urea o aminoácidos, atraviesan sin dificultad el filtro, pasando de la sangre a la luz del túbulo. Sin embargo, las moléculas de mayor tamaño, como las albúminas y otras proteínas plasmáticas, no pasan de la sangre a la luz de la cápsula de Bowman. Aunque no hay un límite fijo, las sustancias que no atraviesan el filtro son aquellas cuyo peso molecular supera, aproximadamente, los 10.000 Da. Como consecuencia de la selectividad del filtro renal, la composición del fluido capsular –que es, en definitiva, la orina primaria- es muy similar a la composición del plasma en lo que se refiere a las sustancias pequeñas, pero difiere absolutamente para las de mayor tamaño.
Un efecto importante de esa permeabilidad diferencial es que al quedar la mayoría de las macromoléculas en el plasma sanguíneo, la presión osmótica de este es superior a la del fluido capsular. A esa diferencia se le denomina presión coloidosmótica de la sangre, porque es debida a coloides sanguíneos, sustancias que se encuentran en suspensión coloidal. Lo relevante de este fenómeno es que esa presión tiende a mover el agua desde el interior del túbulo (cápsula de Bowman en este caso) hacia los capilares glomerulares. Las presiones hidrostáticas de los dos enclaves, sin embargo, mantienen una diferencia de sentido opuesto; es mayor la presión sanguínea y menor la del líquido capsular y en virtud de esa diferencia, el plasma tiende a pasar de los capilares a la luz del túbulo. Así pues, sobre el sistema actúan dos presiones de efectos contrapuestos y, para que se produzca filtración plasmática, la diferencia de presiones hidrostáticas ha de ser superior a la presión coloidosmótica. Para que nos hagamos una idea de las magnitudes del juego de presiones, en los vertebrados utilizados normalmente en los estudios de función renal, la presión hidrostática de la sangre es de 6.7 kPa, la del fluido capsular es de 1.9 kPa, y por lo tanto, la diferencia es de 4.8 kPa. La presión coloidosmótica es de 3.5 kPa, por lo que la presión de filtración es de 1.3 kPa.
Denominamos tasa de filtración al volumen de orina primaria formado en un órgano excretor por unidad de tiempo; si el órgano en cuestión es el riñón de un vertebrado, la llamamos tasa de filtración glomerular (GFR, por sus siglas en inglés). El riñón humano adulto produce 120 ml min-1. A nadie se le escapa que no eliminamos 170 l de orina al día, por lo que resulta evidente que la mayor parte del volumen filtrado es reabsorbido antes de la evacuación de la orina.
Uno de los mecanismos con que cuentan los vertebrados para regular el volumen de orina que producen consiste, precisamente, en ajustar la tasa de filtración glomerular. Y ese ajuste se puede producir mediante dos métodos: (1) modificar el número de nefronas activas y (2) modificar la filtración de plasma en todas las nefronas del riñón. El primer procedimiento es característico de peces, anfibios y reptiles, aves incluidas. El segundo, que es propio de mamíferos, se basa en el ajuste de la presión sanguínea en el glomérulo. Cuanto menor es esa presión, menor es la producción de orina primaria; la presión sanguínea se controla mediante cambios en el diámetro de los vasos sanguíneos aferentes (los que llevan la sangre a las nefronas) y modulando así la resistencia al flujo (cuanto menor es el diámetro, menor es el flujo). No obstante, el volumen de orina que finalmente es expulsado al exterior depende más de procesos que ocurren en la nefrona tras la producción de la orina primaria que mediante el ajuste de la producción de esta.
Conforme avanza a lo largo del túbulo de la nefrona la orina primaria experimenta una serie de cambios tanto en su volumen como en la concentración de los solutos, así como en la concentración osmótica total. La nefrona consta de diferentes segmentos, cada uno con sus características funcionales: dependiendo de las proteínas que expresan las células epiteliales de cada segmento, desempeñarán unas u otras tareas (reabsorción de agua o solutos, o secreción de solutos). Lo normal es que en alguno de esos segmentos una parte más o menos importante del agua sea reabsorbida y pase a la sangre, por lo que el volumen de orina final suele ser bastante menor que el de orina primaria, como ya se ha señalado. Y también se reabsorben e, incluso, secretan solutos activamente (con gasto energético) de y a la luz del túbulo.
Más que los ajustes en el volumen de orina primaria que se forma, son los procesos reseñados en el párrafo anterior los que determinan tanto el volumen de la orina final como su composición y concentración osmótica. Y todo ello está al servicio de la regulación del volumen y composición de los fluidos corporales. De hecho, esta es la principal función de los riñones, más si cabe que la eliminación de restos nitrogenados. La actividad de los epitelios de la nefrona, así como su permeabilidad al agua depende de la acción de ciertas hormonas. Por lo tanto, son esas hormonas las que regulan la actividad global de los riñones y, por lo tanto, el volumen, composición y concentración de los fluidos corporales.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Características básicas de los riñones de vertebrados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Así forman la orina los animales
- Túbulos excretores: protonefridios y metanefridios
- Sistemas nerviosos: el sistema periférico de vertebrados
Geometría de una aceituna deshuesada

Las aceitunas tienen forma de elipsoide de revolución, un volumen que se forma dándole vueltas a una elipse alrededor de su eje mayor. Bueno, alrededor de su eje mayor son los denominados “prolatos”, también se puede construir un elipsoide “oblato” girando la elipse alrededor del eje menor. Ejemplo de los prolatos son las aceitunas y de los oblatos serían las lentejas.
Las aceitunas nacen colgadas de los olivos, y allí crecen hasta que se cosechan. En esa vida inmóvil no existe delante y detrás, no hay ninguna fuerza ni característica en la forma de vida que señale una dirección privilegiada en ese plano, por eso hay simetría de revolución, cualquier dirección en ese plano es igual que otra. En el caso de las personas, y de todos los seres vivos que se desplazan, en realidad, sí hay una dirección especial, la dirección del movimiento. Esa dirección es la que marca el eje delante- detrás. Los órganos perceptores del entorno tienden a colocarse delante, lógicamente, queremos ver y oler lo que tenemos por delante, en cambio queremos dejar detrás lo que ya no nos es útil. Tendemos a excretar hacia atrás. La aceituna es redondeada porque ni se mueve ni excreta; característica que comparte con el árbol que la sostiene y con casi todas las plantas, su ausencia de movimiento las redondea en el plano perpendicular a la gravedad.
No es totalmente redonda porque en el tercer eje sí hay una fuerza que marca un eje privilegiado, se trata de la gravedad. La aceituna está colgada del árbol por un punto; la fuerza que ejerce el rabillo sobre el fruto en ese punto es la que evita que se caiga. El peso de la aceituna tira en un sentido y la reacción del rabillo en el opuesto. Ese tirón en sentidos contrarios de un eje es el que hace que la aceituna se estire y pierda la simetría. Las aceitunas no tiene delante y detrás pero sí arriba y abajo, un eje que comparten con la inmensa mayoría de los seres vivos, por eso hay tan pocos simétricos (o casi) en ese eje, en la tierra nadie se libra de la gravedad. Se sufre bastante menos en el agua, por eso los peces se aproximan mucho más a la simetría arriba abajo que los animales terrestres (con el permiso de algún reptil como las serpientes). En resumen, las aceitunas tienen la simetría que cabría esperar por su desarrollo (se me hace exagerado llamar “forma de vida” a la existencia de una aceituna).
Las aceitunas de la foto están deshuesadas. Han sufrido un proceso industrial que les elimina el hueso que originalmente tenían en el interior. El hueco por el que ha salido el hueso es circular, y si nos fijamos vemos que está en un extremo de la aceituna. Cualquier sección perpendicular al eje mayor del elipsoide es un círculo. Lo es “por definición”, dado que ese es el eje de revolución que genera la figura tridimensional. Así pues parece que el proceso industrial que se sigue para deshuesar aceitunas de alguna forma tiene que incorporar esta característica geométrica para que todas las aceitunas (o casi todas) tengan su agujero redondo en su sitio.

En efecto, los dos procesos más habituales para deshuesar aceitunas incorporan en que el corte se produzca perpendicularmente al eje mayor del elipsoide. En el sistema mecánico más habitual para deshuesar grandes cantidades (Figura 1), los frutos llegan al punto de deshuesado en unos receptáculos que hay en el borde exterior de un carrete. Se toman las aceitunas de una en una y las lleva rodando ese punto. Ahí, por un lado entra una cuchilla circular hueca y por el otro un vástago que se clava en la aceituna hasta el hueso y lo presiona hacia el otro lado. La clave geométrica está en que los frutos van rodando hasta el punto de operación, y la única manera estable que tiene de rodar un elipsoide es alrededor de su eje mayor.
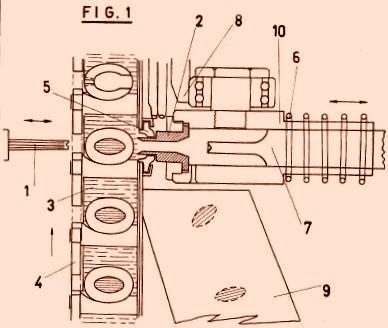
Figura 1 esquema de la máquina automática de deshuesar aceitunas. Fuente.
Hay un segundo proceso de deshuesado, menos automático, en el que los frutos se colocan en unos receptáculos cónicos con un hueco circular en la parte de abajo. Un vástago se clava desde arriba y empuja al hueso, que se desplaza hacia abajo separándose de la carne de la aceituna que está sujeta por el receptáculo y no puede moverse. El hueso sale por el hueco circular de la parte inferior arrastrando una porción de carne que deja en el producto final el característico agujero.
Esa intersección es perfectamente natural si la aceituna se colocó en el receptáculo de deshuesado con el eje mayor perpendicular al plano del agujero. Cualquier sección perpendicular al eje mejor es un círculo… por definición, dado que ese es el eje de revolución que genera la figura tridimensional. En otras direcciones no ocurre, por eso cuando aparece (rara vez, por cierto) una aceituna con el agujero en otro sitio resulta raro. El proceso industrial habrá deformado la carne y algún agujero se habrá hecho, pero al recuperar la forma inicial del elipsoide se pierde la forma circular del hueco. Estos deshuesados forzados son raros porque a la hora de colocar un elipsoide en un hueco cónico la posición de menor energía, la que deja más bajo el centro de gravedad del elipsoide, es con su eje paralelo (coincidente, en realidad) con el del cono. Así que no hay más que lanzar aceitunas a los receptáculos, agitar un poco y de forma “natural” (minimizando la energía del sistema) las aceitunas se colocarán bien.

Figura 2. Fuente
Si miramos la aceituna deshuesada con los ojos de la topología más que un elipsoide lo que tenemos es un donut (un toroide). Antes de deshuesarla la superficie de la aceituna es lisa y sin agujeros, si fuera de plastilina la podríamos deformar poco a poco hasta convertirla en una esfera. Una vez deshuesada eso ya es imposible, ahora tiene un roto que la atraviesa. Por el lado por el que salió el hueso el roto es grande (y circular como decíamos en el párrafo anterior) mientras que por el otro lado el hueco es pequeño, casi siempre con forma de cruz, la forma del perfil del vástago que entró por ahí para presionar y arrancar el hueso. Si este objeto lo imaginamos de plastilina y lo vamos deformando poco a poco, sin pegar lo roto ni romperlo por otros sitios, lo podemos convertir en un donut, un objeto distinto e irreconciliable con la esfera de antes de deshuesar. Ese proceso ha transformado la aceituna topológicamente.
Este post ha sido realizado por Joaquín Sevilla (@Joaquin_Sevilla) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Geometría de una aceituna deshuesada se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La geometría de los ‘cristaloides’, según Léopold Hugo
- La geometría de la obsesión
- Quad: pura geometría
π, así en el cielo como en la Tierra
En una parente paradoja en un día en el que se celebra π, el único conferenciante que habla de π resulta ser el físico Enrique Fernández Borja (Universidad de Córdoba) que nos plantea cómo la irrazonable efectividad de las matemáticas para describrir el universo nos permitiría usarlas como lenguaje común con los extraterrestres.
Enrique F. Borja: ''Pi, así en el cielo como en la Tierra''
El número π es una de las constantes matemáticas más importantes que existen. π es un número fascinante que goza de una gran popularidad e, incluso, de un día propio. Desde el año 1988, cada 14 de marzo se celebra el Día de Pi. Este evento fue idea del físico Larry Shaw, quien lanzó la propuesta añadiendo a su favor que la celebración coincidía con la fecha del nacimiento de Albert Einstein. Además, la forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos del número. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés)
En los últimos años la conmemoración del Día de Pi se ha ido extendiendo hasta convertirse hoy en día en una celebración que sobrepasa el ámbito de las matemáticas. π está presente en física, en el principio de incertidumbre de Heisenberg, la teoría de la relatividad o la ley de Coulomb. En geología hace su aparición a la hora de estimar la longitud de los ríos; en bioquímica, en el estudio de la estructura de una molécula de ADN; en astronomía, en el estudio de la forma del universo y en otras muchísimas aplicaciones de nuestro día a día.
Este 2018 nos unimos de manera especial a la celebración del Día de Pi con el evento BCAM-NAUKAS, que se desarrolló el miércoles 14 de marzo en el Bizkaia Aretoa de UPV/EHU. Este evento fue una iniciativa del Basque Center for applied Mathematics (BCAM) y la Cátedra de Cultura Científica de la Universidad el País Vasco.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo π, así en el cielo como en la Tierra se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El número de taxis de Bilbao y el espionaje en la 2ª guerra mundial
- Así en la Tierra como en Marte: espectrógrafos y espectrómetros de masas
- El universo en un día: El nacimiento de la Tierra, por César Tomé
¿Sirven para algo los enjuagues con clorhexidina?
Un gran número de bacterias están presentes en las bocas humanas y pueden pasar a la sangre cuando se realizan intervenciones como la extracción de algún diente. Los enjuagues con clorhexidina tiene un potente efecto antimicrobiano, pero hay posiciones encontradas sobre su uso en estos casos. Una investigación de la UPV/EHU demuestra que su uso solo evitaría un 12% de los casos de bacteriemia pero, dado su bajo coste y la ausencia de reacciones adversas y complicaciones, es recomendable utilizar estos enjuagues.
La cavidad oral humana está colonizada por una gran variedad de bacterias. Cuando se realizan procedimientos quirúrgicos, como por ejemplo una extracción dental, pueden pasar al torrente circulatorio, causando una bacteriemia generalmente transitoria. No está clara todavía la importancia que esta presencia de bacterias en la sangre tiene en el origen y evolución de procesos infecciosos como endocarditis de las válvulas cardiacas, de prótesis valvulares, de prótesis de articulaciones como cadera y rodilla generalmente y en la infección local.
Numerosos estudios han demostrado que el enjuague con clorhexidina tiene un potente efecto antimicrobiano sobre la microflora salival y la placa bacteriana. “Partiendo de esta hipótesis, podemos suponer que los enjuagues bucales antimicrobianos, utilizados antes de un procedimiento dental, debieran disminuir el número de microorganismos introducidos en el torrente sanguíneo del paciente, sin embargo, existe una gran controversia sobre este aspecto”, señalan los miembros del grupo de personal investigador de la UPV/EHU.
Así, la American Heart Association (AHA), en 1997, sugirió que los pacientes con riesgo de endocarditis infecciosa debieran usar un enjuague bucal antimicrobiano antes de un tratamiento dental. En 2006, la Sociedad Británica de Quimioterapia Antimicrobiana (BSAC) recomendó un único enjuague bucal con clorhexidina al 0,2% (CHX) (10 ml durante 1 minuto) antes de realizar procedimientos dentales asociados con bacteriemia en pacientes con riesgo. Sin embargo, en 2007, la AHA recomendó no utilizar ningún protocolo de profilaxis antiséptica.
Tratando de aportar evidencia científica sobre este asunto, el grupo de investigación de la UPV/EHU del que forman parte Iciar Arteagoitia, Carlos Rodriguez Andrés y Eva Ramos decidió realizar una revisión sistemática y un metanálisis de ensayos controlados aleatorios (ECA), siguiendo la Declaración PRISMA. El objetivo era evaluar la eficacia de la clorhexidina en la prevención de la bacteriemia tras una extracción dental. La investigación se realizó en colaboración con el Departamento de Medicina Preventiva y Salud Pública de la UPV/EHU y ha sido publicado en Plos One la primera revista científica de acceso abierto del mundo, que acepta investigaciones científicas rigurosas e innovadoras.
En el estudio se incluyen 8 ensayos clínicos, con 523 pacientes, 267 en el grupo tratado con clorhexidina, donde se registraron 145 casos de bacteriemia y 256 en el grupo control, en el que se produjeron 156 casos de bacteriemia. Los resultados de la investigación indican, por tanto, que el porcentaje de casos de bacteriemia que se pueden evitar si una población realiza prevención con clorhexidina es del 12%. El NNT, número necesario de pacientes a tratar para prevenir una bacteriemia, es del 16.
Los resultados muestran una eficacia relativa y poco significativa del uso de la clorhexidina a la hora de evitar que las bacterias presentes en la boca se introduzcan en el torrente sanguíneo cuando se practica una extracción dental. “Sin embargo, dado su bajo coste y la ausencia de reacciones adversas y complicaciones, consideramos recomendable realizar un enjuague con clorhexidina, antes de realizar una intervención de este tipo”, concluye el grupo de personal investigador de la UPV/EHU.
Referencia:
Iciar Arteagoitia, Carlos Rodriguez Andres and Eva Ramos (2018) Does chlorhexidine reduce bacteremia following tooth extraction? A systematic review and meta-analysis Plos One doi: 10.1371/journal.pone.0195592
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo ¿Sirven para algo los enjuagues con clorhexidina? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Para qué sirven las matemáticas?
- Marcas de agua digitales, qué son y para qué sirven
- El amor es algo bonito que acaba mal
La ciencia y el sentido de la vida

Otro de los habituales reproches que suelen escuchar los ‘cientifistas’ es que a diferencia de la religión la ciencia no proporciona respuestas a las Grandes Preguntas de la Humanidad, aquellas relacionadas con el sentido de la existencia y con el papel que en ella jugamos cada uno de los mortales. Una vez más como si esto fuese de alguna manera un fallo del proyecto científico, un defecto que de alguna manera invalida o menoscaba el valor que tiene la ciencia. Cuando, una vez más, encontrar el sentido de la vida no ha sido jamás, ni puede serlo, un propósito de la ciencia.
Mirándolo con distancia resulta fascinante y extraña la imperiosa necesidad que sienten los humanos por las narrativas, por disponer de explicaciones hiladas en historias que estructuren y den forma al Universo. Todas las religiones incluyen cosmogonías que explican cuál es el origen del mundo y cómo y por qué se produce su desarrollo, dejando huecos para que todos sus feligreses puedan insertar sus propias vidas y experiencias en una narración con principio, nudo y desenlace, siempre con connotaciones morales que no sólo explican los cómos, sino también los porqués. Cuando se pregunta a las persona religiosas el por qué de su fe una de las respuestas más típicas es que su creencia les ayuda a entender su papel en el Universo, ya que sin ella se sentirían perdidos en un Cosmos carente de sentido o razón. Las cosmogonías religiosas son así una parte fundamental del atractivo de la religión como concepto al proporcionar un sentido a la existencia, un esquema narrativo sobre el que fijar la experiencia humana y darle una estructura sin la cual nos sentimos inseguros. ‘Porque dios quiere’ o ‘porque los planes de la divinidad on complejos e insondables’ se convierten en explicaciones que para los creyentes dotan de sentido incluso a los sucedidos más absurdos o incomprensibles.
La ciencia no hace eso, dicen quienes lo consideran un defecto, y por tanto es insuficiente, está tarada, carece de una pieza esencial. Y tienen toda la razón, solo que no se trata de un defecto sino de una característica esencial: la búsqueda del sentido de la existencia nunca ha formado parte de los objetivos de la ciencia, que no pretende explicar nuestro papel en el Universo sino simplemente describir cómo funciona.
Puede que la confusión provenga del hecho de que la ciencia ha desguazado con datos y conocimiento las cosmogonías de todas las religiones al describir el verdadero origen y desarrollo posterior del cosmos. Quizá sea porque en sus sucesivos saltos de conocimiento la ciencia ha ido desplazando a la Humanidad del centro del Universo, lugar que por definición ocupa en las narrativas de todas las religiones. El caso es que de alguna manera ciertos creyentes han pasado a considerar a la ciencia como una narrativa de tipo religioso más, pero sin que responda a las clásicas dudas existenciales tan típicas de adolescentes y de intoxicados: ¿quiénes somos? ¿De dónde venimos? ¿Cuál es nuestro papel en la Gran Narrativa Universal?
La ciencia no busca ni pretende responder a esas preguntas en el sentido filosófico-moral-religioso en el que suelen hacerse. Para la ciencia en el Universo no hay necesariamente rima, ni razón, ni una narrativa confortable que nos permita comprender con facilidad nuestro papel en el Cosmos. Lo que es es lo que es, sin que quepan deducciones morales ni se pretenda obtenerlas, sin que el papel de la Humanidad sea especial por encima del que cualquier otra especie biológica. De lo que se trata es de entender lo que existe, no de buscar, descubrir y encajar la experiencia humana en un plan o historia universal que no existe. Por eso la ciencia tiene la característica, que no el defecto, de no buscar ni estar interesda por el sentido de la vida. Porque bastante complicado es ya simplemente entender el Cosmos como para buscarle las vueltas.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La ciencia y el sentido de la vida se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas15 El olfato, el sentido menos conocido
- Activa tu neurona – Astronomía. Vida y muerte de una ciencia en España
- La ciencia contra lo obvio
Matemáticos y sin embargo criminales
En la muy recomendable serie Preparados para matar en este Cuaderno de Cultura Científica, Eduardo Angulo ha hablado de diversos perfiles de asesinos, de víctimas de crímenes, de motivos para asesinar, de la evolución de los homicidios, etc.
No quiero hacer la competencia a Eduardo –imposible, él es un maestro–, pero quería aportar al tema los casos de dos criminales matemáticos: uno de ficción y otro real.
James Moriarty
El profesor James Moriarty es un personaje de ficción creado por Arthur Conan Doyle: es el eterno enemigo de Sherlock Holmes. Aparece por primera vez en las Memorias de Sherlock Holmes, en El problema final:
Es el Napoleón del crimen. Es la mente organizativa de la mitad de los hechos depravados de los que se tiene conocimiento y de casi todos los que pasan inadvertidos en esta gran ciudad. Es un genio, un filósofo, un pensador abstracto. Tiene un cerebro de primer orden. Permanece sentado, inmóvil, como una araña en el centro de su red; pero esta red tiene miles de hilos y el conoce muy bien el modo de vibrar de cada uno. Él mismo hace poco. Sólo planea. Pero sus agentes son numerosos y están espléndidamente organizados.
James Moriarty. Fuente: Wikimedia Commons.
Moriarty aparece citado en siete de las novelas de Sherlock Holmes: El problema final, La casa deshabitada, El valle del terror, El cliente ilustre, El tres cuartos desaparecido, El constructor de Norwood y Su último saludo en el escenario.
En El problema final se alude a un tratado sobre el teorema del binomio que Moriarty escribió:
Hizo una carrera extraordinaria. Es un hombre de buena familia y recibió una esmerada educación; tiene, además, por naturaleza, unas excepcionales dotes para las matemáticas. A la edad de veintiún años escribió un tratado sobre el teorema del binomio, que estuvo muy en boga en Europa. Fundándose en esto, ganó una cátedra de matemáticas en una de esas pequeñas universidades nuestras y todo parecía indicar que tenía ante sí una brillantísima carrera.
En El valle del terror se alude al tratado The Dynamics of an Asteroid escrito por Moriarty:
¿No es él el aclamado autor de ‘La Dinámica de un Asteroide’, un libro que asciende a tan raras cuestiones de matemática pura, que se dice que no hay individuo en el medio científico capaz de criticarlo?

The Dynamics of an Asteroid. Fuente: Wikimedia Commons.
A Moriarty lo utilicé para hablar de Una paradoja del infinito: la oferta del diablo por ser un villano de maldad reconocida.
André Bloch (1893-1948)
El matemático André Bloch fue un criminal, esta vezreal. Pasó prácticamente toda su vida en un hospital psiquiátrico tras haber asesinado a tres miembros de su familia en 1917: todas sus brillantes matemáticas fueron redactadas en ese lugar.

André Bloch. Fuente: MacTutor Archive.
Bloch mantuvo correspondencia con varios matemáticos de renombre, entre ellos Georges Valiron, George Pólya, Jacques Hadamard, Gösta Mittag-Leffler, Émile Picard, Paul Montel y Henri Cartan. En sus cartas, ponía como remite “57, Grande rue, Saint-Maurice”, sin mencionar que se trataba de un hospital psiquiátrico, con lo que muchos de sus correspondientes nunca supieron lo extraordinario de su situación.
Según Pólya, Blochtenía como costumbre fechar todas sus cartas el 1 de abril –el día de los inocentes en Francia– independientemente del día en las que las escribiera.
Su mayor contribución fue el teorema de Bloch –no debe confundirse con el teorema de Bloch de física, debido a Felix Bloch– en variable compleja, que afirma la existencia de una cierta constante, llamada constante de Bloch, cuyo valor exacto aún se desconoce.
Según se comenta en [Cartan y Ferrand, pág. 214], al final de su vida, el hermano menor de Bloch le fue a visitar al hospital. El matemático se interesó por el resto de su familia. Al día siguiente, le dijo a su médico:
Es una cuestión de lógica matemática. Había habido enfermedades mentales en mi familia. Debía seguirse inevitablemente la aniquilación de toda esta rama. Comencé mi trabajo en el momento de esa famosa comida. No ha terminado. Quería saber cómo está la situación.
Y ante las protestas del médico, Blochle respondió:
Usted habla un lenguaje emotivo. Por encima, están las matemáticas y sus leyes. Usted sabe muy bien que mi filosofía se inspira en el pragmatismo y el racionalismo absoluto. He aplicado el ejemplo y los principios de una famosa matemática de Alejandría, Hipatia.
A pesar de esta ‘misión asesina’ que guio su triple crimen, Bloch era una persona tranquila, amable, con costumbres regulares. Trabajaba en todo el día en una pequeña mesa, negándose a salir a pasear: Las matemáticas me bastan, argumentaba.
Referencias
-
James Moriarty, The Arthur Conan Doyle Encyclopedia
-
Marta Macho Stadler, Moriarty, matemático y criminal, ZTFNews, 3 febrero 2013
-
Bradley E. Schaeffer (1993). Sherlock Holmes and some astronomical connnections. Journal British Astronomical Association 103 (1) 30-34
-
Henri Cartan et Jacqueline Ferrand, Le cas André Bloch, Cahiers du Séminaire d’histoire des mathématiques t. 9, 211-219, 1988
-
Marta Macho Stadler, Una cuestión de lógica matemática, ZTFNews, 20 noviembre 2013
-
César Tomé López, André Bloch: el asesinato como una cuestión de lógica matemática, Experientia docet, 19 marzo 2011
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Matemáticos y sin embargo criminales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Quipu y yupana, instrumentos matemáticos incas (I)
- Quipu y yupana, instrumentos matemáticos incas (II)
- Repasando algunos objetos matemáticos notables
Cristalografía (5): Copos de nieve, Frankenheim o el nuevo Euclides
Veíamos en la entrega anterior de esta serie que Kepler había mantenido una correspondencia muy interesante con Thomas Harriot y que, en el transcurso de ésta, Harriot le había mencionado a Kepler el problema del empaquetamiento de esferas. También mencionamos que Kepler llegó pronto a la conjetura de su nombre.

Imagen: Alexey Kljatov
Como parte de este proceso, Kepler se dio cuenta que el empaquetamiento compacto de esferas en una sola capa da lugar a estructuras hexagonales que recuerdan a un panal de abeja. Esto le llevó a cuestionarse (y a buscar una respuesta satisfactoria) sobre la forma hexagonal de los copos de nieve en su tratado de 1611 Strena seu de nive sexangula (Un regalo de Año Nuevo de nieve hexagonal). Esto ya de por sí era bastante excepcional, ya que en aquella época no era común el conocimiento sobre la forma de los copos de nieve.

A título de ejemplo del conocimiento de la época tomemos el Historia de gentibus septentrionalibus (Historia de los pueblos del Norte) de Olof Månsson (latinizado Olaus Magnus), publicado en 1555. En él aparece una ilustración de los copos de nieve en la que es evidente que el autor, sueco por más señas, no es consciente de la forma hexagonal de los copos de nieve. Vemos que hay copos de nieve con forma de mano o de ojo o de media luna, por ejemplo.

Kepler llegó a la conclusión de que la forma de los cristales está relacionada con la geometría de los panales de abeja. Este empaquetamiento compacto del panal puede extenderse en las tres dimensiones de la misma forma en que los granos ocupan una granada. La elección de Kepler del copo de nieve (plano) para su explicación en vez de los cristales poliédricos de cuarzo que usó Cardano tiene la ventaja de que no le aplica la refutación de Scaligero (véase la IV entrega). Ni que decir tiene que este razonamiento, desde el punto de vista actual, no es válido: ni la molécula de agua es una esfera ni el empaquetamiento del cristal de agua de origen atmosférico puede ser llamado compacto de ninguna de las maneras. Sin embargo merece la pena detenernos un momento en él.

En el momento de componer De nive sexangula, Kepler ya era un convencido atomista y consideraba la materia como compuesta por átomos esféricos. Había evaluado dos maneras diferentes en las que las esferas se pueden empaquetar en dos dimensiones, cuadrada y hexagonal, comprobando que esta proporcionaba un empaquetamiento más compacto. La extensión de estos empaquetamientos a tres dimensiones llevaba, en el caso del cuadrado, a una disposición cúbica en el que cada esfera está rodeada por otras seis esferas (un empaquetamiento cúbico primitivo), mientras que la disposición hexagonal llevaba a un empaquetamiento más denso, en el que cada esfera tiene doce vecinos. Este es el empaquetamiento que el conjeturó que era el que tenía mayor densidad posible.
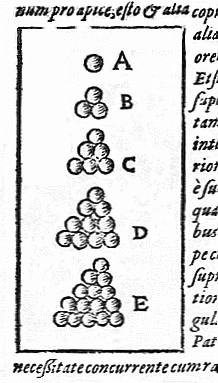
Al igual que Cardano y Kepler, Robert Hooke (del que ya hablamos en la II entrega) también creía que la naturaleza atómica de la materia también podría explicar las formas regulares de los cristales. A diferencia de los primeros, que se dedicaron casi en exclusiva a los hexágonos, Hooke también consideró otras formas y se dio cuenta de que el empaquetamiento compacto de esferas podría explicar toda clase de formas diferentes que se pueden encontrar en los cristales.
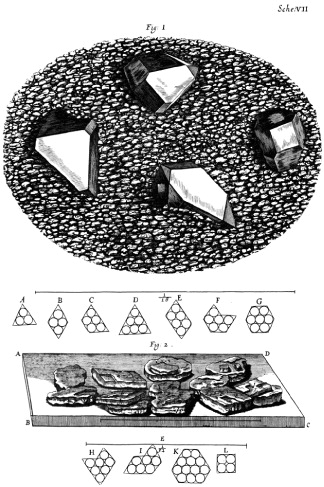
Hooke fue un paso más allá y dibujó en su Micrographia (1665) estudios detallados para intentar determinar cómo se empaquetan los átomos para dar lugar a las distintos cuerpos cristalinos. Su idea era observar detalladamente cristales, naturales y artificiales, para determinar todas las formas posibles, y después tratar de construirlas usando esferas. Fijémonos en que de aquí se sigue con naturalidad la idea de que sólo ciertos ángulos son posibles en los cristales; sin embargo, Hooke nunca dijo tal cosa de forma explícita, por lo que la ley de la constancia de los ángulos se atribuye a Steensen aunque su De solido es de 1669.
Hooke nunca completó su proyecto más ambicioso. De hecho se necesitaron 160 años de observaciones antes de poder intentar una construcción general de formas cristalinas. En 1826 Moritz Ludwig Frankenheim publicó Crystallonomische Aufsätze, su intento de sistematizar la mayoría de los cristales conocidos basándose en sus simetrías. Llegó a la conclusión de que sólo existían 32 combinaciones de operaciones de simetría. Hoy diríamos que sólo existen 32 grupos puntuales cristalográficos que definen 32 clases de cristales. Frankenheim no usó la definición de grupo (Galois, 1829) que no sería de uso generalizado hasta después de 1846.
En algunos textos el descubrimiento de los 32 grupos puntuales cristalográficos aparece atribuido a Johann F.C. Hessel, que lo realizó independientemente cuatro años después de Frankenheim, en 1830, aunque pasó desapercibido hasta que fue redescubierto por Ostwald en 1897; también aparecen atribuciones a Auguste Bravais (1848) y a Axel Gadolin (1867), dependiendo de si el texto es alemán, francés o ruso, respectivamente.
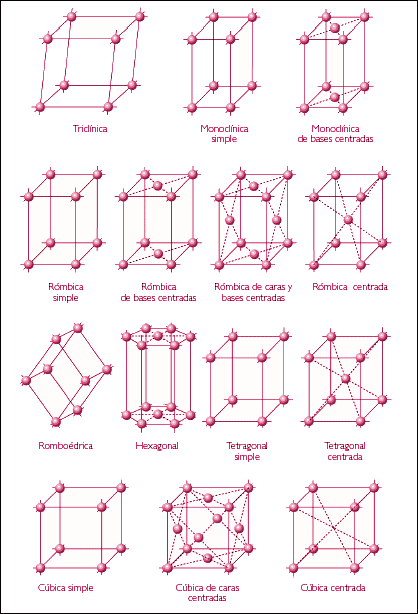
Este primer paso llevó a Frankenheim a considerar las maneras posibles que podría haber de ordenar puntos (átomos esféricos) periódicamente en el espacio euclidiano (hacemos esta puntualización porque los cuasicristales, que son cuasiperiódicos en el espacio euclidiano, son periódicos en espacios de al menos 5 dimensiones, pero este es otro tema). Llegó a la conclusión en 1845 (esta fecha es importante) de que sólo había 15 simetrías diferentes para una disposición periódica de puntos en el espacio, esto es, 15 redes cristalinas.
Frankenheim hizo todo el trabajo, pero otro se llevaría el mérito, una vez más. Como decíamos más arriba la teoría de grupos se popularizó entre los matemáticos a partir de 1846, un año después de la publicación de Frankenheim. En 1848, Auguste Bravais publica sus Études Cristallographiques en el que expone los hallazgos de Frankenheim pero hace notar matemáticamente que dos de las redes de Frankenheim son, de hecho, equivalentes, y que, por lo tanto, el número de redes elementales es 14. Desde entonces se las conoce como redes de Bravais, mientras que reto al amable lector a que busque alguna cita a Frankenheim en algún texto cristalográfico general.
Así, Frankenheim (y Bravais) habían resuelto el problema de disponer puntos en el espacio. Pero, ¿qué pasa si lo que hay que distribuir espacialmente son moléculas que no tienen por qué tener una simetría propia? Esta es la pregunta que al final fue resuelta en 1891 por dos matemáticos que publicaron independientemente las definiciones de los 230 grupos espaciales cristalográficos (si se admite que las copias quirales son distintas; si no, 219), pero que colaboraron en la elaboración de estas ideas, Evgraf Stepánovich Fiodorov y Arthur Moritz Schönflies.
Si bien la forma de los cristales era un buen argumento a favor de la teoría atómica, y que la teoría atómica también era una buena base para las teorías cristalográficas, la oposición al atomismo persistía. El concepto había sido revitalizado a principios del siglo XIX por John Dalton, pero hasta el primer Congreso de Químicos en Karlsruhe (1860) no tuvo una especie de reconocimiento oficial. Con todo, muchos científicos abominaban de la teoría y lo siguieron haciendo hasta entrado el siglo XX. La verdad es que no se les puede acusar de cabezonería o falta de conocimiento, si acaso de rigor excesivo o de dejarse llevar por según qué corriente filosófica. En cualquier caso, las pruebas experimentales definitivas se encontrarían en el siglo XX: la radioactividad, la confirmación de la teoría de Einstein del movimiento browniano y, mire usted por donde, la difracción de los rayos X por los cristales.
Referencias generales sobre historia de la cristalografía:
[1] Wikipedia (enlazada en el texto)
[3] Molčanov K. & Stilinović V. (2013). Chemical Crystallography before X-ray Diffraction., Angewandte Chemie (International ed. in English), PMID: 24065378
[4] Lalena J.N. (2006). From quartz to quasicrystals: probing nature’s geometric patterns in crystalline substances, Crystallography Reviews, 12 (2) 125-180. DOI:10.1080/08893110600838528
[5] Kubbinga H. (2012). Crystallography from Haüy to Laue: controversies on the molecular and atomistic nature of solids, Zeitschrift für Kristallographie, 227 (1) 1-26. DOI: 10.1524/zkri.2012.1459
[6] Schwarzenbach D. (2012). The success story of crystallography, Zeitschrift für Kristallographie, 227 (1) 52-62. DOI: 10.1524/zkri.2012.1453
Este texto es una revisión del publicado en Experientia docet el 12 de diciembre de 2013
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cristalografía (5): Copos de nieve, Frankenheim o el nuevo Euclides se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cristalografía (4): átomos y balas de cañón.
- Cristalografía (3): Goniómetros y óxidos dulces
- Cristalografía (2): Las rocas con lengua y la orina de Hooke
Las ventajas (para ti y para los demás) de ser egoísta de vez en cuando

Fuente: Pixabay
Consideramos el egoísmo un grave fallo de carácter, algo que reprochamos a los demás cuando lo ejercen y un defecto contra el que advertimos a los niños. “Hay que ser generoso”, decimos. “Que persona más generosa”, admiramos. Es casi lo mejor que se puede decir de alguien tras su fallecimiento.
Quizá deberíamos tragarnos nuestras palabras y reconsiderar el egoísmo. Podría ser que el egoísmo no fuese tan malo después de todo. Que un poco de egoísmo ocasional sea el aliño perfecto para tomar decisiones más eficientes.
Es lo que sugiere una investigación llevada a cabo por psicólogos de la Universidad del Estado de Ohio. “La decisión más eficiente es aquella que va a aumentar la cuenta total de beneficios a partir de la solución de un problema, y eso es verdad tanto si la mayor parte de esos beneficios van para ti como si van para otra persona. Por eso a veces tiene sentido ser un poco egoísta si eso va a incrementar el beneficio final total”, explica Paul Stillman, líder del estudio.
El informático que no quiso ayudar a su amigo
Un ejemplo sería el siguiente. Imaginemos un ingeniero informático que está trabajando en un nuevo programa que ayudará a limpiar el ordenador de archivos basura de forma sencilla a aquellos usuarios que no tengan mucha idea de informática. Uno de sus amigos, precisamente poco hábil con el ordenador, le pide ayuda porque tiene un problema que no consigue solucionar. Nuestro protagonista le da amablemente plantón para quedarse en casa programando. Esto es una muestra de egoísmo, pero en realidad se trata de una decisión más eficiente. Sí, es verdad que nuestro ingeniero ha decidido pasar de su amigo para avanzar en su proyecto que, espera, le dará pingües beneficios económicos cuando termine, pero si miramos la decisión con perspectiva, estamos de acuerdo en que es la decisión que más beneficios aporta en conjunto, incluido a su desafortunado amigo, que cuando pueda instalar dicho programa en el ordenador podrá trabajar con él mucho mejor.
Una de las claves para tomar estas decisiones egoístas pero eficientes es precisamente ese mirarlas con perspectiva. El “big picture” en inglés. En este caso, lo que hace nuestro informático al desatender las necesidades de su amigo para centrarse en su gran proyecto.
En definitiva, se trata de crear una distancia psicológica para pensar fríamente y elegir la mejor solución a cada situación. Esa distancia puede darse en forma de tiempo, al planear algo con suficiente antelación, o en forma de desapego personal cuando afecta a personas que no conocemos, o ser simplemente una estrategia mental cuando nos planteamos las situaciones de forma hipotética en vez de real.

Fuente: Pixabay
Pensar con perspectiva
Para estudiar esta cuestión, Stillman y sus colegas llevaron a cabo una serie de experimentos. En uno de ellos, pidieron a 106 estudiantes que llevasen a cabo una tarea que les instaba a pensar con perspectiva o de forma más inmediata. A los primeros, se les pidió una lista de cosas que mejorarían si consiguiesen el objetivo de mejorar su salud, como por ejemplo, vivir más años. Así les hacían pensar con perspectiva. A los segundos, una lista para conseguir ese objetivo de una salud mejor, como por ejemplo, hacer más ejercicio. Así les hacían pensar en el corto plazo y con cercanía.
Pensando en esos objetivos se les pidió participar en un juego económico en el que tenían que tomar nueve decisiones sobre cómo compartir una cantidad de dinero entre ellos mismos y otras cuatro personas. Ninguno de ellos sabría quién había tomado la decisión y ninguno de ellos podría compartir el dinero.
Lo mejor para ti es a veces lo mejor para todos
Para la mitad de los voluntarios, la idea de maximizar los beneficios significaba favorecer a los demás, pero no siempre con buenos resultados. Por ejemplo: por cada dólar que se daban a sí mismos, cada uno de los otros cuatro participantes perdían 9. La situación para la otra mitad de los participantes era la contraria: favorecerse a sí mismos suponía aumentar los beneficios totales.
Al combinar ambos resultados, los investigadores observaron que aquellos participantes a los que se había pedido que pensasen con distancia y perspectivas tenían más probabilidades de tomar decisiones que aumentasen los beneficios generales, tanto si eso significaba beneficiarse antes a sí mismos o a los demás.
En otro de esos experimentos, los investigadores utilizaron otro método para crear distancia entre las decisiones de los participantes y sus efectos: a la mitad de ellos se les dijo que el reparto del dinero que decidiesen se haría efectivo en un año, y a la otra mitad que se haría efectivo al día siguiente. Igual que en el anterior experimento, aquellos que tuvieron que pensar con distancia tenían más probabilidades de tomar decisiones que maximizaban los beneficios totales del grupo, tanto si ellos mismos eran los principales beneficiarios como si no lo eran.
Por eso los autores han sacado la conclusión de que el principal factor a la hora de tomar decisiones eficientes es precisamente la distancia, esa capacidad de pensar en los problemas con perspectiva, del tipo que sea, para prescindir de condicionantes inmediatos y mantener como objetivo el mayor beneficio posible, a veces, para uno mismo.
Referencias:
Paul E. Stillman et al, From “me” to “we”: The role of construal level in promoting maximized joint outcomes, Organizational Behavior and Human Decision Processes (2018)
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Las ventajas (para ti y para los demás) de ser egoísta de vez en cuando se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El pueblo que hablaba con las ballenas, ¿podría enseñarnos su idioma a los demás?
- Cuando “ver para creer” no es suficiente
- ¿Quién llorará por los animales feos cuando desaparezcan?
Hablando se interrumpe la gente

Dicen de los escandinavos que si se les ofrece una taza de té hay que esperar casi un minuto para que te respondan. Muchos creen que las conversaciones entre japoneses están llenas de silencios entre una intervención y la siguiente. O que los italianos mantienen conversaciones muy vivas, plagadas de interrupciones. Algunas de esas creencias tienen alguna justificación, pero solo algunas.
Según Nick Enfield, de la Universidad de Sidney, el tiempo que transcurre entre las intervenciones de dos personas en una conversación es similar en hablantes de diferentes idiomas. En promedio, tardamos en torno a 200 milisegundos –lo que nos lleva un parpadeo- en tomar la palabra en una conversación o responder a una pregunta, aunque necesitamos más tiempo cuando la respuesta es negativa que cuando es afirmativa. Pero no hay grandes diferencias entre los hablantes de distintas lenguas. Los anglohablantes tardan 240 milisegundos en tomar la palabra y cuando lo hacen no se guían por una posible pausa de la otra persona, sino que se atienen a claves gramaticales o a otras señales, como la entonación, para intervenir.
En contra de la creencia antes mencionada, los japoneses prácticamente no dejan pasar nada de tiempo entre las intervenciones de dos contertulios; son los más rápidos: 7 milisegundos. Pero los daneses sí hacen largas pausas entre las intervenciones de dos personas que conversan: necesitan casi medio segundo. Según Enfield, atribuimos a los hablantes de distintas lenguas tiempos de respuesta muy diferentes debido a que la percepción del transcurso del tiempo es subjetiva. Somos tan sensibles a la cadencia temporal del habla, que magnificamos las diferencias, nos parecen mayores de lo que realmente son. El hecho de que no todos experimentemos los tiempos de la misma forma, conduce a desajustes cuando hablan personas que poseen pautas de conversación diferentes. Cuando quienes hablan hacen pausas de diferentes duraciones, es fácil que una de las dos interrumpa a la otra sin pretenderlo. Pero también se producen interrupciones de forma voluntaria.
Hay interrupciones “cooperativas”: se hacen para mostrar acuerdo con quien habla, le ayudan proporcionándole la expresión o palabra que necesita, o piden una aclaración de lo dicho. Otras son “intrusivas”: muestran desacuerdo, se hacen para dominar la conversación (“llevar la voz cantante”), o se usan para cambiar de tema. Al parecer, los occidentales tendemos a interrumpir de forma intrusiva, mientras que para los orientales son más frecuentes las interrupciones cooperativas.
Y también en este aspecto hay diferencias entre hombres y mujeres. Las mujeres se interrumpen más entre sí que los hombres, pero las interrupciones entre mujeres son, sobre todo, del tipo colaborativo. En los intercambios en los que participan hombres y mujeres, ellos tienden a interrumpir a las mujeres con una frecuencia muy superior que a la inversa. Eso ocurre, incluso, cuando la mujer goza de un estatus superior al del hombre. Y ese diferente comportamiento emerge muy pronto en el desarrollo de chicas y chicos. Ya en los primeros años de la escuela, los niños tienden a interrumpir con mayor frecuencia, mientras las niñas tienden a facilitar en mayor medida la participación de los demás en las conversaciones.
Los especialistas en estas cuestiones creen que es muy importante que seamos conscientes de que hay diferencias entre personas de diferente sexo y procedencia geográfica o cultural en la forma de conversar y en la tendencia a interrumpir a los demás. Porque el simple hecho de ser conscientes ya nos hace estar en guardia, evitando interrupciones intrusivas y facilitando el intercambio de puntos de vista. Tengámoslo en cuenta: pocas actividades sociales hay tan útiles como conversar y hacerlo con respeto.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 22 de abril de 2018.
El artículo Hablando se interrumpe la gente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Cuánta gente ha vivido en la Tierra?
- Una nueva investigación muestra que explicar cosas a la gente “normal” puede ayudar a los científicos a ser mejores en su trabajo
- Domesticados
El número de taxis de Bilbao y el espionaje en la 2ª guerra mundial
En esta conferencia, Juan Antonio Cuesta (Universidad de Cantabria) nos revela que tiene una obsesión un poquito particular: contar taxis, mirar sus números de licencia y, a partir de estos datos, estimar el número de licencias en las ciudades que visita. Ocurre que una cosa parecida hacían los servicios de información en la Segunda Guerra Mundial.
Charla de Juan Antonio Cuesta en el día de Pi
El número π es una de las constantes matemáticas más importantes que existen. π es un número fascinante que goza de una gran popularidad e, incluso, de un día propio. Desde el año 1988, cada 14 de marzo se celebra el Día de Pi. Este evento fue idea del físico Larry Shaw, quien lanzó la propuesta añadiendo a su favor que la celebración coincidía con la fecha del nacimiento de Albert Einstein. Además, la forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos del número. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés)
En los últimos años la conmemoración del Día de Pi se ha ido extendiendo hasta convertirse hoy en día en una celebración que sobrepasa el ámbito de las matemáticas. π está presente en física, en el principio de incertidumbre de Heisenberg, la teoría de la relatividad o la ley de Coulomb. En geología hace su aparición a la hora de estimar la longitud de los ríos; en bioquímica, en el estudio de la estructura de una molécula de ADN; en astronomía, en el estudio de la forma del universo y en otras muchísimas aplicaciones de nuestro día a día.
Este 2018 nos unimos de manera especial a la celebración del Día de Pi con el evento BCAM-NAUKAS, que se desarrolló el miércoles 14 de marzo en el Bizkaia Aretoa de UPV/EHU. Este evento fue una iniciativa del Basque Center for applied Mathematics (BCAM) y la Cátedra de Cultura Científica de la Universidad el País Vasco.
El artículo El número de taxis de Bilbao y el espionaje en la 2ª guerra mundial se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Códigos secretos en la primera guerra mundial
- ¿Es normal el número pi?
- 666, el número de la Bestia (1)
Una nueva vía de desarrollo farmacológico para el tratamiento de la fase progresiva de la esclerosis múltiple
Fuente: Esclerosis Múltiple España
La esclerosis múltiple es una enfermedad autoinmune que ataca y destruye la llamada vaina de mielina que recubre los axones de las neuronas y cuya integridad es indispensable en el correcto funcionamiento del encéfalo y de la médula espinal, ya que garantiza la correcta transmisión de la señal nerviosa.
El tratamiento actual de la esclerosis múltiple se basa en modular la actividad del sistema inmunológico, e impedir que sus células accedan al sistema nervioso central, y lo dañen. Estas terapias son eficaces en las fases iniciales de la enfermedad, pero no impiden su avance y el deterioro funcional progresivo.
En la fase progresiva de la enfermedad son las células microgliales del cerebro las principales causantes de la inflamación crónica responsable del deterioro neurológico. Estas células microgliales son las centinelas del encéfalo, y reaccionan ante cualquier daño o infección del mismo. Esta reacción, que es en principio beneficiosa, se convierte en nociva cuando se prolonga en el tiempo dando lugar a una inflamación crónica, y agrava la enfermedad y favorece su avance.
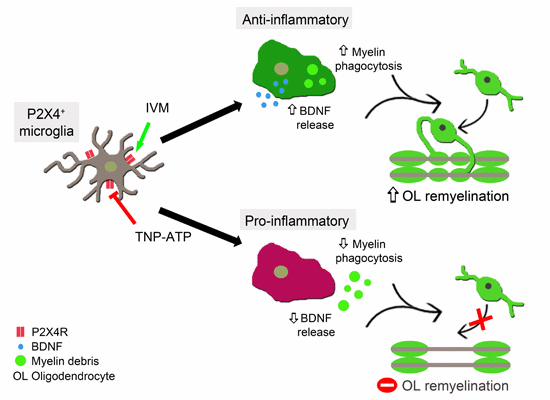
En el trabajo que se acaba de publicar se ha conseguido identificar un receptor denominado P2X4, en las células microgliales que incrementa su potencial anti-inflamatorio, con objeto de disminuir el daño en la esclerosis múltiple y, sobre todo, potenciar las respuestas reparadoras propias del organismo.
Este desarrollo experimental se ha realizado utilizando modelos animales, gracias a los que se ha podido descubrir que los fármacos que activan ese receptor mejoran los síntomas en la fase crónica de la enfermedad, al favorecer la reparación del tejido nervioso.
Según indica la Dra. María Domercq, del Departamento de Neurociencias de la UPV/EHU, que trabaja en el centro de investigación ACHUCARRO de Leioa, “estamos ante un hallazgo que abre una nueva vía de desarrollo farmacológico para el tratamiento de la fase progresiva de la esclerosis múltiple, y con ello, queremos abrir una nueva puerta a la mejora de la calidad de vida de las personas que padecen esclerosis múltiple”.
Referencia:
Alazne Zabala, Nuria Vazquez‐Villoldo, Björn Rissiek, Jon Gejo, Abraham Martin, Aitor Palomino, Alberto Perez‐Samartín, Krishna R Pulagam, Marco Lukowiak, Estibaliz Capetillo‐Zarate, Jordi Llop, Tim Magnus, Friedrich Koch‐Nolte, Francois Rassendren, Carlos Matute, María Domercq (2018) P2X4 receptor controls microglia activation and favors remyelination in autoimmune encephalitis EMBO Molecular Medicine doi: 10.15252/emmm.201708743
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Una nueva vía de desarrollo farmacológico para el tratamiento de la fase progresiva de la esclerosis múltiple se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Análisis de redes de la esclerosis múltiple
- Una posible terapia neuroprotectora y neurorrestauradora para el párkinson
- Una nueva diana terapéutica para el neuroblastoma
La ciencia que deberías saber antes de comprar tu protector solar (2)
En el anterior artículo de esta serie hemos resuelto algunas preguntas frecuentes sobre protección solar. Por ejemplo, si son mejores unos filtros solares que otros, de qué radiación debemos protegernos, cómo afecta la radiación UVA y UVB a nuestra piel, si son seguros los filtros nano y micro o si es cierto que abusar de la protección solar puede afectar a los niveles de vitamina D.
Ese primer artículo de la serie recibió un gran número de consultas, además de las que también nos han llegado a través de las redes sociales mediante la etiqueta #cienciaprotectorsolar. Hoy abordaremos algunas de ellas y, en próximas entregas, resolveremos las que se hayan quedado en el tintero y las nuevas que puedan surgir.
6. ¿Qué es el SPF (factor de protección solar) y cómo se mide?
El factor de protección solar (SPF) viene indicado por un número que figura en el envase y que va del 2 al 50+. El SPF nos indica por cuánto se multiplica el tiempo al que podemos exponernos al sol antes de que aparezca un eritema o enrojecimiento. Así, un SPF 30 multiplica por 30 el tiempo de exposición segura al sol. Si una persona se quemaría en 5 min de exposición directa al sol, con un SPF de 30, bajo esa misma radiación tardaría 30 veces más tiempo en quemarse.
Si un producto tiene SPF, si se especifica en su envase, implica que ha pasado unas pruebas que certifican que ese y no otro es su factor de protección solar. Estas pruebas se hacen in vivo, es decir, sobre piel. Es una de las razones por las que certificar un SPF es algo costoso para los laboratorios cosméticos.
Existen varios métodos de certificación, así que dependiendo del país en el que nos encontremos, el factor de protección solar puede variar y resulta complicado compararlos entre sí, como el FDA americano, el DIN alemán (ya en desuso) o el SAA australiano.
El método europeo es el que más se emplea en la actualidad para certificar el SPF. Se llama método COLIPA.
En 1994 se creó el Sun Proteccion Factor Test Method (método de verificación del factor de protección solar), fruto del estudio de los distintos métodos de evaluación del SPF, con el objetivo de obtener un método validado para todos los países de la Unión Europea, realizado por la Agrupación Europea de Fabricantes de Productos de Cosmética y Perfumería (COLIPA). Por ello es conocido como método COLIPA.
El factor de protección frente a la radiación UVB de un fotoprotector se determina desde 1997 de acuerdo con el estándar de COLIPA. Esto permite una clasificación según el nivel de fotoprotección:
• Bajo: 2, 4, 6.
• Medio: 8, 10, 12.
• Alto: 15, 20, 25.
• Muy alto: 30, 40, 50.
• Ultra: 50+
Para calcular el SFP según el método COLIPA, se valora la dosis mínima de radiación ultravioleta que produce la primera reacción eritemática (o enrojecimiento), perceptible en la piel humana. A esto lo denominamos mínima dosis eritemática (MED). La MED se determina con y sin protección. El cociente entre la MED con y sin protección nos da como resultado el SPF.
Para hacer esta medida se utilizan, dependiendo del método estadístico, entre 10 y 20 personas a los que se irradian 35 cm2 de la piel de la espalda. Para evaluar el SPF se aplican 2 mg de producto por cada cm2 de piel durante 15 min, y se inspecciona la piel también al día siguiente.

La implantación de esta metodología ha permitido unificar criterios, que todos los laboratorios que quieran especificar un SPF deban someterse al mismo método de evaluación. Por este motivo todos los productos con un SPF determinado han pasado la misma certificación, así se vendan en farmacias o en grandes superficies. Unos y otros son igual de fiables. No obstante, aunque tengan el mismo SPF, se diferencian en muchos otros aspectos tanto o más importantes relativos a la formulación del producto: si resisten al agua, si son para niños, si son más o menos cosméticos, si son hidratantes, la textura, la sensación que dejan en la piel, la facilidad de aplicación, la presencia de otros principios activos interesantes como despigmentantes o antioxidantes, etc.
Hay que tener en cuenta que los datos que se obtienen a través del método COLIPA y que figuran en el etiquetado no tienen en cuenta otros factores como la transpiración, la incorrecta aplicación del producto, la intensidad de la radiación y el lugar de exposición al sol. Por eso es tan importante saber qué SPF nos corresponde a nuestro tipo de piel y cómo debemos aplicar el producto.
7. ¿Qué SPF debería utilizar?
El uso de más o menos SPF depende de dos factores. Uno de los factores, el más relevante, es nuestro fototipo de piel. Así, una piel que se quema siempre y nunca se broncea, como suele ser el caso de las personas pelirrojas de ojos claros, necesitan emplear un SPF muy alto, el de 50 o 50+. Estamos ante un fototipo de piel I.
Una persona que se quema a veces, que puede llegar a broncearse, que tiene la piel, los ojos y el pelo claro, tendrá un fototipo de piel II. A estas personas también se les recomienda utilizar SPF 50 o 50+.
Sin embargo, las personas que nunca se queman y se broncean con facilidad, con piel, ojos y cabello oscuro, pueden utilizar un SPF menor. Entre 15 y 20 es suficiente. Son las personas con fototipo de piel IV.
Así que, a menor fototipo, mayor SPF debemos utilizar. Y ante la duda, hay que preguntar al farmacéutico o dermatólogo, y ser preferiblemente conservadores.
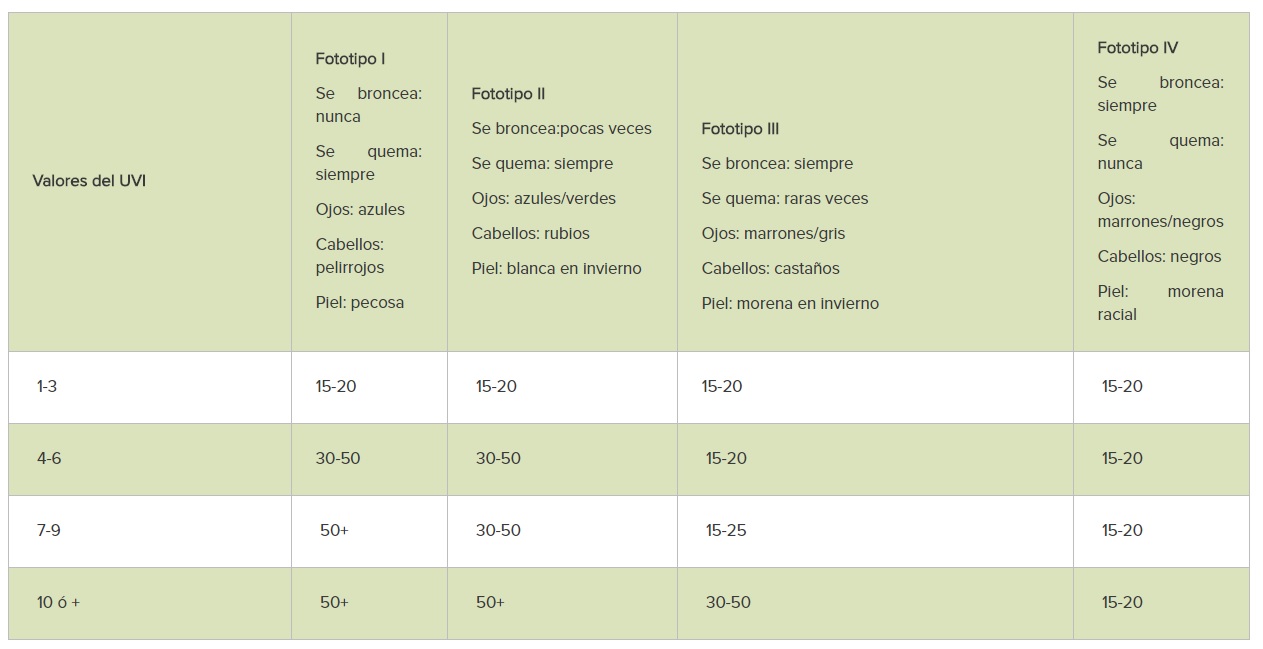
Fuente: AECC.org
El otro factor a tener en cuenta para escoger el SPF adecuado es el índice ultravioleta (UVI). El UVI es la estimación promediada de la radiación UVB solar máxima que llega a la superficie de la tierra. El UVI depende, entre otros factores, de la cantidad de ozono que hay en la columna atmosférica, de la elevación del sol, de la altitud del lugar y de la nubosidad.
El UVI se mide de forma continua con radiómetros de UV en banda ancha en más de veinte estaciones españolas de la Red Radiométrica Nacional de la AEMET, así como por los espectrofotómetros Brewer de la AEMET situados en A Coruña, Zaragoza, Madrid, Murcia, Izaña y Santa Cruz de Tenerife. Fuera de España se utilizan métodos de medida similares.
El UVI se divide en radiación UV baja (valores 1 a 3), radiación media (valores 4 a 6), radiación alta (valores 7 a 9) y radiación extrema (superiores a 10).
En España, los valores máximos de UVI entre 9 y 11 son comunes al mediodía en los días despejados de verano, sobre todo en Canarias. También se observan valores instantáneos muy altos en algunas estaciones incluso en presencia de nubes. En zonas montañosas el UVI puede presentar valores muy elevados. Por ese motivo conviene ser conservadores a la hora de escoger el SPF adecuado.
Al ser una información sujeta a variaciones, debemos consultar el UVI en los medios y aplicaciones que nos facilitan el dato.
8. ¿Hay protectores solares pantalla total, SPF 100 o SPF por encima de 50?
Las denominaciones han ido cambiando a lo largo del tiempo. En la actualidad ya no se utiliza la denominación pantalla total o SPF 100. Tanto una como la otra se corresponden a lo que actualmente llamamos SPF 50+. No es que hayamos rebajado el factor de protección solar, sino que se ha optado por unificar los criterios y denominar SPF 50+ al factor de protección solar más alto que existe.
El método COLIPA establece que el SPF 50+ (o plus) es la reivindicación más alta que se debe incluir en un fotoprotector de uso común. Esta cifra se reserva a los productos con SPF igual o superior a 60, ya que se entiende que, a partir de ahí, es poca la diferencia de absorción real de radiación entre un producto y otro por más que aumente la concentración de filtros.
Hay excepciones todavía permitidas, como productos específicos para intolerancias graves al sol, antecedentes de cáncer de piel o pacientes oncológicos. Por eso en productos de oncocosmética podemos encontrarnos envases en los que se permite el uso de la nomenclatura antigua SPF 100.
Es tu turno
Este es el segundo artículo de una serie que estamos escribiendo para resolver todas las dudas que nos hacéis llegar a través de los comentarios y las redes sociales. Algunas de ellas, las más repetidas, han sido resueltas en esta entrega. Otras las iremos resolviendo en los artículos siguientes, como si la ropa o las sombrillas pueden protegernos de la radiación ultravioleta, qué diferencia hay entre water resistant y waterproof, si podemos utilizar la crema del año pasado, cada cuánto y cómo hay que aplicar y reaplicar los productos, o si existen filtros solares que son perjudiciales para el medioambiente.
Así que, si tienes alguna pregunta más, déjala en un comentario o envíanosla a través de las redes sociales utilizando la etiqueta #cienciaprotectorsolar.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo La ciencia que deberías saber antes de comprar tu protector solar (2) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ciencia que deberías saber antes de comprar tu protector solar (1)
- Así es la mejor crema antiedad según la ciencia
- Saber y saber que se sabe
Los números poéticos
El pasado año 2017 se celebró el centenario del nacimiento de una de las grandes poetas españolas, la madrileña Gloria Fuertes (1917-1998), que además acercó la poesía y la literatura a toda una generación de niños y niñas, entre los que me incluyo, a través de sus poemas y cuentos infantiles.

Portadas de algunos de los libros infantiles de Gloria Fuertes que están en mi pequeña biblioteca personal: La oca loca (Escuela Española, 1978), “La ardilla y su pandilla” (Escuela Española, 1981) y “Yo contento, tu contenta, que bien me sale la cuenta (la tabla en verso)” (Escuela Española, 1984)
Teniendo en cuenta que Gloria Fuertes escribió algunos poemas relacionados con los números, me ha parecido una bonita forma de conmemorar, aunque sea con cierto retraso, el centenario de esta gran poeta, el dedicar algunas entradas de la sección Matemoción del Cuaderno de Cultura Científica a poemas relacionados con los números.
Pero antes de me gustaría empezar por la poeta homenajeada, Gloria Fuertes, y la mejor forma de presentarla, para quienes quizás aún no la conocen, o no mucho, es a través de sus propias palabras, a través de su poema Autobiografía.
Gloria Fuertes nació en Madrid
a los dos días de edad,
pues fue muy laborioso el parto de mi madre
que si se descuida muere por vivirme.
A los tres años ya sabía leer
y a los seis ya sabía mis labores.
Yo era buena y delgada,
alta y algo enferma.
A los nueve años me pilló un carro
y a los catorce me pilló la guerra;
A los quince se murió mi madre, se fue cuando más falta me hacía.
Aprendí a regatear en las tiendas
y a ir a los pueblos por zanahorias.
Por entonces empecé con los amores,
-no digo nombres-,
gracias a eso, pude sobrellevar
mi juventud de barrio.
Quise ir a la guerra, para pararla,
pero me detuvieron a mitad del camino.
Luego me salió una oficina,
donde trabajo como si fuera tonta,
-pero Dios y el botones saben que no lo soy-.
Escribo por las noches
y voy al campo mucho.
Todos los míos han muerto hace años
y estoy más sola que yo misma.
He publicado versos en todos los calendarios,
escribo en un periódico de niños,
y quiero comprarme a plazos una flor natural
como las que le dan a Pemán algunas veces.

Dos fotografías de Gloria Fuertes, del archivo fotográfico de la Fundación Gloria Fuertes
Pero vayamos con algunos de sus poemas relacionados con los números y que aparecen en el libro Obras incompletas (Cátedra, 1980), que es uno de los libros a los que más cariño tengo de la pequeña colección de libros que habitan en mi casa y uno de los primeros libros que compré. El primer poema lleva el título de Palabras y números, y apareció publicado por primera vez en el libro Aconsejo beber hilo (Arquero Colección de Poesía, 1954).
En el cielo una luna se divierte.
En el suelo dos bueyes van cansados.
En el borde del río nace el musgo.
En el pozo hay tres peces condenados.
En el seco sendero hay cuatro olivos,
en el peral pequeño, cinco pájaros,
seis ovejas en el redil del pobre,
—en su zurrón duermen siete pecados—
Ocho meses tarda en nacer el trigo,
nueve días tan solo el cucaracho;
diez estrellas cuento junto al chopo.
Once años tenía,
doce meses hace que te espero,
por este paraguas trece duros pago.
El siguiente poema es Números comparados, que aparece en su Antología poética 1950-1969 (Plaza & Janés, 1970).
Cuéntame un cuento de números,
háblame del dos y el tres
-del ocho que es al revés
igual que yo del derecho-.
Cuéntame tú que te han hecho
el nueve, el cinco y el cuatro
para que los quieras tanto;
anda pronto, cuéntame.
Dime ese tres que parece
los senos de cualquier foca;
dime, ¿de quién se enamora
ese tonto que es el tres?
Ese pato que es el dos,
está navegando siempre;
pero a mí me gusta el siete,
porque es un roto en la vida,
y como estoy descosida,
le digo a lo triste: Vete.
Cuéntame el cuento y muy lenta,
que aunque aborrezco el guarismo,
espero gozar lo mismo
si eres tú quien me lo cuenta.
La siguiente poeta de esta entrada dedicada a los números y la poesía habría cumplido 95 años el pasado 2 de julio. Nos estamos refiriendo a la poeta y traductora polaca Wisława Szymborska (1923-2012), que entre otros galardones recibió el Premio Nobel de Literatura del año 1996.

Fotografía de la poeta Wisława Szymborska
En el mundo de las matemáticas se suele asociar el nombre de la poeta Wisława Szymborska con el número pi, debido al poema que dedica a este popular número y motivo por el cual yo me hice con el libro El gran número, Fin y principio, y otros poemas (Hiperión, 1997), en el que aparecía. En esta traducción se incluye dos libros de la premio nobel de literatura, uno de los cuales es El gran número (1976). El poema que da título al poemario empieza así “Cuatro mil millones de gentes sobre esta tierra, mi imaginación es la que era. No se le dan bien los grandes números…”. Este poema nos habla de los grandes números, pero de uno en particular, la población mundial. La lectura del mismo nos puede producir cierto vértigo, puesto que la población mundial en el momento que escribo estas líneas es de 7.484.398.943, según United States Census Bureau.
El gran libro termina con el poema dedicado al número pi y, aunque que es bastante conocido, lo incluimos a continuación.
Digno de admiración es el número Pi
tres coma catorce.
Todas sus siguientes cifras también son iniciales,
quince noventa y dos porque nunca termina.
No deja abarcar sesenta y cinco treinta y cinco con la mirada,
ochenta y nueve con los cálculos
sesenta y nuevecon la imaginación,
y ni siquiera treinta y dos treinta y ocho con una broma o sea comparación
cuarenta y seiscon nada
veintiséis cuarenta y tres en el mundo.
La serpiente más larga de la tierra después de muchos metros se acaba.
Lo mismo hacen aunque un poco después las serpientes de las fábulas.
La comparsa de cifras que forma el número Pi
no se detiene en el borde de la hoja,
es capaz de continuar por la mesa, el aire,
la pared, la hoja de un árbol, un nido, las nubes, y así hasta el cielo,
a través de toda esa hinchazón e inconmensurabilidad celestiales.
Oh, qué corto, francamente rabicorto es el cometa
¡En cualquier espacio se curva el débil rayo de una estrella!
Y aquí dos treinta y uno cincuenta y tres diecinueve
mi número de teléfono el número de tus zapatos
el año mil novecientos sesenta y tres sexto piso
el número de habitantes sesenta y cinco céntimos
centímetros de cadera dos dedos una charada y mensaje cifrado,
en la cual ruiseñor que vas a Francia
y se ruega mantener la calma,
y también pasarán la tierra y el cielo,
pero no el número Pi, de eso ni hablar,
seguirá sin cesar con un cincoen bastante buen estado,
y un ocho, pero nunca uno cualquiera,
y un siete que nunca será el último,
y metiéndole prisa, eso sí, metiéndole prisa a la perezosa eternidad
para que continúe.

Portada de su libro, en inglés, “Here” (Mariner Books, 2012)
El número pi es un número que causa admiración, como también el número phi o la sucesión de Fibonacci, motivo por el cual nos lo podemos encontrar en el arte. Buscando estos días poemas que podría incluir en esta entrada, descubrí –y no pude evitar comprar por los diferentes poemas que fui leyendo del mismo- el poemario El Libro de mi Selva (PIEdiciones, 2018), primer premio del II Certamen Nacional de Poesía La huella de la palabra, de la poeta bilbaína Manuela Ipiña. Esta bilbaína que estudió derecho, pero aspira a ser psicoterapeura, ha escrito otros dos poemarios Cuando hablan de Creta y yo estoy en Marte (2015) y No importa cuándo si hoy es todavía (2017), publicados en Cuadernos del Laberinto. El libro de mi selva incluye un poema dedicado al número pi, cuyo título es 3,141516.
Este relativo, cargado de incertidumbre,
Te elige como centro invariable de deseo.
Ahora que sabes cómo tiendo a infinito
dime que π nació para nosotros.
3,141516

Fotografía, de su blog, de la poeta bilbaína Manuela Ipiña, en la que está recitando uno de los poemas del poemario “El libro de mi selva” (PIEdiciones, 2018)
Pero regresemos a la premio nobel de literatura polaca Wisława Szymborska, con un poema dedicado a la estadística. Se trata del poema Contribución a la estadística, que aparece en el libro Instante (Ediciones Igitur, 2004).
De cada cien personas,
las que todo lo saben mejor:
cincuenta y dos,
las inseguras de cada paso:
casi todo el resto,
las prontas a ayudar,
siempre que no dure mucho:
hasta cuarenta y nueve,
las buenas siempre,
porque no pueden de otra forma:
cuatro, o quizá cinco,
las dispuestas a admirar sin envidia:
dieciocho,
las que viven continuamente angustiadas
por algo o por alguien:
setenta y siete,
las capaces de ser felices:
como mucho, veintitantas,
las inofensivas de una en una,
pero salvajes en grupo:
más de la mitad seguro,
las crueles
cuando las circunstancias obligan:
eso mejor no saberlo
ni siquiera aproximadamente,
las sabias a posteriori:
no muchas más
que las sabias a priori,
las que de la vida no quieren nada más que cosas:
cuarenta,
aunque quisiera equivocarme,
las encorvadas, doloridas
y sin linterna en lo oscuro:
ochenta y tres,
tarde o temprano,
las dignas de compasión:
noventa y nueve,
las mortales:
cien de cien.
Cifra que por ahora no sufre ningún cambio.
La cuarta poeta de esta entrada es la poeta y traductora catalana Clara Janés. Esta poeta de Barcelona ha recibido varios reconocimientos, como el Premio Nacional de Traducción en 1997 o el Premio Nacional de las Letras Teresa de Ávila en 2007. Además, Clara Janés es académica de la Real Academia de la Lengua, ocupa la silla “U”, desde mayo del 2015.

Clara Janés es académica de la Real Academia de la Lengua, ocupa la silla “U”, desde mayo del 2015
La ciencia, y muy en especial, las matemáticas, están muy presentes en su obra poética. Solo hay que ver lo títulos de algunos de sus libros para comprobarlo. Por ejemplo, entre los libros de Clara Janés que he ido adquiriendo estos últimos años están Paralajes (Tusquets, 2002), Fractales (Pre-textos, 2005), Los números oscuros (Siruela, 2006), Variables ocultas (Vaso roto, 2010) y mi última adquisición El nudo de los vientos (o la mitad perdida de Pitágoras) (Ars Poética, 2017), que es precisamente una selección de sus poemas relacionados con las matemáticas.
Lo cierto es que muchos son los poemas que podríamos traer a esta entrada, pero intentaremos seleccionar unos pocos para ilustrar la poesía de Clara Janés.
Los poemas de El libro de los pájaros (Pre-textos, 1999) son un buen ejemplo. Podemos empezar con el poema número 7 que dice así:
Cruzan las nubes,
saben que el otro lado
es igual que este lado.
Bailan los números impares,
los números pares, los quebrados;
inventan las parábolas,
las hipérbolas.
No ven el cero
que arrastran con sus alas
al infinito
hasta la cascada de las potencias.
Que acompañaremos por los poemas número 24 y 26.
No descubro la ecuación
que invierta
la desencadenada tormenta
que causó
el aleteo de aquella mariposa.
El algoritmo deseado
se esconde entre las nubes.
Y el rayo sonda
que partió a la zaga
de la aparente levedad
se pierde en el infinito
de los puntos sucesivos.
Ni siquiera los astros
alcanzan a contar todos los números
merodeando la oscuridad,
custodia de la cifra inabarcable,
mas en círculo mágico
convocan el uno repetido del ser
mientras el sueño y la muerte
quedan a resguardo
en las formas sumergidas.
El siguiente texto pertenece al poemario Vilanos (Adamar, 2004).
Miraba el desierto y me preguntaba si los números algebraicos podían realmente expresar las arenas. También de noche el compás de los astros se equivocaba. Le pedía al sueño que pusiera de manifiesto la utilidad de las matemáticas. Y tú, que jugabas con los números, dime, ¿qué cifra describe la macla de la rosa?

Portada del libro “El nudo de los vientos (o la mitad perdida de Pitágoras)”, de Clara Janés, publicado por la editorial Ars Poetica en 2017
Y terminemos con algunos poemas en prosa de Los números oscuros (Siruela, 2006). Primero el poema que da nombre al libro, Los números oscuros.
Desde la primera noche hubo un mensaje oscilante, que se mostraba y se ocultaba. Recogí su eco y lo guardé en un cofre: era el primer número oscuro que llegaba a mis manos.
Pero entonces hubo también una respuesta: el segundo de aquellos números. Igualmente lo guardé. Ambos, además, eran candentes y no podían tocarse. No sumé ni resté, dejé que siguieran su curso. Luego llegaron otros. De vez en cuando abría el cofre y veía que habían aumentado y que se trenzaban y destrenzaban, de tal modo que me daba vértigo mirarlos.
Fuera del cofre las ecuaciones eran distintas y algún día pasaba todavía aquel pájaro que llevaba una flor en el pico y la depositaba en mi pelo.
Los números oscuros son cifra de lo incomunicable y a la vez ensanchan la propia visión. Aún no han despejado todas las incógnitas e incluso alguno se ha escapado del cofre, pero actúan como espejos.
Yo sigo sin tocarlos, respetando su orientación. Tampoco he despejado mi incógnita: mis números que son distintos, se perdieron en el bosque de los secretos.
… … …
Cuando el cofre esté lleno no necesitaré hacer operación alguna: sabré que el resultado es cero. Entonces lo lanzaré a las aguas y lo veré alejarse como un barco cargado de amenazantes lanzas.
No sé si ese cero que quede será blanco o negro, no sé si algún día me permitirá volver a ver aquel sueño.
Y el poema De la rosa.
En el libro la rosa se abría en numerosos círculos partiendo del dos, pasando al tres, al cinco…; y su corazón era un círculo negro que se extendía a las distintas secciones creadas, de tamizadas sombras. Eran sombras simples o compuestas. Cada pétalo un nido secreto. Y nadie sabe si existe membrana traslúcida capaz de medir lo que en él se alberga. Acaso el perfume nos dé su medida y la del enigma de sus números.
Para finalizar vamos a incluir un poema en euskera de la traductora en euskera y escritora lekeitiarra Miren Agur Meabe (Lekeitio, 1964). Además de poesía y novela, escribe literatura infantil y juvenil. Entre los muchos premios que ha recibido, está el Premio Euskadi de Literatura Juvenil en tres ocasiones, por las obras Itsaslabarreko etxea (La casa del acantilado, 2002), Urtebete itsasargian (Un año en el faro, 2006) y Errepidea (La carretera, 2011).

La escritora y traductora Miren Agur Meabe. Fotografía Telle
El poema de Miren Agur Meabe que vamos a mostrar en esta entrada (muchas gracias a Goizalde Landabaso por descubrirme este bello poema) es Kalkulua (apuntea kantu baterako), es decir, Cálculo (apunte para una canción).
Problema honetan,
urratsez urrats aztertu dut
ebazpen-prozedura:
zure begiraden estatistika,
zure bularren geometria,
zure bertuteen aritmetika.
Hala ere,
oraindik ez dut faktore
ezezaguna askatu.
Zenbat balio dut nik
zure ametsen ekuazioan?
Y debemos dar las gracias a la misma escritora por la traducción de su poema. La traducción sería la siguiente: En este problema, he analizado paso a paso el procedimiento para hallar la solución: la estadística de tus miradas, la geometría de tus pechos, la aritmética de tus virtudes. Sin embargo, aún no he hallado el factor desconocido. ¿Cuál es mi valor en la ecuación de tus sueños?

“2 x 5” (1919) de la artista alemana Hannah Hoch (1889-1978), miembro del movimiento dadaista
Bibliografía
2.- Sección Poesía y Ciencia, de la web Madrid+d
3.- Blog de Manuela Ipiña, De aquella mirada nacían orgasmos
4.- Clara Janés en la Biblioteca Virtual Miguel de Cervantes
5.- Miren Agur Meabe en El portal de la literatura vasca
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los números poéticos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El origen poético de los números de Fibonacci
- Una conjetura sobre ciertos números en el ‘sistema Shadok’
- El gran cuatro, o los números siguen estando locos
Cristalografía (4): átomos y balas de cañón.
La idea de que la divisibilidad de la materia es finita es contraintuitiva. Ahora nos puede parecer evidente porque hemos crecido con la idea de los átomos, pero no es un concepto en absoluto evidente. A pesar de ello ha estado presente en la filosofía prácticamente desde sus comienzos.

Filosofía no sólo Occidental. Hay muchos que afirman que fue probablemente Kanada, allá por el siglo II a.e.c. (aunque hay fuentes que afirman que vivió en el VI a.e.c.) el que introdujo en el pensamiento hindú el concepto de anu o aṇor (átomo). Lo cierto es que en el Bhagavad-Guitá, con seguridad del siglo II a.e.c o anterior, ya recoge en el capítulo ocho, versículo nueve, lo siguiente (énfasis nuestro):
kaviḿ purāṇam anuśāsitāram aṇor aṇīyāḿsam anusmared yaḥ sarvasya dhātāram acintya-rūpam āditya-varṇaḿ tamasaḥ parastāt
lo que se traduce según Julio Pardilla como
Aquél que medita en el Creador: Gobernador Supremo de todo lo creado desde tiempo inmemorial, más pequeño que el más pequeñito de los átomos y, aun así, abarcando y manteniendo este inmenso universo entero […]

En la filosofía Occidental los padres oficialmente reconocidos del atomismo, ambos del siglo V a.e.c., son Leucipo de Mileto, que creía que todo estaba compuesto por átomos indivisibles que se movían al azar en el vacío, y su discípulo Demócrito de Abdera, que elaboró y diseminó las ideas de su maestro. Aunque, si hemos de creer a Estrabón cuando cita a Posidonio, el primero en proponer la idea del átomo habría sido Mosco de Sidón, posiblemente en el XII o XIII a.e.c.
La teoría atomista encontró desde el comienzo fervorosos defensores y fieros críticos. Entre los primero destacó Lucrecio que, en su De rerum natura, presentó argumentos empíricos muy claros y convincentes para apoyar su visión atomista del universo. Más interesante para lo que nos ocupa ahora es que también señaló que las propiedades físicas como la dureza o la densidad son el resultado de la disposición de los átomos; incluso su idea de “átomos ramosos y enlazados” del Libro II se corresponde muy bien con nuestra idea intuitiva de lo que es un enlace covalente en un sólido.
Deben los cuerpos duros y compactos tener unos átomos más unidos, ramosos y enlazados. Entre los que sobresalen los diamantes, que se burlan de golpes repetidos, el duro pedernal y el fuerte hierro, y los bronces rechinantes de los quicios. (Traducción de José Marchena, adaptada por nosotros)
Loa argumentos de Lucrecio sin embargo no se aceptaron fácilmente. Tanto es así que se necesitaron casi dos milenios para zanjar la cuestión.
Esta idea que se insinúa en Lucrecio de que el empaquetamiento de los átomos (y moléculas) está en la base de la estructura cristalina, y que ésta es la responsable última de las propiedades macroscópicas que presentan los cristales no volvería a retomarse hasta el siglo XVI.

La primera mención de este concepto aparece en De subtilitate libri XXI* (en traducción libre: 21 libros de filosofía trascendental) publicado por Gerolamo Cardano en 1550. En el Libro VII intenta explicar la forma prismática hexagonal de los cristales de cuarzo como resultado del empaquetamiento compacto de partículas esféricas, una propuesta que surge de su estudio de las celdillas de las colmenas. Los cristales están compuestos de partículas esféricas y, dado que se pueden ubicar seis esferas alrededor de una esfera central, el añadir más capas de partículas esféricas debe llevar a un cristal final con forma hexagonal.

Esta hipótesis de Cardano no encontró mucho eco y pronto fue puesta en cuestión por Giulio Cesare Scaligero (o della Scala). Scaligero, aristotélico furibundo, señala que Cardano se ha olvidado de las pirámides hexagonales (las caras romboédricas de los extremos del cristal de cuarzo) que, en su opinión, no son consistentes con el modelo de Cardano. De hecho, a Scaligero le gustó tan poco De subtilitate que terminó publicando en 1557 un texto extensísimo (más de 1000 páginas de folio) para rebatirlo punto por punto: Exotericarum exercitatonium liber XV. De subtilitate, ad Hyeronimun Cardanum. Incidentalmente, este libro, que propugnaba el realismo y el empirismo, tendría una influencia reconocida en Francis Bacon, Johannes Kepler o Gottfried W. Leibniz.
En cualquier caso, este debate filosófico sobre el empaquetamiento de esferas invisibles podía parecer al lector del siglo XVI demasiado próximo a una discusión escolástica sobre el sexo de los ángeles, por lo que, aparte de a los implicados, no despertó mucho interés en general. Hubo que esperar a un escenario más bélico y práctico para que el empaquetamiento de esferas volviese a estudiarse en profundidad.

Mientras preparaba su expedición de 1585 al Nuevo Mundo, Walter Raleigh encomendó a su joven tutor de matemáticas, Thomas Harriot, graduado por Oxford en 1580, la solución de un problema de diseño para sus barcos:
¿Cuál es la forma más eficiente de almacenar las balas de cañón en la cubierta de un barco, de tal manera que se pueda disponer del mayor número posible ocupando el mínimo espacio, ya que probablemente serán de utilidad para tratar con los nativos?
Harriot encontró una solución que hoy llamaríamos empaquetamiento hexagonal compacto y, asumiendo que se apilaba de esta manera, construyó una tabla para calcular el número de balas de cañón en pilas trigonal-piramidales.

La mayor parte del trabajo de Harriot sobre las balas de cañón no se publicó nunca. Y se hubiese perdido en la noche de los tiempos si no hubiese sido por su correspondencia con Johannes Kepler. Esta correspondencia duró dos años (1606-1608), de la que sobreviven cinco cartas, dos de Harriot y tres de Kepler. La correspondencia fue iniciada por Kepler, que estaba interesado en la óptica (con objeto de obtener mediciones astronómicas precisas) y había oído que existían expertos en esta ciencia en Inglaterra.
El intercambio epistolar les llevó pronto a cuestiones más generales, entre ellas la teoría atómica. Harriot era un atomista convencido y trató de convencer a Kepler de la existencia de los átomos explicándole en primer lugar la reflexión y la reflexión de la luz en términos atómicos (lo que Kepler no encontró plausible porque, según él, requería un continuo vítreo); después que incluso el más opaco de los cuerpos, como el oro, se vuelve translúcido si se hace lo suficientemente fino.

Como parte de la argumentación Harriot mencionó el problema del empaquetamiento de esferas, en relación a la forma en que los átomos ocupan el espacio, dejando poco vacío entre ellos. Más tarde Kepler enunciaría la conjetura de su nombre, que ningún empaquetamiento de esferas iguales puede ser más compacto (tener mayor densidad)** que el hexagonal compacto (de Harriot) o su variante el cúbico centrado en las caras.
Kepler, menos belicoso que los ingleses, aplicó este conocimiento al estudio de los copos de nieve. Pero eso será en nuestra próxima entrega.
Notas:
[*] No podemos dejar de mencionar que Cardano también aportó ideas increíblemente avanzadas para su tiempo en cuestiones geológicas en De subtilitate. Entre ellas destaca la idea de que hubo una época en que las montañas estuvieron bajo el mar. Como dice Charles Lyell en Principles of Geology (que se equivoca en la fecha, por cierto):
The title of a work of Cardano’s, published in 1552, De Subtilitate (corresponding to what would now be called transcendental philosophy), would lead us to expect, in the chapter on minerals, many far fetched theories characteristic of that age; but when treating of petrified shells, he decided that they clearly indicated the former sojourn of the sea upon the mountains.
[**] El valor de densidad máxima fue calculado por Carl F. Gauss (π/3√2 ≈ 0,74048) y la prueba de la conjetura de Kepler fue finalmente dada por Thomas Hales en 1998.
Referencias generales sobre historia de la cristalografía:
[1] Wikipedia (enlazada en el texto)
[3] Molčanov K. & Stilinović V. (2013). Chemical Crystallography before X-ray Diffraction., Angewandte Chemie (International ed. in English), PMID: 24065378
[4] Lalena J.N. (2006). From quartz to quasicrystals: probing nature’s geometric patterns in crystalline substances, Crystallography Reviews, 12 (2) 125-180. DOI:10.1080/08893110600838528
[5] Kubbinga H. (2012). Crystallography from Haüy to Laue: controversies on the molecular and atomistic nature of solids, Zeitschrift für Kristallographie, 227 (1) 1-26. DOI: 10.1524/zkri.2012.1459
[6] Schwarzenbach D. (2012). The success story of crystallography, Zeitschrift für Kristallographie, 227 (1) 52-62. DOI: 10.1524/zkri.2012.1453
Este texto es una revisión del publicado en Experientia docet el 05 de diciembre de 2013
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cristalografía (4): átomos y balas de cañón. se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cristalografía (1): Protociencia, del “Homo erectus” a Linneo
- Cristalografía (3): Goniómetros y óxidos dulces
- Cristalografía (2): Las rocas con lengua y la orina de Hooke
Túbulos de Malpigio y recto, el sistema excretor de los insectos
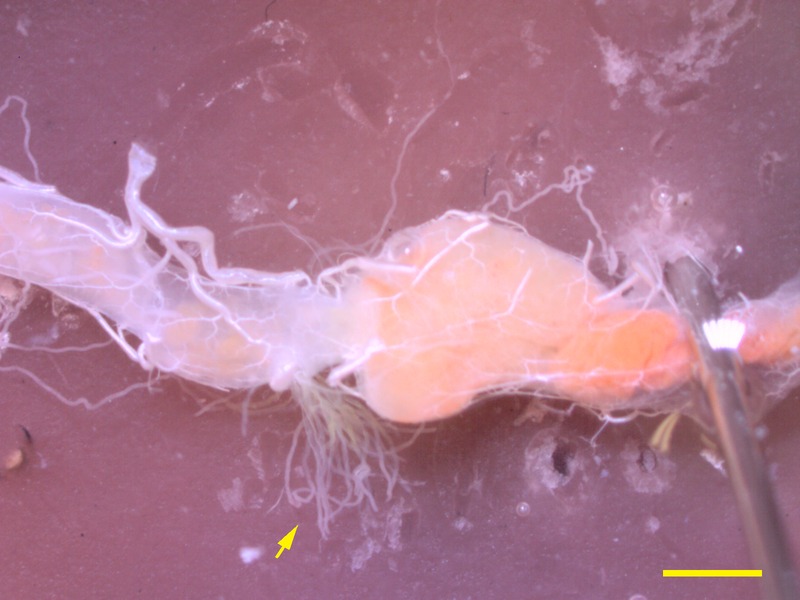
Túbulos de Malpighi o Malpigio (señalados por una flecha) de una cucaracha. La barra amarilla es una referencia para el tamaño: representa 2 mm
Los túbulos de Malpigio son ductos ciegos cuyo epitelio tiene el grosor de una célula. Se encuentran suspendidos en la hemolinfa y desembocan en el intestino posterior, al que vierten sus productos. Se disponen por pares a ambos lados del cuerpo, pudiéndose proyectar unos hacia adelante y otros hacia atrás. El número de túbulos varía con las especies: Drosophila melanogaster, la conocida mosca de la fruta, tiene dos pares, pero la langosta del desierto tiene centenares.
La orina no se forma en los túbulos de Malpigio por filtración, como ocurre en protonefridios y metanefridios, sino que surge a partir de la secreción activa de K+ -y en ocasiones también de Na+– hacia la luz del túbulo. En ese transporte no participa la muy común ATPasa de Na+/K+, sino una ATPasa V, no tan común pero muy antigua. Al parecer, la ATPasa V genera un gradiente de protones entre la luz del túbulo (alta concentración) y la hemolinfa (baja concentración), de manera que el movimiento de protones desde el interior del túbulo hacia el medio interno impulsa el movimiento en sentido contrario de K+ (y Na+), mediante el concurso de transportadores CPA (antiporters catión-protón) localizados en determinadas células epiteliales de los túbulos (en los dípteros son las denominadas células principales). Este dispositivo permite transportar ciertas sustancias contra gradiente gracias a la energía que aporta una sustancia que se mueve a favor de su gradiente de concentración, protones en este caso.
Al acumularse Na+ y K+ en la luz del túbulo, su contenido se vuelve positivo, lo que impulsa el movimiento de iones Cl– a favor de gradiente eléctrico. Se cree que el Cl– atraviesa el epitelio por canales ClC (canales de Cl– activados por Cl–) de las células estrelladas del epitelio tubular, en unas especies, y a través de vías paracelulares, en otras. La acumulación de KCl y en ocasiones de NaCl genera un gradiente de concentración osmótica que impulsa el movimiento de agua desde la hemolinfa hacia la luz del túbulo. Ese movimiento también se puede producir atravesando las células epiteliales, mediante acuaporinas, o a través de los espacios paracelulares. De esa forma surge la orina primaria.
A partir de su generación, esa orina primaria ve modificada su composición debido a la secreción activa –mediante transportadores- o el movimiento pasivo –a través de canales proteicos- de ciertas sustancias. El ácido úrico, que es la molécula de excreción de restos nitrogenados en los insectos, es secretada de forma activa por transportadores específicos. Además de canales y transportadores, en el epitelio de los túbulos de Malpigio hay enzimas detoxificadoras, que están relacionadas con las del hígado de vertebrados, cuyo cometido es, lógicamente, el de eliminar sustancias tóxicas.
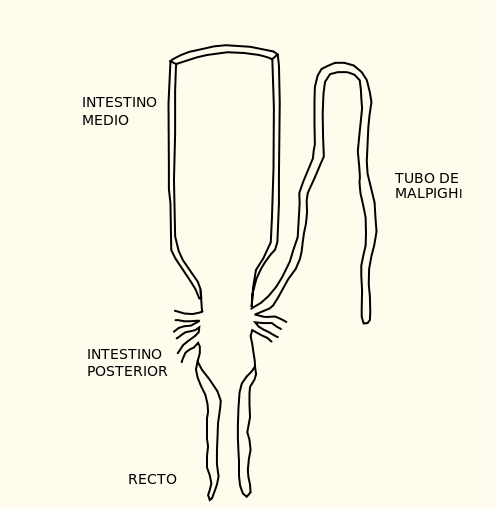
Diagrama estilizado de la sección final del aparato digestivo de un insecto mostrando los tubos de Malpighi (Orthoptera).
El fluido formado en los túbulos llega al intestino posterior con una concentración osmótica similar a la de la hemolinfa, aunque con una composición muy diferente. Ciertas células especializadas del recto pueden seguir modificando las características del fluido antes tubular y ahora rectal. Su papel es especialmente necesario en condiciones de baja disponibilidad de agua. En esos casos se puede producir una intensa reabsorción de agua, en la que está implicado también el KCl, cuya reabsorción en el recto permite que se produzca el movimiento de agua desde la luz rectal a la hemolinfa. Esa reabsorción de agua puede dar lugar a una fuerte elevación de la concentración osmótica, lo que unido a la secreción activa de protones hace que el ácido úrico llega a precipitar, de manera que es expulsado al exterior en forma de uratos sólidos o semisólidos.
Un aspecto especialmente reseñable del funcionamiento del sistema excretor de insectos es que, como veremos que ocurre en aves y en mamíferos, este también es capaz de producir una orina de mayor concentración osmótica que el medio interno. Y esa producción conlleva, por paradójico que resulte, la reabsorción de agua en el recto incluso en contra de fuertes gradientes de concentración osmótica. Esa capacidad paradójica se basa en tres mecanismos alternativos.
En ciertas especies son las denominadas papilas rectales del intestino posterior las responsables de la ejecución de tan asombrosa tarea. En ellas, la disposición microanatómica de sus elementos constituyentes (el epitelio, los espacios intercelulares y los denominados canales infundibulares) permite mantener una especie de flujo circular de KCl (alimentado mediante transporte activo), de manera que el movimiento de la sal “arrastra” agua (provoca su salida de la luz rectal) y posteriormente, una vez generado el flujo, aquella (o sea, la sal) se recupera y se mantiene en el flujo circular conforme el fluido, con una baja concentración salina, retorna a la hemolinfa.
Un segundo dispositivo, propio de especies que viven en ambientes muy secos, es el complejo criptonefridial. Ese complejo se basa en una gran proximidad física entre la zona ciega del túbulo de Malpigio y el epitelio rectal, y en el transporte activo de KCl y NaCl desde la luz del recto hasta la del túbulo. El epitelio del intestino posterior permite el paso del agua, de manera que así se reabsorbe desde el fluido rectal hasta la hemolinfa, pero el agua no puede atravesar el epitelio tubular de la zona implicada en este proceso (porque es impermeable), por lo que se genera un fortísimo gradiente de concentración osmótica entre el túbulo y el recto, debido a su proximidad física. Ese dispositivo actúa como una bomba osmótica de succión de agua.
El tercer mecanismo es característico de las pocas especies que viven en aguas salinas. Y se basa en la secreción activa de sales al fluido rectal, lo que permite, mediante transporte activo una vez más, elevar la concentración de la orina contra gradiente osmótico.
En las especies que utilizan néctar como alimento o en los insectos acuáticos el agua no es un factor limitante, aunque su abundancia podría ser un problema. En esos casos los insectos eliminan abundante orina hipotónica, de menor presión osmótica que la hemolinfa, para lo que el epitelio rectal recupera activamente las sales que han servido para la formación de la orina primaria, sin que ello lleve emparejada reabsorción de agua. Hay también, como es sabido, insectos ectoparásitos, como mosquitos o chinches besuconas, que se alimentan de la sangre de sus hospedadores. Estos llegan a multiplicar por diez la masa corporal gracias a la sangre recién ingerida. Pues bien, estas especies empiezan a producir y a eliminar orina rápidamente, antes incluso de que hayan terminado de comer. Es una orina isosmótica, normalmente, por lo que su eliminación no conlleva especiales complicaciones, pero ha de cursar a gran velocidad, razón por la cual las chinches besuconas llegan a multiplicar por mil la velocidad a la que producen y expulsan la orina.
El sistema formado por los túbulos de Malpigio y el recto es, como hemos visto, muy flexible, puesto que puede dar satisfacción a necesidades muy dispares en lo que al balance hídrico se refiere. Esa flexibilidad se basa en el recurso al transporte activo de sales y a unas disposiciones microanatómicas complejas que permiten recuperar agua en condiciones en que el resto de especies de invertebrados no pueden hacerlo. Es posible que esa gran flexibilidad haya sido una de las claves del gran éxito de este grupo, al que pertenece el mayor número de especies animales existentes.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Túbulos de Malpigio y recto, el sistema excretor de los insectos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Túbulos excretores: protonefridios y metanefridios
- Así forman la orina los animales
- La regulación osmótica e iónica en los teleósteos marinos
Vamos a la piscina

Nadar y otros ejercicios en el agua son una buena práctica de ejercicio físico y, por tanto, recomendables como conducta saludable. Si no es posible hacerlo en la naturaleza, en aguas libres, siempre se puede ir a la piscina, incluso durante todo el año. Allí se hace ejercicio con la natación, con otros deportes acuáticos, o hay diversión con juegos y con otras actividades educacionales o de rehabilitación. Participan personas de toda edad y condición y, por ello, con todo tipo de normas higiénicas. Como cuentan Yuli Ekowati y sus colegas, del Instituto de Educación del Agua de Delft, en Holanda, los riesgos para la salud en las piscinas pueden tener variados orígenes.
En primer lugar, del agua y de los productos químicos que se añaden, sobre todo desinfectantes, para mantenerla limpia y transparente. Y, en segundo lugar, de las sustancias que llegan con los propios bañistas. Son sudor, orina, restos de jabón, cosméticos, aceites bronceadores, protectores solares, saliva, moco, pelo, sangre, materias fecales o vómitos. Allí, en el agua de la piscina, hay restos de todas las sustancias que los bañistas transporten.

Los desinfectantes, la mayoría basados en el cloro o el bromo, son los compuestos más abundantes en el agua de las piscinas. Paro, como aparece en la revisión de Rhys Carter y Cynthia Joll, de la Universidad Curtis Perth, en Australia, son derivados de esos desinfectantes los que pueden ser un riesgo para la salud de los bañistas. Incluso se han detectado alguno de esos compuestos en el aire que se respira en las piscinas cubiertas.
Entre los riesgos para la salud están desde los más habituales, como la dermatitis, irritación ocular o problemas respiratorios, hasta los menos frecuentes como el asma o algunos tipos de cáncer. Hay que resaltar que algunos de estos riesgos se han detectado por estudios epidemiológicos, es decir, porque aparecen a la vez que esos compuestos en el agua de la piscina, pero todavía no se conoce el modo de acción.
Para Francesca Gallè y su grupo, de la Universidad de Nápoles, uno de los problemas más graves son las posibles infecciones por materias fecales o por otros vertidos. La desinfección del agua de la piscina es esencial. Sin embargo, como decía, esos mismos desinfectantes pueden reaccionar con los productos de la piscina y los compuestos resultantes ser también un riesgo para la salud.

Los autores encuentran que, como media, con treinta minutos de ejercicio físico, sea deporte o diversión, en la piscina aparecen 37.1 miligramos de urea.
Para entrar en detalles podemos repasar un estudio sobre el contenido en orina en 250 muestras, tomadas durante tres semanas, de 31 piscinas de Alberta, en Canadá, publicado por el grupo de Lindsay Blackstock, de la Universidad de Alberta en Edmonton. Utilizan de marcador, para conocer la cantidad de orina en el agua, el acesulfamo de potasio, un edulcorante sintético estable, muy utilizado en varios alimentos, y que se elimina en la orina.
Encuentran el edulcorante en el agua de la piscina en concentraciones hasta 570 veces más altas que en el agua potable. Son concentraciones que suponen hasta 75 litros de orina en casi 800000 litros de agua, más o menos el equivalente a un tercio de una piscina olímpica. O sea, que en una piscina olímpica puede haber hasta unos 225 litros de orina. Por lo menos en Alberta, Canadá. O, como dicen los autores, es una “piscina muy dulce”, por lo del edulcorante que encuentran en cantidad.
A pesar de que se considera una conducta tabú, hasta el 19% de los adultos en Estados Unidos reconoce que ha orinado en la piscina por lo menos una vez. Es más, se ha calculado que, de media, la excreción de orina por nadador es de unos 70 mililitros. El grupo de Blackstock termina su estudio con una recomendación a cada uno de los usuarios: “¡Disfruten de la natación y dejen de hacer pis en las piscinas!”.

Es el grupo de Francesca Gallè el que sospecha que una de las causas de que los usuarios orinen en la piscina es que ignoran las reglas que se deben cumplir en estos baños comunitarios. Lo estudian con los bañistas de seis piscinas de Rimini, en Italia. Hacen encuestas a 184 adultos y a 184 niños y adolescentes.
Aunque más del 80% dice conocer las reglas, hay quienes no las cumplen y, así, no llevan gafas protectoras cerca del 20%, tanto jóvenes como adultos; no se lavan los pies antes de entrar en la piscina el 10% de los adultos; o cerca del 3% no utiliza el gorro de baño. Y, por tanto, hay quien orina en la piscina, aunque las reglas digan que no debe hacerlo.
A todas las edades el cumplimiento de las reglas aumenta cuantas más veces se va a la piscina. Entre los adultos, cumplen más las reglas quienes conocen el riesgo para la salud que supone no hacerlo.

En el estudio que he mencionado más arriba, y que lidera Yuli Ekowati, intervienen varios investigadores de Barcelona y Girona y, por ello, los muestreos se hacen en 17 piscinas de centros de deportes y hoteles de Cataluña, en tres días durante el mes de septiembre de 2014, con un total de 51 muestras de agua.
Encuentran 32 medicamentos y 14 protectores solares. Entre los fármacos están, entre otros, el atenolol, para enfermedades cardiovasculares; el paracetamol; el diurético hidroclorotiazida, con las mayores concentraciones; o la carbamazepina, que está en el 53% de las muestras, y se utiliza para los dolores del trigémino o en la depresión y el síndrome bipolar. Alguno de los protectores solares aparece en el 59% de las muestras.
Otra investigación similar en Estados Unidos confirma la presencia de todo tipo de productos en las piscinas. El grupo de ShihChi Weng, de la Universidad Purdue, en Indiana, analizó el agua de tres piscinas utilizadas por estudiantes. Las muestras se tomaron en enero, para la época invernal, y en julio, para el verano. Encontraron hasta 32 compuestos como los que ya conocemos y, en este caso, destacan el ibuprofeno, el paracetamol, la cafeína y el DEET, un conocido y muy utilizado repelente de mosquitos.
Referencias:
Blackstock, L.K.J. et al. 2017. Sweetened swimming pools and hot tubs. Environmental Science and Technology Letters 4: 149-153.
Carter, R.A.A. & C.A. Joll. 2017. Occurrence and formation of diinfection by-products in the swimming pool environment. A critical review. Journal of Environmental Sciences 58: 19-50.
Ekowati, Y. et al. 2016. Occurrence of pharmaceuticals and UV filters in swimming pools and spas. Environmental Science and Pollution Research doi: 10.1007/s11356-016-6560-1
Gallè, F. et al. 2016. Health-related behaviors in swimming pool users: Influence of knowledge of regulations and awareness of health risks. International Journal of Environmental Research and Public Health doi: 10.3390/ijerph13050513
Manasfi, T. et al. 2017. Occurrence, origin, and toxicity of disinfection byproducts in chlorinated swimming pools: An overview. International Journal of Hygiene and Environmental Health 220: 591-603.
Weng, S. et al. 2014. The presence of pharmaceuticals and personal care products in swimming pools. Environmental Science and Technology Letters 1: 495-498.
Zheng, Q. et al. 2017. Keep swimming but stop peeing in the pools. Journal of Environmental Sciences doi: 10.1016/j.jes.2017.03.006
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Vamos a la piscina se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Zientziateka: Blanca Mª Martínez García – La geología fantástica de Verne, Poe y H.P. Lovecraft

La convergencia entre las diferentes áreas de estudio ha supuesto desde siempre una herramienta maravillosa para reflejar de una forma global y fidedigna la realidad de cada tiempo. En este sentido, la conexión entre la naturaleza, la literatura y la ciencia es, quizás, una de las formas más fabulosas que tiene el ser humano para diseñar una ventana desde donde poder contemplar y enseñar el mundo desde múltiples y complementarias perspectivas.
La unión de estas tres áreas de conocimiento fue la temática principal del ciclo de conferencias “Naturaleza, Literatura y Ciencia” que albergó Azkuna Zentroa entre el 10 y el 19 de abril pasados.
Blanca María Martínez García, geóloga e investigadora de la Sociedad de Ciencias Aranzadi, habla de tres grandes autores de literatura fantástica y de terror que emplearon la geología como eje central de sus obras.
‘La geología fantástica de Verne, Poe y H.P. Lovecraft'Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Zientziateka: Blanca Mª Martínez García – La geología fantástica de Verne, Poe y H.P. Lovecraft se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Zientziateka: Déborah García Bello – Elementos a vuelapluma
- Zientziateka: Raúl Ibáñez – El teorema de la rosa
- Zientziateka: Santiago Pérez Hoyos – Explorando el espacio a través de la literatura de ciencia ficción
La ineficiencia de las microglías causa del 100 % de mortalidad de un hongo multirresistente
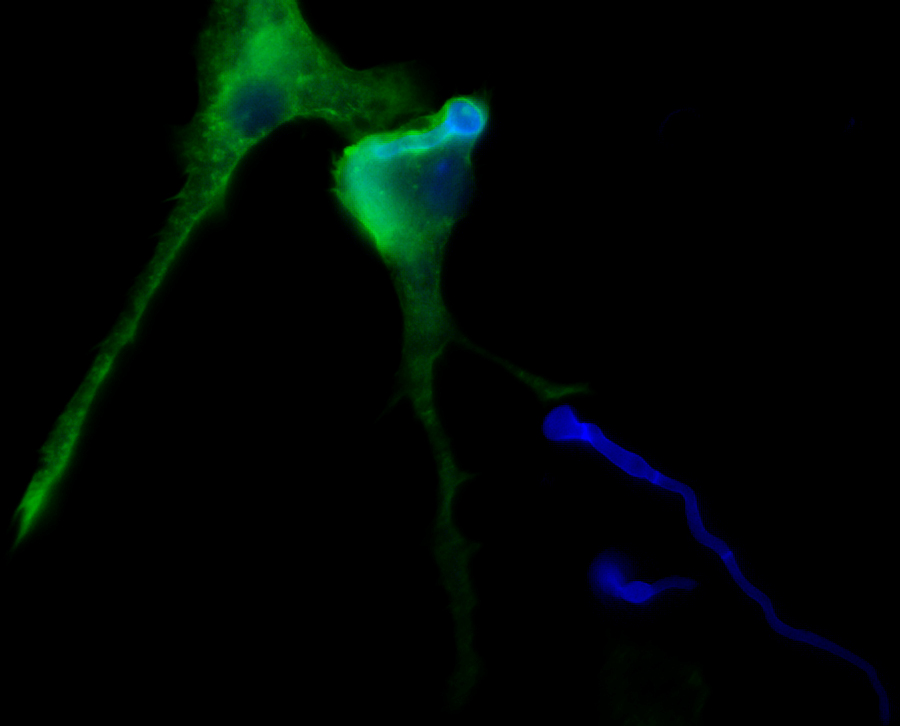
Fagocitosis de “Lomentospora prolificans” por microglías. Tinción de florescencia en la que podemos observar el hongo (en azul) y las células de microglía con los filamentos de actina marcados (en verde). Puede apreciarse que la microglía ha ingerido alguna célula del hongo, pero no todas.
El grupo de investigación de la UPV/EHU Fungal and Bacterial Biomics ha descubierto un nuevo mecanismo de infección que se desconocía hasta el momento en el hongo Lomentospora prolificans . Este microorganismo es multirresistente a los antifúngicos, los antibióticos que combaten los hongos, utilizados actualmente y provoca una mortalidad de entre el 50% (cuando ataca a órganos como los pulmones) y el 100% (cuando ataca el sistema nervioso central) en pacientes con el sistema inmunológico debilitado.
“Es urgente descifrar los mecanismos que utiliza el microorganismo para infectar al ser humano, así como su relación con el sistema inmunitario para poder combatir este tipo de infecciones más eficientemente”, apunta Aize Pellón, miembro del grupo de investigación de la UPV/EHU Fungal and Bacterial Biomics, y actualmente investigador del CIC bioGUNE.
En este novedoso estudio los miembros del grupo de investigación de la UPV/EHU han descubierto que las células del sistema inmunitario del encéfalo “responden pobremente” ante ese hongo.
“Los macrófagos son las células del sistema inmunitario encargadas de eliminar microorganismos y residuos de tejidos mediante su ingestión y eliminación. Estas células son residentes en cada tipo de tejido, pero en todos ellos tienen peculiaridades que los diferencian entre sí. Es decir, no son iguales los macrófagos del cerebro o microglía, que los del intestino, o los del pulmón. Creemos que estas diferencias son las que están detrás de la ineficiencia de la microglía y de que el hongo tenga facilidad de infectar el cerebro, causando un 100% de mortalidad en los pacientes que se infectan. Sin embargo, L. prolificans también debe tener algo especial en su biología que permita esto, ya que la comparación que hacemos en el artículo con otros microbios similares, nos muestra que este hongo es especialmente reacio a ser fagocitado”, explica Aize Pellón.
“Este es un hongo filamentoso que pertenece a un grupo conocido vulgarmente como mohos, algunos de los cuales podemos observar creciendo en la comida en mal estado (fruta, pan, etc.) y que se diferencian de las levaduras unicelulares, tales como Candida albicans o Saccharomyces cerevisiae, que son relevantes en práctica clínica o en la industria alimenticia, respectivamente. El hongo L. prolificans es también común en suelos de ciudades o de zonas industriales. A pesar de estar en contacto con él, no suele producir dolencias en individuos sanos, gracias al sistema inmunológico”, indica Pellón.
Sin embargo, puede producir infecciones muy graves en pacientes con alguna enfermedad subyacente, como la fibrosis quística, o con el sistema inmunológico debilitado, como es el caso de pacientes que están siendo tratados con quimioterapia debido a padecer algún tipo de cáncer, pacientes en los que se ha llevado a cabo algún trasplante de órgano, o que sufren el Síndrome de la Inmunodeficiencia Adquirida (SIDA) por VIH.
“En nuestro grupo de investigación tratamos de enfocar el estudio de la patobiología de microorganismos, resistencia a compuestos antifúngicos y desarrollo de métodos diagnósticos desde puntos de vista diferentes a los que se utilizan habitualmente. Esto nos permite producir nuevo conocimiento básico sobre el funcionamiento de todos estos procesos que permitirán en el futuro mejorar las herramientas terapéuticas y diagnósticas”, explica Pellón.
En este sentido, el grupo de investigación de la UPV/EHU propone nuevas dianas o mecanismos que pueden ser susceptibles de ser objetivos de terapia. “Colaboramos con otros investigadores del Hospital Universitario Vall d’Hebron (Barcelona) o del Centre Hospitalier Universitaire d’Angers (Francia) lo cual nos permite analizar muestras clínicas de pacientes enfermos. Sin embargo, hay que matizar que la aplicación de este conocimiento a una terapia real podría llevar aún unos cuantos años”, adelanta Pellón.
Referencia:
Pellon A, Ramirez-Garcia A, Guruceaga X, Zabala A, Buldain I, Antoran A, Anguita J, Rementeria A, Matute C, Hernando FL. (2018) Microglial immune response is impaired against the neurotropic fungus Lomentospora prolificans Cell Microbiol doi: 10.1111/cmi.12847
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La ineficiencia de las microglías causa del 100 % de mortalidad de un hongo multirresistente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La hiperactividad neuronal impide que las microglías realicen su trabajo
- Un nuevo mecanismo de resistencia antifúngico
- Candida auris, el hongo que ha causado una alerta sanitaria internacional
La ciencia y el materialismo

Una de las más peculiares críticas a la ciencia como empresa es acusarla de materialismo, o fisicismo, como si se tratara de un defecto en lugar de una característica intrínseca. La ciencia es materialista porque no puede, ni pretende, ser otra cosa.
La esencia de la tarea científica es recopilar conocimiento sobre el Universo en el que vivimos. Pero no cualquier tipo de conocimiento: sólo conocimiento objetivo, que se caracteriza por que es independiente del observador y por tanto transmisible. Si yo mido la temperatura de una habitación el valor será igual sujete el termómetro Agamenón o su porquero: lo único que podrá variar es la escala de medida, pero el dato será el mismo. Lo mismo ocurre con un experimento genético o una medida de espectro estelar: si no hay error o malicia el dato tomado por un científico será el mismo que el tomado por otro. Lo cual significa que el segundo puede fiarse del dato obtenido por el primero, porque es objetivo: independiente del observador.
No ocurre lo mismo con una idea, una sensación o un sentimiento, que son por naturaleza y esencialmente subjetivos: dependen de quién los experimenta. El bienestar de la brisa en la cara una tarde de playa, el éxtasis estético de una puesta de sol o la satisfacción y expansión del alma que produce un poema pueden experimentarse, pero no transmitirse; el pintor, el escultor o el escritor lo intentan con su arte, pero sólo pueden conseguirlo de modo limitado. La esencia del idealismo en todas sus formas es la experiencia subjetiva, no transmisible.
Y por eso la ciencia no puede ser más que materialista: porque su objetivo es el conocimiento objetivo, que es el que se puede medir y transmitir con independencia del observador. Curiosamente por el camino del materialismo la ciencia ha acabado llegando a objetos del cosmos que no son materiales: campos, energía, espaciotiempo, materia oscura. Pero siempre desde sus interacciones y relaciones con la materia, el único constituyente del universo que sabemos con certeza (decreciente) que está ahí. Y por eso ‘acusar’ a la ciencia de materialista es proclamar el propio, como mínimo, dualismo.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La ciencia y el materialismo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La geometría de la obsesión
David Mazzucchelli es dibujante de cómic y profesor en la Escuela de Artes Visuales de Nueva York. Es conocido fundamentalmente por su trabajo junto al guionista Frank Miller en los tebeos Batman: Año Uno y Daredevil: Born Again.
La Géométrie de l’obsession –La geometría de la obsesión– es una recopilación de tres historias cortas publicadas anteriormente, en EE. UU., por David Mazzucchelli.

Cada uno de los relatos trata de una obsesión. El protagonista de cada una de las historias vive abstraído en su mundo imaginario, obcecado en su disparatada actividad.
En el primero de los relatos, Manqué de peu –Salvado por los pelos–, el protagonista se obsesiona con la idea del posible impacto de un cometa sobre la Tierra. Cree que se ha librado “por los pelos” de morir en una catástrofe, y huye para esconderse, pensando que el peligro le acecha ineludiblemente.
El tercero de los relatos, Stop the hair nude –Detener el pelo desnudo–, es una historia de estética manga en la que el protagonista se dedica a censurar fotografías de mujeres en las que aparece visible el vello púbico. Esta tarea se apodera de su vida y le lleva irremediablemente a la locura.

El segundo relato, Discovering America –Descubriendo América–, es el que tiene un claro contenido matemático. Utiliza dos colores principales, el rojo teja y azul verdoso, con el negro como nexo de unión entre esos dos tonos. En este cuento, Mazzucchelli traza la historia de un cartógrafo obsesionado por rehacer el globo terráqueo de manera exacta.
La historia comienza con el protagonista, Chris, trabajando en su casa sobre un mapa de Mercator: está intentando transportar con precisión océanos y tierras sobre un enorme globo terráqueo que tiene en su estudio. Lucha, obsesionado, intentado corregir las imperfecciones del mundo:
Es como un rompecabezas, la forma del agua debe encajar con precisión en la forma de la tierra: un ensamblaje perfecto.
Pero el mundo no es perfecto. Por esto existen los mapas, para traer orden a la disposición aleatoria de la naturaleza.
Recordemos que ningún mapa plano, ningún tipo de proyección cartográfica plana, puede preservar de manera fiel todas las variables que entran en juego. En particular, la proyección de Mercator es un tipo de proyección cilíndrica que deforma las distancias entre los meridianos y entre los paralelos sobre todo al acercarse a los polos. La única forma de evitar distorsiones sería usando un mapa esférico… si la Tierra fuera una esfera perfecta.
La geografía es la hermana gemela de la geometría.
Como la lengua o las matemáticas, es un sistema que da sentido al mundo.
Desde la ventana de su casa, Chris observa a su vecina leyendo. Tras una primera cita, la invita a su casa para enseñarle su trabajo:
Soy… el guarda del edificio. Pero es sólo mi trabajo de día. Mi verdadero trabajo, está aquí… ¡esto! Trabajo en ello desde hace cuatro años. Y apenas he empezado el globo.
El problema consiste en llegar a hacer algo tridimensional a partir de objetos de dimensión dos. […]
Por ejemplo, coge un mapa de Mercator… todo se vuelve alargado y grotesco… cerca de los polos.
Es decir, el protagonista está ‘deshaciendo’ las operaciones realizadas para obtener la proyección de Mercator desde una esfera, para reconstruir, de nuevo, el mapa esférico original…
Chris empieza a enamorarse de su vecina, pero lucha contra la irracionalidad de sus sentimientos, retornando a su obsesivo trabajo de corregir mapas:
Todas las medidas eran correctas todos los cálculos eran exactos. Entonces ¿por qué la India estaba en mal sitio?
La Tierra se riza y se encorva con el paso del tiempo, deformando paralelos y meridianos. ¿Están fijados al paisaje, o es la Tierra la que se oculta detrás de ellos, flexible y ondulante? […]
El mejor camino sería el camino más corto, que Euclides definía como la línea recta. Pero no hay líneas rectas sobre un globo. Y además, tampoco sería el camino más corto en tiempo. Todo depende de los vientos, de los caminos. Un camino más largo puede terminar siendo el más corto. Y eso no tiene en cuenta que la ruta menos directa puede también ser la más interesante…
Su amada encuentra un trabajo en Japón y desaparece de su vida. Chris se desmorona al comprobar sobre su globo la distancia que les separará:
El mejor camino es el que puede llevarte en dos direcciones a la vez. Longitudes y latitudes se miden en minutos y en segundos, como si el lugar y el tiempo estuvieran localizados simultáneamente. […]
Todo sistema genera vacíos impenetrables cuando se le empuja al extremo.
Algunos números se vuelven irracionales, otros imaginarios. Las palabras se vuelven contradictorias, inadecuadas, privadas de sentido…
Además, ¿no son todos los números imaginarios?
… Como las proyecciones de Mercator. Esto se presenta tan distorsionado, pero ahora… las configuraciones parecen arbitrarias en este momento… y el retículo tan inamovible… como una gráfica de coordenadas X e Y…
En un ataque de rabia, Chris destroza el globo terráqueo en el que trabaja.
Tras esta crisis, al día siguiente, ya más tranquilo, Chris reinicia su trabajo. Se centra en su globo, vuelve a su rutina, pegando sin tregua piezas de papel sobre la enorme esfera…
La geometría de un globo nos muestra que eligiendo y siguiendo durante suficiente tiempo una dirección, se termina por regresar eventualmente al punto de partida
Referencias:
- David Mazzucchelli, La Géométrie de l’obsession, Éditions Cornelius, 1997
- Marta Macho Stadler, La geometría de la obsesión, de David Mazzucchelli, DivulgaMAT, julio de 2012
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo La geometría de la obsesión se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La botella de Klein: geometría ‘palindrómica’
- La geometría de los ‘cristaloides’, según Léopold Hugo
- La traba de Pascal: geometría proyectiva y literatura

