Azúcar moreno, ¿mejor que el azúcar blanco?

Sabemos que un consumo excesivo de azúcar incrementa el riesgo de padecer enfermedades como diabetes, obesidad y, en consecuencia, cardiopatías. Estos son los principales motivos por los que la Organización Mundial de la Salud recomienda consumir un máximo de 25 g de azúcar al día.
Alcanzar esta cifra es más sencillo de lo que parece, ya que además del azúcar que añadimos al café o a las infusiones, consumimos azúcar añadido en multitud de alimentos. Para algunos, todo esto ha provocado mayor conciencia del azúcar que tomamos y hemos optado por minimizar su consumo y, en algunos casos, sustituirlo por opciones en principio más saludables. Es común que entre estas opciones se encuentre el azúcar moreno como sustituto.
Analicemos si sustituir el azúcar blanco por azúcar moreno es una buena elección.
-
Tipos de azúcar
El azúcar de cualquier tipo, sea blanco o moreno, está constituido principalmente por una sustancia denominada sacarosa. La sacarosa se extrae de dos fuentes: la remolacha azucarera o la caña de azúcar. En los climas cálidos se opta por la caña y en los climas templados por la remolacha. En el sudeste asiático, donde ya se utilizaba azúcar desde hace miles de años, se extrae de la caña; pero en España, por razones climáticas, se obtiene de la remolacha.
En la legislación podemos distinguir dos grandes grupos atendiendo a su composición: azúcar blanco y azúcar moreno. La distinción esencial se hace en función de la cantidad de sacarosa que contienen. El azúcar moreno tiene una pureza media del 85% y el blanco del 95%. Las denominaciones «azúcar natural» o «azúcar integral» no están recogidas en la legislación, sino que se trata de denominaciones coloquiales o publicitarias para denominar al azúcar moreno.
Existen otras denominaciones para el azúcar que hacen referencia a la presentación del producto, además de a su composición. Por ejemplo, el azúcar candi que está tan de moda, se presenta en forma de bloques amorfos. Se hace alargando el proceso de cristalización, añadiendo agua y prensándolo en moldes. Puede estar hecho con azúcar blanco o con azúcar moreno. En cambio, el azúcar glas, que se presenta como azúcar en polvo, de grano muy fino y de color blanco, se hace exclusivamente con azúcar blanco molido.

Azucar candi moreno
-
¿Cómo se produce el azúcar blanco?
El proceso de producción de cualquier tipo de azúcar, sea blanco, moreno, o de cualquier otra denominación, es el mismo en todas las etapas y sólo difiere ligeramente en la última. El proceso es bastante complejo, pero podemos simplificarlo.
Se lava y se trocea la caña o la remolacha y se hace un proceso análogo a una infusión en agua, de forma que se extrae un jugo dulce. Ese jugo contiene una gran cantidad de sacarosa, pero también va acompañado de otras sustancias indeseables que podrían estropearla. Estas sustancias se eliminan añadiendo otros compuestos con los que se combinan fácilmente y terminan depositándose en el fondo del jugo, por lo que se pueden extraer por decantación y filtrado. Gracias a este proceso de separación también se inhibe el crecimiento de bacterias.
Así llegamos a una disolución que es básicamente agua con sacarosa. El agua se evapora -de ahí que las fábricas de azúcar estén envueltas en grandes nubes de vapor de agua- hasta llegar a una disolución saturada. En este punto es donde la sacarosa empieza a formar cristales. Hay una pequeña parte de sacarosa que, por su contenido en agua e impurezas, no llega a cristalizar. Parte de esta sacarosa carameliza hasta volverse amarga y adquirir un color parduzco. Esta fracción es la melaza.
Esta última parte del proceso se repite hasta lograr una separación óptima entre la sacarosa cristalizada y la melaza. La melaza se emplea, entre otras cosas, para producir alcohol etílico.

Melaza
-
Cómo se produce el azúcar moreno
El azúcar moreno se produce de la misma manera que el azúcar blanco, salvo en la etapa final en la que se separa la sacarosa de la melaza. En el azúcar moreno se conserva parte de la melaza. Según la cantidad de melaza que se conserve y la forma de presentación del producto final, podemos distinguir varios tipos (mascabado, turbinado, demerara, etc.) La presencia de más o menos melaza es la responsable de las apreciables diferencias en el aroma y el sabor de los distintos tipos de azúcar moreno. Como la melaza es de color pardo, es la responsable de teñir el azúcar moreno.
Hay dos maneras de producir azúcar moreno: mezclando azúcar blanco con melaza hasta llegar a la proporción deseada, o bien no separar totalmente la sacarosa de la melaza en la última etapa de la producción. Con el modo de mezcla se controlan mejor las proporciones y se reducen costes, ya que es más sencillo fabricar varios tipos de azúcar moreno ajustando las mezclas.
No es cierto que se empleen colorantes para teñir el azúcar, ya que esto no está legalmente permitido. En todos los tipos de azúcar moreno, el color pardo se debe a la melaza. Cuando disolvemos azúcar moreno y éste pierde su color superficial revelando que el interior se asemeja al azúcar blanco, es debido a que es un azúcar moreno producido por mezcla.
-
Diferencias nutricionales entre el azúcar blanco y el azúcar moreno.
Tanto el azúcar blanco como el azúcar moreno aportan 4 kcal por gramo. Estas calorías se denominan «calorías vacías» porque aportan energía, pero no tienen valor desde el punto de vista nutricional. Ambos tipos de azúcar son, esencialmente, sacarosa con una pureza del 85% o más. El pequeño porcentaje restante, que es melaza y agua, contiene una insignificante cantidad de minerales y vitaminas.
La presencia de vitaminas y minerales que porta la melaza del azúcar moreno es lo que suele usarse como razón para sustituir un azúcar por otro. Pero, esta razón no es relevante desde el punto de vista nutricional: la cantidad de minerales o vitaminas que se encuentran en el azúcar moreno es tan baja que, para alcanzar un nivel simbólico para el organismo, habría que consumir mucho más azúcar del recomendado, así que lo que se presenta como virtud, realmente enmascara el verdadero problema: el consumo excesivo de «azúcar libre».
La Organización Mundial de la Salud recomienda no consumir más de 25 g de «azúcar libre» al día. Tanto el azúcar blanco como el azúcar moreno son «azúcar libre».
También hay que tener en cuenta que el azúcar moreno, por su contenido en melaza, que es amarga, tiene un poder edulcorante menor que el azúcar blanco, con lo que resulta tentador utilizar más cantidad para llegar al mismo dulzor. Si a esto le sumamos la errónea convicción de que es más saludable, a muchos no les temblará el pulso y utilizarán más azúcar moreno del que añadirían si se tratase de azúcar blanco.
-
Conclusiones.
No hay diferencias nutricionales relevantes entre el azúcar blanco y el azúcar moreno. Ambos son «azúcar libre» y su consumo según la Organización Mundial de la Salud ha de minimizarse.
Sustituir el azúcar blanco por azúcar moreno perpetúa el problema y, en algunos casos, lo sobredimensiona porque consumimos más, ya que tiene menor poder edulcorante y además es fácil caer en el error de creer que es un sustituto saludable. Si queremos vitaminas y minerales, no los busquemos en el azúcar.
La elección saludable y el esfuerzo que deberíamos hacer, si realmente queremos plantarle cara al problema, es endulzar cada vez menos todo lo que consumimos y comer más productos frescos y menos ultraprocesados, que son los que más azúcar añadido contienen. Si lo logramos, obtendremos una recompensa realmente valiosa: descubrir el auténtico sabor de los alimentos.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Azúcar moreno, ¿mejor que el azúcar blanco? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El azúcar oculto en los alimentos
- El mejor lacón con grelos tiene su ciencia
- Las constantes de Planck y el caballo blanco de Santiago
Aislantes topológicos en sólidos amorfos
Todos sabemos que hay materiales aislantes de la electricidad y otros que la conducen: en un cable eléctrico el cobre del interior es conductor y la protección plástica exterior es aislante. Sin embargo, existen materiales que son aislantes en su conjunto pero que conducen la electricidad en su superficie, son los llamados aislantes topológicos. Esta característica se debe a unos estados cuánticos muy particulares del material en su superficie. Lo interesante del asunto es que estos estados son robustos frente a defectos y otras imperfecciones, lo que hace que estos materiales se estén investigando intensamente porque son potencialmente útiles en computación cuántica y otras aplicaciones.
Todos los aislantes topológicos conocidos son cristales, es decir estructuras tridimensionales perfectamente ordenadas. Ahora, un nuevo trabajo teórico demuestra que los materiales amorfos, los llamados vidrios, también podrían ser aislantes topológicos. Esto podría dar lugar a la búsqueda de nuevos aislantes topológicos entre en abanico muchísimo más amplio de materiales posibles.
Los aislantes topológicos se caracterizan por ciertas simetrías. Por ejemplo, muchos aislantes topológicos son simétricos frente a la inversión del tiempo, lo que significa que las funciones de onda electrónicas que describen el estado no se ven alteradas por un cambio en la dirección del tiempo. Se dice que estas simetrías “protegen” los estados de la superficie, lo que significa que el sistema no puede cambiar a otro estado sin pasar por un cambio de fase. Actualmente la búsqueda de nuevos aislantes topológicos asume que las simetrías deseadas se generan en una estructura reticular ordenada, pero nada se opone a que estas simetrías aparezcan en un material no cristalino.
Los resultados, de momento una posibilidad teórica, sugieren que los aislantes topológicos podrían hacerse mediante la creación de vidrios con un fuerte acoplamiento espín-órbita o colocando al azar átomos de otros elementos en el interior de un aislante normal. De comprobarse que esto es cierto significará una pequeña revolución en el mundo de los materiales que tendrá un gran impacto en el rendimiento y el coste de los dispositivos del futuro.
Referencia:
Adhip Agarwala and Vijay B. Shenoy (2017) Topological Insulators in Amorphous Systems Physical Review Letters doi: 10.1103/PhysRevLett.118.236402
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Aislantes topológicos en sólidos amorfos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El estaño beta es como el grafeno pero en 3D
- La fusión nuclear como fuente de neutrones eficiente
- El calor no es un fluido
Locura instantánea, un rompecabezas con cubos de colores
Locura instantánea es el nombre de un juego de ingenio de la familia de los solitarios. Es un juego que me gusta mucho, que suelo utilizar en algunas de mis charlas y que incluí en mi libro sobre las matemáticas de los juegos de ingenio, Del ajedrez a los grafos, que es el último libro de la colección El mundo es matemático (National Geographic, 2015). Mencioné este juego de pasada en mi entrada del Cuaderno de Cultura Científica, Blanche Descartes y la cuadratura del cuadrado, pero en aquella ocasión no entramos a analizarlo.

Rompecabezas “Locura instantánea”, formado por los cuatro cubos con caras de colores, junto con la caja para guardar los cubos
El rompecabezas Locura instantánea, nombre con el que fue comercializado por la empresa de juguetes Parker Brothers en 1967 y del que se vendieron más de doce millones, consta de cuatro cubos, cada una de cuyas caras está coloreada con uno de los cuatro colores del juego (en la imagen anterior, rojo, azul, verde y amarillo), siguiendo un patrón determinado, que se muestra más abajo.
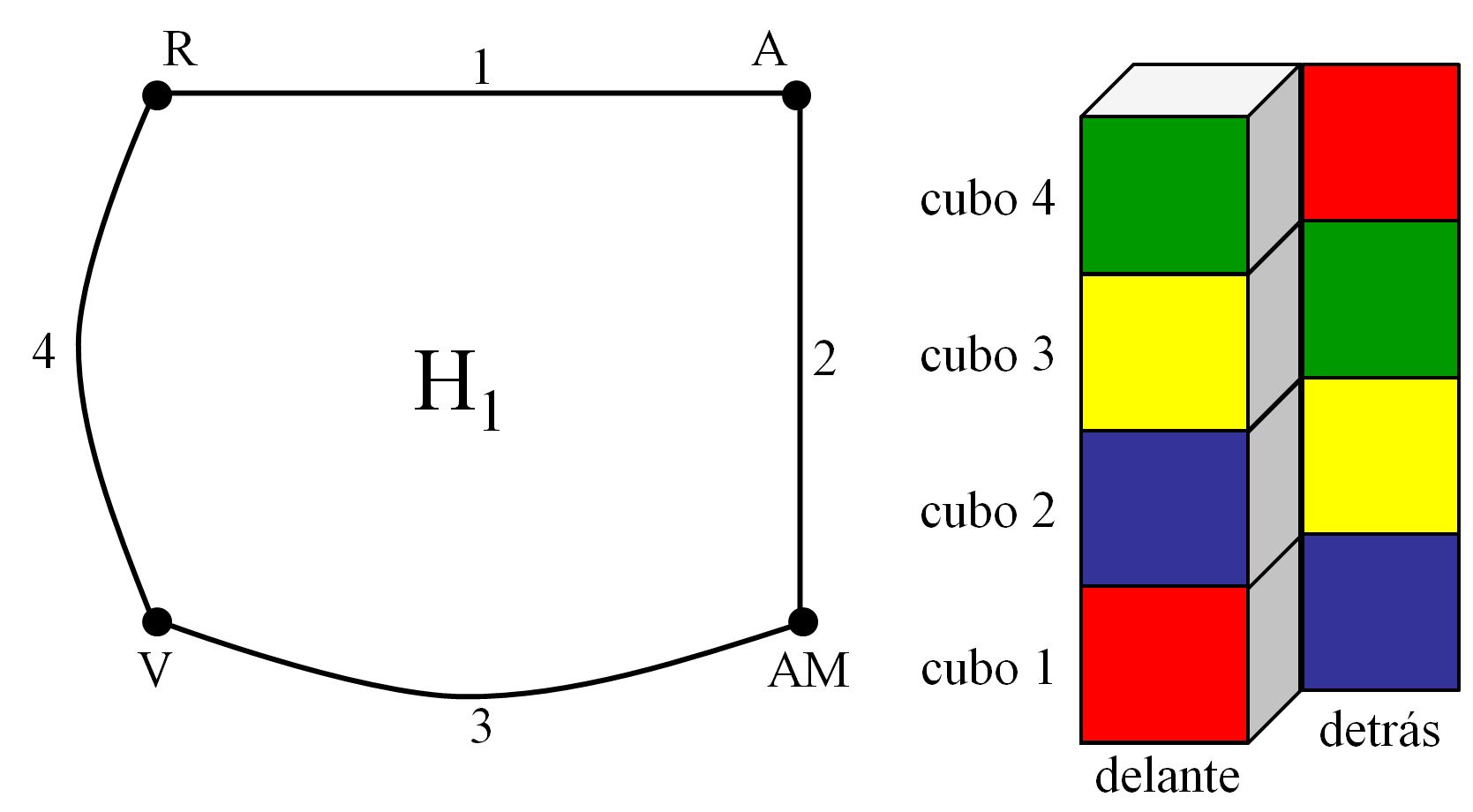
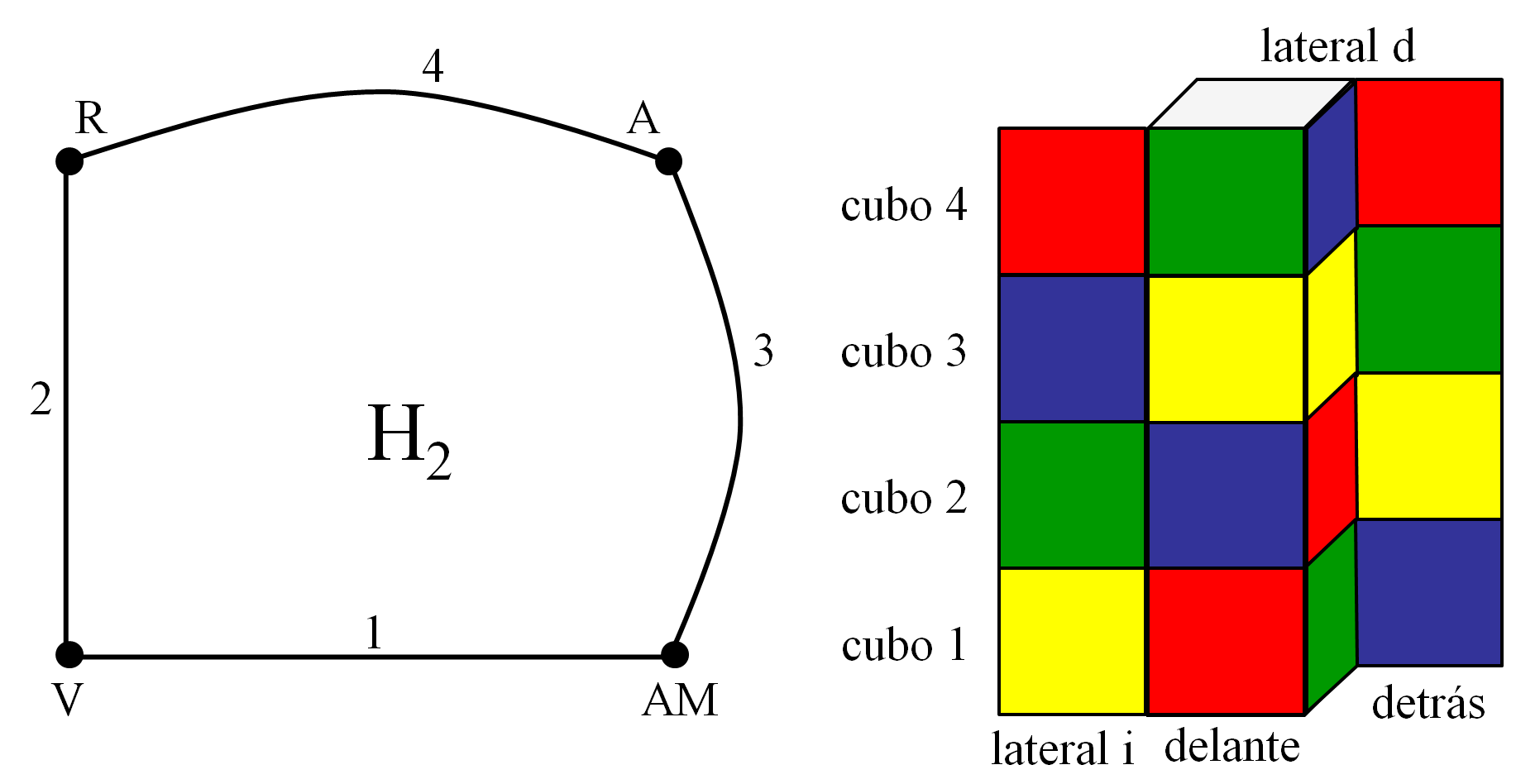
El objetivo del solitario es colocar los cuatro cubos, uno encima (o a continuación) del otro, formando una torre (o un prisma rectangular de tamaño 1 x 1 x 4) de manera que cada uno de los cuatro colores aparece exactamente una vez en cada una de las cuatro caras de la torre.
En la página Sources in recreational mathematics, an annotated bibliography, el matemático estadounidense David Singmaster menciona que este juego aparece por primera vez en 1890, patentado por Frederick A. Schossow (con corazones, picas, tréboles y diamantes, en lugar de colores), con el nombre Katzenjammer (que puede traducirse como conmoción, o también, resaca), y que volvería a aparecer a lo largo del siglo XX con diferentes nombres, en los años 1940 con el nombre El gran suplicio de Tántalo, pero también Cubo 4, Cubo diabólico, Cuatro ases, rompecabezas de Symington y muchos otros.

El rompecabezas “Katzenjammer” (conmoción), patentado por Frederick A. Schossow en 1890, en cuyas caras están los cuatro palos del poker, picas, corazones, rombos y tréboles

El “locura instantánea”, fue utilizado bajo el nombre de “rompecabezas de Symington”, para hacer publicidad de los cubitos de sopa de Symington
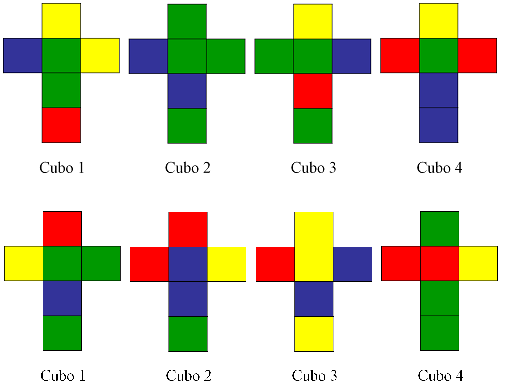
A continuación, mostramos el esquema plano de la distribución de los colores del juego Locura instantánea (exactamente la distribución de los dados de la primera imagen), al desplegar en el plano los cuatro cubos en sus seis caras.
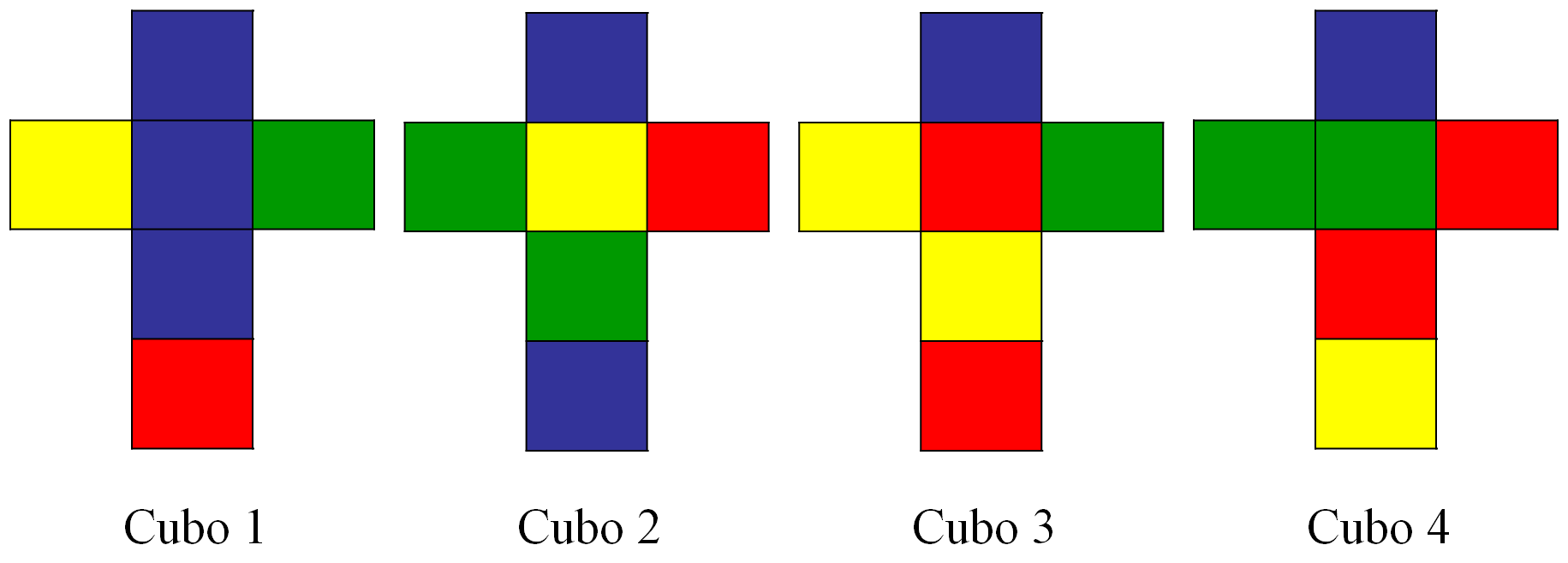
Una primera cuestión que nos podemos plantear en relación a este rompecabezas, antes de ir a lo importante que es jugar y resolver el puzzle, es la siguiente: ¿Cuál es el número de formas distintas (en relación al juego) de colocar los cuatro cubos de colores formando una torre (o una a continuación del otro)? El objetivo del juego es encontrar cual, o cuales, de ellas son una solución del rompecabezas.
Teniendo en cuenta que, de cara a su resolución, lo importante son las cuatro caras de cada cubo que van a quedar en los laterales visibles de la torre, y que es irrelevante el orden de colocación de los cubos, se puede observar que esencialmente hay tres formas distintas de colocar el primer cubo de la torre, dependiendo de cuál de las tres parejas de caras opuestas ocultemos. Y como es la primera pieza en ser colocada, da lo mismo cuál de las dos caras ocultas vaya arriba y cuál abajo.
Una vez colocado el primer cubo, hay veinticuatro formas de colocar el segundo cubo. Seis caras tiene el cubo, luego tenemos seis opciones para la cara de abajo (o equivalentemente, tenemos tres parejas de caras opuestas, pero ahora, fijada ya la posición del primer cubo, si es diferente cual de las caras va debajo), y para cada una de esas seis posiciones, puede rotarse el cubo, dando lugar a cuatro posiciones distintas, ya que hay cuatro caras laterales. Lo mismo ocurre para el tercer y cuatro cubos. En consecuencia, existen 3 x 24 x 24 x 24 = 41.472 formas distintas (desde la perspectiva del solitario) de colocar los cuatro cubos.
El método del ensayo y error, es decir, el ir probando diferentes alternativas de colocación de los cuatro cubos y ver si se ha resuelto el solitario, no parece ser muy apropiado para la resolución de este juego a la vista de las 41.472 configuraciones distintas que existen de los cubos. El recorrido por todas ellas en busca de la solución será tedioso y llevará bastante tiempo. Si utilizásemos unos 5 minutos de media para cada posición, recorrer todas llevaría 3.456 horas, más o menos, dos años y medio, dedicando cuatro horas todos los días.

“Locura instantánea” gigante realizada por el artista griego Dimitris Ioannou, para una exposición en Atenas en 2007. Los cubos están colocados en una posición que no resuelve el solitario ya que en el lado más visible hay tres caras verdes y una roja, es decir, sobran dos verdes y faltan una amarilla y una azul
Si el método de ensayo y error no parece ser el más adecuado, esto nos lleva a plantear algún otro método de resolución del juego. Para empezar podemos intentar conocer más en profundidad este solitario y extraer información útil que nos simplifique la búsqueda o nos ayude a plantear algún método de resolución.
Para empezar, veamos cuántas caras hay de cada color. Si miramos a los cuatro cubos (por ejemplo, en la imagen de los desarrollos planos) se verá que en este solitario hay 7 caras azules, 6 rojas, 5 amarillas y 6 verdes. Puesto que en la solución del rompecabezas cada color aparece una sola vez en cada lateral de la torre, serán cuatro caras de cada color, y el resto permanecerán ocultas, es decir, sabemos que van a tener que quedar ocultas 3 caras azules, 2 rojas, 1 amarilla y 2 verdes.

Versión “Cubos locos” del juego “locura instantánea”, en la cual se utilizaban números en lugar de colores
La anterior información nos da una pista de cómo podríamos intentar resolver el juego, buscando distribuciones de los cubos que oculten 3 caras azules, 2 rojas, 1 amarilla y 2 verdes.
Esta información, y el camino que nos abre, es interesante, pero se necesita complementarla con algún dato más, como por ejemplo, cuales son los pares de caras opuestas de cada cubo (que se mostrarán u ocultarán de forma conjunta, lo cual es relevante). A continuación, detallamos cuales son estos pares de caras opuestas, según su color.
Cubo 1: [azul – azul] + [azul – rojo] + [amarillo – verde]
Cubo 2: [verde – azul] + [verde – rojo] + [amarillo – azul]
Cubo 3: [amarillo – verde] + [amarillo – azul] + [rojo – rojo]
Cubo 4: [verde – rojo] + [verde – amarillo] + [rojo – azul]
Y ya tenemos una información que puede ser muy útil. Ahora, para intentar resolver el rompecabezas, se trata de elegir pares de caras opuestas de cada cubo de forma que sus colores sumen las 3 caras azules, 2 rojas, 1 amarilla y 2 verdes, que son las que deben permanecer ocultas. Es una cuestión combinatoria muy sencilla.
Por ejemplo, la combinación [azul – azul] (cubo 1), [verde – azul] (cubo 2), [rojo – rojo] (cubo 3) y [verde – amarillo] (cubo 4) resulta que, como se observa fácilmente colocando convenientemente los cubos, ya nos genera una solución, de hecho, la única.

Este es un método muy sencillo, que es el que yo utilicé para resolver el Cubo 4 cuando me enfrenté a su resolución. No es tan elegante como la solución con grafos que vamos a mostrar a continuación, ni podemos extraer información muy relevante de cara a posibles generalizaciones o rompecabezas relacionados, pero cumple una de las máximas principales de la resolución de problemas, lo primero es resolverlo. Además, nos ha permitido rápidamente no solo encontrar una solución, sino saber que es única.
Antes de abordar la resolución del juego mediante grafos, recordemos qué es un grafo etiquetado.
Grafo etiquetado: Un grafo al que le asignamos etiquetas a las aristas, o a los vértices, es un grafo etiquetado. Las etiquetas pueden ser números, colores u otras informaciones.
El rompecabezas Locura instantánea puede ser modelizado con grafos etiquetados de la siguiente forma. Los vértices del grafo son cada uno de los colores, rojo, azul, verde y amarillo. Además, para cada cubo, dos vértices van a estar unidos por una arista si esos dos colores están en caras opuestas del cubo. En nuestro caso, los grafos etiquetados (las etiquetas en los vértices son los colores) asociados a los 4 cubos son:
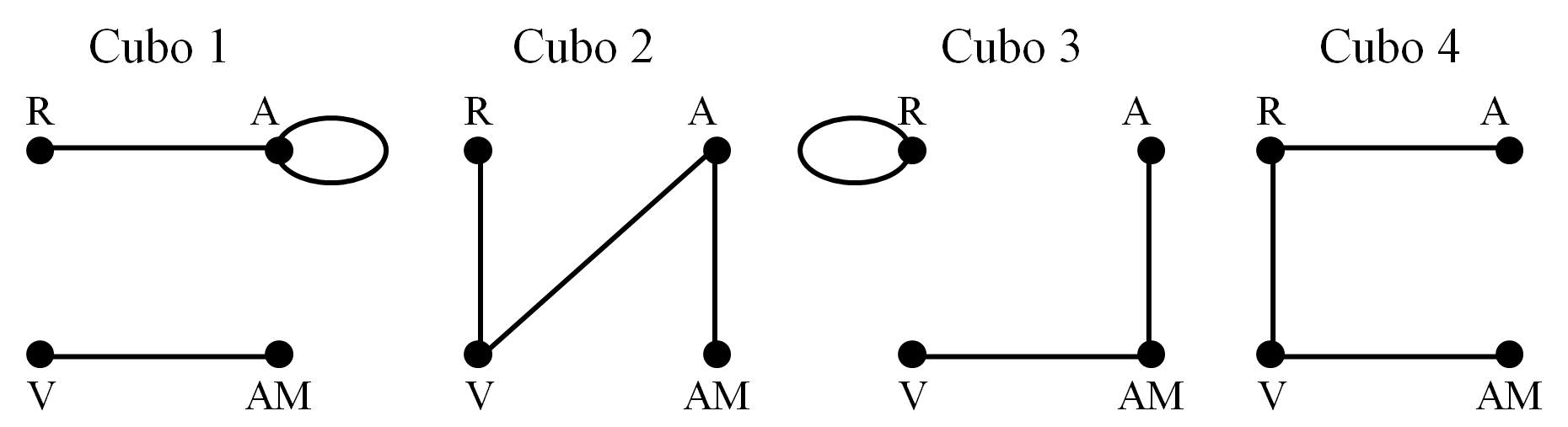
Para juntar toda esa información en un único grafo se etiquetan también las aristas con un número que se corresponde con el del cubo en el que se establece dicha arista. Así, el grafo etiquetado que modeliza El gran suplicio de Tántalo es el siguiente.

Una vez que el rompecabezas ha sido modelizado mediante este grafo, hay que utilizarlo para construir una solución, y en general, estudiar el espacio de soluciones.
Dada una solución del solitario, en particular, los cuatro colores aparecerán en la parte de delante, y también en la de detrás, de la torre. Esto se suele llamar una solución parcial, ya que no se imponen condiciones sobre los laterales de la torre. Y construir una solución parcial del Cubo diabólico es equivalente a encontrar un “subgrafo bueno” del grafo original, es decir, un subgrafo H que contiene los cuatro vértices (colores), con grado 2 (número de aristas que inciden en el vértice) con una arista etiquetada para cada uno de los números (que se corresponden con los cuatro cubos). Como cada vértice en un tal subgrafo bueno H tiene grado 2, cada color aparece exactamente dos veces, y se pueden colocar los cubos para que cada color aparezca una vez en la parte delantera y una en la de atrás.
Subgrafo bueno del grafo etiquetado asociado al rompecabezas “Locura instantánea”, con los correspondientes colores, según el subgrafo bueno, en las caras opuestas, delantera y trasera, de cada cubo
Si ahora podemos encontrar otro subgrafo bueno que no utilice las mismas aristas que el primero, es decir, en cada cubo nos va a dar otra pareja, distinta de la anterior, de caras opuestas, entonces podemos rotar cada cubo de manera que estas parejas aparezcan en las caras laterales de la torre, pero sin deshacer las caras de delante y detrás, lo que resolverá completamente el Cubo 4. Es decir, la solución de El suplicio de Tántalo se corresponde con dos soluciones parciales que encajan bien la una con la otra.
Otro subgrafo bueno, que no comparte aristas con el anterior, y la solución que se genera teniendo en cuenta la información proporcionada por los dos
Puede formularse así el resultado.
Teorema (F. de Canterblanche): El rompecabezas Locura instantánea tiene solución si, y sólo si, el grafo etiquetado asociado admite dos subgrafos buenos que no comparten aristas.
F. de Carteblanche es un seudónimo. En los años 1940, cuatro matemáticos de la Universidad de Cambridge adoptaron el seudónimo Blanche Descartes, y también el de su marido F. de Carteblanche, para publicar sobre matemáticas, pero también sobre poesía y humor matemático. Probaron algunos teoremas sobre teselaciones, publicaron sobre el coloreado de grafos, resolvieron la cuadratura del cuadrado, o descubrieron la disección de Blanche. A ellos se debe el estudio con grafos del (Gran) “suplicio de Tántalo”.
Una vez resuelto el rompecabezas, podemos ver si existen más soluciones al mismo. Calculando todos los subgrafos buenos y viendo qué parejas de subgrafos no comparten aristas obtendríamos todas las soluciones del rompecabezas. En el caso del Conmoción solo hay otro subgrafo bueno, además de los dos anteriores, y comparte aristas con ambos, luego no genera ninguna nueva solución. Es decir, la solución es única, como ya sabíamos.
Tercer subgrafo bueno del grafo asociado a los “Cuatro ases”, pero que no genera ninguna solución
Como hemos estudiado, el Locura instantánea admite una única solución, pero pueden existir otros rompecabezas con cuatro cubos de colores que no admitan soluciones o que admitan varias soluciones, como los dos mostrados en la siguiente imagen.
Estos dos solitarios con cuatro cubos de colores, uno no admite solución y el otro admite tres soluciones, como puede comprobarse analizando los grafos etiquetados asociados, sus subgrafos buenos y cuántos de ellos no comparten aristas dos a dos
Una cuestión interesante relacionada con la creación de este tipo de rompecabezas es el cálculo del número de formas distintas que hay de colorear un cubo con 4 colores (o en general, con un número k de colores), que son los cubos con los que podemos formar, a priori, rompecabezas como el Locura instantánea. Este cálculo es posible gracias al lema de Burnside, pero esa es otra historia y debe ser contada en otra ocasión.

Existen versiones del “Locura Instantánea” incluso con gatitos, como este juego de 1996 llamado “el puzzle del gato”
Bibliografía
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, colección El mundo es matemático, National Geographic, 2015.
2.- David Singmaster, Sources in recreational mathematics, an annotated bibliography
3.- Página web de rompecabezas de James A. Storer
4.- Página web del artista griego Dimitris Ioannou
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Locura instantánea, un rompecabezas con cubos de colores se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba
- El teorema de los cuatro colores (1): una historia que comienza en 1852
- El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema?
Evolución de los sistemas nerviosos: anélidos y artrópodos

Muchos invertebrados segmentados tienen sistemas nerviosos centrales “distribuidos”: están formados por los ganglios de cada segmento corporal. Cada ganglio se ocupa del control del segmento en el que se encuentra y además, quizás, de parte de los adyacentes. Los ganglios intercambian información a través de dos haces o troncos de axones, denominados conectivos. Esa disposición da lugar a un cordón nervioso ventral característico de anélidos y artrópodos. En el extremo anterior una o varias grandes agrupaciones de cuerpos celulares neuronales dan lugar a la formación de un cerebro. Ese cerebro recibe información de los sistemas sensoriales localizados en la cabeza y controla sus movimientos, pero los axones de varios somas neuronales del cerebro se extienden a lo largo del cordón ventral y ejercen un cierto control sobre sus ganglios; así coordina el cerebro los movimientos del conjunto del organismo.
Los anélidos fueron el primer gran grupo zoológico con un sistema nervioso central condensado de un modo significativo. En algunas especies los ganglios están fusionados. Merece la pena citar una curiosa excepción a la disposición general del sistema nervioso central en este grupo: las sanguijuelas tienen, además del cerebro anterior, un cerebro caudal, en el extremo posterior, que es de mayor tamaño que el anterior. En lo que se refiere al sistema nervioso periférico, muchos anélidos cuentan con un sistema somatogástrico muy desarrollado y en los gusanos de tierra hay además una extensa red subepidérmica de nervios finos.
Las formas de comportamiento mejor estudiadas en anélidos son las siguientes: (1) Las respuestas de huida, que son patrones de acción fijados en los que participan interneuronas y motoneuronas del sistema nervioso central con axones gigantes. (2) La regulación del latido cardiaco en los corazones tubulares de sanguijuelas, que constituyen un ejemplo de control nervioso de comportamiento rítmico. En éste participan motoneuronas del sistema periférico cuya actividad puede ser influenciada por inputs sensoriales directos o por interneuronas del sistema central que permiten ajustar el latido a las necesidades del animal. (3) Movimientos locomotores, que están bajo el control de una red del sistema central que recibe señales de receptores sensoriales periféricos (nociceptores, barorreceptores y receptores táctiles).
Los sistemas nerviosos de los artrópodos se asemejan a los de los anélidos. En las formas más primitivas consisten en una cadena de ganglios ventrales unidos por conexiones horizontales. En muchas especies, los ganglios de la cabeza y los del segmento abdominal terminal se forman por fusión de los ganglios de varios segmentos. Los artrópodos más evolucionados, como cangrejos y algunos insectos, presentan una única masa ganglionar torácica, además de la de la cabeza. Se trata de un sistema nervioso muy complejo, con numerosas neuronas y, por lo tanto, muchas conexiones sinápticas. Por ello, es capaz de desarrollar una gran variedad de comportamientos de gran complejidad.
Muchos movimientos de ajuste de la posición corporal y del movimiento de las extremidades están controlados por señales sensoriales que son sometidas a una integración considerable por parte del sistema central, aunque también hay circuitos de ámbito local.
En artrópodos hay comportamientos rítmicos motores y digestivos. Las actividades rítmicas correspondientes a la locomoción, la natación y el vuelo dependen de Generadores Centrales de Modelos formados por redes de neuronas del sistema nervioso central. En estos casos, la retroalimentación sensorial juega un papel importante. En las respuestas rítmicas de huida, como los rápidos movimientos abdominales de los cangrejos de río, participan dos neuronas gigantes motoras cuyos axones recorren toda la longitud del cuerpo y que establecen conexión sináptica mutua en el cerebro, además de otros tres pares de interneuronas con axones gigantes. El vuelo de las langostas es otra forma de comportamiento rítmico que está controlado por un Generador Central de Modelos. Se trata de un comportamiento controlado por el sistema nervioso central y dependiente de inputs sensoriales.
El sistema somatogástrico controla las actividades rítmicas implicadas en el procesamiento del alimento en el sistema digestivo. Estas actividades están reguladas por conjuntos de interneuronas y motoneuronas del ganglio somatogástrico. Su funcionamiento garantiza la correcta secuenciación de los movimientos implicados en la conducción y tratamiento mecánico del alimento.
Además de los rítmicos, los artrópodos tienen comportamientos que no lo son. Los movimientos de huida de las cucarachas constituyen el comportamiento no-rítmico mejor conocido en este filo. En él participan pares de neuronas con axones gigantes, cuyos cuerpos celulares radican en los últimos ganglios abdominales, pero cuyos axones terminan probablemente en los ganglios subesofágicos en la cabeza. Además de estos, la presencia de axones gigantes que participan en movimientos de huida está muy extendida en otros grupos de artrópodos.
Otro ejemplo de comportamiento no-rítmico es el de los movimientos de amartillamiento y salto en langostas y saltamontes. En éstos participan inputs sensoriales de diferentes tipos (visuales, auditivos y táctiles) a través del sistema nervioso central, a la vez que propioceptores y receptores cuticulares del sistema periférico. La red nerviosa implicada, en la que se producen fenómenos de inhibición cruzada, da lugar a la contracción alternativa de músculos flexores y extensores a cargo de sus correspondientes motoneuronas.
En la mayor parte de los comportamientos anteriores participan tan solo unos pocos ganglios. Sin embargo, en los artrópodos se producen comportamientos muy elaborados y se ha demostrado capacidad de aprendizaje. Todos aquellos aspectos del comportamiento que requieran una valoración del inicio, mantenimiento y duración o selección, precisan del concurso de la principal masa nerviosa del cerebro, que suele estar dividido en dos partes, el ganglio subesofágico y el superesofágico. Aunque se desconoce el funcionamiento preciso de estos órganos, se ha comprobado que el superesofágico inhibe la actividad del subesofágico, quien, a su vez, ejerce un efecto excitatorio en muchos comportamientos.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Evolución de los sistemas nerviosos: anélidos y artrópodos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Evolución de los sistemas nerviosos: cnidarios y gusanos no segmentados
- Evolución del tamaño animal
- Historia mínima de la complejidad animal
Carnot y los comienzos de la termodinámica (2)
La máquina ideal de Carnot, tan sencilla como es, explica algunos aspectos fundamentales del funcionamiento de máquinas y motores de todo tipo y permite formular un principio fundamental de la naturaleza.

Las chimeneas anchas de la derecha en realidad son torres de refrigeración. las chimeneas auténticas por las que salen los gases de la combustión del carbón de esta planta de generación eléctrica son las altas y delgadas.
Cualquier máquina que derive su energía mecánica del calor se debe enfriar para eliminar el “desperdicio” de calor a una temperatura más baja. Si hay alguna fricción u otra ineficiencia en la máquina, agregarán más calor residual y reducirá la eficiencia por debajo del límite teórico de la máquina ideal.
Sin embargo, a pesar de las ineficiencias de todas las máquinas reales, es importante saber que nada de la energía total se destruye. Lo que ocurre con la parte de la energía de entrada que llamamos residual es que no se puede emplear para hacer trabajo útil. Así, el calor residual no puede ser reciclado como energía de entrada para hacer funcionar la máquina para producir más trabajo útil y así aumentar la eficiencia del motor a base de reducir la cantidad de energía residual, porque el depósito de calor de entrada está a una temperatura más alta que el de salida, y el calor no fluye por sí mismo de frío a caliente.
La observación de Carnot, que parece tan obvia, esa de que el calor no fluye por sí solo de un cuerpo frío a uno caliente, y que la necesidad de acondicionadores de aire y refrigeradores ilustra tan bien, no es más, si se generaliza, que una forma de expresar un principio fundamental de la naturaleza: la segunda ley de la termodinámica. Esta ley es una de las más potentes que conocemos, dada su capacidad para explicar cosas: desde cómo y en qué sentido ocurren los fenómenos naturales a los límites fundamentales de la tecnología. Volveremos a ella repetidamente en esta serie.
Un ejemplo paradójico del resultado de Carnot
Si quemamos gasóil para calefacción en una caldera en el sótano de nuestro edificio, sabemos que parte del calor se pierde por la chimenea en forma de gases calientes y otra como calor perdido porque el propio quemador no puede estar aislado por completo. Con todo, los recientes avances en tecnología de calderas han dado como resultado calderas con una eficiencia nominal de hasta 0,86, o 86%.
Ahora bien, si preferimos radiadores eléctricos, nos encontramos con que es probable que la compañía de energía eléctrica todavía tenga que quemar petróleo, carbón o gas natural en una caldera, Y después conseguir que esa electricidad generada llegue a nuestra casa. Debido a que los metales se funden por encima de una cierta temperatura (por lo que la sustancia caliente no puede superar la temperatura de fusión de su contenedor) y debido a que el agua de refrigeración nunca puede bajar por debajo del punto de congelación (porque entonces sería sólida y no fluiría, lo que pone un límite inferior de temperatura a nuestra sustancia fría), el hallazgo de Carnot hace imposible que la eficiencia de la generación eléctrica supere el 60%. Dado que la caldera de la compañía de energía también pierde parte de su energía por la chimenea, y dado que existen pérdidas de electricidad en el camino desde la planta que la genera, sólo alrededor de un cuarto a un tercio de la energía que había originalmente en el combustible llega realmente a tu casa. Una eficiencia, en el mejor de los casos, del 33 %. Paradójicamente, la calefacción eléctrica es mucho menos sostenible que una caldera de gasóil si las plantas que generan energía emplean combustibles fósiles.
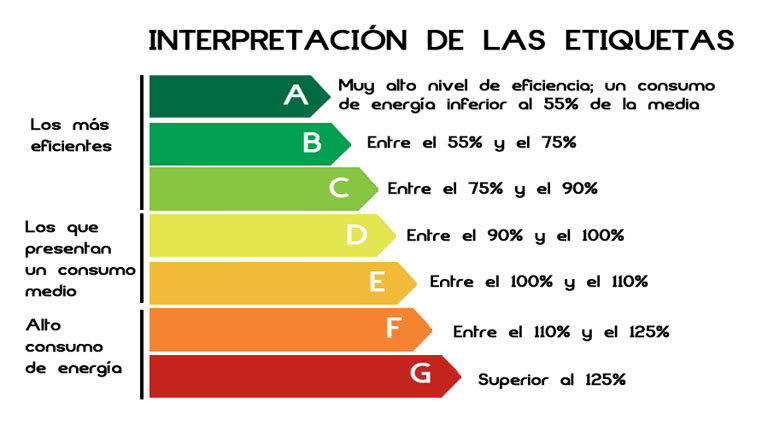
Debido a los límites encontrados por Carnot para las máquinas térmicas, a veces es importante no sólo dar la eficiencia real de una máquina térmica, sino también especificar lo cerca que está del máximo posible. Los aparatos de calefacción domésticos y muchos aparatos eléctricos de gran potencia, como frigoríficos y acondicionadores de aire, vienen ahora con una etiqueta que indica la eficiencia relativa del aparato y el potencial de ahorro anual en coste de electricidad.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Carnot y los comienzos de la termodinámica (2) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Carnot y los comienzos de la termodinámica (1)
- Potencia y eficiencia de una máquina
- La máquina de vapor (1)
Dudas sobre las vacunas: problemas y soluciones
Ignacio López Goñi
Cada vez hay más padres que dudan de los beneficios de la vacunación. ¿Debería ser obligatoria? Los profesionales de la salud son la mejor herramienta contra los anti-vacunas.
Los programas de vacunación han contribuido a que el número de casos y de muertes por enfermedades infecciosas hayan disminuido de forma significativa en el último siglo. Las vacunas han salvado millones de vidas humas, son responsables de la erradicación de la viruela del planeta y de que la polio esté apunto de serlo. En general, las coberturas vacunales o tasas de vacunación infantil siguen creciendo a nivel mundial, lo que indica que la vacunación es una medida de salud pública ampliamente aceptada.
Sin embargo, un número cada vez más creciente de padres (*) perciben la vacunación como algo insano e innecesario. Como las vacunas se administran cuando el niño está sano, nuestro umbral del riesgo es muy bajo. Cualquier duda, aunque sea teórica, sobre la seguridad de las vacunas puede causar que los padres rechacen o retrasen la vacunación de sus hijos. Incluso algunos padres que vacunan a sus hijos suelen tener dudas y temores acerca de la vacunación. Los movimientos anti-vacunas han sido responsables de la disminución de las tasas de aceptación de las vacunas y del aumento de brotes de enfermedades infecciosas que se pueden prevenir con las vacunas. Entre los extremos de los movimientos anti-vacunas que rechazan totalmente la inmunización y los entusiastas pro-vacunas, cada vez hay más padres que dudan: padres que rechazan alguna de las vacunas pero que aceptan otras, que retrasan la vacunación de su hijo porque dudan del calendario vacunal recomendado, o que se sienten inseguros cuando vacunan a sus hijos.
En África entierran a los niños, en Europa enterramos a los ancianos
Por supuesto, la situación es diferente según el contexto y el país. En los países de altos ingresos donde los programas de vacunación están bien establecidos y en gran parte son gratuitos, las vacunas son víctimas de su propio éxito. Como gracias a las vacunas han disminuido radicalmente la frecuencia de enfermedades infecciosas, los padres no perciben el riesgo de esas enfermedades y no ven la necesidad de las vacunas: “¿para que voy a vacunar a mi hijo si ya no hay varicela?”. Se tiene más miedo a la vacuna que a la propia enfermedad. Sin embargo, en los países con ingresos medios o bajos, donde este tipo de enfermedades son todavía más frecuentes, la duda de la inmunización es menor. En países donde la mortalidad infantil es todavía muy alta debido a las enfermedades infecciosas, todavía da más miedo la enfermedad que la vacuna.
Anti-vacunas: desde Jenner hasta Twitter
Los movimientos anti-vacunas no son algo nuevo. Nada más empezar Edward Jenner, a principios de 1800, sus demostraciones de que la viruela de las vacas protegía contra la viruela humana, y a pesar de que más del 30% de los casos de viruela eran mortales, comenzaron las campañas contra la vacuna. Son famosos los dibujos satíricos publicados en 1802 en los que se ridiculizaba la vacunación de Jenner y se mostraban los bulos de sus opositores: que al vacunarte con la viruela de las vacas te salían por el cuerpo apéndices de vaca.

Caricatura publicada en 1802 en “The Punch” por James Gillray de una escena de la inoculación de la vacuna de Jenner en el Hospital de St. Pancras (Londres).
Durante el siglo XIX, en el Reino Unido primero, luego en el resto de Europa y en EE.UU. después, se crearon las primeras Ligas Anti-Vacunación y hubo varias campañas anti-vacunas que lucharon activamente contra las leyes que obligaban a la vacunación y en defensa de la libertad personal. Sin embargo, ya en pleno siglo XX, llegó la edad de oro de las vacunas en las décadas de los 50 y 60, durante las cuáles la aceptación de la inmunización fue máxima. En esos años se introdujeron las vacunas contra la poliomielitis, el sarampión, las paperas y la rubéola, con gran aceptación al comprobar cómo los casos de enfermedades y muertes se reducían de forma espectacular. En los años 70 se comenzó un gran esfuerzo internacional para expandir los programas de vacunación también a los países de bajos ingresos, con el objetivo de acabar con seis grandes asesinos: polio, difteria, tuberculosis, tosferina, sarampión y tétanos. Entonces menos del 5% de la población mundial infantil menor de un año estaba inmunizada contra estos patógenos. En los años 90 cerca del 75% de la población mundial infantil estaba vacunada contra la polio difteria, tétanos y tosferina. Sin embargo, ese periodo de aceptación entusiasta de las vacunas duraría poco tiempo.
A mediados de los 70 los movimientos anti-vacunas resurgieron con fuerza. La controversia comenzó en el Reino Unido con la vacuna contra la tosferina (pertussis en inglés, por estar causada por la bacteria Bordetella pertussis), al publicarse un trabajo que relacionada serios trastornos neurológicos en 36 niños después de haber sido vacunados con la tripe difteria-tétano-pertusis (vacuna DTP). Este trabajo tuvo una gran repercusión mediática e hizo que la cobertura vacunal en el Reino Unido bajara del 77 al 33%, con el consiguiente aumento de los casos de tosferina, algunos de ellos mortales. En EE.UU. la controversia comenzó en 1982 con la emisión de un emotivo documental periodístico “DTP: vaccination roulette” que acusaba al componente pertusis de la DTP de causar daños cerebrales severos y retraso mental. A raíz de tal escándalo se crearon grupos de presión anti-vacunas, se investigaron las empresas fabricantes de vacunas, aumentaron los precios y se redujeron las tasas de vacunación. A pesar de los estudios que se hicieron posteriormente que demostraban que no había relación alguna entre la vacuna DTP y los trastornos neurológicos, la preocupación sobre su seguridad fue un estimulo para el desarrollo de una nueva vacuna de pertusis acelular, menos reactiva y, por lo que se está viendo con el tiempo, con un menor poder protector contra la enfermedad. Quizá lo único bueno de todo aquello fue la creación del Vaccine Adverse Event Report System (VAERS), un programa nacional del CDC y la FDA para recoger, evaluar y publicar de forma transparente todo tipo de información sobre los efectos adversos que puedan ocurrir por la administración de las vacunas en EE.UU.
Unos 25 años después de la controversia sobre la vacuna DTP, el Reino Unido volvió a ser el origen de una de las mayores crisis sobre las vacunas, en esta ocasión relacionando la vacuna tripe vírica sarampión/rubeola/paperas (SRP) con el autismo. La revista The Lancet publicó en 1998 un artículo firmado por Andrew Wakefield y otros doce colegas en el que se sugería una posible asociación entre la vacuna y el autismo. Aunque en el artículo no se probaba una relación causal, las afirmaciones posteriores de Wakefield no dejaban lugar a duda de su opinión y pidió la retirada de la vacuna hasta que se hicieran más estudios. Años después se demostró que los datos de la publicación habían sido sesgados, y que Wakefiled recibió dinero para publicar estos datos contra las empresas farmacéuticas. En 2004, 10 de los 12 coautores del trabajo se retractaron de la publicación. En 2010 el Consejo General Médico inglés expulsó a Wakefield y le prohibió ejercer la medicina en el Reino Unido, y The Lancet tomó la decisión de retirar y retractarse de lo publicado en 1998. Pero habían pasado ya doce largos años. Se han evaluado y revisado más de 20.000 artículos relacionados con esta vacuna y más de 14 millones de casos de niños vacunados y no hay ningún indicio de que la vacuna SRP tenga alguna relación con el autismo infantil. A pesar de ello, la relación de las vacunas con el autismo sigue siendo una de las principales preocupaciones de muchos padres que dudan.
Como hemos comentado, en general las vacunas son mucho mejor recibidas en los países de bajos ingresos. Sin embargo, en los últimos años ha habido también algunas controversias que han hecho disminuir las coberturas vacunales y han supuesto un serio problema para las campañas mundiales de inmunización. En 1990 en Camerún se extendieron rumores de que el objetivo de las campañas de vacunación era la esterilización de las mujeres y en 2003 se boicoteó la vacuna de la polio en el norte de Nigeria también con rumores de que la vacuna era una estrategia para extender el VIH y reducir la fertilidad entre los musulmanes. A consecuencia de estos rumores, la polio resurgió en Nigeria y se extendió en 15 países africanos que ya habían sido declarados libres de la enfermedad.
Desde el año 2000, Internet ha supuesto un cambio de paradigma en la relación médico/paciente. Internet ha acelerado la velocidad de la información y ha roto barreras: la web proporciona información gratis, inmediata y disponible todo el tiempo y anónima. Internet es una oportunidad sin precedentes para los activistas anti-vacunas, para difundir su mensaje a una audiencia cada vez más amplia y reclutar nuevos miembros. Las personas que son contrarias a las vacunas, aunque sean minoría, generan una cantidad desproporcionada de contenidos anti-vacunas.
Cada mes son miles los contenidos que se vierten al ciberespacio sobre la vacunación, la inmensa mayoría subjetivos y de contenido emocional. Internet es una de las principales fuentes de información que emplean los padres para consultas sobre el tema de la vacunación. Desgraciadamente si se examinan los contenidos relacionados con la vacunación en la web o en las redes sociales sobresale la información inexacta e incorrecta. Esto hace que muchos padres pasen de dudar de las vacunas a ser resistentes a la vacunación o incluso claramente opuestos. Muy probablemente ver una web anti-vacunas aumenta los sentimientos negativos contra la inmunización, mientras que las webs pro-vacunas suelen tener un efecto mínimo.
En España no existen movimientos anti-vacunas como en EE.UU. pero el número de padres que dudan aumenta
En España no existen movimientos anti-vacunas bien organizados y beligerantes como los que hay en EE.UU. o en el Reino Unido, pero el número de padres que ponen en duda la efectividad y seguridad de las vacunas aumenta. Además, cada vez tienen más relevancia pública algunos claros anti-vacunas como Josep Pamiés o la monja Forcades, incluso sorprendentemente con la colaboración de grandes medios de comunicación y poderes públicos. También, en los últimos años se han publicado varios libros que claramente ponen en tela de juicio el valor de las vacunas: Vacunas, una reflexión crítica (Enric Costa), Los peligros de las vacunas (Xavier Uriarte), Vacunaciones sistemáticas en cuestión, ¿son realmente necesarias? (Manuel Marín Olmos), o Vacunas las justas (Miguel Jara).
La duda sobre las vacunas es ya un problema de salud pública
Los padres que mantiene una posición claramente anti-vacunas son una minoría, pero la proporción de los que dudan va en aumento. Esto es preocupante porque para el éxito de las campañas de vacunación se debe mantener una cobertura vacunal alta. Se debe conseguir que lo normal sea que un padre vacune a su hijo según el calendario que le corresponde. La vacunación es una medida individual pero que beneficia a la comunidad. A diferencia de otras intervenciones preventivas, si un padre rechaza las vacunas de su hijo no solo pone en riesgo la vida de su hijo sino también de los que le rodean, de los más débiles, otros niños, los enfermos y los ancianos. Luchar contra la oposición o la duda de las vacunas es un problema comunitario.
¿Qué impacto clínico tiene el fenómeno de los anti-vacunas? Quizá el de mayor actualidad sea el aumento de los casos de sarampión, una de las enfermedades infecciosas más contagiosas (ver El sarampión aumente en Europa, en microBIO). Las autoridades sanitarias han alertado que desde febrero de 2016 han aumentado los casos de sarampión en Europa, la mayoría en niños pequeños sin vacunar. La situación en este momento es que de los 53 países de toda la región europea solo han conseguido erradicar la enfermedad 15 países, y en 6 todavía sigue habiendo transmisión endémica. Desde enero de 2017 ya ha habido incluso algunos casos de muertes en Rumanía, Italia y Portugal. La ECDC alerta de que la probabilidad de que se extienda el sarampión a otros países es alta. Casos similares también han ocurrido en el continente americano, libre de sarampión desde el año 2002. En EE.UU. hubo tres grandes brotes en 2013 y lo mismo ocurrió en Canadá. De forma similar en los últimos años ha habido brotes de rubéola, paperas y pertusis en Polonia, Suecia, Holanda, Rumania, Bosnia EE.UU., etc. por la misma causa: personas que no habían sido vacunadas. En 2010, la OMS estimó el número de muertos por enfermedades infecciosas prevenibles por las vacunas (difteria, sarampión, tétanos, pertusis y polio) en unas 400.000. Estas muertes se podrían haber evitado con las vacunas. Es cierto, que más de la mitad ocurren en países donde los problemas de infraestructuras son responsables de la falta de vacunación, pero en otros casos es el rechazo a las vacunas la causa.
Entender las causas y el contexto del que duda
Los grupos anti-vacunas de hoy en día son en su mayoría gente de clase media (o media-alta) con estudios superiores que reclaman su derecho a una decisión informada acerca de las vacunas, prefieren soluciones “naturales”, no les gusta que les califiquen como anti-vacunas (el término “anti” es negativo) y prefieren términos neutros, como grupo pro vacunas seguras. Pero algunos de sus argumentos son los mismos que en 1800: las vacunas no son efectivas; causan enfermedades; son un negocio y se fabrican sólo para beneficio de las farmacéuticas; las vacunas contienen aditivos tóxicos peligrosos para la salud; los daños de las vacunas son ocultados por las autoridades (teorías conspiratorias); la vacunación obligatoria es contraria a la libertad y a los derechos civiles; la inmunidad natural es mucho mejor que la que inducen las vacunas; las vacunas son muchas y se dan demasiado pronto; los productos naturales y alternativos (vida “sana”, homeopatía, vitaminas) son mejores que las vacunas para prevenir las enfermedades; etc. En muchos casos se presentan datos incorrectos, hechos sacados de contexto, ambiguos o medias verdades. En muchas ocasiones apelan a las emociones y presentan historias muy duras del legitimo sufrimiento de padres que creen seriamente que sus hijos han padecidos enfermedades graves por culpa de las vacunas.
El contexto a veces no ayuda. En los últimos años ha aumentado el número de nuevas vacunas, lo que ha complicado los calendarios vacunales. El que no exista un mismo calendario vacunal en distintos países o, lo que es peor, en distintas comunidades autónomas de un mismo país genera percepciones negativas. La falta de transparencia de algunos gobiernos y empresas farmacéuticas y los errores en la forma de afrontar e informar sobre crisis sanitarias también provoca desconfianza y susceptibilidades: la crisis de las vacas locas, la pandemia de gripe aviar o el último brote de Ébola, por ejemplo. Hoy en día los pacientes quieren estar involucrados y participar en sus propias decisiones de salud.
¿Debería ser obligatoria la vacunación?
Esta es la pregunta que hace unos días lance desde mi cuenta de Twitter, y el 94% de las respuestas fue afirmativa. Es verdad que el resultado está sesgado y no es significativo: la mayoría de los seguidores de esa cuenta de Twitter son claramente pro-vacunas, pero algunos comentarios fueron muy sugerentes: “si la vacuna de la rabia es obligatoria para los perros, ¿por qué vacunar a los niños no lo es?”, “si llevar cinturón de seguridad en el coche es obligatorio, ¿por qué no las vacunas?”, “si fumar está prohibido en muchos lugares porque es malo para la salud, ¿por qué las vacunas no son obligatorias si son buenas para la salud?”, “si una persona no vacunada puede poner en riesgo la salud de mi hijo, ¿por qué no obligan a vacunarse en las guarderías?”
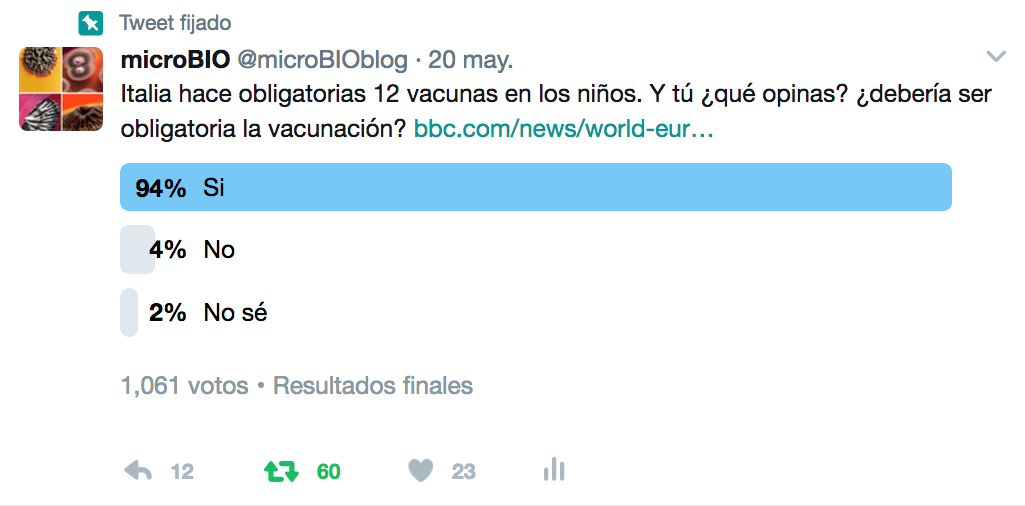
Resultado de la encuesta “¿Debería ser obligatoria la vacunación?” en Twitter.
Los recientes brotes de sarampión y de otras enfermedades evitables por las vacunas han hecho que algunos países cambien su legislación. En Italia ya es obligatoria la vacunación contra doce enfermedades infecciosas para poder matricular a tu hijo en el colegio. En Portugal no son obligatorias, pero sí gratuitas y están preparando una ley para exigir la vacunación. En Alemana, no son obligatorias, pero preparan también una ley para poder multar si no vacunas a tus hijos. En Francia son obligatorias las del tétanos, difteria y polio, y en Bélgica solo la de la polio. ¿Y en España? La vacunación es voluntaria, nuestro ordenamiento no incorpora explícitamente el deber de vacunación y nadie puede, en principio, ser obligado a vacunarse. Ahora bien, hay determinadas situaciones que permiten que los poderes públicos competentes impongan la vacunación forzosa, en caso de brotes o epidemias y de peligro para la salud pública. ¿Debería cambiarse la ley y que la vacunación fuera obligatoria?
Para controlar e incluso llegar a erradicar una enfermedad infecciosa, la OMS recomienda que la cobertura vacunal para esa enfermedad sea de al menos el 95%. Según datos oficiales, las tasas de vacunación en nuestro país en los últimos años son elevadas, superiores al 95%.

Coberturas vacunales en España desde 2006 hasta el 2015. Para más información consultar la web del MSSSI.
En España, a pesar de la no obligatoriedad, la tasa de vacunación es incluso superior a la de países en los que la vacunación es obligatoria. Por ello, el debate planteado podría ser útil si hubiera un descenso de las tasas de vacunación que pusieran en compromiso la protección del efecto rebaño y afectara a la salud pública. Adelantar cambios normativos que impusieran de forma coercitiva la vacunación, podría generar un efecto contrario al pretendido. Obligar quizá, de momento, no sea la solución.
¿Qué podemos hacer?
Para responder a los movimientos anti-vacunas o convencer a los que dudan, algunas estrategias se han basado en campañas de educación (folletos “oficiales” o similar) con información sobre la efectividad y seguridad de las vacunas. Si embargo, aunque necesaria, no parece que ésta sea la forma más efectiva. Educar a la gente tiene poco efecto o impacto en cambiar la actitud anti-vacunas. La información y educación no suelen cambiar por si solas las percepciones. Todos tenemos la tendencia de recibir mejor la información que confirma lo que pensamos y solemos rechazar lo que contradice nuestras creencias. Para muchas personas lo que convence no son los hechos, sino la credibilidad o autoridad de quién lo dice. En este sentido, la pieza fundamental para conseguir la aceptación y confianza pública de las vacunas son los profesionales de la salud (de la medicina y la enfermería). La gente cree y confía más en su médico o enfermera de lo que nos imaginamos. Muchas gente dice que la primera razón para vacunar a su hijo es la recomendación del profesional de la salud en la consulta de pediatria. Promover una buena relación con el paciente es fundamental.
Se han publicado algunas recomendaciones para estos profesiones de la salud, pero que nos pueden ayudar a todos cuando nos enfrentamos a una persona que duda: ¿cómo convencer a unos padres de que no vacunar supone un riesgo mayor?
1. Recuerda por qué nos vacunamos. Hay que explicar cómo las vacunas nos protegen de las infecciones y nos ayudan mantener la salud; reforzar la idea de que la vacunación es una norma social, porque la gente hace lo que cree que todo el mundo debe hacer. Da por hecho que va a vacunar a su hijo, ni si quiera ponlo en duda. Felicítale por vacunarlo (y concreta la fecha para la siguiente cita).
2. No intentes asustar a la gente con mensajes catastrofistas, ya que te puede salir el tiro por la culata. Explica cómo se controla de forma rigurosa la seguridad de las vacunas, algo que no se suele contar a la gente. Las vacunas son uno de los agentes farmacéuticos mejor estudiados y más seguros del mercado. Es frecuente confundir correlación con causalidad: que dos cosas ocurran al mismo tiempo no quiere decir que una sea la causa de la otra. Que el autismo se manifieste los primeros años de vida al mismo tiempo que el calendario vacunal, no demuestra que las vacunas sean la causa del autismo. Pero el sufrimiento de unos padres con un niño autista, … es tremendo.
3. Ten empatía. Evita ser despectivo. Hazte cargo de sus preocupaciones. Si tiene dudas, escucha, deja que hable, deja que acabe de hablar, reconoce el derecho que tiene para dudar y hacerse esas preguntas, sé positivo, responde de forma simple, sencilla, que se te entienda (“Hay más formaldehido en una pieza de fruta que en todas las vacunas que recibe tu niño”). Dedícale tiempo, con respeto, paciencia y confianza. Recuerda aquello de “siempre positivo, nunca negativo”.
4. La verdad es la piedra angular de la aceptación de las vacunas. Explica claramente las posibles reacciones adversas que pueda haber, que no le coja por sorpresa las reacciones locales de la vacuna. Su hijo ha ido a vacunarse estando sano, sin fiebre y las reacciones locales pueden alarmar si no se han explicado antes. La fiebre, el malestar general, un pequeño sarpullido o enrojecimiento local no significan que la vacuna no funcione sino todo lo contrario. Es señal de que la vacuna está activando las defensas. Y explica las posibles reacciones adversas graves muy raras que puede haber (menos de un caso por millón de dosis administradas). Se honesto y claro. Ningún medicamento es 100% seguro y todos tienen efectos secundarios. Reconoce los riesgos, también hay riesgo en tomar un paracetamol, pero distingue claramente las reacciones locales de los casos graves y muy raros. Hay que dar la información a medida, según las dudas y las preocupaciones de los padres.
5. Cuenta tu historia, tu propia experiencia, como profesional de la salud o como padre que vacuna a sus hijos: aquel viejo amigo del colegio que tuvo polio, o por qué tus hijos no han tenido rubéola. Y cuéntalo como una historia de ciencia. Explica que no hay nada más natural que las vacunas que inducen una inmunidad natural, al estimular a tu propio sistema inmune a producir su propia protección. Los anticuerpos que te protegen los produce tu propio cuerpo. La gente que está en riesgo es la que no hace nada.
6. Utiliza las redes sociales. Involúcrate de forma proactiva con los medios de comunicación y en las redes sociales. Proporcionarles información, comentarios independientes, ayuda a los periodistas a entender los datos. Da información, respuestas, historias, videos. Internet puede ser una herramienta muy útil para luchar contra la duda. Los algoritmos que usa Google no ayudan. Google puede darte una información sesgada. Las palabras “clave” que te sugiere y los contendidos web que te ofrece puede estar condicionados por tus propias preferencias y consultas previas. Así, Google puede contribuir a crear, mantener o aumentar tus dudas o a creer que lo que opina una minoría es mucho más frecuente que lo que realmente es. Por ejemplo, los contendidos negativos tienden a proliferar más en internet. ¿Por qué una madre que ha vacunado a su hijo y todo ha ido fenomenal y están los dos sanos y felices va a escribir su experiencia en un blog o va a dejar un comentario en Internet? Por el contario, si ha habido el menor problema, esa madre compartirá sus dudas en fórums o redes sociales y su testimonio se extenderá cómo la pólvora, generando una percepción errónea del problema. Como ya hemos dicho, los contenidos relacionados con la vacunación en la web y redes sociales son principalmente inexactos e incorrectos. Por eso, uno de los “campos de batalla” se libra en internet. Difundir mensajes en blogs, redes sociales, YouTube, … está muy bien, pero es complicado. El reto no solo es que los padres tengan acceso a la información, sino que esta se entienda y sea inteligible para cualquiera. Usa un lenguaje coloquial, muestra empatía y escucha al público.
Conclusión: En España no hay grandes movimientos anti-vacunas pero sí un aumento de padres que dudan de la seguridad y eficacia de las vacunas. De momento, las coberturas vacunales son altas y no se compromete el efecto rebaño. Por ello, imponer de forma coercitiva la vacunación, podría tener un efecto contrario al pretendido. No obstante, es necesaria una vigilancia estrecha del fenómeno anti-vacunas y su efecto en la salud pública. Los profesionales de la salud son la principal fuente de información para los padres que dudan y la forma más efectiva de convencerles de lo peligroso que es no vacunar a sus hijos.
Referencias y más información:
Las vacunas funcionan. Ignacio López-Goñi y Oihana Iturbide. 2015. Phylicom ediciones, Valencia. Colección Pequeñas Guías de Salud. ISBN: 978-84-943440-0-8
Vaccine hesitancy, vaccine refusal and the anti-vaccine movement: influence, impact and implications. Dubé, E., y col. (2015). Expert Rev Vaccines. 14(1):99-117. doi: 10.1586/14760584.2015.964212.
Identifying and addressing vaccine hesitancy. Kestenbaum, L.A., y col. (2015). Pediatr Ann. 44(4):e71-5. doi: 10.3928/00904481-20150410-07.
Promoting vaccine confidence. Smith, M.J. (2015). Infect Dis Clin North Am. 29(4):759-69. doi: 10.1016/j.idc.2015.07.004.
Vaccine hesitancy: A vade mecum v1.0. Thomson, A., y col. (2016). Vaccine. 34(17):1989-92. doi: 10.1016/j.vaccine.2015.12.049.
The impact of the web and social networks on vaccination. New challenges and opportunities offered to fight against vaccine hesitancy. Stahl, J.P., y col. (2016). Med Mal Infect. 46(3):117-22. doi: 10.1016/j.medmal.2016.02.002.
Vaccine Adverse Event Reporting System (VAERS)
El sarampión aumenta en Europa
Coberturas de vacunación en España (MSSSI)
Nota:
(*) Cuando me refiero a “padres” e “hijos” empleo los términos en plural que según el Diccionario de Lengua Española de la Real Academia significan “padre y madre de una persona” y “descendientes”, respectivamente.
Sobre el autor: Ignacio López Goñi es catedrático de microbiología de la Universidad de Navarra y autor del blog microBio.
El artículo Dudas sobre las vacunas: problemas y soluciones se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las ideas erróneas sobre educación entre el profesorado: prevalencia, causas y soluciones
- Vacunas: El arte de salvar vidas
- Sobre la predisposición genética a padecer enfermedades
Un nuevo mecanismo de resistencia antifúngico
El grupo de investigación de la UPV/EHU Fungal and Bacterial Biomics ha demostrado la existencia de un nuevo mecanismo de resistencia que se desconocía hasta el momento en el hongo Lomentospora prolificans (L. prolificans). Este microorganismo es multirresistente a los antifúngicos (antibióticos desarrollados frente a hongos) utilizados actualmente y provoca una mortalidad de entre el 80 y el 100% en pacientes con el sistema inmunológico debilitado. Gracias al estudio se podrán diseñar fármacos más efectivos para luchar contra este hongo.
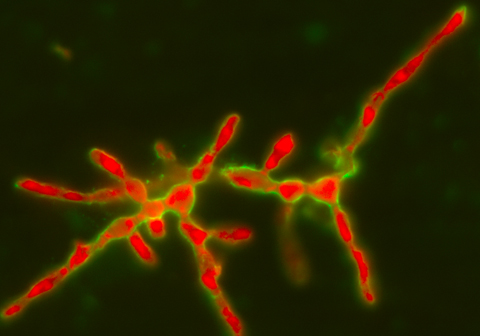
El microorganismo L. prolificans (antes conocido como Scedosporium prolificans) es un hongo filamentoso que pertenece a un grupo conocido vulgarmente como mohos, algunos de los cuales podemos observar creciendo en la comida en mal estado (fruta, pan, etc.) y que se diferencian de las levaduras unicelulares, tales como Candida albicans o Saccharomyces cerevisiae, que son relevantes en práctica clínica o en la industria alimenticia, respectivamente. El hongo L. prolificans es también común y bastante habitual en suelos de ciudades o en zonas industriales. A pesar de estar en contacto con él, no suele producir dolencias en individuos sanos, gracias al sistema inmunológico.
Sin embargo, explica Andoni Ramirez, uno de los autores del artículo, produce “infecciones muy graves” en pacientes con alguna enfermedad subyacente, como la “fibrosis quística”, o con el “sistema inmunológico debilitado”, como es el caso de pacientes que están siendo tratados con quimioterapia debido a padecer algún tipo de cáncer, pacientes en los que se ha llevado a cabo algún trasplante de órgano, o que sufren el Síndrome de la Inmunodeficiencia Adquirida (SIDA) por VIH.
Este hongo, revela la investigación, muestra una gran resistencia a los antifúngicos más habituales como el voriconazol, que es uno de los “fármacos de elección para el tratamiento” de las infecciones causadas por hongos filamentosos. “Este trabajo es muy relevante porque demuestra la existencia de un nuevo mecanismo de resistencia que se desconocía hasta el momento en hongos. Así, observamos una gran modificación de la pared celular en respuesta al antifúngico voriconazol, que es el que se utiliza preferentemente frente a este hongo y frente a otras especies fúngicas. Estas modificaciones se producen tanto en el tamaño como en la composición de su pared celular”, explica.
Este trabajo supone la primera descripción de estas respuestas como mecanismo de defensa frente a un antifúngico, abriendo un nuevo campo de posibilidades de cara al diseño de nuevas moléculas que permitirán un mejor tratamiento de ésta y otras infecciones fúngicas. “A diferencia de lo que ocurre con los agentes antibacterianos, la variedad de los compuestos antifúngicos es muy escasa, y funcionan con pocos mecanismos de acción diferentes. Así, en caso de aparición de cepas o especies resistentes, las opciones que tienen en los hospitales pueden ser a veces muy limitadas. Por tanto, el hallazgo de nuevos mecanismos de resistencia podría, en primer lugar, aumentar el número de dianas frente a las que dirigir fármacos; y en segundo lugar, explicar la resistencia tanto intrínseca como adquirida en otras especies de hongos patógenos”, advierte.
Por el momento, la investigación que está llevando a cabo el grupo de la UPV/EHU Fungal and Bacterial Biomics es básica, es decir, están generando el conocimiento necesario para que en un futuro se puedan diseñar nuevas terapias. “En este sentido, el siguiente objetivo es el de identificar los enzimas necesarios para los cambios que produce el hongo L. prolificans en su pared en respuesta al antifúngico, para así estudiarlos y generar nuevas estrategias terapéuticas”.
Aunque, hay que tener en cuenta que como en cualquier área de la biomedicina, el camino desde el laboratorio hasta el paciente es largo (de varios años) y difícil debido a la cantidad de pruebas que deben hacerse. “Además, al igual que sucede con las denominadas enfermedades raras, las infecciones causadas por este tipo de hongos tienen una baja incidencia en la población y, por tanto, a pesar de la elevada mortalidad que presentan, resulta difícil que haya agentes interesados en invertir en su investigación. Por ello, el avance siempre resulta más dificultoso y lento”, señala Ramírez.
Referencia:
Aize Pellon, Andoni Ramirez-Garcia, Idoia Buldain, Aitziber Antoran, Aitor Rementeria, Fernando L. Hernando.. Molecular and cellular responses of the pathogenic fungus Lomentospora prolificans to the antifungal drug voriconazole. PLOS ONE 12(3): e0174885. DOI: 10.1371/journal.pone.0174885.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un nuevo mecanismo de resistencia antifúngico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una nueva vía para la lucha contra la resistencia a los antibióticos
- La catálisis geométrica como mecanismo de fisión celular
- El mecanismo que bloquea receptores de membrana celular
Migraciones
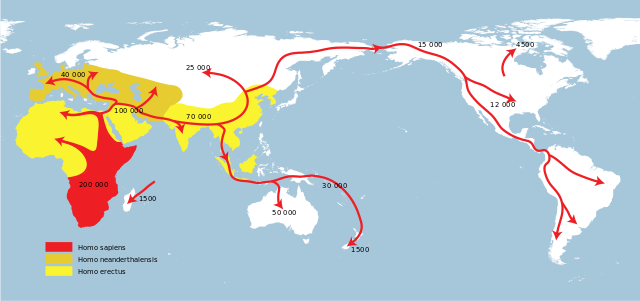
Los seres humanos modernos aparecieron en el este de África hace unos 200.000 años. Hace 75.000 alcanzaron el Oeste del continente. Aunque hubo otros movimientos anteriores hacia Oriente Próximo, hasta hace unos 60.000 no salieron del continente africano para, poco a poco, extenderse hacia otras zonas del planeta. Hace 46.000 años llegaron a Australia y 2.000 después, a Europa. Hace 16.000 años llegaron al continente americano. Hace 11.000 los asentados en el continente europeo avanzaron hacia el Norte el retirarse los hielos de la última glaciación. Y 3.000 después llegaron a nuestro continente los primeros pueblos de agricultores y ganaderos. Hace 1.500 años los seres humanos empezaron a poblar la Polinesia. La mayor parte de esas expansiones eran, seguramente, de carácter “démico”; esto es, fueron ocupaciones graduales de territorios vecinos que iban siendo colonizados poco a poco.
Hace 6.000 años, en Sumeria, las ciudades se convirtieron en los primeros focos de atracción de emigrantes procedentes de localidades de menor tamaño o asentamientos rurales. Y ese proceso impulsó innovaciones culturales, incluidas las tecnológicas. Hace 4.500 años los pastores yamnaya invadieron Europa procedentes de las estepas de Eurasia, y los hunos hicieron lo propio hace unos 1.650, provocando el desplazamiento de pueblos germánicos hacia el interior del Imperio Romano.
Hace unos 1.570 años, anglos y sajones procedentes del norte de Europa colonizaron Gran Bretaña. Los vikingos, 350 años después, siguieron el mismo camino, y en el 980 de nuestra era, viajaron a Islandia, Groenlandia y Terranova. Antes, los árabes ya se habían expandido por Asia Occidental y Norte de África a partir del 632. Y hace ocho siglos los mongoles ocuparon gran parte de Asia.
En 1492 Colón llegó a las Américas, propiciando a partir de esa fecha grandes movimientos migratorios hacia ese continente. En 1520, barcos europeos empezaron a llevar a América esclavos capturados en el África Occidental. En 1820, cuando todavía no se habían producido las migraciones masivas que vendrían más adelante, ya vivían en América 2,6 millones de personas de origen europeo. En 1847, millón y medio de irlandeses huyeron de la hambruna en dirección a Gran Bretaña y Norteamérica. En 1913 la emigración europea hacia las Américas alcanzó su máximo histórico: ese año se desplazaron algo más de dos millones de personas. La revolución bolchevique de 1917 provocó el desplazamiento de más de un millón de seres humanos hacia Europa Occidental. Y en 1945 la Segunda Guerra Mundial desplazó a 30 millones de personas. En 1947 se movieron entre India y Paquistán 18 millones, como consecuencia de la partición india de acuerdo con criterios étnico-religiosos.
Hasta aquí hemos relatado los grandes movimientos de población que se han producido en la historia de la humanidad y de los que tenemos información precisa o, al menos, constancia. Pero, como es sabido, los desplazamientos siguen produciéndose a gran escala. En la actualidad, alrededor de 245 millones de personas viven en países distintos de los que nacieron y, de esos, más de 65 millones han tenido que abandonar su país huyendo de conflictos, violencia o vulneraciones de derechos humanos. Parte de los emigrantes -menos del 10%- son refugiados. El Alto Comisionado de Naciones Unidas para los Refugiados (ACNUR) informa de la existencia de 16,1 millones de personas bajo su jurisdicción, a los que hay que añadir otros 5,2 millones que están al amparo de la Agencia de Naciones Unidas para los Palestinos. En total son más de 21 millones.
Las personas no han dejado de moverse en el Mundo y siempre lo ha hecho por las mismas razones: huyen de la violencia y la persecución o, sencillamente, buscan una vida mejor.
Nota: Las fechas consignadas en el primer párrafo de esta anotación tienen carácter tentativo, por lo que no han de tomarse como definitivas. Cada cierto tiempo se hacen propuestas diferentes para las expansiones. El origen de la especie también está sometido a revisión; esta misma semana Nature ha publicado el hallazgo de fósiles que podrían modificar tanto el origen geográfico como temporal de nuestra especie. La paleoantropología no deja de dar sorpresas.
—————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 26 de marzo de 2017.
El artículo Migraciones se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Arte & Ciencia: Conservación de obras con componentes tecnológicos

El arte y la ciencia son dos formas de conocimiento aparentemente alejadas, en gran medida consecuencia de la especialización profesional y la educación compartimentada. Del estudio de esta impostada separación surgió el estereotipo de las dos culturas, las ciencias y las humanidades, para referirnos a esa brecha de conocimiento. La realidad es que la ciencia y el arte sí están conectadas y que ninguna forma de conocimiento es impermeable a otra. Por poner algunos ejemplos: ¿Cómo podría crearse una obra plástica sin las técnicas propiciadas por la ciencia? ¿Cómo podríamos interpretar la elección de materiales?
Estas y otras cuestiones relacionadas furon tratadas por destacados profesionales -artistas, ilustradores, filósofos y científicos- que han puesto el foco en ese difuso trazo que une la ciencia y el arte. El ciclo Ciencia & Arte se desarrolló, bajo la dirección de Deborah García Bello, a lo largo de cuatro jornadas que se celebraron los jueves días 6 y 27 de abril y 11 y 25 de mayo de 2017 en el auditorio del Museo Guggeheim Bilbao.
Esta actividad de la Cátedra de Cultura Científica de la UPV/EHU se enmarca en el programa TopARTE que conmemora el XX Aniversario del Museo Guggenheim Bilbao.

Primera jornada. 2ª conferencia.
Aitziber Velasco, técnica de Conservación del Museo Guggenheim Bilbao: Conservación de obras con componentes tecnológicos
Las ciencias experimentales juegan un papel esencial en el análisis, tratamiento y conservación de las obras de arte. Estos procesos nos ofrecen, además, información valiosa sobre el contenido de la obra y las circunstancias en las que fue creada. Ciencia y arte tienen una relación mucho más íntima de lo que imaginamos, ya que el conocimiento científico es una herramienta imprescindible para artistas, restauradores y analistas. Les permite conocer las cualidades de los materiales para optar por unos u otros, prever cómo se degradarán los pigmentos o determinar la mejor manera para conservar una escultura.
Conservación de obras con componentes tecnológicosEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Arte & Ciencia: Conservación de obras con componentes tecnológicos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: La importancia de la ciencia para la conservación del arte
- Ciencia, naturaleza y arte: la química y sus metáforas, por Fernando Cossío
- Curso de verano “La ciencia de nuestras vidas”: Arte, literatura y ciencia, por Gustavo A. Schwartz
La carrera hacia la supremacía cuántica

Ordenador IBM Q de 17 cúbits superconductores. Fuente: IBM.
Dos grandes empresas, IBM y Google, compiten entre sí por alcanzar la supremacía cuántica: fabricar un ordenador cuántico capaz de resolver un problema que ningún ordenador clásico del mundo haya sido capaz de resolver hasta ese día. Parece difícil, ya que los superordenadores más poderosos del mundo, que lideran el TOP500, son muy poderosos. Sin embargo, se estima que un ordenador cuántico de propósito general totalmente funcional sería capaz de tal hazaña con tan solo 50 cúbits. Como puedes imaginar, lograr la supremacía cuántica será el final de una carrera y el inicio de otra, la carrera hacia los ordenadores cuánticos comerciales. Permíteme glosar la situación actual de esta carrera entre gigantes.
El término «supremacía cuántica» fue acuñado por el físico John Preskill, que ocupa la cátedra Richard P. Feynman de Física Teórica en el Instituto Técnico de California (Caltech). Lo acuñó en octubre del año 2011 para su charla en la 25º Conferencia Solvay de Física [1]. Un término muy popular hoy en día, aunque resulta políticamente incorrecto para cierta gente [2]. El problema lingüístico es sencillo, en inglés recuerda demasiado al término «supremacía blanca», que se usó durante el apartheid de Sudáfrica entre 1948 y 1991. Para un hispanoparlante, quizás, la asociación con la segregación racial no sea tan obvia. Aun así, el propio Preskill tuvo sus propias dudas al respecto como nos contó en su blog Quantum Frontiers [3]; allí retó a sus lectores a proponer una alternativa; nadie propuso ninguna mejor.
Llamamos «cúbit» (qubit en inglés) a un «dígito binario cuántico» (quantum binary digit), o sea, a un «bit cuántico» (quantum bit). Este término matemático fue acuñado en el año 1993 por el físico Ben Schumacher, del Kenyon College, Ohio (EE.UU.), tras una conversación con uno de los padres de la teoría cuántica de la información, el físico teórico Bill K. Wootters, del Williams College, Massachusetts (EE.UU.) [4]. El concepto matemático de cúbit se puede implementar físicamente mediante cualquier sistema cuántico que presente dos niveles, o estados energéticos, que puedan estar en superposición cuántica. A veces conviene diferenciar entre «cúbit matemático» y «cúbit físico», pero en la práctica el contexto suele aclarar en qué sentido se está usando.
El primer artículo en el que se escribió el término «cúbit» se envió en 1993 a una revista de física, Physical Review A, aunque apareció en abril de 1995 [4]. Un segundo artículo del propio Schumacher, junto al matemático Richard Jozsa, de la Universidad de Cambridge (Reino Unido), que fue enviado más tarde en 1993 a una revista de óptica, acabó apareciendo publicado un poco antes, en 1994 [6]. En poco tiempo el término se hizo muy popular.
Los ordenadores cuánticos se caracterizan por su número total de cúbits, lo que en un ordenador clásico sería equivalente, más o menos, al número total de transistores de su microprocesador. En los ordenadores clásicos el número de bits se usar para otra cosa, el tamaño del bus de datos, es decir, el número de bits que puede recibir o enviar de forma simultánea desde la placa base al microprocesador. Hoy en día lo habitual es que un ordenador use un microprocesador de Intel de 64-bits (un Core i3, Core i5, o Core i7), que tiene unos cientos de millones de transistores. Sin embargo, el primer microprocesador de Intel era de 4-bits, el famoso Intel 4004, que tenía 2300 transistores; luego aparecieron los procesadores de 8-bits, como el 8080, con 4500 transistores; más tarde los de 16-bits, como el famoso 8086, con 29000 transistores; y así sucesivamente.
Un ordenador cuántico con 50 cúbits sería algo así como un ordenador clásico con una memoria capaz de almacenar 50 bits (el equivalente a siete letras de texto en formato ASCII); parece un número ridículamente pequeño, sobre todo hoy en día que los ordenadores tienen gigabytes de memoria; pero la magia cuántica oculta un as bajo la manga, el paralelismo cuántico. En cada paso de la ejecución de cierto algoritmo, el ordenador clásico aplica una operación matemática al contenido almacenado en su memoria clásica de 50 bits, llamada registro, es decir, a un valor numérico concreto de entre 250 posibles valores (uno entre unos mil billones).
Sin embargo, en el ordenador cuántico la información se almacena en un registro cuántico, que para 50 cúbits almacena un estado en superposición cuántica de todos los 250 posibles valores, cada uno con su correspondiente amplitud de probabilidad; gracias a ello, en cada paso de la ejecución del algoritmo cuántico se aplica una operación matemática que cambia de forma simultánea las 250 amplitudes de probabilidad correspondientes a cada uno de los 250 valores en superposición cuántica. Si este proceso se realiza de forma adecuada, el ordenador cuántico puede ser mucho más eficiente que un ordenador clásico; más aún, la simulación en un ordenador clásico del funcionamiento de un ordenador cuántico requerirá usar 250 registros clásicos, o aplicar 250 operaciones sobre un único registro clásico. Aunque estoy obviamente muchas sutilezas técnicas, salta a la vista que un ordenador cuántico con decenas de cúbits puede lograr la supremacía cuántica.
El gran problema de la fabricación de un ordenador cuántico es que no basta tener unos cuantos cúbits físicos para tener un registro cuántico en el que adquieran un estado de superposición cuántica coherente. Además, hay que garantizar que la coherencia cuántica no se pierda durante la aplicación de todas y cada una de las operaciones cuánticas aplicadas a los cúbits del registro cuántico. Cualquier interacción de alguno de los cúbits con su entorno (el sitio donde se encuentre cada cúbit físico) puede resultar en una medida no intencionada de su estado cuántico; la medida destruye (al menos parcialmente) el estado cuántico en superposición y entra en acción la decoherencia cuántica, con lo que el sistema de cúbits pasa a comportarse como un ordenador clásico (probabilístico). Con la tecnología actual aislar 50 cúbits del resto del universo y al mismo tiempo poder operar de forma arbitraria con cualquiera de ellos raya lo imposible. Por eso la carrera hacia la supremacía cuántica está repleta de obstáculos, incluso para gigantes como IBM y Google.
El concepto de supremacía cuántica es relevante en computación cuántica porque, en la práctica, es el único método para asegurarnos de que un supuesto ordenador cuántico con muchos cúbits es realmente un ordenador cuántico. Parece un juego de palabras, pero la diferencia entre un ordenador cuántico y un ordenador clásico probabilístico que usa cúbits como fuente de aleatoriedad es sutil; la eficiencia cuántica requiere que el ordenador sea cuántico de verdad. Con pocos cúbits se puede realizar un estudio experimental sistemático para verificar que el ordenador cuántico se comporta como tal. Pero con decenas de cúbits dicho estudio experimental es inviable.
Por todo ello, la mejor manera de confirmar que un supuesto ordenador cuántico con 50 cúbits es realmente un ordenador cuántico consiste en ejecutar en él un algoritmo que resuelva un problema cuya solución es imposible de lograr con el más potente de los superordenadores clásicos actuales; lo ideal sería que, por supuesto, el problema sea tal que sea fácil comprobar que la solución ofrecida es correcta. Hay muchos problemas así, pero es muy costoso poner a un equipo de investigadores a desarrollar programas y más programas para ejecutar en dicho ordenador esperando, no sin cierta fe, a que alguno demuestre la supremacía cuántica. Aquí es donde entra con pie firme la iniciativa de IBM llamada Quantum Experience [7].
El gigante azul ofreció en el verano de 2016 el acceso gratuito y automático a un ordenador cuántico de 5 cúbits mediante un servicio en la nube (cloud). La iniciativa ha sido todo un éxito y se estima que unos 40000 usuarios de más de 100 países han desarrollado más de 275000 algoritmos cuánticos para dicho ordenador en solo un año; la corrección de los programas se verifica en un simulador clásico, para luego ser ejecutados en la máquina física IBM Q [8]. Gracias a esta ingente cantidad de experimentos se puede validar estadísticamente que este ordenador IBM Q de 5 cúbits se comporta como debe hacerlo un ordenador cuántico de propósito general.
Validar de forma experimental que un ordenador cuántico de 16 cúbits es realmente cuántico, si bien no es imposible, requiere un coste muy elevado en tiempo y recursos. Por ello, desde marzo de 2017, la IBM Q Experience ofrece el acceso gratuito a un supuesto ordenador cuántico de 16 cúbits que usa la misma tecnología que el ordenador anterior de 5 cúbits [7]. Para este nuevo ordenador no existe un simulador clásico eficiente, aunque existe un verificador de la sintaxis del código. Un usuario solo sabrá si su algoritmo funciona correctamente tras ejecutarlo físicamente en la máquina IBM Q. Se espera que gran parte de los usuarios que ya han disfrutado de la experiencia con 5 cúbits se atrevan con la nueva máquina de 16 cúbits. Si toda va bien, dentro de un año habrá un número suficiente de experimentos como para que se pueda verificar de forma estadística que la máquina de 16 cúbits se comporta como debe hacerlo un ordenador cuántico.

Dra. Katie Pooley junto al cilindro del contiene el sistema criogénico que contiene en su interior el ordenador IBM Q de 17 cúbits en el Centro de Investigación Thomas J. Watson de IBM. Fuente: Carl de Torres para IBM.
Permíteme enfatizar la idea del gigante azul: decenas de miles de usuarios trabajarán gratis para IBM demostrando que su máquina funciona. ¡Qué más se puede pedir! Por supuesto, mantener una máquina cuántica de 16 cúbits en funcionamiento continuo en un laboratorio tiene un coste. Por ello, las grandes mentes pensantes de IBM Q han tenido otra idea feliz, que anunciaron el pasado 17 de mayo de 2017 [7]. Su máquina de 16 cúbits tiene 17 cúbits. ¡¿Cómo?! La experiencia IBM Q ofrece acceso gratuito a 16 cúbits, ni uno más; quien quiera usar los 17 cúbits tendrá que pagar por ello. Todas las empresas, industrias, institutos de investigación y demás entes interesados en usar la máquina de 17 cúbits podrán aprender a usarla de forma gratuita, con 16 cúbits, pero para usar la máquina fetén tendrán que abonar por ello. Sin lugar a dudas el gigante azul es gigante por algo.
Seguro que te preguntas, si nadie sabe con seguridad si el ordenador IBM Q de 17 cúbits es realmente cuántico, ¿quién va a pagar por usarlo? Yo no tengo la respuesta. Lo cierto es que lo único importante para IBM Q es que la máquina de 16 cúbits sea tan usada, o más, de lo que ha sido usada la máquina de 5 cúbits en el último año. Así podrá verificar que su tecnología funciona.
El objetivo de IBM Q es fabricar un ordenador cuántico de 50 cúbits antes de 2022 capaz de lograr la supremacía cuántica. Para este proyecto lo ideal es disponer de cientos de miles de algoritmos cuánticos ya implementados y de decenas de miles de programadores cuánticos experimentados en su tecnología. Quizás alguno de esos algoritmos, implementado en 50 cúbits, sea el que logre la supremacía cuántica para IBM. Quizás en los próximos años IBM abra una competición entre sus usuarios con un buen premio en metálico para el primero que logre demostrar la supremacía. Quizás el gigante azul venza en la carrera de la supremacía cuántica contra Google gracias a esos miles de programadores que están trabajando gratis por el mero placer de usar un ordenador cuántico.
Por cierto, Google afirma tener un ordenador cuántico de 8 cúbits, pero no ha demostrado aún que sea cuántico. Ha anunciado que pretende fabricar uno de 50 cúbits antes que IBM [8]. ¿Pero quién programará dicha máquina? ¿Quién trabajará gratis para Google?
Este post ha sido realizado por Francis Villatoro (@Emulenews) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias
[1] John Preskill, “Quantum computing and the entanglement frontier,” 25th Solvay Conference on Physics (“The Theory of the Quantum World”), 19-22 Oct 2011, arXiv:1203.5813 [quant-ph].
[2] Karoline Wiesner, “The careless use of language in quantum information,” arXiv:1705.06768 [physics.soc-ph].
[3] John Preskill, “Supremacy Now?” Quantum Frontiers, 22 Jul 2012. https://goo.gl/KdnD3j
[4] John Preskill, “Who named the qubit?” Quantum Frontiers, 09 Jun 2015. https://goo.gl/EwFDyR
[5] Benjamin Schumacher, “Quantum coding,” Physical Review A 51: 2738 (1995), doi: 10.1103/PhysRevA.51.2738.
[6] Richard Jozsa, Benjamin Schumacher, “A New Proof of the Quantum Noiseless Coding Theorem,” Journal of Modern Optics 41: 2343-2349 (1994), doi: 10.1080/09500349414552191.
[7] IBM Q Experience: https://www.research.ibm.com/ibm-q/
[8] Davide Castelvecchi, “IBM’s quantum cloud computer goes commercial,” Nature 543: 159 (09 Mar 2017), doi: 10.1038/nature.2017.21585.
El artículo La carrera hacia la supremacía cuántica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una puerta cuántica robusta y ultrarrápida
- Cuántica y relatividad por todas partes
- Digitalización universal de la computación cuántica analógica en un chip superconductor
La evaluación mejora el aprendizaje
Marta Ferrero

En el ámbito escolar la evaluación se suele asociar con el proceso de examinar y poner nota a los conocimientos de los estudiantes. Quizá por eso despierta tanto recelo entre muchos alumnos, familias e incluso docentes, hasta el punto de que no son pocas las voces que abogan por desterrarla definitivamente de los centros escolares. Lo que muchos desconocen es que, además de ser un medio para comprobar lo aprendido, la evaluación es un potente medio para aprender.
A mediados de la década de los 70, una revisión de la literatura puso de relieve que el acto de recuperar la información almacenada en la memoria favorece su aprendizaje (Bjork, 1975). Desde entonces, el efecto de la evaluación (o “testing effect” en inglés) ha sido objeto de estudio en innumerables ocasiones y la evidencia recogida hasta el momento apunta de forma consistente en la misma dirección: evaluar a los alumnos propicia un mejor aprendizaje y recuerdo posterior de lo aprendido que otras técnicas de estudio más populares (Adesope y cols., 2017; Bangert y cols., 1991; Phelps, 2012; Roediger y cols, 2006; Rohrer y cols., 2010). De hecho, en contra de lo que la intuición nos pueda dictar, el hecho de enfrentarse a una evaluación tiene más beneficios en el aprendizaje que leer la materia una y otra vez. Y más importante aún, como veremos a continuación, este resultado es robusto bajo una amplia variedad de circunstancias.
En el año 2006, Roediger y colaboradores realizaron una revisión cualitativa sobre el efecto de la evaluación en el aprendizaje. Los resultados mostraron que los beneficios de ésta son constantes independientemente del tipo de tarea que se emplee para ello (por ejemplo, tareas de laboratorio como la asociación de parejas de estímulos o tareas reales como la redacción de un ensayo o responder a preguntas de selección múltiple), del tipo de material objeto de estudio (por ejemplo, listas de palabras o textos) o del contenido y su complejidad. Además, encontraron que estas ganancias se mantienen constantes tanto en los laboratorios como en las aulas. Un meta-análisis de estudios realizados exclusivamente en colegios había alcanzado esta misma conclusión años atrás (Bangert y cols., 1991). En el año 2012, Phelps realizó una nueva síntesis sobre el efecto de la evaluación en el rendimiento académico de los alumnos. En esta ocasión, se incluyeron trabajos cuantitativos y cualitativos realizados entre 1910 y 2010. Una vez más, los resultados mostraron que evaluar mejora el aprendizaje.
Recientemente, Adesope y colaboradores (2017) han realizado un meta-análisis sobre el efecto de la evaluación. Su trabajo de revisión incorpora una serie de mejoras en relación a los anteriores como, por ejemplo, la inclusión de los estudios más recientes o el uso de técnicas de análisis más sofisticadas que permiten una interpretación de los datos más completa y rigurosa. Por todo ello, las conclusiones a las que llega son especialmente relevantes. En primer lugar, los resultados confirman que realizar evaluaciones favorece el aprendizaje. Este efecto es moderado si se compara con otras estrategias de estudio, como la relectura, y es mucho mayor cuando se compara con no hacer nada. En relación al formato de las tareas de evaluación empleadas, se observa que el recuerdo libre, el recuerdo con pistas, las preguntas de selección múltiple y las preguntas de respuestas cortas son las estrategias que conducen a beneficios mayores. Por ello, lo más adecuado es que el docente decida en cada caso qué formato usar en función del tipo de aprendizaje (por ejemplo, preguntas de selección múltiple para retener hechos y preguntas de respuesta corta para contenidos más abstractos y conceptuales). Además, los beneficios de aprendizaje son mayores si el formato de las pruebas finales coincide con el de las pruebas de repaso y también si se combinan diferentes tipos de tarea durante ambos tipos de prueba. Este último resultado justifica una vez más el empleo de diferentes tipos de tarea en función de la materia objeto de aprendizaje. En relación al feedback, los autores concluyen que los beneficios de la evaluación son prácticamente iguales tanto si los alumnos reciben retroalimentación sobre su rendimiento durante las pruebas de repaso como si no. Y, por tanto, recomiendan la evaluación incluso cuando no existe la opción de dar feedback. La evaluación es también eficaz independientemente del intervalo de tiempo que transcurra entre las pruebas de repaso y las finales, aunque las mejoras son mayores si este lapso de tiempo es de 1 a 6 días que si es inferior a 1 día. Y también lo es al margen del nivel académico en el que se encuentren los alumnos. Curiosamente, es preferible que los estudiantes realicen una única prueba de repaso a que realicen varias. Luego, en principio, una pequeña inversión de tiempo es suficiente para obtener mejoras. Por último, al igual que en revisiones previas, este meta-análisis muestra que los efectos de la evaluación se producen tanto en contextos artificiales como en aulas reales.
¿Por qué la evaluación está tan infravalorada en relación a otras estrategias de aprendizaje como la relectura, tan valorada por muchos estudiantes? La relectura de un texto puede propiciar un sentido de familiaridad con el mismo que nos conduce a la falsa sensación de estar aprendiendo (Bjork y cols., 2011). Sin embargo, este aprendizaje es superficial y se traduce en un rendimiento pobre a largo plazo (Roediger et al., 2006). Por el contrario, la evaluación posibilita unas condiciones de aprendizaje que, aunque aparentemente crean cierta dificultad, permiten un aprendizaje más flexible y duradero. Estas dificultades deseables, como las ha denominado Bjork (1994), impulsan los procesos de codificación y recuperación que favorecen el aprendizaje, la comprensión y el recuerdo. Junto con la dificultad que supone ser evaluado, hay otras razones que pueden explicar la mala fama de la evaluación. Por un lado, hay voces que apuntan al estrés que puede causar en los estudiantes una exposición frecuente a evaluaciones (véase, por ejemplo, Acaso, 2014). Sin entrar en más debate, es importante recalcar aquí que evaluación no es necesariamente sinónimo ni de calificación ni de prueba oficial para acceder a estudios superiores. Por otro lado, algunos críticos también apuntan a que la evaluación puede quitar tiempo para hacer otras actividades o para usar el material didáctico de una forma más creativa. Sin embargo, como apuntan Roediger y colaboradores (2006), si los alumnos no han alcanzado un dominio básico de la materia, difícilmente van a poder pensar de forma crítica y creativa sobre la misma. Además, como explican estos autores, hay muchas formas de integrar la práctica de la evaluación en el aula sin interrumpir la rutina de trabajo habitual.
En síntesis, la evidencia demuestra de forma robusta que la evaluación es una herramienta muy valiosa para favorecer el aprendizaje a largo plazo. Los numerosos estudios que se han hecho muestran además que los beneficios de la evaluación se mantienen con independencia de la edad y nivel educativo de los aprendices así como del tipo y complejidad de la materia. A la luz de estos resultados, y a pesar del creciente número de voces críticas, no hay razón para que los centros escolares no mantengan o incorporen la evaluación en sus aulas como práctica habitual.
Referencias:
Acaso, M. (2014). Dopamina, empoderamiento y responsabilidad: sin cambiar la evaluación no cambiaremos la educación.
Adesope, O. O., Trevisan, D. A., & Sundararajan, N. (2017). Rethinking the Use of Tests: A Meta-Analysis of Practice Testing. Review of Educational Research, 87, 1-43.
Bangert-Drowns, R.L., Kulik, J.A., & Kulik, C.L.C. (1991). Effects of frequent classroom testing. Journal of Educational Research, 85, 89-99.
Bjork, R. A. (1975). Retrieval as a memory modifier. In R. Solso (Ed.), Information processing and cognition: The Loyola Symposium (pp. 123-144). Hillsdale, NJ: Erlbaum.
Bjork, R.A. (1994). Memory and metamemory considerations in the training of human beings. In J. Metcalfe & A. Shimamura (Eds.), Metacognition: Knowing about knowing (pp. 185-205). Cambridge, MA: MIT Press.
Bjork, E. J., & Bjork, R. (2011). Making things hard on yourself, but in a good way: Creating desirable difficulties to enhance learning. In M. A. Gernsbacher, R. W. Pew, L. M. Hough, & J. R. Pomerantz (Eds.), Psychology and the real world: Essays illustrating fundamental contributions to society (pp. 56-64). Washington, DC: FABBS Foundation.
Phelps, R. P. (2012). The effect of testing on student achievement, 1910–2010. International Journal of Testing, 12, 21–43.
Roediger, H.L., & Karpicke, J.D. (2006). The Power of Testing Memory: Basic Research and Implications for Educational Practice. Perspectives on Psychological Science, 1, 181-210.
Rohrer D., & Pashler, H. (2010). Recent research in human learning challenges conventional instructional strategies. Educational Research, 39, 406-412.
Sobre la autora: Marta Ferrero es psicopedagoga y doctora en psicología. Actualmente es investigadora posdoctoral en el Deusto Learning Lab de la Universidad de Deusto. Es autora del blog Si tú supieras…
El artículo La evaluación mejora el aprendizaje se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El aprendizaje del inglés es mejor si se usa para aprender otra cosa
- Dejad de propagar el mito de los estilos de aprendizaje
- A favor de la evaluación escolar objetiva
Ciencia: es complicado
Explicaciones hay, y las ha habido siempre; para cada problema humano hay siempre una solución bien conocida, elegante, plausible y equivocada. H. L. Mencken
La mente humana es una máquina maravillosa que está poseída por un insaciable deseo de conocer, de satisfacer su curiosidad, pero como todos los sistemas biológicos tiene sus defectos. Y uno de ellos es particularmente perverso: la vagancia. La mente humana quiere saber, pero el cerebro tiene un infinito anhelo de trabajar lo menos posible. Por eso siempre prefiere una explicación sencilla a una compleja; un razonamiento simple a uno más alambicado, una historia directa y sin demasiados condicionales que otra repleta de apartes, casos particulares y rincones que necesitan explicaciones complementarias. No hablamos aquí de la llamada Navaja de Ockham, un principio metodológico razonable, sino del simple problema de la pereza que hace que los seres vivos prefieran el camino con menos cuestas. Y eso, para la ciencia, es un problema, porque resulta que nuestro Universo es complejo, sutil, a veces contradictorio y siempre anti-intuitivo. Comprender el cosmos es siempre cuesta arriba.
Por eso la respuesta a casi cualquier pregunta realmente interesante se puede resumir igual que esas tortuosas relaciones personales se etiquetan en Facebook: Es Complicado.
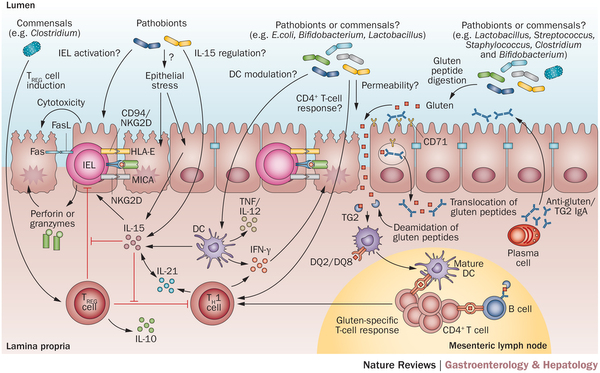
Imagen resumen en la que solo se indica la posible influencia de las bacterias intestinales en la enfermedad celíaca. Nótese la cantidad de interrogantes.
Pongamos un ejemplo relacionado con la actualidad. El pasado domingo 4 de junio de 2017 la periodista Rosa Montero publicó en la revista El País Semanal un artículo sobre intolerancias alimenticias, transgénicos, el poder de la industria farmacéutica y la demonización de la homeopatía. No se trata de desmontar sus numerosos, variados y profundos errores; otros ya lo han hecho, con brillantez. Lo que se pretende aquí es subrayar hasta qué punto este tipo de argumentos revelan el daño que hace el afán de simplicidad enfrentado a la complejidad del conocimiento científico. Porque puramente por casualidad y coincidiendo con el artículo citado la revista The Scientist publicó un amplio repaso de lo que la ciencia conoce ahora mismo sobre la celiaquía, las intolerancias alimentarias no celiacas, su prevalencia, causas y posibles orígenes, además de potenciales avenidas de tratamiento. A diferencia de la elegante, plausible y equivocada explicación defendida por Rosa Montero lo que conocemos es mucho más complejo.
La prevalencia de estas enfermedades está aumentando, es cierto, y no sabemos por qué; pero no se debe a transgénicos (que no están en nuestros campos de cultivo) y mucho menos a que la labor del gran Norman Borlaug y la Revolución Verde crearan nuevos tipos de trigo con un gluten distinto, cosa que no hizo. Sabemos que la verdadera intolerancia celiaca se comporta como una enfermedad autoinmune, creando respuesta de nuestras defensas no sólo contra algunas de las proteínas del gluten, sino sobre células propias del cuerpo. Hay un componente genético, pero resulta que casi el 40% de la población lleva variantes génicas relacionadas con la enfermedad y sólo entre el 1 y el 3% del total la desarrollan, y aún no conocemos el agente detonante que podría ser cualquier cosa en nuestro medio ambiente, tal vez la más insospechada. Existen, además, intolerancias a los cereales que no están relacionadas con el gluten, pero que pueden interactuar modificando el curso de la enfermedad.
Los síntomas abdominales son los más típicos y pueden dañar el intestino, pero ahora están apareciendo otros de síntomas en adultos (osteoporosis, anemia) cuya conexión no conocemos. Sabemos que la composición del microbioma intestinal es diferente en los celiacos, pero no sabemos de qué manera afecta a la enfermedad; aunque resulta que al menos parte del aumento del número de casos podría deberse a nuestra exitosa lucha contra las úlceras de estómago, porque la presencia de Helicobacter pylori (la bacteria que causa muchas de ellas) coincide con menos celiaquía. Y sabemos que en algunas circunstancias la infección deliberada con parásitos, como lombrices intestinales, alivia a algunos enfermos, pero no sabemos cómo ni por qué. Hay pocas certezas y muchos factores en juego. En otras palabras: es complicado.
Sería mucho más sencillo, comprensible y satisfactorio tener un único enemigo contra el que poder luchar. Sería mucho más heroico que ese enemigo tuviese defensores poderosos para así luchar hasta derrotarlos en defensa de la verdad. Sería mucho más elegante y plausible que las cosas tuviesen una explicación sencilla. Pero la realidad no es así. En ciencia muchos fenómenos surgen de la interacción de múltiples factores, lo que complica entenderlos. Por eso uno de los principios metodológicos básicos es el reduccionismo: controlar los factores que participan en un sistema complejo y modificarlos de uno en uno, de modo controlado y sistemático, para detectar cuáles influyen y de qué manera afecta cada uno. Cuando se trata de objetos o seres vivos es fácil realizar este tipo de investigación en un laboratorio. Pero cuando se trata de seres humanos no se pueden hacer experimentos, así que hay que usar los grandes números, las estadísticas y la historia para intentar conseguir los datos. Esto obliga a tratar con múltiples factores y a usar sofisticados métodos de análisis para separar sus efectos. El proceso no es simple y puede conducir a errores que luego hay que corregir, pero es el único disponible.
Esto exige años de estudio, décadas de dedicación, grandes presupuestos, captación de datos a gran escala, y también personas que dedican su carrera y deben vivir con la posibilidad, siempre presente, de que el trabajo de su vida resulte ser uno de esos errores que se descartan en los pies de página de los libros de ciencia. Exige mucho trabajo mental sin ninguna garantía de que el resultado final sea positivo y con la certeza de que, aun siéndolo, la explicación nunca será elegante y sencilla sino retorcida, compleja, llena de excepciones y sutilezas difíciles de entender. La práctica de la ciencia a veces genera la sensación de estar golpeándote la cabeza contra la pared, de estar desperdiciando tu vida dedicándote a pensar con feroz intensidad en resolver un problema que no se puede resolver. Y hacerlo antes de que los chinos, o los estadounidenses, lo consigan antes que tú.
Cuánto más fácil es buscar un culpable, un enemigo malvado, plausible y que explique todo y enfocar en la ira sobre esa imagen, sobre todo cuando lo que se quiere es la explicación de un sufrimiento humano real; cuánto más satisfactorio sentirse seguro y lleno de justicia con una explicación simple y un enemigo claro en lugar de frustrado, inseguro e incluso ignorante. La ciencia no ofrece respuestas sencillas, ni morales, ni justas: busca respuestas reales. El cerebro a veces prefiere ahorrarse el trabajo y las dudas, y es comprensible: siempre es más fácil remar a favor que en contra de la corriente. Pero aunque cueste más trabajo hay que ir donde está la verdad; por eso merece la pena. Aunque sea complicado.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo Ciencia: es complicado se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- De los héroes de la ciencia y sus frágiles teorías
- La ciencia y la duda
- Buscar vida extraterrestre va a ser un poquito más complicado
Cómo el Ártico se volvió salado

El Océano Ártico fue una vez un gigantesco lago de agua dulce. Sólo después de que el puente terrestre entre Groenlandia y Escocia se hubiese sumergido lo suficiente, grandes cantidades de agua salada llegaron desde el Atlántico. Con la ayuda de un modelo climático, investigadores del Instituto Alfred Wegener (Alemania) han demostrado cómo tuvo lugar este proceso, permitiéndonos por primera vez comprender con mayor precisión cómo se desarrolló la circulación atlántica que conocemos hoy.
Cada año, aproximadamente 3.300 kilómetros cúbicos de agua dulce fluyen hacia el océano Ártico. Esto equivale al diez por ciento del volumen total de agua que todos los ríos del mundo transportan a los océanos al año. En el clima cálido y húmedo del Eoceno (hace entre 56 a 34 millones de años), la afluencia de agua dulce probablemente fue aún mayor. Sin embargo, a diferencia de hoy, durante ese período geológico no hubo intercambio de agua con otros océanos. La afluencia de aguas salinas del Atlántico y del Pacífico, que hoy encuentra su camino al Océano Ártico desde el Pacífico a través del estrecho de Bering y desde el Atlántico Norte a través de la cresta Groenlandia-Escocia, no era posible. La región que hoy está sumergida estaba por encima del nivel del mar en ese periodo.
Sólo una vez que desapareció el puente terrestre entre Groenlandia y Escocia, surgieron los primeros pasos oceánicos, conectando el Ártico con el Atlántico Norte y haciendo posible el intercambio de agua. Utilizando un modelo climático, los investigadores han simulado con éxito el efecto de esta transformación geológica en el clima. En sus simulaciones, sumergieron gradualmente el puente terrestre a una profundidad de 200 metros, un proceso tectónico de inmersión que en la realidad duró varios millones de años. Curiosamente, los mayores cambios en los patrones de circulación y las características del Océano Ártico sólo se produjeron cuando el puente de tierra había alcanzado una profundidad de más de 50 metros por debajo de la superficie del océano.
Esta profundidad umbral corresponde a la profundidad de la capa superficial de mezcla, esto es, la capa que determina dónde termina el agua superficial relativamente ligera del Ártico y comienza la capa subyacente de agua densa que entra del Atlántico Norte. Sólo cuando la cresta oceánica se encuentra por debajo de la capa de mezcla superficial puede el agua salina más pesada del Atlántico Norte fluir hacia el Ártico con relativamente poco obstáculo. Por tanto, solo una vez que el puente entre Groenlandia y Escocia había alcanzado esta profundidad crítica, se creó el Océano Ártico salino como lo conocemos hoy. La formación de los pasos oceánicos desempeña un papel vital en la historia del clima global, ya que conlleva cambios en el transporte de energía térmica en el océano entre las latitudes media y polar.
La teoría de que la Cuenca Ártica estuvo una vez aislada se apoya en el descubrimiento de fósiles de algas de agua dulce en los sedimentos de aguas profundas del Eoceno que se obtuvieron durante una campaña de perforación internacional cerca del Polo Norte en 2004. Lo que una vez fue un puente terrestre ahora se encuentra alrededor de 500 metros bajo el océano y está formado casi enteramente de basalto volcánico. Islandia es la única sección que queda por encima de la superficie.
Referencia:
Michael Stärz, Wilfried Jokat, Gregor Knorr, Gerrit Lohmann (2017) Threshold in North Atlantic-Arctic Ocean circulation controlled by the subsidence of the Greenland-Scotland Ridge. Nature Communications. DOI: 10.1038/NCOMMS15681
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Cómo el Ártico se volvió salado se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El óxido de grafeno que se mueve como una oruga y coge cosas como una mano
- Y el Sol se volvió azul
- Cómo usar a las ballenas como detectores de radiación
El teorema de los cuatro colores (y 4): ¿Podemos creer la prueba de la conjetura?
En 1975, el divulgador científico Martín Gardner (1914-2010) publicaba un artículo (ver [1]) en el que afirmaba que el denominado mapa de Mc.Gregor –de 110 regiones– precisaba necesariamente de cinco colores para pintarse, sin que dos regiones adyacentes compartieran color. Es decir, proponía un contraejemplo al teorema de los cuatro colores. ¿Por qué continuaron entonces Appel y Haken intentando demostrar el resultado planteado por Guthrie en 1852?
El artículo de Gardner se publicó el 1 de abril de 1975, el Día de los inocentes en los países anglosajones. Muchos lectores, contrariados, enviaron a Gardner propuestas de coloreado del mapa de Mc.Gregor, para mostrarle que su afirmación era errónea.
El mapa de Mc.Gregor y la propuesta de 4-coloreado de Stan Wagon (1951).
Lo raro es que esos lectores no fueran conscientes de que se trataba de una simple broma; en ese artículo Gardner hablaba de Seis descubrimientos sensacionales que de alguna manera han escapado a la atención pública. En efecto, el divulgador:
-
‘mostraba’ una refutación de la teoría de la relatividad de Einstein, a través de un experimento del físico británico Humbert Pringl;
-
‘anunciaba’ el descubrimiento –en el Codex Madrid I y por parte de Augusto Macaroni de la Universidad Católica de Milán– de que Leonardo de Vinci había inventado el retrete auto-limpiable con el agua de su cisterna;
-
‘comentaba’ la demostración de Richard Pinkleaf –con ayuda del ordenador MacHic– de que en ajedrez, el movimiento de apertura de peón a cuatro torre de rey gana siempre la partida;
-
‘notificaba’ el sorprendente resultado –obtenido por John Brillo de la Universidad de Arizona– de que la base de los logaritmos naturales, el número e,elevado a π(163)½ es el número entero 262.537.412.640.768.744;
-
‘anunciaba’ la construcción –debida al parapsicólogo Robert Ripoff– de un motor funcionando con energía mental; y
-
‘notificaba’ el descubrimiento –por parte del especialista en teoría de grafos William McGregor– del famoso mapa del que hemos hablado antes.
Así que es lógico que, tras el 1 de abril de 1975, se continuara con la búsqueda de una demostración del teorema de los cuatro colores… Durante el largo proceso hasta llegar a su prueba, se desarrollaron teorías matemáticas como la teoría de grafos y de redes. Es decir, ni los errores ni los aciertos intentando demostrar este teorema fueron nimios; todos ellos ayudaron a la puesta a punto de este primer gran teorema demostrado –¿verificado?– usando un ordenador.
Pero, ¿es realmente una demostración? ¿Se puede garantizar la corrección de la compilación realizada por un ordenador? ¿Las computadoras son infalibles? Tras la demostración del teorema de los cuatro colores con ayuda de ordenadores, otras pruebas se apoyaron en este método, como la clasificación de los grupos simples finitos (2004) –que depende de cálculos imposibles de ejecutar con detalle a mano– o la solución de Thomas Hales (1998) del problema de Kepler sobre el empaquetamiento óptimo de esferas. Pero, ¿se puede aceptar como válida una afirmación que sólo una máquina, y no una mente humana, puede comprobar?
¿Qué es una demostración? El filósofo de la ciencia Imre Lakatos (1922-1974) la define (ver [3]) como: “Una sucesión finita de fórmulas de algún sistema dado, donde cada uno de los pasos de la sucesión es o bien un axioma del sistema, una fórmula derivada por una regla del sistema a partir de una fórmula precedente”.
Por su parte, el filósofo Thomas Tymoczko (1943-1996) califica una demostración como algo (ver [6]): convincente –debería persuadir incluso a los escépticos que dudan de la veracidad del resultado–, formalizable –la conclusión debería alcanzarse partiendo de sistemas axiomáticos–, y comprobable.
Este último es el aspecto más controvertido en el caso del teorema de los cuatro colores. ¿Puede estar un teorema probado si no se puede leer (comprobar) su demostración?
Existen dos corrientes principales que intentan responder a este dilema:
Los escépticos opinan que el aspecto de la comprobabilidad es el que pone en duda la credibilidad de la prueba. Si las pruebas deben ser verificadas, parece que entonces una persona –lo opuesto a una máquina– debe completar esta tarea: esto no puede hacerse con la prueba del teorema de los cuatro colores.
El matemático Paul Halmos (1916-2006) opinaba que la demostración realizada con un ordenador tiene la misma credibilidad que si está hecha por un adivino…Y afirmaba: “No puedo aprender nada de la demostración. La prueba no indica la razón por la que sólo se necesitan 4 colores ¿por qué no 13? ¿Qué tiene de especial el número 4?”.
El matemático Pierre Deligne (1954) comentaba: “No creo en una prueba hecha con ordenador. En primer lugar, soy demasiado egocéntrico. Creo en una demostración si la entiendo, si está clara. Un ordenador puede también cometer errores, pero es mucho más difícil encontrarlos”.
Tymockzo afirma que usar un ordenador para establecer una verdad matemática es transformar pruebas en experimentos. Afirma que el teorema de los cuatro colores ha sido confirmado a través de un experimento de física teórica, pero no probado de una manera formal. Aunque se tiene una pequeña idea de lo que el ordenador está testando, no se tiene la seguridad de lo que se está haciendo.
Los no escépticos, por su parte, argumentan del siguiente modo:
-
aunque las equivocaciones cometidas por los ordenadores son más difíciles localizar, los seres humanos fallan con más frecuencia; los ordenadores siguen un programa rígido predeterminado, y no tienen tropiezos motivados por los cambios de humor, el estrés u otros factores externos;
-
la longitud de algunas demostraciones sobrepasa la capacidad de computación humana, pero es perfectamente aceptable por los estándares de las máquinas;
-
la idea de que no pueden usarse ordenadores va a ser cada vez más insólita para las generaciones futuras: los ordenadores serán –¿son?– herramientas como el lápiz y el papel…
-
la prueba de Appel y Haken es, en esencia, tradicional, ya que consiste en una serie de pasos lógicos, que conducen a la conclusión de que la conjetura puede reducirse a una predicción sobre el comportamiento de unos2.000 mapas.
¿Quiénes tienen razón?
Para añadir un poco más de incertidumbre al tema, el filósofo Hud Hudson afirmaba dar en [2] un contraejemplo al teorema de los cuatro colores: presentaba el mapa de Zenopia, una isla formada por seis provincias que necesita seis tonos para colorearse… Entonces, ¿es falso el teorema de los cuatro colores? No, no hay que preocuparse: Zenopia es un mapa con fronteras extrañas, cuya especial geografía queda excluda del enunciado original del teorema…
Bibliografía
[1] Martin Gardner, Mathematical Games: Six Sensational Discoveries that Somehow or Another have Escaped Public Attention, Scientific American 232, 127-131, 1975
[2] Hud Hudson, No basta con cuatro colores, Gaceta de la RSME 8(2), 361-368, 2005.
[3] Imre Lakatos, What does a mathematical proof prove?, Cambridge Univers¡ity Press, 540-551, 1979.
[4] Marta Macho Stadler, Mapas, colores y números, Descubrir las matemáticas hoy: Sociedad, Ciencia, Tecnología y Matemáticas 2006 (2008) 41-68
[5] E.R. Swart, The philosophical implications of the four-colour theorem, American Mathematical Montlhy 87, 697-707, 1980
[6] Thomas Tymoczko, The four-color problem and its philosophical significance, Journal of Philosophy 76, 57-70, 1979
[7]Robin .J. Wilson, Four colors suffice: how the map problem was solved, Princeton University Press, 2002
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo El teorema de los cuatro colores (y 4): ¿Podemos creer la prueba de la conjetura? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba
- El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema?
- El teorema de los cuatro colores (1): una historia que comienza en 1852
Evolución de los sistemas nerviosos: moluscos

El rasgo más característico del sistema nervioso de los moluscos es la gran importancia relativa que tiene su sistema periférico. En todos los grupos de moluscos se da alguna forma de coalescencia de neuronas que dan lugar a ganglios o encéfalos. Cefalópodos y gasterópodos presentan encéfalos bien definidos, aunque de diferente grado de complejidad y desarrollo. Los bivalvos disponen de ganglios, encefálicos y viscerales, que cumplen funciones análogas a las de los encéfalos de los anteriores. Pero además, todos ellos disponen de un extenso sistema periférico que comprende plexos nerviosos subepidérmicos y pequeños ganglios periféricos. Los ganglios periféricos son responsables del control reflejo y del procesamiento sensorial primario de órganos especiales, tales como branquias o palpos de bivalvos, y en numerosas ocasiones ambos sistemas intervienen de forma coordinada en el desarrollo de algunos comportamientos.
La importancia tan grande del sistema periférico parece deberse a la condición de animales de cuerpo blando y al hecho de tener un esqueleto hidrostático. Al disponer de una compleja y bien organizada musculatura en la superficie corporal, un control preciso a cargo del sistema central requeriría de un muy elevado número de neuronas centrales, por lo que resulta mucho más económico, desde el punto de vista de la organización nerviosa disponer de una extensa organización periférica responsable del control local. La ausencia de articulaciones impide disponer de sentidos de posición; sin la información que proporcionan los receptores de estiramiento de uniones articuladas, los cefalópodos desconocen la posición de sus brazos; tampoco puede estimar el peso de un objeto, sólo conocer su textura y tamaño. La gran importancia funcional del sistema periférico es lo que, sin embargo, les permite alcanzar los grandes tamaños propios de algunas especies.
El sistema nervioso central de los gasterópodos está formado por pares de ganglios conectados por células nerviosas; hay ganglios encefálicos, pedales, osfradiales, pleurales y viscerales, y en algunos casos, bucales también. En este grupo han surgido dos líneas principales, la de los opistobranquios, por un lado, y la de los prosobranquios y caracoles pulmonados, por el otro. La primera corresponde a animales que han abandonado las actividades de excavación de sus antecesores y que ramonean y pastan libremente, por lo que cuentan con elaborados sistemas de defensa química. Viven en ambientes simples y su sistema nervioso es simple, por lo que el comportamiento de estos animales se caracteriza por un repertorio limitado de subrutinas.
Los prosobranquios y pulmonados, sin embargo, ocupan nichos más complejos y presentan ganglios encefálicos más desarrollados, a la vez que sistemas sensoriales de alta resolución. Son capaces de desarrollar comportamientos de orden superior, muy elaborados. Un ilustrativo ejemplo de comportamiento elaborado es el del depredador Fusitriton oregonensis, que adhiere su puesta a la roca y patrulla la zona para rechazar a posibles depredadores; los detecta gracias a ojos muy desarrollados y los ataca propinándoles golpes con sus conchas.
Dada la condición sedentaria de la mayoría de los bivalvos, su sistema nervioso es bastante más simple que el del resto de moluscos. Carecen de un encéfalo, y el sistema consiste en una red nerviosa y una serie de pares de ganglios. En la mayoría de bivalvos hay dos ganglios cerebro-pleurales, a cada lado del esófago, los cerebrales controlan los órganos sensoriales y los pleurales la cavidad del manto. Los ganglios pedales controlan el pie, y los viscerales, que se encuentran tras el músculo aductor posterior, pueden llegar a tener gran tamaño en los bivalvos que nadan; los que tienen largos sifones también cuentan con un par de ganglios que los controlan.
Los cefalópodos, por su parte, tienen modos de vida muy activos, viven en un medio tridimensional y son depredadores. Disponen de desarrollados receptores de equilibrio, receptores de posición corporal análogos a la línea lateral de los peces pelágicos, y habilidades fotorreceptoras muy notables; también pueden identificar texturas.
Tienen encéfalos muy desarrollados, con un elevado número de neuronas, y sus comportamientos pueden ser muy elaborados, con alta capacidad de aprendizaje. El sistema periférico también está muy desarrollado. Cada ventosa de un pulpo tiene su propio ganglio periférico, aunque también está comunicado con el sistema nervioso central. Los ganglios realizan integración quimio y mecanorreceptora y son responsables del control motor de la ventosa.
El sistema central y el periférico actúan en serie y en paralelo. Los comportamientos complejos suelen generarse en el central, aunque el periférico puede participar en la recepción del estímulo y en el control motor final. En los moluscos se producen tanto comportamientos fijados como no fijados. Ejemplos relativamente bien conocidos de modelos de acción fijos son la natación de huida del opistobranquio Tritonia, que está basado en un grupo de cuatro neuronas del sistema nervioso central, y el comportamiento ventilatorio de la branquia de Aplysia. Sin embargo, el comportamiento alimenticio –en el que intervienen el encéfalo y los ganglios bucales-, o el de rechazo de alimento de gasterópodos –en el que interviene el ganglio abdominal- son buenos ejemplos de comportamientos no fijados.
Por último, hay plasticidad en el comportamiento y la actividad neural de moluscos debido a fenómenos de plasticidad de los reflejos simples (habituación, sensitización, aprendizaje asociativo) y a la capacidad para modificar taxias y desarrollar comportamientos complejos gracias al aprendizaje asociativo.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Evolución de los sistemas nerviosos: moluscos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Evolución de los sistemas nerviosos: cnidarios y gusanos no segmentados
- Moluscos en el Arte
- Evolución del tamaño animal
Carnot y los comienzos de la termodinámica (1)
Carnot fue uno de de los ingenieros franceses que se propusieron estudiar los principios científicos subyacentes al funcionamiento de la máquina de vapor con el objetivo de lograr la máxima potencia de salida con la máxima eficiencia. Como resultado de sus estudios, Carnot y otros ayudaron a establecer la física del calor, lo que se conoce como termodinámica.

Nicolas Léonard Sadi Carnot (1796-1832), en este imagen vistiendo el uniforme de estudiante de L’École polytechnique, fue hijo de Lazare Carnot, uno de los generales de confianza de Napoléon. Murió a los 36 años como conseuencia de la epidemia de cólera que se extendió por Europa en la época.
Carnot comenzó con la observación experimental de que el calor no fluye por sí solo de un cuerpo frío a uno caliente. Se deduce entonces que si, en una situación dada, se hace fluir calor de lo frío a lo caliente, debe tener lugar algún otro cambio en otra parte. Es decir, debe realizarse algún trabajo. Por ejemplo, un refrigerador o un acondicionador de aire son también “máquinas térmicas”, pero su ciclo funciona de manera inversa a una máquina de vapor o un motor de automóvil. Hace falta trabajo (en forma de energía eléctrica o mecánica) para bombear el calor de un cuerpo frío (desde el interior del compartimento o la habitación fríos) a uno más caliente (la habitación donde está el refrigerador o el aire exterior). Utilizando una argumentación muy elegante1 Carnot demostró que ninguna máquina puede ser más eficiente que una máquina ideal y reversible, y que todas las máquinas de este tipo tienen la misma eficiencia.
¿Y que es una máquina ideal y reversible? De entrada algo que no existe en el mundo real (por eso se llama ideal), pero que es extremadamente útil para entender los límites de las máquinas reales. Íntimamente ligado a la idealidad está el concepto de reversibilidad. Una máquina reversible es aquella en la que el ciclo desde la energía de entrada al trabajo de salida más la energía residual, y vuelta a la energía de entrada, se puede ejecutar en sentido inverso sin ninguna pérdida o ganancia adicional de calor u otras formas de energía.
Como todas las máquinas reversibles tienen la misma eficiencia, sólo se tiene que elegir una versión simple de una máquina reversible y calcular su eficiencia para un ciclo para encontrar un límite superior a la eficiencia de cualquier máquina. Esta máquina simple se representa esquemáticamente en el siguiente diagrama. Durante un ciclo de funcionamiento, la máquina, representada por la C de Carnot, absorbe la energía térmica Q1 del cuerpo caliente a temperatura T1, produce un trabajo útil W, y descarga una cierta cantidad de energía térmica Q2 al cuerpo frío a temperatura T2. El ciclo puede repetirse muchas veces.
Observando el diagrama y empleando la ley de conservación de la energía vemos que se tiene que cumplir que Q2 = Q1 – W; o, dicho en términos coloquiales, el calor que sale es la diferencia entre el que entra menos el trabajo que realiza la máquina. Pero, como la eficiencia vimos que era la proporción entre la energía de salida (ahora añadimos “útil”, esto es, el trabajo) y la energía de entrada, tenemos que ef = W/Q1.
Carnot calculó la eficiencia de este ciclo esquemático y encontró que las proporciones de calor y trabajo en una máquina reversible dependen solamente de la temperatura2 de la sustancia caliente desde la cual la máquina obtiene el calor y la temperatura2 de la sustancia fría que extrae el calor residual de la máquina.
La expresión que encontró Carnot para la eficiencia de las máquinas reversibles es, escrita con nomenclatura actual, ef = W/Q1 = 1 – T2/T1
Démonos cuenta de que la única forma de obtener una eficiencia del 100%, es decir ef = 1, es si hacemos que T2, la temperatura de la sustancia que recibe el calor residual, sea el cero absoluto, algo físicamente imposible, como veremos. Esto significa, de nuevo en términos coloquiales, que toda máquina debe liberar algo de calor residual al exterior antes de volver a tomar más energía del cuerpo caliente. Y esto, tan simple, es de una importancia enorme.
Notas:
1 Una argumentación a la que, por su simplicidad, importancia y valor formativo, dedicaremos una anotación específica.
2 Las temperaturas usadas en este caso se llaman temperaturas absolutas (T), o Kelvin, (por el señor Kelvin que fue el primero en introducir esta escala). En la escala absoluta, las mediciones de temperatura son iguales a las temperaturas (t) en la escala Celsius (°C) más 273. No se usa signo de grado, °, para grados Kelvin, el símbolo utilizado es K. Por tanto, el agua se congela a T = 273 K y cuando T = 0 K hablamos de cero absoluto. Ya explicaremos el origen de esta escala más adelante en la serie.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Carnot y los comienzos de la termodinámica (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Historias de la malaria: Charles Louis Alphonse Laveran y el protozoo

Charles Louis Alphonse Laveran
Fue Alphonse Laveran quien en 1880 identificó correctamente que era un protozoo, al que llamó Oscillaria, el agente causante de la malaria. Nació en 1845 y se licenció en Medicina en 1867. Sirvió como médico militar en la guerra con Prusia en 1870 y en 1874 fue nombrado Director de Enfermedades y Epidemiología en la Escuela de Val de Grâce. En 1878 fue destinado a Argelia donde inició sus estudios sobre la malaria, una de las enfermedades más incapacitantes y extendidas entre los soldados franceses que servían en aquella colonia.
No se conocía su causa y, para aliviar los síntomas, sobre todo los accesos de fiebre, solo era eficaz la quinina. En Bona, Laveran practicó la autopsia a soldados fallecidos por las fiebres, y encontró que padecían anemia y que su sangre tenía un color marrón oscuro por la presencia de un pigmento negro. Todo ello le llevó a estudiar al microscopio muestras de sangre de soldados enfermos, sin preparar la muestra para facilitar el examen como era habitual entonces, algo que no habían probado otros investigadores antes que él.
Ilustración de Laveran de 1880 con sus observaciones del parásito de la malaria en sangre fresca.
En su destino en Bona y, más tarde, en Constantina, detectó que los glóbulos rojos de los enfermos llevaban unos gránulos pigmentados. Poco después descubrió en la sangre fresca de esos enfermos, que, a veces, de esos glóbulos rojos se desprendían partículas de menor tamaño con cilios o flagelos móviles. Fue, según lo relata el propio Laveran, el 6 de noviembre de 1880 y en el Hospital Militar de Constantina, cuando observó “unos filamentos móviles o flagelos, con movimientos muy rápidos y variados que no dejaban duda de su naturaleza”. Dos días después observó lo mismo en la sangre de otro enfermo. De inmediato redactó y envió una nota, de fecha 23 de noviembre, comunicando su descubrimiento a la Academia de Medicina de París.
Ilustración de Laveran C.L.A., “Note sur un nouveau parasite trouvé dans le sang de plusieurs malades atteints de fièvre palustres”. Bull Acad Med 1880; 9: 1235-1236.
En 1881, publicó la revista The Lancet, de Estados Unidos, la confirmación del hallazgo de Laveran. En los meses siguientes, Laveran encontró los mismos organismos en la sangre de 148 de 192 enfermos examinados, incluidos algunos de las marismas de Roma y de otros lugares de Italia.
Viajó a París y convenció a Louis Pasteur y a su colaborador Emile Roux, otro prestigioso microbiólogo de la época, de que era un protozoo el parásito que causaba la malaria. Laveran era un médico militar, fuera de los círculos académicos y destinado en una colonia al otro lado del Mediterráneo, lejos de la capital, y sin contactos con los grupos de investigación de la malaria de finales del siglo XIX. Pero también los italianos Ettore Marchiafava y Angelo Celli, con un microscopio más potente, confirmaron el hallazgo de Laveran y le agradecieron expresamente el descubrimiento del protozoo. Pertenecían a la prestigiosa escuela italiana de estudios de la malaria, encargada de las investigaciones sobre esta enfermedad en las numerosas marismas de Italia. De allí nos llega el término malaria, del italiano “mal aria”, o “mal aire” en traducción directa.
Cuatro años más tarde, en 1884, Laveran ya había estudiado 480 casos y concluyó que el parásito de la malaria penetraba y se desarrollaba en los glóbulos rojos, provocaba su ruptura y liberaba esporas al torrente sanguíneo que, a su vez, invadían otros glóbulos rojos. Lo llamó Oscillaria malariae, nombre que, posteriormente, la escuela italiana cambió a Plasmodium, tal como ahora se conoce.
Era la época de la Microbiología y Pasteur, Koch y otros habían demostrado que la causa de las infecciones y de muchas enfermedades eran las bacterias. Así se había confirmado para, entre otras, el ántrax, la tuberculosis, el tifus o el cólera. Aceptar que había otros organismos causantes de enfermedades, como el protozoo descrito por Laveran, costó que lo aceptaran muchos investigadores. Pero las evidencias eran abrumadoras y Laveran recibió el Premio Nobel en 1907.

Ronald Ross
Uno de los expertos en malaria más críticos, en principio, con los trabajos de Laveran fue el médico militar inglés, de servicio en la India, Ronald Ross. Llevaba años estudiando la malaria y, en 1893, estaba convencido, según lo habitual en la época, de que era una enfermedad intestinal provocada por la toma de agua no potable. Escribió un informe para la revista Medical Reporter en que afirmaba que no era necesario otro parásito, un protozoo según Laveran, como causa de la malaria.
Consideraba que la enfermedad era compleja en síntomas y diagnóstico y, por ello, terminaba su informa con una frase llena de ironía, oculta en el típico lenguaje científico:
“Para la solución de la cuestión de la fiebre india, lo que queremos es una definición clara de las ideas, un escrutinio cuidadoso de todas las suposiciones y una interpretación de sentido común de los fenómenos que tenemos ante nosotros; y están muy equivocados quienes se imaginan que un problema siempre tan grande y variado será resuelto por un solo ‘coup de microscope’.”
Por “un vistazo al microscopio” y, además, en francés, o sea, lo que había propuesto Laveran, en francés, años antes de este escrito de Ross.

Página del cuaderno de notas de Ross en la que identifica en parásito de la malaria
Dos años más tarde, en 1895, y después de los consejos de otro médico inglés, Patrick Manson, Ross observó el “denostado” protozoo en el estómago del mosquito Anopheles y demostró que era el parásito y el vector de la malaria. Y, por estos hallazgos, Ronald Ross recibió el Premio Nobel en 1902.
Además de los conocimientos de Microbiología, típicos de su época, a Laveran le permitieron su descubrimiento y los estudios posteriores sobre el protozoo de la malaria otras mejoras en los métodos de investigación. Por ejemplo, los microscopios cambiaron en la segunda mitad del siglo XIX, con adelantos sustanciales en óptica y en la fabricación de lentes. Eran los años de Ernst Abbe, el especialista en óptica que resolvió los problemas teóricos de la fabricación de lentes. Y Carl Zeiss y Otto Schott, que formaron la empresa Carl Zeiss Inc., que todavía fabrica microscopios de gran calidad. A partir de 1884, junto con la fábrica Nachet, de París, ya comercializaban microscopios que mejoraban sustancialmente el material disponible hasta entonces. Fue sorprendente que, cuando Laveran, en 1880, encontró por vez primera el parásito de la malaria, su microscopio no era precisamente de los mejores y no tenía los aumentos, solo llegaba a 400, que después se consideraron necesarios para describir el protozoo. Pero, a pesar de ello, lo hizo con una precisión que se confirmó en años posteriores y con mejor instrumental. Como diría Pablo Picasso, la inspiración le encontró trabajando, o sea, en este caso mirando por el microscopio.
Otro de los adelantos técnicos que permitió la observación del protozoo de la malaria fue el desarrollo de las técnicas de tinción. No eran fáciles los estudios al microscopio tal como hizo Laveran, con sangre fresca y sin teñir. Fue Dimitri Leonidovich Romanowsky, en 1891, quien publicó una tinción que permitió las observaciones en frotis de sangre sobre portaobjetos que, incluso, permitían guardar las muestras y repetir el estudio al microscopio. Además, utilizaba dos colorantes, eosina y azul de metileno, que teñían diferente al protozoo según la fase de su ciclo vital.
En aquellos años, Wilhelm von Drigalski nos cuenta que en Italia llevaban mucho tiempo estudiando las causas de la malaria, sobre todo en las marismas que rodeaban la capital, Roma. Fueron Camillo Golgi, Marchiafava o Celli quienes completaron el ciclo vital del Plasmodium en la sangre de los enfermos, con buenos microscopios y la tinción de Romanowsky. El primero, Golgi, identificó con precisión los parásitos de la malaria y clasificó el Plasmodium vivax y el P.malariae. Y en 1890, Marchiafava y Celli identificaron el P. falciparum. Así quedó establecido que la malaria no era una enfermedad provocada por un solo parásito sino por cuatro (el P. ovale se identificó en 1922) que, a veces, hasta provocaban las fiebres actuando en conjunto.
Fue en la India donde el también médico militar Ronald Ross planteó la hipótesis, y la demostró en aves, de que el parásito llegaba a la sangre de los enfermos por la picadura de mosquitos.

Giovanni Battista Grassi
Y, finalmente, el italiano Giovanni Battista Grassi mostró todo el ciclo de desarrollo del protozoo, con su paso por el mosquito y el hombre como huéspedes.
La historia del protozoo de la malaria está llena de intensos debates, rencillas personales y amargura. Varios de los científicos dedicaron mucho tiempo a reclamar la prioridad de sus descubrimientos, un aspecto importante en la cultura de la ciencia de la época y hoy, en cambio, un debate casi olvidado. Investigadores franceses, alemanes, ingleses e italianos contribuyeron a los descubrimientos sobre la malaria y, también, polemizaron interminablemente sobre muchos aspectos de lo que se iba encontrando.
Además, todos los estudios de finales del siglo XIX sobre la malaria coinciden, en los grandes países europeos, con las aventuras y las exploraciones de otros continentes, con las colonias y los imperios. En ese momento histórico, la malaria era una enfermedad importante para el control europeo de esas colonias y la explotación de sus recursos naturales y, por tanto, era un asunto prioritario para los gobiernos y para la opinión pública.
En cambio, en Italia la malaria era algo muy cercano y, por ello, su investigación era esencial para la salud pública y como problema social. Era una enfermedad de siempre que mantenía empobrecidas extensas regiones del país. Para ingleses y franceses, la malaria es un problema colonial y, para los italianos, era un asunto interno, sobre todo para el centro y sur del país.
Y, por si fuera poco este sustrato político en la investigación sobre la malaria, estamos en la era de los nacionalismos y, también, son habituales en la ciencia. Parte de la polémica entre Grassi, Ross y Laveran, o del rechazo de ingleses e italianos a los descubrimientos del médico militar francés en Argelia, viene de esta competición patriótica entre científicos. Como ejemplo nos sirve lo que Santiago Ramón y Cajal publicó en aquellos años en sus “Reglas y consejos de investigación científica”, pues entre las “cualidades de orden moral” de un investigador está el patriotismo. Inicia el texto afirmando que
“entre los sentimientos que deben animar al hombre de ciencia merece particular mención el patriotismo. Este sentimiento tiene en el sabio signo exclusivamente positivo: ansía elevar el prestigio de su patria, pero sin denigrar a los demás.”
Es oportuno citar que la cualidad que Ramón y Cajal menciona antes del patriotismo es la “pasión por la gloria” y, de ello se derivan las polémicas sobre la prioridad en los descubrimientos. Hoy, quizá, solo se discute por las patentes derivadas de esos hallazgos.
En mayo de 1922, Alphonse Laveran murió en París a los 76 años. Está enterrado en el Cementerio de Montparnasse, junto a celebridades como el filósofo Jean Paul Sartre, o el líder anarquista Pierre-Joseph Proudhon, el poeta Charles Baudelaire o el escritor Julio Cortázar.
Referencias:
Capanna, E. 2006. Grassi versus Ross: who solved the riddle of malaria? International Microbiology 9: 69-74.
Chernin, E. 1984. The malariatherapy of neurosyphilis. Journal of Parasitology 70: 611-617.
Coleman-Jones, E. 1999. Ronald Ross and the great malaria problem: historical reference in the biological sciences. Journal of Biological Education 33: 181-184.
Earle, D.P. 1979. A history of malaria and its ironies. Transactions of the American Clinical and Climatological Association 90: 1-26.
Hommel, M. 2007. Morphologie, biologie et cycle des Plasmodium parasites de l’homme. Bulletin de l’Academie nationale de medicine 191: 1235-1246.
Laverdant, C. 2007. Le context scientifique contemporain de la découverte de Laveran. Bulletin de l’Academie nationale de medicine 191: 1227-1234.
Ledermann, W. 2008. Laveran, Marchiafava y el paludismo. Revista Chilena de Infectiología 25: 216-221.
Macchi, G. 1999. Camillo Golgi: A clinical pathologist. Journal of History of Neurosciences 8: 141-150.
Ramón y Cajal, S. 1940 (1899). Reglas y consejos sobre investigación científica (Los tónicos de la voluntad). 8ª ed. Librería Beltrán. Madrid. 302 pp.
Ross, R. 1893. Some objections to hematozoic theories of malaria. Medical Reporter 2: 65-71.
Schmidt, G.D. & L.S. Roberts. 1985. Foundations of Parasitology. Times Mirror/Mosby College Publ. St. Louis, Toronto. Santa Clara.
Snowden, F.M. 2006. The conquest of malaria. Italy, 1900-1962. Yale University Press. New Haven & London.
Tan, S.Y. & A. Ahana. 2009. Charles Laveran (1845-1922): Nobel lauréate pioneer of malaria. Singapore Medical Journal 50: 657-658.
von Drigalski, W. 1954. Hombres contra microbios. La victoria de la Humanidad sobre las grandes epidemias. Ed. Labor. Barcelona. 368 pp.
Yoeli, M. 1973. Sir Ronald Ross and the evolution of malaria research. Bulletin of the New York Academy of Medicine 49: 722-735.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Historias de la malaria: Charles Louis Alphonse Laveran y el protozoo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Historias de la malaria: El parásito
- Historias de la malaria: El charlatán y caballero Sir Robert Talbor
- Historias de la malaria: El árbol de la quina
Superelasticidad nanométrica

La superelasticidad es una propiedad física por la que se puede deformar un material en gran medida, hasta un 10 % —un porcentaje muchísimo mayor que en la elasticidad—, de forma que aplicando una tensión a una varilla recta, esta puede formar una U, y al eliminar la tensión aplicada, la varilla recupera completamente su forma inicial. Aunque está más que probada en materiales macroscópicos, “hasta ahora nadie había podido estudiar estas propiedades de superelasticidad en dimensiones micrométricas y nanométricas”, explica José María San Juan, investigador principal y catedrático de la UPV/EHU.
Investigadores del Departamento de Física de la Materia Condensada y de Física Aplicada II de la UPV/EHU han conseguido ver que “el efecto superelástico se mantiene en dispositivos realmente pequeños de una aleación de cobre-aluminio-niquel”. Se trata de una aleación con memoria de forma en la que el equipo de investigación lleva más de 20 años trabajando a nivel macroscópico: Cu-Al-Ni, una aleación que muestra superelasticidad a temperatura ambiente.
Utilizando un equipo denominado Focused Ion Beam, “un cañón de iones que actúa como una especie de cuchillo atómico que talla el material”, explica San Juan, han construido micropilares y nanopilares de esta aleación de diámetros comprendidos entre 2 µm y 260 nm —un micrómetro es una millonésima parte de un metro y un nanómetro es una mil millonésima parte de un metro— a los que han aplicado una tensión con un sofisticado equipo llamado nanoindentador, que “permite aplicar fuerzas extremadamente pequeñas” y han medido su comportamiento.
Los investigadores han constatado y cuantificado por primera vez que en diámetros menores de un micrómetro hay un cambio notable de las propiedades relacionadas con la tensión crítica para la superelasticidad: “El material se empieza a comportar de manera diferente y requiere una tensión mucho más elevada para que se produzca. La aleación sigue presentando superelasticidad pero para tensiones más elevadas”. San Juan remarca la novedad de ese incremento de la tensión crítica con el tamaño, y subraya, además, que han podido explicar la razón de dicho cambio de comportamiento: “Hemos propuesto un modelo atómico que permite entender por qué y cómo cambia la estructura atómica de estos pilares cuando se les aplica una tensión”.
El catedrático de la UPV/EHU destaca la importancia de este descubrimiento, “un comportamiento superelástico espectacular a pequeña escala”, que abre nuevas vías en el diseño de estrategias de aplicación de aleaciones con memoria de forma para el desarrollo de microsistemas y nanosistemas electromecánicos flexibles. “La electrónica flexible está muy presente en el mercado actual, se utiliza cada vez más en prendas de vestir, zapatillas de deporte, en diversos displays…”. Asimismo, afirma que todo ello es de suma importancia para el desarrollo de dispositivos inteligentes médico-sanitarios implantables en el cuerpo humano, del tipo Lab on a chip o laboratorio en un chip: “Se podrán construir pequeñas microbombas o microactuadores que se puedan implantar en un chip, que permitan liberar y regular una sustancia dentro del cuerpo humano para diversos tratamientos médicos”.
Se trata de un descubrimiento que “se espera que tenga una gran repercusión científica y tecnológica y que pueda revolucionar ciertos aspectos en campos afines”, concluye San Juan, y se congratula de que “hemos sido capaces de transferir todo el conocimiento necesario y de conseguir las herramientas de trabajo que tienen los centros más avanzados para abrir una nueva línea de investigación con la capacidad de desarrollarla íntegramente en la UPV/EHU”.
Referencia:
Jose F. Gómez-Cortés, Maria L. Nó, Iñaki López-Ferreño, Jesús Hernández-Saz, Sergio I. Molina, Andrey Chuvilin and Jose M. San Juan. Size effect and scaling power-law for superelasticity in shape-memory alloys at the nanoscale. Nature Nanotechnology. May 2017. DOI: 10.1038/nnano.2017.91.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Superelasticidad nanométrica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una puerta cuántica robusta y ultrarrápida
- La máquina de vapor (1)
- La fusión nuclear como fuente de neutrones eficiente
II Concurso de Cristalización en la Escuela del País Vasco
La final de la segunda edición del Concurso de Cristalización en la Escuela tuvo lugar el pasado 5 de mayo en el Aula Magna de la UPV/EHU en Leioa. En la misma se dieron a conocer los ganadores del concurso quienes, además de un diploma acreditativo, también recibieron un detalle.
El concurso, dirigido a estudiantes de educación secundaria (ESO y bachillerato), tiene el objetivo de acercar el mundo científico al alumnado, aprovechando el atractivo de la cristalografía.
Además de subrayar la importancia que tienen los cristales en la sociedad, el concurso también busca ”fomentar el estudio, el trabajo sistemático, el pensamiento racional y la comunicación, utilizando como base la cristalografía”, tal como explica Begoña Bazán, organizadora del evento.
La edición de este año ha reunido maquetas de todo tipo, desde un parque de atracciones, una réplica del Guggenheim con Puppy incluído, volcanes, fondos marinos, hasta el hundimiento del Titanic pasando por el sistema solar.
Acercar la metodología científica
Para participar en el concurso el alumnado utiliza un kit didáctico que permite hacer crecer cristales de fosfato monoamónico (dihidrógeno fosfato de amonio). El kit permite modificar variables físicas (temperatura solubilidad, concentración, etc.), lo que posibilita variar los procesos de cristalización y obtener distintos resultados.
Los participantes deben presentar, además de una maqueta con los cristales creados, un póster con formato científico en el que se detallan los objetivos, materiales, métodos, resultados y las conclusiones. Por último, también deben presentar un cuaderno de laboratorio con los procesos seguidos y las respuestas obtenidas.
El formato del concurso acerca la metodología científica a los más jóvenes, ya que incluye todos sus elementos empezando por la investigación en el laboratorio hasta la presentación de resultados en un congreso científico creado a tal efecto. Mediante esta actividad amena y visual el alumnado se familiariza con el método científico. También permite introducir la cristalografía y la cristalización en el temario educativo, temas en los que no se suele profundizar o que, directamente, están ausentes.
Implicación docente
La participación no solo atañe a los estudiantes, también requiere el compromiso del profesorado. El concurso tiene una duración aproximada de un curso académico y está dividido en tres fases:
- Fase 1. Curso de formación para el profesorado de secundaria. En esta primera fase el profesorado responsable de cada centro educativo realiza un curso de formación donde personal de la UPV/EHU les dota de las herramientas científico-didácticas para la realización de los experimentos.
- Fase 2. Realización de los proyectos de cristalización y seguimiento del concurso. Durante esta fase el profesorado orienta a los participantes en los experimentos. Esta fase tiene una duración de cinco meses.
- Fase 3. Final del concurso de cristalización. En esta fase se exponen los resultados obtenidos en formato de congreso científico.
Tres grupos de jurados han evaluado los distintos trabajos, valorando cada grupo dos ítems: (i) póster y entusiasmo, (ii) rigor científico y cuaderno y (iii) cristal y montaje. En cuanto a los criterios de evaluación, los principales han sido: la creatividad, la aplicación del método científico, la calidad de los cristales, la originalidad de la maqueta, la claridad en el cuaderno de laboratorio, el conocimiento del procedimiento utilizado para el crecimiento cristalino, utilización del lenguaje cinetífico-técnico apropiado, orden y claridad en el póster…
La edición de Euskadi 2017 ha contado con la participación de 31 centros (24 de Bizkaia, 5 de Gipuzkoa y 2 de Araba). En todo el proceso del concurso más de 1.200 estudiantes han formado parte de la iniciativa.
Por segundo año consecutivo el concurso ha sido organizado por el grupo IMaCris/MaKrisil del departamento de Mineralogía y Petrología de la UPV/EHU, en colaboración con Geobizirik y la Cátedra de Cultura Científica.
—————————-
Agradecemos a Begoña Bazán, profesora de la UPV/EHU y coordinadora del concurso de cristalización, la información proporcionada.
Texto elaborado por Ziortza Guezuraga, periodista y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU.
El artículo II Concurso de Cristalización en la Escuela del País Vasco se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ‘Cristalización en la escuela’, un concurso para fomentar el interés por la ciencia
- LocosxCiencia llega al País Vasco
- Estudio de eficacia escolar en el País Vasco
Cálculo y geometría analítica, de George F. Simmons
En Editoralia lectores, autores o editores presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
Pablo Rodríguez Sánchez, lector

Tenía 18 años, y, aunque yo no me daba cuenta, aún era un poco idiota. Pasando por alto las más elementales leyes de la prudencia, había decidido matricularme en la carrera de física; las enormes dificultades y padecimientos que había sufrido con las matemáticas en el instituto no lograron frenarme.
Necesitaba un libro para preparar la asignatura de cálculo infinitesimal (aquello de las derivadas y las integrales), de modo que acudí a una librería, no muy bien surtida en libros de ciencia, y agarré el primero que vi. Ya he mencionado que entonces era un poco idiota.
El libro que me llevé de la tienda resultó ser una auténtica joya, aunque yo aún tardé unas semanas en abrirlo y darme cuenta.
Me refiero a “Cálculo y geometría analítica”, de George Finlay Simmons. Se trata de una magnífica introducción al cálculo infinitesimal. A primera vista parece un libro normal y corriente, con sus capítulos, sus problemas, etcétera. Pero son varias las cosas las que lo convierten en un libro digno de mención.
Lo primero que llama la atención, debido al uso recuadros de diferente color, es la gran cantidad de notas históricas que se introducen en medio del texto. Estas notas tienen la peculiaridad de que, en lugar de centrarse únicamente aspectos biográficos de matemáticos célebres, conceden tanta o incluso más importancia a un problema matemático clásico (que el lector puede comprender con las herramientas del propio capítulo)1.
Otra curiosidad llamativa: a menudo, en los márgenes aparece dibujada la imagen de una señal de tráfico como esta:

Esta señal indica que el párrafo adyacente debe ser leído despacio y reproduciendo los cálculos uno mismo con lápiz y papel.
Con el tiempo he apreciado otros detalles más sutiles. La estructura es un constante malabarismo entre conceptos teóricos, aplicaciones prácticas y notas históricas casi novelescas. Los métodos analíticos se explican con muchísimo detalle y siempre desde el punto de vista del estudiante, casi se diría que con cariño. Los problemas combinan ejercicios rutinarios con otros muy creativos, y como es tradición, se incluye la solución de todos los ejercicios impares. El lenguaje es elegante y claro sin dejar de ser cercano. Los ejemplos prácticos brillan tanto por su cantidad como por su calidad.
Todos estos detalles responden a un objetivo: enseñar de la forma más clara y duradera posible.
Gracias a este libro empezaron, por fin, a dárseme bien las matemáticas. Sus señales de obra me enseñaron cómo se deben leer las matemáticas. Algunos de sus problemas eran tan entretenidos que aún los recuerdo. Sus notas históricas me enseñaron que la ciencia es una empresa humana y no solamente sus resultados, y además me mantuvieron horas pegado al libro como si de una novela se tratase. Sus lecciones fueron tan duraderas que, salvo por placer, no he tenido que volver a abrir un libro de cálculo jamás. Por todo ello, lo recomiendo a cualquiera que tenga interés.
Referencia: (concretamente leí esta traducción, pero el original está en inglés)
Cálculo y geometría analítica (2ª ed.)
George F. Simmons, 2002
Editorial: S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA
Lengua: CASTELLANO
ISBN: 9788448135911
1 En este sentido cabe mencionar también otro libro del mismo autor, Calculus Gems: brief lives and memorable mathematics, centrado únicamente en la historia de las matemáticas
El artículo Cálculo y geometría analítica, de George F. Simmons se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El primer instrumento logarítmico: la regla de cálculo
- Las matemáticas como herramienta (III): La Ilustración y el nuevo cálculo
- Las matemáticas como herramienta (II): La Revolución Científica y el cálculo

