Encontrando exoplanetas tapando las estrellas
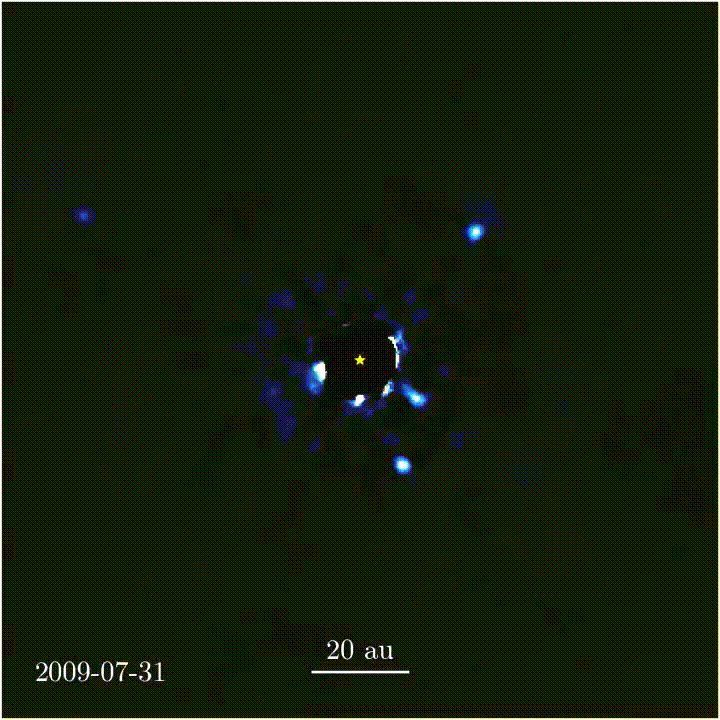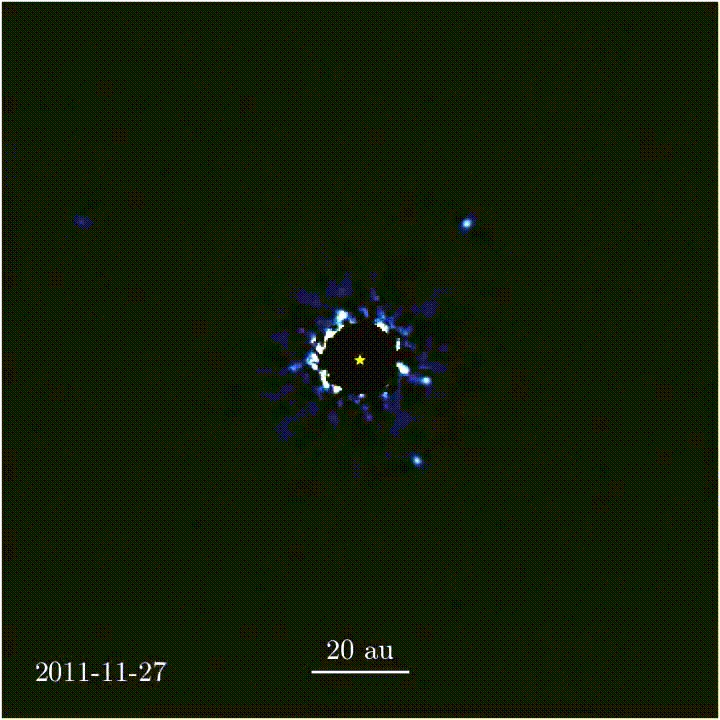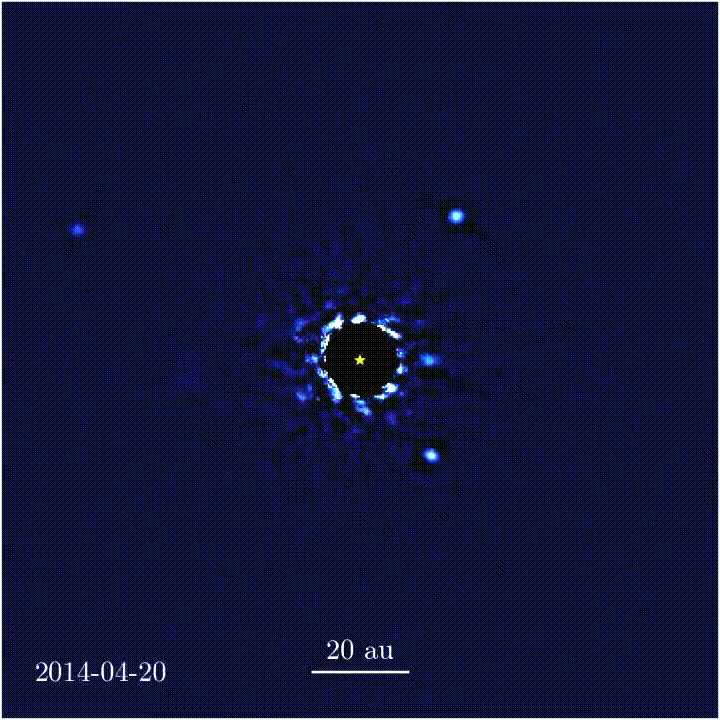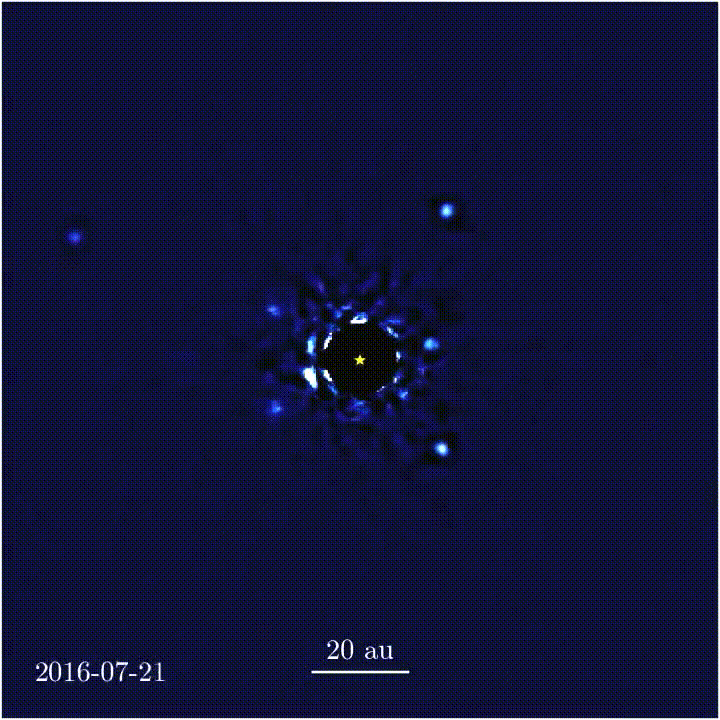
El sistema solar de HR 8799. La imagen se obtuvo con observaciones realizadas con un coronógrafo de vórtice a lo largo de 7 años. Este sistema se encuentra a 129 años luz de distancia de la Tierra.
Un exoplaneta o planeta extrasolar es un planeta que está fuera de nuestro sistema solar. La primera detección confirmada de uno data de 1988, pero ha sido en los últimos años cuando el número de hallazgos confirmados se ha disparado. Los últimos datos oficiales (a cierre de abril) indican que se han encontrado 3.608 planetas en 2.702 sistemas planetarios de los que 610 tienen más de un planeta.
Un número que empieza a ser significativo hace que, por pura probabilidad, empiecen a aparecer planetas con características que los hacen potencialmente habitables, lo que ha acaparado portadas en prensa y que los exoplanetas sean conocidos por el público en general.
Con todo detectar exoplanetas no es precisamente fácil. Y ello se debe, fundamentalmente, a la enorme diferencia de luminosidad entre el planeta y la estrella que orbita, por lo que hay que recurrir a métodos indirectos y renunciar, en muchos casos, a disponer de información de sus atmósferas, por ejemplo, ya que no se pueden “ver”. Pero puede que esto cambie.
Artur Aleksanyan encabeza un grupo de astrónomos de la Universidad de Burdeos (Francia) que a propuesto una mejora a una de las técnicas que se emplean en la búsqueda de exoplanetas, en concreto la coronagrafía, que podría permitir ver directamente los exoplanetas en sistemas con dos o más estrellas, los más habituales en el universo hasta donde sabemos.
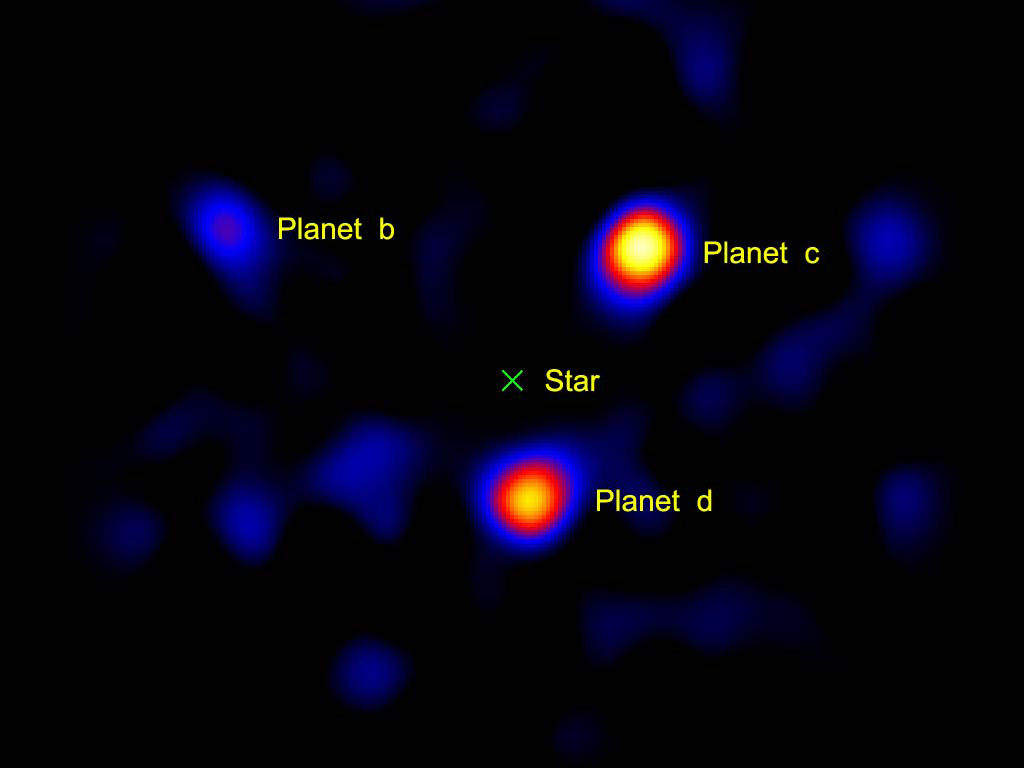
Imagen obtenida por un coronógrafo de vórtice de tres de los cuatro planetas que orbitan HR 8799 (que se encuentra en la posición X y etiquetada como “Star”). Este tipo de imagen se obtuvo por primera vez en 2008.
Un coronógrafo de vórtice fuerza una trayectoria espiral hacia el exterior a la luz entrante desde una fuente puntual en el espacio, “doblando” la luz a lo largo de una ruta que ya no coincide con la cámara del telescopio. Al hacerlo, bloquea la luz de la fuente, permitiendo que los objetos débiles cercanos a la fuente se vuelvan visibles: los fotones de los objetos pasan a través del dispositivo sin obstáculos. Esos objetos incluyen a los exoplanetas que orbitan a las estrellas. Pero los coronógrafos de vórtice actuales sólo pueden atenuar una fuente a la vez, eso está bien para conseguir imágenes de un planeta que tenga una sola estrella anfitriona, pero no para uno con múltiples estrellas.
El coronógrafo de vórtice propuesto por Aleksanyan y sus colaboradores utiliza defectos reconfigurables en un cristal líquido, que son los que fuerzan las trayectorias en espiral a las fuentes puntuales de luz. Los dispositivos tradicionales usan defectos únicos fijos de varios materiales. Usando rayos láser, se pueden escribir y borrar múltiples defectos del cristal líquido rápidamente y con una precisión extraordinaria. Esto permite que el dispositivo se configure fácilmente para cualquier sistema estelar, independientemente del número de estrellas que incluya.
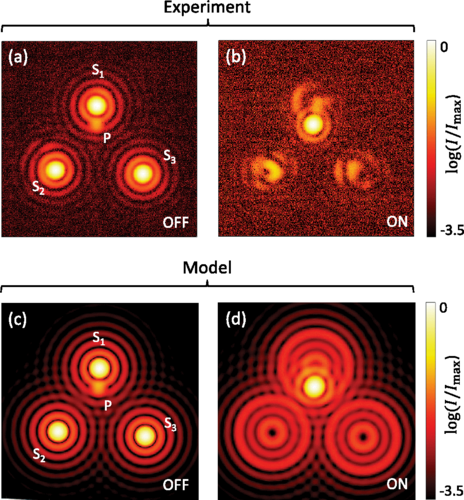
Imagen del experimento con un sistema triple. Nótese an las imágenes de la derecha cómo mejora el detalle del fondo. Abajo la simulación por ordenador del modelo.
Como demostración del principio de funcionamiento, los investigadores simularon un sistema de triple estrella en el laboratorio usando tres haces de luz, y dirigieron los haces hacia un dispositivo con tres defectos. Encontraron que el dispositivo atenuaba drásticamente la luz que llegaba a una cámara procedente de estas estrellas artificiales. El dispositivo podría incluir cualquier número de defectos, ampliando significativamente las capacidades de los coronógrafos de vórtice actuales, multiplicando así el número de exoplanetas que podrían descubrirse y, sobre todo, aumentando la calidad de la información sobre ellos.
Referencia:
Artur Aleksanyan, Nina Kravets, and Etienne Brasselet (2017) Multiple-Star System Adaptive Vortex Coronagraphy Using a Liquid Crystal Light Valve Physical Review Letters doi: 10.1103/PhysRevLett.118.203902
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Encontrando exoplanetas tapando las estrellas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La estructura en común de estrellas de neutrones y aparcamientos
- #Naukas16 Exoplanetas: mundos de ciencia ficción
- La habitabilidad de las exotierras alrededor de estrellas enanas rojas
El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema?
Continuamos con la historia del teorema de los cuatro colores (ver [1] y [2]) cambiando de enfoque: existe una manera dual de abordar este problema, sustituyendo los mapas por grafos. ¿Cómo? Se marca la capital de cada país en el mapa, se unen las capitales de países contiguos y se obtiene el grafo dual del mapa. Colorear el mapa equivale a pintar las capitales (vértices del grafo), asignando distintos tonos a dos capitales unidas por una trayectoria (arista).
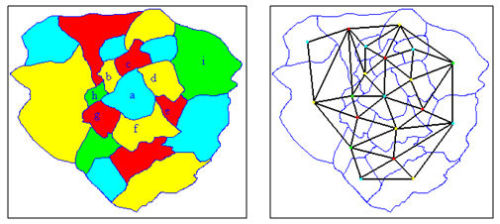
Imagen 1: Mapa y el grafo dual coloreados.
Puede demostrarse que los grafos duales de mapas son siempre planares, es decir, se puede dibujar en el plano una representación concreta del grafo, en la cual las aristas no se cortan excepto en un eventual vértice común (imagen 2).
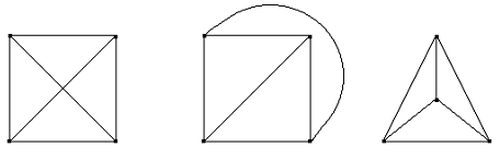
Imagen 2: Un grafo planar y dos representaciones sin cortes entre aristas.
Además, se puede probar que:
-
un mapa es cúbico (ver [1]) si y sólo si su grafo dual es triangular (grafo planar en el que cada cara tiene exactamente tres aristas),
-
el número de regiones colindantes coincide con el grado de cada vértice (número de aristas incidentes), y
-
los grafos duales heredan la fórmula de Euler:
Núm(vértices) – Núm(aristas) + Núm(caras) = 2
Imaginemos por un momento que el teorema fuera falso, es decir, que existen mapas (grafos) que no pueden 4-colorearse. Entre estos mapas (grafos) que necesitan cinco colores o más, debe de haber alguno con el menor número posible de regiones: es un minimal criminal. Así, un minimal criminal no puede 4-colorearse, pero un mapa (grafo) con menos regiones (vértices) sí.
Probar el teorema de los cuatro colores equivale a demostrar que no existen minimales criminales. De hecho, lo que Kempe demostró con su método de cadenas es que un minimal criminal no puede contener digones, triángulos o cuadrados (ver [2], figura 3), y cometió un error al intentar probar que tampoco puede contener pentágonos. Si hubiese conseguido esto último, habría quedado demostrado el teorema.
Los siguientes conceptos sobre grafos son fundamentales en la demostración del teorema:
-
una configuración es un ciclo con vértices internos triangulados;
-
un conjunto inevitable K es una familia finita de configuraciones tal que todo grafo contiene una copia conforme de una de K;
-
k es una configuración reducible, si se puede deducir el coloreado de cualquier grafo que contenga a k, a partir de un grafo menor.
La demostración del teorema de los cuatro colores copia la prueba de Kempe, pero para la inducción, en vez de eliminar un único vértice, se recorta una configuración.
El plan de la prueba consiste en encontrar conjuntos inevitables K; si K estuviese formado sólo por configuraciones reducibles, la demostración del teorema de los cuatro colores estaría terminada, ya que en tal caso no podría existir un minimal criminal.
En 1969, Heinrich Heesch sistematiza la prueba de la reducibilidad, desarrollando un algoritmo que intenta implementar en un ordenador. Realiza diversas pruebas en una máquina CDC1604A y entra en contacto con su alumno Wolfgang Haken (en EE. UU.), comentándole que la demostración necesita estudiar solamente 8.900 configuraciones.
A través de su algoritmo de descarga propone un método de construcción de conjuntos inevitables: Heesch considera el grafo como una red eléctrica; asociando a cada vértice una carga inicial de 6-d(v) (d(v) es el grado del vértice v).Usando la fórmula de Euler, demuestra que la suma de las cargas en un grafo triangulado es 12.
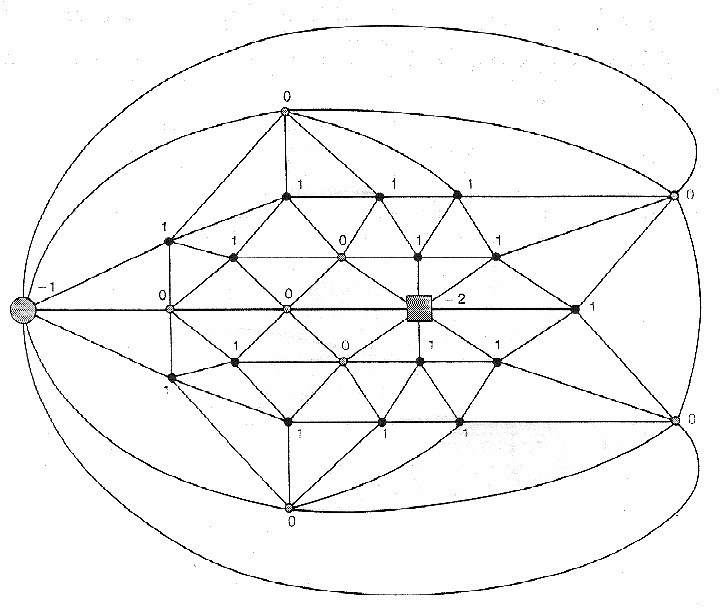
Imagen 3.
Desplazando las cargas eléctricas sobre la red (con su algoritmo de descarga), la suma total no varía: los vértices cargados positivamente pueden ceder cargas, los cargados negativamente pueden recibir y los de carga nula no intercambian. Con este sistema, su objetivo es eliminar de esta red eléctrica los vértices de carga negativa, obteniendo un conjunto de configuraciones con vértices de cargas positivas o nulas. Y como todo grafo triangulado es de carga total 12, debe contener al menos una de las configuraciones (cuya geometría dependerá del proceso de descarga elegido) del anterior conjunto, que forma entonces un conjunto inevitable.
Una vez obtenida la extensa lista de configuraciones inevitables, probando su reducibilidad, se tendría una prueba inductiva del teorema.
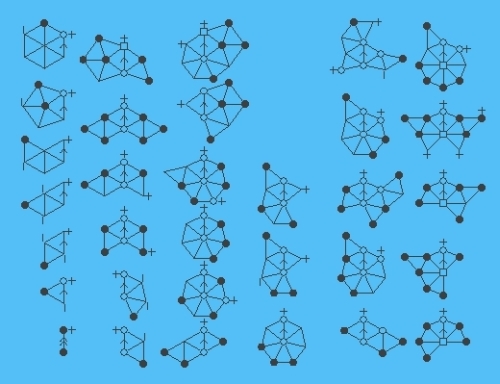
Imagen 4: Una lista de configuraciones inevitables.
En 1976, Ken Appel y Wolfgang Haken dan una prueba cuyos principales ingredientes son precisamente los conceptos de reducibilidad y descarga.
La primera prueba de Appel, Haken y John A. Koch usa un algoritmo de descarga muy sofisticado, que produce una lista de 1.936 configuraciones inevitables, cada una de las cuales se demuestra reducible con la ayuda de un ordenador. Modificando consecutivamente el algoritmo de descarga, encuentran otro (con 300 reglas de descarga) produciendo 1.482 configuraciones inevitables, comprobando su reducibilidad mediante un ordenador programado por Koch: necesita 1.200 horas de cálculo en unIBM 360. Appel y Haken completan la demostración en 1976, tras seis años de duro trabajo: más de 100 páginas impresas, 400 microfilms con dibujos y la verificación de varios miles de casos particulares.
Todo este trabajo precisaba (en 1976) más de cincuenta días de trabajo en los tres ordenadores de la Universidad de Illinois, con un programa de varios miles de líneas… es decir, nadie podía comprobar la veracidad o falsedad del teorema a mano.
La hazaña de estos investigadores mereció un triunfal matasellos en 1977:

Imagen 5.
Appel y Haken reconocieron el papel fundamental de Kempe: Kempe’s argument was extremely clever, and although his “proof” turned out not to be complete, it contained most of the basic ideas that eventually led to the correct proof one century later.
Muchos matemáticos aceptan esta prueba como irrefutable, pero muchos otros argumentan que no se trata de una demostración matemática: la máquina había verificado que una enorme cantidad de mapas podían colorearse usando como mucho cuatro colores, pero, ¿y si existía un mapa que el ordenador no hubiese contemplado?
En 1996, un grupo de investigadores del Instituto de Tecnología de Georgia publicael artículo [6] en el que:
-
reducen las complicaciones, probando que la inevitabilidad de un conjunto reducible puede demostrarse con menos ejemplos que en la prueba de Appel y Haken;
-
su conjunto inevitable es solo de tamaño 633;
-
usan únicamente32 reglas de descarga;
-
la comprobación a mano de la inevitabilidad se reemplaza por una prueba formal verificable con un ordenador;
-
la verificación necesita únicamente tres horas en cualquier ordenador doméstico.
Posteriores investigaciones han ido confirmando cada una de las etapas de esta última prueba utilizando diferentes programas y métodos. Pero…El teorema de los cuatro colores (y 4): ¿Podemos creer la prueba de la conjetura?
Referencias
[1] Marta Macho Stadler, El teorema de los cuatro colores (1): una historia que comienza en 1852, Cuaderno de Cultura Científica, 26 abril 2017
[1] Marta Macho Stadler, El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba, Cuaderno de Cultura Científica, 10 mayo 2017
[3] Marta Macho Stadler, Mapas, colores y números, Descubrir las matemáticas hoy: Sociedad, Ciencia, Tecnología y Matemáticas 2006 (2008) 41-68
[4]K. Appel, W. Haken, Every planar map is four colourable, Part I: discharging, Illinois Journal of Mathematics 21, 429-490, 1977.
[5]K. Appel, W. Haken, J. Koch, Every planar map is four colourable, Part II: reducibility, Illinois Journal of Mathematics 21, 491-567, 1977.
[6]N. Robertson, D.P. Sanders, P. Seymour, R. Thomas, A new proof of the four-colour theorem, Electronic Announcements of the AMS 2, 17-25, 1996.
[7]R.J. Wilson, Four colors suffice: how the map problem was solved, Princeton University Press, 2002.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
Esta entrada participa en la Edición 8.4 “Matemáticas de todos y para todos” del Carnaval de Matemáticas cuyo anfitrión es, en esta ocasión, matematicascercanas.
El artículo El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (1): una historia que comienza en 1852
- El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba
- El problema de Malfatti
El valor de la curiosidad
Muchos atribuyen a la falta de cultura científica el que haya amplios sectores de la población que no aceptan que el clima esté cambiando y que ese fenómeno tenga su origen en la actividad humana. Creen, en consecuencia, que proporcionando una buena educación científica el cambio climático acabará siendo aceptado como un hecho real. Las cosas, como en tantas ocasiones, no parecen ser tan sencillas.
El psicólogo de la Universidad de Bristol (Reino Unido) Stephan Lewandosky ha observado que la actitud de una persona para con el cambio climático depende más de factores emocionales ligados a la ideología que de elementos racionales. Y Dan Kahan -psicólogo también, pero de la Universidad de Yale (EEUU)- ha comprobado que cuanto mayor es el conocimiento científico de una persona más firme es la postura, sea a favor o sea en contra, que mantiene en esa controversia. De hecho, quienes saben manejar información científica suelen elaborar buenos argumentos a favor de sus ideas, a la vez que ignoran los contrarios. Al parecer, la culpa la tiene el llamado “razonamiento motivado”, fenómeno que está en la base de las paradojas que consisten en ignorar las pruebas que respaldan hechos contrastados, mientras se asumen como tales datos anecdóticos que respaldan la posición que mejor se acomoda a nuestros deseos y visión de la realidad.
El razonamiento motivado surte unos efectos tan poderosos que personas capaces de interpretar correctamente información estadística compleja sobre cuestiones variadas, pierden tal capacidad cuando lo que han de considerar son hechos o datos con implicaciones ideológicas. Si a las consecuencias del razonamiento motivado añadimos la influencia de las redes sociales de internet, por la ausencia de filtros de calidad al flujo de información y por su efecto de caja de resonancia de las ideas con las que más nos identificamos, la receta de la posverdad está servida.
En los ejemplos anteriores me he referido a sesgos característicos de perfiles ideológicos conservadores. Pero quienes se consideran a sí mismos progresistas tampoco están a salvo de los efectos del razonamiento motivado. Muchos lo ponen en práctica, por ejemplo, a la hora de evaluar cuestiones tales como los (supuestos) efectos sobre la salud de las radiaciones electromagnéticas de telefonía móvil o redes wi-fi, o los de las plantas transgénicas y del consumo de alimentos procedentes de esas plantas. Y además de las de carácter político, también hay motivaciones ideológicas con otras bases, por supuesto, como la religiosa.
Es fácil caer en la tentación fatalista y aceptar que es inevitable sufrir las consecuencias del razonamiento motivado y, por lo tanto, que estamos condenados, en un futuro de duración incierta, a convivir con la posverdad. Pero eso sería socialmente suicida, pues solo debates basados en datos contrastados pueden ser verdaderamente democráticos y útiles, condición necesaria para el progreso social. La clave está, quizás, en la formación que se dé a los niños y niñas de hoy y de mañana, una formación que debería servir para hacerlos más conscientes del peligro que entraña una comunicación de masas sin mediaciones, de la influencia de los sesgos, y del efecto de las emociones en nuestra capacidad para aprehender la realidad.
En medio de ese panorama, Dan Kahan también ha observado algo alentador: que las personas con curiosidad científica, sea cual sea su orientación ideológica, tienden a aceptar con facilidad hechos contrastados y, lo que es más importante, están más dispuestas a recurrir a fuentes diversas para informarse. El psicólogo norteamericano cree, por ello, que una clave para superar la posverdad puede radicar, precisamente, en la capacidad para cultivar la curiosidad en las generaciones más jóvenes.
El artículo El valor de la curiosidad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ciencia: pasión, asombro y curiosidad.
- Dando valor a los residuos marinos para cuadrar la economía circular
- Zombis éticos
El balance energético
La aptitud de biológica de un animal depende, en última instancia, de su capacidad para dejar tras de sí nuevos individuos cuyo genoma sea, en parte, copia del propio. Esa capacidad depende, en una primera aproximación, de la cantidad de recursos que es capaz de adquirir y destinar a la línea germinal, pues esa es la línea que da lugar a la gestación de nuevos individuos.

La forma más sencilla de abordar esta cuestión de forma analítica es recurrir al balance energético que resulta de la ingestión del alimento, su posterior aprovechamiento y la utilización de la fracción que ha podido aprovecharse para proveer la energía que necesitan las actividades que cada animal ha de desarrollar. No quiere decirse que la energía sea el único término a tener en cuenta si se quiere valorar con rigor el uso de los recursos que requiere y ha de conseguir un animal. Casi todos los elementos que necesita están sometidos a procesos de adquisición y de pérdida, como el nitrógeno, por ejemplo, o los nutrientes minerales, vitaminas, y demás; y con cada uno de ellos podría elaborarse un balance. Es más, un animal puede tener excedentes de carbono o de energía, pero ser deficitario en nitrógeno, o en calcio, por ejemplo. Sin embargo, la energía constituye el limitante principal de la mayoría de animales para generar nueva biomasa. Y esa es la razón por la que aquí recurrimos a ese término, sin olvidar que otros pueden acabar resultando tan o más limitantes que aquella.
Todos los animales han de alimentarse para conseguir los recursos que necesitan. Se incluyen en ese capítulo energía y componentes estructurales. Se alimentan consumiendo alimento. La ingestión o consumo (C) es el término que representa esa función. El alimento ha de ser digerido (fragmentación mecánica y química mediante el concurso de enzimas específicos) para que sus componentes básicos se puedan absorber. Como consecuencia de esos procesos, una parte de lo ingerido (C) es absorbido; a esta parte la denominamos absorción (A). Y otra parte no es absorbida y se elimina en forma de heces. A esta la denominamos egestión (F). Así pues, con los elementos considerados ya disponemos de un primer balance, el que nos da la energía absorbida (A), como A = C – F.
La mayor parte del alimento absorbido es asimilado. La asimilación (A) consiste en su incorporación al conjunto de procesos celulares que pueden incluir su degradación para obtener energía metabólica en forma, principalmente, de ATP, o su participación en vías de síntesis de otras sustancias. En términos de balance energético se suele diferenciar entre los términos “absorción” (tal y como se ha presentado en el párrafo anterior) y “asimilación”. La distinción se basa en la existencia de procesos de desaminación de moléculas que dan lugar a la aparición de restos nitrogenados (NH4+ en primera instancia) que, debido a su toxicidad, han de ser eliminados directamente o tras su conversión en otras sustancias (urea y ácido úrico, principalmente); la energía contenida en esas sustancias se expresa como U. A efectos de balance energético no se establece distinción entre los restos nitrogenados que resultan de la desaminación de sustancias recién absorbidas y los que proceden del permanente recambio (procesos de síntesis y degradación) de macromoléculas nitrogenadas. Así pues, tendríamos aquí un segundo balance: A´= C – F – U.
La energía asimilada tiene, por último, dos posibles destinos. Una parte se disipa en forma de calor; a esa la denominamos Gasto metabólico o, de forma más simple, Metabolismo (H). Y la otra parte es la que se deposita en forma de biomasa propia; a esta última la denominamos Producción (P). Más adelante nos referiremos a los tres usos posibles de la energía producida.
Conviene reparar en el hecho de que el término R tiene una doble cara. Da cuenta, por un lado, de la energía que se pierde por el simple hecho de que en todos los procesos que ocurren en las células animales una parte de la energía química se transforma en calor y se pierde de esa forma. Y por el otro lado, al ser esa disipación de calor consecuencia de las actividades biológicas, constituye un indicador del nivel de actividad del organismo.
Así pues, la energía asimilada puede entrar en las vías catabólicas que conducen a la producción de ATP o, alternativamente, dirigirse a (1) la síntesis de nuevas estructuras (somáticas y reproductivas), (2) la reparación y renovación de las ya existentes; y (3) el almacenamiento de sustancias de reserva.
Por su parte, el ATP producido en las vías metabólicas correspondientes es utilizado para proporcionar la energía que necesitan las actividades biológicas, como son (1) los procesos de biosíntesis para la producción de nuevas estructuras (nuevos tejidos somáticos y gametos) y la reparación o renovación de las existentes (enzimas, estructuras, neurotransmisores, hormonas, etc.); (2) las actividades de regulación (transporte de iones, secreción activa…); (3) otras actividades internas, como contracciones musculares, movimientos ciliares, etc.; y (4) las actividades hacia el exterior (contracciones musculares, movimientos ciliares, etc.
Todas las actividades anteriores conllevan un cierto gasto metabólico pues, como se ha visto, es a su desarrollo a lo que se destina el ATP que se obtiene de las vías catabólicas. Por ello, también podemos categorizar el gasto metabólico de la forma siguiente: (1) costes de mantenimiento del organismo, que son los derivados de las actividades de renovación y reparación de estructuras, las de regulación, y los movimientos internos; (2) costes del crecimiento y la reproducción, que son los asociados a los procesos biosintéticos de producción de biomasa; y (3) costes de la actividad, que son los ligados al desarrollo de actividades hacia el exterior.
La expresión definitiva del balance energético sería, por lo tanto, la siguiente:
P = C – F – U – R.
En teoría, y suponiendo que la energía es la unidad relevante a efectos de producción animal, mediante la determinación experimental de los términos contenidos en esa expresión se puede calcular la producción de un individuo bajo las condiciones experimentales establecidas. También permite analizar la forma en que diferentes factores ambientales (cantidad de alimento disponible, temperatura, etc.) afectan al balance y, por lo tanto, a la aptitud biológica del individuo.
Conviene precisar, para terminar, que la ecuación del balance energético refleja, por su naturaleza, el margen existente para la producción; de hecho, en inglés se denomina scope for growth al valor que resulta de la determinación experimental de sus componentes. Pero la medida de la producción real en condiciones naturales, y la proporción que cada individuo o grupo de individuos destina al crecimiento somático o a la reproducción, están también sometidas a control fisiológico (endocrino). Además, esas magnitudes son, en parte, el resultado de la historia evolutiva de cada linaje, pues son variables características del ciclo de vida, y en su definición intervienen elementos ambientales y demográficos. Pero de estos asuntos ya nos ocuparemos en otra ocasión.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El balance energético se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las actividades animales
- Cuando el ahorro energético salta por la ventana
- El flujo sanguíneo se reorganiza en respuesta a las necesidades
La máquina de vapor (2)
La máquina Newcomen fue ampliamente utilizada en Gran Bretaña y otros países durante el siglo XVIII. Según los estándares modernos, no era una máquina muy buena. Quemaba una gran cantidad de carbón, pero realizaba solo una pequeña cantidad de trabajo a una velocidad lenta y espasmódica. Pero la gran demanda de máquinas para sacar agua de las minas era un buen mercado, incluso para una máquina ineficiente.

James Watt en un retrato de Carl Frederik von Breda, 1792
El trabajo de un escocés, James Watt, condujo a una máquina de vapor muy mejorada y que tendría importantes consecuencias económicas. El padre de Watt era un carpintero con un negocio de éxito dedicado a vender equipamiento a los armadores de buques. Sería en el taller del ático de su padre donde James Watt desarrollaría una considerable habilidad en el uso de herramientas. Quería convertirse en un fabricante de instrumentos y fue a Londres para aprender el oficio. A su regreso a Escocia en 1757, obtuvo un puesto como fabricante de instrumentos en la Universidad de Glasgow.
En el invierno de 1763-1764, Watt fue requerido para reparar un modelo del motor de Newcomen que era utilizado en las clases prácticas de la universidad. Al familiarizarse con el modelo, Watt quedó impresionado por la cantidad de vapor que se requería para hacer funcionar la máquina. Realizó una serie de experimentos sobre el comportamiento del vapor y encontró que un problema importante era la temperatura de las paredes del cilindro. La máquina de Newcomen desperdiciaba la mayor parte de su calor calentando las paredes del cilindro, ya que las paredes se enfriaban en cada ciclo al inyectar agua fría para condensar el vapor y forzar el retorno del pistón con aire a presión.

Máquina de Watt en un gráfico de 1797
A principios de 1765 Watt remedió esta ineficiencia ideando un tipo modificado de máquina de vapor. En retrospectiva, parece una idea tonta de lo simple que es, pero en su momento fue verdaderamente revolucionaria. Después de empujar el pistón hacia arriba, el vapor se hacía pasar a un recipiente separado, llamado condensador, donde el vapor se condensaba a una temperatura baja. Con este sistema, el cilindro que contiene el pistón podía mantenerse caliente permanentemente, y el condensador podía mantenerse frío todo el tiempo.
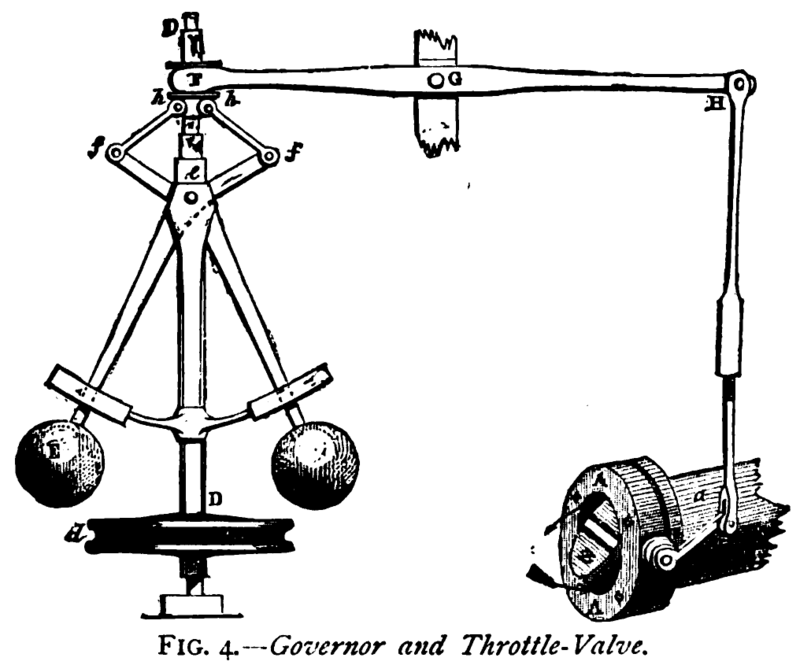
Regulador centrífugo de Watt
El uso de un condensador separado permitía grandes ahorros de combustible. La máquina de Watt podía hacer el doble de trabajo que el de Newcomen con la misma cantidad de combustible. Watt también agregó muchos otros refinamientos, tales como válvulas de control automático que se abrían y cerraban mediante la acción alternativa del propio pistón, así como un regulador centrífugo que controlaba la cantidad de vapor que llegaba a la máquina, lo que permitía mantener una velocidad constante. Esta idea de usar parte de la salida del proceso para regular el proceso en sí, se llama retroalimentación. Es una parte esencial del diseño de muchos sistemas mecánicos y electrónicos modernos.

Al igual que Thomas Edison más tarde, o los emprendedores tecnológicos de éxito en nuestros días, Watt y sus asociados aunaban ser buenos hombres de negocios y excelentes ingenieros. Hicieron una fortuna fabricando y vendiendo las máquinas de vapor mejoradas. Las invenciones de Watt estimularon el desarrollo de máquinas que podían hacer muchos otros trabajos. El vapor movía las máquinas en las fábricas, las locomotoras de ferrocarril, los barcos de vapor, e incluso los primeros coches de vapor, incluyendo maquinaria pesada semoviente. La máquina de Watt dio un estímulo enorme al crecimiento de la industria en Europa y América. Ayudó así a transformar la estructura económica y social de la civilización industrial. El desarrollo generalizado de motores y máquinas revolucionó la producción en masa de bienes de consumo, construcción y transporte.

Máquina agrícola a vapor francesa de mediados del XIX
El nivel de vida medio en Europa Occidental y los Estados Unidos aumentó considerablemente. Es difícil para la mayor parte de nosotros en los países industrializados “desarrollados” imaginar cómo era la vida antes de esta “Revolución Industrial”.
Pero no todos los efectos de la industrialización fueron beneficiosos. De hecho la palabra “medio” del párrafo anterior encubre una enorme desigualdad. El sistema manufacturero del siglo XIX proporcionaba a algunos empleadores codiciosos y crueles la oportunidad de tratar a los trabajadores casi como esclavos. Sin leyes laborales o de protección infantil, esos empleadores obtenían fortunas mientras mantenían a los empleados ya sus familias al borde de la inanición.
Según avanzaba el siglo XIX cada vez más personas abandonan las granjas, voluntariamente o forzadas por la pobreza y las nuevas leyes de propiedad, para trabajar en las fábricas. El conflicto se intensificó entre otra novedad, la clase obrera, formada por empleados, y la clase media, formada por empleadores y profesionales.
Al mismo tiempo, algunos artistas e intelectuales, muchos del movimiento romántico, comenzaron a atacar las nuevas tendencias de esta sociedad. Vieron esta sociedad cada vez más dominada por el comercio, la maquinaria y el énfasis en los bienes materiales. En algunos casos, confundieron la ciencia como tal, con sus aplicaciones técnicas y éstas con el uso comercial de las mismas por parte de empresarios sin escrúpulos. La reacción llevaba a estos intelectuales a echar en cara a los científicos el explicar todos los maravillosos misterios de la naturaleza. Estos artistas denunciaron tanto a la ciencia como a la tecnología, aunque en la mayor parte de los casos se negaban a aprender algo sobre ellas.
Estas actitudes siguen estando a la orden del día y son parte de una vieja tradición, que se remonta a ls antiguos opositores griegos al atomismo de Demócrito. Muchos escritores y artistas románticos atacaron la física galileana y newtoniana por supuestamente distorsionar los valores morales. El mismo tipo de acusación que se escucha hoy por parte de la anticiencia y que es un continuo desde la máquina de vapor.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La máquina de vapor (2) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Ingredientes para la receta: El conejo
“casi ningún otro animal es más difícil de amansar que el gazapo de un conejo de monte, y apenas hay animal más manso que el gazapo del conejo amansado; pero difícilmente puedo suponer que los conejos domésticos hayan sido seleccionados frecuentemente, sólo por mansos, de modo que tenemos que atribuir a la costumbre y al prolongado encierro la mayor parte, por lo menos, del cambio hereditario, desde el extremo salvajismo a la extrema mansedumbre.”
Charles Darwin. El origen de las especies. 1859.

Hablemos del conejo común, también conocido como conejo europeo, y de nombre científico Oryctolagus cuniculus. Lo descubrieron por vez primera y según los textos escritos, primero, los fenicios y, después, los romanos al llegar a la Península Ibérica. Y, por cierto, Iberia deriva del nombre del conejo para los habitantes prerromanos de la Península. Su distribución después de las glaciaciones era relativamente pequeña y restringida al sudoeste de Europa, a la Península Ibérica y el sudeste de Francia. Es posible que llegara también al norte de África entre Marruecos y Túnez.
Son animales sociales que viven en grupos de tamaño medio en madrigueras excavadas en el suelo llamadas conejeras. Son activos, sobre todo, al atardecer y en el crepúsculo aunque no es raro verles de día en zonas con arbustos que les sirven de escondite en caso de peligro. Al anochecer salen a terreno abierto a buscar alimento.
No hace mucho que domesticamos al conejo. Es una especie de lo último que ha llegado a nuestro corral como animal domesticado, aunque durante miles de años, ya lo veremos, lo hemos consumido como caza abundante y fácil de obtener. En el esquema que Don y Patricia Brothwell publicaron con los periodos de domesticación de nuestro ganado, el conejo es el más reciente, como mucho de hace unos 2000 años. Ahora existen más de 100 variedades seleccionadas por el peso, el tamaño o el color del pelaje. Y son alimento, mascota, animal de exposición, con una piel apreciada para el vestido y la moda o, incluso, un estimado animal de laboratorio.

Hay dos subespecies del conejo, la cuniculus cuniculus y la cuniculus algirus. Su distribución en la Península es curiosa pues, si trazamos una diagonal desde Galicia a Murcia, al norte está el cuniculus cuniculus y al sur y en el norte de África el cuniculus algirus. Parece claro que el conejo doméstico viene de la subespecie cuniculus cuniculus.
Son Eudald Carbonell y Cinta Bellmunt, de las universidades Rovira i Virgili y Politécnica de Catalunya, los que cuentan que hay evidencias del consumo de conejo por nuestra especie desde hace más de 300000 años. En el nivel TD10-I de la Gran Dolina de Atapuerca, se alimentaban, entre otras presas, de conejos. Eran los neandertales e, incluso, quizá antecesores de los neandertales.
Los Homo se alimentan de lo que encuentran, animal o vegetal, grande o pequeño, fresco o desechos. Cuando caza en grupo prefiere animales grandes pues alimentan a más individuos, durante más tiempo y proporcionan más energía en forma de grasas. Si fueran conejos, se necesitarían, más o menos, un ejemplar al día por persona. Por todo ello, cuando aparecen restos en yacimientos de más de 50000 años, suelen ser escasos y mezclados con los huesos de animales de mayor tamaño. Todas las especies de homínidos muestran dietas con gran diversidad de alimentos y, aunque haya más restos de una o de pocas presas, habitualmente de gran tamaño y más numerosas, siempre hay otros animales y, entre ellos, está el conejo.
En concreto y en un tiempo más cercano, en el yacimiento de Molí de Salt, Tarragona, era el animal más consumido en la dieta de hace unos 13000 años. Manuel Vaquero y su grupo, de la Universitat Rovira i Virgili, encuentran que hasta el 91% de los restos encontrados en este yacimiento son huesos de conejo.
Como explican John Fa y sus colegas, del Grupo Durrell de Conservación de la Naturaleza de Trinity, en la isla de Jersey, el conejo fue, para los depredadores y para las especies de Homo, neandertales y sapiens, un recurso alimenticio importante. Como antes he mencionado, era una especie abundante y fácil de cazar.
En los yacimientos, los restos de conejo son escasos hasta que las poblaciones de presas de mayor tamaño comienzan a escasear. El consumo de carne de conejo aumenta con el tiempo y se convierte en parte esencial de la dieta de nuestra especie. Los neandertales lo capturaban en menor cantidad y su dieta se centraba en animales de mayor tamaño. Los autores concluyen, después de analizar los restos de 104 excavaciones en 30 yacimientos de la Península y del sur de Francia, que el cambio de dieta hacia el conejo y otras presas pequeñas se produjo hace más de 35000 años, lo que ya había ocurrido en el yacimiento de Molí de Salt.
Y en el interesante libro de Carbonell y Bellmunt, titulado “Recetas Paleo”, nos presentan un conejo a las hierbas al estilo de nuestros ancestros. Dice así, tal cual y sin ayudas entre paréntesis:
“Caza un conejo en el bosque, despelléjalo, lávalo con agua y pártelo en dos. Haz diez partes de una de las mitades.
Excava un agujero en el suelo, de unos dos palmos de ancho y algo más de profundidad. Que tenga sedimentos blandos en el fondo. Echa leña al agujero y quémala; si es posible que sea de olivo, encina o roble.
Para cocinar en conejo ponlo en una piedra cóncava, con ramas de romero y empapado en agua. Tápalo con otra piedra más plana.
Cuando la leña sea brasa y ceniza caliente, mete el recipiente con el conejo y tápalo todo con un recorte cuadrado de césped. Tiene que estar unas tres horas como poco pero, de vez en cuando, destápalo para ver cómo va. Con cuidado, pues la piedra quema, saca el recipiente del agujero y come el conejo con las manos.”

Citado por los fenicios en la Península, los romanos llevaron el conejo primero a su capital, a Roma, y, después, a su imperio. Como ejemplo nos sirve Gran Bretaña adonde lo llevaron los romanos en su conquista del año 43 y, ahora, son unos 40 millones. Y, añado, si le interesa conocer cómo viven los conejos en las Islas Británicas lea “La colina de Watership”, de Richard Adam, merece la pena.
En Roma y en su imperio se adaptaron a vivir en amplios recintos cerrados con paredes de piedra, llamados leporaria, pero no estaban domesticados tal como ahora entendemos el término. Recintos como estos se han encontrado, por ejemplo, en Bretaña y en otros yacimientos romanos de Europa occidental.
Era el siglo I, en la época imperial de Roma, y Marco Gavio Apicio, apreciado gastrónomo, escribió el libro de cocina De Re Coquinaria, que resume la sabiduría culinaria de aquellos años. Y solo nombra el conejo una vez y, además, para hacer albóndigas. Para Apicio, la carne de conejo estaba en tercer lugar como preferencia para las albóndigas, después del pavo real y del faisán, pero, avisa, siempre que se frían de manera que queden tiernos. Sin embargo, de aquella época también son algunos conocidos mosaicos que muestran apetecibles conejos.
Se cree que la domesticación comenzó en los monasterios de la Península Ibérica y, sobre todo, del sur de Francia y se incentivó por la Iglesia desde que, en el siglo VII, el Papa San Gregorio Magno había establecido que el gazapo, la cría del conejo, no era carne y, por tanto, se podía consumir en Cuaresma. Entre los siglos VI y X comenzó la domesticación en los monasterios franceses. En el siglo XVII ya existían varias razas seleccionadas por el color del pelaje.
Una de las diferencias más evidente entre el conejo silvestre y el domesticado es la conducta. El silvestre es un peligroso luchador en defensa de sí mismo y de su grupo. Golpea con las patas traseras y muerde con sus grandes y potentes incisivos. Las luchas de los machos por el control del grupo pueden llegar a las heridas graves y a la muerte del contrincante.

Por el contrario, el conejo doméstico no pelea, es tranquilo y, en general, se deja manipular. Se ha propuesto la hipótesis de que, en el proceso de la domesticación, parte de la información genética perdida o silenciada es la que provoca estos cambios en la conducta agresiva. De ahí la cita de Darwin, en El origen de las especies, que aparece al comienzo de este texto.
Su centro Vavilov, es decir, el área geográfica con mayor variabilidad genética y, por tanto, el origen de la especie domesticada, es la Península Ibérica. Para confirmarlo, Joel Alves y su grupo, de la Universidad de Oporto, han hecho el análisis genético de 471 individuos de 16 razas de conejos y de 13 localidades con conejos silvestres de Francis y del nordeste de España.
Los resultados demuestran que la población original del conejo domesticado, con la mayor diversidad genética, está en la Península. La colonización del sudeste francés, que los autores fechan hace 18000 años, supuso la pérdida del 12% de la variabilidad. La domesticación, mucho más reciente y en periodo histórico, fue hace 1500 años y se origina de los conejos silvestres de Francia. Provocó la pérdida de otro 21% de diversidad genética.
Un estudio similar de Miguel Carneiro y su grupo, del Campus Agrario de Varao, en Portugal, llega a conclusiones parecidas después de analizar 150 ejemplares de las razas más comunes de conejos domesticados. La relación de pérdida de diversidad genética es del 40% con los conejos silvestres de Francia.
Por tanto, el centro Vavilov de la domesticación del conejo está en el nordeste de España y el sudeste de Francia.
Durante muchos años, los conejos se criaron en las casas y cabañas de los campesinos solo para consumo propio. Los alimentaban con hierbas, semillas y restos no utilizables de sus cosechas. Pero en la economía rural más reciente e intensiva, los conejos pasaron a la producción industrial con el objetivo comercial de su venta y consumo para grandes poblaciones, todo ello solo en los países con tradición de consumir este tipo de carne.

El conejo supone carne barata y accesible en épocas de crisis. Así ocurrió en Europa y Estados Unidos en la Gran Depresión y en la Segunda Guerra Mundial. Los conejos se criaban fácilmente en casa, alimentados con restos de plantas y se reproducían rápido y, además, no ocupaban mucho espacio. Sin embargo, cuando pasan las crisis no tardan a recuperar su estatus de “comida para pobres”. Por si fueran pocas las ventajas, su escasez en grasas y colesterol los convierten en un alimento saludable. Los conejos europeos, con su adaptabilidad y enorme capacidad reproductora que llega a las once puestas al año y los gazapos en 8-10 semanas alcanzan la madurez, se han extendido por todos los continentes excepto la Antártida. Los llevaban los marinos y los dejaban en islas y lugares conocidos para, en otros viajes, disponer de carne fresca. En la actualidad se han detectado en más de 800 islas de todos los mares. Así llegaron, como ejemplo muy conocido, a Australia donde, a partir de dos docenas que llegaron en 1859, a los 30 años eran 20 millones y, un siglo después, eran 600 millones. Los australianos importaron el virus de la mixomatosis para controlar la población de conejos y provocaron el desastre contrario, con matanzas enormes. Cuando el virus regresó a Europa, de donde había sido importado, causó la casi extinción del conejo salvaje con la eliminación de entre el 90% y el 99% de los ejemplares. Además, el aspecto sanguinolento y llagado de los conejos enfermos provocaba asco y rechazo y, por ello, el consumo de carne de conejo disminuyó. A pesar de los intentos de reintroducir el conejo salvaje en muchos países de Europa, nunca se han conseguido recuperar las poblaciones anteriores a la mixomatosis.
En un entorno favorable, con mucho alimento y sin depredadores, el éxito del invasor es inevitable. Además, tienen un especial sistema de digestión que les permite aprovechar la celulosa de las plantas aunque no sean rumiantes. Las ingieren y pasan por su digestivo en el que viven bacterias simbiontes del género Anaerobacter. Estas bacterias digieren la celulosa y la convierten en ácidos grasos que el conejo expulsa en las heces que, a su vez, vuelven a ser ingeridas para poder absorber esos ácidos grasos.
Ahora, los mayores criadores de conejos son Francia, Italia, Malta y España. En 2015 la producción global fue de 1680 miles de toneladas. En España se consumieron 62.700 toneladas y a cada habitante le correspondieron 1.3 kilogramos de carne de conejo.
En el interesante libro “Cocina para pobres” del Dr. Alfredo Juderías, hay varias recetas de conejo tomadas directamente de fondas y casas de comida y de cocineros de su casa. Allí aparece este “Conejo adobado”, plato que no es fácil de hallar y probar y que, para terminar con un buen sabor de boca, creo que es apropiado:
“Se avía, se parte en trozos y se pone en una cazuela para que tome, durante un par de horas, más o menos, un adobillo a base de un cuartillo de vino blanco, laurel, ajo, pimienta, tomillo, orégano, sal, etc.
Después de escurridos, se embozan en harina y se echan a un sartén, a la lumbre, con aceite bien caliente.”
Sencillo, rápido y sabroso. Pruébenlo, se lo recomiendo.
Referencias:
Alda, F. & I. Doadrio. 2014. Spatial genetic structure across a hybrid zone between European rabbit subspecies. PeerJ DOI: 10.7717/peerj.582
Alves, J.M. et al. 2015. Levels and patterns of genetic diversity and population structure in domestic rabbits. PLOS ONE 10: e0144687
Apicio, Marco Gavio. 2007. El arte de la cocina. De Re Coquinaria. Comunicación y Publicaciones SA. Barcelona. 119 pp.
Blasco López, R. 2011. La amplitud de la dieta cárnica en el Pleistoceno medio peninsular: una aproximación a partir de la Cova del BOLOMOR (Tavernes de Valldigna, Valencia) y del subnivel TD10-I de Gran Dolina (Sierra de Atapuerca, Burgos). Tesis doctoral. Universitat Rovira i Virgili. Tarragona. 724 pp.
Brothwell, D. & P. Brothwell. 1969. Food in Antiquity. A survey of the diet of early peoples. Johns Hopkins University Press. Baltimore and London. 283 pp.
Callou, C. 1995. Modifications de l’aire de répartition du lapin (Oryctolagus cuniculus) en France et en Espagne, du Pléistocène à l’époque actuelle. État de la question. Anthropozoologica 21: 95-114.
Carbonell, E. & C.S. Bellmunt. 2016. Recetas Paleo. La dieta de nuestros orígenes para una vida saludable. Ed. Planeta. Barcelona. 143 pp.
Carneiro, M. et al. 2011. The genetic structure of domestic rabbits. Molecular Biology and Evolution 28: 1801-1816.
Cheeke, P.R. 2000. Rabbits. En “The Cambridge world history of food, Vol. I”, p. 565-567. Ed. por K.F. Kiple & K.C. Ornelas. Cambridge University Press. Cambridge.
Fa, J.E. et al. 2013. Rabbits and hominin survival in Iberia. Journal of Human Evolution doi: 10.1016/j.jhevol.2013.01.002
Juderías, A. 1980. Cocina para pobres. Ed. SETECO. Madrid. 325 pp.
Martínez Polanco, M.F. et al. 2016. Rabbits as food at the end of the Upper Palaeolithic at Molí del Salt (Catalonia, Spain). International Journal of Osteoarchaeology DOI: 10.1002/oa.2541
Wikipedia. 2017. Oryctolagus cuniculus. 5 abril.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Ingredientes para la receta: El conejo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ingredientes para la receta: el ajo
- Ingredientes para la receta: El arroz
- Preparados para matar: algunas ideas para el debate
Una nueva diana terapéutica para el neuroblastoma
Los cánceres infantiles del sistema nervioso simpático, o neuroblastomas, tienen una tasa anual de mortalidad de 10 por millón, en edades comprendidas entre 0 y 4 años. El trabajo de investigación en el que han participado Investigadores de la UPV/EHU y el centro Achucarro ha servido para identificar algunas mutaciones genéticas que ayudarán a mejorar el tratamiento de esta enfermedad.
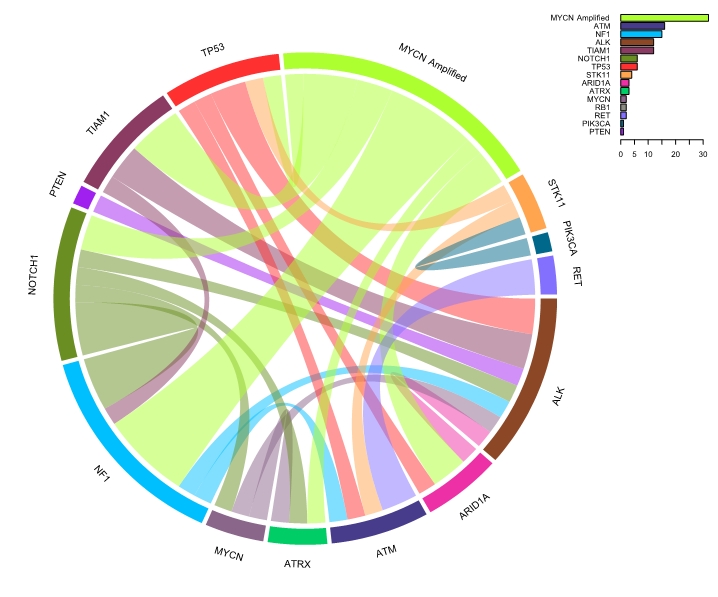
Diagrama Circos que muestra la relación entre genes mutados y/o la amplificación de MYCN.
Investigadores del Instituto de Investigación Sanitaria La Fe de Valencia dirigidos por Jaime Font de Mora, en colaboración con José Luis Zugaza, investigador Ikerbasque en la UPV/EHU y en el centro “Achucarro Basque Center for Neuroscience”, han identificado mediante NGS (Next Generation Sequencing) mutaciones en el gen Tiam1 que predicen un mejor pronóstico a pacientes con neuroblastoma.
El neuroblastoma es el tumor extracraneal sólido más frecuente en la infancia. Representa el 7% de todos los cánceres pediátricos y es la causa del 15% del total de defunciones por procesos oncológicos en la infancia. Su incidencia oscila entre 8 y 10 casos por millón de niños y año. Se han descrito casos familiares de neuroblastoma, pero son muy poco frecuentes. A día de hoy, se desconoce cómo se origina este tipo de cáncer raro.
El estudio revela que estas mutaciones que previenen la progresión de esta enfermedad están localizadas en diferentes dominios de Tiam1 relacionados con las GTPasas Ras y Rac así como con Myc, todas estas proteínas están implicadas en la etiología y progresión de este tipo cáncer.
Los resultados sugieren que el señalosoma controlado por Tiam1 puede ser esencial para el desarrollo del neuroblasoma y, por tanto, Tiam1 se posiciona como una diana que ayude a mejorar la eficacia de la terapia en neuroblastoma.
El siguiente paso es incorporar estos estudios a la práctica clínica para mejorar las herramientas y procedimientos de diagnóstico, en aras a implementar tratamientos más tempranos para los pequeños afectados.
Referencia:
Sanmartín E et al.. (2017) TIAM1 variants improve clinical outcome in neuroblastoma. Oncotarget DOI: 10.18632/oncotarget.16787.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Una nueva diana terapéutica para el neuroblastoma se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ADN para la nueva generación de baterías
- Una nueva vía para la lucha contra la resistencia a los antibióticos
- Biomarcadores para la detección precoz del melanoma
La inteligencia, la herencia y la madre
Todo comenzó hace más de cuatro décadas, a principios de los setenta, cuando el psicólogo Robert Lehrke, del Hospital Estatal de Brainerd, en Minnesota, publicó un artículo que resumía su tesis doctoral y presentaba una teoría, así lo llama el autor, sobre el desarrollo de la inteligencia. Trabajaba en un centro para discapacitados intelectuales y había encontrado que muchos genes relacionados con el desarrollo de la inteligencia y, en concreto, con las habilidades verbales y con la percepción de las relaciones espaciales, se localizaban en el cromosoma X que, de los cromosomas sexuales que todos llevamos, es el que viene de la madre.
Ahora y desde hace un par de años, abundan las noticias en los medios y las entradas en blogs que afirman que los genes más importantes de la inteligencia de los niños se heredan de la madre. En la red esta noticia es viral y, por ello, a muchos nos gustaría conocer que hay de cierto en ella.

De izquierda a derecha, Marie Skłodowska-Curie (premios Nobel de física y química), Irène Joliot-Curie (premio Nobel de química) y Pierre Curie (premio Nobel de Física)
Según esos escritos, los padres tendrían poco que ver en la determinación del cociente de inteligencia (CI) de sus hijos. No hay evidencias claras y rotundas de que exista esta herencia de la inteligencia entre madre e hijo. Los últimos estudios apuntan algo que es evidente: los genes de la inteligencia llegan tanto de la madre como del padre. Sin embargo, seguimos sin conocer con claridad y detalle el proceso debido a lo compleja que es la inteligencia.
Nuestra especie tiene en cada célula, excepto en las reproductoras, 46 cromosomas o, con más precisión, 23 pares de cromosomas, y en cada pareja de cromosomas, uno es del padre y otro es de la madre. Todos los pares están formados por cromosomas iguales y repetidos, excepto el par 23 formado por los cromosomas sexuales, que son diferentes según el sexo de la persona. Si es una mujer, tiene dos cromosomas iguales llamados X, y es por tanto un par XX. En los hombres, los cromosomas son diferentes, uno es X, que viene de la madre, y el otro es Y, que viene de padre y, por tanto, es un par XY. En conclusión, el par de cromosomas 23 de una mujer es XX, y el de un hombre es XY.
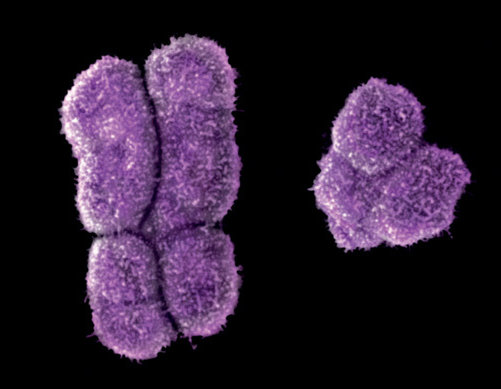
Cromosomas X (izquierda) e Y (derecha)
Por tanto, en un hombre el X viene de la madre y el Y viene del padre. Lehrke dice que hay muchos genes relacionados con la inteligencia en el cromosoma X que, si mutan y no funcionan bien, provocan la discapacidad intelectual en el hombre. Para 2010 ya había unos 300 genes localizados en el cromosoma X y relacionados con la discapacidad intelectual, según la revisión de Ulrich Zechner y su grupo, de la Universidad de Ulm, en Alemania. Ello supone que en el cromosoma X hay seis veces más genes relacionados con la inteligencia que en el resto de cromosomas. Además, suponen el 10% de todos los genes del cromosoma X.
En las mujeres que, repito, tienen dos cromosomas X, si falla un gen en uno de ellos se suple con el funcionamiento del mismo gen en el otro cromosoma X. Solo si falla en los dos cromosomas X aparece la discapacidad intelectual en la mujer. Hay entre un 30% y un 50% más de discapacitados intelectuales entre los hombres y se ha propuesto que es por esta causa: no tienen dos copias de los genes del cromosoma X y, si falla una de ellas, no pueden suplir el funcionamiento del que no lo hace bien. Así lo afirman Gillian Turner y Michael Partington, de los hospitales de Niños Príncipe de Gales de Sidney y de los Suburbios Occidentales de Newcastle, ambos en Australia.
Por cierto, si hay algún gen relacionado con la inteligencia en el cromosoma Y, típico del hombre, y muta, tampoco hay repuesto ya que solo hay una copia de este cromosoma.
También se ha propuesto la hipótesis de que esta presencia de genes relacionados con la inteligencia en el cromosoma X quizá tenga relación con el sexo y, en el proceso de la evolución, se ha seleccionado así porque una mayor inteligencia permite una mejor reproducción y, por tanto, un mayor éxito evolutivo. O sea, los hombres y las mujeres más inteligentes se reproducen mejor. Es otra hipótesis.
También se ha confirmado que la distribución en una gráfica de los CI de hombres y mujeres no es exactamente igual. Ambas tienen forma de campana, con un mayor número de hombres y mujeres con un CI medio y un número mucho menor con un CI muy alto o muy bajo. Pero esta campana en los hombres es más plana y alargada en los dos extremos. Implica que hay menos hombres con un CI medio y más número que en mujeres con un CI muy bajo, que son los discapacitados intelectuales que ya he mencionado, o con un CI muy alto. Se ignora como el cromosoma X, si es que lo hace, interviene para que existan esos CI altos.
Quizá ya ha llegado el momento de ver de qué estamos hablando y, para ello, transcribo una definición de inteligencia fechada en 1997 y apoyada por 52 expertos:
“Inteligencia es una capacidad muy general que, entre otras cosas, incluye la habilidad para razonar, planificar, resolver problemas, pensar en abstracto, comprender ideas complejas, aprender con rapidez y aprender de la experiencia. No es solamente aprender de los libros o la competencia académica o la rapidez en responder tests. Más bien refleja una capacidad amplia y profunda para comprender nuestro entorno, captarlo, dar sentido a las cosas o imaginar lo que son. Inteligencia, así definida, se puede medir, y los tests de inteligencia lo hacen bien.”

A la izquierda Aage Bohr (premio Nobel de física 1975) con su padre Niels (premio Nobel de física 1922)
Según los neurobiólogos y los psicólogos, la inteligencia se hereda de una generación a la siguiente, pero en qué porcentaje se hereda y cuánto varía por causas del entorno como la alimentación, la educación o el ambiente en la infancia y adolescencia, se ignora. El porcentaje, según cada autor, va del 30% al 80%. La inteligencia es compleja en cuanto al número de genes implicados. Sabemos más de lo que perjudica a la inteligencia a causa de genes mutados que no funcionan bien y que llegan a 300 en el cromosoma X, como antes he mencionado. En conclusión, en muchas de las revisiones más recientes ni siquiera se menciona la herencia de la madre pues, aparte de las propuestas de Lehrke, poco más se ha averiguado sobre la función de esta herencia materna en la inteligencia de los hijos.
En un estudio del grupo de Min Zhao, de la Universidad de Pekín, aparece la revisión de la bibliografía sobre los genes relacionados con la inteligencia que conocemos hasta ahora. Hay 158 genes localizados y el 16% están en el cromosoma X.
Para terminar, y como hacen Jozef Gecz y John Mulley, de la Universidad de Adelaida, en Australia, podemos especular que, para conseguir que un órgano tan complejo como el cerebro funcione con normalidad, requiere no uno, ni dos, sino cientos o miles de genes integrados de tal manera que sus productos funcionen coordinados. Además, estas interacciones complejas deben mantenerse en equilibrio incluso bajo una enorme variedad de estímulos del entorno. Por el contrario, el fallo de un solo gen, como ocurre en el cromosoma X, puede romper catastróficamente el equilibrio y provocar una discapacidad más o menos grave.
En muchas entradas de blogs que tratan este asunto y que antes mencionaba, se cita como prueba de la herencia materna un estudio hecho en Glasgow, con 12686 voluntarios entre 14 y 22 años, en el que se compara su CI con el de sus madres, y se llega a la conclusión de que el 15% de la inteligencia de los jóvenes viene de su madre. Parece que es un trabajo del grupo de Ian Deary (grupo que ya he citado dos veces en este texto, en Deary et al, 2010, y Davies et al, 2015), de la Universidad de Edimburgo, que trabaja en neurociencia de la inteligencia desde hace años y con resultados muy interesantes.
Pues bien, este estudio tan citado en los blogs parece que no existe y no lo encuentro ni preguntando a los autores que, por lo que cuentan, tampoco saben cuál es su origen. Lo más parecido, con los 12686 voluntarios, es una investigación de este grupo sobre la relación de la inteligencia del niño con la lactancia materna. Los autores llegan a la conclusión de que la relación es con la inteligencia de la madre y que las madres con el CI alto dan más de mamar a sus hijos. Es la influencia de la alimentación en el desarrollo del niño que antes mencionaba. Pero lo del 15% de herencia materna no lo encuentro ni en esta ni en ninguna otra publicación. Me declaro incapaz de conseguir localizarla.
Referencias:
Davies, G. et al. 2015. Genetic contributions to variation in general cognitive function: a meta-analysis of genome-wide association studies in the CHARGE consortium (N=53949). Molecular Psychiatry 20: 183-192.
Deary, I.J. et al. 2010. The neuroscience of human intelligence. Nature Reviews Neuroscience 11: 201-211.
Der, G. et al. 2006. Effect of breast feeding on intelligence in children: prospective study, sibling pair analysis, and meta-analysis. British Medical Journal doi: 10.1136/bmj.38978.6995583.55
Gecz, J. & J. Mulley. 2016. Genes for cognitive function: developments on the X. Genome Research 10: 157-163.
Lehrke, R. 1972. A theory of X-linkage of major intelectual traits. American Journal of Mental Deficiency 76: 611-619.
Turner, G. & M.W. Partington. 1991. Genes for intelligence on the X chromosome. Journal of Medical Genetics 28: 429.
Zechner, U. et al. 2001. A high density of X-linked genes for general cognitive ability: a run away process shaping human evolution? Trends in Genetics 17: 697-701.
Zhao, M. et al. 2014. A systems biology approach to identify intelligence quotient score related genomic regions, and pathways relevant to potential therapeutic treatments. Scientific Reports 4: 4176.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo La inteligencia, la herencia y la madre se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La búsqueda de la inteligencia artificial, en la próxima zientziateka
- La búsqueda de la inteligencia artificial
- Máquinas inteligentes (II): Inteligencia artificial y robótica
Candida auris, el hongo que ha causado una alerta sanitaria internacional

En los últimos meses, varias agencias nacionales e internacionales han emitido diferentes alertas sobre la expansión de un tipo de hongo, denominado Candida Auris, que causa graves infecciones en pacientes hospitalarios críticos. Se trata de un agente infeccioso difícil de identificar y muy resistente a los fármacos existentes que puede provocar elevadas tasas de mortalidad. Su mayor incidencia hasta la fecha se ha producido en países como España, Dinamarca o EE.UU.
Guillermo Quindós, catedrático de Microbiología en la UPV/EHU, habló sobre este organismo en una conferencia tuvo lugar el pasado 4 de abril en Azkuna Zentroa (Bilbao). Este evento, forma parte del ciclo de conferencias Zientziateka, que organizan todos los meses la Cátedra de Cultura Científica de la UPV/EHU y Azkuna Zentroa para divulgar asuntos científicos de actualidad.
Candida auris, el hongo que ha causado una alerta sanitariaEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Candida auris, el hongo que ha causado una alerta sanitaria internacional se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los ojos que explorarán la superficie de Marte (Mars2020)
- ¿Cómo sienten y piensan los bilingües?
- Investigación con medicamentos en seres humanos: del laboratorio a la farmacia
Catástrofe Ultravioleta #16 RARO

Catástrofe Ultravioleta #16 RARO
En cada uno de nosotros hay pequeñas variaciones genéticas que nos hacen especiales y nos cambian la vida. Todos somos mutantes. El libro de instrucciones de un ser humano tiene alrededor de 3.000 millones de letras entre las que a menudo se cuelan gazapos o saltos de línea. “La mayoría son pequeñísimas mutaciones, de apenas una letra, pero algunas de estas variantes tienen consecuencias patológicas”, nos explica Lluís Montoliu. Pero, ¿cuándo empieza la enfermedad o qué es eso que llamamos “normalidad”?
En en este episodio os explicaremos por qué “todos somos mutantes” y en qué consisten esas pequeñas variaciones que cambian la vida de las personas. Sabremos qué es una enfermedad rara, hablaremos de ratones mutantes y os sumergiremos en las aventuras de un “Retrón ninja” capaz de hacerle una pirueta a su destino y reírse en su cara. Dale al ‘play’ y sumérgete en nuestro programa más “raro”.
Agradecimientos: A Raúl Gay (retrón indómito), Oihana Iturbide y Laura Morrón (Next Door editores), Lluís Montoliu (CNB), Pepe Solves y Patty Bonet. Y a Ray Jaén por prestarnos su voz.
* Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) con el apoyo de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.
Puedes conocernos en nuestra web: Catastrofeultravioleta.com y seguirnos en el twitter Catastrofe_UV. También puedes encontrar todos los capítulos en este enlace.
El artículo Catástrofe Ultravioleta #16 RARO se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Catástrofe Ultravioleta #13 LEVIATÁN
- Catástrofe Ultravioleta #11 – Elefancía
- Catástrofe Ultravioleta #14 VULCANO
Las cartas de Darwin: ¡La geología por encima de todo!
Las cartas de Darwin, una serie para conocer aspectos sorprendentes de la vida del naturalista
Si hablamos de Newton pensamos en física, si hablamos de Galileo pensamos en astronomía, si hablamos de Darwin damos por sentado que hablamos de biología, y es cierto, pero muchos pasan por alto la enorme influencia que la geología tuvo sobre el naturalista.
Sus primeros pasos como científico reconocido fueron como geólogo, recordemos que en el Beagle recolectó pacientemente miles de rocas que fue enviando a Inglaterra durante todo el viaje. Muchos lo consideran un libro de viajes, sin embargo la primera obra publicada enteramente por Darwin, Journal of researches (1839), es esencialmente un libro geológico y el 75% de las anotaciones científicas de su diario pertenecen a este campo.
De hecho, las aportaciones a la geología de Darwin se recogieron en numerosos volúmenes publicados durante los años posteriores al viaje del Beagle: Geological observations on the volcanic islands visited during the voyage of H.M.S. Beagle (1844), Geological observations on South America (1846), o el propio Letters on Geology publicado en 1835 con las cartas que se intercambiaban él y Henslow.
Darwin, reconozcámoslo, fue geólogo antes que biólogo.

Secciones estructurales de la cordillera de los Andes en los pasos de Piuquenes y de Uspallata. Darwin Geological observations on South America, being the third part of the geology of the voyage of the Beagle, under the command of Capt. Fitzroy, R.N. during the years 1832 to 1836, Smith Elder & Co, 1846
Y es curioso que así fuera puesto que durante su estancia en Edimburgo, y según su propia Autobiografía, Darwin reconocía que llegó a aborrecer la geología por culpa de un aburrido profesor llamado Robert Jameson.
“Las rancias lecciones de Jameson me decidieron a no leer en mi vida un libro de Geología ni estudiar esta ciencia por ningún pretexto”
Afortunadamente su posterior estancia en Cambridge, junto a nuevos profesores como Henslow o Sedgwick, y sus frecuentes escapadas y excursiones geológicas, el joven quedó encandilado con esta disciplina. “¡La geología por encima de todo!”, exclamó en una de sus cartas a su hermana Caroline.
Carta de Charles Darwin a su hermana Catherine Darwin [13 noviembre de 1833]
“Desearía que cualquiera de ustedes pudiera penetrar en los sentimientos de placer excesivo que me proporciona la geología, tan pronto como uno comprende en parte la naturaleza de un país”.
Carta de Charles Darwin a John Stevens Henslow [marzo de 1834]
“Estoy encantado con la geología, pero como el animal prudente entre dos haces de heno no sé qué saborear más, si el grupo cristalino de rocas o los suaves lechos fosilíferos. […].
Por cierto que no tengo una idea clara acerca de hendiduras, estratificación, líneas de levantamiento. No tengo libros que me ilustren y lo que dicen no lo puedo aplicar a lo que veo. En consecuencia saco mis propias conclusiones y de seguro que son absolutamente ridículas”.
La humildad de Darwin en sus escritos no era una pose, realmente se acercaba a este campo con dedicación y prudencia, lo cual no le impedía realizar sus propias deducciones y teorías, apoyándolas con razonamientos que, en muchos casos, terminaron siendo válidos y acertados.
Carta de Charles Darwin a John Stevens Henslow [24 julio de 1834]
“Me ha interesado mucho encontrar tanta abundancia de conchas recientes a una altura de 1300 pies. El campo en muchos lugares está cubierto de conchas, pero todas son de litoral. Así supongo yo que la elevación de 1300 pies debe deberse a una sucesión de pequeñas elevaciones como ocurrió en 1822. Con estas pruebas ciertas de la residencia reciente del océano sobre todas las partes bajas de Chile, la línea panorámica y la forma de cada valle poseen un alto interés.
¿Habrá la acción del flujo del agua o del mar formado esta hondonada profunda? Ésta fue una pregunta que me planteé con frecuencia y que, por lo general, se me respondió al encontrar un lecho de conchas recientes en el fondo. No tengo suficientes argumentos, pero no creo que más que una pequeña fracción de la altura de los Andes se haya formado dentro del periodo terciario”.
Carta de Charles Darwin a John Stevens Henslow [12 agosto de 1835]
“Hace poco conseguí el informe sobre los trabajos de M. Dessalines D’Orbigny en S. América. Experimenté un nivel degradante de irritación al comprobar que ya había descrito la geología de la Pampa, y que yo me había estado dando duros paseos a caballo para nada. Sin embargo fue gratificante ver que mis conclusiones fueran las mismas, en la medida que yo puedo deducir, que sus resultados”.[…]
En esa misma carta, Darwin se mostraba exultante con su trabajo geológico:
“Ahora puedo demostrar que ambos lados de los Andes surgieron en un periodo reciente a una considerable altura. Aquí las conchas estaban a 350 pies sobre el nivel del mar”.

Charles Lyell | National Gallery Londres (imagen Javier Peláez)
Mención aparte merece la figura de Charles Lyell en la vida y obra de Darwin.
Carta de Charles Darwin a su primo William Darwin Fox [12 de agosto de 1835]
“Me estoy convirtiendo en un discípulo celoso de los puntos de vista del señor Lyell tal como se conocen por su libro. Hacer de geólogo en Sudamérica hace que me sienta tentado de llevar adelante algunas partes a una amplitud mayor incluso de la que él contempla.
La geología es una ciencia capital para empezar ya que no requiere más que un poco de lecturas, de pensar y de martillar. Tengo reunido un considerable cuerpo de notas, pero es un tema constante de complejidad para mí saber si tienen el valor suficiente para haber utilizado tanto tiempo en ellas”.
El libro al que Darwin alude es, por supuesto, el primer volumen de los Principles of Geology de Charles Lyell que su profesor (y reverendo) John Henslow le había regalado para el viaje con la advertencia de: “Léelo pero no aceptes los puntos de vista ahí declarados”.
Darwin llegaría a declarar en su Autobiografía que “la ciencia de la geología debe mucho a Lyell, mucho más, creo yo, que a cualquier otro hombre que haya vivido”.
Las nociones geológicas de Lyell, la idea de que pequeños cambios durante largos periodos de tiempo pueden dar lugar a grandes cambios y aquel libro de geología que le regaló Henslow fueron parte fundamental de lo que más tarde sería el Darwin biólogo.

Dos de los tres volúmenes de los Principios de Geología de Lyell editados por John Murray
La ingente cantidad de material y notas recogidas por Darwin durante aquella expedición se convertirían en la principal fuente de trabajo durante los próximos 40 años, y así lo intuía el propio naturalista mientras el viaje iba tocando a su fin:
Carta de Charles Darwin a su hermana Caroline Darwin [29 abril de 1836]
“Mi ocupación ahora consiste en reacomodar mis viejas notas geológicas y este reacomodo consiste en volverlas a escribir por completo. Justo ahora estoy empezando a descubrir la dificultad de expresar mis propias ideas en papel. Si solo consiste en describir, esto es muy fácil, pero cuando el razonamiento entra en juego, hacer las conexiones apropiadas, una fluidez clara y moderada es para mí, como ya te dije, una dificultad de la que no tenía ni idea.
Mi espíritu se levanta con la geología e incluso aspiro a pensar que mis observaciones serán consideradas de alguna utilidad por los verdaderos geólogos. Veo con toda claridad que será necesario vivir en Londres durante un tiempo para que, según confío, la mayor parte de mis materiales podrán ser analizados exhaustivamente.”
Darwin no se equivocaba. A su llegada a Londres fue nombrado miembro de la Sociedad Geológica, de la que terminaría siendo Secretario unos años después. Allí conoció personalmente a su admirado Charles Lyell con quien entablaría una sólida amistad hasta el final de sus días.
Si tenéis la oportunidad de visitar la Abadía de Westminster en Londres comprobaréis que la tumba de Charles Darwin se encuentra a solo unos pasos de la de su amigo Charles Lyell.

Las tumbas de Lyell y Darwin en Westminster (imágenes Javier Peláez)
Este post ha sido realizado por Javier Peláez (@irreductible) y es una colaboración deNaukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Las cartas de Darwin: ¡La geología por encima de todo! se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las cartas de Darwin: La vida a bordo de un balandro ataúd
- Las cartas de Darwin: El sueño truncado de Canarias
- Las cartas de Darwin: ¿Dejamos que el chaval se vaya de viaje?
La teoría de la inoculación: usar la desinformación para combatir la desinformación
John Cook
![]()
Como psicólogo que investiga la desinformación, me centro en reducir su influencia. Esencialmente, mi objetivo es quedarme sin trabajo.
Los acontecimientos recientes indican que no lo he estado haciendo muy bien. La desinformación, las noticias falsas y los “hechos alternativos” son más prominentes que nunca. El Oxford Dictionary eligió “post-truth” como la palabra del año 2016 . La ciencia y la evidencia científica están siendo atacadas.
Afortunadamente, la ciencia tiene un medio para protegerse, y proviene de una rama de la investigación psicológica conocida como teoría de la inoculación. Se inspira en la lógica de las vacunas: Un poco de algo malo te ayuda a resistir un caso completo. En mi investigación recientemente publicada, he intentado exponer a la gente a una forma débil de desinformación para inocularlos contra la situación real – con resultados prometedores.
La dos formas en las que la desinformación hace daño
La desinformación se está generando y difundiendo a ritmos prolíficos. Un estudio reciente comparando los argumentos contra la ciencia del clima frente a los argumentos políticos contra la acción sobre el clima encontró que la negación de la ciencia está aumentando relativamente. Y las investigaciones recientes indican que estos tipos de campañas tienen un impacto en las percepciones de las personas y en la cultura científica.
Un estudio reciente llevado a cabo por el psicólogo Sander van der Linden encontró que la desinformación sobre el cambio climático tiene un impacto significativo en la opinión pública sobre el cambio climático.
La información errónea que usaron en su experimento fue el artículo sobre el clima más compartido en 2016. Se trata de una petición, conocida como el Proyecto de Petición Calentamiento Global, en la que 31.000 personas, con un grado en ciencias o superior, habían firmado una declaración diciendo que los humanos no están alterando el clima . Este artículo aislado bajó la percepción de los lectores sobre el consenso científico. La medida en que las personas aceptan que existe un consenso científico sobre el cambio climático es lo que los investigadores llaman una “creencia de entrada“, lo que influye en las actitudes hacia el cambio climático, tales como el apoyo a la acción climática.
Al mismo tiempo que van der Linden estaba llevando a cabo su experimento en los Estados Unidos, estaba en el otro lado del planeta en Australia realizando mi propia investigación sobre el impacto de la desinformación. Por coincidencia, usé el mismo mito, usando texto literal del Proyecto de Petición Calentamiento Global. Después de mostrar la desinformación, pedí a la gente que estimara el consenso científico sobre el calentamiento global causado por el ser humano, con objeto de medir cualquier efecto.
Encontré resultados similares, con la información errónea reduciendo la percepción de la gente del consenso científico. Además, la desinformación afectó a unas personas más que a otras. Cuanto más conservadora políticamente era una persona, mayor era la influencia de la desinformación.
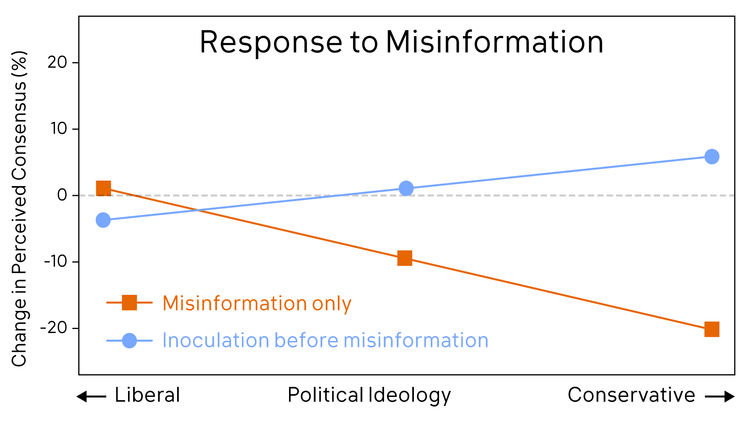
Respuesta a la desinformación sobre el cambio climático. Cook et al. (2017), CC BY-ND (Cambio en el consenso percibido frente a ideología política. Liberal = progresista; Conservative = conservador)
Esto cuadra con otras investigaciones que encuentran que la gente interpreta los mensajes, ya sean información o desinformación, según sus creencias preexistentes. Cuando vemos algo que nos gusta, es más probable que pensemos que es verdad y consecuentemente fortalece nuestras creencias. Por el contrario, cuando nos encontramos con información que está en conflicto con nuestras creencias, es más probable que desacreditemos la fuente.
Sin embargo, hay más en esta historia. Más allá de desinformar a la gente, la desinformación tiene una influencia más insidiosa y peligrosa. En el estudio de van der Linden, cuando se presentaba a la gente tanto los hechos como la información errónea sobre el cambio climático, no había un cambio neto en la creencia. Las dos informaciones en conflicto se cancelaron mutuamente.
El hecho y el “hecho alternativo” son como la materia y la antimateria. Cuando chocan, hay una destello de calor seguido de nada. Esto revela la forma sutil en que la desinformación daña. No sólo desinforma. Impide que la gente crea en los hechos. O como Garry Kasporov lo expresa elocuentemente, la desinformación “aniquila la verdad”.
La respuesta de la ciencia a la negación de la ciencia
El asalto a la ciencia es formidable y, como indica esta investigación, puede ser incluso demasiado eficaz. Convenientemente, la ciencia tiene la respuesta a la negación de la ciencia.
La teoría de la inoculación toma el concepto de vacunación, donde nos exponemos a una forma débil de un virus con el fin de crear inmunidad al virus real, y lo aplica al conocimiento. Medio siglo de investigación ha encontrado que cuando estamos expuestos a una “forma débil de desinformación”, esto nos ayuda a crear resistencia para que no seamos influenciados por la desinformación real.
El texto inoculante necesita de dos elementos. Primero, incluye una advertencia explícita sobre el peligro de ser engañado por la desinformación. En segundo lugar, necesitas proporcionar contraargumentos que explican los fallos en esa desinformación.
En la inoculación de van der Linden éste indicaba que muchos de los signatarios eran falsos (por ejemplo, una Spice Girl aparecía falsamente como signataria), que 31.000 representan una fracción minúscula (menos del 0,3 por ciento) de todos los graduados en ciencias estadounidenses desde 1970 y que menos del 1% de los signatarios tenían experiencia en climatología.
En mi investigación publicada recientemente, también probé la inoculación pero con un enfoque diferente. Mientras inoculaba a los participantes contra el Proyecto Petición, no lo mencioné en absoluto. En cambio, hablé de la técnica de desinformación que hace uso de “expertos falsos” – personas que transmiten la impresión de conocimiento al público en general, pero que no tienen ninguna experiencia relevante real.
Descubrí que explicar la técnica de desinformación neutralizó completamente la influencia de la información errónea, incluso sin mencionar la información errónea específicamente. Por ejemplo, después de que expliqué cómo los expertos falsos se han utilizado en campañas de desinformación pasadas, los participantes no fueron influenciados cuando se enfrentaron a los expertos falsos del Proyecto de Petición. Además, la desinformación se neutralizó en todo el espectro político. Ya seas conservador o progresista, nadie quiere ser engañado por artimañas.
Poner en práctica la inoculación
La inoculación es una forma poderosa y versátil de comunicación científica que se puede utilizar de varias maneras. Mi enfoque ha sido combinar los hallazgos de la inoculación con la psicología cognitiva de la desacreditación, desarrollando el marco Hecho-Mito-Falacia.
Esta estrategia implica explicar los hechos, seguido de la introducción de un mito relacionado con esos hechos. En este punto, las personas se enfrentan a dos informaciones en conflicto. Resuelves el conflicto explicando la técnica que utiliza el mito para distorsionar el hecho.
Hemos utilizado este enfoque a gran escala en un curso en línea gratuito sobre la desinformación sobre el clima, Making Sense of Climate Science Denial. Cada conferencia adopta la estructura Hecho-Mito-Falacia. Comenzamos explicando un solo hecho climático, luego introdujimos un mito relacionado, seguido de una explicación de la falacia empleada por el mito. De esta manera, al mismo tiempo que explicamos los hechos clave del cambio climático, también inoculamos a los estudiantes contra 50 de los mitos climáticos más comunes.

Conferencias Denial101x que siguen la estructura Hecho-Mito-Falacia (Fact-Myth-Fallacy). Denial101x, CC BY-ND
Por ejemplo, sabemos que estamos causando el calentamiento global porque observamos muchos patrones en el cambio climático característicos del efecto invernadero. En otras palabras, las huellas humanas se observan en todo nuestro clima. Sin embargo, un mito sostiene que el clima ha cambiado naturalmente en el pasado antes de que hubiese seres humanos; por lo tanto, lo que está sucediendo ahora debe ser natural también. Este mito comete la falacia de saltar a conclusiones (o non sequitur), donde la premisa no conduce a la conclusión. Es como encontrar un cadáver con un cuchillo asomando por la espalda y argumentar que las personas han muerto de causas naturales en el pasado, por lo que esta muerte debe haber sido por causas naturales también.
La ciencia, en un momento de franqueza, nos ha informado que arrojar más ciencia a la gente no es la respuesta completa a la negación de la ciencia. La desinformación es una realidad que no podemos permitirnos ignorar – no podemos negar la negación de la ciencia. Más bien, debemos verlo como una oportunidad educativa. Abordar conceptos erróneos en el aula es una de las maneras más poderosas de enseñar ciencia.
Resulta que la clave para detener la negación de la ciencia es exponer a la gente solo a un poco de negación de la ciencia.
Sobre el autor:
John Cook es profesor ayudante investigador en el Centro para la Comunicación del Cambio Climático, Universidad George Mason (EE.UU.)
Texto traducido y adaptado por César Tomé López a partir del original publicado por The Conversation el 15 de mayo de 2017 bajo una licencia Creative Commons (CC BY-ND 4.0)
El artículo La teoría de la inoculación: usar la desinformación para combatir la desinformación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Elogio de la teoría
- #Naukas14 ¿Para qué podemos usar el dióxido de carbono?
- Cuando el más pequeño movimiento genera electricidad que puedes usar
Estimada OCU: recuerda que NO se pueden utilizar las cremas solares del año pasado
La semana pasada la OCU (Organización de Consumidores y Usuarios) hizo llegar a diferentes medios de comunicación una nota de prensa titulada «OCU recuerda que se pueden utilizar las cremas solares del año pasado». La nota fue publicada en su web y en importantes diarios nacionales.

En resumen, la nota de prensa nos cuenta que la OCU analizó* seis productos de protección solar a los que sometió al típico trajín veraniego (mantuvieron los envases 15 días al sol, alta temperatura, humedad, etc.) simulando el uso real de los productos. Tras doce meses los analizaron y comprobaron que conservaban sus cualidades originales. De este análisis dedujeron que «los consumidores pueden sentirse tranquilos si utilizan estas cremas de protección solar pasados los 12 meses desde su fecha de apertura, incluso tras haberlas utilizado ya el año anterior».
Que la prueba se haya realizado pasados 12 meses no es un asunto trivial, sino que responde a las recomendaciones habituales de los fabricantes de estos productos cosméticos.
Hay tres informaciones importantes que figuran en la etiqueta de cualquier producto cosmético y que como consumidores deberíamos conocer:
-
Instrucciones de uso. Todos los cosméticos tienen instrucciones, o bien en el envase, o bien en una etiqueta desplegable, o bien remiten a una web, o bien en un prospecto adjunto. El símbolo que hace referencia a que existe información adjunta es el siguiente:

-
Fecha de duración mínima. Es la fecha a partir de la cual el fabricante no puede garantizar que el producto sea efectivo y seguro, incluso sin haber sido utilizado y conservando el embalaje original. Es similar a la fecha de caducidad de los alimentos. Los cosméticos que tienen una caducidad superior a los 30 meses no tienen obligación de poner una fecha de caducidad, pero sí un consumo recomendado una vez abierto (PAO). Suele aparecer acompañada del siguiente símbolo:
-
Periodo después de la apertura (PAO). Es un símbolo de un tarro abierto en el que figura un número seguido de una M. Ese número indica la cantidad de meses que el producto puede utilizarse con seguridad una vez abierto. Más allá de ese plazo el fabricante no puede garantizar la seguridad y efectividad del producto. El símbolo utilizado es como los siguientes:
Gran parte de los productos de protección solar son 12M, es decir que, transcurridos 12 meses tras el primer uso, no podemos tener la garantía de que sean eficaces ni seguros, por lo que la recomendación es utilizar uno nuevo. Por este motivo la OCU decidió hacer la prueba tras 12 meses.
Hay que tener en cuenta que estos productos cosméticos contienen agua y una gran cantidad de nutrientes, además de estar sometidos a bruscos cambios de temperatura, humedad, y que entran en contacto con el aire: son un caldo de cultivo idóneo para la proliferación de microorganismos, con lo que la seguridad y la eficacia del producto puede verse comprometida. El PAO se calcula teniendo esto en cuenta, por eso es tan importante no consumir ningún cosmético más allá de ese tiempo, aunque aparentemente esté en buen estado.
En la nota de prensa de la OCU añaden la recomendación «Si al abrir el bote de crema su color, olor o textura se ha modificado no debería utilizarse». Si el producto es oleoso, su mal estado se detecta con facilidad, porque, con la rotura de emulsiones, se separan las fases y aparece un sobrenadante, que se traduce en líquido sobre el producto. Pero la mayoría de las veces no es así de sencillo y la contaminación de un cosmético no se percibe a simple vista. Utilizar un cosmético en mal estado puede causarnos reacción en la piel, desde una irritación hasta una infección bacteriana. Por eso es una temeridad aconsejar que se use un cosmético más allá de su PAO, aunque «parezca» que está en buen estado.
En la actualidad se ha dado un paso adelante muy acusado con respecto a la concienciación de lo importante que es la protección solar. Según la Asociación Española Contra el Cáncer (AECC) alrededor del 80% de la población española utiliza protección solar cuando va la playa, el 50% cuando practica deporte a la intemperie durante el verano, y el 42% de la población utiliza productos de uso diario para protegerse, como por ejemplo cremas hidratantes o maquillajes con protección solar media o alta. También ha mejorado la profesionalización del mercado: actualmente el 35% de la población adquiere su protección solar en las farmacias y parafarmacias, donde un experto pueda asesorarles.
Durante muchos años hemos vivido ingenuamente despreocupados por la radiación solar, creyendo que los fotoprotectores o bien no servían para nada, o bien dificultaban el bronceado. Incluso en los años 90 había quien tomaba el sol sin protección, embadurnado en potingues grasos y zumos de zanahoria que supuestamente ayudaban a potenciar el moreno. Estas ideas y estas prácticas, aunque todavía no se han erradicado completamente, hoy nos parecen escandalosas. Estamos concienciados y es por ello por lo que confiamos en la eficacia de los productos de protección solar, incluso por encima de cualquier otro producto cosmético.
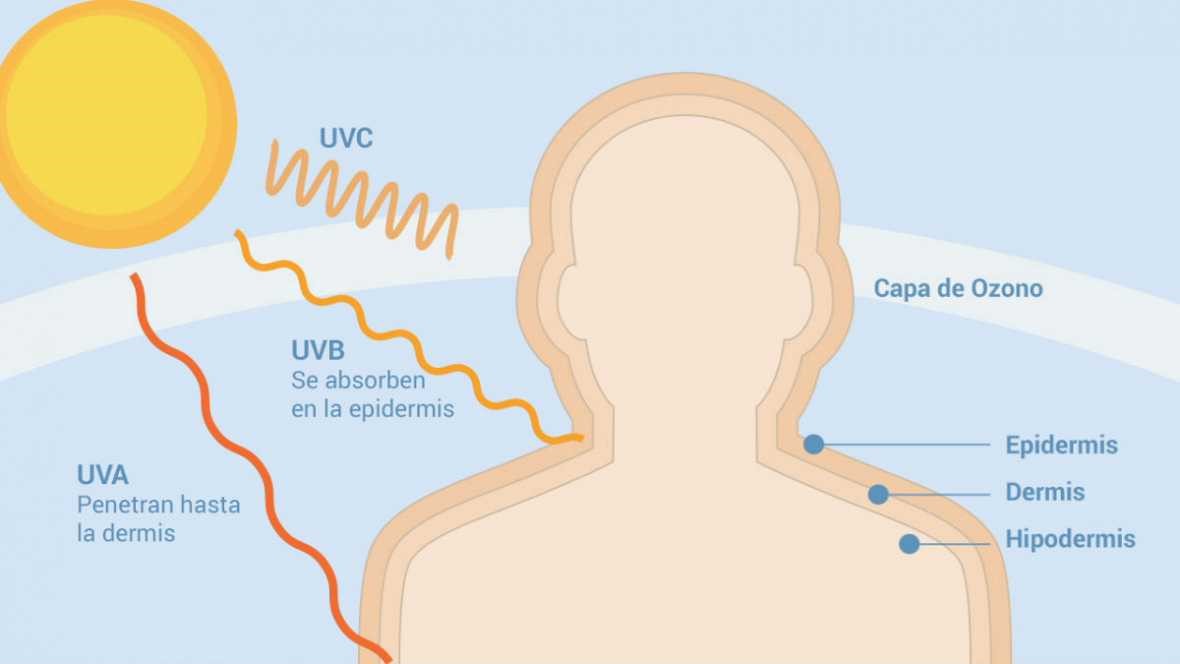
La radiación ultravioleta (tanto la UV-A como la UV-B) es suficientemente energética como para romper enlaces de moléculas y generar fragmentos muy reactivos llamados radicales libres. Estos radicales son tan reactivos que consiguen alterar las moléculas de ADN. Esto se traduce en que la radiación UV es mutagénica, modifica el ADN, y por tanto es potencialmente cancerígena.
Otros problemas cutáneos como la rosácea, algunos tipos de dermatitis y el acné, se agravan a causa de la exposición a la radiación ultravioleta. Por este motivo es importantísimo protegerse de la radiación ultravioleta.
Para protegernos de la radiación ultravioleta, los productos de protección solar contienen, entre otros importantes ingredientes, dos tipos de filtros: filtros químicos y/o filtros físicos. Ambos filtros solares funcionan absorbiendo la radiación ultravioleta y reemitiéndola como radiación visible o térmica, inocua para la piel. Los filtros químicos son compuestos orgánicos cromóforos y los filtros físicos son compuestos minerales fluorescentes.
Los filtros químicos resultan ventajosos frente a los filtros físicos porque son más cosméticos, ya que no dejan rastro blanco en la piel, y permiten formulaciones hidratantes, ya que los filtros físicos son de por sí deshidratantes. En cambio, los filtros físicos presentan la ventaja de ser más estables a lo largo del tiempo que los filtros químicos. Los productos de gama media-alta presentan una combinación de los dos tipos.
La estabilidad de los filtros solares es crucial a la hora de determinar la PAO de estos productos. El uso de un producto cosmético más allá de su PAO no sólo afecta a la seguridad del producto y, por tanto, a nuestra salud, sino también a su eficacia.
La eficacia de un producto de protección solar se mide por su SPF (factor de protección solar: número de veces que el fotoprotector aumenta el tiempo de defensa natural de la piel frente al eritema o enrojecimiento). Los ensayos que permiten verificar el SPF de un cosmético son muy laboriosos. Es más costoso para el laboratorio cosmético verificar un SPF 50 que un SPF 15.
También hay que tener en cuenta que, sobre todo en el caso de los filtros físicos nanoparticulados y en el de los filtros químicos, su estabilidad va mermando, con lo que el SPF sólo puede garantizarse por un periodo de tiempo reducido. De ahí que muchos de ellos sean 12M.
Si un cosmético es 12M es porque no es posible garantizar que la degradación sufrida tras 12 meses tras su primer uso no afecte a la seguridad y a la eficacia del producto original. La PAO no es una medida al azar ni una estrategia de mercadotecnia, tal y como se ha insinuado desde la prensa, sino el resultado del estudio de la degradación del producto cosmético.

Obviamente hay cierto margen: tras «doce meses y un día» el producto no va a sufrir un deterioro repentino notable. Y tampoco sufrirá lo mismo un producto que se haya utilizado una vez, o veinte veces, o cuyo aplicador lo mantenga aislado del aire, o sea un tarro en el que metemos la mano, o le hayan entrado arenas, o agua de mar, o haya estado al sol, o nos lo hayamos dejado mal cerrado en la bolsa de la playa, o tirado en un cajón del armario del baño. Hay múltiples factores que pueden hacer oscilar esta medida y es por ello por lo que debemos ser cautos y siempre tener en cuenta las indicaciones del fabricante.
Aunque el ensayo de la OCU sobre seis productos haya dado como resultado que seguían siendo eficaces, ¿por cuánto tiempo?, ¿son esas condiciones comparables a las de mis productos?, ¿son seis productos reflejo de toda la gama de solares que existen en el mercado? Hay demasiadas cuestiones que quedan en interrogante, demasiada incertidumbre y riesgo que asumir. No vale la pena.
Otro asunto a tener en cuenta, aunque quizá sea menos importante, es que llueve sobre mojado. Esa nota de prensa de la OCU vuelve a arremeter sin pudor contra la industria cosmética, sirviéndose de todos los prejuicios que hay sobre ella, con la excusa de la “defensa del consumidor”. El titular busca el retuit sin sonrojo ni búsqueda de datos ni reflexión. La protección solar no es un asunto baladí que deba usarse para buscar clics fáciles y cuotas de socios. El uso de cosméticos más allá de su PAO pone en peligro nuestra salud. Es como para tomárselo en serio.
Si la OCU pretende defender al consumidor, ofrézcannos buenos consejos sobre el buen uso de los cosméticos. Claro que, es más fácil obtener parabienes arremetiendo contra un enemigo impostado sobre el que ya hay suficientes prejuicios, que ofrecer información útil.
Conclusión
Si un producto cosmético es 12M, no lo uses más allá de 12 meses tras el primer uso. No pongas en riesgo tu salud con algo tan serio como la exposición a la radiación ultravioleta por ahorrarte unos euros rebañando los restos de crema del verano pasado.
Está en juego tu salud, no seas tacaño con eso.
Nota:
*El acceso al estudio está limitado a los socios de la OCU.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Estimada OCU: recuerda que NO se pueden utilizar las cremas solares del año pasado se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las cremas hidratantes no hidratan, pero funcionan
- Combustibles solares por un tubo
- Cuando las algas rojas no pueden gestionar los radicales libres
Cómo sintetizar casi cualquier biomaterial usando ADN

Que el ADN es la molécula en la que se atesora la información que permite hacer un ser vivo es de sobra conocido. Que se puede usar como molde para algunas aplicaciones diferentes a las biológicas, no es tan popular, pero tampoco debería resultar extraño a los lectores de esta sección.
Ahora se ha dado un paso más. Un grupo de investigadores encabezado por Lei Tang, de la Universidad de Duke (EE.UU.) da la receta para usar una enzima para fabricar nuevos biomateriales a partir de ADN. Estas instrucciones permitirán a investigadores de todo el mundo sintetizar moléculas autoensamblables para aplicaciones que van desde el suministro de fármacos a nanohilos.
La maquinaria molecular del cuerpo humano, por ejemplo, normalmente se basa en plantillas genéticas para llevar a cabo la síntesis de moléculas. Por ejemplo, las máquinas moleculares llamadas ADN polimerasas leen el ADN base a base para construir copias precisas.
Hay, sin embargo, algunas ovejas negras en el mundo de la biología molecular que no requieren una plantilla. Una de estas aberraciones, llamada transferasa terminal (TdT), trabaja en el sistema inmune y cataliza la adición sin plantilla de nucleótidos (los componentes unitarios del ADN) a un ADN de una sola hebra (recordemos que el ADN es una doble hebra en forma de doble hélice). Las secuencias de nucleótidos aparentemente aleatorias en una sola cadena de ADN no parecen tener mucho uso biológico, pero los investigadores han descubierto qué hacer con ellas.
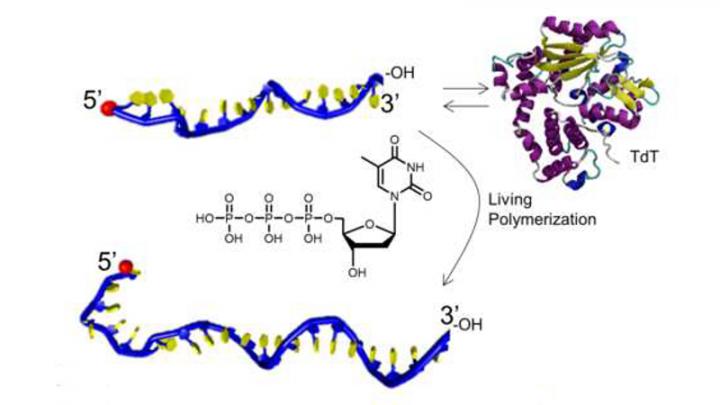
La enzima TdT puede producir estructuras biomoleculares sintéticas precisas de alto peso molecular empleando una fracción del tiempo que los métodos actuales, y en un solo sitio en vez de en un montón de pasos diferentes en una secuencia de síntesis. La síntesis puede adaptarse para crear ADN monocatenario que se autoensambla formando recipientes de tipo bola para administrar fármacos o para incorporar nucleótidos no naturales dando acceso a una amplia gama de posibilidades con utilidad médica.
La TdT tiene la ventaja sobre las reacciones típicas de síntesis en cadena de que continúa añadiendo nucleótidos al final de la cadena de crecimiento siempre y cuando estén disponibles en el medio. Esto abre para los científicos de materiales un amplio espectro para el diseño.
Debido a que todas las enzimas funcionan al mismo ritmo y nunca se detienen, las hebras de ADN resultantes son todas de un tamaño muy parecido, un rasgo importante para controlar sus propiedades mecánicas. Un proceso sin fin también significa que los investigadores pueden alimentar forzadamente a la TdT cualquier nucleótido que quieran, incluso los no naturales, simplemente no proporcionando otras opciones.
Por ejemplo, los nucleótidos no naturales pueden incorporar moléculas diseñadas para facilitar la “química clic“, lo que permite la unión de un conjunto completo de biomoléculas. Los investigadores también pueden iniciar el proceso de síntesis con una base hecha de una secuencia de ADN específica, llamada aptámero, que puede dirigirse a proteínas y células específicas.
La enzima terminal transferasa se conoce desde hace décadas, pero esta es la primera vez que alguien deja de estudiar su papel en el sistema inmunológico humano para encontrar una aplicación tecnológica en la síntesis de polinucleótidos.
Referencia:
Lei Tang et al (2017) High-Molecular-Weight Polynucleotides by Transferase-Catalyzed Living Chain-Growth Polycondensation Angewandte Chemie I.E. doi: 10.1002/anie.201700991
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Cómo sintetizar casi cualquier biomaterial usando ADN se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Usando ADN para sintetizar nanoestructuras de oro
- Cómo mecanizar una pieza de cobre usando bacterias
- Hidrógeno a partir de cualquier biomasa
El rostro humano de las matemáticas
El año 2007, con motivo del centenario de la creación de la Junta de Ampliación de Estudios e Investigaciones Científicas (JAE), germen del actual Consejo Superior de Investigaciones Científicas (CSIC), se celebró el Año de la Ciencia en España.

El médico español Santiago Ramón y Cajal (1852-1934) fue presidente de la Junta de Ampliación de Estudios e Investigaciones Científicas entre 1907 y 1934, pocos años antes de su disolución, en 1939, tras la Guerra Civil Española. Esta imagen pertenece al cómic “Neurocómic”, de Matteo Farinella y Hana Ros (Norma Editorial, 2014)
El objetivo del Año de la Ciencia fue “concienciar a toda la sociedad y muy especialmente a los jóvenes de apoyar y participar en los avances de cualquier rama de la ciencia y la tecnología”.
Como respuesta al llamamiento que la Fundación Española para la Ciencia y la Tecnología (FECyT) y el Ministerio de Educación y Ciencia (MEC) hicieron dentro de la Convocatoria de Ayudas para la Realización de Acciones de Difusión y Divulgación Científico y Tecnológica del Año de la Ciencia 2007, la Real Sociedad Matemática Española (RSME) propuso, entre otras acciones, la creación de una exposición de caricaturas de matemáticos y matemáticas.
Con esta exposición se quería acercar a la sociedad un trozo de la Historia de las Matemáticas, y más concretamente, de los protagonistas de la misma, es decir, a los personajes, hombres y mujeres, que habían desarrollado las matemáticas y descubierto los grandes teoremas y teorías matemáticas.
La mayoría de las personas de nuestra sociedad no tienen ningún problema en nombrar grandes personajes de la historia de las artes gráficas, la literatura, el cine, la música o el deporte, sin embargo, son incapaces de nombrar a diez grandes nombres de la historia de las matemáticas, salvo quizás a Pitágoras o Newton. Incluso estudiantes de Bachillerato, a pesar de que han estudiado los teoremas de Tales y Pitágoras, el triángulo de Pascal o de Tartaglia, la sucesión de Fibonacci, el binomio de Newton, las coordenadas cartesianas (de Descartes), el teorema de Lagrange (o del valor medio) del cálculo o la campana de Gauss de la estadística, entre otros. De hecho, cuando se ven estos temas en clase rara vez se habla al alumnado de quienes eran sus autores, nadie suele hablar de Pitágoras, Tales, Hipatia, Arquímedes, Fibonacci, Cardano, Gauss, Fermat o Kovaleskaya, por citar algunos.
Por otra parte, la exposición tenía como destinatario al público general, por lo que era muy importante tenerlo en cuenta, lo cual significaba adecuar el lenguaje, el medio de transmisión de la información. El arte gráfico de las caricaturasnos permitía acercarnos a los jóvenes y al público en general de una forma atractiva, con un lenguaje moderno que fuese capaz de llegar a todo el mundo, y muy especialmente a los jóvenes. Y cada una de las caricaturas se acompañaría de una breve biografíaescrita en un lenguaje comprensible para todo el mundo, sin tecnicismos, que destacase tanto aspectos humanos, como científicos del matemático o matemática. En resumen, la Historia de las Matemáticas a través de sus personajes con una perspectiva no académica sino atractiva y humana. Además, se realizarían versiones en los diferentes idiomas, además del castellano, el catalán, el euskera, el gallego y el valenciano.
El germen de esta idea de utilizar las caricaturas para acercar a los matemáticos y matemáticas, y por lo tanto, su ciencia, a la sociedad, fueron una serie de caricaturas de matemáticos españoles actuales que se habían realizado unos años antes desde la Comisión de Divulgación de la RSME, y que se colgaron del portal DivulaMAT [www.divulgamat.net]. Aquí podéis ver algunas…

Manuel de León (ICMAT-CSIC, Madrid), caricatura realizada por Enrique Morente

Pilar Bayer (Universidad de Barcelona), caricatura realizada por Enrique Morente
Este proyecto fue coordinado por Antonio Pérez Sanz y por mí (Raúl Ibáñez Torres), y en el mismo participaron, además de nosotros dos, un grupo de personas de la RSME: Santiago Fernández Fernández, Pedro M. González Urbaneja, Vicente Meavilla Seguí, Fco. Javier Peralta Coronado y Adela Salvador Alcaide; así como dos dibujantes del País Vasco: Enrique Morente Luque, Gerardo Basabe Pérez de Viñaspre.

Raúl Ibáñez (Universidad del País Vasco, Bilbao), caricatura realizada por Enrique Morente

Antonio Pérez Sanz (IES Salvador Dalí, Madrid), caricatura realizada por Enrique Morente
La exposición estaba formada por de 31 caricaturas de grandes matemáticos, entre ellos se incluyeron 5 mujeres matemáticas y 5 matemáticos españoles, así como una breve reseña biográfica de cada uno de ellos, destacándose no solamente la parte científica sino también la parte humana, y un elemento gráfico de las matemáticas del trabajo de ese personaje.
La primera parte de la organización de esta acción divulgativa consistió en la elección, nada fácil, de las personas de la Historia de las Matemáticas que iban a estar en la exposición. La lista no era muy grande, por lo que cualquier elección que hiciésemos sería polémica y además había que intentar compensar por épocas y áreas de las matemáticas, y pensar que la exposición estaba destinada al público general y no a la comunidad matemática o científica.
La lista de matemáticos, y matemáticas, que salió después de varias listas de nombres y varios debates fue la siguiente (podían haberse elegido otras personas, pero en aquel momento, esta fue el listado que se confeccionó):
1.- Pitágoras (ca. 585-500 a.C.)
2.- Euclides (ca. 325-265 a. C.)
3.- Arquímedes (ca. 287-212 a.C.)
4.- Apolonio (ca. 262-190 a.C.)
5.- Hipatia (¿?-415)
6.- Mohammed ibn Musa Al-Khwarizmi (s. IX)
7.- Leonardo de Pisa, Fibonacci (ca. 1175-1250)
8.- Niccolò Fontana, Tartaglia (ca. 1499-1557)
9.- Gerolamo Cardano (1501-1576)
10.- René Descartes (1596-1650)
11.- Pierre de Fermat (1601-1665)
12.- Isaac Newton (1642-1727)
13.- Gottfried Wilhelm Leibniz (1646-1716)
14.- Madame de Châtelet (1706-1749)
15.- Leonhard Euler (1707-1783)
16.- Joseph-Louis Lagrange (1736-1813)
17.- Sophie Germain (1776-1831)
18.- Carl Friedrich Gauss (1777-1855)
19.- Augustin-Louis Cauchy (1789-1857)
20.- Niels Henrik Abel (1802-1829)
21.- Évariste Galois (1811-1832)
22.- Bernhard Riemann (1826-1866)
23.- Sofía Kovalévskaya (1850-1891)
24.- Henri Poincaré (1854-1912)
25.- David Hilbert (1862-1943)
26.- Emmy Noether (1882-1935)
27.- Ventura Reyes Prósper (1863-1922)
28.- Julio Rey Pastor (1888-1962)
29.- Pedro Puig Adam (1900-1960)
30.- Lluís Antoni Santaló i Sors (1911-2001)
31.- Miguel de Guzmán Ozámiz (1936-2004)

Pitágoras, caricatura realizada por Gerardo Basabe

Hipatia, caricatura realizada por Enrique Morente
Las reseñas biográficas, con algunos aspectos humanos, debían de ser cortas, de una lectura fácil y rápida, puesto que formaban parte de una exposición, motivo por el cual elegimos una extensión de unos 2.000 caracteres. Además, su tamaño permitía, tanto en el libro como en la exposición on-line, las lecturas individualizadas de las mismas y poder disfrutar de su lectura en situaciones de lo más diversas (desde en una clase de matemáticas a un rato mientras se toma un café tranquilamente).
A continuación, podemos observar los paneles expositivos –caricatura (las tres de Enrique Morente), reseña biográfica y detalle gráfico- correspondientes a Sophie Germain, Carl Friedrich Gauss y Julio Rey Pastor.


“ […] Tenía 19 años en 1795, cuando se fundó la Escuela Politécnica de París. Como las mujeres no eran admitidas (la Escuela Politécnica no admitirá mujeres hasta 1972) consiguió hacerse con apuntes de algunos cursos, entre ellos, los de Análisis de Lagrange. Al final del período lectivo los estudiantes podían presentar sus investigaciones a los profesores, Sophie presentó un trabajo firmándolo como Antoine-Auguste Le Blanc, un antiguo alumno de la escuela. El trabajo impresionó a Joseph Louis Lagrange (1736-1813) por su originalidad y quiso conocer a su autor. Al saber su verdadera identidad, la felicitó personalmente y le predijo éxito como analista, animándola de esta forma a seguir estudiando.
Sus primeros trabajos en Teoría de Números los conocemos a través de su correspondencia con C. F. Gauss, con el que mantenía oculta su identidad bajo el pseudónimo de Monsieur Le Blanc. El teorema que lleva su nombre fue el resultado más importante, desde 1738 hasta 1840, para demostrar el último teorema de Fermat, además permitió demostrar la conjetura para n igual a 5 […]”


“[…]En 1796 demuestra que el heptadecágono, el polígono regular de 17 lados, se puede construir con regla y compás, resolviendo de paso el problema clásico de qué polígonos regulares pueden construirse con regla y compás. A partir de ese momento comienza a llevar su Diario científico donde a lo largo de muchos años anotará sus resultados más importantes. Entre los 19 y 21 años escribió su obra maestra Disquisitiones arithmeticae, publicado en 1801, que convirtió a la Teoría de Números, la Aritmética superior, en una ciencia unificada y sistemática.
En 1801, utilizando su método de mínimos cuadrados va a fijar la órbita de Ceres a partir de las pocas observaciones de Piazzi. En 1807 obtuvo la cátedra de Astronomía en la Universidad de Gotinga y la dirección de su observatorio astronómico, permaneciendo en esos cargos hasta el final de su vida.
Las aportaciones de Gauss en la Matemática fueron extraordinariamente amplias y en todas las ramas que trabajó dejó una huella indeleble. Realizó investigaciones en Álgebra, en 1799 realizó la primera demostración del Teorema Fundamental del Álgebra, en Teoría de Números, Geometría Diferencial (1827, Disquisitiones generales circa superficies curvas), Geometría no Euclídea, Análisis Matemático, Geodesia (triangulación de Hannover), Astronomía Teórica (Theoria motus corporum coelestium), Teoría de la Electricidad y el Magnetismo (Allgemeine Theorie Erdmagnetismus, 1839). […]”


“[…] Nace en Logroño y fallece en Buenos Aires. Suspende el ingreso a la Academia militar y estudia Ciencias Exactas en Zaragoza. Hace el doctorado en Madrid sobre Geometría Proyectiva y participa vivamente en la creación de la Sociedad Matemática Española (1911), de la que es secretario.
Catedrático de Análisis Matemático en Oviedo (1911) y Madrid (1913), sigue su formación en Alemania. En 1915 funda el Laboratorio y Seminario Matemático, origen de nuestra mejor investigación matemática.
La Institución Cultural Española le invita a ir a Buenos Aires, y su magisterio cosecha un gran éxito. Al marchar, desaparece la Revista de la SociedadMatemática Española, y al volver funda la Revista Hispano-Americana.
Tras otros viajes, fija su residencia en Argentina y juega un papel capital en la modernización de su matemática. Alterna luego su actividad con Madrid, salvo de 1936 a 1947 en que permanece en Argentina, y ayuda a instalarse a matemáticos exiliados españoles […]”
A partir del material elaborado se desarrollaron cuatro estructuras distintas:
i) Una exposición de calidad para mover por los Museos de la Ciencia y otros Museos, que visitó por ejemplo, Miramon Kutxaespacio de la Ciencia, la Casa de las Ciencias de A Coruña o la Casa de las Ciencias de Logroño.
ii) Varias copias de exposiciones flexibles para mover por los centros educativos del estado español, y que se estuvo moviendo durante muchos años, y aún hoy día siguen demandándola algunos centros educativos.
iii) Una exposición virtual, que las personas que están leyendo esta entrada del Cuaderno de Cultura Científica pueden ver en el portal divulgamat, en Castellano, Catalá, Euskara, Galego y Valencià.
iv) Y el magnífico libro “El Rostro Humano de las Matemáticas”, que publicó la editorial Nivola en 2008.

Portada del libro El Rostro humano de las matemáticas (Nivola, 2008)
Y terminamos con las caricaturas de otros tres personajes de la exposición El rostro humano de las matemáticas.

Sofía Kovalevskaya, caricatura realizada por Gerardo Basabe

Henri Poincaré, caricatura realizada por Enrique Morente

Lluís Antoni Santaló i Sors, caricatura realizada por Enrique Morente
Los autores de este proyecto, incluidos los dibujantes, también fuimos caricaturizados, y nuestra caricatura aparece en la parte final del libro, así como en las versiones de divulgamat.

Caricaturas de los autores de la exposición y del libro: Santiago Fernández Fernández, Pedro M. González Urbaneja, Raúl Ibáñez Torres, Vicente Meavilla Seguí, Francisco Javier Peralta Coronado, Antonio Pérez Sanz, Adela Salvador Alcaide, Enrique Morente Luque y Gerardo Basabe Pérez de Viñaspre
Bibliografía
1.- Archivo de la Junta de Ampliación de Estudios e Investigaciones Científicas (1907-1939)
2.- Raúl Ibáñez, Antonio Pérez (coordinadores de la edición), El rostro humano de las matemáticas, Nivola, 2008.
3.- Matteo Farinella, Hana Ros, Neurocómic, Norma Editorial, 2014
El artículo El rostro humano de las matemáticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Matemáticas experimentales
- Artistas que miran a las matemáticas
- Muerte entre las ecuaciones (Historias de muerte y matemáticas 1)
Las actividades animales

Los animales pueden ser tratados como sistemas abiertos que intercambian materia y energía con su entorno y que ejercen un cierto control sobre esos intercambios. Agua, sales, elementos estructurales, energía química, oxígeno, calor, así como los restos químicos de sus actividades (CO2, sustancias nitrogenadas,…) son objeto de un trasiego continuo. La capacidad de un animal para que ese flujo, en una y otra dirección (hacia dentro y fuera del organismo), rinda el máximo beneficio energético posible, a la vez que las condiciones estructurales y fisico-químicas internas permiten el mantenimiento de su integridad funcional, es lo que determina su éxito reproductor y, por lo tanto, su aptitud biológica en términos darwinianos.
Cualquier clasificación que se quiera hacer de las actividades animales de acuerdo con las funciones a cuyo servicio se encuentran contiene, necesariamente, algún criterio arbitrario. Eso es así porque varias de esas actividades cumplen funciones en más de un ámbito. A los efectos de lo que nos interesa exponer aquí, las actividades pueden agruparse en las siguientes tres grandes categorías: (1) mantenimiento de la integridad estructural y funcional del organismo; (2) adquisición y procesamiento de los recursos necesarios para producir copias de sí mismo; y (3) control e integración de los procesos implicados en las funciones anteriores y en las relaciones (del tipo que fueren) con el resto de organismos del mismo o de otros linajes.
La primera categoría engloba las actividades implicadas en el mantenimiento de las condiciones que permiten que los procesos fisiológicos cursen de tal forma que el sistema animal en su conjunto mantenga su integridad. En rigor cabría atribuir a esta categoría casi todas las actividades –todas con la única excepción de las reproductivas-, pero algunas de ellas tienen cometidos más específicos, por lo que serán tratadas de acuerdo con su especificidad. La integridad funcional depende de los siguientes elementos: (1) mantenimiento del balance de agua y solutos en las células y en el individuo en su conjunto, incluyendo el concurso del sistema excretor; (2) equilibrio ácido-base de los líquidos corporales; (3) funcionamiento del sistema cardio-vascular como sistema de distribución y transporte de información, gases, nutrientes, deshechos y calor; (4) tareas de defensa; y (5) sistema de captación de O2 y eliminación de CO2 y transporte de estos gases.
La segunda categoría comprende las actividades mediante las cuales se adquieren y procesan los recursos que proporcionan: (1) la energía química que alimenta el conjunto de las actividades animales; y (2) los elementos estructurales que se necesitan para elaborar nuevos tejidos, ya sean para la línea somática o la línea germinal. Incluye, por lo tanto, (1) funciones de adquisición, digestión y absorción del alimento; (2) el metabolismo en su conjunto en su doble vertiente de indicador del nivel de actividad global del organismo y de gasto de energía en forma de calor disipado; y (3) balance energético de los procesos de ganancia y pérdida de energía, del que depende el crecimiento y la reproducción del individuo.
Y en la tercera categoría se incluyen las actividades que permiten: (1) recibir información del estado del organismo y del entorno; (2) procesar esa información y elaborar respuestas; y (3) ejecutar esas respuestas mediante cambios en las funciones fisiológicas internas o mediante actuaciones sobre el entorno. Esta categoría comprende el funcionamiento de los sistemas nervioso, endocrino y de los órganos efectores, especialmente los sistemas musculares.
Para concluir debemos remarcar una idea presentada al comienzo: los animales del presente son los herederos actuales de antecesores que, bajo las específicas circunstancias ambientales en que vivieron, han dejado mayor número de réplicas (parciales) de su información genética que otros muchos miembros de su linaje. Son, por lo tanto, herederos de los animales con mayor aptitud biológica de sus respectivas generaciones. Es a la luz de ese hecho como debe valorarse el modo en que cada individuo animal desarrolla sus actividades.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Las actividades animales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El tamaño relativo de los órganos animales
- Los animales
- El sistema de la difusión social de la ciencia: Efecto de las actividades de difusión científica
La máquina de vapor (1)

Segunda máquina de vapor construida por Newcomen (1714)
El desarrollo de la ciencia moderna del calor estuvo estrechamente ligado al desarrollo de la tecnología moderna de máquinas diseñadas para realizar trabajo. Durante milenios y hasta hace dos siglos la mayor parte del trabajo se realizaba por animales (humanos y de otras especies). El viento y el agua también proporcionaban trabajo mecánico, pero en general no son fuentes de energía fiables, ya que no siempre está disponibles cuando y donde se necesitan.
En el siglo XVIII, los mineros comenzaron a cavar cada vez a más profundidad en su búsqueda de mayores cantidades de carbón. El agua tendía a filtrarse e inundaba estas minas más profundas. Se planteó la necesidad de un método económico para bombear el agua y sacarla de las minas. La máquina de vapor se desarrolló inicialmente para satisfacer esta necesidad concreta.
La máquina de vapor es un dispositivo para convertir la energía térmica del calor que produce un combustible en trabajo mecánico. Por ejemplo, la energía química de la madera, el carbón o el petróleo, o la energía nuclear del uranio, pueden convertirse en calor. La energía térmica a su vez se utiliza para hervir el agua para formar vapor, y la energía en el vapor se convierte en energía mecánica. Esta energía mecánica puede ser utilizada directamente para realizar trabajo, como en una locomotora de vapor, o utilizada para bombear agua, o para transportar cargas, o se transforma en energía eléctrica. En las sociedades post-industriales típicas de hoy, la mayor parte de la energía utilizada en las fábricas y en los hogares proviene de la energía eléctrica. Parte viene de saltos de agua y del viento pero la fuente que garantiza el suministro continuo y a demanda sigue siendo la proveniente de generadores.
Existen otros dispositivos que convierten el combustible en energía térmica para la producción de energía mecánica, como los motores de combustión interna utilizados en automóviles, camiones y aviones, por ejemplo. Pero la máquina de vapor sigue siendo un buen modelo para el funcionamiento básico de toda la familia de los llamados motores térmicos y la cadena de procesos desde la entrada de calor hasta la salida de trabajo y el escape de calor residual es un buen modelo del ciclo básico involucrado en todos los motores térmicos.

Modelo moderno de eolípila
Desde la antigüedad se sabe que el calor se puede utilizar para producir vapor que, a su vez, puede realizar trabajo mecánico. Un ejemplo fue la eolípila, inventada por Herón de Alejandría alrededor del año 100. Se basaba en el mismo principio que hace que giren los aspersores de jardín, excepto en que la fuerza motriz era el vapor en vez de la presión del agua. La eolípila de Herón era un juguete, hecho para entretener más que para hacer un trabajo útil. Quizás la aplicación más “útil” del vapor en el mundo antiguo fue otro de los inventos de Herón. Este dispositivo asombraba a los fieles congregados en un templo al hacer que una puerta se abriera cuando se encendía un fuego en el altar.
No fue hasta finales del siglo XVIII que los inventores empezaron a producir máquinas de vapor con éxito comercial. Thomas Savery (1650-1715), un ingeniero militar inglés, inventó la primera máquina de este tipo, a la que dio en llamarse “la amiga del minero”. Podía bombear el agua de una mina llenando alternativamente un tanque con vapor de alta presión, lo que llevaba vaciaba el agua del tanque empujándola hacia arriba, condensando después el vapor, lo que permitía que entrase más agua en el tanque.

Máquina de Savery (1698)
Desafortunadamente, el uso de vapor de alta presión por parte de la máquina Savery implicaba unimportante riesgo de explosiones de calderas o cilindros. Thomas Newcomen (1663-1729), otro ingeniero inglés, solucionó este defecto. Newcomen inventó una máquina que utilizaba vapor a menor presión. Su máquina era mejor también en otros aspectos. Por ejemplo, podía elevar cargas distintas al agua. En lugar de usar el vapor para forzar el agua dentro y fuera de un cilindro, Newcomen utilizó vapor para forzar un pistón hacia adelante y presión de aire para forzarlo hacia atrás. El movimiento del pistón podía utilizarse para mover una bomba u otro tipo de máquina.
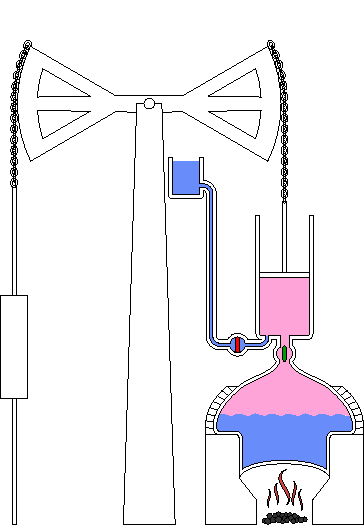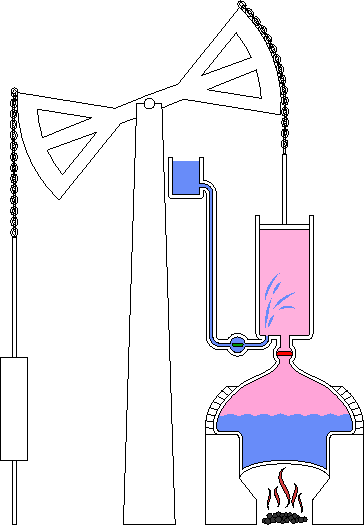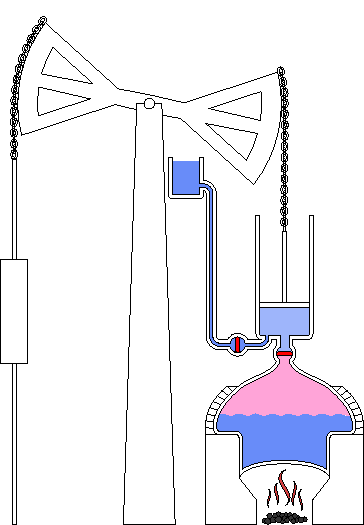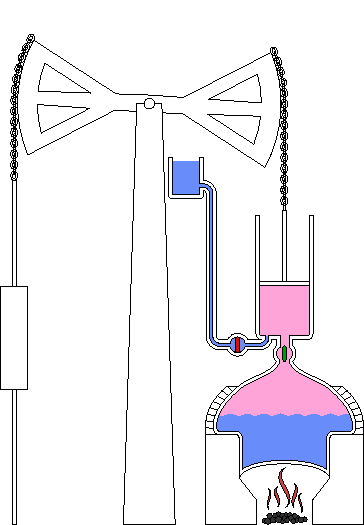
Principio de funcionamiento de la máquina de Newcomen
El movimiento del pistón en una máquina de vapor, hacia adelante y hacia atrás, es uno de los orígenes de la definición de trabajo mecánico, W, como fuerza (F) x distancia (d), W = F·d.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La máquina de vapor (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El terrorismo como sacerdocio

El sufrimiento por las creencias propias facilita que otros compartan las mismas creencias, religiosas y de otro tipo, porque les otorga credibilidad. Esta es la tesis que sostiene Joseph Henrich, de la Universidad de la Colombia Británica (Canada). El prestigio de una persona en el seno de su comunidad facilita considerablemente que las costumbres, ideas y creencias de esa persona sean adoptadas por el resto de sus miembros. Si además de eso, la persona en cuestión está dispuesta a realizar actos costosos o que acarrean sufrimiento en pro de esas costumbres, ideas o creencias, su credibilidad es aún mayor, porque otorgamos mucho valor a ese tipo de actos. Por eso, en las primeras fases de las religiones que tienen éxito suelen aparecer personas de prestigio que los realizan. La gente se fija, sobre todo, en modelos o referencias comunitarias y la credibilidad de su fe es mayor si están dispuestas a sufrir o pasarlo mal para demostrarlo.
Esa es la razón por la que el martirio se convierte en una poderosa herramienta para que las creencias del mártir sean aceptadas por otras personas y para que éstas se comprometan, a su vez, con la causa. Es también el mecanismo que subyace a los votos de castidad y pobreza, o al ayuno, de los líderes religiosos, porque la renuncia (real o aparente) a los correspondientes bienes, supone una muestra de lo genuino de las creencias y promueve su adopción por parte de otras personas.
El mismo argumento vale para los terroristas, sobre todo si son suicidas. Por esa razón, las medidas que puedan adoptar las autoridades para punir determinados comportamientos pueden, en la práctica, servir de estímulo para la aparición de nuevos seguidores de la causa. Los mártires del primer cristianismo son ejemplos claros de ese fenómeno. No es que los terroristas hagan votos de castidad o pobreza, o que ayunen de forma voluntaria, pero ante los potenciales adeptos a su causa aparecen como personas dispuestas a renunciar a bienes, como la libertad o el bienestar material, de los que muchos disfrutan y que tienen en alta estima. Desde ese punto de vista y en sus modalidades menos exageradas, la militancia terrorista bien podría asimilarse a una especie de sacerdocio. Y si los terroristas están dispuestos a arriesgar sus vidas o, incluso, se la quitan a sí mismos como consecuencia inevitable de sus actos, más que sacerdotes, alcanzan la condición de mártires.
Fuente:
Joseph Henrich (2015): The secret of our success. Princeton University Press.
El trabajo original fue publicado por el autor en Evolution and Human Behavior (2009) y se puede consultar aquí.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El terrorismo como sacerdocio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Del relativimo al cientifismo, por Experientia Docet
- La prolongación de la juventud como precarización de lo adulto
- El óxido de grafeno que se mueve como una oruga y coge cosas como una mano
Un espectrómetro Raman portátil mide el punto óptimo de maduración del tomate
Un espectrómetro Raman portátil
El espectrómetro Raman portátil, un equipo que se utiliza en campos tan diversos como la metalurgia, la arqueología o el arte, permite obtener datos sobre la variación de la composición del fruto del tomate en sus diferentes fases de maduración, según los resultados de un estudio realizado en el Departamento de Química Analítica de la UPV/EHU.
El espectrómetro Raman portátil es un instrumento muy utilizado en sectores muy diferentes, ya que es una técnica no invasiva que sirve, por ejemplo, para observar los pigmentos que contiene un cuadro o una escultura sin tener que extraer muestra alguna, preservando así la integridad de la obra en cuestión. En este caso, los investigadores han aplicado el espectrómetro Raman a la investigación culinaria. Según Josu Trebolazabala, autor del estudio, “se trata de un trasvase de esta tecnología, que tenía un uso concreto, a la cocina. Nuestra idea era crear una herramienta que pudiera ayudar al productor a saber cuál es el punto óptimo de maduración del tomate. Con esta técnica se consigue, además, hacerlo sin destruir el fruto”.

Josu Trebolazabala analiza en el laboratorio la composición de un tomate mediante el espectrómetro Raman. Foto: Txetxu Berruezo.
Los resultados ofrecidos por este instrumento portátil han sido comparados con los ofrecidos por un instrumento similar de laboratorio, y “aunque la calidad de los espectros Raman del instrumento de laboratorio ha resultado ser superior, la información obtenida con la instrumentación portátil puede considerarse de suficiente calidad para el objetivo propuesto, es decir, que el productor pueda ir a la huerta con este equipo y, posando la sonda Raman de contacto sobre el fruto del tomate, pueda saber si el tomate está en un punto de recogida óptimo o hay que dejarlo madurar más tiempo”, comenta Josu Trebolazabala.
La monitorización de la composición del fruto del tomate en sus fases de maduración ha permitido observar los cambios que se producen en la composición del tomate en su tránsito desde su estado inmaduro hacia el estado maduro. “Cuando el tomate está verde, los pigmentos mayoritarios son la clorofila (de ahí su color verde) y las ceras cuticulares, que se encuentran en el exterior”, explica Trebolazabala. Pero la presencia de dichos compuestos desciende a medida que el fruto alcanza su punto óptimo de maduración. “Una vez que el color pasa al anaranjado, se observan otro tipo de compuestos; se activan los compuestos carotenoides. El tomate va adquiriendo nutrientes hasta llegar al punto óptimo, es decir, cuando el licopeno (carotenoide de color rojo) está en su máximo. Después, el tomate empieza a perder contenido en carotenoides, como demuestran los análisis realizados en tomates excesivamente maduros”.
Esta innovadora técnica es extrapolable a cualquier otro alimento que cambie de coloración durante su etapa de maduración. “Se han realizado pruebas con el pimiento y con la calabaza, por ejemplo, y también es posible obtener datos sobre su composición”, aclara.
Referencia:
J. Trebolazabala, M. Maguregui, H. Morillas, A. de Diego, J.M. Madariaga.. Portable Raman spectroscopy for an in-situ monitoring the ripening of tomato (Solanum lycopersicum) fruits. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 180: 138-143. DOI: 10.1016/j.saa.2017.03.024.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un espectrómetro Raman portátil mide el punto óptimo de maduración del tomate se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La pantalla de tu móvil solo tiene tres colores
- Otra pieza en el puzle de la fotosíntesis
- La contaminación por metales pesados no llega a los tomates
Sin atajos frente al cáncer

El archiconocido empresario norteamericano Steve Jobs murió a consecuencia de un cáncer de páncreas que no fue operado a tiempo. Si hubiese sido intervenido cuando le fue diagnosticada la enfermedad, el desenlace podría haber sido otro. Sin embargo, Jobs optó por recurrir a terapias alternativas, y retrasó la intervención que, realizada a tiempo, podría quizás haberle salvado. Ese no es, desgraciadamente, el único caso en que la renuncia a las terapias más eficaces de que disponemos conduce a un desenlace fatal.
Aparte de para curarse, también hay quien recurre a remedios supuestamente preventivos. Se promocionan dietas con la pretensión declarada de prevenir la aparición de tumores. Y en el colmo de la desfachatez –por no decir, directamente, de la maldad- hay quienes atribuyen a los enfermos la responsabilidad de su situación, al afirmar que el cáncer tiene origen en algún problema psicológico no resuelto mediante alguna práctica o modo de vida supuestamente indicado a tal efecto.
Proliferan ahora dietas “anti-cáncer”. Una de las más populares es la llamada “dieta alcalina”, que usaré aquí, a modo de ejemplo, para ilustrar el sinsentido de esta y otras falsas terapias. Para entender el fundamento en que supuestamente se basa, hay que tener en cuenta que el entorno de las células cancerosas suele ser ácido y que los promotores de la dieta milagrosa sostienen que esa acidez es la que provoca el cáncer. Creen que hay que neutralizarla ingiriendo una dieta alcalina.
La razón de que las células cancerosas se encuentren en un entorno ácido es que, para obtener energía, tienden a utilizar más glucosa que las sanas, haciendo uso de una vía metabólica llamada glucolisis, sin que esa ruta sea complementada por otras que son las que en muchos tejidos animales proporcionan más energía y acaban requiriendo el concurso del oxígeno que respiramos. En esas condiciones, los productos finales de la glucolisis son sustancias ácidas, y es por eso por lo que el entorno de esas células se acidifica. Algo parecido ocurre, por cierto, con las células de nuestros músculos cuando los sometemos a un esfuerzo muy intenso; bajo esas condiciones la glucosa, tras una serie de etapas, acaba convirtiéndose en ácido láctico.
A la utilización preferente de glucosa por las células cancerosas se le denomina “efecto Warburg”, pues fue Otto Warburg quien lo describió en 1924. De hecho, fue él quien sugirió que el cáncer podía ser una consecuencia del fenómeno descrito. Sin embargo, como hemos visto, la secuencia causal es la opuesta: son las células cancerosas las que provocan la acidificación del entorno, y no al revés. Y en todo caso, conviene aclarar que el grado de acidez del organismo no puede modificarse con la dieta, puesto que está regulado fisiológicamente de forma muy estricta, sin que la acidez de aquélla ejerza ningún efecto.
Los diagnósticos de cáncer son difíciles de aceptar, sobre todo cuando el tratamiento prescrito es agresivo, como suele ocurrir con la quimioterapia. Y por esa razón no es raro que a la hora de afrontar un tratamiento duro, de efectos secundarios muy desagradables e incluso temporalmente incapacitantes, haya quien valore la posibilidad de probar terapias alternativas. No faltan, además, personajes que, valiéndose del sufrimiento de los enfermos, les ofrecen remedios sin los duros efectos de los tratamientos oncológicos habituales. Pues bien, conviene tener siempre presente que son los médicos de nuestro sistema de salud los únicos capacitados para prescribir la terapia más eficaz posible. Cuando el camino a recorrer es muy duro, la tentación de tomar atajos es muy fuerte, también frente a la enfermedad. Pero tampoco frente al cáncer hay atajos.
Adenda:
Tras su publicación en la sección con_ciencia del diario Deia el 29 de enero pasado, este texto recibió comentarios críticos con la idea de que el cáncer que sufría Jobs tuviese mejor pronóstico que la mayoría de los que afectan al páncreas, razón por la cual no debía criticarse su opción por explorar tratamientos alternativos a los que le ofrecía la medicina. Quien suscribe no es especialista en oncología; ni siquiera es médico. Recurro, por ello, a lo que señala la Wikipedia en inglés a ese respecto y que cada cual juzgue:
En octubre de 2003 a Jobs se le diagnosticó cáncer. A mediados de 2004 él anunció a sus empleados que tenía un tumor canceroso en el páncreas. El pronóstico para el cáncer de páncreas es normalmente muy negativo. Jobs especificó que él tenía un tipo de tumor raro, no tan agresivo, conocido como carcinoma de los islotes pancreáticos.
A pesar del diagnóstico, durante nueve meses Jobs no hizo caso a las recomendaciones de sus médicos de que se operase, confiando, por el contrario, en una dieta pseudo-médica para intentar un tratamiento natural para combatir la enfermedad. De acuerdo con el investigador de Harvard Ramzi Amri, su opción por un tratamiento alternativo le condujo a una muerte innecesariamente temprana. El investigador en cáncer y crítico de la medicina alternativa David Gorski disentía de la opinión de Amri, y manifestó que “según mi criterio, Jobs probablemente solo redujo de manera modesta sus posibilidades de sobrevivir”. Barrie R. Cassileth, el jefe del departamento de medicina integrativa del Memorial Sloan Kettering Cancer Center dijo que “la fe de Jobs en la medicina alternativa probablemente le costó la vida…. Él tenía el único tipo de cáncer de páncreas que es tratable y curable… Él, básicamente se suicidó.” De acuerdo con el biógrafo de Jobs, Walter Isaacson, “durante nueve meses él rehusó someterse a una cirugía para su cáncer de páncreas, una decisión que más tarde lamentaría conforme su salud empeoró. En vez de ello, probó una dieta vegana, acupuntura, hierbas y otros tratamientos que encontró en internet, e incluso, consultó a un vidente. El estaba muy influido por un médico que dirigía una clínica que prescribía enemas, ayunos y otros tratamientos carentes de fundamento antes de ser operado en julio de 2004 y de serle extirpado el tumor. Jobs no recibió radioterapia ni quimioterapia.”
—————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Sin atajos frente al cáncer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
