La insoportable levedad del TRES, o sobre la existencia de sistemas numéricos en base 3
En dos entradas anteriores de la sección Matemoción del Cuaderno de Cultura Científica hemos hablado de las palabras para los números que utilizaban diferentes “pueblos primitivos” del mundo.
I) “Los números deben estar locos”
II) “El gran cuatro, o los números siguen estando locos”
En la primera entrada, se contaba como muchos de estos pueblos solamente disponían de dos vocablos para los números básicos “uno” y “dos”, términos que podían combinar para construir las palabras para algunos números más, de forma que para el tres se utilizaba una expresión del tipo “dos uno” o para el cuatro “dos dos”, como mucho hasta el número diez. A este método de contar se le denominaba “contar por pares” y en el libro Numbers through the ages, de Graham Flegg, se citan unos noventa “pueblos primitivos”, de África, Sudamérica, Norteamérica y la zona de Australia y Nueva Guinea, que utilizaban el método de contar por pares, o alguna sencilla variación.
En la segunda entrada, se mostraban algunos ejemplos de lenguas de “pueblos primitivos” que utilizaban métodos de contar por cuartetos, es decir, con el número cuatro como base. Estos no eran tan frecuentes como los métodos basados en el mencionado número 2 (contar por pares), o en los números 5, 10 o 20, muy frecuentes debido a que disponemos de 5 dedos en la mano, 10 en ambas manos o 20 dedos entre manos y pies.

El número 3 está muy presente en la obra de Joan Miró, como por ejemplo, en el cuadro “13, La escalera ha rozado el firmamento” (1940)
En esta entrada vamos a fijarnos en métodos de contar mucho más raros aún, aquellos que tienen como base el número tres. Como se menciona en el artículo Rarities in Numeral Systems, de Harald Hammarström, se han encontrado muy pocos ejemplos de “pueblos primitivos” que utilizaran un método de contar basado en el número tres, aunque alguno hay, en particular, en la zona de Nueva Guinea.
La lengua Ámbulas, que es una de las pertenecientes a la familia de lenguas Ndu de Papua Nueva Guinea, tiene unos 44.000 hablantes de la zona de Maprik, según Patricia Wilson (referencia [4], de 1989). Tiene tres dialectos, uno de ellos el Wingei, que es del que vamos a hablar aquí.
Los números en Wingei se cuentan, esencialmente, en grupos de tres, aunque en el relacionado dialecto Maprik de la lengua Ámbulas se utiliza la base cinco.
A continuación, mostramos una tabla con las palabras de los números en la lengua Ámbulas.

La palabra para el número “seis” es “taabak”, que es la palabra para designar la mano, luego en la lengua Ámbulas la mano se ve como una entidad de seis elementos. Esto quizás, es una especulación, sea debido a que cuentan en la mano cada uno de los cinco dedos, así como la propia mano, luego seis elementos (más abajo se muestra otra posible explicación). Para los números 7, 8 y 9 se suman los números básicos 1, 2, 3 al número 6. Así, el número “ocho” se dice “taabak kaayek vétik”, algo así como “seis más dos”, el número “nueve” es “taabak kaayek kupuk”, mientras que el número “siete” se dice solo “taabak kaayek”, en lugar de la expresión lógica “taabak kaayek nawurak”, como si se sobreentiende que se suma una unidad, ya que se suma algo.
La palabra para el número “doce” es dos manos o dos veces seis, “taaba vétik”. Y a partir de esta palabra se generan las palabras 10 y 11 al restarle 1 o 2. Así, la palabra para “diez” es “vétik taaba vétik”, es decir, 12 “taaba vétik”, menos (al colocarla por delante, como en los número romanos) 2 “vétik”, y la palabra para “once” es “nawurak taaba vétik”. Y así se puede seguir contando hasta el número 24. Y para el número “veinticuatro”, ya que no se puede decir cuatro veces seis, se utiliza una nueva palabra en Wingei, es “nawura mi”, cuya etimología no está clara.

Mujer Wingei en un mitin político
Otro ejemplo de pueblo que utiliza un sistema en base tres son los Waimiri Atroari, o Kinja (como se autodenominan), en la zona del Amazonas en Brasil, que está casi completamente desaparecido como consecuencia de su oposición al progreso que se estableció en su territorio (la construcción de una carretera o la instalación de algunas empresas, minera e hidroeléctrica), como se menciona en esta página sobre pueblos indígenas de Brasil.
Los Waimiri Atroari tenían un sistema en base tres para contar hasta nueve, que era “tres tres tres”. Las palabras para los números eran:
“uno” (1) = awenin (o awini, awinini);
“dos” (2) = typytyna;
“tres” (3) = takynyna, takynynapa;
“cuatro” (4) = typytypytyna (algo así como el doble de dos, ya que había una repeteción, algo así como en el método de contar por pares), o también, takynynapa awenini (que es el más lógico “tres más uno”);
“cinco” (5) = takynynapa typytyna (3 + 2);
“seis” (6) = takynynapa takynynapa (3 + 3);
“siete” (7) = takynynapa takynynapa awenini (3 + 3 + 1);
“ocho” (8) = takynynapa takynynapa typytyna (3 + 3 + 2);
“nueve” (9) = takynynapa takynynapa takynynapa (3 + 3 + 3).

Los Waimiri Atroari del Amazonas (Brasil)
Para terminar, la lengua Bukiyip, otra lengua de Papua Nueva Guinea (de las montañas Torricelli), también conocida como Arapesh de las montañas, que dispone de dos sistemas para contar, uno en base tres y otro en base cuatro, y cual de ellos se utiliza depende de cuales sean los objetos que se cuente. Así, para contar cocos, boniatos pequeños, fardos de leña, días, huevos, pájaros, lagartos, peces, árboles del pan, arcos o flechas se utiliza el sistema en base tres, mientras que el sistema en base cuatro se utiliza para contar nueces de areca, boniatos grandes, troncos (individuales) de leña, lunas (meses), carne de caza, plátanos o escudos.
La palabra para “mano” en la lengua Bukiyip, anauwip, aparece en ambos sistemas para contar. En el sistema en base tres significa “seis” (6) ya que se cuentan los 5 dedos y la base del pulgar, mientras que significa “veinticuatro” (24) en el sistema en base 4, ya que se considera que se multiplica por cuatro cada uno de los seis elementos mencionados de la mano, como se explica en el libro When languages die, de K. David Harrison.

Figura arapesh de las montañas Torricelli, en Papua Nueva Guinea
Bibliografía
1.- Georges Ifrah, Historia universal de las cifras, Espasa Calpe, 2002.
2.- Graham Flegg, Numbers through the ages, Macmillan, Open University, 1989.
3.- Harald Hammarström, Rarities in Numeral Systems, Rethinking universals: How rarities affect linguistic theory 45, 2010, p. 11-53.
4.- Patricia Wilson, Ambulas-Wingei statement, 1989 [http://www-01.sil.org/pacific/png/pubs/50783/Ambulas_Wingei_Stat.pdf]
5.- Diana Green, Diferenças entre termos numéricos em algumas línguas indígenas do Brasil, Boletim do Museu Paraense Emílio Goeldi, Série Antropologia, 1997, p. 179-207.
6.- K. David Harrison, When languages die: the extinction of the world languages and the erosion of human knowledge, Oxford University Press, 2007
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La insoportable levedad del TRES, o sobre la existencia de sistemas numéricos en base 3 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El problema de los tres caballeros y los tres criados
- El Ballet Triádico: un homenaje al número tres
- El Mengenlehreuhr: existencia y unicidad
A mayor tamaño menor intensidad metabólica

En el curso de la evolución han ido surgiendo animales de tamaños cada vez mayores (aquí). Ese mayor tamaño ha ido acompañado por una especialización progresiva en el trabajo biológico, de manera que han ido surgiendo nuevos tejidos y ha aumentado el número de tipos celulares (aquí). Por otra parte, como vimos aquí, los animales de diferente tamaño tienen características estructurales diferentes; la proporción que representa cada componente, órgano o tejido es distinta en animales grandes y animales pequeños. En los pequeños el encéfalo o el tegumento, por ejemplo, son relativamente mayores que en los grandes; y estos tienden a tener osamentas proporcionalmente mayores y más tejidos grasos.
No solo los aspectos estructurales varían de acuerdo con el tamaño. También los aspectos funcionales cambian. Y el que quizás sintetiza de forma más clara ese cambio es el metabolismo. Obviamente, un animal de tamaño grande despliega una mayor actividad metabólica total que uno pequeño, por la simple razón de que el animal grande tiene más biomasa, más células y más mitocondrias. En términos puramente energéticos, el grande disipa una mayor cantidad de calor que el pequeño. Sin embargo, si en vez de considerar el metabolismo total de dos individuos de diferente tamaño atendemos a sus respectivas tasas metabólicas, comprobaremos que los animales pequeños tienen tasas metabólicas mayores que los grandes. La tasa metabólica representa la actividad metabólica por unidad de masa corporal; es pues, una medida de la intensidad relativa del conjunto de las reacciones químicas que tienen lugar en un organismo.
Los animales de menor tamaño desarrollan una mayor actividad biológica por unidad de masa que los grandes, y esto vale tanto si consideramos individuos de la misma especie como si la comparación la hacemos entre animales de distintas especies. Dado que el metabolismo se traduce, al final, en disipación de calor hacia el exterior, se suele decir que si un elefante tuviera la tasa metabólica de un ratón, el elefante ardería; el calor que generaría su actividad no podría disiparse a través de la superficie corporal, se acumularía y, a partir de una determinada temperatura, se echaría a arder1.
En 1883 Max Rubner, a partir de resultados experimentales, propuso que el metabolismo de un animal era proporcional a su superficie corporal, y no a su masa; esa idea era compatible con el hecho de que el calor resultante de la actividad metabólica se disipa a través de la superficie corporal. Hace ahora un siglo, August Krogh, el fisiólogo que recibió el premio Nobel por descubrir el mecanismo (apertura y cierre de arteriolas y capilares) mediante el que los músculos reciben cantidades variables de sangre en función de sus demandas metabólicas, propuso que el metabolismo debería ser una función de la masa del individuo de acuerdo con una ecuación potencial del tipo M = a Wb, en la que M es el metabolismo y W es la masa del animal. Si la idea de Rubner hubiese sido correcta, la potencia de esa ecuación debería valer 0,67 (2/3), ya que la masa es proporción lineal del volumen y 2/3 es la relación superficie:volumen. Sin embargo, Max Kleiber, en 1933 observó que, al menos para animales endotermos, el valor de esa potencia era 0,75 (3/4) y no 0,67. Y en 1960, A. M. Hemmingsen generalizó esa relación a los animales ectotermos.
Desde entonces se han buscado todo tipo de explicaciones para el valor 0,75, pero ninguna ha concitado suficiente acuerdo en la comunidad científica. La última propuesta de cierto éxito se debe a Geoffrey B. West, James H. Brown y Brian J. Enquist (1997) y se trata de una explicación basada en la arquitectura de los sistemas circulatorios. Según un elegante análisis teórico en el que incorporan todas las variables relevantes de los sistemas respiratorios y circulatorios llegan a la conclusión de que la potencia 0,75 (3/4) es una característica de todos los organismos y se deriva de un modelo general que describe el modo en que los materiales esenciales son transportados a través de redes fractales de tubos que al ramificarse van ocupando el espacio interno disponible para tales estructuras. Es un modelo que asume que la energía disipada en esos procesos de transporte se minimiza y que los tubos terminales (capilares en el sistema circulatorio) no varían con el tamaño del animal. El modelo no solo proporciona un valor teórico para la potencia que relaciona el metabolismo con el tamaño; también lo hace para otros parámetros característicos de la fisiología respiratoria y circulatoria que se hallan muy próximos a las determinaciones experimentales.
Sin embargo, aunque cosechó un éxito considerable, tampoco da cuenta precisa de la variabilidad observada. La razón es que conforme se han ido obteniendo datos para más especies y se han ido refinando los análisis, se ha comprobado que la función que relaciona metabolismo y tamaño tiene una mayor curvatura que la que corresponde a una relación potencial o, en otras palabras, que el valor de b de la ecuación M = a Wb se eleva conforme aumenta el tamaño de los animales. Cuando se trata de animales de pequeño tamaño, ese valor se aproxima a 2/3, y en animales de gran tamaño, a 3/4. Y aunque se han propuesto modificaciones al modelo que dan cuenta del fenómeno descrito, en realidad seguimos sin conocer la naturaleza íntima de la relación existente entre metabolismo y tamaño, o sea, la base funcional de tal relación.
En todo caso, y para concluir, si consideramos la enorme variabilidad de tamaños en el mundo animal, no es mala aproximación seguir trabajando con una potencia cuyo valor sea 0,75 (3/4), si bien cuando se dispone de buenos datos para alguna especie, lo lógico es utilizar la ecuación propia de esa especie siempre que sea preciso. Por otra parte, si de lo que se trata es de constatar, sin ulteriores intenciones, que la intensidad metabólica de los animales disminuye conforme aumenta su masa, la ecuación M = a W3/4 es perfectamente adecuada.
Fuentes:
Tom Kolokotrones, Van Savage, Eric J. Deeds & Walter Fontana (2010): Curvature in metabolic scaling. Nature 464, 753-756 (doi: 10.1038/nature08920)
Geoffrey West (2017): Scale, Penguin Press, New York
1Es una imagen muy expresiva, pero en realidad es una exageración, porque el elefante moriría enseguida y la actividad metabólica se detendría antes de que llegase a acumularse tanto calor como para iniciarse la combustión.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo A mayor tamaño menor intensidad metabólica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- A mayor tamaño, mayor complejidad
- El tamaño relativo de los órganos animales
- Evolución del tamaño animal
La primera ley de la termodinámica
Lo que llevamos visto en esta serie, cosas fáciles de entender, macroscópicas, en las que solo hemos empleado algunas relaciones matemáticas muy elementales, nos sobra y nos basta junto con alguna definición adicional para establecer dos de las leyes fundamentales del universo. Así, como suena. En ambos casos son afirmaciones de imposibilidad, es decir, establecen que hay cosas imposibles. veremos en esta entrega la primera y veremos la segunda en la próxima.

Si consideramos al Bugatti Chiron en movimiento como un sistema termodinámico, en él no se cumple la primera ley de la termodinámica. ¿Por qué?
La primera ley de la termodinámica es una generalización de la conservación de la energía en los procesos térmicos. Se basa en la conclusión de Joule de que el calor y la energía son equivalentes. Pero para llegar a ella hay que sortear algunas trampas en el camino.
A partir de la conclusión de Joule podríamos caer en la tentación de llamar al calor energía “interna” asociada con la temperatura. Podríamos entonces agregar calor a las energías potencial y cinética de un sistema, y llamar a esta suma la energía total, que es lo que conservaría. De hecho, esta solución funciona bien para una gran variedad de fenómenos, incluyendo los experimentos de Joule. Los problemas surgen con la idea de “contenido” de calor de un sistema. Por ejemplo, cuando se calienta un sólido hasta su punto de fusión, una “entrada de calor” adicional provoca la fusión pero sin aumentar la temperatura. Con este sencillo experimento vemos que considerar simplemente la energía térmica medida solo por un aumento de temperatura como parte de la energía total de un sistema no dará una ley general completa.
En lugar de “calor”, podemos usar el concepto de energía interna, esto es, una energía en el sistema que puede tomar formas no directamente relacionadas con la temperatura. Podemos entonces usar la palabra “calor” para referirnos solamente a una transferencia de energía entre un sistema y su entorno. De forma análoga, el término trabajo no lo utilizaremos para describir algo contenido en el sistema, sino que describe una transferencia de energía de un sistema a otro. Calor y trabajo son, pues, dos formas en las que la energía se transfiere, no energías.
Estas definiciones no permiten una declaración simplista como “la entrada de calor a un sistema aumenta su energía interna, y el trabajo hecho en un sistema aumenta su energía mecánica”. La entrada de calor a un sistema puede tener efectos distintos al aumento de la energía interna. En un máquina de vapor, por ejemplo, la entrada de calor aumenta la energía mecánica del pistón. Del mismo modo, el trabajo realizado en un sistema puede tener efectos distintos al aumento de la energía mecánica. Al frotarnos las manos en un día frío, por ejemplo, el trabajo que hacemos aumenta la energía interna de la piel de las manos lo que, en este caso, se traduce en un aumento de la temperatura.
En resumen, una ley general de conservación de la energía debe incluir la transferencia de energía como trabajo y la transferencia energía como calor. Además, debe incluir el cambio en la energía total del sistema, pero no con una parte “mecánica” y una parte “interna”.
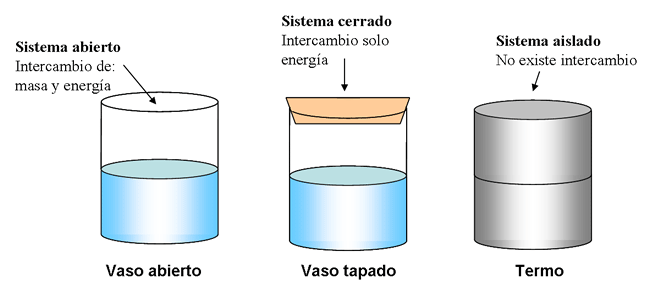
En un sistema aislado, esto es, un sistema que no intercambia materia ni energía con su entorno, la energía total debe permanecer constante. Si el sistema intercambia energía con su entorno pero no materia (lo que se llama sistema cerrado), puede hacerlo solo de dos formas: una transferencia de energía bien en forma de trabajo realizado sobre o por el sistema, bien en forma de calor hacia o desde el sistema. En el caso de que exista transferencia de energía, el cambio en la energía del sistema debe ser igual a la energía neta ganada o perdida por el entorno.
Formalmente*, llamemos W al trabajo realizado sobre o por el sistema (como el cilindro en una máquina de vapor). Si el trabajo lo realiza el sistema, diremos que W es negativo; si el trabajo se realiza sobre el sistema, diremos que W es positivo. De forma similar, llamemos ΔQ a la transferencia neta de calor hacia o desde el sistema. Si la transferencia neta de calor es hacia el sistema, ΔQ será positiva; si la transferencia neta sale del sistema, ΔQ será negativa.
Ya lo tenemos todo para enunciar la primera ley de la termodinámica:
La primera ley de la termodinámica establece que el cambio en la energía total de un sistema cerrado, ΔE, viene dado por la suma del trabajo realizado sobre o por el sistema y la transferencia neta de calor hacia o desde el sistema. Simbólicamente, ΔE = W + ΔQ.
Esta expresión general incluye como casos especiales las versiones preliminares de la ley de conservación de la energía que hemos dado en entregas anteriores de esta serie. Si no hay transferencia de calor en absoluto, entonces ΔQ = 0, y ΔE = W. En este caso, el cambio en la energía de un sistema es igual al trabajo realizado sobre o por él. Por otra parte, si no se realiza trabajo ni sobre ni por el sistema, entonces W = 0 y ΔE = ΔQ. En este caso el cambio en la energía del sistema es igual a la transferencia neta de calor.
Esta ecuación tan sencilla es de una utilidad tremenda. Pero, si bien hemos enunciado la primera ley, aún queda un misterio por resolver, que es la estructura de esa energía interna de la que, de momento, solo sabemos que en algunos casos está relacionada con la temperatura y cómo se relaciona con la enería total del sistema. Lo veremos más adelante en esta serie, cuando tengamos la necesidad de introducir el concepto de átomo. Algo que, hasta ahora no nos ha hecho falta.
Nota:
* Este criterio de signos es importante, ya que varía en función del autor. Nosotros empleamos el criterio más intuitivo, a saber, tomar al sistema como referencia. Por tanto, lo que recibe el sistema es positivo y aumenta su energía total y lo que sale del sistema es negativo y la disminuye. Si usas este texto como apoyo en tus clases comprueba que el criterio de signos es el mismo.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La primera ley de la termodinámica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Carnot y los comienzos de la termodinámica (2)
- Carnot y los comienzos de la termodinámica (1)
- Los experimentos de Joule
Naturaleza, ciencia y cultura en el bicentenario de Henry David Thoreau
Antonio Casado da Rocha

Henry David Thoreau
El escritor norteamericano Henry David Thoreau (Concord, Massachusetts, 1817) es mundialmente conocido por sus méritos literarios (en particular, como detonante del género que luego se ha dado en llamar como nature writing) y por haber inspirado a activistas sociales como Gandhi, Martin Luther King, etc., diferentes prácticas políticas en torno al concepto de “desobediencia civil”. Pero en las numerosas menciones que ha recibido en los medios de comunicación a propósito del bicentenario de su nacimiento, que se celebra este 12 de julio, no abundan las referencias a su trabajo como naturalista ni como crítico de la cultura tecnocientífica. Son estas las que quisiera presentar aquí aunque sólo sea en parte.
Afortunadamente, la revista Nature publicó este 15 de junio una oportuna pieza sobre ese mismo tema. En ella, Randall Fuller describe la evolución del pensamiento de Thoreau con respecto a la ciencia tras la publicación de su obra maestra, Walden, en 1854. Hasta esa fecha, Thoreau se había mantenido más o menos fiel al movimiento trascendentalista, un grupo de intelectuales agrupados en torno a Ralph Waldo Emerson. No es sencillo definirlo, pero por un lado podemos decir (como hace Fuller) que el trascendentalismo surgió como una reacción de descontento con el modo de vida americano en la primera mitad del siglo XIX. Por el otro, cabe añadir que el trascendentalismo fue una forma de adaptar a la cultura americana el idealismo y el romanticismo europeos (como dijo Emerson, es “el idealismo tal como se lo entiende en 1842”).
Ese movimiento trascendentalista tenía una visión peculiar de la naturaleza. En lo que podríamos considerar su manifiesto, el ensayo Nature de Emerson (1836), se la describe como “el símbolo del espíritu”. Para los trascendentalistas el mundo empírico, visible, tenía un aspecto moral y espiritual que era intrínsecamente bueno. De hecho, como para ellos toda naturaleza es humana o aspira a ser humanizada, Emerson y sus seguidores veían el avance de la ciencia moderna y la revolución industrial como algo inevitable y positivo, prueba del progresivo paso del reino de la necesidad al de la libertad, de la asimilación de todo el universo a la racionalidad.

Thoreau habría sido el primer pensador norteamericano en tomar en serio a Darwin, en la imagen.
Emerson, que era teólogo por formación, estaba encantado con la idea. Thoreau, que sabía algo más de ciencia, no tanto. Fuller describe cómo Thoreau se sentía dividido porque sus investigaciones sobre el terreno le alejaban cada vez más de esa visión optimista de la naturaleza. Y lo hace relacionándolo con Darwin, cuyo Origin of Species (1859) leyó en 1860. El artículo de Nature muestra a Thoreau como el primer norteamericano que se tomó en serio a Darwin y puso en práctica sus intuiciones sobre una naturaleza capaz de autodirigirse sin necesidad de acción divina: “un mundo natural ciegamente autónomo, guiado por la lucha y la contingencia, autor de sí mismo”. Darwin reforzó en Thoreau una intuición revolucionaria para su tiempo: que la naturaleza existía al margen de lo humano, y que con eso bastaba para la ciencia (Fuller 2017: 350).
No hay duda de que, efectivamente, Thoreau sintió verdadero entusiasmo por lo esa “teoría del desarrollo” que había encontrado en su lectura de Darwin: una teoría que, a juicio de Thoreau, “implica una fuerza vital mayor en la naturaleza, porque es más flexible y adaptable, y equivale a una especie de nueva creación constante” (18/10/1860). Para Thoreau la ciencia no era una práctica contemplativa y alejada de cuestiones mundanas, sino la mejor herramienta para la lucha por la vida, y admiraba por igual el valor de Darwin, el de Tales en sus observaciones nocturnas y el de Linneo preparándose para una expedición a Laponia (Thoreau 1842: 4-5).

Ahora bien, Nature no tiene mucho espacio para temas de humanidades y el relato que cuenta Fuller carece de matices. Es cierto que Darwin ayudó a poner en marcha el programa de Alexander von Humboldt (brevemente, dar cuenta del mundo de manera generativa y holística, como un cosmos), pero también que lo hizo dentro de una tendencia general hacia la especialización del conocimiento. Y, como explica otra autora (Walls 2010: 97), en ese momento ya se estaba dando en la cultura literaria un similar movimiento de profesionalización. En respuesta a la desintegración de esa “cultura única” en la que ciencias y artes no estaban separadas, la literatura comenzó a independizarse de la ciencia natural. A su vez, esta abandonó sus roles tradicionales de creación estética, conciencia moral y critica social, que fueron progresivamente asumidos por la cultura literaria.

Alexander von Humboldt
Thoreau no fue ajeno a ese fenómeno y, por así decirlo, vio abrirse un abismo a sus pies. Como seguidor de Humboldt, Thoreau quería que la ciencia fuera poética, que la literatura pudiera hablar del mundo natural tanto como del social, y encontraba en la naturaleza intuiciones morales (lo que entonces llamaban la higher law o “ley superior”) desde las que criticar al sistema económico vigente. Pero ni la ciencia ni la poesía iban en esa dirección. De ahí la enorme vacilación o inquietud que atraviesa los 25 años de escritura de su diario. En él, Thoreau se debate con la pregunta de si una descripción científica del mundo puede o no hacer justicia a la pluralidad de la experiencia humana. En un apunte Thoreau duda de que la persona dedicada a la ciencia “descubra un mundo que la mente humana pueda habitar con todas sus facultades” (5 de septiembre de 1851). En otro, elogia al científico porque “la suma de lo que cualquier escritor puede ofrecer es simplemente cierta experiencia humana, ya sea poeta o filósofo u hombre de ciencia. La persona con más ciencia es la persona más viva; su vida es el mayor de los eventos” (6 de mayo de 1854).

El pasaje anterior está escrito poco antes de la publicación de Walden; hasta ese momento, la ciencia era un elemento de la cultura común o colectiva de los EE.UU. y no había una autoridad central que otorgase sus credenciales a quienes luego trabajarían como científicos, a menudo al margen de la universidad. Formado en Harvard, el propio Thoreau colaboró con científicos universitarios como Louis Agassiz, pero la palabra scientist no fue de uso común hasta después de la muerte de Thoreau en 1862. Sin embargo, en esa década de 1850 los “hombres de ciencia” comenzaron a identificarse como un grupo distinto, formado en las universidades.
Durante esos años Thoreau presenció cómo se separaban, entre otras, la cultura de las ciencias y la de las letras. Y lo constata en repetidas ocasiones, afirmando por ejemplo que ya “es imposible que la misma persona vea las cosas desde el punto de vista del poeta y desde el punto de vista del científico” (18 de febrero de 1852). De modo que el diario de Thoreau es de gran interés para estudiar lo que luego se llamó el problema de la separación de “las dos culturas”, por decirlo con la ya muy trivializada distinción de C. P. Snow.

Lago Walden (Concord, Massachusetts, EE.UU.). Fueron los dos años que pasó viviendo en su orilla los que inspiraron a Thoreau su obra “Walden” (1854). Foto: Antonio Casado da Rocha
Mi hipótesis, que aquí no puedo más que esbozar, es que Thoreau se resistió a la separación de esas dos culturas y que esa oposición se refleja en sus escritos sobre la percepción y apreciación del paisaje. En un momento de auge del positivismo y su ideal de completa objetividad, Thoreau desarrolló una visión que no es ni empirista ni idealista. En ella, el paisaje no es algo meramente natural ni cultural, objetivo o subjetivo, sino una relación que se halla entre el sujeto y el objeto, un proceso que le afecta. Un fenómeno que no es independiente del observador, sino que interactúa con él. Este pasaje me parece crucial al respecto:
“Creo que el científico comete un error que también repite la mayoría de la humanidad: prestar toda tu atención únicamente al fenómeno que te interesa, como si fuera algo independiente de ti, y no como si estuviera relacionado contigo. El hecho relevante es su efecto sobre mí. […] El filósofo que pretende reducir el arco iris a su explicación nunca lo ha visto de verdad. Con respecto a esos objetos, observo que lo que me importa no son ellos mismos, ese objeto con el que trafican los científicos, sino que mi punto de interés es algo que está entre los objetos y yo.” (5 de noviembre de 1857)
En esta manera de concebir el paisaje Thoreau no lo construye como un objeto estático, sino como una interacción con el sujeto observador a través de las posibilidades vitales que le ofrece (affordances). Para ilustrarlo podemos acudir a otro pasaje del diario, del 3 de octubre de 1859, en el que advirtió el humo que salía de la chimenea de una granja entre los bosques donde, supuso, alguna familia estaría preparando la cena. “Hay pocas vistas más agradables para el viajero pedestre”, escribió, suponiendo que bajo el humo todo sería felicidad doméstica. Pero también era consciente de que eso solo era una suposición, que de cerca las cosas de la granja no tendrían por qué ser tan idílicas como las imaginaba el viajero. Thoreau se lanza entonces a una larga meditación sobre ese fenómeno de idealizar todo aquello que vemos. Esta es su conjetura:
“¿Por qué nos encantan las perspectivas lejanas? Porque, inmediata e inevitablemente, imaginamos una vida que vivir allí […] Mentalmente, siempre estamos tomando muestras. ¿Por qué siempre nos parecen bellos los valles lejanos, los lagos, las montañas en el horizonte? Porque por un momento nos damos cuenta de que pueden ser la casa del hombre, que la vida humana puede estar en armonía con ellos. […] Creemos que vemos estas hermosas moradas y la alegría nos invade, cuando tal vez solo veamos nuestros propios tejados. Siempre estamos ocupados en alquilar casa y tierras y poblarlas con nuestra imaginación. No hay belleza en el cielo, sino en el ojo que lo ve. La salud, la moral alta, la serenidad: he ahí los grandes paisajistas.”
Es una reflexión inicialmente trascendentalista en su reconocimiento de la belleza como algo subjetivo y como fuente de inspiración moral, pero que al mismo tiempo va más allá y deconstruye en cierto sentido ese sentimiento de idealización, haciéndolo depender de la salud y las circunstancias objetivas del sujeto. Para Thoreau la belleza no está en el cielo, sino en una capacidad que es inmanente a la humanidad. Es una llamada a habitar humanamente la tierra; dicho de otra forma, a sostener las condiciones sociales que hacen posible la vida y su mejora, que Thoreau identifica con la salud y la virtud.
Esa intuición de que la percepción del entorno está relacionada con lo que el entorno nos ofrece en términos de su habitabilidad u otras oportunidades vitales (affordances) ha sido elaborada por la psicología ecológica del siglo XX y puede ser aplicada a la filosofía del paisaje (Menatti y Casado 2016). Esa aplicación permite al menos dos cosas. Por un lado, celebra la pluralidad de la experiencia humana al tiempo que, por el otro, intenta hacer justicia epistémica y dar a la ciencia lo que es de la ciencia: un mundo natural y cultural con límites reales pero que, como escribe Thoreau, “no están fijados ni son más rígidos que la elasticidad de nuestra imaginación” (31 de mayo de 1853). Thoreau explora los límites de la racionalidad, tanto aquella con la que trabajamos los humanos en nuestra toma de decisiones cotidiana, que está acotada por muchos factores que no la hacen perfecta, como la racionalidad colectivamente desplegada sobre el mundo a través de las tecnociencias, que también tiene límites que tenemos que conocer y aprender a aceptar, los propios límites biofísicos del planeta.
Esa racionalidad es en lo que estamos trabajando ahora, en el siglo XXI, buscando algo que ya no puede ser la racionalidad ilusoria o desalmada de los siglos XIX y XX. Ha de ser una racionalidad consciente de sus límites pero tan rica como puede llegar a ser la experiencia humana en toda su pluralidad. Pues no hay una respuesta única a la pregunta sobre la naturaleza, ese conjunto de procesos con los que seguimos traficando, y que no son objetivos ni subjetivos, de ciencia o de letras, o eso al menos parece decirnos aún Thoreau desde la atalaya de sus dos siglos de vida.
En resumen, Thoreau apreció la cultura y la ciencia de su tiempo, de Humboldt a Darwin, y entendió la naturaleza en una clave más empírica o factual que el trascendentalismo de Emerson. Pero no puede decirse que recibiera el darwinismo como un ácido que disuelve toda idea de trascendencia (a la Dennet) sino que mantiene algunos elementos románticos dentro de esa visión intersubjetiva de la percepción humana que hemos esbozado mediante el concepto de affordance, contribuyendo así a una propuesta de racionalidad consciente en la que se aúnan ciencia y experiencia humana.
Referencias:
Casado da Rocha, Antonio. Una casa en Walden y otros ensayos sobre Thoreau y cultura contemporánea. Logroño, Pepitas, 2017.
Fuller, Randall. Thoreau’s debt to Darwin. Nature 546 (15 June 2017): 349-350.
Menatti, Laura, y Antonio Casado da Rocha. Landscape and Health: Connecting Psychology, Aesthetics, and Philosophy through the Concept of Affordance. Frontiers in Psychology 7:571 (2016): 1-17.
Thoreau, Henry David. Natural History of Massachusetts.The Natural History Essays, Edited by Robert Sattelmeyer. Salt Lake City, Peregrine Smith Books, 1980.
Walls, Laura Dassow. Greening Darwin’s Century: Humboldt, Thoreau, and the Politics of Hope. Victorian Review 36:2 (2010): 92-103.
Sobre el autor: Antonio Casado da Rocha es investigador titular en el Departamento de Filosofía de los Valores y Antropología Social de la UPV/EHU
El artículo Naturaleza, ciencia y cultura en el bicentenario de Henry David Thoreau se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La cultura científica como cultura contemporánea: sobre “Ciencia ficción”, de Cristina Blanco
- Ciencia, naturaleza y arte: la química y sus metáforas, por Fernando Cossío
- Ciencia y desarrollo: naturaleza de una relación, por Juan Ignacio Pérez
Riesgo de sufrir los efectos de un vertido de petróleo en el mar de las costas europeas

El profesor Javier Fernández-Macho ha llevado a cabo un estudio con el que propone un método para medir y comparar el riesgo que tienen las regiones costeras europeas de padecer los efectos de un vertido de petróleo en el mar. El modelo estadístico propuesto y probado por el investigador ha fijado un ranking de riesgo relativo o vulnerabilidad de regiones costeras frente a este tipo de polución, que de aplicarlo “podría ayudar a diseñar políticas de protección y reducir la vulnerabilidad de recursos marinos y costeros sensibles”, explica Fernández-Macho.
“El enfoque del índice no es tanto evaluar uno a uno el daño que vaya a causar un vertido, sino poner en relación el riesgo de vertidos relativo de cada región frente al resto de regiones europeas —añade—. Se trata de una ordenación para saber cuáles son las regiones que corren más riesgo, y quizá se tengan que proponer soluciones en los territorios donde corren más riesgo antes que en otros”.
El investigador ha utilizado un modelo computacional que simula el efecto de vertidos de petróleo marinos en toda la costa europea. Para componer este modelo ha considerado cuatro variables relevantes, como son la distancia desde la costa hasta el lugar donde ocurre cada incidente marítimo, la magnitud del vertido liberado como resultado del incidente marítimo, la forma y longitud de la zona costera potencialmente afectada y el efecto de las corrientes oceánicas en el lugar y fecha del incidente.
El modelo se basa en datos de 301 incidentes y accidentes ocurridos en aguas europeas entre 1970 y 2014, obtenidos de la base de datos pública de ITOPF —organización de compañías navieras y diversas instituciones relacionadas con el transporte internacional en aguas oceánicas de todo el mundo—. Con todo ello, se ha evaluado y dibujado en un mapa el riesgo relativo de 429 unidades territoriales y 156 regiones costeras definidas por Eurostat, la Oficina Europea de Estadística.
Los resultados del estudio muestran una alta heterogeneidad entre las regiones costeras europeas, y las áreas con mayor riesgo de vertido marino se encuentran predominantemente en la costa atlántica. En particular, según el estudio, las costas del Reino Unido se ven notablemente afectadas, ya que de las primeras 25 unidades territoriales más expuestas a los vertidos marinos solo hay cinco que no son británicas.
Tal y como señala Fernández-Macho, las conclusiones obtenidas en este estudio han resultado ser de bastante sentido común. Como ejemplo, cita los resultados relacionados con el Reino Unido: “En el Canal de la Mancha existe un gran tráfico marítimo, y debido a la estrechez de algunas zonas es muy lógico que a lo largo del tiempo haya habido más accidentes importantes cercanos a la costa que en otras zonas”. Asimismo, el investigador constata que “mientras no se apliquen políticas de cambio, es muy fácil extrapolar lo conocido históricamente al futuro”, es decir, es muy probable que donde haya habido accidentes graves vuelvan a ocurrir. Por todo ello, el investigador de la UPV/EHU advierte de que “las costas europeas, y sobre todo la costa atlántica, están en gran riesgo, y que es necesario aplicar políticas a nivel europeo, nacional o local para paliar el grave problema que pueden causar los vertidos de petróleo”.
En lo que respecta a las costas vascas, el investigador explica que “no son rutas por las que pasan grandes transportes marítimos y petroleros peligrosos. Nuestra afectación va más bien por el sentido de que las corrientes marinas puedan traer el vertido a nuestras costas. Por lo que nuestros niveles de riesgo son relativamente bajos”.
El estudio ha captado la atención de investigadores internacionales, interesados en ver cómo se podría adaptar el mismo tipo de índice en aguas de otros entornos geográficos.
Referencia:
J. Fernández-Macho.. Risk assessment for marine spills along European coastlines. Marine Pollution Bulletin, vol 113 (2016), pp. 200-210. DOI: 10.1016/j.marpolbul.2016.09.015.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Riesgo de sufrir los efectos de un vertido de petróleo en el mar de las costas europeas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los efectos protectores de la lactancia materna frente a la contamincación atmosférica
- El petróleo, los desastres y la prensa
- La filosofía como actividad de alto riesgo
La ecología de una enfermedad
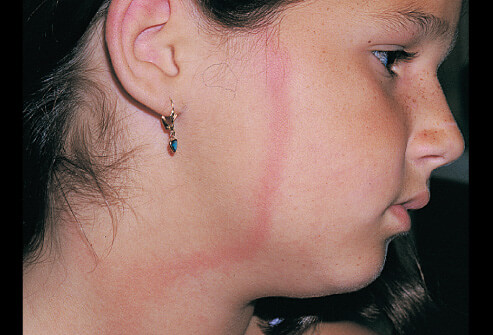
Erythema migrans (literalemente, enrojecimiento que se desplaza) en la cara de una niña a la que ha picado una garrapata en la cabeza.
La borreliosis de Lyme puede ser bastante grave. Es la enfermedad más transmitida por garrapatas en el Hemisferio Norte y, al menos en los Estados Unidos, la que más se contagia a través de una picadura. La contraen unas 300.000 personas al año en Norteamérica y 65.000 en Europa. La causa una bacteria de tipo Borrelia.
El síntoma más normal de la infección es un enrojecimiento de la piel denominado erythema migrans que comienza en el lugar de la picadura una semana después de haberse producido, aunque muchos afectados no lo experimentan. Otros síntomas tempranos incluyen fiebre, dolor de cabeza y sensación de cansancio. En caso de no tratarse a tiempo la enfermedad, puede haber síntomas adicionales, como imposibilidad para mover uno o ambos lados de la cara, dolores articulares, fuertes cefaleas con rigidez de cuello, y palpitaciones, entre otros. Y meses o años más tarde pueden producirse nuevos episodios de algunos de estos síntomas. En esta enfermedad es importantísimo el detectarla cuanto antes porque los tratamientos disponibles son mucho más efectivos en fases tempranas. A día de hoy, la única prevención posible consiste en no exponerse a las garrapatas y, en caso de ser picado por una de ellas, retirarla cuanto antes porque, al parecer, el ácaro necesita varias horas para producir una infección efectiva.
La incidencia de la enfermedad de Lyme no ha dejado de aumentar últimamente; el número de personas contagiadas ha crecido, y cada vez es mayor la extensión del área geográfica en que se dan casos de borreliosis. Ese aumento sería una consecuencia más del aumento global de temperatura, pues este factor tiene una incidencia directa en el ciclo de vida de las garrapatas. La supervivencia de los ácaros y su velocidad de desarrollo son más altas a temperaturas elevadas.
Al igual que ocurre con otras enfermedades infecciosas, también la de Lyme tiene su propia ecología. Los ratones de campo de zonas boscosas son los principales responsables de la extensión de la enfermedad. Las garrapatas se adhieren con facilidad a los roedores y mediante su picadura les transmiten las bacterias. Por esa razón, los años en que cuentan con abundante alimento (bellotas, por ejemplo), sus poblaciones crecen mucho, y las garrapatas tienen muchas posibilidades de encontrar un huésped. De esa forma, los años buenos para los ratones también lo son para las garrapatas que, andando el tiempo, verán aumentar notablemente su población. Las consecuencias para los seres humanos son evidentes: cuantas más garrapatas hay, más probable es que se produzcan picaduras y, por lo tanto, contagios. La relación causal está bien establecida y los especialistas son capaces de predecir con dos años de antelación brotes especialmente importantes de borreliosis a partir de la abundancia de bellotas en los bosques.
La borreliosis no sería tan preocupante si hubiese una vacuna efectiva pero a día de hoy tal vacuna no existe, aunque existió. Se llegó a comercializar una hace algunos años, pero la compañía que la desarrolló decidió retirarla del mercado cuatro años después, como consecuencia de las presiones ejercidas por los grupos anti-vacunas que difundieron la especie de que provocaba artritis; era una acusación sin fundamento.
Es bueno conocer con antelación cuándo aumentará la densidad de garrapatas y, con ella, la posibilidad de contagios. Puede alertarse así a la población de las zonas más afectadas, de manera que extremen los cuidados para evitar la infección o detectarla cuanto antes. Pero la solución más efectiva, sin duda, es la vacuna. El que carezcamos hoy de ella es otra triste victoria de quienes se oponen al progreso de la dignidad y bienestar humanos.
—————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 23 de abril de 2017.
El artículo La ecología de una enfermedad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- En busca de los genes de la enfermedad celíaca
- Celiaquía: el ADN no codificante es clave en el desarrollo de la enfermedad
- Parkinsonia parkinsoni
Arte & Ciencia: La relación entre el desarrollo de la ciencia y la creación artística

El arte y la ciencia son dos formas de conocimiento aparentemente alejadas, en gran medida consecuencia de la especialización profesional y la educación compartimentada. Del estudio de esta impostada separación surgió el estereotipo de las dos culturas, las ciencias y las humanidades, para referirnos a esa brecha de conocimiento. La realidad es que la ciencia y el arte sí están conectadas y que ninguna forma de conocimiento es impermeable a otra. Por poner algunos ejemplos: ¿Cómo podría crearse una obra plástica sin las técnicas propiciadas por la ciencia? ¿Cómo podríamos interpretar la elección de materiales?
Estas y otras cuestiones relacionadas furon tratadas por destacados profesionales -artistas, ilustradores, filósofos y científicos- que han puesto el foco en ese difuso trazo que une la ciencia y el arte. El ciclo Ciencia & Arte se desarrolló, bajo la dirección de Deborah García Bello, a lo largo de cuatro jornadas que se celebraron los jueves días 6 y 27 de abril y 11 y 25 de mayo de 2017 en el auditorio del Museo Guggeheim Bilbao.
Esta actividad de la Cátedra de Cultura Científica de la UPV/EHU se enmarca en el programa TopARTE que conmemora el XX Aniversario del Museo Guggenheim Bilbao.

Segunda jornada. 3ª conferencia
José Ramón Marcaida, especialista en historia de la ciencia e historia del arte de la Edad Moderna de la Universidad de Cambridge : La relación entre el desarrollo de la ciencia y la creación artística
Las primeras ilustraciones de animales y plantas, el coleccionismo de maravillas naturales, el trabajo de los artistas… A lo largo de su historia, el ser humano ha representado la naturaleza de diferentes maneras que han jugado un papel fundamental en la generación de conocimiento científico. Pero esta influencia también se ha dado en la dirección inversa, puesto que los descubrimientos científicos han servido de inspiración y han influido en el desarrollo de técnicas pictóricas y estilos artísticos, marcando el devenir de la historia del arte.
La relación entre el desarrollo de la ciencia y la creación artísticaEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Arte & Ciencia: La relación entre el desarrollo de la ciencia y la creación artística se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: Química y Arte, reacciones creativas
- Arte & Ciencia: La importancia de la ciencia para la conservación del arte
- Arte & Ciencia: Imaginario marino
Sobre la predisposición genética a padecer enfermedades (II)

En un artículo anterior hablábamos de cómo se descubren las variantes genéticas (los polimorfismos de un solo nucleótido ‒SNPs‒, ¿recuerdas?) que podemos relacionar estadísticamente con diversas enfermedades o trastornos mediante estudios de asociación del genoma completo (GWAS, Genome-wide association study). Es importante dejar claro que estas asociaciones nos señalan algunos cambios en el ADN que aumentan la probabilidad de que padezcamos una patología, sin que ello signifique que la vayamos a sufrir necesariamente.
Entonces ya apuntábamos a un problema de estas correlaciones SNP-patología: salvo excepciones, no indican de forma clara la causa concreta de la enfermedad. Sabemos que un nucleótido concreto en una posición específica del genoma aumenta la predisposición a padecer un trastorno determinado, pero poco conocemos sobre los mecanismos celulares y rutas metabólicas que llevan de una variación concreta del ADN a la enfermedad. Y esto es importante si queremos investigar tratamientos efectivos.
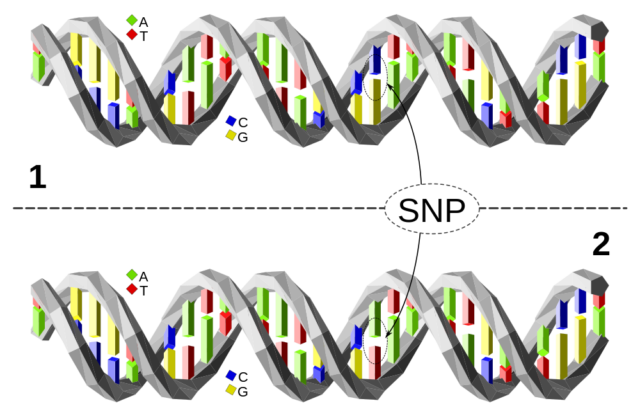
Como ya se explicó en el artículo anterior, un polimorfismo de un solo nucleótido (SNP) no es más que una diferencia en un punto de la secuencia de ADN entre distintos individuos. En la imagen, el individuo 1 tiene un par C-G en la posición señalada, mientras que el individuo 2 tiene el par de nucleótidos A-T. El resto de la secuencia mostrada es idéntica
En algunos casos sí que podemos deducir las causas: si hay un cambio en la secuencia de un gen, este cambio puede afectar a la estructura de la proteína resultante y, según las funciones de esta, podemos tratar de inferir los mecanismos que llevan a sufrir el trastorno. Pero esto sólo ocurre en un 5-10% de los SNPs estudiados y asociados a patologías: el resto de variantes genéticas relacionadas con enfermedades a través de GWAS se encuentran en zonas del genoma que no codifican proteínas (en el mal denominado ADN basura).
¿Qué ocurre en el resto de casos? ¿Cómo puede afectar una variante genética, un pequeño cambio en la secuencia de ADN, al funcionamiento de la célula si no se encuentra directamente implicada en la construcción de proteínas? Pues a través de otros mecanismos, principalmente mediante la regulación de la expresión génica.
Expresión génica
Aunque la secuencia de ADN de todas nuestras células es la misma (salvo mutaciones puntuales), resulta evidente que existen muchos tipos distintos de células: las células que forman los músculos son distintas a las del hígado o el páncreas, a las epiteliales o a las neuronas. Esto se debe a que no se «activan» los mismos genes ni con la misma intensidad en las distintas células.
Recordemos que los genes son secuencias de ADN que contienen la información para fabricar una proteína. Para ello, previamente se transcriben a ARN mediante la acción de la enzima ARN polimerasa, se eliminan fragmentos no codificantes de su interior (los denominados intrones) y las secuencias resultantes (denominadas ARNm) se traducen a proteínas. Un cambio en la secuencia de ADN que define un gen puede conllevar que la proteína se fabrique mal y que aparezca una enfermedad grave.
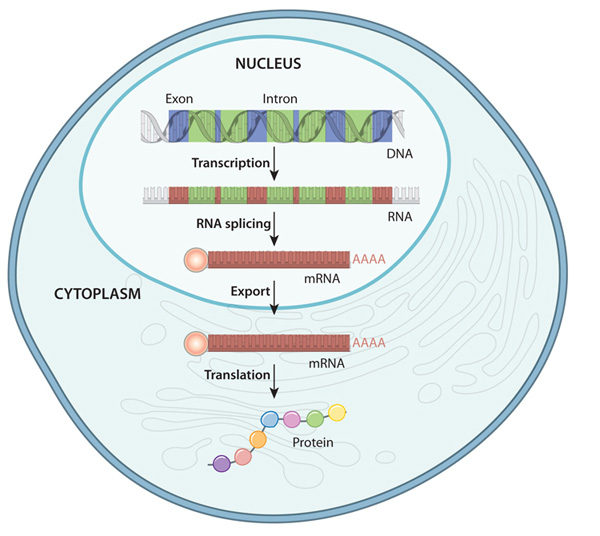
Así pues, un gen contiene la información necesaria para fabricar una proteína, pero no sobre cuándo empezar este proceso, cuánta cantidad de proteína es necesaria y en qué tipo de células se debe llevar a cabo. De esta regulación de la expresión génica, se encargan factores externos, diversos actores en el interior de la célula y, en particular, otras secuencias cromosómicas. Un ejemplo sería la propia secuencia que marca el inicio de transcripción donde se une la enzima ARN polimerasa (promotor). Otros fragmentos de ADN van a actuar como potenciadores de la transcripción o represores. A grandes rasgos, estos fragmentos (que no tienen por qué encontrarse cerca del gen que controlan) regulan el plegamiento de la cadena de ADN como lugares de unión de otros complejos enzimáticos, permitiendo un mejor o peor acceso de la ARN polimerasa al inicio de la transcripción. Una variación en estas secuencias no influye en cómo se construye la proteína, sino en qué condiciones se va a fabricar y en qué magnitud.
Podemos medir la expresión de un gen en un tejido concreto estimando qué cantidad de ARNm se ha fabricado, lo que se conoce como transcriptoma. Avances recientes en secuenciación genética han permitido obtener transcriptomas con una eficacia elevada.
Expression quantitative trait loci
Así pues, resumiendo, podemos utilizar técnicas avanzadas de secuenciación masiva para obtener tanto el genoma de un conjunto de individuos como su transcriptoma. De hecho, empezamos a disponer de grandes bases de datos con ambos datos asociados a patologías y rasgos concretos de los donantes de muestras. Analizando estas bases de datos con potentes herramientas computacionales y estadísticas podemos relacionar variaciones concretas del genoma (en particular, SNPs) en regiones no codificantes, con cambios en la expresión génica. A estas regiones del ADN cuyos cambios afectan a la expresión génica de uno o más genes se les denomina eQTLs (expression quantitative trait loci). Vamos a utilizar esta definición con frecuencia a lo largo de este artículo, así que vamos a explicar con más detalle qué significa.
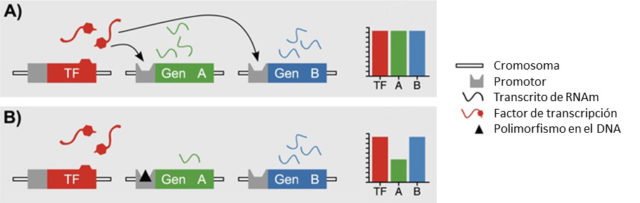
Imagen modificada de Wikipedia Commons.
Un eQTL es una posición concreta del genoma que, en función del nucleótido que se encuentre en ella, va a influir en la predisponibilidad a poseer algún rasgo o padecer enfermedad concreta. Pero no lo va a hacer modificando la estructura de la proteína codificada por un gen, sino alterando la expresión génica. Es decir, las personas que presenten en su genoma un eQTL determinado van a fabricar proteínas de forma correcta, pero en una cantidad distinta de la adecuada para el funcionamiento adecuado de la célula, pudiendo dar lugar a algún trastorno determinado o rasgo específico.
En la figura anterior, un factor de transcripción se une a los promotores de los genes A y B, dando como resultado una cierta cantidad de proteína (A). Si hay una variación en el promotor del gen A (indicada con un triángulo negro en la figura) la cantidad de proteína fabricada disminuye.
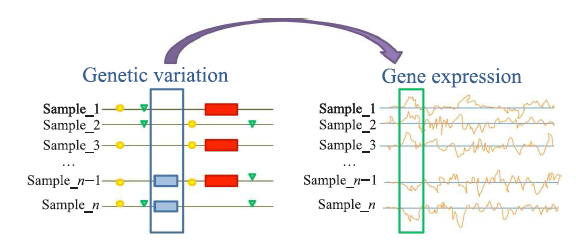
Una variante concreta de un eQTL (señalada con un rectángulo azul a la izquierda) lleva consigo un cambio en la expresión de un gen concreto (rectángulo verde a la derecha).
¿Cómo se localizan eQTLs en el genoma? Primero, se obtienen los SNPs de cada uno de los participantes en el experimento como se explicó en el anterior artículo. En la siguiente figura se toman como ejemplo dos polimorfismos de los cromosomas 4 y 14, marcados como SNP1 y SNP2. Recuerda que un SNP varía de individuo a individuo, aunque en este ejemplo sólo consideraremos dos variantes posibles.
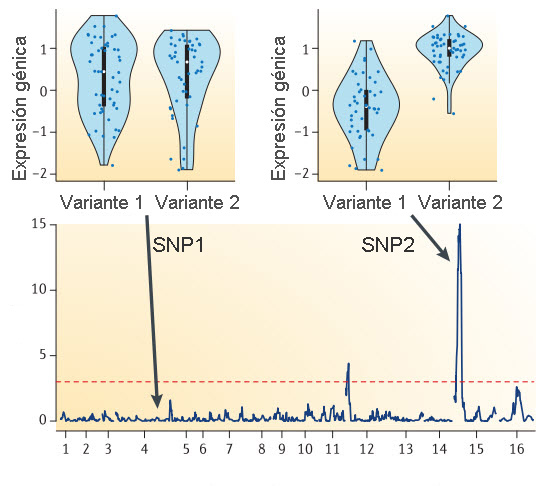
A continuación se obtiene una muestra del tejido de interés (recuerda que la expresión génica depende del tipo concreto de células) y se mide la cantidad de ARNm fabricado de distintos genes (con técnicas como RNA-seq). Podemos representar para cada variante de un SNP la cantidad de ARNm expresada de un gen concreto (en la figura, los puntos negros de las gráficas). Se observa que en el primer SNP no hay apenas variación en el nivel de expresión según se posea una variante u otra (fíjate en las formas de las distribuciones de puntos, destacadas en fondo azul), mientras que en el segundo hay una mayor expresión en la variante 2. Por lo tanto, diríamos que el SNP2 tiene asociados cambios destacables de expresión génica según la variante implicada, por lo que sería un eQTL.
Con este tipo de estudios se han podido localizar un gran número de eQTLs en nuestro genoma. Muchas de estas zonas influyen en la expresión génica por encontrarse cerca del lugar donde se inicia la transcripción del gen: se conocen como cis-eQTL. Hay que tener en cuenta que «cerca» puede significar hasta un millón de nucleótidos de distancia entre el SNP y el inicio del gen. Otras variaciones, sin embargo, son capaces de modificar la expresión de un gen situado a mucha distancia del SNP implicado, e incluso en un cromosoma distinto: son los denominados trans-eQTL.
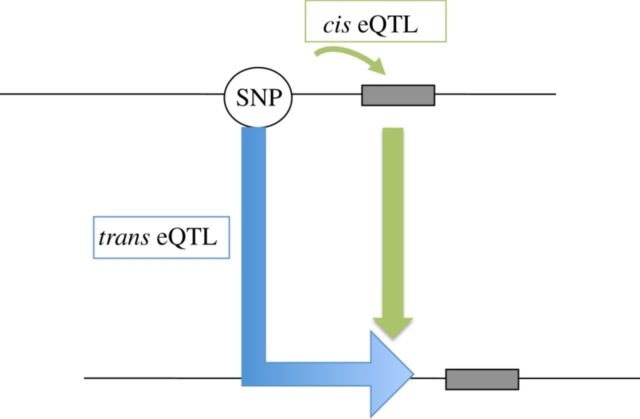
Empezábamos este artículo comentando que conocer que una variante genética esté asociada a una enfermedad no implica que podamos entender cuál es el mecanismo subyacente, lo cual no nos da pistas de cómo tratar el problema. Si descubrimos que esta variante afecta a la expresión de un gen determinado, y conocemos su función celular, sí que podemos investigar nuevos tratamientos.
Pongamos un ejemplo concreto. Recientemente se descubrió un SNP asociado a un menor riesgo de padecer un infarto de miocardio. Se comprobó que la variante menos común de este SNP (la T destacada en azul en la siguiente figura) promueve la expresión de un gen en el hígado que produce sortilina. Estudios posteriores con ratones demostraron que esta proteína disminuye los niveles de colesterol LDL, asociado a riesgo cardíaco.
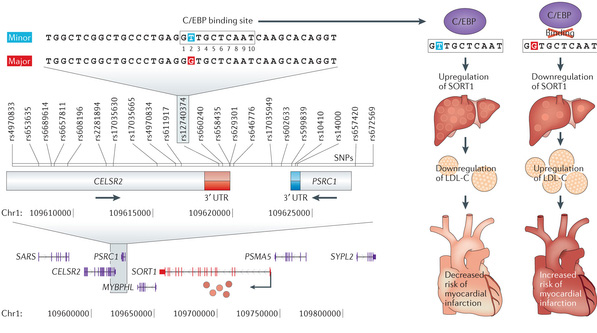
Otros ejemplos de eQTLs recientemente descubiertos han contribuido a explicar la asociaciones de variantes genéticas con enfermedades como el asma infantil, la enfermedad de Crohn o el lupus.
Este post ha sido realizado por Guillermo Peris (@Waltzing_piglet) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias- Gene expression. Scitable (Nature Education).
- The role of regulatory variation in complex traits and disease. Albert, F.A. and Kruglyak, L. (2015) Nature Reviews Genetics 16, 197–212. doi:10.1038/nrg3891
- Expression quantitative trait loci: present and future. Nica A.C. and Dermitzakis E.T. (2013). Philos Trans R Soc Lond B Biol Sci.;368: 20120362
doi: 10.1098/rstb.2012.0362 - The study of eQTL variations by RNA-seq: from SNPs to phenotypes. Majewski, J. and Pastinen, T. (2011) Trends in Genetics 27 (2) , 72-79. doi: 10.1016/j.tig.2010.10.006.
El artículo Sobre la predisposición genética a padecer enfermedades (II) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sobre la predisposición genética a padecer enfermedades
- Dani y Fiti sobre la ingeniería genética
- Dudas sobre las vacunas: problemas y soluciones
Pena de muerte contra el fraude científico

Una de las grandes tendencias en el mundo científico durante las últimas décadas ha sido el imparable avance de China. Decidido a ser una potencia de alcance mundial el gobierno chino ha ejecutado una deliberada estrategia de desarrollo de la ciencia y la tecnología que comenzó hace muchos años, cuando de repente los laboratorios del mundo en múltiples especialidades se llenaron de estudiantes doctorales y postdoctorales provenientes de aquel país con especial hincapié en determinados campos que se consideraron estratégicos. Estos estudiantes regresaron a China, donde montaron laboratorios y centros de investigación conectados a la comunidad científica internacional; miles, centenares de miles de nuevos puestos de trabajo se crearon en estos campos, y se comenzó a desarrollar una verdadera invasión de publicaciones de equipos chinos que después se transformó en un diluvio de nuevas revistas especializadas creadas específicamente para este mercado. El país ha ejecutado un salto científico enorme desde finales del siglo XX como parte de una clara estrategia política: el gobierno ha decidido que la ciencia es clave para el estátus de potencia mundial de China.
El problema es que inevitablemente el fomento por parte de un estado de cualquier cosa provoca el desarrollo paralelo de un fenómeno de picaresca: los espabilados de turno se aferran a la tradicional corta visión de las burocracias para aprovecharse de los incentivos (económicos, profesionales, sociales) que se usan para desarrollar un campo, en este caso la ciencia. Y surge el fraude, en múltiples formas y variedades. La ciencia trucha en China se ha convertido en un auténtico problema, y no sólo para el gobierno local y su despilfarro de recursos en resultados falsos: el volumen de publicación es tal que se corre un riesgo real de que acabe contaminando el avance científico en todo el mundo. Para dar una idea según algunas estimaciones de científicos chinos del área de biomedicina hasta el 40% de todas las publicaciones locales de su sector podrían contener algún tipo de fraude. Esto supone un problema colosal, dado el enorme número de publicaciones que salen hoy de aquel país.
Las instituciones chinas han tomado cartas en el asunto, castigando ejemplarmente los casos que han salido a la luz con penas que incluyen la devolución del dinero concedido en forma de proyectos de investigación. Los departamentos encargados de supervisar el sistema de investigación están preocupados por la reputación internacional de China tras escándalos como la reciente retracción en masa de 107 artículos que se habían publicado en una revista (Tumor Biology) tras pasar una falsa revisión por pares en la que los presuntos revisores no existían. El Ministerio chino de Ciencia y Tecnología ha anunciado una política de ‘tolerancia cero’ con las falsificaciones y los fraudes. Una política que en algunos casos puede acabar con duras penas de prisión para los investigadores responsables de malas conductas científicas, y hasta potencialmente en la pena de muerte.
Sí: en el caso de que se pueda demostrar que una falsificación de datos científicos haya dañado a personas, por ejemplo en pruebas clínicas de medicamentos, el castigo podría llegar hasta la ejecución de los culpables. Según sentencias emitidas por algunos tribunales chinos no hay diferencia entre la falsificación de datos científicos y la falsificación de moneda, por lo que las penas de cárcel están garantizadas; pero en caso de que se perjudique a terceros se podría llegar en principio a la pena de muerte. Cosa que en China no es ninguna tontería: se trata del país con mayor entusiasmo con esta institución penal abolida en muchas partes del mundo, pero que allí se sigue practicando. Se calcula que el país ejecuta a más de 2.o00 prisioneros al año por diversos delitos que incluyen casos graves de soborno o corrupción, aunque las cifras exactas no son conocidas.
El fraude científico es, en esencia, una forma de crimen especialmente poco inteligente, ya que la naturaleza no hace trampas y las posibilidades de que las falsificaciones e invenciones no se descubran (tarde o temprano) es cero. La ciencia como cuerpo de conocimiento a la larga no sale dañado porque los datos espurios son eliminados por posteriores investigaciones: cualquier falsificación sobre el comportamiento del universo acaba por colisionar con la realidad y es eliminada. Para la ciencia es una pérdida de tiempo y una molestia que detrae recursos de los investigadores serios y retrasa el avance. Para las burocracias que financian la actividad científica, sin embargo, se trata de una estafa, pura y simple: el robo de unos recursos obtenidos con premisas falsas y un insulto a la autoridad que concede esos recursos. Por el bien de la ciencia como actividad y como conocimiento es necesario luchar contra el fraude, que supone un desperdicio y una pérdida de tiempo y dinero, y en ese sentido la postura de las autoridades chinas es encomiable. Aunque es obvio que la pena de muerte supone un castigo un tanto excesivo para el fraude científico, y rechazable en cualquier caso.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo Pena de muerte contra el fraude científico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Fraude científico (III). Profundizando en los dos tipos de fraude
- Fraude científico (y V). Resumen y conclusiones
- Fraude científico (I). Una primera aproximación
¿Y si el Sol estuviese cambiando de forma fundamental?

Un estudio del Sol usando ondas sonoras utilizando sugiere que la capa en la que se produce la actividad magnética significativa se ha vuelto más fina en los últimos años. La persistencia de este cambio podría indicar que el Sol habría entrado en una fase de transición hacia no se sabe muy bien qué, todavía. Los resultados de este estudio fueron presentados ayer martes 4 de julio por Yvonne Elsworth, profesora de la Universidad de Birmingham, en un congreso que se está celebrando en la Universidad de Hull.
El Sol es muy parecido a un instrumento musical, excepto en que sus notas típicas están a una frecuencia muy baja – unas 100.000 veces menor que el do central. El estudio de estas ondas de sonido utilizando una técnica llamada heliosismología, nos permite descubrir lo que está pasando en el interior del Sol .
El Sol actúa como una cavidad natural que atrapa el sonido, sonido que se genera por la turbulencia existente en unos pocos cientos de kilómetros más exteriores de la zona de convección. La Universidad de Birmingham es uno de los centros pioneros a nivel mundial en el campo de la heliosismología y los investigadores han estado utilizando la Red Birmingham de Oscilaciones Solares (BISON, por sus siglas en inglés) para estudiar el Sol a través de las ondas sonoras desde 1985. Este período abarca tres ciclos de 11 años de actividad del Sol. En estos ciclos se producen fluctuaciones en el ritmo al que se crean partículas energéticas por la interacción entre el campo magnético del Sol y sus capas exteriores calientes y altamente cargadas.
Los investigadores del equipo de Elsworth han encontrado que el interior del Sol ha cambiado en los últimos años, y que estos cambios persisten en el ciclo actual. Estas observaciones, combinadas con modelos teóricos, sugieren que la distribución del campo magnético en las capas más externas podría haberse vuelto algo más delgada. Otros datos seismológicos apuntan a que la velocidad de rotación del Sol también habría sufrido algunos cambios en lo que se refiere a la forma en la que el material del sol rota a distintas latitudes.
Según Elsworth:
“[…] esto no es lo que solía ser, y la velocidad de rotación ha disminuido un poco en las latitudes alrededor de unos 60 grados. No estamos muy seguros de cuáles serán las consecuencias de esto pero está claro qué nos encontramos en tiempos inusuales. ”
Estos resultados hacen que la idea de que la dinamo del Sol esté en proceso de cambiar fundamentalmente sea menos especulativa de lo que era hace unos años.
Referencia:
R. Howe, G. R. Davies, W. J. Chaplin, Y. Elsworth, S. Basu, S. J. Hale, W. H. Ball, R. W. Komm (2017) The Sun in transition? Persistence of near-surface structural changes through Cycle 24 Mon Not R Astron Soc stx1318. DOI: 10.1093/mnras/stx1318
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo ¿Y si el Sol estuviese cambiando de forma fundamental? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo dejar de usar petróleo y seguir consumiendo sus derivados de forma barata
- El estaño beta es como el grafeno pero en 3D
- Encontrando exoplanetas tapando las estrellas
La máquina calculadora de Nicholas Saunderson
En la entrada Haciendo matemáticas en la oscuridad citábamos al británico Nicholas Saunderson (1682-1739) entre los matemáticos ciegos que, a pesar de su defecto visual, fueron capaces de realizar importantes aportaciones en su disciplina.

Nicholas Saunderson (Wikipedia).
Saunderson perdió la vista al enfermar de viruela con tan solo un año de edad. Su ceguera le permitió adquirir unos excepcionales sentidos del oído y del tacto, y una increíble agilidad mental para los cálculos matemáticos.
Tras muchas negativas, gracias al apoyo del matemático William Whiston y a petición de personajes destacados de la Universidad de Cambridge, la Reina Ana I concedió a Saunderson el cargo de profesor Lucasiano en 1911 –fue el cuarto, tras Isaac Barrow, Isaac Newton y el propio William Whiston–.
Ocupando aquella cátedra, Saunderson enseñó matemáticas con un éxito asombroso; escribió los libros Elements of Algebra (1740, basado en el ábaco del que hableremos más adelante) y The Method of Fluxions (publicado en 1756 por su hijo). Sorprendentemente, dio además clases de óptica, sobre la naturaleza de la luz y de los colores, y acerca de otras materias relativas a la visión y a su órgano.
En 1718, fue admitido en la Royal Society, donde compartió amistad con matemáticos de gran relevancia como Isaac Newton, Edmund Halley, Abraham de Moivre o Roger Cotes.
El filósofo y enciclopedista Denis Diderot le citó en varios fragmentos de su ensayo Lettre sur les aveugles, à l’usage de ceux qui voyent (Carta sobre los ciegos para uso de los que ven, 1749). Al igual que el filósofo William Molyneux (ver [1]), Diderot opinaba que un ciego que empieza a ver de repente –por ejemplo tras una operación– no puede comprender inmediatamente lo que observa, y debería costarle un tiempo hacer el vínculo entre su experiencia con las formas y distancias adquiridas mediantes el tacto, y las imágenes percibidas a través de sus ojos.
Saunderson ideó una especie de ábaco con una serie de agujeros en los que podía introducir clavijas para facilitar su utilización a personas ciegas. Para describirlo, vamos a utilizar las palabras de Diderot extraídas de [4, página 26 y siguientes]:
Es mucho más rápido usar símbolos ya inventados que inventarlos uno mismo, como se está forzado, cuando nos cogen desprevenidos. ¡Cuánto mejor hubiera sido para Saunderson haber encontrado una aritmética palpable, ya preparada, cuando tenía cinco años, en vez de tener que imaginársela a los veinticinco! […] Cuentan de él prodigios y no hay ninguno que sus progresos en las bellas letras y su habilidad en las ciencias matemáticas no puedan hacer creíble.
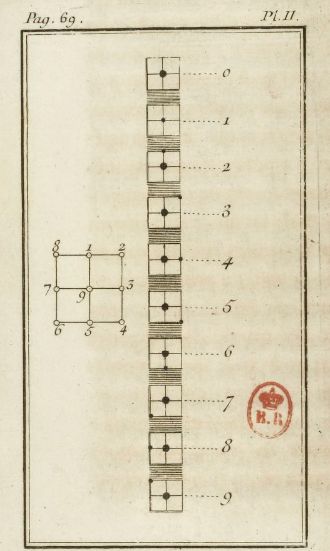
Plancha II (página 69 de [3]).
Una misma máquina le servía para los cálculos algebraicos y para la descripción de las figuras rectilíneas. […] Imaginad un cuadrado como el que veis en la Plancha II, dividido en cuatro partes iguales por líneas perpendiculares a los lados, de suerte que os ofrezca los nueve puntos 1, 2, 3, 4, 5, 6, 7, 8, 9. Suponed este cuadrado perforado por nueve agujeros capaces de recibir alfileres de dos clases, todos de la misma longitud y del mismo grosor, pero unos con la cabeza algo más gruesa que otros. Los alfileres de cabeza gruesa sólo se colocan en el centro del cuadrado; los de cabeza fina, sólo en los lados, excepto en un caso, el del cero. El cero se marca por un alfiler de cabeza gruesa, colocado en el centro del cuadrado pequeño, sin ningún otro alfiler a los lados. La cifra 1 estará representada por un alfiler de cabeza fina, colocado en el centro del cuadrado, sin ningún otro alfiler a los lados. La cifra 2, por un alfiler de cabeza gruesa colocado en el centro del cuadrado y un alfiler de cabeza fina colocado a uno de los lados, en el punto 1. La cifra 3, por un alfiler de cabeza gruesa colocado en el centro del cuadrado y un alfiler de cabeza fina colocado a uno de los lados, en el punto 2. La cifra 4, por un alfiler de cabeza gruesa colocada en el centro del cuadrado y un alfiler de cabeza fina colocado a uno de los lados, en el punto 3. La cifra 5, por un alfiler de cabeza gruesa colocado en el centro del cuadrado y un alfiler de cabeza fina colocado a uno de los lados, en el punto 4. La cifra 6, por un alfiler de cabeza gruesa colocado en el centro del cuadrado y un alfiler de cabeza fina colocado a uno de los lados, en el punto 5. La cifra 7, por un alfiler de cabeza gruesa colocado en el centro del cuadrado y un alfiler de cabeza fina colocado a uno de los lados, en el punto 6. La cifra 8, por un alfiler de cabeza gruesa colocado en el centro del cuadrado y un alfiler de cabeza fina colocado a uno de los lados, en el punto 7. La cifra 9, por un alfiler de cabeza gruesa colocado en el centro del cuadrado y un alfiler de cabeza fina colocado a uno de los lados del cuadrado, en el punto 8.
Estas son diez expresiones diferentes para el tacto, cada una de las cuales responde a uno de nuestros diez caracteres aritméticos. Imaginad ahora una tabla tan grande como queráis, dividida en pequeños cuadrados colocados horizontalmente y separados unos de otros a la misma distancia, como podéis verlo en la Plancha III, y tendréis la máquina de Saunderson.

La máquina calculadora de Nicholas Saunderson
Podréis ver fácilmente que no existen números que no puedan escribirse sobre esa tabla y, por consiguiente, ninguna operación aritmética que no pueda ejecutarse.
Diderot continúa dando un ejemplo de utilización de esta máquina para ilustrar su descripción.
No es el único momento en el que Diderot alude a Saunderson en su ensayo; por ejemplo, para exponer su visión materialista desarrolla un pasaje con una serie de argumentos que atribuye a Saunderson mientras con un sacerdote que intenta demostrar la existencia de Dios a través del espectáculo de la naturaleza (que no puede ver) y posteriormente por la perfección de los órganos humanos.
Referencias
[1] Marta Macho Stadler, Haciendo matemáticas en la oscuridad, Cuaderno de cultura científica, 14 de mayo de 2015
[2] Marta Macho Stadler, Nicholas Saunderson, extraordinario calculador, ZTFNews, 19 de abril de 2014
[3] Lettre sur les aveugles, à l’usage de ceux qui voyent, Gallica
[4] Julia Escobar, Carta sobre los ciegos para uso de los que ven, Fundación ONCE y Editorial Pre-Textos, 2002
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo La máquina calculadora de Nicholas Saunderson se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Evolución de los sistemas nerviosos: el sistema periférico de vertebrados

Como decíamos en la entrega anterior de esta serie, en los sistemas nerviosos diferenciamos el subsistema central y el periférico. Desde un punto de vista funcional, en el sistema periférico se distinguen dos grandes divisiones: la aferente y la eferente. La división aferente es la formada por los nervios que transportan información hacia el sistema nervioso central. En la división eferente la información viaja del sistema central a los órganos efectores, tanto musculares como de otro tipo. Dentro de la división eferente se diferencian, a su vez, dos sistemas, el somático y el visceral o autónomo.
El sistema somático conduce las señales que dan lugar a movimientos corporales y a acciones hacia el exterior del organismo. Está formado por las fibras de las motoneuronas que inervan los músculos esqueléticos; sus cuerpos celulares se encuentran en la médula espinal y un único axón alcanza las fibras musculares que inerva. La acción de estas motoneuronas consiste siempre en la excitación y contracción de los músculos, aunque la actividad muscular puede ser inhibida mediante sinapsis inhibitorias a cargo de neuronas del sistema central. De hecho, la actividad de las motoneuronas puede ser controlada mediante señales presinápticas, tanto excitatorias como inhibitorias. Esas señales pueden proceder de receptores sensoriales periféricos (reflejos espinales) o de diferentes enclaves encefálicos.
El sistema visceral está formado por las fibras que inervan la musculatura lisa, el corazón, las glándulas y otros órganos o tejidos no motores, como la grasa parda. Controla funciones que están sobre todo relacionadas con el mantenimiento de las condiciones del medio interno y también ciertas respuestas de carácter automático a estímulos exteriores. Regula actividades viscerales tales como la circulación, digestión, termorregulación, entre otras. En peces teleosteos, anfibios, aves y mamíferos, el sistema autónomo se subdivide, a su vez en dos divisiones, la simpática y la parasimpática. La mayor parte de los órganos viscerales están inervados tanto por fibras de la división simpática como de la parasimpática. En esos casos suelen ejercer efectos opuestos. Normalmente ambas divisiones mantienen una cierta actividad, pero dependiendo de las circunstancias, se eleva la de uno de los dos a la vez que se reduce la del otro. De esa forma se eleva o se reduce la actividad del órgano en cuestión. Con carácter general se puede decir que la activación de la división simpática prepara al organismo para desarrollar una actividad física muy intensa (eleva la ventilación respiratoria y la actividad cardiaca, activa la circulación periférica, inicia el catabolismo del glucógeno y grasas; dilata las pupilas, ajustando la vista a larga distancia o en oscuridad; en algunas especies promueve la sudoración o el jadeo; y a cambio, reduce las actividades urinaria y digestiva). La división parasimpática domina, por el contrario, en condiciones de tranquilidad, cuando el organismo ha de ocuparse de sus asuntos internos; por esa razón, esta división activa la digestión y la función urinaria.
La inervación a cargo de las dos divisiones proporciona un control más preciso de la funciones reguladas por el sistema autónomo. No obstante, hay unos pocos órganos o glándulas que solo reciben señales de una de las dos divisiones. Arteriolas y venas están inervados por fibras simpáticas (arterias y capilares no están inervados), con la excepción de los vasos que irrigan el pene y el clítoris, que reciben fibras simpáticas y parasimpáticas, lo que permite un control muy preciso de la erección de ambos. La mayoría de las glándulas sudoríparas también están inervadas solo por fibras simpáticas. Y aunque las glándulas salivares reciben fibras simpáticas y parasimpáticas, en este caso sus efectos no son antagonistas; ambas estimulan su actividad.
Algunos textos de fisiología añaden a las dos divisiones anteriores –simpática y parasimpática- una tercera, la división entérica que, aunque mantiene alguna conexión con el sistema central, se halla contenida en el intestino. Consiste en redes neuronales ubicadas en las paredes del intestino. Controla el peristaltismo, la segmentación y otros patrones de contracción de la musculatura lisa de la pared intestinal. Por lo tanto, es la división que se encarga de impulsar el alimento que es procesado dentro del tracto intestinal.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Evolución de los sistemas nerviosos: el sistema periférico de vertebrados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Evolución de los sistemas nerviosos: el sistema central de vertebrados
- Evolución de los sistemas nerviosos: anélidos y artrópodos
- Evolución de los sistemas nerviosos: moluscos
Se establece el principio de conservación de la energía

Este mes de julio se cumplen 170 años de un artículo clave en la historia de la ciencia.
Mayer y Joule fueron sólo dos de al menos una docena de personas que, entre 1832 y 1854, propusieron de alguna forma la idea de que la energía se conserva. Algunos expresaron la idea vagamente; otros con toda claridad. Algunos llegaron al convencimiento principalmente a través de la filosofía; otros a partir de consideraciones prácticas en el uso de motores y máquinas o a partir de experimentos de laboratorio; otros más por una combinación de factores. Muchos, entre ellos Mayer y Joule, trabajando independientemente de todos los demás. Una cosa era evidente, la idea de la conservación de la energía estaba, de alguna manera, “en el aire”.

Hermann Ludwig Ferdinand von Helmholtz en 1848
Pero si hemos de poner fecha al inicio de la aceptación mayoritaria de la ley de la conservación de la energía hemos de referirnos a la publicación de uno de los artículos más influyentes de la historia, no ya de la física, sino de la ciencia, lo que no implica que sea de los más conocidos. Se publicó en 1847, dos años antes de que Joule publicase los resultados de sus experimentos más precisos. El autor, un joven médico alemán que estaba estudiando el metabolismo del músculo llamado Hermann von Helmholtz, tituló su trabajo Über die Erhaltung der Kraft (Sobre la conservación de la fuerza). Helmholtz (usando ” fuerza “en el sentido moderno de “energía”), afirmaba audazmente en él la idea que otros sólo expresaban vagamente, a saber, “que es imposible crear una fuerza motriz duradera a partir de nada “.Con esto rechazaba la existencia de una “fuerza vital” necesaria para el movimiento del músculo, una idea la de la necesidad de la fuerza vital directamente extraída de la Naturphilosophie imperante en la fisiología alemana de la época.
Helmhotz volvería sobre este tema aún más claramente muchos años después en una de sus conferencias de divulgación:
Llegamos a la conclusión de que la Naturaleza en su conjunto posee una reserva de fuerza [energía] que no puede de ninguna manera ser aumentada ni disminuida y que, por lo tanto, la cantidad de fuerza en la Naturaleza es igual de eterna e inalterable que la cantidad de materia. Expresado en esta forma, he llamado a la ley general “El Principio de la Conservación de la Fuerza”.
Así pues, a medidados del siglo XIX queda establecido un principio básico y universal de la ciencia con enormes consecuencias prácticas. Cualquier máquina o motor que realice trabajo (proporciona energía) sólo puede hacerlo si la extrae de alguna fuente de energía. O, de otra forma, la máquina no puede suministrar más energía de la que obtiene de la fuente. Cuando se agote la fuente, la máquina dejará de funcionar. Las máquinas y los motores sólo pueden transformar la energía; no pueden crearla o destruirla.
Esto, que hoy día debería estar asumido, no lo está tanto como debiera. En cualquier caso, con lo que llevamos visto en esta serie de forma tan sencilla, ya podemos formular dos de las leyes que rigen el funcionamiento del universo (así, como suena) y que veremos en las dos próximas entregas de la serie.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Se establece el principio de conservación de la energía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Se intuye la conservación de la energía (1)
- Se intuye la conservación de la energía (2)
- De las leyes de conservación (I)
Cómo regular la velocidad de disolución de los biometales de las prótesis
Los biometales se usan desde hace mucho tiempo en medicina, principalmente en prótesis, pero también en elementos de unión para soldar huesos o en los stents que se emplean para solventar problemas cardiovasculares, entre otros. Los metales más utilizados tradicionalmente —el acero inoxidable y las aleaciones de titanio—presentan ventajas, como su resistencia a la corrosión en el medio fisiológico, pero también inconvenientes, como la disminución de la densidad ósea en las inmediaciones de la prótesis, que produce una pérdida de resistencia del hueso. Además, en muchas ocasiones se hace necesario realizar una segunda intervención para eliminar el material una vez que ha cumplido su función.
Para solventar dichos problemas, se están desarrollando numerosas investigaciones con otros materiales, como la familia del magnesio y sus aleaciones. “Lo que hace que este material sea especialmente atrayente es su capacidad de disolverse en el medio fisiológico, es decir, se iría disolviendo progresivamente, hasta que, una vez cumplida su misión, fuera expulsado del cuerpo de forma natural, a través de la orina”, explica Nuria Monasterio, autora del estudio realizado en la Escuela de Ingeniería de Bilbao de la UPV/EHU. Así, se evitarían segundas intervenciones en los pacientes. Otro punto fuerte del nuevo material consiste en que evita la pérdida de densidad ósea localizada que producen otros materiales más resistentes. “Además, al tratarse de un material abundante en la corteza terrestre, la materia prima tiene un costo razonable, aunque su procesado requiere ciertas precauciones que encarecen la fabricación de las aleaciones. Por lo cual, sus costos finales se sitúan a medio camino entre los del acero inoxidable y las aleaciones de titanio”.
Sin embargo, dicho metal también presenta retos, ya que “su velocidad de disolución es mayor de la deseada. Se disuelve antes de cumplir su función; por ello, el reto es alargar su vida para que esté, de alguna manera, regulada a la medida de la aplicación”, afirma Monasterio.

Aspecto de la superficie de la capa de fosfato de calcio. Foto: Nuria Monasterio. UPV/EHU.
Existen varias técnicas para tratar de alargar la vida de las aleaciones de magnesio; esta investigación de la UPV/EHU ha optado por el recubrimiento del material con fosfato de calcio, aunque “la función del fosfato de calcio no solo es alargar la vida del propio magnesio. Se trata, además, de que el cuerpo humano lo tolere mejor y que aumente la velocidad de generación de tejidos adyacentes, una doble función que consiste en alargar la vida del material y conseguir una mejor integración. Hay que tener en cuenta que, por un lado, es el componente principal de los huesos y, por otro, está comprobado que favorece el crecimiento de los tejidos circundantes”, comenta.
Como medio para adherir la capa de fosfato de calcio a la superficie del metal, se ha empleado la electrodeposición. “Lo que perseguíamos era obtener un depósito uniforme, que no se desprendiera, y que pudiéramos variar su espesor de manera eficaz. Para ello, se han estudiado distintas variables eléctricas, para conseguir adecuar los espesores a la medida de lo que requieran las aplicaciones concretas”. Y el resultado ha sido más que satisfactorio: “además de validar el método utilizado, se ha logrado regular la calidad y el espesor de la capa de manera precisa” destaca Nuria Monasterio.
La investigadora de la UPV/EHU menciona varios retos de cara al futuro, “hemos conseguido afinar el sistema electrolítico, por lo que ahora pretendemos probar con otros biometales. Por otro lado, trabajamos en la fabricación de aleaciones de magnesio de composiciones que no supongan riesgo alguno, ya que la aleación de magnesio utilizada en esta investigación contiene aluminio, un metal perjudicial para la salud”.
Referencia:
N. Monasterio, J.L. Ledesma, I. Aranguiz, A.M. Garcia-Romero, E. Zuza.. Analysis of electrodeposition processes to obtain calcium phosphate layer on AZ31 alloy. Surf. Coat. Technol. 319 (2017) 12-22. doi: 10.1016/j.surfcoat.2017.03.060
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Cómo regular la velocidad de disolución de los biometales de las prótesis se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo mecanizar una pieza de cobre usando bacterias
- Cómo sintetizar casi cualquier biomaterial usando ADN
- Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte
Libros para enamorarse
Daniel Torregrosa, lector

Durante prácticamente toda su vida, el científico y popularizador de la ciencia Carl Sagan dio una gran importancia a la generación de entusiasmo y fascinación en la transmisión de la ciencia a la ciudadanía, algo que veía como una obligación necesaria e ineludible para el beneficio de la civilización global y de nuestra supervivencia como especie. Una faceta que Sagan predicaba con el ejemplo y resumía con su famosa sentencia: «Después de todo, cuando estás enamorado, quieres salir a contarlo a todo el mundo».
Y una forma de «salir a contarlo» puede ser la de recomendar algunos libros que pueden enamoraros de la ciencia. O al menos es mi deseo.
Para enamorarse de la Química

El tío tungsteno. Recuerdos de un químico precoz, de Oliver Sacks. Barcelona, 2003. Editorial Anagrama. Colección compactos.
En este delicioso libro de Oliver Sacks nos encontraremos con la autobiografía adolescente de este famoso neurólogo amalgamada con un buen resumen de la historia general de la química. Aparte de disfrutar y maravillarnos con las vivencias de su infancia descubriremos un relato donde la química, como ciencia apasionante como pocas, cobra un valor original y muy personal. Un viaje iniciático donde la curiosidad de Sacks le lleva a la admiración de héroes y heroínas como Carl Wilhelm Scheele, Lavosier, Marie Curie, Mendeléiev, Moseley y otros personajes conocidos de la historia de la ciencia. Una cuestión menor, pero muy curiosa, de este libro es la que nos revela Sacks como motivo de que abandonara el interés por la química cuando apenas había cumplido 14 años. La respuesta, a todas luces reveladora de la irrepetible figura de Oliver Sacks, la encontrará el lector en sus páginas.
Para enamorarse de la Física

Seis piezas fáciles, de Richard Feynman. Barcelona, 2014. Planeta. Colección Booket Ciencia.
Esta obra es una selección del libro de texto Lecciones de Física (1963) de Richard Feynman, uno de los genios más reconocibles del siglo XX. La ciencia no es una aventura fácil y mucho menos la Física, pero viendo cómo la explicaba Feynman dan ganas de matricularse en un curso avanzado de esta disciplina o directamente en el grado de Física. La forma tan clara y magistral de explicar los conceptos básicos, con ejemplos escogidos sacados de nuestro mundo cotidiano, nos embriaga desde el primer capítulo, el de los átomos en movimiento, hasta llegar al clímax final con la mecánica cuántica. Pero mi pieza favorita es la tercera, la que nos cuenta de forma muy original la relación de la física con el resto de ciencias. La épica y la lírica de la ciencia, tan habituales en Feynman, también tiene cabida en este accesible libro, que constituye una delicia absoluta para neófitos o recién iniciados.
Para enamorarse de las Matemáticas

Cartas a una joven matemática, de Ian Stuart. Barcelona, 2016. Crítica. Drakontos bolsillo.
Mediante una serie de cartas dirigidas a la joven Meg (personaje ficticio), Ian Stuart convierte este libro en toda una apología de las matemáticas, emulando al gran matemático Godfrey H. Hardy. Fresco, divertido e inspirador. Un libro que nos convence de la belleza y la importancia de esta disciplina, nos habla de las nuevas áreas de investigación como la teoría del caos o la geometría fractal, e incluso se adentra en vida académica de los matemáticos profesionales. No es uno de esos libros de introducción formal a las matemáticas, ni de paradojas o desafíos matemáticos, no es aparentemente un libro de divulgación de las matemáticas. Es el libro que te lleva a devorar todos los anteriores.
Para enamorarse de la Biología

Botánica insólita, de José Ramón Alonso con ilustraciones de Yolanda González. Pamplona, 2016. Next Door Publishers.
La primera impresión que ofrece este libro, con solo acariciar su portada, es la de estar frente a una obra maestra de la divulgación científica y el arte.
Y cuando nos sumergimos en sus páginas nos encontramos con unas historias extraordinarias y fascinantes sobre las plantas, contadas con un exquisito lenguaje literario de la mano del profesor y divulgador José Ramón Alonso Peña e ilustradas por Yolanda González.
Semillas con alas aerodinámicas, plantas carnívoras aterradoras, árboles descomunales, la inmortalidad surgida del hielo, la alquimia para detectar moléculas en el aire y modificar su comportamiento, las plantas medicinales de los neandertales y así hasta treinta y seis capítulos maravillosamente ilustrados. Goce intelectual y visual absoluto que nos hará mirar con otros ojos al reino Plantae que nos rodea.
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
El artículo Libros para enamorarse se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¡Explora! Libros de divulgación científica para niños
- Cálculo y geometría analítica, de George F. Simmons
- #Naukas16 Big Van Science
Arte & Ciencia: Imaginario marino

El arte y la ciencia son dos formas de conocimiento aparentemente alejadas, en gran medida consecuencia de la especialización profesional y la educación compartimentada. Del estudio de esta impostada separación surgió el estereotipo de las dos culturas, las ciencias y las humanidades, para referirnos a esa brecha de conocimiento. La realidad es que la ciencia y el arte sí están conectadas y que ninguna forma de conocimiento es impermeable a otra. Por poner algunos ejemplos: ¿Cómo podría crearse una obra plástica sin las técnicas propiciadas por la ciencia? ¿Cómo podríamos interpretar la elección de materiales?
Estas y otras cuestiones relacionadas furon tratadas por destacados profesionales -artistas, ilustradores, filósofos y científicos- que han puesto el foco en ese difuso trazo que une la ciencia y el arte. El ciclo Ciencia & Arte se desarrolló, bajo la dirección de Deborah García Bello, a lo largo de cuatro jornadas que se celebraron los jueves días 6 y 27 de abril y 11 y 25 de mayo de 2017 en el auditorio del Museo Guggeheim Bilbao.
Esta actividad de la Cátedra de Cultura Científica de la UPV/EHU se enmarca en el programa TopARTE que conmemora el XX Aniversario del Museo Guggenheim Bilbao.

Segunda jornada. 2ª conferencia
Clara Cerviño, bióloga e ilustradora: Imaginario marino
Las primeras ilustraciones de animales y plantas, el coleccionismo de maravillas naturales, el trabajo de los artistas… A lo largo de su historia, el ser humano ha representado la naturaleza de diferentes maneras que han jugado un papel fundamental en la generación de conocimiento científico. Pero esta influencia también se ha dado en la dirección inversa, puesto que los descubrimientos científicos han servido de inspiración y han influido en el desarrollo de técnicas pictóricas y estilos artísticos, marcando el devenir de la historia del arte.
Imaginario marinoEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Arte & Ciencia: Imaginario marino se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: La importancia de la ciencia para la conservación del arte
- Arte & Ciencia: Química y Arte, reacciones creativas
- Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte
Parkinsonia parkinsoni

Parkinsonia parkinsoni NHM. Pablo Barrecheguren
Todos tenemos nuestras aficiones y la de James Parkinson eran los fósiles. Nacido en 1755, este médico londinense compaginó su labor médica en Hoxton con los fósiles y llegó a tener una de las colecciones más bellas del país. Es fácil imaginarlo tras una jornada de trabajo paseándose por sus estanterías llenas de piezas bien ordenadas. Como médico ejercía en la zona norte de la ciudad, en un barrio que por la Revolución Industrial pasó de ser una zona ajardinada a una interminable sucesión de edificios de ladrillos. Esto produjo un aumento en la población y por lo tanto de pacientes, entre los cuales James empezó a detectar casos de un trastorno motor desconocido.
- Essay on the Shaking Palsy
En 1817, James Parkinson publicó “Essay on the Shaking Palsy” (Ensayo sobre la parálisis agitante), donde describe la mayoría de los síntomas clásicos motores presentes en la enfermedad de Parkinson. Actualmente es la segunda enfermedad neurodegenerativa, después del alzhéimer, con una prevalencia que aumenta según envejece la población y se estima que afecta al 1-2% de la población mayor de 65 años.
Aunque los temblores son el síntoma que más se suele asociar a la enfermedad, uno de cada cuatro pacientes no desarrolla temblores y además los problemas motores van mucho más allá: rigidez muscular, calambres, dificultad para iniciar o terminar un movimiento, temblores estando en reposo, movimientos lentos, etc. Sin embargo, tal y como el propio James señaló en su ensayo, esta enfermedad es más que un trastorno motor y también existen síntomas no motores como desórdenes en el sueño, y se ha visto que algunos de los pacientes desarrollan demencia o psicosis tras varios años con la enfermedad de Parkinson.
La causa principal de la enfermedad es la degeneración de las neuronas dopaminérgicas en la substantia nigra, que es uno de los núcleos principales de los ganglios basales (los cuales participan en la regulación de la actividad motora). Esta degeneración se debe principalmente a la aparición intracelular de unos depósitos proteicos denominados Cuerpos de Lewy, que interfieren en el funcionamiento neuronal y están compuestos mayoritariamente por α-Sinucleína. Se trata de una proteína presináptica cuya función exacta todavía no está clara, pero las mutaciones que afectan a su regulación son culpables de la mayor parte de casos de Parkinson familiar (que suponen aproximadamente el 5% del total). En el resto de situaciones las causas genéticas de cada caso no están claras, al igual que tampoco lo están los factores ambientales de riesgo (que van desde el consumo de drogas, la exposición a pesticidas o pequeños traumas cerebrales). Pero al igual que en otras enfermedades neurodegenerativas, uno de los factores que más aumenta las posibilidades de desarrollar la enfermedad es la edad: por ejemplo, a los cuarenta padecen la enfermedad aproximadamente el 0,041% de la población mientras que pasados los ochenta se supera el 1,9%.
Pasado el diagnóstico de la enfermedad, que se realiza principalmente mediante la identificación de los síntomas, la esperanza de vida ronda los 15 años. Durante todo ese tiempo el tratamiento principal para atenuar los síntomas es la administración de levodopa. Esta molécula es capaz de llegar al cerebro y allí se convierte en dopamina, por lo que su administración compensa la falta de dopamina provocada por la degeneración de las neuronas dopaminérgicas en la substantia nigra, y como consecuencia los síntomas de la enfermedad remiten. Desgraciadamente, con el paso del tiempo el efecto terapéutico de la levodopa disminuye e incluso es objeto de debate si la administración continuada de levodopa durante años puede también generar problemas en los pacientes. Por ello, también se usan otros fármacos o la estimulación cerebral profunda para combatir los síntomas.
Sin embargo, es importante recordar que todos los actuales tratamientos son paliativos: compensan temporalmente los desajustes pero no actúan sobre la causa del problema. Es como si tuviéramos un coche con el depósito de gasolina agujereado y en vez de arreglar el agujero lo único que pudiéramos hacer es suministrar continuamente más gasolina para que el coche no se pare. Además, hay que tener en cuenta que mantener a un paciente medicado durante años puede generar problemas, especialmente en casos como el párkinson donde es posible que el paciente también desarrolle otro tipo de enfermedades (por ejemplo 1 de cada 3 pacientes con párkinson desarrolla posteriormente alzhéimer) lo cual aumenta la medicación que deben tomar los pacientes, y por lo tanto las posibles complicaciones.
A día de hoy todavía es necesario un gran trabajo en investigación tanto básica como aplicada para comprender mejor la enfermedad y ser capaz de tratar su origen. Y aunque se va a tratar de un trabajo de décadas, tampoco se puede negar que ha habido una mejora sustancial en la calidad de vida de los pacientes gracias a los tratamientos paliativos: hace dos siglos cuando James Parkinson describió la enfermedad no se les podía ofrecer prácticamente ninguna ayuda a los pacientes mientras que ahora, al menos a corto plazo, es posible controlar los síntomas de la enfermedad.
James Parkinson, cuya colección de fósiles por cierto se vendió fragmentada en una subasta tras su muerte en 1824, y la mayoría de las piezas acabaron en un museo geológico de Estados Unidos. Museo donde se perdieron los fósiles a consecuencia de un incendio que destruyó el edificio. James Parkinson, quien moriría sin saber que daría nombre a una de las enfermedades más importantes del siglo XXI pero que curiosamente un año antes de su muerte se le honraría poniendo su nombre a un fósil: Parkinsonia parkinsoni.
Este post ha sido realizado por Pablo Barrecheguren (@pjbarrecheguren) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Parkinsonia parkinsoni se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sobre la predisposición genética a padecer enfermedades
- Una nueva diana terapéutica para el neuroblastoma
- La mutación vasca de la dardarina y el párkinson
Turquía prohíbe la enseñanza de la evolución – pero la ciencia no es un sistema de creencias
James Williams
![]()

Wellcome Images/Wikimedia Commons, CC BY
En los Estados Unidos han habido muchos intentos de eliminar la evolución del currículo escolar o exigir que el creacionismo – la idea de que toda vida fue creada por Dios – se le da el mismo trato en los libros de texto de ciencias. Si bien todos estos han fracasado, el gobierno de Turquía acaba de prohibir la evolución de su plan de estudios nacional.
Los creacionistas estadounidenses quieren que se presenten ambas opiniones, para que los niños decidan qué creer. Los esfuerzos para rechazar esto se caracterizan erróneamente como intentos de coartar el debate o la libertad de expresión para promover una ideología científica, atea, secular, frente a una cosmovisión religiosa más moral, ética y de sentido común.
La decisión de Turquía va mucho más allá. No se trata de reclamar la igualdad de trato, es una prohibición absoluta. El gobierno la justifica alegando que la evolución es “difícil de entender” y “controvertida”. Cualquier controversia, sin embargo, es una fabricada por las comunidades ultra-religiosas que buscan socavar la ciencia. Muchos conceptos en la ciencia son más difíciles que la evolución, pero todavía se enseñan.
Argumentos creacionistas
La evolución, según los creacionistas, es sólo una teoría – no está probada y, por tanto, es debatible. Los árboles evolutivos (especialmente para los seres humanos) se re-dibujan habitualmente después del descubrimiento de nuevos fósiles, demostrando lo pobre que es la teoría. Después de todo, si la teoría fuese correcta, esto no seguiría cambiando. A menudo los creacionistas plantean un reto a la ciencia para que demuestre cómo comenzó la vida, sabiendo que no hay todavía una teoría firme y aceptada. Por último, está el rey de todos los argumentos: si todos evolucionamos de los monos, ¿por qué hay monos todavía?
Estos argumentos están llenos de inexactitudes fácticas y falacias lógicas. La evolución no necesita una explicación de cómo comenzó la vida. Simplemente describe cómo la vida se desarrolla y se diversifica. Los humanos no evolucionaron de los monos – somos grandes simios. Los simios modernos, incluidos los humanos, evolucionaron a partir de especies preexistentes ahora extintas de simios. Estamos emparentados con, no descendimos de, los simios modernos.
Conceptos erróneos fundamentales creacionistas

Darwin lideró un gran avance. Glendon Mellow/Flickr, CC BY-NC-ND
Los creacionistas no comprenden que la evolución misma no es una teoría. La evolución sucede. La vida se desarrolla y diversifica, aparecen nuevas especies. Podemos ver las formas de vida intermedias en este momento, como peces que están en transición de vivir en tierra y los mamíferos terrestres que han realizado la transición a la vida acuática. La “teoría de la evolución” explica cómo se desarrolla la evolución. Charles Darwin y Alfred Russel Wallace describieron por primera vez el mecanismo que impulsa el cambio – la selección natural – en 1858.
Los creacionistas tampoco comprenden la diferencia entre una teoría y una ley en ciencia. Esto es algo que incluso los graduados en ciencia padecen, como he señalado en mi propia investigación. Las teorías explican conceptos científicos. Están respaldadas por pruebas y aceptadas por la comunidad científica. Las teorías son el pináculo de la explicación científica, no sólo un presentimiento o una conjetura. Sin embargo, las leyes tienen un papel diferente, describen fenómenos naturales. Por ejemplo, la ley de la gravedad de Newton no explica cómo ocurre la gravedad, describe los efectos que la gravedad tiene en los objetos. Hay leyes y teorías para la gravedad. En biología, sin embargo, hay pocas leyes, por lo que no hay ley de la evolución. Las teorías no se convierten, si tienen pruebas suficientes, en leyes. No son jerárquicas.
Una tercera cuestión es la falta de comprensión de la naturaleza de la ciencia. La ciencia no pretende encontrar alguna verdad objetiva, sino obtener una explicación de los fenómenos naturales. Todas las explicaciones científicas son provisionales. Cuando se encuentran nuevas pruebas que contradicen lo que pensamos que sabemos, cambiamos nuestras explicaciones, a veces rechazando teorías que antes se creían correctas. La ciencia siempre está trabajando para tratar de falsar ideas. Cuantas más superan esas ideas nuestras pruebas, más robustas son y mayor es nuestra confianza en que son correctas. La evolución se ha comprobado durante casi 160 años. Nunca se ha falsado. La ciencia sólo se ocupa de los fenómenos naturales, no le incumbe ni trata de explicar lo sobrenatural.
¿Por qué la prohibición es peligrosa?
Prohibir la buena ciencia socava toda la ciencia, especialmente teniendo en cuenta el lugar de la evolución como base de la biología moderna, con abundantes evidencias para apoyarla. Para la mayoría de científicos el hecho de que la evolución tenga la lugar no se cuestiona seriamente ni es algo controvertido. Cualquier controversia en las discusiones sobre la evolución trata sobre el papel que la selección natural tiene como motor de la diversidad y el cambio, o el ritmo de ese cambio.
Esta prohibición de enseñar la evolución en las escuelas turcas abre la posibilidad de que ideas alternativas no científicas puedan entrar en la enseñanza de la ciencia, desde aquellos que creen en una tierra plana a los negadores de la gravedad.
¿Cómo tratar el aparente cisma entre la creencia religiosa y la evidencia científica?
Mi investigación y enfoque ha sido distinguir entre religión, un sistema de creencias, y la ciencia, que trabaja en la aceptación de pruebas. Las creencias, incluyendo pero no limitadas a las creencias religiosas, a menudo se mantienen irracionalmente, sin pruebas, y son resistentes al cambio. La ciencia es racional, basada en la evidencia y está abierta al cambio cuando se enfrenta con nuevas pruebas. En ciencia, aceptamos las pruebas, en lugar de “elegir creer”.
La decisión de Turquía de prohibir la enseñanza de la evolución contradice el pensamiento científico y trata de convertir el método científico en un sistema de creencias, como si se tratara de una religión. Busca introducir explicaciones sobrenaturales para los fenómenos naturales y afirmar que existe alguna forma de verdad o explicación para la naturaleza más allá de la naturaleza. La prohibición es anticientífica, antidemocrática y debe oponérsele resistencia.
Sobre el autor:
James Williams es profesor de educación de la ciencia en el Sussex School of Education and Social Work de la Universidad de Sussex (Reino Unido)
Texto traducido y adaptado por César Tomé López a partir del original publicado por The Conversation el 28 de junio de 2017 bajo una licencia Creative Commons (CC BY-ND 4.0)
![]()
El artículo Turquía prohíbe la enseñanza de la evolución – pero la ciencia no es un sistema de creencias se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Evolución de los sistemas nerviosos: el sistema central de vertebrados
- El sistema de la difusión social de la ciencia: Catalizadores del sistema y consideraciones finales
- Ciencia, creencias, política y matar al mensajero
Miel y siropes, ¿son mejores que el azúcar?

A estas alturas, los que nos preocupamos por nuestra salud y tratamos de seguir una dieta equilibrada, sabemos que se consume más azúcar del recomendable, con las consecuencias para la salud que eso acarrea, sobre todo relacionadas con el sobrepeso y la diabetes. Por este motivo, muchos hemos buscado el ansiado sabor dulce en sustitutos del azúcar. Cada vez hay más oferta, desde el azúcar moreno, a edulcorantes como el aspartamo, el eritritol, la sacarina, la estevia, etc.
En el primer artículo de la serie «Azúcar y otros edulcorantes» concluimos que el azúcar moreno no es más saludable que el azúcar blanco. En siguientes artículos analizaremos al resto de edulcorantes. Hoy vamos a ver qué ocurre con los llamados edulcorantes naturales, como la miel y los siropes.
-
¿Qué es la miel?
Las abejas recolectan el néctar de las flores (miel de flores) o las secreciones de partes vivas de plantas o excreciones de insectos chupadores de plantas (rocío de miel), lo transforman gracias a la enzima invertasa que contienen en la saliva y lo almacenan en los panales donde madura hasta convertirse en miel.
La composición de la miel es la siguiente, aunque varía según el origen del néctar y el clima:
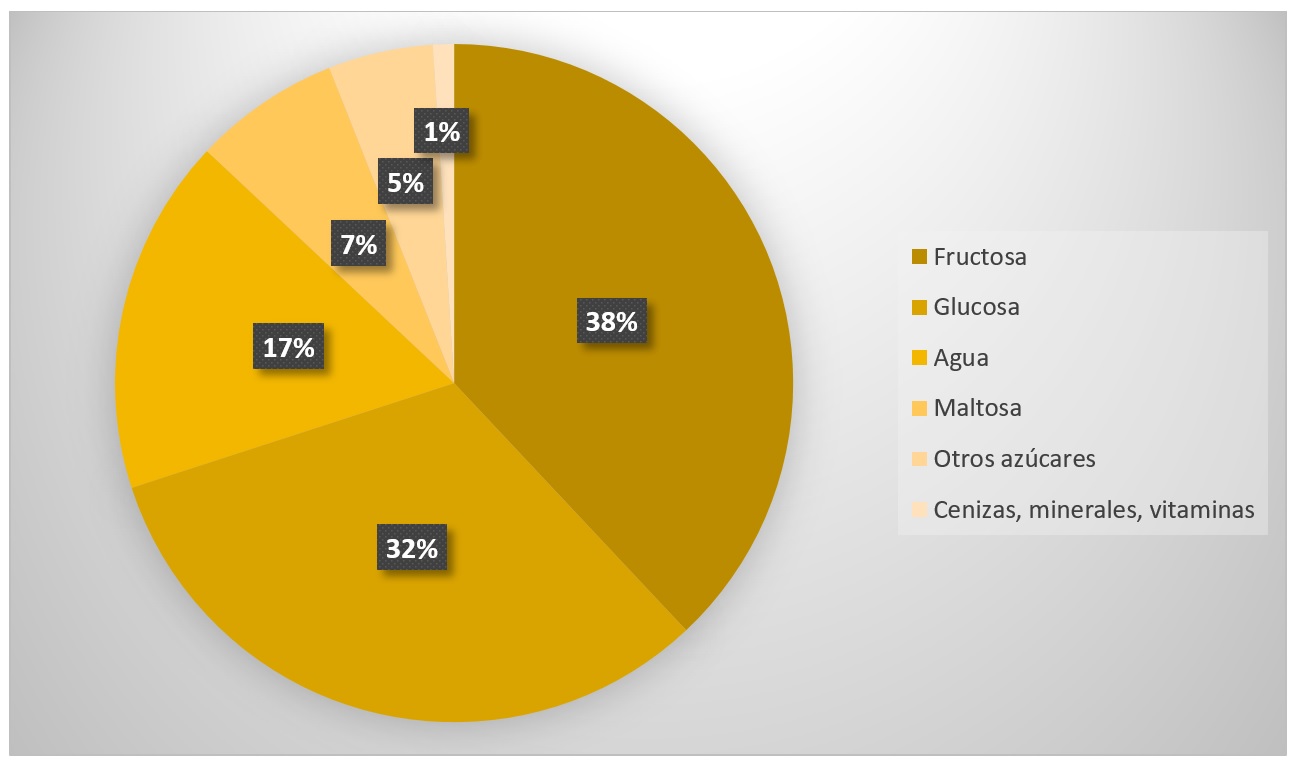
Composición media de la miel
El azúcar blanco y el azúcar moreno son sacarosa al 85-100%. La miel contiene en un 70-80% fructosa y glucosa —los monosacáridos que conforman la sacarosa—. En todos los tipos de miel, los azúcares conforman más de 85% de su composición.
Con respecto al aporte calórico, el azúcar tiene 4 kcal por gramo, mientras que la miel tiene unas 3 kcal por gramo. Esta disminución se debe al agua que contiene.
El índice glucémico (IG) de un alimento es otro valor a tener en cuenta. El IG determina la velocidad con la que un alimento hace aumentar los niveles de glucosa en sangre, de modo que los alimentos de alto IG se restringen en dietas para diabéticos o propensos a padecer diabetes. También reducen la saciedad, por lo que se suelen desaconsejar en dietas para perder peso. La miel tiene un IG de 60-65. El azúcar común tiene un IG de 70. Ambos son valores elevados y similares, así que tampoco es un dato que haga a la miel mejor que al azúcar común.
En la miel encontramos un 1% de otras sustancias que sí tienen valor nutricional, como minerales, vitaminas y aminoácidos, y es por ello por lo que se le atribuyen propiedades antioxidantes, entre otras. También contiene una pequeña porción de agua oxigenada, responsable de que en la antigüedad y en caso de emergencia, se utilizase miel como cicatrizante y bactericida.
La proporción de nutrientes es tan pequeña que necesitaríamos comer grandes cantidades de miel para que el aporte fuera significativo. Y eso es precisamente lo que no debemos hacer. El beneficio que pudiesen suponer sus nutrientes queda eclipsado por la enorme cantidad de azúcares que contiene la miel. Si queremos nutrientes, no los busquemos en la miel.
-
¿Qué son los siropes?
Los siropes o jarabes son jugos que se extraen de diferentes plantas que posteriormente se tratan para eliminar parte del agua y concentrar sus azúcares. Los siropes son disoluciones acuosas con un contenido en azúcares que oscila entre el 70 y el 90%. Los más conocidos son el sirope de arce y el sirope de agave.
El sirope de arce, edulcorante típico canadiense, se extrae del tronco de diferentes tipos de arces. Es el sustituto de la miel que suele emplearse en cocina vegana. Para producir el sirope se extrae el jugo del tronco de los arces y se calienta hasta conseguir la consistencia deseada. Algunos productores además le añaden grasa en forma de manteca.
El sirope de agave se extrae del corazón del agave, planta típica de México. Para su elaboración se corta la planta y se extrae la savia, denominada aguamiel, que es consumida por los nativos como una bebida refrescante. Si la savia se fermenta obtenemos pulque, bebida alcohólica tradicional de México. También se emplea para fabricar tequila. El proceso de obtención del sirope es por degradación enzimática de los carbohidratos, principalmente fructosanos, en azucares simples. Posteriormente se filtra y se concentra por calentamiento hasta alcanzar una viscosidad similar a la miel, de forma muy parecida a cómo se obtiene el sirope de arce o cualquier otro sirope vegetal.
Tanto el sirope de arce como el sirope de agave tienen un IG de 55 y aportan una media de 3 kcal por gramo. La diferencia con el azúcar se debe a la cantidad de agua y a la elevada proporción de fructosa. La composición media de ambos siropes es:
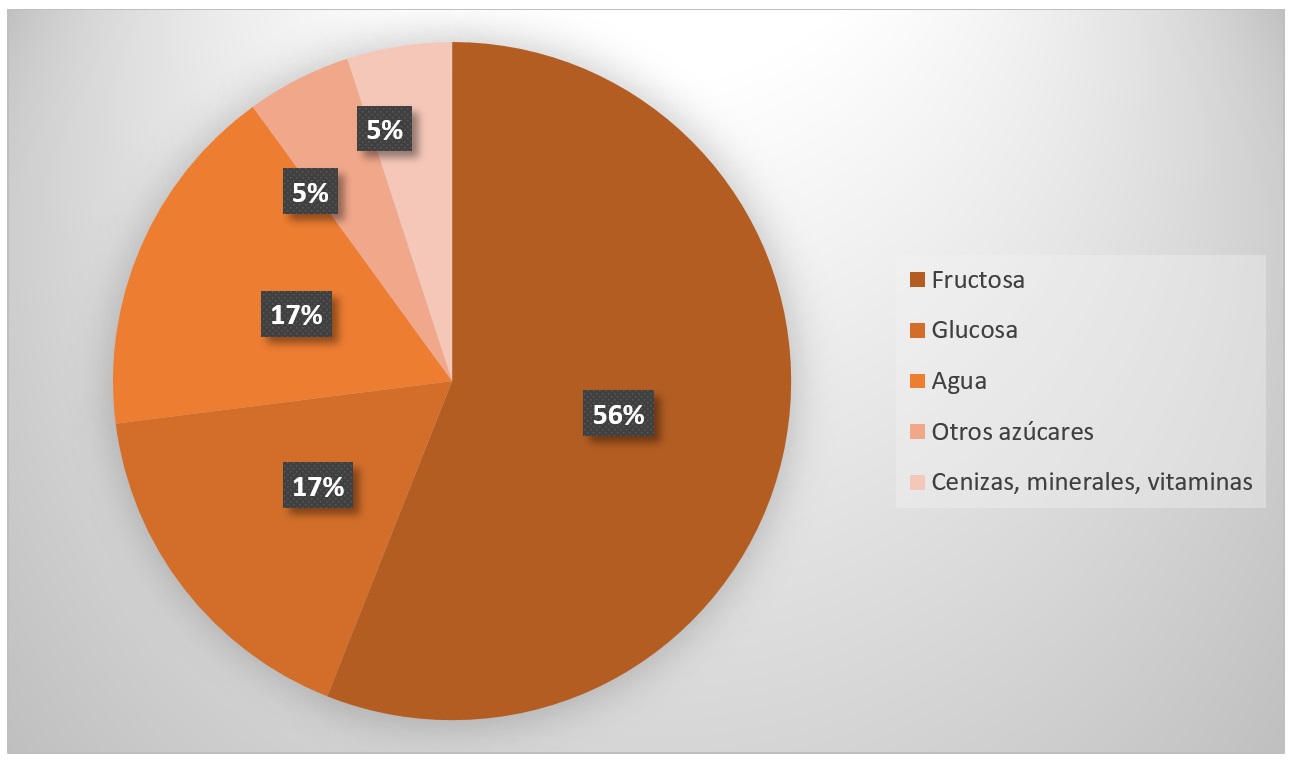
Composición media del sirope de agave y de arce
La principal diferencia entre los siropes y la miel es que los siropes contienen una mayor cantidad media de fructosa. El sirope que más fructosa contiene es el llamado jarabe de maíz, también conocido como jarabe de maíz de alta fructosa. Aunque la fructosa y la glucosa aportan casi las mismas kcal, la fructosa tiene una capacidad edulcorante más potente, por lo que suele emplearse menos cantidad para obtener el mismo dulzor.
De media, el 5% de cualquiera de estos siropes contiene otro tipo de sustancias con valor nutricional, como vitaminas, minerales y aminoácidos, responsables, entre otras cosas, de los diferentes sabores y aromas de los siropes. El porcentaje es muy pequeño como para tenerlo en consideración como aspecto saludable, ya que, como pasaba con la miel o con el azúcar moreno, habría que consumir una elevada cantidad de estos edulcorantes para conseguir una porción significativa de nutrientes. La enorme cantidad de azúcares ensombrece la posible bondad de sus nutrientes.
Para algunos consumidores, la ventaja de este 5% de nutrientes y otras sustancias es organoléptica. De ninguna manera debería aconsejarse el consumo de miel o siropes alegando valor nutricional y otros aspectos saludables, porque no son ni ciertos ni relevantes.
-
Consideraciones metabólicas de siropes, miel y otros edulcorantes de alto contenido en fructosa.
A diferencia de la glucosa, que se absorbe instantáneamente produciendo un aumento y disminución rápida de energía, la fructosa se metaboliza más despacio y en parte es almacenada como reserva por el hígado en forma de glucógeno. El exceso acaba convirtiéndose en grasa. Sin embargo, puesto que la fructosa se transforma en glucosa y produce una elevación glucémica en sangre, no se considera un edulcorante recomendable para las personas con diabetes, tal y como se creía erróneamente en el pasado.
El hecho de que toda la fructosa tenga que ser metabolizada por el hígado (mientras que la glucosa se metaboliza en todo tipo de células) tiene implicaciones sobre la salud. Actualmente se está analizando la relación entre un consumo excesivo de fructosa y algunas patologías como la diabetes tipo II, la obesidad y sus enfermedades cardiovasculares asociadas, el hígado graso no alcohólico y el síndrome metabólico. Patologías que, hasta ahora, asociábamos al consumo excesivo de azúcar común, entre otros, y que hoy en día extendemos a estos otros edulcorantes de elevado contenido en azúcares como la fructosa.
Puede resultar curioso que un alimento con un IG medio, como muchos siropes, esté relacionado con la obesidad. Esto tiene una razón metabólica que lo explica: el hígado focaliza toda la actividad en la fructosa, lo que causa un cese en la actividad digestiva normal. La consecuencia es que se reducen los niveles de insulina y leptina, y aumenta el nivel de la hormona ghrelina, encargada de controlar el apetito, con lo cual, cuando consumimos fructosa, no sentiremos saciedad.
-
Conclusiones
La recomendación de la Organización Mundial de la Salud (OMS) es reducir el consumo de azúcar libre hasta los 25 g diarios (exactamente al 5% de las calorías diarias consumidas). En la recomendación de la OMS se hace una clara distinción entre azúcar libre y azúcar intrínseco. El azúcar intrínseco es el que de serie contienen las frutas y las verduras, y sobre el que no hay restricción de consumo. El azúcar libre es el que sí debemos minimizar. El azúcar libre lo añadimos a los alimentos como azúcar común y es el que se utiliza como un ingrediente más en alimentos procesados (sean aparentemente dulces o no). La OMS también denomina azúcar libre la miel y los siropes, ya que su consumo ocasiona una respuesta metabólica de consecuencias análogas a las que produce el consumo de azúcar común.
Tanto la miel como los siropes tienen un contenido en azúcares elevado, que varía entre el 70% y el 90%. El resto es agua, y una cantidad mínima de nutrientes, vitaminas y minerales. Estos nutrientes son tan escasos que, cualquiera de las propiedades beneficiosas que pudiesen aportarnos, quedan ensombrecidas por el alto contenido en azúcares. Si queremos nutrientes, no los busquemos en la miel o en los siropes.
En definitiva, si la recomendación es disminuir la ingesta de azúcar libre, disminuyámosla, no busquemos soluciones mágicas. Tanto la miel como los siropes son azúcares con nombres y presentaciones atractivas, que evocan salud y naturalidad. Son azúcares con un bonito disfraz.
Principales fuentes consultadas:
- Recomendaciones sobre el consumo de azúcares de la Organización Mundial de la Salud [PDF]
- Wikipedia: Maple syrup.
- Directo al paladar: Qué es el sirope de agave, origen y usos en la cocina.
- Morselli, Mariafranca; Whalen, M Lynn (1996). “Appendix 2: Maple Chemistry and Quality”. In Koelling, Melvin R; Heiligmann, Randall B. North American Maple Syrup Producers Manual. Ohio State University.
- Gominolas de petróleo: ¿Es cierto que la miel no se estropea?
- El comidista: ¿Existen alternativas sanas al azúcar?
- Forristal, Linda (2001). The Murky World of High-Fructose Corn Syrup.
- Teff, K. L.; Elliott, S. S., Tschöp, M., Kieffer, T. J., Rader. D., Heiman, M., Townsend, R. R., Keim, N. L., D’Alessio, D., Havel, P. J. (2004). “«Dietary fructose reduces circulating insulin and leptin, attenuates postprandial suppression of ghrelin, and increases triglycerides in women.» J Clin Endocrinol Metab. 89 (6): 2963-72.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Miel y siropes, ¿son mejores que el azúcar? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El azúcar oculto en los alimentos
- Azúcar moreno, ¿mejor que el azúcar blanco?
- Un modelo para la máquina de coser fluidodinámica, o como untar miel con conocimiento
Nanotubos de carbono y regeneración neuronal
Cuando hablamos de nanotecnología aplicada a la medicina surgen preguntas muy básicas, como ¿qué pasa si permitimos que interactúen neuronas con nanotubos de carbono? ¿Será tóxico, pierden las neuronas sus capacidades, mueren? Precisamente un equipo de investigadores en el que participa Maurizio Prato, profesor Ikerbasque en CIC biomaGune, ha investigado los posibles efectos sobre las neuronas de la interacción con los nanotubos de carbono. Y han encontrado algo tremendamente interesante y potencialmente muy importante.
Los científicos han demostrado que estos nanomateriales pueden mediar en la formación de sinapsis, esas estructuras especializadas a través de las cuales las células nerviosas se comunican, y modular mecanismos biológicos, como el crecimiento de las neuronas, como parte de un proceso autorregulado. Este resultado, que muestra hasta qué punto la integración entre las células nerviosas y estas estructuras sintéticas es estable y eficiente, pone de relieve las grandes potencialidades de los nanotubos de carbono como materiales capaces de facilitar la regeneración neuronal o para crear una especie de puente artificial entre grupos de neuronas cuya conexión se haya visto interrumpida. Las pruebas in vivo ya han comenzado.
Tan espectacular como suena, los nanomateriales representan hoy día la mejor esperanza para el tratamiento de personas con daños en su médula espinal. Estos materiales se usan tanto como andamiaje, dando soporte estructural, como interfaces para permitir la comunicación entre neuronas.
Sin embargo, todavía hay que considerar muchas cuestiones. Entre ellas el impacto en la fisiología neuronal de la integración de estas estructuras nanométricas con la membrana celular. Si, por ejemplo, el mero contacto provocara un aumento vertiginoso del número de sinapsis, estos materiales serían esencialmente inutilizables. Esto es precisamente lo que se ha investigado en este estudio.
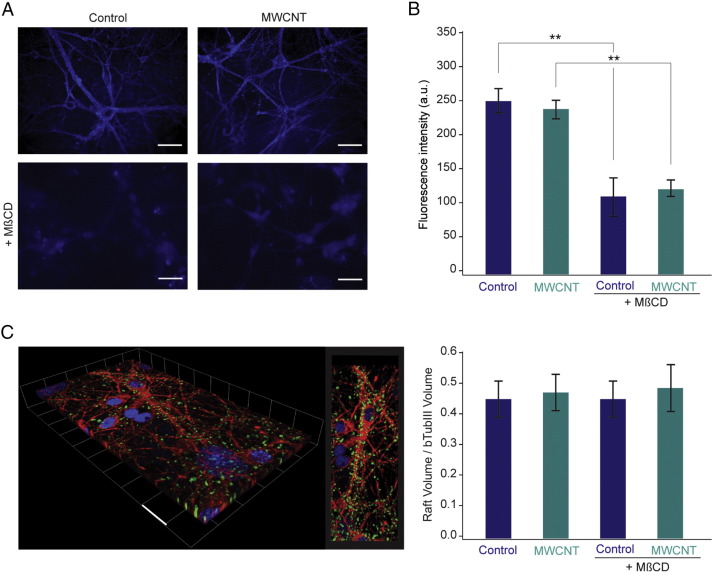
Los resultados de la investigación son muy alentadores: se ha comprobado que los nanotubos no interfieren en la composición de los lípidos, en particular del colesterol, que constituyen la membrana celular en las neuronas; estos lípidos de la membrana juegan un papel muy importante en la transmisión de las señales a través de las sinapsis. Y los nanotubos no parecen influir en este proceso, lo que es muy importante.
La investigación también ha destacado el hecho de que las células nerviosas que crecen sobre el substrato de nanotubos, gracias a esta interacción, se desarrollan y alcanzan la madurez muy rápidamente, llegando finalmente a una condición de homeostasis biológica, es decir, este crecimiento no es indiscriminado e ilimitado sino que se consigue llegar a un equilibrio fisiológico.
La consecución de este equilibrio es un aspecto de fundamental importancia . Efectivamente, no solo los nanotubos de carbono funcionan excelentemente en términos de duración, adaptabilidad y compatibilidad mecánica con el material biológico, también estamos ante una interacción eficiente.
Si las pruebas in vivo salen bien, se habrá dado un paso en una dirección muy prometedora para recuperar funciones neurológicas perdidas.
Referencia:
Niccolò Paolo Pampaloni, Denis Scaini, Fabio Perissinotto, Susanna Bosi, Maurizio Prato, Laura Ballerini (2017) Sculpting neurotransmission during synaptic development by 2D nanostructured interfaces nanomedicine doi: 10.1016/j.nano.2017.01.020
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con N
El artículo Nanotubos de carbono y regeneración neuronal se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo incorporar nanotubos de carbono a un plástico de aviación
- Nanotubos de carbono como canales iónicos artificiales
- Nadar y guardar la ropa: nanotubos en revestimientos epoxis nanoestructurados

