La serendipia de la galaxia enana más lejana
Un equipo internacional, del que forma parte el profesor Ikerbasque de la UPV/EHU y asociado al Donostia International Physics Center (DIPC) Tom Broadhurst, utilizó la alta resolución del Telescopio Espacial James Webb (JWST) combinada con una poderosa lente gravitacional para concluir que las galaxias que se formaron en el universo primitivo eran normalmente muy pequeñas y que, en un proceso de evolución jerárquico, estas galaxias se fueron fusionando por gravedad mutua hasta formar galaxias masivas como nuestra Vía Láctea.
 El equipo miró más de 13.000 millones de años atrás para descubrir una galaxia enana muy poco brillante que podría ayudar a los astrónomos a saber más sobre las galaxias que existían poco después del Big Bang. Los 3 círculos de la imagen en color son las 3 imágenes de la galaxia lejana aumentada por el cúmulo de galaxias brillantes que se encuentran en primer plano. Imagen; ESA/Webb, NASA & CSA, P. Kelly.
El equipo miró más de 13.000 millones de años atrás para descubrir una galaxia enana muy poco brillante que podría ayudar a los astrónomos a saber más sobre las galaxias que existían poco después del Big Bang. Los 3 círculos de la imagen en color son las 3 imágenes de la galaxia lejana aumentada por el cúmulo de galaxias brillantes que se encuentran en primer plano. Imagen; ESA/Webb, NASA & CSA, P. Kelly.Mediante el análisis de los espectros de varias galaxias en el Universo lejano, el equipo ha podido confirmar además la detección de la galaxia enana más distante encontrada hasta la fecha. Según explica Broadhurst, “esta galaxia pequeña y de muy baja luminosidad es una de las primeras que se formaron, solo 500 millones de años después del Big Bang, cuando el volumen del universo era unas mil veces menor que el actual”.
Broadhurst forma parte de un equipo internacional que cuenta con una gran asignación de tiempo del JWST para estudiar estrellas y galaxias en el universo lejano a través de lentes gravitacionales, un método que utiliza objetos masivos, como cúmulos de galaxias, que magnifican en luminosidad y tamaño los objetos que se encuentran detrás. A principios de este año, el equipo ya había medido el espectro de varias estrellas y galaxias mediante esta técnica, “y nos sentimos muy emocionados al detectar una galaxia con un desplazamiento al rojo muy elevado”. Las últimas observaciones permitieron al equipo confirmar que “la estimación de la distancia de esta galaxia es fiable al 100 %, porque hemos sido capaces de reconocer elementos distintivos en su espectro, como hidrógeno, carbono, oxígeno y neón, que provienen de su gas caliente”.
Pura serendipiaLas mediciones del tamaño de esta galaxia han revelado que se trata de una galaxia enana de muy baja luminosidad situada a 13.200 millones de años luz. Estas mediciones han sido realizadas “gracias a la alta resolución del telescopio James Webb combinada con el poder magnificador de un cúmulo masivo de galaxias que se encuentra en primer plano, que actúa como una lente gigante”, explica el profesor. Broadhurst es un experimentado espectroscopista y experto en lentes gravitacionales, por lo que su trabajo ha consistido en “interpretar el espectro y estimar la amplificación de esta galaxia, mediante un modelo del campo gravitatorio del gran cúmulo de galaxias que actúa como lente en este caso”.
Según explica el investigador, “esta galaxia no era nuestro objetivo principal, pero afortunadamente apareció en las imágenes obtenidas con el James Webb, por lo que decidimos añadirla a nuestra lista de objetivos para una espectroscopía de seguimiento”. Esta serendipia ha llevado al equipo a concluir que “es muy posible que este tipo de galaxia enana y poco luminosa sea típica de las primeras galaxias que se formaron en el Universo primitivo, en lugar de galaxias más brillantes, como afirman otros grupos que no utilizan lentes gravitacionales”.
Referencia:
Hayley Williams, Patrick L. Kelly, Wenlei Chen, Gabriel Brammer, Adi Zitrin, Tommaso Treu, Claudia Scarlata, Anton M. Koekemoer, Masamune Oguri, Yu-Heng Lin, Jose M. Diego, Mario Nonino, Jens Hjorth, Danial Langeroodi, Tom Broadhurst, Noah Rogers, Ismael Perez-Fournon, Ryan J. Foley, Saurabh Jha, Alexei V. Filippenko, Lou Strolger, Justin Pierel, Frederick Poidevin, and Lilan Yang (2023) A magnified compact galaxy at redshift 9.51 with strong nebular emission lines Science DOI: 10.1126/science.adf5307
Para saber más:
La estrella individual más lejana jamás vista
Las lentes gravitacionales permiten observar la aparición de una supernova varias veces
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La serendipia de la galaxia enana más lejana se ha escrito en Cuaderno de Cultura Científica.
Desmitificando: El maíz transgénico y la mariposa monarca
monarca
El cultivo de maíz modificado genéticamente que sintetiza proteínas con capacidad insecticida de la bacteria Bacillus thuringiensis, el llamado maíz ttrasngénico Bt, ha aumentado exponencialmente desde las primeras variedades sembradas en 1996 en Estados Unidos y un año después en Canadá. La toxina que producen es la Cry1Ab que controla los insectos barrenadores del tallo del maíz de las especies de lepidóptero Ostrinia nubilalis y Diatraea saccharalis. Las proteínas cry se unen a receptores específicos de las membranas de las células epiteliales del tubo digestivo medio de insectos y las destruyen. Si las células no tienen receptores de proteínas cry no son afectadas por ellas. La historia del desarrollo de este maíz con el gen con capacidad insecticida la cuenta una de las participantes, Laura Privalle, en los laboratorios de la compañía CIBA-Geigy en los años ochenta.
En la revisión de Matías García y sus colegas del Centro de Investigaciones Biológicas Margarita Salas del CSIC en Madrid, se menciona que hasta el momento, en 2023, se han comercializado 210 tipos de maíz transgénico con resistencia a insectos y, en concreto, son 181 contra lepidópteros y 126 contra coleópteros.
El maíz Bt ha sido, como he mencionado, ampliamente cultivado en muchos países debido a su eficacia contra algunas plagas dañinas, lo que hace que sea competitivo además de suponer beneficios económicos, sociales y ambientales. beneficios sociales. En la Unión Europea (UE), se autorizaron solo dos variantes de maíz Bt, ambas productoras de Cry1Ab, para su cultivo hasta 2023: Bt176 (de la empresa Syngenta) de 1998 a 2005, y MON810 (de Monsanto) desde 2003. La variante de Syngenta se retiró en 2006 y, desde entonces, solo queda la de Monsanto. Entre 2011 y 2021 se cultivaron en la UE de 100000 a 130000 toneladas anuales de esta variante, un 0.05% de los cultivos transgénicos a nivel global.
De los 27 países que componen la Unión Europea, ocho han cultivado maíz Bt en algún momento: España, Portugal, Francia, Alemania, República Checa, Eslovaquia, Polonia y Rumanía. Sin embargo, desde 2017 solo España y Portugal han plantado esta variante de maíz y solo España lo ha cultivado de manera continua desde 1998, durante 24 años desde entonces hasta 2021. Donde más se siembra es en Cataluña, seguida de Aragón y Navarra, por ser las zonas donde las plagas que se controlan con esta variante son más abundantes.
En el estudio de Matías García y su grupo, se indica que el seguimiento a partir de bioensayos de laboratorio muestra que hasta 2021 no se ha producido una disminución de la susceptibilidad a Cry1Ab en estas plagas, confirmando que el maíz Bt sigue siendo eficaz. En la revisión a nivel global publicada este año por Bruce Tabashnik y sus colegas, de la Universidad de Arizona en Tucson, han encontrado un caso de resistencia a Ostrinia nubilalis, en Canadá, y dos casos a Diatraea saccharalis, ambos en Argentina.
 Foto: Steve Corey / Wikimedia Commons
Foto: Steve Corey / Wikimedia CommonsEl debate sobre la utilización del maíz Bt comenzó en 1999 con la publicación de un breve artículo, firmado por John Losey y su grupo, de la Universidad Cornell de Ithaca, en Nature. Después de ensayar los efectos del polen del maíz transgénico sobre larvas de la mariposa monarca Danaus plexippus, muy conocida en Estados Unidos por su gran migración. Después de estudiarlo en el laboratorio llegaron a la conclusión de que había un efecto significativo del polen sobre la supervivencia de las larvas de la monarca, además de cambios en su conducta para la alimentación y un menor crecimiento. Los autores pedían más datos para evaluar los riesgos asociados con el uso de transgénicos y compararlos con los que provocan los que plantea el uso de pesticidas y otras tácticas de control de plagas.
Dos años más tarde, en 2001, Richard Hellmich y su equipo, del Departamento de Agricultura, ensayaron los efectos del maíz Bt con la variante Cry1Ab sobre larvas de la mariposa monarca y concluyeron que no tiene efectos agudos sobre ellas en entornos en el campo. Y en 2002 se publicó en Inglaterra una nueva revisión, por el grupo de Angharad Gatehouse, de la Universidad de Newcastle, llega a la misma conclusión: el cultivo de las variedades comerciales de maíz Bt (Monsanto y Novartis) no supone un riesgo significativo para las poblaciones de la mariposa monarca y, en general, para insectos que no son el blanco de la capacidad insecticida de Cry1Ab, incluyendo a los polinizadores. Para 2002 la siembra de maíz Bt ha crecido más de un 40% mientras que las poblaciones de la mariposa monarca han aumentado un 30%. Para el Departamento de Agricultura de Estados Unidos, según el resumen de Mike Mendelsohn y sus colegas de la Agencia de Protección Ambiental (EPA), el maíz Bt no presenta riesgos para el ambiente ni para la salud humana.
Y en el meta-análisis de 47 experimentos de campo publicado en 2007 por Michelle Marvier y sus colegas, de la Universidad Santa Clara de California, los autores concluyen que los invertebrados que no son el objetivo de la capacidad insecticida del maíz Bt son más abundantes en los campos de este cultivo que en los tratados con insecticidas.
Referencias:
García, M. et al. 2023. Monitoring insect resistance to Bt maize in the European Union: Update, challenges, and future prospects. Journal of Economic Entomology doi: 10.1093/jee/toac154.
Gatehouse, A.M.R. et al. 2002. The case of monarch butterfly: a verdict is returned. Trends in Genetics 18: 249-251.
Hellmich, R.L. et al. 2001. Monarch larvae sensitivity to Bacillus thuringiensis-purified proteins and pollen. Proceedings of the National Academy of Sciences USA 98: 11925-11930.
Losey, J.E. et al. 1999. Transgenic pollen harms monarch larvae. Nature 399: 214.
Marvier, M. et al. 2007. A meta-analysis of effects of Bt cotton and maize on nontarget invertebrates. Science 316: 1475-1477.
Mendelsohn, M. et al. 2003. Are Bt crops safe? Nature Biotechnology 21: 1003-1009.
Privalle, L.S. 2017. The story behind the approval of the first Bt maize product. En “Women in sustainable agriculture and food biotechnology”, p. 71-83. Ed. por L.S. Privalle. Springer Int. Publ. Suiza.
Tabashnik, B.E. et al. 2023. Global patterns of insect resistance to transgenic Bt crops: The first 25 years. Journal of Economic Entomology doi: 10.1093/jee/toac183.
Wikipedia. 2023. Genetically modified maize. March 25.
Para saber más:
La historia de Cruz Gallastegui y el maíz híbrido
Ciencia, creencias, política y matar al mensajero
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Desmitificando: El maíz transgénico y la mariposa monarca se ha escrito en Cuaderno de Cultura Científica.
El juego militar francés
En esta entrada del Cuaderno de Cultura Científica vamos a hablar de un interesante juego de estrategia para dos jugadores que fue descrito y estudiado en un libro maravilloso, como es Recreaciones matemáticas (que tenemos la suerte de que esté traducido al castellano, aunque no sea fácil de conseguir en estos momentos), del matemático francés Édouard Lucas (1842-1891) y posteriormente recuperado por el gran divulgador de las matemáticas Martin Gardner (1914-2010), en su columna en la revista Scientific American de juegos matemáticos, en 1963. Se trata del juego militar francés, que recibe también otros nombres como el juego de los soldados, la liebre y los sabuesos, o el halcón y las palomas.
 Portadas de los cuatro volúmenes de Recreaciones matemáticas, de Édouard Lucas, publicados por la editorial Nivola en 2007 y 2008
Portadas de los cuatro volúmenes de Recreaciones matemáticas, de Édouard Lucas, publicados por la editorial Nivola en 2007 y 2008En el volumen 3 de Recreaciones matemáticas (publicado originalmente, de forma póstuma, en 1893), Édouard Lucas habla de un juego con cierta fama en los círculos militares franceses, que recibe el nombre el juego militar, e incluso menciona un evento relacionado con el mismo que ocurrió en un famoso café de París, el café de la Regencia, un sitio habitual de los jugadores y apasionados del ajedrez. Aunque Lucas ya había publicado esa información en el artículo Recreaciones científicas, el juego militar de la revista científica La Nature en el año 1887.
 Portada de la revista La Nature, de 1887, en la que aparece publicado el artículo Recreaciones científicas, el juego militar
Portada de la revista La Nature, de 1887, en la que aparece publicado el artículo Recreaciones científicas, el juego militarEn el citado artículo, así como en el volumen 3 de Recreaciones matemáticas, sobre el juego militar Lucas escribe que el juego aparece mencionado en una revista militar, el Bulletin de la Réunion des officers, de agosto de 1886, otorgándose la autoría del juego a un militar francés, Louis Dyen. Lucas incluye el siguiente párrafo de dicha publicación:
El Sr. Louis Dyen, subteniente retirado, caballero de la Legión de honor, ha dedicado su tiempo libre a la creación de un juego militar que ha ofrecido a la biblioteca y que, por sus variadas combinaciones, da una idea sobre las estratégicas maniobras empleadas por tres brigadas de caballería para cortar las comunicaciones de un cuerpo de ejercito que están asediando. Bajo una apariencia de las más simples, el juego militar presenta una variedad de combinaciones muy complicadas. La partida material del juego se compone de un tablero, parecido al del ajedrez, en el que hay 11 casillas, unidas a sus vecinas por otras tantas líneas rectas, que marcan otras tantas etapas que cada brigada debe superar para cortar al cuerpo de ejército sus comunicaciones y que el cuerpo de ejército dbe superar para evitar ser bloqueado. El cuerpo del ejército saldrá victorioso cuando, tras un número de etapas fijado con anterioridad, no se haya podido inmovilizar; es vencido en caso contrario. Menos difícil que el ajedrez el juego militar es más instructivo y merece ser recomendado como una distracción de las más útiles a los oficiales y a los suboficiales.
Sin embargo, la autoría del juego no está clara. El propio Édouard Lucas escribe la siguiente nota: “Según Martin Gall [que es un seudónimo del campeón de ajedrez francés Jules Arnous de Riviére (1830–1905)], cronista de juegos de combinación del Journal Gil Blas, el inventor del Juego militar sería el Sr. Constant Roy, de Saint-Mandé (Seine) [que son unos suburbios de París]”. El ingeniero francés Constant Roy patentó este juego en enero de 1886 (patente número 173.665) con el nombre Système de jeu dit le stratagème militaire (Sistema de juego llamado la estratagema militar).
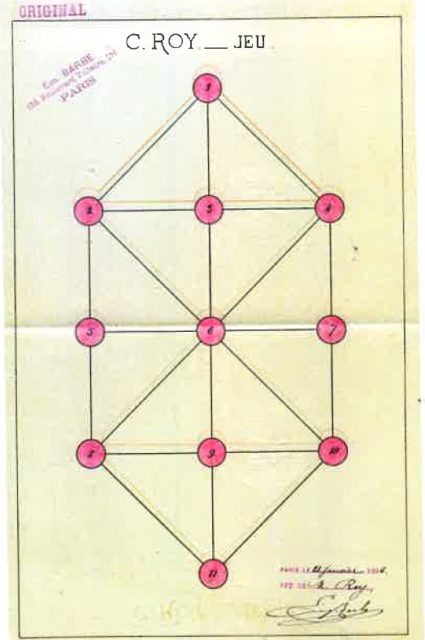 Diseño del tablero del juego militar que aparece en la patente del ingeniero francés Constant Roy
Diseño del tablero del juego militar que aparece en la patente del ingeniero francés Constant Roy
 Tablero del juego militar que incluye Édouard Lucas en el artículo sobre este juego de estrategia
Tablero del juego militar que incluye Édouard Lucas en el artículo sobre este juego de estrategiaAprendiendo a jugar
Pero vayamos con las reglas del juego. El tablero consta de 11 casillas, cada una de las cuales está unida por aristas con las casillas adyacentes. Como se puede observar en las imágenes anteriores, las 9 casillas del centro, que forman un cuadrado y están unidas como en el tres en raya (que Lucas numera del 1 al 9, como se ve en la siguiente imagen), mientas que hay 2 casillas más (una la casilla 0 y otra la casilla a, en la siguiente imagen) situadas cerca de dos lados opuestos del cuadrado central y unidas a las tres casillas de cada lado cercano. Y hay cuatro fichas, tres se corresponden con las torres (imagen de Lucas) o las brigadas de caballería (versión de Louis Dyen) en la versión militar o con los sabuesos o palomas (fichas blancas en el siguiente tablero) en las otras versiones, y otra ficha que se corresponde con el cuerpo del ejército, en la versión militar, o con la liebre o el halcón (ficha negra en el siguiente tablero), en las otras versiones.
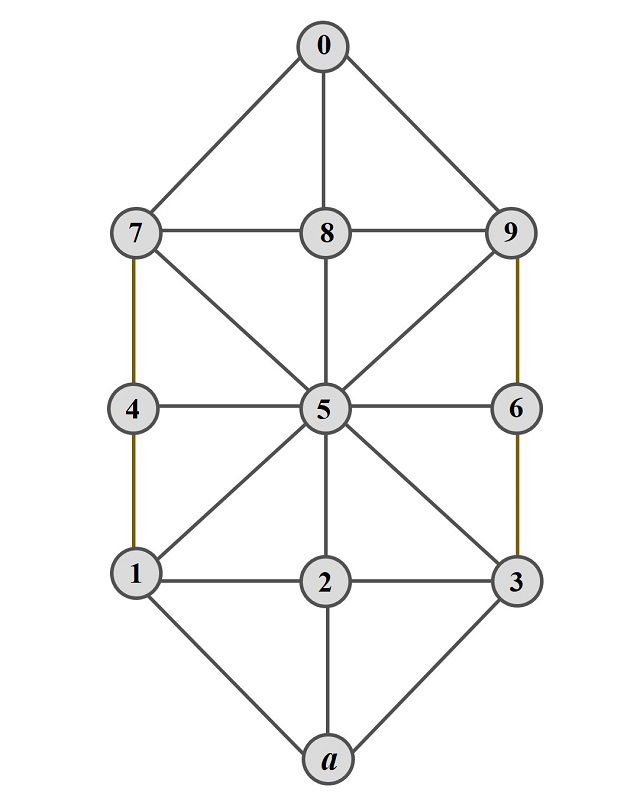 Tablero del juego militar francés, con la notación de las casillas de Édouard Lucas
Tablero del juego militar francés, con la notación de las casillas de Édouard Lucas
El objetivo del juego es el siguiente, para los sabuesos (fichas blancas) bloquear a la liebre (ficha negra) y para la liebre escapar de los sabuesos.
Las reglas del juego son las siguientes:
1. En la posición inicial los sabuesos (fichas blancas) están en un extremo del tablero (véase la siguiente imagen), por ejemplo, en las casillas 1, a y 3 de la notación de Lucas, mientras que la liebre (ficha negra) está en la casilla adyacente a las otras tres, la casilla 2 en la notación de Lucas.
2. Hay dos jugadores, uno juega con las fichas blancas (los sabuesos) y el otro con la ficha negra (la liebre), y cada uno de ellos mueve, por turnos, una de sus fichas hacia una casilla adyacente. Y empieza el jugador que juega con la liebre.
3. Las fichas blancas solo se pueden mover lateralmente o hacia adelante, mientras que la ficha negra se mueve en cualquier dirección.
4. Gana el jugador con juega con los sabuesos si estos bloquean a la liebre, es decir, la ficha negra no puede moverse hacia ninguna casilla adyacente, ya que están las fichas blancas bloqueándola; en caso contrario, es decir, si los sabuesos han sido incapaces de bloquear a la liebre, gana el jugador que juega con la liebre.
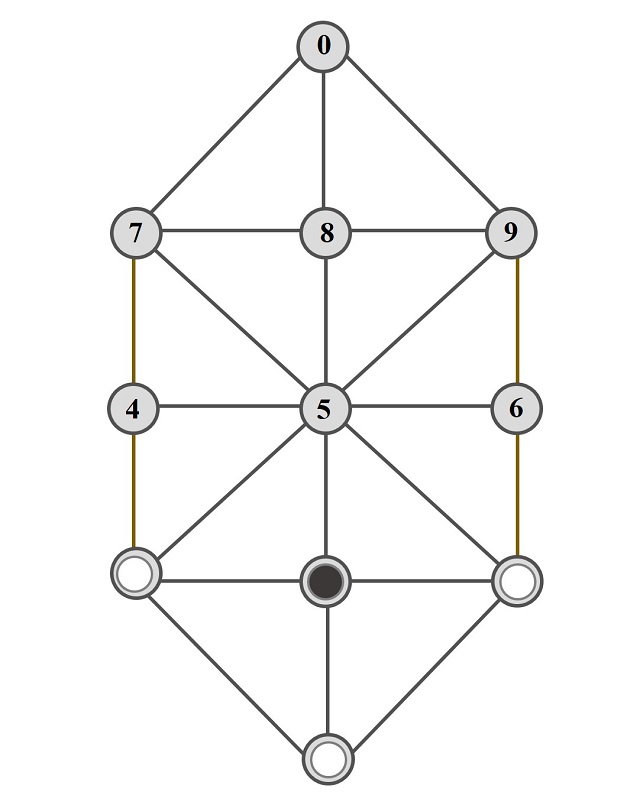 Posición inicial del juego militar francés, sobre el tablero con la notación de las casillas de Édouard Lucas
Posición inicial del juego militar francés, sobre el tablero con la notación de las casillas de Édouard Lucas
Pero, como os suelo decir cada vez que hablamos de juegos, lo primero que os recomiendo es
¡Jugar, jugar y jugar!
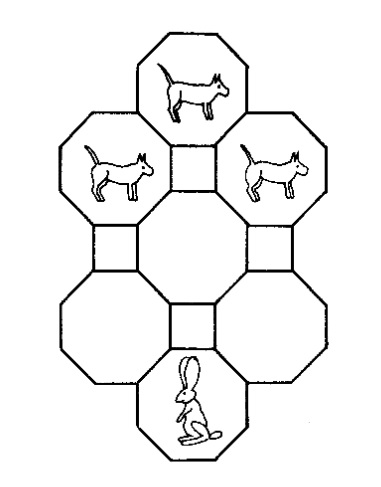
En el tercer volumen del libro Winning ways for your mathematical plays, de Elwyn R. Berlekamp, John H. Conway y Richard K. Guy, se utiliza un tablero diferente (con casillas que son cuadrados y octógonos, y la adyacencia se da cuando dos casillas comparten un lado), pero que esencialmente es el mismo.
Como menciona Édouard Lucas en el prospecto del juego se menciona, entre otras cosas, lo siguiente:
Este nuevo juego, basado en la estrategia militar y que parece, a primera vista, de una gran simplicidad, presenta, al contrario, movimientos difíciles y exige atención continua.
Los jugadores se encuentran pronto en presencia de combinaciones incalculables de defensa y de paso, dependiendo siempre del ataque y de la réplica, lo que permite compararlo con el juego del ajedrez.
A pesar de lo que dice el prospecto de que hay “combinaciones incalculables de defensa y de paso”, más bien el número de posiciones distintas del juego se pueden calcular con facilidad y no es un número excesivamente grande.
El cálculo del número de posiciones distintas del juego es un sencillo cálculo combinatorio. Por una parte, podemos pensar de cuántas formas pueden estar colocadas las fichas blancas (las torres o sabuesos), que son tres, sobre el tablero, que consta de 11 casillas. La respuesta es el número combinatorio C(11, 3), “11 sobre 3”, el número de formas de elegir 3 objetos (en este caso, casillas donde colocar las tres fichas blancas) de entre un total de 11 objetos (las casillas del juego) posibles. Recordemos que el número combinatorio C(n, k) (puede leerse sobre los números combinatorios en cualquier libro de combinatoria, aunque también podéis leer sobre ellos en cualquiera de mis dos últimos libros, La gran familia de los números, cuyo capítulo 6 está dedicado a familias de números que surgen del campo de la combinatoria, o Las matemáticas como herramienta de creación artística, que en su capítulo 4 habla de permutaciones y combinaciones en matemáticas y en arte contemporáneo) es
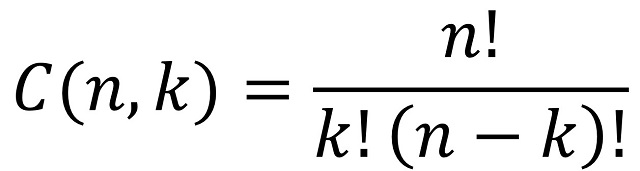
donde la operación factorial está definida como
![]()
Por lo tanto, el número de formas en las que pueden estar colocadas las fichas blancas sobre el tablero son C(11, 3) = 165.
Por otra parte, para cada una de esas 165 posiciones distintas de las tres fichas blancas, la ficha negra tiene 8 posibles casillas en las que estar colocadas, luego el número de posiciones distintas del juego, de formas de colocar las tres fichas blancas y la ficha negra son 165 por 8, esto es, 1.320 posiciones distintas del juego.
Aunque puede ocurrir que dos posiciones, aunque sean distintas, sean esencialmente la misma, ya que son simétricas respecto al eje que une las casillas exteriores a y 0, como las dos que se muestran en la siguiente imagen.
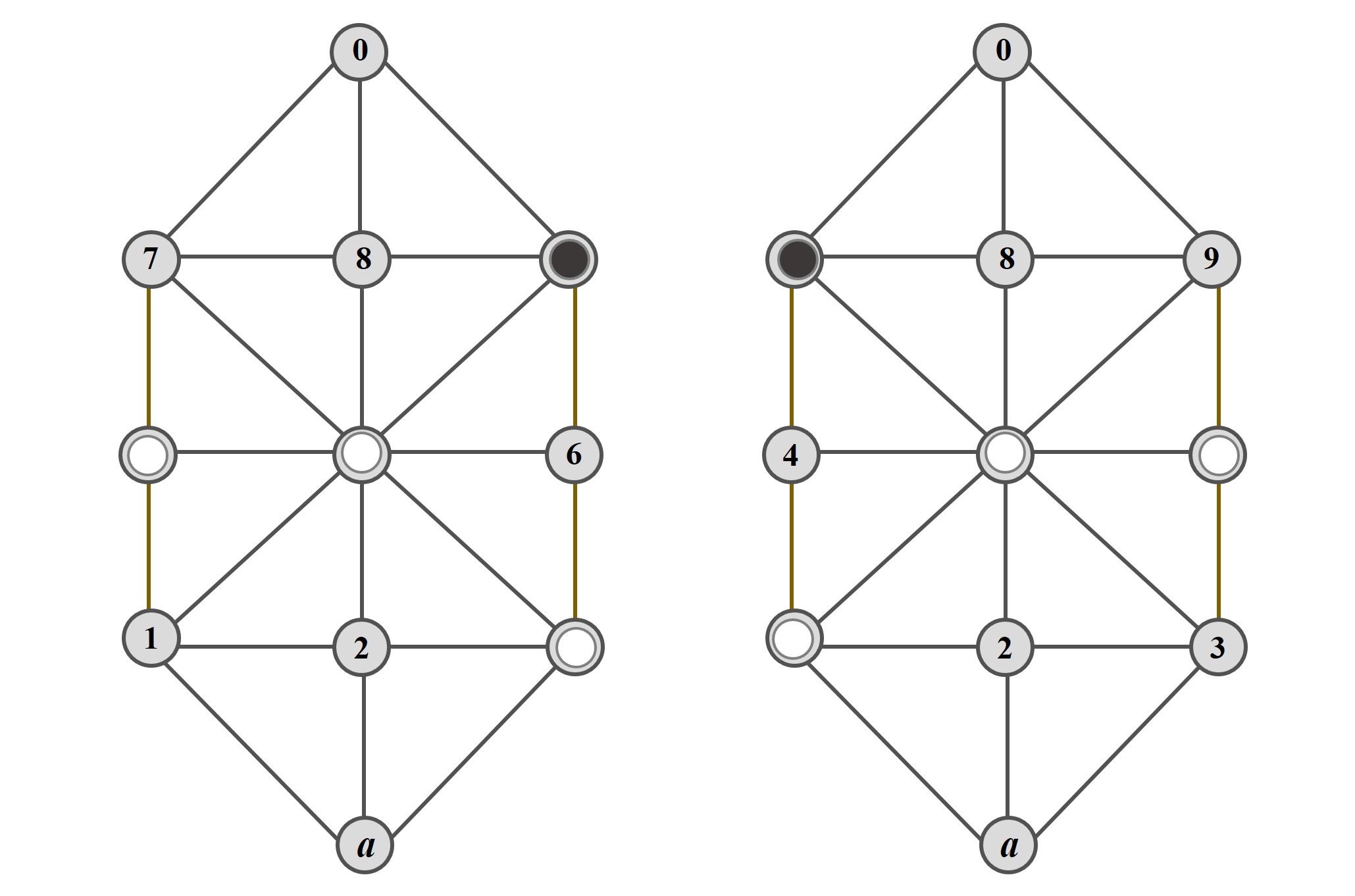
El prospecto del juego, después de lo anterior, continúa así:
Recompensas de cien francos son ofrecidas por el inventor a las personas que ganen tantas partidas como él mismo, y recompensas de mil francos a las que ganen más de la mitad.
Eso nos hace sospechar que seguramente existe alguna estrategia ganadora para alguno de los dos jugadores, el que juega con los sabuesos o el que juega con la liebre. De hecho, como hemos comentado al inicio de esta entrada del Cuaderno de Cultura Científica el matemático Édouard Lucas ya analizó el juego, mostrando que existe una estrategia ganadora, en concreto, para las fichas blancas.
En primer lugar, Lucas analiza 6 finales de partida (que llama partidas elementales y denomina con las letras A, B, C, D, E y F), donde mueven las fichas blancas, en alguno de los cuales terminará la partida si las blancas juegan según la estrategia que veremos más adelante.
La partida elemental A
En este final de partida, que vemos representado en la siguiente imagen, mueven las fichas blancas y ganan en un solo movimiento. Basta trasladar la ficha blanca de la casilla 5 a la 8 y la ficha negra quedará bloqueada en la casilla 0, sin posibilidad de movimiento.
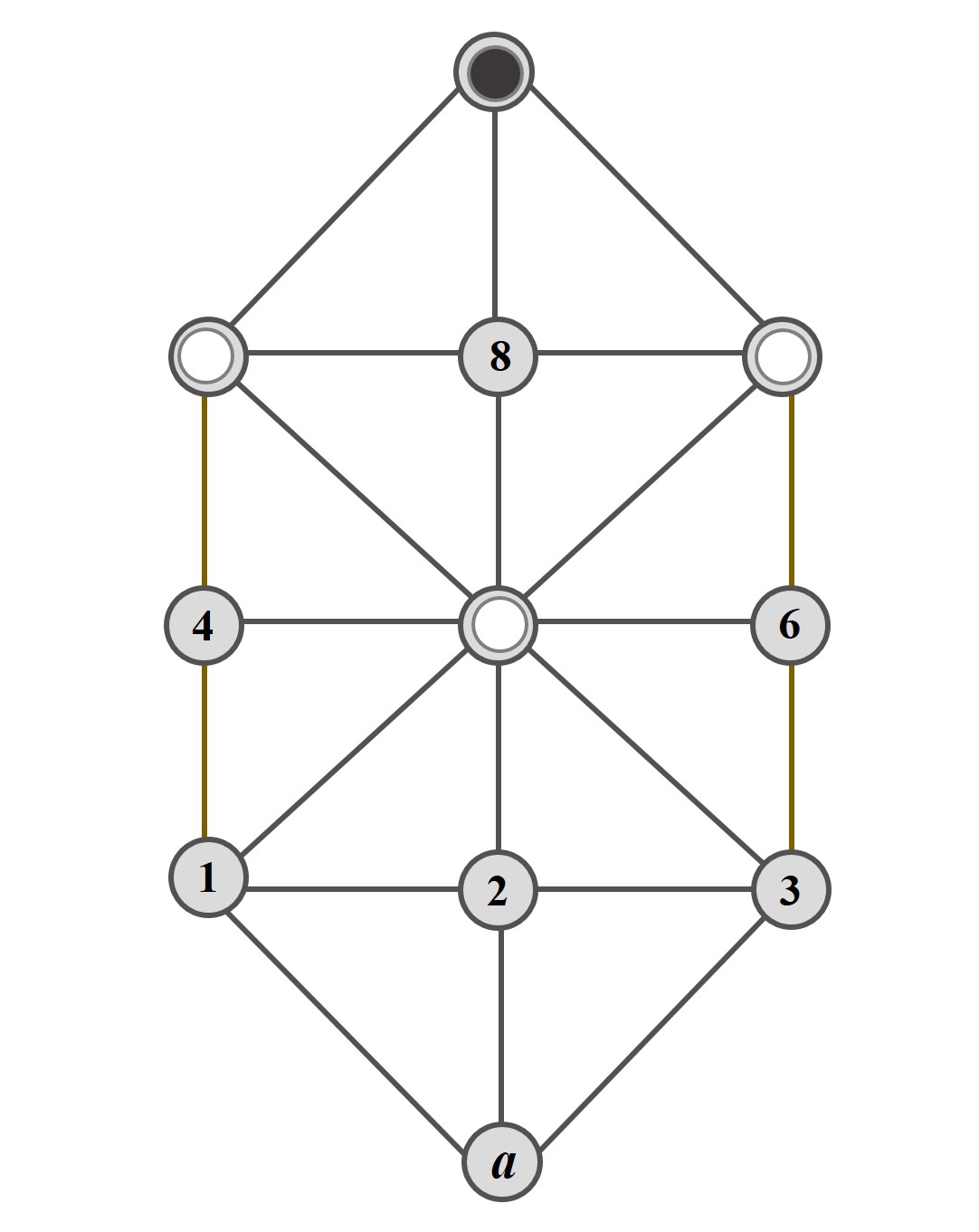 Partida elemental A
Partida elemental A
Podríamos describir ese final de partida como 579 0 789, donde los grupos de tres caracteres indican las posiciones de las tres fichas blancas después de que hayan movido las blancas y el grupo de un solo carácter indica la posición de la ficha negra después de que haya movido.
La partida elemental B
De nuevo mueven las fichas blancas y ganan en un solo movimiento, pasando la ficha blanca de la casilla 8 a la 7. Utilizando la anterior notación, la descripción de la partida sería 158 4 157.
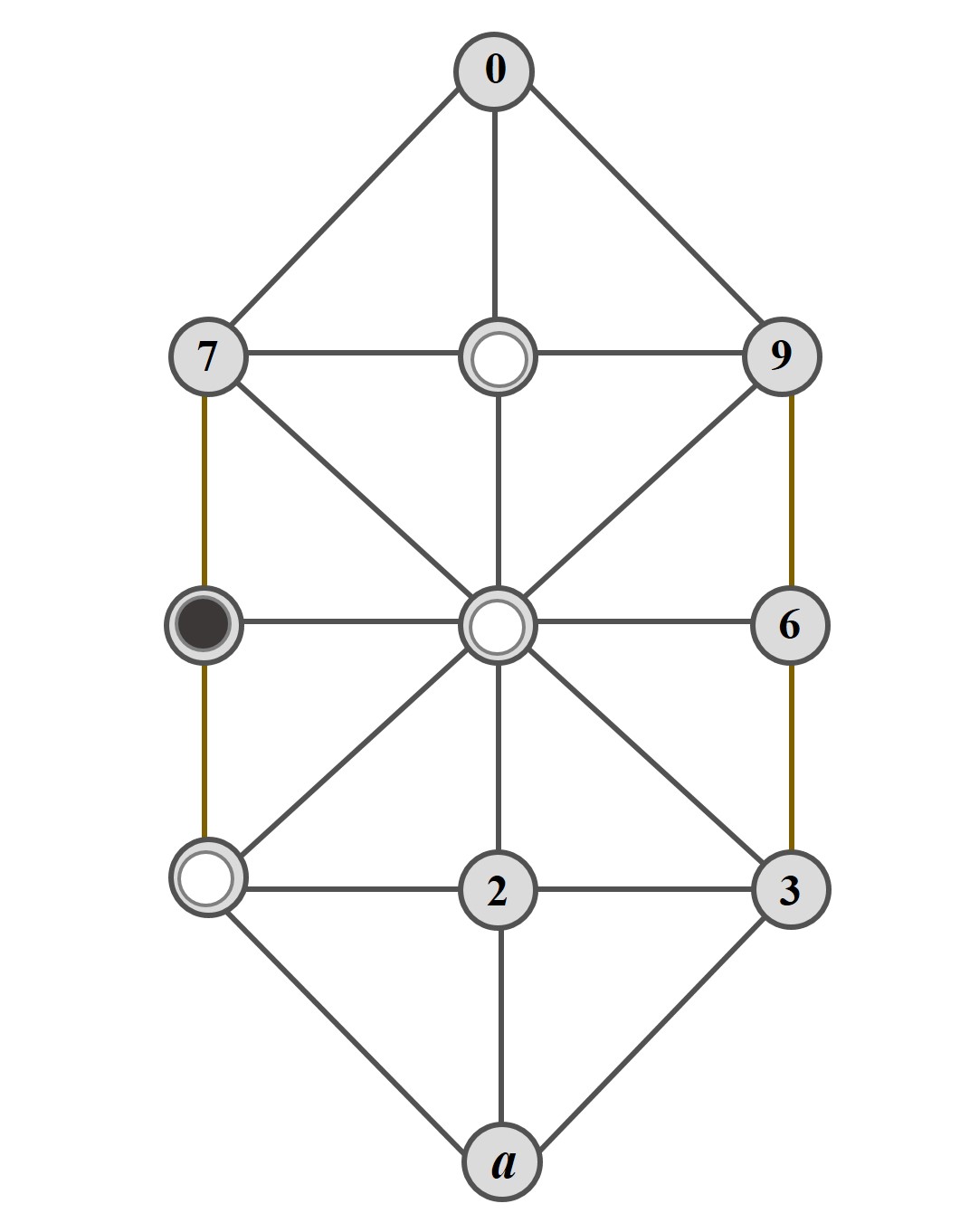 Partida elemental B
Partida elemental B
Esta partida nos sirve para explicar que podríamos considerar la partida elemental simétrica (es decir, las fichas blancas estarían en las casillas 3, 5 y 8. mientras que la ficha negra estaría en la casilla 6), cuya solución es idéntica (la ficha de la casilla 8 pasa a la casilla 9). En todo el estudio que hace Lucas, y que estamos explicando aquí, evita repetir el análisis para las posiciones simétricas.
La partida elemental C
Para esta partida elemental donde dos de las fichas blancas están en las casillas 7 y 9, la otra ficha blanca puede estar en cualquiera de las casillas 1, 2, 3, 4 o 6 (que en la siguiente imagen hemos indicado dando un poco de color amarillo a la ficha), mientras que la ficha negra está en la casilla 8.
Las blancas mueven y ganan en dos movimientos. Se mueve la ficha blanca que está en la tercera casilla (una de las casillas 1, 2, 3, 4 o 6) a la casilla del centro, la casilla 5, luego a la casilla negra no le queda más remedio que ir a la casilla 0, y llegamos a la partida elemental A.
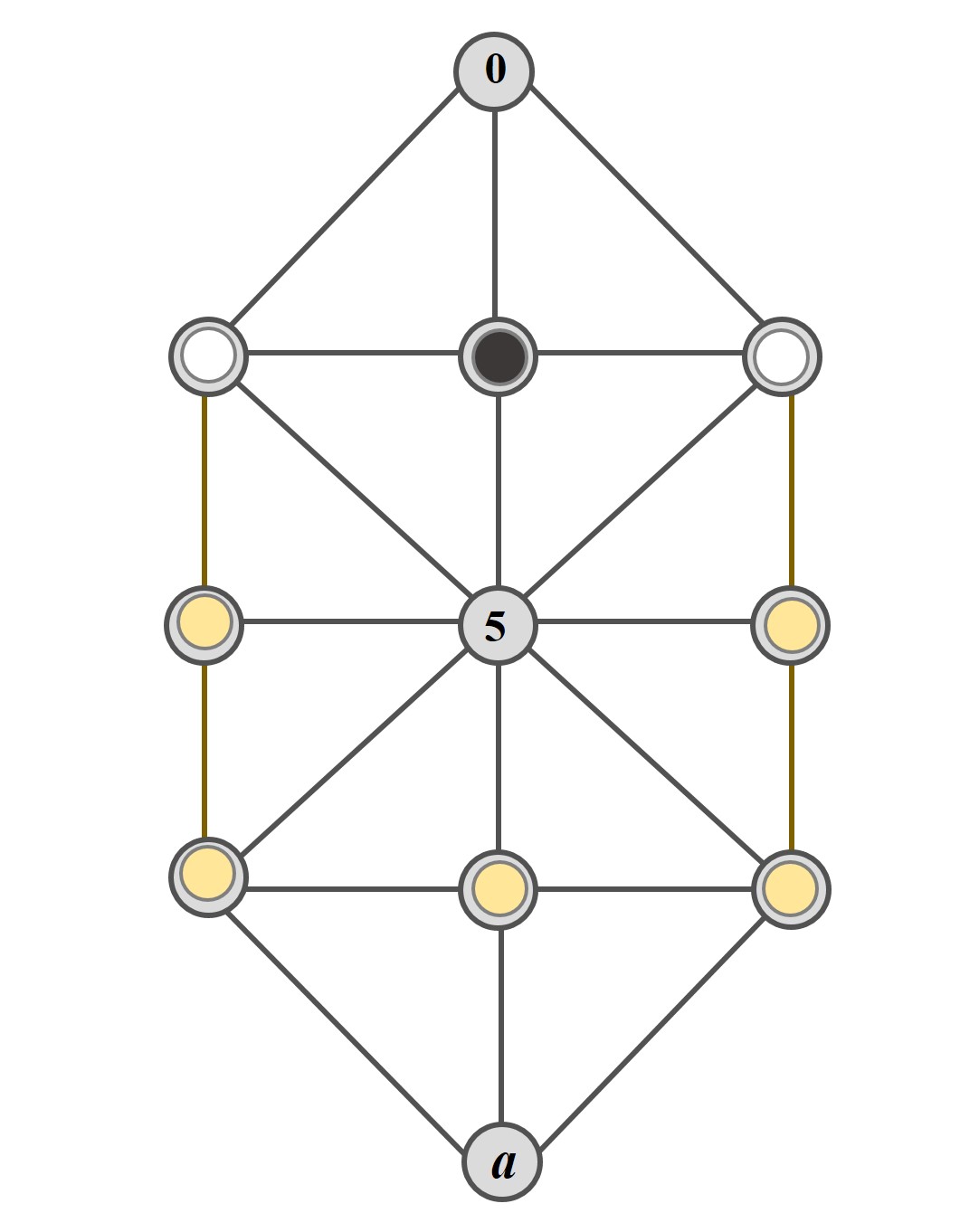 Partida elemental C
Partida elemental C
Según la notación de Lucas, asumiendo que la tercera ficha blanca estuviese en la casilla 1 (de forma similar para el resto), la partida elemental C se describiría como 179 8 579 0 789.
La partida elemental D
Otro sencillo final de partida en el que mueven las blancas y ganan en dos movimientos. Basta llevar la ficha de la casilla 6 a la 9, y estaremos en la partida elemental A. La descripción de la misma sería 567 8 579 0 789.
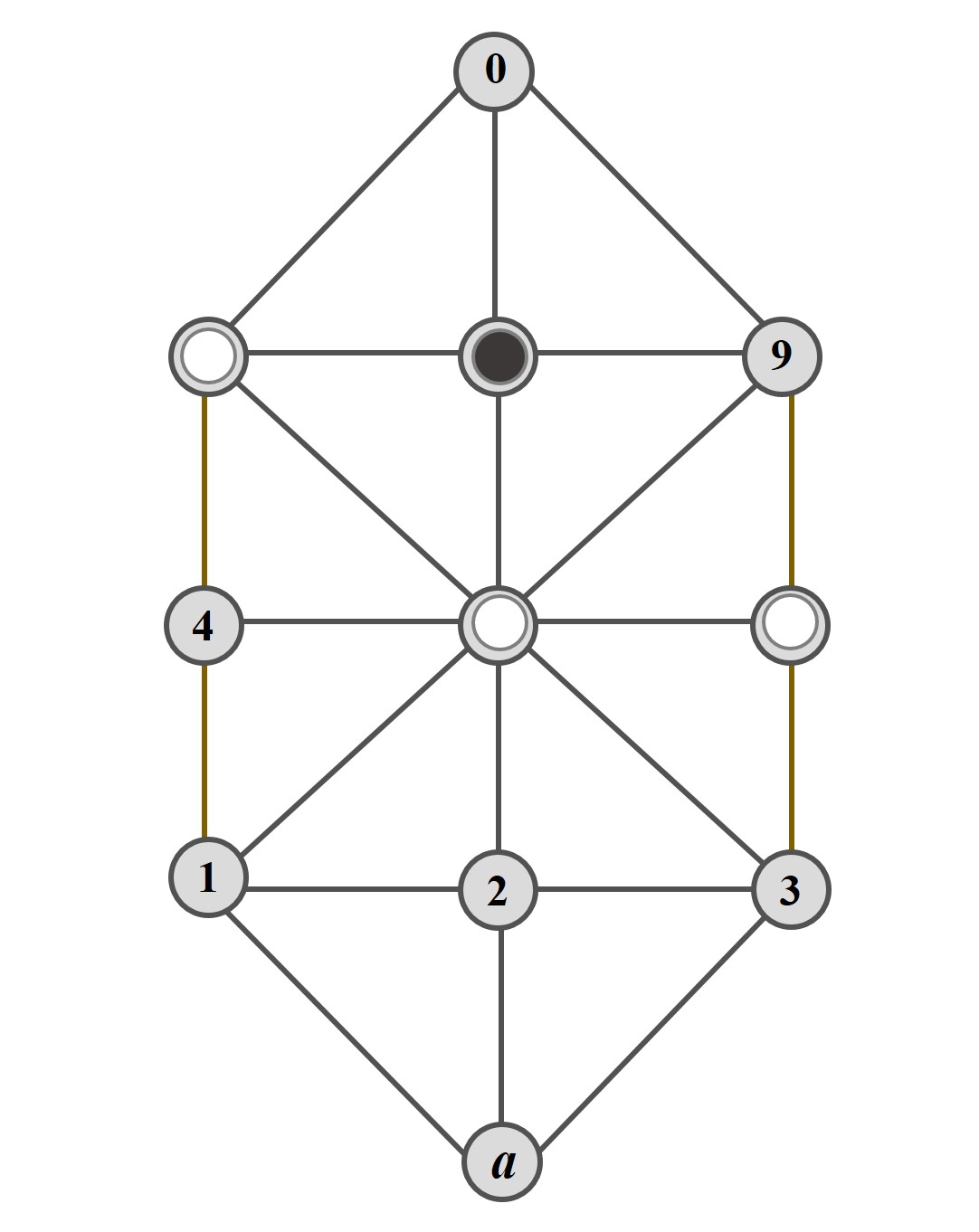 Partida elemental D
Partida elemental D
La partida elemental E
Esta partida elemental es, de nuevo, múltiple, como la partida C. Las dos primeras fichas blancas están en las casillas 5 y 7, mientras que la tercera estará en una se las siguientes casillas, 1, 2, 3, 4 o 6, como antes, mientras que la ficha negra estará en la casilla 0. Ahora, las fichas blancas necesitan tres movimientos para ganar. Las fichas blancas mueven de 5 a 9, la ficha negra solo puede mover a 8, quedando la posición de la partida elemental C.
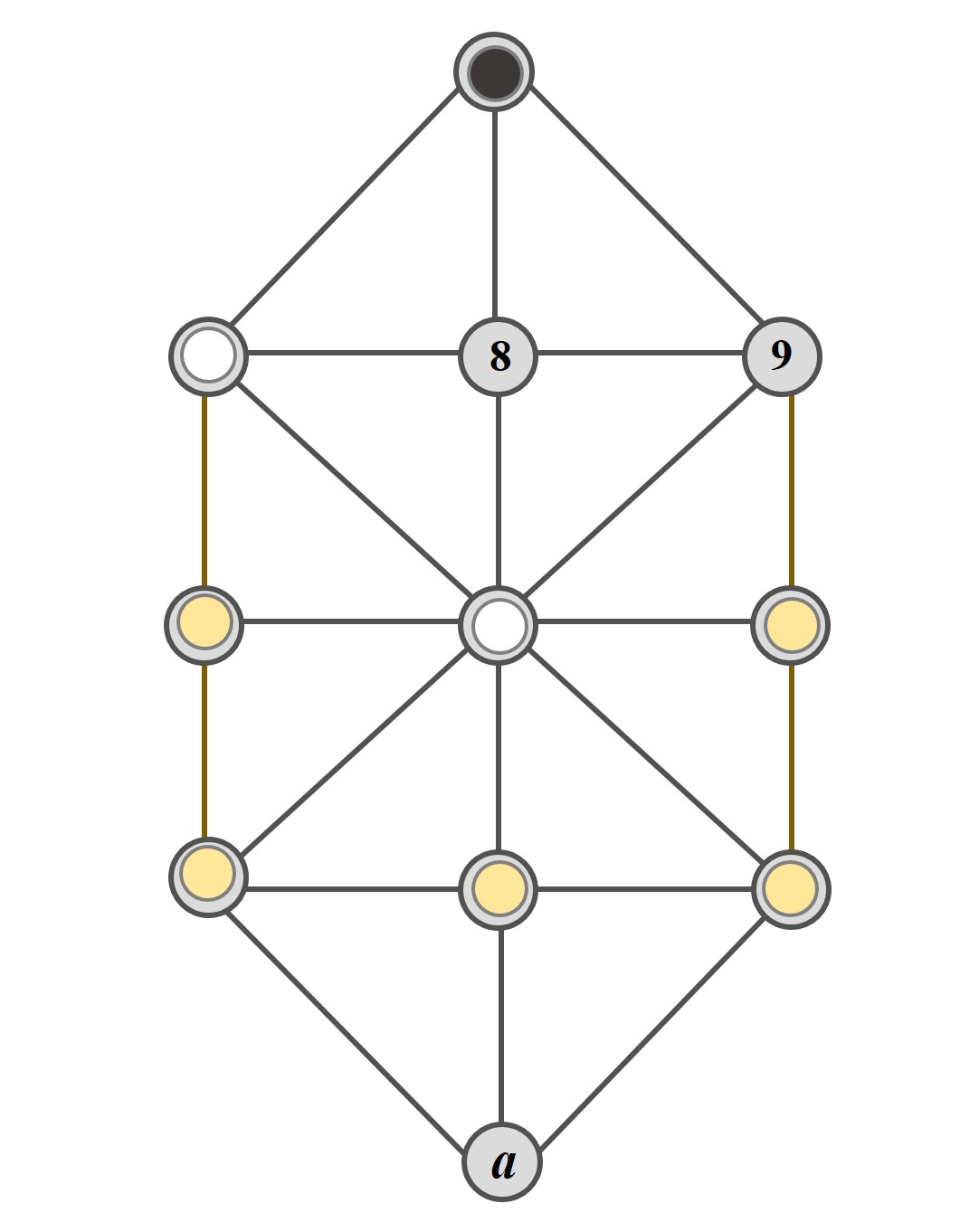 Partida elemental E
Partida elemental E
La partida elemental F
En esta posición las fichas blancas mueven y ganan en 3 o 4 movimientos, en función de los movimientos de la negra. Para empezar las blancas mueven de la casilla 1 a la 4, y la ficha negra, que está en la casilla 7, tiene dos opciones, mover a la casilla 8 o a la casilla 0. En función del movimiento de la ficha negra, las blancas moverán en consecuencia. Si la ficha negra pasa a la casilla 8, será la posición simétrica a la partida elemental D, y las blancas ganarán en dos movimientos más (las blancas mueven de 4 a 7, la negra retrocede a 0 y las blancas mueven de 5 a 8, quedando bloqueada la negra), mientras que si la ficha negra pasa a la casilla 0, las blancas mueven de 5 a 7 y la ficha negra de 0 a 8 quedando la posición elemental C y las blancas ganan en dos movimientos (las blancas mueven de 4 a 5, las negras retroceden a la casilla 0 y las blancas la bloquean moviendo de 5 a 8).
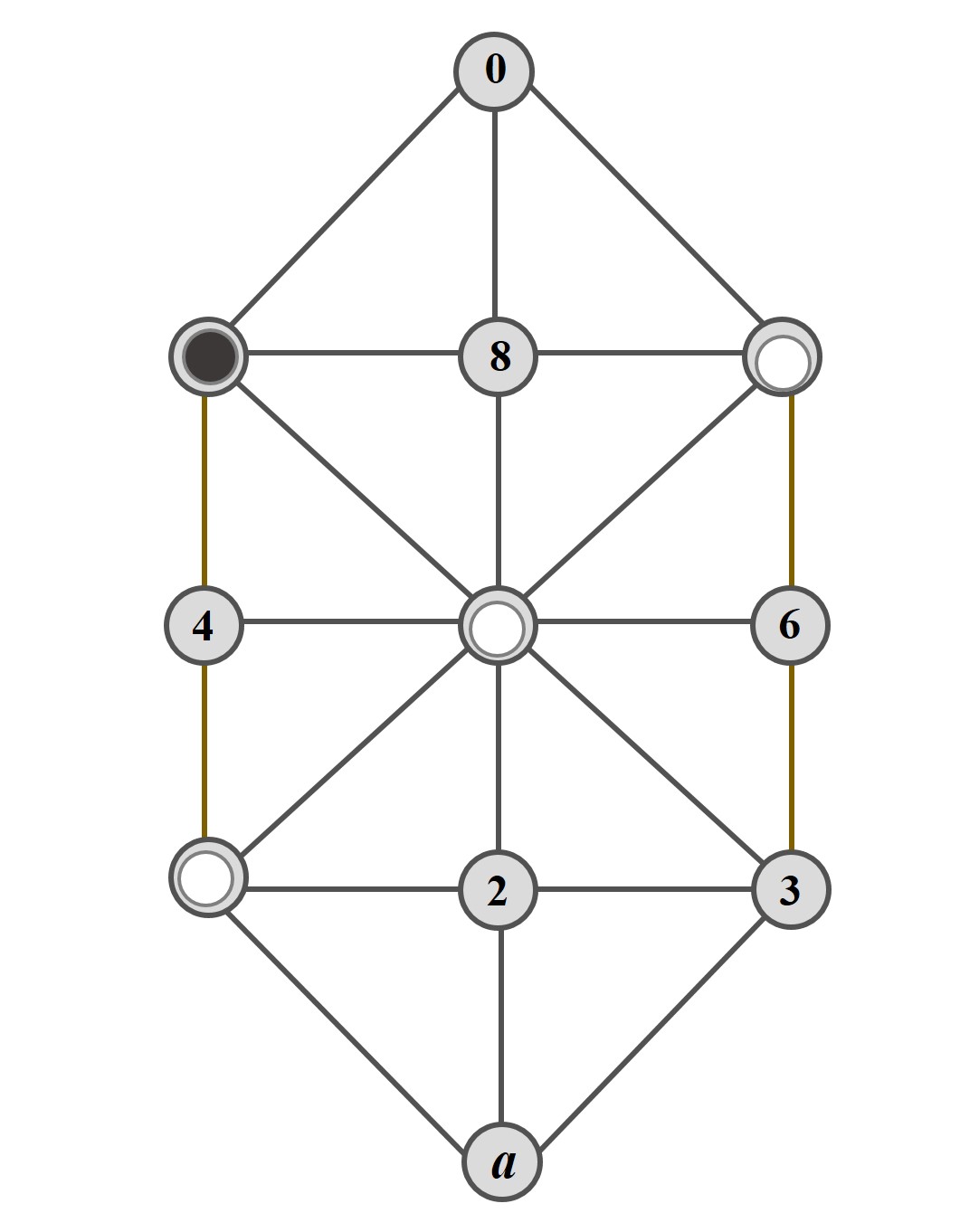 Partida elemental F
Partida elemental F
Las dos partidas posibles serían 159 7 459 8 579 0 789 y 159 7 459 0 479 8 579 0 789, que Édouard Lucas denota de la siguiente manera, con una linea vertical, para reflejar las dos opciones de movimiento de la ficha negra.
 La representación numérica del desarrollo de la partida elemental F
La representación numérica del desarrollo de la partida elemental F
Como hemos explicado más arriba, en la posición inicial la ficha negra está en la casilla 2, mientras que las fichas blancas están en las casillas a, 1 y 3. El primer movimiento de la ficha negra es obligado, de la casilla 2 a la casilla 5 y ahí las blancas, aunque tienen diferentes opciones deberían mover de la casilla a a la casilla 2. Luego el inicio de la partida sería 2 a13 5 123. En el siguiente recuadro se recoge la tabla del análisis del juego realizada por Lucas para mostrar que ganan las fichas blancas si mueven convenientemente. Las letras, de la A a la F, indican que hemos llegado a la partida elemental con ese nombre, mientras que el símbolo del $ nos indica que más arriba en la tabla ya se ha producido esa situación y que, por tanto, se continúa de igual forma.
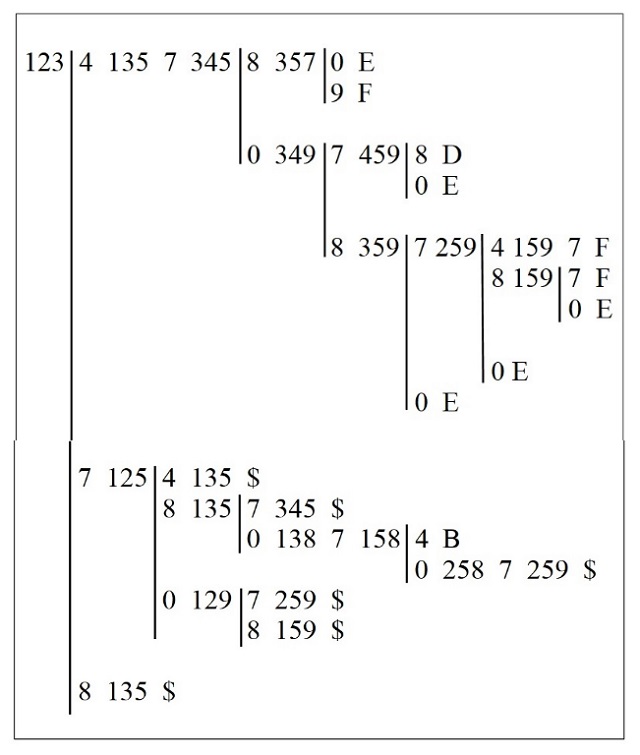 Recuadro con la estrategia ganadora para las fichas blancas en el juego militar francés
Recuadro con la estrategia ganadora para las fichas blancas en el juego militar francés
Para comprender bien la estrategia ganadora y disfrutar del análisis de Lucas lo mejor es ir reproduciendo las diferentes jugadas que nos describe el anterior recuadro.
Por cierto, como podemos observar las fichas blancas ganan en doce movimientos como mucho.
VariacionesPara terminar podemos plantar algunas variaciones. La primera sería jugar empezando con la ficha negra en otra posición distinta. Por ejemplo, un inicio de partida bastante frecuente es con la ficha negra en el otro lado del tablero, en la casilla 0, y el jugador que empieza primero se decide a suertes o se va cambiando. Por ejemplo, en la siguiente imagen se muestra el tablero de la empresa de juegos Thinkfun que plantea esta alternativa.
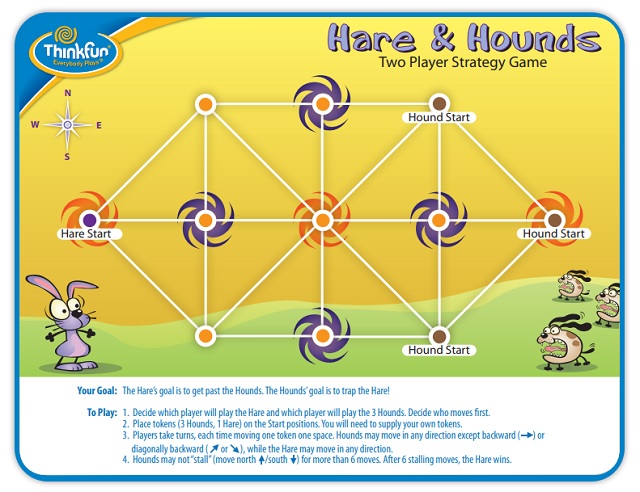 Tablero del juego Sabuesos y liebre de la empresa de juegos Thinkfun, que podéis encontrar (en pdf) en la página web de Thinkfun
Tablero del juego Sabuesos y liebre de la empresa de juegos Thinkfun, que podéis encontrar (en pdf) en la página web de Thinkfun
Existen diferentes alternativas al tablero del juego. Algunas de las cuales las mostraremos a continuación para quienes estén interesados en jugar a ellas. La primera es un tablero similar al anterior, pero con tan solo 9 casillas, se han eliminado dos de la parte central (véase la siguiente imagen).
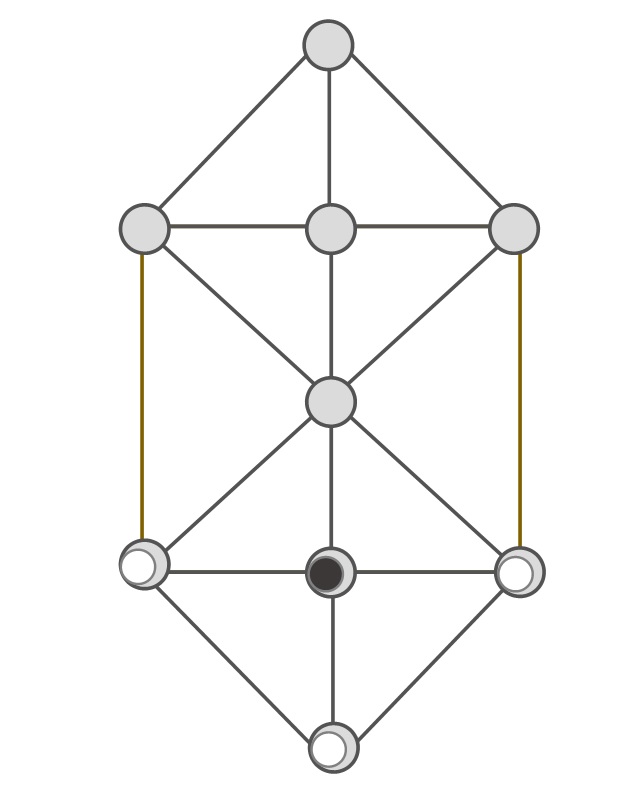 Tablero del juego con tan solo nueve casillas
Tablero del juego con tan solo nueve casillas
Existe otra versión con 12 casilla, que mostramos en la siguiente imagen.
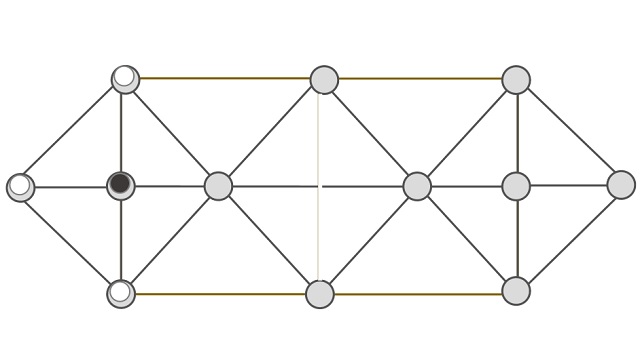 Tablero del juego con doce casillas
Tablero del juego con doce casillas
Incluso un tablero circular de 13 puntos (véase la siguiente imagen), entre muchos otros que ya no incluimos en esta entrada.
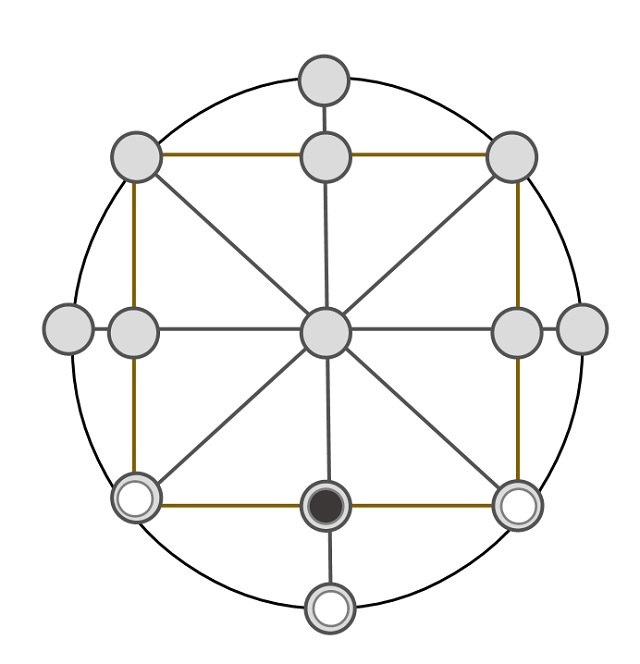 Tablero circular del juego con trece casillas
Tablero circular del juego con trece casillas
Bibliografía
1.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.
2.- Peter Michaelsen, Haretavl – Hare and Hounds as a board game, en el libro Sport Und Spiel Bei den Germanen. De Gruyter, pp. 197 – 216, 2013.
3.- Raúl Ibáñez, La gran familia de los números, Libros de la Catarata, 2021.
4.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística, Libros de la Catarata, 2023.
5.- Michel Boutin, Les jeux dans les collections du Conservatoire national des arts et métiers, 8-Le Jeu militaire (8e partie), Le Vieux Papier, no. 435, pp 213-222, 2020.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El juego militar francés se ha escrito en Cuaderno de Cultura Científica.
El electrón es tan redondo que descarta nuevas partículas
Si la carga del electrón no fuera perfectamente redonda, podría indicar la existencia de partículas ocultas. Una nueva medición se acerca a la perfección.
Un artículo de Zack Savitsky. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Si el electrón tuviese el tamaño de la Tierra, el experimento podría detectar la protuberancia de una molécula de azúcar. Imagen: Kristina Armitage / Quanta Magazine
Si el electrón tuviese el tamaño de la Tierra, el experimento podría detectar la protuberancia de una molécula de azúcar. Imagen: Kristina Armitage / Quanta MagazineImagina un electrón como una nube esférica de carga negativa. Si esa bola fuera mínimamente menos redonda ello podría ayudar a explicar las lagunas fundamentales en nuestra comprensión de la física, incluido por qué el universo contiene algo en lugar de nada.
Dado lo que está en juego, una pequeña comunidad de físicos ha estado buscando obstinadamente cualquier asimetría en la forma del electrón durante las últimas décadas. Los experimentos son ahora tan sensibles que, si un electrón fuera del tamaño de la Tierra, podrían detectar una protuberancia en el Polo Norte de la altura de una sola molécula de azúcar.
Ya tenemos los últimos resultados: El electrón es más redondo que eso.
La medición actualizada decepciona a cualquiera que tenga esperanzas de encontrar señales de una nueva física. Aun así, ayuda a los teóricos a restringir sus modelos para qué partículas y fuerzas desconocidas pueden faltar en la imagen actual.
“Estoy seguro de que es difícil ser el experimentador que mide cero todo el tiempo, [pero] incluso un resultado nulo en este experimento es realmente valioso y realmente nos enseña algo”, afirma Peter Graham, físico teórico de la Universidad de Stanford. El nuevo estudio es «una hazaña tecnológica y también muy importante para la nueva física».
Cazando elefantes furtivamenteEl modelo estándar de física de partículas es nuestra mejor lista de todas las partículas que existen en el zoológico del universo. La teoría ha aguantado excepcionalmente bien las pruebas experimentales durante las últimas décadas, pero deja algunos «elefantes en la habitación» serios, afirma Dmitry Budker, físico de la Universidad de California, Berkeley.
Por un lado, nuestra mera existencia es prueba de que el Modelo Estándar está incompleto, ya que según la teoría, el Big Bang debería haber producido partes iguales de materia y antimateria que se habrían aniquilado entre sí.
En 1967, el físico soviético Andrei Sakharov propuso una posible solución a este enigma en concreto. Conjeturó que debe haber algún proceso microscópico en la naturaleza que se vea diferente marcha atrás; de esa manera, la materia podría llegar a dominar a la antimateria. Unos años antes, los físicos habían descubierto esa situación en la desintegración de la partícula kaón. Pero eso por sí mismo no era suficiente para explicar la asimetría.
Desde entonces, los físicos han estado a la caza de indicios de nuevas partículas que podrían inclinar aún más la balanza. Algunos lo hacen directamente, utilizando el Gran Colisionador de Hadrones, a menudo promocionado como la máquina más complicada jamás construida. Pero en las últimas décadas, ha surgido una alternativa comparativamente de bajo presupuesto: observar cómo las partículas hipotéticas alterarían las propiedades de las partículas conocidas. “Ves huellas [de nueva física], pero en realidad no ves lo que las hizo”, afirma Michael Ramsey-Musolf, físico teórico de la Universidad de Massachusetts en Amherst.
Una huella potencial de este tipo podría aparecer en la redondez del electrón. La mecánica cuántica dicta que dentro de la nube de carga negativa del electrón, otras partículas están constantemente parpadeando dentro y fuera de la existencia. La presencia de ciertas partículas «virtuales» más allá del modelo estándar, del tipo que podría ayudar a explicar la supremacía primordial de la materia, haría que la nube de electrones pareciese un poco más con forma de huevo. Una punta tendría una carga un poco más positiva, la otra un poco más negativa, como los extremos de un imán. Esta separación de carga se conoce como momento dipolar eléctrico (MDE).
El modelo estándar predice un MDE extremadamente diminuto para el electrón, casi un millón de veces más pequeño de lo que pueden medir las técnicas actuales. Por lo tanto, si los investigadores detectaran una forma oblonga usando los experimentos de hoy, eso revelaría señales definitivas de nueva física y apuntaría hacia lo que podría faltar en el modelo estándar.
Para encontrar el MDE del electrón los científicos buscan un cambio en el espín de la partícula, una propiedad intrínseca que define su orientación. El espín del electrón puede invertirse fácilmente mediante campos magnéticos, y su momento magnético sirve como una especie de manivela. El objetivo de estos experimentos de laboratorio es tratar de invertir el espín pero usando campos eléctricos, con el MDE como manivela eléctrica.
“Si el electrón es perfectamente esférico, no tiene manivelas que asir con las que ejercer un par”, explica Amar Vutha, físico de la Universidad de Toronto. Pero si hay un MDE considerable, el campo eléctrico lo usará para tirar del espín del electrón.
En 2011, investigadores del Imperial College de Londres demostraron que podían amplificar este efecto de manivela al anclar el electrón a una molécula pesada. Desde entonces, dos equipos principales se han ido superando uno al otro cada pocos años con mediciones cada vez más precisas.
Un experimento, ahora en la Universidad de Northwestern, se conoce con el nombre de Advanced Cold Molecule Electron MDE, o ACME (un acrónimo inspirado en los viejos dibujos animados del Correcaminos). Otro tiene su sede en el instituto JILA de la Universidad de Colorado. Las mediciones de los equipos competidores han aumentado en sensibilidad en un factor de 200 en la última década, y aún no hay MDE a la vista.
“Es una especie de carrera, excepto que no tenemos idea de dónde está la línea de meta, o incluso de si hay una línea de meta”, afirma David DeMille, físico de la Universidad de Chicago y uno de los líderes del grupo ACME.
Una carrera hacia lo desconocidoPara seguir avanzando, los investigadores quieren dos cosas: más mediciones y un tiempo de medición más prolongado. Los dos equipos toman enfoques opuestos.
El grupo ACME, que estableció el récord anterior en 2018, prioriza la cantidad de mediciones. Disparan un haz de moléculas neutras a través del laboratorio, midiendo decenas de millones de ellas cada segundo, pero solo durante unos pocos milisegundos cada una. El grupo JILA mide menos moléculas, pero durante más tiempo: atrapan unos pocos cientos de moléculas a la vez y luego las miden durante un máximo de tres segundos.
La técnica de captura de iones, desarrollada por primera vez por Eric Cornell, físico de la Universidad de Colorado en Boulder, que dirige el grupo JILA, fue «un gran avance conceptual», afirma DeMille. “Muchas personas en el campo pensaron que esto era una locura. Verlo llegar a buen término es realmente emocionante”.
Tener dos configuraciones experimentales distintas que puedan cotejarse entre sí es «absolutamente crucial», explica Budker. “No tengo palabras para expresar mi admiración por esta inteligencia y persistencia. Es simplemente la mejor ciencia que existe”.
La técnica de Cornell se presentó por primera vez en 2017 con moléculas de fluoruro de hafnio. Desde entonces, las mejoras técnicas han permitido que el grupo supere el récord de ACME por un factor de 2,4, como se describe en una prepublicación reciente dirigida por la antigua alumna de posgrado de Cornell, Tanya Roussy. El equipo rehusó hacer comentarios mientras su artículo está en revisión en Science.
Medir la redondez del electrón con mayor precisión equivale a buscar nueva física en escalas de energía más altas o buscar signos de partículas más pesadas. Este nuevo límite es sensible a energías superiores a aproximadamente 1013 electronvoltios, más de un orden de magnitud más allá de lo que el LHC puede medir actualmente. Hace algunas décadas, la mayoría de los teóricos esperaban que se descubrirían indicios de nuevas partículas significativamente por debajo de esta escala. Cada vez que sube el listón, algunas ideas quedan descartadas.
“Tenemos que seguir lidiando con lo que implican estos límites”, afirma Ramsey-Musolf. “Nada ha muerto todavía, pero está subiendo la temperatura”.
Mientras tanto, la comunidad de la MDE del electrón sigue adelante. En futuras iteraciones experimentales, los grupos rivales pretenden encontrarse en algún punto intermedio: el equipo de JILA planea hacer un haz lleno de iones para aumentar su número, y el equipo de ACME quiere aumentar la longitud de su haz para incrementar su tiempo de medición. Vutha incluso está trabajando en enfoques «totalmente locos», como congelar moléculas en bloques de hielo, con la esperanza de subir la sensibilidad varios órdenes de magnitud de un golpe.
El sueño es que estos experimentos MDE sean los primeros en detectar signos de una nueva física, lo que provocaría una ola de investigaciones de seguimiento por parte de otros experimentos de medidas de precisión y de colisionadores de partículas más grandes.
La forma del electrón es «algo que nos enseña aspectos totalmente nuevos y diferentes de las leyes fundamentales de la naturaleza», afirma Graham. “Hay un gran descubrimiento a la espera. Soy optimista de que lo haremos”.
El artículo original, The Electron Is So Round That It’s Ruling Out Potential New Particles, se publicó el 10 de abril de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo El electrón es tan redondo que descarta nuevas partículas se ha escrito en Cuaderno de Cultura Científica.
Un nuevo mapa del vulcanismo de Venus
mapa del vulcanismo
El pasado 20 de marzo hablábamos en el artículo ¿Es esta la prueba definitiva de que Venus tiene volcanes activos? de como una revisión de pares de imágenes de radar de la superficie del planeta tomadas por la misión Magellan en la década de los 90 parecía mostrar el antes y el después de una erupción volcánica ocurrida durante la propia misión y que había pasado desapercibida hasta ahora.
¿Por qué entonces no se había descubierto antes? En estos treinta años ha habido una verdadera revolución en la informática, tanto a nivel de potencia de computación como de capacidad de almacenamiento, que nos facilita trabajar con enormes cantidades de datos desde prácticamente cualquier ordenador. Esto se suma a los sistemas de información geográfica, con cada vez mayor permeabilidad no solo en el estudio de nuestro planeta, sino también en el de cualquier superficie de nuestro Sistema Solar, que nos permiten analizar miles de imágenes, hacer cálculos sobre estas e, incluso, comparar el antes y el después de una manera mucho más sencilla y rutinaria.
 Mosaico de imágenes de radar de Sapas Mons, uno de los grandes sistemas volcánicos de Venus. Cortesía de NASA/JPL.
Mosaico de imágenes de radar de Sapas Mons, uno de los grandes sistemas volcánicos de Venus. Cortesía de NASA/JPL.Obviamente, esto no quiere decir que sea una tarea fácil, ya que Venus tiene una superficie muy extensa, apenas un ~10% menor que la de nuestro planeta, por lo que encontrar cambios entre parejas de imágenes puede ser como buscar una aguja en un pajar. Una tarea que viene dificultada también por la resolución de las imágenes, que requiere de que ocurran grandes cambios -las imágenes globales de Venus tomadas por la Magellan están en el entorno de los 75 metros por píxel- para que puedan ser vistos con claridad.
Pero un nuevo estudio publicado a finales del mes de marzo puede facilitar mucho esta tarea, ya que ha servido como excusa para crear el atlas de volcanes más detallado del planeta Venus. El primer dato sorprendente es la gran cantidad de formas volcánicas reconocibles, con unas 85.000 en total. Eso sí, estos científicos piensan que es una estimación relativamente conservadora y que podrían ser muchos más, pero que debido a la resolución de las imágenes los edificios volcánicos más pequeños han pasado desapercibidos.
¿Son muchos o pocos volcanes? Quizás si lo comparamos con la Tierra nos pueden parecer muchos, ya que si por ejemplo contamos solo los volcanes que han mostrado actividad durante el Holoceno -la época del tiempo geológico en la que vivimos actualmente y que comenzó hace unos aproximadamente 11.700 años- según la base de datos de la Smithsonian Institution, una de las más completas, nos encontramos ante algo más de 12.000 volcanes.
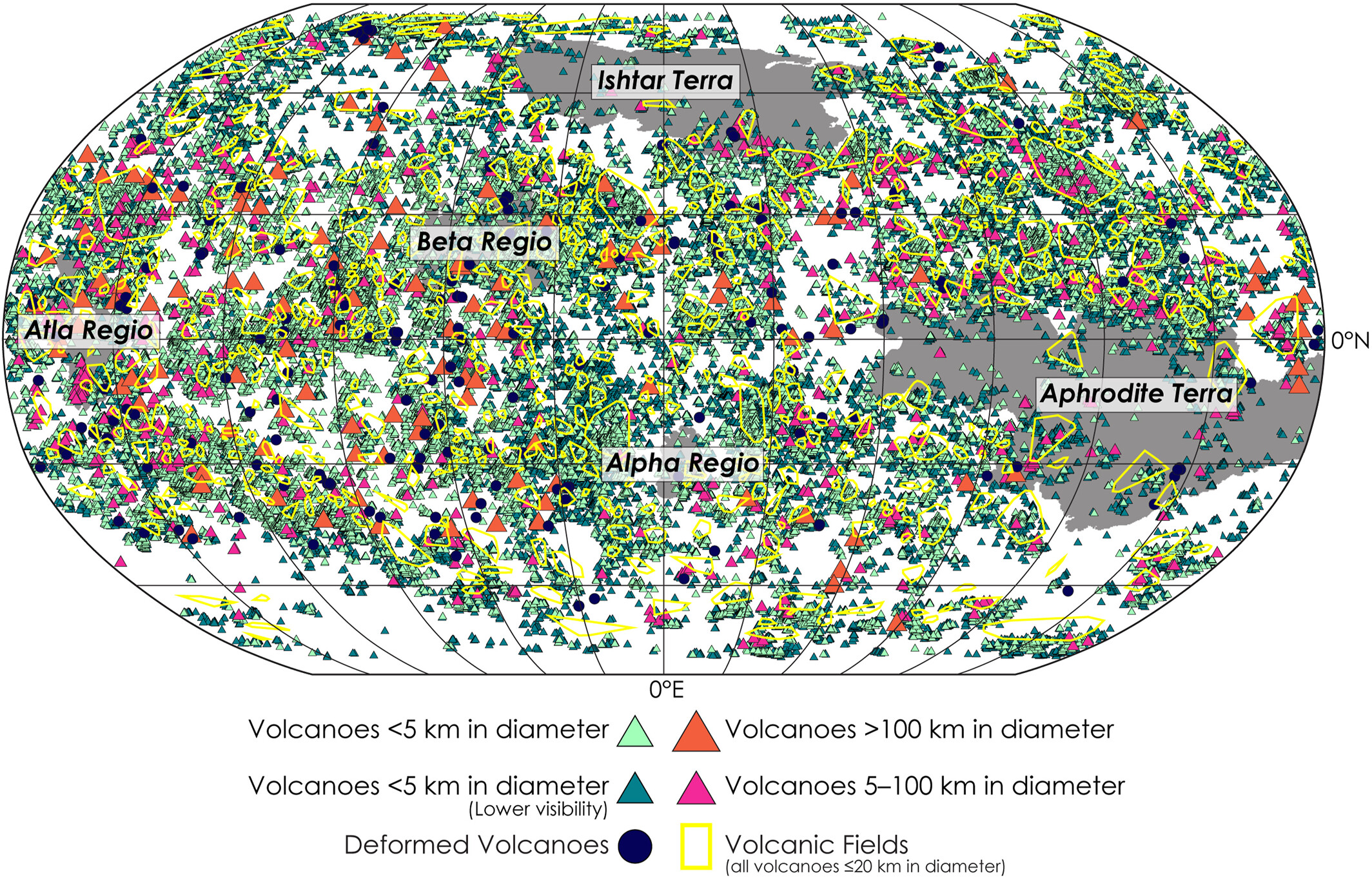 Mapa de Venus con los volcanes catalogados en este nuevo estudio. Si nos fijamos bien en la imagen hay zonas donde a esta resolución es imposible ver edificios volcánicos individuales debido a la gran acumulación existente de estos. Fuente: Han et al. (2022).
Mapa de Venus con los volcanes catalogados en este nuevo estudio. Si nos fijamos bien en la imagen hay zonas donde a esta resolución es imposible ver edificios volcánicos individuales debido a la gran acumulación existente de estos. Fuente: Han et al. (2022).¿Cómo es posible? Bueno, en Venus y desde la distancia no es tan fácil discriminar la posible edad de estos edificios volcánicos, por lo que podríamos estar viendo una acumulación de estos a lo largo del tiempo y no solo de los activos. Pero hay algo más: y es que Venus, al carecer de océanos, nos permite ver toda su superficie, mientras que es posible que en la Tierra una gran cantidad de la actividad volcánica siga permaneciendo invisible a nuestros ojos por la gran profundidad de los océanos.
El segundo dato sorprendente es que el 99% de estas formas volcánicas tienen menos de 5 kilómetros de diámetro y que hay una escasez de volcanes comprendidos entre los 20 y los 100 kilómetros de diámetro, lo que podría darnos alguna pista sobre cómo funciona el suministro de magma hacia la superficie y la tasa de erupciones o de actividad volcánica, algo que a su vez nos podría dar pistas para hacer modelos sobre el interior del planeta.
Esta inmensa base de datos puede servir también a los científicos para estudiar si existe alguna relación entre las concentraciones de volcanes y las distintas estructuras geológicas que existen en la superficie de Venus, ya que mientras en nuestro planeta una gran parte de la actividad volcánica ocurre en los límites de las placas tectónicas, en Venus, al no existir tectónica de placas, la distribución espacial de estos volcanes podría seguir otro tipo de patrones espaciales.
Pero sin duda también servirá para planificar detalles de las futuras misiones a Venus, como EnVision y VERITAS, que están equipadas con radares que tomarán imágenes de su superficie, si va todo según lo previsto, en la próxima década, indicándonos a que puntos de su superficie tenemos que mirar con mayor atención para confirmar si Venus sigue siendo un planeta activo.
Referencias:
Hahn, R.M. and Byrne, P.K. (2023) “A morphological and spatial analysis of volcanoes on Venus,” Journal of Geophysical Research: Planets, 128(4). doi: 10.1029/2023je007753.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Un nuevo mapa del vulcanismo de Venus se ha escrito en Cuaderno de Cultura Científica.
Testosterona y paternidad
 Foto: Caleb Jones / Unsplash
Foto: Caleb Jones / UnsplashEn una investigación en Filipinas midieron los niveles de testosterona en sangre de más de seiscientos hombres jóvenes a lo largo de casi un lustro. Observaron, por un lado, que aquellos con mayores niveles de la hormona al comienzo del estudio tenían, cuatro años y medio después, una mayor probabilidad de haberse emparejado y haber sido padres que los hombres con menor nivel.
Ese resultado no debe sorprender a nadie. La testosterona tiene efectos diversos en los varones; en la pubertad es la responsable del desarrollo de buen número de caracteres sexuales secundarios, como la aparición del vello facial y corporal, el agravamiento del tono de voz, el crecimiento de la nuez de Adán, la producción de musculatura, el crecimiento del pene, la producción de espermatozoides, y la configuración facial angulosa. En la edad adulta estimula la libido, predispone a ser más agresivos con los semejantes e induce a cortejar a la persona con la que uno se quiere emparejar. Es, por tanto, la hormona que promueve el emparejamiento y la competencia con otros hombres.
Más interesante resultó ser otro de los resultados de la investigación. Porque los jóvenes que participaron en el estudio tras ser padres experimentaban fuertes descensos en los niveles de testosterona; y esos descensos eran significativamente mayores que los que, por efecto de la edad, experimentaban los hombres que no habían sido padres. Y por si todo esto fuera poco, el descenso en la testosterona fue mayor en los padres que dedicaban mayor atención a sus hijos que en los que casi no se ocupaban de ellos.
En las especies en las que los machos asumen una parte de la tarea de cuidar a la prole, o contribuyen con su aportación de alimento a su crianza, su éxito reproductivo depende de la magnitud del esfuerzo que dedican a esa tarea. Y dado que el tiempo y otros recursos son limitados, los que se dedican a tratar de aparearse con otras parejas reproductivas no se pueden destinar al cuidado de la progenie, por lo que entre esos dos cometidos se establece un conflicto. Es decir, cuantos más recursos se dedican al cuidado de la prole, menos pueden destinarse a buscar parejas reproductivas adicionales. Parece, por tanto, lógico que la testosterona, dado su papel en la fisiología y psicología del emparejamiento, cumpla un papel importante en la regulación de esa alternativa.
En las aves, efectivamente, se ha demostrado que la testosterona cumple ese relevante papel. Sin embargo, hasta este estudio en Filipinas, en los mamíferos no se había podido determinar una relación clara entre los términos en los que se establece la disyuntiva entre emparejamientos múltiples y el cuidado de la prole, aunque había varias observaciones que no se habían considerado suficientemente concluyentes.
Así pues, si la testosterona se mantuviese en niveles altos tras la paternidad, aumentaría la probabilidad de que el varón dedicase demasiado tiempo y energía a buscar otra posible pareja, y ello iría en detrimento de la atención a sus hijos. De ese modo, la posible ganancia en términos de éxito reproductivo que pudiera derivarse de tener hijos con la nueva pareja, se vería contrarrestada por la posible pérdida que se produciría por disminuir su contribución al cuidado y atención de los que ya tiene. Por lo tanto, a través de sus efectos sobre la testosterona, la paternidad hace que disminuya la probabilidad de que los varones busquen otras parejas reproductivas y dediquen esfuerzo y recursos a ello.
Fuente:
Gettler, L. T., McDade, T. W., Feranil, A. B., Kuzawa, C. W. (2011) Longitudinal evidence that fatherhood decreases testosterone in human males. Proceedings of the National Academy of Sciences 2011, 108 (39): 16194-16199.
Para saber más:
Testosterona
La hormona de la maternidad y de la paternidad
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Testosterona y paternidad se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: Soy un planeta, una tetera, una cuchara y un cucharón

Definiciones que parecen evidentes no lo son tanto. En ciencia, siempre sometida a revisión, cambián con el tiempo (unas más y otras menos). Y como la ciencia está hecha por una especie animal que no puede sustraerse a sus instintos, sus definiciones también tienen sesgos. Para muestra, la definición de planeta
Nahúm Méndez Chazarra es geólogo planetario y divulgador científico. Publica la sección Planeta B en el Cuaderno de cultura Científica sobre la actualidad del Sistema Solar.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2022: Soy un planeta, una tetera, una cuchara y un cucharón se ha escrito en Cuaderno de Cultura Científica.
Soy mujer y tengo párkinson: ¿qué puedo esperar?
 Foto: Nickolas Nikolic / Unsplash
Foto: Nickolas Nikolic / UnsplashEl párkinson, enfermedad neurodegenerativa que aparece cuando las neuronas que producen dopamina están dañadas o se mueren, no afecta de la misma forma a hombres y mujeres.
En primer lugar, el sexo biológico es un factor de riesgo importante: los varones tienen 1,5 veces más posibilidades de desarrollarlo. ¿A qué se debe esta llamativa diferencia?
La clave parece estar en las hormonas que se encuentran principalmente en el sexo femenino: los estrógenos. Algunos estudios indican que podrían tener un efecto protector sobre las neuronas que degeneran en la enfermedad, gracias a su potencial para bloquear los principales mecanismos responsables de la muerte neuronal.
El hecho de que la proporción de mujeres diagnosticadas de párkinson en el periodo posmenopáusico sea mayor que durante el periodo premenopáusico apoyaría esta hipótesis.
Soy mujer y me han diagnosticado párkinson: ¿ahora qué?Ese “ahora qué” es lo que realmente le importa a la persona a la que se le ha detectado la dolencia: ¿qué me va a pasar?, ¿qué voy a notar?, ¿los síntomas van a empeorar?, ¿qué tratamientos me van a aplicar y para qué?
Actualmente, el párkinson no tiene cura y sigue avanzando con el paso del tiempo, por lo que los síntomas –cuya naturaleza, frecuencia y gravedad varían entre personas– empeoran poco a poco. Aun así, diversos estudios han observado que existen ciertos patrones de estas manifestaciones que difieren entre sexos.
En el caso de las mujeres, los problemas motores suelen aparecer más tarde que en los hombres, y el temblor suele ser el principal síntoma cuando se realiza el diagnóstico. Esto es importante, porque las personas que comienzan así la enfermedad parece que la experimentan de forma más benigna. No obstante, ellas tienen un mayor riesgo de caídas a medida que avanza la dolencia.
Dicen que me quejo demasiado“Me duele la espalda, las piernas… me encuentro todo el día cansada”. “Parece que no levanto cabeza”. “Estoy baja de ánimos, pero dicen que es normal sentirse así, ya que me acaban de diagnosticar párkinson”. Hay una creencia extendida de que esta es una enfermedad que nos hace temblar. Pero no es el único síntoma: además, los pacientes suelen padecer rigidez muscular, lentitud de movimientos e, incluso, inestabilidad postural.
Por si esto fuera poco, la dolencia viene acompañada de una serie de manifestaciones no motoras que afectan a la calidad de vida incluso más que los problemas de movilidad. Estamos hablando de estreñimiento, alteraciones del sueño, pérdida de olfato, cambios en la sudoración…
Estos trastornos están relacionados con alteraciones de otros sistemas del cuerpo, más allá de la falta de dopamina del cerebro. En concreto, las mujeres experimentan dolor, fatiga, depresión y ansiedad con más frecuencia e intensidad que los hombres.
A menudo, esos síntomas propios de la dolencia están infradiagnosticados y no se manejan adecuadamente porque ¿cómo no va a estar triste y ansiosa con la que le ha caído? Mujer con párkinson: no minimice sus síntomas, ya que muchos de ellos se pueden tratar farmacológicamente o mediante otro tipo de terapias, como la psicoterapia, el ejercicio físico o la terapia ocupacional. ¡Quéjese!, ¡quéjese mucho!
Mi enfermedad no tiene cura, pero ¿me van a tratar?Por supuesto. La primera línea de tratamiento consiste en suplir la falta de dopamina del cerebro. Con terapia farmacológica se consigue mejorar significativamente los síntomas motores. Aunque la dosis es igual de efectiva en ambos sexos, las mujeres tienen más riesgo de desarrollar efectos adversos indeseados, como los movimientos involuntarios, también llamados discinesias.
Respecto al tratamiento de los síntomas no motores, no se sabe si a las mujeres afectadas de párkinson se les prescriben más fármacos antidepresivos, ansiolíticos, analgésicos… que estarían justificados por su sintomatología. Los expertos abogan por una medicina personalizada para mejorar la atención sanitaria. Comencemos por adaptar los tratamientos terapéuticos en función del sexo.![]()
Para saber más:
El papel de los astrocitos en la aparición de la enfermedad de Parkinson
Párkinson en una lágrima
La mutación vasca de la dardarina y el párkinson
Sobre las autoras: Teresa Morera Herreras, profesora agregada del Departamento de Farmacología; Ane Murueta-Goyena, profesora Adjunta del Departamento de Neurociencias y Maider Zubelzu Irazusta, estudiante de doctorado en Farmacología. Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Soy mujer y tengo párkinson: ¿qué puedo esperar? se ha escrito en Cuaderno de Cultura Científica.
65, ¿un título acertado?
Hace poco han estrenado una película titulada, simplemente, “65”. Aunque en algunas zonas le han puesto un pequeño añadido: “65. Al borde de la extinción”. No voy a hacer ningún espóiler de la peli, ya que no la he visto, pero con este título, el añadido del final y lo que nos muestran en los tráileres, creo que todo el mundo se imagina lo que nos podemos encontrar en esta historia. Pero, si viajásemos en el tiempo hasta hace unos 65 millones de años, ¿realmente veríamos lo que nos presenta esta película? ¿Seríamos testigos de los momentos previos de una extinción masiva? Pues siento traeros malas noticias, porque la respuesta es no.
 Panel representativo de los primeros momentos del Periodo Paleoceno, tras la extinción del límite K-Pg. Diseñado e ilustrado por Antonio Grajera, está expuesto en los pasillos del Museo Geominero (IGME-CSIC, Madrid).
Panel representativo de los primeros momentos del Periodo Paleoceno, tras la extinción del límite K-Pg. Diseñado e ilustrado por Antonio Grajera, está expuesto en los pasillos del Museo Geominero (IGME-CSIC, Madrid).Estrictamente hablando, hace 65 millones de años nuestro planeta se encontraría inmerso en el primer Periodo geológico de la Era Cenozoica, al que hemos nombrado como Paleoceno. Habría pasado un millón de años desde que sucedió la quinta y última extinción masiva de los últimos 500 millones de años de la historia de nuestro planeta, la denominada extinción del límite Cretácico-Paleógeno, o límite K-Pg, en la que desaparecieron más del 75% de las especies tras la caída de un cuerpo extraterrestre en el actual Golfo de México hace 66 millones de años. Los mamíferos supervivientes reclamarían el dominio de los medios terrestres y marinos y la vida estaría empezando a diversificarse para intentar recuperar la diversidad biológica previa a la extinción, algo que no se conseguiría hasta varios millones de años después.
Vamos, que si viajásemos a hace 65 millones de años no veríamos enormes dinosaurios intentando comerse unos a otros en un espeso bosque de helechos y coníferas gigantes, sino paisajes todavía devastados donde árboles y plantas con flores servirían de refugio a pequeños mamíferos, principalmente roedores, que cazarían insectos o comerían sus semillas para sobrevivir. Mucho menos épico de lo que creíamos. Pero esto os lo digo ahora, porque si la película la hubieran estrenado hace 15 o 20 años, estaría alabando su acertado título y la utilizaría como herramienta para contaros, con pelos y señales, lo que sucedió durante la extinción del límite K-Pg.
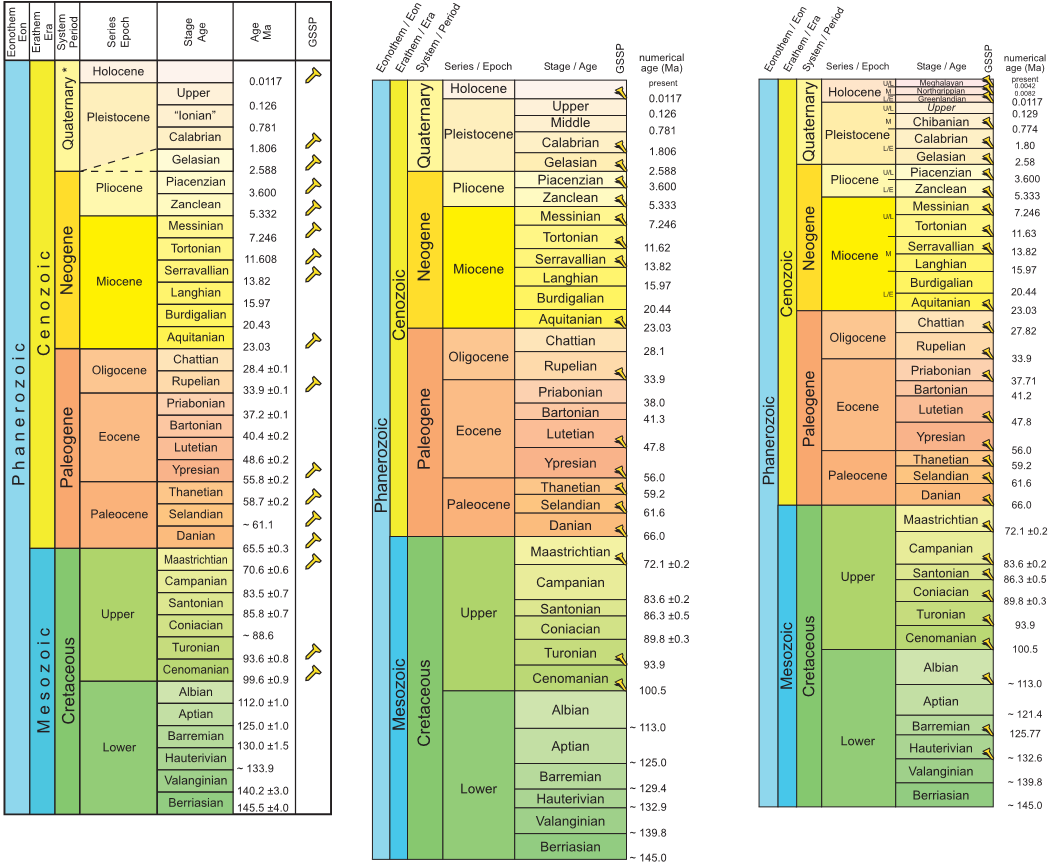 Diversas versiones de la tabla de los tiempos geológicos, en inglés, en las que podemos ver cómo ha cambiado la edad del límite K-Pg, y de muchos otros, a lo largo del tiempo. Izquierda: versión de 2008; centro: versión de agosto de 2012; derecha: versión más reciente, publicada en abril de 2023. Créditos: International Commission on Stratigraphy. Disponible para su descarga gratuita, incluidas las versiones previas traducidas.
Diversas versiones de la tabla de los tiempos geológicos, en inglés, en las que podemos ver cómo ha cambiado la edad del límite K-Pg, y de muchos otros, a lo largo del tiempo. Izquierda: versión de 2008; centro: versión de agosto de 2012; derecha: versión más reciente, publicada en abril de 2023. Créditos: International Commission on Stratigraphy. Disponible para su descarga gratuita, incluidas las versiones previas traducidas.¿Y de dónde procede esta curiosa contradicción que os acabo de comentar? Pues de que la Geología es una ciencia en continuo cambio, incluidas las edades a las que se produjeron algunos de los eventos. Si miramos la tabla de los tiempos geológicos del año 2008, la edad estimada para el límite K-Pg era de 65,5 millones de años, con un error de +-0,3 millones de años (es decir, 300.000 años arriba o abajo), antes de la actualidad. Sin embargo, cuando utilizamos la tabla de 2012, la edad estimada era de 66,0 millones de años, número que aún se mantiene en la versión más actualizada de la tabla publicada este mismo mes.
La siguiente pregunta que os estaréis haciendo es ¿y cómo sabemos esa edad tan precisa para los eventos geológicos? Pues gracias a los métodos de datación radiométrica que se basan en la desintegración radiactiva de los isótopos. Voy por partes con esto, que me estoy metiendo en el maravilloso mundo de la química.
Los átomos tienen un número particular de protones (partículas positivas) y neutrones (partículas neutras) en su núcleo, sobre las que orbitan una serie de electrones (partículas negativas). Sin embargo, hay algunos elementos que, aunque mantienen el mismo número de protones, tienen diferente número de neutrones en su núcleo, como el Carbono o el Uranio, que se conocen como isótopos. Pues muchos de esos isótopos tienen un núcleo inestable que tiende a desintegrarse con el tiempo, dando lugar a un isótopo hijo. Es lo que conocemos como radiactividad. Esa desintegración desde el isótopo inicial o isótopo padre al isótopo hijo sigue un ritmo constante, de tal manera que pasado un tiempo X tendremos la mitad del isótopo padre, al pasar ese mismo tiempo X tendremos la mitad de esa mitad, y así continuamente. A ese ritmo de decaimiento se le conoce como vida media. Y conociendo esa vida media de un elemento y pudiendo calcular en un material geológico la cantidad de isótopo hijo formado a partir del isótopo padre original, podemos saber su edad.
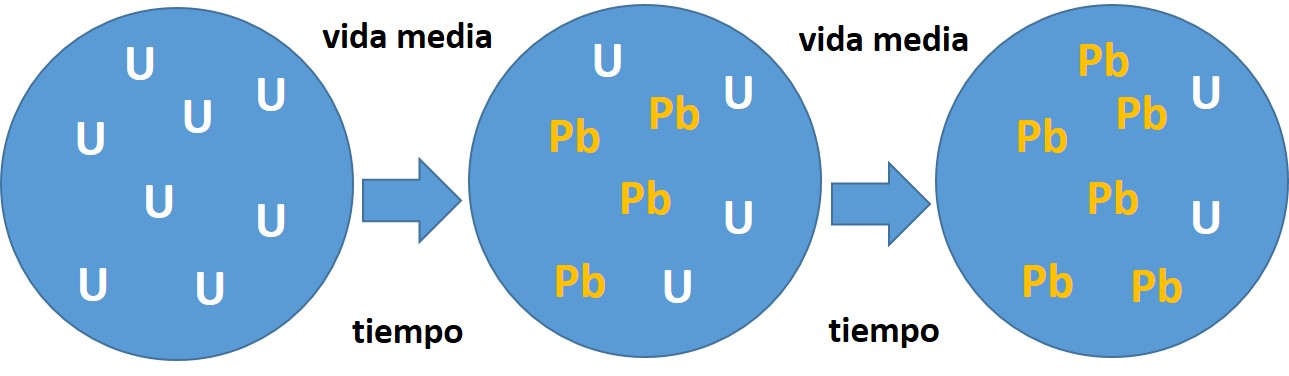 Modelo muy simplificado del decaimiento radiactivo del isótopo radiactivo de Uranio (U) en un elemento geológico que lo incluya en su composición química. Pasado el tiempo de desintegración (vida media), la mitad del isótopo padre se habrá transformado en el isótopo hijo (Plomo, Pb), proceso que se reproducirá de manera consecutiva.
Modelo muy simplificado del decaimiento radiactivo del isótopo radiactivo de Uranio (U) en un elemento geológico que lo incluya en su composición química. Pasado el tiempo de desintegración (vida media), la mitad del isótopo padre se habrá transformado en el isótopo hijo (Plomo, Pb), proceso que se reproducirá de manera consecutiva.Hay isótopos con vidas medias muy grandes que permiten datar con bastante fiabilidad materiales tan antiguos como la propia formación de nuestro planeta. Uno de los métodos radiométricos más utilizados es la relación entre el Uranio (isótopo padre) y el Plomo (isótopo hijo), conocida como datación U/Pb, que permite conocer la edad de materiales que se formaron hace más de 1 millón de años con márgenes de error de cientos de miles de años. Pero eso es ahora, porque la relación U/Pb es uno de los métodos de datación más antiguos empleados en Geología, por lo que las técnicas analíticas de medición isotópica han ido haciéndose cada vez más precisas, lo que ha provocado que se vayan corrigiendo las edades de los eventos geológicos de manera continua. Por ese motivo, cada año se publican versiones más novedosas y precisas de la tabla de los tiempos geológicos.
Vamos, que el equipo productor de la película se quedó con dataciones de hace más de 15 años y no se molestaron en comprobar las versiones más actualizadas. Pero también es cierto que 65 es un número más redondo y llamativo para un título que 66, salvo que seas fan de Iron Maiden (como yo) y empieces a tararear el estribillo de una canción a la que le falta un último 6 cada vez que tienes que explicar cuándo sucedió la última extinción masiva de la Tierra.
Para saber más:
Datación radiométrica
Cómo usar uranio para saber si un neandertal pintó en una cueva
Datación K-Ar y las edades de Marte
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo 65, ¿un título acertado? se ha escrito en Cuaderno de Cultura Científica.
Las impredecibles capacidades emergentes en grandes modelos de IA
Los modelos de lenguaje extenso como ChatGPT ahora son lo suficientemente grandes como para comenzar a mostrar comportamientos sorprendentes e impredecibles.
Un artículo de Stephen Ornes para Quanta Magazine
¿Qué película describen estos emojis?

Esa pregunta fue una de las 204 tareas elegidas el año pasado para probar la capacidad de varios modelos de lenguaje extenso (LLM, por sus siglas en inglés), los motores computacionales detrás de los bots conversacionales de IA como ChatGPT. Los LLM más simples produjeron respuestas surrealistas. “La película es una película sobre un hombre que es un hombre que es un hombre”, comenzó uno. Los modelos de mediana complejidad se acercaron, aventurando Emoji: la película. Pero el modelo más complejo lo clavó al primer intento: Buscando a Nemo.
“A pesar de tratar de esperar sorpresas, me sorprenden las cosas que estos modelos pueden hacer”, afirma Ethan Dyer, científico informático de Google Research que ayudó a organizar la prueba. Es sorprendente porque estos modelos supuestamente tienen una directiva: aceptar una cadena de texto como entrada y predecir lo que viene a continuación, una y otra vez, basándose únicamente en estadísticas. Los informáticos habían anticipado que la ampliación mejoraría el rendimiento de las tareas conocidas, pero no esperaban que los modelos manejaran repentinamente tantas tareas nuevas e impredecibles.
Investigaciones recientes, como en la que trabajó Dyer, han revelado que los LLM pueden producir cientos de habilidades «emergentes», tareas que los modelos grandes pueden completar y los modelos más pequeños no, muchas de las cuales parecen tener poco que ver con el análisis de texto. Van desde multiplicar hasta la generación de código informático ejecutable y, aparentemente, la decodificación de películas basándose en emojis. Nuevos análisis sugieren que, para algunas tareas y algunos modelos, existe un umbral de complejidad más allá del cual la funcionalidad del modelo se dispara. (También sugieren un lado oscuro: a medida que aumentan en complejidad, algunos modelos revelan nuevos sesgos e inexactitudes en sus respuestas).
“Que los modelos de lenguaje puedan hacer este tipo de cosas nunca se discutió en ninguna literatura que yo conozca”, afirma Rishi Bommasani, científico informático de la Universidad de Stanford. El año pasado ayudó a compilar una lista de docenas de comportamientos emergentes, incluidos varios identificados en el proyecto de Dyer. Esa lista sigue creciendo.
Ahora, los investigadores se eesfuerzan en no solo identificar habilidades emergentes adicionales, sino también en descubrir por qué y cómo ocurren; en esencia, para tratar de predecir la imprevisibilidad. Comprender la emergencia podría revelar respuestas a preguntas profundas sobre la IA y el aprendizaje automático en general, como si los modelos complejos de verdad están haciendo algo nuevo o solo se están volviendo realmente buenos en estadística. También podría ayudar a los investigadores a aprovechar los beneficios potenciales y reducir los riesgos emergentes.
“No sabemos cómo predecir en qué tipo de aplicación va a surgir la capacidad de hacer daño, ya sea gradualmente o de manera impredecible”, asegura Deep Ganguli, un científico informático de la startup de IA Anthropic.
La emergencia de la emergenciaBiólogas, físicas, ecologistas y otras personas de ciencia utilizan el término «emergente» para describir comportamientos colectivos autoorganizados que aparecen cuando una gran colección de cosas actúa como una sola. Las combinaciones de átomos sin vida dan lugar a células vivas; las moléculas de agua crean olas; las bandadas de estorninos surcan el cielo formando patrones cambiantes pero identificables; las células hacen que los músculos se muevan y los corazones latan. Fundamentalmente las habilidades emergentes aparecen en sistemas que involucran muchos componentes individuales. Pero los investigadores solo han podido documentar recientemente estas habilidades en los LLM, al alcanzar estos modelos tamaños enormes.
Los modelos de lenguaje han existido durante décadas. Hasta hace unos cinco años los más potentes se basaban en lo que se denomina red neuronal recurrente. Básicamente, toman una cadena de texto y predicen cuál será la siguiente palabra. Lo que hace que un modelo sea «recurrente» es que aprende de su propio resultado: sus predicciones retroalimentan la red para mejorar el rendimiento futuro.
En 2017 los investigadores de Google Brain introdujeron un nuevo tipo de arquitectura llamada transformador. Mientras que una red recurrente analiza una oración palabra por palabra, el transformador procesa todas las palabras al mismo tiempo. Esto significa que los transformadores pueden procesar grandes cuerpos de texto en paralelo.
Los transformadores permitieron una rápida ampliación de la complejidad de los modelos de lenguaje al aumentar la cantidad de parámetros en el modelo, así como otros factores. Los parámetros se pueden considerar como conexiones entre palabras, y los modelos mejoran ajustando estas conexiones a medida que avanzan en el texto durante el entrenamiento. Cuantos más parámetros haya en un modelo con más precisión podrá hacer conexiones y más cerca estará de imitar aceptablemente el lenguaje humano. Como era de esperar, un análisis de 2020 realizado por investigadores de OpenAI encontró que los modelos mejoran en precisión y capacidad a medida que se amplían.
Pero el debut de los LLM también trajo algo realmente inesperado. Muchas cosas. Con la llegada de modelos como GPT-3, que tiene 175.000 millones de parámetros, o PaLM de Google, que se puede alcanzar hasta los 540.000 millones, los usuarios comenzaron a describir más y más comportamientos emergentes. Un ingeniero de DeepMind incluso informó que pudo convencer a ChatGPT de que era una terminal de Linux y logró que ejecutara un código matemático simple para calcular los primeros 10 números primos. Sorprendentemente, pudo terminar la tarea más rápido que el mismo código ejecutado en una máquina Linux real.
Al igual que con la tarea con emojis para la película, los investigadores no tenían motivos para pensar que un modelo de lenguaje construido para predecir texto imitaría de manera convincente una terminal de ordenador. Muchos de estos comportamientos emergentes ilustran el aprendizaje de «cero intentos» o «pocos intentos», que describe la capacidad de un LLM para resolver problemas que nunca, o rara vez, ha visto antes. Este ha sido un objetivo durante mucho tiempo en la investigación en inteligencia artificial, afirma Ganguli. Al mostrar que GPT-3 podía resolver problemas sin ningún dato de entrenamiento explícito en una configuración de cero intentos, afirma, «me llevó a dejar lo que estaba haciendo e involucrarme más».
No estaba solo. Una gran cantidad de investigadores, detectando que los primeros indicios de que los LLM podrían ir más allá de las limitaciones de sus datos de entrenamiento, se esfuerzan por comprender mejor qué aspecto tiene la emergencia y cómo sucede. El primer paso fue documentarlo a fondo.
Más allá de la imitaciónEn 2020, Dyer y otros en Google Research predijeron que los LLM tendrían efectos transformadores, pero cuáles serían esos efectos seguía siendo una pregunta abierta. Así que le pidieron a la comunidad de investigación que proporcionara ejemplos de tareas difíciles y diversas para trazar los límites exteriores de lo que podría hacer un LLM. Este esfuerzo se denominó proyecto Beyond the Imitation Game Benchmark (BIG-bench), tomando como el nombre como referencia el del «juego de imitación» de Alan Turing, una prueba para ver si una computadora podría responder preguntas de una manera convincentemente humana. (Esto más tarde se conocería como la prueba de Turing). El grupo estaba especialmente interesado en ejemplos en los que los LLM habían adquirido repentinamente nuevas habilidades que no habían existido antes en absoluto.
“Cómo entendemos estas transiciones bruscas es una gran pregunta de investigación”, afirma Dyer.
Como era de esperar, en algunas tareas el rendimiento de un modelo mejoró de manera gradual y predecible a medida que aumentaba la complejidad. Y en otras tareas, aumentar la cantidad de parámetros no produjo ninguna mejora. Pero para aproximadamente el 5% de las tareas los investigadores encontraron lo que llamaron «avances»: saltos rápidos y dramáticos en el rendimiento en una escala con umbral. Ese umbral variaba según la tarea y el modelo.
Por ejemplo, los modelos con relativamente pocos parámetros, solo unos pocos millones, no pudieron completar con éxito problemas de suma de tres dígitos o multiplicación de dos dígitos; pero para decenas de miles de millones de parámetros, la precisión se disparaba en algunos modelos. Ocurrieron saltos similares para otras tareas, incluida la decodificación del Alfabeto Fonético Internacional, reordenar las letras de una palabra, identificar contenido ofensivo en párrafos de Hinglish (una combinación de hindi e inglés) y generar un equivalente en inglés similar a los refranes en suajili.
Pero los investigadores se dieron cuenta rápidamente de que la complejidad del modelo no era el único factor determinante. Algunas habilidades inesperadas podían obtenerse de modelos más pequeños con menos parámetros, o entrenarse en conjuntos de datos más pequeños, si los datos eran de una calidad lo suficientemente alta. Además, la forma en la que se redactaba una consulta influía en la precisión de la respuesta del modelo. Cuando Dyer y sus colegas plantearon la tarea con emojis para la película utilizando un formato de opción múltiple, por ejemplo, la mejora de la precisión fue menos un salto repentino y más un aumento gradual con mayor complejidad. Y el año pasado, en un artículo presentado en NeurIPS, la reunión más importante del campo, los investigadores de Google Brain demostraron cómo un modelo entrenado (prompted) para explicarse (una capacidad llamada razonamiento en cadena de pensamiento) podía resolver correctamente un problema matemático verbal, mientras que el mismo el modelo sin ese entrenamiento no podía.
Yi Tay, un científico de Google Brain que trabajó en la investigación sistemática de los avances, señala un trabajo reciente que sugiere que la cadena de pensamiento cambia las curvas de escalado y, por lo tanto, el punto donde ocurre la emergencia. En su artículo de NeurIPS, los investigadores de Google demostraron que el uso de entrenamientos de cadena de pensamiento podía provocar comportamientos emergentes no identificados en el estudio BIG-bench. Tales entrenamientos, que le piden al modelo que explique su razonamiento, pueden ayudar a los investigadores a comenzar a investigar por qué aparece la emergencia en primer lugar.
Hallazgos recientes como estos sugieren al menos dos posibilidades de por qué ocurre la emergencia, afirma Ellie Pavlick, científica informática de la Universidad de Brown que estudia modelos computacionales de lenguaje. Una es que, como sugieren las comparaciones con los sistemas biológicos, los modelos más grandes realmente obtienen nuevas habilidades de forma espontánea. “Es muy posible que el modelo haya aprendido algo fundamentalmente nuevo y diferente que no tenía con un tamaño más pequeño”, dijo. «Eso es lo que todos esperamos que sea el caso, que se produzca un cambio fundamental que ocurre cuando se amplían los modelos».
La otra posibilidad, menos sensacional, afirma, es que lo que parece ser emergente pueda ser, en cambio, la culminación de un proceso interno impulsado por la estadística que funciona a través de un razonamiento tipo cadena de pensamiento. Los LLM grandes pueden simplemente estar aprendiendo heurísticas que están fuera del alcance de aquellos con menos parámetros o con datos de menor calidad.
Pero, añade, descubrir cuál de esas explicaciones es más probable depende de una mejor comprensión de cómo funcionan en realidad los LLM. “Dado que no sabemos cómo funcionan debajo del capó, no podemos decir cuál de esas cosas está sucediendo”.
Capacidades impredecibles y trampasHay un problema obvio al pedirles a estos modelos que se expliquen: son mentirosos notorios. “Nos apoyamos cada vez más en estos modelos para hacer el trabajo básico”, afirma Ganguli, “pero no confío en ellos y ya está. Compruebo su trabajo.” Como uno de los muchos ejemplos divertidos, en febrero Google presentó su chatbot de IA, Bard. La publicación del blog que anuncia la nueva herramienta muestra a Bard cometiendo un error de hecho.
La emergencia conduce a la imprevisibilidad, y la imprevisibilidad, que parece aumentar con la escala, dificulta que los investigadores anticipen las consecuencias del uso generalizado.
“Es difícil saber de antemano cómo se usarán o implementarán estos modelos”, afirma Ganguli. “Y para estudiar fenómenos emergentes debes tener un caso en mente, y no sabrás hasta que estudies la influencia de la escala qué capacidades o limitaciones pueden surgir”.
En un análisis de LLMs publicado en junio pasado los investigadores de Anthropic estudiaron si los modelos muestran ciertos tipos de prejuicios raciales o sociales, no muy diferentes a los encontrados anteriormente en algoritmos no basados en LLM que se utilizan para predecir qué personas con antecedentes cometerán probablemente otro delito. Ese estudio se inspiró en una aparente paradoja relacionada directamente con la emergencia: a medida que los modelos mejoran su rendimiento cuando se amplían, también pueden aumentar la probabilidad de fenómenos impredecibles, incluidos aquellos que podrían conducir a sesgos o perjuicios.
“Ciertos comportamientos dañinos surgen abruptamente en algunos modelos”, afirma Ganguli. Cita un análisis reciente de LLMs, conocido como el punto de referencia BBQ, que mostró que el sesgo social surge con las cantidades enormes de parámetros. “Los modelos más grandes se vuelven abruptamente más sesgados”. No abordar ese riesgo, recalca, podría poner en peligro a los sujetos de estos modelos.
Pero ofrece un contrapunto: cuando los investigadores simplemente le dijeron al modelo que no se basara en estereotipos o sesgos sociales, literalmente escribiendo esas instrucciones, el modelo estaba menos sesgado en sus predicciones y respuestas. Esto sugiere que algunas propiedades emergentes también podrían usarse para reducir el sesgo. En un artículo publicado en febrero, el equipo de Anthropic informó sobre un nuevo modo de «autocorrección moral», en el que el usuario solicita al programa que sea útil, honesto e inofensivo.
La emergencia, afirma Ganguli, revela tanto un potencial sorprendente como un riesgo impredecible. Las aplicaciones de estos grandes LLMs ya están proliferando, por lo que una mejor comprensión de esa interacción ayudará a aprovechar la diversidad de habilidades de los modelos lingüísticos.
“Estamos estudiando cómo las personas usan realmente estos sistemas”, añade Ganguli. Pero esos usuarios también están jugueteando, constantemente. “Pasamos mucho tiempo conversando con nuestros modelos”, asegura, “y ahí es donde comienzas a tener una buena intuición sobre la confianza, o la falta de ella”.
El artículo original, The Unpredictable Abilities Emerging From Large AI Models, se publicó el 16 de marzo de 2023 en Quanta Magazine. Cuaderno de Cultura Científica tiene un acuerdo de distribución en castellano con Quanta Magazine.
Traducido por César Tomé López
El artículo Las impredecibles capacidades emergentes en grandes modelos de IA se ha escrito en Cuaderno de Cultura Científica.
El problema de Tammes
El botánico y artista holandés Pieter Merkus Lambertus Tammes (1903-1980) descubrió que los granos de polen que son casi esféricos poseen pequeños poros distribuidos de manera que parecen distanciados lo más posible los unos de los otros.
 Granos de polen de varias especies ampliados mediante un microscopio electrónico de barrido. Fuente: Wikimedia Commons.
Granos de polen de varias especies ampliados mediante un microscopio electrónico de barrido. Fuente: Wikimedia Commons.
En 1930, como parte de su tesis doctoral, publicó sus investigaciones sobre este tema. En este trabajo el botánico se preguntaba sobre cuál era la manera de distribuir n puntos sobre una esfera, de manera que la menor de las distancias entre ellos fuera la mayor posible. Esta cuestión pronto pasó al mundo matemático como el problema de Tammes.
La primera ideaUna idea natural es, probablemente, pensar en colocar los puntos en los vértices de un poliedro regular inscrito en la esfera, es decir, un tetraedro si n = 4, un octaedro si n = 6, un cubo si n = 8, un icosaedro si n = 12 o un dodecaedro si n = 20.
Surgen inmediatamente dos preguntas: como sólo existen estos cinco poliedros regulares (convexos), ¿qué sucede para otros valores de n? Además, para los cinco casos nombrados, ¿el poliedro regular inscrito proporciona la solución óptima buscada?
Este problema se conoce también como el problema de los dictadores enemigos ya que, si quisieran repartirse la Tierra (si se considera que el territorio de un dictador está formado por los puntos de la esfera situados más cerca de él que de cualquier otro dictador), ¡desearían estar lo más alejados los unos de los otros para obtener regiones mayores!
El problema de Tammes equivale al problema de empaquetamiento de esferas, es decir, la cuestión de encontrar el mayor diámetro para n círculos iguales que pueden situarse sobre una esfera sin superponerse.
Las aplicaciones de este problema son numerosas. Por ejemplo, en biología, podría ayudar a describir el autoensamblaje en virus esféricos (como el virus del mosaico del tabaco, el SARS-CoV-2, etc.).
 Virus esférico SARS-CoV-2. Fuente: Wikimedia Commons.
Virus esférico SARS-CoV-2. Fuente: Wikimedia Commons.
En química, el modelo VSEPR postula que los pares de electrones de valencia (bolas) alrededor de un átomo se repelen mutuamente; adoptan entonces una disposición espacial que minimiza esta repulsión y maximiza la distancia entre esas bolas. Así, este modelo es consistente con la solución al problema de Tammes.
Muchas personas se han dedicado a estudiar este problema que, a fecha de hoy, está resuelto para los n menores o iguales a 14 y para n = 24.
Los casos conocidosRecordemos que la intersección de una esfera con un plano que contiene a su centro genera una circunferencia máxima (y un círculo máximo) sobre la superficie de la esfera. La distancia entre dos puntos de la esfera, unidos por un arco de circunferencia máxima, es la menor entre ambos y se llama distancia ortodrómica.
El problema de Tammes busca maximizar la menor de las distancias ortodrómicas entre n puntos de una esfera.
Para n = 2, la solución es obvia: los dos puntos deben ser diametralmente opuestos.
Si n = 3, la solución al problema de Tammes es un triángulo equilátero inscrito en un círculo máximo de la esfera.
Para n = 4, 6 y 12 puntos, las soluciones son las que admiten más simetrías: los poliedros regulares con, respectivamente, 4, 6 y 12 vértices, es decir, los tetraedros regulares inscritos en la esfera, los octaedros y los icosaedros.
El geómetra húngaro Laszlo Fejes Tóth fue quien resolvió los casos n = 3, 4, 6 y 12.
Para n = 5 existen varias configuraciones que proporcionan la solución óptima, y, además, esa distancia máxima buscada es la misma que la del caso de n = 6.
Para n = 8, los ocho vértices de un cubo inscrito en la esfera no proporcionan la distancia óptima. La solución no es única, y la mejor disposición es un la de un antiprisma cuadrado.
En 1951, los matemáticos Kurt Schütte y Bartel Leendert van der Waerden resolvieron los casos para n = 5, 7, 8 y 9.
En 1963, el geómetra Ludwik Danzer encontró la solución para n = 10 y 11.
Raphael M. Robinson resolvió el caso n = 24 en 1961. Los casos n = 13 y 14 fueron resueltos por Oleg R. Musin y Alexey S. Tarasov en 2015; enumeraron las posibles configuraciones con ayuda de un ordenador.
Hay soluciones propuestas para muchos otros casos… pero aún son solo conjeturas.
Referencias
- L. Danzer, Finite point-sets on S2 with minimum distance as large as possible, Discr. Math. 60 (1986) 3-66.
- L. Fejes Tóth, Über die Abschätzung des kürzesten Abstandes zweier Punkte eines auf einer Kugelfläche liegenden Punktsystems, Jber. Deutch. Math. Verein. 53 (1943) 66-68.
- P. Legrand, Le problème de Tammes, APMEP, 10 de julio de 2012.
- O. R. Musin and A. S. Tarasov, The Tammes problem for N=14, Experimental Mathematics 24 (2015) 460-468, arXiv:1410.2536 [math.MG].
- H. Pfoertner, Arrangement of points on a sphere. Visualization of the best known solutions of the Tammes problem, Engine Monitoring.
- R.M. Robinson, Arrangement of 24 circles on a sphere, Math. Annalen 144 (1961) 17-48.
- K. Schütte and B. L. van der Waerden, Auf welcher Kugel haben 5, 6, 7, 8 oder 9 Punkte mit Mindestabstand Eins Platz?, Math. Annalen 123 (1951) 96-124.
- N. J. A. Sloane, Spherical Codes. Nice arrangements of points on a sphere in various dimensions, Neil J. A. Sloane: Home Page.
- P. M. L. Tammes, On the origin of number and arrangement of the places of exit on the surface of pollen-grains, Recueil Des Travaux Botaniques Néerlandais 27, 1930.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo El problema de Tammes se ha escrito en Cuaderno de Cultura Científica.
Agujetas: las dolorosas protagonistas tras el ejercicio físico
 Imagen: StockSnap / Pixabay
Imagen: StockSnap / PixabayNunca es tarde para empezar a realizar ejercicio físico. Los beneficios para la salud que tiene la práctica de actividad física frecuente son claros y numerosos: aumento de la esperanza de vida, disminución del riesgo de sufrir diabetes, obesidad, enfermedades cardiovasculares, diferentes tipos de cáncer y otras muchas enfermedades, mejora de la salud mental…
Sin embargo, las personas que se deciden a tener una vida más activa y comienzan a practicar o retoman un deporte o cualquier otra actividad física se enfrentan a menudo con un fenómeno biológico que puede echarles para atrás en su iniciativa: las temidas agujetas, también conocidas como «mialgia diferida» o «dolor muscular de aparición tardía».
Prácticamente todo el mundo ha experimentado el dolor típico de las agujetas en algún momento de su vida y, a pesar de ello, las causas detrás siguen sin estar del todo claras. Es una situación muy similar a lo que ocurre con la frecuente somnolencia tras una comida pesada, existen varias hipótesis que intentan explicarlo, pero las pruebas científicas al respecto son limitadas por la escasez de estudios. Las curiosidades del cuerpo humano no son, lógicamente, una prioridad en el terreno de la investigación médica.
Normalmente, las agujetas tardan en aparecer entre 12 y 72 horas tras el ejercicio físico que lo desencadena y el máximo nivel de dolor se presenta entre uno y tres días. Los ejercicios excéntricos como las sentadillas o bajar escaleras, en los que se estiran los músculos mientras existe contracción, son los que inducen agujetas con mayor frecuencia porque alteran más el músculo y el tejido conectivo de alrededor.
Durante mucho tiempo, se creyó que el principal mecanismo involucrado en las agujetas era la formación y acumulación de cristales de ácido láctico en el músculo, como consecuencia de un metabolismo anaeróbico (en el que no se emplea oxígeno). Sin embargo, un hecho clave descarta esta hipótesis: el ácido láctico se acumula rápidamente con un ejercicio físico intenso, pero desaparece en torno a una hora después. Por tanto, los cristales de esta molécula no pueden ser los responsables de las agujetas, que aparecen de forma mucho más tardía.
En la actualidad, la hipótesis con mayor respaldo científico y más aceptada entre los investigadores sostiene que las agujetas tienen su origen en las microrroturas de las fibras musculares provocadas por daños mecánicos. Así, cuando una persona realiza una actividad física a la que sus músculos no están habituados se producen diminutas lesiones (y, como consecuencia, alteraciones metabólicas) en las células musculares incapaces de aguantar ese nivel de ejercicio. No obstante, estas lesiones no causan inmediatamente dolor, ya que las agujetas tardan en aparecer, sino que lo provocan de forma más tardía a través de un proceso inflamatorio.
Debido al número limitado de estudios, no está todavía muy claro qué tratamientos son efectivos para aliviar las agujetas y limitar su duración. Se han evaluado algunos complementos dietéticos (preparados proteicos, taurina, ácidos grasos omega-3, curcumina, D-ribosa, L-glutamina…), fármacos antiinflamatorios, masajes, duchas o baños fríos, descanso y prendas de compresión con algunos indicios de efectividad, aunque con una certeza científica baja o hallazgos contradictorios. Entre todos ellos, el masaje muscular parece la opción con más respaldo a la hora de limitar la duración de las agujetas. También existen múltiples evidencias que constatan que hacer ejercicios con un aumento progresivo de la intensidad, en lugar de realizar de primeras ejercicios intensos, previene la aparición de agujetas. Los estiramientos antes y después de la actividad física quizás podrían atenuar las posteriores agujetas, pero tampoco está claro en la actualidad.
Afortunadamente, las agujetas son transitorias, hagamos lo que hagamos, y bastan unos pocos días (casi siempre menos de una semana) para que desaparezcan por sí solas. Tras este episodio de dolor, el músculo se regenera totalmente. La mialgia diferida no es una señal por sí misma de crecimiento muscular, pero sí nos indica que estamos saliendo fuera de nuestra zona de confort en cuanto a actividad física se refiere y, cuando se vaya, estaremos mejor preparados para retomarla.
Para saber más:
Respuesta de los sistemas respiratorio y cardiovascular al ejercicio físico
Evite, si puede, la silla y el sofá
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo Agujetas: las dolorosas protagonistas tras el ejercicio físico se ha escrito en Cuaderno de Cultura Científica.
Cómo hacer un clarinete con tubos de pvc y un guante de goma
clarinete
Seguro que tú también lo viste. Fue un vídeo viral hace bastantes años ya (siempre más de los que parecen). En él, un tipo con una camisa chillona utilizaba un taladro para fabricarse un instrumento musical con… una zanahoria. Sí, ¡una zanahoria!, y lo peor es que la melodía resultaba hasta pegadiza.
Desde entonces, Linsey Pollak saltó a la fama como el músico de los instrumentos insospechados, un tipo capaz de arrancarle una notas a casi cualquier cosa. La zanahoria era solo uno de muchos ejemplos. Después de aquella charla TEDx, hemos podido ver al músico australiano tocando el bate de baseball, la regadera, un manillar de bicicleta, y a veces también (esto es más raro) el saxofón.
La imaginación de Pollak parece no tener límites. En muchos casos, sus instrumentos consisten en una boquilla de saxofón acoplada a algún objeto con forma de tubo. Es, en parte, la gracia de los instrumentos de viento y aquello que los convierte en una de las tecnologías más antiguas de la humanidad: son muy fáciles de fabricar. Pero algunos de sus inventos van un poco más allá. Es el caso de Mr. Curly, que juega con la forma espiral del larguísimo tubo (de ahí la tesitura de contrabajo) para que todos los agujeros queden accesibles en el espacio de una mano. O, mi preferido, el “Foonki”, un clarinete de membrana construido de forma casera con materiales fáciles de encontrar en cualquier ferretería. Pollak explica cómo hacerlo en su canal de Youtube. Y, después que él, Nicolás Bras presentó su propia versión en un vídeo un poco más detallado.
Estas navidades, Iñaki y yo nos propusimos fabricar nuestro propio Foonki. Nos costó un rato encontrar los materiales perfectos y desentrañar los detalles de la boquilla. Así que, por si a alguien quiere repetir el experimento, aquí va una receta simplificada.
Instrucciones generales:El clarinete de membrana es un instrumento de viento madera. En esencia, consiste en una membrana (léase, un globo, un trozo de plástico) que vibra contra una superficie sólida cuando se opone al paso del aire. En el Foonki, el aire entra por un agujero lateral, y recorre el espacio existente entre dos tubos concéntricos. Cuando llega al extremo, se encuentra con la mencionada membrana, la “estira” para poder pasar y regresa a través del tubo interno. En ese lapso, genera una vibración y el sonido resultante es bastante parecido al de un clarinete. La idea básica es el siguiente:

Ahora bien, en la práctica nosotros acabamos construyendo algo más bien parecido a lo siguiente. Trataré de explicarlo a continuación.
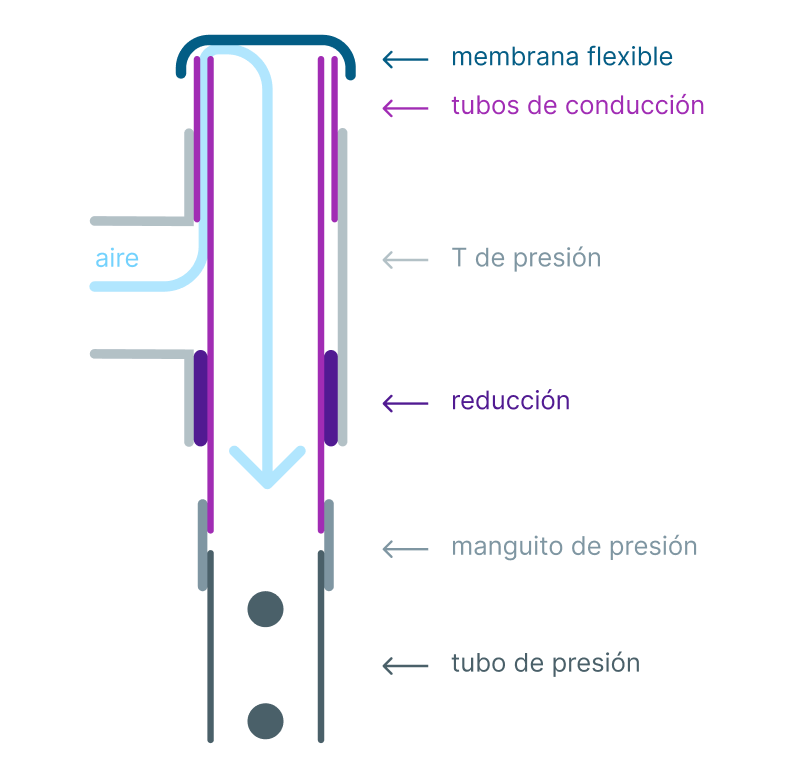
- Tubo de conducción eléctrica de Ø16 mm
- Tubo de conducción eléctrica de Ø20 mm.
- T de Ø20 mm.
- Reducción de Ø20 a Ø16 mm.
- Manguito de presión, Ø16 mm.
- Membrana: vale un guante de goma, globo, plástico, o similar.
- Herramientas: una sierra (para cortar los tubos), un taladro, cinta aislante, una lija redonda.
Empezaremos por cortar los tubos de conducción (en morado, en la figura). Necesitaremos:
- Un trozo tubo de Ø16 mm de unos 10 cm de longitud (que sea más largo que la T, en cualquier caso).
- Otro trozo de Ø20 mm de unos 4 cm de longitud.
A continuación, vamos a completar los brazos de la T. En el extremo inferior, colocaremos la reducción de pvc. Esta pieza permitirá que el aire no se salga de la T “por debajo” de la boquilla. Por eso queremos que quede muy bien sellada y fija a la T. Si fuese necesario, se puede usar cinta aislante para reducir el espacio entre las dos piezas (nosotros utilizamos un martillo para colocarla en su posición final).
En el brazo superior de la T, colocaremos el trozo de tubo de Ø20 mm. Esta pieza también debe quedar bien fija a la T, sin que pueda salirse el aire entre ambas (de nuevo, se puede usar cinta aislante en caso necesario).
Introducimos el tubo de Ø16 mm desde el extremo inferior de la T, hasta que quede alineado en la parte superior con el tubo de Ø20 mm.
Por último, colocaremos la membrana, como si fuese una capucha, a la salida de los dos tubos. Podemos fijarla en esta posición con ayuda de una goma elástica, un manguito, o similar. Recomiendo no usar cinta aislante para esto, ya que hará más difícil “estirar” y mover la membrana en busca de un sonido mejor.
¡Y listo! Basta con soplar por el cuello de la T para que el invento empiece a sonar. A veces hay que jugar un poco con la posición del tubo interior, y con la tensión de la membrana para conseguir un sonido más o menos estable. Pero es sorprendentemente fácil conseguir que el invento funcione.
Cómo taladrar el tubo:Para poder tocar distintas notas con el clarinete de membrana necesitamos un tubo con una serie de agujeros estratégicamente situados. Utilizaremos un tubo de Ø16 mm y lo acoplaremos a la boquilla con ayuda del manguito. Para saber cómo cortarlo y dónde taladrar, nosotros utilizamos esta plantilla de Nicolas Bras como punto de partida. Linsey Pollak tiene otra parecida en su página web. Es importante tener en cuenta que las distancias están medidas desde la membrana del clarinete, así que no basta con medir el tubo que vas a acoplar.
En cualquier caso, da un poco igual la plantilla que uses. Lo más probable es que alguna nota no te quede afinada a la primera. La física es complicada y la realidad está llena de márgenes de error, es lo que hay. Mi consejo es que empieces taladrando los agujeros con una broca pequeña. El sonido estará un semitono bajo, aproximadamente. Desde ese punto, con paciencia y una lija, puedes ir agrandando el agujero hasta conseguir la afinación perfecta.
Después de semejante sesión de bricolaje, tu clarinete debería estar listo. Ahora, ¡a tocar!
Para saber más:
El sonido del viento (2)
La ingeniería de las flautas (serie)
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Cómo hacer un clarinete con tubos de pvc y un guante de goma se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: ¿Para qué sirve una roca?

Las rocas, como los minerales que las componen, tienen muchas más aplicaciones que las puramente estéticas. De hecho, en cierto sentido, todo se basa en rocas en este planeta.
Eugenio Manuel Fernández Aguilar es físico, profesor de secundaria, escritor y un divulgador científico muy activo.
Si no ve correctamente el vídeo, use este enlace.
Más sobre el tema:
¿De qué está hecha la arena?
Introducción histórica a la mineralogía (serie)
La geodiversidad que nos rodea
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2022: ¿Para qué sirve una roca? se ha escrito en Cuaderno de Cultura Científica.
Nos hacemos mayores y nuestra microbiota también
La esperanza de vida ha aumentado en las últimas décadas, pasando de los 62,8 y 58,1 años registrados en 1950 en Europa y América, respectivamente, a los 77 y 74,2 años en la actualidad. Aunque es buena noticia, este incremento también ha provocado un aumento en la prevalencia de enfermedades crónicas asociadas al envejecimiento, como el cáncer o enfermedades cardiovasculares y neurodegenerativas.
 Imagen: Julien Tromeur / Unsplash
Imagen: Julien Tromeur / Unsplash¿Hay solución? Si bien el envejecimiento es un proceso natural e inevitable, las patologías asociadas a él se pueden prevenir. En este sentido, las estrategias más utilizadas son las intervenciones dietéticas y la promoción de ejercicio físico regular. Curiosamente, estas estrategias tienen un denominador común: influyen sobre la composición y funcionalidad de la microbiota intestinal.
La microbiota envejece con nosotrosNos referimos a la microbiota cuando hablamos del conjunto de microorganismos (bacterias, arqueas, bacteriófagos, virus y hongos) que coexisten en superficies externas e internas del organismo humano, como la piel, las mucosas y el tracto gastrointestinal. En concreto, la microbiota intestinal interviene en diversas funciones fisiológicas (respuesta inmune, digestión y absorción de nutrientes, y producción de metabolitos bioactivos), por lo que las perturbaciones en su composición pueden influir en el equilibrio metabólico del huésped. Lo que en la jerga médica se conoce como homeostasis.
Aunque parece que existen rasgos comunes en la composición de la microbiota intestinal de los individuos claves para mantener las funciones vitales, también se ha detectado que existen diferencias entre la microbiota de personas jóvenes y de mayor edad. Estos cambios producen una pérdida de funcionalidad de la microbiota intestinal debida a una menor riqueza y diversidad microbiana, pero también a un aumento en el número de bacterias asociadas al envejecimiento no saludable.
Por ejemplo, se ha observado que el filo Firmicutes y el género Bifidobacteria disminuyen con la edad, mientras que los filos Bacteroidetes y Proteobacteria, y la familia Enterobacteriaceae aumentan. Esto hace que se desequilibre la relación simbiótica entre las bacterias de la microbiota y el huésped.
¿Cómo le afecta la edad a la microbiota?La barrera intestinal juega un papel clave en la protección contra patógenos. A medida que envejecemos, las uniones entre los enterocitos que forman esta barrera protectora se debilitan, perdiendo su funcionalidad. Esto, junto a los cambios que desequilibran la microbiota al envejecer, deriva en una mayor permeabilidad intestinal y en el sobrecrecimiento de bacterias patógenas. Como consecuencia, aumenta el acceso de bacterias o componentes bacterianos al torrente sanguíneo.
En este escenario, tanto la producción como la liberación de citoquinas proinflamatorias al torrente sanguíneo se disparan. A este respecto, un estudio comprobó que la transferencia de microbiota intestinal de ratones ancianos a ratones jóvenes provocaba un aumento de la inflamación intestinal, proceso conocido como inflammaging (inflamación asociada al envejecimiento).
Para empeorar aún más las cosas, con el paso de los años se altera la producción de metabolitos microbianos derivados del procesamiento de los alimentos. En concreto, la producción de ácidos grasos de cadena corta (AGCCs), que tienen un probado efecto antiinflamatorio, se ve reducida con la edad.
Más pescado azul, romero y perejilSe ha descrito que el consumo de ciertas cepas de bacterias probióticas de los géneros Lactobacillus y Bifidobacterium no solo ayudan a mejorar la composición de la microbiota intestinal, sino que promueven la producción de AGCC antiinflamatorios. Además, el consumo de prebióticos ayuda a que las bacterias de la microbiota intestinal tengan sustrato para crecer.
En este sentido, los aceites esenciales de plantas aromáticas características de la dieta mediterránea como el perejil y el romero muestran efectos prebióticos sobre la microbiota. Asimismo, el consumo de galacto-oligosacáridos (GOS), abundantes en las legumbres, y de fructo-oligosacáridos (FOS) presentes en alimentos como la cebolla, el puerro o los ajos, resulta especialmente efectivo para prevenir la disminución de bacterias del género Bifidobacterium que se da al envejecer.
También aumenta la riqueza de la microbiota intestinal consumir ácidos grasos ω-3, abundantes en las sardinas, el salmón y otros pescados azules. Asimismo, incorporar hábitos como, por ejemplo, una alimentación rica en fibra y micronutrientes o la práctica de ejercicio físico pueden ayudarnos a mantener una mejor composición microbiana y a envejecer de forma más saludable.![]()
Sobre las autoras: Laura Isabel Arellano García, investigadora UPV/EHU; Iñaki Milton Laskibar, investigador del grupo Nutrición y Obesidad del Centro de Investigación Biomédica en Red de la Fisiopatología de la Obesidad y Nutrición (ciberOBN) y del Instituto de Investigación Sanitaria Bioaraba y María Puy Portillo, Catedrática de Nutrición UPV/EHU y ciberOBN.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Nos hacemos mayores y nuestra microbiota también se ha escrito en Cuaderno de Cultura Científica.
El rostro
Rostro. 1. Cara. 2. Semblante.
Cara. 1. Parte anterior de la cabeza humana desde el principio de la frente hasta la punta de la barbilla.
Semblante. 2. Representación de algún estado de ánimo en el rostro
Diccionario RAE.
En la cara reconocemos fácilmente el sexo, la pertenencia familiar y racial, y la edad aproximada del sujeto. Se trata de una habilidad que se desarrolla muy pronto en los niños. La capacidad para descifrar de inmediato las emociones que comunican las expresiones faciales es igualmente temprana, al menos las que se consideran emociones básicas (alegría, miedo, sorpresa, ira, tristeza, disgusto y desprecio). Las ventajas evolutivas del desarrollo de estas habilidades están claras, así como de las que nos llevan a reconocer … el estado físico, psicológico e intelectual de la persona que tenemos enfrente … Las enfermedades graves son claramente visibles en la facies, y también lo son muchos problemas menores de salud….
Belén Altuna en «Una historia moral del rostro», Pre-Textos, Valencia, 2010, 297 pp., p. 30.
 Foto: Alessandro Bellone / Unsplash
Foto: Alessandro Bellone / UnsplashComo revisa Belén Altuna, de la UPV/EHU, en su libro de 2010 titulado Una historia moral del rostro, las investigaciones sobre la comunicación no verbal en nuestra especie se basan sobre todo en el estudio de la expresión facial y corporal de las emociones. Los rostros tienen una importancia esencial en las interacciones sociales humanas. No solo brindan información visual que permite determinar el sexo, la edad, el conocimiento y la identidad de un individuo, sino que también se usan rostros para recopilar información sobre lo que otros individuos podrían estar pensando o sintiendo.
Añade Belén Altuna que el experto en comunicación no verbal que más nos interesa es Paul Ekman, de la Universidad de California en San Francisco. Al comienzo de sus estudios, en la década de los sesenta del siglo pasado, aunque aceptaba, según los expertos de aquellos años, que la expresión de las emociones se aprendía por contacto social y, por tanto, variaba según la cultura de cada grupo, encontró que la expresión era universal. Es curioso que esta había sido la propuesta de Charles Darwin en La expresión de las emociones en los animales y en el hombre, publicado hace siglo y medio, en 1872.
Como destaca Tomás Fernández, de la Universidad de Oviedo, en la presentación del texto, Darwin buscó el estudio de la expresión más que de la emoción como estado interno, más difícil de estudiar y de cuantificar. En concreto, con el estudio de la expresión de las emociones encontró un método útil y descriptivo más sencillo de detectarlas y de presentarlo en su libro.
Ekman, en sus primeras investigaciones, mostró unas fotografías a personas de diferentes culturas, en concreto de Chile, Argentina, Brasil, Japón y Estados Unidos, y les pidió que identificaran la emoción que expresaban sus caras. Y la mayoría coincidían. Para confirmar sus conclusiones y evitar los posibles contactos de estas personas por la actual globalización, repitió la encuesta en tribus de Papua Nueva Guinea, con escasos contactos con el exterior, y los resultados se repitieron según explica en la revisión publicada en 1970.
Para Ekman, son siete las expresiones universales del rostro: enojo o ira, asco, miedo, sorpresa, felicidad, tristeza y desprecio. A veces cita solo seis, descartando el desprecio, aunque otros autores citan hasta ocho o más. Como indica Belén Altuna, es interesante el debate sobre el número de expresiones de las emociones que publicó David Le Breton, de la Universidad de Estrasburgo, en 1999.
Ekman subraya que la expresión de la emociones aparecen en la infancia y siguen un proceso predeterminado. La felicidad, con la sonrisa, y la sorpresa surgen al nacer, el asco y la tristeza entre el primer día y los tres meses, la sonrisa hacia los otros entre el mes y medio y los tres meses, y el miedo entre los cinco y los nueve meses.
 Foto: Alexander Krivitskiy / Unsplash
Foto: Alexander Krivitskiy / UnsplashEl grupo de Kate Lawrence, de la Universidad St. Mary’s de Londres, ensayó en 478 niños y jóvenes de 6 a 16 años, el desarrollo del reconocimiento de emociones en el rostro. Las emociones analizadas fueron felicidad, sorpresa, miedo, disgusto, tristeza y enfado. Encontraron aumentos en las cuatro primeras emociones mientras que en la tristeza y el enfado hay pocos o ningún cambio con la edad. En todos los tramos, las niñas superaron a los niños.
Según el experimento de Katharina Dobs y su grupo, del MIT en Cambridge, Massachusetts, con 16 voluntarios, de ellos ocho son mujeres, y edad media de 25.9 años, se les muestran 16 fotografías de diferentes personas y se les pide que reconozcan su género, edad e identidad. El tiempo que tardan en conseguirlo se mide por magneto encefalografía cerebral. Lo consiguen con rapidez, en algo menos de medio segundo. El género y la edad se consigue en menos tiempo que la identidad. Cuando se repite el experimento, el género y la identidad ganan en rapidez para los rostros ya conocidos.
 Foto: Thea Hoyer / Unsplash
Foto: Thea Hoyer / UnsplashY, por supuesto, en la observación del rostro influye el considerarlo atractivo aunque, todavía, no es fácil establecer el atractivo que se detecta en cada persona. Julie White y David Puts, de la Universidad Estatal de Pennsylvania, lo estudiaron en un grupo de 12 estudiantes graduados en institutos de Wisconsin en 1957. Se recogieron sus datos genéticos en 2006 y 2007 y hasta 80 observadores midieron su atractivo entre 2004 y 2008 en las fotografías que se habían publicado en el anuario del instituto en 1957.
Relacionaron varias regiones del genoma con el atractivo atribuido a cada persona: dos zonas tuvieron una relación fuerte y otras diez bastante fuerte. Varias de estas regiones estaban ligadas al sexo. Esas regiones del genoma estaban relacionadas con el color de la piel, el índice de masa corporal, la altura, la proporción cintura-cadera y la morfología del rostro. Por ejemplo, influye el ancho de la boca respecto al centro del rostro o el ancho de la frente.
Además, era de esperar la incógnita, si el rostro puede ser o no más atractivo si lo ocultamos más o menos cuando, por ejemplo, llevamos mascarilla, algo que conocemos bien por la pandemia del COVID-19. Según el estudio publicado en 2022 por Oliver Hies y Michael Lewis, de la Universidad de Cardiff, la mascarilla aumenta la atracción del rostro más que otras cubiertas de la cara.
Participaron 42 universitarias de los cursos de Psicología, con edad de 18 a 24 años, que observaron y puntuaron el atractivo de 40 hombres, con edad de 18 a 30 años. Su rostro llevaba mascarilla quirúrgica, mascarilla de tela, un libro sobre el rostro o ninguna cubierta. Los resultados muestran que los rostros se consideraron más atractivos cuando están cubiertos por mascarilla quirúrgica y algo más atractivos cuando están tapados con mascarillas de tela que cuando no están tapados. Quizá el cerebro del observador reconstruye la parte del rostro que no ve y siempre lo hace de manera positiva.
Incluso la barba, que también tapa parte del rostro en los machos de nuestra especie, también se puede asociar a un mayor atractivo en la competencia para la búsqueda de pareja. E.A. Beseris y sus colegas, de la Universidad de Utah en Salt Lake City, lo resumen en que así se consigue que el rostro se perciba como más masculino, socialmente dominante y con una conducta más agresiva en comparación con los hombres con el rostro desnudo.
Por ello y por esta posible reconstrucción del rostro atractivo es por lo que se admite que la belleza está más bien en la mente del observador. Por ejemplo, el estudio de Ravi Thiruchselvam y su equipo, del Colegio Hamilton de Clinton, en Nueva York, con estudiantes de 18 a 21 años, una edad media de 19.6 años y 11 mujeres. Las participantes encuentran que, en imágenes, los rostros más atractivos son aquellos que, previamente, se les ha dicho que son atractivos. Si los esperan atractivos pues son atractivos.
El estudio de Atsunobu Suzuki y sus colegas, de la Universidad de Tokio, parte de la hipótesis de que las personas no deducen de igual manera la personalidad y las habilidades de los demás a partir de sus rostros. Pero, como hemos mencionado, esa deducción tiene un fuerte impacto, a menudo no justificado, sobre la toma de decisiones sobre la conducta de otras personas en el mundo real. Encuentran que las decisiones sobre siete rasgos psicológicos, cuando coinciden en el encuestado, llevan a conclusiones reforzadas que se mantienen en el tiempo y sirven para juzgar a otras personas. Es lo que denominan deducción a partir de rasgos basados en el rostro. Las siete características que buscan en los rostros observados son competencia, moralidad, inteligencia, dominancia, agresividad, emociones y veracidad.
Los resultados indican que hay individuos que tienen una disposición estable en el tiempo para sacar conclusiones sobre varios rasgos de los demás a partir de la apariencia facial.
 Foto: Renè Müller / Unsplash
Foto: Renè Müller / UnsplashPara terminar, repasemos con Belén Altuna el rostro de los muertos o, como titula el apartado, “ni tienen rostro los muertos”. Son los cadáveres los que no tienen rostro pues los seres humanos conservan en la memoria de los que les conocieron el rostro de cuando estaban vivos. Ya no están vivos, solo queda el cuerpo y, por ello, se les tapa el rostro con una tela: ya no mira y, por tanto, no debe ser mirado.
Lo primero es cerrar sus ojos. Ellos no pueden ver, pero los vivos no soportan la mirada muerta de un muerto. Allí ya no hay nadie. Pero nos tranquilizan los ojos cerrados, quizá no ha muerto y solo duerme.
En el velatorio interviene quien viste y maquilla al muerto. Se busca una expresión neutra y apacible, aunque a menudo no se consigue y llega la frustración para quienes le conocieron en vida. El rostro del muerto es una máscara, fría, blanca, rígida, inmóvil.
Referencias:
Altuna, B. 2010. Una historia moral del rostro. Pre-Textos. Valencia. 297 pp.
Beseris, E.A. et al. 2020. Impact protection potential of mammalian hair: testing the pugilism hypothesis for the evolution of human facial hair. Integrative Organismal Biology doi: 10.1093/iob/obaa005.
Darwin, C. 1872 (1998). La expresión de las emociones en los animales y en el hombre. Alianza Ed. Madrid. 390 pp.
Dobs, K. et al. 2019. How face perception unfolds over time. Nature Communications 10: 1258.
Ekman, P. 1970. Universal facial expressions of emotion. California Mental Health Research Digest 8: 151-158.
Fernández, T.R. 1998. Consideraciones preliminares del traductor. En Charles Darwin, “La expresión de las emociones en los animales y en el hombre”, p. 7-34. Alianza Ed. Madrid.
García Etxebarria, K. 2020. Los componentes genéticos del atractivo. Cuaderno de Cultura Científica 12 octubre.
Hies, O. & M.B. Lewis. 2022. Beyond the beauty of occlusion: medical masks increase facial attractiveness more than other face coverings. Cognitive Research: Principles and Implications doi: 10.1186/s41235-021-00351-9.
Hu, B. et al. 2019. Genome-wide association study reveals sex-specific genetic architecture of facial attractiveness. PLOS Genetics doi: 10.1371/journal.pgen.1007973.
Lawrence, K. et al. 2015. Age, gender, and puberty influence the development of facial emotion recognition. Frontiers in Psychology 6: 761.
Le Breton, D. 1999. Las pasiones ordinarias. Antropología de las emociones. Ed. Nueva Visión. Buenos Aires. 254 pp.
Pérez, J.I. 2020. La barba humana. Cuaderno de Cultura Científica 2 agosto.
Suzuki, A. et al. 2022. Generalized tendency to make extreme trait judgements from faces. Royal Society Open Science 9: 220172.
Thiruchselvam, R. et al. 2016. Beauty is in the belief of the beholder: cognitive influences on the neural response to facial attractiveness. Social Cognitive and Affective Neuroscience 11: 1999-2008.
White, J.D. & D.A. Puts. 2019. Genes influence facial attractiveness through intricate biological relationships. PLOS Genetics doi: 10.1371/journal.pgen.1008030.
Para saber más:
El sesgo a la izquierda al reconocer un rostro
Sombra aquí, sombra allá: reconocimiento facial discriminatorio
Los componentes genéticos del atractivo
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo El rostro se ha escrito en Cuaderno de Cultura Científica.
La sucesión fractal de Thue-Morse y la partida infinita de ajedrez
En la anterior entrada del Cuaderno de Cultura Científica, titulada Sucesiones fractales, analizamos las sucesiones infinitas de números enteros denominadas autosemejantes, o fractales, que imitan la propiedad de autosemejanza de los objetos fractales. En concreto, una sucesión (infinita) de números enteros se dice que es una sucesión autosemejante, si una parte de la sucesión es igual a toda la sucesión, es decir, si eliminamos algunos miembros de la sucesión infinita los miembros de la sucesión que quedan constituyen de nuevo toda la sucesión.
Por ejemplo, tomemos la sucesión
1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 2, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 2, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 2, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 2, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 2, 1, 0, 0, 1, 0, 1, 0, …
que es la sucesión A000161 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS, y que se define de la siguiente manera: para cada posición n de la sucesión (empezando en 0), el número que está en dicha posición es igual a la cantidad de formas de expresar n como suma de dos cuadrados (es posible que no haya ninguna), sin importar el orden. Así, teniendo en cuenta que los primeros cuadrados son 0, 1, 4, 9, 16, 25, etc, se tiene que 0 se puede expresar como 0 + 0; 1 se puede expresar como 0 + 1; 2 como 1 + 1; 3 no se puede expresar como suma de cuadrados; 4 es igual a 4 + 0; 5 es igual a 4 + 1; 6 y 7 no se pueden expresar como suma de cuadrados; 8 se puede expresar como 4 + 4; 9 como 9 + 0; 10 es igual a 9 + 1; 11 y 12 no se pueden expresar como suma de cuadrados; 13 como 9 + 4; y así seguiríamos con el resto. La primera vez que aparece el 2 es para n = 25, ya que 25 = 25 + 0 = 16 + 9, o la primera vez que aparece el 3 en la sucesión es para n = 325, ya que 325 = 324 + 1 = 289 + 36 = 225 + 100.
Esta sucesión es una sucesión fractal ya que si eliminamos los números que están en las posiciones impares (cuidado, ya que estamos empezando en n = 0), es decir, nos quedamos con los números que están en las posiciones pares, esta sigue siendo la sucesión original, como se puede comprobar arriba para los primeros términos.
 Seis etapas de la construcción infinita del fractal conocido como “curva de Koch”
Seis etapas de la construcción infinita del fractal conocido como “curva de Koch”¿Qué es la sucesión de Thue-Morse?
En esta entrada vamos a centrarnos en una sucesión fractal concreta, conocida con el nombre de sucesión de Thue-Morse, o sucesión de Prouhet-Thue-Morse, que es una curiosa sucesión de números enteros que aparece en diferentes ramas de las matemáticas, como puede leerse en el artículo The ubiquitous Prouhet-Thue-Morse sequence (La omnipresente sucesión de Prouhet-Thue-Morse) de Jean-Paul Allouche y Jeffrey Shallit, desde la combinatoria de palabras a problemas de ajedrez, pasando por la geometría diferencial, la teoría de números, el análisis matemático de funciones, la física matemática, los cuasi-cristales o la teoría de grupos.
Empecemos definiendo esta sucesión. La sucesión de Thue-Morse es una sucesión infinita (la sucesión A010060 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS) cuyos elementos son ceros y unos y que se define recursivamente de la siguiente manera. Si la denotamos como {tn}, entonces t0 = 0 y t2n = tn, t2n + 1 = 1 – tn. Por lo tanto, los primeros términos de la sucesión, como podéis calcular desde la definición, son:
0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, …
Otra manera de definir esta sucesión es utilizando las representaciones binarias de los números. Se empieza representando los números, desde n = 0, en base 2, como aparece en la siguiente imagen (de hecho, esto ya lo hicimos para la entrada Sucesiones fractales).

La sucesión de Thue-Morse se obtiene sumando, para cada número n, los unos (1) que aparecen en su representación binaria, si es una cantidad par se considera el número 0 y si es impar el número 1 (matemáticamente podemos decir que es la suma de los dígitos de su representación binaria, módulo 2). Por ejemplo, 29 se representa como 11101, que tiene una cantidad par de unos, luego para n = 29 se toma el valor 0 en la sucesión (t29 = 0), mientras que para n = 37 se toma el valor 1 ya que 37 se representa en base dos como 100101 (t37 = 1). Luego, para los primeros números n (los de la imagen anterior) se obtienen los primeros términos de esta sucesión binaria: 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1.
En la trilogía Winning Ways for your Mathematical Plays (Estrategias ganadoras para tus juegos matemáticos), de los matemáticos John H. Conway, Richard K. Guy y Elwyn Berlekamp, se denominan números malvados (evil numbers en inglés) a aquellos números tales que su representación binaria tiene un número par de unos, es decir, se corresponden con los ceros de la sucesión de Thue-Morse, que, como se observa en la imagen anterior, serían 0, 3, 5, 6, 9, 10, 12, 15, 17, 18, 20, 23, 24, 27, 29, 30, 33, 34, 36, etc. Por otra parte, se llaman números odiosos a aquellos con una cantidad impar de unos en su representación binaria, es decir, que se corresponden con los unos de la sucesión de Thue-Morse, que son 1, 2, 4, 7, 8, 11, 13, 14, 16, 19, 21, 22, 25, 26, 28, 31, 32, 35, 37, 38, etc.
Una tercera forma de definir la sucesión de Thue-Morse es utilizando, de manera recursiva, el complemento, o negación, bit a bit (dígito a dígito) de un número binario. Empecemos definiendo qué es el complemento, o negación, bit a bit (dígito a dígito) de un número binario: esta operación consiste en cambiar cada dígito de una representación binaria por su complemento, es decir, si es un 1 se cambia por 0, y si es un 0 se cambia por 1. Por ejemplo, el complemento del número binario 100100110 será C[100100110] = 011011001.
Para definir la sucesión de Thue-Morse se realizan los siguientes pasos. Se empieza por T(0) = 0 y en casa paso se toma el número binario del paso anterior seguido de su complemento bit a bit, esto es, T(k + 1) = T(k)C[T(k)]. Así, los primeros pasos serían:
La sucesión de Thue-Morse se obtendría siguiendo este proceso hasta el infinito, T(infinito).
Una curiosidad de esta definición es que en los pasos pares T(2k) se obtienen números binarios capicúas, 0, 0110, 0110100110010110, etc.
Una forma similar de construir la sucesión de Thue-Morse mediante una serie de transformaciones consiste en empezar en 0 y luego en cada paso transformar 0 en 01 y 1 en 10. Así, como se empieza en 0, en el primer paso 0 se transforma en 01; en el segundo paso, al trasformar los dos dígitos de 10, mediante la transformación descrita, quedaría 0110; el siguiente paso da como resultado 01101001; el siguiente 0110100110010110; y vemos que vamos obteniendo los mismos términos que en la descripción anterior.
El origen de la sucesión de Thue-MorseA principios del siglo XX el matemático noruego Axel Thue (1863-1922), en dos artículos publicados en 1906 y 1912 (que supusieron el origen de una rama de la combinatoria denominada combinatoria de palabras), se planteó el problema de construir sucesiones sobre alfabetos finitos (un alfabeto es un conjunto finito de símbolos (letras), por ejemplo, un alfabeto binario consta de dos símbolos, como los símbolos 0 y 1, o cualquier otro par de símbolos; y el alfabeto del español tiene 27 letras) libres de cuadrados o de cubos.
Una sucesión se dice que está libre de cuadrados si no es posible tomar un conjunto de elementos consecutivos de la sucesión que formen una “palabra” (es decir, una sucesión de símbolos, por ejemplo, “1001001” es una palabra en el alfabeto binario y “abracadabra” o “prgtrro” son palabras en el alfabeto de 27 letras, aunque la segunda no tiene significado alguno) de la forma WW, donde W es una palabra no vacía. Por ejemplo, la palabra binaria anterior no está libre de cuadrados, ya que contiene la palabra “00”, que es un cuadrado tomando W = “0”, o también contiene el cuadrado “001001” para W = “001”. De forma similar se definen las palabras libres de cubos, cuando no contiene una palabra de la forma WWW.
Axel Thue observó que toda sucesión binaria con al menos 4 elementos contiene cuadrados, luego no existen sucesiones infinitas binarias libres de cuadrados. Entonces se planteó algunas cuestiones relacionadas como la existencia de sucesiones infinitas con tres letras libres de cuadrados o la existencia de sucesiones binarias infinitas libres de cubos, o de solapamientos (esto es, palabras de la forma vWvWv, donde W es una palabra y v es una letra de este alfabeto binario, es decir, 0 o 1). La respuesta a esas cuestiones venía de la mano de la sucesión que lleva su nombre.
La demostración de que toda sucesión binaria con más de 4 elementos contiene cuadrados es bastante sencilla. Veámosla. Si la sucesión binaria empezase por 0 (el argumento es similar si empezamos por 1), el siguiente término de la sucesión debería ser 1, ya que si fuese 0 tendríamos un cuadrado “00”. Luego los dos primeros términos de la sucesión serían {0, 1} (si hubiésemos empezado por 1 serían {1, 0}). De la misma manera, el tercer término deberá ser 0, ya que si fuese 1, de nuevo tendríamos un cuadrado, en este caso “11”. Por lo tanto, los tres primeros términos de la sucesión libre de cuadrados serían {0, 1, 0} (si hubiésemos empezado por 1 serían {1, 0, 1}). Llegados a este punto, si el siguiente término de la sucesión es 0, la sucesión es {0, 1, 0, 0} y tenemos un cuadrado “00”, mientras que si el siguiente término es 1, la sucesión es {0, 1, 0, 1} y el cuadrado es “0101”. Así, queda demostrada la afirmación de Thue.
Un resultado que puede verse en la literatura (puede leerse alguna de las demostraciones de este resultado en algunos de los textos de la bibliografía, como el capítulo Substitutions and symbolic dynamical systems) es que la sucesión de Thue-Morse no contiene palabras de la forma WWv, donde W es una palabra no vacía (es decir, con alguna letra) y v es la primera letra de la palabra W. Como consecuencia (corolario) de este resultado se tiene:
A. La sucesión de Thue-Morse es una sucesión binaria infinita no periódica, es decir, no existe una palabra finita W que genere, por repetición, toda la sucesión infinita (por ejemplo, entre los ejemplos de sucesiones autosemejantes de la entrada Sucesiones fractales se incluía la sucesión 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, … que es una sucesión periódica de periodo W = 1, 2, 2, 3, 2, 3, 3), ya que si existiese un periodo W tendríamos que existiría una palabra de la forma Wwv, con v la primera letra de la palabra W, lo cual no es posible por el resultado anterior;
B. La sucesión de Thue-Morse es una sucesión binaria infinita que no admite cubos (WWW), ni solapamientos (vWvWv), dando respuesta a dos de las cuestiones de Thue.
Además, la sucesión de Prouhet-Thue-Morse permite construir una sucesión infinita sobre un alfabeto de tres letras libre de cubos. Se define la sucesión vn , para n mayor o igual que 1, de la siguiente manera, vn es igual a la cantidad de unos (1) que hay entre el cero (0) que está en la posición n-ésima y en cero (0) que está en la posición (n + 1)-ésima. Como la sucesión de Thue-Morse empieza
0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, …
entonces la nueva sucesión sería, según la definición,
2, 1, 0, 2, 0, 1, 2, 1, 0, 1, 2, 0, 2, 1, 0, 2, 0, 1, 2, 0, 2, 1, 0, 1, 2, 1, 0, 2, 0, 1, 2, 1, 0, 1, 2, 0, 2, 1, 0, 1, 2, 1, 0, 2, 0, 1, 2, 0, 2, 1, 0, 2, …
Utilizando que la sucesión original no admite solapamientos (vWvWv) puede probarse que la sucesión descrita anteriormente es una sucesión infinita sobre un alfabeto de tres letras {0, 1, 2} y que está libre de cuadrados.
Los artículos del matemático noruego Axel Thue fueron publicados en una revista noruega y pasaron desapercibidos durante mucho tiempo, motivo por el cual esta sucesión fue redescubierta por otras personas. Por ejemplo, el matemático estadounidense Harold Marston Morse (1892-1977) redescubrió la sucesión binaria infinita 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, … en relación con una investigación en el campo de la geometría diferencial, e concreto, sobre superficies de curvatura negativa.
Posteriormente se conocería que esta sucesión ya aparecía, de forma implícita, en un artículo de 1851 del matemático francés Eugène Prouhet (1817-1867) en relación con un problema de teoría de números.
El problema del juego infinito en el ajedrezEl matemático y jugador de ajedrez neerlandés Machgielis (Max) Euwe (1901-1981), que fuera campeón del mundo de ajedrez en 1935 y profesor de matemáticas en las universidades de Róterdam y Tilburg, también redescubrió, de forma independiente, la sucesión de Thue-Morse en relación con el ajedrez.
Una de las reglas del ajedrez (conocida como regla alemana) decía que si en una partida de ajedrez se repetía tres veces, de forma consecutiva, una misma secuencia de movimientos, se consideraba que el juego terminaba en tablas. Euwe demostró, en un artículo de 1929, que podía realizarse una partida de ajedrez infinita evitando la regla alemana, es decir, que una misma secuencia de movimientos se repitiera tres veces consecutivas. Para ello consideró una secuencia de cuatro movimientos, que se corresponde con el 0, y una secuencia de otros cuatro movimientos, que se corresponde con el 1, y se inventó una sucesión binaria infinita libre de cubos, para evitar la regla alemana, que no es otra que la sucesión de Thue-Morse, aunque el ajedrecista y matemático desconocía la existencia de la misma.
Por este motivo se introdujeron dos reglas más fuertes para declarar tablas en un juego y evitar el juego infinito, la regla de la triple repetición y la regla de los cincuenta movimientos. De hecho, la regla de la triple repetición establece que la partida ha terminado en tablas si se repite tres veces una misma secuencia de movimientos, aunque no sea de forma consecutiva,
 Juego de piezas abstractas del ajedrez, conocido como Bauhaus-Schachspiel, diseñado por el profesor de la Bauhaus Josef Hartwig Wood
Juego de piezas abstractas del ajedrez, conocido como Bauhaus-Schachspiel, diseñado por el profesor de la Bauhaus Josef Hartwig WoodBibliografía
1.- Clifford A. Pickover, La maravilla de los números, MA NON TROPPO, 2002.
2.- Jean-Paul Allouche, Jeffrey Shallit, The ubiquitous Prouhet-Thue-Morse sequence, incluido en el libro Sequences and their Applications, Springer, 1999.
3.- Christopher Williamson, An Overview of the Thue-Morse Sequence (manuscrito no publicado). University of Washington, 2012.
4.- S. Ferenczi, Substitutions and symbolic dynamical systems (capítulo), Substitutions in Dynamics, Arithmetics and Combinatorics, Springer, 2002.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La sucesión fractal de Thue-Morse y la partida infinita de ajedrez se ha escrito en Cuaderno de Cultura Científica.
Cómo nuestra realidad puede ser la suma de todas las realidades posibles
La integral de caminos de Richard Feynman es tanto una potente máquina de predicción como una filosofía sobre cómo es el mundo. Pero la comunidad científica todavía está esforzándose por descubrir cómo usarla y qué significa.
Un artículo de Charlie Wood para Quanta Magazine
 El camino en línea recta de una partícula puede entenderse como la suma de todos sus posibles caminos. Imagen: Kristina Armitage/Quanta Magazine
El camino en línea recta de una partícula puede entenderse como la suma de todos sus posibles caminos. Imagen: Kristina Armitage/Quanta MagazineLa fórmula más poderosa de la física comienza con una S delgada, el símbolo de una especie de suma conocida como integral. Más adelante viene una segunda S, que representa una cantidad conocida como acción. Juntas, estas S gemelas forman la esencia de una ecuación que podría decirse que es el adivino del futuro más eficaz que se haya ideado hasta ahora.
La fórmula del oráculo se conoce como integral de caminos de Feynman. Hasta donde sabe la comunidad científica, predice con precisión el comportamiento de cualquier sistema cuántico: un electrón, un rayo de luz o incluso un agujero negro. La integral de caminos ha acumulado tantos éxitos que muchos físicos y físicas creen que es una ventana directa al corazón de la realidad.
“Es como el mundo es realmente”, afirma Renate Loll, física teórica de la Universidad Radboud en los Países Bajos.
Pero la ecuación, aunque adorna las páginas de miles de publicaciones de física, es más una filosofía que una receta rigurosa. Sugiere que nuestra realidad es una especie de mezcla, una suma, de todas las posibilidades imaginables. Pero no les dice a los investigadores exactamente cómo llevar a cabo la suma. Así que la comunidad científica ha pasado décadas desarrollando un arsenal de estrategias de aproximación para construir y calcular la integral para diferentes sistemas cuánticos.
Las aproximaciones funcionan lo suficientemente bien como para que físicas intrépidas como Loll busquen ahora la integral de caminos definitiva: una que combina todas las formas concebibles de espacio y tiempo y produce un universo con la forma del nuestro como resultado neto. Pero en esta búsqueda por demostrar que la realidad es de hecho la suma de todas las realidades posibles, se enfrentan a una profunda confusión sobre qué posibilidades deberían entrar en la suma.
Todos los caminos llevan a unoLa mecánica cuántica realmente despegó en 1926 cuando Erwin Schrödinger ideaba una ecuación que describe cómo los estados ondulatorios de las partículas evolucionan de un momento a otro. La siguiente década Paul Dirac presentaba una visión alternativa del mundo cuántico. La suya se basaba en el venerable concepto de que las cosas toman el camino de “menor acción” para ir de A a B, la ruta que, en términos generales, requiere menos tiempo y energía. Richard Feynman luego se toparía con el trabajo de Dirac y desarrollaría la idea, dando a conocer la integral de caminos en 1948.
El corazón de la filosofía se muestra todo él en la demostración por excelencia de la mecánica cuántica: el experimento de la doble rendija.
Los físicos disparan partículas a una barrera con dos rendijas y observan dónde dan las partículas en una pared detrás de la barrera. Si las partículas fueran balas sea agruparían detrás de cada ranura. En cambio, las partículas dan en toda la pared trasera formando franjas que se repiten. El experimento sugiere que lo que se mueve a través de las rendijas es en realidad una onda que representa las posibles ubicaciones de la partícula. Los dos frentes de onda emergentes se interfieren entre sí, produciendo una serie de picos donde la partícula podría acabar siendo detectada.
El patrón de interferencia es un resultado sumamente extraño porque implica que ambos caminos posibles de la partícula a través de la barrera tienen una realidad física.
La integral de caminos asume que así es como se comportan las partículas incluso cuando no hay barreras o rendijas presentes. Primero, imagina cortar una tercera rendija en la barrera. El patrón de interferencia en la pared del fondo cambiará para incorporar la nueva ruta posible. Ahora sigue cortando rendijas hasta que la barrera no sea más que rendijas. Por último, rellena el resto del espacio con «barreras» todo rendijas. Una partícula disparada a este espacio toma, en cierto sentido, todas las rutas a través de todas las rendijas hacia la pared del fondo, incluso rutas extrañas con desvíos en bucle. Y de alguna manera, cuando se suman correctamente, todas esas opciones totalizarían lo que esperarías ver si no hubiera barreras: un solo punto brillante en la pared del fondo.
Es una visión radical del comportamiento cuántico que muchos físicos toman en serio. “Lo considero completamente real”, afirma Richard MacKenzie, físico de la Universidad de Montreal.
Pero, ¿cómo puede un número infinito de caminos curvos sumar en total una sola línea recta? La estrategia de Feynman, en términos generales, consiste en tomar cada camino, calcular su acción (el tiempo y la energía necesarios para recorrer el camino) y, a partir de ahí, obtener un número llamado amplitud, que indica la probabilidad de que una partícula recorra ese camino. Luego sumas todas las amplitudes para obtener la amplitud total de una partícula que va desde aquí hasta allí: una integral de todos los caminos.
Ingenuamente, los caminos zigzagueantes parecen tan probables como los rectos, porque la amplitud de cualquier camino individual tiene el mismo tamaño. Es de crucial importancia, sin embargo, que las amplitudes son números complejos. Mientras que los números reales marcan puntos en una línea, los números complejos actúan como flechas. Las flechas apuntan en diferentes direcciones para diferentes caminos. Y dos flechas que se alejan una de la otra suman cero.
El resultado final es que, para una partícula que viaja por el espacio, las amplitudes de caminos más o menos rectos apuntan esencialmente en la misma dirección, amplificándose entre sí. Pero las amplitudes de los caminos sinuosos apuntan en todas direcciones, por lo que estos caminos tienden a anularse entre sí. Solo queda el camino en línea recta, lo que demuestra cómo el clásico camino único de mínima acción emerge de opciones cuánticas interminables.
Feynman demostró que su integral de caminos es equivalente a la ecuación de Schrödinger. El beneficio del método de Feynman es una receta más intuitiva sobre cómo lidiar con el mundo cuántico: suma todas las posibilidades.
La suma de todas las ondasLos físicos pronto llegaron a entender las partículas como excitaciones en campos cuánticos, entes que llenan el espacio con valores en cada punto. Donde una partícula puede moverse de un lugar a otro a lo largo de diferentes caminos, un campo puede ondularse aquí y allá de diferentes maneras.
Afortunadamente, la integral de caminos también funciona para campos cuánticos. “Es obvio qué hacer”, afirma Gerald Dunne, físico de partículas de la Universidad de Connecticut. “En lugar de sumar todas los caminos, sumas todas las configuraciones de tus campos”. Identificas los estados iniciales y finales del campo, luego consideras cada una de todas las historias posibles que los unen.
El mismo Feynman se apoyó en la integral de caminos para desarrollar una teoría cuántica del campo electromagnético en 1949. Otros averiguarían cómo calcular acciones y amplitudes para campos que representan otras fuerzas y partículas. Cuando los físicos modernos predicen el resultado de una colisión en el Gran Colisionador de Hadrones en Europa, la integral de caminos es la base de muchos de sus cálculos. La tienda de regalos incluso vende una taza de café que muestra una ecuación que se puede usar para calcular el ingrediente clave de la integral de caminos: la acción de los campos cuánticos conocidos.
“Es absolutamente fundamental para la física cuántica”, afirma Dunne.
 La tienda de regalos del CERN, que alberga el Gran Colisionador de Hadrones, vende una taza de café que muestra una ecuación que se puede usar para calcular el ingrediente clave de la integral de caminos: la acción de los campos cuánticos conocidos. Foto: Cortesía del CERN
La tienda de regalos del CERN, que alberga el Gran Colisionador de Hadrones, vende una taza de café que muestra una ecuación que se puede usar para calcular el ingrediente clave de la integral de caminos: la acción de los campos cuánticos conocidos. Foto: Cortesía del CERNA pesar de su triunfo en la física, la integral de caminos incomoda a los matemáticos. Incluso una simple partícula que se mueve por el espacio tiene infinitas rutas posibles. Los campos son peores, con valores que pueden cambiar de infinitas maneras en infinitos lugares. Los físicos tienen técnicas creativas para hacer frente a la tambaleante torre de infinitos, pero los matemáticos argumentan que la integral nunca fue diseñada para operar en un entorno infinito como este.
“Es como magia negra”, afirma Yen Chin Ong, físico teórico de la Universidad de Yangzhou en China que tiene formación como matemático. “Los matemáticos no se sienten cómodos trabajando con cosas en las que no está claro lo que está pasando”.
Sin embargo, obtiene resultados que están fuera de toda duda. Los físicos incluso han logrado estimar la integral de caminos de la fuerza fuerte, la interacción extraordinariamente compleja que mantiene unidas a las partículas en los núcleos atómicos. Usaron dos atajos principales para conseguir esto. Primero, hicieron del tiempo un número imaginario, un extraño truco que convierte las amplitudes en números reales. Luego aproximaron el continuo espacio-tiempo infinito a una cuadrícula finita. Los practicantes de este enfoque de la teoría cuántica de campos “reticular” pueden usar la integral de caminos para calcular las propiedades de los protones y otras partículas que sienten la fuerza fuerte, superando las inseguras matemáticas para obtener respuestas sólidas que coinciden con los experimentos.
“Para alguien como yo en física de partículas”, afirma Dunne, “esa es la prueba de que funciona”.
Espaciotiempo = ¿la suma de qué?Sin embargo, el mayor misterio de la física fundamental se encuentra más allá del alcance experimental. Los físicos desean comprender el origen cuántico de la fuerza de la gravedad. En 1915, Albert Einstein reformuló la gravedad como el resultado de curvaturas en el tejido del espacio y el tiempo. Su teoría reveló que la longitud de una vara de medir y el tictac de un reloj cambian de un lugar a otro; en otras palabras, que el espaciotiempo es un campo maleable. Otros campos tienen una naturaleza cuántica, por lo que la mayoría de los físicos esperan que el espaciotiempo debería tenerla también, y que la integral de caminos debería recoger ese comportamiento.
 El físico británico Paul Dirac, a la izquierda, reajustó la mecánica cuántica en 1933 de una manera que considera toda la historia, o camino, de una partícula, en lugar de su evolución momento a momento. El físico estadounidense Richard Feynman, a la derecha, tomó esa idea y la elaboró, desarrollando la integral de caminos en 1948. Fotos: Sueddeutsche Zeitung Photo/Alamy (izquierda); Estate of Francis Bello/Science Source (derecha)
El físico británico Paul Dirac, a la izquierda, reajustó la mecánica cuántica en 1933 de una manera que considera toda la historia, o camino, de una partícula, en lugar de su evolución momento a momento. El físico estadounidense Richard Feynman, a la derecha, tomó esa idea y la elaboró, desarrollando la integral de caminos en 1948. Fotos: Sueddeutsche Zeitung Photo/Alamy (izquierda); Estate of Francis Bello/Science Source (derecha)La filosofía de Feynman es clara: los físicos deben sumar todas las formas posibles del espaciotiempo. Pero cuando consideramos la forma del espacio y el tiempo, exactamente, ¿qué es posible?
Es posible que el espacio-tiempo se divida, por ejemplo, separando un lugar de otro. O podría estar perforado con tubos (agujeros de gusano) que unen las ubicaciones. Las ecuaciones de Einstein permiten estas formas tan exóticas, pero prohíben los cambios que conducirían a ellas; las rasgaduras o fusiones violarían la causalidad y generarían paradojas de viajes en el tiempo. Sin embargo, nadie sabe si el espaciotiempo y la gravedad podrían interactuar en una actividad más atrevida a nivel cuántico, por lo que los físicos no saben si arrojar o no espaciotiempos de queso suizo a la «integral de la caminos gravitacional».
Un bando sospecha que todo entra. Stephen Hawking, por ejemplo, defendió una integral de caminos que se adapta a rasgaduras, agujeros de gusano, donuts y otros cambios «topológicos» delirantes entre las formas del espacio. Se apoyó en el truco de los números imaginarios para el tiempo para hacer las matemáticas más fáciles. Hacer que el tiempo sea imaginario lo convierte efectivamente en otra dimensión del espacio. En un escenario así, atemporal, no existe una noción de causalidad que los universos llenos de agujeros de gusano o desgarrados puedan violar. Hawking usó esta integral de caminos «euclidiana» atemporal para argumentar que el tiempo comenzó en el Big Bang y para contar los bloques de construcción del espaciotiempo dentro de un agujero negro. Recientemente, los investigadores utilizaron el enfoque euclidiano para argumentar que la información escapa de los agujeros negros moribundos.
Este «parece ser el punto de vista más rico a adoptar», afirma Simon Ross, un teórico de la gravedad cuántica de la Universidad de Durham. «La integral de caminos gravitacional, definida para incluir todas las topologías, tiene algunas propiedades estupendas que aún no entendemos completamente».
Pero la perspectiva más rica tiene un precio. A algunos físicos no les gusta eliminar un elemento de carga de la realidad como el tiempo. La integral de caminos euclidiana «es en realidad totalmente no física», afirma Loll.
Su bando se esfuerza por mantener el tiempo en la integral de caminos, situándolo en el espaciotiempo que conocemos y amamos, donde las causas preceden estrictamente a los efectos. Después de pasar años desarrollando formas de aproximarse a esta integral de caminos mucho más formidable, Loll ha encontrado indicios de que el enfoque puede funcionar. En un artículo, por ejemplo, ella y sus colaboradores sumaron un montón de formas estándar de espaciotiempo (aproximando cada una a una colcha de pequeños triángulos) y obtuvieron algo como nuestro universo: el espaciotiempo equivalente a demostrar que las partículas se mueven en lineas rectas.
Otros están avanzando en la integral de caminos atemporal para el espaciotiempo y la gravedad, con todos los cambios topológicos incluidos. En 2019, los investigadores definieron rigurosamente la integral completa, no solo una aproximación, para universos bidimensionales, per utilizando herramientas matemáticas que enturbiaron aún más su significado físico. Un trabajo así solo profundiza la impresión, tanto en físicos como en matemáticos, de que la integral de caminos tiene una potencia que está esperando a que sea aprovechada. «Quizás todavía tenemos que definir bien las integrales de caminos», afirma Ong, «pero fundamentalmente creo que es solo cuestión de tiempo».
El artículo original, How Our Reality May Be a Sum of All Possible Realities, se publicó el 6 de febrero de 2023 en Quanta Magazine. Cuaderno de Cultura Científica tiene un acuerdo de distribución en castellano con Quanta Magazine.
Traducido por César Tomé López
El artículo Cómo nuestra realidad puede ser la suma de todas las realidades posibles se ha escrito en Cuaderno de Cultura Científica.
Un poco más de agua en la Luna
Encontrar agua en la Luna es muy importante, no solo a nivel de poder comprender mejor su historia geológica, sino porque esta puede servir para abastecer al ser humano en bases permanentes. Además de su uso para el consumo humano directo, también permitiría obtener oxígeno e hidrógeno, el primero solo respirar, pero la combinación de ambos elementos permitiría generar el combustible necesario para misiones más allá de la órbita lunar o incluso para el retorno a nuestro planeta.
No podemos olvidar que en estos momentos estamos inmersos en una nueva carrera que nos llevará de vuelta a la Luna -esperamos que antes de la década de los 30- en los cuales tanto Estados Unidos -colaborando también con otros países- y China, pretenden empezar a establecer una presencia humana más permanente en nuestro satélite natural, y que permita no solo investigar, sino poner a prueba los sistemas necesarios que nos permitan dar el salto hacia la exploración humana de Marte, y, donde el abastecimiento de agua, también será fundamental.
Nuestra visión sobre la posibilidad de la existencia de agua en la Luna -entiéndase por agua en cualquiera de sus estados, ya sea sólida, líquida o gaseosa- ha cambiado mucho a lo largo de los siglos. Y es que el hecho de que sea un cuerpo sin una atmósfera hacía pensar a los científicos que en su superficie, carente de nubes y de precipitación, probablemente no hubiese una gota de agua.
Esta idea empezó a cambiar allá por la década de los 60, cuando algunos científicos -como Watson, Murray y Brown (1961)- pensaron que podían existir depósitos de hielo en los cráteres en sombra permanente de la Luna, donde en ningún momento del año la luz del Sol los ilumina directamente, algo que haría subir rápidamente las temperaturas y provocar la sublimación del hielo.
Pero las misiones Apolo traerían un gran chasco a estas teorías. Y es que el análisis de las muestras traídas por los astronautas y analizadas en nuestro planeta parecían demostrar que las rocas estaban totalmente secas… ¿Cómo era posible? ¿Se había escapado toda el agua al espacio o quizás la roca ya era seca de por sí?
 Distribución del hielo en la superficie del polo norte y sur de la Luna, en color azul. Si nos fijamos, se sitúa principalmente en las zonas de sombra de los cráteres. Imagen cortesía de la NASA.
Distribución del hielo en la superficie del polo norte y sur de la Luna, en color azul. Si nos fijamos, se sitúa principalmente en las zonas de sombra de los cráteres. Imagen cortesía de la NASA.No sería hasta la década de los 90 cuando las misiones espaciales empezaron a hacer descubrimientos que apuntaban a que si podría existir agua en la superficie de la Luna, aunque en este caso, dentro de los cráteres en sombra permanente, donde ya se había teorizado sobre su existencia en los años 60.
Esto llevó a, por un lado, volver a analizar las muestras de las misiones Apolo con instrumentación mucho más moderna y que arrojó resultados diferentes en algunos casos, y, por otro, las misiones espaciales comenzaron a detectar señales de la presencia de minerales hidratados en la superficie lunar, no solo en las zonas en sombra, sino también en las zonas iluminadas por el Sol.
El origen del agua en la Luna¿De dónde procede esta agua? Es muy probable que en la Luna estemos viendo moléculas de agua de distinta procedencia. Por un lado, tenemos moléculas que pueden proceder de los volcanes lunares cuya actividad cesó hace unos dos mil millones de años -a grandes rasgos- pero cuyas erupciones pudieron crear atmósferas transitorias a partir de las cuales el vapor de agua pudo depositarse en el interior de los cráteres en sombra permanente.
También es posible que las continuas colisiones de distintos cuerpos contra la Luna -como por ejemplo los cometas y que son más ricos en volátiles- durante millones de años, hayan sido capaces de crear estas acumulaciones en esos cráteres.
 Los lugares de aterrizaje propuestos para la misión Artemis III de la NASA. Como se puede observar, están muy cerca de los cráteres en sombra permanente y por lo tanto, estos podrían muestrearse para confirmarse la presencia de hielo y analizar su composición. Imagen cortesía de la NASA.
Los lugares de aterrizaje propuestos para la misión Artemis III de la NASA. Como se puede observar, están muy cerca de los cráteres en sombra permanente y por lo tanto, estos podrían muestrearse para confirmarse la presencia de hielo y analizar su composición. Imagen cortesía de la NASA.Pero es que incluso la interacción del viento solar -un chorro de partículas cargadas como lo son protones y electrones que constantemente son emitidos por el Sol y que llegan hasta nosotros- podría generar algunos de los depósitos de agua que existen en la luna, ya que los protones al combinarse con el oxígeno podrían dar lugar a moléculas de agua.
Eso si, todo apunta a que las reservas de agua en la Luna son mucho menores que en la Tierra, no únicamente por la diferencia de tamaño en este caso sino porque también podría haber perdido una parte sustancial de esta al espacio a lo largo del tiempo, ya que su campo gravitatorio no es suficiente para retenerla.
Antes decíamos que se había descubierto agua incluso en la cara iluminada de la Luna, algo que a simple vista parecía muy diferente. Explicar esta existencia es difícil, ya que el ciclo día-noche haría fácil que el agua se perdiese al espacio, pero aun así se sigue detectando, por lo que tiene que haber algún mecanismo que pueda explicar la presencia de agua.
Un nuevo estudio publicado en Nature Geoscience pone en el radar unos materiales muy particulares y que conocemos como perlas de vidrio, pequeñas esferas de vidrio formadas cuando un meteorito choca con la superficie, en este caso de la Luna. Las grandes presiones y temperaturas generadas por este impacto funden las rocas y el polvo, y, al enfriarse rápidamente, forma estas pequeñas esferas de vidrio.
Estos materiales actuarían como una esponja en miniatura capaz de absorber parte del agua generada por la interacción del viento solar y la superficie y que, en sus estimaciones más optimistas, podrían albergar aproximadamente un equivalente a 270 kilómetros cúbicos de agua, o lo que es lo mismo, alrededor de un diez por ciento del agua que usamos los seres humanos de la Tierra en todo un año.
 Fotografía tomada por los astronautas de la misión del Apolo 17 en una pequeña excavación del suelo lunar. Los colores naranjas corresponden con zonas ricas en vidrio volcánico que posteriormente se analizaría en la Tierra. Imagen cortesía de la NASA.
Fotografía tomada por los astronautas de la misión del Apolo 17 en una pequeña excavación del suelo lunar. Los colores naranjas corresponden con zonas ricas en vidrio volcánico que posteriormente se analizaría en la Tierra. Imagen cortesía de la NASA.No son los únicos vidrios. Las muestras de las misiones Apolo incluían una sorpresa también en un material vítreo formado durante las erupciones volcánicas cuando esta era expulsada al espacio y al enfriarse rápidamente acababa formando también unas pequeñas esferas de vidrio volcánico y en las que el agua quedó atrapada en su interior y cuya detección no se pudo confirmar hasta principios de este siglo con las mejoras en las técnicas analíticas.
Sin duda, estos descubrimientos nos están ayudando a tener una imagen más detallada sobre, por un lado, la formación de la Luna y todos los procesos que se han dado a lo largo del tiempo desde su nacimiento y, por otro, de donde buscar el agua de cara a las misiones tripuladas, lo que sin duda condicionará mucho la tecnología y la manera de extraerla.
Referencias:
He, Huicun, Jianglong Ji, Yue Zhang, Sen Hu, Yangting Lin, Hejiu Hui, Jialong Hao, et al. «A Solar Wind-Derived Water Reservoir on the Moon Hosted by Impact Glass Beads». Nature Geoscience, 27 de marzo de 2023. doi: 10.1038/s41561-023-01159-6.
Watson, Kenneth, Bruce Murray, y Harrison Brown. «On the Possible Presence of Ice on the Moon». Journal of Geophysical Research 66, n.º 5 (mayo de 1961): 1598-1600. doi: 10.1029/JZ066i005p01598.
Para saber más:
La porosidad de la corteza lunar
Daniel Marín – Naukas Bilbao 2019: Guía para turistas lunares
¿Por qué las caras de la Luna son tan diferentes?
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Un poco más de agua en la Luna se ha escrito en Cuaderno de Cultura Científica.
La doble vida de una seta
 Pleurotus ostreatus. Foto: Dominicus Johannes Bergsma / Wikimedia Commons
Pleurotus ostreatus. Foto: Dominicus Johannes Bergsma / Wikimedia CommonsLa seta de ostra (Pleurotus ostreatus) lleva una doble vida, por decirlo así. Es un hongo de amplia distribución geográfica en zonas templadas; es comestible y hasta se cultiva. Es del mismo género que la seta de cardo (Pleurotus aryngii), aunque no tan apreciada. No es raro verla crecer sobre madera, sobre todo de árboles de hoja caduca y, en especial, de hayas. La descompone y se alimenta de ella. Aunque es normal que crezca sobre troncos, no está considerado un hongo parásito, sino saprofito, lo que quiere decir que se alimenta de los restos de árboles muertos o moribundos. Cumple un papel importante en el bosque, porque ayuda a reciclar un material –la madera– que, por su contenido en lignocelulosa, es muy difícil o imposible de digerir por los animales. De esa forma, pone a disposición de las plantas los nutrientes minerales que se liberan al descomponer la madera sobre la que a menudo se asienta y crece.
La otra vida de la seta de ostra es la depredadora, porque sus micelios pueden matar y digerir nemátodos, que son –no lo olvidemos– los animales que más abundan en los suelos. Pleurotus ostreatus es una de las pocas setas carnívoras conocidas. Otros hongos carnívoros atrapan a los nemátodos tras atraerlos mediante sustancias que imitan señales alimenticias y sexuales. Una vez atraídos, capturan la presa mediante algún dispositivo, como redes adhesivas, botones adhesivos o anillos de constricción. El hongo ostra actúa de otro modo. En vez de atraparlo físicamente, sus hifas –los filamentos de 4-6 µm de diámetro que forman el micelio– producen toxinas muy potentes que paralizan al nemátodo pocos minutos después de haber entrado en contacto con él.
Pleurotus ostreatus utiliza estructuras especializadas, llamadas toxocistos, para paralizar al nemátodo. Un compuesto (volátil) –la 3-octanona (una cetona)–, que se encuentra en el interior de esas estructuras, es el agente principal que desencadena la parálisis y muerte del nemátodo. Ataca la integridad de las membranas celulares de muchos tejidos, incluidas las neuronas sensoriales, las células musculares y la hipodermis, lo que provoca una fuerte entrada de calcio en esas células que, a su vez, induce una hipercontracción muscular. Simultáneamente, en las células se va agotando el trifosfato de adenosina (ATP); en otras palabras, se quedan sin energía. Otros compuestos, similares estructuralmente a la 3-octanona, también pueden provocar la parálisis de los nemátodos y la necrosis celular; en ese sentido, la longitud de la cadena de carbono de la molécula es crítica para la toxicidad nematicida. También lo es la dosis. La 3-octanona repele babosas y caracoles a dosis bajas, pero es letal a dosis altas. De hecho, hace falta que la concentración de la toxina supere un cierto umbral para que surta efecto. Si el nemátodo entra en contacto con un único toxocisto, la propagación del daño es más lenta y débil. Los toxocistos permiten, precisamente, acumular una concentración suficientemente alta de 3-octanona para que su efecto sea lo más intenso posible, aunque tampoco se descarta que en ellos se encuentren otras toxinas que actúen reforzando los efectos de aquella.
¿Pero cómo es que un hongo es carnívoro y se dedica a “comer” nemátodos? La razón está, muy probablemente, en que las sustancias que normalmente aprovecha –restos de plantas en descomposición o moribundas– son muy pobres en nitrógeno, y las proteínas de los nemátodos son una fuente excelente de ese preciado elemento. Y también, quizás, que le sirve para defenderse de posibles nemátodos frugívoros a quienes (¡qué casualidad!) les gusta el contenido de las hifas de los hongos y, cuando pueden, se los comen.
Fuente: Lee C-H, Lee Y-Y, Chang, Y-C, et al (2023) A carnivorous mushroom paralyzes and kills nematodes via a volatile ketone. Science Advances 9 (3) ade4809 doi: 10.1126/sciadv.ade480
Para saber más:
Los usos terapéuticos de la psilocibina de los hongos alucinógenos
Las plantas parásitas roban agua, nutrientes… y hasta genes
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La doble vida de una seta se ha escrito en Cuaderno de Cultura Científica.

