Los lisosomas: el talón de Aquiles de los macrófagos cerebrales durante el infarto cerebral
El cerebro se compone de células, unidades de vida que hacen posible la función; la matriz extracelular, el andamio alrededor del cual las células se organizan; y los vasos sanguíneos, las autopistas encargadas de transportar combustibles celulares como el oxígeno y los nutrientes. Dentro del cerebro, podemos distinguir dos tipos principales de poblaciones celulares. Las neuronas, células especializadas en la transmisión de la información; y las células gliales, que incluyen los astrocitos, los oligodendrocitos, y la microglía, y se encargan de realizar funciones esenciales que favorecen y optimizan la transmisión de información por las neuronas.
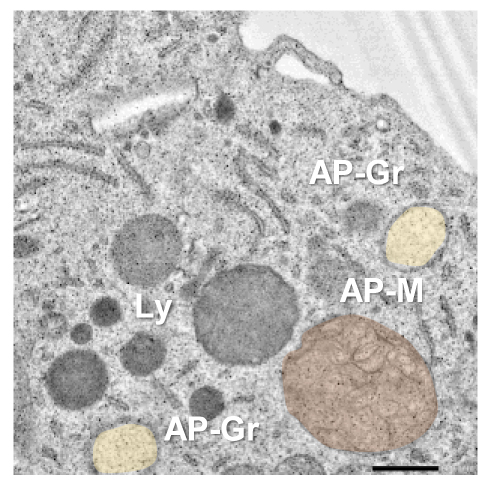 Imágenes por microscopia de barrido electrónico de una microglía. Ly: lisosomas; AP-Gr: autofagosoma con carga granular; AP-M: autofagosoma con carga membranosa.
Imágenes por microscopia de barrido electrónico de una microglía. Ly: lisosomas; AP-Gr: autofagosoma con carga granular; AP-M: autofagosoma con carga membranosa.La microglía es el tipo celular que defiende y protege el cerebro frente a las lesiones. Constituyendo alrededor del 10% de las células cerebrales, la microglía se distingue por poseer un cuerpo pequeño y estático, rodeado de ramificaciones finas y largas que se mueven sin cesar, registrando el ambiente. Para ello, contienen una diversidad de moléculas que detectan, procesan y responden a cambios químicos y/o físicos que ocurren en el ambiente microglial próximo. Tras la activación de estas moléculas, la microglía pone en marcha acciones específicas que favorecen la recuperación del balance tisular. Así, la microglía limpia los residuos tóxicos originados por la función cerebral en un proceso denominado fagocitosis, esencial para el buen funcionamiento del cerebro. Por tanto, es una prioridad promover la función y la salud de la microglía tras una lesión cerebral, como por ejemplo la inducida por el infarto cerebral.
El infarto cerebral de tipo isquémico se produce por la formación de un tapón vascular en una arteria cerebral, produciéndose la interrupción del flujo sanguíneo a las áreas cerebrales irrigadas por dicha arteria. La duración y la intensidad del bloqueo vascular determinan la magnitud de privación de oxígeno y nutrientes que sufren las neuronas y las células gliales del tejido circundante al vaso sanguíneo afectado, pudiendo llegar a producir muerte neuronal. Las neuronas son células con una alta especialización funcional y baja resistencia al estrés, siendo normalmente el primer tipo celular en morir en cantidades significativas. Las células gliales, y más en concreto la microglía, también sufre durante la privación de oxígeno y nutrientes que ocurre durante el infarto cerebral.
En un artículo de investigación reciente1, hemos demostrado que la microglía pierde su habilidad para fagocitar los restos de neuronas muertas tras el infarto cerebral en modelos de ratón y mono. La fagocitosis y eliminación de los residuos neuronales por parte de la microglía es esencial para el mantenimiento de un ambiente cerebral saludable. De hecho, la microglía reconoce, engloba y digiere los despojos de las neuronas muertas de forma muy eficiente en el cerebro sano, no dejando rastro alguno del paso de esas neuronas por el cerebro. Sin embargo, cuando existe un fallo en la limpieza de los cadáveres neuronales por la microglía, las neuronas muertas pierden su integridad física y empiezan a liberar sustancias tóxicas, lo que afecta al bienestar de las células que se encuentran a su alrededor2. La degradación de los cuerpos neuronales fagocitados se lleva a cabo en los lisosomas, los principales orgánulos o compartimentos celulares dedicados a la digestión de moléculas biológicas en células de mamíferos como la microglía. Según nuestra investigación, durante el infarto cerebral, el bloqueo de la fagocitosis ocurre por una reducción de la disponibilidad de los lisosomas en microglía.
Los lisosomas son orgánulos redondeados y sellados con membrana de tamaño pequeño o medio. En su interior, disponen de toda la maquinaria necesaria para degradar cualquier tipo de macromolécula biológica como los carbohidratos, los lípidos, las proteínas y los ácidos nucleicos. Por lo tanto, los lisosomas no solo son capaces de degradar las macromoléculas que vienen desde el exterior celular (por ejemplo, las neuronas muertas internalizadas por la microglía mediante fagocitosis) sino que también tienen la capacidad de digerir contenido intracelular dañado o superfluo. Este último proceso se conoce como autofagia (comerse a uno mismo), y es una respuesta celular que se pone en marcha frente a estrés de tipo metabólico como la falta de oxígeno y nutrientes y promueve la supervivencia celular. En nuestro estudio, hemos observado que durante el infarto cerebral y ante la falta de oxígeno y nutrientes, se intensifica la respuesta autofágica en microglía1, posiblemente con el fin de eliminar las proteínas y los orgánulos tóxicos dañados para adaptarse a las nuevas condiciones metabólicas y finalmente promover la supervivencia de la microglía. Sin embargo, la promoción de la respuesta autofágica durante el infarto cerebral supone un coste para la microglía. De hecho, el incremento del reclutamiento lisosomal con fines autofágicos produce una disminución de la disponibilidad de los lisosomas para otros procesos digestivos, como por ejemplo, la fagocitosis de restos neuronales.
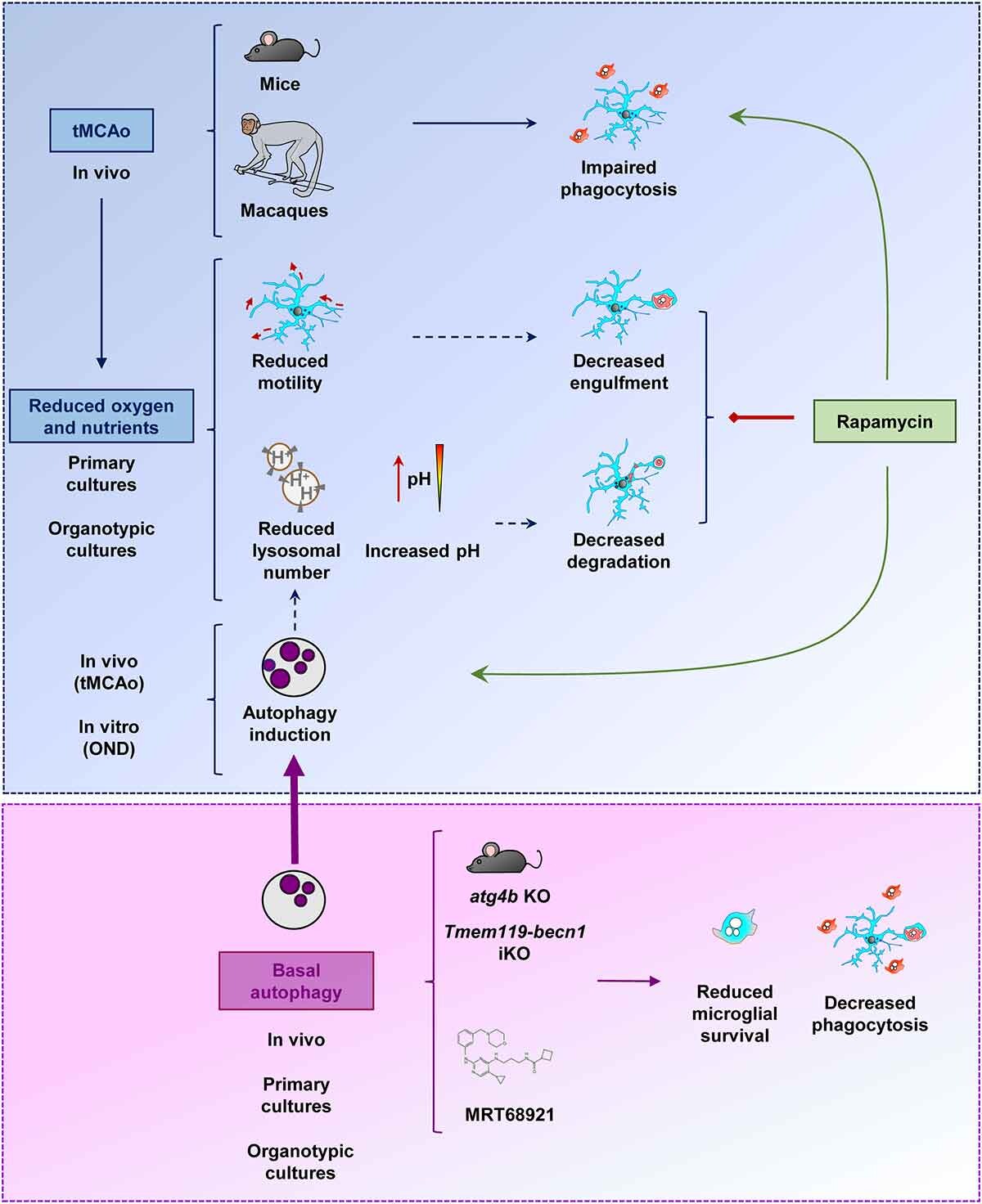
El bloqueo de la fagocitosis microglial en el infarto cerebral produce una acumulación de material tóxico en el cerebro, proceso que empeora la evolución de la enfermedad2. Por lo tanto, las estrategias dedicadas a la recuperación de la actividad fagocítica microglíal podrían suponer un beneficio terapéutico. Según nuestros resultados, cabría esperar que la inhibición de la autofagia liberara un número significativo de lisosomas, aumentando su disponibilidad y promoviendo de forma indirecta la digestión fagocítica microglial. Sin embargo, la inhibición de la autofagia es perjudicial para el estado físico y supervivencia de la microglía1. La estrategia alternativa de estimulación de autofagia mediante administración de rapamicina (un fármaco clásico inductor de autofagia) produce efectos complejos en microglía, que culminan en efectos beneficiosos, neutros, o tóxicos en función del modelo experimental usado para determinar la actividad fagocítica y la supervivencia microglial1. Aunque la modulación de la autofagia resultó ser inefectiva o no concluyente para la modulación de la fagocitosis microglial en este estudio, los datos obtenidos fueron cruciales para entender la complejidad mecanística de las respuestas lisosomales en microglía durante el infarto cerebral y contribuirán al desarrollo de nuevas estrategias terapéuticas enfocadas a aumentar la respuesta protectora microglial durante el infarto cerebral.
Referencias
1Beccari S, Sierra-Torre V, Valero J, Pereira-Iglesias M, García-Zaballa M, Soria FN, De las Heras-García L, Carretero-Guillén A, Capetillo-Zarate E, Domercq M, Huguet PR, Ramonet D, Osman A, Han W, Dominguez C, Faust TE, Touzani O, Pampliega O, Boya P, Schafer D, Mariño G, Canet-Soulas E, Blomgren K, Plaza-Zabala A, Sierra A (2023) Microglial phagocytosis dysfunction in stroke is driven by energy depletion and induction of autophagy. Autophagy 20: 1-30. doi: 10.1080/15548627.2023.2165313
2Abiega O, Beccari S, Díaz-Aparicio I, Nadjar A, Layé S, Leyrolle Q, Gómez-Nicola D, Domercq M, Pérez-Samartín A, Sánchez-Zafra V, Paris I, Valero J, Savage JC, Hui CW, Tremblay ME, Deudero JJ, Brewster AL, Anderson AE, Zaldumbide L, Galbarriatu L, Marinas A, Vivanco Md, Matute C, Maletic-Savatic M, Encinas JM, Sierra A (2016) Neuronal hyperactivity disturbs ATP microgradients, impairs microglial motility, and reduces phagocytic receptor expression triggering apoptosis/microglial phagocytosis uncoupling. PLoS Biol 14:e1002466. doi: 10.1371/journal.pbio.1002466
La versión original de este artículo apareció en inglés en Mapping Ignorance. Traducción de las autoras.
Para saber más:
La hiperactividad neuronal impide que las microglías realicen su trabajo
La microglía es un sensor de mortalidad neuronal
Más allá de las neuronas
Sobre las autoras: Ainhoa Plaza-Zabala1, 2 y Amanda Sierra1,3,4
1 Laboratorio de Biología Celular Glial, Achucarro Basque Center for Neuroscience
2 Dpt. de Farmacología, Universidad del País Vasco (UPV/EHU)
3 Dpt. de Bioquímica y Biología Molecular, Universidad del País Vasco (UPV/EHU)
4 Fundación Ikerbasque
El artículo Los lisosomas: el talón de Aquiles de los macrófagos cerebrales durante el infarto cerebral se ha escrito en Cuaderno de Cultura Científica.
Día de Darwin 2023: La transición a la agricultura y El cerebro humano

¿Cómo ha influido el cerebro en la evolución humana? ¿Cómo funciona y qué lo convierte en un órgano extraordinario? ¿Hechos como la domesticación de las plantas influyeron en la evolución humana? Esas serán algunas de las preguntas que se abordaron el pasado 13 de febrero con motivo del Día de Darwin en la Biblioteca Bidebarrieta de Bilbao.
Con el objetivo de conmemorar el aniversario del nacimiento del naturalista, geólogo y biólogo inglés Charles Darwin la Cátedra de Cultura Científica de la Universidad del País Vasco organizó un evento con dos conferencias con la evolución como eje central en colaboración con el Círculo Escéptico y El Correo.
Por un lado, Amaia Arranz Otaegui, investigadora Ikerbasque y profesora de la Universidad del País Vasco, habló sobre la domesticación de las plantas y el desarrollo de los primeros campos de cultivo en la charla “La transición a la agricultura. ¿revolución o evolución?” Arranz ofreció nuevas perspectivas sobre el cambio que supuso un momento crucial en la historia y puso en contexto el papel que los humanos tuvimos en él.
Por otro lado, el catedrático de Psicobiología de la Universidad Complutense de Madrid, Manuel Martín-Loeches,trató sobre las partes, circuitos y sistemas que componen el encéfalo humano en la charla “El cerebro humano a la luz de la evolución ¿Qué lo hace extraordinario?” Martín-Loeches ofreció detalles sobre las estructuras que nos ayudan a tener más tolerancia social y que hemos desarrollado a lo largo de millones de años.
La charla-coloquio se organiza dentro del ciclo Bidebarrieta Científica, impulsado por la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta.
Amaia Arranz Otaegui
Amaia Arranz Otaegui es investigadora Ikerbasque y profesora de Geografía, Prehistoria y Arqueología de la UPV/EHU. Es especialista en Arqueobotánica (análisis de semillas, frutas, carbón o sobrantes de comida) y ha realizado un amplio campo de su investigación en el sudoeste asiático (Siria, Líbano, Jordania, Irán e Israel). Sus investigaciones se centran en la transición de los pueblos cazadores-recolectores del Epipaleolítico y en las primeras sociedades ganaderas del Neolítico. Entre sus temas de investigación se encuentran el uso y explotación de las plantas, el proceso de domesticación, la dieta vegetal y la reconstrucción del Pleistoceno y el paleopaisaje holoceno.
Manuel Martín-Loeches
Actualmente es catedrático de Psicobiología en la Universidad Complutense de Madrid y en la Universidad de Colorado enseña sobre la neurocognición del arte y su evolución. Sus investigaciones abordan diversos temas, siempre en torno al cerebro y la cognición humana, tanto en pacientes sanos como en los que sufren esquizofrenia. Sus investigaciones incluyen la atención visual, la memoria laboral, las emociones, las creencias religiosas, la estética y el arte y, sobre todo, el lenguaje humano. Todo ello sin perder nunca la visión evolucionista.
Edición realizada por César Tomé López
El artículo Día de Darwin 2023: La transición a la agricultura y El cerebro humano se ha escrito en Cuaderno de Cultura Científica.
¿Quién cree en pseudociencias?
 Foto: Brian McMahon / Unsplash
Foto: Brian McMahon / Unsplash¿Estamos bien inmunizados como sociedad frente a los bulos pseudocientíficos?
Hace un par de meses realizamos una encuesta donde incluimos una medida de aceptación de creencias pseudocientíficas desarrollada por el investigador y especialista en pseudociencias Ángelo Fasce. A partir del panel online de IMOP Insights (pendiente de publicación), solicitamos a población adulta en España su grado de acuerdo o desacuerdo con una lista de aseveraciones relacionadas con bulos o paparruchas pseudocientíficas.
Las afirmaciones podían ir desde que la ciencia ha validado la existencia de habilidades telepáticas o que se ha “demostrado” que las emociones negativas causan cáncer, hasta que los arqueólogos han registrado el encuentro entre antiguas civilizaciones y seres alienígenas.
De manera agregada, una puntuación media mayor en estas creencias suele significar una disposición más propicia a aceptar bulos y creencias pseudocientíficas.
La mayor parte de la población acepta la posibilidad de las pseudocienciasLos datos de la encuesta sugieren que a día de hoy la respuesta típica en España ante bulos pseudocientíficos es de agnosticismo: ni se abrazan, ni se rechazan de frente, sino que se reconoce ignorancia. ¿Está entonces el vaso medio lleno?
Hay razón para pensarse dos veces que realmente sea así. No solo una porción mayoritaria de la población adulta española da prueba de estar abierta a contemplar como plausibles ideas pseudocientíficas, sino que, en algunos casos, un porcentaje muy alto de la ciudadanía abraza directamente dichas creencias, como puede verse en detalle en esta gráfica:
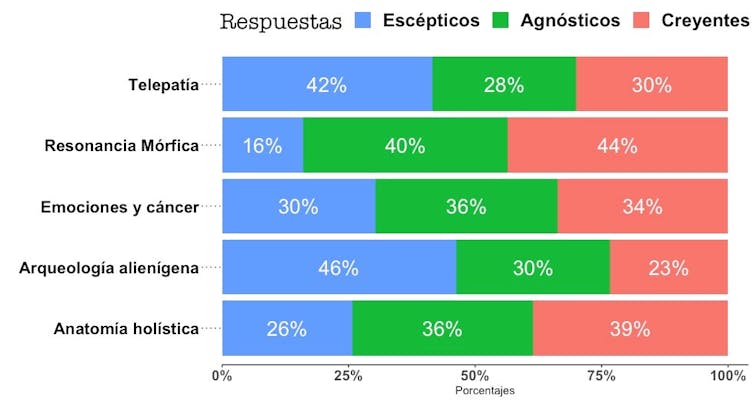 Resultados de la encuesta.
Resultados de la encuesta.Author providedTener estudios universitarios no significa creer menos en pseudociencias
¿Cómo puede ser que un 30% de los adultos en España estén de acuerdo en que la telepatía ha sido demostrada científicamente? ¿O que casi un cuarto de los encuestados afirme que hay pruebas demostradas de contactos prehistóricos con civilizaciones alienígenas?
En nuestra encuesta incluimos las variables demográficas habituales (edad, género, nivel educativo). Respiramos aliviados al comprobar que el nivel educativo predice ligeramente una menor susceptibilidad ante las ideas pseudocientíficas. Pero, aunque estadísticamente significativa, la correlación entre haber completado estudios universitarios y abrazar ideas pseudocientíficas era pequeña. ¿Motivo para congratularse o más bien para la consternación? Después de todo, una formación superior de varios años no parece que inmunice altamente frente a imposturas intelectuales.
Como contraste, la edad (pertenecer a una generación más mayor) era aproximadamente tan predictiva como el nivel educativo: a idéntico nivel educativo, una generación mayor parece más susceptible a aceptar estas creencias.
¿Cómo puede ser que la educación universitaria, ante la que nuestra sociedad y nuestros jóvenes dedican tantos esfuerzos, no sea un factor altamente protector frente a paparruchas pseudocientíficas?
Cuánto sabemos de cienciaEn nuestro estudio también incluimos una medida de comprensión ciudadana de la naturaleza del conocimiento científico. Es decir, medimos cuán familiarizados están los adultos residentes en España con la filosofía del saber científico y la naturaleza de la ciencia como actividad, incluyendo medidas sobre si la gente entiende que un resultado puede ser científico aunque no sea absolutamente concluyente, o si, por ejemplo, la gente entiende lo que es la revisión por pares.
Medidas altas de familiaridad con la filosofía del saber científico sí eran un claro predictor del rechazo de bulos pseudocientíficos. De hecho, en nuestro modelo, la formación universitaria solo era protectora frente a los bulos pseudocientíficos cuando había servido para transmitir un mínimo de comprensión en la filosofía de la ciencia.
De lo contrario, las personas con formación universitaria no son ni menos ni más reacias que el resto a abrazar ideas pseudocientíficas.
Esto sugiere que en España la formación universitaria no está sirviendo para transmitir una mínima comprensión filosófica de la naturaleza de la ciencia en muchos casos.
Factores de riesgoEn nuestra encuesta, ser mujer también aparecía como un factor de riesgo de cara a aceptar creencias pseudocientíficas. Es así aun controlando otras variables. Es decir, a igual nivel educativo o igual nivel de familiaridad con la filosofía de la ciencia, en promedio las mujeres mostraban una susceptibilidad algo mayor. No sabemos por qué es así y el proverbial “estudios ulteriores deberían examinar esta cuestión” se aplica aquí. No obstante, ya que este resultado ha sido replicado en otras encuestas y puede ser clave para afrontar situaciones de vulnerabilidad social, creemos que merece la pena prestar atención a la dimensión de género en esta cuestión.
Como suele ser habitual, dichas diferencias promedio son modestas. En ningún caso supone que un sexo sea más crédulo que otro (en otras encuestas los
varones suelen aparecer como más dispuestos a abrazar teorías de la conspiración, por absurdas que puedan llegar a ser).
Una posibilidad subrayada anteriormente es que la mayor empatía en promedio de la que dan muestra las mujeres las haga más susceptibles. Otra posibilidad más inquietante es que muchas de estas creencias hayan sido manufacturadas o que (como la cepa de un virus que se adapta a su huésped) hayan coevolucionado para captar adeptas más fácilmente entre las mujeres.
Otras encuestas muestran, por ejemplo, que en nuestra sociedad la receptividad a las terapias alternativas (una forma particularmente perniciosa de pseudociencia en algunos casos) está más extendida entre las mujeres.
El camino hacia una sociedad menos crédulaDesde hace unos años contamos en nuestro país con un, en algunos aspectos, envidiable sistema de vigilancia y detección de la epidemia de gripe. Asimismo, la covid-19 ha puesto de relieve la necesidad de contar con sistemas de detección temprana de patógenos para prevenir posibles brotes explosivos y poder actuar a tiempo de cara a contener su difusión. La experiencia y los resultados de algunos estudios nos aconsejarían tomarnos en serio la necesidad de detectar, seguir y modelizar la difusión de bulos pseudocientíficos entre la población.
Comprender qué hace que ciertas ideas perniciosas se extiendan y qué hace a algunos grupos más vulnerables fortalecería nuestra inmunidad ante las pseudociencias y sus consecuencias más perniciosas.
Una sociedad menos crédula es una sociedad menos susceptible a la desinformación y a las prácticas nocivas, y es más probable que tome decisiones con conocimiento de causa sobre su salud, el medio ambiente y otras cuestiones importantes.![]()
Para saber más:
Negacionismo, anticiencia y pseudociencias: ¿en qué se diferencian?
Pseudociencia y arrogancia
Anticiencia (I): la unidad perdida
Sobre los autores: Hugo Viciana, Profesor investigador en la Universidad de Sevilla, especialista en filosofía y ciencias cognitivas, Universidad de Sevilla y Aníbal M. Astobiza, Investigador Posdoctoral, especializado en ciencias cognitivas y éticas aplicadas, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Quién cree en pseudociencias? se ha escrito en Cuaderno de Cultura Científica.
ZientZinema 4: 2001, una odisea del espacio
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsTítulo original: 2001: A space odyssey. 1968, color, 141 minutos. Productor y Director: Stanley Kubrick. Guion: Stanley Kubrick y Arthur C. Clarke, basado en parte en el cuento corto El centinela, publicado en 1951 por Arthur Clarke; en 1968, Clarke publicó una novela con el mismo título de la película basada en el guion suyo y de Kubrick. Efectos especiales: Douglas Trumbull. Fotografía: Geoffrey Unsworth. Música: Richard Strauss, Johann Strauss, Aram Khachaturian, György Ligeti. Intérpretes: Keir Dullea, Gary Lockwood, William Sylvester, Douglas Rain (voz de HAL).
Eres libre de especular, como desees, sobre el significado filosófico y alegórico de Odisea 2001.
Stanley Kubrick.
Comenzaré por el resumen final que supone el comentario de Román Gubern sobre esta película en su texto clásico Historia del cine, publicado en 1989, y que dice así.:Ñ
“Más adelante, Kubrick realizará la impresionante epopeya cósmica 2001 un odisea del espacio (2001, a space odyssey, 1968), escrita en colaboración con Arthur C. Clarke, y que comienza con el proceso de hominización en el cuaternario para concluir en una nueva fase de la futura evolución biológica del hombre. 2001, una odisea del espacio señala la definitiva mayoría del género de la ciencia-ficción y abre excitantes perspectivas a este género hasta ahora tenido por menor”.
Unas páginas después, Gubern extiende su argumento y escribe que:
“En otra órbita muy distinta se movió la muy considerable contribución de Stanley Kubrick al cine moderno. Su epopeya cósmica 2001: una odisea del espacio (2001: A Space Odyssey, 1967), escrita con Arthur C. Clarke, llevó a su cúspide adulta el género de la ciencia ficción, mediante una historia que abarcó la evolución completa de la humanidad, desde el proceso de hominización de los primates en algún lugar de África hasta el estadio posthumano que alcanza el protagonista al cruzar la Puerta de las Estrellas y que le conduce, por mutación biológica, a un estadio superior de la evolución de la especie”.
2001, la odisea humanaLa película relata la evolución de la especie humana desde una especie animal, quizá algún australopiteco por ser la película de 1968 y por lo que entonces se conocía de los homínidos, hasta el Niño de las Estrellas en un proceso dirigido por un artefacto alienígena. Se desarrolla el guion en tres secciones unidas por la imagen de un negro monolito. Parece que viene de una antigua y muy avanzada civilización extraterrestre. Un guion extenso, muy detallado con la precisión habitual de Kubrick y tan complejo que llevó a Clarke a declarar que “si alguien entiende la película por completo, hemos fracasado”. Otro aspecto notable del guion es la escasez de diálogos. Los primeros, desde el episodio de los homínidos, aparecen a los 25 minutos del inicio de la película. Y en total, con más de dos horas de duración, los diálogos ocupan 45 minutos. Además, a menudo son textos poco importantes, casi rutinarios, y hay que destacar que los más emotivos los pronuncia el ordenador HAL cuando es desconectado.
Un monolitoLa primera sección, El amanecer del hombre, y según el análisis de Alberto Lombo, de la Universidad de Zaragoza, comienza con una escena en un desierto pedregoso lleno de rocas y huesos. Una serie de escenas muestra una banda de primates alimentándose, viviendo en cuevas, bebiendo agua de un charco y defendiéndose de los ataques de otro grupo de monos. Por sorpresa, sin un anuncio previo, , una mañana, al amanecer, aparece un monolito negro entre las rocas, y suena una muy especial música coral (es Atmospheres de György Ligeti). Los primates tocan el monolito y pronto descubren que un hueso puede ser una herramienta, una porra, un arma para la caza y para la guerra. En la caza o cuando son atacados por otra banda, uno de los primates usa la porra para matar al más agresivo de los atacantes. El grupo tiene un arma y sabe cómo utilizarla. Eliminan o destierran al otro grupo y cazan, tienen alimento de sobra.
Como escribe Vicente Castellanos, de la Universidad Autónoma Metropolitana de México, la primera parte de la película presenta un homínido, quizá entre Australopithecus y Homo habilis, especie que utilizó herramientas hace cuatro millones de años que, es evidente, demuestra algo para Kubrick, pues es la fecha que menciona en el siguiente apartado para el monolito que encuentran en la Luna. Por otra parte, el grupo de homínidos con herramientas, con las porras como armas, en su lucha con el otro grupo muestra que son bípedos mientas que los otros siguen apoyando los brazos en el suelo. Tienen las manos libres para utilizar el hueso como arma. Y el grupo armado, de alguna manera que Kubrick no explica, se han transmitido el conocimiento y el uso de armas entre ellos. Es, quizá, el nacimiento de la cultura.
En la alegría de la primera victoria, el primate lanza el hueso al aire y, en una escena extraordinaria, Kubrick lo convierte en un cohete que viaja a una estación espacial entre la Tierra y la Luna. Es curioso que también flota en el aire, sin gravedad, un bolígrafo que se le escapa a uno de los viajeros del cohete. Todo ello sugiere que la evolución de la especie humana, por el monolito extraterrestre, lleva a los primates al uso de herramientas y, en último término a los viajes al espacio.
En la Luna, los viajeros estudian un nuevo monolito que, calculan lleva allí enterrado unos cuatro millones de años y les muestra una señal que los dirige a Júpiter. Este viaje, que la película sitúa 18 meses después, lleva a un grupo de astronautas y al ordenador HAL serie 9000, a Júpiter (HAL es un acrónimo de Heuristically Programmed Algorithmic Computer (Computador algorítmico programado heurísticamente para resolver problemas; también se ha propuesto que deriva alfabéticamente de IBM). Después de la pérdida de la nave por la rebelión de HAL, comienza la tercera parte de la película “Júpiter y más allá del infinito”. Kubrick relata la evolución de la humanidad, del astronauta superviviente, hasta una especie más avanzada, el Niño de las Estrellas, que vuelve a la Tierra. Todo ello con imágenes sorprendentes acompañadas de una música extraordinaria, el Así habló Zaratustra de Richard Strauss y composiciones de Ligeti.
Es una película con muchos aspectos que sirven para divulgar temas científicos. Por ejemplo, Leroy Dubeck y sus colegas, de la Universidad Temple de Philadelphia, proponen repasar la formación de gravedad artificial en la estación espacial situada entre la Tierra y la Luna o en la cabina de la nave Discovery que lleva a los astronautas a Júpiter. O, también, la descripción y conducta del ordenador HAL serie 9000 que dirige la nave y que, en un momento de la trama, entra en conflicto por las órdenes contradictorias que recibe. Desconecta sistemas de la nave y provoca la muerte de los astronautas y el único que sobrevive lo desconecta. Es curioso que Kubrick ve el progreso de los ordenadores con un aumento de tamaño cuando la realidad, en la actualidad, nos ha llevado a la miniaturización.
Por otra parte, Kubrick filmó la película como si estuviera preparando un documental y, para ello, grabó muchos metros de película para facilitar el montaje y la versión definitiva. Como en los documentales, el cociente de grabación de película fue de 200 a 1 respecto de lo filmado frente a lo utilizado en el metraje final.
El origen violento de la humanidadEs interesante, en el primer apartado de la película, como Kubrick y Clarke sitúan la humanidad, después de los toques al monolito, en la violencia y la muerte de otro primate de su especie. Fue en 1964 cuando Kubrick contactó por vez primera con Clarke para preparar el guion de una película de ciencia ficción y, en ese guion, terminado en 1966, se incluyen estas escenas de violencia. Entonces, en los estudios sobre la evolución de nuestra especie, se debatían las ideas de Robert Ardrey, dramaturgo, escritor y guionista, que en su libro Génesis en África, publicado en 1961, propone que la especie humana posee un instinto para la agresión y la violencia tal como afirma Nadine Weidman, de la Universidad de Harvard. La especie humana es violenta por naturaleza y es lo que narra Kubrick en la película.
Según el paleoantropólogo sudafricano Raymond Dart, descubridor y estudioso del Australopithecus africanus, que había encontrado hasta 5000 fósiles de esta especie en el yacimiento en cueva Makapan, la violencia ya aparecía en este ancestro de la especie humana. Abundaban los huesos de antílopes y gacelas y algunos podían ser utilizados como porras o, más afilados, como cortadores de carne, y eran diez veces más abundantes que otros fósiles. Fue Dart quien afirmó que los usaron para la caza y, según su propuesta, las armas precedieron al desarrollo de los cerebros de gran tamaño.
Para Ardrey, la especie humana y sus ancestros más cercanos en el tiempo y en la evolución, son animales territoriales y la defensa del territorio está entre los instintos más antiguos. Y ese instinto se mantiene en nuestra especie; la evolución no ha tenido tiempo de cambiarlo, incluso si en la actualidad se puede apuntar que ha dejado de ser ventajoso. Ya no se lucha por una charca sino por la conquista del espacio, por la luna y planetas como Júpiter. Nada ha cambiado en el primate territorial, propone Ardrey. Escribió en 1990 que “el hombre es hombre, y no chimpancé, porque durante millones y millones de años en evolución ha matado para sobrevivir”.
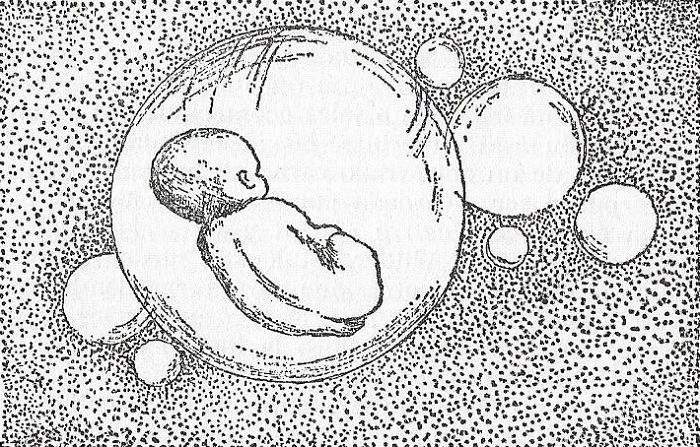 Ilustración en Génesis en África (1961), de Robert Ardrey, realizada por Berdine Ardrey, pareja del autor. Fair use.
Ilustración en Génesis en África (1961), de Robert Ardrey, realizada por Berdine Ardrey, pareja del autor. Fair use. Un fotograma de una de las últimas escenas de 2001 una odisea del espacio (1968), con el Niño de las Estrellas. Fuente: Metro-Godlwyn-Mayer (fair use).
Un fotograma de una de las últimas escenas de 2001 una odisea del espacio (1968), con el Niño de las Estrellas. Fuente: Metro-Godlwyn-Mayer (fair use).
El parecido entre la ilustración en el libro Génesis en África, publicado en 1961, y la última escena de 2001 una odisea del espacio, estrenada en 1968, parece demostrar que Kubrick conocía el libro de Ardrey y, por tanto, su propuesta sobre la violencia y la evolución de la especie humana.
Sin embargo, no hay que evitar la conclusión más interesante de lo que es y significa la ciencia ficción: no representa el futuro sino el entorno en que fue concebida, en este caso la película, y sus transformaciones más inmediatas, más cercanas, más evidentes para sus autores y, también, para los espectadores. El futuro de 2001 es el futuro que ofrecía el presente de 1968, un futuro que ahora, en 2023, ya no es el que se creía que nos alcanzaría.
Referencias:
Ardrey, R. 1969. Génesis en África. La evolución y el origen del hombre. Ed. Hispano Europea. Barcelona. 457 pp.
Castellanos Cerdá, V. 2009. Stanley Kubrick, un evolucionista cinematográfico. Origen y término de la cultura en 2001, una odisea del espacio. Ciencia ergo sum 16: 15-29.
De Miguel, C. 1988. La ciencia ficción. Un agujero negro en el cine de género. Servicio Editorial Universidad del País Vasco. Leioa. 400 pp.
Dubeck, L.W. et al. 1994. Fantastic voyages. Learning science through science fiction films. AIP Press. New York. 327 pp.
Fernández Bobadilla, V. 2021. 2001: Una odisea del espacio (1968). En “Películas y series de ciencia ficción”, p. 30-33. Muy Interesante junio.
Gámez, L.A. 2022. Los extraterrestres que atormentaron a Kubrick. El Correo 26 enero.
Gubern, R. 1989. Historia del cine. Ed. Lumen. Barcelona. 533 pp.
Herranz, P. 1998. Rumbo al infinito. Las 50 películas fundamentales del cine de ciencia-ficción. Midons Ed. Valencia. 223 pp.
Lombo Montañés, A. 2019. Los australopitecos de Kubrick, la teoría de la violencia y los posthumanismos en el imaginario prehistórico. Revista ArkeoGazte Aldizkaria 9: 271-290.
Palacios, J. 2001. Recuerdos del futuro. Cuadernos de Filmoteca Canaria 2: 43 pp.
Telotte, J.P. 2002. El cine de ciencia ficción. Cambridge University Press. Madrid. 278 pp.
Weidman, N. 2011. Popularizing the ancestry of man. Robert Ardrey and the killer instinct. Isis 102: 269-299.
Wikipedia. 2023. Robert Ardrey. March 1.
Para saber más:
En busca del monolito de “2001: una odisea espacial”
Nuestros ancestros asesinos
Máquinas inteligentes (y III): Deep blue, HAL 9000 y más allá
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo ZientZinema 4: 2001, una odisea del espacio se ha escrito en Cuaderno de Cultura Científica.
Sucesiones fractales
Una de las características que definen a los objetos fractales es la autosemejanza (véase la entrada Fractus, arte y matemáticas). Esta consiste en que la estructura de los fractales se repite a diferentes escalas o también podríamos expresarlo como que el objeto fractal es igual a una parte del mismo.
 Trifurcation /trifurcación (2014), del artista Robert Fathauer, basada en el fractal llamado triángulo de Sierpinspi (véase la entrada ¿Conocían los romanos el triángulo fractal de Sierpinski?). Imagen de la página web de Robert Fathauer
Trifurcation /trifurcación (2014), del artista Robert Fathauer, basada en el fractal llamado triángulo de Sierpinspi (véase la entrada ¿Conocían los romanos el triángulo fractal de Sierpinski?). Imagen de la página web de Robert FathauerEsta propiedad de los objetos fractales se ha trasladado al mundo de las sucesiones de números enteros. Esencialmente una sucesión (infinita) de números enteros es una sucesión fractal, también llamada sucesión autosemejante, si una parte de la sucesión es igual a toda la sucesión, es decir, si eliminamos algunos miembros de la sucesión infinita los miembros de la sucesión que quedan constituyen de nuevo toda la sucesión.
Veamos un ejemplo. Consideremos la sucesión finita de números 1, 2, 2, 3, 2, 3, 3 y consideremos la sucesión infinita que consiste en repetir la secuencia anterior de forma infinita, es decir, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, … Esta sucesión de números aparece mencionada en la explicación de la Melodía racional XV (1982) del músico minimalista estadounidense Tom Johnson (1939). Ahora si eliminamos de la sucesión infinita todos los números que están en posiciones pares, los que nos quedan, que son los que están en las posiciones impares, siguen siendo la sucesión original.
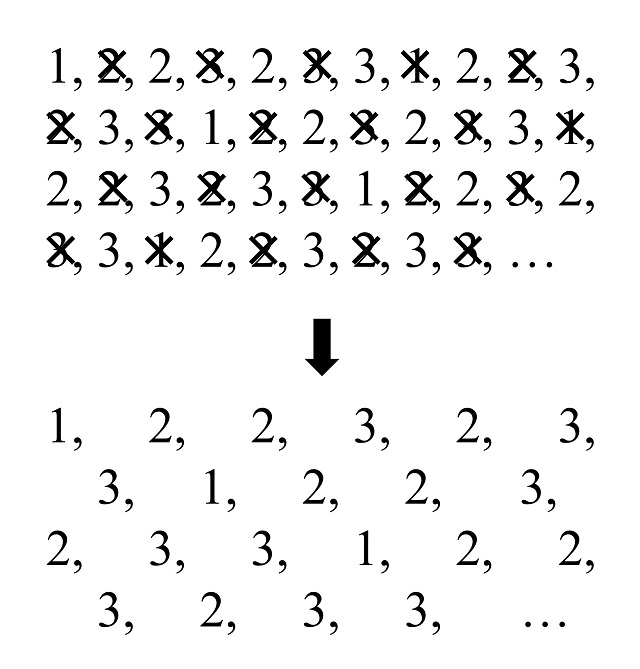
Como este proceso lo podemos repetir de forma infinita podemos decir que la sucesión autosemejante tiene infinitas copias de sí misma, como para los objetos fractales.
Esta sucesión infinita de números se dice que es una sucesión fractal de razón 2. En general, se dice que una sucesión es una sucesión fractal, o autosemejante, de razón d si el subconjunto de la sucesión que no eliminamos son el primer número de la sucesión y los que van apareciendo cada d posiciones, es decir, los números que están en las posiciones que son múltiplos de d más 1 (esto es, posiciones de la forma 1 + d x n. donde n toma valores 0, 1, 2, 3, 4, etc), y de esta forma obtenemos de nuevo la sucesión original.
Por ejemplo, tomemos la siguiente sucesión, que explicaremos más adelante: 0, 1, 2, 1, 2, 3, 2, 3, 4, 1, 2, 3, 2, 3, 4, 3, 4, 5, 2, 3, 4, 3, 4, 5, 4, 5, 6, 1, 2, 3, 2, 3, 4, 3, 4, 5, 2, 3, 4, 3, 4, 5, 4, 5, 6, 3, 4, 5, 4, 5, 6, 5, 6, 7, 2, 3, 4, 3, 4, 5, 4, 5, 6, 3, 4, 5, 4, 5, … podemos observar que si nos quedamos con el primer número y los que aparecen cada tres posiciones, o lo que es lo mismo, los números que están en las posiciones que son múltiplos de 3 más 1 (es decir, las posiciones 1, 4, 7, 10, 13, 16, etc) estos son de nuevo la sucesión original. Por lo tanto, esta sucesión es un ejemplo de sucesión autosemejante de razón 3.
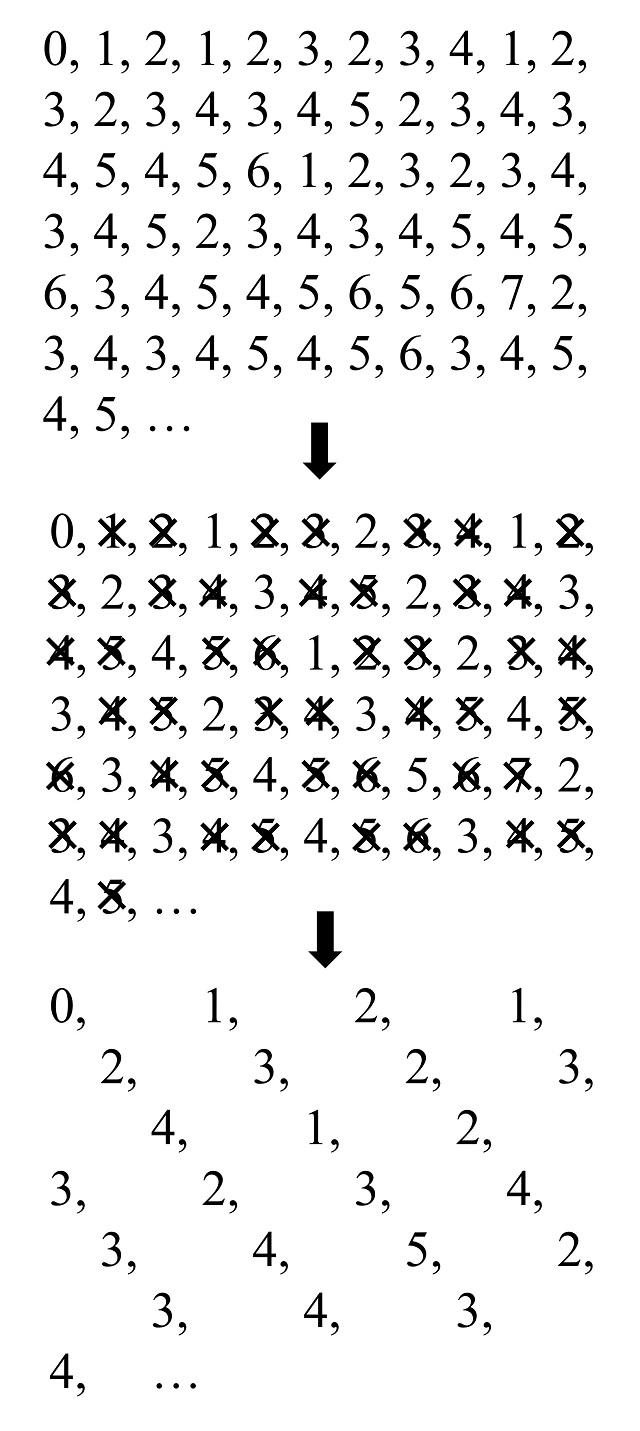
Veamos algunos ejemplos concretos de sucesiones autosemejantes.
La sucesión de unos en la expresión binariaNuestro primer ejemplo es la sucesión que está formada por la cantidad de unos que tienen las expresiones binarias de los números enteros no negativos, es decir, 0, 1, 2, 3, 4, 5, 6, … En la entrada Las bases de numeración o cómo hacer trucos de magia binarios [https://culturacientifica.com/2022/05/04/las-bases-de-numeracion-o-como-hacer-trucos-de-magia-binarios/] ya explicamos cómo se expresan los números en diferentes bases de numeración y cómo calcular esas expresiones, pero recordémoslo brevemente.
El sistema de numeración posicional moderno utilizado en casi todo el mundo es decimal, es decir, que tiene base 10 (véase el libro Los secretos de la multiplicación, de los babilonios a los ordenadores). Por lo tanto, consta de diez cifras básicas, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 y todo número se puede representar con ellas al expresarlo en función de las potencias de 10. Por ejemplo, el número 3.457 tiene el valor de 3 veces la cantidad de 1.000, 4 veces la cantidad de 100, 5 veces la cantidad de 10 y 7 veces la unidad 1, que son las potencias de 10, a saber, 1.000 = 103, 100 = 102, 10 = 101 y 1 = 100.
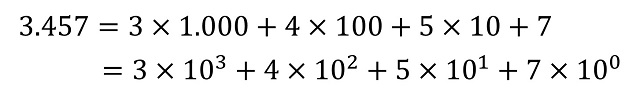
En general, dada una base de numeración b –ya sea esta igual a 2, 3, 12 o 60- la representación posicional de cualquier número en la misma viene dada por una expresión d1d2…dr (donde los dígitos di –para i entre 1 y r– pertenecen a la familia de las b cifras básicas del sistema de numeración, que tienen valores entre 0 y b – 1) teniendo en cuenta que el número puede escribirse, de forma única, como
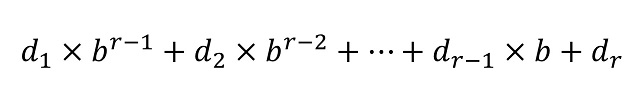
Por lo tanto, la representación del número está ligada a la base elegida. Así, si tomamos el sistema binario (b = 2) el anterior número se representa como (110110000001)2, ya que “3.457” = 211 + 210 + 28 + 27 + 1; en la base octal (b = 8) como (6600)8, porque “3.457” = 6 x 83 + 6 x 82; o en la base hexadecimal (b = 16), donde las cifras básicas son 0, 1, …, 9, A, B, C, D, como (D81)16, puesto que “3.457” = D x 162 + 8 x 16 + 1, donde estamos utilizando el subíndice de las representaciones (2, 8 y 16) para recordar que esa es una representación en esa base de numeración.
Como para la sucesión infinita que queremos calcular se necesitan las expresiones binarias de los números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, entonces escribamos primero estas expresiones para los números.

La sucesión consiste en la cantidad de unos (1) en la expresión binaria de los números, luego la sucesión que se genera es:
0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 1, 2, 2, 3, 2, 3, 3, …
Esta sucesión (que es la sucesión A000120 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS [oeis.org]) resulta ser una sucesión autosemejante de razón 2, como se puede comprobar en la siguiente imagen.
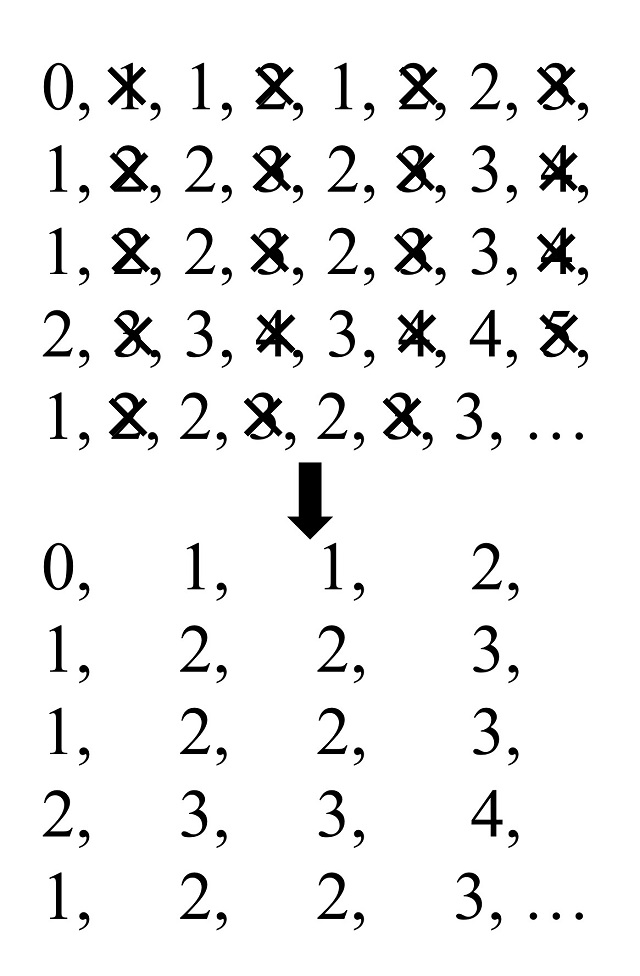
Consideremos ahora la sucesión que consiste en expresar los números enteros no negativos (0, 1, 2, 3, 4, 5, 6, …) en base tres y sumar los dígitos que se han utilizado para expresar cada número. Para ello, empecemos expresando los números en base 3. Recordemos que ahora utilizamos las potencias de 3 y las cifras básicas son 0, 1, y 2.

Ahora sumemos los dígitos, en base 3, de los números, que vemos (para los primeros números) en la imagen anterior. La sucesión que nos queda es: 0, 1, 2, 1, 2, 3, 2, 3, 4, 1, 2, 3, 2, 3, 4, 3, 4, 5, 2, 3, 4, 3, 4, 5, 4, 5, 6, 1, 2, 3, 2, 3, 4, 3, 4, 5, 2, 3, 4, 3, 4, 5, 4, 5, 6, 3, 4, 5, 4, … (que es la sucesión A053735 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS [oeis.org]). Esta es la sucesión que habíamos considerado más arriba y que es una sucesión autosemejante de razón 3.
La sucesión fractal de Clark KimberlingEsta sucesión la vamos a introducir primero siguiendo la explicación del divulgador científico estadounidense Clifford A. Pickover (1957), en su libro La maravilla de los números.
Para cada número natural n se consideran n tarjetas numeradas con los números 1, 2, 3, …, n – 1, n, que utilizaremos para definir el número que está en la posición n de la sucesión. Entonces, se colocan las tarjetas numeradas boca arriba (es decir, con los números para arriba) sobre la mano, ordenadas de forma natural y de manera que la tarjera con el número 1 esté abajo del montón y la tarjeta con el número n arriba. Por ejemplo, para n = 5 se consideran cinco tarjetas y se colocan sobre nuestra mano mirando (los números) hacia arriba, primero la tarjeta 1, sobre nuestra mano, luego la tarjeta 2 sobre la anterior, luego la tarjeta 3, después la 4 y finalmente la tarjeta 5 en la parte de arriba del montón.

A continuación, se realiza el siguiente proceso. Se toma la tarjeta que está arriba del montón y se pasa a la parte de abajo del montón, manteniéndola con la cara (el número) hacia arriba. La siguiente tarjeta en la parte de arriba del montón se coloca sobre la mesa, también con la cara hacia arriba. Y se continua con este doble movimiento. Es decir, la tarjeta de arriba del montón se pasa abajo del montón y la siguiente tarjeta a la mesa, sobre la tarjeta anterior. Y se repite el proceso hasta que las n tarjetas que teníamos sobre la mano pasen a la mesa. Entonces deberemos fijarnos en qué posición del montón de la mesa, empezando desde arriba, está la carta con el número n, que estaba originalmente en la parte de arriba del montón sobre nuestra mano. El número que nos da esa posición es nuestro número de la sucesión que estamos construyendo.
Por ejemplo, si tomamos n = 5 y tenemos las tarjetas numeradas sobre nuestra mano, boca arriba, que podemos expresar como (1, 2, 3, 4, 5), entendiendo que a la izquierda está la tarjeta colocada debajo de las demás y hacia la derecha las que están por encima. En el primer par de movimientos la tarjeta 5 pasa abajo y la tarjeta 4 a la mesa, quedando en nuestra mano (5, 1, 2, 3) y en la mesa (4). En el siguiente par de movimientos la tarjeta 3 pasa abajo, mientras que la tarjeta 2 va a la mesa, quedando en nuestra mano (3, 5, 1) y en la mesa (4, 2). En los dos movimientos siguientes en la mano queda (1, 3) y en la mesa (4, 2, 5). Después quedaría (3) en la mano y (4, 2, 5, 1). Finalmente quedarían las tarjetas sobre la mesa (4, 2, 5, 1, 3). Por lo tanto, nuestro número en la posición 5 de la nueva sucesión es el 3, ya que el número 5 está en la posición 3 desde arriba (en nuestra notación desde la derecha).
La sucesión que se genera de esta forma es
1, 1, 2, 1, 3, 2, 4, 1, 5, 3, 6, 2, 7, 4, 8, 1, 9, 5, 10, 3, 11, 6, 12, 2, 13, 7, 17, 4, 15, 8, 16, 1, …
Esta sucesión es autosemejante ya que si se elimina la primera aparición de cada número nos queda la sucesión original. De hecho, es una sucesión autosemejante de razón 2.
El matemático y músico estadounidense Clark Kimberling (1942) introduce esta sucesión de una forma más matemática, relacionada con las bases de numeración, que explicaremos de forma simplificada. En el caso de esta sucesión se toma la base 2, luego está relacionada con las potencias de 2. Para explicar la construcción de esta sucesión vamos a considerar la potencia de 2 más grande por la que dividimos a un número cualquiera y nos vamos a fijar en el resultado de esa división. Así, como 5 es un número impar no se puede dividir por ninguna potencia de 2, salvo 20 = 1, y el cociente es 5; 12 se puede dividir entre 22 = 4 y el resultado es 3; o 56 se puede dividir por 8 y el resultado es 7.
A continuación, vamos a colocar en la primera fila todos los números cuyo resultado, al dividir por la potencia de 2 más grande posible, es 1, que son todas las potencias de 2; en la segunda fila aquellos números cuyo resultado es 3; en la tercera fila aquellos para los que el cociente es 5; y así para todos los números. En la siguiente imagen se han escrito algunos de los números en sus respectivas filas.
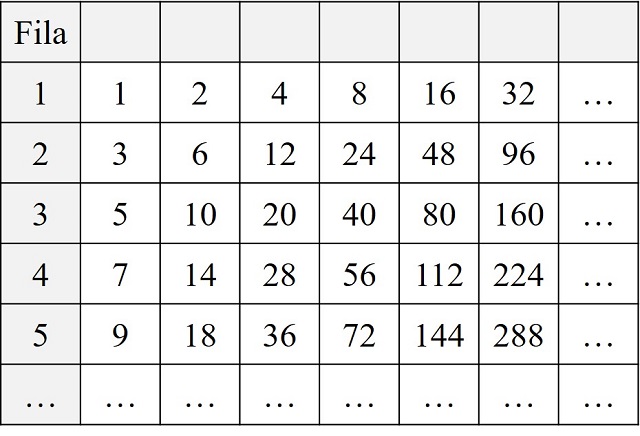
Para crear la sucesión vamos tomando cada número 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, … y nos quedamos con el número de fila en el que está el número, luego nos quedaría la siguiente sucesión 1, 1, 2, 1, 3, 2, 4, 1, 5, 3, 6, 2, … que es la misma sucesión que antes.
Una sucesión “sin razón”Vamos a terminar esta entrada del Cuaderno de Cultura Científica viendo un sencillo ejemplo que nos muestra que no todas las sucesiones autosemejantes son sucesiones autosemejantes de razón d, para ninguna d.
La siguiente sucesión se define de la siguiente forma. Se trata de ir enumerando los números en orden decreciente, hasta 1, a partir de uno dado n. Para n = 1, solo es el número 1; para n = 2, sería 2, 1; para n = 3 tendríamos 3, 2, 1; para n = 4, sería 4, 3, 2, 1; y así se continúa para los demás números. La sucesión consiste en tomar todas esas listas decrecientes de números:
1, 2, 1, 3, 2, 1, 4, 3, 2, 1, 5, 4, 3, 2, 1, 6, 5, 4, 3, 2, 1, 7, 6, 5, 4, 3, 2, 1, 8, 7, 6, 5, 4, 3, 2, 1, 9, 8, 7, 6, 5, 4, 3, 2, 1, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, …
Si se elimina la primera vez que aparece cada número, lo cual ocurre cada vez más lejos, como se muestra en la siguiente imagen, se obtendrá de nuevo la sucesión original. Esta es la sucesión A004736 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS.
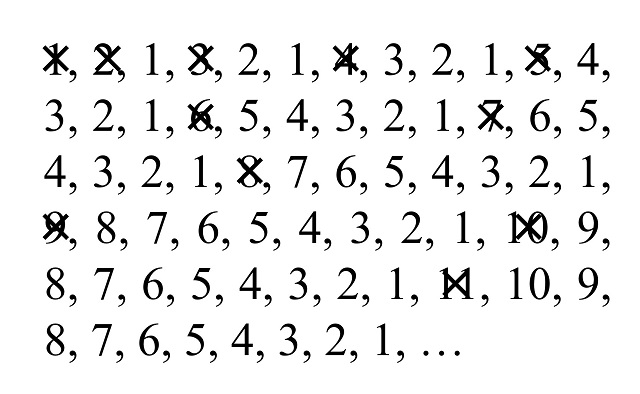
Bibliografía
1.- Tom Johnson, Rational Melodies, Editions 75, 1982.
2.- Carl Kimberling, Self-Containing Sequences, Fractal Sequences, Selection Functions, and Parasequences, Journal of Integer Sequences, Vol. 25, 2022.
3.- Carl Kimberling, Numeration systems and fractal sequences, Acta Arithmetica LXXIII, 2, 1995.
4.- Clifford A. Pickover, La maravilla de los números, MA NON TROPPO, 2002.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Sucesiones fractales se ha escrito en Cuaderno de Cultura Científica.
Rebobinado cuántico
 No existen protocolos de rebobinado en el mundo macroscópico. Foto: Sincerely Media / Unsplash
No existen protocolos de rebobinado en el mundo macroscópico. Foto: Sincerely Media / UnsplashEn el mundo macroscópico, los procesos físicos parecen desarrollarse en una dirección temporal; por ejemplo, los huevos pueden estar batidos pero no “desbatidos”. Sin embargo, en el ámbito cuántico, los procesos se pueden revertir utilizando los llamados protocolos de rebobinado. Aquí hay que tener cuidado con el lenguaje y las analogías macroscópicas. Esa reversión es más una vuelta al estado inicial, un reseteo, que un cambio en la dirección de la flecha del tiempo.
Ahora, David Trillo, estudiante de doctorado del grupo de Miguel Navascués en el Instituto de Óptica Cuántica e Información Cuántica de Viena, y sus colegas han demostrado un protocolo de este tipo para sistemas cuánticos de dos niveles. Mientras que los enfoques anteriores tenían una baja probabilidad de éxito, este se puede hacer que funcione, lo que abre la puerta a aplicaciones prácticas.
El nuevo protocolo funciona haciendo que el sistema de destino evolucione a lo largo de una superposición cuántica de diferentes caminos. En algunos caminos, se permite que el sistema progrese libremente; en los demás, actúa sobre él una operación cuántica desconocida. La posterior interferencia de estos caminos hace que el sistema vuelva a su estado inicial. Sorprendentemente, este protocolo no requiere conocimiento del sistema de destino, su dinámica interna o la operación aplicada. Además, el reseteo es óptimamente eficiente y puede alcanzar una probabilidad de éxito arbitrariamente alta.
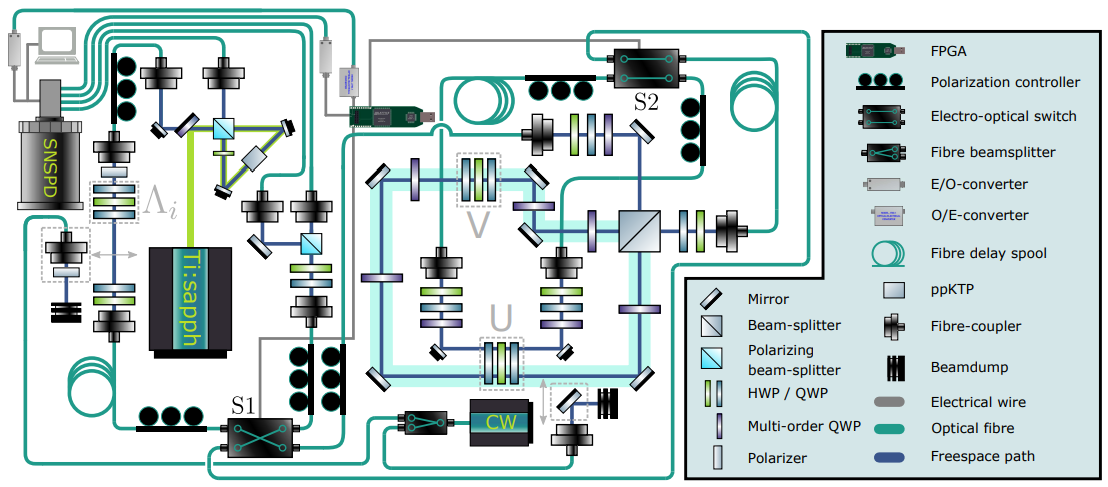
Los investigadores comprobaron el funcionamiento de su protocolo utilizando una compleja configuración óptica, en la que invirtieron la evolución de un sistema de dos niveles en forma de fotón con dos posibles estados de polarización. Destacan, sin embargo, que el enfoque no se limita a las plataformas fotónicas. Sugieren que esta capacidad de devolver un sistema cuántico a un estado pasado, de nuevo, resetear más que hacer que el tiempo cambie de dirección, con éxito garantizado tiene implicaciones para nuestra comprensión de la mecánica cuántica y podría tener aplicaciones en muchas áreas de la tecnología de la información cuántica.
Referencias:
Trillo et al. (2023) Universal quantum rewinding protocol with an arbitrarily high probability of success Phys. Rev. Lett. doi: 10.1103/PhysRevLett.130.110201
D.P. Schiansky et al. (2023) Demonstration of universal time-reversal for qubit processes Optica doi: 10.1364/OPTICA.469109
R. Wilkinson (2023) Hitting Rewind on Quantum Processes Physics 16, s34
F.R. Villatoro (2023) Podcast CB SyR 405: Agujero negro, CARMENES DR1, blázar y rebobinado cuántico La ciencia de la mula Francis
Para saber más:
Un observador cuántico de lo más útil
La carrera hacia la supremacía cuántica
Incompletitud y medida en física cuántica (serie)
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Rebobinado cuántico se ha escrito en Cuaderno de Cultura Científica.
¿Es esta la prueba definitiva de que Venus tiene volcanes activos?
La Tierra y Venus son dos planetas que, a pesar de tener un tamaño y una composición similares, han seguido caminos muy diferentes en cuanto a su evolución geológica y atmosférica, hasta tal punto que en apariencia podríamos decir que se parecen muy poco. Las temperaturas infernales en su superficie -en contraposición a la temperatura de nuestro planeta que permite agua líquida y la presencia de vida-, la ausencia de una tectónica de placas -¿es, precisamente, la tectónica de placas una propiedad emergente en los planetas rocosos o la Tierra es una rareza?- y las escasas pruebas de la existencia de volcanes activos a pesar de que, por sus similitudes con la Tierra todavía debería ser un planeta activo, dibujan una imagen de Venus extraño para lo que esperaríamos de un “gemelo” de nuestro planeta.
En los últimos años -especialmente durante la última década- está empezando a cambiar nuestra visión sobre Venus, no solo a través de los datos de las misiones más recientes, sino también a través del estudio y reinterpretación de datos tomados hace más de treinta años y que empiezan a arrojar algo de luz sobre la actividad geológica de este planeta.
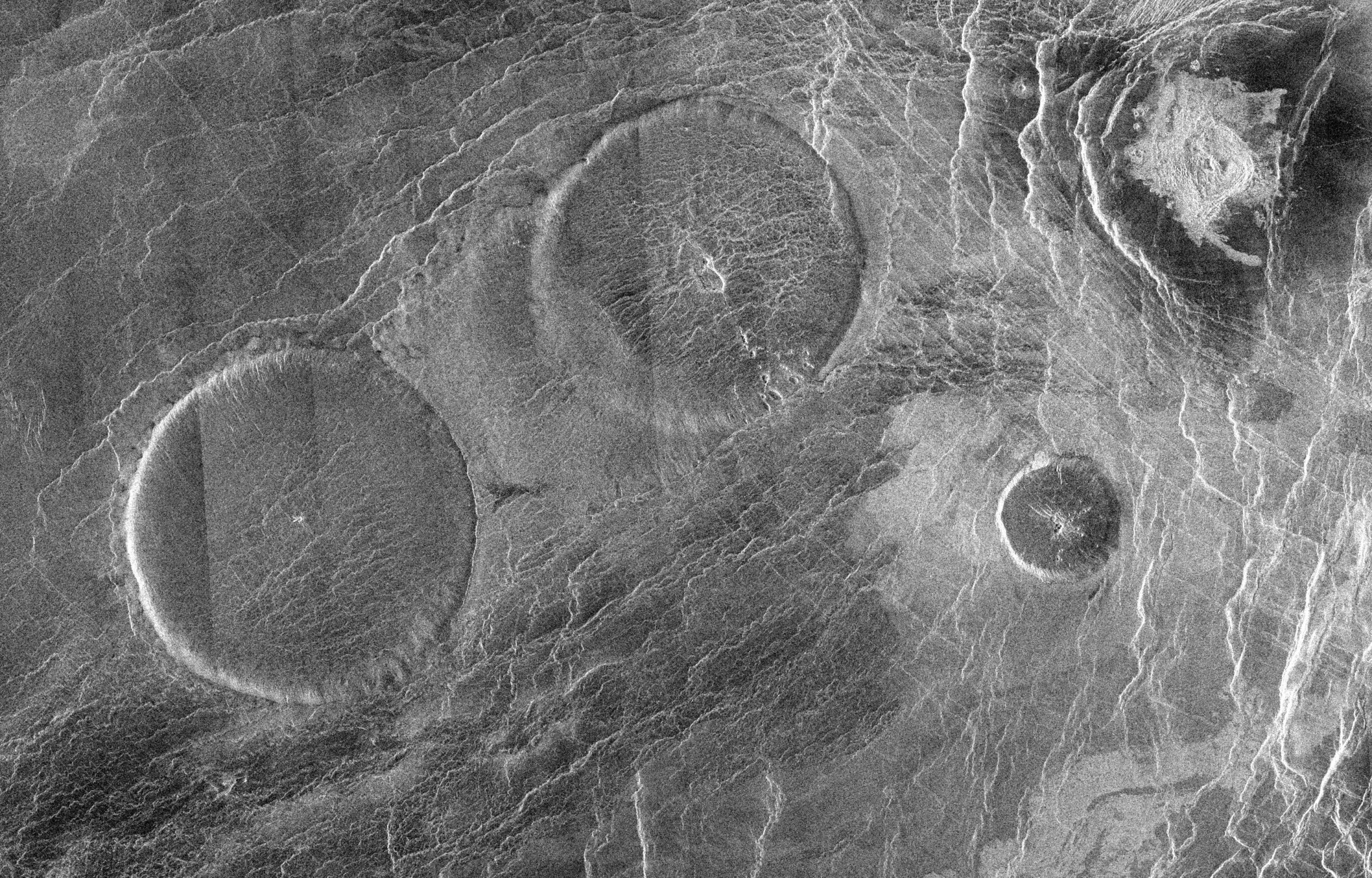 Aunque en algunas cosas seamos similares, hay formas como estas “tortitas” venusianas -llamadas pancake domes en inglés- que no tienen equivalente terrestre, y que se piensa que son domos de lava, que en este caso tienen en torno a unos 65 kilómetros de diámetro y menos de uno de altura, con un techo muy plano. Imagen cortesía de NASA/JPL.
Aunque en algunas cosas seamos similares, hay formas como estas “tortitas” venusianas -llamadas pancake domes en inglés- que no tienen equivalente terrestre, y que se piensa que son domos de lava, que en este caso tienen en torno a unos 65 kilómetros de diámetro y menos de uno de altura, con un techo muy plano. Imagen cortesía de NASA/JPL.Y es que el hecho de que no observemos actividad geológica no significa que esta no exista: Venus supone un verdadero quebradero de cabeza para observar lo que ocurre de una manera directa, ya que su superficie perpetuamente cubierta por las nubes impide la observación en longitudes de onda visibles, por lo que hay que depender de misiones que lleven un radar -capaz de tomar imágenes de su superficie a pesar de las nubes- o de algunas ventanas del infrarrojo.
Hablar de misiones que sean capaces de aterrizar en su superficie todavía es un reto técnico mayúsculo, con temperaturas que pueden superar los 450 °C y una presión atmosférica 90 veces superior a la de la Tierra, lo que limita mucho la vida de este tipo de misiones. De hecho, en los últimos años estamos viendo propuestas no tanto para misiones que se muevan por su superficie, sino a través de la atmósfera -como por ejemplo, globos- donde las condiciones garantizan una mayor supervivencia y desde donde también se podrían tomar una gran cantidad de datos e incluso detectar la actividad geológica a través del uso de infrasonidos.
Lo que si está claro es que en el planeta algo ocurre para que su superficie se vaya rejuveneciendo con el tiempo, y una de las explicaciones más favorables es la de la actividad volcánica, que a través de coladas de lava y otros fenómenos vaya cambiando su aspecto, aunque a pesar de esto los volcanes hayan permanecido muy elusivos a nuestras observaciones.
Y es que desde el año 2010 han ido apareciendo una serie de pistas que apuntan a la existencia en la actualidad de volcanes activos: La existencia de puntos calientes -en el infrarrojo- sobre zonas montañosas similares en morfología a los volcanes terrestres y que indicarían la presencia de coladas recientes en la superficie, la variable concentración de dióxido de azufre en la atmósfera de Venus -un gas que en la Tierra está relacionado con la actividad volcánica- y, por último, el polémico fosfano y que algunos autores sugieren que su origen no tenía nada que ver con la vida y que podría formarse a partir de los gases emitidos a la atmósfera durante erupciones explosivas capaces de inyectar compuestos con fosfato en las capas altas de la atmósfera.
Pero la prueba publicada la pasada semana en la revista Science es una de las evidencias más importantes en favor de la existencia de las erupciones volcánicas en la actualidad. Las imágenes de radar tomadas por la sonda Magellan a principios de la década de los 90, parecían esconder todavía algunas sorpresas.
 Reconstrucción tridimensional de Maat Mons, efectuada con los datos de la misión Magellan. Este volcán en escudo es similar en altura a los volcanes terrestres, pero tiene un diámetro mucho mayor. Imagen cortesía de NASA/JPL-Caltech.
Reconstrucción tridimensional de Maat Mons, efectuada con los datos de la misión Magellan. Este volcán en escudo es similar en altura a los volcanes terrestres, pero tiene un diámetro mucho mayor. Imagen cortesía de NASA/JPL-Caltech.Comparando imágenes tomadas en momentos diferentes por el radar de la sonda, los científicos se dieron cuenta de que entre febrero y octubre de 1991, habían ocurrido una serie de cambios en Maat Mons. Este es un volcán en escudo que se eleva casi 5 kilómetros sobre la llanura que lo circunda y que en los últimos años había atraído el interés científico porque tanto su morfología como la de las coladas que caían ladera abajo parecían indicar actividad en tiempos recientes.
¿Qué tipo de cambios han observado los científicos? Pues entre las dos imágenes se ha podido comprobar como uno de los cráteres del volcán ha cambiado de tamaño y de forma -agrandándose en este caso de una extensión inicial de 2.5 kilómetros cuadrados a unos casi 4 kilómetros cuadrados- y en el que los científicos piensan que podría haber habido un lago de lava durante los ocho meses que separan ambas imágenes.
 Comparación de las dos imágenes de la Magellan donde se pueden observar estos cambios. Se aprecia perfectamente el cambio en la morfología del cráter. Cortesía de Robert Herrick/UAF.
Comparación de las dos imágenes de la Magellan donde se pueden observar estos cambios. Se aprecia perfectamente el cambio en la morfología del cráter. Cortesía de Robert Herrick/UAF.Hay otra explicación alternativa y es que el agrandamiento de este cráter podría haber sido por un simple colapso de sus paredes debido a la propia inestabilidad del edificio volcánico o por un terremoto de origen tectónico, pero en nuestro planeta colapsos de este tipo y tamaño suelen ir cercanos en el tiempo a una erupción volcánica.
También en la segunda imagen, la de octubre, aparecen lo que podrían ser unas nuevas coladas de lava ladera abajo, aunque desgraciadamente, y debido a la resolución y ángulo de incidencia de las imágenes, no se puede descartar que ya estuviesen ahí y que simplemente destaquen más en la segunda imagen.
Si todo va bien, a principios de la próxima década podríamos tener dos nuevas misiones, VERITAS y EnVision en la órbita de Venus capaces de resolver algunas cuestiones sobre la actividad geológica del planeta, con radares de apertura sintética capaces de obtener imágenes de su superficie -y poder estudiar cambios- a una resolución sin precedentes en comparación con las que tenemos de misiones anteriores aunque quien sabe si todavía seremos capaces de encontrar mayores sorpresas escondidas en los datos de antiguas misiones planetarias.
Referencias:
Marcq, Emmanuel, Jean Loup Bertaux, Franck Montmessin, and Denis Belyaev. “Variations of Sulphur Dioxide at the Cloud Top of Venus’s Dynamic Atmosphere.” Nature Geoscience 6, no. 1 (2013): 25–28. https://doi.org/10.1038/ngeo1650.
Bains, William, Oliver Shorttle, Sukrit Ranjan, Paul B. Rimmer, Janusz J. Petkowski, Jane S. Greaves, and Sara Seager. “Only Extraordinary Volcanism Can Explain the Presence of Parts per Billion Phosphine on Venus.” Proceedings of the National Academy of Sciences of the United States of America 119, no. 7 (2022): 2–3. https://doi.org/10.1073/pnas.2121702119.
Herrick, Robert R, and Scott Hensley. “Surface Changes Observed on a Venusian Volcano during the Magellan Mission” 7735 (2023): 1–7. doi: 10.1126/science.abm7735
Shalygin, E. V., A. T. Basilevsky, W. J. Markiewicz, D. V. Titov, M. A. Kreslavsky, and Th Roatsch. “Search for Ongoing Volcanic Activity on Venus: Case Study of Maat Mons, Sapas Mons and Ozza Mons Volcanoes.” Planetary and Space Science 73, no. 1 (2012): 294–301. https://doi.org/10.1016/j.pss.2012.08.018.
Smrekar, Suzanne E., Ellen R. Stofan, Nils Mueller, Allan Treiman, Linda Elkins-Tanton, Joern Helbert, Giuseppe Piccioni, and Pierre Drossart. “Recent Hotspot Volcanism on Venus from VIRTIS Emissivity Data.” Science 328, no. 5978 (2010): 605–8. https://doi.org/10.1126/science.1186785.
Bains, William, Oliver Shorttle, Sukrit Ranjan, Paul B Rimmer, Janusz J Petkowski, Jane S Greaves, and Sara Seager. “Venusian Volcanoes,” 2022, 1–18.
Cordiner, M. A., G. L. Villanueva, H. Wiesemeyer, S. N. Milam, I. de Pater, A. Moullet, R. Aladro, et al. “Phosphine in the Venusian Atmosphere: A Strict Upper Limit From SOFIA GREAT Observations.” Geophysical Research Letters 49, no. 22 (2022). https://doi.org/10.1029/2022GL101055.
Basilevsky, A. T., E. V. Shalygin, D. V. Titov, W. J. Markiewicz, F. Scholten, Th Roatsch, M. A. Kreslavsky, et al. “Geologic Interpretation of the Near-Infrared Images of the Surface Taken by the Venus Monitoring Camera, Venus Express.” Icarus 217, no. 2 (2012): 434–50. https://doi.org/10.1016/j.icarus.2011.11.003.
Zhang, Xi. “On the Decadal Variation of Sulphur Dioxide at the Cloud Top of Venus” 9, no. 2012 (2014): 2–3.
Para saber más:
Los volcanes de Venus
Lo que Venus, el gemelo infernal de la Tierra, podría enseñarnos sobre lo que hace a un planeta habitable
Vulcanismo y habitabilidad planetaria
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Es esta la prueba definitiva de que Venus tiene volcanes activos? se ha escrito en Cuaderno de Cultura Científica.
Ayuno
 Kurt Gödel ayunó hasta morir de inanición.
Kurt Gödel ayunó hasta morir de inanición.Lo primero que ocurre cuando una persona ayuna es que su metabolismo cae. Quienes ayunan reducen su actividad o, incluso, dejan de realizar cualquier actividad que no sea imprescindible. Pero la bajada del metabolismo no solo obedece al descenso de actividad; la tasa metabólica en condiciones de reposo también cae. La frecuencia de latido cardiaco se reduce. La temperatura corporal baja de 37 C a 35,5 C. Los músculos pierden masa; también el cardiaco. El hígado y los riñones también adelgazan. Solo el encéfalo mantiene su volumen. Esto implica que ciertos procesos que, en principio, son necesarios o muy convenientes para el organismo, dejan de ejecutarse o cursan con menor intensidad. La caída de la actividad metabólica es, además, mayor que la que correspondería a la pérdida de masa corporal que, necesariamente, ha de producirse en ayunas. De esta forma se ahorran reservas de energía que pueden resultar esenciales más adelante.
El metabolismo se ralentiza debido, principalmente, a una reducción en la secreción de la hormona tiroidea, especialmente la forma activa llamada T3 o triyodotironina. Es muy probable que este descenso se deba, a su vez, a una menor secreción de leptina por los adipocitos. La leptina es una adipocina, una proteína que informa acerca de la situación de las células que la producen. Los adipocitos son las células que almacenan grasa en el organismo y son, además, los principales productores de leptina. Cuando están cargados de lípidos, la liberan a la sangre, llega al hipotálamo –en el encéfalo– e induce una disminución del apetito. Además, también promueve la liberación, por la glándula hipófisis –vecina y socia del hipotálamo–, de la hormona que estimula la glándula tiroides. Como consecuencia, aumenta la liberación de la T3, por lo que sube el metabolismo y, por ende, la producción de calor. Si bajan los niveles de lípidos en esos mismos adipocitos, estos liberan menos leptina, de manera que el apetito aumenta y el metabolismo disminuye. Quienes ayunan tienen frío.
El glucógeno, que es la reserva de carbohidratos de los animales, se agota en 24 horas en el hígado, que es quien surte al encéfalo de glucosa, y seguramente en una semana en el músculo. Junto con la reducción del metabolismo global, también se ahorran proteínas porque, en proporción a carbohidratos y grasas, se catabolizan menos. Como consecuencia, los depósitos de grasa pasan a ser el principal –casi el único–suministro de energía. De hecho, la supervivencia de las personas que ayunan depende de la magnitud de esos depósitos. Cuando se terminan los lípidos, ya solo quedan proteínas para poder obtener energía, por lo que se produce un rápido uso de estas; y como muchas cumplen funciones esenciales para la supervivencia, la muerte sobreviene rápidamente.
No es fácil prever cuánto tiempo puede permanecer con vida una persona en ayunas, porque hay muchos factores que influyen, especialmente su estado de salud antes del ayuno y el volumen de sus reservas lipídicas. Suponiendo que una persona de 70 Kg y unas reservas de grasa de 18 Kg (el 25% de su peso) decide ayunar. Tendría, de partida, unas reservas de unos 700 megajulios (un megajulio es un millón de julios: MJ); por otro lado, al ayunar, el metabolismo bajaría del valor normal en reposo (10 MJ/día) a 7 MJ/día. Por tanto, las reservas podrían durar alrededor de 100 días. Bobby Sands, un militante encarcelado del IRA que, junto con otros compañeros, hizo una huelga de hambre en 1981, falleció tras 66 días ayunando. Lo más probable es que Sands empezase la huelga con menos grasa que esos 18 Kg considerados en el supuesto teórico.
Para saber más:
Para perder peso y no recuperarlo
Límite energético a la actividad humana
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Ayuno se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: Conexiones meteorológicas

La meteorología influye nuestra vida cotidiana, esto no es ninguna novedad. Pero, en ocasiones, acontecimientos meteorológicos en conjunción con personas extraordinarias dan lugar a conexiones meteorológicas extraordinarias.
José Miguel Viñas es meteorólogo y autor de varios libros de divulgación meteorológica.
Si no ve correctamente el vídeo, use este enlace.
Más sobre el tema:
Pirocúmulos, los temibles aliados de los incendios forestales
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2022: Conexiones meteorológicas se ha escrito en Cuaderno de Cultura Científica.
Podemos prevenir el suicidio
Según el informe que elabora anualmente el Observatorio del Suicidio en España, en 2021 han fallecido por suicidio 4.003 personas, una media de 11 personas al día (75 % hombres, 25 % mujeres). Así, 2021 se convierte en el año con más suicidios registrados desde que se tienen datos (año 1906). Esas cifras suponen un aumento del 1,6 % frente a las de 2020 (cuando ya había habido un aumento del 7,4 % con respecto a 2019). En menores de 15 años ha habido un aumento del 50 % con respecto a 2020 (pasando de 14 a 22 -14 chicos y 8 chicas-). Esa es, en este momento, la principal causa de muerte en la juventud (entre 15 y 29 años).
A las muertes por suicidio hay que añadir los intentos de suicidio y la ideación suicida. Según cálculos de la OMS, existirían unos 20 intentos por cada suicidio, mientras que, según otros estudios epidemiológicos, la ideación podría afectar, a lo largo de la vida, a un porcentaje de entre el 5 % y el 10 % de la población española.
Esos son los datos «duros» del año pasado, datos que ponen en evidencia que el suicidio es un problema de salud pública de primer orden, un problema que está afectando de manera importante a adolescentes y jóvenes, y un problema en el que todas las personas estamos implicadas.
 Foto: Andreea Popa / Unsplash
Foto: Andreea Popa / UnsplashCuando nos asomamos a la realidad de la conducta suicida, tenemos que considerar varias cuestiones fundamentales.
En primer lugar, hay que considerar el ‘continuum’ cuyo final es el suicidio consumado, especialmente porque es en ese ‘continuum’ en el que vamos a poder ayudar a las personas que sufren. Así, hablaríamos de:
- Ideación suicida. Una fase puramente cognitiva, formada por pensamientos acerca del suicidio, como pensar que la vida no merece la pena, tener preocupaciones autolesivas o crear un plan específico de muerte.
- Comunicación suicida. Consiste en la transmisión a otros del deseo, el pensamiento o la intención de acabar con la propia vida. Está situado entre la ideación y la conducta, y se puede realizar de manera verbal o no verbal y sin la aparición de lesiones.
- Conducta suicida. Es el acto propiamente dicho en el que la persona se inflige daño intencionadamente y con el fin de quitarse la vida. Puede que lo consiga o que no lo consiga, tratándose entonces de una tentativa de suicidio.
Además, existen otras conductas como las ‘autolesiones no suicidas’, que son lesiones autoinfligidas de manera intencional con la expectativa de que la lesión conlleve un daño físico leve o moderado. Su misión es aplacar el dolor psicológico (aliviar un sentimiento negativo, resolver una dificultad interpersonal) a través del dolor físico. Muchas veces, esas autolesiones suponen un entrenamiento para soportar el dolor físico y, como tal entrenamiento, suponen un riesgo más para la conducta suicida.
En segundo lugar, no podemos olvidar que el suicidio es un fenómeno multicausal, una conducta compleja y multifactorial, en la que confluyen diferentes factores de riesgo, factores de protección, factores precipitantes, distintas vulnerabilidades, factores contextuales, etc. En cada uno de esos factores existe un espacio de ayuda que puede cambiar la conducta última, porque el suicidio es un fenómeno ambivalente, en el que existe a la vez el deseo de dejar de sufrir (morir) y el deseo de vivir.
Por otro lado, es esencial recordar que, si bien es un acto individual, humano, en él intervienen múltiples factores que no siempre son individuales. Lo que sí nos encontramos siempre es que la persona se ve superada en sus recursos y en sus competencias para afrontar la realidad que le toca vivir; por tanto, y nuevamente, existen espacios de ayuda que pueden ser identificados.
Por último, aunque el paso al acto es impulsivo, el suicidio tiene en la gran mayoría de los casos una planificación previa, que puede ser detectada o no. Muchas veces es difícil de detectar, porque el sufrimiento es privado y la persona intenta superarlo por sus propios medios, aunque no lo consigue. Aprender a detectar las señales de alarma nos ayuda a poder intervenir de manera preventiva, aunque no seamos expertos en salud mental.
Mitos sobre el suicidioExisten también una serie de mitos que funcionan en la sociedad en general. Algunos de esos mitos señalan que «el que se quiere matar no lo dice» y que «el que dice que se va a matar no lo hará». Sin embargo, un número significativo de personas con ideación suicida expresa claramente sus propósitos y otras muchas lo dejan entrever directa o indirectamente. Es fundamental detectar esas señales de alarma. La realidad es que 6 de cada 10 personas piden ayuda de una u otra manera en la misma semana de su suicidio y que 2 de cada 10 la piden el mismo día.
Otro mito es que «quien habla de su intención de morir en realidad lo que hace es una manipulación del entorno o una búsqueda de atención». Algunas personas amenazan o intentan suicidarse como una súplica desesperada para que los demás sepan que tienen un dolor insoportable, que no pueden afrontarlo en soledad y que necesitan ayuda. Es posible que no conozcan otras formas de expresar esos sentimientos, que crean que a nadie le importa o que nadie les puede ayudar. Las personas en crisis suicida necesitan atención y apoyo, independientemente de cómo expresen esa necesidad. También hay quien piensa que «el suicidio es un acto egoísta», cuando la realidad es que muchas personas que intentan suicidarse se sienten una carga para sus familias y precisamente quieren liberarles de ella.
Otra idea compartida socialmente que impide dar una ayuda efectiva es que «quien se quiere matar al final lo va a hacer». Sin embargo, sabemos que los pensamientos suicidas suelen ser a corto plazo y específicos de la situación, por lo que no son permanentes. La desesperanza, que siempre está presente, provoca una constricción en la visión de la vida, en la visión de sí mismo y del entorno, facilitando y potenciando la visión en túnel que señala que no hay salida, que nada va a cambiar y que el dolor será permanente. Podemos ayudar a cambiar esa visión conociendo cuáles son los factores de riesgo y de protección que tiene cada persona, ayudándola a detectar posibles desencadenantes, a encontrar otras alternativas de solución de problemas, a establecer conjuntamente un plan de intervención en crisis. Nadie puede, en soledad, con los avatares de la vida. Frente a la desconexión de la persona en crisis suicida, nuestra convicción de que podemos ayudarle es muchas veces la luz al final del túnel.
Otra creencia errónea, ampliamente compartida por la sociedad en general, es que hablar del suicidio con personas que pueden estar en una situación vital complicada les va a dar ideas que antes no tenían y puede precipitar esa decisión. Sin embargo, hay evidencia de que hablar y escuchar a una persona con ideación suicida puede reducir su miedo y angustia, eliminar la sensación de soledad y aislamiento, reducir el estigma, permitirle buscar ayuda y comenzar un camino hacia la recuperación. Es bueno hacerle saber a alguien que hemos notado que no está bien, que está luchando para estar mejor y preguntarle si tiene pensamientos suicidas. Al ponerlo en común abierta y honestamente estamos ayudando a la persona a dar los primeros pasos para obtener la ayuda que necesita. La escucha activa es crucial para hablar sobre el suicidio.
El suicidio se puede prevenirPor tanto, podemos decir abiertamente que el suicidio sí se puede prevenir. No hace falta ser una persona experta en salud mental, no hace falta ser personal sanitario. Hace falta no mirar para otro lado cuando detectamos a una persona vulnerable, hace falta dejarle hablar, escuchar con respeto, facilitarle que conecte con los recursos de ayuda profesional, a veces puede hacer falta ayudarle a mantenerse a salvo hasta que llegan los recursos especializados y siempre es necesario hacerle saber que no está sola y que podemos ayudarla.
Sobre la autora: Patricia Insúa es profesora titular del Departamento de Procesos Psicológicos Básicos y Directora del Servicio de Atención Psicológica de la UPV/EHU
Este texto apareció originalmente en campusa
Para saber más:
El peor enemigo de la prevención del suicidio
Prevención de la conducta suicida en jóvenes usando perros
El artículo Podemos prevenir el suicidio se ha escrito en Cuaderno de Cultura Científica.
Sellos muy geológicos
En la era de la digitalización en la que nos encontramos, cada vez es menos frecuente tener que enviar cartas o paquetes por correo postal, lo que hace que esas estampitas generalmente rectangulares, con letras, dibujos y colores que llevan impreso su precio y que pegamos, normalmente a lengüetazos, en los sobres también pierdan su función principal, quedando casi relegados a artículos de coleccionismo. Lo cual sería una pena, ya que hasta en los sellos postales podemos encontrar mucha Geología. Y no hace falta tener que irnos muy lejos para encontrarla.
Es muy habitual que, cada año, Correos lance tiradas de sellos conmemorativos celebrando alguna efeméride importante o dedicada a alguna temática en concreto, y desde hace años también se acuerdan de las Ciencias de la Tierra. Así que os voy a llevar a un repaso temporal de la filatelia española más geológica.
 Sellos de la tirada Minerales de España de 1994 con cuatro minerales icónicos en el desarrollo minero e industrial español y la sala central del Museo Geominero de Madrid. Imagen tomada de Correos.es
Sellos de la tirada Minerales de España de 1994 con cuatro minerales icónicos en el desarrollo minero e industrial español y la sala central del Museo Geominero de Madrid. Imagen tomada de Correos.esEntre los años 1994 y 1996 nos encontramos con la primera serie de Minerales de España emitida por la Fábrica Nacional de Moneda y Timbre. La tirada de 1994 consistía en cinco sellos en los que podíamos encontrarnos con la sala principal del Museo Geominero, situado en la sede central del Instituto Geológico y Minero de España (IGME) en Madrid, y con cuatro minerales muy comunes en territorio español y que han marcado nuestro desarrollo minero e industrial a nivel histórico: cinabrio (HgS), pirita (FeS2), esfalerita (ZnS) y galena (PbS). Por su parte, en 1995 fue el turno de la fachada de la Escuela Técnica Superior de Ingeniería (ETSI) de Minas de Madrid y de los minerales dolomita (CaMg(CO3)2) y aragonito (CaCO3). Finalmente, en 2016 se emitió un sello dedicado al mineral fluorita (CaF2) en su variedad ámbar, llamada así por su coloración anaranjada, y a la lámpara de seguridad utilizada en las antiguas minas asturianas.
 Sello homenaje al Plan MAGNA, o Mapa Geológico Nacional, emitido en 2003. Imagen tomada de Correos.es
Sello homenaje al Plan MAGNA, o Mapa Geológico Nacional, emitido en 2003. Imagen tomada de Correos.esLa primera efeméride geológica inmortalizada en forma de sello conmemorativo aparece en 1999. Se trata de la celebración del 150 aniversario de la creación, por parte de la reina Isabel II, de la Comisión para la Carta Geológica de Madrid y General del Reino. Esta comisión fue el germen del actual IGME y su principal función fue la realización del primer mapa geológico de España. Y en 2003 tenemos una nueva conmemoración geológica muy similar con la emisión de un sello homenaje al Plan MAGNA, acrónimo de Mapa Geológico Nacional. Sin entrar mucho en detalle, este plan o proyecto geológico a gran escala consistió en una actualización muy detallada de toda la cartografía geológica de España realizada por el IGME entre los años 1970 y 1971. Este hito geológico también ha quedado, nunca mejor dicho, sellado para la posteridad.
 Sellos emitidos en 2012 por la tirada Ciencia dedicados a la Geología y a la Paleontología. Imagen tomada de Correos.es
Sellos emitidos en 2012 por la tirada Ciencia dedicados a la Geología y a la Paleontología. Imagen tomada de Correos.esHay que dar un pequeño salto en el tiempo, hasta 2012, para encontrarnos de nuevo con las Ciencias de la Tierra decorando los sobres postales. Se produjo con la tirada de la serie Ciencia, en la que se editó un sello dedicado a la Geología, con un diseño de capas de colores que recuerdan a la disposición de las rocas en la corteza terrestre, y otro sello dedicado a la paleontología, con un par de fósiles de trilobites preservados en unos estratos.
 Tirada de sellos dedicada a Dinosaurios Ibéricos emitida en 2016. Imagen tomada de Correos.es
Tirada de sellos dedicada a Dinosaurios Ibéricos emitida en 2016. Imagen tomada de Correos.esPero estos no han sido los únicos fósiles filatélicos de nuestra historia. En el año 2015 se lanzó la primera tirada de la serie Dinosaurios, con unos sellos bastante particulares, ya que todos incluyen realidad aumentada y algunas otras sorpresas. Así nos encontramos con un Triceratops y un Diplodocus en 3D, un Anquilosaurio con efecto escamas y un Tiranosaurio con efecto esqueleto fosforescente. Pero si estos sellos nos parecen bastante particulares, en 2016 se emitió la segunda tirada de esta serie, con cuatro nuevos géneros de dinosaurio, esta vez autóctonos de la Península Ibérica, que tampoco son, precisamente, un trozo de papel impreso sin más. Conocemos así al dinosaurio turolense Europelta, cuyo sello está impreso con una técnica conocida como impresión lenticular, que proporciona una sensación de movimiento a la imagen. Además, tenemos a su paisano Proa, cuya imagen aparece en 3D. Y al Turiasaurus, también oriundo de Teruel y en el que se ha usado una tinta termocrómica que cambia de color cuando se somete a cambios de temperatura. Finalmente, el cuarto dinosaurio de esta serie es un Pelecaniminus oriundo de Cuenca estampado con tinta holográfica.
Para terminar este repaso geofilatélico, en los últimos años ha vuelto a relanzarse la serie de Minerales de España, con la emisión de un sello dedicado al azabache, una variedad de carbón, en el año 2020, y, de nuevo, a la pirita en 2022.
Sin duda la Geología, en todas sus vertientes, está en todo lo que nos rodea. Incluso nos la podemos encontrar en el frontal de un sobre de correos cuando recibimos una carta.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Sellos muy geológicos se ha escrito en Cuaderno de Cultura Científica.
Calculando con los números escritos “a la Cauchy”
«No me imagino una vida más plena que una vida dedicada a la matemática»
Augustin Louis Cauchy (1789-1857) fue un matemático francés, uno de los más prolíficos de todos los tiempos en esta disciplina científica. Investigó en todas las áreas matemáticas de su época, siendo pionero en análisis; entre otros, introdujo las funciones holomorfas, los criterios de convergencia de series y las series de potencias.
 Composición realizada con la imagen de Cauchy (Wikipedia) y capturas de pantalla del artículo que se cita a continuación (Gallica).
Composición realizada con la imagen de Cauchy (Wikipedia) y capturas de pantalla del artículo que se cita a continuación (Gallica).En 1840, en la nota Sur les moyens d’éviter les erreurs de calculs numériques (Sobre la manera de evitar errores de cálculo numérico) publicada en los Comptes-Rendus de l’Académie des Sciences, Cauchy proponía una manera diferente de escribir los números usando dos tipos de dígitos, uno positivo y el otro negativo.
Imaginemos que, en un número escrito en cifras, se coloca el signo sobre la cifra correspondiente a las unidades de cierto orden para expresar que las unidades de ese orden deben tomarse efectivamente con el signo −. Podremos distinguir en cada número dos especies de cifras, algunas positivas, y las otras negativas. […] Con este planteamiento, obviamente podremos escribir cualquier número con dígitos cuyo valor numérico sea como máximo igual a 5.
En esta nueva notación propuesta por Cauchy, los números del 1 al 20 pueden escribirse como se indica en la siguiente tabla:
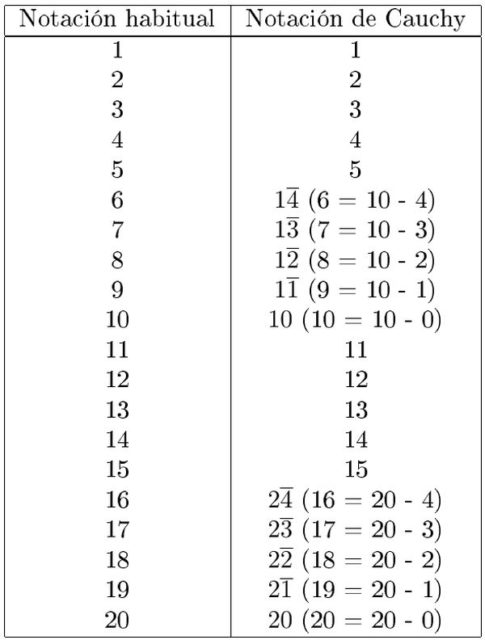 Tabla de los 20 primeros números naturales con la notación de Cauchy.
Tabla de los 20 primeros números naturales con la notación de Cauchy.
La escritura de un número con la notación de Cauchy no es única. Por ejemplo, el número 55 puede escribirse de estas tres maneras diferentes:
![]()
Para encontrar el opuesto de un número con la notación de Cauchy, basta con poner una barra sobre los números que no la tenían y eliminarla de aquellos que sí la llevaban (se cambia el signo de las operaciones indicadas en la escritura de Cauchy, al ser la suma de un número y su opuesto igual a 0).
Sumando números con la notación de CauchySumar no es difícil con la notación propuesta por el matemático francés. Debajo se muestra una tabla de sumar.
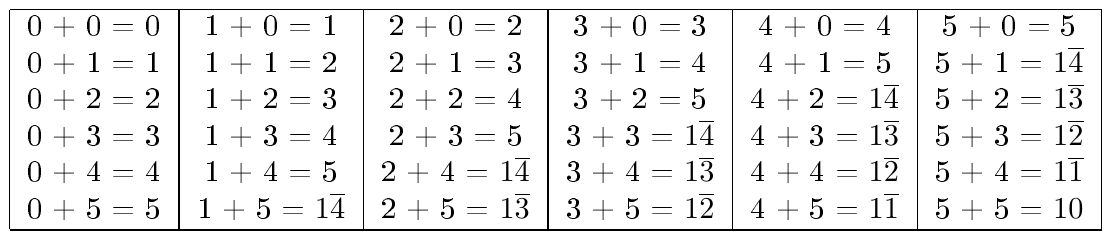
Restar dos números consiste en sumar al minuendo el opuesto del sustraendo. Como ya sabemos la manera de calcular el opuesto de un número con la notación de Cauchy, basta con entender y aplicar las reglas de la suma.
Cambio de una forma de numeración a la otraPara pasar de la notación usual a la notación de Cauchy basta con sustituir en el número dado cada secuencia continua de cifras positivas mayores que 4 por cifras negativas que forman, en valor absoluto, el complemento aritmético de esta sucesión, y añadir a la cifra que la precede una unidad. Si el último dígito de la secuencia es 5, podríamos ignorarlo y excluirlo de ella. Se muestra un ejemplo debajo (los números en la notación usual están en negro y con la notación de Cauchy en rojo para entender mejor la operación):
![]()
Inversamente, para transformar un número con la notación de Cauchy en un número con la notación estándar, basta con reemplazar cada secuencia continua de números negativos por el complementario aritmético de esta secuencia, y disminuir en una unidad la cifra positiva que le precede. Se muestra un ejemplo debajo:
![]()
En su artículo, Cauchy explica que, como con su notación las cifras no sobrepasan el 5, la tabla de multiplicar puede reducirse a la cuarta parte de su extensión habitual, y basta con efectuar multiplicaciones parciales por 2, 3, 4 = 2 x 2 y 5 = 10/2. El matemático recuerda, además, que el producto de dos cifras de la misma especie (ambas positivas o ambas negativas) es siempre positivo, mientras que el producto de dos cifras de distinta especie (uno positivo y otro negativo) será negativo. Así, se obtiene de este modo una sencilla tabla de multiplicar.
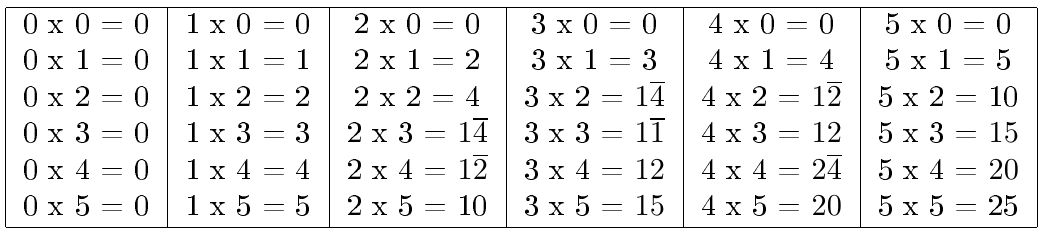
Dos números se multiplican de la misma manera en la que lo hacemos con la notación habitual, y usando las tablas de sumar y multiplicar que se han introducido antes. Para la división, de nuevo, basta con actuar como tenemos costumbre, con las nuevas reglas aprendidas.
¿Por qué esta notación?Cauchy no pretendía sustituir el método clásico de numeración por el suyo, proponía usarlos en paralelo. Comentaba, de hecho, en su nota en los Comptes-Rendus de l’Académie des Sciences:
[…] Para poder ofrecer el resultado de un cálculo como digno de ser adoptado con confianza, lo que debe hacerse no es repetir el mismo cálculo dos veces siguiendo la misma ruta, dado que es bastante natural que uno vuelva a caer en un error ya cometido. Por el contrario, es determinar todo de tal manera que, por medio de dos sistemas de operaciones muy distintos, lleguemos de nuevo a resultados idénticos.
Referencias
-
Gérard Grancher, Compter comme Cauchy ou diviser par 4 la taille des tables de multiplication, Café des maths, Images des mathématiques, 14 de agosto de 2020
-
Augustin Louis Cauchy (1840). Sur les moyens d’éviter les erreurs de calculs numériques, Comptes-Rendus de l’Académie des Sciences 11, 789-798, 826 [en Gallica, Œuvres complètes, série 1, tome 5, 431-442].
Para saber más:
De la grandeur a las matemáticas puras
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Calculando con los números escritos “a la Cauchy” se ha escrito en Cuaderno de Cultura Científica.
Polígonos de sal
En salinas, salares, en desiertos y lagos secos se encuentran patrones de polígonos entrelazados formados por crestas estrechas que crecen sobre un suelo con una costra de sal. El origen de estos polígonos, de unos pocos metros de ancho, no tiene una explicación que justifique su tamaño y forma distintivos. Ahora un equipo de investigación cree que puede explicar cómo se forman estos patrones a través de la interacción entre el fluido que se mueve en el suelo y el fluido que se evapora en la superficie. El nuevo trabajo parece ofrecer una explicación unificadora del crecimiento de estos polígonos en una amplia gama de condiciones físicas diferentes.
 Foto: Mahdi Kalhor / Wikimedia Commons
Foto: Mahdi Kalhor / Wikimedia CommonsLos polígonos de sal se forman en regiones donde la tasa de evaporación del agua del suelo excede significativamente la tasa de precipitación. En esos lugares la evaporación en la superficie se equilibra con un flujo continuo de agua subterránea de fuentes más distantes, como montañas cercanas. Esta agua sube a la superficie y provoca una evaporación continua, incluso en ausencia de lluvias, y deja un residuo de sal. Pero sigue siendo un misterio por qué estos residuos se forman en crestas que trazan patrones poligonales. También es desconcertante por qué los patrones resultan ser tan similares dondequiera que ocurran, a pesar de las diferencias locales en geología, química de la sal y condiciones ambientales.
Para encontrar una explicación los investigadores desarrollaron un modelo matemático de los procesos que ocurren justo debajo de la superficie. Este modelo, basado en la dinámica de fluidos y otros principios geofísicos, predice que el lecho de un lago seco típico desarrollará una capa de fluido muy rica en sal cerca de su superficie como resultado del residuo salado que se encuentra encima.
Esta capa salada densa descansa inestablemente sobre un fluido menos denso que se encuentra debajo. Si la fuerza impulsora de la evaporación es suficientemente fuerte, se desarrolla un flujo convectivo en el fluido: el agua más salada se hunde y el agua menos salada sube, lo que genera columnas de fluido que fluyen hacia arriba y hacia abajo, como las que aparecen en el agua hirviendo. Usando parámetros de fluidos característicos de los lechos de lagos salados reales, los investigadores predicen que estos ciclos convectivos tendrán aproximadamente entre 1 y 2 m de ancho, sospechosamente similares a los tamaños de los polígonos observados.

Las simulaciones muestran que los ciclos convectivos finalmente generan un conjunto de columnas estrechas de agua de alta salinidad que descienden de la superficie. Estos penachos luego forman una red poligonal cerrada de láminas verticales descendentes que rodean zonas de fluido ascendente.
Esta red de ciclos convectivos impulsa la formación de las crestas de sal. En el interior de cada celda de convección, donde el agua de baja salinidad fluye hacia arriba, la costra de sal crece más lentamente porque está en contacto con agua menos salada. En contraste, en los límites de las celdas ubicados directamente sobre las láminas de afloramiento, una mayor cantidad de sal fluye hacia arriba la costra. Como resultado, las crestas estrechas crecen rápidamente y construyen el patrón de red poligonal.
Para comprobar el modelo el equipo realizó simulaciones detalladas y las comparó con las mediciones realizadas en lugares reales. Excavando debajo del patrón de crestas encontraron evidencia de penachos salados que fluyen hacia abajo, exactamente como predice el modelo, con agua menos salada que fluye hacia arriba en los centros planos de los polígonos. En general, los investigadores descubrieron que su modelo podía explicar no solo los patrones emergentes básicos, sino también las escalas de longitud clave: los anchos de las células convectivas y las crestas de sal.
Referencias:
Jana Lasser, Joanna M. Nield, Marcel Ernst, Volker Karius, Giles F. S. Wiggs, Matthew R. Threadgold, Cédric Beaume, and Lucas Goehring (2023) Salt Polygons and Porous Media Convection Phys. Rev. X doi: 10.1103/PhysRevX.13.011025
Mark Buchanan (2023) Why Death Valley Is Full of Polygons Physics 16, 31
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Polígonos de sal se ha escrito en Cuaderno de Cultura Científica.
La fiebre: incomprendida, con mala fama y rodeada de mitos
El cuerpo humano es un sistema biológico extremadamente complejo con multitud de mecanismos de defensa que cumplen un objetivo principal: mantenernos con vida. Sin embargo, no todas las reacciones fisiológicas que suceden en nuestro organismo reciben la comprensión que merecen. La fiebre, por ejemplo, destaca por su mala reputación en casi todo el mundo y por estar acompañada de numerosos mitos que llevan a prácticas sanitarias erróneas para combatirla.
 Foto: Matteo Fusco / Unsplash
Foto: Matteo Fusco / UnsplashSon los padres, especialmente aquellos primerizos, los que más aterrorizados suelen estar con la fiebre si esta se presenta en sus retoños porque la perciben como un riesgo para su vida. Con la idea de mantenerla a raya, muchos progenitores administran a sus hijos medicamentos antitérmicos, que no están precisamente libres de efectos adversos. De hecho, una reciente encuesta nacional realizada en Estados Unidos muestra que uno de cada tres padres dan a sus hijos, de forma injustificada, fármacos para mitigar la fiebre. Este fenómeno no es aislado. En otros muchos países, entre ellos España, los padres también demandan con mucha frecuencia a los pediatras o a los farmacéuticos tratamientos para la fiebre, alentados por un miedo irracional a esta.
En prácticamente casi todos los casos, la fiebre es una reacción natural de defensa frente a infecciones (con frecuencia, provocadas por virus y bacterias). La elevación de la temperatura corporal se produce de forma precisa gracias al termostato del cuerpo (el hipotálamo) y su fin es dar ventaja al sistema inmunitario a la hora de destruir los agentes patógenos y dificultar la proliferación de estos últimos. En otras palabras, la fiebre es un aliado, no un enemigo. Por supuesto, tener fiebre no es un proceso agradable, puede generar malestar general y debilidad. Se trata de un precio a pagar por acortar el proceso infeccioso y tener más opciones frente al microorganismo invasor.
Conforme más se conocen los beneficios de la fiebre, a través de diferentes estudios científicos, más claro resulta que tratar de bajarla, cueste lo que cueste, puede resultar contraproducente. Por esta razón, en medicina cada vez está más extendida la práctica de tratar la fiebre solo cuando esté justificado, ya sea porque esta es demasiado elevada o porque provoca un sufrimiento notable en la persona. En otras palabras, hay que tratar a la persona y no al termómetro. En ese sentido, diferentes instituciones sanitarias como la Asociación Española de Pediatría, la Clínica Mayo o el Instituto Nacional de Salud y Excelencia Clínica de Reino Unido solo recomiendan combatir la fiebre en casos puntuales.
Los mitos más destacados en torno a la fiebreMito 1: La fiebre es peligrosa porque puede provocar daño cerebral e incluso la muerte.
Esto no es así en la casi totalidad de los pacientes con fiebre. Para que este proceso pudiera causar lesiones cerebrales, graves e irreversibles, la elevación de la temperatura corporal tendría que ir más allá de los 42 ºC (para provocar la desnaturalización de diversas proteínas). En estos casos, en los que hay fiebre elevada, sí se recomienda rebajarla con medicamentos antitérmicos, pero normalmente esto no llega a suceder.
Mito 2: La fiebre provoca graves convulsiones en los niños y hay que tratarla para evitar su aparición.
Muchos padres tienen auténtico pavor a las convulsiones que pueden aparecer en algunos menores durante un proceso infeccioso porque perciben que es un signo de alarma. En realidad, las convulsiones en estos casos no son signos de alarma: suelen ser leves y, además, no guardan relación con la temperatura corporal. De hecho, las convulsiones suelen aparecer más con fiebres bajas y los fármacos antitérmicos no previenen su aparición.
Mito 3: La fiebre debe rebajarse con medidas físicas como baños o paños fríos o desnudando a los niños.
Numerosas instituciones médicas desaconsejan estas medidas. Estas acciones suelen ser inútiles para rebajar la temperatura corporal y, en ocasiones, pueden incluso aumentarla al provocar la contracción de los vasos sanguíneos de la piel.
Cuando la fiebre sí es un signo de alarmaPor sí sola, la fiebre es un proceso normal durante una enfermedad infecciosa. Sin embargo, en ocasiones, este signo puede ser motivo de sospecha de que algo no va bien. Estos son los casos en los que la fiebre sí debería preocuparnos y tendríamos que acudir al médico para averiguar qué hay detrás:
Fiebre de origen desconocido.
Una fiebre que dura más de tres semanas, ya sea de forma constante o apareciendo y desapareciendo, sin que existan signos obvios de enfermedad infecciosa es motivo de peso para ir al facultativo.
Fiebre por encima de 40 ºC en cualquier persona o fiebre de 3 o más días de duración en niños.
En estos casos, hay que acudir sin demora a la consulta para que establezca el tratamiento oportuno.
Fiebre en un bebé menor de 3 meses.
Es necesario acudir rápidamente a urgencias para averiguar la causa de la fiebre en un infante de tan corta edad.
Además de estos supuestos, hay determinados signos de alarma que pueden aparecer junto a la fiebre y que justifican ir rápidamente a Urgencias. Entre ellos encontramos la rigidez de nuca (sospecha de meningitis), confusión mental, manchas en la piel o coloración pálida-grisácea, dificultad para respirar, vómitos constantes, dolor al orinar o producción reducida de orina… En otras palabras, a la hora de decidir si una persona con fiebre debe o no acudir al médico, no hay que obsesionarse con lo que marca el termómetro, sino centrarse sobre todo en cómo está la persona.
Para saber más:
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo La fiebre: incomprendida, con mala fama y rodeada de mitos se ha escrito en Cuaderno de Cultura Científica.
Luz al comienzo del túnel
El ser humano tiende a asociar el túnel con el tránsito hacia lo desconocido. Cuando bajamos al prosaico mundo de las infraestructuras, esta concepción tan trascendente no solo se mantiene, sino que adquiere un impacto económico, energético, medioambiental y, por supuesto, sobre la seguridad, de proporciones descomunales. Entrar en un túnel significa entrar en la más absoluta oscuridad, por lo que su iluminación es un reto de primera magnitud que el conductor ni siquiera imagina cuando se aproxima a esas bocas iluminadas que nos adentran en las profundidades de las montañas. Inyectar luz del sol en los túneles es una propuesta audaz, y está en marcha.
 Foto: Daniel Jerez / Unsplash
Foto: Daniel Jerez / UnsplashInvestigadores de la Universidad de Granada y de la Universidad de Sevilla hemos diseñado un modelo novedoso para inyectar la luz solar en los túneles de las carreteras: se trata de un sistema acoplado en el que la captura del flujo luminoso se consigue gracias a colectores de luz (que funcionan a modo de sumideros) situados en el exterior, antes de la entrada del túnel, y su guía se realiza a través de lumiductos a ras de suelo o enterrados bajo los arcenes, hasta el interior del tubo, donde un mecanismo de apertura y distribución del flujo luminoso proyecta la luz hacia la bóveda, en la que una nueva superficie de geometría compleja logra una distribución homogénea de la iluminación sobre la calzada del túnel.
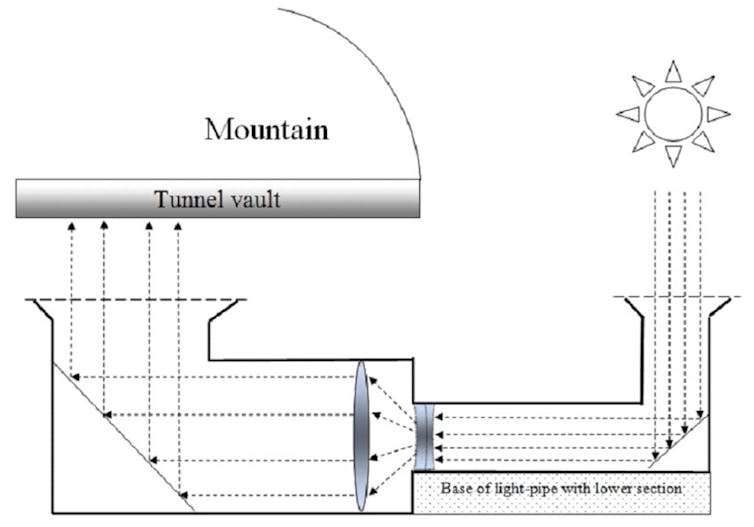
Inyección de luz solar mediante sistema óptico acoplado basado en tierra.
Elsevier, CC BY
Pero ¿por qué es tan relevante la iluminación de túneles y el aprovechamiento de la luz del Sol?
Peligro, trampa mortalAl hablar de infraestructuras del transporte como carreteras, puentes o túneles, partimos de una premisa: sus usuarios no pueden perder la vida por una percepción visual deficiente.
Los accidentes en túneles son más graves porque una salida de la vía conlleva la colisión con una pared de hormigón y, por si fuera poco, se convierten en trampas mortales en caso de incendio. Por tanto, las exigencias visuales y psicológicas son muy altas.
Estas dos razones no son independientes entre sí sino que la primera suele ser consecuencia de la segunda. Por todo esto, la calidad del alumbrado de los túneles es un factor fundamental del que depende nuestra reacción ante cualquier situación de peligro.
Hace falta más luz de día que de nocheComenzamos con una paradoja: en túneles, los conductores precisan niveles de iluminación mucho más altos durante el día que durante la noche. Hablamos de niveles de iluminación aunque en realidad trabajamos con una magnitud física llamada luminancia.
Esta paradoja responde a las características de las células de la retina que transforman la luz en impulsos nerviosos y que nuestro cerebro interpreta como sensaciones visuales. Son de tres tipos: conos, que trabajan a alta luminosidad, bastones, a baja luminosidad, y células ipRGC, de las que aún queda mucho por aprender y que canalizan vías no visuales como los ritmos circadianos, somnolencia, estrés, etc.
En conducción diurna nuestro cerebro recibe información de los conos, mientras los bastones permanecen saturados porque no pueden trabajar con tanta luz. Sin embargo, al pasar a ambientes poco iluminados el cerebro procesa señales de conos y bastones. Al entrar en el túnel los conos no funcionan porque necesitan mucha luz y los bastones están saturados. Es evidente que un conductor que recorre 28 metros cada segundo no puede permitirse esta lentísima adaptación visual. Por eso durante el día es necesario proporcionar una elevada luminancia especialmente en los 100-120 primeros metros del túnel (llamados zona umbral) para que los conos puedan funcionar como en el exterior. Esto conlleva elevados consumos de energía, proyectores, cableado y dispositivos auxiliares, un costoso mantenimiento, reciclado, etc.
La cuestión es si podríamos hacer el alumbrado de túneles más sostenible sin comprometer la seguridad. La respuesta es sí.
Contamos con distintas estrategias para conseguirlo.
Disminuir las necesidades lumínicasPodemos colocar alrededor del portal de entrada al túnel elementos que reflejen poca luz solar, como vegetación o incluso placas fotovoltaicas, que además pueden alimentar dispositivos de balizamiento o emergencia del propio túnel. Así disminuye la luminosidad exterior y la adaptación del conductor al interior requiere menos luz. También se ha propuesto reducir la velocidad máxima de circulación por debajo de 100 km/h por ser ésta proporcional a la luminancia necesaria en el interior.
 Placas solares sobre entrada de túnel para disminuir la luminosidad ambiental.
Placas solares sobre entrada de túnel para disminuir la luminosidad ambiental.Elsevier, Author providedUna inyección de energía en el túnel
También es posible desplazar la zona umbral fuera del túnel mediante estructuras que permitan el paso de cierta cantidad de luz, o inyectándola en el interior mediante sistemas ópticos como guías de luz tipo periscopio (lumiductos), difusores etc.
La primera opción consiste en la instalación de pérgolas o estructuras semitransparentes en la entrada del túnel como complemento lumínico a los proyectores. Aunque el ahorro es notable, el alargamiento del túnel con el consiguiente peligro, el posible deslumbramiento y la falta de uniformidad a ciertas horas del día son inconvenientes a considerar.
 Inyección de luz solar en el túnel de Huashuyan.
Inyección de luz solar en el túnel de Huashuyan.International Journal of Photoenergy, CC BY
Finalmente, la luz solar puede introducirse en túneles mediante sistemas ópticos más o menos sofisticados sin necesidad de alargarlos. En la década pasada, un túnel de Huashuyan (China) incorporó un sistema de distribución de luz solar con lumiductos de fibra óptica.
Los dilemas de la inyección de luz solarUn problema de la inyección es su alto coste al requerir túneles con altura (gálibo) no estándar. Además, el Sol no está permanentemente alineado con la entrada de los lumiductos, lo que reduce drásticamente el flujo luminoso captado y origina reflexiones que bajan aún más el rendimiento.
Para superar estos inconvenientes de la inyección de luz solar, se ha barajado instalar heliostatos exteriores que capten los rayos y los inyecten en los lumiductos en condiciones óptimas, solución no exenta de problemas.
Lo novedoso del sistema que acabamos de proponer para inyectar luz solar en túneles es que acopla colectores, lumiductos y bóveda distribuidora. Los colectores, situados en los laterales de la carretera, captan la luz y la llevan a unos lumiductos con un juego de lentes en su interior. Finalmente, una bóveda de propiedades reflectoras especiales la proyecta sobre la carretera. La ventaja, respecto a otros sistema descritos, es que ofrece la posibilidad de basar los lumiductos en tierra sin suspenderlos en altura. Así no se requiere gálibo especial y se pueden instalar en túneles ya existentes.
El enorme impacto del alumbrado de túneles sobre la seguridad y la sostenibilidad nos lleva a buscar soluciones de las que poco a poco empezamos a beneficiarnos y cuyas perspectivas son realmente prometedoras.![]()
Sobre el autor: Antonio Manuel Peña García, Catedrático del Área de Ingeniería Eléctrica, Universidad de Granada
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Luz al comienzo del túnel se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: Un biólogo con datos sospechosos

¿Cuál es la probabilidad de que unos resultados experimentales salgan tan, tan similares a lo que dice la teoría? ¿No habrá el investigador hecho trampa? El incomparable Juan Antonio Cuesta analiza las estadísticas de un caso real muy famoso.
Juan Antonio Cuesta es catedrático de probabilidad y estadística en la Universidad de Cantabria.
Si no ve correctamente el vídeo, use este enlace.
Más sobre el tema:
Experimentación y evidencia: dos visiones opuestas
No se puede cambiar el azar
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2022: Un biólogo con datos sospechosos se ha escrito en Cuaderno de Cultura Científica.
Influencia de la obesidad de la madre sobre la placenta y el crecimiento fetal
Un equipo de investigación de la UPV/EHU y del Instituto Biocruces-Bizkaia ha estudiado cómo influye el índice de masa corporal de la madre al inicio del embarazo en patrones moleculares de la placenta, y si puede incidir de alguna manera en el desarrollo del feto y posterior salud en la infancia.
 Foto: Vanessa / Unsplash
Foto: Vanessa / UnsplashEl equipo ha realizado un metaanálisis sobre “el impacto del índice de masa corporal de la madre al inicio del embarazo en los perfiles moleculares de la placenta y más concretamente en la metilación del ADN de la placenta (adición de un grupo formado por un carbono y tres hidrógenos, en una posición determinada de la molécula de ADN)”, señala Nora Fernández Jiménez, profesora de la Facultad de Medicina y Enfermería e investigadora del departamento de Genética, Antropología Física y Fisiología de la UPV/EHU. “Se trata del estudio sobre metilación del ADN de la placenta más grande llevado a cabo hasta la fecha, con un total de 2.631 parejas de madres e hijos/as de Europa, Norte América y Australia”, añade Fernández Jiménez.
Al contrario de las más conocidas mutaciones —sustitución de un nucleótido por otro en la secuencia del ADN—, la metilación es una modificación del ADN que regula la expresión génica sin alterar la secuencia. “Estudios recientes señalan que la metilación es el puente entre el ambiente intrauterino y el genoma del feto. Por ejemplo, debido al ambiente puede ocurrir que aumente el nivel de metilación de una región del genoma. Ese aumento generalmente conlleva que el ADN se vuelva más compacto, y, en consecuencia, la maquinaria de transcripción no puede acceder a dichas regiones y se produce un silenciamiento de algunos genes. También podría ocurrir lo contrario, es decir, que en respuesta al ambiente decrezca el nivel de metilación en ciertas regiones del genoma. En ese caso, el ADN obtiene una conformación abierta, a la cual las maquinarias de transcripción tienen una mejor accesibilidad y, por tanto, aumentaría la expresión génica. En ambos casos, la secuencia sigue intacta pero el genoma se comporta de una forma u otra», explica la investigadora de la UPV/EHU.
“En este trabajo hemos identificado 27 sitios en los que se observan variaciones en la metilación del ADN que parecen específicas de la placenta”, señala Fernández. Conviene recordar que la placenta es un órgano fundamental en el crecimiento y desarrollo fetal, porque es el órgano que conecta a la madre con el feto y el órgano a través del cual el feto se alimenta. “Muchos de esos sitios identificados se encuentran cerca de genes relacionados con la obesidad y están enriquecidos en rutas metabólicas del cáncer y del estrés oxidativo. No significa que las criaturas nacidas de madres con problemas de obesidad vayan a desarrollar cáncer, pero sí que es cierto que la placenta tiene un comportamiento similar a un tumor, crece de forma muy rápida, y eso nos hace pensar que existe una repercusión sobre el funcionamiento de la placenta y el crecimiento fetal”, añade Nora Fernández.
Todos estos resultados sugieren que la metilación del ADN de la placenta podría ser uno de los mecanismos por los cuales la obesidad materna se asocia con resultados adversos de salud metabólica en la infancia, aunque Fernández advierte que se necesitarán más estudios para corroborar estos hallazgos.
Referencia:
Fernandez-Jimenez, N., Fore, R., Cilleros-Portet, A. et al. (2022) A meta-analysis of pre-pregnancy maternal body mass index and placental DNA methylation identifies 27 CpG sites with implications for mother-child health. Commun Biol 5, 1313 doi: 10.1038/s42003-022-04267-y
Para saber más:
La obesidad infantil podría iniciarse antes de la concepción
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Influencia de la obesidad de la madre sobre la placenta y el crecimiento fetal se ha escrito en Cuaderno de Cultura Científica.
No olvidar Seveso
Ocurrió el sábado 10 de julio de 1976 a las 12:37 horas, la hora de la comida para los habitantes del lugar. Se escuchó un silbido sordo, amenazador, extraño. Un incendio se había declarado en uno de los edificios de una industria situada en el pueblo de Seveso, a unos 25 kilómetros al norte de Milán, en la Lombardía italiana. Seveso entonces tenía unos 17000 habitantes y algo más de 20000 en la actualidad. Aquel incendio liberó al ambiente, desde la planta, la dioxina TCDD que llegó a zonas pobladas y provocó efectos desastrosos.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsLa planta industrial pertenecía a ICMESA o Industria Chimiche Meda Società, subsidiaria de Givaudan que, a su vez, pertenecía a Hoffmann-La Roche. La población la consideraba no peligrosa pero, en la fábrica se producía, además de aceites esenciales para perfumes y cosméticos, y como subproducto de la fabricación del herbicida conocido como 2,4,5-T y del jabón hexaclorofeno, la dioxina TCDD o 2,3,7,8-tetraclorodibenzo-p-dioxina, sustancia muy peligrosa y con altos niveles de letalidad. Era un defoliante que formaba parte del Agente Naranja. Se había utilizado en la guerra de Vietnam para eliminar la vegetación de la selva y descubrir a los grupos del Vietcong.
El incendio, provocado por un error humano, liberó una nube en forma de aerosol que contenía TCDD en cantidad entre algunos cientos de gramos y hasta algunos kilogramos, además de hidróxido de sodio, glicol y triclorofenato de sodio. De la válvula de seguridad de la chimenea del reactor de TCDD escapaba una nube grisácea compuesta de diminutas partículas, como arena fina, que llovieron alrededor de los obreros de la fábrica. Era una espesa neblina blanca, con olor a medicina y a cloro.
La nube, que se movía hacia el sur, en dirección a Milán, afectó a unos 18 kilómetros cuadrados de los alrededores de factoría. En poco tiempo había recorrido más de cinco kilómetros y la arenilla blanca caía sobre tejados y campos.
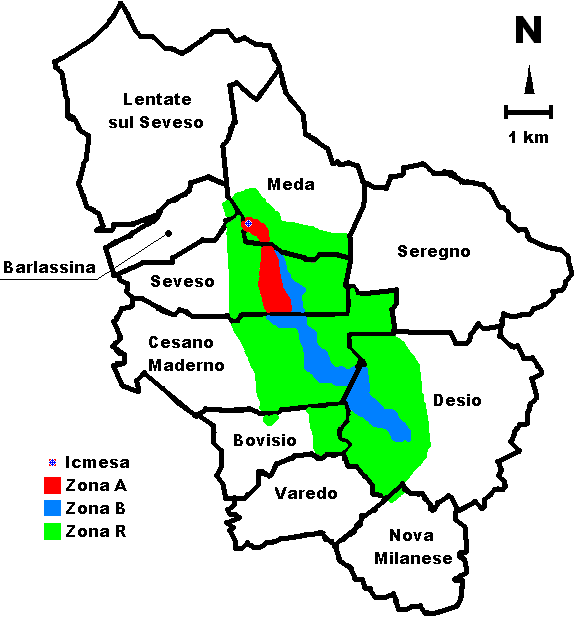 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsLa zona afectada se dividió en tres áreas. El área A, con unos dos kilómetros de longitud y 500 metros de anchura, tenía una concentración de TCDD superior a 50 microgramos por metro cuadrado de suelo y allí vivían 736 residentes que fueron evacuados el sábado 24 de julio. Poco después, el 29 de julio, se amplió la zona a evacuar y otros 600 habitantes fueron trasladados a lugares seguros.
El área B tenía entre 5 y 50 microgramos por metro cuadrado de suelo y vivían 4700 personas. Y en el área R, con menos de 5 microgramos de TCDD por metro cuadrado, vivían 31800 residentes. A todos ellos se les recomendó no tocar o comer vegetales de los cultivos locales ni aves de corral crecidas en la vecindad.
A los cuatro días, el 14 de julio, los médicos detectaron un aumento de erupciones cutáneas extensas tanto en adultos como en niños. Parecía evidente que se debían al paso de la nube de la fábrica, pero no conocían la naturaleza de la contaminación y, por tanto, no sabían cuál era el tratamiento adecuado. Desde la fábrica habían enviado muestras a Suiza, a la central, pero no tenían respuesta todavía. Además, comenzaron a encontrar gallinas y pájaros muertos y mascotas enfermas como gatos o perros, así como tomates quemados en las huertas y conejos sangrando por la nariz y los ojos. Días más tarde se estableció que la mortalidad animal era casi del 90%. En los días siguientes se sacrificaron unos 50000 animales en las zonas A y B. Incluso las abejas y sus panales se destruyeron en un radio de cinco kilómetros de la zona contaminada.
Sin embargo, la situación general no había llamado la atención en la prensa o la radio. Las noticias se propagaron lentamente. Los incidentes con pájaros o animales aparecían dispersos en varios medios de comunicación. En las personas las enfermedades eran bastante leves con erupciones cutáneas o molestias digestivas. Los médicos, más que alarmados estaban molestos por la falta de informaciones creíbles. Los relatos que empezaban a dispersarse entre la población se creían más bien rumores. Pero el viernes a la tarde llegó al hospital una niña de dos años con grandes llagas por todo el cuerpo. Y el sábado eran 18 niños los ingresados en el hospital con llagas, además de varios adultos con acné, náuseas y vómitos.
Para el 20 de julio, diez días después del incendio en la fábrica, comenzaron a aparecer gallinas, patos y conejos muertos en la población de Cesano Maderno, tres kilómetros al sur de Seveso. Entonces los periodistas de Milán comenzaron a tratar de la nube venenosa de Seveso. Parecía una noticia importante y de gran trascendencia.
 El presidente de Ucrania Viktor Yushchenko fue envenenado en 2004 con la dioxina TCDD. Como consecuencia desarrolló cloracné cuyas señales se pueden observar en su cara. Fuente: Wikimedia Commons
El presidente de Ucrania Viktor Yushchenko fue envenenado en 2004 con la dioxina TCDD. Como consecuencia desarrolló cloracné cuyas señales se pueden observar en su cara. Fuente: Wikimedia CommonsEl primer efecto de la exposición a dioxina en la población de Seveso fue el cloracné como único efecto vinculado con certeza con el accidente. La mortalidad y la morbilidad durante el período de 20 años posterior al accidente mostraron un mayor riesgo de neoplasia linfoemopoyética, cáncer del sistema digestivo (recto en hombres y vías biliares entre mujeres) y cáncer del sistema respiratorio (pulmón, entre hombres). En los análisis de incidencia, también el cáncer de tiroides y pleura apareció aumentado. También encontró el grupo de Angela Cecilia Pesatori, de la Universidad de Milán, efectos cardiovasculares (posiblemente vinculados tanto a la exposición química a la dioxina como a la experiencia estresante del desastre), efectos endocrinos (diabetes entre las mujeres) y efectos reproductivos. La exposición de los hombres a TCDD se relacionó con una menor proporción de sexo masculino respecto al femenino en la descendencia.
En estudios epidemiológicos hasta 2009 se encontraron incrementos de la tasa de incidencia de cáncer, no muy elevados, en sangre y mama según la revisión de Angela Cecilia Pesatori publicada en 2009, para 20 años después del accidente. Se centraron en los diagnósticos entre 1977 y 1996 para las zonas A y B.
Una revisión muy completa y con muchos datos sobre las consecuencias del accidente de Seveso la publicaron Brenda Eskenazi y sus colegas de la Universidad de California en Berkeley. El último apartado del texto se titula Lecciones aprendidas y lo resumo a continuación.
Confirman que un desastre ambiental, como el de Seveso, es claramente devastador para la población local e introduce posibles consecuencias ecológicas, económicas y de salud a largo plazo, tanto físicas como psicológicas. Desafortunadamente, una serie de desastres ambientales, tanto provocados por el hombre como naturales, han seguido al de Seveso y, sin duda, otros ocurrirán en el futuro. Seveso proporciona un ejemplo importante de los pasos que pueden tomar los epidemiólogos y los profesionales de la salud después de un desastre para documentar sus efectos en la salud. La investigación epidemiológica solo fue posible en Seveso debido al rápido establecimiento de un programa de vigilancia de la salud a largo plazo en la población, que incluyó, de manera crítica, la recolección y el almacenamiento de muestras biológicas de una gran cantidad de personas afectadas a pesar de que aún no se habían desarrollado métodos para analizar la exposición en esas muestras. Otros pasos importantes incluyeron un seguimiento cuidadoso de las personas con respuestas agudas a la exposición y, en este caso, de niños con cloracné, y el desarrollo o aumento de registros de salud, con los datos de cáncer y defectos de nacimiento, para recoger información sobre los efectos que podrían presentarse tanto en los primeros años como después de la exposición inicial.
A partir de lo ocurrido en Seveso, la Unión Europea instauró en 1996 nuevas y más exigentes normas de seguridad industrial conocidas como Directiva Seveso II (96/82/CE).
Un último dato a añadir a esta historia del accidente de Seveso: Paolo Paoletti, director de producción de la planta ICMESA fue asesinado el 2 de febrero de 1980 en Meda por la organización terrorista de izquierdas Prima Linea.
Referencias:
Eskenazi, B. et al. 2018. The Seveso accident: A look at 40 years of health research and beyond. Environment International 71-84.
Fuller, J.G. 1977. Sección de Libros: Niebla mortal. Selecciones del Reader’s Digest. Noviembre: 161-190.
Pesatori, A.C. et al. 2003. Short- and long-term morbidity and mortality in the population exposed to dioxin after the “Seveso accident”. Industrial Health 41: 127-138.
Pesatori, A.C. et al. 2009. Cancer incidence in the population exposed to dioxin after the “Seveso accident”: twenty years of follow-up. Environmental Health 8: 39.
Wikipedia. 2022. Desastre de Seveso. 20 abril.
Para saber más:
El caso de los enfermos de Minamata
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo No olvidar Seveso se ha escrito en Cuaderno de Cultura Científica.
Sudokus, matemáticas y arte contemporáneo
El día 21 de marzo estará en las librerías mi nuevo libro en la colección Miradas Matemáticas, de la editorial Los libros de la Catarata y la Federación Española de Sociedades de Profesores de Matemáticas (FESPM), cuyo título es Las matemáticas como herramienta de creación artística.
 Portada del libro es Las matemáticas como herramienta de creación artística (Catarata, 2023)
Portada del libro es Las matemáticas como herramienta de creación artística (Catarata, 2023)El capítulo 5, que está dedicado a los cuadrados mágicos y los cuadrados latinos, debía terminar con los sudokus, con un poco de matemáticas (ya que las soluciones de los sudokus son un tipo particular de cuadrados latinos) y de su uso en el arte contemporáneo como herramienta creativa para algunos artistas. Como al final no ha sido posible incluirlo, me ha parecido buena idea hablar de este tema en esta entrada del Cuaderno de Cultura Científica.
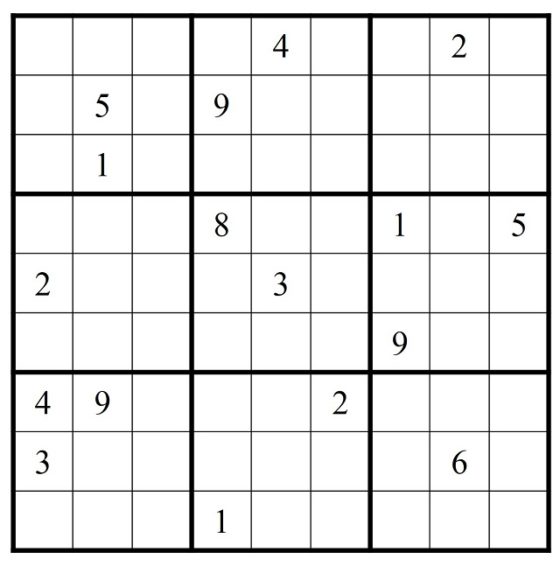 Sudoku de 17 pistas, extraído del libro de Jason Rosenhouse y Laura Taalman, Taking Sudoku Seriously, The Math Behind the World’s Most Popular Pencil Puzzle (Oxford University Press, 2011)El rompecabezas sudoku
Sudoku de 17 pistas, extraído del libro de Jason Rosenhouse y Laura Taalman, Taking Sudoku Seriously, The Math Behind the World’s Most Popular Pencil Puzzle (Oxford University Press, 2011)El rompecabezas sudoku
El sudoku es sin lugar a dudas uno de los rompecabezas más populares de los últimos tiempos, que ha tenido además un desarrollo vertiginoso. Desde que se diera a conocer internacionalmente en 2005, el sudoku se ha convertido en todo un fenómeno de masas. Hay sudokus en los periódicos, revistas y libros de sudokus, sudokus en los dispositivos electrónicos, juguetes de sudokus, programas de ordenador para crearlos, competiciones, versiones infantiles y una enorme cantidad de variantes del original.
El sudoku normal consiste en un retículo cuadrado de tamaño 9 x 9, luego con 81 casillas, dividido en 9 regiones, retículos 3 x 3, de manera que hay que rellenar las 81 casillas con los números del 1 al 9 (partiendo de una situación inicial en la que algunos números, las pistas, ya están colocados en algunas de las casillas), de forma que no se puede repetir ningún número en una misma fila, columna o región. Por lo tanto, la solución de este juego es un tipo especial de cuadrado latino.
Recordemos que un cuadrado latino de orden n es un retículo cuadrado de tamaño n x n en el que cada entrada es un número del 1 al n, aunque bien podrían considerarse n símbolos cualesquiera, por ejemplo, las letras del alfabeto latino que utilizó el matemático suizo Leonhard Euler (1707-1783) o los colores utilizados por el artista suizo Richard Paul Lohse (1902-1988), de tal forma que cada número de {1,…, n} aparece una vez, y solo una vez, en cada fila y cada columna (parta más información véase la entrada Cuadrados latinos, matemáticas y arte abstracto).
 Sin título (1980/1996), de Richard P. Lohse, que es un ejemplo de cuadrado latino de orden 6 con colores (verde, amarillo, naranja, morado, azul oscuro y azul claro). Imagen obtenida de la Galerie Hoffmann
Sin título (1980/1996), de Richard P. Lohse, que es un ejemplo de cuadrado latino de orden 6 con colores (verde, amarillo, naranja, morado, azul oscuro y azul claro). Imagen obtenida de la Galerie HoffmannEl juego denominado sudoku fue creado en la década de 1970 por el arquitecto jubilado y diseñador de pasatiempos Howard Garns (1905-1989) y publicado bajo en nombre “number place” en la revista Dell Pencil Puzzles & Word Games. Maki Kaji, presidente de la editorial Nikoli, especializada en juegos y pasatiempos, en particular, rompecabezas lógicos, lo exportó a Japón y empezó a publicarlo en 1984 en su revista Monthly Nikolist bajo el nombre Suji wa dokushin ni kagiru (los números deben estar solos), que se abrevió a Su Doku. Su expansión por el resto del mundo vino de la mano del juez retirado neozelandés, residente en Hong Kong, Wayne Gould, quien desarrolló un programa de ordenador para crear rápidamente sudokus. En 2004 empezaron a publicarse sudokus en periódicos británicos, como The Times y The Guardian, y acabó convirtiéndose, desde 2005, en un rompecabezas muy popular que aparecía en la mayoría de los periódicos del mundo.
Pueden plantearse diferentes cuestiones matemáticas relacionadas con este rompecabezas. Entre otras:
i) cuántas estructuras de solución, es decir, cuadrados latinos de orden 9 que cumplen la regla de las regiones diferentes, existen. La respuesta es 6.670.903.752.021.072.936.960 (de entre los 5.524.751.496.156.892.842.531.225.600 cuadrados latinos de orden 9 que existen), aunque si tenemos en cuenta las simetrías (permutaciones de filas y columnas, renombramiento de los símbolos, rotaciones y simetrías especulares), estas se reducen a 5.472.730.538 soluciones de sudokus distintas;
ii) dado un cuadrado latino de orden 9 que es solución de sudoku, cuántos rompecabezas sudokus distintos se pueden generar a partir del mismo, es decir, eliminando los números de las casillas hasta dejar una pequeña cantidad inicial, las pistas, que es el punto inicial del juego, y de manera que exista una solución única. Lo cierto es que para esta interesante cuestión no se tiene respuesta;
iii) y cuál es la cantidad mínima de números iniciales (pistas) posibles. Se conocen sudokus con tan solo 17 pistas (véase la primera imagen de la entrada), pero se desconoce si existen con menos pistas.
En general, se pueden considerar sudokus de orden n2 con regiones de tamaño n x n. El caso más sencillo, es el de los shidoku, que son sudokus de tamaño 4 x 4. No es difícil ver que existen 288 soluciones de shidoku distintas, aunque esencialmente son solo dos.
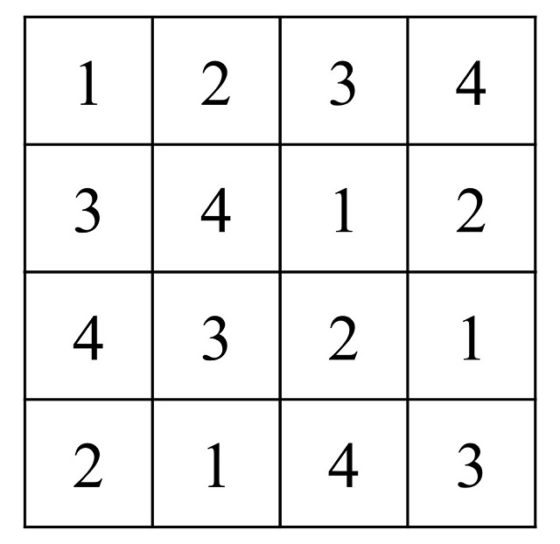 Ejemplo de solución de un shidoku, esto es, un tipo de sudoku de orden 4Los sudokus en el arte contemporáneo
Ejemplo de solución de un shidoku, esto es, un tipo de sudoku de orden 4Los sudokus en el arte contemporáneo
La pasión por los sudokus se extendió a todos los ámbitos de la cultura, en particular, también al arte contemporáneo. Los artistas vieron, y jugaron, a los sudokus en los periódicos y trasladaron este rompecabezas numérico a sus obras de arte.
Algunos artistas relacionados con el arte concreto y el constructivismo los utilizaron para crear pinturas de color al estilo de Richard P. Lohse. En este sentido, cabe destacar al artista y poeta visual austriaco Josef Linschinger (1945), un apasionado de las matemáticas como herramienta creativa, que ha realizado una serie de obras, muy reconocidas, dedicada a los sudokus. Linschinger resuelve los sudokus que aparecen en el periódico y toma estas soluciones como punto de partida para sus obras. Asigna colores a los nueve números (1 = rojo, 2 = rojo-naranja, 3 = naranja, 4 = amarillo-naranja, 5 = amarillo, 6 = amarillo-verde, 7 = verde, 8 = azul-verde, 9 = azul) y crea obras, como Sudoku 03 01 11 (2011) o Sudoku 01 07 11 (2013), formadas por tres lienzos, uno con el cuadrado latino que es solución del sudoku, mientras que los otros dos son una descomposición complementaria del anterior, con las casillas vacías en blanco o negro. En algunas obras prescinde del sudoku solución y solamente presenta los lienzos complementarios, como Sudoku 01 01 11 (2012) o Sudoku 01 08 15 (2015).
 Sudoku 13/1 01 07 11 (2012), del artista Josef Linschinger. Imagen de la página web de Josef Linschinger
Sudoku 13/1 01 07 11 (2012), del artista Josef Linschinger. Imagen de la página web de Josef LinschingerDe forma similar, la artista abstracta venezolana, residente en Madrid, Emilia Azkarate (1964), pintó algunos sudokus que aparecieron en periódicos entre los años 2008 y 2010, cambiando los números por colores. En un lienzo grande el rompecabezas y en un lienzo pequeño la solución.
 Sin título, Sudoku 90 (2009), de la artista Emilia Azkarate. Imagen obtenida en la página web de Emilia Azkarate
Sin título, Sudoku 90 (2009), de la artista Emilia Azkarate. Imagen obtenida en la página web de Emilia AzkaratePor otra parte, el artista digital Rototype, nombre artístico del eslovaco Jaka Bonca (1962), asocia los números con colores y/o formas, entre ellas, figuras geométricas básicas del mismo tamaño o de diferentes tamaños, teselas de Truchet (véase las entradas Los embaldosados de Truchet y el puzle del diamante y El arte de la sencilla baldosa de Truchet), líneas paralelas con diferentes inclinaciones, etc), creando estructuras más complejas, no solo para sudokus 9 x 9, sino también para otros tamaños. Estas obras pueden verse en la página del artista .
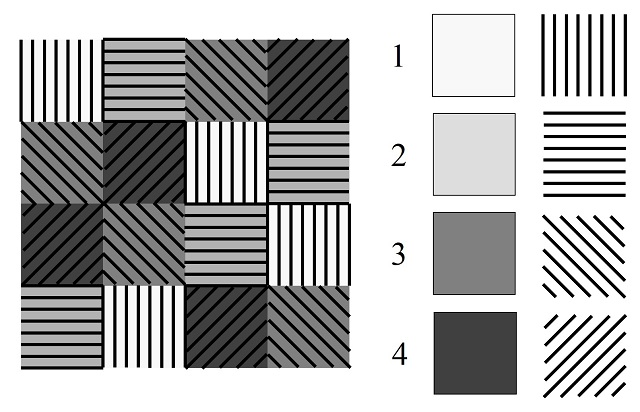 Ilustración, al estilo de Rototype, del shidoku mostrado más arriba, utilizando color (escala de grises) y forma (direcciones de líneas paralelas)
Ilustración, al estilo de Rototype, del shidoku mostrado más arriba, utilizando color (escala de grises) y forma (direcciones de líneas paralelas)
Por último, un hermoso ejemplo de presencia de los shidokus (sudokus 4 x 4), no el rompecabezas sino el cuadrado latino de orden 4 con regiones 2 x 2, en el arte contemporáneo es Dibujo mural #413 (1984), del artista conceptual y minimalista estadounidense Sol Lewitt (1928-2007). Esta obra está formada por 24 shidokus de color (1 = gris, 2 = amarillo, 3 = rojo, 4 = azul), cuya estructura básica es la que aparece en la imagen de más arriba y el resto son las permutaciones de los cuatro números/colores, es decir, 4! = 24 estructuras de color.
 Instalación del Dibujo mural #413 (1984), del artista Sol Lewitt en el MASS MoCA, Museo de Arte Contemporáneo de Massachusetts. Imagen de la página web del MASS MoCA
Instalación del Dibujo mural #413 (1984), del artista Sol Lewitt en el MASS MoCA, Museo de Arte Contemporáneo de Massachusetts. Imagen de la página web del MASS MoCAAdemás, esta obra ha sido utilizada por la artista, compositora, música y directora de cine estadounidense Laurie Anderson (1947) para componer su pieza Quartet for Sol Lewitt (1977).
Bibliografía
1.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística , colección Miradas matemáticas, Catarata, 2023.
2.- Jason Rosenhouse, Laura Taalman, Taking Sudoku Seriously, The Math Behind the World’s Most Popular Pencil Puzzle, Oxford University Press, 2011.
3.- María Merino, Sudokus y modelización, Un paseo por la Geometría 2009/2010, UPV/EHU, 2010.
4.- E. Russell, F. Jarvis, Mathematics of Sudoku II, Mathematical Spectrum, Vol. 39, No. 2, pp. 54-58, 2006/07.
5.- Josef Linschinger, Zahlen und Farben, Matematikum, Modo Verlag GmbH, 2016.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Sudokus, matemáticas y arte contemporáneo se ha escrito en Cuaderno de Cultura Científica.
Un anillo aromático de seis átomos de nitrógeno
Un equipo de investigación acaba de presentar un descubrimiento espectacular para la química del nitrógeno: por primera vez se ha sintetizado un compuesto que contiene anillos aromáticos de seis átomos de nitrógeno. El compuesto de nitrógeno y potasio se produjo bajo presiones y temperaturas extremadamente altas. Tiene una estructura muy compleja, pero su componente principal es un anillo plano de seis átomos de nitrógeno, llamado anión hexazina, ya que tiene carga negativa. La disposición de los átomos de nitrógeno en el anión hexazina es similar a la de los átomos de carbono en el benceno, un anillo aromático que es omnipresente en la naturaleza.
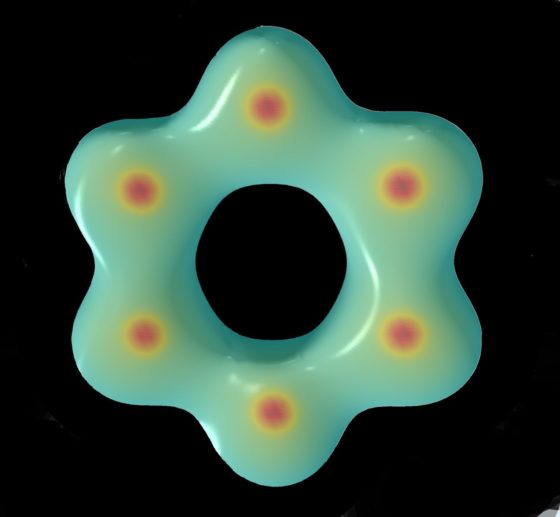 Anillo de hexazina [N₆]⁴⁻. Fuente: (c) Dominique LanielAunque el término «aromático» originalmente se refería al olor, hoy en día su uso en química está restringido a compuestos que tienen propiedades electrónicas, estructurales y químicas concretas. La estabilidad única que poseen estos compuestos se conoce como aromaticidad. Los compuestos aromáticos juegan un papel importante en la química y la biología, así como en numerosas ramas de la industria. Aunque inicialmente se pensó que la aromaticidad era exclusiva de los compuestos cíclicos de carbono, se ha demostrado que numerosos sistemas compuestos por heterociclos de carbono y otros átomos, e incluso compuestos cíclicos de átomos diferentes al carbono, pueden tener un carácter aromático. Sin embargo, la aromaticidad del nitrógeno solo se había encontrado hasta ahora al anión pentazolato [N₅]⁻.
Anillo de hexazina [N₆]⁴⁻. Fuente: (c) Dominique LanielAunque el término «aromático» originalmente se refería al olor, hoy en día su uso en química está restringido a compuestos que tienen propiedades electrónicas, estructurales y químicas concretas. La estabilidad única que poseen estos compuestos se conoce como aromaticidad. Los compuestos aromáticos juegan un papel importante en la química y la biología, así como en numerosas ramas de la industria. Aunque inicialmente se pensó que la aromaticidad era exclusiva de los compuestos cíclicos de carbono, se ha demostrado que numerosos sistemas compuestos por heterociclos de carbono y otros átomos, e incluso compuestos cíclicos de átomos diferentes al carbono, pueden tener un carácter aromático. Sin embargo, la aromaticidad del nitrógeno solo se había encontrado hasta ahora al anión pentazolato [N₅]⁻.
En condiciones extremas de presión y temperatura, el equipo sintetizó el compuesto complejo K₉N₅₆, que contiene anillos de hexazina, [N₆]⁴⁻. La estructura de K₉N₅₆ está compuesta por una disposición compleja de anillos [N₆]⁴⁻ y [N₅]⁻, así como dímeros de nitrógeno neutro. Los investigadores encontraron que la estructura del anillo [N₆]⁴⁻ de hexazina se ajusta a la regla de aromaticidad de los compuestos químicos que lleva el nombre del químico físico Erich Hückel: el anillo es cíclico, plano y tiene (4n + 2) electrones π (es un sistema 10π ). Su carácter aromático está respaldado por consideraciones de longitud de enlace y por cálculos de la densidad de carga electrónica.
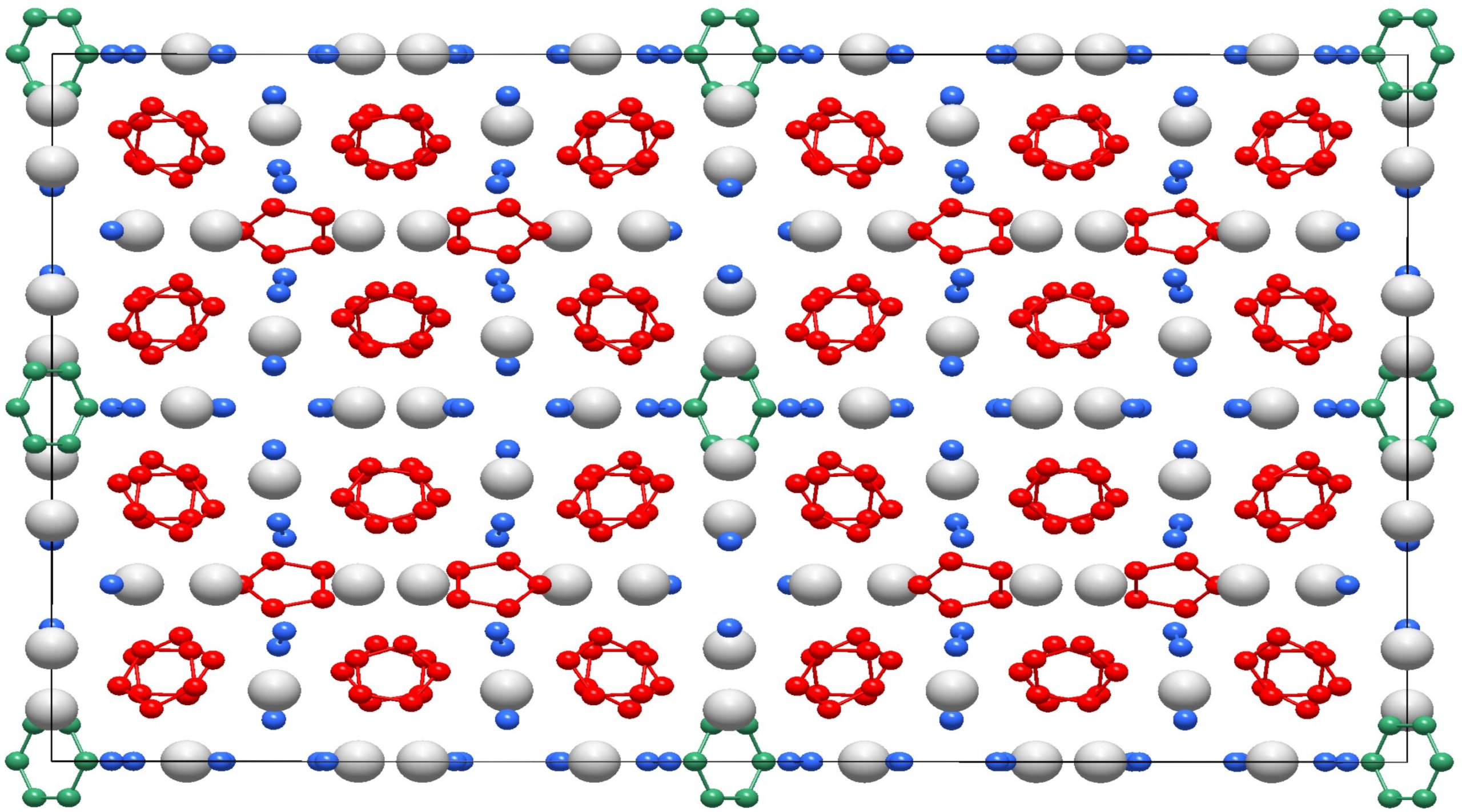 Estructura cristalina del compuesto K₉N₅₆. Fuente: (c) Dominique Laniel
Estructura cristalina del compuesto K₉N₅₆. Fuente: (c) Dominique LanielEl compuesto complejo K₉N₅₆ se formó en condiciones inusuales: la azida de potasio (KN₃) y el nitrógeno molecular (N₂) se comprimieron bajo una presión de más de 400.000 atmósferas y se calentaron a 2.000 grados Celsius con láseres de alta potencia. El siguiente paso fue dilucidar la estructura interna de este nuevo compuesto. Para ello, las muestras se expusieron a un haz de rayos X intenso en dos aceleradores de partículas, la fuente de rayos X PETRA III en el Sincrotrón de Electrones Alemán (DESY) en Hamburgo y la Instalación Europea de Radiación de Sincrotrón (ESRF-EBS) en Grenoble. La estructura atómica del compuesto K₉N₅₆ es, en sí misma, notable, de una complejidad casi nunca observada para sólidos producidos a presiones tan altas. Se compone de una disposición repetitiva de 520 átomos: 72 K y 448 N.
Referencia:
Dominique Laniel et al. (2023) Aromatic hexazine [N₆]⁴⁻ anion featured in complex structure of the high-pressure potassium nitrogen compound K₉N₅₆. Nature Chemistry doi: 10.1038/s41557-023-01148-7
Para saber más:
De la valencia y el enlace químico (y II)
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un anillo aromático de seis átomos de nitrógeno se ha escrito en Cuaderno de Cultura Científica.

