¿Cómo llegan partículas rocosas a los geiseres de Encélado?
Encélado es uno de los satélites más interesantes del Sistema Solar. Buena parte de este interés proviene de la gran actividad geológica que tiene este pequeño cuerpo de apenas 500 kilómetros de diámetro y del que seguimos aprendiendo cosas gracias a los datos que tomo la misión Cassini. Es también uno de los llamados mundos océano que existen en nuestro vecindario, cuerpos que, debajo de una corteza formada principalmente por hielo, tienen un océano de agua líquida debidamente protegido de las condiciones externas -a veces especialmente duras en el entorno de los gigantes gaseosos- y, por lo tanto, lo convierte en uno de los cuerpos también de mayor interés desde el punto de vista de la astrobiología.
 Geiseres en Encélado vistos desde la Cassini. Se aprecian perfectamente por su forma de “chorros”, creando una cortina de gases que sale despedida del pequeño satélite. Imagen cortesía de NASA/JPL-Caltech/Space Science Institute.
Geiseres en Encélado vistos desde la Cassini. Se aprecian perfectamente por su forma de “chorros”, creando una cortina de gases que sale despedida del pequeño satélite. Imagen cortesía de NASA/JPL-Caltech/Space Science Institute.Una de las pruebas más evidentes de la existencia de un océano debajo de su superficie -que no vemos directamente- es la presencia de grandes geiseres que expulsan vapor de agua, nitrógeno, dióxido de carbono, algunas sales, compuestos orgánicos e incluso pequeños granos silicatados.
Aunque también hay otros datos, como los resultantes del estudio de su campo gravitatorio y el movimiento de bamboleo que realiza a lo largo de su órbita alrededor de Saturno y que nos confirman la existencia de este océano y que tendría entre 10 y 30 kilómetros de profundidad, dependiendo de la zona.
Tantas partículas emite a través de los geiseres que uno de los anillos de Saturno, el anillo E está formado por estas partículas, y los científicos calculan que lo hace a un ritmo de unos 200 kilogramos por segundo, tanta que desde su formación hace 4500 millones de años podría haber perdido aproximadamente un 30% de su masa original.
 En esta imagen podemos ver a Encélado dentro del anillo E, al que nutre de partículas en su viaje alrededor de saturno. Imagen cortesía de NASA/JPL/Space Science Institute.
En esta imagen podemos ver a Encélado dentro del anillo E, al que nutre de partículas en su viaje alrededor de saturno. Imagen cortesía de NASA/JPL/Space Science Institute.En 2015 los científicos descubrieron en los datos de la Cassini un detalle muy importante, y es que, al acercarse a Encélado, algunas de las partículas que atrapaba uno de sus instrumentos -el Cosmic Dust Analyzer (o Analizador de Polvo Cósmico) eran en realidad pequeñas partículas de roca muy ricas en silicio, tan minúsculas que las más grandes medían menos de nueve nanómetros.
Estos granos solo podrían provenir de un lugar, del contacto entre el océano y el núcleo rocoso de Encélado, y en la Tierra el ambiente más habitual donde se forman granos de sílice de este tamaño es en las chimeneas hidrotermales, donde aguas muy calientes -de al menos 90ºC- y supersaturadas en sílice sufren una brusca caída en la temperatura al entrar en contacto con el agua del océano. Pero no solo descubrió granos de polvo, sino también hidrógeno, que podría proceder también de la actividad hidrotermal.
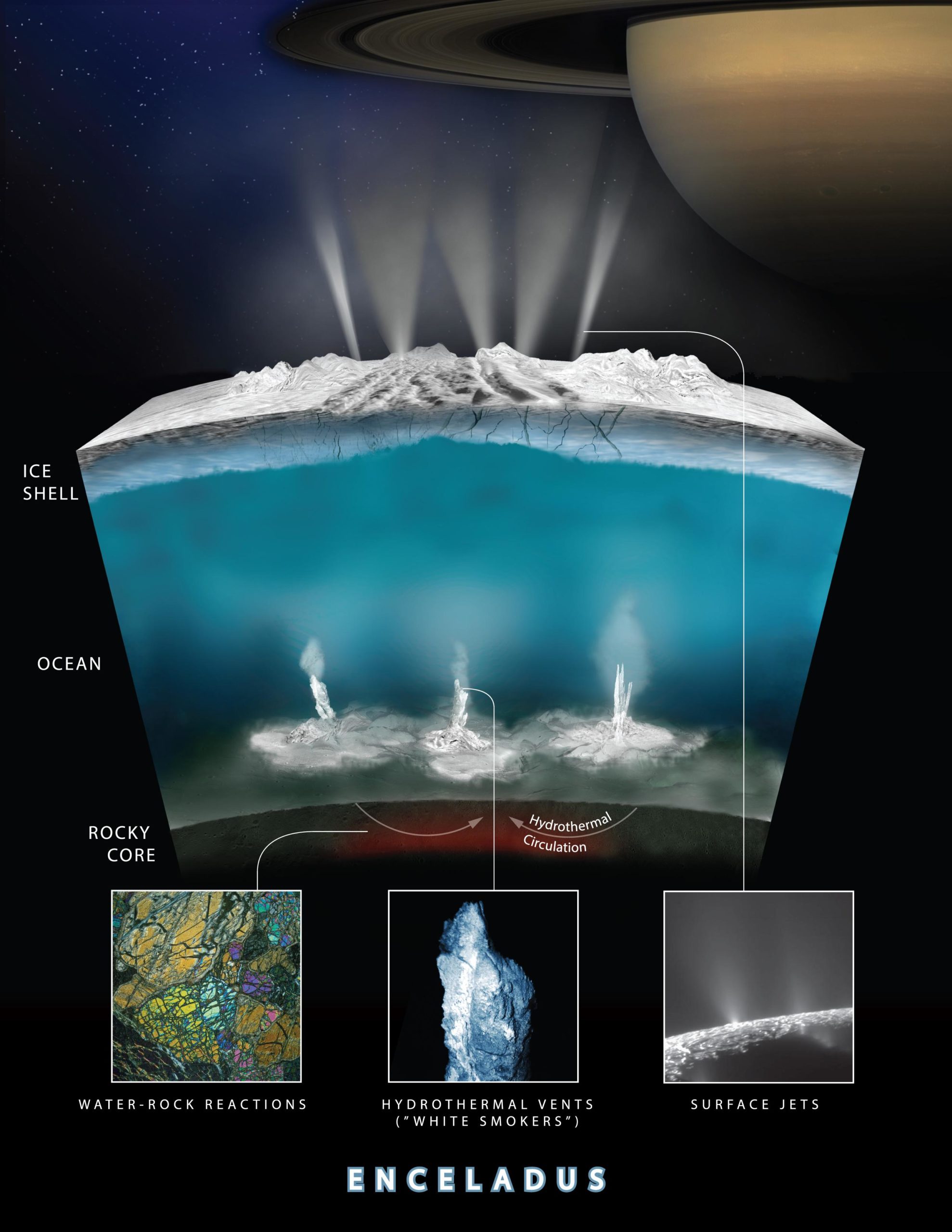 Un esquema de la actividad hidrotermal en Encélado, donde no solo se formarían las partículas rocosas, sino que la interacción entre el agua y la roca generaría el hidrógeno detectado. Imagen cortesía de NASA/JPL-Caltech/Southwest Research Institute.
Un esquema de la actividad hidrotermal en Encélado, donde no solo se formarían las partículas rocosas, sino que la interacción entre el agua y la roca generaría el hidrógeno detectado. Imagen cortesía de NASA/JPL-Caltech/Southwest Research Institute.Pero, ¿Cuánto tiempo tardan estas partículas en salir desde el océano y ser expulsadas por los geiseres? ¿Es un proceso lento o rápido? Un nuevo estudio publicado esta pasada semana en Communications Earth & Enviroment deja entrever que este periodo podría ser de tan solo unos meses.
Encélado tiene una gran actividad geológica en la actualidad porque sufre de un proceso denominado calentamiento de mareas, es decir, que a lo largo de su órbita sufre deformaciones en su parte sólida: es estirada y aplastada -obviamente no de una manera literal-, generando una serie de fricciones que calientan el núcleo rocoso que está en el fondo del océano, de tal manera que se generan unas corrientes verticales que transportan rápidamente las partículas de sílice hasta la superficie.
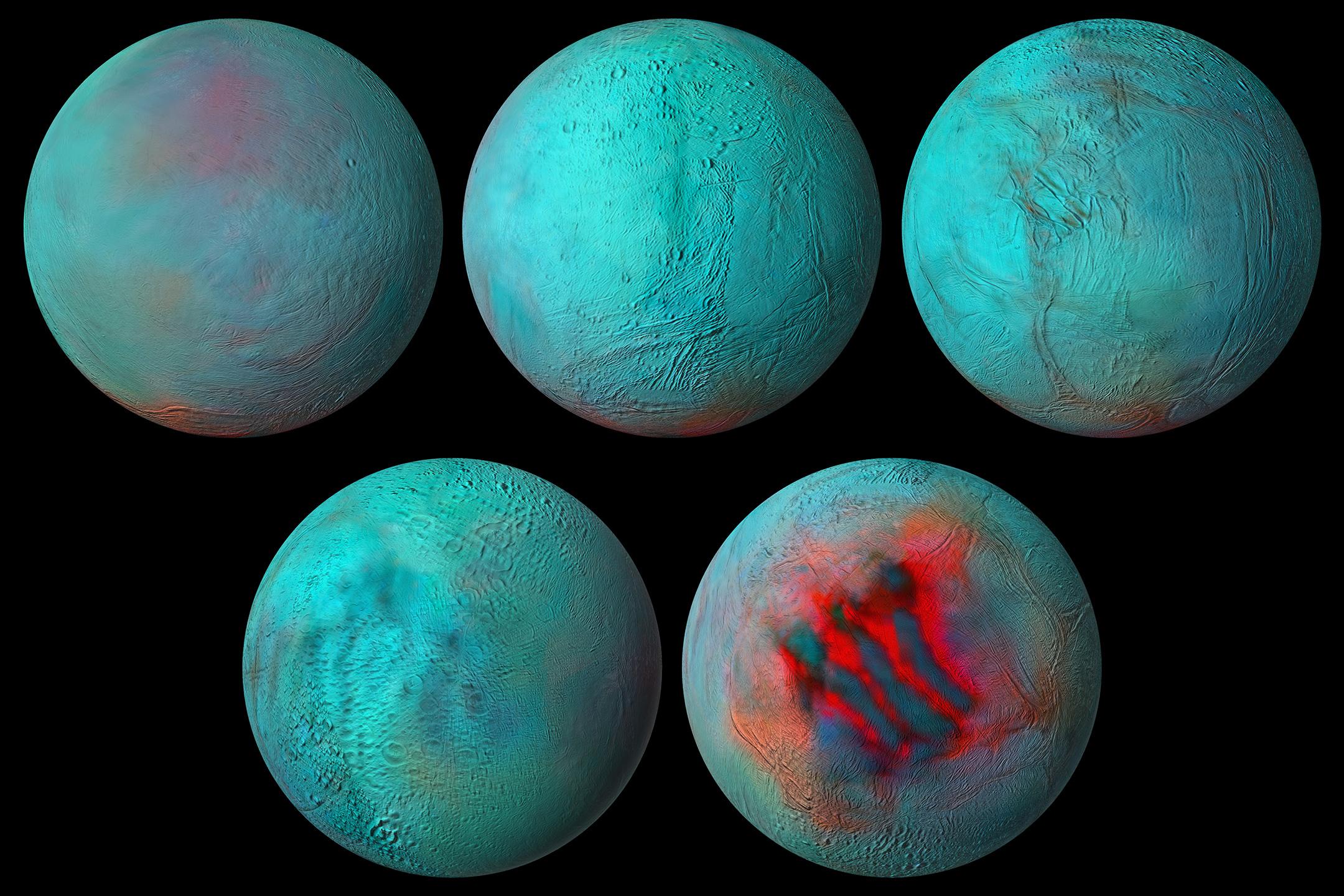 Encélado en el infrarrojo. En azul, las zonas más frías. En rojo, las más cálidas, y donde mayor actividad geológica hay. Es llamativo especialmente el detalle de la última imagen, con esa zona con marcas lineales de una temperatura muy superior al resto: Son las “tiger stripes” (o rayas de tigre, en castellano) donde se concentran la mayor parte de los geiseres. Imagen cortesía de NASA/JPL-Caltech/University of Arizona/LPG/CNRS/University of Nantes/Space Science Institute.
Encélado en el infrarrojo. En azul, las zonas más frías. En rojo, las más cálidas, y donde mayor actividad geológica hay. Es llamativo especialmente el detalle de la última imagen, con esa zona con marcas lineales de una temperatura muy superior al resto: Son las “tiger stripes” (o rayas de tigre, en castellano) donde se concentran la mayor parte de los geiseres. Imagen cortesía de NASA/JPL-Caltech/University of Arizona/LPG/CNRS/University of Nantes/Space Science Institute.También estiman que las “tiger stripes”, el conjunto de fracturas que aparecen en el polo sur de Encélado y donde aparece la mayor actividad del satélite, podrían en realidad ser un conducto casi directo para estas partículas del océano, ofreciendo a los científicos una oportunidad para poder estudiar detalles sobre la composición del océano muestreando con mayor detalle los materiales expulsados por los geiseres.
Y lo más importante, sería una composición representativa del estado del océano actual y de los procesos geoquímicos gracias a estos tiempos de viaje tan cortos entre el fondo del océano y la superficie.
Estudios como estos nos servirán no solo para conocer mejor Encélado y que mecanismos pueden estar operando por debajo de su superficie, sino que podrían ayudarnos también a planificar futuras misiones espaciales, tanto en saber que tenemos que estudiar con más detalle, como para plantearnos que tenemos que buscar y que instrumentos serán necesarios para descubrir todos los secretos de este fascinante satélite.
Referencias:
Hsu, H.-W. et al. (2015) “Ongoing hydrothermal activities within Enceladus,” Nature, 519(7542), pp. 207–210. Doi: 10.1038/nature14262.
Schoenfeld, A.M. et al. (2023) “Particle entrainment and rotating convection in Enceladus’ Ocean,” Communications Earth & Environment, 4(1). Doi: 10.1038/s43247-023-00674-z.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Cómo llegan partículas rocosas a los geiseres de Encélado? se ha escrito en Cuaderno de Cultura Científica.
Antes nacían más en primavera y verano, ya no
nacimientos
 Foto: Valeria Zoncoll / Unsplash
Foto: Valeria Zoncoll / UnsplashAntes de 1960 la frecuencia de nacimientos en España variaba de forma clara a lo largo del año, con dos máximos, uno muy marcado en abril y el otro, mucho más atenuado, en septiembre. Los niños y niñas nacidas en abril habían sido concebidas en junio o julio del año anterior, mientras que los y las que vieron la luz en septiembre, lo habían sido en el diciembre anterior. A partir de 1960, sin embargo, ese ritmo estacional empezó a desvanecerse. Y durante el periodo comprendido entre 1990 y 2000, ya no hubo ritmo estacional alguno en el número de nacimientos. Estos son los resultados principales de un estudio que analizó la estacionalidad de los nacimientos en España desde 1941 hasta 2000. En total, fueron 33421731 nacimientos durante 60 años.
Ese ritmo era similar al que se había observado antes en otros países europeos, y también en Canadá y Australia, aunque en los Estados Unidos solo se producía un máximo claro de nacimientos en el mes de septiembre. También se había observado en otros estudios que la estacionalidad se había atenuado con el paso de los años, con una disminución de la frecuencia de nacimientos en primavera y un aumento en otoño, aunque en ningún otro país se había documentado su desaparición, como ocurrió aquí.
En 1940 España era un país eminentemente rural. La fecundidad no estaba controlada como lo estuvo unas décadas después. A partir de 1960, sin embargo, hubo un desarrollo industrial acelerado, acompañado por un flujo de población masivo hacia las ciudades. En las últimas décadas del siglo XX se generalizó el uso de anticonceptivos eficaces, por lo que las mujeres pudieron decidir el número de hijos e hijas que tendrían y, hasta cierto punto también, el periodo de la concepción.
La disminución de la estacionalidad en las concepciones se empezó a producir con el éxodo hacia las ciudades, aunque su desaparición total seguramente tuvo su causa en el uso de anticonceptivos. Investigaciones anteriores en otros países europeos habían llegado a la conclusión de que ciertos factores ambientales eran los principales responsables de los ciclos de fecundidad antes del desarrollo industrial. Y de entre esos factores, parece que el fotoperiodo (horas diarias de luz) era clave. Así cabe interpretar el máximo primaveral de concepciones. El descenso estival, muy marcado en España en las décadas de los cuarenta y cincuenta, probablemente obedecía al aumento de la temperatura. De hecho, la probabilidad de concepción parece ser inferior a la media por debajo de 5 ºC y por encima de 21 ºC. Y el progresivo descenso en el máximo primaveral a partir de la década de los sesenta era seguramente consecuencia del control creciente de las condiciones ambientales, ligado a la mejora de la situación económica.
Es normal que la actividad reproductora de los animales tenga ciclos estacionales, porque la probabilidad de sacar adelante a la progenie depende, sobre todo, del alimento disponible. El fotoperiodo actúa así como señal ambiental, de manera que, como se ha visto en el caso español y otros países occidentales, el máximo de fecundaciones ocurre cuando los días son largos. Ese ritmo conduce a un mayor número de nacimientos entre marzo y octubre, que es la mitad del año en la que es previsible que haya más alimento disponible para las madres lactantes. Por eso, cuando el régimen de luz se uniformiza por efecto de la iluminación artificial, ese factor deja de ejercer su efecto, de la misma forma que la disponibilidad de alimento deja de variar con el curso estacional. Son las consecuencias del desarrollo.
Fuente: Cancho-Candela, R., Andrés-de Llano, J. M., Ardura-Fernández, J.: Decline and loss of birth seasonality in Spain: analysis of 33 421 731 births over 60 years. J Epidemiol Community Health. 2007 Aug; 61(8): 713–718. doi: 10.1136/jech.2006.050211
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Antes nacían más en primavera y verano, ya no se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: Las cinco vidas de un cazador de planetas

En 1983, cuando aún no se conocía ningún planeta extrasolar, alguien vino con la idea de colocar un telescopio en órbita y observar 13000 estrellas al mismo tiempo e intentar determinar aquellas que sufrían una disminución de su intensidad por el tránsito de un planeta. Aquella idea fructificó en el año 2009 con el lanzamiento del telescopio espacial Kepler. Daniel Marín nos cuenta su historia.
Daniel Marín es doctor en astrofísica y un divulgador de referencia en exploración espacial. Ha sido invitado por la NASA y Roskosmos a asistir a distintos lanzamientos de misiones.
Si no ve correctamente el vídeo, use este enlace.
Más sobre el tema:
25 años de planetas extrasolares
El sucesor del Hubble: el telescopio espacial James Webb
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2022: Las cinco vidas de un cazador de planetas se ha escrito en Cuaderno de Cultura Científica.
Los productos sin gluten no son más sanos
El grupo Gluten 3S de la UPV/EHU está acreditado para conceder el sello de productos sin gluten a los productores. En los últimos nueve años, el grupo ha liderado una amplia investigación de estos productos y ha realizado análisis nutricionales para examinar 200 productos sin gluten. Si bien la calidad de los productos sin gluten ha aumentado considerablemente durante este tiempo, estos productos aún no han llegado a ser equivalentes a los que contienen gluten.
 Foto: Jorge Zapata / Unsplash
Foto: Jorge Zapata / UnsplashCon el paso de los años, cada vez se conocen más casos de celiaquía, con un crecimiento exponencial. Según los expertos, puede haber dos razones para ello. Una, que debido a factores medioambientales el número de celíacos está en aumento, y otra, que los diagnósticos han mejorado y se han incrementado. Además, junto con a celiaquía, el gluten provoca también otros trastornos. El incremento de casos ha llevado a la percepción pública de tal manera que ha generado un problema, ya que la gente considera, erróneamente, que una dieta sin gluten es más sana que una que contiene gluten.
«Se atribuyen a la dieta ciertos atributos que en sí mismos no están relacionados con ella. Los datos demuestran que los productos sin gluten no son más sanos», según Jonatan Miranda Gómez, investigador del grupo de investigación Gluten 3S.
Precisamente, el equipo de Miranda lleva muchos años realizando un análisis nutricional de los productos sin gluten. «En 2014 publicamos un artículo científico bastante innovador», dice Miranda. En él, comparábamos 200 alimentos sin gluten con sus equivalentes con gluten. No eran nutricionalmente equivalentes». Muchos de los productos sin gluten contenían más lípidos saturados (o grasas nocivas) que los productos con gluten, tenían un aporte de fibra más reducido y era necesario controlar su cantidad de sal y proteínas. Pero la situación está cambiando constantemente y acaban de publicarse los resultados de otro estudio.
La evolución de los productos sin glutenLa proporción de celíacos no ha variado y sigue siendo de aproximadamente del 1%. Pero, por un lado, ha aumentado la población y, por otro, han surgido sensibilidades al gluten, con lo que, considerando también a este grupo, el problema afecta a un 10% de la población. «La industria ha sido consciente de ello —dice Miranda—. Por lo tanto, ha desarrollado más productos, lo que ha permitido que la propia industria investigue más y tenga en cuenta otros componentes. De alguna manera, este impulso social y de equipos de investigación ha provocado una evolución en la industria. Y la mejora ha sido notable.
Un ejemplo representativo es el de la pasta. La pasta sin gluten no se elabora con trigo, ya que contiene gluten, sino con maíz. Precisamente la harina de maíz ha sido siempre el ingrediente principal. Esto no ha cambiado en los últimos nueve años. Sin embargo, así como anteriormente el segundo ingrediente en importancia era la harina de arroz, actualmente el más común es el mijo. «Esto ha influido positivamente en la nutrición», señala Miranda. «Para fabricar pasta hay que hacer una extrusión y el mijo permite la extrusión utilizando menos lípidos». Además, distintas iniciativas legislativas en materia alimentaria han contribuido a esta evolución.
En los casos de productos no sólidos, los productores utilizan otras estrategias. La cerveza es un ejemplo. En este caso, en lugar de sustituir al gluten, este se rompe mediante la adición de unas enzimas en el proceso de clarificación (separación de partículas en suspensión del líquido). «Pero este proceso tiene otra limitación —añade Miranda—. Podría ocurrir que queden moléculas nocivas que no se detectan en el análisis rutinario. Los miembros de la Asociación de Celíacos nos dicen a veces que la cerveza sin gluten les sienta mal». Por lo tanto, se ha abierto una nueva línea de investigación para analizar los problemas de estas cervezas.
Para Miranda está claro que el tema es amplio. «En los últimos años, se ha visto en los artículos que otras moléculas pueden ser perjudiciales también y que, aunque se siga una dieta estricta sin gluten, estos productos sin gluten pueden causar malestar. Además, quieren añadir otro enfoque a la investigación, ya que también quieren analizar el aspecto medioambiental. «Queremos conocer el impacto ambiental de los alimentos sin gluten. Suelen tener mayor impacto que el resto, por el hecho de que, por ejemplo, es necesario importar del extranjero algunos ingredientes. Habría que reducir ese impacto. Por ejemplo, hay que estudiar de dónde traer el mijo», dice Miranda.
Referencia:
Mármol-Soler, C.; Matias, S.; Miranda, J.; Larretxi, I.; Fernández-Gil, M.d.P.; Bustamante, M.Á.; Churruca, I.; Martínez, O.; Simón, E. (2022) Gluten-Free Products: Do We Need to Update Our Knowledge? Foods doi: 10.3390/foods11233839
Para saber nmás:
Alternativas para tratar la enfermedad celíaca
De la sal «sin gluten» al champú «sin gluten»: no solo marketing
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Los productos sin gluten no son más sanos se ha escrito en Cuaderno de Cultura Científica.
¿Por qué lo llaman mármol cuando quieren decir caliza?
Es posible que alguna vez hayáis ido a comprar unas losas o una encimera para vuestra casa y encargaseis un precioso mármol de color crema con un vistoso nombre que evocaba fantasías. Sin embargo, cuando os llegó el pedido, os encontrasteis con una roca que tenía un elevado contenido en restos fósiles. Y ahí os saltarían todas las alarmas, ¿cómo es posible?
 A-C) Granitos de diferentes tonalidades y D) gneis empleados como rocas ornamentales en diversos edificios circundantes a la Plaza Moyua de Bilbao (Bizkaia). Foto: Blanca María Martínez
A-C) Granitos de diferentes tonalidades y D) gneis empleados como rocas ornamentales en diversos edificios circundantes a la Plaza Moyua de Bilbao (Bizkaia). Foto: Blanca María MartínezUn mármol es un tipo de roca metamórfica formada por la transformación de una roca sedimentaria carbonatada al ser sometida a un importante régimen de presión y temperatura durante millones de años. Esta transformación, conocida como metamorfismo, consiste en una recristalización y nueva ordenación de los minerales carbonatados originales. Para que nos entendamos, los fósiles que pudiesen haberse preservado en esa roca sedimentaria inicial se destruyen durante el proceso de metamorfismo, por lo que no queda ningún rastro de ellos en el mármol. Dicho esto, ¿nos han engañado en la tienda de rocas ornamentales dándonos caliza por mármol?
Pues la respuesta es no. Esta confusión procede de la clasificación de las rocas ornamentales, que no es exactamente igual a la clasificación geológica de las rocas. Pero voy a empezar por el principio. Las rocas ornamentales son aquellas que se explotan comercialmente en canteras para su uso en la construcción, como enlosado de edificios y monumentos o como material escultórico, principalmente debido a su belleza estética, es decir, gracias a que “son bonitas”. Y, para su clasificación, se tienen en cuenta, principalmente, sus características físicas, tales como su resistencia y durabilidad ante la erosión provocada por las condiciones climáticas, más que su composición química o su origen geológico. De esta manera, nos encontramos con tres grandes grupos o tipos de rocas ornamentales: granitos, mármoles y pizarras.
 Fachada del edificio Bizkaia Aretoa, Paraninfo de la Universidad del País Vasco (UPV/EHU) en Bilbao (Bizkaia), construida con losas de mármol blanco, con ligeros veteados verdosos por el mineral clorita, extraído de las canteras de Macael (Almería). Foto: Blanca María Martínez
Fachada del edificio Bizkaia Aretoa, Paraninfo de la Universidad del País Vasco (UPV/EHU) en Bilbao (Bizkaia), construida con losas de mármol blanco, con ligeros veteados verdosos por el mineral clorita, extraído de las canteras de Macael (Almería). Foto: Blanca María MartínezGeológicamente hablando, un granito es una roca ígnea plutónica, es decir, que se forma por el enfriamiento lento (millones de años) de un magma en el interior de la tierra, por lo que tiene tiempo de formar cristales minerales. Pero en el caso de las rocas ornamentales, el término granito engloba a rocas cristalinas donde los minerales se observan a simple vista, de composición no carbonatada y, en general, muy resistentes al esfuerzo y la erosión. Y en esta denominación se incluyen los granitos en sentido geológico, pero también otras rocas ígneas plutónicas, como la diorita, la sienita o el gabro; rocas subvolcánicas filonianas, formadas por el enfriamiento y la cristalización de un magma o de un fluido caliente y mineralizado que circulaban a través de fracturas, dando lugar a cuerpos de rocas con formas prismáticas, como son las pegmatitas; y rocas ígneas volcánicas, generadas por el enfriamiento rápido del magma al salir a superficie, por lo que no tiene tiempo de cristalizar y presenta elevados contenidos de vidrio volcánico en su composición, como la andesita y el basalto. Pero también nos encontramos con rocas metamórficas de alto grado, es decir, que han sufrido altas presiones y temperaturas durante su formación, tal y como les sucede al gneis y a la migmatita.
 Rocas ornamentales de la fachada del Palacio Chávarri (Bilbao, Bizkaia). En tonos rosados, mármol rojo de Ereño, que es una caliza marina del Cretácico con abundante contenido fósil (de color blanco), principalmente bivalvos, extraída de la cantera de Ereño (Bizkaia). En tonos amarillos, arenisca del Eoceno posiblemente obtenida de alguna antigua cantera de Bizkaia. En tonos verdes, rocas volcánicas del Cretácico formadas por erupciones submarinas durante la apertura del Golfo de Bizkaia, procedentes de algún afloramiento del País Vasco (las marcas blancas son recristalizaciones de carbonato cálcico). Foto: Blanca María Martínez
Rocas ornamentales de la fachada del Palacio Chávarri (Bilbao, Bizkaia). En tonos rosados, mármol rojo de Ereño, que es una caliza marina del Cretácico con abundante contenido fósil (de color blanco), principalmente bivalvos, extraída de la cantera de Ereño (Bizkaia). En tonos amarillos, arenisca del Eoceno posiblemente obtenida de alguna antigua cantera de Bizkaia. En tonos verdes, rocas volcánicas del Cretácico formadas por erupciones submarinas durante la apertura del Golfo de Bizkaia, procedentes de algún afloramiento del País Vasco (las marcas blancas son recristalizaciones de carbonato cálcico). Foto: Blanca María MartínezSi pasamos al grupo de los mármoles ornamentales, aquí se incluyen rocas de composición principalmente carbonatada, con cristales de pequeño tamaño y menos duras y resistentes que las del grupo de los granitos. Así que no solo se refiere al mármol en el sentido geológico, si no que con este término también se denominan un gran número de rocas sedimentarias como la caliza, la dolomía, la toba y el travertino. Además, en muchas ocasiones se describen como mármoles ornamentales rocas no carbonatadas, tales como las sedimentarias arenisca o yeso y las metamórficas cuarcita, anfibolita o serpentinita, esta última formada a partir de la alteración de una roca ígnea plutónica por la circulación de un fluido profundo muy caliente que modifica su composición mineral y su estructura.
Y terminamos con las pizarras. Si atendemos al término geológico, una pizarra es una roca metamórfica de bajo grado formada por la transformación de una roca sedimentaria de composición arcillosa debido a la acción de la presión y la temperatura, generando una recristalización mineral y su disposición en planos de foliación, que no son otra cosa que esas líneas paralelas que apreciamos en las pizarras y que nos permiten separarlas en finas láminas de roca. Pero en el caso del término ornamental, este hace referencia, precisamente, a esta última cualidad de las pizarras, esa capacidad de separarse en lajas más o menos perfectas, por lo que agrupa a varias rocas metamórficas de grado bajo-medio, como son la pizarra, la filita y el esquisto, pero también rocas sedimentarias muy compactadas, incluso ligeramente metamorfizadas, como ciertas lutitas y margas.
 Fachada de la entrada de la Biblioteca Foral de Bizkaia en Bilbao, cubierta de losas de filita, de color verdoso por el mineral clorita, procedentes de China. Foto: Blanca María Martínez
Fachada de la entrada de la Biblioteca Foral de Bizkaia en Bilbao, cubierta de losas de filita, de color verdoso por el mineral clorita, procedentes de China. Foto: Blanca María MartínezEn definitiva, cuando vayamos a comprar alguna roca ornamental no debemos olvidarnos de que el nombre comercial que nos van a dar no tiene por qué concordar con el nombre geológico que le aplicaríamos a esa misma roca. Si queremos conocer estos detalles, deberemos pedir que nos enseñen la ficha técnica de ese material, en donde sí encontraremos una definición muy detallada de la misma, incluida no solo su clasificación geológica, sino también una descripción de su composición, sus propiedades físicas y el lugar en donde se ha extraído. Y con esos datos, incluso, podremos conocer toda la historia geológica de la zona de explotación. Gracias a las rocas ornamentales que decoran fachadas, edificios, aceras y monumentos de nuestros pueblos y ciudades podemos aprender maravillosas historias geológicas que nos transportan a recónditos lugares de todo el mundo y a millones de años atrás en el tiempo, aunque las llamemos a todas mármoles, granitos y pizarras.
Para saber más:
Los volcanes submarinos de Bizkaia y Gipuzkoa
La geodiversidad que nos rodea
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿Por qué lo llaman mármol cuando quieren decir caliza? se ha escrito en Cuaderno de Cultura Científica.
Homenaje alfabético a Georg Cantor
El matemático Georg Cantor (1845-1918) nació un 3 de marzo. Este retrato alfabético es un modesto homenaje a un genial matemático que ha marcado tanto mi investigación como mi docencia a lo largo de mi carrera.
 Georg Cantor. Fuente: Wikimedia Commons.
Georg Cantor. Fuente: Wikimedia Commons.
APEIROFOBIA
Esta palabra procede del término griego «Ápeiron» que fue utilizado por Anaximandro para referirse al «arjé», al elemento primordial de la realidad. Suele traducirse por «ilimitado», «infinito» o «indeterminado».
En la hermosa novela Villa des hommes (2007) de Denis Guedj, el protagonista, Hans Singer (un álter ego de Georg Cantor), se refiere a esta «fobia al infinito» de esta manera: «Cuando comencé con mis investigaciones, la mayor parte de mis colegas, así como los de las generaciones que me habían precedido, sufrían una enfermedad particular: apeirofobia. […] Apeirofobia, señor Matthias, o fobia al infinito».
BLASFEMIA
Cantor fue acusado de blasfemia por algunos colegas que no entendían sus novedosas teorías respecto a la teoría de conjuntos y otros aspectos de las matemáticas. Muchos de ellos, sin duda, padecían «apeirofobia».
CONJUNTO TERNARIO DE CANTOR
Entre 1879 y 1884, Cantor escribió una serie de cinco artículos que contienen, entre otros, el primer tratamiento sistemático de la topología de la recta real. En el quinto artículo de esta serie, introdujo lo que se conoce como el conjunto ternario de Cantor, un conjunto infinito, perfecto y totalmente disconexo. Es un modelo topológico para cierto tipo de espacios en el sentido que indica este teorema: «Todo espacio métrico no vacío, totalmente disconexo, perfecto y compacto es homeomorfo al conjunto ternario de Cantor».
DEPRESIÓN
Cantor sufrió episodios recurrentes de depresión desde 1884 hasta el final de su vida. Algunos de sus biógrafos los atribuyen a un posible trastorno bipolar que se manifestaba, en particular, en momentos en los que sus colegas matemáticos rechazaban sus teorías. En varias ocasiones ingresó en hospitales psiquiátricos, donde no dejó de pensar y escribir sus teorías matemáticas.
ESENCIA (DE LAS MATEMÁTICAS)
Una de las más famosas citas de Georg Cantor es: «La esencia de las matemáticas radica en su libertad».
FILOSOFÍA
Georg Cantor discutió los aspectos filosóficos de sus teorías matemáticas sobre el infinito con diferentes científicos.
GENIO
El matemático David Hilbert describió el trabajo de Georg Cantor como «el mejor producto del genio matemático y uno de los logros supremos de la actividad humana puramente intelectual».
HIPÓTESIS DEL CONTINUO
La hipótesis del continuo es un enunciado relativo a la cardinalidad del conjunto de los números reales; fue formulado como una conjetura por Cantor en 1878. Afirma que no existen conjuntos infinitos cuyo cardinal esté estrictamente comprendido entre el del conjunto de los números naturales y el del conjunto de los números reales.
Fue una conjetura tan notoria que acabó siendo uno de los 23 problemas de Hilbert propuestos en 1900. La hipótesis del continuo es indecidible, es decir, partiendo de los axiomas de la teoría de conjuntos no puede probarse ni refutarse. Kurt Gödel demostró su consistencia (no puede refutarse) en 1940 y Paul Cohen probó su indecibilidad (no puede demostrarse) en 1963.
INFINITO
Antes de las teorías de Cantor, solo se consideraban conjuntos finitos y «el infinito», pensado como un asunto de discusión filosófica más que matemática. Al demostrar que hay una infinidad de posibles «tamaños» para conjuntos infinitos, Cantor mostró que la teoría de conjuntos debía revisarse.
JOURDAIN
Cantor mantuvo correspondencia con el lógico Philip Jourdain sobre la teoría de conjuntos en la que ambos trabajaban.
KRONECKER
Leopold Kronecker fue uno de sus profesores más admirados por Cantor en la Universidad de Berlín. Su radical oposición a las novedosas teorías matemáticas de Cantor provocó una profunda enemistad entre ambos. Kronecker llegó a calificar a su pupilo de «charlatán científico, renegado y corruptor de la juventud».
LO VEO PERO NO LO CREO
Cantor mantuvo correspondencia durante varios años con Richard Dedekind, compartiendo sus ideas y solicitando la opinión de su colega matemático. En 1877, Cantor escribió a Dedekind para compartir su demostración de la existencia de una biyección entre el intervalo [0 ,1] y el espacio n-dimensional. Sorprendido de su propio descubrimiento, Cantor escribió: «Lo veo, pero no lo creo».
MITTAG-LEFFLER
Cantor también mantuvo correspondencia con el matemático sueco Gösta Mittag-Leffler. Fue a partir de 1882 y duró tres años, se interrumpió tras un desencuentro entre ambos científicos. Mittag-Leffler pidió a Cantor que retirara una propuesta de artículo para Acta Mathematica (fundada por el matemático sueco)por considerarla demasiado adelantada a su tiempo, y Cantor decidió dejar de publicar en esa revista.
NÚMEROS
Cantor demostró que los números racionales y los algebraicos son numerables, es decir, pueden ponerse en correspondencia biunívoca con los números naturales. También probó que los números reales no son numerables, usando el conocido como argumento diagonal de Cantor.
 Argumento diagonal de Cantor. Fuente: Wikimedia Commons.
Argumento diagonal de Cantor. Fuente: Wikimedia Commons.
ORDINALES Y CARDINALES
Cantor desarrolló una teoría de conjuntos infinitos, llamados cardinales (y su aritmética) y ordinales (y su aritmética), que ampliaba la aritmética de los números naturales.
PARAÍSO
David Hilbert defendió con vehemencia las teorías de Cantor ante las críticas de otros colegas. En 1926, Hilbert escribía: «Nadie debería poder expulsarnos del paraíso que ha creado Cantor para nosotros».
QUIMERA
Muchos de sus colegas pensaban que las teorías de Cantor eran quimeras, delirios, fantasías.
RELIGIÓN
Cantor estuvo preocupado por preservar la ortodoxia de la relación entre Dios y las matemáticas. En 1905, escribió una obra religiosa tras regresar a casa después de una temporada en un hospital psiquiátrico.
SAN PETERSBURGO
Georg Cantor nació en San Petersburgo y se crio allí hasta los once años. La familia se mudó a Alemania en 1856, al enfermar el padre.
TEORÍA DE CONJUNTOS
El comienzo de la teoría de conjuntos como rama de las matemáticas tiene como origen un artículo de Cantor de 1874 (Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen). En este artículo se encuentra la primera prueba rigurosa de la existencia de más de un tipo de infinito.
UNIVERSIDAD DE HALLE
En 1867, tras defender su tesis (tutelado por Eduard Kummer y Karl Weierstrass) en la Universidad de Berlín, Cantor pasó a ocupar un puesto en la Universidad de Halle, donde desarrolló toda su carrera.
VALLY GUTTMANN
En 1874, Cantor se casó con Vally Guttmann, una amiga de su hermana. El matrimonio tuvo seis hijos.
WILLIAM SHAKESPEARE
Cantor poseía una curiosa creencia literaria; estaba convencido de que Francis Bacon era en realidad el autor de las obras teatrales atribuidas a William Shakespeare. En 1884, durante una de sus estancias en un sanatorio psiquiátrico, comenzó un intenso estudio de la literatura isabelina para intentar probar la teoría baconiana. Publicó dos panfletos sobre este tema en 1896 y 1897.
XIX
El siglo XIX vivió grandes cambios en las matemáticas gracias, en parte, a las propuestas revolucionarias de Georg Cantor.
Y…
… llegamos al final de este homenaje, con la Z, y los conjuntos como protagonistas.
ZERMELO-FRAENKEL
Los axiomas de Zermelo-Fraenkel son un sistema axiomático concebido para formular la teoría de conjuntos. Como ya hemos comentado, la hipótesis del continuo es indecidible en este sistema.
«Me imagino un conjunto como un abismo».
Georg Cantor
Referencias:
-
O’Connor, John J.; Robertson, Edmund F., Georg Cantor, MacTutor History of Mathematics archive, University of St Andrews
-
Joseph Warren Dauben, Georg Cantor: his Mathematics and Phylosophy of the infinite, Princeton University Press, 1990
-
Georg Cantor, Wikipedia
Para saber más:
Apeirofobia
Una mirada topológica al conjunto de Cantor
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Homenaje alfabético a Georg Cantor se ha escrito en Cuaderno de Cultura Científica.
Un cristal de Wigner en una superred de muaré
Comprender y controlar el movimiento cuántico de los electrones permitirá a los científicos construir los dispositivos microelectrónicos del futuro y los qubits robustos necesarios para la computación cuántica. En este sentido, algunas superredes que forman un patrón de muaré resultan ser un entorno óptimo para investigar las interacciones entre electrones. Cuanto más fuertes son estas interacciones, más prominente es la naturaleza mecáno-cuántica de los materiales sólidos. En esta ocasión, un equipo de investigación ha empleado láseres para «observar» el movimiento de los electrones sin los artefactos que abundan en otras técnicas de medición. Y, al hacerlo, ha descubierto un raro estado cuántico de la materia, nunca antes observado en las superredes de muaré.
 Patrón de muaré en el plumaje de un pájaro. Foto: David Clode / Unsplash
Patrón de muaré en el plumaje de un pájaro. Foto: David Clode / UnsplashUn patrón de muaré es un patrón de interferencia que se forma cuando se superponen dos rejillas de líneas, ya sean rectas o curvas, con un cierto ángulo, y tiene como resultado la aparición de bandas oscuras. Un efecto de interferencia similar ocurre cuando se apilan cristales bidimensionales con espacios atómicos que no coinciden. Las superredes de muaré presentan propiedades físicas exóticas, ausentes en las capas que forman los patrones, que tienen su origen en la naturaleza cuántica de los electrones. Las investigadoras han descubierto una nueva propiedad en las superredes de muaré formadas en cristales hechos de diseleniuro de tungsteno/disulfuro de tungsteno (WSe2/WS2). En estos cristales bidimensionales, las interacciones entre los electrones son tan fuertes que los electrones se “congelan” y forman una matriz ordenada.
En los sólidos los niveles de energía que ocupan los electrones forman bandas de energía. Las superredes de muaré alteran la periodicidad atómica “vista” por los electrones y, por lo tanto, las bandas de energía. Los efectos muaré pueden dar lugar a bandas «planas», en las que los niveles de energía se juntan, lo que hace que los electrones reduzcan su energía cinética y sientan su repulsión mutua con más fuerza. El equipo del Laboratorio Nacional Lawrence Berkeley (LBNL, por sus siglas en ingés) utilizó una técnica óptica novedosa para observar el movimiento de los electrones mientras variaba la cantidad de electrones inyectados en la muestra.
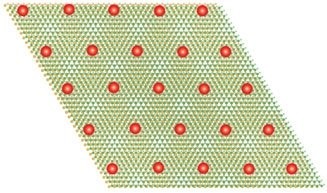 Una superred de muaré formada en cristales hechos de diseleniuro de tungsteno/disulfuro de tungsteno en la que se ha inyectado un portador de carga por celda unidad. Fuente: LBNL
Una superred de muaré formada en cristales hechos de diseleniuro de tungsteno/disulfuro de tungsteno en la que se ha inyectado un portador de carga por celda unidad. Fuente: LBNLCuando solo se inyectó un portador de carga (un nombre genérico para cosas como un electrón) por celda muaré unidad, se esperaba que los electrones se movieran libremente o, dicho de otra manera, que la muestra condujera la electricidad. En cambio, la muestra se convirtió en lo que se conoce como aislante de Mott, en el que los electrones interactúan con tanta fuerza que evitan estar en la misma celda. Si todas las celdas están ocupadas, los electrones dejan de moverse. Un material es un aislante de Mott si según la teoría de bandas debería conducir la electricidad pero, debido a las interacciones electrón-electrón, deja de hacerlo.
La verdadera sorpresa vino cuando se inyectaron menos electrones, de modo que solo la mitad o un tercio de las celdas estaban ocupadas. A estas bajas densidades los científicos esperaban que los electrones sintieran menos la presencia de los demás y tuvieran una gran movilidad. Sin embargo, la muestra resultó ser un aislante. En WSe2/WS2 los electrones interactúan con tanta fuerza que, no solo no puede haber dos electrones por celda unidad, sino que tampoco pueden estar en celdas vecinas. Este raro fenómeno se conoce como cristal electrónico de Wigner.
Los investigadores del LBNL también demostraron que en WSe2/WS2 la luz con la polarización adecuada interactúa de forma diferente con los electrones con distinto espín, lo que hace posible cambiar selectivamente la energía de los electrones en función de su espín. Al hacerlo, observaron que las excitaciones de espín persistían un tiempo órdenes de magnitud más largo que las excitaciones de carga. Esto abre la puerta a una futura investigación de estados de espín exóticos, como el líquido de espín cuántico, un sistema de espines cuyas orientaciones fluctúan incluso en el cero absoluto de temperatura .
Referencia:
Regan, E.C., Wang, D., Jin, C. et al. (2020) Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature. doi: 10.1038/s41586-020-2092-4
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un cristal de Wigner en una superred de muaré se ha escrito en Cuaderno de Cultura Científica.
El consumo del alcohol no mata a las neuronas, pero sí las trastorna
alcohol
 Foto: Kelsey Knight / Unsplash
Foto: Kelsey Knight / UnsplashLas bebidas alcohólicas irrumpieron en las sociedades humanas en épocas muy tempranas de la historia. La hipótesis más plausible sostiene que el descubrimiento de la fermentación alcohólica se dio poco después del nacimiento de la agricultura, hace unos 10.000 años. Los efectos agudos del consumo de esta droga sobre el cuerpo humano fueron los primeros en conocerse por ser evidentes: desinhibición, euforia, depresión del sistema nervioso central, descoordinación de los movimientos, lagunas de memoria, vómitos, náuseas…
Sin embargo, conocer los efectos de la ingesta de bebidas alcohólicas sobre la salud a largo plazo es una tarea mucho más complicada y, aún hoy, seguimos sin saber bien toda su magnitud. Según la monografía «Alcohol 2021. Consumo y Consecuencias», del Ministerio de Sanidad, la ingesta de bebidas alcohólicas se asocia con más de 200 problemas de salud y lesiones, incluyendo enfermedades cardiovasculares, hepáticas y neuropsiquiátricas, entre otras.
Discapacidad, cáncer y muertesPor su parte, los estudios poblacionales muestran que el consumo de alcohol es un factor que incrementa el riesgo de discapacidad y de muerte por diversas causas. En España concretamente, este hábito es la segunda causa evitable de mortalidad prematura y cada año fallecen en nuestro país unas 15.000 personas por enfermedades relacionadas con la ingesta de alcohol.
Además, el alcohol es una sustancia cancerígena (por alterar el ADN), aunque se tome a dosis moderadas. A mayor consumo, mayor riesgo de aparición de tumores, sin que exista una cantidad mínima segura. La «copita de vino saludable» sencillamente no existe, pues cualquier ingesta de alcohol, por mínima que sea, incrementa el riesgo de aparición de cáncer en diversos lugares: boca, faringe, laringe, esófago, colorrectal, mama e hígado. De hecho, el consumo de alcohol es la segunda causa evitable, tras el tabaco, de cáncer en el mundo. La Organización Mundial de la Salud (OMS) estimó que 750.000 casos de cáncer (el 4 % del total) en 2020 se debían al consumo de bebidas alcohólicas.
El alcohol altera el funcionamiento del encéfaloPor otro lado, en la cultura popular está bastante extendida la idea de que tomar alcohol mata directamente a las neuronas del cerebro. Aunque el consumo de esta molécula altera el funcionamiento de este órgano vital, esto no se produce mediante la destrucción de neuronas, sino a través de otros mecanismos.
En primer lugar, el alcohol puede dañar las conexiones entre neuronas al lesionar las dendritas y los axones (las prolongaciones de dichas células), lo que complica el envío de señales entre ellas. El consumo elevado y crónico de esta droga provoca inflamación en el cerebro que, a la larga, destroza la vaina de mielina que recubre los axones de las neuronas y dificulta la transmisión del impulso nervioso.
Por otro lado, el alcohol provoca importantes cambios en el normal funcionamiento de los neurotransmisores (las moléculas mensajeras de las neuronas), en especial del ácido gamma aminobutírico (más conocido como GABA). El GABA es el principal neurotransmisor inhibidor del cerebro (inhibe la transmisión de las señales nerviosas) y su mayor actividad por el consumo de alcohol provoca los típicos efectos sedantes. Estos efectos sedantes se ven potenciados, a su vez, por la inhibición de neurotransmisores excitadores del sistema nervioso central como el glutamato. La alteración conjunta de los niveles de diversos neurotransmisores en cada persona determinará que aparezcan ira, bajo estado de ánimo, euforia o agresividad, entre otros estados de ánimo.
En los alcohólicos crónicos, en los que se da un consumo elevado de alcohol mantenido en el tiempo, la alteración de la actividad de los neurotransmisores puede perpetuarse y aparecer cambios crónicos e incluso modificaciones estructurales en el cerebro con atrofia en diferentes regiones. Esto puede desencadenar problemas emocionales, de equilibrio y de memoria. Si el consumo de alcohol se da durante el embarazo, se pueden generar alteraciones en el desarrollo cerebral del embrión/feto que se traduzcan en déficit de atención e hiperactividad (TDAH) o en discapacidad intelectual, uno de los signos del síndrome alcohólico fetal.
Por supuesto, el alcohol también puede provocar lesiones cerebrales (y, por tanto, daño neuronal) de forma indirecta al aumentar el riesgo de sufrir accidentes (de tráfico, por caídas o golpes…), coma e ictus. Si se tiene en cuenta todos los datos anteriores, queda claro que la única bebida alcohólica saludable es aquella que no se toma.
Para saber más:
Daños estructurales por consumo de alcohol en el cerebro humano
«Una copita de vino es buena para el corazón». Claro que sí, guapi.
Alcohol y sandía
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo El consumo del alcohol no mata a las neuronas, pero sí las trastorna se ha escrito en Cuaderno de Cultura Científica.
Una mirada a los modos de pensar la ciencia
pensar la ciencia
Por si toda la trayectoria de la humanidad no hubiera sido suficiente para despejar cualquier duda, el premio Nobel Max Perutz nos proporcionó la respuesta. Lo hizo en 1989, en su libro ¿Es necesaria la ciencia?.
La respuesta la seguimos encontrando a nuestro alrededor, en nuestra vida cotidiana. Sin ciencia no existiría la electrónica. No tendríamos internet, ¡ni redes sociales! Y no habríamos salido de la pandemia de covid-19 como lo hemos hecho.
Aun así, sin duda son muchas las personas que aún se preguntarán que para qué sirve la ciencia. Y quizás lo hagan mientras leen este artículo en su dispositivo móvil –una caja que encierra mucha ciencia– o toman su medicación –auténticas píldoras de ciencia concentrada– durante el desayuno.
 Foto: SpaceX / UnsplashPensar la ciencia
Foto: SpaceX / UnsplashPensar la ciencia
Cada cual tenemos unas ideas, una percepción, una imagen, unas actitudes, con respecto a la ciencia. En definitiva, un modo de pensar la ciencia.
Recientemente se ha llevado a cabo el estudio Estilos de pensar la ciencia: diagnóstico y prevalencia, dirigido desde la Unidad de Investigación en Ciencia, Tecnología y Sociedad del Ciemat. En él hemos escuchado a una muestra de la población española para mirar, desde diferentes prismas, a esos diversos modos de pensar la ciencia.
Para ello hemos empleado el cuestionario LAIC (Lente conformada por la Actitud y la Ideología hacia la Ciencia). Se trata de una investigación innovadora, que experimenta sobre el modo en que se aborda el estudio de la percepción de la ciencia.
Por un lado, supera las aproximaciones estrictamente psicológicas o sociológicas: pone el foco en el individuo, sin olvidar la influencia del contexto. Además, tiene en cuenta las dimensiones actitudinal e ideológica.
La actitud tiene que ver con la valoración o sentir de cada persona, con lo que sentimos con respecto al objeto que analizamos: por ejemplo, gusto o disgusto, interés, o la percepción de sus riesgos y beneficios.
La ideología hace referencia a las ideas clave que cada uno tenemos, las que nos definen o caracterizan, a lo que consideramos importante: por ejemplo, a las creencias, los valores o la orientación política.
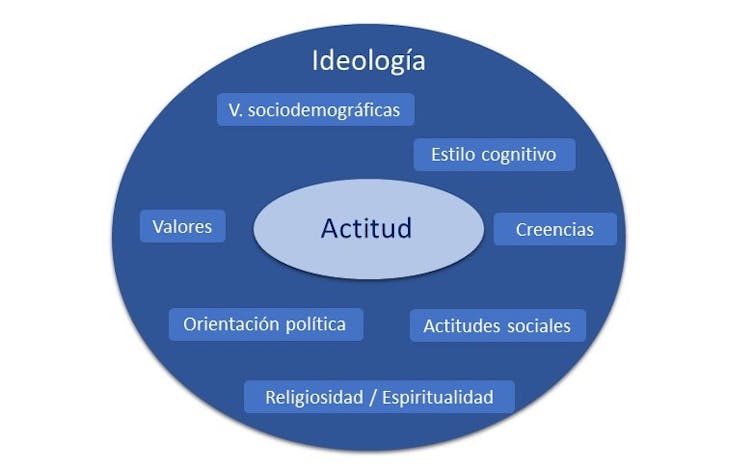 Áreas del cuestionario LAIC (Lente conformada por la Actitud y la Ideología hacia la Ciencia).
Áreas del cuestionario LAIC (Lente conformada por la Actitud y la Ideología hacia la Ciencia).Author providedPensar la crisis ecológica
Nos hemos preguntado antes para qué sirve la ciencia. Podemos identificar tres utilidades genéricas, no excluyentes:
- la ciencia como fuente de conocimiento;
- la ciencia práctica, que proporciona respuestas concretas a problemas específicos;
- y la ciencia orientada a la obtención de beneficios.
Como fuente de conocimiento, la ciencia permite entender lo que ocurre en la naturaleza. Y en su faceta práctica, proporcionar soluciones para enfrentar los problemas del medio ambiente. Dejaremos los beneficios económicos derivados de ello para otra ocasión.
No nos detendremos aquí en los problemas ambientales resultantes de la actividad humana: calentamiento global, contaminación, sobreexplotación de los recursos naturales, pérdida de biodiversidad, etc. Las evidencias científicas sobre su ocurrencia son cada vez más abundantes y explícitas. Y sus efectos, cada vez más evidentes.
Pero la percepción que la ciudadanía tiene tanto de la ciencia como de la crisis ecológica no se elabora únicamente con datos y evidencias.
La imagen de la ciencia tiene un doble componente, individual y contextual: depende de la propia persona, de la lente con la que procesa la información, así como del contexto en el que vive. Y a su vez está influida por la imagen de la ciencia que tiene el conjunto de la sociedad.
Lo mismo ocurre con la percepción y la imagen del calentamiento global y la crisis climática y ecológica. Esta imagen puede ser perfilada o condicionada por fenómenos ambientales. Pero también por acontecimientos políticos y sociales, y por su cobertura mediática.
Entre los distintos aspectos estudiados se encuentra la percepción de las consecuencias de la actividad humana sobre la naturaleza, de la crisis ecológica y del papel de la ciencia para hacer frente a los problemas medioambientales.
Cinco de las preguntas incluidas en el cuestionario presentaban afirmaciones sobre estos temas. Las personas encuestadas debían señalar su grado de acuerdo con ellas (de 0 nada de acuerdo a 10 totalmente de acuerdo).
Los resultados indican que la ciudadanía española muestra un elevado grado de acuerdo con que “el impacto de nuestras acciones sobre la naturaleza tiene consecuencias desastrosas” y “los impactos de la industria ponen en peligro el equilibrio de la naturaleza”. Y están poco de acuerdo con que “la crisis ecológica se ha exagerado”.
Estas opiniones enlazan con una percepción positiva de la ciencia. La mayoría de las personas encuestadas creen que “descubre leyes que representan exactamente lo que ocurre en la naturaleza” y que “proporcionará soluciones para hacer frente a los problemas del medio ambiente”.
Relación con nuestra ideologíaHemos explorado en qué medida esta percepción está relacionada con variables individuales, sociodemográficas e ideológicas. Para ello, hemos identificado cinco perfiles poblacionales de percepción de la ciencia y la crisis ecológica.
El resultado más relevante es que la lente con la que cada cual miramos e interpretamos la ciencia, el entorno que nos rodea y los efectos de nuestras acciones sobre él, está relacionada con la ideología, concretamente política y religiosa. Más que con la edad, el género, el nivel y área de estudios, o el número de habitantes de la población de residencia.
Los detalles de esta relación pueden consultarse en el capítulo 6 del libro Pensar la ciencia. Una mirada desde diferentes prismas. En él se muestran y discuten los resultados del estudio y sus implicaciones.
Niveles de reflexión y actuaciónConocer las opiniones, imágenes, representaciones y creencias que los ciudadanos tienen sobre la ciencia y la crisis ecológica tiene un doble ámbito de importancia: ético y político, individual y colectivo.
Las actuaciones políticas en defensa y promoción de la ciencia y en relación con el equilibrio entre la explotación del planeta y su conservación, discurren por el ámbito de lo colectivo. Están orientadas, o al menos así debería ser, al bien común.
La ética apela al individuo, al igual que la espiritualidad y la religión, y por tanto a sus actitudes, acciones y responsabilidades. En los sistemas plenamente democráticos, además, la agregación de lo individual tiene un efecto más o menos intenso en la configuración de lo político-colectivo a través de los mecanismos de participación.
Así pues, conocer esas opiniones, imágenes, representaciones y creencias puede ayudar a informar y configurar la acción colectiva frente a la crisis ecológica, ya sea en uno u otro sentido. Al igual que, no seamos ingenuos, puede contribuir a desinformarla y manipularla.
Las posturas frente al calentamiento global y la crisis ecológica no deberían guiarse por la ideología o los intereses políticos o económicos. O al menos no preferentemente, por más que las posturas más negacionistas, recalcitrantes y reaccionarias se empeñen en mantenerse.
Los datos disponibles y las evidencias proporcionadas por la ciencia son cada vez más abundantes, indiscutibles e incontestables. Y por tanto, inexcusablemente deben tenerse en cuenta en un diálogo equilibrado. Los intereses políticos y económicos no deberían determinar qué conocimiento puede o no hacerse público, y qué acciones deben o no acometerse para prevenir y mitigar la crisis ecológica y la degradación de las condiciones de vida en el planeta.![]()
Sobre los autores: Jesús Rey Rocha, Investigador Científico. Grupo de investigación ‘Ciencia, vida y sociedad’, Instituto de Filosofía (IFS-CSIC); Ana Muñoz van den Eynde, Responsable de la Unidad de Investigación CTS (Ciencia, Tecnología y Sociedad) del Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas (CIEMAT) y Emilio Muñoz Ruiz, Profesor de Investigación. Unidad de Investigación CTS (Ciencia, Tecnología y Sociedad) del CIEMAT, Instituto de Filosofía (IFS-CSIC).
Este artículo fue publicado originalmente en The Conversation. Artículo original.
Para saber más:
Los males de la ciencia (serie)
Los valores de la ciencia (serie)
Goethe, pensar la ciencia con el espíritu del arte
Anticiencia (I): la unidad perdida
El artículo Una mirada a los modos de pensar la ciencia se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: Un telescopio de oro

El telescopio espacial James Webb lleva 48 gramos de oro en forma de una capa de solo 100 nanómetros de espesor, recubriendo los espejos hexagonales que aparecen en el cartel anunciador del evento. Y ¿por qué de oro? Eso nos lo explica Ángel Gómez Roldán en su charla.
Ángel Gómez Roldán ha sido durante muchos años operador de telescopio en el Observatorio del Teide del Instituto de Astrofísica de Canarias, es autor y coautor de varios libros de divulgación astronómica, pertenece a multitud de sociedades y ha recibido varios premios por su tarea divulgativa a lo largo de los años. Es el director y editor de la revista Astronomía.
Si no ve correctamente el vídeo, use este enlace.
Más sobre el tema:
El sucesor del Hubble: el telescopio espacial James Webb
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2022: Un telescopio de oro se ha escrito en Cuaderno de Cultura Científica.
Apibioma y antropización
El conjunto de microorganismos de una colmena de abejas melíferas (el apibioma) varía considerablemente dependiendo del grado de transformación que haya ejercido el ser humano (antropización) sobre el entorno. Tras trasladar colmenas de un entorno agrícola a uno seminatural en tan solo 16 días el desequilibrio microbiano disminuye.
 Foto: Maxime Bouffard / Unsplash
Foto: Maxime Bouffard / UnsplashLa abeja melífera occidental (Apis mellifera) está en peligro debido a muchos de los factores de estrés que sufren en zonas dependientes de los seres humanos, como la mala nutrición, los pesticidas y los patógenos. “Desde hace varios años se está evidenciando que la mortalidad de las abejas ha aumentado mucho; es por eso que hace unos 6 años empezamos a investigar qué factores influyen en la microbiota de la abeja y qué relación tiene esto con las enfermedades o la salud de las abejas”, explica Iratxe Zarraonaindia, investigadora Ikerbasque del grupo Applied Genomics and Bioinformatics de la UPV/EHU.
En colaboración con tres universidades croatas el grupo ha tenido la oportunidad de investigar algunas colmenas situadas en la isla croata de Unije, lejos de la influencia humana. Durante diez años estas colmenas no han recibido tratamiento alguno; se sabía que sus abejas tenían una larga supervivencia a pesar de la presencia del ácaro Varroa destructor, causante de una enfermedad mortal para las abejas. La idea era estudiar cómo influye la antropización en la microbiota de las abejas. Para ello, se han comparado las colmenas de la isla de Unije con la microbiota de dos colmenas situadas en zonas rurales.
Para que las dos colmenas de la zona agrícola fueran comparables, se han utilizado «hermanas genéticas» (colmenas formadas por abejas que contienen el mismo material genético que las de la zona agraria), una de las cuales se ha trasladado a una zona seminatural. “Hemos visto claramente que la antropización tiene un impacto importante, ya que sólo 16 días después detectamos que el desequilibrio microbiano por estrés agrícola se había atenuado en la colmena trasladada a la zona seminatural”, explica Zarraonaindia. Esto demostraría que la microbiota de las abejas melíferas tiene una gran capacidad de adaptación. “No suponíamos que la composición de la microbiota fuera a cambiar tan rápido”, dice.
Los investigadores han encontrado un claro gradiente relacionado con el grado de antropización y la comunidad microbiana de la colmena: “La microbiota de la colmena de la isla Unije está más equilibrada, su proporción de microorganismos beneficiosos es mayor y en ambiente seminatural la proporción va reduciéndose, mientras que en el ámbito agrícola la colmena tiene una composición muy desequilibrada, se encuentran más bacterias oportunistas y es más sensible a las enfermedades”, explica Zarraonaindia. Según la investigadora, “en las zonas agrícolas los factores de estrés están muy activados”.
 Las investigadoras del grupo Applied Genomics and Bioinformatics Andone Estonba e Iratxe Zarraonaindia en la isla Unije, preparando las colmenas para el estudio, junto a sus colegas croatas. Foto: Marin Kovačić / Universidad de OsijekInvestigación del apibioma
Las investigadoras del grupo Applied Genomics and Bioinformatics Andone Estonba e Iratxe Zarraonaindia en la isla Unije, preparando las colmenas para el estudio, junto a sus colegas croatas. Foto: Marin Kovačić / Universidad de OsijekInvestigación del apibioma
Estas conclusiones han permitido al grupo investigador determinar biomarcadores que aportarán información sobre la salud de las abejas. Por ejemplo, los investigadores han detectado que una bacteria determinada, Arsenophonus, es muy abundante en las zonas agrícolas, que está menos presente en las zonas seminaturales, y que apenas aparece en las zonas naturales.
Han estudiado la colmena en su totalidad, no sólo las abejas. Esta es una de las claves más importantes de esta investigación: “Este enfoque es innovador. Hemos estudiado el apibioma: el conjunto de microorganismos en los nichos presentes en la colmena. Hemos estudiado el intestino de las abejas, la entrada de la colmena, el pan de abeja (la sustancia de la que se alimentan las abejas) y el aire interior de la colmena”. Como se ha comentado anteriormente, la bacteria Arsenophonus es la más frecuente en la zona agrícola, y se trata de una tendencia que se ha encontrado en todos los nichos. Por lo tanto, es un biomarcador muy adecuado para medir el impacto de la agricultura en las colmenas y medir su salud; además, “este método no es invasivo, ya que se puede llevar a cabo tomando una muestra de la entrada de la colmena”.
La investigación recogida en el artículo de referencia solo representa un primer año de trabajo. Las investigaciones continúan: “Ahora hemos trasladado la colmena de la zona seminatural a una zona natural para observar si se le equilibra la microbiota y llega a ser la misma que la de las abejas de la zona natural. Esto nos permitirá conocer el alcance tanto de la contribución genética como de la contribución ambiental”.
Referencia:
June Gorrochategui Ortega, Marta Muñoz Colmenero, Marin Kovačić, Janja Filipi, Zlatko Puškadija, Nikola Kezić, Melanie Parejo, Ralph Büchler, Andone Estonba, Iratxe Zarraonaindia (2022) A short exposure to a seminatural habitat alleviates the honey bee hive microbial imbalance caused by agricultural stress Scientific Reports DOI: 10.1038/s41598-022-23287-6
Para saber más:
Qué puedes hacer tú para proteger a las abejas
La mente de una abeja
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Apibioma y antropización se ha escrito en Cuaderno de Cultura Científica.
Los invasores: La perca del Nilo
 Perca del Nilo (Lates niloticus). Fuente: Wikimedia Commons
Perca del Nilo (Lates niloticus). Fuente: Wikimedia CommonsEs un invasor de otros hábitats, no de nuestro entorno más cercano y, sin embargo, desde aquí subvencionamos esa invasión. Y, es curioso, ahora ni eso pues ha desaparecido, que sepamos, de nuestros mercados. Es un pez de gran tamaño, de agua dulce y hasta 1.80 metros de longitud y 200 kilogramos de peso, que vive en África central y oriental y que, para promocionar la pesca, se ha introducido en lagos y ríos de ese continente. Durante un tiempo, era habitual verlo a la venta en pescaderías y supermercados de nuestro entorno pero en poco tiempo ha desaparecido. Ya no se vende porque adquirió mala fama pues era típico que se ofreciera sustituyendo a otras especies como, por ejemplo, el mero, en los menús del día de muchos restaurantes. En el estudio de José Luis Horreo y sus colegas de la Universidad Complutense con 77 platos de pescado en el menú de 53 restaurantes de Madrid, publicado en 2019, siete especies y el 30% de las muestras están mal etiquetadas en cuanto a la especie que indican. Y entre ellas varios platos de mero, Epinephelus marginatus, contienen perca del Nilo cuyo parecido con esa especie es muy alto.
Además, un estudio detallado que lleva varios años en marcha ha encontrado que los cíclidos del lago Victoria están desapareciendo al ser alimento para la perca del Nilo, un depredador voraz.
Los cíclidos son peces de agua dulce del hemisferio sur, sobre todo de África, y muy populares entre los aficionados a los acuarios; entre ellos están los discos o los peces ángel. Los que habitan en Lago Victoria son únicos y han aparecido en una radiación evolutiva única entre los vertebrados. Antes de llegar la perca había más de 300 especies que ocupaban una gran variedad de nichos y, por ello, cada hábitat del lago tenía su propia comunidad de cíclidos.
La perca del Nilo, un “elefante” del agua dulce por su tamaño, fue introducido en el norte del lago y avanza hacia el sur alimentándose de los cíclidos. Donde se ha hecho dominante, más de la mitad de las especies de cíclidos han desaparecido. Ha sido introducida en otros lagos africanos y como decía, en el caso mejor conocido, en el Lago Victoria al que llegó en la década de los cincuenta para reforzar la pesca y promocionar la pesca deportiva para turistas.
 Ejemplar de perca del Nilo capturado en el lago Victoria, en aguas de Uganda. Habida cuenta del efecto de la perspectiva la longitud de la perca es aproximadamente la altura del hombre. Fuente: Wikimedia Commons
Ejemplar de perca del Nilo capturado en el lago Victoria, en aguas de Uganda. Habida cuenta del efecto de la perspectiva la longitud de la perca es aproximadamente la altura del hombre. Fuente: Wikimedia CommonsEs un lago con una superficie de 68.000 kilómetros cuadrados y su costa se reparte entre tres países con el 51% en Tanzania, el 43% en Uganda y el 6% en Kenia. En 2007, alrededor de tres millones de personas dependían de la pesca en el lago.
Para 1980, la perca suponía el 2% de la pesca en el Lago Victoria; para 1986, era el 80%. Fue en los años 1983-84 cuando se detectó un crecimiento dramático de las poblaciones de perca del Nilo. Además, la pesca en el lago era de 100.000 toneladas anuales en los sesenta y, tres décadas después, en los noventa e incluyendo la perca del Nilo, llegaba a las 500.000 toneladas. Mas datos de la pesquería en Uganda muestran que los peces nativos pasaron de casi el 92% a casi cero entre 1981 y 1985 y, por el contrario, la perca pasó, en esas fechas, del 5% al 96%.
El número de pescadores aumentó un 32% en 2002, las embarcaciones lo hicieron en un 24%, las redes en el 50% y el número de anzuelos de palangre se dobló. Incluso la potencia de los motores fuera borda de las embarcaciones de los pescadores creció un 47%. El número de barcos pasó de 12.000 en 1983 a 23.000 en 1990 y 42.000 en 2000. Todo ello es, concluye John Balirwa, del Instituto Nacional de Recursos Pesqueros de Uganda en Jirja, un caso claro de síntomas de sobreexplotación.
Además, la perca capturada se destinó a ser fileteada para la exportación mientras que para los habitantes de la costa solo quedaban los desechos como los esqueletos, las cabezas o las colas o, también los ejemplares de tamaño pequeño. Los salarios han caído, el sistema tradicional de pesca familiar casi ha desaparecido, escasea la alimentación adecuada y el número de personas que sufren hambre había crecido un 25% en los últimos diez años según datos de 2007.
Por todo ello, la perca del Nilo aparece en la lista de las 100 especies invasoras más peligrosas del planeta.
La perca del Nilo, Lates niloticus, es una especie de agua dulce con una distribución original por África tropical y nativa del Congo, Senegal, Níger y, en concreto, en el Nilo, el lago Chad, Volta o Turkana. Es parte sustancial de la economía y la alimentación de África Oriental. Puede alcanzar gran tamaño y en la madurez llega a una longitud de 1.20-1.40 metros, con un peso de hasta 200 kilogramos. Crece entre 21 y 28 centímetros por año y hay datos de que puede llegar a los 40 centímetros anuales. Es un predador feroz que ocupa todos los ambientes con suficiente oxígeno y se alimenta de peces, incluso ejemplares de su propia especie, así como crustáceos, moluscos e insectos. Habitualmente se mueve en grupo como sistema de defensa ante otros predadores, entre ellos los de su especie.
Probaremos la perca del Nilo con una receta fácil de la cocina de Tanzania según la experta Eva Pendaeli-Sarakikya. Vamos a freír unos filetes de perca.
 Filetes de perca del Nilo fritos servidos en un hotel de Zambia. Fuente: Wikimedia Commons
Filetes de perca del Nilo fritos servidos en un hotel de Zambia. Fuente: Wikimedia CommonsMezclamos harina, sal y pimienta y, a la vez, limpiamos los filetes de perca con un trapo limpio hasta que estén secos. Recubrimos los filetes con la mezcla de harina. Para freír usaremos grasa animal, quizá manteca. La calentamos y freímos los filetes por ambos lados, bajamos el fuego y seguimos hasta que estén marrón dotado. Los servimos en caliente, quizá adornados con rodajas de limón.
Introducida de forma activaLlegó al Lago Victoria, en África Oriental, a Uganda, según relata Robert Pringle, de la Universidad de Oxford, en la década de los cincuenta del siglo pasado, hacia 1954 por iniciativa de funcionarios británicos de la colonia. El objetivo era contrarrestar la caída de los stocks de peces nativos que comenzaban a escasear debido a la sobrepesca. En los sesenta, la mayoría de las especies de peces de gran tamaño del Lago Victoria estaban sobreexplotadas. La respuesta de las autoridades fue la introducción de la perca. Sin embargo, contribuyó a la extinción de más de 200 especies endémicas por depredación y competencia por el alimento.
Además, la acción de la perca provocó la invasión de algas y, sobre todo, del jacinto acuático o Euchornia crassipes. Así disminuyó el oxígeno en las aguas del lago lo que ayudó a la extinción de más especies de cíclidos. Para Tijs Goldschmidt y sus colegas, de la Universidad de Leiden, en Holanda, el 18% de los cíclidos se alimentaban de fitoplancton y hasta el 31% lo hacían de detritos. En total, calculan que más del 58% de su alimento son fitoplancton y detritos. La desaparición de estas especies aumentó la turbidez de las aguas del lago con más fitoplancton, mayor escasez de oxígeno y contribuyó a la colonización por el jacinto acuático.
El aumento de población de la perca del Nilo se detectó a finales de los setenta en Kenia, a principios de los ochenta, un par de años después, en Uganda, y a mediados de esta década en Tanzania, según la revisión publicada en 2008 por Kees Goudswaard y sus colegas, también de la Universidad de Leiden, en Holanda.
 Puesto de pescadería en la orilla ugandesa del lago Victoria. En primer plano, piezas de perca del Nilo.La perca del Nilo cambió la economía local
Puesto de pescadería en la orilla ugandesa del lago Victoria. En primer plano, piezas de perca del Nilo.La perca del Nilo cambió la economía local
Además, la introducción y pesca de la perca del Nilo cambió el sistema socioeconómico de los habitantes del lago. Muchos de los habitantes han sido desplazados de sus ocupaciones tradicionales en la pesca y el comercio de los productos pesqueros y se han visto obligados a entrar en las empresas que se dedican a la preparación y exportación de perca del Nilo. Son, en este momento, refugiados económicos. La preparación de la perca no es la habitual para los cíclidos. Tiene más componentes grasos y no funciona bien el secado al sol y, además, necesita el ahumado. Por tanto, necesita madera para quemar en una región con problemas de deforestación.
Todo ello se refleja en el documental La pesadilla de Darwin, estrenado en 2004, y dirigido por Hubert Sauper. En la película aparece el comercio en tres etapas que se ha desarrollado con la exportación de la perca del Nilo a Europa en aviones de Rusia que, una vez descargado el pescado en Europa, viajan a Rusia y cargan armas que llevan al centro de África y surten a las numerosas guerrillas que allí operan. En el lago ahora se reúnen pescadores locales, ejecutivos financieros internacionales, ministros africanos, niños sin hogar, comisarios de la Unión Europea, pilotos rusos y prostitutas locales. Para su director, Hubert Sauper, el documental “es una historia sobre seres humanos del norte y del sur, sobre la globalización y sobre pescado”. Es un buen resumen.
En 2003 las exportaciones a la Unión Europea llegaron a 169 millones de euros. Sin embargo, las exportaciones totales de perca del Nilo en el comercio mundial cayeron casi un 30% en 2020. Entre los exportadores están Tanzania, Uganda, con el 65% del total, y Kenia, países que rodean el Lago Victoria. Entre los importadores están y pertenecen a la Unión Europea, Polonia, Rumania y Grecia, con el 23% del total. España, en 2020, importó el 6.50%.
Hay que añadir que la pesca deportiva de perca del Nilo atrae a numerosos turistas a Uganda, Tanzania y Kenia. También se ha propuesto la introducción de la perca del Nilo en Australia pero expertos como Christopher Barlow y Allan Lisle, de la Estación de Investigación de Walkamin, se oponen a ello y argumentan con datos de lo que ha supuesto la perca en el lago Victoria para la fauna indígena. Los riesgos asociados se consideran muy superiores a los futuros beneficios. Se ha abandonado la propuesta.
Pero, años después, en 2013, biólogos de la Universidad de Leiden, en Holanda, descubren que, más o menos, un 25% de las especies de cíclidos se han recuperado del “desierto” que provocó la perca e, incluso, algunas de las especies recuperadas son ahora más abundantes que en el pasado. Algunas de esas especies recuperadas han cambiado en parte su morfología y son más ágiles y rápidas para huir de los depredadores, entre ellos, de la perca del Nilo.
Y para terminar no hay nada mejor que una buena receta, algo más complicada que la anterior. Es perca al curry, un plato que muestra la influencia de la cocina de la India, al otro lado del Océano Índico, sobre el África Oriental.
Primero cortar en cubos un filete grueso de perca. Después pelar y picar ajo, cebolla y tomate. Mezclar pimentón, ralladura de coco, zumo de limón, sal y curry en polvo. Calentar aceite o manteca en la sartén y freír al ajo y la cebolla y añadir la mezcla anterior. Solo unos minutos y añadir el tomate y cocinar algo más. Añadir los cubos de perca, leche y agua y cocinar suave un cuarto de hora o algo más hasta que el pescado esté hecho. Servir caliente.
Referencias:
Altimira i Palau, J. 2007. Efectos socioeconómicos y medioambientales de la introducción de la Perca del Nilo (Lates niloticus) en el Lago Victoria. Ecología Política 32: 111-114.
Balirwa, J.S. 2007. Ecological, environmental and socioeconomic aspects of the Lake Victoria’s introduced Nile perch fishery in relation to the native fisheries and the species culture potential: lessons to learn. African Journal of Ecology 45: 120-129.
Barlow, C.G. & A. Lisle. 1987. Biology of the Nile perch Lates niloticus (Pisces: Centropomidae) with reference to its proposed role as a sport fish in Australia. Biological Conservation 39: 269-289.
Chapman, L.J. et al. 2008. Biodiversity conservation in African inland waters: Lessons of the Lake Victoria region. Verhandlungen des Internationalen Verein Limnologie 30: 16-34.
De Zeeuw, M.P. et al. 2013. Two new species of zooplanktivorous haplochromine cichlids from Lake Victoria. ZooKeys 256: 1-34.
Goldschmidt, T. et al. 1993. Cascading effects of the introduced Nile Perch on the detritivorous/phytoplanktivorous species in the sublittoral areas of Lake Victoria. Conservation Biology 7: 686-700.
Goudswaard, K. (P.C.) et al. 2008. The invasion of an introduced predator, Nile perch (Lates niloticus, L.) in Lake Victoria (East Africa): chronology and causes. Environmental Biology of Fishes 81: 127-139.
Horreo, J.L. et al. 2019. Amplification of 16S rDNA reveals important fish mislabeling in Madrid restaurants. Food Control 96: 146-150.
IUCN. 2000. 100 of the World’s worst invasive alien species. A selection from the Global Invasive Species Database. University of Auckland. New Zealand. 10 pp.
Mercadal Orfila, R. 2005. La pesadilla de Darwin. Making of: cuadernos de cine y educación 35: 16-21.
Pendaeli-Sarakikya, E. 1978. Tanzania cookbook. Tanzania Publ. House. Dar Es Salaam. 165 pp.
Prados, L. 1999. El mayor lago de África se muere por la introducción de especies foráneas. El País 21 noviembre.
Pringle, R.M. 2005. The origins of the Nile Perch in the Lake Victoria. BioScience 55: 780-787.
Wanink, J.H. 1991. Survival in a perturbed environment: the effects of Nile perch introduction on the zooplanktivorous fish community of Lake Victoria. En “Terrestrial and aquatic ecosystems: perturbation and recovery”, p. 268-275. Ed. por O. Ravera. Ellis Horwood Ltd. Chichester.
Wikipedia. 2023. Nile perch. 23 January.
Wilson, E.O. 1995. La diversidad de la vida. En defensa de la pluralidad biológica. Círculo de Lectores. Barcelona. 561 pp.
Para saber más:
Catástrofe Ultravioleta #18 INVASORES
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Los invasores: La perca del Nilo se ha escrito en Cuaderno de Cultura Científica.
Dibujando grafos sobre la banda de Moebius
La banda de Moebius es un sorprendente objeto geométrico, y más concretamente topológico (véase la entrada La topología modifica la trayectoria de los peces), que ha cautivado a personas de dentro y fuera de las matemáticas. En el Cuaderno de Cultura Científica hemos hablado en varias ocasiones, tanto de sus sorprendentes propiedades matemáticas, como de su utilización en el arte (algunas interesantes entradas sobre la misma son: Poesía retorcida sobre banda de Möbius, De menú para hoy, dos novelas gráficas negras con salsa matemática, Arte Moebius (I), Arte Moebius (II), En busca de la banda de Moebius más corta posible).
 Libertas quae sera tambem (2021), del artista brasileño Valin Branco. Triánngulo, curva de Moebius con corte central. Madera dura: Caoba. Dimensiones: 34cm x 30cm x 17cm. Imagen de la cuenta de instagram de Valin Branco
Libertas quae sera tambem (2021), del artista brasileño Valin Branco. Triánngulo, curva de Moebius con corte central. Madera dura: Caoba. Dimensiones: 34cm x 30cm x 17cm. Imagen de la cuenta de instagram de Valin BrancoPodéis leer más sobre la banda de Moebius y su utilización en el arte contemporáneo en el libro Las matemáticas como herramienta de creación artística (R. Ibáñez, colección Miradas matemáticas, Catarata, 2023), que estará en las librerías a finales del mes de marzo.
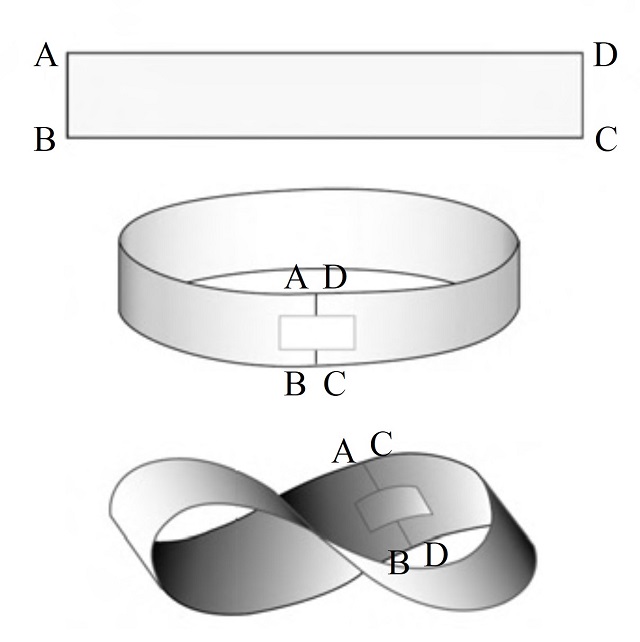
Pero en esta entrada del Cuaderno de Cultura Científica queremos hablar de una curiosa propiedad de la banda de Moebius, que tiene que ver con la teoría de grafos. Aunque esta superficie es un objeto matemático de sobra conocido, no está de más volver a recordar su construcción. Una banda de Moebius es una banda retorcida que podemos construir de forma sencilla de la siguiente forma. Si tomamos una tira de papel y pegamos los extremos se obtiene una banda normal con dos caras y dos bordes, pero si primero giramos uno de los extremos del papel media vuelta y después juntamos los extremos se obtiene la banda de Moebius, una superficie que solo tiene una cara y un solo borde (como se observa en la siguiente imagen).
Por otra parte, la teoría de grafos es la rama de las matemáticas que estudia los grafos, estructuras formadas por puntos –llamados vértices– y líneas uniendo pares de puntos –llamadas aristas–, que son estructuras matemáticas muy sencillas, pero a la vez muy versátiles, con muchas aplicaciones en ciencia y tecnología (véase, por ejemplo, El problema de los tres caballeros y los tres criados, El grafo de Marion (Gray) o El juego de Sim, entre otros).
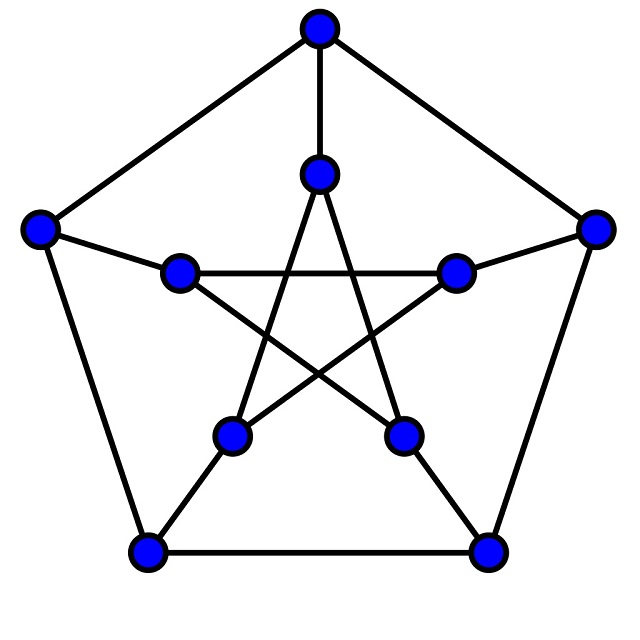 El conocido grafo de Petersen, con 10 vértices y 15 aristas. Imagen: Leshabirukov / Wikimedia Commons
El conocido grafo de Petersen, con 10 vértices y 15 aristas. Imagen: Leshabirukov / Wikimedia CommonsAntes de adentrarnos en la mencionada propiedad de los grafos sobre la banda de Moebius, primero vamos a plantear un sencillo problema sobre grafos en el plano.
Problema: ¿Cual es el mayor número de puntos (vértices) que puede unirse mediante líneas (aristas), sin que estas se crucen unas con otras y de manera que todos los pares de puntos queden unidos por líneas?
Si tomamos un trozo de papel y empezamos a pintar puntos y líneas uniendo esos puntos, es fácil ver que el problema es trivial para 2, 3 y 4 puntos del plano, como se muestra en la siguiente imagen.
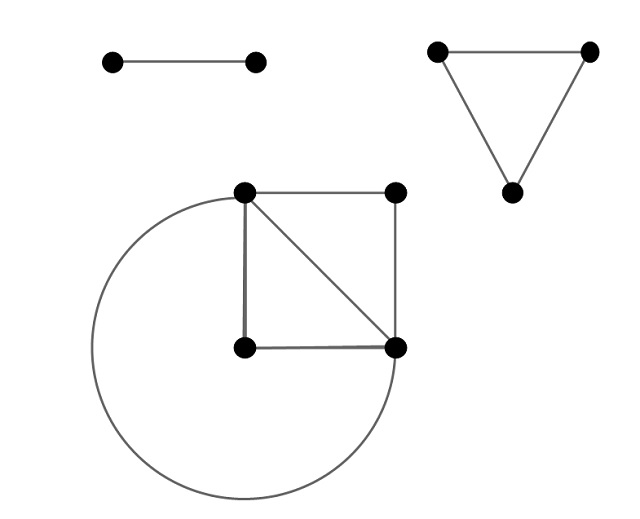
Pero parémonos a pensar un momento qué ocurre para 5 puntos. Empecemos dibujando el grafo de 5 puntos con todas las aristas posibles que unen dos de esos puntos, es lo que en matemáticas, en concreto, en teoría de grafos, se denomina el “grafo completo” de 5 vértices (y se denota como K5).
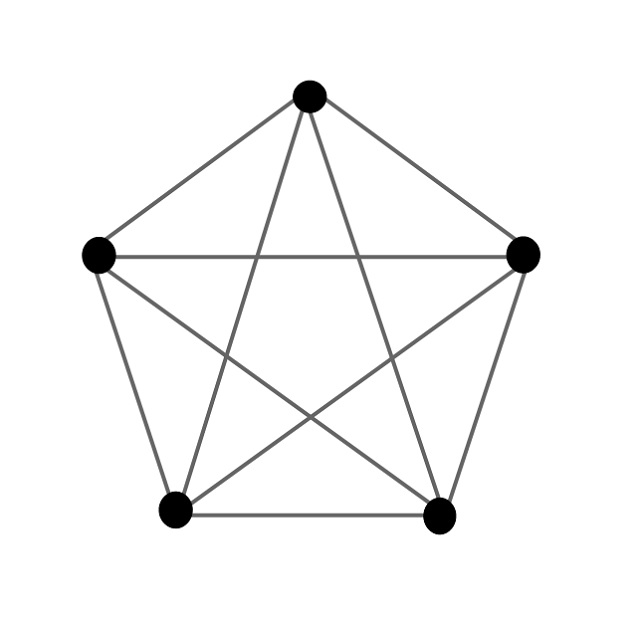
En el dibujo que hemos realizado del grafo completo de 5 vértices. Observamos que las aristas se cruzan entre ellas y nos planteamos si será posible redibujar las aristas de tal manera que estas no se crucen, como hemos visto que sí es posible para el grafo completo de 4 vértices, K4. Por cierto, esto es lo que en teoría de grafos se dice que es un “grafo plano”, un grafo que podemos dibujar en el plano sin que las aristas se crucen. Luego nuestro problema consiste en averiguar si el grafo completo de 5 vértices es plano, o no. La respuesta es negativa. Veamos una idea de cómo demostrarlo.
Para probar que el grafo completo de 5 vértices no es plano se hace uso de la fórmula de Euler. Esta establece que para los grafos planos “conexos” (esto quiere decir que cada par de vértices está conectado por un camino de aristas que empieza y termina en esos dos vértices) con v vértices, a aristas y c caras (se incluye también como cara la zona exterior no acotada) se verifica la fórmula:
![]()
Por ejemplo, el grafo de Goldner-Harary, que vemos en la siguiente imagen, es un grafo plano y se verifica la fórmula de Euler (v = 11, a = 27 y c = 17).
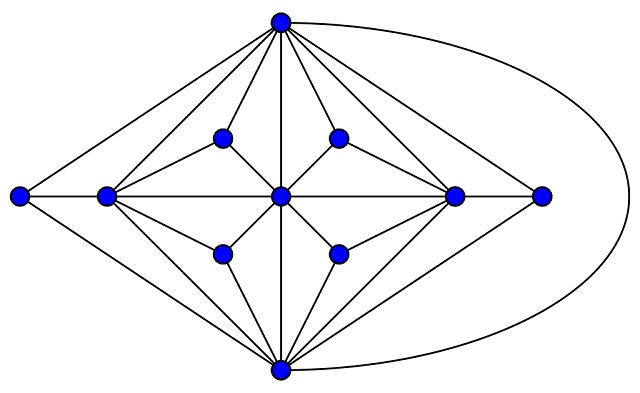 Grafo de Goldner-Harary. Imagen: David Eppstein / Wikimedia Commons
Grafo de Goldner-Harary. Imagen: David Eppstein / Wikimedia Commons
Ahora, si tenemos un grafo plano y simple (esto quiere decir que en ese grafo no hay bucles, es decir, aristas que unan un vértice consigo mismo, ni tampoco hay aristas múltiples, esto es, que no hay dos aristas distintas que unan los mismos dos vértices) con más de dos vértices, la fórmula de Euler permite afirmar (la prueba es simple) que
![]()
A partir de esta fórmula se demuestra que el grafo completo de 5 vértices no es plano, ya que v = 5, pero el número de aristas, al ser completo, es a = 10, y no se verifica la anterior desigualdad. Por lo tanto, queda demostrado que el grafo completo de 5 vértices K5 no es plano.
¿Pero qué ocurre si consideramos el problema sobre la banda de Moebius?
Problema: Dados 5 puntos en la banda de Moebius, ¿pueden unirse mediante líneas, sin que estas se crucen unas con otras y de manera que todos los pares de puntos queden unidos por líneas? ¿Es el grafo completo de 5 vértices sobre la banda de Moebius un “grafo plano”, es decir, cuyas aristas pueden trazarse de forma que no se crucen?
Antes de abordar esta cuestión, una pequeña reflexión sobre el concepto de superficie, ya que la banda de Moebius es una superficie (matemáticamente hablando). Esto es algo trivial, a priori, pero para entender bien este concepto, lo primero que hay que comprender es que una superficie matemática “ideal” no tiene grosor, luego sus puntos están “dentro” de la misma, no “sobre” ella. Para visualizar esto pensemos en una superficie transparente (por ejemplo, acetato) sobre la que se pinta un punto, este podrá verse “desde los dos lados”, lo cual nos permite entender qué significa que el punto está en la superficie, pero no sobre uno de sus lados. De hecho, podríamos decir que la superficie matemática no tiene “lados” en sí misma, sino que estos son una manifestación de la relación de la superficie con el espacio tridimensional que la contiene. En conclusión, a la hora de resolver el problema anterior sobre la banda de Moebius, es conveniente que pensemos en la banda de Moebius como si fuese una superficie transparente sobre la que pintamos las aristas.
Ahora, contrariamente a lo que ocurría para el plano, dados 5 puntos en la banda de Moebius sí se pueden trazar líneas que unan todas las parejas de puntos sin que se crucen entre ellas, como se muestra en la siguiente imagen (se realiza el dibujo sobre la tira de papel estirada, teniendo en cuenta que luego los extremos se unen después de medio giro, por eso la línea que pasa por y en el lado AB, arriba a la izquierda, continua por abajo a la derecha en el lado CD).
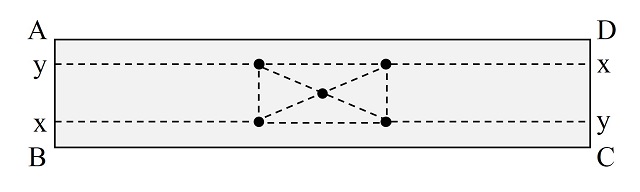 El grafo completo K5 de 5 puntos es un grafo “plano” en la banda de Moebius
El grafo completo K5 de 5 puntos es un grafo “plano” en la banda de MoebiusEl siguiente paso sería ver si es posible lo mismo para 6 puntos, es decir, si el grafo completo de 6 vértices es un grafo “plano” en la banda de Moebius.
Problema: Dados 6 puntos en la banda de Moebius, ¿pueden unirse mediante líneas, sin que estas se crucen unas con otras y de manera que todos los pares de puntos queden unidos por líneas?
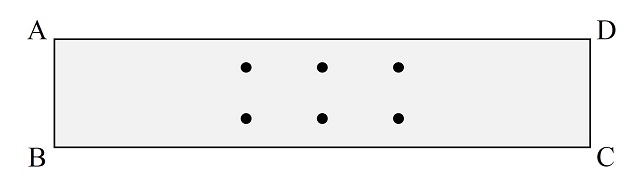
Este problema queda para quienes queráis divertiros intentando resolverlo. No olvidéis que estáis sobre una banda de Moebius, es decir, una tira de papel cuyos extremos se unen después de dar media vuelta a la misma. ¡Que os divirtáis!
El problema anterior está relacionado con un pasatiempo matemático clásico, el problema del agua, el gas y la electricidad, también conocido como problema de los tres servicios. Este problema aparece recogido en el libro Amusements in mathematics (1917), que fue publicado en castellano en tres partes, con el nombre conjunto de Diversiones Matemáticas (El acertijo del mandarín, Los gatos del hechicero y El misterio del muelle), del experto inglés en matemática recreativa Henry E. Dudeney (1857-1930). Aunque ya lo había publicado con anterioridad, en 1913, en la revista The Strand Magazine. Dudeney dice que es un pasatiempo matemático muy antiguo, que él ha bautizado como el problema del agua, el gas y la electricidad, aunque es más antiguo que la utilización de la electricidad para iluminar las casas. El problema, traducido del original de Dudeney, dice así.
El problema del agua, el gas y la electricidad: El rompecabezas consiste en tender agua, gas y electricidad, desde W, G y E, a cada una de las tres casas, A, B y C, sin que ninguna tubería se cruce con otra. Coge tu lápiz y dibuja líneas que muestren cómo hacerlo. Pronto te encontrarás con dificultades.
Según vayáis intentando resolver este problema clásico os daréis cuenta de que nos encontramos ante una cuestión similar a la anterior, que era intentar dibujar el grafo completo K5 de 5 vértices sin que se crucen las líneas. Sin embargo, ahora el grafo asociado al problema del agua, el gas y la electricidad, que es el grafo bipartito completo K3,3 (que aparece en la siguiente imagen), es decir, está formado por dos conjuntos de vértices, en este caso, de 3 vértices cada uno, y están todas las aristas que unen los vértices de un conjunto con los del otro.
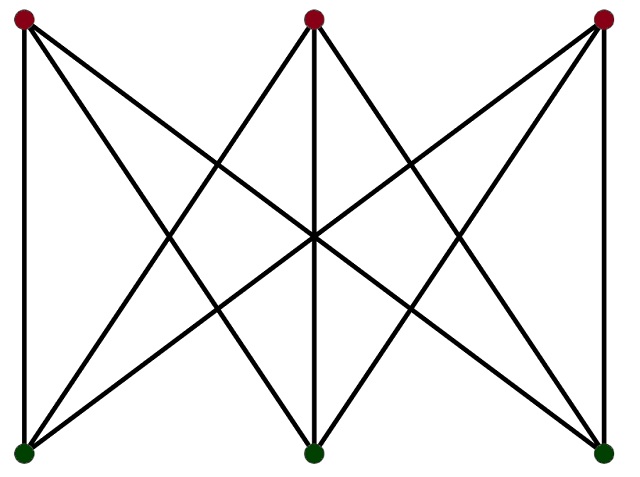 El grafo bipartito completo K3,3, que es el grafo asociado al pasatiempo del agua, la electricidad y el gas
El grafo bipartito completo K3,3, que es el grafo asociado al pasatiempo del agua, la electricidad y el gasUtilizando de nuevo la fórmula que es consecuencia de la fórmula de Euler puede demostrarse que el grafo bipartito completo K3,3 no es plano y el problema del agua, el gas y la electricidad no tiene solución.
Para terminar…
Problema: ¿es posible resolver el problema del agua, el gas y la electricidad para la banda de Moebius?
 Curva clásica de Moebius (2021), del artista brasileño Valin Branco. Madera dura: Cedro. Dimensiones: 21cm x 20cm x 13cm. Imagen: Instagram de Valin Branco
Curva clásica de Moebius (2021), del artista brasileño Valin Branco. Madera dura: Cedro. Dimensiones: 21cm x 20cm x 13cm. Imagen: Instagram de Valin BrancoBibliografía
1.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística , colección Miradas matemáticas, Catarata, 2023.
2.- Clifford A. Pickover, La banda de Möbius, Almuzara, 2009.
3.- Martin Gardner, Festival mágico-matemático, Alianza editorial, 1984.
4.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
5.- David E. Kullman, The utilities problem, Mathematics Magazine, 52 (5), pp. 299–302, 1979.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Dibujando grafos sobre la banda de Moebius se ha escrito en Cuaderno de Cultura Científica.
Un bombeo intermitente ahorra energía
El bombeo intermitente de un fluido por una tubería reduce significativamente el coste de transporte.
 Foto: Pedro Netto / Unsplash
Foto: Pedro Netto / UnsplashEn un estudio de prueba de concepto, los investigadores utilizaron simulaciones numéricas para demostrar que, cuando se conecta y se apaga periódicamente una bomba, el flujo sigue cambiando entre un estado turbulento y otro laminar. Esto redujo los costes de energía hasta en un 22%, una cifra que, según los investigadores, puede optimizarse aún más.
Los flujos laminares, como el que se ve cuando se abre lentamente un grifo, son regulares, ocupan el menor espacio posible y son energéticamente eficientes. Los flujos turbulentos, por otro lado, como cuando un grifo abre a tope, son caóticos y desperdician energía.
Si inyectamos tinta en un flujo laminar en una tubería transparente, veremos una línea bien definida de tinta moviéndose por la tubería. Con un flujo turbulento, sin embargo, veremos a la tinta dispersarse a medida que cada partícula de fluido toma un camino impredecible. Este movimiento caótico a pequeña escala da como resultado que se pierda mucha energía. Los flujos laminares son ideales para el transporte de fluidos, pero cuando los fluidos viscosos se mueven rápido y a gran escala, el sistema evoluciona naturalmente hacia un estado turbulento.
En el estudio, los investigadores codificaron un modelo que, usando un superordenador, pudo simular un flujo turbulento estandarizado. Los científicos ejecutaron diferentes escenarios, cambiando la duración del tiempo en que la bomba estaba encendida, su intensidad (la velocidad a la que acelera el fluido) y la duración total de cada ciclo de encendido y apagado de la bomba.
Descubrieron que los ciclos caracterizados por un bombeo breve e intenso que aceleraba rápidamente el fluido seguido de una fase larga en la que se apagaba la bomba y el fluido se ralentizaba funcionaban mejor para mantener el fluido en un estado laminar durante la mayor cantidad de tiempo.
Reducir la turbulencia y, por lo tanto, los costes de mover fluidos a través de tuberías podría generar numerosos beneficios económicos y ambientales. El transporte de fluidos constituye una parte importante del costo final del combustible, por lo que el hidrógeno líquido podría volverse más barato para los países desarrollados. Para los países en desarrollo que aún no pueden hacer el cambio a la energía verde, el petróleo y el gas natural podrían convertirse en una alternativa energética más asequible a la leña, cuyo uso contribuye a la deforestación y produce más contaminantes nocivos que los combustibles fósiles.
Referencia:
Foggi Rota, G., Monti, A., Rosti, M.E. et al. (2023) Saving energy in turbulent flows with unsteady pumping. Sci Rep 13, 1299. doi: 10.1038/s41598-023-28519-x
Para saber más:
Un modelo para la máquina de coser fluidodinámica, o como untar miel con conocimiento
¿Por qué moja el agua? La física de fluidos inunda nuestras vidas
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un bombeo intermitente ahorra energía se ha escrito en Cuaderno de Cultura Científica.
Meteoritos con una pizca de sal
Los meteoritos son una de las fuentes fundamentales en nuestro conocimiento sobre el Sistema Solar, que nos permiten reconstruir distintos aspectos de la historia de nuestro sistema planetario, desde los más dinámicos hasta los geoquímicos, pasando incluso por los ambientales en algunos casos, ya que nos traen muestras de otros cuerpos sin necesidad de ir a recogerlos con una compleja misión de retorno de muestras.
Obviamente esto tiene su parte negativa, porque nosotros no escogemos en ningún caso lo que queremos muestrear. Además, quien sabe si en estos meteoritos que recogemos de la superficie de nuestro planeta podrían existir algunos sesgos de preservación o incluso temporales, habiendo familias composicionales que ya serían difíciles de encontrar porque hace mucho que cayeron y desaparecieron de nuestro entorno cercano. Y es que cuanto más tiempo pasa un meteorito en la superficie de nuestro planeta, más sufre de procesos de alteración que pueden cambiar su composición y provocar la aparición de nuevos minerales. Incluso puede experimentar una fragmentación que acelere estos procesos de alteración.
 Imagen de un meteorito metálico en la superficie de Marte. Estos meteoritos son muy fáciles de observar en su superficie por el fuerte contraste con las rocas autóctonas. Cortesía de NASA/JPL-Caltech/LANL/CNES/IRAP/LPGNantes/CNRS/IAS/MSSS.
Imagen de un meteorito metálico en la superficie de Marte. Estos meteoritos son muy fáciles de observar en su superficie por el fuerte contraste con las rocas autóctonas. Cortesía de NASA/JPL-Caltech/LANL/CNES/IRAP/LPGNantes/CNRS/IAS/MSSS.Recientemente se ha estimado que sobre la superficie de la Tierra caen unos 6000 meteoritos al año, de los cuales en torno a unos 2000 caerían sobre tierra firme, sin embargo, un número muy pequeño de estos es recuperado para su estudio y en ocasiones pasa mucho tiempo entre la caída y el descubrimiento, especialmente en el caso de fragmentos muy pequeños. Cada instante que pasa en la superficie sin proteger, la alteración avanza.
Y es que un análisis recién publicado sobre el meteorito de Winchcombe, que cayó en febrero de 2021 en el Reino Unido y el primero en ser recuperado en este país en casi 30 años, ha puesto de manifiesto la gran velocidad a la que los procesos de alteración tienen lugar, independientemente de lo rápido que se recuperen los fragmentos.
De hecho, los primeros fragmentos fueron recuperados tan solo unas horas después de la caída gracias a que lo hicieron sobre una carretera, y otra gran parte de estos en los primeros seis días después sobre un pasto de ovejas. Hasta al menos septiembre de 2021 se estuvieron encontrando fragmentos de este meteorito en distintos lugares.
Un nuevo estudio pone de manifiesto que, a pesar de la rápida recuperación de los meteoritos, sobre estos habían aparecido ya minerales fruto de la interacción entre el meteorito y la humedad del ambiente. Gracias al uso de técnicas como la microscopía electrónica y la espectroscopía de tipo Raman, los investigadores han podido estudiar con un gran nivel de detalle la superficie de algunos de los meteoritos y caracterizar su mineralogía. Concretamente estudiaron dos fragmentos: uno recogido de la carretera y otro del pasto de ovejas.
Durante la reentrada, los meteoritos suelen desarrollar lo que denominamos costra de fusión: debido a las altas temperaturas que sufre el meteorito en su contacto con la atmósfera debido a la gran velocidad que lleva con respecto a nuestro planeta, su superficie empieza a fundirse. Cuando el meteorito ha frenado, empieza a enfriarse y este fundido que queda se transforma en una capa vitrificada y que muchas veces ayuda a los científicos a distinguir en el campo lo que es un meteorito de lo que no.
 El famoso meteorito ALH84001, conocido por la posibilidad de haber preservado formas de vida microscópicas -y muy discutidas-, deja entrever parte de su costra de fusión, como una fina capa negra de un color y textura distinta al meteorito original que cubre parte de este. Imagen cortesía del JSC.
El famoso meteorito ALH84001, conocido por la posibilidad de haber preservado formas de vida microscópicas -y muy discutidas-, deja entrever parte de su costra de fusión, como una fina capa negra de un color y textura distinta al meteorito original que cubre parte de este. Imagen cortesía del JSC.En el meteorito recogido del pasto de las ovejas, los análisis descubrieron minerales como el sulfato de calcio y calcita, pero estos aparecían fuera de la costra de fusión, por lo que lo más posible es que se formaran después de su caída por la exposición a las condiciones de humedad del pasto.
 Una de las secciones del meteorito de Winchcombe analizadas. Señalados por flechas podemos ver las apariciones de sulfatos y de calcita de origen terrestre. Imagen cortesía de la Universidad de Manchester.
Una de las secciones del meteorito de Winchcombe analizadas. Señalados por flechas podemos ver las apariciones de sulfatos y de calcita de origen terrestre. Imagen cortesía de la Universidad de Manchester.Sin embargo, el fragmento recuperado de la carretera se cortó en secciones que se pulieron en el laboratorio, y en estas secciones se dieron cuenta de que aparecía halita -el mineral que forma la sal común- de tal manera que este mineral tendría que haber aparecido después del corte y el pulido por la interacción con el propio aire del laboratorio.
¿Qué nos quiere decir este estudio? Pues hay varias cosas a tener en cuenta: Lo primero es que por muy rápido que recuperemos el meteorito, lo normal es esperar que haya algo de alteración, incluso si solo han pasado unas horas.
Lo segundo, pone de manifiesto que es importante que preservemos los meteoritos en unas condiciones lo más inertes posibles, es decir, con la mejor presencia posible de gases como el oxígeno o el dióxido de carbono, que pueden reaccionar muy rápidamente con los meteoritos, así como las muestras que traigamos de asteroides, satélites y planetas.
Y por último, la importancia de discriminar en los meteoritos cuáles de los minerales son de origen terrestre y cuáles originales del propio meteorito, especialmente en aquellos que hayan pasado prolongados tiempos expuestos a las condiciones ambientales de nuestro planeta, porque no podemos olvidar que los meteoritos pueden también haber sufrido previamente procesos de alteración por colisiones o por su historia en el cuerpo progenitor.
Este estudio podría sentar las bases para nuevas directrices que nos permiten preservar mejor las colecciones de meteoritos y muestras de otros cuerpos de cara al futuro, para que las siguientes generaciones de científicas puedan estudiarlos tal y como si estuviesen recién caídos.
Bibliografía:
Jenkins, L. E., Lee, M. R., Daly, L., King, A. J., Floyd, C. J., Martin, P. E., Almeida, N. V., & Genge, M. J. (2023). Winchcombe: An example of rapid terrestrial alteration of a chondrite. Meteoritics & Planetary Science. doi: 10.1111/maps.13949
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Meteoritos con una pizca de sal se ha escrito en Cuaderno de Cultura Científica.
¿Cómo se mide un sentimiento?
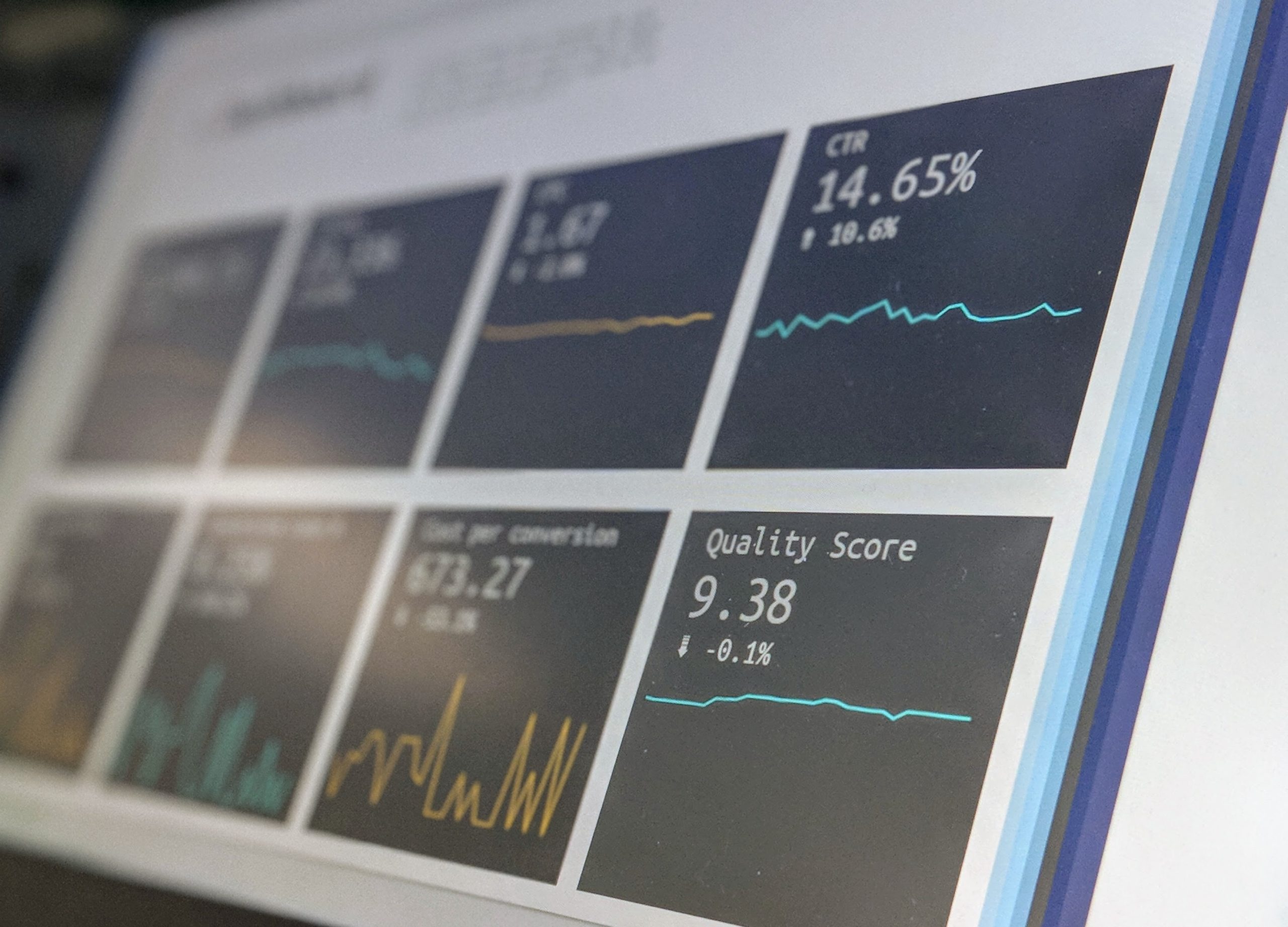 Foto: Stephen Dawson / Unsplash
Foto: Stephen Dawson / Unsplash¿Se puede medir un sentimiento? Me refiero a su intensidad. ¿Qué tal está usted? ¿Cuán satisfecho está con la vida? ¿Cómo es la relación con su pareja? ¿Cuánto le satisface vivir donde vive? Estas son preguntas a las que, en ocasiones, se nos pide que respondamos con un número. Cuando se encuesta a la gente para conocer su nivel de satisfacción con diferentes aspectos de la vida, normalmente en el marco de una investigación científica o un estudio sociológico, se le suele pedir que lo cuantifiquen. Ocurre lo mismo cuando se nos pide que valoremos de 1 a 5 (por ejemplo) el grado de satisfacción con el servicio prestado por los empleados de una empresa. Lo normal es que lo hagamos, aunque en este caso el valor otorgado suele ser –por razones que no hace falta explicitar– muy alto o máximo.
Pues bien, cuando estas encuestas se hacen en el contexto de una investigación, es normal que surjan dudas acerca de la fiabilidad de la calificación numérica otorgada. Sospecho que a la mayoría nos parece que la intensidad de un sentimiento es algo demasiado subjetivo como para que se le pueda asignar un valor numérico fiable. Por esa razón, dos miembros del Centro de Investigación en Bienestar (Universidad de Oxford, Reino Unido) han hecho un estudio para valorar hasta qué punto hay una correspondencia entre el número (entero, sin decimales) con el que las personas encuestadas valoran ciertos sentimientos, y la probabilidad de que esas mismas personas actúen más adelante en consonancia con la valoración otorgada. La probabilidad de que actúen se refiere a si toman, o no, decisiones del tipo “get-out-of-here” (sácame de aquí).
En economía del trabajo ya habían comprobado, por ejemplo, que un bajo nivel de satisfacción con el trabajo es un predictor muy bueno de la decisión de abandonarlo y buscar otro. Ese es un buen ejemplo de una decisión “sácame de aquí”. En la investigación que nos ocupa han estudiado la vinculación entre el sentimiento de satisfacción (o insatisfacción) y las decisiones posteriores (hasta un año después) relativas a asuntos correspondientes a cuatro dominios de la experiencia humana: vivienda, pareja, trabajo, y salud. En el estudio han recurrido a bases de datos –recogidos durante años en tres países (Reino Unido, Alemania y Australia) por administraciones públicas y organismos internacionales– sobre los sentimientos y decisiones de decenas de miles de personas a las que se ha encuestado con diferentes motivos a lo largo de cuatro décadas. Han utilizado del orden de setecientos mil datos, aproximadamente.
Los resultados del estudio fueron muy claros. En los cuatro dominios examinados, el número entero con el que las personas cuantifican un sentimiento tiene un mayor poder predictivo que un conjunto de variables económicas y sociales objetivas. Además, hay una relación inversa entre las acciones “sácame-de-aquí” y los valores asignados a los correspondientes sentimientos. Así, la probabilidad de cambiar de vivienda es mayor cuanto menor es la satisfacción con aquella en que se vive; la de romper una relación disminuye con el grado de satisfacción con la pareja; la de cambiar de trabajo se reduce con la satisfacción con el que se tiene; y la de acudir a hospitales cae con la satisfacción con el estado de salud. La relación entre los sentimientos y la probabilidad de actuar para cambiar las cosas es prácticamente linear (y negativa).
En resumidas cuentas, los seres humanos podemos usar una escala numérica fiable para asignar un valor a sentimientos que, en principio, son inmensurables. No sabemos cómo, pero lo hacemos. O, dicho de forma más castiza, “sabemos lo que queremos”.
Fuente: C. Kaiser, A. J. Oswald, The scientific value of numerical measures of human feelings. Proc. Natl. Acad. Sci. U.S.A. 119, e2210412119 (2022). doi: 10.1073/pnas.2210412119
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo ¿Cómo se mide un sentimiento? se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: La fina línea

Es posible que, en alguna ocasión, un sentimiento homicida te haya invadido ante según qué plantemientos de tu profesor de matemáticas. Sentimiento este que podría verse correspondido desde el momento en que para algún matemático el asesinato es la única salida lógica a determinadas cuestiones. Este matemático ingresó en un manicomio, pero su fama empezó ahí, precisamente. Juan Antonio Prado nos cuenta su historia.
Juan Antonio Prado Bassas es profesor titular del departamento de Análisis Matemático y vicedecano de Innovación Docente y Divulgación Científica de la Facultad de Matemáticas de la Universidad de Sevilla.
Si no ve correctamente el vídeo, use este enlace.
Más sobre el tema:
André Bloch: el asesinato como una cuestión de lógica matemática
Matemáticos y sin embargo criminales
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2022: La fina línea se ha escrito en Cuaderno de Cultura Científica.
El impacto de la violencia en la incertidumbre de vida
La duración de la vida en países con altas tasas de violencia es menos predecible y la esperanza de vida de los jóvenes puede ser hasta 14 años más corta en comparación con los países pacíficos, según un nuevo estudio realizado por un equipo internacional, liderado por la Universidad de Oxford y en el que ha participado el investigador Ikerbasque en la UPV/EHU, Tim Riffe.
 Foto: Tengyart / Unsplash
Foto: Tengyart / UnsplashSegún la investigación, las muertes violentas son responsables en una alta proporción del diferente nivel de incertidumbre de vida entre los países violentos y los pacíficos. La incertidumbre de vida hace referencia a la dispersión en las edades de mortalidad; cuanto mayor es la dispersión, mayor incertidumbre. El impacto de la violencia en la mortalidad va más allá de acortar vidas, ya que cuando, debido a la violencia se pierden vidas de forma continuada, las personas supervivientes tienen mayor incertidumbre sobre quién será la siguiente víctima. En palabras de los autores de la investigación lo más sorprendente de este estudio ha sido constatar que la incertidumbre sobre la vida tiene una mayor asociación con la violencia que la esperanza de vida, de ahí su importancia para analizar los cambios en los patrones de mortalidad
Utilizando los datos de mortalidad de 162 países y el Índice de Paz Interna entre 2008 y 2017, el estudio muestra que los países más violentos también son aquellos con mayor incertidumbre de vida. En el caso de Oriente Medio son las muertes relacionadas con el conflicto a edades tempranas las que más contribuyen a la percepción de incertidumbre elevada. Asimismo, en América Latina se observa un patrón similar resultado de los homicidios y de la violencia interpersonal. En el otro extremo nos encontramos que la incertidumbre de vida fue «notablemente baja» entre 2008 y 2017, en la mayoría de los países del norte y sur de Europa.
En los países de ingresos altos la reducción de la mortalidad temprana por cáncer ha influido en reducir la incertidumbre de vida. Sin embargo, en las sociedades más violentas, la incertidumbre de vida es incluso experimentada por aquellos que no están directamente involucrados en la violencia. El informe recoge que “Los ciclos de pobreza, inseguridad y violencia magnifican los patrones estructurales preexistentes de desventaja para las mujeres. En algunos países de América Latina, los asesinatos a mujeres han aumentado en las últimas décadas y la exposición a entornos violentos tiene consecuencias sociales y de salud, en particular para niños y mujeres”. Según los autores del estudio «Si bien los hombres son las principales víctimas directas de la violencia, las mujeres tienen más probabilidades de experimentar sus consecuencias en contextos violentos»
Según el informe la esperanza de vida más baja suele estar asociada con una mayor incertidumbre de vida. Además, vivir en una sociedad violenta crea vulnerabilidad e incertidumbre y eso, a su vez, puede conducir a un comportamiento más violento. Los países con altos niveles de violencia tienen una esperanza de vida más baja que los más pacíficos. Se estima una brecha de alrededor de 14 años en la esperanza de vida entre los países menos y más violentos. Así, en países como El Salvador, Honduras, Guatemala o Colombia la brecha en la esperanza de vida con los países de altos ingresos se explica principalmente por el alto nivel de mortalidad debido a los homicidios.
Según el investigador Ikerbasque de la UPV/EHU, Tim Riffe, autor del estudio, es importante mostrar en un sentido amplio los efectos que la violencia tiene para la salud de la población, de modo que pueda considerarse un problema de salud pública y, por lo tanto, pueda ser susceptible de programas de prevención. La violencia como causa de muerte resulta, en principio, más fácil de prevenir que otras grandes causas, como puede ser el cáncer, y los beneficios de hacerlo son tanto inmediatos como duraderos. De hecho, existen muchos ejemplos de sociedades que transitaron de una situación de elevada violencia a otra de paz prolongada.
El estudio está basado en el uso masivo de datos y se fundamenta, en parte, en estimaciones de mortalidad modeladas por el proyecto Global Burden of Disease. Muchas de las poblaciones incluidas no tienen información demográfica directa sobre la mortalidad, debido a que, en gran parte del mundo, los sistemas de registro vital, que permiten desarrollar una investigación como esta de forma directa, están aún por desarrollar o requieren de mejoras significativas.
Referencia:
José Manuel Aburto, Vanessa di Lego, Tim Riffe, Ridhi Kashyap, Alyson van Raalte, and Orsola Torrisi (2023) A global assessment of the impact of violence on lifetime uncertainty Science Advances doi: 10.1126/sciadv.add9038
Para saber más:
Serie Preparados para matar
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El impacto de la violencia en la incertidumbre de vida se ha escrito en Cuaderno de Cultura Científica.
Geóloga, ¿una especie en peligro de extinción?
Geóloga
El sábado once de febrero se celebró el Día Internacional de la Mujer y la Niña en la ciencia. Este evento pretende visibilizar el papel femenino en las disciplinas científicas y técnicas, buscando crear referentes entre las más jóvenes, de tal manera que puedan plantearse su futuro como profesionales en este ámbito, incluidas las Ciencias de la Tierra.
De manera general, la Geología siempre se ha considerado como una ciencia muy masculinizada. En la sociedad, tanto en el pasado como en la actualidad, nunca se ha visto como “muy femenino” una profesión que implica ir al campo a llenarse de barro, dar martillazos a rocas y cargar en la espalda con una mochila llena de muestras durante largos paseos en mitad del monte. Como mucho, se normalizaba más la presencia de mujeres en el laboratorio, procesando esas muestras de roca, apretando botoncitos en máquinas y dejándose la vista ante un microscopio contando minerales y fósiles microscópicos. De hecho, generalmente nuestro papel era el de “secretarias” que pasaban a limpio las sesudas divagaciones y complejos esquemas realizados por los compañeros varones. Pero sin darnos la opción de pensar en hipótesis demasiado complejas para nuestro limitado conocimiento científico. Y sin que se nos pasase por la cabeza la remota posibilidad de redactar, ni siquiera firmar, publicaciones científicas resultantes de esas investigaciones.
Pero esta imagen dista mucho de la realidad. Hace más de doscientos años que las mujeres han ido realizando importantísimos descubrimientos que han permitido avanzar en el conocimiento de la historia de nuestro planeta, sentando las bases de la Geología tal y como la conocemos en la actualidad, aunque su nombre se haya cubierto con el polvo del paso del tiempo. Por eso, uno de los deberes de aquellas que, muchas veces sin saberlo, seguimos sus pasos es coger nuestro martillo geológico y retirar esas capas de roca que cubren su legado hasta desvelar sus nombres y trabajos al mundo.
 Portada del libro “GEAS, Mujeres que estudian la Tierra” en su versión en castellano.
Portada del libro “GEAS, Mujeres que estudian la Tierra” en su versión en castellano.Con este objetivo nació la Comisión Mujeres y Geología en el seno de la Sociedad Geológica de España. Y una de sus últimas actividades ha sido la colaboración en la publicación del libro “GEAS, Mujeres que estudian la Tierra”. Escrito por Rosa Mateos y Ana Ruiz Constán, geólogas del Instituto Geológico y Minero de España (IGME-CSIC) y bellamente ilustrado por Nívola Uyá, recoge las biografías de doce pioneras de las Ciencias de la Tierra que han cambiado el mundo de la Geología en los dos últimos siglos. Sin hacer muchos spoilers, descubriremos como antes de que Charles Lyell animase a otro Charles, Darwin, a lanzar su teoría de la evolución, una joven medio analfabeta inglesa había descubierto cómo cambiaban las especies fósiles con el tiempo, dándole a Lyell las pruebas que necesitaba para sustentar sus hipótesis. O cómo una geofísica danesa descubrió que el núcleo interno es sólido mientras que el núcleo externo es líquido, algo básico para que se forme el campo magnético terrestre y se sustente la vida en nuestro planeta. Incluso, conoceremos a la geóloga marina que, dibujando los mapas de los fondos marinos, dio con la clave de la tectónica de placas, a pesar de que se burlasen de sus descubrimientos sus propios compañeros de laboratorio. Este libro, traducido a más de diez idiomas, también se ha convertido en una exposición itinerante solicitada por varios museos, instituciones y centros educativos, para trasladar su legado a todos los rincones posibles.
 Paneles que componen la exposición itinerante de “GEAS, Mujeres que estudian la Tierra” colocados en el Parque de las Ciencias de Granada, donde permanecerán todo el mes de febrero.
Paneles que componen la exposición itinerante de “GEAS, Mujeres que estudian la Tierra” colocados en el Parque de las Ciencias de Granada, donde permanecerán todo el mes de febrero.Pero el trabajo de la Comisión Mujeres y Geología no termina aquí. Dos cosas que tenemos muy claras es que no debemos caer en el error de transmitir a las futuras generaciones que para ser geóloga debes ser brillante y hacer un descubrimiento que cambie los pilares de la ciencia, ni tampoco que esta visibilización de nuestro trabajo deba realizarse únicamente un día al año. Por este motivo pusimos en marcha la iniciativa Geocharlas, que consisten en charlas, conferencias, talleres y paseos geológicos ofertados de manera totalmente gratuita a centros educativos, museos, instituciones y asociaciones de diversa índole durante todo el año. Así, las geólogas pertenecientes a la Comisión nos desplazamos a los centros demandantes para hablar de nuestro trabajo y nuestra disciplina científica a un público muy diverso, principalmente estudiantes de niveles preuniversitarios, para aumentar su conocimiento en Ciencias de la Tierra y crear referentes cercanos para las más jóvenes: nosotras mismas.
 Taller didáctico ofertado como una Geocharla ante alumnado de educación primaria.
Taller didáctico ofertado como una Geocharla ante alumnado de educación primaria.Crear vocaciones científicas es una tarea ardua y muy noble, pero al igual que cuando siembras una semilla hay que regarla y cuidarla continuamente para que se desarrolle la planta, también debemos mantener y potenciar el interés por la Geología en las jóvenes. Con este propósito surgió una de las últimas iniciativas que hemos desarrollado en la Comisión, el “Programa de Mentorización Geólogas en Red” (GERMEN). Se trata de un programa en el que geólogas experimentadas de diferentes disciplinas, ámbitos de conocimiento y puestos laborales, no solo relacionados con la investigación, actuamos como mentoras de jóvenes que inician su camino como profesionales de las Ciencias de la Tierra y buscan una mano amiga para que las guíe y aconseje. Realmente, hemos creado una red de apoyo en la que todas podemos ayudarnos mutuamente a mejorar en nuestra profesión.
 Reunión de bienvenida de las mentoras y mentorizadas de la última edición del “Programa de Mentorización Geólogas en Red”.
Reunión de bienvenida de las mentoras y mentorizadas de la última edición del “Programa de Mentorización Geólogas en Red”.Todas estas actividades no serían posibles si no remásemos todas en la misma dirección, compartiendo objetivos comunes que nos dan la capacidad de aumentar nuestros esfuerzos y dedicación. Salvo que las geólogas queramos acabar extinguiéndonos en unas pocas décadas.
Si queréis conocer con más detalle las actividades que realizamos en la Comisión Mujeres y Geología, solicitarnos alguna Geocharla o uniros a nuestra lista de distribución de información, no dejéis de visitar nuestra página web. Estaremos encantadas de atenderos.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Geóloga, ¿una especie en peligro de extinción? se ha escrito en Cuaderno de Cultura Científica.
Sophie Bryant, matemática y educadora irlandesa
Sophie Bryant fue la primera mujer de Gran Bretaña e Irlanda que obtuvo un doctorado en cualquier disciplina: ocurrió en 1884. También fue la primera mujer que publicó un artículo científico en las actas de la London Mathematical Society: sucedió en 1885. Y, además, fue la primera mujer irlandesa que publicó un libro de texto de matemáticas: ocurrió en 1897, era el primero de varios tomos sobre la geometría de Euclides.
 Sophie Bryant. Fuente: Wikimedia Commons.
Sophie Bryant. Fuente: Wikimedia Commons.
Sophie Willock nació el 15 de febrero de 1850 en Dublín (Irlanda). Era la tercera de los seis hijos de Sophie Morris y el reverendo William Alexander Willock, miembro del Trinity College de Dublín donde enseñaba matemáticas. Fue educada en su casa por su padre y por institutrices privadas. Estas últimas eran francesas o alemanas y, gracias a ellas, Sophie consiguió hablar con fluidez ambas lenguas.
En 1863 William Alexander Willock fue nombrado titular de la Cátedra de Geometría de la Universidad de Londres y la familia se mudó a esta ciudad. Sophie pudo ingresar en 1866 en el Bedford College gracias a la concesión de una beca Arnott para ciencias. Al año siguiente se presentó al examen local de Cambridge que acababa de abrirse a mujeres; sus buenos resultados en matemáticas la colocaron en la primera clase.
En 1869 se casó con un cirujano, William Hicks Bryant, diez años mayor que Sophie. El médico enfermó y falleció un año más tarde. Sophie Bryant comenzó a trabajar entonces como maestra en una escuela para mujeres en Highgate, cerca de Londres. Pero no abandonó sus propios estudios.
La influencia de Frances Mary BussSophie conoció a la educadora Frances Mary Buss (1827-1894) en 1867, cuando se presentó al examen local de Cambridge para mujeres. Buss, que había fundado en 1850 la North London Collegiate School, animó a Bryant a continuar con su educación tras la muerte de su marido.
En 1875, la invitó a formar parte del personal del colegio para niñas que dirigía, trabajando como profesora de matemáticas. En realidad, Sophie no poseía ningún título universitario, ya que las mujeres no podían obtenerlos en ese momento. Finalmente, en 1878, la Universidad de Londres abrió sus puertas a las mujeres; Buss volvió a animar a Bryant a continuar con sus estudios. Aunque Sophie debió salvar previamente algunas carencias en su formación; su educación en casa no había incluido el aprendizaje del latín, y esa materia era necesaria para ser admitida en la universidad. Así que tuvo que recurrir de nuevo a clases particulares para aprender esa lengua y completar también sus conocimientos en alguna otra materia como la biología. En 1881 consiguió un grado con honores de primera clase en ciencias mentales y morales (filosofía) y honores de segunda clase en matemáticas. Tres años más tarde consiguió un doctorado sobre filosofía mental y moral, convirtiéndose en la primera mujer en Inglaterra en obtener este título.
 Frances Mary Buss y Sophie Bryant. Fuente : Wikimedia Commons.
Frances Mary Buss y Sophie Bryant. Fuente : Wikimedia Commons.
En 1882, Bryant fue admitida como miembro de la London Mathematical Society; fue la tercera mujer en entrar en esa sociedad científica tras la geómetra algebraica Charlotte Angas Scott (1858-1931) y la lógica Christine Ladd-Franklin (1847-1930), que ingresaron en 1881.
Bryant fue la primera mujer en publicar un artículo en la revista Proceedings of the London Mathematical Society. Fue en 1884; el trabajo se titulaba On the Ideal Geometrical Form of Natural Cell-Structure. En él investigaba la forma hexagonal de los panales de abejas. Su enfoque era lógico y descriptivo, no era demasiado matemático para los estándares actuales, aunque su manera de proceder era una práctica común en la época. En su artículo, Bryant explicaba cómo la forma de los panales podría deberse a la actividad natural de las abejas, a su intuición usando el método de prueba y error. Argumentaba que era necesario que cada abeja excavara su propia celda, aproximadamente al mismo ritmo que las demás, y concluía que los semidodecaedros rómbicos alargados eran la forma natural de las celdas de los panales de abeja.
En 1895 Frances Mary Buss falleció y Bryant la sucedió como directora de la North London Collegiate School, ocupando este cargo hasta que se jubiló en 1918. Durante esos años escribió sobre temas de educación y de educación matemática.
Pionera en la educación de las mujeres, nacionalista irlandesa y feministaEntre otras muchas actividades, Sophie Bryant jugó un papel decisivo en la creación del Cambridge Training College for Women, ahora llamado Hughes Hall.
Fue miembro de la London Ethical Society, una de las primeras comunidades humanistas que defendía una vida moral al margen de la religión. Además, apoyó abiertamente el sufragio femenino, aunque defendió su aplazamiento hasta que las mujeres tuvieran una mejor educación.
Interesada en la política irlandesa y entusiasta nacionalista, Bryant escribió varios libros sobre la historia de Irlanda y la antigua ley irlandesa.
Falleció practicando senderismo en los Alpes: su cadáver fue descubierto el 28 de agosto de 1922, tras permanecer dos semanas desaparecida. Algunas noticias apuntaban a un asalto para robar sus pertenencias.
Referencias
-
Sophie Willock Bryant, MacTutor History of Mathematics Archive, St Andrews University
-
Patricia Rothman, ‘So work the honey bees… building roofs of gold’. The Story of Sophie Bryant, The London Mathematical Society Newsletter 311 (2003) 22-24
-
Patricia Rothman, A biography of Sophie Bryant, Chalkdust Magazine,18 octubre 2017
-
Peter Berresford Ellis, Sophie Bryant (part 1) y Sophie Bryant (part 2), Irish Democrat
-
Sophie Bryant, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Sophie Bryant, matemática y educadora irlandesa se ha escrito en Cuaderno de Cultura Científica.

