Ártico y Antártico se calientan a la vez
Fernando Prieto
Las temperaturas récord en el Ártico y en el Antártico, unidas al desprendimiento de la plataforma Conger de 1.200 kilómetros cuadrados el 15 de marzo en la Antártida oriental, son una seria llamada a priorizar las medidas para proteger el clima. Este hecho nunca había sucedido. Es una advertencia que debería poner en alerta a los políticos y decisores para, de una vez, reducir las emisiones de gases de efecto invernadero y tomar medidas de adaptación de una vez por todas.
 En Groenlandia, las anomalías alcanzaron los 10 ºC por encima de la media, y en la región Ártica llegaron hasta los 30ºC. Además en el Ártico esta subida de temperaturas continuada, unida al aumento de olas de calor registrado, está relacionada con el deshielo del permafrost. Foto: Pixabay
En Groenlandia, las anomalías alcanzaron los 10 ºC por encima de la media, y en la región Ártica llegaron hasta los 30ºC. Además en el Ártico esta subida de temperaturas continuada, unida al aumento de olas de calor registrado, está relacionada con el deshielo del permafrost. Foto: PixabayLa ola de calor de la segunda semana de marzo tanto en el Ártico como en el Antártico llevó a temperaturas de hasta 40 °C por encima de lo habitual para esta época del año. Hasta ahora este fenómeno se había registrado solo en el Ártico, pero no había llegado a la Antártida y jamás en los dos polos a la vez. Así lo señala una de las autoridades mundiales en el campo, Carlos Duarte, de la Tarek Ahmed Juffali Research Chair in Red Sea Ecology.
En Groenlandia, las anomalías alcanzaron los 10 °C por encima de la media, y en la región Ártica llegaron hasta los 30 °C por encima de los valores habituales. La disminución del albedo hace que aumente la radiación absorbida y, como consecuencias, las temperaturas.
En el Ártico, esta subida de temperaturas continuada, unida al aumento de olas de calor registrado, está relacionada con el deshielo del permafrost que aumentará las emisiones de metano y puede desencadenar uno de los temidos puntos de no retorno.
En la Antártida, en la base de Concordia, situada a 75 grados sur de latitud, se registraron 40 grados de temperatura por encima de la media. Si por esas fechas lo habitual son unos -55 °C, el pasado 18 de marzo los termómetros marcaron -12 °C. Si este aumento de temperaturas sucede de manera continuada produciría una fusión masiva del hielo que aumentaría la cantidad de agua líquida en el océano y, en consecuencia, un aumento del nivel del mar.
Así como en el Ártico no existe ninguna duda sobre el proceso, en la Antártida sí ha habido polémica entre la comunidad científica sobre la variación de las masas de hielo, si bien las últimas investigaciones publicadas en Nature entre 1992 y 2017 apuntan a que a largo plazo existe una disminución del hielo.
La Antártida perdió 2.720 ± 1.390 mil millones de toneladas de hielo entre 1992 y 2017, lo que corresponde a un aumento del nivel medio del mar de 7,6 ± 3,9 milímetros. El desprendimiento citado de la plataforma de hielo coincide con el hecho de que la extensión de hielo marino en la Antártida mostró su nivel más bajo desde que hay registros para el mes de febrero de 2022. Se encontraría por debajo de los 2 millones de kilómetros cuadrados, según cita la Oficina Meteorológica de Australia.
Efectos cascada en otras partes del planetaLa consecuencia de que se desestabilice el clima en las zonas polares puede ser un efecto dominó de cambios a escala planetaria. Esto puede generar un cambio climático abrupto, ya que estas regiones tienen un papel crítico en la regulación al sistema climático global, así como respecto al nivel del mar.
Los eventos meteorológicos extremos son pruebas del calentamiento global y como este puede originar cambios irreversibles. Si se mantiene en el tiempo el aumento de las temperaturas detectadas en los polos, cambiará la circulación de las masas de aire y tendrá repercusiones en latitudes medias.
En concreto, en la Península y en el Mediterráneo, además del aumento de temperaturas generalizado, puede haber un aumento de los fenómenos meteorológicos extremos como olas de calor, inundaciones, mayor irregularidad de precipitaciones, sequías o inundaciones.
La ciencia climática es todavía incapaz de predecir los puntos de no retorno, pero estas señales sí pueden indicar que podemos estar cerca de alguno de ellos, que como su propio nombre sugiere, pueden ser graves para la humanidad.
 Evolución de la plataforma Conger entre el 22 de febrero y el 21 de marzo de 2022. Fuente: NASA Earth ObservatoryLas consecuencias climáticas de la guerra en Ucrania
Evolución de la plataforma Conger entre el 22 de febrero y el 21 de marzo de 2022. Fuente: NASA Earth ObservatoryLas consecuencias climáticas de la guerra en Ucrania
Por otra parte, las primeras estimaciones de las consecuencias de la guerra en Ucrania indican que las emisiones pueden subir un 14 % en el año 2022. Asimismo, ha determinado una falta de interés en todo el proceso del cambio climático, lo que ha generado una ruptura de acuerdos internacionales y de medidas conjuntas climáticas por parte de todos los países.
El primer informe importante del Panel Intergubernamental de Expertos sobre el Cambio Climático (IPCC) es de 1990 y desde entonces y hasta abril de 2022 se han sucedido hasta seis grandes de ellos recogiendo las mejores investigaciones mundiales con los mejores científicos sobre el clima. En 1997 se firmó el protocolo de Kioto con la finalidad de reducir las emisiones. En 2015 el Acuerdo de París y se aprobaron los 17 Objetivos de Desarrollo Sostenible. En noviembre de 2021 se celebró la 26 Cumbre del Clima de Glasgow con el mismo objetivo y en los últimos meses se ha presentado el último informe del IPCC con resultados cada vez más alarmantes.
Mientras, en 1990 la concentración de CO₂ en la atmosfera era de 350 ppm (partes por millón), lo que se considera un valor seguro. En la actualidad ya son más de 419, lo cual ya es un valor preocupante y no hace más que incrementar los efectos del cambio climático que se hacen notar en todos los rincones del mundo.
Las emisiones de CO₂ en 1990 a la atmosfera eran de 22,7 gigatoneladas (Gt) según Carbon Project y en 2020 ya se han alcanzado más de 36.4 Gt de CO₂, solo un 0.8 % menor que los valores pre pandemia que fueron de 36,7 Gt CO₂ en 2019. Con la guerra ya se está quemando mucho más carbón, más gas y países como el Reino Unido ya han anunciado que volverán a las perforaciones para extraer más petróleo del Mar del Norte.
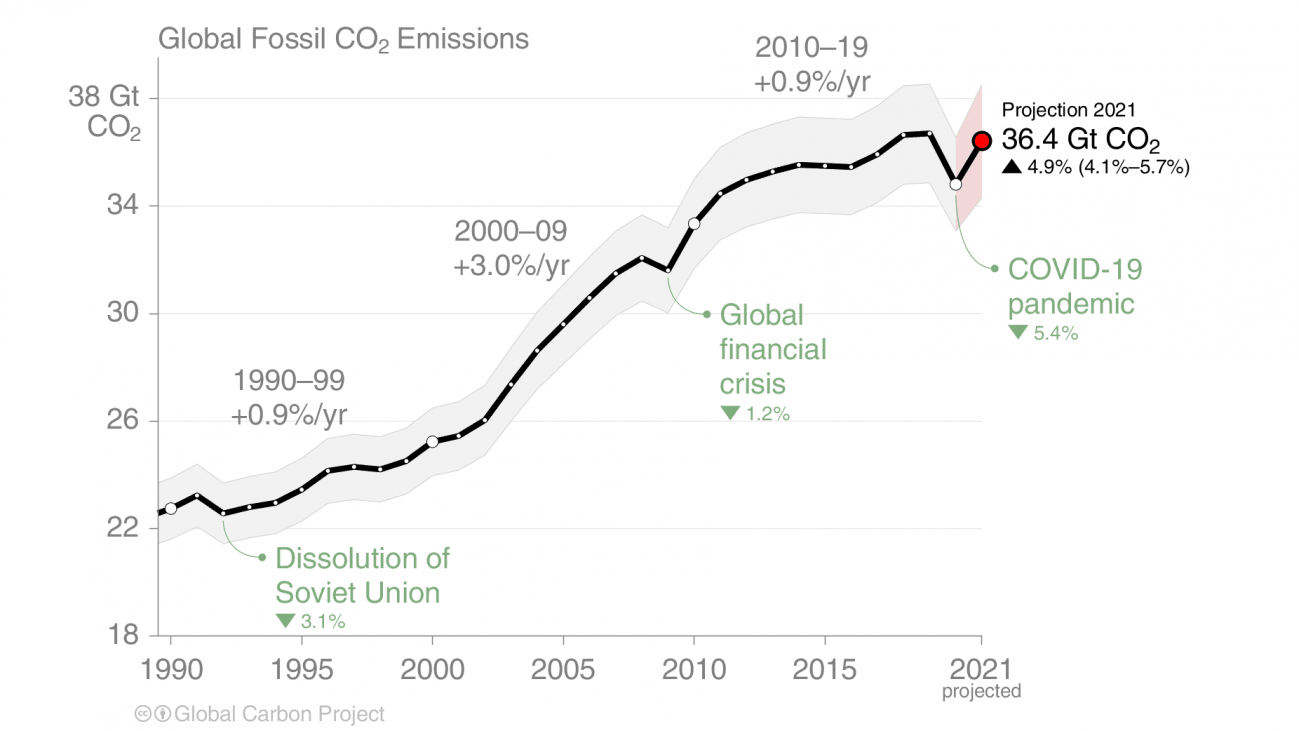 Fuente: Global Carbon ProjectLa historia de un fracaso
Fuente: Global Carbon ProjectLa historia de un fracaso
Es sabido que las emisiones de combustibles fósiles son responsables de estos récords de temperaturas y del cambio climático. Sin embargo, las emisiones han seguido aumentando desde que existen datos, excepto en periodos muy puntales como la crisis de la antigua Unión Soviética, la crisis de Lehman Brothers o la reciente pandemia de la covid-19. Por todo ello, es evidente que es necesario reducir todas estas emisiones y volver a mirar arriba para replantearse los temas realmente importantes.
En resumen, hasta la actualidad, es la historia de un gran fracaso. Es hora de reducir las emisiones de una forma radical y sobre todo de adaptarnos con políticas valientes y basadas en la ciencia, para aumentar la resiliencia sobre todo con señales tan alarmantes como anomalías térmicas en ambos polos simultáneamente, señal clara de disrupciones del sistema climático global. Parar la guerra y mirar arriba para resolver los problemas del sistema climático son, sin duda, la única salida y la opción más inteligente.
Sobre el autor: Fernando Prieto es doctor en Ecología y director del Observatorio de la Sostenibilidad.
Una versión de este artículo se publicó en SINC.
El artículo Ártico y Antártico se calientan a la vez se ha escrito en Cuaderno de Cultura Científica.
El arte de la sencilla baldosa de Truchet
En la anterior entrada del Cuaderno de Cultura Científica Los embaldosados de Truchet y el puzle del diamante estuvimos hablando del diseño de patrones de embaldosado realizados con una sencilla baldosa, la conocida con el nombre de “baldosa de Truchet”. Esta es una baldosa cuadrada dividida por la diagonal en dos zonas triangulares de dos colores distintos, por ejemplo, gris y negro, como la que aparece en la imagen.
 Baldosa de Truchet
Baldosa de Truchet
En el siglo XVIII los religiosos franceses, interesados por las matemáticas, Sébastien Truchet –en su artículo Memoria sobre las combinaciones (1704)– y Dominique Doüat –en su libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722)– tomaron las cuatro orientaciones posibles de esta baldosa cuadrada bicolor, que vemos en la siguiente imagen, y realizaron un análisis combinatorio de los posibles patrones de teselados que se podían construir con ellas, del que hemos hablado en la anterior entrada.
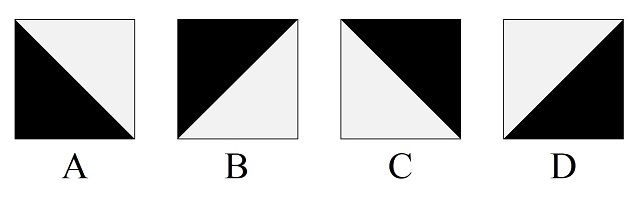 Las cuatro orientaciones posibles de la tesela de Truchet, nombradas por Doüat como A, B, C y D
Las cuatro orientaciones posibles de la tesela de Truchet, nombradas por Doüat como A, B, C y D
Y como comentábamos entonces, el estudio de los patrones de embaldosado o teselado, y en particular también los realizados con la baldosa de Truchet, es un tema con interés tanto en el ámbito de la ciencia y la tecnología, como del arte y el diseño. De hecho, tanto Truchet, como Doüat, no solo realizaron el estudio combinatorio de estos patrones de teselados, sino que se preocuparon de mostrar hermosos diseños realizados con esta baldosa, como los que aparecen en la siguiente imagen.
 Una página del libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722), de Dominique Doüat, con ilustraciones de patrones de embaldosado, con una baldosa de Truchet
Una página del libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722), de Dominique Doüat, con ilustraciones de patrones de embaldosado, con una baldosa de Truchet
Es sorprendente como con un elemento tan sencillo se pueden realizar tan hermosos y complejos diseños de patrones de embaldosado. El propio Sébastien Truchet explicaba en su artículo Memoria sobre las combinaciones (1704) que para su estudio combinatorio se había inspirado en las baldosas de cerámica utilizadas para la decoración de un castillo que había visitado en uno de sus viajes, como hemos recogido en la entrada Los embaldosados de Truchet y el puzle del diamante. En la siguiente imagen se muestran, aunque no los azulejos que vio el religioso matemático en su viaje, sí unos azulejos decorativos antiguos. Pertenecen a la Catedral Santa María de la Huerta de Tarazona, edificio religioso que empezó a construirse a mediados del siglo XII, que como en la mayoría de edificaciones de este tipo tuvo sus etapas de destrucción y reconstrucción. Los azulejos pertenecen a las reconstrucciones de los siglos XV y XVI, de estilo mudéjar.
 Fotografía de los azulejos de la Catedral Santa María de la Huerta de Tarazona, perteneciente a la entrada Simetrías I en la Catedral de Tarazona del blog MateTurismo, de Angel Requena
Fotografía de los azulejos de la Catedral Santa María de la Huerta de Tarazona, perteneciente a la entrada Simetrías I en la Catedral de Tarazona del blog MateTurismo, de Angel Requena
Así mismo, en la anterior entrada comentamos la presencia de estos cuadrados bicolor en el arte textil de los quilts. Pero también podemos ver como algunas artistas contemporáneas han utilizado, y siguen utilizando, estas ideas en sus obras de arte.
Las baldosas de Truchet en el arte contemporáneoPor ejemplo, la artista noruega Josefine Lyche ha diseñado dos instalaciones con los patrones de teselado de las baldosas de Truchet que están relacionadas con el teorema del diamante en su versión 2 x 2 (véase Los embaldosados de Truchet y el puzle del diamante), que son The 2×2 Case (Diamond Theorem). After Steven H. Cullinane (2011) y The 2×2 Case (Diamond Theorem) II. After Steven H. Cullinane (2011). Estas obras consisten en la realización de los 24 diseños de embaldosados cuadrados de tamaño 2×2 que contienen las cuatro orientaciones distintas (A, B, C y D) de la baldosa cuadrada bicolor. La primera de ellas –que vemos en la siguiente imagen- realizada sobre una pared blanca con espejos que reflejan la luz dirigida hacia ellos en el lugar de exposición, una sala a oscuras, mientras que la segunda versión consiste en piezas realizadas en pintura acrílica sobre lienzo, en lugar de espejos.
 The 2×2 Case (Diamond Theorem). After Steven H. Cullinane (2011), de la artista noruega Josefine Lyche. Imágenes de la página web de Josefine Lyche
The 2×2 Case (Diamond Theorem). After Steven H. Cullinane (2011), de la artista noruega Josefine Lyche. Imágenes de la página web de Josefine LycheLa artista abstracta estadounidense Heather Jones, cuyo trabajo está inspirado en los diseños geométricos de los quilts tradicionales elaborados por las mujeres de ciertas regiones de Estados Unidos, ha creado algunas obras con esta estructura cuadrada dividida en dos triángulos coloreados. Por ejemplo, en la reciente exposición Storytellers / Contadoras de historias (2022) en el centro de arte contemporáneo de Dayton (Ohio), The Contemporary Dayton, dedicada a las mujeres desarrollaron el arte textil de los quilts, se ven algunas de estas obras, como las que vemos en la siguiente imagen: One way or another / De una manera u otra (2021), realizada en algodón cosido, destacando el color negro, y A time for change / Un tiempo para el cambio (2021), también en algodón cosido, destacando el color rojo.
 Fotografía de la exposición Storytellers / Contadoras de historias (2022) en The Contemporary Dayton, en la que se pueden ver las obras One way or another / De una manera u otra (2021) y A time for change / Un tiempo para el cambio (2021), de la artista abstracta estadounidense Heather Jones
Fotografía de la exposición Storytellers / Contadoras de historias (2022) en The Contemporary Dayton, en la que se pueden ver las obras One way or another / De una manera u otra (2021) y A time for change / Un tiempo para el cambio (2021), de la artista abstracta estadounidense Heather Jones
O también, en la reciente exposición To Hold Tender This Land / Mantener joven esta tierra (2022) en la Galería David Richard de Nueva York se ha podido disfrutar de obras como la siguiente, titulada There was always light / Siempre hubo luz (2022).
 Fotografía de la exposición To Hold Tender This Land (2022), de la artista estadounidense Heather Jones, en la Galería David Richard de Nueva York. La obra de la derecha es There was always light / Siempre hubo luz (2022). Imagen de la página GalleriesNow
Fotografía de la exposición To Hold Tender This Land (2022), de la artista estadounidense Heather Jones, en la Galería David Richard de Nueva York. La obra de la derecha es There was always light / Siempre hubo luz (2022). Imagen de la página GalleriesNow
Otra artista que utiliza este tipo de teselaciones es la francesa Ode Bertrand (1930) cuyo trabajo artístico está relacionado con la abstracción geométrica y el arte concreto, y que según sus palabras pretende “poner orden en el caos”. En una serie de obras, como la pintura Sin título (2015) que podemos ver en la siguiente imagen, añade a las cuatro teselas cuadradas bicolor blanco/negro, las dos teselas monocromáticas relacionadas, la tesela blanca y la negra.
 Sin título (2015), de la artista francesa Ode Bertrand. Imagen de la Galerie Wagner
Sin título (2015), de la artista francesa Ode Bertrand. Imagen de la Galerie Wagner
Una artista que sigo a través de Instagram y cuyas obras, realizadas en lápiz sobre papel, son de una belleza geométrica inspiradora es la alemana Christiane Kaufmann (1983). Muchas de sus sencillas y hermosas creaciones nos recuerdan a la baldosa de Truchet, aunque muchos de sus cuadrados a lápiz son monocolor. En particular, la serie de obras titulada azul/rojo, de la que destaco esta pieza azul/rojo [25/10/2021],
 Pintura azul/rojo [25/10/2021], de la artista alemana Christiane Kaufmann, realizada con lápices de colores sobre papel
Pintura azul/rojo [25/10/2021], de la artista alemana Christiane Kaufmann, realizada con lápices de colores sobre papel
que nos recuerda al diseño con baldosas de Truchet siguiente.

Preparando esta entrada del Cuaderno de Cultura Científica se me ocurrió una idea para realizar una obra plástica basada en la baldosa de Truchet y el número pi, cuyo boceto explico en las siguientes líneas. Para empezar, renombramos las cuatro orientaciones de la baldosa cuadrada tricolor –antes nombradas A, B, C y D- como 1, 2, 3, 0, como se muestra en la imagen.
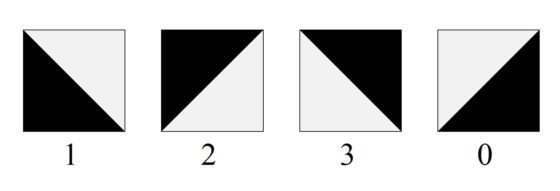
La idea es realizar un patrón de embaldosado cuadrado de tamaño 12 x 12 que formará la estructura visual de la obra. Para determinar la colocación de las cuatro baldosas de Truchet orientadas utilizaré el número pi, es decir, el diseño no depende de mis preferencias personales. Con este fin, consideramos la expresión decimal de esta constante matemática (sobre esta puede leerse la entrada ¿Es normal el número pi?), pero no en la base decimal que utilizamos normalmente, sino en base cuatro (en la que utilizamos las cuatro cifras básicas 1, 2, 3, 0), ya que solo tenemos cuatro orientaciones posibles. La expresión del número pi en base cuatro es la siguiente (en una futura entrada del Cuaderno de Cultura Científica explicaremos cómo determinar la expresión del número pi, o cualquier otro número, en una base de numeración cualquiera, por ejemplo, cuatro):
3,02100333122
220202011220
300203103010
301212022023
200031300130
310102210002
103200202022
121330301310
000200232332
221203230103
212302021101
102200201321…
Solo hemos incluido los 144 primeros dígitos del número pi, en base cuatro, ya que nuestro patrón es un cuadrado de tamaño 12 x 12 y utilizaremos 12 x 12 = 144 baldosas cuadradas. Estas estarán determinadas por el correspondiente dígito de pi, en base cuatro, recorriendo el cuadrado fila a fila, de arriba a la izquierda, hacia la derecha en cada fila, hasta abajo a la derecha. Así la primera fila de nuestro diseño de embaldosado utiliza las baldosas que se corresponden con los primeros doce dígitos 3 0 2 1 0 0 3 3 3 1 2 2, como puede observarse en el diseño final que hemos obtenido y que se muestra en la siguiente imagen.
 Idea para una obra basada en los patrones de embaldosado con baldosas de Truchet y el número pi.
Idea para una obra basada en los patrones de embaldosado con baldosas de Truchet y el número pi.
En esta entrada solamente hemos considerado el caso de los diseños con la sencilla baldosa de Truchet, aunque podríamos considerar las baldosas de Truchet en un sentido más amplio, pero eso será en otra ocasión. Mientras os animo a realizar vuestros propios diseños con cuadrados bicolor, ya sea con telas, lápices de colores, pinturas o con el ordenador.
Bibliografía:
1.- Cyril Stanley Smith (con la traducción del texto de Truchet por Pauline Boucher), The Tiling Patterns of Sebastian Truchet and the Topology of Structural Hierarchy, Leonardo, vol. 20, n. 4, pp. 373-385, 1987.
2.- Dominique Doüat, Méthode pour faire une infinité de desseins différents avec des carreaux mi-partis de deux couleurs par une ligne diagonale : ou observations du Père Dominique Doüat, Religieux Carme de la Province de Toulouse, sur un mémoire inséré dans l’Histoire de l’Académie Royale des Sciences de Paris l’année 1704, présenté par le Révérend Père Sébastien Truchet religieux du même ordre, Académicien honoraire [Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal], París, 1922.
* Facsímil (extractos) e introducción de Jacques André
* Obra completa en Gallica – Bibliothèque nationale de France
3.- Sebastien Truchet, Memoir sur les Combinaisons, Histoire de l’Académie Royale des Sciences de Paris, 363-372 (1704).
* Obra completa en Gallica – Bibliothèque nationale de France
4.- Angel Requena, Simetrías I en la Catedral de Tarazona, del blog MateTurismo, 2018.
5.- Página web de Josefine Lyche
6.- Página web de Heather Jones
7.- Página web de Christiane Kaufmann
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El arte de la sencilla baldosa de Truchet se ha escrito en Cuaderno de Cultura Científica.
Einstein y su educación formal
En contra de las leyendas populares, Einstein fue en realidad un buen estudiante. Lo que sí es cierto es que el sistema de educación convencional, que él calificaba como dictatorial, le frustraba y que su rebeldía contra él era una manifestación de su propia creatividad. Muchas de las personas que intentaron enseñar a Einstein durante su educación formal se encontraron frente a un joven muy inteligente, pero quizás demasiado aficionado a discutir.

Antes siquiera de que Einstein empezase el colegio, su madre, con objeto de darle un empujoncito para que comenzase con buen pie, contrató a una profesora particular. Einstein se aburría mortalmente con las lecciones y, todavía en esa época de la vida en la que las rabietas se entienden como normales, le tiró una silla a la maestra. No volvería y la madre terminó contratando a otra.
En el Volksschule (colegio público de primaria), para alegría de su madre, le fue bastante bien y, aunque la leyenda quiere que suspendiese matemáticas, la realidad es que fue un estudiante muy bueno.
Las cosas cambiaron un poco cuando empezó a asistir al Luitpold Gymnasium (colegio de secundaria que prepara para la universidad) en Múnich. Según Einstein, los profesores tenían “una naturaleza dictatorial”. Uno de ellos llegó a decir que la sonrisa arrogante de Einstein ya era irrespetuosa. Pero, a pesar del hecho de que Einstein, al igual que muchas personas de inclinaciones intelectuales, odiaba el deporte (área fundamental en la educación alemana), pasó por el colegio bastante bien.
Mucho del estímulo intelectual lo conseguía Einstein fuera de clase. Su tío Jakob procuraba que su sobrino se distrajese enseñándole álgebra. Un amigo de la familia, Max Talmey (en aquella época, Max Talmud), un pobre estudiante de medicina en la Universidad de Múnich, judío polaco acogido por la comunidad judía local, cenaba muchas noches con la familia Einstein, y le hablaba al joven Albert de medicina, matemáticas, ciencia y filosofía. No sólo eso, sino que también le prestaba libros: entre ellos el “sagrado librito de geometría” (los Elementos de Euclides) y la Crítica de la razón pura de Kant. [Talmey, ya con su apellido adaptado al ambiente anglosajón, terminaría siendo oftalmólogo en la ciudad de Nueva York y un gran divulgador de la obra científica de Einstein.]
La educación de Einstein tuvo un giro inesperado en 1894. El negocio de su padre quebró, por lo que la familia partió hacia Pavía (Italia) donde había un encontrado un empleo. Einstein se quedó en Múnich con la idea de terminar la educación secundaria. El joven Albert, sin guía y expuesto a la rigidez militar de sus profesores, no lo soportó mucho tiempo, por lo que dejó el colegio y sorprendió a sus padres presentándose en la puerta de su casa en Italia.
La educación universitaria de EinsteinSu madre, posiblemente preocupada porque su vástago no triunfase en la vida como le correspondía por su valía, movió todos los hilos que pudo para conseguir que a Einstein se le permitiese presentarse al examen de entrada del Eidgenössische Technische Hochschule (ETH), la Escuela Politécnica Federal de Zúrich (Suiza). Estos hilos no eran fáciles de mover. Fue finalmente un amigo de la familia, Gustav Maier, el que convenció al director, Albin Herzog, de que merecía la pena dejar que aquel “niño prodigio” lo intentase. Einstein se presentó al examen y, a pesar de tener dos años menos de la edad habitual de entrada (18) y carecer de un certificado de escuela secundaria, aprobó las secciones de matemáticas y ciencia, pero suspendió las demás.
La familia decidió entonces que Einstein se matricularía en la escuela cantonal de Argovia (Suiza) [Aargau en alemán]. Tras un año de estudios en el que se hospedó en casa de su profesor Jost Winteler, consiguió aprobar la Maturitätsprüfung, la prueba de madurez establecida como final de la educación secundaria y que le daba acceso al ETH [en la imagen el certificado; usa el sistema de calificación suizo de la época, en el que la máxima nota posible es un 6].
Einstein se unió al Departamento VI, la “Escuela de profesores especializados en las asignaturas de matemáticas y ciencias” del ETH, cuando todavía le faltaban seis meses para tener la edad mínima oficial de acceso. Einstein era uno de los cinco estudiantes de física en la universidad. La Politécnica había sido fundada en 1855 y en la época en la que se inscribió Einstein se la consideraba de inferior categoría a otras escuelas, especialmente a las alemanas, aunque fuera por el solo hecho de que no podía otorgar doctorados.
Los primeros años fueron muy buenos para el joven Einstein. Los resultados de los exámenes lo colocaban siempre en los primeros puestos de su clase pero, conforme se acercaba el final de sus estudios, su incapacidad para soportar la autoridad volvió a aparecer. Especialmente difícil fue su relación con Heinrich Weber que, según Einstein contase a su biógrafo Carl Seelig, llegó a decir: “Es usted un muchacho inteligente, Einstein, muy inteligente. Pero tiene usted un gran defecto: no deja usted que se le diga nada”.
Einstein había comenzado ya una relación amorosa con Mileva Marić cuando en 1900 la pareja dedicó las vacaciones de primavera a preparar sus disertaciones finales de graduación. Sus calificaciones fueron de mediocres a malas. Sobre un máximo de 6, Einstein obtuvo un 4,5 y Mileva un 4,0. Los exámenes finales no fueron mejores. El sistema de evaluación final tenía en cuenta las calificaciones en exámenes y los trabajos presentados. Einstein aprobó, el cuarto de cinco alumnos, con un 4,91. Mileva suspendió con un 4,0.
El testarudo y joven físico se sintió desilusionado con el mundo académico, pero sí continuó trabajando en su tesis doctoral. La ETH no ofrecía doctorados, pero se podía obtener uno simplemente mandando una tesis a la Universidad de Zúrich. En septiembre de 1901 Einstein envió una tesis sobre un tema de la teoría cinética de gases. Esta tesis no prosperó. Se desconoce si Einstein la retiró o si no fue aceptada (los historiadores no han podido encontrar la respuesta de la universidad).
Mientras Einstein luchaba por encontrar un empleo, y subsistía dando clases particulares, siguió trabajando en su segunda tesis. El tema esta vez era sobre cómo usar el movimiento browniano para medir el tamaño de los átomos. Con la estabilidad que le daba el empleo que había encontrado en la Oficina Federal de Patentes en Berna, pudo avanzar en ella. Envió finalmente la tesis a la Universidad de Zúrich a comienzos de 1905. Paralelamente, Einstein mandó una versión de la misma a la principal revista alemana, Annalen der Physik, que fue publicada prácticamente a la vez que era aceptada por la Universidad de Zúrich, en abril de 1905. Einstein tenía finalmente su doctorado.
Einstein le contó la siguiente anécdota a Seelig: “Un día recibí un sobre grande en la oficina [de patentes], que contenía una elegante hoja de papel con algunas palabras en una tipografía pintoresca (creo incluso que era latín) que me pareció impersonal y carente de interés, por lo que terminó en la papelera”. Solo más tarde alguien le diría que aquella hoja de papel era su título de doctor y que, además, en el sobre había una carta invitándole a la ceremonia de graduación.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 4 de julio de 2010.
El artículo Einstein y su educación formal se ha escrito en Cuaderno de Cultura Científica.
¿Por qué las caras de la Luna son tan diferentes?
Creo que sin excepción todos hemos mirado alguna vez a nuestra Luna y nos ha llamado la atención las irregularidades que incluso a simple vista son evidentes. Quizás la más vistosa de todas es la presencia de dos colores bien diferenciados, el blanco y el gris, que salpican la superficie creando formas caprichosas, acompañadas de numerosos cráteres de impacto.
Pero desgraciadamente, desde la Tierra solo podemos ver una parte de la superficie, la que conocemos como «cara visible», y menos de un veinte por ciento de la que llamamos «cara oculta”, cuya geografía y geología es muy diferente de la primera.
No fue hasta el año 1959 cuando pudimos ver por primera vez la cara oculta de la Luna gracias a las imágenes tomadas por la sonda soviética Luna 3. A lo largo de los años sesenta, especialmente a partir de la segunda mitad, la pudimos estudiar con un mayor nivel de detalle gracias al creciente número de misiones lunares y una mejor tecnología.
Las diferencias entre las caras de la Luna Comparación entre las caras visible y oculta de la Luna con imágenes de la Lunar Reconaissance Orbiter. Imagen cortesía de NASA/GSFC/Arizona State University.
Comparación entre las caras visible y oculta de la Luna con imágenes de la Lunar Reconaissance Orbiter. Imagen cortesía de NASA/GSFC/Arizona State University.
Al examinar estas imágenes los científicos se dieron cuenta de que había grandes diferencias entre ambas caras. Propusieron distintas explicaciones a este hecho, a veces no exentas de controversia, pero que anticipaban que la historia de la Luna iba a ser mucho más interesante de lo que habíamos pensado a priori.
¿Y cuáles son estas diferencias? La más evidente es la proporción entre los mares lunares y las zonas más claras del terreno. Mientras que en la cara visible los mares representan aproximadamente un tercio de su superficie, en la cara oculta únicamente cubren alrededor de un uno por ciento. Además, la menor presencia de mares lunares hacía de la geografía de la cara oculta un lugar mucho más agreste y aparentemente con un mayor número de cráteres.
¿Pero qué son los mares? Los mares lunares, lejos de ser mares de agua como serían los de nuestro planeta, en realidad son grandes llanuras cubiertas por lava formadas como resultado de grandes colisiones de asteroides contra la superficie de la Luna y las erupciones volcánicas provocadas por estos.
 Salvo por cráteres de impacto posteriores a su formación y algunas montañas, los mares lunares son extraordinariamente llanos, como podemos ver en esta imagen tomada desde el módulo de comando de la misión Apolo XVI. Imagen cortesía de NASA.
Salvo por cráteres de impacto posteriores a su formación y algunas montañas, los mares lunares son extraordinariamente llanos, como podemos ver en esta imagen tomada desde el módulo de comando de la misión Apolo XVI. Imagen cortesía de NASA.
Tenemos que imaginarnos que las colisiones más energéticas y violentas eran capaces no solo de crear cráteres de grandes dimensiones, sino que podían fracturar la corteza lunar, facilitando que partes fundidas del manto fluyesen hacia la superficie, y rellenando estos cráteres con el material que ascendía.
Pero, entonces, ¿cómo podemos explicar esta diferencia? ¿Acaso no habrían ocurrido grandes impactos en la cara oculta de la Luna o es que hay otro mecanismo en juego y que no hemos podido atisbar hasta ahora?
El misterio de la Cuenca AitkenLa pasada semana se publicaba un artículo en la revista Science Advances que intenta dar una respuesta definitiva a estas preguntas: En el polo sur de la Luna existe la llamada Cuenca Aitken, un gigantesco cráter de impacto que alcanza los casi 2500 kilómetros de diámetro por más de 6 kilómetros de profundidad, y que se formó hace unos 4300 millones de años. De hecho, es el cráter más grande de la Luna y uno de los más grandes del Sistema Solar, probablemente el segundo más grande de todos los que conocemos.
Los autores afirman que la virulencia de este impacto fue tan grande que la energía liberada en forma de calor habría sido suficiente para alterar los patrones de circulación del manto lunar, debido a que el brusco aumento de la temperatura se habría ido propagando desde el lugar del impacto a todo el interior de la Luna.
A pesar de que fue un impacto de dimensiones realmente grandes, provocado por un cuerpo en el entorno de los 100 kilómetros de diámetro, sabemos que no llegó a profundizar más allá de la corteza lunar y, por lo tanto, llegar hasta el manto.
¿Cómo sabemos este detalle? Pues bien, las distintas misiones espaciales que han podido analizar la composición de esa zona de la Luna han podido comprobar que realmente todas las rocas que se ven tienen un mayor parecido composicional a las de la corteza que a las del manto, por lo que, de haber sido un impacto que realmente hubiese llegado hasta el manto, veríamos rocas con una composición diferente tanto dentro del cráter como desperdigadas hacia afuera del cráter, expulsadas por la brutal energía del impacto.
Esto quiere decir que el impacto probablemente ocurrió con un ángulo muy oblicuo y no “de frente”. Si se hubiese producido con un ángulo mucho más vertical, probablemente si hubiese llegado hasta el manto, haciendo que numerosas rocas quedasen exhumadas y otras fueran lanzadas a gran distancia.
Contados estos detalles del impacto, puede parecer que no tienen nada que ver con nuestra historia, pero probablemente condicionaron lo que ocurrió posteriormente. Justo debajo de la corteza lunar se estaban acumulando un conjunto de elementos químicos que conocemos como KREEP, y que se llaman así porque agrupan al potasio (K), tierras raras (REE) y fósforo (P). Junto a estos, también viajarían otros capaces de generar calor por el efecto de la desintegración radioactiva, como, por ejemplo, el torio.
Como dijimos antes, al ocurrir el impacto, el calor producido por este alteraría la circulación normal en el manto lunar, de tal manera que estos elementos que justo se acumulaban debajo de la corteza “se montaron” en esa nueva corriente de circulación por el manto y habrían llegado hasta la cara visible de la Luna.
Este hecho casa muy bien con las observaciones de la geoquímica lunar, tanto que concentraciones anómalas de estos elementos se pueden encontrar en algunos lugares de nuestro satélite, como Oceanus Procellarum, uno de los mares lunares más grandes.
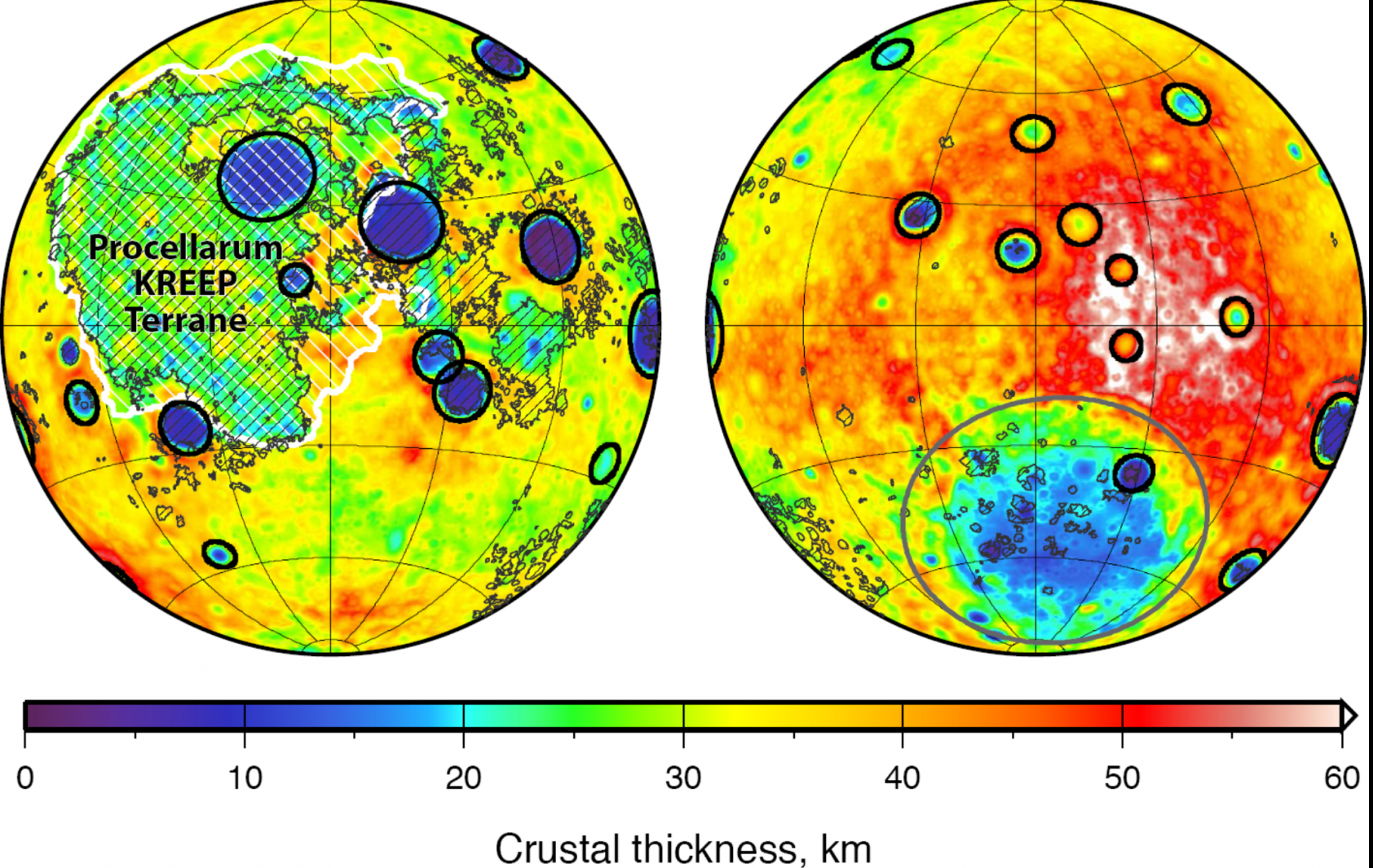 Mapa de espesor cortical de la Luna. En este puede apreciarse como en la cara visible, además de los grandes cráteres de impacto, la zona de Océanos Procellarum destaca por su menor espesor. Imagen cortesía de NASA/JPL-Caltech/S. Miljkovic.
Mapa de espesor cortical de la Luna. En este puede apreciarse como en la cara visible, además de los grandes cráteres de impacto, la zona de Océanos Procellarum destaca por su menor espesor. Imagen cortesía de NASA/JPL-Caltech/S. Miljkovic.
Y es que, gracias al calor extra aportado por estos elementos, se habría producido un mayor grado de fusión en los materiales del manto, lo que, a su vez, habría generado un mayor volumen de magma disponible para salir a la superficie y acabar formando los mares a través de los sistemas de fracturas generados por los impactos de asteroides.
Sin duda es una hipótesis muy interesante y que a grandes rasgos parece cuadrar muy bien con las observaciones, aunque todavía falta mucho por conocer de la geología lunar, y por ejemplo, comprender por qué el espesor de la corteza de nuestro satélite es mayor en la cara oculta que en la visible, y si esto también fue un factor importante a la hora de que una esté más cubierta por mares que la otra.
Referencia:
Jones, M. J., Evans, A. J., Johnson, B. C., Weller, M. B., Andrews-Hanna, J. C., Tikoo, S. M., & Keane, J. T. (2022). A south pole–aitken impact origin of the lunar compositional asymmetry. Science Advances, 8(14).doi: 10.1126/sciadv.abm8475
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Por qué las caras de la Luna son tan diferentes? se ha escrito en Cuaderno de Cultura Científica.
Solo respira el domingo
 Foto: Vitaly Sokol / Wikimedia Commons
Foto: Vitaly Sokol / Wikimedia Commons“Por anómalo que parezca este es el caso exactamente de la ballena, que vive sistemáticamente con intervalos de una hora entera y más (cuando está sumergida) sin inhalar un solo respiro, ni absorber de ningún modo una partícula de aire, pues recordemos que no tiene branquias.” (Moby Dick, capítulo LXXXV).
La historia de la obsesión del capitán Ahab con la gran ballena blanca que al final provocó su muerte, el naufragio del Pequod, así como la pérdida de la tripulación (salvo Ismael), es una epopeya trágica. Pero es también una crónica de la vida en los balleneros del siglo XIX y, aunque pueda sorprender, un tratado de historia natural. Quizás por reunir en una sola obra tal diversidad temática, la novela de Herman Melville es el texto de mayor densidad de vocabulario de que se tiene constancia. En ningún otro hay tantas palabras diferentes en comparación con el total de vocablos. Moby Dick contiene abundante y, en gran parte, correcta información biológica, como la que encabeza este texto.
Los cachalotes se sumergen, en promedio, a unos 400 m de profundidad, inmersiones que se prolongan alrededor de 40 minutos. Pero pueden llegar hasta los 3000 m y permanecer bajo el agua casi dos horas. Gracias a ello dan caza, incluso, a calamares gigantes. Son grandes depredadores. A pesar de haber sido diezmados de forma severa por la caza a que fueron sometidos durante el siglo XIX y gran parte del XX, consumen, en la actualidad, unas cien mil toneladas de pescado al año, el equivalente a lo que pescamos los seres humanos.
Se necesitan características muy especiales para conseguir esas inmersiones, algunas compartidas con el resto de mamíferos, aunque desarrolladas en mayor grado, como el reflejo de inmersión. Al sumergirnos, el corazón late más lentamente y consume así menos oxígeno. A la vez, la circulación periférica se limita o suprime, dirigiéndose la sangre, sobre todo, al encéfalo, pulmones y corazón; la subida de presión arterial que podría producirse la contrarresta la menor frecuencia de latido y, en los mamíferos marinos, una expansión de la aorta que funciona como cámara de compensación. Además, el bazo, que alberga en su interior muchos glóbulos rojos llenos de oxígeno, se contrae y los vierte al sistema circulatorio.
En comparación con otros mamíferos, los cetáceos exhiben rasgos específicamente adaptados al buceo a gran profundidad. Antes de sumergirse respiran varias veces y, a continuación, expulsan todo el aire de sus pulmones. Minimizan así la formación de burbujas de nitrógeno en la sangre al despresurizarse en el retorno a la superficie. A cambio, cuentan con varios “depósitos de oxígeno”. Ya hemos citado los glóbulos rojos extra que aporta el bazo. Además, tienen más sangre que los demás mamíferos; y esa sangre tiene un hematocrito -concentración de glóbulos rojos- muy alto. Su concentración de mioglobina es diez veces más alta que la nuestra; la mioglobina es una proteína similar a la hemoglobina, localizada en las células musculares. Lo mismo cabe decir de la citoglobina (en diferentes tejidos) y neuroglobina (en el tejido nervioso).
Los cachalotes pasan la mitad de su tiempo haciendo inmersiones profundas, la cuarta parte sumergiéndose a poca profundidad, y la otra cuarta parte algo por debajo o por encima de la superficie del agua. Moby Dick era un cachalote de tamaño enorme, por lo que seguramente superaba los periodos de una hora de inmersión que le atribuye Melville y, lo que es más significativo, resulta ser cierto, metafóricamente, lo que el propio autor escribió en el mismo capítulo LXXXV: “el cachalote solo respira cerca de la séptima parte, el domingo de su tiempo.”
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Solo respira el domingo se ha escrito en Cuaderno de Cultura Científica.
Día de Pi con BCAM Naukas 2022: María Ángeles García-Ferrero – Imágenes matemáticas

La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han suamdo a la celebración, organizando la tercera edición del evento BCAM-NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
María Ángeles García Ferrero, que es investigadora postdoctoral en el BCAM, se dedica, entre otras cosas, a los problemas inversos. En esta charla nos presenta algunos en forma de imágenes, desde ingeniosos pasatiempos japoneses a sistemas biológicos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de Pi con BCAM Naukas 2022: María Ángeles García-Ferrero – Imágenes matemáticas se ha escrito en Cuaderno de Cultura Científica.
Párkinson en una lágrima
Un estudio piloto liderado por la Dra. Elena Vecino, catedrática de Biología Celular y directora del grupo de investigación GOBE de la UPV/EHU, ha detectado potenciales biomarcadores de diagnóstico del párkinson en tan solo una lágrima.
 Foto: Luis Gálvez / Unsplash
Foto: Luis Gálvez / UnsplashLa enfermedad de Parkinson es la segunda enfermedad neurodegenerativa más común después de la enfermedad de Alzheimer. Uno de los principales retos en el tratamiento de las enfermedades neurodegenerativas es encontrar marcadores clínicos que permitan la clasificación temprana de los pacientes y ayuden a monitorizar la progresión de la enfermedad. Actualmente una de las pruebas de detección de marcadores de párkinson se realiza mediante punción lumbar y extracción de líquido cefalorraquídeo, pero un estudio dirigido por la UPV/EHU intenta detectarlo por otra vía menos invasiva. “Como el párkinson afecta a varios sistemas no motores y a los nervios periféricos, la secreción lagrimal podría estar alterada en estos pacientes, y la composición de las proteínas lagrimales podría mostrar un perfil característico en estos pacientes que podría servir como biomarcador de diagnóstico”, explica la Dra. Elena Vecino, catedrática de Biología Celular de la UPV/EHU.
El grupo de investigación GOBE ha analizado por primera vez las lágrimas de pacientes con párkinson con el fin de detectar biomarcadores tempranos de la enfermedad. Se trata de un estudio pionero en la detección en cantidades muy pequeñas (unos 5 microlitros), dirigido por la Dra. Elena Vecino y codirigido por la Dra. Arantxa Acera, investigadora Ikerbasque, en el que ha sido fundamental la participación del neurólogo del Hospital de Cruces Dr. Juan Carlos Gómez y su equipo además de especialistas en Oftalmología del Hospital de Cruces, y el servicio de proteómica del CIC Biogune (la proteómica es el estudio a gran escala de las proteínas).
Este estudio piloto se ha realizado mediante el análisis comparado de las lágrimas de 27 personas control y 27 pacientes con párkinson en distintos estadios de la enfermedad. Los resultados apuntan a una alteración en una serie de proteínas implicadas en la función de los lisosomas, orgánulos celulares responsables de la degradación de sustancias en el interior de la célula. “Hemos localizado estos marcadores (proteínas) sobreexpresados en las lágrimas de pacientes con párkinson”, señala Vecino.
Según explica la catedrática, “la córnea, la parte transparente del ojo, es la estructura más inervada del organismo; la lágrima que baña esta estructura retiene, entre otras sustancias, las proteínas necesarias para mantener el estado de lubricación de nuestros ojos. Entre los cientos de proteínas, casi miles de proteínas, que se pueden detectar en una lágrima, hemos visto que hay una tendencia en unas cuantas a sobreexpresarse, es decir, que aparecen en mayor cantidad en los pacientes de párkinson”.
Detectar el párkinson en una lágrimaEste estudio ha sido el germen de un Proyecto Elkartek, liderado por la UPV/EHU, en el que, además del Hospital de Cruces, se han incorporado los servicios de Neurología y Oftalmología del Hospital Donostia para ampliar el número de pacientes participantes. Además, también se ha incorporado la empresa Tecnalia, con el objetivo de desarrollar un test de detección temprana de la enfermedad con los biomarcadores que sean caracterizados en el estudio de proteómica. Vecino destaca que en el estudio es fundamental la participación de los pacientes; “en particular es de especial importancia la participación de familias afectadas por párkinson congénito. En el País Vasco hay varias familias afectadas por mutaciones que inducen esta enfermedad y el conocimiento de los marcadores tempranos son de especial importancia para el conocimiento de las causas y posterior estudio del tratamiento”.
En opinión de la doctora, “la novedad de este estudio estriba en el análisis individualizado, porque vamos hacia la personalización de la detección de las enfermedades”. Pero afirma que todavía queda mucho por hacer: “Ahora tenemos que mirar por qué sucede la citada sobreexpresión, por qué las neuronas de los pacientes bloquean el mecanismo de los lisosomas. Pero eso lo tenemos que demostrar con más pacientes”. La investigadora se muestra optimista: “Hemos sido los primeros en detectar en una lágrima todas las proteínas que hay y queremos llegar a poder detectar precozmente la patología”. Asimismo, la investigadora afirma que “si esta metodología funciona, el siguiente paso sería poderla aplicar a alzhéimer y a otras enfermedades neurodegenerativas”, concluye.
Referencia:
Arantxa Acera, Juan Carlos Gómez-Esteban, Ane Murueta-Goyena, Marta Galdos, Mikel Azkargorta, Felix Elortza, Noelia Ruzafa, Oliver Ibarrondo, Xandra Pereiro, and Elena Vecino Potential Tear Biomarkers for the Diagnosis of Parkinson’s Disease—A Pilot Study Proteomes 2022 10,4 DOI: 10.3390/proteomes10010004
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Párkinson en una lágrima se ha escrito en Cuaderno de Cultura Científica.
Taxones, paranormal activity en paleontología
En ciencia en general y en geología en particular, cuando queremos ponerle un nombre a algún proceso o estructura, buscamos un término que sea auto-explicativo. Es decir, que ya solo con oírlo, nos hagamos una idea de lo que estamos hablando, sin necesidad de una descripción más profunda. Pero, a veces, somos demasiado literales a la hora de elegir esos nombres. Y aquí os voy a mostrar unos ejemplos, con los que no sabremos si estamos hablando de términos paleontológicos o si queremos contar una película de terror con tintes rockeros.
Pero antes de entrar en detalles, es necesario que haga algunas aclaraciones. Los estudios paleontológicos se basan en la información preservada en el registro fósil, es decir, en los restos de organismos del pasado que se han conservado transformados en rocas. Pero es extremadamente difícil que un resto orgánico se convierta en fósil, la mayor parte de ellos acaban desapareciendo sin dejar huella. Por eso solemos decir que el registro fósil es “incompleto”. Con esto no pretendemos afirmar que sea malo o que no sirva para nada, más bien al contrario, es una manera de recordarnos que nos faltan muchas piezas del puzle que, poco a poco, tenemos que ir completando. Y esto cobra especial relevancia en los estudios evolutivos basados en organismos del pasado, por ese motivo se siguen descubriendo especies fósiles nuevas cada día y se van corrigiendo algunas creencias, incluso certezas, que pensábamos que teníamos ya aseguradas. Es aquí donde entran los protagonistas de hoy.
Taxones Elvis, Lázaro y hasta zombisComo buena amante de la música heavy metal y hard rock, voy a empezar hablando del Rey del Rock, el gran Elvis Presley. Aunque el Rey fue único e inigualable, desde su muerte no han dejado de aparecer cientos de imitadores por medio mundo. Pues esto también les puede suceder a los taxones, que es el término científico para referirse a los grupos faunísticos, a lo largo de la historia evolutiva de nuestro planeta. Podemos encontrarnos con organismos más modernos que son muy similares, casi idénticos a veces, a otros organismos más antiguos. Esto nos lleva a pensar que se trata de sus descendentes evolutivos, pero en realidad no tienen nada que ver. Sus semejanzas morfológicas son fruto de un proceso denominado convergencia evolutiva, mediante el cual dos organismos desarrollan estructuras morfológicas muy parecidas y con unas funciones casi iguales, pero sus líneas evolutivas se han desenvuelto por separado. A estos organismos más modernos que desarrollan esas semejanzas con los grupos más antiguos, llegando incluso a imitarlos, y que nos llevan a la confusión de creer que están estrechamente emparentados, se les conoce como taxones Elvis.
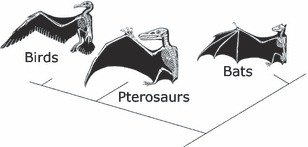 Convergencia evolutiva en las alas de las aves, los pterosaurios (reptiles) y los murciélagos (mamíferos). Los tres grupos han desarrollado un elemento morfológico muy similar y con unas funciones prácticamente idénticas, pero tienen líneas evolutivas diferentes. Imagen tomada de: Seed, A., Emery, N. y Clayton, N. (2009). Intelligence in Corvids and Apes: A Case of Convergent Evolution? Ethology 115, 401-420.
Convergencia evolutiva en las alas de las aves, los pterosaurios (reptiles) y los murciélagos (mamíferos). Los tres grupos han desarrollado un elemento morfológico muy similar y con unas funciones prácticamente idénticas, pero tienen líneas evolutivas diferentes. Imagen tomada de: Seed, A., Emery, N. y Clayton, N. (2009). Intelligence in Corvids and Apes: A Case of Convergent Evolution? Ethology 115, 401-420.Pasamos ahora al mundo de los muertos vivientes. Y voy a comenzar con los taxones Lázaro. Este nombre, basado en la historia bíblica, se refiere a esos grupos faunísticos que se creían extintos hace miles o millones de años, ya que no han dejado restos fósiles a partir de un momento determinado de la historia geológica. Pero, de repente, se descubren nuevos restos fósiles más modernos o, incluso, ejemplares vivos en la actualidad, alargando así su línea evolutiva en el tiempo. El principal ejemplo de un taxón Lázaro es el celacanto, un pez que habita en aguas muy profundas y que se suponía extinto hace unos 66 millones de años, ya que no se habían encontrado evidencias del mismo desde finales del Cretácico. Hasta que, hace casi un sigo, se capturó un ejemplar vivo en las costas sudafricanas. Esto nos muestra lo extremadamente difícil que es que un resto orgánico deje su huella en el registro fósil.
 Arriba, ejemplar fósil de celacanto (millones de años) y, abajo, ejemplar actual de celacanto (vivo). Fuente: Wikimedia Commons
Arriba, ejemplar fósil de celacanto (millones de años) y, abajo, ejemplar actual de celacanto (vivo). Fuente: Wikimedia CommonsY, continuando con la temática anterior, el último término que os voy a introducir es el del taxón Zombi. Este término se refiere a un grupo faunístico ya extinto, pero cuyos restos fósiles, debido a procesos de erosión, transporte y sedimentación, pueden ser extraídos de los materiales rocosos en los que se encontraban incluidos y acaban formando parte de materiales geológicos más modernos. Estos ejemplares redepositados nos dan una información muy valiosa sobre los procesos geológicos acontecidos en ese medio ambiente (por ejemplo, nos informan sobre la zona de la que proceden los ríos o arroyos que desembocaban en antiguos lagos). Pero, si no tenemos mucho cuidado al hacer un estudio de los organismos fósiles presentes en esas rocas, identificando los restos más antiguos como removidos, podríamos cometer el error de alargar la historia evolutiva de los mismos, creyendo que dichas especies pervivieron hasta épocas más recientes cuando, en realidad, ya estaban extintos. Vamos, auténticos zombis que se levantan de sus tumbas rocosas para darse un paseo por ambientes más modernos.
El estudio de la evolución de la vida en la Tierra únicamente se puede hacer a partir de la información aportada por el registro fósil. Pero no es una tarea tan sencilla como podría parecer. Por eso está en continuo cambio y actualización y es preciso seguir haciendo estudios paleontológicos cada vez más precisos. Si queremos saber de dónde venimos y hacia dónde vamos, tenemos que fijarnos en los testigos rocosos que tenemos a nuestro alrededor. De ahí que sea vital conservar, preservar y proteger los afloramientos fósiles en todo el mundo, para no perder ninguna de las piezas del puzle de la vida que aún nos quedan por encajar.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Taxones, paranormal activity en paleontología se ha escrito en Cuaderno de Cultura Científica.
Victor Thébault y sus tres teoremas
Personalmente le tengo en alta estima por su destacado talento como matemático, como lo demuestran las numerosas e ingeniosas aportaciones a lo que se denomina geometría elemental, fuente inagotable de problemas cuya solución requiere un don de invención muy especial.
Maurice d’Ocagne.
 Victor Thébault y algunas de sus aportaciones matemáticas.
Victor Thébault y algunas de sus aportaciones matemáticas.
Victor Thébault nació el 6 de marzo de 1882 en Ambrières-les-Grands, en Mayenne, Francia. Estudió en Laval entre 1898 y 1901. Tras su graduación enseñó durante tres años en Pré-en-Pail hasta que obtuvo un puesto de profesor en la escuela técnica de Ernée. En 1909 obtuvo la primera plaza en un concurso que le habilitó para trabajar como profesor de ciencia para docentes. Considerando que el sueldo era insuficiente para mantener a su gran familia (su esposa y él tuvieron cinco hijos y una hija), abandonó la enseñanza para trabajar como superintendente en una fábrica en Ernée entre 1910 y 1923. En 1924 pasó a ser inspector jefe de seguros en Le Mans, puesto que ocupó hasta su jubilación en 1940. Falleció el 19 de marzo de 1960 tras un grave accidente vascular.
A pesar de su alejamiento del mundo de la enseñanza, Thébault nunca dejó de interesarse por las matemáticas, siendo sus principales áreas de interés la teoría de números y la geometría. Publicó numerosos artículos en revistas matemáticas, contribuyendo también en muchas de ellas proponiendo problemas —llegó a proponer unos mil— y soluciones a enunciados de otros colegas. En la sección de problemas de la revista American Mathematical Monthly se contabilizan más de seiscientos problemas y soluciones debidas a Thébault.
La mayor parte de sus propuestas trataban sobre la geometría del triángulo y del tetraedro; justo en el momento de su fallecimiento estaba preparando un escrito sobre el arbelos.
En reconocimiento a todas sus contribuciones fue nombrado Officier de l’Instruction Publique, en 1932, a propuesta del ingeniero y matemático Maurice d’Ocagne. La cita que abre este escrito procede precisamente de las palabras de d’Ocagne destacando la importante labor de Thébault.
En 1935 fue nombrado Chevalier de l’Ordre de la Couronne de Bélgica por sus actividades relacionadas con la Sociedad Científica de Bruselas, en particular en sus revistas Annales y Mathesis.
Es sobre todo conocido por tres hermosos teoremas que enunciamos a continuación.
Primer teorema de ThébaultEste problema de geometría euclidiana puede considerarse como “una versión cuadrada” del teorema de Napoleón y un caso particular del teorema de van Aubel. Se enuncia de la siguiente manera:
Consideremos un paralelogramo cualquiera ABCD y los cuatro cuadrados exteriores construidos sobre los lados del paralelogramo. Si denotamos por M, N, O y P los centros de esos cuadrados, entonces MNOP es un cuadrado.
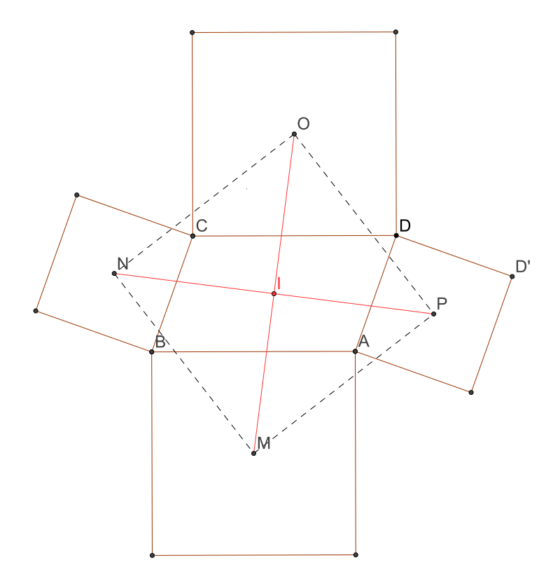 Imagen representando el primer problema de Thébault. Wikimedia Commons.
Imagen representando el primer problema de Thébault. Wikimedia Commons.
Segundo teorema de Thébault
Consideremos un cuadrado ABCD. Construimos dos triángulos equiláteros sobre dos lados consecutivos del cuadrado, ambos exteriores o ambos interiores. Por ejemplo, ABL y BCM. Entonces, el triángulo LMD es equilátero.
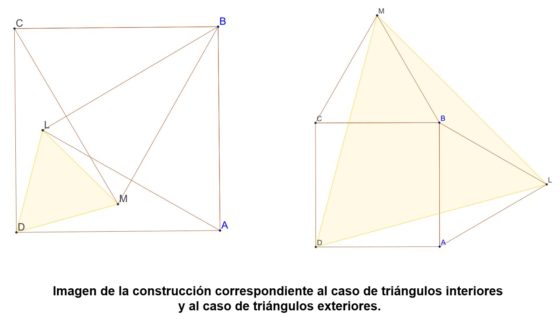 Imagen representando el segundo problema de Thébault. Wikimedia Commons.
Imagen representando el segundo problema de Thébault. Wikimedia Commons.
Tercer teorema de Thébault
Consideremos un triángulo arbitrario ABC y D un punto en el lado [BC]. Sean Q el centro del círculo inscrito en ABC y K el círculo circunscrito al triángulo. Sean, finalmente, N el centro del círculo tangente a [DC], [DA] y K y P el centro del círculo tangente a [DB], [DA] y K.
Entonces, P, Q y N están alineados.
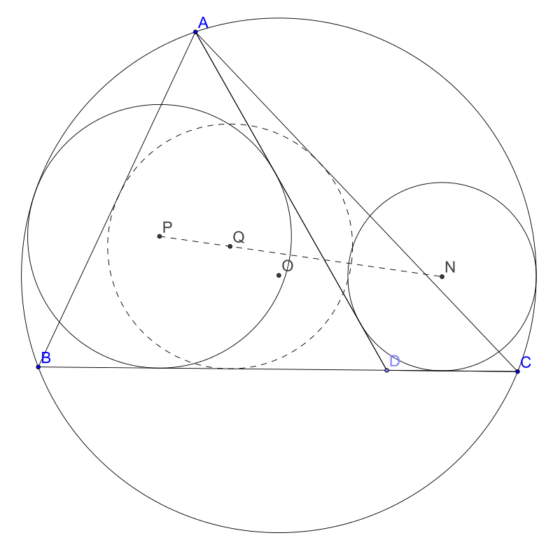 Imagen representando el tercer problema de Thébault. Wikimedia Commons.
Imagen representando el tercer problema de Thébault. Wikimedia Commons.
Los dos primeros problemas fueron planteados en 1937 y resueltos en poco tiempo. El tercer teorema de Thébault fue publicado en la American Mathematical Monthly en 1938 y demostrado por el matemático Hendrik Streefkerk en 1973. En 2003, Jean-Louis Ayme, estudioso de la geometría del triángulo, descubrió que Y. Sawayama, instructor de la Escuela Militar Central de Tokio, había propuesto y resuelto este problema ya en 1905.
Estas propuestas de matemática “recreativa” no son nada sencillas de resolver. El solo proceso de reflexionar sobre ellas ayuda, sin duda, a entender y aprender mucho sobre geometría. El propio Thébault lamentaba el desprecio con el que algunos matemáticos profesionales miraban estos problemas matemáticos:
Algunos matemáticos muestran una tendencia, no del todo libre de cierto desdén, a ver en tales problemas sólo pequeñeces insignificantes. Nimiedades, por favor, pero cuya solución a menudo exige no menos penetración de la mente, ingenio y artificio sutil que muchas preguntas de significado supuestamente más profundo. Además, el estudio de una proposición elemental exige a veces un esfuerzo nada desdeñable, que constituye un excelente ejercicio intelectual, y que conduce a algo verdaderamente valioso.
Referencias-
W. E. Byrne, E. P. Starke and N. A. Court, N. A. (1947). A Distinguished Contributor to the Monthly. The American Mathematical Monthly 54(8), 443-446. doi:10.1080/00029890.1947.11991862
-
C. W. Trigg (1960) Victor Thébault (1882-1969), Mathematics Magazine 33 (5)
-
Théorème de Thébault, Wikipédia (consultado el 8 de abril de 2022)
-
Thébault’s theorem, Wikipedia (consultado el 8 de abril de 2022)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Victor Thébault y sus tres teoremas se ha escrito en Cuaderno de Cultura Científica.
Einstein y Marcel Grossmann
Marcel Grossmann fue, además de compañero de clase en la universidad, un amigo muy cercano a Albert Einstein hasta su muerte en 1936, a pesar de las marcadas diferencias en personalidad. En la universidad, Grossmann era formal y respetuoso mientras que Einstein era impredecible y rebelde. Él mismo un científico consumado, presidente de la Sociedad Matemática Suiza en 1916, Grossmann trabajó con Einstein en las teorías de la gravitación de este, publicando juntos en 1913.
 Marcel Grossman. Fuente: ETH Zürich
Marcel Grossman. Fuente: ETH ZürichLa principal colaboración entre Einstein y Marcel Grossmann se conoce como el artículo Einstein-Grossmann, un paso en la dirección de lo que sería la teoría general de la relatividad, publicado en 1913. La contribución de Grossmann estuvo en la base matemática para apoyar las tesis de Einstein (Grossmann era un geómetra experto, que dominaba la geometría analítica y el cáculo tensorial). Grossmann fue el primero de una serie de colaboradores que tenían un dominio de las matemáticas muy superior al que tenía el propio Einstein. El artículo no ha pasado a la historia por ser una gran aportación: aunque fue un paso importante en el camino hacia la teoría final, el artículo Einstein-Grossmann está salpicado de razonamientos no demasiado consistentes.
Pero este es solo un ejemplo de toda una vida de ayuda a Einstein por parte de Grossmann. Grossmann le dejaba a Einstein usar sus metódicos apuntes de clase, y éste sacó tanto provecho de ellos a lo largo de todos sus años universitarios que no pudo menos que dedicar su tesis doctoral a su amigo.
Tras la graduación Einstein no tuvo ningún éxito en la búsqueda de empleo como profesor; incluso le llegó a pedir consejo a Grossmann sobre si debía ocultar sus orígenes judíos (Grossmann también lo era). Al final, Grossmann tuvo que acudir al rescate. Convenció a su padre (un industrial muy bien relacionado) para que hablase con Friedrich Haller, el director de la Oficina de Patentes Suiza, para que este contratase a Einstein. Después de un año en paro, un enchufe permitió a Einstein conseguir su primer trabajo. Un año después Grossmann se unía a su amigo en la oficina de patentes para, poco más tarde, abandonarla para irse de profesor al Politécnico de Zúrich.
Por su parte, tras su annus mirabilis, Einstein fue aceptando trabajos que no se ajustaban a sus necesidades, culminando con el puesto que se le ofreció para enseñar en Praga. Einstein odiaba la ciudad por lo que, cuando Grossman le ofreció un puesto de profesor en el Politécnico de Zúrich, donde ya ocupaba puestos de gestión, Einstein se apresuró a aceptarlo. Pero la búsqueda del puesto perfecto continuó, y solo un año después Einstein dejaba Zúrich, a pesar lo que eso significaba para su gran amigo, para hacerse cargo de un puesto en Berlín.
La marcha de Einstein no afectó demasiado ni a su amistad ni a su colaboración. Sus teorías fueron publicadas en 1913, y Grossmann continuó siendo la mente matemática con la que Einstein prefería contrastar sus ideas. Es a través de las cartas entre ambos como conocemos en qué estaba trabajando Einstein en un momento dado, ya que Einstein siempre mantuvo a Grossmann al corriente de sus investigaciones y Grossmann respondía con críticas constructivas (de hecho, parece demostrado que fue Grossmann el que sugirió el uso del cálculo tensorial para la relatividad general). Así, por ejemplo, en 1901, Einstein estaba investigando la teoría cinética de los gases, el movimiento de la materia con respecto al éter o el concepto de una fuerza molecular universal.
Tristemente, sin embargo, la enfermedad hizo su aparición en la vida de los dos amigos. Grossmann desarrolló esclerosis múltiple en los años 20. El hombre que era el apoyo de Einstein, desde pasarle los apuntes de las clases de matemáticas para que él pudiese asistir a otras más interesantes, hasta cuidar de su hijo Eduard cuando fue hospitalizado con síntomas de esquizofrenia, pasando por conseguirle una entrevista de trabajo en más de una ocasión, murió en 1936.
Einstein escribió a la mujer de Grossmann para expresarle sus sentimientos: “Recuerdo nuestros días de estudiante. Él, el estudiante irreprochable, yo mismo, desordenado y soñador. Él, en buenos términos con los profesores y entendiéndolo todo, yo un paria, descontento y poco amado. Pero éramos buenos amigos y nuestras conversaciones delante de un café helado en el Metropole cada pocas semanas están entre mis recuerdos más felices”.
A pesar de la temprana muerte de su amigo, Einstein le guardó un cariño inmenso hasta el final de su vida. En 1955, poco antes de morir, Einstein redactó un texto autobiográfico, algo que odiaba hacer, pero que escribió, tal y como aparece en la dedicatoria, como homenaje a su amigo: “la necesidad de expresar al menos una vez en mi vida mi gratitud a Marcel Grossmann me dio el valor para escribir esto”.
Como homenaje a la contribución de Marcel Grossmann al desarrollo de la teoría, la comunidad de relativistas (ICRANet) organiza cada tres años los encuentros Marcel Grossmann y concede los premios Marcel Grossmann.
Referencia:
Einstein, A. & Grossmann, M. (1913). Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation Zeitschrift für Mathematik und Physik, 62, 225-265
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 30 de agosto de 2009.
El artículo Einstein y Marcel Grossmann se ha escrito en Cuaderno de Cultura Científica.
Todo cabe en el encéfalo
 Foto: Richard Lee / Unsplash
Foto: Richard Lee / UnsplashHasta los perdigones. Por lo menos es una de las conclusiones del estudio de Anders Pape Moller y Johannes Erritzoe, de las universidades de París-Saclay y de Christianfeld, en Dinamarca, sobre la caza de aves en este país nórdico. Revisan las aves disecadas en los talleres de taxidermistas del entorno de Christianfeld entre los años 1960 y 2015. Toman sus datos e incluyen el peso del encéfalo y la causa de la muerte. De un total de 3781 ejemplares examinados, un 7%, o sea, 299, murieron por disparos. El análisis de los datos lleva a los autores a confirmar que les disparan más a los ejemplares de más peso, lo que es coherente ya que se trata de animales cazados, y los más grandes son los más codiciados pues se buscan por su tamaño y, también, son los que más blanco ofrecen a los cazadores. Pero igualmente detectan que se dispara más a los animales con el encéfalo más pequeño. La probabilidad de recibir un tiro aumenta hasta 30 veces con el encéfalo de menor tamaño. No conozco un estudio similar para la especie humana.
Por cierto y entre paréntesis, en una publicación muy reciente, los mismos autores encuentran un resultado similar que relaciona el tamaño del encéfalo de las aves con los accidentes de tráfico: con el encéfalo más pequeño hay una mayor probabilidad de ser atropellado. Quizá las aves con el encéfalo más grande se adaptan mejor a conductas que les permiten evitar los accidentes.
También influye el tamaño del encéfalo de las aves en su muerte por mal tiempo. Por lo menos en algunas especies como, por ejemplo, la golondrina risquera, Petrochelidon pyrrhonata, que se encuentra en América. Gigi Wagnon y Charles Brown, de la Universidad de Tulsa, estudiaron esta especie en varias colonias de Nebraska desde 1982 a 2018. Recogieron los ejemplares muertos por diversas causas incluyendo varias olas de frío y lluvia. Con ese clima no hay insectos que son el componente principal de la dieta de las golondrinas risqueras.
En 1996, con una ola de frío extremo, murió el 53% de la población en un periodo de seis días. En total, los autores estudiaron el encéfalo de algo más de 1000 ejemplares. La conclusión fue que las golondrinas que morían de hambre durante la ola de frío tenían el encéfalo más pequeño que las que morían por otras causas.
Miedo, mucho miedoNo solo los perdigones, también el miedo se esconde en el encéfalo. Nos lo explicó María José Moreno hace unos meses en Cuaderno de Cultura Científica, según estudios de la Universidad Politécnica de Madrid y de la Universidad Autónoma de Barcelona. El miedo está, es un decir, en la amígdala, en el centro del encéfalo, una en cada hemisferio. El miedo es una emoción seleccionada en la evolución ya que ayuda a la supervivencia al detectar peligros y provocar respuestas rápidas y precisas para evitarlos.
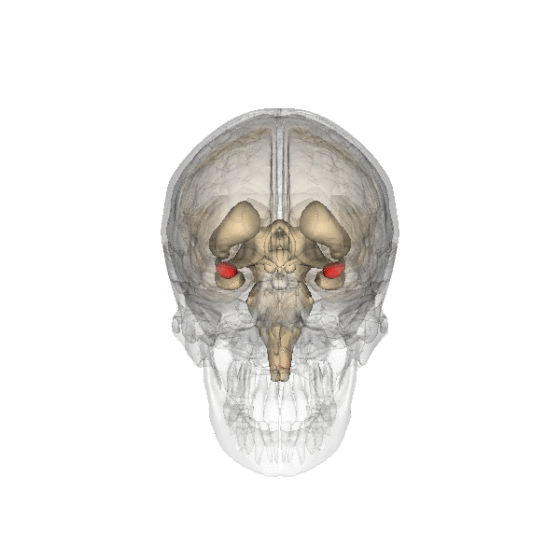 En rojo posición de los cuerpos amigdalinos en el encéfalo humano. Fuente: Anatomography / Life Science Databases (LSDB) / Wikimedia Commons
En rojo posición de los cuerpos amigdalinos en el encéfalo humano. Fuente: Anatomography / Life Science Databases (LSDB) / Wikimedia CommonsEs la amígdala la que procesa esa respuesta rápida a las posibles amenazas que nos llegan del entorno a través de los sentidos: la imagen que nos parece una serpiente venenosa; el estruendo que podría ser una piedra o un árbol que cae y nos puede herir y, en la actualidad, hemos aprendido a evitar el ruido que provoca el motor de un vehículo, aunque todavía no sabemos detectar a los vehículos eléctricos y silenciosos; en un bosque húmedo y sombrío, esa criatura misteriosa que se vislumbra entre las hojas y, quizá, es un depredador o, quien sabe, si el Bigfoot, el Yeti o Basajaun. En el cine es el temido plano dorsal o de espalda. El protagonista se mueve por un decorado oscuro, incluso tenebroso. Y la cámara le sigue, muestra lo que tiene delante, pero no conoce lo que está a su espalda. Seguro que es algo peligroso y el miedo llega al espectador que, sin remedio, espera el susto, quizá una mano que se apoya en hombro del protagonista.
También provoca una respuesta rápida ver un rostro que refleja miedo, lo que nos avisa de que algo peligroso está ocurriendo. En este caso, la respuesta de la amígdala puede darse en 74 milisegundos. Y la respuesta se da aunque la imagen del rostro con miedo sea algo borrosa.
El funcionamiento habitual es que, poco después, en unos milisegundos, la imagen se enfoca y lo que vemos nos dará una información más precisa. Pero, para entonces, la respuesta primaria, rápida y dirigida por la amígdala y el miedo ya se habrá producido y, si era un peligro, ha dado la oportunidad de evitarlo.
Es en la amígdala donde almacenamos recuerdos que tienen que ver con el miedo. Allí están las imágenes de serpientes, arañas o cucarachas. En ratones se han identificado algunas neuronas, llamadas Tac2, que almacenan estos miedos. En un experimento de Raúl Andero, de la Universidad Autónoma de Barcelona, con ratones se ha conseguido que estas neuronas Tac2 sean sensibles a la luz. Cuando se iluminan, se activan y el ratón recuerda aquello que le asustó y siente miedo.
Placebo, empatía, racismoPero, además del miedo, en el encéfalo está el placebo, es decir, la respuesta positiva, sobre todo contra el dolor, a un tratamiento que, en realidad, no existe. El equipo de Pascal Tétreault, de la Universidad del Noroeste en Chicago, trabaja con voluntarios que tienen osteoartritis en las rodillas, con dolores continuos y tratamiento analgésico habitual. Les dan, a un grupo de voluntarios, su medicación y, a un segundo grupo, unas píldoras que son placebo. A la vez escanean su encéfalo para conocer que se activa en caso de responder al placebo.
En los experimentos, la mitad de los enfermos responden al placebo y la otra mitad no siente un alivio del dolor. En el encéfalo es el giro frontal medio del cerebro, situado a la altura de la frente en el hemisferio derecho, la zona que se activa y mejor identifica a los pacientes que responden al placebo. Es notable que el medicamento contra el dolor provoca en la mitad de los pacientes un aumento la sensación de placebo, según la respuesta cerebral que se detecta, y, a la otra mitad, les disminuye la sensación de dolor por acción del medicamento.
Y todavía más conductas caben en el giro frontal medio como, por ejemplo, la empatía. Giovanni Novembre y su grupo, de la Escuela Superior Internacional de Estudios Avanzados de Trieste, han encontrado, con imágenes de escáner del encéfalo de voluntarios, que la respuesta a la exclusión social, a lo que denominan “dolor social”, es decir, la empatía ante lo que el otro siente, está incluida en la misma zona del cerebro que responde al dolor físico y que, si se observa en otros, también despierta empatía. Por tanto, tanto el dolor físico como el “dolor social” provocan empatía y disparan las mismas zonas del cerebro. Es una respuesta que, desde la selección evolutiva, sentir el dolor del otro tiene gran importancia para mantener la cohesión del grupo.
En trabajo reciente, Yoni Ashar y sus colegas, de la Universidad de Colorado, han estudiado las imágenes del giro frontal medio de voluntarios cuando se les provoca empatía para ayudar y empatía para evitar, con la aparición de disgusto y, quizá, de miedo. La empatía para ayudar, concepto habitual en nuestros sentimientos, se localiza en el nucleus accumbens, mientras que la empatía para evitar es cuestión de la corteza relacionada con la información sensorial y con el sistema motor. Es evidente que la empatía de disgusto lleva al movimiento y la huida.
Pero no solo la empatía, también el racismo encuentra acomodo en el encéfalo. Además, se localiza en la amígdala. En un experimento publicado en el 2000 por Allen Hart y su equipo, del Colegio Amherst, en Estados Unidos, se detectó que, cuando voluntarios blancos veían rostros de blancos y de negros, aparecía en la amígdala una respuesta más fuerte ante la imagen de un negro. La potencia de la respuesta se relaciona con el conservadurismo político y el apoyo a la diferencia entre razas de cada voluntario.
Una respuesta semejante han encontrado Kelly Correa y sus colegas, de la Universidad de Illinois en Chicago, cuando analizaron la reacción ante hispanos y blancos. Sin embargo, también encuentran que la sensación de amenaza ante los hispanos depende en parte de experiencias previas de los participantes.
Y, por hoy ya es suficiente, ya tenemos el encéfalo lleno, muy lleno, repleto.
ReferenciasAndero, R. et al. 2016. Amygdala-dependent molecular mechanisms of the Tac2 pathway in fear learning. Neuropsychopharmacology doi: 10.1038/npp.2016.77
Ashar, Y.K. et al. 2017. Empathic care and distress: Predictive brain markers and dissociable brain systems. Neuron doi: 10.1016/j.neuron.2017.05.014
Correa, K.A. et al. 2022. Ethnic differences in behavioral and physiological indicators of sensitivity to threat. Journal of Anxiety Disorders 85: 102508.
Hart, A.J. et al. 2000. Differential response in the human amygdala to racial outgroup vs. ingroup face stimuli. NeuroReport 11: 2351-2355.
Karaki, S. 2017. Inside the racist brain. Scientificus Europaeus 2 March.
Méndez Bertolo, C. et al. 2016. A fast pathway for fear in human amygdala. Nature Neuroscience 19: 1041-1049.
Moller, A.P. & J. Erritzoe. 2016. Brain size and the risk of getting shot. Biology Letters 12: 20160647
Moller, A.P. & J. Erritzoe. 2017. Brain size in birds is related to traffic accidents. Royal Society Open Science DOI: 10.1098/rsos.161040
Moreno, M.J. 2016. El miedo se esconde en el cerebro. Cuaderno de Cultura Científica octubre 20.
Novembre, G. et al. 2015. Empathy for social exclusion involves the sensory-discriminative component of pain: a within-subject fMRI study. SCAN 10: 153-164.
Tétreault, P. et al. 2016. Brain connectivity predicts placebo response across chronic pain clinical trials. PLOS Biology 14: e1002570
Wagnon, G.S. & C.R. Brown. 2020. Smaller brained cliff swallows are more likely to die during harsh weather. Biology Letters 16: 20200264.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Todo cabe en el encéfalo se ha escrito en Cuaderno de Cultura Científica.
Los organoides: órganos humanos en miniatura
Isidoro Martínez González, Isabel Liste y Salvador Resino García
El uso de organoides ayuda a entender mejor cómo funciona la biología del ser humano, pero también cómo se producen y desarrollan las enfermedades y ensayar fármacos o terapias frente a ellas.
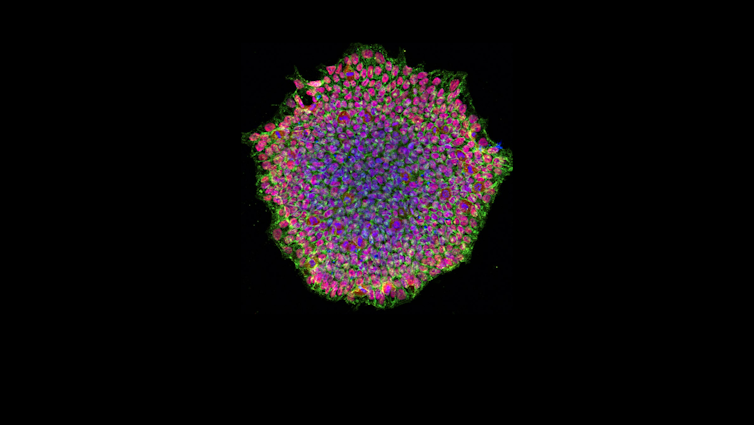 Colonia de células madre pluripotentes inducidas humanas. A partir de ellas se forman organoides. Fuente: National Eye Institute/NIH – Wikimedia Commons
Colonia de células madre pluripotentes inducidas humanas. A partir de ellas se forman organoides. Fuente: National Eye Institute/NIH – Wikimedia Commons
Para entender cómo funciona el cuerpo humano, cómo se producen las enfermedades y cómo se pueden tratar, los científicos necesitamos hacer experimentos. Por razones obvias, la gran mayoría de esos experimentos no se pueden hacer en los seres humanos.
Para resolver este problema, la ciencia usa lo que se llaman “modelos”, en los cuales sí se pueden hacer experimentos. Por ejemplo, dos modelos clásicos utilizados en biomedicina son las líneas celulares y los animales de experimentación.
A diferencia de las células normales de un organismo, las líneas celulares tienen la capacidad de crecer indefinidamente in vitro, es decir pueden “cultivarse” en un laboratorio. Estas células, también llamadas “inmortales”, han sido obtenidas en su mayoría a partir de tumores. Aunque funcionan en muchos aspectos como las células no tumorales, en otros muchos se comportan de forma diferente, y esto es una limitación muy importante para determinados estudios.
Los animales de experimentación (los más utilizados son los ratones) presentan problemas similares. Aunque se trata de organismos vivos en los que se pueden hacer experimentos más complejos, la biología de los animales de experimentación difiere también en muchos aspectos de la biología humana. Además, el uso de animales presenta problemas éticos.
En los últimos años se han empezado a desarrollar modelos de experimentación que solucionan gran parte de los inconvenientes de los modelos basados en líneas celulares o animales de experimentación. Los más atractivos son los organoides, sobre los cuales se han conseguido avances muy importantes en la última década.
Qué son y cómo se producen los organoidesUn organoide es una versión reducida y simplificada de un órgano que se fabrica en el laboratorio mediante métodos de cultivo específicos. Están formados por muchas células diferentes que se organizan en estructuras tridimensionales de tamaño reducido (de micrómetros a centímetros), similares a los tejidos u órganos vivos correspondientes (ej. pulmón, hígado, etc). Es decir, los organoides pueden llegar a tener características estructurales y funcionales de los órganos humanos.
Se producen a partir de una o unas pocas células denominadas “células madre” o “células troncales”. Estas células se caracterizan por ser pluripotentes, es decir, además de crecer in vitro, tienen la capacidad de “diferenciarse”, esto es, de generar células especializadas de diferentes tipos, similares a las que forman los órganos verdaderos.
Las células troncales pluripotentes son fundamentalmente de dos tipos:
- Células troncales embrionarias. Se obtienen justo después de la fecundación del óvulo.
- Células troncales pluripotentes inducidas. Se obtienen a partir de células de un tejido concreto (la piel, por ejemplo) mediante determinados tratamientos. Una vez que las células adquieren la capacidad de ser pluripotentes, se pueden volver a diferenciar a células especializadas de distintos órganos mediante cultivo con diferentes nutrientes y factores de crecimiento. Dependiendo de la composición de esos nutrientes y de los factores de crecimiento, las células se diferenciarán a un órgano u otro.
Existen también las “células troncales adultas”, que se pueden obtener a partir de tejidos con capacidad regenerativa (el hígado, por ejemplo). Sin embargo, estas células tienen un limitado potencial de diferenciación y dan lugar a organoides menos complejos.
 La importancia en el estudio de enfermedades
La importancia en el estudio de enfermedades
Hasta el momento, los investigadores han conseguido generar organoides de hígado, cerebro, retina, oído interno, pulmón, intestino, próstata, páncreas y ovario, entre otros.
Los organoides tienen importantes ventajas:
- Se pueden producir en un laboratorio de forma controlada y pueden ser manipulados con relativa facilidad.
- Constan de más de un tipo de célula, por lo que son más complejos y reproducen mejor el ambiente y lo que realmente ocurre en el organismo vivo.
- Son de origen humano.
- Son seguros y asequibles.
Por todo ello, el uso de organoides ayuda a entender mejor cómo funciona la biología del ser humano, pero también cómo se producen y desarrollan las enfermedades (cáncer, enfermedades genéticas, enfermedades infecciosas, etc.) y ensayar fármacos o terapias frente a ellas. También pueden ser usados en trasplantes y medicina regenerativa.
Además, permiten reducir el uso de animales de experimentación.
No obstante, los organoides también tienen importantes limitaciones, sobre todo en estudios que implican la participación de diferentes órganos y su coordinación. Por ejemplo, carecen de sistema vascular o de intercambio de gases. Además, suelen ser inmaduros y tienen una vida limitada.
Todos estos problemas están siendo abordados por científicos e ingenieros y, en algunos casos, parecen haberse encontrado soluciones imaginativas. Por ejemplo, se han podido generar redes vasculares usando impresoras 3D.
 Esquema de creación de tejidos con hidrogel termorresistente y generación de biotintas que son utilizadas para la impresión de parches vascularizados y estructuras celulares complejas. Fuente: 3D Printing of Personalized Thick and Perfusable Cardiac Patches and Hearts_, Advanced Science, 15 April 2019.
Esquema de creación de tejidos con hidrogel termorresistente y generación de biotintas que son utilizadas para la impresión de parches vascularizados y estructuras celulares complejas. Fuente: 3D Printing of Personalized Thick and Perfusable Cardiac Patches and Hearts_, Advanced Science, 15 April 2019.En definitiva, aunque los organoides tienen algunas limitaciones, la intensa investigación que se está llevando a cabo en este campo y los continuos progresos harán que se extienda su aplicación en la clínica y que el conocimiento que se adquiera con su uso resulte cada vez más valioso para entender la biología del ser humano y tratar enfermedades.![]()
Sobre los autores: Isidoro Martínez González, Científico Titular; Isabel Liste, Investigadora principal y Salvador Resino García, Investigador Científico de OPIs, Instituto de Salud Carlos III
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Los organoides: órganos humanos en miniatura se ha escrito en Cuaderno de Cultura Científica.
Día de Pi con BCAM Naukas 2022: Adolfo Quirós – El número pi y la muralla de Cartago

La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han suamdo a la celebración, organizando la tercera edición del evento BCAM-NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
Los reyes y las reinas se enfrentan a problemas matemáticos muy interesante. Tomemos el caso de Elisa, llamada Dido, la errante. Tiene una cuerda hecha con tiras de una piel de buey y su problema es qué forma tiene que adoptar la curva que forme con esa cuerda para maximizar el área encerrada entre la curva y la línea de costa que asumimos recta Efectivamente, estamos hablando de la fundación de Birsa, la «ciudad nueva», Cartago en el idioma local. Adolfo Quirós, profesor titular de la Universidad Autónoma de Madrid, nos plantea el problema de Dido, la solución matemática y la que encontró Dido para construir las murallas.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de Pi con BCAM Naukas 2022: Adolfo Quirós – El número pi y la muralla de Cartago se ha escrito en Cuaderno de Cultura Científica.
Trigos de alto rendimiento capaces de inhibir la nitrificación del suelo
La hibridación de variedades comerciales consigue trigos de alto rendimiento capaces de inhibir la nitrificación del suelo. El estudio ha merecido el premio Cozzarelli 2021.
 Foto: Pixabay
Foto: PixabayEl trigo es uno de los pilares de la alimentación mundial. Alrededor de 250 millones de hectáreas se dedican al cultivo de este cereal, cuya demanda y producción están en aumento. Por otra parte es impensable conseguir altas producciones con calidad de grano sin la aplicación de fertilizantes, especialmente los nitrogenados. La combinación de ambos factores da como resultado que el trigo consuma la quinta parte de los fertilizantes nitrogenados producidos en el mundo.
El nitrógeno es aplicado al cultivo en forma de amonio o nitrato, sin embargo, no todo el que se aporta es absorbido por los cultivos. Por un lado, el amonio se convierte rápidamente en nitrato por el proceso de nitrificación del suelo, y al ser el nitrato muy soluble en agua, llega a las aguas subterráneas y ríos, y puede producir eutrofización (la pérdida de calidad del agua provocada por el exceso de nutrientes que hace que aumente tanto el número de organismos que terminan agotando el oxígeno disuelto en el agua). Por otro lado, parte del nitrógeno se puede emitir a la atmósfera en forma de óxido nitroso, un gas con efecto invernadero mucho más potente que el CO2.
Nos encontramos con que el continuo crecimiento de la población mundial hace necesaria una agricultura altamente productiva que, inevitablemente, precisa de fertilizantes, pero ello debe convivir con el hecho de que es imprescindible mitigar los efectos dañinos para el medioambiente y el cambio climático producidos por la agricultura.
Una de las soluciones pasa por optimizar la toma de los fertilizantes por parte de las plantas. Para ello se han empleado diversas técnicas, encaminadas a que la planta utilice más eficientemente el nitrógeno: por ejemplo, utilizar fertilizantes de liberación lenta o inhibidores de síntesis química que ralenticen la conversión del amonio a nitrato en el suelo. Otra más interesante sería usar la capacidad que tienen algunas especies vegetales para producir y secretar por las raíces moléculas que inhiben la oxidación del amonio a nitrato en el suelo. Con ello se consigue mantener durante más tiempo el nitrógeno en el suelo, lo que permite que las plantas lo tomen de manera más eficiente. El problema es que muchas de estas especies que producen inhibidores biológicos de la nitrificación (IBN) son poco productivas agronómicamente.
Trigos de alto rendimiento capaces de inhibir la nitrificación del sueloUn estudio reciente, en el que colaboran grupos de investigación de la UPV-EHU, del CIMMYT (Centro Internacional de Mejoramiento de Maíz y Trigo, de México), del JIRCAS (Japan International Research Center for Agricultural Sciences) y de la Universidad Nihon (Japón), ha caracterizado el segmento cromosómico que confiere una alta capacidad de liberación de IBN en la planta silvestre Leymus racemosus. Esta especie está emparentada evolutivamente con el trigo, y, a través de cruces con diversos trigos de alto rendimiento capaces de producir 10.000 kg por hectárea, los investigadores consiguieron transferir la capacidad de liberación de moléculas IBN a estas variedades.
“El proceso permite, al mismo tiempo, producir más trigo y, además, reducir las emisiones de gases de efecto invernadero y la contaminación de las aguas continentales causada por la lixiviación del nitrato” afirma Carmen González Murua, catedrática de fisiología vegetal, investigadora principal del grupo NUMAPS de la UPV/EHU.
Este trabajo ha merecido el Premio Cozzarelli, en la categoría de Biología aplicada, Agricultura y Ciencias ambientales. El galardón se concede anualmente por el Consejo Editorial de Proceedings of the National Academy of Sciences (PNAS).
Referencia:
Guntur V. Subbarao, Masahiro Kishii, Adrian Bozal-Leorri, Ivan Ortiz-Monasterio, Xiang Gao, Maria Itria Ibba, Hannes Karwat, M. B. Gonzalez-Moro, Carmen Gonzalez-Murua, Tadashi Yoshihashi, Satoshi Tobita, Victor Kommerell, Hans-Joachim Braun, and Masa Iwanaga (2021) Enlisting wild grass genes to combat nitrification in wheat farming: A nature-based solution PNAS, doi: 10.1073/pnas.2106595118
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Trigos de alto rendimiento capaces de inhibir la nitrificación del suelo se ha escrito en Cuaderno de Cultura Científica.
Vida y muerte de una estrella
 Una viñeta de Quino.
Una viñeta de Quino.Tras calcular la distancia que le separa de los países que rodean su isla, nuestro náufrago se prepara para emigrar. Le gustaría nadar hacia algún país donde se invierta en ciencia e investigación; un país con futuro, vaya. Por suerte, las facturas de su playa le han dado una pista sobre la base de la economía de cada país y el grado de desarrollo en que se encuentra, si le espera un largo porvenir o si se avecina una temible crisis.
Algo parecido es lo que nos cuenta la composición química de una estrella. Podemos saber en qué momento de su ciclo vital se encuentra si averiguamos cuál es su “combustible”, aquello que mantiene su energía. Pero vayamos por partes. ¿A qué nos referimos con “combustible” en este caso?
Bien, a grandes rasgos, una estrella es un inmenso reactor nuclear, que fusiona distintos átomos y libera la energía sobrante en forma de radiación. La mayoría de ellas nacen en el seno de una nube molecular, una región del espacio donde abunda el hidrógeno en su forma molecular. Este es el “combustible” primario de todas las estrellas, ya que los átomos de hidrógeno pueden fusionarse y formar helio más un exceso de energía. Por ese motivo, estas nubes de gas y polvo espacial se conocen también como “viveros de estrellas”, un precioso nombre que nos invita a imaginar el arte de la jardinería espacial. En ocasiones, atraída por la gravedad, la nube puede comprimirse hasta colapsar bajo su propio peso y formar una protoestrella.
En este punto, si la masa es menor que 0,08 masas solares (0.08 M☉), la protoestrella no se comprimirá lo suficiente y no alcanzará la temperatura necesaria para empezar a fusionar el hidrógeno. Terminará convertida en una enana marrón de poca luminosidad y se irá apagando y enfriando poco a poco con el tiempo. En cambio, las protoestrellas que superan este umbral de masa y temperatura (unos 10 millones Kelvin) empiezan a fusionar hidrógeno en su núcleo. Pasan entonces a formar parte de la secuencia principal, aquella rama especialmente visible del diagrama Hertzsprung-Russell (el mapa de historias de las estrellas). La presión de radiación causada por las reacciones de fusión y la propia gravedad de la estrella darán lugar a un equilibrio de fuerzas que definirá su tamaño y la situará en un punto determinado de dicha rama1.
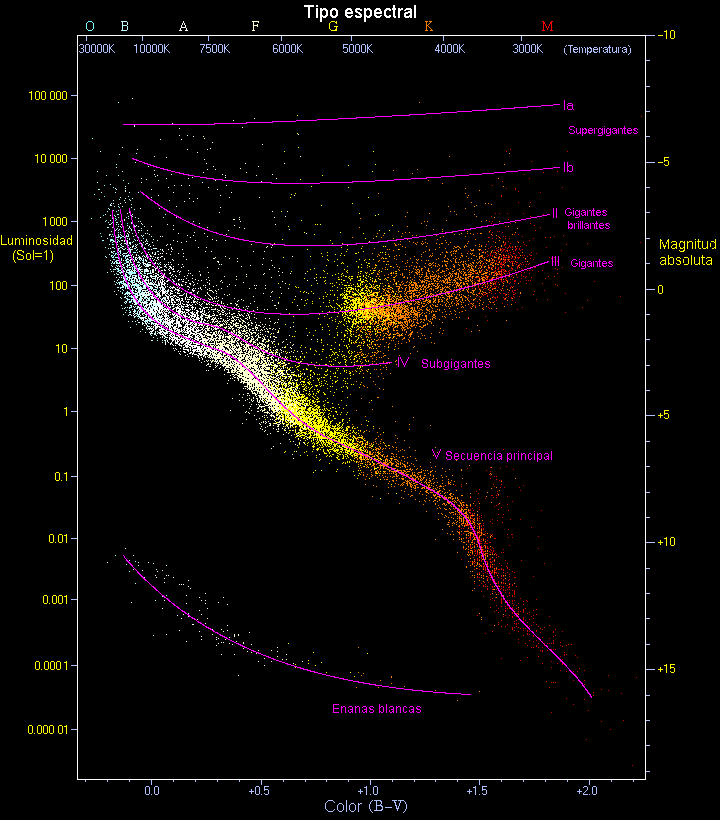 Diagrama de Hertzsprung-Russell. Fuente: Wikimedia Commons
Diagrama de Hertzsprung-Russell. Fuente: Wikimedia CommonsLas estrellas pasan la mayor parte de su vida sobre la secuencia principal, mientras queman el hidrógeno de su núcleo. Estas reacciones de fusión, van dando lugar poco a poco a otros elementos más pesados, que pueden convertirse a su vez en combustible nuclear. Primero aparece el helio, luego el berilio, el carbono, el oxígeno… hasta que finalmente se forman átomos de hierro, los más pesados. Una estrella alcanza la vejez cuando se agotan las fuentes de hidrógeno de su núcleo. Es en ese momento cuando se separa de la secuencia principal y busca otro rincón del mapa donde pasar su jubilación. Pero la dirección de este desplazamiento, su velocidad y su destino dependen de la masa inicial de la estrella.
La muerte de las estrellas depende de su masaSi la estrella tiene una masa baja o intermedia (menor que 9 M☉), no alcanzará la temperatura suficiente como para quemar el helio que se forme en su núcleo de manera inmediata. Tras agotar su núcleo, seguirá quemando hidrógeno en capas cada vez más alejadas del centro y al hacerlo se expandirá hasta formar una gigante roja. Se piensa que este es el futuro que le espera a nuestro Sol. Dentro de unos pocos miles de millones de años, engullirá a Mercurio, a Venus y quizás también a la Tierra.
Tras esta inmensa expansión, es posible que la gigante empiece a devorar también el helio de su núcleo. Esta fase recibe el nombre de apelotonamiento rojo debido a la concentración de este tipo de estrellas en el diagrama H-R. Una vez el helio del núcleo se agota, la estrella vuelve a consumirse en capas cada vez más externas. En el proceso se expande, y se enfría (se vuelve cada vez más gigante y más roja), recorriendo el diagrama hacia arriba y hacia la derecha. La estrella alcanza su mayor tamaño justo antes de extinguirse. Hasta que, finalmente, expulsa sus capas externas (las menos atraídas por la fuerza gravitatoria) y queda convertida en una nebulosa planetaria con una enana blanca en su centro.
Las estrellas un poco más grandes (entre 9 y 30 M☉) tienen un origen similar. También ellas nacen en viveros y pasan su juventud consumiendo el hidrógeno de su núcleo. Pero cuando este combustible se agota, pueden seguir quemando helio sin problema. En el proceso, su luminosidad no varía, pero debido a la pérdida de masa, su temperatura (su color) disminuye rápidamente y se desplazan a la derecha en el diagrama. De azules pasan a blancas, luego amarillas, hasta que se convierten en supergigantes rojas, las estrellas más grandes del universo. Cuando agotan todo su combustible, el colapso gravitatorio de su enorme masa genera una supernova, con un remanente estelar en forma de estrella de neutrones.
Las estrellas más masivas de todas (mayor a 30 M☉) tienen una historia similar, salvo por un detalle, y es que la estrella pierde masa a un ritmo tan elevado que nunca llega a convertirse en una supergigante roja. Una vez consume todo su combustible, la estrella colapsa y da lugar a una supernova y a un agujero negro como remanente estelar.
Son historias fascinantes de objetos remotos, a distancias inabarcables incluso para nuestra imaginación. Lo fascinante es que hoy podamos contarlas con solo mirar la luz de las estrellas. Gracias a siglo y medio de investigación, hemos aprendido descifrar su mensaje. Hemos atravesado por fin la superficie de la bóveda celeste, y al otro lado hemos encontrado un profundo relato formado de tiempo, hidrógeno y gravedad.
 Grabado Flammarion. Fuente: Wikimedia CommonsNota:
Grabado Flammarion. Fuente: Wikimedia CommonsNota:
1Este equilibrio de fuerzas era el que hacía oscilar el tamaño de las cefeidas, la regla de medir universos que ayudó a encontrar Henrietta Leavitt.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Vida y muerte de una estrella se ha escrito en Cuaderno de Cultura Científica.
Los embaldosados de Truchet y el puzle del diamante
El estudio de los patrones de embaldosado o teselado es un interesante tema con interés tanto en el ámbito de la ciencia y la tecnología, como del arte y el diseño. En la entrada de hoy del Cuaderno de Cultura Científica vamos a centrarnos en los patrones de teselado con un único tipo de baldosa –o tesela-, pero que además es de una gran sencillez, la conocida como “baldosa de Truchet”. Es la baldosa cuadrada dividida por la diagonal en dos zonas triangulares de dos colores distintos, por ejemplo, gris y negro, como la que aparece en la imagen.
 Baldosa de Truchet
Baldosa de TruchetEn el libro El sentido del orden (1979) del historiador del arte británico de origen austriaco Ernst H. Gombrich (1909-2001), conocido entre otras obras por su famosa Historia del Arte (1950), se reproducen algunos de los diseños de patrones de teselados realizados con esta baldosa que aparecen en el libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722), del padre carmelita francés Dominique Doüat (siglo XVIII).

 Ilustraciones de patrones de embaldosado, con una baldosa de Truchet, del libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722), de Dominique Doüat
Ilustraciones de patrones de embaldosado, con una baldosa de Truchet, del libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722), de Dominique Doüat
Estos son solamente dos de los setenta y dos diseños de patrones de embaldosados incluidos en el libro de Doüat (véase en la bibliografía un enlace a una edición facsímil con extractos y otro a la obra completa que pueden consultarse), que es un texto en el que se realiza un análisis combinatorio de los embaldosados que pueden generarse con esa baldosa. El padre Doüat empieza nombrado las cuatro orientaciones de la baldosa como A, B, C y D, como se muestra en la imagen.
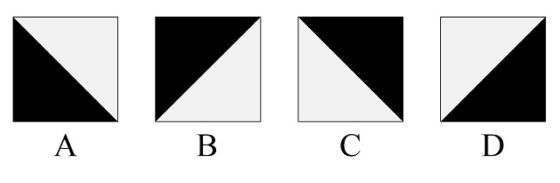 Las cuatro orientaciones posibles de la tesela de Truchet, nombradas por Doüat como A, B, C y D
Las cuatro orientaciones posibles de la tesela de Truchet, nombradas por Doüat como A, B, C y D
A partir de ese momento, el carmelita se dedica a realizar un análisis combinatorio con las letras A, B, C y D, empezando por los casos más sencillos, que es la única forma de clasificar con cierto orden, entre las páginas 20 y 189 (en muchas ocasiones son páginas con listados de letras). Por ejemplo, los posibles embaldosados con tan solo dos baldosas (en horizontal) serían dieciséis (cuatro posibilidades para cada posición, cuatro al cuadrado): AA, BB, CC, DD, AB, BA, CA, DA, AC, BC, DC, AD, BD, CD, DC. Al final de la obra se incluyen ilustraciones relacionadas con ese análisis combinatorio. Por ejemplo, en la siguiente ilustración se recogen los cuatro embaldosados de una sola baldosa (que son las cuatro orientaciones posibles) y de dos baldosas (en horizontal), que son las que se corresponden con el listado anterior de dieciséis.
 Página del libro del padre carmelita Dominique Doüat que contiene los embaldosados con una sola baldosa, o con dos baldosas, mediante la tesela de Truchet
Página del libro del padre carmelita Dominique Doüat que contiene los embaldosados con una sola baldosa, o con dos baldosas, mediante la tesela de Truchet
El siguiente análisis que se realiza es el de los posibles embaldosados con tres baldosas (en horizontal), que es igual a 43 = 64 (cuatro posibilidades –A, B, C, D- para cada posición), como se muestra en la siguiente tabla.
 Página del libro de Dominique Doüat que contiene los embaldosados con tres baldosas utilizando la tesela cuadrada bicolor
Página del libro de Dominique Doüat que contiene los embaldosados con tres baldosas utilizando la tesela cuadrada bicolor
Mientras que los posibles patrones de teselado con cuatro baldosas (en horizontal) son 44 = 256. Aprovechemos este análisis para comentar cuales serían los posibles patrones de embaldosado de un pavimento cuadrado 2 x 2 utilizando cuatro baldosas cuadradas bicolor. Si pensamos en ello, podemos observar que tenemos cuatro posiciones posibles para nuestras baldosas, arriba a la izquierda, arriba a la derecha, abajo a la izquierda y abajo a la derecha, luego se trata de analizar las posibles formas de colocar baldosas de Truchet, con sus cuatro orientaciones (A, B, C y D) en esas cuatro posiciones. La solución es exactamente el análisis de Doüat, luego los posibles patrones de teselado del pavimento cuadrado 2 x 2 serían también 256.
Veamos algunos de estos patrones. Por ejemplo, si consideramos embaldosados del pavimento cuadrado 2 x 2 con las cuatro teselas distintas, es decir, aparecen las cuatro baldosas orientadas A, B, C y D, se obtienen 24 patrones de teselado distintos, las permutaciones de (A, B, C, D): ABCD, ABDC, ACBD, ACDB, ADBC, ADCB, BACD, BADC, BCAD, BCDA, BDAC, BDCA, CABD, CADB, CBAD, CBDA, CDAB, CDBA, DABC, DACB, DBAC, DBCA, DCAB y DCBA. Y las ilustraciones (teselados concretos) que se corresponden con estos códigos de letras son los siguientes.


Estos son los 24 patrones de embaldosado con las cuatro baldosas distintas, pero si podemos repetir baldosas, llegamos hasta los 256 mencionados. Unos pocos más los mostramos en la siguiente imagen.

Cuanto más grande sea nuestro pavimento, más complejo será el análisis. A continuación, incluimos algunas ilustraciones de embaldosados de 12 x 12 baldosas pertenecientes al libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal, junto con su expresión mediante las letras A, B, C y D.

Respecto a la clasificación general de los patrones de embaldosado, claramente, la cantidad de patrones distintos para un pavimento con n baldosas es 4n, que podemos describirlas con las correspondientes cadenas de letras.
 Ilustración de un patrón de embaldosado, con una baldosa de Truchet, del libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722), de Dominique Doüat
Ilustración de un patrón de embaldosado, con una baldosa de Truchet, del libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722), de Dominique DoüatLos embaldosados de Truchet
Aunque el trabajo de investigación sobre los patrones de embaldosado con la sencilla tesela cuadrada de dos colores divididos por la diagonal lo inició el sacerdote dominico francés Sebastien Truchet (1657-1729) en su publicación Memoria sobre las combinaciones, publicada en Histoire de l’Académie Royale des Sciences de Paris, en 1704.
El propio Sebastien Truchet explica al inicio de su trabajo cómo se le ocurrió empezar a investigar la combinatoria de estos patrones de embaldosados:
Durante el último viaje que hice al canal de Orleans por orden de Su Alteza Real, en un castillo llamado Motte St. Lye, 4 leguas a este lado de Orleans, encontré varias baldosas de cerámica que estaban destinadas a embaldosar el suelo de una capilla y de varios otros apartamentos. Eran de forma cuadrada, divididas por una línea diagonal en dos partes coloreadas. Para poder formar diseños y dibujos agradables mediante la disposición de estas baldosas, primero examiné el número de formas en que estas baldosas podían unirse por parejas, siempre en disposición de damero […].
Desde el punto de vista histórico debemos de tener en cuenta que, aunque algunos conceptos y técnicas de la combinatoria se han estudiado desde la antigüedad, el origen de la combinatoria moderna podemos establecerlo en los siglos XVII y XVIII, gracias al trabajo de matemáticos como el francés Blaise Pascal (1623-1662), el alemán Gottfried Wilhelm Leibniz (1646-1716), quien publicara el texto De Arte Combinatoria (1666), el británico Isaac Newton (1643-1727), el suizo Jacob Bernoulli (1655-1705) o el suizo Leonhard Euler (1707-1783), quien inició o desarrolló el estudio de muchos ámbitos de la combinatoria (la teoría de grafos, los cuadrados greco-latinos, las particiones, el problema del recorrido del caballo, etc), entre otros. Por lo tanto, los trabajos de Sebastien Truchet y Dominique Doüat aparecieron en pleno desarrollo de la teoría de la combinatoria.
 Ilustración de un patrón de embaldosado, con una baldosa de Truchet, de la publicación Memoria sobre las combinaciones (1704), de Sebastien Truchet
Ilustración de un patrón de embaldosado, con una baldosa de Truchet, de la publicación Memoria sobre las combinaciones (1704), de Sebastien Truchet
Claramente, la mejor forma de conseguir patrones hermosos –como podemos ver, por ejemplo, en muchos textos sobre diseños para quilts- es trabajar directamente con las baldosas cuadradas bicolor en las cuatro orientaciones (A, B, C y D), pero desde el punto de vista matemático trabajar con las letras, como hizo Doüat, permite un mejor análisis de las posibilidades combinatorias y ayuda a distinguir unas de otras, puesto que el listado de letras se convierte en el código que nos permite identificar cada embaldosado.
 Quilt realizado con “cuadrados de Truchet” –o triángulos de medios cuadrados, como se cuelen denominar en los manuales sobre quilt-. Imagen de la página Carried Away Quilting
Quilt realizado con “cuadrados de Truchet” –o triángulos de medios cuadrados, como se cuelen denominar en los manuales sobre quilt-. Imagen de la página Carried Away Quilting
Otra cuestión que podemos tener en cuenta a la hora de estudiar los patrones de teselados es qué tipo de simetría tienen. Por ejemplo, si continuamos con los pavimentos cuadrados 2 x 2, aunque solo prestamos atención a los 24 patrones de embaldosado (de los 256 que hay en total) con las cuatro baldosas distintas que hemos descrito arriba, podemos observar que existen diferentes tipos de simetrías. Por ejemplo, los patrones ABCD, CDBA, BCAD y DACB se mantienen invariantes, es decir, no cambian, aunque realicemos rotaciones sobre ellos de 90, 180 o 270 grados. Tienen una simetría rotacional de 90 grados.

Los patrones ADBC, CBDA, BACD y DCAB se mantienen invariantes mediante rotaciones de 180 grados. Tienen una simetría rotacional de 180 grados. Aunque observemos que si realizamos un giro de 90 grados no se obtiene el mismo patrón, sino un patrón similar con cambio de los colores (girando 90 grados ADBC se obtiene CBDA y viceversa, y girando 90 grados BACD se obtiene DCAB y viceversa, que son patrones con los colores cambiados).
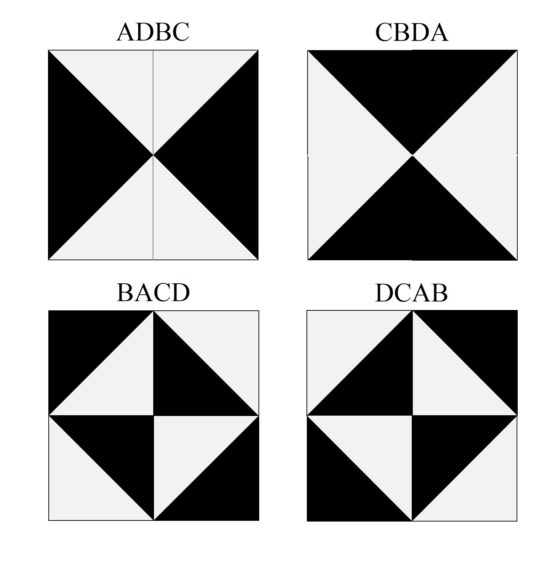
Otro tipo de simetrías que podemos considerar son las simetrías (especulares) respecto a una recta, es decir, lo que hay a un lado y a otro respecto a la recta es igual (su imagen especular, como si la recta fuera el espejo). Por ejemplo, el patrón DABC tiene simetría respecto a la recta vertical que pasa por el centro, como se muestra en la imagen.

En este sentido, tenemos que los patrones DACB y BCAD, que sabemos que tienen una simetría rotacional de 90 grados por lo visto anteriormente, tienen simetría especular respecto a cuatro rectas que pasan por el centro del cuadrado, las dos rectas horizontal y vertical, así como las dos diagonales del cuadrado.
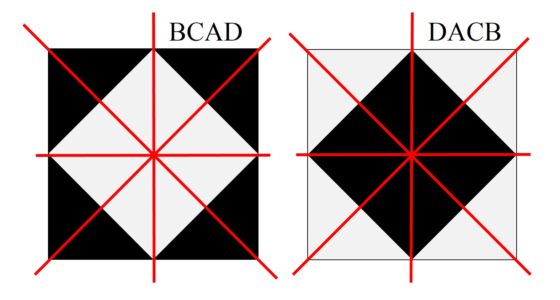
Los patrones BACD y DCAB tienen simetría especular respecto a las dos diagonales, los patrones ADBC y CBDA respecto a las rectas vertical y horizontal que pasan por el centro del cuadrado, los patrones ACBD, BDAC, CABD y DBCA respecto a la recta horizontal que pasa por el centro y BCDA, CBAD, DABC y ADCB respecto a la vertical que pasa por el centro. En total, catorce patrones son simetría especular respecto a rectas, los que aparecen en la siguiente imagen.

En resumen, de los 24 patrones de embaldosado con las cuatro baldosas distintas, tenemos que 16 tienen alguna simetría rotacional o especular, que son las “simetrías normales”, mientras que hay 8 patrones (los que vemos en la siguiente imagen) que no tienen ninguna de estas simetrías.
Vistos juntos estos 8 patrones, podemos percibir que tienen cierto tipo de simetría. En concreto, tienen simetría con cambio de color. Los cuatro primeros patrones tienen una simetría especular respecto a la recta horizontal que pasa por el centro, pero con cambio de color, es decir, las zonas que en un lado son blancas, en el lado opuesto son negras, y al revés. Mientras que los cuatro últimos patrones tienen una simetría especular respecto a la recta vertical que pasa por el centro.
En conclusión, todos los patrones de teselado para un pavimento cuadrado de tamaño 2 x 2 tienen simetría normal o simetría con cambio de color. Esta es precisamente la versión sencilla del conocido como teorema del diamante, que describimos a continuación.
Teorema del diamanteTeorema del diamante (versión 2 x 2): Sea D la figura formada por el diamante negro, construido con las cuatro orientaciones distintas de la baldosa bicolor de Truchet, que se muestra en la siguiente imagen:

Si G es el grupo de las 24 permutaciones de los cuatro cuadrados (baldosas) de D, entonces la imagen de D mediante cualquiera de los elementos del grupo G da lugar a una figura que tiene simetría normal o simetría con cambio de color.
Pero esta solo es una versión sencilla, que nos va a permitir entender mejor la versión normal, del verdadero teorema del diamante, que explicamos a continuación.
Sea ahora D la figura de cuatro diamantes negros sobre un cuadrado 4 x 4 que mostramos en la siguiente imagen y cuyo código de letras es DADACBCBDADACBCB,

y sea G el grupo de las 322.560 transformaciones generado por las permutaciones de dos filas cualesquiera del cuadrado 4 x 4, las permutaciones de dos columnas cualesquiera o las permutaciones de dos cuadrantes 2 x 2 cualesquiera. Por ejemplo, si a la figura D le aplicamos la permutación de las columnas del medio, luego la permutación de las filas del medio, después la permutación de los cuadrantes de abajo a la izquierda y de arriba a la derecha y finalmente la permutación de las dos filas exteriores, el resultado es la siguiente figura.

El teorema del diamante, del matemático estadounidense Steven H. Cullinane (1942), dice lo siguiente.
Teorema del diamante: Todas las imágenes que se obtienen mediante alguna de las 322.560 transformaciones del grupo G de la figura D tienen simetría normal o simetría con cambio de color.
Por ejemplo, la anterior imagen tiene simetría especular con cambio de color respecto a las rectas horizontal y vertical que pasan por el centro.
O la siguiente figura que se obtiene permutando las dos primeras filas, luego las dos columnas de la derecha, después el cuadrante de arriba a la izquierda con el de abajo a la derecha y finalmente, las dos columnas centrales, tiene una simetría rotacional de 180 grados con cambio de color.

O, por ejemplo, la siguiente figura tiene simetrías rotacionales y especulares.

Pero no hemos dicho cómo obtener la figura anterior a partir de la figura original de los cuatro diamantes negros. Este es un problema, o una diversión, que el propio Steven H. Cullinane plantea como rompecabezas y que bautiza con el nombre de “rompecabezas diamante 16”.
Rompecabezas diamante 16: Primero construir 16 baldosas bicolor de Truchet sobre cartulina, obtener alguna de las figuras de la columna de la izquierda, en la siguiente imagen, e intentar transformarla en la correspondiente figura de la columna de la derecha, utilizando las transformaciones del teorema del diamante, es decir, permutaciones de dos filas cualesquiera, de dos columnas cualesquiera o de dos cuadrantes 2 x 2 cualesquiera.

Si no queréis construir las teselas de Truchet y jugar con ellas al rompecabezas diamante 16, podéis hacerlo en la versión online que está incluida en la bibliografía.
Terminamos con la imagen de un quilt realizado utilizando un diseño de teselado con la estructura cuadrada bicolor, con los dos colores separados por la diagonal, la baldosa de Truchet.
 Quilt titulado “Blue tango” del blog de Louisa Enright
Quilt titulado “Blue tango” del blog de Louisa EnrightBibliografía:
1.- Cyril Stanley Smith (con la traducción del texto de Truchet por Pauline Boucher), The Tiling Patterns of Sebastian Truchet and the Topology of Structural Hierarchy, Leonardo, vol. 20, n. 4, pp. 373-385, 1987.
2.- Dominique Doüat, Méthode pour faire une infinité de desseins différents avec des carreaux mi-partis de deux couleurs par une ligne diagonale : ou observations du Père Dominique Doüat, Religieux Carme de la Province de Toulouse, sur un mémoire inséré dans l’Histoire de l’Académie Royale des Sciences de Paris l’année 1704, présenté par le Révérend Père Sébastien Truchet religieux du même ordre, Académicien honoraire [Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal], París, 1922.
Facsímil (extractos) e introducción de Jacques André
Obra completa en Gallica – Bibliothèque nationale de France
3.- Sebastien Truchet, Memoir sur les Combinaisons, Histoire de l’Académie Royale des Sciences de Paris, 363-372 (1704).
Obra completa en Gallica – Bibliothèque nationale de France
4.- Steven H. Cullinane, The Diamond Theorem, eprint arXiv:1308.1075, 2013.
5.- Steven H. Cullinane, The Diamond Theorem
6.- 5.- Steven H. Cullinane, The Diamond 16 puzzle
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los embaldosados de Truchet y el puzle del diamante se ha escrito en Cuaderno de Cultura Científica.
Einstein y Jules Henri Poincaré
El matemático Jules Henri Poincaré ha pasado a la historia como el hombre que casi descubrió la relatividad. Todo indica que Einstein empleó muchas horas revisando las teorías de Poincaré antes de tener la idea feliz que llevaría a su famoso artículo de 1905 sobre el asunto. Durante un tiempo se discutió si Einstein debería haber citado las ideas de Poincaré, pero el análisis posterior muestra que Einstein llegó a un nivel de comprensión de las implicaciones físicas del trabajo de Poincaré que este mismo no alcanzó.
 Fotografía de la primera Conferencia Solvay (1911). Poincaré está sentado hablando con Marie Curie, Einstein está de pie detrás de ellos, a la derecha.
Fotografía de la primera Conferencia Solvay (1911). Poincaré está sentado hablando con Marie Curie, Einstein está de pie detrás de ellos, a la derecha.Einstein y Henri Poincaré mantuvieron una relación notablemente fría. Poincaré nunca aceptó públicamente la teoría de la relatividad de Einstein y Einstein nunca dijo claramente que se había basado en el trabajo de Poincaré. Por otra parte, Poincaré sí recomendó a Einstein para uno de sus primeros empleos, llamándole “una de las mentes más originales con las que nunca me haya tropezado”.
En los primeros años del siglo XX, el francés era uno de los matemáticos más destacados del mundo. Desarrolló la teoría cualitativa moderna de sistemas dinámicos, contribuyó notablemente al establecimiento de un nuevo campo de investigación en matemáticas, la topología, y lo usó para probar que el Sistema Solar es estable, aparte de ser el presidente del Bureau des Longitudes y coautor de sus extraordinariamente precisos mapas.
Por lo que respecta a la relatividad, Poincaré y el físico holandés Hendrik Antoon Lorentz intercambiaban teorías y artículos regularmente sobre la naturaleza del tiempo. Lorentz había creado ecuaciones en las que el tiempo parecía diferente para diferentes observadores. Sin embargo, Lorentz vio esta suposición como una herramienta matemática, no como una verdadera representación de la realidad. Poincaré intentó plantear a qué correspondería en el mundo real este cambio en el tiempo dentro de las ecuaciones. Sugirió que podían interpretarse como relojes sincronizados por señales de luz; dado que la luz tomaría un tiempo finito para viajar entre un reloj y el otro, los relojes en diferentes sistemas mostrarían tiempos diferentes.
¿El principio de relatividad de Einstein y Poincaré?En 1904, Poincaré incluyó una sección dedicada al principio de la relatividad (la idea de que cosas como el tiempo eran relativas dependiendo de en qué sistema está el observador) en una conferencia llamada “Sobre el estado presente y futuro de las física matemática”. Su transcripción fue el primer texto en el que se trata el concepto y aparece el nombre de la relatividad. Pero, durante la conferencia, Poincaré se retractó de esta idea, sumándose a la original de Lorentz de que solo existe un “tiempo real”. Escribió, “los relojes sincronizados de esta manera no muestran por lo tanto el tiempo real, sino lo que podríamos llamar ‘tiempo local’ de tal forma que uno está retrasado con respecto al otro. Esto no importa mucho, ya que no tenemos forma de determinarlo”. (Esta conferencia de 1904 de Poincaré también incluía otros indicios sobre el futuro desarrollo de la física. Poincaré señaló por primera vez que la velocidad de la luz podría jugar un papel principal en la física, estructurando la teoría no solo en óptica y electrodinámica sino también en la mecánica).
En esa época, Einstein estaba trabajando en la Oficina Suiza de Patentes en Berna, y se encontraba en medio de conversaciones muy estimulantes con su amigo Michele Besso, así como con sus otros amigos Conrad Habitch y Maurice Solovine en su esperpéntica Academia Olímpica. Solovine luego comentaría que Einstein hizo que la academia emplease varias semanas revisando La science et l’hypothèse de Poincaré. El libro de Poincaré reducía el éter a una hipótesis que era simplemente “conveniente para la explicación de los fenómenos” e incluso predecía que “un día el éter sería indudablemente descartado como innecesario”.
Así, el cerebro de Einstein estaba filtrando toda esta información conforme discutía con sus amigos y pensaba acerca de la naturaleza de la luz. Sin embargo, cuando publicó la teoría especial de la relatividad (cuando de repente todo encajó en su cabeza y anunció una mañana a sus amigos que no se preocuparan, que había resuelto completamente el problema) la única nota a pie de página fue de agradecimiento a Besso. Al defender su falta de atribuciones, Einstein afirmó que no conocía ni el artículo de 1904 de Lorentz ni el de Poincaré de 1905 que discutía la relatividad. “En ese sentido”, argumentaba Einstein, “mi artículo de 1905 fue independiente”.
La teoría de la relatividad de Einstein se divulgó rápidamente en toda la comunidad científica, y la mayoría de los científicos la aceptaron sin dilación. Pero Poincaré se mantuvo especialmente callado. No rechazó las ideas de Einstein activamente; simplemente las ignoró. Los dos hombres solo se encontraron una vez, en la Primera Conferencia Solvay, en 1911. Después Einstein escribiría, “Poincaré fue simplemente negativo [hacia la teoría de la relatividad] y a pesar de toda su perspicacia mostró poca comprensión de la situación”.
Poincaré fallecería en 1912 con tan solo 58 años. Mucho después de su muerte, Einstein habló de él en una conferencia en la Academia Prusiana de Ciencias, pero no hizo referencia a la relatividad. En vez de eso, ensalzó al “agudo y profundo Poincaré” que supo unir física y geometría.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 5 de julio de 2009.
El artículo Einstein y Jules Henri Poincaré se ha escrito en Cuaderno de Cultura Científica.
¿Hay terremotos de origen volcánico en Marte?
Uno de los grandes retos de la geología moderna sigue siendo el de poder conocer con detalle la estructura interna de los planetas: como son estas capas –si son monolíticas o si están muy fracturadas-, en qué estado están -sólidas o líquidas-, y cuál es su composición. Y no es un dato baladí, ya que nos abriría una puerta a una mejor comprensión de el origen y evolución de estos y, quizás, a responder por qué los planetas no gaseosos somos en apariencia tan diferentes entre sí.
Desgraciadamente no podemos abrir una ventana y mirar al interior de los planetas y la única manera que tenemos de poder saber que hay dentro es mediante métodos indirectos, pero fuera de la Tierra no es una tarea fácil. De hecho, una de las mejores ventanas, y disculpen la paradoja, que teníamos para mirar al interior de planetas y asteroides eran los meteoritos.
 Los cráteres nos dejan ver algo del interior de los planetas, pero no mucho. NASA/JPL/ASU.
Los cráteres nos dejan ver algo del interior de los planetas, pero no mucho. NASA/JPL/ASU.Una de las consecuencias más evidentes de las colisiones de los distintos cuerpos que se mueven en nuestro Sistema Solar es la formación de los cráteres de impacto, que a veces nos permiten tener a la vista unos pocos cientos de metros e incluso algunos kilómetros hacia el interior de la corteza.
Al mismo tiempo que se producen estos choques puede ocurrir que, debido a la violencia del impacto, algunos trozos de esos planetas salgan despedidos con tal velocidad que escapen a su propio planeta y no vuelvan a caer sobre este, sino que queden vagando por el espacio en órbita alrededor del Sol.
Eventualmente, puede ocurrir que estos fragmentos expulsados de un planeta acaben encontrándose a lo largo de su camino con otros planetas, como la Tierra, cayendo como meteoritos que podemos recuperar y que a veces nos ayudan a inferir propiedades de la corteza y manto del planeta del que provienen.
Esto resulta insuficiente. Tenemos que acercarnos más si queremos obtener más detalles sobre el interior de los planetas. Desde la segunda mitad del siglo XX hemos tenido la oportunidad de poder enviar sondas a distintos cuerpos de nuestro Sistema Solar, y estas nos han permitido conocer mejor los interiores planetarios gracias al estudio de su campo gravitatorio y magnético, que nos da algunas pistas sobre la distribución de la masa en el interior de estos y sobre el estado de los materiales en el interior.
Escuchando los terremotos de MartePero si queremos saber más, tenemos que llegar hasta la superficie de los planetas e instalar instrumentos lo suficientemente sensibles que nos permitan escuchar de una manera inequívoca el latido de los planetas: los terremotos.
Para detectar y estudiar estos hacemos uso de unos sensores que llamamos sismómetros, que miden la amplitud del desplazamiento del suelo, no solo debido a los terremotos, sino al viento, el oleaje, las explosiones o incluso el tráfico, entre muchas otras causas naturales y artificiales.
Estudiando como se propagan las ondas a través del planeta, como cambian de velocidad y de amplitud e incluso como sufren fenómenos de refracción y reflexión de estas ondas al atravesar las distintas capas podemos hacernos una imagen mucho más detallada del interior de los planetas y construir un modelo mucho más preciso, tanto a nivel físico como químico.
 Una reconstrucción de la misión InSight totalmente desplegada en la superficie de Marte. El sismómetro es ese aparato con forma de cúpula en primer plano. NASA/JPL.
Una reconstrucción de la misión InSight totalmente desplegada en la superficie de Marte. El sismómetro es ese aparato con forma de cúpula en primer plano. NASA/JPL.Hasta el momento, tres son los sismómetros que ha viajado a Marte: Dos en los años setenta a bordo de los módulos de aterrizaje de las misiones Viking 1 y 2, y que desgraciadamente no sirvieron de mucho y otro a bordo de la misión InSight, que aterrizó en Marte en noviembre de 2018 y que todavía está en funcionamiento y recabando datos. Para que nos hagamos una idea del salto cualitativo y cuantitativo, mientras las Viking detectaron inequívocamente un único evento de origen sísmico, la InSight ha detectado ya a lo largo de su misión unos 500 terremotos y más de 800 eventos de corta duración que probablemente estén asociados a la rotura de la roca por los cambios de temperatura.
¿Y si en Marte hubiesen terremotos de origen volcánico?En Marte, obviamente, solo esperamos terremotos de origen natural –salvo cuando aterriza o choca alguna misión contra su superficie- pero principalmente generados por la tensión acumulada en las rocas y que al no poder seguir acomodando como deformación, acaba rompiéndolas y liberando toda esa energía en forma de ondas sísmicas.
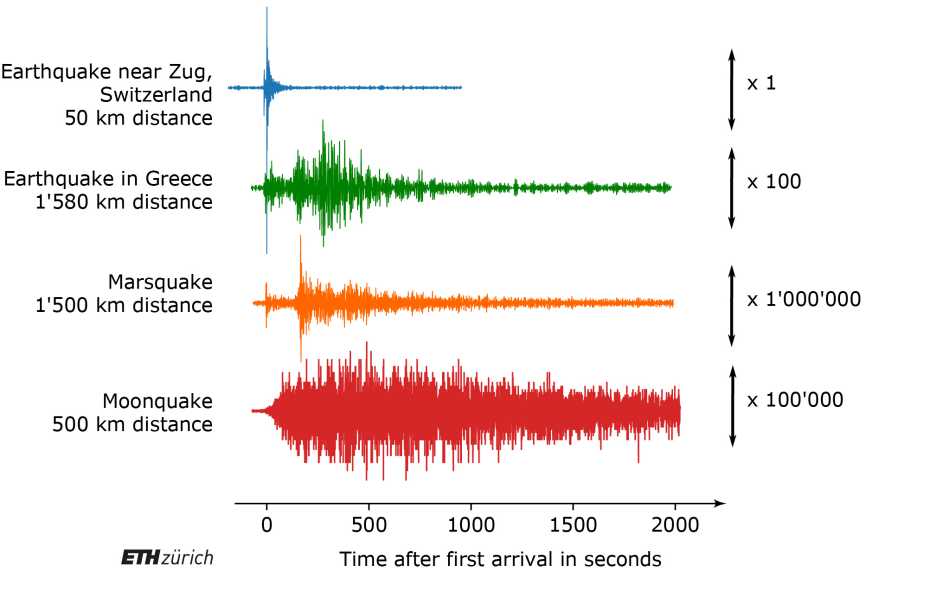 Imagen de la señal de terremotos en distintos lugares del Sistema Solar. Los dos primeros en ocurrieron en la Tierra, el tercero a Marte y el cuarto a la Luna. ETZ Zürich.
Imagen de la señal de terremotos en distintos lugares del Sistema Solar. Los dos primeros en ocurrieron en la Tierra, el tercero a Marte y el cuarto a la Luna. ETZ Zürich.Pero, ¿y si en Marte hubiesen terremotos también de origen volcánico? Lo cierto es que cuando miramos al planeta rojo, vemos un planeta frío, yermo, cuyo principal agente geológico en superficie es el viento. Al menos, desde que tenemos capacidad para estudiar Marte de una manera más o menos continua no hemos observado nada que se parezca a una erupción volcánica.
Marte tiene algunos de los volcanes más grandes de nuestro Sistema Solar, especialmente aquellos que están situados en la región de Tharsis, donde entre otros se encuentra Olympus Mons, que supera los 20 kilómetros de altura, pero que en la actualidad no tienen actividad, muy probablemente debido al enfriamiento del interior del planeta, a diferencia de lo que ocurre en nuestro la Tierra, cuya dinámica interna queda patente a través de un importante nivel de vulcanismo en superficie.
Pero hay una zona en Marte denominada Cerberus Fossae, relativamente próxima a la zona de aterrizaje de la misión InSight, y que parece tener un nivel de actividad importante. Este lugar es un sistema de fracturas que supera los 1200 kilómetros de longitud y que en algunos puntos está rodeado de unos halos oscuros, como si algo hubiese salido de esas fracturas y hubiese “manchado” el terreno circundante.
 Una pequeña porción de Cerberus Fossae en falso color para mostrar las diferencias composicionales entre el exterior y el interior. NASA/JPL/ASU.
Una pequeña porción de Cerberus Fossae en falso color para mostrar las diferencias composicionales entre el exterior y el interior. NASA/JPL/ASU.Precisamente Cerberus Fossae es un sistema de fisuras extensional, donde la corteza se está separando, parecido a lo que ocurre en el valle del Rift, en África, por poner un ejemplo cercano a nosotros, y donde hay un vulcanismo muy activo.
Los estudios más recientes sugieren que en esa zona podría haber habido fenómenos de vulcanismo activo en los últimos millones de años, quizás hace menos de diez según algunos autores, e incluso alrededor de los 50.000 años por otros autores, reciente en términos geológicos y muy reciente si tenemos en cuenta el grado de actividad geológica que apreciamos en Marte hoy día.
Bueno, ¿y qué tiene que ver esto con los terremotos? Los fenómenos volcánicos son uno de los mayores generadores de terremotos naturales en nuestro planeta: los movimientos del magma y otros fluidos moviéndose y emplazándose por la corteza pueden fracturar las rocas debido al aumento de presión, y también pueden aparecer vibraciones continuas fruto de un movimiento más asísmico, de estos fluidos por conductos más desarrollados (algo así como si tocamos una tubería de agua mientras esta circula por dentro).
La misión InSight lleva más de tres años vigilando los terremotos marcianos y algunos de estos parecen provenir de Cerberus Fossae, pero la causa de los terremotos que han sido detectados no está muy clara: o son por el propio enfriamiento del planeta, que al “encoger” somete a mucho esfuerzo a las rocas y acaban partiéndose, o se deben a otras fuerzas que están generando esas fracturas que se abren formando Cerberus Fossae, o a la migración de distintos fluidos por el interior de Marte o al movimiento de magma.
El último estudio publicado sobre este tema, Sun, W., & Tkalčić, H. (2022) Repetitive marsquakes in Martian upper mantle, ha estudiado todo el registro sísmico de la misión InSight descubriendo un mayor número de terremotos del detectado inicialmente gracias al uso de técnicas más avanzadas para encontrar las señales de menor amplitud que podían haber pasado desapercibidas.
Es importante saber que en la superficie de Marte sopla el viento y a pesar de que el sismómetro está relativamente aislado, este viento genera una señal continua en forma de vibración que puede enmascarar los eventos más pequeños, por lo que a veces cuesta detectarlos. Algo así como cuando vamos al cine y tenemos a alguien comiendo palomitas a nuestro lado: nos cuesta escuchar los diálogos de la película. Pues bien, el viento es una fuente de ruido para la señal sísmica igual que lo es el masticar de las palomitas para nosotros en el cine.
Estos nuevos terremotos parecen no seguir un patrón, sino que ocurren de una manera más o menos continua e incluso algunos podrían estar asociados con terremotos de mayor magnitud previamente detectados.
Los autores del estudio interpretan que estos nuevos terremotos se parecen a los que ocurren en nuestro planeta por el movimiento del magma, generando enjambres de terremotos relacionados con la migración lateral y vertical del magma.
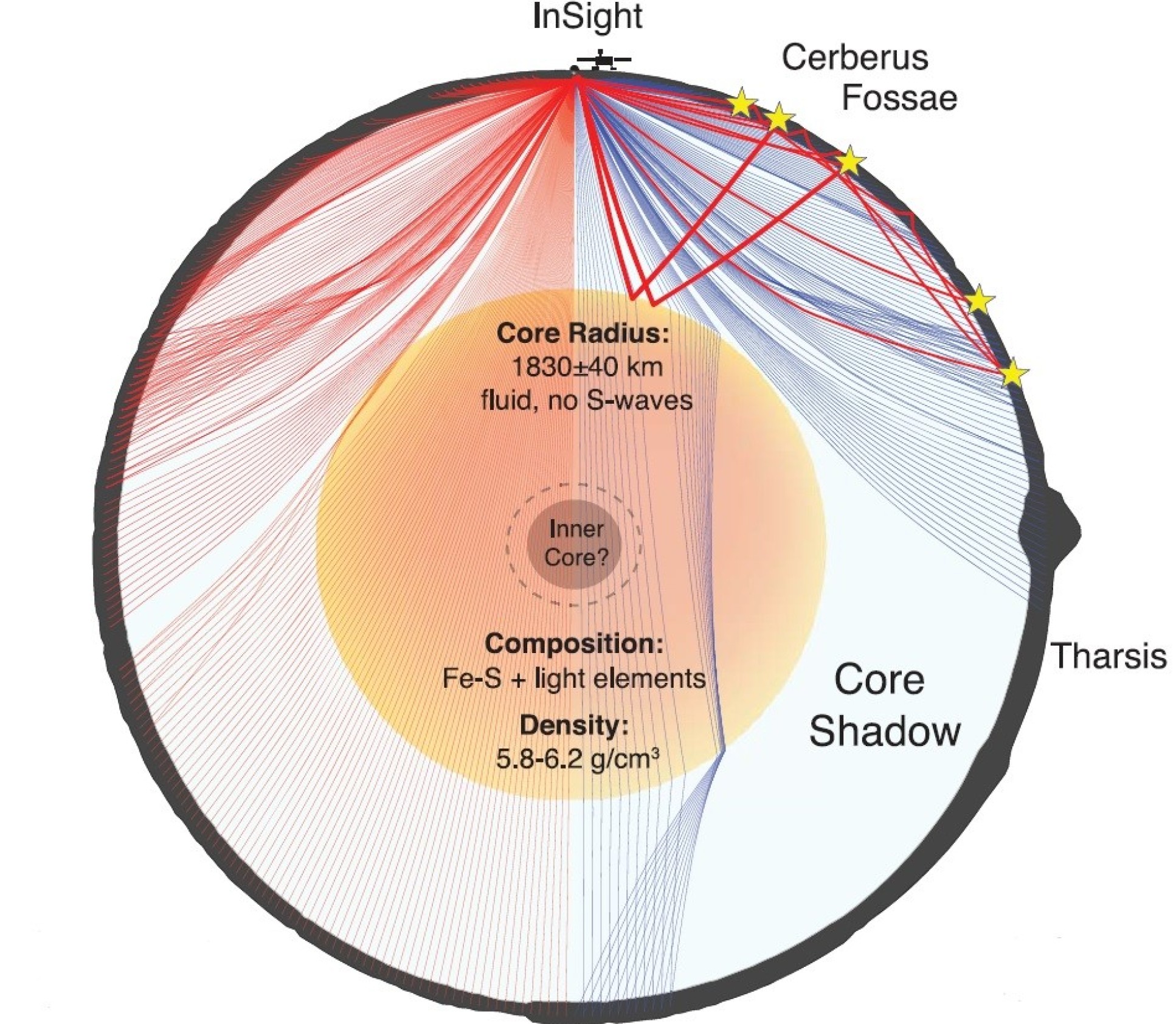 Este modelo del interior de Marte ha sido desarrollado a partir de las ondas sísmicas recogidas por la misión InSight. La trayectoria y los cambios de velocidad de las ondas nos ayudan a reconstruir como son las distintas capas de su interior. Khan et al. (2021).
Este modelo del interior de Marte ha sido desarrollado a partir de las ondas sísmicas recogidas por la misión InSight. La trayectoria y los cambios de velocidad de las ondas nos ayudan a reconstruir como son las distintas capas de su interior. Khan et al. (2021).En este caso, parece que los terremotos ocurrirían en el manto de Marte, demostrando que en su interior podría quedar más calor del que pensábamos. Eso sí, es muy probable que debido al grosor de la corteza de Marte –que se encuentra entre los 24 y 70 kilómetros-, el magma tendría muchas dificultades para aflorar en superficie y provocar una erupción volcánica, explicando la baja actividad volcánica que vemos en la actualidad.
Sin duda, una teoría apasionante que pone de manifiesto cuanto nos queda por saber y aprender de Marte… y quien sabe si nos abre a la posibilidad de que algún día veamos una erupción volcánica en Marte.
ReferenciasSun, W., & Tkalčić, H. (2022). Repetitive marsquakes in Martian upper mantle. Nature Communications, 13(1), 1695. doi:10.1038/s41467-022-29329-x
Horvath, D. G., Moitra, P., Hamilton, C. W., Craddock, R. A., & Andrews-Hanna, J. C. (2021). Evidence for geologically recent explosive volcanism in Elysium Planitia, Mars. Icarus, 365, 114499. doi: 10.1016/j.icarus.2021.114499
Khan, A., Ceylan, S., van Driel, M., Giardini, D., Lognonné, P., Samuel, H., Schmerr, N. C., Stähler, S. C., Duran, A. C., Huang, Q., Kim, D., Broquet, A., Charalambous, C., Clinton, J. F., Davis, P. M., Drilleau, M., Karakostas, F., Lekic, V., McLennan, S. M., … Banerdt, W. B. (2021). Upper mantle structure of Mars from InSight seismic data. Science, 373(6553), 434-438. doi: 10.1126/science.abf2966
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Hay terremotos de origen volcánico en Marte? se ha escrito en Cuaderno de Cultura Científica.
Más con menos
 Scarabaeus sacer (escarabajo pelotero sagrado) tenía estatus de dios en el Antiguo Egipto.
Scarabaeus sacer (escarabajo pelotero sagrado) tenía estatus de dios en el Antiguo Egipto.Cuenta Beth Shapiro en su último libro que al comienzo del Holoceno, en Beringia, la región que comprende los extremos noroccidental de América y nororiental de Asia, la tundra esteparia fue sustituida por el actual ecosistema de tundra, que es menos productivo que el anterior. Ello se debe, en parte, a que los grandes herbívoros que antes habían reciclado los nutrientes, dispersado las semillas y removido el suelo, habían desaparecido a causa, sobre todo, de la caza por seres humanos. La intervención humana no solo redujo las poblaciones de grandes mamíferos de manera directa como consecuencia de la caza, sino que también lo hizo indirectamente, al reducir su efecto beneficioso sobre la productividad de la tundra, y limitar de esa forma el aporte de materia vegetal para alimentar a aquellos.
Es esta una noción hasta cierto punto paradójica. Porque lo que acabo de decir es que cuando hay menos animales, disponen estos también de menos comida, algo que, a primera vista, puede resultar contradictorio. Pero no lo es. En un ecosistema muy productivo se produce mucha biomasa vegetal y, sin embargo, si los herbívoros que lo ocupan consumen esa biomasa rápidamente, lo normal es que no haya mucha. Se obtiene más (producción) con menos (biomasa).
La clave está en la función que cumplen los herbívoros, los organismos que descomponen la materia muerta y los que se comen a los anteriores que, tras asimilar el alimento, eliminan los desechos que contienen las sustancias minerales de las que depende el crecimiento de las plantas. Cuanto mayor sea la cantidad de nutrientes minerales que se reciclan por unidad de tiempo, mayor disponibilidad de ellos habrá para su reutilización por los vegetales, también por unidad de tiempo. Me refiero a sustancias tales como compuestos de nitrógeno y de fósforo o minerales como el hierro que usan las plantas para hacer nuevos tejidos.
En lo que a moluscos bivalvos se refiere, el enclave costero más productivo que conozco es la Ría de Arosa. Como en otras rías, los que allí se cultivan y los que habitan en las explanadas de sedimento y arenas en la zona entre mareas crecen muy rápidamente. Pues bien, la concentración de microalgas en las aguas de la ría de Arosa suele ser inferior a la de otros estuarios que conozco donde también crecen poblaciones de esos moluscos.
Algo similar ocurre con las ballenas (cetáceos misticetos) cuyo alimento más importante es el krill, un pequeño crustáceo. Antes de que las poblaciones de cetáceos fueran diezmadas y llevadas al borde de la extinción, las aguas antárticas eran mucho más productivas que lo son ahora. Las ballenas barbadas consumían ingentes cantidades de krill, lo que aceleraba el ciclo de los nutrientes -en especial el hierro- y permitía una alta productividad de las microalgas de fitoplancton y, como consecuencia, gran producción de krill. Ahora esos mares son mucho menos productivos, porque las pocas ballenas que quedan no pueden realizar un reciclaje tan intenso del hierro.
En Australia tuvieron que importar escarabajos peloteros africanos para que se comiesen las boñigas del ganado y ayudasen a liberar los nutrientes contenidos en ellas, restaurando así la productividad de los pastos. Al parecer, a los escarabajos australianos no les interesaban las boñigas de los herbívoros foráneos, solo querían las de los canguros, de manera que la producción de las praderas se vio muy mermada.
La naturaleza tiene sus reglas, y los seres humanos, a pesar de ser parte de ella, intervenimos a menudo en sus cosas sin calibrar los efectos últimos de nuestra intervención. A veces estamos a tiempo de corregir desmanes. Solo a veces.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Más con menos se ha escrito en Cuaderno de Cultura Científica.
Día de Pi con BCAM Naukas 2022: Carmen Quinteiro – Sembrando cuadrados, cosechando árboles

La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han suamdo a la celebración, organizando la tercera edición del evento BCAM-NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
Carmen Quinteiro, que es profesora titular de matemáticas en la Universidad de Vigo, partiendo del teorema del punto fijo de Brower no enseña como se pueden obtener árboles a partir de un cuadrado. Esta charla se complementa especialmente bien con esta anotación de Raúl Ibáñez: Paseando entre árboles de Pitágoras.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de Pi con BCAM Naukas 2022: Carmen Quinteiro – Sembrando cuadrados, cosechando árboles se ha escrito en Cuaderno de Cultura Científica.

