Instantáneas en tiempo real de la formación y crecimiento de polímeros 2D
Investigadores del grupo del profesor Ikerbasque Aurelio Mateo-Alonso en POLYMAT y en la UPV-EHU, en colaboración con investigadores de KU Leuven (Bélgica) y la Universidad de Aveiro (Portugal), han conseguido, literalmente, instantáneas en tiempo real de la formación y crecimiento de polímeros 2D, molécula por molécula. Los resultados se han publicado en Nature.
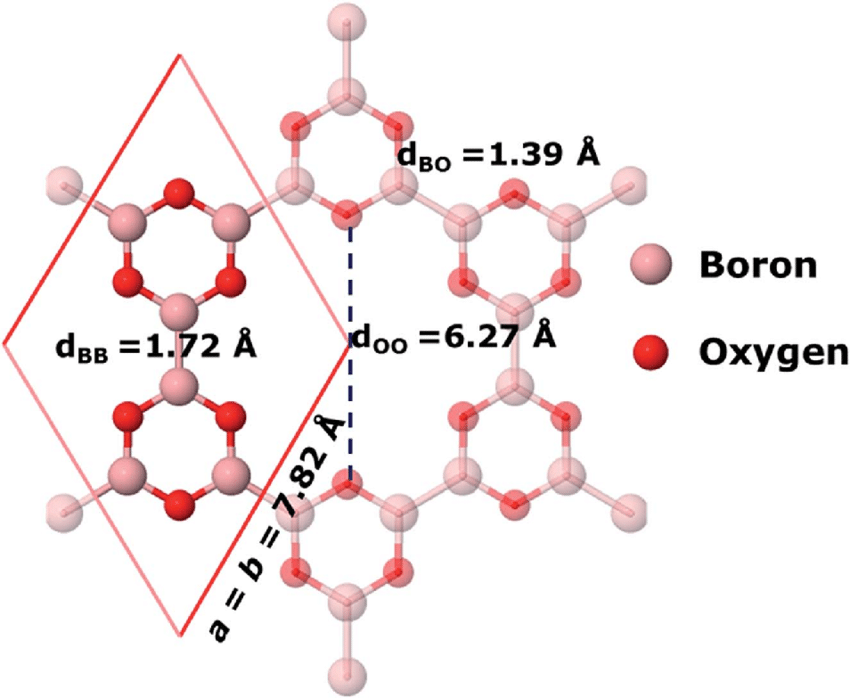 Boroxina bidimensional. Fuente: Ullah et al (2019)
Boroxina bidimensional. Fuente: Ullah et al (2019)Ya no podemos imaginar la vida sin polímeros. Los productos hechos de polímeros están a nuestro alrededor, desde ropa hecha de fibras sintéticas hasta lentes de plástico en gafas. Los polímeros se forman cuando pequeñas moléculas llamadas monómeros se unen para formar largas cadenas. Si un monómero reacciona con más de dos monómeros, se pueden formar láminas con una estructura interna periódica, denominadas polímeros bidimensionales (2D). Algunos de estos polímeros 2D son porosos y podrían usarse como membranas. Otros tipos son prometedores para la electrónica avanzada.
Cómo se forman exactamente estos polímeros 2D sigue siendo un misterio. Es importante conocer su mecanismo de formación para potenciar el tamaño y la perfección estructural de estos interesantes materiales.
Los científicos emplearon microscopía de túnel de barrido, un tipo avanzado de microscopía no óptica, para seguir en tiempo real, a medida que se forman y se rompen los enlaces, molécula por molécula, el nacimiento y crecimiento de un polímero 2D de boroxina en un soporte sólido inmerso en una solución reactiva. Con el apoyo de la teoría, demostraron que coexisten varios mecanismos de crecimiento y controlarlos conduce a la formación de láminas de polímero de gran tamaño y alta calidad.
Referencia:
Gaolei Zhan, Zhen-Feng Cai, Karol Strutyński, Lihua Yu, Niklas Herrmann, Marta Martínez-Abadía, Manuel Melle-Franco, Aurelio Mateo-Alonso & Steven De Feyter (2022) Observing polymerization in 2D dynamic covalent polymers Nature doi: 10.1038/s41586-022-04409-6
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Instantáneas en tiempo real de la formación y crecimiento de polímeros 2D se ha escrito en Cuaderno de Cultura Científica.
Aguas que no vemos, pero aguas que bebemos
El pasado 22 de marzo se celebró el Día Mundial del Agua, una efeméride que pretende concienciar sobre la importancia y necesidad de hacer un uso racional y sostenible del líquido elemento si queremos que la vida siga desarrollándose en la Tierra. Y es que, aunque se la conozca como “el planeta azul” por la abundante presencia de agua en la misma, en realidad se trata de un bien muy escaso, ya que el agua dulce, esa que podemos aprovechar de manera directa los seres humanos, representa menos del 3% del total del agua de nuestro planeta. Además tampoco es tan fácil acceder a las reservas de agua dulce, ya que aproximadamente el 66% está congelada en glaciares y casquetes polares, un 30% son aguas subterráneas y solo un 4% la encontramos en ríos y lagos. Y este año las protagonistas del Día Mundial del Agua han sido las aguas subterráneas, buscando “hacer visible lo invisible”.
 Foto: Michael Behrens / Unsplash
Foto: Michael Behrens / UnsplashLas aguas subterráneas siempre han sido las más desconocidas y han generado mitos y leyendas tenebrosas que han quedado grabadas en el imaginario colectivo, llegando incluso a darnos pavor su mención al asociarlas, en muchas ocasiones, con la muerte. Solo hay que recordar ese río de los muertos que debían cruzar los egipcios o el tránsito de las almas de los griegos por la Laguna Estigia. Pero dejemos de lado la mitología y veamos lo que nos dice la Geología sobre ellas.
Aguas subterráneas en poros, no en ríosLas aguas subterráneas son las que se infiltran en el terreno y se acumulan y circulan bajo tierra. Pero, a diferencia de lo que cuentan las leyendas, no se suelen encontrar en enormes túneles subterráneos por los que se mueven como grandes ríos. Estos grandes conductos solo están presentes en algunos tipos de rocas como, por ejemplo, las calizas, formadas principalmente por carbonato cálcico (CaCO3). Cuando el agua de lluvia, que es ligeramente ácida porque tiene disuelto algo de CO2 atmosférico, entra en contacto con estas rocas carbonatadas, reacciona químicamente y las disuelve hasta formar cuevas y cavidades en las que se forman lagos y ríos subterráneos.
Realmente, la mayor parte del agua subterránea se almacena y se desplaza a través de unos orificios microscópicos que tienen algunas rocas y sedimentos y que conocemos como poros. Esta porosidad convierte a estos materiales en permeables, es decir, permite que el agua circule a través de ellos. En Geología denominamos a estos materiales como acuíferos. Estas aguas subterráneas vuelven a salir al exterior alimentando a los ríos o a través de surgencias o manantiales. De esta forma, tanto el agua superficial como la subterránea acaban desembocando en los océanos, cerrando así el ciclo hidrológico.
Pero hay ocasiones en que el agua subterránea circula a mucha profundidad a través de fallas o fracturas en el terreno o bien discurre cerca de zonas volcánicas. Esto hace que su temperatura, al alcanzar la superficie, sea elevada. Así es como se forman las aguas hidrotermales. Esta agua caliente tiene la capacidad de captar elementos químicos de las rocas que atraviesa y transportarlos en disolución. Cuando esa agua asciende hacia la superficie a través de fracturas del terreno, se va enfriando y pierde la capacidad de transportar esos elementos, por lo que los va liberando por el camino y acaban reaccionando químicamente con las rocas que atraviesa, dando lugar a diferentes tipos de mineralizaciones que pueden tener un interés comercial.
 Surgencia de agua dulce subterránea en la playa de Castro Urdiales (Cantabria). Foto: Blanca María HernándezLos antiguos sí que sabían
Surgencia de agua dulce subterránea en la playa de Castro Urdiales (Cantabria). Foto: Blanca María HernándezLos antiguos sí que sabían
Nuestros antepasados ya se dieron cuenta del potencial del uso del agua subterránea para su propia subsistencia. Los romanos y los musulmanes preferían utilizar el agua subterránea, antes que la de los ríos, para garantizar el abastecimiento de grandes ciudades como Roma, Sevilla o Mérida. Siempre nos ha sorprendido que captasen agua de manantiales alejados de las urbes y la transportasen empleando enormes acueductos a pesar de estar ubicadas junto a grandes ríos. Pero estas civilizaciones conocían los rigores del clima mediterráneo, con grandes reducciones de caudal de los ríos durante las épocas de sequía y con momentos de arrastre y acumulación de sedimentos y residuos durante las épocas de lluvias intensas, disminuyendo la calidad del agua. Por ello, preferían utilizar el agua subterránea que no se veía influenciada por estos factores. Y también les dieron un buen uso a las aguas hidrotermales, empleándolas en las termas y baños públicos precursores de los balnearios modernos. Incluso, en los últimos siglos hemos llegado a embotellar y comercializar esta agua mineral procedente de surgencias hidrotermales.
En la época actual, en la que el agua dulce apta para el consumo humano se ha convertido en un recurso de primera necesidad que es cada vez más escaso debido a los efectos de la emergencia climática, la contaminación y alteración de los ambientes acuáticos y la sobreexplotación del agua de ríos, arroyos, lagos y embalses, los estudios geológicos centrados en las aguas subterráneas son básicos para nuestro desarrollo. Conocer dónde están los acuíferos, por dónde se va a mover o va a salir al exterior el agua y cuál puede ser su composición química, nos permite planificar cómo explotarla de manera sostenible y mantenida en el tiempo para asegurarnos un suministro futuro de agua. Pensad en esta última reflexión la próxima vez que abráis el grifo y os bebáis un vaso de ese líquido vital formado por moléculas compuestas por dos átomos de hidrógeno unidos a uno de oxígeno.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Aguas que no vemos, pero aguas que bebemos se ha escrito en Cuaderno de Cultura Científica.
Mujeres matemáticas de Budapest
Hace unos días participé en el XLII Seminario de Historia de la Matemática de la UCM (organizado por el profesor Miguel Ángel Gómez Villegas) hablando de seis mujeres matemáticas nacidas en Budapest.
 Primera diapositiva de “Mujeres matemáticas de Budapest”
Primera diapositiva de “Mujeres matemáticas de Budapest”
Cuando Miguel Ángel me propuso intervenir en el seminario con este tema, consulté el repositorio MacTutor y encontré a 42 personas nacidas en la capital de Hungría. Por supuesto, este listado no es exhaustivo; la búsqueda en otros lugares puede proporcionar algunos nombres diferentes. Pero MacTutor es, para mí, un repositorio de referencia, muy completo y bien documentado. En este listado de personas nacidas en Budapest aparecían solo dos mujeres, Rózsa Péter y Vera T. Sós. Aunque sí figuraban los maridos de cuatro de las seis mujeres citadas en mi conferencia: John von Neumann (esposo de Klára Dán von Neumann, Dán es su apellido de soltera), Alfréd Rényi (marido de Kató Rényi, de soltera Katalin Schulhof), George Szekeres (esposo de Esther Szekeres, apellidada Klein antes de casarse) y Paul Turán (marido de Vera T. Sós).
¿Queréis conocer un poco mejor a estas seis mujeres nacidas en Budapest?
Esther y Márta, una amistad duraderaIntroduje a Esther Klein (1910-2005) a través del denominado (por Paul Erdős) problema del final feliz, del que ya hablamos en este blog. Esther Klein y Márta Wachsberger nacieron en 1910, ambas en el seno de familias judías. Desde pequeñas destacaron en matemáticas, compartiendo aula de secundaria en Budapest y manteniendo su temprana y estrecha amistad durante toda su vida. Las limitaciones impuestas a los judíos en Hungría a finales de la década de 1920 solo permitían que dos estudiantes de su clase pudieran cursar carreras de ciencias en la Universidad de Budapest: Márta eligió la plaza de matemáticas y Esther optó por la de física.
Esther conoció a George Szekeres en la universidad; se casaron en 1937, y ella pasó a ser Esther Szekeres. Huyendo de la amenaza nazi, el matrimonio viajó en 1939 a China donde permanecieron hasta 1948, cuando la Universidad de Adelaida ofreció un puesto a George. Durante los primeros tres años de estancia en Australia los Szekeres compartieron un pequeño apartamento con sus amigos George y Márta Svéd (Márta Wachsberger de soltera). Parte de la historia de Esther puede leerse en [1]; y también parte de la de Márta. Junto a su marido, el ingeniero George Svéd, huyó en 1939 a Australia debido a su procedencia judía. Márta fue profesora, realizó alguna contribución matemática, y escribió el original libro Journey into Geometries, que ofrece una introducción informal a las geometrías no euclidianas a través de una serie de diálogos entre Alicia, su tío Lewis Carroll y un visitante del siglo XX, el Dr. Whatif. Alicia modera las discusiones entre Carroll, que defiende la geometría euclidiana, y Whatif que realiza preguntas controvertidas y perspicaces.
 Portada de Journey into Geometries (Mathematical Association of America, 1991).
Portada de Journey into Geometries (Mathematical Association of America, 1991).
Con 75 años, Márta defendió su tesis doctoral On Finite Linear And Baer Structures en la Universidad de Adelaida. Falleció 20 años más tarde, dos días después que su amiga Esther.
Vera y Kató, trayectorias cruzadasNo es fácil encontrar una amistad tan duradera como la de Esther y Márta. En matemáticas existen varios teoremas “de la amistad”; uno de ellos fue demostrado por Paul Erdős, Alfréd Rényi y Vera T. Sós; su enunciado puede leerse en este blog.
Vera T. Sós (1930) es una matemática húngara cuya investigación se ha centrado fundamentalmente en teoría de números y combinatoria. Su currículum investigador es impresionante: ha colaborado con numerosos matemáticos, publicando más de 100 artículos en revistas matemáticas. En la década de 1950 demostró el famoso teorema de tres distancias, resultado conjeturado por Hugo Steinhaus y demostrado independientemente por Stanisław Świerczkowski. Puede leerse algo más de ella en [2].
 Kató Renyi, Paul Turan, Vera Sós y Paul Erdős. Imagen tomada del blog de Gil Kalai
Kató Renyi, Paul Turan, Vera Sós y Paul Erdős. Imagen tomada del blog de Gil Kalai
Katalin Schulhof (1924-1969) comenzó sus estudios universitarios en 1942 en Budapest (allí fue alumna de Turán, quien posteriormente se casó con Vera Sós) y, a partir de 1945, los continuó en Szeged, donde conoció a Alfred Rényi, su futuro esposo. El matrimonio pasó dos años en Leningrado (hoy San Petersburgo) y regresaron a Budapest, donde Kató Rényi terminó la universidad en 1949. En 1950, se convirtió en profesora en la Universidad Eötvös Loránd. Fue una docente muy apreciada; por ello, en su honor, la Sociedad Matemática János Bolyai fundó el Premio Conmemorativo Kató Rényi concedido a resultados de investigación originales de estudiantes de pregrado.
Kató estaba interesada en la teoría de números y contribuyó a la teoría de funciones analíticas complejas. De su investigación en matemáticas resultaron 21 artículos científicos, algunos de ellos compartidos con su marido, conocido especialista en probabilidad y combinatoria. De hecho, su último trabajo conjunto (The Prüfer Code for k-Trees, 1970) se publicó en Combinatorial Theory and its Applications después del fallecimiento de Kató en agosto de 1969. Alfred preparó el artículo final, indicando en un pie de página que parte de los resultados de la investigación eran exclusivos de Kató…
Klára y Rozsda, “atrapadas” por la computaciónKlára Dán Von Neumann, como Kató Rényi, vivió a la sombra de un científico brillante. Aunque no tenía formación matemática posterior a la del instituto, aprendió a programar de manera autodidacta. Nació en 1911 en el seno de una familia acomodada. Conoció a John von Neumann antes del comienzo de la Segunda Guerra Mundial; en 1938 el matemático se divorció de su esposa y Klara Dán de su marido, y se casaron. El matrimonio emigró a EE. UU., donde von Neumann ocupó una cátedra en Princeton.
Entre otras aportaciones, Klára trabajó en la máquina ENIAC para producir el primer pronóstico meteorológico con ayuda de una computadora. Tradujo a código de programación las ecuaciones simplificadas de la dinámica atmosférica y, en 1950, se realizó la primera predicción del tiempo por ordenador. Enseñó al equipo de meteorólogos a programar la ENIAC y revisó el programa final. Von Neumann, Jule Charney y Ragnar Fjörtoft publicaron en 1950 el artículo Numerical Integration of the Barotropic Vorticity Equation con los detalles de este experimento. Klára no firmó ese trabajo y quedó al margen de los reconocimientos. Solo aparecía como Mrs. K. VON NEUMANN, invisibilizada, en los agradecimientos finales. Puede leerse más sobre su trabajo en [4].
También trabajó en computación Rózsa Péter. Nacida en 1905, por imposición de su padre, empezó a estudiar química para trabajar junto a su hermano mayor, que cursaba medicina. En su primer año de carrera, descubrió en las clases de Lipót Fejér su gusto por las matemáticas. Y se cambió de grado.
 Portadas de dos de los libros de Rózsa Péter
Portadas de dos de los libros de Rózsa Péter
Es muy conocida por su libro Jugando con el Infinito, una reflexión sobre temas relacionados con la geometría, la lógica y la teoría de números dirigida a un público no experto.
Rózsa trabajó fundamentalmente en funciones recursivas, tanto de manera teórica como en su importancia en computación. Puede leerse más sobre ella en [5].
Esther, Márta, Vera, Kató, Klára y Rózsa fueron seis matemáticas, nacidas en Budapest, que se cruzaron de diferentes maneras a lo largo de sus vidas. Aunque estas últimas palabras son de Rózsa Péter, estoy segura todas ellas las compartían:
Me encantan las matemáticas no sólo por sus aplicaciones técnicas, sino sobre todo porque son hermosas.
Referencias
[1] Marta Macho Stadler, Esther Szekeres y Márta Svéd, unidas por las matemáticas y una larga amistad, Mujeres con ciencia, 5 de mayo de 2020.
[2] Marta Macho Stadler, Vera T. Sós, especialista en combinatoria, Mujeres con ciencia, 10 de abril de 2019.
[3] Gil Kalai, The last paper of Catherine Rényi and Alfréd Rényi: Counting k-Trees, Combinatorics and more, 1 de mayo de 2019.
[4] Marta Macho Stadler, Klára Dán Von Neumann, desconocida pionera de la programación, Mujeres con ciencia, 6 de enero de 2021.
[5] Teresa E. Pérez Fernández, Rocío Raya Prida y Evangelina Santos Aláez, Rózsa Péter (1905-1977). Jugando con el infinito, Mujeres con ciencia, 21 de diciembre de 2017.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Mujeres matemáticas de Budapest se ha escrito en Cuaderno de Cultura Científica.
Einstein y el condensado de Bose-Einstein
En los años 20 del siglo XX, Albert Einstein amplió las ideas del físico indio Satyendra Nath Bose para predecir que, a temperaturas extremadamente frías, los átomos se unirían en una nueva fase de la materia (diferente a líquido, gas, sólido o plasma) conocida como condensado de Bose-Einstein.
 Foto Robert Zunikoff / Unsplash
Foto Robert Zunikoff / UnsplashEn 1924, Bose vivía en Calcuta y no conseguía llamar la atención de sus colegas europeos sobre su trabajo. Se decidió a escribir a Einstein, adjuntándole un artículo que usaba una nueva forma de estadística para deducir la ley de Planck, la famosa ecuación que representa la intensidad de la radiación de un cuerpo negro como función de la temperatura. Einstein quedó impresionado con la mecánica estadística de fotones de Bose, calificándola como “una avance significativo”. Tradujo personalmente el artículo al alemán e intervino para que se publicase [1] en Zeitschrift Für Physik en 1924.
La nueva estadística de Bose ofrecía más información sobre cómo comprender el comportamiento de los fotones. Bose demostró que si un fotón alcanzaba un estado cuántico específico (un conjunto de variables que incluye la energía que tiene el fotón), entonces existía una pequeña tendencia a que el siguiente fotón alcanzase el mismo estado. Es como si cada vez que golpeases una bola de billar americano hubiese más probabilidad de que fuese a la tronera (bolsillo) donde ya hay una bola.
 Satyendra Nath Bose en 1925. Fuente: Wikimedia Commons
Satyendra Nath Bose en 1925. Fuente: Wikimedia CommonsBose había aplicado su estadística a un “gas” de fotones. Esto indujo a Einstein a considerar la aplicación de la estadística de Bose a un gas ideal de átomos o moléculas; Einstein quería ver qué pasaba cuando uno trataba con materia de verdad. Basándose en el trabajo de Bose, Einstein terminó deduciendo un conjunto de fórmulas que predecían cómo los átomos de un gas deberían comportarse, que resulta ser correcto para cierto tipo de partículas, entre ellas protones y neutrones, que ahora se conocen, apropiadamente, como bosones.
Como consecuencia de estas nuevas ideas surgía una predicción de lo que les ocurriría a los átomos a temperaturas extremadamente bajas, cercanas al cero absoluto. En 1925, Einstein descubrió que si a un gas se le baja la temperatura hasta aproximarla al cero absoluto, una temperatura a la que los átomos casi no se muevan, todos alcanzarán exactamente el mismo estado cuántico.
Volviendo a la mesa de billar, podemos imaginar que dejamos caer 20 bolas sobre la mesa y vemos cómo ruedan cada una hasta terminar en troneras diferentes. Esta clase de rodar aleatorio es lo que ocurre a temperaturas normales: cada átomo en un estado cuántico específico. Pero cerca del cero absoluto, esas bolas dejadas caer irían, una tras otra, a la misma tronera. En el cero absoluto, los átomos se “bloquean” en el mismo estado cuántico y van uno detrás de otro sin discusión. Se unen en un nuevo estado de la materia que se denomina condensado de Bose-Einstein. Todos los átomos en un condensado de Bose-Einstein pierden su identidad individual. Marchan al unísono, actuando como un solo superátomo. De hecho, los condensados de Bose-Einstein interaccionan entre sí como una partícula con otra: se repelen o atraen igual que los átomos individuales.
Einstein publicó su trabajo en dos artículos en 1925 [2][3], cuando tenía 46 años. No es habitual que un científico haga una contribución de este calibre en un campo completamente nuevo cuando ya tiene más de 40 años y, de hecho, esta fue la última gran contribución de Einstein a la física. Setenta años más tarde el condensado de Bose-Einstein fue observado experimentalmente en átomos de rubidio.
Referencias[1] Bose, S.N . (1924). Plancks Gesetz und Lichtquantenhypothese Zeitschrift für Physik, 26 (1), 178-181 DOI: 10.1007/BF01327326
[2] Einstein, A. (1925). Quantentheorie des einatomigen idealen Gases.I Sitzungsberichte Akad. Berlin DOI: 10.1002/3527608958.ch27
[3] Einstein, A. (1925). Quantentheorie des einatomigen idealen Gases.II Sitzungsberichte Akad. Berlin DOI: 10.1002/3527608958.ch28
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 23 de mayo de 2010.
El artículo Einstein y el condensado de Bose-Einstein se ha escrito en Cuaderno de Cultura Científica.
Desmitificando: Los plásticos
Un mundo sin plásticos parece inimaginable en la actualidad, a pesar de que, como se menciona a menudo, su producción y uso a gran escala comenzó no hace mucho tiempo, hacia la década de los 50 del siglo pasado. Los plásticos son omnipresentes en la vida actual y están ampliamente dispersos en el medio ambiente. Los orígenes materiales e históricos de los plásticos siguen siendo oscuros, simplificados en exceso e incomprendidos, lo que da como resultado varios mitos. El repaso de Rebecca Altman, periodista científica del Washington Post, sirve para aclarar algunos de esos mitos.
 Foto: Francesco La Corte / Unsplash
Foto: Francesco La Corte / UnsplashPublicaciones como National Geographic y Nature han señalado 1950 como el año en que comenzó la producción masiva de plásticos. Pero 1950, en realidad, marca el primer año en que se recogieron datos de fabricación global, según el estudio de Roland Geyer y sus colegas, de la Universidad de California en Santa Barbara. El primer plástico sintético, la baquelita, apareció en 1907 y todavía se utiliza en la carcasa de teléfonos fijos y de radios vintage.
¿Cuánto plástico hay?La producción comercial de baquelita, el primer plástico sintético, comenzó en Alemania y en Estados Unidos en 1910. La Comisión de Aranceles de EE. UU. contó 1 millón de toneladas en 1921, aumentando a 15 millones en 1931, y a más de 60 millones unos años después.
Los datos del grupo de Roland Geyer, publicados en su artículo de 2017, permiten calcular algunas cifras sobre la producción de plásticos. Hasta 2015, el total de la producción mundial acumulada había sido de 8300 millones de toneladas. Y ese año 2015 el total de basura plástica vertido desde 1950, era de 6300 millones de toneladas; solo el 9% había sido reciclado, el 12% incinerado y el 79% acumulado en vertederos o en el medio ambiente. Los autores calcularon que para 2050 cerca de 12000 millones de toneladas de basura de plásticos se habían tirado en el entorno.
Los datos de Geyer ayudaron al público a comprender la magnitud de los plásticos producidos: aproximadamente 2 millones de toneladas en 1950, lo que nos parece escaso en comparación con la actualidad. (En 2019 la producción mundial se acercó a los 368 millones de toneladas).
La Segunda Guerra Mundial aceleró aún más el crecimiento de los plásticos: los contratos de guerra ampliaron la infraestructura para los plásticos existentes (p. ej., acrílicos, fenólicos, PVC y poliestireno), y la Armada ayudó a DuPont y Union Carbide a obtener las licencias necesarias para comenzar la producción de polietileno (entonces una industria emergente), desarrollado en Inglaterra y Estados Unidos.
Como resultado, en la década de 1940, la producción en Estados Unidos aumentó más de seis veces. Este crecimiento ha quedado reflejado en los sedimentos marinos según el estudio de Jennifer Brandon y sus colegas, de la Universidad de California en San Diego. En muestras tomadas cerca de la costa de California, los plásticos y las fibras plásticas son aparecen incluso en las capas sedimentarias de antes de la guerra, creciendo después de 1945 a un ritmo en que se dobla la cantidad cada 15 años, a medida que los plásticos llegaron a los consumidores.
 Foto: Michael Dziedzic / UnsplashLos plásticos son persistentes, no estáticos
Foto: Michael Dziedzic / UnsplashLos plásticos son persistentes, no estáticos
Muchas publicaciones, incluida una de la NOAA, abordan el problema de estimar el tiempo que el plástico tarda en degradarse. Dicen, por ejemplo, que un vaso de plástico dura 50 años o una botella de plástico llega a los 450 años o una red de pesca a los 600 años o un pañal desechable a los 450 años.
Sin embargo, algunos expertos cuestionan la precisión de estas cifras pues la resistencia de los plásticos es una función de su entorno. Eso podría variar desde la superficie del mar brillante y salobre hasta el interior oscuro de un intestino rico en ácido, las capas subterráneas de paisajes terrestres o las profundidades presurizadas de una fosa de aguas profundas. Los plásticos son una clase diversa de contaminantes que contienen mezclas complejas de alrededor de 10 000 monómeros, aditivos y coadyuvantes de procesamiento diferentes, lo que dificulta estimar la longevidad, aunque grupos como Ali Chamas y sus colegas, de la Universidad de California en Santa Barbara, o Colin Ward y Christopher Reddy, del Instituto Oceanográfico de Woods Hole, llevan tiempo pidiendo más estudios y precisión en las cifras que se publican como definitivas.
Puede ser difícil afirmar con rotundidad que «los plásticos son para siempre«, como escribe en un artículo Bruce Gibb, de la Universidad Tulane de Nueva Orleans, aunque algunos se depositan en sedimentos y ya se recuperan como hallazgos arqueológicos. Muchos plásticos resisten la degradación pero no son estáticos. Los encargados de los museos que preservan los artefactos plásticos saben muy bien que se decoloran, secan, agrietan, rompen, y pasan por cambios físicos, que incluyen, sobre todo, convertirse en partículas a escala micro e incluso nanométrica. Así se convierten en contaminantes persistentes, de larga vida, móviles y que se acumulan y entran en los sistemas y ciclos de la Tierra. Estos fragmentos también cambian químicamente, liberando lixiviados y productos de degradación que pueden actuar como disruptores endocrinos.
Para terminar, la contaminación plástica está más allá de la capacidad de remediación de los sistemas tecnológicos, escribe el experto en plásticos Max Liboiron, de la Universidad de Terranova y Labrador, en Canadá. La mayoría de los plásticos son fragmentos minúsculos que se distribuyen por debajo de la superficie del mar, en la atmósfera, o están enterrados en sedimentos o arenas costeras. Otros plásticos se han propagado a través de los sistemas de agua dulce o la tierra. Algunos expertos como Hans Peter Arp y su grupo, de la Universidad Noruega de Ciencia y Tecnología de Trondheim, proponen que los suelos pueden contener cantidades aún mayores de microplásticos que los océanos. Además de los propios plásticos, sus contaminantes asociados como ftalatos o retardantes de llama con bromo también están en muchos entornos. Todos ellos podrían interferir con la capacidad de la Tierra para albergar vida, como concluyen Arp y sus colegas.
ReferenciasAltman, R. 2022. Five myths about plastics. Washington Post January 14.
Arp, H.P.H. et al. 2021. Weathering plastics as a planetary boundary threat: Exposure, fate, and hazards. Environmental Science & Technology 55: 7246-7255.
Brandon, J.A. et al. 2019. Multidecadal increase in plastic particles in coastal ocean sediments. Science Advances 5: eaax0587.
Chamas, A. et al. 2020. Degradation rates of plastics in the environment. ACS Sustainable Chemistry & Engineering 8: 3494-3511.
Geyer, R. et al. 2017. Production, use, and fate of all plastics ever made. Science Advances 3: e1700872.
Gibb, B.C. 2019. Plastics are forever. Nature Chemistry 11: 394-395.
Ward, C.P. & C.M. Reddy. 2020. We need better data about the environmental persistence of plastic goods. Proceedings of the National Academy of Sciences USA 17: 14618-14621.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Desmitificando: Los plásticos se ha escrito en Cuaderno de Cultura Científica.
Pulpos, una reproducción que les cuesta la vida
Eduardo Almansa Berro y Catalina Perales-Raya
 Imagen submarina de un pulpo en su medio natural. Lugar: Islas Canarias. Foto: C. Perales-Raya.
Imagen submarina de un pulpo en su medio natural. Lugar: Islas Canarias. Foto: C. Perales-Raya.
Una vez en la vida, así se reproducen los pulpos. El pulpo común vive apenas un año, y su ciclo vital queda completado tras un único evento reproductivo.
No es algo único de los pulpos, sino una estrategia que sucede en la mayoría de las especies de cefalópodos, con la única excepción de los nautilos (se reproducen varias veces a lo largo de su vida, que puede durar más de 20 años).
La maduración sexual en cefalópodos es poco conocida aunque se sabe que está controlada por hormonas producidas en una parte del cerebro llamada glándula óptica.
Al igual que en muchos otros animales, esta glándula integra información sobre el crecimiento del animal, reservas corporales y factores ambientales como el fotoperíodo y la temperatura que permiten seleccionar el momento adecuado, tanto para iniciar la maduración como para depositar los huevos.
La hembra deja de comer y muere tras cuidar los huevosSin embargo, una característica que diferencia a los cefalópodos de la mayoría de los animales es que esta regulación está muy integrada con la regulación del apetito, hasta el punto de que la hembra deja de alimentarse una vez depositados los huevos, lo que conduce inevitablemente a su muerte por inanición tras cuidar de la puesta.
Esta especie de “suicidio programado” parece ocurrir también en los machos, pues una vez cumplida su edad máxima programada (normalmente un año o año y medio) también dejan de alimentarse.
Almacenan espermatóforos de varios machosEl cortejo en los cefalópodos se produce con ayuda de llamativos y elaborados cambios en su coloración y patrón corporal, aunque en el caso de los pulpos no suele haber tanto juego previo.
Los machos “empaquetan” el esperma en unas cápsulas llamadas espermatóforos, que son transferidas a la hembra gracias a la modificación de uno de sus brazos (hectocótilo).
En el pulpo común, el hectocótilo del macho se forma en el extremo del tercer brazo derecho y permite depositar los espermatóforos en la glándula oviductal de la hembra, donde permanecerá almacenada hasta que se den las condiciones adecuadas para la reproducción.
Observaciones llevadas a cabo en nuestro laboratorio han mostrado que las hembras son capaces de almacenar el esperma durante varios meses antes de usarlo para fecundar los ovocitos e iniciar la puesta.
Estudios genéticos han mostrado que una hembra puede almacenar esperma de varios machos, dando lugar a puestas con múltiple paternidad, aunque cada uno de ellos intentará eliminar los espermatóforos depositados por los machos anteriores.
Una progenie numerosa y huérfanaEl cuidado y dedicación que la hembra de pulpo aplica a su puesta es otro comportamiento que no suele encontrarse en el reino animal.
 Paralarva de pulpo común en el momento de la eclosión bajo luz polarizada. Ampliación: 80X. Foto: C. Perales-Raya.
Paralarva de pulpo común en el momento de la eclosión bajo luz polarizada. Ampliación: 80X. Foto: C. Perales-Raya.Las hembras cuelgan los huevos (varios cientos de miles) agrupados en racimos dentro en un lugar seguro. Normalmente utilizan un hueco u oquedad de la roca con el tamaño y oscuridad adecuados, pero pueden usar cualquier lugar con similares características, como algunas trampas para pulpo frecuentes en pesquerías artesanales dirigidas a esta especie.
Durante varias semanas la hembra protege los huevos de posibles depredadores, a la vez que los limpia con sus ventosas y los mantiene aireados y en movimiento mediante chorros de agua producidos con su sifón. Este proceso se ha conseguido replicar en laboratorio sin la presencia de la hembra.
La temperatura es fundamental y afecta tanto a la duración como a la calidad del desarrollo embrionario. Se ha observado que aumentos de temperatura compatibles con el cambio climático reducen la calidad de la puesta.
 Detalle de la mandíbula de una paralarva de pulpo, bajo el microscopio electrónico. Foto: I. Molto y A. Lancha
Detalle de la mandíbula de una paralarva de pulpo, bajo el microscopio electrónico. Foto: I. Molto y A. LanchaUna vez terminado el desarrollo embrionario, eclosionan miles de pequeñas “paralarvas” de unos 2 mm de longitud, dotadas de mandíbulas (o picos) con dientes para cazar, y que viajarán en mar abierto llevadas por las corrientes oceánicas hasta su asentamiento final como juveniles.
Avances hacia una producción sostenibleEl aumento de la demanda en el consumo de pulpo en el mundo se suma a otras amenazas sobre las poblaciones salvajes como la sobrepesca, la contaminación o el cambio climático. Todo ello ha llevado a la búsqueda de alternativas que garanticen una producción sostenible, entre las que se incluye el desafío afrontado en las últimas décadas: su producción acuícola.
El principal cuello de botella para conseguirlo han sido desde siempre las primeras fases de vida. En esos primeros momentos, es muy complejo conseguir que las paralarvas tengan alimentación y nutrición adecuadas. También tienen requerimientos especiales que tienen que ver con factores ambientales como la luz.
Siguiendo estas líneas de investigación, los últimos avances llevados a cabo por el Instituto Español de Oceanografía en sus centros de Vigo y Tenerife han permitido mejorar su cría en cautividad. Lograr su reproducción en cautividad abre la puerta a una mejor gestión de su producción para el consumo humano, tanto a nivel acuícola como pesquero, ya que también facilita el estudio de su biología y ecología.
No obstante, aún quedan importantes retos relacionados con una producción sostenible y que asegure el bienestar animal. Este ha sido en todo momento el objetivo de proyectos científicos de nuestro grupo OCTOWELF o la red europea CephsInAction. La producción sostenible y el bienestar animal han de seguir siendo un objetivo prioritario en futuros proyectos de investigación.![]()
Sobre los autores: Eduardo Almansa Berro es Científico Titular y Catalina Perales-Raya, Científica Titular, del Instituto Español de Oceanografía (IEO – CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Pulpos, una reproducción que les cuesta la vida se ha escrito en Cuaderno de Cultura Científica.
Día de PI con BCAM NAUKAS 2022: Pablo Rodríguez Sánchez – Con matemáticas en los ojos

La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han suamdo a la celebración, organizando la tercera edición del evento BCAM-NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
La visión humana es básicamente un conjunto de problemas matemáticos. Pablo Rodríguez Sánchez, que es matemático aplicado en el Netherlands eScience Center, nos lo cuenta en esta interesantísima charla.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de PI con BCAM NAUKAS 2022: Pablo Rodríguez Sánchez – Con matemáticas en los ojos se ha escrito en Cuaderno de Cultura Científica.
Respuestas a preguntas en lenguaje natural, el nuevo paradigma de los buscadores basados en inteligencia artificial
 VIGICOVID es un prototipo para extraer información mediante preguntas y respuestas en lenguaje natural de un conjunto actualizado de artículos científicos publicados por la comunidad investigadora mundial. Fuente: 123rf
VIGICOVID es un prototipo para extraer información mediante preguntas y respuestas en lenguaje natural de un conjunto actualizado de artículos científicos publicados por la comunidad investigadora mundial. Fuente: 123rfLa comunidad investigadora biosanitaria mundial está realizando un gran esfuerzo en la generación de conocimiento en torno a la COVID-19 y al SARS-CoV-2. Este esfuerzo se traduce en una producción ingente y muy rápida de publicaciones científicas, lo cual dificulta la consulta y el análisis de toda esa información. Por ello, resulta necesario proporcionar sistemas de información a las personas expertas y a las autoridades responsables en la toma de decisiones, que les permitan adquirir el conocimiento necesario.
Eso es, precisamente, lo que han desarrollado en el proyecto VIGICOVID un equipo de investigación del Centro HiTZ de la UPV/EHU, del grupo NLP & IR de la UNED y de la Unidad de Inteligencia Artificial en el ámbito lingüístico de Elhuyar, gracias a la financiación a través del Fondo Supera COVID-19 otorgada por la CRUE. Con la coordinación del grupo de investigación de la UNED, el resultado ha sido un prototipo para extraer información mediante preguntas y respuestas en lenguaje natural de un conjunto actualizado de artículos científicos publicados por la comunidad investigadora mundial en torno a la COVID-19 y el SARS-CoV-2.
“El paradigma de las búsquedas de información está cambiando gracias a la inteligencia artificial. Hasta ahora, para buscar información en la red, se introduce una pregunta, y la respuesta se debe buscar en los documentos que nos muestra el sistema. Sin embargo, en función del nuevo paradigma, cada vez están más extendidos los sistemas que ofrecen directamente la respuesta, sin necesidad de leer todo el documento”.
Eneko Agirre, director del Centro HiTZ de la UPV/EHU
En este sistema, “la persona usuaria no solicita la información mediante palabras clave, sino que formula directamente una pregunta”, explica el investigador de Elhuyar Xabier Saralegi. El sistema busca las respuestas a esa pregunta en dos fases: “En primer lugar, recupera los documentos que pueden contener la respuesta a la pregunta realizada, utilizando una tecnología que combina palabras clave y preguntas directas. Para eso hemos investigado arquitecturas neuronales”, añade el doctor Saralegi. Han utilizado arquitecturas neuronales profundas alimentadas con ejemplos: “Eso significa que los modelos de búsqueda y los modelos de respuesta a las preguntas se entrenan a través del aprendizaje automático profundo”.
Una vez extraída la serie de documentos, se vuelven a procesar mediante un sistema de preguntas y respuestas, para así obtener respuestas concretas: “Hemos construido el motor que responde a las preguntas; proporcionándole una pregunta y un documento, el motor es capaz de detectar si la respuesta se encuentra o no en el documento, y en caso afirmativo, dice exactamente dónde se encuentra”, explica el doctor Agirre.
Un prototipo fácilmente comercializableLos investigadores creen que los resultados obtenidos son muy prometedores: “De las técnicas y las evaluaciones que hemos analizado en nuestros experimentos, hemos llevado al prototipo aquellas que han dado mejores resultados”, señala el investigador de Elhuyar. Han establecido una base tecnológica sólida, y han publicado varios artículos científicos al respecto. “Hemos conseguido otra manera de realizar búsquedas para casos de necesidad de información urgente, que facilita el proceso de consumo de información. A nivel de investigación hemos demostrado que la tecnología propuesta funciona, y que el sistema da buenos resultados”, apunta Agirre.
“Nuestro resultado es un prototipo de un proyecto de investigación básica. No se trata de un producto comercial”, destaca Saralegi. Pero este tipo de prototipos se puede escalar fácilmente y en poco tiempo, lo que permitiría comercializarlos y ponerlos al alcance de la sociedad. Los resultados abundan en la tendencia de que la inteligencia artificial permitirá disponer de instrumentos cada vez más potentes para trabajar con grandes bases de documentos. “Estamos avanzando muy rápidamente en este ámbito. Y, además, todo lo que se investiga llega fácilmente al mercado”, concluye el investigador de la UPV/EHU.
Referencia:
Arantxa Otegi, Iñaki San Vicente, Xabier Saralegi, Anselmo Peñas, Borja Lozano, Eneko Agirre (2022) Information retrieval and question answering: A case study on COVID-19 scientific literature Knowledge-Based Systems doi: 10.1016/j.knosys.2021.108072
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Respuestas a preguntas en lenguaje natural, el nuevo paradigma de los buscadores basados en inteligencia artificial se ha escrito en Cuaderno de Cultura Científica.
El mapa de historias de las estrellas
El primer sistema de clasificación estelar del Observatorio de Harvard atendía principalmente a su color. Fue definido por la astrónoma Annie Jump Canon y utilizaba siete letras (OBAFGKM) que, según se supo más tarde, identificaban la temperatura de las estrellas. Sin embargo, pronto resultó evidente que aquel catálogo unidimensional resultaba insuficiente para representar la diversidad del cielo nocturno y Antonia Maury fue la primera astrónoma que se atrevió a ampliarlo. Reparó en que las líneas espectrales de algunas estrellas estaban mucho más definidas que otras. Aunque en un primer momento el origen de aquellas diferencias no estaba claro, su apreciación permitió añadir una segunda dimensión al catálogo astronómico de Harvard. Y fue entonces cuando todas las piezas empezaron a encajar. Como un mapa que se despliega y revela rutas insospechadas, las estrellas empezaron a dibujar sus historias sobre el papel.
Esto es precisamente lo que representa el diagrama Hertzsprung-Russell. Se trata de un mapa de historias estelares, la foto de los caminos que comparten. En él, las estrellas aparecen representadas en función de su color (en horizontal) y su magnitud absoluta (en vertical). Las letras del sistema de Harvard sirven para graduar el eje horizontal, mientras que el eje vertical es el que ayudó a descubrir Maury.
Resultó que las diferencias que había observado en las líneas espectrales de las estrellas dependían, precisamente, de su luminosidad. En concreto, cuando una estrella es más densa y tiene más presión en su atmósfera, presenta un ensanchamiento de las líneas espectrales correspondientes al gas que se encuentra en su superficie. Existen otros factores que pueden producir este efecto, como la abundancia de cierto elemento químico, por ejemplo, no es un puzzle que se pueda resolver a partir de una única variable. Pero aquella observación fue la primera pista que más tarde permitiría identificar diferencias en la gravedad, la densidad y la presión atmosférica de una estrella, en función de su espectro.
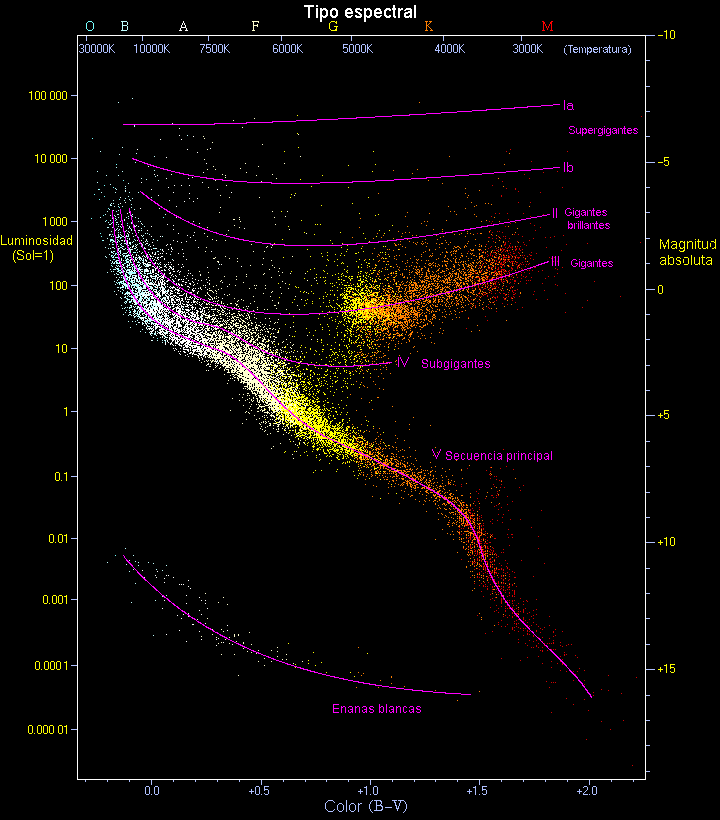 Diagrama de Hertzsprung-Russell. Fuente: Wikimedia Commons
Diagrama de Hertzsprung-Russell. Fuente: Wikimedia CommonsUn mapa de historias
¿Pero por qué digo que este diagrama es un mapa de historias? Bien, resulta que no todas las estrellas tienen el mismo ciclo de vida. Todas nacen, se consumen y mueren, pero lo que les sucede en el camino y el modo en que finalmente desaparecen depende crucialmente de su masa. De hecho, cuando uno representa las estrellas en función de su magnitud y su temperatura, es fácil ver que no se distribuyen al azar. La mayoría se sitúan sobre ciertas líneas o ramas.
Son estas líneas las que nos cuentan su evolución y las que recoge el sistema de clasificación de Yerkes. Se trata de un sistema de clasificación que fue introducido en 1943 por William Wilson Morgan, Philip C. Keenan y Edith Kellman (se lo conoce también como MKK, por las siglas de estos autores) y cataloga las estrellas en varios tipos y subtipos situados sobre distintas ramas sobre el diagrama.
En el extremo superior, por ejemplo, encontramos las estrellas hipergigantes (tipo 0). Son las estrellas más luminosas que existen, al menos 30 veces más masivas que el Sol y son extremadamente raras. Queman combustible a una gran velocidad, hasta que colapsan bajo su propio peso y estallan en forma de supernova. Con semejante ritmo de vida, son estrellas con una esperanza de vida muy corta (corta para una estrella, se entiende). Mueren tras unos pocos millones de años, cerca de su lugar de formación, y pueden dejar como remanente un agujero negro tras de sí. Nuestro Sol, por comparación, vivirá miles de millones de años.
En el extremo opuesto encontramos las enanas blancas. Su historia es muy diferente. Suelen ser el núcleo inerte de estrellas viejas que han agotado sus fuentes de energía. Como ya han alcanzado pacíficamente la jubilación, estas estrellas se enfrían lentamente a lo largo de miles de millones de años moviéndose hacia la derecha del diagrama.
De entre todas las estrellas, las más frecuentes son las estrellas enanas (tipo V) que dan forma a la línea más visible del diagrama Hertzsprung-Russell. Se trata de la secuencia principal, que acoge a nuestro propio Sol desde hace 4500 millones de años y que lo seguirá haciendo durante al menos otro 4500 millones más. Sobre esta rama se encuentra la infancia de todas las estrellas, la época inicial de su vida donde se alimentan principalmente de hidrógeno. Pero hablaremos de ellas con más detalles en la próxima y última entrada de esta serie.
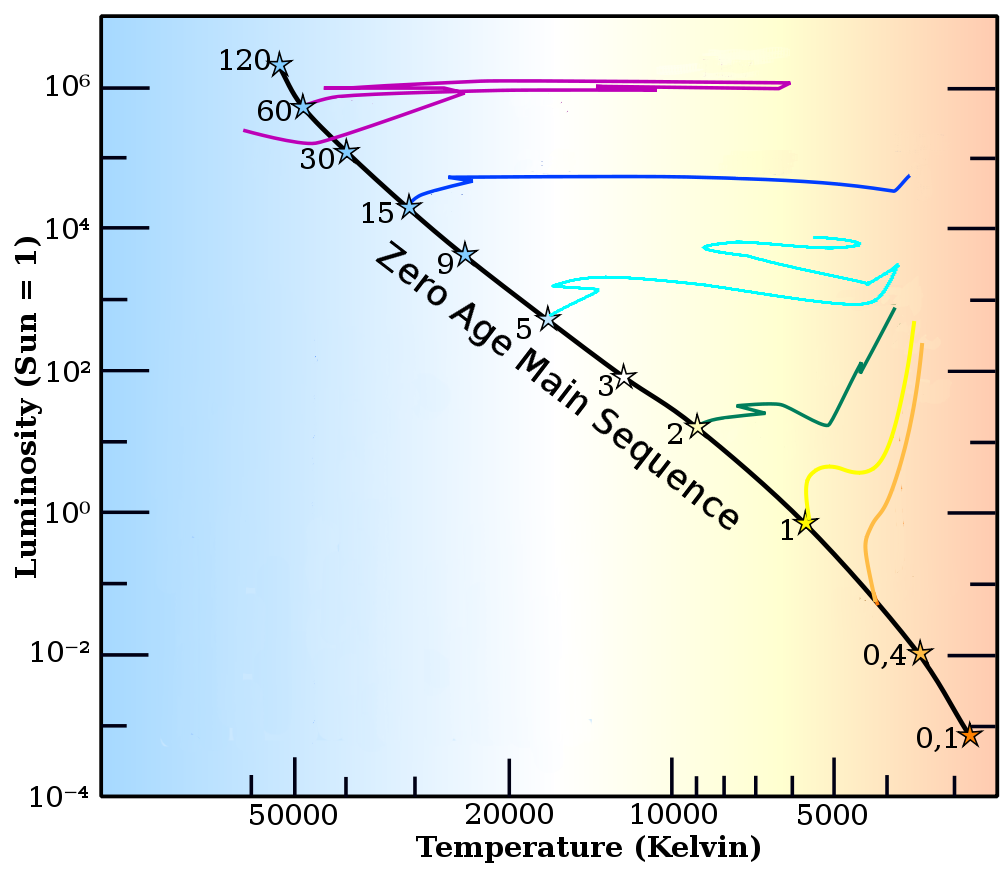 Evolución de las estrellas a lo largo de la Secuencia Principal. Fuente: Wikimedia Commons.
Evolución de las estrellas a lo largo de la Secuencia Principal. Fuente: Wikimedia Commons.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El mapa de historias de las estrellas se ha escrito en Cuaderno de Cultura Científica.
Fútbol, sorteos y matemáticas
El fútbol es un deporte que levanta pasiones. Por este motivo, no es de extrañar que cuando un equipo de fútbol se clasifica para una final, las personas aficionadas de ese equipo muevan cielo y tierra para conseguir una entrada para el partido. Una entrada para la final se convierte en un pequeño tesoro.
 Diego Maradona levantando la Copa Mundial de Fútbol de 1986 en México. Foto: El Gráfico / Wikimedia Commons
Diego Maradona levantando la Copa Mundial de Fútbol de 1986 en México. Foto: El Gráfico / Wikimedia Commons
La historia que vamos a contar en esta entrada del Cuaderno de Cultura Científica tuvo lugar hace ya unos años, cuando cierto equipo de fútbol se clasificó para una final importante. Como es comprensible, su afición estaba deseosa de asistir a la misma, pero las entradas para el partido escaseaban. El Club, que disponía de una cierta cantidad de entradas para la final, realizó un sorteo de las mismas entre sus socios, en el que me vi implicado sin ser yo una persona muy aficionada al fútbol.
Al día siguiente del sorteo, un periodista que había estado presente en el desarrollo del mismo se puso en contacto conmigo para que analizáramos juntos algunas de sus cifras, ya que no le cuadraban. A pesar de que yo estaba preparándome para asistir esa misma tarde a un espectáculo del Circo del Sol, saqué el tiempo suficiente para que nos reuniéramos y me explicara todo el asunto.
 Imagen del cartel del espectáculo Varekai del Circo del Sol
Imagen del cartel del espectáculo Varekai del Circo del Sol
El club sorteaba 14.800 entradas y se inscribieron 33.301 socios a través de 25.746 solicitudes, ya que cada solicitud podía llevar agrupados hasta cuatro socios distintos, con lo cual si salía elegido su número de solicitud les corresponderían tantas entradas como socios agrupados. De esta forma, puesto que se contabilizaron 25.746 solicitudes de 33.301 socios, se sabía de inicio que había 33.301 – 25.746 = 7.555 socios agrupados como segundo, tercero o cuarto socio de alguna de las solicitudes (que podemos denominar “socios agrupados extra”).
Algo andaba mal
La siguiente información que me proporcionó el periodista, fue que el club había informado el segundo día del plazo para la inscripción que ya se habían apuntado 19.654 socios en un total de 13.449 solicitudes, es decir, ya había 6.205 agrupados extra. La primera conclusión que se podía extraer de esta información, puesto que había en total 7.555 socios agrupados extra, fue que entre los números de las solicitudes 13.450 y 25.746 – es decir, después del segundo día- solamente podía haber 7.555 – 6.205 = 1.350 socios agrupados extra. Este dato resultó ser trascendental para descubrir que algo andaba mal.
Además, el sorteo fue un poco enrevesado. En el mismo se sacaban cinco números y se entregaban 2.960 entradas (1/5 de las 14.800 entradas en total a repartir) a partir de cada uno de ellos, teniendo además en cuenta que había solicitudes con socios agrupados y para una misma solicitud podían corresponderle hasta cuatro entradas. Por lo que las cuentas no cuadraban y así lo reflejó el periodista –que realizó un magnífico trabajo de investigación- en el artículo publicado al día siguiente en el periódico para el que trabajaba:
“Las entradas repartidas entre el número 18.428 y el 19.956 (ambos inclusive) son, según las bases del sorteo, 2.960. Como quiera que ahí solo aparecen 1.529 números de agraciados resulta que en teoría hay 1.431 agrupadas en esta horquilla. Aquí aparece el primer problema matemático. Son 81 más de las en teoría 1.350 asignadas para todos los números situados por encima del registro 13.449.
Entre los números 20.299 y el 24.903, ambos inclusive, hay un total de 4.605 solicitudes para 8.880 entradas, dado que al haberse superpuesto tres números agraciados (20.299, 21.549 y 22.496) a este grupo le corresponden el triple. La resta entre el número disponible y la cifra de solicitudes afortunadas revela que aquí se han agrupado 4.275 personas. Si sumamos esta cifra a los agrupados entre el 18.428 y el 19.956 resulta que los socios ‘concentrados’ desde el segundo día son 5.706, cuando según datos oficiales del club en ningún caso podía ser mayor de 1.350.”
Es decir, podíamos deducir por la información suministrada por el club en el sorteo que la cantidad de socios agrupados extra, con números por encima de 13.450, que habían recibido entradas para la final eran 5.706, pero resulta que solo había 1.350 agrupados extra por encima de 13.450. En conclusión, esta cuenta nos decía que, al menos, 5.706 – 1.350 = 4.356 entradas estaban asignadas a socios agrupados extra inexistentes. Se desconocía que había pasado con ellas. Al día siguiente el club dio a conocer que se había producido un error informático en la asignación de entradas.

La ventaja de empezar por 2
Por otra parte, el método de realización del sorteo también tenía su propio interés matemático. El sorteo no era un sorteo de los llamados “justo”, puesto que no todas las solicitudes, todos los números, tenían las mismas probabilidades de salir elegidos.
Como había 25.746 solicitudes, el club decidió poner 5 urnas. La primera (para las decenas de millar) con 3 bolas -0,1,2-, y las demás con 10 bolas –del 0 al 9- (unidades de millar, centenas, decenas y unidades), aunque con correcciones durante el sorteo, ya que si, por ejemplo, la primera bola era un 2, se quitaban las bolas 6, 7, 8 y 9 de la siguiente urna, ya que la segunda bola solo podía tomar valores entre 0 y 5 (puesto que el número más alto posible era el 25.746), y de forma similar para el resto de urnas.
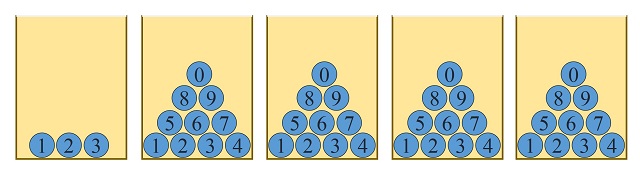
El club no se dio cuenta, a la hora de elegir el método de sorteo, de que con el que se había propuesto, los números que empezaban por 2 tenían más posibilidades de salir que los que empezaban por 0 o 1. Para entenderlo mejor, simplifiquemos un poco y supongamos que tenemos que sacar un número premiado con ese método sobre un total de 20.001 solicitudes. Fijémonos en dos números, A = 13.437 y B = 20.001, ¿tendrán las mismas probabilidades de salir? Para empezar en la primera urna, cada número -0,1,2- tiene las mismas probabilidades de salir (de hecho, 1/3). Si la primera bola es 1, entonces la probabilidad de que salga el número A es de 1 entre 10.000, ya que hay 10.000 números que empiezan por 1 –desde el 10.000 al 19.999-, pero si sale 2 en la primera urna, B tiene una probabilidad del 50% -1 entre 2- de salir, puesto que solamente hay dos números que empiezan por 2 –20.000 y 20.001-.
Efectivamente, el sorteo no era justo, no todos los números tenían la misma probabilidad de salir. De hecho, de los cinco números que se sacaron, tres empezaban por 2.
 Pavimento con forma de balón de fútbol en Friburgo de Brisgovia (Alemania). Foto: Andreas Schwarzkopf / Wikimedia Commons
Pavimento con forma de balón de fútbol en Friburgo de Brisgovia (Alemania). Foto: Andreas Schwarzkopf / Wikimedia Commons
Bibliografía:
1.- Raúl Ibáñez, Leer el periódico con ojos matemáticos, ConCIENCIAS.digital: revista de divulgación científica de las Facultad de Ciencias de Zaragoza, no. 8, 2011, págs. 48-57.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Fútbol, sorteos y matemáticas se ha escrito en Cuaderno de Cultura Científica.
Einstein y el experimento de Michelson-Morley
Llevado a cabo en 1887, el experimento de Michelson-Morley se considera el trabajo definitivo que terminó eliminando la creencia decimonónica de que las ondas luminosas viajaban a través de un medio llamado éter. La historia estándar que se cuenta es que una vez que el experimento de Michelson-Morley probó que el éter era falso, todo el mundo supo que había una crisis, a la que puso fin Einstein cuando intervino resueltamente para resolver el problema con la teoría especial de la relatividad en 1905. Pero esta es una versión demasiado simplificada de lo que realmente ocurrió…
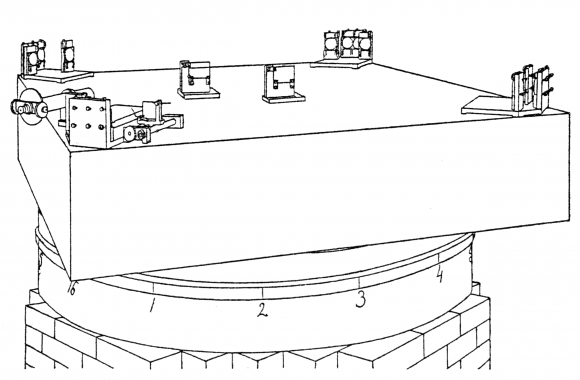 Esquema del experimento de Michelson-Morley. Fuente: Wikimedia Commons
Esquema del experimento de Michelson-Morley. Fuente: Wikimedia CommonsAlbert Abraham Michelson comenzó a trabajar en la búsqueda del éter cuando era un joven estudiante en Berlín con un permiso de la Marina de los Estados Unidos. Más tarde, cuando se convirtió en profesor de física en el Colegio Case de Ciencia Aplicada de Cleveland, formó equipo con Edward Williams Morley, un químico también estadounidense que trabajaba en la cercana Universidad Western Reserve. Morley tenía fama de gran experimentador, y a Michelson le atraía el reto de crear un experimento meticuloso para medir la velocidad de la Tierra a través del éter que se suponía que llenaba el espacio. Las mediciones tenían que ser tan precisas que muchos dijeron que no podían hacerse. (Más tarde Michelson le diría a Einstein que había empleado tanta energía para conseguir la precisión necesaria simplemente porque era “divertido”).
James Clerk Maxwell fue el primero en describir la luz como una onda electromagnética. En esa época, los físicos comprendían las ondas bastante bien. Las ondas del sonido, por ejemplo, se crean cuando un objeto que vibra comprime y descomprime alternativamente el medio que le rodea. En el aire, paquetes de aire más y menos densos viajan al oído y son interpretados por el cerebro. Las ondas en el agua tienen crestas y valles en vez de diferencias de densidad. Pero tanto el agua como el aire son medios necesarios para la propagación del sonido. Maxwell creía que la luz igualmente debía emplear un medio, una misteriosa sustancia llamada éter. Según la teoría, el éter estaría en reposo con respecto a un espacio absoluto del universo, y la Tierra, naturalmente, viajaría por él. Maxwell propuso que, por lo tanto, debería existir un “viento de éter” de algún tipo, que soplaría en la cara de un observador que mirase en el sentido del movimiento de la Tierra, y en su espalda si miraba en sentido contrario. Cabría esperar entonces que la luz viajase a diferentes velocidades dependiendo de la dirección en la que se moviese a través del éter, parecido a una persona que se mueve más fácilmente con el viento a favor que en contra. La idea de que la luz se puede mover con velocidades diferentes, en un mismo medio en idénticas condiciones, dependiendo solo de la dirección de propagación, está en el corazón mismo del experimento de Michelson-Morley. Y esta es la idea que Einstein terminaría haciendo desaparecer.
El experimento
El experimento que se cita oficialmente como el experimento de Michelson-Morley tuvo lugar en 1887 [1] y utilizaba un diseño bastante innovador que se basaba en una técnica desarrollada por Michelson, la interferometría (Michelson recibiría el premio Nobel de física en 1907 por sus instrumentos ópticos de precisión y las mediciones realizadas con ellos). La interferometría depende del hecho de que cuando dos ondas se cruzan forman patrones muy concretos. Un experimento de interferometría comienza dividiendo un haz de luz, haciendo después que cada uno de los dos nuevos rayos viajen caminos distintos, para luego unirlos en una pantalla. Analizando los patrones resultantes se puede obtener información sobre la velocidad y la distancia recorrida por la luz. Michelson ya había usado la interferometría tanto para conseguir la medición más precisa hasta la fecha de la velocidad de la luz como para determinar la longitud oficial del metro para la Oficina Nacional de Estándares de los Estados Unidos.
Para su experimento, Michelson y Morley hicieron que dos rayos de luz viajasen en ángulo recto uno del otro: uno viajaba en la misma dirección que el éter y el otro la cruzaba. Imaginemos dos personas nadando en un río, una va corriente arriba y luego a favor de corriente, mientras que la otra nada directamente a un punto al otro lado del río y vuelta. Ambos nadadores se tienen que enfrentar a la corriente pero de forma diferente y, consecuentemente, el tiempo que emplean para recorrer exactamente la misma distancia será diferente. Si la Tierra viaja a través del éter, el éter crea una corriente (como un río), y un rayo de luz que viaje en contra y luego a favor debería tardar menos en recorrer una distancia determinada que otro que la atraviese en ángulo recto. Esta era la hipótesis que Michelson y Morley intentaban confirmar con su experimento.
El experimento estaba muy bien diseñado, pero por mucho que repitieron la medición, ambos rayos empleaban la misma cantidad de tiempo en sus viajes. La pareja comprobó y recomprobó el dispositivo experimental y repitieron las mediciones varias veces después de cada comprobación, siempre con el mismo resultado. El dispositivo, que se encontraba en un sótano con paredes de ladrillo, estaba instalado sobre un bloque de mármol que flotaba sobre una balsa de mercurio, lo que permitía girarlo para estudiar todos los ángulos posibles con respecto al “viento de éter”; ningún ángulo probado dio un resultado diferente. La reputación enorme de la que gozaban Michelson y Morley en la comunidad científica hizo que los físicos más famosos de la época aceptaran como válido un resultado tan inesperado. Claramente, había un problema con la teoría del éter.
Sin embargo, el concepto del éter, no fue completamente descartado en ese momento. El consenso era que la hipótesis no estaba completa. El mismo Michelson repitió el experimento en numerosas ocasiones a lo largo de su vida, cambiando incluso la localización del dispositivo (lo llevó a lo alto de una montaña) para ver si había variaciones en la intensidad del presunto “viento de éter” que permitiesen detectar diferencias en las mediciones. [3]
¿Qué sabía Einstein?
Aunque había físicos que conocían el trabajo de Michelson y Morley, y sabían que sus resultados debían incorporarse a una nueva teoría de la luz, no está claro que Einstein, el que finalmente proporcionó esa teoría, tuviese conocimiento de él. Su artículo sobre la relatividad especial está claro que no hace referencia a los resultados del experimento, si bien es cierto que este artículo no hace referencia a casi nada, ya que lo que se proponía era tan novedoso que Einstein podía afirmar que no se basaba en el trabajo de nadie.
Años más tarde Einstein se contradiría a sí mismo sobre el asunto de si conocía el experimento de Michelson-Morley. Dijo muchas veces que no tenía noticias de él y, de hecho, no lo menciona en sus Notas autobiográficas en las que describe cómo desarrolló sus teorías. Ya mayor afirmó, sin embargo, que la primera referencia del experimento la obtuvo del estudio del trabajo de Lorentz en 1895, y en algunas de sus primeras cartas (1899) que se conservan discute un artículo de Wien que contiene una referencia al experimento.
Independientemente de si Einstein conocía el experimento mismo de Michelson-Morley, lo que si parece claro es que desarrolló su teoría de la relatividad especial creyendo firmemente que el éter no existía. Esta convicción no fue apriorística. La lectura de otros grandes científicos de su época, muchos de los cuales ciertamente conocían el experimento, habría influido con toda seguridad en las convicciones de Einstein.
Después de la publicación de la teoría especial de la relatividad, Einstein tuvo conocimiento fehaciente del trabajo de Michelson y Morley [2] y, de hecho, estuvo en contacto con Michelson. Poco antes de su fallecimiento, en 1931, Michelson asistió a una cena en honor a Einstein en California. En su discurso Einstein dijo:
“Usted, honorable Dr. Michelson, comenzó este trabajo cuando yo era un jovenzuelo que no levantaba un metro del suelo. Fue usted el que guio a los físicos por nuevos caminos, y gracias a su maravilloso trabajo experimental preparó el terreno para el desarrollo de la teoría especial de la relatividad”.
El comentario honraba a Michelson a la vez que eludía el asunto de si Einstein se había basado en su trabajo.
Después de la muerte de Michelson, en honor al 70 aniversario de Einstein, el famoso físico norteamericano Robert Millikan, que era uno de los protegidos de Michelson, escribió un artículo en el que establecía una conexión directa entre la teoría de la relatividad y la anterior búsqueda del éter de Michelson. Millikan escribió:
“Se puede ver la teoría de la relatividad especial como basada esencialmente en una generalización del experimento de Michelson” [no nombra a Morley]. A continuación dice que tras la demostración de que no había éter “…los físicos de la luz andaban en tinieblas” buscando una nueva teoría de la luz. Millikan añade, “Entonces Einstein nos llamó a todos, ‘Aceptemos simplemente esto como un hecho experimental establecido y a partir de ahí veamos cuáles son sus consecuencias inevitables’, y él mismo se dispuso a la tarea con una energía y una capacidad que poca gente posee en esta Tierra. Así nació la teoría especial de la relatividad”.
De la misma forma que Atenea surgió hecha y derecha de la cabeza de Zeus, así describió Millikan la teoría de Einstein como surgida del trabajo de Michelson.
La ciencia real, igual que la historia real, no es tan sencilla, pero la idea de que el experimento de Michelson-Morley llevó directa y claramente a la teoría especial de la relatividad es algo que pertenece al folklore de Einstein desde entonces, como es fácilmente comprobable en cualquier libro de texto.
Referencias:
[1] Michelson,AA, & Morley,EW (1887). On the Relative Motion of the Earth and the Luminiferous Ether The American Journal of Science, 34 (203), 833-845
[2] F.R. Villatoro (2009) ¿Conocía Einstein el experimento de Michelson-Morley en 1905 y le influyó en su teoría? La ciencia de la mula Francis
[3] Una reflexión filosófica interesante y pertinente a este respecto puede encontrarse aquí: El experimento crucial que nunca existió
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 16 de agosto de 2009.
El artículo Einstein y el experimento de Michelson-Morley se ha escrito en Cuaderno de Cultura Científica.
Los glaciares olvidados de Marte
Cuando observamos Marte, ya sea desde nuestros telescopios terrestres o bien desde las misiones espaciales en órbita alrededor de este, una de las cosas más llamativas y que más contrastan con ese ubicuo color rojo de su superficie es la presencia de dos casquetes polares que cubren las latitudes más altas del planeta y que de algún modo nos recuerdan a nuestro planeta.
 Marte desde el telescopio espacial Hubble en Mayo de 1999. Créditos: NASA, ESA, STScI y AURA
Marte desde el telescopio espacial Hubble en Mayo de 1999. Créditos: NASA, ESA, STScI y AURA
Desde el punto de vista geológico, los glaciares son uno de los grandes agentes de erosión, transporte y sedimentación que se ocurren en la superficie de los planetas, ya que el fluir del hielo es capaz con el paso del tiempo de ir esculpiendo grandes valles y al mismo tiempo transportar los restos de la roca que va rasgando a su paso -y cayendo sobre estos- a veces a grandes distancias, donde se depositarán.
Pero los glaciares también nos pueden aportar una gran cantidad de información sobre el clima de los planetas. Estudiando las capas de hielo que forman los glaciares, ya sea viendo como se superponen unas a las otras, analizando la composición de las pequeñas burbujas de aire que queden atrapadas o fijándonos en las capas de polvo o ceniza que pueden depositarse entre estas, podemos hacer inferencias sobre el clima en el cual se formaron estos glaciares. Son, por lo tanto, un magnífico indicador del cambio climático que ocurre en un planeta.
 El glaciar Viedma desemboca en el lago del mismo nombre. En la imagen podemos ver como confluyen distintos glaciares, marcados por unas líneas negras llamadas morrenas, unas acumulaciones de restos de suelo y rocas transportadas por el glaciar. Fuente: Programa Copernicus de la Unión Europea.
El glaciar Viedma desemboca en el lago del mismo nombre. En la imagen podemos ver como confluyen distintos glaciares, marcados por unas líneas negras llamadas morrenas, unas acumulaciones de restos de suelo y rocas transportadas por el glaciar. Fuente: Programa Copernicus de la Unión Europea.Hoy sabemos, que salvo en los polos y las regiones más próximas a estos, probablemente solo a partir de la latitud 60º, las condiciones de Marte no permiten la existencia de hielo, en este caso de hielo de agua, en la superficie, ya que este rápidamente se sublima, pasando del estado sólido al gaseoso.
Sin embargo, en algunos lugares de Marte, como puede ser la región de Tharsis, hogar de algunos de los volcanes más altos del Sistema Solar, aparecen formas sobre su superficie que nos recuerdan a los depósitos de sedimentos dejados en nuestro planeta por glaciares en retroceso, marcando distintas etapas en las que el hielo se ha ido retirando y dejando sobre el suelo aquellos materiales que transportaba.
Además, estas formas que vemos en Marte y nos recuerdan a los glaciares son relativamente recientes, es decir, que se formaron hace poco en tiempo geológico. ¿Cómo sabemos eso? Puesto que no podemos ir a tomar muestras para ponerles una edad en un laboratorio, a través de las imágenes podemos datar las superficies de una manera más o menos absoluta contando el número y el tamaño de los cráteres que hay en esa zona.
Me explico: Cuando se forma una nueva superficie en un planeta, pongamos por ejemplo una colada de lava, sobre esta no hay cráteres. Para que se formen, tendrán que impactar sobre la colada cuerpos que provengan del espacio, como asteroides y meteoroides.
Cuanto más tiempo pase desde que se formó la colada de lava, más probabilidades tendrá de que se hayan podido formar cráteres. Obviamente, en nuestro planeta no es una buena forma de datar las superficies ya que los procesos atmosféricos y la tectónica de placas se encargan de ir renovando la superficie a un ritmo importante, pero en cuerpos sin atmósfera como la Luna, o con una atmósfera muy tenue, como Marte, se han podido desarrollar escalas temporales basadas en cuantos cráteres y que tamaños encontramos en una superficie, de tal manera que cuantos más cráteres tenga un lugar, por norma general, más antiguo será.
La estabilidad del hielo
Hecha esta breve acotación, decíamos que estos glaciares marcianos parecían ser recientes, ¿pero cómo es posible si las condiciones actuales de la superficie hacen que el hielo no sea estable?
Durante años se pensaba que muchos de los glaciares, o los restos de estos, que veíamos en la superficie, en realidad estaban formados por el movimiento del hielo que hay debajo de la superficie, en suelos congelados muy ricos en hielo de agua donde este sería más estable a lo largo del tiempo debido a la protección que le ofrecerían los materiales que hay por encima.
Pero lo cierto es que hoy en día se sabe que muchos de estos glaciares en realidad se formaron por la acumulación y movimiento de hielo a partir de la nieve que caía desde la atmósfera, como ocurre en la actualidad en la Tierra, ya que las formas que vemos en el terreno sugieren la existencia de precipitaciones.
Algo tuvo que ocurrir a lo largo de los últimos millones de años en Marte (y quizás más tiempo), que permitiese la existencia de nieve y con esta la formación de glaciares en latitudes alejadas de los polos, incluso cercanas al ecuador. Quizás una pequeña edad del hielo marciana. Y eso que Marte ya es frío por si solo.
La teoría más plausible apunta a que la inclinación del eje de rotación de Marte varía mucho a lo largo del tiempo. Ahora mismo, se encuentra en unos 25º, y el de nuestro planeta, para comparar, en unos 23,5º. Pero hay momentos en los que su inclinación puede superar los 45º.
Esto provoca que en los momentos de mayor inclinación de su eje, los polos reciban mucha más insolación, aumentando la temperatura y provocando que se transforme parte del hielo de agua y de dióxido de carbono en gas, que en primer lugar aumentan la presión de la atmósfera, logrando que en una mayor parte del planeta Marte el hielo pueda ser estable en superficie.
Por otro, el vapor de agua podría condensarse formando nubes en latitudes más bajas y acabar precipitando en forma de nieve, acumulándose en algunos lugares que darían lugar poco a poco a los glaciares. Probablemente los glaciares que vemos en la superficie no se hayan formado en un único episodio de inclinación extrema, sino que necesitaran de múltiples episodios para alcanzar las dimensiones que observamos.
Con el tiempo, el hielo más próximo a la superficie iría sublimándose y desapareciendo, dejando únicamente los depósitos sedimentarios que hoy somos capaces de reconocer en las imágenes… pero esto no es todo.
Resulta que en latitudes medias, a partir de los 30º, si existe en la actualidad hielo bajo la superficie. Tanto que podríamos cubrir Marte con una capa de hielo de un metro solo con el que existe entre la latitud 30º y 50º.
 La erosión nos permite ver uno de estos depósitos de hielo en la superficie de Marte como si le hubiésemos hecho un corte. El hielo, aquí en color azul, se encuentra protegido por una capa de polvo y rocas de color blanquecino, que evita su rápida sublimación. Fuente: NASA/JPL/UArizona..
La erosión nos permite ver uno de estos depósitos de hielo en la superficie de Marte como si le hubiésemos hecho un corte. El hielo, aquí en color azul, se encuentra protegido por una capa de polvo y rocas de color blanquecino, que evita su rápida sublimación. Fuente: NASA/JPL/UArizona..Si lo comparamos con el agua de la Tierra, nos parecerá poco, ya que ese volumen se corresponde aproximadamente con una diezmilésima parte del agua que hay en nuestros océanos, pero si pensamos en el futuro de la exploración humana del espacio, son unas reservas muy importantes de cara a permitirnos explotar ese recurso in situ, y que pueda abastecer a futuras bases o colonias y que permitan una estancia prolongada del ser humano en el planeta rojo.
El caso es que ese hielo que hoy observamos en las latitudes medias y que conocemos gracias a imágenes y datos de radar, sigue existiendo hoy día pese a que las condiciones no le son favorables gracias a que está cubierto por una capa de polvo y rocas que evita que se vaya sublimando.
Estos depósitos podrían también representar distintos momentos de acumulación y por lo tanto, diferentes momentos temporales y climáticos del planeta y su estudio de detalle, ya sea con técnicas robóticas más sofisticadas y precisas que de las que disponemos hoy día, o in situ por seres humanos en el futuro, podría abrirnos una ventana a conocer mejor la evolución reciente del clima marciano.
Referencias:
Fastook, J. L., Head, J. W., Marchant, D. R., & Forget, F. (2008). Tropical mountain glaciers on Mars: Altitude-dependence of ice accumulation, accumulation conditions, formation times, glacier dynamics, and implications for planetary spin-axis/orbital history. Icarus, 198(2), 305-317. doi: 10.1016/j.icarus.2008.08.008
Forget, F., Haberle, R. M., Montmessin, F., Levrard, B., & Head, J. W. (2006). Formation of Glaciers on Mars by Atmospheric Precipitation at High Obliquity. Science, 311(5759), 368-371. doi: 10.1126/science.1120335
Karlsson, N. B., Schmidt, L. S., & Hvidberg, C. S. (2015). Volume of Martian midlatitude glaciers from radar observations and ice flow modeling. Geophysical Research Letters, 42(8), 2627-2633. doi: 10.1002/2015GL063219
The HRSC Co-Investigator Team, Head, J. W., Neukum, G., Jaumann, R., Hiesinger, H., Hauber, E., Carr, M., Masson, P., Foing, B., Hoffmann, H., Kreslavsky, M., Werner, S., Milkovich, S., & van Gasselt, S. (2005). Tropical to mid-latitude snow and ice accumulation, flow and glaciation on Mars. Nature, 434(7031), 346-351.doi: 10.1038/nature03359
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Los glaciares olvidados de Marte se ha escrito en Cuaderno de Cultura Científica.
La benevolencia social tiene más de una cara
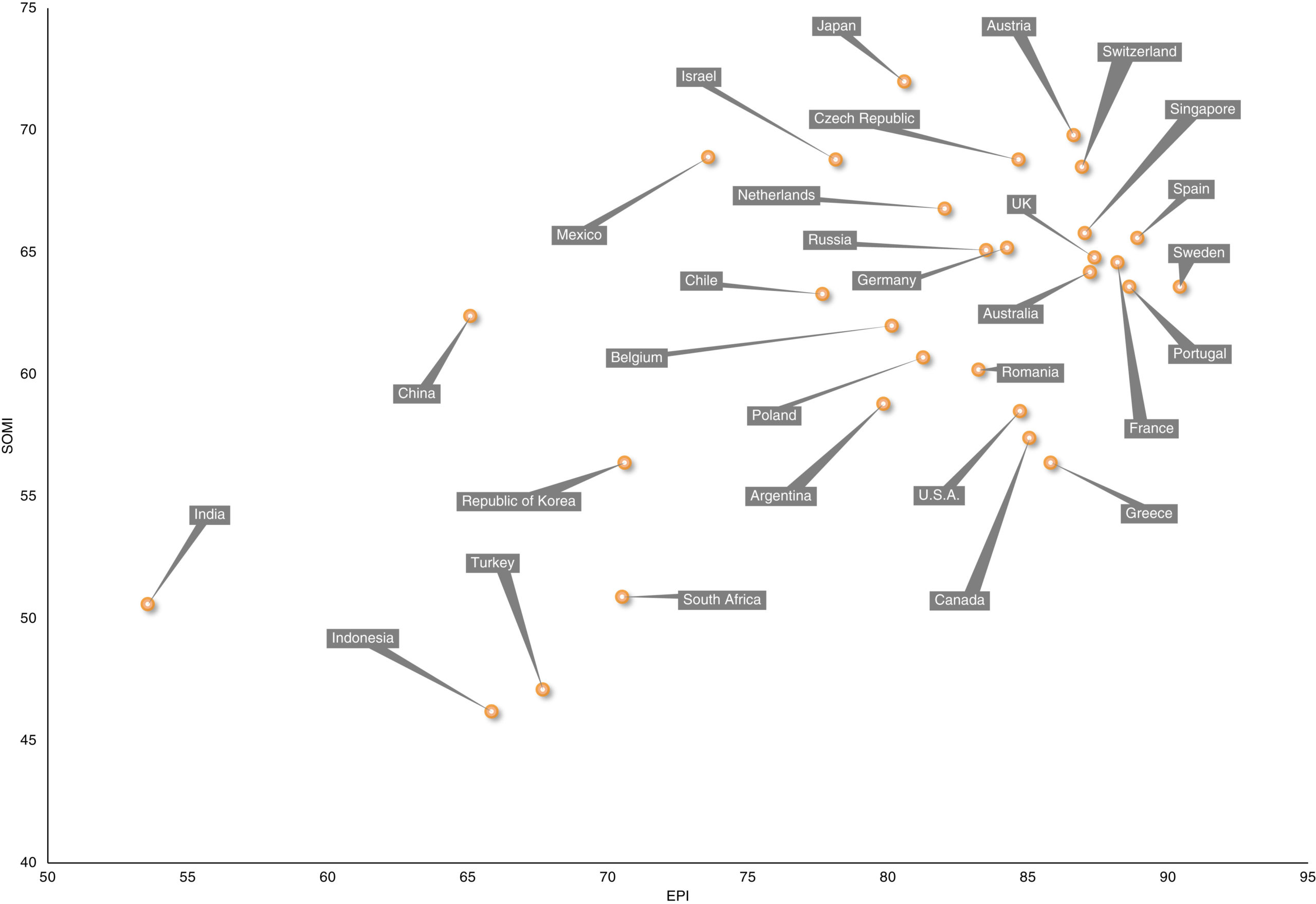 Conciencia social (SoMi) frente al Índice de Actuación Ambiental (EPI) para una selección de países. Véase el texto para una explicación. Fuente: Van Doesum et al (2021)
Conciencia social (SoMi) frente al Índice de Actuación Ambiental (EPI) para una selección de países. Véase el texto para una explicación. Fuente: Van Doesum et al (2021)En ciertas áreas de psicología y de economía son habituales experimentos en los que se valora el grado de prosocialidad de las personas. En esos experimentos la generosidad, el altruismo o la cooperación conllevan algún coste, ya sea de tiempo, dinero o esfuerzo, para favorecer a los demás, o para castigarlos.
Sin embargo, en la vida hay comportamientos que también pueden ser calificados de prosociales sin que conlleven coste o esfuerzo alguno para quien los practica o, si acaso, suponen alguna pequeña molestia. Se trata de gestos cotidianos que denotan una cierta benevolencia o amabilidad para con los demás, que hacen la convivencia más agradable, pero que no modifican sustancialmente la calidad de vida de quienes se benefician de ellos. Quienes se han ocupado de estos asuntos lo llaman social mindfulness, algo así como conciencia social.
Imagine una situación en la que llega tarde a una fiesta y usted sabe que otra persona llegará algo más tarde aún, y que solo queda una copa de vino blanco y varias de tinto. Puede usted optar por tomar una de las copas de tinto o por la de blanco. En el primer caso, la segunda persona seguirá teniendo, como usted, posibilidad de elegir; en el segundo, sin embargo, no podrá hacerlo. Si se encuentra usted una bufanda en el suelo paseando puede dejarla donde está o, alternativamente, colocarla en un lugar como un banco o un seto en posición bien visible. La segunda opción casi no le cuesta nada, es apenas un gesto. En la vida hay infinidad de situaciones como estas.
Pues bien, resulta que cuando se evalúa este tipo de comportamientos en diferentes países mediante experimentos que simulan las condiciones relatadas para la fiesta a la que dos personas llegan tarde, aparecen diferencias muy grandes entre unos países y otros, asombrosamente grandes diría yo. También hay diferencias entre individuos, claro.
En un estudio internacional de gran alcance, con más de ocho mil personas pertenecientes a treinta países industrializados de muy diversas culturas, han evaluado el grado de asociación entre la conciencia o benevolencia social y un buen número de características demográficas, políticas y económicas. En general, hay una cierta correspondencia entre la prosocialidad costosa, esa cuyo ejercicio conlleva un cierto esfuerzo, y esta forma de benevolencia social, tanto entre individuos como entre países, aunque la correlación no es muy alta. No obstante, el resultado más sobresaliente de esta investigación es la fuerte asociación que se observa en la comparación entre países entre esa conciencia social y un índice de desempeño ambiental, que refleja el grado de proximidad que tienen los países a los objetivos de política ambiental establecidos. El posible efecto del resto de factores se desvanece al considerar este.
Lo que sugiere la existencia de ese fuerte vínculo es que las tendencias prosociales no solo se manifiestan en una orientación generosa o benévola hacia otras personas, sino también en forma de una preocupación más amplia para con la calidad del entorno. Quienes han hecho esta investigación sostienen que esa benevolencia proviene de un capital social que también se proyecta en el interés por la protección del ambiente, quizás reflejando alguna forma de acción colectiva. La consecuencia sería que el grado de atención a los demás no solo se manifiesta en actos amables o generosos para con nuestros coetáneos, sino también en forma de interés activo por quienes nos sucederán.
Lo más sorprendente de esta investigación es que sus autores desconocen cuáles pueden ser los factores que subyacen a la relación observada, dado que otras variables socioeconómicas o culturales no parecen influir.
Referencia:
Van Doeasum et al (2021) Social mindfulness and prosociality vary across the globe PNAS doi: 10.1073/pnas.2023846118
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La benevolencia social tiene más de una cara se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: José Ramón Alonso – ¿Hay algo mejor para un científico que ganar el premio Nobel?
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.
La pregunta del titular se podría reformular de la siguiente manera: ¿existe algo más influyente que un maestro? José Ramón Alonso en un merecido reconocimiento a la labor de todas las personas que se dedican con vocación y entusiasmo a la docencia.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: José Ramón Alonso – ¿Hay algo mejor para un científico que ganar el premio Nobel? se ha escrito en Cuaderno de Cultura Científica.
Revertir y prevenir la obesidad modulando el uso de la metionina
El grupo de investigación Lipids & Liver de la UPV/EHU ha demostrado que modificando de manera específica el uso de metionina en el hígado de ratones obesos, a través del silenciamiento del gen Mat1a, se obtiene un efecto global sobre el organismo: se previene y revierte la obesidad, desaparecen la resistencia a la insulina y el exceso de lípidos circulante y se consumen los lípidos del hígado.
 La obesidad es una enfermedad muy compleja, que no solamente concierne al hígado o al tejido adiposo, también está implicado el cerebro. Imagen: lightwise/123rf.
La obesidad es una enfermedad muy compleja, que no solamente concierne al hígado o al tejido adiposo, también está implicado el cerebro. Imagen: lightwise/123rf.La obesidad es un importante problema de salud pública con una prevalencia creciente en todo el mundo. Se considera que para el 2030 entre un 50-60 % de la población va a ser obesa. La obesidad es un factor de riesgo establecido para diversas enfermedades como la enfermedad del hígado graso no alcohólico, ahora también conocida como esteatosis hepática metabólica, la diabetes tipo 2 y la dislipemia (alteración de los niveles de lípidos y proteínas en sangre), entre otras. La pérdida de peso mediante tratamientos farmacológicos, intervenciones en el estilo de vida o incluso la cirugía son eficaces para tratar las comorbilidades relacionadas con la obesidad. Sin embargo, sigue siendo necesario comprender mejor la conexión entre los diferentes trastornos metabólicos relacionados con la obesidad para poder proponer nuevas terapias.
La investigadora principal del grupo Lipids & Liver de la UPV/EHU Patricia Aspichueta se muestra muy satisfecha con los resultados obtenidos en la investigación, que son “importantes y clarísimos”. Tras cinco años de exhaustiva investigación colaborativa, este grupo ha obtenido “información de cómo el hígado puede regular la obesidad y las enfermedades asociadas a esa obesidad; cómo modulando o restringiendo el uso de metionina (un aminoácido esencial que se obtiene únicamente a través de la dieta) dentro del hígado, conseguimos mejorar el estado corporal: mejorar la obesidad y las enfermedades asociadas a ella. Aportamos datos importantes y esperanzadores en este camino. Sin embargo, no está todo descubierto y hay que aportar mucho más”, afirma la investigadora.
En el estudio liderado por Aspichueta se ha conseguido, en ratones obesos, prevenir y revertir la obesidad, así como la resistencia a la insulina y la hepatosteatosis (acumulación de grasa en el hígado) asociadas, aumentando el gasto energético, además de reducir los lípidos en el suero y del hígado. Según explica la doctora, “modificando de manera específica en el hígado el uso de la metionina, a través del silenciamiento del gen Mat1a, obtenemos un efecto global sobre el organismo: el hígado genera una molécula que se secreta al torrente circulatorio y tiene efectos sobre otros tejidos debido a su alta capacidad para modular el metabolismo de todo el organismo. Entre otros, uno de los tejidos que regula es la grasa parda; al activarse esta grasa parda, se activa el consumo de grasas del organismo en este tejido, dando lugar a una serie de efectos beneficiosos: los ratones bajan de peso, desaparece la resistencia a insulina, desaparece el exceso de lípidos circulante en sangre y disminuyen los lípidos del hígado”.
No obstante, Aspichueta enfatiza que este es un paso más: “Nosotros hemos realizado un análisis en modelos animales; pero todavía queda mucho por hacer: hay que investigar sobre posibles efectos adversos, antes de llevar todo esto a un ensayo clínico. Se puede restringir el uso de la metionina en el hígado, pero nunca se debe inhibir. Esta restricción produce una serie de cambios a nivel del metabolismo hepático, y hay que tener cuidado. Hay que mantener todo en equilibrio, porque si mantienes una inhibición muy larga, también puede tener un efecto perjudicial”. La obesidad es una enfermedad muy compleja, que no solamente concierne al hígado o al tejido adiposo, también está implicado el cerebro. “Es una enfermedad tan compleja que tiene mecanismos compensatorios. Esta investigación es, por tanto, un granito de arena más; una información importante para saber cómo funciona todo el metabolismo en esta enfermedad tan compleja”, afirma.
La prevalencia de la obesidad, del sobrepeso, cada vez es más elevada. Entre un 70-80 % de pacientes con obesidad, tienen problemas de esteatosis hepática metabólica, es decir, de enfermedad hepática. En algunos de estos pacientes, progresa, se complica y acaba en una hepatitis por grasa, o incluso en cáncer hepático. “Nuestro objetivo es poder determinar cómo parar la generación de esta enfermedad en el hígado y su progresión. Y si conseguimos de alguna manera detener o revertir esta obesidad y todos estos efectos nocivos, podremos ayudar a disminuir quizá la prevalencia del cáncer. Si conseguimos conocer cómo modular esta obesidad y con ello todas las enfermedades asociadas, podremos ralentizar la progresión hacia este problema de alta prevalencia”, concluye.
Referencia:
Diego Sáenz de Urturi, Xabier Buqué, Begoña Porteiro, Cintia Folgueira, Alfonso Mora, Teresa C. Delgado, Endika Prieto-Fernández, Paula Olaizola, Beatriz Gómez-Santos, Maider Apodaka-Biguri, Francisco González-Romero, Ane Nieva-Zuluaga, Mikel Ruiz de Gauna, Naroa Goikoetxea-Usandizaga, Juan Luis García-Rodríguez, Virginia Gutierrez de Juan, Igor Aurrekoetxea, Valle Montalvo-Romera, Eva M. Novoa, Idoia Martín-Guerrero, Marta Varela-Rey, Sanjay Bhanot, Richard Lee, Jesus M Banales, Wing-Kin Syn, Guadalupe Sabio, María L. Martínez-Chantar, Rubén Nogueiras, Patricia Aspichueta (2022) Methionine adenosyltransferase 1a antisense oligonucleotides activate the liver-brown adipose tissue axis preventing obesity and associated hepatosteatosis Nature Communications doi: 10.1038/s41467-022-28749-z
El artículo Revertir y prevenir la obesidad modulando el uso de la metionina se ha escrito en Cuaderno de Cultura Científica.
Perlas avinagradas
 El banquete de Cleopatra, obra de 1652 realizada por el artista Jan de Bray. Fuente: The Royal Collection Trust
El banquete de Cleopatra, obra de 1652 realizada por el artista Jan de Bray. Fuente: The Royal Collection TrustCuenta Plinio el Viejo en uno de los tomos de su gran obra Historia Natural una anécdota muy curiosa entre la reina de Egipto, Cleopatra, y el general romano más famoso del momento, Marco Antonio. Resulta que Cleopatra quería impresionar a Marco Antonio para que se convirtiera en su aliado militar y político y, ya de paso, en su amante particular. Para ello se le ocurrió hacer una apuesta con el general romano, asegurándole que le invitaría al banquete más suntuoso y caro al que habría asistido en su vida. Cuando llegó la celebración del ansiado festejo, las cosas no estaban saliendo como Cleopatra esperaba, ya que el romano no parecía en absoluto impresionado con lo que le estaban ofreciendo. Incluso, con cierto sarcasmo, Marco Antonio le dejó caer a la reina egipcia que se estaba aburriendo. Cleopatra reaccionó rápido y con la chulería que parece que la caracterizaba. Pidió a uno de sus esclavos que le llevase una copa de vinagre de vino, se quitó una de las enormes perlas que decoraban sus pendientes, la dejó caer en la copa, esperó unos segundos a que se disolviese y se la bebió. Eso sí impresionó a Marco Antonio, que ya no se separó de la reina egipcia hasta el momento de su muerte.
La historia es muy bonita, pero veamos qué dice la ciencia sobre esta anécdota. Por un lado, tenemos una perla. Las perlas son unas estructuras compuestas por carbonato cálcico (CaCO3) cristalizado en forma de un mineral llamado aragonito, y por una proteína orgánica denominada conquiolina. Estas estructuras son segregadas por algunos moluscos bivalvos, como las ostras, para proteger su cuerpo blando cuando entra alguna partícula externa, a la que van envolviendo de manera progresiva en carbonato hasta asegurarse de que dicha partícula ya no representa ningún peligro para su integridad. Por otro lado, tenemos vinagre de vino. El vinagre es básicamente ácido acético (CH3COOH) diluido, un ácido considerado débil. En definitiva, tenemos una base (la perla) y un ácido (el vinagre) que vamos a mezclar.
Si recordamos un poco las clases de química del instituto, en esa reacción se produce una sal en estado sólido, dióxido de carbono en forma gaseosa y agua líquida. Es decir, que la perla de Cleopatra acabaría reaccionando con el vinagre generando una sustancia sólida carbonatada mezclada con agua en una copa burbujeante, que sería lo que se habría bebido la reina egipcia. Pero hay algo que no hemos tenido en cuenta, ¿esta reacción habría sucedido en unos segundos? Pues aquí es donde entra la leyenda. El hecho de que el acético sea un ácido débil determina el tiempo de la reacción. Para poder disolver el carbonato cálcico de la perla habrían pasado varios días y, además, habrían tenido que ir añadiendo más vinagre cada cierto tiempo.
Vamos, que parece inviable que Marco Antonio se quedase sentado esperando a que terminase la reacción durante unos cuantos días, así que esta historia bien podría ser un simple mito. Eso, o Cleopatra se tragó una enorme perla utilizando vinagre de vino para acompañarla, después de engañar al romano tras generar un poquito de espuma en una copa, que tampoco lo descarto.
Hasta aquí he hablado de historia, leyendas y química. Pero ahora le toca el turno a la geología. Y es que los geólogos empleamos diferentes ácidos para que reaccionen con sustancias minerales de manera controlada y facilitarnos el trabajo en numerosas ocasiones. Un ejemplo es su utilización como mecanismos de extracción química de fósiles en el ámbito de la paleontología. Y el ácido acético diluido es uno de los más empleados para disolver las rocas y los sedimentos carbonatados cuando realizamos estudios de restos fósiles de vertebrados.
 Proceso de trabajo en micropaleontología de vertebrados por disolución química. A: reacción química entre el ácido acético y los restos carbonatados. B: lavado del material resultante tras la reacción química para concentrar los restos óseos fosfáticos. Fotografías de Oier Suarez Hernando.
Proceso de trabajo en micropaleontología de vertebrados por disolución química. A: reacción química entre el ácido acético y los restos carbonatados. B: lavado del material resultante tras la reacción química para concentrar los restos óseos fosfáticos. Fotografías de Oier Suarez Hernando.Los restos óseos tienen una composición fosfática que resiste mucho mejor el ataque del ácido acético que los materiales conformados por carbonato cálcico. La metodología de trabajo es simple, se sumerge la muestra de matriz carbonata que incluye los fósiles fosfáticos en ácido acético diluido y se deja actuar durante varias horas, incluso días. A continuación, se lava abundantemente con agua corriente, hasta eliminar la mayor parte del compuesto carbonatado resultante de la reacción química, y se deja secar al aire. Este proceso se puede repetir sucesivas veces hasta que nos quedemos únicamente con los restos óseos que nos interesan analizar.
Y aunque este proceso es lento y laborioso, por suerte los geólogos tenemos más paciencia que Marco Antonio (y sabemos un poco más de química que él).
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Perlas avinagradas se ha escrito en Cuaderno de Cultura Científica.
No se puede cambiar el azar
Érase una vez un lejano y extraño lugar en el que los nacimientos de niñas y niños sucedían exactamente en la misma proporción: los bebés eran niñas en un 50 % de los alumbramientos y niños en el 50 % restante. No se conocía ninguna época en la que este hecho hubiera sido diferente. Es decir, desde el principio de los tiempos, el sexo de los bebés se comportaba como si se decidiera al azar lanzando, por ejemplo, una moneda equilibrada.
 Foto: Pixabay
Foto: PixabayEl Gobierno decidió que solo las parejas con al menos una niña recibirían una gran suma de dinero al llegar su jubilación. En respuesta a esta medida, y después de pensarlo concienzudamente, cada pareja adoptó la siguiente estrategia para garantizar una jubilación tranquila:
-
si su primer bebé era una niña, decidían no tener más descendencia;
-
si el primer hijo era un varón, la pareja tenía un segundo bebé que sería el último si era una niña;
-
y actuaban de este modo sucesivamente: cada pareja tenía descendencia hasta que llegaba una hija, que era entonces su último retoño.
Esta estrategia tenía dos consecuencias obvias:
-
no había familias sin hijas en este lejano y extraño lugar, y
-
una de cada dos familias no tenía hijos.
Esto parecía favorecer claramente a las niñas. Sin embargo, después de unos años tras haber sido adoptada esta medida, el Ministerio de Estadística del Gobierno de ese lejano y extraño lugar revisó los datos de nacimientos, y comprobó, con sorpresa, que había habido casi tantos nacimientos de niños como de niñas. ¿Cómo explicar esta paradoja?
La realidad, y aunque parezca sorprendente, es que la estrategia adoptada por las familias no tiene ninguna influencia en la proporción de niñas nacidas. En efecto, la probabilidad de que un bebé sea niña es siempre del 50 %; lo que ha sucedido en el pasado no influye sobre el siguiente nacimiento, según se declara al principio de esta historia. La afirmación inicial implica que, en media, nace una niña por cada dos alumbramientos. No importan las estrategias elegidas por las parejas que desean tener hijas: la proporción de niñas y niños nacidos seguirán siendo las mismas.
Para convencernos, vamos a hacer un cálculo suponiendo, por simplificar, que las familias tienen un máximo de cinco descendientes. Puede repetirse el cálculo con cualquier cantidad máxima de nacimientos, o incluso sin limitaciones en la cantidad de prole:
-
La probabilidad de que una familia tenga un único descendiente es de 1/2. Será entonces una niña.
-
La probabilidad de que una pareja tenga dos descendientes es de 1/4. Serán niño-niña.
-
La probabilidad de que una familia tenga tres descendientes es de 1/8. Y serán niño-niño-niña.
-
La probabilidad de que una pareja tenga cuatro descendientes es de 1/16, siendo entonces niño-niño-niño-niña.
-
Finalmente, la probabilidad de que una familia tenga cinco descendientes es de 1/32, siendo el orden de nacimientos niño-niño-niño-niño-niña.
Es decir, de 32 familias, hay un promedio de 16 familias de tipo [niña], 8 de tipo [niño-niña], 4 de tipo [niño-niño-niña], 2 de tipo [niño-niño-niño-niña], 1 de tipo [niño-niño-niño-niño-niña] y 1 de tipo [niño-niño-niño-niño-niño].
Esto hace un total de 16 + 8 + 4 + 2 + 1 = 31 niñas y 0 + 8 + 8 + 6 + 4 + 5 = 31 niños.
El afán de cada pareja por tener una hija no cambia la proporción de niños y niñas. Aunque es cierto que la mayoría de las familias son más felices porque tienen al menos una hija: en el ejemplo que hemos dado, 31 parejas de las 32 tienen una hija, y aseguran su pequeña fortuna en el momento de la jubilación.
La situación comentada en este ejemplo es, por supuesto, ficticia. Solo pretende ilustrar lo contraintuitivos que resultan algunos argumentos relacionados con la teoría de la probabilidad.
De hecho, como explica Marta Bueno Saz en el artículo Mujeres que no llegaron a existir: abortos selectivos e infanticidio de niñas, la realidad es que nacen menos niñas que niños en el mundo: la mayoría de los países poseen la proporción de 103-108 bebés masculinos por cada 100 femeninos.
El economista Amartyan Sen (1933) definió en 1990 la noción de mujeres desaparecidas aludiendo a aquellas féminas que podrían estar vivas si no existieran los abortos selectivos en función del sexo del feto, el infanticidio femenino o la menor atención a las niñas que provoca una mayor mortalidad que en el caso de los niños.
Los datos de la última década indican que China es el país que posee la proporción más sesgada de nacimientos, con 112 niños nacidos frente a 100 niñas. Esto no tiene nada que ver con el azar, es un asunto de pura discriminación.
Referencia
Jean-Paul Delahaye, S’opposer au hasard des naissances, Accromath 17, hiver – printemps 2022, 30-31.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo No se puede cambiar el azar se ha escrito en Cuaderno de Cultura Científica.
Einstein y Michele Besso
Michele Besso fue un amigo, una caja de resonancia y un poco el hermano mayor de Einstein. Besso era seis años mayor, y no sólo le ayudó con algunas de sus teorías científicas, sino que también se vio envuelto directamente en su vida personal.
 Michele Besso. Fuente: ETH-Bibliothek Zürich, Bildarchiv
Michele Besso. Fuente: ETH-Bibliothek Zürich, BildarchivEn 1905 Michele Besso, ingeniero mecánico de formación, trabajaba con Einstein en la Oficina Suiza de Patentes. Los dos hombres solían pasear por las calles de Berna discutiendo las posiciones filosóficas de Ernst Mach (que Einstein conoció por Besso), debatiendo sobre gustos musicales, hablando de judaísmo (Besso era sefardí, Einstein asquenazí) y analizando los problemas candentes de la física. Las teorías que se estaban proponiendo de la luz y de la mecánica mantenían a Einstein despierto durante las noches, intentando comprender como podrían reconciliarse alguna vez. En un momento dado, Einstein pidió ayuda a Besso, y durante diecisiete días los dos hombres discutieron cada aspecto del problema.
Entonces, una noche, la inspiración llegó y encontró a Einstein trabajando. Einstein apareció a primera hora de la mañana siguiente ante la puerta de Besso y, sin decirle hola siquiera, le espetó: “¡Gracias! ¡He resuelto completamente el problema!”. Einstein había resuelto sus problemas con la luz desarrollando su teoría especial de la relatividad. Besso fue la primera persona en escuchar la explicación de Einstein de una teoría que cambiaría las bases de la física.
Ya en ese momento tanto Einstein como Besso parece que eran conscientes de que la teoría era “especial”. El artículo de Einstein sobre ella fue extraordinario en claridad y concisión, y más tarde Einstein diría que las cinco semanas que le llevó escribirlo y prepararlo para publicación fue un tiempo feliz. Aunque Besso no era de los que se quedaba atrás en su comprensión de la física y las matemáticas necesarias, está claro que la teoría especial era de Einstein y solo de Einstein. El mérito de Besso estuvo en su habilidad para escuchar y en su capacidad técnica para absorber y criticar unas ideas revolucionarias provenientes de uno de los científicos más creativos que han existido. Einstein después se referiría a Besso como “la mejor caja de resonancia de Europa [para las ideas científicas]”. En el artículo sobre la teoría especial Einstein supo ser agradecido: “Para terminar, me gustaría decir que mi amigo y colega, M. Besso, me ha ofrecido constantemente sus valiosos consejos mientras estuve trabajando en este problema, y que estoy en deuda con él por sus muchas sugerencias interesantes”.
Einstein y Besso se mantuvieron en contacto por escrito durante el resto de sus vidas, aunque nunca colaboraron en un artículo. Su relación fue más la de dos hermanos. Einstein pedía consejo a menudo a Besso y Besso solía regañar a Einstein por su comportamiento. Las cartas entre los dos hombres contienen muchísima información personal sobre Einstein.

Los dos hombres se conocieron en 1895 cuando Einstein se hospedaba en la casa de su profesor Jost Winteler en Aarau (Suiza), mientras finalizaba el instituto. En aquella época Einstein desarrolló lazos muy fuertes con las personas del círculo de los Winteler: Paul, el hijo mayor, fue su primer gran amigo y posterior marido de su hermana Maja; Marie, la hija pequeña, fue su primera novia; y Besso, que también se hospedaba allí. Besso formalizaría su relación con los Winteler en 1898 al casarse con Anna, la hija mayor.
Una vez casado, Besso se trasladó a Milán como consultor técnico de la Sociedad para el Desarrollo de la Industria Eléctrica en Italia. Influyó en la compañía para que contrataran a Einstein para un pequeño trabajo consistente en un estudio de cómo la electricidad irradia durante la corriente alterna. Einstein le devolvería el favor más tarde cuando avisó a Besso de la existencia de una vacante de examinador de patentes de segunda clase en la Oficina Suiza de Patentes. En esa época Einstein era examinador de patentes de tercera clase y, de hecho, él mismo solicitó el puesto. Pero no parece que le ocasionara ningún problema que escogieran a Besso antes que a él. De hecho, Besso fue claramente bienvenido a la comunidad de Einstein en Berna.
Durante la década siguiente la relación de Einstein con su esposa Mileva se fue deteriorando. El traslado de la familia a Berlín fue la gota que colmaría el vaso. Einstein se mudó a la capital prusiana, entre otras razones, para estar cerca de su amante, Elsa. No es sorprendente, por tanto, que Mileva se deprimiese en Berlín. Solo aguantó allí el tiempo necesario para que Besso pudiese organizarse, recogerla a ella y a sus dos hijos pequeños y llevarlos de vuelta a Suiza.
De esta manera, en 1914, Besso se convirtió en el intermediario entre Mileva y Einstein. El divorcio fue largo y amargo, con crueldad por ambas partes. Mileva estaba destrozada, Einstein distante, y ambos lloraban en el hombro de Besso. Besso supo mantener la cabeza fría. Censuró a Einstein por su comportamiento con su mujer, y protegió a este de las posiciones más dramáticas de ella. En esa época Besso vivía en Zurich, a donde había trasladado Mileva con los niños, lo que le permitió actuar como “tío” de Hans Albert y Eduard.
Besso también estuvo allí cuando tuvo lugar la segunda gran crisis de la familia: el diagnóstico de la enfermedad mental de Eduard. Besso de nuevo asumió el papel de hermano mayor: gestionó toda la parte médica de la enfermedad de Eduard, mantuvo informado a Einstein, regañándole cuando no ayudaba, y consoló, junto a su mujer, a Mileva.
A pesar de todos estos líos familiares, la ciencia estaba casi siempre presente en las comunicaciones entre Einstein y Besso: el rechazo de algunos postulados de la mecánica cuántica, la nueva astronomía y el desarrollo de la teoría general de la relatividad son algunos ejemplos de cuestiones que discutieron los dos amigos.
Besso murió solamente unos meses antes que Einstein. Y si bien éste sintió profundamente la pérdida, supo recurrir a la ciencia como bálsamo. En la carta que envió en marzo de 1955 a Anna, su viuda, escribió: “Se me ha adelantado un poco a la hora de abandonar este mundo extraño. Esto no significa nada. Para nosotros los físicos creyentes [en la física] la distinción entre pasado, presente y futuro solo tiene el significado de una terca ilusión”.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 25 de octubre de 2009.
El artículo Einstein y Michele Besso se ha escrito en Cuaderno de Cultura Científica.
La hora de la comida
Tenemos un ritmo circadiano, un ritmo de 24 horas, como tantos seres vivos, dirigido por el ciclo luz-oscuridad que regula el sol. Este reloj se localiza en el cerebro y se han encontrado ciclos similares, quizá dirigidos por medio de mensajeros y hormonas desde el ciclo del cerebro, en muchos órganos como el hígado, el tubo digestivo o el tejido adiposo. Una de las funciones que dirigen estos ciclos es la digestión. Los cambios en su ciclo, según Daniela Jakubowicz y sus colegas, de la Universidad de Tel Aviv, pueden llevar a la sobrealimentación y a la obesidad.
 Foto: Rachel Park / Unsplash
Foto: Rachel Park / UnsplashEl grupo de Jakubowicz trabaja con 93 mujeres obesas o con sobrepeso, con una edad media de 45.8 años, y un rango de edades de 30 a 57 años. Siguen una dieta de adelgazamiento durante 12 semanas y se controla la composición del desayuno, que se toma entre las 6 y las 9 horas de la mañana, de su comida, entre las 12 y las 15 horas, y de la cena, entre las 18 y las 21 horas. Forman dos grupos que toman una dieta con las mismas kilocalorías, 1400 en total, pero distribuidas con distinto horario a lo largo del día. Uno de los grupos de voluntarias toma un desayuno fuerte, con 700 kilocalorías, una comida media, con 500 kilocalorías, y una cena ligera, con 200 kilocalorías. La dieta del segundo grupo de voluntarias es la misma pero distribuida en un desayuno ligero, una comida media y una cena fuerte.
Los resultados demuestran que todas las voluntarias pierden peso y reducen el diámetro de la cintura, pero las voluntarias del desayuno fuerte lo hacen 2.5 veces más rápido que las voluntarias del desayuno ligero. Los desayunos fuertes bajan, de media, de 86 a 76 kilogramos en las 12 semanas que dura el estudio. Las de desayuno ligero bajan de 86 a 83 kilogramos en el mismo tiempo. Con el desayuno fuerte también bajan la glucosa en sangre y los triglicéridos en un 33% mientras que con el desayuno ligero se elevan un 14%.
En conclusión, un desayuno fuerte y una cena suave ayudan a controlar el peso.
Solo con el cambio de una hora en el esquema de tiempo de las comidas se detectan variaciones en la grasa corporal. Elizabeth Thomas y sus colegas, de la Universidad de Colorado, lo ensayan en 83 voluntarios con sobrepeso y obesidad, variando los horarios durante siete días y tomando datos cada día. Con una hora de retraso en la comida hay un aumento de 1.35% en la grasa corporal.
Incluso no desayunar puede llevar a un aumento de peso y aparición de sobrepeso. El grupo de Julia Wichersky, de la Universidad de Bielefeld, en Alemania, revisaron nueve estudios publicados antes de septiembre de 2020. De ellos, seis se revisaron y tres se incluyeron en un meta-análisis. Los resultados muestran que, si no se desayuna tres o más días a la semana, hay un 11% de riesgo de aumento de peso.
Poco después, el grupo de Marta Garaulet, de la Universidad de Murcia, amplió el estudio sobre el horario de la comida a 420 voluntarios durante 20 semanas, con el 49.5% de mujeres, y 42 años de media. Cambian el protocolo y, en primer lugar, entrevistan a los voluntarios y los dividen en dos grupos: los que comen temprano y hacen la comida del mediodía antes de las 15 horas, y los que comen tarde y la hacen después de las 15 horas.
Los comedores tempranos pierden más peso y lo hacen en menos tiempo que los que comen más tarde. A los autores les sorprende que, en ambos grupos, no es diferente la ingestión de calorías, la composición de la dieta, el gasto de energía, las hormonas relacionadas con el apetito o la duración del sueño. Solo cambia la hora de la comida.
Un estudio publicado en 2021 por el grupo de Kelly Allison, de la Universidad de Pennsylvania, confirma resultados anteriores. Con 12 voluntarios adultos, de edad media de 26.3 años, peso normal y con cinco mujeres en el grupo. Después de un seguimiento de ocho días con dos grupos y, uno de ellos, con horario de comidas de 8.00 a 19.00 horas, y el segundo grupo de 12.00 a 23.00 horas. El grupo que come más temprano muestra tendencia a la pérdida de peso.
El mismo grupo de Marta Garaulet ha hecho un seguimiento durante seis años a pacientes obesos operados con cirugía bariátrica. Son 270 pacientes, con el 70% mujeres y una edad media de 52 años. El 68% han respondido bien a la cirugía y pierden peso, el 11% no reacciona después de la cirugía, y el 21.5% que primero responde bien con el paso del tiempo deja de hacerlo.
Cuando relacionan los investigadores estas tres respuestas con la hora de la comida del mediodía, antes o después de las 15 horas, encuentran que los que comen tarde son hasta el 70% de los que responden mal a la cirugía y pierden poco peso. La respuesta adecuada a la cirugía se corresponde, por lo tanto, a los resultados del ejercicio anterior. Es mejor una hora temprana de la comida del mediodía.
Para averiguar cuál es la causa de estas variaciones en el peso según la hora de la comida, Christopher Morris y sus colegas, del Hospital Brigham and Women de Boston, estudiaron la termogénesis, o gasto de energía para producir calor. Es este proceso metabólico el que mantiene nuestra temperatura a unos 37 °C. La termogénesis también sigue un ciclo diario y es menor a la tarde y a la noche.
Para detectar si la dieta influye en este gasto de energía cíclico, los autores trabajan con 30 voluntarios en un seguimiento de 8 días y con turnos de sueño cambiados y, así, unos duermen de noche y otros duermen de día. La termogénesis la miden una hora y cuarto después de la comida, a las 8 de la mañana para los que duermen de noche y a las 8 de la noche para los que duermen de día.
En los que duermen de noche, con un ciclo que se puede denominar como normal, la termogénesis es un 44% mayor a la mañana que a la tarde y la noche. Por tanto, gastamos más energía de día que en la tarde y la noche y, sobre todo, gastamos más a la mañana temprano. Comemos más fuerte a la mañana y gastamos más energía y, si comemos más fuerte a la noche y no gastamos energía a esas horas pues la almacenamos y no se pierde tanto peso como a la mañana.
Nuestro metabolismo no está preparado para procesar alimentos y utilizar su energía de forma eficaz por la tarde y por la noche, lo hace mejor por la mañana. Los expertos aconsejan no comer nada durante 12 horas de las 24 horas de un día, y que ese ayuno sea, preferiblemente, por la noche, durante el sueño. Lo adecuado es no comer entre la cena y el desayuno del día siguiente. Durante la evolución de nuestra especie, como ocurrió en otras muchas especies, nuestra biología se ha adaptado a un fenómeno superior e inevitable: la salida puesta del sol y, por tanto, al ciclo luz-oscuridad cada 24 horas. Así nos hemos adaptado a comer de día y ayunar y dormir de noche. La luz artificial y las neveras de nuestro tiempo, llenas a cualquier hora, nos empujan a cambiar el ciclo y debemos recuperarlo para regular más adecuadamente el metabolismo.
Referencias:
Allison, K.C. et al. 2021. Prolonged, controlled daytime versus delayed eating impacts weight and metabolism. Current Biology 31: 650-657.
Garaulet, M. et al. 2013. Timing of food intake predicts weight loss effectiveness. International Journal of Obesity 37: 604-611.
Jakubowicz, D. et al. 2013. High caloric intake at breakfast vs. dinner differentially influences weight loss of overweight and obese women. Obesity 21: 2504-2512.
Laber-Warren, E. 2016. Eres cuando comes. Selecciones del Reader’s Digest septiembre: 14-17.
Morris, C.J. et al. 2015. The human circadian system has a dominating role in causing the morning/evening difference in diet-induced thermogenesis. Obesity 23: 2053-2058.
Ruiz-Lozano, T. et al. 2016. Timing of food intake is associated with weight loss evolution in severe obese patients after bariatric surgery. Clinical Nutrition doi: 10.1016/j.clnu.2016.02.007
Thomas, E.A. et al. 2021. Later meal and sleep timing predicts higher percent body fat. Nutrients 13: 73.
Wichersky, J. et al. 2021. Association between breakfast skipping and body weight – A systematic review and meta-analysis observational longitudinal studies. Nutrients 13: 272.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo La hora de la comida se ha escrito en Cuaderno de Cultura Científica.
La Estación Espacial Internacional ante la posible retirada de Rusia
Miguel Bello Mora
 Estación Espacial Internacional fotografiada desde una nave Soyuz tras su desacoplamiento. Fuente: NASA/Roscosmos
Estación Espacial Internacional fotografiada desde una nave Soyuz tras su desacoplamiento. Fuente: NASA/RoscosmosHoy en día la Estación Espacial Internacional (ISS) depende completamente de Rusia para mantenerse en órbita. Las naves de Space X, que contrata la NASA, transportan astronautas pero no pueden impulsar a la ISS para que mantenga su altura. Se espera que sí pueda hacerlo una nueva nave americana, Cygnus, que ya ha realizado con éxito un test de propulsión.
La Estación Espacial Internacional (ISS en inglés) es con diferencia la mayor estructura espacial construida en órbita. Tiene el tamaño de un campo de fútbol, orbita a 400 km de altura y se mueve con una velocidad de cerca de 30.000 km/h para dar una vuelta a la Tierra cada 90 minutos.
Comenzó su andadura en 1998 y fue diseñada para durar 15 años en órbita. Hoy ya lleva más de 21 años habitada permanentemente. Hay un compromiso formal de los socios que la construyeron −Estados Unidos (EEUU), Rusia, Europa, Canadá y Japón− para continuar las operaciones hasta 2024, aunque EEUU ya ha propuesto seguir hasta 2028 como mínimo.
La nueva situación generada por la guerra en Ucrania puede cambiar este escenario, con la amenaza de Rusia de abandonar la estación como respuesta a las sanciones de occidente. Pero, ¿cuál sería el efecto en la ISS si se produce el abandono de Rusia?
Afortunadamente la situación hoy está mucho mejor que hace tan solo dos años, desde que la nave Dragon, de Space X, bajo el programa de vuelos comerciales de la NASA, es capaz de llevar y traer astronautas al complejo orbital.
Durante nueve años, tras el abandono de los vuelos del transbordador espacial de la NASA, el Space Shutle, y hasta la entrada en operación de las naves de Space X en 2020, la única forma de volar a la ISS era con las naves rusas, de forma que la dependencia de la ISS de Rusia era total.
La NASA llegaba a pagar hasta 80 millones de dólares a Rusia para comprar estos billetes espaciales para sus astronautas. De hecho esta actividad era la más lucrativa del programa espacial ruso. Gracias a Space X, esta dependencia ya no existe y no habría problema en el abandono de Rusia para poder habitar la ISS.
Pero las naves rusas son también importantes para la ISS porque son las que han proporcionado hasta hoy la propulsión necesaria para su mantenimiento en órbita.
La ISS necesita propulsión para tres funciones vitales. Una es el mantenimiento de la altura orbital. La ISS pierde de media dos kilómetros de altura cada mes −en realidad esta caída es variable y depende de la actividad solar, que tiene ciclos de 11 años−; la nave rusa Progress le proporciona impulso para ganar altura cada cierto tiempo, cuando está anclada a la ISS. Sin el impulso de las Progress la ISS caería a Tierra en aproximadamente dos años −este tiempo puede variar dependiendo del ciclo solar.
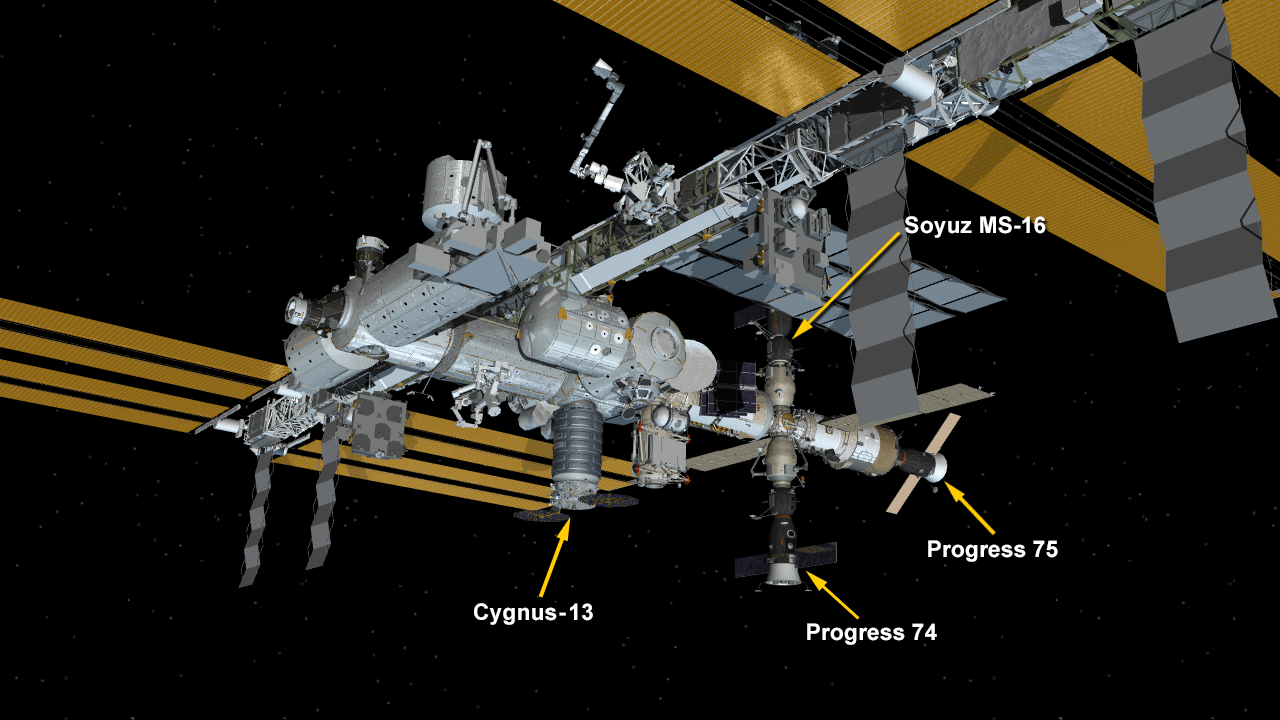 Configuración de la ISS en abril de 2020 con cuatro naves espaciales unidas a la estación: la nave de carga estadounidense Cygnus de Northrop Grumman, las naves de reabastecimiento rusas Progress 74 y 75, y la nave de tripulación Soyuz MS-16. Fuente: NASA
Configuración de la ISS en abril de 2020 con cuatro naves espaciales unidas a la estación: la nave de carga estadounidense Cygnus de Northrop Grumman, las naves de reabastecimiento rusas Progress 74 y 75, y la nave de tripulación Soyuz MS-16. Fuente: NASALa propulsión también es clave para evitar basura espacial. La basura espacial es un grave problema que origina la necesidad de realizar maniobras evasivas con cierta periodicidad para evitar colisiones fatales, dada la gran velocidad de estos objetos.
En noviembre de 2021 la ISS hizo una maniobra para subir su altura más de un kilómetro, y evitar así una zona congestionada de basura debido a una fragmentación intencionada de China de un satélite Fenyung hace años. Estas maniobras hasta ahora se realizan con naves rusas Progress.
Al final de su vida operativa, que la NASA ya estima para 2028 para luego ser reemplazada por un programa de vuelos comerciales, es necesario hacer una reentrada de la ISS en la atmósfera de manera controlada.
Si se deja caer la estación de manera incontrolada, puede hacerlo en cualquier lugar de la Tierra entre 51º de latitud Sur y 51º de latitud Norte, donde se encuentra la inmensa mayoría de la población terrestre (dado que su inclinación orbital con respecto al Ecuador es 51º).
Aunque la mayor parte de la superficie terrestre es océano y es menos probable que caiga sobre tierra, esta es una probabilidad que no se puede permitir porque se sabe que al igual que las estaciones precedentes Skylab o MIR, los restos de la ISS no se desintegrarían completamente en la atmósfera (como casi todos los satélites y restos de basura), sino que partes importantes de su estructura caerían sobre la Tierra y podrían generar un serio peligro para personas o propiedades.
Para evitar esto se utiliza primero la caída natural debido a la resistencia atmosférica durante un periodo de aproximadamente 2 años y después una maniobra final para asegurar que va a caer en un punto determinado del océano. La NASA ha seleccionado el ‘Point Nemo’ como punto para la caída de la ISS, un lugar en el Pacífico Sur que está a una distancia de 2.700 km de la costa más cercana. En principio esta maniobra final para la reentrada controlada de la ISS debería ser realizada por las naves rusas.
En resumen, la para mantener la altura, para evitar colisiones con basura espacial y para evitar un accidente al final de la vida útil de la ISS. La nave europea ATV, que tenía también la capacidad de propulsión ya no está operativa desde 2014.
Sin embargo una nueva nave americana, Cygnus de Northrop Grumman, tiene capacidad para atracar en la ISS y ya ha realizado con éxito un test de propulsión. De esta forma también USA puede realizar maniobras en la ISS y la dependencia de Rusia desaparecería por completo.
La amenaza rusa de abandonar la ISS no sería ahora un grave peligro para los socios occidentales. Tan solo habría que cerrar los módulos rusos y seguir operando con la nave Dragon de Space X para la tripulación y la nave Cygnus de Northrop Grumman para la propulsión.
Sobre el autor: Miguel Bello Mora es Director General (CEO) de AIR Centre, organismo intergubernamental para el uso de la tecnología espacial para la sostenibilidad y el cambio climático.
Artículo publicado originalmente en SINC.
El artículo La Estación Espacial Internacional ante la posible retirada de Rusia se ha escrito en Cuaderno de Cultura Científica.

