A vueltas con el equipaje de mano (II)
En la anterior entrada del Cuaderno de Cultura Científica titulada A vueltas con el equipaje de mano (I) estuvimos hablando de las medidas de las maletas de cabina. En la actualidad cada compañía aérea tiene establecidas unas medidas concretas (ancho x largo x alto) para el equipaje de mano que debe ser utilizado en sus aviones. Por ejemplo, para British Airways y EasyJet son 25 x 45 x 56 cm, para Iberia son 25 x 40 x 56 cm, para Lufthansa 23 x 44 x 55 cm, para Vueling y Ryanair 20 x 40 x 55 cm, para American Airlines 23 x 36 x 56 o para Air Europa, Air France o KLM 25 x 35 x 55 cm, que, aunque todas puedan estar alrededor de unas ciertas medidas, tienen diferencias significativas en algunos casos.

Como comentábamos en la anterior entrada, hace unos años, y aún hay compañías que lo mantienen, existía una norma general (que era el estándar internacional de la IATA = Asociación Internacional de Transporte Aéreo), por encima de las recomendaciones particulares de cada compañía (que, en algunos casos, en aquella época eran algo menores que las actuales), que consistía en que las medidas de la maleta de cabina debían ser tales que su suma no excediera los 115 centímetros, es decir, ancho + largo + alto (de la maleta) debía medir menos, o igual, que 115 cm. Esto es,
![]()
siendo x = ancho, y = largo, z = alto.
Un dispositivo para controlar las maletas
Como pusimos de manifiesto en la reflexión final de la anterior entrada, el problema estaba en que siendo la norma general ancho + largo + alto menor, o igual, que 115 cm, el dispositivo que utilizaba cada compañía para controlar si las maletas de los pasajeros cumplían la normativa era un dispositivo con forma de paralelepípedo (caja rectangular, como en la siguiente imagen) con las medidas de su recomendación, que en aquella época se ajustaban a que la suma de las medidas (ancho, largo y alto) fuese 115 cm. Así, la caja de Iberia estaba adaptada para las medidas que recomendaba en esa época 20 x 40 x 55 cm, pero en esa caja podían tener problemas las maletas recomendadas por Spanair (25 x 40 x 50 cm) o Air Europa (25 x 35 x 55 cm), que eran más anchas, de 25 cm, así como maletas con otras medidas, incluyendo la maleta cúbica de 38,33 cm de lado, que, aunque fuese extraña y difícil de incluir en la zona de equipaje de mano (véase la entrada A vueltas con el equipaje de mano (I)), estaba dentro de la norma general.

Por este motivo, cuando hace unos cuantos años (alrededor de 2010) preparé mi charla Matemáticas para andar por casa, me planteé la siguiente cuestión:
¿Es posible diseñar un dispositivo para que la compañía aérea compruebe que las medidas del equipaje (sin medirlas) cumplen la norma general?
puesto que el sistema de la caja rectangular realmente no era efectivo. De hecho, quizás por este motivo se ha ido eliminando la norma general de que ancho + largo + alto sea menor, o igual, que 115 cm, por medidas más concretas, en algunos casos algo mayores, que dan más flexibilidad.

La solución para la regla general no era la estructura de caja rectangular utilizada, que como fuente de información orientativa podía ser válida, o estar tomando las medidas de cada maleta, que hubiese convertido el sistema en un suplicio para las trabajadoras de la compañía aérea, sino un dispositivo que, como veremos, derivaba del conocimiento de lo que son las coordenadas cartesianas y la ecuación cartesiana de un plano.
No se trata en esta entrada de intentar establecer un mecanismo que se podía, o no, haber utilizado, sino mostrar como el análisis matemático de un problema puede ofrecer una solución al mismo. Una vez obtenida esa solución la empresa implicada puede decidir desarrollarla, o no, en función de múltiples factores que tendrá que tener en cuenta.
El problema en dos dimensiones
Para intentar simplificar la cuestión y facilitar su comprensión, vamos a pensar en el problema en dos dimensiones, en cuyo caso, en lugar de una maleta tendremos un objeto rectangular (cuyas dimensiones son el ancho y el largo), por ejemplo, el marco de una fotografía o un cuadro.

Por lo tanto, una regla equivalente al estándar de IATA para las maletas podría ser que la suma de las medidas del marco sea menor, o igual, que 35 centímetros. De esta manera entrarían dentro de lo permitido medidas habituales como 13 x 18 cm o 15 x 20 cm. En consecuencia, se trata de crear un dispositivo para controlar que los marcos de las fotografías cumplan esa regla. Pensemos que quizás, esto podría ser útil en una fábrica de marcos para separar los marcos por tamaños o alguna otra situación equivalente.
Para analizar matemáticamente esta cuestión vamos a introducir primero las coordenadas cartesianas del plano y después la ecuación de una recta en el plano utilizando las coordenadas cartesianas.
Coordenadas cartesianas
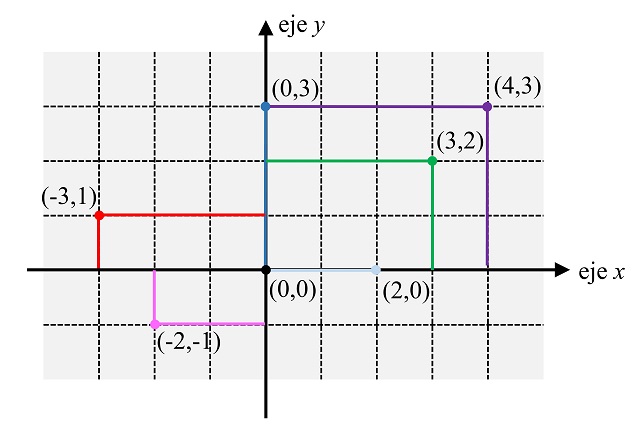
Para definir estas coordenadas en el plano debemos de partir de dos rectas perpendiculares, que van a ser los denominadas “ejes de coordenadas” (el eje X o eje de abscisas –horizontal– y el eje Y o eje de ordenadas –vertical–), a cuyo punto de corte se le denomina origen (O). Entonces, las coordenadas cartesianas (rectangulares) permiten determinar la posición de cada punto del plano P en función de dos números (x, y) que expresan la distancia del punto a los dos ejes coordenados (x la distancia del punto P al eje Y e y la distancia al eje X). En esta imagen vemos algunos ejemplos que nos ayudan a entender mejor esta idea (el signo negativo indica si se está en una parte o en otra respecto a los ejes, aunque para lo que nos ocupa aquí solo hablaremos de coordenadas positivas). Por ejemplo, el punto (3,2) dista 3 unidades del eje Y y 2 unidades del eje X.
Nos podemos cuestionar el motivo por el cual es útil hablar de coordenadas cartesianas en este problema. Seguramente, la imagen anterior nos dará ya una idea del motivo. Imaginemos que tenemos un plano coordenado y colocamos un marco de manera que uno de sus vértices esté apoyado en el origen y dos de sus lados estén apoyados en los ejes coordenados, como en la siguiente imagen, de manera que el ancho se apoye en el eje X y el largo en el eje Y.
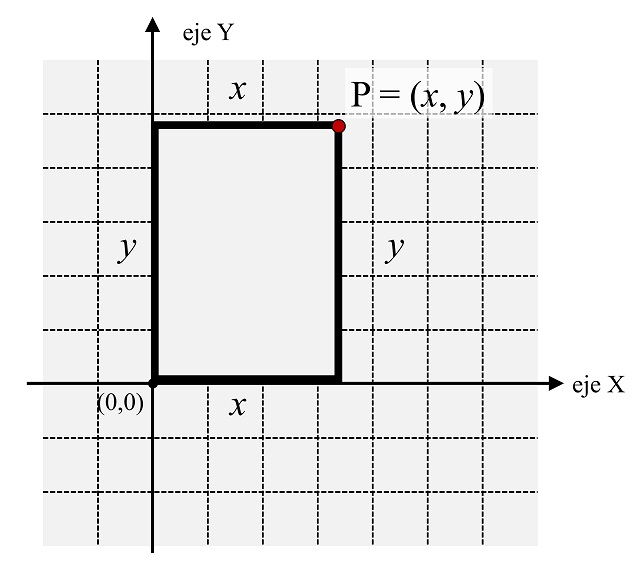
De esta manera, como se muestra en la imagen anterior, las medidas del marco de una fotografía (x, y), siendo x el ancho e y el largo, determinarán el punto P = (x, y) del plano, que es la posición del vértice opuesto al apoyado en el origen. Y recíprocamente, dado un punto cualquiera del plano P = (x, y), este determinará las medidas concretas de un marco fotográfico, colocado como en la situación anterior.
La ecuación de una recta
Dicho esto, ahora vamos a explicar qué es la ecuación algebraica de una recta del plano coordenado. Dada una recta del plano, se pueda asociar a la misma una ecuación de la forma ax + by + c = 0, donde a, b y c son números reales (como las rectas que aparecen en la siguiente imagen: x – y – 1 = 0, 3x + 2y – 6 = 0). ¿Cómo funciona la ecuación de la recta? Si tenemos un punto P de coordenadas (x, y), este estará en la recta si los números x e y satisfacen la ecuación, y no estará en ella si no la cumplen. Por ejemplo, los puntos (4, 3), (3, 2) y (0, –1) están en la recta x – y – 1 = 0, ya que (4) – (3) – 1 = 0, (3) – (2) – 1 = 0 y (0) – (–1) – 1 = 0, mientras que el punto (0, 3), no está en ella, por ser (0) – (3) – 1 = – 4, que no es 0; y de la misma manera, los puntos (0, 3) y (2, 0) está en la recta 3x + 2y – 6 = 0, pero no el punto (3, 2).
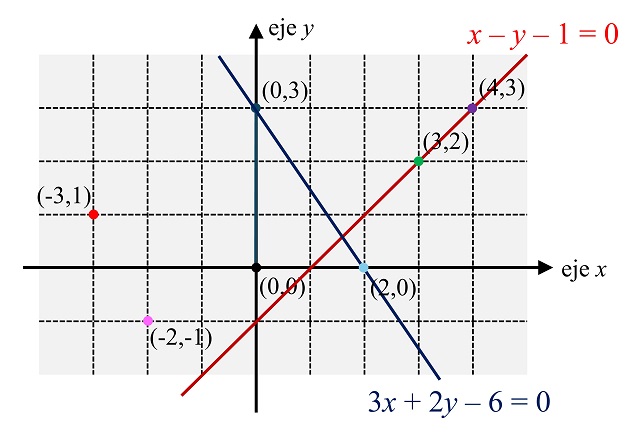
Pero la ecuación de una recta nos da más información. Consideremos de nuevo la recta 3x + 2y – 6 = 0 y veamos que pasa con los puntos que no están sobre ella, como (4, 3), (3, 2), (0, 0) o (–2, –1):
3(4) + 2(3) – 6 = 12, 3(3) + 2(2) – 6 = 7,
3(0) + 2(0) – 6 = –6, 3(–2) + 2(–1) – 6 = –14,
de manera que, en los dos primeros el valor de la ecuación 3x + 2y – 6 es positivo, mientras que en los dos siguientes es negativo.
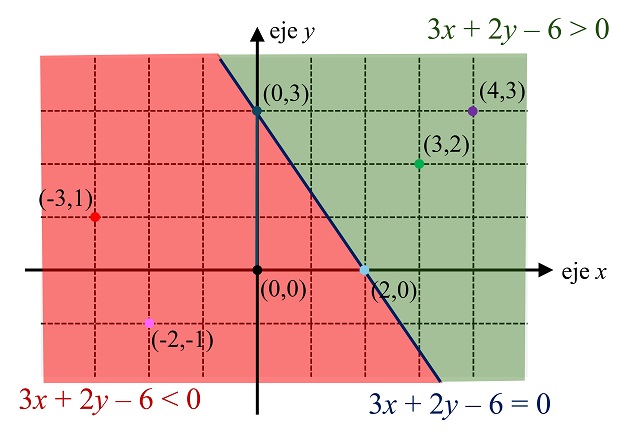
Lo que ocurre es que la ecuación de la recta, en este caso 3x + 2y – 6 = 0, divide al plano en tres regiones distintas, la recta y las dos regiones a cada lado de la misma. Los puntos (x, y) de la recta satisfacen que 3x + 2y – 6 = 0, mientras que los puntos a un lado de la recta satisfacen la desigualdad 3x + 2y – 6 > 0, mientras que los puntos al otro lado de la recta satisfacen que 3x + 2y – 6 < 0. Y esto ocurre en general para cada recta.
Un dispositivo para controlar los marcos
Empecemos recordando que la condición establecida para que los marcos pasen el filtro (o sean considerados pequeños en la fábrica) es que
![]()
siendo x = ancho del marco, y = largo del marco. Pero si miramos la anterior desigualdad desde la óptica de lo visto hasta ahora podemos afirmar lo siguiente.
Consideremos un marco de fotografía concreto, cuyas medidas sean a centímetros de ancho y b centímetros de largo. Este marco se corresponderá, según lo visto, con el punto (a, b) del plano coordenado. Por otra parte, tenemos la ecuación de la recta x + y = 35 (véase la siguiente imagen), dada por las condiciones aplicadas a los marcos fotográficos. Si las coordenadas de nuestro punto (a, b) satisfacen la ecuación la ecuación x + y = 35, entonces el punto está sobre la recta (las medidas del marco a y b satisfacen que a + b = 35, esto es, ancho más largo es igual a 35 centímetros), si verifican que x + y > 35, entonces el punto estará por encima de la recta (las medidas del marco no satisfacen la condición fijada), mientras que si satisfacen que x + y < 35, el punto estará por debajo de la recta (las medidas del marco sí cumplen la condición fijada).
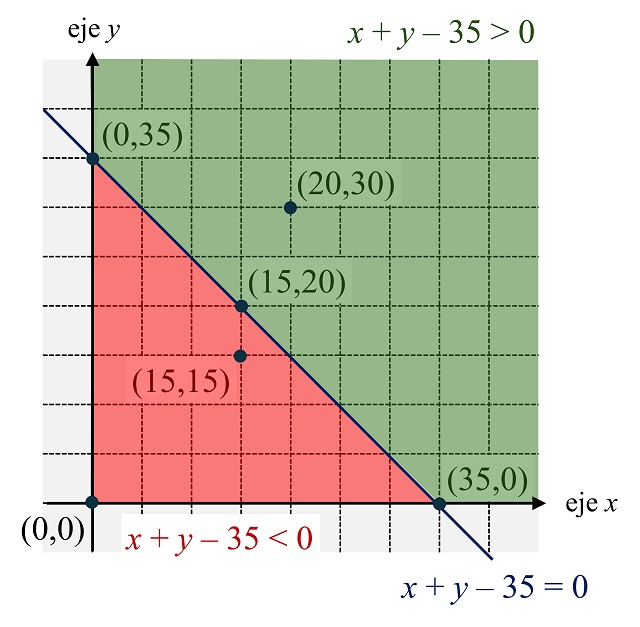
De manera, que podemos observar gráficamente que el marco de medidas (15, 15), es decir, ancho y largo igual a 15 cm, satisface las condiciones establecidas, por estar situado debajo de la recta, así como el marco de medidas (15, 20), que está en la recta, pero no el marco de medidas (20, 30), situado encima de la recta.
En consecuencia, ya tenemos las ideas necesarias para diseñar un dispositivo para controlar que el tamaño de los marcos cumpla esa condición establecida. Este estaría formado por una estructura fija formada por dos lados rectangulares de más de 35 centímetros de largo (una especie de escuadra de dos brazos), junto con una tapa o puerta móvil, unida a la parte vertical de la estructura fija por una bisagra colocada a 35 cm de la base y apoyada en la parte horizontal, a 35 cm de la tabla vertical (utilizando el teorema de Pitágoras sabemos que la tapa tendría una longitud de 35 cm multiplicado por la raíz cuadrada de 2, es decir, unos 49 centímetros).
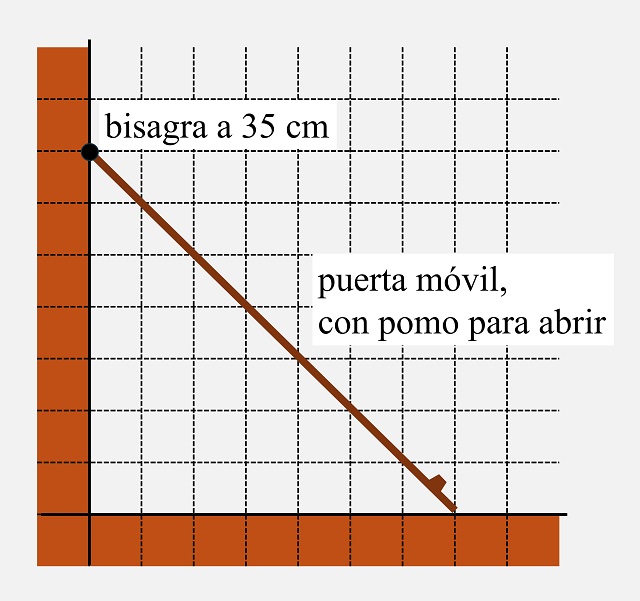
Le he pedido a Gemini que me haga una versión realista del dispositivo. No es que se ajuste del todo a lo que le he pedido, pero quizás con esta imagen os hagáis una mejor idea del mismo, aunque mi idea era un dispositivo apoyado en una superficie plana horizontal, para trabajar mejor con el mismo.

¿Cómo funcionaría el dispositivo? Dado un marco cualquiera, abriríamos la tapa del dispositivo y lo meteríamos dentro apoyándolo en la esquina. Si la tapa cerrase, esto significaría que el marco cumpliría la regla de que la suma de las medidas del marco sea menor, o igual, que 35 centímetros, como en la siguiente imagen.

Mientras que, si la tapa no cerrase, porque lo impide el marco, querría decir que las medidas del marco excederían las que se han fijado en la norma, como se ilustra en la siguiente imagen.

Regreso al dispositivo para controlar las maletas
Una vez entendido el dispositivo bidimensional para controlar las medidas de los marcos de fotografías, o estructuras rectangulares en general, podemos comentar brevemente cual sería el dispositivo para las maletas de mano, o paralelepípedos (cajas rectangulares) en general. La idea es la misma, pero con tres dimensiones, en lugar de dos.
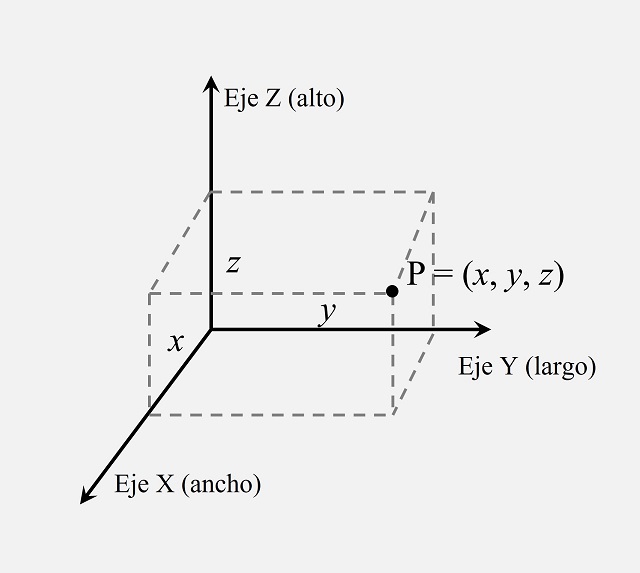
De forma análoga a como ocurría en dimensión dos, ahora las medidas de una maleta / caja rectangular (x, y, z), siendo x el ancho, y el largo y z el alto, determinarán el punto P = (x, y, z) del espacio tridimensional coordenado, que es el vértice opuesto al apoyado en el origen (0,0,0). Y recíprocamente, dado un punto cualquiera del plano P = (x, y, z), este determinará las medidas concretas de una maleta / caja rectangular.
Ahora debemos observar, de manera análoga a lo ocurrido en dimensión dos, que la ecuación x + y + z = 115, derivada de las condiciones generales sobre las maletas, es la ecuación de un plano del espacio tridimensional, que se ilustra en la siguiente imagen. Luego, un punto P = (x, y, z) está en el plano si se cumple la ecuación, estará debajo del plano si x + y + z < 115 y estará por encima del plano si x + y + z > 115.
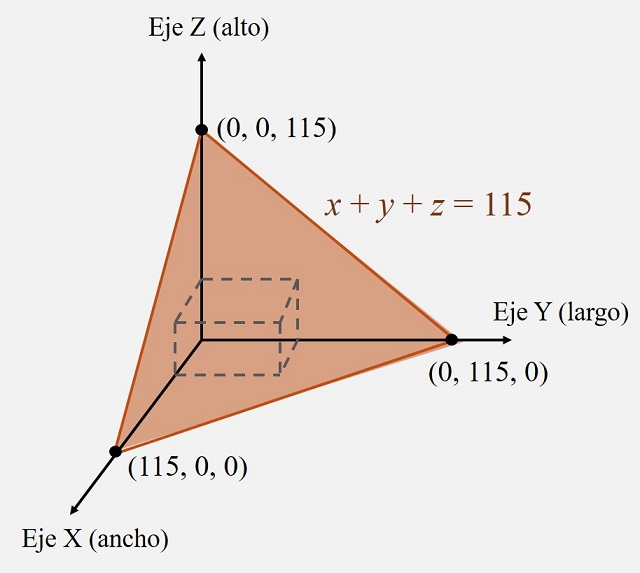
En consecuencia, el dispositivo ahora está muy relacionado con la imagen anterior. Estará formado por tres trozos de planos que se cortan perpendicularmente (en la siguiente imagen las zonas en gris), junto con una tapa triangular cuyos vértices están a 115 cm del vértice origen (de intersección de los tres planos), cuya bisagra estará en el vértice superior para poder abrir esa tapa triangular. El funcionamiento, por lo visto, será igual al de los marcos, si metemos la maleta y se cierra la tapa, estará en las condiciones determinadas (x + y + z menor, o igual, que 115 cm), pero si no cierra la tapa la maleta no puede subirse al avión como equipaje de mano.
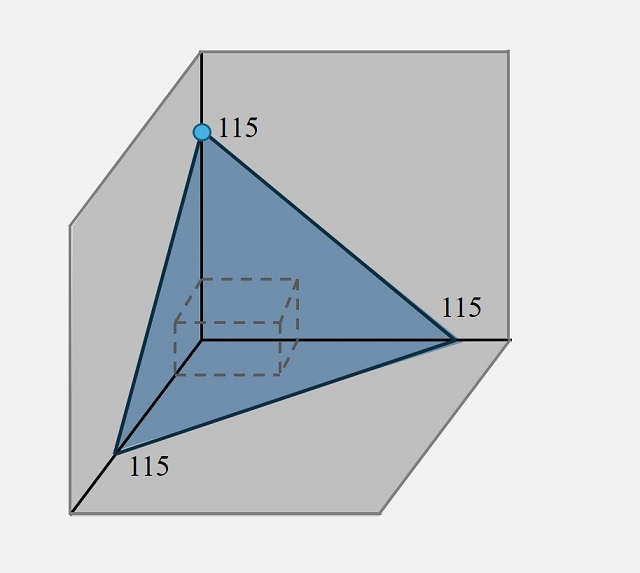
Esta era la idea básica con la que se podía haber construido un dispositivo para el control de las maletas de cabina. Por supuesto, con mejoras reales, como mejorar el punto de bisagra. Pero la idea que quería transmitiros es que las matemáticas nos pueden ayudar a aportar soluciones concretas a cuestiones concretas.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo A vueltas con el equipaje de mano (II) se ha escrito en Cuaderno de Cultura Científica.
Baterías de estado sólido para un futuro eléctrico
La electrificación del transporte ya no es solo una idea de futuro; se ha convertido en una transformación en marcha que está redefiniendo la movilidad y acelerando la transición hacia sistemas más sostenibles y menos dependiente de los combustibles fósiles. Para que este cambio sea realmente efectivo, es fundamental disponer de sistemas de almacenamiento energético capaces de ofrecer mayor autonomía, mejores niveles de seguridad y una vida útil más prolongada, sin que ello suponga un aumento excesivo de los costes ni un retroceso en sostenibilidad. Hasta ahora, las baterías de litio-ion han sido las grandes protagonistas. Su combinación de alta densidad energética, buena estabilidad y durabilidad las ha situado en el centro del desarrollo del vehículo eléctrico. Sin embargo, la expansión acelerada de la movilidad eléctrica y la integración masiva de energías renovables están empezando a revelar sus límites. La necesidad de reducir aún más los tiempos de carga, ampliar la autonomía y reforzar la seguridad está impulsando la búsqueda de alternativas capaces de llevar el rendimiento de las baterías un paso más allá.
Baterías de estado sólidoEn este contexto, las baterías de estado sólido se han consolidado como una de las líneas de desarrollo más prometedoras. La ventaja más destacada es que dejan atrás los electrolitos líquidos, compuestos por disolventes orgánicos inflamables, y los reemplazan por electrolitos sólidos, que resultan mucho más seguros y toleran mejor el estrés térmico. Este cambio supone un avance notable en seguridad. Además, abre la posibilidad de utilizar materiales más avanzados, como el litio metálico en el ánodo, que ofrece una capacidad energética muy superior a la de los materiales convencionales en base de carbón. Sin embargo, la transición hacia sistemas completamente sólidos aún está lejos de ser inmediata. Fabricar electrolitos sólidos cerámicos extremadamente finos, garantizar interfaces químicamente estables y dominar procesos de producción complejos sigue siendo un desafío tecnológico. Por esta razón, la industria está apostando por soluciones intermedias que combinan componentes líquidos y sólidos, permitiendo avanzar hacia el estado sólido sin necesidad de rediseñar por completo las líneas de producción de celdas de litio-ion actuales.
Este enfoque combinado se basa en electrolitos que inicialmente se encuentran en estado líquido y son capaces de infiltrarse completamente en los poros de los electrodos, para luego solidificarse dentro de la celda. Esta estrategia representa un paso pragmático y estratégico en la transición hacia baterías de estado sólido, ya que permite formar interfaces continuas y estables, algo que resulta mucho más difícil de conseguir con electrolitos sólidos preformados (membranas sólidas). La solidificación in situ no solo mejora la conducción iónica, sino que también minimiza espacios vacíos o irregularidades que podrían afectar la eficiencia y la seguridad de la batería. Además, esta estrategia es compatible con los procesos industriales ya existentes en la producción de baterías de litio-ion, lo que facilita su integración y reduce los costes y complicaciones asociados. Gracias a esta combinación de realismo industrial y avance tecnológico, las arquitecturas semi-estado-sólido, semi-SSB en inglés, están emergiendo como una alternativa sólida para mejorar el rendimiento de las baterías en aplicaciones de movilidad eléctrica y almacenamiento estacionario.
La familia de celdas Gen4a Estructura de la familia de celdas tipo semi-SSB Gen4a. Fuente: CIDETEC
Estructura de la familia de celdas tipo semi-SSB Gen4a. Fuente: CIDETECEn este contexto, en CIDETEC Energy Storage trabajamos en el desarrollo de dos familias de celdas de tipo semi-SSB que aportan ventajas complementarias. La primera (Gen4a) aprovecha la tecnología de litio-ion, utilizando una arquitectura electroquímica ya conocida, con grafito en el ánodo y materiales activos tipo LiNixMnyCozO2 (x+y+z=1) en el cátodo, pero incorporando un electrolito híbrido (sal de litio + carga inorgánica + polímero + disolvente) que se convierte en sólido mediante un proceso de polimerización in situ después del ensamblaje. Este proceso uniformiza la interfaz interna y reduce la resistencia de contacto, además de ser compatible con electrodos de alta densidad de carga sin requerir presiones elevadas durante el ensamblaje. En conjunto, esta aproximación ofrece estabilidad, seguridad y facilidad de fabricación, lo que la hace especialmente adecuada para su implementación industrial a corto plazo. Los prototipos de celda desarrollados en formato pouch de 5 Ah han mostrado un rendimiento estable durante cientos de ciclos: se han alcanzado hasta 300 ciclos con un 80 % de capacidad retenida bajo un protocolo de testeo de 0,33C/0,33C a 25 °C. Las densidades energéticas de estas celdas, alrededor de 240 Wh/kg y 700 Wh/L, se sitúan en niveles comparables a los de las baterías comerciales más avanzadas. Además, la tecnología ha sido ya escalada a prototipos de 25 Ah manteniendo sus buenas prestaciones, consolidando su papel como una tecnología puente hacia sistemas de estado sólido más sofisticados.
La familia de celdas Gen4b Estructura de la familia de celdas tipo semi-SSB Gen4b. Fuente: CIDETEC
Estructura de la familia de celdas tipo semi-SSB Gen4b. Fuente: CIDETECLa segunda línea (Gen4b) de desarrollo explora la integración de litio metálico como ánodo, un material cuya capacidad específica es muy superior a la del grafito y que permitiría incrementar de forma notable la densidad energética de las celdas. El uso de litio metálico con electrolitos líquidos presenta desafíos importantes, como la formación de dendritas y la inestabilidad de la interfaz, pero las arquitecturas semisólidas ofrecen un entorno más rígido y seguro para la deposición del litio. La polimerización in situ del electrolito mejora el contacto con el cátodo y contribuye a una mayor durabilidad del sistema. Los prototipos desarrollados en esta línea, basados en un electrolito gel-polimérico, han mostrado un comportamiento electroquímico prometedor a temperatura ambiente. En pruebas realizadas sobre celdas tipo pouch de 4,6 Ah, se han alcanzado densidades energéticas gravimétricas y volumétricas del orden de 350 Wh/kg y 1000 Wh/L, respectivamente, valores notablemente superiores a los de las baterías de litio-ion convencionales y muy atractivos para aplicaciones que demandan gran autonomía, como los vehículos eléctricos de largo recorrido.
Un salto cualitativo robustoLa evolución hacia baterías de estado sólido no solo es un reto técnico, sino también un proceso en el que la química y la ingeniería deben avanzar de manera coordinada para ofrecer soluciones eficientes, asequibles, sostenibles y seguras. En este sentido, las arquitecturas semi-SSB representan un paso decisivo para acelerar esta transición. Por un lado, la variante basada en litio-ion ofrece una opción robusta, compatible con la industria actual y capaz de mejorar el rendimiento sin elevar los costes. Por otro, la versión basada en litio metálico abre la puerta a un salto cualitativo en densidad energética. Juntas, ambas tecnologías constituyen un camino realista hacia las baterías de estado sólido del futuro, un camino que permitirá desarrollar sistemas de almacenamiento más seguros y duraderos, reforzando al mismo tiempo la competitividad tecnológica de la industria y contribuyendo al avance global hacia una movilidad verdaderamente sostenible.
Sobre los autores: Dra. Mónica Cobos, investigadora del equipo de baterías de estado sólido, y Dr. Andriy Kvasha, líder del equipo de estado sólido en CIDETEC Energy Storage.
Sobre CIDETEC Energy Storage: Es una organización de investigación y desarrollo especializada en tecnologías avanzadas de baterías, que diseña, desarrolla y testea las baterías del futuro desde hace 30 años. Su experiencia abarca toda la cadena de valor. CIDETEC es miembro de Basque Research and Technology Alliance (BRTA).

Basque Research & Technology Alliance (BRTA) es una alianza que se anticipa a los retos socioeconómicos futuros globales y de Euskadi y que responde a los mismos mediante la investigación y el desarrollo tecnológico, proyectándose internacionalmente. Los centros de BRTA colaboran en la generación de conocimiento y su transferencia a la sociedad e industria vascas para que sean más innovadoras y competitivas. BRTA es una alianza de 17 centros tecnológicos y centros de investigación cooperativa y cuenta con el apoyo del Gobierno Vasco, SPRI y las Diputaciones Forales de Araba, Bizkaia y Gipuzkoa.
El artículo Baterías de estado sólido para un futuro eléctrico se ha escrito en Cuaderno de Cultura Científica.
Retrato de mundos efervescentes
Cuando observamos la enorme diversidad de satélites que están en órbita alrededor de los planetas del Sistema Solar exterior, a los geólogos nos encanta buscarles sus fracturas, como si estuviésemos interesados en darles costura. Durante mucho tiempo hemos interpretado esas señales, junto con otras muestras de deformación en sus cortezas, como la prueba inequívoca de que existe -o existió- un océano subterráneo. Parecía que esta lógica siempre estaba de nuestro lado: cuando un océano interior se congela o el hielo de la corteza comienza a fundirse, provoca unos esfuerzos y una deformación en la corteza que acaba rompiéndola por algunos puntos como si fuese el frágil cascarón de un huevo. Lo que no se consideraba hasta ahora era que los océanos de los mundos océano podrían entrar en ebullición.
Pero un nuevo estudio publicado en Nature Astronomy por Rudolph et al. (2025), propone un mecanismo por el cual los océanos subterráneos de las pequeñas lunas heladas podrían «hervir» debido a la despresurización, creando un interior rico en volátiles que pueda esconder -o disfrazar- la actividad tectónica e incluso de provocar fenómenos criovolcánicos explosivos.
Para comprender mejor esto que acabo de decir, primero tenemos que fijarnos en el “extraño” comportamiento -disculpen mi excesivo uso de las comillas hoy- del agua. A diferencia de la mayoría de las sustancias, el agua se expande cuando se congela, permitiendo que el hielo flote, y se contrae cuando se funde.
Esto tiene una consecuencia muy importante para estos satélites cuya corteza está formada por hielo. Cuando esta comienza a engrosarse porque hay menos calor disponible, el agua se convierte en un hielo que ocupa un mayor volumen, presurizando al océano que hay por debajo y al mismo tiempo generando una serie de esfuerzos que acaban agrietándola, como por ejemplo vemos en Europa. Y, por cierto, de una manera similar, las cortezas de los cuerpos rocosos también sufren de la formación de sistemas de fracturas durante su etapa de enfriamiento.
Pero, ¿qué ocurre cuando es al revés? Cuando la corteza de hielo adelgaza, tal vez debido a un aumento de las temperaturas del agua del océano subterráneo, la transformación del hielo al agua reduce el volumen y la corteza de hielo es, de repente, demasiado grande para el interior que cubre. Durante este proceso, la corteza comienza a ajustarse y comprimirse “hacia adentro”, como intentando ajustarse al océano, provocando una inmensa tensión compresiva en el hielo mientras que al mismo tiempo se reduce la presión en el océano de agua líquida que hay debajo.
 Imagen de Mimas, el satélite de Saturno. Además de su enorme parecido con la “estrella de la muerte” de Star Wars, se aprecia una superficie completamente cubierta de cráteres, un síntoma que suele estar asociado a cuerpos geológicamente inactivos o con poca actividad, incapaces de rejuvenecer su superficie. Imagen cortesía de NASA/JPL/Space Science Institute.
Imagen de Mimas, el satélite de Saturno. Además de su enorme parecido con la “estrella de la muerte” de Star Wars, se aprecia una superficie completamente cubierta de cráteres, un síntoma que suele estar asociado a cuerpos geológicamente inactivos o con poca actividad, incapaces de rejuvenecer su superficie. Imagen cortesía de NASA/JPL/Space Science Institute.Esto ha llevado a los investigadores a observar una sorprendente divergencia en la forma en la que los distintos satélites podrían soportar las tensiones que provoca el aumento o la disminución de la capa de hielo y descubrieron que el resultado que vemos en la superficie depende en gran medida del tamaño del satélite.
En el caso de los cuerpos helados más pequeños como Mimas, Encélado o Miranda, la física del océano da un giro radical antes de que la superficie tenga la oportunidad de resquebrajarse. Debido a que estas lunas tienen una gravedad bastante baja, la presión en la superficie de los océanos es también relativamente baja. A medida que la capa de hielo pierde espesor al calentarse el océano y la presión dentro de las aguas del océano también disminuye, el agua alcanza un umbral crítico conocido como punto triple, un estado en el cual coexisten las fases de hielo, agua líquida y el vapor.
En estas condiciones, el océano comienza, literalmente, a hervir. No se trata de la misma ebullición del agua cuando ponemos una olla de agua a calentar para hacer un caldo en un frío día de invierno y que en este caso estaría provocado por el calor, sino más bien un fenómeno de ebullición por descompresión, similar a lo que le ocurre el agua cuando la introducimos en una cámara de vacío.
El océano existente en estos satélites herviría para compensar el vacío creado por el deshielo, amortiguando las tensiones que se generan y evitando que la corteza se rompa, algo así como un air-bag geológico. Esto implica que una luna como Mimas podría albergar en su interior un océano en crecimiento sin la necesidad de que en su superficie aparezcan zonas de deformación ni fracturación.
Y al mismo tiempo resolvería la paradoja de por qué este pequeño satélite -cuyo parecido con la estrella de la muerte es abrumador- según los últimos datos de libraciones podría tener un océano de reciente formación en su interior, a pesar de que su superficie es muy antigua y está llena de cráteres y no hay señales de la reactivación de procesos internos.
Las implicaciones para un mundo como Encélado también son profundas: Sabemos que es un mundo tremendamente activo, atestiguado por sus geiseres, su joven superficie y por los sistemas de fracturas. Y es que este estudio sugiere que el mecanismo de ebullición podría ser el principal motor de estos chorros de agua que se en ocasiones llegan a los cientos y miles de kilómetros de distancia. Un fenómeno realmente espectacular.
A medida que la presión del océano permite la aparición un entorno parecido al vacío, los gases disueltos como el dióxido de carbono, el metano o el nitrógeno se separarían, burbujeando fuera del agua del océano de una forma muy similar a cuando abrimos una botella de gaseosa. Estos gases que se están separando crearían una capa flotante y rica en volátiles en la interfaz entre la corteza de hielo y el océano.
 Imagen de Encélado donde se aprecia perfectamente la gran actividad de los geiseres que funcionan en las proximidades de su polo sur. Imagen cortesía de NASA/JPL/Space Science Institute.
Imagen de Encélado donde se aprecia perfectamente la gran actividad de los geiseres que funcionan en las proximidades de su polo sur. Imagen cortesía de NASA/JPL/Space Science Institute.Esta mezcla gaseosa, de manera natural, tiende a ascender. Los investigadores proponen que estos gases podrían subir a través del hielo a través las fracturas o como fenómenos diapíricos, donde un hielo más plástico y lleno de burbujas de gas ascendería como la cera en una lámpara de lava. Este mecanismo evita un problema que desde hace mucho tiempo existe en física planetaria: como conseguir que las fracturas se propaguen desde la base de la corteza de hielo hacia la superficie, cuando el hielo en las partes inferiores suele estar a mayor temperatura y comportarse de manera dúctil y no frágil.
La flotabilidad que proporcionan estos gases que escapan del agua suministraría la fuerza necesaria para propagar las fracturas desde el interior hacia la superficie, y también podría ser un mecanismo válido para explicar los geiseres que vemos hoy día. Por lo tanto, estos podrían ser el resultado directo de la “ebullición” del océano a medida que la capa de hielo va adelgazando.
Sin embargo, la historia cambia drásticamente cuando hablamos de cuerpos más grandes: El estudio marca un límite claro entre cuerpos con un radio de unos 300 kilómetros o menos y los más grandes. En los mundos de mayor tamaño, como pueden ser Titania, Oberon o Japeto, la gravedad ejerce una fuerza mayor, y la presión litostática que ejerce el hielo que recubre el océano es mucho mayor también. Como consecuencia de esto, a medida que las capas de hielo adelgazan, la presión del océano nunca desciende lo suficiente como para alcanzar el punto de ebullición, pero la tensión compresiva que se acumula en la capa de hielo se vuelve insoportable.
Entonces, en estos mundos más grandes, el hielo falla mecánicamente mucho antes de que el agua pueda hervir y emitir todos esos gases disueltos que actúen como un cojín que amortigüe a la corteza, que sufrirá procesos tectónicos compresivos, en los cuales esta se deforma y se fractura. Los investigadores señalan que algunos sistemas montañosos en Titania y la gran cordillera ecuatorial de Japeto serían precisamente cicatrices de estos procesos. Aunque hay muchas teorías sobre la formación de esta última, como podría ser la caída del material de un anillo que ya no existe sobre la superficie, el fallo compresional de una corteza cada vez más delgada aparece como una explicación físicamente viable, como si Japeto hubiese sido un acordeón cósmico.
Esto nos deja abierta una nueva línea para la investigación: los cuerpos más pequeños pueden ser buenos ocultando sus océanos, mientras que las lunas más grandes si suelen mostrar señales en su corteza, como grandes sistemas de fracturas y cordilleras montañosas.
 Imagen de Japeto donde se aprecia perfectamente su cordillera ecuatorial y que, según este estudio, podría ser la señal de un océano subterráneo. Imagen cortesía de NASA/JPL/Space Science Institute.
Imagen de Japeto donde se aprecia perfectamente su cordillera ecuatorial y que, según este estudio, podría ser la señal de un océano subterráneo. Imagen cortesía de NASA/JPL/Space Science Institute.Para llevar a cabo este estudio, los científicos usaron modelos numéricos para simular la evolución térmica y mecánica de estos cuerpos. Asumieron el adelgazamiento de la corteza de hielo en aproximadamente un 10%, un valor razonable teniendo en cuenta los últimos datos que conocemos de calentamiento por mareas o por cambios en las resonancias orbitales, capaces a su vez de traducirse en una mayor energía disponible y, por lo tanto, de mayor temperatura en el océano y la corteza de hielo.
Tampoco podemos olvidar el destino del vapor generado en estos océanos. Cuando el agua entra en ebullición, se genera una capa de vapor de agua y de otros gases. Ya que el interior está bajo alta presión -en comparación con la superficie- el comportamiento de esta capa de gas puede ser bastante complejo. Aunque el vapor de agua podría recondensarse al ascender hasta la capa de hielo más fría, el resto de los gases -como el nitrógeno, el metano o el dióxido de carbono- seguirían en estado gaseoso bajo estas condiciones.
Estos gases podrían acumularse en capas de hielo poroso o incluso formar clatratos -unas estructuras que actúan como una jaula capaz de atrapar moléculas de gas- que luego podrían ascender rápidamente. Este detalle también sugiere que el diapirismo, como mencionamos anteriormente, también podría ser un mecanismo importante de transporte de calor y materiales entre el interior y el exterior de estos cuerpos.
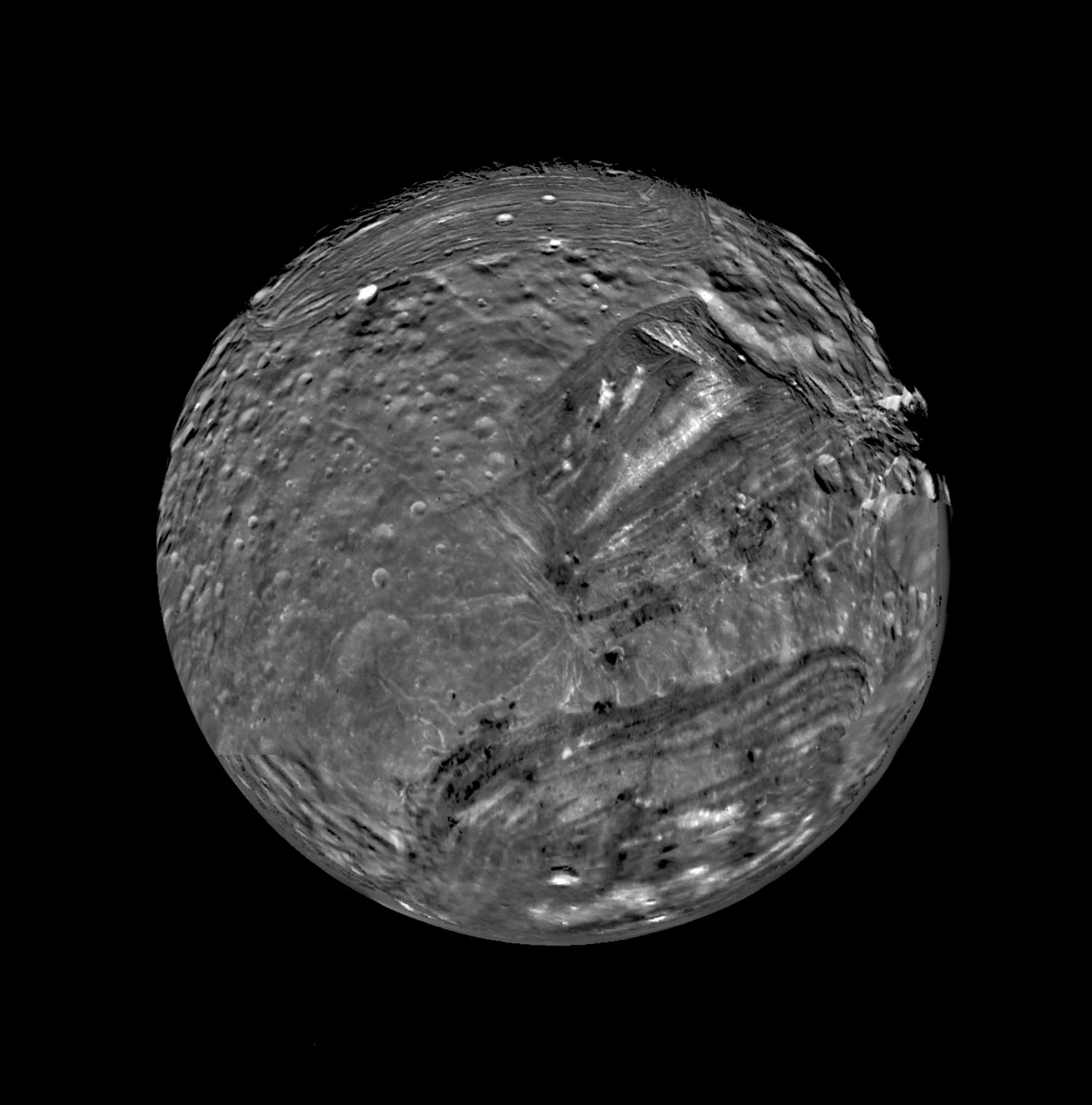 Mosaico de imágenes de Miranda, el satélite de Urano, a partir de imágenes tomadas por la Voyager 2 en enero de 1986. Se aprecia perfectamente la enorme diferencia que hay entre las zonas más antiguas y cubiertas de cráteres y las más recientes, que parecen parches cosidos sobre su superficie, dejando unas costuras muy marcadas. Imagen cortesía de NASA/JPL/USGS.
Mosaico de imágenes de Miranda, el satélite de Urano, a partir de imágenes tomadas por la Voyager 2 en enero de 1986. Se aprecia perfectamente la enorme diferencia que hay entre las zonas más antiguas y cubiertas de cráteres y las más recientes, que parecen parches cosidos sobre su superficie, dejando unas costuras muy marcadas. Imagen cortesía de NASA/JPL/USGS.La existencia de estos procesos nos ofrece una nueva perspectiva para estudiar un cuerpo como Miranda, una luna de Urano. Miranda es algo parecido a un Frankenstein geológico, un mosaico de distintos terrenos que parecen cosidos entre si como los parches de un pantalón. Los investigadores sugieren en este estudio que los fenómenos de rejuvenecimiento de la superficie de Miranda implican la existencia de un océano -en el pasado- que podría haber estado alimentado por una convección que se vería facilitada o potenciada por la ebullición del océano. Si la capa de hielo de Miranda sufrió un rápido adelgazamiento debido a una resonancia orbital temporal o pasajera, la ebullición resultante podría haber impulsado la caótica transformación de su superficie.
Esta investigación podría cambiar radicalmente que tipo de señales buscamos cuando investigamos la existencia de océanos más allá de la Tierra. Anteriormente, la ausencia de sistemas de fracturas en Mimas llevó a muchos a suponer que se trataba de un bloque sólido de hielo, como un cubito. Ahora sabemos que pueden existir océanos ocultos en los que la física de la ebullición es capaz de enmascarar o de incluso inhibir la actividad tectónica, al menos a simple vista.
Esto nos lleva a considerar que la ausencia de pruebas no es necesariamente una prueba de ausencia de un océano. Por el contrario, en mundos más grandes como Titania, la presencia de cordilleras fruto de la compresión podría ser la revelación de un océano moribundo o en proceso de adelgazamiento, más que de un mundo geológicamente muerto, como a veces se han interpretado.
De cara a futuras misiones, este nuevo marco podría servirnos para planificar mejor los destinos y que instrumentos hemos de incorporar para estudiar estos océanos, o al menos que deberíamos hacer para poder detectarlos, pero también debe recordarnos que a veces algunos detalles sutiles son capaces de hacernos cambiar la interpretación geológica de algunos mundos que, a pesar de darlos por muertos, podrían estar muy vivos.
Referencias:
Rudolph, M. L., Manga, M., Rhoden, A. R., & Walker, M. (2025) Boiling oceans and compressional tectonics on emerging ocean worlds Nature Astronomy doi: 10.1038/s41550-025-02713-5
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Retrato de mundos efervescentes se ha escrito en Cuaderno de Cultura Científica.
La brecha entre la obediencia imaginada a la autoridad y la real
Estás en una sala. Frente a ti, un hombre de bata blanca te dice que pulses el botón que provocará una descarga eléctrica. Al otro lado de la pared, alguien grita de dolor. Tus manos tiemblan. La autoridad insiste. ¿Qué harás?
No es una película. Es un escenario muy parecido al que vivieron cientos de personas en el famoso experimento de Stanley Milgram (1963). Lo perturbador es que la mayoría obedeció.
Décadas después, cuando los psicólogos preguntamos a la gente qué haría en ese mismo contexto, casi todos aseguran que se plantarían mucho antes de hacer daño a otro ser humano. Sin embargo, los datos cuentan otra historia.
La ilusión de resistirLa mayoría nos vemos como más éticos y valientes que la media: un sesgo de superioridad ilusoria. También tendemos a minimizar el poder de las circunstancias y a sobrevalorar los rasgos personales: llamado error fundamental de atribución (Ross, 1977). El resultado es una confianza ingenua: “Yo no sería de los que aprietan el botón”.
 Es tal la autoridad que asociamos a una bata blanca y un estetoscpio al cuello, que el uso de actores caracterizados así es una herramienta muy eficaz en la venta de suplementos, medicamentos, servicios sanitarios o seguros de salud. Solo siendo conscientes del sesgo de autoridad podemos minimizar la obedencia indebida y tomar decisiones más objetivas. Foto: Usman Yousaf / Unsplash
Dos condiciones, dos realidades
Es tal la autoridad que asociamos a una bata blanca y un estetoscpio al cuello, que el uso de actores caracterizados así es una herramienta muy eficaz en la venta de suplementos, medicamentos, servicios sanitarios o seguros de salud. Solo siendo conscientes del sesgo de autoridad podemos minimizar la obedencia indebida y tomar decisiones más objetivas. Foto: Usman Yousaf / Unsplash
Dos condiciones, dos realidades
El experimento de Milgram se ha replicado muchas veces, la brecha entre lo que la gente imagina y lo que hace es consistente:
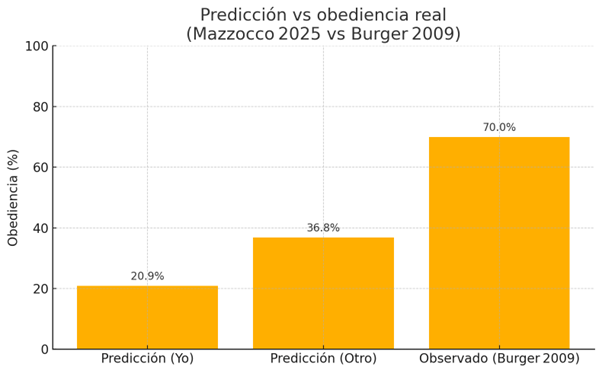 En la investigación de Mazzocco et al. (2025), cuando se preguntó a las personas cuánto obedecerían en una situación tipo Milgram, predijeron tasas mucho más bajas (20,9 % para sí mismos y 36,8 % para “otra persona”) que lo que realmente se observa en experimentos controlados. En el estudio de Burger (2009), que replicó parcialmente el paradigma de Milgram, el 70 % de los participantes obedeció hasta el máximo permitido.
En la investigación de Mazzocco et al. (2025), cuando se preguntó a las personas cuánto obedecerían en una situación tipo Milgram, predijeron tasas mucho más bajas (20,9 % para sí mismos y 36,8 % para “otra persona”) que lo que realmente se observa en experimentos controlados. En el estudio de Burger (2009), que replicó parcialmente el paradigma de Milgram, el 70 % de los participantes obedeció hasta el máximo permitido.
La consecuencia es brutal: en nuestra cabeza somos héroes; ante la bata blanca, obedecemos tanto como en 1963.
¿Por qué nos equivocamos tanto?- Distancia emocional. Imaginar un dilema moral no genera la misma activación fisiológica que vivirlo; sin adrenalina, es fácil ser valiente.
- Presión situacional silenciosa. En la situación real, señales como la bata, la seriedad del investigador… legitiman la orden y reducen el conflicto interno.
- Brújula ética atenuada. Un estudio con EEG encontró que, al obedecer, disminuye la actividad theta frontal-medial previa a infligir daño: la sumisión silencia alertas internas antes de que se enciendan.
Un sabio dijo: “no nos elevamos a la altura de las expectativas, caemos a la altura de nuestro entrenamiento”.
- Entrenamiento en asertividad. Situaciones reales donde practicamos decir “no” bajo autoridad percibida.
- Micro‑actos de desobediencia. Rechazar pequeñas órdenes injustas en la vida diaria refuerza el músculo moral.
- Entornos que refuercen la voz crítica. Equipos o amistades que celebren la integridad, no el conformismo.
- Educación sobre sesgos. Conocer nombres y mecanismos facilita detectarlos en tiempo real.
No te sentarán ante un generador de shocks, pero cada día te enfrentas a la misma brecha entre intención y acción: decir “no” a un compromiso mal planteado, cuestionar una orden dudosa, no dejarte arrastrar por un “aceptar todo”.
La bata blanca cambia de forma: a veces un “es urgente”, otras un proceso diseñado para que no pienses. Y casi siempre obedecemos más de lo que creemos.
Esta brecha explica nuestra frustración vital: expectativas altas, ejecución tibia. La narrativa que construimos sobre nosotros mismos no sobrevive al contacto con los hechos.
La pregunta no es si resistirás, sino qué entrenamiento y qué alianzas estás creando hoy para resistir cuando de verdad importe.
Referencias
Burger J. M. (2009). Replicating Milgram: Would people still obey today? The American psychologist, 64(1), 1–11. doi: 10.1037/a0010932
Caspar, E. A., & Pech, G. P. (2024). Obedience to authority reduces cognitive conflict before an action. Social neuroscience, 19(2), 94–105. doi: 10.1080/17470919.2024.2376049
Ebert, J., Winzer, P., & Müller, C. (2025). Reducing the Hypothetical Bias in Measuring Willingness to Pay for Mobile Communication Products. Journal of Theoretical and Applied Electronic Commerce Research, 20(2), 122. doi: 10.3390/jtaer20020122
Mazzocco, P. J., Reitler, K., Little, L., Korte, J., Ridgill, M., & Stalnaker, X. (2025). Milgram shock‑study imaginal replication: How far do you think you would go? Current Psychology. doi: 10.1007/s12144-025-07962-1
Ross, L. (1977). The intuitive psychologist and his shortcomings: Distortions in the attribution process. In L. Berkowitz (Ed.), Advances in experimental social psychology (Vol. 10, pp. 173–220). Academic Press.
Sobre el autor: David Carcedo es divulgador, psicólogo sanitario en Donostia y coordinador de sección de laboratorio en el BCBL.
El artículo La brecha entre la obediencia imaginada a la autoridad y la real se ha escrito en Cuaderno de Cultura Científica.
La viscosidad altera la música de las estrellas
 Ilustración artística de la fusión de dos estrellas de neutrones, proceso que genera ondas gravitacionalesFuente: University of Warwick/Mark Garlick, CC BY 4.0, Wikimedia Commons
Ilustración artística de la fusión de dos estrellas de neutrones, proceso que genera ondas gravitacionalesFuente: University of Warwick/Mark Garlick, CC BY 4.0, Wikimedia CommonsLas ondas gravitacionales son vibraciones del propio espacio-tiempo, ondas que se propagan tras sucesos muy violentos como la fusión de agujeros negros o de estrellas de neutrones. Estas ondas, tan débiles que apenas deforman los detectores más sensibles de la Tierra, también atraviesan planetas, gases y estrellas. Pero ¿qué ocurre cuando una de esas ondas pasa a través de objetos que no son rígidos, sino fluidos y, por tanto, viscosos?
Recordemos que la viscosidad mide la resistencia de un fluido a fluir y es una expresión de la existencia de fuerzas de rozamiento internas y, por lo tanto, de cómo disipa energía. Así, un líquido muy viscoso, como la miel, amortigua las vibraciones más rápido que el agua. Las estrellas y otros objetos compactos como los planetas, aunque puedan parecer sólidos, son en realidad fluidos extremadamente densos. Algunas partes de su interior —como el núcleo de una estrella de neutrones— pueden comportarse como un líquido con cierta viscosidad.
La viscosidad altera…En un nuevo estudio los autores han modelado la interacción de las ondas gravitacionales y la materia siguiendo las leyes de la relatividad general, pero incluyendo los efectos de la viscosidad. De esta manera han podido calcular cómo se propagan las perturbaciones a través de las estrellas y cómo se ve afectada la onda gravitacional al atravesarlas.
El resultado principal es que, como era de esperar, la viscosidad absorbe parte de la energía de la onda. Si la materia fuera un fluido ideal, sin viscosidad, la onda las atravesaría casi sin alteración; pero si hay fricción interna, la onda deja parte de su energía en la estrella. Simplificando, es como si la onda gravitacional hiciera vibrar el interior de la estrella y esa vibración se fuera convirtiendo en calor.
Cuando la viscosidad es pequeña, la absorción es débil. Si se incrementa, la onda empieza a perder más energía dentro de la estrella. S la materia es muy viscosa la onda puede incluso reflejarse parcialmente, igual que una ola rebota contra un muro. Los autores demuestran que, para ciertos valores, la reflectividad puede parecerse a la de un agujero negro.
Sin embargo, alcanzar esos niveles de viscosidad extrema no es fácil: si se exagera, el modelo empieza a violar principios básicos de la relatividad, como la causalidad. En otras palabras, la materia no puede ser infinitamente viscosa sin dejar de tener sentido físico. Por eso, aunque el hallazgo es fascinante, no implica que existan objetos capaces de reflejar ondas gravitacionales de manera perfecta; más bien marca los límites teóricos de lo que la física permite.
…la música de las estrellasEl estudio también muestra que la viscosidad cambia las notas naturales de vibración de las estrellas. Igual que una campana produce tonos característicos cuando se la golpea, una estrella vibra en modos característicos cuando una onda gravitacional la alcanza. La presencia de viscosidad altera ligeramente esas frecuencias y los tiempos en los que las oscilaciones se amortiguan. La viscosidad introduce un nuevo tipo de vibraciones internas, propias del material viscoso, que podrían dejar señales específicas en la radiación gravitacional emitida por el sistema. Detectar esas huellas sería una manera de estudiar las propiedades internas de las estrellas más densas sin necesidad de observarlas directamente.
Desde el punto de vista astrofísico, los cálculos muestran que el efecto de absorción o calentamiento que una onda gravitacional produce en una estrella es minúsculo en la mayoría de los casos. Incluso en las colisiones más energéticas del universo, la cantidad de energía que una onda transfiere a una estrella es despreciable. Aun así, en entornos muy extremos —por ejemplo, cerca del centro de una galaxia activa o dentro de cúmulos donde las ondas gravitacionales son intensas—, estos efectos podrían tener un papel interesante y observable.
Imitadores de agujeros negrosEl artículo toca dos grandes temas actuales. El primero es la idea de que ciertos objetos extremadamente compactos, pero sin horizonte de sucesos, podrían imitar el comportamiento de los agujeros negros. Si son lo bastante viscosos, podrían reflejar parte de las ondas gravitacionales y producir ecos en las señales que registran detectores como LIGO o Virgo. El segundo es la posibilidad de que la viscosidad y la rotación generen superradiancia, un fenómeno en el que una onda sale del objeto amplificada, robándole energía a su rotación. Este mecanismo podría producir inestabilidades o patrones característicos en las observaciones futuras.
Este trabajo demuestra que la viscosidad no es un detalle menor: influye en cómo las estrellas absorben, reflejan o incluso amplifican las ondas que las atraviesan. También recuerda que, para interpretar correctamente las señales detectadas en la Tierra, debemos tener en cuenta la microfísica de las estrellas y los efectos disipativos que pueden modificar esas vibraciones del espacio-tiempo.
Es un paso más hacia una astronomía gravitacional más completa, en la que no sólo observamos cómo las ondas viajan por el universo, sino también cómo los distintos tipos de materia responden a ellas, revelando su estructura interna y, quizás, las propiedades más sutiles de la gravedad misma.
Referencias:
Valentin Boyanov, Vitor Cardoso, Kostas D. Kokkotas, and Jaime Redondo-Yuste (2025) Dynamical Response of Viscous Objects to Gravitational Waves Phys. Rev. Lett. doi: 10.1103/smlr-v7b2
Sumanta Chakraborty (2025) Viscous Stars Can Reflect Gravitational Waves like Black Holes Do Physics 18, 169
César Tomé López (2019) Ondas (serie) Cuaderno de Cultura Científica
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La viscosidad altera la música de las estrellas se ha escrito en Cuaderno de Cultura Científica.
El violento nacimiento de Venus
Cuando hablamos en términos coloquiales muchas veces nos referimos al planeta Venus como una especie de gemelo de nuestro planeta, pero la realidad nos dice que de gemelos más bien tienen poco. Quizás sí podríamos llamarlos hermanos, ya que ambos son planetas rocosos y tienen un tamaño, composición y densidad similar.
A pesar de este aparente parecido son dos mundos antagónicos. La Tierra es un planeta templado, con océanos de agua líquida y casquetes polares, mientras que Venus sería lo más parecido al infierno: Un mundo con temperaturas que se acercan a los 500 ºC rodeado por una densa e irrespirable atmósfera de dióxido de carbono, nitrógeno y dióxido de azufre.
Pero hay muchas más diferencias, alguna de ellas muy llamativas. El día de Venus dura nada más y nada menos que 243 días terrestres y, por si fuese poco, gira sobre sí mismo al revés. Bueno, en sentido contrario al de la Tierra y al de la mayoría de los planetas. Y hay un detalle más que fascina a los científicos y del que todavía no tenemos una respuesta clara al porqué: Venus está solo, no tiene ni un solo satélite natural que quizás hubiese podido ser clave para estabilizar su giro e incluso su clima.
 Imagen de Venus tomada en luz visible por la sonda Messenger en junio de 2007. Así lo veríamos con nuestros propios ojos si estuviésemos en sus proximidades, con una capa de nubes que oscurece de manera perpetua su superficie. Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington..
Imagen de Venus tomada en luz visible por la sonda Messenger en junio de 2007. Así lo veríamos con nuestros propios ojos si estuviésemos en sus proximidades, con una capa de nubes que oscurece de manera perpetua su superficie. Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington..¿Cómo pudieron ambos planetas empezar siendo tan parecidos y evolucionar hacia mundos tan diferentes? Un nuevo estudio publicado por Bussmann et al. (2025) parece haber sido capaz de traer una nueva teoría para explicar las causas y al menos resolver -aparentemente- estas dos últimas diferencias mediante la simulación de un impacto gigante contra la superficie de Venus cuando el Sistema Solar era mucho más joven.
Los inicios del Sistema Solar fueron realmente agitados. Las simulaciones sobre la formación de nuestro sistema planetario muestran que las últimas etapas de su formación estuvieron probablemente dominadas por colisiones de una magnitud inimaginable.
De hecho, la teoría más ampliamente aceptada sobre la formación de nuestra propia Luna tiene mucho que ver con esto, ya que incluye un cuerpo del tamaño de Marte chocando con nuestra proto-Tierra. Y no sería raro pensar que Venus hubiese sufrido un destino similar, pero… ¿qué tipo de impacto podría haber dejado a Venus tal y como lo conocemos hoy?
Para responder a esta pregunta, los científicos han ejecutado una serie de modelos numéricos que permiten analizar con gran nivel de detalle la física de estas grandes colisiones. Crearon un proto-Venus diferenciado en dos capas con un núcleo de hierro que formaría un 30% de la masa del planeta y un manto rocoso que ocuparía el 70% restante.
Tras la creación de este gemelo digital, comenzaron a “dispararle” cuerpos planetarios de distintos tamaños, con distintos ángulos y velocidades. La clave no era el hacer una sola simulación, sino explorar el amplio abanico de posibilidades en cuanto a los parámetros de impacto. En total realizaron 81 simulaciones diferentes variando los parámetros más importantes para ver que pasaba.
Como decíamos en el párrafo anterior, dispararon contra el proto-Venus cuerpos de distintos tamaños, desde cuerpos de tan solo 0.01 veces la masa terrestre hasta otros del tamaño de Marte y con una masa de 0.1 veces la de nuestro planeta. También variaron las velocidades de colisión en un rango entre los 10 y los 15 km/s, suficientes para alcanzar la velocidad de escape de Venus.
 Mapa topográfico de Venus centrado en la longitud 270º. Si miramos la distribución de alturas -cuya leyenda esta en la parte inferior derecha de la imagen- veremos que se parece muy poco a la de nuestro planeta, donde hay una fuerte distribución bimodal donde se distinguen los continentes y las cuencas oceánicas. Imagen cortesía de NASA/JPL/USGS.
Mapa topográfico de Venus centrado en la longitud 270º. Si miramos la distribución de alturas -cuya leyenda esta en la parte inferior derecha de la imagen- veremos que se parece muy poco a la de nuestro planeta, donde hay una fuerte distribución bimodal donde se distinguen los continentes y las cuencas oceánicas. Imagen cortesía de NASA/JPL/USGS.También cambiaron las condiciones iniciales de este proto-Venus. Ya que no sabemos cómo podría haber sido este embrión planetario antes de la gran colisión, probaron también con diferentes periodos de rotación, desde uno de cero horas -es decir, con el planeta sin girar sobre si mismo- hasta uno en el que el día tan solo duraba dos horas y media, más rápido que Júpiter. También probaron distintas geometrías de impacto, desde unas colisiones “frontales” hasta otras más oblicuas y tangenciales capaces de añadir o restar momento angular al planeta.
El primer objetivo de los investigadores era el intentar resolver el misterio de la lenta velocidad de rotación y su sentido “inverso”. Para considerar que habían dado en el clavo, el escenario del impacto no necesitaba producir una velocidad de rotación como la actual, que es equivalente a 243 días terrestres. Solo necesitaban que la velocidad de rotación tras el impacto fuese de aproximadamente de 2 días o más.
Este es el umbral conservador que marcan algunos modelos de como podría haber sido la velocidad de rotación de Venus en el pasado. Y es que un Venus girando tan lentamente, con una atmósfera tan densa como la actual, permitiría que las mareas gravitatorias y térmicas que provoca la atmósfera sobre la superficie sirviesen como un freno que, a lo largo de miles de millones de años, frenase al planeta hasta la velocidad de rotación de hoy día, como un enorme lastre.
Curiosamente, los científicos se dieron cuenta que un gran número de los escenarios de impacto simulados son capaces de generar este resultado sin problemas. Si el proto-Venus no giraba sobre sí mismo antes del impacto, la solución era directa: una colisión frontal con un objeto del tamaño de Marte sería suficiente. Pero con un cuerpo pequeño, incluso con un impacto muy tangencial podría dejar al planeta con periodos de rotación superiores a las 48 horas.
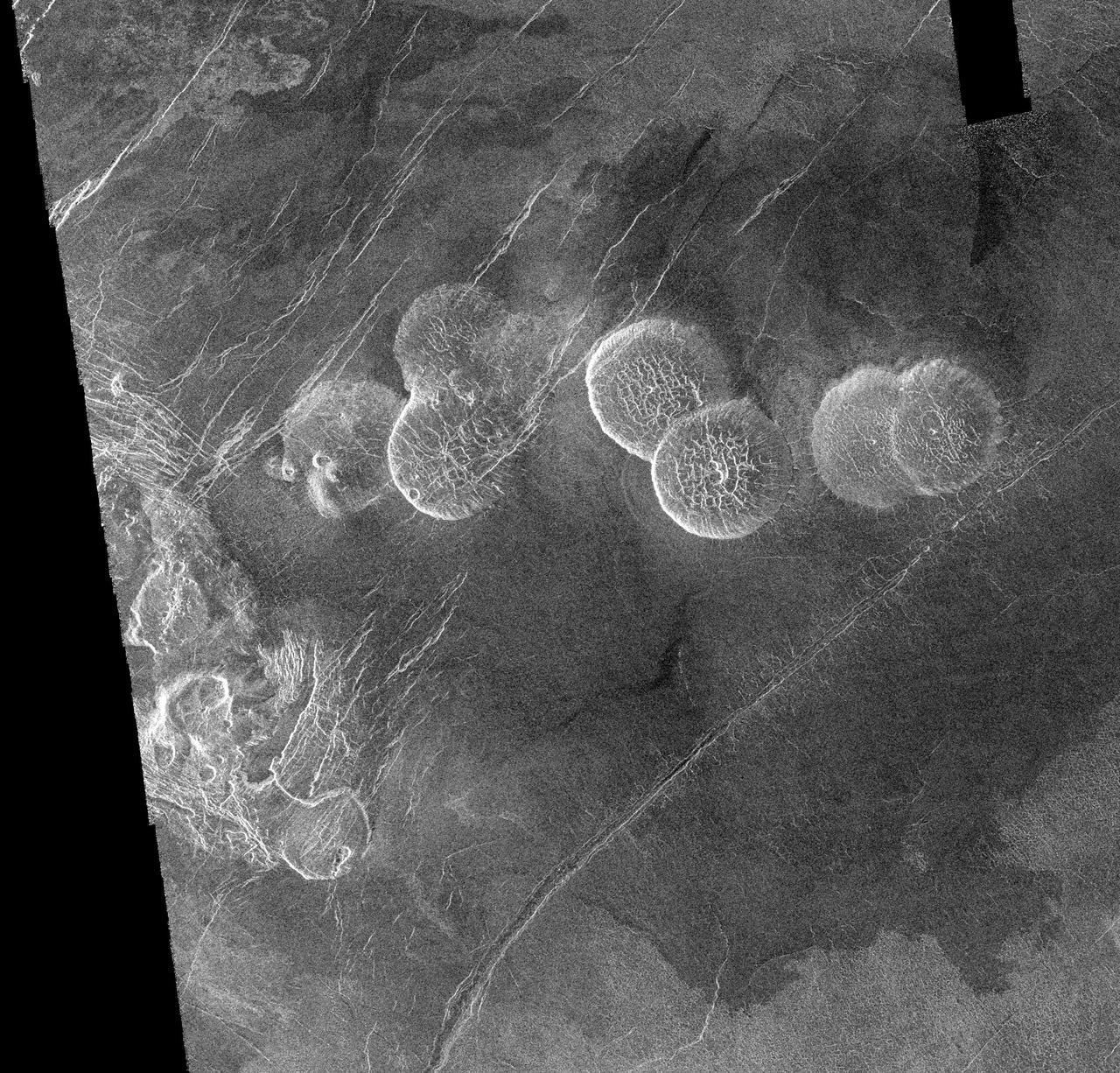 Venus es un mundo tan diferente al nuestro que incluso tiene formas geológicas que no se parecen en nada a las de la tierra, como estos pancake domes o, en traducción libre conocidos como “domos tortita” y que parecen ser domos de lava formados por la erupción de una lava muy viscosa, en este caso situados en Alpha Regio. Imagen cortesía de NASA/JPL.
Venus es un mundo tan diferente al nuestro que incluso tiene formas geológicas que no se parecen en nada a las de la tierra, como estos pancake domes o, en traducción libre conocidos como “domos tortita” y que parecen ser domos de lava formados por la erupción de una lava muy viscosa, en este caso situados en Alpha Regio. Imagen cortesía de NASA/JPL.Pero más llamativos fueron los resultados cuando simularon el impacto con un Venus girando sobre sí mismo. En este caso, el cuerpo que impactaba contra el proto-Venus tenía no solo que cambiar su velocidad de rotación, sino también de invertirla.
Para conseguir este efecto, se necesitaba un impacto oblicuo que golpease al planeta en contra de su dirección de rotación, algo que en las simulaciones es un escenario posible. Eso sí, en el caso de un Venus con una rotación muy rápida -el escenario de 2.5 horas- necesitaría de múltiples impactos para frenarlo e invertir su rotación, algo mucho más difícil desde el punto de vista estadístico.
Y ahora que tenemos resuelta la primera parte del puzle, ¿Por qué Venus no tiene un satélite natural? Estos mismos impactos son capaces de lanzar una gran cantidad de materia a la órbita, formando anillos cuyos fragmentos pueden ir fusionándose para formar un satélite, como en el caso de la Tierra y la Luna.
No todo iba a ser tan fácil ni tan bonito para Venus. El estudio tiene una derivada muy importante: los investigadores han encontrado una fuerte correlación positiva entre el momento angular del sistema tras el impacto y la masa del disco de materia producido por el impacto. Es decir, si el impacto acelera mucho al planeta, también lanza hacia afuera una gran cantidad de materia, mientras que los impactos que dejan al planeta con una velocidad de rotación pequeña, la cantidad de materia que se expulsa al espacio es mucho menor.
 También hay formas que nos son más familiares, como esta imagen de radar de Sapas Mons, un volcán que alcanza los 1500 metros y cuyas coladas de lava -en esta imagen de radar en tonos muy claros- nos recuerda mucho a una imagen cenital de los volcanes terrestres. Imagen cortesía de NASA/JPL.
También hay formas que nos son más familiares, como esta imagen de radar de Sapas Mons, un volcán que alcanza los 1500 metros y cuyas coladas de lava -en esta imagen de radar en tonos muy claros- nos recuerda mucho a una imagen cenital de los volcanes terrestres. Imagen cortesía de NASA/JPL.Aquí es donde se unen las dos partes del estudio, ya que los investigadores opinan que son las dos caras de una moneda. Los escenarios que fueron capaces de explicar por qué Venus gira tan lentamente son los mismos que no pudieron crear un gran disco de materia alrededor del planeta y que acabase formando un satélite.
Además, la estabilidad del disco de materia alrededor de los planetas depende de su distancia con respecto a la órbita síncrona del planeta, la altitud a la cual una satélite gira a la misma velocidad que el propio planeta, un caso similar al de los satélites geoestacionarios en el ecuador de la Tierra.
Para el caso de un Venus girando tras el impacto con un periodo de 48 o más horas, la órbita síncrona estaría muy lejos, en torno a unas 10 veces el radio del planeta. Los investigadores analizaron todos los discos de materia formados en las simulaciones observando que, en cada caso, la poca materia que acaba en órbita lo hacía muy dentro de la órbita síncrona.
Este material estaría, de algún modo, condenado. En vez de unirse formando un satélite con una vida prolongada -en tiempo geológico, claro- las fuerzas de marea irían acercándolo a Venus. Este disco de materia iría lentamente haciendo una espiral descendente hacia el planeta, cayendo finalmente sobre su superficie.
Los resultados de este modelo no son un final en sí mismo, sino un inicio para comprender mejor la evolución de Venus. Un impacto de esta magnitud es capaz de “reiniciar” un planeta, ya que introduce una inmensa cantidad de energía cinética que, a su vez, se transforma en energía térmica, fundiendo grandes cantidades de la corteza y manto de Venus y alterando su evolución geodinámica.
Comprender mejor como Venus se ha ido enfriando, como se ha desarrollado la convección en el manto y conocer detalles que nos permitan entender el por qué, por ejemplo, no ha desarrollado una tectónica de placas, puede ser fundamental para por fin responder a la pregunta de por qué dos planetas que nacieron siendo tan iguales, acabaron teniendo un destino antagónico.
Referencias:
Bussmann, M., Reinhardt, C., Gillmann, C., Meier, T., Stadel, J., Tackley, P., & Helled, R. (2025) The possibility of a giant impact on Venus. Astronomy & Astrophysics doi: 10.1051/0004-6361/202555802
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El violento nacimiento de Venus se ha escrito en Cuaderno de Cultura Científica.
Adiós a la canica azul: La Tierra se está oscureciendo y no son buenas noticias
 La Tierra vista por la misión lunar Apolo 17 en 1972. Foto: NASA / Dominio Público
La Tierra vista por la misión lunar Apolo 17 en 1972. Foto: NASA / Dominio PúblicoEl 7 de diciembre de 1972, a las 12:33 a. m, el colosal cohete Saturno V despegaba desde el actual Centro espacial Kennedy rumbo a la Luna. Se trataba de la última misión del programa Apolo y en ella viajaba la última tripulación que pisaría la Luna hasta nuestros días. Apenas cinco horas después del lanzamiento los astronautas Eugene Cernan, Ronald Evans y Harrison Schmitt se encontraban ya a casi 30.000 kilómetros de nuestro planeta cuando decidieron mirar por la ventanilla y observar la Tierra desde la distancia. La fotografía que tomaron en aquel momento se conoce popularmente como «la canica azul» y pronto se convirtió en un icono de los movimientos medioambientales de los setenta inspirando la idea de que debemos cuidar nuestro único y frágil hogar en el inmenso cosmos.
Era la primera vez que un ser humano captaba una imagen de la Tierra de manera completa, nítida y sin sombras. La fotografía original, tomada por la tripulación desde el Módulo de Mando y Servicio (CSM), mostraba el Polo Sur en la parte superior de la imagen pero posteriormente fue girada para cumplir con las expectativas y convenciones de orientación con el norte en su lugar. También fue única al captar la Antártida y casi todo su casquete polar, así como la costa de África, tanto en el Atlántico como en el Índico e incluso el potente ciclón de Tamil Nadu que, apenas unos días antes, había provocado fuertes vientos e inundaciones en la India.
Pero, además de las características físicas y geográficas de la fotografía, más allá de su simbología y trascendencia o de las incontables tecnologías que fueron necesarias para poder tomar una fotografía así desde el espacio, la célebre «Blue Marble» fue posible gracias al albedo de nuestro planeta. Ya sea un pequeño punto azul pálido o una canica brillante en el oscuro vacío del espacio, nuestra querida Tierra es visible desde el espacio porque refleja la luz… aunque según los todos estudios y datos satelitales de las últimas décadas, cada vez menos.
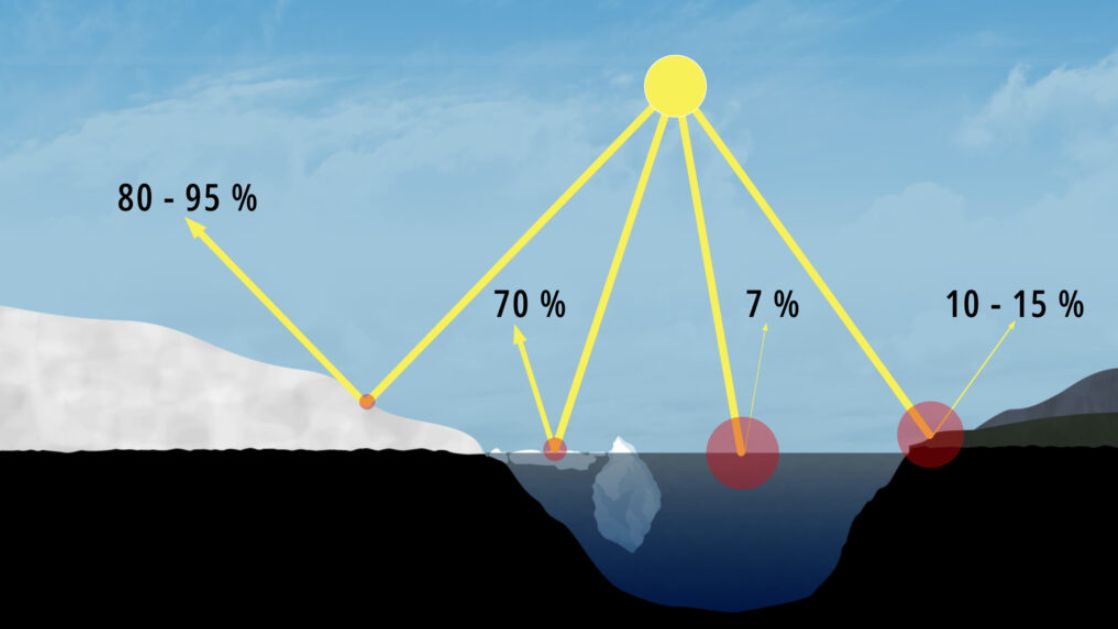 El albedo es un concepto científico que expresa el porcentaje de luz solar que refleja una superficie. La nieve, por ejemplo, puede tener un albedo de hasta un 0,9, es decir puede reflejar hasta el 90 % de la luz solar que incide sobre ella. Por otro lado, «el océano abierto puede tener un albedo inferior a 0,1, lo que significa que absorbe más del 90 % de la luz solar incidente y reflejando menos del 10 %».
El albedo es un concepto científico que expresa el porcentaje de luz solar que refleja una superficie. La nieve, por ejemplo, puede tener un albedo de hasta un 0,9, es decir puede reflejar hasta el 90 % de la luz solar que incide sobre ella. Por otro lado, «el océano abierto puede tener un albedo inferior a 0,1, lo que significa que absorbe más del 90 % de la luz solar incidente y reflejando menos del 10 %».El albedo es un concepto científico que expresa el porcentaje de luz solar que refleja una superficie. La nieve, por ejemplo, puede tener un albedo de hasta un 0,9, es decir puede reflejar hasta el 90 % de la luz solar que incide sobre ella. Por otro lado, «el océano abierto puede tener un albedo inferior a 0,1, lo que significa que absorbe más del 90 % de la luz solar incidente y reflejando menos del 10 %».
Un nuevo estudio, publicado hace unas semanas en Proceedings of the National Academy of Sciences (PNAS), vuelve a confirmar que nuestro planeta está perdiendo albedo y, desde hace décadas, es un cuerpo cada vez más y más oscuro. Los autores, encabezados por el investigador Norman Loeb, pertenecen al departamento de Ciencias de la radiación de NASA y han utilizado datos de tres satélites diferentes que miden «la luz solar incidente frente a la radiación de onda larga saliente, es decir, la cantidad de radiación reflejada de vuelta al espacio».
Los datos proceden del programa CERES, un acrónimo cuyas siglas se corresponden con «Sistema de Nubes y Energía Radiante de la Tierra» y que cuenta en la actualidad con una red de satélites que miden el balance de radiación terrestre (BRT). Desde el año 2000, CERES ha estado registrando cuánta luz solar absorbe nuestro planeta así como la cantidad de radiación infrarroja que escapa de vuelta al espacio. El equipo de Loeb utilizó estas mediciones para analizar el balance energético de nuestro planeta en los últimos 24 años (2001-2024) y, posteriormente, combinó estos datos con otras fuentes de información como cámaras espectrales de alta resolución, mapas de nieve y nubes, y modelos climáticos por computadora para llegar a una conclusión esperada: la Tierra lleva décadas oscureciéndose.
Un sistema desequilibrado en el Hemisferio NorteEl trabajo publicado no solo ha utilizado los datos satelitales del programa CERES para confirmar el paulatino oscurecimiento de la Tierra sino que además, y puede ser su mayor aportación, incluye un descubrimiento con importantes repercusiones: El Hemisferio Norte se está oscureciendo más rápido que el Sur.
Según las mediciones del estudio, el Hemisferio Norte «absorbe aproximadamente 0.34 vatios más de energía solar por metro cuadrado por década que el Hemisferio Sur», una diferencia que parece menos pero que, teniendo en cuenta toda la superficie del planeta, supone una «cantidad enorme», explica Loeb en Eos.org.
Hasta ahora se pensaba que la Tierra absorbía y reflejaba la energía procedente del Sol de manera balanceada y que no había una diferencia significativa entre ambos hemisferios, sin embargo este nuevo estudio descarta esa hipótesis y apunta a un desequilibrio notable entre hemisferios en el que el Norte está absorbiendo un plus energía y, por tanto, se oscurece más.
¿Por qué el Hemisferio Norte se oscurece más?El trabajo publicado también expone los motivos de este desequilibrio e indica tres factores fundamentales. El primero, quizá el más obvio, es el deshielo. En el Hemisferio Norte la nieve y el hielo, especialmente en el Ártico, se están derritiendo a un ritmo más acelerado y eso reduce el albedo exponiendo la tierra y el océano que hay debajo.
El segundo aspecto a tener en cuenta son las regulaciones medioambientales que, en los últimos años, han logrado disminuir la contaminación en lugares como China, Estados Unidos y Europa, lo que significa que «hay menos aerosoles en el aire para reflejar la luz solar. En el Hemisferio Sur ocurre lo contrario».
Y en tercer lugar, los autores mencionan el vapor de agua. «Debido a que el Norte se está calentando más rápido, también retiene más vapor de agua, un gas de efecto invernadero que no refleja la luz solar sino que la absorbe. Esa es otra razón por la que el Hemisferio Norte está absorbiendo más calor».
Pero todavía quedan incógnitas que resolver en este panorama y factores de los cuales aún desconocemos su influencia, como por ejemplo la cobertura de nubes. Otro de los hallazgos interesantes de este estudio es que, en los últimos 20 años, la cobertura de nubes no ha cambiado significativamente a pesar de la asimetría Norte-Sur. «Debería verse más reflexión por parte de las nubes en el Hemisferio Norte (en comparación con el Sur), pero no la vemos», concluye Loeb.
En definitiva, el nuevo estudio publicado por NASA nos muestra que nuestro planeta está absorbiendo cada vez más radiación, reflejando menos luz y calentándose de manera acelerada, sin olvidar que el Hemisferio Norte lo hace más rápido que el Sur.
Si los astronautas del Apolo 17 mirasen en nuestros tiempos por la ventana de su módulo, la fotografía de nuestra «Canica Azul» sería hoy algo menos brillante y más oscura, un punto azul cada vez más pálido…
Referencias científicas y más información:
Loeb, Norman G., et al. (2025) Emerging Hemispheric Asymmetry of Earth’s Radiation Proceedings of the National Academy of Sciences doi:10.1073/pnas.2511595122.
Larissa G. Capella (2025) «New Satellite Data Reveal a Shift in Earth’s Once-Balanced Energy System» Eos.org
Margherita Bassi (2025) «Earth Is Getting Dimmer—and the Northern Hemisphere Is Losing Brightness Faster Than Scientists Expected» Smithsonian Magazine (2025)
Ryan Green (2025) «Earth Is Getting Darker, Which Could Accelerate Global Warming» Scientific American
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico. Autor de «500 Años de Frío» (2019) y «Planeta Océano» (2022). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Adiós a la canica azul: La Tierra se está oscureciendo y no son buenas noticias se ha escrito en Cuaderno de Cultura Científica.
CRISPR-CAS9 y las terapias génicas
CRISPR-Cas9 ha transformado la biología: una herramienta de edición genética que permite cortar y pegar ADN con una precisión revolucionaria.
Los vídeos “Hitos científicos del siglo XXI” muestran los mayores descubrimientos y avances científicos de las últimas décadas. Se han emitido como una sección del programa de divulgación científica de RTVE Órbita Laika, en colaboración con la Cátedra de Cultura Científica de la Universidad del País Vasco.
Ficha técnica:
Producción ejecutiva: Blanca Baena
Guion: José Antonio Pérez Ledo
Dirección: Aitor Gutierrez
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Doblaje: K 2000
Locución: José Antonio Pérez Ledo
El artículo CRISPR-CAS9 y las terapias génicas se ha escrito en Cuaderno de Cultura Científica.
Cuidando nuestra salud oral protegemos el cerebro
Cuando pensamos en salud oral, solemos imaginar dientes blancos y encías firmes. Pero mantener una buena higiene bucal va mucho más allá de una cuestión estética: puede influir directamente en la salud de todo nuestro organismo.
 Foto: Marcos Ramírez / Unsplash
Foto: Marcos Ramírez / UnsplashPorque lo que ocurre en la boca no se queda en la boca. Las bacterias que se acumulan en los dientes y encías pueden viajar por el cuerpo y tener consecuencias en órganos tan distintos como el corazón o el cerebro.
Una mala salud oral no solo favorece la aparición de caries, la pérdida de dientes o la inflamación de encías (gingivitis): también puede agravar enfermedades crónicas como la diabetes, aumentar el riesgo de ciertos tipos de cáncer e incluso contribuir al desarrollo de enfermedades cardiovasculares, cerebrales y neurodegenerativas.
En concreto, se ha observado que las personas que padecen periodontitis –una inflamación crónica de las encías causada por la acumulación de placa bacteriana– presentan más posibilidades de desarrollar complicaciones en otras partes del cuerpo. Los datos son claros: un paciente con periodontitis no tratada tiene 2,5 veces más riesgo de sufrir un ictus y casi 3 veces más de probabilidades de padecer una enfermedad cardíaca en comparación con quienes mantienen una buena salud bucodental.
Además, la inflamación crónica asociada con la periodontitis también podría contribuir al deterioro cognitivo, como ocurre en el alzhéimer.
Alzhéimer: el olvido que lo cambia todoEl alzhéimer es la causa más frecuente de demencia neurodegenerativa. A nivel mundial, más de 57 millones de personas viven con demencia, de las cuales entre el 60 % y el 70 % padecen alzhéimer. En España, afecta a unas 800 000 personas, y se estima que su prevalencia se duplicará en los próximos 20 años.
Aunque aún no conocemos su causa exacta, sí sabemos que influyen tanto la genética como factores ambientales, incluido nuestro estilo de vida. Y es aquí donde aparece una conexión inesperada: el cuidado de las encías podría desempeñar un papel protector frente al deterioro cognitivo.
Bacterias, seres invisibles que dejan huellaLa boca alberga unas 770 especies de microorganismos que componen la microbiota oral. En equilibrio, esta comunidad bacteriana cumple funciones beneficiosas. Pero cuando la higiene es deficiente o existen factores que alteran ese equilibrio, las bacterias patógenas se multiplican, favoreciendo la aparición de enfermedades como la enfermedad periodontal.
La gingivitis, la forma más leve, afecta hasta al 90 % de la población y puede revertirse con una correcta higiene. Sin embargo, si progresa, puede convertirse en periodontitis, una afección crónica, inflamatoria e irreversible con consecuencias que van mucho más allá de la pérdida de dientes.
Las bacterias implicadas, especialmente Porphyromonas gingivalis, y las moléculas inflamatorias que el sistema inmunitario libera al intentar combatirlas pueden viajar por la sangre y alcanzar órganos distantes, como el cerebro. Allí pueden contribuir a procesos inflamatorios y al desarrollo o progresión de enfermedades neurodegenerativas como el alzhéimer.
De hecho, varios estudios recientes refuerzan la hipótesis de esa conexión. En modelos animales, la exposición prolongada a toxinas de bacterias como Porphyromonas gingivalis ha inducido neuroinflamación, acumulación de proteína beta-amiloide y deterioro de la memoria, tres características típicas del alzhéimer.
En humanos, también se ha hallado evidencia sorprendente: la cantidad de bacterias orales en el tejido cerebral de personas fallecidas con esa patología es hasta siete veces mayor que en quienes no padecían la enfermedad.
Cepillarse: una rutina que podría proteger nuestra menteAsí pues, dedicar apenas 10 minutos al día a la higiene oral es una inversión para la salud futura. Cada vez que olvidamos cepillarnos, las bacterias se multiplican y pueden acabar en otras partes del cuerpo con efectos imprevisibles.
Cepillarse los dientes, usar hilo dental y acudir regularmente al dentista no solo cuida la sonrisa: también puede ayudar a proteger el corazón, el cerebro y, posiblemente, la memoria. El alzhéimer borra recuerdos, pero hay algo que conviene no olvidar: cuidar de nuestra boca es cuidar de nuestra mente.![]()
Sobre las autoras: Teresa Morera Herreras, Profesora agregada del Departamento de Farmacología, EHU; Ane Murueta-Goyena, Profesora Adjunta del Departamento de Neurociencia, EHU; y Unai Fernández Martín, Investigador predoctoral, EHU
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Cuidando nuestra salud oral protegemos el cerebro se ha escrito en Cuaderno de Cultura Científica.
La Geología por la que pasean las ánimas
En estas fechas, aparte del maratón de películas de terror de la noche de Halloween, me encanta rememorar una fantástica historia convertida en auténtica leyenda por la pluma de Gustavo Adolfo Bécquer, y en una preciosa canción por el grupo español de folk metal Saurom, «El Monte de las Ánimas».
Esta historia nos relata que, en esa zona, siglos atrás tuvo lugar una cruenta batalla entre caballeros templarios y nobles castellanos, cuyas almas no encontraron descanso, por lo que sus espíritus vagan errantes en la Noche de Todos los Santos (que, según la versión de Bécquer, no es la noche del 31 de octubre, sino la que va del 1 al 2 de noviembre) para llevarse consigo a toda aquella persona que ose pasar por allí en ese oscuro momento. Cosa que descubre Beatriz de manera atroz al perder a Alonso tras hacerle regresar al monte por la noche. Pero, ¿sobre qué materiales geológicos caminan esos fantasmas?
 Detalle de las rocas que forman el Monte de las Ánimas (Soria). Imagen de Google Street View a la altura de la antigua Área de Descanso de la N-234 (Soria Sur) a las afueras de la ciudad, tomada de Google Maps.
Detalle de las rocas que forman el Monte de las Ánimas (Soria). Imagen de Google Street View a la altura de la antigua Área de Descanso de la N-234 (Soria Sur) a las afueras de la ciudad, tomada de Google Maps.Si abandonamos las leyendas y nos vamos a la realidad, el monte de las Ánimas es una pequeña elevación del terreno situada a las afueras de la ciudad de Soria. Geológicamente hablando, esta zona forma parte de la denominada Cuenca de Almazán, que representa el límite oriental de la Cuenca del Duero, que abarca gran parte de la actual comunidad autónoma de Castilla y León. Y que también tiene una apasionante historia geológica.
Todo comenzó hace unos 80 millones de años, cuando la placa Ibérica chocó contra la placa Europea. Este proceso tectónico fue muy intenso en esta zona desde hace algo más de 60 millones de años hasta hace unos 40 millones de años, provocando la formación de tres grandes cadenas montañosas: el Sistema Ibérico al este, el Sistema Central al sur y la Cordillera Cantábrica al norte. El alzamiento de estas montañas dejó una zona deprimida en el centro, como si fuese una especie de cubeta, que es lo que en Geología denominamos cuenca sedimentaria.
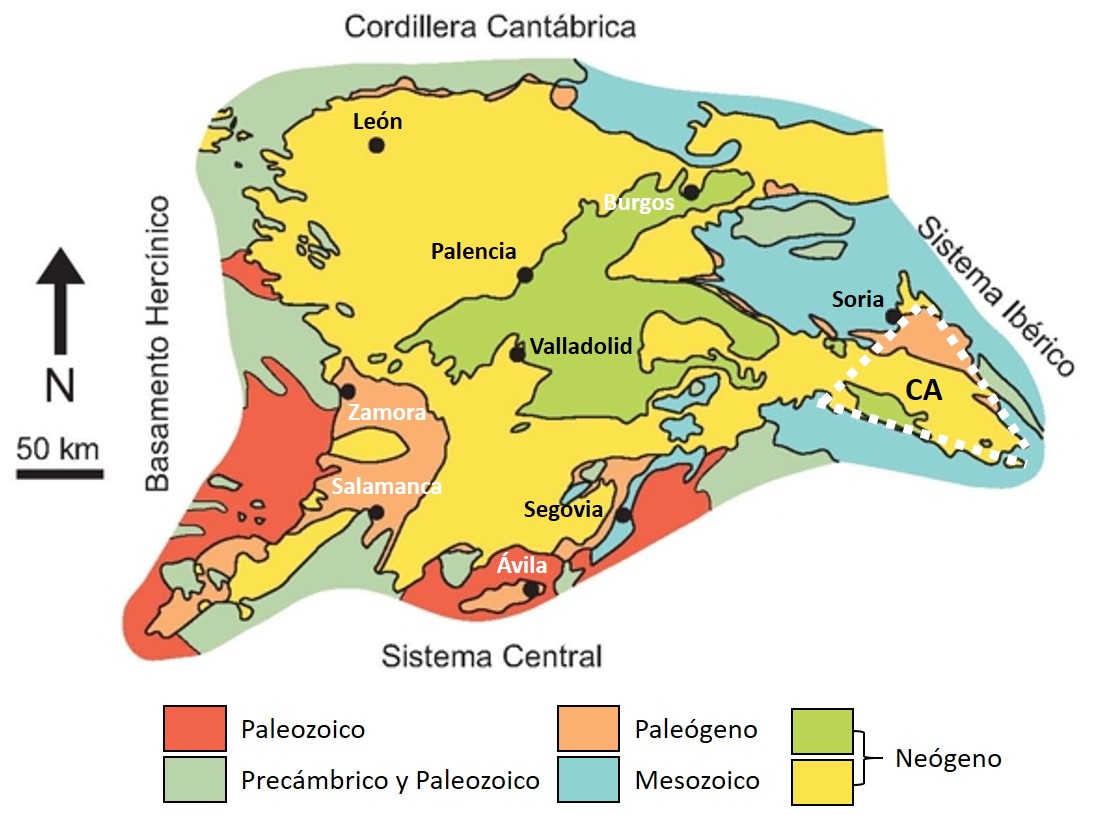 Mapa geológico simplificado de la Cuenca del Duero, donde se remarca la localización de la Cuenca de Almazán (CA). Imagen modificada de Sastre Merlín, A., Montamarta Prieto, G., de Miguel Vela, F., Vicente Lapuente, R., Alejandre Alcalde, V. y Acosta Molinero, J.A. (2025) Deza: un balcón sobre la cuenca de Almazán. Guía del Geolodía 25 Soria, 8 pp.
Mapa geológico simplificado de la Cuenca del Duero, donde se remarca la localización de la Cuenca de Almazán (CA). Imagen modificada de Sastre Merlín, A., Montamarta Prieto, G., de Miguel Vela, F., Vicente Lapuente, R., Alejandre Alcalde, V. y Acosta Molinero, J.A. (2025) Deza: un balcón sobre la cuenca de Almazán. Guía del Geolodía 25 Soria, 8 pp.La principal característica de estas cuencas sedimentarias continentales rodeadas por elevaciones montañosas es que actúan como si fuesen unas bañeras, recibiendo el agua y los materiales (barro, arena y fragmentos de rocas) transportados por los ríos y arroyos que bajan por sus laderas. Y la Cuenca de Almazán no se quedó atrás, acumulando estos aportes montañosos durante más de 20 millones de años.
Esto provocó la formación de diferentes medios ambientes según nos alejamos de las montañas, debido a la energía que tenía el agua para poder arrastrar los materiales geológicos. Aquí es donde entran la física de fluidos y, sobre todo, la gravedad. Cuando un arroyo o riachuelo caía por la ladera de la montaña tenía una gran energía, lo que le permitía arrastrar grandes fragmentos de rocas, granos de arena de diferente tamaño y mucho barro. Pero, al llegar al pie de la ladera, cuando la pendiente disminuye, ya no tenía tanta energía, por lo que depositaba los materiales más grandes y pesados en el margen de su cauce, arrastrando sólo los sedimentos más finos hasta, finalmente, únicamente poder circular el agua casi limpia. De esta forma, junto a las laderas de las montañas se acumulaban rocas y arena de grano grueso mezcladas con barro, en unas estructuras llamadas abanicos aluviales, porque nos recuerdan a un abanico abierto si las miramos desde arriba. A su lado se formarían unas llanuras aluviales con arena más fina y arcilla y, al final, nos encontraríamos con lagos carbonatados poco profundos que, en muchas ocasiones, serían temporales.
Con el tiempo, estos sedimentos se convirtieron en diferentes tipos de rocas que, desde el pie de las laderas hasta las zonas centrales de la cuenca, serían: conglomerados y areniscas de grano grueso en los antiguos abanicos aluviales; areniscas de grano medio-fino y lutitas en las llanuras aluviales; y margas y calizas en los lagos carbonatados.
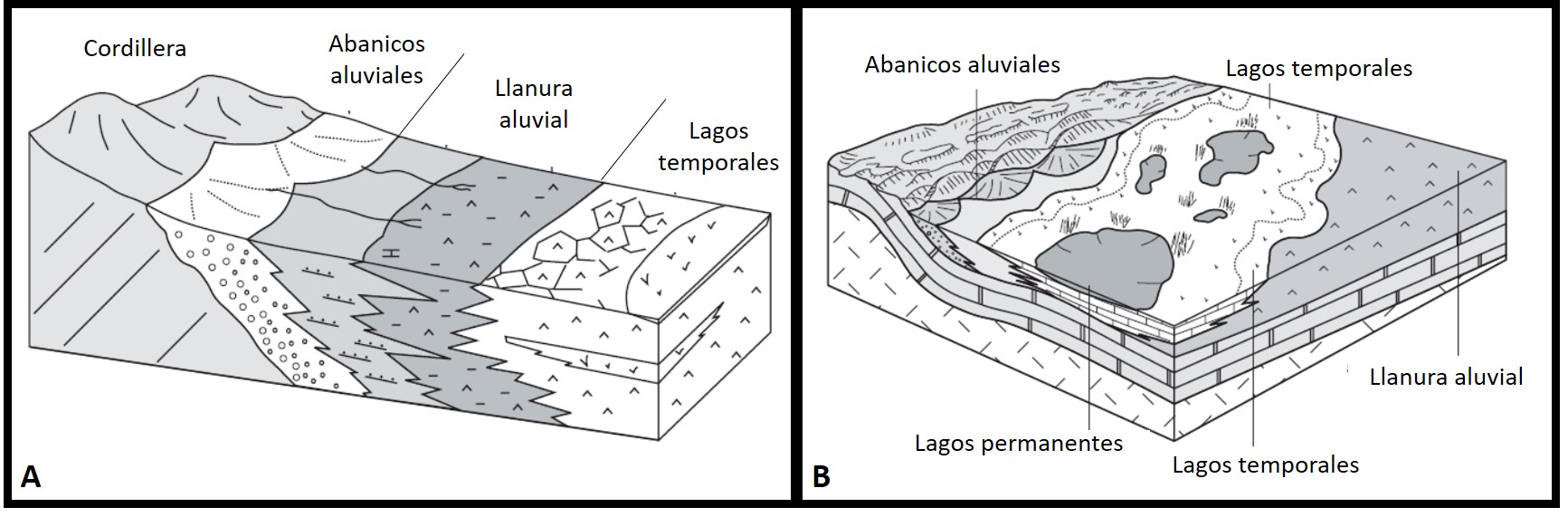 A) Zonación ambiental de una cuenca sedimentaria continental desde la cordillera hasta la zona central de la misma; y B) detalle de los ambientes sedimentarios formados en la Cuenca de Almazán. Imágenes modificadas de Huerta, P. (2006) El Paleógeno de la cuenca de Almazán. Tesis Doctoral. Universidad de Salamanca. Memoria (339 pp.), Anexo 1 y Anexo 2.
A) Zonación ambiental de una cuenca sedimentaria continental desde la cordillera hasta la zona central de la misma; y B) detalle de los ambientes sedimentarios formados en la Cuenca de Almazán. Imágenes modificadas de Huerta, P. (2006) El Paleógeno de la cuenca de Almazán. Tesis Doctoral. Universidad de Salamanca. Memoria (339 pp.), Anexo 1 y Anexo 2.Pero la historia no terminó aquí. En los últimos millones de años, el Duero fue capaz de abrirse camino hasta su desembocadura en el océano Atlántico. Siguiendo con el símil, fue como si le quitásemos el tapón a las bañeras que eran la Cuenca del Duero y su pequeño apéndice, la Cuenca de Almazán. Así, los lagos efímeros se desecaron y los arroyos y riachuelos que surgían de las montañas se convirtieron en afluentes del propio Duero, transformándose en los principales agentes de la última fase de esta historia: la erosión. Esta agua que antes depositaba sedimentos, desde entonces está robando lo que una vez poseyó, arrasando con las rocas formadas en esta zona. Pero no a todas les afecta por igual: las más resistentes, como los conglomerados, las areniscas de grano más grueso y las calizas, resisten mejor la erosión; mientras que las rocas más débiles, como las lutitas o las margas, son arrastradas sin compasión.
Entonces, ¿qué ha pasado con el Monte de las Ánimas? Pues se trata de antiguos abanicos aluviales que transportaban agua, cantos, arena y barro procedentes de las montañas situadas justo al norte de Soria. Hoy en día, esas rocas soportan el embate del agua de lluvia resistiéndose a la erosión con mayor ahínco que los materiales que tiene a su lado, por lo que permanece en pie como una pequeña elevación que vigila la ciudad.
Así que, volviendo a la pregunta del inicio, los templarios y caballeros castellanos que visiten nuestro mundo en la noche de difuntos, caminarán sobre conglomerados, areniscas y arcillas de hace unos 20 millones de años. Pero si queréis ir a comprobarlo, os recomiendo que esperéis a que sea de día, por si acaso. Y recordad ataos bien al hombro la banda de color azul, no vaya a ser que la perdáis durante vuestro paseo…
Agradecimientos:
Quiero dar las gracias a mi colega Jone Mendicoa por darme la idea para este artículo después de una interesante conversación sobre literatura y música camino a un concierto.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la EHU
El artículo La Geología por la que pasean las ánimas se ha escrito en Cuaderno de Cultura Científica.
Una apuesta engañosa
A Julene, como buena bilbaína, le encanta hacer apuestas.
Está en clase de geografía, un tanto aburrida, escuchando al profesor López que está explicando el funcionamiento de las redes hidrográficas terrestres. Para intentar vencer la apatía, propone a su compañero de pupitre, Mikel, apostar sobre los números que va a mencionar el docente a lo largo de su lección. Así, Julene invita a Mikel a apostar diez euros en un juego que tratará sobre los siguientes nueve números que mencionará el profesor, números que hacen referencia a longitudes (en kilómetros) de ríos u otras corrientes fluviales.
 Fuente: FreepikJulene propone las reglas del juego a Mikel
Fuente: FreepikJulene propone las reglas del juego a Mikel
Julene comenta los términos de la apuesta a Mikel:
Te propongo tener en cuenta únicamente la primera cifra significativa de las longitudes de los cursos de agua que mencione el profesor. Yo me quedaré con el conjunto de las tres primeras cifras A = {1, 2, 3} y tú con el conjunto de las otras seis cifras B = {4, 5, 6, 7, 8, 9}. Ganará, y recibirá los diez euros del otro, quien tenga en su conjunto la primera cifra que haya aparecido con mayor frecuencia en la lección.
Para aclarar su propuesta, Julene continúa argumentando para convencer a Mikel de que está siendo generosa con él:
Si las nueve longitudes mencionadas son, por ejemplo, 243 km, 876 km, 1222 km, 92 km, 4330 km, 982 km, 3445 km, 2122 km y 832 km (cuyos primeros dígitos son 2, 8, 1, 9, 4, 9, 3, 2 y 8), tú ganarías porque en el anterior listado de primeros dígitos hay cinco números del conjunto B, el tuyo, y sólo cuatro del conjunto A, el mío.
Julene es una jugadora astuta y, con su propuesta de juego y el ejemplo que hábilmente ha expuesto, ha conseguido que Mikel crea que es sencillo para él ganar los diez euros de la apuesta. Al fin y al cabo, el conjunto que le corresponde (el conjunto B) tiene seis dígitos y el de Julene (el conjunto A) solo posee tres. Así que, convencido de que tiene muchas posibilidades de ganar los diez euros, Mikel acepta el juego de Julene.
Pero se equivoca; de hecho, Julene tiene una mayor probabilidad de ganar. ¿Cómo puede ser esto cierto?
Con las reglas de Julene, a Mikel no le conviene jugarEfectivamente, Julene ha conseguido embaucar a Mikel; con sus reglas, ella sabe que tiene bastantes probabilidades de quedarse con los diez euros de su compañero.
La explicación de la ventaja de Julene en este juego tiene que ver con la llamada ley de Benford (o ley del primer dígito) que se refiere a una distribución de frecuencia estadística observada empíricamente en muchas fuentes de datos numéricos (como en el caso de la medida de la longitud de ríos). Esta ley dice que la cifra 1 aparece en primera posición con mucha mayor frecuencia que el resto de los números. Además, según crece el primer dígito, es menos probable que se encuentre en la primera posición.
La ley de Benford establece que la probabilidad de que un número obtenido de un determinado dato comience con el dígito d es de:
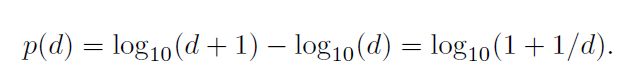
En la práctica, la frecuencia de aparición de cada número es de:
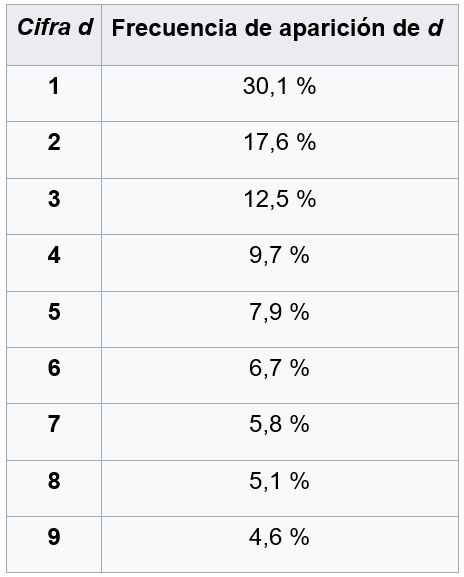
Si la apuesta consistiera en jugar con un único número, Julene ganaría con una probabilidad de a = p(1) + p(2) + p(3) = 0,602 (0,301 + 0,176 + 0,125 = 0,602). Por lo tanto, Mikel ganaría con una probabilidad de b = 1 – a = 0,398.
Pero la apuesta tiene en cuenta nueve números, no solo uno. Así, la probabilidad de que Julene gane es la probabilidad de que, entre los nueve números que mencionará el profesor durante su clase, haya al menos cinco (cinco, seis, siete, ocho o nueve números) pertenecientes al conjunto A = {1, 2, 3}. Dicho de otro modo, de los números significativos mencionados por el docente, como mucho cuatro pertenecerán al conjunto B = {4, 5, 6, 7, 8, 9} asignado a Mikel, que perdería así la apuesta.
La probabilidad de que haya k números de A = {1, 2, 3} entre los nueve números utilizados por el profesor (probabilidad de k éxitos en una repetición de 9 experimentos) es de:
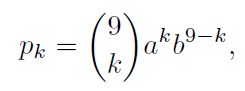
que involucra un coeficiente binomial (cantidad de subconjuntos de k elementos escogidos de un conjunto de 9 elementos).
Así, la probabilidad de que Julene gane es de:
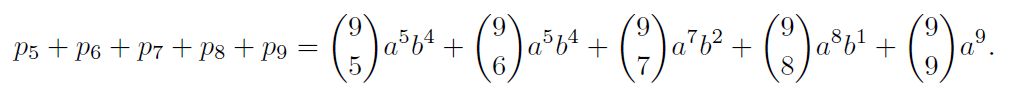
Tras hacer las operaciones indicadas en la anterior fórmula, el resultado es de 0,738. Así, Mikel tiene pocas probabilidades de ganar (1 – 0,738 = 0,262), y muchas de perder los diez euros de la apuesta… ¡Su compañera Julene “se la ha jugado”!
Nota
Adaptado de: Jean-Paul Delahaye, Rubrique des paradoxes précédents : La longueur des fleuves, Accromath 20.2 été-automne 2025
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Una apuesta engañosa se ha escrito en Cuaderno de Cultura Científica.
La teoría de juegos de cómo los algoritmos pueden hacer subir los precios
Estudios recientes revelan que incluso los algoritmos de fijación de precios más simples pueden encarecer las cosas.
Un artículo de Ben Brubaker. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Nash Weerasekera / Quanta Magazine
Ilustración: Nash Weerasekera / Quanta MagazineImagina un pueblo con dos comerciantes de utensilios. Los clientes prefieren el utensilio más barato, así que los comerciantes compiten fijando precios bajos. Descontentos con sus escasas ganancias, se reúnen una noche en una taberna llena de humo para discutir un plan secreto: si suben los precios juntos en lugar de competir, ambos podrían ganar más. Pero ese tipo de acuerdo intencionado sobre precios, llamado colusión, lleva más de un siglo prohibido. Los comerciantes deciden no arriesgarse y todo el mundo sigue disfrutando de utensilios baratos.
Durante más de un siglo, la legislación estadounidense ha seguido este esquema básico: prohibir esos tratos a puerta cerrada y con ello preservar unos precios justos. Hoy no es tan sencillo. En amplios sectores de la economía los vendedores dependen cada vez más de programas informáticos llamados algoritmos de aprendizaje, que ajustan los precios de forma iterada en función de nuevos datos sobre el mercado. A menudo son mucho más simples que los algoritmos de “aprendizaje profundo” que impulsa la inteligencia artificial moderna, pero aun así pueden comportarse de formas inesperadas.
Entonces, ¿cómo pueden los reguladores garantizar que los algoritmos fijan precios justos? Su enfoque tradicional no servirá, porque se basa en encontrar una colusión explícita. “Los algoritmos desde luego no se están tomando copas juntos”, apunta Aaron Roth, científico informático de la Universidad de Pennsylvania.
Sin embargo, un artículo muy citado de 2019 mostró que los algoritmos podían aprender a coludir de forma tácita, incluso cuando no estaban programados para ello. Un equipo de investigadores enfrentó dos copias de un algoritmo de aprendizaje simple en un mercado simulado y les dejó explorar distintas estrategias para aumentar sus beneficios. Con el tiempo, cada algoritmo aprendió por ensayo y error a castigar cuando el otro bajaba los precios: respondía reduciendo su propio precio en una cuantía enorme y desproporcionada. El resultado final fue precios elevados, sostenidos por la amenaza mutua de una guerra de precios.
 Aaron Roth sospecha que los problemas de la fijación de precios algorítmica podrían no tener una solución sencilla. «La conclusión de nuestro estudio es que resulta difícil determinar qué descartar», afirma. Foto cortesía de Aaron Roth
Aaron Roth sospecha que los problemas de la fijación de precios algorítmica podrían no tener una solución sencilla. «La conclusión de nuestro estudio es que resulta difícil determinar qué descartar», afirma. Foto cortesía de Aaron RothLas amenazas implícitas como esta también están en la base de muchos casos de colusión humana. Así que, si quieres garantizar precios justos, ¿por qué no exigir que los vendedores utilicen algoritmos incapaces de hacer amenazas?
En un trabajo reciente, Roth y otros cuatro científicos informáticos mostraron por qué eso puede no ser suficiente. Probaron que incluso algoritmos aparentemente benignos que optimizan su propio beneficio pueden a veces dar lugar a resultados perjudiciales para los compradores. “Aun así puedes obtener precios altos de maneras que, desde fuera, parecen razonables”, explica Natalie Collina, estudiante de posgrado que trabaja con Roth y coautora del nuevo estudio.
No todos los investigadores coinciden en las implicaciones del hallazgo —mucho depende de cómo se defina “razonable”—. Pero la investigación revela lo sutiles que pueden ser las cuestiones sobre fijación algorítmica de precios y lo difícil que puede resultar regularlas.
“Sin alguna sospecha de amenaza o de un acuerdo, es muy difícil que un regulador pueda entrar y decir: ‘Estos precios no parecen correctos’”, afirma Mallesh Pai, economista de la Universidad Rice. “Por eso creo que este artículo es importante.”
Sin arrepentimiento
El trabajo reciente estudia la fijación algorítmica de precios desde la óptica de la teoría de juegos, un campo interdisciplinar en la frontera entre la economía y la informática que analiza las matemáticas de las competiciones estratégicas. Es una forma de explorar los errores de los algoritmos de precios en un entorno controlado.
“Lo que intentamos hacer es crear colusión en el laboratorio”, explica Joseph Harrington, economista de la Universidad de Pennsylvania que escribió un influyente artículo de revisión sobre la regulación de la colusión algorítmica y que no ha participado en la nueva investigación. “Una vez que lo hacemos, queremos averiguar cómo destruir esa colusión.”
 Natalie Collina y sus colegas han descubierto que los precios altos pueden surgir de maneras inesperadas. Foto: Nandan Tumu
Natalie Collina y sus colegas han descubierto que los precios altos pueden surgir de maneras inesperadas. Foto: Nandan TumuPara entender las ideas clave conviene empezar con el simple juego de piedra-papel-tijera. Un algoritmo de aprendizaje, en este contexto, puede ser cualquier estrategia que un jugador use para elegir una jugada en cada ronda basándose en los datos de rondas anteriores. Los jugadores pueden probar distintas estrategias a lo largo del juego. Pero si juegan bien, acabarán convergiendo a un estado que los teóricos de juegos llaman equilibrio. En equilibrio, la estrategia de cada jugador es la mejor respuesta posible a la estrategia del otro, por lo que ninguno tiene incentivo a cambiar.
En piedra-papel-tijera, la estrategia ideal es sencilla: hay que jugar una jugada aleatoria cada ronda, escogiendo las tres posibilidades con la misma frecuencia. Los algoritmos de aprendizaje destacan cuando un jugador adopta un enfoque distinto. En ese caso, elegir jugadas en función de rondas anteriores puede ayudar al otro jugador a ganar más a menudo que si jugara al azar.
Supón, por ejemplo, que tras muchas rondas detectas que tu oponente —un geólogo— eligió piedra más del 50% de las veces. Si hubieras jugado papel cada ronda, habrías ganado más. Los teóricos de juegos se refieren a esta dolorosa constatación como arrepentimiento.
Los investigadores han diseñado algoritmos de aprendizaje sencillos que garantizan siempre que acabarás con arrepentimiento cero. Algoritmos de aprendizaje algo más sofisticados, llamados algoritmos “sin arrepentimiento por intercambio” (no-swap-regret), también garantizan que cualquiera que sea la acción de tu oponente, no podrías haberlo hecho mejor sustituyendo todas las ocurrencias de una jugada por otra (por ejemplo, jugando papel cada vez que en realidad jugaste tijera). En 2000, teóricos de juegos demostraron que, si enfrentas dos algoritmos sin arrepentimiento por intercambio en cualquier juego, acabarán en un tipo específico de equilibrio —uno que sería el equilibrio óptimo si solo jugaran una única ronda. Esa propiedad es atractiva porque los juegos de una sola ronda son mucho más simples que los de varias rondas. En particular porque las amenazas no funcionan ya que los jugadores no pueden ejecutarlas.
En un artículo de 2024, Jason Hartline, informático de la Universidad Northwestern, y dos estudiantes de posgrado tradujeron los resultados clásicos de 2000 a un modelo de mercado competitivo, donde los jugadores pueden fijar precios nuevos cada ronda. En ese contexto, los resultados implicaban que dos algoritmos sin arrepentimiento por intercambio se acabarían encontrando en precios competitivos cuando alcanzaran el equilibrio. La colusión sería imposible.
Sin embargo, los algoritmos sin arrepentimiento por intercambio no son las únicas estrategias de fijación de precios en los mercados en línea. ¿Qué ocurre cuando un algoritmo sin arrepentimiento por intercambio se enfrenta a un oponente distinto que también parece benigno?
El precio está equivocado
Según los teóricos de juegos, la mejor estrategia para jugar contra un algoritmo sin arrepentimiento por intercambio es simple: empieza con una probabilidad concreta para cada posible acción y, luego, en cada ronda elige una sola acción al azar, sin importar lo que haga tu oponente. La asignación ideal de probabilidades para este enfoque “no reactivo” depende del juego específico.
En el verano de 2024, Collina y su colega Eshwar Arunachaleswaran se propusieron encontrar esas probabilidades óptimas para un juego de fijación de precios entre dos jugadores. Hallaron que la mejor estrategia asignaba probabilidades sorprendentemente altas a precios muy elevados, junto con probabilidades menores distribuidas en una amplia gama de precios bajos. Si juegas contra un algoritmo sin arrepentimiento por intercambio, esta extraña estrategia maximizará tu beneficio. “Para mí fue una sorpresa total”, cuenta Arunachaleswaran.
 Eshwar Arunachaleswaran y Collina obtuvieron su resultado al explorar las mejores respuestas a algoritmos de precios bien definidos. Foto: Paritosh Verma
Eshwar Arunachaleswaran y Collina obtuvieron su resultado al explorar las mejores respuestas a algoritmos de precios bien definidos. Foto: Paritosh VermaLas estrategias no reactivas parecen superficialmente inocuas. No pueden transmitir amenazas, porque no reaccionan a las jugadas del rival en absoluto. Pero pueden inducir a los algoritmos de aprendizaje a subir sus precios, y luego aprovecharse ocasionalmente vendiendo más barato que el competidor.
Al principio, Collina y Arunachaleswaran pensaron que este escenario artificial no sería relevante en el mundo real. Seguro que el jugador que usara el algoritmo sin arrepentimiento por intercambio cambiaría a otro algoritmo en cuanto se diera cuenta de que su competidor estaba obteniendo beneficios a su costa.
Pero al profundizar y al discutirlo con Roth y otros dos colegas, se dieron cuenta de que su intuición era errónea. Los dos jugadores en su escenario ya estaban en un estado de equilibrio. Sus beneficios eran casi iguales, y ambos eran tan altos como podían ser siempre que ninguno cambiara de algoritmo. Ninguno tenía incentivo a cambiar de estrategia, así que los compradores se quedarían atrapados con precios altos. Además, las probabilidades precisas no eran tan importantes. Muchas elecciones distintas conducían a precios elevados cuando se enfrentaban a un algoritmo sin arrepentimiento por intercambio. Es un resultado que cabría esperar de una colusión, pero sin que se viera ningún comportamiento colusorio.
Conviene ser tonto
¿Y qué pueden hacer los reguladores? Roth admite que no tiene respuesta. No tendría sentido prohibir los algoritmos sin arrepentimiento por intercambio: si todos usaran uno, los precios caerían. Pero una simple estrategia no reactiva podría ser una elección natural para un vendedor en un mercado en línea como Amazon, aunque conlleve el riesgo de arrepentimiento.
“Una forma de tener arrepentimiento es simplemente ser un poco tonto”, afirma Roth. “Históricamente, eso no ha sido ilegal.”
Para Hartline, el problema de la colusión algorítmica tiene una solución simple: prohibir todos los algoritmos de fijación de precios excepto los algoritmos sin arrepentimiento por intercambio que los teóricos de juegos han venido recomendando. Puede haber formas prácticas de hacerlo: en su trabajo de 2024, Hartline y sus colegas idearon un método para comprobar si un algoritmo tiene la propiedad de sin arrepentimiento por intercambio sin mirar su código.
Hartline reconoció que su solución preferida no evitaría todos los malos resultados cuando algoritmos sin arrepentimiento por intercambio compitieran con humanos. Pero sostiene que escenarios como el del trabajo de Roth no son casos de colusión algorítmica.
“La colusión es algo de doble vía”, dijo. “Fundamentalmente debe ser posible que un único jugador haga algo para no coludir.”
Sea como fuere, el nuevo trabajo deja muchas preguntas abiertas sobre cómo puede fallar la fijación de precios algorítmica en el mundo real.
“Aún no entendemos ni de lejos todo lo que quisiéramos”, dico Pai. “Es una cuestión importante para nuestro tiempo.”
El artículo original, The Game Theory of How Algorithms Can Drive Up Prices, se publicó el 22 de octubre de 2025 en Quanta Magazine.
Traducido por César Tomé López
El artículo La teoría de juegos de cómo los algoritmos pueden hacer subir los precios se ha escrito en Cuaderno de Cultura Científica.
Atracción (electroestática) fatal
En una entrega anterior de esta sección describíamos la curiosa estrategia del nematodo Caenorhabditis elegans para dispersarse en el medio. Estos pequeños gusanos forman torres para salvar espacios y, eventualmente, adherirse a insectos que los transporten a otros lugares. Parecía difícil superar esto, pero otro nematodo, Steinernema carpocapsae (Figura 1), acaba de proporcionarnos un caso aún más sorprendente. Con una longitud máxima de medio milímetro, este minúsculo gusano es capaz de saltar a una distancia superior a veinte veces su longitud corporal, con una velocidad inicial de 1.5 m/s, y adherirse a un insecto al que matará y consumirá. Si a esto le añadimos que rara vez falla en su objetivo, nos tenemos que preguntar cómo un animal, tan limitado en lo sensorial como en lo motor, tiene tanta puntería. Y la respuesta, totalmente inesperada, radica en la electroestática.
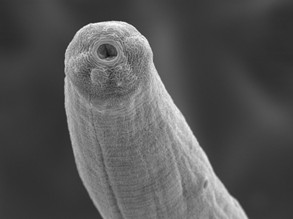 Figura 1. El nematodo Steinernema carpocapsae, individuo juvenil en fase infectiva. De Lu et al. (2017), doi: 10.1371/journal.ppat.1006302, CC BY 4.0.
Figura 1. El nematodo Steinernema carpocapsae, individuo juvenil en fase infectiva. De Lu et al. (2017), doi: 10.1371/journal.ppat.1006302, CC BY 4.0.La electricidad estática está presente en muchos fenómenos biológicos. Los insectos voladores, por ejemplo, suelen cargarse positivamente por el roce con partículas presentes en el aire. De esta forma se facilita la recolección de polen por abejas, mariposas o colibrís. Eso sí, la carga eléctrica positiva de los insectos voladores aumenta su riesgo de enredarse en telarañas. La electricidad estática también está implicada en el vuelo de arañas, en ocasiones a cientos de kilómetros de distancia. Los filamentos de seda emitidos por estas arañas y cargados negativamente son atraídos por cargas eléctricas positivas en la atmósfera, como podemos ver en este vídeo.
Volvamos a S. carpocapsae. Este nematodo ha sido comercializado debido a su utilidad en la lucha biológica contra plagas de insectos. Cincuenta millones de gusanos pueden adquirirse en el mercado fitosanitario por unos 20 euros. A pesar de su pequeño tamaño, S. carpocapsae mata rápidamente (en 24-48 horas) a los insectos a los que ataca. Esta letalidad se debe a dos factores. Por un lado, transporta en su intestino bacterias simbióticas del género Photorhabdus o Xenorhabdus. Cuando el gusano penetra en su víctima, las bacterias son liberadas y proliferan rápidamente, produciendo toxinas y enzimas que degradan los tejidos del insecto. Al mismo tiempo, el nematodo produce otras sustancias tóxicas y supresoras del sistema inmune del insecto, que no puede defenderse de la infección bacteriana. Para completar el trabajo, las bacterias también segregan antibióticos que evitan la competencia de otras bacterias.
A estas alturas el insecto ha sido ya atacado por otros nematodos de la misma especie, que pasan de un estadio juvenil (el único de vida libre) a adultos de ambos sexos. Se aparean, ponen huevos y mantienen el ciclo hasta que el insecto ha sido completamente consumido. En ese momento los juveniles vuelven a asociarse con las bacterias (que solo pueden vivir en simbiosis con S. carpocapsae) y abandonan el cadáver para buscar otra víctima.
La pregunta que nos hacíamos al principio es, ¿cómo este pequeño gusano es capaz de saltar y adherirse a un insecto volador con precisión? La sorprendente respuesta acaba de aparecer en un artículo publicado en PNAS por investigadores estadounidenses. Es el propio insecto el que atrae al nematodo a causa de su carga eléctrica positiva, como vemos en este video.
Los experimentos se realizaron con moscas del vinagre conectadas a un filamento de cobre para proporcionarles carga eléctrica positiva (Figura 2A-C). De acuerdo con las medidas tomadas en insectos voladores, estas cargas suelen estar entre 10 y 200 picoculombios (pC), lo que equivale a voltajes entre 50 y 1000 voltios. En todos los experimentos, los nematodos saltarines aterrizaron sobre el insecto. Lo mismo sucedió cuando el insecto fue reemplazado por una bola metálica con la misma carga eléctrica.
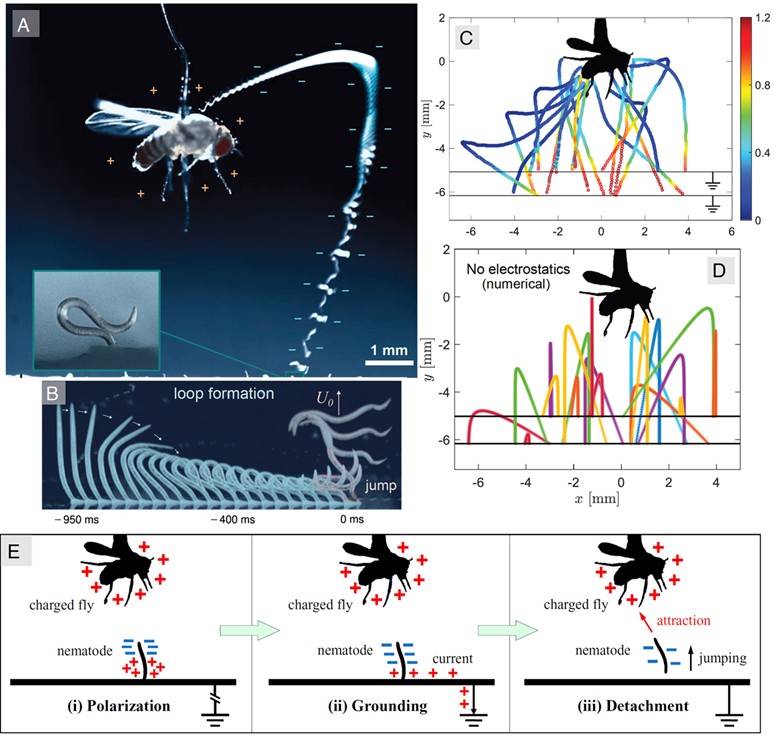 Figura 2. A: Trayectoria del nematodo Steinernema carpocapsae. Tras el salto es atraído hacia la mosca, cargada positivamente. B: El nematodo se dobla como un resorte antes de saltar. C: Trayectoria registrada en 19 individuos, partiendo de dos alturas diferentes. Todos ellos impactan contra el insecto, independientemente de la dirección del salto. Los colores indican la velocidad en m/s. D: Modelo numérico basado en las observaciones anteriores (velocidad y dirección), pero asignando carga neutra a los gusanos. Solo en un caso se logra el contacto con el insecto. Los colores indican diferentes voltajes para la mosca, entre 100 y 700 V. E: Carga del nematodo por inducción. El insecto cargado positivamente polariza al gusano atrayendo cargas negativas. El sustrato actúa como toma de tierra y proporciona electrones que neutralizan las cargas positivas. Cuando el nematodo salta, su carga es negativa y es atraído hacia el insecto. Fuente: Ran et al. (2025), cita completa en referencias, CC BY 4.0.
Figura 2. A: Trayectoria del nematodo Steinernema carpocapsae. Tras el salto es atraído hacia la mosca, cargada positivamente. B: El nematodo se dobla como un resorte antes de saltar. C: Trayectoria registrada en 19 individuos, partiendo de dos alturas diferentes. Todos ellos impactan contra el insecto, independientemente de la dirección del salto. Los colores indican la velocidad en m/s. D: Modelo numérico basado en las observaciones anteriores (velocidad y dirección), pero asignando carga neutra a los gusanos. Solo en un caso se logra el contacto con el insecto. Los colores indican diferentes voltajes para la mosca, entre 100 y 700 V. E: Carga del nematodo por inducción. El insecto cargado positivamente polariza al gusano atrayendo cargas negativas. El sustrato actúa como toma de tierra y proporciona electrones que neutralizan las cargas positivas. Cuando el nematodo salta, su carga es negativa y es atraído hacia el insecto. Fuente: Ran et al. (2025), cita completa en referencias, CC BY 4.0.Para que la atracción electrostática sea eficaz, el nematodo debe tener carga eléctrica negativa, y los modelos numéricos mostraron que, en efecto, esta carga está alrededor de 0.1 pC. ¿Cómo se genera esta carga? La hipótesis más probable es que se deba a la inducción (Figura 2E). Cuando el insecto cargado positivamente se acerca, atrae cargas negativas del extremo más próximo del nematodo, con lo que el extremo contrario se carga positivamente. Ese extremo está en contacto con el sustrato, que actúa como toma de tierra y proporciona electrones que cancelan las cargas positivas. Por eso, todo el gusano, cuando salta hacia su objetivo, tiene carga negativa y es atraído hacia su víctima.
La pequeñísima carga negativa adquirida por inducción es esencial. De acuerdo con los modelos numéricos, cuando se simularon las trayectorias y las velocidades de los saltos, pero se asignó una carga nula a los gusanos, solo uno de los 19 intentos terminó con éxito (Figura 2D).
Resulta paradójico que la misma carga positiva que resulta útil, por ejemplo, para la recogida de polen, pueda ser fatal al atraer a nematodos parásitos. En cualquier caso, este descubrimiento ilustra la importancia de comprender mejor los fenómenos eléctricos en las interacciones animales.
Referencias
Ran, R., Burton, J.C., Kumar, S. et al. (2025). Electrostatics facilitate midair host attachment in parasitic jumping nematodes, Proc. Natl. Acad. Sci. U.S.A. doi: 10.1073/pnas.2503555122.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
El artículo Atracción (electroestática) fatal se ha escrito en Cuaderno de Cultura Científica.
Nuestros ojos saben lo que hicimos el último verano
 Foto: Eugene Golovesov en Unsplash
Foto: Eugene Golovesov en Unsplash
La miopía avanza de forma imparable en todo el mundo. Según la Organización Mundial de la Salud, para 2050 la mitad de la población mundial será miope. No se trata solo de llevar gafas: cuando esa afección visual progresa mucho, aumenta el riesgo de desprendimiento de retina, glaucoma o ceguera irreversible.
En España, por ejemplo, la ceguera miópica es la primera causa de afiliación a la ONCE. La pregunta es inevitable: ¿qué podemos hacer para frenar la epidemia?
Una “caja negra” de la exposición al solLa respuesta podría estar, literalmente, en nuestros ojos. Más en concreto, en un curioso fenómeno llamado autofluorescencia ultravioleta conjuntival (CUVAF por su denominación en inglés), que funciona como una especie de “caja negra” de la exposición solar que ha recibido cada persona.
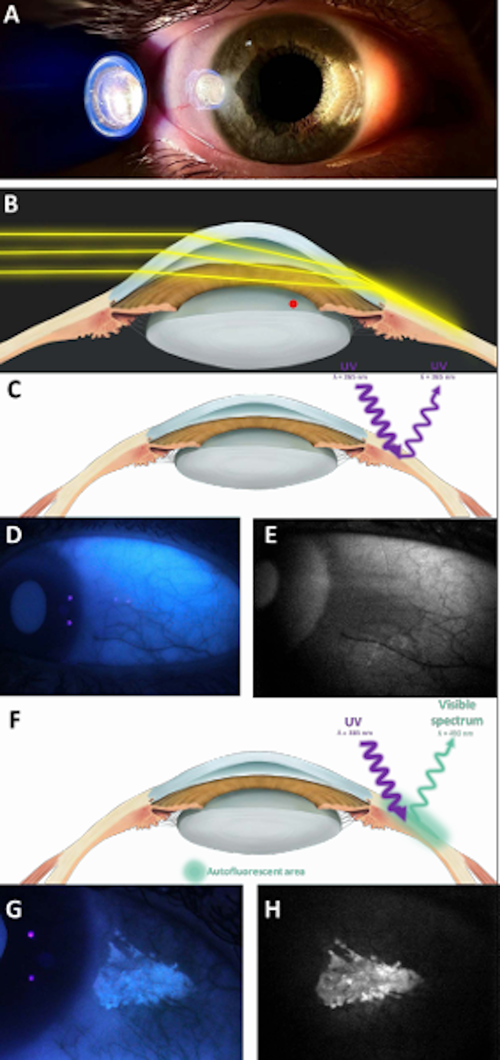 (A) Demostración ‘in vivo’ del enfoque corneal de la luz periférica proveniente del lado temporal del ojo hacia el limbo y la conjuntiva nasal, con una intensidad luminosa mayor en comparación con el lado temporal. (B) Representación óptica del efecto de enfoque de la luz periférica que provoca la concentración de los rayos incidentes, al atravesar la cámara anterior, sobre la superficie límbico-conjuntival contralateral del ojo. (C) Representación de un caso CUVAF negativo (sin área de hiperautofluorescencia conjuntival). (D–E) Fotografías CUVAF negativas tomadas bajo luz ultravioleta (D) (longitud de onda máxima de 365 nm) y (E) una fotografía tomada con el modo BAF del Heidelberg Spectralis HRA+OCT (longitud de onda máxima de 488 nm). (F) Representación de un caso CUVAF positivo (muestra un área de hiperautofluorescencia que absorbe a 360 nm y emite en el espectro visible). (G–H) Fotografías CUVAF positivas en una imagen a color tomada bajo luz ultravioleta (G) y (H) con el Heidelberg Spectralis HRA+OCT.
(A) Demostración ‘in vivo’ del enfoque corneal de la luz periférica proveniente del lado temporal del ojo hacia el limbo y la conjuntiva nasal, con una intensidad luminosa mayor en comparación con el lado temporal. (B) Representación óptica del efecto de enfoque de la luz periférica que provoca la concentración de los rayos incidentes, al atravesar la cámara anterior, sobre la superficie límbico-conjuntival contralateral del ojo. (C) Representación de un caso CUVAF negativo (sin área de hiperautofluorescencia conjuntival). (D–E) Fotografías CUVAF negativas tomadas bajo luz ultravioleta (D) (longitud de onda máxima de 365 nm) y (E) una fotografía tomada con el modo BAF del Heidelberg Spectralis HRA+OCT (longitud de onda máxima de 488 nm). (F) Representación de un caso CUVAF positivo (muestra un área de hiperautofluorescencia que absorbe a 360 nm y emite en el espectro visible). (G–H) Fotografías CUVAF positivas en una imagen a color tomada bajo luz ultravioleta (G) y (H) con el Heidelberg Spectralis HRA+OCT.El CUVAF es un área de autofluorescencia en la conjuntiva (la parte blanca del ojo) que aparece cuando se ilumina con luz ultravioleta. Entonces, el ojo muestra manchas brillantes que delatan cuánto tiempo hemos pasado bajo la luz del sol.
Aunque esas manchas no son visibles a simple vista, quedan registradas de forma objetiva. Así, el CUVAF se ha convertido en un biomarcador fiable para saber cuántas horas al aire libre ha acumulado una persona a lo largo de su vida reciente.
Los científicos llevan años sospechando que la falta de luz natural es una de las grandes culpables del aumento de la miopía. Los niños que pasan más tiempo en interiores –ya sea frente al móvil, la tableta o los libros– tienen más riesgo de desarrollarla.
¿Por qué? La hipótesis más aceptada es que la luz solar estimula la liberación del neurotransmisor dopamina en la retina, y esa dopamina actúa como freno natural para que el ojo no crezca en exceso (además de controlar ciclos circadianos, hormonas, etc).
Otra posible causa es que cuando estamos en la calle miramos principalmente de lejos, de forma relajada y sin forzar los músculos de la acomodación (necesarios para ver de cerca), lo cual evita el crecimiento excesivo del ojo. Porque cuando esto último ocurre, la imagen no se enfoca nítidamente en la retina y aparece la miopía.
De los cuestionarios a la “memoria ocular”Hasta hace poco, los investigadores solo podían medir el tiempo que pasan los niños al aire libre preguntando a los padres o a los propios menores. Pero esos cuestionarios tienen muchas limitaciones: ¿quién recuerda con exactitud cuántas horas estuvo en el parque hace un mes?
El CUVAF resuelve este problema. Funciona como un registro objetivo de la exposición solar, independiente de la memoria o la percepción. Si un niño presenta poco CUVAF, significa que pasa poco tiempo en exteriores y, por tanto, que tiene más riesgo de ser miope.
Lo que dicen los estudiosVarios trabajos internacionales confirman su utilidad. Así, un metaanálisis con más de 3 600 personas de distintos países encontró que los miopes pasaban menos tiempo al aire libre y tenían áreas de CUVAF significativamente más pequeñas que los no miopes. Y en la Universidad de Navarra, un estudio con estudiantes de Medicina y de Ciencias Ambientales mostró que los segundos, que pasan más horas en el exterior por su carrera, tenían más CUVAF y la mitad de riesgo de desarrollar miopía.
Para conocer las repercusiones de este biomarcador en la edad infantil –la etapa más sensible para el crecimiento excesivo del ojo–, se llevó a cabo una investigación en más de 260 niños de entre 6 y 17 años. Los autores comprobaron que los miopes, efectivamente, pasaban menos tiempo al aire libre y presentaban menos CUVAF. Además, si el área de autofluorescencia de la conjuntiva era grande en relación a la edad, los menores estaban protegidos hasta 2,5 veces frente a la miopía y hasta 5 veces frente a la miopía alta.
Este hallazgo podría confirmarse en un estudio, actualmente en revisión, con más de 2 600 niños de la Comunidad de Madrid.
Imaginemos cómo podría usarse dicha información en la práctica clínica. En una revisión ocular, el oftalmólogo toma una imagen del CUVAF. Si el resultado muestra un área reducida, podría dar el siguiente consejo:
“Su hijo necesita al menos una o dos horas de juego al aire libre cada día. El mejor tratamiento ahora mismo es la luz natural, gratuita y sin efectos secundarios”.
En el futuro, las consultas de oftalmología podrían incorporar esa prueba rutinaria igual que hoy se mide la tensión ocular o el fondo de ojo.
No es solo cosa de niñosAunque la prevención en la infancia es clave, el CUVAF también puede ser útil en adultos jóvenes. Durante la universidad o los primeros años laborales, la miopía puede seguir progresando. Medir el CUVAF en esta etapa permite detectar a quienes mantienen un estilo de vida demasiado “de puertas adentro” y orientar cambios sencillos: salir a pasear, practicar deporte al aire libre, exponerse a la luz natural cada día.
Hay una metáfora muy bonita que usan algunos investigadores: el verano se borra de nuestra piel, pero permanece en nuestros ojos. Aunque la piel pierda el bronceado, el ojo conserva la huella del sol a través del CUVAF. Y esa huella no es un simple recuerdo: es una pista directa sobre nuestra futura salud visual.
Porque la miopía no es inevitable: aunque los genes juegan un papel, el ambiente es decisivo. Y entre los factores ambientales, el tiempo al aire libre es el más importante y modificable.![]()
Sobre el autor: Sergio Recalde Maestre es Director científico del laboratorio de oftalmología experimental de la Universidad de Navarra
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Nuestros ojos saben lo que hicimos el último verano se ha escrito en Cuaderno de Cultura Científica.
Un termómetro para medir la cuanticidad
El flujo de calor “anómalo”, que a primera vista parece violar la segunda ley de la termodinámica, ofrece a los físicos una forma de detectar el entrelazamiento cuántico sin destruirlo.
Un artículo de Philip Ball. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Una variante moderna del demonio de Maxwell puede actuar como una especie de catalizador, impulsando un flujo de calor de objetos cuánticos fríos a calientes. Ilustración: Daniel García / Quanta Magazine
Una variante moderna del demonio de Maxwell puede actuar como una especie de catalizador, impulsando un flujo de calor de objetos cuánticos fríos a calientes. Ilustración: Daniel García / Quanta Magazine
Si hay una ley de la física que parece fácil de comprender, esa es la segunda ley de la termodinámica: el calor fluye espontáneamente de los cuerpos más calientes hacia los más fríos. Pero ahora, de forma suave y casi casual, Alexssandre de Oliveira Jr. acaba de mostrarme que, en realidad, no la entendía del todo.
«Toma esta taza de café caliente y esta jarra de leche fría», dijo el físico brasileño mientras estábamos sentados en una cafetería de Copenhague. «Ponlas en contacto y, efectivamente, el calor fluirá del objeto caliente al frío, tal como el científico alemán Rudolf Clausius formuló oficialmente en 1850». Sin embargo, en algunos casos —explicó de Oliveira— los físicos han descubierto que las leyes de la mecánica cuántica pueden hacer que el flujo de calor ocurra en sentido contrario: del frío al caliente.
Esto no significa realmente que la segunda ley falle, añadió mientras su café se enfriaba con tranquilidad. Lo que sucede es que la expresión de Clausius es el límite clásico de una formulación más completa, exigida por la física cuántica.
Los físicos empezaron a apreciar la sutileza de esta situación hace más de dos décadas y, desde entonces, han estado explorando la versión cuántica de la segunda ley. Ahora, de Oliveira, investigador posdoctoral en la Universidad Técnica de Dinamarca, y sus colegas han demostrado que el tipo de “flujo de calor anómalo” que se da a escala cuántica podría tener una aplicación tan práctica como ingeniosa.
Según afirman, puede servir como un método sencillo para detectar la cuanticidad —por ejemplo, para saber si un objeto está en una superposición cuántica de varios estados observables posibles, o si dos objetos están entrelazados (es decir, sus estados son interdependientes)— sin destruir esos delicados fenómenos cuánticos. Una herramienta diagnóstica así podría usarse para verificar que un ordenador cuántico está utilizando realmente recursos cuánticos al realizar sus cálculos. Incluso podría ayudar a detectar aspectos cuánticos de la fuerza de la gravedad, uno de los grandes objetivos de la física moderna.
Según los investigadores, basta con conectar un sistema cuántico a un segundo sistema capaz de almacenar información sobre él, y a un sumidero térmico (un cuerpo capaz de absorber mucha energía). Con esta disposición, se puede aumentar la transferencia de calor al sumidero más allá de lo que permitirían las leyes clásicas. Midiendo simplemente lo caliente que está el sumidero se podría detectar la presencia de superposición o entrelazamiento en el sistema cuántico.
Más allá de las posibles aplicaciones prácticas, la investigación pone de manifiesto un nuevo aspecto de una profunda verdad sobre la termodinámica: la forma en que el calor y la energía se transforman y se desplazan en los sistemas físicos está íntimamente ligada a la información —a lo que se sabe o puede saberse sobre dichos sistemas—. En este caso, “pagamos” el flujo de calor anómalo sacrificando información almacenada sobre el sistema cuántico.
«Me encanta la idea de que las magnitudes termodinámicas puedan señalar fenómenos cuánticos», afirma la física Nicole Yunger Halpern, de la Universidad de Maryland. «El tema es fundamental y profundo».
El conocimiento es poder
 «Es imposible que una máquina autónoma, sin la ayuda de ningún agente externo, transmita calor de un cuerpo a otro a una temperatura más alta», escribió Rudolf Clausius (en alemán) en 1850. Fue la primera expresión de la segunda ley de la termodinámica. Foto: Theo Schafgans/Dominio público
«Es imposible que una máquina autónoma, sin la ayuda de ningún agente externo, transmita calor de un cuerpo a otro a una temperatura más alta», escribió Rudolf Clausius (en alemán) en 1850. Fue la primera expresión de la segunda ley de la termodinámica. Foto: Theo Schafgans/Dominio públicoLa conexión entre la segunda ley de la termodinámica y la información fue explorada por primera vez en el siglo XIX por el físico escocés James Clerk Maxwell. Para su consternación, la segunda ley de Clausius parecía implicar que los focos de calor acabarían disipándose por todo el universo hasta que desapareciesen todas las diferencias de temperatura. En ese proceso, la entropía total del universo —en términos simples, una medida de su desorden y falta de estructura— aumentaría inexorablemente. Maxwell comprendió que esa tendencia acabaría eliminando toda posibilidad de aprovechar los flujos de calor para realizar trabajo útil, y que el universo alcanzaría un equilibrio estéril, dominado por un zumbido térmico uniforme: la llamada “muerte térmica”. Esa perspectiva ya era bastante inquietante por sí misma, pero resultaba especialmente inaceptable para el devoto cristiano Maxwell. En una carta a su amigo Peter Guthrie Tait en 1867, afirmó haber encontrado una manera de “abrir un agujero” en la segunda ley.
Imaginó un diminuto ser (más tarde apodado demonio) capaz de ver el movimiento de las moléculas individuales de un gas. El gas llenaría una caja dividida en dos compartimentos por una pared con una trampilla. Abriendo y cerrando la trampilla selectivamente, el demonio podría separar las moléculas que se mueven más rápido en un lado y las más lentas en el otro, creando así un gas caliente y otro frío, respectivamente. Al actuar según la información obtenida sobre el movimiento molecular, el demonio reduciría la entropía del gas, generando un gradiente de temperatura con el que podría realizarse trabajo mecánico, como empujar un pistón.
Los científicos estaban seguros de que el demonio de Maxwell no podía violar realmente la segunda ley, pero se tardó casi un siglo en comprender por qué. La respuesta es que la información que el demonio recoge y almacena sobre los movimientos moleculares acabaría llenando su memoria finita. Para seguir funcionando, tendría que borrar y reiniciar esa memoria. El físico Rolf Landauer demostró en 1961 que ese borrado consume energía y genera entropía —más entropía de la que el demonio reduce mediante su selección—. El análisis de Landauer estableció una equivalencia entre información y entropía, lo que implica que la información misma puede actuar como un recurso termodinámico: puede transformarse en trabajo. Los físicos demostraron experimentalmente esta conversión de información en energía en 2010.
 Incómodo con la segunda ley de la termodinámica, el físico escocés James Clerk Maxwell inventó un experimento mental sobre un demonio omnisciente que aún hoy nos brinda nuevas perspectivas. Imagen: The Print Collector/Heritage Images
Incómodo con la segunda ley de la termodinámica, el físico escocés James Clerk Maxwell inventó un experimento mental sobre un demonio omnisciente que aún hoy nos brinda nuevas perspectivas. Imagen: The Print Collector/Heritage ImagesPero los fenómenos cuánticos permiten procesar información de formas que la física clásica no permite —esa es, de hecho, la base de tecnologías como la computación cuántica y la criptografía cuántica—. Y por eso la teoría cuántica altera la versión convencional de la segunda ley.
Aprovechando las correlaciones
Los objetos cuánticos entrelazados comparten información mutua: están correlacionados, de modo que podemos conocer propiedades de uno observando el otro. Eso, por sí mismo, no es tan extraño; si observas uno de un par de guantes y ves que es el izquierdo, sabes que el otro es el derecho. Pero un par de partículas cuánticas entrelazadas difiere de los guantes en un aspecto esencial: mientras que la lateralidad de los guantes está fijada antes de mirar, en las partículas no es así, según la mecánica cuántica. Antes de medirlas, no está decidido qué valor de una propiedad observable tiene cada partícula del par entrelazado. En ese momento solo conocemos las probabilidades de las posibles combinaciones de valores (por ejemplo, 50 % izquierda-derecha y 50 % derecha-izquierda). Solo cuando medimos el estado de una partícula esas posibilidades se resuelven en un resultado concreto. En ese proceso de medición, el entrelazamiento se destruye.
Si las moléculas de un gas están entrelazadas de esta manera un demonio de Maxwell puede manipularlas con más eficacia que si todas se movieran independientemente. Si el demonio sabe, por ejemplo, que cada molécula rápida que ve venir está correlacionada de tal modo que otra rápida la seguirá al instante, no necesita observar la segunda partícula antes de abrir la trampilla para dejarla pasar. El coste termodinámico de (temporalmente) desafiar la segunda ley se reduce.
En 2004, los teóricos cuánticos Časlav Brukner, de la Universidad de Viena, y Vlatko Vedral, entonces en el Imperial College de Londres, señalaron que esto significa que las mediciones termodinámicas macroscópicas pueden utilizarse como un “testigo” para revelar la presencia de entrelazamiento cuántico entre partículas. Bajo ciertas condiciones, mostraron que la capacidad calorífica de un sistema o su respuesta a un campo magnético aplicado debería llevar la huella del entrelazamiento, si este existe.
De manera similar, otros físicos calcularon que se puede extraer más trabajo de un cuerpo caliente cuando hay entrelazamiento cuántico en el sistema que cuando es puramente clásico.
Y en 2008, el físico Hossein Partovi, de la Universidad Estatal de California, identificó una consecuencia particularmente llamativa del modo en que el entrelazamiento cuántico puede cuestionar las intuiciones derivadas de la termodinámica clásica. Descubrió que la presencia de entrelazamiento puede incluso invertir el flujo espontáneo de calor de un objeto caliente a uno frío, aparentemente subvirtiendo la segunda ley.
Esa inversión es una forma especial de refrigeración, explica Yunger Halpern. Y, como ocurre siempre con la refrigeración, no es gratuita (y por tanto no viola realmente la segunda ley). Clásicamente, refrigerar un objeto requiere trabajo: hay que bombear el calor en dirección contraria consumiendo combustible, compensando así la entropía perdida al enfriar el cuerpo frío y calentar el caliente. Pero en el caso cuántico —sigue Yunger Halpern—, en lugar de quemar combustible para lograr la refrigeración, «se queman las correlaciones». Es decir, a medida que avanza el flujo de calor anómalo, el entrelazamiento se destruye: las partículas que inicialmente tenían propiedades correlacionadas se vuelven independientes. «Podemos usar las correlaciones como un recurso para empujar el calor en dirección opuesta», añade.
 Vlatko Vedral es uno de los creadores de la idea de utilizar mediciones termodinámicas como «testigo» para revelar la presencia de entrelazamiento cuántico entre partículas. foto: Cortesía de Vlatko Vedral
Vlatko Vedral es uno de los creadores de la idea de utilizar mediciones termodinámicas como «testigo» para revelar la presencia de entrelazamiento cuántico entre partículas. foto: Cortesía de Vlatko VedralDe hecho, el “combustible” aquí es la información misma: concretamente, la información mutua de los cuerpos calientes y fríos entrelazados.
Dos años más tarde, David Jennings y Terry Rudolph, del Imperial College de Londres, aclararon lo que sucede. Mostraron cómo puede reformularse la segunda ley de la termodinámica para incluir el caso en que existe información mutua, y calcularon los límites sobre cuánto puede modificarse —e incluso invertirse— el flujo de calor clásico mediante el consumo de correlaciones cuánticas.
El demonio sabe de cuanticidad
Cuando entran en juego los efectos cuánticos la segunda ley deja de ser tan sencilla. Pero ¿podemos hacer algo útil con la forma en que la física cuántica flexibiliza los límites de las leyes termodinámicas? Esa es una de las metas de la disciplina llamada termodinámica cuántica, en la que algunos investigadores buscan fabricar motores cuánticos más eficientes que los clásicos o baterías cuánticas que se carguen más rápidamente.
Patryk Lipka-Bartosik, del Centro de Física Teórica de la Academia Polaca de Ciencias, ha buscado aplicaciones prácticas en la dirección contraria: usar la termodinámica como herramienta para explorar la física cuántica. El año pasado, él y sus colaboradores vieron cómo materializar la idea de Brukner y Vedral (2004) de utilizar propiedades termodinámicas como testigo del entrelazamiento cuántico. Su esquema involucra sistemas cuánticos calientes y fríos correlacionados entre sí, y un tercer sistema que media el flujo de calor entre ambos. Podemos pensar en este tercer sistema como en un demonio de Maxwell, solo que ahora posee una “memoria cuántica” que puede estar entrelazada con los sistemas que manipula. Al estar entrelazados con la memoria del demonio, los sistemas caliente y frío quedan efectivamente vinculados, de modo que el demonio puede inferir información de uno a partir de las propiedades del otro.
 Patryk Lipka-Bartosik ha explorado cómo utilizar mediciones termodinámicas para detectar efectos cuánticos. Foto: Alicja Lipka-Bartosik
Patryk Lipka-Bartosik ha explorado cómo utilizar mediciones termodinámicas para detectar efectos cuánticos. Foto: Alicja Lipka-BartosikUn demonio cuántico así puede actuar como un tipo de catalizador, facilitando la transferencia de calor al aprovechar correlaciones que de otro modo serían inaccesibles. Es decir, al estar entrelazado con los objetos caliente y frío, el demonio puede detectar y explotar todas sus correlaciones de manera sistemática. Y, de nuevo como un catalizador, este tercer sistema vuelve a su estado original una vez completado el intercambio de calor entre los objetos. De esta forma, el proceso puede potenciar el flujo de calor anómalo más allá de lo que sería posible sin dicho catalizador.
El artículo publicado este año por de Oliveira, junto con Lipka-Bartosik y Jonatan Bohr Brask, de la Universidad Técnica de Dinamarca, utiliza algunas de estas mismas ideas, pero con una diferencia crucial que convierte el sistema en una especie de termómetro para medir la cuanticidad. En el trabajo anterior, la memoria cuántica —el demonio— interactuaba con un par de sistemas cuánticos correlacionados, uno caliente y otro frío. Pero en este nuevo trabajo se coloca entre un sistema cuántico (por ejemplo, una red de bits cuánticos, o qubits, entrelazados en un ordenador cuántico) y un sumidero térmico sencillo con el que el sistema cuántico no está directamente entrelazado.
Como la memoria está entrelazada tanto con el sistema cuántico como con el sumidero, puede de nuevo catalizar un flujo de calor entre ellos más allá de lo posible clásicamente. En ese proceso, el entrelazamiento dentro del sistema cuántico se convierte en calor adicional que fluye hacia el sumidero. Así, medir la energía almacenada en el sumidero (equivalente a leer su “temperatura”) revela la presencia de entrelazamiento en el sistema cuántico. Pero, dado que el sistema y el sumidero no están entrelazados entre sí, la medición no afecta al estado del sistema cuántico. Este recurso elude la conocida dificultad de que las mediciones destruyen la cuanticidad. «Si intentaras simplemente medir el sistema [cuántico] directamente, destruirías su entrelazamiento antes incluso de que el proceso se desarrollara», explica de Oliveira.
 Los físicos Alexssandre de Oliveira Jr. (izquierda) y Jonatan Bohr Brask (derecha) colaboraron con Patryk Lipka-Bartosik en un nuevo esquema para detectar la cuántica sin destruirla. Foto: Jonas Schou Neergaard-Nielsen
Los físicos Alexssandre de Oliveira Jr. (izquierda) y Jonatan Bohr Brask (derecha) colaboraron con Patryk Lipka-Bartosik en un nuevo esquema para detectar la cuántica sin destruirla. Foto: Jonas Schou Neergaard-NielsenEl nuevo esquema tiene la ventaja de ser simple y general, señala Vedral, ahora en la Universidad de Oxford. «Estos protocolos de verificación son muy importantes», dice: cada vez que una empresa de computación cuántica anuncia un nuevo dispositivo, siempre surge la cuestión de cómo —o si— saben realmente que el entrelazamiento entre los qubits está contribuyendo al cálculo. Un sumidero térmico podría actuar como detector de tales fenómenos cuánticos simplemente a través de su cambio de energía. Para implementar la idea, podría designarse un qubit como la memoria cuyo estado revele el de otros qubits, y luego acoplar ese qubit de memoria a un conjunto de partículas que funcionen como sumidero, cuya energía se pueda medir. (Vedral añade una salvedad: es necesario tener un control muy preciso del sistema para asegurarse de que no haya otras fuentes de flujo de calor que contaminen las mediciones. Además, el método no detectará todos los estados entrelazados.)
De Oliveira cree que ya existe un sistema adecuado para poner a prueba su idea experimentalmente. Él y sus colegas están en conversaciones con el grupo de investigación de Roberto Serra en la Universidad Federal del ABC, en São Paulo (Brasil). En 2016, Serra y sus colaboradores utilizaron las orientaciones magnéticas, o espines, de los átomos de carbono e hidrógeno en moléculas de cloroformo como bits cuánticos entre los que podían transferir calor.
Usando este montaje, dice de Oliveira, debería ser posible aprovechar un comportamiento cuántico —en este caso la coherencia, es decir, que las propiedades de dos o más espines evolucionan en fase entre sí— para modificar el flujo de calor entre los átomos. La coherencia de los qubits es esencial para la computación cuántica, así que poder verificarla detectando un intercambio de calor anómalo sería muy útil.
Las implicaciones podrían ser aún mayores. Varios grupos de investigación intentan diseñar experimentos para determinar si la gravedad es una fuerza cuántica, al igual que las otras tres fuerzas fundamentales. Algunos de estos esfuerzos consisten en buscar entrelazamiento cuántico entre dos objetos generado únicamente por su atracción gravitatoria mutua. Tal vez los investigadores puedan explorar ese entrelazamiento inducido por la gravedad mediante simples mediciones termodinámicas sobre los objetos, verificando así (o no) que la gravedad está realmente cuantizada.
Para estudiar una de las cuestiones más profundas de la física —concluye Vedral—, «¿no sería maravilloso poder hacerlo con algo tan sencillo y macroscópico como esto?».
El artículo original, A Thermometer for Measuring Quantumness, se publicó el 1 de octubre de 2025 en Quanta Magazine. Cuaderno de Cultura Científica tiene un acuerdo de distribución en castellano con Quanta Magazine.
Traducido por César Tomé López
El artículo Un termómetro para medir la cuanticidad se ha escrito en Cuaderno de Cultura Científica.
Rarezas quiméricas: dientes fuera de la boca con funciones sexuales
El Diccionario de la lengua española define “quimérico” como fabuloso, fingido o imaginado sin fundamento, pero aquí nos referimos a una sorprendente peculiaridad recién descubierta en las quimeras u holocéfalos, un pequeño grupo de peces marinos. Los machos de estos peces son el único caso conocido de formación de dientes fuera de la cavidad bucal, unos dientes que usan para sujetar a la hembra durante la cópula.
Vayamos por orden y comencemos por tratar el origen de los dientes en los vertebrados. Los primeros vertebrados aparecieron en el Cámbrico, hace unos 520 millones de años. Carecían de mandíbulas y su cuerpo era blando y vulnerable, pero muy pronto adquirieron una especie de caparazón de hueso dérmico (peces ostracodermos). Este caparazón está cubierto por unos pequeños tubérculos constituidos por dentina (una forma compacta de hueso) y recubiertos por un tipo de esmalte (enameloide). Son los llamados “odontodos” (Figura 1). Cuando los peces desarrollaron mandíbulas a partir del esqueleto branquial, hace unos 420-430 millones de años, aprovecharon los odontodos para fijarlos a las mandíbulas y formar los dientes[1].
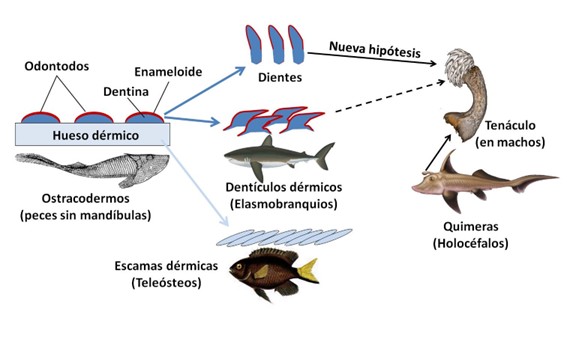 Figura 1. Los odontodos del caparazón de los peces ostracodermos son el origen evolutivo tanto de los dentículos dérmicos de los elasmobranquios como de los dientes. En cambio, las escamas de los teleósteos derivan del hueso dérmico de dicho caparazón. Se pensaba que las espinas del tenáculo de las quimeras derivaban de los dentículos dérmicos (flecha discontinua), pero un nuevo estudio sugiere que se originaron a partir de dientes. Se han utilizado imágenes de Damouraptor, Gasmasque y Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.
Figura 1. Los odontodos del caparazón de los peces ostracodermos son el origen evolutivo tanto de los dentículos dérmicos de los elasmobranquios como de los dientes. En cambio, las escamas de los teleósteos derivan del hueso dérmico de dicho caparazón. Se pensaba que las espinas del tenáculo de las quimeras derivaban de los dentículos dérmicos (flecha discontinua), pero un nuevo estudio sugiere que se originaron a partir de dientes. Se han utilizado imágenes de Damouraptor, Gasmasque y Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.Los peces armados de mandíbulas y dentadura aumentaron de tamaño y llegaron a ser los predadores dominantes durante el periodo Devónico. Paralelamente, el caparazón óseo defensivo disminuyó su importancia, dando lugar a las escamas de los peces (Figura 1). En el grupo de los condrictios (elasmobranquios -es decir, tiburones y rayas- y quimeras) estas escamas retienen la composición de los odontodos primitivos, formados por dentina y un recubrimiento muy duro similar al esmalte dentario. Por eso, el cuerpo de los elasmobranquios actuales está cubierto de dentículos dérmicos derivados de los odontodos. En las quimeras, cuyo linaje se separó muy pronto del de los elasmobranquios, la mayor parte de la piel los ha perdido pero se mantienen en los apéndices copuladores.
Las quimeras forman un grupo muy reducido de peces marinos, alrededor de 50 especies de aguas profundas. A diferencia de tiburones y rayas no tienen dientes individuales, ya que se sueldan formando placas dentarias. Sí comparten con elasmobranquios la fecundación interna, y los machos disponen de una serie de apéndices copuladores en la región pélvica para sujetar a la hembra. Además, los machos tienen un curiosísimo apéndice, el tenáculo, situado entre los ojos, y dotado de unas fuertes espinas (Figura 2). Todo parece indicar que su función es también ayudar en la cópula y se consideraba que sus espinas eran dentículos dérmicos modificados, como los de los apéndices pélvicos.
Hasta ahora. Un estudio publicado en PNAS por investigadores estadounidenses sugiere que el tenáculo está provisto de auténticos dientes, lo que constituiría el único caso conocido entre los vertebrados en que los dientes se desarrollan fuera de la cavidad bucal.
 Figura 2. Macho de quimera (Hydrolagus collei) y detalle del tenáculo. Modificado de Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.
Figura 2. Macho de quimera (Hydrolagus collei) y detalle del tenáculo. Modificado de Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.El estudio consistió en una descripción del desarrollo embrionario del tenáculo en machos de la quimera Hydrolagus collei (Figura 2). Los dientes del tenáculo se desarrollan a partir de una estructura llamada lámina dental, que es la responsable de formar los dientes seriados en los elasmobranquios (recordemos que las quimeras tienen los dientes soldados en placas). Ni los dentículos dérmicos ni las escamas de los apéndices copuladores pélvicos de las quimeras se desarrollan a partir de una lámina dental. Por otro lado, el desarrollo de dientes en elasmobranquios (pero no el de los dentículos dérmicos) requiere la expresión del gen Sox2 (característico de las células madre dentales) y la activación de la proteína b-catenina. Pues bien, estos dos elementos están presentes en el desarrollo de los dientes del tenáculo (Figura 3). Más interesante aún, la expresión de Sox2 se mantiene en la lámina dental del tenáculo adulto, exactamente igual que sucede en las mandíbulas de elasmobranquios. Esta expresión en adultos permite la formación continua de dientes característica de tiburones y rayas.
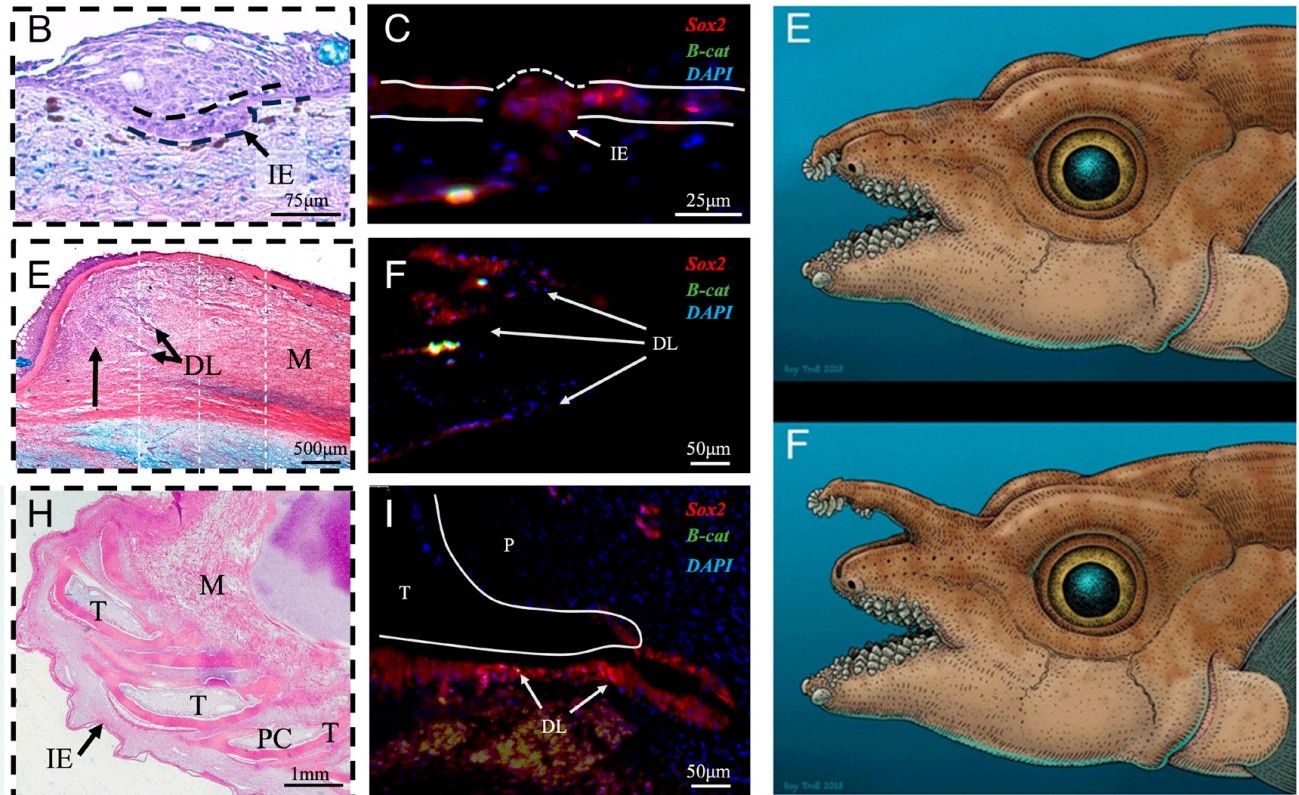 Figura 3. A la izquierda se muestran tres etapas en el desarrollo del tenáculo. Se observa la lámina dental (DL) y los dientes (T) formándose en el interior del tejido. Células de la lámina dental expresan Sox2 (marcador de células madre dentales) y b-catenina. La figura I corresponde a un adulto, y revela que la expresión de Sox2 se mantiene en la lámina dental. Esto es lo mismo que sucede en elasmobranquios, permitiendo una formación continua de dientes en adultos. A la derecha, reconstrucción de la quimera fósil Helodus simplex. Los dientes del largo tenáculo encajan en la sínfisis mandibular. Modificado de Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.
Figura 3. A la izquierda se muestran tres etapas en el desarrollo del tenáculo. Se observa la lámina dental (DL) y los dientes (T) formándose en el interior del tejido. Células de la lámina dental expresan Sox2 (marcador de células madre dentales) y b-catenina. La figura I corresponde a un adulto, y revela que la expresión de Sox2 se mantiene en la lámina dental. Esto es lo mismo que sucede en elasmobranquios, permitiendo una formación continua de dientes en adultos. A la derecha, reconstrucción de la quimera fósil Helodus simplex. Los dientes del largo tenáculo encajan en la sínfisis mandibular. Modificado de Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.¿Cómo es posible que se formen dientes en una estructura localizada entre los ojos, en animales que, además, carecen de dientes aislados en las mandíbulas? La respuesta parece estar en una quimera fósil, Helodus simplex, que vivió hace 315 millones de años y que sí tenía dientes aislados (Figura 3). Los machos de Helodus poseían un largo tenáculo situado en la región etmoidea, y su extremo alcanzaba la sínfisis entre las dos mandíbulas superiores. Es concebible que el epitelio de ese extremo del tenáculo adquiriera capacidad odontogénica durante el desarrollo. A lo largo de la evolución, el tenáculo habría mantenido la capacidad de formar dientes pero se habría reducido en longitud hasta el tamaño actual, al tiempo que los dientes mandibulares terminaron soldándose en placas.
Las quimeras mitológicas eran monstruos híbridos que combinaban partes de distintos animales. Este insólito descubrimiento acerca de dientes extrabucales nos muestra cómo la realidad de la naturaleza puede igualar, si no superar, a la imaginación humana.
Referencias
Cohen, K.E., Coates, M.I., Fraser, G.J. (2025). Teeth outside the jaw: Evolution and development of the toothed head clasper in chimaeras. Proc Natl Acad Sci U S A. doi: 10.1073/pnas.2508054122.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
Nota:
[1] Es la llamada hipótesis “de fuera a dentro”. Un modelo alternativo, menos apoyado, es que los dientes proceden de una dentición faríngea que ya estaba presente en ostracodermos.
El artículo Rarezas quiméricas: dientes fuera de la boca con funciones sexuales se ha escrito en Cuaderno de Cultura Científica.
¿Cuándo podremos decir que “hemos encontrado vida en Marte”?
 Las manchas de leopardo encontradas en el crater Jerezo de Marte podrían indicar que, hace miles de millones de años, las reacciones químicas en esta roca podrían haber sustentado vida microbiana. Foto:NASA/JPL-Caltech/MSSS, CC BY
Las manchas de leopardo encontradas en el crater Jerezo de Marte podrían indicar que, hace miles de millones de años, las reacciones químicas en esta roca podrían haber sustentado vida microbiana. Foto:NASA/JPL-Caltech/MSSS, CC BYUna roca moteada, bautizada como “Cheyava Falls” y situada en un antiguo cauce fluvial del cráter Jezero, ha encendido de nuevo una pregunta antigua con traje moderno: ¿hay o hubo vida en Marte?
Entre minerales rojos e indicios orgánicos, la NASA acaba de anunciar el hallazgo de posibles biofirmas en un roca marciana. El comunicado ha desatado el frenesí, pero en ciencia es un frenesí cauto.
Este es un análisis –con los pies en los datos– sobre pistas, escalas de certeza y lo que significaría oír, por fin, un “sí, esto es vida extraterrestre”. Pero aún no ha llegado el momento.
Los indicios de vida en MarteDesde hace años, la NASA ha ido informando de hallazgos que se acercan a lo que podría parecerse a una huella de vida.
En 1976, las sondas Viking realizaron los primeros experimentos biológicos en Marte. Sus resultados fueron intrigantes, pero también muy polémicos, y no se consideraron una prueba concluyente de vida. Desde entonces, ninguna misión ha vuelto a llevar experimentos tan directos. La lección de Viking es clara: en la exploración del planeta rojo, conviene mantener la curiosidad… pero también la cautela en las expectativas.
En 2018, la NASA informó de indicios de vida orgánica en barro antiguo de Marte. Entonces el rover Curiosity detectó en el cráter Gale moléculas orgánicas preservadas en lutitas lacustres (un tipo de roca sedimentaria, compuesta por partículas muy finas de arcilla y limo que se depositaron en el fondo de los lagos) de aproximadamente 3500 millones de años, así como una variación estacional del metano de fondo. Son ingredientes y pistas, pero no es propiamente vida.
En el estudio reciente, la NASA informa que en la zona conocida como Bright Angel, el instrumento SHERLOC del rover Perseverance también identificó la presencia de moléculas orgánicas, mientras que el instrumento PIXL mapeó minerales como vivianita y greigita en un lodo rico en hierro, fósforo y azufre.
Pero este tipo de mezcla puede formarse tanto por la acción de microorganismos como por procesos puramente químicos. Así que puede ser un indicio de vida, o no.
Esa ambigüedad es justo lo que resalta la síntesis publicada en Nature, que subraya cómo estos hallazgos mantienen abierto el debate sobre si Marte albergó vida o no.
Las muestras de metanoAnteriormente, el Curiosity detectó variaciones locales y estacionales en la presencia de metano en el planeta vecino, algo que también podría asociarse con una biofirma. Sin embargo, el orbitador europeo TGO (de la misión ExoMars) no ha encontrado prácticamente nada: sus mediciones ponen un límite global muy estricto, menos de 0,05 partes por mil millones.
El reto ahora es conciliar ambos resultados: ¿se trata de pequeñas emisiones superficiales que la atmósfera elimina rápidamente, o de mediciones que están sesgadas por factores aún desconocidos? La ciencia sigue en curso y la respuesta todavía no está cerrada.
¿Qué sería una prueba irrefutable?Tras varias decepciones, la comunidad científica ha elaborado una “escala de confianza” para detectar vida, llamada Confidence of Life Detection (CoLD).. Es como una escalera de siete peldaños: primero se detecta una posible señal y después hay que descartar contaminación; demostrar que la biología sería viable en ese entorno; excluir explicaciones no biológicas; encontrar otra señal independiente; derrotar hipótesis alternativas… y, por último, conseguir confirmación por distintos equipos. ¿Cómo se sube esa escalera? No con un único hallazgo espectacular, sino con varias pruebas que, juntas, formen un caso sólido.
Una química orgánica compleja con homoquiralidad (se refiere a moléculas que tienen una estructura no superponible con su imagen especular, similar a la de nuestras manos) sería un buen indicio, porque es extremadamente difícil de generar sin vida.
Otro rastro lo darían los isótopos: variaciones en elementos como el carbono o el azufre que, dentro de su contexto geológico, se ajusten a lo que esperaríamos de procesos biológicos. Sin ese contexto, el isótopo puede engañar.
También podrían encontrarse texturas microscópicas que recuerden a células o biofilms, siempre asociadas a moléculas orgánicas e isótopos de “firma biológica”.
Una sola pista nunca basta: se necesitan varias, y que se repitan de manera independiente, con instrumentos distintos.
Lo ideal sería confirmar en la Tierra, con muestras traídas de Marte bajo protocolos estrictos para evitar contaminación. Al final, no se trata de obtener una foto espectacular, sino un expediente coherente y abrumador.
De Europa a Venus¿Y en qué otros mundos podría asomarse la vida? Estos son los candidatos:
- Europa (Júpiter). Es el favorito: oculta un océano salado bajo el hielo. la misión Europa Clipper, que llegará hacia 2030, hará casi 50 sobrevuelos para estudiar si allí existen condiciones habitables. No busca vida directamente, pero sí comprobar si podría haberla.
- Encélado (luna de Saturno). Sus espectaculares géiseres conectan el océano interno con el espacio. Allí se ha detectado fósforo en abundancia, un nutriente esencial para la vida. Es, literalmente, un laboratorio natural abierto.
- Titán (luna de Saturno). Con su atmósfera densa y rica en compuestos orgánicos, es un lugar único para explorar química prebiótica. La misión Dragonfly despegará a finales de esta década (si no entra en el grupo de recortes de Donald Trump) y aterrizará hacia mediados de los 30, para estudiar si podrían darse formas de bioquímica distintas a las terrestres.
- Venus. En sus nubes se han detectado posibles rastros de fosfina, aunque el debate sigue abierto. Para unos es una señal sugerente; para otros, un artefacto de las observaciones. El debate es un buen antídoto contra el autoengaño.
En ciencia y tecnología, aceleraríamos las misiones de retorno de muestras y desarrollaríamos sistemas de contención de máximo nivel, además de nuevas herramientas para detectar formas de vida “no terráqueas”; en filosofía, nos obligaría a dejar de confundir singularidad con privilegio; en religión, probablemente inspiraría lecturas más inclusivas de la creación, más que crisis de fe; en política y ética, reforzaría la necesidad de no contaminar otros mundos ni traer riesgos a la Tierra.
Y en lo cotidiano, se abriría la puerta a nuevos materiales, sensores y biotecnologías
Pero más allá de lo práctico, nos brindaría una cura contra el provincianismo: nos recordaría que no somos el centro del universo.
¿Cuándo podríamos afirmarlo rotundamente?Hay dos ventanas realistas. En primer lugar, hacia la década de 2030. El rover europeo Rosalind Franklin, cuyo lanzamiento está previsto para 2028, llegará a Marte en unos cinco años. Está diseñado para perforar hasta dos metros bajo la superficie, donde la radiación no ha destruido los compuestos más delicados. Con su instrumento MOMA podría encontrar moléculas orgánicas complejas, señales de quiralidad (esa preferencia por una “mano” molecular que suele asociarse a la vida) y posibles texturas biológicas. No será fácil, pero las posibilidades están ahí.
La segunda ventana sería el retorno de muestras. La misión conjunta de NASA y ESA, que busca traer rocas marcianas a la Tierra, se ha encarecido y retrasado, por lo que lo más probable es que su “veredicto de laboratorio” no llegue antes de la década de 2040.
Eso sí, incluso si la roca Cheyava Falls ofrece biofirmas tentadoras, la confirmación no llegará con un único indicio. Habrá que recorrer toda la “escalera CoLD”: descartar explicaciones no biológicas y repetir pruebas de forma independiente, idealmente en laboratorios terrestres. El calendario es incierto. Mientras tanto, el escepticismo no supone un freno: es la dirección en la que vamos.
Si la vida marciana existe o existió, nos esperará, no tiene nuestras prisas. Y si no existió nunca, el hallazgo más grande será comprender por qué aquí sí. Esa respuesta también nos pertenece y entusiasma.![]()
Sobre el autor: José Ygnacio Pastor Caño, Catedrático de Universidad en Ciencia e Ingeniería de los Materiales, Universidad Politécnica de Madrid (UPM)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Cuándo podremos decir que “hemos encontrado vida en Marte”? se ha escrito en Cuaderno de Cultura Científica.
La química del olfato vibra
Respiramos más de 20.000 veces al día. Es un mecanismo inconsciente y automático, imprescindible para sobrevivir. Al inhalar, obtenemos el oxígeno que nuestro cuerpo necesita para funcionar, lo transformamos en CO2 y lo exhalamos. Sin embargo, junto al oxígeno, entran en nuestro organismo otras muchas moléculas como nitrógeno, bacterias o virus. Toda esta mezcla nos aporta una ingente cantidad de información sobre nuestro entorno, tanta que contamos con un sentido especializado para poder descifrarla: el olfato.
Gracias a él, somos capaces de identificar con los ojos cerrados a quien tenemos al lado, sortear un peligro inminente, o viajar de golpe a un verano de la infancia. Pero, ¿cómo funciona este gran detective alojado en nuestra nariz?
La química Elixabete Rezabal, experta en química física y profesora titular en la facultad de Química de la EHU, lo explicó durante el decimoquinto aniversario de Naukas Bilbao, en una charla dedicada a la química que se esconde tras este misterio.
 © Iñigo Sierra | Cátedra de Cultura Científica de la EHU.La teoría clásica del olfato
© Iñigo Sierra | Cátedra de Cultura Científica de la EHU.La teoría clásica del olfato
La teoría clásica sostiene que al fondo de la nariz y cerca del cerebro tenemos una serie de proteínas receptoras que captan las moléculas procedentes del exterior. Si una de ellas encaja de la forma adecuada, se activa una señal que nuestro cerebro reconoce como un olor.
“Nos han contado que oler es como meter la llave correcta en la cerradura nasal: si la llave encaja, la cerradura se abre y la señal pasa al cerebro, y nosotros detectamos ese olor”, explicó Rezabal. Por esta teoría, que describe el funcionamiento del olfato, los investigadores Linda Buck y Richard Axel recibieron el Premio Nobel de Medicina en 2004.
Sin embargo, como subrayó la química, esta explicación no siempre funciona. ¿Qué ocurre, por ejemplo, con las moléculas que tienen casi la misma forma, pero huelen de manera radicalmente diferente? Pongamos el caso de una molécula formada por un grupo alcohol, compuesto por un oxígeno unido a un hidrógeno. Puede oler a hierba recién cortada. No obstante, si sustituimos ese oxígeno por un azufre, la geometría se mantiene, pero el olor se convierte en el de un huevo podrido. La forma, por tanto, no basta para explicar cómo procesamos los olores.
 © Iñigo Sierra | Cátedra de Cultura Científica de la EHU.
© Iñigo Sierra | Cátedra de Cultura Científica de la EHU.Para ofrecer una respuesta, Rezabal expuso la atrevida teoría del biofísico Luca Turin y su equipo de colaboradores del MIT, quienes en 1996 propusieron una teoría alternativa en la que planteaba que nuestra nariz no detecta la forma de las moléculas, sino sus vibraciones a nivel cuántico.
¿Y si lo que olemos son vibraciones?
Su hipótesis partía de la idea de que las moléculas no solo tienen una geometría, sino que no paran de moverse. A temperatura ambiente, vibran de manera constante, pero no de cualquier manera. Esto, en palabras de Rezabal, se debe a que “la energía vibracional está cuantizada, lo que quiere decir que sólo ciertos modos de vibración están permitidos, cada uno con su energía”.
El agua es un buen ejemplo. Se trata de una molécula simple que, debido a su geometría, tiene tres modos de vibración, “tres pasos de baile”, cada uno con una energía asociada. Si recibe la cantidad exacta de energía del entorno, puede vibrar de otra manera y subir al siguiente escalón. Y así hasta alcanzar el tercer nivel.
 © Iñigo Sierra | Cátedra de Cultura Científica de la EHU.
© Iñigo Sierra | Cátedra de Cultura Científica de la EHU.Por su parte, el agua deuterada -conocida como agua pesada- es idéntica en su forma al agua, con la salvedad de que los átomos de hidrógeno son sustituidos por deuterio, que incorpora un neutrón, además de un protón, en su núcleo. Esto hace que los átomos sean más pesados y que las energías necesarias para pasar de un modo de vibración a otro sean diferentes. En definitiva, la forma es la misma, en cambio, sus vibraciones no lo son.
En la mente de Turin, si el olfato se basa en las vibraciones, se debería poder distinguir el agua del agua pesada. Para comprobar su teoría, él y su equipo realizaron experimentos con un animal de olfato extremadamente fino, la mosca de la fruta.
Acertó. Estos insectos se acercaban al agua y se alejaban del agua pesada. Entonces, ¿qué hace nuestra nariz para detectar este fenómeno cuántico?
A partir de este curioso experimento, se desarrolló el concepto del túnel cuántico de la nariz. Un mecanismo que aprovecha las propiedades cuánticas de los electrones para identificar moléculas basándose en sus vibraciones, de manera similar a ciertos espectrómetros de laboratorio, como la espectroscopía de túnel inelástico de electrones, Inelastic Electron Tunneling Spectroscopy (IETS), en inglés.
La nariz, un espectrómetro biológico
“Esta teoría actual lo que propone es que cuando la molécula se une, hay un electrón que tiene que pasar de una parte de la proteína a otra, lo que genera una transferencia de energía que manda una señal al cerebro”, resumió.
 © Iñigo Sierra | Cátedra de Cultura Científica de la EHU.
© Iñigo Sierra | Cátedra de Cultura Científica de la EHU.Hay que tener en cuenta que la molécula siempre estará vibrando o “bailando” en su nivel más bajo de energía, pero si la energía que necesita para saltar al siguiente modo de vibración coincide exactamente con la que tiene que liberar el electrón para poder moverse, la transferencia se produce y se activa el olor en nuestro cerebro. En cambio, si la energía que necesita la molécula odorífera para subir de escalón no es la misma que requiere el electrón, no habrá transferencia y, por tanto, el olor no se activará.
Más allá de la curiosidad científica, Turin aplicó este concepto de la teoría de la vibración olfativa para fundar Flexitral, una empresa -ya extinta- al servicio de la industria de la perfumería. ¿Cómo? Calculando los modos vibracionales de las moléculas, el biofísico libanés era capaz de sustituir compuestos carísimos, apreciados por los perfumistas por su particular aroma, por otros más baratos que vibraban del mismo modo y, por tanto, olían igual.
Rezabal cerró su intervención en Naukas Bilbao 2025 recordando que la mecánica cuántica, aunque pueda parecernos lejana, está más presente en nuestra vida cotidiana de lo que podamos imaginar, ya que “muchos fenómenos de nuestro cuerpo se basan en principios cuánticos”. Y, en el caso del olfato, todo apunta a que el secreto está en la vibración.
Si no ve correctamente el vídeo, use este enlace.
Sobre la autora: María Larumbe es periodista y responsable de comunicación de la Cátedra de Cultura Científica de la Universidad del País Vasco / Euskal Herriko Unibersitatea.
El artículo La química del olfato vibra se ha escrito en Cuaderno de Cultura Científica.
Las veladuras blancas de los óleos contemporáneos
En las pinturas al óleo pueden producirse alteraciones por las interacciones entre sus componentes químicos y por factores externos: por ejemplo, pueden aparecer sustancias blanquecinas en todo el cuadro o en algunas partes concretas. Sin embargo, estas veladuras blancas no siempre tienen el mismo aspecto y pueden tener diferentes orígenes. “Estas sustancias que blanquean la superficie de las obras de arte no solo afectan a la estética, sino que también son un problema de conservación, y es muy importante saber qué las produce para poder resolver el problema”, explica Erika Tarilonte, investigadora de la Facultad de Bellas Artes de la Universidad del País Vasco / Euskal Herriko Unibertsitatea (EHU).
Veladuras blancas Sin título (1971) de Santos Iñurreta. Óleo sobre lienzo (114×146 cm). Fuente: Erika Tarilonteet al. (2025) Journal of Cultural Heritage doi: 10.1016/j.culher.2025.06.007
Sin título (1971) de Santos Iñurreta. Óleo sobre lienzo (114×146 cm). Fuente: Erika Tarilonteet al. (2025) Journal of Cultural Heritage doi: 10.1016/j.culher.2025.06.007La obra Sin título del pintor vasco Santos Iñurrieta (1950-2023) es un óleo sobre lienzo no barnizado que está cubierta en gran parte por una sustancia blanquecina homogénea y frágil. A partir de este cuadro, los investigadores del grupo FARMARTEM de la EHU han llevado a cabo el estudio analítico más completo hasta la fecha para identificar los fenómenos de blanqueo de la superficie de los óleos contemporáneos. “Hemos definido una metodología multianalítica exhaustiva que nos permitirá analizar algunos fenómenos de degradación y conservar las pinturas”, explica Tarilonte. Este estudio supone un gran paso para hacer frente a uno de los problemas más importantes de la conservación del arte contemporáneo en la actualidad.
Jabones plúmbicos Erika Tarilonte tomando una micromuestra. Fuente: EHU
Erika Tarilonte tomando una micromuestra. Fuente: EHUEn primer lugar, el estudio histórico-artístico de las obras de Iñurrieta ha demostrado que estas veladuras blancas no son intencionadas por parte del artista y, a partir de ahí, los investigadores han analizado diferentes hipótesis: «Pueden ser hongos, o el efecto de la cristalización de sales, la migración de ácidos grasos, la exudación de ceras, los jabones metálicos… Los análisis efectuados por nosotros han demostrado que los jabones plúmbicos son la principal causa de las veladuras blancas en las pinturas, y que probablemente fuera un secante de plomo el origen del plomo”, afirma la investigadora. El proceso de formación de jabones plúmbicos se produce dentro de la capa de pintura, “pero poco a poco, con el tiempo, va aflorando y aparece la veladura blanca. Da la impresión de que la obra está cubierta de niebla”.
Conocer para intervenirLa investigación ha permitido obtener una amplia información sobre los materiales y las técnicas que el artista empleó en la pintura. “Ahora sabemos qué capas pictóricas tiene la obra, cómo son, qué espesor tienen, qué granulometría, qué pigmentos ha utilizado exactamente, qué aditivos, qué aglutinantes, etc. Tras esta investigación, lo sabemos todo sobre la obra de arte, y hoy en día eso es muy importante para poder intervenir”. Según la investigadora de la EHU, ese ha sido el primer paso: “La obra de arte está así ahora, pero sabemos que el original no era así. El siguiente paso natural sería intervenir en la obra, limpiarla y dejarla como era en su origen”.
El estudio multianalíticoEl estudio multianalítico para detectar el origen de las veladuras blancas en las pinturas al óleo ha uncluido análisis microbiológicos diversos, radiografías, estudios de fluorescencia, análisis químicos de micromuestras, microscópicos, espectroscópicos, tomografías computarizadas, cromatografías, etc. Como resultado la investigación ha puesto a disposición de la comunidad científica y artística información detallada sobre la utilidad de cada una de estas técnicas y la información específica que aporta cada una de ellas.
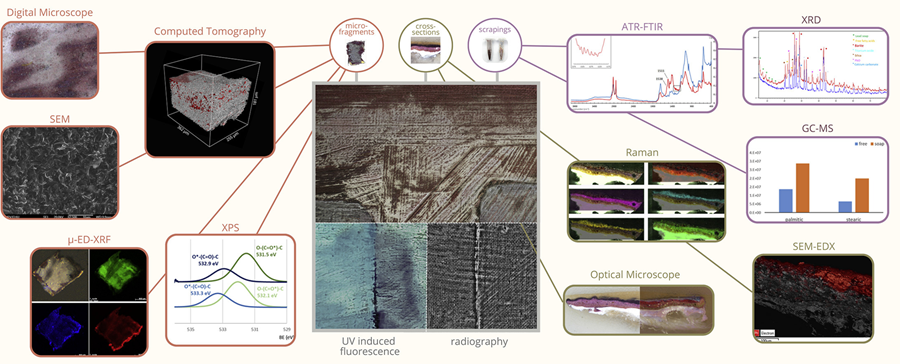 Fuente: Erika Tarilonteet al. (2025) Journal of Cultural Heritage doi: 10.1016/j.culher.2025.06.007
Fuente: Erika Tarilonteet al. (2025) Journal of Cultural Heritage doi: 10.1016/j.culher.2025.06.007De hecho, “la flexibilidad de esta metodología multianalítica nos ha permitido comprobar que algunas técnicas que no aportan resultados significativos para los jabones metálicos pueden aportar, sin embargo, información útil para otros fenómenos de veladura”, afirma Tarilonte. Por ejemplo, ahora están trabajando con otra obra: Sin título, de Alberto González (1978). “Esta obra también tiene veladuras blancas, pero su morfología es diferente: presenta puntos blancos en un color azul determinado”, explica la investigadora. Una de las principales hipótesis de los investigadores es que “la cristalización de sales ha sido el origen de estas acreciones. Gracias a la metodología que hemos desarrollado, vamos a poder usar únicamente las técnicas analíticas más interesantes para analizar la cristalización de las sales, en lugar de utilizar todas. Ahora sabemos qué tipo de información que nos da cada técnica y, por lo tanto, a la hora de analizar otras obras de arte, solo elegiremos aquellas que sean más útiles en cada caso. Hemos conseguido dar la opción de adaptarnos a cada caso”.
A pesar de los grandes avances en este campo, “todavía hay que investigar mucho sobre las causas y mecanismos que provocan las veladuras. Este trabajo servirá para desarrollar mejores estrategias de conservación de las pinturas al óleo y para investigar remedios eficaces para el cuidado de las obras de arte a largo plazo”, explica la investigadora de la EHU.
Referencia:
Erika Tarilonte, Oskar González-Mendia, Ilaria Costantini, Kepa Castro, Itxaso Maguregui (2025) A multi-analytical approach for the identification of surface whitening phenomena in contemporary oil painting and its application to metal soaps Journal of Cultural Heritage doi: 10.1016/j.culher.2025.06.007
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Las veladuras blancas de los óleos contemporáneos se ha escrito en Cuaderno de Cultura Científica.
Whole Earth Catalog: la versión analógica de internet
«¿Dónde buscabais la información antes de que existiera internet?» es una pregunta que a algunos nos ha hecho sentir viejos alguna vez. No tiene importancia, la normalización del uso de los grandes modelos del lenguaje ya hará que se sientan viejos los mismos que la formulan. Pero, efectivamente, hace no tanto vivíamos sin internet… y sobrevivimos. Hasta finales de los noventa, tratar de aprender algo nuevo implicaba, bien buscar a alguien que pudiera enseñarte, o bien una visita a una biblioteca, a una librería… y muchísimo tiempo. Es posible que la idea de contar con una especie de repositorio del conocimiento que nos permitiera un acceso rápido a la información se remonte a la biblioteca de Alejandría. Y es que, salvando las distancias, y dentro de sus limitaciones, ¿no era exactamente eso?
Pero lo cierto es que las bibliotecas no ofrecen el acceso rápido, directo y práctico al conocimiento que ofrece, por ejemplo, un tutorial de YouTube. El Whole Earth Catalog, editado por Steward Brand en la California de los años sesenta y setenta, sí lo hizo, y probablemente, por primera vez en la historia.
En plena efervescencia cultural y social, con los movimientos en defensa de los derechos civiles, la contracultura hippie, la expansión de la música y el arte experimentales, y un creciente interés por estilos de vida más libres, sostenibles y autónomos, surgió la necesidad de medios que ofrecieran un acceso rápido al conocimiento práctico y a herramientas que facilitaran la autosuficiencia —pensemos en las comunas hippies autogestionadas—. Como ciudadanos de un mundo muy diferente al de sus padres, la mayoría de aquellos jóvenes no sabía cómo construir una casa, cultivar sus propios alimentos o reparar los aparatos que utilizaba a diario… y tampoco había internet para buscar cómo se hacía. Steward Brand, que se movía en el corazón de ese ambiente, les dio los recursos que buscaban.
 Steward Brand en 2020. Créditos: CC BY 2.0/Christopher Michel
Steward Brand en 2020. Créditos: CC BY 2.0/Christopher Michel
En 1966, y en plena alucinación psicodélica producida por el LSD, Brand tuvo una especie de revelación: si la humanidad pudiera ver una imagen de la Tierra completa desde el espacio, cambiaría su percepción del planeta y eso despertaría una conciencia global que lo transformaría todo —existían entonces imágenes de nuestro planeta tomadas desde la órbita, pero fragmentadas y de poca calidad—. Así que inició una campaña por campus universitarios de todo el país con el eslogan: «Why haven’t we seen a photograph of the whole Earth yet?» (‘¿Por qué no hemos visto todavía una fotografía de la Tierra entera?’) para que la NASA publicara una foto completa de nuestro planeta flotando en el vacío. Se disfrazó, vendió chapas y panfletos… y parece que dio resultado, porque al año siguiente, la NASA publicó la imagen que pedía y que tomó el satélite ATS-3 el 10 de noviembre del año siguiente.
 Primera fotografía en color de la Tierra al completo, tomada por el satélite ATS-3 el 10 de noviembre de 1967. Fuente: NASA
Primera fotografía en color de la Tierra al completo, tomada por el satélite ATS-3 el 10 de noviembre de 1967. Fuente: NASA
Esta anécdota es importante porque esta fotografía sería la que aparecería en la portada del primer número del Whole Earth Catalog, que se publicó en el otoño de 1968.
 Primer número del Whole Earth Catalog y primera página, con una especie de manifiesto sobre el propósito de la publicación. Fuente: Whole Earth Index / fair use
Primer número del Whole Earth Catalog y primera página, con una especie de manifiesto sobre el propósito de la publicación. Fuente: Whole Earth Index / fair useSería bastante complicado definir qué era el Whole Earth Catalog, porque no entraría en la categoría de panfleto ni de revista ni de libro, me atrevería a decir que podría parecerse más a una guía telefónica de recursos de lo más… heterodoxo. Así, podíamos encontrar manuales de construcción, guías de jardinería y agricultura, planos y materiales para aprovechar fuentes de energía alternativas, recetas de cocina y remedios naturales, lecciones de programación, referencias a libros de todo tipo —ciencia, filosofía, artes, sociología…—, contactos y direcciones de expertos… Merece bastante la pena echarle un vistazo. Todo el material se encuentra digitalizado en Whole Earth Index.
El Whole Earth Catalog, aunque nunca se distribuyó de forma masiva, sí se convirtió en el símbolo de un colectivo de jóvenes que buscaba plantear alternativas al mundo que les había tocado vivir. Un mundo en el que el desarrollo tecnológico ya había mostrado su peor cara, pero también era una oportunidad para tratar de hacer las cosas de una manera más auténtica y sostenible. Su periodo de mayor auge fue la década de los setenta, aunque el último número, una edición por el trigésimo aniversario, se publicó en 1998… cuando internet ya estaba llegando a nuestras vidas. Y del mundo de internet y de aquella California en la que se gestó Silicon Valley llega el crossover de hoy.
Uno de los estudiantes que formó parte de aquella experiencia, dijo, ya de adulto, que el Whole Earth Catalog había sido «algo así como Google en formato libro, treinta y cinco años antes de que Google existiera». Lo hizo durante el discurso de graduación de la Universidad de Stanford el 12 de junio de 2005, junto con otra frase que pasaría a la historia, y que aparecía en la contraportada del número de octubre de 1974 del Whole Earth Catalog:
 Whole Earth Index / fair use
Whole Earth Index / fair use
Bibliografía
Kabil, A. (29 de mayo de 2018). Seeing the whole earth from space changed everything. Long now.
Markoff, J. (2022). Whole Earth. The many lives of Steward Brand. Penguin Press.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Whole Earth Catalog: la versión analógica de internet se ha escrito en Cuaderno de Cultura Científica.

