Faringe, esófago y buche
Cavidad bucal, faringe, esófago y, si es el caso, buche conforman lo que podemos considerar como sistema digestivo anterior. Tras este conjunto de estructuras se encuentra el sistema digestivo medio. La boca ya se trató en la anotación anterior, por lo que en esta nos ocuparemos de la faringe, el esófago y el buche. Los sistemas digestivos mejor conocidos son el de insectos y, sobre todo, el de vertebrados, por lo que en adelante nos referiremos a esos sistemas, principal, pero no exclusivamente.

El sistema digestivo anterior de los insectos, llamado estomodeo, comienza en la boca y en él se diferencian la faringe (que es parte de la boca), el esófago (de forma tubular), el buche, que es un ensanchamiento de la parte final del esófago, y los proventrículos. La válvula estomodeal regula el paso del alimento y jugos digestivos del estomodeo al sistema digestivo medio, llamado mesenterón en los insectos. Una membrana gruesa, de cutícula, tapiza el interior del estomodeo; puede tener pliegues y proyecciones, o cerdas o espículas. Cada vez que muda el insecto se renueva.
En el sistema digestivo de los vertebrados la faringe es la parte de la garganta que sigue a las cavidades bucal y nasal, y precede al esófago y la laringe. Es una vía común al sistema digestivo y al respiratorio. Al acto de tragar el alimento se denomina deglución en terminología técnica.
La fase orofaríngea de la deglución en vertebrados empieza cuando la lengua (que es precisamente una adquisición de los cordados) empuja al bolo alimenticio hacia la parte trasera de la cavidad bucal y la faringe. Los barorreceptores de la faringe, al ser estimulados por la presión que ejerce el bolo, envían señales al centro de deglución que se encuentra en la médula (en el tronco encefálico), lo que desencadena una respuesta refleja por parte del citado centro y que es la que activa los músculos implicados. La musculatura actúa de manera que, a la vez que desplaza el alimento hacia la faringe y de ahí hacia el esófago, evita que retorne a la cavidad bucal, se eleve hacia la cavidad nasal y se dirija hacia la laringe y la tráquea. Para ello, hace lo siguiente:
- La posición de la lengua contra el paladar evita el retorno a la cavidad bucal.
- El velo del paladar (proyección colgante trasera) se eleva y cierra el acceso de la faringe a la cavidad nasal.
- La laringe se eleva y se produce el cierre hermético de las cuerdas vocales1 a lo largo de la glotis (apertura de la laringe). Además, el bolo alimenticio empuja a la epiglotis2 hacia abajo, de manera que cubre la glotis y refuerza su cierre.
- En humanos los movimientos respiratorios están inhibidos durante el breve periodo de tiempo que dura la deglución.
- La musculatura faríngea empuja el bolo hacia el esófago mientras se mantienen sellados laringe y tráquea.
La fase esofágica viene a continuación. El esófago es un tubo recto muscular que se extiende desde la faringe hasta el estómago. Hay especies en las que la musculatura del esófago es lisa (aves y humanos, por ejemplo), en otras es estriada (rumiantes y perros, por ejemplo); en gatos y caballos es esquelética (estriada) las dos terceras partes iniciales y lisa la tercera última parte.
Dos esfínteres cierran el esófago por sus dos extremos. El superior (faringoesofágico) se mantiene cerrado para evitar el paso de aire hacia el las zonas inferiores del sistema digestivo, pero se abre al llegar el bolo alimenticio. En ese momento, al contactar el bolo con la mucosa esofágica, el centro de deglución provoca una onda peristáltica primaria que se desplaza todo a lo largo del tubo empujando el bolo hacia el estómago3. En humanos la onda peristáltica se prolonga entre 5 y 9 s y su velocidad es controlada por el centro de deglución a través del nervio vago4.
Pero puede ocurrir que el bolo, por su tamaño y consistencia, se atasque y la onda peristáltica primaria sea incapaz de empujarlo. En ese caso, los receptores de presión del propio esófago activan una respuesta que consiste en la distensión de la pared y la generación de una onda peristáltica secundaria, más fuerte que la primaria. En este reflejo no interviene el centro de deglución, sin que se produce por mediación del plexo nervioso local que, además, da lugar a un aumento de la producción de saliva para lubrificar más el bolo y ayudar a su progresión.
El esfínter del extremo inferior (gastroesofágico) permanece normalmente contraído (cerrado) para evitar el reflujo de jugos gástricos hacia el esófago pero, como es lógico, se relaja de forma refleja al llegar el bolo para que pueda pasar al estómago.
En varios grupos (anélidos, gasterópodos, insectos y algunos dinosaurios, incluidas algunas aves) el esófago presentan un engrosamiento que da lugar a una especie de bolsa a la que llamamos buche. Cumple funciones de almacenamiento y es especialmente importante en los insectos que se alimentan de fluidos, como sangre o néctar. Suelen tener un buche bien desarrollado las aves granívoras y piscívoras, y no tanto las insectívoras y las rapaces.
En las especies con buche, el bolo alimenticio puede o bien quedar retenido temporalmente allí, o proseguir hasta el complejo proventrículo-molleja. La estancia del alimento en el buche se ajusta al tiempo de vaciado del complejo proventrículo-molleja, y todo ello es regulado a través del nervio vago.
En las palomas las células epiteliales del buche son sensibles a la hormona prolactina, la misma que promueve la síntesis de leche en mamíferos. Durante la incubación de los huevos, tanto machos como hembras experimentan una elevación de los niveles de prolactina circulantes en la sangre, lo que da lugar a una proliferación de las células epiteliales citadas. Esas células tienen un contenido lipídico muy alto. Al eclosionar los huevos se desprenden del epitelio y, junto con otros materiales almacenados en el buche, se utilizan para, regurgitándolos en su esófago, alimentar a los polluelos. A esa sustancia lipídica se la denomina “leche del buche”.
Notas:
1 En ese momento las cuerdas vocales cumplen, de hecho, un función que nada tiene que ver con la producción de sonidos.
2 Lámina cartilaginosa que en reposo se encuentra orientada hacia arriba.
3 El estómago, por cierto, puede estar por encima de la boca, como en los casos en los que el animal baja el cuello para comer.
4 Nervio perteneciente a la división parasimpática del sistema nervioso autónomo.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Faringe, esófago y buche se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El pulmón de los mamíferos
- Sistemas nerviosos: moluscos
- Sistemas nerviosos: el sistema periférico de vertebrados
¿Anti-oxidantes o pro-oxidantes?
Saioa Gómez Zorita, Andrea Mosqueda Solís & Jenifer Trepiana
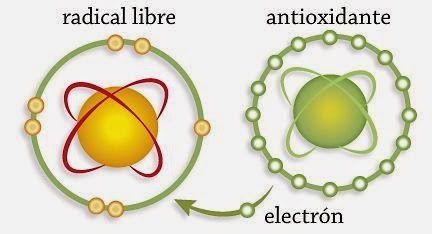
Para comprender qué son y cómo actúan los radicales libres hay que tener en cuenta que las moléculas están formadas por átomos, y que estos tienen alrededor protones (carga positiva) y electrones (carga negativa). Estos electrones pueden compartirse con otros átomos para que la molécula resultante sea más estable. Si alguno de estos electrones no se aparea (comparte) o son impares, se forma un radical libre. Por consiguiente, los radicales libres son moléculas muy inestables al contener un electrón desapareado, y por ello reaccionan con otras moléculas con el fin de encontrar otro electrón (agente oxidante) para de este modo poder convertirse en moléculas estables. También pueden sustraer un electrón a otra molécula, la cual quedará inestable convirtiéndose de este modo en un nuevo radical libre, ya que quedará con un electrón no apareado, que a su vez podrá hacer lo mismo con otra molécula. Así, se inicia una cascada o reacción en cadena que puede dañar nuestras células.
Los radicales libres provienen principalmente del oxígeno, el nitrógeno y el azufre, dando lugar así a especies reactivas de oxígeno (ERO o ROS en inglés), de nitrógeno o de azufre respectivamente. Entre los radicales de oxígeno se encuentran: el anión superóxido (O2•-), y los radicales hidroxilo (HO•), peroxilo (RO2•), y alcoxilo (RO•). Así mismo, encontramos moléculas no-radicales que también se comportan como agentes oxidantes entre los que se hayan: el peróxido de hidrógeno (H2O2), el ácido hipocloroso (HOCl), el ozono (O3) y el oxígeno simple (1O2). De entre todas las ERO, el radical hidroxilo es el más peligroso y el responsable de la mayor parte de los daños celulares relacionados con el estrés oxidativo. Para entenderlo mejor, podemos definir el estrés oxidativo como el incremento de los niveles de radicales libres, debido a una disminución en la eliminación de éstos por parte de las defensas antioxidantes. Las ERO se forman de manera natural en las células como consecuencia de la respiración celular en las mitocondrias, por la oxidación de los ácidos grasos para conseguir energía, en el proceso de fagocitosis, o por enzimas encargadas de eliminar productos tóxicos para el organismo. Además, otros factores externos como el alcohol, el tabaco, los rayos ultravioletas, la actividad física excesiva, o los pesticidas promueven una mayor producción de radicales libres.
Tenemos que tener en cuenta que los radicales libres de oxígeno, cumplen numerosas funciones en el organismo actuando como mensajeros en la señalización celular, el crecimiento, la diferenciación celular, la eliminación de células infectadas o malignas, y la destrucción de organismos patógenos. No obstante, las ERO se deben mantener en niveles adecuados, ya que su producción excesiva puede generar estrés oxidativo y daño celular que se asocia con un mayor riesgo de desarrollar enfermedades crónicas como el cáncer, enfermedades cardiovasculares o trastornos neurológicos y metabólicos.
¿Qué daño producen los radicales libres sobre las moléculas?
-
En el caso de los lípidos, dañan las estructuras ricas en ácidos grasos como las membranas celulares, alterándose la permeabilidad de las mismas y provocando edemas y la muerte celular. Además, oxidan las lipoproteínas de baja densidad (LDL) generando placas de ateroma. Es importante señalar, que el ácido graso, al oxidarse, se convierte en radical de ácido graso con capacidad de oxidar a otras moléculas, con lo que se propaga el proceso oxidativo o peroxidación lipídica. Se generan numerosos subproductos como el malondialdehído, que es uno de los métodos de evaluar o cuantificar el estrés oxidativo.
-
En lo que respecta a las proteínas, los radicales libres pueden oxidar los aminoácidos que forman estas moléculas, como la cisteína y tirosina entre otros, provocando cambios en su estructura y/o función que puede desencadenar la inactivación de las proteínas, y como consecuencia imposibilita el desarrollo de sus funciones: transporte, receptores y mensajeros celulares, enzimas que regulan el metabolismo, etc.
-
Otra molécula que puede ser dañada es el ADN, lo que tiene serias consecuencias en el desarrollo de mutaciones y carcinogénesis. Como resultado de los daños provocados en el material genético, el ciclo celular de las células se puede ver alterado, lo que puede acarrear la parada de la división celular o incluso la muerte de la célula.
-
No únicamente las moléculas anteriores pueden ser dañadas, así mismo los glúcidos también pueden ser alterados y degradados perdiendo su función y pudiendo inducir el proceso de inflamación.
Por consiguiente, es de gran importancia mantener un equilibrio entre la producción y la eliminación de radicales libres en el organismo. El cuerpo cuenta con dos mecanismos internos, denominados antioxidantes, para protegerse de los efectos nocivos de estas especies: un sistema enzimático y otro no enzimático. Entre los sistemas enzimáticos se encuentra la glutatión peroxidasa, que cataliza la reducción del peróxido de hidrógeno (H2O2) a agua, utilizando como agente reductor el glutatión reducido, en el citoplasma de las células; la catalasa, que transforma el peróxido de hidrógeno en oxígeno y agua, en los peroxisomas; y la superóxido dismutasa, que transforma el anión superóxido en peróxido de hidrógeno, manteniendo las concentraciones del anión superóxido lo suficientemente bajas para evitar la formación de peroxinitrito. Por otro lado, entre los sistemas no enzimáticos, se encuentran los antioxidantes como la vitamina A, la coenzima Q10 y el glutatión. A pesar de que poseamos estos dos métodos antioxidantes para neutralizar los radicales libres, en ocasiones resulta insuficiente por lo que los antioxidantes exógenos como los ingeridos en la dieta juegan un papel importante para mantener la homeostasis (equilibrio) ya que refuerzan los mecanismos internos.
Los antioxidantes están presentes de manera natural en algunos alimentos que tomamos en mayor o menor medida a través de la dieta, como la fruta y la verdura, que contienen polifenoles, ascorbato (vitamina C), α-tocoferol (vitamina E) o β-caroteno entre otros. No obstante, también están presentes en alimentos de origen animal como el pescado que puede ser rico en ácidos grasos poliinsaturados de cadena larga n-3.

¿Cómo actúan los antioxidantes?
-
Como quelantes de metales pro-oxidantes, como son el hierro y el cobre. Estos metales no pueden ser metabolizados por el organismo, donde persisten y pueden ejercer efectos tóxicos. Así, estos metales inducen daño oxidativo, por reacciones catalizadoras, que generan excesivos radicales libres. Los quelantes se unen a los metales dando lugar a una molécula más estable, lo que evitará la formación de radicales libres.
-
Como secuestradores de radicales, que cumplen la función de eliminarlos, evitando así que ataquen las moléculas diana.
-
Como inhibidores de oxidasas, como la lipoxigenasa, la ciclooxigenasa, la mieloperoxidasa, la NADPH oxidasa y la xantina oxidasa. De esta manera se evita la generación de ERO, así como de hidroperóxidos orgánicos.
-
Como inhibidores de enzimas involucradas indirectamente en los procesos oxidativos, como la fosfolipasa A2.
-
Como estimulantes de enzimas con propiedades antioxidantes, como son la catalasa, la glutatión peroxidasa y la superóxido dismutasa.
¿Qué ocurre para que siempre no sean tan beneficiosos los antioxidantes?
Los radicales libres se consideran pro-oxidantes, ya que como hemos mencionado anteriormente, son sustancias químicas que inducen estrés oxidativo, normalmente mediante la formación de especies reactivas o por inhibición de los sistemas antioxidantes. Al igual que los radicales libres, los antioxidantes también pueden tener un comportamiento pro-oxidante dependiendo de diversos factores como son: la dosis (cantidad ingerida), el tipo de antioxidante y la matriz (componentes de los alimentos) en la que se encuentre. Por tanto, como podemos imaginar, son numerosos los estudios que muestran los efectos beneficiosos del empleo de antioxidantes pero también algunos muestran el efecto contrario.
Uno de los ejemplos más conocidos es el del estudio del efecto del β-caroteno sobre el cáncer de pulmón. Numerosos estudios mostraban que alimentos ricos en β-caroteno prevenían el cáncer de pulmón, por lo que a los pacientes del estudio se les suministró β-caroteno aislado. Dicha intervención tuvo que suspenderse ya que entre los fumadores la suplementación estaba incrementando el cáncer de pulmón (Omenn GS, 1996).
También se han estudiado, algunos de los mecanismos a través de los cuales los flavonoides, compuestos fenólicos que podemos encontrar en frutas, verduras, así como en el vino, pueden ejercen acciones pro-oxidantes, incluyendo la reducción temporal de Cu (II) a Cu (I), (Brown, 1998) la generación de ERO, (Sahu, 1997), así como la afectación de las funciones de los componentes del sistema de defensa antioxidante nuclear: glutatión y glutatión-S transferasa (Sahu, 1996). En concreto, se ha visto que el flavonoide quercetina, puede actuar como pro-oxidante al producir daño en el ADN mediante el ciclo redox Cu(II)/Cu(I) capaz de generar ERO y lesionar el material genético mediante oxidación (Yoshino, 2002).

Entonces… ¿qué hacemos?
Es muy probable que cuando los antioxidantes forman parte de los alimentos y se ingieren dentro de una dieta equilibrada, predominen los efectos beneficiosos; en cambio, en forma de suplementos que generalmente emplean altas concentraciones de antioxidantes, éstos pueden actuar como pro-oxidantes.
Como norma general, con una dieta equilibrada rica en fruta y verduras, se cubren los requerimientos de antioxidantes lo que a su vez puede contribuir a la prevención de enfermedades y al incremento de la esperanza de vida. Además, en cuanto al tratamiento de las patologías, no se puede pensar que ayudan o curan cualquier enfermedad ni que aquellos más de “moda” son los más efectivos.
A pesar de lo dicho anteriormente, hay grupos de población, como los ancianos, los deportistas, los bebedores y los fumadores, en los que el empleo de determinados suplementos antioxidantes podría ser beneficioso. No obstante, en el caso de los deportistas los radicales libres juegan un papel importante en las adaptaciones a la actividad física, y por tanto según en qué fase de la “temporada” se encuentren, la suplementación con antioxidantes podría ser beneficioso o perjudicial al inhibir parcialmente las adaptaciones. Por consiguiente, tanto en deportistas como en cualquier otro colectivo, en caso de administrar suplementos antioxidantes de este modo, se debe tener en cuenta al menos la historia clínica (hábitos) y el análisis bioquímico (estrés oxidativo, niveles de antioxidantes, etc).
¿Consumir más vitaminas es MEJOR o PEOR?
Por sus propiedades y funciones, la vitamina C, el β-caroteno (principal fuente de vitamina A) y la vitamina E son considerados antioxidantes, ya que son los únicos nutrientes esenciales que atrapan directamente radicales libres, y debido a esto, pueden proteger a las células al reducir el daño oxidativo provocado por las ERO. La vitamina C es soluble en agua (hidrosoluble), ubicándose en el citoplasma celular; mientras que la vitamina E y el β-caroteno son solubles en lípidos (liposolubles) actuando como antioxidante a nivel de las membranas celulares.
Los antioxidantes son añadidos con frecuencia a alimentos comerciales y suplementos deportivos con el fin de extender su vida útil. Sin embargo, la principal fuente natural son los alimentos, como verduras, frutas cítricas, nueces, granos, semillas y aceites. La dosis diaria recomendada de vitamina A, C y E, son distintas para cada etapa de la vida. A continuación, en las tablas podrás observar las cantidades recomendadas y los alimentos con alto contenido de estas vitaminas. Así, podrás observar cómo la suplementación de ciertas vitaminas no es necesaria si se tiene una alimentación adecuada.
Dosis diaria recomendada de vitamina A (National Institutes of Health, 2017):
Etapa de la vida
Límite máximo recomendado
Bebés hasta los 12 meses de edad
2.000 UI
Niños de 1 a 3 años
2.000 UI
Niños de 4 a 8 años
3.000 UI
Niños de 9 a 13 años
5.667 UI
Adolescentes de 14 a 18 años
9.333 UI
Adultos
10.000 UI
UI: Unidades internacionales. El contenido en vitamina A de los alimentos se mide como equivalentes de actividad de retinol (EAR). Un EAR es igual a la actividad de 1 mg de retinol (1 mg de retinol es igual a 3,33 unidades internacionales [UI]).
Alimentos con alto contenido de vitamina A:
Vitamina A (EAR)
Alimento
15.534
200 g pavo
5.553
150 g zanahoria cruda
6.882
150 g espinacas cocinadas
2.337
100 g verduras mixtas congeladas
725
150 g brócoli cocinado
450
150 g tomates
430
150 g coles
Adultos, cantidad diaria recomendada = 700-900 EAR/día, dependiendo del sexo.
Dosis diaria recomendada de vitamina C (National Institutes of Health, 2017):
Etapa de la vida
Cantidad recomendada
Bebés hasta los 6 meses de edad
40 mg
Bebés de 7 a 12 meses de edad
50 mg
Niños de 1 a 3 años de edad
15 mg
Niños de 4 a 8 años de edad
25 mg
Niños de 9 a 13 años de edad
45 mg
Adolescentes (varones) de 14 a 18 años de edad
75 mg
Adolescentes (niñas) de 14 a 18 años de edad
65 mg
Adultos (hombres)
90 mg
Adultos (mujeres)
75 mg
Adolescentes embarazadas
80 mg
Mujeres embarazadas
85 mg
Adolescentes en período de lactancia
115 mg
Mujeres en período de lactancia
120 mg
Alimentos con alto contenido de vitamina C:
Vitamina C
Alimento
190 mg
1 taza de pimiento verde
137 mg
2 Kiwis
132 mg
1 cabeza pequeña de brócoli
128 mg
1 cabeza pequeña de coliflor
122 mg
1 mango
120 mg
1 taza de pimiento verde
108 mg
1 taza de chile
88 mg
1 taza de papaya
85 mg
1 taza de fresas
80 mg
1 taza de col rizada
79 mg
1 taza de piña
75 mg
Coles de Bruselas
67 mg
½ naranja
Dosis recomendada de vitamina E (National Institutes of Health, 2017):
Etapa de la vida
Cantidad recomendada
Bebés hasta los 6 meses de edad
4 mg (6 UI)
Bebés de 7 a 12 meses de edad
5 mg (7.5 UI)
Niños de 1 a 3 años de edad
6 mg (9 UI)
Niños de 4 a 8 años de edad
7 mg (10.4 UI)
Niños de 9 a 13 años de edad
11 mg (16.4 UI)
Adolescentes de 14 a 18 años de edad
15 mg (22.4 UI)
Adultos
15 mg (22.4 UI)
Mujeres y adolescentes embarazadas
15 mg (22.4 UI)
Mujeres y adolescentes en período de lactancia
19 mg (28.4 UI)
Alimentos con alto contenido de vitamina E:
Vitamina E
Alimento
35 mg
100 g de pipas de calabaza
26 mg
100g de almendras
15 mg
100g de avellanas
5,6 mg
1 cucharada de aceite de girasol
3,8 mg
100 g de aceitunas
2,1 mg
½ aguacate
2,0 mg
100 g de espinaca
1,5 mg
100 g de brócoli
100 g de puré de calabaza
Se pueden encontrar diversos estudios científicos sobre la toxicidad provocada por una ingesta elevada de las vitaminas anteriormente descritas. Dosis excesivas de vitamina A (de más de 100 veces la cantidad necesaria) de forma persistente superan la capacidad del hígado de almacenar dicha vitamina y pueden producir intoxicación. Además, esto puede conllevar cambios en el color de la piel y producir exfoliación. Por otra parte, la vitamina C es uno de los suplementos utilizados con más frecuencia en EE.UU. Los efectos adversos de dosis elevadas de esta vitamina son trastornos digestivos y diarreas. Además, puede aumentar el riesgo de formar cálculos renales de oxalato. Referente a la vitamina E, aunque ingestas elevadas de vitamina E parecen ser bien toleradas por el organismo, dosis elevadas puede reducir la capacidad del cuerpo de utilizar otras vitaminas liposolubles. Asimismo, en los últimos años, se han publicado datos contradictorios acerca del aporte complementario de vitamina E en dosis altas y sus efectos adversos, con los que debería estudiarse en profundidad (Gerss J, 2009).
En lo referente a la complementación en la actividad deportiva, no existe evidencia científica consistente de mejoría en el desempeño físico tras una suplementación con antioxidantes.
Nieman et al., realizó un estudio en corredores donde midió la influencia de la suplementación con vitamina C y un placebo en cambios oxidativos e inmunitarios antes y después de una maratón y concluyó que dicha suplementación no puede utilizarse como variable para observar cambios oxidativos y del sistema inmunitario en atletas.
Otro estudio realizado para determinar el efecto de la suplementación de vitamina C sobre la frecuencia, duración y gravedad de las infecciones de las vías respiratorias en nadadores adolescentes, observó que no había efectos considerables para disminuir los resfriados que aparecen con frecuencia en la población estudiada. Por otro lado, los efectos de una suplementación de 400mg de acetato de α-tocoferol (vitamina E) diariamente durante seis semanas comparado con un grupo placebo, observó que las adaptaciones al entrenamiento mejoraron la función fisiológica y el rendimiento físico, pero no fue así en el grupo suplementado con la vitamina.
Como hemos visto, el consumo excesivo de antioxidantes puede provocar efectos pro-oxidantes. Una suplementación excesiva de vitamina E (800 UI/día) durante dos meses en combinación con un entrenamiento prolongado y de intensidad alta incrementa el estrés oxidativo y la reacción inflamatoria durante el ejercicio.
Sujetos no entrenados recibieron suplementación de 1000 mg al día de vitamina C durante un programa de entrenamiento de 8 semanas y se demostró una mejoría muy baja en su capacidad aeróbica.
Investigadores como Yftanti, sugieren que la administración de vitamina C y vitamina E en personas que no tengan una deficiencia vitamínica previa no presentan ningún efecto en las adaptaciones físicas al entrenamiento de resistencia.
Recuerda que todo es cuestión de balance, nunca excederte ya que todo tiene un efecto secundario en nuestro organismo.
Referencias:
Brown JE, Khodr H, Hider RC, Rice-Evans CA. Structural dependence of flavonoids interactions with Cu2+ ions: implications for their antioxidant properties. Biochem J 1998;330:1173-8.
Omenn, G. S., Goodman, G., Thornquist, M., Barnhart, S., Balmes, J., Cherniack, M., … & Meyskens Jr, F. (1996). Chemoprevention of lung cancer: the beta-Carotene and Retinol Efficacy Trial (CARET) in high-risk smokers and asbestos-exposed workers. IARC scientific publications, (136), 67.
Sahu SC, Gray GC. Pro-oxidant activity of flavonoids: effects on glutathione and glutathione-S transferase in isolated rat liver nuclei. Cancer Lett 1996;104:193-6
Sahu SC, Gray GC. Lipid peroxidation and DNA damage induced by morin and naringenin in isolated rat liver nuclei. Food Chem Toxicol 1997;35:4436-47.
Yoshinoa M, Haneda M, Naruseb M, Htay H.H, Iwata S, Tsubouchi R, Murakami K. Prooxidant action of gallic acid compounds: copper-dependent strand breaks and the formation of 8-hydroxy-2′-deoxyguanosine in DNA. Toxicology in Vitro 2002; 16: 705-709.
Gerss J, Kopcke W: The questionable association of vitamin E supplementation and mortality—inconsistent results of different meta-analytic approaches, Cell Mol Biol 55:1111S, 2009.
L.K. Mahan, S Escott-Stump, JL Raymond. Krause dietoterapia. 13ª edición. Ed. Elsevier España; 2012.
Gomez-Cabrera MC, et al. Oral administration of vitamin c decreases muscle mitochondriak biogénesis and hampers training-induced adaptations in endurance performance. Am J Clin Nutr. 2008 Jan; 87 (1):142-9.
Burke L. Practial Sport Nutrition 1st edition. Human kinetics; 2007.
Yfanti C, et al. Antioxidant supplementation does not alter endurance-training adaptation. Med Sci Sports Exerc. 2010;42(7):1388-95
Mastalouidis A, et al. Antioxidant supplementation prevents exercise-induced lipid peroxidation, but not inflammation in ultra marathon runners. Free Radic Biol Med. 2004 May 15;36 (10) 1329-41
Sobre las autoras:
Saioa Gómez Zorita (@saioasgz) es doctora en farmacia, Andrea Mosqueda Solís (@andreamoss87) es doctora en nutrigenómica y nutrición personalizada y Jenifer Trepiana es doctora en biología molecular y biomedicina. Trabajan en el grupo de fisiopatología de la obesidad y nutrición (CIBERobn) del Instituto de Salud Carlos III y en el Departamento de Farmacia y Ciencias de los Alimentos de la Facultad de Farmacia de la UPV/EHU.
El artículo ¿Anti-oxidantes o pro-oxidantes? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Color de las lechugas y antioxidantes
- Una planta amazónica podría acabar con las células tumorales hepáticas
- 10 aditivos alimentarios que proceden de la naturaleza y quizá no lo sabías
Carlos Briones – Naukas Bilbao 2018: Os voy a contar una historia (en imágenes)

El pasado 15 de septiembre, durante Naukas Bilbao 2018, Carlos Briones ofreció una de las charlas de divulgación más impactantes, por diferente, desde el inicio de estos eventos divulgativos. Además de investigador del Centro de Astrobiología del CSIC, Briones es músico y un gran aficionado al arte, y combina su erudición renacentista para contarte la historia del universo como nunca te la habían contado. Y en 10 minutos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Carlos Briones – Naukas Bilbao 2018: Os voy a contar una historia (en imágenes) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Pro 2017: Carlos Briones y el origen de la vida
- El universo en un día: El origen de la vida, por Carlos Briones
- Naukas Bilbao 2017 – Laura Morrón: La gran divulgadora
Un hidrogel de almidón/grafeno, conductor y antibacteriano, para implantes neurológicos

Los hidrogeles son redes poliméricas capaces de retener grandes cantidades de líquido en entornos acuosos sin perder su estabilidad dimensional. Se utilizan en numerosas aplicaciones, y al incorporarles diferentes componentes, adquieren propiedades específicas, como la conductividad eléctrica. Esta ha sido la vía seguida por el grupo de investigación Materiales+Tecnología del Departamento de Ingeniería Química y del Medio Ambiente de la Escuela de Ingeniería de Gipuzkoa de la UPV/EHU para un hidrogel para el que han elegido un biopolímero que no se había utilizado hasta la fecha para ese tipo de aplicaciones: el almidón.
En la creación del nuevo hidrogel los miembros del grupo tenían en mente su utilización en interfases neuronales, es decir, las partes encargadas de la conexión eléctrica en los implantes que interactúan con el sistema nervioso. “Los electrodos tradicionales de las interfases neuronales, de platino u oro, por ejemplo, al ser rígidos, requieren de revestimientos poliméricos conductores para acercar su flexibilidad a la de los tejidos neuronales. Actualmente, sin embargo, se demandan dispositivos más pequeños, así como que cuenten con mejores propiedades mecánicas, eléctricas y biológicas”, explica la investigadora Kizkitza Gonzalez Munduate. Los hidrogeles desarrollados “responden muy bien a esas demandas”.
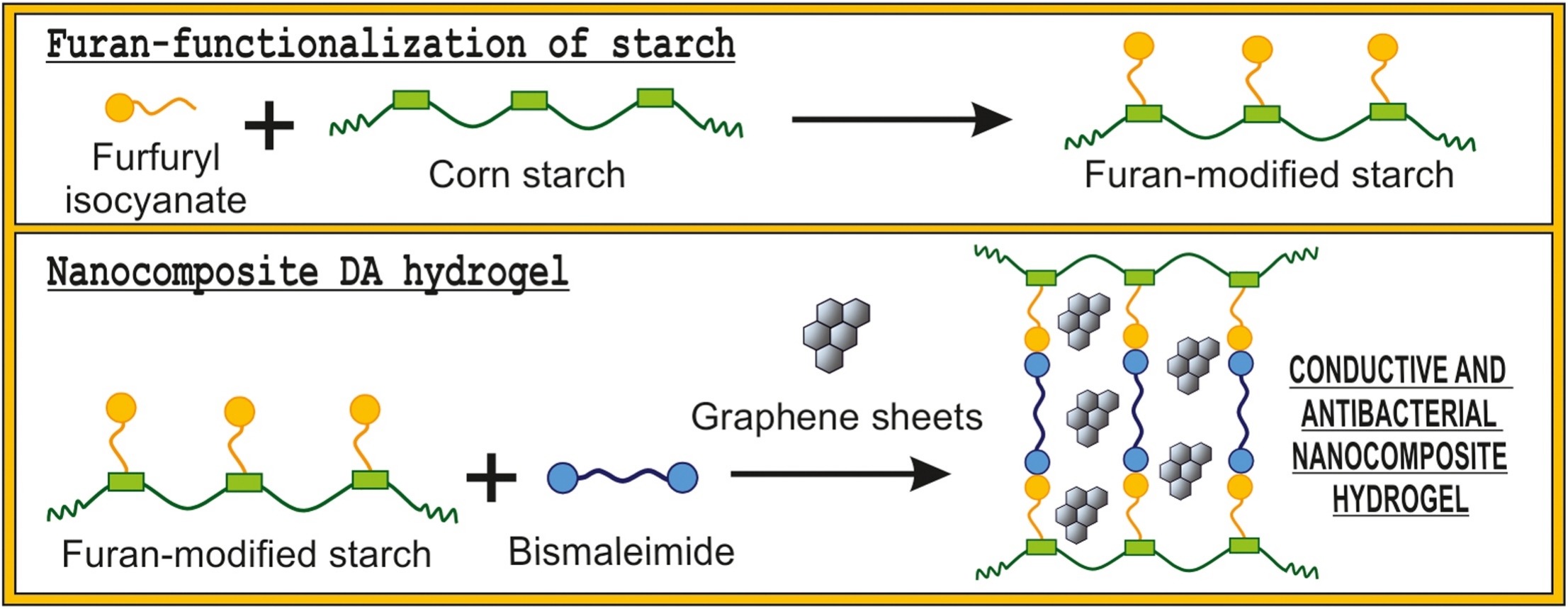
Para dotar al hidrogel de conductividad eléctrica, los investigadores recurrieron al grafeno, “un material de gran interés. Proporciona unas propiedades eléctricas muy adecuadas al hidrogel, pero también presenta un inconveniente: no se estabiliza muy fácilmente en agua. Para superar ese obstáculo, y hacer al grafeno estable en un medio acuoso, utilizamos extractos de salvia. Estos extractos, además, hacen al hidrogel aún más adecuado, si cabe, para ser utilizado en medicina, ya que también tienen propiedades antimicrobianas y antiinflamatorias”, añade Gonzalez Munduate.
Una de las características distintivas de esta investigación ha sido la utilización de la denominada química click para la elaboración del hidrogel. “Es una estrategia que en los últimos años está acaparando la atención de la comunidad científica, porque a diferencia de otras vías de síntesis, la química click generalmente no utiliza catalizadores en las reacciones; además no se generan subproductos, y son reacciones de gran rendimiento”, explica la investigadora.
Aunque ha sido diseñado para una aplicación muy específica, Gonzalez Munduate reconoce que este producto de bioingeniería debe recorrer un largo camino todavía hasta que pueda llegar a ser utilizado con pacientes: “Ha sido una investigación de nivel inicial, centrada en la parte de la ingeniería, relacionada con el material. A partir de ahora, se deberían ir superando niveles paulatinamente y diseñando los correspondientes ensayos”.
Referencia:
Kizkitza González, Clara García-Astrain, Arantzazu Santamaria-Echart, Lorena Ugarte, Luc Avérous, Arantxa Eceiza, Nagore Gabilondo (2018) Starch/graphene hydrogels via click chemistry with relevant electrical and antibacterial properties Carbohydrate Polymers doi: 10.1016/j.carbpol.2018.09.007
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un hidrogel de almidón/grafeno, conductor y antibacteriano, para implantes neurológicos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Polímeros biocompatibles para integrar dispositivos electrónicos en nuestro cuerpo
- Naukas Pro 2017: Amaia Zurutuza y el grafeno
- Un atlas para materiales 2D
Los parabenos usados en cosmética son seguros

Recientemente el CIR (Cosmetic Ingredient Review), que es el panel de expertos en EEUU en materia de cosmética, ha publicado la última revisión sobre los parabenos y su uso en cosmética. El CIR es el organismo análogo al SCCS europeo. Ambos organismos se han encargado de recopilar todos los estudios científicos independientes relativos al uso de parabenos en cosmética y así poder hacer una evaluación exhaustiva de sus implicaciones en la salud. Los dos organismos están libres de conflictos de interés y actúan de forma completamente independiente.
Los parabenos se utilizan en cosmética como conservantes. Tienen actividad antimicrobiana y antifúngica, por lo que protegen al producto de la degradación y por tanto, protegen al consumidor. Su uso se ha puesto en entredicho desde 2004, cuando se publicó un estudio realizado en una universidad de Reino Unido en el que se habían detectado parabenos en tejido tumoral mamario. Aunque las conclusiones de este estudio no fueron que los parabenos estuviesen implicados en el cáncer de mama, muchos medios de comunicación lo contaron así. Después de ese estudio se hicieron cientos de estudios más para tratar de encontrar alguna relación entre el cáncer y el uso de parabenos en cosmética. Todos los estudios científicos realizados hasta la fecha han desestimado esta relación. La evidencia científica nos dice que los parabenos usados en cosmética son seguros.
El panel de expertos del CIR está compuesto por dermatólogos, toxicólogos, químicos, defensores de la protección del consumidor y expertos en salud pública que han sido nominados públicamente por grupos de consumidores, científicos y médicos, agencias gubernamentales e industrias. La Administración de Alimentos y Medicamentos de EEUU (FDA), la Federación de Consumidores de América (CFA) y la industria participan como miembros sin derecho a voto en las deliberaciones del panel de expertos del CIR.
En esta última revisión sobre los parabenos se ha evaluado su posible efecto como disruptores endocrinos, el efecto de la bioacumulación y uso prolongado, y las diferentes fuentes de exposición, no solo cosmética, sino a través de fármacos y alimentos. La conclusión a la que han llegado es clara: los parabenos usados en cosmética son seguros.
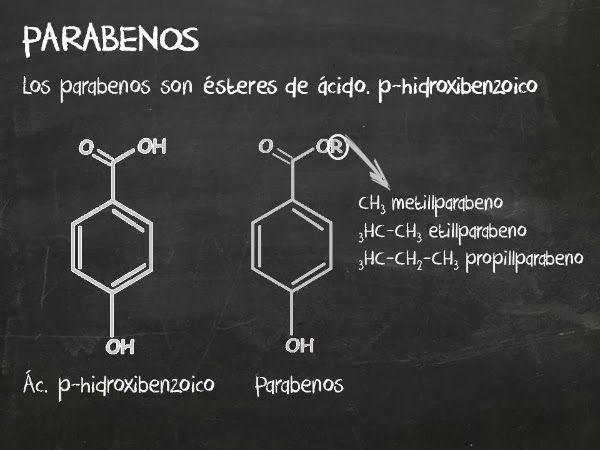 Imagen de www.cosmeticosaldesnudo.com
Imagen de www.cosmeticosaldesnudo.comCuando hablamos de parabenos, nos referimos a una familia de compuestos muy amplia. Los parabenos son derivados del ácido para-hidroxibenzoico (PHBA) que se produce de forma natural en muchas frutas y verduras, como pepinos, zanahorias, cerezas, arándanos y cebollas, así como en la descomposición de algunos aminoácidos en nuestro organismo. Sin embargo, los parabenos que utilizamos en los cosméticos son de síntesis, por lo que no se malgastan plantas ni alimentos en su fabricación. Producimos PHBA a través de la reacción modificada de Kolbe-Schmitt entre el dióxido de carbono y el benzoato de potasio, que a su vez se obtiene del ácido benzoico que podemos extraer del petróleo. Es un proceso relativamente sencillo y que produce menor impacto medioambiental que su extracción de plantas.
En cosmética solo se utilizan el metil, etil, propil y butilparaben y sus sales. Es decir, no todos los compuestos denominados parabenos pueden emplearse en cosmética. De hecho, en el Reglamento de la UE es donde se especifica los compuestos que podemos usar en cosmética y en qué cantidades. En ese reglamento aparecen estos parabenos. En el anexo V encontramos los parabenos permitidos en cosmética y la concentración a la que se pueden emplear. 0,8% en el caso de mezclas de parabenos y 0,4% en el caso de usar un único parabeno. Los parabenos permitidos en cosmética los denominamos “parabenos de cadena corta” para diferenciarlos de los parabenos que sí han demostrado cierto efecto estrogénico, los “parabenos de cadena larga”. Por cierto, los parabenos de cadena larga no se emplean en cosmética.

Para que un compuesto llegue a formar parte de la lista de ingredientes permitidos en un cosmético debe demostrar que su uso está justificado, es decir, que cumple una función coherente dentro del producto, y debe demostrar que su uso es seguro. Para ello se hacen estudios toxicológicos. En los estudios toxicológicos se mide qué cantidades se pueden emplear sin que supongan un riesgo para la salud. Se tienen en cuenta los efectos acumulativos, es decir, cómo influiría un uso prolongado, y el llamado “efecto cóctel”, es decir, cómo interfiere con otros ingredientes. Para la evaluación toxicológica se emplean varios parámetros, como el MoS, que es la relación existente entre el valor del NOAEL (No Observed Adverse Effects Level: cantidad máxima de producto administrado con la que no se observan efectos adversos, 10.000 veces por debajo del DL50), y la SED (Dosis de Exposición Sistémica). Es decir, se mide. A partir de estos y otros parámetros se calculan las concentraciones permitidas, que están muy por debajo de las dosis con efectos tóxicos detectables. Así que cuando se determina el 0,8% de concentración máxima de parabenos en un cosmético, estamos siendo extremadamente prudentes.
Llevamos utilizando parabenos en cosmética casi 80 años. La razón es que son muy versátiles y estables en prácticamente cualquier tipo de formulación cosmética. Combaten la proliferación de un amplio espectro de hongos y bacterias, por lo que son muy seguros. Funcionan a baja concentración, por lo que se emplean dosis muy bajas y siguen siendo efectivos. Esto lo vemos en los ingredientes de los cosméticos, ya que aparecen como los últimos de la lista, es decir, como los componentes minoritarios, ya que las listas de ingredientes van de mayor a menor cantidad en el producto. Y además no son considerados alérgenos, por lo que los encontramos en productos denominados hipoalergénicos y en formulaciones específicas para pieles sensibles y reactivas. Son los mejores conservantes que conocemos.
Desgraciadamente la desinformación y la incultura científica nos ha llevado a la situación actual. Los consumidores no quieren parabenos. No saben lo que son, pero saben que no los quieren. Esa es la razón por la que muchos laboratorios tomaron la decisión de dejar de utilizarlos y poner otros conservantes en su lugar. Si el consumidor tiene un miedo, sea o no infundado, la industria le pone remedio. Por eso en la UE resulta casi imposible encontrar un cosmético que no se publicite como “sin parabenos”.
En lugar de parabenos se emplean otros conservantes como el phenoxyethanol, el sodium benzoate con potassium sorbate, el dehydracetic acid, o el gluconodactone con sodium benzoate. Es decir, otros compuestos que en conjunto dan un resultado similar al de los parabenos. Normalmente se utiliza una combinación de varios para cubrir todo el espectro que antes cubrían los parabenos, y en más concentración, para que la actividad sea equivalente a la de los parabenos. Todos ellos también son seguros.
Afortunadamente la industria llegó a alternativas que respondieron a la presión social contra los parabenos. Para ello no solo tuvieron que cambiar unos conservantes por otros, sino que estos cambios afectaron a la formulación de productos enteros. Por eso la composición de algunos cosméticos en EEUU (donde muchos siguen conteniendo parabenos y a nadie le importa) no es la misma que en Europa. En Europa, el miedo hacia los parabenos fue un monstruo mucho más grande que en EEUU.
Conclusiones
-
Los parabenos son conservantes. Su uso está permitido.
-
La seguridad de los parabenos fue puesta en entredicho por la incorrecta interpretación de un estudio científico publicado en 2004. Ese fue el origen del miedo hacia estos compuestos.
-
Los laboratorios que decidieron dejar de utilizar parabenos no lo hicieron por una razón sanitaria sino por presión social. Tuvieron que reformular sus productos para poder utilizar conservantes diferentes a los parabenos.
-
El CIR ha publicado un trabajo en el que se ha revisado toda la literatura científica acerca de los parabenos. Se ha evaluado su efecto como disruptores endocrinos y su relación con el cáncer, y su efecto bioacumulativo teniendo en cuenta todas las fuentes de exposición, no solo la fuente cosmética. La conclusión es rotunda: los parabenos son seguros.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Los parabenos usados en cosmética son seguros se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ciencia en la cosmética o el triunfo del absurdo
- La ciencia que deberías saber antes de comprar tu protector solar (2)
- Los champús sin sulfatos y la libertad de decidir
Y tú, ¿cómo cuentas con los dedos? (1)
En mi última entrada de la sección Matemoción del Cuaderno de Cultura Científica, titulada Construye tu propia calculadora de sumas y restas, hablábamos de construir una sencilla calculadora mecánica para sumar y restar. Aunque, sin lugar a dudas, la primera calculadora de la que dispusieron los seres humanos fueron sus manos. Estas se han utilizado, desde hace muchos, muchos milenios, cuando la humanidad empezó a introducir el concepto de número, para contar, así como para realizar las operaciones aritméticas básicas, lo cual ha quedado reflejado en el hecho de que la mayoría de los sistemas de numeración son decimales.
Por este motivo, me ha parecido que podía ser interesante abordar en esta entrada cómo contamos las personas con los dedos de nuestras manos y cómo han contado, utilizando sus manos, los diferentes pueblos a lo largo de la historia de la humanidad.
Lo primero que me planteé fue cómo cuento yo mismo, si para ello utilizo los dedos de las manos, y cómo lo hacen las personas de mi entorno. Yo cuento de la siguiente manera. Empiezo con la mano izquierda cerrada y con la zona de los dedos hacia arriba, y voy levantando los dedos, mientras cuento, en el siguiente orden, primero el pulgar para el uno, el índice para el dos, el corazón para el tres, el anular para el cuatro y el meñique para el cinco, manteniéndolos levantados. Después, mientras mantengo la mano izquierda extendida, paso a la mano derecha, con la misma postura, el mismo método y en el mismo orden, contando desde el pulgar, que extiendo para contar el seis, índice, siete, corazón, ocho, anular, nueve, hasta el meñique, para el diez.
 Forma en la que yo cuento, del 1 al 10, con los dedos de las manos. Empiezo por la izquierda, extendiendo los dedos desde el pulgar al meñique, para contar del uno al cinco, y luego paso a la derecha, mientras mantengo la izquierda abierta para mantener el valor del cinco, extendiendo de nuevo los dedos del pulgar al meñique, para los números del seis al diez
Forma en la que yo cuento, del 1 al 10, con los dedos de las manos. Empiezo por la izquierda, extendiendo los dedos desde el pulgar al meñique, para contar del uno al cinco, y luego paso a la derecha, mientras mantengo la izquierda abierta para mantener el valor del cinco, extendiendo de nuevo los dedos del pulgar al meñique, para los números del seis al diezPero, ¿será este el método habitual para contar con las manos para las personas que están en mi entorno? Más aún, empecé a plantearme otras cuestiones más o menos sencillas, pero lógicas. ¿Existirá una forma estándar de contar con los dedos? ¿Por qué mano empezamos a contar? ¿Y, de hecho, qué dedo utilizamos primero en dicha mano? ¿Empleamos el mismo método, de forma simétrica, con las dos manos, como hacía yo mismo o cambiamos en la segunda mano? Y otras preguntas similares.
Me pareció que el problema planteado requería de un pequeño trabajo de campo. Por este motivo, pregunté a varias personas de mi entorno laboral y personal “cómo contaban (del uno al diez) con los dedos de las manos”. En total fueron 48 personas encuestadas, incluido yo mismo. Obviamente, esta no es una encuesta realizada de forma científica, de la que podamos extraer información concluyente, pero me sirve para tener una ligera idea de las cuestiones que me había planteado.
Una de las primeras cosas que llamó mi atención fue que no parecía existir una relación directa entre ser diestro o zurdo y la mano con la que se empezaba a contar. Al parecer, la gente empieza indistintamente con la mano derecha o la izquierda, aunque normalmente quien lo hace por una de ellas, por ejemplo, yo con la mano izquierda, casi siempre inicia el conteo con esa mano. De las 48 personas entrevistadas, 23 empezaron con la mano derecha y 25 con la mano izquierda. La mayoría de las personas entrevistadas eran diestras, pero no se veía un patrón en ninguno de los dos grupos.
Respecto al dedo de inicio para contar los números desde el uno en adelante, la mayoría de las personas empezaban por el dedo pulgar o el meñique, aunque algunas empezaron por el dedo índice. Las cifras fueron las siguientes: con el pulgar, 19 personas, con el meñique, 24 de las entrevistadas, y con el índice, tan solo 5.
 Escultura de manos gigantes durante la Bienal de Venecia de 2017, del artista italiano Lorenzo Quinn. Imagen de la Galería Halcyon, en Venecia, extraída de la página de Lorenzo Quinn
Escultura de manos gigantes durante la Bienal de Venecia de 2017, del artista italiano Lorenzo Quinn. Imagen de la Galería Halcyon, en Venecia, extraída de la página de Lorenzo QuinnTambién me fijé en que la mayoría de las personas entrevistadas, en concreto, 32 de las 48, utilizaban el mismo método en ambas manos y en el mismo orden, como lo hacía yo mismo. Sin embargo, había 12 personas que utilizaban el mismo método, pero en el sentido opuesto. Por ejemplo, si una persona empezaba por la mano izquierda con el mismo método que yo, desplegando los dedos desde el pulgar (1) al meñique (5), en la mano derecha desplegaba los dedos desde el meñique (6) hasta el pulgar (10). Y había algunos casos, 4, en los que se cambiaba de método de una mano a otra.
Respecto al método utilizado para contar, el más común, que me mostraron 34 de las 48 personas participantes en la encuesta, ha sido “desplegar los dedos de cada mano”, con algunas variaciones.
Analicemos las variantes dentro del grupo de desplegar los dedos de cada mano. Esencialmente hay dos grupos, los que empiezan a contar con el pulgar, como yo, o los que empiezan a contar con el meñique (como muestra la siguiente imagen), en ambos casos pueden empezar por la mano izquierda o la derecha, aunque como comentábamos, quien lo hace con una mano, casi siempre lo hace con esa misma mano. Una curiosidad de este método es que era el elegido por la mayoría de las personas que empezaban a contar con el pulgar, 17 de las 19 comentadas más arriba. Mientras que solo 12 de las 24 que empezaban con el meñique, lo hacían con la técnica de desplegar los dedos.
La otra variación es que utilicen el mismo orden de despliegue en las dos manos o que cambien de orden, como en la siguiente imagen, que en la mano izquierda se cuenta desplegando de meñique (1) a pulgar (5), mientras que en la derecha se despliegan los dedos de pulgar (6) a meñique (10).
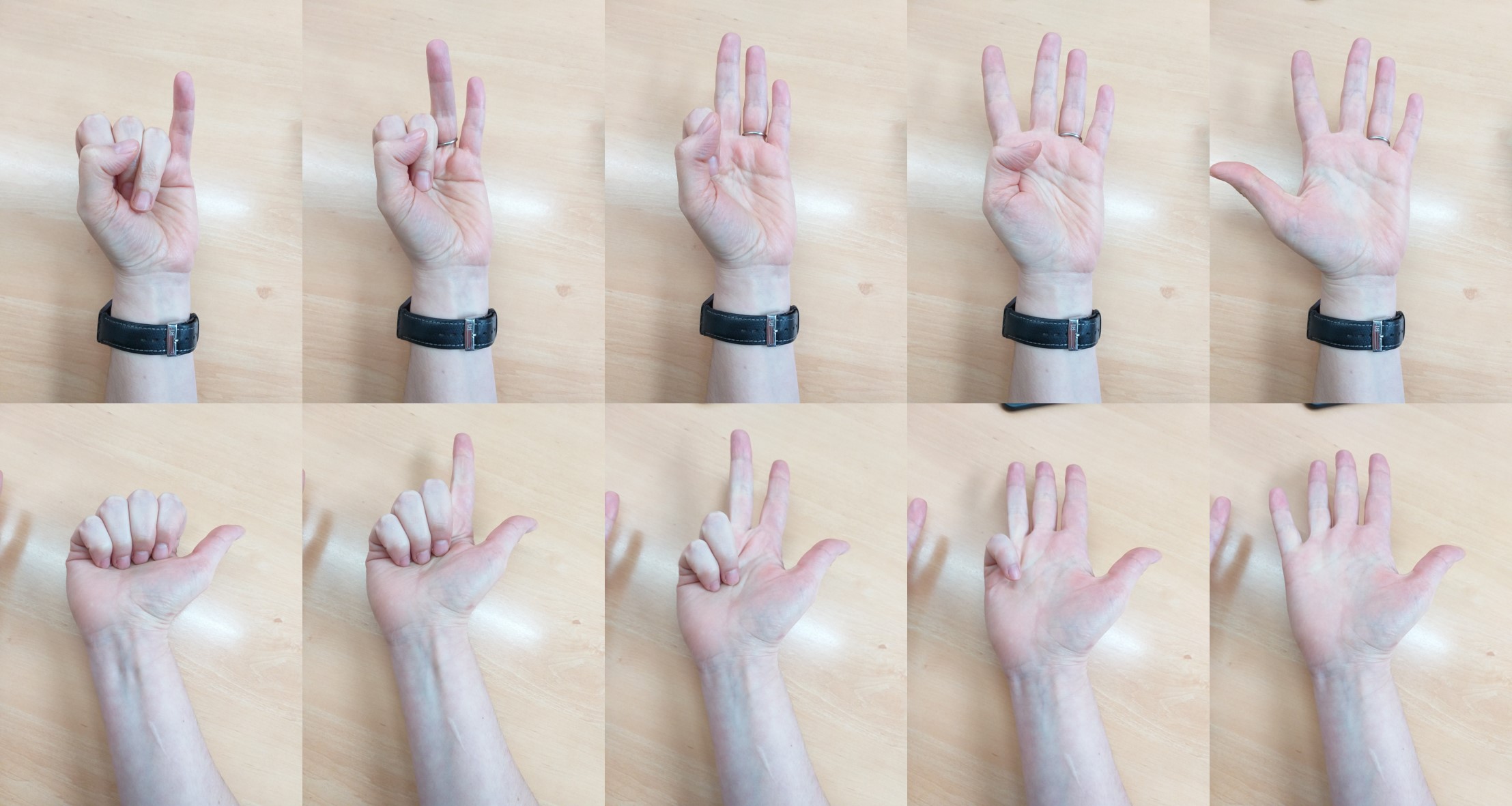 Esta es la manera en la que cuenta mi compañera María Merino, del Departamento de Matemática Aplicada, Estadística e Investigación Operativa, de la Facultad de Ciencia y Tecnología (UPV/EHU). Empieza por la mano izquierda, extendiendo los dedos desde el meñique al pulgar, para contar del uno al cinco, y luego pasa a la derecha, mientras mantiene la izquierda abierta, para mantener el valor del cinco, extendiendo de nuevo los dedos, pero ahora en sentido opuesto, del pulgar al meñique, para los números del seis al diez
Esta es la manera en la que cuenta mi compañera María Merino, del Departamento de Matemática Aplicada, Estadística e Investigación Operativa, de la Facultad de Ciencia y Tecnología (UPV/EHU). Empieza por la mano izquierda, extendiendo los dedos desde el meñique al pulgar, para contar del uno al cinco, y luego pasa a la derecha, mientras mantiene la izquierda abierta, para mantener el valor del cinco, extendiendo de nuevo los dedos, pero ahora en sentido opuesto, del pulgar al meñique, para los números del seis al diezPor otra parte, las cinco personas que empezaron a contar por el dedo índice utilizaron el método de desplegar los dedos. Dos de ellas, iniciaron el conteo por la mano derecha, aunque podría haber sido con la izquierda, y desplegaron los dedos en este orden, índice (1), corazón (2), anular (3), meñique (4) y pulgar (5), y después siguieron con la otra mano, en el mismo sentido, índice (6), corazón (7), anular (8), meñique (9) y pulgar (10). Mientras que otras dos personas contaron igual que antes en la primera mano, pero en la segunda empezaron por el pulgar, así pulgar (6), índice (7), corazón (8), anular (9) y meñique (10).
La quinta persona planteó una variante curiosa. Empezó con la mano derecha cerrada. Primero levantó el índice para 1, que le acompañó el corazón para el 2, mientras que para el 3 cambió de dedos y levantó corazón, anular y meñique (debido a la dificultad para mantener índice, corazón y anular levantados a la vez), a los que añadió el índice para el 4 y el pulgar para el 5, como se muestra en la siguiente imagen. Para contar los números del 6 al 10, mantuvo la mano derecha extendida, y utilizó la misma técnica con la mano izquierda.
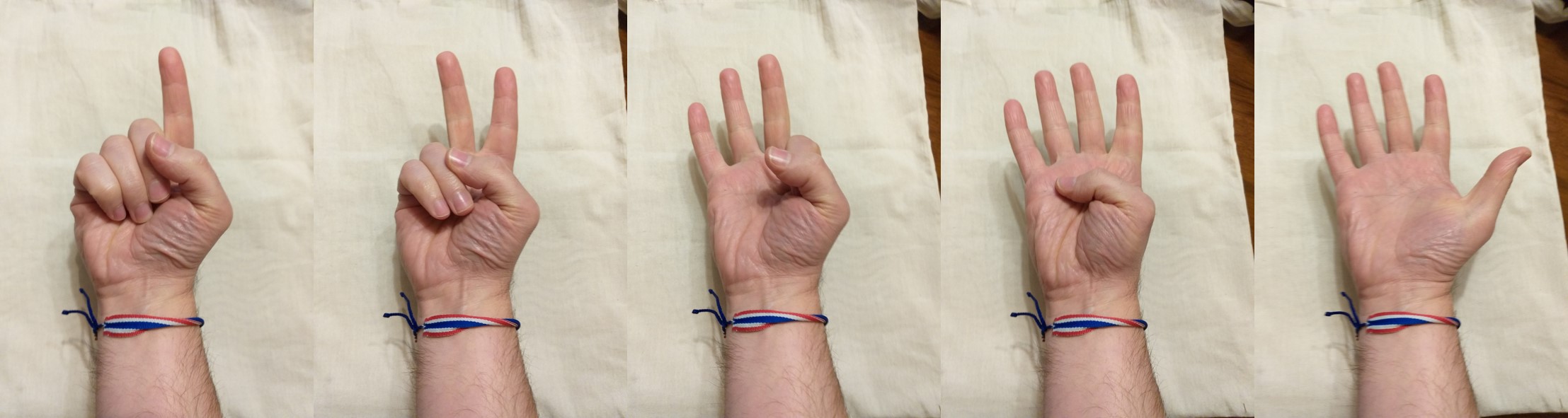 Forma de contar del 1 al 5, representada por mí, de una de las personas entrevistadas. Despliega los dedos, empezando por el índice, aunque en un orden particular. Para los números del 6 al 10 se mantiene la mano derecha extendida y se continúa contando con la izquierda de la misma forma que en la imagen
Forma de contar del 1 al 5, representada por mí, de una de las personas entrevistadas. Despliega los dedos, empezando por el índice, aunque en un orden particular. Para los números del 6 al 10 se mantiene la mano derecha extendida y se continúa contando con la izquierda de la misma forma que en la imagen  Escultura La mano (1995) del artista colombiano Fernando Botero, que está ubicada en el Paseo de la Castellana, en Madrid. Fotografía de Manuel González Olaechea
Escultura La mano (1995) del artista colombiano Fernando Botero, que está ubicada en el Paseo de la Castellana, en Madrid. Fotografía de Manuel González OlaecheaLa otra técnica utilizada mayoritariamente, después de desplegar los dedos, para contar con los dedos de las manos ha consistido en tocar, o incluso agarrar, los dedos de una mano con otro dedo de la otra mano, o de la misma. En total, 12 personas de las 48 entrevistadas contaron utilizando alguna variante de “tocar los dedos con otro dedo”, de las que podríamos decir que 7 indicaban con el dedo índice de la otra mano y 5 con el pulgar de la misma mano. Como curiosidad mencionemos que la mayoría de las personas entrevistadas que utilizaron esta técnica, empezaron por el meñique, lo cual no deja de ser significativo.
Veamos primero un ejemplo de este método, en la variante de indicar con el dedo índice de una mano, los dedos, mientras se cuentan, de la otra.
 Esta es la manera en la que cuenta mi compañera Marta Macho, del departamento de matemáticas de la Facultad de Ciencia y Tecnología (UPV/EHU). Con el índice de la mano derecha va indicando, mientras cuenta, los dedos de la mano izquierda, desde el meñique al pulgar, para contar del uno al cinco, y luego pasa a la derecha, contando con el índice de la mano izquierda, del meñique al pulgar, para los números del seis al diez
Esta es la manera en la que cuenta mi compañera Marta Macho, del departamento de matemáticas de la Facultad de Ciencia y Tecnología (UPV/EHU). Con el índice de la mano derecha va indicando, mientras cuenta, los dedos de la mano izquierda, desde el meñique al pulgar, para contar del uno al cinco, y luego pasa a la derecha, contando con el índice de la mano izquierda, del meñique al pulgar, para los números del seis al diezEn este grupo sí encontramos cierta relación con la lateralidad. De las siete personas que, más o menos, están en este grupo, las seis que son diestras empiezan utilizando el dedo índice de la mano derecha para contar sobre la izquierda (pueden empezar por el dedo meñique o el pulgar, incluso hay una persona que no solo los toca con el dedo índice, sino que los agarra con el índice y el pulgar) y después cambian, el dedo índice de la izquierda cuenta tocando los dedos de la mano derecha. Y la única persona zurda de este grupo, lo hace justo al revés, empieza utilizando el índice de la mano izquierda para contar sobre la mano derecha.
Una de las personas entrevistadas y que hemos incluido en este grupo, utiliza una variación curiosa para la segunda mano, que consiste en establecer una relación uno a uno entre los dedos de las dos manos. Cuenta así. Para empezar, con el índice de la mano derecha toca, mientras cuenta, los dedos de la mano izquierda, meñique (1), anular (2), corazón (3), índice (4) y pulgar (5). Y para la mano derecha, el meñique de la mano izquierda toca por detrás al meñique de la mano derecha, para indicar el 6, el anular de la mano izquierda toca por detrás el anular de la mano derecha, para indicar el 7, y así sigue con el corazón (8), índice (9) y pulgar (10).
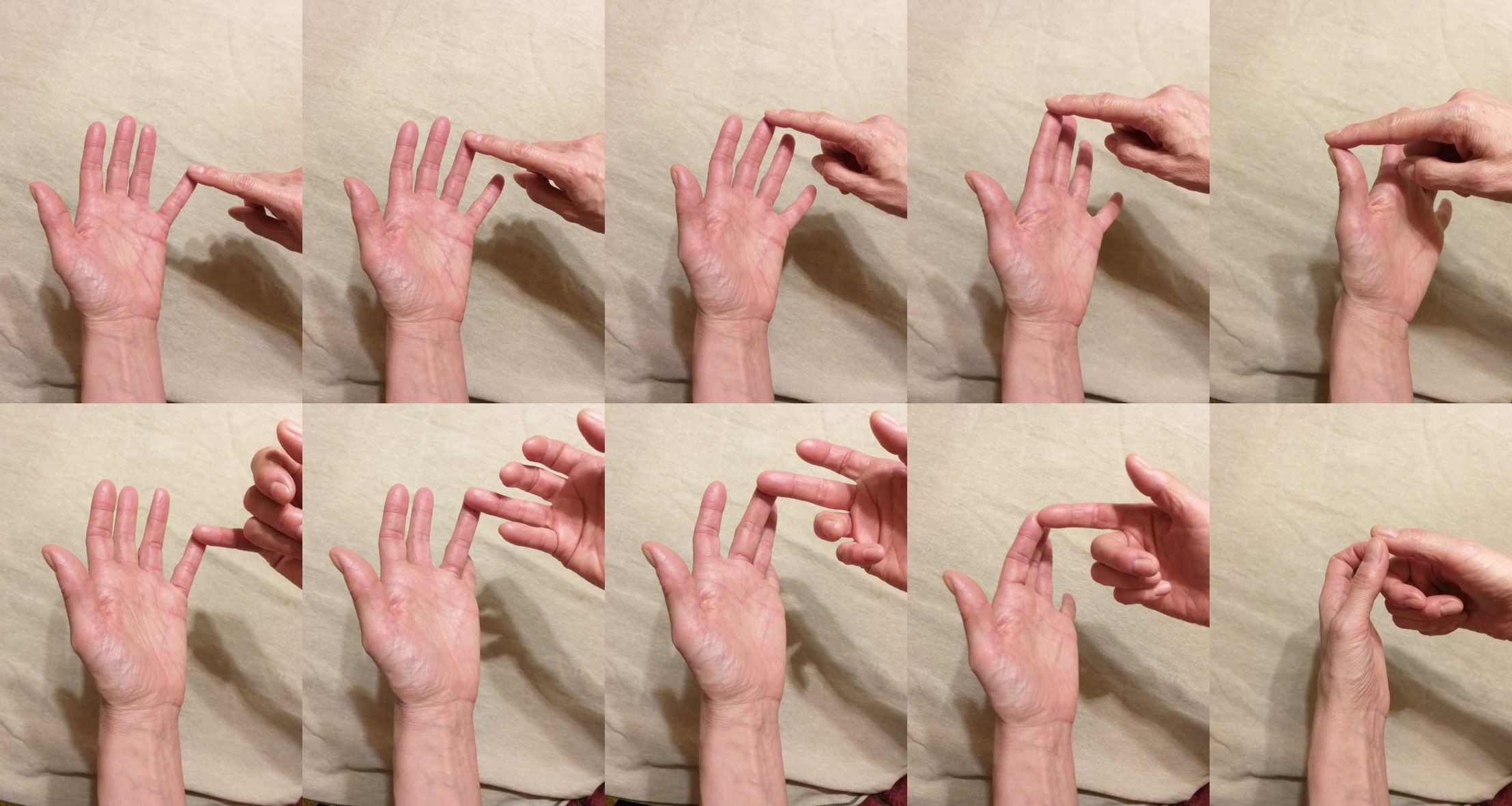 Forma de contar mixta que consiste en contar con el índice de la mano derecha tocando los dedos de la izquierda, del meñique (1) al pulgar (5), y los dedos de la segunda mano, la derecha, se cuentan tocando desde abajo con el correspondiente dedo de la mano izquierda, en una correspondencia uno a uno, así el meñique de la mano izquierda toca por detrás al meñique de la mano derecha (6), el anular de la mano izquierda toca el anular de la derecha (7), hasta el pulgar izquierdo tocando al pulgar derecho (10)
Forma de contar mixta que consiste en contar con el índice de la mano derecha tocando los dedos de la izquierda, del meñique (1) al pulgar (5), y los dedos de la segunda mano, la derecha, se cuentan tocando desde abajo con el correspondiente dedo de la mano izquierda, en una correspondencia uno a uno, así el meñique de la mano izquierda toca por detrás al meñique de la mano derecha (6), el anular de la mano izquierda toca el anular de la derecha (7), hasta el pulgar izquierdo tocando al pulgar derecho (10)Por otra parte, mi amigo Luis Javier Rodríguez, físico del Departamento de Electricidad y Electrónica, de la Facultad de Ciencia y Tecnología de la UPV/EHU, utiliza una mezcla de los dos métodos principales. El método de tocar con el índice de la mano derecha los dedos de la izquierda (también es diestro), para contar del 1 al 5, mientras que en la mano derecha despliega los dedos, para contar del 6 al 10, como vemos en el siguiente video que me ha enviado.
https://culturacientifica.com/app/uploads/2018/11/contar-con-los-dedos.mp4 
Dentro de este grupo de “tocar los dedos con otro dedo”, tenemos aquellas personas, 5 de las 12 de este grupo, que tocan los dedos que van contando con el pulgar de la misma mano. De nuevo, en este grupo no encontramos ninguna relación con la lateralidad, seguramente porque se está contando con el pulgar de la misma mano, y empiezan a contar indistintamente por la derecha o la izquierda.
En este caso, con el pulgar de la mano por la que se empieza a contar se toca al meñique (1), anular (2), corazón (3) e índice (4), y aquí llegan las pequeñas variaciones, hay quienes en este punto abren la mano entera para contar 5, quienes encogen el pulgar como señalándose a sí mismo o quienes señalan la base del meñique o del índice. En la otra mano se realiza la misma operación para contar del 6 al 10.
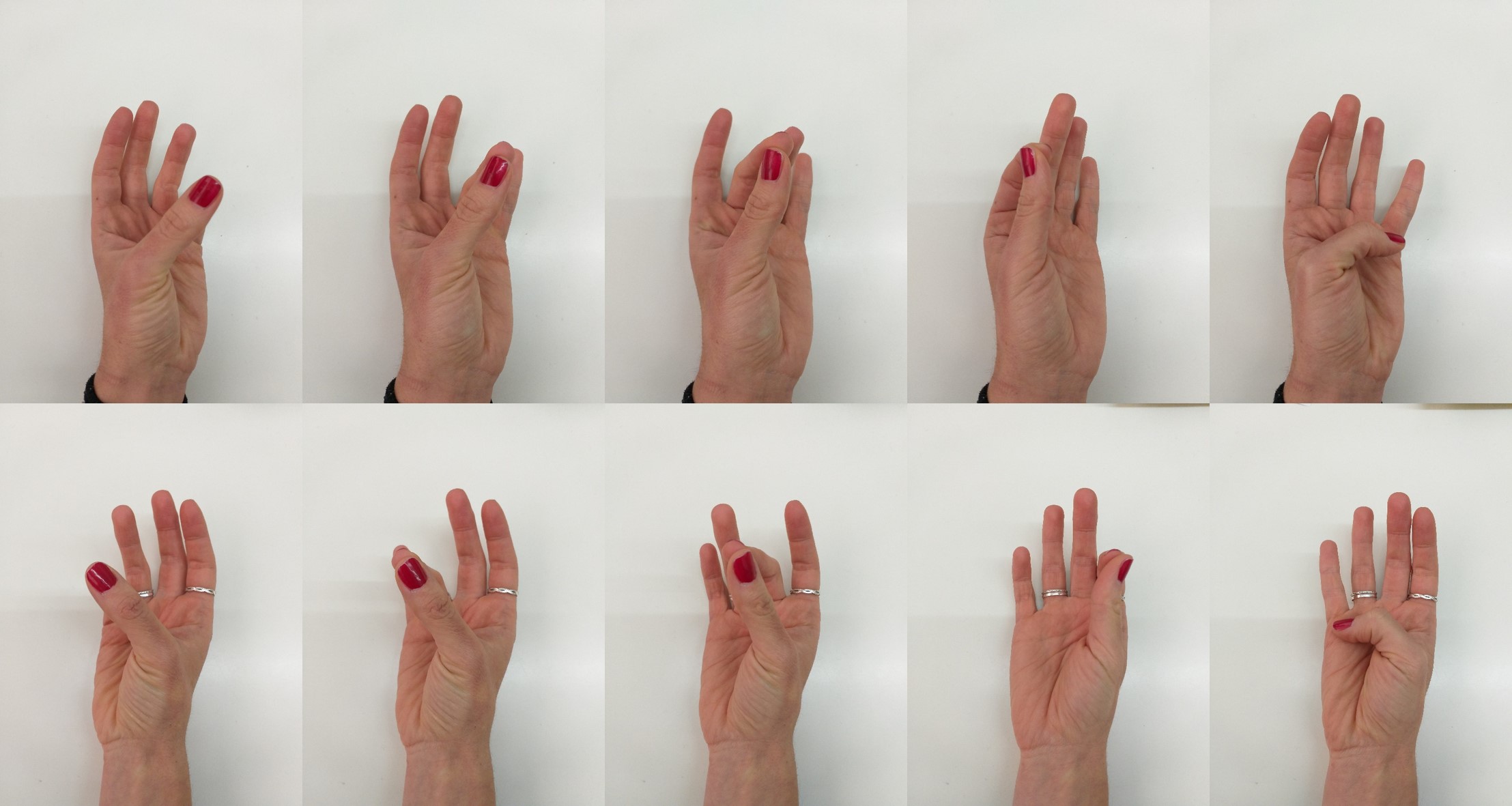 Esta es la manera en la que cuenta mi compañera Naiara Arrizabalaga, del departamento de matemáticas de la Facultad de Ciencia y Tecnología (UPV/EHU). Con el pulgar de la mano izquierda va tocando, mientras cuenta, los dedos de esa misma mano, meñique (1), anular (2), corazón (3), índice (4) y finalmente la base del meñique para contar 5. Con la mano derecha realiza una operación simétrica, para los números del 6 al 10
Esta es la manera en la que cuenta mi compañera Naiara Arrizabalaga, del departamento de matemáticas de la Facultad de Ciencia y Tecnología (UPV/EHU). Con el pulgar de la mano izquierda va tocando, mientras cuenta, los dedos de esa misma mano, meñique (1), anular (2), corazón (3), índice (4) y finalmente la base del meñique para contar 5. Con la mano derecha realiza una operación simétrica, para los números del 6 al 10Para terminar, entre las 48 personas entrevistadas, solo una de ellas ha utilizado un método del que pensé que habría más ejemplos. Mi amigo Ángel Ordóñez, que es periodista, empieza con las manos extendidas y va replegando los dedos. En su caso empieza por la mano izquierda, replegando desde el meñique, para el 1, hasta el pulgar, para el 5, y luego pasa a la mano derecha, donde repliega de igual forma para los números del 6, el meñique, al 10, el pulgar.
 Cueva de las manos, Cañadón del Río Pinturas, Santa Cruz, Argentina. Fotografía de PabloGimenez.com
Cueva de las manos, Cañadón del Río Pinturas, Santa Cruz, Argentina. Fotografía de PabloGimenez.comDespués de analizar los resultados de esta pequeña encuesta, podemos extraer algunas conclusiones informales, aunque nada rigurosas, puesto que la encuesta ha sido más un mero juego, que una encuesta diseñada y ejecutada de forma rigurosa.
Mirando a mi entorno más cercano, existen esencialmente dos formas de contar, desplegando los dedos de las manos y tocando los dedos de las manos con otro dedo, ya sea de la otra mano (que suele ser el índice) o de la misma mano (el pulgar). No existe una uniformidad respecto a la mano con la que se empieza a contar, derecha o izquierda, salvo en el caso de contar con el dedo índice indicando los dedos de la otra mano, en cuyo caso los diestros empiezan a contar con el índice de la mano derecha sobre los dedos de la izquierda y los diestros al revés. Se suele empezar a contar mayoritariamente por el dedo pulgar o el meñique. Las personas que despliegan los dedos se inclinan un poco más por empezar por el pulgar, mientras que entre los que tocan los dedos de la mano con otro dedo suelen empezar con el meñique.
 Fotografía de la iniciativa Arroces del Mundo que tiene lugar en el barrio bilbaíno de Bilbao La Vieja. Fotografía de Naiz
Fotografía de la iniciativa Arroces del Mundo que tiene lugar en el barrio bilbaíno de Bilbao La Vieja. Fotografía de NaizAyer, cuando terminé de escribir lo que acabáis de leer, me pregunté cómo contarían en la actualidad las personas de otras partes del mundo. Teniendo en cuenta que yo vivo en el barrio Bilbao La Vieja, el barrio más antiguo de Bilbao, y este es realmente una pequeña copia del mundo, me animé a bajar a la calle y preguntar a unas pocas personas de diferentes procedencias cómo contaban ellas con los dedos de las manos. Estas fueron las respuestas que obtuve.
En primer lugar, les pregunté a dos hombres de Nigeria, que como ellos mismos me dijeron en nuestra conversación, este país africano es el país del mundo con más negros. Ellos contaban contrayendo los dedos de las manos. Empezaron con la mano derecha extendida, contrayendo el pulgar (1), el índice (2), el corazón (3), el anular (4) y finalmente, el meñique (5), para acabar con la mano cerrada. Entonces, mientras mantenían la mano derecha cerrada, continuaron contando con la mano izquierda, y de la misma forma, contaron del 6, contrayendo el dedo pulgar, hasta el 10, contrayendo el dedo meñique.
 Representación de la forma en la que contaban dos personas de Nigeria con las que hablé, mientras contaban contraían los dedos de las manos, primero de la derecha y luego de la izquierda, empezando por el dedo pulgar
Representación de la forma en la que contaban dos personas de Nigeria con las que hablé, mientras contaban contraían los dedos de las manos, primero de la derecha y luego de la izquierda, empezando por el dedo pulgarUn joven de Senegal a quien también pregunté resultó que utilizaba el mismo método para contar con los dedos que los dos hombres de Nigeria, pero él empezaba por la mano izquierda y en el sentido contrario, primero el meñique y terminando en el pulgar, en cada mano.
Otro joven africano, pero este de Guinea Bisáu, contaba con el mismo método descrito antes que consiste en tocar con el dedo índice de una mano los dedos de la otra mano. De hecho, lo hacía de la forma usual vista más arriba. Con el índice de la mano derecha tocaba desde el meñique de la izquierda, para contar uno, siguiendo el orden natural hasta el pulgar, para el cinco, y continuaba con la otra mano, utilizando el índice de la mano izquierda para señalar desde el meñique al pulgar de la derecha, para contar del 6 al 10.
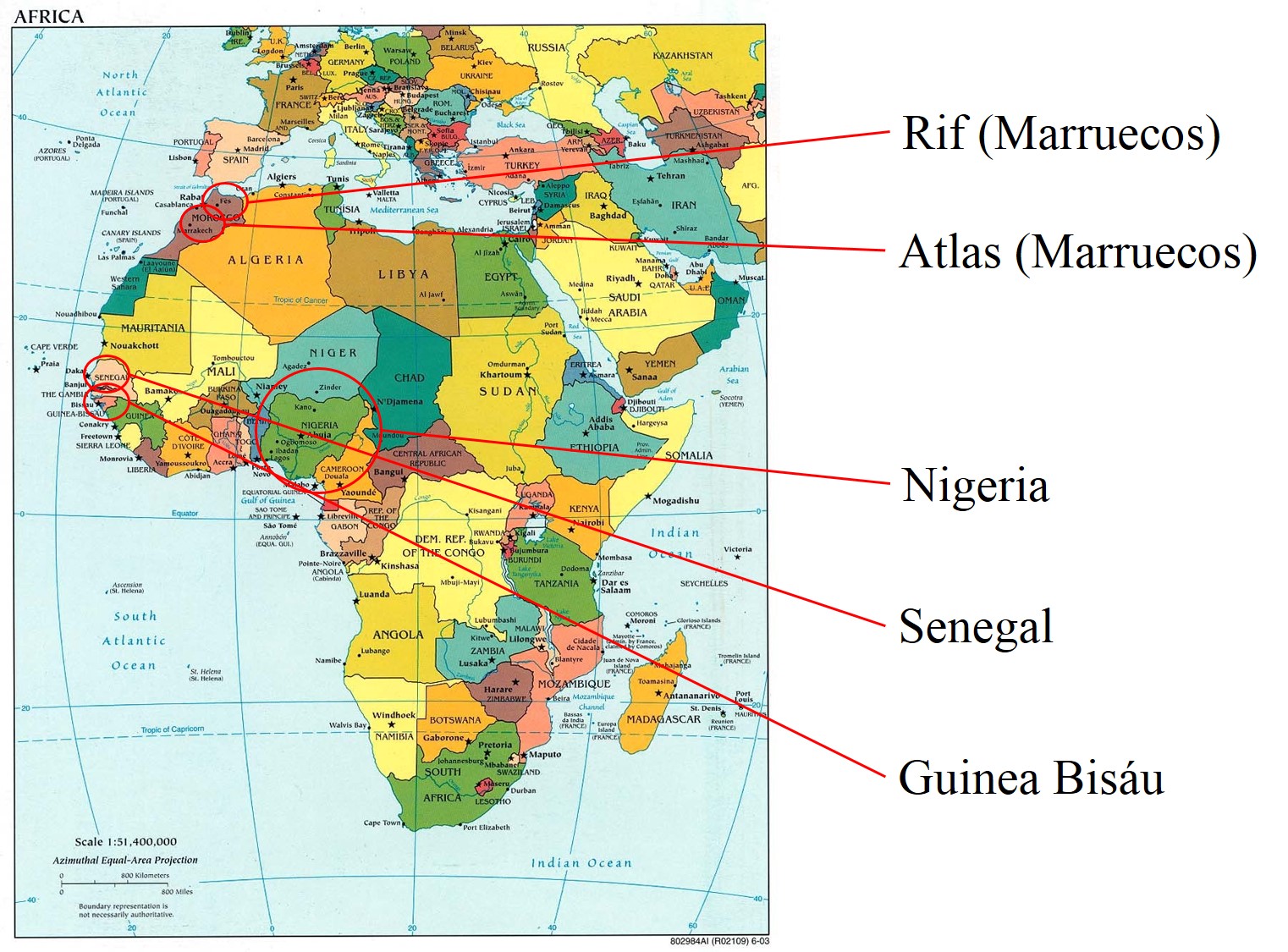 Mapa político de África en el que están destacados los lugares de procedencia de las personas del continente africano que he entrevistado
Mapa político de África en el que están destacados los lugares de procedencia de las personas del continente africano que he entrevistadoEn el Berebar de la calle San Francisco de Bilbao pregunté a un joven bereber, originario de la zona de las montañas del Rif en Marruecos, en concreto de la ciudad de Alhucemas. Utilizaba una singular manera de contar. Empezó con la mano derecha cerrada, con los dedos mirando hacia arriba, y fue extendiendo los dedos desde el meñique hasta el pulgar, para contar del 1 al 5, al llegar al cinco la mano quedaba extendida, y continuó contando con esa misma mano, pero ahora recogiendo los dedos, desde el pulgar (6) hasta el meñique (10). Después, continuaba contando con la mano izquierda, mediante la misma técnica, para contar desde el 11 hasta el 20. Es decir, este joven bereber contaba hasta el número 20 con sus dos manos. Era el primer ejemplo que me encontraba, posiblemente relacionado con la base 20, entre las personas a las que había preguntado.
 Fotografía del exterior del Restaurante Berebar, en la calle San Francisco de Bilbao, en la que podemos ver al escritor bilbaíno Jon Arretxe, autor de la saga de libros del detective Touré, un detective muy particular del barrio bilbaíno de Bilbao La Vieja, burkinés, emigrante africano, sin papeles, que hace de todo para poder vivir y que en muchas ocasiones se pasa por el Berebar
Fotografía del exterior del Restaurante Berebar, en la calle San Francisco de Bilbao, en la que podemos ver al escritor bilbaíno Jon Arretxe, autor de la saga de libros del detective Touré, un detective muy particular del barrio bilbaíno de Bilbao La Vieja, burkinés, emigrante africano, sin papeles, que hace de todo para poder vivir y que en muchas ocasiones se pasa por el BerebarUn compañero de mi departamento, Abdelmalik Moujahid, que también es bereber y cuya familia es de la zona montañosa del Atlas en Marruecos, me contó la forma en la que su padre y su madre, y muchas de las personas del lugar del que es originaria su familia, contaban.
Esta forma de contar, que de hecho se ha utilizado en muchos países cuya religión es el islam, tiene su origen en una práctica religiosa. Es la forma que tienen los musulmanes de enumerar los 99 nombres, o atributos divinos, de Alá (se le atribuye a Mahoma la frase “Dios tiene noventa y nueve nombres, cien menos uno. Quien los cuente entrará en el Paraíso. Él es el singular, y le gusta el non (número impar)”) o también a modo de rosario, cuando no se tiene este, para rezar.
Pero expliquemos como se cuenta. Como vemos en la imagen de abajo, se cuenta señalando cada una de las tres falanges de los dedos de la mano (aunque el pulgar solo tiene dos falanges, se considera como si tuviese tres). Se utiliza primero la mano derecha (aunque podría empezarse por la izquierda), contando en cada dedo las falanges (o también, las articulaciones) de abajo a arriba, empezando por el meñique. Por lo tanto, de esta forma puede contarse 15 con cada mano, luego 30 con las dos manos. Según me ha dicho Abdelmalik, para contar los 99 nombres se cuenta tres veces las dos manos, es decir, tres veces treinta, y luego se cuenta 9 más.
 Esta es la forma en la que se contaba en la zona del Atlas en Marruecos, de donde es originaria la familia de mi compañero Abdelmalik Moujahid, del departamento de matemáticas de la Facultad de Ciencia y Tecnología (UPV/EHU). Se cuentan las 15 falanges de cada mano (considerando que el pulgar también tuviese tres falanges), empezando por el meñique y de abajo a arriba, luego 30 con las dos manos
Esta es la forma en la que se contaba en la zona del Atlas en Marruecos, de donde es originaria la familia de mi compañero Abdelmalik Moujahid, del departamento de matemáticas de la Facultad de Ciencia y Tecnología (UPV/EHU). Se cuentan las 15 falanges de cada mano (considerando que el pulgar también tuviese tres falanges), empezando por el meñique y de abajo a arriba, luego 30 con las dos manosEn algunos otros lugares de religión musulmana, lo que se cuentan son los nudillos de los dedos de las manos, es decir, por la parte dorsal. De nuevo, cada dedo tiene tres nudillos, salvo el pulgar, aunque también se le considera como si tuviese tres.
Otra variante a la hora de recitar los 99 nombres de Alá, o de rezar, es que se cuenta primero 33, contando después del 30, las puntas de los tres dedos (meñique, anular y corazón) de la segunda mano, y esto se repite tres veces, es decir, 3 33 = 99.
Seguí preguntando a mis vecinos de barrio. La siguiente persona a la que pregunté era de Pakistán. Este hombre empezó a contar con la mano izquierda abierta y la palma hacia arriba, levantando ligeramente cada dedo para contar del 1 al 5, meñique (1), anular (2), corazón (3), índice (4) y pulgar (5). Y la misma operación con la mano derecha para contar del 6 al 10.
Y la última persona a la que pregunté, aunque me habría gustado que fuesen muchas más, era una de las personas que trabaja en una pequeña frutería que hay cerca de mi casa. Él es originario de Bangladesh, el país situado al este de la India. El método que utiliza para contar también es muy interesante.
Utiliza la mano derecha para contar de 1 a 20, indicando con el dedo índice de la otra mano, cada una de las posiciones. Cada dedo, desde el meñique al pulgar, está dividido en cuatro zonas, separadas por las articulaciones de la mano. Aunque el pulgar solo tiene tres, él considera que también tiene cuatro zonas. Por lo tanto, 5 4 = 20 zonas. Cuando le pedí que contase los números desde el uno, empezó a contar por el meñique, desde la zona de abajo hacia arriba, del 1 al 4, luego el anular, del 5 al 8, el corazón del 9 al 12, el índice del 13 al 16 y finalmente, el pulgar, del 17 al 20, como se muestra en la imagen.
 El frutero de Bangladesh de mi barrio utiliza la mano derecha para contar del 1 al 20, señalando con el índice de la mano izquierda las zonas que hay en cada dedo separadas por las articulaciones (considerando que en el pulgar también hay cuatro zonas, y no tres), que se muestran en la imagen
El frutero de Bangladesh de mi barrio utiliza la mano derecha para contar del 1 al 20, señalando con el índice de la mano izquierda las zonas que hay en cada dedo separadas por las articulaciones (considerando que en el pulgar también hay cuatro zonas, y no tres), que se muestran en la imagenPero la cantidad de números que puede contar no termina ahí, como me comentó, puesto que utiliza la otra mano, la izquierda, para indicar los múltiplos de 20. Si se toca a la zona del 1 es 20, si se toca el 2 es 40, el 3 sería 60, etcétera. De esta forma para contar el número 52 se tocaría con el índice de la mano derecha la segunda posición, desde abajo, del meñique de la izquierda (2 20 = 40) y después con el índice de la izquierda se tocaría en la zona de arriba del dedo corazón de la mano derecha (12), como indica la imagen.
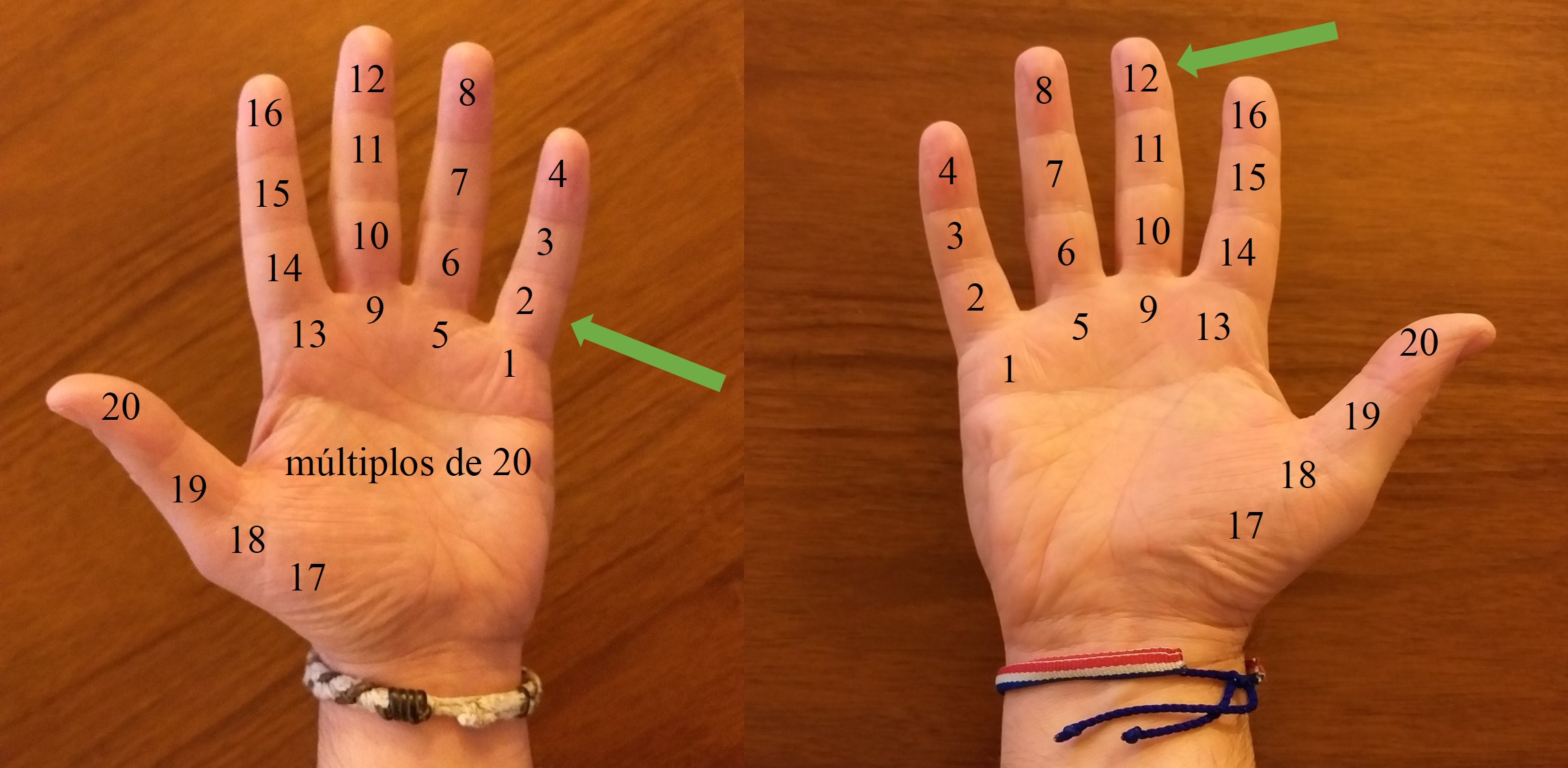 El frutero de Bangladesh de mi barrio utiliza la mano derecha para contar del 1 al 20, y la mano izquierda para los múltiplos de 20, así las flechas de la imagen están indicando el número 52, que es 2 veces 20 y 12
El frutero de Bangladesh de mi barrio utiliza la mano derecha para contar del 1 al 20, y la mano izquierda para los múltiplos de 20, así las flechas de la imagen están indicando el número 52, que es 2 veces 20 y 12Este sistema para contar, de mi frutero de Bangladesh, es claramente un sistema de numeración de base 20.
Estas son algunas de las formas en las que hoy en día seguimos contando con los dedos de las manos, pero… y tú, ¿cómo cuentas con los dedos?
 El caballero de la mano en el pecho (aprox. 1580), del artista toledano, nacido en la isla griega de Creta, Doménikos Theotokópoulos, conocido como El Greco. Cuadro perteneciente a la colección del Museo del Prado. Fotografía del Museo, a través de Wikimedia Commons.
El caballero de la mano en el pecho (aprox. 1580), del artista toledano, nacido en la isla griega de Creta, Doménikos Theotokópoulos, conocido como El Greco. Cuadro perteneciente a la colección del Museo del Prado. Fotografía del Museo, a través de Wikimedia Commons.En mi próxima entrada de la sección Matemoción del Cuaderno de Cultura Científica, haremos un repaso a diferentes formas de contar con los dedos de las manos, a lo largo de la historia.
Bibliografía
1.- Levi Leonard Conant, Counting, The world of mathematics, volumen 1, James Newman (editor), Dover, 1956.
2.- Georges Ifrah, Historia universal de las cifras, Ensayo y pensamiento, Espasa, 2002 (quinta edición).
3.- Página web del artista Lorenzo Quinn
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Y tú, ¿cómo cuentas con los dedos? (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La morra, jugando a contar con los dedos
- La insoportable levedad del TRES, o sobre la existencia de sistemas numéricos en base 3
- El gran cuatro, o los números siguen estando locos
Cuando las ondas se encuentran

Con los conceptos que hemos visto ya estamos en disposición de explorar un territorio fascinante. Hasta ahora hemos considerado ondas individuales. ¿Qué ocurre cuando se encuentran dos ondas en el mismo medio? Supongamos que dos ondas se aproximan la una a la otra en una cuerda, una se desplaza hacia la derecha y la otra hacia la izquierda. La serie de imágenes de la Figura 1 muestra lo que sucedería si hiciéramos este experimento. Las ondas se atraviesan la una a la otra sin sufrir modificación alguna. ¿Te sorprende? No debería.
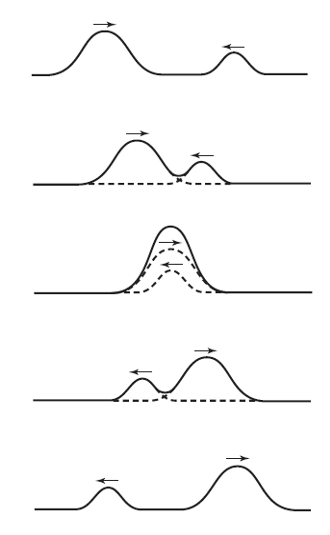 Figura 1.
Figura 1.Después del encuentro, cada onda tiene el mismo aspecto que antes del mismo y sigue avanzando como antes. (¡Algo completamente diferente al encuentro de dos partículas!). Este fenómeno de ondas que se atraviesan sin ser alteradas se puede observar con todos los tipos de ondas. Se puede ver experimentalmente muy fácilmente en las ondulaciones superficiales en el agua. También ocurre con las ondas de sonido, la prueba la tenemos en que alrededor de una mesa pueden mantenerse varias conversaciones al mismo tiempo sin que se distorsionen entre sí, no digamos ya en una discoteca.
¿Qué sucede durante el tiempo en que en el que las dos ondas estás superpuestas? Los desplazamientos que provocan se suman en cada punto del medio. Dicho de otra manera, el desplazamiento de cualquier punto en la región de superposición es solo la suma de los desplazamientos que serían causados en ese momento por cada una de las dos ondas por separado, como se muestra en la Figura 1. En esta figura vemos dos ondas que se desplazan en sentidos opuestos en una cuerda. Una tiene un desplazamiento máximo de 0,4 cm hacia arriba y la otra un desplazamiento máximo de 0,8 cm hacia arriba. El desplazamiento total máximo hacia arriba de la cuerda en un punto en el que estas dos ondas se cruzan será de 1,2 cm.
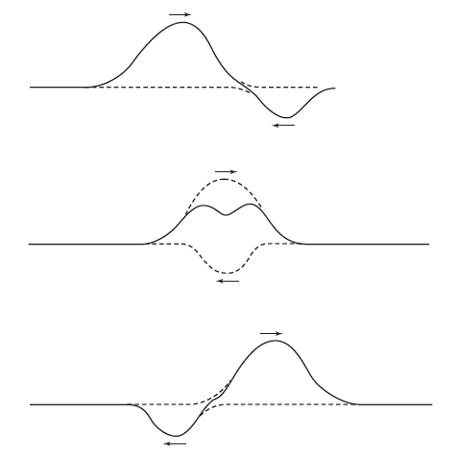 Figura 2.
Figura 2.Este comportamiento de las ondas es muy simple y facilita mucho las cosas. Veámoslo. Cada onda avanza a lo largo de la cuerda haciendo su propia contribución al desplazamiento de la cuerda sin importar lo que haga cualquier otra onda. Esta propiedad de las ondas se llama superposición. Usándolo podemos determinar fácilmente de antemano qué aspecto tendrá la cuerda en cualquier momento dado. Todo lo que hay que hacer es sumar los desplazamientos que causará cada onda en cada punto a lo largo de la cuerda en ese instante. La figura 2 muestra una superposición de ondas más general, en la que una de ellas provoca desplazamientos negativos; los desplazamientos se siguen sumando, cada uno con su signo. Esto significa que si los desplazamientos son en sentidos opuestos tienden a cancelarse entre sí.
El principio de superposición se aplica sin importar cuántas ondas o perturbaciones individuales estén presentes en el medio. En los ejemplos que acabamos de ver solo había dos ondas. Pero, experimentalmente se comprueba (en la discoteca mismo) que el principio de superposición funciona igual de bien para tres, diez o cualquier cantidad de ondas. Cada una hace su propia contribución, y el resultado neto es simplemente la suma de todas las contribuciones individuales (Figura 3).
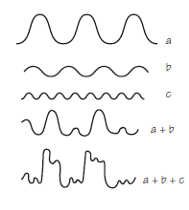 Figura 3.
Figura 3.Si las ondas se agregan como acabamos de describir, de ahí se sigue que podemos considerar cualquier onda compleja como la suma de un conjunto de ondas (sinusoidales) simples. En 1807, el matemático francés Augustin Jean Fourier presentó un teorema muy útil. Fourier afirmó que cualquier oscilación periódica continua, por compleja que sea, puede analizarse como la suma de movimientos de onda más simples.
Esto también se demuestra experimentalmente. Los sonidos de los instrumentos musicales también se pueden analizar de esta manera y este análisis de Fourier (o análisis armónico) permite “imitar” los instrumentos electrónicamente combinando y emitiendo las proporciones correctas de vibraciones simples, que corresponden a tonos puros.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cuando las ondas se encuentran se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Hablar de lo que pasa y de lo que pasó
Hubo una época en la que el ser humano no dudaba de su inteligencia privilegiada como especie sobre las demás. Pero luego fuimos aprendiendo sobre las distintas habilidades de otros animales y esto de la inteligencia única y especial hubo que ponerlo en cuarentena.
Resulta que muchos otros animales pueden comunicarse entre sí a través de distintos sistemas. A las hienas se les da muy bien contar y comparar el tamaño de un grupo invasor con el del suyo. Primates como gorilas y chimpancés saben fabricar y utilizar herramientas para conseguir lo que buscan, casi siempre comida. Los cetáceos se comunican con distintos idiomas según el grupo en el que han crecido, es decir, tienen algo similar a lo que nosotros llamamos cultura. Todo apunta a que los elefantes lloran a sus muertos. Animales tan diversos como urracas y macacos han demostrado tener conciencia de sí mismos y reconocerse ante un espejo.
Los orangutanes también hablan del pasado

Recientemente, otra habilidad que creíamos exclusiva del ser humano ha demostrado no serlo: la capacidad de hablar del pasado. Los orangutanes también saben hacerlo.
Cuando los orangutanes divisan a un depredador, hacen un sonido, como el chasquido de un beso muy fuerte. Ese sonido hace saber al depredador que ha sido detectado, y avisa a otros orangutanes de que el peligro está cerca. Ahora, un grupo de científicos asegura que ha oído a los orangutanes hacer ese mismo sonido un buen rato después de que el depredador se hubiese marchado, y lo consideran la primera evidencia de que estos primates, además de los humanos, son capaces de hablar de lo que ya ha pasado.
“Una de las características que define a un idioma son las referencias desplazadas, es decir, la capacidad de transmitir información sobre algo que no está presente o sobre un evento ocurrido en el pasado o que ocurrirá en el futuro. Es algo muy raro en la naturaleza [pero que se da en todos los idiomas humanos] y que hasta ahora no habíamos visto en ningún primate no humano, lo cual ha hecho más confuso el estudio de los precursores y la evolución del lenguaje”, explican los autores en el estudio.
Hay que aclarar que muchos otros mamíferos y aves tienen señales de alarma, algunas muy completas que incluyen información sobre el tipo y tamaño del depredador, su posición y distancia y el nivel de peligro que suponen. Pero hasta ahora, nunca se había oído a un animal anunciando el peligro después de que ocurriese. Sí se sabe que los cercopitecos verdes, un tipo de mono que vive en el África subsahariana, emite señales de alarma en ausencia de depredadores, pero estas llamadas se consideran estrategias de engaño y no referencias desplazadas.
Un caso aparte son las abejas, capaces de indicar a sus compañeras la dirección y distancia de un lugar con alimento abundante, algo que también se puede considerar una referencia desplazada. En este caso se considera más el resultado de un proceso de inteligencia colectiva y convergencia de distintos procesos que una representación de la comunicación entre individuos como tal.
Silencio ante el peligro… y señal de alarma después
Para llegar a estas conclusiones, los propios investigadores hicieron de depredadores. En la jungla de Ketambe en Sumatra, donde se ha estudiado a los orangutanes durante décadas, el estudiante postdoctoral Adriano Reis e Lameira desarrolló un sencillo experimento para analizar las señales de alarma de estos primates: un miembro del equipo vestido con un traje de rayas como si fuera un tigre debía caminar a cuatro patas por la jungla, justo bajo las ramas de los árboles donde hembras solitarias de orangután se encontraban sentadas, a una altura de entre 5 y 20 metros.
Una vez que sabían que ellas les habían visto, el falso tigre rondaba el lugar un par de minutos antes de desaparecer de la vista. Lameira esperaba oír su señal de alarma en ese momento, pero no fue así. La primera orangután con la que probaron no hizo ni un ruido. “Dejó lo que estaba haciendo, cogió a su cría, defecó (una señal de estrés y miedo) y comenzó a trepar árbol arriba en silencio”.
Esperaron y esperaron… y finalmente, 20 minutos después, llegó la alarma. Pero no fue un solo chasquido. “Estuvo alertando durante más de una hora”.
Esperar ante un estímulo, una señal de inteligencia

Esa fue la ocasión en la que más tuvieron que esperar. De media la alarma llegaba unos 7 minutos después de que pasase el peligro. Lameira explica que no cree que el motivo fuese que estuviesen petrificadas de miedo, porque no habían dudado en agarrar a las crías y trepar a más altura donde se sintiesen a salvo.
El investigador cree que el silencio era una forma de no atraer la atención de lo que creían que era un depredador. Una vez fuera de peligro, la señal de alarma servía no solo para avisar a otros orangutanes, sino también para enseñar a su cría y educarla sobre el peligro que acababan de evitar.
No responder inmediatamente a un estímulo sino desarrollar una estrategia teniendo en cuenta el mejor resultado para sí mismas y para sus crías se considera una señal de inteligencia, un talento que encaja con otras habilidades antes observadas en los grandes simios, como la memoria a largo plazo, la comunicación intencional y el control afinado de los músculos de la laringe, capacidades que eventualmente llevaron a la evolución del lenguaje, argumenta el investigador.
Referencias:
Hyenas can count like monkeys – Nature
La cultura de los cetáceos: la forma en que las ballenas hacen cosas – Whales.org
Do animals experience grief? – Smithsonian magazine
Mirror-Induced Behavior in the Magpie (Pica pica): Evidence of Self-Recognition – PLOS biology
Danza de la abeja – Wikipedia
Time-space–displaced responses in the orangutan vocal system – Science Advances
Orangutans are the only great apes—besides humans—to ‘talk’ about the past – Science Magazine
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Hablar de lo que pasa y de lo que pasó se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La fusión a un paso gracias al hidrógeno líquido
- ¿Qué pasa si me río de todo?
- #Naukas16 Qué pasa cuando le das un péndulo a una máquina
Poca influencia genética en el desempeño educativo

Hasta hace unos años, la forma de saber en qué medida dependía un determinado rasgo de su configuración genética y en qué medida del entorno en que se desarrolla el individuo era estudiar cómo difiere ese rasgo entre individuos que siendo gemelos procedentes del mismo óvulo, son criados en familias distintas. Aunque los gemelos univitelinos pueden experimentar condiciones ligeramente diferentes en el seno materno, no se consideran de la suficiente entidad como para propiciar diferencias significativas. Simplificando algo y con algunas salvedades que no vienen al caso, ese procedimiento permite fijar la componente genética, de manera que las diferencias que se observan a lo largo de la vida de los individuos pueden ser atribuidas a los efectos del entorno.
Hoy las cosas son diferentes, porque las técnicas que permiten conocer el orden preciso de las moléculas que conforman la cadena de ADN -la macromolécula que codifica la información que se transmite en herencia a la descendencia- han experimentado un desarrollo espectacular y se han abaratado mucho. Eso hace posible estudiar en detalle las diferencias entre unos individuos y otros, y caracterizar así distintas variantes genéticas. Y puede hacerse, además, para un gran número de individuos. En algunos casos es posible conocer con precisión cuál es el proceso o procesos en los que se encuentra implicado un determinado gen, pero en la mayor parte de los casos, no.
Hace unos meses se han publicado los resultados de un análisis de asociación entre la configuración genética de los individuos de una muestra de gran tamaño y el nivel educativo alcanzado por esos mismos individuos. La muestra estaba formada por más de un millón cien mil personas. Los investigadores identificaron 1.271 variantes –polimorfismos de nucleótido único, en lenguaje técnico- que, en conjunto, mostraron una asociación significativa con el nivel formativo, tal y como queda reflejado en el número de años de permanencia en el sistema educativo.
Gran parte de la variabilidad ligada al desempeño educativo afecta a genes implicados en procesos de desarrollo cerebral y en la comunicación entre las neuronas que se establece mediante las denominadas conexiones sinápticas. Se trata de las uniones que permiten transmitir la información a las neuronas vecinas y se produce mediante el concurso de moléculas que actúan como mensajeras.
Curiosamente, el efecto de las variantes genéticas varía de unos países a otros y aunque los investigadores no pudieron precisar la causa de esos diferentes efectos, muy probablemente tienen que ver con las diferencias que hay entre los sistemas educativos de los países en lo relativo a las competencias o habilidades que se promueven en cada uno de ellos. Es posible que determinadas configuraciones sean más propicias para la resolución de problemas, mientras otras lo son para el aprendizaje memorístico, por ejemplo.
La asociación genética global es de escasa entidad: entre un 11% y un 13% de la variabilidad en el desempeño educativo se asocia a la variabilidad genética. Eso quiere decir que la incidencia de factores ambientales, como las características de la familia, el nivel educativo de los padres o factores ligados al entorno escolar, ejercen un efecto cuantitativamente mayor. Además, en este tipo de caracteres la configuración genética, más que determinar ciertos rasgos, lo que hace es transmitir la predisposición a desarrollarlos, lo que significa que hay amplio margen para que se produzcan diferencias asociadas a la influencia ambiental.
No es una consecuencia menor si tenemos en cuenta que el desempeño educativo ejerce efectos de gran importancia y largo alcance, como son el bienestar económico, el estado de salud en la vida adulta e, incluso, la esperanza de vida.
Fuente: J. J. Lee, R. Wedow, […] & D. Cesarini (2018): Gene discovery and polygenic prediction from a genome-wide association study of educational attainment in 1.1 million individuals. Nature Genetics 50: 1112-1121.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 9 de septiembre de 2018.
El artículo Poca influencia genética en el desempeño educativo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Genética en las aulas
- Contra el furtivismo, genética molecular
- Al menos de 24 siglos de continuidad genética
Diálogos en la frontera: Física y relato

¿Qué relación puede existir entre formas de conocimiento aparentemente tan dispares como la física y la literatura? Aunque la relación entre las diferentes formas de conocimiento puede parecer imposible, lo cierto es que en muchas ocasiones el vínculo entre ellas es necesario e inevitable. Las artes y las ciencias son el vivo ejemplo de la conexión que existe entre las distintas áreas de estudio. Y aunque puede resultar complicado pensar cómo pueden convivir la creación artística y la investigación científica, lo cierto es que hay profesionales que combinan estas disciplinas en su trabajo diario.
La novela de Javier Argüello “A propósito de Majorana” sobre la extraña desaparición en 1938 del físico Ettore Majorana, conocido por sus estudios sobre física de partículas, sirve de punto de partida de la segunda edición de “Diálogos en la frontera”. En este caso ciencia y literatura aunarán esfuerzos y mostrarán las múltiples relaciones existentes entre ambas a la hora de dar respuesta a la incertidumbre y a las preguntas que nos rodean. El evento contó con la participación del escritor argentino Javier Argüello, la catedrática de física teórica Pilar Hernández Gamazo y el físico y escritor Juan José Gómez Cadenas, que fue el encargado de moderar el coloquio.
El evento se enmarca en el ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
Pilar Hernández Gamazo es catedrática de Física Teórica por la Universidad de Valencia y experta en física de partículas elementales. Hernández Gamazo obtuvo su doctorado en la Universidad Autónoma de Madrid y desde entonces ha trabajado en centros internacionales de relevancia como la Universidad de Harvard y el Laboratorio Europeo de Física de Partículas (CERN). En la actualidad, trabaja en el Instituto de Física Corpuscular (IFIC), un centro mixto del Consejo Superior de Investigaciones Científicas (CSIC) y la Universidad de Valencia.
Javier Argüello es un destacado autor argentino residente en Barcelona desde 2001. Entre sus obras más emblemáticas se encuentran “El mar de todos los muertos” (Lumen, 2008), “La música del mundo” (Galaxia Gutenberg, 2011) o la que abrirá el debate del próximo 26 de septiembre, “A propósito de Majorana” (Literatura Random House, 2015), una novela dedicada a la extraña desaparición del físico italiano Ettore Majorana, famoso por su labor sobre neutrinos. Actualmente colabora con el periódico El País, con diversas agencias de publicidad y ejerce de profesor en la Escuela de Letras del Ateneo Barcelonés.
El físico, divulgador científico y escritor murciano Juan José Gómez Cadenas ha trabajado durante ocho años en el Laboratorio Europeo de Física de Partículas (CERN), así como en las Universidades de Harvard y Massachusetts. Actualmente compagina labores de docencia en el CSIC y el Donostia International Physics Center (DIPC). Asimismo, es director del grupo de Física de Neutrinos del Instituto de Física Corpuscular y se encuentra trabajando en un experimento internacional sobre neutrinos llamado NEXT, en el Laboratorio Subterráneo de Canfranc. Como escritor, colabora en la revista Jot Down y ha publicado cuentos y novelas como el thriller científico “Materia Extraña” ( Espasa, 2008) o “Los Saltimbanquis” (Encuentro, 2018).
Edición realizada por César Tomé López.
El artículo Diálogos en la frontera: Física y relato se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Diálogos en la frontera: Matemáticas y procesos creativos
- #NaukasKids14 Física y ciencia ficción
- Ciencia, arte y cultura callejera: física y música
La importancia del agua en un biomarcador contra el cáncer
El Departamento de Química Física de la UPV/EHU y el Instituto Biofísikala, entre otros centros, han realizado un estudio multidisciplinar del antígeno Tn que aparece en el 90 % de los cánceres. Se han estudiado dos variantes aparentemente similares pero que tienen conformaciones muy diferentes en agua. Los resultados podrían facilitar el diseño de herramientas de detección tumoral más eficaces.
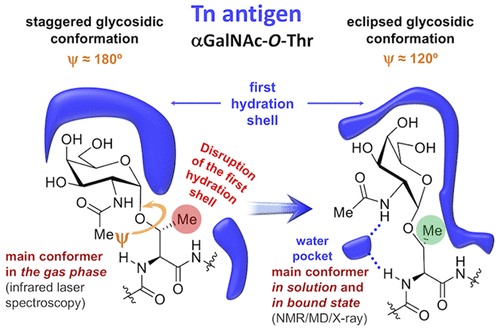
El antígeno Tn aparece en el 90 % de los cánceres y está asociado con la metástasis. Por eso, “son unos biomarcadores muy prometedores para identificar células cancerígenas y se han convertido en dianas muy atractivas para terapias contra el cáncer”, explica Emilio José Cocinero, miembro del Departamento de Química Física de la UPV/EHU y del Instituto de Biofísika, uno de los autores principales del trabajo. Los antígenos son moléculas que inducen la formación de anticuerpos, debido a que el sistema inmune las reconoce como una amenaza, pudiendo desencadenar por tanto una respuesta inmunitaria.
En este trabajo se estudian dos variantes aparentemente similares de antígenos Tn, que difieren sólo en un aminoácido de serina o treonina. Sin embargo, “hemos observado, que tienen un comportamiento muy diferente en agua”, señala Emilio José Cocinero. “Utilizando un enfoque tanto experimental como computacional, hemos demostrado que el antígeno Tn unido a la treonina asume una forma rígida en disolución gracias a una molécula de agua que contribuye a estabilizar la estructura. Por el contrario, el antígeno Tn unido a la serina carece del elemento estructural y es flexible en disolución”, comenta el investigador de la UPV/EHU. “Estas diferencias no se observaron en los estudios de fase gaseosa y ambas moléculas se comportan exactamente igual, lo ha permitido conocer, por primera vez, y de forma inequívoca, el papel del agua en la estructura tridimensional de estas moléculas”, añade.
Para conocer más de cerca el papel activo del agua, “hemos ido añadiendo las moléculas de agua de una en una para ver cómo se comportaba el antígeno Tn. Hemos observado que añadiendo una sola molécula de agua era suficiente para que cambiara la estructura de los dos antígenos, y de hecho, el agua se localizaba en diferentes partes de la molécula”, explica Cocinero.
Emilio José Cocinero señala que “es probable que las diferentes conformaciones del antígeno Tn den lugar a interacciones distintas con receptores celulares y anticuerpos, y la compresión de estas estructuras puede facilitar el diseño de herramientas de detección más eficaces y fármacos anticancerígenos”. “Este trabajo en concreto —añade Cocinero— está dentro de un proyecto a largo plazo que está encaminado a intentar generar potenciales vacunas contra el cáncer”.
“El gran problema que tiene esta molécula, el antígeno Tn, es que también lo tenemos naturalmente en el cuerpo, con lo cual la respuesta inmune del cuerpo es muy baja porque nuestro cuerpo no lo ve como un agente extraño”, subraya el autor del trabajo. Sin embargo, “sí que hemos observado que si aumenta la concentración de esta molécula, se trata de que el cáncer está desarrollado. Podemos seguir la evolución de esta molécula para conocer el nivel de desarrollo del cáncer”, añade Cocinero.
Según Cocinero, “en un futuro lo ideal sería que se pudieran crear moléculas sintéticas que no estuvieran en nuestro cuerpo y que tuvieran la misma estructura que el antígeno Tn, para que de esta manera el cuerpo la viera como un agente extraño, desencadenando así una respuesta inmune mayor contra las células tumorales”.
Referencia:
Iris A. Bermejo, Imanol Usabiaga, Ismael Compañon, Jorge Castro-López, Aran Insausti, José A. Fernández, Alberto Avenoza, Jesús H. Busto, Jesús Jiménez-Barbero, Juan L. Asensio, Jesús M. Peregrina, Gonzalo Jiménez-Oses, Ramón Hurtado-Guerrero, Emilio J. Cocinero, Francisco Corzana (2018) Water Sculpts the Distinctive Shapes and Dynamics of the Tumor-Associated Carbohydrate Tn Antigens: Implications for Their Molecular Recognition J.A.C.S. doi: 10.1021/jacs.8b04801
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La importancia del agua en un biomarcador contra el cáncer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La batalla contra el cáncer: la importancia de la alimentación
- Avances contra la enfermedad de hígado graso no alcohólica
- Inteligencia contraterrorista contra el cáncer
El meme más antiguo de la historia
El tema de Corelli, de las variaciones de Rachmaninov, el tema que inspiró a Vangelis y esta misma serie de posts se llama La Folía y en mi cabeza tiene forma de catedral. No es más que una metáfora, evidentemente, pero seguidme a través de la imagen que evoca, merecerá la pena. Vamos a empezar desde abajo, por la base: analizando simplemente, su melodía.

Si hubiese que escoger una palabra, sería sencillez: se caracteriza, precisamente, por una nota repetida que forma lo que en música llamaríamos un motivo. Ese motivo se escucha hasta 4 veces en una frase musical y esa frase, a su vez, se repite casi sin ninguna alteración (sólo cambia el cierre o cadencia) hasta completar 16 compases.
Hasta aquí ya tenemos los tres primeros pisos de la catedral sonora: una nota repetida (x2) que forma un motivo. Un motivo repetido (x4) que forma una frase. Una frase repetida (x2) que forma un tema. Existen más simetrías y patrones dentro del tema pero por el momento… vamos a intentar que no nos explote la cabeza.
Desde el punto de vista de la armonía, el tema comienza oscuro (en re menor), coquetea fugazmente con la luz (compás 5, acorde de fa, relativo mayor) y vuelve enseguida a las tinieblas iniciales, doblemente vencido. Puedes escucharlo, en el segundo 50 de este vídeo: notarás que la melodía asciende y, de repente, suena más optimista, como si sonriese. Sin embargo, 10 segundos más tarde, el desenlace vuelve a ser oscuro. Esto es, en parte, gracias a la armonía (acordes mayores, de luz y menores, de sombra).
Retomando ahora las variaciones de Rachmaninov, veremos que tienen, a su vez, una peculiaridad. De las 20 variaciones, las 13 primeras conforman una primera parte de la obra más bien oscura, (en tono menor). Sin embargo, hacia la mitad de la obra (11’30’’), se hace la luz. Es un momento absolutamente mágico: de repente, la variación 14 modula a una tonalidad mayor y el cambio es… dulcísimo, lo llena a uno de optimismo. Sin embargo, es una cambio fugaz: la variación 16 (14’30”) regresa la tonalidad inicial (re menor) y con ella la oscuridad, esta vez sin solución posible.
Sombra, luz efímera, sombra: de alguna manera, las variaciones repiten, a mayor escala, la estructura internet del mismo tema. Con esta nueva simetría, ascendemos hasta el cuarto piso de la catedral.
Pero el quinto piso… el quinto piso es, sin duda, mi preferido. Porque sólo se ve a vista de pájaro, cuando uno levanta los ojillos por encima de la historia, es entonces cuando aparece.
Hace dos semanas decíamos que este tema no lo compuso Vangelis, ni Rachmaninov, ni siquiera Corelli… porque Corelli lo utilizó, efectivamente, en una Sonata para violín y continuo que compuso en 1700. Pero claro… el tema de Corelli no era, precisamente, original. De hecho, ya lo había utilizado Gaspar Sanz, en España, en una obra para guitarra de 1675. Pero claro… el tema de de Sanz no era, precisamente, original. Lo había usado antes Lully, en Francia, en 1672 y también Marin Marais.
A su vez, en tiempos de Corelli, encontramos variaciones sobre el mismo tema de Vivaldi (1705) en una sonata para dos violines y bajo continuo, y de Scarlatti (1710) en una obra para clave. Incluso Johann Sebastian Bach lo utiliza en una cantata de 1742. Y la lista continúa: Purcell, Boccherini, Salieri, Paganini, Grieg, Liszt, Berlioz, Joaquín Rodrigo… básicamente, todo el mundo y su gato compone algo basado en este tema (literalmente, cientos de compositores, yo he incluido sólo algunos en esta lista de Spotify). Y quien no escribe variaciones sobre La Folía de forma literal, se inspira en ella, consciente o inconscientemente. Como Beethoven, que la cita en su quinta sinfonía:
O, probablemente, el caso más conocido: el de la Sarabanda de Haendel. Si bien esta obra no tiene exactamente la misma estructura de la Folía, el parecido es evidente. Además, es una obra especialmente conocida por repetirse hasta la saciedad en la banda sonora de Barry Lyndon, así que no podía faltar en esta serie.
Y bien, si ninguno de estos compositores es el autor original del tema, ¿de dónde salen estas notas?, ¿a quién pertenece su melodía? Pues bien: La Folía es una melodía que no es de nadie y que, probablemente por ese mismo motivo, pudo ser utilizada durante siglos por todos estos compositores, convirtiéndose, quizás, en el mayor meme de la historia de la música.
Es un tema popular cuyos orígenes se remontan a mediados del s.XV. Por su forma y por su nombre, se piensa que podría haber surgido cerca de Portugal o bien en el antiguo Reino de León, en una zona de influencia gallega. Este es el motivo por el que Vangelis se basa en ella para componer la banda sonora de la película de Ridley Scott: “1492: Conquest of Paradise” relata el descubrimiento de América por Colón y está ambientada en la España de aquella época. Aunque, de hecho, es probable que la folía del siglo XV no fuese exactamente igual a como la conocemos ahora. Desde su aparición y durante al menos dos siglos evolucionó y se extendió también por Italia y Francia conocida como “folía española”. No es hasta mediados del del s. XVII cuando cobra su forma definitiva y se vuelve realmente popular gracias a Jean-Baptiste Lully.
Durante todo este tiempo, lo más probable es que fuese una danza festiva y, hasta cierto punto, “loca” (esto es lo que significa “folía”; locura). Un texto de 1611, la describe como una danza rápida y confusa, en la que los bailarines debían llevar sobre sus hombros a hombres vestidos de mujer. Debía de ser todo un espectáculo…
Curiosamente, cuando lo oímos hoy, no parece un tema demasiado loco. Más bien lo contrario, a mí en concreto me inspira solemnidad. Pero quizás suceda con La Folía como con el Quijote de Menard, que cambia de significado según la época en que se escribe. O quizás, la locura radica, precisamente, en su repetición. Es ese carácter cíclico que permite repetir el mismo tema una y otra vez, como una melodía pegadiza interminable, variando y adquiriendo nuevas caras, acelerándose y deformándose, hasta la obsesión, hasta la locura…
Yo, personalmente, prefiero pensar en ella como una catedral. Me parece tan bonito… pensar en esa nota repetida, en un motivo repetido, en un tema repetido dentro de miles de variaciones escritas por cientos de compositores diferentes. Es tan bonito visualizar esa especie de obra colectiva y fractal, construida a lo largo de los siglos… e imaginar que la historia misma de la música está escrita sobre sus paredes, cantando siempre el mismo tema, de un origen tan humilde. Pero lo más bonito es saber que, aún hoy, esa catedral sigue creciendo. Aún hoy, la Folía sigue transformándose, adquiriendo nuevos significados cada vez que se repite.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El meme más antiguo de la historia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El arte de la repetición
- Tema y variaciones
- El teorema de los cuatro colores (1): una historia que comienza en 1852
La paradoja del asno de Buridán
Jean Buridan (hacia 1292-hacia 1363) fue un filósofo escolástico francés, instigador del escepticismo religioso en Europa.
 Historieta satírica estadounidense (hacia 1900) sobre la indecisión del Congreso entre la elección de la ruta del canal de Panamá o del canal de Nicaragua y aludiendo a la paradoja de Buridán. Imagen: Wikimedia Commons.
Historieta satírica estadounidense (hacia 1900) sobre la indecisión del Congreso entre la elección de la ruta del canal de Panamá o del canal de Nicaragua y aludiendo a la paradoja de Buridán. Imagen: Wikimedia Commons.Una leyenda –propagada por la Balada de las damas de antaño del poeta François Villon (1431-1463¿?) y popularizada por el cantautor Georges Brassens– asociaba a Buridan –equivocadamente– con el escándalo de la torre de Nesle:
Y ¿dónde está, si no, la reina
que a Buridán hizo meter
en un saco y lo tiró al Sena?
¿Dónde están las nieves de ayer?
¿En un saco y lo tiró al Sena?
¿Dónde están las nieves de ayer?
Fragmento extraído de ‘Brassens en castellano’ (traducido por Ramón García Toga)
Su nombre se asocia también a un experimento mental conocido como ‘la paradoja del asno de Buridán’, a pesar de que no se recoge en ninguna de las obras conocidas de este filósofo. Sin embargo, un problema similar aparece en el tratado Sobre el cielo de Aristóteles (384 a. C.-322 a. C.), en un momento en el que su autor se preguntaba sobre cómo un hombre sediento y hambriento, situado a la misma distancia de una mesa llena de alimentos y otra llena de bebidas, se las arreglaría para escoger entre ambas ofertas… Y concluía que necesariamente, ¡se mantendría inmóvil!
En su comentario sobre el anterior tratado del polímata griego, Buridan cambiaba a la persona por un perro confrontado a este cruel dilema. Aludía a esta posibilidad como a la de una alternativa sin sentido comparable ‘a la que debería sopesar los méritos de la gravedad terrestre y del objeto pesado que se somete a ella.’
Buridan no discutió este problema en particular, pero aludía en su obra a la existencia de un determinismo moral en el que un ser humano que se enfrenta a posibles decisiones, siempre debe elegir el mayor bien, aunque la voluntad puede demorar la elección.
 L’âne de Buridan entre deux opinions (1859) por A-C-H de Noé. Imagen: Wikimedia Commons.
L’âne de Buridan entre deux opinions (1859) por A-C-H de Noé. Imagen: Wikimedia Commons.Posteriormente se satirizó esta visión por medio de la historia de un asno sediento y hambriento, situado a la misma distancia entre un cubo de agua y otro de avena… y que acababa muriendo, incapaz de elegir el cubo por el que le convenía.
Más que una paradoja, esta historia podría catalogarse como un dilema llevado al absurdo, ambos rasgos caracterizando el fenómeno del doble vínculo.
Parece que Baruch Spinoza (1632-1677) fue el primero en hablar de la Buridani asina –la asna de Buridán… en efecto, no el asno– en su Ethica (traducción de Vidal Peña):
[…] Puede objetarse que si el hombre no obra en virtud de la libertad de su voluntad, ¿qué sucederá si está en equilibrio, como el asna de Buridán? ¿Perecerá de hambre y sed? Si lo admito, parecería que pienso en un asno, o en una estatua de hombre, y no en un hombre, pero si lo niego, entonces el hombre se determinará a sí mismo y, por consiguiente, tendrá la facultad de dirigirse a donde quiera y hacer lo que quiera. […] Concedo por completo que un hombre, puesto en tal equilibrio (a saber, sin otras percepciones que las de la sed y el hambre, y las de tal y cual comida y bebida que están a igual distancia de él), perecerá de hambre y sed. Si me preguntan: ¿acaso tal hombre no debe ser estimado más bien como un asno que como un hombre?, respondo que no lo sé, como tampoco sé cómo ha de ser estimado el que se ahorca, o cómo han de ser estimados los niños, los necios, los locos, etc.
Buridan y Spinoza difieren en sus conclusiones. Para el primero, el asno moriría, pero un ser humano enfrentado a la misma situación sería capaz de elegir arbitrariamente… para el segundo el hombre actuaría de la misma manera que el animal… ¿Qué opináis?
Referencias:
Jean Buridan, Wikipédia (consultado el 19 de noviembre de 2018)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo La paradoja del asno de Buridán se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Fase y ecuación de onda
 En determinados estamentos se da mucha importancia al concepto de fase. Como en este caso muestran los cadetes de la Escuela de Suboficiales del Sargento 2° Daniel Rebolledo Sepúlveda (Chile).
En determinados estamentos se da mucha importancia al concepto de fase. Como en este caso muestran los cadetes de la Escuela de Suboficiales del Sargento 2° Daniel Rebolledo Sepúlveda (Chile).El concepto de fase no es en sí mismo complicado. La palabra fase suele emplearse habitualmente para indicar cada uno de los distintos estados sucesivos de un fenómeno natural (o histórico). Decimos habitualmente, pero hemos de ser conscientes de que no siempre para evitar errores. Así, por ejemplo, también se llama fase a una parte homogénea con límites bien definidos de un sistema heterogéneo, un concepto que, si bien tiene su origen en el uso habitual (el agua solida al calentarse pasa sucesivamente a una fase líquida y después a una fase vapor, por ejemplo), es un concepto actualmente independiente de la idea de estado sucesivo.
El concepto de fase es fundamental para entender el funcionamiento de una onda periódica. El siguiente diagrama representa una onda periódica que pasa a través de un medio. En él aparecen marcados conjuntos de puntos que se mueven “a la vez y de la misma forma” a medida que pasa la onda periódica. Los puntos cresta C y C’ han alcanzado posiciones máximas hacia arriba. Los puntos valle D y D’ han alcanzado posiciones máximas hacia abajo. Los puntos C y C’ tienen desplazamientos y velocidades idénticos en cualquier instante de tiempo. Sus vibraciones son idénticas y van al unísono. Lo mismo ocurre con los puntos D y D’. De hecho hay infinitos pares de puntos a lo largo del medio que vibran de manera idéntica cuando pasa esta onda. Démonos cuenta de que C y C’ están separados una distancia igual a una longitud de onda, λ, al igual que D y D’.
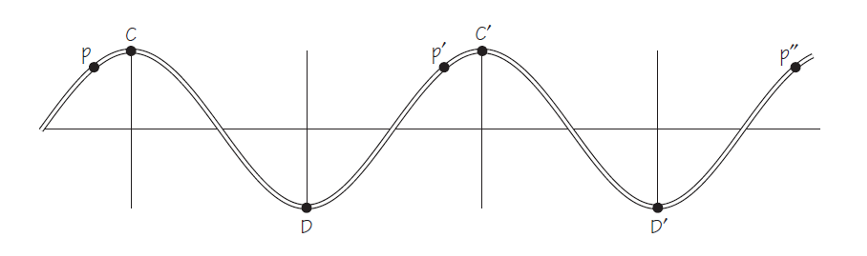
Los puntos que se mueven al unísono, como C y C’, se dice que están en fase entre sí. Los puntos D y D’ también se mueven en fase. De hecho, los puntos separados entre sí por distancias de λ, 2λ, 3λ,. . . o, en general, nλ (siendo n cualquier número entero) están todos en fase entre sí. Estos puntos pueden estar en cualquier lugar (fase) a lo largo de la longitud de la onda. No necesitan corresponderse solo con los puntos más altos o más bajos. Así, puntos como P, P’, P”, están todos en fase entre sí. Cada uno de estos puntos está separado por una distancia λ del siguiente que está en fase con él.
Por otro lado, también podemos ver que algunos pares de puntos están fuera de sincronía. Por ejemplo, el punto C alcanza su máximo desplazamiento hacia arriba al mismo tiempo que D alcanza su máximo desplazamiento hacia abajo. En el instante en que C comienza a bajar, D comienza a subir (y viceversa). Puntos como estos están medio período fuera de fase entre sí. C y D’ también están medio período fuera de fase. Cualquiera dos puntos separados entre sí por distancias de 1⁄2λ , 3/2λ , 5⁄2 λ, etc., están medio período fuera de fase.
En esta serie hacemos hincapié en las ideas, pero entendemos que las matemáticas son la mejor forma de expresarlas de forma eficaz y eficiente, auqnue no nos metamos a fondo con ellas. Si pretendemos representar una onda periódica y sus características en un plano XY, entonces la posición (x,y) de un punto cualquiera en función del tiempo, t, viene dada por la siguiente ecuación de onda:
y(x, t) = A sen (ωt + kx + δ),
donde A es la amplitud, ω es la velocidad angular dada por ω = 2π/T (donde T es el periodo), k es el número de onda dado por k = 2π/λ y δ el desfase. La fórmula parece que es ciencia infusa, pero con los conceptos que hemos visto y este fantástico vídeo de José Luis Crespo, la entenderás perfectamente (incluso sin tener ni idea de trigonometría):
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Fase y ecuación de onda se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Características de una onda periódica
- Propagación de una onda
- Incompletitud y medida en física cuántica (VI): la onda piloto
La boca
 Boca de una lamprea marina (Petromyzon marinus)
Boca de una lamprea marina (Petromyzon marinus)La boca es la entrada al sistema digestivo y puesto que hay una gran diversidad de modalidades de alimentación, existen también muy diferentes tipos de bocas. Los animales que se alimentan de fluidos biológicos tienen una anatomía bucal apta para succionar los líquidos (como algunos insectos fitófagos), aunque pueden necesitar también dispositivos adicionales para perforar tejidos e incluso para anestesiar a su huésped en el caso de los ectoparásitos de animales. Los micrófagos, como bivalvos, suelen tener aparatos filtradores para retener las minúsculas partículas en que consiste su alimento o, si comen sedimentos, dispositivos para seleccionar las de alto valor nutricional de las partículas de escaso o nulo valor. Hay animales macrófagos que engullen animales enteros, sin desmenuzarlos, como algunas serpientes, pero la mayoría han de fragmentar los pedazos de alimento y su boca suele estar dotada de dientes, con los que lo cortan en trozos pequeños. Las aves, sin embargo, han prescindido de los dientes y se han dotado de pico, una estructura dura con una diversidad anatómica y funcional enorme en las diferentes especies.
En los mamíferos la apertura bucal está bordeada por los labios, que aparte de para cerrar la boca o mantener sellado su contorno sobre la superficie mamaria en la lactación, también sirve a algunas especies como herramienta prensil. La bóveda de la cavidad bucal es el paladar, que la separa de las vías respiratorias nasales. La mayor parte de los anfibios, reptiles (aves incluidas) y mamíferos tienen lengua, que es una estructura muscular que cumple variadas funciones. En ciertas especies es el órgano que atrapa el alimento, como en algunas ranas y camaleones; en otras, como los rumiantes, sirve para coger el alimento; perros y gatos la utilizan para beber. Y a muchas especies, como la nuestra, les sirve para conducir el alimento y moverlo durante la masticación. En la lengua hay, además, un gran número de papilas gustativas, aunque también las hay en el paladar, y en la garganta.
El primer tratamiento que recibe la comida en la mayoría de macrófagos (no en las especies que engullen sus presas enteras) es la masticación. Masticando el alimento, se fragmenta en trozos muy pequeños, lo que además de aumentar la superficie expuesta a la acción digestiva1, facilita su posterior ingestión. Además, ayuda a mezclar la comida con la saliva. Y también estimula los receptores de las papilas gustativas, lo que desencadena reflejos de secreción de saliva en la cavidad bucal y de jugos gástricos, pancreáticos y biliares en órganos inferiores del sistema.
Los dientes de peces, anfibios y reptiles están especializados para sujetar y desgarrar los pedazos de alimento. Muchas especies renuevan sus piezas dentales a lo largo de la vida, como hacen tiburones, dinosaurios (estos hacían, claro) y reptiles no aviares (las aves carecen de dientes, como se ha dicho antes), aunque hay grandes diferencias de frecuencia de cambio entre unas especies y otras2. En las serpientes venenosas los colmillos contienen sendos depósitos de veneno. Y hay vertebrados (los misticetos) cuyos dientes vestigiales son reabsorbidos y sustituidos por las ballenas3, que utilizan como filtro para retener los crustáceos eufasiáceos (krill) que les sirve de alimento.
 La saliva de la boca de las sanguijuelas contiene apirasa, que impide la coagulación de la sangre en la herida.
La saliva de la boca de las sanguijuelas contiene apirasa, que impide la coagulación de la sangre en la herida.La saliva es producida por las glándulas salivares. Entre sus funciones se encuentran las siguientes:
(1) Humectación, para lubricar el alimento y facilitar su ingestión.
(2) Digestión, dado que en la mayor parte de animales la saliva contiene amilasa, la enzima que degrada el polisacárido almidón al disacárido maltosa.
(3) En algunas especies la saliva ejerce funciones de defensa, pues (a) contiene lisozima, una enzima que ataca las paredes bacterianas; (b) contiene aglutinina, una glucoproteína que forma complejos con anticuerpos IgA para unirse después a las bacterias; (c) lactoferrina, que se une al hierro que necesitan las bacterias para duplicarse; y (d) arrastrando material que podría ser fuente de alimento para las bacterias.
(4) La saliva es un disolvente para muchas moléculas que estimulan los receptores de las papilas gustativas. Si no están en disolución no surten efectos gustativos.
(5) Suele ser rica en tampón bicarbonato, por lo que neutraliza muchos ácidos de los alimentos, así como los que producen las bacterias.
(6) Puede cumplir también funciones de termorregulación en los animales que no recurren a la sudoración para disipar calor por evaporación en caso de necesidad. Hay animales que incluso impregnan de saliva su superficie corporal con ese propósito.
(7) La saliva de los ectoparásitos como vampiros, insectos y sanguijuelas contiene apirasa, que previene la agregación de plaquetas al degradar ADP; ejerce por lo tanto función anticoagulante.
(8) Las glándulas salivares de muchos insectos y algunos vertebrados liberan feromonas.
A diferencia del resto de secreciones digestivas, que están controladas por el sistema nervioso y el endocrino, la secreción de saliva en vertebrados4 está sometida a control nervioso únicamente. En los mamíferos, la estimulación permanente y de baja intensidad de las terminaciones nerviosas del subsistema parasimpático5 que inervan las glándulas salivares provoca la producción constante de saliva. Gracias a esa secreción la boca y la garganta se mantienen húmedas de forma permanente. La tasa basal de secreción de saliva en humanos es de 0,5 ml min-1, aunque puede elevarse rápidamente hasta los 5 ml min-1 bajo ciertos estímulos. Esas cifras, no obstante, empalidecen al lado de las de los rumiantes: una vaca produce 140 l de saliva diarios y la mitad del agua corporal pasa cada día de las glándulas salivares al rumen.
Además de la producción continua de un volumen limitado de saliva, hay dos reflejos que pueden provocar una elevación en su secreción. Uno es el reflejo simple o no-condicionado, que es el que se produce cuando los quimiorreceptores y barorreceptores de la cavidad bucal responden a la presencia de alimento. Esos receptores envían señales al centro salivar de la médula6 y esta, a su vez, responde enviando a las glándulas salivares las correspondientes señales para elevar la producción de saliva. El otro es el reflejo salivar condicionado, que ocurre sin que haya estimulación oral; es un reflejo aprendido que consiste en la insalivación en respuesta a un estímulo que indica que en breve habrá alimento disponible para comer.
Un rasgo que diferencia a las glándulas salivares del resto de órganos regulados por el sistema autónomo es que es el único caso en que los subsistemas simpático y parasimpático no tienen efectos antagonistas. Ambas divisiones estimulan la producción de saliva. La división parasimpática, que es dominante, provoca un aumento del flujo de sangre a las glándulas y, por consiguiente, da lugar a una abundante producción de saliva serosa. La simpática, sin embargo, reduce el flujo sanguíneo y, aunque mantiene un cierto nivel de producción salivar, esta es de menor volumen y de consistencia más mucosa. Bajo esa circunstancia suele experimentarse la sensación de boca seca característica de condiciones de estrés.
Fuente:
Lauralee Sherwood, Hillar Klandorf & Paul H. Yancey (2005): Animal Physiology: from genes to organisms. Brooks/Cole, Belmont.
Notas:
1 La superficie acumulada total de una misma masa o volumen de cualquier material es mayor cuando se encuentra fragmentada en muchos trozos de pequeño tamaño que en pocos de gran tamaño.
2 En la mayor parte de los tiburones se renuevan cada dos semanas, y en los cocodrilos cada dos años.
3 Las conocidas coloquialmente como barbas, que son largos filamentos de queratina dispuestos en paralelo.
4 Y con la excepción de los rumiantes, en los que la saliva es secretada de forma permanente por la glándula parótida sin que responda a estímulos nerviosos.
5 En la anotación dedicada al sistema nervioso periférico tratamos del subsistema parasimpático.
6 En El tronco encefálico y el cerebelo, hicimos referencia a la médula como parte del tronco encefálico.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La boca se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Modalidades de alimentación
- El balance energético animal
- Túbulos de Malpigio y recto, el sistema excretor de los insectos
Hace 16 años ya: el hundimiento del Prestige

“May day, may day. Soy el capitán del Prestige, un petrolero de 243 metros de eslora que transporta 77000 toneladas de fuel desde el Báltico con destino a Gibraltar. Perdimos el control y estamos escorados 25 grados a estribor. Necesito ayuda para evacuar a la tripulación.”
Capitán Apostolos Mangouras, 14.15 horas, 13 de noviembre de 2002.
El petrolero Prestige se hundió el 19 de noviembre de 2002, entre las 11.45 y las 16.18 horas.
“El último resto del Prestige yace bajo el fondo del mar desde las 16.18 de ayer, a unas 133 millas marinas (250 kilómetros) de la costa gallega… A las ocho de la mañana se partió en dos. A las 11.45 se hundió la popa, y cuatro horas y media después el Atlántico terminó de tragarse la proa.”
El País, 20 de noviembre de 2002.
“No se puede hablar de marea negra, son manchas negras y dispersas.”
José Luis López Sors, Director General de la Marina Mercante. 17 de noviembre de 2002.
“Se piensa que el fuel está aún enfriándose, salen unos pequeños hilitos, hay cuatro en concreto, los que se han visto, cuatro regueros solidificados con aspecto de plastilina en estiramiento vertical.”
Mariano Rajoy, Vicepresidente del Gobierno. 5 de diciembre de 2002.

El 13 de noviembre de 2002 se recibió el primer aviso del Prestige: fue la primera petición de ayuda. Se encontraba frente a las costas de Galicia, luchando con un fuerte temporal. Seis días más tarde, el 19 de noviembre, se hundió a unos 250 kilómetros al oeste de la costa gallega. Ahora, estos días de noviembre, celebramos el 16 aniversario de la catástrofe que provocó el vertido y el desastre ambiental que todos conocemos. Vamos a repasar algunos aspectos de las consecuencias que tuvo el accidente en el futuro o, mejor, en nuestro presente.
Hasta 2007, cinco años después del hundimiento, más de 300 investigadores de 42 centros de investigación colaboraron en proyectos relacionados con el Prestige. Organizaron 45 campañas de muestreos y recorrieron más de 2000 kilómetros de costa, en 10 barcos y durante 170 días. Nueve de esos investigadores eran de la UPV/EHU.
La primera conclusión de todos estos estudios, tal como cuentan Beatriz Morales Nin y sus colegas, de la Universidad de las Islas Baleares, es de sorpresa y alivio. A pesar de las alarmas que se activaron en muchos sectores afectados por el fuel vertido por el petrolero, el océano y las costas se recuperaron con una rapidez inesperada. Sin embargo, los científicos avisaron de que no hay que descuidar la vigilancia en el futuro pues, para esa fecha, en 2007, no se conocía, ni se conoce en la actualidad, donde están parte de las 77000 toneladas que llevaba el petrolero. Y pueden afectar a los ecosistemas en el futuro, aunque sea, como alguno aseguró en rueda de prensa, plastilina y no chapapote.
Galicia es una región a vigilar con un seguimiento continuo. Ha sufrido ocho episodios de vertidos de petróleo y productos químicos y, por ello, es la región costera del mundo con el mayor número de accidentes de este tipo. El primero de esta serie fue el Yanxilas en 1965, y el último el Prestige en 2002.

Entre los estudios sobre los efectos del fuel derramado por el Prestige, nos sirven de ejemplo los muestreos de mejillones que, desde el norte de Portugal, por el Cantábrico y hasta la costa de Francia, mostraron que el impacto más fuerte se detectó cerca de puertos como Avilés, Gijón, Santander o Bilbao, y en las zonas más cercanas al vertido, como la Costa da Morte y Corrubedo en Galicia. Pero la concentración de productos del fuel del Prestige descendió a los pocos meses del vertido. Además, no es posible comparar con datos anteriores al vertido para certificar la recuperación del medio pues esos datos, en la mayoría de los casos, no existen pues no había estudios ni seguimientos detallados anteriores.
A los dos años, en 2003 y 2004, los mejillones mostraban recuperación en varios marcadores de células y tejidos, según el grupo de Miren Cajaraville, de la UPV/EHU. Los animales proceden de 22 puntos de muestreo en las costas de Galicia y del Cantábrico. Una revisión de los datos del ecosistema marino recogidos entre 2003 y 2006, y con cinco índices diferentes de salud ambiental tratados en conjunto por el grupo de Ionan Marigómez, de la UPV/EHU, confirma la recuperación de los mejillones.
Esta disminución de concentraciones también la ha detectado el grupo de Dario Monaco, de la Universidad de Nápoles. Después del accidente, la concentración de petróleo en el fondo y en la superficie, en las costas de Galicia, era de 300 kilogramos por metro cuadrado en enero de 2003. Casi dos años después, en octubre de 2004, había bajado a 0.5 kilogramos por metro cuadrado. Como otras autores, avisan de que, aunque bajen las concentraciones, no se sabe donde está el petróleo que falta del vertido del Prestige, aunque, añaden, expertos y pescadores lo han visto en el fondo del mar y cerca de la costa.
Los autores han medido las concentraciones de hidrocarburos y metales pesados en las rías de Vigo y Pontevedra y en las islas Cíes. Los resultados indican que las mayores concentraciones se encuentran en la mitad interior de las rías y su origen está en la actividad humana habitual y no en vertidos grandes.
Un resultado similar ha encontrado en el estuario de Urdaibai el grupo de Eunate Puy, de la UPV/EHU. La contaminación por hidrocarburos en las rías de Galicia y en Urdaibai es habitual en muchos estuarios por la actividad humana. Los autores de la investigación de Galicia recomiendan un seguimiento continuo para detectar vertidos e iniciar, si se considera necesario, procesos de estudio y recuperación de los ecosistemas.
Entre los métodos de futuro, quizá ya en el presente, para el seguimiento y detectar y controlar los vertidos está la ciencia ciudadana tal como proponen Kieran Hyder y sus colegas, del Centro de Ciencias del Ambiente, Pesquerías y Acuicultura de Lowestoft, en Inglaterra. Los programas de detección de ciencia ciudadana, con la participación de muchas personas interesadas, son muy útiles para los vertidos en pequeña escala o los de mayor importancia pero con dispersión del contaminante en muchas manchas pequeñas, tal como ocurrió con el chapapote del Prestige (quizá a esto se refería López Sors en sus proféticas declaraciones). Estos vertidos dispersos a menudo no son detectados y son igualmente dañinos para el ambiente.

Siempre queda el riesgo de que la catástrofe se repita. Como decía al principio, entre 1965 y 2002, son ocho los vertidos graves desde buques que han contaminado las costas de Galicia. Es decir, uno cada casi cinco años y, por ello, estadísticamente ya toca otro accidente. Javier Fernández Macho, de la UPV/EHU, ha elaborado un índice que calcula el riesgo de vertidos en las costas europeas. Ha utilizado datos de 301 accidentes, ocurridos entre 1970 y 2014, en 156 regiones costeras de Europa.
De las 25 regiones con más riesgo, 20 están en Gran Bretaña, un grupo de islas cercano al continente y con muchos puertos y gran movimiento de barcos. Galicia y el estrecho de Gibraltar están entre las regiones con más riesgo de vertidos, también por el numeroso tráfico y, además, muchos de los barcos transportan productos contaminantes y peligrosos.
Para terminar, el coste económico del accidente del Prestige en Galicia tal como lo ha calculado María Loureiro y su grupo, de la Universidad de Santiago. Es un estudio fechado en 2006 y suma las pérdidas y gastos a corto plazo de los sectores económicos afectados, por la limpieza y recuperación, y por los daños ambientales conocidos en esa fecha.
El total es de algo más de 770 millones de euros, con el valor del euro de 2001. Recomiendan comparar esta cifra de gasto con los fondos que costaría la aplicación de medidas preventivas y de otros planes que eviten o mitiguen los vertidos. Otro estudio, publicado en las mismas fechas, y centrado en el sector pesquero de la Ría de Vigo, da cifras parecidas. Publicado por Dolores Garza y su grupo, de la Universidad de Vigo, calcula que, solo en el año 2003, las pérdidas alcanzan los 100 millones de euros.
Todavía quedan por conocer, y los grupos de investigación está en ello, los daños a largo plazo, tal como nos enseña el accidente del petrolero Exxon Valdez en las costas de Alaska, que ocurrió en 1989, y casi 30 años después todavía se observan daños en organismos marinos. Como recordaba antes, el petróleo del Prestige, o por lo menos mucho de ese petróleo, todavía está en el mar, casi seguro en el fondo, y sigue descargando compuestos peligrosos en el océano que, es fácil suponer, siguen influyendo en el funcionamiento de especies y ecosistemas.
Referencias:
Cajaraville, M.P. et al. 2006. Signs of recovery of mussels health two years after the Prestige oil spill. Marine Environmental Research Suppl 1: S337-S341.
Fernández Macho, J. 2016. Risk assessment for marine spills along European coast lines. Marine Pollution Bulletin doi: 10.1016/j.marpolbul.2016.09.015
Garza, M.D. et al. 2006. Assessment of economic damages from the Prestige oil spill. Marine Policy 30: 544-551.
Hyder, K. et al. 2017. The role of citizen science in monitoring small-scale pollution events. Marine Pollution Bulletin 120: 51-57.
Loureiro, M.L. et al. 2006. Estimated costs and admisible claims linked to the Prestige oil spill. Ecological Economics 59: 48-63.
Marigómez, I. et al. 2013. Marine ecosystem health status assessment through integrative biomarker indices: a comparative study after the Prestige oil spill “Mussel Watch”. Ecotoxicology 22: 486-505.
Monaco, D. et al. 2017. Spatial distribution of heavy hydrocarbons, PAHs and metals in polluted sea. The case of “Galicia”, Spain. Marine Pollution Bulletin doi: 10.1016/j.marpolbul.2017.06.003
Morales Nin, B. et al. 2007. Ciencia & Prestige. La investigación desarrollada a raíz del accidente del Prestige. Oficina Técnica de Vertidos Marinos. Universidad de Vigo. 67 pp.
Puy Azurmendi, E. et al. 2010. Origin and distribution of polycyclic aromatic hydrocarbon pollution in sediment and fish from the Biosphere Reserve of Urdaibai (Bay of Biscay, Basque country, Spain). Marine Environmental Research 70: 142-149.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Hace 16 años ya: el hundimiento del Prestige se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Prestige: impacto biológico
- El 70% de los varones del País Vasco desciende de un antepasado que vivió hace 4.500 años
- Flores en su tumba, hace 16.000 años
Diálogos en la frontera: Matemáticas y procesos creativos

Aunque la relación entre las diferentes formas de conocimiento puede parecer imposible, lo cierto es que en muchas ocasiones el vínculo entre ellas es necesario e inevitable. Las artes y las ciencias son el vivo ejemplo de la conexión que existe entre las distintas áreas de estudio. Y aunque puede resultar complicado pensar cómo pueden convivir la creación artística y la investigación científica, lo cierto es que hay profesionales que combinan estas disciplinas en su trabajo diario.
Ejemplo de ello son la artista donostiarra Esther Ferrer y el compositor minimalista estadounidense Tom Johnson, los protagonistas de la primera edición del programa “Diálogos en la frontera”, que se celebró el pasado 12 de marzo en la Biblioteca Bidebarrieta de Bilbao.
El evento, cuyo principal objetivo es crear un espacio para el diálogo entre las artes y las ciencias, congregó en la capital vizcaína a los profesores de la Universidad del País Vasco/Euskal Herriko Unibertsitatea Josu Rekalde (Bellas Artes) y Raúl Ibáñez (Ciencia y Tecnología), que conversaron con Ferrer y Johnson sobre la utilización de las matemáticas en los procesos creativos de ambos artistas.
El evento se enmarca dentro del ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
La artista donostiarra Esther Ferrer es pionera del arte de la performance y una de sus máximas representantes en España. Su trabajo ha sido reconocido con múltiples galardones como el Premio Nacional de Artes Plásticas (2008), el Premio Gure Artea (2012) y el premio Marie Claire de l’Art Contemporain (2014). En sus obras, expuestas por todo el mundo, aparecen múltiples referencias a las matemáticas (números primos, el infinito en el número pi, la geometría, espacio y tiempo…) y se relacionan con el minimalismo, el arte conceptual y el feminismo.
El músico Tom Johnson es un compositor minimalista y teórico de la música estadounidense. Para sus composiciones utiliza formas simples, escalas limitadas y elementos matemáticos como la combinatoria, las simetría, los números o los fractales. Entre sus obras destacan la famosa La ópera de las cuatro notas (1972), Melodías Racionales (1982) y Kientzy Loops, premiada con el premio nacional francés “Victoires de la musique 2000”; o melodías más recientes como Galileo (2001), Mosaicos (2002) o Ritmos de Vertmon (2008).
Edición realizada por César Tomé López.
El artículo Diálogos en la frontera: Matemáticas y procesos creativos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia, arte y cultura callejera: materiales y obra artística
- Ciencia, arte y cultura callejera: física y música
- Las matemáticas de la desigualdad
Vida artificial en un ordenador cuántico IBM
El grupo de investigación Quantum Technologies for Information Science (QUTIS), liderado por el Profesor Ikerbasque Enrique Solano del Departamento de Química Física de la UPV/EHU ha desarrollado un protocolo de biomimética que reproduce los procesos característicos de la evolución darwiniana adaptado a la computación cuántica. Los investigadores prevén que en el futuro se conjugarán el autoaprendizaje de las máquinas, la inteligencia artificial y la vida artificial a escala cuántica.

En un escenario de vida artificial los modelos de organismos simples serían capaces de experimentar las diferentes etapas de la vida en un entorno virtual controlado. Eso es lo que ha diseñado el grupo QUTIS pero en un escenario de ordenadores cuánticos: un protocolo de vida artificial, que codifica comportamientos propios de sistemas vivos, como la autorreplicación, la mutación, la interacción entre individuos, el nacimiento, la muerte, y lo ha ejecutado en el ordenador cuántico en la nube de IBM ibmqx4.
Se trata de la primera realización experimental de un algoritmo de vida artificial siguiendo las leyes evolutivas de Darwin en un ordenador cuántico. El algoritmo sigue un protocolo biomimético, que codifica comportamientos cuánticos simulando los mismos comportamientos de los sistemas vivos. La biomimética cuántica consiste en reproducir en sistemas cuánticos algunas propiedades exclusivas de los seres vivos, y este grupo de investigación anteriormente había conseguido imitar mediante sistemas cuánticos la vida, la selección natural, el aprendizaje y la memoria. El objetivo de esta investigación es, tal como relatan los propios autores, “diseñar una serie de algoritmos cuánticos basados en la imitación de procesos biológicos, que se dan en organismos complejos, y llevarlos a la escala cuántica, por lo que solamente tratamos de imitar los aspectos claves de estos procesos”.
En el escenario de vida artificial que han diseñado, una serie de modelos de organismos simples son capaces de llevar a cabo las fases más comunes de la vida en un entorno virtual controlado,. Los investigadores han probado que los sistemas cuánticos microscópicos pueden codificar características cuánticas y comportamientos biológicos que normalmente se asocian con sistemas vivos y la selección natural.
Los modelos de organismo se han diseñado como unidades de vida cuántica, cada una compuesta por dos cúbits, que hacen las veces de genotipo y fenotipo, respectivamente,. El genotipo contiene la información que describe el tipo de unidad viviente, información que se transmite de generación en generación, mientras que el fenotipo, las características que muestran efectivamente los individuos, viene determinado tanto por la información genética como por la interacción de los propios individuos con el medioambiente.
Las características básicas de la evolución darwiniana que han simulado con estos sistemas, para poder considerarlos como organismos de vida artificial, han sido el nacimiento, el desarrollo, la autorreplicación (que incluye las mutaciones, que se materializan en rotaciones al azar de cúbits individuales), la interacción entre los individuos y con el medioambiente. Esta interacción va degradando el fenotipo del individuo conforme va avanzando en edad hasta que llega a un estado que representa la muerte.
Esta prueba experimental representa la consolidación del marco teórico de la vida artificial cuántica en un sentido evolutivo, pero conforme vayan escalando el modelo a sistemas más complejos, podrán “realizar emulaciones cuánticas más precisas con una complejidad creciente hacia la supremacía cuántica”, tal como comentan los autores.
De la misma forma, esperan que estas unidades de vida artificial y sus posibles aplicaciones tengan profundas implicaciones en la comunidad de la simulación cuántica y la computación cuántica en diversidad de plataformas cuánticas, sean iones atrapados, sistemas fotónicos, átomos neutros o circuitos superconductores.
Según Enrique Solano “se han sentado las bases para plantearse diferentes niveles de complejidad clásica y cuántica. Por ejemplo, se podría considerar el crecimiento de poblaciones de individuos cuánticos con criterios de género, sus objetivos vitales tanto individuales como colectivos, comportamientos automatizados sin control externos, procesos de robótica cuántica, sistemas cuánticos inteligentes, hasta llegar a superar el umbral de la supremacía cuántica donde solo un ordenador cuántico podría llegar. A partir de allí surgen preguntas terriblemente arriesgadas como conjeturar el origen microscópico de la vida misma, el desarrollo inteligente de los individuos y sus sociedades, o plantearse el origen de la conciencia y la creatividad animal y humana. Esto es solo el principio, estamos a inicios del siglo XXI y tendremos muchos sueños y preguntas fantásticas que podremos responder”.
Referencia:
U. Alvarez-Rodriguez, M. Sanz, L. Lamata, E. Solano (2018) Quantum Artificial Life in an IBM Quantum Computer Scientific Reports doi: 10.1038/s41598-018-33125-3
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Vida artificial en un ordenador cuántico IBM se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La vida cuántica
- #Quantum13 El timo del ordenador cuántico comercial
- Un simulador cuántico de fenómenos imposibles
Pros y contras de los nuevos semáforos nutricionales

Las compañías Coca-Cola, Mondelez, Nestlé, Pepsico y Unilever se han puesto de acuerdo para incluir un nuevo etiquetado en el frontal de sus alimentos. Lo han llamado «Etiquetado Nutricional Evolucionado» (ENL en sus siglas en inglés) y recuerda al que se emplea en Reino Unido. El sistema de basa en una suerte de semáforo nutricional (verde, ámbar y rojo) que servirá como indicador de la cantidad de calorías, grasas, azúcares y sal presentes en una porción de alimento.
La iniciativa impulsada por estas cinco compañías llega en un momento en el que países como Francia o Bélgica ya han optado por apostar por otro sistema diferente llamado Nutri-Score. El Nutri-Score se basa en una calificación global de la calidad nutricional del alimento que va de la A a la E, siendo la A la mejor puntuación (color verde) y la E la peor posible (color rojo). Todas las medidas se presentan con respecto a 100 g de producto (no por porción) y hay elementos cuya presencia suma (frutas, verduras, frutos secos, fibra y proteínas) y otros que restan (grasas saturadas, azúcar, sal y calorías).
Los sistemas Nutri-Score y el ENL son de carácter voluntario a la espera de que la Comisión Europea armonice la información nutricional adicional. En España, el Ministerio de Sanidad, Consumo y Bienestar Social, ha informado recientemente que aplicará el modelo Nutri-Score.

Eroski lleva años utilizando el semáforo nutricional en sus alimentos de marca blanca. A finales de 2018 pretende añadir también el sistema Nutri-Score.
Para algunos, este colorido etiquetado frontal favorece la comprensión nutricional de los productos. Para otros, esto es un coladero que permitirá pasar por buenos a alimentos de escaso valor nutricional.
Estos etiquetados son un extra, puesto que la información obligatoria que debe presentar cualquier alimento envasado es la lista de ingredientes (ordenados de mayor a menor cantidad en el producto) y la tabla nutricional, en la que se desglosa, por cada 100 g de alimento, el aporte calórico, los carbohidratos (de los cuales se indica cuántos gramos son azúcares), las grasas (de las cuales de indica cuántas son saturadas), fibra, proteínas y sal.
Tampoco es obligatorio mostrar la tabla nutricional por porción de alimento, sino solo por cada 100 g de producto. La principal controversia del ENL surge precisamente de la definición de «porción de alimento». Por ejemplo, en el caso de un yogur o postre lácteo, la definición de «porción» es evidente, pero en el caso de cereales, galletas, frutos secos… u otros alimentos que se venden en paquetes grandes de los cuales tú eliges cuánto consumir, la elección del tamaño de la porción es arbitraria. Al ser arbitraria podríamos encontrarnos que un alimento con alto valor calórico, rico en grasas saturadas, azúcares y sal, como por ejemplo la mayoría de las galletas, podrían mostrar un semáforo nutricional en el que primase el verde y el ámbar. No porque sea un alimento saludable, sino porque la medida se ha hecho en función de una porción muy pequeña.
Además, la cantidad de azúcares, grasas o sal se compara con la «ingesta de referencia de un adulto medio», es decir, con el total de lo que podrías consumir en un día. Por este motivo, si la porción es de dos o tres galletas supondrá un porcentaje pequeño, lo que se traduce en un semáforo aparentemente benévolo.
La solución a esto sería llegar a un consenso sobre qué es una «porción de alimento», para así poder comparar las cualidades nutricionales de diferentes cereales, panecillos, galletas, etc. Sin embargo, esto ya se hace al dorso: la tabla nutricional se hace obligatoriamente por 100 g de producto. Algunos fabricantes incluyen voluntariamente una columna más en la tabla nutricional «por ración». Esa ración puede ser un puñado de 30 g de avellanas o un envase de yogur de 125 g.
Con el sistema Nutri-Score, este problema desaparece, ya que siempre se da el dato con respecto a 100 g de producto.
Otra fuente de controversia es que podríamos entrar en comparaciones absurdas. Por ejemplo, en el semáforo nutricional ENL de la mayoría de los frutos secos aparecerá en rojo y ámbar el contenido calórico y de grasas. Los consumidores podrían pensar que se trata de un alimento insano, cuando la realidad es que los frutos secos son siempre una opción saludable.
Si comparásemos el semáforo nutricional de unas galletas con el de unas nueces, las nueces podrían parecer una opción menos saludable, ya que su contenido en grasas seguramente será mayor. La realidad es que unas nueces siempre serán una opción saludable, y unas galletas, salvo limitadas excepciones, no lo serán.

El sistema Nutri-Score no presenta este problema de comparaciones absurdas, ya que premia y penaliza por familia de alimentos. No analiza solo sus componentes, sino que tiene en cuenta el alimento completo. Los frutos secos tendrán buena calificación en Nutri-Score y la bollería no.
El contenido en azúcares también es complicado de evaluar con los semáforos nutricionales. Por ejemplo, un producto lácteo contendrá azúcares en forma de lactosa. Estos azúcares propios de la leche son saludables y no deberían condicionar la compra. Los azúcares añadidos son los que sí deberíamos evitar para mantener una alimentación saludable, no los que forman parte de la matriz del alimento.

Por ejemplo, el semáforo nutricional de un vaso de leche (200 ml), mostrará en ámbar los azúcares y en rojo las grasas, cuando ni los azúcares ni las grasas de la leche deberían preocuparnos, ya que la leche es un alimento a todas luces saludable. Por eso en el sistema Nutri-Score la leche tendrá una valoración positiva, mientras que con el ENL resulta engorroso saber si se trata o no de un buen alimento.
En la tabla nutricional obligatoria se indica qué cantidad de carbohidratos son azúcares, pero no se especifica si estos azúcares son añadidos o intrínsecos. Esto complica la elección de compra. Por ejemplo, un yogur natural sin azucarar contendrá entre 4 y 5 g de azúcares. Estos azúcares son la lactosa que contenía la leche con la que se fabricó el yogur, así que todos los yogures tendrán como mínimo entre 4 y 5 g de azúcares. Estos azúcares son saludables, pero en el semáforo y en la tabla nutricional suman como cualquier otro azúcar insalubre, lo que con frecuencia da lugar a malinterpretaciones.

Para saber si un yogur tiene azúcar añadido tenemos que buscar la palabra «azúcar» entre la lista de ingredientes. Si no aparece, quiere decir que ese yogur no tiene azúcar añadido. Si aparece la palabra «azúcar» (o equivalente, como jarabe de glucosa, miel, panela, etc.) tendremos que ir a la tabla nutricional para ver cuánto contiene. A esa cantidad le restamos unos 4-5 g, y ya tendremos la cantidad de azúcar añadido. Complicado.
Por este motivo algunos exigimos que en la tabla nutricional aparezca desglosado el azúcar en azúcar libre e intrínseco. Al igual que las grasas se desglosan en saturadas e insaturadas.
-
Conclusión
La incorporación de etiquetados frontales basados en el sistema de colores tipo semáforo nutricional como el ENL tiene pros y contras. Por un lado, nos permite saber de un vistazo si el contenido en grasas saturadas, azúcares, sal y calorías de un alimento es elevado. Por otro lado, este método puede inducir a error fácilmente, ya que una porción pequeña de un alimento insano puede mostrar un semáforo aparentemente benévolo. Tampoco sirve para diferenciar azúcares intrínsecos de azúcares añadidos, que es un problema todavía sin resolver en el etiquetado obligatorio basado en la lista de ingredientes y la tabla nutricional. También propicia comparaciones absurdas: unas galletas insanas pueden mostrar un semáforo más indulgente que el de unos frutos secos, aun cuando los frutos secos son una opción saludable.
La buena noticia es que el sistema Nutri-Score que ya han incorporado Bélgica y Francia, y al que pronto se sumará España, aunque no es perfecto, sí palía la mayor parte de los contras que presenta el semáforo nutricional ENL.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Pros y contras de los nuevos semáforos nutricionales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El azúcar oculto en los alimentos
- Miel y siropes, ¿son mejores que el azúcar?
- Lo dicen en la tele: un alimento natural no lleva aditivos
Construye tu propia calculadora de sumas y restas
Puede parecer raro que, en la actualidad, cuando tenemos calculadoras en nuestro teléfono móvil, tablet u ordenador, calculadoras on-line en internet que permiten realizar todo tipo de operaciones, ya sea con números, vectores o matrices, y sofisticadas calculadoras, que cada vez se parecen más a un ordenador de mano, planteemos en esta entrada del Cuaderno de Cultura Científica construir una calculadora mecánica para realizar sumas y restas.
 Máquina de sumar y restar, Addometer PAMOMA, modelo B estándar, construido en 1900 en Palma de Mallorca, 29 x 6 cm. Imagen de Antiguos instrumentos de cálculo
Máquina de sumar y restar, Addometer PAMOMA, modelo B estándar, construido en 1900 en Palma de Mallorca, 29 x 6 cm. Imagen de Antiguos instrumentos de cálculo Máquina de sumar y restar de mesa, Desk Calcumeter, diseñada en 1901 por el físico estadounidense James J. Walsh. Esta versión, con 6 diales, debe ser posterior, puesto que tiene tecla de “reseteado”. Imagen de Antiguos instrumentos de cálculo
Máquina de sumar y restar de mesa, Desk Calcumeter, diseñada en 1901 por el físico estadounidense James J. Walsh. Esta versión, con 6 diales, debe ser posterior, puesto que tiene tecla de “reseteado”. Imagen de Antiguos instrumentos de cálculoA finales del siglo XIX y principios del XX se diseñaron varias calculadoras mecánicas, del tipo de la Pascalina (máquina calculadora mecánica diseñada, haciendo uso de ruedas dentadas, por el matemático francés Blaise Pascal en 1642), de pequeño tamaño, que permitían realizar sumas y restas de forma sencilla, como las dos mostradas arriba.
Estas máquinas estaban diseñadas con una serie de ruedas dentadas, en las que se representaban las 10 cifras básicas de nuestro sistema de numeración, junto con un mecanismo sencillo, que variaba de unos diseños a otros, para incorporar la “llevada” de la suma al mecanismo.
Para explicar su funcionamiento, veamos un diseño simple de una máquina de sumar mecánica que podemos realizar en casa, o en clase, con algunos materiales que podemos tener a mano, como cartón, plástico o madera.
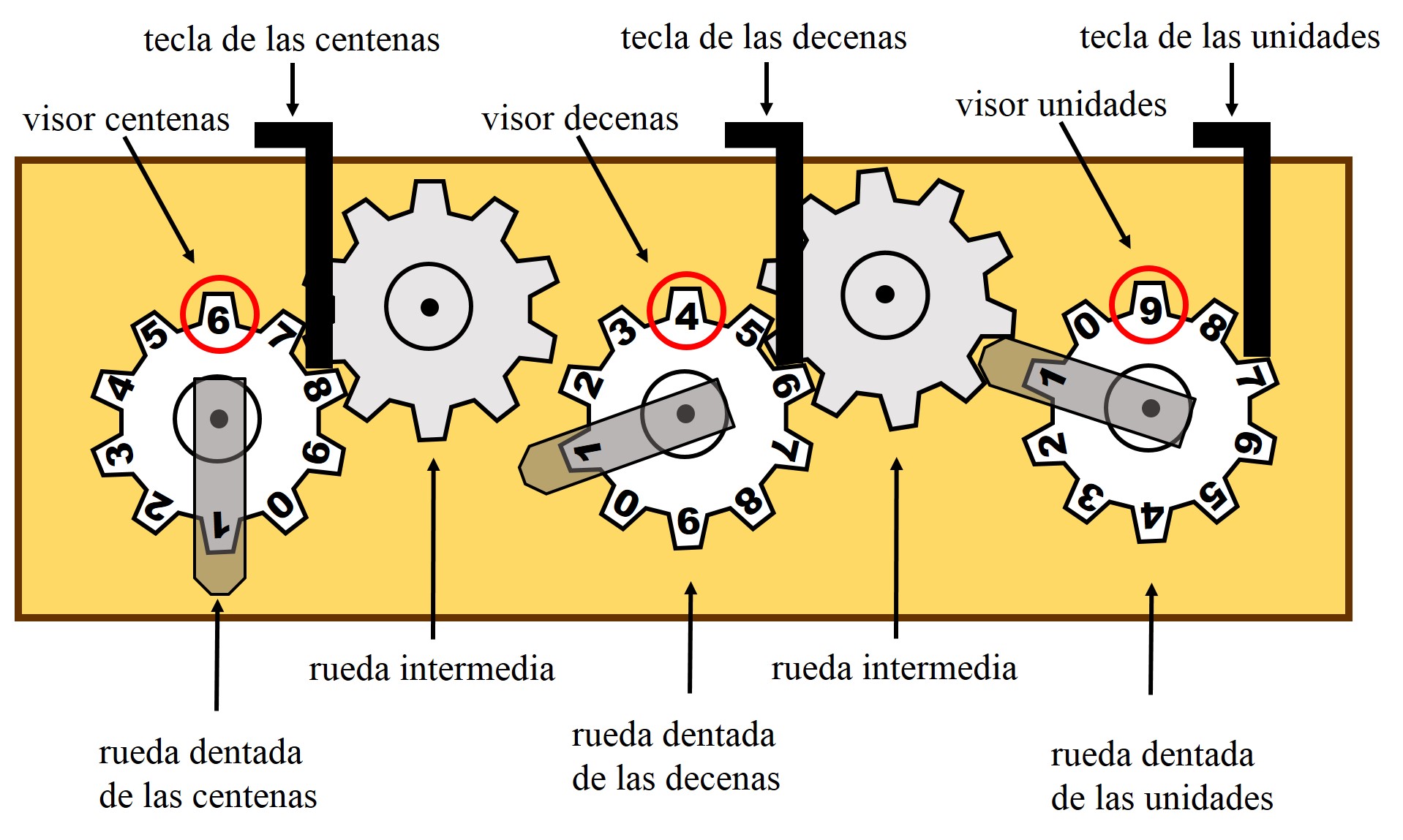 Diseño básico de una máquina de sumar mecánica, de tres ruedas dentadas, para construir uno mismo. Puede taparse el mecanismo, dejando libre la parte de las teclas, para poder accionarlas, y realizando unos agujeros en la parte de los visores para poder observar las cifras de las operaciones a realizar
Diseño básico de una máquina de sumar mecánica, de tres ruedas dentadas, para construir uno mismo. Puede taparse el mecanismo, dejando libre la parte de las teclas, para poder accionarlas, y realizando unos agujeros en la parte de los visores para poder observar las cifras de las operaciones a realizarComo vemos en la imagen anterior, esta calculadora mecánica de sumas está formada por tres ruedas dentadas con las diez cifras básicas, de 0 a 9, en cada una de ellas, lo que permite representar números de tres cifras. Aunque podemos construirla con más cantidad de ruedas dentadas, como en los ejemplos anteriores, para representar números mayores.
Para representar un número se presionan las teclas de las unidades, decenas y centenas, tantas veces como indique la cifra de la correspondiente posición. Así, para representar el número 649 que está en la imagen, se presiona 9 veces la tecla de las unidades, 4 la de las decenas y 6 la de las centenas (las ruedas dentadas girarán en el sentido de las agujas del reloj), viéndose en los visores de unidades, decenas y centenas las cifras del número 649.
Si ahora le queremos sumar el número 135 al número 649, es decir, queremos realizar la suma 649 + 135, se marcarán las cifras, desde las unidades a las centenas, con las correspondientes teclas, del número 135. ¿Qué es lo que va a ocurrir para que nos de la suma de esos dos números? Bastante simple. Al presionar 5 veces la tecla de las unidades, se están sumando las unidades, es decir, 9 + 5 (que son 14), de forma que cuando la rueda dentada da una vuelta completa, es decir, se pasa del 9 al 0 en el visor, la palanca alargada de la rueda de las unidades, que está colocada en el diente de la cifra 1, mueve la rueda dentada intermedia, la cual produce, a su vez, un movimiento de una posición en la rueda de las decenas (es la llevada de la suma de las unidades). Por lo tanto, en el visor de las unidades queda un 4, y en el de las decenas, se ha pasado del 4 al 5.
A continuación, se presiona 3 veces la tecla de las decenas, que pasa del 5 al 8, al sumar 3 al 5. Y finalmente, se presiona 1 vez la de las centenas, que pasa del 6 al 7. En los visores se verán las cifras 7 (centenas), 8 (decenas) y 4 (unidades), es decir, la suma es 784.
649 + 135 = 784.
La siguiente imagen es un ejemplo real de una máquina mecánica para sumar de este tipo. Es una máquina para realizar sumas rápidas para las compras, con los dos primeros números de la izquierda para los peniques y los dos siguientes para las libras. Teniendo en cuenta que cada libra son cien peniques, es como utilizar números de cuatro cifras en el sistema de numeración posicional decimal moderno, es decir, el sistema de numeración indo-arábigo que utilizamos en la actualidad.
 Sumador rápido para las compras, que cuenta libras y peniques. Fabricado en Hong Kong por FORDA, probablemente en la década de 1970. Es una máquina realmente pequeña, su tamaño es 7 x 3,5 x 1,5 cm. Imagen de Rechnen ohne Strom – Historische Rechenmaschinen
Sumador rápido para las compras, que cuenta libras y peniques. Fabricado en Hong Kong por FORDA, probablemente en la década de 1970. Es una máquina realmente pequeña, su tamaño es 7 x 3,5 x 1,5 cm. Imagen de Rechnen ohne Strom – Historische RechenmaschinenLa estructura interna de este pequeño sumador para las compras es similar a la del diseño básico explicado más arriba, aunque en este diseño se ahorran las ruedas intermedias al disponer las cifras en las ruedas dentadas en sentidos contrarios de forma alterna, unidades y centenas en el sentido contrario de las agujas del reloj, y decenas y unidades de mil, en el sentido de las agujas del reloj. De esta forma, la llevada se traslada directamente de una rueda dentada a la siguiente.
 Mecanismo interno del sumador rápido para las compras. Imagen de Rechnen ohne Strom – Historische Rechenmaschinen
Mecanismo interno del sumador rápido para las compras. Imagen de Rechnen ohne Strom – Historische Rechenmaschinen Con la máquina básica de sumas cuyo diseño hemos mostrado arriba, o con la que acabamos de mostrar para compras rápidas, se pueden realizar también restas. La idea para realizar una resta es considerar el complemento del sustraendo (el número que se resta) respecto a la potencia de 10 inmediatamente superior al minuendo (el número al que se le resta el sustraendo) y sumarlo al minuendo.
Veamos algún ejemplo. Para realizar la resta 93 – 57 en la sumadora anterior, se suma al sustraendo, 93, el complemento del minuendo, 57, respecto a 100, es decir, 43 (= 100 – 57). Al realizar la suma con la calculadora mecánica nos queda 93 + 43 = 136. No debemos de tener en cuenta el 1 inicial, que se corresponde con la llevada, y se obtiene el resultado, 36:
93 – 57 = 36.
Tengamos en cuenta que 93 + 43 = 93 + (100 – 57) = 100 + (93 – 57).
Otro ejemplo. Si queremos realizar la resta 723 – 235, debemos sumarle al sustraendo, 723, el complementario, respecto de 1000, del minuendo, 235, que es 1000 – 235 = 765. Por lo tanto, se realiza la suma 723 + 765 = 1488, y el resultado es 488.
723 – 235 = 488.
 Sumador rápido de pulsera. Frabricado en Hong Kong para la empresa estadounidense Kass Merchandise Co. Inc., en la década de 1970. Tamaño 6,5 x 5,5 x 2,3 cm y peso 39 gr. (con paquete). Imagen de Rechnen ohne Strom – Historische Rechenmaschinen
Sumador rápido de pulsera. Frabricado en Hong Kong para la empresa estadounidense Kass Merchandise Co. Inc., en la década de 1970. Tamaño 6,5 x 5,5 x 2,3 cm y peso 39 gr. (con paquete). Imagen de Rechnen ohne Strom – Historische RechenmaschinenEl problema de la resta es que tenemos que calcular el complementario del sustraendo, aunque realmente esto es fácil. Para calcular el complemento de un número respecto a una potencia de 10 más alta, solo hay que calcular el complemento de cada cifra, respecto a 9 o 10, dependiendo de su posición. Si la cifra es la de las unidades el complemento es respecto de 10, pero si es de las decenas, centenas o cualquier otra superior, el complemento es respecto de 9. Veamos algunos ejemplos.
El complemento del 75 respecto de 100 es 25, ya que 7 + 2 = 9 y 5 + 5 = 10; el complemento del 387 respecto de 1000 es 613, ya que 3 + 6 = 9, 8 + 1 = 9 y 7 + 3 = 10; o el complemento de 253 respecto de 10.000 es 9747, ya que 0 + 9 = 9, 2 + 7 = 9, 5 + 4 = 9 y 3 + 7 = 10.
 Antiguo teléfono con dial giratorio
Antiguo teléfono con dial giratorioEn el diseño básico de la máquina de sumar que hemos mostrado arriba, podemos sustituir las teclas para introducir las cifras de los números por discos con las diez cifras básicas sobre cada una de las ruedas de las unidades, las decenas, las centenas, etcétera. Más aún, estos discos, con los que introduciremos ahora las cifras de los números, pueden ser diales con diez agujeros, del tipo de un teléfono antiguo (como el que se muestra en la anterior imagen). Para introducir la cifra 3 giramos, mediante un dedo si los agujeros son grandes o mediante un lápiz si son pequeños, que suele ser el caso, en el sentido de las agujas del reloj, desde donde esté pintado el 3 hasta el tope, es decir, tres posiciones. Este es el diseño de la segunda calculadora que hemos mostrado en esta entrada.
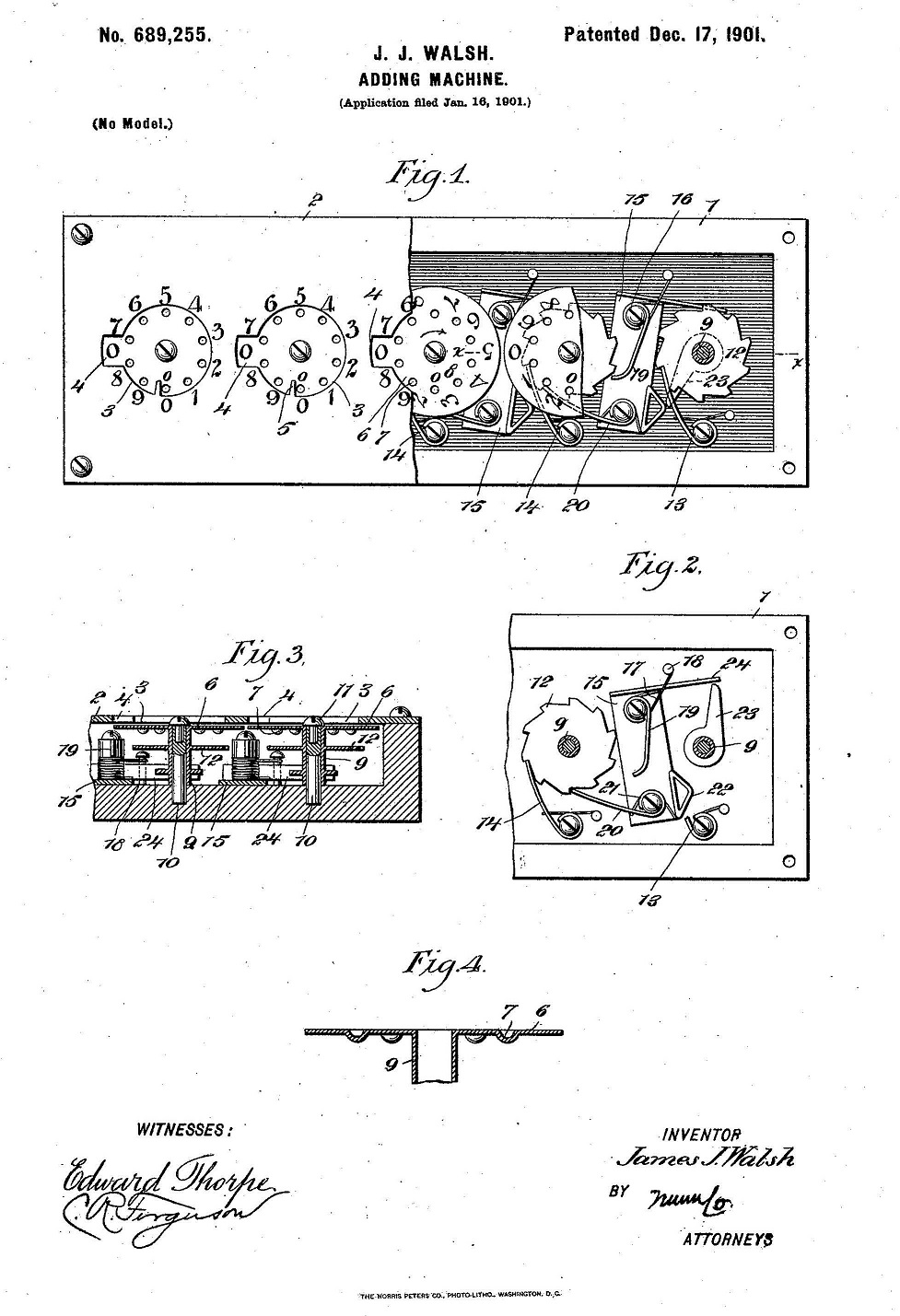 Página de la patente US 689.255 en Estados Unidos del “Calcumeter Desk”. Dispone de una rueda a la derecha para poner a cero el mecanismo. Imagen de History of computers.
Página de la patente US 689.255 en Estados Unidos del “Calcumeter Desk”. Dispone de una rueda a la derecha para poner a cero el mecanismo. Imagen de History of computers.En la siguiente imagen se muestra el diseño, para nuestra máquina mecánica básica de sumar mostrada arriba, de la rueda dentada con el dial para girar el disco y la tapa que iría delante de la rueda. Este diseño sería para cada rueda dentada.
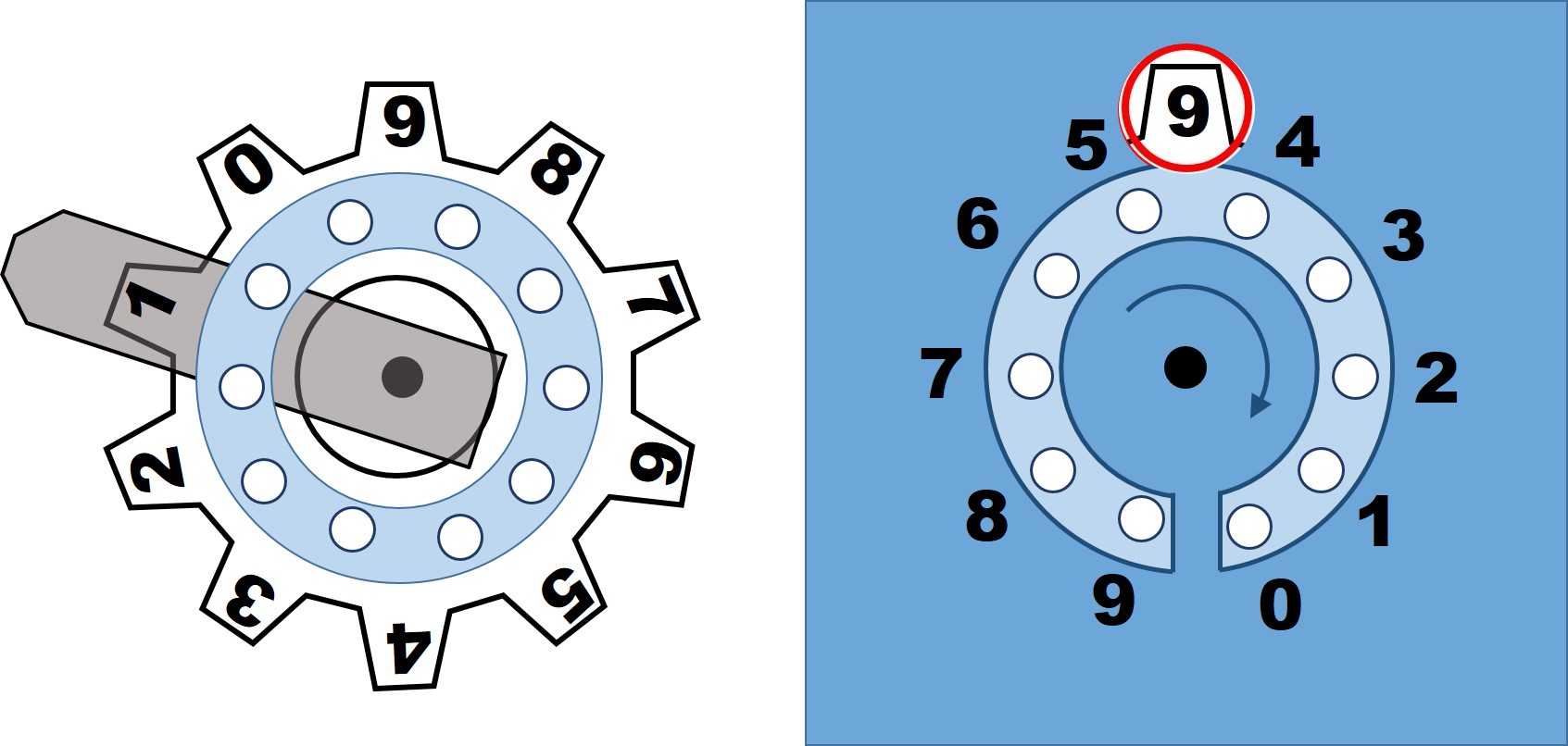 A la izquierda, el diseño de la rueda dentada de tipo dial correspondiente a nuestro diseño básico anterior de una máquina mecánica de sumar, y a la derecha, diseño de la tapa de la misma, donde se nos indican los números para el dial, desde donde se marca cada cifra como en un teléfono antiguo. La tapa nos deja ver la rueda dentada tanto por el visor, como en la parte central el dial con los diez agujeros
A la izquierda, el diseño de la rueda dentada de tipo dial correspondiente a nuestro diseño básico anterior de una máquina mecánica de sumar, y a la derecha, diseño de la tapa de la misma, donde se nos indican los números para el dial, desde donde se marca cada cifra como en un teléfono antiguo. La tapa nos deja ver la rueda dentada tanto por el visor, como en la parte central el dial con los diez agujeros Este sistema nos permite introducir cada cifra de una sola vez, mediante el dial, en cada rueda dentada y no hace falta estar presionando cada tecla tantas veces como indica la cifra correspondiente.
Además, una de las ventajas de este diseño de diales para introducir las cifras de nuestros números es que nos va a permitir realizar restas. Si para sumar en cada cifra, hay que girar el dial en el sentido de las agujas del reloj, utilizando para ello los números negros pintados en el exterior del dial), de forma que el mecanismo tiene en cuenta las llevadas, para la resta habrá que girar en el sentido contrario de las agujas del reloj, utilizando para ello los números rojos pintados en el interior del dial, y el mecanismo sigue teniendo en cuenta las llevadas para la resta.
 Diseño de la tapa de las ruedas dentadas de la máquina básica de sumar, con los números negros para sumar, girando el dial en el sentido de las agujas del reloj, y con los números rojos para restar, girando el dial en el sentido contrario a las agujas del reloj
Diseño de la tapa de las ruedas dentadas de la máquina básica de sumar, con los números negros para sumar, girando el dial en el sentido de las agujas del reloj, y con los números rojos para restar, girando el dial en el sentido contrario a las agujas del relojVeamos como realizar la resta 649 – 372 en nuestro mecanismo (véase en la siguiente imagen el interior del mecanismo en la versión de los diales, así como las tapas con los números en negro y rojo). Primero se introduce el número 649 en la calculadora mecánica. Se gira, en el sentido de las agujas del reloj, el dial de las unidades (el de la izquierda) desde el 9 negro, quedando marcado el 9 en el visor de arriba. Después se hace lo mismo para las decenas, segundo dial desde la derecha, girando en el sentido de las agujas del reloj desde el 4 negro. Y de forma similar el dial de las centenas, en el que se marca la cifra 6. Quedando en los visores el número 649, como en la imagen.
 Interior del diseño básico de una máquina de sumar mecánica, de tres ruedas dentadas, con diales para girar las ruedas dentadas, a derecha –para sumar– o izquierda –para restar–, como se indica en las tapas que irían sobre cada rueda dentada y que mostramos en la parte inferior de la imagen, utilizando los números negros y rojos como el dial de un teléfono antiguo que permite girar en los dos sentidos
Interior del diseño básico de una máquina de sumar mecánica, de tres ruedas dentadas, con diales para girar las ruedas dentadas, a derecha –para sumar– o izquierda –para restar–, como se indica en las tapas que irían sobre cada rueda dentada y que mostramos en la parte inferior de la imagen, utilizando los números negros y rojos como el dial de un teléfono antiguo que permite girar en los dos sentidosAhora le vamos a restar el número 372. Hay que tener en cuenta que como es una resta se utilizarán los números rojos y el giro es en el sentido contrario a las agujas del reloj. Como en las unidades del sustraendo tenemos un 2, giramos el dial de las unidades desde el 2 rojo en el sentido contrario a las agujas del reloj, quedando un 7 en el visor. En las decenas tenemos un 7, luego se gira el segundo dial desde el 7 rojo y en el sentido contrario a las agujas del reloj, en el visor se pasa del 4 al 7. Pero en este giro, cuando en el visor se pasa del 0 al 9 (es decir, necesitamos una llevada para la resta), la palanca que está en el 1, hace girar en el sentido de las agujas del reloj a la siguiente rueda dentada intermedia, que a su vez hace girar una posición a la rueda dentada de la izquierda (las centenas), en el sentido contrario a las agujas del reloj, y en el visor pasa del 6 al 5 (la llevada). Finalmente, en las centenas, que ahora hay un 5, se gira desde el 3 rojo, en el sentido contrario a las agujas del reloj, y queda un 2. Si miramos a los visores tendremos el resultado de la resta, 277.
649 – 372 = 277.
Una máquina calculadora mecánica para sumar y restar con ruedas dentadas y diales, como la que acabamos de describir, es la sumadora de bolsillo Kesling, también conocida, como sumadora de bolsillo Kes-Add, que fue diseñada en la década de 1940 por el dentista e inventor Elmer G. Kesling (1881-1961) y construida por la compañía The Hart Vance Company hacia 1954.
 Máquina mecánica de sumar, y restar, de bolsillo de Kelsing, construida hacia 1954 por la The Hart Vance Company, diseñada con ruedas dentadas y diales. Su tamaño es 1 x 13,7 x 5 cm. Esta acompañada de su lápiz para girar los diales a derecha o izquierda, y su bolsa para guardarla. Imagen de Jaap’s Mechanical Calculators Page
Máquina mecánica de sumar, y restar, de bolsillo de Kelsing, construida hacia 1954 por la The Hart Vance Company, diseñada con ruedas dentadas y diales. Su tamaño es 1 x 13,7 x 5 cm. Esta acompañada de su lápiz para girar los diales a derecha o izquierda, y su bolsa para guardarla. Imagen de Jaap’s Mechanical Calculators Page  Sumadora de bolsillo de Kesling desmontada. Se pueden observar las ruedas dentadas y el mecanismo de unión entre ellas para poder efectuar sumas y restas, como se ha descrito en esta entrada. Imagen de Aus der Rechenmaschinen-Werkstatt
Sumadora de bolsillo de Kesling desmontada. Se pueden observar las ruedas dentadas y el mecanismo de unión entre ellas para poder efectuar sumas y restas, como se ha descrito en esta entrada. Imagen de Aus der Rechenmaschinen-Werkstatt 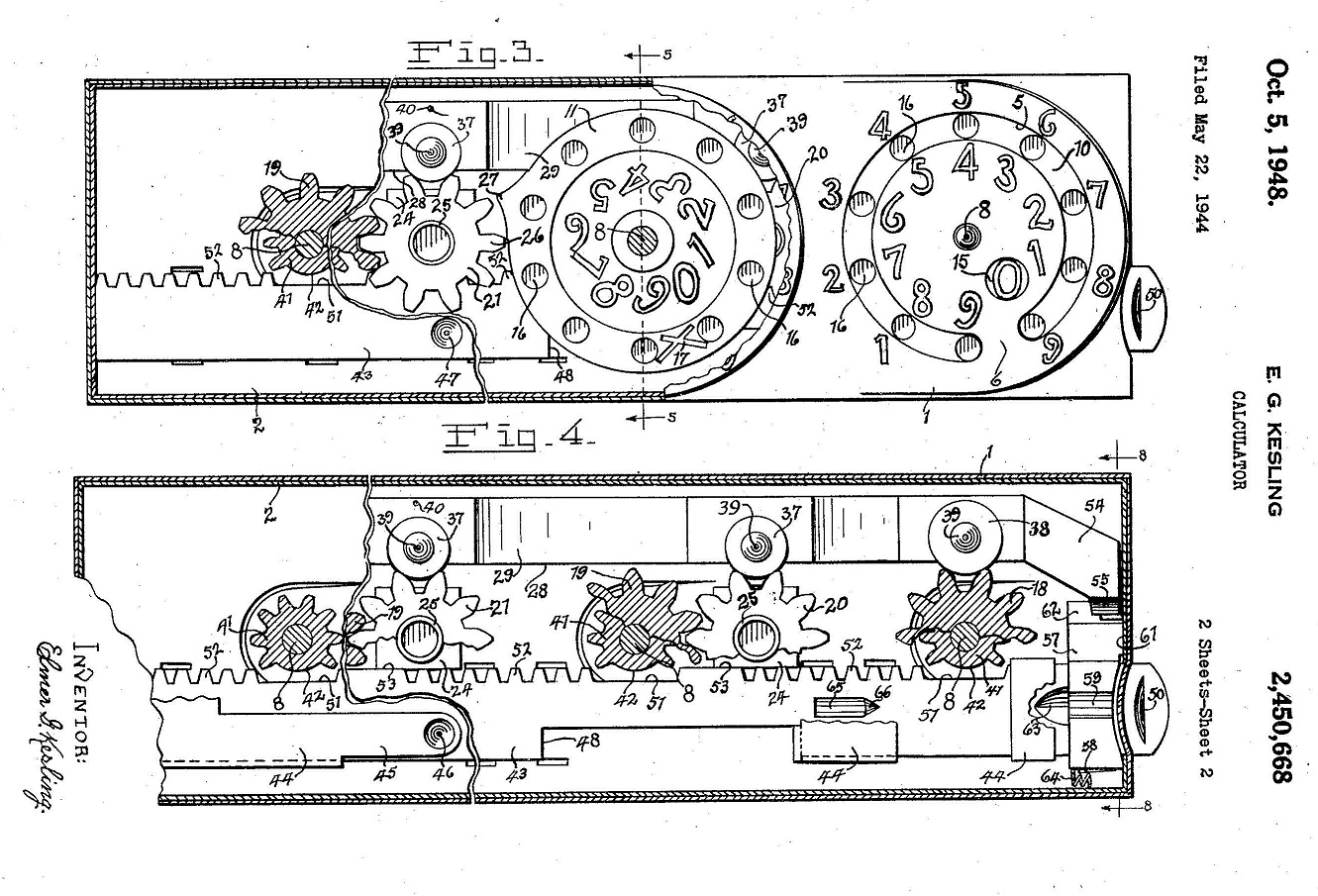 Página de la patente US 2.450.668 en Estados Unidos de la Sumadora de bolsillo de Kesling. Imagen de la página de patentes en Google
Página de la patente US 2.450.668 en Estados Unidos de la Sumadora de bolsillo de Kesling. Imagen de la página de patentes en GoogleY terminamos mostrando otra máquina similar, la máquina de sumar de Groesbeck, patentada en 1870 por John Groesbeck (1834-1884).
 Exterior e interior de la máquina de sumar de Groesbeck. Imagen de History of computers
Exterior e interior de la máquina de sumar de Groesbeck. Imagen de History of computers
Biblioteca
1.- Theodor Ziegler, Juegos de calcular, 38 sugerencias para utilizar el “Juego del ábaco”, Interduc/Schroedel, 1977.
2.- Antonio Pérez-Prados, Antiguos instrumentos de cálculo
3.- W. Denz, Rechnen ohne Strom – Historische Rechenmaschinen (Cálculo sin electricidad – Calculadoras históricas)
4.- Jaap Scherphuis, Jaap’s Mechanical Calculators Page
5.- Georgi Dalakov, History of computers
6.- Detlev Bölter, Aus der Rechenmaschinen-Werkstatt
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Construye tu propia calculadora de sumas y restas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
