Catástrofe Ultravioleta #21 PHARMA
Catástrofe Ultravioleta #21 PHARMA
En este capítulo nos disponemos a recorrer, desde cero, todos los pasos que se necesitan para descubrir un nuevo medicamento. Entraremos en docenas de laboratorios y conoceremos de primera mano en qué consiste la investigación farmacéutica.
Agradecimientos: Javier Burgos (FIBAO), Juan Diego Unciti (Nanogetic), Manuel Bioque, José Marqués, Pedro Torres y José Riquelme de la fundación AVITE.
* Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) con el patrocinio parcial de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.
El artículo Catástrofe Ultravioleta #21 PHARMA se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Preparados para una Catástrofe Ultravioleta
- Catástrofe Ultravioleta #01 Expedición
- Catástrofe Ultravioleta #14 VULCANO
Acciones policiales proactivas bajo la lupa científica

Los protagonistas de Mindhunter dan a la investigación policial un enfoque científico. Fuente: Mindhunter/Netflix
En la serie Mindhunter, estrenada recientemente en Netflix y que recomiendo a todo el mundo que vea ya, ahora mismo (en cuanto termine de leer este artículo que con tanto cariño he escrito, obviamente), dos agentes del FBI comienzan en los años 70 a analizar desde una perspectiva científica el comportamiento de determinados criminales.
Lo que estos agentes intentan es aplicar un conocimiento metódico, estadístico, sólido y fiable a la prevención de determinados crímenes utilizando como objetos de estudio a aquellos que los han cometido anteriormente. Además del guion y los personajes, especialmente los malos, basados por cierto en criminales reales, lo interesante de la serie es ver cómo las intervenciones policiales comienzan a seguir criterios científicos.
La historia está basada en hechos reales. Se inspira en un libro Mind Hunter: Inside FBI’s Elite Serial Crime Unit escrito por Mark Olshaker y John E. Douglas, dos exagentes del FBI que llevaron a cabo precisamente la labor que realizan los protagonistas en la serie. Un buen ejemplo de cómo la ciencia se aplica a la investigación criminal.
No solo los crímenes pueden someterse a la meticulosa lupa científica. También las intervenciones de la propia policía. Recientemente las Academias Nacionales de Ciencias, Ingeniería y Medicina de Estados Unidos han publicado un informe en el que analizan cuáles de las llamadas prácticas policiales proactivas realmente funcionan para reducir la incidencia del crimen en una zona y cuáles no. Se trata de aumentar la eficacia de los cuerpos policiales y mejorar sus resultados yendo más allá de la mera intuición y aportando una visión estadística rigurosa.

Acciones policiales proactivas, las que funcionan y las que no. Fuente: EFE/Nigel Roddis
El informe se refiere a las técnicas policiales proactivas, aquellas que se emplean para eliminar y reducir los crímenes, en oposición a las técnicas reactivas, aquellas que se limitan a investigar y resolver crímenes ya cometidos. En cada una de ellas han tratado de responder a varias preguntas: cuál es su impacto en los índices de criminalidad en la zona donde se implementan, cuál es la reacción que producen en la población de la zona, si se están utilizando de forma ética y legal y si existe en su aplicación algún sesgo racial.
Las técnicas policiales que sí reducen el crimen
Un ejemplo es el llamado en inglés hot spots policing o policía en puntos calientes. Esta técnica trata de reducir la criminalidad haciendo que siempre haya agentes apostados en aquellas zonas donde se concentra un mayor número de crímenes. Según los estudios analizados en el informe, esta técnica hace que se reduzcan los delitos cometidos en ese punto sin desplazarlos a las zonas de alrededor.

Evolución de los puntos calientes de crímenes con armas en Portland. Fuente: Portland State University

Los puntos calientes de los crímenes con armas en Portland de 2009 a 2013. Fuente: Portland State University
También ha demostrado su eficacia la acción policial orientada a los problemas (problem-oriented policing). Esta técnica trata de determinar qué causas subyacen en los crímenes de una zona y actuar sobre ellas, ya sea mejorando la iluminación en un punto concreto, arreglando mobiliario urbano o aportando alternativas de ocio para la juventud que de otra forma serían carne de cañón.
Otra técnica analizada es la que llaman de disuasión focalizada (focused deterrence), un intento por mantener controlados a delincuentes reincidentes analizando las causas subyacentes de la criminalidad (marginación, tráfico y consumo de drogas, pobreza, falta de alternativas) e implementando programas que impliquen a las fuerzas de seguridad, a los vecinos y a los servicios sociales en conjunto.
Las técnicas policiales con menos impacto
Algunas de las acciones policiales analizadas no han demostrado ser tan eficaces. Es el ejemplo del alto-interrogación-cacheo (stop-question-frisk), una técnica que consiste en dar el alto por la calle, interrogar y registrar a sospechosos habituales. Los resultados señalan que cuando esta técnica se emplea en puntos concretos con altos índices de criminalidad y sobre criminales con alto riesgo de reincidencia sí parece ser eficaz a corto plazo, pero no existen evidencias sólidas que señalen ese mismo efecto a largo plazo.

La teoría de las ventanas rotas defiende que evitar los pequeños actos de vandalismo previene y reduce la criminalidad. Fuente: Wikipedia
Tampoco parece muy clara la efectividad de la técnica de las ventanas rotas (broken-window policing). Está basada en la teoría de que vigilar y controlar entornos urbanos evitando crímenes leves como vandalismo, basura en las calles o consumo de alcohol en público evita que la criminalidad escale y aumente en número e intensidad. Según el informe, esta técnica tiene un impacto a corto plazo, pero pequeño o nulo en la reducción de la criminalidad cuando se aplica de forma agresiva aumentando las detenciones por delitos menores.
La última técnica examinada se llama en inglés procedural justice policing y podríamos traducirla como lo justo de los procedimientos policiales. Se trata de poner el foco en las interacciones policiales con el público y los habitantes de un lugar concreto para transmitir la legitimidad de las acciones policiales, consiguiendo así que la población se involucre y colabore con la policía, consiguiendo una reducción del crimen. Aunque son positivas para mejorar la imagen de la policía en una zona determinada, según el informe no hay evidencias suficientes que confirmen la eficacia de estas iniciativas.
La relación de la policía con el público
El informe de las Academias de Ciencias, Ingeniería y Medicina analiza también cómo la implementación de estas políticas policiales afecta a las relaciones de los cuerpos de seguridad con la población.

¿Cómo afectan estas técnicas a la imagen que el público tiene de la policía?
Las investigaciones disponibles que las intervenciones policiales en lugares donde se concentra el crimen, como su presencia en puntos calientes, no suelen tener efectos negativos a corto plazo sobre la comunidad en la que se realizan, pero tampoco mejoran la imagen de la policía en esa comunidad. Por eso hacen falta más estudios que permitan entender cuáles son sus efectos a largo plazo.
En cambio, las intervenciones policiales que analizan y tratan de resolver las causas subyacentes del crimen sí que muestran de forma consistente una mejora entre pequeña y moderada de la opinión que la población tiene de la policía. Eso no quita para que siga siendo necesario estudiar las consecuencias a medio y largo plazo.
¿Son técnicas racistas?
El informe ha tratado de determinar si la aplicación de estas políticas policiales proactivas deja entrever un patrón racista. Según sus conclusiones, cuando la policía actúa sobre gente o zonas de alto riesgo, algo común en estas técnicas, son muy probables las disparidades raciales en las interacciones entre los agentes y los ciudadanos. Sin embargo, considera que esto no sirve para establecer de forma concluyente hasta que punto son resultado de una anomalía estadística, un sesgo implícito del observador o un verdadero ánimo racista por parte de los cuerpos policiales.
Por eso hace un llamamiento a ampliar las investigaciones en este campo, de forma que las comunidades y departamentos de policía preocupados por una posible desigualdad racista puedan contar con datos fiables sobre los que actuar. Lo mismo ocurre con los datos a medio y largo plazo sobre la eficacia de estas técnicas, así como la eficacia a mayor escala, observando no solo por zonas sino por ciudades: que no existen.
Referencia:
National Academies of Sciences, Engineering, and Medicine (2017) Proactive Policing: Effects on Crime and Communities. Washington, DC: The National Academies Press. doi: 10.17226/24928.
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Acciones policiales proactivas bajo la lupa científica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Nubes bajo el sol
- La ciencia bajo el totalitarismo
- Ciencia en la cocina: Frutas bajo el volcán de caseínas
Trepar o correr

Caza de persistencia actual en Nuevo México (Estados Unidos)
Los chimpancés tienen fama de forzudos y, dependiendo de cómo se mire, es una fama merecida. Un kilogramo de músculos de chimpancé desarrolla más fuerza que la misma masa muscular de un ser humano. Ahora bien, nosotros somos de mayor tamaño que ellos, y eso compensa la diferencia. En otras palabras, aunque siempre se ha pensado que un chimpancé puede destrozar a un hombre en una pelea, la realidad no es tan dramática.
Es cierto, no obstante, que los músculos de nuestros primos son más fuertes que los nuestros, un 50% más por unidad de masa. Una pequeña parte de esa diferencia –la correspondiente a un 15%- parece obedecer a factores de carácter anatómico, pero la mayor parte –el 35%- se debe al tipo de fibras musculares de una y otra especie. Simplificando algo las cosas, se puede decir que hay dos tipos de fibras, unas son de contracción rápida y otras de contracción lenta. Y resulta que dos terceras partes de las fibras de los chimpancés son de contracción rápida y, por ello, desarrollan más fuerza. Pero en humanos, en general, las proporciones no son tan diferentes; por esa razón, al tener más fibras lentas, nuestros músculos desarrollan menos fuerza.
La mayor fuerza de los chimpancés tiene una clara contrapartida: sus fibras musculares se fatigan antes. Volviendo a simplificar algo las cosas, se puede afirmar que las fibras de contracción rápida se fatigan con facilidad y las de contracción lenta son muy resistentes a la fatiga. Y lo normal, como suele ocurrir en estos casos, es que esas diferencias tengan relación con el modo de vida o con la práctica de alguna actividad física: los corredores de largas distancias suelen tener mucha mayor proporción de fibras de contracción lenta y resistentes, mientras que los velocistas tienen más fibras rápidas y fatigables.
Por otra parte, si tenemos en cuenta el modo de vida de los chimpancés, entenderemos fácilmente que sus músculos, con abundantes fibras rápidas, son muy adecuados para trepar a los árboles, balancearse y saltar de rama en rama. Que esos músculos se fatiguen con facilidad no constituye una limitación de importancia, porque sus saltos, balanceos y movimientos, en general, no se suelen prolongar durante largo tiempo.
Humanos y chimpancés tuvimos un antepasado común que vivió hace entre siete y ocho millones de años. Su modo de vida era mayoritariamente arbóreo, por lo que es de suponer que su musculatura era similar a la de los chimpancés actuales. Los seres humanos, sin embargo, adoptamos un modo de vida diferente, caracterizado principalmente por la bipedestación. Somos homínidos andarines y se nos da muy bien correr largas distancias, sobre todo bajo las altas temperaturas que han predominado en las horas centrales del día en las sabanas de África durante los tres o cuatro últimos millones de años. Fue precisamente, esa capacidad la que nos proporcionó una ventaja decisiva con respecto a otros animales y la que nos permitió desarrollar la caza de persistencia. Pero esa capacidad dependía críticamente de dos rasgos fisiológicos claves: Uno es la posibilidad de disipar calor mediante la evaporación del sudor, y eso explica que perdiésemos el pelaje al colonizar la sabana, porque el sudor que se evapora en el pelaje apenas enfría la piel. Y el otro es la resistencia a la fatiga; por eso en nuestros músculos hay una proporción mayor de fibras lentas y resistentes que en los chimpancés. Al fin y al cabo, ellos pertenecen a un linaje cuyos miembros trepan y saltan de rama en rama, pero los del nuestro tuvieron que andar y correr sin descanso durante horas.
—————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 16 de julio de 2017.
El artículo Trepar o correr se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sistemas nerviosos: el sistema periférico de vertebrados
- Sistemas nerviosos: la médula espinal
- Sistemas respiratorios: la ventilación de los pulmones de mamíferos
Naukas Pro 2017: Lluis Montoliu y el albinismo

El pasado 14 de septiembre de 2017 se celebró la primera edición de Naukas Pro, en el que Centros de Investigación, Laboratorios, científicos de renombre o equipos de trabajo contaron con 20 minutos para explicar a un público general en qué consiste su trabajo.
6ª Conferencia: Lluis Montoliu, Centro Nacional de Biotechología (CNB-CSIC)
LLuis Montoliu explica su trabajo en biotecnologíaEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Pro 2017: Lluis Montoliu y el albinismo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Pro 2017: Carlos Briones y el origen de la vida
- Naukas Pro 2017: Manuel Collado y las células madre
- Naukas Pro 2017: Javier Burgos y el alzhéimer
Los beneficios de las prendas de compresión para los jugadores de fútbol

A pesar de que se hayan publicado numerosos estudios científicos sobre los procesos subyacentes a la recuperación post-ejercicio, el conocimiento de los procesos de recuperación permanece en un estadio de subdesarrollo científico en comparación con el avance experimentado en el área del entrenamiento para el fútbol. Actualmente, se están estudiando los efectos de algunas estrategias de recuperación de la fatiga o del daño muscular inducido por el ejercicio en futbolistas, pero, hasta la fecha, ningún trabajo había evaluado los beneficios de llevar diferentes tipos de prendas de compresión durante partidos de futbol y el posterior periodo de recuperación. La tesis doctoral de Diego Marqués Jiménez, ‘Efectividad de las prendas de compresión como modalidad de recuperación de la fatiga muscular en jugadores de fútbol’, viene s suplir esta carencia.
La tesis hace un compendio de cuatro investigaciones, entre las que hay una revisión de los principales mecanismos de fatiga y daño muscular en fútbol, así como consideraciones a tener en cuenta para la evaluación del proceso de recuperación en fútbol, una revisión sistemática con meta-análisis sobre los efectos de la terapia compresiva en la recuperación del daño muscular por ejercicio y dos estudios experimentales que analizan la influencia de jugar partidos de fútbol llevando diferentes prendas de compresión, y la de las mismas durante los tres días posteriores al partido.
Las demandas competitivas y las elevadas y variables exigencias físicas a las que es sometido el futbolista pueden derivar en un gran nivel de fatiga y estrés en los sistemas fisiológicos, pudiendo afectar al tiempo para recuperarse por completo después de la competición y tener una incidencia en el rendimiento en los días posteriores al partido. Además, y dado que el deportista pasa más tiempo recuperando que entrenando, optimizar el periodo de recuperación mediante la aplicación de diferentes estrategias de recuperación es un procedimiento esencial en la preparación del próximo partido o entrenamiento. Así, esta tesis doctoral aporta más información sobre una estrategia que puede optimizar dichos procesos de recuperación.
Los resultados de la revisión sistemática con meta-análisis muestran que las prendas de compresión pueden favorecer la recuperación después del ejercicio, pero los resultados necesitan corroboración y son poco concluyentes, ya que la mayoría de los estudios incluidos tienen una alta heterogeneidad, de modo que deben ser interpretados con cautela. Los resultados de los estudios experimentales muestran que, a pesar de la poca significación estadística alcanzada, los diferentes tipos de prendas de compresión podrían tener un efecto positivo tanto en la atenuación de las respuestas provocadas tanto por la fatiga como por el daño muscular inducido por el ejercicio.
En respuesta a los síntomas de la fatiga, las perneras de compresión parecen ser más efectivas y, en respuesta a los síntomas del daño muscular, las perneras y musleras de compresión parecen ser las más efectivas. En cualquier caso, y como el autor señala, “la alta variabilidad en la respuesta física del futbolista a las exigencias de un partido de futbol pone de manifiesto la necesidad de nuevos estudios en situaciones reales de juego, que permitan establecer conclusiones prácticas y que sean aplicables teniendo en cuenta dicha la variabilidad”. Esto permitiría verificar la influencia de esta estrategia de recuperación en las respuestas físicas, fisiológicas y perceptivas en futbolistas.
Referencias:
Marqués-Jiménez, D., Calleja-González, J., Arratibel, I., Delextrat, A., Terrados, N. ‘Fatigue and recovery in soccer: evidence and challenges’. The Open Sports Sciences Journal, 10, (Suppl 1: M5) 52-70 (2017).
Marqués-Jiménez D, Calleja-González J, Arratibel I, Delextrat, A., Terrados, N. ‘Are compression garments effective for the recovery of exercise-induced muscle damage? A systematic review with meta-analysis’. Physiology y Behavior, 153: 133–484. (2016).
Marqués-Jiménez D, Calleja-González J, Arratibel I, Delextrat, A., Uriarte, F., Terrados, N. ‘Physiological and physical responses to wearing compression garments during soccer matches and recovery’. J Sports Med Phys Fitness (2017). Doi: 10.23736/S0022-4707.17.07831-8.
Marqués-Jiménez D, Calleja-González J, Arratibel I, Delextrat, A., Uriarte, F., Terrados, N. ‘Influence of different types of compression garments on exercise-induced muscle damage markers after a soccer match’. Research in Sports Medicine (2017) (aceptado y pendiente de publicación).
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Los beneficios de las prendas de compresión para los jugadores de fútbol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La condición física de los árbitros de fútbol
- Fórmulas matemáticas y números: cómo ayuda la economía al fútbol
- Algoritmos de triaje para readmitidos en urgencias
12000 francos para conquistar el mundo
No hay duda de que Napoleón era un hombre con una mente brillante. Pero a conquistar medio mundo no se llega sino subiéndose a hombros de gigantes.
Napoleón conquistó tierras, derrotó ejércitos, sentía que podía con todo… menos con las bacterias y el escorbuto que sufrían sus soldados debido a una alimentación basada básicamente en carne cocida y algo de pan. Carne, además, en dudoso estado porque no conseguían que durase más de 3 o 4 días.
Como hombre listo que era, Napoleón sabía que sus soldados debían estar sanos y bien alimentados para enfrentarse a la batalla en sus mejores condiciones. Permanecían largas temporadas fuera de Francia y el abastecimiento era complicado. Necesitaba una solución.
Esa solución se la dio Nicolás Appert, pastelero francés interesado en conseguir que los alimentos se conservaran durante más tiempo. Este pastelero revolucionó el mundo con un método que hoy todos utilizamos y que lleva su nombre, apertización. Puede que esta palabra no les suene, pero ¿y si les digo “conservas”? Todos tenemos alguna lata de tomate o atún en nuestra casa y se lo debemos a él.

Nicolás Appert consiguió que los alimentos se mantuvieran en perfectas condiciones durante largas temporadas aunque no sabía bien por qué, ya que en aquella época no tenía medios para averiguarlo. Para ello utilizó botellas de vidrio con la boca ancha donde introducía los alimentos y que sumergía parcialmente dentro de cazuelas con agua hirviendo (al baño maría). Antes las cerraba especialmente bien con corcho y cera, sujetándolas con alambres para evitar que el aire entrara en ellas. Estudió los tiempos, cantidad y temperatura dependiendo del alimento. Se dio cuenta de la importancia de una estricta higiene a la hora de manipular los alimentos y de que un cierre hermético era clave para que su método funcionara correctamente.
Él no fue consciente en ese momento, pero acababa de descubrir la esterilización por calor. Posteriormente Louis Pasteur consiguió dar una explicación científica a los experimentos de Nicolás Appert. Al igual que Napoleón, Pasteur se subió a hombros de este gigante y le agradeció sus experimentos, ya que gracias a ellos llegó a tirar por tierra la teoría de la “generación espontánea” e inventó la hoy llamada pasteurización. Eso sí, 54 años después que Appert.

Botella de conservas de Appert
El método de Appert llamó la atención de Napoleón, como no podía ser de otra manera, y comenzó a usarlo para abastecer a la marina francesa. Otorgó a Nicolás el premio de 12.000 francos fruto de un concurso creado para aquel que encontrara una manera eficaz de conservar alimentos (dudosa manera de invertir en ciencia, no lo cuenten por ahí, no vaya a ser que les copien). Con esos 12.000 francos Appert abrió la primera fábrica de conservas que, pese a que fue quemada y destruida en la guerra franco-prusiana, estuvo en activo hasta 1933. No hizo mal negocio Napoleón: 12.000 francos por conquistar el mundo.
Appert era un hombre inquieto y no dejó nunca de hacer experimentos y, por supuesto, de proporcionarle soluciones a las tropas napoleónicas. Quizá por casualidad se dio cuenta de que, eliminando completamente el agua de un caldo, obtenía una pasta (él la llamaba “cubo de caldo”) a la que si se le incorporaba nuevamente agua, aunque fuera mucho tiempo después, volvía a convertirse en un caldo similar al original. Nicolás Appert inventó el caldo concentrado que tan explotado ha sido posteriormente como recurso para potenciar el sabor en los guisos o simplemente convertirlo de nuevo en caldo.

Recipiente metálico para cubo de caldo de la primera mitad del siglo XX (Museo del Objeto. Ciudad de México).
Como se podrán imaginar, esto fue otra gran revolución para facilitar la alimentación del ejército. Napoleón estaba realmente encantado con Nicolás Appert. Sus descubrimientos consiguieron unas tropas bien alimentadas, que junto a una gran estrategia le llevaron a construir un imperio de unas magnitudes asombrosas.
Basándose siempre en diferentes momentos de la desecación de productos, Appert llegó también a inventar el concentrado de leche, es decir, la leche condensada. Gran cantidad de nutrientes, altamente calórica, de fácil conservación y duradera. Un manjar para quien se encuentra en el frente.

Con alimentos en conserva, comenzando por legumbres, siguiendo por frutas y verduras, con caldo concentrado con el que podían aportar nutrientes en una sopa calentita y la leche condensada, la marina de Napoleón tenía una importante ventaja añadida sobre las tropas de otros países. No había quien pudiera con ellos. Napoleón, gracias a Nicolás Appert había vencido al gran ejército de bacterias que consumían sus alimentos y a terribles enfermedades como el escorbuto que mermaban los recursos humanos de sus contrincantes.
Esto llevó a Nicolás Appert a convertirse en héroe nacional, ganando la medalla de oro de la Société d’Encouragement pour l’Industrie Nationale por facilitar el acceso a este tipo de alimentos no sólo a la marina y ejército sino a toda la población francesa.
Pero no todo iba a ser fácil para Napoleón, es evidente que no finalizó con éxito su conquista mundial (si no, estaría leyendo esto en francés), y todo comenzó en Rusia. Allí los métodos de Nicolás Appert encontraron un fallo: las botellas en las que se conservaban los alimentos eran frágiles y se rompían, además no se podían apilar con facilidad. Cuando conseguían alcanzar su destino, muchas de ellas llegaban rotas y no se podían aprovechar los alimentos que contenían. Este declive, unido a las adversas condiciones rusas, fue el principio del fin de Napoleón.
Mientras tanto, sus enemigos se habían fijado en el método de Appert, lo mejoraron y encontraron una solución para la fragilidad de los envases. El inglés Durant le pide al rey Jorge la patente del método para conservar alimentos tan sólo dos meses después de que Nicolás publicara el libro “Le livre de tous les ménages ou L’Art de conserver, pendant plusieurs années, toutes les substances animales et végétales” (El libro de todos los hogares o El arte de preservar, durante varios años, todas las sustancias animales y vegetales). Durant, que nunca llegó a fabricar ni una sola lata, vendió esta patente a Bryan Donkin y John Hall, dueños de una fundición donde comienzan a fabricar latas de hierro cubiertas de estaño. Desde luego que era un método más cómodo y práctico para el envío de alimentos a los soldados e igual de eficaz.

Appert también lo intentó, pero ya era tarde, los ingleses ya eran capaces de fabricar alimentos en conserva y con mayores ventajas. Aunque no crean que los ingleses eran tan listos. Tuvieron que pasar 45 años hasta que un americano Ezra J. Warner, inventara el abrelatas. Hasta ese momento se utilizaban navajas o bayonetas, o incluso disparos de fusil para abrir las dichosas latitas.
Nicolás Appert no patenta ninguno de sus métodos anteponiendo las necesidades de la población a sus propios intereses económicos. Lamentablemente muere solo y arruinado en 1841 a los 92 años. Su cadáver es enterrado en una fosa común. Triste final para el pastelero que ayudó a Napoleón a conquistar medio mundo.
Hoy en día nos queda su legado: el caldo concentrado, la leche condensada, la obtención de gelatina y los inicios de lo que posteriormente sería el autoclave: básico para la esterilización tanto de objetos como de las propias conservas.
Aunque no conozcamos el nombre de su método, la apertización, lo utilizamos con frecuencia en nuestros hogares cuando preparamos conservas caseras (háganlo con cuidado, si no cierran herméticamente el envase, puede contaminarse con bacterias peligrosas como el Clostridium botulinum).
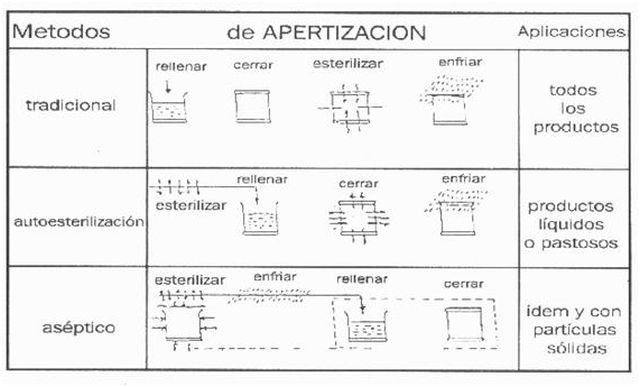
Imagen: Mundolatas.com
Ahora, cada vez que añadan un poco de caldo concentrado al guiso o calienten un tarro al baño maría para hacer una conserva, acuérdense del pastelero que revolucionó la conservación de alimentos durante la Revolución francesa y ayudó a ganar a Napoleón la guerra más importante, la de la alimentación.
Este post ha sido realizado por Gemma del Caño (@FarmaGemma) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias:
Historia y Biografías. Nicolás Appert
Historia de la alimentación militar en Europa durante los siglos XIX y XX. Miguel Krebs. 2008
El gran libro de las conservas. Carol W. Costenbader
Fundación Cotec para la innovación tecnológica. DOCUMENTOS COTEC SOBRE NECESIDADES TECNOLÓGICAS. Conservas Vegetales.
Tatiana Díaz. Octubre 2014. Napoleón y las conservas de alimentos, el inicio militar de un avance científico-tecnológico.
El artículo 12000 francos para conquistar el mundo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Libros para enamorarse
- El consumo de alcohol para el corazón y las dificultades de divulgar ciencia
- #Naukas14: Experimentos para entender el mundo
Por qué la filosofía es tan importante para la educación científica
Subrena E. Smith

La misión Cassini fue una consecuencia directa de los experimentos mentales de Albert Einstein. Imagen: JPL/NASA
Cada semestre, enseño cursos sobre filosofía de la ciencia a estudiantes de grado en la Universidad de New Hampshire. La mayoría de los estudiantes se matriculan en mis cursos para satisfacer los requisitos de educación general, y la mayoría de ellos nunca antes han asistido una clase de filosofía.
El primer día del semestre, trato de darles una idea de lo que va la filosofía de la ciencia. Comienzo por explicarles que la filosofía aborda cuestiones que no pueden resolverse solo con los hechos, y que la filosofía de la ciencia es la aplicación de este enfoque al campo de la ciencia. Después de esto, explico algunos conceptos que serán centrales para el curso: inducción, pruebas y método en la investigación científica. Les digo que la ciencia procede por inducción, las práctica de recurrir a observaciones pasadas para hacer afirmaciones generales sobre lo que aún no se ha observado, pero que los filósofos consideran que la inducción está inadecuadamente justificada y, por lo tanto, es problemática para la ciencia. Luego me refiero a la dificultad de decidir qué prueba se ajusta a cada hipótesis de manera única, y por qué es vital para cualquier investigación científica tener esto claro. Les hago saber que “el método científico” no es singular y directo, y que existen disputas básicas sobre cómo debería ser la metodología científica. Por último, hago hincapié en que, aunque estos temas son “filosóficos”, sin embargo tienen consecuencias reales sobre cómo se hace ciencia.
En este punto, a menudo me hacen preguntas como: “¿Cuáles son sus credenciales?””¿A qué universidad asistió?” y “¿Es usted una científica?”
Tal vez hacen estas preguntas porque, como filósofa de extracción jamaicana, encarno un grupo de identidades poco común, y sienten curiosidad por mí. Estoy segura de que eso es en parte así, pero creo que hay más, porque he observado un patrón similar en un curso de filosofía de la ciencia impartido por un profesor más estereotípico. Como estudiante de posgrado en la Universidad de Cornell en Nueva York, trabajé como profesora asistente en un curso sobre la naturaleza humana y la evolución. El profesor que lo impartía daba una impresión física muy diferente a la mía. Era blanco, varón, barbudo y de unos 60 años: la imagen misma de la autoridad académica. Pero los estudiantes eran escépticos sobre sus puntos de vista sobre la ciencia, porque, como algunos decían, desaprobantes: “No es un científico”.
Creo que estas respuestas tienen que ver con dudas sobre el valor de la filosofía en comparación con el de la ciencia. No es de extrañar que algunos de mis alumnos duden de que los filósofos tengan algo útil que decir acerca de la ciencia. Son conscientes de que científicos prominentes han declarado públicamente que la filosofía es irrelevante para la ciencia, si no completamente inútil y anacrónica. Saben que la educación STEM (ciencia, tecnología, ingeniería y matemáticas, por sus siglas en inglés) tiene una importancia mucho mayor que cualquier cosa que las humanidades puedan ofrecer.
Muchos de los jóvenes que asisten a mis clases piensan que la filosofía es una disciplina confusa que solo se ocupa de cuestiones de opinión, mientras que la ciencia se dedica al descubrimiento de hechos, a proporcionar pruebas y la difusión de verdades objetivas. Además, muchos de ellos creen que los científicos pueden responder a las preguntas filosóficas, pero los filósofos no tienen nada que aportar a las científicas.
¿Por qué los estudiantes universitarios tratan tan a menudo a la filosofía como completamente distinta y subordinada a la ciencia? En mi experiencia, destacan cuatro razones.
Una tiene que ver con la falta de conciencia histórica. Los estudiantes universitarios tienden a pensar que las divisiones departamentales reflejan divisiones precisas en el mundo, por lo que no pueden darse cuenta de que la filosofía y la ciencia, así como la supuesta división entre ellas, son creaciones dinámicas humanas. Algunos de los temas que ahora se etiquetan como “ciencia” en algún momento estuvieron bajo encabezados diferentes. La física, la más segura de las ciencias, estuvo una vez el ámbito de la “filosofía natural”. Y la música correspondía naturalmente a la facultad de matemáticas. El alcance de la ciencia se ha reducido y ampliado, dependiendo de la época y el lugar y los contextos culturales donde se practicó.
Otra razón tiene que ver con los resultados concretos. La ciencia resuelve problemas del mundo real. Nos da tecnología: cosas que podemos tocar, ver y usar. Nos da vacunas, cultivos transgénicos y analgésicos. La filosofía no parece, para los estudiantes, tener elementos tangibles que mostrar. Pero, por el contrario, los tangibles filosóficos son muchos: los filosóficos experimentos mentales de Albert Einstein hicieron posible la Cassini. La lógica de Aristóteles es la base de la informática, que nos dio ordenadores portátiles y teléfonos inteligentes. Y el trabajo de los filósofos sobre el problema mente-cuerpo preparó el terreno para el surgimiento de la neuropsicología y, por lo tanto, de la tecnología de imagenes del encéfalo. La filosofía siempre ha estado trabajando silenciosamente a al sombra de la ciencia.
Una tercera razón tiene que ver con las preocupaciones sobre la verdad, la objetividad y el sesgo. La ciencia, insisten los estudiantes, es puramente objetiva, y cualquiera que desafíe esa visión debe estar equivocado. No se considera que una persona sea objetiva si aborda su investigación con un conjunto de supuestos previos. Por contra, sería “ideológica”. Pero todos somos “parciales” y nuestros prejuicios alimentan el trabajo creativo de la ciencia. Este problema puede ser difícil de abordar, ya que la concepción ingenua de la objetividad está muy arraigada en la imagen popular de lo que es la ciencia. Para abordarlo, invito a los estudiantes a mirar algo cercano sin ningún prejuicio. Luego les pido que me digan lo que ven. Se paran … y luego reconocen que no pueden interpretar sus experiencias sin recurrir a ideas anteriores. Una vez que se dan cuenta de esto, la idea de que puede ser apropiado hacer preguntas sobre la objetividad en la ciencia deja de ser tan extraña.
La cuarta fuente de incomodidad para los estudiantes proviene de lo que ellos consideran que es la educación científica. Una tiene la impresión de que piensan que la ciencia consiste principalmente en enumerar las cosas que existen -los “hechos” – y que la educación científica es enseñarles cuáles son estos hechos. Yo no respondo a estas expectativas. Pero como filósofa, me preocupa principalmente cómo se seleccionan e interpretan estos hechos, por qué algunos se consideran más importantes que otros, las formas en que los hechos están empapados de prejuicios, y así sucesivamente.
Los estudiantes a menudo responden a estas cuestiones declarando con impaciencia que los hechos son hechos. Pero decir que una cosa es idéntica a sí misma no es decir nada interesante acerca de ella. Lo que los estudiantes quieren decir con “los hechos son hechos” es que una vez que tenemos “los hechos” no hay lugar para la interpretación o el desacuerdo.
¿Por qué piensan de esta manera? No es porque esta sea la forma en que se practica la ciencia sino, más bien, porque así es como normalmente se enseña la ciencia. Hay una cantidad abrumadora de hechos y procedimientos que los estudiantes deben dominar para llegar a ser competentes científicamente, y solo tienen un tiempo limitado para aprenderlos. Los científicos deben diseñar sus cursos para mantenerse al día con un conocimiento empírico en rápida expansión, y no tienen el placer de dedicar horas de clase a preguntas que probablemente no están capacitados para abordar. La consecuencia involuntaria es que los estudiantes a menudo salen de sus clases sin darse cuenta de que las preguntas filosóficas son relevantes para la teoría y la práctica científica.
Pero las cosas no tienen por qué ser así. Si se establece la plataforma educativa adecuada, los filósofos como yo no tendrán que trabajar a contracorriente para convencer a nuestros estudiantes de que tenemos algo importante que decir acerca de la ciencia. Para esto necesitamos la ayuda de nuestros colegas científicos, a quienes los estudiantes ven como los únicos proveedores legítimos de conocimiento científico. Propongo una división explícita del trabajo. Nuestros colegas científicos deberían continuar enseñando los fundamentos de la ciencia, pero pueden ayudar dejando claro a sus alumnos que la ciencia está repleta de importantes cuestiones conceptuales, interpretativas, metodológicas y éticas que los filósofos están en una posición única para abordar, y que lejos de ser irrelevantes para la ciencia, los asuntos filosóficos se encuentran en su núcleo.
Sobre el autor: Subrena E. Smith es profesora ayudante de filosofía en la Universidad de New Hampshire (Estados Unidos).
Texto traducido y adaptado por César Tomé López a partir del original publicado por Aeon el 13 de noviembre de 2017 bajo una licencia Creative Commons (CC BY-ND 4.0).
![]()
El artículo Por qué la filosofía es tan importante para la educación científica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La importancia de la educación científica, por Juan Carlos López
- La educación no es la materia prima de la mano de obra
- Heinrich Rohrer: Priorizar la educación para garantizar la calidad, por P. M. Etxenike y J. M. Pitarke
El Rubius hace un vídeo de química y la lía parda

El último vídeo que el Rubius subió a su canal ha superado los 6 millones de reproducciones en sólo cuatro días. Se trata de la primera entrega de lo que será una serie de vídeos sobre experimentos científicos. Y para experimentos científicos chulos, están las reacciones químicas redox. Eso es lo que hace el Rubius durante todo el vídeo, diferentes versiones de la reacción redox conocida como «pasta de dientes de elefante».
Es una reacción química muy atractiva que muchos profesores de ciencias y divulgadores hemos hecho más de una vez. Es un triunfo asegurado. Existen varias versiones, pero el resultado de todas ellas es que el agua oxigenada se oxida. No es una redundancia. Cuando el agua oxigenada se oxida, libera oxígeno gaseoso.
El agua oxigenada se denomina peróxido de hidrógeno o, como también la llama el Rubius, «esta vaina loca». El agua oxigenada que normalmente tenemos en casa, la de uso sanitario, suele ser peróxido de hidrógeno disuelto en agua con una concentración del 3-4%. El agua oxigenada que el Rubius utiliza para este experimento está más concentrada, es peróxido de hidrógeno al 12%. Es imprescindible que el agua oxigenada tenga una concentración superior al 9% para que el experimento sea vistoso. Por eso hay que tener especial precaución al manipularla. El Rubius se pone guantes y gafas protectoras, siguiendo las advertencias de seguridad del envase. El pictograma de peligrosidad que figura en la etiqueta es el de sustancia corrosiva. Efectivamente el peróxido de hidrógeno es capaz de producir quemaduras en la piel y en los ojos.
El agua oxigenada se descompone de forma natural en agua y oxígeno, pero esto sucede tan lentamente que no se percibe. Para favorecer esta reacción se pueden utilizar varios métodos. O bien añadir una sustancia que sirva de catalizador, es decir, una sustancia que acelera esa descomposición. O bien añadir una sustancia oxidante (con un potencial de oxidación mayor que el del agua oxigenada).
Como catalizador se suele emplear un yoduro (normalmente la sal yoduro potásico). El yoduro reacciona con el peróxido de hidrógeno liberando agua e hipoyodito, y el hipoyodito reacciona con el peróxido de hidrógeno liberando oxígeno y volviendo a su estado inicial de yoduro. Es decir, que el yoduro empieza y termina la reacción de la misma manera, mientras que el peróxido de hidrógeno se transforma en agua y oxígeno. Cuando una sustancia es capaz de provocar una reacción química sin alterarse, se denomina catalizador. Si la sustancia cambia, ya no sería un catalizador, sino un reactivo.
El Rubius no utiliza un catalizador de yoduro, sino que utiliza otra sustancia como reactivo llamada permanganato potásico. El permanganato potásico es un fuerte oxidante de un intenso color violeta. En contacto con el peróxido de hidrógeno consigue oxidarlo a agua y oxígeno. Por su parte, el permanganato potásico sufre una reducción, la reacción inversa a la oxidación. Esta reducción se aprecia en el cambio de color de violeta a marrón.
Cuando una sustancia se oxida ocurre a costa de que otra sustancia de reduzca. Por eso a este tipo de reacciones químicas las llamamos reacciones redox.
En el envase del permanganato que el Rubius muestra a cámara figuran dos pictogramas de peligro. El primero indica que se trata de una sustancia comburente, es decir, que puede provocar o agravar un incendio o explosión. El segundo pictograma, el que llama más la atención del Rubius es el que contiene un signo de exclamación. Él lo llama «hazardous, hazard», que significa peligroso, peligro. Efectivamente eso es lo que significa ese pictograma: peligroso para la salud. La etiqueta también incluye como advertencias de seguridad el uso de guantes y gafas. El permanganato puede provocar quemaduras en los ojos y en la piel.

En la primera parte del experimento, el Rubius hecha una cucharada de permanganato en una botella de vidrio a la que llama «instrumento 100tífiko». Sobre este polvo de permanganato vierte directamente un vaso de peróxido de hidrógeno. El Rubius dice «No sé si es buena idea, así que me voy a apartar un poco». Instantáneamente sale disparado un chorro de gas de la botella. Por suerte para el Rubius ese gas no es peligroso, ya que se trata de oxígeno y vapor de agua. «Esto no lo había hecho antes. No sabía que iba a reaccionar así». Aquí es cuando los técnicos en prevención y riesgos laborales se ponen nerviosos.
A continuación, hace un nuevo experimento utilizando unas sustancias más: agua, jabón y colorante azul. Primero hecha una cucharada de permanganato, añade un poco de agua y agrega un chorro de fairy. Agita la botella hasta que todo esté completamente mezclado y el permanganato disuelto. En las paredes internas del cuello de la botella hecha un poco de colorante azul. «Espero que esto funcione. No sé qué coño va a pasar. Sólo he visto tutoriales en Youtube, sinceramente».
Sobre esta mezcla añade un vaso de peróxido de hidrógeno. Inmediatamente sale disparada una columna de espuma blanca. Esta espuma va arrastrando parte del permanganato, que la tiñe de rosa y marrón, y parte del colorante, que la tiñe de azul. El Rubius exclama «¡Loco, qué bonito!».

La reacción que ha ocurrido es la misma que la anterior, una reacción redox en la que el peróxido de hidrógeno se oxida a agua y oxígeno, y el permanganato se reduce. Lo que sucede esta vez es que el gas oxígeno que se forma se queda atrapado en la disolución jabonosa, formando una gran cantidad de espuma. Cuanto más espumante contenga el jabón (ya sea fairy o cualquier otro jabón), saldrá más cantidad de espuma y de mayor densidad.
«Según Google no pasaría nada si lo toco, pero nunca os fieis de Google». Aun así, el Rubius toca la espuma. Dice que está calentita y que le recuerda al puré de patatas.
A continuación, el Rubius repite el experimento a mayor escala en la terraza de su casa. Os animo a verlo. Pero antes de terminar, como química debo hacer una advertencia de seguridad para que nadie la líe parda: por muchos tutoriales de Youtube que hayas visto, si no sabes nada de química jamás hagas un experimento con sustancias peligrosas. Porque como dice el Rubius, “no sabes qué coño va a pasar”.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo El Rubius hace un vídeo de química y la lía parda se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El microondas es seguro, lo que hace es calentar
- Los cimientos de la química neumática al estilo van Helmont (y 3)
- El lenguaje de la química
¿Y si la Gran Oxidación tuvo un origen geológico?

Si uno se interesa por el origen de la vida en Tierra tarde o temprano se encuentra con el fenómeno conocido como la Gran Oxidación, hace unos 2400 millones de años. La Gran Oxidación fue un cambio radical en la atmósfera de la Tierra en el que ésta empezó a contener cantidades importantes de oxígeno o, como dicen los químicos, pasó de ser reductora a oxidante. La vida, tal y como la conocemos hoy día, es consecuencia de la adaptación a esta circunstancia y habrían sido otras formas de vida, las cianobacterias, las que hace 2800 millones de años habrían provocado ese cambio atmosférico al ser las primeras criaturas fotosintéticas capaces de producir oxígeno molecular.
Pero, ¿y si esto, que está en cualquier libro de texto, no hubiera sido así? Un equipo internacional encabezado por Ho-kwang “Dave” Mao, de la Carnegie Institution (EE.UU.), propone otra idea basada en un fenómeno puramente geológico. En este fenómeno solo interviene el agua el hierro y las altas presiones y temperaturas del interior de la Tierra.
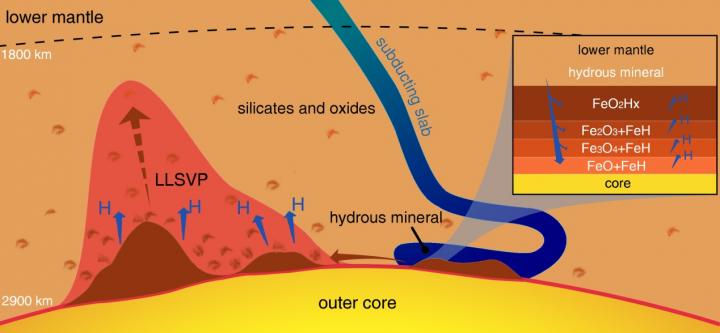
Cuando la acción de la tectónica de placas lleva minerales que contienen agua hacia el interior del planeta hasta encontrarse con el núcleo de hierro de la Tierra, las condiciones extremas de presión y temperatura hacen que el hierro tome átomos de oxígeno de las moléculas de agua y libere los átomos de hidrógeno. El hidrógeno escapa a la superficie, pero el oxígeno queda atrapado formando dióxido de hierro cristalino, FeO2, que solo puede existir a estas presiones y temperaturas tan intensas.
Utilizando cálculos teóricos y experimentos de laboratorio para recrear el entorno del límite núcleo-manto, el equipo determinó que el dióxido de hierro puede crearse efectivamente, utilizando para ello una celda de yunque de diamante calentada por láser para exponer los materiales a entre 950 y 1 millón de veces la presión atmosférica normal y 2000 ºC de temperatura.
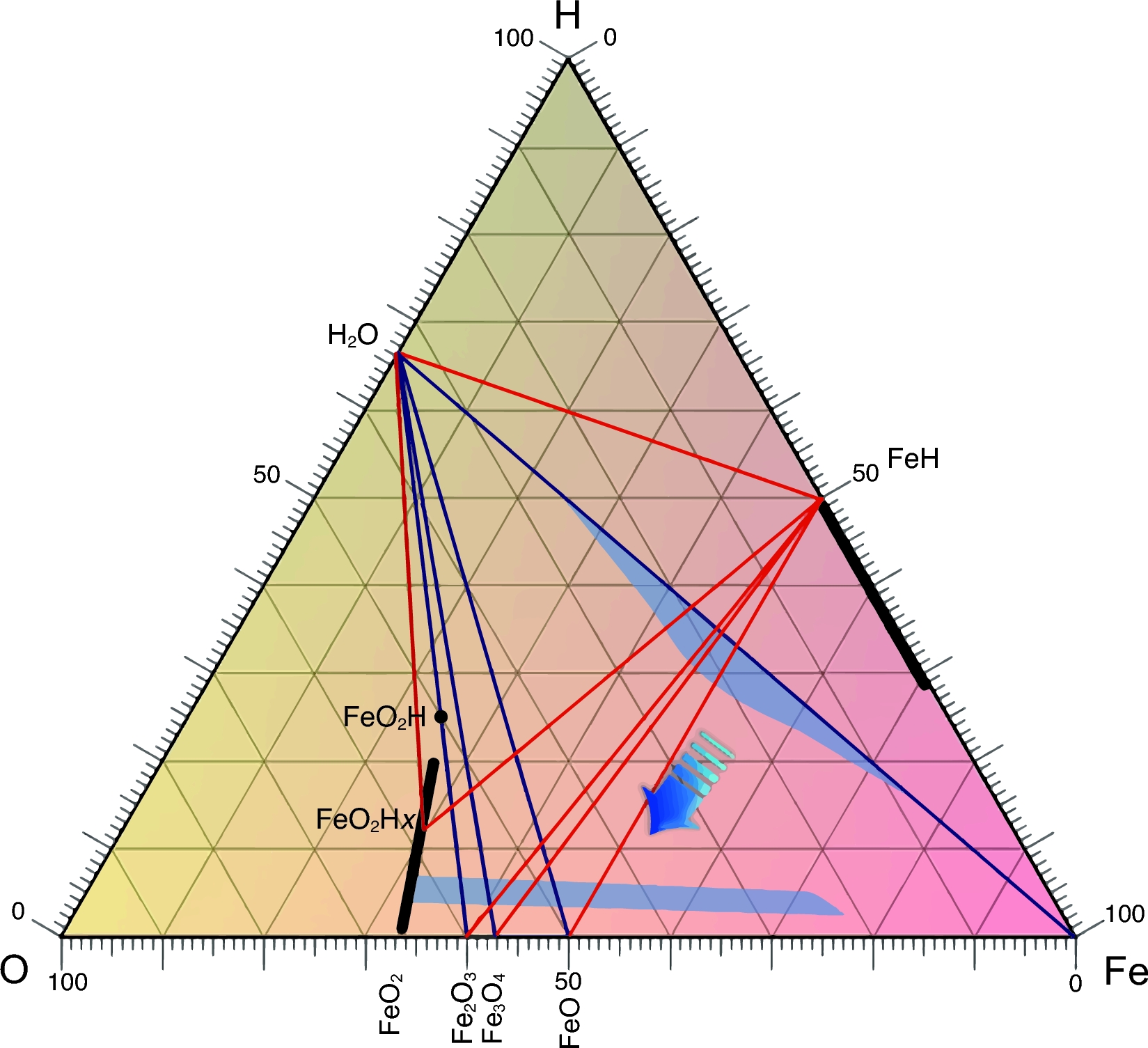
Los investigadores calculan que se podrían estar transportando 300 millones de toneladas de agua hasta el hierro del núcleo y generando enormes rocas de dióxido de hierro cada año. Estas rocas extremadamente ricas en oxígeno podrían acumularse año tras año por encima del núcleo, creciendo hasta alcanzar tamaños colosales, como los de un continente. Un acontecimiento geológico que calentara estas rocas de dióxido de hierro podría causar una erupción masiva, liberando repentinamente una gran cantidad de oxígeno a la superficie.
Los autores plantean la hipótesis de que si una explosión de oxígeno de este tipo podría inyectar una gran cantidad del gas en la atmósfera de la Tierra, nada impediría que esta fuese la causa de la Gran Oxidación, impulsora de la vida dependiente del oxígeno que conocemos.
Este descubrimiento puede tener muchas más consecuencias para la geoquímica. Esta hidrólisis, el término que los químicos usamos para referirnos a la rotura de la molécula de agua, a alta presión y tempertaura afectaría a la geoquímica desde las profundidades de la Tierra hasta, como hemos visto, la atmósfera. Hay que revisar muchas teorías.
Referencia:
Ho-Kwang Mao et al (2017) When water meets iron at Earth’s core–mantle boundary National Science Review doi: 10.1093/nsr/nwx109
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo ¿Y si la Gran Oxidación tuvo un origen geológico? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Otra pieza en el puzle de la fotosíntesis
- Un origen químico de la vida elegantemente simple
- Un mecanismo que explica el origen de la homoquiralidad biológica
El disputado voto del Señor Condorcet (I)
En nuestra sociedad hay innumerables ocasiones en las que un colectivo de personas debe tomar decisiones sobre diferentes alternativas que se le plantean, como quién debe ser la persona que preside una nación, quien el candidato o candidata de un partido político, dónde se celebrarán los siguientes juegos olímpicos, cuál ha sido la mejor película, o libro, del año, qué empresa debe contratar una comunidad de vecinos para arreglar la fachada de su casa o qué política debe de seguir determinado gobierno, partido político o empresa, y muchas otras cuestiones similares.
Ante lo cual se nos plantea la cuestión trascendental de cómo elegir la propuesta que mejor represente las preferencias de los individuos del colectivo, es decir, cómo convertir las preferencias individuales en una preferencia colectiva, de la mejor forma posible.

Portada del libro “El disputado voto del Señor Cayo” (Destino, 1978), del escritor Miguel Delibes, y cartel de la película homónima de 1986 del director Antonio Giménez-Rico
Aunque pueda parecer lo contrario, ya que las votaciones son algo habitual en nuestra vida cotidiana, la cuestión no es precisamente sencilla. Para ilustrar esto vamos a mostrar dos ejemplos clásicos interesantes.
El primero es la paradoja de Condorcet. Marie-Jean-Antoine
Nicolás de Caritat, Marqués de Condorcet (1743-1794) fue un filósofo, matemático y político francés, que tuvo un papel relevante durante la Revolución francesa.

Marie-Jean-Antoine Nicolás de Caritat, Marqués de Condorcet (1743-1794)
Supongamos que se está decidiendo cuál de las tres ciudades, Bilbao, Donosti y Gasteiz, va a ser la capital del País Vasco, y se designa una comisión de expertos internacional, formada por 12 personas, para tal fin.
Tras un tiempo de estudio del problema y las consiguientes deliberaciones llega la votación, obteniéndose un empate entre las tres candidaturas, con cuatro votos cada una. Ante lo cual, se pide a los expertos que indiquen su orden de preferencia entre las tres ciudades, obteniéndose las siguientes preferencias:
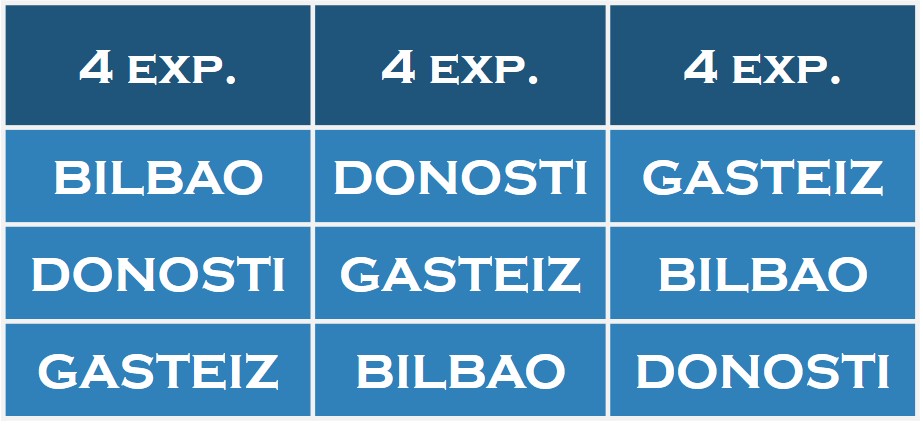
El alcalde de Bilbao que está en la reunión, como representante de la capital de Bizkaia, toma la palabra y dice lo siguiente:
“Si comparamos solamente las ciudades de Bilbao y Donosti observaremos que 8 de los 12 expertos prefieren Bilbao a Donosti. Por otra parte, si comparamos ahora Donosti y Gasteiz, observaremos que, de nuevo, 8 de los 12 expertos prefieren Donosti a Gasteiz. En conclusión, los expertos prefieren Bilbao a Donosti, y Donosti a Gasteiz, por lo tanto, la ciudad preferida es Bilbao, que debería ser la capital del País Vasco.”
Pero entonces, el alcalde de Vitoria-Gasteiz, que también está presente en la reunión, manifiesta lo siguiente:
“Querido alcalde de Bilbao, quizás antes de tomar ninguna decisión deberíamos tener en cuenta también la comparación entre Bilbao y Gasteiz, y veremos que la mayoría de los expertos, de nuevo 8 de 12, prefiere Gasteiz a Bilbao. En consecuencia, vuestro razonamiento queda así anulado.”
Como podemos ver en este ejemplo, se ha producido una preferencia cíclica, cuando se comparan las candidaturas dos a dos la mayoría de los expertos prefiere Bilbao a Donosti, Donosti a Gasteiz, y Gasteiz a Bilbao, por lo que no podemos determinar cuál es la ciudad preferida por los expertos, y por tanto, la capital del País Vasco. Esto es lo que se conoce con el nombre de paradoja de Condorcet.

Pero vayamos con un segundo ejemplo, más esclarecedor aún. Imaginemos que hay que elegir la sede de los siguientes Juegos Olímpicos, y que las ciudades candidatas a ser la sede de los mismos son Barcelona (BCN), Johannesburgo (JNB), Los Ángeles (LAX), Sydney (SYD) y Tokio (TYO).
El COI – Comité Olímpico Internacional, que es el “organismo encargado de promover el olimpismo en el mundo y coordinar las actividades del Movimiento Olímpico”, es también quien se encarga de la elección de las sedes de los Juegos Olímpicos.
Supongamos que el número de compromisarios del COI que pueden tomar parte en la votación para la elección de la sede de las Olimpiadas es 55 (aunque en realidad son del orden de cien), y que para conocer mejor la opinión personal de cada uno de los compromisarios respecto al problema de la elección de la sede de los JJ. OO., se les pide en esta ocasión que ordenen las ciudades candidatas en función de sus preferencias, primero la ciudad que piensan que debería ser la sede, después su segunda opción, seguida de la tercera, la cuarta y finalmente, la última opción. E imaginemos que el resultado de las votaciones ha sido el siguiente:
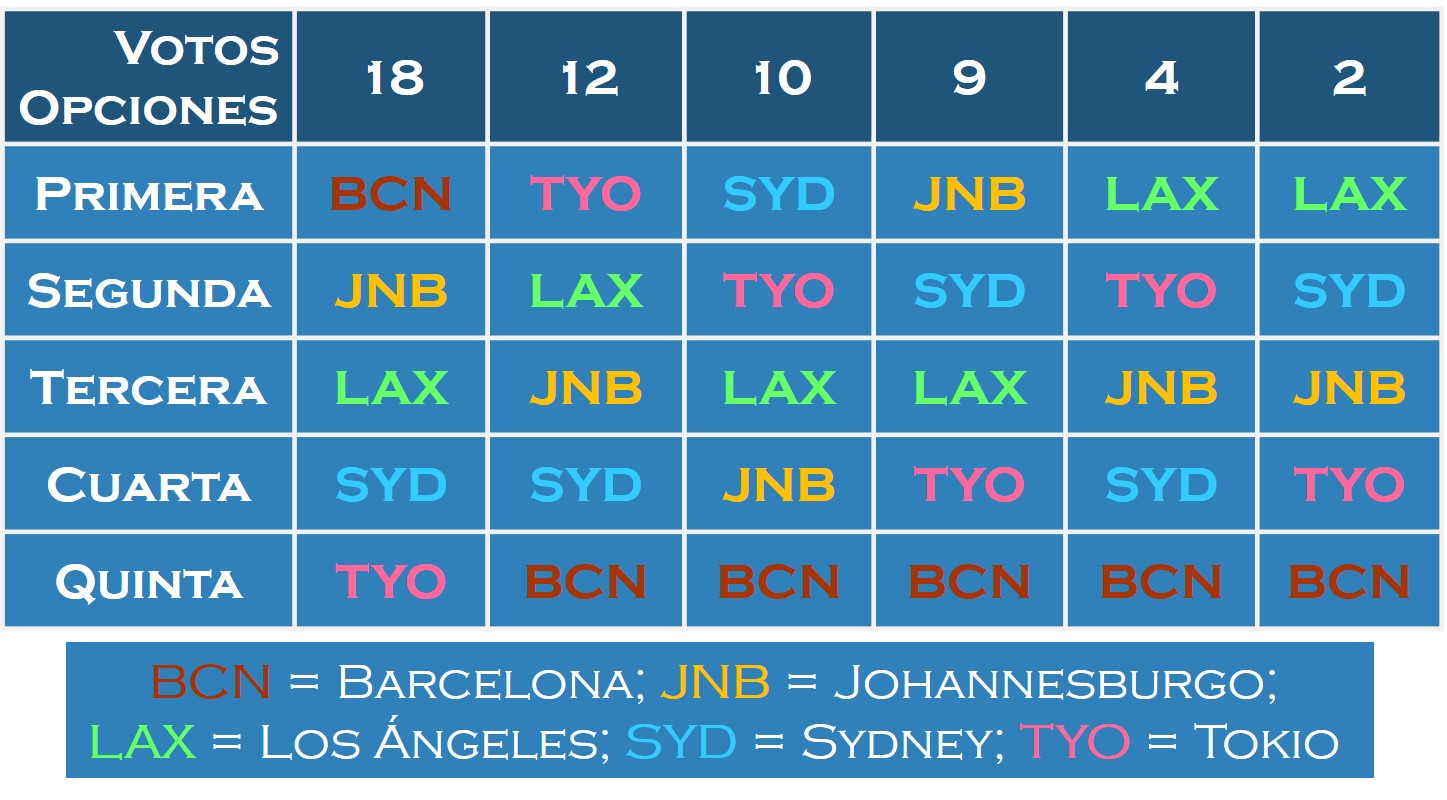
Por ejemplo, 18 de los compromisarios han ordenado las ciudades de la siguiente forma: Barcelona es su opción preferida, su segunda opción es Johannesburgo, la tercera es Los Ángeles, seguida de Sydney y por último, Tokio. Y de forma similar, como se indica en la tabla anterior, el resto de compromisarios.
Una vez que tenemos fijadas las preferencias individuales de los miembros del Comité Olímpico Internacional, debemos de decidir cuál es la ciudad ganadora, es decir, establecer la preferencia colectiva.
A. Método de votación “mayoría simple”.
Este método, conocido también como “método de pluralidad”, es el método de votación más antiguo y sencillo que existe. Cada votante expresa su preferencia individual votando por su candidatura preferida y al final se cuentan los votos que recibe cada una de las opciones que se han presentado, y la que ha obtenido más apoyos, más votos, es la ganadora.
Este sencillo sistema es uno de los más utilizados, sobre todo en grandes votaciones. Por ejemplo, es el sistema utilizado en las elecciones presidenciales de Canadá, EE.UU., México, Venezuela, Palestina, Panamá o Ruanda, entre muchos otros países. Así mismo, también suele ser el sistema utilizado en las elecciones primarias de muchos partidos políticos.
Papeleta electoral general de las elecciones de las elecciones de 2016 a Presidente y Vice-presidente de los Estados Unidos de América
Entre los inconvenientes de este sistema de votación está el que puede ganar una candidatura para nada deseada por la mayoría de las personas del colectivo de votantes, si hay varias opciones similares que hacen que el voto se divida dentro de esas opciones parecidas. Es un sistema que permite desarrollar estrategias para manipular el resultado, por ejemplo, si hay dos opciones de voto y quien convoca las elecciones teme que pierda su opción, puede plantear dividir la opción contraria en dos opciones parecidas que se deriven de ella, para que se divida el voto. Por ejemplo, en las elecciones para la salida de Gran Bretaña de la Unión Europea, Brexit, donde había dos opciones SI (salir de la UE) y NO (permanecer), podría haber tenido tres opciones del siguiente estilo:
A. salir de la UE, manteniendo una alianza estratégica con ella;
B. salir de la UE, rompiendo toda relación;
C. permanecer en la UE.
Quizás así el voto del SI se podría haber dividido entre las opciones A y B. Es un ejemplo simple, pero nos sirve para ilustrar la idea.
Utilizando este sistema de votación, el de la mayoría simple, los resultados para la elección de la sede de los siguientes Juegos Olímpicos habrían sido estos:

Es decir, Barcelona (BCN), 18 votos; Tokio (TYO), 12 votos; Sydney (SYD), 10 votos; Johannesburgo (JNB), 9 votos; y Los Ángeles (LAX), 6 votos. Por lo tanto, la ciudad ganadora, y en consecuencia, sede de los siguientes JJ.OO. habría sido

B. Método de votación “segunda vuelta”.
Otro de los métodos de votación utilizado en muchas elecciones presidenciales, como en Francia, Brasil, Portugal, Polonia, Rusia, Colombia, Argentina, Chile, Perú o Indonesia, es el método de segunda vuelta, también llamado “balotaje” (que viene del vocablo francés ballottage).
Este consiste en lo siguiente. Si tras la primera votación, en la que cada persona vota por su candidatura preferida como en el sistema de mayoría simple, alguna de las candidaturas ha alcanzado la mayoría absoluta, es decir, más del 50% de los votos, entonces es la ganadora. En caso contrario, las dos opciones más votadas pasan a la segunda vuelta, produciéndose entonces una votación únicamente entre estas dos opciones.
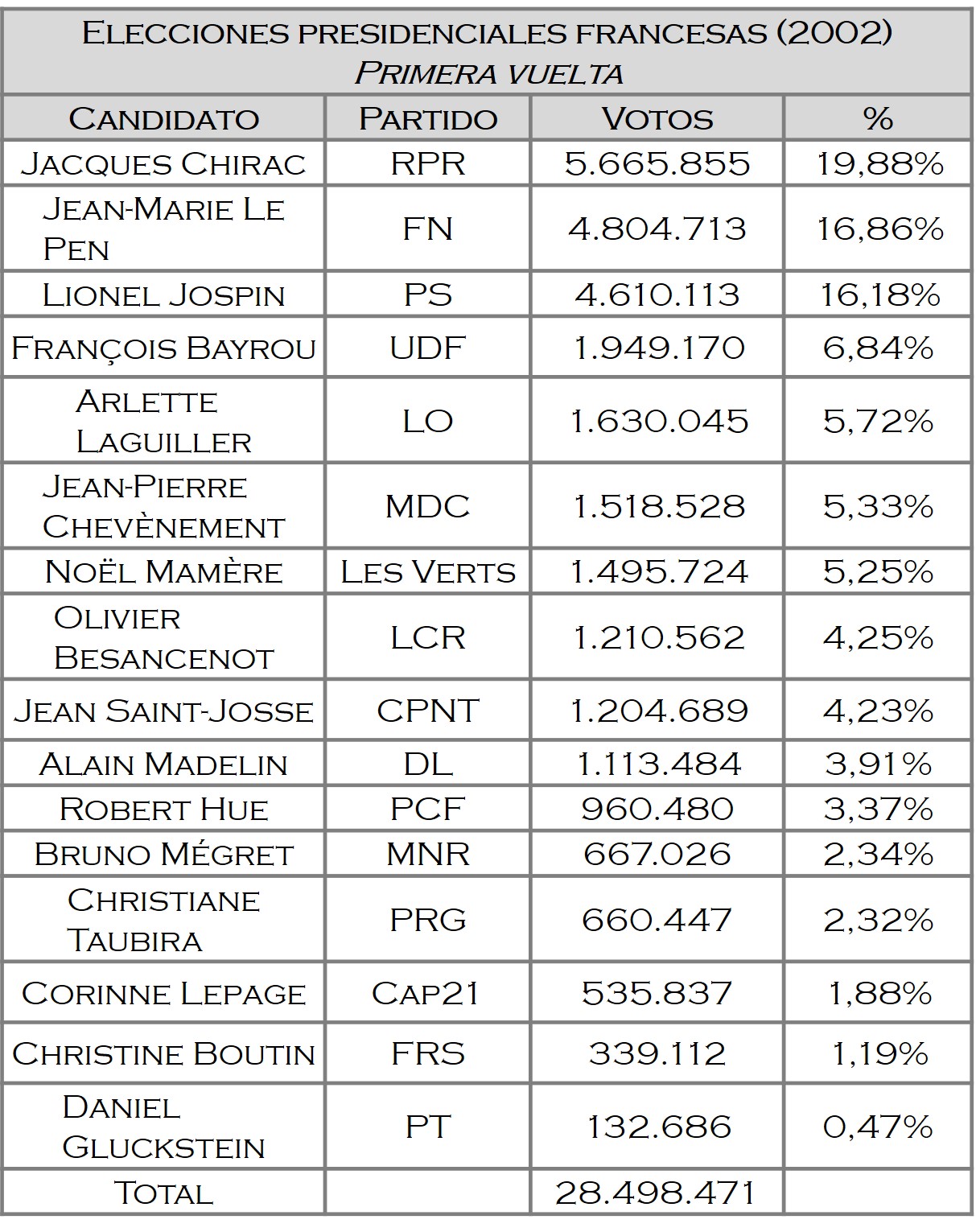
Veamos un caso real, las elecciones francesas de 2002, en las cuales había 16 candidatos a la presidencia de la República Francesa. En la primera vuelta los resultados fueron:
Los dos candidatos que pasaron a la segunda vuelta fueron Jacques Chirac (del RPR – Agrupación por la República, partido conservador francés neo-gaullista) y Jean-Marie Le Pen (del FN – Frente Nacional, partido político de extrema derecha francés). Jean-Marie Le Pen dejó fuera de la segunda vuelta, por un pequeño porcentaje, al socialista Lionel Jospin, que era a priori el candidato natural para pasar a la segunda vuelta.
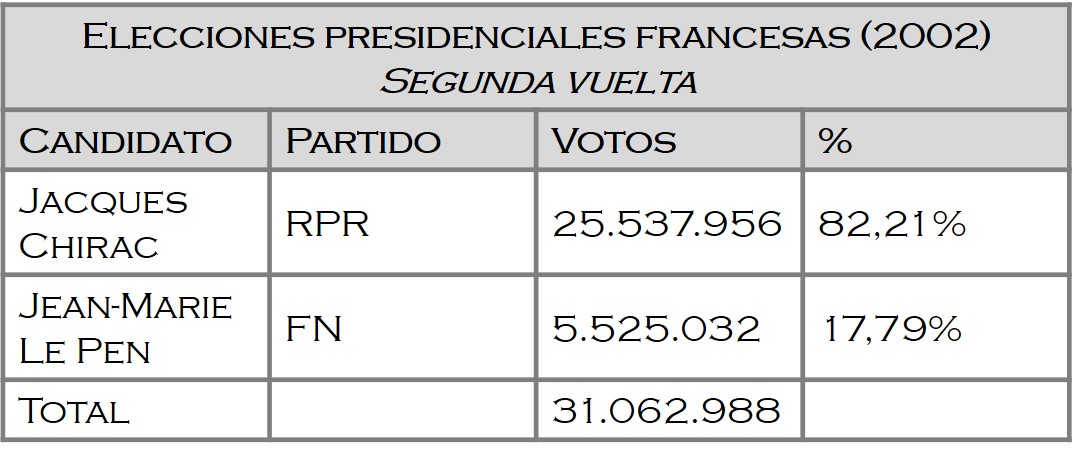
En la segunda vuelta el resultado de la votación entre Jacques Chirac y Jean-Marie Le Pen fue
con un triunfo aplastante de Jacques Chirac, mientras que Jean-Marie Le Pen no obtuvo un incremento significativo en el porcentaje de votos.
Volviendo a nuestro ejemplo, si observamos los resultados de la votación por parte de los miembros del COI, las dos candidaturas más votadas han sido Barcelona, con 18 votos –que son el 32% de los votos– y Tokio, con 12 votos –que son el 21,8% de los votos–. Como ninguna de las candidaturas ha obtenido mayoría absoluta, esas dos ciudades, Barcelona y Tokio, pasan a la segunda vuelta. Y se produce por tanto una segunda votación.
En la vida real, entre la primera y la segunda votación pueden producirse cambios en la opinión de los votantes. Los motivos pueden ser muy diversos. Por ejemplo, puede que haya votantes que estén desencantados o cansados de las elecciones, o puede que las candidaturas que han pasado a la segunda vuelta no tengan el atractivo suficiente para algunos votantes, o que algunos votantes modifiquen su intención de voto en la segunda vuelta por sugerencia de quienes apoyaban la candidatura por la que habían votado en la primera.
Es decir, en la vida real la cuestión es más complicada que en este ejemplo, donde ya tenemos la intención de voto en la segunda vuelta marcada por las preferencias de la votación realizada. En cualquier caso, si miramos a la tabla de preferencias anterior y vemos cuales son las preferencias de los compromisarios en la votación entre Barcelona y Tokio (en la siguiente tabla hemos dejado solamente las dos ciudades) …
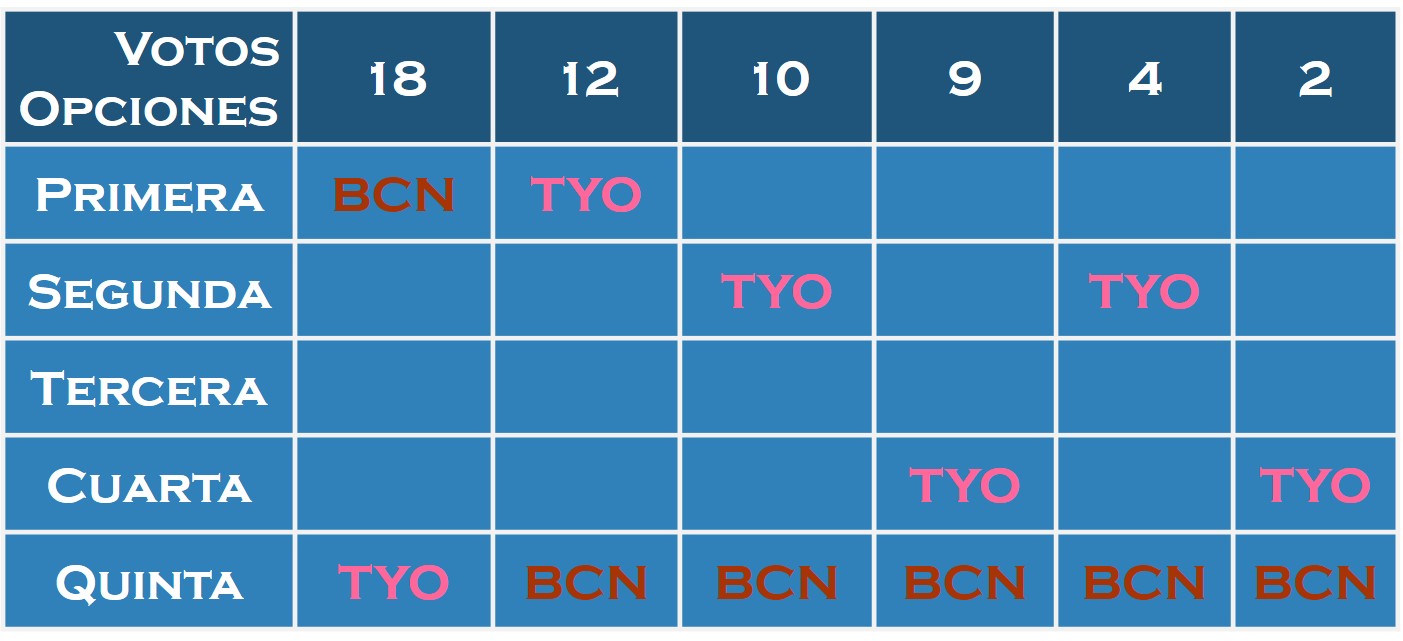
… observamos que el resultado de la segunda vuelta será: Barcelona, 18 votos, y Tokio, 37 votos, puesto que todos los compromisarios que no votaron por Barcelona en la primera vuelta, prefieren Tokio a Barcelona. La ciudad ganadora y, en consecuencia, sede de los siguientes JJ.OO. será

C. Método de votación “eliminación de los perdedores”.
Este es el sistema que utiliza realmente el Comité Olímpico Internacional, con la salvedad de que nosotros estamos contando con la intención de voto desde el inicio para determinar lo que votará cada compromisario en las diferentes vueltas que se van a producir, mientras que, en la realidad, entre una votación y la siguiente, cada compromisario puede cambiar de opinión, ya sea de forma libre, con la intención de manipular el resultado a favor de una opción débil e intentando eliminar alguna candidatura rival con posibilidades o como consecuencia del juego político que se desarrolla en esos momentos “entre bastidores”.
El método de “eliminación de los perdedores” consiste en lo siguiente. Cada votante da su voto a la candidatura que piensa que es la mejor de todas, como en las anteriores, pero después del recuento de votos se elimina la candidatura menos votada. Entonces, se produce la segunda ronda, en la que se vota entre todas las candidaturas, menos la que ha sido eliminada, se cuentan los votos y se elimina la candidatura con menos votos. Así se continúa hasta que solamente queda una candidatura, que será la ganadora de la votación.
Por ejemplo, en octubre de 2009 se produjo la elección de la sede de los JJ.OO. de 2016. Las ciudades candidatas fueron Río de Janeiro, Madrid, Tokio y Chicago. En la primera vuelta los resultados de la votación dentro del COI fueron:
Río de Janeiro, 26 votos; Madrid, 28 votos; Tokio, 22 votos; y Chicago, 19 votos.
Por el método de la mayoría simple habría ganado Madrid. Sin embargo, como utilizan el método de la “eliminación del perdedor” se eliminó a Chicago en esa primera ronda. Los resultados de la segunda votación fueron:
Río de Janeiro, 46 votos; Madrid, 29 votos; Tokio, 20 votos .
Observemos que Tokio no solo no subió en votos, sino que perdió dos de los votos de la primera ronda. Pasaron a la siguiente ronda Río de Janeiro y Madrid, donde perdió Madrid por 66 frente a 32 votos.
En nuestro ejemplo, tenemos que los resultados de las votaciones en cada una de las rondas, siguiendo la intención de voto que han manifestado inicialmente (véase el cuadro de arriba), serían…
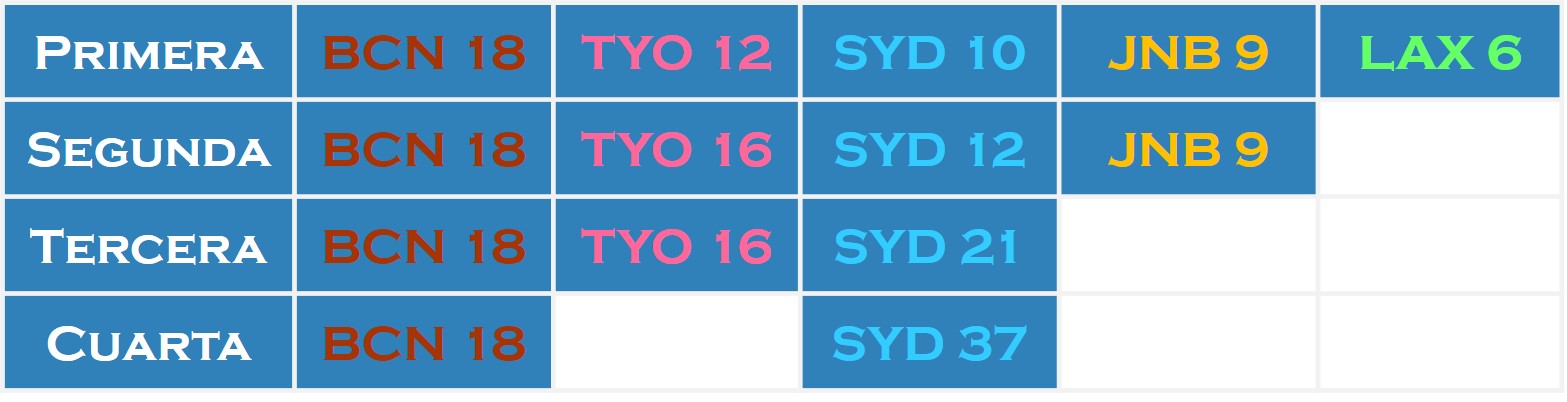
Las ciudades eliminadas en cada ronda serían Los Ángeles, Johannesburgo, Tokio y finalmente Barcelona, quedando como ciudad ganadora y, en consecuencia, sede de los siguientes JJ.OO.

D. Método de votación “recuento de Borda”.
Este sistema de votaciones, propuesto por el matemático, físico, navegante y político francés Jean-Charles de Borda (1733-1799), se utiliza, por ejemplo, en las elecciones primarias de Podemos, en las elecciones presidenciales de Kiribati en el océano Pacífico, o se utilizó también en el proceso de pacificación de Irlanda.
Este método consiste en darle peso a las preferencias de los votantes sobre las candidaturas, mediante la asignación de puntos según el orden de preferencia. De esta forma se prima a las primeras preferencias sobre las últimas.
Así, en nuestra votación para la sede de los JJ.OO. se conceden 5 puntos a la ciudad preferida del votante, 4 puntos a la segunda opción, 3 puntos a la tercera, 2 puntos a la cuarta y 1 punto a la última, como se observa en la imagen.
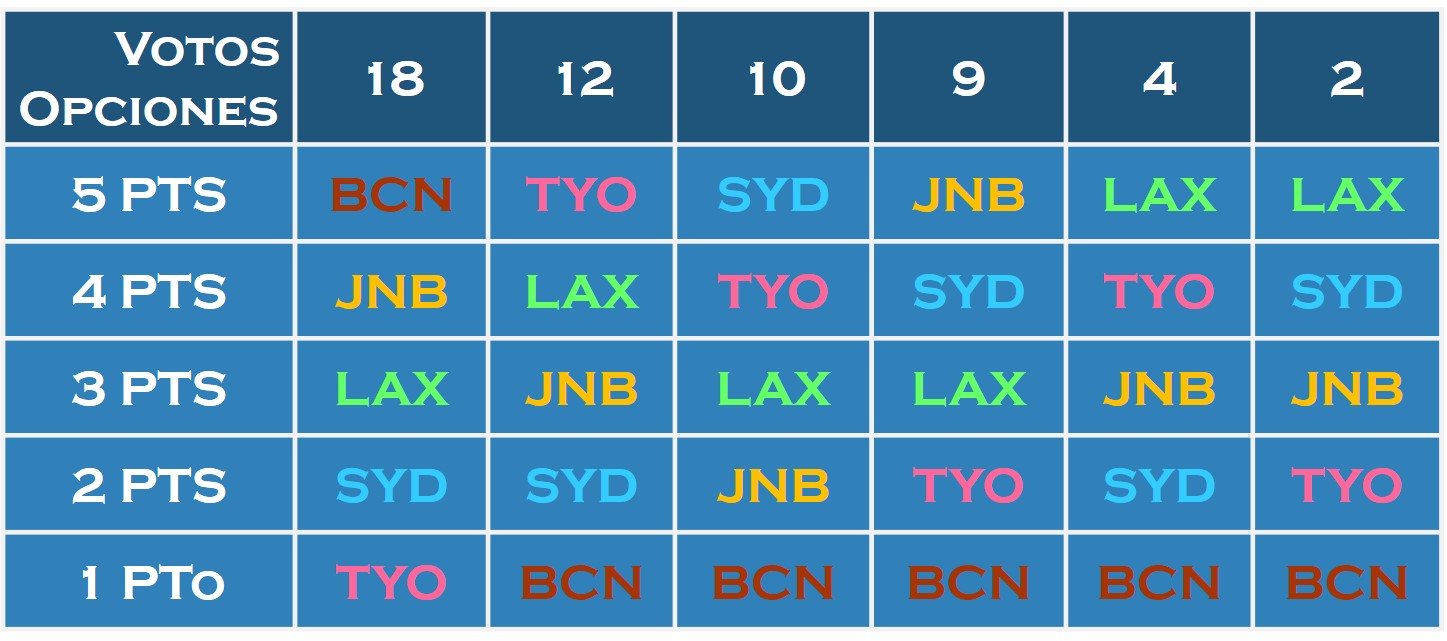
De esta forma, el número de puntos de cada candidatura es:

En consecuencia, la ciudad ganadora y sede de los siguientes JJ.OO. sería

E. Método de votación “de Condorcet”.
El método de Condorcet, como ya se anticipaba en la paradoja que lleva su nombre, es el de los enfrentamientos dos a dos, por parte de todas las candidaturas, es decir, cada candidatura se compara con el resto de candidaturas, y la que “gane” más enfrentamientos gana las elecciones.
En nuestro ejemplo, como tenemos 5 ciudades candidatas a sede de los siguientes juegos olímpicos, el número de enfrentamientos dos a dos será 10. Cada ciudad se enfrenta a cuatro ciudades.
Por ejemplo, si enfrentamos a Los Ángeles y Sydney, el resultado de la votación de los compromisarios si solo votan por una de las dos es (miremos la tabla anterior de preferencias): Los Ángeles, 36 votos; Sydney, 19 votos.
La única ciudad que, en este ejemplo, gana todos sus enfrentamientos es Los Ángeles. En concreto, LAX 28 – JNB 27; LAX 36 – SYD 19; LAX 33 – TYO 22; y LAX 37 – BCN 18. Por lo tanto, la ciudad ganadora de estas elecciones y sede de los siguientes JJ.OO. sería


Cuadro “Voting Line” del artista americano Charly “Carlos” Palmer
Este ejemplo nos ilustra como el ganador de la anterior votación no lo determinan únicamente las preferencias individuales de los votantes, sino también el método de votación elegido. Con unas mismas preferencias individuales (las que hemos recogido en la tabla inicial) se obtiene que cada ciudad candidata podría ganar las elecciones en función del sistema de votación elegido.
Por lo tanto, habrá que tratar de elegir el método de votación que permita determinar la preferencia colectiva que mejor represente las preferencias individuales de los votantes. Este será el tema de nuestra siguiente entrada del Cuaderno de Cultura Científica.
Para terminar, una cita del filósofo, matemático y político francés, Nicolás de Condorcet. Tras la Revolución Francesa, la Asamblea Nacional estuvo trabajando sobre los Derechos del Hombre y del Ciudadano, dejando fuera a las mujeres. Una de las personas que pidió el reconocimiento de los derechos de las mujeres fue precisamente el Marqués de Condorcet.
Quien vota en contra del derecho de otro ser, sean cuales sean su religión, el color de su piel o su sexo, renuncia a los suyos desde ese preciso momento.
“Sobre la admisión de las mujeres al derecho de ciudadanía”
Marqués de Condorcet, 1790
Bibliografía
1.- VV. AA., Las matemáticas en la vida cotidiana, Addison-Wesley/Universidad Autónoma de Madrid, 1999.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El disputado voto del Señor Condorcet (I) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- “La cultura científica o la misteriosa identidad del señor Gauss” por Raúl Ibáñez
- La insoportable levedad del TRES, o sobre la existencia de sistemas numéricos en base 3
- Uno, dos, muchos
Sistemas respiratorios: la emergencia de un doble sistema circulatorio

No todos los animales cuentan con lo que puede considerarse, con propiedad, un sistema circulatorio. Y muchos animales, aunque tienen bomba o bombas de impulsión, tienen sistemas circulatorios abiertos. En los sistemas abiertos la sangre o hemolinfa bombeada se vierte a una amplia cavidad interna a través de un sistema de arterias que se ramifican de forma sucesiva. Luego es recogida por un sistema de venas equivalente al anterior y devuelto a la bomba de impulsión. Los sistemas abiertos ejercen un menor control que los cerrados sobre el flujo de sangre a los diferentes órganos, aunque en cualquier caso las demandas de los tejidos son satisfechas de manera conveniente.
El sistema abierto más complejo que se conoce es el de algunos crustáceos, que alcanzan un desarrollo muy similar al de los sistemas cerrados. El sistema arterial llega hasta el final de las extremidades, la hemolinfa se vierte en pequeños espacios abiertos y de ellos es recogida por unos senos a modo de pequeños canales que la devuelven al corazón, no sin antes pasar por las branquias. Así pues, en estos crustáceos la sangre se oxigena en su trayecto de vuelta a la bomba de impulsión.
Las cosas son diferentes en los animales que tienen sistemas cerrados. Los cefalópodos son los únicos moluscos con sistema cerrado. En estos la sangre también pasa por las branquias antes de alcanzar el corazón sistémico o corazón principal, de donde se distribuye al resto de órganos y tejidos. A diferencia de los crustáceos, los moluscos cefalópodos tienen dos corazones branquiales que bombean la sangre venosa procedente de los tejidos a las branquias. Así se oxigena y se descarga de CO2 antes de llegar al corazón sistémico. Una característica notable de este sistema es que al trabajar con sangre venosa, los corazones auxiliares trabajan en condiciones virtualmente anóxicas, con muy escaso aporte de oxígeno.
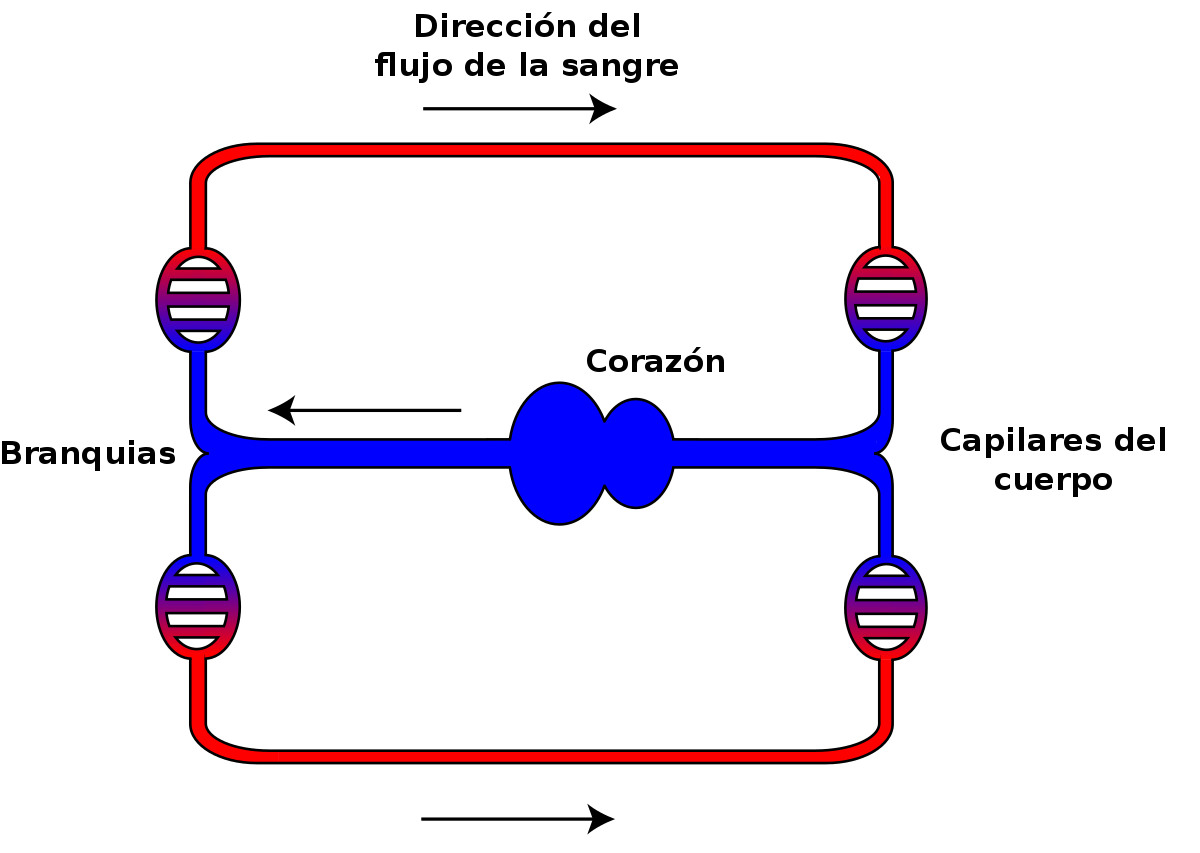
Esquema del sistema circulatorio de los peces. Fuente: Lennert B. / Wikimedia Commons
Los sistemas circulatorios cerrados más desarrollados son los de los vertebrados, y hay una gran variedad de disposiciones anatómicas en este grupo. Lo más probable es que los de los primeros vertebrados consistieran en un circuito muy simple que siguiera, más o menos, la secuencia: corazón, arteria, branquias, aorta, arterias, arteriolas, capilares, vénulas, venas y corazón. Este sistema es diferente de los anteriores porque en aquellos la sangre circulaba de las branquias al corazón y en este circula del corazón a las branquias. Es un buen dispositivo a efectos de oxigenar la sangre, pero reduce mucho la velocidad de circulación desde el corazón a los tejidos, porque al pasar por los capilares branquiales, estos, por su pequeño calibre, ofrecen una gran resistencia al paso de la sangre y la ralentizan. Los peces mantienen las características generales de este sistema, aunque en algunos casos incorporan alguna bomba auxiliar antes del corazón sistémico.
La transición al medio terrestre trajo importantes novedades. La aparición de órganos respiratorios distintos de las branquias complicó de forma notable la arquitectura del circuito. Como vimos aquí, hay peces que son capaces de respirar en aire a través de estructuras tales como la cavidad bucal, el intestino, la vejiga natatoria o la cloaca. En los primeros que desarrollaron esa capacidad el órgano respiratorio recibe sangre del circuito sistémico, lo que da lugar a que, una vez oxigenada, se mezcle con la desoxigenada que procede del resto de los tejidos antes de entrar en el corazón. Por lo tanto, cuando respiran en aire los tejidos sistémicos reciben sangre parcialmente oxigenada, porque las branquias, en caso de ser funcionales, aportan muy poco oxígeno. Esa particularidad, que ha sido tradicionalmente considerada una desventaja de esos peces, tiene sin embargo una ventaja por comparación con los que respiran en agua a través de las branquias: como la sangre que llega al corazón está parcialmente oxigenada, el corazón toma de ella el oxígeno que necesita.
A diferencia de los anteriores, en los peces pulmonados –y en concreto, en el respirador aéreo obligado Protopterus aethiopicus– la sangre procedente de los pulmones no se mezcla con la procedente de los tejidos antes de entrar en el atrio (aurícula) del corazón, sino que entra en este directamente. Y por otro lado, la configuración anatómica del corazón de estos peces es tal que permite que la sangre procedente de los pulmones y la que llega del resto de los tejidos solo se mezclen en una pequeña proporción, de manera que la que viene de los pulmones se dirige preferentemente a la circulación sistémica, y la que procede de los tejidos a los pulmones. Aunque anatómicamente no hay una separación clara entre los dos circuitos, el sistémico o general, y el pulmonar, funcionalmente se produce una cierta diferenciación, lo que constituye un anticipo de los sistemas totalmente diferenciados que aparecieron posteriormente en otros vertebrados.

Esquema del sistema circulatorio de los anfibios. Fuente: Lennert B. / Wikimedia Commons
Los anfibios que respiran en aire tienen ya dos cámaras auriculares separadas. La sangre oxigenada procedente de los pulmones entra en la aurícula izquierda, mientras la sangre sistémica venosa entra en la derecha a través del seno venoso. Ambas sangres están separadas hasta que llegan al ventrículo. Pero, gracias a las características ventriculares, tampoco en este se mezclan en una medida significativa. En anfibios, además, hay que introducir la irrigación de la piel en el análisis, dado que puede contribuir de forma significativa al intercambio de gases. El caso de la rana toro (Rana catesbeiana) es muy ilustrativo. Prácticamente toda la sangre oxigenada procedente de los pulmones llega a la aurícula izquierda y sale hacia la circulación sistémica, se descarga de O2 en los tejidos y vuelve al corazón, donde entra por la aurícula derecha; la mayor parte de esa sangre venosa desoxigenada se dirige a la vía pulmo-cutánea (dos tercios a los pulmones, y el otro tercio a la piel). Lo curioso es que la sangre (oxigenada) que procede de la piel se mezcla con la procedente de los tejidos antes de llegar al corazón.
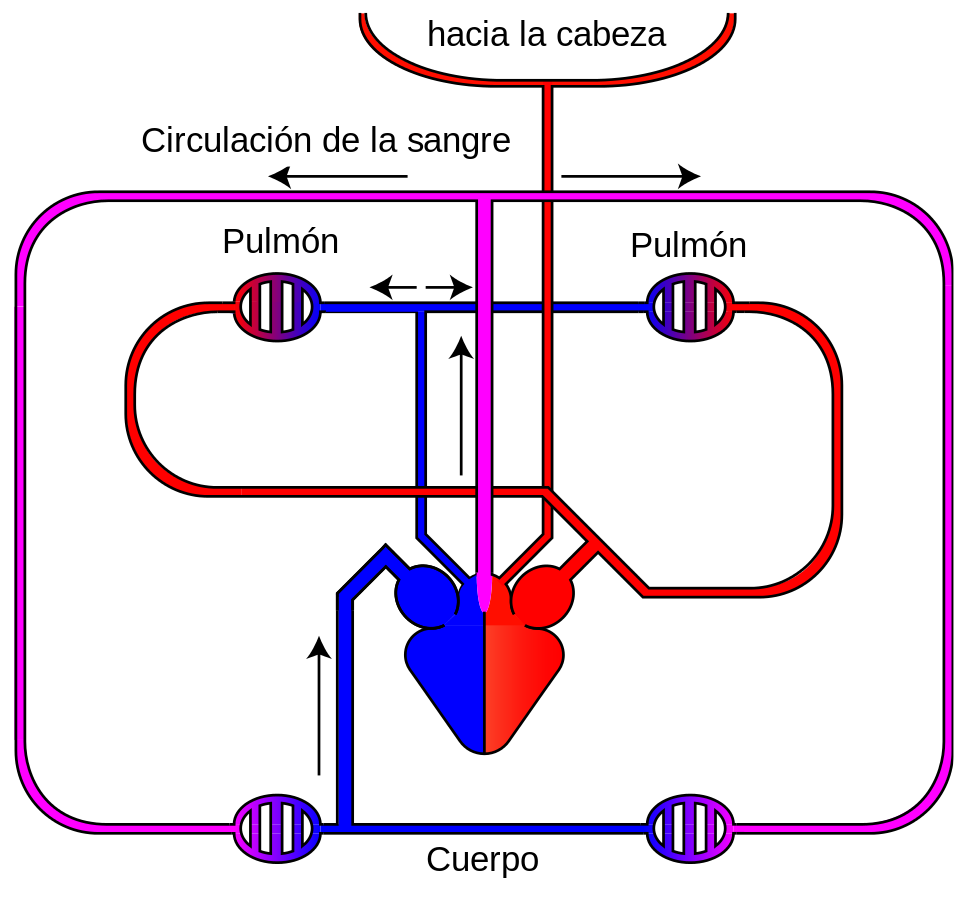
Esquema del sistema circulatorio de los reptiles. Fuente: Basquetteur. / Wikimedia Commons
Los reptiles no cocodrilianos (tortugas, serpientes y lagartos) tienen el ventrículo parcialmente separado en tres cámaras, y aunque la separación no es total, también en estos hay poca mezcla de sangre oxigenada y desoxigenada. No se conoce bien el mecanismo, pero las arterias pulmonares reciben preferentemente sangre desoxigenada. En los cocodrilianos el ventrículo está completamente dividido en dos cámaras por un septo. Del ventrículo izquierdo sale la arteria pulmonar y una arteria sistémica, la izquierda, y del ventrículo izquierdo sale la aorta sistémica derecha; sendas válvulas controlan el flujo a través de ambas aortas y están, además, conectadas nada más salir del corazón. Ese sofisticado dispositivo no solo propicia una distribución selectiva de la sangre desoxigenada a los pulmones prácticamente perfecta, sino que durante el buceo permite limitar el flujo de sangre a los pulmones cuando estos se han quedado sin oxígeno.
Los diferentes dispositivos vistos en peces (de respiración aérea), anfibios y reptiles son funcionales en animales que no tienen garantizado un alto contenido en oxígeno en sus pulmones de manera permanente. Permiten dirigir la sangre desoxigenada y oxigenada hacia diferentes destinos dependiendo de las circunstancias; por ejemplo, dependiendo de la disponibilidad ambiental de O2 y, por ello, de su concentración en el órgano respiratorio. Por eso, la adquisición de un doble sistema, pulmonar y sistémico, por parte de aves y mamíferos no debe entenderse como un “último” paso en la evolución de los sistemas respiratorios hacia una hipotética configuración ideal. La disposición en serie del circuito sistémico y del pulmonar obliga a que los flujos hacia uno y el otro sean idénticos. Ello impide generar flujos diferentes en un y otro circuito, pero en aves y mamíferos no hay tal necesidad, pues, como se ha dicho, estos grupos tienen elevadas concentraciones de oxígeno en sus pulmones de forma permanente.
Por otro lado, esa configuración permite generar presiones hidrostáticas muy diferentes en cada circuito: en el sistémico son necesarias altas presiones para vencer la resistencia que ofrece el sistema capilar, pero en el pulmonar la presión no ha de ser muy alta, pues de lo contrario saldría plasma sanguíneo hacia los espacios extracelulares e, incluso, al interior de los alveolos, lo que aumentaría peligrosamente la longitud de la vía de difusión. Como consecuencia de esa disposición en serie, ambos circuitos se mantienen completamente separados en el corazón. En animales con muy altas demandas metabólicas, como aves y mamíferos, eso es ventajoso pues permite garantizar que sangres con diferentes contenidos de O2 no se mezclan en ningún momento, lo que favorece el transporte de oxígeno a los tejidos. Pero que ese dispositivo resulte muy ventajoso para aves y mamíferos no quiere decir que los animales que carecen de él tengan, a esos efectos, una configuración incompleta. Como hemos visto, el resto de vertebrados que respiran en aire en la práctica también han conseguido evitar la mezcla de sangres, aunque no de forma completa, y disponen, además de otras funcionalidades de las que carecen los dos grupos homeotermos.
Nota:
En las siguientes anotaciones hemos tratado otros aspectos de los sistemas circulatorios que complementan lo expuesto aquí:
La distribución del agua animal y el curioso caso del potasio
Un viaje a través del sistema circulatorio humano
El flujo sanguíneo se reorganiza en respuesta a las necesidades
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Sistemas respiratorios: la emergencia de un doble sistema circulatorio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un viaje a través del sistema circulatorio humano
- Sistemas respiratorios: el pulmón de los mamíferos
- Sistemas respiratorios: los límites a la difusión de los gases
La teoría de la invariancia

El color del oro es inexplicable si no se tiene en cuenta la relatividad
Tras el triunfo de Newton, su forma de plantear la ciencia física se expandió no solo a la mecánica, sino también a las otras ramas de la ciencia, en especial a la electricidad y el magnetismo. Este trabajo culminó a finales del siglo XIX con una nueva teoría de la electricidad y el magnetismo basada en la idea de campos eléctricos y magnéticos. James Clerk Maxwell, quien formuló la nueva teoría del campo electromagnético, demostró que lo que observamos como luz puede entenderse como una onda electromagnética.
La física de Newton y la teoría de Maxwell explican casi todo lo que observamos en el mundo físico cotidiano que nos rodea. Los movimientos de los planetas, los automóviles y los proyectiles, la luz y las ondas de radio, los colores, los efectos eléctricos y magnéticos y las corrientes, ya sean eléctricas o de masas de agua, encajan dentro de la física de Newton, Maxwell y sus contemporáneos. Además, su trabajo hizo posible las muchas maravillas de la nueva era eléctrica que extende por gran parte del mundo desde finales del siglo XIX. No es de extrañar que para 1900 algunos físicos muy distinguidos creyeran que la física estaba casi completa, y que solo eran necesarios algunos ajustes menores.

Albert Einstein en 1904
No es de extrañar, tampoco, que se quedasen estupefactos cuando, apenas 5 años después, un desconocido empleado de patentes suizo, que se había graduado en el Instituto Politécnico Federal de Zúrich en 1900, presentase cuatro trabajos de investigación que desencadenaron una transformación en la física de tal envergadura que todavía está en curso . Uno estos documentos proporcionó la teoría definitiva buscada desde hace tiempo para la existencia de átomos y moléculas y otro inició el desarrollo de la teoría cuántica de la luz.
En el tercer y cuarto artículos, este jovenzuelo de 26 años llamado Albert Einstein introducía una teoría que el llamaba de la invariancia. En esta serie que hoy comenzamos presentaremos la que después sería conocida como teoría de la relatividad y algunas de sus consecuencias.
Aunque la teoría de la relatividad representaba una ruptura con el pasado, fue una ruptura muy suave. Como el mismo Einstein diría en 1954 en “Ideas y opiniones”:
No tenemos aquí ningún acto revolucionario, sino la continuación natural de una línea que puede rastrearse a través de los siglos. El abandono de ciertas nociones relacionadas con el espacio, el tiempo y el movimiento hasta ahora tratadas como fundamentales no debe considerarse como arbitrario, sino solo condicionado por los hechos observados.
Como decíamos antes, la “física clásica” de Newton y Maxwell todavía está plenamente vigente hoy día para lo que observamos en el mundo cotidiano a escala humana, algo nada sorprendente, ya que está física se derivó y diseñó para el mundo cotidiano. Sin embargo, cuando nos alejamos del día a día, necesitamos usar la teoría de la relatividad (para velocidades cercanas a la velocidad de la luz y para densidades extremadamente altas de la materia, como las que se encuentran en estrellas de neutrones y agujeros negros) o la teoría cuántica (para comprender lo que ocurre a escala de átomos y moléculas), o la combinación de ambos conjuntos de condiciones (por ejemplo, para tener en cuenta las los efectos de las velocidades muy altas a escala atómica).
Lo que hace que esta nuevas teoría de la invariancia sean tan asombrosa, y aparentemente difícil de entender, es que nuestras ideas y suposiciones más familiares sobre conceptos básicos como el espacio, el tiempo, la masa y la causalidad deben revisarse desde perspectivas que no nos son tan familiares. Con todo, son fácilmente comprensibles y ni siquiera son necesarias matemáticas más complejas de lo que se estudian en primaria. Iniciamos un viaje para entender una nueva visión del universo que marcó el siglo XX y que en el XXI nos abre posibilidades de conocimiento inimaginables aún.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La teoría de la invariancia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los antecedentes de la teoría cinética
- La teoría cinética y la segunda ley de la termodinámica
- La teoría de bandas de los sólidos se hace topológica
El factor de adecuación f

Rita Levi-Montalcini, premio Nobel de Medicina o Fisiología 1986, el día de la celebración de su centenario en 2009.
La gente más inteligente tiene, por regla general, mayor calidad de vida, mejor salud y vive más años. Siempre se ha pensado que eso es debido a que las personas más inteligentes toman mejores decisiones sobre sus hábitos de vida. Sin embargo, es posible que además de ese factor, en esa relación intervengan otros elementos, como han sugerido estudios que han encontrado sorprendentes relaciones entre la inteligencia general (factor G) y otras variables.
Uno de los estudios da cuenta de la existencia de una correlación altamente significativa (en términos estadísticos) entre dos variables que en principio, y según sus autores, no tienen nada que ver entre sí, que son la calidad del semen y la inteligencia. Los autores plantean la hipótesis de que exista un factor de éxito o adecuación “f” (de fitness) que subyace a características diversas y que hace que éstas covaríen. Éxito debe entenderse en este contexto como una suerte de propensión estadística a la supervivencia y el éxito reproductivo. Y en otro, observaron correlación negativa entre la inteligencia y la presencia de algunas anomalías o malformaciones de base genética, algo que sería igualmente consecuencia de la existencia de ese factor “f” general de éxito o adecuación.
Los autores proponen dos posibles explicaciones para la existencia de ese tipo de asociaciones entre rasgos en principio independientes. Una sería que el fenómeno se deba a la existencia de genes con efectos pleiotrópicos, o sea, con efectos múltiples en más de un carácter fenotípico. Y la otra es que sea el resultado de lo que en inglés se conoce como “assortative mating” y que podría traducirse como emparejamiento según un conjunto (un surtido) de criterios definidos. La covariación de distintos rasgos sería el resultado de que a lo largo de generaciones personas pertenecientes a determinados grupos de población hayan preferido sistemáticamente esos rasgos en sus parejas y, por lo tanto, se hayan seleccionado a la vez. En este caso habrían sido la inteligencia y otros que reflejan lo que podría considerarse como calidad genética del individuo, muestra de la cual serían la calidad espermática y la ausencia de anomalías.
Los autores de estos trabajos, conscientes de lo impopulares que son los estudios que atribuyen a factores hereditarios rasgos como los aquí tratados, se curan en salud de un tipo de posibles críticas con el párrafo final del segundo trabajo. Transcribo, según traducción propia:
“El campo de la epidemiología cognitiva debiera ocuparse de todas las posibles relaciones causales entre inteligencia y salud, y no solo entre inteligencia fenotípica, estilo de vida, ambientes sociales y salud. La eliminación de las desigualdades de salud es uno de los objetivos que se asigna a la epidemiología cognitiva. Si nuestra hipótesis del factor de éxito es correcta, habría que ver las desigualdades de salud bajo un prisma algo diferente. Puede que algunas disparidades entre grupos socio-económicos no sean evidencia de una sociedad disfuncional, sino que reflejen una variabilidad genética en la carga de mutaciones que afecta tanto a la salud física como a la inteligencia en general (que, a su vez, influye en el éxito socio-económico). La misma evolución puede, mediante mutaciones pleiotrópicas y emparejamientos de acuerdo con un surtido de criterios definidos, maximizar el rango de calidad genética entre individuos y la intensidad de las correlaciones genéticas entre caracteres, con el efecto colateral de que se maximiza la aparente injusticia de la situación médica, educativa y económica. Sin embargo, esto no debiera causar pesadumbre. La evolución también nos ha proporcionado perspicacia, comprensión, empatía y un sentido de la justicia. Las buenas personas, equipadas con una buena comprensión del mundo tal y como es, siempre han encontrado oportunidades para reducir el sufrimiento evitable haciendo uso de esos dones.”
Referencias:
Rosalind Arden, Linda S. Gottfredso, Geoffrey Miller, Aran Pierce (2009): Intelligence and semen quality are positively correlated. Inteligence 37 (3): 277-282
Rosalind Arden, Linda S. Gottfredso, Geoffrey Miller (2009): Does a fitness factor contribute to the association between intelligence and health outcomes? Evidence from medical abnormality counts among 3654 US Veterans. Intelligence 37 (6): 581-591
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El factor de adecuación f se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Curso de verano “La ciencia de nuestras vidas”: La cultura como factor evolutivo, por Juan Ignacio Pérez
- El altruismo en las mujeres se ve recompensado
- Cuestión de contrastes
El tamaño importa en organismos, empresas, ciudades y economías
Juan Ignacio Pérez Iglesias, lector

En biología animal y fisiología nos interesamos por cómo varía la velocidad o intensidad de los procesos con el tamaño de los organismos que estudiamos. Del estudio de esa fuente de variación hemos descubierto que fenómenos tales como el metabolismo, el latido cardiaco, la proporción de grasa corporal o el tamaño del encéfalo no son funciones lineales de la masa corporal. Son funciones potenciales de la misma. Y el valor de la potencia de la ecuación que las relaciona con la masa puede ser mayor o menor que 1. Si fuera 1 la relación sería lineal, por supuesto.
Geoffrey West es un físico al que, hace más de veinte años y por razones que se encarga de explicar él mismo, le empezaron a interesar las relaciones entre ciertas variables y el tamaño de los organismos. Se asoció con otros científicos del campo de la ecología evolutiva y más adelante de otras áreas, e inició una línea de trabajo que a la postre ha resultado ser muy fructífera. Tanto, que además de un ramillete de artículos en algunas de las mejores revistas científicas, ha escrito un libro divulgativo en el que da cuenta de los resultados cosechados. El libro se titula Scale, en versión breve, y Scale: The universal laws of growth, innovation, sustainability, and the pace of life in organisms, cities, economies and companies en toda su extensión.
Como no le resultaban satisfactorias las hipótesis acerca de los factores que determinan esas dependencias de tamaño, propuso una nueva que, todo hay que decirlo, hoy es la que más aceptación tiene, aunque con alguna variación. La hipótesis en cuestión se basa en el carácter fractal de las ramificaciones de los sistemas de distribución de gases, nutrientes y demás sustancias de interés fisiológico en el interior de los organismos animales. A partir de consideraciones puramente geométricas desarrolló, junto con sus colegas, modelos que predecían cuál había de ser el valor de la potencia de las relaciones entre funciones diversas y el tamaño. Y los resultados le satisficieron.
Tras ocuparse de los animales, su metabolismo, su alimentación, sus corazones, el latido cardiaco y demás, pasó a las plantas, al modo cómo se distribuye la savia y llega hasta las hojas. Y no contento con los árboles, siguió con las ciudades: su funcionamiento, la velocidad a la que anda la gente por ellas, el volumen de combustible que consumen, la longitud de las redes de cables, su intensidad innovadora, y bastantes más rasgos cuantitativos que permiten caracterizar cómo funcionan los sistemas urbanos. También se ha ocupado de las empresas, aunque en menor medida.
Partiendo, en todos los casos, de una serie de premisas relativamente sencillas –las relacionadas con la fractalidad de los procesos analizados-, West y colaboradores realizan predicciones que vienen a cumplirse con un alto grado de acierto1 y que básicamente permiten definir una serie de magnitudes muy simples que caracterizan el funcionamiento de organismos o ciudades en función de sus dimensiones. Resumiendo mucho se puede decir que en los organismos las cosas van más lentas cuanto más grandes son, mientras en las ciudades ocurre lo contrario: en las de mayor tamaño casi todo va más rápido.
Lo más notable de los resultados de West es el carácter universal de las relaciones encontradas. Él sostiene que esos resultados reflejan, de hecho, la existencia de leyes que gobiernan el modo en que funcionan organismos de diferente naturaleza en función de su tamaño. Se trataría, según él de leyes de la Naturaleza equivalentes a otras leyes que la ciencia ha ido descubriendo a lo largo de su historia.
Como suele ocurrir en estos caso, no todo lo que he leído en Scale me ha gustado. No me gusta la actitud condescendiente del autor en relación para con sus colegas de otras disciplinas. Tampoco me han convencido algunas explicaciones de índole fisiológica; West es físico y los colegas con los que ha trabajado las materias biológicas son ecólogos y eso, cuando habla de fisiología, se nota. El texto es, a mi juicio, demasiado largo porque ha dedicado mucho espacio a explicar nociones muy básicas; es posible que haya lectores que lo agradezcan, pero no ha sido mi caso. Y por último, tampoco me ha parecido buena idea el ejercicio de prospectiva que hace hacia el final en un línea neomalthusiana. Porque el futuro sigue sin ser predecible.
Pero dicho lo anterior, Scale es un libro muy interesante porque los fenómenos que analiza y la aproximación seguida lo son. Además, para las gentes de ciencia resulta muy gratificante encontrar el tipo de regularidades universales que documenta. A mí, en concreto, me ha resultado muy sugerente, sobre todo lo relativo a las ciudades; creo que entiendo mejor la forma en que funcionan los sistemas urbanos después de leerlo. Es un libro que hace pensar, “thought provoking”, como dicen inglés.
Ficha:
Autor: Geoffrey West
Título: Scale: The universal laws of growth, innovation, sustainability, and the pace of life in organisms, cities, economies and companies.
Año: 2017
Editorial: Penguin Random House/Orion
Nota:
1 De otra forma, imagino que los trabajos no se habrían publicado.
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
El artículo El tamaño importa en organismos, empresas, ciudades y economías se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas14 El tamaño sí importa…sobre todo en el nanomundo
- De los organismos
- Evolución del tamaño animal
Naukas Pro 2017: Inma Estévez y la producción animal

El pasado 14 de septiembre de 2017 se celebró la primera edición de Naukas Pro, en el que Centros de Investigación, Laboratorios, científicos de renombre o equipos de trabajo contaron con 20 minutos para explicar a un público general en qué consiste su trabajo.
5ª Conferencia: Inma Estévez, departamento de producción animal de Neiker Tecnalia
Inma Estévez explica cómo se trabaja en la producción animalEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Pro 2017: Inma Estévez y la producción animal se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Pro 2017: Julián Estévez y la inteligencia computacional
- Naukas Pro 2017: Leni Bascones y los superconductores
- Naukas Pro 2017: Manuel Collado y las células madre
La compleja transición de cazador-recolector a agricultor
Los investigadores han recuperado 180 genomas de Hungría, Alemania y España de hace entre 8.000 y 4.000 años. Su estudio pone de manifiesto que los primeros agricultores en Europa se entrecruzaron con los cazadores locales durante nada menos que 3.000 años.

Imagen: Dan Burr
El cambio del modo de vida cazador-recolector a agricultor representa la mayor transición demográfica experimentada por el ser humano en millones de años. La agricultura surge en Oriente Próximo hace unos 10.000 años y posteriormente se expande hacia Europa, donde en pocos miles de años reemplaza a los cazadores mesolíticos (el primer genoma mesolítico, secuenciado hace apenas tres años, es el del hombre de La Braña, en León). Aunque desde hace algunos años sabemos que ambos grupos eran genéticamente distintos, las dinámicas locales de dicho proceso de reemplazamiento eran hasta ahora poco conocidas.
Un equipo internacional de investigadores, entre los que se encuentran Javier Fernández Eraso y José Antonio Mujika Alustiza, del Departamento de Geografía, Prehistoria y Arqueología de la Universidad del País Vasco/Euskal Herriko Unibertsitatea, ha logrado secuenciar numerosas muestras antiguas procedentes de tres regiones de Europa (Hungría, Alemania y España). “Gracias a esta secuenciación se ha podido determinar que en los tres casos, después de la llegada inicial de los primeros agricultores, éstos se entrecruzaron con los cazadores locales a lo largo de varios siglos”, han explicado desde el equipo investigador. Es decir, los genomas de los agricultores del neolítico medio, final y del calcolítico de la península Ibérica muestran cerca de un 25% de componente genético procedente de cazadores afines a La Braña, pero los de Europa central muestran afinidades con cazadores de esa región.
En algunos casos, especialmente en Europa central, se detectan individuos con ancestralidades mixtas e incluso cazadores que se incorporan a vivir a las comunidades agrícolas y son enterrados allí. “Este descubrimiento dibuja un panorama más complejo del que existía hasta ahora sobre el proceso de neolitización, que ya no puede considerarse únicamente una migración de agricultores ni un proceso demográfico uniforme”, señalan.
El análisis de más individuos de la prehistoria de la península ibérica ayudará a completar este panorama y a entender los cambios genómicos que tuvieron lugar con posterioridad, con la llegada de los metales e incluso con migraciones que ocurrieron en tiempos históricos. En estos momentos, se dispone de cerca de 400 genomas ibéricos antiguos de todas las regiones y períodos, desde el mesolítico hasta la edad media, que siguen mostrando cambios genéticos posteriores que podrán correlacionarse con cambios a nivel arqueológico.
Referencia:
Mark Lipson et al (2017) ‘Parallel palaeogenomic transects reveal complex genetic history of early European farmers’. Nature doi: 10.1038/nature24476.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La compleja transición de cazador-recolector a agricultor se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Si Felipe fuese nutricionista hablaría de la transición nutricional
- #Naukas15 El cazador de cerebros
- #Naukas13 Tractor, azada y bacterias. Las herramientas del agricultor
Microbiota y cáncer
El impacto de la microbiota en las infecciones bacterianas durante el tratamiento del cáncer
Las infecciones son uno de los grandes temores y riesgos que tiene un paciente que está siendo tratado contra el cáncer y pueden llegar a ser una causa importante de su fallecimiento. Esto suele ser debido a los efectos colaterales de la quimioterapia y radioterapia que dañan la mucosa intestinal (lo que se denomina mucositis), y a la medicación inmunosupresora que debilita el sistema inmune, las defensas, lo que favorece la susceptibilidad a padecer infecciones. La pérdida de la integridad de las mucosas aumenta mucho el riesgo de que las bacterias patógenas la atraviesen y causen bacteriemia (presencia de bacterias en sangre). Por eso, los enfermos suelen además recibir un tratamiento antibiótico intenso, lo que puede alterar no sólo la microbiota intestinal del propio paciente, sino también las barreras y mucosas epiteliales. Este mismo ambiente oncológico favorece también la proliferación de bacterias resistentes a los antibióticos.
Los pacientes oncológicos sufren una gran cantidad de infecciones
Depende del tipo de cáncer, pero, por ejemplo, hasta un 15% de los trasplantados de médula ósea pueden padecer complicaciones con infecciones, que pueden llegar a ser mortales. Las infecciones más frecuentes en un enfermo oncológico suelen ser las neumonías, especialmente en los pacientes con cáncer de pulmón. También es frecuente que un paciente oncológico lleve un catéter intravenoso durante largos periodos de tiempo, lo que favorece las infecciones relacionadas con el uso de catéteres o sondas. En los cánceres hematológicos son frecuentes las bacteriemias. Las enterocolitis por Clostridium difficile son hasta un 30% más frecuentes en enfermos oncológicos que en pacientes normales, y, además, la infección por esta bacteria aumenta la mortalidad un 20%. Como hemos dicho, el tratamiento antibiótico aumenta el problema, y en un paciente con cáncer son típicas las infecciones por bacterias Gram positivas como Staphylococcus o Enterococcus, o por Gram negativas como Escherichia coli, Pseudomonas aeruginosa, Klebsiella pneumoniae, Enterobacter o Acinetobacter, muchas de ellas resistentes a los antibióticos como carbapenems, meticilina, vancomicina, etc. Además, estas bacterias pueden acceder y colonizar lugares estériles por haberse roto las barreras epiteliales.
Se necesitan nuevas estratégicas y tratamientos alternativos para evitar todas estas infecciones en los pacientes oncológicos
Hoy sabemos que los microbios que habitan en nuestro cuerpo en condiciones normales (la microbiota) influyen de forma muy importante en la fisiología y la patología del huésped. Entre las funciones de la microbiota está la de prevenir la colonización e infección de bacterias patógenas oportunistas, inducir componentes específicos del sistema inmune, promover una tolerancia inmune intestinal, balancear el proceso inflamatorio, mejorar la barrera epitelial, etc. En general, una microbiota intestinal con una gran diversidad de microorganismos es un indicador de buena salud, y la pérdida de diversidad microbiana suele ser frecuente durante la quimioterapia. Además, el uso de antibióticos para evitar infecciones en los pacientes oncológicos e inmunocomprometidos, no solo favorece la aparición de resistencias a los antibióticos sino que causa también una alteración de la propia microbiota.
Nuestra salud depende también de nuestros microbios.
Cada vez conocemos mejor la composición y función de nuestra microbiota, y hay más estudios que demuestran una correlación entre la microbiota del paciente oncológico y una infección durante el tratamiento con quimioterapia. Se han descrito cambios en la diversidad de la microbiota intestinal que preceden a una eventual infección. La razón es que una microbiota “saludable” puede proteger de una colonización y establecimiento del patógeno, bien porque la microbiota produzca alguna sustancia que inhiba al patógeno (como las bacteriocinas) o por su función moduladora del sistema inmune. Mantener una microbiota diversa y heterogénea en los pacientes con cáncer antes del inicio del tratamiento puede explicar por qué algunos pacientes son más susceptibles a padecer infecciones durante el tratamiento.
Una microbiota “sana” puede proteger del establecimiento de un patógeno
Aunque actualmente no sabemos exactamente qué especies bacterianas podrían prevenir el aumento o predominio de un determinado patógeno, algunos ensayos sugieren, por ejemplo, que un aumento de la bacteria Clostridium scindens en el intestino previene la infección por Clostridium difficile o que la colonización por Barnesiella, un tipo de Bacteroidete, confiere protección frente a Enterococcus. Se sabe que muchas bacterias comensales de la microbiota mejoran la función del epitelio como barrera. Algunos Bacteroides, Bifidobacterium, Faecalibacterium o Lactobacillus aumentan las uniones entre las células del epitelio, reducen la permeabilidad intestinal, aumentan la reparación de los epitelios y la producción de moco protector. Por ejemplo, la producción de butirato por parte de la microbiota ha sido asociada a la producción de mucina (componente principal del moco) que interviene en la integridad del epitelio y de las uniones entre las células epiteliales. Por tanto, algunas bacterias intestinales son muy beneficiosas para evitar infecciones.
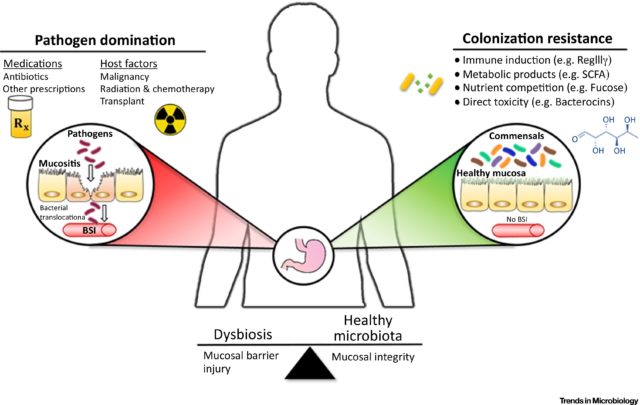
En los pacientes con cáncer existe un balance entre una microbiota “saludable” y el desarrollo de una infección gastrointestinal que depende de la integridad de la barrera mucosal (Fuente: ref 1)
Modificar la microbiota intestinal para mejorar la calidad de vida de los pacientes con cáncer
Todavía son necesarios muchos más ensayos clínicos y la investigación está en sus comienzos, pero ya se están proponiendo algunas soluciones terapéuticas basadas en modificaciones de la microbiota intestinal para mitigar las infecciones y mejorar la calidad de vida de los pacientes con cáncer. Por ejemplo, el trasplante de microbiota intestinal (también conocido con el repulsivo nombre de trasplante fecal) se ha utilizado para reducir el riesgo de infección recurrente por Clostridium difficile. Hay ya estudios de su eficacia vía enemas, endoscopias, tubo nasogástrico o cápsulas liofilizadas, pero todavía faltan estudios en pacientes con cáncer y existe la duda de que pueda ser una forma de introducir nuevas infecciones en pacientes inmunocomprometidos. De momento es necesario estandarizar las técnicas y evaluar su efectividad clínica, pero es probable que en el futuro el trasplante de microbiota sea más común de lo que nos imaginamos. También se están proponiendo nuevos diseños de probióticos (una mezcla concreta y bien definida de microbios “saludables”) o de prebióticos (oligosacáridos o ácidos grasos de cadena corta que promuevan la proliferación y colonización de bacterias propias que eviten los patógenos invasores).
Medicina “a la carta” teniendo en cuenta también a tus microbios
Pero, manipular la microbiota y restaurarla en caso de alguna enfermedad, a través de trasplantes, probióticos o prebióticos es mucho más complicado que lo que podíamos imaginar. La razón de esta dificultad puede ser que la microbiota supone un complejo consorcio con millones de interacciones entre los propios microbios y nuestras células. Es necesario seguir investigando para entender mejor los mecanismos por los que la microbiota mantiene la salud o desencadena la enfermedad. Los pacientes con cáncer necesitan estos estudios, es urgente avanzar en el conocimiento del efecto de la microbiota en la infección de estos pacientes.
Lo que sí podemos predecir es que en un futuro muy próximo el análisis del microbioma humano se incorporará a los protocolos de medicina personalizada de precisión. Una medicina “a la carta” que propondrá un tratamiento personalizado teniendo en cuenta los millones de datos del genoma, metabolismo, sistema inmune y microbioma de cada paciente individual. Cuando vayas al hospital, el médico secuenciará y analizará tu genoma, con los datos de tu ARN y proteínas, definirá tu metabolismo y analizará tu sistema inmune. Pero además, estudiará la composición de tu microbiota y su función, identificará microorganismos oportunistas potencialmente patógenos en tu cuerpo, posibles deficiencias y cómo tus microbios pueden afectar al tratamiento. Con todos esos datos tuyos, podrá estudiar tu susceptibilidad genética a padecer una enfermedad, podrá predecir tu respuesta a un tratamiento y posibles reacciones adversas, incluso recomendar un cóctel de microbios concreto, podrá en definitiva diseñar una terapia personalizada para ti: medicina “a la carta”, pero teniendo en cuenta también tu microbiota, porque (no lo olvides) … ¡somos microbios!
En resumen: los tratamientos contra el cáncer alteran la microbiota y favorecen la aparición de infecciones. Es necesario seguir investigando nuevas soluciones terapéuticas basadas en la manipulación de la microbiota en este tipo de enfermos para mitigar las infecciones y mejorar su calidad de vida.
Este post ha sido realizado por Ignacio López-Goñi (@MicrobioBlog) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias científicas y más información:
(1) Impact of the microbiota on bacterial infections during cancer treatment. Galloway-Peña, J., y col. Trends in Microbiology. July 17, 2017. DOI: http://dx.doi.org/10.1016/j.tim.2017.06.006
https://es.wikipedia.org/wiki/Mucositis
https://es.wikipedia.org/wiki/Bacteriemia
https://es.wikipedia.org/wiki/Colitis_seudomembranosa
https://es.wikipedia.org/wiki/Bacteriocina
https://es.wikipedia.org/wiki/Mucina
http://microbioun.blogspot.com.es/2014/09/trasplante-fecal.html
http://www.cell.com/trends/microbiology/fulltext/S0966-842X(17)30151-8
El artículo Microbiota y cáncer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Soy esa bacteria que vive en tu intestino, mejor vídeo de divulgación “On zientzia”
“Soy esa bacteria que vive en tu intestino” de Julio Ruiz Monteagudo es el vídeo ganador del premio al mejor vídeo de divulgación de la 6ª edición de los premios On Zientzia. Este vídeo musical de animación ofrece en menos de cuatro minutos una introducción al proceloso mundo de las bacterias que viven en ese cuerpo que llamamos nuestro, pero que, en puridad democrática, es de ellas.
¿Tienes una idea genial para explicar un concepto científico en un vídeo? ¿Quieres ver tu trabajo emitido en televisión? La Fundación Elhuyar y el Donostia International Physics Center (DIPC) han organizado la octava edición de On zientzia, un concurso de divulgación científica y tecnológica enmarcado en el programa Teknopolis, de ETB. Este certamen pretende impulsar la producción de vídeos cortos y originales que ayuden a popularizar el conocimiento científico.
On zientzia tendrá tres categorías. El mejor vídeo de divulgación recibirá un premio de 3.000 euros. Para impulsar la producción de piezas en euskera, existe un premio de 2.000 euros reservado a la mejor propuesta realizada en ese idioma. Por último, con el objetivo de impulsar la participación de los estudiantes de ESO y Bachillerato, hay un premio dotado con 1.000 euros para el mejor vídeo realizado por menores de 18 años.
Los vídeos han de tener una duración inferior a los 5 minutos, se pueden realizar en euskera, castellano o inglés y el tema es libre. Deben ser contenidos originales, no comerciales, que no se hayan emitido por televisión y que no hayan resultado premiados en otros concursos. El jurado valorará la capacidad divulgativa y el interés de los vídeos más que la excelencia técnica.
Las bases las encuentras aquí. Puedes participar desde ya hasta el 25 de abril de 2018.
Edición realizada por César Tomé López
El artículo Soy esa bacteria que vive en tu intestino, mejor vídeo de divulgación “On zientzia” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Keats vs Feynman, mejor vídeo de divulgación “On zientzia”
- On Zientzia, un concurso para divulgadores audiovisuales
- OnZientzia: Una joya de bacteria
Verdad científica y verdad jurídica
El ingeniero estadounidense Mark Jacobson acaba de demandar por difamación a la Academia Nacional de las Ciencias de Estados Unidos y a un investigador que publicó en la reputada revista PNAS (editada por la academia) un estudio que criticaba el trabajo de Jacobson. La demanda pide 10 millones de dólares por daños a su reputación y la retirada y retracción de un artículo publicado en 2017 en PNAS por el matemático Christopher Clack y 20 autores más analizando la metodología de otro artículo publicado por Jacobson en 2015. La crítica llegaba a la conclusión de que los errores metodológicos de Jacobson invalidaban sus conclusiones; el ingeniero considera que se trata de un infundado ataque a su carrera y prestigio profesional y ha llevado el asunto a los tribunales. Una vez más un tribunal de justicia se verá forzado, en la práctica, a determinar cuál es la verdad entre dos alternativas científicas; una vez más el asunto está ligado a un tema políticamente candente, en este caso la política energética e indirectamente el calentamiento global y sus potenciales soluciones. Una vez más será un desastre porque la verdad científica no es democrática ni puede ser determinada por la vía legal.

Fotograma de “Inherit the wind” (1960) de Stanley Kramer
Los tribunales no buscan la verdad, sino la justicia; término de difícil definición pero que desde luego no está relacionado con el funcionamiento del universo, sino en todo caso con el de las sociedades humanas. El cosmos no es justo, ni injusto; simplemente es, y al intentar describir su funcionamiento la ciencia prescinde por completo de cualquier noción de justicia. El rayo no cae donde castiga al malo y favorece al bueno, sino donde la diferencia de potencial se acumula en un grado suficiente. La gacela no puede recurrir a un juez para que la salve del leopardo, como este no puede demandar a la bacteria que infecta la herida de su pata y le va a causar la muerte. Carece por completo de sentido intentar proyectar ideas humanas como responsabilidad o moralidad, sobre un mundo que funcionaría del mismo exacto modo sin la presencia de humanos. Hacerlo tiene nombre: la falacia patética, y el hecho de que se cometa con frecuencia no la hace menos falaz.
Al revés la situación es más compleja porque a menudo la justicia sí que necesita establecer la verdad (o falsedad) de un hecho con el fin de poder juzgar adecuadamente su adecuación a las leyes. Ahí la ciencia frecuentemente ayuda a la justicia dado que proporciona herramientas y métodos para demostrar, o falsear, hechos o vinculaciones entre hechos y personas que ayudan a establecer responsabilidades y a facilitar el cumplimiento de las leyes. Especialmente en estos tiempos de CSIs y de análisis de ADN parece que la administración de justicia está colonizada de científicos y que los abogados necesitan estudiar más biología y menos Derecho Romano. La relación entre ciencia y justicia no es aquí demasiado problemática.
Cuando esta relación se transforma en un verdadero desastre es cuando se exige a la administración de justicia que adjudique cuál es la verdad científica de entre dos puntos de vista contrarios. Y esto es así porque ni la metodología ni el objetivo de los sistemas jurídicos es establecer cuál es la verdad, sino resolver los conflictos entre personas. Y a la verdad científica las personas le importan (le deben importar) poco. Lo que es es lo que es, aunque moleste, aunque no sea justo, aunque no sea democrático. La descripción de lo real no depende de sujeción alguna a normas morales, mucho menos legales.
Demasiadas veces se ha producido y se produce esta anomalía de que un tribunal de justicia sea llamado a dilucidar qué es verdad científica y qué no, a menudo en casos relacionados con conflictos políticos (como el de la demanda de Jacobson) o bien con la existencia de charlatanes que se benefician de curar enfermedades que no existen (hipersensibilidad química o electromagnética), o de vender pseudoterapias (reiki, homeopatía, etc). Ningún tribunal de justicia tiene la capacidad de decidir por sí mismo sobre la veracidad de una proposición científica, de modo que se ve obligado a depender de expertos externos. Si estos expertos están sesgados la sentencia del tribunal será legal, pero no reflejará la realidad del universo. Con lo que podemos llegar a la absurda situación de que una sentencia judicial (una verdad legal) esté dando soporte a una falsedad científica. Y ya ha ocurrido.
Existen, por ejemplo, sentencias judiciales que reconocen grados de invalidez a ciertas personas y que se usan como pruebas de que la hipersensibilidad electromagnética es real. Pero al igual que ocurrirá en el caso de Jacobson una vez sea juzgado la administración de justicia no tiene capacidad para determinar la existencia o inexistencia de un fenómeno: la verdad judicial (se ajusta, o no, a la ley) no tiene nada que ver con la científica (existe, o no), por lo que cualquier intento de usar el dominio legal para demostrar la existencia (o inexistencia) de un fenómeno estará condenado al fracaso. Puede ser que una persona merezca una pensión de invalidez (verdad jurídica) al mismo tiempo que la enfermedad que cree padecer no existe (verdad científica). Y cualquier intento, como la demanda de difamación, para forzar que la justicia determine cuál es la verdad científica tan sólo puede crear confusión y mala ciencia. Por muy buena que sea la sentencia legal.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo Verdad científica y verdad jurídica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:En Marte el viento crea montañas
Si le preguntas al geólogo de guardia cómo se forman las montañas es probable que te diga que los procesos que intervienen están asociados con movimientos a gran escala de la corteza terrestre (lo que se llama tectónica de placas). Te hablará posiblemente de plegamientos, fallas, actividad volcánica, intrusión ígnea y metamorfismo. Será muy interesante, sin duda, pero el único problema es que esto aplica a un planeta, la Tierra. Y es que en Marte las montañas las forma el viento. Algunas, al menos.
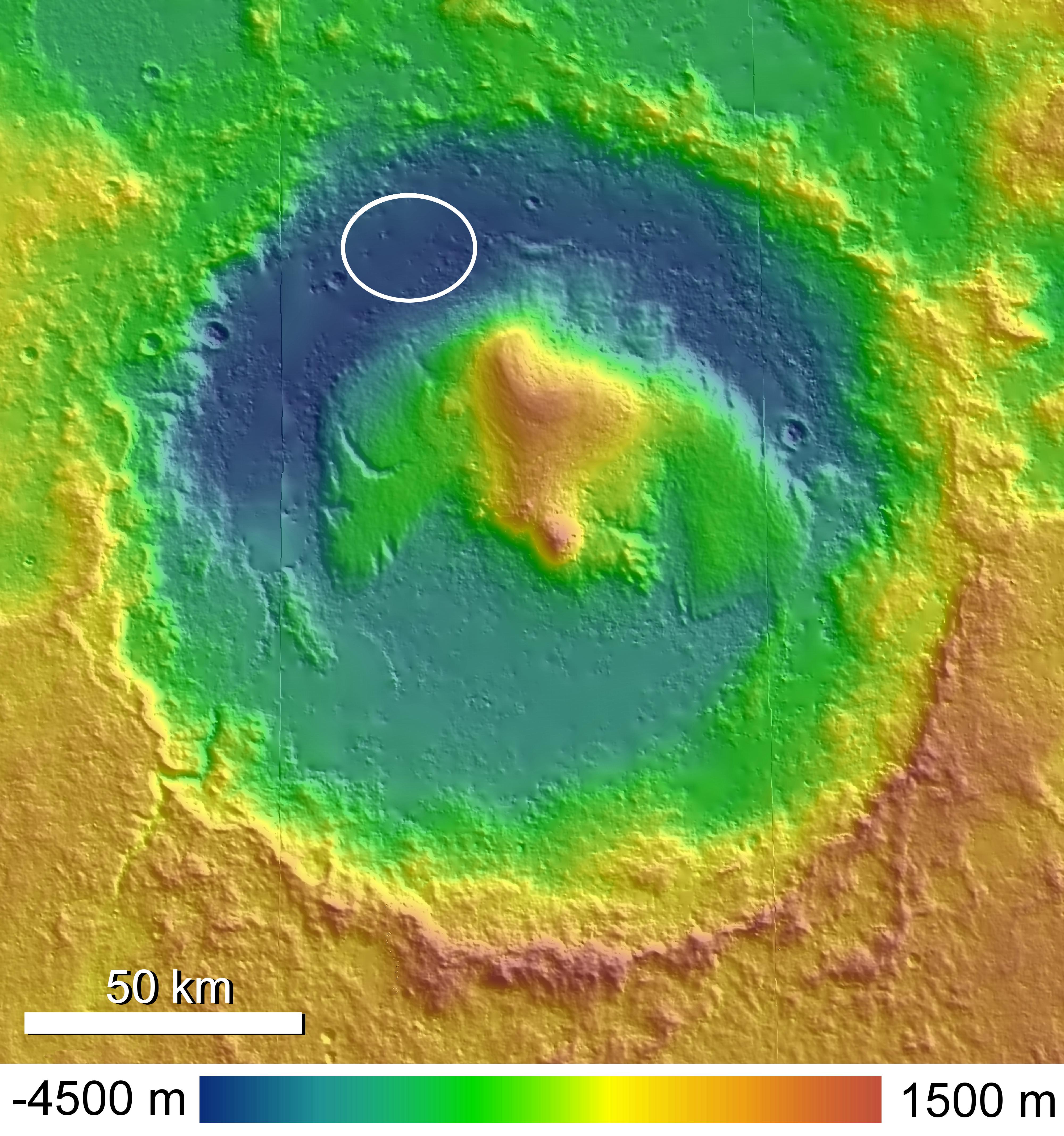
Mapa topográfico del cráter Gale (Marte). El círculo indica la zona de aterrizaje del rover Curiosity.
El cráter Gale en Marte tiene 154 km de diámetro y una montaña en su interior de 5.500 m de altitud, Aeolis Mons. Curiosity es un ingenio humano del tamaño de un coche utilitario que está explorando las estribaciones de Aeolis Mons desde agosto de 2012. El Gale es un cráter creado por impacto de un meteorito hace unos 3.700 millones de años que fue llenándose de sedimentos durante 500 millones de años, probablemente porque llegó a a ser un enorme lago cuando Marte aún era cálido y húmedo.
Cuando este lago se secó, no había montaña en su interior, sino una caldera colmatada de sedimentos. Según las simulaciones de William Anderson (Universidad de Texas en Dallas) y Mackenzie Day (Universidad de Washington en Seattle) habrían sido remolinos de viento dentro de las paredes del cráter los que habrían excavado una región con forma de rosquilla, dejando una montaña en el centro. Como los vientos excavarían un lado de cráter más rápido que el otro, ello resultaría que la montaña no está en el centro del cráter, sino ligeramente desplazada del centro.
Usando simulaciones de dinámica de fluidos, Day y Anderson estudiaron los patrones de flujo de viento sobre cuatro geometrías de cráter idealizadas: un cráter lleno, un cráter lleno con un foso poco profundo, un cráter con un foso profundo alrededor de los comienzos de una montaña, y un cráter vacío. Estos cráteres idealizados tenían los rasgos principales de Gale y cráteres marcianos similares.
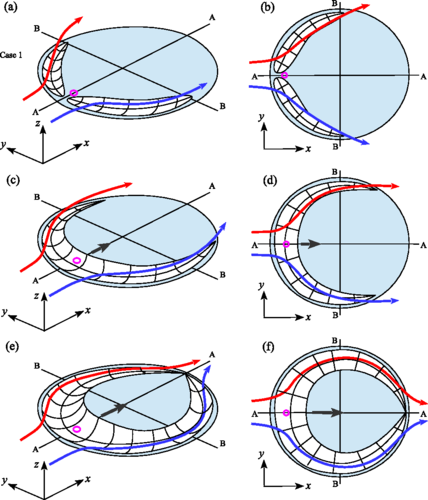
Analizando los patrones de viento los investigadores observaron que los vientos se focalizaban debido a las características topográficas. Los vórtices a pequeña escala se desarrollan cuando el viento golpea por primera vez el borde exterior del borde del cráter. Estos vórtices fluyen sobre el borde hacia el cráter y luego se dividen en dos corrientes que se propagan a sotavento (hacia donde sopla el viento), una corriente a cada lado del borde del cráter. A medida que el foso se profundiza y se alarga, los vórtices aumentan de intensidad.
Las simulaciones indican que la erosión comienza en el lugar donde los vórtices entran en el lado de barlovento (de donde sopla el viento) del cráter. El viento inicialmente crea una depresión en forma de media luna que luego se alarga y profundiza hasta que sus dos extremos se unen, creando un foso completo. El lugar donde el viento golpea por primera vez el cráter experimenta la erosión más duradera, por lo que el foso en ese extremo de la cuenca es más ancho, y la montaña termina situada a sotavento del centro del cráter.
Los resultados muestran que la erosión eólica puede explicar la formación y posición de las montañas dentro de los cráteres de impacto en Marte. Tener un escenario plausible para la evolución del cráter de Gale en los últimos 3 mil millones de años ayudará a interpretar los datos de geología que está siendo recolectados por el rover Curiosity y en la reconstrucción de la historia geofísica de Marte.
Referencia:
William Anderson and Mackenzie Day (2017) Turbulent flow over craters on Mars: Vorticity dynamics reveal aeolian excavation mechanism Phys. Rev. E doi: 10.1103/PhysRevE.96.043110
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo En Marte el viento crea montañas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los ojos que explorarán la superficie de Marte (Mars2020)
- Datación K-Ar y las edades de Marte
- H. pylori crea túneles en la mucosa del estómago

