Polvaredas y sonidos en Jezero (Marte)
 Secuencia de levantamiento de polvo causado por una fuerte ráfaga de viento a mediodía. El área que se ve en las imágenes ocupa una superficie de unos 4 km2. Autor: NASA/Caltech-JPL/ASU/MSSS/SSI
Secuencia de levantamiento de polvo causado por una fuerte ráfaga de viento a mediodía. El área que se ve en las imágenes ocupa una superficie de unos 4 km2. Autor: NASA/Caltech-JPL/ASU/MSSS/SSIEl 18 de febrero de 2021 llegó a Marte la misión Mars 2020 de la NASA y sobre la superficie del cráter Jezero comenzó a operar el rover Perseverance, un auténtico laboratorio móvil. Uno de sus instrumentos es la estación meteorológica MEDA, desarrollada en el Centro de Astrobiología-INTA en Madrid y en la que colaborado el Grupo de Ciencias Planetarias de la Universidad del País Vasco, que dirige el catedrático Agustín Sánchez Lavega. El análisis de los datos que va proporcionando MEDA está permitiendo profundizar en uno de los aspectos clave de la atmósfera del planeta rojo: como se levanta el polvo de la superficie.
“Podemos decir que ahora empezamos a comprender las condiciones necesarias para levantar el polvo de la superficie de Marte. Y este es un elemento clave, porque el ciclo de polvo del planeta rojo nos ayudará a entender mejor la meteorología global de Marte”, explica Ricardo Hueso, segundo autor del artículo publicado en Science Advances por el grupo.
 Remolino de polvo o dust devil observado por las camaras Mastcam-Z. Autor: NASA/Caltech-JPL/ASU/MSSS/SSI
Remolino de polvo o dust devil observado por las camaras Mastcam-Z. Autor: NASA/Caltech-JPL/ASU/MSSS/SSIAl ser la atmósfera marciana unas 150 veces menos densa que la terrestre, el polvo en suspensión determina muchas de sus propiedades térmicas y cómo se calienta y se enfría. Este nuevo trabajo estudia los fenómenos que levantan el polvo en la superficie de Marte, incluyendo los remolinos de polvo llamados ‘dust devils’ y los vientos racheados capaces de producir grandes polvaredas. De hecho, gracias a los datos recopilados sobre el viento, polvo, temperatura y otras variables atmosféricas, el equipo internacional que colabora en la investigación ha concluido que el cráter Jezero, elegido como lugar de estudio de la misión Mars 2020 porque, aunque hoy es un desierto, hace miles de millones de años estaba totalmente inundado, es uno de los lugares más activos y favorables para levantar grandes cantidades de polvo de su superficie.
 Serie de imágenes capturadas por las cámaras Navcam que muestran varios «dust devils» en movimiento en Jezero. Autor: NASA/Caltech-JPL/ASU/MSSS/SSI
Serie de imágenes capturadas por las cámaras Navcam que muestran varios «dust devils» en movimiento en Jezero. Autor: NASA/Caltech-JPL/ASU/MSSS/SSILos vientos diurnos son ascendentes y, en general, intensos, mientras que de noche los vientos detectados son descendentes y más débiles. “Es la interacción de estas corrientes de viento con la superficie la que produce estos fenómenos de levantamiento de polvo masivo”, indica Hueso. El polvo de la atmósfera de Marte, al depositarse sobre la superficie, puede cubrir paneles solares e imposibilitar el funcionamiento de algunas misiones espaciales de superficie. Sin embargo, este no es un aspecto preocupante para el rover Perseverance, que utiliza energía nuclear para sus operaciones.
“Conocer la atmosfera de Marte hoy no solo es fundamental para entender su pasado cuando Marte era un planeta potencialmente habitable, sino también para preparar la exploración humana de Marte que esperamos pueda desarrollarse en las próximas décadas”
Ricardo Hueso.
Primeras grabaciones de sonidosPor otra parte, Nature publica esta semana ‘In situ recording of Mars soundscape’, que recoge las primeras grabaciones de sonido en la fina atmósfera de Marte. En el artículo ha participado el grupo IBeA de la UPV/EHU, que dirige el catedrático Juan Manuel Madariaga, así como uno de los firmantes del artículo anterior, el estudiante de doctorado Asier Muguira.
Como desvelan las grabaciones, en la tenue atmósfera de Marte se producen fenómenos acústicos diferentes a los terrestres, como, por ejemplo, la dispersión del sonido en diferentes frecuencias del espectro audible humano, o una mayor atenuación del sonido con la distancia debido de nuevo a la baja densidad atmosférica.
El artículo está basado en los datos del micrófono del instrumento SuperCam, en cuyo desarrollo ha participado el grupo IBeA, y recoge sonidos naturales producidos por el viento en el cráter Jezero. Así mismo, se pueden escuchar sonidos artificiales producidos por las aspas del helicóptero Ingenuity, el compresor del instrumento MOXIE y los del rover y sus ruedas al desplazarse por Marte, así como los sonidos producidos por la ablación que genera el láser del instrumento LIBS (parte de SuperCam), de cuyo análisis se pueden inferir propiedades de los materiales examinados en Marte.
Referencias:Newman, Hueso, Lemmon, Munguira et al. (2022) The dynamic atmospheric and aeolian environment, of Jezero crater, Mars Science Advances doi: 10.1126/sciadv.abn3783
Maurice, S., Chide, B., Murdoch, N. et al. (2022) In situ recording of Mars soundscape Nature doi: 10.1038/s41586-022-04679-0
Para saber más:Sería buena noticia que no hubiera vida en Marte ni la hubiese habido nunca
Marte y el enigma de la vida: el gran desembarco robótico de 2021
Los glaciares olvidados de Marte
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Polvaredas y sonidos en Jezero (Marte) se ha escrito en Cuaderno de Cultura Científica.
Y, sin embargo, se mueven
Hace 110 años, el físico y meteorólogo alemán Alfred Wegener propuso una curiosa idea que presentó a la comunidad científica, unos años después, con la publicación de su obra “El Origen de los Continentes y Océanos”. En ella, Wegener planteaba una concepción movilista de nuestro planeta, argumentando que hace millones de años todos los continentes estuvieron unidos en una gran masa de tierra a la que denominó Pangea (del griego “todas las tierras”), que a su vez estaba rodeada por un único y enorme océano al que llamó Panthalassa (también del griego “todos los mares”). Pero, en algún momento, este gran supercontinente se fracturó y entonces los continentes se desplazaron sobre el océano hasta alcanzar la posición actual.
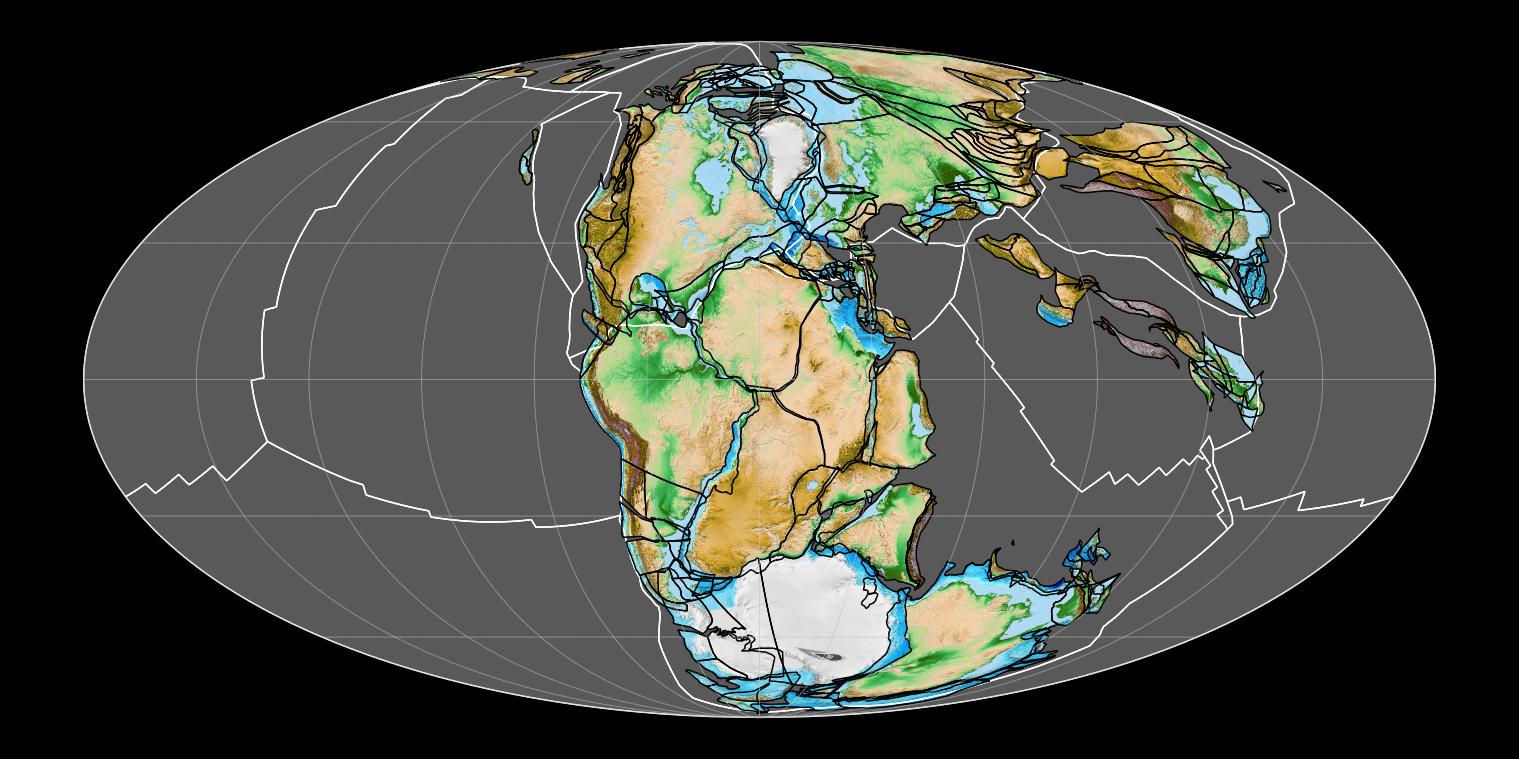 Pnagea hace 200 millones de años. Fuente: Wikimedia Commons
Pnagea hace 200 millones de años. Fuente: Wikimedia CommonsPara sustentar su hipótesis, Wegener se basó en ciertas evidencias geológicas. Observó que los perfiles continentales de Europa, África y América encajaban casi a la perfección, como si fuesen las piezas de un puzle, y encontró que algunos materiales geológicos, rocas, fósiles y cordilleras se continuaban a un lado y otro del Atlántico, aseverando que, en algún momento del tiempo geológico, esas zonas estuvieron unidas y posteriormente se separaron. Sin embargo, no fue capaz de explicar cómo se produjo ese movimiento de las masas continentales. Hasta que, en los años 60, gracias a los avances en la investigación geofísica de los fondos oceánicos, se descubrió el motor que realmente mueve nuestro planeta, la tectónica de placas. Ahora sabemos que los continentes no se desplazan sobre los océanos, son los fragmentos en los que está dividida la litosfera o capa más externa de nuestro planeta, a los que llamamos placas tectónicas, los que se mueven sobre la astenosfera, que es la capa que tienen justo por debajo.
Pero no voy a entrar ahora en detalles sobre cómo o por qué se mueven las placas tectónicas. Lo que vamos a ver es desde cuándo lo hacen. Es decir, responder a una pregunta que igual no os habéis hecho nunca: ¿Ha habido una sola Pangea en la historia de la Tierra?
Pues vamos a viajar al pasado más remoto de nuestro planeta y veamos lo que nos dice la evidencia científica. La Tierra tiene casi 4600 millones de años y hace al menos 3800 millones de años que se formó una litosfera estable, con las primeras placas tectónicas y las primeras masas continentales. Fue entonces cuando se le dio al botón de encendido de los movimientos tectónicos y, por suerte, tenemos registros geológicos del devenir de las placas desde entonces. Y parece que tienen un comportamiento muy cíclico: en primer lugar, las placas tectónicas formadas por masas continentales acaban convergiendo entre sí dando lugar a un supercontinente. Pasados millones de años, los movimientos tectónicos provocan la fragmentación de esa gran masa terrestre en continentes menores y su separación progresiva. Finalmente, las placas tectónicas vuelven a converger, dando lugar a un nuevo supercontinente. Y así sucesivamente. Es lo que se conoce como Ciclo Supercontinental de Wilson.
No hubo un único supercontinenteAhora que sabemos que no ha habido una sola Pangea en el pasado geológico, se nos plantean dos nuevas preguntas: ¿Cuántos supercontinentes han existido?, y ¿cuándo se formaron y se disgregaron esos supercontinentes? Para responder a ambas cuestiones, vamos a hacer un pequeño listado lleno de nombres curiosos.
El supercontinente más antiguo del que tenemos evidencias se formó hace entre 3600 y 2750 millones de años y se le conoce como Supercontinente Vaalbará. Le sigue el Supercontinente Kenorland, que comenzó a constituirse hace unos 2750 millones de años y se fracturó hace 2500 millones de años. El tercer supercontinente del que nos quedan evidencias se conformó hace entre 2500 y 2100 millones de años y se le conoce como Supercontinente Arctica. Hace entre 2100 y 1800 millones de años nos encontramos con el Supercontinente Atlantica. El quinto fue el Supercontinente Columbia, que se generó hace unos 1800 millones de años y se desmembró hace unos 1300 millones de años. A continuación, hace entre 1250 y 650 millones de años, tenemos el Supercontinente Rodinia. Y terminamos este repaso con el Supercontinente Pannotia, formado hace unos 600 millones de años y fracturado hace 540 millones de años. Por tanto, el Supercontinente Pangea (hace entre 335 y 175 millones de años) es, como mínimo, el octavo supercontinente de la historia geológica de nuestro planeta.
 Ilustración del aspecto que ofrecería la Tierra vista desde el espacio hace 600 millones de años, con el supercontinente Pannotia
Ilustración del aspecto que ofrecería la Tierra vista desde el espacio hace 600 millones de años, con el supercontinente PannotiaVamos, que la Tierra no ha estado quieta prácticamente desde que se formó. La tectónica de placas evidencia una serie de movimientos cíclicos de colisión y separación de grandes continentes que seguirá produciéndose mientras exista dinámica litosférica en nuestro planeta. ¿Significa esto que en el futuro volverá a formarse un nuevo supercontinente? La respuesta es sí. Se estima que, dentro de algo más de 200 millones de años, las actuales masas continentales confluirán de nuevo entre sí. Aunque se han propuesto hasta cuatro hipótesis sobre el aspecto de dicho supercontinente, ya que no es tan sencillo estimar el verdadero movimiento futuro de las placas tectónicas basándonos en las actuales orientaciones y velocidades de desplazamiento de las mismas. Al menos los nombres propuestos para esos posibles futuros supercontinentes siguen siendo muy evocadores: Pangea Ultima, Novapangea, Aurica y Amasia.
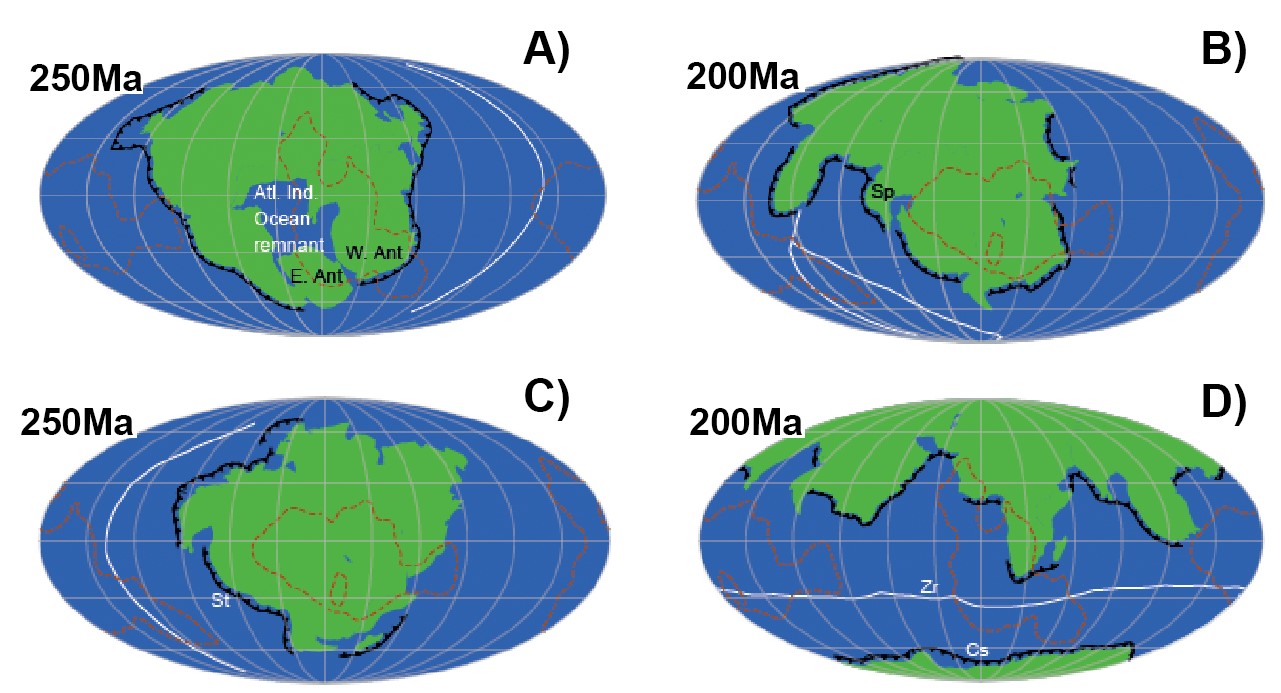 Aspectos hipotéticos del futuro supercontinente global dentro de 200-250 millones de años (Ma). A) Pangea Ultima, B) Novapangea, C) Aurica y D) Amasia. Imágenes modificadas de Davies, H.S., Green, M. y Duarte, J.C. (2018). Back to the future: Testing different scenarios for the next supercontinent gathering. Global and Planetary Change doi: 10.1016/j.gloplacha.2018.07.015Para saber más:
Aspectos hipotéticos del futuro supercontinente global dentro de 200-250 millones de años (Ma). A) Pangea Ultima, B) Novapangea, C) Aurica y D) Amasia. Imágenes modificadas de Davies, H.S., Green, M. y Duarte, J.C. (2018). Back to the future: Testing different scenarios for the next supercontinent gathering. Global and Planetary Change doi: 10.1016/j.gloplacha.2018.07.015Para saber más:
Historia de la tectónica de placas [vídeo breve]
De la tectónica de placas
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Y, sin embargo, se mueven se ha escrito en Cuaderno de Cultura Científica.
Dos más dos son cinco
La libertad es poder decir libremente que dos y dos son cuatro. Si se concede esto, todo lo demás vendrá por sus pasos contados.
George Orwell, 1984 (capítulo VII)
 Imagen generada con Powerpoint. Fuente: Marta Macho
Imagen generada con Powerpoint. Fuente: Marta Macho
¿Pero dos más dos no han sido siempre cuatro? No necesariamente; ya vimos en la anotación Algunas observaciones someras relativas a las propiedades aerodinámicas de la suma que el resultado de esa suma puede depender de la velocidad del viento…
Bromas aparte, el lógico y filósofo Bertrand Russell (1872-1970) utilizó este enunciado matemático para explicar que es posible llegar a demostrar cualquier propiedad si se comienza con una proposición falsa. Como parte de esta anécdota, se comenta que, con escepticismo, alguien increpó a Russell de este modo:
¿Quiere usted decir que si 2 + 2 = 5, entonces es usted el Papa?
Russell asintió y pasó a demostrar que, efectivamente él era el obispo de Roma:
Supongamos que 2 + 2 = 5. Restemos 3 de cada uno de los miembros de la identidad; obtenemos 1 = 2. Por simple simetría, 1 = 2 implica que 2 = 1. Ahora, dado que el Papa y yo somos dos personas distintas, y dado que 2 = 1, el Papa y yo somos uno. Como resultado de ello, yo soy el Papa.
George Orwell y Radiohead
La banda británica de rock Radiohead lanzó en 2003 el tema «2 + 2 = 5 (The Lukewarm)», aludiendo a la novela 1984 del escritor británico George Orwell (1903-1950):
Cogió el libro de texto infantil y miró el retrato del Gran Hermano que llenaba la portada. Los ojos hipnóticos se clavaron en los suyos. Era como si una inmensa fuerza empezara a aplastarle a uno, algo que iba penetrando en el cráneo, golpeaba el cerebro por dentro, le aterrorizaba a uno y llegaba casi a persuadirle que era de noche cuando era de día. Al final, el Partido anunciaría que dos y dos son cinco y habría que creerlo. Era inevitable que llegara algún día al dos y dos son cinco. La lógica de su posición lo exigía. Su filosofía negaba no sólo la validez de la experiencia, sino que existiera la realidad externa. La mayor de las herejías era el sentido común. Y lo más terrible no era que le mataran a uno por pensar de otro modo, sino que pudieran tener razón. Porque, después de todo, ¿cómo sabemos que dos y dos son efectivamente cuatro? O que la fuerza de la gravedad existe. O que, el pasado no puede ser alterado. ¿Y si el pasado y el mundo exterior sólo existen en nuestra mente y, siendo la mente controlable, también puede controlarse el pasado y lo que llamamos la realidad? […] La libertad es poder decir libremente que dos y dos son cuatro. Si se concede esto, todo lo demás vendrá por sus pasos contados.
«2 + 2 = 5» es parte de un eslogan comunista que se popularizó en la Unión Soviética y que buscaba “convencer” de que, a través del esfuerzo de las personas asalariadas, el trabajo realizado en dos años (1929 y 1930) y otros dos años más (1931 y 1932) podía llegar a equivaler al trabajo realizado en 5 años.
 Cartel de Yakov Guminer (1931) en el que se puede leer «La aritmética de un plan alternativo industrial-financiero: 2 + 2 más el entusiasmo de los trabajadores = 5». Fuente: Wikimedia Commons.
Cartel de Yakov Guminer (1931) en el que se puede leer «La aritmética de un plan alternativo industrial-financiero: 2 + 2 más el entusiasmo de los trabajadores = 5». Fuente: Wikimedia Commons.
George Orwell alteró el significado del eslogan comunista para transformarlo en dogma y aludir a la manipulación del Gran Hermano, el fundador del Partido que todo lo controla de la novela 1984, de tal forma que lo promulgado estuviera por encima de lo verdadero.
La canción «2 + 2 = 5 (The Lukewarm)» comienza con estos versos:
¿Eres tan soñador
como para enderezar al mundo?
Me quedaré para siempre en casa,
donde dos y dos siempre suman cinco.
Antes que George Orwell, en 1895, el periodista y humorista francés Alphonse Allais (1854-1905) ya había utilizado esta expresión. Deux et deux font cinq fue el título que eligió para una colección crónicas absurdas.
 Portada de Deux et deux Font cinq de Alphonse Allais. Fuente: Wikimedia Commons.
Portada de Deux et deux Font cinq de Alphonse Allais. Fuente: Wikimedia Commons.
Prueba (o no) de que 2 + 2 = 5
Vamos a demostrar (o no) que 2 + 2 = 5 de una manera sencilla. Sean a = b = 1. Entonces, a = b. Multiplicando ambos miembros de la anterior igualdad por a, se obtiene que a2 = ab. Si restamos b2 en ambos lados, a2 – b2 = ab – b2; de otra manera (a – b)(a + b) = (a – b)b. Dividiendo por (a – b) ambos miembros de la ecuación, se deduce que a + b = b. Y como hemos supuesto que a = b = 1, se deduce que 2 = 1. Sumando 3, queda que 5 = 4 o, de otra manera, 5 = 2 + 2.
Quizás sería conveniente repasar la prueba antes de creérsela. Aunque para aquellas personas que deseen realmente que 2 + 2 sean 5, podríamos limitarnos a “valores grandes de 2”…
Referencias
- 2 + 2 = 5, Wikipedia (consultado el 19 de mayo de 2022)
- 2 + 2 = 5 (canción), Wikipedia (consultado el 19 de mayo de 2022)
- Sobre 2+2=5 en Radiohead, Blog de la Biblioteca de Matemáticas, UCM, 18 enero 2010
- George Orwell, 1984, versión online UCM
- Alphonse Allais, Deux et deux Font cinq, Gallica
- What is meant by «Two plus two equals five”?, Quora, 2019
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Dos más dos son cinco se ha escrito en Cuaderno de Cultura Científica.
Einstein y Erwin Schrödinger
Erwin Schrödinger fue un físico austriaco que ayudó a crear los fundamentos de la mecánica cuántica. Al igual que Einstein, Schrödinger no estuvo de acuerdo con los extremos a los que otros llevaron la nueva ciencia. Fue uno de los pocos científicos que se alinearon con Einstein en contra de los “giros estrafalarios” que estaba adoptando la mecánica cuántica, intentando buscar una teoría unificada que mejorase las teorías que todos los demás apoyaban. Hasta que ocurrió un terrible malentendido.
 Schrödinger. Fuente: Wikimedia Commons
Schrödinger. Fuente: Wikimedia CommonsEinstein y Schrödinger trabajaron juntos en los primeros años 30 como profesores del Instituto Kaiser Wilhelm en Berlín. Ambos destacaron en esta institución extremadamente rígida y formal como profesores que trataban a sus alumnos como iguales. Los dos disfrutaban de paseos juntos, a pie y en velero, y llegaron a ser amigos íntimos.
Como muchos de sus contemporáneos, Einstein y Schrödinger comenzaron a escribirse acerca de su trabajo mucho antes de conocerse en persona. En los años veinte toda la comunidad de físicos se concentró en una nueva clase de ciencia que había dado en llamarse mecánica cuántica, ya que estaba basada en la idea de que la luz y la energía no eran flujos continuos, sino que estaba formada por paquetes discretos llamados cuantos. Einstein fue el primero en sugerir que la luz estaba hecha de cuantos, por lo que participó en el desarrollo de la mecánica cuántica desde el principio. Pero este campo estaba empezando a adquirir lo que Einstein y Schrödinger estaban de acuerdo en llamar un giro estrafalario.
Cuanto más y más se aprendía, más parecía que la mecánica cuántica eliminaba las leyes de la causalidad, insistiendo en que los procesos atómicos eran tan aleatorios que no se podía predecir exactamente lo que ocurriría a continuación. En 1925 Werner Heisenberg propuso una nueva clase de matemáticas matriciales que podían usarse para hacer predicciones probabilísticas acerca de cómo un átomo podría comportarse en una situación dada. Este trabajo fue saludado, y con razón, como una gran ayuda para la incipiente teoría, pero también implicaba la idea de que solamente se podían hacer “conjeturas” acerca del comportamiento del átomo.
Al año siguiente, Schrödinger publicó lo que esperaba que fuese una alternativa mejor. Ideó otro conjunto de herramientas matemáticas para que sirvieran de ayuda con la mecánica cuántica, la llamada mecánica ondulatoria. Einstein se alegró mucho con la noticia. Las matemáticas de Schrödinger, haciendo referencia a las cualidades físicas de las ondas como hacían, parecían dar esperanza a la idea de que había una razón física tras las rarezas del comportamiento atómico. Einstein, que estaba muy a disgusto con las probabilidades de Heisenberg, escribió a su amigo Michele Besso en mayo de 1926: “Schrödinger ha aparecido con un par de artículos fantásticos sobre las reglas cuánticas”.
Pero la euforia de Einstein no duraría mucho. Casi inmediatamente, se demostró que las matemáticas de Schrödinger, tan diferentes de las de Heisenberg a primera vista, eran de hecho equivalentes. Schrödinger había venido a confirmar esencialmente la inherente aleatoriedad que otros científicos estaban pidiendo ávidamente. El austriaco estaba tan contrariado por el giro de los acontecimientos como el propio Einstein, llegando a decir que si hubiera sabido lo que sus artículos iban a desencadenar no los habría publicado.
Con todo, la cuestión de si era mejor usar la mecánica matricial de Heisenberg o la ondulatoria de Schrödinger se convirtió en un debate acalorado. Aunque no le gustase la forma en la que otros interpretaban sus matemáticas, Schrödinger entró en la refriega defendiendo su propio trabajo, lo que fastidió a Heisenberg, que escribió a su amigo Wolfgang Pauli diciendo: “Cuanto más pienso en la parte física de la teoría de Schrödinger, más repulsiva la encuentro […] Lo que Schrödinger escribe acerca de la visualizabilidad de su teoría ‘es probablemente no demasiado correcto’, en otras palabras, son chorradas”. [*]
A pesar de su importante contribución a su desarrollo, Schrödinger tuvo reservas sobre la mecánica cuántica toda su vida. En su famoso experimento mental conocido como el gato de Schrödinger, trataba de burlarse de una ciencia que insistía en que nada en el mundo atómico puede conocerse a no ser (y hasta) que se mida. Lo absurdo que le resultaba a Schrödinger pensar que el gato pudiese estar a la vez vivo y muerto le convencía de que la teoría de la mecánica cuántica no era todavía comprendida del todo, la misma posición que mantenía Einstein.
Independientemente de la frustración con la que veían cómo otros científicos se entregaban a los absurdos de la mecánica cuántica, tanto Einstein como Schrödinger sabían que la teoría hacía un fantástico trabajo a la hora de predecir las probabilidades de los acontecimientos atómicos. El trabajo de Schrödinger con la mecánica ondulatoria era una parte crucial de ese éxito, y Einstein fue uno de los que nominaron a Schrödinger al premio Nobel varias veces. Schrödinger ganó el premio de física en 1933.
¿El campo unificado de Schrödinger?Dado que Schrödinger, como Einstein, no creía que la física cuántica estuviese completa, se unió a Einstein en la búsqueda de una nueva teoría. Einstein se refería a ella como la teoría del campo unificado, ya que sería la teoría omnicomprensiva que uniría toda la física. Consecuentemente, en los años 40, cuando Einstein vivía en Princeton y Schrödinger había dejado el odio de Alemania para vivir en Irlanda, Schrödinger era una de las pocas personas con las que Einstein compartía sus ideas. “No envío esto a nadie más”, escribió Einstein en 1946, “ya que tú eres la única persona que conozco que no lleva anteojeras en lo que respecta a las cuestiones fundamentales de nuestra ciencia”.
Pero la colaboración tomó un rumbo inesperado cuando Schrödinger anunció que él había resuelto el problema completamente. Estaba convencido de que había encontrado la teoría del campo unificado gracias al uso de la geometría afín. Anunció sus hallazgos el 27 de enero de 1947, no en una revista científica, sino a bombo y platillo en una rueda de prensa a la que asistió el primer ministro de Irlanda, Éamon de Valera.
Einstein se quedó estupefacto: el trabajo era idéntico a lo que él le había enviado. Si bien Schrödinger se las había ingeniado para hallar una nueva forma de derivarlas, las ecuaciones que había anunciado eran las mismas que Einstein había encontrado y que, a esas alturas, ya había descartado por incompletas. Einstein hizo unas feroces declaraciones al New York Times en las que venía a afirmar que una publicidad exagerada como la de Schrödinger hacían un flaco favor a la ciencia, ya que “el lector tiene la impresión de que cada cinco minutos hay una revolución en la ciencia, algo así como un golpe de estado en alguna de esas pequeñas repúblicas inestables”.
Schrödinger mandó una disculpa a Einstein, intentando explicar como podía haber cometido ese error colosal, pero Einstein no cambió de opinión. Einstein escribió a Schrödinger para decirle que deberían tomarse un descanso en su carteo y concentrarse en sus trabajos. Pasarían tres años (hasta poco antes del fallecimiento de Einstein) antes de que reanudasen su correspondencia.
Nota:[*] Hoy día el más usado es el enfoque de Schrödinger. Tanto es así que un estudiante de química, por ejemplo, puede terminar su grado, e incluso su máster, sin saber siquiera que existe algo que no sea la ecuación de Schrödinger para el tratamiento de los sistemas cuánticos.
Para saber más:Serie de artículos de introducción a los conceptos básicos de la mecánica cuántica, asumiendo conocimientos previos muy elementales: Cuantos
Serie de artículos de introducción a los problemas interpretativos de la mecánica cuántica: Incompletitud y medida en física cuántica
El artículo Einstein y Erwin Schrödinger se ha escrito en Cuaderno de Cultura Científica.
Ingredientes para la receta: El tomate
En tiempo de tomate, no hay mala cocinera.
Dicho popular a orillas del Bidasoa.
Cómo no os queda nada? Ay un puchero,
con chorizo, con baca, y con carnero,
con tozino, que alegra los gaznates,
con su salsa picante de tomates,
ya picadas sus verengenitas,
con sus garbanzos, y sus verduritas,
y para que acabéis unos buñuelos.
Agustín Moreto (1676) en el «Entremés de la Mariquita», tomado de Blanca y Cañizares, 2021.
 Foto: Avin CP / Unsplash
Foto: Avin CP / UnsplashHablamos de la planta llamada tomatera y de su fruto el tomate, con nombre científico Solanum lycopersicum. El término de la especie, lycopersicum, se podría traducir por melocotón de lobo. Según leyendas germánicas, brujas y magos utilizaban los frutos de la belladona para convertirse en hombres lobo. La belladona pertenece a la familia Solanacea, como el tomate. Cuando llegó a Europa el tomate, sus frutos recordaban a los de la belladona y, además, sin llegar a madurar eran tóxicos por su contenido en el alcaloide tomatina. Por ello, se conocían como melocotón de lobo. El fruto lleva minerales como potasio, fósforo y magnesio, vitaminas B y C, carotenoides como licopeno y beta-caroteno, y polifenoles, todos ellos componentes ideales para las dietas actuales.
Es el segundo cultivo hortícola más importante después de la patata. En Asia es donde más se siembra, seguido de África, Europa, América y Oceanía.
La flor de la tomatera de la especie original tiene un estilo largo que supera la altura del cono de estambres lo que favorece la fecundación cruzada, con el polen de otra flor, por insectos o el viento. Con el tiempo aparecieron variedades con el estilo corto y autofecundación obligada.
El nombre del tomate deriva de tomatl, en nahuatl, idioma de los antiguos mexicanos. Formaba parte importante de la dieta antes de la llegada de Colón. Y no solo de los mexicanos sino de muchas tribus de América como los sioux, los apaches o de los indígenas peruanos y bolivianos. La referencia más antigua que conocemos sobre el tomate se fecha entre 1335 y 1347 en los Códices de Xocimilco, durante el gobierno de la reina Tlazocilhuapilli, interesada en el ambiente y en la dieta de sus gobernados. Inventó, entre otros platos, el tonalchilli o chile güero en tomate, que lleva chile amarillo, tomate y clavo.
Llegó a Europa con Colón en 1523 y la primera mención se atribuye a Pier Andrea Mattioli, médico y botánico italiano, en 1544, o a Mathiolus en el mismo año (sospecho que son el mismo con el apellido traducido a otro idioma, quizá al latín). Mattioli describía lo que consideraba una nueva berenjena. Recomendaba cocinarlo con sal, pimienta y aceite. En Francia se conocía en 1660 como planta ornamental y hacia 1778 también como hortaliza formando parte de la dieta.
El tomate más antiguo conocido conservado en un herbario es de 1551 y está en Bolonia, Italia, y fue preparado por Ulisse Aldrovandi. Hay otros 17 ejemplares de tomate del siglo XVI en herbarios que se encuentran en Italia, Alemania, Francia, Suiza y Países Bajos. Ocho de los ejemplares tienen frutos.
Ya en 1580, en el Libro Quinto de Plantas Medicinales de Francisco Hernández se menciona el tomate en un texto que publica Pilar Iglesias y que nos ayudará a conocer el tomate, sus variedades y los usos medicinales. Dice así
Aparte de las demás especies de solano de las cuales hablamos al tratar de las plantas de nuestro Viejo Mundo, hay en este otras cuyos frutos, llamados tomatl porque son redondos, están encerrados en una membrana, son de naturaleza seca y fría en primer grado y participan de alguna acidez. Los más grandes de ellos se llaman xitomatl, es decir, tomatl, con forma de calabaza y rugosos; los más chicos, miltomatl, es decir, de siembra, porque se acostumbra sembrarlos al mismo tiempo que el tlaolli o grano indio. Algunos de los primeros son de hermoso aspecto, un poco mayores que nueces, de color verde al principio y después amarillo pálido, y se llaman coatomatl, o sea, de culebra. Otros son de la misma forma y tamaño, pero se vuelven al fin rojos; otros se vuelven de verdes a amarillos y tienen casi el tamaño de la llamada naranja, con uno y otro lado ligeramente comprimidos e irregularmente rugosos desde la parte en que se adhieren al pedúnculo hasta su mitad; otros son rojos cuando han madurado por completo, pasando antes también por el verde, el amarillo pálido y el rojizo, y son casi del mismo tamaño y figura que los anteriores, pero, además de ser rugosos, tienen ciertas protuberancias irregulares que no solo semejan las partes femeninas, sino también hemorroides y cuanto de horrible y obsceno pueda verse en las mujeres. Entre los menores, algunos son del tamaño de nueces y de color verde; otros, llamados izhoatomatl, son mayores que avellanas, aunque menores que las nueces, están encerrados en una membrana a modo de vejiga, de donde les viene el nombre, y pasan del verde al amarillo pálido o al púrpura; los llamados miltomatl son del tamaño de avellanas y del mismo color que los precedentes, así como el coztomatl y el tomatl, que llamamos xalatlacense por el lugar en que se hace, los cuales están llenos de unas semillas como pajitas, y se cuentan principalmente entre los medicamentos dotados de calor. Hay otras especies, de las que hablaremos separadamente, pues tienen nombre propios y especiales naturalezas. Por lo que ve a las antes citadas, todas parecen ser semejantes al solano y aun especies suyas; pero las que dan fruto más grande son también mayores y con hojas aserradas, en tanto que las de fruto menor son más pequeñas. Los farmacéuticos europeos que han conocido algunos de estos frutos los han llamado frutos de amor. En suma, la figura de la planta, las propiedades del fruto, sus membranas y a veces su forma de tal modo corresponden a las especies de solano, que sería necio no convenir con los que clasifican todos los tomates entre las variedades del mismo. Se hace de ellos, molidos y mezclados con chili, una salsa muy agradable que mejora el sabor de casi todas las viandas y alimentos y estimula el apetito. Su naturaleza es fría, seca y algo picante. Tanto las hojas como los frutos son muy eficaces, untados, contra los fuegos de San Antón: curan aplicados las fístulas lagrimales y los dolores de cabeza, alivian los ardores de estómago, y untados con sal resuelven las paperas. Su jugo es bueno contra las inflamaciones de la garganta, y cura las úlceras reptantes mezclado con albayalde, aceite rosado y litargirio. Para las fístulas lagrimales se mezcla con pan; para la irritación de los niños que llaman soriasis, con aceite rosado; se agrega en vez de agua a los colirios, se unta en vez de huevo contra los flujos agudos, y alivia instilado el dolor de oídos. Aplicado en una venda detiene los flujos menstruales excesivos, y mezclado con estiércol de gallina y aplicado en una mecha es un remedio excelente para las fístulas lagrimales. Nacen en cualesquiera regiones, pero principalmente en las cálidas, ya espontáneamente, ya cultivados.
Las primeras recetas con tomates impresas en Europa se publicaron en Nápoles en 1692. El autor era Antonio Latini y una de la recetas era un estofado con codorniz, ternera, pollo y tomate. La segunda receta era una salsa de tomate que llamó al estilo español. Rudolf Grewe la tradujo al inglés y decía así
Toma media docena de tomates que estén maduros, y ponlos a asar en las brasas, y cuando estén chamuscados quítales la piel con diligencia y pícalos finamente con un cuchillo- Agrega tomillo y cebollas, picadas finamente, a discreción y agrega pimientos picantes también picados finamente. Después de mezclar todo junto, ajustarle un poco de sal, aceite y vinagre, es una salsa muy rica, tanto para platos hervidos, como para cualquier otra cosa.
El ancestro silvestre del tomate son pequeñas bayas con semillas que son dispersadas por las aves. Resisten el paso por el tubo digestivo que, además, influye en la capacidad de germinación. Si ayuda el clima y el entorno, se pueden encontrar plantas de tomate en lugares donde no se ha sembrado como cerca de desagües, junto a muros y cercas o en cunetas.
Existe apenas una docena de especies de tomate silvestre pero solo una, Solanum lycopersicum, fue domesticada y, al parecer, solo ocurrió una vez hace unos 2500 años. La especie silvestre es originaria de los Andes en Perú y Ecuador, pero no interesó a los nativos y se extendió, quizá como mala hierba, hacia el norte y fue domesticada en México donde comenzó su cultivo. En el siglo XVI lo cultivaban los mayas. Las variedades que llegaron a Europa se parecen a las cultivadas en México más que a las de la región de los Andes. También fueron los españoles los que llevaron, desde la costa occidental de México, el tomate a Filipinas desde donde se extendió el cultivo por Asia.
En el siglo XVI, Fray Bernardino de Sahagún encontró una gran variedad de tomates en el mercado de Tenochtitlán, y como Francisco Hernández, también lo dejó por escrito
El que trata en tomates suele vender los que son de muchos y diversos géneros … como son los tomates amarillos, colorados y los que están bien maduros. El que es mal tratante en esto vende los que están pudridos y machucados, y los que están azedos. Vende también los que aún no están bien maduros sino muy verdes, y cuando se comen revuelven el estómago, ni dan sabor alguno, sino que provocan las reumas.
Las variedades cultivadas más grandes, como el tomate Corazón de Buey, pueden ser hasta cien veces mayores que las bayas ancestrales. El tamaño va desde la variedad Cherry, de 1-2 centímetros de diámetro, hasta el mencionado Corazón de Buey de más de 10 centímetros. El tamaño comercial mas habitual se de 5-6 centímetros de diámetro.
La selección de variedades de tomate, según cuenta Jonathan Silvertown, con la domesticación original y el transporte de variedades entre diferentes lugares supuso el paso de, por lo menos, tres cuellos de botella genéticos y, en cada uno de ellos, solo un pequeño número de ejemplares consiguió pasar a la siguiente fase.
Los primeros tomates domesticados en México solo contenían una parte de los genes de las poblaciones silvestres. En el siglo XVI, esos tomates domesticados viajaron a Europa. Más tarde, las variedades europeas volvieron a México y solo llevaban el 5% de la dotación genéticas de los tomates silvestres. Pero tenían suficientes posibilidades de variar como permitir selección artificial que se aceleró.
La selección de nuevas variedades se aceleró a partir del siglo XIX y se favoreció por el traslado geográfico por nuestra especie, la disminución de insectos polinizadores y la promoción de variedades autofecundantes.
Las variedades más recientes, conocidas como de larga vida y desarrolladas en primer lugar en Israel a finales de los ochenta y principios de los noventa tienen una duración que permite la cosecha y su envío a mercados lejanos en buen estado de conservación. Sin embargo, en muchas de estas variedades falta el típico aroma del tomate, tan importante para el consumidor.
Los estudios para recuperar y mejorar el aroma han aumentado en el último medio siglo. La revisión de Miriam Distefano y su equipo, de la Universidad de Catania, revela que, en las bases de datos de publicaciones científicas, el número de artículos sobre los componentes volátiles del tomate, es decir, de su aroma, han pasado de 20 en la década de los setenta del siglo pasado, a casi 1000 entre 2011 y 2022. Es una muestra del aumento de interés en conocer mejor el aroma de los tomates.
Son estudios técnicamente difíciles pues en el aroma se han encontrado más de 400 compuestos volátiles. Intervienen muchos genes y el proceso se ve influido por factores externos tanto durante el crecimiento y la maduración del fruto como después de la cosecha en el transporte hasta el consumidor. La revisión de Distefano indica que lo poco que se empieza a conocer se centra, sobre todo, en los factores que actúan durante el crecimiento y después de la cosecha.
El grupo de José Blanca, de la Universidad Politécnica de Valencia, publicó en 2022 el análisis genético de 1254 muestras de variedades de tomate tanto tradicionales como modernas, y algunas de las primeras variedades domesticadas y silvestres.
Las variedades más antiguas tienen escasa variabilidad genética pero, en España e Italia, a donde llegó en primer lugar el tomate desde América, hay dos grupos con una variabilidad alta. En general, hay variedades que muestran un patrón de migraciones, movimientos geográficos debidos a nuestra especie, e hibridaciones muy complejo.
El grupo de Hamid Razifard, de la Universidad de Massachusetts en Amherst, en una publicación en 2020, menciona que la evolución del tomate se acepta muy simplificada, con dos transiciones principales: la primera es desde la especie Solanum pimpinellifolium, pequeña, silvestre y con el fruto del tamaño de un arándano, a un intermedio domesticado, S. lycopersicum var. cerasiforme, que ocurrió en Sudamérica; y la segunda transición desde esta var. cerasiforme al tomate domesticado S. lycopersicum var. lycopersicum, en América Central.
Sin embargo, el estudio por el grupo de Rafizard del genoma de 166 muestras de tomates cultivados en México y semicultivados en América Central revela un proceso más complejo. Por ejemplo, la var. cerasiforme apareció en Ecuador hace 80000 años como especie salvaje. Fue cultivada en Perú y Ecuador con frutos de tamaño mediano. Y, según los autores, se expendió hacia el norte por América Central hasta México como mala hierba acompañando a otros cultivos.
El debate continúa pues un fruto con muchas formas, colores, tamaños y sabores. El grupo de Michael Alonge, de la Universidad Johns Hopkins, analizó el genoma de 100 variedades y encontró nada menos que 238490 variaciones. Con combinaciones múltiples de estas variantes se modifica el aroma, el tamaño y la producción de frutos. Por ejemplo, encontraron un gen que da sabor ahumado al tomate y consiguieron cambiar su tamaño. En un último ensayo de diferentes combinaciones facilitaron la recolección sin disminuir la cosecha.
Hipótesis sobre la domesticación del tomateLa revisión más reciente de la domesticación del tomate la han propuesto José Blanca y sus colegas. Analizan 628 secuencias, incluyendo las publicadas en seis estudios previos. Como en el estudio de Hamid Razifard parten de las tres especies y variedades implicadas, es decir, de Solanum pimpinellifolium, Solanum lycopersicum cerasiforme y Solanum lycopersicum lycopersicum.
Mencionan tres hipótesis: la de José Blanca y colegas publicada en 2012; la ya comentada de Hamid Razifard; y la que proponen en esta revisión de 2022.
Las dos primeras proponen el movimiento de especies y variedades desde Perú y Ecuador hacia el norte, a México a través de Centroamérica. En la primera hipótesis solo llega la variedad cerasiforme a México, y en la segunda llega una cerasiforme de pequeño tamaño, y ambas, en México evolucionan a la variedad domesticada. En la hipótesis de 2022, José Blanca propone el paso hacia el norte, la vuelta a Sudamérica, con aumento de tamaño, y el regreso hacia el norte para llegar a la lycopersicum domesticada.
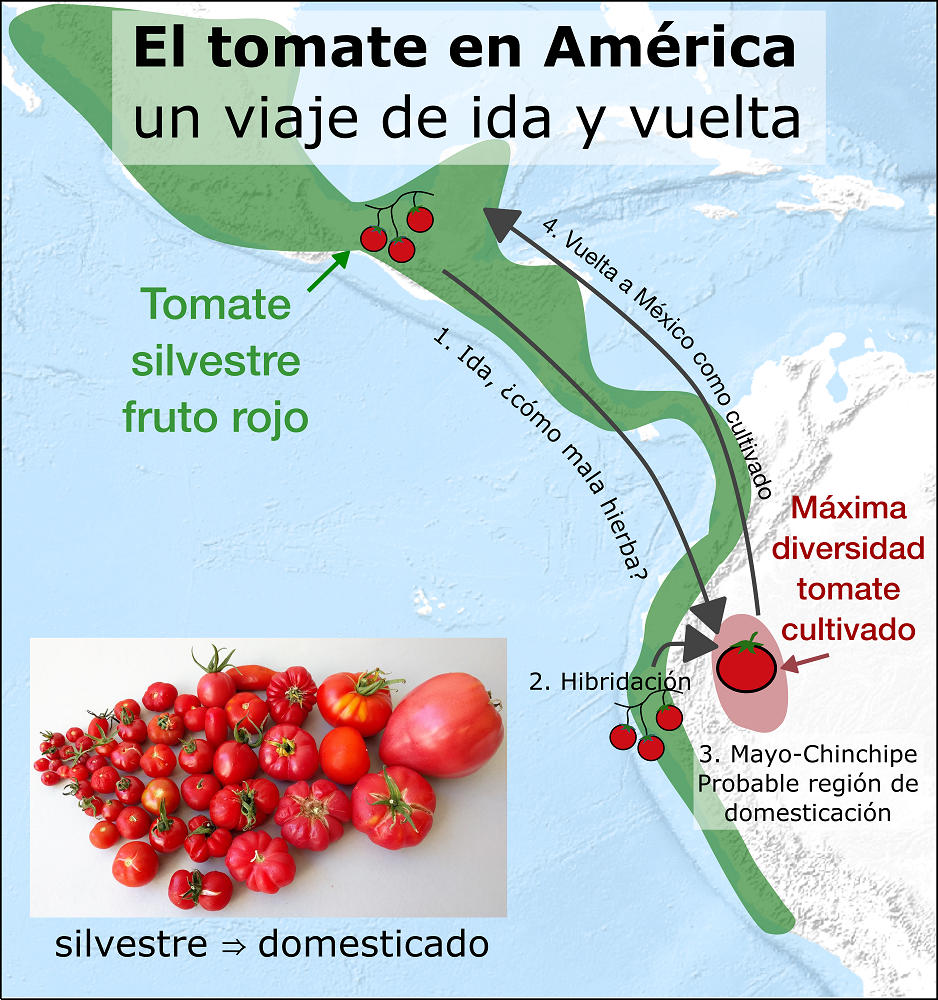 Fuente: Blanca & Cañizares (2022) The Conversation
Fuente: Blanca & Cañizares (2022) The ConversationPara celebrar lo que sabemos del tomate no hay nada mejor que degustarlo y, propongo, una receta de la Cocina para pobres de Alfredo Juderías. Este es el Pisto Carretillero que ilustra el refrán popular que dice que “Tomates y pimientos, siempre amigos y siempre revueltos”.
Echar en una sartén a la lumbre con aceite unos pimientos verdes partidos en dados. Cuando estén a medio freír agregar un calabacín y unos tomates algo escaldados y pelados y troceados. Cocer lentamente hasta que el agua del calabacín y del tomate se haya consumido. Espolvorear con sal, un pelín de azúcar si se quiere, algo de pimienta y que aproveche.
Y si queremos conservar los tomates podemos seguir a Juan de Altamiras y la edición de 1767 de su libro Nuevo Arte de la Cocina Española. El autor era fraile franciscano, aragonés de nacimiento, y cocinero del Convento de San Cristóbal, hoy en ruinas, junto a Tauste, en Zaragoza. La receta nos la ofrece Vicky Hayward en su libro publicado en 2017.
Una vez maduros los tomates, Fray Juan escribe que
Quando estén medio crudos, echalos en aceyte frío, y los mantendrás todo el año, como si se cogieran entonces de la mata; pero los has de coger antes de salir el Sol; y el aceyte sirve para cualquier cosa.
Así Fray Juan, como dice, tiene tomates para todo el año.
Como curiosidad y para estar al día en el gusto de los consumidores, hay que mencionar una de las variantes de salsa de tomate más conocidas y utilizadas es el kétchup que, según el Diccionario, está condimentada con vinagre, azúcar y especias. Es de origen chino y la comercializó en Estados Unidos Henry Heinz en 1878. Lleva tomate, agua, azúcar, vinagre, fécula, sal, especias, conservantes y acidulantes.
Referencias:Alonge, M. et al. 2020. Major impacts of widespread structural variation on gene expression and crop improvement in tomato. Cell 182: 145-161.
Bai, Y. & P. Lindhout. 2007. Domestication and breeding of tomatoes: What have we gained and what can we gain in the future? Annals of Botany 100: 1085-1094.
Barath, H. 2020. Las numerosas mutaciones del tomate. Investigación y Ciencia octubre: 7.
Blanca, J. et al. 2012. Variation revealed by SNP genotyping and morphology provides insight into the origin of the tomato. PLOS One 7: e48198.
Blanca, J. et al. 2022. Haplotype analyses reveal novel insights into tomato history and domestication driven by long-distance migrations and latitudinal adaptations. Horticulture Research 9: uhac030.
Blanca, J. et al. 2022. European traditional tomatoes galore: a result of farmers’ selection of a few diversity-rich loci. Journal of Experimental Botany doi: 10.1093/jxb/erac072.
Blanca, J. & J. Cañizares. 2021. El tomate no es natural, es un tesoro creado por el ingenio humano. El País 3 diciembre.
Blanca, J. & J. Cañizares. 2022. La domesticación del tomate en América: un viaje de ida y vuelta. The Conversation 28 febrero.
Distefano, M. et al. 2022. Aroma volatiles in tomato fruits: the role of genetic, preharvest and postharvest factors. Agronomy 12: 376.
Grewe, R. 1988. The arrival of the tomato in Spain and Italy: Early recipes. Journal of Gastronomy 3: 67-81.
Hayward, V. 2017. Nuevo Arte de la Cocina Española de Juan Altamiras. Círculo de Lectores. Barcelona. 493 pp.
Iglesias, P. 1988. El libro del tomate. Alianza Ed. Madrid. 143 pp.
Juderías, A. 1994. Cocina para pobres. Undécima edición. Ed. SETECO. Madrid.325 pp.
Razifard, H. et al. 2020. Genomic evidence for complex domestication history of the cultivated tomato in Latin America. Molecular Biology and Evolution 37: 1118-1132.
Sahagún, Fray Bernardino de. 1830 (1677). Historia natural de las cosas de Nueva España. Biblioteca Laurenciana. Florencia.
van Andel, T. et al. 2022. Sixteenth-century tomatoes in Europe: who saw them, what they looked like, and where they come from.PeerJ 10: e12790.
Vergani Guralazzi, R. 1997. Lycopersicum esculentum: Una breve historia del tomate. Alquibia 3: 105-111.
Wikipedia. 2022. Kétchup. 16 febrero.
Wikipedia. 2022. Solanum lycopersicum. 7 marzo.
Para saber másUn espectrómetro Raman portátil mide el punto óptimo de maduración del tomate
La contaminación por metales pesados no llega a los tomates
Así es la química de una buena pizza
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Ingredientes para la receta: El tomate se ha escrito en Cuaderno de Cultura Científica.
Tú no sabes por qué sale cara, pero la moneda sí
Javier Fernández Panadero
 Foto: ZSun Fu / Unsplash
Foto: ZSun Fu / Unsplash
El uso y la costumbre nos hace olvidar que el mundo es muy diferente a lo que de primeras pudiera parecer, así cómo qué herramientas hemos elegido para (intentar) entenderlo. En la aproximación científica al conocimiento intentamos ser empíricos. Nuestro criterio para evaluar la verdad de una proposición es su acuerdo con las observaciones del mundo natural, más allá de opiniones, teorías, gurús o tradiciones. Construimos modelos que serían capaces de explicar los hechos observados, intentando que sean lo más sencillos posibles (navaja de Ockham) y expliquen cuántas más cosas, mejor. Repito, modelos.
Modelos simples, pero sin pasarseAlgunos muy exitosos, son asombrosamente “falsos” por simplificados. Te pondré un ejemplo, el gas ideal. Este modelo considera que los átomos o moléculas que forman el gas son puntuales (de tamaño cero) y que no interaccionan entre ellos. Estas obvias falsedades son tan aproximadamente ciertas para muchas situaciones que es un modelo que funciona estupendamente. Piensa que, debido a su simplicidad, las ecuaciones que se derivan son también sencillas y manejables. ¿Eso significa que existe ese gas? ¿Cómo puede ser que las moléculas ocupen un volumen cero? No, no existe. Es un modelo que aproxima la realidad con precisión suficiente para nuestras aplicaciones. Fin.
Estas ideas suelen estar bastante claras. Lo llamativo es que a veces olvidemos que con el azar pasa algo parecido. Me explicaré.
El comportamiento de una moneda no ES azaroso. La moneda es un objeto que sigue obediente las leyes de Newton del movimiento, las ecuaciones del sólido rígido, experimenta la gravedad, la reacción de la mesa, el movimiento del aire circundante… Podemos plantear las ecuaciones correspondientes e intentar derivar soluciones. El problema es que nos encontraremos con que resulta muy difícil predecir el comportamiento por la gran influencia de pequeñas variaciones en los futuros posibles.
En cambio, si analizamos los resultados de múltiples lanzamientos veremos que se PARECE mucho al que se obtendría de un sistema que, al azar, pudiera dar dos valores de salida. De hecho, haciendo un poco de estadística podríamos incluso modelizar monedas asimétricas con probabilidades distintas del 50% entre sus dos posibilidades. Por lo tanto, decir que una moneda es un sistema que devuelve al azar un valor de dos posibles es un excelente MODELO, no que estemos diciendo que sale cara porque existe un proceso necesariamente aleatorio en su comportamiento esencial. Volviendo al título. La moneda “siente” la gravedad, la reacción de la mesa, SABE muy bien quien la ha empujado en qué dirección y por qué cae como cae… eres tú el que no lo sabe y no podría saberlo.
Si piensas en una molécula que se mueve en un líquido de nuevo sabe muy bien con quién se ha chocado o con qué pared y por qué lleva la velocidad que lleva. Ella sí. Nosotros, no. Por eso hacemos mecánica estadística con estupendos resultados. Pensemos, si quieres, en la salida de una boca del metro en hora punta vista desde arriba. Se parece mucho a un líquido que se desborda y probablemente responda estupendamente a ese modelo. ¿Significa eso que cada persona que sale no sepa donde va y por qué? No, significa que nos resulta difícil hacer esa cuenta y que un modelo más simple explica suficientemente el comportamiento observado.
Y ahora, dejadme que me pare un momento sobre estas dos frases:
“El comportamiento de una moneda no ES azaroso.”
“(…) se PARECE mucho al que se obtendría de un sistema que, al azar, pudiera dar dos valores (…)”
En un esquema de pensamiento empírico, donde sabemos de las cosas por cómo se presentan a los sentidos, ¿cuál es la diferencia entre SER y PARECER?
Cuando solo tratamos con EFECTOS, ¿cómo podemos distinguir entre algo que PARECE todo el tiempo de una manera y algo que lo FUERA?
No podemos. Son indistinguibles. Desde el conocimiento empírico accedemos a la “esencia” de las cosas por sus efectos en el mundo observable.
Otra cosa sería un objeto que se comporta casi siempre de una manera, pero en situaciones especiales lo hace de otra. Ahí podría distinguirlos… pero sería de nuevo por los efectos, por esos comportamientos excepcionales.
Por lo tanto, clásicamente el comportamiento azaroso es un modelo más, aproximado, no una característica esencial de los sistemas.
¿Es el mundo cuántico esencialmente azaroso?
Veamos…
Por un lado, la cuántica es un modelo más de la naturaleza, aproximado, y que trata de explicar los comportamientos y los efectos que percibimos. Ahí adolecería también de la renuncia a una explicación esencialista como en los modelos clásicos.
De hecho, la evolución de los sistemas cuánticos es determinista, lo que significa que dado un estado del sistema podemos saber su evolución futura. Otra cosa diferente es que el estado de un sistema no tenga “detalladas” todas sus propiedades o que no sean “accesibles”.
Estamos familiarizados con esa versión del principio de incertidumbre de Heisenberg donde el hecho de conocer con más precisión la posición nos añade incertidumbre en el momento lineal y viceversa. Así que, habrá cosas imposibles de saber (una “trayectoria”, por ejemplo. Se convierten en “nube de probabilidad”) o cosas que no podrán saberse a la vez con tanta precisión como se quiera.
También podríamos pensar en estados cuánticos que no tienen un valor definido para un observable (una “magnitud”). Por ejemplo, un electrón cuyo spin en un eje sea una combinación lineal de “arriba” y “abajo”, dos partículas entrelazadas*, etc.
¿Cómo o quién decide el valor concreto que saldrá cuando se produzca una medida?
Cuando mida el espín de ese electrón, ¿qué hará que dé ½ o -½ en la medida de cada partícula concreta?
En las partículas entrelazadas, ¿por qué al medir una me sale un valor y no el opuesto? ¿Existe un mecanismo microscópico no percibido (similar a lo que le pasaba a la moneda) o es un proceso esencialmente aleatorio?
La mejor respuesta que puedo daros es que la pregunta no tiene sentido… y que no importa, en tanto que los resultados son indistinguibles y nosotros somos empiristas.
Quizá a alguno les suene la Teoría de Variables Ocultas donde se pretendía que había variables que no estábamos midiendo y que marcaban los resultados que podíamos apreciar.
Los científicos se pusieron a idear experimentos en los que una teoría y la interpretación más habitual de la cuántica arrojaran resultados distintos. Porque esa es la única manera desde el empirismo. Los científicos siguen el mandato bíblico Por sus obras los conoceréis.
Finalmente consiguieron idearlos y llevarlos a cabo. Con ello probaron que la Teoría de Variables Ocultas, tal y como se planteaba, era incompatible con los experimentos. Así que ahora queda la disyuntiva: ¿Es la naturaleza cuántica esencialmente azarosa o muestra un comportamiento que puede modelizarse bien por el azar? Pero, como os digo, la respuesta a eso es que desde el empirismo no tiene demasiado sentido la pregunta.
Concluimos, por lo tanto, que las matemáticas son una sorprendentemente buena manera de modelizar el mundo que percibimos de forma aproximada, y que las descripciones que incluyen el azar y lo probabilístico son solo otras herramientas matemáticas a nuestra disposición. Y, aunque suponga cierta insatisfacción filosófica, recordamos que el empirismo renuncia a conocer la esencia de las cosas más que por sus comportamientos, diluyendo así la diferencia entre SER y PARECER.
Nota:
*Entrelazamiento cuántico. Curioso fenómeno, sin análogo clásico, donde dos sistemas tienen una propiedad cuyo valor en uno y otro están “ligados”. Por ejemplo, dos electrones con valor de spin en un eje igual a cero, de forma que uno tendrá un valor ½ y el otro -½, pero no está fijado cuál tiene cuál. Si preparas muchos estados así, al medir en uno te saldrá un valor y en el otro se concretará el valor contrario, y viceversa.
Para saber más:
Serie de artículos de introducción a los conceptos básicos mencionados en el texto, asumiendo conocimientos previos muy elementales: Cuantos
Serie de artículos de introducción a los problemas interpretativos de la mecánica cuántica: Incompletitud y medida en física cuántica
Sobre el autor: Javier Fernández Panadero es físico y profesor de secundaria, además de un prolífico autor de libros de divulgación científica.
El artículo Tú no sabes por qué sale cara, pero la moneda sí se ha escrito en Cuaderno de Cultura Científica.
IV Jornada Nacional de Evolución y Neurociencias: Julio Sanjuán – El mono creativo: sueños, alucinanciones y locura

¿Estamos realmente diseñados para conectar con los demás? Si es así, ¿por qué siguen existiendo los psicópatas? ¿Se pueden tratar trastornos delirantes como la paranoia desde el punto de vista de la evolución? O ¿cómo ha cambiado la atracción sexual desde la época de nuestros ‘abuelos’ homínidos hasta ahora?
A estas y otras cuestiones relativas a la evolución del comportamiento humano se trató de dar respuesta durante la IV Jornada Nacional de Evolución y Neurociencias, evento organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Red de Salud Mental de Bizkaia, que tuvo lugar los días 28 y 29 de abril en el Bizkaia Aretoa – UPV/EHU de Bilbao.
Desde que en 2017 un grupo de psiquiatras de la Red de Salud Mental de Bizkaia organizara la primera edición de esta jornada, la cita se ha convertido en un punto de encuentro para profesionales de distintos ámbitos científicos como la psiquiatría, la psicología, la biología o la filosofía con un interés común: la conducta humana desde una perspectiva evolucionista y su divulgación científica en un formato accesible y ameno para todos los públicos, a la par que riguroso y actualizado.
La evolución no nos ha hecho perfectos del todo. Nuestro encéfalo a veces no compila o computa como se espera de él. Nos lo explica Julio Sanjuán, profesor de psiquiatría en la Facultad de Medicina de la Universidad de Valencia.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo IV Jornada Nacional de Evolución y Neurociencias: Julio Sanjuán – El mono creativo: sueños, alucinanciones y locura se ha escrito en Cuaderno de Cultura Científica.
La luz y el caudal regulan el metabolismo de los ríos
Los factores que regulan el metabolismo de los ríos son la luz y el caudal. Esa es la conclusión que se extrae del análisis de millones de datos de las estaciones de medida de 222 ríos estadounidenses. Estos resultados son importantes para escalar y modelizar la dinámica de los ecosistemas fluviales, e incluso pueden cambiar la forma de estudiarlos. En el estudio ha participado una investigadora del Departamento de Biología Vegetal y Ecología de la UPV/EHU.
 Foto: Maite Arroita / UPV/EHU
Foto: Maite Arroita / UPV/EHULa temperatura y las precipitaciones determinan gran parte de la variación de la productividad en los ecosistemas terrestres, y se utilizan para definir los biomas. “En tierra se conocen muy bien los cambios que se producen en el metabolismo de los ecosistemas tanto a nivel estacional como a nivel de sistema. Sabemos que los principales factores que controlan dichos cambios son la temperatura y la precipitación, y en base a eso sabemos qué tipo de vegetación y fauna nos encontraremos, qué fisionomía tendrán, podemos predecir cómo funcionará un ecosistema, etc. Sin embargo, con los ríos no pasa lo mismo. Teníamos un hándicap importante, sobre todo porque carecíamos de datos”, explica Maite Arroita, doctora del grupo de investigación Stream Ecology de la UPV/EHU.
En ese sentido, la investigadora del Departamento de Biología Vegetal y Ecología de la UPV/EHU Maite Arroita ha colaborado con varias universidades de EE. UU. en un estudio en el que han concluido que el metabolismo de los ríos está regulado por la luz y el caudal fluvial. En este estudio se han utilizado millones de datos extraídos de las estaciones de medida de la calidad del agua de 222 ríos estadounidenses. “La temperatura, la concentración de oxígeno, el caudal, el pH, la conductividad, etc., son parámetros que se miden a menudo, en función de cada estación: cada 10 o 15 minutos, cada media hora, etc., durante varios años. De todos esos datos hemos calculado el metabolismo fluvial; hemos analizado la estacionalidad de los ríos y hemos buscado patrones, para ver cuáles son los factores que marcan esas diferencias espaciales y temporales”, explica.
La importancia del caudal“La fotosíntesis es uno de los principales procesos metabólicos. Sin luz no hay fotosíntesis. La disponibilidad de luz varía mucho de unas estaciones a otras, pero también de un sistema a otro, en función de la topografía, el clima, la cobertura de los bosques de ribera, la turbidez, etc. Esta variabilidad de la luz explica la mayor proporción de los cambios que suceden en el metabolismo”, detalla la investigadora.
Por otra parte, otra de las características más importantes de los ríos es el caudal o el régimen hidrológico. La investigadora lo explica así: “El caudal puede afectar al metabolismo de varias formas. Por un lado, tras una tormenta aumenta la llegada de sedimentos a los ríos; aumenta la turbidez y disminuye la disponibilidad de luz. Además, cuando se producen lluvias torrenciales, el efecto del caudal puede ser aún mayor, ya que puede mover incluso los sedimentos y los seres vivos que los habitan. Entonces, se produce una disminución de la biomasa, al ser arrastrada aguas abajo. Cuando el caudal es muy variable, estas alteraciones son muy frecuentes, y se limita considerablemente la biomasa acumulada”.
Este trabajo viene a cubrir un vacío existente hasta ahora. Con un esquema de clasificación basado en estos dos factores, “se puede avanzar mucho en la ciencia fluvial, ya que ahora comprendemos mejor qué es lo que realmente controla el metabolismo de los ríos. Además, puede servir de base para la gestión de los ríos, ya que se mejora la capacidad de escalar y modelizar la dinámica de los ecosistemas fluviales, y puede cambiar sustancialmente la forma de investigar los ríos”, afirma Arroita. El cambio climático tendrá un gran impacto en el funcionamiento de los ecosistemas fluviales “y los resultados obtenidos permitirán predecir mejor los cambios o consecuencias que se producirán y cómo evitarlos”.
Con las metodologías y herramientas utilizadas en este trabajo, la Dra. Arroita quiere analizar la base de datos de los ríos guipuzcoanos: “La Diputación Foral de Gipuzkoa cuenta con una base de datos muy amplia. Disponemos de datos tomados durante 20 años en 13 estaciones de medida ubicadas en diferentes ríos de Gipuzkoa. En ningún otro lugar existe una base de datos tan grande en lo que respecta al tiempo. Quiero analizar los cambios temporales, para determinar, por ejemplo, la historia de los ríos y los cambios que se han producido, para hacer previsiones, etc.”.
Referencia:
Emily S. Bernhardt, Phil Savoy, Michael J. Vlah, Alison P. Appling, Lauren E. Koenig, Robert O. Hall Jr., Maite Arroita, Joanna R. Blaszczak, Alice M. Carter, Matt Cohen, Judson W. Harvey, James B. Heffernan, Ashley M. Helton, Jacob D. Hosen, Lily Kirk, William H. McDowell, Emily H. Stanley, Charles B. Yackulic, and Nancy B. Grimm (2022) Light and flow regimes regulate the metabolism of rivers PNAS doi: 10.1073/pnas.2121976119
Para saber más:
Todo lo que se puede medir en un río
La contribución global de los ríos intermitentes al ciclo del carbono
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La luz y el caudal regulan el metabolismo de los ríos se ha escrito en Cuaderno de Cultura Científica.
Un, dos, tres… mucho
Desde que nacemos, los seres humanos compartimos con muchas otras especies animales la capacidad de estimar pequeñas cantidades sin necesidad de utilizar números. Es lo que coloquialmente entendemos como “contar a ojo” y que técnicamente se denomina “subitización”, por lo “súbitamente” que sucede. La subitización solo es precisa hasta cifras sorprendentemente pequeñas, más allá del cuatro y el cinco, los montones empiezan a parecerse entre sí y ya no podemos cuantificarlos a golpe de ojo (intenta visualizar once puntos, por ejemplo, en vez de tres, para entender a qué me refiero). Contar con números, en cambio, requiere siempre recitar un listado de palabras o símbolos (uno, dos, tres, cuatro…), lo que consume más tiempo, y también un mayor esfuerzo cognitivo.
 Foto: Dorelys Smits / Unsplash
Foto: Dorelys Smits / UnsplashVeréis, pensar es malísimo. En mis charlas de divulgación sobre percepción y diseño, suelo provocar al público advirtiendo que “pensar da cáncer”. Espero que no, sinceramente, o escribir estos artículos estará poniendo en riesgo mi esperanza de vida. Pero lo cierto es que los humanos, en general, procuramos evitar hacer esfuerzos cognitivos siempre que no sean estrictamente necesarios. Y contar con números (esto es, recitar una serie de símbolos cuantitativos) supone un esfuerzo mucho mayor que estimar cantidades a ojo, o subitizar. Esto ha hecho que los pequeños números, generalmente hasta el tres o el cuatro, aquellos que nos evitan la necesidad de “contar”, hayan dejado su huella en la lengua de muchas culturas.
En 1992, los investigadores Stanislas Dehaene y Jacques Mehler publicaron un estudio1 donde analizaban la frecuencia con que distintas palabras relacionadas con números se utilizaban en siete idiomas distintos; inglés, catalán, holandés, francés, japonés, kannada (una lengua del sur de la India) y español. Salvando algunas cifras redondas que tienden a agrupar cantidades aproximadas cercanas (como cien, mil, millón, etcétera, que a menudo designan cierto orden de magnitud, más que una cantidad exacta), descubrieron que el uso de los números disminuye con su magnitud. La palabra “tres” se usa con menos frecuencia que “dos” y esta, aún menos que “uno”. Lo mismo sucedía con los ordinales (primero, segundo, tercero) y con la representación arábiga de esos mismos números.
Según la hipótesis de los investigadores, esta tendencia no sería necesariamente un reflejo del mundo que nos rodea. No es que a nuestro alrededor las cosas se agrupen en dúos o tríos de manera preferente. Más bien, se trataría de un sesgo impuesto por nuestros sistemas perceptivo y cognitivo2, que manejan estas cantidades con mayor facilidad y condicionan nuestras posibles representaciones mentales del entorno. Así lo explica Dehaene en “El cerebro matemático”3:
“El lenguaje humano está profundamente influido por una representación no verbal de los números que compartimos con los animales y los bebés. Creo que esto, por sí solo, explica la reducción universal de la frecuencia de las palabras según el tamaño del número. Expresamos los números pequeños con mucha más asiduidad que los grandes porque nuestra recta numérica mental representa los números con una precisión decreciente. Cuanto más grande es una cantidad, más confusa es nuestra representación mental de ella, y menos frecuente la necesidad de referirnos a ella de manera exacta”.
Los números uno, dos y tres no son solo los más frecuentes. En algunos idiomas son los únicos que existen. Se han descubierto culturas que solo usan las palabras “uno”, “dos” y “muchos”, haciendo literal aquello de que “tres son multitud”. Un ejemplo son los warlpiris, una tribu de Australia que únicamente añaden la palabra “pocos” a este reducido léxico cuantitativo. Los Munduruku, en Brasil, son un grupo bastante sofisticado en comparación: tienen nombres hasta el cinco. En su mundo, más allá de los dedos de una mano, no es posible contar. Todas las cantidades se vuelven “montones”.
Los pirahãs, en la selva del Amazonas, plantean un caso especialmente restrictivo. Tras convivir durante años con ellos, Daniel Everett concluyó que no usaban números en absoluto4:
“Al principio pensé que usaban los números uno, dos y ‘muchos’, un sistema bastante común alrededor del mundo. Pero después me di cuenta de que lo que yo, y otros previamente, habíamos considerado números, no eran sino cantidades aproximadas”.
Tras observar con más atención, Everett confirmó su error inicial:
“[Los pirahã] podían usar la palabra ‘dos’ (eso creía que significaba) para designar un par de peces pequeños o uno solo relativamente más grande, contradiciendo mi entendimiento de lo que significaba ‘dos’ y confirmando mi nueva idea sobre los ‘números’ como referencias de volumen relativo”.
Los miembros de aquella tribu nunca contaban, tampoco usaban los dedos para indicar cantidades, ni ningún otro artilugio que permitiese hacer cálculos, ni siquiera de manera sencilla. En medio de la selva, tampoco les había hecho falta.
Referencias y notas:
1Dehaene, Stanislas, y Jacques Mehler. 1992. «Cross-Linguistic Regularities in the Frequency of Number Words». Cognition 43 (1): 1-29.
2Hablo sobre sobre cómo este sesgo afecta, también, a ciertos aspectos de la musicalidad humana en: Martín Castro, Almudena. 2022. La lira desafinada de Pitágoras. Cómo la música inspiró a la ciencia para entender el mundo. HarperCollins Ibérica.
3Un libro altamente recomendable. Dehaene, Stanislas. 2011. The Number Sense. How the mind creates Mathematics. Estados Unidos: Oxford University Press. Existe una traducción al castellano titulada El cerebro matemático, de Siglo Veintiuno Editores Argentina.
4Everett, Daniel. 2008. Don’t Sleep, There Are Snakes: Life and Language in the Amazonian Jungle. Profile Books
Para saber más:
Los números deben de estar locos
El gran cuatro, o los números siguen estando locos
Y tú, ¿cómo cuentas con los dedos? (1)
Y tú, ¿cómo cuentas con los dedos? (2)
Contar hasta un millón con los dedos de las manos
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Un, dos, tres… mucho se ha escrito en Cuaderno de Cultura Científica.
Sobre cómo escribir el número pi en base cuatro
En la entrada del Cuaderno de Cultura Científica titulada Las bases de numeración o cómo hacer trucos de magia binarios hablamos de las distintas bases de un sistema de numeración posicional como el que nosotros utilizamos de forma habitual y cómo pasar de la representación posicional de un número natural (o entero) cualquiera en la base usual, la decimal, a otra base de numeración no decimal, y viceversa.
En particular, comentamos que dada una base de numeración b –ya sea esta igual a 2, 3, 10, 12 o 60- la representación posicional de cualquier número natural en la misma viene dada por una expresión d1d2…dr (donde los dígitos di –para i entre 1 y r– pertenecen a la familia de las b cifras básicas del sistema de numeración, que tienen valores entre 0 y b – 1) teniendo en cuenta que el número puede escribirse, de forma única, como
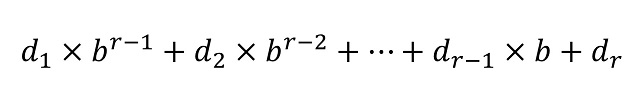
Así, el número que en la base decimal representamos como 3.457, es decir, que tiene el valor de 3 veces la cantidad de 1.000 (= 103), 4 veces la cantidad de 100 (= 102), 5 veces la cantidad de 10 (= 101) y 7 veces la unidad 1 (= 100), tendrá diferentes representaciones en función de la base b elegida. Así, si tomamos el sistema binario (b = 2) el anterior número se representa como (110110000001)2, ya que “3.457” = 211 + 210 + 28 + 27 + 1; en la base octal (b = 8) como (6600)8, porque “3.457” = 6 x 83 + 6 x 82; o en la base hexadecimal (b = 16), donde las cifras básicas son 0, 1, …, 9, A, B, C, D, como (D81)16, puesto que “3.457” = D x 162 + 8 x 16 + 1, donde estamos utilizando el subíndice de las representaciones (2, 8 y 16) para recordar que esa es una representación en esa base de numeración.
En esta entrada vamos a estudiar la representación de cualquier número real, no solamente natural, es decir, que tiene parte “fraccionaria” (la que va a la derecha de la coma, como 1415 en el número 13,1415). Al igual que la representación en el sistema de numeración posicional de base b para los números naturales se basaba en la expresión de estos números en función de las potencias (no negativas) de la base b0, b1, b2, b3, … para los números reales, no enteros, es decir, aquellos con parte fraccionaria (“con coma”) la representación en la base b se basa en la expresión en función de todas las potencias de la base b, incluidas ahora las negativas b-1 = 1/b, b-2 = 1/b2, b-3 = 1/b3, …
El sistema de numeración babilónicoPara ilustrar el primer ejemplo, vamos a considerar el sistema de numeración posicional babilónico (véase la entrada ¿Sueñan los babilonios con multiplicaciones eléctricas?). Como menciono en mi libro Los secretos de la multiplicación, de los babilonios a los ordenadores (Catarata, 2019), hacia el 2.000 a. n. e. se introdujo en Babilonia el que parece ser el primer sistema de numeración posicional de la historia de la humanidad, el sistema sexagesimal de los eruditos babilonios, conocido por este nombre porque era el utilizado por matemáticos y astrónomos.
La primera diferencia con el sistema de numeración moderno es que este último es decimal, luego tiene diez cifras básicas, del 0 al 9, mientras que el sistema babilónico, al ser sexagesimal, necesitaba de sesenta cifras básicas. Durante mucho tiempo no existió un símbolo para el cero y simplemente dejaban un hueco vacío, lo cual creaba cierta confusión. Las 59 cifras del sistema de numeración babilónico, excluido el cero, no eran todas diferentes, como ocurre en el sistema moderno, sino que su notación se basaba en la acumulación de unidades, que eran los clavos verticales, y decenas, que eran espigas, como se ve en la siguiente imagen, heredados de los números cuneiformes sumerios. Cuando se empezó a representar el cero, se hizo como un doble clavo inclinado o una doble espiga, con un tamaño más pequeño que el de las otras cifras.
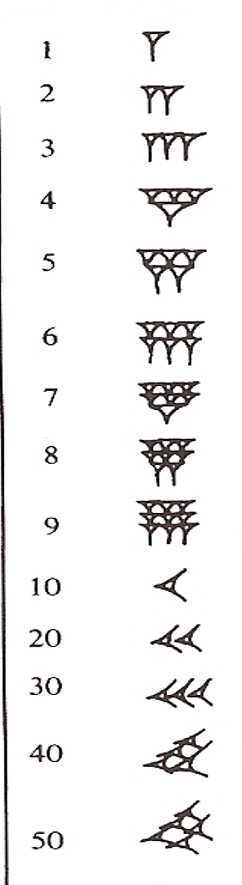 Representación de las 59 cifras básicas del sistema de numeración babilónico, utilizando clavos (unidades) y espigas (decenas).
Representación de las 59 cifras básicas del sistema de numeración babilónico, utilizando clavos (unidades) y espigas (decenas).
Así, el número que nosotros representamos como 1.859, en la base decimal, los babilonios lo representaban, como se observa en la siguiente imagen, como tres espigas, es decir, 30, seguido de cinco espigas y nueve clavos, es decir, 59, puesto que 1.859 = 30 x 60 + 59. En esta entrada, para no tener que dibujar los clavos y las espigas, escribiremos que es el número de dos dígitos [30; 59] en el sistema babilónico.
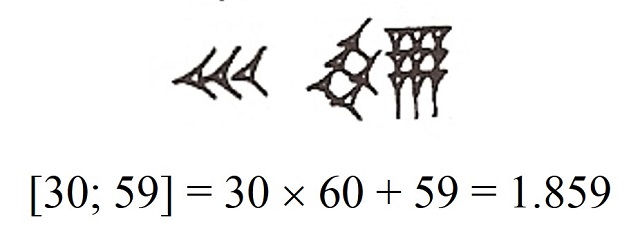 Representación con espigas y clavos del número 1.859
Representación con espigas y clavos del número 1.859
Por ejemplo, dos números que se representan en la tablilla de arcilla BM13901, que se conserva en el Museo Británico de Londres y que es uno de los textos matemáticos babilónicos más antiguos, son 64.000 y 424.000. El primero, 64.000, está representado como [17; 46; 40], aunque con las cifras babilónicas de clavos y espigas, es decir, 17 x 602 + 46 x 60 + 40, mientras que el segundo, 424.000, está representado como [1; 57; 46; 40], esto es, 1 x 603 + 57 x 602 + 46 x 60 + 40.
 Tablilla de arcilla BM13901, que se conserva en el Museo Británico de Londres. Copyright The Trustees of the British Museum
Tablilla de arcilla BM13901, que se conserva en el Museo Británico de Londres. Copyright The Trustees of the British Museum
Los babilonios también manejaron los números racionales, las fracciones. Como ya hemos recordado más arriba, las cifras a la derecha de la coma expresan las potencias negativas de la base b. Así, el número racional 23,14, en nuestro sistema de numeración posicional decimal, tiene el valor 3,14 = 3 + 1 x 0,1 + 4 x 0,01 = 3 + 1 x 10–1 + 4 x 10–2. Mostremos un ejemplo para los números babilónicos.
 Anverso y reverso de la tablilla YBC 7289, de la Universidad de Yale, que contiene la expresión numérica [1; 24; 51; 10], con clavos y espigas (que se ha marcado con los números para situar la expresión), que es una aproximación de la raíz de 2. Imagen del Yale Peabody Museum of Natural History
Anverso y reverso de la tablilla YBC 7289, de la Universidad de Yale, que contiene la expresión numérica [1; 24; 51; 10], con clavos y espigas (que se ha marcado con los números para situar la expresión), que es una aproximación de la raíz de 2. Imagen del Yale Peabody Museum of Natural History
La tablilla de arcilla babilónica YBC7289, de la Universidad de Yale, contiene la aproximación de la raíz de 2 siguiente [1; 24; 51; 10], que está expresada en el sistema de numeración babilónico (en su versión original con clavos y espigas), cuyo valor sería: 1 + 24 x 60–1 + 51 x 60–2 + 10 x 60–3 = 1,41421296… aunque la notación babilonia respecto al lugar donde se sitúa la coma era confusa, y solo el contexto del problema o la situación la resolvían.
Expresión decimal de un númeroAl igual que en el ejemplo anterior, del sistema de numeración babilónico, obtener la expresión decimal de un número real, que tiene parte fraccionaria, es sencillo. Veamos algunos ejemplos.
Consideremos el siguiente número racional expresado en base binaria como
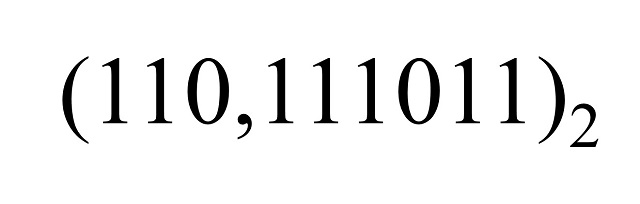
Para ver cuál es el valor de este número binario necesitamos las potencias de 2. Por una parte, las no negativas, 22 = 4, 21 = 2, 20 = 1, para los tres dígitos de la izquierda de la coma, y las negativas, 2−1 = 1∕2 = 0,5; 2−2 = 1∕4 = 0,25; 2−3 = 1∕8 = 0,125; 2−4 = 1∕16 = 0,0625; 2−5 = 1∕32 = 0,03125 y 2−6 = 1∕64 = 0,015625, para los dígitos de la derecha de la coma.
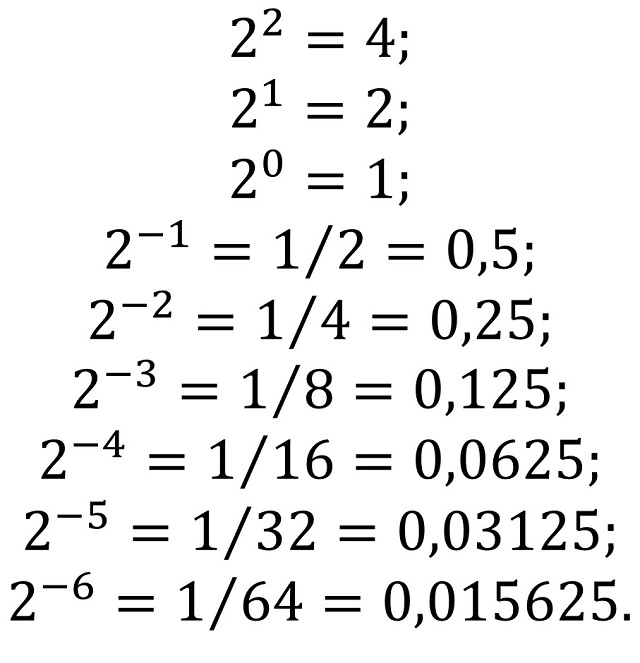
Por lo tanto, el número binario (110,111011)2 tiene el valor de 6,921875 (expresado en el sistema decimal), ya que:
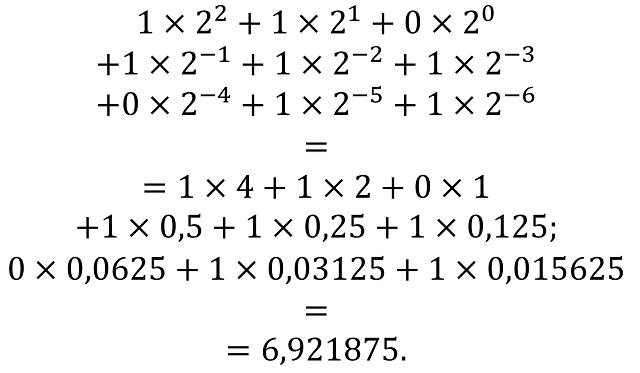
Veamos un nuevo ejemplo para la base b = 4, en concreto, consideremos el número que en base 4 se escribe como (3,021003331)4. Para ver su valor, la expresión en el sistema decimal, necesitamos las potencias negativas de 4, desde – 1 hasta – 9, que aparecen en la siguiente imagen.

Por lo tanto, el número (3,021003331)4 toma el valor 3.141590118408203125, ya que:

Como podemos observar el número racional dado por la expresión (3,021003331)4 es una aproximación al número pi, en base 4. Si hubiésemos tomado (3.02100333122220202011)4 tendríamos una mejor aproximación 3.14159265358921402366.
 Distribución aleatoria de cuadrados utilizando los decimales del número π, 50% de dígitos impares azul, 50% de dígitos pares rojo (1963-2016), del artista francés François Morellet. Imagen de la página ARTNews
Distribución aleatoria de cuadrados utilizando los decimales del número π, 50% de dígitos impares azul, 50% de dígitos pares rojo (1963-2016), del artista francés François Morellet. Imagen de la página ARTNewsConversión de la base decimal a otra base
Como en la entrada anterior, empecemos por la base binaria, b = 2. Si tenemos un número con parte fraccionaria, en la base decimal, y queremos pasarlo a la base binaria, sabemos que tenemos que expresarlo en función de las potencias de 2. Por ejemplo, tomemos el número 0,375. Como las potencias de 2 negativas son 2−1 = 1∕2 = 0,5; 2−2 = 1∕4 = 0,25; 2−3 = 1∕8 = 0,125; 2−4 = 1∕16 = 0,0625; 2−5 = 1∕32 = 0,03125 y 2−6 = 1∕64 = 0,015625, etc, entonces si vemos cómo escribir ese número como suma de estas podemos ver que
0,375 = 0,25 + 0,125 = 2−2 + 2−3
luego el número decimal 0,375 se escribe en base binaria como (0,011)2.
Aunque, al igual que vimos para los números naturales, podemos desarrollar un algoritmo para determinar la expresión binaria del número. Si el número que queremos convertir en binario tiene parte no fraccionaria (por ejemplo, en 197,703125 sería el 197), para esa parte utilizaremos el algoritmo visto en la entrada Las bases de numeración o cómo hacer trucos de magia binarios, que consiste en dividir por 2 e ir considerando los restos. Como vimos en esa entrada el número 197 se expresa en la base binaria como (11000101)2. Mientras que para la parte fraccionaria (en nuestro ejemplo sería 0,703125) utilizaremos un algoritmo basado en dividir por 0,5 = 1/2 = 2–1. Veámoslo con un ejemplo.
El algoritmo consiste en dividir nuestro número 0,703125 por 0,5 (que es como multiplicar por 2), si lo hacemos nos queda 1,40625. De este nos quedamos la unidad 1, que nos va a aportar un 1 en la representación binaria, y volvemos a dividir 0,40625 por 0,5. Al hacerlo nos queda 0,8125, que nos aporta un 0 en la representación binaria y lo volvemos a dividir por 0,5. En total:

De donde la expresión binaria de 0,703125 es (0,101101)2. El motivo es que este procedimiento nos permite obtener la expresión del número en función de las potencias de 2 negativas, como vemos en la siguiente imagen.
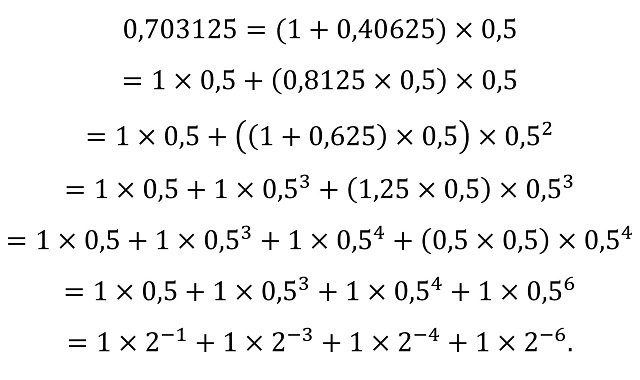
En conclusión, el número (decimal) 197,703125 se expresa en la base binaria como (11000101,101101)2.
Al igual que lo hemos hecho para la base binaria lo podríamos hacer para cualquier otra base.
Un patrón artístico en base cuatroEn la entrada del Cuaderno de Cultura Científica titulada El arte de la sencilla baldosa de Truchet utilizábamos los primeros dígitos del número pi en base 4 (con las cuatro cifras básicas 1, 2, 3, 0) para crear un patrón de embaldosado particular que pudiésemos utilizar para crear una pintura abstracta. Vamos a terminar esta entrada con una idea similar, creando otro patrón basado en la expresión de la raíz de 2 en base 4.
Los primeros 12 x 12 = 144 dígitos del número raíz de 2 en base 4 son los siguientes (que yo he obtenido con un conversor online de la Université Cote d’Azur).

Además, ahora las cuatro orientaciones de la baldosa cuadrada de Truchet que asociamos a las cuatro cifras básicas, 1, 2, 3, 0, son las que se muestran en la imagen (en esta ocasión le hemos añadido color).
Por lo tanto, el patrón de teselado con las cuatro orientaciones de la baldosa de Truchet basado en el número raíz de 2, en base 4, es el siguiente.
 Idea para una obra basada en los patrones de embaldosado con baldosas de Truchet y la expresión del número raíz de 2 en base 4
Idea para una obra basada en los patrones de embaldosado con baldosas de Truchet y la expresión del número raíz de 2 en base 4
Bibliografía:
1.- Raúl Ibáñez, Los secretos de la multiplicación, de los babilonios a los ordenadores, Catarata, 2019.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Sobre cómo escribir el número pi en base cuatro se ha escrito en Cuaderno de Cultura Científica.
Einstein y Sigmund Freud
Cuando se hace una lista de las mentes más influyentes del siglo XX, Einstein y Freud aparecen invariablemente en ella. Las teorías de Einstein crearon la época de la física moderna y las de Freud, aunque pseudocientíficas, la de la psicología [1]. Colaboraron sólo una vez, escribiendo un ensayo que apoyaba una visión de la política internacional que favorecía la paz sobre la guerra.
 Edición alemana de «¿Por qué la guerra?», publicada por la Sociedad de Naciones (Völkerbund) en 1933. Imagen: Wikimedia Commons
Edición alemana de «¿Por qué la guerra?», publicada por la Sociedad de Naciones (Völkerbund) en 1933. Imagen: Wikimedia CommonsAlbert Einstein y Sigmund Freud se encontraron cara a cara en el Berlín de antes de la Segunda Guerra Mundial. Freud había ido a visitar a su familia por Janucá (fiesta religiosa judía de las luces, que suele anteceder, y a veces coincidir, con las de la Navidad) en 1926, y Einstein y su mujer, Elsa, visitaron al famoso psicoanalista. En una carta a un amigo, Freud describió su encuentro como una charla agradable, aunque sí añadió que “[Einstein] entiende tanto de psicología como yo de física”.
Quedaron en buenos términos y mantuvieron un contacto distante durante muchos años. La apertura de Einstein a las teorías de Freud sobre el significado de los sueños y del subconsciente es un poco llamativa, teniendo en cuenta que Einstein le tenía pavor a la enfermedad mental y, enfáticamente, no tenía interés en el psicoanálisis. A este respecto dijo una vez: “Me gustaría permanecer en la oscuridad de no haber sido analizado”. Pero al igual que Einstein, Freud lo cuestionaba todo [2], incluso sus propias ideas, lo que le gustaba a Einstein. Además, tenían otro punto en común: ambos eran judíos conocidos por criticar abiertamente la religión.
No dejaron de ser meros conocidos hasta 1932. Ese año, la Sociedad de Naciones le pidió a Einstein que escogiera a alguien con quien reflexionar sobre alguna cuestión candente. En esa época el militarismo en Alemania estaba en auge, y de ahí vino el tema que Einstein eligió: “¿Hay alguna manera de librar a la humanidad de la amenaza de la guerra?” Como compañero de discusión Einstein eligió a Freud.
Freud era bien conocido por su teoría de que existen un bien y un mal absolutos, publicando visiones muy pesimistas sobre la propensión a errar favoreciendo al segundo. Pero la respuesta de diecisiete páginas de Freud a la pregunta de una línea de Einstein fue sorprendentemente optimista.
Freud expuso la idea de que la humanidad está dividida entre un impulso vital y un ansia por la muerte. Escribió que, a veces, nuestra agresión podría empujarnos a la guerra, pero que el impulso del amor lo evitaría. Einstein respondió que las leyes podrían compensar el impulso humano hacia la violencia, y apoyó vehementemente un cuerpo internacional que limitase los excesos del nacionalismo y resolviese los conflictos.
El diálogo entre los dos llevó a la publicación del libro Warum Krieg? (¿Por qué la guerra?). El Instituto Internacional de Cooperación Intelectual de la Sociedad de Naciones, a la que pertenecía Einstein a instancias de Marie Curie, lo publicó simultáneamente en inglés, francés y alemán en 1933. Sin embargo, el objetivo del libro, alentar la paz en el mundo, no se cumpliría. Ese mismo año, 1933, Hitler llega al poder en Alemania y ejemplares de este libro, como del resto de trabajos de Einstein y Freud, son quemados públicamente por los nacionalsocialistas.
Además de por su colaboración directa, Einstein y Freud están unidos en la conciencia colectiva por ser ambos pensadores extraños y profundos en un tiempo crucial en la historia del mundo, además de por estar también juntos en la lista de los judíos que consiguieron escapar de la persecución nazi.
Notas:
[1] Esta frase dice lo que dice y no otra cosa. Esto es, Freud convierte a la psicología en una rama del conocimiento de pleno derecho, si bien ello no implica que la psicología moderna se base en las ideas de Freud que, como hemos indicado, no son científicas.
[2] Cuestionar todo no significa que se haga con una actitud científica. Véase enlace en [1].
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 1 de agosto de 2009.
El artículo Einstein y Sigmund Freud se ha escrito en Cuaderno de Cultura Científica.
¿Y si pudiésemos llegar al océano de Europa sin necesidad de atravesar toda la corteza?
Si algo nos ha enseñado la geología planetaria en la segunda mitad del siglo XX y en estos principios del siglo XXI, es que el Sistema Solar es un lugar mucho más diverso y dinámico de lo que soñábamos.
Y es que, más allá de la cotidianidad de los mundos rocosos de nuestro Sistema Solar interior, encontramos una suerte de sistemas planetarios en miniatura girando en torno a los gigantes gaseosos.
Estos satélites en la mayoría de ocasiones son mundos helados, es decir, cuerpos cuya corteza, lo que nosotros vemos, no está formada por roca, sino por hielo, y deben su dinámica interna, precisamente, y a diferencia de los planetas interiores del Sistema Solar, al agua y el hielo que circula -o circuló, si ya no tienen actividad- por su interior.
La presencia de agua y de procesos que sean capaces de mantenerla en estado líquido en el interior de estos cuerpos a lo largo del tiempo geológico hace que sean lugares con un gran potencial astrobiológico, ya que en nuestro planeta el agua es un ingrediente fundamental para la vida tal y como la conocemos.
Con esto no queremos decir, obviamente, que haya tenido lugar el desarrollo de vida, pero que sin duda los hacen lugares muy interesantes para estudiar esta posibilidad. Y precisamente, uno de los candidatos que más ha despertado el interés de los científicos es Europa, satélite de Júpiter.
El asombrosamente plano Europa Europa, satélite de Júpiter, observada por la sonda Galileo. Imagen cortesía de NASA/JPL-Caltech/SETI Institute.
Europa, satélite de Júpiter, observada por la sonda Galileo. Imagen cortesía de NASA/JPL-Caltech/SETI Institute.Con un radio de 1560 kilómetros, es el sexto satélite en tamaño de nuestro Sistema Solar y precisamente antecedido por nuestra Luna, pero, a diferencia de esta, es un cuerpo asombrosamente plano, sin apenas cráteres de impacto ni cadenas montañosas.
La escasez de cráteres ya nos quiere decir algo: que su superficie es joven y ha ido cambiando a lo largo del tiempo acaecido tras su formación, ya que, si nada modificase su superficie, estaría completamente cubierta de cráteres.
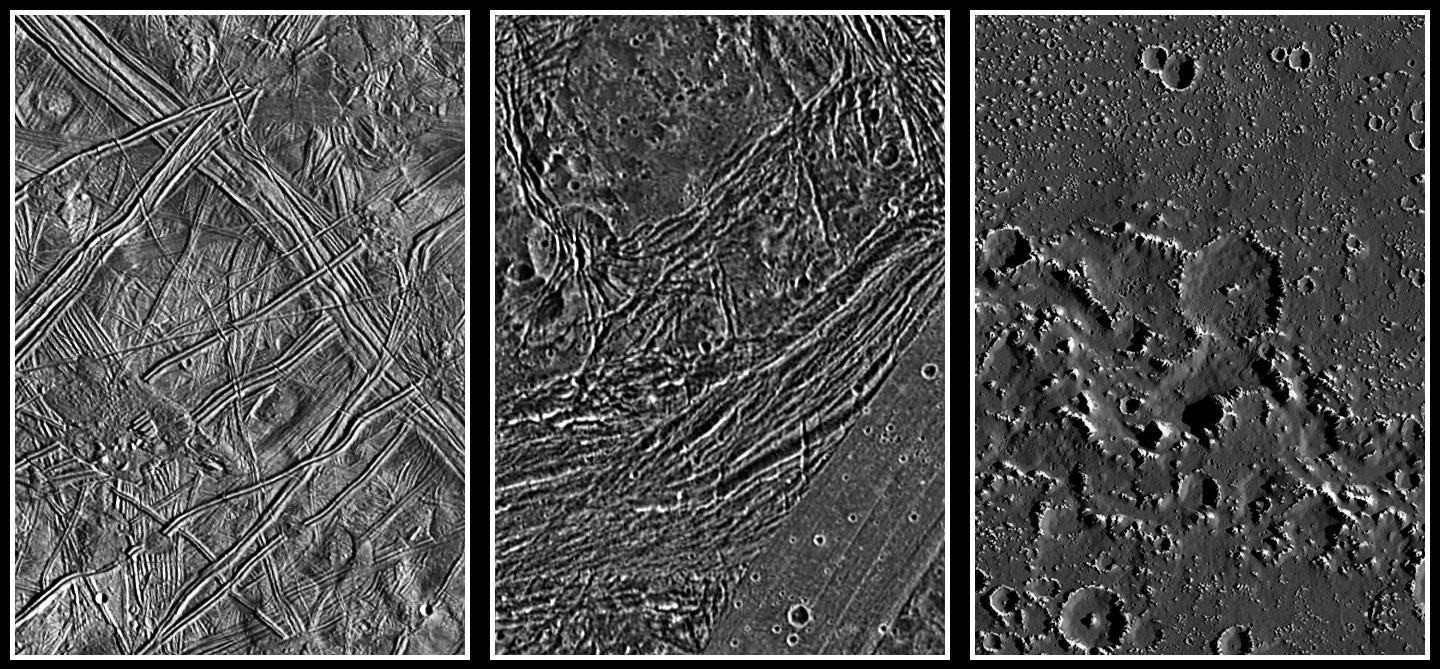 Comparación de imágenes de alta resolución de las superficies de Europa, Ganímedes y Calisto. Como se puede apreciar, la superficie de Europa, en comparación con la de los otros dos satélites, luce casi completamente sin cráteres. Imagen cortesía de NASA/JPL/DLR.
Comparación de imágenes de alta resolución de las superficies de Europa, Ganímedes y Calisto. Como se puede apreciar, la superficie de Europa, en comparación con la de los otros dos satélites, luce casi completamente sin cráteres. Imagen cortesía de NASA/JPL/DLR.
Y en el caso de Europa, esta transformación no procede de fenómenos externos, como el viento o la lluvia a los que tanto estamos acostumbrados en la Tierra, sino de un activo interior que se manifiesta renovando el aspecto de este satélite.
Esta actividad aparente nos hace pensar -junto con otros datos- que hay un océano bajo su corteza y que pone en contacto su núcleo con el agua, que la calienta y la hace ascender hacia la corteza, empujando al hielo y obligándole a adoptar nuevas formas, un papel similar al que tiene nuestro manto terrestre.
 Gráfico en el que se superponen los datos del telescopio espacial Hubble a una imagen de Europa mostrando el lugar donde se detectaron las moléculas de vapor de agua en el año 2021. Imagen cortesía de NASA/ESA/L. Roth/SWRI/University of Cologne.
Gráfico en el que se superponen los datos del telescopio espacial Hubble a una imagen de Europa mostrando el lugar donde se detectaron las moléculas de vapor de agua en el año 2021. Imagen cortesía de NASA/ESA/L. Roth/SWRI/University of Cologne.
El telescopio espacial Hubble también detectó moléculas de vapor de agua escapándose, y distintos modelos geofísicos atestiguan que Europa tiene una corteza de hielo que tiene un espesor del entorno de los 30 kilómetros, y de muy difícil acceso si algún día tuviésemos la capacidad para perforar y adentrarnos para ver que ocurre en su interior.
Pero no todo está perdido. Una de las formas del relieve más comunes en Europa podemos verla en prácticamente toda su superficie: un juego doble de crestas separadas por un pequeño valle y que llega a medir de centenares de kilómetros de longitud.
Hasta ahora, se habían propuesto distintos mecanismos de formación, desde el criovulcanismo hasta el ascenso de penachos de hielo en un estado más plástico y que se emplazaban en la corteza, pero ninguno de estos modelos parecía satisfacer todas las morfologías que se observaban.
 Comparación entre este relieve en Europa (izquierda) y Groenlandia. Imagen de Culberg et al. (2022).
Comparación entre este relieve en Europa (izquierda) y Groenlandia. Imagen de Culberg et al. (2022).
Pero resulta que en nuestro planeta hay unas formas similares y que hasta ahora habían pasado desapercibidas, concretamente en Groenlandia. Allí se forman cuando pequeñas bolsas de agua permiten que esta suba a través de las fracturas del propio hielo. El agua acaba congelándose de nuevo, formando un dique vertical que traza el camino del agua y que, al expandirse, genera más fracturas y deformación en el hielo.
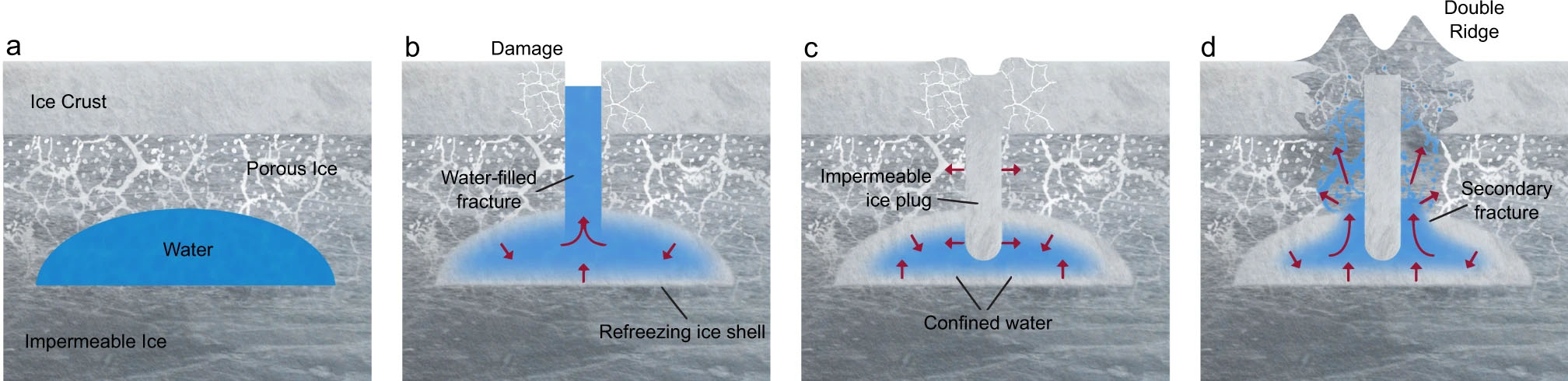 Mecanismo de formación de las crestas dobles. Como se puede apreciar en el esquema en cuatro pasos, la repetición de procesos de fracturación, congelación y presurización de las bolsas de agua serían capaces de generar estas morfologías. Imagen de Culberg et al. (2022).
Mecanismo de formación de las crestas dobles. Como se puede apreciar en el esquema en cuatro pasos, la repetición de procesos de fracturación, congelación y presurización de las bolsas de agua serían capaces de generar estas morfologías. Imagen de Culberg et al. (2022).
Si este proceso se repite en el tiempo, gracias a las nuevas fracturas generadas alrededor del dique de hielo, de nuevo ascenderá el agua, deformando la superficie y fracturándola todavía más. En este proceso se generan estas formas de crestas y valles tan parecidas a las que hay en Europa.
Este mecanismo se ha podido verificar gracias a las observaciones de georradar, que permiten observar la estructura del subsuelo -en este caso, bajo el hielo- y ver las distintas capas y discontinuidades que existen, algo que todavía no podemos hacer en Europa.
Pero en 2023, si todo va según lo previsto, despegará la misión JUICE (Jupiter Icy Moons Explorer), con una llegada prevista al sistema joviano en 2031, y que llevará también un radar que permitirá, desde la órbita, poder estudiar y quizás dilucidar el mecanismo de formación de estas crestas.
¿Y por qué es tan importante este hallazgo?. Los autores estiman que, en Europa, estas bolsas de agua se encontrarían a unos 5 kilómetros de profundidad, mucho más cerca de la superficie que el océano subterráneo, por lo que acceder hasta este punto sería mucho más fácil para una futura sonda.
Pero todavía más importante, ¿de dónde vendría el agua líquida que rellena estas bolsas? Eso es lo más interesante, ya que, si no hay mecanismos que expliquen una fusión del hielo en el interior de la corteza, estas bolsas podrían formarse por el ascenso de agua desde el océano hacia la superficie por distintos sistemas de fracturas, permitiéndonos muestrear el contenido de esas aguas, por lo que este hallazgo mejora mucho las perspectivas de cara al diseño y desarrollo de futuras misiones astrobiológicas a este satélite.
Referencia:
Culberg, R., Schroeder, D.M. & Steinbrügge, G. (2022) Double ridge formation over shallow water sills on Jupiter’s moon Europa. Nat Commun doi: 10.1038/s41467-022-29458-3
Para saber más:
La presencia de sales podría hacer que exista una tectónica de placas en Europa
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Y si pudiésemos llegar al océano de Europa sin necesidad de atravesar toda la corteza? se ha escrito en Cuaderno de Cultura Científica.
Ruido, veneno para la mente
 Foto: John Onaeko / Unsplash
Foto: John Onaeko / UnsplashLas autoridades de varias ciudades francesas, París incluida, se proponen instalar aparatos para identificar a los vehículos que sobrepasan el nivel de ruido permitido e imponerles sanciones. El sistema que planean implantar está siendo probado en siete ciudades y, si los resultados acompañan, próximamente se empezarán a instalar. Se dará al ruido un tratamiento equivalente al que se da a la velocidad, de manera que a quienes sobrepasen los límites establecidos se les impondrá una multa de 135€.
La medida es la respuesta que se quiere dar al creciente malestar ciudadano motivado por el ruido que producen de noche las motocicletas. De acuerdo con estimaciones hechas por Bruitparif, una entidad que se dedica a monitorizar el ruido en el área metropolitana de París, una sola motocicleta trucada puede llegar a despertar hasta a 10000 personas en una noche.
Pero el nocturno no es el único ruido que soportamos quienes vivimos en entornos urbanos. Según un informe ya clásico de la Organización Mundial de la Salud (OMS), la contaminación acústica es, tras la atmosférica, el segundo factor ambiental que más daña la salud de la población.
De acuerdo con el informe “Ruido en Europa 2020”, publicado por la Agencia Europea de Medio Ambiente (AEMA), una de cada cinco personas está expuesta a diario a niveles que son nocivos para la salud. Se estima que del orden de 113 millones (M) de personas se ven afectadas por el ruido (más de 55 dB) provocado por el tráfico rodado en nuestro continente. A esa cifra habría que añadir 22 M expuestos al ferroviario, 4 M al del tráfico aéreo, y 1 M al de origen industrial.
A la exposición a ruido intenso de manera prolongada se atribuyen 48000 casos de accidente cardiovascular y 12000 muertes prematuras por esa causa cada año en Europa. El vínculo entre el ruido y las afecciones cardiovasculares es la hipertensión. Un estudio danés estimó que el riesgo de sufrir infarto de miocardio se eleva en un 12% por cada incremento de 10 dB del ruido callejero. Pero según otro estudio, esta vez en los EEUU, publicado por un equipo de la Universidad de Harvard, el riesgo de sufrir «ataques al corazón, ictus y otros problemas coronarios serios» aumenta en un 34% por cada subida de 5 dB.
Según el informe “Ruido en Europa 2020” antes citado, 22 M de personas sufren irritación crónica a causa del ruido y 6,5 M padecen trastornos severos del sueño, también de forma permanente. Por otro lado, el provocado por las aeronaves en las maniobras de despegue y aterrizaje próximas a poblaciones es responsable de los problemas de aprendizaje de 12500 niños y niñas, y de deterioro cognitivo en general. El informe de la OMS citado antes también señala que el ruido es responsable de muchos casos de acúfenos (tinnitus), esos molestos sonidos que, sin tener origen físico real, se perciben de forma persistente.
En el estudio de la Universidad de Harvard ya citado también hallaron que la exposición a altos niveles de ruido está asociada a un incremento de la actividad en la amígdala, una zona del encéfalo que se activa en condiciones de estrés, miedo y ansiedad. La salud mental también se ve seriamente afectada por este factor. Por ello, no es sorprendente que quienes lo soportan de forma constante tiendan a encontrarse, como se ha dicho, más irritables, tengan actitudes agresivas, experimenten síntomas depresivos, sufran problemas de concentración y tengan, en general, un menor rendimiento académico y laboral. Y es que, como dice una gran amiga mía, el ruido es veneno para la mente.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Ruido, veneno para la mente se ha escrito en Cuaderno de Cultura Científica.
IV Jornada Nacional de Evolución y Neurociencias: Laura Morán – Evolución de la atracción sexual

¿Estamos realmente diseñados para conectar con los demás? Si es así, ¿por qué siguen existiendo los psicópatas? ¿Se pueden tratar trastornos delirantes como la paranoia desde el punto de vista de la evolución? O ¿cómo ha cambiado la atracción sexual desde la época de nuestros ‘abuelos’ homínidos hasta ahora?
A estas y otras cuestiones relativas a la evolución del comportamiento humano se trató de dar respuesta durante la IV Jornada Nacional de Evolución y Neurociencias, evento organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Red de Salud Mental de Bizkaia, que tuvo lugar los días 28 y 29 de abril en el Bizkaia Aretoa – UPV/EHU de Bilbao.
Desde que en 2017 un grupo de psiquiatras de la Red de Salud Mental de Bizkaia organizara la primera edición de esta jornada, la cita se ha convertido en un punto de encuentro para profesionales de distintos ámbitos científicos como la psiquiatría, la psicología, la biología o la filosofía con un interés común: la conducta humana desde una perspectiva evolucionista y su divulgación científica en un formato accesible y ameno para todos los públicos, a la par que riguroso y actualizado.
Una cosa es la atracción sexual y otra el deseo sexual. Esta distinción es fundamental, tal y como explica Laura Morán, psicóloga y sexóloga.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo IV Jornada Nacional de Evolución y Neurociencias: Laura Morán – Evolución de la atracción sexual se ha escrito en Cuaderno de Cultura Científica.
Conversión de frecuencias de fotones individuales
 Tras excitar ópticamente el hidrógeno en su interior, la luz incidente cambia de frecuencia (color) al atravesar la fibra óptica antirresonante. Fuente: UPV/EHU
Tras excitar ópticamente el hidrógeno en su interior, la luz incidente cambia de frecuencia (color) al atravesar la fibra óptica antirresonante. Fuente: UPV/EHUActualmente, estamos viviendo una segunda revolución cuántica en la que la mecánica cuántica está pasando de ser una fuente de paradojas a una herramienta del mundo real. Ejemplo de ello son las tecnologías basadas en la manipulación de la luz, tecnologías que son capaces de abordar los retos que existen actualmente en las comunicaciones, hasta ahora insuperables con las tecnologías convencionales. Este es el caso de la conversión de frecuencias y el transporte a larga distancia de fotones individuales y pares de fotones entrelazados.
Las fibras ópticas son como tuberías para la luz. Una investigación liderada por David Novoa, investigador Ikerbasque en la Escuela de Ingeniería de Bilbao de la UPV/EHU, ha desarrollado un nuevo tipo de fibra óptica micro-estructurada que, a diferencia de las fibras convencionales como las que llevan internet a nuestras casas, guía la luz en un canal hueco con una atenuación extremadamente baja. Lo que hace únicas a estas nuevas fibras es que sus propiedades ópticas son reconfigurables cuando se llenan de gases a distintas presiones. Esto las convierte en unas plataformas muy versátiles, capaces de operar en un rango espectral sin precedentes, desde el ultravioleta hasta el infrarrojo.
En este trabajo los investigadores han llenado la fibra con hidrógeno, la molécula más ligera de la naturaleza y, por tanto, la que posee una frecuencia fundamental de vibración más alta. Por medio del conocido como efecto Raman estimulado, se pueden excitar ópticamente las moléculas del núcleo gaseoso de la fibra de manera que oscilen sincronizadas de forma muy precisa. En palabras de David Novoa, “es en esta coreografía molecular donde reside la belleza de nuestro sistema: Las fuentes de luz cuánticas (los fotones) son capaces, bajo determinadas circunstancias, de extraer la energía vibracional de esas moléculas oscilantes para aumentar su propia energía y así cambiar de frecuencia (color)”.
Sistemas complejos como, por ejemplo, las redes cuánticas, están compuestos por diferentes subsistemas cuya frecuencia óptima de operación no suele coincidir. Es por ello que una técnica capaz de conseguir la conversión de frecuencias ópticas a nivel cuántico en un amplio espectro sin afectar las propiedades de las fuentes de luz originales sería extremadamente útil. Estos resultados muestran precisamente la mejora de un proceso crítico en las tecnologías cuánticas relacionadas con la luz, como es la conversión cuántica de frecuencias.
Referencia:
R. Tyumenev, J. Hammer, N. Y. Joly, P. St.J. Russell and D. Novoa (2022) Tunable and state-preserving frequency conversion of single photons in hydrogen Science, doi: 10.1126/science.abn1434
Para saber más:
Una fibra óptica de plástico actúa como concentrador solar luminiscence
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Conversión de frecuencias de fotones individuales se ha escrito en Cuaderno de Cultura Científica.
Testigos del pasado
Seguro que en algunas películas y en noticias de índole geológica y climatológica habéis oído o leído que los científicos están estudiando núcleos de hielo, sedimento o roca y os ha entrado la curiosidad sobre qué son esas cosas. En primer lugar, aquí no se llaman núcleos. Este término resulta de una traducción literal de la palabra inglesa “core” que, efectivamente, significa núcleo. Pero, en castellano, a estas herramientas geológicas las denominamos testigos de sondeo.
 Extracción de testigos de sondeo de hielo en la Antártida. Imagen: NASA.
Extracción de testigos de sondeo de hielo en la Antártida. Imagen: NASA.Un sondeo es un método de perforación del terreno, es decir, consiste en hacer un agujero en el suelo, ya sea sobre tierra firme, en el hielo o en el fondo del mar, con un tubo de metal o plástico para poder reconocer lo que se encuentra en profundidad. Y se denomina testigo al cilindro de material (hielo, sedimento o roca) que se puede extraer cuando se hace el sondeo y que quedaría encapsulado dentro del tubo.
Los métodos de perforación pueden agruparse en tres tipos. Por un lado, encontramos los sondeos mecánicos por percusión, que consisten en atravesar el terreno o bien dejando caer el tubo de sondeo desde una altura considerable y aprovechar así la fuerza de la gravedad, o bien hincándolo a base de golpes repetitivos hasta conseguir enterrarlo. Por otro lado, tenemos los sondeos de rotación, que consisten en acoplar al tubo de sondeo una cabeza, llamada corona, que tiene un filo cortante de carburo de diamante o de wolframio y es capaz de girar a gran velocidad gracias a un motor externo, por lo que, haciendo un pequeño símil, atraviesa el terreno a dentelladas. Finalmente, el tercer tipo sería una mezcla de los dos anteriores, es decir, existen sondeadoras que, a la vez que van enterrando el tubo por presión, tienen incorporada una corona dentada que va girando rompiendo el terreno.
Los testigos de sondeo tienen un valor científico extraordinario. En su interior, contienen un registro de la evolución geológica de una zona durante los últimos cientos, miles e, incluso, millones de años. Zonas que están enterradas bajos nuestros pies y a las que no podríamos acceder de otra manera más que haciendo estas perforaciones, tales como los mantos y casquetes de hielo o el fondo oceánico.
 Testificadora de sondeos por percusión y detalle del tubo de sondeo a bordo del Buque Oceanográfico Pourquois Pas? del instituto Francés de Investigación para la Exploración Marina (IFREMER). Foto: Blanca María Martínez
Testificadora de sondeos por percusión y detalle del tubo de sondeo a bordo del Buque Oceanográfico Pourquois Pas? del instituto Francés de Investigación para la Exploración Marina (IFREMER). Foto: Blanca María MartínezEn la Antártida o Groenlandia encontramos enormes espesores de hielo que se han formado por la acumulación de agua congelada durante cientos de miles de años. Si nos fijamos más en detalle, estas masas están formadas por la superposición de finas capas de hielo, dispuestas una encima de las otras, donde cada una representa la precipitación producida en un año. Además, cada capa de hielo corresponde con una mini cápsula del tiempo en la que han quedado preservadas las características de la atmósfera en ese momento. Así, al estudiar los testigos de sondeo de hielo extraídos en la Antártida y Groenlandia se han podido reconstruir las variaciones temporales de gases como el dióxido de carbono (CO2) o el metano (CH4) y de la temperatura atmosférica durante los últimos 800.000 años con una precisión anual.
 Obtención de testigos de sondeo por percusión en una laguna de Bardenas Reales de Navarra. Foto: Blanca María Martínez
Obtención de testigos de sondeo por percusión en una laguna de Bardenas Reales de Navarra. Foto: Blanca María MartínezEstos estudios climáticos de hielo se complementan con los registros marinos. En las zonas oceánicas más profundas se acumulan capas de sedimentos finos (limos y arcillas) que apenas sufren alteraciones por las corrientes marinas de fondo. Así que, de manera similar a las capas de hielo, estas capas de sedimento irían recogiendo la historia oceánica de los últimos cientos de miles de años de manera continua. Sin embargo, no tienen una precisión temporal tan grande como el hielo, el registro sedimentario aporta una periodicidad decadal, rara vez anual.
La obtención de testigos de sondeo de sedimento marino no es tan sencilla como la de los testigos de sondeo de hielo. En este caso, los equipos de testificación deben ir a bordo de buques oceanográficos, que son auténticos laboratorios científicos flotantes, y, para llegar a tocar el fondo marino, hay que librar los cientos y miles de metros de espesor que tiene la columna de agua. Una vez hecho esto, la sondeadora debe perforar el fondo marino y hay que conseguir que el testigo de sondeo vuelva al buque sin perderlo por el camino. Pero estas operaciones tan complicadas, merecen la pena. El estudio minucioso del sedimento obtenido en los testigos de sondeo marinos nos aporta información sobre la variación temporal de parámetros como la temperatura, salinidad o pH de las masas de agua y nos permite conocer cambios en la circulación de las corrientes oceánicas durante los últimos cientos de miles de años.
 Muestreo del sedimento de un testigo de sondeo para su estudio geológico. Foto: Blanca María Martínez
Muestreo del sedimento de un testigo de sondeo para su estudio geológico. Foto: Blanca María MartínezLa combinación de los estudios climáticos de los testigos de sondeo de hielo y de sedimento marino, han sido básicos para conocer como ha cambiado el clima, de manera detallada, en los últimos milenios. Estos registros nos dan una idea global de la variabilidad climática de nuestro planeta, sirviendo como base de comparación de cualquier estudio paleoambiental actual realizado en cualquier ambiente, ya sea continental o marino, como, por ejemplo, los estudios de testigos de sondeo de sedimentos de lagos y estuarios. Esta comparativa con los registros globales permite identificar, con mucho detalle, eventos climáticos o condiciones ambientales locales, que sólo afectaron a zonas geográficas restringidas y que no tuvieron una influencia climática a nivel mundial.
Sin estos testigos del pasado, o chivatos del pasado, como los queramos llamar, sería imposible poder conocer cómo ha cambiado el clima en los últimos milenios, lo cual es clave para poder aventurar cómo cambiará en el futuro más próximo para poder adelantarnos y adaptarnos a lo que está por llegar.
Para saber más:
Los volcanes submarinos de Bizkaia y Gipuzkoa
Un estudio paleoceanográfico apunta a que los ciclos naturales de cambio climático están siendo alterados
Geología, Antropoceno y cambio climático
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Testigos del pasado se ha escrito en Cuaderno de Cultura Científica.
La curiosa identidad de Proizvolov
La conocida como identidad de Proizvolov fue propuesta por el matemático Vyacheslav Proizvolov en forma de problema en las Olimpiadas Matemáticas Soviéticas de 1985:
Consideremos el conjunto de los primeros 2N enteros positivos,
CN = {1, 2, 3, …, 2N − 1, 2N},
y una partición de él en dos subconjuntos de N elementos cada uno de ellos:
AN = {a1, a2, …, aN-1, aN} y BN = {b1, b2, …, bN-1, bN}.
Ordenemos los elementos de ambos conjuntos de la siguiente manera:
![]()
Se pide probar que la siguiente suma de valores absolutos
|a1 – b1| + |a2 – b2| + … + |aN-1 – bN-1| + |aN – bN|
es igual a N2.
Un ejemplo
Para entender mejor el enunciado, vamos a ver un ejemplo. Si N = 10, tenemos el conjunto de los veinte primeros números naturales
C10 = {1, 2, 3, …, 19, 20}.
Elegimos las particiones (hemos ordenado los números de la primera partición de manera creciente y los de la segunda de manera decreciente):
A10 = {1, 3, 4, 7, 8, 9, 10, 18, 19, 20}, y
B10 = {17, 16, 15, 14, 13, 12, 11, 6, 5, 2},
Es decir, a1 = 1, a2 = 3, a3 = 4, …, a9 = 19, a10 = 20, b1 = 17, b2 = 16, b3 = 15, …, b9 = 5 y b10 = 2.
Entonces,
|a1 – b1| + |a2 – b2| + … + |a9 – b9| + |a10 – b10| =
|1 – 17| + |3 – 16| + |4 – 15| + |7 – 14| + |8 – 13| + |9 – 12| + |10 – 11| + |18 – 6| + |19 – 5| + |20 – 2| =
16 + 13 + 11 + 7 + 5 + 3 + 1 + 12 + 14 + 18 = 100 = 102.
Una demostración sencilla de la identidad de Proizvolov
Observemos en primer lugar que |a – b| = máx{a,b} – mín{a,b}. En efecto, si a > b, es |a – b| = a – b = máx{a, b} – mín{a, b}, y si a
En segundo lugar, para cada i en {1, 2…, N − 1, N}, se verifica que uno de los números del par {ai, bi} está en el conjunto A = {1, 2…, N − 1, N} y el otro en el conjunto B = {N + 1, N + 2, …, 2N − 1, 2N}.
En efecto, si esta propiedad no fuera cierta, supongamos, por ejemplo, que los números ai y bi pertenecen ambos al conjunto A. Es decir, ai i N que pertenecen a A (ya que a1 2 i N también en A) y al menos N − i + 1 elementos del conjunto BN que pertenecen a A (ya que N + 1> bi > bi+1 > … > bN-1 > bN y podría haber algún otro elemento de BN también en A). Es decir, en el conjunto A habría al menos i + (N – i + 1) = N + 1 elementos de CN. Pero eso es imposible, porque A solo posee N elementos. Un argumento similar prueba que tampoco puede suceder que ai y bi pertenezcan ambos al conjunto B.
Es decir, efectivamente, para cada i en {1, 2…, N − 1, N}, se verifica que uno de los números del par {ai, bi} está en el conjunto A = {1, 2…, N − 1, N} y el otro en el conjunto B = {N + 1, N + 2, …, 2N − 1, 2N}. De aquí se deduce que para cada i en {1, 2…, N − 1, N}, es mín{ai, bi} i, bi} > N. Es decir, de otra manera,
A = {1, 2…, N − 1, N} = {mín{ai, bi}: i en {1, 2…, N − 1, N}}, y
B = {N + 1, N + 2, …, 2N − 1, 2N} = {máx{ai, bi}: i en {1, 2…, N − 1, N}}.
Por lo tanto,
|a1 – b1| + |a2 – b2| + … + |aN-1 – bN-1| + |aN – bN| =
(máx{a1, b1} – mín{a1, b1}) + (máx{a2, b2} – mín{a2, b2}) + … + (máx{aN-1, bN-1} – mín{aN-1, bN-1}) + (máx{aN, bN} – mín{aN, bN}) =
(máx{a1, b1} + máx{a2, b2} + … + máx{aN-1, bN-1} + máx{aN, bN}) – (mín{a1, b1} + mín {a2, b2} + … + mín{aN-1, bN-1} + mín{aN, bN}) =
((N + 1) + (N + 2) + … + (2N – 1) + 2N) – (1 + 2 + … + (N – 1) + N) =
((N + 1) – 1) + ((N + 2) – 2) + … + ((2N – 1) – (N – 1)) + (2N – N) =
N + N + … + N = N2. QED
Una generalización de la identidad de Proizvolov
Grégoire Nicollier propuso en 2015 la siguiente generalización de la identidad de Proizvolov:
Consideremos un conjunto de números reales,
CN = {c1, c2, …, c2N-1, cN},
y una partición de él en dos subconjuntos de N elementos cada uno de ellos:
AN = {a1, a2, …, aN-1, aN} y BN = {b1, b2, …, bN-1, bN}.
Ordenemos los elementos de estos conjuntos de la siguiente manera:
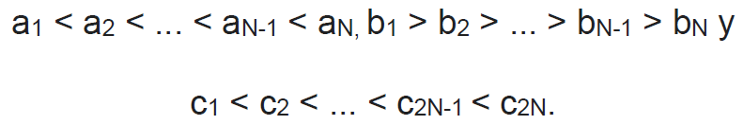
Entonces, la suma
|a1 – b1| + |a2 – b2| + … + |aN-1 – bN-1| + |aN – bN|
es independiente de las particiones elegidas AN y BN.
Para probar esta propiedad, basta con observar, con un argumento similar al realizado antes, que para cualquier par {ai, bi}, uno de los elementos es menor que cN + 1 y el otro es mayor que cN. Entonces,
{c1, c2, …, cN-1, cN} = {mín{ai, bi}: i en {1, 2…, N − 1, N}}, y
{cN+1, cN+2, …, c2N-1, c2N} = {máx{ai, bi}: i en {1, 2…, N − 1, N}}.
Y por lo tanto:
|a1 – b1| + |a2 – b2| + … + |aN-1 – bN-1| + |aN – bN| =
(máx{a1, b1} – mín{a1, b1}) + (máx{a2, b2} – mín{a2, b2}) + … + (máx{aN-1, bN-1} – mín{aN-1, bN-1}) + (máx{aN, bN} – mín{aN, bN}) =
(máx{a1, b1} + máx{a2, b2} + … + máx{aN-1, bN-1} + máx{aN, bN}) – (mín{a1, b1} + mín {a2, b2} + … + mín{aN-1, bN-1} + mín{aN, bN}) =
(c2N + c2N-1 + … + cN+2 + cN+1) – (c1 + c2 + … + cN-1 + cN),
que es la misma cantidad para cualquier partición elegida. QED
Además, Grégoire comentaba en el artículo que esta propiedad sigue siendo cierta aunque los números del conjunto C no sean todos diferentes.
¡Curiosas propiedades!
Referencias
-
Proizvolov’s Identity, Futility Closet, 21 agosto 2014
-
Proizvolov’s Identity, Cut the Knot
-
Grégoire Nicollier, A generalisation of Proizvolov’s identity, The Mathematical Gazette 99 (546) (2015): 525-526
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo La curiosa identidad de Proizvolov se ha escrito en Cuaderno de Cultura Científica.
Einstein y el movimiento browniano
El mismo año en el que Einstein publicó la teoría especial de la relatividad también publicó un artículo igualmente revolucionario sobre los movimientos aleatorios de las moléculas, algo habitualmente conocido como movimiento browniano. El movimiento de una partícula en un líquido es aparentemente algo mucho menos espectacular que los movimientos en el espaciotiempo o la afirmación de que la masa es una forma de energía o que la luz está constituida por partículas, por lo que la explicación de Einstein del movimiento browniano ha sido completamente eclipsada por sus otras teorías. Sin embargo, si Einstein solo hubiese publicado el por qué las partículas se mueven como lo hacen, habría merecido el premio Nobel por ello: esta modelo permitió confirmar, sin ningún género de dudas, que los átomos existen.

En 1827 Robert Brown estudió el movimiento de los granos de polen en un líquido usando un microscopio. Descubrió que se movían al azar y sin nada aparentemente que les hiciese moverse. Antes ya había habido observaciones de este movimiento (entre ellas las realizadas por Jan Ingenhousz en 1785), pero nadie lo había estudiado de forma tan amplia, probando que los granos no se movían porque estuviesen vivos, y que partículas de vidrio o de granito exhibían el mismo comportamiento. Hoy, la idea de que las partículas intercambien el sitio con las moléculas en un líquido y, como consecuencia, se mueven al azar no parece tan extraña. Ello se debe a que estamos familiarizados con las ideas de molécula y átomo, pero en la época de Brown los científicos desconocían su existencia. En los años en los que Einstein comenzó a estudiar ciencia, la física y la química, en ese momento campos con relativamente poco en común, habían comenzado a incorporar la idea de átomo en sus teorías, pero había una gran división entre los científicos sobre si realmente existían. Quizás, pensaban algunos, los átomos y las moléculas eran simplemente una forma matemáticamente conveniente de describir ciertos fenómenos, pero no eran una representación verdadera de la realidad.
Einstein tenía muy claro que los átomos existían. Tanto es así que muchos de sus primeros trabajos de investigación asumían que la materia podía dividirse en partículas discretas. Hizo su tesis doctoral “Una nueva determinación de las dimensiones moleculares” sobre cómo determinar el tamaño de las moléculas midiendo su movimiento browniano en un líquido. Una versión de esta tesis se publicó en Annalen der Physik en abril de 1905, y es uno de los primeros artículos en mostrar de forma definitiva que las moléculas no son artificios matemáticos, sino entes reales.
Movimiento browniano y teoría estadísticaOnce días más tarde, Einstein publicó un artículo sobre el movimiento browniano mismo. El artículo se titulaba “Sobre el movimiento de pequeñas partículas suspendidas en líquidos en reposo requerido por la teoría cinético-molecular del calor”, por lo que no indicaba que se tratase del movimiento browniano. Simplemente decía en su párrafo de apertura que iba a describir el movimiento de las moléculas suspendidas en un líquido, y que quizás este fenómeno era idéntico a un fenómeno del que había oído hablar, el movimiento browniano. Desde ese punto de partida, continuó demostrando que podía usar las teorías del calor en vigor para describir cómo la energía térmica, incluso a temperatura ambiente, provocaría que las moléculas del líquido estuviesen en continuo movimiento. Este movimiento haría a su vez que cualquier partícula suspendida en el líquido resultase empujada. Einstein acababa de ofrecer la primera explicación del movimiento browniano (Marian Smoluchowski llegaría a un resultado similar en 1906 de forma independiente).
A continuación Einstein daba una descripción matemática de cómo se moverían las partículas en el seno del líquido. Usó el análisis estadístico para calcular el camino promedio de dichas partículas. Si bien el movimiento de la partícula sería al azar, desplazándose brevemente a la izquierda para hacerlo después hacia la derecha, Einstein demostró que se podía determinar una dirección básica para el movimiento. Es análogo al movimiento de un borracho, que va para allá y después para acá, tropieza con el banco, cruza la calle tres veces, se abraza a la farola, pero en términos generales se dirige hacia su casa. Una observación del borracho permite determinar la zona hacia la que se dirige y hacer predicciones sobre el tiempo que tardará en llegar, incluso sin saber exactamente con cuantos objetos tropezará durante el trayecto. Se puede obviar el azar a corto plazo para hacer predicciones acerca de lo que sucederá a largo.
El artículo de Einstein ofrecía una explicación del movimiento browniano, pero fueron otros científicos los que llevaron a cabo los experimentos que demostraron que las moléculas existían realmente, y que era la transmisión de calor la que causaba su movimiento en un líquido. En 1908, Jean Baptiste Perrin estudió la forma en la que las partículas sedimentan en el agua por la influencia de la gravedad. La sedimentación encuentra la oposición de los choques de las moléculas desde abajo, por lo que el movimiento browniano se opone a la atracción gravitatoria. Perrin usó este descubrimiento para calcular el tamaño de las moléculas de agua basándose en las ecuaciones de Einstein. Por este trabajo recibió el premio Nobel de física en 1926.
Toda esta investigación sobre el movimiento browniano resolvió el problema que enfrentaba a físicos y químicos sobre si la materia era fundamentalmente continua o estaba constituida por partículas. Con su tesis doctoral, su trabajo sobre el movimiento browniano, y su artículo sobre el efecto fotoeléctrico, Einstein fue crucial para la aceptación de la existencia de átomos y moléculas. Y, sin embargo, Einstein no volvería a trabajar con nada relacionado directamente con moléculas en el resto de su carrera científica.
Referencia:
Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. AdP 17, 549 (1905) Annalen der Physik, 14 (S1), 182-193 DOI: 10.1002/andp.200590005
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 20 de junio de 2010.
El artículo Einstein y el movimiento browniano se ha escrito en Cuaderno de Cultura Científica.
Primer catálogo de materiales de banda plana
Una colaboración internacional ha creado un catálogo de materiales que podría ser muy útil para el desarrollo de las tecnologías cuánticas. Se trata del primer catálogo del mundo de materiales de banda plana, que podría reducir la influencia del azar en la búsqueda de nuevos materiales con propiedades cuánticas exóticas, tales como el magnetismo y la superconductividad. Estos materiales tendrían aplicaciones en dispositivos de memoria o en el transporte de energía sin disipación a través de largas distancias. Este trabajo, que se enmarca dentro de la iniciativa IKUR 2030 del Gobierno Vasco, ha sido publicado en Nature.
 Representación artística de las dispersiones de banda en un material. En negro, las diferentes bandas, siendo el eje vertical la energía cinética. En el centro tenemos dos bandas planas que se originan a partir de la estructura del material.
Representación artística de las dispersiones de banda en un material. En negro, las diferentes bandas, siendo el eje vertical la energía cinética. En el centro tenemos dos bandas planas que se originan a partir de la estructura del material.Encontrar los ingredientes adecuados para crear materiales con propiedades cuánticas exóticas ha sido una quimera para los científicos experimentales, debido a las numerosas combinaciones posibles de elementos a sintetizar. A partir de ahora, la creación de este tipo de materiales podría ser menos aleatoria gracias a una colaboración internacional liderada por Andrei Bernevig, profesor visitante Ikerbasque en el Donostia International Physics Center (DIPC) y profesor de la Universidad de Princeton, y Nicolas Regnault, de la Universidad de Princeton y la Ecole Normale Supérieure Paris, CNRS, con la participación de Luis Elcoro de la Universidad del País Vasco (UPV/EHU).
El equipo realizó una búsqueda sistemática de posibles candidatos en una enorme base de datos de 55.000 materiales. El proceso de eliminación se inició con la identificación de los llamados materiales de banda plana, es decir, estados electrónicos con energía cinética constante, donde el comportamiento de los electrones se rige principalmente por las interacciones con otros electrones. Sin embargo, los investigadores se dieron cuenta de que tener banda plana no es el único requisito, ya que cuando los electrones están demasiado unidos al átomo, éstos no pueden moverse y crear estados interesantes de la materia, aun estando en una banda plana. “La idea es que los electrones se vean entre sí, lo que se puede lograr asegurándonos de que estén extendidos en el espacio. Eso es exactamente lo que aportan las bandas topológicas”, según Nicolas Regnault.
La topología, como lo sugieren los tres premios Nobel de 1985, 1997 y 2016, juega un papel crucial en la física de la materia condensada moderna, ya que implica que algunas funciones de onda cuánticas estén extendidas, haciéndolas insensibles a perturbaciones locales, como por ejemplo impurezas. Esto a su vez hace que algunas propiedades físicas, tales como la resistencia, estén cuantificadas o generen estados superficiales perfectamente conductores. Afortunadamente, el equipo ha estado a la vanguardia de la caracterización de las propiedades topológicas de las bandas a través de su enfoque conocido como «química cuántica topológica«, proporcionándoles tanto una gran base de datos de materiales, como las herramientas teóricas para buscar bandas planas topológicas.
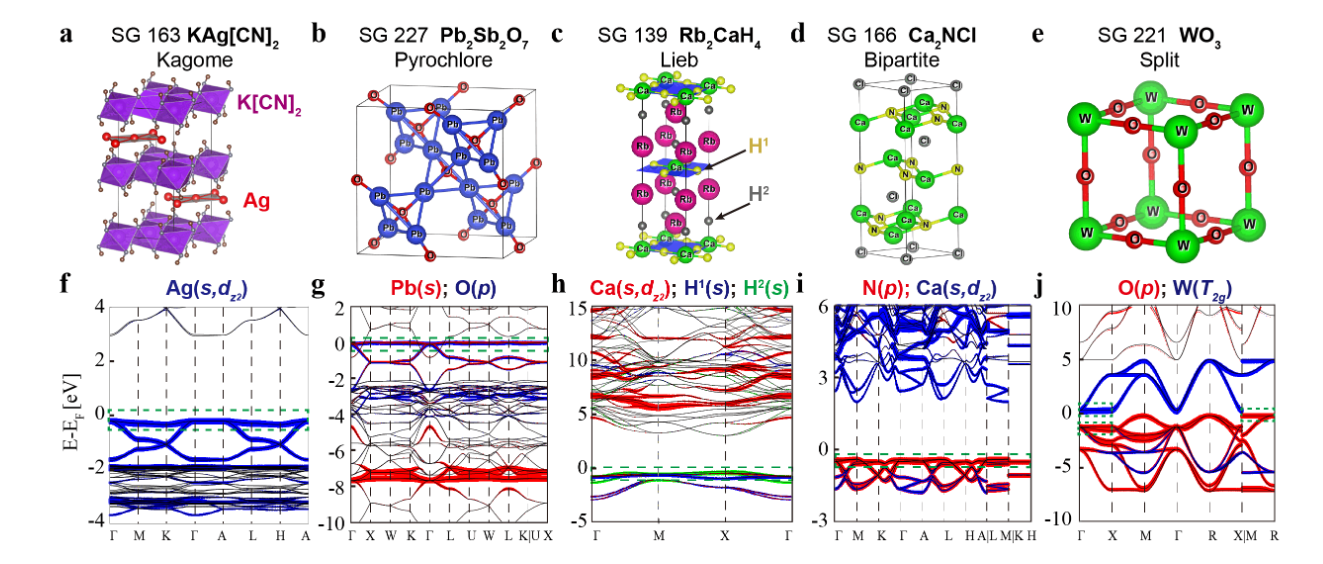
Mediante el empleo de herramientas que van desde métodos analíticos hasta búsquedas por fuerza bruta, el equipo encontró todos los materiales de banda plana que se conocen actualmente en la naturaleza. Este catálogo de materiales de banda plana está disponible en https://www.topologicalquantumchemistry.fr/flatbands e incluye su propio buscador.
“La comunidad científica puede ahora buscar bandas topológicas planas en los materiales. Hemos encontrado alrededor de 700 materiales (de los 55.000 materiales estudiados) que muestran bandas planas con un interés potencial”, dice Yuanfeng Xu, de la Universidad de Princeton y el Instituto Max Planck de Física de Microestructuras, uno de los dos autores principales del estudio. «Nos hemos asegurado de que los materiales que identificamos son candidatos prometedores para la síntesis química», enfatiza Leslie Schoop del departamento de química de Princeton. El equipo ha ido más allá en la clasificación de las propiedades topológicas de estas bandas, mostrando además qué tipo de electrones deslocalizados albergan.
Ahora que este gran catálogo está completo, el equipo comenzará a trabajar con los materiales más prometedores para descubrir experimentalmente el potencial de nuevos estados de interacción. “Ahora que sabemos dónde buscar, necesitamos fabricar estos materiales”, dice Claudia Felser del Instituto Max Planck de Física Química de Sólidos. “Tenemos un equipo experimental excepcional trabajando con nosotros. Están ansiosos por medir las propiedades físicas de estos materiales candidatos potenciales y ver qué excitantes fenómenos cuánticos surgen”.
El catálogo de bandas planas representa el fruto de años de investigación del equipo. “Muchas personas, muchas instituciones y universidades a las que presentamos el proyecto nos dijeron que esto era demasiado difícil y que nunca se podría hacer. Nos tomó varios años, pero lo logramos”, dice Andrei Bernevig.
Referencia:
Nicolas Regnault, Yuanfeng Xu, Ming-Rui Li, Da-Shuai Ma, Milena Jovanovic, Ali Yazdani, Stuart S. P. Parkin, Claudia Felser, Leslie M. Schoop, N. Phuan Ong, Robert J. Cava, Luis Elcoro, Zhi-Da Song & B. Andrei Bernevig (2022) Catalogue of flat-band stoichiometric materials Nature doi: 10.1038/s41586-022-04519-1
Más información:
A powerful search engine for flatband stoichiometric materials
Química Cuántica Topológica Magnética
Un catálogo de estructuras magnéticas topológicas
La teoría de bandas de los sólidos se hace topológica
Edición realizada por César Tomé López a partir de materiales suministrados por DIPC
El artículo Primer catálogo de materiales de banda plana se ha escrito en Cuaderno de Cultura Científica.
ADN en cuevas, puerta a nuestra historia evolutiva
Por primera vez se ha conseguido obtener ADN nuclear de varios individuos neandertales a partir de sedimentos de cuevas prehistóricas europeas. Se abre así la puerta al conocimiento de la historia de poblaciones homínidas antiguas, incluso en ausencia de registro fósil.
Los restos esqueléticos encontrados en yacimientos arqueológicos son fuente fundamental de ADN. La secuenciación de este ADN ha servido para revelar aspectos importantes de nuestro pasado evolutivo. Pero encontrar restos óseos es extremadamente raro, ya que el registro fósil es realmente escaso, lo que deja grandes lagunas en la comprensión de la historia evolutiva humana.
El ADN nuclear (ADNn) está en el núcleo de cada célula formando los cromosomas (23 pares, uno por pareja de cada progenitor), y el ADN mitocondrial (ADNmt) es una pequeña molécula circular localizada en las mitocondrias que son pequeños orgánulos repartidos por la célula responsables de producir la energía. Las mitocondrias poseen varias copias de ADNmt y en cada célula existe un gran número de mitocondrias, así que las células contienen múltiples copias de ADNmt. Esta abundancia hace que sean más altas las posibilidades de recuperar ADNmt a partir de restos arqueológicos antiguos o muy degradados que las de recuperar ADNn. Además, el hecho de que el ADNmt sea una molécula circular hace que sea menos susceptible a la degradación.
Por todo ello, y porque el ADNmt se hereda exclusivamente de la madre, este es una herramienta valiosísima en el estudio de genética de poblaciones. Todos los familiares relacionados por vía materna comparten la misma secuencia de ADNmt. Pero, por esta misma razón, tiene un valor limitado, ya que sólo representa el linaje materno.
Hasta ahora, únicamente se había conseguido recuperar ADNmt de homínidos a partir de sedimentos de cuevas del Pleistoceno. Aunque el ADNn contiene mucha más información, su recuperación de los sedimentos supone numerosos problemas. Se encuentra en mucha menor cantidad que el mitocondrial y muchos otros mamíferos cohabitaron con nuestros antepasados por lo que no todo el ADN presente en los sedimentos es de homínido.
Para facilitar la recuperación del ADNn se han seguido estrategias en las que se buscaba enriquecer el escaso ADNn de homínido. Para ello se han desarrollado sondas de hibridación, que son pequeños fragmentos de ADN que se “emparejan” con puntos concretos del genoma nuclear homínido. Así, el equipo de investigación internacional del que forma parte la UPV/EHU ha conseguido recuperar ADNn de sedimentos de dos yacimientos en el sur de Siberia (cuevas Denisova y Chagyrscaya) y de la Galería de las Estatuas en Atapuerca (Burgos).
 ADN en cuevas. Los sedimentos de cuevas prehistóricas contienen ADN mitocondrial y nuclear de homínidos que se puede enriquecer, secuenciar y analizar para conocer la historia genética de quienes las ocuparon, incluso en ausencia de sus restos esqueléticos. Ilustración: Nuria González Santiago
ADN en cuevas. Los sedimentos de cuevas prehistóricas contienen ADN mitocondrial y nuclear de homínidos que se puede enriquecer, secuenciar y analizar para conocer la historia genética de quienes las ocuparon, incluso en ausencia de sus restos esqueléticos. Ilustración: Nuria González Santiago
En los dos primeros sitios ya se conocía el ADN de varios huesos, y los resultados filogenéticos del ADN del sedimento fueron consistentes con los resultados publicados anteriormente de los restos esqueléticos. En la Galería de las Estatuas el único hueso de un dedo de neandertal no había sido suficiente para secuenciar su ADN, pero el ADNn extraído de los sedimentos reveló que 2 poblaciones neandertales habían vivido en la cueva. Así pues, se ha logrado averiguar que la primera población neandertal que vivió hace 135.000 años fue reemplazada por otra población de perfil genético muy diferente (105.000 años aprox. de antigüedad). Los dos linajes estaban separados por unos 35.000 años de evolución.
Este trabajo abre la posibilidad de estudiar la historia de las poblaciones de homínidos a pesar de no existir, o ser extremadamente escaso, el registro fósil en muchos asentamientos arqueológicos.
Referencias consultadas:
Vernot B. et al., (2021). Unearthing Neanderthal population history using nuclear and mitochondrial DNA from cave sediments. Science, 372. DOI: 10.1126/science.abf1667.
Cardoso S., Valverde L., Palencia L., López Quintana J. C., Guenaga Lizasu A., Martínez de Pancorbo M. (2011). Análisis de ADN Mitocondrial en los restos humanos de la cueva de Santimamiñe (Kortezubi, Bizkaia). KOBIE Serie Bizkaiko Arkeologi Indusketak, nº 1: 383-392 Bizkaiko Foru Aldundia, Bilbao – 2011 ISSN 0214-7971.
Autora: Nuria González Santiago (@lanuri_). Licenciada en Biología. Especialista en Ilustración Científica, UPV/EHU. Curso 20/21.
Articulo Original: ADN nuclear de varios individuos neandertales a partir de sedimentos Cuaderno de Cultura Científica, 16 de abril de 2021
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión centrada en la propia ilustración
El artículo ADN en cuevas, puerta a nuestra historia evolutiva se ha escrito en Cuaderno de Cultura Científica.

