Einstein y Sigmund Freud
Cuando se hace una lista de las mentes más influyentes del siglo XX, Einstein y Freud aparecen invariablemente en ella. Las teorías de Einstein crearon la época de la física moderna y las de Freud, aunque pseudocientíficas, la de la psicología [1]. Colaboraron sólo una vez, escribiendo un ensayo que apoyaba una visión de la política internacional que favorecía la paz sobre la guerra.
 Edición alemana de «¿Por qué la guerra?», publicada por la Sociedad de Naciones (Völkerbund) en 1933. Imagen: Wikimedia Commons
Edición alemana de «¿Por qué la guerra?», publicada por la Sociedad de Naciones (Völkerbund) en 1933. Imagen: Wikimedia CommonsAlbert Einstein y Sigmund Freud se encontraron cara a cara en el Berlín de antes de la Segunda Guerra Mundial. Freud había ido a visitar a su familia por Janucá (fiesta religiosa judía de las luces, que suele anteceder, y a veces coincidir, con las de la Navidad) en 1926, y Einstein y su mujer, Elsa, visitaron al famoso psicoanalista. En una carta a un amigo, Freud describió su encuentro como una charla agradable, aunque sí añadió que “[Einstein] entiende tanto de psicología como yo de física”.
Quedaron en buenos términos y mantuvieron un contacto distante durante muchos años. La apertura de Einstein a las teorías de Freud sobre el significado de los sueños y del subconsciente es un poco llamativa, teniendo en cuenta que Einstein le tenía pavor a la enfermedad mental y, enfáticamente, no tenía interés en el psicoanálisis. A este respecto dijo una vez: “Me gustaría permanecer en la oscuridad de no haber sido analizado”. Pero al igual que Einstein, Freud lo cuestionaba todo [2], incluso sus propias ideas, lo que le gustaba a Einstein. Además, tenían otro punto en común: ambos eran judíos conocidos por criticar abiertamente la religión.
No dejaron de ser meros conocidos hasta 1932. Ese año, la Sociedad de Naciones le pidió a Einstein que escogiera a alguien con quien reflexionar sobre alguna cuestión candente. En esa época el militarismo en Alemania estaba en auge, y de ahí vino el tema que Einstein eligió: “¿Hay alguna manera de librar a la humanidad de la amenaza de la guerra?” Como compañero de discusión Einstein eligió a Freud.
Freud era bien conocido por su teoría de que existen un bien y un mal absolutos, publicando visiones muy pesimistas sobre la propensión a errar favoreciendo al segundo. Pero la respuesta de diecisiete páginas de Freud a la pregunta de una línea de Einstein fue sorprendentemente optimista.
Freud expuso la idea de que la humanidad está dividida entre un impulso vital y un ansia por la muerte. Escribió que, a veces, nuestra agresión podría empujarnos a la guerra, pero que el impulso del amor lo evitaría. Einstein respondió que las leyes podrían compensar el impulso humano hacia la violencia, y apoyó vehementemente un cuerpo internacional que limitase los excesos del nacionalismo y resolviese los conflictos.
El diálogo entre los dos llevó a la publicación del libro Warum Krieg? (¿Por qué la guerra?). El Instituto Internacional de Cooperación Intelectual de la Sociedad de Naciones, a la que pertenecía Einstein a instancias de Marie Curie, lo publicó simultáneamente en inglés, francés y alemán en 1933. Sin embargo, el objetivo del libro, alentar la paz en el mundo, no se cumpliría. Ese mismo año, 1933, Hitler llega al poder en Alemania y ejemplares de este libro, como del resto de trabajos de Einstein y Freud, son quemados públicamente por los nacionalsocialistas.
Además de por su colaboración directa, Einstein y Freud están unidos en la conciencia colectiva por ser ambos pensadores extraños y profundos en un tiempo crucial en la historia del mundo, además de por estar también juntos en la lista de los judíos que consiguieron escapar de la persecución nazi.
Notas:
[1] Esta frase dice lo que dice y no otra cosa. Esto es, Freud convierte a la psicología en una rama del conocimiento de pleno derecho, si bien ello no implica que la psicología moderna se base en las ideas de Freud que, como hemos indicado, no son científicas.
[2] Cuestionar todo no significa que se haga con una actitud científica. Véase enlace en [1].
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 1 de agosto de 2009.
El artículo Einstein y Sigmund Freud se ha escrito en Cuaderno de Cultura Científica.
¿Y si pudiésemos llegar al océano de Europa sin necesidad de atravesar toda la corteza?
Si algo nos ha enseñado la geología planetaria en la segunda mitad del siglo XX y en estos principios del siglo XXI, es que el Sistema Solar es un lugar mucho más diverso y dinámico de lo que soñábamos.
Y es que, más allá de la cotidianidad de los mundos rocosos de nuestro Sistema Solar interior, encontramos una suerte de sistemas planetarios en miniatura girando en torno a los gigantes gaseosos.
Estos satélites en la mayoría de ocasiones son mundos helados, es decir, cuerpos cuya corteza, lo que nosotros vemos, no está formada por roca, sino por hielo, y deben su dinámica interna, precisamente, y a diferencia de los planetas interiores del Sistema Solar, al agua y el hielo que circula -o circuló, si ya no tienen actividad- por su interior.
La presencia de agua y de procesos que sean capaces de mantenerla en estado líquido en el interior de estos cuerpos a lo largo del tiempo geológico hace que sean lugares con un gran potencial astrobiológico, ya que en nuestro planeta el agua es un ingrediente fundamental para la vida tal y como la conocemos.
Con esto no queremos decir, obviamente, que haya tenido lugar el desarrollo de vida, pero que sin duda los hacen lugares muy interesantes para estudiar esta posibilidad. Y precisamente, uno de los candidatos que más ha despertado el interés de los científicos es Europa, satélite de Júpiter.
El asombrosamente plano Europa Europa, satélite de Júpiter, observada por la sonda Galileo. Imagen cortesía de NASA/JPL-Caltech/SETI Institute.
Europa, satélite de Júpiter, observada por la sonda Galileo. Imagen cortesía de NASA/JPL-Caltech/SETI Institute.Con un radio de 1560 kilómetros, es el sexto satélite en tamaño de nuestro Sistema Solar y precisamente antecedido por nuestra Luna, pero, a diferencia de esta, es un cuerpo asombrosamente plano, sin apenas cráteres de impacto ni cadenas montañosas.
La escasez de cráteres ya nos quiere decir algo: que su superficie es joven y ha ido cambiando a lo largo del tiempo acaecido tras su formación, ya que, si nada modificase su superficie, estaría completamente cubierta de cráteres.
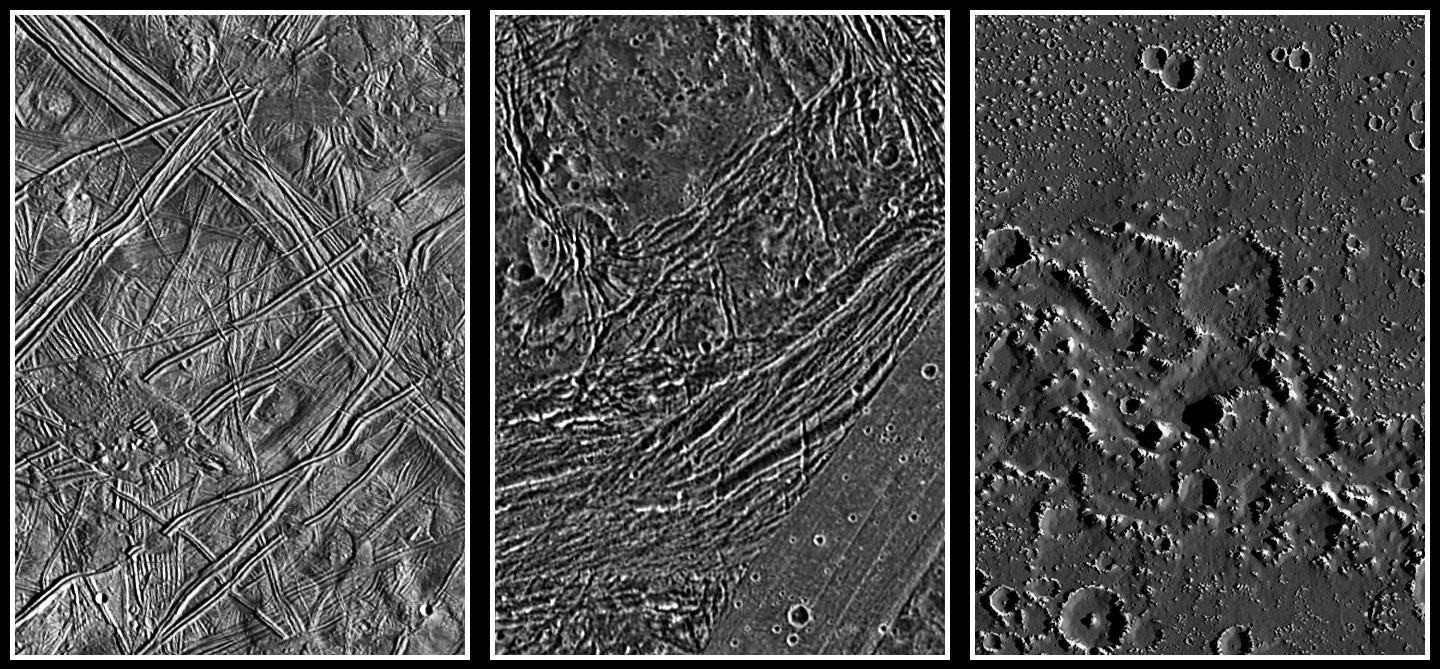 Comparación de imágenes de alta resolución de las superficies de Europa, Ganímedes y Calisto. Como se puede apreciar, la superficie de Europa, en comparación con la de los otros dos satélites, luce casi completamente sin cráteres. Imagen cortesía de NASA/JPL/DLR.
Comparación de imágenes de alta resolución de las superficies de Europa, Ganímedes y Calisto. Como se puede apreciar, la superficie de Europa, en comparación con la de los otros dos satélites, luce casi completamente sin cráteres. Imagen cortesía de NASA/JPL/DLR.
Y en el caso de Europa, esta transformación no procede de fenómenos externos, como el viento o la lluvia a los que tanto estamos acostumbrados en la Tierra, sino de un activo interior que se manifiesta renovando el aspecto de este satélite.
Esta actividad aparente nos hace pensar -junto con otros datos- que hay un océano bajo su corteza y que pone en contacto su núcleo con el agua, que la calienta y la hace ascender hacia la corteza, empujando al hielo y obligándole a adoptar nuevas formas, un papel similar al que tiene nuestro manto terrestre.
 Gráfico en el que se superponen los datos del telescopio espacial Hubble a una imagen de Europa mostrando el lugar donde se detectaron las moléculas de vapor de agua en el año 2021. Imagen cortesía de NASA/ESA/L. Roth/SWRI/University of Cologne.
Gráfico en el que se superponen los datos del telescopio espacial Hubble a una imagen de Europa mostrando el lugar donde se detectaron las moléculas de vapor de agua en el año 2021. Imagen cortesía de NASA/ESA/L. Roth/SWRI/University of Cologne.
El telescopio espacial Hubble también detectó moléculas de vapor de agua escapándose, y distintos modelos geofísicos atestiguan que Europa tiene una corteza de hielo que tiene un espesor del entorno de los 30 kilómetros, y de muy difícil acceso si algún día tuviésemos la capacidad para perforar y adentrarnos para ver que ocurre en su interior.
Pero no todo está perdido. Una de las formas del relieve más comunes en Europa podemos verla en prácticamente toda su superficie: un juego doble de crestas separadas por un pequeño valle y que llega a medir de centenares de kilómetros de longitud.
Hasta ahora, se habían propuesto distintos mecanismos de formación, desde el criovulcanismo hasta el ascenso de penachos de hielo en un estado más plástico y que se emplazaban en la corteza, pero ninguno de estos modelos parecía satisfacer todas las morfologías que se observaban.
 Comparación entre este relieve en Europa (izquierda) y Groenlandia. Imagen de Culberg et al. (2022).
Comparación entre este relieve en Europa (izquierda) y Groenlandia. Imagen de Culberg et al. (2022).
Pero resulta que en nuestro planeta hay unas formas similares y que hasta ahora habían pasado desapercibidas, concretamente en Groenlandia. Allí se forman cuando pequeñas bolsas de agua permiten que esta suba a través de las fracturas del propio hielo. El agua acaba congelándose de nuevo, formando un dique vertical que traza el camino del agua y que, al expandirse, genera más fracturas y deformación en el hielo.
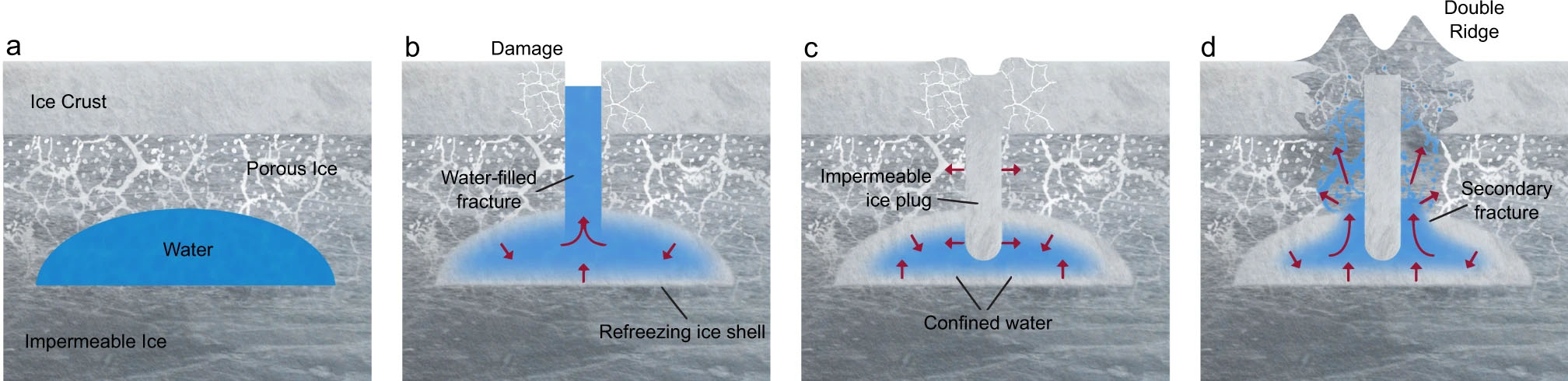 Mecanismo de formación de las crestas dobles. Como se puede apreciar en el esquema en cuatro pasos, la repetición de procesos de fracturación, congelación y presurización de las bolsas de agua serían capaces de generar estas morfologías. Imagen de Culberg et al. (2022).
Mecanismo de formación de las crestas dobles. Como se puede apreciar en el esquema en cuatro pasos, la repetición de procesos de fracturación, congelación y presurización de las bolsas de agua serían capaces de generar estas morfologías. Imagen de Culberg et al. (2022).
Si este proceso se repite en el tiempo, gracias a las nuevas fracturas generadas alrededor del dique de hielo, de nuevo ascenderá el agua, deformando la superficie y fracturándola todavía más. En este proceso se generan estas formas de crestas y valles tan parecidas a las que hay en Europa.
Este mecanismo se ha podido verificar gracias a las observaciones de georradar, que permiten observar la estructura del subsuelo -en este caso, bajo el hielo- y ver las distintas capas y discontinuidades que existen, algo que todavía no podemos hacer en Europa.
Pero en 2023, si todo va según lo previsto, despegará la misión JUICE (Jupiter Icy Moons Explorer), con una llegada prevista al sistema joviano en 2031, y que llevará también un radar que permitirá, desde la órbita, poder estudiar y quizás dilucidar el mecanismo de formación de estas crestas.
¿Y por qué es tan importante este hallazgo?. Los autores estiman que, en Europa, estas bolsas de agua se encontrarían a unos 5 kilómetros de profundidad, mucho más cerca de la superficie que el océano subterráneo, por lo que acceder hasta este punto sería mucho más fácil para una futura sonda.
Pero todavía más importante, ¿de dónde vendría el agua líquida que rellena estas bolsas? Eso es lo más interesante, ya que, si no hay mecanismos que expliquen una fusión del hielo en el interior de la corteza, estas bolsas podrían formarse por el ascenso de agua desde el océano hacia la superficie por distintos sistemas de fracturas, permitiéndonos muestrear el contenido de esas aguas, por lo que este hallazgo mejora mucho las perspectivas de cara al diseño y desarrollo de futuras misiones astrobiológicas a este satélite.
Referencia:
Culberg, R., Schroeder, D.M. & Steinbrügge, G. (2022) Double ridge formation over shallow water sills on Jupiter’s moon Europa. Nat Commun doi: 10.1038/s41467-022-29458-3
Para saber más:
La presencia de sales podría hacer que exista una tectónica de placas en Europa
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Y si pudiésemos llegar al océano de Europa sin necesidad de atravesar toda la corteza? se ha escrito en Cuaderno de Cultura Científica.
Ruido, veneno para la mente
 Foto: John Onaeko / Unsplash
Foto: John Onaeko / UnsplashLas autoridades de varias ciudades francesas, París incluida, se proponen instalar aparatos para identificar a los vehículos que sobrepasan el nivel de ruido permitido e imponerles sanciones. El sistema que planean implantar está siendo probado en siete ciudades y, si los resultados acompañan, próximamente se empezarán a instalar. Se dará al ruido un tratamiento equivalente al que se da a la velocidad, de manera que a quienes sobrepasen los límites establecidos se les impondrá una multa de 135€.
La medida es la respuesta que se quiere dar al creciente malestar ciudadano motivado por el ruido que producen de noche las motocicletas. De acuerdo con estimaciones hechas por Bruitparif, una entidad que se dedica a monitorizar el ruido en el área metropolitana de París, una sola motocicleta trucada puede llegar a despertar hasta a 10000 personas en una noche.
Pero el nocturno no es el único ruido que soportamos quienes vivimos en entornos urbanos. Según un informe ya clásico de la Organización Mundial de la Salud (OMS), la contaminación acústica es, tras la atmosférica, el segundo factor ambiental que más daña la salud de la población.
De acuerdo con el informe “Ruido en Europa 2020”, publicado por la Agencia Europea de Medio Ambiente (AEMA), una de cada cinco personas está expuesta a diario a niveles que son nocivos para la salud. Se estima que del orden de 113 millones (M) de personas se ven afectadas por el ruido (más de 55 dB) provocado por el tráfico rodado en nuestro continente. A esa cifra habría que añadir 22 M expuestos al ferroviario, 4 M al del tráfico aéreo, y 1 M al de origen industrial.
A la exposición a ruido intenso de manera prolongada se atribuyen 48000 casos de accidente cardiovascular y 12000 muertes prematuras por esa causa cada año en Europa. El vínculo entre el ruido y las afecciones cardiovasculares es la hipertensión. Un estudio danés estimó que el riesgo de sufrir infarto de miocardio se eleva en un 12% por cada incremento de 10 dB del ruido callejero. Pero según otro estudio, esta vez en los EEUU, publicado por un equipo de la Universidad de Harvard, el riesgo de sufrir «ataques al corazón, ictus y otros problemas coronarios serios» aumenta en un 34% por cada subida de 5 dB.
Según el informe “Ruido en Europa 2020” antes citado, 22 M de personas sufren irritación crónica a causa del ruido y 6,5 M padecen trastornos severos del sueño, también de forma permanente. Por otro lado, el provocado por las aeronaves en las maniobras de despegue y aterrizaje próximas a poblaciones es responsable de los problemas de aprendizaje de 12500 niños y niñas, y de deterioro cognitivo en general. El informe de la OMS citado antes también señala que el ruido es responsable de muchos casos de acúfenos (tinnitus), esos molestos sonidos que, sin tener origen físico real, se perciben de forma persistente.
En el estudio de la Universidad de Harvard ya citado también hallaron que la exposición a altos niveles de ruido está asociada a un incremento de la actividad en la amígdala, una zona del encéfalo que se activa en condiciones de estrés, miedo y ansiedad. La salud mental también se ve seriamente afectada por este factor. Por ello, no es sorprendente que quienes lo soportan de forma constante tiendan a encontrarse, como se ha dicho, más irritables, tengan actitudes agresivas, experimenten síntomas depresivos, sufran problemas de concentración y tengan, en general, un menor rendimiento académico y laboral. Y es que, como dice una gran amiga mía, el ruido es veneno para la mente.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Ruido, veneno para la mente se ha escrito en Cuaderno de Cultura Científica.
IV Jornada Nacional de Evolución y Neurociencias: Laura Morán – Evolución de la atracción sexual

¿Estamos realmente diseñados para conectar con los demás? Si es así, ¿por qué siguen existiendo los psicópatas? ¿Se pueden tratar trastornos delirantes como la paranoia desde el punto de vista de la evolución? O ¿cómo ha cambiado la atracción sexual desde la época de nuestros ‘abuelos’ homínidos hasta ahora?
A estas y otras cuestiones relativas a la evolución del comportamiento humano se trató de dar respuesta durante la IV Jornada Nacional de Evolución y Neurociencias, evento organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Red de Salud Mental de Bizkaia, que tuvo lugar los días 28 y 29 de abril en el Bizkaia Aretoa – UPV/EHU de Bilbao.
Desde que en 2017 un grupo de psiquiatras de la Red de Salud Mental de Bizkaia organizara la primera edición de esta jornada, la cita se ha convertido en un punto de encuentro para profesionales de distintos ámbitos científicos como la psiquiatría, la psicología, la biología o la filosofía con un interés común: la conducta humana desde una perspectiva evolucionista y su divulgación científica en un formato accesible y ameno para todos los públicos, a la par que riguroso y actualizado.
Una cosa es la atracción sexual y otra el deseo sexual. Esta distinción es fundamental, tal y como explica Laura Morán, psicóloga y sexóloga.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo IV Jornada Nacional de Evolución y Neurociencias: Laura Morán – Evolución de la atracción sexual se ha escrito en Cuaderno de Cultura Científica.
Conversión de frecuencias de fotones individuales
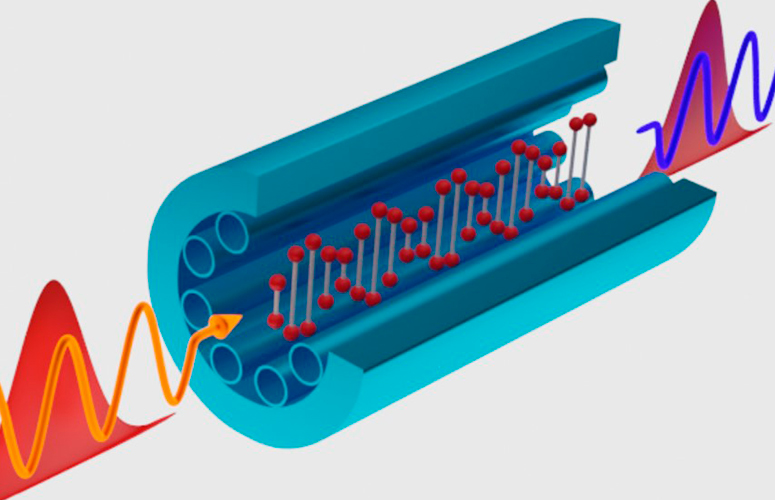 Tras excitar ópticamente el hidrógeno en su interior, la luz incidente cambia de frecuencia (color) al atravesar la fibra óptica antirresonante. Fuente: UPV/EHU
Tras excitar ópticamente el hidrógeno en su interior, la luz incidente cambia de frecuencia (color) al atravesar la fibra óptica antirresonante. Fuente: UPV/EHUActualmente, estamos viviendo una segunda revolución cuántica en la que la mecánica cuántica está pasando de ser una fuente de paradojas a una herramienta del mundo real. Ejemplo de ello son las tecnologías basadas en la manipulación de la luz, tecnologías que son capaces de abordar los retos que existen actualmente en las comunicaciones, hasta ahora insuperables con las tecnologías convencionales. Este es el caso de la conversión de frecuencias y el transporte a larga distancia de fotones individuales y pares de fotones entrelazados.
Las fibras ópticas son como tuberías para la luz. Una investigación liderada por David Novoa, investigador Ikerbasque en la Escuela de Ingeniería de Bilbao de la UPV/EHU, ha desarrollado un nuevo tipo de fibra óptica micro-estructurada que, a diferencia de las fibras convencionales como las que llevan internet a nuestras casas, guía la luz en un canal hueco con una atenuación extremadamente baja. Lo que hace únicas a estas nuevas fibras es que sus propiedades ópticas son reconfigurables cuando se llenan de gases a distintas presiones. Esto las convierte en unas plataformas muy versátiles, capaces de operar en un rango espectral sin precedentes, desde el ultravioleta hasta el infrarrojo.
En este trabajo los investigadores han llenado la fibra con hidrógeno, la molécula más ligera de la naturaleza y, por tanto, la que posee una frecuencia fundamental de vibración más alta. Por medio del conocido como efecto Raman estimulado, se pueden excitar ópticamente las moléculas del núcleo gaseoso de la fibra de manera que oscilen sincronizadas de forma muy precisa. En palabras de David Novoa, “es en esta coreografía molecular donde reside la belleza de nuestro sistema: Las fuentes de luz cuánticas (los fotones) son capaces, bajo determinadas circunstancias, de extraer la energía vibracional de esas moléculas oscilantes para aumentar su propia energía y así cambiar de frecuencia (color)”.
Sistemas complejos como, por ejemplo, las redes cuánticas, están compuestos por diferentes subsistemas cuya frecuencia óptima de operación no suele coincidir. Es por ello que una técnica capaz de conseguir la conversión de frecuencias ópticas a nivel cuántico en un amplio espectro sin afectar las propiedades de las fuentes de luz originales sería extremadamente útil. Estos resultados muestran precisamente la mejora de un proceso crítico en las tecnologías cuánticas relacionadas con la luz, como es la conversión cuántica de frecuencias.
Referencia:
R. Tyumenev, J. Hammer, N. Y. Joly, P. St.J. Russell and D. Novoa (2022) Tunable and state-preserving frequency conversion of single photons in hydrogen Science, doi: 10.1126/science.abn1434
Para saber más:
Una fibra óptica de plástico actúa como concentrador solar luminiscence
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Conversión de frecuencias de fotones individuales se ha escrito en Cuaderno de Cultura Científica.
Testigos del pasado
Seguro que en algunas películas y en noticias de índole geológica y climatológica habéis oído o leído que los científicos están estudiando núcleos de hielo, sedimento o roca y os ha entrado la curiosidad sobre qué son esas cosas. En primer lugar, aquí no se llaman núcleos. Este término resulta de una traducción literal de la palabra inglesa “core” que, efectivamente, significa núcleo. Pero, en castellano, a estas herramientas geológicas las denominamos testigos de sondeo.
 Extracción de testigos de sondeo de hielo en la Antártida. Imagen: NASA.
Extracción de testigos de sondeo de hielo en la Antártida. Imagen: NASA.Un sondeo es un método de perforación del terreno, es decir, consiste en hacer un agujero en el suelo, ya sea sobre tierra firme, en el hielo o en el fondo del mar, con un tubo de metal o plástico para poder reconocer lo que se encuentra en profundidad. Y se denomina testigo al cilindro de material (hielo, sedimento o roca) que se puede extraer cuando se hace el sondeo y que quedaría encapsulado dentro del tubo.
Los métodos de perforación pueden agruparse en tres tipos. Por un lado, encontramos los sondeos mecánicos por percusión, que consisten en atravesar el terreno o bien dejando caer el tubo de sondeo desde una altura considerable y aprovechar así la fuerza de la gravedad, o bien hincándolo a base de golpes repetitivos hasta conseguir enterrarlo. Por otro lado, tenemos los sondeos de rotación, que consisten en acoplar al tubo de sondeo una cabeza, llamada corona, que tiene un filo cortante de carburo de diamante o de wolframio y es capaz de girar a gran velocidad gracias a un motor externo, por lo que, haciendo un pequeño símil, atraviesa el terreno a dentelladas. Finalmente, el tercer tipo sería una mezcla de los dos anteriores, es decir, existen sondeadoras que, a la vez que van enterrando el tubo por presión, tienen incorporada una corona dentada que va girando rompiendo el terreno.
Los testigos de sondeo tienen un valor científico extraordinario. En su interior, contienen un registro de la evolución geológica de una zona durante los últimos cientos, miles e, incluso, millones de años. Zonas que están enterradas bajos nuestros pies y a las que no podríamos acceder de otra manera más que haciendo estas perforaciones, tales como los mantos y casquetes de hielo o el fondo oceánico.
 Testificadora de sondeos por percusión y detalle del tubo de sondeo a bordo del Buque Oceanográfico Pourquois Pas? del instituto Francés de Investigación para la Exploración Marina (IFREMER). Foto: Blanca María Martínez
Testificadora de sondeos por percusión y detalle del tubo de sondeo a bordo del Buque Oceanográfico Pourquois Pas? del instituto Francés de Investigación para la Exploración Marina (IFREMER). Foto: Blanca María MartínezEn la Antártida o Groenlandia encontramos enormes espesores de hielo que se han formado por la acumulación de agua congelada durante cientos de miles de años. Si nos fijamos más en detalle, estas masas están formadas por la superposición de finas capas de hielo, dispuestas una encima de las otras, donde cada una representa la precipitación producida en un año. Además, cada capa de hielo corresponde con una mini cápsula del tiempo en la que han quedado preservadas las características de la atmósfera en ese momento. Así, al estudiar los testigos de sondeo de hielo extraídos en la Antártida y Groenlandia se han podido reconstruir las variaciones temporales de gases como el dióxido de carbono (CO2) o el metano (CH4) y de la temperatura atmosférica durante los últimos 800.000 años con una precisión anual.
 Obtención de testigos de sondeo por percusión en una laguna de Bardenas Reales de Navarra. Foto: Blanca María Martínez
Obtención de testigos de sondeo por percusión en una laguna de Bardenas Reales de Navarra. Foto: Blanca María MartínezEstos estudios climáticos de hielo se complementan con los registros marinos. En las zonas oceánicas más profundas se acumulan capas de sedimentos finos (limos y arcillas) que apenas sufren alteraciones por las corrientes marinas de fondo. Así que, de manera similar a las capas de hielo, estas capas de sedimento irían recogiendo la historia oceánica de los últimos cientos de miles de años de manera continua. Sin embargo, no tienen una precisión temporal tan grande como el hielo, el registro sedimentario aporta una periodicidad decadal, rara vez anual.
La obtención de testigos de sondeo de sedimento marino no es tan sencilla como la de los testigos de sondeo de hielo. En este caso, los equipos de testificación deben ir a bordo de buques oceanográficos, que son auténticos laboratorios científicos flotantes, y, para llegar a tocar el fondo marino, hay que librar los cientos y miles de metros de espesor que tiene la columna de agua. Una vez hecho esto, la sondeadora debe perforar el fondo marino y hay que conseguir que el testigo de sondeo vuelva al buque sin perderlo por el camino. Pero estas operaciones tan complicadas, merecen la pena. El estudio minucioso del sedimento obtenido en los testigos de sondeo marinos nos aporta información sobre la variación temporal de parámetros como la temperatura, salinidad o pH de las masas de agua y nos permite conocer cambios en la circulación de las corrientes oceánicas durante los últimos cientos de miles de años.
 Muestreo del sedimento de un testigo de sondeo para su estudio geológico. Foto: Blanca María Martínez
Muestreo del sedimento de un testigo de sondeo para su estudio geológico. Foto: Blanca María MartínezLa combinación de los estudios climáticos de los testigos de sondeo de hielo y de sedimento marino, han sido básicos para conocer como ha cambiado el clima, de manera detallada, en los últimos milenios. Estos registros nos dan una idea global de la variabilidad climática de nuestro planeta, sirviendo como base de comparación de cualquier estudio paleoambiental actual realizado en cualquier ambiente, ya sea continental o marino, como, por ejemplo, los estudios de testigos de sondeo de sedimentos de lagos y estuarios. Esta comparativa con los registros globales permite identificar, con mucho detalle, eventos climáticos o condiciones ambientales locales, que sólo afectaron a zonas geográficas restringidas y que no tuvieron una influencia climática a nivel mundial.
Sin estos testigos del pasado, o chivatos del pasado, como los queramos llamar, sería imposible poder conocer cómo ha cambiado el clima en los últimos milenios, lo cual es clave para poder aventurar cómo cambiará en el futuro más próximo para poder adelantarnos y adaptarnos a lo que está por llegar.
Para saber más:
Los volcanes submarinos de Bizkaia y Gipuzkoa
Un estudio paleoceanográfico apunta a que los ciclos naturales de cambio climático están siendo alterados
Geología, Antropoceno y cambio climático
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Testigos del pasado se ha escrito en Cuaderno de Cultura Científica.
La curiosa identidad de Proizvolov
La conocida como identidad de Proizvolov fue propuesta por el matemático Vyacheslav Proizvolov en forma de problema en las Olimpiadas Matemáticas Soviéticas de 1985:
Consideremos el conjunto de los primeros 2N enteros positivos,
CN = {1, 2, 3, …, 2N − 1, 2N},
y una partición de él en dos subconjuntos de N elementos cada uno de ellos:
AN = {a1, a2, …, aN-1, aN} y BN = {b1, b2, …, bN-1, bN}.
Ordenemos los elementos de ambos conjuntos de la siguiente manera:
![]()
Se pide probar que la siguiente suma de valores absolutos
|a1 – b1| + |a2 – b2| + … + |aN-1 – bN-1| + |aN – bN|
es igual a N2.
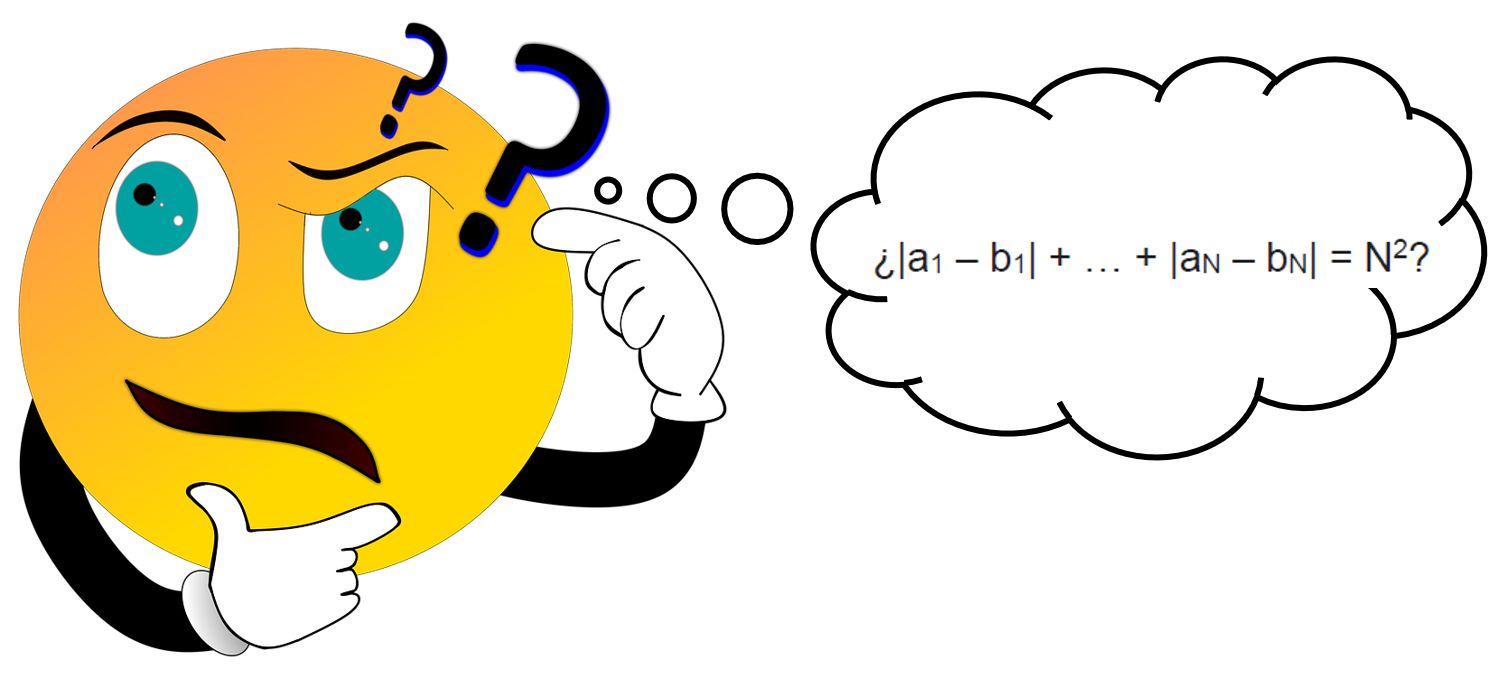
Un ejemplo
Para entender mejor el enunciado, vamos a ver un ejemplo. Si N = 10, tenemos el conjunto de los veinte primeros números naturales
C10 = {1, 2, 3, …, 19, 20}.
Elegimos las particiones (hemos ordenado los números de la primera partición de manera creciente y los de la segunda de manera decreciente):
A10 = {1, 3, 4, 7, 8, 9, 10, 18, 19, 20}, y
B10 = {17, 16, 15, 14, 13, 12, 11, 6, 5, 2},
Es decir, a1 = 1, a2 = 3, a3 = 4, …, a9 = 19, a10 = 20, b1 = 17, b2 = 16, b3 = 15, …, b9 = 5 y b10 = 2.
Entonces,
|a1 – b1| + |a2 – b2| + … + |a9 – b9| + |a10 – b10| =
|1 – 17| + |3 – 16| + |4 – 15| + |7 – 14| + |8 – 13| + |9 – 12| + |10 – 11| + |18 – 6| + |19 – 5| + |20 – 2| =
16 + 13 + 11 + 7 + 5 + 3 + 1 + 12 + 14 + 18 = 100 = 102.
Una demostración sencilla de la identidad de Proizvolov
Observemos en primer lugar que |a – b| = máx{a,b} – mín{a,b}. En efecto, si a > b, es |a – b| = a – b = máx{a, b} – mín{a, b}, y si a
En segundo lugar, para cada i en {1, 2…, N − 1, N}, se verifica que uno de los números del par {ai, bi} está en el conjunto A = {1, 2…, N − 1, N} y el otro en el conjunto B = {N + 1, N + 2, …, 2N − 1, 2N}.
En efecto, si esta propiedad no fuera cierta, supongamos, por ejemplo, que los números ai y bi pertenecen ambos al conjunto A. Es decir, ai i N que pertenecen a A (ya que a1 2 i N también en A) y al menos N − i + 1 elementos del conjunto BN que pertenecen a A (ya que N + 1> bi > bi+1 > … > bN-1 > bN y podría haber algún otro elemento de BN también en A). Es decir, en el conjunto A habría al menos i + (N – i + 1) = N + 1 elementos de CN. Pero eso es imposible, porque A solo posee N elementos. Un argumento similar prueba que tampoco puede suceder que ai y bi pertenezcan ambos al conjunto B.
Es decir, efectivamente, para cada i en {1, 2…, N − 1, N}, se verifica que uno de los números del par {ai, bi} está en el conjunto A = {1, 2…, N − 1, N} y el otro en el conjunto B = {N + 1, N + 2, …, 2N − 1, 2N}. De aquí se deduce que para cada i en {1, 2…, N − 1, N}, es mín{ai, bi} i, bi} > N. Es decir, de otra manera,
A = {1, 2…, N − 1, N} = {mín{ai, bi}: i en {1, 2…, N − 1, N}}, y
B = {N + 1, N + 2, …, 2N − 1, 2N} = {máx{ai, bi}: i en {1, 2…, N − 1, N}}.
Por lo tanto,
|a1 – b1| + |a2 – b2| + … + |aN-1 – bN-1| + |aN – bN| =
(máx{a1, b1} – mín{a1, b1}) + (máx{a2, b2} – mín{a2, b2}) + … + (máx{aN-1, bN-1} – mín{aN-1, bN-1}) + (máx{aN, bN} – mín{aN, bN}) =
(máx{a1, b1} + máx{a2, b2} + … + máx{aN-1, bN-1} + máx{aN, bN}) – (mín{a1, b1} + mín {a2, b2} + … + mín{aN-1, bN-1} + mín{aN, bN}) =
((N + 1) + (N + 2) + … + (2N – 1) + 2N) – (1 + 2 + … + (N – 1) + N) =
((N + 1) – 1) + ((N + 2) – 2) + … + ((2N – 1) – (N – 1)) + (2N – N) =
N + N + … + N = N2. QED
Una generalización de la identidad de Proizvolov
Grégoire Nicollier propuso en 2015 la siguiente generalización de la identidad de Proizvolov:
Consideremos un conjunto de números reales,
CN = {c1, c2, …, c2N-1, cN},
y una partición de él en dos subconjuntos de N elementos cada uno de ellos:
AN = {a1, a2, …, aN-1, aN} y BN = {b1, b2, …, bN-1, bN}.
Ordenemos los elementos de estos conjuntos de la siguiente manera:
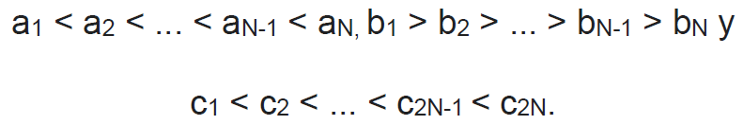
Entonces, la suma
|a1 – b1| + |a2 – b2| + … + |aN-1 – bN-1| + |aN – bN|
es independiente de las particiones elegidas AN y BN.
Para probar esta propiedad, basta con observar, con un argumento similar al realizado antes, que para cualquier par {ai, bi}, uno de los elementos es menor que cN + 1 y el otro es mayor que cN. Entonces,
{c1, c2, …, cN-1, cN} = {mín{ai, bi}: i en {1, 2…, N − 1, N}}, y
{cN+1, cN+2, …, c2N-1, c2N} = {máx{ai, bi}: i en {1, 2…, N − 1, N}}.
Y por lo tanto:
|a1 – b1| + |a2 – b2| + … + |aN-1 – bN-1| + |aN – bN| =
(máx{a1, b1} – mín{a1, b1}) + (máx{a2, b2} – mín{a2, b2}) + … + (máx{aN-1, bN-1} – mín{aN-1, bN-1}) + (máx{aN, bN} – mín{aN, bN}) =
(máx{a1, b1} + máx{a2, b2} + … + máx{aN-1, bN-1} + máx{aN, bN}) – (mín{a1, b1} + mín {a2, b2} + … + mín{aN-1, bN-1} + mín{aN, bN}) =
(c2N + c2N-1 + … + cN+2 + cN+1) – (c1 + c2 + … + cN-1 + cN),
que es la misma cantidad para cualquier partición elegida. QED
Además, Grégoire comentaba en el artículo que esta propiedad sigue siendo cierta aunque los números del conjunto C no sean todos diferentes.
¡Curiosas propiedades!
Referencias
-
Proizvolov’s Identity, Futility Closet, 21 agosto 2014
-
Proizvolov’s Identity, Cut the Knot
-
Grégoire Nicollier, A generalisation of Proizvolov’s identity, The Mathematical Gazette 99 (546) (2015): 525-526
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo La curiosa identidad de Proizvolov se ha escrito en Cuaderno de Cultura Científica.
Einstein y el movimiento browniano
El mismo año en el que Einstein publicó la teoría especial de la relatividad también publicó un artículo igualmente revolucionario sobre los movimientos aleatorios de las moléculas, algo habitualmente conocido como movimiento browniano. El movimiento de una partícula en un líquido es aparentemente algo mucho menos espectacular que los movimientos en el espaciotiempo o la afirmación de que la masa es una forma de energía o que la luz está constituida por partículas, por lo que la explicación de Einstein del movimiento browniano ha sido completamente eclipsada por sus otras teorías. Sin embargo, si Einstein solo hubiese publicado el por qué las partículas se mueven como lo hacen, habría merecido el premio Nobel por ello: esta modelo permitió confirmar, sin ningún género de dudas, que los átomos existen.

En 1827 Robert Brown estudió el movimiento de los granos de polen en un líquido usando un microscopio. Descubrió que se movían al azar y sin nada aparentemente que les hiciese moverse. Antes ya había habido observaciones de este movimiento (entre ellas las realizadas por Jan Ingenhousz en 1785), pero nadie lo había estudiado de forma tan amplia, probando que los granos no se movían porque estuviesen vivos, y que partículas de vidrio o de granito exhibían el mismo comportamiento. Hoy, la idea de que las partículas intercambien el sitio con las moléculas en un líquido y, como consecuencia, se mueven al azar no parece tan extraña. Ello se debe a que estamos familiarizados con las ideas de molécula y átomo, pero en la época de Brown los científicos desconocían su existencia. En los años en los que Einstein comenzó a estudiar ciencia, la física y la química, en ese momento campos con relativamente poco en común, habían comenzado a incorporar la idea de átomo en sus teorías, pero había una gran división entre los científicos sobre si realmente existían. Quizás, pensaban algunos, los átomos y las moléculas eran simplemente una forma matemáticamente conveniente de describir ciertos fenómenos, pero no eran una representación verdadera de la realidad.
Einstein tenía muy claro que los átomos existían. Tanto es así que muchos de sus primeros trabajos de investigación asumían que la materia podía dividirse en partículas discretas. Hizo su tesis doctoral “Una nueva determinación de las dimensiones moleculares” sobre cómo determinar el tamaño de las moléculas midiendo su movimiento browniano en un líquido. Una versión de esta tesis se publicó en Annalen der Physik en abril de 1905, y es uno de los primeros artículos en mostrar de forma definitiva que las moléculas no son artificios matemáticos, sino entes reales.
Movimiento browniano y teoría estadísticaOnce días más tarde, Einstein publicó un artículo sobre el movimiento browniano mismo. El artículo se titulaba “Sobre el movimiento de pequeñas partículas suspendidas en líquidos en reposo requerido por la teoría cinético-molecular del calor”, por lo que no indicaba que se tratase del movimiento browniano. Simplemente decía en su párrafo de apertura que iba a describir el movimiento de las moléculas suspendidas en un líquido, y que quizás este fenómeno era idéntico a un fenómeno del que había oído hablar, el movimiento browniano. Desde ese punto de partida, continuó demostrando que podía usar las teorías del calor en vigor para describir cómo la energía térmica, incluso a temperatura ambiente, provocaría que las moléculas del líquido estuviesen en continuo movimiento. Este movimiento haría a su vez que cualquier partícula suspendida en el líquido resultase empujada. Einstein acababa de ofrecer la primera explicación del movimiento browniano (Marian Smoluchowski llegaría a un resultado similar en 1906 de forma independiente).
A continuación Einstein daba una descripción matemática de cómo se moverían las partículas en el seno del líquido. Usó el análisis estadístico para calcular el camino promedio de dichas partículas. Si bien el movimiento de la partícula sería al azar, desplazándose brevemente a la izquierda para hacerlo después hacia la derecha, Einstein demostró que se podía determinar una dirección básica para el movimiento. Es análogo al movimiento de un borracho, que va para allá y después para acá, tropieza con el banco, cruza la calle tres veces, se abraza a la farola, pero en términos generales se dirige hacia su casa. Una observación del borracho permite determinar la zona hacia la que se dirige y hacer predicciones sobre el tiempo que tardará en llegar, incluso sin saber exactamente con cuantos objetos tropezará durante el trayecto. Se puede obviar el azar a corto plazo para hacer predicciones acerca de lo que sucederá a largo.
El artículo de Einstein ofrecía una explicación del movimiento browniano, pero fueron otros científicos los que llevaron a cabo los experimentos que demostraron que las moléculas existían realmente, y que era la transmisión de calor la que causaba su movimiento en un líquido. En 1908, Jean Baptiste Perrin estudió la forma en la que las partículas sedimentan en el agua por la influencia de la gravedad. La sedimentación encuentra la oposición de los choques de las moléculas desde abajo, por lo que el movimiento browniano se opone a la atracción gravitatoria. Perrin usó este descubrimiento para calcular el tamaño de las moléculas de agua basándose en las ecuaciones de Einstein. Por este trabajo recibió el premio Nobel de física en 1926.
Toda esta investigación sobre el movimiento browniano resolvió el problema que enfrentaba a físicos y químicos sobre si la materia era fundamentalmente continua o estaba constituida por partículas. Con su tesis doctoral, su trabajo sobre el movimiento browniano, y su artículo sobre el efecto fotoeléctrico, Einstein fue crucial para la aceptación de la existencia de átomos y moléculas. Y, sin embargo, Einstein no volvería a trabajar con nada relacionado directamente con moléculas en el resto de su carrera científica.
Referencia:
Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. AdP 17, 549 (1905) Annalen der Physik, 14 (S1), 182-193 DOI: 10.1002/andp.200590005
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 20 de junio de 2010.
El artículo Einstein y el movimiento browniano se ha escrito en Cuaderno de Cultura Científica.
Primer catálogo de materiales de banda plana
Una colaboración internacional ha creado un catálogo de materiales que podría ser muy útil para el desarrollo de las tecnologías cuánticas. Se trata del primer catálogo del mundo de materiales de banda plana, que podría reducir la influencia del azar en la búsqueda de nuevos materiales con propiedades cuánticas exóticas, tales como el magnetismo y la superconductividad. Estos materiales tendrían aplicaciones en dispositivos de memoria o en el transporte de energía sin disipación a través de largas distancias. Este trabajo, que se enmarca dentro de la iniciativa IKUR 2030 del Gobierno Vasco, ha sido publicado en Nature.
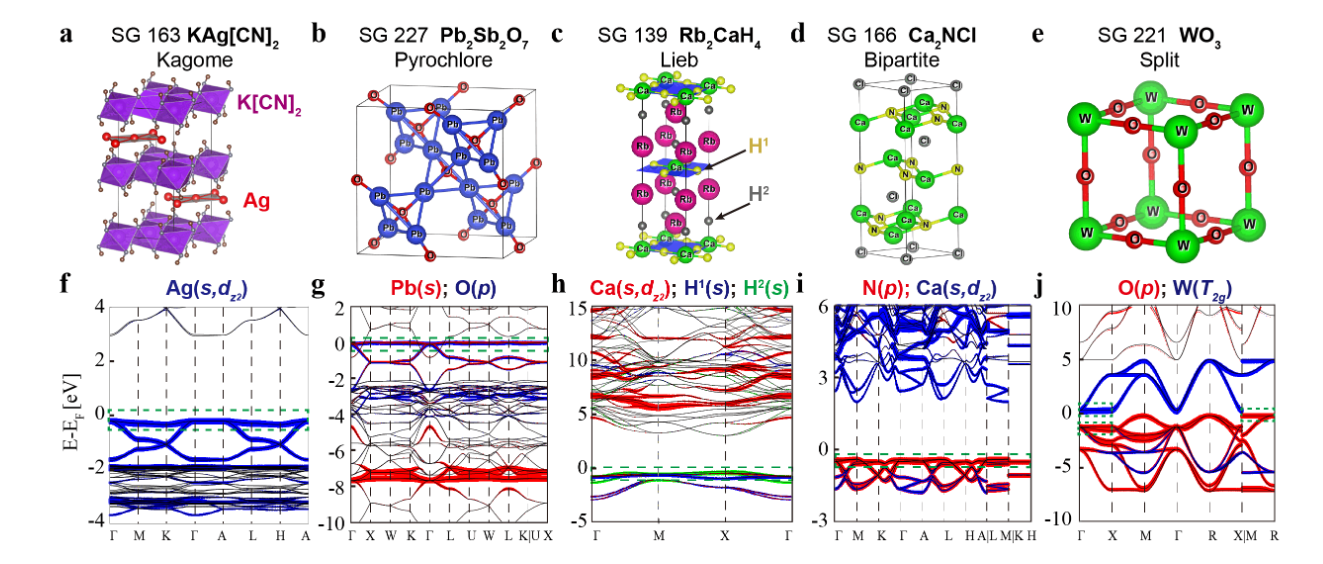
 Representación artística de las dispersiones de banda en un material. En negro, las diferentes bandas, siendo el eje vertical la energía cinética. En el centro tenemos dos bandas planas que se originan a partir de la estructura del material.
Representación artística de las dispersiones de banda en un material. En negro, las diferentes bandas, siendo el eje vertical la energía cinética. En el centro tenemos dos bandas planas que se originan a partir de la estructura del material.Encontrar los ingredientes adecuados para crear materiales con propiedades cuánticas exóticas ha sido una quimera para los científicos experimentales, debido a las numerosas combinaciones posibles de elementos a sintetizar. A partir de ahora, la creación de este tipo de materiales podría ser menos aleatoria gracias a una colaboración internacional liderada por Andrei Bernevig, profesor visitante Ikerbasque en el Donostia International Physics Center (DIPC) y profesor de la Universidad de Princeton, y Nicolas Regnault, de la Universidad de Princeton y la Ecole Normale Supérieure Paris, CNRS, con la participación de Luis Elcoro de la Universidad del País Vasco (UPV/EHU).
El equipo realizó una búsqueda sistemática de posibles candidatos en una enorme base de datos de 55.000 materiales. El proceso de eliminación se inició con la identificación de los llamados materiales de banda plana, es decir, estados electrónicos con energía cinética constante, donde el comportamiento de los electrones se rige principalmente por las interacciones con otros electrones. Sin embargo, los investigadores se dieron cuenta de que tener banda plana no es el único requisito, ya que cuando los electrones están demasiado unidos al átomo, éstos no pueden moverse y crear estados interesantes de la materia, aun estando en una banda plana. “La idea es que los electrones se vean entre sí, lo que se puede lograr asegurándonos de que estén extendidos en el espacio. Eso es exactamente lo que aportan las bandas topológicas”, según Nicolas Regnault.
La topología, como lo sugieren los tres premios Nobel de 1985, 1997 y 2016, juega un papel crucial en la física de la materia condensada moderna, ya que implica que algunas funciones de onda cuánticas estén extendidas, haciéndolas insensibles a perturbaciones locales, como por ejemplo impurezas. Esto a su vez hace que algunas propiedades físicas, tales como la resistencia, estén cuantificadas o generen estados superficiales perfectamente conductores. Afortunadamente, el equipo ha estado a la vanguardia de la caracterización de las propiedades topológicas de las bandas a través de su enfoque conocido como «química cuántica topológica«, proporcionándoles tanto una gran base de datos de materiales, como las herramientas teóricas para buscar bandas planas topológicas.
Mediante el empleo de herramientas que van desde métodos analíticos hasta búsquedas por fuerza bruta, el equipo encontró todos los materiales de banda plana que se conocen actualmente en la naturaleza. Este catálogo de materiales de banda plana está disponible en https://www.topologicalquantumchemistry.fr/flatbands e incluye su propio buscador.
“La comunidad científica puede ahora buscar bandas topológicas planas en los materiales. Hemos encontrado alrededor de 700 materiales (de los 55.000 materiales estudiados) que muestran bandas planas con un interés potencial”, dice Yuanfeng Xu, de la Universidad de Princeton y el Instituto Max Planck de Física de Microestructuras, uno de los dos autores principales del estudio. «Nos hemos asegurado de que los materiales que identificamos son candidatos prometedores para la síntesis química», enfatiza Leslie Schoop del departamento de química de Princeton. El equipo ha ido más allá en la clasificación de las propiedades topológicas de estas bandas, mostrando además qué tipo de electrones deslocalizados albergan.
Ahora que este gran catálogo está completo, el equipo comenzará a trabajar con los materiales más prometedores para descubrir experimentalmente el potencial de nuevos estados de interacción. “Ahora que sabemos dónde buscar, necesitamos fabricar estos materiales”, dice Claudia Felser del Instituto Max Planck de Física Química de Sólidos. “Tenemos un equipo experimental excepcional trabajando con nosotros. Están ansiosos por medir las propiedades físicas de estos materiales candidatos potenciales y ver qué excitantes fenómenos cuánticos surgen”.
El catálogo de bandas planas representa el fruto de años de investigación del equipo. “Muchas personas, muchas instituciones y universidades a las que presentamos el proyecto nos dijeron que esto era demasiado difícil y que nunca se podría hacer. Nos tomó varios años, pero lo logramos”, dice Andrei Bernevig.
Referencia:
Nicolas Regnault, Yuanfeng Xu, Ming-Rui Li, Da-Shuai Ma, Milena Jovanovic, Ali Yazdani, Stuart S. P. Parkin, Claudia Felser, Leslie M. Schoop, N. Phuan Ong, Robert J. Cava, Luis Elcoro, Zhi-Da Song & B. Andrei Bernevig (2022) Catalogue of flat-band stoichiometric materials Nature doi: 10.1038/s41586-022-04519-1
Más información:
A powerful search engine for flatband stoichiometric materials
Química Cuántica Topológica Magnética
Un catálogo de estructuras magnéticas topológicas
La teoría de bandas de los sólidos se hace topológica
Edición realizada por César Tomé López a partir de materiales suministrados por DIPC
El artículo Primer catálogo de materiales de banda plana se ha escrito en Cuaderno de Cultura Científica.
ADN en cuevas, puerta a nuestra historia evolutiva
Por primera vez se ha conseguido obtener ADN nuclear de varios individuos neandertales a partir de sedimentos de cuevas prehistóricas europeas. Se abre así la puerta al conocimiento de la historia de poblaciones homínidas antiguas, incluso en ausencia de registro fósil.
Los restos esqueléticos encontrados en yacimientos arqueológicos son fuente fundamental de ADN. La secuenciación de este ADN ha servido para revelar aspectos importantes de nuestro pasado evolutivo. Pero encontrar restos óseos es extremadamente raro, ya que el registro fósil es realmente escaso, lo que deja grandes lagunas en la comprensión de la historia evolutiva humana.
El ADN nuclear (ADNn) está en el núcleo de cada célula formando los cromosomas (23 pares, uno por pareja de cada progenitor), y el ADN mitocondrial (ADNmt) es una pequeña molécula circular localizada en las mitocondrias que son pequeños orgánulos repartidos por la célula responsables de producir la energía. Las mitocondrias poseen varias copias de ADNmt y en cada célula existe un gran número de mitocondrias, así que las células contienen múltiples copias de ADNmt. Esta abundancia hace que sean más altas las posibilidades de recuperar ADNmt a partir de restos arqueológicos antiguos o muy degradados que las de recuperar ADNn. Además, el hecho de que el ADNmt sea una molécula circular hace que sea menos susceptible a la degradación.
Por todo ello, y porque el ADNmt se hereda exclusivamente de la madre, este es una herramienta valiosísima en el estudio de genética de poblaciones. Todos los familiares relacionados por vía materna comparten la misma secuencia de ADNmt. Pero, por esta misma razón, tiene un valor limitado, ya que sólo representa el linaje materno.
Hasta ahora, únicamente se había conseguido recuperar ADNmt de homínidos a partir de sedimentos de cuevas del Pleistoceno. Aunque el ADNn contiene mucha más información, su recuperación de los sedimentos supone numerosos problemas. Se encuentra en mucha menor cantidad que el mitocondrial y muchos otros mamíferos cohabitaron con nuestros antepasados por lo que no todo el ADN presente en los sedimentos es de homínido.
Para facilitar la recuperación del ADNn se han seguido estrategias en las que se buscaba enriquecer el escaso ADNn de homínido. Para ello se han desarrollado sondas de hibridación, que son pequeños fragmentos de ADN que se “emparejan” con puntos concretos del genoma nuclear homínido. Así, el equipo de investigación internacional del que forma parte la UPV/EHU ha conseguido recuperar ADNn de sedimentos de dos yacimientos en el sur de Siberia (cuevas Denisova y Chagyrscaya) y de la Galería de las Estatuas en Atapuerca (Burgos).
 ADN en cuevas. Los sedimentos de cuevas prehistóricas contienen ADN mitocondrial y nuclear de homínidos que se puede enriquecer, secuenciar y analizar para conocer la historia genética de quienes las ocuparon, incluso en ausencia de sus restos esqueléticos. Ilustración: Nuria González Santiago
ADN en cuevas. Los sedimentos de cuevas prehistóricas contienen ADN mitocondrial y nuclear de homínidos que se puede enriquecer, secuenciar y analizar para conocer la historia genética de quienes las ocuparon, incluso en ausencia de sus restos esqueléticos. Ilustración: Nuria González Santiago
En los dos primeros sitios ya se conocía el ADN de varios huesos, y los resultados filogenéticos del ADN del sedimento fueron consistentes con los resultados publicados anteriormente de los restos esqueléticos. En la Galería de las Estatuas el único hueso de un dedo de neandertal no había sido suficiente para secuenciar su ADN, pero el ADNn extraído de los sedimentos reveló que 2 poblaciones neandertales habían vivido en la cueva. Así pues, se ha logrado averiguar que la primera población neandertal que vivió hace 135.000 años fue reemplazada por otra población de perfil genético muy diferente (105.000 años aprox. de antigüedad). Los dos linajes estaban separados por unos 35.000 años de evolución.
Este trabajo abre la posibilidad de estudiar la historia de las poblaciones de homínidos a pesar de no existir, o ser extremadamente escaso, el registro fósil en muchos asentamientos arqueológicos.
Referencias consultadas:
Vernot B. et al., (2021). Unearthing Neanderthal population history using nuclear and mitochondrial DNA from cave sediments. Science, 372. DOI: 10.1126/science.abf1667.
Cardoso S., Valverde L., Palencia L., López Quintana J. C., Guenaga Lizasu A., Martínez de Pancorbo M. (2011). Análisis de ADN Mitocondrial en los restos humanos de la cueva de Santimamiñe (Kortezubi, Bizkaia). KOBIE Serie Bizkaiko Arkeologi Indusketak, nº 1: 383-392 Bizkaiko Foru Aldundia, Bilbao – 2011 ISSN 0214-7971.
Autora: Nuria González Santiago (@lanuri_). Licenciada en Biología. Especialista en Ilustración Científica, UPV/EHU. Curso 20/21.
Articulo Original: ADN nuclear de varios individuos neandertales a partir de sedimentos Cuaderno de Cultura Científica, 16 de abril de 2021
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión centrada en la propia ilustración
El artículo ADN en cuevas, puerta a nuestra historia evolutiva se ha escrito en Cuaderno de Cultura Científica.
Día de Darwin 2022: el lenguaje antes del lenguaje y normas sociales

¿Qué papel tienen las normas sociales dentro de la evolución humana? ¿Garantizan una adaptación exitosa al medio natural y social o por el contrario pueden suponer un freno? ¿Cómo llevamos a cabo el proceso de adquisición y aprendizaje del lenguaje? Estas son algunas de las cuestiones a las que se trató de dar respuesta durante la decimosexta edición del Día de Darwin, que tuvo lugar el pasado 14 de febrero. Desde 2007, la Cátedra de Cultura Científica de la Universidad del País Vasco y el Círculo Escéptico conmemoran el nacimiento de Charles Darwin, científico y autor de la teoría de la evolución por selección natural, mediante conferencias centradas en distintos aspectos de la evolución humana dirigidas a amantes de la ciencia y del conocimiento. La Biblioteca Bidebarrieta de Bilbao fue de nuevo el escenario de esta cita con la evolución.
En esta nueva edición del Día de Darwin, las dos conferencias programadas se centrarán en la evolución desde dos perspectivas diferentes: por un lado, la de la adquisición del lenguaje y su desarrollo; y, por otro, sobre el papel de las normas sociales en la evolución humana.
Durante la primera conferencia, “La ontogénesis del lenguaje: el lenguaje antes del lenguaje”, Núria Sebastián Gallés explica cómo funciona la adquisición del lenguaje, un proceso que desarrollamos desde el periodo prenatal hasta los dos años de vida y que nos hace pasar en un corto periodo de tiempo de ser unos aprendices a contar con un conocimiento especializado.
Núria Sebastián Gallés es catedrática de Psicología en la Universidad Pompeu Fabra y directora del grupo de investigación Speech Acquisition and Perception en la misma institución. Se doctoró en Psicología Experimental en la Universidad de Barcelona. Entre 2013 y 2016 fue miembro del Consejo Científico del European Research Council y entre 2014 y 2016 fue una de sus vicepresidentas. En 2016 fue elegida Fellow de la British Academy.
La segunda conferencia, “Normas sociales y evolución humana”, a cargo de Joseba Ríos Garaizar, aborda la evolución humana desde el punto de vista de las normas sociales, es decir, el conjunto de reglas o normas que deben seguir las personas para tener una mejor convivencia en sociedad. Sin embargo, en algunas ocasiones, estas decisiones o normas no han permitido una adaptación exitosa, así lo demuestran algunos restos arqueológicos encontrados. Durante la charla se reflexiona sobre el papel que las normas sociales han tenido dentro de la evolución humana a través de algunos ejemplos paradigmáticos de la arqueología paleolítica.
Joseba Ríos Garaizar es doctor en Historia por la Universidad de Cantabria, arqueólogo especialista en prehistoria y técnico arqueólogo en el Arkeologi Museoa de Bilbao. Sus proyectos más destacados son las investigaciones arqueológicas en los yacimientos de Arlanpe (Lemoa), Aranbaltza (Barrika) y Amalda III (Zestoa) y ha colaborado en numerosos artículos científicos destacando sus estudios sobre la tecnología y la cultura de los neandertales.
Nota: si bien la bienvenida y presentación iniciales son en euskera, ambas conferencias son en castellano. La primera conferencia comienza en el minuto 7:00 del vídeo, y la segunda en el 48:40.
Edición realizada por César Tomé López a partir de materiales suministrados por Bidebarrieta Kulturgunea
El artículo Día de Darwin 2022: el lenguaje antes del lenguaje y normas sociales se ha escrito en Cuaderno de Cultura Científica.
Mejorando la vida de la batería de sodio-aire
Un equipo de investigación de la UPV/EHU en colaboración con CIC energiGUNE ha demostrado que añadiendo una sal de cesio en el electrolito de las baterías de sodio-aire (Na-O2) aumenta notablemente la vida del dispositivo, lo que impactaría notablemente en la autonomía del vehículo eléctrico.
 Foto: Matteo Paganelli / Unsplash
Foto: Matteo Paganelli / UnsplashLas baterías de metal-aire son una tecnología prometedora para suceder a las actuales baterías de iones de litio convencionales. Entre las ventajas que cuentan las baterías de metal-aire la más significativa reside en contar con una mayor densidad de energía que las de iones de litio, por lo que este tipo de baterías ofrecería al automóvil una mayor autonomía, uno de los condicionantes fundamentales para la adopción de este tipo de vehículos.
“Las baterías de metal-aire se encuentran entre las más sostenibles ya que los materiales que se utilizan son más respetuosos con el medio ambiente. Estas baterías toman oxígeno del aire, realizan sus procesos electroquímicos para generar la electricidad y cuando hay que volver a cargar la batería vuelven a emitir el oxígeno; es decir, funcionan consumiendo oxígeno y liberando oxígeno. Por eso, se conocen también como las baterías que respiran”, comenta Idoia Ruiz de Larramendi, investigadora del departamento de Química Orgánica e Inorgánica de la Facultad de Ciencia y Tecnología de la UPV/EHU.
Sin embargo, “no todo son ventajas. Uno de los problemas asociados a estas baterías es que presentan una pobre ciclabilidad, es decir, hacen pocos ciclos de carga y descarga”, dice Ruiz de Larramendi. Por ello, “en este trabajo de investigación nos hemos centrado en el diseño racional de electrolitos para su implementación en baterías de sodio-aire. En la actualidad, la mayoría de las baterías del mercado son de iones de litio. Sin embargo, el litio es un metal de abundancia limitada restringida en solo unos pocos países, por lo que en los últimos años se ha despertado el interés en el desarrollo de baterías basadas en sodio como alternativa, ya que se trata de un elemento más abundante, barato y sostenible”, señala la investigadora de la UPV/EHU.
“El electrolito es el encargado de dar movilidad a los iones dentro de la batería. Nuestro objetivo ha sido conseguir que esa movilidad sea la óptima. Para ello, en este estudio hemos trabajado con dos aditivos: el tetrabutilamonio (TBA) y el cesio (Cs) y hemos evaluado el potencial que presentan para mover los aniones de oxígeno por la batería. Ambos cationes son iones de gran tamaño, más grandes que los cationes de sodio que tenemos en el electrolito. Aplicando los principios de la química y apoyándonos en estudios teóricos entendíamos que se iban a unir mejor a los aniones de oxígeno, y así ha sido en ambos casos”, dice Ruiz de Larramendi. “Sin embargo —continúa—, los cationes de cesio han demostrado tener mayor potencial y ser más eficaces que los cationes de TBA porque la carga del Cs es más accesible para el oxígeno. Al añadir una sal de cesio hemos conseguido mejorar la ciclabilidad y llegar hasta más de 90 ciclos de carga y descarga. A día de hoy puede parecer que es poco, pero supone un gran avance hacia la futura comercialización de estos dispositivos”.
Según el equipo, “gracias al correcto diseño del electrolito es posible optimizar la operación de las baterías de sodio-aire. Obviamente, es mejorable y tenemos que seguir trabajando en ello, pero este trabajo es un importante paso en el que se demuestra que con una estrategia tan sencilla como la de añadir una sal de cesio en el electrolito mejoramos notablemente su ciclabilidad, lo que nos permite soñar con una nueva generación de vehículos eléctricos de mayor autonomía.”
Referencia:
Idoia Ruiz de Larramendi, Iñigo Lozano, Marina Enterría, Rosalía Cid, María Echeverría, Sergio Rodríguez Peña, Javier Carrasco, Hegoi Manzano, Garikoitz Beobide, Imanol Landa-Medrano, Teófilo Rojo y Nagore Ortiz-Vitoriano (2021) Unveiling the Role of Tetrabutylammonium and Cesium Bulky Cations in Enhancing Na-O2 Battery Performance Advanced Energy Materials doi: 10.1002/aenm.202102834
Para saber más:
Ionogeles para baterías de sodio
Las baterías ion sodio, la alternativa estacionaria
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Mejorando la vida de la batería de sodio-aire se ha escrito en Cuaderno de Cultura Científica.
Arpa de boca: De las clases de Beethoven al spaghetti western
Si alguna vez has oído hablar del arpa de boca, probablemente asocies su sonido a los dibujos animados, a los muelles, o quizás, con suerte, a las películas del oeste. Es ese instrumento que hace doing doing doing —o boing boing o wuaaaang wuaang, según el modelo que tengas— cada vez que algo rebota. Acompaña a menudo al coyote en su eterna persecución del correcaminos, a Bugs Bunny cuando salta en un trampolín o a Tom y Jerry, cada vez que que el pobre gato recibe algún golpe o pinchazo lo bastante flexible.
 Jongen met mondharp / Joven con arpa de boca (1621) de Dirk van Baburen (1595 – 1624). Fuente: Centraal Museum Utrecht.
Jongen met mondharp / Joven con arpa de boca (1621) de Dirk van Baburen (1595 – 1624). Fuente: Centraal Museum Utrecht.Donde probablemente no te esperabas oír un sonido así es en medio de un concierto clásico y, probablemente por eso, esta composición te sorprenderá:
Si has escuchado la obra desde el principio, al llegar al minuto 1 quizás has pensado que se trataba de una broma. Cuando hace su aparición, el timbre de este instrumento resulta tan contrastante que casi parece una parodia, como si un personaje de los Looney Tunes se hubiese colado en la sala de conciertos para asustar a señoras elegantes y epatar a “le bourgeois”. Pero no, no es una broma. Se trata de una de las pocas partituras que se conservan escritas por Johann Georg Albrechtsberger, un célebre compositor austriaco del siglo XVIII. Fue, quizás, uno de los teórico musicales más reconocido de su tiempo, y pasó a la historia como profesor de otros grandes compositores, entre ellos, Ludwig van Beethoven.
Entre 1769 y 1771, Albrechtsberger escribió al menos siete conciertos para arpa de boca y orquesta de cuerda. Y lo hizo sin ironía, sin despeinarse su tupida peluca, porque a fin de cuentas, el arpa de boca pertenecía a una larga tradición musical dentro de su país. El Maultrommel (que se podría traducir, literalmente, como tambor de boca) se llevaba usando desde hacía siglos y era particularmente popular en la música folclórica de Austria y otros países de habla alemana. Y para ubicarla, aquí va otro vídeo que probablemente os sorprenderá:
No es, ni de lejos, la única tradición musical que incluye este peculiar instrumento, ni tampoco la más antigua. La primera representación de alguien tocando lo que parece ser un arpa de boca es un dibujo chino del siglo III a. C. Pero se cree que una serie de huesos curvos del año 1800 a.C., descubiertos en Shaanxi, China, podrían haberse utilizado con fines musicales. Esto convertiría al arpa de boca en uno de los instrumentos musicales más antiguos conservados. Y también uno de los más universales: está presente, con más de 900 nombres diferentes, en culturas de todo el planeta, desde China a Europa, Siberia, Japón, el Sureste asiático (Taiwan, Vietnam, Filipinas, Indonesia…) y Polinesia. En español se conoce también como guimbarda, trompe o birimbao.
Siberia
Hecho de bambú.
Su sencillez podría explicar su antigüedad, y también su popularidad. Basta una lámina flexible, lo bastante alargada como para producir un tono más o menos reconocible. Esta lámina suele estar hecha de metal, hueso o madera. Pero también te puedes hacer un arpa de plástico, si tienes un poco de mañana y una tarjeta de crédito que no vayas a usar. Al flexionar la lámina y soltarla, esta intenta regresar a su posición inicial, y en el camino produce una vibración sonora. La frecuencia está definida por la forma de la lámina, y es siempre la misma (por eso, en la tradición austriaca, van alternando entre varias arpas para cambiar de nota). Pero aquí viene la magia: el arpista utiliza su boca para amplificar este sonido y para filtrarlo. Cambiando la posición de su mandíbula y sus mejillas1, puede resaltar los distintos armónicos y formar melodías reconocibles.
El resultado es una sonoridad ciertamente exótica, con un tono fundamental y una melodía difusa que va flotando sobre la base. Algo parecido a lo que sucede en el canto difónico. Resulta sorprendente, muy reconocible, y al mismo tiempo está basada en una técnica que a todos nos resulta familiar: las resonancias de nuestra propia boca, las mismas que utilizamos en nuestro día a día para hablar y para expresarnos. Por eso, quizás no debería sorprendernos que su uso sea tan popular, desde la antigua China, y hasta el salvaje Oeste.
Cuando el siglo XX, Ennio Morricone decidió buscar una nueva sonoridad para las narrativas del lejano Oeste que le encargaban recrear, empezó a combinar los timbres de la orquesta, con otros más humildes y populares. Sonidos como el de la ocarina y el arpa de boca, que probablemente resonaron en aquel paisaje remoto. Gracias a él, el arpa de boca volvió a encontrarse con la orquesta, y quedó grabada en nuestra memoria, desde entonces, asociada al spaghetti western.
Nota:
1Para ver a qué me refiero, puedes probar a darte pequeños golpes con los dedos en la mejilla. Si cambias la posición de la boca (como pronunciando una u, o una a) observarás cómo el sonido se vuelve más grave o más agudo.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Arpa de boca: De las clases de Beethoven al spaghetti western se ha escrito en Cuaderno de Cultura Científica.
Las bases de numeración o cómo hacer trucos de magia binarios
En la anterior entrada del Cuaderno de Cultura Científica titulada El arte de la sencilla baldosa de Truchet hablábamos de la expresión del número pi en base cuatro, en la que utilizamos las cuatro cifras básicas 1, 2, 3, 0, y dejamos para una entrada futura, que es la que hoy tenéis delante, explicar las diferentes bases de numeración y cómo obtener las expresiones de cada número en dichas bases.
 Idea para una obra basada en los patrones de embaldosado con baldosas de Truchet y la expresión del número pi en base 4
Idea para una obra basada en los patrones de embaldosado con baldosas de Truchet y la expresión del número pi en base 4
Para empezar, recordemos que el sistema de numeración posicional moderno utilizado en casi todo el mundo es decimal, es decir, que tiene base 10 (véase el libro Los secretos de la multiplicación, de los babilonios a los ordenadores). Por lo tanto, consta de diez cifras básicas, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 y todo número se puede representar con ellas al expresarlo en función de las potencias de 10. Por ejemplo, el número 3.457 tiene el valor de 3 veces la cantidad de 1.000, 4 veces la cantidad de 100, 5 veces la cantidad de 10 y 7 veces la unidad 1, que son las potencias de 10, a saber, 1.000 = 103, 100 = 102, 10 = 101 y 1 = 100.
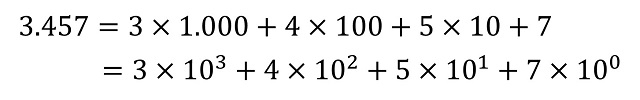
En general, dada una base de numeración b –ya sea esta igual a 2, 3, 12 o 60- la representación posicional de cualquier número en la misma viene dada por una expresión d1d2…dr (donde los dígitos di –para i entre 1 y r– pertenecen a la familia de las b cifras básicas del sistema de numeración, que tienen valores entre 0 y b – 1) teniendo en cuenta que el número puede escribirse, de forma única, como
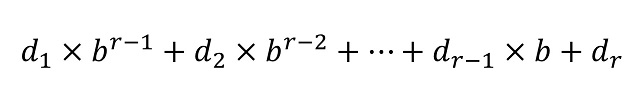
Por lo tanto, la representación del número está ligada a la base elegida. Así, si tomamos el sistema binario (b = 2) el anterior número se representa como (110110000001)2, ya que “3.457” = 211 + 210 + 28 + 27 + 1; en la base octal (b = 8) como (6600)8, porque “3.457” = 6 x 83 + 6 x 82; o en la base hexadecimal (b = 16), donde las cifras básicas son 0, 1, …, 9, A, B, C, D, como (D81)16, puesto que “3.457” = D x 162 + 8 x 16 + 1, donde estamos utilizando el subíndice de las representaciones (2, 8 y 16) para recordar que esa es una representación en esa base de numeración.
La base de numeración binariaVeamos esto más despacio para el caso de la base binaria, b = 2. En este caso solamente hay dos cifras básicas, 0 y 1, y expresar un número N en el sistema binario es escribirlo como suma de potencias de 2, donde cada dígito nos dice cuántas veces se toma esa potencia (como las cifras básicas son solo 0 y 1, entonces cada dígito nos dice si está o no dicha potencia). Así, si tenemos una expresión binaria como (101101)2, podemos saber cuál es su valor viendo qué potencias de 2 nos indica esa expresión que aparecen. Como el número binario tiene 6 dígitos, eso quiere decir que las potencias implicadas son 25 = 32, 24 = 16, 23 = 8, 22 = 4, 21 = 2 y 20 = 1 y los dígitos nos dicen si la correspondiente potencia está o no, como se muestra a continuación,

entonces, el número expresado con la representación binaria (101101)2 es 1 x 32 + 0 x 16 + 1 x 8 + 1 x 4 + 0 x 2 + 1 x 1 = 32 + 8 + 4 + 1 = 45.
De hecho, este es el método general para pasar de un número binario a su expresión decimal, que es la que nosotros entendemos mejor. Esto es, se cuentan cuántos dígitos r hay implicados –por ejemplo, en la expresión binaria 1110100001011001 hay 16 dígitos- y se van considerando qué potencias de 2, desde 2r-1 hasta 20 = 1, aparecen en función de si hay un 1 o un cero en la correspondiente posición, empezando por la derecha (aunque también podríamos realizar esa lectura empezando por la izquierda y tomando las potencias desde 20 = 1 hasta 2r-1) –por ejemplo, en la expresión binaria anterior, 1110100001011001, aparecen las potencias 215 = 32.768, 214 = 16.384, 213 = 8.192, 211 = 2.048, 26 = 64, 24 = 16, 23 = 8 y 20 = 1, por lo tanto, el número representado en forma binaria por (1110100001011001)2 es el número representado en el sistema decimal como 59.481.
 La ceramista estadounidense Laura C. Hewitt crea cerámicas con números binarios, con tipografías de máquinas de escribir, como este hermoso cuenco con una espiral binaria. La imagen pertenece a su tienda de Etsy
La ceramista estadounidense Laura C. Hewitt crea cerámicas con números binarios, con tipografías de máquinas de escribir, como este hermoso cuenco con una espiral binaria. La imagen pertenece a su tienda de Etsy
Recíprocamente, si queremos ver cuál es la representación binaria de un número N, por ejemplo, el número N = 197, tendremos que ver cómo expresarlo como suma de potencias de 2. Como las potencias de 2 que pueden verse implicadas son 27 = 128, 26 = 64, 25 = 32, 24 = 16, 23 = 8, 22 = 4, 21 = 2 y 20 = 1, ya que 28 = 256 ya es mayor que el número en cuestión, tenemos que ver cómo expresar el número 197 como suma de estas. Para empezar, en nuestra expresión aparecerá 27 = 128, además, 197 – 128 = 69; por lo tanto, también aparecerá 26 = 64; como 69 – 64 = 5, no aparecerán 25 = 32, 24 = 16, ni 23 = 8, pero sí 22 = 4; por último, 5 – 4 = 1, que es 20. En conclusión, 197 = 128 + 64 + 4 + 1 y la expresión binaria es (11000101)2.
Podemos dar un algoritmo general teniendo en cuenta el conocido como teorema de la división o lema de la división de Euclides, que nos dice que si tenemos un número natural a (dividendo), que queremos dividirlo por un número natural b (divisor), nos dará como resultado un cierto número natural c (cociente) y nos quedará de resto un número r, que toma valores entre 0 y b – 1, que ya no se puede dividir por b, de manera que podemos expresar la división como a = b x c + r. El lema de la división de Euclides es el que nos permite afirmar que todo número N puede expresarse, de forma única, como suma múltiplos de potencias de la base, es decir, como
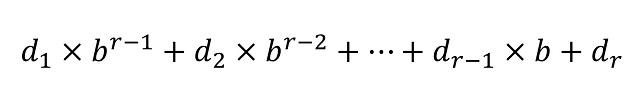
La idea del algoritmo de cambio de base está en utilizar, hasta que ya no podemos hacerlo más, el teorema de la división. Dado un número N que queremos cambiar de la base decimal a la base b se aplica el lema, primero considerando N como dividendo y después, en cada paso, el dividendo será el cociente del paso anterior. Veámoslo con un ejemplo concreto, por ejemplo, el número anterior N = 197.
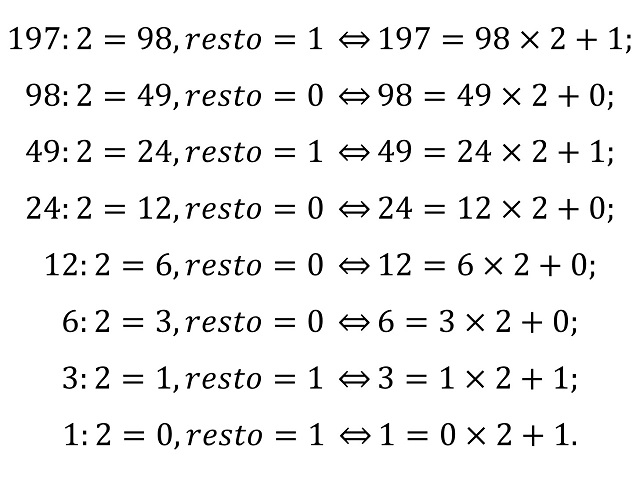
De forma que, si tomamos las raíces y las colocamos de izquierda a derecha, es decir, empezando por las unidades, obtenemos la expresión binaria del número, en este caso, de 197, así: 11000101, como ya habíamos visto antes.
Esto se debe a que, de nuevo en este ejemplo, aunque es algo general, aplicando el teorema de la división se obtiene
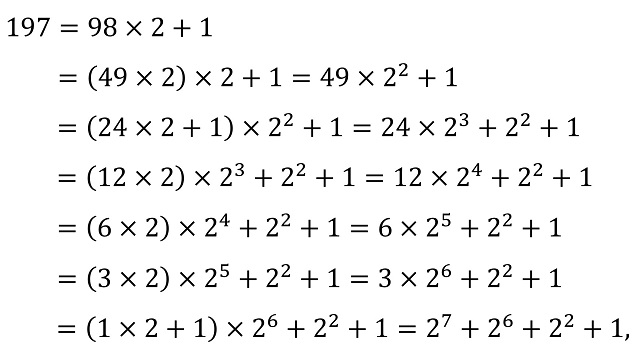
es decir, la expresión de N en las potencias de 2.
 Escultura Código binario, del artista italiano Hector & Hector. Imagen de su página web en Saatchiart
Escultura Código binario, del artista italiano Hector & Hector. Imagen de su página web en SaatchiartUn truco de magia binario
Existe un sencillo truco de magia relacionado con los números binarios. Es muy sencillo y podéis hacérselo a vuestros familiares y amistades. Es un truco relativamente conocido, que incluso alguna empresa ha utilizado para su publicidad, como el siguiente ejemplo “Estas cartas son mágicas” de la empresa Coca Cola.
 Parte delantera del tríptico de la publicidad de Coca Cola con el truco de magia relacionado con los números binarios. Las dos partes de la izquierda son la parte trasera de las seis tarjetas que se utilizan para el truco, que simplemente llevaban publicidad, mientras que la parte de la derecha era la presentación de la publicidad, con el nombre “These cards are magic / Estas cartas son mágicas”
Parte delantera del tríptico de la publicidad de Coca Cola con el truco de magia relacionado con los números binarios. Las dos partes de la izquierda son la parte trasera de las seis tarjetas que se utilizan para el truco, que simplemente llevaban publicidad, mientras que la parte de la derecha era la presentación de la publicidad, con el nombre “These cards are magic / Estas cartas son mágicas”
 Parte trasera del tríptico de la publicidad de Coca Cola con el truco de magia relacionado con los números binarios. La parte de la izquierda explica brevemente el truco de magia, mientras que las dos partes de la derecha son son la parte frontal de las seis tarjetas que se utilizan para el truco
Parte trasera del tríptico de la publicidad de Coca Cola con el truco de magia relacionado con los números binarios. La parte de la izquierda explica brevemente el truco de magia, mientras que las dos partes de la derecha son son la parte frontal de las seis tarjetas que se utilizan para el truco
Expliquemos en qué consiste el truco de magia de las tarjetas numéricas. Se le pide a una persona que piense en un número del 1 al 63. Aunque también se puede complicar esto un poco y hacer un poco de espectáculo, es decir, podemos inventarnos cualquier acción para que alguien del público acabe obteniendo un número del 1 al 63, pero que nosotros debemos desconocer.
Una vez que esa persona del público tiene en la cabeza el número, entre 1 y 63, determinado, que nadie más conoce, se le muestran las siguientes seis tarjetas y se le pide que nos diga en cuál de ellas está el número que ha elegido. Le vamos preguntando “¿está en esta tarjeta?” y nos irá contestando “sí” o “no”. Si contesta “sí” sumamos el número de la esquina de la tarjeta correspondiente y si contesta “no” no lo sumamos. Al para todas las tarjetas el resultado final de la suma será el número que esa persona tiene en la cabeza. Las tarjetas son las siguientes:






Por ejemplo, imaginemos que una persona nos contesta lo siguiente al mostrarle las tarjetas: sí, sí, no, sí, no y sí, entonces el número que ha pensado es 1 + 2 + 8 + 32 = 43.
¿Cuál es la base de este truco? Como podemos imaginar la base es el sistema binario de numeración, como vamos a explicar brevemente. Empezando por el final, cuando la persona del público nos va diciendo en cada tarjeta si el número está –dice “sí”- o no está –dice “no”-, realmente nos está dando la representación binaria del número que ha pensado. Por ejemplo, en el caso anterior (sí, sí, no, sí, no y sí), sería (1 0 1 0 1 1)2 –ya que las hemos mostrado desde las unidades- que no es otro que 25 + 23 + 2 + 1 = 43.
Esto es así porque a la hora de crear las tarjetas, en la primera tarjeta, la que tiene un 1 en la esquina, están todos los números que tienen un 1 en la primera posición de la derecha de su representación binaria, que son todos los impares. Podemos comprobarlo en la siguiente lista con las representaciones binarias de los números entre 1 y 63.
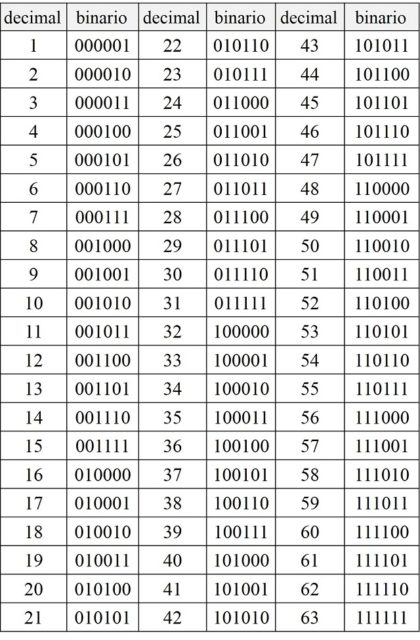
En la segunda tarjeta están los números que tienen un 1 en la segunda posición de la derecha de su representación binaria (2, 3, 6, 7, 10, 11, 14, 15, …, 62, 63), en la tercera los que tienen un 1 en la tercera posición de la derecha de su representación binaria (4, 5, 6, 7, 12, 13, 14, 15, …, 60, 61, 62, 63) y así hasta la última tarjeta.
 Fotografía del proyecto The Binary Graffiti Club (más información en The Binary Graffiti Club), un proyecto de arte performativo y social diseñado para cada ciudad o lugar, del artista británico Stanza. Imagen de la página del proyecto
Fotografía del proyecto The Binary Graffiti Club (más información en The Binary Graffiti Club), un proyecto de arte performativo y social diseñado para cada ciudad o lugar, del artista británico Stanza. Imagen de la página del proyectoLa base duodecimal
A lo largo de esta entrada hemos hecho hincapié en el cambio de base del sistema binario, pero todo lo comentado sirve para cualquier otra base, ya sea la base 12 (del sistema duodecimal, del que hablamos algo en la entrada El sistema duodecimal, o si los humanos hubiésemos tenido seis dedos en las manos), la base 60 (que utilizaban los babilonios y del que hablamos algo en la entrada ¿Sueñan los babilonios con multiplicaciones eléctricas?) o cualquier otra base.
Terminemos con un ejemplo para la base 12, la duodecimal. Denotaremos las cifras básicas de este sistema de numeración como 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B (donde A tiene el valor de 10 y B de 11). Consideremos en número 13.762 y expresémosle en base 12. Si consideramos el algoritmo de la división de Euclides, tenemos que:
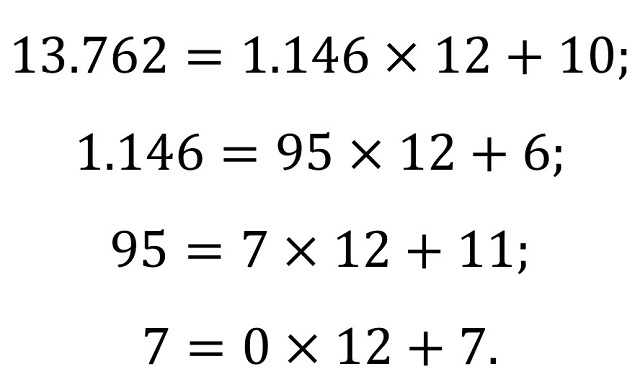
Por lo tanto, los restos son 10, 6, 11 y 7, que, si recordamos que el primero corresponde a las unidades (parte derecha de la representación duodecimal), nos da la representación del número 13.762 en base 12 como
![]()
La siguiente cuestión será cómo representar los números que no son naturales (ni enteros), como 0,25; 3,7675 o el número pi, pero de eso hablaremos en la siguiente entrada del Cuaderno de Cultura Científica.
Bibliografía:
1.- Raúl Ibáñez, Los secretos de la multiplicación, de los babilonios a los ordenadores, Catarata, 2019.
2.- George Gheverghese Joseph, La cresta del pavo real, las matemáticas y sus raíces no europeas, Pirámide, 1996.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Las bases de numeración o cómo hacer trucos de magia binarios se ha escrito en Cuaderno de Cultura Científica.
Einstein y Ernst Mach
Ernst Mach es más conocido hoy por dar su nombre a la velocidad del sonido en la atmósfera terrestre, pero para Einstein fue el hombre que estableció la base para la relatividad y un héroe admirado que empleó una considerable cantidad de tiempo pensando cómo se debería hacer ciencia.
 Ernst Mach en 1905. Fuente: Wikimedia Commons
Ernst Mach en 1905. Fuente: Wikimedia CommonsEinstein leyó a Mach cuando era estudiante y ya era seguidor suyo en 1902, cuando vivía en Zúrich y se reunía regularmente con sus amigos Conrad Habicht y Maurice Solovine. Einstein insistió para que el grupo leyese los dos libros de Mach publicados hasta esa fecha: El desarrollo de la mecánica y El análisis de las sensaciones.
Mach fue un ejemplo de una clase de profesor que se hizo cada vez más escasa en el siglo XX: un científico cuyos intereses cubrían un amplio abanico de materias, desde la óptica y la mecánica a la filosofía, pasando por la dinámica de ondas, las experiencias sensoriales o la teoría cognitiva. Fue la filosofía lo primero que llamó la atención de Einstein. Mach era abiertamente un positivista extremo, es decir, mantenía que sólo se pueden extraer conclusiones de lo que se puede percibir directamente. Las teorías científicas, según Mach, no pueden pretender ser más que un resumen de hechos observables. Hacer inferencias que no fuesen directamente atribuibles a algo que se pudiese ver, tocar o percibir de alguna manera, era entrar en el mundo de la fantasía.
Todos los científicos estarían de acuerdo, por supuesto, en que las teorías están basadas en último extremo en lo que podemos percibir, pero Mach llevó esta posición mucho más lejos que los demás. Por ejemplo, durante años se negó a creer en la existencia de los átomos ya que serían demasiado pequeños para ser percibidos directamente con nuestros propios ojos.
Los estudios de Mach sobre la mecánica y la inercia también tuvieron su impacto en Einstein. Dado que Mach creía solamente en cantidades que se pudiesen tocar, afirmó enfáticamente que el “tiempo” no tiene ningún significado real. Escribió que era una idea abstracta, producto de la mente humana y sujeta, por lo tanto, a sus caprichos. Este rechazo del “tiempo absoluto” parece que liberó el pensamiento del joven Einstein; cuando se publicó la teoría especial de la relatividad de Einstein en 1905, se apoyaba directamente en el concepto de que no existe ni tiempo ni espacio absolutos. De hecho, todo lo que hay en la teoría especial de la relatividad se deriva directamente de la percepción humana; dado que la gente en diferentes marcos de referencia experimenta diferentes cosas, Einstein afirmó que la realidad misma era diferente en esos marcos de referencia. Una actitud genuinamente positivista que Mach no pudo menos que aprobar.
De hecho, Mach tuvo ideas parecidas cuando joven. Einstein siempre creyó que Mach había estado en el camino correcto para descubrir la relatividad en parte de sus trabajos de juventud, y que la única razón por la que no lo había hecho fue porque la época no fue la propicia. Einstein comenzó a pensar en el problema en un momento en el que las miradas de la comunidad científica estaban puestas en el hecho de que la velocidad de la luz era constante, mientras que Mach lo hizo dos décadas antes. La constancia de la velocidad de la luz fue un importante punto de partida para el desarrollo de la relatividad, y uno al que Mach no tuvo acceso.
Einstein también usó el trabajo de Mach unos diez años más tarde cuando estaba escribiendo la teoría general de la relatividad. Mach había hecho una propuesta, a la que Einstein se refería como el principio de Mach, según la cual la causa de que cualquier objeto permanece en reposo o continúa moviéndose es directamente atribuible a su relación con todos los demás objetos del universo. Esto constituía una modificación de la ley de la inercia de Newton: un objeto en reposo tiende a estar en reposo, y un objeto en movimiento tiende a estar en movimiento. Mach quería determinar simplemente por qué la ley de Newton era así, y su respuesta fue que la responsable era la distribución de masa en el universo. Se puede ver como, si la idea de que la masa afecta a la inercia se introdujo en el cerebro de Einstein, le pudo haber ayudado a crear su teoría general de la relatividad, que afirma que, básicamente, la masa crea la gravedad.
Einstein, un metafísico para MachEinstein siempre reconoció la obra de Mach como el catalizador de su teoría de la relatividad. Pero Mach eligió distanciarse del trabajo de Einstein. Para cuando se publicó la teoría general de la relatividad en 1915, Einstein había ido demasiado lejos en la dirección a la que Mach se refería como “conceptos metafísicos”. La teoría general de la relatividad explica la gravedad postulando la curvatura de algo llamado espaciotiempo; para Mach la teoría era demasiado abstracta para ser aceptable.
Einstein, sin embargo, nunca admitió del todo que su héroe había rechazado la relatividad, achacando a la vejez la actitud de Mach. A pesar de ello, Einstein también se apartó de su estricta adhesión al trabajo de Mach. Así, se hizo cada vez más evidente que el principio de Mach no tenía, de hecho, mucho que ver con la relatividad general; el primero tenía que ver con la inercia, el segundo con la gravedad. No solo eso, a pesar de la reticencia inicial de Einstein a la idea, la relatividad permite un universo sin ninguna masa. En su última década de vida, Einstein había dejado completamente de asociar el principio de Mach con su propio trabajo. En una carta de 1954 escribió “uno no debería hablar más en absoluto del principio de Mach”.
Einstein también dejó, bastante enfáticamente, de seguir el positivismo de Mach. Aunque apoyarse solamente en los sentidos le ayudó a crear su primera teoría de la relatividad, Einstein abandonó esta actitud tan rígida con el paso del tiempo. Conforme se desarrollaba la mecánica cuántica la mayor parte de la comunidad científica comenzaba a aceptar una teoría que se basaba solamente en la medición directa del mundo atómico. Pero la teoría todavía albergaba complejidades innatas que Einstein pensaba que estaban aún por resolver: la medición directa no era suficiente.
Mach también rechazó la mecánica cuántica, porque si bien se basaba solamente en mediciones para sacar conclusiones, estas mediciones eran de un tipo demasiado abstracto. ¿Quién, después de todo, ha visto un electrón con sus ojos? Sin experiencia sensible, Mach no tenía interés en esta nueva rama de la ciencia.
A pesar de sus diferencias científicas, Einstein siempre consideró a Mach una de las grandes influencias en su vida. En 1916, Einstein escribió un obituario sobre Mach en el que alababa al hombre que había empleado tanto tiempo estudiando, como una ciencia en sí misma, cómo la ciencia debería hacerse. Sin ese autoexamen, escribía Einstein, “los conceptos que han probado ser útiles para ordenar las cosas adquieren fácilmente una autoridad tal sobre nosotros que olvidamos sus orígenes terrenos y los aceptamos como axiomas inalterables… La senda del avance científico se hace a menudo infranqueable durante mucho tiempo por esos errores”.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 11 de julio de 2009.
El artículo Einstein y Ernst Mach se ha escrito en Cuaderno de Cultura Científica.
¿Cómo se esculpe el paisaje de Titán?
La llegada de la sonda Cassini al sistema de Saturno en julio de 2004 marcó el inicio de una nueva revolución en cuanto a nuestro conocimiento del sistema del gigante gaseoso. Especialmente interesante resultó la geología de los satélites, que en los casos particulares de Encélado y Titán resultaron ser mucho más activos a nivel geológico de lo que se había imaginado hasta el momento.
 En esta imagen creada a partir de mediciones en el infrarrojo cercano tomadas por la sonda Cassini se aprecia la luz del sol reflejándose en los mares de metano y etano de Titán. Imagen cortesía de NASA / JPL-Caltech / University of Arizona / University of Idaho.
En esta imagen creada a partir de mediciones en el infrarrojo cercano tomadas por la sonda Cassini se aprecia la luz del sol reflejándose en los mares de metano y etano de Titán. Imagen cortesía de NASA / JPL-Caltech / University of Arizona / University of Idaho.Pero el pastel tenía una guinda. El aterrizaje de la sonda Huygens sobre Titán y los sucesivos sobrevuelos de la Cassini descubrieron que este satélite, uno de los más grandes de nuestro Sistema Solar, y además con una atmósfera más densa que la de nuestro planeta, no es que tuviese una geología interna activa, sino que además tenía procesos externos relacionados con la atmósfera y las estaciones que esculpían su superficie.
No solo eso. Titán, junto con la Tierra, es el único cuerpo del Sistema Solar del que tengamos pruebas fehacientes de que tenga un ciclo hidrológico. Eso sí, en el sentido laxo de la palabra, ya que la temperatura media en su superficie ronda los -180 ºC, por lo que el ciclo hidrológico en realidad está constituido por compuestos orgánicos, como el metano, que pueden encontrarse en fases líquidas y gaseosas en ese rango de temperaturas, lo que permite la presencia de nubes desde las que llueven estos.
 Redes fluviales en Titán desembocando sobre una llanura. Imagen cortesía de ESA/NASA/JPL/University of Arizona.
Redes fluviales en Titán desembocando sobre una llanura. Imagen cortesía de ESA/NASA/JPL/University of Arizona.La lluvia de estos compuestos orgánicos erosiona la superficie, formando redes fluviales como las que vemos en la Tierra o Marte, y acaban acumulándose en lagos y mares, algunos de los cuales vuelven a evaporarse a la atmósfera, dejando un depósito mineral como en las salinas terrestres donde se fabrica la sal común, pero con una química muy distinta.
Pero no solo eso, en Titán también hay desiertos, desiertos de arena que desde la órbita parecen como los terrestres o los marcianos. La sonda Huygens aterrizó en una rambla seca cubierta de guijarros de distintos tamaños, redondeados por el transporte a lo largo del tiempo.
 La rambla sobre la que aterrizó la sonda Huygens. Como podemos ver, se aprecian numerosos cantos redondeados fruto de la acción fluvial sobre materiales más finos, con un parecido extraordinario al de las ramblas terrestres. Imagen cortesía de ESA/NASA/JPL/University of Arizona.La superficie de Titán es de hielo, no de roca
La rambla sobre la que aterrizó la sonda Huygens. Como podemos ver, se aprecian numerosos cantos redondeados fruto de la acción fluvial sobre materiales más finos, con un parecido extraordinario al de las ramblas terrestres. Imagen cortesía de ESA/NASA/JPL/University of Arizona.La superficie de Titán es de hielo, no de roca
Estos hechos también nos parecerían normales si no fuese porque la superficie de Titán no es rocosa, como la de los planetas interiores, sino que está formada por hielo, un hielo que a simple vista se comporta de una manera similar a como lo haría la roca… pero, ¿qué procesos permiten que el hielo acabe formando un paisaje similar al de nuestro planeta?
Un equipo de investigadores ha publicado recientemente un artículo en Geophysical Research Letters que pretende responder a estas cuestiones usando la arena como un mecanismo formador del relieve que observamos en los polos y en las latitudes medias de Titan. Sorprendente, ¿verdad?.
En nuestro planeta, la formación de dunas viene precedida por la formación, valga la redundancia, de depósitos sedimentarios costeros o fluviales de un material fino que permite que el viento sea capaz de moverlo. En Titán podría haber muchos más mecanismos que sean capaces de generar partículas de ese tamaño: por ejemplo, tenemos la erosión de las capas de hielo superficial a partir de la lluvia o los cauces fluviales, la aglutinación de partículas de compuestos orgánicos desde la atmósfera, la erosión de los depósitos evaporíticos que quedan en el lecho de los mares y lagos cuando estos se evaporan…
 Campos de dunas sobre la superficie de Titán… ¿no os recuerdan mucho a las dunas terrestres?. Imagen cortesía de NASA/JPL-Caltech.
Campos de dunas sobre la superficie de Titán… ¿no os recuerdan mucho a las dunas terrestres?. Imagen cortesía de NASA/JPL-Caltech.Uno de los mayores problemas de los científicos a la hora de entender los procesos relacionados con la arena de Titán es que se pensaba que durante la formación de las distintas partículas que conforman la arena, poco a poco estas irían disminuyendo de tamaño a causa del transporte por el simple hecho de ir desgastándose. En cambio, parece que no es el caso y que, durante su movimiento, son capaces de mantener, al menos parcialmente, su tamaño al ir aglutinándose con otras partículas.
Si no, con el paso del tiempo y sin un gran aporte de nuevos granos de arena, entiéndase en este caso arena formada por pequeños cristales de hielo y no por minerales como en nuestro planeta, estos granos irían menguando tanto que las dunas, probablemente, desaparecerían durante su migración.
En Titán aparecen las dunas de arena en dos lugares muy diferentes: por un lado, en los polos y, por otro, en las llanuras de las latitudes medias. Es muy probable que la mayor parte de esta arena se forme en el ecuador, donde sabemos que hay un régimen de viento suficiente como para erosionar y transportar los granos de estas zonas a las latitudes adyacentes.
A las latitudes medias llegarían estos granos que podrían ir uniéndose por fenómenos de aglutinación de tal forma que las partículas tendrían cada vez un tamaño más y más grande, siendo finalmente incapaces de moverse con el viento y pudiendo, con el paso del tiempo, dar lugar a la topografía que vemos, como si fuésemos uniendo cubitos de hielo hasta formar un iceberg, pero a gran escala.
En cambio, en los polos, la situación parece más compleja, y el transporte de la arena desde latitudes ecuatoriales no parece una posibilidad. En estas zonas polares aparece un relieve muy característico denominado “terreno laberíntico” cuyo origen se discute, y que podría ser debido a zonas elevadas que han sido erosionadas por ríos de metano, que han sufrido procesos de disolución como en las zonas kársticas de la Tierra o que, por procesos tectónicos, han quedado zonas elevadas y hundidas unas con respecto a las otras.
 Terreno laberíntico en Titán (izquierda) y en la Tierra (derecha). Imagen cortesía de NASA JPL-Caltech ASI.
Terreno laberíntico en Titán (izquierda) y en la Tierra (derecha). Imagen cortesía de NASA JPL-Caltech ASI.Los autores de este estudio se inclinan a pensar que este relieve en realidad se parece más a las zonas kársticas y que lo que vemos es el resultado del colapso del terreno fruto de la disolución de unas areniscas, también en sentido laxo, formadas por compuestos orgánicos.
¿Cómo se formarían estas areniscas que a su vez forman el terreno laberíntico tras su disolución?. En nuestro planeta, las areniscas son rocas formadas principalmente por granos de roca de tamaño arena (entre 0.0625 a 2 mm de diámetro), pero si no hay una fuente de arena que alimente esta zona, ya hemos dicho antes que desde el ecuador no podían transportarse, ¿de dónde vienen?
Es cierto que en los polos el régimen de vientos es mucho más débil que en el ecuador, pero a cambio tienen una mayor formación de tormentas y, por lo tanto, de escorrentía, por lo que la erosión y el transporte pueden llevarse a cabo mediante los compuestos orgánicos en estado líquido. Estas arenas transportadas por los ríos irían acumulándose con el tiempo, formando extensos depósitos que con el tiempo sufrirían los procesos de disolución y que darán lugar al terreno laberíntico.
Dicho todo esto, y como concluyen los propios autores del estudio, mediante este modelo se puede explicar muy bien la distribución de los distintos tipos de terreno a ambos lados del ecuador de Titán usando únicamente un modelo sedimentario en el que la abrasión de las partículas, lo que permite generar la arena, por un lado y, por otro, los fenómenos de aglutinación que permiten generar los paisajes uniendo los granos, son los fenómenos fundamentales.
Sin duda, este mecanismo activo de depósito de sedimentos y formación de relieves en Titán pone de manifiesto que la geología del Sistema Solar todavía tiene muchas sorpresas y procesos que, aunque den relieves y formas que nos resultan muy habituales y cotidianas, en el fondo son muy diferentes.
Referencias
Lapôtre, M. G. A., Malaska, M. J., & Cable, M. L. (2022). The role of seasonal sediment transport and sintering in shaping Titan’s landscapes: A hypothesis. Geophysical Research Letters, 49, e2021GL097605 doi: 10.1029/2021GL097605
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Cómo se esculpe el paisaje de Titán? se ha escrito en Cuaderno de Cultura Científica.
La brújula de los salmones
 Foto: Marcos Paulo Prado / Unsplash
Foto: Marcos Paulo Prado / UnsplashEl salmón nada hacia el fondo del Golfo de Bizkaia. Lo guía, según todos los indicios, el campo magnético terrestre, aunque al aproximarse a la costa, es el “olor” que emana del agua del Bidasoa el que le marca el camino y lo conduce hasta la desembocadura de su río natal. A partir de ese momento no necesitará orientarse: ya ha llegado. Solo le falta hacer el esfuerzo supremo, nadando río arriba y superando obstáculos, hasta llegar al lecho de grava donde desovará.
La señal que lo orienta a través de centenares de millas es geomagnética. Los salmones no son los únicos animales capaces de orientarse y navegar haciendo uso del campo magnético terrestre. Abejas, otros peces, varias aves y ratones, al menos, también la tienen, aunque no acabamos de conocer bien el mecanismo que lo hace posible. La hipótesis más aceptada es que hay unos orgánulos celulares con cristales de magnetita que interaccionan con el campo magnético. Esa interacción daría lugar a la generación y emisión de señales nerviosas que se procesan en el encéfalo u órgano equivalente para guiar el movimiento. Según esa hipótesis, los cristales de magnetita serían similares a los de mineral de hierro sintetizados por unas bacterias magnetotácticas -las llamamos así- que los utilizan para alinearse, de forma pasiva, con las líneas del campo magnético y de ese modo poder desplazarse en una misma dirección.
La magnetita, único material de propiedades magnéticas producido por los seres vivos, ha sido hallada en tres reinos: bacterias (organismos unicelulares sin núcleo ni compartimentos internos complejos), protistas (organismos unicelulares con núcleo y compartimentos internos complejos) y animales. Sus cristales se disponen en estructuras lineales envueltas en membranas, denominadas magnetosomas, que funcionan como barras o agujas biológicas imantadas. La estructura general de los magnetosomas es muy similar en los tres grupos de seres vivos citados. Aunque ocupan un volumen muy reducido en el interior de los organismos, tienen una gran sensibilidad para con fluctuaciones y variaciones espaciales muy leves del campo geomagnético de fondo al que están expuestos.
En un trabajo de investigación recién publicado han encontrado que las células del epitelio olfativo de los salmones (su órgano del olfato) contienen cristales de magnetita organizados en grupos compactos. Es muy significativo que esas células estén en la misma estructura que recibe la información olfativa, la que proporcionan las sustancias químicas que sirven a los salmones para identificar el río concreto al que se dirigen. Coincide, por tanto, la disposición de las estructuras para orientarse en el camino de vuelta al río natal -mediante magnetorrecepción- y la de las que les permiten precisar la ubicación de su desembocadura -mediante quimiorrecepción-, para iniciar el ascenso a la cabecera.
Los genes que controlan la producción de magnetita en las células olfativas magnéticas comparten ascendencia con los implicados en la misma tarea en ciertos microorganismos. Once de esos genes se encuentran en numerosos animales y nueve están presentes en un grupo de arqueas (organismos unicelulares sin núcleo ni compartimentos internos complejos, pero distintos de las bacterias) emparentado con los antecesores de los organismos superiores. Según los autores de la investigación, los magnetosomas habrían surgido en un grupo de bacterias hace entre dos mil y tres mil millones de años; y hace unos mil millones de años algunos de esos magnetosomas se habrían introducido en el interior de los primeros eucariotas (seres unicelulares con estructuras internas complejas) que, procedentes de un grupo de arqueas, acabarían dando lugar a los organismos multicelulares complejos, como esos salmones que tras pasar un tiempo en el mar, engordando, vuelven a su río a desovar.
Fuente: M. Renee Bellinger, Jiandong Wei, Uwe Hartmann, Hervé Cadiou, Michael Winklhofer, Michael A. Banks (2022): Conservation of magnetite biomineralization genes in all domains of life and implications for magnetic sensing. PNAS, 119 (3) e2108655119; DOI: 10.1073/pnas.2108655119
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La brújula de los salmones se ha escrito en Cuaderno de Cultura Científica.
Día de Pi con BCAM Naukas 2022: Almudena M. Castro – El último puzle de Bach

La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han suamdo a la celebración, organizando la tercera edición del evento BCAM-NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
Almudena M. Castro, es pianista, licenciada en bellas artes, graduada en física y divulgadora científica. En esta charla nos cuenta como un canon musical es como las matemáticas: tú das unas reglas y unas propiedades y después miras a ver qué sale. Esa lógica permite resolver el último puzle de Bach.
Para saber más:
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de Pi con BCAM Naukas 2022: Almudena M. Castro – El último puzle de Bach se ha escrito en Cuaderno de Cultura Científica.
Prevención de la conducta suicida en jóvenes usando perros
Un estudio piloto realizado por un equipo de las facultades de Psicología y Medicina y Enfermería de la UPV/EHU evalúa por primera vez un tratamiento para prevenir la conducta suicida en jóvenes mediante terapia asistida por animales. Tras la intervención, los jóvenes presentaron una reducción de la conducta suicida y de las autolesiones no suicidas, así como una mayor predisposición a buscar ayuda.
 Los perros ayudan a las personas que con conducta suicida fomentando lazos afectivos, reduciendo los sentimientos de rechazo y promoviendo la comunicación espontánea. Foto: 123rf
Los perros ayudan a las personas que con conducta suicida fomentando lazos afectivos, reduciendo los sentimientos de rechazo y promoviendo la comunicación espontánea. Foto: 123rf
El suicidio juvenil es un problema de salud pública de carácter global. Según datos de la Organización Mundial de la Salud (OMS), el suicidio es la cuarta causa de muerte en el grupo de edad de entre 15 y 29 años, después de las lesiones por accidentes de tráfico, la tuberculosis y la violencia interpersonal. La reducción de la mortalidad por suicidio es uno de los objetivos prioritarios de la OMS.
Se han realizado diversos estudios que han aplicado la psicoterapia asistida por animales con jóvenes que presentan problemas de salud mental. Sin embargo, “en este trabajo hemos aplicado por primera vez la terapia asistida por animales, en nuestro caso perros, para tratar un fenómeno tan complejo como la conducta suicida en adolescentes y jóvenes”, indica Alexander Muela, primer autor del estudio.
La población joven que presenta una conducta suicida no siempre es capaz de exteriorizar o compartir con sus familiares o amigos su malestar emocional, y en muchas ocasiones tampoco buscan ayuda o desconfían de los tratamientos tradicionales. “Lo que hemos observado es que el hecho de incluir animales en la intervención favorece la motivación y adherencia al tratamiento. Además, ayuda a establecer un clima de seguridad y confianza porque el animal ejerce de lubricante social. Los perros que utilizamos están especialmente entrenados y preparados. Son animales dóciles, muy sociables y con gran flexibilidad ante estímulos estresantes. Son animales perfectos para ayudar a las personas que presentan una conducta suicida, ya que fomentan los lazos afectivos, reducen los sentimientos de rechazo y estigmatización, y promueven la comunicación espontánea, favoreciendo el efecto del tratamiento”, cuenta el investigador de la UPV/EHU.
“Después del tratamiento asistido con animales —continúa Muela— los jóvenes mostraron reducciones en la ideación suicida y en las autolesiones no suicidas, así como una mayor predisposición a buscar ayuda. Esta percepción de que podían pedir ayuda si la necesitaban puede reflejar un aumento de su confianza para recurrir a recursos de apoyo comunitarios en otros en momentos de gran sufrimiento emocional”.
“A través del tratamiento hemos observado que los jóvenes han aprendido a detectar las señales de alarma del suicidio y han aprendido estrategias de regulación emocional más recomendables que las autolesiones no suicidas.”, afirma Muela. “Aprender a manejar esas señales de alarma, a ser capaces de buscar y pedir ayuda, y conseguir un sentido vital más esperanzador son las claves de este tipo de intervenciones”, añade.
Según el investigador, “Los resultados preliminares obtenidos en este estudio piloto permiten afirmar que el programa puede resultar efectivo para reducir la conducta suicida y las autolesiones no suicidas en jóvenes con altos factores de riesgo de suicidio”. “Una de las principales consecuencias de la presencia de animales es que facilitan las intervenciones de aprendizaje socioemocional y representan un factor añadido que maximiza su impacto”, concluye el investigador de la UPV/EHU.
Referencia:
Alexander Muela, Nekane Balluerka, Eneko Sansinenea, Juan Manuel Machimbarrena, Jon Garcia-Ormaza, Nekane Ibarretxe, Ane Eguren y Patxi Baigorri. (2021) A Social-Emotional Learning Program for Suicide Prevention through Animal-Assisted Intervention Animals doi: 10.3390/ani11123375
Para saber más:
El peor enemigo de la prevención del suicidio
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Prevención de la conducta suicida en jóvenes usando perros se ha escrito en Cuaderno de Cultura Científica.
Armas extraterrestres
En la película “La novia de acero”, dirigida por Gordon Douglas y estrenada en 1952, el protagonista encarga a un herrero que le fabrique un cuchillo muy especial, ya que le pide que utilice los restos de un meteorito para fortalecer la hoja.
Esto que podría parecer mera ficción, se basa en algo mucho más habitual de lo que nos imaginamos. Y es que, entre esas masas rocosas procedentes del espacio exterior que acaban impactando contra nuestro planeta y que comúnmente denominamos meteoritos, existe un tipo muy especial, el de los meteoritos metálicos.
 Daga encontrada en la tumba del faraón Tutankamón, cuya hoja está forjada con hierro procedente de un meteorito metálico. Imagen: Wikimedia Commons
Daga encontrada en la tumba del faraón Tutankamón, cuya hoja está forjada con hierro procedente de un meteorito metálico. Imagen: Wikimedia CommonsLos meteoritos metálicos están formados principalmente por hierro y níquel, acompañados en mucha menor proporción por otros elementos metálicos, como el cobalto. Su principal interés científico radica en que aportan una valiosa información sobre la composición y formación de los núcleos metálicos de los planetas rocosos, incluido el nuestro. De manera un poco poética, tener un meteorito metálico entre nuestras manos sería lo más cercano a tocar el centro de la Tierra.
Pero si algo ha caracterizado la evolución social de nuestra especie ha sido el uso de diferentes materiales para fabricar utensilios y herramientas, entre ellos el hierro. Y si, literalmente, te cae del cielo una gran masa de hierro, no te lo piensas dos veces antes de aprovechar ese metal. Sobre todo, si le aportas connotaciones místicas a la pieza que construyas con ese hierro enviado desde las estrellas, máxime si se trata de armas.
Uno de estos objetos tan particulares es una daga encontrada en la tumba del faraón egipcio Tutankamón, cuya hoja está fabricada con metal procedente de un meteorito. Que esta arma forme parte de su ajuar funerario remarca el alto estatus del fallecido, ya que en la época en la que vivió el uso del hierro no estaba muy extendido por Egipto y estas piezas se reservaban como regalos reales. Además, el uso de un meteorito para su construcción relaciona directamente al faraón con las estrellas, algo muy importante en la cultura egipcia.
Si damos un salto de varios milenios, encontramos un caso similar en Colombia. El 20 de abril de 1810, cayó un meteorito metálico en la localidad de Bocayá, al que dieron el nombre de meteorito de Santa Rosa de Viterbo. Pues un fragmento de este meteorito fue empleado para forjar una espada portada por Simón Bolívar durante las campañas militares para la independencia de varias naciones sudamericanas. La parte más mítica de esta espada la encontramos en la dedicatoria que le haría el naturalista francés Jean-Baptiste Boussingault: “Esta espada ha sido hecha con hierro caído del cielo para defensa de la libertad”.
 Fragmentos del meteorito Gibeon expuestos en la plaza del mercado de Windhoek, Namibia. Fotografía de Raymond M. Coveney Jr. / Wikimedia Commons
Fragmentos del meteorito Gibeon expuestos en la plaza del mercado de Windhoek, Namibia. Fotografía de Raymond M. Coveney Jr. / Wikimedia CommonsPero no siempre se les ha dado esta faceta mística a las armas construidas con metal procedente de meteoritos. A comienzos del siglo XIX se encontró en una pequeña región de Namibia un meteorito al que denominaron Gibeon, en honor a la localidad más cercana al lugar de hallazgo. Este meteorito, que debió impactar en la tierra hace cientos de millones de años, había sido utilizado durante generaciones por los pueblos cercanos para construir todo tipo de herramientas, incluidas sus armas.
Aunque los pueblos namibios empleasen los fragmentos del meteorito Gibeon simplemente como una abundante fuente de hierro de gran calidad para elaborar sus utensilios habituales, en épocas más recientes se les ha vuelto a dar cierto carácter exclusivo a las armas producidas con este metal. Hace unas décadas, el maestro artesano japonés Yoshindo Yoshiwara forjó con uno de esos fragmentos la “katana Tentetsutou” o “espada del cielo”, recordando de nuevo la procedencia del material con el que está hecha. Esta espada se considera como uno de los tesoros más modernos de Japón y se encuentra en exposición permanente en el Instituto de Tecnología de la Prefectura de Chiba, en Tokyo.
 Pareja de pistolas fabricadas en su totalidad con fragmentos del meteorito Gibeon. Imagen tomada de Cabot Guns
Pareja de pistolas fabricadas en su totalidad con fragmentos del meteorito Gibeon. Imagen tomada de Cabot GunsHasta ahora he hablado de armas blancas, pero también existen armas de fuego construidas a partir del metal obtenido de fragmentos del meteorito Gibeon. En 2015, la armería estadounidense Cabot Guns lanzó al mercado una serie de pistolas hechas íntegramente de este material y que, además, funcionan. Estas armas reciben el sugerente nombre de “The Big Bang Set”, haciendo alusión al año de formación de este meteorito, estimado en más de 4000 millones de años, en los albores de la formación de nuestro sistema solar.
Los seres humanos siempre hemos dependido de los materiales que tenemos a nuestro alrededor para poder avanzar como especie y como sociedad, pero a veces estos materiales que encontramos a nuestra disposición no proceden de nuestro propio planeta, sino que vienen directamente del espacio. Estos visitantes del exterior deberían ser conservados como patrimonio geológico para poder conocer mejor los orígenes tanto de la Tierra como del propio Universo, aunque ahora muchos formen parte de nuestro patrimonio cultural e histórico.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Armas extraterrestres se ha escrito en Cuaderno de Cultura Científica.

