Cuaderno de Cultura Científica

La foto que abre esta entrada es bastante popular. Más que por la foto en sí, por una aplicación que permite escribir en la pizarra lo que cada cual quiera. Y, sin embargo, esta foto tiene una historia cuando menos curiosa que nos va a permitir explorar someramente la idea de curvatura y cómo expresarla usando una herramienta matemática tremendamente útil en física, los tensores, a la par que rememorar un momento muy interesante en la historia de la cosmología.

En una época anterior a internet, las fotos de las noticias eran enviadas por las agencias de prensa por correo ordinario urgente a los distintos periódicos. Cada fotografía llevaba anexa su historia escrita por la agencia de noticias adherida a la parte posterior, de esa forma el periódico no tenía que complicarse a la hora elaborar el pie de foto.

La foto de Einstein fue tomada el 14 de enero de 1931 durante su visita al complejo del Observatorio del Monte Wilson en California (Estados Unidos). Sin embargo, se hizo pública 24 años después, con motivo de la muerte de Einstein el 18 de abril de 1955. El pie de foto con el que apareció en prensa decía: “Dr. Albert Einstein writes an equation for the density of the Milky Way on the blackboard at the Carnegie Institute, Mt. Wilson Observatory headquarters in Pasadena, Calif., in this Jan. 14, 1931.”  En español se tradujo tal cual, por ejemplo: “Einstein escribe una ecuación sobre la densidad de la Vía Láctea en un pizarrón del Observatorio Monte Wilson, en Pasadena, California, en 1931”. Pero, ¿desde cuándo una densidad se expresa con subíndices y con la letra R? ¿La densidad de la Vía Láctea es cero? No parece tener sentido.

La historia anexa a la foto que mandó la agencia de noticias podría ayudarnos a desvelar esta posible contradicción. El original es el siguiente:

Vemos que “density” era originalmente “destiny”. ¿Podría haber ocurrido que el avezado reportero de la agencia de noticias se limitase a reflejar la frase que entendió y le llamó la atención y que, en algún paso intermedio, alguien decidiese que el “destino” no puede expresarse en una ecuación y que lo que quería decir es “densidad”? Podría ser. Parecería incluso más probable que Einstein lo que hacía era escribir sobre la curvatura del espaciotiempo. Pero, en realidad, lo que estaba haciendo es considerar el problema de la existencia de la constante cosmológica. Vamos a verlo, que es muy fácil de entender intuitivamente.

Si cortas una naranja por la mitad, quitas la pulpa del interior, e intentas aplanar el hemisferio de piel resultante, terminas rajándolo. Si tratas de aplanar algo con la forma de una silla de montar, como una patata frita (de las de bolsa) revenida, te encuentras con el problema contrario: hay “demasiada” superficie y se te forman pliegues. Si tomas, sin embargo, un rollo de papel de cocina y deseas aplanarlo, no hay nada más fácil, con desenrollarlo, listo. Las superficies como las esferas se dice que están curvadas positivamente, las que tienen la forma de una silla de montar que lo están negativamente, y las que son como el papel de cocina son, simplemente, planas (démonos cuenta de que son planas en este sentido aunque no estén en un plano). Esto es así porque la curvatura se define en términos de “geometría intrínseca” de una superficie, en la que la distancia se mide en función de los caminos que están dentro de la superficie.

Hay varias maneras de hacer precisa esta noción de curvatura y hacerla cuantitativa, de tal manera que a cada punto de la superficie se pueda asociar un número que diga “cómo de curvada” está en ese punto. Para poder hacer esto es necesario que se cumplan determinadas condiciones matemáticas que permitan determinar las longitudes de los caminos, es lo que se llama una métrica riemanniana. La noción de curvatura puede ser generalizada a un mayor número de dimensiones, de tal forma que se habla de la curvatura en un punto en una variedad riemanniana de d dimensiones. Sin embargo, cuando la dimensión es mayor de dos, es decir, no es un plano lo que se curva sino un espacio, las posibilidades de curvatura en un punto se hacen tan complicadas que ya no pueden ser expresadas por un número sino por algo llamado el tensor de Ricci.

Un tensor no es más que la extensión del concepto de vector a dimensiones adicionales. Un escalar, un número, aparece en un gráfico como un punto, un objeto de cero dimensiones. Un vector, que tiene magnitud y dirección, aparecería en un gráfico como una línea, es decir, como un objeto de una dimensión. El tensor extiende esta idea a las dimensiones adicionales. Esto podemos interpretarlo como un conjunto de vectores relacionados, moviéndose en múltiples direcciones en un plano.

Lo veremos mejor de otra manera. En vez de pensar en un vector como un conjunto de coordenadas, lo podemos considerar una operación, es decir, un vector lo que haría es asociar una dirección a un número. Lo importante desde el punto de vista matemático es que la operación es lineal y homogénea. Gracias a esto, un vector queda completamente determinado por sus proyecciones en d direcciones, donde d es el número de dimensiones del espacio en el que se define. Por tanto, un vector se puede expresar como un conjunto de números que son en realidad sus proyecciones en un sistema de ejes coordenados.

Un vector es realmente un tensor de rango 1, asocia 1 dirección a un número. Un escalar, es un tensor de rango 0, asocia 0 direcciones a un número. Por tanto un tensor de rango 2 (un tensor ya por derecho propio), asocia dos direcciones arbitrarias a un número. Si quisiéramos expresarlo en términos de las d coordenadas, como se hace con los vectores, necesitaríamos d x d números. Para un tensor de rango q, por tanto, necesitaríamos nq números.

Veamos ahora desde el punto de vista formal las ecuaciones de campo de la relatividad general. Si has llegado leyendo hasta aquí no te asustará demasiado, después de todo no es más que una igualdad tensorial en la que se relacionan un conjunto de tensores 4 x 4 (simétricos, pero en esto no vamos a entrar ahora), para un espaciotiempo de 4 dimensiones. Así:

Donde Rμν es el tensor de curvatura de Ricci del que hablábamos más arriba, R es la curvatura escalar (simplificando, la curvatura entendida en el sentido que hablábamos más arriba, un número asociado a un punto del espacio), gμν es el tensor métrico (una generalización del campo gravitatorio y principal objeto de interés), Λ es la constante cosmológica, G es la constante gravitacional de Newton, c la velocidad de la luz en el vacío y Tμν el tensor de energía-impulso.

Los índices en los tensores son etiquetas, es una forma de llamarlos. En este caso empleamos la notación abstracta de Penrose. Se puede usar cualquier símbolo conveniente para los índices de los tensores. Tradicionalmente, las letras latinas se usan para indicar que se están usando coordenadas espaciales (x, y, z), mientras que las griegas se emplean para indicar coordenadas espaciotemporales (x, y, z, t). En la época de la foto esta convención no se había establecido.

Una simple observación de la ecuación de campo nos dice que podría haber algo similar con lo que escribe Einstein en la pizarra: el tensor de Ricci. Efectivamente, existe un caso especial de la ecuación de campo en el que se postula que Tμν = 0, es decir, que la energía y el momento se conservan localmente. En este caso, y por las propiedades de los tensores, solo existe una posibilidad para que Rμν= 0 o, usando la notación de Einstein, Rik = 0, y es que Λ = 0. En definitiva, que el pie de foto podría ser “El Dr. Einstein discutiendo [por lo de la interrogación] la posibilidad de que la constante cosmológica sea cero”.

Para saber más:

Las ecuaciones de campo de la relatividad general

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 17 de diciembre de 2010.

El artículo Einstein y la pizarra del Observatorio del Monte Wilson se ha escrito en Cuaderno de Cultura Científica.

Francisco José Esteban Ruiz

Foto: TheOtherKev / Pixabay

Sin entrar en el debate de si la obesidad debe o no considerarse una enfermedad, y siendo conscientes de que sus causas pueden ser múltiples, nos enfrentamos a un verdadero problema de salud pública que aumenta tanto la morbilidad (enfermar) como la mortalidad (morir debido a ello).

Independientemente de lo que nos lleve a pasarnos del peso que se considera dentro de lo normal, esos kilos de más nos afectan de un modo u otro. Existen pruebas irrefutables de que la obesidad es un importante factor de riesgo para padecer otras enfermedades como hipertensión, dislipemia (alteración de la cantidad de lípidos en sangre, como el colesterol), diabetes, enfermedades cardiacas e infartos cerebrales, piedras en la vesícula, artrosis, ovario poliquístico, síndrome de apnea del sueño y algunos tipos de cáncer. Y nos hemos quedado cortos, pues se considera que la obesidad y el sobrepeso incrementan el riesgo y favorecen el desarrollo de más de 200 enfermedades crónicas.

Además, y desafortunadamente, desde el inicio de la pandemia debida al coronavirus se hizo patente el hecho de que la obesidad empeoraba la situación. Sí, desde hace años se conoce que las personas obesas son más vulnerables a las infecciones y a las complicaciones derivadas de las mismas. En el caso concreto de la covid-19, y según un estudio de la Sociedad Española de Obesidad, el 80% de las personas con manifestaciones severas por coronavirus en España eran obesas.

La acumulación de grasa enferma al tejido

¿A qué se debe que el ser obeso aumente el riesgo de contraer otras enfermedades? La investigación en biología celular, bioquímica y genética nos ayuda a responder.

La principales células responsables del almacenamiento de grasa en nuestro cuerpo son los adipocitos, que forman parte del llamado tejido adiposo. En este tejido también hay otros tipos celulares, como los linfocitos y los macrófagos del sistema inmune, y el buen estado de salud del tejido depende de que exista un equilibrio funcional entre todos los tipos de células.

Pues bien, en la base de la obesidad se encuentra la adiposopatía, que podemos decir que es una alteración que se produce debido a que, por diferentes causas, ingerimos más calorías de las que gastamos. Esto da lugar a una alteración anatómica (deposición anormal de grasa) y funcional (inmune y hormonal) del tejido adiposo que puede causar o empeorar una enfermedad metabólica.

¿Y qué es una enfermedad metabólica? Sencillamente un daño debido a la alteración de nuestras vías metabólicas, como la del colesterol, la insulina y las hormonales, que a su vez dan lugar a enfermedades como arterioesclerosis, la hipertensión, la diabetes y un aumento de hormonas masculinas en mujeres y su disminución en hombres.

La grasa se acumula donde no debe

Cuando los adipocitos comienzan a acumular más grasa de lo normal también se produce deposición de grasa más allá de donde debería, por ejemplo, en el hígado y en el músculo. Junto a la adiposopatía, este hecho provoca una alteración en la secreción de hormonas, como la leptina, y de toda una serie de proteínas proinflamatorias, como las citoquinas.

Además, la obesidad da lugar a una deposición anormal de grasa alrededor del corazón. Un estudio reciente realizado sobre casi 7 000 participantes ha puesto de manifiesto que el aumento de la grasa pericárdica se asocia con el riesgo de fallo cardiaco.

El aumento en la secreción de citoquinas debido a la obesidad no sólo reduce la capacidad de responder a la infección respiratoria causada por el coronavirus, sino que provoca que todo empeore. Más aún, la asociación de la obesidad con una disminución de la función inmune hace que estos pacientes sean más susceptibles a todo tipo de infecciones.

En cuanto al tratamiento, en los obesos disminuye la respuesta a los antivirales y son menos eficaces las vacunas.

El novelista Charles Dickens dijo que “cuanto más engorda uno, más prudente se vuelve. Prudencia y barriga son dos cosas que crecen simultáneamente”. Visto lo visto, más vale que seamos prudentes y no hagamos crecer la barriga.

Sobre el autor: Francisco José Esteban Ruiz  es profesor titular de biología celular en la Universidad de Jaén

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo Por qué la obesidad es un imán para otras enfermedades se ha escrito en Cuaderno de Cultura Científica.

Foto:  Brett Jordan / Unsplash

La búsqueda de información en Google ofusca la percepción acerca del origen de lo que sabemos o creemos saber. Al demandar a Google datos, historias, piezas de conocimiento del tipo que sea, tendemos a considerar como propio el origen de la información que nos da el buscador. Esto es, tendemos a pensar que ya disponíamos de ella, y así sobrevaloramos nuestros recursos y capacidades cognitivas. Esta es la principal conclusión de un estudio publicado hace unas semanas en la revista PNAS.

El hecho en sí, el recabar conocimiento ajeno, no es inhabitual en absoluto. Nadie lo sabe todo. Dependemos del conocimiento de familiares, amistades, colegas. Configuramos con esas personas sistemas cognitivos compartidos que nos permiten atender, procesar y recordar información de forma colectiva. No necesitamos saberlo todo; lo que necesitamos es saber quién sabe qué cosas. La ciencia, por ejemplo, funciona así, sobre la base de un conocimiento y comprensión de los fenómenos de la naturaleza compartidos de forma parcial por centenares de miles de personas, muchas de las cuales ni siquiera viven en la actualidad. La cognición humana no es individual; el pensar, recordar y conocer son, muy a menudo, colaborativos, el producto de la interacción entre recursos cognitivos propios y ajenos.

En las últimas décadas, a los mecanismos clásicos de cooperación cognitiva se ha sumado la internet y sus sistemas de búsqueda rápida. La red permite expandir la mente dotándonos de una memoria externa que se puede consultar cada vez que se necesita. Lo sabe casi todo y está siempre a nuestra disposición; nos proporciona la información que deseamos en el instante en que la solicitamos, sin esfuerzo por nuestra parte, con mayor facilidad, incluso, que si la obtuviésemos de nuestra misma mente. No tenemos que acudir a la biblioteca o consultar con un colega por teléfono. Es esa particularidad, esa facilidad para acceder a ella, la ausencia de otros actos intermedios, lo que, al parecer, hace que se difuminen las fronteras entre el conocimiento interno y el externo. Tendemos a pensar que el conocimiento de internet es nuestro conocimiento.

Como se difumina la frontera entre conocimiento externo e interno, quienes recurren con mayor frecuencia a internet para buscar información tienen más confianza en su memoria. A menudo olvidan, incluso, que habían recurrido a Google para saber algo. Creen que las respuestas obtenidas de internet procedían de su propia memoria.

Sabíamos del denominado “efecto Google”: cuando obtenemos información fácilmente en internet, tendemos a no almacenarla en nuestra memoria o, incluso, a olvidarla con facilidad. Pues bien, el estudio citado antes ha revelado la existencia de un segundo efecto Google, uno que no se refiere a lo que la gente sabe, sino a lo que cree saber. Como consecuencia, en un mundo en el que la búsqueda en internet es con frecuencia más rápida y fácil que bucear en la memoria propia, la gente puede llegar a saber menos, aunque crea saber más.

Las implicaciones de este fenómeno pueden ser variadas e importantes. Al aumentar la confianza de las personas en su conocimiento y comprensión, puede distorsionar su juicio acerca del aprendizaje y la motivación para aprender. Puede también otorgar mayor (e injustificada) confianza en el criterio propio a la hora de tomar ciertas decisiones. Y puesto que somos poco dados a cuestionar lo que consideramos conocimiento propio, al borrarse la frontera con el que obtenemos de la red, es más difícil detectar informaciones erróneas, con las consecuencias que se pueden derivar de ello.

¿Se imagina un mundo lleno de ignorantes que creen saberlo casi todo? Sé que exagero, pero quizás no demasiado. Piénselo.

Fuente: Ward, A. F. (2021): People mistake the internet’s knowledge for their own. Proceedings of the National Academy of Sciences, 118 (43) e2105061118.

 

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Ignorantes que creen saberlo todo se ha escrito en Cuaderno de Cultura Científica.

El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

Ningún tiempo pasado fue mejor que hoy en términos sanitarios. Sin embargo, la pandemia ha puesto de manifiesto la existencia de una parte de la sociedad que es presa fácil de los enemigos de la medicina de base científica; que es, por cierto, la única medicina (las alternativas, por definición, no tienen base científica). Esther Samper, que es doctora en medicina regenerativa y comunicadora, lidia con estos enemigos a diario.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2021: Esther Samper – Eran otros tiempos se ha escrito en Cuaderno de Cultura Científica.

Fuente: Fundación Valle Salado de Añana

El Valle Salado de Añana es una zona muy biodiversa, en la que las especies acuáticas son especialmente llamativas. Los análisis realizados por el grupo de investigación MikroIker, de la Universidad del País Vasco/Euskal Herriko Unibertsitatea, han aportado información sobre la existencia de una nueva especie microbiana. La nueva especie bacteriana aislada en el agua del manantial de Santa Engracia ha sido bautizada como Altererythrobacter muriae, y, por el momento, solo ha sido identificada en ese lugar.

“Los estudios poblacionales microbianos realizados durante los últimos años en el Valle Salado de Añana nos están permitiendo conocer la evolución y la relación entre las especies detectadas en ese ambiente. Hemos observado cómo existe la posibilidad de estar ante algunas nuevas especies bacterianas no descritas anteriormente que sean únicas de ese ecosistema, lo que cerciora la biodiversidad exclusiva del lugar aumentando su valor ecológico”.

Ilargi Martinez-Ballesteros.

Los ambientes hipersalinos se consideran ambientes metabólicamente extremos y son habitados por un grupo diverso de microorganismos con capacidad para sobrevivir en concentraciones variables (2-30 %) de cloruro sódico (sal), denominados halófilos. El Valle Salado de Añana se emplaza sobre una gran burbuja de sal que procede de la desecación de un antiguo mar de hace 200 millones de años. El agua dulce de lluvia atraviesa las capas más profundas de halita o sal gema disolviéndola y aflora en forma de manantiales hipersalinos, ofreciendo así hábitat a una gran diversidad de microorganismos halófilos y halotolerantes.

Existe una amplia variedad de halófilos (pertenecientes a los tres dominios principales de la vida, Archaea, Bacteria y Eukarya), que transforman una amplia gama de sustratos en los hábitats hipersalinos. Además, los distintos mecanismos de haloadaptación desarrollados por los microorganismos en esas condiciones extremas han derivado en la producción de compuestos útiles para la supervivencia microbiana que, a su vez, han resultado ser de gran interés en los ámbitos de la biomedicina, la biorremediación o la industria alimentaria.

“Los microorganismos son indispensables en el mantenimiento de la biosfera, ya que regulan los ciclos biogeoquímicos de los principales elementos, participan en los procesos de descomposición de materia orgánica, favorecen el ciclaje de nutrientes, y degradan compuestos contaminantes, procesos indispensables en el mantenimiento de los ecosistemas”.

Ilargi Martinez-Ballesteros.

A la hora de comprender la diversidad microbiana en ambientes extremos, como es el Valle Salado de Añana, es importante estudiar la composición de las comunidades procariotas (bacterias y arqueas) tanto en los manantiales salinos de los que se extrae sal en distintos puntos del valle, como de afluentes salobres que afloran en otros puntos del valle. “Esto permitirá generar conocimiento básico sobre las poblaciones microbianas allí presentes, sus patrones de distribución y su potencial uso biotecnológico en beneficio de la salud tanto humana como medioambiental. Los métodos de análisis microbiológicos convencionales y quimiotaxonómicos o la genómica comparativa han permitido ya el reconocimiento de tipos interesantes y numéricamente importantes de halófilos y halotolerantes”, concluye Ilargi Martinez-Ballesteros.

Referencia:

Maia Azpiazu-Muniozguren, Ilargi Martinez-Ballesteros, Javier Gamboa, Sergio Seoane, Rodrigo Alonso, Lorena Laorden, Javier Garaizar, Joseba Bikandi Altererythrobacter muriae sp. nov., isolated from hypersaline Añana Salt Valley spring water, a continental thalassohaline-type solar saltern  (2021) International Journal of Systematic and Evolutionary Microbiology doi: 10.1099/ijsem.0.004734

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Una nueva especie extremófila en el Valle Salado de Añana se ha escrito en Cuaderno de Cultura Científica.

 

Reconstrucción de un sinápsido, grupo precursor de los mamíferos, de finales del Pérmico. Autor: U. Kikutani

Hace unos 252 millones de años se produjo la mayor extinción masiva de los últimos 500 millones de años de historia de nuestro planeta, la extinción del límite Pérmico-Triásico. En poco menos de 1 millón de años, desaparecieron aproximadamente el 95% de las especies que había en la Tierra. Se vio el final de todas las especies de trilobites que habitaban los mares y océanos, se extinguieron muchas especies de los helechos y coníferas gigantes que formaban enormes bosques pantanosos y desaparecieron más del 70% de las especies de reptiles y sinápsidos, grupo precursor de los actuales mamíferos, que dominaban la tierra firme. Por eso a esta extinción se la suele denominar “La Gran Mortandad” y se toma como un punto de inflexión tan importante en la historia evolutiva del planeta, que da fin a la Era Paleozoica y comienzo a una nueva etapa, la Era Mesozoica. Poniéndonos poéticos, prácticamente la podríamos denominar como un apocalipsis biótico en el que el contador evolutivo casi se puso a 0. Por suerte, la vida siempre se abre camino y, si superó la extinción del Pérmico-Triásico, puede soportar casi cualquier cosa que se le ponga por delante.

Meseta de Putorana, incluida dentro de los Trap Siberianos, formada por la acumulación de rocas volcánicas. Foto:  jxandreani / Wikimedia Commons

Son varias las causas a las que se aluden para intentar explicar los motivos que provocaron esta extinción biótica. Por un lado, en la actual Siberia, se encuentran unos enormes depósitos volcánicos, denominados los Trap Siberianos, que se formaron por sucesivas erupciones acontecidas a finales del Pérmico. Estas gigantescas erupciones debieron liberar toneladas de gases de efecto invernadero a la atmósfera, que rápidamente cubrieron todo el globo y dieron lugar a un intenso calentamiento global que, literalmente, achicharró la Tierra. Por otro lado, en los mares y océanos se registró un descenso generalizado de los niveles de oxígeno disuelto en el agua, lo que produjo condiciones anaerobias en el fondo que dieron lugar a la expulsión de enormes cantidades de sulfuro de hidrógeno a la atmósfera, gas nocivo para la biota y que, además, es capaz de afectar a la capa de ozono. Y también se descongelaron los depósitos de hidratos de metano que se encontraban enterrados en el sedimento de los fondos oceánicos, liberando toneladas de este gas de efecto invernadero a la atmósfera. Por último, recientemente se especula con un posible impacto de un cuerpo extraterrestre a finales del Pérmico tras el descubrimiento de un cráter meteorítico en la Antártida, aunque aún se está investigando esta hipótesis ante la necesidad de realizar una datación temporal más precisa de este hallazgo.

Pero ahora es cuando todo se pone más interesante. Y aviso de que voy a hacer algunos spoilers. En 1934, la escritora británica Agatha Christie publicó una de sus obras más famosas, Asesinato en el Orient Express. En esta novela, el detective belga más admirado a nivel mundial, Hércules Poirot, se enfrenta al asesinato de un conocido hombre de negocios norteamericano sucedido durante uno de los viajes de este famoso tren y tiene que descubrir al asesino mientras esperan a que los rescaten tras acabar varados debido en un alud de nieve. Ahora es cuando debéis dejar de leer este artículo si no conocéis la novela, puesto que voy a destriparos el final. Y es que lo que descubre Poirot es que todos los pasajeros son los asesinos, ya que tenían una relación entre ellos y un motivo para acabar con la víctima, así que entre todos terminaron con su vida apuñalándole de uno en uno.

Y algo similar es lo que parece que sucedió a finales del Pérmico en nuestro planeta. Las causas que os he descrito previamente, cada una por sí sola, no serían capaces de acabar con cerca del 95% de las especies de nuestro planeta. Pero todas juntas y de manera combinada, sí. Las erupciones volcánicas provocarían un efecto invernadero generalizado en todo el planeta que daría lugar a un aumento de la temperatura del agua marina, que a su vez provocaría las condiciones anóxicas del fondo, con la generación de sulfuro de hidrógeno y la descongelación de los hidratos de metano. Estos dos gases, una vez liberados a la atmósfera, aumentarían el efecto invernadero, retroalimentando las condiciones de calentamiento global. Incluso la hipótesis del impacto extraterrestre tendría cabida en este juego, ya que sería factible que las ondas de choque provocadas por el mismo fueran las desencadenantes del vulcanismo siberiano. A esta hipótesis que une las posibles casusas de la extinción del Pérmico-Triásico como auto desencadenantes una de la otra, se la ha denominado “Efecto Asesinato en el Orient Express”, en honor a la gran novela de Agatha Christie.

Como podéis comprobar, en geología siempre nos encanta hacer homenajes a la cultura popular poniendo nombres de este tipo a las cosas que descubrimos. Y aunque esta hipótesis aún está en estudio, el nombre es más que apropiado, ya que por sí mismo explica lo que pudo suceder en nuestro planeta hace unos 252 Millones de años durante la mayor crisis biótica de nuestra historia.

Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU

El artículo Una extinción de novela policiaca se ha escrito en Cuaderno de Cultura Científica.

 

Vera Stepen nació en Chicago (Estados Unidos) el 5 de marzo de 1931. Sus padres eran judíos rusos que habían emigrado a Estados Unidos: su madre, Helen Blinder, era dentista, y su padre, Lyman Stepen, joyero. Deseaban que su única hija disfrutara de los beneficios en educación que se ofrecían en este país, y la incentivaron a estudiar.

Vera Pless. Fuente: Wikimedia Commons.

 

Cuando Vera tenía unos 12 años, un amigo de la familia, estudiante de posgrado en la Universidad de Chicago, le enseñó cálculo. Observó que poseía un verdadero talento matemático, pero Vera no estaba demasiado interesada en las matemáticas en ese momento. Tocaba el violonchelo en la orquesta de su escuela, y soñaba con llegar a ser una instrumentista destacada. Pero su padre tenía otros planes para ella, y la obligó a abandonar la escuela secundaria dos años antes.

Vera ingresó en la Universidad de Chicago donde obtuvo una licenciatura en solo tres años. Seguía sin tener un interés especial por convertirse en matemática, a pesar de tener cerca varias personas que la inspiraron.

No tenía la ambición de convertirme en matemática; las chicas en ese momento aspiraban a ser esposas (de hombres exitosos) y madres. Tal vez algunas chicas «desafortunadas» no se casaron e hicieron una carrera; pero, en lo que respecta a las mujeres matemáticas, nunca vi una durante mi época de estudiante. Sin embargo, conocía el trabajo de Emmy Noether y tal vez influyó en mi elección de área, álgebra; aunque creo que la enseñanza de Irving Kaplansky fue lo que realmente me inspiró.

Vera Pless, AMS Notices

Efectivamente, Emmy Noether (1882-1935) e Irving Kaplansky (1917-2006) eran especialistas en álgebra abstracta, en teoría de anillos y, sin duda alguna, dos personas realmente inspiradoras. Así, Vera continuó sus estudios en la Universidad de Chicago preparando su maestría. En esa época conoció a su futuro esposo, un estudiante de física, en la universidad y se casaron en 1952, dos semanas antes de su examen de maestría. Vera Stepen pasó a llamarse Vera Pless.

Vera comenzó a trabajar con un grupo de física en la Universidad de Chicago mientras su esposo preparaba su doctorado en física experimental de altas energías. Poco después consiguió una beca para estudiar en la Universidad Northwestern y comenzó a trabajar en su tesis doctoral bajo la supervisión de Alex Rosenberg (1926-2007), un antiguo alumno de Kaplanski.

Cuando su marido terminó su doctorado, le ofrecieron un puesto en el Instituto de Tecnología de Massachusetts y Vera se mudó con él a Cambridge. Rosenberg se mostró dispuesto a que Pless terminara su tesis doctoral a distancia; Vera regresó en junio de 1957 a la Universidad Northwestern para defender su trabajo doctoral Quotient Rings of Continuous Transformation Rings. Dos semanas más tarde nació prematuramente su primera hija, y Vera se quedó en casa cuidando de la pequeña; era lo que se esperaba de ella.

En 1959 llegó su segundo hijo, un niño. Cuando el pequeño tuvo la edad suficiente para asistir a la guardería, en 1962, Pless comenzó a impartir cursos en la Universidad de Boston.

Todavía sentía que mi primera responsabilidad eran mis hijos pequeños. Incluso con mi docencia, encontré esta vida agobiante. Teníamos poco dinero, por lo que no podíamos contratar niñeras ni ayuda doméstica. Mi esposo era muy ambicioso, trabajaba muchas horas, y no sentía que debía ayudar de todos modos, algo que era común en esa época.

Vera Pless, AMS Notices

Cuando el menor de sus hijos tuvo la edad suficiente para comenzar la escuela primaria, Vera Pless comenzó a buscar puestos de tiempo completo. Pero no tuvo éxito: aunque tenía experiencia docente, había interrumpido su investigación. Era consciente de que la discriminaban; de hecho, en algunas instituciones le decían abiertamente que la universidad no era el lugar adecuado para una mujer.

En ese momento, en 1963, el Laboratorio de Investigación de Cambridge de la Fuerza Aérea Estadounidense buscaba matemáticos para trabajar en el área emergente de códigos correctores de errores. Aunque Vera desconocía a que se dedicaba este campo, su experiencia algebraica se consideró suficiente para incorporarse en el equipo. Trabajó allí hasta 1972, con un breve permiso maternal cuando nació su tercer hijo. Se convirtió en una de las principales expertas mundiales en teoría de códigos.

Publicó varios artículos sobre códigos correctores de errores, y otros que continuaban con la investigación que había realizado para su doctorado.

En 1973, la llamada enmienda Mansfield limitó las asignaciones para investigación en defensa solo a proyectos que tuvieran una aplicación militar directa. Vera Pless dejó su puesto para trabajar, durante tres años, como investigadora asociada en el Instituto de Tecnología de Massachusetts en el proyecto MAC sobre matemáticas y computación. En 1975 fue nombrada profesora titular en la Universidad de Illinois en Chicago. Su esposo y su hijo menor se quedaron a vivir en la zona de Boston; el matrimonio se divorció en 1980.

Portada de Introduction to the theory of error-correcting codes.

 

En 1982 publicó un libro sobre la teoría de la codificación, Introduction to the theory of error-correcting codes, diseñado como un curso de un semestre para estudiantes universitarios. Trataba sobre teoría de codificación algebraica, y fue especialmente apreciado por incluir demostraciones claras y sencillas. Sus publicaciones de investigación suman más de un centenar.

Se jubiló en 2006 y falleció el 2 de marzo de 2020 a la edad de 88 años.

Mirando atrás, creo que tuve mucha suerte. Trabajé en codificación desde sus inicios, y se ha convertido en un tema matemático fascinante. He apreciado la oportunidad de trabajar con muchos matemáticos maravillosos, en particular Richard Brualdi, John Conway y Neil Sloane. Era capaz de cuidar a mis hijos en sus años más jóvenes en un entorno de baja presión. […] Nuestra disciplina no es la única que exige mucho. Mi hija, médica residente con una hija pequeña, tiene mucho que decir sobre las largas horas demandadas a los residentes. Lamentablemente, nuestra sociedad está perdiendo probablemente valiosas contribuciones de las mujeres por estas razones. Y muchas mujeres están pagando un gran precio emocional, ya sea renunciando a carreras o no dedicando tanto tiempo a sus familias como creen que deberían.

Vera Pless, AMS Notices

Referencias

• Su página web, Universidad de Illinois en Chicago
• Vera Pless (1991). In Her Own Words, AMS Notices 38 (7) 705-706
• O’Connor, John J.; Robertson, Edmund F., Vera Pless, MacTutor History of Mathematics archive, University of St Andrews
• Vera Pless, Biographies of Women Mathematicians, Agnes Scott College

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo Vera Pless, de especialista en álgebra abstracta a experta en teoría de códigos se ha escrito en Cuaderno de Cultura Científica.

Foto: Bermix Studio / Unsplash

“Solo sé que no sé nada”. ¿Cuántas veces habremos oído esta frase atribuida a Sócrates como justificación de la ignorancia? Sin embargo, esta sentencia no aparece en ninguno de los escritos en los que se cita al que era más sabio que ningún otro humano, parafraseando a la Pitia. De hecho, la comprobación de lo que en realidad quería decir nos desvelará que Sócrates estaba en realidad probablemente sujeto a un prejuicio cognitivo, el efecto Dunning-Kruger.

El dicho se suele atribuir al Sócrates de Platón. Sócrates no dejó nada escrito, de ahí que lo que conocemos de él es lo que escribieron sus contemporáneos, especialmente Platón. En ninguna de las referencias de Platón a Sócrates aparece la expresión “Solo sé que no sé nada”.

Sin embargo, en la Apología, la versión idealizada de la defensa que hizo Platón de Sócrates en el juicio a este, encontramos: “Este hombre, por una parte, cree que sabe algo a pesar de no saber nada. Por otra, yo, igualmente ignorante, no creo saber algo”. Esta es la frase a partir de la cual se produce el salto, lógicamente falaz, del “no creo saber algo” al “no sé nada”. El autor no dice que no sepa algo sino que no puede, que nadie puede, saber con absoluta certeza, pero que puede tener confianza acerca del conocimiento de ciertas cosas (por ejemplo, de que el otro no sabe nada). Como es obvio, esta conclusión no la extraemos de esta frase aislada sino sobre el análisis del conjunto de la obra sobre Sócrates que han realizado varios autores.

Vemos pues que la ignorancia o, mejor, su admisión, no es una resultante sino un punto de partida para el conocimiento. Es la base del método socrático que se ilustra mejor en los primeros diálogos de Platón. El método consiste en simular ignorancia, la llamada ironía socrática, o admitirla como base sobre la que construir el conocimiento y establecer un diálogo con un supuesto experto, cuya confiada afirmación de conocer terminará siendo destruida. A partir de aquí ya se pueden desarrollar ideas más adecuadas.

Así, en Menón, un diálogo de Platón, aparece Sócrates diciendo: “Por eso ahora no sé lo que es la virtud; quizás tu lo supieses antes de que me contactases, pero ahora eres ciertamente como uno que no sabe”. En este punto el objetivo de Sócrates está claro, cambiar la posición de Menón, que era un firme creyente en su propia opinión y cuya afirmación de conocimiento Sócrates acaba de probar que es infundada.

Estamos ante el origen de la filosofía occidental que terminará resultando en lo que hoy conocemos como ciencia: Sócrates comienza toda sabiduría con el autocuestionamiento, con la propia admisión de ignorancia.

Pero veamos la misma cuestión desde un punto de vista diferente. En los diálogos socráticos de Platón el sabio es el que duda, el que se cuestiona, mientras que el verdadero ignorante es el que tiene muy clara cuál es la verdad, a la que ha llegado en muchos casos por sí mismo sin preocuparse demasiado de donde surge el conocimiento. Por otra parte, estos “sabios” no siempre reconocen su error, están pagados de sí mismos y se creen superiores a los demás. Estamos ante una ilustración del efecto Dunning-Kruger.

El efecto Dunning-Kruger se puede expresar de la siguiente manera: los peores trabajadores/estudiantes/participantes son los que menos conscientes son de su propia incompetencia. Toma su nombre de un estudio de 2003 que realizaron Dunning, Kruger y otros con estudiantes universitarios con respecto a los resultados de sus exámenes. Después los resultados han sido reproducidos en varias ocasiones, por ejemplo con estudiantes de medicina a la hora de evaluar su capacidad para hacer entrevistas de diagnóstico, con administrativos evaluando su rendimiento o con técnicos de laboratorios médicos calibrando su nivel de dominio del trabajo.

La razón de fondo parece estar en que los que peor lo hacen son incapaces de aprender de sus errores.

Una solución aparentemente simple es decirle directamente al incompetente que lo es y por qué. Pero no funcionará. Desafortunadamente, el incompetente habrá estado recibiendo ese tipo de respuesta durante años y no habrá sido capaz de enterarse. A pesar de los exámenes suspensos, los trabajos mal hechos, las risas, burlas y sesudas contraargumentaciones a sus comentarios en redes sociales y la irritación que provocan sistemáticamente en los demás, el incompetente sigue sin creerse que lo sea.

Como Sócrates, las personas con verdadero talento tienden a subestimar lo buenos que son. Es la parte simétrica de este prejuicio: las personas inteligentes tienden a asumir que para los demás las cosas son tan fáciles y evidentes como para ellos, cuando lo que están haciendo es proyectar su propia luz y creer que ven un reflejo de la misma en los demás.

Estas ideas se conocen desde mucho antes que Dunning-Kruger y los demás investigadores las cuantificasen. Se pueden encontrar muchas citas al respecto, como esta de Bertrand Russell en la que se refiere a su tiempo, pero que como sabemos que es otro prejuicio cognitivo, podemos extrapolar a cualquiera:

“Una de las cosas dolorosas de nuestra época es que aquellos que se sienten ciertos son estúpidos, y aquellos con algo de imaginación y comprensión están llenos de dudas e indecisión”.

En el mundo de Internet lo anterior tiene una consecuencia práctica inmediata: No alimentes al comentarista manifiestamente incompetente, es solo una versión de trol que busca llamar la atención. Su problema es que no sabe, ni puede llegar a saber, que lo es.

Para saber más:

Lo que los sabelotodos no saben, o la ilusión de competencia
 

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 13 de junio de 2012.

El artículo Sócrates y el efecto Dunning-Kruger en redes sociales se ha escrito en Cuaderno de Cultura Científica.

Ilustración: María Lezana

La gacela de Thomson (Eudorcas thomsonii) es un antílope de pequeño tamaño (pesa entre 20 y 30 kg) que habita en los pastizales de las sabanas de Tanzania y Kenia, donde es una de las presas preferidas de leones, guepardos, leopardos y cocodrilos.

Puede alcanzar velocidades de hasta 80 km/h, normalmente cuando huye de alguno de sus depredadores habituales, aunque difícilmente supera los 40 km/h en carrera sostenida durante varios minutos.

Tras huir de un depredador -quizás del más rápido de ellos, el guepardo-, durante un tiempo de unos 5 min, y suponiendo que no haya sido atrapada, ha generado una gran cantidad de calor debido al esfuerzo realizado. Ese calor no se disipa inmediatamente, de manera que provoca un aumento de la temperatura corporal bien por encima de la habitual. La sangre arterial puede elevarse de los 38 °C o 39 °C normales hasta los 44 °C. La gacela de Thomson, a pesar de ser un animal homeotermo, pierde así de manera transitoria la capacidad para mantener constante su temperatura corporal como consecuencia del esfuerzo.

Al huir despavorida a toda velocidad, el gasto metabólico de la gacela se multiplica por cuarenta. Además del efecto del esfuerzo, la temperatura ambiental es alta, muy alta, tanto quizás como la corporal. Así pues, a la gacela le resulta muy difícil disipar el calor que produce, por lo que la temperatura sanguínea sube rápidamente. Además, es posible que esa temperatura corporal tan alta sirva a la gacela para que sus músculos se contraigan más rápidamente y pueda así huir con mayor facilidad del depredador.

La elevación de la temperatura corporal no se debe a que fallen los sistemas de disipación de calor. De hecho, la gacela jadea a muy alta frecuencia, tanto para tomar más oxígeno como para refrigerar la sangre facilitando la evaporación del líquido que cubre las superficies respiratorias. El problema es que bajo las condiciones en que se encuentra no es posible mantener la temperatura en los valores normales, incluso aunque los sistemas de termorregulación mantengan plena integridad funcional. La carga de calor es demasiado alta y la gacela no puede disipar todo el que genera.

Pero ocurre que la elevación de la temperatura no se produce por igual en todo el organismo, ya que gracias precisamente al jadeo, la gacela de Thomson puede mantener su encéfalo más fresco que el resto de órganos. De hecho, mientras el cuerpo alcanza los 44 °C, el encéfalo no pasa de 41 °C, temperatura por encima de la cual las neuronas sufrirían graves daños.

El mecanismo de refrigeración se basa en una rete mirabile (red maravillosa). En su camino hacia el encéfalo, la sangre que circula por la arteria carótida se distribuye entre centenares de arteriolas o capilares, para volver a agruparse justo antes de alcanzarlo. Esas arteriolas constituyen una rete mirabile, un dispositivo especialmente apto para intercambiar calor. El intercambio se produce porque los vasos arteriales atraviesan un seno que se encuentra lleno de sangre venosa, que procede, precisamente, de la zona nasal de la gacela, donde ha tenido lugar la evaporación del líquido superficial y, como consecuencia, el enfriamiento de la que circula por allí. De esa forma se enfría la sangre que circula por las arteriolas, cediendo calor a la venosa que procede de la nariz. Al atravesar el seno, la sangre arterial reduce su temperatura en unos 2 o 3 °C.

En la anotación anterior de la sección Animalia, sobre la irrigación de la musculatura de algunos peces (atunes y lenguados), vimos cómo funcionaba una rete mirabile como esta, con la diferencia de que aquella red servía para calentar la sangre que irrigaba los músculos que impulsan al atún y ésta para enfriar la sangre que irriga el encéfalo. En ambos casos se producen intercambios de calor mediante un dispositivo en contracorriente, aunque con objetivos opuestos.

En inglés denominan “selective brain cooling” al mecanismo, basado en el jadeo, de que hace uso la gacela de Thomson. Aunque no es el único animal que lo utiliza, pues bastantes ungulados domésticos también recurren a él cuando lo necesitan. De todos ellos cabría decir aquello de que mantienen la cabeza fría y, en este caso, las pezuñas calientes.

 

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Pezuñas calientes, cabeza fría se ha escrito en Cuaderno de Cultura Científica.

Dirección: Roland Emmerich. USA. 2004. 124 min. Intérpretes: Dennis Quaid (Profesor Jack Hall), Jake Gyllenhaal (Sam Hall), Ian Holm (Terry Rapson), Emmy Rossum (Laura), Sela Ward (Dra. Lucy Hall), Dash Mihok (Jason Evans), Jay O. Sanders (Frank Harris), Austin Nichols (J.D.), Arjay Smith (Brian Parks), Tamlyn Tomita (Janet Tokada). Guion: Roland Emmerich y Jeffrey Nachmanoff; basado en un argumento de Roland Emmerich. Producción: Mark Gordon y Roland Emmerich. Música: Harald Kloser. Fotografía: Ueli Steiger. Montaje: David Brenner. Diseño de producción: Barry Chusid. Dirección artística: Martin Gendron, Michele Laliberte, Claude Paré, Réal Proulx, Tom Reta y Gerald Sullivan.

¿Y si estuviéramos al borde de una nueva era glacial? Éste es el asunto que obsesiona al climatólogo Jack Hall (Dennis Quaid). Las investigaciones llevadas a cabo por Hall indican que el calentamiento global del planeta podría desencadenar un repentino y catastrófico cambio climático de la Tierra. Las perforaciones realizadas en la Antártida muestran que es algo que ya ha ocurrido con anterioridad, hace diez mil años. Y ahora está alertando a los dirigentes de que podría ocurrir de nuevo si no se adoptan medidas de forma inmediata. Pero sus advertencias llegan demasiado tarde. Todo empieza cuando Hall presencia cómo un bloque de hielo del tamaño de Rhode Island se desgaja completamente de la masa de hielo de la Antártida. Posteriormente, una serie de fenómenos climatológicos cada vez más drásticos empiezan a ocurrir en distintas partes del globo: granizos del tamaño de una ciruela destrozan Tokio, vientos huracanados que rompen todos los récords machacan Hawai; la nieve cae en Nueva Delhi; una serie de devastadores tornados azotan la ciudad de Los Ángeles. Una llamada de teléfono de un colega suyo de Escocia, el profesor Terry Rapson, confirma los peores temores de Jack: estos intensos fenómenos meteorológicos son síntomas de un cambio climatológico masivo y, además, se ha detectado una bajada súbita de la temperatura en las aguas del Atlántico Norte. El derretimiento de la capa de hielo polar ha vertido recientemente demasiada agua dulce a los océanos y ha afectado a las corrientes que dan estabilidad a nuestro sistema climático. La disminución de la salinidad en el mar provoca que la corriente se detenga, la temperatura global cae y lleva al planeta a una nueva edad glacial. El cambio climático ha puesto el planeta al borde del precipicio y, en la película, todo ocurrirá durante una supertormenta de extensión planetaria.

La premisa central del guion se basa en una hipótesis científica legítima pero adornada con episodios de obvias inexactitudes científicas: tornados que destruyen Los Angeles; inundación de Nueva York con olas gigantes; y, sobre todo, el enfriamiento del planeta se completa en una semana.

La película de Emmerich combina con acierto melodrama y cine de catástrofes en un intento de comprometer a los espectadores cognitiva y emocionalmente con una historia espectacular sobre un abrupto cambio climático, escribía en 2012 Alexa Weik von Mossner, de la Universidad de Klagenfurt, en Austria.

La recaudación que obtuvo el film después de su estreno muestra que tuvo gran aceptación, no solo de críticos y periodistas, sino también de climatólogos, sociólogos, ecologistas y miembros del gobierno y la administración. Fue una película alabada, criticada e, incluso, despreciada. Pero, además, fue la primera película popular que promocionó el interés público por el cambio climático. Para la autora, el interés de la película está en que apela al pensamiento racional y, también, a las emociones cuando relata el rápido y catastrófico cambio climático.

El guion se basa en propuestas de la década de los noventa sobre la emisión de dióxido de carbono, su disolución en el agua del mar y su influencia sobre las corrientes marinas tal como aparece en el artículo de 1997 de Thomas Stocker y Andreas Schmitter en Nature. El estudio de los cambios en las corrientes se inició con la del Golfo y se amplió a todos los movimientos de agua en los océanos. Anuncian cambios en 100 años si la emisiones de dióxido de carbono aumentan con rapidez y provocarían la detención permanente de las corrientes. Si la emisión de dióxido de carbono disminuye, las corrientes no se detendrán pero serán más lentas.

La conocida Corriente del Golfo es parte de un sistema de corrientes del Atlántico que, en conjunto, se conocen como AMOC (en inglés, Atlantic Meridional Overturning Circulation, o Circulación Meridional de Retorno del Atlántico). Está compuesta por corrientes superficiales y profundas, como explica Montserrat Alonso, de la Universidad de Salamanca, en El País.

Las aguas superficiales del hemisferio sur pasan por el trópico donde se calientan, llegan al Caribe, se dirigen al norte por la costa este de Norteamérica, cruzan el Atlántico por el sur de Groenlandia y llegan a Europa frente a Noruega. Parte de este sistema es la Corriente del Golfo que sale del Caribe, se mueve hacia el norte paralela a la costa de Norteamérica y se convierte en la corriente Noratlántica.

Todo este sistema de movimientos de agua llega al Atlántico subpolar, se enfría, y como las aguas son muy salinas y con menos temperatura, se hunden y retornan hacia el sur como corrientes profundas. Por eso se le llama circulación de retorno: las aguas del sur, calientes, llegan a la zona polar, se enfrían y vuelven al sur.

Además de agua, AMOC mueve energía en forma de cambios de temperatura del agua. Según estudios recientes, todo el sistema se ha ralentizado en un 15% desde la mitad del siglo pasado. Sin embargo, en 2006 faltaban evidencias de que la circulación fuese más lenta, como escribía Richard Kerr en Science. En una reunión de expertos se constató que más del 95% de los asistentes consideraba que no había cambios significativos en las corrientes atlánticas. Añadían que no había pruebas de un riesgo inmediato y piden más datos, durante quizá décadas, para demostrar la circulación lenta por el cambio climático.

En aquellos años hay más expertos que consideran que una nueva edad glaciar en Europa no es un escenario probable a corto o medio plazo. Carl Wunsch, del MIT, plantea que la corriente del Golfo se produce por el sistema de vientos a gran escala del Atlántico y por el movimiento de rotación del planeta. Por tanto concluye que o se detiene el sistema de vientos o la rotación de la Tierra, o ambos a la vez, para llegar a una nueva edad glaciar dentro de millones de años.

La táctica del director se basa en los efectos especiales de un guion que relata la historia de un científico cuyos avisos de lo que puede ocurrir son ignorados. La ciencia avisa, es una profecía, y cuando se cumple es la visión del desastre lo que vemos en la pantalla. Algunos modelos predicen que si Groenlandia se deshiela, la corriente podría detenerse lo que haría caer la temperatura en el sur de Europa. En la película, en enfriamiento ocurre en cuestión de horas. Es poco probable pero puede comenzar una época más fría, una nueva edad de hielo.

El mismo año del estreno comenzó el debate la película. Bogi Hansen y su grupo, del Laboratorio de Pesquerías de las Islas Feroe, escriben, en 2004, que el debilitamiento de la AMOC durante este siglo puede tener efectos sobre el clima, quizá con el enfriamiento del norte de Europa como aparece en la película. El grupo de Hansen tiene datos de temperaturas más bajas en el mar, con la salinidad en aumento desde mediados de los 70 y menos flujo de agua, hasta un 20% desde 1950. Sin embargo, como muchos otros expertos concluyen que faltan datos a más largo plazo.

Para 2018 comienza a aceptarse, con datos y modelos, que AMOC se ha debilitado. Levke Caesar y su grupo, del Instituto Postdam de Investigación sobre el Impacto del Clima, en Alemania, plantean que la reducción es del 15% desde mediados del siglo XX. Añaden, para el futuro, que si continua el calentamiento global, seguirá debilitándose la AMOC, con cambios en los flujos de agua, pérdidas en la cubierta de hielo de Groenlandia y caída de las temperaturas en el Atlántico Norte.

La propuesta del grupo de Caesar se confirma con los datos de David Thornalley y su equipo, del Colegio Universitario de Londres, con participación de Pablo Ortega del Centro de Biocomputación de Barcelona. Es un estudio sobre el Mar del Labrador, entre Groenlandia y Norteamérica y, para los autores, las evidencias apuntan a los últimos 150 años, desde 1850, al final de la Pequeña Edad del Hielo, con una reducción de la corriente en 15%-20%. Sugieren más datos para delimitar el papel de la variabilidad natural del clima y de la actividad humana con el resultado actual del debilitamiento de la AMOC. Aunque también encuentran que los cambios en la AMOC no coinciden siempre con las variaciones en la temperatura. Parece que la AMOC responde a los cambios en el clima pero que no los dirige.

De nuevo Levke Caesar y su grupo, ahora desde la Universidad de Maynooth, en Irlanda, confirmaron que AMOC había perdido fuerza según la revisión de 11 series de datos desde el año 400 a la actualidad. Al principio, AMOC permanecía estable hasta comienzos del siglo XIX. Después, se acelera el proceso desde mediados del siglo XX hasta la actualidad.

Para resumir, en 2021, Niklas Boers, después de analizar ocho índices de la AMOC sobre la temperatura en la superficie del mar y la salinidad en el Atlántico, concluye que hay evidencias empíricas consistentes de que, en el pasado siglo, AMOC ha pasado de condiciones estables a un punto crítico de transición a una circulación más lenta que puede provocar un impacto severo en el sistema climático del planeta.

Una revisión final, publicada en 2021, sobre los indicadores del cambio climático en los océanos la firma Carlos García-Soto, del Instituto Español de Oceanografía en Santander, con otros once expertos y, entre ellos, Ainhoa Caballero, de AZTI en Pasaia.Según esta:

– La temperatura del agua en la superficie del mar ha crecido, de media, 0.062ºC al año en los últimos 120 años. En la última década, de 2010 a 2019, el aumento se ha acelerado a los 0.280ºC al año.

– El contenido de calor del océano en los 2000 metros superiores, de media y a nivel mundial, ha sido de 0.35 watios por metro cuadrado en los últimos 65 años. Durante la última década, de 2010 a 2019, la tasa es el doble con 0.70.

– El pH global de la superficie del océano ha disminuido, de media, 0.1 unidades desde 1770 con la revolución industrial. El nivel medio global del mar ha aumentado de 1993 a 2019 una tasa de 3.17 milímetros por año. Entre 1900 y 2015, en 115 años, ha aumentado en 19 centímetros.

– Los niveles de oxígeno disuelto han bajado el 2% en los últimos 50 años. La extensión de hielo marino en el Ártico ha disminuido un 13.1% por década en verano y un 2.6% por década en invierno.

– Y la AMOC está en su punto más débil de varios cientos de años y se ha ralentizado más en el último siglo.

Después del estreno en Gran Bretaña, el grupo de Thomas Lowe, de la Universidad de East Anglia en Norwich, organizó un estudio para conocer si los espectadores, después de la película, diferenciaban en ella la ciencia y la ficción. Los autores preguntan a los espectadores sobre su concepto del calentamiento global antes y después del film, así como su percepción sobre si la ciencia que aparece se basa en hechos. Entrevistan a 301 espectadores, de 12 a 60 años o más, y son mujeres el 55%.

La audiencia no consigue determinar la precisión de la ciencia que aparece en la película. Según los autores, los espectaculares efectos especiales y su gran calidad hacen difícil distinguir dónde termina la ciencia y comienza la ficción. Para el 30%, los efectos especiales les ayudan a entender los hechos y, por ello, aumentó su compromiso con lo que significa el cambio climático. Casi el 44% está dispuesto a hacer algo para reducir el cambio climático.

Otro estudio sobre el efecto de la película en el público y su percepción del cambio climático lo firma Anthony Leiserowitz, de la Universidad de Yale, e incluye entrevistas a 529 espectadores. Encuentra cambios en su percepción del riesgo, los modelos conceptuales del cambio climático, las intenciones de su conducta, las prioridades políticas e, incluso, en su intención de voto en futuras elecciones. En conclusión, la representación en una película popular de riesgos ambientales puede influir en la actitud y la conducta de los ciudadanos.

Uno de los cambios en que está implicada la temperatura del agua y la AMOC es la distribución de las especies pesqueras. Ocurre, por ejemplo, con las migraciones de anguilas y angulas desde Europa y Norteamérica al Mar de los Sargazos para la reproducción. La deriva hacia el norte de la isoterma de 22.5ºC, que marca el límite norte de la reproducción de las anguilas, más la disminución del viento y la mezcla de temperaturas en profundidad afectan a la distribución de las larvas. Según Kevin Friedland y sus colegas, del Servicio Nacional de Pesquerías Marinas de Estados Unidos, la relación entre estos datos y los cambios en la AMOC sugiere que la caída en el número de angulas y anguilas que llegan a nuestros ríos en Europa y, quizá, en Norteamérica, está causada, por lo menos en parte, por el cambio climático.

En conclusión, esta película busca provocar en los espectadores una reacción ante el desastre global que puede suponer el cambio climático y, en parte, lo consigue.

Referencias:

Alonso García, M. 2021. ¿Han cambiado la temperatura y la dirección de la corriente del Golfo? El País 3 marzo.

Boers, N. 2021. Observation-based early-warning signals for a collapse of the Atlantic Meridional Overturning Circulation. Nature Climate Change 11: 680-688.

Caesar, L. et al. 2018. Observed fingerprint of a weakening Atlantic Ocean Overturning Circulation. Nature 556: 191-198.

Caesar, L. et al. 2021. Current Atlantic Meridional Overturning Circulation weakest in last millenium. Nature Geoscience 14: 118-120.

Criado, M.A. 2018. El sistema circulatorio del planeta se debilita. El País 12 abril.

Cubitt, S. 2005. Eco Media. Rodopi. Amsterdam-New York. 168 pp.

Friedland, K.D. et al. 2007. Oceanic changes in the Sargasso Sea and declines in recruitment of the European eel. ICES Journal of Marine Science 64: 519-530.

García-Soto, C. et al. 2021. An overview of ocean climate change indicators: sea surface temperature, ocean heat content, ocean pH, dissolved oxygen concentration, Arctic Sea ice extent, thickness and volume, sea level and strength of the AMOC (Atlantic Meridional Overturning Circulation). Frontiers in Marine Science doi: 10.3389/fmars.2021.642372.

Hansen, B. et al. 2004. Already the Day After Tomorrow? Science 305: 953-954.

Kerr, R.A. 2006. Fake alarm: Atlantic conveyor belt hasn’t slowed down after all. Science 314: 1064.

Kirby, D.A. 2011. Lab coats in Hollywood. Science, scientists, and cinema. MIT Press. Cambridge & London. 265 pp.

Leiserowitz, A.A. 2004. Before and after The Day After Tomorrow: a U.S. study of climate risk perception. Environment 46: 23-37.

Lomborg, B. 2008. En frío. La guía del ecologista escéptico para el cambio climático. Ed. Espasa-Calpe. Pozuelo de Alarcón. 284 pp.

Lowe, T. et al. 2006. Does tomorrow ever come? Disaster narrative and public perceptions of climate change. Public Understanding of Science 15: 435-457.

Mulet, J.M. 2021. Ecologismo real. Ed. Destino. Barcelona. 3,83 pp.

Stocker, T.F. & A. Schmittner. 1997. Influence of CO2 emission rates on the stability of the thermohaline circulation. Nature 388: 862-865.

Thornalley, D.J.R. et al. 2018. Anomalously weak Labrador Sea convection and Atlantic overturning during the past 150 years. Nature 556: 227-232.

Weik von Mossner, A. 2012. Facing The Day After Tomorrow: Filmed disaster, emotional engagement, and climate risk perception. En “American environments: Climate-Cultures-Catastrophe”, p. 97-115. Ed. por C. Mauch & S. Mayer. Universitätverlag Winter. Heidelberg.

Wunsch, C. 2004. Gulf Stream safe if wind blows and Earth turns. Nature 428: 601.

Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.

El artículo ZientZinema 2: El día de mañana se ha escrito en Cuaderno de Cultura Científica.

El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

Amanda Sierra es neurocientífica y lidera el laboratorio de biología de las células glía del Achucarro Basque Center for Neuroscience. Pero en esta charla no habla de neurociencia, sino que aporta tres mensajes muy sencillos para ayudarnos a diferenciar entre ciencia y pseudociencia, entre datos contrastados y bulos.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2021: Amanda Sierra – Elogio de la incertidumbre se ha escrito en Cuaderno de Cultura Científica.

Bautizado como Txikispora philomaios, pertenece a un linaje cercano al punto evolutivo en el que organismos unicelulares se diferenciaron para formar animales y hongos.

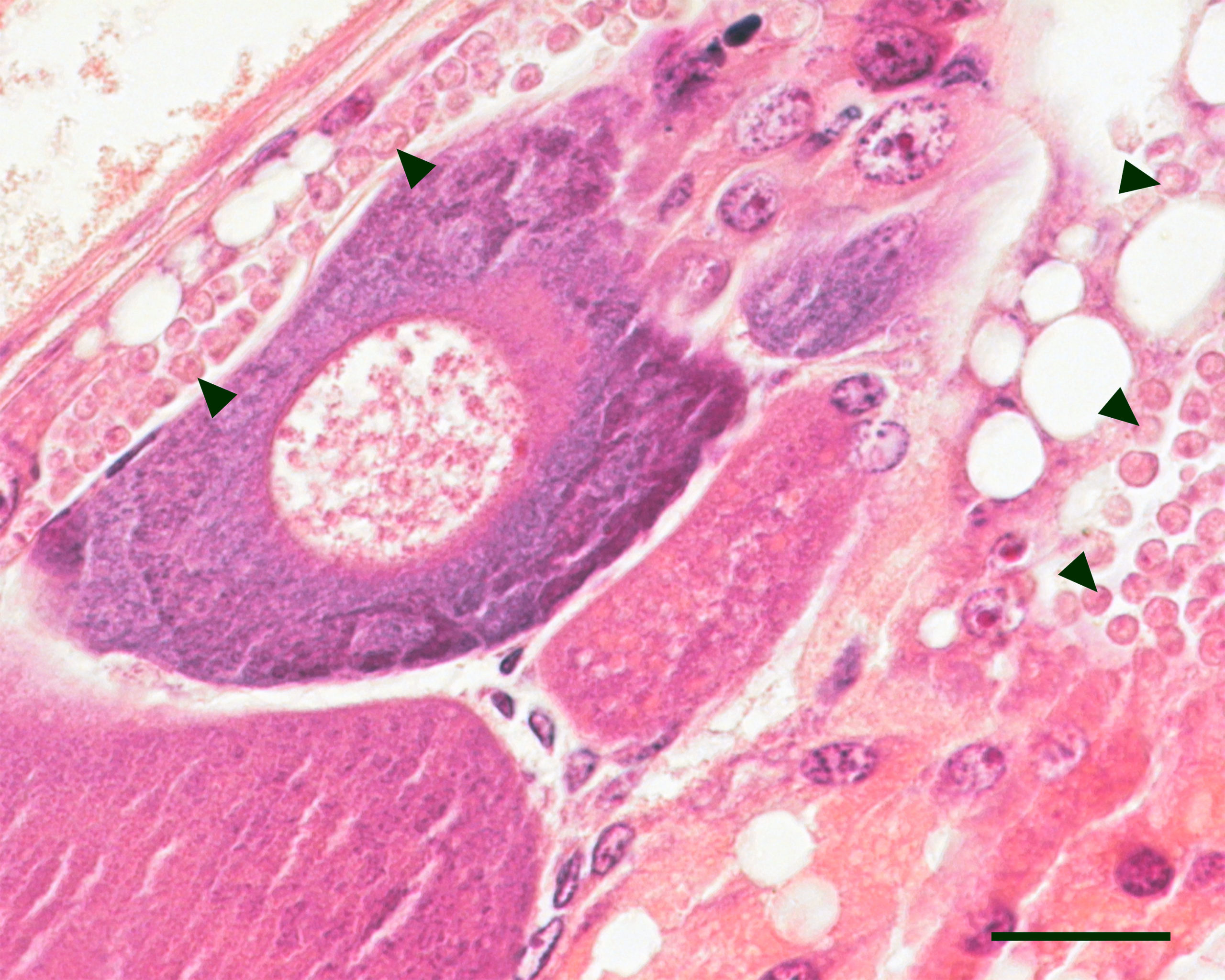Imagen microscópica de Txikispora philomaios parasitando hemocitos, tejidos conectivos y gónadas femeninas de un anfípodo. Imagen:  Ander Urrutia / UPV/EHU

El investigador Ander Urrutia del grupo de investigación Biología Celular en Toxicología Ambiental de la UPV/EHU y de Patología Animal en CEFAS/OIE, (Centre for Environment, Fisheries, and Aquaculture Science, Reino Unido) se dedica a estudiar la gran diversidad aun desconocida de organismos parasíticos unicelulares que existe en la zona intermareal en los ecosistemas costeros de climas templados. Una herramienta muy útil para ello es el ADN ambiental: se trata de una técnica que consiste en “extraer el ADN contenido bien en una matriz orgánica o ambiental, como, por ejemplo, en un organismo o en muestras de agua marina previamente filtradas”. Urrutia la usa para ver qué organismos parasitan a los invertebrados: “Existen muchísimos parásitos sin identificar; encontramos nuevas secuencias de ADN e inferimos su comportamiento en base a su similitud genética con otros parásitos, pero realmente no sabemos lo que son”, comenta el investigador.

En la tarea de clasificar los parásitos unicelulares encontrados en las muestras, Urrutia encontró un parásito a priori poco común, que en base a sus características no casaba en ningún grupo existente hasta el momento. “Tuvimos que hacer unos análisis moleculares, que nos confirmaron que era un organismo distinto. Una vez realizados varios árboles filogenéticos, es decir, una vez comparado el ADN de este organismo con sus posibles parientes más cercanos, pudimos ver que se trata de un organismo perteneciente a un linaje primitivo, que se sitúa cerca del punto en el que se diferenciaron los animales y los hongos. Está cerca del momento evolutivo en el que un organismo unicelular se diferenció para dar a todos los animales que existen, poco después de que otro organismo celular parecido se diferenciara para terminar evolucionando en todos los hongos que existen”, explica Urrutia.

El parásito, bautizado como Txikispora philomaios, es un protista (organismo eucariota unicelular) que evolucionó poco después de la división del ancestro común de animales y hongos antes de desarrollar su multicelularidad. “Todos los animales y los hongos del mundo vienen de un mismo organismo celular que presumiblemente estaba en el océano hace cientos de millones de años. En algún momento este comenzó a agregarse y duplicarse, mientras sus células se especializaban formando tejidos, y eventualmente un cuerpo, desde una microscópica medusa hasta una enorme ballena azul”, explica el investigador.

Puesto que a menudo la reordenación genética sufrida por los parásitos difiere de sus parientes de vida libre, el estudio de este parásito y su genoma contribuirá a entender cómo se desarrolló la multicelularidad animal; “es decir, en qué momento y cómo las células empezaron a comunicarse, juntarse, o especializarse entre ellas, formando organismos cada vez más complejos. El desarrollo de la multicelularidad animal es muy importante desde el punto de vista de biología básica”, añade Urrutia, que ha realizado la investigación a caballo entre CEFAS en el Reino Unido, la Estación Marina de Plentzia (PIE) y el Instituto de Biología Evolutiva (IBE/CSIC).

Según explica Urrutia, “Txikispora no solo es una especie nueva, sino que da nombre a un género nuevo, una familia nueva, y un orden nuevo. Es decir, ahora tenemos a la nueva familia Txikisporidae, una familia con bastantes secuencias crípticas, es decir, trozos de ADN desconocidos que se parecen mucho a Txikispora, que también podrían pertenecer a parásitos, pero que ni sabemos dónde están ni qué animales podrían parasitar. Muchas de ellas están en ecosistemas acuáticos de Europa, pero no sabemos nada más acerca de ellos. Esa es otra línea de investigación que me gustaría seguir”.

Los investigadores de la UPV/EHU han sido los encargados de poner nombre a dicho parásito. El nombre de Txikispora es debido a que se trata de una pequeña (txiki) espora, y philomaios es debido a que el parásito solo aparecía unos pocos días durante mayo: ‘amante de mayo’. A la dificultad de ubicarlo filogenéticamente en su correspondiente grupo se ha sumado la dificultad de encontrarlo en aguas marinas: “Estuvimos dando palos de ciego hasta darnos cuenta de que solo se encuentra en la comunidad de anfípodos unos pocos días durante este mes; es como si el resto del año el parásito desapareciera”, explica Urrutia.

Referencia:

Ander Urrutia, Konstantina Mitsi, Rachel Foster, Stuart Ross, Martin Carr, Georgia M. Ward, Ronny van Aerle, Ionan Marigomez, Michelle M. Leger, Iñaki Ruiz-Trillo, Stephen W. Feist, David Bass (2021) Txikispora philomaios n. sp., n. g., a micro-eukaryotic pathogen of amphipods, reveals parasitism and hidden diversity in Class Filasterea Journal of Eukaryotic Microbiology doi: 10.1111/jeu.12875

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Un parásito que contribuirá a explicar el origen de la multicelularidad animal se ha escrito en Cuaderno de Cultura Científica.

Fuente: Wikimedia Commons

“Un misionero de la Edad Media dice haber encontrado el punto en el que el cielo se encuentra con la tierra”. Esta es la leyenda que acompaña a una de las imágenes más icónicas de la historia de la astronomía. El conocido como grabado Flammarion ilustra un pasaje de L’Atmosphere: Météorologie Populaire, un libro publicado por el astrónomo Camille Flammarion en 1888. En él, el autor describe las concepciones antiguas del mundo, con el cielo apoyado como una tienda de campaña sobre la tierra.

Durante siglos, nuestra visión del cielo nocturno fue muy parecida a esta. Las primeras representaciones del cosmos pintan el firmamento como una bóveda salpicada de luces. Todas las estrellas se sitúan a la misma distancia del observador, las constelaciones son dibujos planos sobre una pared.

Como el protagonista del grabado de Flammarion, con el paso de los siglos los astrónomos fueron asomándose más allá de esa aparente bóveda y empezaron a hacerse preguntas que les permitieron entender la lógica que daba sentido a todos esos dibujos de luz en la noche. Descubrieron que, lejos de formar una bóvida, cada estrella se sitúa a distinta profundidad y desarrollaron métodos para medir distancias cada vez más inimaginables.

Uno de los más antiguos es el método de paralaje. Se trata de un efecto visual que se produce cuando un observador se mueve. Al hacerlo, los objetos más cercanos parecen cambiar de posición en relación con los más distantes. Es un fenómeno especialmente fácil de reproducir, gracias a los dos ojos (dos puntos de observación) de nuestra cara. Basta con que extiendas tu brazo, con el pulgar alzado, y guiñes alternativamente uno de los dos ojos. El desplazamiento aparente del dedo respecto a los objetos del fondo depende de la distancia que lo separe de tus ojos y se puede usar para calcularla de manera precisa. De hecho, esto es lo que hace tu propio cerebro para que tú percibas el espacio en tres dimensiones. La diferencia entre las imágenes obtenidas desde tus dos puntos de observación (los dos ojos) es suficiente para estimar la distancia a la que se sitúan los objetos de manera intuitiva. Otros animales, con los ojos en lados opuestos de la cabeza y dos campos de visión que no se superponen, por tanto, deben utilizar el movimiento de la propia cabeza o el cuerpo para obtener este efecto del paralaje y poder ver en 3D.

Los astrónomos no tienen los ojos lo suficientemente separados como para percibir la profundidad del cielo nocturno. En cambio, aprovechan el movimiento de la propia Tierra para invocar este mismo principio y determinar la distancia a estrellas relativamente cercanas. Al igual que la punta del dedo, las estrellas que están más cerca de la Tierra cambian de posición en relación con las más distantes, que parecen fijas. Es posible medir de manera precisa el ángulo de desplazamiento de estas estrellas a lo largo del año, y así, conociendo cuánto se ha movido la Tierra (el tamaño de su órbita), calcular la distancia de la estrella usando geometría.

En términos astronómicos, el paralaje solo nos permite calcular distancias relativamente cortas. Pero gracias a él, los astrónomos pueden estimar la profundidad de otros objetos más lejanos y calibrar distintas escalas de medición. Este es el caso de las llamadas “candelas estándar”. Se trata de objetos luminosos cuya magnitud absoluta es conocida, como las cefeidas que mencionamos en el capítulo anterior de esta serie. Comparando su verdadero brillo con su magnitud aparente, es posible conocer a qué distancia se sitúan. No obstante, para calibrar esta escala, primero es necesario calcular la distancia a una cefeida cercana y determinar la relación entre su magnitud absoluta y su periodo de pulsación.

Las cefeidas son estrellas especialmente brillantes, por lo que son visibles en galaxias que se encuentran a decenas de millones de años luz de distancia. Para galaxias aún más distantes, los astrónomos confían en otro tipo de estrellas en explosión conocidas como supernovas de tipo A. Al igual que sucede con las cefeidas, la velocidad a la que se iluminan y se desvanecen estas supernovas está relacionada con su magnitud absoluta, que se puede utilizar para calcular su distancia. Pero esta técnica también requiere una buena calibración utilizando paralaje y cefeidas. Sin conocer la distancia precisa a algunas supernovas, no hay forma de determinar su brillo absoluto.

Otro tipo de método útil para calcular distancias tiene que ver con las variaciones en la propia luz de las estrellas que se alejan de nosotros: el desgaste de la botella debido al viaje del que hablábamos en el capítulo anterior. Hoy sabemos que el universo está en expansión y que las galaxias más lejanas se alejan de nosotros a mayor velocidad que las más cercanas. Esta velocidad provoca un fenómeno conocido como “desplazamiento hacia el rojo” (red shift), debido al efecto Doppler. Las longitudes de onda de la radiación electromagnética tienden a alargarse debido a que su fuente se aleja de nosotros. Si conocemos la frecuencia percibida y la frecuencia original, podemos calcular a qué velocidad se aleja su fuente1.

Para objetos celestes del espacio profundo (a partir de 10 megaparsecs, o 32 millones de años luz, que se dice pronto), la ley de Hubble2 afirma que el corrimiento al rojo de la radiación es proporcional a la distancia que nos separa de su fuente. Esta ley se considera la primera base observacional del paradigma de un universo en expansión, una de las evidencias de la teoría del Big Bang. Se diría que los astrónomos se han asomado tanto a través de la cúpula celeste, que han conseguido ver sus orígenes, quizás no su base, pero sí el punto que vio nacer nuestro cielo nocturno.

Referencias:

1P. A. Tipler, G. Mosca. Física para la ciencia y la tecnología. 6ª Edición. 2012.

2 E. Hubble. A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae. 1929.

Para saber más: De la paralaje

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo La distancia a las estrellas (III) se ha escrito en Cuaderno de Cultura Científica.

 

Los números capicúas, aquellos números tales que sus cifras leídas de izquierda a derecha y de derecha a izquierda son las mismas, llaman profundamente nuestra atención, hasta el punto que solemos buscarlos, e incluso coleccionarlos, en las matrículas de los coches, los décimos de lotería, los billetes de medios de transporte, los billetes de la moneda de cualquier país o cualquier otro lugar en el que aparezcan números de cuatro, o más dígitos. De la misma forma, cuando una fecha lleva asociada una expresión numérica capicúa nos parece una fecha curiosa y solemos prestarle atención, comentarlo e incluso darle cierta relevancia a la misma. Por este motivo, no he podido evitar empezar esta entrada del Cuaderno de Cultura Científica mencionando que ayer fue 22 de febrero de 2022, es decir, 22/02/2022, luego una fecha capicúa puesto que el número asociado a la misma, 22.022.022, es un número capicúa. Además, en esta fecha el número 22 tiene especial relevancia, ya que aparece tres veces el número 22, separado cada uno de los otros por un 0 (sobre el número 22 véase la entrada El misterioso número 22).

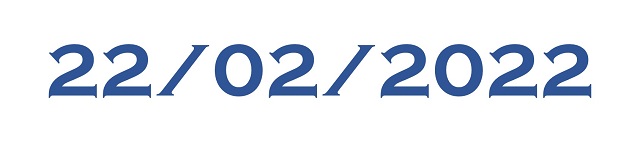
¿Qué pasa con el día de hoy, el 23/02/2022? Obviamente no es un número capicúa. Sin embargo, podemos obtener fácilmente un número capicúa a partir del mismo, con el simple proceso de sumarle el número simétrico, 23.022.022 + 22.022.032 = 45.044.054. Este es el algoritmo “invierte el orden y suma” del que hemos hablado en la entrada El secreto de los números que no querían ser simétricos (véase también el libro La gran familia de los números, Libros de la Catarata, 2021).

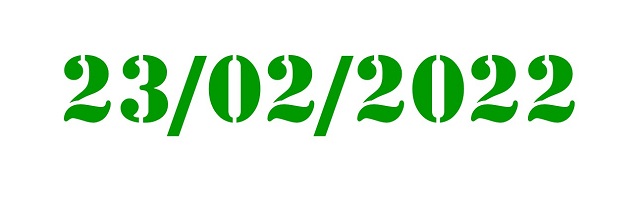
Pero, sigamos con el número asociado al día de hoy, 23.022.022 y pensemos qué propiedades numéricas tiene. Para empezar, este número se puede escribir como producto de tres números primos distintos, 23.022.022 = 2 x 79 x 145.709, es lo que se conoce en matemáticas con el nombre de “número esfénico”. Por lo tanto, tiene 8 divisores (incluyendo el 1 y él mismo: 1, 2, 79, 158, 145.709, 291.418, 11.511.011 y 23.022.022) y la suma de sus divisores propios es 11.948.378, que es una cantidad menor que nuestro número 23.022.022, luego este es un número deficiente (véase la entrada Los números enamorados o el libro La gran familia de los números). Además, es un “número aritmético” ya que, si se realiza la media aritmética de los divisores del número 23.022.022 el resultado es un número natural, en concreto, la media de los divisores de este número

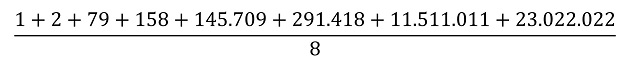
es 4.371.300.

Trivialmente, no es un número primo, ya que es par, pero tampoco es un número “potencialmente primo”, ya que no se puede obtener un número primo sin más que cambiar uno de sus dígitos (por ejemplo, el número 144 es “potencialmente primo” ya que si cambiamos su último dígito obtenemos un número primo, 149).

Más aún, 23.022.022 es un número trapezoidal, ya que puede expresarse como suma de dos, o más, números consecutivos, mayores que 1. Así, nuestro número puede expresarse como suma de los números consecutivos desde 72.697 hasta 73.012. Y se dice que 2 elevado a 23.022.022 es un número apocalíptico ya que incluye el número de la bestia, 666, entre sus dígitos.

Finalmente, el número que se corresponde con el día de hoy, 23.022.022, es un “número congruente”. Y este es el concepto que analizaremos brevemente en esta entrada.

El concepto de número congruente está relacionado con el teorema de Pitágoras. Por lo tanto, como es nuestra costumbre, empecemos recordando este resultado geométrico: “dado un triángulo rectángulo, entonces el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos” (la famosa expresión a2 + b2 = c2, si a y b son los catetos y c la hipotenusa). De hecho, el teorema dice algo más, también es cierto el recíproco, es decir, que “dado un triángulo para el cual el cuadrado de uno de sus lados es igual a la suma de los cuadrados de los otros dos, entonces el triángulo es rectángulo”.

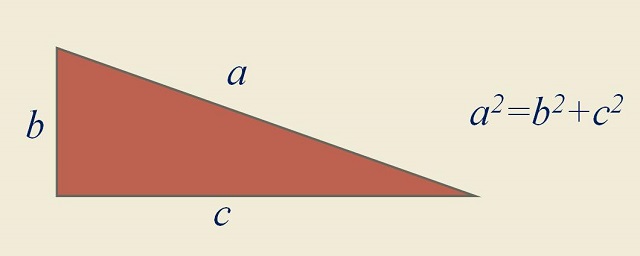
Por lo tanto, un número se llama congruente si es igual al área de un triángulo rectángulo cuyos lados, hipotenusa y catetos, son números racionales (recordemos que un número es racional si es el cociente a / b de dos números enteros a y b, como 0,5 = 1 / 2 ó 1,4 = 7 / 5). Por ejemplo, el triángulo egipcio, es decir, el triángulo rectángulo de lados (3, 4, 5), tiene área igual a 6, por lo tanto, el número 6 es un número congruente. Como puede verse en la siguiente imagen, los números 5, 6 y 7 son números congruentes (de hecho, los primeros).

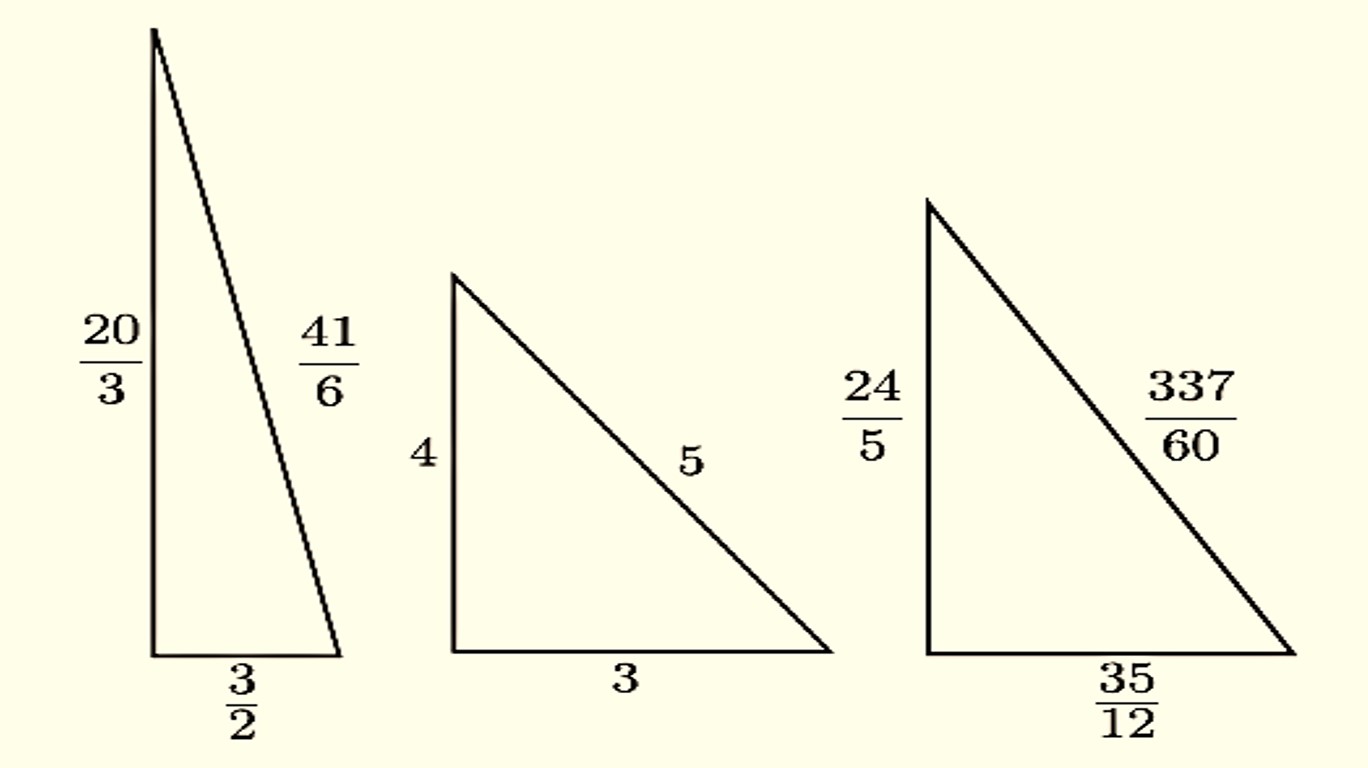
Como se indica en el libro History of the Theory of Numbers (volumen II), del matemático estadounidense Leonard Eugene Dickson (1874-1954), la historia de los números congruentes se inicia con el matemático griego Diofanto (siglo III). Aunque su estudio fue el tema central de dos manuscritos árabes del siglo X, en los que ya aparecen mencionados los números 5 y 6 como números congruentes. El matemático italiano Leonardo de Pisa (aprox. 1170-1240), conocido como Fibonacci, descubrió que el 7 también es un número congruente y afirmó, aunque sin demostrarlo, que el número 1 no es un número congruente, luego ningún número cuadrado lo es (ya que si m2 fuese un número congruente con triángulo rectángulo asociado (a, b, c), entonces 1 sería un número congruente con triángulo rectángulo asociado (a / m, b / m, c / m)). El matemático francés Pierre de Permat (1601-1665) fue el primero en demostrar que el número 1 no es un número congruente –y, por lo tanto, tampoco todos los números cuadrados-, ni tampoco los números 2 y 3.

Teorema (Fermat, 1640): El número 1 no es un número congruente.

La demostración de este resultado se realiza mediante la técnica del descenso infinito de Fermat. La idea es la siguiente. Para empezar, supongamos que existe un triángulo rectángulo, de lados racionales, cuya área sea igual a 1. Entonces renombrando los lados del triángulo rectángulo como a / d, b / d y c / d, con a, b, c y d números enteros, se tiene una 4-tupla de números enteros (a, b, c, d) tales que

A continuación, si tenemos una 4-tupla de números enteros (a, b, c, d) tales que satisfacen las ecuaciones (1), entonces puede demostrarse que a y b son coprimos (es decir, a no tienen divisores comunes, salvo el 1).

Entonces, el método del descenso infinito de Fermat consiste en demostrar que si tenemos una 4-tupla de números enteros (a, b, c, d) tales que satisfacen (1) y a y b son coprimos, puede construirse otra 4-tupla de números enteros (a’, b’, c’, d’) tales que satisfacen (1) y a’ y b’ son coprimos, con 0 c’ c (es decir, que el nuevo número c’ es más pequeño que c). Si seguimos realizando este proceso llegamos a una contradicción, puesto que es imposible realizar este proceso de forma infinita, ya que c es un número positivo (finito). Por lo tanto, no existe un triángulo rectángulo de lados racionales y área igual a 1.

Para quienes estén interesados en leer la demostración completa, y no solo este bosquejo, pueden consultar, por ejemplo, el artículo The Congruent Number Problem, del matemático Keith Conrad.

Caricatura de Pierre de Fermat, realizada por Gerardo Basabe de Viñaspre, para la exposición de la Real Sociedad Matemática Española, El rostro humano de las matemáticas (2008)

 

La sucesión de números congruentes está recogida en la Enciclopedia On-line de Sucesiones de Números Enteros (OEIS) como la sucesión A003273, cuyos primeros elementos son:

5, 6, 7, 13, 14, 15, 20, 21, 22, 23, 24, 28, 29, 30, 31, 34, 37, 38, 39, 41, 45, 46, 47, 52, 53, 54, 55, 56, 60, 61, 62, 63, 65, 69, 70, 71, 77, 78, 79, 80, 84, 85, 86, 87, 88, 92, 93, 94, 95, 96, 101, 102, 103, 109, 110, 111, 112, 116, 117, 118, 119, 120, …

Por otra parte, volviendo al concepto de número congruente, podemos observar que la condición de que un número N sea congruente es equivalente a que exista un número racional u tal que u2 – N y u2 + N son también cuadrados, que es como consideraron originalmente el problema Diofanto, los matemáticos árabes o Fibonacci. La justificación es sencilla. Si tenemos que N es un número congruente, entonces existen números racionales (a, b, c) tales que a2 + b2 = c2 y N = ab / 2, luego u = c / 2, ya que:

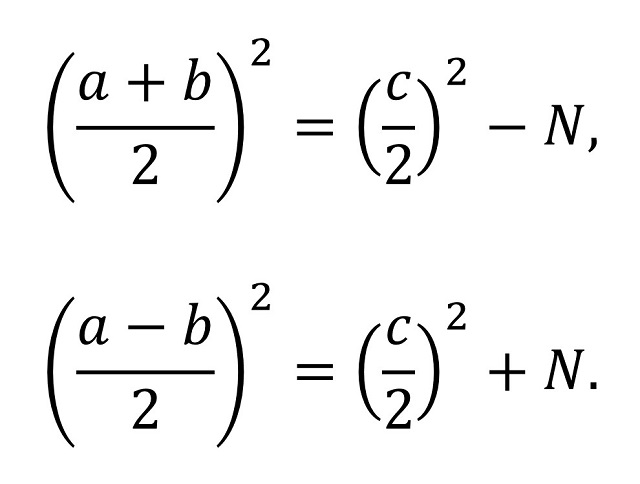
De forma análoga el recíproco. Es decir, estamos diciendo que la condición de que N sea un número congruente es equivalente a que existan números racionales u, p y q tales que

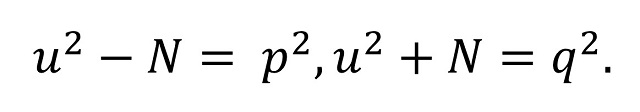
Teniendo en cuenta que u, p y q son racionales, luego cocientes de números enteros, se puede probar fácilmente que la condición de que un número N sea congruente es equivalente a que existan números enteros a, b, x, y tales que

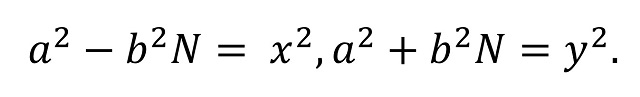
Caricatura de Leonardo de Pisa, Fibonacci, realizada por Enrique Morente, para la exposición de la Real Sociedad Matemática Española, El rostro humano de las matemáticas (2008)

 

Obtener ejemplos de números congruentes no es difícil, basta con tener una terna o triple pitagórico, es decir, una terna de tres números enteros (a, b, c) que satisfacen la ecuación del teorema de Pitágoras a2 + b2 = c2, siendo uno de los números a o b par, ya que en ese caso el número N = ab / 2 es un número congruente.

Por ejemplo, si consideramos la fórmula de Euclides para generar ternas pitagóricas, es decir, dados dos números enteros n y m tales que m > n > 0, entonces

es una terna pitagórica y b siempre es par. En conclusión, a partir de este método se obtienen ejemplos de números congruentes.

Así, en la siguiente tabla podemos observar algunos ejemplos de ternas pitagóricas generadas con la fórmula de Euclides y el número congruente obtenido.

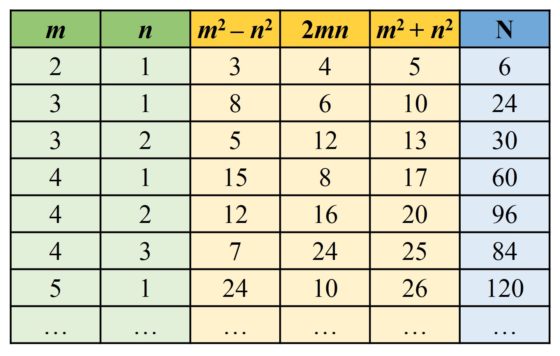
Existen otros métodos de generar ternas pitagóricas, aunque esto solo nos da algunos números congruentes, que además están generados mediante los lados enteros –no racionales en general- de un triángulo rectángulo.

Sin embargo, la cuestión importante, y más compleja, es conocer, dado un número entero cualquiera, si es, o no, un número congruente. Este es el conocido como el problema del número congruente. Este es uno de los problemas de la teoría de números que aún continúa abierto.

El problema de si un número N es congruente está relacionado con las soluciones de la ecuación y2 = x3 – N2 x (que es un ejemplo de lo que se conoce como “curva elíptica”, aunque de eso no hablaremos hoy). De hecho, estudiando esta ecuación, el matemático estadounidense Jerrold B. Tunnell (1950) obtuvo una resolución parcial del problema del número congruente.

Teorema de Tunnell: Sea N un número entero, libre de cuadrados (si es múltiplo de un número cuadrado sabemos que no es congruente, por el teorema de Fermat), y sean los conjuntos

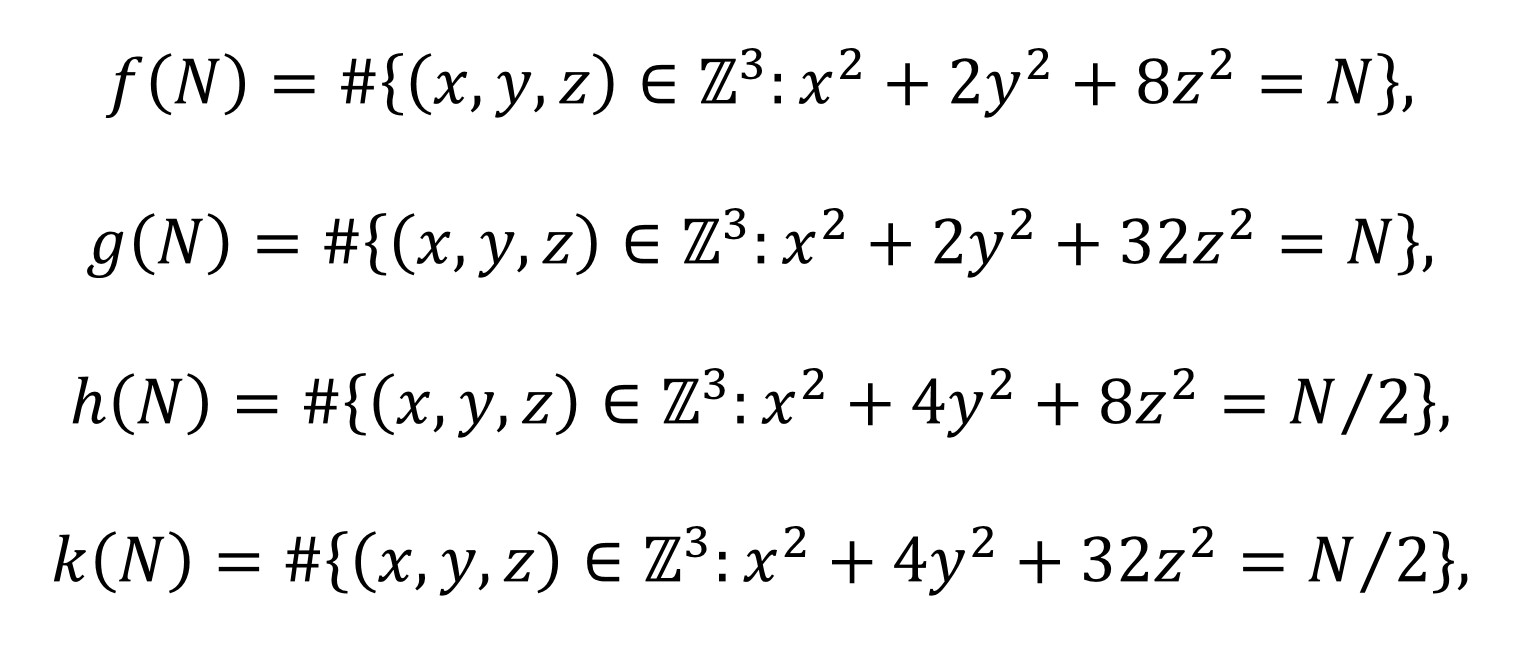
donde el símbolo # indica la cantidad de elementos del conjunto, es decir, soluciones enteras de la correspondiente ecuación diofántica de cada conjunto. Entonces, si N es un número congruente impar, entonces f(N) = 2 g(N), y si N es un número congruente par, entonces h(N) = 2 k(N).

Además, si se verifica la conjetura de Birch y Swinnerton-Dyer (que es uno de los 7 problemas del milenio del Instituto Clay de Matemáticas, aunque en esta entrada no hablaremos de este tema) para la curva elíptica y2 = x3 – N2 x, se verificaría el recíproco, es decir, las igualdades anteriores son suficientes para afirmar que N es congruente.

En particular, si la conjetura de Birch y Swinnerton-Dyer fuese cierta, se tendría que todos los números N congruentes con 5, 6 o 7, módulo 8 (véase la entrada Un código detector de errores: la letra del DNI), serían números congruentes. En particular, los primeros números N congruentes con 5, 6 o 7, módulo 8, son: 5, 6, 7, 13, 14, 15, 21, 22, 23, 29, 30, 31, 37, 38, 39, 45, 46, 47, 53, 54, 55, … que, como podemos observar en la lista anterior, son números congruentes.

Una cuestión curiosa es la distribución de los números congruentes dentro de los números naturales. Si consideramos los 2.500 números naturales, representados en espiral, como en la espiral de Ulam (véase la entrada El poema de los números primos), y pintamos de rojo los cuadrados que se corresponden con números congruentes y de un color claro los que no lo son, la imagen que nos queda es la siguiente:

Espiral con los números congruentes, y no congruentes, hasta 2.500. Imagen de la página Numbers Aplenty

 

Para terminar, el número correspondiente al día de hoy, 23.022.022, se escribe en el sistema de numeración binario como:

1010111110100100111000110.

Bibliografía

1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata, 2021.

2.- Página web: Numbers Aplenty.

3.- Keith Conrad, The Congruent Number Problem

4.- Wikipedia: congruent number

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo El teorema de Pitágoras y los números congruentes se ha escrito en Cuaderno de Cultura Científica.

¿Hasta qué punto nuestras decisiones están determinadas por las circunstancias? Es probable que respondas que bastante pero porque asumes que eres consciente de esas circunstancias y que las sopesas, también conscientemente, a la hora de tomar una decisión que tú crees racional. Permíteme que te lo plantee de una forma ligeramente diferente: ¿hasta qué punto influye en tu posicionamiento político o en tus preferencias a la hora de elegir pareja la silla en la que estás sentado? ¿Te parece absurda la pregunta? Si influyese de alguna manera, ¿qué nos diría eso de tu libertad individual? Sigue leyendo, puede que te sorprendas.

En los últimos años se han realizado experimentos en los que se ha tratado de dilucidar cómo hechos circunstanciales, aparentemente intrascendentes, afectan a nuestra interpretación de las intenciones de los demás y a nuestra toma de decisiones, reforzando la idea (como si hiciese falta) de que buena parte de nuestros juicios y decisiones se toman a nivel inconsciente, por algo que alguien describió como automatismos de mamífero. Así, si a una persona se le ofrece una bebida con hielo en circunstancias en las que una caliente también tendría sentido, esta interpreta que los presentes no la acogen, mientras que si se le ofrece una caliente se siente bienvenida. Si esto suena extraño aún lo es más el que si haces que votantes se sienten en sillas que se inclinan hacia la izquierda consigues que simpaticen más con políticas asociadas con la izquierda [1].

Otro estudio [2] encabezado por David Kille, de la Universidad de Waterloo (Canadá), que también se centra en el efecto del mobiliario, sugiere que algo tan trivial como la estabilidad de sillas y mesas tiene su efecto en nuestras percepciones y deseos.

Los investigadores pidieron a la mitad de sus 47 voluntarios, estudiantes sin vínculos sentimentales, que se sentasen en una silla ligeramente coja frente a una mesa tampoco demasiado estable mientras realizaban la tarea asignada. La otra mitad se sentaron en sillas frente a mesas que eran idénticas a las del otro grupo pero sin que ni unas ni otras cojeasen.

Una vez sentados los participantes tenían que juzgar la estabilidad de las relaciones de cuatro parejas de famosos: Barack y Michelle Obama, David y Victoria Beckham, Jay-Z y Beyoncé y Johnny Depp y Vanessa Paradis [esta pareja existía en el momento del estudio]. Para emitir su juicio los participantes valoraban en una escala del 1 al 7 la probabilidad de que la pareja se rompiese en los próximos cinco años, siendo 1 “muy poco probable” y 7 “con toda probabilidad”.

Tras haber hecho esto, los participantes tenían que calificar sus preferencias por varios rasgos de una posible pareja. Los rasgos incluían algunos que un estudio piloto previo indicaba que se asociaban con el sentido de estabilidad psicológica (por ejemplo, digna de confianza o responsable), otros asociados con inestabilidad psicológica (espontánea, aventurera) y un tercer grupo sin asociación con la estabilidad o la inestabilidad (cariñosa, divertida). Los sujetos valoraron cada rasgo en una escala del 1 al 7, con 1 siendo “para nada deseable” y 7 “extremadamente deseable”.

Los resultados ponen de manifiesto que, igual que las bebidas frías nos llevan a la percepción de que las condiciones sociales también lo son, las sensaciones de inestabilidad física nos llevan a percepciones de inestabilidad social. Los participantes que se sentaron en sillas cojas a mesas cojas otorgaron a las parejas de famosos una puntuación de estabilidad promedio de 3,2, mientras que los que usaron mobiliario estable dieron un 2,5.

Pero lo que llama particularmente la atención es que los que se sentaban en las sillas inestables no solo veían inestabilidad en las relaciones de los demás, sino que valoraban más la estabilidad en las propias. Dieron a los rasgos que se relacionan con la estabilidad en sus posibles parejas un promedio de 5,0, mientras que los que utilizaron mobiliario estable dieron a estos mismos rasgos 4,5. No es una gran diferencia, pero es estadísticamente significativa.

Si solamente un poco de inestabilidad ambiental parece favorecer el deseo de una roca emocional a la que aferrarse, no quiero ni pensar lo que pueden estar pasando algunas parejas en los tiempos en que vivimos.

Referencias:

[1] Daniel M. Oppenheimer, & Thomas E. Trail1 (2010). Why Leaning to the Left Makes You Lean to the Left: Effect of Spatial Orientation on Political Attitudes Social Cognition, 28 (5), 651-661 : 10.1521/soco.2010.28.5.651

[2] David R. Kille, Amanda L. Forest, Joanne V. Wood (2012) Tall, Dark, and Stable: Embodiment Motivates Mate Selection Preferences Psychological Science doi: 10.1177/0956797612457392

Una versión anterior de este artículo se publicó en Experientia Docet el 7 de julio de 2012.

El artículo La estabilidad de la silla y tu pareja ideal se ha escrito en Cuaderno de Cultura Científica.

Bárbara Álvarez González

Efecto de las lentes gravitacionales fuertes observado por el Telescopio espacial Hubble en el cúmulo de galaxias Abell 1689 que indica la presencia de materia oscura. Fuente: Wikimedia Commons / NASA / ESA

 

¿Ha llegado la hora de considerar que la materia oscura no existe?
¿Es el momento de buscar otras alternativas para explicar de qué está hecho el 80 % del Universo desconocido? En estos momentos, algunos científicos consideran la posibilidad de que la materia oscura no sea materia, sino un artefacto causado por la incompleta comprensión de la teoría de la gravedad.

En el origen del Universo

A día de hoy, existe consenso entre los científicos acerca de que la teoría que mejor describe el origen del Universo es la del Big Bang. Así, el Universo nació hace unos 13 800 millones de años a partir de una singularidad infinitamente densa que explotó. La explosión generó una gran cantidad de energía y materia. Y todo aquello ha estado expandiéndose desde entonces.

Sorprendentemente, solo conocemos y comprendemos un 5 % de la materia que existen en el Universo. Incluso de este pequeño porcentaje hay aspectos que no hemos conseguido explicar, como la diferencia entre materia y antimateria.

La física de partículas elementales y el estudio de las interacciones entre ellas intenta desvelar el estado y la evolución del Universo. Y entre todas las incógnitas por resolver, determinar la naturaleza de la materia oscura es una de las más importantes de la cosmología moderna y la física de partículas.

Sabemos que el Universo está hecho de materia visible y materia oscura. En especial, la materia visible, también conocida como materia ordinaria o materia bariónica, es todo aquello formado por leptones (partículas elementales) y bariones (formados por quarks, que son también partículas elementales). De este tipo es tan solo el 20 % de la materia del Universo, el 80 % restante es materia oscura.

Además de su composición, sabemos que debe existir un agente que explique la expansión acelerada del Universo, que por el momento se atribuye a la llamada energía oscura.

El hallazgo de Vera Rubin

La materia oscura junto con la energía oscura componen prácticamente el 95 % del Universo. No la podemos ver, ya que no emite ningún tipo de radiación electromagnética.

Muchas de las evidencias de su existencia provienen del estudio de los movimientos de las galaxias. El análisis del fondo cósmico de microondas también aporta información sobre la cantidad de materia visible y oscura que existe.

En 1933 Fritz Zwicky propuso la existencia de una masa invisible que podía influir en la velocidad de rotación de las galaxias. La pionera Vera Rubin, con sus medidas sobre la curvatura de la velocidad de rotación de las estrellas dentro de galaxias espirales, descubrió que estas curvas se mantienen planas.

El hallazgo de Vera Rubin contradecía el modelo teórico que predecía que las estrellas más alejadas del centro de la galaxia tendrían menor velocidad. Este hecho no se puede explicar solo con la existencia de materia visible y su masa gravitacional asociada, sino que tiene que existir otra forma de materia que proporcione también energía gravitacional. Esta es la evidencia más directa y robusta de la existencia de materia oscura.

A partir de ese momento, y durante las décadas posteriores, se han recopilado más evidencias relacionadas con la materia oscura, hasta el punto de que hoy la gran mayoría de los científicos aceptan su existencia.

Experimentos de primer nivel en busca de la materia oscura

La materia oscura está compuesta por partículas que no absorben, reflejan, o emiten luz, no puede ser vista directamente, y desconocemos su composición.

Los científicos han diseñado diferentes estrategias para encontrar estas posibles partículas candidatas a materia oscura. Dar con ellas es uno de los mayores desafíos actuales de la física.

Existen diferentes estrategias de búsqueda de materia oscura, directa, indirecta o con aceleradores de partículas.

El progreso tecnológico en las últimas décadas ha sido enorme. Hay decenas de experimentos activos dedicados a comprender la naturaleza de la materia oscura con instrumentos de alta precisión y sensibilidad.

Estos experimentos están repartidos por todo el mundo, incluso hay uno en la Estación Espacial Internacional (ISS), y son parte de colaboraciones internacionales de decenas de científicos.

Los experimentos ANAIS, DAMA, XENON100 y LUX utilizan técnicas de detección directa; MAGIC, HESS, VERITAS, Fermi y AMS (en la ISS), entre otros, se basan en técnicas indirectas, para la observación de lo que ocurre en la naturaleza buscando partículas elementales.

En el primer caso, a partir de medias directas, se estudian partículas que surgen de colisiones de partículas de materia visible con partículas de materia
oscura, y en el segundo caso, a partir de medias indirectas, se estudian partículas de colisiones entre partículas de materia oscura exclusivamente.

El LHC “fabrica” partículas de materia oscura

En aceleradores de partículas tan energéticos como el Gran Colisionador de Hadrones (LHC) del CERN, Organización Europea para la Investigación Nuclear, se pueden recrear las condiciones de segundos después del Big Bang y producir o “fabricar” partículas de materia oscura a partir de colisiones de protones muy energéticos.

Los aceleradores son dispositivos que permiten incrementar la energía cinética de las partículas cargadas estables.

El LHC es el último de una cadena de aceleradores que consigue alcanzar energías de hasta los casi 7 TeV (tera electrón voltios) por cada haz de protones. Alrededor de los puntos de colisión se colocan los detectores que pueden medir e identificar las partículas que se producen en cada colisión, para luego poder estudiarlas.

Los experimentos ATLAS y CMS son los encargados de estas búsquedas en el LHC del CERN. Estos experimentos son los mismos que tras una larga búsqueda descubrieron el bosón de Higgs en 2012 completando así el Modelo Estándar de la Física de Partículas y abriendo una nueva era en el campo.

Este logro fue reconocido en 2013 con el Premio Nobel de Física y con el premio Príncipe de Asturias de Investigación Científica y Técnica.

La dificultad que tiene el identificar partículas candidatas a materia oscura en estos tipos de experimentos es que la materia oscura interacciona muy débilmente con la materia y es prácticamente imposible en estos casos encontrar su rastro o traza.

Compact Muon Solenoid (CMS) es uno de los grandes experimentos del LHC. Es un gran detector entre cuyos objetivos está la búsqueda de las partículas que forman la materia oscura.
CERN

Indagando en procesos desconocidos

Incorporando teorías más allá del modelo estándar como la supersimetría, modelos simplificados con bosones escalares, o modelos del sector oculto o sector oscuro, se llevan a cabo búsquedas a partir de sus desintegraciones en partículas ordinarias que sí se pueden observar. Estas búsquedas nos llevan a estudiar procesos desconocidos que quizá sean los que al fin nos permitan comprender la composición de la materia oscura, algo que sobrepasaría la frontera del conocimiento actual.

Hasta la fecha no se ha encontrado nada acerca de los posibles candidatos a materia oscura, es una gran incógnita, un misterio aún sin resolver que lleva décadas sin respuesta. Y entre los físicos empieza a haber opiniones discordantes.

No tenemos ningún resultado concluyente en ninguna de las estrategias de búsquedas empleadas en acelerados o astropartículas y todas las posibilidades están abiertas.

Hay científicos que empiezan a plantearse que no existe

El año pasado se publicó un artículo en The Astrophysical Journal que proponía definir la materia oscura como una modificación de la gravedad. Este artículo proponía que en realidad no hay materia oscura, sino que hay partes de la fuerza de la gravedad que no entendemos bien. Su publicación generó un enorme revuelo y entusiasmo, pero enseguida se publicaron respuestas señalando incongruencias que los autores del artículo no tenían en cuenta. Así que por ahora seguimos pensando que hay materia oscura.

Hay grandes expectativas para la detección de materia oscura en los próximos años, aunque, muy probablemente, la respuesta no vendrá de uno solo de estos estudios sino del conjunto de todos ellos. La búsqueda continúa.

Sobre la autora: Bárbara Álvarez González es investigadora Ramón y Cajal del Grupo Experimental de Altas Energías de la Universidad de Oviedo

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo El problema difícil de la materia oscura se ha escrito en Cuaderno de Cultura Científica.

Fuente: Wikimedia Commons

Hace cinco mil trescientos años, en el ocaso de la Edad del Cobre y los albores de la del Bronce, surgió, al norte de los mares Negro y Caspio, la que hoy denominamos cultura yamna, también llamada “del sepulcro”. El grupo humano que la desarrolló experimentó una gran expansión geográfica; los yamnaya se extendieron hacia el este hasta el territorio de la actual Mongolia y hacia el oeste por todo el subcontinente europeo. A la Península Ibérica llegaron hace, aproximadamente, cuatro mil trescientos años, diez siglos después de su aparición. Su legado genético se encuentra hoy en prácticamente toda Europa y parte de Asia. Tan grande fue su éxito demográfico.

Hasta hace relativamente poco tiempo, la mayor parte de la información relativa a esta cultura se había obtenido de investigaciones arqueológicas, por su característico método de enterramiento; de ahí el nombre “cultura del sepulcro”. Hacían las inhumaciones en túmulos (kurganes), unos sepulcros excavados en el suelo en los que se colocaba el cadáver boca arriba y con las rodillas dobladas. Además, los cuerpos eran cubiertos con ocre.

En algunos enterramientos se han hallado restos de animales domesticados y, por otro lado, los restos más antiguos de carros con ruedas se han encontrado en Europa Oriental en un kurgán en Ucrania perteneciente a la cultura yamna, precisamente. A partir de esos elementos, a los yamnaya se les ha considerado nómadas o seminómadas, que se desplazaban en carros de dos ruedas o vagones de cuatro, pastoreaban ganado y adquirieron la capacidad para consumir leche. A esas adquisiciones se les ha atribuido su fenomenal éxito demográfico.

Las dudas que pudiera haber acerca de los elementos que impulsaron su expansión se han empezado a disipar tras la publicación reciente de los resultados de una investigación. En ella han examinado el sarro de los dientes de restos humanos procedentes del periodo inmediatamente anterior al comienzo de la expansión yamnaya, durante su inicio y tras haberse producido. Han estudiado restos dentales de 56 individuos que vivieron en un periodo de tiempo que va desde hace unos 6600 a 3700 años. Y el examen ha consistido en la caracterización de los restos de proteínas presentes en ese sarro y la determinación de su origen.

Diez de los once individuos procedentes del final de la Edad del Cobre carecían de rastros de haber consumido leche o productos lácteos. Solo uno presentaba restos de proteínas lácteas, debido quizás a su consumo ocasional. Sin embrago, en quince de los dieciséis individuos procedentes del comienzo de la Edad del Bronce, la dentadura contenía abundantes restos lácteos, prueba fiable de su consumo habitual.

Además, algunas de las muestras analizadas en los restos de individuos procedentes del comienzo de la Edad del Bronce contenían proteínas de leche de yegua. Ese dato, junto con otras evidencias arqueológicas, sugiere que los yamnaya no solamente consumían leche de vacas, ovejas y cabras, sino que, además, domesticaron el caballo, lo utilizaron para cabalgar y tirar de carros de dos ruedas, y llegaron incluso a consumir leche de yegua.

Todos estos elementos refuerzan la idea de que la domesticación del caballo y el pastoreo de rebaños de diferentes especies fueron los elementos que impulsaron una transición demográfica muy intensa que permitió la expansión de los jinetes de las estepas hacia Mongolia, el norte del subcontinente indio y el extremo occidental del europeo. El genetista David Reich sostiene que los varones yamnaya llegaron incluso a sustituir la práctica totalidad de los varones de otros linajes en la Península Ibérica hace unos cuatro mil quinientos años. De ser cierta esa conjetura, pocos linajes habrían tenido un éxito tan “arrollador”.

Fuente: Wilkin, S., Ventresca Miller, A., Fernandes, R. et al. Dairying enabled Early Bronze Age Yamnaya steppe expansions. Nature (2021).

 

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Yamnaya se ha escrito en Cuaderno de Cultura Científica.

El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

Las probabilidades de que una concepción termine resultando en un nacimiento son muchísimo más bajas de los que te imaginas. Sergio Pérez Acebrón nos presenta qué ocurre en las primeras 6 semanas del embarazo, esos momentos en que ni siquiera muchas mujeres sospechan que pueden estar embarazadas,



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2021: Sergio Pérez Acebrón – El comienzo más difícil se ha escrito en Cuaderno de Cultura Científica.

Ivan Gomez-Lopez, Maitane González-Arceo y María P. Portillo

Durante el cocinado los alimentos son susceptibles de sufrir muchos cambios de color, olor y/o sabor. Estos cambios se deben a la formación de diferentes sustancias químicas que no siempre son beneficiosas, como es el caso de la acrilamida. Ésta se forma gracias a la reacción de Maillard, que se da a altas temperaturas en presencia del aminoácido asparagina e hidratos de carbono. Por ello, los alimentos en los que se puede encontrar mayor cantidad de acrilamida son los elaborados a base de patata y cereales, además del café, entre otros. Este compuesto está clasificado como probable cancerígeno por la Agencia Internacional de Investigación contra el Cáncer (IARC, International Agency for Research on Cancer), pudiendo producir efectos negativos sobre la salud. La única manera de reducir su ingesta es previniendo la formación de la misma, ya que es fácil de identificar debido al cambio de color que producen los alimentos. No obstante, cabe destacar que, siguiendo una dieta variada y equilibrada, su ingesta no debería suponer una preocupación mayor.

Foto: Leti Kugler / Unsplash

Introducción

La mayoría de los alimentos que consumimos hoy en día sufren una serie de procesos que modifican muchas de sus características. Estos procesos no solo se dan en la industria alimentaria; el cocinado de los alimentos que realizamos en el hogar es un procesamiento térmico con el que se producen cambios en características como el olor, el color, la textura y/o el sabor. También se puede reducir el valor nutricional de los alimentos, por ejemplo, por pérdida de vitaminas. No obstante, también se producen efectos positivos como la eliminación de microorganismos patógenos [1].

Durante el cocinado de los alimentos se dan una serie de reacciones químicas que, en ciertos casos, desencadenan en la formación compuestos tóxicos. A veces estos compuestos son fácilmente detectables a simple vista ya que van asociados a cambios de color de los alimentos. Este es el caso de la acrilamida, una sustancia química que se crea de forma natural en los productos alimenticios que contienen almidón durante procesos culinarios cotidianos a altas temperaturas, como la fritura, el tostado, el asado u otros procesos térmicos a más de 120 ºC y a baja humedad [2]. ¿Quién no ha oído decir que una tostada quemada o la carne muy hecha provoca “cáncer”? Pero, ¿Hasta qué punto es esto cierto?

¿Cómo se forma la acrilamida?

Mientras se da el procesamiento térmico de un alimento, los colores del mismo tienden a pardearse, debido a la reacción de Maillard. Esta reacción es la responsable de la formación de compuestos que dan color, sabor y olor al alimento cocinado a temperaturas altas. Además de estos cambios que hacen atractivos y apetecibles los alimentos, se puede generar, entre otros compuestos, la acrilamida. Para la formación de la acrilamida, el alimento debe tener una serie de características. En primer lugar, es necesario que el alimento sea rico en hidratos de carbono y en segundo lugar, se requiere la presencia del aminoácido asparagina (Figura 1). Cabe destacar, que la formación de este compuesto va asociado al tiempo y temperatura de cocción [3]. Cuanto más tiempo cocinamos una patata frita, particularmente mediante fritura y en menor grado en el caso del horneado, más oscura se vuelve, formándose mayor cantidad de acrilamida.

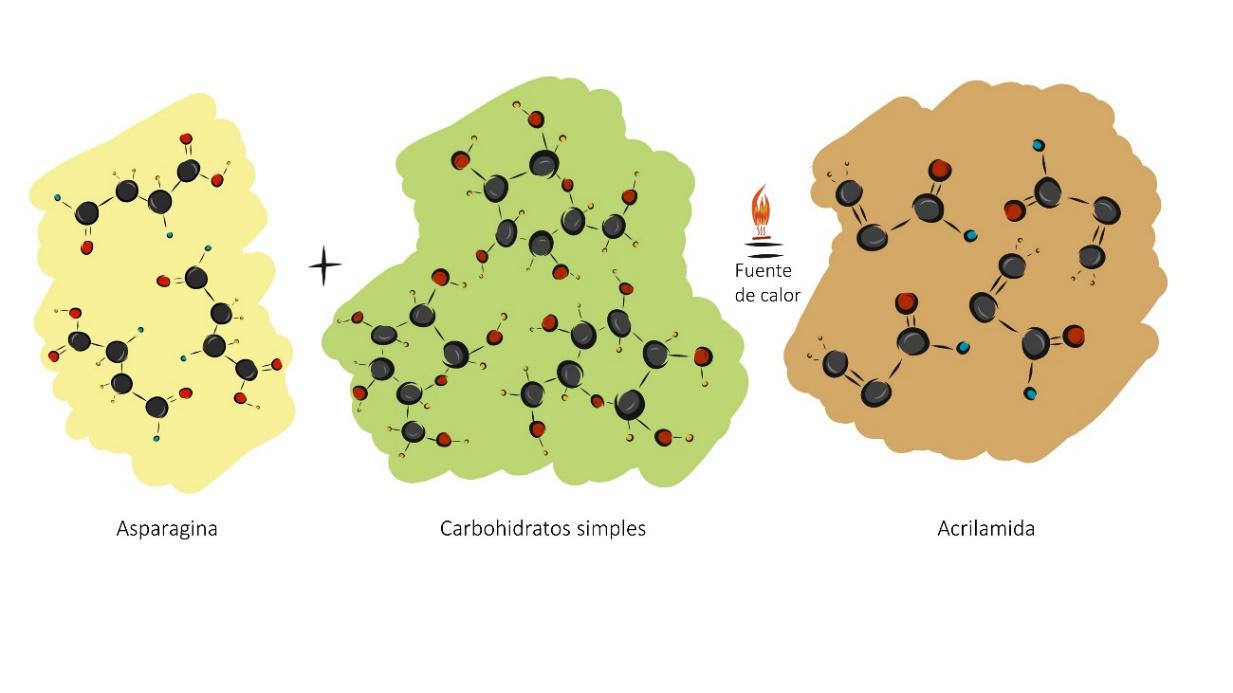Figura 1. Representación de formación de la acrilamida. Fuente: Los autores.

 

¿En qué alimentos se puede encontrar y qué presencia tiene la acrilamida en nuestra dieta?

Las fuentes más comunes de acrilamida son las patatas fritas o los productos fritos a base de patata, cereales y sus derivados como galletas, bizcochos y pan y el café tostado. En un reciente estudio de la AESAN (Agencia Española de Seguridad Alimentaria y Nutrición) se muestra que la patata y sus derivados son los alimentos que más contribuyeron a la ingesta de acrilamida en adultos, adolescentes y niños mayores de 1 año, representando un 49-62% de la exposición. En bebés menores de un año, los principales contribuyentes son los alimentos que no provienen ni de patata ni de cereales (Figura 2) [2].

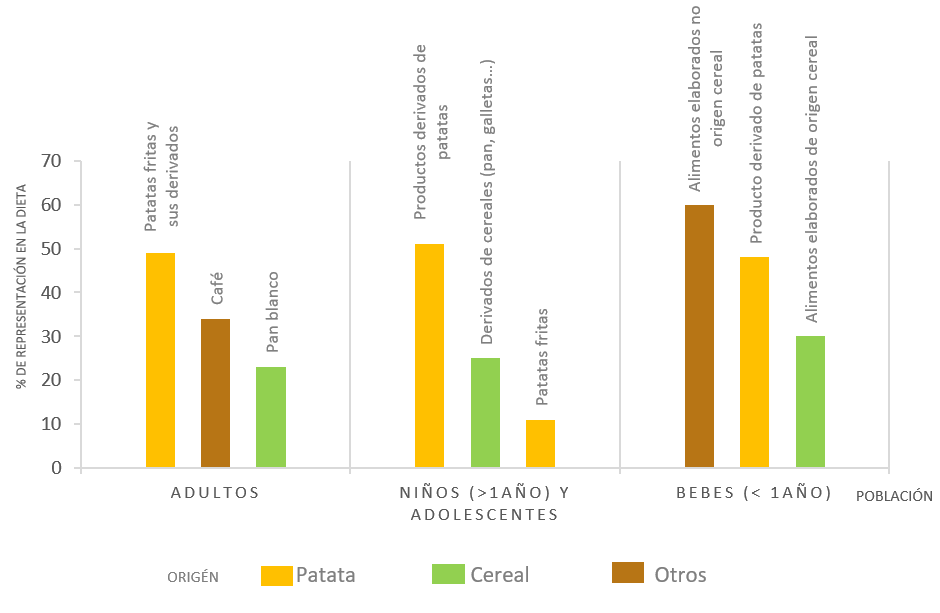Figura 2. Porcentaje de contribución de diversos alimentos a la ingesta de acrilamida según edad. Datos obtenidos de la Agencia Española de Seguridad Alimentaria y Nutrición, 2020. Fuente: Los autores.

 

¿Cuáles son los efectos negativos de la acrilamida?

La Agencia Internacional de Investigación contra el Cáncer (IARC, International Agency for Research on Cancer) ha clasificado la acrilamida como “probable cancerígeno para los humanos” [4].Pero, hasta el momento, el potencial carcinógeno (que produce cáncer o favorece su aparición) y genotóxico (que daña el ADN) de la acrilamida solo ha sido demostrado en modelos animales. Dado que en humanos sólo se han realizado unos pocos estudios epidemiológicos, no se puede establecer una clara asociación entre la exposición a la acrilamida mediante la dieta y el desarrollo del cáncer. Otros estudios preclínicos apuntan que la acrilamida tiene efectos sobre la reproducción, el sistema nervioso y el hígado [5].

Aunque es importante hacer hincapié en que estos efectos tóxicos solo se han demostrado en animales, sin embargo, es preferible actuar con precaución y tratar de reducir la exposición a la acrilamida, por ejemplo, minimizando su presencia en los alimentos.

¿Existe una “dosis tolerable” de acrilamida?

Puesto que cualquier nivel de exposición a una sustancia genotóxica puede dañar el ADN y contribuir a la aparición de cáncer, los científicos de la Autoridad Europea de Seguridad Alimentaria (EFSA, European Food Safety Authority) concluyen que no se puede establecer una ingesta diaria tolerable de acrilamida en alimentos [6]. Por ello, deberíamos reducir su ingesta lo máximo posible. La Organización de las Naciones Unidas para la Agricultura y la Alimentación (FAO, Food and Agriculture Organization) publicó en 2009 un Código de Prácticas para intentar reducir el contenido de acrilamida en los alimentos [7].

¿Cómo podemos reducir la formación e ingesta de acrilamida?

Entre otras, la Administración de Medicamentos y Alimentos de Estados Unidos (FDA, Food and Drug Administration) hace una serie de recomendaciones que se pueden seguir en casa a la hora de cocinar alimentos para minimizar la formación de acrilamida [8]:

1. Reducir el tiempo de fritura y controlar la temperatura en la medida de lo posible.

2. En el caso concreto de las patatas, se recomienda guardarlas en un lugar seco y oscuro y evitar la nevera.

3. El color es un buen indicador de la cantidad de acrilamida, por lo que se deben retirar los alimentos de la fuente de calor cuando tienen un color dorado, y evitar las tonalidades marrones oscuras (Figura 3).

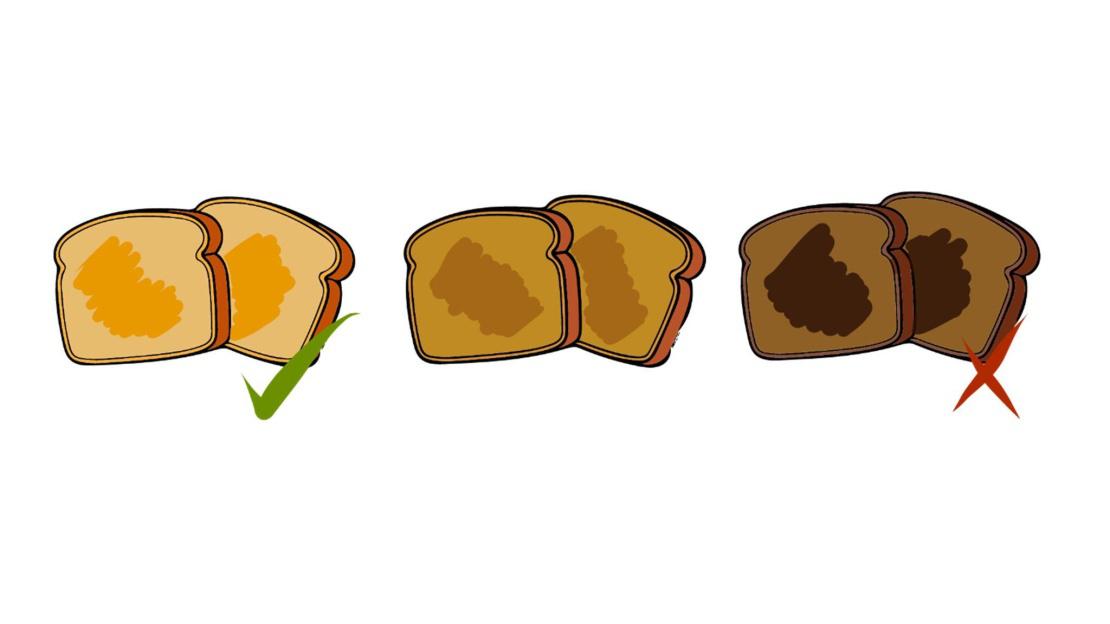Figura 3. Representación de los diferentes colores de tostado obtenido según el tiempo de cocinado del pan. Siendo la más oscura la que mayor cantidad de acrilamida alberga. Fuente: Los autores.

 

Como conclusión, cabe destacar que, aunque los alimentos citados en el presente artículo puedan contener una gran cantidad de acrilamida, dado que si llevamos una dieta variada y equilibrada no van suponer la base de nuestra alimentación, la ingesta de acrilamida no debería preocuparnos en exceso.

 

 

Bibliografía

5. Rifai L y Saleh FA. A Review on Acrylamide in Food: Occurrence, Toxicity, and Mitigation Strategies. International Journal of Toxicology, 39(2):93-102 (2020). doi: 10.1177/1091581820902405

6. Aesan (Agencia Española de Seguridad Alimentaria y Nutrición). Con la acrilamida no desentones, elige dorado, elige salud. (21/12/2020).

7. Teodorowicz M, van Neerven J, y Savelkoul H. Food Processing: The Influence of the Maillard Reaction on Immunogenicity and Allergenicity of Food Proteins. Nutrients, 9(8), 835 (2017). doi: 10.3390/nu9080835

8. Agencia Internacional para la Investigación en Cáncer (IARC). IARC monographs on the evaluation of carcinogenic risk to humans. Some industrial chemicals. Volumen 60 (1994).

9. Perera DN, Hewavitharana GG y Navaratne SB. Comprehensive Study on the Acrylamide Content of High Thermally Processed Foods. BioMed Research International (2021). doi: 10.1155/2021/6258508

10. Autoridad europea de seguridad alimentaria (EFSA). Scientific Opinion on acrylamide in food. EFSA Journal 13(6):4104 (2015).

11. Organización de las Naciones Unidas para la Agricultura y la Alimentación (FAO). Código de prácticas para reducir el contenido de acrilamida en los alimentos. CAC/RCP 67-2009 (2009).

12. FDA (Food and Drug Administration). You Can Help Cut Acrylamide in Your Diet (14/03/2016). 

Sobre los autores:

Ivan Gomez-Lopez 1,2 , Maitane González-Arceo1, María P. Portillo1,3

1 Grupo de Nutrición y Obesidad, Departamento de Farmacia y Ciencias de los Alimentos, Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU)

2 Grupo de fitoquímica y funcionalidad de productos vegetales, Departamento de Biotecnología y Microbiología de los Alimentos, Instituto de investigación en ciencias de la alimentación (CIAL) (CSIC-UAM)

3 Centro de Investigación Biomédica en Red de la Fisiopatología de la Obesidad y Nutrición (CiberObn)

El artículo En busca de El Dorado (en los alimentos) se ha escrito en Cuaderno de Cultura Científica.

 

En la primera generación de videojuegos de Pokémon nos encontrábamos con unos objetos curiosos cuando visitábamos la región de Kanto: un par de fósiles y un fragmento de ámbar o resina fósil. Hasta aquí podíamos considerarlo una anécdota, pero venía acompañada por una parte más fantasiosa. Una vez que conseguíamos esos objetos, podíamos acudir con ellos a un laboratorio científico para que reviviesen a los Pokémon que habían dejado esos restos fósiles. En el último caso, incluso, extrayendo una muestra de ADN preservado en el ámbar, al más puro estilo de la novela de Michael Crichton “Parque Jurásico”.

Esta idea de completar nuestra colección de Pokémon con ejemplares extintos reanimados por la ciencia tuvo una fantástica acogida entre los fanáticos de esta saga, de tal manera que los diseñadores decidieron incluir más fósiles en casi todas las nuevas generaciones de videojuegos. Pero el diseño de estas criaturas fósiles no surgió simplemente de una imaginación desbordada, sino que tiene una base científica sólida. Así que vamos a sacar nuestra Pokédex paleontológica y analicemos esos organismos tan particulares, considerando primero los invertebrados para pasar, a continuación, a los vertebrados.

Diseño de las cartas del juego de mesa Pokémon Trading Card Game con una agrupación de restos fósiles inidentificados y con los científicos que se dedican a buscar y revivir Pokémon fósiles. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.

Uno de los primeros Pokémon fósiles que podíamos revivir era Kabuto, cuya morfología responde a una mezcla entre un cangrejo herradura y un trilobites, un grupo de artrópodos marinos extintos hace unos 250 millones de años.

También podíamos hacernos con Anorith, criatura casi calcada a los Anomalocaris, un grupo de organismos relacionados con los artrópodos que poblaron los mares cámbricos hace entre 510 y 530 millones de años.

Aspecto del Pokémon Anorith. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.

Por otro lado, nos encontrábamos con Omanyte, Pokémon directamente basado en unos cefalópodos marinos también extintos llamados ammonites.

Aspecto del Pokémon Omanyte. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.

Pero un ejemplar que podía confundirnos sobre su grupo taxonómico de origen era Lileep. Considerado de tipo planta, además de roca, lo conseguíamos a partir del fósil raíz, lo que nos hacía pensar que se trataría de algún tipo de vegetal pretérito. Pero su morfología está basada en los crinoideos, un grupo de equinodermos marinos comúnmente conocidos como “lirios de mar” porque de un simple vistazo recuerdan a una planta, pero se trata de animales.

El primer Pokémon fósil vertebrado lo encontrábamos a partir de ese ADN antiguo conservado en ámbar, ya que revivíamos a un Aerodactyl, cuyo nombre y forma recuerdan enormemente a Pterodactylus, un género de reptiles voladores mesozoicos.

En cuanto a los reptiles acuáticos, podíamos hacernos con Tirtouga, que está basado en el género extinto de tortugas marinas cretácicas Protostega, la segunda tortuga de mayor tamaño de la historia, solo superadas por el género Archelon, extintas también a finales del Cretácico. Y sí, la evolución de Tirtouga, Carracosta, mucho más grande y fuerte, tiene su inspiración precisamente en este último género de tortugas gigantes.

Por supuesto, no podían faltar los Pokémon originados a partir de géneros extintos de dinosaurios. Por un lado, revivíamos a Cranidos, una criatura similar a los paquicefalosáuridos, un grupo que tenía fusionados los huesos frontal y parietal, lo que le aportaba una resistente protuberancia ósea en la cabeza. Por su parte, Shieldon se inspira en los ceratópsidos, un grupo de dinosaurios que desarrollaron una estructura ósea en la parte trasera de la cabeza a modo de collar protector. Y no podía faltar el Pokémon basado en el Tyrannosaurus rex, Tyrunt.

Aspecto del Pokémon Cranidos. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.

Con Amaura también podíamos equivocarnos en su clasificación faunística, como en el caso de Lileep. Y es que revivía a partir del fósil aleta, por lo que nos podríamos imaginar que está inspirado en algún tipo de reptil marino. Pero, en realidad, su desarrollo está basado en la especie Amargasaurus cazaui, un dinosaurio saurópodo que tenía una hilera de espinas dorsales desde la cabeza hasta la punta de la cola.

Finalmente encontramos a Archen, la versión Pokémon de Archaeopteryx, género considerado como una forma de transición entre los dinosaurios y las aves.

Aspecto del Pokémon Archen. Crédito: Nintendo/Creatures Inc./GAME FREAK inc.

Pero estas criaturas no son las únicas herramientas didácticas de paleontología aparecidas en la saga de videojuegos. En la región de Hoenn descubrimos un Pokémon que se creía extinto y al que consideran un fósil viviente, Relicanth. Esta criatura es un homenaje a los celacantos, un grupo de peces que se consideraban extintos desde finales del Cretácico ya que no se tenían evidencias ni de restos fósiles más modernos ni de su presencia en la actualidad, al habitar aguas profundas y de difícil acceso, hasta que se capturó un ejemplar vivo hace décadas.

Y el último guiño geológico lo aportan los juegos de octava generación. Aquí podemos combinar fósiles en grupos de dos piezas para revivir Pokémon híbridos. Así conseguimos un Dracozolt, que es mitad un dromeosáurido, dinosaurio de baja estatura y con el cuerpo emplumado, y mitad un estegosáurido, dinosaurio con placas óseas dorsales. Arctozolt es la combinación de un dromeosáurido y un plesiosaurio, un reptil marino. Por su parte, Dracovish representa una mezcla entre un Dunkleosteus, un género de peces acorazados de la Era Paleozoica, y un estegosáurido. Y, por último, podemos revivir a un Arctovish, parte Dunkleosteus y parte plesiosaurio.

Esta mezcla de géneros y grupos faunísticos rememora los comienzos de la paleontología de vertebrados, cuando los naturalistas de finales del s. XVIII y comienzos del s. XIX se empeñaban en montar esqueletos completos en cada yacimiento fósil, incluso mezclando restos de especies y géneros diferentes, dando lugar a formas que nunca existieron en la naturaleza.

Sin duda, la saga de videojuegos Pokémon es una manera de lo más divertida de aprender paleontología. Ahora sólo nos queda hacernos con todos los fósiles que aparecen en los mismos.

Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU

El artículo Pokepaleontología se ha escrito en Cuaderno de Cultura Científica.