Revertir y prevenir la obesidad modulando el uso de la metionina
El grupo de investigación Lipids & Liver de la UPV/EHU ha demostrado que modificando de manera específica el uso de metionina en el hígado de ratones obesos, a través del silenciamiento del gen Mat1a, se obtiene un efecto global sobre el organismo: se previene y revierte la obesidad, desaparecen la resistencia a la insulina y el exceso de lípidos circulante y se consumen los lípidos del hígado.
 La obesidad es una enfermedad muy compleja, que no solamente concierne al hígado o al tejido adiposo, también está implicado el cerebro. Imagen: lightwise/123rf.
La obesidad es una enfermedad muy compleja, que no solamente concierne al hígado o al tejido adiposo, también está implicado el cerebro. Imagen: lightwise/123rf.La obesidad es un importante problema de salud pública con una prevalencia creciente en todo el mundo. Se considera que para el 2030 entre un 50-60 % de la población va a ser obesa. La obesidad es un factor de riesgo establecido para diversas enfermedades como la enfermedad del hígado graso no alcohólico, ahora también conocida como esteatosis hepática metabólica, la diabetes tipo 2 y la dislipemia (alteración de los niveles de lípidos y proteínas en sangre), entre otras. La pérdida de peso mediante tratamientos farmacológicos, intervenciones en el estilo de vida o incluso la cirugía son eficaces para tratar las comorbilidades relacionadas con la obesidad. Sin embargo, sigue siendo necesario comprender mejor la conexión entre los diferentes trastornos metabólicos relacionados con la obesidad para poder proponer nuevas terapias.
La investigadora principal del grupo Lipids & Liver de la UPV/EHU Patricia Aspichueta se muestra muy satisfecha con los resultados obtenidos en la investigación, que son “importantes y clarísimos”. Tras cinco años de exhaustiva investigación colaborativa, este grupo ha obtenido “información de cómo el hígado puede regular la obesidad y las enfermedades asociadas a esa obesidad; cómo modulando o restringiendo el uso de metionina (un aminoácido esencial que se obtiene únicamente a través de la dieta) dentro del hígado, conseguimos mejorar el estado corporal: mejorar la obesidad y las enfermedades asociadas a ella. Aportamos datos importantes y esperanzadores en este camino. Sin embargo, no está todo descubierto y hay que aportar mucho más”, afirma la investigadora.
En el estudio liderado por Aspichueta se ha conseguido, en ratones obesos, prevenir y revertir la obesidad, así como la resistencia a la insulina y la hepatosteatosis (acumulación de grasa en el hígado) asociadas, aumentando el gasto energético, además de reducir los lípidos en el suero y del hígado. Según explica la doctora, “modificando de manera específica en el hígado el uso de la metionina, a través del silenciamiento del gen Mat1a, obtenemos un efecto global sobre el organismo: el hígado genera una molécula que se secreta al torrente circulatorio y tiene efectos sobre otros tejidos debido a su alta capacidad para modular el metabolismo de todo el organismo. Entre otros, uno de los tejidos que regula es la grasa parda; al activarse esta grasa parda, se activa el consumo de grasas del organismo en este tejido, dando lugar a una serie de efectos beneficiosos: los ratones bajan de peso, desaparece la resistencia a insulina, desaparece el exceso de lípidos circulante en sangre y disminuyen los lípidos del hígado”.
No obstante, Aspichueta enfatiza que este es un paso más: “Nosotros hemos realizado un análisis en modelos animales; pero todavía queda mucho por hacer: hay que investigar sobre posibles efectos adversos, antes de llevar todo esto a un ensayo clínico. Se puede restringir el uso de la metionina en el hígado, pero nunca se debe inhibir. Esta restricción produce una serie de cambios a nivel del metabolismo hepático, y hay que tener cuidado. Hay que mantener todo en equilibrio, porque si mantienes una inhibición muy larga, también puede tener un efecto perjudicial”. La obesidad es una enfermedad muy compleja, que no solamente concierne al hígado o al tejido adiposo, también está implicado el cerebro. “Es una enfermedad tan compleja que tiene mecanismos compensatorios. Esta investigación es, por tanto, un granito de arena más; una información importante para saber cómo funciona todo el metabolismo en esta enfermedad tan compleja”, afirma.
La prevalencia de la obesidad, del sobrepeso, cada vez es más elevada. Entre un 70-80 % de pacientes con obesidad, tienen problemas de esteatosis hepática metabólica, es decir, de enfermedad hepática. En algunos de estos pacientes, progresa, se complica y acaba en una hepatitis por grasa, o incluso en cáncer hepático. “Nuestro objetivo es poder determinar cómo parar la generación de esta enfermedad en el hígado y su progresión. Y si conseguimos de alguna manera detener o revertir esta obesidad y todos estos efectos nocivos, podremos ayudar a disminuir quizá la prevalencia del cáncer. Si conseguimos conocer cómo modular esta obesidad y con ello todas las enfermedades asociadas, podremos ralentizar la progresión hacia este problema de alta prevalencia”, concluye.
Referencia:
Diego Sáenz de Urturi, Xabier Buqué, Begoña Porteiro, Cintia Folgueira, Alfonso Mora, Teresa C. Delgado, Endika Prieto-Fernández, Paula Olaizola, Beatriz Gómez-Santos, Maider Apodaka-Biguri, Francisco González-Romero, Ane Nieva-Zuluaga, Mikel Ruiz de Gauna, Naroa Goikoetxea-Usandizaga, Juan Luis García-Rodríguez, Virginia Gutierrez de Juan, Igor Aurrekoetxea, Valle Montalvo-Romera, Eva M. Novoa, Idoia Martín-Guerrero, Marta Varela-Rey, Sanjay Bhanot, Richard Lee, Jesus M Banales, Wing-Kin Syn, Guadalupe Sabio, María L. Martínez-Chantar, Rubén Nogueiras, Patricia Aspichueta (2022) Methionine adenosyltransferase 1a antisense oligonucleotides activate the liver-brown adipose tissue axis preventing obesity and associated hepatosteatosis Nature Communications doi: 10.1038/s41467-022-28749-z
El artículo Revertir y prevenir la obesidad modulando el uso de la metionina se ha escrito en Cuaderno de Cultura Científica.
Perlas avinagradas
 El banquete de Cleopatra, obra de 1652 realizada por el artista Jan de Bray. Fuente: The Royal Collection Trust
El banquete de Cleopatra, obra de 1652 realizada por el artista Jan de Bray. Fuente: The Royal Collection TrustCuenta Plinio el Viejo en uno de los tomos de su gran obra Historia Natural una anécdota muy curiosa entre la reina de Egipto, Cleopatra, y el general romano más famoso del momento, Marco Antonio. Resulta que Cleopatra quería impresionar a Marco Antonio para que se convirtiera en su aliado militar y político y, ya de paso, en su amante particular. Para ello se le ocurrió hacer una apuesta con el general romano, asegurándole que le invitaría al banquete más suntuoso y caro al que habría asistido en su vida. Cuando llegó la celebración del ansiado festejo, las cosas no estaban saliendo como Cleopatra esperaba, ya que el romano no parecía en absoluto impresionado con lo que le estaban ofreciendo. Incluso, con cierto sarcasmo, Marco Antonio le dejó caer a la reina egipcia que se estaba aburriendo. Cleopatra reaccionó rápido y con la chulería que parece que la caracterizaba. Pidió a uno de sus esclavos que le llevase una copa de vinagre de vino, se quitó una de las enormes perlas que decoraban sus pendientes, la dejó caer en la copa, esperó unos segundos a que se disolviese y se la bebió. Eso sí impresionó a Marco Antonio, que ya no se separó de la reina egipcia hasta el momento de su muerte.
La historia es muy bonita, pero veamos qué dice la ciencia sobre esta anécdota. Por un lado, tenemos una perla. Las perlas son unas estructuras compuestas por carbonato cálcico (CaCO3) cristalizado en forma de un mineral llamado aragonito, y por una proteína orgánica denominada conquiolina. Estas estructuras son segregadas por algunos moluscos bivalvos, como las ostras, para proteger su cuerpo blando cuando entra alguna partícula externa, a la que van envolviendo de manera progresiva en carbonato hasta asegurarse de que dicha partícula ya no representa ningún peligro para su integridad. Por otro lado, tenemos vinagre de vino. El vinagre es básicamente ácido acético (CH3COOH) diluido, un ácido considerado débil. En definitiva, tenemos una base (la perla) y un ácido (el vinagre) que vamos a mezclar.
Si recordamos un poco las clases de química del instituto, en esa reacción se produce una sal en estado sólido, dióxido de carbono en forma gaseosa y agua líquida. Es decir, que la perla de Cleopatra acabaría reaccionando con el vinagre generando una sustancia sólida carbonatada mezclada con agua en una copa burbujeante, que sería lo que se habría bebido la reina egipcia. Pero hay algo que no hemos tenido en cuenta, ¿esta reacción habría sucedido en unos segundos? Pues aquí es donde entra la leyenda. El hecho de que el acético sea un ácido débil determina el tiempo de la reacción. Para poder disolver el carbonato cálcico de la perla habrían pasado varios días y, además, habrían tenido que ir añadiendo más vinagre cada cierto tiempo.
Vamos, que parece inviable que Marco Antonio se quedase sentado esperando a que terminase la reacción durante unos cuantos días, así que esta historia bien podría ser un simple mito. Eso, o Cleopatra se tragó una enorme perla utilizando vinagre de vino para acompañarla, después de engañar al romano tras generar un poquito de espuma en una copa, que tampoco lo descarto.
Hasta aquí he hablado de historia, leyendas y química. Pero ahora le toca el turno a la geología. Y es que los geólogos empleamos diferentes ácidos para que reaccionen con sustancias minerales de manera controlada y facilitarnos el trabajo en numerosas ocasiones. Un ejemplo es su utilización como mecanismos de extracción química de fósiles en el ámbito de la paleontología. Y el ácido acético diluido es uno de los más empleados para disolver las rocas y los sedimentos carbonatados cuando realizamos estudios de restos fósiles de vertebrados.
 Proceso de trabajo en micropaleontología de vertebrados por disolución química. A: reacción química entre el ácido acético y los restos carbonatados. B: lavado del material resultante tras la reacción química para concentrar los restos óseos fosfáticos. Fotografías de Oier Suarez Hernando.
Proceso de trabajo en micropaleontología de vertebrados por disolución química. A: reacción química entre el ácido acético y los restos carbonatados. B: lavado del material resultante tras la reacción química para concentrar los restos óseos fosfáticos. Fotografías de Oier Suarez Hernando.Los restos óseos tienen una composición fosfática que resiste mucho mejor el ataque del ácido acético que los materiales conformados por carbonato cálcico. La metodología de trabajo es simple, se sumerge la muestra de matriz carbonata que incluye los fósiles fosfáticos en ácido acético diluido y se deja actuar durante varias horas, incluso días. A continuación, se lava abundantemente con agua corriente, hasta eliminar la mayor parte del compuesto carbonatado resultante de la reacción química, y se deja secar al aire. Este proceso se puede repetir sucesivas veces hasta que nos quedemos únicamente con los restos óseos que nos interesan analizar.
Y aunque este proceso es lento y laborioso, por suerte los geólogos tenemos más paciencia que Marco Antonio (y sabemos un poco más de química que él).
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Perlas avinagradas se ha escrito en Cuaderno de Cultura Científica.
No se puede cambiar el azar
Érase una vez un lejano y extraño lugar en el que los nacimientos de niñas y niños sucedían exactamente en la misma proporción: los bebés eran niñas en un 50 % de los alumbramientos y niños en el 50 % restante. No se conocía ninguna época en la que este hecho hubiera sido diferente. Es decir, desde el principio de los tiempos, el sexo de los bebés se comportaba como si se decidiera al azar lanzando, por ejemplo, una moneda equilibrada.
 Foto: Pixabay
Foto: PixabayEl Gobierno decidió que solo las parejas con al menos una niña recibirían una gran suma de dinero al llegar su jubilación. En respuesta a esta medida, y después de pensarlo concienzudamente, cada pareja adoptó la siguiente estrategia para garantizar una jubilación tranquila:
-
si su primer bebé era una niña, decidían no tener más descendencia;
-
si el primer hijo era un varón, la pareja tenía un segundo bebé que sería el último si era una niña;
-
y actuaban de este modo sucesivamente: cada pareja tenía descendencia hasta que llegaba una hija, que era entonces su último retoño.
Esta estrategia tenía dos consecuencias obvias:
-
no había familias sin hijas en este lejano y extraño lugar, y
-
una de cada dos familias no tenía hijos.
Esto parecía favorecer claramente a las niñas. Sin embargo, después de unos años tras haber sido adoptada esta medida, el Ministerio de Estadística del Gobierno de ese lejano y extraño lugar revisó los datos de nacimientos, y comprobó, con sorpresa, que había habido casi tantos nacimientos de niños como de niñas. ¿Cómo explicar esta paradoja?
La realidad, y aunque parezca sorprendente, es que la estrategia adoptada por las familias no tiene ninguna influencia en la proporción de niñas nacidas. En efecto, la probabilidad de que un bebé sea niña es siempre del 50 %; lo que ha sucedido en el pasado no influye sobre el siguiente nacimiento, según se declara al principio de esta historia. La afirmación inicial implica que, en media, nace una niña por cada dos alumbramientos. No importan las estrategias elegidas por las parejas que desean tener hijas: la proporción de niñas y niños nacidos seguirán siendo las mismas.
Para convencernos, vamos a hacer un cálculo suponiendo, por simplificar, que las familias tienen un máximo de cinco descendientes. Puede repetirse el cálculo con cualquier cantidad máxima de nacimientos, o incluso sin limitaciones en la cantidad de prole:
-
La probabilidad de que una familia tenga un único descendiente es de 1/2. Será entonces una niña.
-
La probabilidad de que una pareja tenga dos descendientes es de 1/4. Serán niño-niña.
-
La probabilidad de que una familia tenga tres descendientes es de 1/8. Y serán niño-niño-niña.
-
La probabilidad de que una pareja tenga cuatro descendientes es de 1/16, siendo entonces niño-niño-niño-niña.
-
Finalmente, la probabilidad de que una familia tenga cinco descendientes es de 1/32, siendo el orden de nacimientos niño-niño-niño-niño-niña.
Es decir, de 32 familias, hay un promedio de 16 familias de tipo [niña], 8 de tipo [niño-niña], 4 de tipo [niño-niño-niña], 2 de tipo [niño-niño-niño-niña], 1 de tipo [niño-niño-niño-niño-niña] y 1 de tipo [niño-niño-niño-niño-niño].
Esto hace un total de 16 + 8 + 4 + 2 + 1 = 31 niñas y 0 + 8 + 8 + 6 + 4 + 5 = 31 niños.
El afán de cada pareja por tener una hija no cambia la proporción de niños y niñas. Aunque es cierto que la mayoría de las familias son más felices porque tienen al menos una hija: en el ejemplo que hemos dado, 31 parejas de las 32 tienen una hija, y aseguran su pequeña fortuna en el momento de la jubilación.
La situación comentada en este ejemplo es, por supuesto, ficticia. Solo pretende ilustrar lo contraintuitivos que resultan algunos argumentos relacionados con la teoría de la probabilidad.
De hecho, como explica Marta Bueno Saz en el artículo Mujeres que no llegaron a existir: abortos selectivos e infanticidio de niñas, la realidad es que nacen menos niñas que niños en el mundo: la mayoría de los países poseen la proporción de 103-108 bebés masculinos por cada 100 femeninos.
El economista Amartyan Sen (1933) definió en 1990 la noción de mujeres desaparecidas aludiendo a aquellas féminas que podrían estar vivas si no existieran los abortos selectivos en función del sexo del feto, el infanticidio femenino o la menor atención a las niñas que provoca una mayor mortalidad que en el caso de los niños.
Los datos de la última década indican que China es el país que posee la proporción más sesgada de nacimientos, con 112 niños nacidos frente a 100 niñas. Esto no tiene nada que ver con el azar, es un asunto de pura discriminación.
Referencia
Jean-Paul Delahaye, S’opposer au hasard des naissances, Accromath 17, hiver – printemps 2022, 30-31.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo No se puede cambiar el azar se ha escrito en Cuaderno de Cultura Científica.
Einstein y Michele Besso
Michele Besso fue un amigo, una caja de resonancia y un poco el hermano mayor de Einstein. Besso era seis años mayor, y no sólo le ayudó con algunas de sus teorías científicas, sino que también se vio envuelto directamente en su vida personal.
 Michele Besso. Fuente: ETH-Bibliothek Zürich, Bildarchiv
Michele Besso. Fuente: ETH-Bibliothek Zürich, BildarchivEn 1905 Michele Besso, ingeniero mecánico de formación, trabajaba con Einstein en la Oficina Suiza de Patentes. Los dos hombres solían pasear por las calles de Berna discutiendo las posiciones filosóficas de Ernst Mach (que Einstein conoció por Besso), debatiendo sobre gustos musicales, hablando de judaísmo (Besso era sefardí, Einstein asquenazí) y analizando los problemas candentes de la física. Las teorías que se estaban proponiendo de la luz y de la mecánica mantenían a Einstein despierto durante las noches, intentando comprender como podrían reconciliarse alguna vez. En un momento dado, Einstein pidió ayuda a Besso, y durante diecisiete días los dos hombres discutieron cada aspecto del problema.
Entonces, una noche, la inspiración llegó y encontró a Einstein trabajando. Einstein apareció a primera hora de la mañana siguiente ante la puerta de Besso y, sin decirle hola siquiera, le espetó: “¡Gracias! ¡He resuelto completamente el problema!”. Einstein había resuelto sus problemas con la luz desarrollando su teoría especial de la relatividad. Besso fue la primera persona en escuchar la explicación de Einstein de una teoría que cambiaría las bases de la física.
Ya en ese momento tanto Einstein como Besso parece que eran conscientes de que la teoría era “especial”. El artículo de Einstein sobre ella fue extraordinario en claridad y concisión, y más tarde Einstein diría que las cinco semanas que le llevó escribirlo y prepararlo para publicación fue un tiempo feliz. Aunque Besso no era de los que se quedaba atrás en su comprensión de la física y las matemáticas necesarias, está claro que la teoría especial era de Einstein y solo de Einstein. El mérito de Besso estuvo en su habilidad para escuchar y en su capacidad técnica para absorber y criticar unas ideas revolucionarias provenientes de uno de los científicos más creativos que han existido. Einstein después se referiría a Besso como “la mejor caja de resonancia de Europa [para las ideas científicas]”. En el artículo sobre la teoría especial Einstein supo ser agradecido: “Para terminar, me gustaría decir que mi amigo y colega, M. Besso, me ha ofrecido constantemente sus valiosos consejos mientras estuve trabajando en este problema, y que estoy en deuda con él por sus muchas sugerencias interesantes”.
Einstein y Besso se mantuvieron en contacto por escrito durante el resto de sus vidas, aunque nunca colaboraron en un artículo. Su relación fue más la de dos hermanos. Einstein pedía consejo a menudo a Besso y Besso solía regañar a Einstein por su comportamiento. Las cartas entre los dos hombres contienen muchísima información personal sobre Einstein.

Los dos hombres se conocieron en 1895 cuando Einstein se hospedaba en la casa de su profesor Jost Winteler en Aarau (Suiza), mientras finalizaba el instituto. En aquella época Einstein desarrolló lazos muy fuertes con las personas del círculo de los Winteler: Paul, el hijo mayor, fue su primer gran amigo y posterior marido de su hermana Maja; Marie, la hija pequeña, fue su primera novia; y Besso, que también se hospedaba allí. Besso formalizaría su relación con los Winteler en 1898 al casarse con Anna, la hija mayor.
Una vez casado, Besso se trasladó a Milán como consultor técnico de la Sociedad para el Desarrollo de la Industria Eléctrica en Italia. Influyó en la compañía para que contrataran a Einstein para un pequeño trabajo consistente en un estudio de cómo la electricidad irradia durante la corriente alterna. Einstein le devolvería el favor más tarde cuando avisó a Besso de la existencia de una vacante de examinador de patentes de segunda clase en la Oficina Suiza de Patentes. En esa época Einstein era examinador de patentes de tercera clase y, de hecho, él mismo solicitó el puesto. Pero no parece que le ocasionara ningún problema que escogieran a Besso antes que a él. De hecho, Besso fue claramente bienvenido a la comunidad de Einstein en Berna.
Durante la década siguiente la relación de Einstein con su esposa Mileva se fue deteriorando. El traslado de la familia a Berlín fue la gota que colmaría el vaso. Einstein se mudó a la capital prusiana, entre otras razones, para estar cerca de su amante, Elsa. No es sorprendente, por tanto, que Mileva se deprimiese en Berlín. Solo aguantó allí el tiempo necesario para que Besso pudiese organizarse, recogerla a ella y a sus dos hijos pequeños y llevarlos de vuelta a Suiza.
De esta manera, en 1914, Besso se convirtió en el intermediario entre Mileva y Einstein. El divorcio fue largo y amargo, con crueldad por ambas partes. Mileva estaba destrozada, Einstein distante, y ambos lloraban en el hombro de Besso. Besso supo mantener la cabeza fría. Censuró a Einstein por su comportamiento con su mujer, y protegió a este de las posiciones más dramáticas de ella. En esa época Besso vivía en Zurich, a donde había trasladado Mileva con los niños, lo que le permitió actuar como “tío” de Hans Albert y Eduard.
Besso también estuvo allí cuando tuvo lugar la segunda gran crisis de la familia: el diagnóstico de la enfermedad mental de Eduard. Besso de nuevo asumió el papel de hermano mayor: gestionó toda la parte médica de la enfermedad de Eduard, mantuvo informado a Einstein, regañándole cuando no ayudaba, y consoló, junto a su mujer, a Mileva.
A pesar de todos estos líos familiares, la ciencia estaba casi siempre presente en las comunicaciones entre Einstein y Besso: el rechazo de algunos postulados de la mecánica cuántica, la nueva astronomía y el desarrollo de la teoría general de la relatividad son algunos ejemplos de cuestiones que discutieron los dos amigos.
Besso murió solamente unos meses antes que Einstein. Y si bien éste sintió profundamente la pérdida, supo recurrir a la ciencia como bálsamo. En la carta que envió en marzo de 1955 a Anna, su viuda, escribió: “Se me ha adelantado un poco a la hora de abandonar este mundo extraño. Esto no significa nada. Para nosotros los físicos creyentes [en la física] la distinción entre pasado, presente y futuro solo tiene el significado de una terca ilusión”.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 25 de octubre de 2009.
El artículo Einstein y Michele Besso se ha escrito en Cuaderno de Cultura Científica.
La hora de la comida
Tenemos un ritmo circadiano, un ritmo de 24 horas, como tantos seres vivos, dirigido por el ciclo luz-oscuridad que regula el sol. Este reloj se localiza en el cerebro y se han encontrado ciclos similares, quizá dirigidos por medio de mensajeros y hormonas desde el ciclo del cerebro, en muchos órganos como el hígado, el tubo digestivo o el tejido adiposo. Una de las funciones que dirigen estos ciclos es la digestión. Los cambios en su ciclo, según Daniela Jakubowicz y sus colegas, de la Universidad de Tel Aviv, pueden llevar a la sobrealimentación y a la obesidad.
 Foto: Rachel Park / Unsplash
Foto: Rachel Park / UnsplashEl grupo de Jakubowicz trabaja con 93 mujeres obesas o con sobrepeso, con una edad media de 45.8 años, y un rango de edades de 30 a 57 años. Siguen una dieta de adelgazamiento durante 12 semanas y se controla la composición del desayuno, que se toma entre las 6 y las 9 horas de la mañana, de su comida, entre las 12 y las 15 horas, y de la cena, entre las 18 y las 21 horas. Forman dos grupos que toman una dieta con las mismas kilocalorías, 1400 en total, pero distribuidas con distinto horario a lo largo del día. Uno de los grupos de voluntarias toma un desayuno fuerte, con 700 kilocalorías, una comida media, con 500 kilocalorías, y una cena ligera, con 200 kilocalorías. La dieta del segundo grupo de voluntarias es la misma pero distribuida en un desayuno ligero, una comida media y una cena fuerte.
Los resultados demuestran que todas las voluntarias pierden peso y reducen el diámetro de la cintura, pero las voluntarias del desayuno fuerte lo hacen 2.5 veces más rápido que las voluntarias del desayuno ligero. Los desayunos fuertes bajan, de media, de 86 a 76 kilogramos en las 12 semanas que dura el estudio. Las de desayuno ligero bajan de 86 a 83 kilogramos en el mismo tiempo. Con el desayuno fuerte también bajan la glucosa en sangre y los triglicéridos en un 33% mientras que con el desayuno ligero se elevan un 14%.
En conclusión, un desayuno fuerte y una cena suave ayudan a controlar el peso.
Solo con el cambio de una hora en el esquema de tiempo de las comidas se detectan variaciones en la grasa corporal. Elizabeth Thomas y sus colegas, de la Universidad de Colorado, lo ensayan en 83 voluntarios con sobrepeso y obesidad, variando los horarios durante siete días y tomando datos cada día. Con una hora de retraso en la comida hay un aumento de 1.35% en la grasa corporal.
Incluso no desayunar puede llevar a un aumento de peso y aparición de sobrepeso. El grupo de Julia Wichersky, de la Universidad de Bielefeld, en Alemania, revisaron nueve estudios publicados antes de septiembre de 2020. De ellos, seis se revisaron y tres se incluyeron en un meta-análisis. Los resultados muestran que, si no se desayuna tres o más días a la semana, hay un 11% de riesgo de aumento de peso.
Poco después, el grupo de Marta Garaulet, de la Universidad de Murcia, amplió el estudio sobre el horario de la comida a 420 voluntarios durante 20 semanas, con el 49.5% de mujeres, y 42 años de media. Cambian el protocolo y, en primer lugar, entrevistan a los voluntarios y los dividen en dos grupos: los que comen temprano y hacen la comida del mediodía antes de las 15 horas, y los que comen tarde y la hacen después de las 15 horas.
Los comedores tempranos pierden más peso y lo hacen en menos tiempo que los que comen más tarde. A los autores les sorprende que, en ambos grupos, no es diferente la ingestión de calorías, la composición de la dieta, el gasto de energía, las hormonas relacionadas con el apetito o la duración del sueño. Solo cambia la hora de la comida.
Un estudio publicado en 2021 por el grupo de Kelly Allison, de la Universidad de Pennsylvania, confirma resultados anteriores. Con 12 voluntarios adultos, de edad media de 26.3 años, peso normal y con cinco mujeres en el grupo. Después de un seguimiento de ocho días con dos grupos y, uno de ellos, con horario de comidas de 8.00 a 19.00 horas, y el segundo grupo de 12.00 a 23.00 horas. El grupo que come más temprano muestra tendencia a la pérdida de peso.
El mismo grupo de Marta Garaulet ha hecho un seguimiento durante seis años a pacientes obesos operados con cirugía bariátrica. Son 270 pacientes, con el 70% mujeres y una edad media de 52 años. El 68% han respondido bien a la cirugía y pierden peso, el 11% no reacciona después de la cirugía, y el 21.5% que primero responde bien con el paso del tiempo deja de hacerlo.
Cuando relacionan los investigadores estas tres respuestas con la hora de la comida del mediodía, antes o después de las 15 horas, encuentran que los que comen tarde son hasta el 70% de los que responden mal a la cirugía y pierden poco peso. La respuesta adecuada a la cirugía se corresponde, por lo tanto, a los resultados del ejercicio anterior. Es mejor una hora temprana de la comida del mediodía.
Para averiguar cuál es la causa de estas variaciones en el peso según la hora de la comida, Christopher Morris y sus colegas, del Hospital Brigham and Women de Boston, estudiaron la termogénesis, o gasto de energía para producir calor. Es este proceso metabólico el que mantiene nuestra temperatura a unos 37 °C. La termogénesis también sigue un ciclo diario y es menor a la tarde y a la noche.
Para detectar si la dieta influye en este gasto de energía cíclico, los autores trabajan con 30 voluntarios en un seguimiento de 8 días y con turnos de sueño cambiados y, así, unos duermen de noche y otros duermen de día. La termogénesis la miden una hora y cuarto después de la comida, a las 8 de la mañana para los que duermen de noche y a las 8 de la noche para los que duermen de día.
En los que duermen de noche, con un ciclo que se puede denominar como normal, la termogénesis es un 44% mayor a la mañana que a la tarde y la noche. Por tanto, gastamos más energía de día que en la tarde y la noche y, sobre todo, gastamos más a la mañana temprano. Comemos más fuerte a la mañana y gastamos más energía y, si comemos más fuerte a la noche y no gastamos energía a esas horas pues la almacenamos y no se pierde tanto peso como a la mañana.
Nuestro metabolismo no está preparado para procesar alimentos y utilizar su energía de forma eficaz por la tarde y por la noche, lo hace mejor por la mañana. Los expertos aconsejan no comer nada durante 12 horas de las 24 horas de un día, y que ese ayuno sea, preferiblemente, por la noche, durante el sueño. Lo adecuado es no comer entre la cena y el desayuno del día siguiente. Durante la evolución de nuestra especie, como ocurrió en otras muchas especies, nuestra biología se ha adaptado a un fenómeno superior e inevitable: la salida puesta del sol y, por tanto, al ciclo luz-oscuridad cada 24 horas. Así nos hemos adaptado a comer de día y ayunar y dormir de noche. La luz artificial y las neveras de nuestro tiempo, llenas a cualquier hora, nos empujan a cambiar el ciclo y debemos recuperarlo para regular más adecuadamente el metabolismo.
Referencias:
Allison, K.C. et al. 2021. Prolonged, controlled daytime versus delayed eating impacts weight and metabolism. Current Biology 31: 650-657.
Garaulet, M. et al. 2013. Timing of food intake predicts weight loss effectiveness. International Journal of Obesity 37: 604-611.
Jakubowicz, D. et al. 2013. High caloric intake at breakfast vs. dinner differentially influences weight loss of overweight and obese women. Obesity 21: 2504-2512.
Laber-Warren, E. 2016. Eres cuando comes. Selecciones del Reader’s Digest septiembre: 14-17.
Morris, C.J. et al. 2015. The human circadian system has a dominating role in causing the morning/evening difference in diet-induced thermogenesis. Obesity 23: 2053-2058.
Ruiz-Lozano, T. et al. 2016. Timing of food intake is associated with weight loss evolution in severe obese patients after bariatric surgery. Clinical Nutrition doi: 10.1016/j.clnu.2016.02.007
Thomas, E.A. et al. 2021. Later meal and sleep timing predicts higher percent body fat. Nutrients 13: 73.
Wichersky, J. et al. 2021. Association between breakfast skipping and body weight – A systematic review and meta-analysis observational longitudinal studies. Nutrients 13: 272.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo La hora de la comida se ha escrito en Cuaderno de Cultura Científica.
La Estación Espacial Internacional ante la posible retirada de Rusia
Miguel Bello Mora
 Estación Espacial Internacional fotografiada desde una nave Soyuz tras su desacoplamiento. Fuente: NASA/Roscosmos
Estación Espacial Internacional fotografiada desde una nave Soyuz tras su desacoplamiento. Fuente: NASA/RoscosmosHoy en día la Estación Espacial Internacional (ISS) depende completamente de Rusia para mantenerse en órbita. Las naves de Space X, que contrata la NASA, transportan astronautas pero no pueden impulsar a la ISS para que mantenga su altura. Se espera que sí pueda hacerlo una nueva nave americana, Cygnus, que ya ha realizado con éxito un test de propulsión.
La Estación Espacial Internacional (ISS en inglés) es con diferencia la mayor estructura espacial construida en órbita. Tiene el tamaño de un campo de fútbol, orbita a 400 km de altura y se mueve con una velocidad de cerca de 30.000 km/h para dar una vuelta a la Tierra cada 90 minutos.
Comenzó su andadura en 1998 y fue diseñada para durar 15 años en órbita. Hoy ya lleva más de 21 años habitada permanentemente. Hay un compromiso formal de los socios que la construyeron −Estados Unidos (EEUU), Rusia, Europa, Canadá y Japón− para continuar las operaciones hasta 2024, aunque EEUU ya ha propuesto seguir hasta 2028 como mínimo.
La nueva situación generada por la guerra en Ucrania puede cambiar este escenario, con la amenaza de Rusia de abandonar la estación como respuesta a las sanciones de occidente. Pero, ¿cuál sería el efecto en la ISS si se produce el abandono de Rusia?
Afortunadamente la situación hoy está mucho mejor que hace tan solo dos años, desde que la nave Dragon, de Space X, bajo el programa de vuelos comerciales de la NASA, es capaz de llevar y traer astronautas al complejo orbital.
Durante nueve años, tras el abandono de los vuelos del transbordador espacial de la NASA, el Space Shutle, y hasta la entrada en operación de las naves de Space X en 2020, la única forma de volar a la ISS era con las naves rusas, de forma que la dependencia de la ISS de Rusia era total.
La NASA llegaba a pagar hasta 80 millones de dólares a Rusia para comprar estos billetes espaciales para sus astronautas. De hecho esta actividad era la más lucrativa del programa espacial ruso. Gracias a Space X, esta dependencia ya no existe y no habría problema en el abandono de Rusia para poder habitar la ISS.
Pero las naves rusas son también importantes para la ISS porque son las que han proporcionado hasta hoy la propulsión necesaria para su mantenimiento en órbita.
La ISS necesita propulsión para tres funciones vitales. Una es el mantenimiento de la altura orbital. La ISS pierde de media dos kilómetros de altura cada mes −en realidad esta caída es variable y depende de la actividad solar, que tiene ciclos de 11 años−; la nave rusa Progress le proporciona impulso para ganar altura cada cierto tiempo, cuando está anclada a la ISS. Sin el impulso de las Progress la ISS caería a Tierra en aproximadamente dos años −este tiempo puede variar dependiendo del ciclo solar.
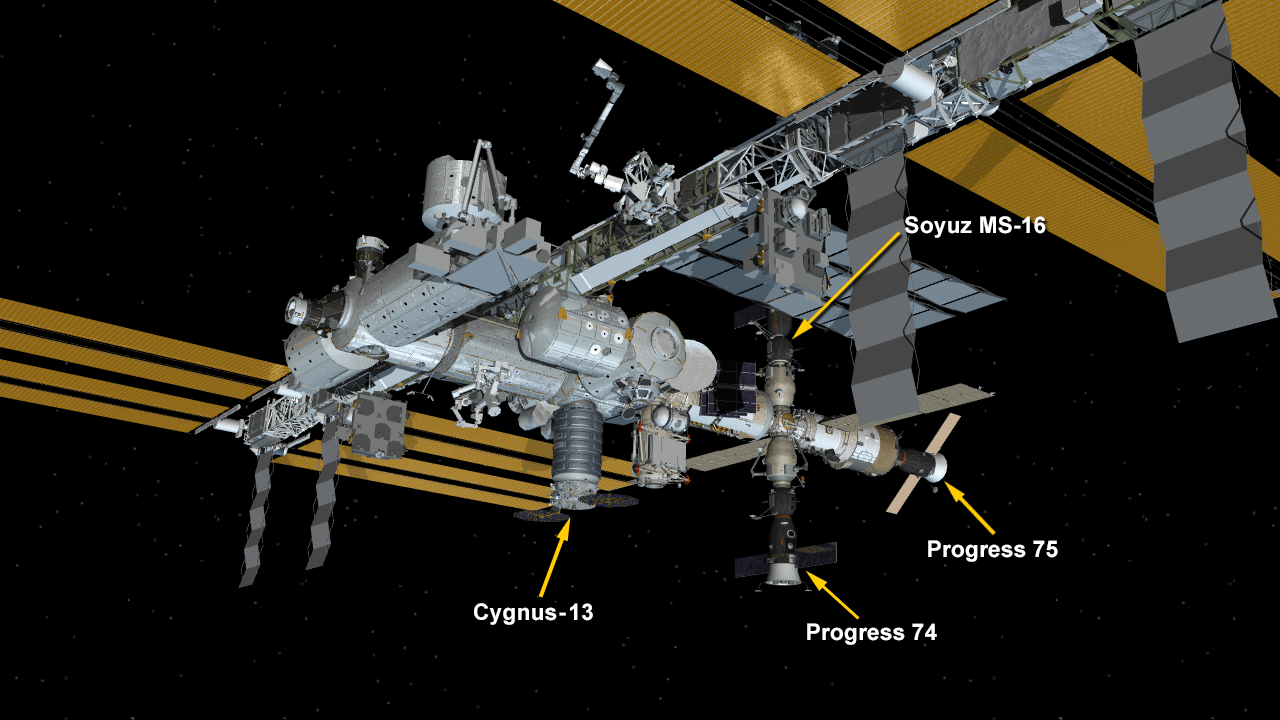 Configuración de la ISS en abril de 2020 con cuatro naves espaciales unidas a la estación: la nave de carga estadounidense Cygnus de Northrop Grumman, las naves de reabastecimiento rusas Progress 74 y 75, y la nave de tripulación Soyuz MS-16. Fuente: NASA
Configuración de la ISS en abril de 2020 con cuatro naves espaciales unidas a la estación: la nave de carga estadounidense Cygnus de Northrop Grumman, las naves de reabastecimiento rusas Progress 74 y 75, y la nave de tripulación Soyuz MS-16. Fuente: NASALa propulsión también es clave para evitar basura espacial. La basura espacial es un grave problema que origina la necesidad de realizar maniobras evasivas con cierta periodicidad para evitar colisiones fatales, dada la gran velocidad de estos objetos.
En noviembre de 2021 la ISS hizo una maniobra para subir su altura más de un kilómetro, y evitar así una zona congestionada de basura debido a una fragmentación intencionada de China de un satélite Fenyung hace años. Estas maniobras hasta ahora se realizan con naves rusas Progress.
Al final de su vida operativa, que la NASA ya estima para 2028 para luego ser reemplazada por un programa de vuelos comerciales, es necesario hacer una reentrada de la ISS en la atmósfera de manera controlada.
Si se deja caer la estación de manera incontrolada, puede hacerlo en cualquier lugar de la Tierra entre 51º de latitud Sur y 51º de latitud Norte, donde se encuentra la inmensa mayoría de la población terrestre (dado que su inclinación orbital con respecto al Ecuador es 51º).
Aunque la mayor parte de la superficie terrestre es océano y es menos probable que caiga sobre tierra, esta es una probabilidad que no se puede permitir porque se sabe que al igual que las estaciones precedentes Skylab o MIR, los restos de la ISS no se desintegrarían completamente en la atmósfera (como casi todos los satélites y restos de basura), sino que partes importantes de su estructura caerían sobre la Tierra y podrían generar un serio peligro para personas o propiedades.
Para evitar esto se utiliza primero la caída natural debido a la resistencia atmosférica durante un periodo de aproximadamente 2 años y después una maniobra final para asegurar que va a caer en un punto determinado del océano. La NASA ha seleccionado el ‘Point Nemo’ como punto para la caída de la ISS, un lugar en el Pacífico Sur que está a una distancia de 2.700 km de la costa más cercana. En principio esta maniobra final para la reentrada controlada de la ISS debería ser realizada por las naves rusas.
En resumen, la para mantener la altura, para evitar colisiones con basura espacial y para evitar un accidente al final de la vida útil de la ISS. La nave europea ATV, que tenía también la capacidad de propulsión ya no está operativa desde 2014.
Sin embargo una nueva nave americana, Cygnus de Northrop Grumman, tiene capacidad para atracar en la ISS y ya ha realizado con éxito un test de propulsión. De esta forma también USA puede realizar maniobras en la ISS y la dependencia de Rusia desaparecería por completo.
La amenaza rusa de abandonar la ISS no sería ahora un grave peligro para los socios occidentales. Tan solo habría que cerrar los módulos rusos y seguir operando con la nave Dragon de Space X para la tripulación y la nave Cygnus de Northrop Grumman para la propulsión.
Sobre el autor: Miguel Bello Mora es Director General (CEO) de AIR Centre, organismo intergubernamental para el uso de la tecnología espacial para la sostenibilidad y el cambio climático.
Artículo publicado originalmente en SINC.
El artículo La Estación Espacial Internacional ante la posible retirada de Rusia se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Conchi Lillo – MicroCellfie
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.
El virus SARS-CoV-2 no solo existe, sino que hasta le han hecho retratos. Conchi Lillo nos enseña como se hacen los micro-selfis.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Conchi Lillo – MicroCellfie se ha escrito en Cuaderno de Cultura Científica.
¿Cómo se conserva una pintura mural sin tocarla?
Entre 1909 y 1916, el pintor de la emblemática obra ‘El grito’, Edvard Munch, realizó por encargo 11 pinturas murales monumentales de gran tamaño (de entre los 4 y 11 metros) para el Aula Magna de la Universidad de Oslo. La profesora de la Facultad de Farmacia de la UPV/EHU Maite Maguregui forma parte del grupo que analiza la técnica utilizada por el pintor noruego.
 Foto: Maite Maguregui
Foto: Maite MagureguiLa profesora noruega Tine Frøysaker perteneciente al Departamento de Arqueología, Conservación e Historia (IAKH) de la Universidad de Oslo (UiO) ha contado con la colaboración de la profesora titular de Química Analítica de la UPV/EHU y miembro del grupo de investigación IBeA Maite Maguregui para el análisis de estas pinturas monumentales, con del uso de metodologías que permiten conocer la técnica pictórica de Edvard Munch y el estado de conservación de los murales. En dicho estudio, también ha participado el doctor Francesco Caruso del Instituto Suizo de Estudios de Arte (SIK-ISEA) de Zúrich.
En concreto, el proyecto MAP (The Munch Aula Paintings Project) busca conocer la gran variedad de materiales empleados por Edvard Munch en dichas pinturas, monitorizar su estado de conservación y llevar a cabo su limpieza como medida de conservación preventiva. “El problema actual al que se enfrentan es la disposición continua de material particulado en suspensión (polvo y otras partículas) que accede desde el exterior, lo que muestra el problema de la contaminación urbana que también afecta a ciudades como Oslo, aunque las obras de arte no estén directamente expuestas a esa contaminación por no estar ubicadas en el exterior”, señala la investigadora Maite Maguregui.
De momento, han tenido que analizar las obras, siempre evitando generar cualquier tipo de daño durante el estudio. “Siempre estamos muy limitados por el muestreo, muchas veces el muestreo incluso está prohibido”, explica Maguregui. Por esa razón, cada vez resulta más interesante encontrar métodos de análisis in situ que no afecte a la obra, problemas que puede plantear el muestreo, por ejemplo.
En este sentido es clave el papel de la profesora Maguregui, ya que está especializada en el desarrollo de metodologías de análisis basadas en el uso de técnicas portátiles y de laboratorio no invasivas. En concreto, en las obras de Munch, se ha utilizado un instrumento portátil basado en espectroscopia Raman. “La técnica permite analizar una superficie pictórica colocando una sonda en contacto con la superficie a analizar, no siendo necesario realizar una toma de muestra. En caso de que el muestreo se permita, las muestras que nosotros tomamos en una pintura son micrométricas y las magnificamos bajo el microscopio”.
En este momento, el grupo de investigación al que pertenece Maguregui se centra en obtener los primeros resultados e interpretaciones, para, en un futuro cercano, poder desarrollar nuevos materiales sostenibles que permitan la conservación de estas obras y otras superficies decoradas.
El proyecto de análisis y conservación de las pinturas monumentales del Aula Magna, llamado ‘Munch Aula Painting Project’, comenzó en 2005, con el objetivo de averiguar la técnica pictórica de Edvard Munch, considerada de gran complejidad. En 2009 se llevó a cabo la primera restauración de los cuadros, que fueron retirados del espacio hasta que en 2011 fueron recolocados. Las mediciones han arrojado la acumulación de material particulado que desde 2011 ha vuelto a aparecer en las obras pictóricas.
La serie de 11 obras de Edvard Munch es el resultado de un encargo que la Universidad de Oslo le hizo al pintor en 1916, después de no haber ganado la convocatoria para las pinturas monumentales en la que competía contra el muralista Emmanuel Vigeland. El Aula es un espacio que se usa como Paraninfo de la Universidad de Oslo y en el que se han entregado los Premios Nobel desde 1947 hasta 1989.
La presencia de la investigadora en Oslo también le ha permitido colaborar en el estudio de esculturas medievales en madera decorada pertenecientes al Museo de Historia Cultural (KHM) de la Universidad de Oslo.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo ¿Cómo se conserva una pintura mural sin tocarla? se ha escrito en Cuaderno de Cultura Científica.
Antonia Maury, la astrónoma rebelde
 Antonia Maury. Fuente: Wikimedia Commons.
Antonia Maury. Fuente: Wikimedia Commons.Cuando Pickering las contrató como calculadoras, todo lo que buscaba era ahorrarse unos cuantos dólares. Pero la cosa no salió como esperaba. Resulta que aquellas mujeres, con “destreza para realizar trabajos repetitivos, no creativos” según él creía, terminaron teniendo iniciativa propia. A Henrietta Leavitt le dio por encontrar una regla con la que medir distancias astronómicas. Williamina Fleming se puso descubrir cosas, nebulosas, estrellas variables, la primera enana blanca. Annie Jump Cannon inventó un nuevo sistema de clasificación estelar. Pero entre todas ellas, la palma se la llevó Antonia Maury. Ella fue quien terminó por sacarle de sus casillas1.
La tarea que se le había encomendado era sencilla. Maury solo debía clasificar las estrellas según el sistema desarrollado por Annie Jump Cannon. Pero a ella le dio por pensar. Era una de las “calculadoras” con más formación previa en astronomía del observatorio, había estudiado en el Vassar College y se había graduado bajo la tutela de la astrónoma Maria Mitchell. Estaba acostumbrada a estudiar y reflexionar por su cuenta y le pareció que el esquema propuesto para el catálogo era demasiado simple para recoger toda la complejidad que ella había visto en las líneas espectrales de las estrellas. Por eso empezó a sub-clasificarlas, atendiendo a la anchura y la nitidez de las líneas. Pero lo hizo sin consultarlo primero con el profesor Pickering, y este, en lugar de incentivarla o valorar su esfuerzo, se mostró irritado por su desobediencia.
Maury, por lo demás, no debía de tener un carácter demasiado dócil. Así que sus constantes roces con el profesor forzaron la salida de la astrónoma del Observatorio de Harvard en 1891. Cuando, tiempo después, Pickering le pidió que regresara para completar sus observaciones (o para delegarlas en una nueva calculadora), ella le contestó que no deseaba volver si sus aportaciones no eran plenamente reconocidas2:
No creo que sea justo que tenga que dejar mi trabajo en otras manos hasta que pueda ser reconocido como un trabajo hecho por mí. Desarrollé mi teoría a costa de mucho esfuerzo y mediante muchas comparaciones, y creo que debería obtener todo el crédito por mi teoría de las relaciones de los espectros estelares y también por mis teorías con respecto a Beta Lyrae.
Pickering le contestó de forma seca, afirmando que “es la práctica habitual de este Observatorio dar reconocimiento a los autores de ciertas secciones en sus publicaciones”. Pero Maury quería más. Cuando regresó a Harvard en 1893 y nuevamente en 1895 para completar sus observaciones, utilizó su propio sistema de clasificación. Además, su catálogo, publicado en 1987, fue el primero claramente acreditado a una mujer. En el subtítulo de «Espectros de estrellas brillantes fotografiados con el telescopio Draper de 11 pulgadas” al fin figuraba su propio nombre: “Discutido por Antonia C. Maury bajo la dirección de Edward C. Pickering”.
¿Pero en qué consistía aquella clasificación que tanto enfrentó a la astrónoma con el profesor? Si bien el sistema de Cannon, con sus siete letras (O B A F G K M) resultaba adecuado para catalogar las estrellas en función de su color (y, por tanto, de su temperatura), Maury se dio cuenta de que el tamaño de las estrellas (su magnitud absoluta) también dejaba una huella distinguible sobre el espectro. Añadió así una segunda dimensión al sistema de clasificación de Oxford que resultaría clave, más tarde, para identificar el ciclo de vida de diferentes estrellas en función de su tamaño.
Sus ideas tuvieron el reconocimiento que merecían solo unas décadas más tarde. En 1911, Ejnar Hertzsprung y por Henry Norris Russell publicaron el diagrama que hoy lleva sus nombres y que se había basado, en parte, en las observaciones de Maury. En 1922, la Unión Astronómica Internacional modificó su sistema de clasificación para adoptar un método mucho más afín, en su planteamiento, al ideado por la astrónoma. Para entonces, y tras la muerte de Pickering, Maury había regresado al Observatorio de Harvard a trabajar como ayudante. Permaneció allí, bajo la dirección del nuevo director, el profesor Shapley, hasta que se jubiló por completo en 1948. En su retiro, Antonia se convirtió en una ornitóloga apasionada y una conservacionista que luchó para salvar los bosques de secuoyas de su país. Murió el 8 de enero de 1952.
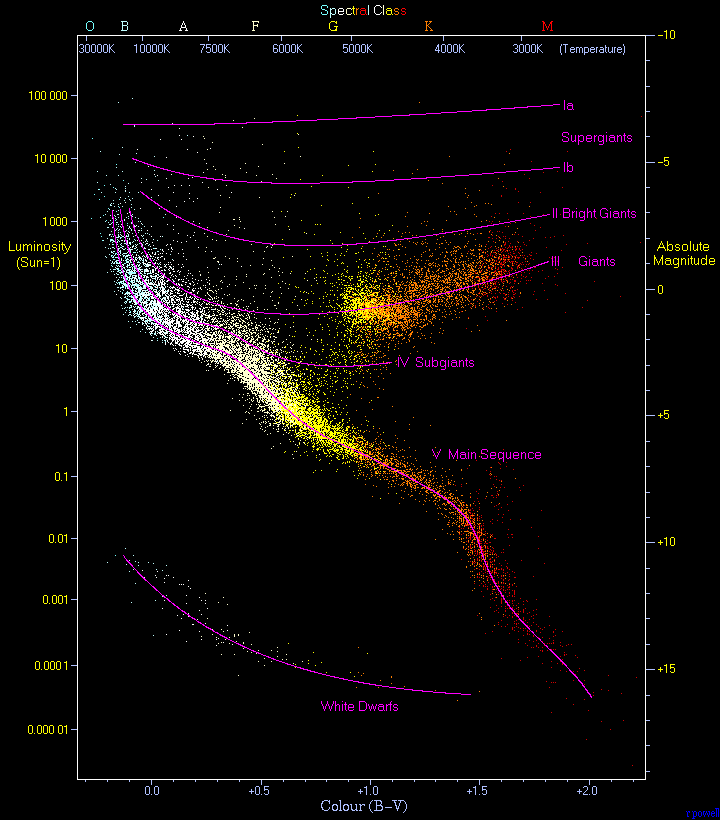 Diagrama Hertzsprung–Russell. Fuente Wikimedia Commons.
Diagrama Hertzsprung–Russell. Fuente Wikimedia Commons.
Referencias:
1Masegosa, J. (11 de marzo de 2013). El harén de Pickering: Antonia C. Maury. El diario secreto de Henrietta S. Leavitt. Consultado el 7 de marzo de 2022.
2Carta del 7 de mayo de 1892. Citada por Hoffleit, D. (1991). The Evolution Of The Henry Draper Memorial. Vistas in Astronomy Volume, 34(Part 1), 107-162.
Para saber más:
Razkin, Uxue (2019) Antonia Maury (1866-1952): la mujer que conocía las estrellas. Mujeres con Ciencia
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Antonia Maury, la astrónoma rebelde se ha escrito en Cuaderno de Cultura Científica.
Premios matemáticos, de las Medallas Fields a los Problemas del Milenio
Hace unas pocas semanas se anunciaba en los medios de comunicación que el Premio Fundación BBVA Fronteras del Conocimiento en Ciencias Básicas, en su XIV edición, había sido concedido a dos matemáticos, el estadounidense Charles Fefferman y el francés François Le Gall, “por sus contribuciones fundamentales en dos áreas de las matemáticas con numerosas ramificaciones, que incluyen numerosas aplicaciones en distintos campos” (para más información sobre el premio y los galardonados puede leerse lo escrito en la página web de los Premios Fronteras del Conocimiento). Leyendo sobre los dos matemáticos galardonados pude observar que eran matemáticos que ya habían recibido, como es normal, varios reconocimientos previos. Entre otros premios, Charles Fefferman había recibido la Medalla Fields en 1978, el Premio Bôcher en 2008 o el Premio Wolf en 2017, mientras que François Le Gall había recibido el Premio Fermat en 2005 o el Premio Wolf en 2018.
 Los matemáticos Charles Fefferman, estadounidense, y François Le Gall, francés, Premio Fundación BBVA Fronteras del Conocimiento en Ciencias Básicas, en su XIV edición. Fotografías de la página web de los Premios Fronteras del Conocimiento
Los matemáticos Charles Fefferman, estadounidense, y François Le Gall, francés, Premio Fundación BBVA Fronteras del Conocimiento en Ciencias Básicas, en su XIV edición. Fotografías de la página web de los Premios Fronteras del Conocimiento
La mayoría de nosotros sabemos que no existe Premio Nobel de Matemáticas, aunque el motivo por el cual no existe no esté del todo claro (pero no es la entrada de hoy la que dedicaremos a este tema), y seguro que conocemos la existencia de algunos premios matemáticos, como las Medallas Fields o los Premios Abel, que han sido considerados desde su origen equivalentes al “Premio Nobel de las Matemáticas”, aunque seguro que no conocemos la existencia de otros premios como, por ejemplo, el Premio Wolf o el Premio Fermat. En esta entrada del Cuaderno de Cultura Científica nos gustaría realizar una pequeña presentación de algunos de los premios que existen y que se conceden por investigaciones matemáticas.
Medalla Fields.
El origen de este premio matemático se encuentra precisamente en la inexistencia de un Premio Nobel de las Matemáticas, que la comunidad matemática quiso resolver instaurando este reconocimiento internacional a la investigación en matemáticas. Las Medallas Fields, que han sido consideradas desde su origen como el Nobel de las Matemáticas, son un galardón entregado cada cuatro años con motivo de la celebración del Congreso Internacional de Matemáticos (ICM), organizado por la Unión Matemática Internacional (IMU). Este evento, que se celebra desde 1897, reúne cada cuatro años a los matemáticos de todo el mundo y todas las disciplinas. A partir de 1936, y por iniciativa del matemático canadiense John C. Fields (1863-1932), quien dejó su fortuna para que fuese posible este premio, se entrega el que durante mucho tiempo ha sido considerado el más alto galardón de la ciencia de Pitágoras.
La cantidad de medallas que pueden concederse en cada edición de los ICM puede ir de dos a cuatro y reconoce “logros sobresalientes en Matemáticas”. De hecho, el nombre real de estas medallas es “Medalla Internacional para Descubrimientos Sobresalientes en Matemáticas”. Se concede a matemáticos o matemáticas de menos de 40 años, aunque esta es una norma no escrita, y esto es debido a que en el testamento de Fields se destaca “aunque la concesión del premio debe basarse en trabajo ya realizado, debe al mismo tiempo servir para animar futuros logros de los galardonados y como estímulo para el esfuerzo renovado de otros”.
El premio consiste en una medalla, diseñada por el escultor canadiense R. Tait McKenzie, y 15.000 dólares canadienses. En el anverso de la medalla puede verse al matemático griego Arquímedes (aprox. 287 – 212 a.n.e.), con la inscripción en latín “Transire suum pectus mundoque potiri” (Elevarse por encima de uno mismo y agarrar el mundo), del poeta romano Marcus Manilius (siglo I). En el reverso hay una inscripción en latín que dice algo así como “Matemáticos reunidos de todo el mundo han otorgado [este premio] por escritos sobresalientes”.
 Anverso y reverso de la Medalla Fields que se concede a las personas galardonadas con esta distinción. Fotografía de Stefan Zachow para la Unión Matemática Internacional (IMU)
Anverso y reverso de la Medalla Fields que se concede a las personas galardonadas con esta distinción. Fotografía de Stefan Zachow para la Unión Matemática Internacional (IMU)
Las dos primeras medallas se concedieron en Oslo (Noruega) en 1936 a los matemáticos Lars Ahlfors (1907-1996), finlandés, y Jesse Douglas (1897-1965), estadounidense, aunque no se volvieron a conceder hasta 1950 y desde entonces se han entregado siempre cada cuatro años, durante la celebración de los ICM. Desde entonces se han galardonado a grandes matemáticos como el francés Laurent Schwartz (1915-2002), el japonés Kunihiko Kodaira (1915-1997), el francés Jean-Pierre Serre (1926), que fue es matemático más joven hasta la fecha en recibir la Medalla Fields con tan solo 27 años, el estadounidense John Milnor (1931), el inglés Michael Atiyah (1929-2019), el ruso Sergei Novikov (1938), que no pudo viajar a recoger el galardón por la prohibición sobre él del gobierno soviético, el francés Alain Connes (1947), el estadounidense Willian Thurston (1946-2012), el estadounidense William Witten (1951), el primer físico en recibir esta distinción, el ruso-estadounidense Efim Zelmanov (1955), el australiano Terence Tao (1975) o el francés Cédric Villani (1973), todos ellos matemáticos muy reconocidos en la comunidad matemática.
La matemática iraní Maryam Mirzajani (1977-2017) ha sido la primera mujer en recibir este galardón, que le fue concedido en 2014 en Seúl (Corea del Sur), “por sus destacadas contribuciones a la dinámica y la geometría de las superficies de Riemann y sus espacios moduli”.
Por otra parte, la Medalla Fields le fue concedida al ruso Gregori Perelman (1966), en el Congreso Internacional de Matemáticos de Madrid 2006, por “sus contribuciones a la geometría y sus ideas revolucionarias sobre la estructura analítica y geométrica del flujo de Ricci”, que estaban detrás de su demostración de la conjetura de Poincaré, pero el matemático ruso rechazó el galardón y declaró “no estoy interesado en el dinero o la fama; no quiero estar en exhibición como un animal en un zoológico”.
 El matemático francés Cédric Villani recibió la Medalla Fields en 2010 (fotografía de Marie-Lan Nguyen / Wikimedia Commons) y la matemática iraní Maryam Mirzajani en 2014.
El matemático francés Cédric Villani recibió la Medalla Fields en 2010 (fotografía de Marie-Lan Nguyen / Wikimedia Commons) y la matemática iraní Maryam Mirzajani en 2014.
El Congreso Internacional de Matemáticos 2022 tenía previsto celebrarse en la ciudad rusa de San Petersburgo, sin embargo, la Unión Matemática Internacional ha decidido, ante la invasión rusa de Ucrania, que este importante evento matemático sea totalmente virtual y albergado fuera de Rusia. Por su parte, las Medallas Fields se entregarán en una ceremonia fuera de Rusia, aunque el lugar está aún por determinar.
La lista completa de las personas galardonadas con la Medalla Fields puede verse en la página web de la Unión Matemática Internacional.
Premio Abel.
El matemático noruego Sophus Lie (1842-1899), tras enterarse de que Alfred Nobel no tenía la intención de incluir a las matemáticas entre los premios que estaba estableciendo (se haría público en 1897), propuso la creación de un Premio Abel de las Matemáticas. El rey Oscar II accedió a financiar un premio de matemáticas en honor de Abel y dos matemáticos noruegos, Ludwig Sylow y Carl Størmer, diseñaron los estatutos y las normas del premio. La intención era que la presentación del premio fuera parte de las celebraciones del primer centenario del nacimiento del matemático noruego Niels Henrik Abel (1802-1826) en 1902. Sin embargo, la muerte de Sophus Lie en 1899 y la disolución de la Unión entre Suecia y Noruega en 1905 desbarataron el primer intento de crear el Premio Abel.
Tuvo que pasar un siglo para que, hacia 2001, empezara a subir la presión ejercida sobre el gobierno noruego para que creara el Premio Abel, y este accedió a concederlo, con la intención de que el primer galardón se concediera en 2002, con motivo del bicentenario del nacimiento de Abel. Finalmente, el primer Premio Abel (con una cuantía económica de unos 750.000 euros, similar al Premio Nobel) llegó en 2003 y fue concedido al matemático francés Jean Pierre Serre (1926), uno de los grandes matemáticos vivos.
 Fotografías de algunos matemáticos que han recibido el Premio Abel de matemáticas, como Sir Michael Francis Atiyah, Mijaíl Grómov, Endre Szemerédi y Andrew Wiles. Imágenes de la página web del Premio Abel
Fotografías de algunos matemáticos que han recibido el Premio Abel de matemáticas, como Sir Michael Francis Atiyah, Mijaíl Grómov, Endre Szemerédi y Andrew Wiles. Imágenes de la página web del Premio Abel
Desde entonces el premio ha sido concedido a 24 personas, entre los que están el matemático indio Srinivasa Varadhan (1940), el matemático ruso-francés Mijaíl Grómov (1943), el matemático húngaro Endre Szemerédi (1940), el matemático estadounidense John Forbes Nash (1928-2015), sobre quien trata la película Una mente maravillosa, quien desgraciadamente murió en un accidente de coche cuando regresaba de recoger el premio, el matemático inglés Andrew Wiles (1953), matemático que había demostrado el famoso Ultimo Teorema de Fermat, la matemática estadounidense Karen Uhlenbeck (1942), la primera matemática en recibir este galardón, el matemático canadiense Robert Langlands (1936) o el matemático israelí Grigori Margulis (1946), de nuevo, todos ellos matemáticos muy reconocidos en la comunidad matemática.
La lista completa de las personas galardonadas con el Premio Abel puede verse en la página web del Premio Abel .
 Fotografía de la matemática estadounidense Karen Keskulla Uhlenbeck, que recibió el Premio Abel en 2019. Imagen del Heidelberg Laureate Forum
Fotografía de la matemática estadounidense Karen Keskulla Uhlenbeck, que recibió el Premio Abel en 2019. Imagen del Heidelberg Laureate Forum
Premio Wolf.
El tercer premio más prestigioso en el mundo de las matemáticas es el Premio Wolf, concedido por la Fundación Wolf de Israel. Esta fundación fue creada por la familia judía Wolf, en concreto por el inventor, diplomático y filántropo Ricardo Wolf (1887-1981), nacido en Alemania y que emigró a Cuba antes de la Primera Guerra Mundial, y su mujer, la tenista española Francisca Subirana Wolf (1900-1981).
Como puede leerse en su página web, la fundación tiene como objetivo “promover la ciencia y el arte en beneficio de la humanidad”. Con este objetivo creó un premio que desde 1978 se concede a “destacados científicos y artistas de todo el mundo, por sus logros y contribuciones en interés de la humanidad y de las relaciones fraternas entre los pueblos, sin distinguir raza, genero, religión o tendencias políticas».
Los Premios Wolf se otorgan en seis campos: Agricultura, Química, Matemáticas, Medicina, Físicas y Artes (Arquitectura, Música, Pintura y Escultura). En el campo de las matemáticas, entre las personas galardonadas están muchos de los matemáticos que ya hemos mencionado en los anteriores premios. En el año 1978 los matemáticos premiados fueron el matemático ruso Izrail Moiséyevich Gelfand (1913-2009) y el matemático alemán Carl Ludwig Siegel (1896-1981). Desde entonces ha habido más de sesenta premiados, entre los que tenemos grandes nombres de las matemáticas, como el matemático francés André Weil (1906-1998), el matemático ruso Andréi Kolmogórov (1903-1987), el matemático húngaro Paul Erdös (1913-1996), el matemático polaco Samuel Eilenberg (1913-1998), el matemático ruso Vladímir Arnold (1937-2010), el matemático estadounidense Stephen Smale (1930), el matemático británico Simon Donaldson (1957) o el matemático rumano-estadounidense George Lusztig (1946).
 Fotografías de Israel M. Gelfand, André Weil, Andréi Kolmogórov y Paul Erdös, de la página web de los Premios Wolf en la Fundación Wolf
Fotografías de Israel M. Gelfand, André Weil, Andréi Kolmogórov y Paul Erdös, de la página web de los Premios Wolf en la Fundación Wolf
El listado completo de los matemáticos galardonados con el Premio Wolf puede verse en la página de la Fundación Wolf, en concreto en la parte de los Premios Wolf.
Continuemos con otros premios creados y concedidos por la Unión Matemática Internacional (IMU).
La Medalla Abaccus IMU (hasta 2018 Premio Nevanlinna).
Otro premio de otorga la Unión Matemática Internacional durante la celebración del Congreso Internacional de Matemáticos (ICM) es la Medalla Abaccus IMU, que hasta el último ICM en Río de Janeiro (2018), llevaba el nombre de Premio Nevanlinna por el matemático finés Rolf Nevalinna. Como se explica en el artículo de Antonio Córdoba, en Materia (El País): “Aunque la IMU no ha hecho públicas sus razones, la Universidad de Helsinki confirma que se trata del papel de Nevanlinna en la Segunda Guerra Mundial. Fue miembro del partido Nacionalista Finlandés (ultraconservador y supremacista); presidió el comité de dirección del “Batallón de voluntarios fineses de las Waffen-SS” y aceptó, durante los años 1936-37, un puesto en la universidad alemana de Göttingen, reemplazando a los ilustres matemáticos de origen judío (como Edmund Landau, Hermann Weyl y Richard Courant) expulsados por los nazis bajo el auspicio de las leyes racistas de Nuremberg”.
El Premio Nevanlinna, ahora Medalla Abaccus, fue creado por la Unión Matemática Internacional en 1981, para premiar “las contribuciones más importantes en los aspectos matemáticos de la Sociedad de la Información, incluyendo:
a) Aspectos matemáticos de la informática, teoría de la complejidad, lenguajes de programación, análisis de algoritmos, criptografía, visión por computador, patrones, procesamiento de la información y modelización de la inteligencia;
b) Computación científica y análisis numérico. Aspectos computacionales de optimización y teoría de control. Álgebra computacional”.
El primer premiado, en 1982, fue el matemático y científico computacional estadounidense Robert Tarjan (1948), al que le han seguido otros nueve premiados, el último (hasta que se conceda el siguiente este mismo año 2022) ha sido el científico computacional teórico griego Constantinos Daskalakis (1981), “por transformar nuestra comprensión de la complejidad computacional de problemas fundamentales de los mercados, las subastas, los equilibrios y otras estructuras económicas. Su trabajo proporciona tanto algoritmos eficientes como límites sobre lo que puede realizarse eficientemente en estos dominios”.
 Fotografía de Constantinos Daskalakis. Fuente: Wikimedia Commons
Fotografía de Constantinos Daskalakis. Fuente: Wikimedia Commons
Premio Leelavati.
Uno de los últimos premios creados en el seno de la Unión Matemática Internacional ha sido el Premio Leelavati (o Lilavati), que se concede a aquellas personas que han realizado una contribución destacada en la difusión pública de las matemáticas. El nombre viene del tratado Lilavati, del matemático indio Bhaskara Acharia o Bhaskara II (1114-1185). Existe una interesante edición (a cargo de Ángel Requena Fraile y de Jesús Malia) en castellano Lilavati, matemática en verso del siglo XII, publicada dentro de la colección Biblioteca de Estímulos Matemáticos, de la editorial SM y la Real Sociedad Matemática Española, que os recomiendo.
Las personas premiadas hasta el momento han sido: en 2010, el escritor, físico y divulgador de las matemáticas británico Simon Singh (1964), autor de libros tan famosos como El enigma de Fermat, sobre el que dirigiría un documental homónimo (premiado con el premio BAFTA en 1996), Los códigos secretos, o Los Simpson y las matemáticas, así como realizador y productor de documentales para la BBC; en 2014, el matemático, periodista y divulgador científico argentino Adrián Paenza, que es conocido tanto por su serie de libros de divulgación matemática que llevan el título Matemática… ¿Estás ahí?, otros libros de divulgación matemática como ¿Pero esto también es matemática?, Matemática para todos o Matemagia, o los programas de televisión Científicos, Industria Argentina y Alterados por pi; y en 2018, el matemático turco Ali Nesin “por sus destacadas contribuciones para aumentar la conciencia pública sobre las matemáticas en Turquía, en particular por su incansable trabajo en la creación de la «Ciudad Matemática» como un lugar excepcional y pacífico para la educación, la investigación y la exploración de las matemáticas para todos”.
 Fotografía de Simon Singh con una bufanda de Moebius. Imagen de Robert Sharp / English PEN / Wikimedia Commons.
Fotografía de Simon Singh con una bufanda de Moebius. Imagen de Robert Sharp / English PEN / Wikimedia Commons.
Medalla Chern.
La Medalla Chern ha sido creada por la Unión Matemática Internacional y se concede en el Congreso Internacional de Matemáticos desde el ICM de 2010 en la India, como el Premio Leelavati. El nombre de la medalla es en honor al matemático chino-estadounidense Shiing-Shen Chern (1911-2004), que trabajaba en el área de la geometría y la topología y era considerado por muchas personas como “el padre de la geometría diferencial moderna”. Por cierto, que Chern fue uno de los matemáticos que recibió el Premio Wolf. La Medalla Chern consiste en 250.000 dólares y se concede “en reconocimiento a los logros destacados de toda una vida dedicada al estudio de las matemáticas en su más alto nivel”.
 Fotografía del matemático chino-estadounidense Shiing-Shen Chern. Imagen de Konrad Jacobs, perteneciente a la colección del Instituto Oberwolfach
Fotografía del matemático chino-estadounidense Shiing-Shen Chern. Imagen de Konrad Jacobs, perteneciente a la colección del Instituto Oberwolfach
Los primeros premiados han sido, en 2010, el matemático canadiense-estadounidense Louis Nirenberg (1925-2020), “por su papel en la formulación de la teoría moderna de las ecuaciones en derivadas parciales elípticas no lineales y por ser el mentor de numerosos estudiantes y postdoctorales en esta área”; en 2014, el matemático estadounidense Phillip A. Griffiths (1938), “por su desarrollo innovador y transformador de los métodos trascendentales en la geometría compleja, en particular su trabajo seminal en la teoría de Hodge y los períodos de variedades algebraicas”; en 2018, el matemático japonés Masaki Kashiwara (1947), “por sus destacadas y fundacionales contribuciones al análisis algebraico y a la teoría de la representación sostenidas a lo largo de casi 50 años”.
 Fotografía del matemático canadiense-estadounidense Louis Nirenberg. Imagen de los archivos de la New York University
Fotografía del matemático canadiense-estadounidense Louis Nirenberg. Imagen de los archivos de la New York University
 Fotografía del matemático estadounidense Phillip A. Griffiths. Imagen del Institute for Advanced Study en Princeton
Fotografía del matemático estadounidense Phillip A. Griffiths. Imagen del Institute for Advanced Study en Princeton
Premio Carl Friedrich Gauss.
El último premio de entre los que concede la Unión Matemática Internacional, pero en esta ocasión en colaboración con la Sociedad Matemática Alemana, es el Premio Carl Frederich Gauss, en honor del matemático alemán Carl Frederich Gauss (1777-1855), uno de los matemáticos más importantes de toda la historia de las matemáticas, conocido como “el príncipe de los matemáticos”. Este premio, que se concede desde el ICM de 2006, en el Congreso Internacional de Matemáticos celebrado en Madrid, se otorga por “contribuciones matemáticas destacadas que han encontrado aplicaciones significativas fuera de las matemáticas”.
Los cuatro premiados han sido el matemático japonés Kiyosi Itô (1915-2008), el matemático francés Yves Meyer (1939), el matemático estadounidense Stanley Osher (1942) y el matemático estadounidense David Donoho (1957).
 Fotografía del matemático japonés Kiyosi Itô. Imagen de la Sociedad Matemática Japonesa
Fotografía del matemático japonés Kiyosi Itô. Imagen de la Sociedad Matemática Japonesa
Premio de los Problemas del Milenio.
Los premios que hemos mencionado hasta el momento son premios que se conceden de forma periódica, pero estos que mencionamos a continuación son premios asociados a la resolución de siete importantes problemas matemáticos, los conocidos como Premios del Milenio del Instituto Clay de Matemáticas (EEUU).
El Instituto Clay de Matemáticas de Cambridge (Massachusetts, Estados Unidos) es una fundación privada sin ánimo de lucro dedicada a incrementar y difundir el conocimiento matemático, fundada en 1998 gracias al patrocinio del empresario de Boston Landon T. Clay y de Lavinia D. Clay. En el año 2000 el Instituto Clay de Matemáticas seleccionó siete importantes problemas abiertos, denominados Problemas del Milenio, que fueron elegidos como representación de algunos de los mayores desafíos a los que se enfrentaban los matemáticos y matemáticas en el nuevo milenio. El premio por la resolución de alguno de los problemas del milenio es de un millón de dólares.
Los problemas del milenio son:
1.- La conjetura de Birch y Swinnerton-Dyer, en teoría de números algebraica;
2.- La conjetura de Hodge, en geometría algebraica;
3.- La solución de las ecuaciones de Navier-Stokes de la mecánica de fluidos;
4.- El problema P = NP, en ciencias de la computación;
5.- La conjetura de Poncaré, en topología;
6.- La hipótesis de Riemann, en análisis complejo y teoría de números primos;
7.- El problema de la masa en la teoría de Yang-Mills, en la teoría cuántica de campos.
De los siete problemas del milenio planteados solo uno ha sido resuelto hasta la fecha, la conjetura de Poincaré. El matemático ruso Gregori Perelman, que ya había rechazado la Medalla Fields en el ICM Madrid 2006, posteriormente rechazó el premio de un millón de dólares del Instituto Clay de Matemáticas. Toda esta historia merece una entrada propia en el futuro.
 El matemático ruso Gregori Perelman resolvió uno de los siete problemas del milenio, la conjetura de Poincaré, pero rechazó la Medalla Fields del ICM2006, así como el millón de dólares del Instituto Clay de Matemáticas
El matemático ruso Gregori Perelman resolvió uno de los siete problemas del milenio, la conjetura de Poincaré, pero rechazó la Medalla Fields del ICM2006, así como el millón de dólares del Instituto Clay de Matemáticas
Para más información sobre los problemas del milenio del Instituto Clay de Matemáticas puede leerse el artículo del matemático Manuel de León, Los problemas del milenio, o más extensamente el monográfico Los problemas del milenio de la Revista Métode.
Pero estos son solo algunos pocos premios matemáticos que existen, pero el listado es muy amplio (Premio Fermat, Premio George Polya, Medalla Euler, Premio Erdös, Premios de la Sociedad Europea de Matemáticas, Premio Sophie Germain, etcétera) y lo podéis ver en la Wikipedia: List of mathematics awards, quizás volveremos a hablar de ellos en una futura entrada del Cuaderno de Cultura Científica.
 La matemática ucraniana Maryna Viazovska (1984), quien ha recibido varios premios, entre otros el Premio Europeo de Combinatoria en 2017, el Premio Fermat en 2019 o el Premio de la Sociedad Europea de Matemáticas-EMS en 2020, entre otros
La matemática ucraniana Maryna Viazovska (1984), quien ha recibido varios premios, entre otros el Premio Europeo de Combinatoria en 2017, el Premio Fermat en 2019 o el Premio de la Sociedad Europea de Matemáticas-EMS en 2020, entre otrosSobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Premios matemáticos, de las Medallas Fields a los Problemas del Milenio se ha escrito en Cuaderno de Cultura Científica.
Einstein y la pizarra del Observatorio del Monte Wilson
La foto que abre esta entrada es bastante popular. Más que por la foto en sí, por una aplicación que permite escribir en la pizarra lo que cada cual quiera. Y, sin embargo, esta foto tiene una historia cuando menos curiosa que nos va a permitir explorar someramente la idea de curvatura y cómo expresarla usando una herramienta matemática tremendamente útil en física, los tensores, a la par que rememorar un momento muy interesante en la historia de la cosmología.
En una época anterior a internet, las fotos de las noticias eran enviadas por las agencias de prensa por correo ordinario urgente a los distintos periódicos. Cada fotografía llevaba anexa su historia escrita por la agencia de noticias adherida a la parte posterior, de esa forma el periódico no tenía que complicarse a la hora elaborar el pie de foto.
La foto de Einstein fue tomada el 14 de enero de 1931 durante su visita al complejo del Observatorio del Monte Wilson en California (Estados Unidos). Sin embargo, se hizo pública 24 años después, con motivo de la muerte de Einstein el 18 de abril de 1955. El pie de foto con el que apareció en prensa decía: “Dr. Albert Einstein writes an equation for the density of the Milky Way on the blackboard at the Carnegie Institute, Mt. Wilson Observatory headquarters in Pasadena, Calif., in this Jan. 14, 1931.” En español se tradujo tal cual, por ejemplo: “Einstein escribe una ecuación sobre la densidad de la Vía Láctea en un pizarrón del Observatorio Monte Wilson, en Pasadena, California, en 1931”. Pero, ¿desde cuándo una densidad se expresa con subíndices y con la letra R? ¿La densidad de la Vía Láctea es cero? No parece tener sentido.
La historia anexa a la foto que mandó la agencia de noticias podría ayudarnos a desvelar esta posible contradicción. El original es el siguiente:

Vemos que “density” era originalmente “destiny”. ¿Podría haber ocurrido que el avezado reportero de la agencia de noticias se limitase a reflejar la frase que entendió y le llamó la atención y que, en algún paso intermedio, alguien decidiese que el “destino” no puede expresarse en una ecuación y que lo que quería decir es “densidad”? Podría ser. Parecería incluso más probable que Einstein lo que hacía era escribir sobre la curvatura del espaciotiempo. Pero, en realidad, lo que estaba haciendo es considerar el problema de la existencia de la constante cosmológica. Vamos a verlo, que es muy fácil de entender intuitivamente.
Si cortas una naranja por la mitad, quitas la pulpa del interior, e intentas aplanar el hemisferio de piel resultante, terminas rajándolo. Si tratas de aplanar algo con la forma de una silla de montar, como una patata frita (de las de bolsa) revenida, te encuentras con el problema contrario: hay “demasiada” superficie y se te forman pliegues. Si tomas, sin embargo, un rollo de papel de cocina y deseas aplanarlo, no hay nada más fácil, con desenrollarlo, listo. Las superficies como las esferas se dice que están curvadas positivamente, las que tienen la forma de una silla de montar que lo están negativamente, y las que son como el papel de cocina son, simplemente, planas (démonos cuenta de que son planas en este sentido aunque no estén en un plano). Esto es así porque la curvatura se define en términos de “geometría intrínseca” de una superficie, en la que la distancia se mide en función de los caminos que están dentro de la superficie.
Hay varias maneras de hacer precisa esta noción de curvatura y hacerla cuantitativa, de tal manera que a cada punto de la superficie se pueda asociar un número que diga “cómo de curvada” está en ese punto. Para poder hacer esto es necesario que se cumplan determinadas condiciones matemáticas que permitan determinar las longitudes de los caminos, es lo que se llama una métrica riemanniana. La noción de curvatura puede ser generalizada a un mayor número de dimensiones, de tal forma que se habla de la curvatura en un punto en una variedad riemanniana de d dimensiones. Sin embargo, cuando la dimensión es mayor de dos, es decir, no es un plano lo que se curva sino un espacio, las posibilidades de curvatura en un punto se hacen tan complicadas que ya no pueden ser expresadas por un número sino por algo llamado el tensor de Ricci.
Un tensor no es más que la extensión del concepto de vector a dimensiones adicionales. Un escalar, un número, aparece en un gráfico como un punto, un objeto de cero dimensiones. Un vector, que tiene magnitud y dirección, aparecería en un gráfico como una línea, es decir, como un objeto de una dimensión. El tensor extiende esta idea a las dimensiones adicionales. Esto podemos interpretarlo como un conjunto de vectores relacionados, moviéndose en múltiples direcciones en un plano.
Lo veremos mejor de otra manera. En vez de pensar en un vector como un conjunto de coordenadas, lo podemos considerar una operación, es decir, un vector lo que haría es asociar una dirección a un número. Lo importante desde el punto de vista matemático es que la operación es lineal y homogénea. Gracias a esto, un vector queda completamente determinado por sus proyecciones en d direcciones, donde d es el número de dimensiones del espacio en el que se define. Por tanto, un vector se puede expresar como un conjunto de números que son en realidad sus proyecciones en un sistema de ejes coordenados.
Un vector es realmente un tensor de rango 1, asocia 1 dirección a un número. Un escalar, es un tensor de rango 0, asocia 0 direcciones a un número. Por tanto un tensor de rango 2 (un tensor ya por derecho propio), asocia dos direcciones arbitrarias a un número. Si quisiéramos expresarlo en términos de las d coordenadas, como se hace con los vectores, necesitaríamos d x d números. Para un tensor de rango q, por tanto, necesitaríamos nq números.
Veamos ahora desde el punto de vista formal las ecuaciones de campo de la relatividad general. Si has llegado leyendo hasta aquí no te asustará demasiado, después de todo no es más que una igualdad tensorial en la que se relacionan un conjunto de tensores 4 x 4 (simétricos, pero en esto no vamos a entrar ahora), para un espaciotiempo de 4 dimensiones. Así:
![]()
Donde Rμν es el tensor de curvatura de Ricci del que hablábamos más arriba, R es la curvatura escalar (simplificando, la curvatura entendida en el sentido que hablábamos más arriba, un número asociado a un punto del espacio), gμν es el tensor métrico (una generalización del campo gravitatorio y principal objeto de interés), Λ es la constante cosmológica, G es la constante gravitacional de Newton, c la velocidad de la luz en el vacío y Tμν el tensor de energía-impulso.
Los índices en los tensores son etiquetas, es una forma de llamarlos. En este caso empleamos la notación abstracta de Penrose. Se puede usar cualquier símbolo conveniente para los índices de los tensores. Tradicionalmente, las letras latinas se usan para indicar que se están usando coordenadas espaciales (x, y, z), mientras que las griegas se emplean para indicar coordenadas espaciotemporales (x, y, z, t). En la época de la foto esta convención no se había establecido.
Una simple observación de la ecuación de campo nos dice que podría haber algo similar con lo que escribe Einstein en la pizarra: el tensor de Ricci. Efectivamente, existe un caso especial de la ecuación de campo en el que se postula que Tμν = 0, es decir, que la energía y el momento se conservan localmente. En este caso, y por las propiedades de los tensores, solo existe una posibilidad para que Rμν= 0 o, usando la notación de Einstein, Rik = 0, y es que Λ = 0. En definitiva, que el pie de foto podría ser “El Dr. Einstein discutiendo [por lo de la interrogación] la posibilidad de que la constante cosmológica sea cero”.
Para saber más:
Las ecuaciones de campo de la relatividad general
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 17 de diciembre de 2010.
El artículo Einstein y la pizarra del Observatorio del Monte Wilson se ha escrito en Cuaderno de Cultura Científica.
Por qué la obesidad es un imán para otras enfermedades
Francisco José Esteban Ruiz
 Foto: TheOtherKev / Pixabay
Foto: TheOtherKev / PixabaySin entrar en el debate de si la obesidad debe o no considerarse una enfermedad, y siendo conscientes de que sus causas pueden ser múltiples, nos enfrentamos a un verdadero problema de salud pública que aumenta tanto la morbilidad (enfermar) como la mortalidad (morir debido a ello).
Independientemente de lo que nos lleve a pasarnos del peso que se considera dentro de lo normal, esos kilos de más nos afectan de un modo u otro. Existen pruebas irrefutables de que la obesidad es un importante factor de riesgo para padecer otras enfermedades como hipertensión, dislipemia (alteración de la cantidad de lípidos en sangre, como el colesterol), diabetes, enfermedades cardiacas e infartos cerebrales, piedras en la vesícula, artrosis, ovario poliquístico, síndrome de apnea del sueño y algunos tipos de cáncer. Y nos hemos quedado cortos, pues se considera que la obesidad y el sobrepeso incrementan el riesgo y favorecen el desarrollo de más de 200 enfermedades crónicas.
Además, y desafortunadamente, desde el inicio de la pandemia debida al coronavirus se hizo patente el hecho de que la obesidad empeoraba la situación. Sí, desde hace años se conoce que las personas obesas son más vulnerables a las infecciones y a las complicaciones derivadas de las mismas. En el caso concreto de la covid-19, y según un estudio de la Sociedad Española de Obesidad, el 80% de las personas con manifestaciones severas por coronavirus en España eran obesas.
La acumulación de grasa enferma al tejido
¿A qué se debe que el ser obeso aumente el riesgo de contraer otras enfermedades? La investigación en biología celular, bioquímica y genética nos ayuda a responder.
La principales células responsables del almacenamiento de grasa en nuestro cuerpo son los adipocitos, que forman parte del llamado tejido adiposo. En este tejido también hay otros tipos celulares, como los linfocitos y los macrófagos del sistema inmune, y el buen estado de salud del tejido depende de que exista un equilibrio funcional entre todos los tipos de células.
Pues bien, en la base de la obesidad se encuentra la adiposopatía, que podemos decir que es una alteración que se produce debido a que, por diferentes causas, ingerimos más calorías de las que gastamos. Esto da lugar a una alteración anatómica (deposición anormal de grasa) y funcional (inmune y hormonal) del tejido adiposo que puede causar o empeorar una enfermedad metabólica.
¿Y qué es una enfermedad metabólica? Sencillamente un daño debido a la alteración de nuestras vías metabólicas, como la del colesterol, la insulina y las hormonales, que a su vez dan lugar a enfermedades como arterioesclerosis, la hipertensión, la diabetes y un aumento de hormonas masculinas en mujeres y su disminución en hombres.
La grasa se acumula donde no debe
Cuando los adipocitos comienzan a acumular más grasa de lo normal también se produce deposición de grasa más allá de donde debería, por ejemplo, en el hígado y en el músculo. Junto a la adiposopatía, este hecho provoca una alteración en la secreción de hormonas, como la leptina, y de toda una serie de proteínas proinflamatorias, como las citoquinas.
Además, la obesidad da lugar a una deposición anormal de grasa alrededor del corazón. Un estudio reciente realizado sobre casi 7 000 participantes ha puesto de manifiesto que el aumento de la grasa pericárdica se asocia con el riesgo de fallo cardiaco.
El aumento en la secreción de citoquinas debido a la obesidad no sólo reduce la capacidad de responder a la infección respiratoria causada por el coronavirus, sino que provoca que todo empeore. Más aún, la asociación de la obesidad con una disminución de la función inmune hace que estos pacientes sean más susceptibles a todo tipo de infecciones.
En cuanto al tratamiento, en los obesos disminuye la respuesta a los antivirales y son menos eficaces las vacunas.
El novelista Charles Dickens dijo que “cuanto más engorda uno, más prudente se vuelve. Prudencia y barriga son dos cosas que crecen simultáneamente”. Visto lo visto, más vale que seamos prudentes y no hagamos crecer la barriga.![]()
Sobre el autor: Francisco José Esteban Ruiz es profesor titular de biología celular en la Universidad de Jaén
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Por qué la obesidad es un imán para otras enfermedades se ha escrito en Cuaderno de Cultura Científica.
Ignorantes que creen saberlo todo
 Foto: Brett Jordan / Unsplash
Foto: Brett Jordan / UnsplashLa búsqueda de información en Google ofusca la percepción acerca del origen de lo que sabemos o creemos saber. Al demandar a Google datos, historias, piezas de conocimiento del tipo que sea, tendemos a considerar como propio el origen de la información que nos da el buscador. Esto es, tendemos a pensar que ya disponíamos de ella, y así sobrevaloramos nuestros recursos y capacidades cognitivas. Esta es la principal conclusión de un estudio publicado hace unas semanas en la revista PNAS.
El hecho en sí, el recabar conocimiento ajeno, no es inhabitual en absoluto. Nadie lo sabe todo. Dependemos del conocimiento de familiares, amistades, colegas. Configuramos con esas personas sistemas cognitivos compartidos que nos permiten atender, procesar y recordar información de forma colectiva. No necesitamos saberlo todo; lo que necesitamos es saber quién sabe qué cosas. La ciencia, por ejemplo, funciona así, sobre la base de un conocimiento y comprensión de los fenómenos de la naturaleza compartidos de forma parcial por centenares de miles de personas, muchas de las cuales ni siquiera viven en la actualidad. La cognición humana no es individual; el pensar, recordar y conocer son, muy a menudo, colaborativos, el producto de la interacción entre recursos cognitivos propios y ajenos.
En las últimas décadas, a los mecanismos clásicos de cooperación cognitiva se ha sumado la internet y sus sistemas de búsqueda rápida. La red permite expandir la mente dotándonos de una memoria externa que se puede consultar cada vez que se necesita. Lo sabe casi todo y está siempre a nuestra disposición; nos proporciona la información que deseamos en el instante en que la solicitamos, sin esfuerzo por nuestra parte, con mayor facilidad, incluso, que si la obtuviésemos de nuestra misma mente. No tenemos que acudir a la biblioteca o consultar con un colega por teléfono. Es esa particularidad, esa facilidad para acceder a ella, la ausencia de otros actos intermedios, lo que, al parecer, hace que se difuminen las fronteras entre el conocimiento interno y el externo. Tendemos a pensar que el conocimiento de internet es nuestro conocimiento.
Como se difumina la frontera entre conocimiento externo e interno, quienes recurren con mayor frecuencia a internet para buscar información tienen más confianza en su memoria. A menudo olvidan, incluso, que habían recurrido a Google para saber algo. Creen que las respuestas obtenidas de internet procedían de su propia memoria.
Sabíamos del denominado “efecto Google”: cuando obtenemos información fácilmente en internet, tendemos a no almacenarla en nuestra memoria o, incluso, a olvidarla con facilidad. Pues bien, el estudio citado antes ha revelado la existencia de un segundo efecto Google, uno que no se refiere a lo que la gente sabe, sino a lo que cree saber. Como consecuencia, en un mundo en el que la búsqueda en internet es con frecuencia más rápida y fácil que bucear en la memoria propia, la gente puede llegar a saber menos, aunque crea saber más.
Las implicaciones de este fenómeno pueden ser variadas e importantes. Al aumentar la confianza de las personas en su conocimiento y comprensión, puede distorsionar su juicio acerca del aprendizaje y la motivación para aprender. Puede también otorgar mayor (e injustificada) confianza en el criterio propio a la hora de tomar ciertas decisiones. Y puesto que somos poco dados a cuestionar lo que consideramos conocimiento propio, al borrarse la frontera con el que obtenemos de la red, es más difícil detectar informaciones erróneas, con las consecuencias que se pueden derivar de ello.
¿Se imagina un mundo lleno de ignorantes que creen saberlo casi todo? Sé que exagero, pero quizás no demasiado. Piénselo.
Fuente: Ward, A. F. (2021): People mistake the internet’s knowledge for their own. Proceedings of the National Academy of Sciences, 118 (43) e2105061118.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Ignorantes que creen saberlo todo se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Esther Samper – Eran otros tiempos
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

Ningún tiempo pasado fue mejor que hoy en términos sanitarios. Sin embargo, la pandemia ha puesto de manifiesto la existencia de una parte de la sociedad que es presa fácil de los enemigos de la medicina de base científica; que es, por cierto, la única medicina (las alternativas, por definición, no tienen base científica). Esther Samper, que es doctora en medicina regenerativa y comunicadora, lidia con estos enemigos a diario.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Esther Samper – Eran otros tiempos se ha escrito en Cuaderno de Cultura Científica.
Una nueva especie extremófila en el Valle Salado de Añana
 Fuente: Fundación Valle Salado de Añana
Fuente: Fundación Valle Salado de AñanaEl Valle Salado de Añana es una zona muy biodiversa, en la que las especies acuáticas son especialmente llamativas. Los análisis realizados por el grupo de investigación MikroIker, de la Universidad del País Vasco/Euskal Herriko Unibertsitatea, han aportado información sobre la existencia de una nueva especie microbiana. La nueva especie bacteriana aislada en el agua del manantial de Santa Engracia ha sido bautizada como Altererythrobacter muriae, y, por el momento, solo ha sido identificada en ese lugar.
“Los estudios poblacionales microbianos realizados durante los últimos años en el Valle Salado de Añana nos están permitiendo conocer la evolución y la relación entre las especies detectadas en ese ambiente. Hemos observado cómo existe la posibilidad de estar ante algunas nuevas especies bacterianas no descritas anteriormente que sean únicas de ese ecosistema, lo que cerciora la biodiversidad exclusiva del lugar aumentando su valor ecológico”.
Ilargi Martinez-Ballesteros.
Los ambientes hipersalinos se consideran ambientes metabólicamente extremos y son habitados por un grupo diverso de microorganismos con capacidad para sobrevivir en concentraciones variables (2-30 %) de cloruro sódico (sal), denominados halófilos. El Valle Salado de Añana se emplaza sobre una gran burbuja de sal que procede de la desecación de un antiguo mar de hace 200 millones de años. El agua dulce de lluvia atraviesa las capas más profundas de halita o sal gema disolviéndola y aflora en forma de manantiales hipersalinos, ofreciendo así hábitat a una gran diversidad de microorganismos halófilos y halotolerantes.
Existe una amplia variedad de halófilos (pertenecientes a los tres dominios principales de la vida, Archaea, Bacteria y Eukarya), que transforman una amplia gama de sustratos en los hábitats hipersalinos. Además, los distintos mecanismos de haloadaptación desarrollados por los microorganismos en esas condiciones extremas han derivado en la producción de compuestos útiles para la supervivencia microbiana que, a su vez, han resultado ser de gran interés en los ámbitos de la biomedicina, la biorremediación o la industria alimentaria.
“Los microorganismos son indispensables en el mantenimiento de la biosfera, ya que regulan los ciclos biogeoquímicos de los principales elementos, participan en los procesos de descomposición de materia orgánica, favorecen el ciclaje de nutrientes, y degradan compuestos contaminantes, procesos indispensables en el mantenimiento de los ecosistemas”.
Ilargi Martinez-Ballesteros.
A la hora de comprender la diversidad microbiana en ambientes extremos, como es el Valle Salado de Añana, es importante estudiar la composición de las comunidades procariotas (bacterias y arqueas) tanto en los manantiales salinos de los que se extrae sal en distintos puntos del valle, como de afluentes salobres que afloran en otros puntos del valle. “Esto permitirá generar conocimiento básico sobre las poblaciones microbianas allí presentes, sus patrones de distribución y su potencial uso biotecnológico en beneficio de la salud tanto humana como medioambiental. Los métodos de análisis microbiológicos convencionales y quimiotaxonómicos o la genómica comparativa han permitido ya el reconocimiento de tipos interesantes y numéricamente importantes de halófilos y halotolerantes”, concluye Ilargi Martinez-Ballesteros.
Referencia:
Maia Azpiazu-Muniozguren, Ilargi Martinez-Ballesteros, Javier Gamboa, Sergio Seoane, Rodrigo Alonso, Lorena Laorden, Javier Garaizar, Joseba Bikandi Altererythrobacter muriae sp. nov., isolated from hypersaline Añana Salt Valley spring water, a continental thalassohaline-type solar saltern (2021) International Journal of Systematic and Evolutionary Microbiology doi: 10.1099/ijsem.0.004734
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Una nueva especie extremófila en el Valle Salado de Añana se ha escrito en Cuaderno de Cultura Científica.
Una extinción de novela policiaca
 Reconstrucción de un sinápsido, grupo precursor de los mamíferos, de finales del Pérmico. Autor: U. Kikutani
Reconstrucción de un sinápsido, grupo precursor de los mamíferos, de finales del Pérmico. Autor: U. KikutaniHace unos 252 millones de años se produjo la mayor extinción masiva de los últimos 500 millones de años de historia de nuestro planeta, la extinción del límite Pérmico-Triásico. En poco menos de 1 millón de años, desaparecieron aproximadamente el 95% de las especies que había en la Tierra. Se vio el final de todas las especies de trilobites que habitaban los mares y océanos, se extinguieron muchas especies de los helechos y coníferas gigantes que formaban enormes bosques pantanosos y desaparecieron más del 70% de las especies de reptiles y sinápsidos, grupo precursor de los actuales mamíferos, que dominaban la tierra firme. Por eso a esta extinción se la suele denominar “La Gran Mortandad” y se toma como un punto de inflexión tan importante en la historia evolutiva del planeta, que da fin a la Era Paleozoica y comienzo a una nueva etapa, la Era Mesozoica. Poniéndonos poéticos, prácticamente la podríamos denominar como un apocalipsis biótico en el que el contador evolutivo casi se puso a 0. Por suerte, la vida siempre se abre camino y, si superó la extinción del Pérmico-Triásico, puede soportar casi cualquier cosa que se le ponga por delante.
 Meseta de Putorana, incluida dentro de los Trap Siberianos, formada por la acumulación de rocas volcánicas. Foto: jxandreani / Wikimedia Commons
Meseta de Putorana, incluida dentro de los Trap Siberianos, formada por la acumulación de rocas volcánicas. Foto: jxandreani / Wikimedia CommonsSon varias las causas a las que se aluden para intentar explicar los motivos que provocaron esta extinción biótica. Por un lado, en la actual Siberia, se encuentran unos enormes depósitos volcánicos, denominados los Trap Siberianos, que se formaron por sucesivas erupciones acontecidas a finales del Pérmico. Estas gigantescas erupciones debieron liberar toneladas de gases de efecto invernadero a la atmósfera, que rápidamente cubrieron todo el globo y dieron lugar a un intenso calentamiento global que, literalmente, achicharró la Tierra. Por otro lado, en los mares y océanos se registró un descenso generalizado de los niveles de oxígeno disuelto en el agua, lo que produjo condiciones anaerobias en el fondo que dieron lugar a la expulsión de enormes cantidades de sulfuro de hidrógeno a la atmósfera, gas nocivo para la biota y que, además, es capaz de afectar a la capa de ozono. Y también se descongelaron los depósitos de hidratos de metano que se encontraban enterrados en el sedimento de los fondos oceánicos, liberando toneladas de este gas de efecto invernadero a la atmósfera. Por último, recientemente se especula con un posible impacto de un cuerpo extraterrestre a finales del Pérmico tras el descubrimiento de un cráter meteorítico en la Antártida, aunque aún se está investigando esta hipótesis ante la necesidad de realizar una datación temporal más precisa de este hallazgo.
Pero ahora es cuando todo se pone más interesante. Y aviso de que voy a hacer algunos spoilers. En 1934, la escritora británica Agatha Christie publicó una de sus obras más famosas, Asesinato en el Orient Express. En esta novela, el detective belga más admirado a nivel mundial, Hércules Poirot, se enfrenta al asesinato de un conocido hombre de negocios norteamericano sucedido durante uno de los viajes de este famoso tren y tiene que descubrir al asesino mientras esperan a que los rescaten tras acabar varados debido en un alud de nieve. Ahora es cuando debéis dejar de leer este artículo si no conocéis la novela, puesto que voy a destriparos el final. Y es que lo que descubre Poirot es que todos los pasajeros son los asesinos, ya que tenían una relación entre ellos y un motivo para acabar con la víctima, así que entre todos terminaron con su vida apuñalándole de uno en uno.
Y algo similar es lo que parece que sucedió a finales del Pérmico en nuestro planeta. Las causas que os he descrito previamente, cada una por sí sola, no serían capaces de acabar con cerca del 95% de las especies de nuestro planeta. Pero todas juntas y de manera combinada, sí. Las erupciones volcánicas provocarían un efecto invernadero generalizado en todo el planeta que daría lugar a un aumento de la temperatura del agua marina, que a su vez provocaría las condiciones anóxicas del fondo, con la generación de sulfuro de hidrógeno y la descongelación de los hidratos de metano. Estos dos gases, una vez liberados a la atmósfera, aumentarían el efecto invernadero, retroalimentando las condiciones de calentamiento global. Incluso la hipótesis del impacto extraterrestre tendría cabida en este juego, ya que sería factible que las ondas de choque provocadas por el mismo fueran las desencadenantes del vulcanismo siberiano. A esta hipótesis que une las posibles casusas de la extinción del Pérmico-Triásico como auto desencadenantes una de la otra, se la ha denominado “Efecto Asesinato en el Orient Express”, en honor a la gran novela de Agatha Christie.
Como podéis comprobar, en geología siempre nos encanta hacer homenajes a la cultura popular poniendo nombres de este tipo a las cosas que descubrimos. Y aunque esta hipótesis aún está en estudio, el nombre es más que apropiado, ya que por sí mismo explica lo que pudo suceder en nuestro planeta hace unos 252 Millones de años durante la mayor crisis biótica de nuestra historia.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Una extinción de novela policiaca se ha escrito en Cuaderno de Cultura Científica.
Vera Pless, de especialista en álgebra abstracta a experta en teoría de códigos
Vera Stepen nació en Chicago (Estados Unidos) el 5 de marzo de 1931. Sus padres eran judíos rusos que habían emigrado a Estados Unidos: su madre, Helen Blinder, era dentista, y su padre, Lyman Stepen, joyero. Deseaban que su única hija disfrutara de los beneficios en educación que se ofrecían en este país, y la incentivaron a estudiar.
 Vera Pless. Fuente: Wikimedia Commons.
Vera Pless. Fuente: Wikimedia Commons.
Cuando Vera tenía unos 12 años, un amigo de la familia, estudiante de posgrado en la Universidad de Chicago, le enseñó cálculo. Observó que poseía un verdadero talento matemático, pero Vera no estaba demasiado interesada en las matemáticas en ese momento. Tocaba el violonchelo en la orquesta de su escuela, y soñaba con llegar a ser una instrumentista destacada. Pero su padre tenía otros planes para ella, y la obligó a abandonar la escuela secundaria dos años antes.
Vera ingresó en la Universidad de Chicago donde obtuvo una licenciatura en solo tres años. Seguía sin tener un interés especial por convertirse en matemática, a pesar de tener cerca varias personas que la inspiraron.
No tenía la ambición de convertirme en matemática; las chicas en ese momento aspiraban a ser esposas (de hombres exitosos) y madres. Tal vez algunas chicas «desafortunadas» no se casaron e hicieron una carrera; pero, en lo que respecta a las mujeres matemáticas, nunca vi una durante mi época de estudiante. Sin embargo, conocía el trabajo de Emmy Noether y tal vez influyó en mi elección de área, álgebra; aunque creo que la enseñanza de Irving Kaplansky fue lo que realmente me inspiró.
Vera Pless, AMS Notices
Efectivamente, Emmy Noether (1882-1935) e Irving Kaplansky (1917-2006) eran especialistas en álgebra abstracta, en teoría de anillos y, sin duda alguna, dos personas realmente inspiradoras. Así, Vera continuó sus estudios en la Universidad de Chicago preparando su maestría. En esa época conoció a su futuro esposo, un estudiante de física, en la universidad y se casaron en 1952, dos semanas antes de su examen de maestría. Vera Stepen pasó a llamarse Vera Pless.
Vera comenzó a trabajar con un grupo de física en la Universidad de Chicago mientras su esposo preparaba su doctorado en física experimental de altas energías. Poco después consiguió una beca para estudiar en la Universidad Northwestern y comenzó a trabajar en su tesis doctoral bajo la supervisión de Alex Rosenberg (1926-2007), un antiguo alumno de Kaplanski.
Cuando su marido terminó su doctorado, le ofrecieron un puesto en el Instituto de Tecnología de Massachusetts y Vera se mudó con él a Cambridge. Rosenberg se mostró dispuesto a que Pless terminara su tesis doctoral a distancia; Vera regresó en junio de 1957 a la Universidad Northwestern para defender su trabajo doctoral Quotient Rings of Continuous Transformation Rings. Dos semanas más tarde nació prematuramente su primera hija, y Vera se quedó en casa cuidando de la pequeña; era lo que se esperaba de ella.
En 1959 llegó su segundo hijo, un niño. Cuando el pequeño tuvo la edad suficiente para asistir a la guardería, en 1962, Pless comenzó a impartir cursos en la Universidad de Boston.
Todavía sentía que mi primera responsabilidad eran mis hijos pequeños. Incluso con mi docencia, encontré esta vida agobiante. Teníamos poco dinero, por lo que no podíamos contratar niñeras ni ayuda doméstica. Mi esposo era muy ambicioso, trabajaba muchas horas, y no sentía que debía ayudar de todos modos, algo que era común en esa época.
Vera Pless, AMS Notices
Cuando el menor de sus hijos tuvo la edad suficiente para comenzar la escuela primaria, Vera Pless comenzó a buscar puestos de tiempo completo. Pero no tuvo éxito: aunque tenía experiencia docente, había interrumpido su investigación. Era consciente de que la discriminaban; de hecho, en algunas instituciones le decían abiertamente que la universidad no era el lugar adecuado para una mujer.
En ese momento, en 1963, el Laboratorio de Investigación de Cambridge de la Fuerza Aérea Estadounidense buscaba matemáticos para trabajar en el área emergente de códigos correctores de errores. Aunque Vera desconocía a que se dedicaba este campo, su experiencia algebraica se consideró suficiente para incorporarse en el equipo. Trabajó allí hasta 1972, con un breve permiso maternal cuando nació su tercer hijo. Se convirtió en una de las principales expertas mundiales en teoría de códigos.
Publicó varios artículos sobre códigos correctores de errores, y otros que continuaban con la investigación que había realizado para su doctorado.
En 1973, la llamada enmienda Mansfield limitó las asignaciones para investigación en defensa solo a proyectos que tuvieran una aplicación militar directa. Vera Pless dejó su puesto para trabajar, durante tres años, como investigadora asociada en el Instituto de Tecnología de Massachusetts en el proyecto MAC sobre matemáticas y computación. En 1975 fue nombrada profesora titular en la Universidad de Illinois en Chicago. Su esposo y su hijo menor se quedaron a vivir en la zona de Boston; el matrimonio se divorció en 1980.
 Portada de Introduction to the theory of error-correcting codes.
Portada de Introduction to the theory of error-correcting codes.
En 1982 publicó un libro sobre la teoría de la codificación, Introduction to the theory of error-correcting codes, diseñado como un curso de un semestre para estudiantes universitarios. Trataba sobre teoría de codificación algebraica, y fue especialmente apreciado por incluir demostraciones claras y sencillas. Sus publicaciones de investigación suman más de un centenar.
Se jubiló en 2006 y falleció el 2 de marzo de 2020 a la edad de 88 años.
Mirando atrás, creo que tuve mucha suerte. Trabajé en codificación desde sus inicios, y se ha convertido en un tema matemático fascinante. He apreciado la oportunidad de trabajar con muchos matemáticos maravillosos, en particular Richard Brualdi, John Conway y Neil Sloane. Era capaz de cuidar a mis hijos en sus años más jóvenes en un entorno de baja presión. […] Nuestra disciplina no es la única que exige mucho. Mi hija, médica residente con una hija pequeña, tiene mucho que decir sobre las largas horas demandadas a los residentes. Lamentablemente, nuestra sociedad está perdiendo probablemente valiosas contribuciones de las mujeres por estas razones. Y muchas mujeres están pagando un gran precio emocional, ya sea renunciando a carreras o no dedicando tanto tiempo a sus familias como creen que deberían.
Vera Pless, AMS Notices
Referencias
- Su página web, Universidad de Illinois en Chicago
- Vera Pless (1991). In Her Own Words, AMS Notices 38 (7) 705-706
- O’Connor, John J.; Robertson, Edmund F., Vera Pless, MacTutor History of Mathematics archive, University of St Andrews
- Vera Pless, Biographies of Women Mathematicians, Agnes Scott College
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Vera Pless, de especialista en álgebra abstracta a experta en teoría de códigos se ha escrito en Cuaderno de Cultura Científica.
Sócrates y el efecto Dunning-Kruger en redes sociales
 Foto: Bermix Studio / Unsplash
Foto: Bermix Studio / Unsplash“Solo sé que no sé nada”. ¿Cuántas veces habremos oído esta frase atribuida a Sócrates como justificación de la ignorancia? Sin embargo, esta sentencia no aparece en ninguno de los escritos en los que se cita al que era más sabio que ningún otro humano, parafraseando a la Pitia. De hecho, la comprobación de lo que en realidad quería decir nos desvelará que Sócrates estaba en realidad probablemente sujeto a un prejuicio cognitivo, el efecto Dunning-Kruger.
El dicho se suele atribuir al Sócrates de Platón. Sócrates no dejó nada escrito, de ahí que lo que conocemos de él es lo que escribieron sus contemporáneos, especialmente Platón. En ninguna de las referencias de Platón a Sócrates aparece la expresión “Solo sé que no sé nada”.
Sin embargo, en la Apología, la versión idealizada de la defensa que hizo Platón de Sócrates en el juicio a este, encontramos: “Este hombre, por una parte, cree que sabe algo a pesar de no saber nada. Por otra, yo, igualmente ignorante, no creo saber algo”. Esta es la frase a partir de la cual se produce el salto, lógicamente falaz, del “no creo saber algo” al “no sé nada”. El autor no dice que no sepa algo sino que no puede, que nadie puede, saber con absoluta certeza, pero que puede tener confianza acerca del conocimiento de ciertas cosas (por ejemplo, de que el otro no sabe nada). Como es obvio, esta conclusión no la extraemos de esta frase aislada sino sobre el análisis del conjunto de la obra sobre Sócrates que han realizado varios autores.
Vemos pues que la ignorancia o, mejor, su admisión, no es una resultante sino un punto de partida para el conocimiento. Es la base del método socrático que se ilustra mejor en los primeros diálogos de Platón. El método consiste en simular ignorancia, la llamada ironía socrática, o admitirla como base sobre la que construir el conocimiento y establecer un diálogo con un supuesto experto, cuya confiada afirmación de conocer terminará siendo destruida. A partir de aquí ya se pueden desarrollar ideas más adecuadas.
Así, en Menón, un diálogo de Platón, aparece Sócrates diciendo: “Por eso ahora no sé lo que es la virtud; quizás tu lo supieses antes de que me contactases, pero ahora eres ciertamente como uno que no sabe”. En este punto el objetivo de Sócrates está claro, cambiar la posición de Menón, que era un firme creyente en su propia opinión y cuya afirmación de conocimiento Sócrates acaba de probar que es infundada.
Estamos ante el origen de la filosofía occidental que terminará resultando en lo que hoy conocemos como ciencia: Sócrates comienza toda sabiduría con el autocuestionamiento, con la propia admisión de ignorancia.
Pero veamos la misma cuestión desde un punto de vista diferente. En los diálogos socráticos de Platón el sabio es el que duda, el que se cuestiona, mientras que el verdadero ignorante es el que tiene muy clara cuál es la verdad, a la que ha llegado en muchos casos por sí mismo sin preocuparse demasiado de donde surge el conocimiento. Por otra parte, estos “sabios” no siempre reconocen su error, están pagados de sí mismos y se creen superiores a los demás. Estamos ante una ilustración del efecto Dunning-Kruger.
El efecto Dunning-Kruger se puede expresar de la siguiente manera: los peores trabajadores/estudiantes/participantes son los que menos conscientes son de su propia incompetencia. Toma su nombre de un estudio de 2003 que realizaron Dunning, Kruger y otros con estudiantes universitarios con respecto a los resultados de sus exámenes. Después los resultados han sido reproducidos en varias ocasiones, por ejemplo con estudiantes de medicina a la hora de evaluar su capacidad para hacer entrevistas de diagnóstico, con administrativos evaluando su rendimiento o con técnicos de laboratorios médicos calibrando su nivel de dominio del trabajo.
La razón de fondo parece estar en que los que peor lo hacen son incapaces de aprender de sus errores.
Una solución aparentemente simple es decirle directamente al incompetente que lo es y por qué. Pero no funcionará. Desafortunadamente, el incompetente habrá estado recibiendo ese tipo de respuesta durante años y no habrá sido capaz de enterarse. A pesar de los exámenes suspensos, los trabajos mal hechos, las risas, burlas y sesudas contraargumentaciones a sus comentarios en redes sociales y la irritación que provocan sistemáticamente en los demás, el incompetente sigue sin creerse que lo sea.
Como Sócrates, las personas con verdadero talento tienden a subestimar lo buenos que son. Es la parte simétrica de este prejuicio: las personas inteligentes tienden a asumir que para los demás las cosas son tan fáciles y evidentes como para ellos, cuando lo que están haciendo es proyectar su propia luz y creer que ven un reflejo de la misma en los demás.
Estas ideas se conocen desde mucho antes que Dunning-Kruger y los demás investigadores las cuantificasen. Se pueden encontrar muchas citas al respecto, como esta de Bertrand Russell en la que se refiere a su tiempo, pero que como sabemos que es otro prejuicio cognitivo, podemos extrapolar a cualquiera:
“Una de las cosas dolorosas de nuestra época es que aquellos que se sienten ciertos son estúpidos, y aquellos con algo de imaginación y comprensión están llenos de dudas e indecisión”.
En el mundo de Internet lo anterior tiene una consecuencia práctica inmediata: No alimentes al comentarista manifiestamente incompetente, es solo una versión de trol que busca llamar la atención. Su problema es que no sabe, ni puede llegar a saber, que lo es.
Para saber más:
Lo que los sabelotodos no saben, o la ilusión de competencia
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 13 de junio de 2012.
El artículo Sócrates y el efecto Dunning-Kruger en redes sociales se ha escrito en Cuaderno de Cultura Científica.
Pezuñas calientes, cabeza fría
 Ilustración: María Lezana
Ilustración: María LezanaLa gacela de Thomson (Eudorcas thomsonii) es un antílope de pequeño tamaño (pesa entre 20 y 30 kg) que habita en los pastizales de las sabanas de Tanzania y Kenia, donde es una de las presas preferidas de leones, guepardos, leopardos y cocodrilos.
Puede alcanzar velocidades de hasta 80 km/h, normalmente cuando huye de alguno de sus depredadores habituales, aunque difícilmente supera los 40 km/h en carrera sostenida durante varios minutos.
Tras huir de un depredador -quizás del más rápido de ellos, el guepardo-, durante un tiempo de unos 5 min, y suponiendo que no haya sido atrapada, ha generado una gran cantidad de calor debido al esfuerzo realizado. Ese calor no se disipa inmediatamente, de manera que provoca un aumento de la temperatura corporal bien por encima de la habitual. La sangre arterial puede elevarse de los 38 °C o 39 °C normales hasta los 44 °C. La gacela de Thomson, a pesar de ser un animal homeotermo, pierde así de manera transitoria la capacidad para mantener constante su temperatura corporal como consecuencia del esfuerzo.
Al huir despavorida a toda velocidad, el gasto metabólico de la gacela se multiplica por cuarenta. Además del efecto del esfuerzo, la temperatura ambiental es alta, muy alta, tanto quizás como la corporal. Así pues, a la gacela le resulta muy difícil disipar el calor que produce, por lo que la temperatura sanguínea sube rápidamente. Además, es posible que esa temperatura corporal tan alta sirva a la gacela para que sus músculos se contraigan más rápidamente y pueda así huir con mayor facilidad del depredador.
La elevación de la temperatura corporal no se debe a que fallen los sistemas de disipación de calor. De hecho, la gacela jadea a muy alta frecuencia, tanto para tomar más oxígeno como para refrigerar la sangre facilitando la evaporación del líquido que cubre las superficies respiratorias. El problema es que bajo las condiciones en que se encuentra no es posible mantener la temperatura en los valores normales, incluso aunque los sistemas de termorregulación mantengan plena integridad funcional. La carga de calor es demasiado alta y la gacela no puede disipar todo el que genera.
Pero ocurre que la elevación de la temperatura no se produce por igual en todo el organismo, ya que gracias precisamente al jadeo, la gacela de Thomson puede mantener su encéfalo más fresco que el resto de órganos. De hecho, mientras el cuerpo alcanza los 44 °C, el encéfalo no pasa de 41 °C, temperatura por encima de la cual las neuronas sufrirían graves daños.
El mecanismo de refrigeración se basa en una rete mirabile (red maravillosa). En su camino hacia el encéfalo, la sangre que circula por la arteria carótida se distribuye entre centenares de arteriolas o capilares, para volver a agruparse justo antes de alcanzarlo. Esas arteriolas constituyen una rete mirabile, un dispositivo especialmente apto para intercambiar calor. El intercambio se produce porque los vasos arteriales atraviesan un seno que se encuentra lleno de sangre venosa, que procede, precisamente, de la zona nasal de la gacela, donde ha tenido lugar la evaporación del líquido superficial y, como consecuencia, el enfriamiento de la que circula por allí. De esa forma se enfría la sangre que circula por las arteriolas, cediendo calor a la venosa que procede de la nariz. Al atravesar el seno, la sangre arterial reduce su temperatura en unos 2 o 3 °C.
En la anotación anterior de la sección Animalia, sobre la irrigación de la musculatura de algunos peces (atunes y lenguados), vimos cómo funcionaba una rete mirabile como esta, con la diferencia de que aquella red servía para calentar la sangre que irrigaba los músculos que impulsan al atún y ésta para enfriar la sangre que irriga el encéfalo. En ambos casos se producen intercambios de calor mediante un dispositivo en contracorriente, aunque con objetivos opuestos.
En inglés denominan “selective brain cooling” al mecanismo, basado en el jadeo, de que hace uso la gacela de Thomson. Aunque no es el único animal que lo utiliza, pues bastantes ungulados domésticos también recurren a él cuando lo necesitan. De todos ellos cabría decir aquello de que mantienen la cabeza fría y, en este caso, las pezuñas calientes.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Pezuñas calientes, cabeza fría se ha escrito en Cuaderno de Cultura Científica.
ZientZinema 2: El día de mañana

Dirección: Roland Emmerich. USA. 2004. 124 min. Intérpretes: Dennis Quaid (Profesor Jack Hall), Jake Gyllenhaal (Sam Hall), Ian Holm (Terry Rapson), Emmy Rossum (Laura), Sela Ward (Dra. Lucy Hall), Dash Mihok (Jason Evans), Jay O. Sanders (Frank Harris), Austin Nichols (J.D.), Arjay Smith (Brian Parks), Tamlyn Tomita (Janet Tokada). Guion: Roland Emmerich y Jeffrey Nachmanoff; basado en un argumento de Roland Emmerich. Producción: Mark Gordon y Roland Emmerich. Música: Harald Kloser. Fotografía: Ueli Steiger. Montaje: David Brenner. Diseño de producción: Barry Chusid. Dirección artística: Martin Gendron, Michele Laliberte, Claude Paré, Réal Proulx, Tom Reta y Gerald Sullivan.
¿Y si estuviéramos al borde de una nueva era glacial? Éste es el asunto que obsesiona al climatólogo Jack Hall (Dennis Quaid). Las investigaciones llevadas a cabo por Hall indican que el calentamiento global del planeta podría desencadenar un repentino y catastrófico cambio climático de la Tierra. Las perforaciones realizadas en la Antártida muestran que es algo que ya ha ocurrido con anterioridad, hace diez mil años. Y ahora está alertando a los dirigentes de que podría ocurrir de nuevo si no se adoptan medidas de forma inmediata. Pero sus advertencias llegan demasiado tarde. Todo empieza cuando Hall presencia cómo un bloque de hielo del tamaño de Rhode Island se desgaja completamente de la masa de hielo de la Antártida. Posteriormente, una serie de fenómenos climatológicos cada vez más drásticos empiezan a ocurrir en distintas partes del globo: granizos del tamaño de una ciruela destrozan Tokio, vientos huracanados que rompen todos los récords machacan Hawai; la nieve cae en Nueva Delhi; una serie de devastadores tornados azotan la ciudad de Los Ángeles. Una llamada de teléfono de un colega suyo de Escocia, el profesor Terry Rapson, confirma los peores temores de Jack: estos intensos fenómenos meteorológicos son síntomas de un cambio climatológico masivo y, además, se ha detectado una bajada súbita de la temperatura en las aguas del Atlántico Norte. El derretimiento de la capa de hielo polar ha vertido recientemente demasiada agua dulce a los océanos y ha afectado a las corrientes que dan estabilidad a nuestro sistema climático. La disminución de la salinidad en el mar provoca que la corriente se detenga, la temperatura global cae y lleva al planeta a una nueva edad glacial. El cambio climático ha puesto el planeta al borde del precipicio y, en la película, todo ocurrirá durante una supertormenta de extensión planetaria.
La premisa central del guion se basa en una hipótesis científica legítima pero adornada con episodios de obvias inexactitudes científicas: tornados que destruyen Los Angeles; inundación de Nueva York con olas gigantes; y, sobre todo, el enfriamiento del planeta se completa en una semana.
La película de Emmerich combina con acierto melodrama y cine de catástrofes en un intento de comprometer a los espectadores cognitiva y emocionalmente con una historia espectacular sobre un abrupto cambio climático, escribía en 2012 Alexa Weik von Mossner, de la Universidad de Klagenfurt, en Austria.
La recaudación que obtuvo el film después de su estreno muestra que tuvo gran aceptación, no solo de críticos y periodistas, sino también de climatólogos, sociólogos, ecologistas y miembros del gobierno y la administración. Fue una película alabada, criticada e, incluso, despreciada. Pero, además, fue la primera película popular que promocionó el interés público por el cambio climático. Para la autora, el interés de la película está en que apela al pensamiento racional y, también, a las emociones cuando relata el rápido y catastrófico cambio climático.
El guion se basa en propuestas de la década de los noventa sobre la emisión de dióxido de carbono, su disolución en el agua del mar y su influencia sobre las corrientes marinas tal como aparece en el artículo de 1997 de Thomas Stocker y Andreas Schmitter en Nature. El estudio de los cambios en las corrientes se inició con la del Golfo y se amplió a todos los movimientos de agua en los océanos. Anuncian cambios en 100 años si la emisiones de dióxido de carbono aumentan con rapidez y provocarían la detención permanente de las corrientes. Si la emisión de dióxido de carbono disminuye, las corrientes no se detendrán pero serán más lentas.
La conocida Corriente del Golfo es parte de un sistema de corrientes del Atlántico que, en conjunto, se conocen como AMOC (en inglés, Atlantic Meridional Overturning Circulation, o Circulación Meridional de Retorno del Atlántico). Está compuesta por corrientes superficiales y profundas, como explica Montserrat Alonso, de la Universidad de Salamanca, en El País.
Las aguas superficiales del hemisferio sur pasan por el trópico donde se calientan, llegan al Caribe, se dirigen al norte por la costa este de Norteamérica, cruzan el Atlántico por el sur de Groenlandia y llegan a Europa frente a Noruega. Parte de este sistema es la Corriente del Golfo que sale del Caribe, se mueve hacia el norte paralela a la costa de Norteamérica y se convierte en la corriente Noratlántica.
Todo este sistema de movimientos de agua llega al Atlántico subpolar, se enfría, y como las aguas son muy salinas y con menos temperatura, se hunden y retornan hacia el sur como corrientes profundas. Por eso se le llama circulación de retorno: las aguas del sur, calientes, llegan a la zona polar, se enfrían y vuelven al sur.
Además de agua, AMOC mueve energía en forma de cambios de temperatura del agua. Según estudios recientes, todo el sistema se ha ralentizado en un 15% desde la mitad del siglo pasado. Sin embargo, en 2006 faltaban evidencias de que la circulación fuese más lenta, como escribía Richard Kerr en Science. En una reunión de expertos se constató que más del 95% de los asistentes consideraba que no había cambios significativos en las corrientes atlánticas. Añadían que no había pruebas de un riesgo inmediato y piden más datos, durante quizá décadas, para demostrar la circulación lenta por el cambio climático.
En aquellos años hay más expertos que consideran que una nueva edad glaciar en Europa no es un escenario probable a corto o medio plazo. Carl Wunsch, del MIT, plantea que la corriente del Golfo se produce por el sistema de vientos a gran escala del Atlántico y por el movimiento de rotación del planeta. Por tanto concluye que o se detiene el sistema de vientos o la rotación de la Tierra, o ambos a la vez, para llegar a una nueva edad glaciar dentro de millones de años.
La táctica del director se basa en los efectos especiales de un guion que relata la historia de un científico cuyos avisos de lo que puede ocurrir son ignorados. La ciencia avisa, es una profecía, y cuando se cumple es la visión del desastre lo que vemos en la pantalla. Algunos modelos predicen que si Groenlandia se deshiela, la corriente podría detenerse lo que haría caer la temperatura en el sur de Europa. En la película, en enfriamiento ocurre en cuestión de horas. Es poco probable pero puede comenzar una época más fría, una nueva edad de hielo.
El mismo año del estreno comenzó el debate la película. Bogi Hansen y su grupo, del Laboratorio de Pesquerías de las Islas Feroe, escriben, en 2004, que el debilitamiento de la AMOC durante este siglo puede tener efectos sobre el clima, quizá con el enfriamiento del norte de Europa como aparece en la película. El grupo de Hansen tiene datos de temperaturas más bajas en el mar, con la salinidad en aumento desde mediados de los 70 y menos flujo de agua, hasta un 20% desde 1950. Sin embargo, como muchos otros expertos concluyen que faltan datos a más largo plazo.
Para 2018 comienza a aceptarse, con datos y modelos, que AMOC se ha debilitado. Levke Caesar y su grupo, del Instituto Postdam de Investigación sobre el Impacto del Clima, en Alemania, plantean que la reducción es del 15% desde mediados del siglo XX. Añaden, para el futuro, que si continua el calentamiento global, seguirá debilitándose la AMOC, con cambios en los flujos de agua, pérdidas en la cubierta de hielo de Groenlandia y caída de las temperaturas en el Atlántico Norte.
La propuesta del grupo de Caesar se confirma con los datos de David Thornalley y su equipo, del Colegio Universitario de Londres, con participación de Pablo Ortega del Centro de Biocomputación de Barcelona. Es un estudio sobre el Mar del Labrador, entre Groenlandia y Norteamérica y, para los autores, las evidencias apuntan a los últimos 150 años, desde 1850, al final de la Pequeña Edad del Hielo, con una reducción de la corriente en 15%-20%. Sugieren más datos para delimitar el papel de la variabilidad natural del clima y de la actividad humana con el resultado actual del debilitamiento de la AMOC. Aunque también encuentran que los cambios en la AMOC no coinciden siempre con las variaciones en la temperatura. Parece que la AMOC responde a los cambios en el clima pero que no los dirige.
De nuevo Levke Caesar y su grupo, ahora desde la Universidad de Maynooth, en Irlanda, confirmaron que AMOC había perdido fuerza según la revisión de 11 series de datos desde el año 400 a la actualidad. Al principio, AMOC permanecía estable hasta comienzos del siglo XIX. Después, se acelera el proceso desde mediados del siglo XX hasta la actualidad.
Para resumir, en 2021, Niklas Boers, después de analizar ocho índices de la AMOC sobre la temperatura en la superficie del mar y la salinidad en el Atlántico, concluye que hay evidencias empíricas consistentes de que, en el pasado siglo, AMOC ha pasado de condiciones estables a un punto crítico de transición a una circulación más lenta que puede provocar un impacto severo en el sistema climático del planeta.
Una revisión final, publicada en 2021, sobre los indicadores del cambio climático en los océanos la firma Carlos García-Soto, del Instituto Español de Oceanografía en Santander, con otros once expertos y, entre ellos, Ainhoa Caballero, de AZTI en Pasaia.Según esta:
– La temperatura del agua en la superficie del mar ha crecido, de media, 0.062ºC al año en los últimos 120 años. En la última década, de 2010 a 2019, el aumento se ha acelerado a los 0.280ºC al año.
– El contenido de calor del océano en los 2000 metros superiores, de media y a nivel mundial, ha sido de 0.35 watios por metro cuadrado en los últimos 65 años. Durante la última década, de 2010 a 2019, la tasa es el doble con 0.70.
– El pH global de la superficie del océano ha disminuido, de media, 0.1 unidades desde 1770 con la revolución industrial. El nivel medio global del mar ha aumentado de 1993 a 2019 una tasa de 3.17 milímetros por año. Entre 1900 y 2015, en 115 años, ha aumentado en 19 centímetros.
– Los niveles de oxígeno disuelto han bajado el 2% en los últimos 50 años. La extensión de hielo marino en el Ártico ha disminuido un 13.1% por década en verano y un 2.6% por década en invierno.
– Y la AMOC está en su punto más débil de varios cientos de años y se ha ralentizado más en el último siglo.
Después del estreno en Gran Bretaña, el grupo de Thomas Lowe, de la Universidad de East Anglia en Norwich, organizó un estudio para conocer si los espectadores, después de la película, diferenciaban en ella la ciencia y la ficción. Los autores preguntan a los espectadores sobre su concepto del calentamiento global antes y después del film, así como su percepción sobre si la ciencia que aparece se basa en hechos. Entrevistan a 301 espectadores, de 12 a 60 años o más, y son mujeres el 55%.
La audiencia no consigue determinar la precisión de la ciencia que aparece en la película. Según los autores, los espectaculares efectos especiales y su gran calidad hacen difícil distinguir dónde termina la ciencia y comienza la ficción. Para el 30%, los efectos especiales les ayudan a entender los hechos y, por ello, aumentó su compromiso con lo que significa el cambio climático. Casi el 44% está dispuesto a hacer algo para reducir el cambio climático.
Otro estudio sobre el efecto de la película en el público y su percepción del cambio climático lo firma Anthony Leiserowitz, de la Universidad de Yale, e incluye entrevistas a 529 espectadores. Encuentra cambios en su percepción del riesgo, los modelos conceptuales del cambio climático, las intenciones de su conducta, las prioridades políticas e, incluso, en su intención de voto en futuras elecciones. En conclusión, la representación en una película popular de riesgos ambientales puede influir en la actitud y la conducta de los ciudadanos.
Uno de los cambios en que está implicada la temperatura del agua y la AMOC es la distribución de las especies pesqueras. Ocurre, por ejemplo, con las migraciones de anguilas y angulas desde Europa y Norteamérica al Mar de los Sargazos para la reproducción. La deriva hacia el norte de la isoterma de 22.5ºC, que marca el límite norte de la reproducción de las anguilas, más la disminución del viento y la mezcla de temperaturas en profundidad afectan a la distribución de las larvas. Según Kevin Friedland y sus colegas, del Servicio Nacional de Pesquerías Marinas de Estados Unidos, la relación entre estos datos y los cambios en la AMOC sugiere que la caída en el número de angulas y anguilas que llegan a nuestros ríos en Europa y, quizá, en Norteamérica, está causada, por lo menos en parte, por el cambio climático.
En conclusión, esta película busca provocar en los espectadores una reacción ante el desastre global que puede suponer el cambio climático y, en parte, lo consigue.
Referencias:
Alonso García, M. 2021. ¿Han cambiado la temperatura y la dirección de la corriente del Golfo? El País 3 marzo.
Boers, N. 2021. Observation-based early-warning signals for a collapse of the Atlantic Meridional Overturning Circulation. Nature Climate Change 11: 680-688.
Caesar, L. et al. 2018. Observed fingerprint of a weakening Atlantic Ocean Overturning Circulation. Nature 556: 191-198.
Caesar, L. et al. 2021. Current Atlantic Meridional Overturning Circulation weakest in last millenium. Nature Geoscience 14: 118-120.
Criado, M.A. 2018. El sistema circulatorio del planeta se debilita. El País 12 abril.
Cubitt, S. 2005. Eco Media. Rodopi. Amsterdam-New York. 168 pp.
Friedland, K.D. et al. 2007. Oceanic changes in the Sargasso Sea and declines in recruitment of the European eel. ICES Journal of Marine Science 64: 519-530.
García-Soto, C. et al. 2021. An overview of ocean climate change indicators: sea surface temperature, ocean heat content, ocean pH, dissolved oxygen concentration, Arctic Sea ice extent, thickness and volume, sea level and strength of the AMOC (Atlantic Meridional Overturning Circulation). Frontiers in Marine Science doi: 10.3389/fmars.2021.642372.
Hansen, B. et al. 2004. Already the Day After Tomorrow? Science 305: 953-954.
Kerr, R.A. 2006. Fake alarm: Atlantic conveyor belt hasn’t slowed down after all. Science 314: 1064.
Kirby, D.A. 2011. Lab coats in Hollywood. Science, scientists, and cinema. MIT Press. Cambridge & London. 265 pp.
Leiserowitz, A.A. 2004. Before and after The Day After Tomorrow: a U.S. study of climate risk perception. Environment 46: 23-37.
Lomborg, B. 2008. En frío. La guía del ecologista escéptico para el cambio climático. Ed. Espasa-Calpe. Pozuelo de Alarcón. 284 pp.
Lowe, T. et al. 2006. Does tomorrow ever come? Disaster narrative and public perceptions of climate change. Public Understanding of Science 15: 435-457.
Mulet, J.M. 2021. Ecologismo real. Ed. Destino. Barcelona. 3,83 pp.
Stocker, T.F. & A. Schmittner. 1997. Influence of CO2 emission rates on the stability of the thermohaline circulation. Nature 388: 862-865.
Thornalley, D.J.R. et al. 2018. Anomalously weak Labrador Sea convection and Atlantic overturning during the past 150 years. Nature 556: 227-232.
Weik von Mossner, A. 2012. Facing The Day After Tomorrow: Filmed disaster, emotional engagement, and climate risk perception. En “American environments: Climate-Cultures-Catastrophe”, p. 97-115. Ed. por C. Mauch & S. Mayer. Universitätverlag Winter. Heidelberg.
Wunsch, C. 2004. Gulf Stream safe if wind blows and Earth turns. Nature 428: 601.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo ZientZinema 2: El día de mañana se ha escrito en Cuaderno de Cultura Científica.


