Sigue Naukas Bilbao 2025

Un año más -y ya van quince- el mayor espectáculo de divulgación científica a nivel estatal, Naukas Bilbao, regresa con su fórmula única para acercar el conocimiento científico de manera sencilla y desenfadada. Organizado por la plataforma de divulgación científica Naukas en colaboración con la Cátedra de Cultura Científica de la EHU, el evento reunirá del 19 al 20 de septiembre a más de medio centenar de divulgadores del panorama científico local y estatal.
Durante dos días, el público podrá disfrutar de monólogos de 10 minutos, espectáculos y experimentos científicos. Esta edición especial aniversario promete grandes novedades. Entre ellas, destaca la incorporación al programa general de Naukas Pro, propuesta en la que científicos y miembros de centros de investigación comparten sus investigaciones y experiencias. Entre otras, la psiquiatra Eva Garnica (RSMB) explicará ante el público la relación entre la microbiota y la salud mental, y la matemática Judith Rivas (EHU) mostrará la fascinante conexión entre las danzas vascas y las matemáticas.
Junto a las nuevas incorporaciones, también participarán en el decimoquinto aniversario del evento rostros conocidos para el público de Naukas Bilbao como el biólogo Luisma García Escudero (Universidad de Sevilla), que pondrá el foco en las dobleces de los ojos de los insectos, o el físico Daniel Marín, que hablará sobre la conquista del espacio por parte de tecnoligarcas como Elon Musk y Jeff Bezos.
Además, el periodista Antonio Martínez Ron conversará con Eloísa del Pino, presidenta del Consejo Superior de Investigaciones Científicas (CSIC), desde el auditorio del Euskalduna Bilbao.
Lo ideal es que vivas la experiencia en persona, pero, si no puedes acudir, recurre al streaming a través de EiTB y en su canal de Youtube. Programa
VIERNES 19 DE SEPTIEMBRE – SESIÓN DE MAÑANA
10:00 a 10:10 – Daniel Torregrosa – Mr. Tompkins en el país de las magufadas cuánticas
10:10 a 10:20 – Eva Garnica – ¿Se puede trasplantar la enfermedad mental?
10:20 a 10:30 – Sara Barja – H2Ohhh: Las fascinantes propiedades del agua
10:30 a 10:40 – Miguel García – Perspectivas cartográficas: imposiciones narrativas
10:40 a 10:50 – Estibaliz Díaz – Las anguilas nacen donde les da la gana
10:50 a 11:00 – Luis María Escudero – Doblez
11:00 a 11:20 – Antonio Martínez Ron entrevista a Eloísa del Pino, presidenta del CSIC (20 minutos)
11:20 a 11:30 – Isabel Moreno – No eres yo, soy tú… o ¿cómo era?
11:30 a 11:40 – Judith Rivas – Pasos de baile a ritmo de matemáticas
11:40 a 12:00 – Descanso de 20 minutos
12:00 a 12:10 – Juan Antonio Cuesta – Matemáticas avanzadas para hacer buenas hamburguesas
12:10 a 12:20 – Álvaro Bayón – Bahía Botánica
12:20 a 12:30 – Laura Morán – Perfectamente imperfectas
12:30 a 12:40 – Marc Ruiz de Minteguía – Tengo miedo a dar una charla en Naukas
12:40 a 12:50 – Iván Rivera – La bomba lenta que arrasó América
12:50 a 13:00 – Carlos Lobato – Rock Stars
VIERNES 19 SEPTIEMBRE – SESIÓN DE TARDE
17:00 a 17:20 – Almudena M. Castro, Iñaki Úcar y Daahoud Abdul Salim Álvarez – Balas y baladas (20 minutos)
17:20 a 17:30 – Oskar González – La mano de Sofonisba
17:30 a 17:40 – Carmen Agustín Pavón – Neuronas viejóvenes
17:40 a 17:50 – Laura Gómez Zamanillo – Cuando las máquinas aprenden a ver bichos
17:50 a 18:00 – Conchi Lillo – Lo nunca visto
18:00 a 18:10 – Daniel Marín – Cómo los tecnoligarcas tomaron el cosmos
18:10 a 18:20 – Francis Villatoro – La teoría del invariante
18:20 a 18:30 – Lorena Pérez Hernández – El lenguaje es la mejor medicina. Sin efectos secundarios
18:30 a 18:40 – Joaquín Sevilla – Revisando la ciencia del botijo
18:40 a 19:00 – Descanso (20 minutos)
19:00 a 19:10 – Eparquio Delgado – Guía inútil para enfadarse como un argentino y llorar como un coreano
19:10 a 19:20 – Raquel Sastre – Ver… Comprobar para creer
19:20 a 19:30 – Javier Armentia – Eclipses, ocultaciones y apagones
19:30 a 19:40 – Ricardo Moure – Hasta el ñoco de El Rey León
19:40 a 19:50 – Pedro A. León – Las cacas de la Luna
19:50 a 20:00 – Javier Pedreira (Wicho) – El culebrón de decidir cuál fue el primer ordenador
SÁBADO 20 DE SEPTIEMBRE – SESIÓN DE MAÑANA
10:00 a 10:10 – Javier Panadero – Con estas manitas y algo más
10:10 a 10:20 – Virginia Arechavala Gomeza – No es una cura. Es un experimento
10:20 a 10:30 – Nahúm Méndez Chazarra – ¿Puede la geología dar respuesta a la paradoja de Fermi?
10:30 a 10:40 – Gemma Marfany – El misterio de la momia maldita
10:40 a 10:50 – Ujué Agudo – Los efectos «colaterales» de la toma de decisiones con IA
10:50 a 11:00 – Clara Peñalver – T-Di. Mi muy querido y temido cerebro
11:00 a 11:10 – Imanol Ituiño (Festival JA!) – ¡Rayos! Houdini y Nueva York, mano a mano
11:10 a 11:20 – Teresa Valdés Solís – Las 4 Rs
11:20 a 11:30 – Fernando Frías – La sábana doblada
11:30 a 11:40 – Elixabete Rezabal – ¿Hueles vibraciones?
11:40 a 12:00 – Descanso de 20 minutos
12:00 a 12:10 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 1
12:10 a 12:20 – Alberto García Salido – El día que fuimos Brad Pitt
12:20 a 12:30 – Iñigo Careaga – Cocinando baterías: recetas de ayer y de hoy (y de mañana)
12:30 a 12:40 – Antonio Martínez Ron – Curso rápido de perspectiva
12:40 a 12:50 – Carlos Briones – Sumando y restando
12:50 a 13:00 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 2
SÁBADO 20 SEPTIEMBRE – SESIÓN DE TARDE
17:00 a 17:10 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 3
17:10 a 17:20 – Gemma del Caño – Misterio en Riverside, cuando la química rozó la ciencia ficción
17:20 a 17:30 – Ana Tamayo – Al manicomio por lavarse las manos
17:30 a 17:40 – Elena Casado – Del castigo bíblico al pinchazo moderno
17:40 a 17:50 – Anabel Forte – To Bayes or not to Bayes
17:50 a 18:00 – Lluis Montoliu – ¿Para qué quieren desextinguir el mamut?
18:00 a 18:10 – Manuel Vicente – El telescopio de los nobeles
18:10 a 18:20 – Sergio Pérez Acebrón – Emergencia celular
18:20 a 18:40 – Miguel Santander y Pablo Rodríguez – Perversión por pares
18:40 a 19:00 Descanso (20 minutos)
19:00 a 19:10 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 4
19:10 a 19:20 – Helena Matute – Experimentos con humanos e IAs: 2ª temporada
19:20 a 19:30 – Eva Caballero – Kit de primeros auxilios para conversaciones incómodas
19:30 a 19:40 – Javier S. Burgos – Caballeros, esto no es una farsa
19:40 a 19:50 – Miguel Ángel Cajigal (El Barroquista) – Cuando Bernini casi destruye el Vaticano
19:50 a 20:00 – ENTREGA PREMIO TESLA 2025 + Despedida y cierre
Esta actividad forma parte de Bilbo Zientzia Plaza 2025, una iniciativa de divulgación científica organizada por la Cátedra de Cultura Científica de la EHU, con el patrocinio del Ayuntamiento de Bilbao y Euskampus Fundazioa, y la colaboración del Departamento de Ciencia, Universidades e Innovación del Gobierno Vasco, Donostia International Physics Center (DIPC), Metro Bilbao y EiTB.
El artículo Sigue Naukas Bilbao 2025 se ha escrito en Cuaderno de Cultura Científica.
Viendo a los electrones moldear las reacciones químicas
Imagina capturar en una fotografía un momento efímero: el movimiento de un electrón durante una reacción química. Desde los albores de la química moderna, la idea de «ver» cómo se desplazan estas partículas subatómicas parecía un sueño imposible, o en todo caso, el capricho de un novelista de ciencia ficción poco riguroso. Sin embargo, un equipo dirigido por Ian Gabalski, de la Universidad de Stanford, ha logrado un avance decisivo para convertirlo en realidad. Su estudio demuestra por primera vez que es posible observar directamente la dinámica de los electrones de valencia —aquellos que participan activamente en las reacciones químicas— en tiempo real.
 Fuente: I. Gabalski / Stanford University / SLAC National Accelerator Laboratory¿Por qué es tan complicado observar los electrones de valencia?
Fuente: I. Gabalski / Stanford University / SLAC National Accelerator Laboratory¿Por qué es tan complicado observar los electrones de valencia?
Las reacciones químicas se inician cuando los electrones más externos de los átomos, conocidos como electrones de valencia, se reorganizan: rompen enlaces existentes y forman nuevos. Estos electrones determinan cómo comienza una reacción y qué productos finales se obtienen. El desafío radica en que, en experimentos con rayos X, los electrones internos —los más cercanos al núcleo atómico y no involucrados en las reacciones— dominan la señal detectada, eclipsando las sutiles variaciones producidas por los electrones de valencia.
¿Cómo lo han logrado?El secreto reside en el uso de pulsos de rayos X ultracortos, cada uno de aproximadamente 30 femtosegundos (30 × 10⁻¹⁵ segundos), generados por el Linac Coherent Light Source (LCLS) en el Laboratorio Nacional de Aceleradores SLAC, en California.
El experimento comienza con un pulso de luz ultravioleta que excita una molécula de amoníaco (NH₃)*, alterando su geometría: de una estructura piramidal pasa a una planar. Esta transformación facilita que uno de los tres átomos de hidrógeno se desprenda, llevándose consigo un electrón de valencia que formaba parte del enlace. Dado que el hidrógeno no posee electrones internos (su único electrón es de valencia), este proceso deja expuesta la dinámica de los electrones de valencia sin la interferencia de señales de electrones centrales.
Inmediatamente después, el pulso de rayos X incide sobre la molécula. Los fotones de rayos X se dispersan en ángulos que dependen de la distribución espacial de los electrones (la densidad electrónica). Al capturar estos fotones dispersados en un detector bidimensional, los investigadores reconstruyen una «instantánea» de la densidad electrónica en ese momento preciso.
Dos caminos distintosGracias a esta técnica, el equipo identificó dos vías diferentes por las que el átomo de hidrógeno puede separarse de la molécula. En cada vía, la densidad de los electrones de valencia —es decir, la «forma» probabilística de su distribución en el espacio— era única. Estas diferencias se mantuvieron durante más de 200 femtosegundos. Al comparar los resultados experimentales con simulaciones cuánticas detalladas, los científicos confirmaron que estaban capturando con precisión la evolución de los electrones de valencia a lo largo de la reacción.
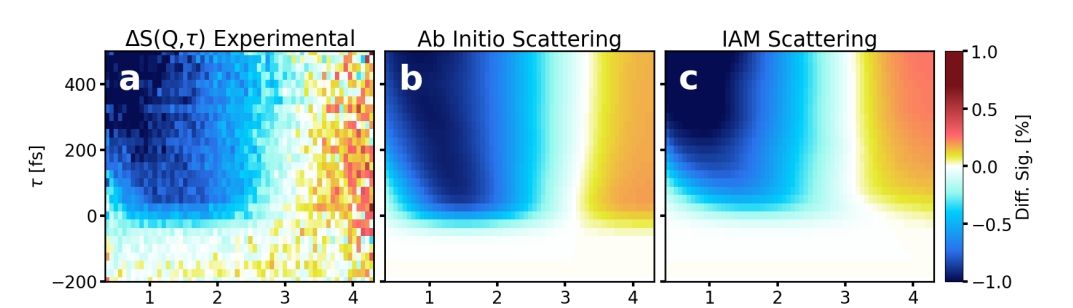 Resultado experimental (a) y los de las dos simulaciones realizadas (b,c). Fuente: Ian Gabalski et al (2025) Phys. Rev. Lett. doi: 10.1103/53h3-vyklComparación con otras técnicas
Resultado experimental (a) y los de las dos simulaciones realizadas (b,c). Fuente: Ian Gabalski et al (2025) Phys. Rev. Lett. doi: 10.1103/53h3-vyklComparación con otras técnicas
Una alternativa para generar «películas moleculares» es la difracción electrónica ultrarrápida, que emplea electrones de alta energía en lugar de rayos X como sonda. Este método permite visualizar estructuras atómicas en movimiento, pero su resolución temporal es inferior: típicamente superior a 50 femtosegundos. En contraste, la dispersión de rayos X ultrarrápida ofrece una vista más nítida y veloz de la dinámica electrónica, acercándose incluso a resoluciones por debajo de 10 femtosegundos.
¿Qué implicaciones tiene este avance?Este logro permite visualizar directamente cómo la dinámica de los electrones de valencia influye en el desarrollo de una reacción química. Hasta ahora, solo podíamos inferir estos movimientos mediante modelos teóricos —como una película imaginaria en nuestra mente—, pero ahora estamos empezando a obtener imágenes reales que la materializan.
Mediante esta combinación innovadora de pulsos láser ópticos y rayos X ultrarrápidos, estamos penetrando en el mundo microscópico para observar cómo los electrones actúan en tiempo real durante una reacción. Es como fotografiar el delicado ritmo de un enlace químico en transformación: lo que antes era invisible, ahora emerge y se deja capturar. Estos conocimientos podrían revolucionar el diseño de procesos industriales más eficientes y sostenibles, medicamentos más precisos o materiales con propiedades inéditas.
Los retos futurosEl próximo objetivo es alcanzar resoluciones temporales en la escala de attosegundos (10⁻¹⁸ segundos) para estudiar fenómenos aún más fugaces, como la migración de cargas o el movimiento correlacionado de electrones. Esto parece factible gracias al desarrollo de fuentes de rayos X de attosegundos en instalaciones como el LCLS-II en Estados Unidos o el European X-Ray Free-Electron Laser en Alemania. Otro desafío es extender estas técnicas a moléculas más complejas, donde los electrones internos podrían seguir ocultando señales, posiblemente mediante detectores que discriminen energías para aislar las contribuciones de los electrones de valencia.
(*) Nota: Siendo estrictos, amoniaco deuterado, esto es, amoniaco en el que los tres hidrógenos son deuterios.
Referencia:
Ian Gabalski et al (2025) Imaging Valence Electron Rearrangement in a Chemical Reaction Using Hard X-Ray Scattering Phys. Rev. Lett. doi: 10.1103/53h3-vykl
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Viendo a los electrones moldear las reacciones químicas se ha escrito en Cuaderno de Cultura Científica.
El metamorfismo como fuente de habitabilidad
La llegada de la sonda Dawn a Ceres en el año 2015 demostró que el cinturón de asteroides era un lugar mucho más diverso e interesante de lo que podríamos haber soñado. Ya en ese momento, Ceres había dejado de ser un asteroide cualquiera: en 2006 pasó a ser un “planeta enano” según la nueva nomenclatura de la IAU ya que no cumplía uno de los tres requisitos para ser planeta, el de haber limpiado su vecindario orbital.
Pero bajo -y bueno, sobre- su superficie escondía muchos más secretos. Cuando buscamos vida más allá de la Tierra, una parte de esta búsqueda se centra en lo que llamamos mundos “océano” u “oceánicos”, cuerpos que albergan o albergaron océanos de agua líquida bajo su superficie en algún momento de su existencia.
En nuestro sistema solar existen satélites como Europa o Encélado que son magníficos ejemplos de este tipo de cuerpos en los que, si bien es cierto que no hemos podido acceder a sus aguas -ya no es solo una cuestión de distancia a ello, sino de dificultad tecnológica- sabemos que albergan océanos por las distintas pruebas que estos dejan, entre otros lugares, en su superficie, pero también por pruebas indirectas como los datos gravimétricos o magnéticos.
 Ceres tal y como lo veríamos con nuestros ojos. En esta imagen tomada por la sonda Dawn, desde fuera, parece un cuerpo aburrido, cubierto de cráteres. Pero son solo las apariencias, y esconde una historia fascinante. Fuente: NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.
Ceres tal y como lo veríamos con nuestros ojos. En esta imagen tomada por la sonda Dawn, desde fuera, parece un cuerpo aburrido, cubierto de cráteres. Pero son solo las apariencias, y esconde una historia fascinante. Fuente: NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.Es cierto que es muy difícil que, a día de hoy, Ceres todavía tenga un importante océano de agua líquida bajo su superficie. Pero sí podría ser un buen ejemplo de una clase de objetos existentes en nuestro Sistema Solar que sean el reflejo de mundos que pudieron ser habitables, ya no por la propia energía del Sol o por la que generan las mareas, sino por el calor que podría haber ido liberando poco a poco su núcleo rocoso, pero no de la manera que esperaríamos en lugares como nuestro planeta. Más tarde entraremos en eso.
Ya sabemos que Ceres fue probablemente un mundo océano en parte gracias a distintos detalles que se han ido descubriendo en las últimas décadas: una baja densidad que hace ver que no es un cuerpo puramente rocoso, una mineralogía de su superficie rica en carbonatos y arcillas, evidencias de criovulcanismo…
Y es que, si realmente fue un mundo océano, también es de lógica pensar que contenía una gran parte de los ingredientes necesarios para la formación de la vida. Pero, sin embargo, quedaba por solucionar un problema: ¿de dónde saldría la energía para que esa vida pudiese florecer?
Me explico: para que la vida pueda surgir y mantenerse en un océano oscuro al que no llega la luz del Sol -imaginemos que sobre este océano habría una capa de hielo de varios kilómetros que actuaría como una capa totalmente opaca- se necesita una fuente de energía química que sea duradera en el tiempo. Y es aquí donde un nuevo estudio publicado por Courville et al. (2025) parece haber encontrado una respuesta que permitiría a Ceres mantener un ambiente habitable durante más de mil millones de años… el metamorfismo.
Para quienes no sean familiares con el término, el metamorfismo es un proceso geológico -o más bien una serie de procesos- por el cual las rocas sufren una transformación a nivel mineral, de textura y de la propia estructura de la roca cuando sufren un aumento en las condiciones de presión, temperatura y por la presencia de fluidos capaces de reaccionar con la propia roca. Esta alteración ocurre con la roca en estado sólido, al menos en su mayor parte, sin fundirse. En esta nueva situación los minerales se ven obligados a adquirir estructuras más estables bajo las nuevas condiciones, dando como resultado una nueva roca.
Volviendo al estudio, los autores detallan un nuevo modelo de evolución térmica y química de Ceres desde su nacimiento hasta hoy, presentándolo como un cuerpo formado por un 90% de roca y un 10% de hielo de agua, una composición similar a las condritas de tipo CI, unos meteoritos primitivos -y raros, en el sentido de poco abundantes- pero que han sufrido la alteración por el agua cuando formaban parte de un cuerpo más grande.
 En esta imagen en la que podemos apreciar el horizonte de Ceres. Si se fijan bien, verán una especie de “verruga” cerca de la zona central del horizonte… es Ahuna Mons, uno de los relieves que hay en el planeta enano y que podrían estar relacionados directamente con fenómenos criovolcánicos. Fuente: ASA/JPL-Caltech/UCLA/MPS/DLR/IDA.
En esta imagen en la que podemos apreciar el horizonte de Ceres. Si se fijan bien, verán una especie de “verruga” cerca de la zona central del horizonte… es Ahuna Mons, uno de los relieves que hay en el planeta enano y que podrían estar relacionados directamente con fenómenos criovolcánicos. Fuente: ASA/JPL-Caltech/UCLA/MPS/DLR/IDA.Durante los primeros momentos de su existencia, el principal motor del cambio en el planeta enano fueron los isótopos radioactivos de vida corta, especialmente el aluminio-26. Este potente, pero efímero, isótopo servía como una fuente de calor extraordinaria para fundir el hielo acumulado en los primeros millones de años de su historia, provocando uno de los eventos geológicos más importantes de su infancia: la diferenciación. En este proceso, los materiales más densos y rocosos se hundieron por efecto de su propia densidad hacia el núcleo de Ceres, mientras que el agua líquida subió para formar un gran océano oculto bajo una capa de hielo que comenzaría a crecer.
Este océano “primordial” probablemente era más cálido y alcalino que el que podría existir hoy día. Y, a pesar de que podría satisfacer las necesidades básicas para la aparición de la vida, en este estudio se sugiere que el periodo más prometedor para que fuese habitable vendría mucho después. Cuando los isótopos de corta vida acabasen su trabajo, el núcleo continuaría calentándose por la desintegración de otros isótopos como los del potasio, uranio y torio. A lo largo de cientos de millones de años, este lento proceso de calentamiento aumentaría la temperatura del núcleo hasta un umbral crítico, llegando a aproximadamente unos 280ºC, cuando comenzaría una nueva y profunda transformación.
En ese momento comenzarían a producirse procesos metamórficos en el núcleo. Los silicatos hidratados que componían el núcleo y que se habían formado por la interacción entre el agua y la roca, se volvieron inestables por el aumento de la temperatura y la presión. Entonces, comenzaron a deshidratarse, liberando las moléculas de agua que estaban atrapadas en el interior de su estructura cristalina.
 Imagen del cráter Occator de Ceres donde se aprecian unas manchas de un color blanco muy llamativo. En estas se ha encontrado carbonato de sodio, arcillas y sulfato de magnesio y, probablemente, se formaron a causa de la actividad hidrotermal que llegaba hasta la superficie a través de sistemas de fracturas. Fuente: NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.
Imagen del cráter Occator de Ceres donde se aprecian unas manchas de un color blanco muy llamativo. En estas se ha encontrado carbonato de sodio, arcillas y sulfato de magnesio y, probablemente, se formaron a causa de la actividad hidrotermal que llegaba hasta la superficie a través de sistemas de fracturas. Fuente: NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.No se trataba simplemente de “echar” el agua de los minerales, sino de la generación de fluidos hidrotermales. Estos fluidos eran diferentes a nivel químico si los comparamos con el agua del océano que había por encima: estaba sobrecargado de compuestos disueltos, favoreciendo un desequilibrio químico que la vida podría aprovechar.
Precisamente, el modelo que presentan en este artículo se centra en una de las rutas metabólicas más antiguas y básicas que se conocen en nuestro planeta: la metanogénesis. Los fluidos que se liberaban fruto del metamorfismo eran probablemente ricos en hidrógeno disuelto y dióxido de carbono. A medida que estos migraban hacia arriba a través de poros y fisuras hacia el fondo del océano -mucho más frío- el desequilibrio químico también se iba desplazando. Para visualizar este ambiente, tenemos que imaginar algo similar a las chimeneas hidrotermales que existen en el fondo de nuestros océanos.
La reacción que permite formar el metano se volvió energéticamente favorable, ofreciendo una fuente de alimento “gratuita” para cualquier organismo quimiótrofo que pudiese existir y pudiese catalizar estas moléculas. El factor limitante de esta ruta metabólica era la abundancia de hidrógeno, lo que transformaba al suministro de estos fluidos metamórficos en un control fundamental de la habitabilidad dentro del océano.
La ventana de habitabilidad no fue algo fugaz ni efímero. El modelo también indica que el periodo en el que ocurría el metamorfismo en el núcleo y, por lo tanto, la liberación de los fluidos hacia el océano habría durado entre 500 y 2000 millones de años tras la formación de Ceres.
Los autores calculan que la tasa de liberación de fluidos por deshidratación sería de más de 300 kilogramos por segundo y, suponiendo unos requisitos energéticos similares a los de los microbios anaerobios de nuestro planeta, podría haber sostenido una biomasa total de unas 10^17 células. Es decir, que si se distribuyera por todo el océano, habría unas 1000 células por kilo de agua.
 Las apariencias engañan. Bajo un aspecto casi lunar y quizás anodino, Ceres esconde una historia realmente fascinante. Fuente: de NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.
Las apariencias engañan. Bajo un aspecto casi lunar y quizás anodino, Ceres esconde una historia realmente fascinante. Fuente: de NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.Aunque nos pueda parecer una densidad muy poca si la comparamos con las comunidades microbianas de la Tierra -que pueden alcanzar cifras de mil millones de células por kilo- no es para nada insignificante y nos sugiere que podría haber sido posible, con estas condiciones, una biosfera a escala planetaria.
Sin embargo, este escenario está basado en un equilibrio muy complicado: la migración de fluidos ascendente es fundamental para suministrar energía, pero una fuerte circulación hidrotermal también habría sido perjudicial, ya que un sistema muy activo habría transportado el calor fuera del núcleo muy rápido, enfriándolo de una manera prematura y apagando este motor metamórfico.
Pero, eventualmente, este motor interno tuvo que detenerse. A medida que los radioisótopos iban desintegrándose y disminuyendo la producción de calor, el núcleo de Ceres comenzó a enfriarse. El metamorfismo se detuvo y se interrumpió el suministro de energía química necesaria para la vida. Desde la superficie el océano siguió congelándose, sus aguas se enfriaron progresivamente y se concentraron más en sales con poder anticongelante como el amoniaco, y transformándose en una salmuera que quizás sea inhóspita para la vida.
A mi juicio, si me lo permiten, las implicaciones de este estudio van mucho más allá de Ceres. El modelo presentado podría servir para otros cuerpos helados de tamaño medio en el Sistema Solar, como algunos satélites de los planetas exteriores y quizás otros planetas enanos -para aquellos descubiertos y otros no-. Los objetos de un diámetro entre 500 y 1000 km podrían haber sufrido procesos similares y el metamorfismo del núcleo podría ser una etapa común en el desarrollo de estos cuerpos y quizás también de las condiciones habitables.
Y, de nuevo, observamos como las condiciones de habitabilidad no son una constante, sino algo que puede ir cambiando a lo largo de la historia de los sistemas planetarios y que, incluso temporalmente, las ventanas de habitabilidad no tienen por que coincidir… ¿qué nuevas sorpresas nos traerán esos cuerpos de nuestro Sistema Solar que todavía solo son un punto de luz en nuestros telescopios?
Referencias:
Courville, S. W., Castillo-Rogez, J. C., Daswani, M. M., Robare, J., & O’Rourke, J. G. (2025). Core metamorphism controls the dynamic habitability of mid-sized ocean worlds—The case of Ceres Science Advances doi: 10.1126/sciadv.adt3283
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El metamorfismo como fuente de habitabilidad se ha escrito en Cuaderno de Cultura Científica.
Desinformación sobre salud mental en TikTok: qué sabemos y qué funciona para corregirla
TikTok concentra una parte relevante de la conversación sobre salud mental. La evidencia muestra dos cosas: (a) abundan contenidos inexactos; (b) intervenciones simples orientadas a influencers pueden aumentar el contenido basado en evidencia.
 Imagen: David Farfan / Pixabay
Imagen: David Farfan / PixabaySe estima que TikTok tiene 1.590 Millones de usuarios activos [1]. El 65.5% de los usuarios buscan en TikTok consejos de salud [2]. Cuando se trata de buscar tratamiento para una enfermedad, uno de cada cinco prefiere abrir la app, antes que acudir al médico [3]. El resultado: un torrente de información que se siente cercana, humana, incluso urgente… pero que en más de la mitad de los casos es imprecisa. [4]
Lo que dice la evidenciaThe Guardian buscó los 100 vídeos más populares publicados bajo el hashtag #mentalhealthtips en TikTok y los compartió con psicólogos, psiquiatras y expertos académicos, quienes evaluaron si los contenidos contenían desinformación.
Los expertos determinaron que 52 de los 100 vídeos que ofrecían consejos para afrontar el trauma, la neurodivergencia, la ansiedad, la depresión y las enfermedades mentales graves contenían algún tipo de desinformación, y que muchos otros eran vagos o poco útiles.
En ciertos temas, la precisión es una rareza. En los vídeos sobre autismo, por ejemplo, solo el 27% se ajusta al consenso científico. [5]
Por qué ocurre estoEl problema es que, en TikTok, la verdad compite en desventaja. El algoritmo no discrimina entre la evidencia y el mito; solo mide el tiempo que pasas mirando.
Existe un desajuste de incentivos: los algoritmos de recomendación optimizan señales de rendimiento inmediato porque son medibles y predicen retención.
En la economía de la atención, los mensajes breves, simples y de alta activación emocional suelen obtener mejores métricas que las explicaciones matizadas. El resultado no implica mala fe: el sistema amplifica lo que retiene, no necesariamente lo que es cierto.
Consecuencias de consumir información errónea sobre salud mentalResumiendo la desinformación te hace menos capaz de regularte, más vulnerable al error y más dependiente de atajos que no funcionan, veamos por qué.
Imagina una joven llamada Laura.
Laura empezó a sentir una presión constante en el pecho. No era insoportable, así que se dijo a sí misma que “no era para tanto”. Semanas después, navegando por TikTok, encontró un vídeo que hablaba de “ataques de ansiedad” y decidió que eso era lo que tenía. Se tranquilizó: ya sabía el nombre. Lo que no sabía era que esa certeza retrasaría meses el diagnóstico correcto: angina de pecho.
Ahora imagina a un joven llamado Pablo
Pablo vio un anuncio que aseguraba que su falta de motivación se debía a que tenía TDAH. Lo que comenzó como una hipótesis se convierte en identidad: “tengo TDAH”. Esa frase le ayudó a sentirse mejor porque ya “sabía lo que tenía” pero le dejó sin poder hacer nada para mejorar.
Estas historias son ficticias, pero en terapia veo todas las semanas jóvenes que traen consigo un guion aprendido en las redes: la promesa de una cura rápida. Cuando la realidad no sigue el ritmo de las historias virales, la frustración crece y la salida fácil es abandonar el tratamiento porque “no funciona”.
En este ciclo, los consejos de “cortar por lo sano” o evitar el malestar se convierten en atajos que parecen proteger, pero en realidad desgastan nuestra capacidad para regularnos.
Herramientas prácticas para identificar y evitar la desinformaciónLa buena noticia: hay maneras concretas de romperlo. No requieren un máster en psicología ni conocimientos técnicos; solo práctica deliberada.
Sospecha de lo que te atrape demasiado rápido: Si un vídeo te provoca una reacción intensa (miedo, esperanza, indignación), pausa antes de creerlo. Los títulos sensacionalistas y las promesas de soluciones milagrosas son red flags clásicas
Pregúntate quién está hablando y por qué: ¿El creador es un profesional acreditado? ¿O alguien que relata su experiencia personal como si fuera una verdad universal? Verifica su historial y su formación
Contrasta con fuentes externas: Antes de compartir o aplicar un consejo, búscalo en webs de organizaciones reconocidas en salud mental. Si no aparece, o la versión que encuentras es distinta, probablemente no sea fiable
Evita autoevaluaciones rápidas: Que un vídeo describa algo que te ha pasado no significa que tengas un trastorno.
ConclusiónCuando yo tenía 16 años no existía TikTok, pero las historias impactantes se extendían con la misma viralidad de ahora, aunque no fuesen verdad. Todos oímos el rumor de que las gominolas están hechas de petróleo o la anécdota de Ricky Martin, Sorpresa Sorpresa, el armario y la mermelada.
El problema es que ahora es nuestra salud la que está en juego.
Pero no todo es malo, el mismo megáfono que se utiliza para enviar información engañosa puede utilizarse para propagar información basada en evidencia.
En marzo de 2023, un grupo de investigadores de Harvard envió a 105 creadores de TikTok un archivo PDF [6]. No era un contrato, ni un guion para un anuncio. Eran consejos prácticos para hablar de salud mental… pero con respaldo científico. No había promesas de dinero ni contratos publicitarios. Solo instrucciones claras y, sobre todo, verificadas.
Lo curioso es que funcionó. Los creadores que recibieron ese material empezaron a producir más vídeos con contenido basado en evidencia, y sus publicaciones atrajeron millones de visualizaciones adicionales.
La lección es doble. Como usuarios tenemos que asumir nuestra responsabilidad en el consumo de desinformación, al mismo tiempo debemos recordar a los influencers que tienen que pagar un precio por su alcance masivo, ese precio la responsabilidad de divulgar con sentido.
Esto, en el terreno de la salud mental, puede significar la diferencia entre un mito viral… y un consejo que salve vidas.
Referencias
[1] Singh, S. (2025, 31 de julio). How Many People Use TikTok (Users Statistics 2025). DemandSage. Recuperado el 25 de agosto de 2025, de https://www.demandsage.com/tiktok-user-statistics/
[2] Kirkpatrick, C. E., & Lawrie, L. L. (2024). TikTok as a Source of Health Information and Misinformation for Young Women in the United States: Survey Study. JMIR infodemiology, 4, e54663. doi: 10.2196/54663
[3] CharityRx News. (2022, 21 de septiembre). The shifting role of influence and authority in the Rx drug & health supplement market. Recuperado el 25 de agosto de 2025, de https://www.charityrx.com/blog/the-shifting-role-of-influence-and-authority-in-the-rx-drug-health-supplement-market/
[4] Hall, R., & Keenan, R. (2025, 31 de mayo). More than half of top 100 mental health TikToks contain misinformation, study finds. The Guardian. Recuperado el 25 de agosto de 2025, de https://www.theguardian.com/society/2025/may/31/more-than-half-of-top-100-mental-health-tiktoks-contain-misinformation-study-finds
[5] Aragon-Guevara, D., Castle, G., Sheridan, E., & Vivanti, G. (2025). The Reach and Accuracy of Information on Autism on TikTok. Journal of autism and developmental disorders, 55(6), 1953–1958. doi:10.1007/s10803-023-06084-6
[6] Motta, M., Liu, Y., & Yarnell, A. (2024). «Influencing the influencers:» a field experimental approach to promoting effective mental health communication on TikTok. Scientific reports, 14(1), 5864. doi: 10.1038/s41598-024-56578-1
Sobre el autor: David Carcedo es divulgador, psicólogo sanitario en Donostia y coordinador de sección de laboratorio en el BCBL.
El artículo Desinformación sobre salud mental en TikTok: qué sabemos y qué funciona para corregirla se ha escrito en Cuaderno de Cultura Científica.
Especies humanas en nuestro genoma y altruismo primate en el Día de Darwin 2025
El 12 de febrero la la Cátedra de Cultura Científica de la Universidad del País Vasco y el Círculo Escéptico celebraron una nueva edición del Día de Darwin en la Biblioteca Bidebarrieta de Bilbao. La sesión contó con dos conferencias centradas en la convivencia de especies humanas diferentes, por un lado, y el origen del altruismo social, por otro; con el objetivo de ampliar la mirada en torno a la singularidad de nuestra especie a través de la evolución.

El Día de Darwin conmemora cada 12 de febrero el nacimiento del biólogo y geólogo inglés Charles Darwin. Nacido en 1809, su figura ha quedado ligada a la historia tras la publicación en 1859 del libro ’El Origen de las Especies’ y su teoría sobre la evolución. Gracias a ella sabemos que todos los seres vivos procedemos de un antepasado común, que las especies varían a lo largo del tiempo, variación a la que se denomina evolución y que se produce por efecto de un mecanismo al que denominamos selección natural.
ProgramaEl Día de Darwin 2025 contó con las conferencias de Conchi de la Rúa, catedrática de Antropología Biológica en la Universidad del País Vasco-Euskal Herriko Unibertsitatea; de Ignacio Martínez, catedrático de Antropología Física en la Universidad de Alcalá; y de Mercedes Conde, doctora en Antropología Física de la Universidad de Alcalá.
Conchi de la Rúa impartió la conferencia “La huella de especies humanas del pasado en nuestro genoma” e Ignacio Martínez y Mercedes Conde la charla titulada “Primate altruista”. Ambas exposiciones muestran los resultados de las investigaciones que se están llevando a cabo en la actualidad en el ámbito de la evolución humana, gracias a las cuales tenemos la posibilidad de entender la historia de nuestra especie y la génesis de algunas de las características propias de los seres humanos.
ContenidoEn la conferencia “La huella de especies humanas del pasado en nuestro genoma” la investigadora de la UPV/EHU Conchi de la Rúa explica que el estudio del ADN fósil ha permitido conocer que en el pasado existieron encuentros entre especies humanas diferentes. Gracias a la paleogenómica, se sabe que neandertales y denisovanos convivieron con los primeros sapiens que llegaron a Eurasia hace unos 40 000 mil años, procedentes de sucesivas oleadas desde África, y que hubo intercambios genéticos entre ellos. Estos hallazgos han posibilitado una mirada más amplia sobre la unicidad de nuestra especie.
Por su lado, en la charla “Primate altruista” Ignacio Martínez y Mercedes Conde, investigadores de la Universidad de Alcalá, abordan una de las cuestiones más debatidas en biología evolutiva: el origen del altruismo. El altruismo es una de las características más extraordinarias de los seres humanos y conocer su historia evolutiva es importante para entender a la humanidad. El origen del altruismo está directamente relacionado con el de los cuidados a personas vulnerables. Este aspecto puede rastrearse en el registro fósil y los restos humanos que arrojan más luz sobre esta cuestión han aparecido en dos yacimientos españoles: Atapuerca (Burgos) y Cova Negra (Valencia).
ConferenciantesConcepción de la Rúa Vaca es licenciada en Medicina y en Biología y catedrática de Antropología Biológica en la Universidad del País Vasco. Es profesora e investigadora de la Facultad de Ciencia y Tecnología de la UPV/EHU, en la cual promovió la creación de un laboratorio de ADN antiguo en los inicios de esta disciplina. Es directora del grupo de investigación consolidado del sistema universitario vasco Biología Evolutiva Humana de la UPV/EHU. En su carrera profesional ha desarrollado y liderado proyectos de investigación interdisciplinares, destacando, entre otros, estudios paleogenómicos de humanos antiguos. En la actualidad, trabaja en un proyecto sobre la domesticación del lobo.
Ignacio Martínez Mendizábal es catedrático de Antropología Física de la Universidad de Alcalá. Pertenece desde 1984 al Equipo Investigador de los Yacimientos Pleistocenos de la Sierra de Atapuerca, que fue galardonado con el Premio Princesa de Asturias de Investigación Científica y Técnica del año 1997. Es especialista en el campo de la evolución humana, área en la que tiene una dilatada trayectoria profesional, siendo autor de artículos científicos de impacto y conferenciante de proyección internacional. Entre otros, es autor del libro ‘El primate que quería volar’ y co-autor, junto a Juan Luis Arsuaga, de los libros ‘La Especie Elegida’, ‘Amalur’, y ‘Atapuerca’ y la ‘Evolución Humana’.
Mercedes Conde Valverde es doctora en Antropología Física y profesora del Área de Antropología Física del Departamento de Ciencias de la Vida de la Universidad de Alcalá. Dirige la Cátedra de Investigación (HM Hospitales – Universidad de Alcalá) de Otoacústica Evolutiva y Paleoantropología. Es además Research Affiliate del Departamento de Antropología de Binghamton University (SUNY-USA), y profesora invitada de la Universidad de Buenos Aires. Miembro del equipo de investigación de Atapuerca desde 2012. Su actividad investigadora ha estado centrada en el estudio de la evolución del oído y el origen del lenguaje. Entre otros, ha participado en artículos científicos publicados en revistas de gran prestigio y es autora del libro ‘El lenguaje. En busca de las primeras palabras’.
Edición realizada por César Tomé López
El artículo Especies humanas en nuestro genoma y altruismo primate en el Día de Darwin 2025 se ha escrito en Cuaderno de Cultura Científica.
El arca de la microbiota
 Las muestras son conservadas en condiciones de frío extremo en el Institute of Medical Microbiology de la Universidad de Zúrich. Fuente: Microbiota Vault Initiative
Las muestras son conservadas en condiciones de frío extremo en el Institute of Medical Microbiology de la Universidad de Zúrich. Fuente: Microbiota Vault Initiative
Puesta en marcha hace cuatro años, la iniciativa Microbiota Vault –también conocida como Arca de la Microbiota o Cámara de Seguridad de la Microbiota– tiene un objetivo tan ambicioso como necesario: conservar la diversidad microbiana de nuestro planeta para las generaciones futuras.
Los expertos ya han creado en su primera fase un biobanco con más de 1 200 muestras fecales humanas y 190 de alimentos fermentados. El proyecto se inspira en el Banco Mundial de Semillas de Svalbard, en Noruega, que protege la diversidad genética de los cultivos.
Las muestras, que proceden de colecciones de Benín, Brasil, Etiopía, Ghana, Laos, Tailandia y Suiza, se conservan congeladas a −80 °C en el Instituto de Microbiología Médica de la Universidad de Zúrich (Suiza). Su ubicación no es definitiva, ya que otros países con climas fríos, como Canadá, lo podrían albergar en el futuro.
Su meta es alcanzar las 20 000 microbiotas de personas, animales, plantas y ecosistemas en riesgo. Además, el proyecto facilitará la secuenciación de los genomas microbianos y su publicación en bases de datos de acceso abierto.
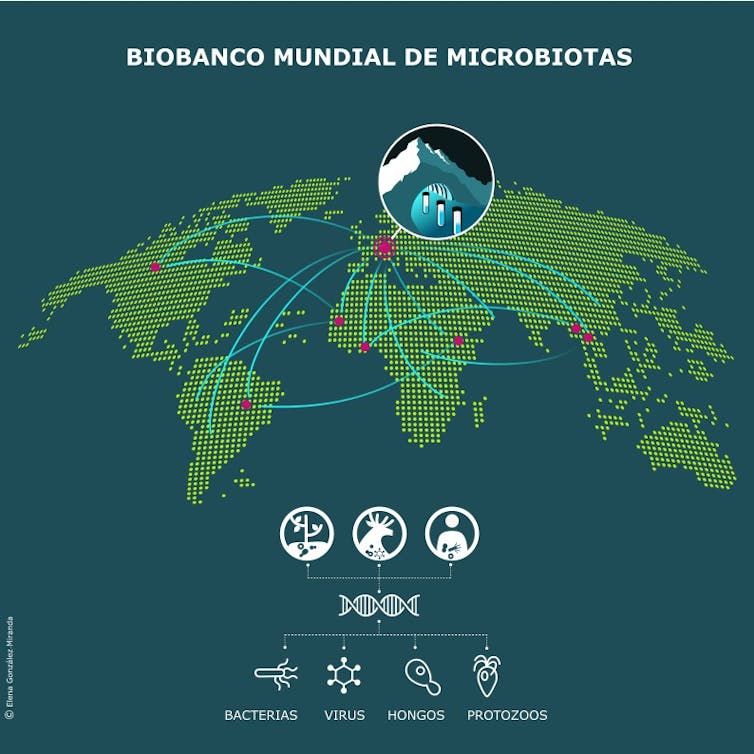 Biobanco mundial de Microbiotas Ilustración: Elena González MirandaUna extinción silenciosa
Biobanco mundial de Microbiotas Ilustración: Elena González MirandaUna extinción silenciosa
Los microbios –arqueas, bacterias, hongos, protozoos y virus– han evolucionado durante millones de años en estrecha relación con los demás seres vivos, configurando una diversidad esencial para el equilibrio de los ecosistemas. A pesar de su importancia, muchas de estas especies nunca han sido cultivadas en el laboratorio. El conocimiento sobre sus genomas sigue siendo limitado.
Aunque los microorganismos son vitales para la salud de personas y animales, la fertilidad del suelo o la regulación del clima, este mundo invisible está en grave peligro de desaparecer debido a la actividad humana.
Sin ir mas lejos, nuestra microbiota nos protege frente a patógenos, refuerza el sistema inmunitario, estimula el sistema nervioso y participa en la biosíntesis de vitaminas y otros metabolitos necesarios.
El uso excesivo de antibióticos, el aumento de las cesáreas, la disminución de la lactancia materna, el consumo de alimentos ultraprocesados o el estrés de la vida urbana alteran nuestros ecosistemas microbianos interiores.
Las consecuencias de esta disbiosis son importantes. Así, la desaparición de las bacterias Bifidobacterium longum variedad infantis, Treponema succinifaciens o Helicobacter pylori se ha relacionado con el aumento de enfermedades crónicas como alergias, diabetes o asma.
Adicionalmente, la pérdida de microbios del suelo compromete la resiliencia de los ecosistemas terrestres y marinos. Por ejemplo, Methanoflorens stordaliensis y otros microorganismos adaptados al permafrost (capa de suelo congelado permanentemente) ayudan a regular las emisiones de metano, y las acinetobacterias son cruciales en el ciclo del carbono. La desaparición de estos microorganismos acelera la liberación de gases de efecto invernadero y el cambio climático.
Tampoco hay que olvidar que los microbios pueden ser aliados terapéuticos. Algunos tratamientos con microbiomas, como el trasplante de heces, se están empleando en medicina con resultados prometedores. También hay propuestas esperanzadoras para su uso en agricultura y conservación ambiental.
Equidad y colaboración internacionalMicrobiota Vault se define como un proyecto internacional, privado y sin ánimo de lucro, respetuoso con el protocolo de Nagoya. Es decir, cada grupo participante decide libremente si desea compartir información genética, intercambiar muestras o colaborar en estudios conjuntos.
Como han manifestado la microbióloga María G. Dominguez-Bello y sus colaboradores en un reciente artículo, se trata de un esfuerzo global basado en la equidad, el respeto a los derechos de las comunidades indígenas y la colaboración internacional para fortalecer las redes de investigación sobre microbiota y apoyar la formación de científicos de países con menos recursos.
Los resultados y propuestas de la colaboración de personas expertas en campos tan diversos como microbiología, antropología, ética, salud pública o bioinformática se comparten en los congresos de la Red Mundial del Microbioma (Global Microbiome Network, GloMiNe).
La financiación podría ser un reto importante: como sucede con otros biobancos, estos proyectos no son prioritarios para los gobiernos. Además, las donaciones privadas son inestables y dependen de modas pasajeras o de los incentivos fiscales disponibles en cada momento.
One Health y microbiomaEsta iniciativa se alinea con el concepto de Salud Global (One Health) de la Organización Mundial de la Salud, basado en la interdependencia entre la salud de las personas, los animales y el medio ambiente.
Todavía no está demostrado que las microbiotas almacenadas puedan ser beneficiosas o reintroducirse con fines terapéuticos, ni contamos con la tecnología para hacerlo de forma segura. Sin embargo, su conservación permitirá futuras terapias cuando tengamos una sólida base científica.
Microbiota Vault se suma a otras propuestas de protección de la biodiversidad. Entre ellas se encuentran colecciones de cultivos microbianos como la Colección Española de Cultivos Tipo, el Banco Mundial de Semillas o la Conservación Global del Microbioma. Estas iniciativas podrían frenar la biopiratería y evitar que empresas y gobiernos poco escrupulosos se apropien de nuestra herencia microbiana sin permiso. También son clave para proteger el legado de las comunidades indígenas.
La esperanza dentro de la caja de PandoraNuestro mundo se enfrenta a múltiples crisis sanitarias, económicas y ecológicas. Por esto, la protección de la invisible vida microbiana es esencial. La conservación de esta biodiversidad microbiana mantendrá la esperanza de que en un futuro cercano podamos comprender mejor la vida en todas sus formas, curar enfermedades que hoy no tienen tratamiento y restaurar ecosistemas esenciales que se hayan perdido.![]()
Sobre el autor: Guillermo Quindós-Andrés, Catedrático de Microbiología Médica, Departamento de Inmunología, Microbiología y Parasitología, Facultad de Medicina y Enfermería, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El arca de la microbiota se ha escrito en Cuaderno de Cultura Científica.
El oro de las montañas rojizas que derrumbaron los romanos
Entre las zonas que, desgraciadamente, están siendo afectadas por los aterradores incendios que invaden la geografía ibérica, se encuentra la comarca leonesa de El Bierzo, en donde se localiza una joya natural que aúna, de manera ejemplar, el desarrollo social humano, la Arqueología y la Geología: Las Médulas.
 Panorámica de Las Médulas. Foto: Rafael Ibáñez Fernández / Rayet, CC BY-SA 3.0, / Wikimedia Commons
Panorámica de Las Médulas. Foto: Rafael Ibáñez Fernández / Rayet, CC BY-SA 3.0, / Wikimedia CommonsDeclaradas “Patrimonio de la Humanidad” por la UNESCO en 1997, Las Médulas son una extraordinaria muestra de cómo las actividades humanas pueden modelar por completo el paisaje natural. Y para conocer esta increíble historia, debemos viajar en el tiempo hasta hace unos 2000 años. Cuando los romanos llegaron al noroeste de Hispania en el siglo I de nuestra era, observaron que los pueblos autóctonos obtenían oro bateando la arena del cauce del río Sil. Entonces, decidieron remontar sus aguas, buscando el origen de ese preciado metal amarillo, encontrándolo en unas colinas de colores rojizos y parduzcos, donde el oro se encontraba incrustado entre las rocas de tipo areniscas, gravas y conglomerados que se extendían por toda esta zona.
 Detalle de los tipos de rocas presentes en Las Médulas, con conglomerados rojizos en la parte superior y areniscas anaranjadas en la inferior. Foto: A. Sánchez del Corral / Inventario Español de Lugares de Interés Geológico / Instituto Geológico y Minero de España (IGME-CSIC)
Detalle de los tipos de rocas presentes en Las Médulas, con conglomerados rojizos en la parte superior y areniscas anaranjadas en la inferior. Foto: A. Sánchez del Corral / Inventario Español de Lugares de Interés Geológico / Instituto Geológico y Minero de España (IGME-CSIC)Los ingenieros romanos no se vieron amedrentados ante la dificultad de sacar el oro de esas rocas tan duras y compactas. Al contrario, pusieron en marcha todo su ingenio hasta dar con la técnica minera más impresionante, a la vez que destructiva, del mundo antiguo: la “ruina montium”, cuya traducción, “derrumbe de montes”, ya nos está dando una clave de en qué consiste. Entrando en detalle, este sistema minero consistía en excavar una serie de canales y represas que traían el agua de las elevaciones cercanas hasta acumularlas por encima de las montañas que contenían el oro. Entonces seguían con las excavaciones, en este caso en forma de galerías verticales en el interior de las rocas que formaban esas colinas. Al terminar, estos conductos abrían los muros de las presas, dejando caer por ellos el agua a presión, lo que provocaba la rotura mecánica de las rocas y su arrastre hasta unas balsas de decantación excavadas al pie de las laderas. Allí, bateaban los sedimentos resultantes para separar, de manera manual, el oro del resto de materiales.
 Esquema de las fases de la técnica minera roma “ruina montium”. Ilustración: Hugo Prades / Fundación Las Médulas
Esquema de las fases de la técnica minera roma “ruina montium”. Ilustración: Hugo Prades / Fundación Las MédulasLa explotación aurífera de Las Médulas por parte de los romanos estuvo activa de manera ininterrumpida durante casi 200 años, desde comienzos del siglo I hasta comienzos del siglo III, afectando a una superficie de unas 540 ha en la que se removieron más de 93.000.000 m3 de materiales que permitieron extraer unos 5.000 kg de oro. Pero también cambió para siempre el paisaje, generando un sistema complejo de cárcavas, barrancos, pináculos o columnas de roca cuyo origen se encuentra, exclusivamente, en la mano del ser humano.
Pero, ¿cómo se formó ese oro? Hace meses os expliqué el origen de algunos de los depósitos de oro que actualmente se explotan en Alaska, pues aquí tenemos algo muy parecido. Para conocer este proceso debemos volver a hacer un viaje en el tiempo, pero esta vez del tipo geológico, llegando a hace más de 300 millones de años. En estos momentos, se estaban produciendo diversas colisiones tectónicas que dieron como resultado la formación del último gran supercontinente de la historia de la Tierra, Pangea. En este contexto compresivo, en la zona donde nos encontramos con Las Médulas actuales se produjo el ascenso de un magma en el interior del terreno, pero este material fundido no llegó a salir a la superficie, se quedó enterrado a varios kilómetros de profundidad. Cuando los fluidos subterráneos circulaban cerca de este magma, se calentaban, aumentando su capacidad de “robar” elementos químicos de las rocas que atravesaban, entre ellos el oro, llevándolos en disolución. Hasta que encontraban alguna fractura del terreno que les permitía fluir hacia la superficie, lo que provocaba que se fuesen enfriando poco a poco, perdiendo esa capacidad de disolución, teniendo entonces que “soltar” los elementos químicos que transportaban. Sí, incluido el oro. Así se formaron unas mineralizaciones ricas en oro que atravesaban el terreno a las que denominamos diques.
 Aspecto general de Las Médulas, donde se observa el paisaje de origen humano formado por cárcavas, pináculos, columnas y escarpes. Foto: A. Sánchez del Corral / Inventario Español de Lugares de Interés Geológico / Instituto Geológico y Minero de España (IGME-CSIC)
Aspecto general de Las Médulas, donde se observa el paisaje de origen humano formado por cárcavas, pináculos, columnas y escarpes. Foto: A. Sánchez del Corral / Inventario Español de Lugares de Interés Geológico / Instituto Geológico y Minero de España (IGME-CSIC)Pues hace unos 20 millones de años, con la tectónica ya más tranquilita, los agentes meteorológicos tomaron el protagonismo. Así, el agua de lluvia se encargó de erosionar los diques con mineralizaciones de oro que se encontraban en las montañas situadas al sur de Las Médulas, transportándolo ladera abajo, hasta depositarlo en capas acumuladas entre la arena, el barro y los fragmentos de rocas que arrastraban. El paso de los millones de años hizo entonces su trabajo, transformando estos sedimentos en rocas duras (las areniscas, gravas y conglomerados que os mencionaba al principio) ricas en depósitos de oro.
Hace dos milenios, esas rocas rojizas también sufrieron la erosión del agua que se llevaba el oro hasta acumularlo en el cauce del Sil, donde lo recogían las poblaciones autóctonas antes de la invasión romana. Pero los romanos no tuvieron paciencia, así que decidieron acelerar el proceso erosivo del agua con su técnica minera nunca antes vista en este lugar.
En los últimos siglos, tras el abandono de la explotación minera, la naturaleza recuperó parte de su terreno original, creciendo una tupida masa boscosa entre los restos de la destrucción provocada por el ser humano. Ahora, ese hermoso manto verde, es el que estamos viendo arder. Posiblemente pasen décadas antes de que la vegetación vuelva a cubrir esta hermosa zona, pero lo que no se ha perdido es su riqueza geológica y arqueológica. Y esta increíble historia que nos cuentan las rocas y el paisaje sigue siendo uno de los mayores reclamos turísticos de la zona. No dejemos de visitar Las Médulas, apoyando a los comercios locales de la comarca berciana, porque ese pequeño grano de arena puede significar mucho para la población.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la EHU
El artículo El oro de las montañas rojizas que derrumbaron los romanos se ha escrito en Cuaderno de Cultura Científica.
El ARN es el sistema de alerta de emergencia de la célula
¿Cómo sabe una célula que ha sido dañada? Una alarma molecular, activada por ARN mutado y colisiones ribosómicas, señala el peligro.
Un artículo de Dan Samorodnitsky. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Wei-An Jin / Quanta Magazine
Ilustración: Wei-An Jin / Quanta Magazine¿Qué ocurre cuando el sol brilla sobre tu piel? ¿Y qué ha fallado cuando se produce una quemadura?
Detrás de ese dolor se esconde la respuesta de emergencia celular al daño en el ADN. Cuando un agente nocivo, como la luz ultravioleta, la radiación ionizante o ciertos productos químicos, daña el ADN, la célula debe reaccionar a toda velocidad. Idealmente, repara el daño en su repositorio de información genética o se sacrifica mediante un proceso de muerte celular controlada. Si no actúa con rapidez, corre el riesgo de una consecuencia más peligrosa: la necrosis, una muerte celular explosiva y descontrolada que daña a las células vecinas, o la transmisión de ADN mutado a sus descendientes, lo que podría derivar en cáncer.
Por tanto, es urgente que la célula identifique el daño en el ADN lo antes posible. Pero el genoma es enorme; cuando el ADN muta, la mutación puede no detectarse a tiempo —o incluso no detectarse en absoluto—. Para mantener el control de su destino, la célula necesita algún tipo de sistema de alarma frente al daño en el ADN.
Investigadores han identificado ahora ese sistema de alarma celular, que sorprendentemente no implica directamente al ADN. En su lugar, cuando se acumulan moléculas mutadas de ARN —el primo cercano del ADN— e interfieren con los procesos moleculares, se activa una vía de señalización que alerta de que algo va terriblemente mal en el código genético y que debe resolverse con urgencia. Estos hallazgos se publicaron en la revista Cell en 2024.
Recientemente, un equipo dirigido por Anna Constance Vind, bióloga molecular de la Universidad de Copenhague, ha confirmado que el ARN está en el centro de esta rápida e intrincada respuesta al daño en células de mamíferos —específicamente en células de ratones con quemaduras solares—, lo que sugiere que ocurre también en células humanas. Este trabajo se publicó en Molecular Cell.
 La investigación de Anna Vind sobre el sistema de alarma de emergencia de las células revela otro papel fundamental del ARN en la biología celular. «Ahora se está viendo que el ARN sí importa», afirma. Foto: Anton Willemann / Københavns Universitet
La investigación de Anna Vind sobre el sistema de alarma de emergencia de las células revela otro papel fundamental del ARN en la biología celular. «Ahora se está viendo que el ARN sí importa», afirma. Foto: Anton Willemann / Københavns Universitet«Lo que intenta hacer la célula es decidir si vive o muere en función de cuán dañado esté el ADN. Si el ADN está demasiado deteriorado, habrá mutaciones que se heredarán», dice Rachel Green, bióloga especializada en ARN en la Universidad Johns Hopkins y coautora del estudio en Cell. «Pero lo asombroso es que es el ARN quien da la señal. Eso es lo realmente sorprendente».
Curso de colisiónLos científicos también son susceptibles a los mitos. La idea extendida era que el daño en el ADN lo detectaban proteínas que interactúan directamente con él. A medida que estas proteínas se desplazaban por la hebra de ADN, podían atascarse en lesiones, enlaces cruzados o mutaciones, como cuando uno pasa un hilo entre los dedos hasta encontrar un nudo. Entonces la célula intentaba reparar el ADN dañado, pero si la lesión era demasiado grave, iniciaba la apoptosis: una forma de suicidio celular ordenado, en la que la célula empaqueta su contenido y se elimina de manera segura sin perjudicar a las vecinas.
Pero esa historia nunca termina de encajar. Debido al enorme tamaño del genoma y al hecho de que el ADN solo se copia y explora en una fase específica del ciclo celular, cualquier sistema de alarma basado en el ADN sería lento y torpe. Los mecanismos internos de reparación del ADN pueden tardar entre 16 y 24 horas. Pero una vez que el ADN se daña, la célula toma una decisión trascendental mucho más rápido que eso.
«La decisión de vivir o morir se toma en 15 a 30 minutos», afirma Niladri Sinha, investigador posdoctoral en el laboratorio de Green y autor principal del estudio en Cell. «No quieres que el problema se extienda; tomas la decisión de detenerlo cuanto antes».
Además, nunca se ha establecido con firmeza una relación causal directa entre el daño en el ADN y la respuesta inflamatoria del sistema inmunitario en un organismo vivo.
Para resolver estas discrepancias, Vind necesita dañar intencionadamente el ADN en el laboratorio y observar cómo responde la célula. Así que su equipo provoca quemaduras solares en ratones: afeitan a dos grupos de ratones y los exponen a luz ultravioleta (UV). El primer grupo está formado por ratones normales, o «salvajes». El segundo grupo consiste en ratones modificados genéticamente para carecer de una proteína llamada ZAK.
ZAK está asociada a los ribosomas, las fábricas celulares encargadas de traducir ciertos tipos de ARN para producir proteínas. Es parte de un conjunto de proteínas que ayudan al ribosoma, por ejemplo, cargándolo con ARN, asistiendo en la síntesis proteica y supervisando su progreso. Además, ocupa una posición central en una cascada de señalización que transmite información del ribosoma al resto de la célula. Tras años de investigación, se ha establecido que ZAK desempeña un papel clave en una red de respuesta celular frente a los daños provocados por la radiación UV. Esos hallazgos se basan en estudios con células y gusanos en cultivo; Vind quiere comprobar cómo se desarrolla esta vía en un organismo complejo y más parecido al humano.
Cuando la luz UV penetra en las células, puede mutar el ADN; y lo que es crucial, provoca mutaciones similares en el ARN. En las células cutáneas de los ratones quemados por el sol, el grupo de Vind observa que los ribosomas tropiezan con ARN dañado. Los ribosomas no pueden interpretar ciertas mutaciones y avanzan con cautela por los obstáculos físicos provocados por daños más severos. Disminuyen su velocidad, dejan de funcionar y comienzan a colisionar entre sí.
 Una investigación dirigida por la bióloga Rachel Green sitúa el ARN mutado y el colapso de los ribosomas en el centro de una rápida respuesta al daño celular. Cortesía de Rachel Green
Una investigación dirigida por la bióloga Rachel Green sitúa el ARN mutado y el colapso de los ribosomas en el centro de una rápida respuesta al daño celular. Cortesía de Rachel GreenEs entonces cuando los investigadores ven a ZAK entrar en acción. Esta proteína permanece inactiva hasta que dos ribosomas entran en contacto físico —es decir, colisionan—. En las células cutáneas de los ratones salvajes, a las seis horas de la exposición a la UV, ZAK pone en marcha una serie de reacciones celulares en respuesta a la desaceleración y colisiones ribosómicas. Cualquiera que haya sufrido una quemadura solar conoce estas reacciones: inflamación debida a la llegada masiva de células inmunitarias al área afectada, lo que causa hinchazón y enrojecimiento.
«ZAK inicia una vía de señalización como una alarma», explica Sinha. «El grado de activación marca el compromiso con la muerte». Cuantos más ribosomas colisionan, más señales emite ZAK. Cuando alcanza un umbral crítico, la célula opta por la apoptosis en lugar de arriesgarse a una necrosis o al cáncer. La célula intenta así proteger a sus vecinas, al propio organismo y a su ADN: la información que se transmitirá a la siguiente generación.
Sin embargo, los ratones sin ZAK reaccionan de forma completamente distinta. Seis horas después del tratamiento con UV, no muestran inflamación alguna. La respuesta rápida al daño solar brilla por su ausencia. Pasan uno o dos días hasta que estos ratones se enrojecen e inflaman como los salvajes.
Estos resultados demuestran que ZAK es necesario para que las células detecten rápidamente el daño en el ADN. Y lo hace detectando no el daño en el ADN directamente, sino en el ARN.
Todo o nadaLos síntomas de una quemadura solar se deben a que el sistema de alarma ribosómico de la célula activa un sistema de protección aguda conocido como respuesta al estrés ribotóxico (RSR, por sus siglas en inglés). Cuando una célula percibe que sus ribosomas se comportan de forma anómala —por ejemplo, colisionando entre sí, algo que normalmente no hacen—, ralentiza su metabolismo para decidir entre intentar una reparación o iniciar una muerte celular controlada.
Lo que hace del RSR un buen sistema de alarma rápido es la frecuencia con la que la célula utiliza el ARN: constantemente. Las células están casi siempre generando, manipulando o interactuando con ARN en alguna de sus formas. Puede tratarse de ARN mensajero (ARNm) que se traduce en proteínas, ARN no codificante que regula la expresión génica, o ARN ribosómico utilizado para construir las máquinas moleculares —una necesidad constante de las células y una de sus actividades que más energía consume.
«Lógicamente, que el ribosoma se atasque es un sistema mucho más sensible para detectar daños, porque los ribosomas están densamente distribuidos en el ARN», dice Craig Kaplan, biólogo del ARN en la Universidad de Pittsburgh, quien no ha participado en los estudios. «Que el ribosoma se atasque es la forma más rápida de detectar daños, y lo que estos estudios están revelando es que es el mecanismo dominante».
No es solo la familiaridad de la célula con el ARN lo que lo convierte en una molécula ideal para emitir alarmas, sino también su ubicuidad, abundancia, plasticidad y bajo coste de producción.
«Puedes pensar en [la respuesta al estrés ribotóxico] como una amplificación de la alarma», señala Lydia Contreras, bióloga molecular de la Universidad de Texas en Austin, que tampoco ha participado en los estudios. «Puedes hacer muchas copias de un ARN, así que es como un altavoz… Es una de las formas más baratas, molecularmente hablando», de generar una señal, añade. «Te comunicas rápidamente porque los estás produciendo muy rápido».
Además, tiene todo el sentido que un ribosoma detenido sea una señal de alarma para una célula. Un ribosoma bloqueado no ha terminado de fabricar su proteína, y las proteínas inacabadas pueden interferir con las sanas, lo que puede ser tóxico e incluso letal. Estos son desórdenes que la célula prefiere resolver antes de que se acumulen y generen problemas graves.
Más allá de las quemaduras solares, el RSR es la vía que lanza la señal de “todo o nada” ante casi cualquier desafío celular. Se activa cuando una célula sufre inanición. Se activa cuando una célula es envenenada con ricina. Se activa cuando un virus la invade. Detectar las colisiones ribosómicas y mantener un sistema de traducción proteica saludable es, por tanto, esencial para todas las células, en cualquier etapa de la vida y en casi cualquier circunstancia.
Para Kaplan, el RSR es un ejemplo maravilloso del lenguaje interno de la célula y de las formas indirectas en que puede evolucionar para acceder a la información necesaria para sobrevivir. «Las células no tienen un pequeño operario que dirija el tráfico y les explique en palabras lo que está ocurriendo. No usan ese tipo de lenguaje. Una de las cosas fascinantes de la biología es que la evolución ha vinculado un evento concreto» —como la colisión entre ribosomas— «con una consecuencia determinada» —una posible emergencia física y celular.
«A veces detectas cosas de forma indirecta», afirma. «Eso es lo que hace la evolución».
El artículo original, RNA Is the Cell’s Emergency Alert System, se publicó el 14 de julio de 2025 en Quanta Magazine. Cuaderno de Cultura Científica tiene un acuerdo de distribución en castellano con Quanta Magazine.
Traducido por César Tomé López
El artículo El ARN es el sistema de alerta de emergencia de la célula se ha escrito en Cuaderno de Cultura Científica.
La implantación del embrión en el útero, ex vivo y en directo
Las primeras etapas del desarrollo embrionario de los mamíferos son excepcionales en el mundo animal. La razón de esto se encuentra en otra característica única. El óvulo de los mamíferos placentados, humanos incluidos, carece de vitelo, es decir, de las sustancias nutritivas que necesita el embrión para su desarrollo. Por ello, necesita imperiosamente recibir cuanto antes nutrientes de la madre.
Cuando el óvulo es fecundado se divide varias veces y forma el blastocisto, compuesto por las células del futuro embrión y el trofoectodermo (figura 1). Para que el desarrollo pueda continuar, el blastocisto debe quedar implantado en el endometrio, la capa interna del útero. El trofoectodermo es el responsable de la implantación, se adhiere al epitelio uterino y comienza la invasión de los tejidos maternos. A consecuencia de la invasión se forman lagunas con sangre materna y se acondiciona el endometrio para organizar la futura placenta.
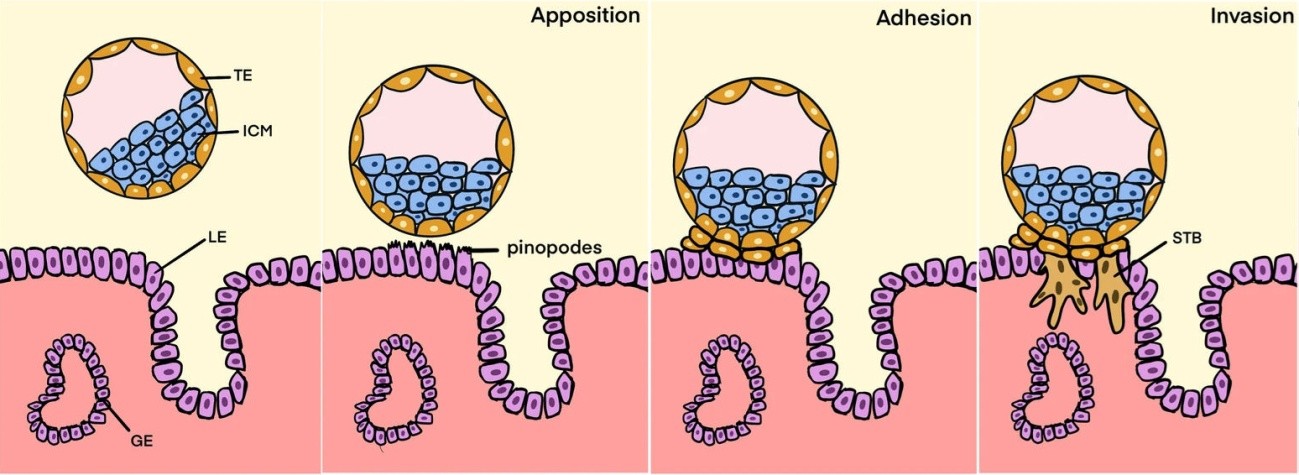 Figura 1. Etapas de la implantación. El blastocisto está formado por el trofoectodermo (TE) y la masa celular interna (ICM) de la que deriva el embrión. El trofoectodermo rompe el epitelio luminal del endometrio (LE) e invade la pared uterina formando el sincitiotrofoblasto (STB). GE=epitelio glandular uterino. Fuente: Li et al. (2022) Reproductive Biology and Endocrinology doi: 10.1186/s12958-022-00973-8 CC BY 4.0.
Figura 1. Etapas de la implantación. El blastocisto está formado por el trofoectodermo (TE) y la masa celular interna (ICM) de la que deriva el embrión. El trofoectodermo rompe el epitelio luminal del endometrio (LE) e invade la pared uterina formando el sincitiotrofoblasto (STB). GE=epitelio glandular uterino. Fuente: Li et al. (2022) Reproductive Biology and Endocrinology doi: 10.1186/s12958-022-00973-8 CC BY 4.0.La implantación es un momento crítico para que la gestación progrese. En la reproducción asistida humana, un 50-60% de los blastocistos fracasan a la hora de implantarse en el útero. Sin embargo, si la implantación tiene lugar, la tasa de abortos desciende al 15%.
Lo que conocíamos de la implantación procede de los estudios hechos sobre tejido fijado y modelos transgénicos de ratón. De esta forma se ha podido identificar un número de genes implicados en el proceso. Sin embargo, no ha sido posible, hasta ahora, observar directamente el proceso de implantación. Estamos hablando de un blastocisto que tiene unas 200 células, mide menos de 0,2 mm y puede implantarse en cualquier punto del útero. No es algo que pueda verse fácilmente.
Esto ha cambiado gracias a la técnica desarrollada por un equipo de investigación de la universidad de Osaka (Japón), que ha conseguido implantar blastocistos de ratón ex vivo, es decir, en una placa de cultivo.
La técnica, desarrollada tras múltiples ensayos, consiste en obtener pequeños fragmentos de útero de ratonas preñadas y, por otro lado, blastocistos de otras ratonas. En los dos casos el tiempo de obtención se ajustó a 3,75 días tras el apareamiento con machos. Los blastocistos se colocaron sobre el endometrio de los fragmentos uterinos y se cubrieron con un polímero de silicona (polidimetilsiloxano) biocompatible y muy permeable a los gases. Después de ensayar diversos medios de cultivo se seleccionó uno que contenía dosis muy precisas de estradiol y progesterona, hormonas necesarias para la gestación.
Más del 90% de los blastocistos así tratados se habían adherido al endometrio pasadas 24 h. A las 36 h, el trofoectodermo ya había roto el epitelio materno y comenzado la invasión de la pared uterina. Esta invasión era completa a las 48 h del comienzo del experimento. Al mismo tiempo, el embrión progresaba normalmente expresando los genes correspondientes a su estado de desarrollo (figura 2).
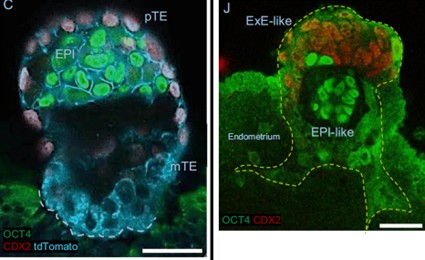 Figura 2. Implantación del blastocisto en el modelo ex vivo descrito en el texto. Izquierda y derecha: 24 y 48 horas tras la colocación sobre el fragmento de útero. El futuro embrión está marcado en verde, el trofoectodermo polar en rojo y el trofoectodermo mural en azul. El trofoectodermo mural es el que genera el sincitiotrofoblasto invasivo. La línea amarilla discontinua muestra el contorno de la invasión. Fuente: Hiraoka et al. (2025), (2025) Nat Commun. doi: 10.1038/s41467-025-60610-x CC BY-NC-ND 4.0.
Figura 2. Implantación del blastocisto en el modelo ex vivo descrito en el texto. Izquierda y derecha: 24 y 48 horas tras la colocación sobre el fragmento de útero. El futuro embrión está marcado en verde, el trofoectodermo polar en rojo y el trofoectodermo mural en azul. El trofoectodermo mural es el que genera el sincitiotrofoblasto invasivo. La línea amarilla discontinua muestra el contorno de la invasión. Fuente: Hiraoka et al. (2025), (2025) Nat Commun. doi: 10.1038/s41467-025-60610-x CC BY-NC-ND 4.0.Desafortunadamente, este sistema no permitió alcanzar mucho más allá de un desarrollo correspondiente a los 5,5 días post coitum. Sin embargo, sí permitió hacer algunos experimentos para conocer mejor el proceso de implantación. El más llamativo fue la investigación del papel desempeñado por la ciclooxigenasa-2 (COX-2) en dicho proceso. Esta enzima cataliza la producción de prostaglandinas, moléculas implicadas en la inflamación y el dolor. Precisamente la aspirina, como otros antiinflamatorios no esteroideos (AINEs), ejerce su función analgésica y antiinflamatoria mediante la inhibición de la COX-2.
Desde hace tiempo se sabe que la COX-2 es necesaria para la implantación del blastocisto, y que es producida por células del endometrio, aunque se ignoraba su mecanismo de actuación. El grupo japonés confirmó en su modelo ex vivo que la inhibición de la COX-2 con celecoxib (un AINE) impedía la correcta implantación del blastocisto. El modelo permitió comparar la expresión génica de blastocistos en presencia de celecoxib y blastocistos control, que se implantaban normalmente. El resultado fue que un importante regulador de múltiples vías de señalización celular llamado AKT (o proteína kinasa B) no se activaba en el blastocisto si COX-2 no era operativa en el endometrio (figura 3).
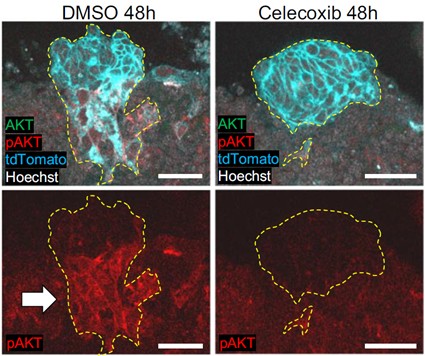 Figura 3. Este experimento realizado sobre el modelo ex vivo de implantación muestra el mecanismo de actuación de la ciclooxigenasa-2 (COX-2) en el proceso. A la derecha, el tratamiento con celecoxib (inhibidor de la COX-2) frena la invasión del endometrio. Abajo podemos ver cómo la forma activada de la enzima AKT (pAKT) se reduce fuertemente en el blastocisto tras el tratamiento con celecoxib, revelando la importancia de esta vía de señalización en la implantación. Fuente: Hiraoka et al. (2025), (2025) Nat Commun. doi: 10.1038/s41467-025-60610-x CC BY-NC-ND 4.0.
Figura 3. Este experimento realizado sobre el modelo ex vivo de implantación muestra el mecanismo de actuación de la ciclooxigenasa-2 (COX-2) en el proceso. A la derecha, el tratamiento con celecoxib (inhibidor de la COX-2) frena la invasión del endometrio. Abajo podemos ver cómo la forma activada de la enzima AKT (pAKT) se reduce fuertemente en el blastocisto tras el tratamiento con celecoxib, revelando la importancia de esta vía de señalización en la implantación. Fuente: Hiraoka et al. (2025), (2025) Nat Commun. doi: 10.1038/s41467-025-60610-x CC BY-NC-ND 4.0.Esto se confirmó mediante inhibidores farmacológicos de AKT, que bloquearon también la implantación en el modelo ex vivo. Por otro lado, si se inducía la activación permanente de AKT, se soslayaba la necesidad de una COX-2 funcional en el endometrio. Por tanto, se demostró que las señales reguladas por la activación de AKT en el blastocisto son esenciales para su normal implantación.
El modelo ex vivo de implantación desarrollado por el grupo japonés ha demostrado ser una técnica del mayor interés para conocer los detalles de este momento crítico de la gestación. Los resultados que se deriven de su utilización pueden ser de mucha utilidad en el tratamiento de la infertilidad femenina.
Referencias
Hiraoka, T., Aikawa, S., Mashiko, D. et al. (2025). An ex vivo uterine system captures implantation, embryogenesis, and trophoblast invasion via maternal-embryonic signaling. Nat Commun. doi: 10.1038/s41467-025-60610-x.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
El artículo La implantación del embrión en el útero, ex vivo y en directo se ha escrito en Cuaderno de Cultura Científica.
La doble (y desconocida) historia del cuerpo humano
Ramón Muñoz-Chápuli, autor
¿Hasta qué punto conocemos nuestro cuerpo? No me refiero a poder indicar la localización de nuestros órganos internos, ni a recitar de carrerilla el nombre de los huesos o músculos principales. Estoy hablando de la historia de nuestro cuerpo, de cada uno de sus elementos. Detrás de todos ellos se esconde una historia fascinante o, mejor dicho, dos historias. Por un lado, cada componente de nuestro cuerpo es el resultado de innovaciones evolutivas que se han sucedido en el linaje de nuestros antepasados a lo largo de millones de años. Pero nuestro cuerpo también es el producto final de una historia que transcurre dentro del vientre de nuestra madre: un desarrollo embrionario a lo largo de nueve meses.
Ambas historias son muy poco conocidas. A lo largo de cuatro décadas enseñando evolución animal y anatomía comparada, he podido constatar la sorpresa de mis estudiantes cuando les desvelaba el origen de alguno de los componentes del cuerpo humano.
 Fuente: Shackleton Books
Fuente: Shackleton BooksVeamos algunos ejemplos. Un momento crucial de la evolución de los vertebrados fue el desarrollo de las mandíbulas. Parece una cuestión secundaria, pero a esta innovación debemos numerosas características de nuestro cuerpo actual. Los primeros peces, habitantes de los mares del Cámbrico hace unos 500 millones de años, no tenían mandíbulas y se alimentaban por filtración a través de una gran faringe branquial. Esto limitaba su tamaño, que raramente superaba los 30 cm. Los depredadores de la época suponían una amenaza, y por ello el cuerpo de estos peces primitivos estaba cubierto por hueso dérmico.
El desarrollo de mandíbulas a partir del esqueleto branquial supuso un cambio radical en la forma de vida de los vertebrados. Los peces ya podían ser depredadores, y esto supuso un gran aumento de tamaño. Al mismo tiempo, los huesos dérmicos que protegían el cuerpo ya no eran tan necesarios y se redujeron a zonas corporales en los que cumplían alguna función. Nuestra bóveda craneana, protectora del encéfalo, nuestras mandíbulas, los dientes y las clavículas son derivados de aquel caparazón protector, y se siguen desarrollando en nuestra dermis de la misma forma que ocurría en nuestros antepasados.
El abandono del sistema primitivo de filtración a través de la faringe tuvo otra consecuencia curiosa. El órgano productor de mucus con el que se atrapaban las partículas alimenticias dio lugar a una glándula controladora del metabolismo. Me refiero a la tiroides, que recapitula su origen evolutivo al formarse a partir de un surco de la faringe embrionaria.
Otro momento estelar de la evolución de los vertebrados fue la transición del agua al medio aéreo. Conservamos numerosos rastros en nuestro cuerpo de los cambios que fueron necesarios para culminar esta transición. Por ejemplo, el esternón que refuerza la caja torácica, el ilion que conecta las patas posteriores a las vértebras sacras, o el estribo del oído medio, que deriva de un arco branquial modificado. Sin olvidar la profunda remodelación del corazón, que se vio enfrentado a la necesidad de atender a dos circuitos sanguíneos diferentes (el general del cuerpo y el pulmonar).
Podríamos seguir enumerando ejemplos acerca de los miembros, la musculatura facial, los riñones o los conductos reproductivos. Cada parte de nuestro cuerpo encierra esa doble historia que antes mencionaba, su origen evolutivo y su desarrollo embrionario. Parecen historias independientes, pero no es así.
Desde hace algunas décadas sabemos que el desarrollo embrionario está regulado por un conjunto relativamente pequeño de genes. Estos genes constituyen una especie de “caja de herramientas” compartida por todos los animales. Su funcionamiento es responsable de la construcción de cada organismo durante el desarrollo. Modificaciones en la forma en que estos genes se aplican a su tarea constructiva pueden generar novedades que terminen siendo integradas en el proceso evolutivo. Este nuevo concepto ha supuesto una importante ampliación de la Teoría de la Evolución.
La nueva forma de contemplar la evolución no se había aplicado todavía al caso del cuerpo humano. Por este motivo, y por el deseo de compartir las historias sorprendentes que explican cada componente de nuestro cuerpo, decidí escribir El cuerpo, una historia por partes.
El enfoque singular de este libro llevará a sus lectores a descubrir que su espalda corresponde al vientre de la mayor parte de los animales. También que las neuronas y la piel tienen una estrecha relación, tanto en su evolución como en su desarrollo. O que la hipófisis probablemente deriva de un ancestral órgano sensorial, hoy perdido en los vertebrados.
A pesar de tratar temas complejos como la evolución o la biología del desarrollo, a lo largo del texto se utiliza un lenguaje sencillo y fácilmente comprensible, apoyado en numerosas ilustraciones. El cuerpo, una historia por partes proporciona una visión insólita y sorprendente de algo que no puede ser más personal y cercano: el cuerpo humano.
Descarga el índice, prólogo y primer capítulo de este libro
Ficha:
Título: El cuerpo, una historia por partes
Autor: Ramón Muñoz-Chápuli
Editorial: Shackleton Books, 2025
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga y autor de Vida fascinante en el Cuaderno de Cultura Científica
El artículo La doble (y desconocida) historia del cuerpo humano se ha escrito en Cuaderno de Cultura Científica.
Participación social y desarrollo local en el Geoparque Las Loras

¿Qué tienen en común un paisaje espectacular, un fósil milenario y una cantera abandonada? Todos forman parte del patrimonio geológico, un testimonio de la historia de la Tierra con un gran valor científico, educativo, cultural y estético, y base del patrimonio natural. Sin embargo, su importancia continúa siendo poco apreciada.
Para acercar las distintas aproximaciones del patrimonio geológico a la sociedad, los días 26, 27 y 28 de marzo se celebró la quinta edición de las jornadas divulgativas “Geología para poetas, miopes y despistados. Patrimonio patrimonio”. Organizadas por el grupo de investigación consolidado Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco (UPV/EHU), estas jornadas contaron con la colaboración del Vicerrectorado del Campus de Bizkaia, la Cátedra de Cultura Científica de la UPV/EHU, el Geoparque de la Costa Vasca / Geoparkea y el Ente Vasco de la Energía (EVE).
Los geoparques no son solo curiosidades científicas, también son motores de desarrollo de las áreas donde se implantan. José Ángel Sánchez describe en esta conferencia los programas que se realizan en el Geoparque Las Loras (Burgos, Palencia).
José Ángel Sánchez es el director científico de la Asociación para la Reserva Geológica de Las Loras (ARGEOL).
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Participación social y desarrollo local en el Geoparque Las Loras se ha escrito en Cuaderno de Cultura Científica.
Poniéndole cara a una muestra de ADN
Un estudio de la Universidad del País Vasco / Euskal Herriko Unibertsitatea (EHU) ha descubierto una fuerte relación entre diez marcadores genéticos con la morfología de la cara de personas españolas. La investigadora Belén Navarro, autora del trabajo, destaca la importancia de realizar investigaciones en poblaciones específicas, para conseguir modelos de predicción con los que poder reconstruir el rostro de una persona a partir de muestras de ADN.
 Las zonas marcadas en color señalan aquellas específicas donde se ha encontrado que algún marcador genético tiene asociación. El color muestra el desplazamiento del tejido blando del rostro en función del genotipo. Para un genotipo específico, el azul indica movimiento hacia el interior y el rojo hacia el exterior. Por ejemplo, en las figuras de la nariz, el color rojo señala una nariz que sobresale más hacia fuera, pero con las fosas nasales más recogidas hacia dentro; por tanto, sería una nariz más proyectada hacia fuera y estrecha. Fuente: Belén Navarro / EHU
Las zonas marcadas en color señalan aquellas específicas donde se ha encontrado que algún marcador genético tiene asociación. El color muestra el desplazamiento del tejido blando del rostro en función del genotipo. Para un genotipo específico, el azul indica movimiento hacia el interior y el rojo hacia el exterior. Por ejemplo, en las figuras de la nariz, el color rojo señala una nariz que sobresale más hacia fuera, pero con las fosas nasales más recogidas hacia dentro; por tanto, sería una nariz más proyectada hacia fuera y estrecha. Fuente: Belén Navarro / EHULa obtención de datos de la apariencia física puede ayudar a guiar la búsqueda de sospechosos en casos penales o a la identificación de personas desaparecidas, por lo que es muy interesante poder llegar a predecir las características externas humanas y en particular la forma de la cara mediante análisis de una muestra de ADN.
El análisis de ADN es una herramienta esencial en biología forense, ya que permite la identificación individual mediante la comparación de perfiles genéticos de los vestigios con muestras de referencia. Los últimos avances en el campo de la genética forense buscan determinar las características externamente visibles a partir del ADN que puedan facilitar la identificación. Sin embargo, la morfología de la cara es un rasgo muy complejo.
Ponerle cara al ADNLa investigadora Belén Navarro, del grupo BIOMICs de la EHU, explica que la finalidad “es utilizar ciertos marcadores concretos para poder predecir la forma de la cara de una persona en una escena del crimen o cuando se quiere identificar a alguien y se encuentran solo restos óseos. En las muestras forenses el ADN es muy limitante. No se pueden analizar todos los marcadores que se quieran”. Por ello, es importante “intentar reducir al máximo y quedarse con aquellos marcadores que son más significativos o que tienen más peso”, añade.
Recientes estudios de asociación de todo el genoma han arrojado luz sobre posibles marcadores asociados con los rasgos de la cara. En un trabajo llevado a cabo por el grupo de investigación BIOMICs de la Universidad del País Vasco, que se dedica entre otros ámbitos a la genética forense, han seleccionado un conjunto de 116 posibles marcadores del ADN y han estudiado cómo se asocian con los rasgos faciales en unas 500 personas de diferentes lugares de la península ibérica. “Hemos seleccionado genes y marcadores genéticos que ya se habían asociado con la morfología facial en otras poblaciones a nivel europeo, y lo hemos probado aquí, para ver si había diferencias —explica la investigadora de BIOMICs—. Hemos querido analizar todos y filtrar cuáles de ellos serían los más informativos en nuestra población, para, en caso de tener que utilizar este sistema, centrarnos solamente en ciertos marcadores. Eso es muy útil cuando no se tiene tanto ADN como para poder mirar todos”.
El equipo de investigación de la EHU escaneó el rostro de las personas voluntarias, y así “tomamos una serie de puntos de referencia cefalométricos y estudiamos cómo varían los rasgos del rostro (los ojos, la nariz, caras más anchas, más estrechas, la frente, la barbilla…), llegando a analizar regiones muy concretas de la cara”. A partir de las muestras de saliva estudiaron los citados marcadores genéticos y “luego analizamos si había asociación entre esa variación facial con los marcadores que teníamos”, añade Navarro. El equipo de investigación ha conseguido ver de esta manera, “por ejemplo, que hay una zona de la frente que está un poco más hundida cuanto se tiene un determinado genotipo (o conjunto de genes) para un marcador, o que cuando se tiene otro la frente es más sobresaliente, etc.”, relata la investigadora.
Los resultados han revelado asociaciones significativas dentro de diferentes segmentos faciales: “En particular, diez de los marcadores han presentado una fuerte asociación dentro de esta población local, y algunos de estos han revelado correlaciones con regiones faciales que no habían sido detectadas en investigaciones anteriores”, afirma Navarro.
La importancia de los estudios en poblaciones de referencia pequeñas
Estos hallazgos resaltan “la importancia de analizar marcadores candidatos en diversas poblaciones de referencia para identificar marcadores robustos que a la vez proporcionen información precisa”, dice la investigadora. Si bien gran parte de la investigación realizada hasta ahora se ha centrado en las poblaciones europeas como un grupo homogéneo, “nuestro trabajo muestra que la población que hemos estudiado puede presentar diferencias. Estos resultados sugieren que podría ser valioso no solo realizar estudios europeos a gran escala, sino también considerar estudios específicos de subpoblaciones más pequeñas”, añade. Este enfoque podría ayudar en la consecución de futuros modelos predictivos.
En este camino es fundamental hilar fino: “Ahora habría que validar nuestros resultados con más personas. Habría que probar en otras poblaciones para ver si, por ejemplo, estos resultados se enmarcan a todo el sur europeo o solo a nuestro entorno”. Actualmente el grupo sigue adelante con esta investigación utilizando otros métodos de medida de las características faciales: “Ahora estamos utilizando distintas medidas que están definidas antropológicamente: distancia entre los ojos, entre la nariz y la boca, entre las dos comisuras, etc.”, añade la investigadora. Un siguiente paso sería “intentar conseguir modelos de predicción, que revelen por ejemplo una determinada distancia en el rostro de una persona cuando se detecte ciertos genotipos”. Así sí que se podría “reconstruir más o menos el rostro de una persona. Pero para conseguirlo es necesario seguir validando estos avances en una población mucho más amplia”, concluye Navarro.
Referencia:
Belén Navarro-López, Franziska Wilke, Victoria Suárez-Ulloa, Miriam Baeta, Rubén Martos-Fernández, Olatz Moreno-López, Iñigo Olalde, Begoña Martínez-Jarreta, Susana Jiménez, Susan Walsh, Marian M. de Pancorbo (2025) Exploring the association between SNPs and facial morphology in a Spanish population. Sci Rep doi: 10.1038/s41598-025-98748-9
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Poniéndole cara a una muestra de ADN se ha escrito en Cuaderno de Cultura Científica.
La kriptonita ¡existe!
Vale… tal vez el título de este artículo sea un poco sensacionalista, pero kriptonita es lo que le apareció en 2007 en los resultados de búsqueda a Chris Stanley, mineralogista y geólogo del Museo de Historia Natural de Londres, cuando introdujo la composición de un mineral recientemente descubierto en una mina de Jadar (Serbia). Se trataba de un hidróxido de silicato de boro, litio y sodio —LiNaSiB₃O₇(OH)—, muy similar a un exótico material que aparecía expuesto en el Museo de Historia Natural de Metrópolis en la película Superman Returns, estrenada el año anterior.
 La composición de la kriptonita en Superman Returns es muy similar a la del mineral que Chris Stanley estaba analizando en 2007, salvo porque aquella también contenía flúor. Fuente: Warner Brothers / fair use
La composición de la kriptonita en Superman Returns es muy similar a la del mineral que Chris Stanley estaba analizando en 2007, salvo porque aquella también contenía flúor. Fuente: Warner Brothers / fair use
Los orígenes de la kriptonita se remontan al propio creador de Superman, Jerry Siegel, quien parece ser que ya mencionó algo así en una historia inédita de 1940 titulada «El K-Metal de Kripton», que nunca se llegó a publicar. La primera aparición oficial se produjo algo después: bien en 1943, o bien en 1945 —existen dos capítulos candidatos— en el serial radiofónico Las aventuras de Superman. No fue, sin embargo, hasta 1949 cuando hizo su aparición en el universo de los cómics del superhéroe.
Desde entonces, la kriptonita, el único talón de Aquiles de Superman, ha tomado diversas formas y colores, y ha mostrado diferentes propiedades. Empezó siendo roja, pero también la ha habido azul, negra, rosa, carmesí, dorada, plateada, blanca… y, por supuesto, verde, que es la que primero se nos viene a la cabeza a la mayoría. Sobre su composición nunca se habían dado demasiados detalles, aunque hay quien llegó a especular con que el gas noble kriptón podría estar involucrado en su fórmula…. hasta 2006, cuando apareció descrita en Superman Returns como «hidróxido de silicato de boro y litio y sodio con flúor».
 La kriptonita verde es la variante más popular. Fuente: Canva/whitehoune
La kriptonita verde es la variante más popular. Fuente: Canva/whitehoune
Seguramente, la coincidencia debió de ser una sorpresa para Chris Stanley, pero, lejos de aprovechar la conyuntura para bautizar el nuevo mineral que tenía entre manos como kriptonita —en realidad, hubiera sido confuso, ya que el mineral que tenía entre manos no contenía kriptón— se quedó con el nombre de jadarita, dado su lugar de procedencia.
Hubiera sido fantástico que la jadarita presentara un aspecto similar al de la kriptonita, pero lo cierto es que las similitudes entre ambas acaban en la fórmula. A la jadarita le falta el flúor en su composición —¡a ver si va a ser ese el ingrediente secreto!— y, aunque también tiene estructura cristalina, el tamaño de sus cristales es del orden de micras, por lo que su textura es más bien terrosa. Por otro lado, es blanca mate, en lugar de verde brillante — salvo si la irradiamos con luz ultravioleta, en cuyo caso muestra un suave brillo rosa anaranjado—, y no emite ningún tipo de radiactividad, así que parece que Superman, por el momento, no tendría de qué preocuparse.
 Muestra de jadarita. La jadarita y la kriptonita, a la hora de la verdad, no se parecen demasiado. Foto: Dungodung – Own work, CC BY-SA 4.0 / Wikimedia Commons
Muestra de jadarita. La jadarita y la kriptonita, a la hora de la verdad, no se parecen demasiado. Foto: Dungodung – Own work, CC BY-SA 4.0 / Wikimedia Commons
Sin embargo, y lejos de limitarse a una mera curiosidad geológica, la jadarita, como la kriptonita, tiene un potencial oculto: es muy rica en litio y en boro, dos elementos fundamentales en la transición energética y el desarrollo tecnológico e industrial. La mina de Jadar, donde se encuentra, es uno de los mayores depósitos de litio —y boro— del mundo, lo que la convierte en un posible recurso estratégico sin precedentes para Europa… pero cuya explotación podría conllevar daños medioambientales sin precedentes también. Un conflicto de intereses bastante propio de una película de Superman, por cierto.
El hallazgo de la jadarita, en cualquier caso, fue toda una sorpresa, y apareció en la revista Time como uno de los diez mejores descubrimientos científicos de 2007; la BBC, por su parte, lo reconoció como una de las historias más populares del año. Y nosotros… bueno, es que si hay una historia fantástica —en varias de las acepciones de la palabra— de por medio es imposible resistirse a escribir sobre ella.
Bibliografía
Stanley, Christopher J., Jones, Gary C., Rumsey, Michael S., Blake, Christopher, Roberts, Andrew C., Stirling, John A.R., Carpenter, Graham J.C., Whitfield, Pamela S., Grice, Joel D., Lepage, Yvon (2007) Jadarite, LiNaSiB3O7(OH), a new mineral species from the Jadar Basin, Serbia. European Journal of Mineralogy, 19 (4) 575-580 doi:10.1127/0935-1221/2007/0019-1741
BBC News (24 de abril de 2007). ‘Kryptonite’ discovered in mine. BBC News.
Stanley, C. (s. f.). Dr Chris Stanley. Natural History Museum
Reuters (25 de abril de 2007). Scientists unearth Superman’s “kryptonite”. Reuters.
Paul, A. (14 de julio de 2025). Yes, Superman’s kryptonite is (sort of) real. Popular Science.
Ríos, O. (17 de marzo de 2022). Superman y los diferentes tipos de kriptonita. Comicverso.
Singer, B. (Director). (2006). Superman Returns [Película]. Warner Bros. Pictures.
Stiefel, K. E. (15 de marzo de 2018). Kryptonite in Superman. Science On.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo La kriptonita ¡existe! se ha escrito en Cuaderno de Cultura Científica.
Tiras cómicas de Moebius (I)
En la sección Matemoción del Cuaderno de Cultura Científica somos unos apasionados de la banda de Moebius y de los cómics. Por este motivo, no puede extrañar a ninguna de las personas que habitualmente leéis las entradas de esta sección que nos interesemos por el uso de la banda de Moebius en los cómics.
En la entrada Matemática punk, un homenaje a Calpurnio se mostraba un ejemplo de como la banda de Moebius puede aparecer en el humor gráfico, a través de una de las viñetas de El bueno de Cuttlas titulada La banda de Moebius, del ilustrador, historietista, guionista, animador y videojockey aragonés Calpurnio, seudónimo de Eduardo Pelegrín Martínez de Pisón (1959-2022), publicado en 20 Minutos.
 El bueno de Cuttlas (La banda de Moebius), de Calpurnio, publicado en 20 Minutos
El bueno de Cuttlas (La banda de Moebius), de Calpurnio, publicado en 20 Minutos
Una novela gráfica en la que se utiliza la banda de Moebius de una forma metafórica, como símbolo del cambio de fortuna en la vida de su protagonista, de la buena a la mala fortuna, es el cómic El número 73304-23-4153-6-96-8 (La cúpula, 2008), del historietista suizo Thomas Ott, sobre la que podéis leer en la entrada De menú para hoy, dos novelas gráficas negras con salsa matemática.
 Página de la obra El número 73304-23-4153-6-96-8, de Thomas Ott, en la que su protagonista se dirige a una tienda de empeños, pawn shop, en cuyo escaparate, arriba a la izquierda, podemos observar la imagen de la banda de Moebius
Página de la obra El número 73304-23-4153-6-96-8, de Thomas Ott, en la que su protagonista se dirige a una tienda de empeños, pawn shop, en cuyo escaparate, arriba a la izquierda, podemos observar la imagen de la banda de Moebius
Por otra parte, un ejemplo muy bonito de la presencia de la banda de Moebius en un cómic es Promethea (1999-2005), del mítico guionista Alan Moore y el dibujante James H. Williams III, donde la banda de Moebius es un camino infinito de piedra por el que pasean dos de las encarnaciones de Promethea, Sophie y Barbara. Sobre las muchas matemáticas que hay en este cómic podéis leer la entrada Guía matemática para el cómic Promethea.
 Ilustración de doble página que muestra a las dos Prometheas, encarnadas por Sophie y Margaret, paseando por un camino, sin fin, con forma de banda de Moebius
Ilustración de doble página que muestra a las dos Prometheas, encarnadas por Sophie y Margaret, paseando por un camino, sin fin, con forma de banda de Moebius
En esta entrada del Cuaderno de Cultura Científica vamos a hablar de un tipo de uso diferente de la banda de Moebius en el cómic, cuando la estructura del mismo está dada por la propia superficie de Moebius, generando lo que podemos llamar una tira cómica de Moebius.
Tira cómica de Moebius
Preparando mi charla Leyendo cómics con una mirada matemática, que impartí a finales de mayo en la librería Joker de Bilbao, librería especializada en cómic que recibió el Premio Librería Cultural 2023, compartí con el público una interesante tira cómica de Moebius de la artista estadounidense Katherine Myers (@katemyyers.art en instagram).
 Portada de la presentación de la conferencia Leyendo cómics con una mirada matemática (Librería Joker, Bilbao)
Portada de la presentación de la conferencia Leyendo cómics con una mirada matemática (Librería Joker, Bilbao)
Pero antes de la tira cómica, vayamos con lo elemental, qué es una banda de Moebius (aunque muchas de las personas que estáis leyendo esta entrada quizás ya lo conocéis, nunca está de más recordar los conceptos básicos). Una banda de Moebius es una banda retorcida que podemos construir de forma sencilla de la siguiente forma. Si tomamos una tira de papel y pegamos los extremos se obtiene una banda normal, que es una superficie con dos caras (el interior y el exterior) y dos bordes (el de arriba y el de abajo), pero si primero giramos uno de los extremos del papel media vuelta y después juntamos los extremos se obtiene la banda de Moebius, una superficie que solo tiene una cara y un solo borde (como se observa en la siguiente imagen), y propiedades muy curiosas (véase el libro Las matemáticas como herramienta de creación artística (Catarata, 2023) o las entradas Arte Moebius (I) o Arte Moebius (II)).
Una de las técnicas habituales para comprobar que la banda de Moebius solo tiene una cara es empezar a pintar la tira de papel longitudinalmente, de manera que cuando lleguemos al punto de partida habremos pintado toda la superficie retorcida, es decir, la única cara de esta superficie. De hecho, si se realiza esta misma operación sobre la banda normal, sin retorcer antes de pegar los extremos, solamente pintaremos una de las caras, la exterior o la interior.
Por otra parte, una tira cómica es una historieta corta, de unas pocas viñetas, e incluso una única viñeta, cuyo formato suele ser rectangular alargado (apaisado), aunque la estructura y longitud es variable, y que se suelen publicar en periódicos y revistas. Algunos conocidos ejemplos de tiras cómicas son Mafalda (del historietista argentino Quino, Joaquín Salvador Lavado Tejón (1932-2020)), como la de la siguiente imagen, Garfield (del autor de cómics estadounidense Jim Davis), Snoopy (del historietista estadounidense Charles Schulz (1922-2000)), las tiras cómicas de Forges (el humorista gráfico madrileño Antonio Fraguas de Pablo (1942-2018)), las distintas tiras cómicas de Max (el artista catalán Francesc Capdevila), como Bardín, el superrealista, El bueno de Cuttlas de Calpurnio o las tiras cómicas, publicadas en diferentes periódicos, de El Perich (el humorista gráfico catalán Jaume Perich Escala (1941-1995)), entre muchos otros.
 Ejemplo de tira cómica de Mafalda, del historietista argentino Quino, Joaquín Salvador Lavado Tejón (1932-2020)
Ejemplo de tira cómica de Mafalda, del historietista argentino Quino, Joaquín Salvador Lavado Tejón (1932-2020)
La tira cómica de Moebius es también una historieta corta, de unas pocas viñetas, pero con algunas diferencias significativas, que funciona de la siguiente manera.
1.- Para empezar, la tira cómica de Moebius se imprime, por las dos caras, en una tira de papel apaisada, pero en la segunda cara la orientación de impresión es la contraria a la de la primera cara, es decir, girada 180 grados.
2.-Cuando se toma la tira de papel apaisada y se juntan los extremos, pero dando primero media vuelta a uno de ellos, entonces la tira de papel sobre la que está impresa la tira cómica se convierte en una banda de Moebius, de manera que solo tiene una cara.
3.-La historieta se ha impreso en las dos caras de la tira de papel apaisada, como hemos dicho, cambiando la orientación de la cara de atrás, de manera que cuando se juntan los extremos formando la banda de Moebius, la historieta que se iniciaba en la primera “cara” se continúa en la segunda “cara” sin necesidad de dar la vuelta a la “tira”.
4.-Por lo tanto, disponemos de una historieta continua que tiene el doble de longitud, pero al llegar a la parte final, como se regresa al inicio de nuevo (no olvidemos que es una superficie de Moebius, de una única cara) se puede continuar leyendo el cómic otra vez, sin interrupción, de manera que si se construye una historia circular (como veremos en la tira cómica de Moebius de la artista estadounidense Katherine Myers) tendremos una historieta infinita.
5.-Por último, mencionar que la tira cómica de Moebius, a diferencia de la tira cómica clásica, tiene una existencia independiente del periódico o revista en la que se pudiera publicar, ya que para poderla leer bien habría que cortarla del periódico y pegar sus extremos formando la tira cómica de Moebius (en la siguiente imagen se muestra la creación de Myers).
 Fotografía de la tira cómica de Moebius, creada por la artista estadounidense Katherine Myers en 2024
Fotografía de la tira cómica de Moebius, creada por la artista estadounidense Katherine Myers en 2024Una tira cómica de Moebius, por Katherine Myers
Aunque lo mejor para entender qué es una tira cómica de Moebius es ver un ejemplo concreto.
Pero antes de mostrar esta historieta infinita creada sobre una estructura tan particular, la superficie de Moebius, presentemos brevemente a la artista que la creó, Katherine Myers. Como ella misma se describe en su página web (Kate Myers), ha estudiado el grado de Animación y Efectos Especiales en la Escuela de Arte de la Universidad Carnegie Mellon (Pittsburgh, Pensilvania, EE.UU.). En su trabajo, se centra en contar historias, utilizando las convenciones de género que se encuentran a menudo en el terror y la ciencia ficción para expresarse de una manera atractiva y visceral. Le fascina la fisicalidad del cuerpo humano y emplea estrategias como los medios basados en el tiempo, el arte secuencial y los efectos prácticos para recrear texturas y formas corporales en contextos anormales e investigar temas como la mortalidad y el yo. Le encanta la accesibilidad que ofrecen tanto el cine como los medios impresos: quiere que su trabajo sea lo más accesible posible. Dirige Full Tilt Comics con su socia Maddie Smoyer y también crea efectos prácticos y de maquillaje para Just a Head Productions.
 Fotografía de Kate Myers en el PIE 2025 – Pittsburgh Indie Expo, del año 2025, en el stand de Full Tilt Comics, donde se observan algunas de sus tiras cómicas de Moebius
Fotografía de Kate Myers en el PIE 2025 – Pittsburgh Indie Expo, del año 2025, en el stand de Full Tilt Comics, donde se observan algunas de sus tiras cómicas de Moebius
Presentemos finalmente la tira cómica de Moebius de la artista Kate Myers. Está formada por seis viñetas, tres que irán impresas en la primera cara (la fila de viñetas de arriba en la siguiente imagen) y las otras tres, pero giradas 180 grados, en la segunda cara (la fila de abajo de la siguiente imagen) de la tira de papel. En la historieta aparecen dos personajes, uno de ellos es una joven que le cuenta a su interlocutora cómo le ha ido en su última cita. Veamos las seis viñetas.
 Las viñetas que van impresas en la “cara” superior y en la “cara” inferior de la tira de papel con la que se forma la tira cómica de Moebius de la artista Kate Myers
Las viñetas que van impresas en la “cara” superior y en la “cara” inferior de la tira de papel con la que se forma la tira cómica de Moebius de la artista Kate Myers
Por lo tanto, cuando la tira cómica de Moebius ya está montada, la lectura de las viñetas es la evidente y que explicamos a continuación. Primero se leen las tres viñetas de la parte de arriba de la anterior imagen. Pero después de la tercera viñeta, en la tira de Moebius, la siguiente es la primera viñeta de la parte de abajo (por el medio giro de la tira antes de pegar los extremos). Por lo tanto, se continúa la lectura con las tres viñetas de abajo. Aunque al llegar a la tercera viñeta de abajo, la siguiente en la tira de Moebius es, de nuevo, la primera viñeta de arriba, por lo que se puede continuar leyendo la historieta de una forma circular e infinita.
A continuación, incluyo una traducción del texto de la tira cómica de Moebius de Kate Myers.
Primera viñeta:
– Recientemente tuve una primera cita muy mala.
– ¿Sí?
Segunda viñeta:
– De lo único que habló fue sobre lo que cree que sucede después de morir.
Tercera viñeta:
– Él piensa que vivimos nuestras vidas una y otra vez como en un circuito cerrado.
Cuarta viñeta:
– Aunque me gusta la idea. Es reconfortante.
– ¿En qué sentido?
Quinta viñeta:
– Ya hemos tenido esta conversación antes, y la volveremos a tener de nuevo. Para siempre.
Sexta viñeta:
– ¡Guau!
– ¡Sí!
 Un montón de tiras cómicas de Moebius de la artista estadounidense Kate Myers
Un montón de tiras cómicas de Moebius de la artista estadounidense Kate MyersSobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Tiras cómicas de Moebius (I) se ha escrito en Cuaderno de Cultura Científica.
Uno de los sólidos más comunes en el universo, el LDA, no es del todo amorfo como se creía
El agua en estado sólido se supone que puede formar un vidrio, lo que se conoce como hielo amorfo de baja densidad (LDA, por sus siglas en inglés). Durante décadas el LDA ha sido considerado un sólido desordenado, casi una “instantánea congelada” del agua líquida. Sin embargo, un nuevo estudio demuestra algo notable: este tipo de hielo no sería completamente amorfo, sino que contendría cristales diminutos en su seno. Las implicaciones de algo aparentemente tan trivial son enormes.
Dos modelos y un experimento muy ingeniosoEl equipo de investigación recurrió a dos modelos computacionales muy utilizados en las simulaciones de las masas de agua para recrear el LDA. Ambos modelos —uno que simula el enfriamiento desde agua líquida y otro que reproduce el proceso de vitrificación desde un estado cristalino— no lograron generar un sólido totalmente caótico, amorfo. En cambio, en los dos casos surgieron nanocristales dispersos en la estructura amorfa.
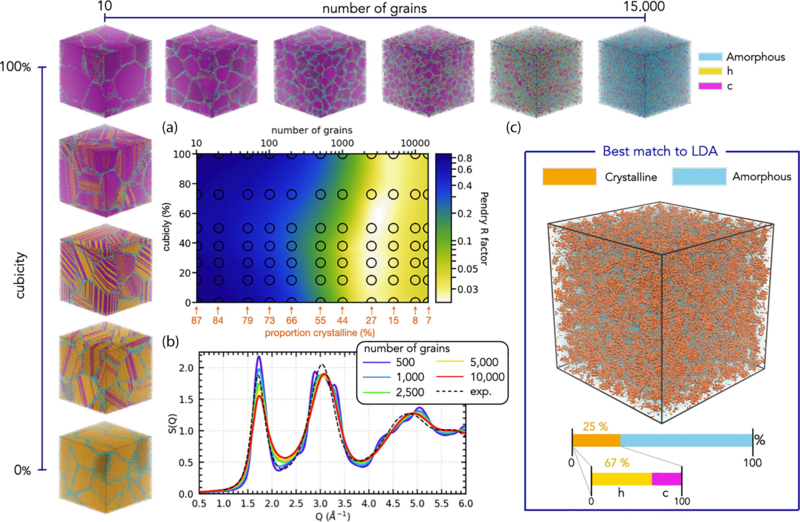 Fuente: M.B. Davies et al (2025) Physical Review B doi: 10.1103/PhysRevB.112.024203
Fuente: M.B. Davies et al (2025) Physical Review B doi: 10.1103/PhysRevB.112.024203Para validar estos resultados, los científicos complementaron las simulaciones con experimentos en el laboratorio muy ingeniosos. Produjeron hielo LDA a partir de dos rutas distintas: como deposición de vapor a muy baja temperatura y como calentamiento de hielo amorfo de alta densidad. Si el LDA fuese verdaderamente amorfo ambas rutas deberían obtener el mismo resultado. Sin embargo, comprobaron que, tras recristalizar, cada muestra mostraba diferencias en la proporción de estructuras cristalinas hexagonales. Esta “memoria” de la ruta de formación solo es posible si existen cristales microscópicos en el material
Este enfoque combinado, datos experimentales y modelado computacional, apunta a que el LDA no es un vidrio puro sino una forma parcialmente cristalina de hielo. Según los autores, la proporción estimada de cristales puede alcanzar hasta un 20 % del volumen total del material.
El LDA es uno de los sólidos más comunes del universo¿Por qué importa este hallazgo? En primer lugar, porque revela la verdadera naturaleza de uno de los sólidos más comunes en el universo. El LDA se encuentra en cometas, nubes moleculares del espacio profundo e incluso en las capas superiores de las atmósferas planetarias. Si su estructura es parcialmente cristalina, esto puede alterar cómo interactúa con la luz, cómo se funde y cómo influye en la química del entorno.
LDA y las anomalías del aguaEn segundo lugar, esta conclusión tiene implicaciones para entender las famosas “anomalías” del agua — fenómenos como su máxima densidad a 4 °C o la existencia de dos posibles estados líquidos en condiciones extremas. El hecho de que el LDA carezca de un equivalente líquido perfectamente correspondiente desafía ciertas teorías sobre el comportamiento del agua superenfriada En otras palabras, la existencia de estos nanocristales pone en entredicho el papel del LDA como referencia estructural para estudiar el agua en condiciones extremas.
Este hallazgo no solo refina nuestra comprensión del agua en condiciones extremas, sino que también invita a reevaluar qué entendemos por estructuras amorfas. Incluso en los sistemas aparentemente más desordenados, la naturaleza parece esconder un grado inesperado de organización.
Referencias:
M.B. Davies et al (2025) Low-density amorphous ice contains crystalline ice grains Physical Review B doi: 10.1103/PhysRevB.112.024203
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Uno de los sólidos más comunes en el universo, el LDA, no es del todo amorfo como se creía se ha escrito en Cuaderno de Cultura Científica.
Las anaranjadas perlas de la Luna
A nuestra escala -la de la humanidad- la Luna ha permanecido en el cielo como un cuerpo gris e inmutable. Su rostro, completamente cubierto de cráteres, nos hace pensar en un mundo geológicamente muerto, casi fósil. Pero no siempre fue así. Nuestra Luna, al igual que la Tierra, también tuvo una juventud fiera y volátil.
Hace unos 3500 millones de años, ocurrieron sobre la superficie lunar fenómenos volcánicos como las fuentes de lava, impulsadas por la expansión de burbujas de gas que procedían del interior del manto lunar. Estas erupciones -que estaban ocurriendo en el casi vacío del espacio- eran muy diferentes a las que ocurren en la Tierra. Gracias a los minúsculos restos de vidrio formados durante estos eventos, los científicos están comenzando a descifrar algunos secretos lunares que hasta ahora habían pasado desapercibidos.
Un nuevo estudio publicado en Icarus por Williams et al. (2025) ofrece una nueva perspectiva sobre este tipo de erupciones gracias al estudio a escala microscópica de unas pequeñas “perlas” de vidrio volcánico que trajeron a nuestro planeta los astronautas de la misión Apolo 17 y que ha permitido reconstruir la presión, la temperatura y la composición de la nube de gases volcánicos fruto de una erupción, abriéndonos la puerta a comprender mejor los mecanismos eruptivos en la Luna.
 Imagen de una de las “trincheras” excavadas para que aflorasen mejor las perlas de color anaranjado. Destaca mucho la diferencia de color entre el regolito de color gris y el anaranjado que hay por debajo de la capa superficial. Imagen cortesía de la NASA.
Imagen de una de las “trincheras” excavadas para que aflorasen mejor las perlas de color anaranjado. Destaca mucho la diferencia de color entre el regolito de color gris y el anaranjado que hay por debajo de la capa superficial. Imagen cortesía de la NASA.La historia del estudio de vidrios lunares comienza en 1972, en el valle de Taurus-Littrow. Los astronautas de la misión Apolo 17 Eugene Cernan y Harrison Schmitt hicieron un descubrimiento asombroso e inesperado en el llamado cráter Shorty: una pequeña zona anaranjada como un oasis entre el infinito gris del regolito lunar.
Schmitt: ¡Oh, hey! ¡Espera un momento!
Cernan: ¿Qué?
Schmitt: ¿… dónde están esos reflejos? Ya me han engañado en otras ocasiones. ¡Hay tierra de color naranja!
Cernan: ¡Bien, no te muevas hasta que no lo vea!
Schmitt: ¡Está por todas partes! ¡Naranja!
Cernan: No te muevas hasta que lo vea.
Schmitt: Lo he removido con mis pies.
Cernan: ¡Hey, aquí está! ¡Puedo verlo desde aquí!
Schmitt: ¡Es naranja!
Cernan: Espera un momento, que subo la visera. ¡Sigue siendo naranja!
Schmitt: ¡Claro que lo es! ¡Que locura! ¡Naranja! Tengo que excavar una trinchera, Houston.
Este suelo naranja al que se refieren en la transcripción de la conversación, junto con el suelo más oscuro de alrededor, estaba formado por incontables pequeñas “perlas” de vidrio anaranjado, restos de un magma enfriado rápidamente y arrojados al cielo durante la erupción mediante fuentes de lava. Los astronautas recogieron estas muestras en tubos de muestras, los sellaron y protegieron de la contaminación de la atmósfera terrestre para su posterior estudio.
Durante décadas, los científicos habían pensado que estas perlas tenían algo de especial. Mientras las gotas de roca fundida viajaban a través del gas expulsado por la erupción, funcionaban como una especie de esponja en miniatura. Conforme estas gotas se alejaban de la parte central de la pluma de gases emitidos por la erupción, mucho más densa y caliente, algunos elementos se condensaron directamente sobre la superficie de estas perlas, recubriéndolas.
Estas coberturas, conocidas como sublimados, son como una especie de “fantasma” de la pluma de gases volcánica, aportándonos un registro directo de su química. Pero hasta ahora, el problema era leer su mensaje, ya que, con menos de 100 nanómetros de espesor, estas capas de minerales son muy frágiles, reactivas con la atmósfera terrestre y, por lo tanto, muy difíciles de analizar.
 El astronauta y geólogo norteamericano Harrison Schmitt es uno de los protagonistas de esta historia. Aquí lo podemos ver con un gigantesco bloque de roca fragmentado que probablemente provenga de la formación de un cráter de impacto. Imagen cortesía de NASA.
El astronauta y geólogo norteamericano Harrison Schmitt es uno de los protagonistas de esta historia. Aquí lo podemos ver con un gigantesco bloque de roca fragmentado que probablemente provenga de la formación de un cráter de impacto. Imagen cortesía de NASA.Es en esta dificultad del estudio de estas muestras donde destaca este nuevo estudio. Los autores han podido trabajar con las muestras de unas perlas de vidrio oscuro que nunca han sido expuestas al aire de la atmósfera terrestre y que aparecen también junto a las anaranjadas.
Mediante unas técnicas de estudio microscópico han podido hacer observaciones tanto a nivel morfológico como químico. No ha sido una tarea fácil, ya que, desde la apertura del tubo donde estaba esta muestra hasta el moverlas entre los distintos instrumentos, se ha tenido que hacer en una atmósfera de nitrógeno puro o en vacío. Algo que no es precisamente pan comido, pero necesario para poder realizar el estudio con las garantías de que al menos no habría alteraciones químicas en la superficie de las perlas.
Este meticuloso análisis ha conseguido descifrar una historia escrita en las distintas capas de las perlas. Una de las cosas que más han llamado la atención de los científicos es la aparición de unos “montículos” microscópicos y con forma semiesférica. Estos están formados por la esfalerita policristalina, un sulfuro de cinc.
Para que se forme la esfalerita, la nube de gas volcánico tiene que contener -obviamente- azufre y cinc. Pero más importante es este otro detalle: su formación apunta directamente a otro elemento, el hidrógeno. Los modelos termodinámicos nos cuentan que en una nube de gas pobre en hidrógeno, el cinc prefiere enlazarse con el cloro para formar cloruro de cinc. La prevalencia del sulfuro de cinc en estas perlas es una fuerte evidencia de que el gas volcánico era rico en hidrógeno en comparación con los elementos halógenos (flúor, cloro, bromo, yodo y astato). Esta prueba sirve como apoyo a la teoría de que el manto lunar no está totalmente seco, sino que contiene grandes cantidades de elementos volátiles que eran capaces de impulsar estas erupciones.
Pero cuando los investigadores pudieron observar más de cerca estos montículos de esfalerita, descubrieron también un gradiente químico muy sutil, pero consistente entre los montículos: en la base, donde se unen a la perla de vidrio, estaban especialmente enriquecidos en hierro con respecto a la cima del montículo. Esta distribución, según interpretan los autores, nos cuenta la historia del viaje de la perla por la nube de gas.
Los modelos muestran que el sulfuro de hierro se condensa a temperaturas más altas y menores presiones que el sulfuro de cinc. Esto significa que conforme la perla sale disparada de la fisura volcánica, pasa primero por una región más densa y caliente donde se enriquecería en el hierro.
Conforme viajara hacia afuera de la nube de gas, hacia las zonas más frías y con menor presión, este cambio en las condiciones favorecería el depósito de las capas ricas en cinc sobre las anteriores. Esto sirve como una especie de registro de las condiciones de presión y temperatura dentro de la misma nube de gas, y del rápido viaje de la perla a través de esta.
 Imagen de las “perlas” de color anaranjado vistas al microscopio. Las más grandes de la imagen están en torno a las 40 micras. Cortesía de NASA/JSC.
Imagen de las “perlas” de color anaranjado vistas al microscopio. Las más grandes de la imagen están en torno a las 40 micras. Cortesía de NASA/JSC.Los investigadores han encontrado otras morfologías sobre la superficie que se habrían superpuesto sobre los montículos, lo que también sugiere que hay un orden en el depósito de otros minerales sobre las perlas. Y este detalle implicaría lo siguiente: No todas las perlas siguieron la misma trayectoria, sino que unas pudieron seguir una más corta antes de caer sobre la superficie y en la que solo dio tiempo a formar los montículos y otras que salieron disparadas mucho más altas y que por lo tanto tuvieron tiempo de quedar recubiertas de una manera más compleja al pasar más tiempo por la pluma de gases de la erupción.
Y, por último, nos falta la interpretación de la propia erupción a partir de estos datos. Los científicos han comparado las perlas de color oscuro con las famosas perlas naranjas. Mientras que las oscuras están recogidas de aproximadamente medio metro de profundidad, las naranjas estaban a muy pocos centímetros de la superficie. Los investigadores piensan que el depósito de estos materiales volcánicos ocurrió en una sola erupción, y por lo tanto su posición estratigráfica es importante: las perlas oscuras se depositaron antes que las naranjas.
Los análisis que se habían realizado anteriormente de las perlas naranjas habían mostrado que los sublimados no estaban compuestos principalmente por sulfuro de cinc, sino por cinc metálico que posteriormente había reaccionado para dar lugar a otros minerales. Los modelos termodinámicos muestran que para que se precipite el cinc nativo en vez de la esfalerita, la presión del gas en la nube tuvo que ser extremadamente baja, órdenes de magnitud por debajo a la presión a la que se forma el sulfuro de cinc.
Esto nos da una pista fundamental sobre la erupción: es posible que comenzase con una presión muy alta, creando una densa nube de gas que provocó el depósito rico en sulfuro de hierro y cinc sobre las primeras perlas de vidrio negro. Con el tiempo, la fuerza de la erupción fue disminuyendo -como ocurre en las erupciones terrestres-, la nube de gas comenzó a ser menos densa y las perlas naranjas se fueron recubriendo del cinc en estado nativo.
Los diferentes recubrimientos de las perlas, separadas por apenas unas decenas de centímetros en el regolito lunar, sirven como un testimonio de la variación en la intensidad de la erupción a lo largo del tiempo, como si pudiésemos ver una película que ha quedado registrada en minúsculos detalles de la geología lunar.
Este trabajo nos abre una ventana para refinar los modelos de funcionamiento del vulcanismo lunar y de la composición de su interior, pero también demuestra que la Luna era un mundo con sistemas volcánicos que evolucionaban y eran químicamente diversos. Y nos debe recordar que, aunque no hayamos vuelto a la Luna -el ser humano, me refiero-, las muestras que se tomaron durante las misiones Apolo todavía tienen mucho que contarnos… ¿Qué secretos aguardarán a ser descubiertos?
Referencias:
Williams, T. A., Parman, S. W., Saal, A. E., Akey, A. J., Gardener, J. A., & Ogliore, R. C. (2025). Lunar volcanic gas cloud chemistry: Constraints from glass bead surface sublimates Icarus, 438, 116607. doi: 10.1016/j.icarus.2025.116607
Fuente de la conversación: N.G. Bai ley and G.E. Ulrich (1975) APOLLO 17 VOICE TRANSCRIPT Pertaining to the geology of the landing site U.S. Geological Survey – Branch of Astrogeology
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Las anaranjadas perlas de la Luna se ha escrito en Cuaderno de Cultura Científica.
Confirmado: El «hombre dragón» es denisovano
 Reconstrucción artística de la apariencia que tendría un denisovano. Ilustración: Chuang Zhao
Reconstrucción artística de la apariencia que tendría un denisovano. Ilustración: Chuang Zhao
Hay quien suele imaginar el camino evolutivo del ser humano como una línea recta que se mueve directa desde nuestros orígenes en África hasta la actualidad, en nuestras ciudades, con ordenadores, coches y teléfonos. Es bastante conocida la viñeta que muestra una ordenada sucesión de figuras, desde el primate encorvado hasta el señor erguido vistiendo orgulloso un traje. A veces se representa la evolución como un árbol, con un tronco común del que nacen diferentes ramas que se extiende de manera independiente creciendo o cortándose abruptamente. La realidad es mucho más compleja y difícil de visualizar, una especie de embrollada madeja con docenas de hilos que no solo se enredan, se anudan o se cruzan, sino que pueden mezclarse dando lugar a nuevos hilos. Homo sapiens, Homo habilis, Homo rudolfensis, Homo heidelbergensis, Homo neanderthalensis, Homo floresiensis, Homo naledi, Homo denisovensis… las hebras son tan variadas y traviesas que se enmarañan con el tiempo y representan un quebradero de cabeza para los científicos que, además, a menudo se ven obligados a trabajar con solo un trocito de ellas.
Uno de los cabos sueltos en ese confuso ovillo de especies del género Homo apareció no hace mucho. En 2008, un equipo de investigadores del Max Planck encabezados por Svante Pääbo, que diez años más tarde ganaría el Premio Nobel de Medicina, analizó un pequeño fragmento de hueso del dedo meñique de una niña, encontrado en las cuevas de Denísova, en los montes Altái de Siberia. Los resultados genéticos fueron sorprendentes. El ADN mitocondrial de aquella niña ofrecía pistas de linajes bien conocidos pero no se podía clasificar claramente como sapiens o como neandertal. La madeja se enredaba aún más. Más adelante, cuando se logró secuenciar su genoma nuclear completo, la conclusión apuntaba a que esa niña estaba más emparentada con los neandertales, con quienes compartió un antecesor común, antes de divergir hace aproximadamente unos 400.000 años. La cueva se convirtió en un buen filón de pistas y, desde entonces, se han encontrado diferentes artefactos y herramientas, así como otros restos humanos. Un molar (bastante grande), varios dientes más, y un puñado de pequeños fragmentos óseos pertenecientes a diferentes estratos y, por tanto a diferentes épocas. Posteriores estudios ayudaron a concluir que nos encontrábamos ante un linaje de humanos diferente al que, en honor a la cueva donde se descubrieron, se bautizó como los denisovanos. La escasez de restos fósiles obligó a aguzar el ingenio de los investigadores y el Homo denisovanis se convirtió en la primera especie humana que se catalogó utilizando ADN y descubriendo que los denisovanos no solo convivieron con sapiens y neandertales, sino llegaron a tener descendencia con ambos.
Lo que no podían sospechar todos los científicos que luchaban por trabajar con esos limitados y escasos restos es que existía un gran cráneo denisovano, oculto desde hace décadas, sin que nadie lo supiera. En 1933, setenta y cinco años antes del primer descubrimiento denisovano, un hombre participaba en la construcción de un puente cerca de la ciudad de Harbin, en China. Por aquel entonces el ejército japonés ocupaba el norte de China y obligaba a un grupo de soldados chinos capturados a trabajar en aquella infraestructura. De entre los escombros, surgió una calavera, incompleta, extraña y diferente. Uno de los soldados chinos la cogió y la escondió de sus enemigos, pensando que tenía en su poder algo valioso. Durante décadas no compartió su hallazgo con nadie, incluso llegó a ocultarla en un pozo cerca de su casa para que no se la quitaran y así pasaron los años. Poco antes de su muerte, aquel hombre reunió a su familia y les habló del pozo y del «precioso tesoro» que guardaba, seguía creyendo que ese insólito cráneo tenía un gran valor. En 2018, sus nietos herederos lo encontraron, lo sacaron del pozo y, lejos de hacerse ricos con él, lo donaron a la Universidad GEO de Hebei.
El soldado había fallecido sin aclarar el lugar exacto donde había encontrado el cráneo y el equipo de paleoantropólogos de Hebei, liderados por Quian Ji, junto a otros expertos en datación y geocronología de la Universidad Griffith, en Australia, tuvieron que esforzarse para confirmar su procedencia. Analizaron isótopos de estroncio incrustados en las fosas nasales del cráneo con una capa específica de sedimentos alrededor del puente y pudieron llegar a una primera aproximación de su edad, entre 138.000 y 309.000 años. Más tarde llegarían estudios de datación por uranio que lo situaban, como mínimo, en 146.000 años.
Realmente era un cráneo extraño, visiblemente más grande que cualquiera que se hubiera encontrado jamás. Realizaron una reconstrucción del cráneo encontrado en Harbin y llegaron a la conclusión de que «pertenecía a un varón de mejillas planas, boca ancha y carente de barbilla. Una imponente frente colgaba sobre sus ojos hundidos y su nariz bulbosa. Y dentro de su enorme cráneo había un cerebro descomunal, que medía un 7 % más que el cerebro medio de un ser humano actual».
 El cráneo encontrado en el puente cerca de Harbin, China en 1933 | Qiang Ji, Wensheng Wu et al. (2021) Cell doi: 10.1016/j.xinn.2021.100132 CC BY-ND 4.0
El cráneo encontrado en el puente cerca de Harbin, China en 1933 | Qiang Ji, Wensheng Wu et al. (2021) Cell doi: 10.1016/j.xinn.2021.100132 CC BY-ND 4.0
En 2021, los investigadores publicaron sus resultados en Cell, describiendo el cráneo e indicando que correspondía a «un homínido extinto masivo en tamaño con una longitud craneal máxima muy grande, tanto en longitud nasiooccipital como en anchura del toro supraorbitario; bóveda craneal larga y baja, con frontal retraído, contorno parietal uniformemente curvado y contorno occipital redondeado; sin quilla sagital; cara superior extremadamente ancha, con órbitas grandes y casi cuadradas; altura facial baja en relación con la anchura facial superior; toro supraorbitario ancho, masivamente desarrollado y suavemente curvado». Estaban entusiasmados y concluyeron que ese cráneo, con todos esos rasgos diferenciados, debía pertenecer a una especie propia. La llamaron Homo longi, en honor a Longjian, la región donde se encontró el cráneo. Longjian significa gran dragón y, consecuentemente, al gran cráneo datado en el Pleistoceno medio tardío se le terminó conociendo como «el hombre dragón», un suculento nombre que abrió muchas portadas por aquellos años.
 Reconstrucción virtual en 3D del cráneo del «hombre dragón» encontrado en el puente de Harbin, China. Fuente: Xijun Ni et al (2021) The Innovation doi: 10.1016/j.xinn.2021.100130 CC BY-ND 4.0
Reconstrucción virtual en 3D del cráneo del «hombre dragón» encontrado en el puente de Harbin, China. Fuente: Xijun Ni et al (2021) The Innovation doi: 10.1016/j.xinn.2021.100130 CC BY-ND 4.0
El sueño de cualquier paleontólogo es descubrir una nueva especie, ser recordado por encontrar y bautizar un nuevo hilo de la compleja madeja humana, sin embargo ese anhelo puede desembocar, y de hecho así ocurre frecuentemente, en prisas y confusiones. La emoción por el nuevo descubrimiento pronto fue sustituido por críticas en diversos medios especializados y muchos expertos expresaron sus dudas al artículo publicado en Cell. Entre ellos destaca la voz autorizada de María Martinón (CENIEH) que, en un artículo publicado en Science en 2021, afirmaba que «es prematuro nombrar una nueva especie, especialmente un fósil sin contexto y con contradicciones en el conjunto de datos». Cuanto más se analizaba más fuerza tomaba la idea de que el «hombre dragon» podría representar no una nueva especie humana, sino el primer cráneo de un denisovano.
Por supuesto, cada vez que surge una hipótesis en ciencia también aparecen científicos dispuestos a corroborarla o echarla por tierra. La primera en saltar al escenario fue Qiaomei Fu, una genetista china del Instituto de Paleoantropología de Pekin que trabajaba en el primer ADN denisovano procedente del pequeño hueso de Siberia. Comparar ese ADN denisovano de la niña de la cueva de Denísova con el ADN del cráneo del «hombre dragón» despejaría todo el misterio. Intentaron extraer material genético de una parte del cráneo llamada hueso petroso (que suele ser una buena fuente) y también de un diente adherido a la mandíbula superior (la inferior no se ha conservado). No lo consiguieron, pero sí lograron secuenciar fragmentos de 95 proteínas antiguas que compararon con secuencias de humanos modernos, neandertales y, cómo no, sus muestras del hueso denisovano. No encontraron correlación con los dos primeros pero sí descubrieron una secuencia proteica idéntica, tanto en la niña de Denísova como en el cráneo de Harbin… Esto sugería que el «hombre dragón» sí que podría ser denisovano… pero sin ADN que lo confirmase, no era suficiente.
 En rojo la localización de los 0,3 mg de cálculo dental extraídos del cráneo de Harbin, donde se capturó y secuenció el ADNmt. Fuente: Qiaomei Fu, Peng Cao, et al. (2025) Cell doi:10.1016/j.cell.2025.05.040 CC BY-ND 4.0
En rojo la localización de los 0,3 mg de cálculo dental extraídos del cráneo de Harbin, donde se capturó y secuenció el ADNmt. Fuente: Qiaomei Fu, Peng Cao, et al. (2025) Cell doi:10.1016/j.cell.2025.05.040 CC BY-ND 4.0
Qiaomei Fu no se dio por vencida y, unos años más tarde, lo ha conseguido. «En lugar de buscar material genético en el propio cráneo, ella y su equipo rasparon un pequeño fragmento de placa dental fosilizada, o cálculo dental, de la raíz ennegrecida del único molar restante del cráneo». Aunque el cálculo contiene menos ADN antiguo que el que se encuentra habitualmente en huesos o dientes, su estructura mineral permite preservar mejor su contenido. Fue un momento emocionante. El equipo de Fu logró raspar apenas 0,3 miligramos de cálculo de ese diente. Puede parecer muy poco, y mucho menos si tenemos en cuenta que «casi cuatro quintas partes de ese material genético extraído provenían de contaminación moderna», pero con lo que quedó pudieron conseguir el ADN que necesitaban. Sus resultados se han publicado hace unos días en la Revista Cell y confirman que coinciden con el ADN mitocondrial de genomas denisovanos previamente secuenciados, lo que confirma que «el hombre dragón» es de hecho un denisovano.
Referencias científicas y más información:
Qiaomei Fu, Peng Cao, et al. (2025) Denisovan mitochondrial DNA from dental calculus of the >146,000-year-old Harbin cranium Cell doi:10.1016/j.cell.2025.05.040
Marshall, Michael (2025) Who Were the Ancient Denisovans? Fossils Reveal Secrets about the Mysterious Humans Nature doi:10.1038/d41586-025-01549-3.
Lewis, Dyani (2025) First Ever Skull from ‘Denisovan’ Reveals What Ancient People Looked Like Nature DOI:10.1038/d41586-025-01899-y.
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico multimedia. Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Confirmado: El «hombre dragón» es denisovano se ha escrito en Cuaderno de Cultura Científica.
Sobrarbe-Pirineos: qué hacemos en un geoparque de montañas

¿Qué tienen en común un paisaje espectacular, un fósil milenario y una cantera abandonada? Todos forman parte del patrimonio geológico, un testimonio de la historia de la Tierra con un gran valor científico, educativo, cultural y estético, y base del patrimonio natural. Sin embargo, su importancia continúa siendo poco apreciada.
Para acercar las distintas aproximaciones del patrimonio geológico a la sociedad, los días 26, 27 y 28 de marzo se celebró la quinta edición de las jornadas divulgativas “Geología para poetas, miopes y despistados. Patrimonio patrimonio”. Organizadas por el grupo de investigación consolidado Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco (UPV/EHU), estas jornadas contaron con la colaboración del Vicerrectorado del Campus de Bizkaia, la Cátedra de Cultura Científica de la UPV/EHU, el Geoparque de la Costa Vasca / Geoparkea y el Ente Vasco de la Energía (EVE).
Los geoparques no son solo curiosidades científicas, también son motores de desarrollo de las áreas donde se implantan. Los geoparques de montaña son muy particulares. Ánchel Belmonte las describe en esta conferencia.
Ánchel Belmonte Ribas es doctor en Geología y Coordinador de la Comisión Científico Asesora del Geoparque Mundial UNESCO Sobrarbe-Pirineos.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Sobrarbe-Pirineos: qué hacemos en un geoparque de montañas se ha escrito en Cuaderno de Cultura Científica.
PCSK9, sospechoso habitual
La proteína PCSK9 (del inglés Proprotein Convertase Subtilisin/Kexin type 9) es miembro de una familia de proteínas llamadas proproteínas convertasas. Dentro de la familia, PCSK9 fue la última en descubrirse y difiere de las demás por su comportamiento. Aquellas personas que tienen problemas de hipercolesterolemia probablemente tengan conocimiento de su existencia puesto que las personas que no responden a tratamientos clásicos como las estatinas se medican con inhibidores de PCSK9.
¿Qué hace PCSK9?PCSK9 es una enzima que tiene la capacidad de cortar otras proteínas como si fuera una tijera, pero en la mayoría de las ocasiones no hace uso de esa cualidad más que consigo misma. Antes de que se produzca el corte, PCSK9 no es funcional; de ahí la importancia de que se corte a sí misma para que se vuelva activa. La proteína, una vez procesada, funciona principalmente como transportadora. Se une a otras proteínas para llevarlas a orgánulos determinados donde son procesadas.
PCSK9 en la hipercolesterolemia
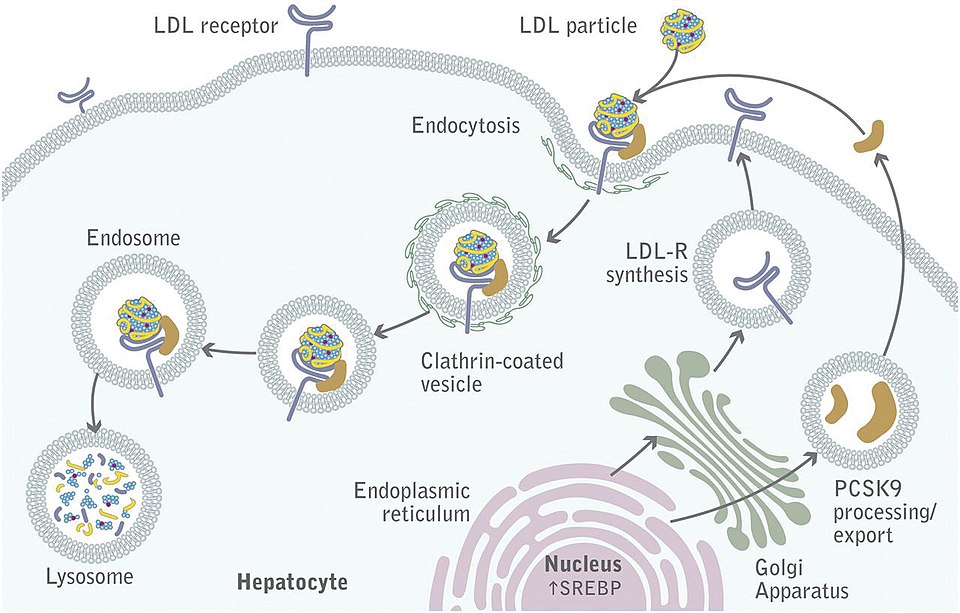 PCSK9 en los hepatocitos. Fuente: Gilles Lambert, Barbara Sjouke, Benjamin Choque, John J.P. Kastelein, G. Kees Hovingh – doi: 10.1194/jlr.R026658 CC BY 4.0 / Wikimedia Commons
PCSK9 en los hepatocitos. Fuente: Gilles Lambert, Barbara Sjouke, Benjamin Choque, John J.P. Kastelein, G. Kees Hovingh – doi: 10.1194/jlr.R026658 CC BY 4.0 / Wikimedia CommonsEn el caso de la hipercolesterolemia se ha visto que PCSK9 se une al receptor del colesterol LDL (lipoproteína de baja densidad, del inglés low density lipoprotein); también llamado coloquialmente colesterol malo por su papel en la ateroesclerosis; en los hepatocitos del hígado. El hígado es el órgano que procesa el colesterol que circula por la sangre. Para ello, los hepatocitos que son las células funcionales del hígado tienen unas proteínas que se llaman receptores, los cuales son específicos para diferentes tipos de moléculas. Uno de estos receptores es el del colesterol LDL. Este receptor capta el colesterol LDL de la sangre y se procesa dentro del hepatocito. La proteína PCSK9 tiene la capacidad de unirse al receptor del colesterol LDL que se encuentra anclado sobre la membrana del hepatocito y lo transporta al lisosoma, orgánulo donde se da la degradación del receptor. De esta manera, un alto contenido de PCSK9 celular provoca la destrucción de los receptores de colesterol LDL de los hepatocitos; el colesterol LDL no se internaliza y se acumula en la sangre.
PCSK9 y cáncer
La hipercolesterolemia no es la única patología en la cual se ha identificado a PCSK9. También se ha observado que algunos tumores poseen grandes cantidades de esta proteína. En algunos tipos de tumores como es el caso del cáncer colorrectal, el cáncer de estómago o el cáncer del cuello del útero, se ha visto que PCSK9 también realiza el papel de transportador. En estos casos transporta la proteína MHC I (del inglés Major Histoconpatibiity Complex type I) o complejo mayor de histocompatibilidad clase I. Este complejo formado por proteínas aparece en todas nuestras células nucleadas y su función es presentar antígenos a las células del sistema inmune. Los antígenos son pequeños trozos de proteínas capaces de producir una reacción inmunitaria. Si nuestro cuerpo detecta un antígeno que no es propio como puede ser un fragmento de la proteína de un virus, las células del sistema inmune lo reconocerán y comenzará la respuesta inmunitaria. De esta manera cuando un tumor se va desarrollando, las células aberrantes expresan antígenos modificados también llamados neoantígenos que son presentados a través del MHC I y las células del sistema inmune los reconocen como extraños y atacan a las células tumorales. Tal y como ocurre con el receptor del colesterol LDL, PCSK9 transporta el complejo MHC I a los lisosomas donde se degrada y las células tumorales no visibilizan sus neoantígenos, de esa manera los tumores se vuelven invisibles para las células del sistema inmune y de ahí su agresividad.
Tratamientos contra PCSK9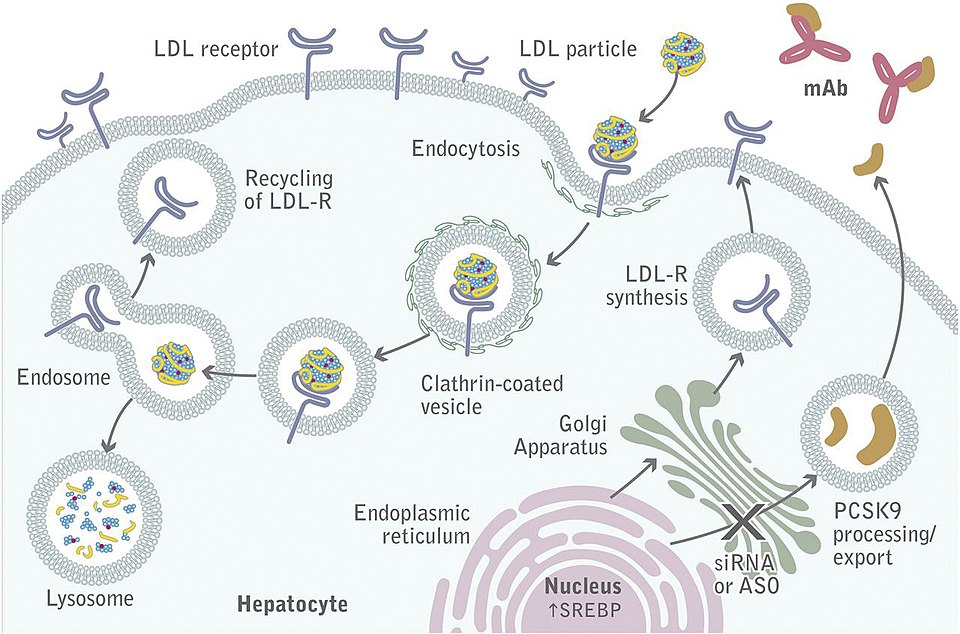 Los anticuerpos monoclonales (mAb) bloquean la acción de PCSK9 permitiendo el reciclado del receptor de LDL. Fuente: Gilles Lambert, Barbara Sjouke, Benjamin Choque, John J.P. Kastelein, G. Kees Hovingh – doi: 10.1194/jlr.R026658 CC BY 4.0 / Wikimedia Commons
Los anticuerpos monoclonales (mAb) bloquean la acción de PCSK9 permitiendo el reciclado del receptor de LDL. Fuente: Gilles Lambert, Barbara Sjouke, Benjamin Choque, John J.P. Kastelein, G. Kees Hovingh – doi: 10.1194/jlr.R026658 CC BY 4.0 / Wikimedia CommonsLos primeros tratamientos que se desarrollaron contra PCSK9 se diseñaron para atajar los problemas de hipercolesterolemia. Se desarrollaron anticuerpos que bloqueaban la acción de PCSK9 impidiendo su unión a los receptores de colesterol LDL o más recientemente se ha usado la tecnología del pequeño ARN interferente, que permite el silenciamiento a nivel de ARN. Es evidente que, visto el papel de PCSK9 en el cáncer, nos puede surgir la pregunta de si estos medicamentos pueden ser también útiles contra esta enfermedad. Por ello, la investigación actual parece ir en la línea de describir nuevas aplicaciones para estos inhibidores de PCSK9 dado que, al haber superado ya todas las medidas de seguridad requeridas por las agencias que regulan la comercialización de los medicamentos, su utilización como terapia antitumoral podría aplicarse de forma segura en mucho menos tiempo que los nuevos medicamentos.
Bibliografía
Xinjian Liu, Xuhui Bao, Mengjie Hu, Hanman Chang, Meng Jiao, Jin Cheng, Liyi Xie, Qian Huang, Fang Li, Chuan-Yuan Li (2020) Inhibition of PCSK9 potentiates immune checkpoint therapy for cancer Nature doi: 10.1038/s41586-020-2911-7
Roth EM, Davidson MH (2018) PCSK9 Inhibitors: Mechanism of Action, Efficacy, and Safety Rev Cardiovasc Med doi: 10.3909/ricm19S1S0002
Melendez QM, Krishnaji ST, Wooten CJ, Lopez D. (2017) Hypercholesterolemia: The role of PCSK9 Arch Biochem Biophys. doi: 10.1016/j.abb.2017.06.001
Sobre los autores: Ander Martín es doctor en biotecnología e investigador en la Facultad de Medicina y Enfermería de la UPV/EHU, e Iker Badiola Etxaburu es doctor en biología, Profesor Pleno en la Facultad de Medicina y Enfermería de la UPV/EHU, y director de la Cátedra de Cultura Científica de la UPV/EHU
El artículo PCSK9, sospechoso habitual se ha escrito en Cuaderno de Cultura Científica.
Un volcán escondido… a la vista de todos
En los últimos cuatro años, el rover Perseverance ha estado investigando la inmensa cuenca formada por el cráter Jezero buscando signos de la existencia de vida en el pasado remoto del planeta Marte, cuando este lugar era muy diferente y albergaba un profundo lago al que llegaban las aguas desde distintos ríos y en el que incluso existía un delta cuya forma todavía se intuye desde el espacio. Pero al comenzar su andadura, el rover descubrió que todas las rocas del fondo no eran sedimentarias -como uno podría esperar del fondo de un lago- sino que también había rocas ígneas, formadas a partir de un magma que se enfría.
Esta primera sorpresa ayudó a los científicos a confirmar la hipótesis de que el cráter Jezero no solo había sido transformado por la actividad del agua, sino que también existían otros procesos activos. Y es que, si el fondo del cráter estaba cubierto por materiales volcánicos, ¿de dónde procedían? Porque tampoco es que hubiese ningún volcán cercano… al menos en apariencia.
Pero en un nuevo estudio publicado por Cuevas-Quiñones et al. (2025) en Communications Earth & Enviroment parece haber encontrado un volcán que habría permanecido escondido a la vista de todos, aunque suene contradictorio. Este, en realidad, estaría en una montaña que aparece en el borde sureste del cráter Jezero y que oficialmente se denomina Jezero Mons.
 En el centro de la imagen podemos ver el cráter que se encuentra sobre la cima de Jezero Mons, con una forma ovalada y una abertura. En la esquina inferior izquierda podemos observar también una parte del perfil del cráter Jezero, notable especialmente por su superficie más llana y suave que el terreno que le rodea. Imagen cortesía de NASA/JPL/ASU.
En el centro de la imagen podemos ver el cráter que se encuentra sobre la cima de Jezero Mons, con una forma ovalada y una abertura. En la esquina inferior izquierda podemos observar también una parte del perfil del cráter Jezero, notable especialmente por su superficie más llana y suave que el terreno que le rodea. Imagen cortesía de NASA/JPL/ASU.Desde el sitio de aterrizaje del Perseverance, Jezero Mons domina una buena parte del horizonte sureste gracias a sus dos kilómetros de altura. Durante años, los mapas creados a partir de los datos orbitales tomados por las distintas sondas clasificaban esta inmensa mole como parte de lo que llamamos basamento, la corteza antigua y completamente cubierta de cráteres que forma el borde del cráter y sobre el que este fue excavado.
Pero la forma y el tamaño de este “monte” ya había levantado anteriormente la suspicacia de algunos científicos, pero se necesitaban más datos para confirmar que podríamos estar ante algo más que un simple relieve. Para ello, en esta investigación se han ayudado de los datos tomados por misiones anteriores para poder comprender mejor a este sospechoso. Pero, ¿qué pistas han encontrado en estos datos? Os las desgrano una a una.
El primer aspecto en el que se fijaron es la morfometría -término bajo el que se esconde el estudio de la forma de la montaña. Jezero Mons es una estructura prácticamente cónica con unos 21 kilómetros de diámetro y con un cráter desfigurado -poco circular en este caso, y con una abertura- en su cima. No solo se quedaron aquí, sino que aprovecharon para medir las pendientes de las laderas, la proporción entre su anchura y la altura y el tamaño del cráter de su cima con relación a la base para poder comparar edificios volcánicos en la Tierra y en Marte.
Los resultados fueron apabullantes. Jezero Mons se ajustaba a la perfección al perfil de otros volcanes compuestos -o estratovolcanes- marcianos como Zephyria Tholus y Apollinarus Tholus y también es muy parecido al del monte Sidley, un gran pico volcánico -bueno, de hecho el volcán más alto- de nuestra Antártida terrestre.
Pero en lo que desde luego no se parece en nada es a los volcanes en escudo, con sus bases muy anchas y sus suaves laderas -como Mauna Loa, en Hawái- y que dominan el espectro volcánico de Marte, ni tampoco se parece a un cráter en pedestal -esos cráteres “formados” sobre una meseta elevada-. Así que parece que su forma dice a gritos la palabra estratovolcán, esos que en nuestro planeta pueden dar lugar a violentas erupciones volcánicas.
 En esta imagen podemos ver perfectamente el perfil de Jezero Mons visto desde la posición del Perseverance en los primeros 100 días de su misión. Es llamativo como ocupa la mayor parte del horizonte, ya que no solo es una forma prominente, sino que se encuentra elevado por estar situado sobre las tierras altas de Marte, mientras que el Perseverance está en el interior de un cráter excavado sobre estas. Imagen cortesía de NASA/JPL/NASA/ASU/MSSS.
En esta imagen podemos ver perfectamente el perfil de Jezero Mons visto desde la posición del Perseverance en los primeros 100 días de su misión. Es llamativo como ocupa la mayor parte del horizonte, ya que no solo es una forma prominente, sino que se encuentra elevado por estar situado sobre las tierras altas de Marte, mientras que el Perseverance está en el interior de un cráter excavado sobre estas. Imagen cortesía de NASA/JPL/NASA/ASU/MSSS.La segunda pista en la que se han fijado los científicos es en sus propiedades “térmicas”. Y me explico: Usando los datos del instrumento THEMIS de la sonda Mars Odyssey han medido lo que conocemos como inercia térmica, la capacidad de los materiales para retener el calor. El basamento rocoso de Marte, sólido y denso, se calienta de día y sigue caliente durante la noche marciana, dando valores de inercia térmica altos. En contraste, los materiales sueltos y de grano fino como pueden ser la arena o la ceniza volcánica no son buenos conductores, de tal forma que se calientan y enfrían muy rápidamente, lo que da como resultado valores bajos de inercia térmica.
La superficie de Jezero Mons tiene una inercia térmica baja muy característica. Esto sugiere que no está formada por coladas de lava sólidas y endurecidas, sino que está cubierta por una potente capa de materiales finos y poco consolidados, un detalle que es una señal perfecta de depósitos de ceniza formados a partir de erupciones explosivas.
La tercera y última pista sobre la que se apoya este descubrimiento es la mineralogía. Gracias al instrumento CRISM de la Mars Reconaissance Orbiter, se pueden distinguir minerales por como reflejan la luz -al fin y al cabo es un espectrómetro- permitiendo a los científicos crear un mapa de la composición química de la montaña. Y han descubierto que sus laderas son ricas en piroxenos, un mineral que es uno de los más habituales en las rocas volcánicas de tonos oscuros que cubren la superficie de Marte.
Y, además, se han encontrado también minerales de alteración alrededor del cráter de la cima. Los investigadores han hallado arcillas e incluso un área con sílice opalino (sílice hidratada). Estos minerales no serían productos volcánicos primarios, sino que se forman cuando los gases volcánicos, el agua y la roca caliente interactúan entre sí.
De hecho, su presencia sugiere la existencia en el pasado de actividad hidrotermal, con quizás aguas termales y fumarolas sobre la cima. Estos ambientes están considerados hoy día como objetivos primordiales en la búsqueda de vida, ya que nos aportan unos ingredientes importantes para el desarrollo de esta: agua, energía, y nutrientes.
Si ya de por sí estas tres pistas parecen apuntar claramente al origen volcánico de Jezero Mons, todavía queda quizás una de las evidencias más fuertes: una relación física entre el fondo del cráter y el volcán. Las imágenes de alta resolución muestran varios depósitos amplios con formas lobuladas que parecen fluir desde el flanco noroeste de la montaña y desparramarse sobre la llanura que forma el fondo del cráter.
 Detalle del cráter de la cima de Jezero Mons. Si nos fijamos, el número de cráteres de impacto que hay sobre este es excepcionalmente bajo si lo comparamos con los terrenos circundantes, lo que quiere decir que probablemente su formación es más reciente o que al menos su superficie ha sido renovada por otros procesos… como puede ser el vulcanismo. Imagen cortesía de NASA/JPL/Universidad de Arizona.
Detalle del cráter de la cima de Jezero Mons. Si nos fijamos, el número de cráteres de impacto que hay sobre este es excepcionalmente bajo si lo comparamos con los terrenos circundantes, lo que quiere decir que probablemente su formación es más reciente o que al menos su superficie ha sido renovada por otros procesos… como puede ser el vulcanismo. Imagen cortesía de NASA/JPL/Universidad de Arizona.Estos depósitos se superponen sobre el terreno fracturado y antiguo del fondo del cráter y tienen un aspecto de debris flows, o flujos de derrubios en castellano. Bajo este nombre se esconden procesos en los que masas de tierra empapadas en agua y fragmentos de roca fluyen ladera abajo, pero también podrían ser la señal de flujos piroclásticos -corrientes de gas y materiales volcánicos a altas temperaturas- que descienden por las laderas de los volcanes durante una erupción explosiva.
Esta conexión física da un sentido a cómo podrían haber llegado los materiales volcánicos al centro del cráter Jezero. Y es que este volcán no sería simplemente una montaña lejana, sino que era un proceso activo capaz de depositar grandes cantidades de ceniza y otros materiales a la cuenca del lago que albergó antaño el cráter.
Identificar Jezero Mons como un volcán no solo nos ayuda a resolver un enigma geológico, sino que aporta una visión totalmente diferente a como era el ambiente en este lugar. No era solo un lago tranquilo, era un paisaje cambiante en el que la actividad volcánica podría enriquecer el agua con minerales y calor, haciéndolo más adecuado para el desarrollo de la vida.
Pero hay todavía una ramificación más para este estudio y que entronca con la misión del Perseverance: El rover está recogiendo muestras que en algún momento vendrán a nuestro planeta -aún no sabemos cuándo-, pero si algunas de estas están directamente relacionadas con Jezero Mons, su valor científico se dispara: Son muestras de un volcán marciano concreto.
Y es que ese detalle nos permitiría datar con precisión cuál es su edad gracias a las técnicas de datación radiométrica, pero, además, también contemporizar mejor los materiales que vemos en el fondo del cráter Jezero y a calibrar nuestras escalas de edad de la superficie de Marte que actualmente dependen de contar cráteres, ya que no hemos podido traer muestras todavía a la Tierra.
¿Qué más sorpresas nos deparará la misión del Perseverance? La verdad es que no lo sabemos, pero, por si acaso, mantengamos los ojos bien abiertos… Marte siempre está dispuesto a sorprendernos incluso a plena luz del día.
Bibliografía:
Cuevas-Quiñones, S. C., Wray, J. J., Rivera-Hernández, F., & Adler, J. B. (2025). Evidence for a composite volcano on the rim of Jezero crater on Mars. Communications Earth & Environment, 6(1), 340. doi: 10.1038/s43247-025-02329-7
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Un volcán escondido… a la vista de todos se ha escrito en Cuaderno de Cultura Científica.

