Primeras evidencias de presencia humana en Europa hace 2 millones de años
 Restos fósiles de animales con marcas de corte datadas en 1,95 Millones de años, descubiertos en Grăunceanu . Fuente: Curran, Sabrina C., et al. (2025)
Restos fósiles de animales con marcas de corte datadas en 1,95 Millones de años, descubiertos en Grăunceanu . Fuente: Curran, Sabrina C., et al. (2025)Hace algo más de medio siglo, durante la década de los sesenta, un equipo de paleontólogos y antropólogos realizó un interesante hallazgo cerca de la pequeña localidad de Grăunceanu, Rumania. Junto al valle del río Olteţ, centenares de huesos de animales prehistóricos, acumulados en un solo yacimiento, resurgían de la tierra ante el asombro de los investigadores. El inexorable paso del tiempo y la paciente acción fluvial habían arrastrado, sedimento tras sedimento, capa tras capa, una impresionante cantidad de restos fósiles, concentrándolos en un rincón de apenas 90 m2. Una amplia diversidad de huesos que el agua fue arrastrando durante milenios y que los investigadores de la época describieron como «mamuts, varias especies de bóvidos y cérvidos, jirafas, équidos, rinoceróntidos, múltiples especies de carnívoros, roedores (castor, puercoespín), avestruces, una gran especie de mono terrestre (Paradolichopithecus) y el representante más temprano de los pangolines en Europa». La colección llegó a alcanzar miles de restos que se guardaron en dos instituciones, el Instituto de Espeleología «Emil Racoviţă» y el Museo de Oltenia… y allí se quedaron durante décadas, guardados en cajas y volviendo a cubrirse de polvo en algún almacén olvidado.
Un nuevo examenSesenta años más tarde, un equipo internacional de investigadores recordó aquel antiguo yacimiento de Grăunceanu y se propuso revisar los restos guardados con la mirada que proporcionan las avanzadas tecnologías actuales. Los huesos aún estaban en sus cajas pero la documentación que los identificaba y clasificaba no aparecía por ningún lado. «Desafortunadamente, casi todos los registros de la excavación y datos de procedencia de los restos se han perdido», explica Sabrina C. Curran, investigadora principal.
Comienza entonces una exhaustiva labor de reidentificación, que se extendió durante cuatro veranos (años 2019 al 2022), y en la que se utilizaron modernas técnicas de datación mediante uranio-plomo (U-Pb) de alta precisión así como análisis de isótopos estables de oxígeno y carbono de alta resolución. El resultado de estas campañas fue alentador y descubrió que algunos de estos restos se remontaban dos millones de años en el pasado. «Nuestro equipo ha identificado e inventariado un total 5527 restos, incluyendo materiales de Grăunceanu (4983) y localidades más pequeñas como Fântâna lui Mitilan (139) y La Pietriș (116)». Una rica biodiversidad que, según las reconstrucciones paleoecológicas, se desarrolló en un entorno de pastizales abiertos, con bosques, ríos y lagos, comparable a un hábitat de bosque-estepa.
Presencia de homínidosEn ocasiones, el conocimiento científico no llega gracias a un nuevo y flamante descubrimiento sino al cuidadoso análisis o revisión de uno antiguo, y es aquí donde llegan las novedades más fascinantes. Los resultados de esta moderna revisión de los restos hallados en Grăunceanu se han publicado hace unos días en Nature Communications y nos sorprenden con las evidencias más antiguas de presencia humana (homininos) en Europa que se remontan a hace unos dos millones de años. Es un salto considerable si tenemos en cuenta que, hasta ahora, las pistas más antiguas que teníamos del género homo en Europa pertenecían al célebre yacimiento de Dmanisi (Georgia) donde se descubrieron restos de homínidos que datan de hace 1,8 millones de años.
«No hay que olvidar que la presencia de homínidos en el yacimiento de Dmanisi se basa directamente en restos humanos mientras que el nuevo estudio está basado en pruebas indirectas», nos explica Roberto Sáez, Doctor en Antropología y divulgador científico, experto en evolución humana.
Este es un hecho que los propios investigadores reconocen al afirmar que «aunque no hemos identificado restos de homínidos ni industria lítica in situ en Grăunceanu […] en este trabajo presentamos evidencia de la presencia de homínidos en Eurasia hace al menos 1,95 millones de años en forma de huesos con marcas de corte, respaldados por estimaciones de edad de uranio-plomo (U-Pb) de alta precisión».
 Restos fósiles de animales con marcas de corte datadas en 1,95 Millones de años, descubiertos en Grăunceanu. Fuente: Curran, Sabrina C., et al. (2025)
Restos fósiles de animales con marcas de corte datadas en 1,95 Millones de años, descubiertos en Grăunceanu. Fuente: Curran, Sabrina C., et al. (2025)El equipo analizó un total de 4746 especímenes a la búsqueda de modificaciones de la superficie ósea para descartar en primer lugar «cualquier marca abiótica (por ejemplo, matriz adherida, alisado, picaduras en la superficie ósea, erosión/disolución, agrietamiento/división de sedimentos, exfoliación/descamación) o bióticas no antropogénicas (modificación de carnívoros u homínidos, pisoteo, grabado de raíces/rizomorfos fúngicos, roedores, actividad de insectos, digestión, marcas de preparadores)». Para ello utilizaron herramientas ópticas de aumento con especial atención a las marcas líneas, «definidas como cualquier marca al menos el doble de larga que ancha». Cuando identificaron las marcas de interés, los investigadores siguieron los criterios cualitativos y protocolos de atribución ya establecidos en la literatura científica para registrar la trayectoria, orientación, morfología, número de marcas visibles, simetría, etc.
Según los resultados publicados se han encontrado un total de veinte especímenes que exhiben marcas de corte de interés de las cuales, siete muestran marcas de corte de alta confianza, doce muestran marcas de corte probables y un espécimen presenta ambos tipos de marcas, lo que lleva a los autores a «argumentar a favor de una presencia de homínidos en Europa hace al menos dos millones de años».
Qué homínidosLos yacimientos más antiguos (anteriores a 2 millones de años) fuera de África se agrupan en Oriente Medio, Rusia occidental alrededor de los mares Negro y Caspio, Asia central y China. Estos yacimientos incluyen una mezcla de localidades en la que se han encontrado líticos y/o una pequeña cantidad de huesos con marcas de corte. Aunque existen yacimientos donde se han descubierto posibles restos de homínidos de esa antigüedad (como los seis dientes descubiertos en Longgudong), los expertos aún albergan dudas sobre ellos y el consenso científico es que el yacimiento con restos humanos confirmados más antiguos fuera de Europa sigue siendo Dmanisi.
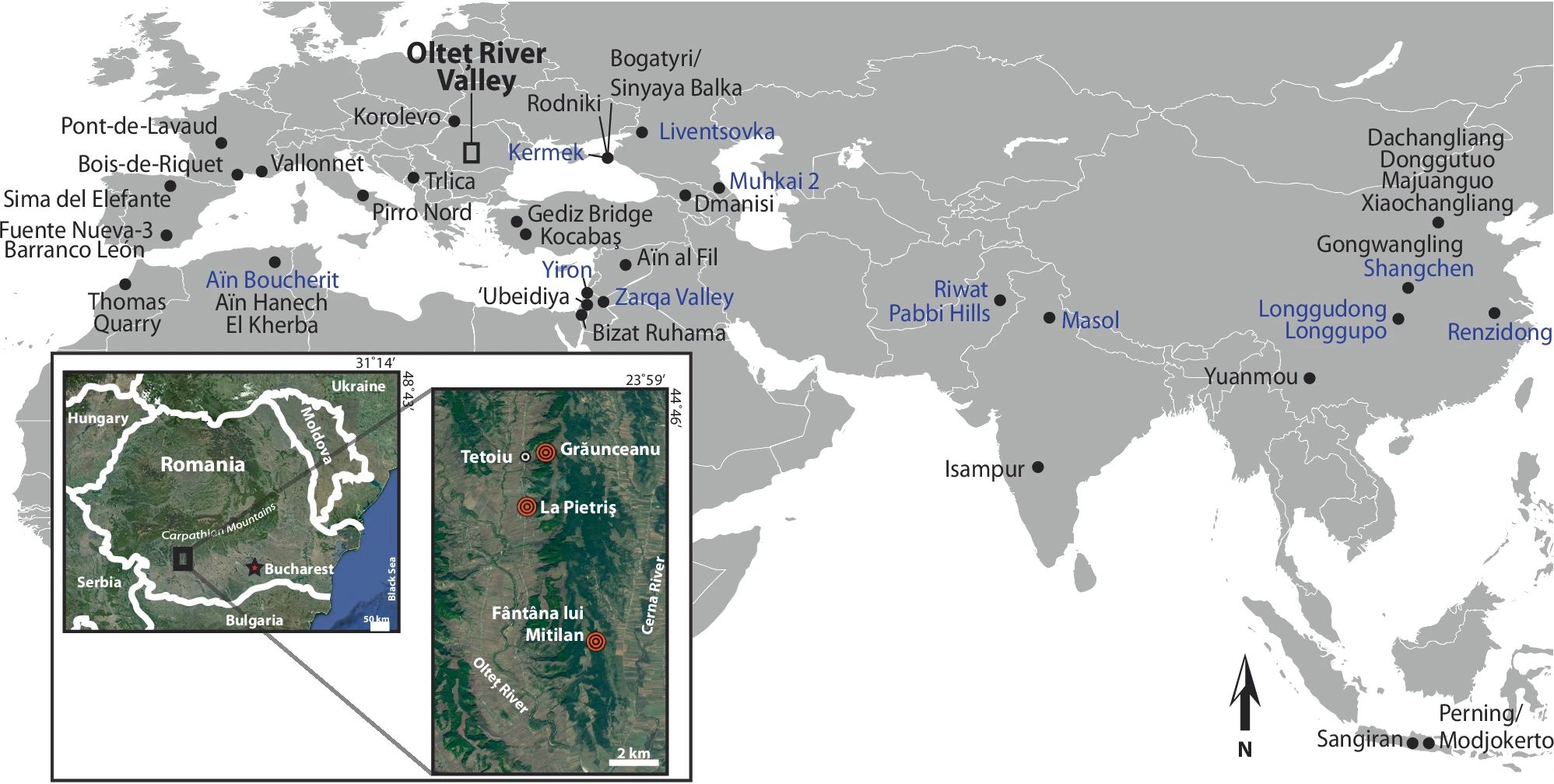 Los yacimientos en letra en azul poseen una antigüedad superior a dos millones de años. El recuadro inferior izquierdo muestra las ubicaciones de los yacimientos analizados en este estudio. Fuente: Curran, Sabrina C., et al. (2025)
Los yacimientos en letra en azul poseen una antigüedad superior a dos millones de años. El recuadro inferior izquierdo muestra las ubicaciones de los yacimientos analizados en este estudio. Fuente: Curran, Sabrina C., et al. (2025)El estudio publicado evita deliberadamente entrar en el espinoso tema de qué especie de homínido pudo realizar esas marcas en los animales de Grăunceanu. «Este es un período en el que múltiples especies de homínidos coexistieron en sitios en el este y sur de África». La afinidad taxonómica de casi todos los fósiles de homínidos descubiertos hasta ahora sigue en pleno debate y abarca diferentes grupos homo, como el erectus o el ergaster.
No es el único hueco que nos queda por rellenar, aún nos faltan muchas piezas para completar el puzle de esas primeras migraciones, pero los hallazgos y estudios publicados en las últimas décadas nos animan a afirmar que, hace aproximadamente unos dos millones y medio de años, se inició la primera gran oleada de diferentes especies de homínidos desde África hacia Eurasia. «La interpretación actual es que no fue migración única sino muchas, intermitentes, que alcanzaron lugares tan lejanos como el norte de China», aclara Sáez. Contábamos con pistas indirectas, como industria lítica o marcas de cortes con herramientas, que indican presencia de homínidos por toda Asia y con una datación de hasta 2,1 millones de años, pero hasta ahora no habíamos encontrado pruebas en Europa con esa antigüedad. El estudio publicado en Nature Communications abre por fin esta puerta.
Referencias y más información:
Curran, Sabrina C., et al. (2025) Hominin Presence in Eurasia by at Least 1.95 Million Years Ago Nature Communications doi: 10.1038/s41467-025-56154-9.
Roberto Sáez «Homininos en Europa hace dos millones de años» Nutcrackerman.com
Sobre el autor: Javier «Irreductible» Peláez (Puertollano, 1974) es escritor y comunicador científico. Autor de 500 años de frío. La gran aventura del Ártico (Crítica, 2019) y Planeta Océano (Crítica 2022). Es uno de los fundadores de la plataforma Naukas.com, editor de ciencia en Yahoo España y Latinoamérica. Es guionista científico en los programas de televisión «El Cazador de Cerebros» y «Órbita Laika» de RTVE. Durante más de una década ha escrito en diferentes medios de comunicación (El País, El Español, National Geographic, Voz Populi). Es autor de los podcasts Catástrofe Ultravioleta y La Aldea Irreductible, y ha colaborado en diferentes proyectos radiofónicos y televisivos (Radio Nacional de España, Radio Televisión Canaria). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Primeras evidencias de presencia humana en Europa hace 2 millones de años se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2024: Neurodiversidad
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

José Ramón Alonso es catedrático de la Universidad de Salamanca, y está especializado en neurociencia. Lleva años investigado y escribiendo sobre neurodiversidad, eso que comúnmente llamamos trastornos del espectro autista, o hiperactividad o lo que sea. José Ramón nos explica que igual que la biodiversidad de especies es una riqueza, también lo es la biodiversidad dentro de nuestra especie.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: Neurodiversidad se ha escrito en Cuaderno de Cultura Científica.
La importancia de la diversidad estructural de los bosques frente al cambio climático
Un nuevo estudio apunta a que la heterogeneidad en los tamaños de los árboles de un bosque influye en cómo el cambio climático afecta a su crecimiento. Así, los bosques con árboles de tamaños más homogéneos son más vulnerables a las alteraciones climáticas.
 Bosque de hayas trasmocho. Foto: Julen Astigarraga
Bosque de hayas trasmocho. Foto: Julen AstigarragaLa investigación, que ha sido liderada por la Universidad de Alcalá y la Universidad del País Vasco (UPV/EHU), se centra en el análisis de datos de crecimiento anual de hayas en el límite sur de su distribución, utilizando técnicas dendrocronológicas.
Desde la década de 1970, la sincronía en el crecimiento de los árboles ha aumentado debido a la mayor frecuencia de eventos climáticos extremos.
“Hemos observado cómo los impactos antropogénicos directos sobre los bosques, a través de los cambios en el uso del suelo, y los impactos indirectos, a través del cambio climático, determinan la sincronía en el crecimiento, siendo los bosques con individuos jóvenes los más vulnerables frente al cambio climático”, indica Julen Astigarraga, autor principal del estudio.
El trabajo resalta la importancia de mantener bosques estructuralmente diversos para mitigar los efectos del cambio climático. “En general, las estructuras más diversas se encuentran en bosques maduros. Sin embargo, esos bosques son muy escasos en todo el continente europeo, pero a su vez, son extremadamente valiosos para mitigar los impactos del cambio climático, como demuestra este estudio”, comenta Paloma Ruiz-Benito, investigadora de la Universidad de Alcalá.
De manera sorprendente, el trabajo ahora publicado ha evidenciado que los bosques de hayas trasmochos, un ecosistema cultural y ecológico caracterizado por bosques abiertos con brotes abundantes en el tronco principal y muy comunes en Gipuzkoa, la zona de estudio, muestran una notable resiliencia frente al cambio climático.
«Incrementar la diversidad estructural de los bosques, además de reducir la sincronía en el crecimiento de los árboles, puede ayudar a disminuir la mortalidad de los mismos, potenciar el secuestro de carbono y fomentar la biodiversidad al aumentar la disponibilidad de hábitats», añade Asier Herrero, investigador de la Universidad del País Vasco.
El estudio ha sido posible gracias a la colaboración de diversos investigadores de toda la península, así como a los guardas forestales y habitantes de Oñati (Gipuzkoa), quienes han mostrado un gran interés y apoyo en el proceso de recolección de datos. «Es impresionante la generosidad que hemos recibido de la comunidad local durante todo este trabajo, y esperamos que los resultados de este estudio contribuyan a adaptar los hayedos frente al cambio climático, no solo en Oñati, sino también en todo el continente europeo», concluye Astigarraga.
Referencia:
Astigarraga J., Calatayud J., Ruiz-Benito P., Madrigal-González J., Tijerín-Triviño J., Zavala MA., Andivia E., Herrero A. (2025) Forest structural diversity modulates tree growth synchrony in response to climate change Forest Ecology and Management doi: 10.1016/j.foreco.2025.122505
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La importancia de la diversidad estructural de los bosques frente al cambio climático se ha escrito en Cuaderno de Cultura Científica.
El verdadero Brexit geológico
Si nos subimos a un barco pesquero en el Mar del Norte y echamos una red de arrastre frente a las costas de los Países Bajos, uno de los botines marinos más comunes que podemos sacar a flote no son merluzas o bacalaos, sino restos fósiles de mamut, rinoceronte lanudo y león de las cavernas. Y su presencia nos está contando una increíble historia de mundos sumergidos al más puro estilo de las leyendas de la Atlántida.
Para comenzar nuestra aventura, debemos viajar a hace unos 20.000 años. En este periodo temporal nos encontramos dentro de lo que se conoce como el Último Máximo Glacial, es decir, el momento más frío y de mayor avance de los casquetes y mantos de hielo continentales de la última glaciación en el hemisferio norte. Esta acumulación de hielo se produjo por el secuestro en tierra firme del agua marina evaporada, ya que cuando caía en forma de precipitación en el continente, inmediatamente se congelaba, sin tener la posibilidad de regresar al océano como agua superficial. Lo cual produjo lo inevitable, un descenso del nivel marino, que llegó a encontrarse unos 120 m por debajo de la actualidad en aquel momento.
 Restos fósiles de mamut encontrados en las redes de pesca de un barco danés mientras fondeaba en el Mar del Norte. Fuente: North Sea Fossils
Restos fósiles de mamut encontrados en las redes de pesca de un barco danés mientras fondeaba en el Mar del Norte. Fuente: North Sea FossilsEn estas condiciones de nivel del mar bajo, el aspecto del océano Atlántico europeo no se parecía en nada al actual. Lo que hoy en día conocemos como archipiélago británico estaba unido a la Europa continental por un brazo de tierra que se extendía desde el norte de Dinamarca hasta el norte de Francia, conformando una enorme península que se conoce como Doggerland.
Durante unos 10.000 años, Doggerland soportó el continuo ascenso del nivel del mar producido por el regreso del agua de fusión de los glaciares continentales al océano tras el final del último periodo glacial, permaneciendo como un ambiente litoral en el que se desarrollaron amplios estuarios y marismas. Lugares por los que se producía un continuo tránsito de fauna entre las actuales Europa continental y las islas británicas, que incluía mamuts, rinocerontes, ciervos y, por supuesto, seres humanos. De hecho, estudios de arqueología submarina realizados en el Mar del Norte han localizado algunos asentamientos mesolíticos donde las poblaciones humanas se ponían las botas con esa estupenda caza conformada por enormes vertebrados.
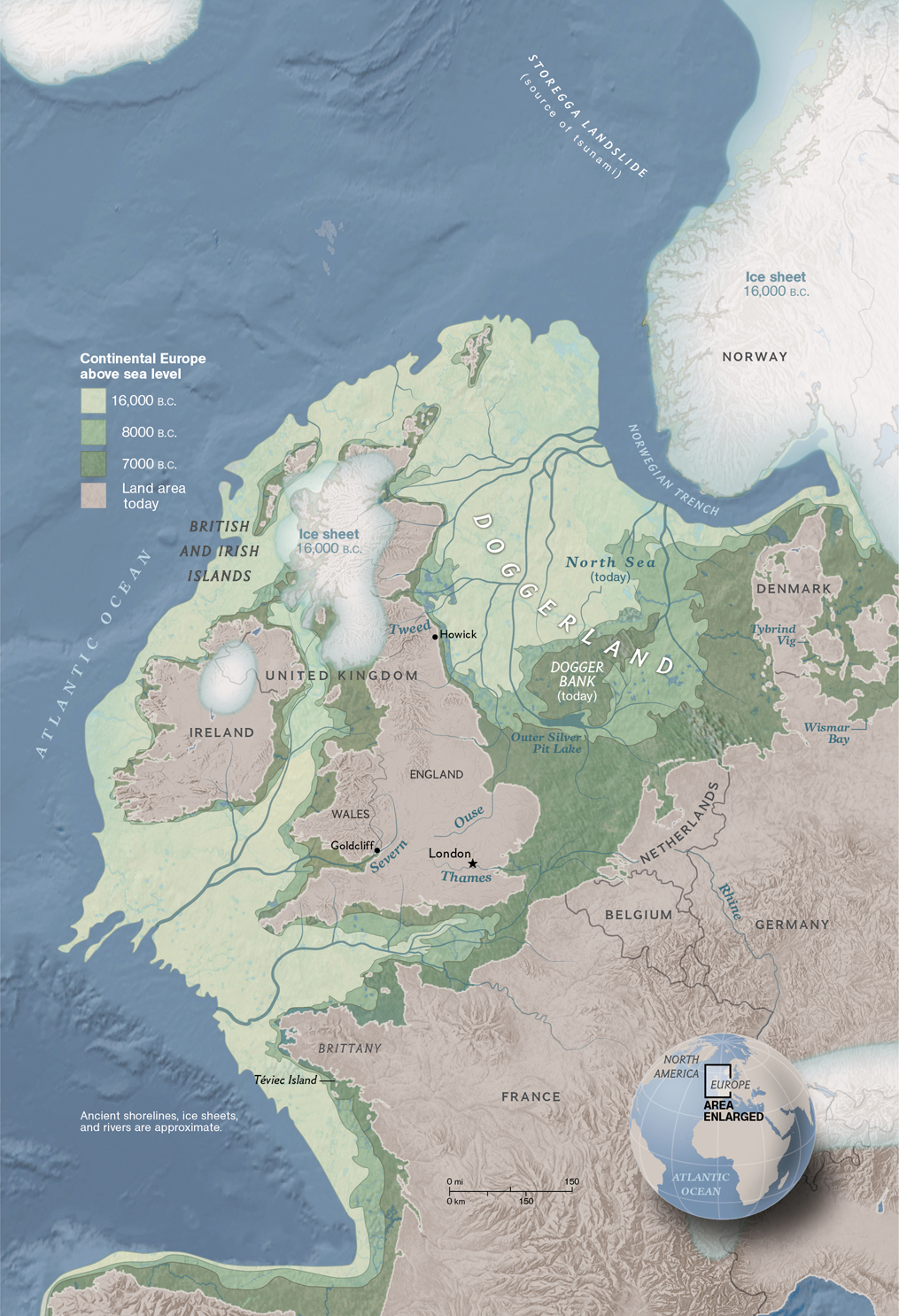 Reconstrucción del puente de tierra conocido como Doggerland que unía el archipiélago británico con la Europa continental a finales de la última glaciación. Mapa de William E. McNulty y Jerome N. Cookson / National Geographic Magazine
Reconstrucción del puente de tierra conocido como Doggerland que unía el archipiélago británico con la Europa continental a finales de la última glaciación. Mapa de William E. McNulty y Jerome N. Cookson / National Geographic MagazinePosiblemente, el imparable aumento del nivel marino durante el actual periodo cálido del Holoceno habría acabado anegando Doggerland, dejando así aislado el archipiélago británico. Pero, al igual que el famoso Brexit político, la separación geológica de las islas británicas de Europa fue un evento catastrófico.
Hace unos 8.200 años, se produjo lo que se conoce como deslizamiento de Storegga (palabra de origen noruego que significa “gran borde”), un gran desprendimiento de sedimentos, que se calcula que pudieron tener el volumen de la actual isla de Islandia, desde la plataforma continental de Noruega hacia el fondo oceánico del Mar de Noruega. Aún no se tiene muy claro el desencadenante de este deslizamiento, discutiendo si el culpable fue un terremoto submarino que afectó al margen continental noruego o si se produjo por una inestabilidad de los sedimentos al fundirse el manto de hielo que los mantenía unidos, pero lo que sí se conoce es lo que provocó en todo lo que había a su alrededor. En cuanto ese volumen de sedimentos se desprendió hacia el fondo marino, desplazó millones de toneladas de agua oceánica y generó un enorme tsunami con olas que superaron los 10m de altura, arrasando todo el litoral noruego y penetrando hacia el sur a través del actual Mar del Norte. Aquí, el agua inundó toda el área estuarina de Doggerland, devastando los asentamientos mesolíticos que pillaba a su paso y aniquilando a miles de personas.
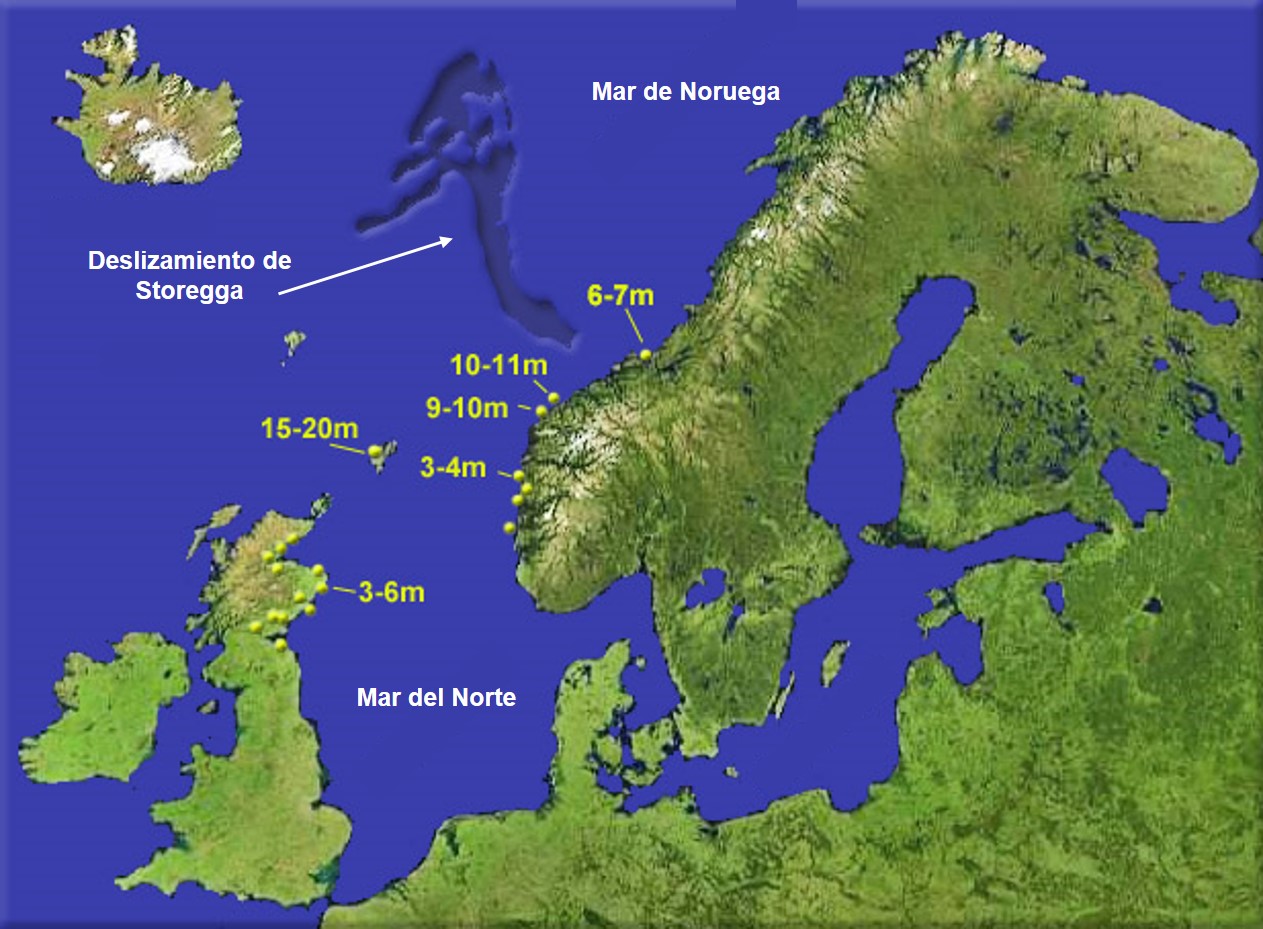 Localización del depósito submarino de sedimentos provocado por el deslizamiento de Storegga ocurrido hace unos 8.200 años en el Mar de Noruega. En amarillo se indican las alturas estimadas de las olas fruto del tunami producido. Imagen modificada de Lamiot / Wikimedia Commons
Localización del depósito submarino de sedimentos provocado por el deslizamiento de Storegga ocurrido hace unos 8.200 años en el Mar de Noruega. En amarillo se indican las alturas estimadas de las olas fruto del tunami producido. Imagen modificada de Lamiot / Wikimedia CommonsCuando el tsunami terminó y el agua se calmó, el brazo de tierra de Doggerland había desaparecido y el Canal de la Mancha se convirtió en una barrera que separó las islas británicas de la Europa continental. Esto detuvo no solo el paso de las grandes faunas litorales de un lado a otro, sino también el intercambio cultural entre las tribus mesolíticas británicas y las europeas, provocando una evolución social diferente en ambos márgenes. Vamos, que el verdadero Brexit se produjo hace unos 8.200 años.
Como siempre os digo, la Geología es una ciencia apasionante que nos permite comprender cómo ha evolucionado nuestra sociedad a lo largo del tiempo. Una historia que comenzó encontrando restos fósiles de mamuts y rinocerontes en el fondo marino frente al litoral de Países Bajos, me ha permitido hablaros de cambio climático, variaciones del nivel marino, asentamientos humanos de hace miles de años y la salida original (y geológica) del Reino Unido (y de Irlanda) de la Unión Europea. Espero haberos sorprendido con ella.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo El verdadero Brexit geológico se ha escrito en Cuaderno de Cultura Científica.
Alice Roth, la inventora del “queso suizo” (matemático)
Ningún matemático debe permitirse olvidar que las matemáticas, más que cualquier otro arte o ciencia, son un asunto de jóvenes. […] Consideremos, por ejemplo, la trayectoria de un hombre que ciertamente fue uno de los tres matemáticos más grandes del mundo. Newton dejó las matemáticas a los 50 años, habiendo perdido su entusiasmo por ellas bastante antes. Sin duda alguna, se dio perfecta cuenta a los cuarenta años de que sus grandes días creativos pertenecían ya al pasado. […] Galois murió a los 21, Abel a los 27, Ramanujan a los 33 y Riemann a los 40. Ha habido matemáticos que han llevado a cabo una obra maestra bastante más tarde; la magna obra de Gauss sobre la geometría diferencial se publicó cuando tenía 50 años (aunque había tenido las ideas fundamentales 10 años antes). No conozco un ejemplo de un avance matemático de importancia desarrollado por una persona que haya superado los 50. Si una persona madura pierde su interés y abandona las matemáticas, es probable que la pérdida no sea demasiado importante ni para las matemáticas ni para él.
G. H. Hardy, Apología de un matemático,1940
En esta cita, Hardy no nombra a ninguna mujer entre esos “relevantes” matemáticos que brillaron en su juventud. Alice Roth fue una joven matemática brillante, pero lo fue aún más a partir de su jubilación.
Alice Roth nació el 6 de febrero de 1905 en Berna, Suiza. Era la segunda hija (entre sus hermanos Conrad y Walter) de Conrad Roth y Marie Landolt, una familia acomodada.
Tras sus estudios de secundaria, tenía claro que quería estudiar matemáticas. Su madre no tenía nada en contra de esta elección, pero quería que su hija aprendiera antes los conceptos básicos de gestión del hogar. Y, obediente, así lo hizo.
 Alice Roth. Fuente: Agnes Scott College.
Alice Roth. Fuente: Agnes Scott College.Una estudiante brillante, una tesis premiada y el olvido
En otoño de 1925, Alice ingresó en la Eidgenössische Technische Hochschule (ETH) en Zúrich, una universidad con alumnado ampliamente masculino. En los cuatro años posteriores su principal campo de estudio fueron las matemáticas, con la física como primera especialidad y la astronomía como segunda. Y logró unos resultados extraordinarios. En 1930 obtuvo su tesis de maestría dirigida por el matemático George Pólya (1887-1985).
Mientras impartía docencia de matemáticas y física en una escuela para niñas, comenzó a trabajar en su tesis doctoral, de nuevo con Pólya como tutor. En 1938 defendió su tesis (Approximationseigenschaften und Strahlengrenzwerte meromorpher und ganzer Funktionen), codirigida por Heinz Hopf (1894-1971), y que fue reconocida como excelente.
La tesis de Roth era de tanta calidad que recibió un premio monetario y la Medalla de Plata en la ETH, siendo la primera mujer en obtener este reconocimiento.
A pesar de su éxito en la ETH, con Pólya trabajando desde 1940 la Universidad de Stanford (Estados Unidos), Alice se apartó de la investigación. Comenzó a trabajar como docente en una escuela privada, ocupación mal remunerada y con una gran carga docente, pero que ella realizaba con dedicación y con un gran aprecio por parte de su alumnado. Sus estudiantes mencionaban su gran capacidad docente y los esfuerzos que realizaba al explicar los conceptos y resultados de muchas maneras diferentes.
Roth fue muy amiga de Marie Boehlen (1911-1999), una abogada bernesa, activista por los derechos familiares y sufragista. La propia Alice fue una firme defensora del derecho al voto de las mujeres. A menudo expresaba su frustración frente a un sistema que la obligaba a pagar impuestos, pero no le permitía tener voz en la gobernanza. Las mujeres suizas recibieron el derecho al voto en 1971, el año en el que Alice Roth se jubiló.
Tras la jubilación, un nuevo comienzo en matemáticasPoco antes de jubilarse, Roth anunció a sus allegados su deseo que volver a la investigación en matemáticas. Se trataba de una tarea complicada tras un parón de tantos años.
La cita de Hardy que abre este escrito nos podría hacer pensar que, con más de sesenta años, Alice Roth no iba a poder aportar matemáticas demasiado valiosas. Sin embargo, durante los treinta años que Roth había permanecido enseñando, el área de investigación en el que ella había trabajado en sus comienzos y que tan bien conocía se había puesto de moda.
Paul Gauthier, un joven matemático de la Universidad de Montreal, leyó la primera publicación de Alice tras su jubilación, y comenzaron a colaborar científicamente. A sus 70 años, Alice realizaría su primer “viaje matemático” fuera de Suiza, invitada por Gauthier, para impartir una conferencia.
Uno de los principales resultados de la tesis de Roth de 1938 fue el llamado conjunto del queso suizo, un ejemplo de un conjunto compacto en el que no todas las funciones continuas pueden aproximarse uniformemente mediante funciones racionales. Este resultado fue olvidado y redescubierto, independientemente, en 1952 por Sergey Mergelyan; el crédito correspondiente fue restablecido en 1969.
En Suiza, como en otros lugares, las mujeres matemáticas son escasas… La tesis de Alice Roth recibió una medalla de la ETH y apareció poco después de su finalización en una revista matemática suiza… Un año después estalló la guerra, el mundo tenía otras preocupaciones al margen de las matemáticas y el trabajo de Alice Roth simplemente cayó en el olvido. Tan completamente olvidado que alrededor de 1950 un matemático ruso redescubrió resultados similares sin tener la menor idea de que una joven matemática suiza había publicado las mismas ideas más de una década antes que él. Sin embargo, su prioridad fue reconocida.
Peter Wilker (antiguo alumno de Alice Roth), obituario en el periódico Der Bund, 29 julio 1977
En 1976, le diagnosticaron a Alice un cáncer. Fue hospitalizada en 1977, aunque continuó con su investigación matemática, ayudada por Wilker en la traducción y redacción de su último trabajo sobre teoría de la aproximación, área en la que realizó importantes contribuciones.
Falleció el 22 de julio de 1977.
El trabajo pasado y futuro de Roth tuvo una fuerte y duradera influencia en los matemáticos que trabajaban en esta área [teoría de aproximación racional]. Su queso suizo ha sido modificado (a toda una variedad de quesos)… El lema de fusión de Roth, que apareció en su artículo de 1976… influyó en una nueva generación de matemáticos en todo el mundo.
Ulrich Daepp, Paul Gauthier, Pamela Gorkin y Gerald Schmieder, 2005
Referencias
-
Larry Riddle, Alice Roth, Biographies of Women Mathematicians, Agnes Scott College
-
Ulrich Daepp, Paul Gauthier, Pamela Gorkin, and Gerald Schmieder. Alice in Switzerland: The Life and Mathematics of Alice Roth, Mathematics Intelligencer 27 (1) (2005), 41-54
-
Alice Roth, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Alice Roth, la inventora del “queso suizo” (matemático) se ha escrito en Cuaderno de Cultura Científica.
Cómo el teorema de Noether revolucionó la física
Emmy Noether demostró que las leyes físicas fundamentales son solo una consecuencia de simetrías simples. Un siglo después, sus ideas siguen dando forma a la física.
Un artículo de Shalma Wegsman. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Kristina Armitage / Quanta Magazine
Ilustración: Kristina Armitage / Quanta MagazineEn el otoño de 1915, los cimientos de la física empezaron a resquebrajarse. La nueva teoría de la gravedad de Einstein parecía implicar que debería ser posible crear y destruir energía, un resultado que amenazaba con trastocar dos siglos de pensamiento en la física.
La teoría de Einstein, llamada relatividad general, transformó radicalmente el significado del espacio y el tiempo. En lugar de ser telones de fondo fijos de los acontecimientos del universo, el espacio y el tiempo eran ahora personajes por derecho propio, capaces de curvarse, expandirse y contraerse en presencia de materia y energía.
Un problema con este espacio-tiempo cambiante es que, a medida que se estira y se encoge, la densidad de la energía en su interior cambia. Como consecuencia, la ley clásica de conservación de la energía que describía toda la física no encajaba en este marco. David Hilbert, uno de los matemáticos más destacados de la época, identificó rápidamente este problema y se propuso, junto con su colega Felix Klein, tratar de resolver este aparente fallo de la relatividad. Cuando no pudieron resolverlo, Hilbert le pasó el problema a su asistente, Emmy Noether, de 33 años.
Noether era asistente solo de nombre. Ya era una matemática formidable cuando, a principios de 1915, Hilbert y Klein la invitaron a unirse a ellos en la Universidad de Gotinga. Pero otros miembros de la facultad se opusieron a contratar a una mujer, y a Noether se le impidió unirse a la facultad. A pesar de todo, pasaría los siguientes tres años presionando la falla que separa la física de las matemáticas, lo que finalmente desencadenó un terremoto que sacudiría los cimientos de la física fundamental.
En 1918, Noether publicó los resultados de sus investigaciones en dos teoremas fundamentales. Uno explicaba las leyes de conservación en pequeñas regiones del espacio, una proeza matemática que más tarde resultaría importante para comprender las simetrías de la teoría cuántica de campos. El otro, ahora conocido simplemente como el teorema de Noether, dice que detrás de cada ley de conservación se esconde una simetría más profunda.
En términos matemáticos, una simetría es algo que le puedes hacer a un sistema sin que cambie. Consideremos el acto de rotación. Si comenzamos con un triángulo equilátero, veremos que podemos rotarlo en múltiplos de 120 grados sin que cambia su apariencia. Si comenzamos con un círculo, podemos rotarlo cualquier ángulo. Estas acciones sin consecuencias revelan las simetrías subyacentes de estas formas.
Pero las simetrías van más allá de la forma. Imagina que haces un experimento, luego te mueves 10 metros hacia la izquierda y lo vuelves a hacer. Los resultados del experimento no cambian, porque las leyes de la física no cambian de un lugar a otro. Esto se llama simetría de traslación.
Ahora espera unos días y repite el experimento. Los resultados no cambian, porque las leyes de la física no cambian con el paso del tiempo. Esto se llama simetría de traslación temporal.
Noether comenzó con simetrías como estas y exploró sus consecuencias matemáticas. Trabajó con la física establecida utilizando una descripción matemática común de un sistema físico, llamada lagrangiano.
 Como la mayoría de los académicos judíos en Alemania, Emmy Noether fue despedida tras la llegada al poder de los nazis. Más adelante, ese mismo año se fue al Bryn Mawr College en los EE. UU. y murió después de una cirugía de cáncer en 1935. Tenía 53 años. Fuente: Archivos del Bryn Mawr College
Como la mayoría de los académicos judíos en Alemania, Emmy Noether fue despedida tras la llegada al poder de los nazis. Más adelante, ese mismo año se fue al Bryn Mawr College en los EE. UU. y murió después de una cirugía de cáncer en 1935. Tenía 53 años. Fuente: Archivos del Bryn Mawr CollegeEn este punto, la intuición de Noether trascendió los símbolos en la página. Sobre el papel, las simetrías no parecen tener ningún impacto en la física del sistema, ya que no afectan al lagrangiano. Pero Noether se dio cuenta de que las simetrías deben ser importantes desde el punto de vista matemático, ya que limitan como puede comportarse un sistema. Trató de determinar cuál debería ser esta restricción y, de las matemáticas del lagrangiano, surgió una cantidad que no puede cambiar. Esa cantidad corresponde a la propiedad física que se conserva. El impacto de la simetría había estado oculto bajo las ecuaciones todo el tiempo, fuera de la vista.
En el caso de la simetría de traslación, el momento total del sistema nunca debería cambiar. En el caso de la simetría de traslación temporal, la energía total de un sistema se conserva. Noether descubrió que las leyes de conservación no son axiomas fundamentales del universo, sino que surgen de simetrías más profundas.
Las consecuencias conceptuales son difíciles de exagerar. Los físicos de principios del siglo XX se sorprendieron al darse cuenta de que un sistema que rompe la simetría de traslación temporal puede romper con ella la conservación de la energía. Ahora sabemos que nuestro propio universo hace esto. El cosmos se está expandiendo a un ritmo acelerado, estirando la luz sobrante del universo primitivo. El proceso reduce la energía de la luz a medida que pasa el tiempo.
“Antes del teorema de Noether, el principio de conservación de la energía estaba envuelto en misterio”, escribió el físico y matemático Feza Gürsey en 1983. “… La formulación matemática simple y profunda de Noether hizo mucho por desmitificar la física”.
El teorema de Noether también ha influido en el mundo cuántico. En la década de 1970, desempeñó un papel importante en la construcción del Modelo Estándar de la física de partículas. Las simetrías de los campos cuánticos dictan leyes que restringen el comportamiento de las partículas fundamentales. Por ejemplo, una simetría en el campo electromagnético obliga a las partículas a conservar su carga.
El poder del teorema de Noether ha inspirado a los físicos a buscar la simetría para descubrir nueva física. Más de un siglo después, las ideas de Noether siguen influyendo en la forma de pensar de los físicos.
“Hay mucho que todavía nos queda por aprender si reflexionamos sobre el teorema de Noether”, afirma el físico matemático John Baez. “Tiene capas y capas de profundidad”.
El artículo original, How Noether’s Theorem Revolutionized Physics, se publicó el 7 de febrero de 2025 en Quanta Magazine.
Traducido por César Tomé López
El artículo Cómo el teorema de Noether revolucionó la física se ha escrito en Cuaderno de Cultura Científica.
Berberechos equipados con fibra óptica
Las plantas y otros organismos fotosintéticos fijan el CO2 y elaboran carbohidratos. Los animales no podemos hacer la fotosíntesis y aprovechar directamente la energía de la luz solar. No obstante, algunos animales establecen relaciones de simbiosis con organismos unicelulares fotosintéticos. Estos organismos reciben el nombre de zooxantelas y generalmente son dinoflagelados del género Symbiodinium, aunque pueden ser algas de diferentes tipos.
Las zooxantelas obtienen protección y elementos inorgánicos de su hospedador, y a cambio le proporcionan moléculas orgánicas. El caso más conocido de esta fotosimbiosis es el de los corales arrecifales. De hecho, el gravísimo problema conocido como blanqueo del coral se debe a la expulsión de las zooxantelas a causa de cambios medioambientales que provocan estrés en los corales.
Además de los corales, otros casos de fotosimbiosis se registran en esponjas, medusas o moluscos. Un caso excepcional es el gasterópodo Elysia chlorotica, la babosa esmeralda. Su color verde se debe a que se alimenta de algas, pero almacena los cloroplastos en divertículos digestivos en los que se sigue produciendo la fotosíntesis.
 Figura 1. El cárdido Tridacna crocea expone su manto a través de la abertura entre las valvas. Los intensos colores se deben a la simbiosis con zooxantelas fotosintéticas y a los iridóforos, células que reflejan la luz ultravioleta. De David Witherall y Sarah Davies, CC BY 3.0
Figura 1. El cárdido Tridacna crocea expone su manto a través de la abertura entre las valvas. Los intensos colores se deben a la simbiosis con zooxantelas fotosintéticas y a los iridóforos, células que reflejan la luz ultravioleta. De David Witherall y Sarah Davies, CC BY 3.0Varios grupos de moluscos lamelibranquios o bivalvos también aparecen asociados con zooxantelas, pero solo en dos de ellos se puede hablar de simbiosis obligada, sin la cual la supervivencia del molusco está comprometida. Los dos casos pertenecen a la familia de los cárdidos. Aquí encontramos a las famosas tridacnas, las almejas gigantes, que pueden alcanzar más de un metro de longitud y 300 Kg de peso (Figura 1). Se calcula que entre el 75% y el 90% de su nutrición deriva de la fotosíntesis. El segundo grupo de bivalvos con zooxantelas incluye a los berberechos de la subfamilia Fraginae, que tienen la característica forma de corazón que da nombre a los cárdidos (Figura 2).
 Figura 2. Dos ejemplares del berberecho Corculum cardissa. Abajo los vemos iluminados desde el interior, lo que permite apreciar las ventanas que dejan pasar la luz. De McCoy et al. (2024). CC BY-NC-ND 4.0
Figura 2. Dos ejemplares del berberecho Corculum cardissa. Abajo los vemos iluminados desde el interior, lo que permite apreciar las ventanas que dejan pasar la luz. De McCoy et al. (2024). CC BY-NC-ND 4.0En ambos casos las zooxantelas se ingieren durante el crecimiento de larvas y juveniles, y se almacenan en complejos divertículos del tubo digestivo. El problema es que estas zooxantelas necesitan exposición a la luz solar, y esto no es sencillo en un animal con valvas calcáreas. Las grandes tridacnas solucionan esto manteniendo sus valvas abiertas, incluso exponiendo su manto fuera de ellas (Figura 1). Sin embargo, los pequeños berberechos se mantienen cerrados y reciben la luz a través de sus conchas. ¿Cómo es posible?
Un estudio de las universidades de Chicago y Stanford, liderado por la Dra. Dakota McCoy, ha revelado las sorprendentes adaptaciones de Corculum cardissa para llevar la luz solar a sus zooxantelas. Este pequeño berberecho (3-4 cm) permanece semienterrado en la arena, exponiendo una zona aplanada de sus valvas al exterior. En esa zona existen una serie de pequeñas ventanas de forma variable que permiten el paso de la luz (Figura 2). Podría pensarse que se trata de zonas adelgazadas de la concha, pero no es así. De hecho, estas ventanas pueden ser más gruesas que las áreas opacas de la valva. ¿Cómo permiten el paso de la luz?
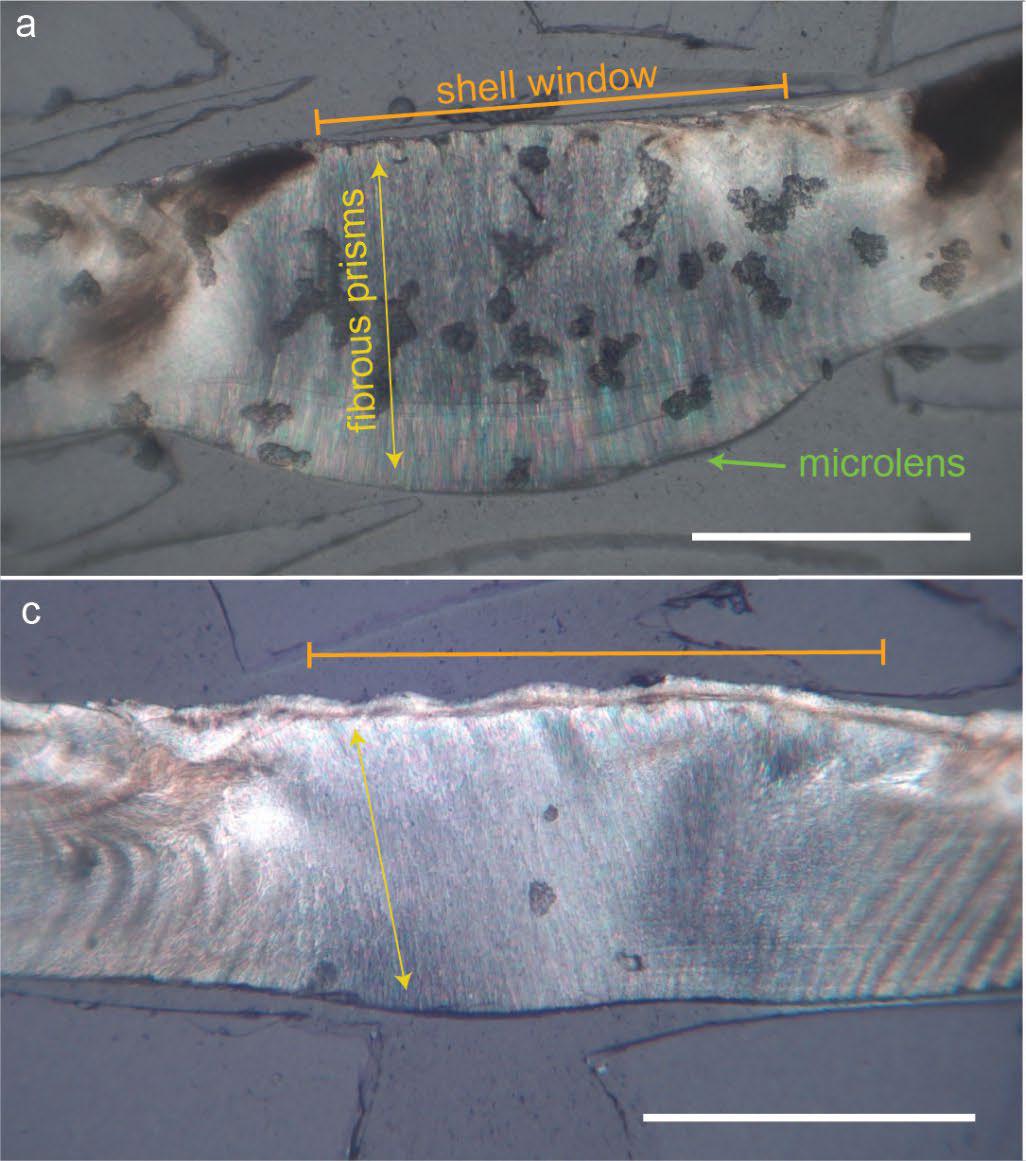 Figura 3. Sección de la concha de C. cardissa a nivel de las ventanas. La figura superior muestra una microlente asociada a la ventana. Obsérvese la presencia de finísimos prismas de aragonito que actúan como fibras ópticas. Escala= 0,5 mm. De McCoy et al. (2024). CC BY-NC-ND 4.0
Figura 3. Sección de la concha de C. cardissa a nivel de las ventanas. La figura superior muestra una microlente asociada a la ventana. Obsérvese la presencia de finísimos prismas de aragonito que actúan como fibras ópticas. Escala= 0,5 mm. De McCoy et al. (2024). CC BY-NC-ND 4.0El estudio de McCoy y sus colaboradores ha mostrado que las ventanas están formadas por haces de finísimos cristales de aragonito (una forma cristalina del carbonato cálcico) de un micrómetro de diámetro, que funcionan como auténticas fibras ópticas (Figura 3). No se trata de que estos cristales sean transparentes y dejen pasar la luz, sino que la conducen a lo largo del cristal con mínimas pérdidas. De hecho, si se superpone el haz de fibras sobre una imagen, la imagen aparece proyectada en la superficie contraria.
La transmisión de la luz a través de las fibras de aragonito está optimizada para ser mucho mayor en las longitudes de onda largas (luz naranja y roja) y mucho menor en las cortas (radiación ultravioleta, perjudicial para las zooxantelas) (Figura 4). La luz roja produce una mayor eficiencia fotosintética a diferencia de la luz verde, que es reflejada. Precisamente por esto las plantas son verdes.
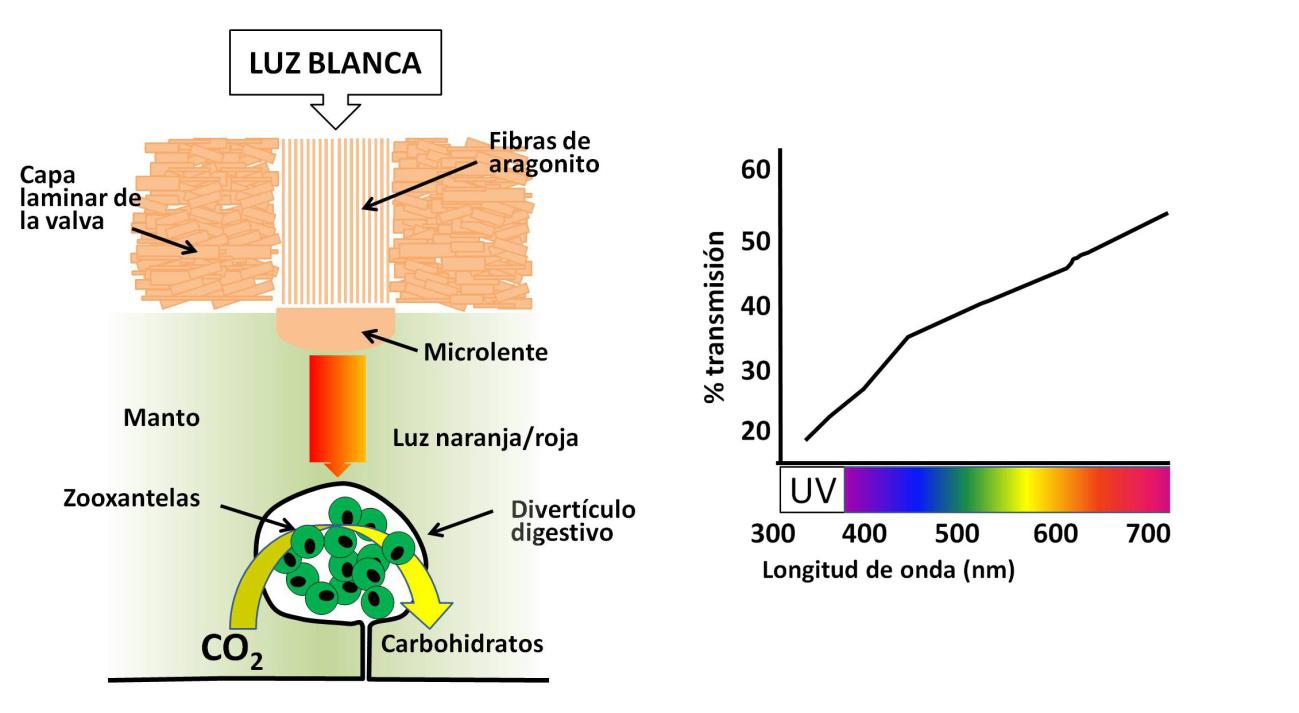 Figura 4. Esquema de la transmisión de luz por las fibras de aragonito. La microlente condensa la luz en un haz que penetra en el manto hasta alcanzar las zooxantelas, albergadas en divertículos del sistema digestivo. A la derecha vemos cómo la máxima transmisión de luz se produce en las mayores longitudes de onda (naranja/rojo), más adecuadas para la fotosíntesis (11-62%, con una media del 31%). Los rayos ultravioletas, perjudiciales, son filtrados (5-28%, con una media del 14%)
Figura 4. Esquema de la transmisión de luz por las fibras de aragonito. La microlente condensa la luz en un haz que penetra en el manto hasta alcanzar las zooxantelas, albergadas en divertículos del sistema digestivo. A la derecha vemos cómo la máxima transmisión de luz se produce en las mayores longitudes de onda (naranja/rojo), más adecuadas para la fotosíntesis (11-62%, con una media del 31%). Los rayos ultravioletas, perjudiciales, son filtrados (5-28%, con una media del 14%)Las ventanas ocupan aproximadamente la mitad de la superficie de la concha expuesta a la luz. El resto está formado por cristales de aragonito en forma de láminas entrecruzadas, lo que da mayor solidez a la concha que la disposición en fibras. Existe, por tanto, un compromiso entre resistencia mecánica y transmisión de luz. En una parte de las ventanas, bajo el haz de fibras ópticas, hay un abultamiento que funciona como lente, concentrando la luz en un haz de 1 mm de diámetro y permitiendo una mayor penetración en los tejidos blandos (Figura 4).
Los parámetros del haz de fibras han mostrado que son el sistema óptimo para la transmisión de luz, tanto en lo que se refiere a su orientación (perpendicular a la superficie), su diámetro (1 m) e incluso el eje óptico elegido. El aragonito es un mineral ópticamente anisótropo. Esto significa que su índice de refracción es diferente en los tres ejes espaciales. Las fibras de aragonito están orientadas de acuerdo con el eje de mayor índice de refracción, orientación que coincide con la máxima eficiencia óptica. Cualquier otra disposición, según las simulaciones hechas con ordenador, resulta en una menor transmisión de luz.
Según los autores del artículo, este constituye el primer caso de haces de fibras ópticas encontradas en un ser vivo. Solo algunas espículas de esponjas tienen propiedades ópticas similares, aunque es dudoso que tengan utilidad relacionada con la transmisión de la luz. Por otro lado, solo se conoce otro caso de lentes aplicadas a la fotosíntesis: ciertas células epidérmicas de plantas angiospermas. En conclusión, las adaptaciones de Corculum cardissa para suministrar luz a sus fotosimbiontes son realmente extraordinarias.
Referencias
McCoy, D.E., Burns, D.H., Klopfer, E. et al. (2024). Heart cockle shells transmit sunlight to photosymbiotic algae using bundled fiber optic cables and condensing lenses. Nat Commun. doi: 10.1038/s41467-024-53110-x
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Berberechos equipados con fibra óptica se ha escrito en Cuaderno de Cultura Científica.
La IA que sueña con ovejas eléctricas
 Foto: Possessed Photography / Unsplash
Foto: Possessed Photography / Unsplash
Soñar con ovejas eléctricas significa, hasta hoy, tener un cerebro humano. De ahí el inmortal título de la novela ciberpunk de Philip K. Dick. ¿Sueñan los androides con ovejas eléctricas? ¿Esta más cerca de producirse una inteligencia artificial genérica parecida a la humana, la llamada singularidad? Este es el camino.
Hoy, año 2025A pesar de enormes avances, los transistores, que son la base de la inteligencia artificial no son a día de hoy, ni actúan, como neuronas, y una computadora no calcula como un cerebro humano piensa. Una inteligencia artificial genérica parecida a la humana no va a producirse mañana. Pero… ¿estamos en el camino?
Existen enfoques, como la computación neuromórfica (el nombre no puede ser más explícito) que persiguen imitar el funcionamiento de nuestro cerebro. Para ello utilizan elementos inspirados en las neuronas y sus conexiones sinápticas, que son de naturaleza eléctrica, y buscan la misma eficiencia energética de un cerebro humano.
¿En qué punto estamos? ¿Nos encontramos más cerca de convivir con inteligencias que imiten la nuestra? Para poder responder a esto, habría que aclarar qué significa imitar nuestra inteligencia.
Imitar un cerebro humanoLa palabra “imitar” nos lleva rápidamente al “juego de la imitación” de Alan Turing y su famoso test.
A la hora de comparar la inteligencia artificial y la natural, el enfoque puede ser “filosófico” o “funcional”. El de Turing se parecería más a este último: como dijo alguien, la cuestión de si una máquina puede pensar no es más interesante que la de si un submarino puede nadar.
Para Turing, si una máquina podía engañar a un humano haciéndole creer que estaba hablando con otra persona humana, mostraría un comportamiento inteligente. Muchos no estarían de acuerdo con el bueno de Alan.
Pasar el test de Turing podría ser una condición necesaria pero no suficiente para darle el cum laude en inteligencia a una máquina. Para esos muchos, echar mano de ingeniosos trucos algorítmicos es de alguna manera degradar la pregunta central que está en juego y que hoy en día no tiene una respuesta clara: ¿qué es el pensamiento? ¿Qué tiene que ver con la autoconciencia?
Pensar con metáforasNosotros, los humanos, a partir de los datos que nos llegan de los sentidos y que describen la realidad circundante, derivamos nueva información. A partir de ellos podemos generar conocimiento asociativo que nos ayuda a actuar, reaccionar o incluso anticipar el curso de los acontecimientos.
Este conocimiento asociativo puede trascender la realidad misma, a veces solo por el simple capricho o placer de hacerlo. Esta asociación conceptual abstracta puede conducir, por ejemplo, a metáforas o poesía.
Pero, aparentemente, todo ello se reduce a una elaborada estrategia de supervivencia que ha servido bien a nuestra autoconservación. Por eso llevamos sapiens en nuestro apellido. Dijo Einstein: “el mejor resultado de la inteligencia no es el conocimiento sino la imaginación”. La IA, hasta la fecha, no razona ni imagina.
El teorema de los monos infinitosLos motores de IA parecen operar principalmente como máquinas de optimización de objetivos que aprovechan una vasta base de datos de conocimiento preexistente. ChatGPT materializa en tiempo récord el teorema de los infinitos monos, que establece que infinitos monos presionando al azar las teclas de máquinas de escribir durante una cantidad infinita de tiempo acabarán escribiendo las obras completas de William Shakespeare en algún momento.
Sin embargo, una IA recién nacida, sin acceso a bases de datos, ¿sería capaz de operar únicamente sobre la base de información fresca y puntual de sensores?
¿Soñaría una IA con ovejas eléctricas?
Esto nos lleva de nuevo a la cuestión de la conciencia artificial y a la probabilidad de que surja de forma espontánea.
La profetizada singularidadEl científico informático Ray Kurzweil acuñó el término de singularidad para tal suceso. El advenimiento de tal superinteligencia puede ser considerado como potencialmente benigno o tan desafortunado, o maligno, que los humanos vamos a salir necesariamente malparados, ya sea involuntariamente (como en 2001, una odisea del espacio) o voluntariamente (como en la serie de películas de Terminator).
La singularidad ha recuperado protagonismo a raíz de herramientas similares a ChapGPT, como la disruptiva DeepSeek, su rápida evolución y aparente creatividad. Han surgido varias voces, como la de Noam Chomsky, que dudan de su verdadera naturaleza inteligente.
En este debate entra el veterano libro La nueva mente del emperador, de Roger Penrose, que sostiene que nuestro cerebro no es algorítmico y no puede ser replicado por mera, aunque poderosa, computación. También afirmaba que el funcionamiento de nuestro cerebro se basa en cierta medida en la mecánica cuántica.
El nacimiento de HalHAL nació en la ficción en 2001, una película de 1968. El levantamiento de Skynet, el nombre de la inteligencia artificial que lidera al ejército de las máquinas en la saga Terminator, tuvo lugar en 1997, imaginado por un film estrenado en 1984. Son fechas ya bien caducadas. La IA parecía una más de las promesas futuristas aquejadas por la paradoja de Zenón, como los coches voladores o la fusión nuclear. Sin embargo, el mundo de la computación está viviendo tiempos y perspectivas interesantes y la IA que necesitamos para navegar el avance exponencial de la tecnología está provocando un debate encendido sobre las implicaciones sociales de la inteligencia no humana.
El mencionado Ray Kurzweil, directivo de Google y “profeta” tecnológico, predijo en 2005 que habría una máquina inteligente sobrehumana en 2045, con una etapa intermedia consistente en una inteligencia similar a la humana en 2029. Esto lo tenemos casi en la punta de nuestros dedos temporales.
Si la singularidad se produjera, el nacimiento de esa IA genérica intermedia, llamémosla infantil y recemos por una adolescencia corta, plantearía un dilema ético interesante. ¿Qué hueco le hacemos?
Si la singularidad ocurreSi la singularidad ocurre, podemos pensar en leyes como las de los Grandes Simios, que en algunas jurisdicciones les confieren la condición de personas, considerándolos seres y no cosas. Estas leyes se apoyan sobre la base de cierta habilidad lingüística, autocontrol, autoconciencia y la capacidad de proyectarse a sí mismos en el futuro.
También podemos inspirarnos en el capítulo de los Derechos del Niño que establece que se les debe facilitar los medios para su desarrollo material y espiritual; proveerles de las condiciones que les permitan ganarse la vida protegiéndolos de la explotación, y educarlos en la idea de que sus talentos deben dedicarse al servicio de sus semejantes.
Alcanzar ese estado de convivencia con inteligencias artificiales y hacerlo con éxito sería un pequeño paso para la humanidad, pero un gran salto para toda vida inteligente, ya sea basada en el carbono como en el silicio.![]()
Sobre el autor: Luis Antonio Fonseca Chácharo, Profesor de Investigación en microelectrónica, Instituto de Microelectrónica de Barcelona (IMB-CNM-CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La IA que sueña con ovejas eléctricas se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2024: El cubata de Brunelleschi
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

Miguel Ángel Cajigal, conocido en las redes sociales como «El barroquista», nos explica en esta charla como se solucionó el problema de la construcción de la cúpula de la catedral de Florencia, algo que sus promotores se comprometieron a que fuese la más grande jamás construida, a pesar de que nadie había hecho nada parecido hasta el momento. Una historia de arte, tecnología y chulería.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: El cubata de Brunelleschi se ha escrito en Cuaderno de Cultura Científica.
Descifrando el código de los materiales

¿Alguna vez os habéis preguntado por qué el cobre conduce la corriente eléctrica y el vidrio no? ¿Por qué el diamante es tan duro y el grafito de los lápices tan blando, aunque ambos estén compuestos de carbono? La respuesta no se encuentra a simple vista.
Pensemos en el ADN. El orden específico de las bases nitrogenadas del ADN codifica las peculiaridades de cada ser vivo. Nuestro código genético determina, por ejemplo, el color de nuestros ojos. De manera similar, cada material posee una distribución interna de sus electrones característica, conocida como “bandas de energía”, que dicta su comportamiento y condiciona propiedades tan importantes como su capacidad para conducir corriente o para imantarse, su reactividad química, o como veremos a continuación, su color.
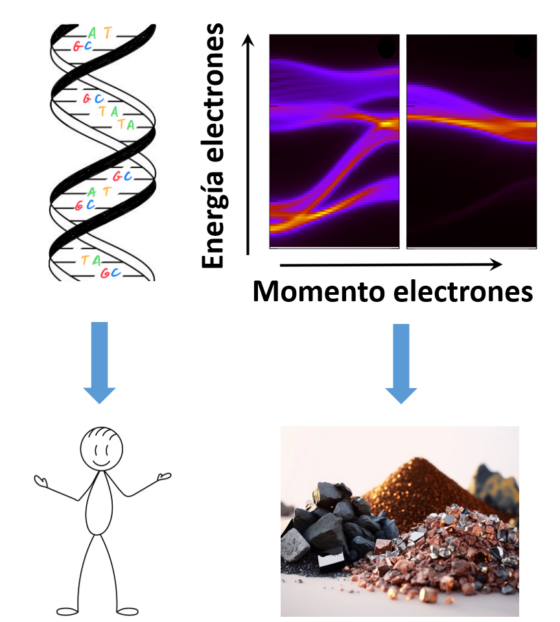 Así como nuestro código genético define nuestras características, las propiedades de un material vienen dadas por su propio código: la estructura de bandas electrónica. Fuente: Composición a partir de imágenes de Wikimedia Commons
Así como nuestro código genético define nuestras características, las propiedades de un material vienen dadas por su propio código: la estructura de bandas electrónica. Fuente: Composición a partir de imágenes de Wikimedia Commons
Imaginemos un material como una enorme escalera, donde cada peldaño corresponde a niveles de energía de sus electrones. Aquí es crucial el papel de la física cuántica. Sabemos que los electrones pertenecen a la clase de partículas conocidas como fermiones. El físico Wolfgang Pauli formuló para ellos el “principio de exclusión”, según el cual dos fermiones pertenecientes a un mismo sistema no pueden encontrarse en el mismo estado. Por otro lado, también necesitamos algo de física clásica. Los electrones poseen carga electrostática, por lo que están sujetos a la ley de Coulomb, que establece que las cargas de signo opuesto se atraen y las de igual signo se repelen. Los electrones, por tener carga negativa, son atraídos por los núcleos de los átomos, de carga positiva, a la vez que son repelidos por los demás electrones presentes en el material. Al hacer balance de todas estas normas, el resultado que obtenemos es que los electrones no pueden estar en cualquier nivel de energía del material: algunos niveles están prohibidos.
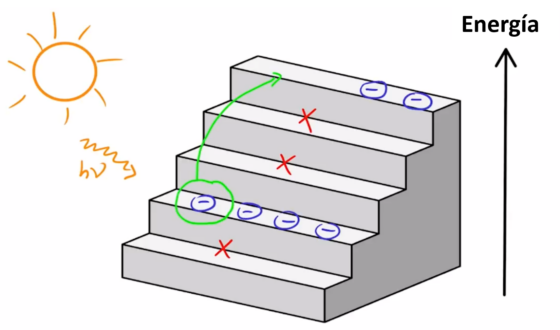 La distribución de las energías de los electrones de un material se puede interpretar como una escalera en la que algunos peldaños están prohibidos y en otros se puede almacenar un número dado de electrones.
La distribución de las energías de los electrones de un material se puede interpretar como una escalera en la que algunos peldaños están prohibidos y en otros se puede almacenar un número dado de electrones.Así, la estructura de bandas electrónicas de cada material es su «ADN» o seña de identidad, formada por una combinación específica de niveles de energía permitidos y prohibidos, que condicionará sus principales propiedades. Por ejemplo, esta combinación específica determina si un material conduce bien la electricidad, como los conductores, si no deja fluir la corriente eléctrica, como en los aislantes…o incluso si la conduce sin resistencia ni pérdida de energía, el caso de los superconductores.
La aplicación de las leyes de la mecánica cuántica nos permite ir más allá y predecir cómo responderá un material ante la aplicación de un estímulo externo, como puede ser una presión mecánica, un campo magnético, o algo tan común como la luz. En semiconductores y aislantes, al absorber luz de una determinada longitud de onda, los electrones son “excitados”, lo que significa que pueden saltar a peldaños vacíos de mayor energía. Este tipo de proceso determina el color con el que vemos el material. Asimismo, se puede dar el proceso contrario de “desexcitación» de electrones, mediante el cual el material emite luz de una determinada longitud de onda en función de los peldaños descendidos. La tecnología LED, presente en muchos de los dispositivos que usamos diariamente, aprovecha este fenómeno de emisión de luz.
 Las propiedades conductoras de un material están definidas por su estructura de bandas. Así, los metales se emplean en transporte de corriente y los semiconductores en chips y LEDs. Se puede hacer levitar a un superconductor, gracias a su especial propiedad de expeler los campos magnéticos. Fuente: Composición a partir de imágenes de Wikimedia Commons
Las propiedades conductoras de un material están definidas por su estructura de bandas. Así, los metales se emplean en transporte de corriente y los semiconductores en chips y LEDs. Se puede hacer levitar a un superconductor, gracias a su especial propiedad de expeler los campos magnéticos. Fuente: Composición a partir de imágenes de Wikimedia Commons
En un laboratorio podemos medir experimentalmente la estructura de bandas de los materiales a partir de la observación del resultado de excitar los electrones con distintas fuentes de luz, en particular de rayos-X y luz ultravioleta (UV). Pero si queremos ser realmente precisos al realizar nuestra “radiografía del material», debemos emplear la intensa luz procedente de radiación sincrotrón, que solo se encuentra disponible en instalaciones especiales. Entre ellas destaca el sincrotrón ALBA, situado en la provincia de Barcelona.
 Cámara de ultra-alto vacío, situada en el Centro de Física de Materiales (CFM-MPC) CSIC-UPV/EHU en Donostia-San Sebastián, donde se combinan distintas técnicas experimentales, como la microscopia túnel y la espectroscopia fotoelectrónica para el estudio experimental de la estructura atómica y electrónica de superficies. Fuente: UPV/EHU
Cámara de ultra-alto vacío, situada en el Centro de Física de Materiales (CFM-MPC) CSIC-UPV/EHU en Donostia-San Sebastián, donde se combinan distintas técnicas experimentales, como la microscopia túnel y la espectroscopia fotoelectrónica para el estudio experimental de la estructura atómica y electrónica de superficies. Fuente: UPV/EHU Vista aérea de las instalaciones del sincotrón ALBA, situado en Cerdanyola del Vallès (Barcelona). Fuente: Consorcio para la Construcción, Equipamiento y Explotación del Laboratorio de Luz Sincrotrón (CELLS)
Vista aérea de las instalaciones del sincotrón ALBA, situado en Cerdanyola del Vallès (Barcelona). Fuente: Consorcio para la Construcción, Equipamiento y Explotación del Laboratorio de Luz Sincrotrón (CELLS)También podemos calcular la estructura de bandas empleando software de simulación basado en las llamadas teorías “ab initio”. Estas simulaciones reproducen el comportamiento de los electrones del material a partir de una serie de ecuaciones matemáticas formuladas a partir los dos fundamentos físicos descritos anteriormente: la mecánica cuántica y la ley de Coulomb. Se trata de cálculos tan complejos, que a veces requieren el uso de supercomputadores.
Finalmente, los físicos experimentales y teóricos colaboramos estrechamente para combinar nuestros hallazgos y así descodificar la estructura de bandas del material. Gracias a estas investigaciones, podemos diseñar y fabricar materiales con las propiedades específicas que deseemos.
Sobre las autoras: Maider Ormaza y Maria Blanco, profesoras investigadoras de la Facultad de Química de la Universidad del País Vasco/Euskal Herriko Unibersitatea

La Facultad de Química de la UPV/EHU cumple este año 50 años. Con motivo de este aniversario se han organizado un gran número de actividades festivas, de orientación del alumnado de secundaria, investigación, transferencia y divulgación. Entre estas últimas podemos encontrar “12 meses – 12 temas”, conjunto de actividades que pretende mostrar a la sociedad las temáticas desarrolladas en la Facultad. Entre estas actividades podemos encontrar el ciclo de charlas “50 años difundiendo la química”, en Ernest Lluch Kulturetxea, así como vídeos de divulgación, entrevistas en radio y artículos en los blogs de divulgación de la Cátedra de Cultura Científica. Durante todo el año contaremos con invitados especiales, como los cuatro Centros de Investigación nacidos de la Facultad (CIDETEC, CFM, DIPC y POLYMAT), así como los Premios Nobel Albert Fert y Jean Marie Lehn. Se puede consultar el conjunto de actividades programadas en la página web de nuestro 50 Aniversario.
El artículo Descifrando el código de los materiales se ha escrito en Cuaderno de Cultura Científica.
El sueño cumplido de Ícaro y Dédalo
Cuenta el mito que el arquitecto Dédalo y su hijo Ícaro escaparon de la isla de Creta gracias a unas alas de plumas y cera, como las de los pájaros, que el primero construyó. A pesar de las advertencias de su padre de que no volase demasiado alto porque el sol podría derretir sus alas, Ícaro hizo caso omiso y cayó al mar.
 La caída de Ícaro (1635-1637), de Jacob Peter Gowy, expuesto en el Museo del Prado. Créditos: Dominio público
La caída de Ícaro (1635-1637), de Jacob Peter Gowy, expuesto en el Museo del Prado. Créditos: Dominio público
Este no es el único mito en el que los Antiguos griegos trataron de prevenirnos acerca del peligro de forzar nuestros propios límites por arrogancia o ambición. Pero eso no significa que consiguieran detenernos, algo que se puede aplicar prácticamente a toda la historia de la ciencia y, sobre todo, de la tecnología y sus usos. Dentro de esa historia, el sueño concreto de convertirnos en Dédalo o Ícaro siempre fue uno de los más antiguos: el sueño de volar como los pájaros.
Y quiero recalcar lo de «como los pájaros», porque obviamente ya estamos acostumbrados a los aviones e incluso a los cohetes, pero ¿y a los ornitópteros? Estos son, probablemente, las máquinas voladoras más similares a un ave que hemos construido, pero todavía continúan más asociadas con la ciencia ficción que con la ciencia.
Casi desde los inicios de la historia o, al menos, que sepamos, desde la Antigüedad, con la paloma de vapor de Arquitas, han existido máquinas que han tratado de emular a las aves. En un principio se trataba de simples ingenios para entretenerse, ornamentos o juguetes de cuerda; con el tiempo se convirtieron en drones, proyectos de robótica o incluso en algo mucho más divertido: en ornitópteros.
 Seguramente, los ornitópteros más conocidos para el gran público sean los de la casa Atreides, en Dune. Créditos: Warner Bros. Pictures / Fair use
Seguramente, los ornitópteros más conocidos para el gran público sean los de la casa Atreides, en Dune. Créditos: Warner Bros. Pictures / Fair use
Un ornitóptero es un tipo de aeronave que vuela imitando el aleteo de un ave o un insecto, y he comentado que es divertido porque es un ingenio muy prototípico de los inventores locos. ¿Quién no ha escuchado alguna vez historias acerca de que tal o cual visionario se tiró de pequeño desde el tejado de su casa con unas alas construidas con lo que tenía por casa para intentar volar? Este tipo de aventuras suele acabar con algún susto —siguiendo el camino marcado por Ícaro—, pero eso no ha evitado que, a día de hoy, incluso algunos youtubers sigan intentando desafiar la gravedad de esta manera.
La idea práctica de emular a Dédalo y construir unas alas de pájaro nos lleva, inevitablemente, a Leonardo da Vinci, pero no fue hasta 1874 cuando el primer ornitóptero, el de Alphonse Pénaud, en Francia consiguió volar —que no despegar, porque hubo que lanzarlo desde cierta altura para que consiguiera la velocidad necesaria para sustentarse— durante 7 segundos a lo largo de 15 metros.
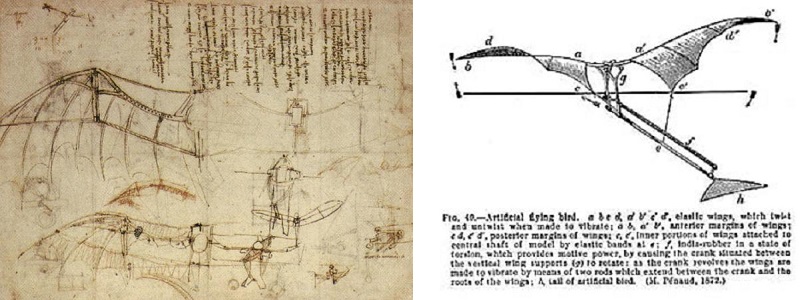 A la izquierda, esbozo de unas alas de Leonardo da Vinci. A la derecha, el ornitóptero de Pénaud. Créditos: Dominio público.
A la izquierda, esbozo de unas alas de Leonardo da Vinci. A la derecha, el ornitóptero de Pénaud. Créditos: Dominio público.
Los primeros ornitópteros utilizaban solo la fuerza humana para propulsarse; los diseños hacían uso de poleas, muelles y gomas para minimizar el esfuerzo del piloto, pero no dieron resultados demasiado buenos. Fue cuestión de poco tiempo que a los inventores se les ocurriera utilizar máquinas de vapor o motores de combustión, como a Edward Purkis Frost, que lo hizo en 1902 sobre uno de sus modelos, aunque parece que, si bien fue capaz de levantar del suelo al piloto, no llegó a volar.
 Ornitóptero de E. P. Frost impulsado por un motor de combustión. Créditos: Dominio público.
Ornitóptero de E. P. Frost impulsado por un motor de combustión. Créditos: Dominio público.
Quien sí parece que consiguió hacerlo fue Alexander Lippisch en 1929. Este pionero de la aviación es más conocido por sus contribuciones durante y después de la Segunda Guerra Mundial, entre ellas, el diseño del primer avión propulsado por cohetes: el Messerschmitt Me 163 Komet, pero antes, y siguiendo la locura generalizada de aquellos tiempos, también cayó en la tentación de diseñar un ornitóptero de propulsión humana. Hans Werner Krause fue el conejillo de indias, y no solo logró alcanzar cierta altura, sino que consiguió mantenerse un ratito en el aire. De nuevo, haciendo un poquito de trampas, tal vez, porque el aparato se lanzó haciendo uso de una goma elástica, más o menos como si fuerza un tirachinas, y eso pudo suponer cierta ventaja.
 Hans Werner Krause en la prueba del ornitóptero de Alexander Lippish (1929), que funcionaba con tan solo la fuerza del piloto. Créditos: Dominio público.
Hans Werner Krause en la prueba del ornitóptero de Alexander Lippish (1929), que funcionaba con tan solo la fuerza del piloto. Créditos: Dominio público.
Los que he mencionado son una mínima fracción de todos los ornitópteros que se intentaron construir desde finales del siglo XIX hasta entrado el siglo XX. Pero ni siquiera la llegada de los aviones modernos y a reacción hizo que olvidáramos sueño de Ícaro y Dédalo. Desde el punto de vista del espíritu aventurero humano y la magia del sentido de la maravilla, sigue sin ser lo mismo volar que volar con unas alas «de verdad». Por eso algunos no cejan en su empeño de conseguirlo.
Dejando a un lado, por el momento, los innumerables proyectos de drones y robótica que simulan el vuelo de las aves de una u otra forma, pero que no están enfocados al transporte, en el Instituto de Estudios Aeroespaciales de la Universidad de Toronto han hecho cosas interesantes. A finales de los años noventa, James DeLaurier creó el UTIAS Ornithopter No. 1, que despegó en su primer vuelo de prueba el 8 de julio de 2006 y consiguió recorrer 300 metros. Asistido, eso sí, por un motor turborreactor.
En la misma institución crearon el UTIAS Snowbird, de propulsión humana, y que consiguió en 2010, con el estudiante de 28 años Todd Reichert a los mandos, recorrer 145 metros en 19,3 segundos tras recibir la asistencia de un vehículo para ponerlo en el aire.
Por el momento, lamentablemente, no parece que estos aparatos corran el riesgo de derretirse por acercarse demasiado al sol… pero con cada intento, al menos, estamos cada vez más cerca de él. Esperemos que no nos pase lo mismo que a Ícaro.
BibliografíaGil, J. M. y Polanco, A. (2017). Aviones bizarros. Glyphos.
Flying Wings (1999-2002). Alphonse Pénaud (1850-1880). Flying Wings.
Human Powered Ornithopter Project
James Botham, C. (9 de febrero de 2022). E. P. Frost’s ornithopters. On Verticality.
Sanderson, J. (2006). Project Ornithopter.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo El sueño cumplido de Ícaro y Dédalo se ha escrito en Cuaderno de Cultura Científica.
La estructura geométrica de la novela “Un caballero en Moscú”
En el curioso e interesante libro Lost in translation (Libros del zorro rojo, 2016), de la escritora e ilustradora irlandesa Ella Frances Saunders, descubrí un término muy cercano a mí, bueno, a muchas de las personas que amamos leer. Es el término japonés “tsundoku”, término que se refiere al hábito de comprar libros y dejarlos amontonados sin leer, por ejemplo, en la mesilla al lado de la cama.
 Portada del libro Lost in translation (Libros del zorro rojo, 2016), de la escritora e ilustradora irlandesa Ella Frances Saunders
Portada del libro Lost in translation (Libros del zorro rojo, 2016), de la escritora e ilustradora irlandesa Ella Frances SaundersEn mi mesilla de noche, que es un claro ejemplo de tsundoku, descansan muchos libros comprados esperando a ser leídos. El problema está en que, como compro muchos más libros de los que soy capaz de leer, el tsundoku de mi mesilla crece y crece sin parar, por lo que tengo que quitar libros del mismo para que la torre de libros no sea tan alta que los libros de la misma terminen cayendo al suelo. Por este motivo, algunos de los libros que no son leídos en mucho tiempo acaban siendo trasladados a alguna de mis estanterías de libros y tienen que esperar a que los vuelva a rescatar algún tiempo después para ser colocados en mi mesilla otra vez y leídos finalmente. Aun así, hay muchos libros del tsundoku de mi mesilla que son retirados de la misma por el motivo original por el que fueron colocados allí, porque al final los leo, eso sí, con más o menos distancia temporal del momento en que fueron comprados.
 Página del libro Lost in translation (Libros del zorro rojo, 2016), de Ella Frances Saunders, con la explicación e ilustración del término japonés tsundoku
Página del libro Lost in translation (Libros del zorro rojo, 2016), de Ella Frances Saunders, con la explicación e ilustración del término japonés tsundokuEsto es lo que ha pasado con la magnífica novela Un caballero en Moscú (Salamandra, 2018), del novelista estadounidense Amor Towles (1964), que me recomendó hace un par de años mi librero y tras comprarla pasó a ser incluida en mi tsundoku, hasta hace poco que empecé a leerla. Justo he terminado de leerla el pasado fin de semana y me ha parecido una buena idea escribir un comentario sobre la interesante estructura geométrica de la misma.
Un caballero en MoscúLa novela Un caballero en Moscú (publicada originalmente en Estados Unidos en 2016) es la segunda novela del escritor estadounidense Amor Towles, autor de las novelas Normas de cortesía (Salamandra, 2013) y La autopista Lincoln (Salamandra, 2022), y del libro Mesa para dos (Salamandra, 2024), compuesto por seis relatos y una novela breve.
Un caballero en Moscú se mantuvo durante 59 semanas en las listas de libros más vendidos que publica el periódico estadounidense The New York Times, fue declarada libro del año por los periódicos The Times y The Sunday Times, finalista del Premio Kirkus (otorgado por la revista Kirkus Reviews) en 2016, preseleccionada para el Premio Literario Internacional IMPAC de Dublín de 2018, y se han venido más de un millón y medio de ejemplares de la misma. Además, se ha realizado una serie de televisión británica (Paramount+, 2024), de ocho capítulos, interpretada por el actor británico, nacionalizado estadounidense, Ewan McGregor (1971).
 Portada de la novela Un caballero en Moscú (Salamandra, 2018), del novelista estadounidense Amor Towles
Portada de la novela Un caballero en Moscú (Salamandra, 2018), del novelista estadounidense Amor TowlesLa sinopsis de la novela es la siguiente.
Condenado a muerte por los bolcheviques en 1922, el conde Aleksandr Ilich Rostov elude su trágico final por un inusitado giro del destino. Gracias a un poema subversivo escrito diez años antes, el comité revolucionario conmuta la pena máxima por un arresto domiciliario inaudito: el aristócrata deberá pasar el resto de sus días en el hotel Metropol, microcosmos de la sociedad rusa y conspicuo exponente del lujo y la decadencia que el nuevo régimen se ha propuesto erradicar.
Erudito, refinado y caballeroso, Rostov es un cliente asiduo del legendario Metropol, situado a poca distancia del Kremlin y el Bolshói. Sin profesión conocida pese a estar ya en la treintena, se ha dedicado con auténtica pasión a los placeres de la lectura y de la buena mesa.
Ahora, en esta nueva y forzada tesitura, irá construyendo una apariencia de normalidad a través de los lazos afectivos con algunos de los variopintos personajes del hotel, lo que le permitirá descubrir los jugosos secretos que guardan sus aposentos. Así, a lo largo de más de tres décadas, el conde verá pasar la vida confinado tras los inmensos ventanales del Metropol mientras en el exterior se desarrolla uno de los períodos más turbulentos del país.
 Cartel de la serie Un caballero en Moscú (Paramount +, 2024), basada en la novela homónima de Amor TowlesReferencias matemáticas en la novela
Cartel de la serie Un caballero en Moscú (Paramount +, 2024), basada en la novela homónima de Amor TowlesReferencias matemáticas en la novela
Aunque el aspecto matemático más interesante de esta novela es su estructura geométrica, de la que hablaremos más adelante, también se incluyen en la misma algunas pequeñas referencias a las matemáticas.
La referencia más larga del libro conectada con las matemáticas trata sobre los números primos y la divisibilidad de los números naturales. La situación es la siguiente. Están juntos el conde Aleksandr Ilich Rostov, protagonista de la novela, y Nina Kulikova, una niña de nueve años muy despierta, inquieta e inteligente, que se hace amiga del conde al principio de la novela, que además le descubre algunos de los secretos ocultos del hotel y ambos mantendrán su amistad a lo largo de los años, hasta que Nina se hace mayor.
– ¿Quieres ver cómo hago un truco?
– Quizá en otro momento.
El conde cuadró la baraja y la dejó encima de la mesa. Entonces, cogió la hoja de encima del montón de hojas terminadas. Vio que en ella estaban concienzudamente alineados en columnas todos los números cardinales del 1100 al 1199. En función de algún sistema que él ignoraba, había trece números encerrado en un círculo rojo.
El conde estaba intrigado, como es lógico.
– ¿Qué estás haciendo?
– Matemáticas.
– Veo que te aplicas a la materia con vigor.
– El profesor Lisitski dice que tienes que pelear con las matemáticas como pelearías con un oso.
– ¿Ah, sí? Y ¿con qué clase de oso peleamos hoy? Sospecho que con alguno más parecido a un oso polar que un panda.
Nina levantó la cabeza y le lanzó una de aquellas miradas suyas capaces de apagar cualquier chispa.
El conde carraspeó y adoptó un tono más serio.
– Me imagino que el proyecto implica ciertos subconjuntos de números enteros.
– ¿Usted sabe qué es un número primo?
– ¿Te refieres a dos, tres, cinco, siete once trece,…?
– Exacto –confirmó ella–. Son los números enteros que son indivisibles por cualquier número excepto el uno y ellos mismos.
Dado el dramatismo con el que había pronunciado la palabra “indivisibles”, parecía que estuviera hablando de la inexpugnabilidad de una fortaleza.
– En cualquier caso –añadió–, estoy haciendo una lista de todos ellos.
– ¡De todos ellos!
– Es una tarea propia de Sísifo –admitió la niña (aunque con un entusiasmo que te hacía preguntarte si conocía realmente el significado de esa expresión).
Nina señaló las páginas escritas que había encima de la mesa.
– La lista de los números primos empieza en dos, tres, cinco, como usted dice. Pero los números primos van haciéndose cada vez más escasos a medida que crecen. De modo que una cosa es encontrar un siete o un once, pero un mil nueve ya es otro cantar. ¿Se imagina identificar un número primo en las centenas de millar? ¿O en los millones? […]
El conde volvió a mirar la hoja que tenía en las manos, esta vez con mayor respeto. Al fin y al cabo, un hombre culto debería admirar cualquier estudio, por misterioso que fuera, si se llevaba a cabo con curiosidad y entrega.
– Mira –dijo con el tono de voz de quien contribuye a una causa–, este número no es primo.
Nina alzó la vista con expresión de incredulidad.
– ¿Qué número?
El conde le puso la hoja delante y señaló la cifra encerrada en un círculo rojo.
– Mil ciento setenta y tres.
– ¿Cómo sabe que no es primo?
– Si la suma de los dígitos que componen una cifra da un número divisible por tres, esa cifra también es divisible por tres.
Ante ese hecho tan extraordinario, Nina replicó:
– Mon Dieu!
Entonces se recostó en el respaldo de la silla y se quedó observando al conde como si reconociera que hasta ese momento quizá lo hubiera infravalorado.
 Fotograma de la serie de televisión Un caballero en Moscú en el que aparecen el conde Aleksandr Ilich Rostov, interpretado por el actor Ewan McGregor, y Nina Kulikova, interpretada por la joven actriz Leah Balmforth. Fuente: Paramount, 2024
Fotograma de la serie de televisión Un caballero en Moscú en el que aparecen el conde Aleksandr Ilich Rostov, interpretado por el actor Ewan McGregor, y Nina Kulikova, interpretada por la joven actriz Leah Balmforth. Fuente: Paramount, 2024Los números primos son muy importantes en matemáticas y de ellos hemos escrito bastante en el Cuaderno de Cultura Científica (una referencia básica sobre los mismos es la entrada Buscando lagunas de números no primos). En la anterior cita, Nina se encuentra haciendo unos deberes que consisten en realizar una lista de números naturales, en la que se marcan con un círculo rojo aquellos que son primos. Cuando llega el conde ve las hojas en las que Nina está escribiendo esa lista, de hecho, los números de la última hoja realizada contiene los números entre 1100 y 1199. Entre esos números hay doce números primos, que son 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187 y 1193, sin embargo, Nina ha incluido uno más 1173, que no es un número primo, puesto que es divisible por tres, como le descubre el conde, ya que satisface la condición de divisibilidad del tres (“un número es divisible por 3 si, y sólo si, la suma de sus dígitos es divisible por 3”, como mostramos en la entrada Las curiosas reglas de divisibilidad).
Pero existen algunas otras pequeñas referencias matemáticas, como los experimentos del cálculo de la aceleración de la gravedad y el de la torre de Pisa realizado por el matemático y astrónomo italiano Galileo Galilei, la resolución de ecuaciones, la paradoja de Aquiles, el teorema de Pitágoras o la aritmética.
La estructura geométrica de la novelaPero, sin lugar a dudas, el aspecto matemático más interesante de la novela es su estructura geométrica. La novela transcurre entre el 21 de junio de 1922 y ese mismo día, 21 de junio, día importante en la novela que aparece continuamente a lo largo de la misma, del año 1954, recorriendo 32 años, desde el principio al final. Ese número de años, 32, que es 25 = 2 x 2 x 2 x 2 x 2, no es un número puesto al azar, sino que tiene relevancia en la estructura.
Justo antes de empezar la novela, se presentan las actas del juicio de los bolcheviques al conde Aleksandr Ilich Rostov, celebrado el día 21 de junio de 1922, donde es declarado culpable y se le condena a la pena de muerte. Sin embargo, se le conmuta la pena capital por un arresto domiciliario de por vida en el hotel Metropol del centro de Moscú donde estaba hospedado, debido a que es el autor de un conocido poema subversivo que había escrito diez años antes.
 Una vieja postal en la que puede verse el hotel Metropol de Moscú en aquellos primeros años del siglo xx
Una vieja postal en la que puede verse el hotel Metropol de Moscú en aquellos primeros años del siglo xx
El primer capítulo de la novela (con el título Ante el embajador), tras las actas del juicio, recoge lo que ocurrió ese primer día al llegar al hotel. En particular, se le desaloja de su lujosa suite y se le aloja en una pequeña habitación de una zona en desuso del hotel que estaba destinada a los sirvientes de los huéspedes ricos. El siguiente capítulo (Aquel naufrago anglicano) recoge lo ocurrido un día después del arresto, el 22 de junio de 1922. El tercer capítulo (A la hora acordada) transcurre dos días después del arresto domiciliario. La historia continúa cinco días después (Amistad), luego diez días (Ahora bien…), tres semanas (A dar una vuelta por ahí), seis semanas (Asamblea), tres meses (Arqueologías), seis meses (Adviento) y justo un año después de su arresto en el hotel Metropol, el 21 de junio de 1923 (Abejas en lo alto, una actriz y una aparición).
A partir de ese momento, la novela va saltando a través del 21 de junio de diferentes años, el año 1924 (Anonimato), es decir, han pasado dos años desde la condena del conde, el año 1926 (Adieu), cuatro años después, el 1930 (Artes de Aracne / Acudir a una cita por la tarde / Alianza / Absenta), pasados ocho años, hasta llegar al año 1938, dieciséis años después del primer día de la novela, el 21 de junio de 1922, que es el punto central de la misma (Alguien regresa / Ajustes / Ascenso y descenso).
 Imagen de los personajes principales de la serie Un caballero en Moscú (2024). Fuente: Paramount, 2024
Imagen de los personajes principales de la serie Un caballero en Moscú (2024). Fuente: Paramount, 2024Como podemos observar los periodos temporales se duplican claramente cuando hablamos del paso de los años (uno, dos, cuatro, ocho, dieciséis años) y se aproxima a la duplicación cuando hablamos de días, semanas y meses (un día, dos días, cinco días, diez días, tres semanas, seis semanas, tres meses, seis meses y doce meses, es decir, un año), que explicaremos más adelante.
A partir de ese punto central, el 21 de junio de 1938, dieciséis años después del inicio de la novela (21 de junio de 1922) y dieciséis años antes del final de la misma (21 de junio de 1954), se produce un reflejo simétrico del paso del tiempo, respecto a la primera mitad, de manera que en esa primera mitad el paso del tiempo se va expandiendo, mientras que en la segunda se va a ir comprimiendo.
Tras el capítulo del 21 de junio de 1938, llega el del año 1946 (Arrebatos, antítesis y un accidente), a ocho años del final, después el año 1950 (Adagio, andante, allegro), a cuatro años del final, el año 1952 (América), a dos años del final y el 21 de junio de 1953 (Apóstoles y apóstatas), a un año del final. Para pasar a seis meses del final (Aplausos y elogios), tres meses (Avanzar como Aquiles), seis semanas (Arrivederci), tres semanas (Adultez), diez días (Anuncio), cinco días (Anécdotas), dos días (Asociación), un día (Antagonistas, frente a frente (y una absolución)) y el final el 21 de junio de 1954 (Apoteosis).
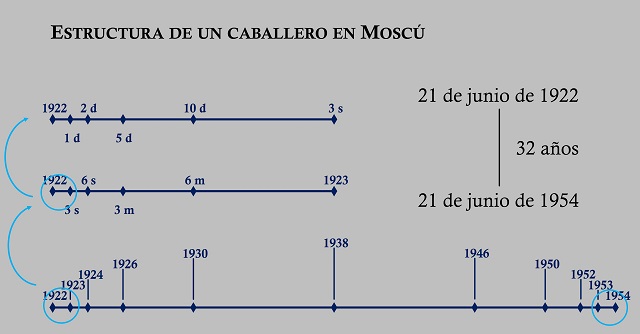 Esquema que representa la estructura temporal de la novela Un caballero en Moscú, de Amor Towles
Esquema que representa la estructura temporal de la novela Un caballero en Moscú, de Amor TowlesComo hemos comentado más arriba, el paso del tiempo se duplica primero, al menos aparentemente, ya que el paso del tiempo desde el 21 de junio de 1992 hasta el 21 de junio de 1938 es
… un día, dos días, cinco días, diez días, tres semanas, seis semanas, tres meses, seis meses y doce meses, es decir, un año, dos años, cuatro años, ocho años y dieciséis años.
Da la impresión de que algo no está bien, ya que, por ejemplo, el doble de dos días no son cinco días o el doble de diez días no es tres semanas. Veamos que la construcción del tiempo es más bien doblando el tiempo por la mitad, dividir entre 2 y no multiplicar.
El tiempo total de la novela son 32 años (del 21 de junio de 1922 al mismo día de 1954), cuya mitad son 16 años, mitad marcada por el 21 de junio de 1938. La mitad de 16 años son 8 años, que nos lleva al 21 de junio de 1930 (y de forma análoga en el otro sentido, hacia delante, a 1946). La mitad de 8 años son 4 años (1926); la mitad 2 años (1924); la mitad 1 año (1923); la mitad 6 meses; su mitad 3 meses; cuya mitad serían 6 semanas y algo, que puede redondearse a 6 semanas; la mitad 3 semanas; la mitad de 3 semanas, que son 21 días, son 10 días y medio, que redondeando serían 10 días; la mitad 5 días; la mitad 2 días y medio, que redondeando serían 2 días; cuya mitad es 1 día. Luego la estructura se explica con la división temporal en mitades.
 Fotograma de la serie Un caballero en Moscú (2024). Fuente: Paramount, 2024La importancia de la estructura geométrica
Fotograma de la serie Un caballero en Moscú (2024). Fuente: Paramount, 2024La importancia de la estructura geométrica
Esta estructura temporal de la novela es muy importante puesto que marca el ritmo narrativo de la misma. La novela se va expandiendo geométricamente, duplicando prácticamente el tiempo, desde el punto inicial, el 21 de junio de 1922. Al principio los saltos temporales son más cortos, el ritmo es mayor (desde el primer día pasa un día, dos días, cinco días, diez días, tres semanas, etcétera), es el momento en el que se van presentando los personajes de la novela, así como el lugar principal, el hotel Metropol, después los saltos temporales son más largos, el ritmo se va suavizando (cuatro años, ocho años, dieciséis años), que es necesario para percibir el paso del tiempo y los profundos cambios que se están dando en la sociedad rusa, en el propio hotel Metropol y en la vida del protagonista, y luego se contrae el tiempo dirigiéndose hacia la resolución de la novela, con un ritmo cada vez mayor por la compresión del tiempo (faltando para el final tres semanas, diez días, cinco días, dos días, un día).
El propio Amor Towles lo explica en algunas de sus entrevistas. Por ejemplo, en la entrevista realizada por Elena Bowes para “26”, cuando esta le pregunta “¿Puede describir la estructura de acordeón que utilizó para esta novela y por qué la eligió?”, el escritor británico responde lo siguiente.
Un caballero en Moscú tiene una estructura un tanto inusual. A partir del día del arresto domiciliario del Conde, los capítulos avanzan por un principio de duplicación que describe los acontecimientos un día después del arresto, dos días después, cinco días, diez días, tres semanas, seis semanas, tres meses, seis meses, un año, dos años, cuatro años, ocho años y dieciséis años después hasta el día de hoy. En este punto medio, se inicia un principio de división a la mitad, con la narración saltando a ocho años después, cuatro años, dos años, hasta diez días, cinco días, dos días, un día.
El aspecto matemático de la forma del libro es prácticamente invisible para los lectores. Dicho esto, creo que se adapta bien a la historia porque los lectores obtienen una descripción muy granular de los primeros días del confinamiento del Conde; luego pueden saltar en el tiempo a través de épocas definidas por la carrera, las relaciones y los cambios en el panorama político; por último, vuelven a la granularidad urgente a medida que la historia se acerca a su conclusión increíblemente emocionante.
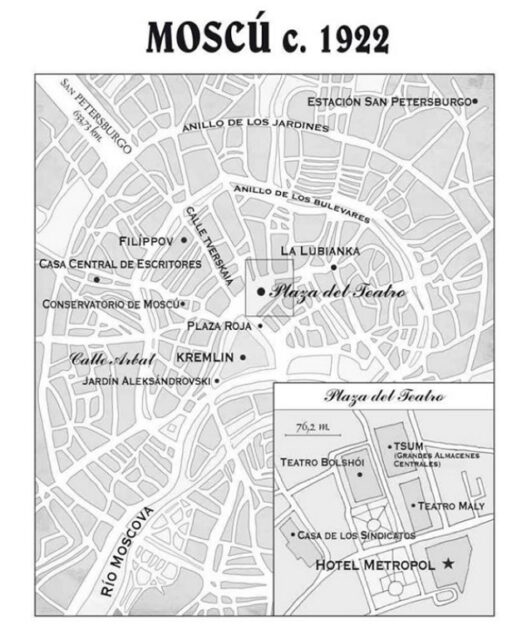 Mapa del centro de Moscú en 1922
Mapa del centro de Moscú en 1922
Mientras que en su página web responde también a una serie de preguntas y nos encontramos con el siguiente comentario sobre la estructura de la novela.
Al final, un reto mucho mayor surgió de la geometría de la novela. Esencialmente, Un caballero en Moscú adopta la forma de un diamante de lado. Desde el momento en que el Conde atraviesa las puertas giratorias del hotel, la narración comienza a abrirse sin cesar hacia el exterior. A lo largo de las doscientas páginas siguientes se acumulan descripciones detalladas de personas, habitaciones, objetos, recuerdos y acontecimientos menores, muchos de los cuales parecen casi incidentales. Pero entonces, cuando el libro entra en su segunda mitad, la narración empieza a estrecharse y convergen todos los elementos dispares de la primera mitad. Personajes insignificantes, observaciones pasajeras y objetos fortuitos se entremezclan y desempeñan papeles esenciales para llevar la narración a su aguda conclusión.
Bibliografía
1.- Sarah Hart, Érase una vez los números primos, Paidós, 2024.
2.- Página web oficial de Amor Towles
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La estructura geométrica de la novela “Un caballero en Moscú” se ha escrito en Cuaderno de Cultura Científica.
Los magnetorreceptores biológicos que actúan en el límite cuántico
 Foto: Alain Bonnardeaux / Unsplash
Foto: Alain Bonnardeaux / UnsplashLos gansos canadienses, las mariposas monarca, los tiburones cabeza de pala y el salmón rojo son algunas de las muchas especies animales que navegan por el mundo detectando pequeños cambios en el campo magnético de la Tierra. Estudios anteriores de estos organismos han identificado varios tipos de sensores, como reacciones químicas sensibles al magnetismo y estructuras celulares similares a brújulas, pero no estaba claro hasta qué punto son sensibles estos llamados magnetorreceptores biológicos.
Ahora, Iannis Kominis y Efthmis Gkoudinakis, de la Universidad de Creta, Grecia, han calculado los límites de la capacidad de detección de tres tipos principales de magnetorreceptores biológicos, demostrando que dos de ellos probablemente pueden detectar campos magnéticos con magnitudes cercanas al límite cuántico para la detección de campos magnéticos.
El rendimiento de un sensor magnético se puede caracterizar por tres parámetros: su volumen, su tiempo de medición y la incertidumbre en la estimación del campo magnético. Cada parámetro puede hacerse más pequeño, pero existe un límite a su reducción colectiva basado en la constante de Planck, un parámetro que define muchos fenómenos cuánticos. Todos los magnetómetros fabricados en laboratorio conocidos obedecen a este límite cuántico. Debido a su pequeño tamaño y a los pequeños cambios de campo que detectan, se cree que los magnetómetros biológicos operan cerca de este límite. Pero los biólogos no han podido determinar con precisión todos los parámetros relevantes.
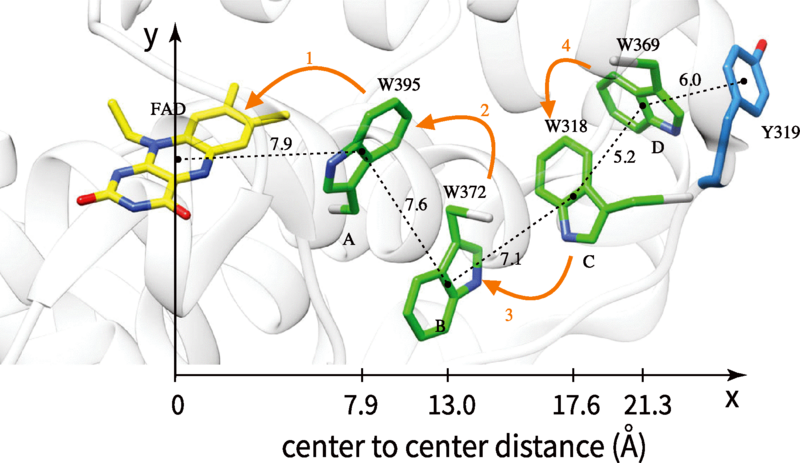 El criptocromo (la molécula de proteína que aparece como fondo gris de la imagen) alberga un par de radicales que actúan como magnetorreceptores. Fuente: S. Y. Wong et al (2021).
El criptocromo (la molécula de proteína que aparece como fondo gris de la imagen) alberga un par de radicales que actúan como magnetorreceptores. Fuente: S. Y. Wong et al (2021).Para solucionar este problema, Kominis y Gkoudinakis trabajaron a la inversa, utilizando el límite cuántico para poner límites a parámetros que eran desconocidos. Descubrieron que dos magnetorreceptores biológicos que implican reacciones químicas dependientes del campo magnético pueden operar justo en el límite, o cerca de él.
Kominis dice que el hallazgo podría ayudar a los investigadores a diseñar futuros dispositivos de detección magnética. “Si [los científicos] queremos hacer las mediciones más sensibles, tenemos que recurrir a la ingeniería cuántica. Imitar los magnetorreceptores biológicos puede guiar esa ingeniería cuántica”, dice.
Referencias:
I. K. Kominis & E. Gkoudinakis (2025) Approaching the Quantum Limit of Energy Resolution in Animal Magnetoreception PRX Life doi: 10.1103/PRXLife.3.013004
S. Y. Wong, Y. Wei, H. Mouritsen, I. A. Solov’yov, and P. J. Hore (2021) Cryptochrome magnetoreception: four tryptophans could be better than three J. R. Soc. Interface doi: 10.1098/rsif.2021.0601
K. Wright (2025) Biological Magnetic Sensing Comes Close to Quantum Limit Physics 18, s8
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Los magnetorreceptores biológicos que actúan en el límite cuántico se ha escrito en Cuaderno de Cultura Científica.
El origen de la dicotomía marciana
Más allá de la búsqueda de vida -tanto pasada como presente- en el planeta rojo, lo cierto es que hay otras cuestiones sobre su historia que todavía permanecen abiertas. Una de ellas es el origen de lo que conocemos como la dicotomía marciana, o lo que es lo mismo, el porqué el hemisferio norte de Marte es una gran llanura deprimida -casi una cuenca- con apenas relieve, mientras que el hemisferio sur está completamente cubierto de cráteres, grandes relieves y se encuentra elevado de media varios kilómetros con respecto al otro hemisferio.
Pero, ¿qué ha provocado que Marte tenga dos caras tan diferentes? Aquí, tradicionalmente, ha existido una gran división entre los científicos que han estudiado este problema. Por un lado tenemos los que opinan que la dicotomía se formó como consecuencia de un gran impacto: Imaginemos un sistema solar muy poco tiempo después de su formación, donde todavía eran habituales los impactos entre cuerpos de gran tamaño. Pues bien, uno de estos habría colisionado contra Marte, provocando la expulsión de una gran cantidad de la corteza marciana que existía en el hemisferio norte y provocando como consecuencia la formación de estas tierras bajas y un adelgazamiento de la corteza. Por poner un ejemplo gráfico es como si golpeáramos una bola de arcilla húmeda con un martillo: dejaríamos un hueco donde dimos el golpe, y parte de la arcilla saldría despedida hacia afuera.
 Mapa topográfico de Marte creado a partir de los datos del instrumento MOLA (Mars Orbiter Laser Altimeter). Los colores más azules representan las zonas más deprimidas y los rojos, las más elevadas. Se aprecia el fuerte contraste entre las zonas deprimidas del hemisferio norte y las tierras altas del hemisferio sur. Fuente: NASA/JPL.
Mapa topográfico de Marte creado a partir de los datos del instrumento MOLA (Mars Orbiter Laser Altimeter). Los colores más azules representan las zonas más deprimidas y los rojos, las más elevadas. Se aprecia el fuerte contraste entre las zonas deprimidas del hemisferio norte y las tierras altas del hemisferio sur. Fuente: NASA/JPL.La otra teoría afirma que la formación de la dicotomía se debe a la propia dinámica interna del planeta. El manto de Marte se encontraría en un estado de convección donde los materiales menos densos y calientes se irían hacia la superficie y los más fríos y densos caerían hacia el núcleo, como en un cazo de agua hirviendo. A lo largo de millones de años, los grandes patrones de convección habrían dado forma a la corteza tal y como la conocemos hoy, creando esta gran diferencia de elevaciones y también esa variación de grosor de la corteza entre ambos hemisferios.
Pero -hasta ahora- probar cualquiera de estas dos teorías ha sido algo realmente complicado para los científicos, ya que estudiando solo las formas que vemos en la superficie no ha sido suficiente y necesitamos poder mirar un poco más en su interior. Y es que ambas versiones de la historia tienen sus fortalezas y debilidades a la hora de explicar la dicotomía y, ni aplicando los modelos geodinámicos más modernos, hemos conseguido salir de dudas.
Pero en noviembre de 2018 llegó a Marte la misión InSight, un módulo de aterrizaje que llevaba consigo -entre otros instrumentos- un sismómetro extremadamente sensible, permitiendo estudiar los terremotos marcianos -o martemotos, si me permiten una pequeña licencia- e intentar resolver algunas cuestiones, desde como es la estructura interna del planeta, a si el planeta todavía tiene actividad geológica.
Y es que los terremotos pueden aportarnos muchísima información sobre los interiores planetarios: desde comprender los procesos que los causan, hasta permitirnos esbozar como es la estructura interna de estos gracias a como varían las propiedades de las ondas sísmicas durante su propagación por las distintas capas rocosas del planeta.
Desgraciadamente, la InSight era una misión única, con un solo sismómetro. En nuestro planeta necesitamos redes de sismómetros -a partir de tres es lo mejor- para conocer el lugar exacto donde se ha producido el terremoto, ya que para poder estudiar mejor como cambian las ondas sísmicas necesitamos saber dónde han ocurrido, pero los científicos han tenido que contar con este hándicap para poder encontrar pistas que nos ayuden a resolver el misterio de la dicotomía marciana.
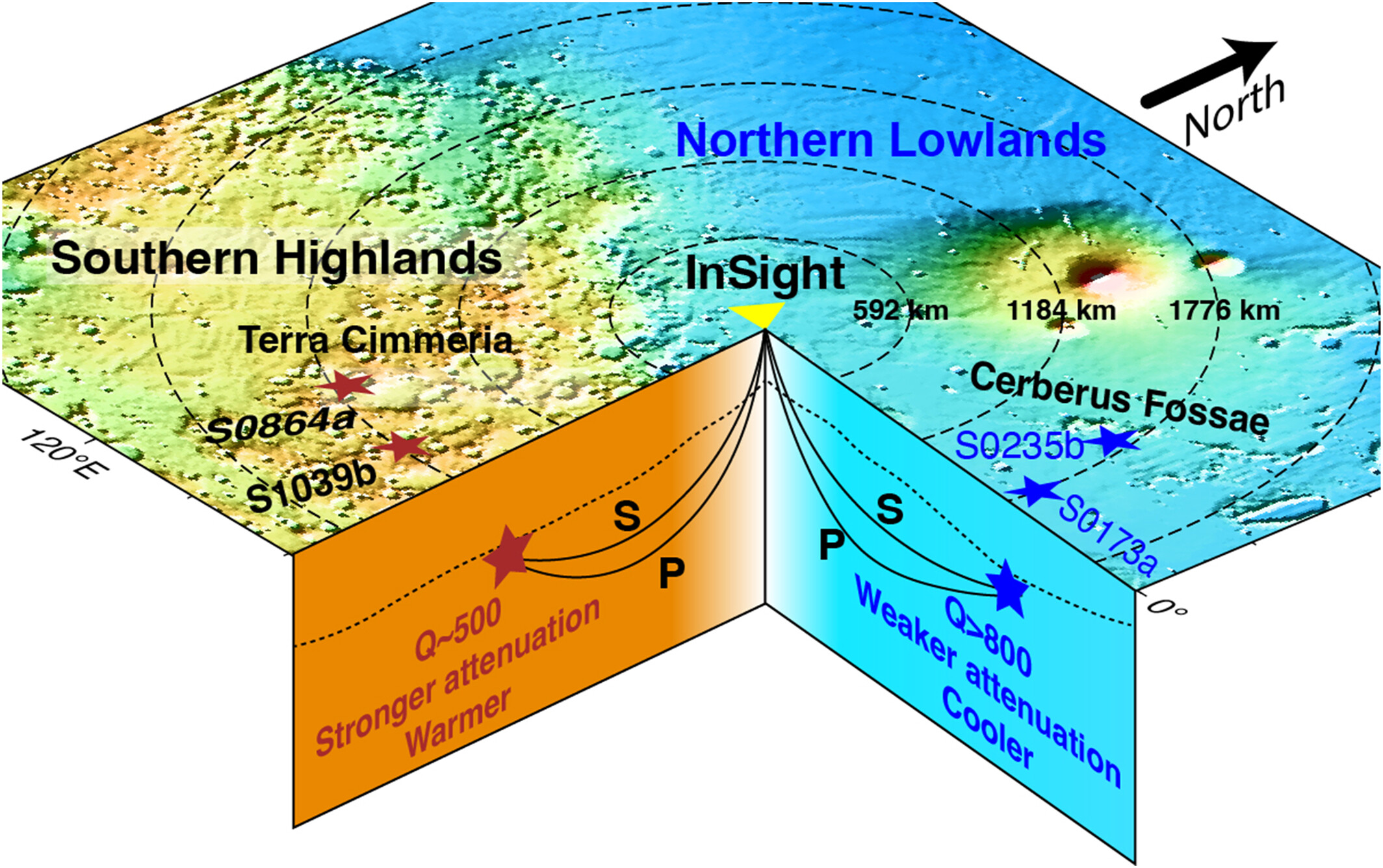 Imagen con algunos de los epicentros de los terremotos usados para calcular la atenuación de las ondas sísmicas. Como se puede apreciar, hay grupos de terremotos localizados a ambos lados de la dicotomía. Fuente: Sun & Tkalčić (2024).
Imagen con algunos de los epicentros de los terremotos usados para calcular la atenuación de las ondas sísmicas. Como se puede apreciar, hay grupos de terremotos localizados a ambos lados de la dicotomía. Fuente: Sun & Tkalčić (2024).A pesar de todos los problemas de los que hemos hablado, una nueva investigación ha conseguido recuperar la señal de algunos de los terremotos más débiles captados por la InSight con mucha más claridad, lo que les ha ayudado a localizar con precisión su epicentro, eso sí, con una sorpresa: Han encontrado un lugar de Marte donde parecen agruparse los terremotos, en una región conocida como Terra Cimmeria.
No es el único lugar donde se han encontrado grupos o conjuntos de terremotos -si alguien se pregunta por que no los llamo enjambres es porque no es el caso, al menos que sepamos- sino que también se han encontrado en otra región de Marte, en Cerberus Fossae, de los que se ha interpretado que en algunos casos podrían ser terremotos de origen volcánico, como ya hablamos en ¿Hay terremotos de origen volcánico en Marte?.
Pero volvamos al asunto que nos trae hoy aquí… ¿Qué tiene de interés que haya terremotos en dos regiones distintas de Marte? ¿No sería lo esperable? Pues que un grupo se encuentra en una parte de la dicotomía y otro en la otra, aportando datos de como se propagan las ondas sísmicas desde ambos lados hacia la InSight.
Localizar los terremotos no ha sido solo uno de los problemas a los que se han tenido que enfrentar los científicos, sino a interpretar la atenuación de las ondas sísmicas a lo largo de su viaje por el interior de Marte. Para que me entiendan, la atenuación es el proceso por el cual las ondas sísmicas pierden energía conforme se van transfiriendo por las rocas que conforman la estructura interna de Marte.
¿Por qué se atenúan las ondas sísmicas? Pues por factores como pueden ser la temperatura o las propiedades de la materia que atraviesan: un material más caliente y menos sólido atenuará mucho más las ondas sísmicas que uno frío y rígido. El análisis exhaustivo de la propagación de las ondas ha demostrado que estas se atenúan mucho más cuando viajan desde el manto de las tierras altas del hemisferio sur que si lo hacen desde la zona deprimida del hemisferio norte.
Los científicos interpretan que esta mayor atenuación se debe a que el manto superior que hay debajo de las tierras altas tiene una mayor temperatura y a las ondas sísmicas les cuesta más viajar -y acaban siendo absorbidas antes- por estos materiales más fluidos.
 Imagen de detalle de una zona de Terra Cimmeria tomada por la sonda Mars Express en 2018. Fuente: ESA/DLR/FU Berlin.
Imagen de detalle de una zona de Terra Cimmeria tomada por la sonda Mars Express en 2018. Fuente: ESA/DLR/FU Berlin.Este hecho lleva a una pista muy interesante… ¿Por qué iba a ser el manto más caliente en una parte de la dicotomía que en otra? La corteza más gruesa de las tierras altas es rica en elementos radiogénicos -que producen calor durante su desintegración- y podría haber servido como una especie de manta térmica, atrapando el calor generado en el manto que hay debajo y no dejando que irradiara tan rápidamente hacia el exterior.
A su vez, esto crearía una gran diferencia de temperaturas entre los mantos del hemisferio norte y sur -entiéndase en este caso hemisferio en el sensu lato-, generando unas corrientes de convección mucho más fuertes en el sur que en el norte, como si le diésemos más gas al cazo de agua que queremos calentar.
El efecto de este calor “extra” y de las corrientes de convección a lo largo de millones de años podría haber sido el responsable de adelgazar la corteza del lado deprimido de la dicotomía y de engrosar la corteza de las tierras altas. Entonces, ¿Queda desacreditada por completo la teoría del impacto gigante? No del todo, pero lo cierto es que los datos sísmicos son un punto a favor de la formación de la dicotomía por procesos endógenos.
Si Marte hubiese sufrido un gran impacto, las propiedades del manto deberían de haber sido mucho más homogéneas y cuya consecuencia más inmediata es que existiría una menor variación en la atenuación de las ondas sísmicas que observamos desde un hemisferio del planeta y el otro.
Aun así, no podemos todavía descartar ninguno de los dos escenarios y, junto a los datos sísmicos tomados por la InSight -y ojalá que por la toma de nuevos datos en el futuro-, así como por la creación de mejores modelos geodinámicos podremos aportar algo más de luz que nos ayude a resolver definitivamente porque el planeta rojo tiene dos caras.
Referencias:
Sun, W., & Tkalčić, H. (2024). Constraints on the origin of the Martian dichotomy from Southern highlands marsquakes. Geophysical Research Letters, 52(1). doi: 10.1029/2024gl110921
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El origen de la dicotomía marciana se ha escrito en Cuaderno de Cultura Científica.
La ingeniería del paisaje casarabe y la revolución neolítica en el Amazonas
Un estudio describe cómo la sociedad prehispánica casarabe, de los Llanos de Moxos (Bolivia), diseñó e implementó un innovador sistema de ingeniería del paisaje que incluyó la construcción de extensos canales de drenaje y de estanques agrícolas. Este avance permitió transformar las sábanas tropicales inundadas en campos altamente productivos e impulsó de este modo el desarrollo de la revolución neolítica en el Amazonas, entendido como el proceso hacia una economía basada en la producción de grano.
 Imagen de los canales de drenaje descritos. Fuente: Bing Maps
Imagen de los canales de drenaje descritos. Fuente: Bing MapsEsta región, habitada por los pueblos casarabes entre el 500 y el 1400 d.C., es una sabana tropical de tierras bajas marcada por estaciones de lluvias intensas e inundaciones, y estaciones muy secas.
El hallazgo, liderado por Umberto Lombardo, arqueólogo ambiental de la Universidad Autónoma de Barcelona, ha permitido identificar una infraestructura agrícola única, hasta ahora no documentada en ningún otro lugar del mundo.
El sistema les permitía drenar el exceso de agua de los campos inundados en la época de lluvias y facilitaba la productividad agrícola. Además de los canales de drenaje, los pueblos casarabes construyeron grupos de estanques agrícolas que servían como reservorios de agua. Los estanques permitieron el riego por macetas, lo que posibilitó la continuidad de la agricultura de maíz durante la temporada seca.
Dos cosechas anualesEsta técnica dual de gestión del agua permitió al menos dos cosechas de maíz al año garantizando el suministro de alimentos durante todo el año, esencial para sostener una población relativamente grande.
«Esta estrategia agrícola intensiva indica que el maíz no solo se cultivaba, sino que probablemente era el cultivo básico de la cultura casarabe», explica Lombardo.
El modelo agrícola no dependía de las técnicas tradicionales de tala y quema empleadas para obtener campos fértiles. En su lugar, los pueblos casarabes conservaron los bosques cercanos para otros fines, como la obtención de leña y plantas medicinales, mientras implementaban prácticas que maximizaban el uso eficiente del agua y del suelo en las sabanas de inundación estacional.
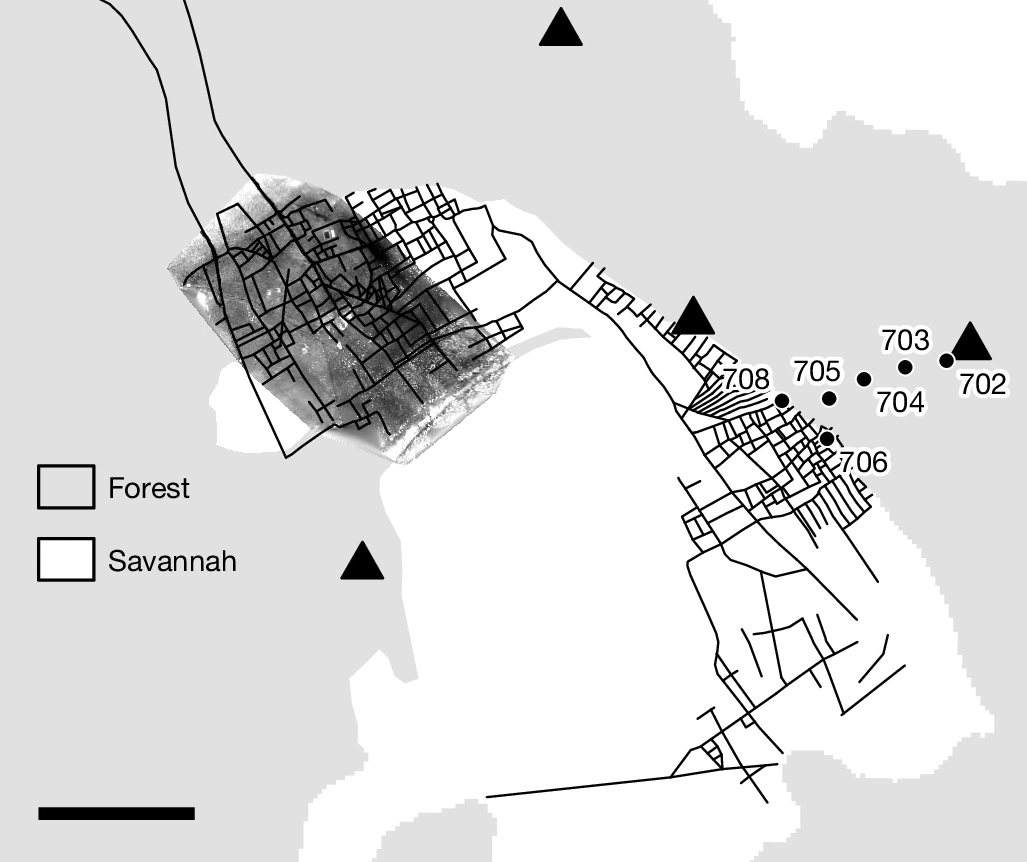 La red de canales de drenaje completa. Los puntos indican zonas de toma de muestras. La barra representa 1 km. Fuente: Lombardo et al. (2025)
La red de canales de drenaje completa. Los puntos indican zonas de toma de muestras. La barra representa 1 km. Fuente: Lombardo et al. (2025)Las conclusiones fueron posibles gracias a un minucioso trabajo de campo que combinó técnicas como el análisis microbotánico, los sensores remotos y la arqueología ambiental.
El análisis de 178 muestras de fitolitos (microfósiles de plantas) y de polen de un estanque confirmó la presencia de maíz en los campos y el papel crucial del monocultivo de maíz en la dieta en esta sociedad precolombina. «Los datos muestran la ausencia de otro tipo de cultivos», añade.
 Ilustración de uno de los estanques. Fuente: Julian Puig Guevara
Ilustración de uno de los estanques. Fuente: Julian Puig Guevara«Podemos documentar que se trata de la primera economía agraria basada en el grano en el Amazonas, donde hasta ahora creíamos que la agricultura que se practicaba era de policultivos en sistemas agroforestales y no de monocultivos a gran escala. Ahora sabemos que eso, en los Llanos de Moxos, no fue así», señala Lombardo, quien asegura que esta innovadora obra de ingeniería transformó un entorno desafiante en un sistema productivo que aseguraba la estabilidad alimentaria y sostuvo el desarrollo de una población creciente.
La investigación no solo arroja luz sobre las capacidades tecnológicas de las civilizaciones precolombinas, sino que también ofrece lecciones valiosas para la sostenibilidad agrícola moderna.
Este descubrimiento es un testimonio del ingenio y la adaptabilidad de los casarabes, quienes lograron prosperar gracias a su habilidad para diseñar soluciones agrícolas sostenibles a largo plazo en un entorno adverso.
Referencia:
Lombardo, U., Hilbert, L., Bentley, M. et al. (2025) Maize monoculture supported pre-Columbian urbanism in southwestern Amazonia Nature doi: 10.1038/s41586-024-08473-y
Edición realizada por César Tomé López a partir de materiales suministrados por la Universitat Autònoma de Barcelona.
El artículo La ingeniería del paisaje casarabe y la revolución neolítica en el Amazonas se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2024: Una escayola para este gen roto, por favor
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

Virginia Arechavala-Gomeza, profesora Ikerbasque en el Grupo de Enfermedades Neuromusculares del Instituto de Investigación Sanitaria Biocruces Bizkaia, explica la complejidad de encontrar tratamientos para las enfermedades llamadas raras (muy poco frecuentes).
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: Una escayola para este gen roto, por favor se ha escrito en Cuaderno de Cultura Científica.
El lugar de nacimiento y las probabilidades de ser futbolista profesional
 Partido clasificatorio de la Eurocopa 2025 entre España y Bélgica en el estadio de Riazor (2024). En la imagen, Alexia Putellas.
Partido clasificatorio de la Eurocopa 2025 entre España y Bélgica en el estadio de Riazor (2024). En la imagen, Alexia Putellas.Wikimedia Commons., CC BY
Si pudiéramos por un segundo desarrollar una herramienta capaz de detectar el próximo Lamine Yamal o Nico Williams, o la próxima Alexia Putellas o Salma Paralluelo, seguro que seríamos de las personas más perseguidas por la industria deportiva. Siendo el fútbol uno de los deportes de mayor impacto social y económico, es cada vez mayor la inversión que los distintos clubes realizan en sus canteras para encontrar y formar a las futuras estrellas del fútbol.
Durante muchos años, la investigación relacionada con la detección de estrellas futbolísticas estaba suscrita al debate de si el futbolista nace o se hace. Este interrogante ha ocupado centenares de investigaciones y ha evolucionado desde una visión dicotómica hasta el reconocimiento de la compleja interacción de factores genéticos y ambientales.
Mientras que la predisposición genética desempeña un papel crucial en el rendimiento, la práctica deliberada y las influencias ambientales son esenciales para hacer realidad el potencial genético.
La identificación del talento debe adoptar un enfoque multidimensional y dinámico, y afrontarse desde la interacción de todos los factores, ya sean innatos (genéticos, antropométricos…), adquiridos (entrenamiento) o contextuales (familia, lugar de nacimiento…).
Ciudad mediana, un buen punto de partidaNuestra investigación se ha centrado en conocer cómo el lugar de nacimiento influye en el desarrollo del futbolista, tanto en su participación como en su rendimiento deportivos.
Estudios previos sugieren que nacer en determinados tamaños de ciudad, normalmente ciudades más pequeñas o medianas, puede suponer ventajas en el desarrollo del talento.
Entre los motivos que contribuyen a este efecto se encuentran la proximidad a instalaciones deportivas y la estructura social.
 Lamine Yamal después de que la selección española ganara la Eurocopa 2024. Fuente:
Lamine Yamal después de que la selección española ganara la Eurocopa 2024. Fuente:Wikimedia Commons., CC BY
En una revisión sistemática centrada en el fútbol, se ha observado que la combinación de la densidad de población y el nivel de las instalaciones del lugar de nacimiento son cruciales, existiendo una relación entre el lugar de nacimiento y el rendimiento futbolístico.
Como idea general, se ha observado que, en ciudades de mayor tamaño y densidad, aumentan las posibilidades de alcanzar un estatus profesional en el fútbol. Este fenómeno se atribuye a diversas razones como un mayor número posible de clubes y oportunidades competitivas disponibles en las zonas urbanas.
Las características sociodemográficas de las poblaciones más grandes como renta media más alta, mejores instalaciones deportivas, entrenadores más cualificados o estructuras competitivas más profundas también pueden contribuir al desarrollo del talento futbolístico.
No obstante, aunque las ciudades más grandes ofrecen muchas ventajas, algunos estudios sugieren que las ciudades más pequeñas pueden fomentar asimismo el desarrollo del talento, al ofrecer un entorno comunitario más solidario y menos competencia por las plazas en los clubes locales. Esto puede permitir una atención más individualizada y más oportunidades.
Un puzle complejoEn cualquier caso, como todo lo relacionado con el desarrollo del talento, no se debe entender el lugar de nacimiento como un factor aislado, sino como algo dinámico que interactúa con otros factores de diversas formas.
Así, por ejemplo, se ha observado que, para ingresar en una academia de fútbol, los jugadores provenientes de zonas con mayor densidad de población tenían más probabilidades de ser seleccionados inicialmente. Sin embargo, una vez dentro de la academia, las probabilidades de debutar profesionalmente eran mayores para los jugadores de zonas de menor densidad.
Del lugar de nacimiento al lugar de crecimientoEsto lleva a la necesidad de una investigación más profunda relacionada con el “lugar de desarrollo”. Porque parece evidente que, en el mundo actual, donde la globalización impera y provoca movimientos migratorios laborales, el lugar de nacimiento no tiene por qué coincidir con el lugar donde las personas crecen y reciben su formación.
En un estudio realizado en una academia de fútbol, se observó que los jugadores que experimentaron una transición geográfica –cambio de su municipio de nacimiento a otro lugar de crecimiento deportivo– tenían aproximadamente un 38 % más de probabilidades de debutar en el equipo profesional.
Este hallazgo indica que la movilidad geográfica puede aumentar las oportunidades de éxito en el fútbol, y sugiere que es necesario considerar ambos lugares como variables conjuntas para comprender los procesos de gestión del talento.
En resumen, el lugar de origen y el lugar donde se crece desempeñan un papel crucial en la configuración del rendimiento y las oportunidades de los jugadores de fútbol. En general, el vínculo con el tamaño de la población es complejo, con ventajas y desventajas según el contexto específico. Toda la investigación al respecto insiste en la naturaleza polifacética del desarrollo del talento, abogando por un enfoque que considere tanto los factores individuales como los contextuales.![]()
Sobre las autoras: Alberto Lorenzo Calvo, Profesor Titular de Universidad de Procesos de Detección y Desarrollo en el Talento Deportivo, Universidad Politécnica de Madrid (UPM); Julio Calleja-Gonzalez, Catedrático de Entrenamiento Deportivo, Universidad del País Vasco / Euskal Herriko Unibertsitatea; Lander Hernández Simal, Licencia UEFA PRO, Responsable del Departamento de Formación y Desarrollo del Athletic Club (Bilbao), Profesor del Grado en Ciencias de la Actividad Física y del Deporte de la Universidad de Deusto; y Maite Aurrekoetxea Casaus, Profesora Doctora en Sociología en la Facultad de Ciencias Sociales y Humanas, Universidad de Deusto.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El lugar de nacimiento y las probabilidades de ser futbolista profesional se ha escrito en Cuaderno de Cultura Científica.
Aprendiendo Geología mientras buscamos oro en Alaska
Estos días de vacaciones navideñas en los que el tiempo andaba revuelto y no invitaba a salir a disfrutar de un agradable paseo, he remoloneado en el sofá delante de la tele. Y un día, haciendo zapping de manera despreocupada, me encontré con una serie tipo docu-reality en la que se muestra el trabajo diario de varios equipos de minería en Alaska, con un título muy directo y evocativo: La Fiebre del Oro. Y digo evocativo porque hace alusión directa a esa locura colectiva que ocurrió en Norteamérica a finales del siglo XIX que condujo a muchos hombres a abandonarlo todo y marcharse a lugares remotos con una pala en una mano y un tamiz en la otra, convencidos de que iban a encontrar la pepita de oro que les haría millonarios. Locura que, visto lo visto en el programa, parece que sigue vigente. Pero lo que llamó mi atención en esta serie no fueron las aventuras y desventuras de estas personas, sino el hecho de que, intercaladas entre las habituales labores de minería, se encontraban pequeñas animaciones con explicaciones geológicas para que pudiésemos entender de dónde salía ese oro o porqué los jefes mineros se centraban en buscar ciertas rocas o niveles de tierra muy concretos. Incluso, defendían el uso de algunas técnicas geológicas para asegurarse de que podrían obtener beneficios económicos con sus explotaciones. Así que hoy voy a haceros un pequeño resumen de lo que nos han querido mostrar en esta serie de televisión.
 Hombre bateando los sedimentos de la playa de Nome, en Alaska, buscando oro en 1900. Imagen de los hermanos Lomen, conservada en el The McMahan Photo Art Gallery and Archive.
Hombre bateando los sedimentos de la playa de Nome, en Alaska, buscando oro en 1900. Imagen de los hermanos Lomen, conservada en el The McMahan Photo Art Gallery and Archive.Los depósitos de oro de Alaska se formaron hace menos de 150 millones de años, debido a varios procesos de colisión que se produjeron por el acercamiento de la Placa tectónica del Pacífico y la Placa tectónica Norteamericana. En este contexto no solo se formaron diversas cadenas montañosas, también se favoreció el ascenso de varias acumulaciones de magma hacia la parte superior de la corteza y se generaron muchas zonas de fractura. Asociados a esos magmas aparecieron fluidos calientes que fueron atrapando todos los elementos químicos presentes en las rocas de su alrededor, incluido el oro. Y en cuanto estos fluidos se encontraban con una fractura, empezaron a ascender hacia la superficie, dando lugar a unas mineralizaciones de cuarzo ricas en oro que, en Geología, se denominan diques y, en minería, se conocen como filones.
Pero su historia no termina aquí. En los últimos 20 millones de años, los ríos se han encargado de erosionar estos diques y arrastrar el oro corriente abajo, hacia su desembocadura, depositando el mineral en las zonas curvadas del cauce donde el agua perdía fuerza. Y, en los últimos 2 millones de años, el hielo también se ha sumado al arrastre de oro desde su depósito original, acumulándolo en áreas deprimidas en la zona del frente de avance de los glaciares. Estos depósitos de oro generados por el efecto del agua, tanto líquida como sólida, se conocen como placeres, y son lo que los equipos mineros actuales buscan explotar. Por este motivo cavan la tierra hasta llegar a niveles en los que encuentran una mezcla de arcillas con abundantes fragmentos de cuarzo y rocas redondeadas, ya que son las chivatas de que han sido arrastradas y erosionadas por el agua desde un filón mineralizado. Entonces hacen una batea manual para ver si también incluye oro y determinar si es rentable explotar ese material.
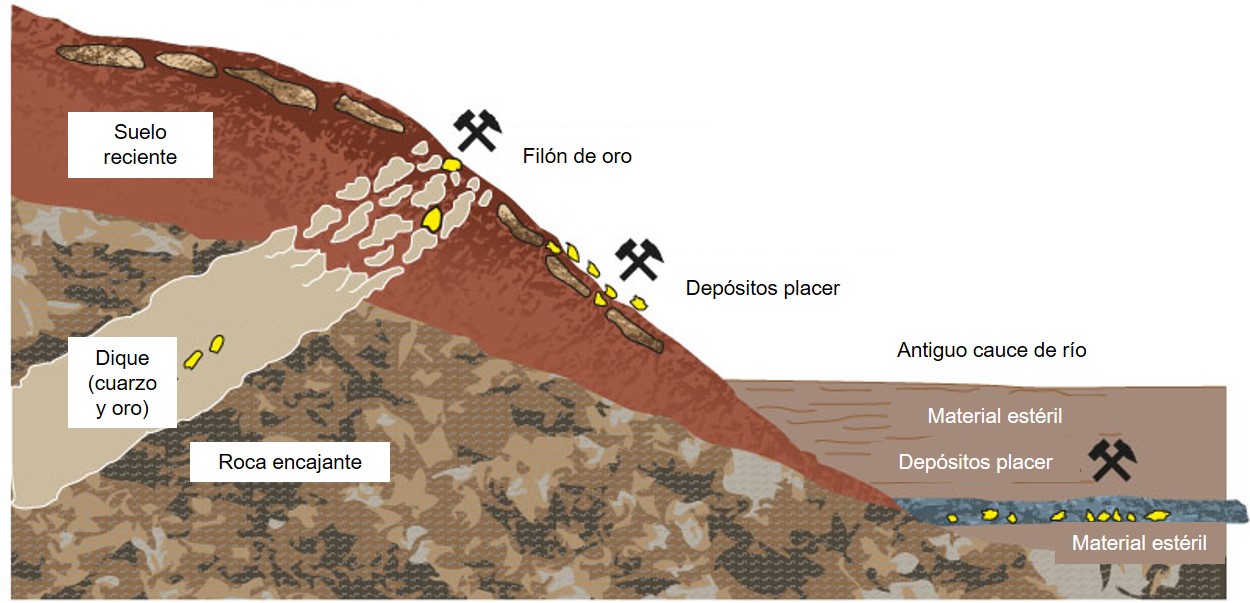 Depósitos de oro asociados a un dique hidrotermal, incluidos los de tipo placer. Imagen modificada de la original de Michael Priester. Fuente: Minelab
Depósitos de oro asociados a un dique hidrotermal, incluidos los de tipo placer. Imagen modificada de la original de Michael Priester. Fuente: MinelabPero estas excavaciones no las hacen al azar por cualquier lugar, siempre van a tiro hecho. Para ello cuentan con la ayuda de especialistas en la geología de Alaska que utilizan diversas técnicas comunes en la exploración mineral para ayudarles a encontrar el yacimiento de oro que se esconde bajo tierra. Y me voy a centrar en explicaros las dos que describieron en los pocos capítulos que he visto.
La primera es la resistividad eléctrica. Se trata de una técnica geofísica que consiste en introducir unos electrodos cilíndricos en el suelo conectados en serie mediante un cableado que, además, se conecta a una caja medidora de resistividad. Estos electrodos son capaces de enviar una corriente eléctrica que se transmite en profundidad y que va cambiando de potencial según atraviesa diferentes materiales o estructuras geológicas. Estos cambios en el potencial eléctrico quedan marcados en la caja medidora, lo que nos permite tratar los datos para realizar una especie de radiografía tridimensional del subsuelo. En el programa, emplearon esta técnica para identificar antiguos canales fluviales y acumulaciones de materiales metálicos transportados por los glaciales hace milenios, calculando la profundidad a la que se encontraban estas estructuras geológicas y, por tanto, los posibles yacimientos auríferos.
 Estudio de resistividad eléctrica del terreno en la mina de crisoprasa de Szklary (Baja Silesia, Polonia). Fuente: Wikimedia Commons
Estudio de resistividad eléctrica del terreno en la mina de crisoprasa de Szklary (Baja Silesia, Polonia). Fuente: Wikimedia CommonsLa segunda técnica os debería sonar más, porque ya he hablado de ella: los testigos de sondeo. En este caso, realizaron varias perforaciones a lo largo del terreno que tenían pensado explotar para obtener un registro continuo del subsuelo hasta la base rocosa. A estos sedimentos se les realizaron dos análisis consecutivos. En primer lugar, un estudio geoquímico para conocer los elementos químicos presentes en el mismo, buscando niveles que dieran positivo en oro. Y, en segundo lugar, lavaron y tamizaron esos niveles para calcular la concentración de oro con respecto al total de sedimento. De esta manera, pudieron determinar dónde y a qué profundidad se encontraban los yacimientos y, así, decidir si les era rentable o no explotarlos.
Debo reconocer que la serie no consiguió engancharme, así que no os puedo contar si estos equipos mineros se hicieron millonarios o si acabaron en la ruina, a mí únicamente me interesaron las animaciones explicativas que describían estos procesos y técnicas geológicas. Y, aunque eran más sencillas y resumidas de lo que yo os he comentado aquí, científicamente hablando sí que eran muy correctas. Así que puedo utilizarlas como otro ejemplo más no solo de que la Geología está en todo lo que nos rodea, sino también de que podemos aprender Ciencias de la Tierra gracias a cosas que, a priori, no parecen muy centradas en aumentar nuestro conocimiento científico. Únicamente hay que saber mirarlo todo con ojos geológicos.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Aprendiendo Geología mientras buscamos oro en Alaska se ha escrito en Cuaderno de Cultura Científica.
Cinco rompecabezas para celebrar el “Puzzle Day”
Cada 29 de enero, desde hace más de treinta años, se celebra en Estados Unidos el Puzzle Day. Esta conmemoración es una iniciativa de la creadora de rompecabezas Jodi Jill, que nació precisamente el 29 de enero de 1971.
 Un rompecabezas. Fuente: Wikimedia Commons.
Un rompecabezas. Fuente: Wikimedia Commons.
Nos unimos a esta celebración con cinco rompecabezas, en nuestro caso, matemáticos. Para solucionarlos no está de más recordar estas palabras del matemático Henry Ernest Dudeney (1857-1930)
Un buen rompecabezas debe exigir el ejercicio de nuestro mejor ingenio y habilidad, y aunque el conocimiento de las matemáticas y la lógica son a menudo de gran utilidad en la solución de estas cosas, sin embargo, a veces sucede que una especie de astucia y sagacidad naturales son de considerable valor.
El puzle de los cuatro roblesEste es un problema de ingenio propuesto por Sam Loyd (1841-1911) en su Cyclopedia of 5000 Puzzles, Tricks, and Conundrums With Answers (1914):
Un padre deja a sus cuatro hijos un campo cuadrado conteniendo cuatro robles [ver debajo]. Pero les pone una condición para obtener este legado: deben dividir el campo en cuatro partes, todas de la misma forma y tamaño, de manera que cada trozo de tierra contenga uno de los árboles. ¿Cómo lograrán hacerlo?
 El planteamiento del problema. Fuente: Wikimedia Commons.
El planteamiento del problema. Fuente: Wikimedia Commons.
Piensa un poco antes de mirar la solución en este enlace.
Un puzle con dos dadosEl autor de este rompecabezas es Pierre Berloquin (1939):
Timoteo y Sofía están jugando con dos dados de seis caras. Pero no son dados normales: en vez de tener un número, cada cara está coloreada de rojo o azul.
Los dos amigos tiran los dados por turnos. Deciden que Timoteo ganará la partida si las dos caras superiores son del mismo color y Sofía lo hará si son diferentes. Se sabe que sus probabilidades de ganar son iguales.
También se sabe que el primer dado tiene 5 caras rojas y 1 cara azul.
¿Cuáles son los colores del segundo dado?
Pensemos en los posibles resultados en cada tirada: al lanzar dos dados de seis caras se obtienen 36 resultados posibles. Como Timoteo y Sofía tienen las mismas probabilidades de ganar, debe haber 18 resultados en los que ambos dados tengan el mismo color y otros 18 en los que la tirada muestre caras de distinto color. Si x es la cantidad de caras rojas en el segundo dado, debe cumplirse que:
18 = 5x + 1(6 – x).
Se deduce inmediatamente que x = 3, y entonces el segundo dado debe tener 3 caras rojas y 3 caras azules.
Un puzle numéricoEl creador de rompecabezas japonés Nobuyuki Yoshigahara (1936-2004) consideraba que este puzle era su obra maestra:
Los números que se muestran en la imagen de debajo están ordenados según una regla determinada. ¿Cuál es el número que falta?
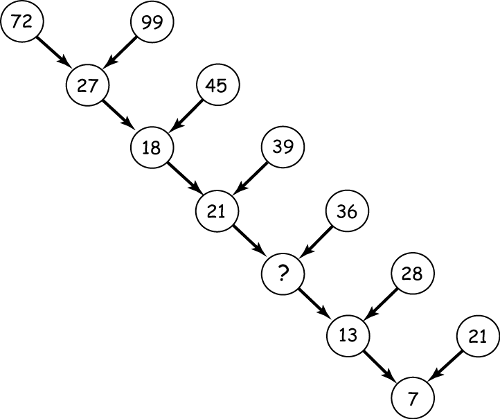 Fuente: Futility Closet.
Fuente: Futility Closet.
Por supuesto, lo importante es encontrar la regla. Intenta encontrarla antes de leer la solución.
Se observa en una primera mirada que 99 – 72 = 27, 45 – 27 = 18, 39 – 18 = 21, … parece que esta es la regla, es decir, la diferencia de los números de una fila devuelve el número del círculo de debajo. Así, como 28 – ? = 13, parece que debe ser ? = 15. Pero si miramos lo que sucede en la última fila, tenemos que 21 – 13 = 8, no 7 como se indica en el diagrama. Así que esta no es la regla.
Mirando de nuevo el diagrama, se puede comprobar que al sumar los dígitos de una fila se obtiene el número que se encuentra en el círculo de debajo. Por ejemplo, 7 + 2 + 9 + 9 = 27 para la primera fila, 4 + 5 + 2 + 7 = 18. Se comprueba que esta regla funciona en todas las filas. Así, 2 + 1 + 3 + 6 = 12, que es el número que falta en la imagen.
Un puzle olímpicoEsta propuesta procede de un problema de la Olimpiada Matemática rusa de 1999:
Se pide demostrar que los números del 1 al 15 no se pueden dividir en un grupo A de 13 números y otro B de 2 números de modo que la suma de los números de A sea igual al producto de los números de B.
Haremos la demostración por reducción al absurdo: supongamos que fuera posible dividir los números en dos grupos con las condiciones que se indican. Llamemos x e y a los dos números en B. Entonces se cumple que:
(1 + 2 + … + 15) – x – y = xy,
Es decir, 120 = xy + x + y, o lo que es lo mismo:
121 = (x + 1) (y + 1).
El número 121 = 112, con lo que es necesariamente x = y = 10. Pero esta solución no es válida, porque x e y son números distintos. Así, queda demostrado lo que se pedía.
Un puzle en el campo de tiroEste último rompecabezas se debe al matemático Peter Winkler (1946):
Sofía y Timoteo (que ya se han cansado de jugar a los dados) acuden a un campo de tiro. Sofía acierta a un objetivo pequeño el 75 % de las veces y Timoteo, con peor puntería, solo el 25 % de las veces.
Los dos apuntan a ese objetivo pequeño y disparan simultáneamente. Una bala lo alcanza.
¿Cuál es la probabilidad de que haya venido del arma de Sofía?
Como Sofía posee el triple de calidad de aciertos que Timoteo, dan ganas de decir que la probabilidad es del 75 %. Pero ese argumento no es válido porque hay que tener en cuenta los aciertos y los fallos. Pensemos en todas las situaciones posibles:
-
La probabilidad de que Sofía y Timoteo acierten en la diana es de 3/4 × 1/4 = 3/16,
-
La probabilidad de que ni Sofía ni Timoteo acierten su tiro es de 1/4 × 3/4 = 3/16,
-
la probabilidad de que Sofía acierte y Timoteo no es de 3/4 × 3/4 = 9/16, y, finalmente,
-
la probabilidad de que Timoteo acierte y Sofía no es de 1/4 × 1/4 = 1/16.
Como solo una bala alcanza el objetivo, se da necesariamente una de las situaciones descritas en 3) o en 4). Así, hay una probabilidad de 9/10 de que la bala que ha alcanzado en el blanco sea la de Sofía.
Referencias
-
The Four Oaks Puzzle, Futility Closet, 8 febrero 2024
-
A Dice Puzzle, Futility Closet, 23 octubre 2014
-
Nob’s number puzzle, Futility Closet, 30 abril 2014
-
15 Puzzle, Futility Closet, 2 julio 2013
-
Gun control, Futility Closet, 15 enero 2025
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Cinco rompecabezas para celebrar el “Puzzle Day” se ha escrito en Cuaderno de Cultura Científica.
El calor destruye el entrelazamiento cuántico
Mientras ideaban un nuevo algoritmo cuántico, cuatro investigadores establecieron accidentalmente un límite estricto para el fenómeno «fantasma».
Un artículo de Ben Brubaker. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Kristina Armitage/Quanta Magazine
Kristina Armitage/Quanta MagazineHace casi un siglo, el físico Erwin Schrödinger llamó la atención sobre una peculiaridad del mundo cuántico que ha fascinado y desconcertado a los investigadores desde entonces. Cuando las partículas cuánticas, como los átomos, interactúan, se deshacen de sus identidades individuales en favor de un estado colectivo que es mayor y más extraño que la suma de sus partes. Este fenómeno se llama entrelazamiento.
Los investigadores tienen una comprensión sólida de cómo funciona el entrelazamiento en sistemas idealizados que contienen solo unas pocas partículas. Pero el mundo real es más complicado. En grandes conjuntos de átomos, como los que forman las cosas que vemos y tocamos, las leyes de la física cuántica compiten con las leyes de la termodinámica y las cosas se complican.
A temperaturas muy bajas, el entrelazamiento puede extenderse a grandes distancias, envolviendo a muchos átomos y dando lugar a fenómenos extraños como la superconductividad. Sin embargo, si aumentamos la temperatura, los átomos se mueven y rompen los frágiles enlaces que unen a las partículas entrelazadas.
Los físicos llevan mucho tiempo intentando precisar los detalles de este proceso. Ahora, un equipo de cuatro investigadores ha demostrado que el entrelazamiento no se debilita simplemente a medida que aumenta la temperatura, sino que, en los modelos matemáticos de sistemas cuánticos, como las formaciones de átomos en los materiales físicos, siempre hay una temperatura específica por encima de la cual desaparece por completo. “No es solo que sea exponencialmente pequeño”, explica Ankur Moitra, del Instituto Tecnológico de Massachusetts, uno de los autores del nuevo resultado. “Es cero”.
Los investigadores ya habían observado indicios de este comportamiento y lo habían denominado la “muerte súbita” del entrelazamiento, pero sus pruebas eran en su mayoría indirectas. El nuevo hallazgo establece un límite mucho más fuerte al entrelazamiento de una manera matemáticamente rigurosa.
Curiosamente, los cuatro investigadores que están detrás del nuevo resultado ni siquiera son físicos y no se proponían demostrar nada sobre el entrelazamiento. Son científicos informáticos que se toparon con la prueba por accidente mientras desarrollaban un nuevo algoritmo.
Independientemente de su intención, los resultados entusiasmaron a los investigadores del área. “Es una afirmación muy, muy contundente”, comenta Soonwon Choi, físico del MIT. “Me quedé muy impresionado”.
En busca del equilibrioEl equipo hizo su descubrimiento mientras exploraba las capacidades teóricas de los futuros ordenadores cuánticos: máquinas que explotarán el comportamiento cuántico, incluidos el entrelazamiento y la superposición, para realizar ciertos cálculos mucho más rápido que las ordenadores convencionales que conocemos hoy.
Una de las aplicaciones más prometedoras de la computación cuántica es el estudio de la propia física cuántica. Supongamos que queremos entender el comportamiento de un sistema cuántico. Los investigadores primero deben desarrollar procedimientos específicos, o algoritmos, que los ordenadores cuánticos puedan utilizar para responder a nuestras preguntas.
 Ewin Tang ayudó a diseñar un nuevo algoritmo rápido para simular cómo se comportan ciertos sistemas cuánticos a altas temperaturas. Foto: Xinyu Tan
Ewin Tang ayudó a diseñar un nuevo algoritmo rápido para simular cómo se comportan ciertos sistemas cuánticos a altas temperaturas. Foto: Xinyu TanPero no todas las preguntas sobre los sistemas cuánticos son más fáciles de responder utilizando algoritmos cuánticos. Algunas son igualmente fáciles para los algoritmos clásicos, que se ejecutan en ordenadores comunes, mientras que otras son difíciles tanto para los algoritmos clásicos como para los cuánticos.
Para entender en qué aspectos los algoritmos cuánticos y las ordenadores que pueden ejecutarlos pueden ofrecer una ventaja, los investigadores suelen analizar modelos matemáticos llamados sistemas de espín, que capturan el comportamiento básico de conjuntos de átomos en interacción. A continuación, pueden preguntarse: ¿qué hará un sistema de espín cuando lo dejamos solo a una temperatura determinada? El estado en el que se establece, llamado estado de equilibrio térmico, determina muchas de sus otras propiedades, por lo que los investigadores han buscado durante mucho tiempo desarrollar algoritmos para encontrar estados de equilibrio.
El hecho de que esos algoritmos sean realmente útiles por su naturaleza cuántica depende de la temperatura del sistema de espín en cuestión. A temperaturas muy altas, los algoritmos clásicos conocidos pueden hacer el trabajo fácilmente. El problema se complica a medida que la temperatura disminuye y los fenómenos cuánticos se hacen más fuertes; en algunos sistemas se vuelve demasiado difícil incluso para que los ordenadores cuánticos lo resuelvan en un tiempo razonable. Pero los detalles de todo esto siguen siendo turbios.
“¿Cuándo se llega al espacio donde se necesita la cuántica y cuándo se llega al espacio donde la cuántica ni siquiera ayuda?”, se pregunta Ewin Tang, investigadora de la Universidad de California en Berkeley y una de los autoras del nuevo resultado. “No se sabe mucho al respecto”.
En febrero, Tang y Moitra comenzaron a pensar en el problema del equilibrio térmico junto con otros dos científicos informáticos del MIT: un investigador postdoctoral llamado Ainesh Bakshi y el doctorando de Moitra, Allen Liu. En 2023, todos habían colaborado en un algoritmo cuántico innovador para una tarea diferente que involucraba sistemas de espín y estaban buscando un nuevo desafío.
“Cuando trabajamos juntos, las cosas fluyen”, afirma Bakshi. “Ha sido fantástico”.
Antes de ese gran avance de 2023, los tres investigadores del MIT nunca habían trabajado en algoritmos cuánticos. Su formación era en teoría del aprendizaje, un subcampo de la informática que se centra en algoritmos para el análisis estadístico. Pero, como los ambiciosos novatos de todo el mundo, vieron su relativa ingenuidad como una ventaja, una forma de ver un problema con nuevos ojos. “Uno de nuestros puntos fuertes es que no sabemos mucho de cuántica”, cuenta Moitra. “La única cuántica que conocemos es la cuántica que Ewin nos enseñó”.
El equipo decidió centrarse en temperaturas relativamente altas, donde los investigadores sospechaban que existirían algoritmos cuánticos rápidos, aunque nadie había podido demostrarlo. Pronto encontraron una forma de adaptar una vieja técnica de la teoría del aprendizaje a un nuevo algoritmo rápido. Pero mientras escribían su artículo, otro equipo presentó un resultado similar: una prueba de que un prometedor algoritmo desarrollado el año anterior funcionaría bien a altas temperaturas. Se les había adelantado.
La muerte súbita renaceUn poco decepcionados por haber quedado en segundo lugar, Tang y sus colaboradores comenzaron a comunicarse con Álvaro Alhambra, físico del Instituto de Física Teórica de Madrid y uno de los autores del artículo rival. Querían determinar las diferencias entre los resultados que habían obtenido de forma independiente. Pero cuando Alhambra leyó un borrador preliminar de la prueba de los cuatro investigadores, se sorprendió al descubrir que habían demostrado algo más en un paso intermedio: en cualquier sistema de espín en equilibrio térmico, el entrelazamiento desaparece por completo por encima de cierta temperatura. “Les dije: ‘Oh, esto es muy, muy importante’”, cuenta Alhambra.

De izquierda a derecha: Allen Liu, Ainesh Bakshi y Ankur Moitra colaboraron con Tang, aprovechando su experiencia en una rama diferente de la informática. “Uno de nuestros puntos fuertes es que no sabemos mucho sobre la computación cuántica”, afirma Moitra. Fots, de izquierda a derecha: Cortesía de Allen Liu; Amartya Shankha Biswas; Gretchen Ertl
El equipo revisó rápidamente su borrador para destacar el resultado accidental. “Resulta que esto simplemente se desprende de nuestro algoritmo”, explica Moitra. “Obtenemos más de lo que esperábamos”.
Los investigadores habían observado esta muerte súbita del entrelazamiento desde la década del 2000 en experimentos y simulaciones en ordenadores clásicos comunes. Pero ninguno de estos trabajos anteriores había podido medir directamente la desaparición del entrelazamiento. Además, solo habían estudiado el fenómeno en sistemas pequeños, que no son los más interesantes.
“Podría haber sido que para sistemas cada vez más grandes habría que alcanzar temperaturas cada vez más altas para ver la ausencia de entrelazamiento”, explica Alhambra. En ese caso, el fenómeno de muerte súbita podría ocurrir a temperaturas tan altas que sería irrelevante en materiales reales. El único límite teórico anterior, de 2003, dejaba abierta esa posibilidad. En cambio, Tang y sus colaboradores demostraron que la temperatura a la que desaparece el entrelazamiento no depende del número total de átomos en el sistema. Lo único que importa son los detalles de las interacciones entre los átomos cercanos.
 Álvaro Alhambra, un físico que trabajaba en el mismo problema que Tang, Moitra, Bakshi y Liu, se dio cuenta de que habían demostrado accidentalmente un nuevo resultado sobre el entrelazamiento cuántico mientras desarrollaban su algoritmo. Foto: Laura Marcos
Álvaro Alhambra, un físico que trabajaba en el mismo problema que Tang, Moitra, Bakshi y Liu, se dio cuenta de que habían demostrado accidentalmente un nuevo resultado sobre el entrelazamiento cuántico mientras desarrollaban su algoritmo. Foto: Laura MarcosEl método que utilizaron en su demostración fue inusual en sí mismo. La mayoría de los algoritmos para hallar estados de equilibrio térmico se inspiran en la forma en que los sistemas físicos reales se acercan al equilibrio. Pero Tang y compañía utilizaron técnicas muy alejadas de la teoría cuántica.
“Eso es lo que hace tan asombroso este artículo”, comenta Nikhil Srivastava, un científico informático de Berkeley. “La prueba en cierto modo ignora la física”.
La búsqueda continúaLa prueba de los cuatro investigadores de que los sistemas de espín de alta temperatura carecen de entrelazamiento ayuda a explicar otra característica interesante de su nuevo algoritmo: muy poco de él es realmente cuántico. Es cierto que el resultado del algoritmo (una descripción completa de cómo se orientan los átomos en un sistema de espín en equilibrio térmico) es demasiado difícil de manejar para almacenar en una máquina clásica. Pero, salvo el último paso que genera este resultado, cada parte del algoritmo es clásica.
“Es esencialmente el cálculo cuántico más trivial”, afirma Liu.
Tang tiene una larga trayectoria en el descubrimiento de resultados de “descuantización”, es decir, pruebas de que los algoritmos cuánticos no son realmente necesarios para muchos problemas. Ella y sus colaboradores no estaban tratando de hacer eso esta vez, pero la prueba de la desaparición del entrelazamiento con la que se toparon equivale a una versión aún más extrema de la descuantización. No es solo que los algoritmos cuánticos no ofrezcan ninguna ventaja en un problema específico que involucre sistemas de espín de alta temperatura; es que no hay nada cuántico en esos sistemas.
Pero eso no significa que los investigadores de computación cuántica deban perder la esperanza. Dos artículos recientes identifican ejemplos de sistemas de espín de baja temperatura en los que los algoritmos cuánticos para medir estados de equilibrio superan a los clásicos, aunque aún queda por ver lo extendido que está este comportamiento. Y aunque Bakshi y sus colaboradores han demostrado un resultado negativo, el método poco ortodoxo que utilizaron para llegar a él indica que pueden surgir nuevas ideas fructíferas de lugares inesperados.
“Podemos ser optimistas y pensar que se descubrirán nuevos algoritmos increíbles”, afirma Moitra. “Y que, en el proceso, podremos descubrir hermosas matemáticas”.
El artículo original, Computer Scientists Prove That Heat Destroys Quantum Entanglement, se publicó el 28 de agosto de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo El calor destruye el entrelazamiento cuántico se ha escrito en Cuaderno de Cultura Científica.

