Naukas Bilbao 2024: 18 de enero de 1902
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

Oskar González Mendía (autor de kimikArte) doctor en químicas y profesor en la Facultad de Bellas Artes de la UPV/EHU se dedica, entre otras cosas, a resolver misterios. Entre ellos por qué el 18 de enero de 1902, un día en el que no pasó absolutamente nada, es interesante.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: 18 de enero de 1902 se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #522
Ezjakintasunaren kartografian astean zehar Mapping Ignorance blogean ingelesez argitaratutako artikuluen mamia euskaraz biltzen duen gehigarria da.
Ustezko paleodieta modan daramatza pare bat hamarkada. Gure arbasoek jaten zutena erreproduzitzen duela suposatzen da. Ikerketa berri batek agerian uzten du hau guztia ipuin bat besterik ez dela. ‘Paleo’ diet narrative challenged
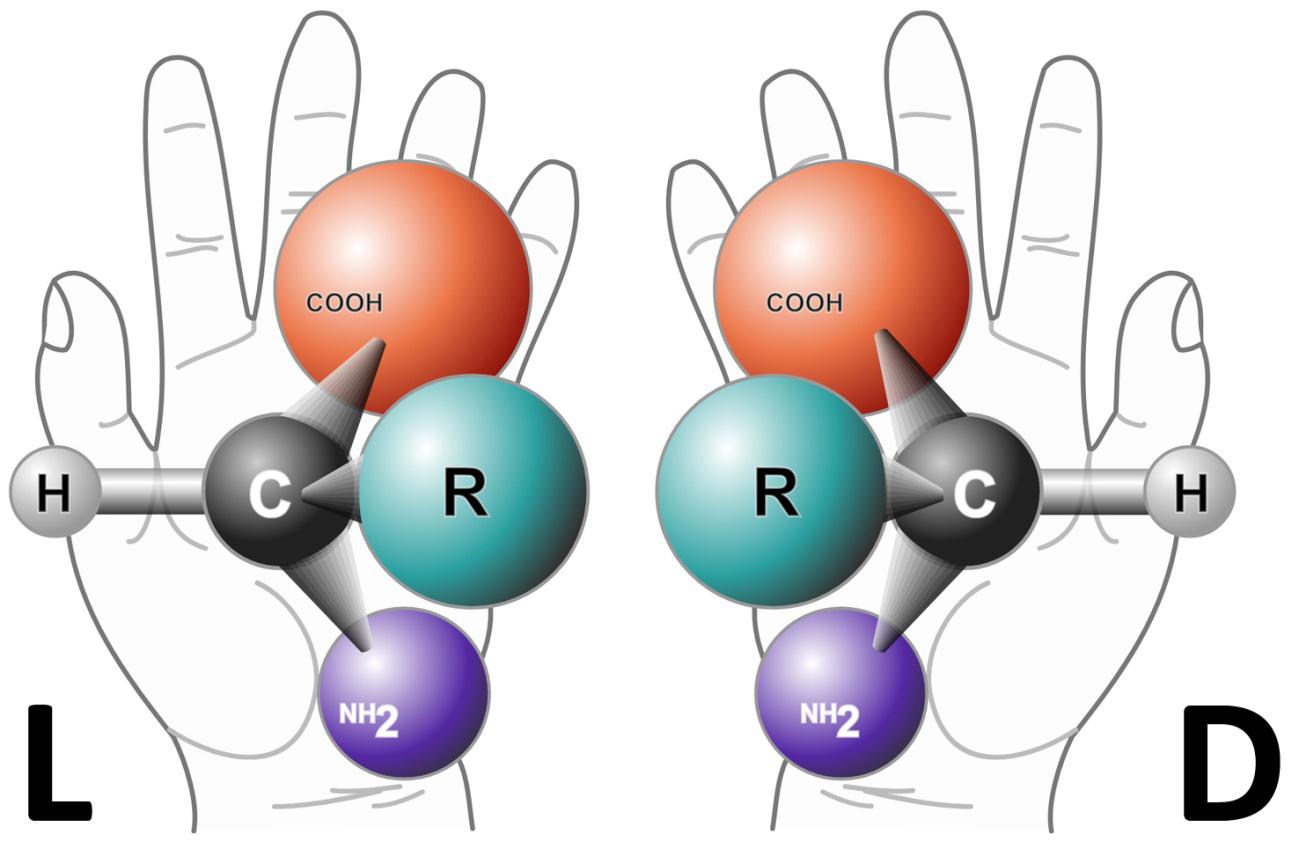
Ezagutzen dugun bizitza molekula kiral mota bakar batean oinarritzen da: ispiluaren alde bat bakarrik da zuzena. Batzuek bizitzaren molekulak eta bizitza bera sortzen saiatzen ari dira beste aldeko molekulak erabiliz. Zenbateraino da hori bizitzarako arriskutsua? Ramón Muñoz-Muchpulik gaia aztertzen du Life Through the Looking Glass: An Unprecedented Threat?
Argitan egoteak korronte elektrikoa eragiten du zenbait materialetan, kanpo eremu elektriko baten beharrik gabe. Hori bereziki interesgarria da grafenozko geruza biratuetan. DIPCko jendeak: Photogalvanic effects in twisted bilayer graphene
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #522 appeared first on Zientzia Kaiera.
Las ballenas ven en blanco y negro
 Ojo de una ballena yubarta, de la familia Balaenopteridae Foto: Rachel Moore via Instagram
Ojo de una ballena yubarta, de la familia Balaenopteridae Foto: Rachel Moore via InstagramEn la Facultad de Medicina de la Universidad del País Vasco hemos analizando los ojos de tres rorcuales varados en diferentes playas de España entre 2019 y 2021. Y su estudio nos ha ayudado a saber cómo ven las ballenas.
Las tres ballenas que han servido para nuestra investigación tenían medidas similares, alrededor de 18 metros de largo, y pesaban 20 toneladas. Cada ojo era del tamaño de una pelota de balonmano (13 cm de diámetro) y pesaba un kilo.
Ojos para sobrevivir en las profundidadesLos rorcuales, pertenecientes a la familia Balaenopteridae, son cetáceos conocidos por su velocidad e hidrodinámica, lo que les ha valido el apodo de “galgos de los mares”.
Estos animales marinos carecen de dientes y se alimentan filtrando krill en las zonas superficiales del océano. Su adaptación al medio marino ha dotado a sus órganos, especialmente los ojos, de características únicas que les permiten sobrevivir en las profundidades.
Ballenas varadasEl primer ojo provenía de un rorcual común que varó en Sopelana (Vizcaya, País Vasco) tras la borrasca Helena en febrero de 2019. Tener acceso a sus ojos nos permitió realizar estudios anatómicos y moleculares, además de cultivar las neuronas ganglionares y las células gliales de la retina, conocidas como glía de Müller.
El segundo ojo, de un rorcual boreal, se obtuvo en la playa de Tapia de Casariego (Asturias) durante la borrasca Filomena en enero de 2021. Este material permitió confirmar los hallazgos previos e inmortalizar las células de Müller para investigaciones futuras.
El tercer ojo correspondía a un rorcual que varó en Tavernes (Valencia) en mayo de 2021. En este caso, el ojo de la ballena nos sirvió para corroborar nuevamente los estudios anatómicos y moleculares realizados con los otros ejemplares. Los resultados se publicaron en varias revistas científicas.
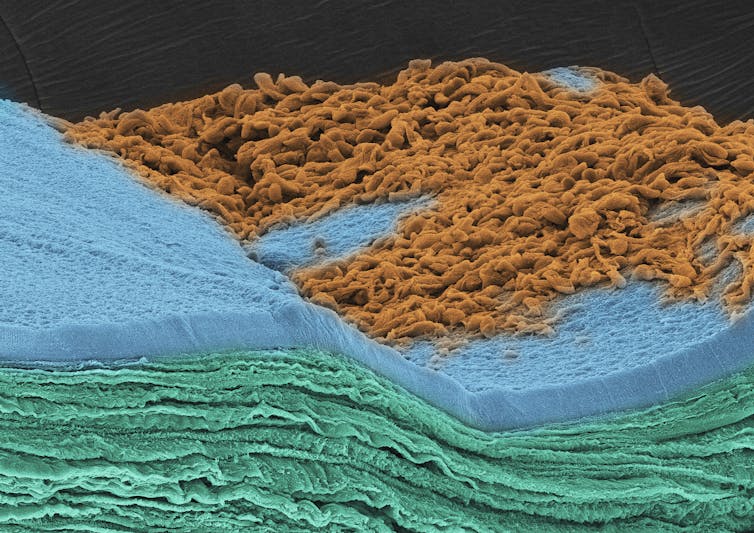 Fotografía de microscopía electrónica de barrido de la córnea del ojo de una de las ballenas. Fotografía premio de la Sociedad Española de Oftalmología.
Fotografía de microscopía electrónica de barrido de la córnea del ojo de una de las ballenas. Fotografía premio de la Sociedad Española de Oftalmología.Elena Vecino y Luis LópezAdaptaciones anatómicas del ojo
En los ojos de los rorcuales encontramos adaptaciones extraordinarias que les permiten resistir las altas presiones y la escasa luz de las profundidades marinas:
- La córnea, que permite la entrada de luz al ojo, es hasta cuatro veces más gruesa que la humana. Este refuerzo, junto con la esclera, protege al órgano visual contra las presiones extremas en el hábitat marino profundo.
- El cristalino en los rorculaes es esférico, para facilitar la visión bajo el mar, a diferencia de los mamíferos terrestres, que es lenticular.
- La esclera, o parte blanca del ojo, es extremadamente gruesa en estos cetáceos: llega a medir hasta 4 centímetros, en contraste con el medio milímetro en humanos. Está formada por colágeno endurecido, lo que protege la retina como si estuviera dentro de un cofre.
- El cuerpo cavernoso es un tejido que rodea el nervio óptico y contiene numerosos vasos sanguíneos y músculo liso. En la ballena, cuando se llena de sangre, impulsa el ojo hacia el exterior, permitiendo enfocar de un modo similar a como lo hace un telescopio.
Estos resultados han sido publicados en el capítulo ¿Cómo ven las ballenas? del libro Mamíferos marinos.
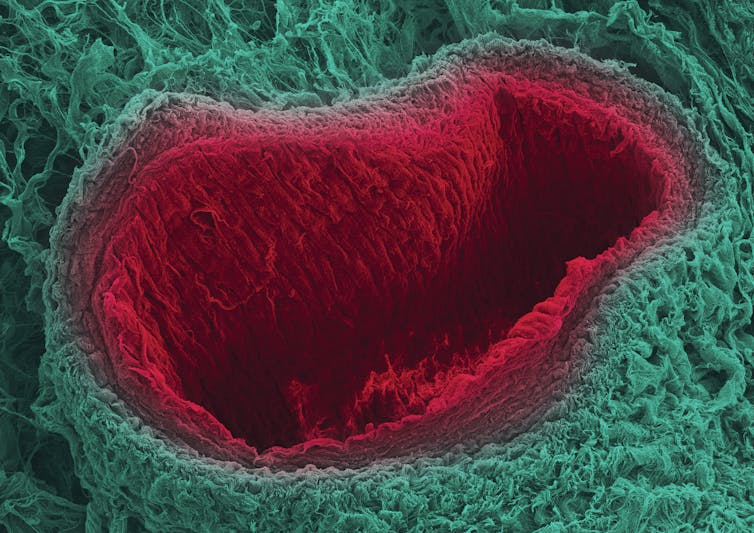 Vaso del cuerpo cavernoso del ojo de la ballena, rodeado de fibras de colágeno. Fotografía de microscopía electrónica de barrido.
Vaso del cuerpo cavernoso del ojo de la ballena, rodeado de fibras de colágeno. Fotografía de microscopía electrónica de barrido.Elena Vecino y Luis LópezCaracterísticas visuales: visión en blanco y negro
Nuestro análisis reveló que la retina de los rorcuales carece de conos, las células responsables de percibir colores y luz intensa. Por el contrario, está compuesta únicamente por bastones, que son sensibles a bajas intensidades lumínicas y funcionan en condiciones de poca luz.
Esto indica que las ballenas solo ven en blanco y negro, una adaptación al entorno oscuro del océano.
Además, las neuronas melanopsínicas, responsables de informar al cerebro sobre los ciclos de luz/oscuridad (denominados ritmos circadianos), están muy desarrolladas en las ballenas. Esto nos revela que tienen alta sensibilidad a la luz y pueden percibir las intensidades lumínicas variables en los distintos hemisferios, lo que les podría ayudar a orientarse.
Aunque los ojos de las ballenas son grandes, su densidad de neuronas ganglionares, encargadas de procesar la información visual y enviarla al cerebro, es muy baja. Esto significa que la cantidad de señales visuales que llegan al cerebro es limitada y da como resultando una visión reducida, como indicamos en el estudio publicado en Frontiers in Anatomy. Metafóricamente hablando, las ballenas podrían llevar el pin de baja visión.
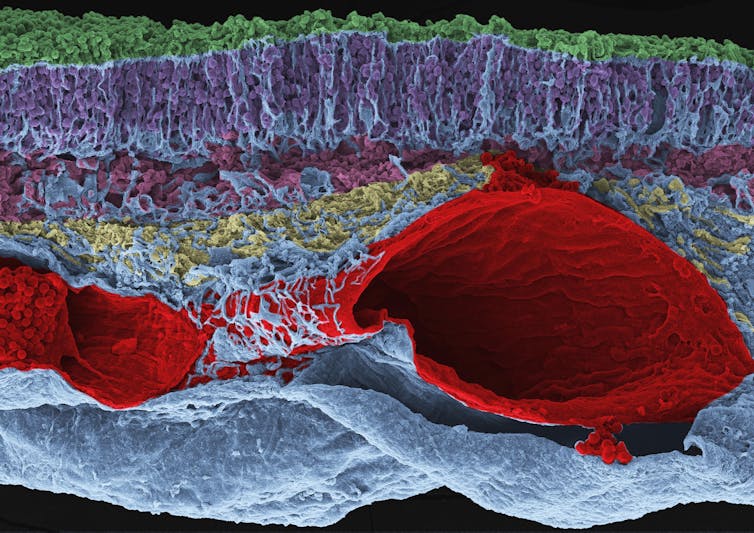 Microscopía electrónica de barrido de la retina de una ballena, coloreada digitalmente. Premio Scientific American NeuroArt de la SENC.
Microscopía electrónica de barrido de la retina de una ballena, coloreada digitalmente. Premio Scientific American NeuroArt de la SENC.Elena Vecino Cordero y Luis López VecinoReconocimientos artísticos
Además de su valor científico, las imágenes obtenidas durante esta investigación han sido reconocidas por su belleza y han ganado varios premios nacionales e internacionales, entre ellos, el de Scientific American NeuroArt.
Estas fotografías se han expuesto en siete museos marítimos, de fotografía y galerías de arte nacionales e internacionales. En la actualidad está en el Museo Nacional de Ciencias Naturales de Madrid, donde permanecerá hasta finales de mayo.
Las exposiciones han sido adaptadas a personas invidentes y con baja visión, incorporando fotografías texturizadas, audioguías y recorridos señalizados con cintas podotactiles. Además, hemos editado tres vídeos que cuentan la historia de la investigación desde el comienzo hasta la exposición: Elena y la ballena; ¿Cómo ven las ballenas? y Cómo adaptar una exposición fotográfica a personas que no ven.
El estudio de los ojos de estos tres rorcuales ha permitido conocer en profundidad las adaptaciones anatómicas y funcionales que posibilitan su vida en el medio marino. Estas investigaciones no solo arrojan luz sobre la biología de estos cetáceos: llevadas al museo, permiten destacar la importancia de preservar y estudiar la biodiversidad de nuestros océanos.![]()
Sobre las autoras: Elena Vecino Cordero, Catedrática de Biología Celular (UPV/EHU), Licenciada en Bellas Artes, Life Member, Clare Hall Cambridge (UK). Directora del Grupo Oftalmo-Biología Experimental (GOBE), Universidad del País Vasco / Euskal Herriko Unibertsitatea y Luis López Vecino, Profesor asociado del Grado en desarrollo de aplicaciones 3D interactivas y videojuegos, Universidad de Salamanca
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Las ballenas ven en blanco y negro se ha escrito en Cuaderno de Cultura Científica.
Purnima Sinha, zientziatik eta artetik abiatuta buztina landu zuen fisikaria
Indiako zoruetan aurki daitezkeen buztinen ikerketa izan zen Purnima Sinha zientzialariaren karrerako interes handietako bat; izan ere, X izpien teknikak erabiltzen zituen horien egiturak aztertzeko. Baina materialen eta beren koloreen analisiak ez zuen soilik fisikariaren arrazoibide zientifikoa pizten, haren inspirazio artistikoa ere erakartzen zuen. Horiek horrela, buztina modelatzen hasi zen, eskulturak sortzeko. Bi alderdi horietan dedikazio eta talentu handia erakutsi zuen, harentzat zientzia eta artea jakin-min beraren bi adierazpen bailiran.
Purnima Sinha 1927ko urriaren 12an jaio zen Kalkutan (India); garai hartan kolonia britainiarra zen. Senar-emazte liberal batzuen alaba zen. Aita abokatua zen, 1917ko Errusiako iraultzaren jarraitzailea, eta joera komunistak zituen. Besteak beste, defendatzen zuen emakumeek heziketarako eskubidea zutela, eta sexuen arteko berdintasunean sinesten zuen.
 1. irudia: Purnima Sinha Kalkutako Unibertsitatean fisikako doktoregoa eskuratu zuen lehenengo emakumea izan zen. (Iturria: Mujeres con Ciencia)
1. irudia: Purnima Sinha Kalkutako Unibertsitatean fisikako doktoregoa eskuratu zuen lehenengo emakumea izan zen. (Iturria: Mujeres con Ciencia)Hori dela eta, Sinhak eta bere ahizpek karrera akademikoak eta zientifikoak egin ahal izan zituzten matematikaren, kimikaren eta ekonomiaren esparruetan. “Trantsizioko zientzialariak” deritzenaren parte izan ziren. Izan ere, horien oinarrizko heziketa erregimen kolonial britainiarraren pean gauzatu bazen ere, karrera zientifikoak India jada independentea zenean egin zituzten. Sinhak fisikaren alde egin zuen.
Fisikako lehenengo emakumezko doktorea Kalkutako UnibertsitateanBere familian emakume batek baino gehiagok jaso zuten prestakuntza zientifikoa, baina Indian ez zen batere ohikoa 40ko hamarkadan emakumeek halako prestakuntzarik jasotzea. 1955ean, Sinha Kalkutako Unibertsitatean fisikako doktoregoa eskuratu zuen lehenengo emakumea izan zen. Sinharen zuzendaria Satyendra Nath Bose izan zen, garai hartako fisikari ospetsua, fisika kuantikoaren eremuan ekarpen handiak egin zituena. Boseri buruzko legatu biografiko gehiena Sinharen beraren eskutik jaso dugu; izan ere, zenbait liburu argitaratu zituen bere maisuari buruz.
 2. irudia: Paul Dirac, Purnima Sinha eta Satyendra Nath Bose (Kolkata, 1954). (Iturria: Mujeres con Ciencia)
2. irudia: Paul Dirac, Purnima Sinha eta Satyendra Nath Bose (Kolkata, 1954). (Iturria: Mujeres con Ciencia)Hala ere, Sinharen lantaldeak fisikaren beste eremu bat aztertzen zuen: buztinetako kristal egiturak ikertzen zituzten, X izpien difrakzioa erabilita. India independizatu berri zen garai hartan, herrialdeak ez zuen baliabide nahikorik ekipo eguneratuak zituzten ikerketa laborategiak ezartzeko. Ikerketa zientifikoa artearen, artisautzaren, asmakuntzaren eta miaketa sistematikoaren arteko erdibidean zegoen.
Tresna zientifikoak makineria militar zaharretik abiatutaSinhak berak kontatuko zuenez, lan egiten zuen laborategian hamar ikertzaile zeuden, eta bakoitzak bere tresnak eraiki behar zituen, haren ikerketaren premien arabera. Horretarako, Sinhak eta bere kideek Bigarren Mundu Gerraren ostean abandonatutako makina militar zaharren piezak eta ikerketa tresna zaharrak erabiltzen zituzten. Eta, horri esker, Indiako hainbat eremutako buztin materialen berrogeita hamar bat motaren sailkapen zehatza egin ahal izan zuten, eta bi artikulu argitaratu zituzten Nature aldizkarian horren berri emateko.
Aurrerago, Stanfordeko Unibertsitatera (Kalifornia) joan zen, Biofisika Sailera, eta bertan ikerketak egin zituen hain ondo ezagutzen zituen buztinaren kristal egitura horiek alderatzeko interesgarriak iruditzen zitzaizkion DNA patroiekin, Origins of Life proiektu orokorraren baitan. Garai hartan, halaber, zenbait konferentzia eman zituen Indiako musikari buruz Chicagoko Unibertsitatean. Eta gerora, liburu batean bildu ziren.
Buztina, zientziaren eta artearen erdibideanIndiara itzuli zenean, Indiako Zundaketa Geologikoan eta JCB Bose Institutuan lan egin zuen; baina, azkenean Kristalaren eta Zeramikaren Ikerketarako Institutu Nagusian sartu zen, kolore ezberdinetako zeramiken fisika aztertzeko.
Interes zientifikoa eta joera artistikoak uztartuta, garai hartan buztina modelatzen hasi zen. Eta musikarekiko bere interesari eta gaitasunari jarraikiz, tabla izeneko musika tresna jotzen ikasi zuen. Eskuarki, gizonezkoek jotzen zuten tresna hori Indiako musika klasikoko taldeetan. Horrez guztiaz gain, hainbat esparrutako erakusketa eta esposizio antolatu zituen, baita horietan parte hartu ere, hala nola zeramika, zura, buztina eta pintura.
 3. irudia: Purnima Sinha tabla jotzen. (Iturria: Mujeres con Ciencia)
3. irudia: Purnima Sinha tabla jotzen. (Iturria: Mujeres con Ciencia)Zientziari eta arteei buruzko liburu asko idatzi zituen, ingelesez zein bengaleraz, irmoki uste baitzuen zientzia tokiko hizkuntzetan irakatsi eta zabaldu ahal zela. Hain zuzen, garai hartako zenbait obra zientifiko ere itzuli zituen bengalerara, hala nola Erwin Schrödingerren Mind and Matter liburua, haren irismena zabaltzeko asmoz.
Bere senarrarekin batera (Surajit Chandra Sinha antropologoa) ere lan egin zuen talde tribaletako haurren hezkuntzarako sarbidea zabaltzeko; eta, horretarako, eskolak, ikastetxeak eta goi mailako hezkuntza programak sortu zituzten komunitate horientzat.2015eko uztailaren 11n zendu zen.
Iturriak:- Rajinder Singhs and Suprakash C. Roy, Purnima Sinha and her Doctoral Work Under Professor S.N. Bose, Science and Culture 85 (7-8) (2019) 243-253.
- Suprakash C Roy, Purnima Sinha. A Role Model for All, en Vigyan Vidushi: 75 Women Trailblazers of Science, 42-53
- Dr Purnima Sinha, the first female physicist from C.U., who did her PhD way back in the 1950s, Get Bengal, 2023ko otsailaren 26a
- Purnima Sinha and Supurna Sinha, Like mother, like daughter, Lilavati’s daughters: The Women Scientists of India, 305-309
- Rinchen Norbu Wangchuk, The Forgotten Scientist Who Broke The Glass Ceiling For Indian Women in Physics, The Better India, 2019ko azaroaren 15a
- The physicist who built her career on clay, Asia Research News, 2020ko apirilaren 7a
- Purnima Sinha, Wikipedia
Rocío Benavente (@galatea128) zientzia kazetaria da.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2024ko urriaren 24an: Purmina Sinha, la física que trabajó con arcilla desde la ciencia y desde el arte.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Purnima Sinha, zientziatik eta artetik abiatuta buztina landu zuen fisikaria appeared first on Zientzia Kaiera.
La impredecibilidad de la sencillez: autómatas celulares
Pocos, como el matemático húngaro John von Neumann, fueron capaces de vislumbrar que el próximo gran giro de guion de la ciencia no vendría de la mano, esta vez, de los campos de la «energía, el trabajo, la fuerza o el movimiento», sino del «control, la programación, el procesamiento de la información, las comunicaciones, la organización y los sistemas» (Burks 1969). Con la llegada de los primeros computadores tras la Segunda Guerra Mundial, o, en otras palabras, las primeras máquinas sofisticadas utilizadas para ayudarnos con tareas mentales en lugar de físicas, se puso sobre la mesa, de manera realista, la posibilidad de recrear artificialmente la vida. Así nació la cibernética, propuesta por Norbert Wiener durante la década de los años cuarenta del siglo XX, y así nacieron los primeros modelos computacionales que buscaban simular procesos que solo se encontraban en la naturaleza a través de operaciones lógicas.
Konrad Zuse, ingeniero alemán y pionero de la computación moderna ya hizo alguna aproximación al problema. Poco después, en el Laboratorio Nacional de Los Álamos, John Von Neumann, por un lado, empezó a explorar la idea de que un sistema computacional pudiera replicarse a sí mismo de forma autónoma; y Stanislaw Ulam, por otro, trató de averiguar si era posible que, de reglas matemáticas sencillas, pudieran surgir estructuras, patrones o comportamientos complejos. Ulam utilizó para ello cuadrículas bidimensionales en las que representaba datos marcando —o no— diferentes celdas. Raúl Ibánez puso, recientemente, un magnífico ejemplo del trabajo del matemático de origen polaco en «Números felices para siempre». Von Neumann utilizó el método de Ulam para crear uno de sus sistemas autorreplicantes. No obstante, y aunque fue el primer autómata celular que se conoce, aquel modelo pasó sin pena ni gloria y quedó olvidado durante décadas.
 Hay pocas ramas de las matemáticas, la física y la computación en las que John von Neumann (1903-1957) no realizara aportaciones fundamentales. En este caso, junto con su colega en Los Álamos Stanislaw Ulam.
Hay pocas ramas de las matemáticas, la física y la computación en las que John von Neumann (1903-1957) no realizara aportaciones fundamentales. En este caso, junto con su colega en Los Álamos Stanislaw Ulam.Créditos: Los Álamos National Laboratory y dominio público
No fue hasta la década de los setenta cuando, en la sección de matemática recreativa de Scientific American, Martin Gardner planteó, a modo de juego, una ocurrencia, sencilla pero fascinante, que había tenido el matemático inglés John Conway. Con el nombre de «juego de la vida», por su semejanza con las dinámicas de evolución de poblaciones de organismos, se regía por unas reglas muy sencillas.
Para jugar al juego de la vida solo se necesita una cuadrícula en la que podamos marcar casillas —puede ser un tablero de ajedrez o de go y algunas piezas, papel y lápiz… aunque lo más fácil e ilustrativo a día de hoy es utilizar un ordenador—. Las casillas marcadas serían el equivalente a organismos o células que podemos hacer evolucionar de forma completamente autónoma en nuestro Mundo Cuadrícula, a partir de una configuración geométrica inicial, con tan solo aplicar una y otra vez las siguientes reglas:
-
Supervivencia: una célula con dos o tres vecinas sobrevivirá en la próxima generación.
-
Muertes:
-
Una célula con cuatro o más vecinas morirá por superpoblación.
-
Una célula con una o ninguna vecina morirá por aislamiento.
-
-
Nacimientos: si una celda vacía está rodeada por tres células, en la siguiente generación nacerá ahí una nueva.
Y nada más, si nos fijamos, en realidad el juego «se juega a sí mismo». Nosotros solo decidimos la configuración inicial de células.
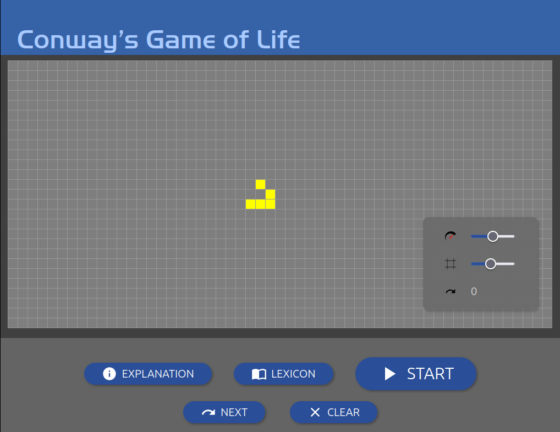 Existen numerosos sitios de internet en los que se puede jugar al juego de la vida, como https://playgameoflife.com/. Existen también librerías de patrones y todo un universo alrededor de las posibles evoluciones que se pueden conseguir a partir de diversas configuraciones iniciales.
Existen numerosos sitios de internet en los que se puede jugar al juego de la vida, como https://playgameoflife.com/. Existen también librerías de patrones y todo un universo alrededor de las posibles evoluciones que se pueden conseguir a partir de diversas configuraciones iniciales.Como el modelo que planteó Von Neumann, el juego de la vida es un autómata celular, aunque algo más sencillo. La popularización de la idea a través de una revista de divulgación científica llevó a matemáticos tanto aficionados como profesionales a experimentar con infinitud de configuraciones iniciales y a descubrir fenómenos muy interesantes; desde patrones estables —no cambian de una generación a otra— y ciclos que se repiten, hasta figuras —«planeadores»— que se deslizan por la cuadrícula dando la sensación de movimiento e incluso estructuras que se replican a sí mismas. Hay auténticas obras de arte geométricas generadas con este sencillo juego en internet —huevo de Pascua: probad a buscar en Google «juego de la vida»—.
 De izquierda a derecha: a) Configuración estable. b) Configuración cíclica (púlsar). c) Planeador (da la sensación de deslizarse por la pantalla). d) Cañón de planeadores de Gosper. Existen numerosos archivos de patrones, por ejemplo: https://conwaylife.appspot.com/library/. Créditos: a), b), c) Dominio público. d) CC BY-SA 3.0/Lucas Vieira.
De izquierda a derecha: a) Configuración estable. b) Configuración cíclica (púlsar). c) Planeador (da la sensación de deslizarse por la pantalla). d) Cañón de planeadores de Gosper. Existen numerosos archivos de patrones, por ejemplo: https://conwaylife.appspot.com/library/. Créditos: a), b), c) Dominio público. d) CC BY-SA 3.0/Lucas Vieira.
Los trabajos de Von Neumman, Ulam y Conway llevaron en los años ochenta al físico Stephen Wolfram a investigar estos autómatas celulares, en esta ocasión, unidimensionales —consisten únicamente en una fila de celdas y se conocen como «elementales»—, y los clasificó en función de la complejidad de su comportamiento en:
-
Clase 1: alcanzan estados estables.
-
Clase 2: generan patrones oscilatorios o periódicos.
-
Clase 3: generan patrones seudoaleatorios o caóticos.
-
Clase 4: generan estructuras complejas pero ordenadas.
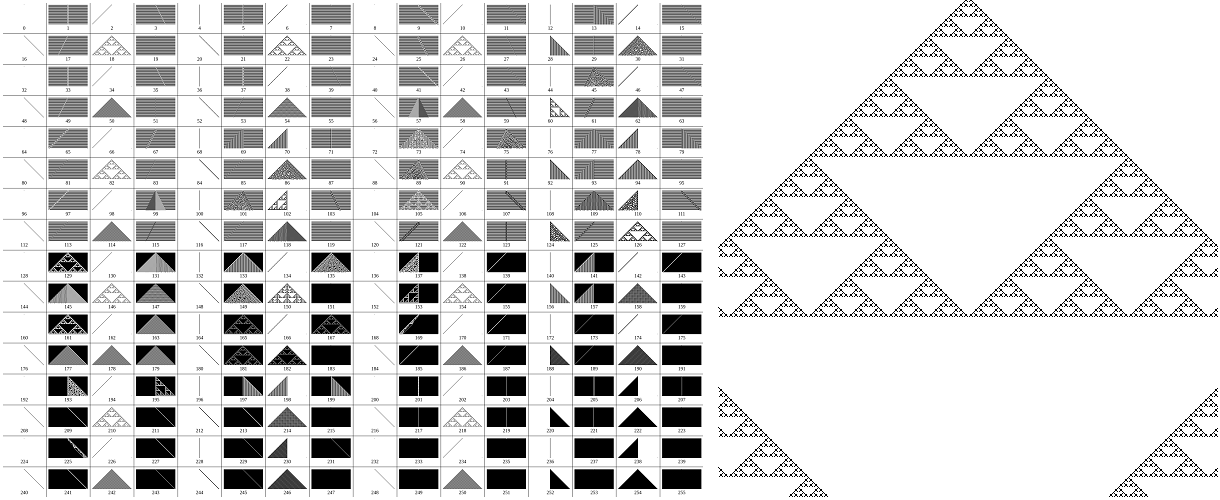 Stephen Wolfram hizo una clasificación de diversas reglas para los autómatas celulares elementales. De algunas de ellas se pueden obtener patrones realmente complejos y, por qué no, bellos, como el fractal que se obtiene tras aplicar la regla 90 (ampliado la derecha). Créditos: CC BY-SA
Stephen Wolfram hizo una clasificación de diversas reglas para los autómatas celulares elementales. De algunas de ellas se pueden obtener patrones realmente complejos y, por qué no, bellos, como el fractal que se obtiene tras aplicar la regla 90 (ampliado la derecha). Créditos: CC BY-SADe nuevo quedó patente que un sistema de reglas muy sencillo en una cuadrícula podía dar lugar a patrones complejos. Esto llevó a Wolfram a aplicar la teoría de autómatas celulares, de una forma cada vez más elaborada, al campo de la física, y a plantear que tal vez el universo podría describirse con un modelo computacional de este tipo… no sin la controversia que suelen despertar este tipo de aseveraciones en el mundo de la física.
Ya se tomen los autómatas celulares como un juego o se pretendan aplicar a campos más tangibles, lo cierto es que son una fuente de sorpresas matemáticas. Su potencial y, seguramente, también su belleza inspiraron al escritor de ciencia ficción Greg Egan para escribir en 1994 su novela Ciudad Permutación, un espectacular homenaje a las matemáticas, la computación y la vida.
 Última edición en inglés de Ciudad Permutación, de Greg Egan (Gollancz). Se publicó en español en 1998, lamentablemente, está descatalogada.
Última edición en inglés de Ciudad Permutación, de Greg Egan (Gollancz). Se publicó en español en 1998, lamentablemente, está descatalogada.
Bibliografía
Burks, A. W. (1969). Von Neumann’s self-reproducing automata. University of Michigan. Computer and Communication Sciences Department. https://fab.cba.mit.edu/classes/MAS.865/topics/self_replication/Burks.pdf
Gardner, M. (octubre de 1970). The fantastic combinations of John Conway’s new solitaire game “life”. Scientific American, 223(4), 120-123.
Wolfram, S. (2002). A new kind of science. Wolfram Media.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo La impredecibilidad de la sencillez: autómatas celulares se ha escrito en Cuaderno de Cultura Científica.
Fisioterapia tratamenduen eragina endometriosiak sortzen duen minean
Endometriosia emakumeetan eratu daitekeen gaixotasun ginekologikoa da. Gaixotasun honetan uteroa inguratzen duen ehuna, endometrioa, uterotik kanpo agertzen da. Horrek, hantura kronikoa eragiten du eta, askotan, endometrioaren gehiegizko garapena eta uteroz kanpoko metaplasia muskularrarekin batera agertzen da. Endometriosiaren patogenesia ezezaguna da, halaber, gaixotasunaren patogenesia azaltzeko hainbat hipotesi proposatu dira. Hipotesi batzuk besteak baino argiagoak dira, hala ere, ez da proposatu hipotesi bat endometriosiaren patogenesia azaltzeko gai dena gaixotasunaren modu guztietan.
Sintoma nagusiak min pelbikoa eta antzutasuna dira, bizi kalitatean eragin handia izaten dutenak. Dena den, minarekin batera beste sintomak ager daitezke, hala nola, dismenorrea (hileroko mina), min pelbikoa, dispareunia sakona (min sakona harreman sexualetan), diskezia (sabelusteko zailtasunak) eta disuria (mina pixa egiterakoan).
 Irudia: endometriosiaren aurrean fisioterapiaren helburuak mina arintzea, inplante endometrialek edo ebakuntzek eragindako adherentziak askatzea, gaixotasunaren progresioa murriztea eta endometriosia pairatzen duten emakumeen bizi kalitatea hobetzea dira. (Argazkia: Sora Shimazaki -Pexels lizentziapean- Iturria: Pexels.comMina endometriosian
Irudia: endometriosiaren aurrean fisioterapiaren helburuak mina arintzea, inplante endometrialek edo ebakuntzek eragindako adherentziak askatzea, gaixotasunaren progresioa murriztea eta endometriosia pairatzen duten emakumeen bizi kalitatea hobetzea dira. (Argazkia: Sora Shimazaki -Pexels lizentziapean- Iturria: Pexels.comMina endometriosian
Mina esperientzia sentsorial eta emozional desatsegina da, ehunen kalte erreal edo potentzialarekin lotuta dagoena. Endometriosian ematen den mina mekanismo periferikoarengatik eta mekanismo zentralarengatik ematen da. Mina eremu anatomiko zehatz batean hauteman ohi den arren, minaren esperientzia kontzientea garunetik sortzen da nerbio-sistema zentralaren barruko jarduera koordinatuaren ondorioz. Minak berak ere nerbio-sistema zentralaren egitura eta funtzioa aldatzen ditu, eta sarritan sentsibilizazio zentralera eramaten du; honek eragiten du estimulu periferikoak sentikorragoak bihurtzea, baita mina sortzea lesio kaltegarri periferikorik gabe.
Zein da endometriosiaren tratamendua?Endometriosiak ez dauka tratamendu sendatzailerik, beraz, tratamendua sintomen eta bizi kalitatearen hobekuntzan oinarritzen da. Izan ere, gaixotasun honen tratamendu sintomatologikoa multidiziplinarra da, tratamendu medikua, nutrizionala, psikologikoa eta fisioterapeutikoa barneratzen dituena, eta, haien artean konbinatu daitezke. Hori dela eta, tratamendu sintomatologikoa planteatu baino lehen, lehenengo minaren jatorria aztertu behar da eta, ondoren, garrantzitsua da zehaztea mina ehunaren lesioarekin lotuta egon daitekeen edo beste faktore batzuengatik sortu den.
Fisioterapia tratamenduei dagokionez, endometriosian ematen den minean duen eraginari buruzko ikerketa askorik ez egon arren, min pelbikoa kronikoari buruz hainbat ikerketa eta berrikuspen sistematiko argitaratu dira azkenengo urteetan. Min pelbikoa endometriosian ematen den sintoma nagusienetarikoa da, izan ere, kasu askotan kronifikatu egiten da. Hortaz, min pelbiko kronikoari buruzko ikerketetan ateratako ondorioak endometriosiarekin erlazio handia izan dezakete.
Gaixotasun honen aurrean fisioterapia pelbiperioneologikoaren helburuak mina arintzea, inplante endometrialek edo ebakuntzek eragindako adherentziak askatzea, gaixotasunaren progresioa murriztea eta endometriosia pairatzen duten emakumeen bizi kalitatea hobetzea dira. Horretarako, Fisioterapia-metodo eta -teknika desberdinak egon daitezke, hala nola, masoterapia (perineala, abdominala, orbainetakoa), osteopatia estrukturala zein biszerala, indukzio miofasziala, berreziketa posturala, arnas teknika fisioterapikoak eta erlaxazio teknikak. Dena den, fisioterapia tratamendu asko enpirikoak dira, beraz, fisioterapia tratamenduei buruzko ebidentzia zientifikoa aztertu nahi izan da.
Berrikuspen sistematikoa egin ondoren eta azken urteetako literatura aztertu ondoren, ikerketak erabilitako fisioterapia metodoak Thiele masajea, TENS-a (kutaneoa eta akupuntura modukoa), nerbio bagoaren elektroestimulazioa eta akupuntura dira. Emaitzei dagokionez, azterlan guztiek minaren hobekuntza estatistikoki esanguratsuak adierazi zituzten. Hala eta ere, tratamenduen eraginkortasuna zehazteko meta-analisi bat egin beharko litzateke, eta, hori hurrengo pausua izango litzateke. Azkenik, berrikuspen sistematiko honek barneratzen dituen ikerketen ezaugarriengatik ezin izan dira ondorio sendoak atera eta etorkizunean ikerketa gehiago, kontrolatuagoak eta lagin handiagoekin gehiago beharko lirateke.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 45
- Artikuluaren izena: Fisioterapia tratamenduen eragina endometriosiak sortzen duen minean: berrikuspen sistematikoa
- Laburpena: Endometriosia emakumeetan agertzen den gaixotasun ginekologiko kroniko, ohiko, onbera, hanturazkoa eta estrogeno menpekoa da. Gaixotasun horretan funtzionalki aktiboa den ehun endometriala uterotik kanpo eratzen da, eta horrek hantura kronikoa eragiten du. Sintoma nagusiak min pelbikoa eta antzutasuna dira, bizi kalitatean eragin handia izaten dutenak. Ikusita askotan gaixotasun honen tratamendurako fisioterapiaren erabilera enpirikoa dela, berrikuspen sistematiko hau egin nahi izan da. Alde batetik, endometriosia diagnostikatuta duten emakumeen minaren tratamendurako zer fisioterapia-tratamendu dauden ikusteko eta, bestetik, horiek lortutako emaitzak aztertzeko ebidentzia zientifikoaren arabera. Bilaketa bibliografikoa egin zen «Endometriosis», «Physical Therapy Modalities» eta «Physical Therapy Specialty» terminoekin osasunarekin lotutako 6 datu-basetan. Bertan, endometriosia diagnostikatuta duten mina tratatzeko fisioterapia metodo edo teknikak erabili zituzten ausazko entsegu klinikoak bilatu ziren, ingelesez edo gaztelaniaz idatziak. Kalitate metodologikoaren balorazioa PEDro eskalaren bidez egin zen. Azkenean, 7 azterlan aukeratu ziren, horien kalitate metodologikoa egokia edo ona izanik; batek bakarrik kalitate metodologiko eskasa zuen. Guztira 320 parte-hartzaile aztertu zituzten, eta aztertutako fisioterapia metodoak, Thiele masajea, TENSa (kutaneoa eta akupuntura modukoa), nerbio bagoaren elektro-estimulazioa eta akupuntura izan ziren. Azterlan guztiek minaren edo minarekin erlazionatutako sintometan hobekuntza estatistikoki esanguratsuak aurkitu zituzten. Endometriosiak sortutako min sintomen tratamendurako dauden fisioterapia-tratamenduak ebidentzia zientifikoan oinarrituta Thiele masajea, TENSa (kutaneoa eta akupuntura modukoa), nerbio bagoaren elektroestimulazioa eta akupuntura dira, eta guztiek minaren gutxipena eragin zuten ebidentzia zientifikoaren arabera.
- Egileak: Ismene Rodriguez, Izaro Esain, Iraia Bidaurrazaga-Letona, Miriam Urquiza eta Iratxe Duñabeitia
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 51-70
- DOI: 10.1387/ekaia.24979
Ismene Rodriguez, Izaro Esain, Iraia Bidaurrazaga-Letona, Miriam Urquiza eta Iratxe Duñabeitia UPV/EHUko Medikuntza eta Erizaintza Fakultateko Fisiologia Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.
The post Fisioterapia tratamenduen eragina endometriosiak sortzen duen minean appeared first on Zientzia Kaiera.
Números felices para siempre
Como comentaba en mi anterior entrada del Cuaderno de Cultura Científica, titulada Algunas propiedades matemáticas del número 2025, algunas personas del ámbito de las matemáticas nos dedicamos a buscar propiedades matemáticas del número al que corresponde el nuevo año, en este caso le tocaba el turno al 2.025, para incluir alguna de ellas en nuestras felicitaciones navideñas para compartir en las redes sociales, enviar a nuestros contactos por whatsapp o para diseñar nuestras tarjetas navideñas físicas. Por este motivo, dediqué esa entrada a algunas propiedades matemáticas del mencionado número, el dos mil veinticinco.
En particular, utilicé para mi tarjeta de año nuevo que el número 2.025 puede escribirse como la suma de los cubos de todas las cifras básicas de nuestro sistema de numeración, es decir, todos los números de un solo dígito:
13 + 23 + 33 + 43 + 53 + 63 + 73 + 83 + 93 = 2.025,
donde no incluí el cero ya que cero elevado al cubo es cero. Pero, además, se comentaba en dicha entrada que este número es un número cuadrado (de hecho, es el cuadrado de un número triangular, 45), suma de números triangulares consecutivos, un número trapezoidal (o cortés), que puede expresarse como suma de números naturales consecutivos de catorce maneras distintas, un número octogonal centrado, un número deficiente, un número tau, un número duffiniano o un número de Harshad. Sin embargo, se podría haber ampliado esta familia de propiedades a otras, como escribir el 2.025 con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potencias, como aparece en la siguiente imagen, que es el típico problema de ingenio, aunque para diferentes números.
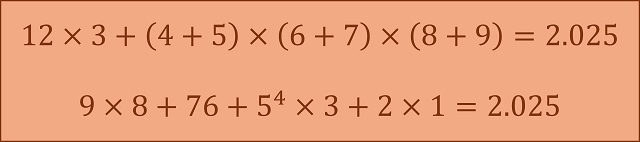 El número 2.025 expresado con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potencias
El número 2.025 expresado con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potenciasEl año 2.026 también tendrá su tarjeta de año nuevo
Cuando compartí en las redes sociales el enlace de la entrada titulada Algunas propiedades matemáticas del número 2025, algunas personas me comentaron que sería difícil encontrar otro año con tantas propiedades matemáticas como el 2.025. Lo cierto es que, aunque haya años, bueno, los números de los años, con más propiedades matemáticas o propiedades más sorprendentes que otros, podemos obtener curiosas propiedades para todos los números. Así, de cara al año que viene, el 2.026 también verifica algunas curiosas propiedades. Por ejemplo, podemos expresar el 2.026 con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potencias, que podéis ir reservando para dentro de un año.
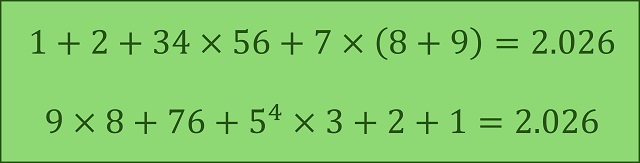 El número 2.026 expresado con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potencias
El número 2.026 expresado con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potencias
Pero como comentaba, este número tiene muchas otras propiedades. Por ejemplo, puede expresarse como suma de números naturales consecutivos
2.026 = 505 + 506 + 507 + 508,
o también pertenece a la familia de números naturales de la que vamos a hablar en esta entrada, los números felices. Es decir, el 2.026 es un número feliz.
Números felicesDefinición: Un número es feliz (en algunos textos también se han sido llamados números elegantes) si al sumar los cuadrados de sus dígitos, repetir esta misma operación sobre el resultado obtenido e iterar el proceso suficientes veces, la sucesión de números resultante alcanza en algún momento el número 1. En caso contrario, se dice que el número es infeliz o triste.
Por ejemplo, el número 7 es un número feliz ya que si consideramos la sucesión de resultados del algoritmo “sumar los cuadrados de sus dígitos” de manera recursiva nos queda lo siguiente:
7, 49, 97 (= 42 + 92), 130 (= 92 + 72), 10 (= 12 + 32 + 02), 1 (= 12 + 02),
es decir, la sucesión se estaciona en el número 1. Sin embargo, si consideramos el número 5 la sucesión que se genera con el anterior algoritmo es
5, 25, 29 (= 22 + 52), 85 (= 22 + 92), 89 (= 82 + 52), 145 (= 82 + 92), 42 (= 12 + 42 + 52), 20 (= 42 + 22), 4 (= 22 + 02), 16 (= 42), 37 (= 12 + 62), 58 (= 32 + 72), 89 (= 52 + 82), …
que, como podemos observar, se mete en un ciclo sin fin, formado por los números 89, 145, 42, 20, 4, 16, 37 y 58, por lo tanto, el número 5 no es un número feliz.
Más aún, como comentábamos más arriba, el número 2.026 es un número feliz, puesto que la sucesión de resultados de aplicar de manera recursiva el algoritmo “sumar los cuadrados de sus dígitos” al 2.026 y después a los respectivos resultados que se van obteniendo es 2.026, 44, 32, 13, 10 y 1. Por lo tanto, la sucesión llega al 1, donde se estanca, en cinco pasos. De manera que las próximas navidades se podría decir que el nuevo año “es un año feliz”, trasladando la propiedad del número al año. El anterior año feliz fue el 2.019 y el siguiente será el 2.030.
Además, de la definición se deduce fácilmente que, dado un número feliz, cualquier otro número que se obtenga como permutación de sus dígitos sigue siendo feliz. Por ejemplo, como 2.026 es un número feliz, también lo son 226, 262, 622, 2.062, 2.206, 2.260, 2.602, 2.620, 6.022, 6.202 y 6.220.
El origen de estos números es incierto. En una de las referencias clásicas sobre los mismos, el libro de Richard Guy Unsolved Problems in Number Theory, se menciona que llamaron la atención del matemático inglés Reg Allenby, cuando su hija le mostró que se los habían enseñado en la escuela. Aunque parece ser que tienen su origen en Rusia.
No es difícil calcular, a mano o con una calculadora, los primeros números felices. En concreto, los menores de 200 son 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167, 176, 188, 190, 192, 193. De hecho, los números felices son la sucesión A007770 de la enciclopedia on-line de sucesiones de números enteros. Al realizar el algoritmo para los números menores de 200 se observará que para los demás números, los infelices, la sucesión termina siempre en el bucle del 89. De hecho, estas son las dos únicas posibilidades que existen, como aparece mencionado en el libro de Richard Guy, aunque demostrado mucho antes, en 1945, en el artículo de Arthur Porges titulado A Set of Eight Numbers (Un conjunto de ocho números).
Teorema: Si para cada número natural se considera la sucesión de números formada por los resultados del algoritmo “sumar los cuadrados de sus dígitos” considerado de forma iterada a partir de dicho número, esta se estacionará en el número 1 o entrará en el ciclo infinito formado por los ocho números 89, 145, 42, 20, 4, 16, 37 y 58.
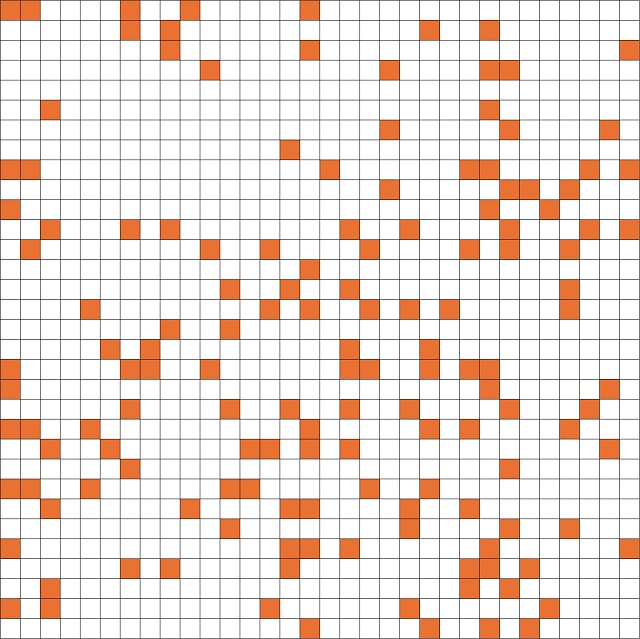 Números felices en la espiral de Ulam. La espiral de Ulam es una estructura geométrica plana, de tipo reticular, en la que los números naturales son escritos en espiral, empezando en el 1 y en el sentido contrario a las agujas del reloj, destacando los números primos (en este caso, los números felices), de tamaño 32 x 32, 1.024 celdas
Números felices en la espiral de Ulam. La espiral de Ulam es una estructura geométrica plana, de tipo reticular, en la que los números naturales son escritos en espiral, empezando en el 1 y en el sentido contrario a las agujas del reloj, destacando los números primos (en este caso, los números felices), de tamaño 32 x 32, 1.024 celdas
Otra curiosa propiedad del algoritmo “sumar los cuadrados de sus dígitos” es que para cualquier número natural n siempre existe otro número natural m tal que el resultado de aplicar el algoritmo “sumar los cuadrados de sus dígitos” a m nos genera n. Esto es muy fácil de demostrar puesto que, en particular, podemos tomar m igual al número formado por n unos (111…111), que trivialmente nos da n al aplicarle el algoritmo.
¿Cuántos números felices hay?Lo primero que nos podríamos plantear es si existe un número infinito de números felices. La respuesta es trivialmente afirmativa, ya que es muy fácil construir familias infinitas de números felices, sin más que añadir ceros a un número que es feliz. Por ejemplo, el 1 es feliz, así como los números 10, 100, 1.000, 10.000, 100.000, …, en general, 10n es un número feliz para cualquier número natural n, que es una familia infinita.
La siguiente cuestión relacionada con esta pregunta es la densidad de números felices dentro de los naturales, es decir, cuál es el porcentaje de números felices dentro de los números naturales. Si miramos la anterior lista de números felices, hay 20 dentro de los 100 primeros, luego un porcentaje del 0,2. Si continuamos con los números felices menores, o iguales, que las potencias de 10, tenemos que hay 143 dentro de los 1.000 primeros (un porcentaje del 0,143); 1.442 dentro de los 10.000 primeros (un porcentaje del 0,1442); 14.377 dentro de los 100.000 primeros (un porcentaje del 0,14377); 143.071 dentro de los 1.000.000 primeros (un porcentaje del 0,143071); y así podemos continuar con los primeros datos, que aparecen en la siguiente tabla.
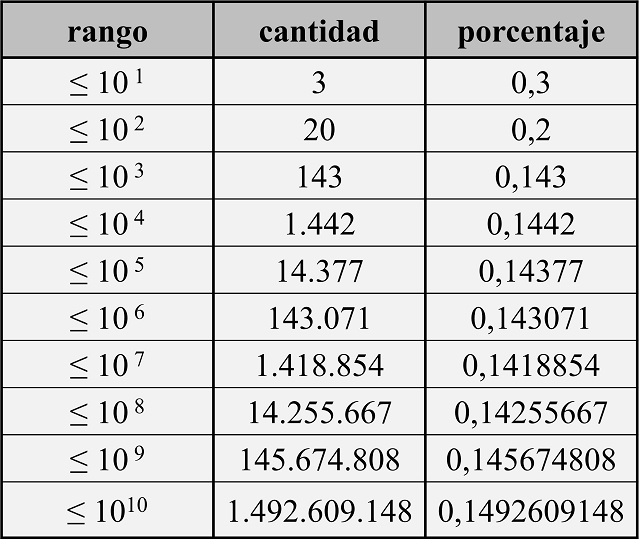
La lista de los porcentajes para números menores, o iguales, que las potencias de 10 (lo que podríamos denominar densidad relativa) empieza con las siguientes cantidades:
1; 0,3; 0,2; 0,143; 0,1442; 0,14377; 0,143071; 0,1418854; 0,14255667; 0,145674808; 0,1492609148; 0,15091199357; 0,149121303586; 0,1443278000870; 0,13770853279685; 0,130660965862333; 0,1245219117260664; 0,12024696404768025; 0,118226055080025491; 0,1183229962059381238; 0,12005034444292997294; etc…
que, salvo las primeras, está en un rango entre 0,118 y 0,151. Richard Guy mencionaba en su libro Unsolved Problems in Number Theory que “parece que 1/7 de los números naturales es feliz” (1 de cada 7), sin embargo, no parece que esto sea realmente así, no existe una densidad “límite”. De hecho, en el artículo On the density of happy numbers, del matemático estadounidense Justin Gilmer, publicado en la revista Integers (2013), se muestra un gráfico (véase la siguiente imagen) en el que se muestra cómo el porcentaje de números felices crece y decrece sin confluir a una cantidad fija.
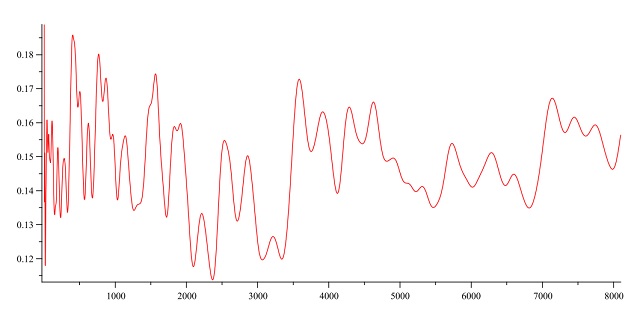 Densidad relativa de números felices menores que 10n
Densidad relativa de números felices menores que 10nDe hecho, Gilmer demuestra que la densidad superior está por encima de 0,18577 y la densidad inferior por debajo de 0,1138.
Números felices consecutivosSi se mira la lista anterior de los números felices menores que 200, se puede observar que existen algunos números felices consecutivos, como 31-32, 129-130 y 192-193, de hecho, existen infinitas parejas de números felices consecutivos. En el libro La gran familia de los números se incluye una actividad relacionada con esto mismo, que ya apareció en el libro Desafíos Matemáticos, propuestos por la Real Sociedad Matemática Española (SM-RSME, 2012), el siguiente sencillo y divertido desafío, que dejo aquí para vuestra diversión.
Problema: Encontrar infinitas parejas de números felices consecutivos.
Si se continuan buscando cadenas de números felices consecutivos se descubrirá que el primer trío es el formado por los números 1.880, 1.881 y 1.882, los tres números felices, como puede comprobarse; el primer cuarteto es el formado por los números 7.839, 7.840, 7.841 y 7.842; mientras que el primer quinteto de números felices consecutivos es el formado por los números 44.488, 44.489, 44.490, 44.491 y 44.492, que aparecen citados por Richard Guy en su libro Unsolved Problems in Number Theory, quien se cuestiona además si existen cadenas de números felices consecutivos de cualquier longitud.
Los matemáticos saudíes Esam El-Sedy y Samir Siksek demostraron, en su artículo On happy numbers, publicado en la revista Rocky Mountain Journal of Mathematics (2000), que la respuesta es afirmativa, es decir, existen cadenas de números felices consecutivos de cualquier longitud.
Una reflexión finalVamos a terminar aquí esta entrada del Cuaderno de Cultura Científica, aunque podríamos haber continuado por dos caminos distintos. El primero hablando de números felices que además satisfacen otras propiedades matemáticas, como ser primos, cuadrados, triangulares, capicúas, de Fibonacci u otras propiedades.
Por ejemplo, los números felices primos menores que 500 son: 7, 13, 19, 23, 31, 79, 97, 103, 109, 139, 167, 193, 239, 263, 293, 313, 331, 367, 379, 383, 397, 409 y 487, sucesión que aparece mencionada en el episodio titulado 42 (el séptimo de la tercera etapa) de la serie británica Doctor Who, emitido en 2017, donde se necesita introducir un número para abrir una puerta, que es el siguiente a la sucesión 313, 331, 367… (véase la siguiente imagen) y la respuesta es 379, que es el siguiente número feliz primo.
 Fotograma del episodio 42 de la serie británica Doctor Who
Fotograma del episodio 42 de la serie británica Doctor WhoMientras que el segundo camino, interesante también, hablando de que la felicidad de los números depende de la base de numeración en la que estén representados (hasta ahora nosotros hemos trabajado en la base natural, la base 10) y no es una característica del propio número. Por ejemplo, el número 160 que no es feliz en la base 10, sí lo es en base 6. Como 160 = 4 36 + 2 6 + 4 1, se representa en dicha base como 424, que al hacer la suma de sus dígitos al cuadrado sale 10 (36 en base decimal) y repitiendo la operación queda 1. El número 5, que no era feliz en base 10, tampoco lo es en base 6, ya que la sucesión asociada, expresada en la base 6, es 5, 41, 25, 45, 105, 42, 32, 21, 5, produciéndose un bucle infinito, que es el único que existe para esta base. O el 7, que es un número feliz en base decimal, no lo es en base senaria, ya que cae en el ciclo del 5.
Bibliografía
1.- Ibáñez, La gran familia de los números, Libros de la Catarata, 2021.
2.- Página web: Numbers Aplenty.
3.- Richard Guy, Unsolved problems in number theory, Springer-Verlag, Berlin, 1994.
4.- Arthur Porges, A Set of Eight Numbers, American Mathematical Monthly 52, p. 379-382, 1945.
5.- Justin Gilmer, On the density of happy numbers, Integers, vol, 13, n. 2, pp. 689-713, 2013.
6.- Esam El-Sedy y Samir Siksek, On happy numbers, Rocky Mountain Journal of Mathematics, vol. 30, n.2, pp. 565-570, 2000.
7.- R. Ibáñez, Números elegantes, en el libro Desafíos Matemáticos, propuestos por la Real Sociedad Matemática Española (coordinado por A. Quirós), SM-RSME, 2012.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Números felices para siempre se ha escrito en Cuaderno de Cultura Científica.
Manhattan proiektuko giza softwarea
Gaur egun, asko txunditzen du konturatzeak duela gutxiko historiako zientziaren eta teknologiaren arloko mugarri garrantzitsuenetako batzuk arazo batean lan egiteko eskuragarri zeuden giza garunen kopuruak mugatutako gaitasun konputazional baten bidez lortu zirela. Baina, kontua da ikerketa zentro batzuetan garun horiek askoz hobeto antolatuta zeudela eskura izan zezaketen edozein makina baino. Horixe izan zen, hain zuzen ere, 1943 inguruan, Manhattan proiektuan zehar Los Alamos konputazio instalazioen kasua.
Kontu horretan garrantzitsuena izan zen XX. mendeko 40ko hamarkadan, alde batera utzita lehen bonba atomikoaren sorrera finantzatzea eragin zuten inguruabar zientifiko, politiko eta belikoak, halako tresna bat garatzeko beharrezkoak ziren kalkuluak ez zirela hutsalak, ezta gutxiagorik ere. Batez ere mekanismoaren diseinuari eta plutonio bonbaren ―Trinity testean probatu zen eredua― inplosio hidrodinamikari buruzko kalkuluak; izan ere, besteak beste, gailuak zenbat energia askatuko zuen zehaztu behar zen. Ezin zenez frogarik egin, batez ere hasieran, deribatu partzial ez-linealetan ekuazio diferentzialak ebatzi beharreko eredu matematikoekin egin behar zen lan, eta, horiekin trebatuta ez dagoen edozeinentzat, nahiko lan zaila zen ordenagailurik izan ezean.
 1. irudia: Los Alamos laborategian, giza ordenagailuek (normalean emakumezkoak) eskuz egiten zituzten bonba atomikoa garatzeko beharrezkoak ziren kalkuluak, argazkiko Marchant kalkulagailu elektromekanikoaren antzekoen bidez. (Iturria: Cuaderno de Cultura Científica)
1. irudia: Los Alamos laborategian, giza ordenagailuek (normalean emakumezkoak) eskuz egiten zituzten bonba atomikoa garatzeko beharrezkoak ziren kalkuluak, argazkiko Marchant kalkulagailu elektromekanikoaren antzekoen bidez. (Iturria: Cuaderno de Cultura Científica)Une hartan, batez ere Bigarren Mundu Gerraren aurretik, nagusiki hiru kalkulagailu mota zeuden: idazmahaiko kalkulagailu elektromekanikoak, txartel zulatuen tabulagailuak eta analizatzaile diferentzialak (Vannevar Bush-ek MITen eraiki zuenaren antzeko ordenagailu analogikoa). Manhattan proiektuan batez ere lehenengo biak erabili ziren. Analizatzaile diferentziala gerran artilleriako taulak egiteko erabili zen.
1943. urtearen hasieran, Stanley P. Frankel eta Edred Nelson Los Alamosera iritsi ziren matematika lan teoriko guztia antolatzeko. Berkeleyko Lawrence laborategian esperientzia jasoa zuten uranioaren isotopoak bereiztearekin lotutako kalkuluak egiten eta kate erreakzioari eusteko beharrezkoa zen masa kritikoa zenbatesten. Mexiko Berrian, hasiera batean, uraniozko bonbarekin lotutako kalkulu balistikoez arduratuko ziren; aurrerago, berriz, 1944 aldera eta John von Neumannek ikuspegia aldatu behar zela behin eta berriro errepikatu ondoren, uraniozko bonbarekin eta haren inplosio mekanismoarekin lotutakoekin arduratu ziren.
Horretarako, idazmahaiko hainbat Marchant eta Friends kalkulagailu eta Monroe batzuk eskatu zituzten, eta prozesuaz arduratuko ziren “giza ordenagailuen” artean (emakumezkoak gehienetan) banatu zituzten. Aurrerago, tabulagailuak erabiltzeko aukera aztertzen hasi ziren eta 1944ko martxoan, besteak beste, IBM 601en errefortzua iritsi zen.
 2. irudia: IBM 601 tabulagailu bat zen, eta bertan txartel zulatuen bidez sartzen ziren bi zenbaki biderkatzeko gai zen, ez zatikatzekoa, ordea. 1944. urtearen amaieran, Los Alamos laborategian halako lau instalatu ziren, bai eta beste aplikazio batzuk zituzten IBM ereduko beste batzuk ere. Sistemak, guztira, zortzi makina zituen. (Iturria: Cuaderno de Cultura Científica)
2. irudia: IBM 601 tabulagailu bat zen, eta bertan txartel zulatuen bidez sartzen ziren bi zenbaki biderkatzeko gai zen, ez zatikatzekoa, ordea. 1944. urtearen amaieran, Los Alamos laborategian halako lau instalatu ziren, bai eta beste aplikazio batzuk zituzten IBM ereduko beste batzuk ere. Sistemak, guztira, zortzi makina zituen. (Iturria: Cuaderno de Cultura Científica)Hemen eten bat egin behar da. Aski ezaguna da, konputazioaren historiaren hasieran, emakumeak arduratzen zirela lehenengo ordenagailuak programatzeko lanez. Manhattan proiektuari dagokionez, batez ere, ehuneko handi batean, han lan egiten zuten zientzialarien emazteek programatzen zituzten. Horiek horrela, izen hauek topa ditzakegu: Mary Frankel, kalkulu talde bat gainbegiratu zuena, edo Mici Teller, zeinen ezkon abizenak ez liratekeen ezezagunak izan beharko. Aipagarriak dira, halaber, gerra amaitu ondoren, Klara Dan von Neumman-ek ENIACekin egindako lanak. Zenbatesten da hirurehun emakume baino gehiago aritu zirela Manhattan proiektuko lanpostu teknikoetan. Los Alamosen kasuan, gainera, familia osoak jaso zituen miniaturazko hiri bat zen leku hura, eta emakume horien lana sustatu zen aktiboki. Horietako asko etxekoandreak ziren eta hainbat laguntza jaso zituzten, normalean etxearen eta seme-alaben zaintzarekin lotutakoak.
 3. irudia: Mary Frankel (X214) eta Mici Teller (X169) Los Alamosen lan egiten zuten emakume kalkulatzaile ugarietako bi izan ziren. (Iturria: Cuaderno de Cultura Científica)
3. irudia: Mary Frankel (X214) eta Mici Teller (X169) Los Alamosen lan egiten zuten emakume kalkulatzaile ugarietako bi izan ziren. (Iturria: Cuaderno de Cultura Científica)Hala ere, Frankel-en eta Nelson-en konputazio taldearen alderdirik deigarriena ez ziren ez emakume kalkulatzaileak, ez erabiltzen zituzten makinak, antolaketa baizik. Kalkuluak egiteko tabulagailuak erabiltzea balioesten hasi zirenean, kalkuluak azkarrago egiteko sistema bat pentsatu zuten. Ekuazio baten ebazpen prozesua urrats sinpleetan banatzen zuen “programa” edo fluxu diagrama moduko sistema bat sortu zuten. Ezin izan zuten zuzenean probatu IBMak izan arte; hortaz, simulazio bat egin zuten emakume kalkulatzaileen taldea erabilita. Prozesua nahiko intuitiboa zen. Marchant-a mahai gainean zutela, bakoitzak urratsetako bat egiten zuen: batek biderketak egiten zituen, beste batek zatiketak, beste batek erro karratuak… beti urrats bera, eta emaitzak txartel batean pasatzen zituzten hurrengo mahaira, beste lankide batek kalkuluaren bere partea egin zezan. Sistemak izugarri ondo funtzionatu zuen, pertsona bakar batek ekuazio osoa, urratsez urrats, ebatzi izan balu baino askoz hobeto eta efizienteago.
Guztiaren erdian, hogeita sei urteko fisikari gazte bat zegoen, zeina etorkizunean ezagunagoa izan baitzen bongoak jotzeagatik Nobel saria irabazteagatik baino: Richard Feynman. Marchant kalkulagailuak matxuratzen zirenean, haiek konpontzeaz arduratzen ziren fisikarietako bat zen (izan ere, ez zegoen fabrikatzaileari bidali eta hark noiz itzuliko zain egoteko denborarik) eta oso ondo ezagutzen zuen guztiaren funtzionamendua. Lehenengo IBMak iritsi zirenean, 1944ko apirilean, Frankeli eta Nelsoni muntatzen lagundu zien ―Manhattan proiektuarekin zerikusia zuen guztiaren inguruko muturreko sekretismoa zela eta, hasiera batean, IBMko langile bakar batek ere ez zuen lortu Los Alamosera joateko baimena―.
Dena prest egon zenean, jakina, Feynmanek bere ideia bitxietako bat izan zuen: emakume kalkulatzaileak eta tabulagailuak lan bera egiten jartzea eta elkarren artean lehian aritzea. Nork emango zuen denbora gutxien arazo bat ebazteko? Gaur egun, esango genuke ordenagailu batek behar zuela denbora gutxien, baina, garai hartan, emakumeek irabazi zuten. Desabantaila bat baino ez zuten izan: kalkulu prozesu bera erabilita, emakumeak nekatu egin ziren, IBMak ez bezala, jakina.
Giza “programa” horrek, dagoeneko operatibo zeuden tabulagailuekin batera, izugarri areagotu zuen errendimendua, eta, gainera, ikusi zuten horrela ez zutela zertan aldi bakoitzean kalkulu bakarra egin, baizik eta aldi berean bi edo hiru eragiketa egin zitzaketela. Koloretako txartelak erabiliz gero, lanpostu bakoitzean beti urrats bera egiten zen, baina hainbat eginkizunetarako, bakoitza kolore batekin identifikatuta.
Bitxia da, halaber, hain oinarrizkoak ziren makina haiek burua galarazi ziotela Stanley Frankeli; izan ere, erosi ziren xederako ez bestetarako erabiltzen hasi zen ―merkatuko azken zehaztapenak dituen PC bat erosten duten geekak bezala―, zer egiteko gai ziren aztertzeko. Feynmanek ordezkatu zuen lanpostuan eta oso antolatzaile ona zela erakutsi zuen. Tabulagailuekin lan egiten zuen taldeak ―institututik ateratako gazteek osatua, zeinak teknikaren eta ingeniaritzaren arloko ezagutzaren bat zuten― ez zekien zertarako ziren kalkulu horiek guztiak. Feynmanek horren berri emateko baimena lortu zuen, eta, berriro ere, produktibitateak nabarmen egin zuen gora: gazte haiek prozesuak hobetzeko eta arintzeko moduak aztertzen hasi ziren gau eta egun. Tabulagailuen eta giza softwarearen aurretik bederatzi hilabetetan hiru arazo ebazten baziren, hiru hilabetetan bederatzi arazo ebaztera iritsi ziren.
Sinestezina da arkatza, papera eta talentua bakarrik erabilita zientzialariek etekin hori guztia ateratzea oinarrizko makina haiei, eta atomoaren sekreturik korapilatsuenetako bat argitzeko gai izatea.
 4. irudia: Esposizio ona duen Trinity eztandaren koloretako argazki bakarra, Jack Aebyk hartua. (Iturria: Wikimedia Commons)Erreferentzia bibliografikoak:
4. irudia: Esposizio ona duen Trinity eztandaren koloretako argazki bakarra, Jack Aebyk hartua. (Iturria: Wikimedia Commons)Erreferentzia bibliografikoak:
- Archer, B. J. (2021). The Los Alamos computing facility during the Manhattan Project. Nuclear technology, 204, pp. S190-S203. doi: 10.1080/00295450.2021.1940060
- Feynman, R. P. (2018 [1987]). ¿Está usted de broma, Sr. Feynman? Aventuras de un curioso personaje. Alianza Editorial.
- Howes, R. y Herzenberg, C. L. (1999). Their day in the sun. Women of the Manhattan Project labor and social change. Temple University Press.
Gisela Baños zientzia, teknologia eta zientzia fikzioaren dibulgatzailea da.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko ekainaren 27an: El software humano del Proyecto Manhattan.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Manhattan proiektuko giza softwarea appeared first on Zientzia Kaiera.
La temperatura en el límite entre el núcleo interno sólido y el núcleo externo líquido de la Tierra
En ocasiones, experimentos hechos en un laboratorio, combinados con un poco de lógica nos permiten tener una idea bastante aproximada de lo que ocurre en lugares inaccesibles para el ser humano y su tecnología. Como el interior del núcleo de la Tierra. Al medir la temperatura de fusión del hierro sometido a una alta presión transitoria, un equipo de investigación ha establecido un valor máximo a la temperatura en el límite entre los núcleos interno y externo.
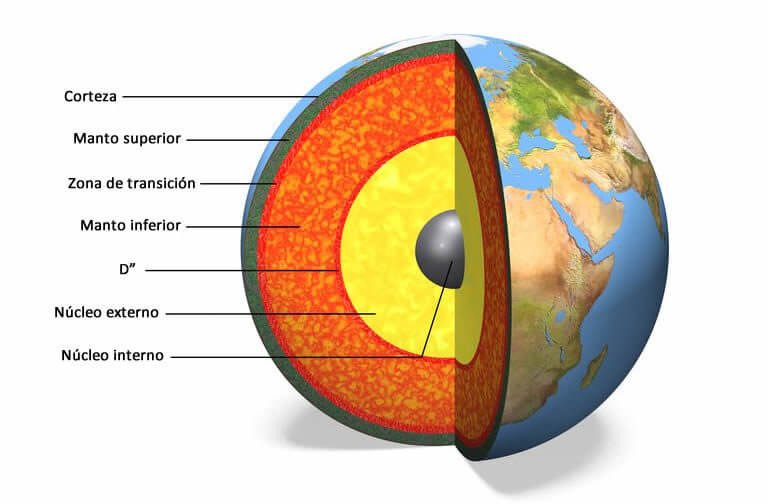 Fuente: capasdelatierra.org
Fuente: capasdelatierra.orgPara comprender el funcionamiento de la dinamo de la Tierra y otros procesos internos del planeta es necesario saber cómo se comporta el hierro (el componente principal del núcleo de la Tierra) bajo altas presiones y temperaturas. Sucesivos estudios han permitido obtener partes del diagrama de fases de presión y temperatura para el hierro utilizando una combinación de teoría y experimentación, pero como las condiciones más extremas solo se pueden producir en el laboratorio de manera fugaz (si es que se pueden producir), aún quedan grandes lagunas e incertidumbres.
Ahora, Sofia Balugani, del Centro Europeo de Radiación Sincrotrón (Francia), y sus colegas han sometido una muestra de hierro puro a una presión de 270 gigapascales (GPa), cerca de los 330 GPa que se encuentran en el límite del núcleo interno de la Tierra, y han medido su temperatura a medida que se fundía. Dado que el hierro del núcleo está mezclado con níquel y otros elementos que reducen su punto de fusión, el resultado establece un límite superior para la temperatura en el límite entre el núcleo interno sólido y el núcleo externo líquido.
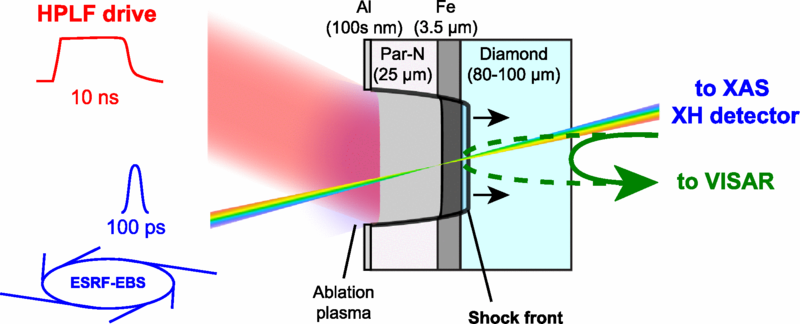 Fuente: S. Balugani et al. (2024)
Fuente: S. Balugani et al. (2024)Los investigadores suelen producir presiones estáticas de cientos de gigapascales utilizando celdas de yunque de diamante. Sin embargo, combinar estas presiones con altas temperaturas requiere un enfoque dinámico. En estudios anteriores los investigadores comprimieron las muestras aplicándoles pulsos láser breves e intensos mientras caracterizaban su estructura mediante difracción de rayos X. Balugani y sus colegas también utilizaron compresión láser, pero la combinaron con espectroscopia de absorción de rayos X, una técnica que es sensible tanto a la estructura como a la temperatura.
La muestra comenzó a fundirse sometida a 240 GPa a 5345 K. Extrapolando, los investigadores dedujeron que la temperatura en el límite del núcleo interno no debe ser mayor que 6202 K. También descartaron una transición cristalina (de empaquetamiento compacto hexagonal a cúbico centrado en el cuerpo) que se había predicho que ocurriría cerca de esa temperatura.
Referencias:
S. Balugani et al. (2024) New constraints on the melting temperature and phase stability of shocked iron up to 270 GPa probed by ultrafast x-ray absorption spectroscopy Phys. Rev. Lett. doi: 10.1103/PhysRevLett.133.254101
M. Stephens (2024) Taking the Temperature of Earth’s Core Physics 17, s139
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La temperatura en el límite entre el núcleo interno sólido y el núcleo externo líquido de la Tierra se ha escrito en Cuaderno de Cultura Científica.
Loaren erregulartasunaren garrantziaz ohartarazi dute
Lo patroi irregularra izateak bihotzeko arazo larriak izateko arriskua %26 handitu dezakeela ondorioztatu du korrelazioan oinarritutako ikerketa batek.
Urtetan zehar pilatutako zientzia ebidentziak aditzera ematen du gauzak horrela direla, eta sen arruntak ere ondo ulertzen du hori: argi dago gutxi lo egitea osasunerako oso kaltegarria izan daitekeela. Hori dela eta, loaren iraupenean eta kalitatean oinarritu dira orain arte lo ohituren eta osasunaren arteko harremanen inguruko ikerketak, baina ez dira asko izan loaren erregulartasunaren gainean egin direnak; hots, ohera joateko eta ohetik altxatzeko antzeko ordutegia erabiltzen ote den aztertzen dutenak.
Familia, lana, oporrak edo bestelako aisialdia izan daitezke ohera joateko orduan ohiko ordutegiak aldatzea ekarri dezaketenak, eta agian aldagarritasun hori guztiz kaltegabea dela eman dezake. Alabaina, gauzak oso bestelakoak izan daitezkeelako zantzuak dituzte zientzialariek. Journal of Epidemiology & Community Health aldizkarian argitaratutako ikerketa baten arabera, erregularrak ez diren lo ordutegiak izateak ondorio negatiboak izan ditzake osasun fisiko eta mentalean.
 1. irudia: Ikerketa honen arabera, gomendatutako loaldiaren luzera baino, askoz garrantzitsuagoa da ordu jakin batzuetan oheratzea eta esnatzea. (Argazkia: Greg Pappas / Unsplash)
1. irudia: Ikerketa honen arabera, gomendatutako loaldiaren luzera baino, askoz garrantzitsuagoa da ordu jakin batzuetan oheratzea eta esnatzea. (Argazkia: Greg Pappas / Unsplash)Ez da aurreneko aldia horrelako planteamendu bat mahai gainean jartzen dena, zientzialariek aspalditik dakitelako loaren aldakortasunak erritmo zirkadianoei eragiten diela. Alabaina, eragin hori norainokoa den jakitea ez da erraza. Orain hori argitzen ahalegindu dira, eta, zalantza barik, emaitzak zeharo harrigarriak dira.
Erloju biologiko baten funtzioa betetzen dute erritmo zirkadianoek, eta loaren patroiak zehazten dituzte, baina bestelako prozesutan ere ezinbestekoak dira. Loa arautzeaz gain, besteak beste, digestioan, hormonen sorreran edota gorputzaren tenperaturaren arautzean eragina ere badute.
Bada, zientzialari talde honek berretsi duenez, erritmo zirkadianoak sarritan eteteak ondorio kaltegarriak izan ditzake. Besteak beste nahasmendu metabolikoak edo gaitz kardiobaskularrak izateko arriskuak handitzen dituelakoan daude zientzialariak. Are, osasunerako epe luzerako ondorioak uste baino larriagoak izan daitezkeela sinetsita daude ikertzaileak.
Datu andana esku artean izan dituzte Ottawako Unibertsitateko (Kanada) ikertzaileek: 40 eta 79 urte arteko 72.269 pertsonarenak. Horien guztien lo patroien inguruko jarraipen datuak erabili dituzte. Aukeratutako pertsona horiek ez zeukaten aurretik bihotzeko arazo nabarmenik. Erresuma Batuko Biobankuan bildutako datuak dira horiek.
Parte hartzaile horien loaren jarraipena zazpi egunen egina zieten, eta, modu horretan, pertsona bakoitzaren Loaren Erregulartasun Indizea kalkulatzeko gai izan dira. Adierazle honetan 87 puntu baino gehiago dituztenek lo patroi erregularra dutela ebatzi dute; 72 baino gutxiago dituztenak, berriz, irregulartasunaren barruan sailkatu dituzte. Tartean direnak, erdibideko eremu batean sartu dituzte ikertzaileek.
 2. irudia: Erritmo zirkadianoek erloju biologiko baten funtzioa betetzen dute, eta, besteak beste, loaren patroiak zehazten dituzte. (Argazkia: Catherine Hughes / Unsplash)
2. irudia: Erritmo zirkadianoek erloju biologiko baten funtzioa betetzen dute, eta, besteak beste, loaren patroiak zehazten dituzte. (Argazkia: Catherine Hughes / Unsplash)Loari buruzko datu horiek heriotza erregistroekin alderatu dituzte, bai eta loaren neurketa egin ondorengo zortzi urteetan zehar jasotako ospitaleratze datuekin ere. Horiek arakatzean arreta berezia jarri diete bihotzari lotutako arazoei. Atera duten ondorio esanguratsuenetakoa izan da lo ordutegi iraunkorra jarraitu ez dutenek osasun kalteak izateko arrisku gehiago izan dituztela. Kontrara, lo egiteko ohitura egonkorragoak izan dituztenek osasun egoera hobea dutela ikusi dute, bai alde fisikoan zein mentalean. Besteak beste, aldaketarik gabeko ordutegiak jarraitu ez dituztenek hantura gehiago izan dituzte, eta hau lotuta dago hainbat gaitz kroniko izateko arriskuarekin: diabetesa, hipertentsioa edota bihotzeko gaitzak, esaterako.
Parametro fisikoetan ez ezik, loaren ordutegien alterazioak buruko gaitzei ere eragiten die, antsietatearekin eta depresioarekin lotu dituztelarik. Erritmo zirkadianoek metabolismoa eta immunitatea arautzen dituztenez, azken horietan ere asaldurak gertatzen direlakoan daude ikertzaileak. Atzean dagoen arrazoia da erritmo zirkadianoak egunaren iraupenarekin batera joan ohi diren prozesu fisiologikoak direla, eta, beraz, egunaren argira eta gauaren iluntasunera egokitu ohi direla. Erritmo hauetan oreka galtzen denean, estresa sortzen da, eta glukosaren arautzea ere eten egiten da.
Hormonei dagokienez, serotonina eta dopaminaren produkzioan eragiten dute erritmo zirkadianoek, eta zientzialariek uste dute horrek antsietatea eta depresioa sortzen dituela. Neurotransmisore hauek aldartean zuzeneko eragina daukatenez, arazoak osasun mentalean zuzeneko eragina duelakoan daude zientzialariak, horiek gainera iraunkor bilakatu daitezkeelako.
Halako ikerketa baten aurrean burura ohi datorren galdera logikoa da ea noraino kontuan hartu izan diren bestelako faktoreek zeresanik ote duten harreman horretan. Adibidez, lo egiteko ohitura duen pertsona batek seguru aski dieta orekatuagoa izan dezake, eta estres gutxiago. Zentzu horretan, ikerketa nahiko irmoa da, beste hainbat aldagairen eragin posiblea ere kontuan hartu dutelako. Besteak beste, adina, jardun fisikoa, pantailen aurreko denbora, dieta, txandakako lanaldia, botiken erabilera, osasun arazoak edota kafearen, tabakoaren edo alkoholaren kontsumoa.
Ikertutakoen artean, oro har, modu erregularrean lo egiten duten gehienek gomendatutako loaldien luzerak mantendu dituzte (% 61). Modu irregularrean egiten zutenen artean, berriz, ehunekoa 48 % izan da. Gauzak hala izanik ere, azken hauen artean, berdin nahikoa lo egin ala ez, istripu zerebrobaskularra gutxiegitasun kardiakoa edota bihotzekoa izateko arriskua bere horretan mantendu da, % 26 horretan. Erdibidean egon direnen artean, hau da, loaldi partez irregularra izan dutenen kasuan, arriskua %8 handitzen da. Beraz, egileek nabarmendu dute jaso dituzten emaitzek iradokitzen dutela loaldiaren erregulartasuna loaldiaren iraupen minimoa baino garrantzitsuagoa izan daitekeela.
Logikoa denez, argi dago zein izan daitekeen arrisku hauek guztiak arintzeko modua: lo ohitura iraunkorra mantentzea, eta ohera joateko eta altxatzeko ordutegi zehatzak izatea, baita asteburuetan ere. Kontu honetan Jean-Philippe Chaput egile nagusia nahiko irmoa da, eta ordu erdiko zehaztasun batekin lokartzea eta esnatzea gomendatu du. “Zero aldakortasunik gero eta gertuago egon, orduan eta hobeto” nabarmendu du, baita “asteburuetan ere”. Chaputek garrantzi gehiago eman dio esnatzeko orduari, ohera joateko orduari baino.
Erreferentzia bibliografikoa:Chaput, Jean-Philippe; Biswas, Raaj Kishore; Ahmadi, Matthew; Cistulli, Peter A.; Rajaratnam, Shantha M. W.; Bian, Wenxin; St-Onge, ;arie-Pierre; Stamatakis, Emmanuel (2024). Sleep regularity and major adverse cardiovascular events: a device-based prospective study in 72 269 UK adults. J Epidemiol Community Health, Published Online First. DOI: 10.1136/jech-2024-222795
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Loaren erregulartasunaren garrantziaz ohartarazi dute appeared first on Zientzia Kaiera.
¿Cuál es la verdadera edad de la Luna?
Damos por hecho que, aparte de la Tierra, la historia geológica de la Luna es la que mejor conocemos. Al fin y al cabo, puesto que es el objeto astronómico más cercano a la Tierra ha facilitado que también sea el más visitado ya no solo por misiones robóticas, sino también por el propio ser humano. Y al mismo tiempo es también uno de los pocos de los que hemos podido traer muestras de su superficie de vuelta a nuestro planeta, algo fundamental para poder estudiarlas en los mejores laboratorios y exprimir los párrafos de su historia escritos en sus rocas.
A pesar de esta mayor facilidad para estudiar la Luna en comparación con otros cuerpos astronómicos, existe una discrepancia en los distintos cálculos de su edad, que abarcan más de 150 millones de años entre unas dataciones y otras, y que es francamente difícil de explicar. Y no, no tiene nada que ver con que las dataciones de las rocas estén mejor o peor hechas, sino de que quizás la historia geológica de nuestro satélite haya sido más turbulenta de lo que pensábamos. Y un nuevo estudio publicado en Nature por Nimmo et al. (2024) parece dar una explicación a esta discrepancia. Pero antes, empecemos por el nacimiento de la Luna…
 La superficie de la Luna vista desde la misión Apolo 17. En esta imagen podemos ver el fuerte contraste en color entre los “mares” lunares, de color gris oscuro, y las tierras altas, con unos tonos mucho más claros y cubiertas de cráteres. Cortesía de NASA/JSC.
La superficie de la Luna vista desde la misión Apolo 17. En esta imagen podemos ver el fuerte contraste en color entre los “mares” lunares, de color gris oscuro, y las tierras altas, con unos tonos mucho más claros y cubiertas de cráteres. Cortesía de NASA/JSC.La teoría más aceptada sobre el origen de nuestro satélite es la “teoría del gran impacto”, en la cual, durante la infancia de nuestro sistema solar, un objeto del tamaño aproximado al de Marte -y que conocemos como Tea- chocó con nuestro planeta. Este impacto lanzó al espacio una gran cantidad de material a la órbita de la Tierra y, parte de esa materia, iría uniéndose hasta formar nuestra Luna.
Esta teoría explica algunas características de nuestra Luna, como una menor densidad de la Luna -en comparación con la Tierra- y la similitud entre las proporciones isotópicas entre las rocas lunares y terrestres, lo que indicaría un origen “común” para la mayor parte de los materiales. Pero, ¿Cuándo ocurrió realmente este impacto? ¿Fue muy pronto o quizás un poco más tarde?
Para conocer la edad de la Luna, los científicos se basan en la datación radiométrica de las muestras lunares y de los meteoritos procedentes de esta. Esta técnica se basa en medir la desintegración de los elementos radioactivos que forman parte de los minerales de las rocas y que, de algún modo, son un reloj natural. Si nada altera -a nivel químico- esos minerales, podemos confiar en que nos den una fecha fiable.
¿Y qué rocas podrían representar la edad de formación de la Luna? Suponemos que nuestro satélite, al igual que nuestro planeta, después de su formación estaba, si no por completo, mayormente en un estado fundido, en lo que conocemos como la etapa del océano de magma, que podría ser una fase común entre los planetas rocosos de nuestro sistema solar.
Conforme este océano fue enfriándose y formando la primera corteza lunar, aparecieron una serie de rocas de tonos muy claros y que en geología conocemos como anortositas. La edad de estas rocas, junto con la de otras similares, indicaban una formación tardía de la Luna, situando su nacimiento en hace aproximadamente 4350 millones de años, casi 200 millones de años después de la propia formación de nuestro sistema solar.
 Una anortosita traída a la Tierra por la misión Apolo 15. A esta roca se la conoce la roca del “Génesis”, porque se pensaba que formaba parte de la corteza original de la Luna, pero resultó ser un poco más joven, de tan solo unos 4100 millones de años. Imagen cortesía de NASA/JSC.
Una anortosita traída a la Tierra por la misión Apolo 15. A esta roca se la conoce la roca del “Génesis”, porque se pensaba que formaba parte de la corteza original de la Luna, pero resultó ser un poco más joven, de tan solo unos 4100 millones de años. Imagen cortesía de NASA/JSC.Bien, si la edad de esas rocas es la que es, asunto zanjado. Esa sería la edad de nuestro satélite. Al fin y al cabo, la datación radiométrica es una técnica que conocemos bastante bien y, al mismo tiempo, bastante precisa. Pero no vayamos tan rápido porque hay un pero.
Hay un mineral muy resistente -y a veces diminuto- que aparece dentro de algunas rocas lunares y que nos cuenta una historia un tanto diferente: los circones. Estos minerales, gracias a su resistencia a la meteorización y a la temperatura, pueden guardar el registro de su formación, incluso aunque sufran grandes eventos geológicos, hasta cierto límite. Y es precisamente en estos donde aparece la discordia: algunos de los circones tienen una fecha de unos 4510 millones de años… y para que estén ahí la Luna ya tenía que haberse formado o, al menos, parte de esta haberse enfriado lo suficiente para que los minerales se hubiesen podido formar a partir del magma.
¿Cómo es posible resolver esta discrepancia? Porque está claro que la Luna no puede haber cambiado su partida de nacimiento. Aquí es donde los autores del artículo explican cómo es posible que se hayan calculado dos edades diferentes, pero solo una apunte al verdadero nacimiento de nuestro satélite.
Viajemos de nuevo al pasado, hasta hace unos 4350 millones de años aproximadamente. En este momento, nuestra Luna estaba experimentando un fenómeno que conocemos “calentamiento de mareas”, un proceso fruto de la interacción gravitatoria entre dos o más cuerpos.
Para comprender mejor como es este fenómeno, pensemos en la órbita de la Luna: Aunque nos parezca un círculo perfecto, no es así, sino que es ligeramente elíptica, de tal manera que, al recorrer la órbita, la distancia entre la Tierra y la Luna va cambiando y, por lo tanto, la atracción gravitatoria que ejerce nuestro planeta sobre ella.
Básicamente, es como si estrujásemos y dejásemos de estrujar una pelota antiestrés. Solo que con este ciclo repetido en el que la Luna se ve obligada a cambiar de forma, se generan unas enormes fricciones en las rocas de su interior que acaban transformándose en calor, algo similar a lo que ocurre en Ío, el satélite de Júpiter.
En este momento, el gran calentamiento de mareas que estaba sufriendo la Luna, habría sido suficiente para crear un importante porcentaje de volumen de roca fundido en su interior, que continuamente ascendía hasta la corteza, calentando las rocas ya frías de la corteza y reiniciando el reloj -en este caso los relojes radioactivos que nos permiten datar las rocas- de muchas de las rocas de la Luna, haciendo pasar las rocas por más jóvenes.
Esto explicaría por qué encontramos tantas rocas con una edad de alrededor de 4350 millones de años, y que los científicos de este estudio interpretan no como la edad de formación de la Luna, sino el momento en el que la Luna sufrió este periodo de gran calentamiento por mareas que alteró los sistemas geoquímicos de algunos minerales, como el de los circones.
 El astronauta Harrison Schmitt recoge muestras de lo que parece un bloque de roca lanzado por el impacto de un cuerpo contra la superficie de la Luna durante la misión Apolo 17. Imagen cortesía de NASA/JSC.
El astronauta Harrison Schmitt recoge muestras de lo que parece un bloque de roca lanzado por el impacto de un cuerpo contra la superficie de la Luna durante la misión Apolo 17. Imagen cortesía de NASA/JSC.Esto tiene una consecuencia y es que, si están en lo cierto, la Luna se formó mucho antes y su edad podría coincidir con la de los circones que tienen una edad de alrededor de 4510 millones de años, colocando su “nacimiento” dentro del calendario de nuestro sistema solar en las primeras decenas de millones de años tras la formación de este. Los circones de esta edad serían los minerales relictos de esas primeras rocas que no habrían sufrido un reinicio de su edad como consecuencia del calentamiento.
Aun así, queda mucho trabajo por hacer. Trabajo que probablemente necesite de nuevas muestras lunares, nuevos modelos matemáticos y estudios geológicos que puedan llevar a los científicos a encontrar rocas que hayan sobrevivido a esa vigorosa etapa de la Luna y que nos permita, en definitiva, dar una edad certera para su origen.
Referencias:
Nimmo, Francis, et al. (2024) Tidally Driven Remelting around 4.35 Billion Years Ago Indicates the Moon Is Old Nature doi: 10.1038/s41586-024-08231-0
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Cuál es la verdadera edad de la Luna? se ha escrito en Cuaderno de Cultura Científica.
Higgs-en eremuak nola ematen dien masa (benetan) oinarrizko partikulei
Matt Strassler fisikariak Waves in an Imposible Sea (Uhinak ezinezko itsaso batean) liburu berritik egokitutako artikulu honetan azaltzen duenez, masak unibertsoan duen jatorriak zerikusi handia du musikarekin.
2012an Higgsen bosoia Hadroien Talkagailu Handian aurkitu izanak berretsi egin zuen partikulen fisikariok aspalditik susmatzen genuena: kosmosa sartzen den eta oinarrizko partikulen masak sortzen dituen eremu bat dagoela. Zoritxarrez, fisikarientzat zaila izan da gainerakoei azaltzea Higgsen eremu deitzen den horrek nola betetzen duen bere zeregin handia.
 1. irudia: masak unibertsoan duen jatorriak zerikusi handia du musikarekin. (Ilustrazioa: Michele Sclafani – Copyright lizentziapean. Iturria: Quanta Magazine)
1. irudia: masak unibertsoan duen jatorriak zerikusi handia du musikarekin. (Ilustrazioa: Michele Sclafani – Copyright lizentziapean. Iturria: Quanta Magazine)Ikuspegi komun bat istorio fantastiko bat kontatzea izan da. Hona hemen bertsio bat:
Bada substantzia bat, zopa baten modukoa, unibertsoa betetzen duena; hori Higgsen eremua da. Partikulak mugitzen diren heinean, zopak balaztatu egiten ditu, eta horrela hartzen dute masa partikulek.
Beste bertsio batzuk Higgsen eremua melaza bat, sastraka bat, jende asko edo elur hedadura baten antzeko zerbaiten moduko gisa deskribatzen dute.
Hala ere, istorio horiek guztiak ez datoz bat fisikariok lehen urteko unibertsitate ikastaroen lehen asteetan irakasten dugunarekin. Higgsen eremuak egindako erresistentziaren eraginez masa sortzen duela iradokitzean, Newtonen mugimenduaren lehen eta bigarren legeak hausten dira. Beste hondamendi batzuen artean, erresistentzia horrek aspaldi eragingo zuen Lurra Eguzkirantz kiribil batean erortzea. Gainera, Higgsen eremua benetan substantzia bat balitz, gure mugimendu absolutua neurtzeko konparazio puntu bat izango litzateke, Galileoren eta Einsteinen erlatibitatearen printzipioak urratuz.
Egia esan, Higgsen eremuak ez du zerikusirik mugimenduarekin, ezta desazelerazioarekin ere; bere historia guztia bibrazioaren ingurukoa da.
Eremuen teoria kuantikoak, partikulen fisika modernoaren esparru ahaltsuak, unibertsoa eremuz beteta dagoela dio. Horren adibide dira eremu elektromagnetikoa, grabitazio eremua eta Higgsen eremua bera. Eremu bakoitzerako, dagokion partikula mota bat dago, eremu horretako uhin txiki gisa hobeto ulertzen dena. Eremu elektromagnetikoaren uhinak argi uhinak dira, eta haien uhin leunenak argi partikulak dira, eta horiei fotoi deitzen diegu. Era berean, elektroiak uhinak dira elektroien eremuan, eta Higgsen bosoia uhin txiki bat da Higgsen eremuan.
 2. irudia Waves in an Impossible Sea. How Everyday Life Emerges from the Cosmic Ocean liburuaren azala. (Iturria: Quanta Magazine)
2. irudia Waves in an Impossible Sea. How Everyday Life Emerges from the Cosmic Ocean liburuaren azala. (Iturria: Quanta Magazine)Elektroi egonkor bat, gitarra soka baten bibrazioa bezala, uhin geldikor bat da, nahi duen maiztasunarekin bibratzen duena, erresonantzia maiztasun gisa ezagutzen dena. Erresonantzia bibrazio hori ohikoa eta familiarra da. Pultsatutako gitarra soka batek erresonantzia maiztasuna etengabe jotzen duenez, beti tonu bera sortzen du. Era berean, pendulu kulunkatzaile baten maiztasun finkoak bihurtzen du erloju bat eraginkor. Printzipio beraren arabera, elektroi egonkor bakoitzak eremu elektronikoaren erresonantzia maiztasunarekin bibratzen du.
Unibertsoko eremu gehienek erresonantzia maiztasunak dituzte. Zentzu batean, kosmosak musika tresna baten antza du; biek dituzte maiztasun bereizgarriak, eta horietan errazago bibratzen dute.
Niretzat, pertsonalki, errealitatearen oinarria erresonantzia izateak atsegina eta harridura sortzen dit. Musikari eta konpositore afizionatua naizen aldetik, aspalditik ezagutzen dut pianoen, klarineteen eta gitarren barne funtzionamendua. Baina erabat harrituta geratu nintzen, graduondoko ikaslea nintzenean, unibertsoaren egiturek, baita neure gorputzaren barruan ere, antzeko printzipioen arabera funtzionatzen dutela ezagutzean.
Hala ere, gure kosmosaren musikaltasun sekretu hori ezinezkoa litzateke Higgsen eremuagatik ez balitz.
Eremuen teoria kuantikoan, Einsteinen fisika kuantikoaren eta erlatibitatearen konbinazio batek erresonantzia maiztasun baten eta oinarrizko partikula baten masaren arteko erlazio erabakigarri batera garamatza: partikula geldikor batek zenbat eta azkarrago bibratu, orduan eta handiagoa da bere masa. Erresonantzia maiztasunik ez duten eremuak masarik ez duten partikulei dagozkie; partikula horiek, eremu elektromagnetikoko fotoiak barne, ezin dute inoiz egonkorrak izan.
Higgsen eremuari buruzko fantasiazko ipuinek masa oinarrizko partikulen desazeleraziotik sortzen dela iradokitzen badute ere, melazaren antzeko substantzia batengatik, egia esan, Higgsen eremu indartsuago batek oinarrizko partikulak maiztasun altuagoetan bibrarazten ditu, eta horrek masa handitzen du. Beraz, Higgsen eremua errefortzuko eragile kosmiko moduko bat dela esan daiteke, beste eremu batzuetako erresonantzia maiztasunak handitzea helburu duena.
Nola alda dezake eremu batek bestearen maiztasuna? Pendulu xumeak adibide erraz bat eskaintzen digu.
Demagun pilota bat soka baten muturrean jartzen dugula espazio sakonean, non grabitazio eremua ia nulua den. Pilotak norabide finkorik gabe flotatuko du. Pixka bat bultzatzen badugu, bere posizioa poliki-poliki alda daiteke, baina ez du bibraziorik izango.
Hala ere, pendulu inprobisatua zero ez den grabitazio eremu batean jartzen bada, dena aldatzen da. Bola zuzen zintzilikatzen da beherantz, eta mugitzen bada, kulunkatu egiten da.
 Iluztrazioa: Mark Belan Quanta Magazine-rako Copyright lizentziapean.
Iluztrazioa: Mark Belan Quanta Magazine-rako Copyright lizentziapean.Pilota geldirik dagoenean, orekan dagoela esaten da: egonkorra, orekatua eta mugitzeko arrazoirik gabe. Pilota eskuinerantz mugitzen bada, grabitateak ezkerrerantz kulunkatzea eragingo du, eta alderantziz. Pilotaren posizioak oreka puntura itzultzeko duen joerak, leheneratze efektu gisa ezagutzen denak, kulunkatzea eragingo du.
Kasu horretan, grabitazio eremuak errefortzu eragile gisa jokatzen du: pendulua zurrunago bihurtzen du, eta horrek erresonantzia maiztasun bat ematen dio, zero ez dena. Grabitazio eremua zenbat eta indartsuagoa izan, orduan eta indartsuagoa izango da berreskuratze efektua, eta penduluaren erresonantzia maiztasuna handiagoa izango da.
Era berean, Higgsen eremuak leheneratze efektua sortzen du oinarrizko beste eremu batzuetan, eta horrek duten bibratzeko modua aldatzen du. Nahiz eta edozein eremuk izan ditzakeen mugitzen diren uhinak, urmael bat zeharkatzen dutenak bezalakoak, leheneratze efektu batek ahalbidetzen du eremu batek uhin geldikorrak izatea, gitarra soka batean agertzen diren uhin geldikorren antzekoak. Lehen aipatu dudan bezala, uhin geldikor horiek geldirik dauden oinarrizko partikulak besterik ez dira, bakoitza bere eremuan kulunkatuz.
Ideia hori Peter Higgs (Higgen eremuaren homonimoa) fisikari britainiarra zenak eta haren lehiakideek 1960ko hamarkadan adierazi zutenaren muinean dago: eremu batek beste eremu batzuk indartu ditzake, eta, horrela, uhinek beren lekuan erresonantzia maiztasunarekin bibratzen dute; eta, horrek, beren partikulei masa ematen die. Higgsen bosoiaren ikerketa esperimentalek, Hadroien Talkagailu Handian, baieztatzen dute hori dela hain zuzen ere Higgsen eremuak egiten duena. Partikulen fisikaren eredu estandarraren matematika erabiliz (ezagutzen diren oinarrizko partikula guztiak eta unibertsoko eremuen arteko elkarrekintzak deskribatzen dituen eremuen teoria kuantikoa), zientzialariek Higgsen bosoiaren portaerari buruzko iragarpenak egiten dituzte, eta esperimentuekin guztiz bat datoz. Ez dago zalantzarik: Higgsen eremuak leheneratze efektua sortzen du beste eremu askotan.
Beraz, Higgsen eremua sakonago ulertuta, beste istorio bat iradokiko dizuet:
Bazen behin existitu zen unibertso bat. Bero kiskalgarria, oinarrizko partikulaz gainezka. Bere eremuen artean Higgsen eremua zegoen, hasiera batean itzalita zegoena. Baina unibertsoa hedatu eta hoztu ahala, Higgsen eremua bat-batean aktibatu zen, zero ez zen indar bat garatuz. Hori gertatu zenean, eremu asko zurrun bihurtu ziren eta, ondorioz, haien partikulek erresonantzia maiztasunak eta masa hartu zuten. Horrela bihurtu zen unibertsoa, Higgsen eremuaren eraginaren bidez, gaur egun den musika tresna kuantikoa.
Jatorrizko artikulua:Matt Strassler (2024). How the Higgs Field (Actually) Gives Mass to Elementary Particles, Quanta Magazine, 2024ko irailaren 3a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post Higgs-en eremuak nola ematen dien masa (benetan) oinarrizko partikulei appeared first on Zientzia Kaiera.
Naturaleza humana con números complejos
La Humanidad ha estudiado su propia naturaleza desde tiempo inmemorial. La Naturaleza Humana es uno de los saberes más complejos y fascinantes para cualquier persona dedicada al pensamiento, sea desde las Humanidades, las Artes, las Ciencias Sociales o las Ciencias Naturales. Los porqués de nuestras formas de pensar, sentir y actuar se han intentado explicar desde nuestra codificación genética, pero resulta evidente que la expresión de nuestros genes depende tanto o más de nuestra interacción con la sociedad en la que vivimos, el ejemplo familiar que observamos al crecer, o la educación que recibimos, en el sentido amplio de la palabra.
A los científicos nos gusta medir los fenómenos naturales. De momento, no parece posible medir la naturaleza humana, pero podemos intentar aportar alguna pequeña idea a este campo.
 Foto: Jake Nackos / UnsplashLa ecuación de onda
Foto: Jake Nackos / UnsplashLa ecuación de onda
Personas dedicadas a la matemática, la física y otras ciencias pudieron modelar matemáticamente el fenómeno de las ondas a lo largo de la historia de la ciencia. Resulta que explicar las ondas mecánicas que se observan lanzando una piedra a un estanque o tocando un instrumento musical, permitió en el siglo XVIII establecer una ecuación diferencial en derivadas parciales que describía muy bien las ondas medidas. A mediados del siglo XIX, las ecuaciones del electromagnetismo de J.C. Maxwell incluyeron la predicción de la existencia de ondas electromagnéticas, sorprendentes entidades que nadie había medido aún. Poco después, H. Hertz observó en su laboratorio la existencia real de dichas ondas electromagnéticas que seguían la ecuación de onda que puede deducirse de las ecuaciones de Maxwell.
En 1926, E. Schrödinger postuló su ecuación de onda, cuya solución permite describir el estado cuántico de ciertas partículas, y dos años después P. Dirac propuso la primera ecuación de onda capaz de conjugar la mecánica cuántica con la relatividad especial. Por otro lado, la relatividad general de A. Einstein predijo la existencia de ondas gravitatorias, que se lograron medir directamente en septiembre de 2015, a través del experimento internacional LIGO, quizás el más emocionante de los desarrollados en el primer cuarto del siglo XXI.
FasoresEn su época de Berlín en 1748, L. Euler publicó una de sus más importantes obras: “Introductio in analysin infinitorum”. De entre sus numerosísimas aportaciones al análisis matemático, nos centramos aquí en el capítulo VIII “De quantitatibus transcendentibus ex Circulo ortis”, en donde Euler extrae casi mágicamente “cantidades transcendentales” del Círculo. Nos referimos aquí a la exponencial compleja, quizás la fórmula más famosa y útil para todas las ciencias e ingenierías. Además, expresada en el caso particular para el ángulo llano, estamos ante la ecuación más bella de las de Euler: eiπ+1=0.
Usando la fórmula de Euler para cualquier ángulo en un círculo, podemos expresar gráficamente los números complejos a través de vectores de fase. Componiendo ambos lexemas, a esas entidades las llamamos Fasores. Todas las ecuaciones de onda se benefician de los números complejos y de la exponencial compleja de Euler, para poder caracterizar las magnitudes que definen las ondas, como la amplitud, la frecuencia y en el caso que ahora nos ocupa, la fase.
Conflicto de visionesEn su blog “Lecturas y Conjeturas” J.I. Pérez Iglesias publicó en mayo de 2024 una excelente y muy ilustrativa reseña [1] sobre las visiones humanas en conflicto que el economista Thomas Sowell describía en su interesantísimo libro [2]. Este estudio de la naturaleza humana trata de describir las diferencias ideológicas de las personas. Se trata de un problema muy complejo pero apasionante, para discutir las razones de las diferencias de lo que llamamos “progresismo” o “conservadurismo”, “izquierda” o “derecha”, “social” o “individual”. Sowell presenta unas bases muy convincentes del fondo de esta cuestión.
Aunque las explicaciones de Sowell pueden ser incompletas, y no se trata de un teorema matemático, su tratamiento científico de la naturaleza humana es brillante, y nos permite concebir una cierta posibilidad de clasificar la ideología humana e incluso podemos intentar explicar algunas de nuestras propias contradicciones.
Escala de naturaleza humanaNo sabemos aún medir la naturaleza humana, pero sí podemos establecer una posible escala de medida usando algunas de las ideas de Sowell. Si tomamos el plano complejo con el círculo de Euler y lo reorientamos, podemos hacer coherentes las indicaciones de un simple fasor con nuestro lenguaje ordinario al describir las ideologías humanas.
En la Figura ilustramos una manera de ordenar el conflicto de visiones, junto con alguna terminología más clara del psicólogo Steven Pinker, que prefiere utilizar la visión “Trágica” vs la visión “Utópica” en lugar de la denominación menos ilustrativa de Sowell (“Restringida” vs “No restringida”).
Si partimos del extremo superior de la ilustración (medida 0º), estamos en una ideología central, moderada y humanista, conscientes de que nuestra sociedad requiere cierto mercado y una imposición. Si somos partidarios de que el mercado se liberalice y nos bajen los impuestos, nos alejamos por la derecha (medida >0º). En caso contrario, si queremos que el mercado se regule más y creemos en los impuestos, nos vamos por la izquierda (medida <0º).
Claramente, a +90º tenemos visión Trágica, lo que llamamos conservadora, de derecha o de visión individual. A -90º nuestra visión es Utópica, lo que denominamos progresista, de izquierda o de visión social.
Si recorremos más allá la medida hacia la parte inferior de la ilustración y nos acercamos a los +180º o a los -180º, somos extremistas. Desaparece nuestro carácter Trágico o Utópico, y somos de la misma ideología: autoritaria, violenta, irracional y antidemocrática. La fórmula de Euler nos indica que, a todos los efectos, en un oscilador la fase +180º o -180º (+π, -π) es idéntica.
 Posible escala de visiones humanas. Nótese que la flecha indicadora de este “naturalezómetro humano” es un vector de fase (fasor)
Posible escala de visiones humanas. Nótese que la flecha indicadora de este “naturalezómetro humano” es un vector de fase (fasor)
No tenemos un instrumento para medir exactamente la naturaleza de una persona, pero aun con cierto nivel de ruido en nuestra propia medida, si somos sinceros con nosotros mismos, el nivel señal/ruido de nuestro medidor puede ser suficiente como para podernos colocar en un cierto sector del círculo.
Si simpatizamos con una tendencia ideológica, podemos criticar fuertemente el extremismo contrario, pero a veces justificamos o comprendemos el extremo propio. Esta es una contradicción humana muy común, pero recordemos que ambas visiones, si son extremas, no están en conflicto: son la misma.
Referencias
[1] Juan Ignacio Pérez Iglesias (2024) Dos visiones en conflicto de la naturaleza humana. Substack.
[2] Thomas Sowell (2007) A conflict of visions. Basic Books ISBN: 978-0465004669
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo Naturaleza humana con números complejos se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #514
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

AEBko antzinako zohikaztegietako molekula fosilak aztertuta, ikertzaile batzuek Deccan bolkanismoaren erupzioen eta Chicxulubeko kraterra sortu zuen asteroidearen talkaren bitarteko tenperaturak argitu dituzte. Deccan bolkanismoaren erupzio masiboek klima 5 ºC hoztu zuten 10.000 urtez, asteroidearen talka baino 30.000 urte lehenago. Gasek eguzki-izpiak blokeatu zituzten, baina tenperatura berehala leheneratu zen, eta erupzioek ez zuten eragin erabakigarririk izan dinosauroen desagerpenean. Asteroidearen talkak, berriz, hondamendi globala eragin zuen: hozte bizkorra, suteak, tsunamiak eta lurrikarak. Hori dela eta, ikertzaileek ondorioztatu dute dinosauroen galera asteroidearen talkak eragin zuela nagusiki. Emaitzak Science Advances aldizkarian argitaratu dituzte. Azalpenak Elhuyar aldizkarian.
Adimen artifizialaUPV/EHUko eta Pauko Unibertsitateko ikertzaileek eginiko azterlan batek erakutsi du Adimen Artifizialak (AA) % 70eko zehaztasunarekin irakasleen ebaluazioak kopiatu ditzakeela. 507 irakasle eta AA sistemek (ChatGPT, Gemini, Copilot) parte hartu zuten esperimentuan, Lehen Hezkuntzako ikasleen testuak ebaluatuz. ChatGPT izan zen gizakien ebaluazioetara gehien hurbildu zena. Ondorioek adierazi dute AAren zehaztasuna prestakuntza mailarekin lotuta dagoela, baina generoak eta maila akademikoak ez dute eraginik. AA tresna lagungarria izan daiteke irakasleentzako, ebaluazio lanak arintzeko eta beste zereginetarako denbora gehiago eskaintzeko. Datu guztiak Zientzia Kaieran.
KimikaMunduko txoko askotan su artifizialak jaurtiz ematen zaio hasiera urte berriari. Horren harira Leire Sangroniz eta Ainara Sangroniz kimikariak kolorez eta soinuz betetako suziri hauen atzean dagoen kimika azaldu dute Zientzia Kaieran. K.a. 250ean Txinan asmatu ziren, eta bolbora beltzaren aurkikuntzarekin garatu ziren. Koloreak gatz metalikoen bidez sortzen dira: sodioak horia, barioak berdea, eta kobreak urdina. Zarata, bestalde, konposatu kimikoen errekuntzaz lortzen da, danbadak aluminioz eta txistu-hotsak nitrokonposatuez eraginez. Oinarrizko osagaiak erregaia, oxidatzailea, koloratzailea eta aglomeratzailea dira. XIX. mendetik aurrera su artifizialak asko hobetu ziren, gaur egungo ikuskizunak sortuz.
BiologiaIkerketek erakutsi dute aitaren dietak eragin epigenetikoa izan dezakeela seme-alaben osasun metabolikoan, sncRNA molekulen bidez. Gantz ugariko dieta jarraitzen duten sagu arren ondorengoek diabetesaren sintomak garatzen dituzte; efektu hori dieta normala berriro hartzean desagertzen da. Eragina epididimoan zehar espermatozoideak heltzen direnean gertatzen da, mitokondrietako sncRNA maila handitzearen ondorioz. Gizakietan, obesitateak eta gorputz-masaren indize altuak ere sncRNA mailak aldatzen dituzte, seme-alaben obesitate eta osasun metabolikorako arriskuak bikoiztuz. Hortaz, osasuntsu jatea garrantzitsua da, batez ere ugalketa unean. Informazioa Zientzia Kaieran.
ArkitekturaLandare-fatxadek lorategi bertikalen izaera emulatzen dute eta eraikinen isolamendu termikoa nabarmen hobetzen dute. Substratu batekin egituratutako sistema hauetan, landareek ura eta mantenugaiak jasotzen dituzte. Azterketa batean, landare-fatxada baten eta oinarrizko hormaren portaera termikoa alderatu da. Landare-fatxada instalatuta, isolamendu-ahalmena % 30 handitu zen, transmisio termikoa 0.75 W/(m²·ºC) izatetik 1.22 W/(m²·ºC) izatera pasatuz. Udaran, kanpoko geruzaren hozte efektua nabarmendu zen, beroa pasiboki murriztuz. Berrikuntzak eraginkorrak dira bero-galerak minimizatzeko eta energia aurrezteko. Informazio gehiago Zientzia Kaieran.
AstrofisikaNASAren Parker zundak Eguzkitik inoizko gertuen igarotzea lortu du, 6,1 milioi kilometroko distantziara. Objektu artifizialik hurbilenak, 692.000 km/h-ko abiaduran, Eguzkiaren atmosferaren datu baliotsuak bildu ditu. Misio honek Eguzkia hobeto ulertzea ahalbidetuko du, eta teknologikoki garrantzitsua da, adibidez, eguzki-ekaitzak iragarri eta horien eragina prebenitzeko. 2018an jaurtitako zundak grabitazio-bultzadak erabiliz hurbildu da pixkanaka Eguzkira, eta azken igarotzea arrakastaz gauzatu du, sistemak kaltetu gabe. Datuak Elhuyar aldizkarian.
Zientziaren komunikazioaGureikerrek egindako ikerketaren arabera, komunikabideetan parte hartu duten ikertzaileen % 51k erasoak jasan dituzte, bereziki COVID-19 eta klima-aldaketarekin lotutako gaiengatik. Sare sozialak dira eraso gehienen gune, eta emakume zientzialariek jasaten dituzte irain eta zalantza gehien, genero estereotipoen ondorioz. Hala ere, dibulgazioa ezinbestekoa da desinformazioari aurre egiteko. Zientzialariek diote erronkak gorabehera, gizartearekiko ardura dutenez jarduera hori ezin dela baztertu. Ondorioz, erasoak gelditzeko eta segurtasuna bermatzeko neurriak eskatu dituzte. Azalpen guztiak Berria egunkarian.
Egileaz:Enara Calvo Gil kazetaria da eta UPV/EHUko Kultura Zientifikoko Katedraren komunikazio digitaleko teknikaria.
The post Asteon zientzia begi-bistan #514 appeared first on Zientzia Kaiera.
Naukas Bilbao 2024: El verdadero valor de un traje espacial
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

La doctora en biología molecular del cáncer Sara García Alonso consiguió la fama mediática al ser seleccionada como astronauta de reserva por la ESA. En Naukas Bilbao 2024 algunos descubrimos, además, que es una fantástica comunicadora científica. En El verdadero valor de un traje espacial explica la importancia de la investigación y desarrollo tecnológico espaciales.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: El verdadero valor de un traje espacial se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #521
Urteko azkena da aste honetako Ezjakintasunaren kartografia, eta pixka bat berezia egitea erabaki dugu. Jarraian lau artikulurik irakurrienak.

1. Ez duzu gezurrik esango. Eta zientzialaria bazara are gutxiago. Izan ere, politikaria izanez gero gezurra esateari iritzi-aldaketa esaten zaio, tradizio marxistarik onenean (Groucho Marxen tradizioan), eta bidean gorantz egiten duzu; baina zientzialaria bazara, zure atzetik ibiliko dira. Juan Trilloren eskutik: The deceiving scientist: an evil to tackle.
2. Ordenagailu-simulazio batean bizitzeko probabilitate ez nulua bada. Eta TILKUTek badaki kodea erabiltzen duten izakiek zer egingo luketen baieztatzen badugu. Virtual reality

3. Sumendi batek lurperatutako papiro bat irakurri ahal izatea zientzia-fikzioa da. Juan F. Trilloren Herculaneum Papyri talking from the ashes
4. Gutxieneko espazioan egia biribilak kontatzeko gai da bineta bat. Translaton. TILKUTena.

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #521 appeared first on Zientzia Kaiera.
¿Dónde están las calzadas romanas que impulsaron la civilización mediterránea?
 Puente de Alcántara, Cáceres (España). Fuente: Estevoaei/Shutterstock, CC BY-SA
Puente de Alcántara, Cáceres (España). Fuente: Estevoaei/Shutterstock, CC BY-SA
En el colegio se nos decía en clase de historia que la mayor aportación que había dejado la civilización romana en la península ibérica había sido su red de carreteras, un tejido de comunicaciones que permitió el desarrollo de la civilización mediterránea.
 El imperio romano en tiempos de Adriano (117-138), con la red de las principales calzadas romanas. Fuente: DS28/Wikimedia Commons, CC BY-SA
El imperio romano en tiempos de Adriano (117-138), con la red de las principales calzadas romanas. Fuente: DS28/Wikimedia Commons, CC BY-SAA pesar de ello, la mayor parte de aquellas han desaparecido o han sido profundamente alteradas. Pero no todo está perdido. Algunos estudios recientes han impulsado su conocimiento y se han descubierto nuevos tramos.
Solo se conserva un 10 % de las calzadasUn nuevo estudio de la Universidad de Copenhague ha demostrado que los lugares con una mayor densidad de calzadas romanas poseen una mayor actividad económica actual. Esto se debe a que la perduración de dichas infraestructuras incentivó el surgimiento de las ciudades de mercado medievales, siendo éstas el origen de la mayor parte de las ciudades modernas europeas.
A pesar de la importancia que han tenido, no han sido tratadas como elementos patrimoniales de relevancia y se conservan pocos kilómetros de ellas. Isaac Moreno, ingeniero e historiador galardonado con la medalla Frontino por sus investigaciones sobre ingeniería romana, ha constatado que solo se conservan en torno a un 10 % de las mismas.
Por una parte, existen caminos que no siendo romanos han sido señalizados como tales por algunas administraciones. La razón es que se ha denominado calzada romana o puente romano a las calzadas y puentes de piedra, aunque no fueran de ese origen. Es cierto que la piedra fue un material importante en las construcciones romanas, pero para que una estructura sea considerada “romana”, las técnicas y métodos de construcción empleados en ella deben ser romanos también.
Por otra parte, los caminos verdaderamente romanos han sufrido la aceleración de su destrucción durante los últimos cien años debido a la ejecución de obras modernas. Dichas acciones se han producido por el desconocimiento de la composición de las calzadas romanas y las características de su trazado.
Herramientas usadas para localizar calzadas desconocidasLas fuentes geográficas históricas que se han utilizado para el estudio de las vías romanas en la península ibérica han sido fundamentalmente los itinerarios romanos. Estos itinerarios han llegado a nuestros días en códices manuscritos medievales.
Los itinerarios romanos son una serie de rutas que discurrían por las calzadas del Imperio y que se describen a partir de las ciudades por las que transcurren, conocidas como estaciones o mansiones. En el caso de algunos itinerarios aparecen también las distancias entre ellas.
Sirva como ejemplo el primer tramo de la ruta entre Asturica (Astorga) y Caesaraugusta (Zaragoza) del Itinerario de Antonino, que pasaba por:
- Brigeco (?), a 40 m.p. (millas romanas, unos 1 480 metros)
- Intercatia (?): 20 m.p.
- Tela (?): 22 m.p.
- Pintiam (Padilla de Duero): 24 m.p.
- Raudam (Roa): 11 m.p.
- Cluniam (Peñalba del Castro): 26 m.p., 16 m.p.
Para saber por dónde iban los itinerarios se necesita conocer la posición de las estaciones por las que pasaban. Y como se ve en las interrogaciones anteriores, hay muchas estaciones de ubicación desconocida. La razón es que las coordenadas geográficas que dan los códices antiguos no son suficientemente precisas.
Además, en algunas rutas existen errores en las distancias y ausencia de estaciones. Esto hace que algunos de estos itinerarios sean interpretados de maneras diferentes por los investigadores, de tal manera que las rutas propuestas por distintos autores para un mismo itinerario pasan por distintas localidades.
Nuevas formas de localizar las calzadas romanasEn el trabajo “Vías romanas en Castilla y León”, dirigido por Isaac Moreno, se realizó un proyecto pionero para la localización de vías romanas en esta comunidad española.
Así, para la interpretación de los itinerarios se realizó un estudio de arqueología apoyado en conocimientos de ingeniería y se analizaron fotos aéreas de la zona en diferentes años y épocas del año para visualizar la huella de las vías bajo los campos. Esto se completó con excavaciones arqueológicas en la propia calzada.
La mayoría de los trabajos dedicados al estudio de las calzadas romanas que han realizado excavaciones arqueológicas se habían centrado en un tramo de una vía. En este caso, el estudio se extendió a una localización geográfica amplia: la submeseta norte.
Gracias a ello ahora conocemos más kilómetros de vías romanas verdaderas y sabemos cuál es la composición y técnica constructiva de la vía.
En los últimos años otros autores han hecho estudios similares para la identificación de tramos de vías romanas en la península ibérica. Entre ellos, cabe destacar los estudios de la Sociedad de Ciencia Aranzadi sobre la carretera romana de Roncesvalles y los realizados sobre la Vía Augusta en Ciudad Real.
Beneficios del conocimiento de la red viaria romanaEl conocimiento de los vestigios que nos quedan de este patrimonio de la ingeniería civil permite tenerlos en cuenta en las obras civiles actuales.
En este sentido, en España se ha llevado a cabo una actuación pionera en Europa. En la construcción de la autovía de Soria (Castilla y León) se modificó el proyecto para reducir su afección a la calzada romana que pasa por allí y se acondicionó esta última para poder ser disfrutada por los turistas culturales. Esto permite que los viajeros que se acercan a Soria para visitar la mítica Numancia se den un paseo por una calzada romana auténtica.
Para evitar la destrucción de los escasos kilómetros de vías romanas verdaderas que se conservan sería interesante un estudio similar a los arriba mencionados aplicado al resto de comunidades de España. Y lo que es no menos importante, la defensa por parte de las administraciones públicas de las vías identificadas por el mismo.![]()
Sobre las autoras: Jesús María Romera Aguayo, Profesor agregado de la Escuela de Ingeniería, UPV/EHU; Amaia Santamaría León, Profesora Titular de Universidad en Hormigón, UPV/EHU y Marcos Larrauri Gil, Profesor en ingeniería de la construcción, UPV/EHU.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Dónde están las calzadas romanas que impulsaron la civilización mediterránea? se ha escrito en Cuaderno de Cultura Científica.
Ane Paniagua, adimen artifizialeko ikaslea: “Aukera izan dut nire eremutik atera eta gauza berriak ikasteko”
Ane Paniagua Gonzalez de Txabarri Adimen Artifizialeko gradua egiten ari da EHUn. Gehiengoak bezala, unibertsitateko ikasketak aukeratzean, ez zeukan oso garbi zer egin nahi zuen: “Ate irekien jardunaldian, informatika eta beste ingeniaritza batzuk erakarrita joan nintzen. Han jakin nuen adimen artifizialeko gradua zegoela, eta, artean ez nekien arren zer zen, horren alde egin nuen”. Eta, aitortu duenez, asmatu egin zuen.
Hain zuzen, oso gustuko zuen informatika, baita matematika ere. Baina matematikako gradua teorikoegia iruditzen zitzaion. Eta ingeniaritzetan fisika eta kimika ere bazeuden. “Adimen artifizialean, berriz, ez zeuden bi ikasgai horiek. Hori alde batera utzita, ez nekien gauza handirik. 2020an batxilergoko bigarren mailan nengoen, eta 2021ean hasi nintzen. Oso berria zen dena, eta horrek ere bultzatu ninduen. Pentsa, oraindik ez zegoen gradua egin zuen inor —gu bigarren belaunaldia gara—, eta chatGPT ez zen existitzen. Siri eta itzultzaile automatikoa eta halakoak bakarrik ezagutzen genituen”, gogoratu du.
 Irudia: Ane Paniagua Gonzalez de Txabarri Adimen Artifizialeko gradua egiten ari da. (Argazkia: Elhuyar)
Irudia: Ane Paniagua Gonzalez de Txabarri Adimen Artifizialeko gradua egiten ari da. (Argazkia: Elhuyar)Ikasgaiek eta berritasunak ez ezik, beste zerbaitek ere lagundu zion erabakia hartzen: irakasle emakumezkoen jarrerak. Izan ere, onartu du bazegoela informatikarien gainean estereotipo jakin bat: bideojokoen zalea, frikia… Eta jendeak esaten ziola bera ere halakoa bilakatuko zela. “Nik, ordea, ez nuen horrelakorik ikusi. Gainera, zer du txarra frikia izateak? Bestalde, nire karreran, neskak eta mutilak nahiko orekatuta gaude. Ingeniaritza informatikoan agian mutil gehiago daude, baina ate irekietan gugana berehala hurbildu ziren irakasle pare bat, emakumeak biak, animatzera, eta, beraz, ondo hartuak sentitu ginen”.
Eta Ane Zelaia Jauregi irakasleak animatu zuen karrerako ikasgaiez aparteko proiektu bat egitera, beste bi lagunekin batera. Hala, Badok eta Musikasten euskal musika-taldeei buruzko webguneetako datuak hartu, eta Wikidatara eraman zituzten, Wikipediaren datu-basera. “Oraindik datu pila falta dira, baina guk, pixka bat osatu genituen, eta, batez ere, egitura eman genien. Horri esker, sistematikoki kontsulta daitezke, eta nazioarteko beste leku batzuetakoekin alderatu daitezke”. Adibidez, euskal musikarien rankinga osatu daiteke, argitaratutako album-kopuruaren arabera, edo argitaratu diren dataren araberako denbora-diagramak egin daitezke.
Atzerriko esperientzia eta etorkizuneko galdera-markaGauza berriak egiteko bulkada horrek berak eraman zuen Ljubljanara, Esloveniako hiriburura. Erasmusen bidez izan da han, eta, etorri berritan, balorazio ezin hobea egin du hango esperientziaz, nahiz eta azterketak egiteko dituen oraindik. “Jende asko etxetik kanpo joaten da karrera ikastera, baina ni etxean geratu nintzenez, gogoa neukan kanpora ateratzeko, eta ikusteko zer ikasten duten beste unibertsitate batzuetan adimen artifizialeko karreran”.
Izan ere, arlo berria denez, ikasgaiak nahiko desberdinak dira batean eta bestean. Ljubljanan, hasiera batean, masterreko ikasgaiak aukeratu zituen, baina gero karrerakoak hartzeko gomendatu zioten, bestela lan-karga handiegia izango zelakoan. “Hasieran beste asmo bat neukan arren, oso gustura ibil naiz. Gauza desberdinak ikasi ditut, eta aukera bat izan da nire eremutik ateratzeko eta zerbait berria ikasteko”. Ikasgaiak alde batera utzita, bidaiatzeko eta herrialde askotako jendea ezagutzeko aukera izan du, eta balorazio ezin hobea egiten du esperientzia osoaz.
Bukatzeko, etorkizuna nola ikusten duen galdetuta, hau da bere erantzuna: “Galdera-marka handi bat”. Ikasten jarraitu nahiko lukeela dio. Esaterako, gustuko du irudi-prozesamendua. “Iazko udan praktikak egin nituen DIPCn (Donostia International Physics Center), eta oso gustura aritu nintzen. Itzulitakoan, haiekin jarraituko dut. Hizkuntzaren inguruan ere badago master bat oso interesgarria, baina uste dut irudiak gehiago erakartzen nauela. Beste aukera bat kanpora joatea da, baina ez dakit”. Tarte batean pentsakor geratu ondoren, errepikatu du: “Galdera-marka da hori”.
Egileaz:Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar aldizkariko zuzendarikidea.
Elhuyar aldizkariarekin lankidetzan egindako atala.

The post Ane Paniagua, adimen artifizialeko ikaslea: “Aukera izan dut nire eremutik atera eta gauza berriak ikasteko” appeared first on Zientzia Kaiera.
Landare-fatxaden eraginkortasun termikoa
Landare-fatxada modular bertikal bat eraikitzea lorezaintzaren eta paisajismoaren esparruan egin beharreko konposizio konplexuenetako bat da, lorategi tradizional baina era perpendikularrean ezaugarriak emulatzea baitu helburu, eta horregatik lorategi bertikal ere deitzen zaio.
Lorategi bertikalen eraketan, ordea, substratu bat ezartzen den egitura bat erabiltzen da, non landaredia eta landareak sustraitzeko gai diren eta horren bidez ura eta horiek garatzeko behar diren mantenugaiak jasotzen dituzten.
 Irudia: landare-fatxadek eraginkortasun termikoa nabarmen handitu dezakete. (Argazkia: manuel m. v. – CC BY 2.0 lizentziapean. Iturria: Flickr.com)
Irudia: landare-fatxadek eraginkortasun termikoa nabarmen handitu dezakete. (Argazkia: manuel m. v. – CC BY 2.0 lizentziapean. Iturria: Flickr.com)Azterketa honetan landare-fatxada baten karakterizazio termikoa egiten da, isolamendu naturalaren gaitasuna egiaztatzeko, eta, beraz, tenperatura atseginagoak ematen dituzten edo ez, bai neguan, bai udan.
Konparazioa fatxada biluziko hormarekin egin zen, eta horma horren gainean landare-fatxada instalatu zen birgaitze energetiko gisa.
Hona hemen lortutako emaitza adierazgarrienak:
MLWn, ezaugarri termikoek hobekuntzak erakusten dituzte. Kasu honetan, oinarrizko hormaren 0.75 W/(m2 ºC)-tik 1.22 W/(m2 ºC)-ra transmisio termikoko balioetara igaro zen honek isolatzeko ahalmena % 30 handituz.
Udako urtaroen kasuan lortutako balioak aztertuz, hau da, erosotasunaren interesa fatxadaren kanpoko geruza hoztean datzanean erradiazioa maximoetara eta kanpoko tenperaturetara iristen baita. Hormaren tenperatura murriztea landare fatxadak eragiten du, eta horrek tenperatura modu pasiboan murrizteko gailu egokiak bihurtzen ditu. Itxitura bat berritu nahi bada bero-galerak murrizteko, komeni da isolamendu-geruza bat gehitzea oinarrizko horman, landaredun fatxadaren aurretik.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 45
- Artikuluaren izena: Eraikin pasiboen karakterizazio termikoa: landare-fatxada modular baten kasu-azterketa.
- Laburpena: Sistema berdeak sendotzen ari dira hirietako eskari termikoa murrizteko eta, aldi berean, hiriko bizitzaren kalitatea hobetzeko. Sistema berdeei lotutako onurak hainbat dira: biodibertsitatea handitzea, ekaitz-uren kontrola, energia aurreztea, tenperatura erregulatzea eta zarata arintzea. Landaredun sistema bertikalek errendimendu energetikoari egiten dioten ekarpenari buruzko ezagutza lortzeko, landaredun fatxada bati proba metodologikoak egin zaizkio Paslink zelda batean. Helburua landare-fatxada modular baten berokuntza- eta hozte-eskaria ezaugarritzea da. Emaitza nagusia isolamenduaren hobekuntza izan da. Erreferentziako fatxada 0.75 W/(m2 °C) baliotik abiatzen zen, eta 1.22 W/(m2 °C)-ko transmisio termikoko balioetara igaro zen landare-fatxadari esker; horrek esan nahi du isolamendu-ahalmena % 30 handitu zela. Fatxada berdeek energia aurrezteko potentzialtasun handia dutela ondoriozta daiteke.
- Egileak: Zaloa Azkorra-Larrinaga, Koldobika Martín-Escudero eta Naiara Romero-Antón
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 259-278
- DOI: 10.1387/ekaia.24600
Zaloa Azkorra-Larrinaga, Koldobika Martín-Escudero eta Naiara Romero-Antón UPV/EHUko Bilboko Ingeniaritza Eskolako Energetika Eraikuntzan Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.
The post Landare-fatxaden eraginkortasun termikoa appeared first on Zientzia Kaiera.
Aitaren dietak eraginda du semearen osasun metabolikoan
Espermatozoidearen geneek modu erabakigarrian laguntzen diote obulua ernaldu ondoren sortuko den banakoari. Gizakien kasuan, aitaldeko 23 kromosomak amaldeko kromosomen kopuru berarekin konbinatzen dira izaki berri bat sortzeko. Ba al dago, aitaldeko kromosomen ekarpenaz bestelako ekarpenik? Baieztatu egiten da mitokondriak (beren gene kopurua duten horiek ere) ez direla aitaren aldetik transmititzen eta herentzia mitokondriala amaldekoa baino ez dela. Hori ez da erabat zuzena; izan ere, espermatozoidearen mitokondria batzuk obulura iristen dira, baina mitokondria horiek zein haien DNA ezabatu egiten dira zenbait mekanismoren bidez.
 1. irudia: espermatozoidearen mitokondria batzuk obulura iristen dira, baina mitokondria horiek zein haien DNA ezabatu egiten dira zenbait mekanismoren bidez. (Argazkia: Kelly Sikkema – Unplash lizentziapean. Iturria: Unplash)
1. irudia: espermatozoidearen mitokondria batzuk obulura iristen dira, baina mitokondria horiek zein haien DNA ezabatu egiten dira zenbait mekanismoren bidez. (Argazkia: Kelly Sikkema – Unplash lizentziapean. Iturria: Unplash)Duela gutxi jakin dugu badagoela espermatozoidearen beste ekarpen bat, eta orain hasi gara haren garrantzia ezagutzen. sncRNA (small non-coding RNA, azido erribonukleiko ez kodifikatzailearen sekuentzia txikiak) izenez ezagutzen ditugun molekulak dira. 200 nukleotido baino gutxiagoko luzera dute eta transferentziako RNAren edo erribosomikoaren zatietatik eratortzen dira. RNA horien egitekoa da, hurrenez hurren, polipeptidoa mihiztatzeko aminoazidoa garraiatzea eta mihiztaketa hori gertatzen den erribosoma antolatzea.
Espermatozoideak obuluari ematen dion sncRNA multzoa, bere nukleoarekin batera, konplexua, dinamikoa eta ingurumen eraginekiko sentikorra da. Halaber, badakigu enbrioiaren garapenean eta helduen ezaugarrietan (fenotipoa) eragiten duela. Hemen aurki dezakegu gaiari buruzko azken berrikuspena. sncRNAek helduen fenotipoan duten eragin hori maila epigenetikoan gertatzen da, hau da, ez dute aldaketarik eragiten DNAren sekuentzian. Espermatozoidetik transferitutako sncRNAek ondorengoaren geneen adierazpena modulatu dezakete, eta aldaketa fenotipikoak eragin. Hortaz, ingurumen faktoreek eragindako herentzia epigenetikoaz ari gara.
Alemaniako eta Austriako ikertzaile talde batek Nature aldizkarian duela gutxi argitaratutako artikulu batean erakutsi du, saguetan, estaltze unean aitaren dietak eragina duela ondorengo arren osasun metabolikoan eta eragin hori maila epigenetikoan gertatzen dela, sncRNAen ekarpen espermatikoaren bidez.
Lehenengo esperimentuan, sagu arrak bi astez elikatu ziren gantz ugariko dietaren bidez. Sagu horiek emeekin estali ziren, eta egiaztatu zen ondorengo arren % 30 inguruk intsulinarekiko erresistentzia eta glukosarekiko intolerantzia garatu zutela, hau da, II motako diabetesaren zeinu bereizgarriak. Bigarren saiakuntzan, gantz ugariko dietarekin bi aste igaro ostean, saguek dieta normala jaso zuten berriro ere hilabete batez. Estalketaren ondoren, ondorengoek ez zuten garatu inolako arazo metabolikorik. Ikertzaileek ondorioztatu zuten dietak eragina zuela epididimoan espermatozoideak heltzen ziren garaian. Lasaiago azalduko dugu.
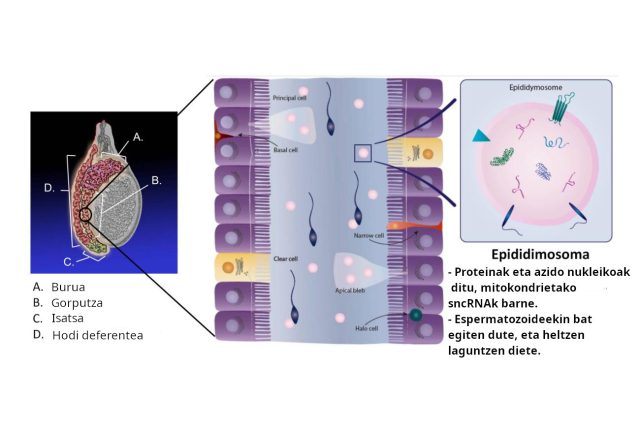 2. irudia: ezkerraldean, epididimoak testikuluaren gainean duen posizioa erakusten da, bere zati guztiekin. (Norena: KDS444, CC BY-SA 3.0). Eskuinaldean, epididimoaren epitelioak epididimosomak askatzen dituela ikusten da, hau da, heltzen ari diren espermatozoideetara proteinak, DNA eta RNA garraiatzen dituzten besikula estrazelularrak. (Norena: ER James et al. Int. J. Mol. Sci. 2020, CC BY 4.0)
2. irudia: ezkerraldean, epididimoak testikuluaren gainean duen posizioa erakusten da, bere zati guztiekin. (Norena: KDS444, CC BY-SA 3.0). Eskuinaldean, epididimoaren epitelioak epididimosomak askatzen dituela ikusten da, hau da, heltzen ari diren espermatozoideetara proteinak, DNA eta RNA garraiatzen dituzten besikula estrazelularrak. (Norena: ER James et al. Int. J. Mol. Sci. 2020, CC BY 4.0)Espermatozoideak testikuluan sortzen dira, zelula germinaletatik abiatuta, gaitasun proliferatibo handia duten aitzindarietatik. Osatu ondoren, epididimo izeneko hodi egitura luzea zeharkatzen dute1. Saguaren espermatozoideek astebete behar izaten dute metro luze den hodi hori zeharkatzeko. Zeharkatzen ari direla, espermatozoideek epididimosomak (epididimoaren epiteliotik datozen molekulaz kargatutako besikulak) jasotzen dituzte, hala nola sncRNAk, eta ondoren lobulura transferituko dituzte (2. irudia).
Nature aldizkariko azterlanak erakutsi zuen gantz ugariko dieta espermatozoideak epididimoan sartu aurretik eteten bazen, ondorengoek ez zutela ondoriorik izango. Hau da, gantz ugariko dietaren eragina/eragin kaltegarria epididimoa zeharkatzean gertatzen zela. Eta horren erantzule transferitutako sncRNAk ziren. Izan ere, gantz ugariko dietak mitokondrietako sncRNAen maila igoarazten zuen ehun guztietan, epididimoa barne. Aldaketa hori dieta normalera itzuli ondoren leheneratzen zen.
Modu independentean, ikertzaileek bi generen (Mrpl23 eta Ndufb8) mutazioen ondorioak aztertu zituzten, mitokondrietako RNAren zati ez kodifikatzaileak areagotzen zituztenak. Mutazio horiek zituzten sagu arren ondorengoek gantz ugariko dietaren bidez elikatutako sagu arren ondorengoen aldaketa metaboliko berberak zituzten.
Ikerketaren egileek saguetan lortutako emaitzek eragin klinikorik izan zezakeen aztertu zuten. Egiaztatu zuten transferentziako eta mitokondrietako RNAren zatien mailak lotuta zeudela gizonen gorputz-masaren indizearekin. Aldi berean, egiaztatu zuten sorkuntzaren unean aitak gainpisua izateak bikoiztu egiten duela semeek obesitatea izateko arriskua eta arriskuan jartzen duela haien osasun metabolikoa. Espermak duen sncRNA karga izan liteke bi behaketa horien arteko lotura.
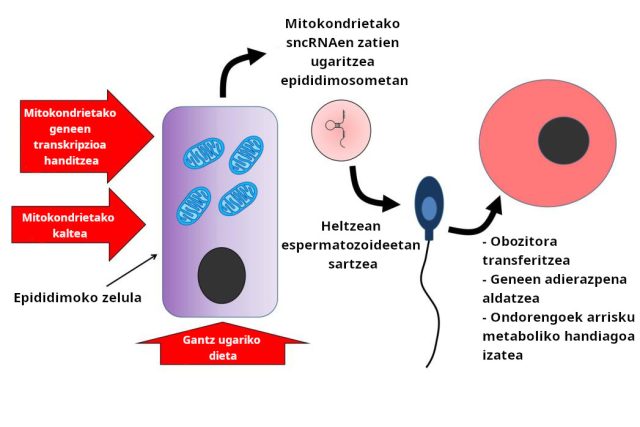 3. irudia. Tomar et al.-ek proposatutako eredua, aitaren gantz ugariko dietaren eragin epigenetikoa azaltzeko. Mitokondrietako kalteak mitokondrietako geneen eta sncRNAen kargaren transkripzioa handiagotuko luke epididimosometan. RNA horiek espermatozoideetara eta ondoren obozitoetara transferitzeak aldatu egingo luke gene adierazpena garapenean , eta, ondorioz, areagotu egingo litzateke ondorengoen arrisku metabolikoa.
3. irudia. Tomar et al.-ek proposatutako eredua, aitaren gantz ugariko dietaren eragin epigenetikoa azaltzeko. Mitokondrietako kalteak mitokondrietako geneen eta sncRNAen kargaren transkripzioa handiagotuko luke epididimosometan. RNA horiek espermatozoideetara eta ondoren obozitoetara transferitzeak aldatu egingo luke gene adierazpena garapenean , eta, ondorioz, areagotu egingo litzateke ondorengoen arrisku metabolikoa.Nature aldizkariko artikuluan aipatzen den egoera batek proposatzen du gantz ugariko dietarekiko esposizioak mitokondrien funtzioa kaltetuko lukeela, eta hori mitokondrietako geneen transkripzio handiagoarekin konpentsatu beharko litzatekeela. Horren ondorioz, RNAn zelulen edukia handitzeak sncRNAen zati gehiegi sortuko lituzke, eta espermatozoideek garraiatu eta obozitoetara iritsiko lirateke. Oraindik ez dakigu, ordea, zati horiek nola modulatzen duten enbrioien geneen adierazpena, modulazio epigenetiko horrek nola eragiten dituen ondorioak ondorengoen metabolismoan eta zergatik dituzten semeek arrisku metaboliko gehiago alabek baino.
Laburbilduz, beti da gomendagarria dieta osasuntsu bat izatea eta gorputzaren pisuari maila egokietan eustea; are gomendagarriagoa da, ordea, gizonezkoentzat sorkuntza unean.
Oharra:1 Testikuluaren gainean dagoen giza epididimoaren bitxikeria bat: 4-5 zentimetro luze da, baina zabaldu egingo balitz, 6 metro luze izango litzateke.
Erreferentzia bibliografikoak:Cai, Chen; Chen, Qi (2024). Father’s diet influences son’s metabolic health through sperm RNA. Nature. DOI: 10.1038/d41586-024-01502-w
Tomar, A.; Gómez-Velázquez, M; Gerlini, R. et al. (2024) Epigenetic inheritance of diet-induced and sperm-borne mitochondrial RNAs. Nature. DOI: 10.1038/s41586-024-07472-3
Egileaz:Ramón Muñoz-Chápuli Oriol Animalien Biologiako Katedraduna (erretiratua) da Malagako Unibertsitatean.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko uztailaren 15ean: La dieta del padre influye en la salud metabólica del hijo.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Aitaren dietak eraginda du semearen osasun metabolikoan appeared first on Zientzia Kaiera.
Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- …
- hurrengoa ›
- azkena »


