LP 791-18d, el planeta cubierto de volcanes
LP 791-18d
Una de las carreras más importantes que se están desarrollando en el campo de la astronomía hoy en día es la búsqueda de un planeta similar en tamaño y características a la Tierra, algo que desde el punto de vista de la geología nos podría ayudar mucho a saber que “ingredientes” son necesarios para la formación de planetas como el nuestro. De momento no hemos encontrado un planeta b, y es posible que tardemos en encontrarlo por dos cuestiones principales: por las dificultades propias de la observación de planetas tan relativamente “pequeños” y porque no sabemos todavía cómo de raros son los planetas como el nuestro -si es que hay más.
Pero el ir completando el catálogo de planetas extrasolares -aquellos que giran en torno a una estrella diferente a nuestro Sol- está aportándonos una visión sobre la enorme diversidad de planetas existentes, muchos de los cuales no tienen una representación directa en nuestro Sistema Solar.
 Figura 1. Reconstrucción artística de LP 791-18d. El punto azul en la lejanía correspondería con el LP 791-18c. Imagen cortesía de NASA’s Goddard Space Flight Center/Chris Smith/KRBwyle.
Figura 1. Reconstrucción artística de LP 791-18d. El punto azul en la lejanía correspondería con el LP 791-18c. Imagen cortesía de NASA’s Goddard Space Flight Center/Chris Smith/KRBwyle.Recientemente, se ha publicado un nuevo estudio en la revista Nature hablándonos de cómo podría ser un planeta de un tamaño similar al de la Tierra (1.03 radios terrestres) llamado LP 791-18d, situado a unos 90 años-luz de nuestro planeta y que gira en torno a una enana roja junto a otros dos planetas, estos dos últimos ya descubiertos en 2019.
Pero, ¿qué tiene de especial este planeta? Los científicos piensan que podría tener una gran actividad volcánica distribuida por toda su superficie, algo similar a lo que ocurre en Ío, un satélite de Júpiter. La actividad volcánica es muy importante en planetas rocosos, ya que puede ayudar a generar una atmósfera -los gases más importantes que emiten los volcanes son el vapor de agua, el dióxido de carbono y el de azufre, entre otros- y a ir rellenándola en el caso de que esta pueda sufrir pérdidas por cualquier motivo, como la carencia de un campo magnético o el propio viento estelar.
Además, las atmósferas de los planetas, si se dan las condiciones adecuadas, pueden permitir la existencia de agua líquida en la superficie, algo que, como sabemos, es de gran importancia para la astrobiología y la búsqueda de la vida más allá de nuestras fronteras.
Al mismo, tiempo, los volcanes son capaces de llevar a la superficie elementos que de otro modo estarían atrapados en su interior, pudiendo crear un ciclo de transferencia y reciclaje entre la corteza y el interior del planeta. También podrían incluso aportar calor a zonas más frías, como el fondo de posibles océanos, permitiendo ambientes menos hostiles.
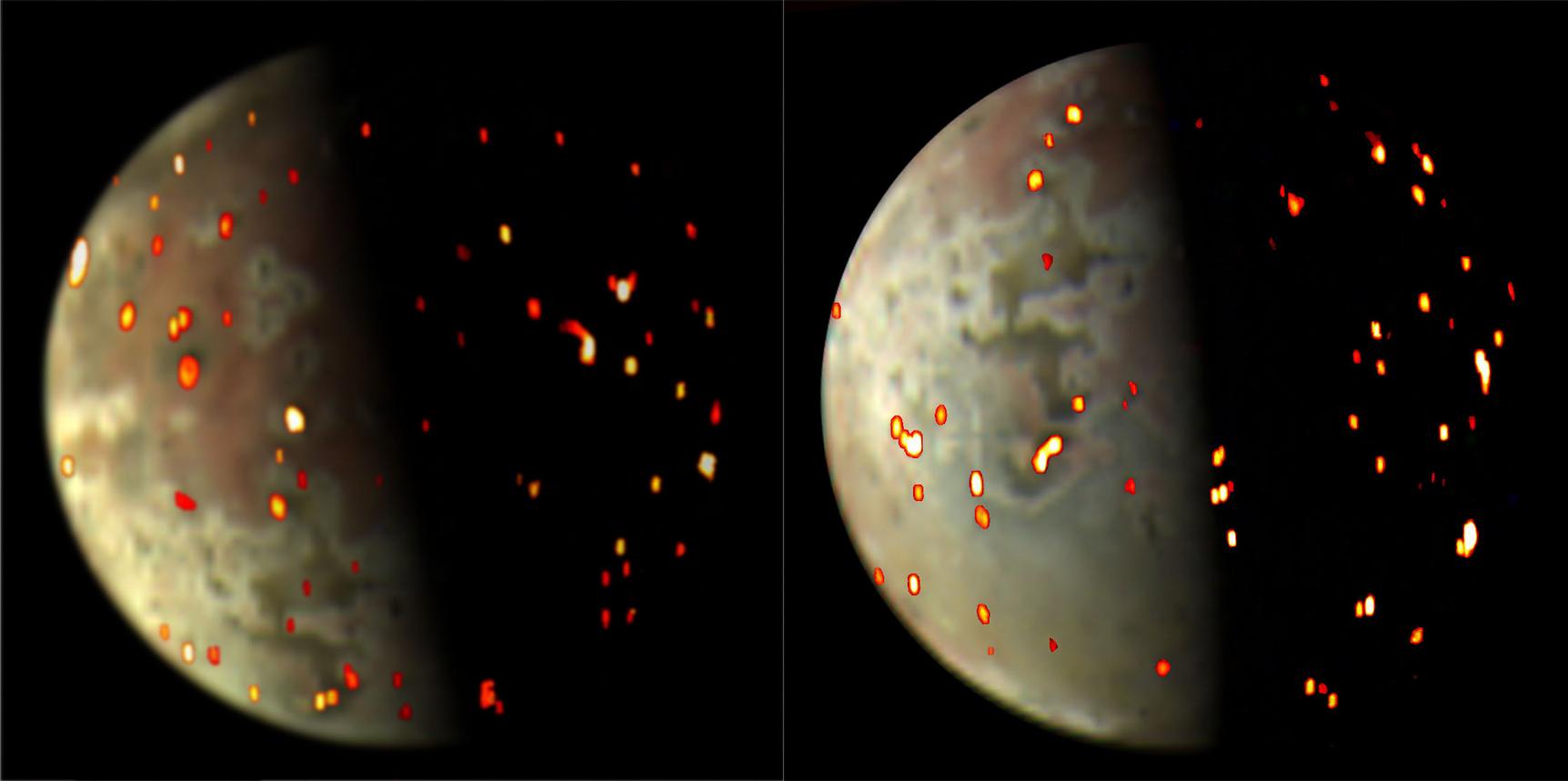 Figura 2. Dos imágenes de Ío tomadas el 14 de diciembre de 2022 y el 1 de marzo de 2023 desde la sonda Juno. En color podemos ver la superficie de Ío, y los puntos rojos, amarillos y blancos corresponden con puntos que tienen una elevada temperatura y que probablemente correspondan con puntos de emisión volcánica recientes o actuales. Cortesía de NASA/JPL-Caltech/SwRI/ASI/INAF/JIRAM.
Figura 2. Dos imágenes de Ío tomadas el 14 de diciembre de 2022 y el 1 de marzo de 2023 desde la sonda Juno. En color podemos ver la superficie de Ío, y los puntos rojos, amarillos y blancos corresponden con puntos que tienen una elevada temperatura y que probablemente correspondan con puntos de emisión volcánica recientes o actuales. Cortesía de NASA/JPL-Caltech/SwRI/ASI/INAF/JIRAM.¿De dónde sacaría este planeta la energía interna suficiente como para poder estar cubierto de volcanes? La respuesta está en la existencia de uno de los otros planetas, el c, que tiene una masa de aproximadamente nueve veces la de la Tierra. Conforme van haciendo órbitas alrededor de su estrella, los planetas c y d pasan cerca el uno del otro, de tal forma que el c es capaz de modificar ligeramente la órbita del d, haciéndola más elíptica.
Esta deformación en la órbita es suficiente como para que el planeta sufra un fenómeno que conocemos como calentamiento de marea, de tal forma que a lo largo de su órbita el planeta sufre una deformación en su superficie y su interior diferente en cada punto de la órbita debido a la atracción gravitatoria de su estrella y de los otros planetas del sistema.
Para que podamos entendernos, imagina que tienes una pelota antiestrés en las manos y que empiezas a comprimirla y a dejar que vuelva a su forma. Después de un rato, verás que esta ha aumentado ligeramente su temperatura y esto se debe en parte a la energía que transfiere el movimiento de tu mano sobre la propia pelota.
De una manera parecida, cuando un cuerpo masivo ejerce una fuerza de atracción gravitatoria sobre otro más pequeño, acaba provocando que el más pequeño sufra un proceso de deformación en el cual se comprime y se estira, parecido a lo que has hecho con la pelota. Esto ocurre normalmente porque la fuerza de atracción de la gravedad en un lado, el que mira al objeto más masivo, es más fuerte, y más débil su efecto sobre el lado opuesto.
 Figura 3. En los planetas con acoplamiento de mareas no hay ciclo día-noche. Solo un lado donde hay oscuridad y otro donde es un día perpetuo. Imagen cortesía de la NASA y el JSC.
Figura 3. En los planetas con acoplamiento de mareas no hay ciclo día-noche. Solo un lado donde hay oscuridad y otro donde es un día perpetuo. Imagen cortesía de la NASA y el JSC.Este proceso, si ocurre en repetidas ocasiones, genera una serie de fricciones que a su vez se traducen en calor, a veces suficiente para generar magmas que pueden dar lugar a erupciones volcánicas, y como decíamos anteriormente, es el mismo proceso que ocurre sobre la luna de Júpiter Ío, y que lo convierte en uno de los objetos con mayor actividad del Sistema Solar.
Otro de los detalles aportados en el estudio sobre este planeta indica que sufre un acoplamiento de mareas con su estrella y que, por lo tanto, siempre tiene la misma cara apuntando a su estrella -algo parecido a lo que ocurre en nuestro planeta con la Luna, en la que el periodo de rotación es igual al orbital- y esto a su vez se traduce en que su cara diurna probablemente tenga una temperatura muy alta, aunque dependiendo de su atmósfera, el agua podría ser estable en su cara nocturna, donde las temperaturas serían menores.
Eso si no ha sufrido un proceso evolutivo como el de Venus, donde los volcanes han sido capaces de generar una atmósfera muy importante, capaz de equilibrar la temperatura en su lado nocturno y diurno, y volviendo totalmente inhabitable cualquier parte del planeta.
Pero precisamente este hecho abre otra cuestión muy importante de cara a entender la habitabilidad de la Tierra. Podríamos suponer que Venus y la Tierra tienen una actividad volcánica similar a grandes rasgos… entonces, ¿por qué Venus ha seguido sumando gases de efecto invernadero? Una de las posibles respuestas a esta pregunta es la existencia de una tectónica de placas capaz de almacenar parte de estos gases -obviamente, no en estado gaseoso sino transformado en otras sustancias químicas- dentro de su corteza o su manto, donde seguirá un ciclo en el que se vaya incorporando al interior del planeta y posteriormente siendo expulsado por los volcanes.
En nuestro planeta este ciclo viene regulado por la tectónica de placas, pero al menos aparentemente no hay una en Venus, y quizás tampoco lo exista en este exoplaneta, por lo que la tectónica de placas podría ser un condicionante para conseguir unas condiciones más habitables en los planetas. O quien sabe si hay algún detalle o mecanismo que todavía desconozcamos por completo a la hora de regular estos ciclos en otros planetas.
Sea como fuere, el estudio de los exoplanetas va a seguir aportándonos una importante visión no solo sobre la diversidad de mundos que pueblan nuestra galaxia, sino también ayudarnos a contestar aquellas preguntas que todavía tenemos sobre nuestro propio Sistema Solar.
Bibliografía:
Crossfield, I.J. et al. (2019) ‘A super-earth and sub-neptune transiting the late-type M dwarf LP 791-18’, The Astrophysical Journal Letters, 883(1). doi: 10.3847/2041-8213/ab3d30.
Peterson, M.S. et al. (2023) ‘A temperate Earth-sized planet with tidal heating transiting an M6 star’, Nature, 617(7962), pp. 701–705. doi: 10.1038/s41586-023-05934-8.
Para saber más:
25 años de planetas extrasolares
El valle de la evaporación de planetas
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo LP 791-18d, el planeta cubierto de volcanes se ha escrito en Cuaderno de Cultura Científica.
Ingredientes para la receta: la vid
20. Noé se dedicó a la labranza y plantó una viña.
21. Bebió del vino, se embriagó, y quedó desnudo en medio de su tienda.
22. Vio Cam, padre de Canaán, la desnudez de su padre, y avisó a sus dos hermanos.
23. Entonces Sem y Jafet tomaron el manto, se lo echaron al hombro los dos, y andando hacia atrás, vueltas las caras, cubrieron la desnudez de su padre sin verla.
Biblia de Jerusalén, Génesis, 9: 20-23.
… El dios hijo de Zeus
da sin distinción al rico y al miserable
el goce apaciguador del vino.
Eurípides, Las bacantes, 405 a.C.
Porque con ser la vid un árbol tan pequeño, no es pequeño el fruto que da. Porque da uvas casi para todo el año, da vino que mantiene, esfuerza y alegra el corazón del hombre, da vinagre, da arrope, da pasas, que es mantenimiento sabroso y saludable para sanos y enfermos.
Fray Luis de Granada (1504-1588).
 Foto: José Alfonso Sierra / Unsplash
Foto: José Alfonso Sierra / UnsplashTanto las uvas silvestres como las cultivadas se mencionan en la Biblia hasta en 72 capítulos o, también, en 12 del Corán. Por supuesto, solo hay que recordar a Noé, que también aparece su producto derivado más conocido, el alcohol, resultado de la fermentación de los azúcares de la uva, y el vino como objetivo final. Por todo ello, la vid es la planta más citada en los textos sagrados. Y también la cita Stephen Harris, de la Universidad de Oxford, entre las 50 plantas legendarias que cambiaron el mundo.
Las uvas silvestres, Vitis sylvestris, son autóctonas del Asia Menor y el Cáucaso donde se inició la viticultura y se difundió por el Mediterráneo, según Jules Janick, de la Universidad Purdue, en Estados Unidos. Se han encontrado semillas de uva en yacimientos prehistóricos de Europa y, en concreto, en Grecia, los Balcanes, Italia, Suiza, Alemania y Francia. La distribución de la vid silvestre va de Portugal al oeste hasta Turkmenistán al este, y desde Alemania al norte hasta Túnez en el sur.
Por tanto, se encuentra en la Península Ibérica, excepto en el norte y en Pirineos, como lo muestran los hallazgos de sus pepitas desde el Neolítico. Los datos confirman, según Ramón Buxó, de la Universidad Pompeu Fabra, que la vid es una planta indígena en todo el Mediterráneo y las pepitas de vid cultivada se han recuperado a partir de la Edad del Bronce.
Todavía está abierto el debate que propone que, dada la extensión de la vid silvestre por la cuenca mediterránea, es posible que la vid doméstica se originara en más de un lugar de la región y no solo de Oriente Medio y el Cáucaso. Rosa Arroyo-García y sus colegas del Instituto Nacional de Investigación y Tecnología Agraria y Alimentaria de Madrid, han estudiado el ADN de los cloroplastos de 1201 muestras de vid silvestre y doméstica de toda el área de su distribución. Los resultados, según los autores, muestran que el 70% de las muestras de la Península Ibérica llevan cloroplastos que son únicamente compatibles con material derivado de poblaciones occidentales de la vid silvestre.
Otra investigación, centrada en los cloroplastos de las variedades silvestre y doméstica de la meseta de Castilla La Vieja, del grupo de José Carlos Santana, de la Universidad de Valladolid, diferencia hasta 121 genotipos diferentes. Es interesante que muchos de ellos muestran cruces entre la vid silvestre autóctona y vides domésticas de Francia que los autores sitúan en variedades que llegaron por el comercio a través del Camino de Santiago.
8000 años de vid domésticaAntes del 5000 a. C., la uva doméstica, Vitis vinifera , llegó de Anatolia a Oriente Próximo, desde el sur del Cáucaso, entre los mares Negro y Caspio y el Creciente Fértil, el valle del Jordán y Egipto, según el análisis genético de 1000 muestras de vides silvestres y domesticadas publicado por Sean Myles y su grupo, de la Universidad Cornell en Ithaca.
La fecha de la domesticación se sitúa hace entre 6000 y 8000 años atrás. Hay semillas de uva de la Edad del Bronce en Mesopotamia, Israel, Siria, Egipto, el Egeo y en lagos de Suiza, y también se han encontrado en América. Solo hay que recordar que cuando el vikingo Leif Erikson llegó a las costas de Labrador llamó Vinland, País del Vino, a aquel país por la abundancia de vides silvestres de la especie Vitis riparia, habitual en América del Norte.
De hace 4000 años, en la Edad del Bronce, se han encontrado vasijas para almacenar vino y pasas. En el yacimiento de Tel Kabri, en Israel, en un local se recuperaron hasta 40 vasijas con restos de compuestos típicos del vino como ácido tartárico, resinas, miel, aceite de cedro o de ciprés. Es, según Andrew Koh y sus colegas, de la Universidad Brandeis de Estados Unidos, una habitación donde se almacenaban vasijas con vino, es decir, una bodega, una de las más antiguas conocidas hasta ahora.
El estudio, reciente y publicado hace unas semanas, y dirigido por Yang Dong, de la Universidad Agrícola de Yunnan, en China, con 84 autores, se analizan datos genéticos de 3525 variedades de uva silvestre y uva cultivada de todo el planeta. Los resultados revelan los efectos del clima, en concreto de las glaciaciones, en los tamaños de población históricos, sugieren domesticaciones simultáneas de vino y uvas de mesa e identifican variantes asociadas con rasgos de domesticación como el color de la baya y la palatabilidad.
En el Pleistoceno, las condiciones climáticas empujaron a la selección de ecotipos de uva silvestre a lo que ayudó la fragmentación del hábitat. La domesticación ocurrió simultáneamente hace unos 11.000 años en Asia occidental y el Cáucaso para producir vides de frutas de mesa y vino. Las domesticadas de Asia occidental se dispersaron en Europa con los primeros agricultores, y se cruzaron con antiguos ecotipos occidentales salvajes y, posteriormente, se diversificaron ayudados por las migraciones humanas a finales del Neolítico.
Y de por entonces son los Mejillones con uvas que nos presentan Eudald Carbonell y Cinta Bellmunt con las fotografías de María Ángeles Torres desde la Universidad Rovira i Virgili y el grupo de Atapuerca. Es receta sencilla y rápida y un buen entrante para una comida en el campo.
Recolectamos los mejillones en las rocas de la costa más cercana y los tostamos a la hoguera encima de una piedra. Cuando se abran ponemos una uva en cada concha y los comemos a la vez, mejillón y uva.
La vid en AméricaUn ejemplo revelador de la difusión del cultivo de la vid nos llega desde América después de la llegada de Cristóbal Colón. Según lo resume Julio Luelmo, cuando llegaron los europeos encontraron muchas variedades de vid que crecían espontáneamente, sobre todo Vitis riparia, aunque no hay evidencias de que se utilizaran para obtener vino o cualquier otro líquido fermentado a pesar del nombre que los vikingos dieron al Labrador. La viticultura se introdujo en América con la importación de las cepas europeas. Los cultivos de vid resultaron en México, California y, sobre todo, en Sudamérica. En cambio, fracasaron al este de las Montañas Rocosas y en las Antillas donde lo había intentado Colón en 1493.
Hasta el siglo XIX no se conoció que fracasaron por la acción de un insecto de la especie Daktulosphaira vitifoliae, parásito de las especies americanas que ya estaban inmunizadas. Sin embargo, atacaba a las variedades europeas y, cuando llegó al Atlántico europeo, casi acaba con la viticultura en el continente durante el siglo XIX. Su recuperación llegó con injertos de la vid europea en troncos de la vid americana resistente.
Con la domesticación se seleccionan el aumento del tamaño de las uvas y su contenido en azúcar, los varios colores de la piel y la ausencia de semillas, importante para las uvas de mesa y las pasas. Según Stephen Harris, en la actualidad se conocen hasta 10000 cultivares distintos de uva y pocas de ellas llegan hasta el gran comercio. Muchas quedan en exclusiva para pequeños productores. Todo ello influye en la fermentación del mosto de la uva y la obtención del vino. La levadura convierte los azúcares del zumo de uva, glucosa y fructosa, en etanol y dióxido de carbono. Entre la levadura y otras bacterias se sintetizan compuestos aromáticos variados que darán la personalidad típica a cada vino.
Una de las pruebas arqueológicas más antiguas que conocemos de la producción de vino se ha encontrado en una aldea datada en el Neolítico de las montañas Zagros, en el norte de Irán. El grupo de Patrick McGovern, de la Universidad de Pennsylvania, encontró una vasija, fechada hace 7000 años, con residuos de ácido tartárico y de una resina del árbol Pistacia que se utiliza para mezclar con el vino y detener la formación de vinagre.
Las antocianinas son las responsables principales del color rojo en el vino. Se encuentran en la capa exterior de la piel de la uva y se extrae durante la maceración. La mayoría de los mostos, incluso los de uvas negras, son incoloros, y por ello la maceración es un proceso importante para la coloración de los vinos. El color rojo o rosado depende, por tanto, de la extracción de las antocianinas de la piel de la uva durante el proceso de fermentación. También se ha encontrado antocianina en vasijas fechadas hace 8000 años recuperadas de la excavación de Areni, en Armenia, y por tanto, otro de los más antiguos restos que indican la presencia de vino según Hans Barnard y sus colegas, de la Universidad de California en Los Angeles. Confirman la obtención de vino en el Cáucaso ya como ya se conocía de las montañas Zagros de Irán.
 Foto: Jaime Casap / Unsplash
Foto: Jaime Casap / UnsplashEs interesante que nuestro gastrónomo romano de hace más de 15 siglos, Marco Gavio Apicio, destaque qué hacer para cambiar el color del vino y, en concreto, de vino tinto a vino blanco. Su consejo es “Pones en la botella harina de habas o bien tres claras de huevo y lo mezclas durante un buen rato. Al día siguiente, el vino será blanco. Las cenizas blancas de viña también pueden producir esta transformación”. Espero que le sea útil a quien le interese.
Es una receta de Juan Altamiras en su texto Nuevo arte de la cocina española. Así recomienda cocinar la Ternera estofada en vino blanco, que publicó en 1758. Era fraile franciscano y había nacido en 1709 en La Almunia de Doña Godina, Zaragoza. La fecha original de publicación de su libro era 1745 y es importante pues presenta la cocina española de la época anterior a la influencia de la cocina francesa a finales del siglo XVIII y en el siglo XIX. La receta aparece en la reciente edición sobre Altamiras publicada por Vicky Hayward.
De lo magro de la ternera cortarás pedazos como nuezes: freirás tocino, y con su pringue has de freír los trozos de ternera: echarás la carne en la olla, con el pringue que te quedó freirás cebolla menuda, y echarás con la carne, pondrás un poco de vino blanco, dos granos de ajos majados, sal, todas especias; peregil y unas hojas de laurel: después de este recado, la pondrás a fuego manso, con un papel en la boca del puchero, para que no levante el hervor, y con un pucherito, que la tape, con agua. Harás un poco masseta, y la pondrás en la circunferencia de la olla principal, de modo que no se exhale, dexala cocer dos horas: así sacarás poco, pero buen caldo, y muy gustoso.
El cultivo de la vid implica un extenso laboreo y la poda anual de los sarmientos. Es el arte de la poda lo que distingue al buen viñador. Y es la base de un plato típico de La Rioja: Chuletillas de cordero al sarmiento.
Una receta para celebrar en cualquier celebración que tenga lugar en tierras riojanas o en cualquier sitio al aire libre. Se trata básicamente de chuletas de cordero asadas, a las que habremos echado sal gorda. Aunque se pueden hacer, por supuesto, en una chimenea, estas chuletas se suelen asar al aire libre, usando para ello una parrilla puesta al fuego, prendido con sarmientos, es decir, ramas secas de vid. Las chuletas se colocan cuando el fuego ya se ha extinguido y sólo quedan las brasas. Es la temperatura ideal para asar las chuletillas. Hay quien les echa un chorro de vino de Rioja poco antes de sacarlas de la parrilla.
Las uvas se conservan secándolas al sol para producir pasas, o transformando el mosto de la uva en vino. Es la bebida alcohólica de difusión universal y, según Jean-François Revel, lo es por su capacidad de viajar y, también, por su gran variedad y, siendo siempre el zumo fermentado de la uva, mantiene características propias del lugar de origen por su sabor, aroma y color. Es una bebida que depende de la habilidad y perspicacia del viticultor y, en último término, de la capacidad y la memoria del catador. Para Revel, la degustación del vino es una partida de ajedrez de infinitas soluciones jamás agotadas.
Una vez probado el vino, el catador queda hechizado. El vino se asocia al amor y a la falta de amor, a la alegría y a la tristeza, al éxito y al fracaso, a la amistad, a los negocios, a la guerra y a la paz, al reposo y a la violencia, y a tantos otros sentimientos y conductas. Incluso el vino se asocia, inevitablemente, a la templanza, aunque Revel menciona civilizaciones donde dejar de beber vino es casi como renunciar a toda otra actividad, a todo intercambio, incluso supone dejar de pensar. Es lo que el ensayista, escritor y crítico literario Jean-François Revel opina sobre el vino en su historia literaria de la sensibilidad gastronómica.
 Foto: Juan Ugarte / Pixabay
Foto: Juan Ugarte / PixabaySin embargo, después de los elogios al vino llega el debate actual sobre los beneficios y daños que provoca el alcohol en la salud humana. Como ejemplo sirve una publicación reciente de Aitor Hernández y sus colegas de la Universidad de Navarra sobre la relación en la ingesta de alcohol y la hipertensión. Son datos de la encuesta “Seguimiento Universidad de Navarra” que, desde octubre de 2015, hace un seguimiento de 14651 participantes con encuestas bianuales durante 14 años. Según los resultados, si el consumo de alcohol sigue las pautas de la dieta mediterránea se asocia con un menor riesgo cardiovascular, aunque todas las relaciones no son significativas según la estadística. En conclusión, se necesitan más datos.
Hace unos años, Jonathan Silvertown, de la Universidad de Edimburgo, escribía que la afinidad entre los humanos y el alcohol, y la levadura, de la especie Saccharomyces cerevisiae, que lo produce, es muy profunda. El alcohol posee el poder transformador de una droga que altera el estado mental. Eleva o deprime el ánimo, inspira o nubla el razonamiento, enciende la pasión, disminuye la pericia, induce la agresión y la violencia o, también, provoca el sueño.
El alcohol ata a los humanos con nudos difíciles, para muchos imposibles, de deshacer. En resumen, el alcohol es una toxina para la que tenemos una cierta tolerancia. Además, es una toxina sin otro equivalente funcional en el metabolismo humano, como pueden ser las que provocan los opioides que son el producto final de nuestro sistema de recompensa cerebral. Pero nuestra especie ha estado expuesta al alcohol resultado de la fermentación de azúcares, sobre todo en frutas maduras, incluso antes de la aparición de Homo. Nuestros ancestros comunes desde hace cinco millones de años ya comían abundante fruta que, al madurar y por la levadura, ya transformaban los azúcares en alcohol. Donde hay fruta madura hay levadura, y donde hay levadura habrá alcohol.
En Bilbao, a los mejillones se les llama mojojones o, con más precisión, se les llamaba así. Ahora mojojón es, me parece, una palabra moribunda. Ni siquiera aparece en el Diccionario de la Lengua y, en Bilbao, a los antiguos mojojones con tomate antes y ahora se les llama tigres. Sin embargo, aquí va una receta con mojojones. La incluye Íñigo Azpiazu en su libro sobre la cocina tradicional vasca y la titula como Mojojones bilbotarras, o sea, mejillones bilbaínos. Dice así, más o menos:
Necesitamos mojojones, puerros, chacolí, harina, limón, perejil, sal y pimienta. Hay quien le añade mostaza. Lavamos los mojojones y los ponemos al fuego en una cazuela grande para que se abran. Entonces los pasamos a otra cazuela grande, quitamos media concha y los regamos con el caldo de la primera hervida. Rehogamos en aceite los puerros picados muy finos, añadimos una cucharada de harina, y juntamos los mojojones y un vaso de chacolí. Hervimos unos diez minutos y añadimos el zumo de medio limón y un poco de pimienta. Dejar que se enfríen y ponemos una buena cantidad de perejil por encima, y a servir.
ReferenciasApicio, M.G. 2007. De re coquinaria. El arte de la cocina. Recetas de la Roma Imperial. Comunicaciones y Publicaciones. Barcelona. 119 pp.
Arroyo-García, R. et al. 2006. Multiple origins of cultivated grapevine (Vitis vinifera L. ssp. sativa) based on chloroplast DNA polymorphisms. Molecular Ecology 15: 3707-3714.
Azpiazu, I. 1989. La cocina tradicional vasca. Ed. Iru. Barcelona. 64 pp.
Barnard, H. et al. 2010. Chemical evidence for wine production around 4000 BCE in the Late Chalcolithic Near Eastern highlands. Journal of Archaeological Science doi: 10.1016/j.jas.2010.11.012.
Biblia de Jerusalén. 1967. Desclée de Brouwer Eds. Bilbao. 1693 pp.
Brothwell, D. & P. Brothwell. 1998. Food in Antiquity. A survey of the diet of early peoples. Johns Hopkins University Press. Baltimore and London. 283 pp.
Buxó, R. 1997. Arqueología de las plantas. La explotación económica de las semillas y los frutos en el marco mediterráneo de la Península Ibérica. Crítica. Barcelona. 367 pp.
Carbonell, E. et al. 2016. Recetas paleo. La dieta de nuestros orígenes para una vida saludable. Ed. Planeta. Barcelona. 143 pp.
Dong, Y. et al. 2023. Dual domestications and origin of traits in grapevine evolution. Science 379: 892-901.
Granada, Fray Luis de. 1947. Maravillas de las plantas y de los animales. Apostolado de la Prensa. Madrid. 184 pp.
Harris, S. 2021. Plantas legendarias: 50 plantas que cambiaron el mundo. Rey Naranjo Eds. Barcelona. 358 pp.
Hayward, V. 2017. Nuevo arte de la cocina española de Juan Altamiras. Círculo de Lectores. Barcelona. 493 pp.
Hernández-Hernández, A. et al 2023. Mediterranean alcohol-drinking pattern and arterial hypertension in the “Seguimiento Universidad de Navarra” (SUN) prospective cohort study. Nutrients doi: 10.3390/nu15020307.
Janick, J. 2007. Fruits of the Bibles. HortScience 42: 1072-1076.
Koh, A. J. et al. 2014. Characterizing a Middle Bronze palatial wine cellar from Tel Kabri, Isr ael. PLOS One 9: e106406.
Luelmo, J. 1975. Historia de la agricultura en Europa y América. Ed. Istmo. Madrid. 469 pp.
McGovern, P.E. et al. 1996. Neolithic resonated wine. Nature 381: 480-481.
Myles, S. et al. 2011. Genetic structure and domestication history of the grape. Proceedings of the National Academy of Sciences USA 108: 3530-3535.
Payo, A. 2023. Los ciclos glaciares determinaron la domesticación de la uva y la aparición del vino. Boletín SiNC 2 marzo.
Piqueras Haba, J. 2005. La filoxera en España y su difusión espacial: 1878-1926. Cuadernos de Geografía 77: 101-136.
Revel, J.-F. 1996. Un festín de palabras. Historia literaria de la sensibilidad gastronómica desde la Antigüedad hasta nuestros días. Tusquets Eds. Barcelona. 289 pp.
Santana, J.C. et al. 2010. Genetic structure, origins, and relationships of grapevine cultivars from the Castilian Plateau of Spain. American Journal of Enology and Viticulture 61: 214-224.
Silvertown, J. 2019. Cenando con Darwin. Tras las huellas de la evolución en nuestros alimentos. Crítica. Barcelona.285 pp.
Wikipedia. 2023. Vino. 14 marzo.
Zohary, D. & P. Spiegel-Roy. 1975. Beginnings of fruit growing in the Old World. Science 187: 319-327.
Para saber más:El consumo del alcohol no mata a las neuronas, pero sí las trastorna
La podredumbre noble: Cuando una infección mejora un vino
«Una copita de vino es buena para el corazón». Claro que sí, guapi.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Ingredientes para la receta: la vid se ha escrito en Cuaderno de Cultura Científica.
BCAM-Naukas 2023: Las sencillas matemáticas de nuestro universo
Quizás sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que existen en el mundo, estudiada por el ser humano desde hace más de 4.000 años. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
La fascinación que ha suscitado durante siglos es tal que el popular número cuenta con su propio día en el calendario, así el mes de marzo se celebra el Día de Pi en todo el planeta.

Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han sumado a la celebración, organizando la cuarta edición del evento BCAM NAUKAS, que tuvo lugar el 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
Las distribuciones normales, las famosas campanas de Gauss, aparecen tanto al hacer mediciones como en aquellos lugares del universo donde podamos hablar de poblaciones en sentido amplio. Laura Toribio nos explica qué son las funciones normales y nos da ejemplos de donde encontrarlas.
Laura Toribio San Cipriano es investigadora postdoctoral en el CIEMAT en cosmología. Licenciada en matemáticas por la Universidad de Salamanca, obtuvo su doctorado en astrofísica por la Universidad de la Laguna. Es una activa divulgadora científica.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo BCAM-Naukas 2023: Las sencillas matemáticas de nuestro universo se ha escrito en Cuaderno de Cultura Científica.
Células solares de perovskitas más estables
Los integrantes de la familia de compuestos, incluyendo sintéticos, que tienen el mismo tipo de fórmula química básica (ABX3, donde A y B son dos cationes y X es un anión, muchas veces un óxido) y estructura cristalina que el mineral perovskita CaTiO3, se conocen como perovskitas. En esta estructura se pueden integrar muchos cationes diferentes, lo que permite el desarrollo de diversos materiales de ingeniería.
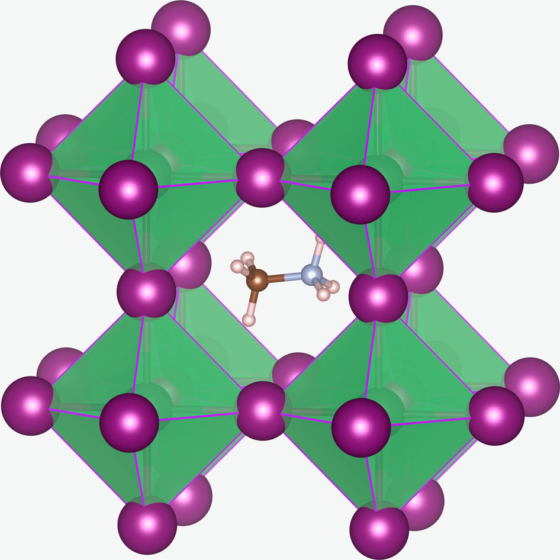 Estructura cristalina de una perovskita de CH3NH3PbX3 (X= I, Br, Cl). El catión metilamonio CH3NH3+ está rodeado por octaedros de PbX6
Estructura cristalina de una perovskita de CH3NH3PbX3 (X= I, Br, Cl). El catión metilamonio CH3NH3+ está rodeado por octaedros de PbX6Las células solares de perovskitas podrían ser la alternativa a las de silicio cristalino comercializadas actualmente, ya que presentan ventajas importantes frente a los paneles convencionales, como una mayor eficiencia (superior al 25%) y un menor coste. Las células de perovskita se fabrican mediante un proceso de deposición y cristalización a partir de una disolución (en esencia, de la misma forma que se obtiene la sal en una salina), lo que resulta económicamente mucho más barato y menos contaminante que la purificación del silicio.
Pero existe un motivo por el que las perovskitas aun no han reemplazado al silicio comercialmente: su estabilidad. Es en esta área donde actualmente se concentra la investigación científica.
Un equipo de investigadores de la Universidad de Oxford liderados por Henry Snaith (Universidad de Oxford, Reino Unido) y Juan Luis Delgado (Ikerbasque, POLYMAT y la Universidad del País Vasco, España) han unido fuerzas para investigar la utilización de aditivos de última generación para obtener células solares de alta eficiencia y estabilidad.
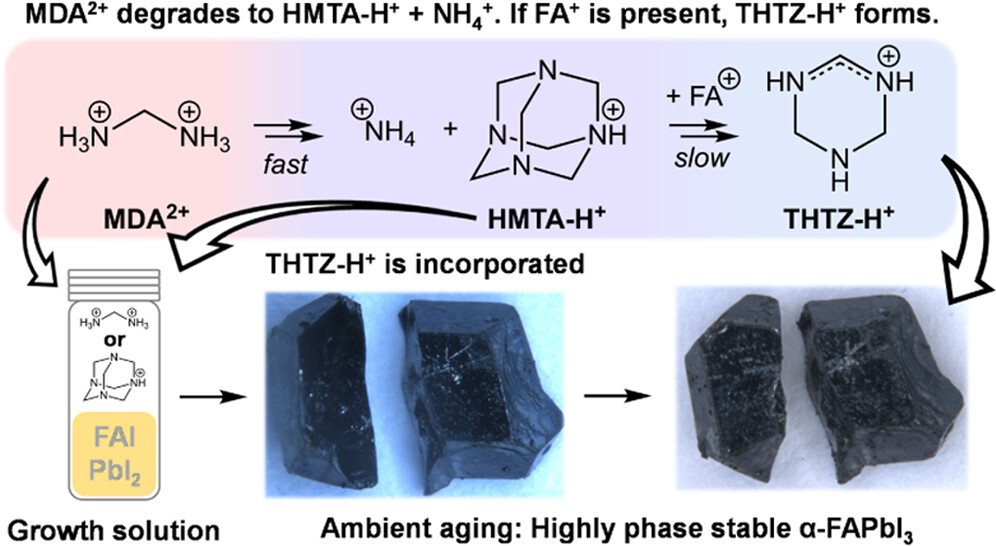
En los últimos tres años varios grupos de investigación han descrito células solares de perovskitas altamente eficientes mediante la incorporación de una pequeña cantidad de aditivo (dicloruro de metilendiamonio) hasta lograr la mayor eficiencia certificada hasta ahora para células solares de perovskitas (25,7% PCE). El equipo de investigación ha explorado los mecanismos tras este logro y cómo afecta el aditivo a la estabilidad. Para ello se ha centrado en el papel del aditivo durante el crecimiento de los cristales de la perovskita. Ha encontrado que este aditivo se descompone en el tiempo a formas químicas más estables que confieren una estabilidad mejorada a la perovskita (>1 año expuesta al aire).
Estos resultados tendrán consecuencias directas para el futuro desarrollo de dispositivos fotovoltaicos de perovskitas estables y de alta eficiencia.
Para saber más:
Paneles solares orgánicos…y de colores
Materiales tipo perovskita como contacto en pilas de combustible de óxido sólido
Referencia:
Elisabeth A. Duijnstee, Benjamin M. Gallant, Philippe Holzhey, Dominik J. Kubicki, Silvia Collavini, Bernd K. Sturdza, Harry C. Sansom, Joel Smith, Matthias J. Gutmann, Santanu Saha, Murali Gedda, Mohamad I. Nugraha, Manuel Kober-Czerny, Chelsea Xia, Adam D. Wright, Yen-Hung Lin, Alexandra J. Ramadan, Andrew Matzen, Esther Y.-H. Hung, Seongrok Seo, Suer Zhou, Jongchul Lim, Thomas D. Anthopoulos, Marina R. Filip, Michael B. Johnston, Robin J. Nicholas, Juan Luis Delgado, and Henry J. Snaith (2023) Understanding the Degradation of Methylenediammonium and Its Role in Phase-Stabilizing Formamidinium Lead Triiodide J. Am. Chem. Soc.https://doi.org/10.1021/jacs.3c01531
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Células solares de perovskitas más estables se ha escrito en Cuaderno de Cultura Científica.
Leyendas volcánicas
Los volcanes siempre han supuesto una fascinación para el ser humano. Temblores de tierra, fracturas del terreno de la que surgen grandes nubes de gases que oscurecen el día y enormes fragmentos de rocas negras y fuego brillante escupidos al cielo, lava que luego fluye por las laderas de las montañas como ríos candentes. ¿Quién no se asombraría viendo todo esto? Si encima le sumamos que, cuando ocurre una erupción en zonas habitadas las pérdidas sociales, económicas y, desgraciadamente, en muchas ocasiones también de vidas humanas son cuantiosas, ¿quién no se preguntaría si puede tratarse de algún tipo de castigo contra la población?
Esa atracción por el evento natural, unido al miedo a perder la vida, ha provocado que las sociedades humanas, a lo largo de la historia, hayan buscado una explicación para las erupciones volcánicas. Y si por algo se caracteriza nuestra especie es por inventar historias lo más épicas y llamativas posibles cuando el conocimiento científico no está lo suficientemente desarrollado como para dar un razonamiento basado en la evidencia. Así es como nacen los mitos y leyendas que se van transmitiendo de generación en generación.
 La Fragua de Vulcano, obra pintada por Diego Rodríguez de Silva y Velázquez en el año 1630 que está expuesta en el Museo del Prado (Madrid). Imagen: Museo Nacional del Prado
La Fragua de Vulcano, obra pintada por Diego Rodríguez de Silva y Velázquez en el año 1630 que está expuesta en el Museo del Prado (Madrid). Imagen: Museo Nacional del PradoEs probable que os suene el nombre de Hefesto, el dios griego del fuego, la forja y la metalurgia. Según algunas leyendas, Hefesto estableció sus fraguas en el interior de varias montañas del Sur de las actuales Grecia e Italia, aunque parece que tenía preferencia por quedarse bajo el monte Etna. Allí, el dios se dedicaba a crear armas, ingenios mecánicos y regalos metálicos para otras divinidades y algunos semidioses como Aquiles o Heracles. Y las manifestaciones en superficie de sus martillazos y templados del material forjado eran los temblores de tierra, los ruidos ensordecedores, la expulsión de gases y la salida de lava ardiente que ocurrían, de vez en cuando, en estas montañas. Puede que os suene un poco más todo esto si os digo que los romanos, tras algunos pequeños retoques en la historia, llamaron a este dios Vulcano, del que procede la palabra volcán.
Pero la mitología griega clásica tiene un montón de versiones de la misma historia. Hay una reinterpretación de esta leyenda en la que se cuenta que, bajo estos volcanes mediterráneos, están encerrados algunos de los gigantes que se rebelaron contra los dioses en los primeros tiempos de dominio de los olímpicos. Y esas manifestaciones propias de una erupción volcánica son los lamentos, el aliento de fuego y los golpes contra los muros de la prisión propinados por estos gigantes en sus intentos de liberarse de su cautiverio.
 Póster promocional de la película “El Señor de los Anillos: El Retorno del Rey”, estrenada en 2003, dirigida por Peter Jackson y distribuida por New Line Cinema, donde se representa el paisaje volcánico de Mordor. Imagen propiedad de New Line Cinema, tomada de tolkiengateway.net
Póster promocional de la película “El Señor de los Anillos: El Retorno del Rey”, estrenada en 2003, dirigida por Peter Jackson y distribuida por New Line Cinema, donde se representa el paisaje volcánico de Mordor. Imagen propiedad de New Line Cinema, tomada de tolkiengateway.netAunque tampoco hay que retroceder milenios en nuestra historia para encontrar leyendas similares. En el mundo fantástico creado por el escritor J. R. R. Tolkien en pleno siglo XX podemos encontrarnos una tierra baldía y negra, en la que mora el mal más tenebroso, llamada Mordor, en cuya parte central se alza una imponente montaña conocida como el Monte del Destino, en cuyo interior Sauron forjó el Anillo Único. Como os podéis imaginar, el Monte del Destino es un enorme volcán y las llanuras de Mordor están formadas por materiales volcánicos, principalmente coladas de lava enfriadas y piroclastos (es decir, fragmentos solidificados de lava que salen expulsados del cráter volcánico en las erupciones explosivas) de diferentes tamaños acumulados erupción tras erupción. Pero es que el propio escritor reconoció que se basó en el Estrómboli y el aspecto de las cuencas volcánicas del margen mediterráneo europeo para dar forma a estas tierras fantásticas. Creo que no hace falta decir en quién estaba pensando cuando puso a Sauron a forjar el anillo.
 Volcanes Popocatépetl (que significa “Montaña Humeante”), al fondo de la imagen, e Iztaccíhuatl (traducido como “Mujer Dormida”), en primer término. Imagen cortesía de Diario Cambio (México)
Volcanes Popocatépetl (que significa “Montaña Humeante”), al fondo de la imagen, e Iztaccíhuatl (traducido como “Mujer Dormida”), en primer término. Imagen cortesía de Diario Cambio (México)Supongo que no os he sorprendido mucho hasta el momento con estas leyendas bastante conocidas. Por eso ahora quiero contaros otra que, espero, no os suene tanto. Aprovechando que el volcán Popocatépetl está despertando, manteniendo en vilo a miles de personas en México, os voy a contar la bonita, a la par que triste, historia azteca sobre su formación.
Cuenta la leyenda que una joven princesa azteca estaba prometida a un joven cacique que la amaba con pasión. Pero el muchacho tuvo que ir a la guerra con otros pueblos cercanos, momento que aprovechó un rival en el amor de la chica para engañarla contándole que su prometido había muerto en batalla. Tras romperle el corazón con la noticia, el traidor la prometió en matrimonio con la excusa de consolar su dolor. Pero, como no podía ser de otra manera, nuestro héroe volvió victorioso de la batalla y, al enterarse del engaño del rival, le retó a un combate para recuperar su honor y el de su amada. Por supuesto, el protagonista de la historia venció en la lucha, haciendo que el traidor huyese, quedando como un embustero y, a la vez, un cobarde. Aunque ahora viene el giro dramático. Cuando el héroe corrió para encontrarse con su amada, la encontró tendida en el suelo de un frondoso valle. La muchacha se había quitado la vida al sentirse deshonrada por el vil mentiroso. Entonces el héroe se arrodilló a su lado y lloró amargamente. Este dolor hizo estremecerse a los propios dioses, que expresaron su rabia haciendo que la tierra temblase, se abriese en dos y surgieran fuego y rocas que llegaron a oscurecer el día. Cuando la ira de los dioses se calmó, los habitantes de la zona descubrieron que, en lo que antes era un valle tranquilo, habían surgido dos enormes montañas: una con la figura de una mujer dormida (Iztaccíhuatl) y otra con la de un guerrero arrodillado a su lado (Popocatépetl).
Si queréis oír una versión más bonita y poética de esta historia, en la que una erupción volcánica dio origen a dos montañas formadas por la acumulación de lava solidificada y piroclastos, os recomiendo la canción “La Mujer Dormida (La Leyenda de Popocatépetl y Iztaccíhuatl)” del grupo español de folk metal Saurom (en este caso, terminado en la letra eme, aunque me permite relacionar todas las historias entre sí, aunque sea un poco “por los pelos”).
Hoy en día, gracias a los avances en la investigación y el conocimiento geológicos podemos darle una explicación científica al vulcanismo que, además, nos permite anticiparnos a las erupciones más peligrosas para prevenir los riesgos en la población. Pero a mí me sigue gustando recordar estas historias mitológicas cuando veo imágenes de erupciones en directo, porque me permiten ponerme en la piel de las civilizaciones pasadas, que alucinaban igual que yo con el tremendo poder de la naturaleza que representa un volcán activo, buscando una explicación de lo que estaban presenciando. Y, encima, son historias curiosas, emotivas y muy bonitas.
Para saber más:
Montañas y mitos
La Geología según Heracles
Los volcanes submarinos de Bizkaia y Gipuzkoa
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Leyendas volcánicas se ha escrito en Cuaderno de Cultura Científica.
Grande, pero no infinito
De un tiempo a esta parte
el infinito
se ha encogido
peligrosamente.
Quién iba a suponer
que segundo a segundo
cada migaja
de su pan sin límites
iba así a despeñarse
como canto rodado
en el abismo.
 Nina Rassen, Laws of the Creation: Law 3. Fuente: Wikimedia Commons.
Nina Rassen, Laws of the Creation: Law 3. Fuente: Wikimedia Commons.En matemáticas, la idea de infinito es difícil de aprehender; no hay un único infinito. Por ejemplo, los conjuntos de los números enteros y de los números reales son infinitos, pero el primero es numerable y el segundo no lo es. Ambos son conjuntos infinitos, pero “de distinto tamaño”.
Cuando hablamos de manera informal, mencionamos al infinito para referirnos a algo “muy grande”, a algo inalcanzable o lejano, a algo que no termina nunca. El infinito puede producir desasosiego; incluso existen personas que padecen de apeirofobia, de fobia al infinito.
Las dos propuestas siguientes involucran números muy grandes, pero no infinitos.
La biblioteca de BabelEl universo (que otros llaman la Biblioteca) se compone de un número indefinido, y tal vez infinito, de galerías hexagonales, con vastos pozos de ventilación en el medio, cercados por barandas bajísimas. Desde cualquier hexágono se ven los pisos inferiores y superiores: interminablemente.
Así comienza el cuento La Biblioteca de Babel de Jorge Luis Borges, que describe más adelante la composición de cada uno de los libros que la forman:
[…] cada libro es de cuatrocientas diez páginas; cada página, de cuarenta renglones; cada renglón, de unas ochenta letras de color negro.
[…] El número de símbolos ortográficos es veinticinco.
La biblioteca es enorme, aunque no infinita: si todos los libros se limitan a 410 páginas, tenemos 410 x 40 x 80 = 1 312 000 caracteres por libro. Cada carácter puede tomar 25 valores, con lo que hay más de 251312000 libros diferentes. Escribir esta cantidad de libros requiere unas 1 834 100 cifras (este es el valor aproximado de 1 312 000 log(25), donde log(b)=a si b=10a). Y, efectivamente, se trata de un número muy grande; para imaginarlo, pensemos que 10p se escribe con p+1 cifras…
Este desasosegante relato finaliza de esta manera:
[…] sospecho que la especie humana –la única– está por extinguirse y que la Biblioteca perdurará: iluminada, solitaria, infinita, perfectamente inmóvil, armada de volúmenes preciosos, inútil, incorruptible, secreta.
En esa biblioteca, por supuesto, no se aloja El libro de arena. No cumple las reglas respecto al número de páginas, de renglones y de letras; este libro sí es infinito:
El número de páginas de este libro es exactamente infinito. Ninguna es la primera; ninguna la última. No sé por qué están numeradas de ese modo arbitrario. Acaso para dar a entender que los términos de una serie infinita admiten cualquier número.
Que(ved)(n)eauQue(ved)(n)eau es el título de un poemario de la escritora Sofía Rhei en el que rinde homenaje a los escritores Francisco de Quevedo y Raymond Queneau (para comprender el título, “eau” se pronuncia como la vocal “o” en castellano).
De Quevedo, Sofía Rhei toma el soneto Amor constante, más allá de la muerte:
Cerrar podrá mis ojos la postrera
sombra que me llevare el blanco día,
y podrá desatar esta alma mía
hora a su afán ansioso lisonjera;
mas no, de esotra parte, en la ribera,
dejará la memoria, en donde ardía:
nadar sabe mi llama la agua fría,
y perder el respeto a ley severa.
Alma a quien todo un dios prisión ha sido,
venas que humor a tanto fuego han dado,
medulas que han gloriosamente ardido,
su cuerpo dejará, no su cuidado;
serán ceniza, mas tendrá sentido;
polvo serán, mas polvo enamorado.
Y de este poema imita las rimas. Además, se inspira en Cent mille milliards de poèmes de Queneau para estructurar su poemario.
 Cómo leer Cent mille milliards de poèmes. Fuente: Marta Macho Stadler.
Cómo leer Cent mille milliards de poèmes. Fuente: Marta Macho Stadler.Que(ved)(n)eau consta de diecinueve sonetos (dos cuartetos y dos tercetos) que se imprimen sobre diecinueve páginas –uno por página–. Después se recortan en tiras los catorce versos de cada uno de los diecinueve poemas.
De esta manera, se pueden crear nuevos sonetos decidiendo, por ejemplo, leer el primer verso del séptimo poema, seguido del segundo verso del décimo, del tercero del segundo, etc. ¿Cuántos sonetos podrían generarse de esta manera?
Hay diecinueve posibles maneras de elegir primer verso, diecinueve modos de seleccionar el segundo de manera independiente, y así hasta el catorce. Son, por lo tanto, 1914 = 799 006 685 782 884 096 posibles sonetos, aproximadamente 799 × 1015, es decir, 799 000 billones de poemas.
En Cent mille milliards de poèmes de Queneau, que incluye 1014 sonetos, el autor realiza un cálculo aproximado del tiempo que se precisaría para leer todos los poemas posibles contenidos. Tiene en cuenta las siguientes suposiciones: se necesitan 45 segundos para leer un poema, 15 segundos para cambiar las tiras, 8 horas de lectura al día y 200 días de lectura al año. Según la estimación de Queneau, la lectura de cada poema –incluido el cambio de tiras– precisaría un minuto; ocho horas de lectura durante doscientos días significan 96 000 minutos invertidos cada año. Y 1014 / 96 000 son aproximadamente 1 042 000 000 años. Es decir, se necesitarían 10 420 000 siglos para completar la lectura del libro.
Que(ved)(n)eau precisaría aún más tiempo. Según las reglas de Queneau serían necesarios 1914 / 96 000 años de lectura, más de 8,3 × 1012 años, es decir, más de 8,3 × 1010 siglos. Sin duda mucho tiempo para nuestras cortas vidas, aunque no sea infinito… Por cierto, Quevedo ya se había encontrado con el infinito en su soneto satírico A una nariz, donde describe la nariz de Luis de Góngora. El terceto final no deja lugar a dudas sobre el tamaño:
[…] Érase un naricísimo infinito,
muchísimo nariz, nariz tan fiera
que en la cara de Anás fuera delito.
Referencias
VV. AA. Textos potentes. Atlas de literatura potencial 2. Pepitas de Calabaza, 2019
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Grande, pero no infinito se ha escrito en Cuaderno de Cultura Científica.
Los recuerdos ayudan a los encéfalos a reconocer los nuevos eventos que merecen recordarse
Los recuerdos pueden afectar lo bien que aprenderá el encéfalo sobre eventos futuros al cambiar nuestras percepciones del mundo.
Un artículo de Yasemin Saplakoglu. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Los recuerdos de eventos pasados significativos sintonizan nuestras percepciones con eventos relacionados en el futuro y nos preparan para recordar más sobre ellos. Ilustración: Kristina Armitage / Quanta Magazine
Los recuerdos de eventos pasados significativos sintonizan nuestras percepciones con eventos relacionados en el futuro y nos preparan para recordar más sobre ellos. Ilustración: Kristina Armitage / Quanta MagazineLos recuerdos son sombras del pasado pero también linternas para el futuro.
Nuestros recuerdos nos guían por el mundo, afinan nuestra atención y dan forma a lo que aprendemos más adelante en la vida. Los estudios en humanos y animales han demostrado que los recuerdos pueden alterar nuestras percepciones de eventos futuros y la atención que les damos. “Sabemos que la experiencia pasada cambia las cosas”, afirma Loren Frank, neurocientífico de la Universidad de California en San Francisco. «Cómo sucede exactamente esto no siempre está claro».
Un nuevo estudio publicado en la revista Science Advances ofrece ahora parte de la respuesta. Trabajando con caracoles, los investigadores han examinado cómo los recuerdos consolidados hacen que los animales tengan más probabilidades de formar nuevos recuerdos a largo plazo de eventos futuros relacionados que, de otro modo, podrían haber ignorado. El mecanismo simple que han descubierto hace esto alterando la percepción que el caracol tiene de estos eventos.
Los investigadores redujeron el fenómeno de cómo el aprendizaje pasado influye en el aprendizaje futuro «hasta una sola célula», explica David Glanzman, biólogo celular de la Universidad de California en Los Ángeles, que no participó en el estudio. Lo describe como un ejemplo atractivo «de usar un organismo simple para tratar de comprender los fenómenos de comportamiento que son bastante complejos».
Aunque los caracoles son criaturas bastante simples, la nueva información lleva a los científicos un paso más cerca de comprender la base neuronal de la memoria a largo plazo en animales de orden superior como los humanos.
Aunque a menudo no somos conscientes del reto, la formación de la memoria a largo plazo es «un proceso increíblemente energético», afirma Michael Crossley, investigador principal de la Universidad de Sussex y autor principal del nuevo estudio. Dichos recuerdos dependen de que forjemos conexiones sinápticas más duraderas entre las neuronas, y las células encefálicas necesitan reclutar muchas moléculas para hacer eso. Por lo tanto, para conservar recursos, un encéfalo debe ser capaz de distinguir cuándo vale la pena el coste de formar un recuerdo y cuándo no. Esto es cierto ya sea el encéfalo de un ser humano o el de un «pequeño caracol con un presupuesto energético ajustado», explica.
En una videollamada reciente, Crossley mostró uno de esos caracoles, un molusco Lymnaea del tamaño de un pulgar con un encéfalo que llamó «hermoso». Mientras que el encéfalo humano tiene 86 mil millones de neuronas, el del caracol tiene solo 20 000, pero cada una de sus neuronas es 10 veces más grande que las nuestras y son mucho más accesibles para el estudio. Estas neuronas gigantes y su circuitería encefálica bien mapeada han hecho de los caracoles un tema favorito de la investigación neurobiológica.
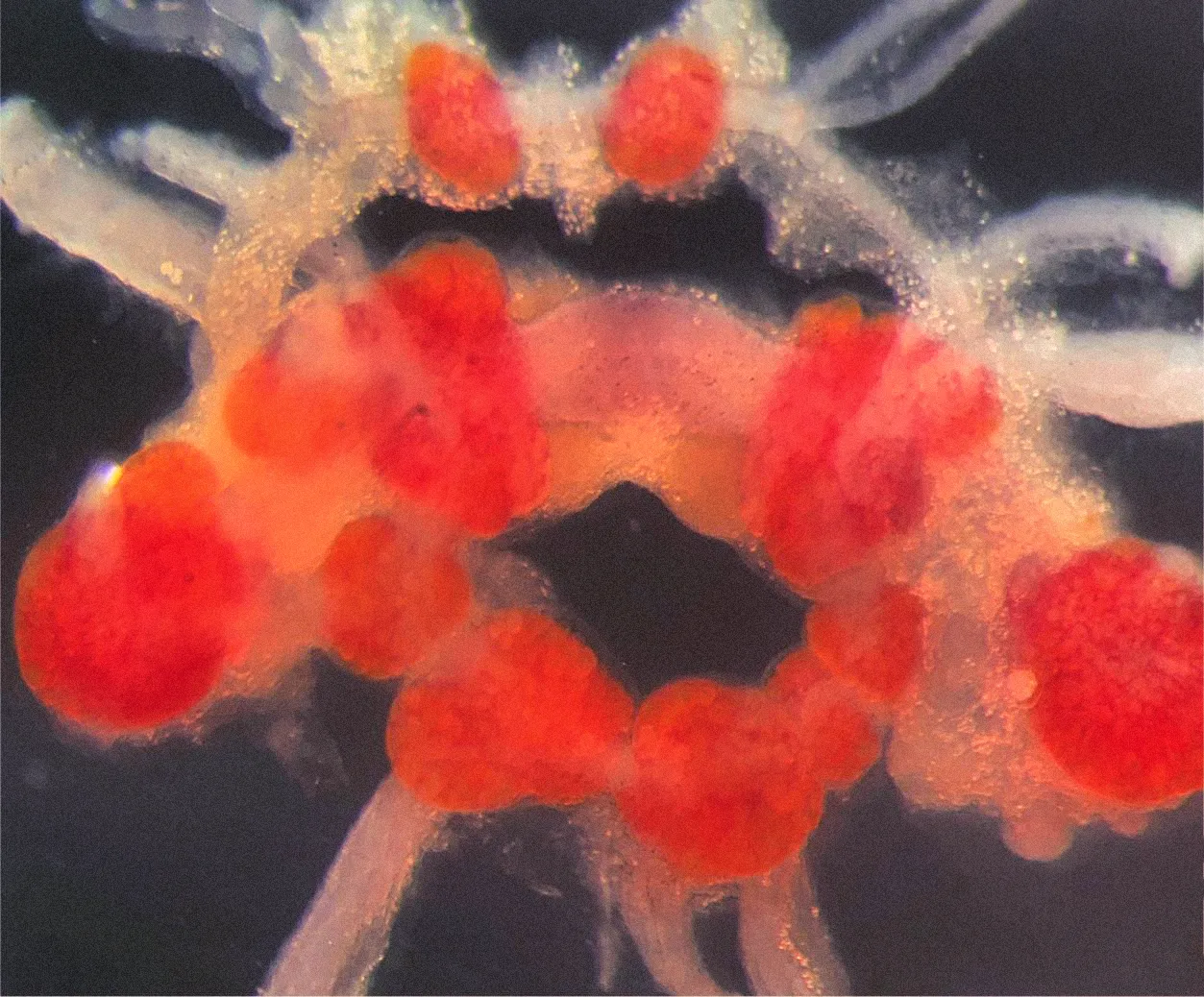 Investigadores de la Universidad de Sussex rastrearon un comportamiento aprendido en los caracoles Lymnaea hasta un circuito de solo cuatro neuronas en su encéfalo. Fuente: Michael Crossley and Kevin Staras
Investigadores de la Universidad de Sussex rastrearon un comportamiento aprendido en los caracoles Lymnaea hasta un circuito de solo cuatro neuronas en su encéfalo. Fuente: Michael Crossley and Kevin StarasLos pequeños recolectores también son «aprendices notables» que pueden recordar algo después de una sola exposición, continúa Crossley. En el nuevo estudio, los investigadores han observado profundamente los encéfalos de los caracoles para descubrir qué sucede a nivel neurológico cuando están creando recuerdos.
Recuerdos persuasivosEn sus experimentos, los investigadores dieron a los caracoles dos formas de entrenamiento: fuerte y débil. En un entrenamiento fuerte, primero rociaban a los caracoles con agua con sabor a plátano, que los caracoles tratan como neutral en su atractivo: tragan un poco pero después escupen un poco. Luego, el equipo les daba azúcar a los caracoles, que devoran con avidez.
Cuando comprobaron los caracoles hasta un día después, los caracoles demostraron que habían aprendido a asociar el sabor del plátano con el azúcar a partir de esa única experiencia. Los caracoles parecían percibir el sabor como más deseable: estaban mucho más dispuestos a tragar el agua.
Por el contrario, los caracoles no aprendieron esta asociación positiva en una sesión de entrenamiento débil, en la que a un baño con sabor a coco le sigue un postre de azúcar mucho más diluido. Los caracoles continuaron tragando y escupiendo el agua.
Hasta este punto, el experimento era esencialmente una versión para caracoles de los famosos experimentos de condicionamiento de Pavlov, en los que los perros aprendían a babear cuando escuchaban el sonido de una campana. Pero entonces los científicos observaron lo que sucedía cuando daban a los caracoles un entrenamiento fuerte con sabor a plátano seguido horas después por un entrenamiento débil con sabor a coco. De repente, los caracoles también aprendían del entrenamiento débil.
Cuando los investigadores cambiaron el orden e hicieron primero el entrenamiento débil, nuevamente falló en crear un recuerdo. Los caracoles aún formaban un recuerdo del entrenamiento fuerte, pero eso no tuvo un efecto de fortalecimiento retroactivo en la experiencia anterior. Intercambiar los sabores utilizados en los entrenamientos fuertes y débiles tampoco tuvo efecto.
Los científicos concluyen que el entrenamiento fuerte lleva a los caracoles a un período «rico en aprendizaje» en el que el umbral para la formación de recuerdos es más bajo, lo que les permite aprender cosas que de otro modo no aprenderían (como la asociación del entrenamiento débil entre un sabor y azúcar diluida). Un mecanismo así podría ayudar al encéfalo a dirigir los recursos hacia el aprendizaje en los momentos oportunos. La comida podría hacer que los caracoles estén más alerta ante posibles fuentes de alimento cercanas; los roces con el peligro podrían agudizar su sensibilidad a las amenazas.
Un caracol Lymnaea que asocia agua aromatizada con azúcar abre y cierra rápidamente la boca para tragarla (derecha). Un caracol que no ha aprendido esa asociación mantiene la boca cerrada (izquierda). Fuemte: Michael Crossley y Kevin StarasSin embargo, el efecto sobre los caracoles es fugaz. El período rico en aprendizaje persistía solo de 30 minutos a cuatro horas después del entrenamiento fuerte. Después de eso, los caracoles dejaban de formar recuerdos a largo plazo durante la sesión de entrenamiento débil, y no era porque hubieran olvidado su entrenamiento fuerte, el recuerdo persistió durante meses.
Tener una ventana crítica para el aprendizaje mejorado tiene sentido porque si el proceso no cesa, «eso podría ser perjudicial para el animal», explica Crossley. No solo podría el animal invertir demasiados recursos en el aprendizaje, sino que podría aprender asociaciones dañinas para su supervivencia.
Percepciones alteradasUsando electrodos, los investigadores descubrieron qué sucede dentro del encéfalo de un caracol cuando forma recuerdos a largo plazo durante los entrenamientos. Se producen dos ajustes paralelos en la actividad encefálica. El primero codifica el recuerdo en sí. El segundo está “estrictamente dedicado a alterar la percepción del animal de otros eventos”, afirma Crossley. “Cambia la forma en que ve el mundo en función de sus experiencias pasadas”.
También descubrieron que podían inducir el mismo cambio en la percepción de los caracoles al bloquear los efectos de la dopamina, la sustancia química encefálica producida por la neurona que activa el comportamiento de escupir. En efecto, esto apaga la neurona para escupir y deja encendida constantemente la neurona para tragar. La experiencia tuvo el mismo efecto de arrastre que el entrenamiento fuerte tuvo en los experimentos anteriores: horas más tarde, los caracoles formaron un recuerdo a largo plazo a partir del entrenamiento débil.
Los investigadores trazan completa y elegantemente un mapa del proceso desde «el comportamiento hasta los fundamentos electrofisiológicos de esta interacción entre los recuerdos pasados y nuevos», comenta Pedro Jacob, becario postdoctoral en la Universidad de Oxford que no participó en el estudio. «Tener el conocimiento de cómo sucede esto mecánicamente es interesante porque probablemente se conserve entre las especies».
Frank, sin embargo, no está completamente convencido de que el hecho de que los caracoles no hayan ingerido agua aromatizada después del entrenamiento débil signifique que no recordaban nada. Puedes tener un recuerdo pero no actuar basándote en él, afirma, por lo que hacer esta distinción puede requerir experimentos de seguimiento.
Los mecanismos trás el aprendizaje y la memoria son sorprendentemente similares en moluscos y mamíferos como los humanos, afirma Glanzman. Hasta donde saben los autores, este mecanismo exacto no se ha demostrado en humanos, explica Crossley. “Podría ser una característica ampliamente conservada y, por lo tanto, una que merece más atención”, concluye.
Sería interesante estudiar si un cambio en la percepción podría hacerse más permanente, comenta Glanzman. Sospecha que esto podría ser posible si a los caracoles se les da un estímulo aversivo, algo que los ponga enfermos en lugar de algo que les guste.
Por ahora, Crossley y su equipo sienten curiosidad por saber qué sucede en el encéfalo de estos caracoles cuando realizan múltiples comportamientos, no solo abrir o cerrar la boca. “Estas son criaturas fascinantes”, dice Crossley. «Realmente no te esperas que estos animales puedan realizar este tipo de procesos complejos».
El artículo original, Memories Help Brains Recognize New Events Worth Remembering, se publicó el 17 de mayo de 2023 en Quanta Magazine.
Traducido por César Tomé López
Nota del editor de Quanta: Loren Frank es investigador de la Iniciativa de Investigación del Autismo de la Fundación Simons (SFARI). La Fundación Simons también financia Quanta como revista editorialmente independiente. Las decisiones de financiación no tienen influencia en nuestra cobertura.
El artículo Los recuerdos ayudan a los encéfalos a reconocer los nuevos eventos que merecen recordarse se ha escrito en Cuaderno de Cultura Científica.
No, un metabolismo basal más lento no es el culpable de que ganes kilos con los años
metabolismo basal
El sobrepeso y la obesidad son dos graves problemas de salud pública que causan de, forma directa o indirecta, en torno a 130.000 muertes al año en España. Estas enfermedades se han convertido en unos de los principales riesgos para la salud, al aumentar de forma significativa el riesgo de sufrir diabetes tipo 2, enfermedades cardiovasculares, dolencias articulares, apnea del sueño, trastornos del ánimo y otros muchos problemas para la salud.
 Foto: Towfiqu barbhuiya / Unsplash
Foto: Towfiqu barbhuiya / UnsplashDesde hace décadas, las cifras de sobrepeso y obesidad han ido incrementándose de forma progresiva hasta el punto de que en la actualidad más del 25 % de la población española sufre sobrepeso u obesidad. Todo apunta a que los casos de exceso de peso corporal irán a más en un futuro próximo. De seguir el ritmo actual, un estudio publicado en la Revista Española de Cardiología anticipa que el 55 % de las mujeres y el 80 % de los hombres serán obesos en nuestro país en 2030.
Las razones detrás de este fenómeno son múltiples y están interrelacionadas. Un factor de peso que contribuye a ello es el creciente sedentarismo entre los ciudadanos de nuestro país. Según el Eurobarómetro de 2022, el 58 % de los españoles nunca o raramente hace ejercicio físico o deporte. Por otro lado, en España se come cada vez peor: la dieta de gran parte de la población ha empeorado con el tiempo, con una presencia cada vez mayor de alimentos ultraprocesados (hipercalóricos, ricos en azúcares, grasas saturadas y sal), en detrimento de frutas, verduras y legumbres.
Sin embargo, tras el sedentarismo y una mala alimentación hay, en realidad, numerosos factores (determinantes sociales de la salud) que predisponen a caer en estos comportamientos: la falta de recursos económicos, el tiempo limitado para hacer la compra y cocinar, la publicidad de alimentos insanos, el predominio del ocio frente a las pantallas entre los jóvenes…
En la gran mayoría de los casos, el sobrepeso y la obesidad no aparece de la noche a la mañana, sino que se desencadenan de forma lenta, con la acumulación progresiva de kilos a lo largo de los años. En ese sentido, existe un mito muy extendido entre las sociedades occidentales: los adultos engordan, en parte, por un metabolismo más lento conforme se van cumpliendo años. De esta forma, aunque mantengamos el mismo nivel de actividad física y la misma dieta, ganar kilos es inevitable. ¿Qué hay de cierto en ello?
En primer lugar, lo que se conoce como metabolismo basal o tasa metabólica basal (TMB) es la energía que consume el organismo para realizar las funciones vitales básicas como el mantenimiento de la temperatura corporal, la respiración, la contracción cardíaca, el peristaltismo intestinal, la actividad cerebral, la producción de orina por parte de los riñones, la reparación o regeneración de los tejidos… En otras palabras, es el gasto calórico mínimo necesario para simplemente mantenernos con vida, sin considerar la actividad física.
Entonces, ¿cómo varía la TMB a lo largo de la vida? ¿»Quema» lo mismo un bebé, que un universitario o un anciano? Gracias a un extenso estudio, publicado en la revista Science en 2021, ahora conocemos muy bien cómo cambia nuestro metabolismo basal conforme vamos cumpliendo años. En esta investigación se analizó el gasto energético diario de más de 6.400 personas de 29 países diferentes y con edades que iban desde los 8 días tras el nacimiento hasta los 95 años. El gasto energético se evaluó gracias al agua doblemente marcada a partir de isótopos estables, no radiactivos, un método bastante preciso para este fin.
Los científicos descubrieron que, efectivamente, el metabolismo basal ajustado por el peso puede variar bastante a lo largo de la vida. No obstante, esto solo ocurre en cuatro etapas muy específicas. Los recién nacidos tienen un consumo metabólico equivalente a los adultos, pero a lo largo del primer año de vida experimentan un drástico incremento en su metabolismo, hasta el punto de que es un 50 % superior al de los adultos. Ya a partir del primer año y hasta los 20 años se produce un enlentecimiento progresivo del metabolismo (en torno a un 3 % al año). Entre los 20 y 60 años el consumo metabólico se mantiene estable y, a partir de los 60, este desciende un 0,7 % al año hasta llegar a un descenso del 20 % del gasto a los 95 años. Además, no hay diferencias evidentes entre el metabolismo de hombres y mujeres tras considerar la masa muscular y el tamaño corporal. En todo caso, sí que hay individuos que pueden tener un gasto energético considerablemente menor o mayor a lo esperado para su edad (25 % superior o inferior).
En otras palabras, un metabolismo basal más lento no es el culpable de que los adultos vayan ganando peso con la edad entre los 20 y 60 años, porque este metabolismo apenas varía en dicha etapa. ¿Por qué, entonces, tanta gente engorda a lo largo de la vida adulta? Generalmente, porque conforme se van cumpliendo años muchas personas tienden a tener una vida más sedentaria, comiendo lo mismo, lo que lleva irremediablemente a acumular grasa con el paso del tiempo por el menor gasto calórico total. Por esta y otras razones, fomentar la práctica de ejercicio físico y de deporte en nuestro país, a partir de múltiples y ambiciosas iniciativas por parte de las autoridades políticas y sanitarias, resulta esencial para limitar la «epidemia» de sobrepeso y obesidad a la que nos enfrentamos.
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo No, un metabolismo basal más lento no es el culpable de que ganes kilos con los años se ha escrito en Cuaderno de Cultura Científica.
Disponibilidad de alimento y fecundidad humana
 Jean-François Millet (1857) Des ganeuses / Las espigadoras. Óleo sobre lienzo. Fuente: Wikimedia Commons
Jean-François Millet (1857) Des ganeuses / Las espigadoras. Óleo sobre lienzo. Fuente: Wikimedia CommonsEn la especie humana, como en el resto de animales, la cantidad de alimento de que disponen los individuos –en el caso de nuestra especie, sobre todo las mujeres– influye de forma decisiva en la fecundidad. Esto, que parece obvio, no ha sido tan fácil de documentar, sobre todo porque en las sociedades desarrolladas contemporáneas la reproducción está sujeta a un control bastante efectivo por parte de las parejas y las decisiones reproductivas obedecen a razones de muy diversa índole.
Afortunadamente, se ha podido utilizar información histórica relativa a sociedades preindustriales para indagar acerca de estos asuntos. Un equipo de investigación ha recurrido a registros parroquiales para evaluar si existe alguna relación entre la fecundidad, por un lado, y el estatus socioeconómico, la disponibilidad de alimento y otros factores, por el otro. Para ello, han trabajado con registros parroquiales de zonas agrícolas de Finlandia que van de 1649 a 1900, y también han contado con datos relativos a las cosechas de centeno, el principal cereal y fuente de alimento del área en que se encontraban las parroquias estudiadas. Los investigadores estaban interesados en saber si el tiempo transcurrido desde el matrimonio hasta el primer alumbramiento puede considerarse un indicador adecuado de las condiciones nutricionales bajo las que vivían las parejas.
En promedio, el tiempo que transcurría entre el matrimonio y el nacimiento del primer hijo era de 25,9 meses, pero había diferencias significativas entre las tres clases socioeconómicas definidas por los investigadores, alta, media y baja. La mujeres pobres daban a luz a su primer hijo 2,6 meses después que las más acomodadas y 3,0 meses después que las de nivel intermedio. Las diferencias entre las mujeres de estos dos niveles, medio y alto, no eran significativas.
Las condiciones nutricionales –tal y como quedan reflejadas en la cosecha de grano de cada año– incidían en el tiempo transcurrido entre el casamiento y el primer nacimiento, pero solo en el caso de las mujeres de nivel económico bajo. Por lo tanto, las mujeres pobres eran las que sufrían las consecuencias de una menor disponibilidad de alimento sobre su capacidad para concebir. Las mujeres de nivel medio o alto, sin embargo, habrían gozado de recursos adicionales que les habrían permitido evadir o neutralizar los efectos de las malas cosechas.
Este estudio permitió al equipo de investigación llegar algo más lejos de donde se habían propuesto, ya que vieron que la duración del intervalo entre el casamiento y el primer alumbramiento estaba relacionada con otras variables reproductivas. Así, cuanto más corto era ese intervalo, la vida reproductiva era más prolongada, los intervalos entre nacimientos, más breves y, por lo tanto, el éxito reproductor global era mayor. Así pues, las mujeres con menos recursos no solo daban a luz más tarde, sino que tenían hijos durante un periodo de años más corto y los intervalos de tiempo transcurridos entre cada nacimiento eran más largos.
La función reproductiva es muy dependiente de la cantidad de alimento de que se dispone o se puede obtener. Incluso cuando las condiciones nutricionales no son tan severas como para influir en el ciclo menstrual, los niveles de las hormonas esteroideas se ven afectados por esas condiciones. Debido a ello, la probabilidad de concebir disminuye cuando las condiciones alimenticias empeoran. En poblaciones africanas de agricultores que no disponen de medios de control de natalidad, los niveles de esteroides de la mujeres en edad fértil antes de la cosecha son inferiores a los niveles que se registran tras la misma. Y esas variaciones explican el patrón estacional de nacimientos en esas poblaciones. Este fenómeno tiene un claro valor adaptativo, pues favorece la concepción en las épocas del año –tras la cosecha– en que el balance energético es positivo y hay recursos suficientes para satisfacer las elevadas demandas energéticas de un feto en desarrollo.
Normalmente no suele estudiarse el efecto que ejercen sobre la fecundidad las variaciones de la cantidad de alimento no demasiado pronunciadas. Se conocen mucho mejor los efectos de grandes hambrunas, que se saldan con caídas importantes de la tasa de nacimientos en el conjunto de la población. Son particularmente bien conocidos los efectos de las hambrunas de Finlandia del periodo 1866-1868, y las de la holandesa de 1944-1945, que consistieron en fuertes descensos de la fecundidad en mujeres de todos los niveles sociales, aunque de mayor magnitud en los más bajos.
Estudios como este ilustran esas relaciones entre variables demográficas y factores nutricionales. Y lo hacen, además, mostrando que la relación entre unas variables y otras no solo se manifiesta cuando se dan condiciones extremas –las hambrunas antes citadas–, sino también cuando son de menor magnitud. Conviene recordar que la selección natural opera mediante las variaciones y diferencias en el éxito reproductivo, por lo que este tipo de estudios sirve para arrojar luz sobre los mecanismos que han actuado y actúan en la evolución de nuestra especie. Sí, también de la nuestra.
Fuente:
Nenko I, Hayward A D, Lummaa V (2014): The effect of socio-economic status and food availability on first birth interval in a pre-industrial human population. Proc. R. Soc. B 281.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Disponibilidad de alimento y fecundidad humana se ha escrito en Cuaderno de Cultura Científica.
BCAM-Naukas 2023: Cómo calcular el número π a hostias
Quizás sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que existen en el mundo, estudiada por el ser humano desde hace más de 4.000 años. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
La fascinación que ha suscitado durante siglos es tal que el popular número cuenta con su propio día en el calendario, así el mes de marzo se celebra el Día de Pi en todo el planeta.

Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han sumado a la celebración, organizando la cuarta edición del evento BCAM NAUKAS, que tuvo lugar el 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
El número pi no solo aparece en geometría, el lugar que podemos entender como natural, sino en las ramas más insospechadas de las matemáticas. Tanto es así que existen formas muy variadas de calcularlo, unas más eficientes que otras y algunas extremadamente originales. De una de estas últimas nos habla Miguel Camarasa: como calcular pi a base de hacer que choquen cosas.
Miguel Camarasa es alumno de doctorado en BCAM. Además de poseer un grado y un máster en matemáticas por la Universidad de Valencia, es graduado en ingeniería aeronáutica y aeroespacial por la Universidad Politénica de Valencia. También es un conocido divulgador de las matemáticas en YouTube con su canal Mates Mike.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo BCAM-Naukas 2023: Cómo calcular el número π a hostias se ha escrito en Cuaderno de Cultura Científica.
¿Tenemos todos personalidad múltiple?
personalidad múltiple
Entre 1998 y 1999, Koldo Larrañaga acabó con la vida de la abogada Begoña Rubio y del empresario Agustín Ruiz, aunque la policía siempre sospechó que cometió dos asesinatos más. Una despiadada carrera criminal ha colocado a este asesino en serie en un capítulo muy destacado de la crónica negra de Álava. Su valoración más técnica la realizó durante el juicio por estos hechos el psiquiatra Miguel Gutiérrez, cuyo informe forense concluía que Larrañaga era un psicópata.
Sin embargo, una de las declaraciones que más sorprendió al Dr. Gutiérrez fue cuando el acusado, sin mostrar el más mínimo remordimiento por los asesinatos cometidos, manifestó que lo “único que le preocupaba era qué iba a pensar su hijo”.
Un individuo que fue capaz de asestar 17 puñaladas a la abogada Begoña Rubio, a la que no conocía de nada, parecía en ese momento un padre preocupado. ¿Cómo es esto posible?
 Fuente: CampusaUn psicópata, ¿es todo el rato un psicópata?
Fuente: CampusaUn psicópata, ¿es todo el rato un psicópata?
La intuición nos sugiere que, si una persona es extraordinariamente perversa, lo es en todas las esferas de su vida. Y, por lo tanto, afecta a todas sus relaciones sociales y familiares. Pero, como acabamos de observar, la personalidad de Koldo Larrañaga no respondía a esta lógica.
Y no es el único. En la práctica profesional forense podemos conocer individuos despiadados y crueles que, no obstante, pueden adorar a sus madres, desvivirse por el bienestar de un hermano, entristecerse con los achaques de su mascota, etc.
Basta tomar como ejemplo al sanguinario Amon Goeth, el asesino más infame de la Alemania nazi. Este comandante de Hitler mostró compasión por la prisionera judía Natalia Karp después de su interpretación de un nocturno de Chopin al piano. Tanto es así que le perdonó la vida el mismo día de su llegada al campo de concentración de Płaszów, donde había sido trasladada para ser fusilada.
Todos tenemos “personalidad múltiple”…Estas paradojas incomprensibles solo parecen cobrar sentido bajo el prisma de la teoría de la personalidad modular. Esta teoría sugiere que todos poseemos lo que popularmente se conoce como personalidad múltiple. Es decir, una personalidad dividida en varios “yoes” diferentes que prestan atención a distintos tipos de información y recuerdan experiencias pasadas diferentes. También pueden albergar sentimientos dispares sobre el mismo asunto y, quizás, aspiran a objetivos vitales muy diversos.
Lo fascinante es que existe una base neurológica para explicar esta “compartimentación” de la personalidad. Un estudio de 1991 de los neurocientíficos J. Grigsby y J. L. Schneiders, confirmado por trabajos posteriores, sostiene que el comportamiento humano puede comprenderse mejor a la luz de los datos actuales sobre la organización estructural del sistema nervioso central. El cerebro, desde este enfoque, estaría organizado como un sistema modular en constante interacción con el entorno.
Una buena noticia que podemos añadir a este hallazgo es que nuestras variopintas contradicciones cotidianas tendrían una explicación científica. Como también las de los criminales.
… pero no todos tenemos un trastorno de identidadDe hecho, trasladando esta idea de la personalidad modular hasta un extremo patológico, nos encontraríamos ante un desorden psíquico conocido como trastorno de identidad disociativo.
En cierto modo, lo podríamos considerar un mecanismo de defensa, ya que, en ocasiones, este trastorno se presenta en menores víctimas de maltrato severo o abuso sexual continuado. El estrés de una guerra o una catástrofe natural también pueden generar un trastorno disociativo. En todos estos casos, sería un recurso psicológico para postergar el trauma vivido a un “alter ego” (a otro yo).
Esta enfermedad mental se manifiesta como una perturbación de la identidad caracterizada por dos o más personalidades bien definidas. Cada una de ellas puede tener un nombre, una historia personal y características propias. Un inconexo rompecabezas que genera un perturbador malestar psicológico.
También delata una evidente desestructuración y discontinuidad de la identidad, que es lo que marca una de las diferencias más relevantes con los individuos que no padecemos el trastorno disociativo, aunque compartamos la citada personalidad múltiple.
Por lo general, los humanos disfrutamos de la sensación de que nuestras experiencias conscientes están enlazadas en un único flujo continuo e indisoluble que llamamos “yo”. Sin embargo, todo parece indicar que la idea de un cerebro “global” con áreas totalmente interconectadas al mando de nuestro aprendizaje y de nuestra forma de gestionar los recuerdos no es del todo precisa.
Una aproximación criminológicaDebemos admitir que la teoría de la personalidad modular, de alguna forma, nos obliga a salir de una especie de “zona de confort mental” desde la que se entiende mejor el mundo, es más previsible y resulta más fácil simplificar para formular juicios y dictar condenas. Esa que nos hace asumir que si alguien tiene un comportamiento antisocial, “es” solo una persona antisocial. Que si alguien roba, “es” sólo un ladrón. Y que si alguien mata, no “es” nada más que un asesino.
Pero la realidad suele ser bastante menos simple. Desde una aproximación criminológica, debemos analizar la conducta delictiva de un individuo teniendo en cuenta su contexto y antecedentes. Y desde esta perspectiva, tomar en consideración sus creencias, sus pensamientos y vivencias.
Debemos analizar, en definitiva, qué “función” cumple el crimen en el escenario que ha sido llevado a cabo y contrastarlo con el repertorio de conductas no criminales de la persona evaluada.
Es muy comprensible el efecto catártico que conlleva calificar a un criminal como un “monstruo”. Lamentablemente, este “diagnóstico” no nos va a ayudar mucho a resolver el problema. Todos somos poliédricos. Y coexisten lados de oscuridad, con lados, quizás, de esperanza.![]()
Sobre el autor: César San Juan es profesor de Psicología Criminal, Dpto. Psicología Social, UPV/EHU
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Tenemos todos personalidad múltiple? se ha escrito en Cuaderno de Cultura Científica.
La importancia del pulso de Shostakovich
El pulso mide los latidos de nuestro corazón, y es una de las bases de nuestra existencia: si no hay pulso en el cuerpo humano, no hay vida. Todos los ritmos musicales provienen del pulso y el ritmo es la base de la música. Quizás aún más importante que la melodía o la armonía, debemos primero establecer el fundamento del ritmo en cualquier composición musical.
El gran compositor ruso Dmitri Shostakovich (1906-1975) era muy consciente de la importancia del pulso de su música. Gracias a su talento y la cuidadosa escritura de sus obras, consiguió no solo sobrevivir en durísimas circunstancias vitales, sino finalmente llegar a ser uno de los más reconocidos músicos del siglo XX. Como dicen los anglosajones, el diablo está en los detalles, y en las monumentales partituras de Shostakovich, sus detalladas indicaciones de tempo marcan la diferencia.
 Momento de la representación de la ópera Lady Macbeth de Mtsensk en el Teatro Comunale de Bolonia (Italia) en 2014 por parte de Helikon Opera Moscow. Foto: Lorenzo Gaudenzi / Wikimedia Commons
Momento de la representación de la ópera Lady Macbeth de Mtsensk en el Teatro Comunale de Bolonia (Italia) en 2014 por parte de Helikon Opera Moscow. Foto: Lorenzo Gaudenzi / Wikimedia CommonsEn su excelente investigación sobre el metrónomo de Beethoven, Almudena Martín Castro e Iñaki Ucar arrojan luz sobre la controversia en torno a las obras de Beethoven y concluyen que lo más probable es que el compositor malinterpretó su medidor [1]. El caso de Shostakovich es diferente, pero de nuevo queda claro que los tempi marcados en sus partituras no solo implican la velocidad, sino que, en combinación de ritmo, melodía, armonía y orquestación, los tempi son capaces de modificar la percepción global de sus obras musicales.
Shostakovich estudió piano y composición en el Conservatorio de Petrogrado (luego Leningrado y actualmente de nuevo el original San Petersburgo). A los 19 años presentó su Primera Sinfonía como obra de graduación final en el conservatorio, que fue estrenada con gran éxito. Su talento traspasó las fronteras y el propio Bruno Walter estrenó esta obra en la sede de la Filarmónica de Berlin en febrero de 1928, y Leopold Stokowski, titular de la Orquesta de Filadelfia, interpretó y grabó esta sinfonía este mismo año.
Como tantos jóvenes instruidos y perspicaces, Shostakovich en su veintena, pleno de saberes, nuevas ideas y fuerzas, fue más allá de su annus mirabilis y, queriendo ejercer libertad intelectual, pudo crear múltiples obras de gran repercusión. Quizás la más importante de esta época es su ópera “Lady Macbeth de Mtsensk”, estrenada el 22 de enero de 1934 en Leningrado y dos días después en el Bolshoi de Moscú. En 1936, esta ópera se había representado casi doscientas veces entre los teatros de Leningrado y Moscú, y además se emitió por radio en múltiples ocasiones. A los dos años de su estreno, Lady Macbeth se había representado ya en Nueva York, Estocolmo, Londres, Zúrich, Copenhague, Argentina y Checoslovaquia. Dentro de la Unión Soviética, el compositor se convirtió en una celebridad [2].
El 26 de enero de 1936 la Nomenklatura en pleno asistió a la representación de Lady Macbeth en el Bolshoi y abandonaron el teatro tras el primer acto. El 28 de enero de 1936, Pravda publicó un editorial titulado “Caos en lugar de música”, comentando entre otras cosas que “Varios teatros han presentado al culturalmente maduro público soviético la última ópera de Shostakovich, Lady Macbeth de Mtsensk, como un logro. La crítica musical aduladora ensalza la ópera y la pone por las nubes. En lugar de críticas prácticas y serias que puedan ayudarle en sus futuras obras, el joven compositor sólo escucha cumplidos entusiastas”. Diez días después, el 6 de Febrero de 1936 Pravda publicó otro editorial titulado “Falsedad en Ballet”. En este caso, el resultado fue primero retirar de cartel “El arroyo cristalino”, el criticado ballet de Shostakovich en este segundo editorial, y después el libretista de dicho ballet, Adrian Piotrovsky, fue arrestado, sentenciado a muerte y ejecutado.
 Artículo editorial en Pravda 28 de Enero de 1936. Traduccion al inglés.
Artículo editorial en Pravda 28 de Enero de 1936. Traduccion al inglés.
Shostakovich hubo de sobrevivir: retiró todas sus obras, incluyendo la Cuarta Sinfonía que estaba terminando, y comenzó la composición de una Quinta. Recordando el famoso tema de los primeros compases de la Quinta de Beethoven “la llamada del destino”, la Quinta de Shostakovich abre el primer movimiento también en modo menor, oscuro y premonitorio. El segundo movimiento es irónico y quebradizo, y el tercero un profundo canto de dolor. Como bien sabía el compositor, lo importante era el mensaje final, de modo que escribió el largo último movimiento con un preciso arco de marcas metronómicas empezando en negras a 88 pulsaciones por minuto, acelerando a 104, 108, 120, 126, 132, 184, y luego bajando de 160 a 108, 116 y 92. De forma sorprendente, la coda final del último movimiento de la sinfonía puede entenderse tanto como una marcha fúnebre o como una marcha triunfal, solamente cambiando marcas de tempo. El patrón rítmico de la coda, iniciado con timbales, se basa en corcheas y Shostakovich colocó la clara indicación de que debía interpretarse a ♪ = 184, un tempo moderado equivalente a 92 pulsos por negra. Sin embargo, la marcha final que interpretó el director Yevgeny Mravinsky en el estreno fue en modo triunfal y no fúnebre, a casi la máxima velocidad de un metrónomo ordinario, con marca ♩ = 184. Esto funcionó, y Shostakovich salvó la vida.
La controversia de los tempi de Shostakovich se extendieron a buena parte de sus obras. Muchos editores posteriores de sus partituras modificaron o intentaron corregir las “erratas” del autor. También grandes directores en los estrenos internacionales con sus orquestas, tacharon o modificaron marcas o pidiendo instrucciones al autor por carta. Intérpretes como la pianista Alice Shapiro llegaron a llamar por teléfono al compositor para aclarar los tempi de su segundo trío con piano. Hoy día la enorme capacidad de las marcas metronómicas de Shostakovich para modificar la percepción y significado de sus obras, sigue en vigor.
Volviendo a su Quinta Sinfonía, Shostakovich pudo componer una obra maestra, permitir interpretaciones correctas o no para salvar la vida y aceptar públicamente la censura “justa”. El 25 de Enero de 1938 su contrita declaración fue publicada en el diario vespertino de Moscú (Vechernyaya Moskva) con título “Mi Respuesta Creativa”. Sus comentarios respecto al reciente estreno en Moscú de su nueva sinfonía decían: “Entre las críticas, que a menudo analizaban la obra en profundidad, una me causó especial placer, al afirmar que la Quinta Sinfonía era la respuesta creativa del artista soviético a la crítica justa”.
 Vechernyaya Moskva el 25 de Enero de 1938: “Mi Respuesta Creativa”, por D. Shostakovich
Vechernyaya Moskva el 25 de Enero de 1938: “Mi Respuesta Creativa”, por D. Shostakovich
La brutal falta de libertad del joven Shostakovich probablemente cambió su psique, y con total seguridad su carrera y las obras que podría haber legado a la humanidad. Sin embargo, no es bueno escuchar opiniones puramente políticas de su vida, sino usar documentación original como sus cartas [3] o el conocimiento y tratamiento independiente con el compositor, su familia y sus amigos músicos directos [4].
¿Cuál es el tempo que Shostakovich quiso realmente para la coda final del último movimiento de la Quinta Sinfonía? Si hacemos caso a las grabaciones de esta obra dirigidas por Maxim Shostakovich, hijo del compositor, director de orquesta y pianista, o las dirigidas por los dos grandes músicos y amigos del compositor, Mstislav Rostropovich y Vladimir Ashkenazi, podemos concluir que el tempo lento, que conduce a una marcha fúnebre final, es lo que el compositor concibió, aunque en el estreno y aún hoy día los tempi rápidos y los finales triunfales se siguen prodigando.
El gran director de orquesta rumano Sergiu Celibidache, que presentó al público alemán por primera vez en 1946 esta Quinta Sinfonía dirigiendo a la Filarmónica de Berlín, refirió que escribió una carta a Shostakovich desde Suiza en la que le preguntaba: “¿Es correcta la marca de tempo ♪ = 184 al final de la Quinta Sinfonía?”. Recibió una postal de Moscú, sin firma, en la que había una sola palabra: “Correcto”.
Referencias:
[1] Martín-Castro A., Ucar I. (2020). Conductors’ tempo choices shed light over Beethoven’s metronome. PLOS ONE 15 (12): e0243616. doi: 10.1371/journal.pone.0243616
[2] Laurel E. Fay. (1999) Shostakovich: A Life. Oxford University Press. 978-0195182514
[3] Laurel E. Fay. (Ed) (2004) Shostakovich and his world. Princeton University Press. 978-0691120690
[4] Elizabeth Wilson (2006) Shostakovich: A Life Remembered (2nd Ed.). Faber and Faber. 978-0571220502
También del autor:
Lutería y acústica (serie)
Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo La importancia del pulso de Shostakovich se ha escrito en Cuaderno de Cultura Científica.
Sucesiones fractales: del número a la nota musical
Hace unas semanas hablamos en el Cuaderno de Cultura Científica de las llamadas sucesiones fractales, o sucesiones autosemejantes, en la entrada titulada Sucesiones fractales], que continuamos con la entrada La sucesión fractal de Thue-Morse y la partida infinita de ajedrez, en la que mostrábamos una sucesión autosemejante concreta, conocida con el nombre de sucesión de Thue-Morse, o sucesión de Prouhet-Thue-Morse, que es una curiosa sucesión de números enteros que aparece en diferentes ramas de las matemáticas. El objetivo de la presente entrada es mostrar algunos ejemplos de cómo el compositor minimalista estadounidense Tom Johnson utiliza estas sucesiones para componer algunas de sus composiciones musicales.
 Josu Rekalde, Tom Johnson, Esther Ferrer y yo mismo, Raúl Ibáñez, conversando sobre la utilización de las matemáticas en los procesos creativos de la artista Esther Ferrer y el compositor Tom Johnson, dentro del programa Diálogos en la frontera organizado por la Cátedra de Cultura Científica, en marzo de 2018
Josu Rekalde, Tom Johnson, Esther Ferrer y yo mismo, Raúl Ibáñez, conversando sobre la utilización de las matemáticas en los procesos creativos de la artista Esther Ferrer y el compositor Tom Johnson, dentro del programa Diálogos en la frontera organizado por la Cátedra de Cultura Científica, en marzo de 2018Empecemos recordando qué son las sucesiones fractales o autosemejantes. Una sucesión (infinita) de números enteros se dice que es una sucesión autosemejante, si una parte de la sucesión es igual a toda la sucesión, es decir, si eliminamos algunos miembros de la sucesión infinita los miembros de la sucesión que quedan siguen siendo toda la sucesión.
Pongamos un ejemplo de sucesión autosemejante, en particular, aprovechemos para mostrar un nuevo ejemplo, no comentado en las entradas anteriores. Se trata de la sucesión de la cantidad de maneras que existen de expresar los cuadrados de los números enteros positivos, 0, 1, 2, 3, 4, 5, 6, …, como suma de dos cuadrados (sin importar el orden), a cuyos miembros vamos a denotar por a(n). Para calcular los primeros términos de esta sucesión nos viene muy bien tener en cuenta la sucesión de los números cuadrados (0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, …) y ver cómo expresar el cuadrado de cada número entero no positivo como suma de dos de los cuadrados de esa lista.
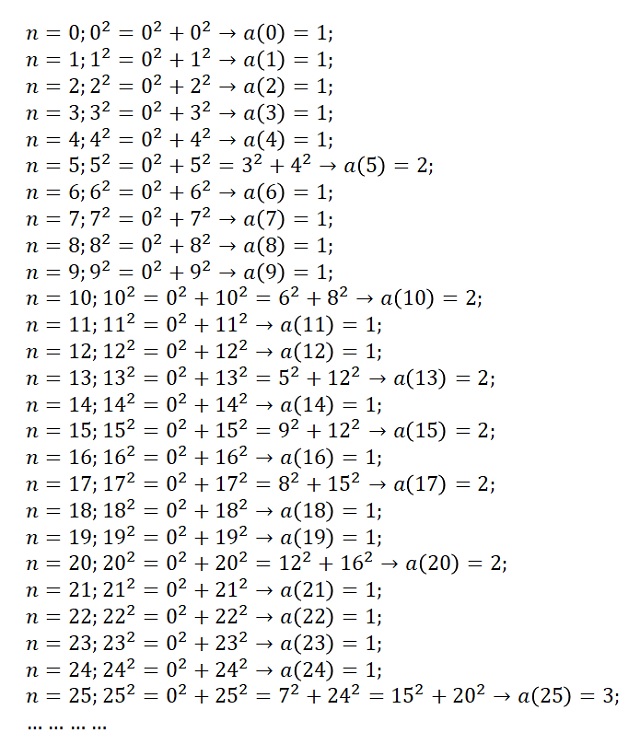
En la imagen anterior hemos obtenido los miembros de la sucesión hasta a(25), que son: 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 2, 1, 2, 1, 2, 1, 1, 2, 1, 1, 1, 1, 3. Esta sucesión infinita, que es la sucesión A063014 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS, cuyos primeros términos son
1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 2, 1, 2, 1, 2, 1, 1, 2, 1, 1, 1, 1, 3, 2, 1, 1, 2, 2, 1, 1, 1, 2, 2, 1, 2, 1, 2, 2, 2, 1, 1, 1, 2, 1, 1, 1, 1, 3, 2, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 1, 5, 1, 1, 2, 1, 2, 1, 1, 2, 2, 3, 1, 1, 2, 1, 2, 1, 2, 1, 1, 5, 1, 2, 1, 2, 2, 2, 1, 1, 1, 2, 1, 2, 1, 1, 3, 2, 2, …
es una sucesión autosemejante. De hecho, es una sucesión fractal de razón 2, como se muestra en la siguiente imagen. Recordemos que una sucesión infinita se dice que es una sucesión fractal de razón d si nos quedamos con un primer número de la sucesión y los que van apareciendo cada d posiciones, es decir, eliminamos el resto, y seguimos obteniendo la sucesión infinita inicial.

Luego, efectivamente es una sucesión autosemejante de razón 2. Pero, curiosamente, también es una sucesión autosemejante de razón 3, como vemos en la siguiente imagen.

Empecemos presentando al compositor del que vamos a hablar en esta entrada, Tom Johnson, del que ya hemos hablado en algunas otras entradas, como Las vacas de Narayana, la versión hindú de los conejos de Fibonacci o Teselaciones rítmicas perfectas.
Tom Johnson (Greeley, Colorado, EE.UU., 1939), es un compositor minimalista y teórico de la música estadounidense. Se graduó en la Universidad de Yale, donde obtuvo además su grado avanzado en música. Viajó a Nueva York en 1967 y fue alumno del compositor Morton Feldman (1926-1987), uno de los artífices, junto con John Cage (1912-1992), de la música aleatoria. Entre 1971 y 1983 fue crítico de música en The Village Voice, el primer periódico semanal alternativo (EEUU) de noticias y cultural. En 1983 se trasladó a París, donde vive con su mujer, la artista donostiarra Esther Ferrer.
Es un compositor minimalista, ya que trabaja con formas simples, escalas limitadas y de manera general, con material reducido. Y dentro del minimalismo destaca por el uso de las matemáticas en su proceso creativo. Sucesiones de números (Fibonacci, Narayana, autosemejantes, …), autómatas, números (contar), números binarios, números primos (Mersenne), geometría, trigonometría, simetrías, teselaciones, curvas fractales, grafos, combinatoria (permutaciones, combinaciones, cuadrados latinos, cuadrados mágicos, el problema de las colegialas de Kirkman, teoría de bloques, …), el triángulo de Pascal, cuadrados mágicos geométricos, son algunas de las teorías matemáticas que utiliza en sus composiciones.
Tom Johnson ha escrito de su música: “quiero encontrar la música, no componerla”, o como decía su maestro Morton Feldman “Deja a la música hacer lo que quiere hacer”. Mientras John Cage, o Morton Feldman, realizan esta búsqueda mediante el azar, Tom Johnson lo hace mediante las matemáticas.
En su artículo Found Mathematical Objects / Objetos matemáticos encontrados (2001) Tom Johnson explica su filosofía artística y empieza así:
La idea es sencilla. Encuentra un objeto, cualquier objeto, decláralo obra de arte, y es una obra de arte. El arte se convierte en algo verdaderamente objetivo, sólo un objeto, las técnicas artísticas se vuelven innecesarias y, al mismo tiempo, se siembran las semillas del arte «no intencional». Este principio de Marcel Duchamp, el «readymade» o el «objet trouvé», se reconoce ahora en todas partes como una forma perfectamente válida de hacer arte. Una generación de artistas Fluxus desarrolló este punto de vista, John Cage lo adaptó para componer música mediante operaciones fortuitas, y ahora es bastante natural que un compositor o artista pueda elegir trabajar con un objeto matemático encontrado, como el triángulo de Pascal o la serie Narayana o algún autómata, lo mismo que con un urinario, una rueda de bicicleta, un peine o un botellero.
 Imagen del compositor Tom Johnson explicando una de sus composiciones musicales en uno de los videos de la serie Illustrated Music de su canal de YouTube
Imagen del compositor Tom Johnson explicando una de sus composiciones musicales en uno de los videos de la serie Illustrated Music de su canal de YouTubeEntre sus obras encontramos óperas como Riemannoper (1988), Trigonometría (1997) o la más famosa La ópera de las cuatro notas (1972), que fue representada en España en 2015 por Vania Produccions bajo la dirección de Paco Mir (que muchos conoceréis por ser uno de los miembros del trío Tricicle) o composiciones musicales muy creativas e interesantes, como Una hora para piano (1972), Nueve campanas (1979), Simetrías (1981), Dúos para contar (1982), Melodías racionales (1982), Melodías infinitas (1982), Música para 88 (1988), Las vacas de Narayana (1989), Kentzy Loops (2000), Galileo (2001), Mosaicos (2002), Combinations for String Quartet (2003) o Ritmos de Vermont (2008).
Ha escrito libros como la colección de artículos de crítica musical The voice of the new music (Apollohuis, 1989), Self-similar Melodies (Editions 75, 1996), Looking at numbers (Birkhauser, 2014) o Finding Music. Writings 1961-2018 (MusikTexte, 2019).
 Portada de los libros Self-similar Melodies, Looking at numbers y Finding Music. Writings 1961-2018La melodía racional XV
Portada de los libros Self-similar Melodies, Looking at numbers y Finding Music. Writings 1961-2018La melodía racional XV
El compositor Tom Johnson utiliza las sucesiones autosemejantes de formas diferentes para componer sus obras musicales. En esta entrada vamos a mostrar dos ejemplos, La melodía racional XV y la pieza La vie est si court.
La melodía racional XV está compuesta a partir de una sucesión autosemejante de razón 2. Esta composición pertenece a un grupo de veintiuna melodías racionales que el compositor minimalista Tom Johnson compuso en 1982 bajo el título Rational Melodies / Melodías Racionales.
De forma paralela a como suelo sugerir, cuando hablamos de juegos matemáticos, que lo primero es jugar, ahora recomiendo escuchar algunas de las melodías racionales (por ejemplo, las melodías racionales I, II, X y XIII, para empezar) y, en particular, la melodía racional XV, de la que vamos a hablar. Puedes escucharlas en diferentes plataformas (YouTube, Spotify, etc), en particular, en el canal de YouTube de Eberhard Blum o de Dedalus, que hacen dos interpretaciones diferentes de las melodías racionales.
Aquí os dejo la versión, para flauta, de Eberhard Blum de la melodía racional XV:
Y aquí os dejo la versión, para cello y violín, de Dedalus de la melodía racional XV:
En la introducción de la publicación de las partituras de las Melodías Racionales, que recordemos que publica en 1983, su autor escribe lo siguiente:
La racionalidad o, más precisamente, la lógica deductiva se ha usado rara vez como factor de control en la composición musical. Normalmente los compositores están más interesados en inspiración, intuición, sentimientos y expresión interna. Últimamente, sin embargo, ha aparecido una tendencia por parte de los compositores a renunciar al control individual sobre cada nota confiando en factores externos. Existen, por ejemplo, piezas controladas por el viento, por el azar, por la idiosincrasia de los magnetófonos o por variaciones impredecibles en un circuito eléctrico, y creo que componer adhiriéndose rigurosamente a premisas lógicas implica un proceso similar de pensamiento.
La autosemejanza ha sido un concepto central en la obra de Tom Johnson. Empezó a trabajar con sucesiones autosemejantes entre 1979 y 1980. Tres fueron las influencias que le llevaron hacia este tema. Por una parte, el matemático polaco, nacionalizado francés y estadounidense, Benoit Mandelbrot (1924-2010) publicó su libro Fractals: Form, Chance and Dimension en 1977 que fue leído con mucho interés por Tom Johnson. La segunda fue la lectura, años después de su publicación, del artículo sobre la “curva dragón” publicado por el divulgador estadounidense Martin Gardner (1914-2010) en su columna de Juegos Matemáticos de la revista Scientific American, en 1967. Y finalmente, su encuentro con el matemático y músico David Feldman, en 1979, con quien realizó un pequeño estudio de “melodías que se presentan a si mismas en dos (o más) tempi a la vez”, es decir, melodías autosemejantes.
 Carátula de la grabación de las Melodías Racionales de Tom Johnson por el ensemble Dedalus, en New World Records, en 2010
Carátula de la grabación de las Melodías Racionales de Tom Johnson por el ensemble Dedalus, en New World Records, en 2010La melodía racional XV, junto al resto de las melodías racionales, fueron publicadas en 1983, pero realmente las compuso dos y tres años antes de su publicación.
Empecemos por la sucesión autosemejante que utiliza Tom Johnson en esta pieza. Si miramos a la primera línea de la partitura (véase la siguiente imagen) veremos el “germen” de la sucesión infinita fractal de razón 2.

Si denotamos por números las diferentes notas obtenemos la sucesión finita
1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5,
donde cada número natural se corresponde con una nota musical cada vez más grave (1 = La, 2 = Sol, 3 = Fa, 4 = Mi, 5 = Re), es decir, más baja en el pentagrama. Esta sucesión finita es el “germen” de una sucesión infinita autosemejante que se obtiene poniendo infinitas copias de la misma, una a continuación de la otra, como se muestra en la siguiente imagen.

Esta sucesión es autosemejante de razón 2 como se puede observar fácilmente, ya que al eliminar los números que están en las posiciones pares, lo que queda (posiciones impares) sigue siendo la misma sucesión infinita. Es decir, la sucesión infinita está dentro de ella misma.

Si nos fijamos en las dos primeras líneas de la anterior imagen, que son dos copias de la sucesión finita germen [1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5, 1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5], al eliminar los números que están en las posiciones pares, nos queda una copia de la sucesión germen [1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5, 1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5], y así ocurre para el resto.
Para entender cómo transforma Tom Johnson esta sucesión fractal en una composición musical debemos de darnos cuenta que podemos ver el anterior proceso desde un punto de vista diferente, añadir números en lugar de quitarlos. De esta forma, partimos de la sucesión infinita y entre cada par de números consecutivos introducimos un número (los que antes quitábamos), de esta forma construimos una sucesión más grande que contiene a la anterior, pero que resulta que es exactamente igual a ella misma. Veámoslo de forma sencilla con una sola copia de nuestra sucesión germen:
[1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5].
Y vamos a incluir entre cada dos números consecutivos los números que antes quitábamos, que si nos fijamos bien primero son los que están en posiciones pares (2, 3, 4, 5, 3, 5, 5) y luego están en posiciones impares (1, 2, 2, 3, 2, 4, 3, 5), quedando (hemos indicado con negrita los números que hemos incluido):
[1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5, 1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5],
es decir, dos copias de la sucesión germen, que incluyen a esta en su interior (los números que NO están en negrita). Y es precisamente este proceso que acabamos de ejemplificar el que utiliza Tom Johnson para componer la melodía racional XV.
La primera línea de la partitura mostrada arriba, que es la versión musical de la sucesión germen 1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5 (1 = La, 2 = Sol, 3 = Fa, 4 = Mi, 5 = Re), es la melodía base de la melodía racional XV, con silencios entre cada dos notas (que pan a ser las posiciones donde se van a incluir las nuevas notas). Entonces en cada nueva línea se va incluyendo una nueva nota (número) intermedio, como se muestra en la siguiente imagen de la partitura (yo he añadido los números, azules en la melodía inicial y rojos los que se corresponden con las notas añadidas), que muestra la mitad del proceso.

Al final del proceso, que se muestra en la siguiente imagen, se concluye con dos copias de la melodía (sucesión germen) de la composición, pero tocadas el doble de rápido, ya que ahora no hay silencios intermedios.

Si ahora volvéis a escuchar la melodía racional XV podréis escuchar el proceso descrito.
La vie est si courteEn 1998 Tom Johnson compuso la obra La vie est si courte / La vida es tan corta, que está compuesta de variaciones sobre un bucle de 20 tiempos que gira continuamente alrededor de los ocho instrumentos, flauta, clarinete, trompeta, trombón, marimba, violín, viola y violonchelo.
 Parte inicial de la partitura de la obra La vie est si courte / La vida es tan corta (1998), del compositor Tom Johnson
Parte inicial de la partitura de la obra La vie est si courte / La vida es tan corta (1998), del compositor Tom JohnsonEn su libro Finding Music, Writings 1961-2018, Tom Johnson escribe de la composición La vie est si courte lo siguiente:
Cuando escribí por primera vez la melodía de esta pieza, parecía música vocal e incluso tenía un texto que la acompañaba.
Después de muchas páginas de esbozos vocales tipo madrigal, me di cuenta de que las cosas polirrítmicas que quería hacer eran en realidad mucho más apropiadas para instrumentos, y que esto sería un buen material para una pieza que me acababan de encargar para Musica Temporale. Sin embargo, decidí conservar parte del texto como título para la pieza instrumental. Las palabras siempre nos ayudan a recordar las melodías y, de hecho, puede ser una buena idea que los músicos canten el tema una vez para el público antes de empezar la composición propiamente dicha.
El texto de la pieza, como se puede ver en la partitura es “La vie est si courte. La mort est si longue” (La vida es tan corta. La muerte es tan larga).
Si miramos al inicio de la partitura (primera línea, en clave de Sol) podremos observar cual es la sucesión finita germen, en la cual se incluyen los silencios, que genera la sucesión infinita fractal, mediante la repetición infinita de la sucesión germen. La sucesión finita germen tiene 20 números (20 tiempos en la partitura, que se pueden ver indicados en la siguiente imagen que el propio Tom Johnson ha incluido en su video de la serie Illustrated Music de YouTube) son, siendo 0 el número que se corresponde con un silencio,
1, 0, 2, 0, 3, 4, 2, 0, 3, 0, 5, 0, 3, 0, 2, 4, 3, 0, 2, 0,
donde 1 = Mi, 2 = Sol, 3 = La, 4 = Si, 5 = Re.
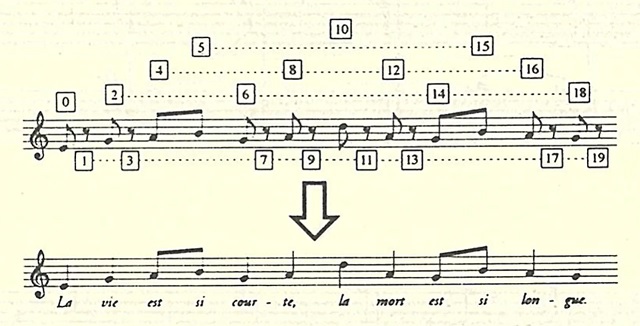
La sucesión numérica infinita que se genera a partir de la sucesión germen de 20 números es efectivamente autosemejante de razón 3, como se observa en la siguiente imagen.

Esta propiedad puede verse en la partitura, ya que el segundo instrumento (segunda línea de la partitura) toca una de cada tres notas de la melodía del primer instrumento (primera línea), pero en clave de Fa, y como la sucesión es autosemejante de razón 3, entonces interpreta la misma melodía, pero tres veces más lenta.
Volviendo a la sucesión infinita, no solo es autosemejante de razón 3, sino que también es autosemejante de razón 7, como se muestra a continuación.

La autosemejanza de razón 3 de la anterior sucesión es el elemento a partir del cual Tom Johnson estructura toda la obra, que es una composición para ocho instrumentos. La explicación al detalle la podéis encontrar en el video de la serie Illustrated Music de su canal de YouTube titulado Illustrated Music #9, La Vie est si courte [https://www.youtube.com/watch?v=F7KBTIXNkc8].
La representación gráfica de Tom JohnsonVamos a terminar esta entrada del Cuaderno de Cultura Científica mostrando la forma en la que el compositor Tom Johnson representa las sucesiones autosemejantes que se generan a partir de una sucesión finita germen.
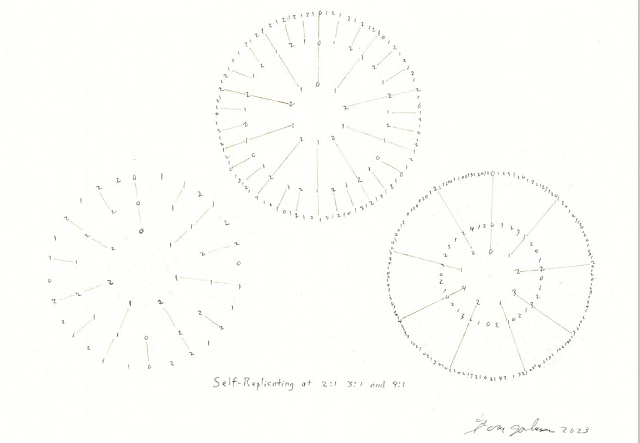 Dibujo de Tom Johnson representando circularmente tres sucesiones autosemejantes de razones 2, 3 y 4, realizado en 2013
Dibujo de Tom Johnson representando circularmente tres sucesiones autosemejantes de razones 2, 3 y 4, realizado en 2013
Para empezar, en el centro de la representación dibuja, de forma circular, la sucesión finita germen. Al ser una representación circular es como si repitiéramos la misma sucesión finita de forma infinita generándose así la sucesión infinita. Por ejemplo, la representación de la izquierda en la anterior imagen se corresponde con la sucesión autosemejante de razón 2 que tiene como sucesión germen 0, 1, 1, 2, 1, 2, 2 (esta sucesión ya aparece en su libro Self-Similar Melodies, de 1996, aunque expresada como 1, 2, 2, 3, 2, 3, 3). Si en la circunferencia central se representa la sucesión germen (en este caso, 0, 1, 1, 2, 1, 2, 2), en la segunda circunferencia se van añadiendo los números intermedios, aquellos que eliminaríamos de la sucesión autosemejante, los que están en posiciones pares, ya que esta sucesión es de razón 2, pero manteniendo la posición de los números de la sucesión germen, lo cual se indica con un segmento radial. Es decir, si indicamos con corchetes los números añadidos, en la segunda circunferencia quedaría 0, [1], 1, [2], 1, [2], 2, [0], 1, [1], 2, [1], 2, [2], que genera dos copias de la sucesión germen, como se muestra en la siguiente imagen. Aunque podemos hacer una lectura de fuera hacia dentro, si en la segunda circunferencia eliminamos uno de cada dos números (por ser de razón 2), se obtiene la circunferencia interior.
 Representación gráfica, de Tom Johnson, de la sucesión autosemejante de razón 2 cuya sucesión germen es 0, 1, 1, 2, 1, 2, 2
Representación gráfica, de Tom Johnson, de la sucesión autosemejante de razón 2 cuya sucesión germen es 0, 1, 1, 2, 1, 2, 2
Si ahora se añade la tercera circunferencia concéntrica exterior añadiendo de nuevo los números intermedios, se obtienen cuatro copias de la sucesión germen.
Si la sucesión autosemejante es de razón 3, como la que mostramos en la siguiente imagen (la sucesión germen es 0, 1, 2, 1, 2, 1, 2, 1), que es la central de la imagen que hemos mostrado arriba, entre dada dos números hay que incluir dos números (que son los excluidos en el proceso inverso).
 Representación gráfica, de Tom Johnson, de la sucesión autosemejante de razón 3 cuya sucesión germen es 0, 1, 1, 2, 1, 2, 2
Representación gráfica, de Tom Johnson, de la sucesión autosemejante de razón 3 cuya sucesión germen es 0, 1, 1, 2, 1, 2, 2
En mi opinión es una hermosa manera de representar las sucesiones autosemejantes, que surgen de una sucesión finita germen.
Mozart, como no…Como escribe Emmanuel Amiot, en su artículo Self Similar Melodies, Tom Johnson “es probablemente el primer compositor que hizo uso de esto [la autosimilitud] de forma consciente y extensa, en obras como La vie est si court o Loops for orchestra”. Sin embargo, se pueden encontrar pequeños ejemplos de autosimilitud en obras más antiguas, como el conocido bajo Alberti (que es un tipo de acompañamiento repetitivo de cuatro notas, grave, agudo, medio, agudo -que en números podríamos representar como 1, 3, 2, 3-, que fue muy utilizado en el clasicismo, pero también en el romanticismo, que debe su nombre al compositor italiano Domenico Alberti (aprox. 1710/17 – 1740)) que se encuentra en el inicio de la Sonata para piano n. 16 en do mayor, K. 545 (1788) del gran Wolfgang Amadeus Mozart (1756-1791).
 Apertura de la Sonata para piano n. 16, K. 545 (1788) de Wolfgang Amadeus Mozart, que contiene el conocido bajo Alberti
Apertura de la Sonata para piano n. 16, K. 545 (1788) de Wolfgang Amadeus Mozart, que contiene el conocido bajo AlbertiLa sucesión infinita que se genera a partir de la repetición del motivo 1, 3, 2, 3 es autosemejante de razón 3 (también de razón 5 o cualquier otro número impar).
Bibliografía
1.- Tom Johnson, Rational Melodies, Editions 75, 1982.
2.- Tom Johnson, Self-similar Melodies, Editions 75, 2014.
3.- Tom Johnson, Finding Music, Writings 1961-2018, MusikTexte, 2019.
4.- Tom Johnson, Found Mathematical Objects, Seminaire Entretemps: Musique, Mathematiques et Philosophies, Paris, Ircam, 2001.
5.- Tom Johnson, Self-Similar Structures in my Music: an Inventory, lecture presented in the MaMuX seminar, IRCAM, Paris, 2006.
6.- Emmanuel Amiot, Auto Similar melodies, Journal of Mathematics and Music, vol. 3, n. 1, pp. 1-26, 2009.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Sucesiones fractales: del número a la nota musical se ha escrito en Cuaderno de Cultura Científica.
La física diminuta tras las inmensas erupciones cósmicas
Una nueva teoría describe cómo las interacciones de partículas alimentan la reconexión magnética rápida, el proceso detrás de las erupciones solares y otros chorros astrofísicos.
Un artículo de Zack Savitsky. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
Dos simulaciones de un agujero negro acreciente. A la izquierda, el plasma se modela como un fluido. A la derecha, se trata como un conjunto de partículas, lo que produce diferencias evidentes en la densidad del plasma (púrpura) y las líneas del campo magnético (blanco). Cortesía de Alisa GalishnikovaEn arrebatos fugaces, el sol arroja de vez en cuando una cantidad colosal de energía al espacio. Llamadas erupciones solares, estas erupciones duran solo unos minutos y pueden desencadenar apagones catastróficos y auroras deslumbrantes en la Tierra. Pero nuestras principales teorías matemáticas sobre cómo funcionan estas llamaradas no logran predecir la fuerza y la velocidad de lo que observamos.
En el corazón de estos estallidos hay un mecanismo que convierte la energía magnética en poderosas explosiones de luz y partículas. Esta transformación está catalizada por un proceso llamado reconexión magnética, en el que los campos magnéticos en colisión se rompen y se realinean instantáneamente, arrojando material al cosmos. Además de impulsar las erupciones solares, la reconexión puede estar detrás de las partículas rápidas y de alta energía expulsadas por las estrellas que explotan, el brillo de los chorros de agujeros negros dándose un festín y el viento constante que sopla el sol.
A pesar de la ubicuidad del fenómeno, los científicos se han esforzado por comprender cómo funciona de manera tan eficiente. Una teoría reciente propone que cuando se trata de resolver los misterios de la reconexión magnética, la física diminuta juega un papel importante. En concreto explica por qué algunos eventos de reconexión son tan asombrosamente rápidos y por qué los más fuertes parecen ocurrir a una velocidad característica. Comprender los detalles microfísicos de la reconexión podría ayudar a los investigadores a construir mejores modelos de estas erupciones energéticas y dar sentido a las rabietas cósmicas.
“Hasta ahora, esta es la mejor teoría que conozco”, afirma Hantao Ji, físico del plasma de la Universidad de Princeton que no ha participado en el estudio. “Es un gran logro”.
Buscando a tientas con fluidos
Casi toda la materia conocida en el universo existe en forma de plasma, una abrasadora sopa de gas donde las temperaturas infernales han reducido los átomos a partículas cargadas. A medida que se desplazan, esas partículas generan campos magnéticos, que luego guían los movimientos de las partículas. Esta interacción caótica teje un revoltijo de líneas de campo magnético que, como bandas elásticas, almacenan más y más energía a medida que se estiran y retuercen.
En la década de 1950, los científicos propusieron una explicación a cómo los plasmas expulsan su energía acumulada, un proceso que se denominó reconexión magnética. Cuando las líneas de campo magnético que apuntan en direcciones opuestas chocan, pueden romperse y conectarse de forma cruzada, lanzando partículas como una honda de doble cara.
Pero esta idea estaba más cerca de una pintura abstracta que de un modelo matemático completo. Los científicos querían comprender los detalles de cómo funciona el proceso: los eventos que influyen en la descarga, la razón por la que se libera tanta energía. Pero la interacción desordenada de gas caliente, partículas cargadas y campos magnéticos es difícil de dominar matemáticamente.
La primera teoría cuantitativa, descrita en 1957 por los astrofísicos Peter Sweet y Eugene Parker, trata los plasmas como fluidos magnetizados. Sugiere que las colisiones de partículas con carga opuesta dibujan líneas de campo magnético y desencadenan una cadena descontrolada de eventos de reconexión. Su teoría también predice que este proceso ocurre a un ritmo particular. Las tasas de reconexión observadas en plasmas relativamente débiles creados en el laboratorio coinciden con su predicción, al igual que las tasas de chorros más pequeños en las capas inferiores de la atmósfera solar.
Pero las erupciones solares liberan energía mucho más rápido de lo que puede explicar la teoría de Sweet y Parker. Según sus cálculos, esas llamaradas deberían ocurrir a lo largo de meses en lugar de en minutos.
Más recientemente, las observaciones de los satélites magnetosféricos de la NASA identificaron que esta reconexión más rápida ocurría incluso más cerca de casa, en el propio campo magnético de la Tierra. Estas observaciones, junto con los resultados de décadas de simulaciones por ordenador, confirman esta tasa de reconexión «rápida»: en plasmas más energéticos, la reconexión ocurre aproximadamente al 10% de la velocidad a la que se propagan los campos magnéticos, órdenes de magnitud más rápido de lo que predice la teoría de Sweet y Parker. .
La tasa de reconexión del 10 % se observa tan universalmente que muchos científicos la consideran “un número dado por Dios”, afirma Alisa Galishnikova, investigadora de Princeton. Pero invocar lo divino contribuye poco a explicar por qué la reconexión es tan rápida.
El número de DiosEn la década de 1990, los físicos dejaron de tratar los plasmas como fluidos, lo que había resultado ser demasiado simplista. De cerca una sopa magnetizada en realidad está compuesta de partículas individuales. Y cómo interactúan esas partículas entre sí marca una diferencia crucial.
“Cuando llegas a las microescalas, la descripción como fluido comienza a fallar”, explica Amitava Bhattacharjee, físico del plasma en Princeton. «La imagen [microfísica] tiene cosas que la imagen a base de fluidos nunca puede capturar».
Durante las últimas dos décadas, los físicos han sospechado que un fenómeno electromagnético conocido como efecto Hall podría tener el secreto de la reconexión rápida: los electrones con carga negativa y los iones con carga positiva tienen masas diferentes, por lo que viajan a lo largo de las líneas del campo magnético a diferentes velocidades. Ese diferencial de velocidad genera un voltaje entre las cargas separadas.
En 2001, Bhattacharjee y sus colegas demostraron que solo los modelos que incluían el efecto Hall producían tasas de reconexión apropiadamente rápidas. Pero precisamente cómo ese voltaje producía el mágico 10% seguía siendo un misterio. «No nos mostró el ‘cómo’ y el ‘por qué'», comenta Yi-Hsin Liu, físico del plasma en Dartmouth College.
Ahora, en dos artículos teóricos publicados recientemente, Liu y sus colegas han intentado completar los detalles.
El primer artículo, publicado en Communications Physics, describe cómo el voltaje induce un campo magnético que extrae electrones del centro de las dos regiones magnéticas en colisión. Esa desviación produce un vacío que succiona nuevas líneas de campo y las pellizca en el centro, lo que permite que la honda magnética se forme más rápidamente.
“Esa imagen pasó desapercibida… [pero] nos estaba mirando a la cara”, afirma Jim Drake, físico del plasma de la Universidad de Maryland. “Este es el primer argumento convincente que he visto”.
En el segundo artículo, publicado en Physical Review Letters, Liu y su asistente de investigación de pregrado, Matthew Goodbred, describen cómo surge el mismo efecto de vacío en plasmas extremos que contienen diferentes ingredientes. Alrededor de los agujeros negros, por ejemplo, se cree que los plasmas consisten en electrones y positrones de igual masa, por lo que el efecto Hall ya no ocurre. Sin embargo, “mágicamente, la reconexión sigue funcionando de manera similar”, explica Liu. Los investigadores proponen que dentro de estos campos magnéticos más fuertes, la mayor parte de la energía se gasta acelerando partículas en lugar de calentarlas, creando nuevamente una disminución de la presión que produce la divina tasa del10%.
“Es un hito teórico importante”, afirma Lorenzo Sironi, astrofísico teórico de la Universidad de Columbia que trabaja en simulaciones por ordenador de chorros de plasma de alta energía. «Esto nos da confianza… de que lo que estamos viendo en nuestras simulaciones no es una locura».
Escogiendo partículasLos científicos no pueden modelar cada partícula individual en simulaciones de plasma a gran escala. Hacerlo produciría miles de millones de terabytes de datos y tardaría cientos de años en completarse, incluso utilizando los superordenadores más avanzados. Pero los investigadores han descubierto recientemente cómo tratar un sistema tan difícil de manejar como un conjunto de partículas más pequeño y manejable.
Para investigar la importancia de considerar partículas individuales, Galishnikova y sus colegas compararon dos simulaciones de un agujero negro acreciente: una que trata el plasma como un fluido homogéneo y la otra que arroja aproximadamente mil millones de partículas a la mezcla. Sus resultados, publicados en marzo en Physical Review Letters, muestran que la incorporación de la microfísica conduce a cuadros claramente diferentes de las llamaradas, aceleraciones de partículas y variaciones en el brillo de un agujero negro.
Ahora, los científicos esperan que los avances teóricos como el de Liu conduzcan a modelos de reconexión magnética que reflejen con mayor precisión la naturaleza. Pero aunque su teoría apunta a resolver el problema de la tasa de reconexión, no explica por qué algunas líneas de campo chocan y desencadenan la reconexión pero no otras. Tampoco describe cómo la energía que fluye se divide en chorros, calor y rayos cósmicos, o cómo funciona todo esto en tres dimensiones y a escalas más grandes. Aún así, el trabajo de Liu muestra cómo, en las circunstancias adecuadas, la reconexión magnética puede ser lo suficientemente eficiente como para provocar estallidos efímeros pero violentos en el cielo.
«Tienes que responder a la pregunta ‘por qué’, esa es una parte crucial para avanzar con la ciencia», afirma Drake. “Tener la confianza de que entendemos el mecanismo nos da una capacidad mucho mejor para tratar de averiguar qué está pasando”.
El artículo original, The Tiny Physics Behind Immense Cosmic Eruptions, se publicó el 15 de mayo de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo La física diminuta tras las inmensas erupciones cósmicas se ha escrito en Cuaderno de Cultura Científica.
La edad de los anillos de Saturno
Desde nuestra perspectiva humana, en muchas ocasiones parecemos tener la impresión de que nuestro Sistema Solar ha sido siempre tal y como lo observamos ahora. Incluso en ocasiones nos pasa con nuestro propio planeta, del que si no fuese por el rápido ritmo de cambio al que le somete el ser humano a veces tendríamos una falsa sensación de inmovilidad que poco se corresponde con la realidad. En las últimas décadas nos hemos dado cuenta de que el dinamismo planetario existente en nuestro Sistema Solar a todos los niveles -atmósferas, procesos externos, internos…- y del que hemos hablado en otras ocasiones en esta misma sección, es muy importante, especialmente en aquellos cuerpos que todavía conservan calor interno y pueden transformar su superficie. En concreto hay lugares cuya gran dinámica nos suscita muchas preguntas: los anillos planetarios. Y es que todavía desconocemos muchos detalles sobre ellos, como cuando se formaron -si lo hicieron al mismo tiempo que el planeta o son un ornamento posterior- o si estos son «para siempre».
 Los majestuosos anillos de Saturno, vistos desde la sonda Cassini. Imagen cortesía de NASA/JPL-Caltech/Space Science Institute
Los majestuosos anillos de Saturno, vistos desde la sonda Cassini. Imagen cortesía de NASA/JPL-Caltech/Space Science InstituteLa misión Cassini nos permitió conocer mucho más de cerca los anillos de Saturno, especialmente en los últimos momentos de su misión, ya que tuvo la oportunidad de pasar entre el planeta y los anillos, tomando imágenes y datos que fueron fundamentales para realizar nuevos modelos que nos han permitido conocer un poco mejor su composición y funcionamiento. Datos que especialmente en los últimos cinco años nos han traído distintos puntos de vista sobre la edad de los anillos.
Hoy día la teoría más reciente sobre la formación de los anillos nos dice que probablemente un satélite de Saturno, y formado principalmente por hielo, se acercó demasiado al planeta, de tal manera que la gravedad de Saturno acabó por desintegrarlo y sus fragmentos acabaron formando los anillos que hoy conocemos, ocurriendo este hecho hace aproximadamente 160 millones de años (Wisdom et al. (2022)).
Unos años antes, en 2019, se publicó un artículo (Iess et al. (2019)) que estimaba la edad de los anillos entre los 10 y los 100 millones de años, algo que ponía de manifiesto que los anillos podrían haber sido unos recién llegados en términos geológicos, aunque más jóvenes que en el estudio mencionado anteriormente, y que estábamos teniendo mucha suerte de poder observarlos durante nuestra vida, teniendo en cuenta que el Sistema Solar tiene unos 4500 millones de años y que por lo tanto los anillos podrían haberse formado mucho antes.
 Un detalle de los anillos de Saturno. Obsérvese su color claro destacando en la imagen y debido a las partículas de hielo, ya que son muy eficientes reflejando la luz. Cortesía de NASA/JPL-Caltech/Space Science Institute.
Un detalle de los anillos de Saturno. Obsérvese su color claro destacando en la imagen y debido a las partículas de hielo, ya que son muy eficientes reflejando la luz. Cortesía de NASA/JPL-Caltech/Space Science Institute.Pero, ¿son estos rangos de edad los correctos? Un nuevo estudio publicado en mayo de este mismo año pone un límite superior a la edad de los anillos de Saturno: 400 millones de años. ¿Cómo han llegado a esta conclusión tan tajante los investigadores?
Hay partículas de roca que se mueven por nuestro Sistema Solar continuamente, pudiendo acumularse en las superficies planetarias o en este caso que nos ocupa, sobre el hielo de los anillos de Saturno, y si me permiten la analogía, es algo parecido a lo que ocurre en nuestras casas cuando no la limpiamos y vemos como se cubre todo de polvo.
Desde 2004 a 2017, el Cosmic Dust Analyzer de la sonda Cassini se dedicó a estudiar los pequeños granos de polvo que atravesaban el sistema de Saturno, detectando 163 granos de polvo que no estaban en órbita al planeta, sino que se habían cruzado con el planeta. Este instrumento es un espectrómetro que permitía calcular el tamaño, velocidad y composición de las partículas que impactaban en la sonda.
Los anillos de Saturno están compuestos principalmente por hielo de agua, pero entre el 0.1% y el 2% es material rocoso y probablemente una gran parte de estos granos provengan de fuera del propio sistema de Saturno. Conforme pasa el tiempo no solo irá cambiando esta proporción entre el hielo y las partículas de roca, sino que también los anillos se irán oscureciendo por la acumulación de polvo.
 Los anillos de Saturno son un lugar muy complejo en el que hay múltiples interacciones, como las que algunos satélites como Dafnis, en la imagen, ejercen sobre las partículas del anillo, moldeándolo y creando esas ondulaciones por efecto de su gravedad. . Cortesía de NASA/JPL-Caltech/Space Science Institute.
Los anillos de Saturno son un lugar muy complejo en el que hay múltiples interacciones, como las que algunos satélites como Dafnis, en la imagen, ejercen sobre las partículas del anillo, moldeándolo y creando esas ondulaciones por efecto de su gravedad. . Cortesía de NASA/JPL-Caltech/Space Science Institute.Con estos datos se ha podido calcular la velocidad a la cual los anillos de Saturno van ganando este polvo -las partículas rocosas- y con ello averiguar la horquilla de edades de formación más probables, aproximadamente entre los 100 y los 400 millones de años.
Eso si, los anillos no serán para siempre, ya que lentamente las partículas que los forman van cayendo sobre el planeta, de tal manera que, en aproximadamente 100 millones de años, podrían desaparecer por completo si no hay ningún mecanismo que vaya regenerando estos.
A pesar de que estos artículos recientes vayan en la línea de un sistema de anillos jóvenes, otros autores han sugerido que quizás si hay procesos que rejuvenecen el aspecto de los anillos, como una eliminación preferente de las partículas rocosas y de los compuestos orgánicos y que por lo tanto, los anillos serían mucho más antiguos y su juventud un mero espejismo.
Sin duda, la edad de los anillos de Saturno seguirá siendo un tema candente gracias a la reinterpretación de los datos tomados por la misión Cassini, pero, sea cual sea su edad, somos unos verdaderos afortunados por haber podido disfrutar en el momento adecuado del sistema de anillos más majestuoso de nuestro Sistema Solar.
Bibliografía:
Iess, L. et al. (2019) ‘Measurement and implications of Saturn’s Gravity Field and ring mass’, Science, 364(6445). doi: 10.1126/science.aat2965.
Kempf, S. et al. (2023) ‘Micrometeoroid infall onto Saturn’s rings constrains their age to no more than a few hundred million years’, Science Advances, 9(19). doi: 10.1126/sciadv.adf8537.
Wisdom, J. et al. (2022) ‘Loss of a satellite could explain Saturn’s obliquity and young rings’, Science, 377(6612), pp. 1285–1289. doi:10.1126/science.abn1234.
Para saber más:
¿Y si los dinosaurios se hubieran extinguido antes de que se formaran los anillos de Saturno?
Saturno en un vaso de aceite
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo La edad de los anillos de Saturno se ha escrito en Cuaderno de Cultura Científica.
Referencias científicas en la salsa
Las expresiones culturales en Latinoamérica son tan diversas como Latinoamérica en sí misma. Esto se debe en gran medida al génesis de nuestra historia (el origen del son* y el vacilón). La llegada de los europeos, el comercio triangular esclavista y la presencia de nuestros ancestros americanos generan una confluencia de culturas que hacen de este territorio un lugar único, donde tres visiones del mundo se conectan generando formas de arte únicas, exquisitas, pero sobre todo diversas. Un gran ejemplo de esta pluralidad es uno de los géneros musicales más apasionantes que existen: la salsa.
¿Qué es la salsa?, es una pregunta difícil de abordar y que puede generar mucha controversia. Pero inicialmente se podría decir que es un elemento de identidad cultural transversal en la vida de muchos latinos de distintas generaciones. Una forma de interactuar con el mundo, la música perfecta para la guachafita*, para la juma1, para la pachanga2, la música ideal pa’l bailador3. En palabras de Izzy Sanabria (maestro de ceremonias de la Fania All Stars)4:
La salsa es sabor y condimento. La salsa es el alma latina. La salsa es ritmo. Comenzó en África con la conga (piel sobre madera) “El bongo”. De África pal Caribe, Puerto Rico, Santo Domingo, Cuba, México y toda Sudamérica. Aquí se mezcló con el Indígena: “El timbal”, “El güiro”, “Las maracas” y la base de la salsa: “la clave”. De Europa: las 88 teclas “El piano”. Sus hijos viajaron a los Estados unidos y con la influencia del Jazz, “los instrumentos de viento”. ¡Esto es la salsa!
Ahora bien, dentro del Olimpo de la salsa podemos encontrar desde Puerto Rico, gigantes como Ismael Rivera “El sonero Mayor”, Héctor Lavoe “El rey de la puntualidad”, Cheo Feliciano, Richie Ray Y Bobby Cruz, El gran combo de Puerto Rico. Desde Cuba, Celia Cruz, Miguel Quintana, La Sonora Matancera, Buena Vista Social Club. Desde Colombia, Joe Arroyo, Fruko y sus Tesos, el grupo Niche, desde Panamá, el gran Rubén Blades, desde Venezuela Oscar de León y en New York, (el lugar donde la salsa nace como género musical) Willie Colon, Ray Barreto, Eddie Palmieri, Jonny Pacheco y el sello discográfico más importante: “La Fania”. De nuevo demostrando que, en términos de complejidad y diversidad, la salsa no tiene nada que envidiarles a otros géneros musicales (incluso me atrevería a decir que rivaliza en complejidad con muchos conceptos científicos abstractos).
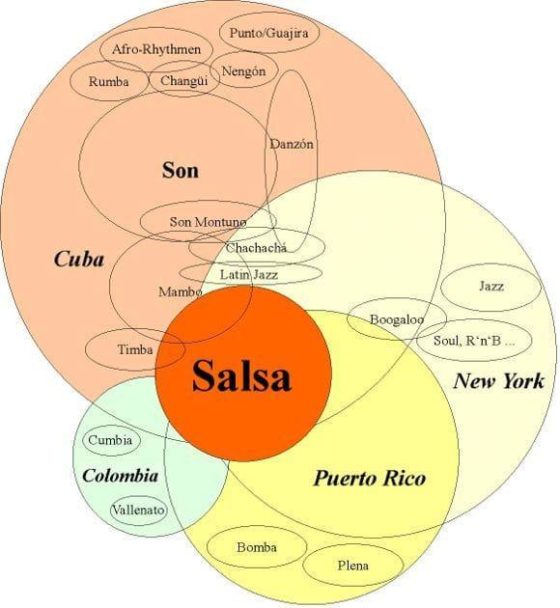 Fuente
Fuente
Por otro lado, existen muchos tópicos en lo que a las letras respecta y en palabras de Ismael Miranda5 :
“Para componer un son, se necesita un motivo y un tema constructivo y también inspiración”
Los temas son igualmente diversos, pero sobre todo apasionados: el amor6, el desamor7, la murga*8, nuestras raíces indígenas9, la vida bucólica10, la santería11, el sandungueo12, el tumbao13, el zaperoco14, la soledad15, la resiliencia16, reivindicaciones históricas17, denuncias sociales18, amores de telenovela19, etc. Pero, dentro de toda esta diversidad y saoco*, ¿existen referencias científicas en la salsa?
Indudablemente, la salsa con su variedad y complejidad tiene un espacio para la ciencia. El primer ejemplo lo podemos encontrar en una canción del Maestro Rubén Blades, nacido en Panamá, uno de los máximos exponentes del género, conocido por grandes clásicos de la salsa como: “Pedro Navaja”, “Plástico”, “Decisiones”, “Amor y control” y “Maestra vida”. En su álbum siembra, el más vendido en la historia, existe una canción llamada “Buscando Guayaba”20, en la cual se usa la guayaba (fruta redonda, amarilla por fuera y rosa por dentro) como una metáfora: la búsqueda de una mujer joven y atractiva. Ahora bien, “quien logre conquistarla, sabrá que, a falta de guitarra, lo mejor sería brindarle un solo de boca” (besos)21. El coro de esta canción menciona una sustancia química, el mentol22.

Así pues, ¿hay mentol en la guayaba? El mentol es un monoterpeno identificado por primera vez en la menta con propiedades sensitivas de frescor causadas por la depolarizacion en el canal iónico TRPM8, encargado entre otras cosas de la termorregulación23. Varios estudios químicos muestran que esta fruta contiene una gran variedad de terpenos (alrededor de 150), pero entre ellos no se encuentra el mentol24,25. Por otro lado, hay versiones de la canción que sugieren que la palabra en el coro no es mentol sino “mendo”26,27. Palabra cubana que hace referencia a la capacidad para hacer las cosas de la mejor manera21. En cualquier caso, se puede concluir que las guayabas son difíciles de encontrar, pero siempre habrá que seguir buscándolas.
El segundo ejemplo, lo podemos encontrar en otro de los grandes del género. Siendo esta una canción esencial de su repertorio: “Temperatura” por los Hermanos Lebrón28. Con un coro inolvidable, este tema describe la incapacidad de un hombre para declarar su amor. La forma que su enamorada lo hace sentir y al mismo tiempo la frustración por no tener la valentía suficiente para confesarlo. Y como esto hace que la temperatura suba más y más.
 Fuentes: Britannica.com y El Universo
Fuentes: Britannica.com y El UniversoDesde la química del estado gaseoso, la temperatura se puede relacionar con el movimiento de las partículas. A mayor movimiento de las partículas mayor probabilidad de choques y si aumentan los choques, entonces la temperatura también aumentara. ¿Cómo se relaciona esto con la salsa? La respuesta podría estar en el baile. La relación entre la salsa y el baile es innegable (razón por la cual muchos la evitan). Así pues, es posible que los Lebrón hagan referencia de una u otra manera a esta relación: El baile representa movimiento, a su vez el movimiento causará choques y a medida que la fiesta avance, la temperatura seguirá subiendo más y más.
Otro caso muy curioso se encuentra en el álbum “No Te voy a Querer” publicado en 1987 por la Orquesta Caribe en Puerto Rico liderada por el trompetista Hector Rivera29.

La segunda canción del lado B se titula “La ciencia”. Esta canción, es una fuerte reclamación a la ciencia en general, pregunta la razón por la cual siendo la ciencia digna de tanto asombro y generadora de tantas maravillas aun no logra resolver uno de los misterios más grandes en la historia del ser humano: el amor.
“La ciencia inventa tantas cosas que son milagros de gran admiración, yo digo la ciencia no ha podido con todo su adelanto inventar el amor”
Después de una busqueda rigurosa en bases de datos (donde se encuentran las mejores revistas científicas), después de consultar con varios colegas y profesores de diferentes ramas científicas, se puede concluir que es una pregunta que sigue en pie. Por lo visto el amor nunca será comprendido en totalidad, o como lo sugiere la canción, nunca terminará de inventarse.
Un cuarto ejemplo, en el cual se hace mención al amor de una manera interesante fue escrito por el sonero* puertorriqueño Primi Cruz. En su álbum homónimo de 1993, en el cual se encuentra la canción “La misma Química”30,31.

La palabra “química” es ampliamente usada para definir la compatibilidad entre dos personas. Si hay química entonces habrá afinidad y por lo tanto es muy probable que la relación llegue a buen puerto. Ahora bien, lo interesante (o gracioso) es que una reacción química no implica necesariamente algo bueno. Por ejemplo, los explosivos y los venenos son reacciones químicas que no están relacionadas en forma alguna con algo saludable o benéfico. Pero por alguna razón en la cultura popular esta palabra hace referencia a la afinidad que se puede llegar a tener o no con una persona y es precisamente lo que menciona esta canción:
“Tienes la misma química que yo…tenemos la misma química tu y yo”
Así pues, ¿qué significa la afinidad en la química? ¿Como podemos saber que puede haber o no una reacción? La respuesta esta en una de las ramas mas odiadas de la química la “termodinámica”; más específicamente la energía libre de Gibbs. La afinidad en este contexto esta asociada a una reacción química. Entonces, si hay afinidad la reacción procede, sino la hay no procederá. Con esto en mente, la energía libre es una noción que permite saber si una reacción procede (si es espontanea). Esta ecuación relaciona a su vez otros dos conceptos interesantes: “La entalpia” (energía que se produce o se libera) y “la entropía” asociada la temperatura (energía no aprovechable)32. Es decir, la relación entre estas tres variables nos permite saber si hay o no afinidad: ΔG = ΔH+TΔS
Cuando se miran estas tres variables al mismo tiempo se puede tener una predicción sobre la reacción. Si ΔG es positivo o igual a cero no hay afinidad y si es negativo hay afinidad (o reacción). Por lo tanto, en lo que a la canción respecta, para que haya “química” entre dos personas es necesario que la energía libre de Gibbs de estas sea negativa de tal manera que el proceso sea espontaneo.
La última canción no hace alusión a una rama científica, teoría, ley o concepto como las anteriores. Hace referencia a una ecuación. De hecho, una de las ecuaciones más famosas de la historia, la cual hace parte de la teoría de relatividad general y demuestra que la masa es una propiedad inherente a la energía, es decir, un indicador de la cantidad energía en un punto del espacio33 . En otras palabras, demuestra la equivalencia entre materia y energía: E=mc2. Lo que Albert Einstein no esperaba, es que su ecuación fuera usada por otro de los grandes de la salsa: Willie Colon. Con éxitos revolucionarios como “Idilio”, “El gran varón” o “Tiempo pa matar”. Willie Colon publica en 1975 el que sería su último trabajo con Héctor Lavoe y la primera colaboración con Rubén Blades, inspirado en una película western34: “The Good, the Bad and the Ugly” contiene en el lado A35, la canción titulada “MC2”. Un tema instrumental donde se puede apreciar la magistral improvisación de Yomo Toro en el cuatro con el acompañamiento en la guitarra eléctrica de Elliot Randall y un solo de Bongo por Jose Mangual Jr. A pesar que la canción no tiene letra, es interesante oír la mezcla entre un instrumento típico del rock y uno típico de la música latina y de la misma forma en la que esta ecuación muestra una equivalencia entre masa y energía, en la canción, se puede encontrar una “equivalencia musical” entre dos instrumentos diferentes, pero de alguna u otra manera equiparables.

Como todo tiene su final y para concluir. La ciencia y la salsa (en apariencia) están muy lejos una de otra, dado que la salsa no es considerada académica o intelectual (a pesar que fue creada por muchos músicos de academia e intelectuales), es algo que no viene en los libros, que no se enseña en la academia. Es un género conocido principalmente por su alegría, por las ganas de vivir que infunde en todo aquel que la oye, porque le imprime sabor a cualquier ocasión, es un lenguaje que genera un sin numero de emociones. No obstante, dentro de su gran variedad es posible encontrar pequeños visos a las ciencias, recordándonos que siempre que siga la clave* y siempre que se toque un buen son*, la salsa tendrá muchos temas para cantar y bailar. Es decir, siempre habrá un sonido bestial.
Para E.M, te conocí bailando salsa
Glosario21:
- Aguzar: Mantenerse en la jugada para que la vida no tome a la persona por sorpresa. Un llamado a ponerse mosca y salirle adelante a cualquier peligro o adversidad. ¡Escucha la voz cuando dice que te están velando!
- Clave: Figura rítmica cubana identificada por cinco golpes marcados en sentido 2:3 o 3:2.
- Guachafita: Situación en la que se forma tremenda algarabía cuando la gente canta, baila o chotorrea sin importar que el volumen incomode a los vecinos. Generalmente es propio de alguna celebración insospechada en la que todos son bienvenidos, aunque no haya cama pa’ tanta gente.
- Juma: Borrachera producto del exceso de licor y una buena rumba.
- Murga:Expresión artística que combina la música y el teatro. Se realiza en tiempos de carnaval con el fin de poner a reír y bailar al pueblo.
- Pachanga: Ritmo surgido en Cuba y popularizado en Nueva York a finales de los años cincuenta, con un sonido similar al de la charanga y el Cha-cha-cha. Combina elementos del son montuno y el merengue con letras en las que predomina un contenido picaresco.
- Rumba: Baile popular afrocubano que se ejecuta acompañado de instrumentos de percusión. Sinónimo de fiesta.
- Sandunguero: Persona que vive la rumba y tiene una soltura a la hora de echar pide. Aquel que con sus movimientos sensuales y ritmo seductor atrapa las miradas en la pista de baile
- Santería: Religión de la diáspora africana que se desarrolló en Cuba a finales del siglo xix.
- Saoco: Persona con chispa y estilo. Viste a la moda, le gusta la rumba buena y sabe gozarse el momento a donde quiera que vaya.
- Son: Ritmo asociado al baile profano, sensual y festivo que surgió en Cuba a finales del siglo XIX. Se interpreta con tres cubano, maraca, bongo, clave y marimbula. Sus versos coloquiales y anecdóticos son entonados por toda la agrupación.
- Sonero: Cantante con estilo propio, destrezas en la improvisación de coros e ingenio en el momento de improvisar. No todos los intérpretes dominan la clave y tienen la facultad de acelerar y desacelerar los fraseos. Su cantar contempla escenas propias del momento, conjuga las letras de distintas canciones y atiza el clamor del público con sus rimas.
- Tumbao: Ritmo propio de la mixtura de sonoridades afrocubanas y latinas que se interpreta a base de conga y bajo en la rumba y son. También se refiere a la candencia y sensualidad al momento de caminar o bailar.
- Vacilón: Rumba en la que se baila frenéticamente hasta gastar las suelas de los zapatos y olvidar los desengaños de la vida.
- Zaperoco: Alboroto que se arma cuando la rumba esta por la maceta.
Referencias:
1. Henry Fiol – La Juma de Ayer – YouTube. https://www.youtube.com/watch?v=i4PA7rvpvhk&ab_channel=Severo2007.
2. La Pachanga Se Baila Asi – YouTube. https://www.youtube.com/watch?v=Cyarz2Sil_Y&ab_channel=CharliePalmieri-Topic.
3. Joe Arroyo – Pal Bailador (Official Music Video) – YouTube. https://www.youtube.com/watch?v=IsmUixSq_hE&ab_channel=JoeArroyo.
4. WHAT is SALSA? – YouTube. https://www.youtube.com/watch?v=DhV5Hf0oHnc&ab_channel=IzzySanabria.
5. Ismael Miranda – Asi Se Compone Un Son – YouTube. https://www.youtube.com/watch?v=hkerFGjASWE&ab_channel=FaniaRecords.
6. Ismael Rivera – Soy Feliz (Official Visualizer) – YouTube. https://www.youtube.com/watch?v=uO50AU6Np6o&ab_channel=IsmaelRivera.
7. Hector Lavoe – Periodico De Ayer – YouTube. https://www.youtube.com/watch?v=qYkpURie5cU&ab_channel=FaniaRecords.
8. Willie Colon & Hector Lavoe – La Murga (Lyrics/Letras) – YouTube. https://www.youtube.com/watch?v=OIHcQ_-S3m0&ab_channel=FaniaRecords.
9. Gan Gan y Gon Gon – YouTube. https://www.youtube.com/watch?v=jAli0gCaXW4&ab_channel=Ricardo%22Richie%22Ray-Topic.
10. Willie Colón — “Guajira Ven” (Official Visualizer) – YouTube. https://www.youtube.com/watch?v=ebmc4qNJlE0&ab_channel=FaniaRecords.
11. El Hijo de Obatalá – YouTube. https://www.youtube.com/watch?v=gjDFU7y2nP0&ab_channel=RayBarretto-Topic.
12. Los Van Van – Sandunguera (Lyric Video) – YouTube. https://www.youtube.com/watch?v=806zEzy0X6c&ab_channel=LosVanVan.
13. Bajo Con Tumbao’ – YouTube. https://www.youtube.com/watch?v=Xqfi2oS_ao4&ab_channel=EddiePalmieri-Topic.
14. El Rincón – Conjunto Sensación – YouTube. https://www.youtube.com/watch?v=QngapmdsRUc&ab_channel=SalsaSoloParaColeccionistas-VinylLandStore.
15. Willie Colon ft Hector Lavoe – Ausencia – YouTube. https://www.youtube.com/watch?v=jNOyGRbdHGs&ab_channel=FaniaRecords.
16. Ray Barretto – Indestructible – YouTube. https://www.youtube.com/watch?v=ZCLeS1ICPuo&ab_channel=FaniaRecords.
17. Joe Arroyo – Rebelion (Audio) – YouTube. https://www.youtube.com/watch?v=KNcaw0Ye69g&ab_channel=JoeArroyo.
18. Ruben Blades & Willie Colon – Plantacion Adentro (Letras/Lyrics) – YouTube. https://www.youtube.com/watch?v=zx6qSntme3o&ab_channel=FaniaRecords.
19. Maria Teresa y Danilo ORIGINAL VIDEO – Hansel y Raul – YouTube. https://www.youtube.com/watch?v=d6HgXyQuNGo&ab_channel=HanselyRaul.
20. Willie Colon & Ruben Blades – Buscando Guayaba (Letras/Lyrics) – YouTube. https://www.youtube.com/watch?v=b3_onR65taQ.
21. Pantoja Junior. Diccionario Salsero. (Salsa sin Miseria y Editorial Quimbombo, 2021).
22. Letra de la canción Buscando guayaba – Rubén Blades. https://www.cancioneros.com/letras/cancion/102809/buscando-guayaba-ruben-blades.
23. Xu, L. et al. Molecular mechanisms underlying menthol binding and activation of TRPM8 ion channel. doi:10.1038/s41467-020-17582-x.
24. Silva Maiolini, T. C. et al. Essential Oils from Different Myrtaceae Species from Brazilian Atlantic Forest Biome – Chemical Dereplication and Evaluation of Antitrypanosomal Activity. Chem Biodivers 19, e202200198 (2022).
25. Weli, A. et al. Chemical composition and biological activities of the essential oils of Psidium guajava leaf. J King Saud Univ Sci 31, 993–998 (2019).
26. Buscando Giayaba – Rubén Blades – LETRAS.COM. https://www.letras.com/ruben-blades/746970/.
27. Willie Colón & Rubén Blades – Buscando Guayaba Lyrics | Genius Lyrics. https://genius.com/Willie-colon-and-ruben-blades-buscando-guayaba-lyrics.
28. Lebrón Brothers – Temperatura (Audio Oficial) – YouTube. https://www.youtube.com/watch?v=7uaenjSPhyE&ab_channel=LeBr%C3%B3nBrothers.
29. Orquesta Caribe – No Te Voy A Querer (1987, Vinyl) – Discogs. https://www.discogs.com/release/6471230-Orquesta-Caribe-No-Te-Voy-A-Querer.
30. Primi Cruz – Primi Cruz | Releases | Discogs. https://www.discogs.com/master/1325895-Primi-Cruz-Primi-Cruz.
31. La Misma Química – Primi Cruz [Official Video] – YouTube. https://www.youtube.com/watch?v=Tj0fLuGVI40&ab_channel=JNMusicGroup.
32. Conceptos Teóricos Energía Libre de Gibbs.
33. The Real Meaning of E=mc2 – YouTube. https://www.youtube.com/watch?v=Xo232kyTsO0&ab_channel=PBSSpaceTime.
34. Willie Colon – The Good, The Bad, The Ugly | Releases | Discogs. https://www.discogs.com/master/393977-Willie-Colon-The-GoodBadUgly.
35. MC2 Theme Realidades Willie Colón – YouTube. https://www.youtube.com/watch?v=8AF-YDTMvdk&ab_channel=Luckylouie522.
Sobre el autor: Daniel Arias Ramírez es investigador en el Laboratorio de espectrometría ICP-Ms, adjunto a la vicedecanatura de investigación en la Universidad de los Andes (Bogotá, Colombia).
El artículo Referencias científicas en la salsa se ha escrito en Cuaderno de Cultura Científica.
BCAM-Naukas 2023: Defendiendo a Newton
Quizás sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que existen en el mundo, estudiada por el ser humano desde hace más de 4.000 años. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
La fascinación que ha suscitado durante siglos es tal que el popular número cuenta con su propio día en el calendario, así el mes de marzo se celebra el Día de Pi en todo el planeta.

Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han sumado a la celebración, organizando la cuarta edición del evento BCAM NAUKAS, que tuvo lugar el 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
En Defendiendo a Newton, Anabel Forte reivindica la figura colosal de Newton quien, antes de presentar sus leyes y teorías físicas, tuvo que demostrar todas las matemáticas necesarias. Anabel Forte es profesora titular en el Departamento de Estadística e Investigación Operativa de la Universidad de Valencia y autora del blog de divulgación científica Bayesana: Estadística casi por todas partes.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo BCAM-Naukas 2023: Defendiendo a Newton se ha escrito en Cuaderno de Cultura Científica.
Terapias ARN, un presente con mucho futuro
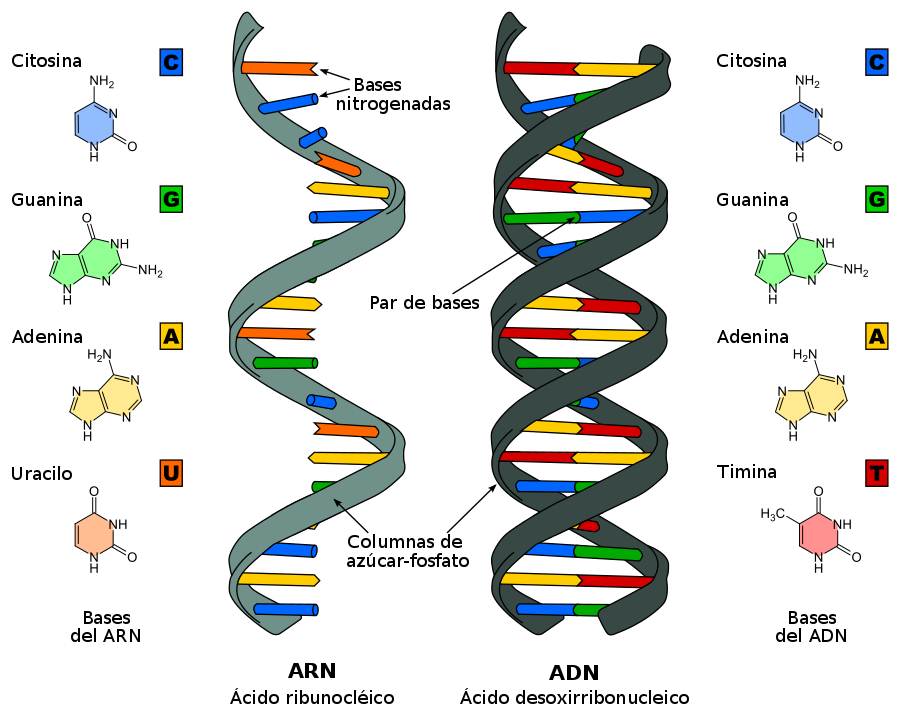 Diferencias en la estructura básica de ARN y ADN. Fuente: Wikimedia Commons
Diferencias en la estructura básica de ARN y ADN. Fuente: Wikimedia CommonsLa expresión “llevar algo en el ADN” es un reflejo de cuán extendido está el conocimiento sobre el ADN o ácido desoxirribonucleico en la sociedad. Sin embargo, el ARN o ácido ribonucleico es mucho menos conocido. Hasta hace poco se le conocía como una ‘copia’ del ADN que llevaba información para sintetizar proteínas, pero ahora sabemos que hay muchos tipos de ARN como el mensajero (ARNm), los de interferencia siARN (del inglés short interfering), los microARNs (miARN) y muchos otros que presentan diferentes funciones relacionadas con la síntesis de proteínas en el organismo.
Cada una de esas funciones representa una nueva diana con la que es posible interaccionar para alterar la expresión de proteínas, tanto evitando la expresión de proteínas perjudiciales como permitiendo la expresión de otras necesarias. Esa amplia gama de actividad explica que los diseños de nuevas terapias ARN tengan un elevado potencial tanto para la prevención como para el tratamiento de enfermedades muy diversas. La aplicación clínica de esas terapias se ha realizado de manera generalizada a la población debido a la pandemia de la COVID-19. La inmunización frente al coronavirus SARS-CoV-2 se ha realizado con vacunas de ácidos nucleicos, incluyendo las basadas en ARN. En ese sentido, la elevada eficacia obtenida y, sobre todo, el excelente perfil de seguridad mostrado, está fomentando el auge de nuevas terapias ARN.
Las posibilidades que ofrecen las terapias ARN han revolucionado la manera de afrontar el tratamiento de numerosas enfermedades, ofreciendo incluso nuevas opciones a aquellas para las que actualmente no hay terapias disponibles. Las enfermedades candidatas a ser tratadas mediante ARN pueden ser hereditarias (como, por ejemplo, las enfermedades de depósito lisosomal, las distrofias musculares o la fibrosis quística) o adquiridas (como el cáncer, enfermedades infecciosas, degeneración macular o enfermedades neurológicas como el Parkinson o el Alzheimer, entre otras).
Aunque la mayoría de esos nuevos medicamentos estén aún en desarrollo, además de las vacunas ARN, existen ya varios productos aprobados para el tratamiento de enfermedades poco frecuentes, como la atrofia muscular espinal o la distrofia muscular de Duchenne, pero también para otras mucho más frecuentes, como terapias para la prevención cardiovascular y manejo de las dislipemias. Se espera que en los próximos años se desarrollen muchas más terapias ARN: una nueva clase de medicamentos con grandes ventajas por ser muy específicos en su mecanismo de acción. Sin embargo, uno de los principales obstáculos para el desarrollo de esos medicamentos es la obtención de un sistema de administración eficaz y seguro, capaz de proteger el ARN terapéutico y acceder al lugar de acción, permitiendo que ejerza su efecto.
El mayor problema para la aplicación de las terapias ARNLa eficacia de las terapias ARN está condicionada por sus dificultades para superar las barreras anatómicas y extracelulares, que limitan su acceso y, por tanto, su efecto en una célula concreta. No es igual de accesible el ojo (un tejido muy bien delimitado y pequeño) o la sangre (fácilmente accesible), que el músculo (un tejido muy extenso y protegido por muchas barreras físicas) o el cerebro (protegido por la barrera hematoencefálica). Las nanopartículas lipídicas, empleadas en las vacunas COVID-19, han mostrado ser un sistema altamente seguro y eficaz para administrar esos medicamentos de forma local, y también se han utilizado para terapias ARN dirigidas al hígado. Sin embargo, es necesario el desarrollo de nuevos sistemas con el fin de administrar terapias que necesitan distribuirse de manera generalizada a otros tejidos (como, por ejemplo, el músculo y el tejido óseo) o llegar a órganos de difícil acceso (como el cerebro).
Recientemente se celebró en Bizkaia Aretoa el congreso internacional organizado por la UPV/EHU y DARTER COST (Acción de Cooperación Europea en Ciencia y Tecnología), que contó con la partición de 160 personas de 17 países europeos. La red de investigadoras e investigadores DARTER, liderada por Virginia Arechavala, aglutina a más de 450 investigadoras e investigadores de toda Europa con el interés común de resolver el mayor problema para la aplicación de las terapias ARN: su mala distribución dentro del organismo. Durante tres días, personal experto en diversos ámbitos (estudio de las enfermedades y posibles tejidos diana, química de esos ácidos nucleicos, terapias avanzadas, nanomedicina, y diseño y evaluación de nuevos sistemas de administración de fármacos) han compartido su conocimiento para fomentar la diseminación de resultados y la búsqueda de sinergias en investigación. Participantes en el congreso (entre quienes se encontraba personal investigador, representantes de asociaciones de pacientes y empresas) destacaron la calidad de las más de 80 presentaciones orales y 60 posters con los que se ha buscado favorecer la colaboración multidisciplinar en ese ámbito.
Para saber más:
Buscando terapias para enfermedades poco frecuentes
‘Hackers’ están diseñando los próximos fármacos
Sobre las autoras:
Mª Ángeles Solinís Aspiazu. Profesora de la Facultad de Farmacia de la Universidad del País Vasco. Investigadora del grupo PharmaNanoGene de la UPV/EHU y del IIS Bioaraba.
Ainara Vallejo Illarramendi. Investigadora permanente del Departamento de Pediatría de la Universidad del País Vasco. Jefa del grupo Neurociencias de la UPV/EHU e investigadora del IIS Biodonostia.
Olatz Villate. Investigadora del grupo Oncología Pediátrica del IIS Biocruces-Bizkaia.
Virginia Arechavala Gomeza. Investigadora Ikerbasque Professor. Jefa del grupo Terapias de Ácidos Nucleicos para Enfermedades Raras (NAT-RD), IIS Biocruces Bizkaia.
El artículo Terapias ARN, un presente con mucho futuro se ha escrito en Cuaderno de Cultura Científica.
Geolodía, la fiesta de la divulgación geológica
El pasado fin de semana, sábado 6 y domingo 7 de mayo, se celebró el Geolodía 23, el mayor evento de divulgación de la Geología de España y, sin ánimo de parecer grandilocuente, de todo el mundo.
 Logotipo del Geolodía 23. Imagen: Sociedad Geológica de España.
Logotipo del Geolodía 23. Imagen: Sociedad Geológica de España.El Geolodía consiste, principalmente, en excursiones geológicas, ya sea en entornos urbanos o por el campo, a razón de una por provincia, guiadas por profesionales de las Ciencias de la Tierra, totalmente gratuitas y abiertas a todo tipo de público, que se realizan el mismo fin de semana en toda España. El principal objetivo es llevar a la gente a nuestro laboratorio natural y que aprendan a ver, con ojos geológicos, el paisaje que les rodea. Y también que comprendan la labor que realizamos todas las personas que nos dedicamos a las Ciencias de la Tierra: búsqueda de recursos, prevención de riesgos, gestión del terreno, obra civil, conservación del medio, regeneración ambiental y un larguísimo etcétera. Incluso, en el año 2019 se decidió realizar esta labor divulgativa durante todo el año con la puesta en marcha, a iniciativa de la Comisión Mujeres y Geología de la Sociedad Geológica de España, de las Geocharlas, que consisten en conferencias, talleres y paseos geológicos conducidos por profesionales de las Ciencias de la Tierra que se ofrecen, también de manera gratuita, a centros educativos y asociaciones de diversa índole.
 Detalle de las explicaciones realizadas por compañeros de la Universidad de Granada (UGR) en un taller ofertado como una de las Geocharlas realizadas en el CEIP Medina Elvira (Atarfe, Granada) el viernes 10 de febrero, con motivo de la celebración del “11F, Día Internacional de la Mujer y la Niña en la Ciencia”.
Detalle de las explicaciones realizadas por compañeros de la Universidad de Granada (UGR) en un taller ofertado como una de las Geocharlas realizadas en el CEIP Medina Elvira (Atarfe, Granada) el viernes 10 de febrero, con motivo de la celebración del “11F, Día Internacional de la Mujer y la Niña en la Ciencia”.Pero la pandemia acabó con la principal característica de estas actividades didácticas, la presencialidad. En ese momento, desde la Sociedad Geológica de España decidimos aplicar la lección que nos enseñaron los dinosaurios hace 66 millones de años: o te adaptas, o te extingues. Así, en 2020 virtualizamos el evento, realizando vídeos de los recorridos desde nuestros propios hogares. Y resultaron todo un éxito, lo que hizo que, desde el año 2021, el Geolodía haya adquirido un formato mixto. Las actividades presenciales son las protagonistas, pero se complementan con conferencias online, recorridos virtuales, concursos en las redes sociales y videojuegos.
El pasado fin de semana, más de 8000 personas asistieron a las 54 excursiones realizadas por toda España, que se suman a los más de 2000 participantes en las Geocharlas desde que comenzó el curso escolar en septiembre. Y las actividades virtuales han cosechado decenas de miles de impactos en redes, que seguirán aumentando con el paso del tiempo. Esto convierte al Geolodía en la actividad de divulgación dedicada a una única ciencia que reúne a más personas, tanto de manera presencial como online. Y no sólo como público asistente, ya que participan más de 600 profesionales de la Geología en la organización y realización de las actividades, e involucra a más de 300 instituciones, asociaciones, empresas, centros educativos y de investigación que colaboran para hacerlas posibles.
 Explicaciones de un compañero de la Universidad de Coimbra (Portugal), exalumno de la Universidad de Huelva, a uno de los grupos asistentes a la excursión presencial realizada en la provincia de Huelva el sábado 6 de mayo. Fotografía de Juan Antonio Morales.
Explicaciones de un compañero de la Universidad de Coimbra (Portugal), exalumno de la Universidad de Huelva, a uno de los grupos asistentes a la excursión presencial realizada en la provincia de Huelva el sábado 6 de mayo. Fotografía de Juan Antonio Morales.Imagino lo que os estaréis preguntando: ¿Son necesarias estás actividades de divulgación de la Geología? ¿Merece la pena este enorme esfuerzo por parte de tanta gente e instituciones para transmitir este conocimiento científico? Pues, por desgracia, sí. Parece mentira que, en esta era digital en la que vivimos, que nos proporciona información con un simple “click” del ratón del ordenador, nos encontremos con un predominio cada vez más preocupante de la anticiencia en el ámbito geológico. A los enemigos ya conocidos, como el terraplanismo o el negacionismo de la evolución biológica, se unen el negacionismo del cambio climático y de la influencia antrópica en sus ciclos naturales, la creencia de que eventos naturales como los terremotos son producidos por pruebas armamentísticas dignas de películas de ciencia ficción, propuestas aún más peliculeras como taponar con cemento el cráter de un volcán en erupción para frenar el ascenso del magma, considerar que el núcleo de nuestro planeta puede llegar a detenerse sin que nos enteremos, asegurar que se puede extraer agua subterránea sin control porque nunca se va a agotar o, más recientemente, solicitar que se ponga barreras a los ríos para evitar que descarguen el agua que transportan al mar porque “se está desperdiciando”.
Aunque todas estas ideas peregrinas, por llamarlas de alguna manera fina y delicada, nos hagan reír un rato, son muy serias para tomarlas a broma, ya que reflejan la necesidad de transmitir el conocimiento geológico a la sociedad, intentando hacer más ruido que todas aquellas personas que fomentan todas estas creencias acientíficas. Por eso es tan necesario mantener ese formato cercano, informal y lúdico del Geolodía, donde la gente de todas las edades y nivel de conocimiento previo puede tener un contacto directo con profesionales de las Ciencias de la Tierra para plantearnos todas sus dudas, mientras aprenden Geología sin darse cuenta. Por eso, nos seguiréis encontrando liando la mejor fiesta de la divulgación geológica año tras año. Nos vemos en el próximo Geolodía.
Agradecimientos:
Geolodía es un proyecto coordinado por la Sociedad Geológica de España (SGE) que cuenta con la colaboración de la Fundación Española para la Ciencia y la Tecnología – Ministerio de Ciencia e Innovación, la Asociación Española para la Enseñanza de las Ciencia de la Tierra (AEPECT), el Instituto Geológico y Minero de España (IGME-CSIC), la International Association of Sedimentologists (IAS), la Asociación de Geólogos y Geofísicos Españoles del Petróleo (AAGEP), Repsol y más de 300 instituciones. Sin su apoyo, así como la participación desinteresada de más de 600 profesionales de las Ciencias de la Tierra, este proyecto no podría llevarse a cabo. Y, como no, hay que agradecer la asistencia, comentarios, participación y colaboración de todas las personas asistentes a las actividades, que generan un ambiente lúdico e informal que favorece la transmisión de conocimiento y el debate en donde se producen aprendizajes bidireccionales.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Geolodía, la fiesta de la divulgación geológica se ha escrito en Cuaderno de Cultura Científica.
Cecilia Payne-Gaposchkin, la autora de «la tesis doctoral más brillante jamás escrita en astronomía»
La astrónoma Cecilia Payne-Gaposchkin (1900-1979) nació tal día como hoy hace 123 años. Le rendimos homenaje a través de este retrato alfabético.
 Cecilia Payne-Gaposchkin. Fuente: Wikimedia Commons.
Cecilia Payne-Gaposchkin. Fuente: Wikimedia Commons.
ASTRONOMÍA
Aunque la astronomía no fue su primera opción de estudio, una conferencia (ver la letra E) la conduciría hacia esta disciplina.
BOTÁNICA
Estudió botánica, física y química en la Universidad de Cambridge.
COSTURERA
Katherine, su hija, la recordaba como «una costurera inspirada, una tejedora inventiva y una lectora voraz». Con 75 años realizó un bordado representando el remanente de supernova Cassiopeia A inspirado en la imagen de la portada de la revista Scientific American de diciembre de 1975.
Dorothy Dalglish
Dorothy Dalglish fue una de las profesoras de ciencias de Cecilia en el St Mary’s College de Paddington en Londres. Tenía en ese momento 12 años y muchas ganas de aprender en un centro escolar que apenas dedicaba tiempo a la ciencia. Dalglish intentó suplir estas carencias, prestándole sus libros de física y llevándola a museos.
Cuando tenía seis años Cecilia había asistido a una escuela local en Wendover (donde vivía entonces la familia). En ese centro, dirigido por Elizabeth Edwards, recibió una buena educación. Con 12 años, Cecilia hablaba francés y alemán, tenía conocimientos básicos de latín y dominaba la aritmética. También estudió allí geometría y álgebra.
EDDINGTON, ARTHUR
El interés de Cecilia por la astronomía comenzó tras asistir a una conferencia impartida por el astrofísico Arthur Eddington (1882-1944). El científico hablaba sobre la expedición que había realizado a la isla de Príncipe (Golfo de Guinea) para observar y fotografiar las estrellas durante el eclipse solar del 29 de mayo de 1919. Las observaciones del astrónomo confirmaron la teoría de la relatividad general de Albert Einstein.
FEYNMANN, JOAN
Cecilia Payne fue una inspiración para muchas personas como la astrofísica Joan Feynman (1927-2020). La madre y la abuela de Feynman pensaban que las mujeres no eran capaces de entender conceptos científicos y habían desanimado a Joan en su deseo de formarse en esas disciplinas. Afortunadamente, Feynman se inspiró en Cecilia Payne leyendo sobre su trabajo en un libro de astronomía.
Gaposchkin, Sergei
Conoció a Sergei Gaposchkin (1898-1984) en Gotinga, durante un congreso. Cecilia, que residía en aquel momento en Estados Unidos, le ayudó a obtener un visado para emigrar a ese país y huir de la persecución nazi. Se casaron en 1934 y Cecilia adoptó el apellido Payne-Gaposchkin. A partir de 1935 comenzaron a colaborar en sus investigaciones sobre astronomía estelar. Su primer libro conjunto fue Variable Stars (1938).
HIDRÓGENO (Y HELIO)
En su tesis demostró que el hidrógeno es el principal componente de las estrellas (donde también hay helio, pero menor proporción), afirmación que contradecía la teoría de la época que afirmaba que las estrellas tendrían una composición similar a la Tierra. Llegó a esta conclusión aplicando la teoría de la ionización desarrollada por el astrofísico Meghnad Saha (1893-1956) con la que pudo relacionar la clasificación espectral de las estrellas con sus temperaturas absolutas.
INVESTIGACION
En 1976 recibió el Premio Henry Norris Russell de la Sociedad Astronómica Estadounidense. En su conferencia, Payne habló de su pasión por la investigación: «La recompensa del joven científico es la emoción de ser la primera persona en la historia del mundo en ver o entender algo. Nada se puede comparar con esa experiencia. […] La recompensa del viejo científico es la sensación de haber visto un vago esbozo convertirse en un paisaje magistral».
JUBILACIÓN
Incluso tras su jubilación las estrellas continuaron siendo una parte importante de su vida. Trabajó en el Observatorio Astrofísico Smithsoniano desde 1967 hasta su fallecimiento.
KNOWLES, JEREMY
Jeremy Knowles(1935-2008), decano de la Facultad de Artes y Ciencias de la Universidad de Harvard, comentaba en febrero de 2002 en unos actos de homenaje a Cecilia Payne-Gaposchkin: «La aportación científica más espectacular de Payne-Gaposchkin fue el descubrimiento de que el hidrógeno es millones de veces más abundante que cualquier otro elemento del universo. Todo estudiante de secundaria sabe que Newton descubrió la gravedad, que Darwin descubrió la evolución, incluso que Einstein descubrió la relatividad. Pero cuando se trata de la composición de nuestro universo, los libros de texto se limitan a decir que el elemento más abundante en el universo es el hidrógeno. Y nadie se pregunta cómo lo sabemos… Tras doctorarse, dio clases en el departamento de astronomía, pero sus no figuraban en el catálogo de cursos. Dirigió investigaciones de posgrado sin estatus; no tenía permiso de investigación; y su pequeño salario estaba categorizado por el departamento como «equipamiento». Sin embargo, sobrevivió y prosperó».
LIBROS
Publicó varios libros a lo largo de su carrera, entre otros The Stars of High Luminosity (1930), Variable Stars (1938) y Variable Stars and Galactic Structure (1954).
MENZEL, DONALD
Tras conocer al astrónomo Harlow Shapley (1885-1972), Payne viajó a Estados Unidos para cursar un postgrado en astronomía en el Observatorio del Harvard College. Fue la segunda estudiante, tras Adelaide Ames (1900-1932), en unirse a un programa de becas en el Observatorio para animar a las mujeres a estudiar allí. Cuando Donald Menzel (1901-1976) se convirtió en director del Observatorio en 1954, trató de mejorar las condiciones laborales de Payne-Gaposchkin; en 1956 se convirtió en la primera mujer en ser promovida a profesora titular en la Facultad de Artes y Ciencias de Harvard.
NEWNHAM COLLEGE
A partir de 1919, en el Newnham College de la Universidad de Cambridge, Payne estudió botánica, física y química, pero abandonó la botánica después de su primer año.
OBSERVATORIO DE HARVARD
En 1923, gracias a una beca, viajó a la Universidad de Harvard en Cambridge, Massachusetts, y se afilió a su Observatorio.
PAYNE, Edward John Y PERTZ, EMMA LEONORA HELENA
Cecilia era hija del abogado Edward John Payne y Emma Leonora Helena Pertz.
Su padre falleció cuando Cecilia tenía cuatro años. Le encontraron ahogado en un canal en Wendover en circunstancias poco claras. Cecilia tenía un hermano y una hermana, Humfry (1902-1936) y Leonora Florence Mary (1904-1996).
RECHAZO
Sus conclusiones innovadoras sobre la composición de las estrellas (ver la letra H) fueron rechazadas inicialmente al contradecir las teorías aceptadas en ese momento que afirmaban que no había diferencias significativas entre la composición del Sol y la Tierra. Estudios posteriores demostraron que Payne tenía razón.
SHAPLEY
Cecilia Payne comprendió que la única opción de carrera en el Reino Unido era convertirse en maestra, por lo que buscó subvenciones que le permitieran viajar a Estados Unidos. Abandonó su país natal en 1923 para incorporarse al programa de postgrado en astronomía del Observatorio del Harvard College, dirigido en ese momento por Harlow Shapley. Cecilia había conocido al astrónomo en Inglaterra y él la animó a unirse al Observatorio a través de un programa de becas destinadas a mujeres.
 Fuente: Universidad de Harvard.
Fuente: Universidad de Harvard.
TESIS
Harlow Shapley convenció a Payne–Gaposchkin para que escribiera una tesis doctoral. Cecilia se convirtió en 1925 en la primera persona en obtener un doctorado en astronomía en el Radcliffe College de la Universidad de Harvard con la memoria titulada Stellar Atmospheres, A Contribution to the Observational Study of High Temperature in the Reversing Layers of Stars. El astrónomo Otto Struve (1897-1963) la describiría años más tarde como «la tesis doctoral más brillante jamás escrita en astronomía».
Al revisar la memoria de Payne–Gaposchkin, el astrónomo Henry Norris Russell (1877-1957) la disuadió de concluir que la composición del Sol era fundamentalmente hidrógeno porque contradecía el consenso científico aceptado entonces. Cecilia agregó un comentario a sus (correctas) conclusiones, temiendo que su tesis no fuera aprobada: «Es casi seguro que las enormes abundancias derivadas de esos elementos en la atmósfera estelar no son reales. Probablemente el resultado pueda considerarse, para el hidrógeno, como otro aspecto de su comportamiento anormal… y el helio… posiblemente se desvía por razones similares».
Algún tiempo más tarde Russell se dio cuenta de que ella estaba en lo cierto cuando obtuvo los mismos resultados por diferentes medios. En 1929, publicó sus conclusiones en el artículo On the Composition of the Sun’s Atmosphere en el que reconocía brevemente el trabajo y descubrimiento anterior de Payne.
UNIVERSIDAD
Sus cursos no fueron registrados en el catálogo de la Universidad de Harvard hasta 1945. En 1967 se convirtió en Profesora Emérita de esta institución.
VIA LÁCTEA
Después de su tesis, Payne continuó estudiando estrellas de alta luminosidad para comprender la estructura de la Vía Láctea. Más tarde, junto a su marido, examinó todas las estrellas más brillantes que la décima magnitud. También estudió estrellas variables, realizando con sus asistentes más de 1 250 000 observaciones. Después investigó las Nubes de Magallanes, añadiendo otras 2.000.000 de observaciones de estrellas variables. Estos datos se utilizaron para determinar los caminos de la evolución estelar.
WENDOVER
Nació en Wendover, localidad situada en el condado de Buckinghamshire, en Inglaterra.
X, RAYOS
Cecilia (ver la letra C) bordó el remanente de supernova Cassiopeia A a partir de una imagen tomada por rayos X y que aparecía en la portada de la revista Scientific American.
Y
Y… llegamos al final.
ZURDA
Era zurda, pero la obligaron a escribir con la mano derecha. A pesar de todas las dificultades que tuvo a lo largo de su carrera, su legado queda. Falleció el 7 de diciembre de 1979, a los 79 años.
Referencias
-
Aitziber Lopez, Cecilia Payne-Gaposchkin: “La astrónoma que descubrió la composición de las estrellas”, Mujeres con ciencia, Vidas científicas, 12 abril 2017
-
Marta Macho Stadler, Cassiopeia A, bordada por Cecilia Payne-Gaposchkin, Mujeres con ciencia, Ciencia y más, 20 octubre 2017
-
Cecilia Payne, la mujer que cambió la receta del universo, SINC, 8 de mayo de 2014
-
Cecilia Payne-Gasposchkin, Wikipedia
- John J. O’Connor and Edmund F. Robertson, Cecilia Payne-Gaposchkin, MacTutor History of Mathematics archive, University of St Andrews
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Cecilia Payne-Gaposchkin, la autora de «la tesis doctoral más brillante jamás escrita en astronomía» se ha escrito en Cuaderno de Cultura Científica.
Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- …
- hurrengoa ›
- azkena »

