Saturno tiene el sistema de nieblas en capas más extenso observado en el Sistema Solar
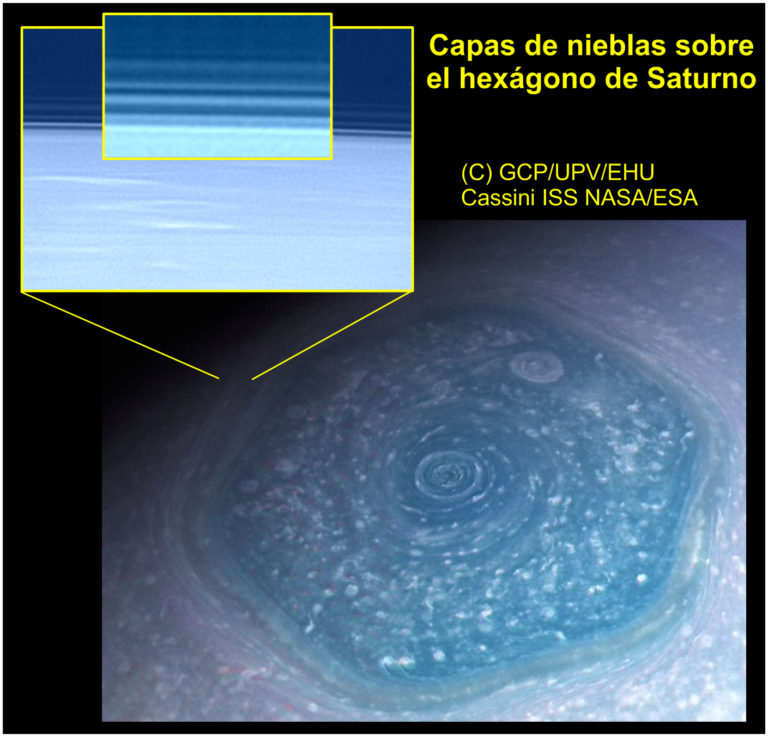
En la extensa atmósfera de hidrógeno del planeta Saturno, un mundo gigante, con unas diez veces el tamaño de la Tierra, se desarrollan fenómenos meteorológicos muy diversos cuyo estudio nos permite comprender mejor los de la atmósfera terrestre. Entre ellos destaca por su singularidad el conocido “hexágono”, una estructura ondulante que rodea a la región polar norte del planeta cuya forma parecería haber sido trazada por un geómetra.
Descubierta en 1980 por las naves espaciales Voyager 1 y 2 de la NASA, ha sido observada ininterrumpidamente desde entonces, a pesar del intenso y largo ciclo de estaciones del planeta. Por el interior de esta gigantesca onda planetaria fluye una estrecha y rápida corriente en chorro en donde los vientos alcanzan velocidades máximas de unos 400 km/hora. Mientras, curiosamente, la onda en sí misma permanece casi estática; es decir, apenas se desplaza con respecto a la rotación del planeta. Todas estas propiedades hacen que el “hexágono” sea un fenómeno altamente atractivo para los meteorólogos e investigadores de las atmósferas de los planetas.
La nave Cassini, que estuvo en órbita del planeta entre los años 2004 y 2017, tomó una inmensa cantidad de imágenes desde muy variadas distancias al planeta y ángulos de visión. En junio del año 2015, su cámara principal obtuvo imágenes del limbo del planeta a muy alta resolución, capaces de resolver detalles de 1-2 km, que capturaban las nieblas situadas sobre las nubes que trazan la onda hexagonal. Además, utilizó muchos filtros de color, desde el ultravioleta hasta el infrarrojo cercano, permitiendo así estudiar la composición de estas nieblas. Como apoyo para este estudio se usaron también imágenes del Telescopio Espacial Hubble tomadas 15 días más tarde y que muestran al hexágono no en el limbo sino visto desde arriba. “Las imágenes de Cassini nos han permitido descubrir que, como si formaran un “sandwich”, el hexágono tiene un sistema multicapa de, al menos, siete neblinas que se extienden desde la cima de sus nubes hasta más de 300 km de altura sobre ellas”, ha declarado el profesor Agustín Sánchez Lavega, quien lidera el estudio. “Otros mundos fríos como el satélite Titán de Saturno o el planeta enano Plutón tienen también capas de nieblas, pero no en tal número, ni tan regularmente espaciadas”.
Cada capa de niebla tiene entre 7 y 18 kilómetros de espesor en vertical y de acuerdo con el análisis espectral contienen partículas muy pequeñas con radios del orden de 1 micra. Su composición química es exótica para nuestros estándares terrestres, ya que, debido a las bajas temperaturas en la atmósfera de Saturno, entre 120 °C y 180 °C bajo cero, pudieran estar compuestas por cristalitos de hielo de hidrocarburos como el acetileno, propino, propano, diacetileno, o incluso butano en el caso de las nieblas más altas.
Otro de los aspectos que el equipo ha estudiado es la regularidad en la distribución vertical de las nieblas. La hipótesis que proponen es que las nieblas están organizadas por la propagación vertical de ondas de gravedad que generan oscilaciones en la densidad y temperatura de la atmósfera, fenómeno bien conocido en la Tierra y otros planetas. Los investigadores plantean que es la propia dinámica del hexágono y su intensa corriente en chorro la que puede estar detrás de la formación de estas ondas de gravedad. En la Tierra también se han observado este tipo de ondas generadas por la corriente en chorro ondulante que con velocidades de 100 km/h se dirige de Oeste a Este en las latitudes medias. El fenómeno pudiera ser semejante en ambos planetas, si bien las peculiaridades de Saturno hacen que este sea un caso único en el sistema solar. Este es un aspecto que queda pendiente para futuras investigaciones.
Referencias:
A. Sánchez-Lavega, A. García-Muñoz, T. del Río-Gaztelurrutia, S. Pérez-Hoyos, J. F. Sanz-Requena, R. Hueso, S. Guerlet & J. Peralta (2020) Multilayer hazes over Saturn’s hexagon from Cassini ISS limb images Nature Communications doi: 10.1038/s41467-020-16110-1
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Saturno tiene el sistema de nieblas en capas más extenso observado en el Sistema Solar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- A vueltas con el hexágono de Saturno
- Planeta X, en busca del inquilino invisible del sistema solar
- Día de Darwin 2020: Evolución del Sistema Solar + Teoría evolutiva y medicina
El ferrocarril metropolitano ante la COVID-19
Iván Rivera
 Cercanías entrando en la estación de Atocha, Madrid. Foto: Iván Rivera
Cercanías entrando en la estación de Atocha, Madrid. Foto: Iván RiveraLa pandemia provocada por SARS-CoV-2, el virus informal y metonímicamente conocido como coronavirus, está suponiendo un reto complejo de afrontar para una enorme cantidad de sistemas de organización y tecnológicos cuya rentabilidad, tanto social como económica, ha dependido hasta ahora de su rendimiento medido en número de personas servidas por unidad de medida temporal o de tamaño.
Entre estos sistemas destaca por méritos propios el transporte público metropolitano. Esencial para garantizar la movilidad en los entornos urbanos, el transporte público es el gran igualador de oportunidades para amplios segmentos de la población. Por ello, la respuesta de los sistemas de transporte, y en particular los ferroviarios, frente a la crisis de la epidemia de COVID-19 ha suscitado gran atención y preocupación.
Los límites del distanciamiento
Hasta ahora, ésta ha pivotado mayoritariamente en torno a medidas destinadas a aumentar el distanciamiento social. En términos prácticos, el distanciamiento social en el transporte se traduce en separación física entre usuarios: una distancia recomendada de seguridad de más de un metro [1], lo que significa que en un recinto cerrado y suponiendo una disposición óptima hexagonal y un área personal —el área físicamente ocupada por cada individuo— de 0,28 m², la densidad máxima alcanzable está por debajo de las 0,45 personas/m². Los límites físicos del recinto —mamparos, paramentos verticales— introducirían una corrección al alza en esta estimación.
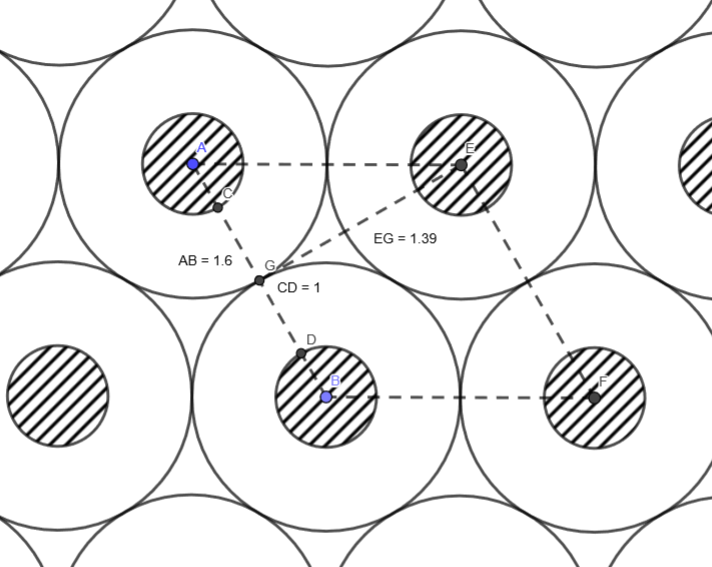 Celda unitaria del modelo de empaquetamiento óptimo para personas, considerando un espacio individual ocupado circular de radio 0,3 metros. Imagen: Iván Rivera
Celda unitaria del modelo de empaquetamiento óptimo para personas, considerando un espacio individual ocupado circular de radio 0,3 metros. Imagen: Iván RiveraLa recomendación de mantener una distancia de seguridad de un metro de distancia, emitida por la Organización Mundial de la Salud, choca con otras estimaciones superiores. El CDC (Centers for Disease Control and Prevention, Centros para el Control y la Prevención de Enfermedades) estadounidense recomienda una separación social de dos metros, lo que coincide con la recomendación del administrador de infraestructuras ferroviarias español, Adif. Recientes estudios acerca de la propagación de nubes de gotículas [2] han llegado a medir velocidades de hasta 30 metros por segundo en el estornudo, lo que establecería una cota superior para la distancia de riesgo en el rango de los 7-8 metros en la dirección frontal.
Incluso sin tener en cuenta la influencia de los estornudos en la posible propagación de patógenos, estos resultados chocan frontalmente con los cálculos de capacidad realizados por organismos reguladores como el Consorcio de Transportes de Madrid, que estima un máximo de 4 personas por metro cuadrado, o incluso con los de operadores como Metro de Madrid, que ha llegado a establecer su oferta de transporte en función de capacidades máximas de 6 personas por metro cuadrado [3].
El modelo de separación de seguridad con empaquetamiento óptimo sugiere que habría que multiplicar por nueve —en el mejor de los casos— la oferta de plazas en el momento más desfavorable, la hora punta. Aunque los sistemas ferroviarios metropolitanos han optado mayoritariamente por mantener o incluso aumentar las frecuencias de paso de los enlaces considerados estratégicos, no es posible aumentar la capacidad de transporte de una línea de metro o cercanías que esté operando cerca de su máximo de tráfico. Este viene fijado por sistemas de señalización que podrían modernizarse en algunos casos, pero nunca más allá de los máximos teóricos ofrecidos por los sistemas de bloqueo más avanzados, como CBTC o ERTMS nivel 3.
Como vemos, ampliar el espacio disponible por pasajero mediante el aumento de la capacidad de transporte es un enfoque con una potencia muy limitada para responder a las nuevas exigencias de seguridad de un mundo post-pandémico. Teniendo esto en cuenta, los gestores del transporte ferroviario han trabajado en propuestas adicionales que ha recogido la UIC (Union Internationale des Chemins de Fer, Unión Internacional de Ferrocarriles) en un documento de trabajo [4]. Estas medidas están clasificadas en tres grupos: relativas al contacto físico persona a persona, relativas al contacto objeto a persona, y de comunicación hacia los pasajeros.
Medidas propuestas por la UIC
Ya hemos visto cómo el contacto físico persona a persona es una característica definitoria de todo el transporte público, que basa su eficiencia precisamente en la compartición del espacio dedicado a la prestación del servicio. Por ello, toda medida basada en el distanciamiento social tendrá necesariamente un recorrido escaso y requerirá ser apoyada por acciones externas al propio sistema de transporte. En este sentido, la limitación de aforos en las estaciones es fundamental, pero como toda limitación de acceso, puede resultar en la denegación del servicio para una parte de los usuarios. Esto se puede paliar mediante la laminación de la hora punta, obligando a los diferentes usuarios a distribuir sus horas de entrada y salida del trabajo en un intervalo lo más amplio posible. El fomento del teletrabajo es también una medida con impacto tanto sobre el transporte público como privado que puede reducir la presión sobre los espacios compartidos.
La adopción obligatoria de mascarillas es otra de las medidas que ofrece el potencial de entorpecer los flujos de gotículas que transmiten el virus SARS-CoV-2, entre otros. Se ha observado que existe una relación entre la eficacia filtrante de la mascarilla, la frecuencia de su uso por parte de la población y el número de reproducción básico R₀ de un patógeno [5]. Esta relación hace posible que el uso de mascarillas de relativa baja eficacia, pero portadas por fracciones cercanas al total de los usuarios, resulte en una medida eficaz para permitir reducir las distancias de seguridad en espacios cerrados y, por consiguiente, aumentar los pasajeros-kilómetro transportados con un grado de seguridad epidemiológica aceptable.
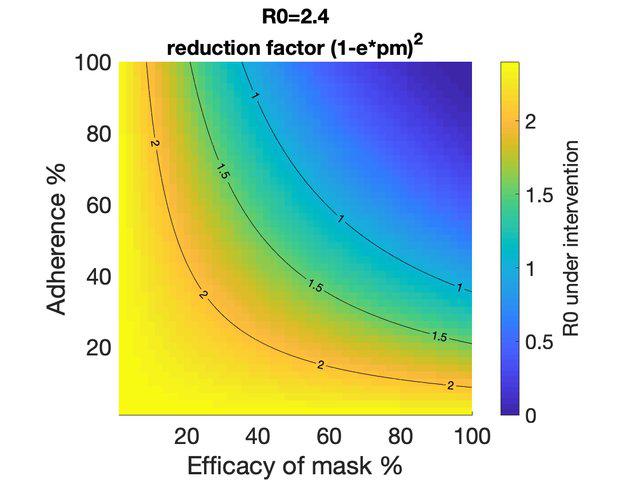 Impacto del uso de mascarillas en función de la frecuencia de su uso y su eficacia protector. El color indica el número de reproducción básico resultante (Rₒ), partiendo de un valor inicial de 2,4. Imagen tomada de [5].Otras actuaciones que pueden resultar en una mejora de la seguridad epidemiológica del transporte colectivo son la adopción de señalización específica tanto en estaciones como embarcada para recordar a los usuarios las distancias de seguridad; la disponibilidad generalizada de dispensadores automáticos de gel hidroalcohólico —si es posible, cuya operación sea sin contacto físico—; así como medidas que favorezcan la trazabilidad de los usuarios: billetes nominativos, controles masivos de temperatura mediante termografía o cuestionarios de síntomas. Este último grupo de intervenciones, sin embargo, plantea riesgos importantes en lo referente a los derechos fundamentales de privacidad de los usuarios [6]. Por ello, su implantación generalizada está llevándose a cabo en estados donde estos derechos no son reconocidos por la legislación, como China.
Impacto del uso de mascarillas en función de la frecuencia de su uso y su eficacia protector. El color indica el número de reproducción básico resultante (Rₒ), partiendo de un valor inicial de 2,4. Imagen tomada de [5].Otras actuaciones que pueden resultar en una mejora de la seguridad epidemiológica del transporte colectivo son la adopción de señalización específica tanto en estaciones como embarcada para recordar a los usuarios las distancias de seguridad; la disponibilidad generalizada de dispensadores automáticos de gel hidroalcohólico —si es posible, cuya operación sea sin contacto físico—; así como medidas que favorezcan la trazabilidad de los usuarios: billetes nominativos, controles masivos de temperatura mediante termografía o cuestionarios de síntomas. Este último grupo de intervenciones, sin embargo, plantea riesgos importantes en lo referente a los derechos fundamentales de privacidad de los usuarios [6]. Por ello, su implantación generalizada está llevándose a cabo en estados donde estos derechos no son reconocidos por la legislación, como China.
Existe, por último, la posibilidad de introducir mejoras en los sistemas de ventilación de estaciones y, sobre todo, coches de viajeros. Por ejemplo, el operador de transporte japonés Japan Rail East reporta haber incorporado nuevos protocolos de revisión más exhaustiva de los dispositivos de aire acondicionado, con limpiezas más frecuentes de los elementos filtrantes. Los ciclos de trabajo también están siendo reducidos en la medida de lo posible, renovando el aire de la cabina en intervalos menores (de 6 a 8 minutos). Por su parte, los ferrocarriles iraníes se han embarcado en un interesante proyecto para utilizar luz ultravioleta de alta frecuencia (UV-C, entre 200 y 280 nm) en componentes clave de los sistemas de ventilación. El uso de luz ultravioleta de alta frecuencia como fungicida, bactericida y viricida está avalado por la práctica en laboratorios de alta seguridad biológica [7], si bien el entorno ferroviario requerirá asegurar la ausencia de exposición de los pasajeros y los operarios a la radiación UV-C, así como dimensionar adecuadamente el sistema en función de las características del patógeno SARS-CoV-2 frente a este tratamiento.
Respecto del contacto y posible transmisión de la enfermedad entre objetos y usuarios, la UIC recomienda acortar los ciclos de limpieza y desinfección de los diferentes recintos, disponer de contenedores apropiados para desechar residuos potencialmente contaminados (como las propias mascarillas) y reducir en la medida de lo posible el contacto físico entre las manos de los pasajeros y los diferentes elementos de interacción de su entorno, como billetes —que deberán ser sustituidos por elementos sin contacto, como tarjetas o móviles con tecnología NFC— y también botones de apertura de puertas. La apertura de puertas deberá ser automática en la medida de lo posible, aunque también puede recurrirse allá donde sea una opción a su operación con partes del cuerpo distintas de la mano, como el codo, apoyándose en señalización ex profeso.
Finalmente, no debemos olvidar las medidas de comunicación. Una política abierta y clara de difusión de riesgos, reglas y consejos es fundamental para reducir la inseguridad del público respecto de sus sistemas de transporte. Para ello, todos los soportes comunicativos de los que disponen los administradores de infraestructuras del transporte y sus encomiendas de gestión deben ponerse al servicio de esta misión: megafonía, cartelería, señalética y sistemas avanzados de vídeo. Es preciso que esta comunicación pueda ser bidireccional, habilitando para ello los canales precisos en redes sociales y, presencialmente, en las mismas instalaciones a través del personal encargado del mantenimiento y seguridad, quienes deberán recibir formación específica.
Qué no hacer
La respuesta de los sistemas de transporte ferroviario a las necesidades inducidas por la pandemia de la COVID-19 tiene todavía aspectos importantes que deberán ser refinados con la práctica. No es una opción, sin embargo, prescindir del ferrocarril metropolitano como medio de transporte de alta capacidad y fomentar en su lugar el uso del automóvil privado como refugio seguro más que en casos aislados y siempre temporalmente.
Esto es así por varias razones. En primer lugar, el problema de las emisiones del transporte privado no desaparecerá mágicamente cuando la crisis de la pandemia pase. Fomentarlo acríticamente dañará los objetivos de limitación de emisiones de CO₂ y otros gases de efecto invernadero que están arrastrando las temperaturas medias del planeta en su actual curso ascendente, con las consecuencias previstas en los modelos climáticos a largo plazo y que estamos comenzando a comprobar en forma de una mayor siniestralidad debida a fenómenos atmosféricos extremos, así como la subida del nivel del mar.
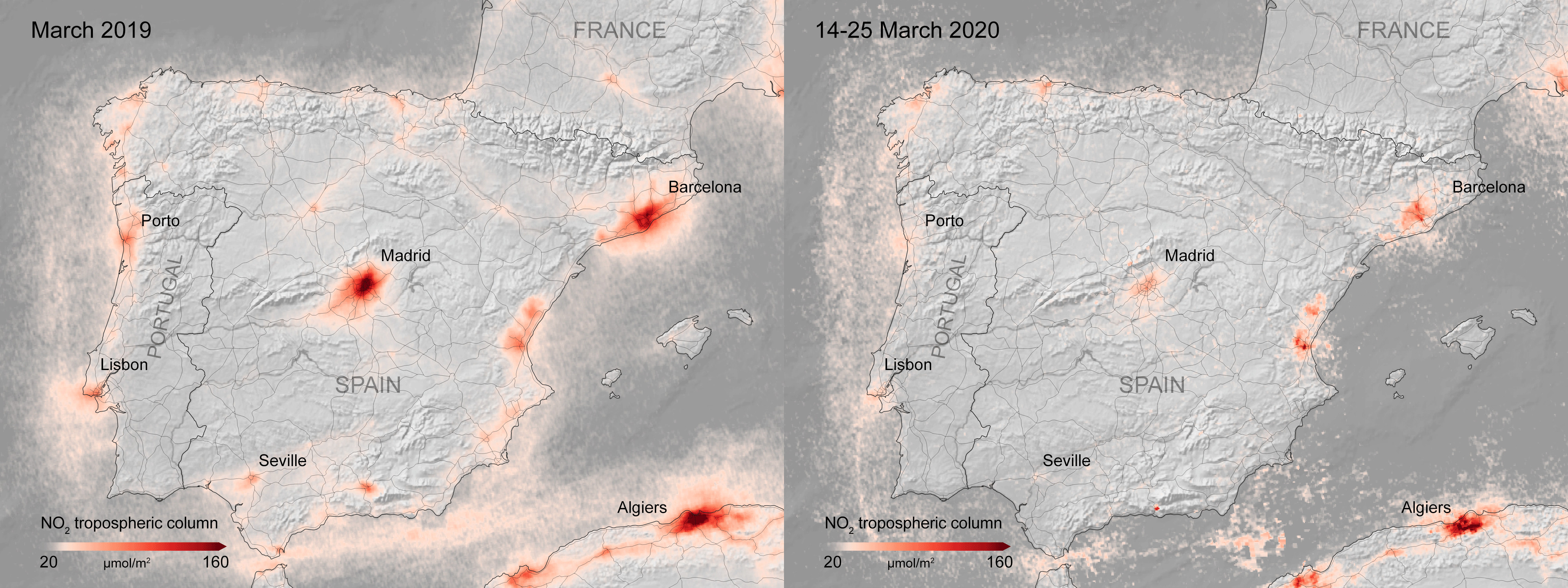 Concentraciones de la columna troposférica de NO₂ sobre la península Ibérica en marzo de 2019 y marzo de 2020. Imagen tomada de [8].En segundo lugar, la lista de contaminantes debidos al automóvil privado no finaliza con el CO₂. Los óxidos de nitrógeno y las partículas en suspensión también son relevantes para establecer la calidad del aire de los grandes núcleos urbanos. Los datos del satélite Copernicus Sentinel-5P, tratados por científicos del Real Instituto Meteorológico de los Países Bajos (KNMI) mediante filtros para eliminar la variación meteorológica intradía, muestran claramente que la disminución de la actividad industrial y del tráfico debida a las medidas de confinamiento y cierre tomadas por los diferentes gobiernos nacionales tienen un impacto inmediato sobre la atmósfera [8]. La primera fase del confinamiento en Madrid, por ejemplo, ocurrió en un contexto meteorológico de bajas temperaturas durante el que las calefacciones estuvieron mayoritariamente activas. Pese a ello, la contaminación atmosférica disminuyó considerablemente, lo que apunta a un origen mayoritario en el transporte no electrificado y en la industria. La relación de la contaminación del aire por partículas en suspensión, óxidos de nitrógeno y otros es responsable, según la literatura disponible, de un 3 % de la mortalidad anual en España, unas 10000 personas [9].
Concentraciones de la columna troposférica de NO₂ sobre la península Ibérica en marzo de 2019 y marzo de 2020. Imagen tomada de [8].En segundo lugar, la lista de contaminantes debidos al automóvil privado no finaliza con el CO₂. Los óxidos de nitrógeno y las partículas en suspensión también son relevantes para establecer la calidad del aire de los grandes núcleos urbanos. Los datos del satélite Copernicus Sentinel-5P, tratados por científicos del Real Instituto Meteorológico de los Países Bajos (KNMI) mediante filtros para eliminar la variación meteorológica intradía, muestran claramente que la disminución de la actividad industrial y del tráfico debida a las medidas de confinamiento y cierre tomadas por los diferentes gobiernos nacionales tienen un impacto inmediato sobre la atmósfera [8]. La primera fase del confinamiento en Madrid, por ejemplo, ocurrió en un contexto meteorológico de bajas temperaturas durante el que las calefacciones estuvieron mayoritariamente activas. Pese a ello, la contaminación atmosférica disminuyó considerablemente, lo que apunta a un origen mayoritario en el transporte no electrificado y en la industria. La relación de la contaminación del aire por partículas en suspensión, óxidos de nitrógeno y otros es responsable, según la literatura disponible, de un 3 % de la mortalidad anual en España, unas 10000 personas [9].
En tercer lugar, existen resultados preliminares, pendientes de confirmación, que indican que son precisamente los altos niveles de contaminación ambiental los que correlacionan con la letalidad de la COVID-19 [10]. Serán necesarios más estudios en esta dirección para confirmar, en su caso, esta posible relación, así como para determinar los mecanismos que puedan explicarla. Parece, sin embargo, que el tan justamente denostado principio de precaución podría aquí mostrarse relevante: optar por medidas que supongan aumentos indiscriminados de la contaminación ambiental, de la que ya sabemos que tiene impactos inmediatos en la salud pulmonar de los ciudadanos, no parece lo más inteligente en plena pandemia de un patógeno nuevo que también afecta al sistema respiratorio.
El ferrocarril metropolitano se enfrenta a la ardua tarea de recuperar la confianza de millones de usuarios. Este objetivo solo podrá cumplirse afianzando la seguridad epidemiológica del entorno del transporte. Para ello, deben aplicarse con rigor aquellas todas las acciones y políticas que tengan un impacto reconocido por la comunidad científica. Pero, a la vez, es necesario redoblar esfuerzos en la investigación para probar nuevas ideas y medir el efecto de otras que, de modo concebible, puedan rendir beneficios y mejoras. Solo así los operadores de transporte ferroviario podrán mantener el ferrocarril de nuestros grandes núcleos urbanos como la opción sostenible y de futuro que, incluso en el nuevo contexto epidémico, sigue siendo.
Agradecimientos
El autor quiere agradecer su ayuda en la elaboración de este texto a Conchi Lillo, profesora titular del área de Biología Celular en la Facultad de Biología de la Universidad de Salamanca e investigadora del Instituto de Neurociencias de Castilla y León (INCYL).
Referencias:
[1] Coronavirus disease (COVID-19) advice for the public, World Health Organization. Visitado el 07/05/2020 en https://www.who.int/emergencies/diseases/novel-coronavirus-2019/advice-for-public.
[2] Bourouiba, L. (2020). Turbulent Gas Clouds and Respiratory Pathogen Emissions. Jama. doi: 10.1001/jama.2020.4756. Visitado el 07/05/2020 en https://jamanetwork.com/journals/jama/fullarticle/2763852.
[3] León, P. (11/02/2019). Metro satura sus vagones para ofertar más plazas sin aumentar los trenes. El País. Visitado el 07/05/2020 en https://elpais.com/ccaa/2019/02/10/madrid/1549808836_600403.html.
[4] Management of COVID-19 — Potential measures to restore confidence in rail travel following the COVID-19 pandemic, Union Internationale des Chemins de Fer. (04/2020). Visitado el 07/05/2020 en https://uic.org/IMG/pdf/potential_measures_to_restore_confidence.pdf.
[5] Howard, J., Huang, A., Li, Z., Tufekci, Z., Zdimal, V., Westhuizen, H.-M. V. D., … Rimoin, A. W. (04/2020). Face Masks Against COVID-19: An Evidence Review. doi: 10.20944/preprints202004.0203.v1. Visitado el 07/05/2020 en https://www.researchgate.net/publication/340603522_Face_Masks_Against_COVID-19_An_Evidence_Review.
[6] Comunicado de la AEPD en relación con la toma de temperatura por parte de comercios, centros de trabajo y otros establecimientos, Agencia Española de Protección de Datos. (30/04/2020). Visitado el 07/05/2020 en https://www.aepd.es/es/prensa-y-comunicacion/notas-de-prensa/comunicado-aepd-temperatura-establecimientos.
[7] La función de las lámparas UV-C como germicida en instalaciones de HVAC, Ingeniarg SA. (02/02/2016). Visitado el 07/05/2020 en http://www.in4geniarg.com/blog/24-la-funcion-de-las-lamparas-uv-c-como-germicida-en-instalaciones-de-hvac.
[8] Coronavirus lockdown leading to drop in pollution across Europe, European Space Agency. (2020, March 27). Visitado el 07/05/2020 en https://www.esa.int/Applications/Observing_the_Earth/Copernicus/Sentinel-5P/Coronavirus_lockdown_leading_to_drop_in_pollution_across_Europe.
[9] La contaminación del aire, protagonista del Día Mundial del Medio Ambiente: muertes prematuras evitables, Instituto de Salud Carlos III. (06/06/2019). Visitado el 07/05/2020 en https://repisalud.isciii.es/bitstream/20.500.12105/7937/1/2019_06_04_LaContaminaci%c3%b3nDelAire.pdf.
[10] Travaglio, M., Yu, Y., Popovic, R., Leal, N. S., & Martins, L. M. (04/2020). Links between air pollution and COVID-19 in England. doi: 10.1101/2020.04.16.20067405. Visitado el 07/05/2020 en https://www.medrxiv.org/content/10.1101/2020.04.16.20067405v3.
Sobre el autor: Iván Rivera (@brucknerite) es ingeniero especializado en proyectos de innovación de productos y servicios para ferrocarriles.
El artículo El ferrocarril metropolitano ante la COVID-19 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los límites del ferrocarril
- El electromagnetismo ante la mente matemática (1)
- El electromagnetismo ante la mente matemática (y 2)
Vida de Galileo
Quien no conoce la verdad, es sólo un zoquete. Pero quién la conoce y la llama mentira, ¡es un criminal!
Vida de Galileo, Bertold Brecht
Vida de Galileo es una obra de teatro de Bertold Brecht (1898-1956) escrita entre 1938 y 1939, durante su exilio en Dinamarca. El dramaturgo escribió otras dos versiones, una entre 1945 y 1947 –adaptada a los gustos del público estadounidense–, y la última en 1955 –la llamada «versión berlinesa»–.
Esta pieza –una biografía novelada de Galileo–se centra en los últimos años de vida del investigador. Simboliza la lucha de la verdad contra el oscurantismo; defiende el racionalismo y el espíritu científico.
SINOPSIS: En su hogar en Florencia, Galileo transmite parte de sus conocimientos a Andrea, el hijo de su casera. Cuando el científico anuncia sus descubrimientos sobre el Sistema Solar, recibe la condena de la Inquisición. Galileo debe retractarse de sus ideas temiendo la tortura y la pérdida de sus privilegios. Pero, al mismo tiempo, difunde en secreto sus descubrimientos entre sus colaboradores.
 Galileo, por Justus Sustermans. Imagen: Wikimedia Commons.
Galileo, por Justus Sustermans. Imagen: Wikimedia Commons.
Recorremos brevemente la obra a través de algunas citas extraídas de la traducción de Miguel Sáenz.
La obra comienza en 1609, en el gabinete de estudio de Galileo, que comenta a Andrea sus descubrimientos:
GALILEO. Yo predigo que, antes de que hayamos muerto, se hablará de astronomía en los mercados. Hasta los hijos de las pescaderas irán a las escuelas. Porque a los hombres de nuestras ciudades, ansiosos de novedades, les gustará que una nueva astronomía empiece a moverse sobre la Tierra. Siempre se ha dicho que los astros estaban fijos en una bóveda de cristal para que no pudieran caerse. […] Y la Tierra gira alegremente alrededor del Sol, y las pescaderas, mercaderes, príncipes y cardenales, y hasta el mismo Papa, giran con ella.
Galileo presenta su telescopio en Venecia:
GALILEO. ¡Excelencia, señorías! Como profesor de matemáticas de vuestra Universidad de Padua y director de vuestro Gran Arsenal, aquí en Venecia, siempre he considerado mi deber, no sólo el cumplir con mi alta labor docente, sino también procurar beneficios excepcionales a la República de Venecia por medio de útiles inventos. […] Hoy puedo presentaros y entregaros un instrumento totalmente nuevo, mi anteojo de larga vista o telescopio, construido en vuestro Gran Arsenal, famoso en el mundo entero, de acuerdo con los más altos principios científicos y cristianos y fruto de diecisiete años de paciente investigación de este vuestro devoto servidor. […] Ésos creen haber recibido una baratija lucrativa, pero es mucho más. Ayer enfoqué el tubo hacia la Luna.
 Galileo enseñando al dux de Venecia el uso del telescopio, por Giuseppe Bertini. Imagen: Wikimedia Commons.
Galileo enseñando al dux de Venecia el uso del telescopio, por Giuseppe Bertini. Imagen: Wikimedia Commons.
Junto a su amigo Sagredo, Galileo observa la Luna:
GALILEO. ¡No hay soportes en el Cielo, no hay nada fijo en el Universo! ¡Júpiter es otro sol! […] Lo ves no lo había visto nadie. ¡Tenían razón!
SAGREDO. ¿Quiénes? ¿Los copernicanos?
GALILEO. ¡Y el otro también!i ¡El mundo entero estaba contra ellos y ellos tenían razón! […] Sí, ¡y no que todo el gigantesco Universo, con todos sus astros, gira en torno a nuestra minúscula Tierra, como piensan todos!
SAGREDO. ¡Es decir, que sólo hay astros!… ¿Y dónde está Dios? […]
GALILEO. ¿Soy teólogo acaso? Soy matemático. […] ¡Tengo fe en los hombres, lo que quiere decir que tengo fe en su razón!
En la corte de Florencia, Galileo no consigue convencer a los científicos de la utilidad de las observaciones realizadas con su telescopio:
EL FILÓSOFO. […] Señor Galilei, antes de utilizar su famoso tubo quisiéramos tener el placer de una discusión. Tema: ¿pueden existir esos planetas?
EL MATEMÁTICO. Una discusión en regla.
GALILEO. Yo había pensado que miraran simplemente por el anteojo y se convencieran. […]
EL MATEMÁTICO. Claro, claro… Naturalmente, usted sabe que, según la opinión de los antiguos, no es posible que existan estrellas que giren en torno a otro centro que no sea la Tierra, ni que no su apoyo en el Cielo. […] Se sentiría la tentación de responder que su anteojo, al mostrar lo que no puede ser, no es muy de fiar, ¿no? […] Sería mucho más provechoso, señor Galilei, que nos diera las razones que le inducen a suponer que, en las más altas esferas del Cielo inmutables, los astros pueden moverse libremente.
EL FILÓSOFO. ¡Razones, señor Galilei, razones!
GALILEO. ¿Razones? ¿Cuándo una ojeada a las propias estrellas y a mis anotaciones demuestran el fenómeno? Señor mío, la discusión me parece de mal gusto.
En 1616 el colegio romano confirma los descubrimientos de Galileo:
EL PEQUEÑO MONJE. Señor Galilei, el padre Clavius dijo antes de irse: ¡ahora tendrán que ver los teólogos cómo recomponen las esferas celestes! Usted ha vencido.
GALILEO. ¡Ha vencido! ¡No yo, sino la razón!
Pero la Inquisición rechaza sus teorías:
PRIMER SECRETARIO. El Santo Oficio ha decidido la pasada noche que la teoría de Copérnico, según la cual el Sol es el centro del Universo y está inmóvil, y la Tierra no es el centro del Universo y se mueve, es demencial, absurda y herética. Se me ha encargado que le exhorte a renunciar a esa opinión.
GALILEO. […] ¿Y los hechos? Creí entender que los astrónomos del Collegium Romanum reconocieron la exactitud de mis anotaciones. […] Pero los satélites de Júpiter, las fases de Venus…
BELLARMINO. La Santa Congregación ha tomado su decisión sin tener en cuenta esos detalles.
GALILEO. Eso significa que toda investigación científica ulterior…
 Galileo ante el Santo Oficio, por Cristiano Banti. Imagen: Wikimedia Commons.
Galileo ante el Santo Oficio, por Cristiano Banti. Imagen: Wikimedia Commons.
Galileo conversa con un monje, que explica los motivos por los que ha abandonado el estudio de la Astronomía:
EL PEQUEÑO MONJE. He conseguido penetrar en la sabiduría de ese decreto. Me ha descubierto los peligros que encierra para la Humanidad una investigación sin freno, y he decidido renunciar a la Astronomía. […] ¿Qué dirían los míos si yo les dijera que se encuentran en un pequeño conglomerado rocoso, que gira incesantemente en el espacio vacío y se mueve en torno a otro astro, uno de muchos, bastante insignificante? […]
GALILEO: ¡Cómo puede suponer nadie que la suma de los ángulos de un triángulo pueda contradecir sus necesidades! Pero si no se movilizan y aprenden a pensar, ni los más hermosos sistemas de riego les servirán para nada.
La llegada de un nuevo Papa, Urbano VIII, anima a Galileo a volver a investigar:
GALILEO. Empecemos a observar por nuestra cuenta y riesgo esas manchas solares que nos interesan. […] Mi intención no es demostrar que he tenido razón hasta ahora, sino saber si realmente la he tenido. […] Quizá sean vapores, quizá sean manchas, pero antes de suponer que son manchas, lo que nos vendría muy bien, supondremos que son colas de pez. Efectivamente, lo pondremos en duda todo, todo otra vez. […]. Y lo que hoy encontremos, lo borraremos mañana de la pizarra y sólo volveremos a anotarlo cuando lo encontremos de nuevo. […]. ¡Quitad el paño al anteojo y apuntadlo a Sol!
Molestos por los panfletos contra la Biblia difundidos por el pueblo, los inquisidores culpan a Galileo. El Papa es un hombre ilustrado, pero no tiene poder contra la Inquisición:
EL PAPA. ¡No haré que se rompan las tablas de cálculo! ¡No!
EL INQUISIDOR. […] Es la inquietud de sus propios cerebros la que aplican a la Tierra, a esta Tierra inmóvil. Y gritan: ¡Los números hablan! ¿Pero de dónde vienen esos números? Todo el mundo sabe que vienen de la duda. […] Y entonces van esos gusanos de matemáticos y apuntan sus anteojos al cielo y comunican al mundo que también allí, en el único lugar que no se os discutía, la posición es difícil.
El 22 de junio de 1633, Galileo se retracta de su teoría sobre el movimiento de la Tierra, ante la desilusión, entre otros, de Andrea:
ANDREA. Lo matarán. No terminará de escribir los “Discorsi” […] Porque no se retractará jamás. […] ¡No se atreverán! Y aunque lo hicieran, no se retractará. “Quien no conoce la verdad, es sólo un zoquete. Pero quién la conoce y la llama mentira, ¡es un criminal! […]
VOZ DEL PREGONERO. “Yo Galileo Galilei, profesor de Matemáticas y de Física en Florencia, abjuro de lo que he enseñado: que el Sol es el centro del mundo y que está inmóvil en su lugar, y que la Tierra no es el centro y no está inmóvil. Abjuro, maldigo y abomino, con corazón sincero y fe no fingida, de todos esos errores y herejías, así como de cualquier otro error y cualquier otra opinión contrarios a la Santa Iglesia”. […]
ANDREA: ¡Pobre del país que no tiene héroes! […] ¡Tonel de vino! ¡Devorador de caracoles! ¿Has salvado tu querido pellejo? […]
GALILEO. No. Pobre del país que necesita héroes.
 Portada de los Discorsi. Imagen: Wikimedia Commons.
Portada de los Discorsi. Imagen: Wikimedia Commons.
Desde 1633 hasta su muerte en 1642, Galileo vive en una casa cerca de Florencia, prisionero de la Inquisición. Recibe la visita de Andrea, que ya es un hombre de mediana edad, y se dirige a Holanda para trabajar en ciencia:
GALILEO. He terminado los “Discorsi”.
ANDREA. ¿Qué? ¿Los “Discursos sobre dos nuevas ciencias: la Mecánica y las leyes de la gravitación”? […] “Mi propósito es presentar una ciencia muy nueva sobre un tema muy viejo: el movimiento. Por medio de experimentos he descubierto algunas de sus propiedades, que son dignas de ser conocidas.” […] ¡Y nosotros que pensábamos que había desertado! ¡Mi voz fue la que más alto se alzó contra usted!
GALILEO. […] Yo sostengo que el único objetivo de la Ciencia es aliviar las fatigas de la existencia humana. Si los científicos, intimidados por los poderosos egoístas, se contentan por acumular Ciencia por la Ciencia misma, se la mutilará, y vuestras nuevas máquinas significarán sólo nuevos sufrimientos. […] Si yo hubiera resistido, los hombres dedicados a las ciencias naturales hubieran podido desarrollar algo así como el juramento de Hipócrates de los médicos: ¡la promesa de utilizar la Ciencia únicamente en beneficio de la Humanidad! […]
Andrea sale de Italia en 1937, con el manuscrito de Galileo:
EL GUARDIA. ¿Por qué deja usted Italia?
ANDREA. Soy científico.
Nota:
i Se refiere a Giordano Bruno.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Vida de Galileo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- 42, la respuesta definitiva a la vida, el universo y todo lo demás
- Galileo vs. Iglesia Católica redux (y VII): Balanzas
- Galileo vs. Iglesia Católica redux (V): Reconvención
Impurezas dopantes
 Es equivalente decir que las burbujas de aire suben como que el agua baja. Foto: Martin Str / Pixabay
Es equivalente decir que las burbujas de aire suben como que el agua baja. Foto: Martin Str / PixabayEl uso más importante de los semiconductores, como el silicio o el germanio, incluido su uso como transistores, surge de su comportamiento cuando, después de estar suficientemente purificados de átomos distintos del elemento básico (esto es, silicio o germanio), se introducen cantidades muy pequeñas de impurezas muy concretas.
Si bien los métodos para purificar primero y agregar pequeñas cantidades de impurezas después al germanio estuvieron disponibles tras la Segunda Guerra Mundial, la investigación sobre la purificación y la introducción controlada de impurezas para el silicio no tuvo éxito hasta finales de la década de 1950. Como el silicio es más abundante que el germanio y otros semiconductores, pronto reemplazó al germanio como el semiconductor preferido.
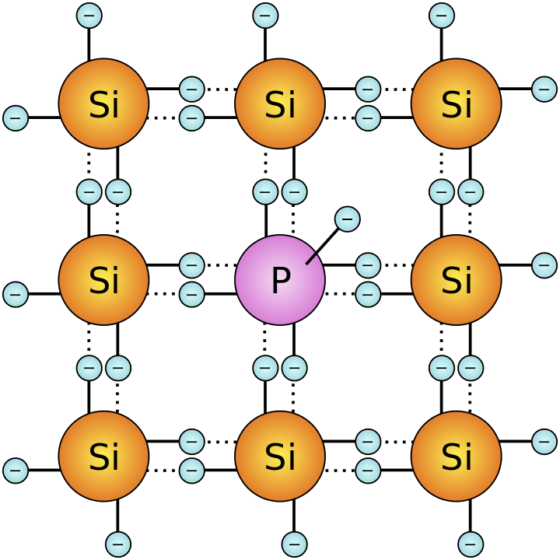
El germanio (elemento 32) y el silicio (elemento 14) tienen ambos cuatro electrones de valencia, que llenan la banda de valencia cuando estos metales forman un cristal. El elemento 33, el arsénico, tiene cinco electrones de valencia, al igual que el elemento 15, el fósforo. Si se agrega una cantidad muy pequeña de arsénico al germanio a medida que se forma el cristal de germanio, los átomos de arsénico sustituirán a varios átomos de germanio en la red. Lo mismo sucede cuando se agrega una pequeña cantidad de fósforo al silicio. Las pequeñas cantidades se controlan cuidadosamente en el proceso de producción y son solo alrededor del 0,0001% del total de átomos.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsEste proceso se llama dopaje, y las impurezas se llaman dopantes. Cuando el dopante correspondiente se introduce en la red de germanio o silicio, cuatro de sus electrones de valencia se unen a los otros átomos en la red, dejando el quinto electrón ”suelto”. Estos electrones de valencia extra de los dopantes están tan ligeramente unidos a sus átomos que con muy poca energía de vibración saltan a la banda de conducción del semiconductor. Tanto es así que, a temperatura ambiente, todos se encuentran en la banda de conducción, lo que significa que el semiconductor dopado ahora actúa como un conductor. Dado que los electrones, que tienen carga negativa, donados por las impurezas permiten que el material conduzca, estos tipos de semiconductores se denominan semiconductores de tipo n.
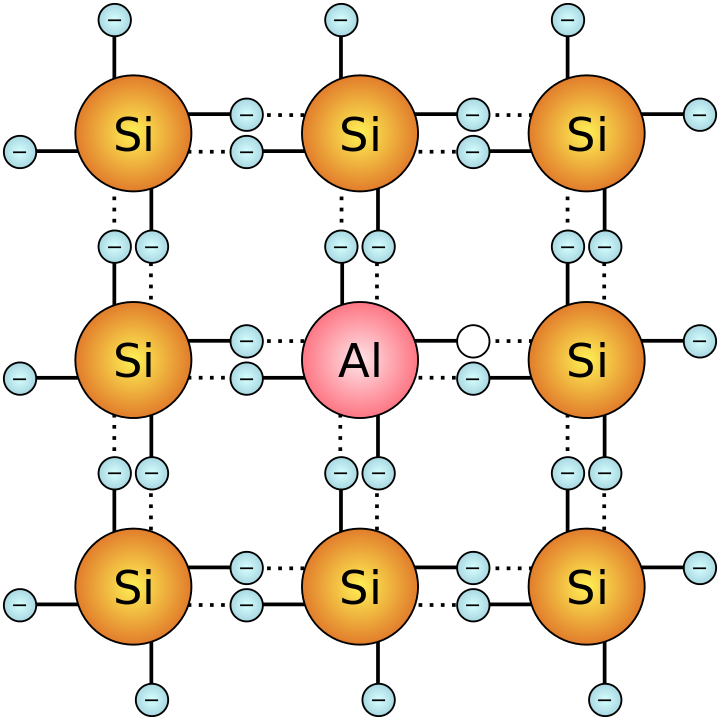
Una situación similar ocurre cuando los semiconductores se dopan con impurezas de elementos que están un peldaño más abajo en la tabla periódica, es decir, cuando el silicio (14) se dopa con el elemento 13, aluminio, y el germanio (32) se dopa con el elemento 31, galio. Los dopantes tienen solo tres electrones de valencia. Eso hace que, cuando están incorporados a la red de silicio o germanio, generen un espacio en la banda de valencia, un espacio que puede aceptar un electrón de un átomo de silicio o germanio vecino. Este espacio es lo que se conoce como hueco [1]. El hueco se comporta de manera similar a una burbuja de aire en un vaso de agua con gas [2].
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsCuando se activa un campo eléctrico externo, los electrones de los átomos vecinos, que normalmente no tienen lugar al que moverse, ahora pueden cambiar de átomo para llenar el hueco. Pero esto deja un hueco en el átomo que han dejado, que puede ser llenado por su vecino, y así sucesivamente. Del mismo modo, el movimiento ascendente de la burbuja de aire en un vaso de agua con gas en realidad implica el flujo descendente del agua hacia el espacio ocupado por la burbuja, que es la que a simple vista parece la única en moverse. En el semiconductor, si el campo mueve los electrones a la izquierda, por ejemplo, el hueco parecerá migrar a la derecha. Al moverse hacia la derecha, se comporta como lo haría una carga positiva, aunque solo sea un espacio.
Es decir, debido al movimiento de carga negativa hacia la izquierda, el efecto físico es el mismo que si hubiese cargas positivas fluyendo hacia la derecha (en nuestro ejemplo) en la banda de valencia, por debajo de la banda de conducción, donde anteriormente no podían fluir cargas. Una vez más, la introducción muy cuidadosa de pequeñas cantidades de impurezas ha convertido el semiconductor en un conductor. Como las cargas conductoras parecen ser positivas, estos semiconductores se conocen como semiconductores de tipo p.
Estos semiconductores dopados podrían usarse como cualquier otro conductor, pero no merece la pena, ya que podemos producir conductores como los cables de cobre de manera mucho más fácil y económica. En cambio, se reconoció durante y después de la Segunda Guerra Mundial que las aplicaciones realmente útiles de este tipo de semiconductores aparecen cuando se colocan físicamente uno al lado del otro dentro de dispositivos electrónicos.
Notas:
[1] Podría llamarse hueco, boquete, bujero u oquedad, pero no, se llama hueco de electrón.
[2] O de refresco, o de cerveza, o de champán. Captas la idea. Elegimos agua porque las alternativas no son buenas para la salud en comparación.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Impurezas dopantes se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Semiconductores
- El modelo clásico de electrones libres de Drude-Lorentz
- La teoría de bandas explica la conducción eléctrica
Geología, industrialización y transporte del mineral de hierro en el entorno de la Ría de Bilbao
 Imagen 1: la ría de Bilbao entre Portugalete y Getxo. (Fotografía: LBM1948 – bajo licencia Creative Commons Attribution-Share Alike 4.0 International. Fuente: Wikimedia Commons)
Imagen 1: la ría de Bilbao entre Portugalete y Getxo. (Fotografía: LBM1948 – bajo licencia Creative Commons Attribution-Share Alike 4.0 International. Fuente: Wikimedia Commons)El desarrollo económico, tecnológico y social de Bizkaia, surgido en la segunda mitad del siglo XIX y que alcanzó su máximo esplendor a finales del mismo y principios del XX, tuvo lugar como consecuencia de la suma de una serie de factores:
- Unas características geológicas muy favorables. La existencia de una importante mineralización de hierro aflorante, muy próxima a una geomorfología facilitadora de la explotación y transporte de los minerales.
- La creación de unas condiciones económicas y legislativas que impulsaron la explotación y exportación de grandes cantidades de mineral.
- La existencia de una mano de obra abundante y barata, procedente del entorno local y de regiones cercanas, que si bien trabajaron a destajo y bajo condiciones, en algunos casos infrahumanas, tuvieron también la valentía y el orgullo de organizarse en movimientos asociativos de gran valor y trascendencia social. En 1910 había unas 13.000 personas trabajando en las minas.
- El desarrollo empresarial minero, que tuvo la facilidad, oportunidad y visión de crear negocios locales, pero de ámbito económico más amplio, que a su vez generaron el desarrollo de otros sectores (bancos, compañías de seguros, siderúrgicas, de ferrocarriles, astilleros, navieras, etc…).
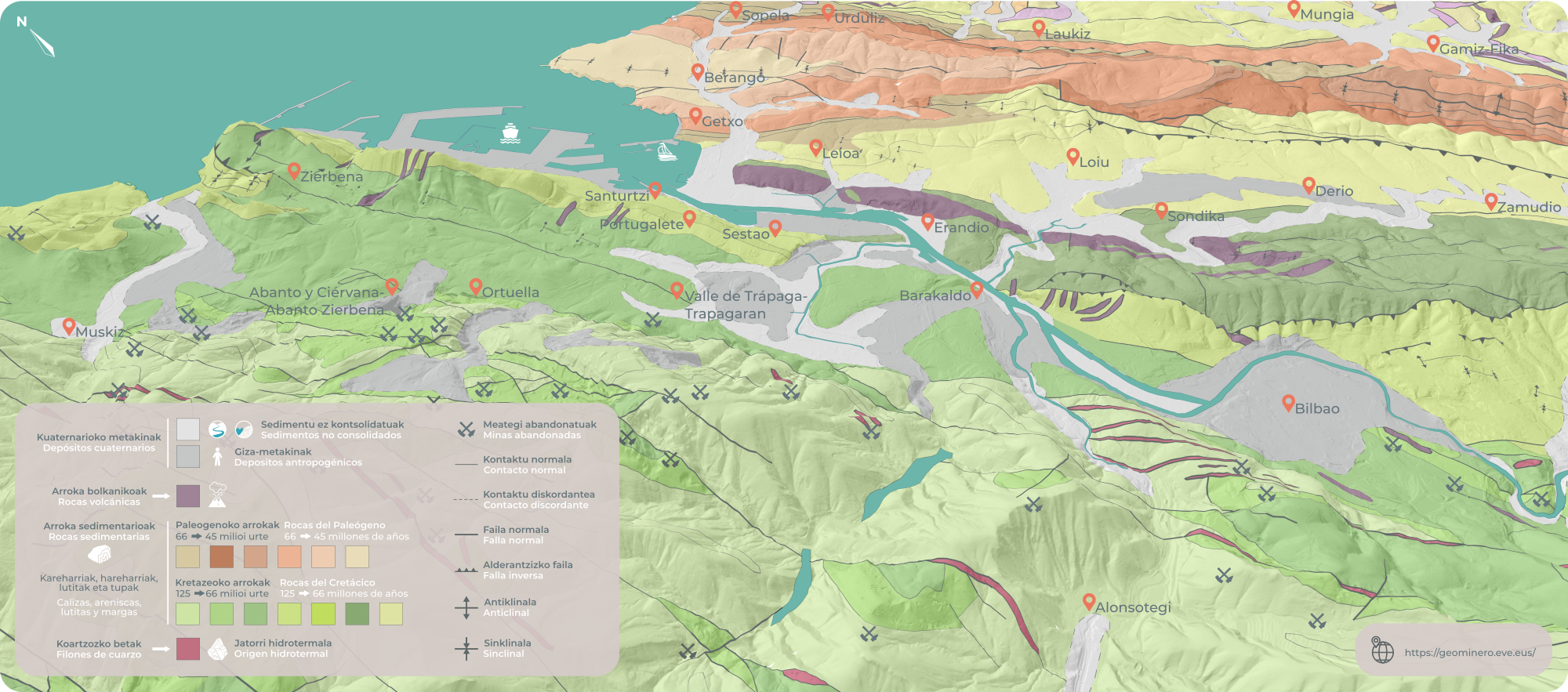 Ilustración 1: características de la geología de la ría del Nervión y sus inmediaciones. (Ilustración: NorArte Studio)
Ilustración 1: características de la geología de la ría del Nervión y sus inmediaciones. (Ilustración: NorArte Studio)Vamos a centrarnos en uno de estos factores, las características geológicas, tanto desde su vertiente de contener los yacimientos de hierro como desde la de facilitar la creación de una geomorfología adecuada para el desarrollo de los medios de transporte que sirvieron para el traslado de los minerales tanto a nivel interno como para su exportación.
El subsuelo del área que rodea la ría de Bilbao se halla compuesto mayoritariamente por rocas sedimentarias. Son el resultado de la acumulación, litificación, plegamiento y erosión de materiales detríticos y biogénicos (areniscas, lutitas, calizas, margas y margocalizas principalmente) en una cuenca sedimentaria, Cuenca Vasco-Cantábrica, que tuvo su origen en la apertura del Océano Atlántico Norte y del Golfo de Bizkaia.
Dicha cuenca ha evolucionado desde momentos con una elevada tasa de acumulación de sedimentos marinos, pasando por situaciones de erosión o de sedimentación continental, hasta terminar por recibir presiones laterales (debidas al choque y ligera rotación de las placas ibérica y euroasiática durante la Orogenia Alpina), que provocaron el plegamiento, fracturación y posterior erosión de las rocas preexistentes, hasta llegar a la situación actual.
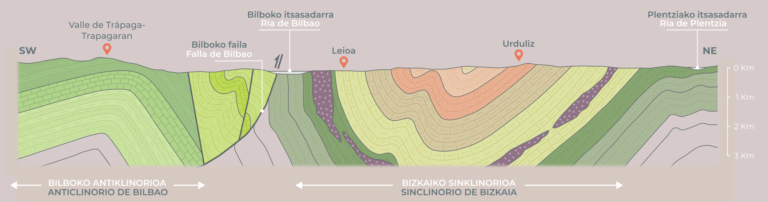 Ilustración 2: bajo el suelo del entorno de la ría de Bilbao existe una gran variedad de materiales y estructuras. Calizas, areniscas, volcánicas, lutitas y margas, así como una falla normal y otra inversa. (Ilustración: NorArte Studio)
Ilustración 2: bajo el suelo del entorno de la ría de Bilbao existe una gran variedad de materiales y estructuras. Calizas, areniscas, volcánicas, lutitas y margas, así como una falla normal y otra inversa. (Ilustración: NorArte Studio)Durante este largo proceso de evolución de la Cuenca Vasco-Cantábrica se han registrado multitud de eventos geológicos superpuestos, si bien son dos los que adquieren mayor relevancia para el tema que nos ocupa:
- La formación de los yacimientos de hierro y su enriquecimiento por oxidación.
- La creación de una geomorfología adecuada para el desarrollo del transporte fluvial.
Las mayores mineralizaciones de hierro del entorno de Bilbao se encuentran encajadas en calizas de edad Cretácico inferior (Aptiense y Albiense, entre 125 y 90 millones de años de antigüedad). Se agrupan en dos franjas más o menos paralelas que corresponden con los flancos norte y sur de una estructura anticlinal de entidad regional, el Anticlinal de Bilbao. La zona mineralizada se extiende entre las localidades de Basauri y Mioño (Cantabria).
Su génesis está sometida a diferentes interpretaciones. No todos los yacimientos pertenecen a la misma tipología, pero podrían clasificarse en dos grupos, las masivas y las filonianas.
Las masivas corresponden a reemplazamientos de las calizas. Son masas de siderita (FeCO3) albergadas en las calizas (CaCO3), con ankerita, calcita y algunos sulfuros. Los volúmenes involucrados en el reemplazamiento pueden ser muy variables. La Mina Bodovalle, en Gallarta, cerrada en 1993 tenía cubicadas 50 Mt de reservas.
 Ilustración 3: las calizas del Cretácico inferior (~125-90 millones de años), presentes en ambos flancos del Anticlinal de Bilbao, fueron enriquecidas con hierro mediante diferentes procesos de mineralización. (Ilustración: NorArte Studio)
Ilustración 3: las calizas del Cretácico inferior (~125-90 millones de años), presentes en ambos flancos del Anticlinal de Bilbao, fueron enriquecidas con hierro mediante diferentes procesos de mineralización. (Ilustración: NorArte Studio)Las filonianas son también muy abundantes. Los filones presentan orientación preferente NO-SE. Se asocian a fracturas de escala regional. Pueden presentar potencias (grosores) desde centimétricas a métricas (filones explotables). La mineralogía es similar a la que presentan las mineralizaciones masivas: siderita, cuarzo, ankerita y como minerales accesorios sulfuros.
En algún momento, cuando las calizas estaban ya sedimentadas y compactadas, o en vías de estarlo, pero no deformadas por las fases compresivas Alpinas, a favor de fracturas y planos de estratificación se introdujeron soluciones hidrotermales (calientes), salinas, clorurado-sódicas, capaces de transportar los cationes disueltos. Suministraron el hierro, produciéndose el reemplazamiento del catión Ca++ por el catión Fe++, formando siderita y ankerita. La mayor parte de los filones con mineralización representan el relleno de las propias fracturas por las que ascendieron los fluidos hidrotermales.
Durante el proceso de plegamiento, y asociado al ascenso y erosión de los sedimentos suprayacentes, las rocas mineralizadas entraron en contacto con el oxígeno ambiental generando una alteración en las zonas superficiales, lo que provocó la transformación de los minerales carbonatados (siderita principalmente), en óxidos e hidróxidos de hierro (hematites, goethita y limonita), cuyo contenido en hierro y la facilidad de su tratamiento metalúrgico es muy superior.
Durante los primeros años de explotación se produjo una doble ventaja competitiva. Por una parte los minerales más ricos en hierro (óxidos e hidróxidos) se explotaron a cielo abierto y por otra no era necesario un tratamiento previo para su incorporación a los hornos altos. En años posteriores, ya bien entrado el siglo XX, empezaron a explotarse los carbonatos, cuya extracción se producía a mayor profundidad, en muchos casos mediante minería subterránea, y además era necesario su tratamiento previo mediante hornos de calcinación para poder enriquecer su contenido en hierro y evitar problemas metalúrgicos.
El segundo de los factores decisivos para el desarrollo económico de Bizkaia, desde el punto de vista geológico, ha sido la evolución geomorfológica del subsuelo, con la creación del estuario de Bilbao, que ha actuado y sigue funcionando como puerto natural. Ya desde la Edad Media y hasta el siglo XIX, la ría actuó como eje vertebrador y comercial de los productos procedentes de Castilla, y es a mediados del siglo XIX y durante el siglo XX cuando se desarrolló la actividad económica minera y su industria asociada.
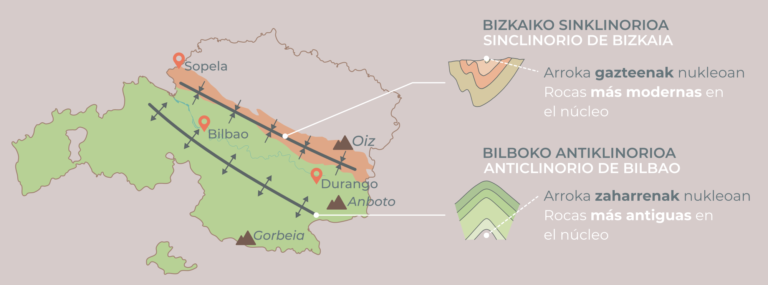 Ilustración 4: trazado de las grandes estructuras cartográficas del estuario de Bilbao, coincidentes con la dirección general del cauce fluvial. (Ilustración: NorArte Studio)
Ilustración 4: trazado de las grandes estructuras cartográficas del estuario de Bilbao, coincidentes con la dirección general del cauce fluvial. (Ilustración: NorArte Studio)Basta con observar desde una cierta distancia la morfología rectilínea y la orientación NW-SE del estuario de Bilbao para percatarse de que esta disposición no es casual. La dirección de los plegamientos principales (anticlinorio y sinclinorio) es totalmente coincidente con la dirección general del cauce fluvial. La alternancia de materiales competentes, calizas y areniscas principalmente, con sedimentos mucho más blandos, lutitas y margas, facilitó que por éstos últimos, y a favor de los accidentes estructurales principales, fallas, planos de debilidad, diaclasas, contactos estratigráficos, fluyeran las aguas que originaron el encauzamiento y redireccionaron los flujos procedentes de los cauces afluentes (Cadagua, Nervión, Ibaizabal).
Todo ello configuró un estuario que, en la zona cercana a su desembocadura, donde los ríos pierden su capacidad erosiva y el sistema se hallaba muy influenciado por los cambios mareales, se produjeron grandes acúmulos de sedimentos que originaron ecosistemas de marismas en los que los cauces fluviales pasaron de una disposición rectilínea a una meandriforme.
 Ilustración 5: ubicación de los cargaderos de mineral que existían a lo largo de la orilla de la ría de Bilbao. (Ilustración: NorArte Studio)
Ilustración 5: ubicación de los cargaderos de mineral que existían a lo largo de la orilla de la ría de Bilbao. (Ilustración: NorArte Studio)Pese a existir una magnífica red de transporte a través de los cauces fluviales, éstos tenían en muchos casos un calado insuficiente y variable en función de cada temporada o incluso eran estacionales. Fue necesario actuar para encauzar los ríos de forma artificial, asegurar su calado y permitir la construcción de cargaderos estables. Llegaron a existir decenas de cargaderos de mineral a lo largo de la margen izquierda del estuario, que representa las vías de ferrocarril que transportaban el mineral hasta los cargaderos.
Sobre el autor: Alex Franco San Sebastián es geólogo y Responsable del Área de Geología y Minería del Ente Vasco de la Energía – EVE
El proyecto «Ibaizabal Itsasadarra zientziak eta teknologiak ikusita / La Ría del Nervión a vista de ciencia y tecnología» comenzó con una serie de infografías que presentan la Ría del Nervión y su entorno metropolitano vistos con los ojos de la ciencia y la tecnología. De ese proyecto han surgido una serie de vídeos y artículos con el objetivo no solo de conocer cosas interesantes sobre la ría de Bilbao y su entorno, sino también de ilustrar como la cultura científica permite alcanzar una comprensión más completa del entorno.
El artículo Geología, industrialización y transporte del mineral de hierro en el entorno de la Ría de Bilbao se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La geología y sus superpoderes
- Naukas Bilbao está en marcha
- Geología, ver más allá de lo que pisamos
¿De qué se muere la gente en el mundo?
 Foto: Davide Ragusa / Unsplash
Foto: Davide Ragusa / UnsplashEn el mundo mueren cada año unas 56 millones (en adelante, M) de personas. La principal causa de muerte son las enfermedades cardiovasculares; por su culpa mueren casi 18 M, cerca de la tercera parte del total. Y si se agrupan en una única categoría, los cánceres son los responsables de casi 10 M de muertes. En conjunto, el 73% fallece a causa de enfermedades no contagiosas.
Los fallecimientos debidos a enfermedades infecciosas representan hoy el 19%. En ese grupo entran, sobre todo, afecciones del aparato respiratorio (2,56 M) y del digestivo (2,38 M), incluidas las diarreas (1,6 M). Hace un cuarto de siglo el porcentaje de muertes debidas a enfermedades infecciosas era del 33% y, en general, es más alto en los países pobres. La bajada del 33% al 19% es consecuencia del progreso. Cuanto más pobre es un país mayor es el porcentaje de muertes debidas a enfermedades infecciosas. Lo contrario ocurre con las no infecciosas. La otra gran categoría de muertes corresponde a las producidas por golpes o heridas, pero estas apenas varían con el tiempo y representan un 8% (9% 25 años antes).
Casi un 4% de los niños y niñas mueren antes de cumplir cinco años. En otras palabras: cada año fallecen 5,5 M. La principal causa de muerte de esas criaturas son las infecciones respiratorias (unas 800.000). De hecho, una de cada tres personas muertas por ese motivo es menor de 5 años. 650.000 bebés (menores de un mes) fallecen por patologías o complicaciones neonatales. Y las diarreas son también una causa de muerte infantil importante; aunque ha bajado mucho su número, alrededor de medio millón de niños y niñas mueren por esa razón. En conjunto estas afecciones son responsables de una gran pérdida de años de vida. También lo son los accidentes de tráfico (1,2 M de muertes, muchos de ellos de adolescentes y jóvenes), y el síndrome de inmunodeficiencia adquirida (SIDA), a causa del cual pierden la vida casi 1 M de personas (el 84% menores de 50 años). De las 800.000 personas que se quitan la vida cada año, 460.000 son menores de 50 años.
En el extremo opuesto están las distintas formas de demencia, que son responsables de 2,5 M de muertes anuales. Esa cifra ha subido mucho y seguirá subiendo conforme siga aumentando la esperanza de vida por la disminución, sobre todo, de las muertes debidas a enfermedades infecciosas. Pero precisamente por esa razón, no provoca la pérdida de muchos años de vida.
Hay tres causas de muerte que no tienen la relevancia cuantitativa de las anteriores pero que, sin embargo, reciben una gran atención mediática; son los homicidios, los atentados terroristas y las catástrofes naturales. Fallecen por homicidio unas 400.000 personas al año, y 26.000 por actos terroristas. Las catástrofes naturales solo provocan 9.600 muertes.
Cuando hablamos de causas de muerte nos referimos a las causas próximas o inmediatas, a las enfermedades que las provocan, pero como es sabido, hay hábitos o modos de vida que aumentan o disminuyen la probabilidad de contraer enfermedades que pueden resultar fatales. Cada año 8 M de personas mueren a causa del tabaco, y la obesidad es responsable de casi 5 M de muertes; en ambos casos, la mitad son menores de 70 años. Por culpa del alcohol fallecen 2,8 M (2 M son menores de 70).
Están, por último, los factores ambientales: la contaminación atmosférica provoca la muerte de 3,4 M, y la del hogar, de 1,6 M. Y es que la contaminación sí mata, la atmosférica también.
Nota: En las cifras anteriores no están incluidas las muertes debidas a Covid19. A fecha 9 de mayo, se habían producido 274.290 muertes confirmadas por esa causa, aunque la cifra real es seguramente muy superior. A modo de ejemplo, en España, los fallecimientos que constan en los registros civiles son, desde la llegada de la pandemia, del orden de un 56% más que en el mismo periodo de otros años. Es de suponer que ese exceso de muertes se debe a los efectos de Covid19, por lo que las muertes reales por esa causa representan del orden de un 30% más de las reportadas oficialmente.
Fuente: Our World in Data
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo ¿De qué se muere la gente en el mundo? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- No habrá solución sin más conocimiento
- ¿Cuánta gente ha vivido en la Tierra?
- La ecología de una enfermedad
Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
Tras dejar claro que es mejor integrar que derivar, esta charla «presenta el problema del año [2019]: la discrepancia a más de cinco sigmas entre la constante de Hubble calculada integrando el modelo cosmológico y extrapolando la pendiente de la escalera de distancias usando supernovas Ia y cefeidas. En la charla explico las razones que me llevan a desconfiar de la estimación astrofísica, que creo está dominada por errores sistemáticos no considerados, y preferir la estimación cosmológica, aunque esté basada en un modelo teórico.» en palabras del propio Francis Villatoro.
.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Francisco R. Villatoro – Naukas Bilbao 2018: El ángulo mágico del grafeno
- Naukas Bilbao 2017 – Francisco R. Villatoro: El espín para irreductibles
- José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos
Generada en plataformas eólicas marinas, desembarcada como hidrógeno
Investigadores de la Escuela de Ingeniería de Vitoria-Gasteiz de la UPV/EHU han propuesto utilizar la energía generada en las plataformas eólicas marinas para producir hidrógeno in situ en lugar de transportarla por cable a tierra. Han demostrado que es técnicamente posible y económicamente viable. Además, han comprobado que la incorporación de ciertos elementos de muy bajo coste mejora notablemente la eficiencia de los aerogeneradores.

En las plataformas eólicas marinas, o parques eólicos offshore, la generación de energía es muy elevada, ya que se instalan aerogeneradores de gran potencia y los regímenes de viento son mucho más estables que en tierra. “Toda esta energía generada puede ser transportada a tierra mediante dos vías: la creación de una infraestructura enorme, para hacer llegar la red de potencia eléctrica hasta ella, y transportar por cable la electricidad generada, o la generación de hidrógeno allí mismo, mediante hidrólisis, utilizando la energía generada en el terreno, y el transporte de ese hidrógeno a tierra para ser utilizado como combustible. Nosotros hemos apostado por la segunda opción y el objetivo de esta investigación ha sido buscar una forma de mejorar ese proceso”, explica Ekaitz Zulueta Guerrero, investigador del Departamento de Ingeniería de Sistemas y Automática de la Escuela de Ingeniería de Vitoria-Gasteiz de la UPV/EHU.
Al poner en marcha la investigación, los investigadores, del Departamento de Ingeniería de Sistemas y Automática y del Departamento de Ingeniería Nuclear y Mecánica de Fluidos de la Escuela de Ingeniería de Vitoria-Gasteiz, buscaban reducir el coste energético del proceso de generación de hidrógeno. “Con el fin de mejorar la aerodinámica de los aerogeneradores, quisimos probar el efecto de dos componentes utilizados para controlar el flujo de la turbina. Uno es un generador de vórtices y, el otro, unas láminas (conocidas como Gurney Flaps) que se colocan en la pala, que mejoran mucho la fuerza de sustentación y, por tanto, la aerodinámica”, explica Unai Fernández-Gámiz, miembro del Departamento de Ingeniería Nuclear y Mecánica de Fluidos. Además, “son muy baratos y se colocan fácilmente en los aerogeneradores”.
En un segundo paso, quisieron ver si “es viable, tanto técnica como económicamente, la generación de hidrógeno en las propias plataformas eólicas offshore, a partir de esa energía generada, mediante hidrólisis, y así poderlo transportar a tierra para que pueda ser utilizado como combustible —añade Fernández-Gámiz—. De hecho, la generación de hidrógeno permitiría su transporte a tierra en barco y, además, la energía acumulada ofrecería una gran flexibilidad al sistema eléctrico, teniendo en cuenta que en la actualidad la producción de electricidad debe ser acorde con la demanda”.
Las pruebas se llevaron a cabo en el laboratorio nacional de energías renovables de Estados Unidos (NREL), en una turbina de 5 MW, cuyas características técnicas, geometrías y demás parámetros son públicos. “Se ha comprobado que la producción anual de energía de las turbinas es alrededor de un 2,5 % superior. No es un incremento muy elevado, pero teniendo en cuenta la gran potencia de los aerogeneradores que se instalan en el mar, se genera una gran cantidad de energía adicional”, ha explicado Zulueta. Los investigadores también han calculado la cantidad de hidrógeno que se podría producir con esta generación adicional de energía: más de 130.000 Nm3. Es decir, “la cantidad de combustible que necesitarían un millón de coches impulsados por hidrógeno para recorrer 100 kilómetros —detallan los investigadores en el artículo—. Y esto gracias a los elementos de control de flujo añadidos, que apenas implican costes adicionales”.
Una vez comprobado que técnicamente es posible y económicamente viable, el siguiente paso sería, según los investigadores, “que algún desarrollador de plataformas eólicas se pusiera en contacto con nosotros para probar, medir y adaptar en sus sistemas lo conseguido en la planta de Estados Unidos”.
Referencia:
Aitor Saenz-Aguirre, Unai Fernández-Gámiz, Ekaitz Zulueta, Iñigo Aramendia, Daniel Teso-Fz-Betoño (2020) Flow control based 5 MW wind turbine enhanced energy production for hydrogen generation cost reduction International Journal of Hydrogen Energy doi: 10.1016/j.ijhydene.2020.01.022
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Generada en plataformas eólicas marinas, desembarcada como hidrógeno se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo obtener hidrógeno a partir de una placa de circuitos impresos
- Hidrógeno a partir de composites de fibra de carbono
- Un microrreactor para producir hidrógeno 100 veces más pequeño
El océano en una caracola
 Voluta musica, llamada así por los adornos de su concha similares a una partitura.
Voluta musica, llamada así por los adornos de su concha similares a una partitura.Ilustración de Charles Kiener, Louis Charles (1835). Fuente Wikimedia Commons
“Me han traído una caracola.
Dentro le canta
un mar de mapa.
Mi corazón
se llena de agua
con pececillos
de sombra y plata.
Me han traído una caracola”.
Caracola, Canciones para niños de Federico García Lorca.
En el océano hay una caracola que contiene un océano entero.
Durante generaciones, la gente creyó que al presionar una concha marina contra su oído, lo que oía era el rugido del mar. Pocos relatos de la cultura popular resultan tan evocadores y, al mismo tiempo, tan erróneos. No existe ninguna relación entre el mar y ese sonido característico, más allá de la asociación mental entre la caracola y su lugar de origen que probablemente dio lugar a este relato popular. Sin embargo, como las mejores metáforas, esta nos puede servir de excusa para explicar una historia real.
El hecho es que vivimos rodeados de olas. Son olas de aire, eso sí, pequeñas variaciones en la densidad de ese fluido en el que inadvertidamente vivimos sumergidos. Normalmente resultan inaudibles, su constante presencia hace que las ignoremos. Pero cuando acercamos una caracola a nuestro oído, estas olas empiezan a rebotar contra sus paredes rígidas y algunas de sus frecuencias llegan a nuestro tímpano amplificadas. El cambio de color nos hace reparar en un sonido que hasta entonces había pasado desapercibido. La caracola nos revela la rugosidad de nuestro ambiente, los terremotos del mundo mosquito, el rugido de las polillas salvajes.
Cualquier cavidad resonante produce el mismo efecto, en realidad. Si uno se coloca un vaso o una tetera en la oreja (cualquier tipo de envase rígido en realidad), se oye el mismo sonido. Sin embargo, sugerir que se oye el mar dentro de un bote de garbanzos probablemente resulta mucho menos evocador, así que ese relato no trascendió. En cambio, en un entorno totalmente silencioso, el mismo experimento quedaría sin ningún efecto. No oiríamos nada porque no habría nada que amplificar.
El parecido entre el sonido de la caracola y el del mar, se debe a que ambos son sonidos amplios, con un gran ancho de banda, una especie de ruido blanco indefinido. En ellos conviven todo tipo de frecuencias, graves y agudas, más o menos en igual proporción. Sin embargo, dentro de la caracola no todas las frecuencias están igualmente representadas. Cuando el sonido atraviesa su cavidad resonante, esta refuerza solo algunas frecuencias: aquellas que coinciden con sus propios modos normales de vibración, que vienen dados por sus dimensiones, su forma y, sobre todo, por su longitud. Puede que una caracola no parezca a priori un objeto muy alargado, pero se puede pensar en ella como una especie de tubo cónico y enrollado, cerrado por uno de sus extremos. En ese sentido, sus modos de vibración son equiparables a los de una cuerda, un tubo, o a los de cualquier otro instrumento de viento. La caracola tiene una frecuencia fundamental característica y otras más agudas, correspondientes a su serie armónica. El resultado de todas ellas combinadas es un tono musical. Gracias a su forma alargada y enrollada, la caracola está afinada en una determinada nota. Por eso, distintas caracolas dan lugar a océanos sonoros ligeramente distintos según su tamaño (océano en do, océano en la bemol…).
 Grabado atribuido a Giorgio Ghisi (1520–1582). Fuente: MET Museum
Grabado atribuido a Giorgio Ghisi (1520–1582). Fuente: MET MuseumEsta peculiaridad convirtió a las caracolas en uno de los instrumentos musicales más antiguos y también en uno de los más universales. Probablemente, el primer instrumento de viento metal de la historia: basta hacer vibrar labios contra su punta un poco rota, como haciendo una pedorreta, para producir un sonido sorprendentemente poderoso, brillante, rotundo. Desde hace miles de años, las caracolas se han utilizado en culturas de todo el mundo como un tipo de trompeta, un símbolo de poder y un instrumento vinculado a los dioses. El ejemplo que nos pilla más cerca quizás es el de Tritón, que utilizaba el sonido de una concha para controlar las olas y el viento. Ese mismo viento que agita y hace llegar a nuestros oídos el sonido del mar.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El océano en una caracola se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los enigmas que nos cantan desde el fondo del océano
- El sonido del viento (2)
- ¿Por qué suena triste el modo menor?
Cancelaciones anómalas
No hace mucho tiempo escribí una entrada para esta sección del Cuaderno de Cultura Científica titulada Números errores de impresión en la cual estuvimos hablando de ciertos números que, aunque se produzca un cierto error tipográfico, siguen manteniendo su valor. Recordemos un ejemplo. Supongamos que queremos escribir en un artículo o una entrada de un blog el número “2 elevado a 5 multiplicado por 9 elevado a 2”, es decir, 25 92, pero se produce un error tipográfico y no quedan reflejadas las potencias, es decir, se queda escrito 2592. En general, esto produciría un error, ya que el valor de la expresión matemática no coincidiría con el valor del número, sin embargo, en este caso el resultado de 25 92 es, si realizamos las operaciones, 2592, luego sorprendentemente se mantiene inalterado. A estos números se les llama números errores de impresión.
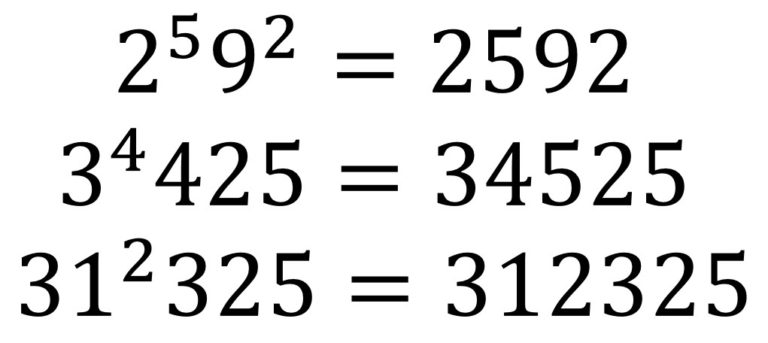
En esta entrada vamos a centrar nuestra atención en una serie de fracciones tales que, a pesar de producirse un error que podríamos calificar de matemático, en concreto, una cancelación anómala, el valor de la fracción se mantiene correcto. Veamos en qué consisten exactamente.
Empecemos con una sencilla fracción como es 12/15 (cuyo valor es 0,8). Como nos han enseñado cuando estudiábamos fracciones en la escuela, las fracciones como esta se pueden simplificar si tenemos en cuenta que 12 = 3 x 4 y 15 = 3 x 5, dividiendo el numerador y el denominador por un divisor común, en este caso, el 3. Es decir, “cancelamos” arriba y abajo el divisor común, luego 12/15 se transforma en 4 / 5 (cuyo valor sigue siendo 0,8).
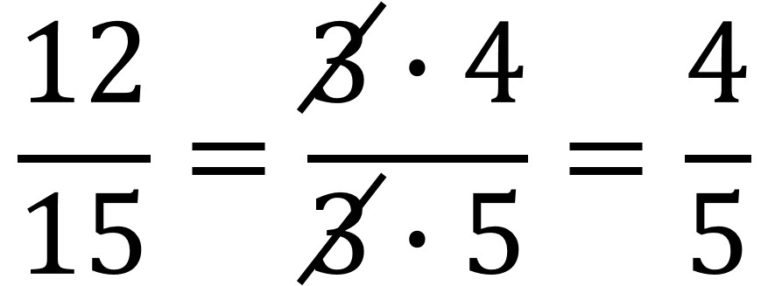
En las llamadas cancelaciones anómalas lo que ocurre es que se cancelan dígitos del numerador y del denominador como si fuesen divisores de los mismos. Esa cancelación que a priori daría lugar a un resultado completamente diferente, sin embargo, en el caso de las llamadas cancelaciones anómalas, lo que ocurre es que el resultado sorprendentemente no varía. Vamos a mostrar dos casos en los que se cancela un dígito del numerador y del denominador, viendo que en el primero el resultado es distinto, mientras que en el segundo el resultado es el mismo, obteniendo así un ejemplo de cancelación anómala.
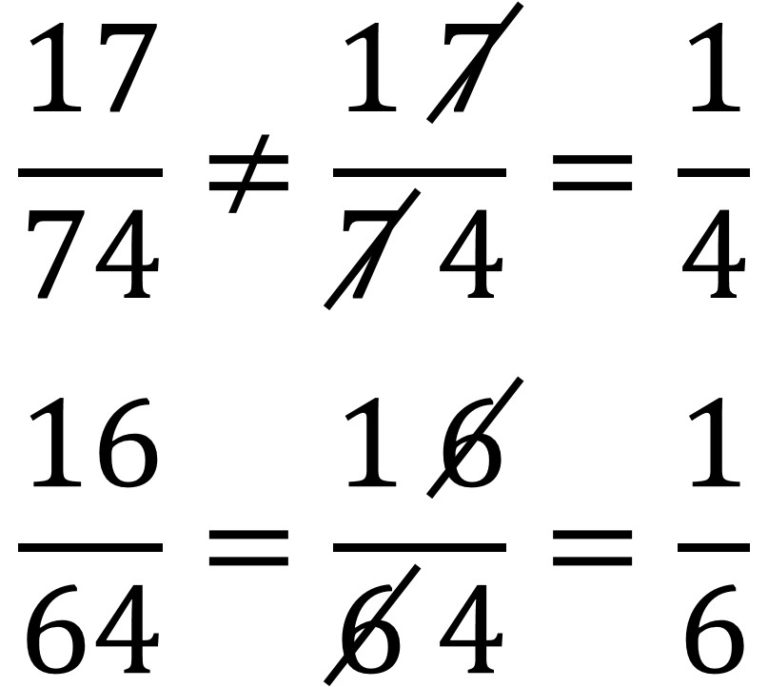
Una vez que hemos entendido cuando una fracción (consideraremos las fracciones propias, es decir, aquellas cuyo valor es menor que 1, lo cual se produce si el numerador es menor que el denominador) es una cancelación anómala, podemos buscar más ejemplos de las mismas. Así, nos planteamos el siguiente problema: encontrar las cancelaciones anómalas en las que numerador y denominador tengan solo dos dígitos.
Veamos cómo se puede resolver este problema. Buscamos una fracción cuyo numerador tenga dos dígitos, luego sea de la forma ac, por lo que su valor es (a.10 + c), y cuyo denominador, con dos dígitos, tiene que ser de la forma cb, luego su calor es (c.10 + d), para que se produzca la cancelación, por tanto, ac / cb = a / b (como es una fracción propia a es menor que b). Es decir,
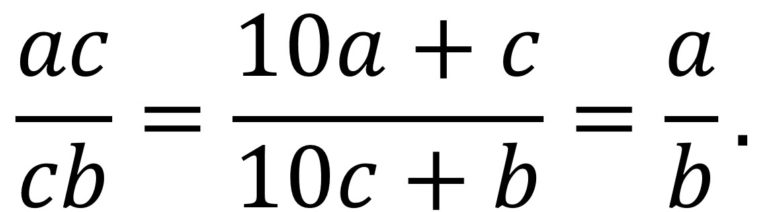
La solución del problema consiste, por lo tanto, en averiguar para qué valores de a, b y c, entre 0 y 9, se satisface la anterior igualdad.
Para empezar, de la igualdad (la segunda) de la expresión matemática anterior, se puede expresar el número que se cancela c en función de los otros dos, a y b.
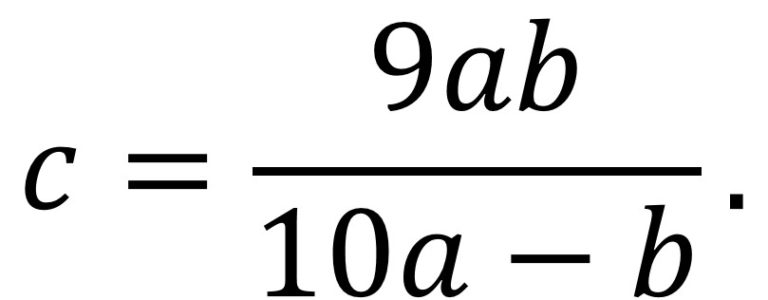
En consecuencia, dados a y b, esa expresión 9 a b / 10 a – b, es un número natural. Más aún, a partir de esa expresión, teniendo en cuenta que c es menor o igual que 9, se puede derivar la siguiente desigualdad.
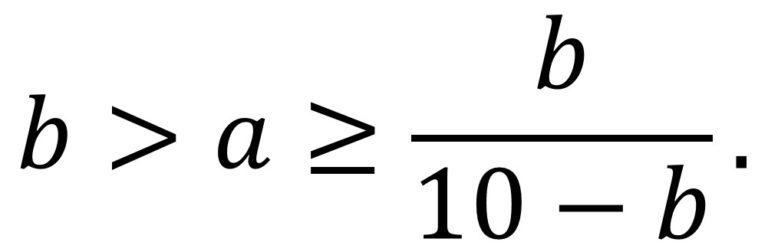
Por lo tanto, se trata de ver para qué números a y b (el primero más pequeño, a b), tales que verifican la desigualdad anterior, se satisface que el valor calculado anteriormente para c, es decir, 9 a b / 10 a – b, es un número natural. Puede verse fácilmente que las únicas soluciones posibles para el par de número (a, b) son (1, 4), (1, 5), (2,5) y (4,8), que se corresponden con las únicas cancelaciones anómalas con números de dos dígitos.
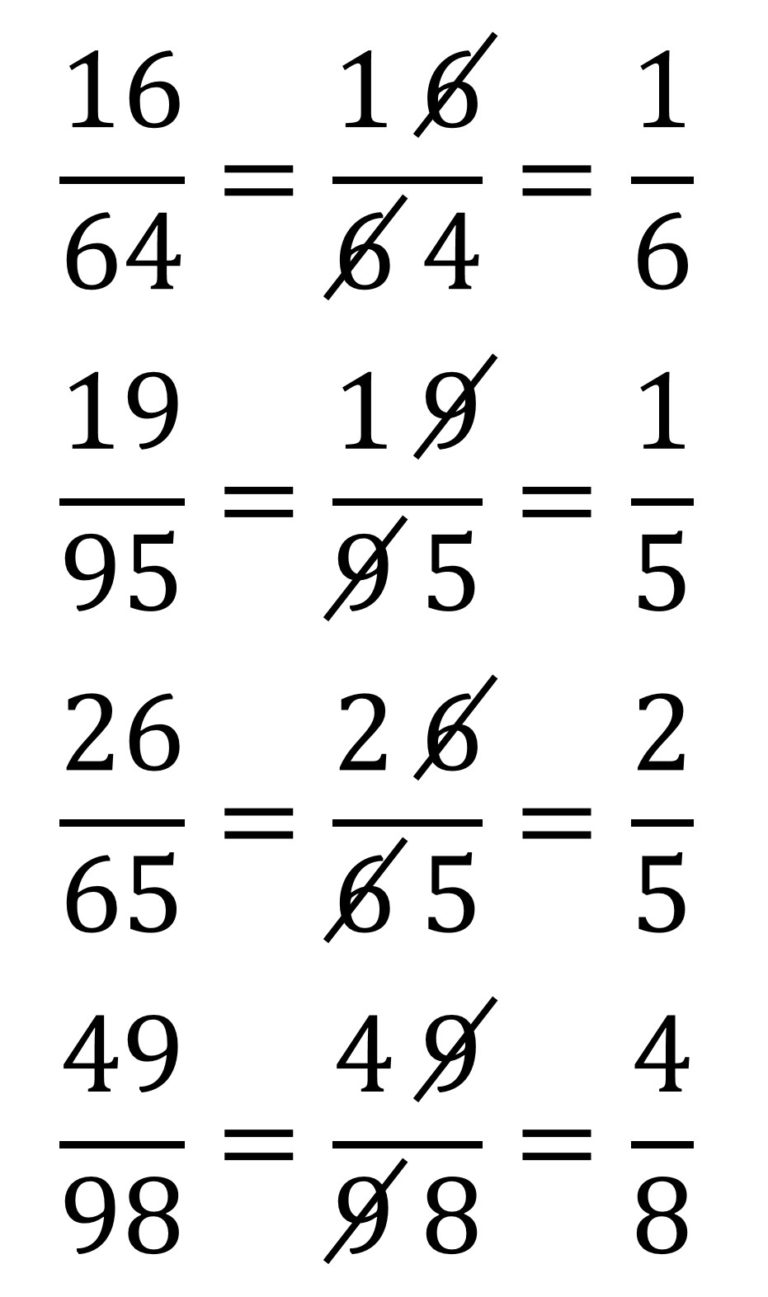
Más aún, a partir de esos cuatro ejemplos sencillos se derivan fácilmente cuatro cadenas de cancelaciones anómalas.

Las primeras menciones, según la literatura matemática, a las cancelaciones anómalas son dos artículos del matemático Alfred Moessner publicados en la revista de la Universidad Yeshiva (Nueva York) Scripta Mathematica, alrededor del año 1950. La siguiente referencia es el artículo Anomalous Cancellation del matemático estadounidense R. P. Boas, publicado en el libro Mathematical Plums (Ross Honsberger (editor). MAA, 1979), en el que se abordaba el problema para números con dos dígitos, pero en una base de numeración arbitraria b. Expliquemos un segundo esto. Teniendo en cuenta que en las cancelaciones anómalas, se “cancelan” dígitos de los números, entonces esta propiedad no depende de los números en sí mismo, sino de su representación en la base de numeración (normalmente la decimal, como hemos estudiado, pero podrían considerarse otras bases).
Pero existen más ejemplos de fracciones propias que son cancelaciones anómalas, con números con más dígitos. Por ejemplo, en el artículo sobre cancelaciones anómalas de la página Wolfram MathWorld se muestran algunas, con números de tres y cuatro dígitos.
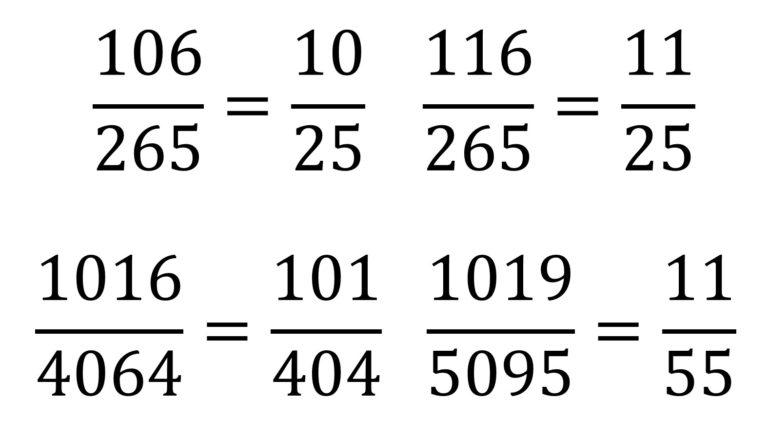
En este último ejemplo se “cancelaban” dos dígitos del numerador y del denominador. Veamos algunos ejemplos más con diferentes características.
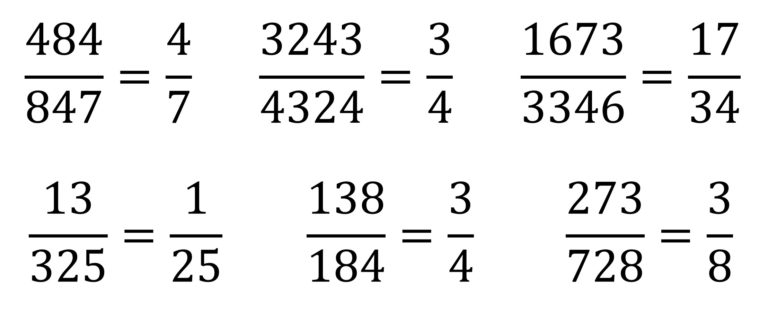
En el libro The Penguin Dictionary of Curious and Interesting Numbers, del matemático y divulgador británico David Wells, se muestra un ejemplo de una cadena con números inicialmente más grandes.

Más aún, en este libro se muestran dos variantes curiosas de cancelaciones, cuando los dígitos que se cancelan son los de las potencias.
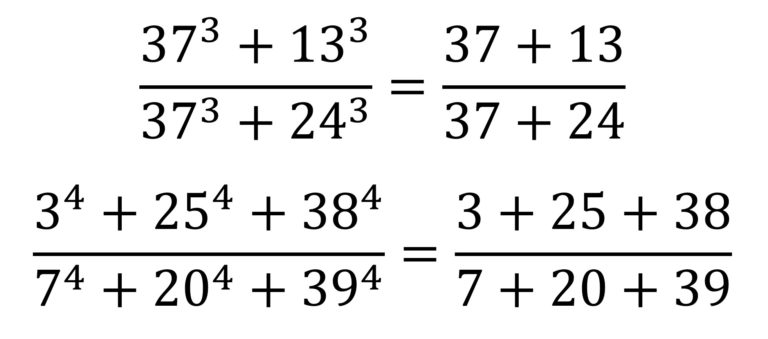
Para terminar, como en otras ocasiones acabaremos con una obra de arte relacionada con los números.
 Counter painting on Kimono (2013), del artista japonés Tatsuo Miyajima. Imagen de la página del artista.
Counter painting on Kimono (2013), del artista japonés Tatsuo Miyajima. Imagen de la página del artista.Bibliografía
1.- David Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Press, 1998.
2.- Wolfram MathWorld: Anomalous Cancellation
3.- N. J. A. Sloane, The On-line Encyclopedia of Integer Sequences
4.- Proof Wiki: Anomalous Cancellation on 2-Digit Numbers
5.- Fun with Numbers: Fractions, Anomalous Cancellation
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Cancelaciones anómalas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Números primos gemelos, parientes y sexis (2)
- El secreto de los números que no querían ser simétricos
- Números errores de impresión
Semiconductores
 foto: Luis Quintero / Unsplash
foto: Luis Quintero / UnsplashEl uso más frecuente hoy en día de los semiconductores es en forma de transistores, los componentes básicos electrónicos de todos los «componentes electrónicos de estado sólido» y los microchips de ordenador. Los semiconductores son los materiales más importantes en la revolución digital y en el desarrollo de otros dispositivos electrónicos. Estas aplicaciones que disfrutamos hoy surgieron hace casi un siglo, a partir de la década de 1930, a partir de la mecánica cuántica de la estructura en bandas de los sólidos.
Los semiconductores más comunes están hechos de silicio o germanio, los elementos 14 y 32 en la tabla periódica. A pesar de que forman estructuras cristalinas muy estables que deberían ser aislantes, en realidad son conductores débiles de la electricidad. ¿Cómo es esto posible?
En ambos elementos el número de electrones es suficiente para llenar completamente una banda de energía. Esta es la razón por la que deberían ser aislantes y, de hecho, cerca del cero absoluto, 0 K, son aislantes (no superconductores). A muy baja temperatura, las vibraciones de la red en el silicio y el germanio son mínimas, y los electrones en la parte superior de la banda de valencia no pueden obtener suficiente energía de las vibraciones de la red como para saltar la brecha de energía a la siguiente banda y convertirse en conductor. Sin embargo, la brecha con la siguiente banda es muy pequeña, de solo 0,7 eV en el germanio y 1,1 eV en el silicio. Debido a que estas brechas son tan pequeñas, a temperaturas algo superiores al cero absoluto los electrones pueden captar suficiente energía de las vibraciones de la red cristalina como para saltar a la banda de conducción vacía. A temperatura ambiente, estos elementos, que por su estructura deberían ser aislantes, en realidad son conductores débiles.
Como aislantes fallidos y conductores pobres, el silicio y el germanio no encontraron mucha utilidad en la electrónica hasta la década de 1950, cuando se hicieron avances en la introducción controlada de ciertas impurezas en la estructura reticular [1]. El uso masivo de estos dos elementos no comenzaría, sin embargo, hasta la década de 1980 con la introducción de métodos de producción a escala industrial de capas de silicio súper delgadas estructuradas microscópicamente, y (en menor medida) cristales de germanio, que, cuando se disponen adecuadamente pueden actuar como transistores. Hoy en día, las obleas de silicio, cuando se convierten en microtransistores mediante la introducción de impurezas y se descomponen en «chips», son la base de las industrias de la informática y la electrónica. [2]
El germanio puro se usó al principio en células fotoeléctricas. Un fotón externo puede golpear un electrón en la banda de valencia del germanio [3], proporcionando al electrón suficiente energía para alcanzar la banda de conducción. Si nos fijamos esto no es más que un “efecto fotoeléctrico interno”. Para que esto ocurra, la energía del fotón debe ser de, al menos, 0,7 eV para el germanio y 1,1 eV para el silicio. Como la energía de un fotón es E = hf, resulta que estas energías se corresponden con fotones que poseen frecuencias en el rango infrarrojo de las ondas electromagnéticas. Cualquier fotón con frecuencia en el rango infrarrojo o superior, lo que incluye luz visible, hará que los electrones salten a la banda de conducción y produzcan una corriente.
Notas:
[1] Curiosamente, dado que el germanio y el silicio son tan sensibles a las impurezas, su uso a gran escala como semiconductores no se produjo hasta que se desarrollaron métodos para producir grafito ultra puro para los reactores nucleares y germanio ultra puro para los circuitos electrónicos durante la Segunda Guerra Mundial. De las impurezas hablamos en la siguiente entrega de esta serie.
[2] Toda esta revolución social digital y las empresas mayores del mundo hoy día dependen de unos pequeños saltos de energía. Como los huracanes y el batir de alas de una mariposa, solo que facturable. Esta es una reflexión que te podrá ser útil en tu próxima charla con amigos.
[3] Esto también aplica al silicio, pero su uso fue más tardío.
[4] Este tipo de conductividad inducida por la luz tiene aplicaciones evidentes. Se puede usar, por ejemplo, para detectores de movimiento. Un haz de luz que incide sobre una fotocélula integrada en un circuito generará una corriente constante. Si alguien atraviesa el haz interrumpirá la corriente, lo que puede o activar una alarma o abrir una puerta automática para que la persona salga o entre sin usar sus manos. Los controles automáticos de las luces de los coches o de las farolas de las calles pueden utilizar el mismo principio. Dado que las fotocélulas son sensibles incluso a los rayos infrarrojos, siempre que haya suficiente luz natural la célula producirá una corriente. Cuando se pone el sol, la corriente se detiene, lo que proporciona la señal para encender las luces.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Semiconductores se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La teoría de bandas explica la conducción eléctrica
- Se intuye la conservación de la energía (1)
- Potencia y eficiencia de una máquina
Virus en el sistema de publicaciones científicas
Joaquín Sevilla, Alberto Nájera López y Juan Ignacio Pérez Iglesias
 Unsplash/Vlad Kutepov, CC BY-SA
Unsplash/Vlad Kutepov, CC BY-SAEl sistema de publicaciones científicas afronta una situación tan comprometida a causa de la COVID-19 que podría acabar desembocando en su transformación. No sería prudente hacer predicciones acerca de la forma en que se comunicarán los resultados científicos cuando la pandemia haya pasado, pero no cabe descartar ninguna posible evolución. La situación que atraviesa el sistema es de verdadera crisis.
El camino habitual para comunicar resultados científicos consiste en publicarlos en revistas especializadas. Para ello, una propuesta de artículo ha de pasar un proceso, generalmente lento, de revisión por pares. Durante este, otros especialistas en el campo, ajenos a los autores y anónimos para ellos, juzgan su calidad y lo aceptan, rechazan o proponen cambios.
Este proceso ganó peso a lo largo del siglo XX (aunque a Einstein no le gustaba nada) y hoy es un elemento inexcusable de una revista científica de calidad.
Publica o perece
En los últimos años el sistema de publicaciones científicas está sufriendo unas tensiones enormes. Por un lado, el progreso en la carrera científica se basa cada vez más en las publicaciones. Esto ha generado una práctica, condensada en la máxima “publica o perece”, que revela una preocupante confusión entre fines y medios.
Por otro, la irrupción de internet ha transformado el sistema de acceso y manejo de la información científica. La presión generada por las redes ha modificado drásticamente el mercado de todos los productos susceptibles de digitalizarse (música, cine, series y periódicos). A pesar de los cambios, el sistema de publicaciones científicas mantiene una estructura análoga a la que vivió Einstein.
Este contraste entre la transformación del sistema de acceso a los contenidos y el mantenimiento de la estructura editorial genera fuertes tensiones, hasta el punto de que se habla incluso de que “la máquina de hacer ciencia está rota”.
Las tensiones afloran por muchos sitios, lo que da lugar a problemas preocupantes y a diversos “males de la ciencia”. Hay una crisis de revisores, pues cada vez menos científicos están dispuestos a dedicar su tiempo a una labor ingrata, que no reporta ningún beneficio directo (ni económico ni de reconocimiento). Ante esto, muchos editores han optado por pedir a los propios autores que sugieran revisores, cosa que ha dado lugar a comportamientos fraudulentos.
Los conflictos de intereses entre autores y revisores son un problema intrínseco del sistema, pero que se ve agravado por las presiones. La importancia que para el sistema de ciencia tienen las editoriales de las revistas consideradas de prestigio hace que se comporten como un cartel, manteniendo unos precios y sistemas de tarificación que están provocando la cancelación de la suscripción a revistas por países enteros.
Éramos pocos y llegó el SARS-CoV-2
La pandemia de COVID-19 bien pudiera ser el elemento que abra la grieta definitiva en un sistema de publicaciones científicas ya tensionado y aquejado, como hemos visto, de diversos problemas serios.
Una de las características más obvias de la revisión por pares es que es lenta. Por rápido que se quiera hacer, desde que se envía un trabajo, es aceptado para su revisión, tres especialistas lo leen y consensuan su juicio para, finalmente ser aceptado (o rechazado), es difícil que pase menos de un mes. Ese tiempo, que puede ser razonable en condiciones normales, es una eternidad en tiempos de pandemia. La investigación, en estado de frenética actividad, no puede esperar semanas para conocer lo que otros equipos están haciendo, máxime cuando el valor que en realidad aporta la revisión al producto final tampoco es esencial.
No solo se retrasan los artículos científicos que podríamos denominar “estándar” con resultados experimentales, sino también otro tipo de contribuciones que permiten enriquecer el desarrollo científico, como son las cartas, comentarios, editoriales y perspectivas. Muchas revistas, ante la imposibilidad de atender todas las propuestas, han limitado su número o no los aceptan. Alguna, incluso, indica que este tipo de contribuciones se harán por iniciativa propia de la revista o consejo editorial, limitando mucho el acceso a ese tipo de formatos a la comunidad científica.
Esta situación conduce a que la comunidad científica que investiga el SARS-CoV-2, en todos sus ámbitos, genere conocimiento mucho más rápido de lo que el sistema editorial puede asimilar. Por eso se ha visto obligado a buscar alternativas.
El papel ¿mojado? de la prepublicación
En una sociedad donde la comunicación no tiene límites, la científica no puede verse encorsetada por un mundo editorial incapaz de dar respuesta en tiempo y forma. Así que muchos autores se han visto obligados a acudir a plataformas de prepublicaciones (preprints) como ArXiv, medRxiv, bioRxiv, Queios y OSFpreprints para dar a conocer los resultados de sus investigaciones.
Son sitios web donde los autores publican sus artículos para que se puedan leer mientras son revisados en las revistas. Esos sitios existen desde hace décadas y se crearon originalmente para mitigar el problema de posibles robos de ideas por parte de revisores poco éticos. Algunos ponen algunas limitaciones y un consejo “editorial” hace de filtro, otros son mucho más flexibles. Casi todos ofrecen la asignación de un DOI (Digital Object Identifier) que permite identificar el contenido, de forma similar al ISBN.
Algunos de estos espacios permiten que otros científicos, previa acreditación con su ORCID (Open Researcher and Contributor ID“ o «Identificador Abierto de Investigador y Colaborador” en español) discutan y revisen públicamente el contenido de la contribución. El número de científicos que pueden “revisar” un artículo será muchísimo mayor que el ofrecido por un sistema de revisión por pares. ¿Estamos ante un cambio de paradigma hacia una verdadera y plena Open Science?
Quizás lo estemos, pero hay que ser cautelosos. En estos días de ciencia frenética, la gran demanda social de conocimiento hace que estudios de bajísima credibilidad adquieran una importante relevancia pública. Por esa razón, en cualquier caso, cualquier alternativa a la revisión por pares a priori deberá garantizar una mínima calidad de lo que se publique.
Situaciones desesperadas requieren medidas desesperadas
El poner una prepublicación en un repositorio público antes de su aceptación formal no implica que la publicación tenga la misma validez de un artículo en una revista de prestigio. Pero ¿acaso la comunidad científica necesita el dictamen de consejos editoriales y revisores para decidir qué es científicamente aceptable o no? Son unas normas y manera de funcionar tradicionales que, por diversas razones, parecen hacer aguas en una situación de emergencia como la que vivimos.
Una prepublicación solo reconoce, de alguna manera, la autoría de una idea. Algo así como colocar el trabajo en la “pole” en una carrera, pero que, al final, podrá ganar otro si se publica antes. Algunos científicos están prefiriendo compartir sus resultados o ideas para que contribuyan al conocimiento lo antes posible, antes que recibir ese reconocimiento de un “aceptado” editorial porque saben que, por encima del curriculum vitae, estamos hablando de vidas.
La pregunta de si nos encontramos ante un nuevo paradigma no tiene una respuesta fácil. Pero no debemos descartar que la situación actual alumbre un nuevo modelo de comunicación de los resultados de la investigación. Más de una vez ha ocurrido a lo largo de la historia que un sistema débil ha perdurado en el tiempo, por inercia, en tanto no ha habido amenazas exteriores que forzasen su transformación o sustitución. Podemos estar en una coyuntura similar. Es posible que la gran cantidad de información generada con motivo de la pandemia sea la amenaza que acabe propiciando la transformación del sistema de publicaciones científicas. Su crisis sería por tanto, la antesala de un nuevo sistema.![]()
Sobre los autores:Joaquín Sevilla responsable de divulgación del conocimiento y profesor de tecnología electrónica en la Universidad Pública de Navarra; Alberto Nájera López es profesor contratado doctor de radiología y medicina física en la Universidad de Castilla-La Mancha; Juan Ignacio Pérez Iglesias es catedrático de fisiología en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Virus en el sistema de publicaciones científicas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Hacia un nuevo sistema de publicaciones científicas
- Las publicaciones científicas
- #Naukas14 Acceso abierto a las publicaciones científicas
Homeostasis y crisis del coronavirus
Juan Luis Arsuaga y María Martinón-Torres
 maradon 333 / shutterstock
maradon 333 / shutterstockHomeostasis es una palabra poco común, que se utiliza en biología, pero que podría ser útil en el contexto de la epidemia que estamos padeciendo. La homeostasis tiene que ver con el equilibrio y a la vez con el desequilibrio. Nos habla, en definitiva, de un desequilibrio equilibrado, o de un desequilibrio estable. La vida es una pura paradoja.
El ser humano ha tenido siempre la sensación de vivir en un mundo estable. Nunca sucede nada y las montañas no cambian de sitio. Y es cierto, pero solo a la escala de la generación humana. Hubo un tiempo en que esas montañas que sostienen el horizonte fueron el fondo de un mar, o una gigantesca cámara de magma subterráneo.
Tampoco los continentes han estado jamás quietos. En realidad siguen moviéndose. La tierra se separa, se junta, se quiebra. Se trata de fenómenos geológicos, movidos por fuerzas gigantescas que operan en el interior de la Tierra, donde se encuentra la caldera de su motor. También el clima ha cambiado, y de eso sí alcanzamos a ser testigos. Hace solo un siglo, los glaciares se extendían mucho más que ahora. Lo podemos comprobar en postales antiguas. Sin saberlo, nuestros abuelos y bisabuelos vivían al final de una pequeña glaciación.
Pero la realidad es que tampoco hay estabilidad en biología, a ninguna escala. Las especies están permanentemente enfrentadas a crisis, no conocen otro tipo de existencia. Podríamos afirmar que los seres vivos están siempre sufriendo una crisis o recuperándose de ella. Podríamos ir más allá y asegurar que una especie está continuamente a punto de extinguirse. La extinción consiste, simplemente, en no haber sido capaz de superar la última crisis.
La vida consiste en resolver problemas
En esa lucha continua, los organismos, como individuos, tampoco dejan de estar sometidos a tensiones. El filósofo Karl Popper acertó con su definición de la vida: consiste en resolver problemas. Los minerales y los muertos no tienen problemas que puedan resolver y por eso nunca cambian. Nuestros átomos cambian, nuestras moléculas cambian, nuestras células cambian, pero nosotros permanecemos.
Y es aquí donde entra la palabra homeostasis. Homeostasis es la capacidad de un organismo de reajustarse después de una grave alteración. Los organismos viven en equilibrios dinámicos, no estáticos. El acueducto de Segovia está en equilibrio estático, arquitectónico. Si se cae un solo pilar se hunde una parte de la canalización y el agua deja de circular, con lo que el acueducto se vuelve inútil por completo. No hay forma de que el propio acueducto segregue un nuevo pilar. El equilibrio (o el desequilibrio) constante es inherente a estar vivo.
Así, una bacteria es un sistema muy complejo, con numerosas estructuras internas bien diferenciadas que se reparten el trabajo. Cualquier célula de nuestro cuerpo es todavía más compleja, y la complejidad será mayor en los tejidos, en los órganos y en lo que en biología se denominan propiamente los sistemas, tales como el sistema respiratorio, el nervioso, el circulatorio, el locomotor, el inmune, el digestivo, el reproductor o el excretor. Finalmente, el individuo (una planta, un animal, una persona) es un sistema de sistemas de sistemas de sistemas. Pero no acaba ahí.
Por encima del individuo está el sistema social que los filósofos, a partir de Platón, han comparado con un organismo biológico. También el cuerpo social tiene homeostasis y eso es lo que, precisamente, le permite superar las crisis. En contra de lo que suele pensarse, la caída de un imperio, como el romano de Occidente (no el de Oriente) o el maya, no se produjo por una crisis única, sino por una serie de perturbaciones encadenadas y muy seguidas a las que el imperio no pudo hacer frente. La resiliencia consiste, simplemente, en recuperarse lo bastante rápido como para que la siguiente perturbación nos pille en equilibrio.
Otras crisis vendrán
El coronavirus ha provocado una crisis sanitaria, económica y social que superaremos sin ninguna duda. Otras crisis vendrán en el futuro y probablemente serán muy distintas, porque habremos aprendido a prevenir esta y otras parecidas. Como no podemos adivinar la naturaleza del siguiente embate, lo único que nos queda es reforzar la homeostasis de nuestra sociedad, que es cada vez más global.
Eso no quiere decir que debamos permanecer estáticos, sino todo lo contrario. Se trata de mejorar nuestra capacidad de alcanzar equilibrios dinámicos que permitan afrontar cualquier perturbación sin perder la estabilidad. No es cuestión de imitar a los acueductos romanos, sino a los organismos biológicos.
En su monumental “La montaña mágica”, Thomas Mann recoge en boca del joven Hans Castorp la definición de la vida como una “fiebre de la materia” que se balancea en precario equilibrio “dentro de este complejísimo y febril proceso de descomposición y renovación”. Nuestra sociedad aun herida, está viva. Tras los golpes, de los objetos inanimados solo quedan añicos; a los seres vivos les salen cicatrices.
Y esa es la lección política, en el mejor sentido de la palabra, que podemos extraer de la crisis del COVID-19. La homeostasis solo se logra si el organismo está bien organizado, si no incuba en su seno distorsiones que lo hagan inestable. Superaremos esta crisis, y la siguiente, y la siguiente, y la siguiente, si nos preocupamos ahora de reducir los desajustes internos en educación, salud, medio ambiente, democracia, riqueza, cultura, ciencia, justicia, solidaridad y sensibilidad.
Homeostasis es, por lo tanto, la palabra oportuna. Si nuestra sociedad mantiene sus equilibrios internos, es seguro que sobrevivirá a todas las crisis. Preocupémonos de que la cuerda sobre la que hacemos equilibrios no sea demasiado floja.![]()
Sobre los autores: Juan Luis Arsuaga, es catedrático de paleontología de la Universidad Complutense de Madrid, y trabaja en el Centro Mixto ISCIII-UCM de Evolución y Comportamiento Humanos y en el Museo de Evolución Humana de Burgos; María Martinón-Torres es directora del CENIEH, Centro Nacional de Investigación sobre la Evolución Humana (CENIEH).
Este artículo fue publicado originalmente en The Conversation. Artículo original
El artículo Homeostasis y crisis del coronavirus se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- De la homeostasis
- El coronavirus de Wuhan, ¿qué sabemos hasta ahora?
- La oreja de oso, una joya del Pirineo que guarda el secreto de la resurrección
Nahúm Méndez Chazarra – Naukas Bilbao 2019: Marcianos, extraterrestres y la zona habitable
 Foto: Daniel Olah / Unsplash
Foto: Daniel Olah / UnsplashConforme se han ido descubriendo exoplanetas el concepto de zona habitable a aparecido cada vez más en los titulares de prensa. Sin embargo, la zona habitable es un término mucho más relativo de lo que solemos pensar. Nahúm Méndez explica en apenas diez minutos todos los matices que encierra.
.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Nahúm Méndez Chazarra – Naukas Bilbao 2019: Marcianos, extraterrestres y la zona habitable se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Álex Méndez: Luz de luna
- José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos
- Naukas Bilbao 2017 – Déborah García Bello: Saboer
El rojo y los cambios climáticos
 La Sala Roja de la cueva de Goikoetxe. Foto: G.E. ADES
La Sala Roja de la cueva de Goikoetxe. Foto: G.E. ADESEn muestras tanto geológicas como arqueológicas el color rojo suele deberse a la presencia de distintos óxidos de hierro, que tiñen de manera muy intensa minerales y rocas. Sin embargo, “en el caso de las estalagmitas de la Cueva de Goikoetxe, localizada en la Reserva de la Biosfera de Urdaibai, el color rojo se debe a la presencia de sustancias orgánicas derivadas de la descomposición de la cobertura vegetal en los suelos situados encima de la cueva”, señala Virginia Martínez Pillado, investigadora del departamento de Mineralogía y Petrología de la UPV/EHU. La intensidad del color rojo de las estalagmitas serviría, por tanto, de registro para determinar cambios climáticos.
“En toda la zona de la cornisa cantábrica existe mucha precipitación y vegetación, por lo que se crea una gran cobertura vegetal encima de la cueva; cuando dicha vegetación se degrada estas sustancias orgánicas, fundamentalmente ácidos húmicos y fúlvicos, son arrastradas al interior de la cueva por el agua de la lluvia, y tiñen de rojo los espeleotemas al incorporarse a la red de la calcita que los forma”, explica Virginia Martínez Pillado.
Los investigadores han combinado diferentes técnicas de análisis sobre varias estalagmitas de diferentes coloraciones, como la datación radiométrica por series de uranio, la petrografía, la fluorescencia de rayos X, la espectroscopía y la luminiscencia con luz ultravioleta. “Para la realización de los análisis se han utilizado dos técnicas espectroscópicas llamadas Raman y FTIR que sirven para la identificación de diferentes tipos de moléculas y compuestos. Estas técnicas han sido las que han determinado la presencia de compuestos orgánicos derivados de la degradación de materia vegetal en el interior de las estalagmitas”, indica Martínez Pillado.
Además, “hemos realizado fotografías mediante luz ultravioleta a las mismas estalagmitas, y la respuesta de la calcita frente a la radiación ultravioleta ha mostrado ser cíclica. Es decir, dentro de las estalagmitas rojas, únicamente en las rojas —subraya la investigadora— han aparecido ciertos ciclos en los que hay mayor y menor incorporación de las substancias orgánicas; en los momentos que hay mayor incorporación orgánica parece ser que hay una cobertura vegetal muchísimo más densa. Probablemente sea porque hay una mayor cantidad de precipitaciones, aunque esto es algo que aún habría que estudiar más en profundidad”. Lo que sí está claro es “que la cobertura vegetal y la producción de suelos es muchísimo más intensa en ciertos momentos que en otros a lo largo de todo el Holoceno medio, entre hace 7.000 y 5.000 años, y esto está estrechamente ligado a las condiciones climáticas del exterior de la cueva”.
Estos ciclos detectados, relacionados con el llamativo color rojo, han permitido a los investigadores comenzar nuevas investigaciones para reconstruir la evolución climática en la costa cantábrica en ese periodo.
Referencia:
V. Martínez-Pillado, I. Yusta, E. Iriarte, A. Álvaro, N. Ortega, A. Aranburu, J.L.Arsuaga (2020) The red coloration of Goikoetxe Cave´s speleothems (Busturia, Spain): An indicator of paleoclimatic changes Quaternary International (2020) doi: 10.1016/j.quaint.2020.04.006
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El rojo y los cambios climáticos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los efectos climáticos de un calentamiento sin precedentes en el Mediterráneo
- Verdín, eucaliptos y cambio climático
- El ocre rojo de la antigüedad y los porqués de sus propiedades
El cuadrante Pasteur español y el efecto Dreadnought
Xabier Irigoien
Todo gestor científico conoce el cuadrante Pasteur, y lo usa en sus presentaciones. Arriba a la izquierda, ilustrada por Bohr y la física cuántica, está la ciencia básica que hacemos para entender la naturaleza, que quizás tenga aplicación algún día pero no es obvia cuando se empieza. Arriba a la derecha, están Pasteur y las vacunas, investigación básica pero ya orientada a un objetivo. Y abajo a la derecha queda Edison, investigación aplicada, con un claro producto como objetivo. A todos los gobiernos del mundo el cuadrante que más les gusta es el de abajo a la derecha, el de la investigación aplicada, el que se traduce en productos que pueden vender las empresas y generar negocio. De hecho a todos los gobiernos les gustaría poder prescindir de financiar los otros cuadrantes, pero son conscientes de que no hay ciencia aplicada sin ciencia básica.
 Cuadrante Pasteur (Stokes 1997)
Cuadrante Pasteur (Stokes 1997)Sin embargo, nos queda la casilla de abajo a la izquierda, que esta vacía. ¿ Que se supone que va ahí ? Stokes, que es quien produjo el ejemplo del cuadrante Pasteur en 1997, habla del cuadrante Peterson, investigación guiada por la curiosidad pero sin utilidad alguna. Es probable que en versiones posteriores se haya quedado vacío porque la idea de que la investigación guiada por la curiosidad sea inútil es bastante discutible. Así que en España hemos hecho algo mejor, hemos creado nuestro propio cuadrante, el cuadrante Unamuno: el de que inventen ellos.
 Cuadrante Pasteur versión española
Cuadrante Pasteur versión españolaObviamente, llamarlo así quedaba mal, por lo que hemos decidido ponerle como titulo el de “Innovación”. A lo que antes le llamábamos I+D, investigación y desarrollo, ahora le llamamos I+D+i, investigación + desarrollo + innovación. Y vamos a ser justos, no es un invento nacional, como veremos Europa está en lo mismo, y todo lo que aquí se menciona vale también para gran parte de Europa. Pero en España tenemos un personaje para ponerle nombre al cuadrante. Y también vamos a distinguir, hay “innovación disruptiva” e “innovación”. Crear la bombilla a partir de conocimiento existente cuando las casas se alumbraban con gas o aceite de ballena es innovación disruptiva, cambiar el color de las bombillas porque hay un mercado para bombillas de colores es innovación.
No todo tiene que ser inventar la bombilla, vamos a explorar una pequeña innovación disruptiva que puso el ordenador personal al alcance de todo el mundo, la interfase grafica (GUI), las ventanas que uso en la pantalla de mi ordenador en vez de escribir líneas de comandos (¿ alguien se acuerda de MS-DOS ?). El inventor fue Douglas Engelbart, en 1968 en la Universidad de Stanford. La primera GUI la desarrollo el Xerox Palo Alto Research Center (PARC), lo que en España llamaríamos un centro tecnológico, en Palo Alto (California) hacia 1973. Steve Jobs visitó PARC en 1979 y Apple incorporó la GUI a sus ordenadores en 1984. De Stanford a Palo Alto hay 3 km, y de Palo Alto a Cupertino 16. Es decir que en el sistema de transferencia más eficiente del mundo, Silicon Valley, desde una de las mejores universidades del mundo a una de las empresas más innovadoras se tardó unos 20 años para llevar una invención muy aplicada a su comercialización, a la velocidad de 1 km por año de la universidad a la empresa.
Por ponernos en contexto, en Estados Unidos, paradigma de llevar la investigación al mercado, se dedican unas 70 000 millones de dólares al año a la investigación, de esos unas 40 000 millones (57 %) vienen de fondos federales, 5 000 millones (7%) de la industria y 25 000 (36 %) millones de otras fuentes (estados, fundaciones etc). Esto se traduce en 15 000 solicitudes de patentes, 800 nuevos productos y la creación de 1000 start-ups al año (Figura 3, AUTM licensing survey 2017, www.autm.net). España con una inversión real de alrededor de 10 000 millones tiene lógicamente los resultados escalables, por ejemplo 1800 patentes al año. Pero lo que España (ni gran parte de Europa) no consigue es generar el tipo de innovación disruptiva que surge en los EEUU (o por ejemplo Corea).
 Investigación y resultados en los EEUU. Fuente: www.autm.net
Investigación y resultados en los EEUU. Fuente: www.autm.net
En mi opinión esto se debe a que España, siguiendo la tradición unamunoniana, no cree en la ciencia y conocimiento como generadores de nuevo negocio. Realmente nuestra sociedad (nuestros dirigentes son un reflejo de la sociedad) cree que inventarán otros, y que nosotros lo único que necesitamos hacer es mejorar esos inventos, es decir innovar a secas.
Con honrosas excepciones, la universidad española es tradicionalmente mediocre. El Unamuno de “inventen ellos” era a la vez el rector de una de las mejores universidades españolas de la época, la de Salamanca, y eso es un reflejo de nuestra tradición. Siempre se discuten las clasificaciones y es obvio que no somos los EEUU con Stanford, MIT y parecidos. Pero Suiza, un país de 8.5 millones de habitantes, menor que Cataluña, tiene 5 universidades entre las 100 mejores del mundo. España ninguna. Y Suiza no solo son bancos, también es el país de Nestlè, Novartis y Roche entre otras multinacionales basadas en la ciencia. Para cubrir las deficiencias tradicionales de la universidad Española en la transferencia del conocimiento, en las ultimas décadas han proliferado los centros tecnológicos, primero en Euskadi y Cataluña, y luego en el resto del Estado. Estos intentan reproducir el papel del PARC, o, para ser más precisos, toman como modelo el Fraunhofer alemán. Eso sí, sin tener institutos del nivel del Max Planck para generar el conocimiento básico en el que apoyarse.
Sin embargo, aunque han tenido un impacto positivo, a esos centros tecnológicos (CCTT) no se les ha dotado de misiones concretas y presupuestos estables, sino que se ha dejado que crezcan y se multipliquen a medio camino entre lo privado y lo público. Obviamente, cualquier organización que debe autosostenerse, aunque sea sin lucro, busca sus propios mercados, y muchos CCTT han acabado ocupando terrenos que serían mas propios de empresas, como pueden ser los servicios.
Sin embargo, tanto en España como en la UE, una tendencia con todavía peor efecto es la presión cada vez mayor para que universidades y sobre todo centros tecnológicos se acerquen a la empresas. Se les pide que hagan su investigación aplicada atendiendo a las necesidades de las empresas. De hecho cada vez más se pide que las empresas sean parte de los proyectos de investigación y se evalúa tanto el potencial impacto del proyecto como el interés científico del proyecto. Esto acaba convirtiendo a los CCTT en departamentos de I+D de las empresas. Pero también tiene un efecto más pernicioso, al que me gusta denominar efecto Dreadnought (Figura 4).
En 1906, el primer Lord del Mar, John «Jackie» Fisher, lanzó el Dreadnought, lo que hoy en día llamaríamos un caso de escuela de innovación disruptiva. Nada era un invento nuevo, pero al reunir las tecnologías más avanzadas de la época en motores, coraza y artillería, el Dreadnought dejó obsoletos de un plumazo a todos los buques de guerra contemporáneos. Incluidos los de la armada más poderosa en ese momento, la Armada británica. Como resultado, todas las armadas estaban niveladas y comenzó la carrera armamentista naval con Alemania.
 El HMS Dreadnought. Fuente: Wikimedia Commons
El HMS Dreadnought. Fuente: Wikimedia CommonsComo hemos dicho, España y la UE tienen un problema reconocido con la innovación: la ciencia básica no se traduce en el mercado de la manera que ocurre, no solo en los EE.UU, sino también en países como Corea y otros. El problema es de tal magnitud que la UE ha incluido para los proyectos de investigación H2020 el requisito de tener PYMES en el consorcio y la participación de las partes interesadas se requiere desde la redacción de la propia propuesta. Además, la propuesta generalmente necesita incluir un plan de negocio, y lo más importante es que el impacto potencial es tan importante como la ciencia en el proceso de evaluación. Esta tendencia se está incorporando a los programas de financiación de investigación nacionales y autonómicos.
Sin embargo, debido al efecto Dreadnought, las compañías ya existentes no promoverán a sabiendas la investigación que conduzca a la innovación disruptiva, ya que de hecho alteraría su estructura de producción y, lo que es más importante, pondrían a los competidores al mismo nivel. Las compañías de gas que iluminaban las calles en el siglo XIX no estaban invirtiendo en la investigación de Menlo Park sobre electricidad (solo por la anécdota, la frase completa de Unamuno en El pórtico del tiempo, 1906, es: “Inventen, pues, ellos y nosotros nos aprovecharemos de sus invenciones. Pues confío y espero en que estarás convencido, como yo lo estoy, de que la luz eléctrica alumbra aquí tan bien como allí donde se inventó”) .Los beneficios que obtenía Bayer por las sulfonamidas no estaban en la base del descubrimiento de los antibióticos e incluso los productos de una empresa famosa por su capacidad innovadora generalmente están en un campo diferente al de su negocio principal.
En realidad, el iPhone es un buen ejemplo de un efecto Dreadnought: Nokia estaba haciendo una excelente investigación para mejorar sus teléfonos móviles cuando la innovación disruptiva proveniente de una compañía de computadoras personales lo sacó del mercado de un solo golpe. Por otro lado, aunque Apple fue el primero en el nuevo mercado, el producto niveló tanto el campo para los competidores que hoy en día, marcas de las que uno nunca había oído hablar, están al frente del mercado. Hay que observar que las gigantescas empresas que asustan a Europa por su dominio global, como Google, Amazon y otros, no tienen en su origen una I+D+i financiada y orientada por una empresa, sino a jóvenes emprendedores que abandonaron la academia y pusieron los últimos conocimientos generados en los laboratorios directamente en el trabajo.
El enfoque adoptado en los proyectos H2020, así como en los programas nacionales y autonómicos, seguramente ayudará a las empresas de la UE y nacionales a seguir siendo competitivas, pero solo hasta que la innovación disruptiva proveniente de otro lugar las borre creando un mercado completamente nuevo. Y como se indicó anteriormente, al tener compañías y partes interesadas estrechamente vinculadas al proyecto desde la concepción del mismo, este enfoque desalienta intrínsecamente la innovación disruptiva.
Por otro lado, toda una serie de estudios en los EEUU sugieren que el mayor retorno de la inversión en ciencia no se genera a través de patentes o secretos industriales, sino a través de la creación de nuevas empresas, start-ups (Valdivia 2013). En lugar de solicitar a las empresas que participen en los proyectos, evaluando el impacto potencial y creando planes comerciales desde la etapa de propuesta, lo que deberíamos promover es la generación de nuevas empresas a partir de proyectos de investigación. Hay que tener en cuenta que no se puede construir un plan comercial sensato para una innovación disruptiva que crea un mercado completamente nuevo, pero en algunas convocatorias se podría omitir la participación empresarial y la evaluación de impacto potencial simplemente solicitando a los proyectos que reserven parte del presupuesto para ayudar a iniciar nuevas empresas. Esto crearía el incentivo para que los proyectos apunten a una investigación disruptiva y al mismo tiempo motivaría a las investigadoras e investigadores jóvenes a correr el riesgo de abandonar la academia para entrar en la empresa. Obviamente, la mayoría de los proyectos no crearán nada disruptivo, pero los resultados siempre seguirán estando disponibles para las empresas existentes como patentes o pequeñas empresas que se pueden adquirir, y al mismo tiempo se establecerán los incentivos adecuados para sembrar las empresas disruptivas que nos faltan hoy en día en España y la UE
Esto debería de ir acompañado de una concienciación de la sociedad sobre el papel real de la ciencia como generador de nuevo negocio. De manera que la sociedad presione para que nuestra universidad mejore significativamente, no solo en su financiación como suelen demandar los rectores, pero también en su organización interna, búsqueda de la excelencia y sobre todo el nivel de autoexigencia. A la vez hay que diseñar mejor el papel de los centros tecnológicos, sus campos de actuación deben de estar claramente definidos. Lógicamente hay que apoyar a la empresa existente, pero también hay que pedirles que ejerzan ese papel de intermediario entre ciencia básica y producto, acercándose tanto a los generadores de conocimiento como se han acercado a las empresas.
Mientras sigamos viviendo en el cuadrante de Unamuno, pensando en que la bombilla la inventen ellos que ya haremos alguna mejora aquí, la luz nos alumbrará, pero nos seguirá sorprendiendo que nuestras empresas sean barridas por algo que viene de fuera y de paso deja sus beneficios e impuestos también fuera.
Referencias:
Stokes, Donald E. (1997). Pasteur’s Quadrant – Basic Science and Technological Innovation. Brookings Institution Press. pp. 196. ISBN 9780815781776.
Valdivia, Walter D. «University start-ups: Critical for improving technology transfer.» Center for Technology Innovation at Brookings. Washington, DC: Brookings Institution (2013).
Sobre el autor: Xabier Irigoien es director científico de AZTI-BRTA
El artículo El cuadrante Pasteur español y el efecto Dreadnought se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El efecto Roseto
- Cristalografía (13): Fiat Pasteur
- Nanopartículas para la consolidación del fuerte español de Bizerta
El problema del final feliz
Casi todos los domingos del invierno de 1933, un pequeño grupo de estudiantes se reunía en algún lugar (un parque o un café) de Budapest para hablar de matemáticas. El especial grupo al que me refiero estaba formado, entre otras personas, por Paul Erdős (1913-1996), Esther Klein (1910-2005), Márta Svéd (¿1910?-2005), George Szekeres (1911-2005) y Pál Turán (1910-1976).
 En esta imagen aparecen tres de los protagonistas citados arriba, pero con algunos años más. De izquierda a derecha: Carole Lacampagne, Roger Eggleton, Esther Szekeres (Klein de nacimiento), Paul Erdös, George Szekeres y John Selfridge en 1984.
En esta imagen aparecen tres de los protagonistas citados arriba, pero con algunos años más. De izquierda a derecha: Carole Lacampagne, Roger Eggleton, Esther Szekeres (Klein de nacimiento), Paul Erdös, George Szekeres y John Selfridge en 1984.©The University of Newcastle; UON Photographer.
En una de estas reuniones, Esther propuso el siguiente problema:
Dados cinco puntos en el plano en posición general, demostrar que cuatro de ellos forman un cuadrilátero convexo.
Tras dejar al resto del grupo un tiempo para reflexionar sobre el problema, Esther explicó a sus colegas la demostración que ella había pensado.
En 1935 Erdős y Szekeres publicaron un artículo en el que se generalizaba el resultado de Esther (ver [1]); es uno de los trabajos fundamentales de la geometría combinatoria. Paul Erdős denominó el problema original como “El problema del final feliz” porque Esther y George se casaron en 1937… ¿tras conocerse mejor gracias a este enunciado?
Empecemos por aclarar los conceptos involucrados en la proposición de Esther. Que varios puntos del plano estén en posición general significa que no existe ningún subconjunto formado por tres de ellos que sean colineales. Un cuadrilátero es convexo si todos sus ángulos interiores son menores que 180 grados.
La solución de Esther se basaba en que existen tres formas diferentes en las que un polígono convexo encierra cinco puntos. Dicho de otra manera, dados cinco puntos en posición general, su envolvente convexa puede ser uno de los tres polígonos siguientes:
-
puede ser un cuadrilátero cuyos vértices son cuatro de los puntos del conjunto inicial y que deja en su interior el punto restante. En este caso, la solución ya es inmediata;
-
la envolvente convexa puede ser un pentágono cuyos vértices son los cinco puntos dados. Entonces cuatro de esos puntos pueden conectarse para formar un cuadrilátero convexo;
-
finalmente, si la envolvente es un triángulo, los dos puntos que quedan dentro de la figura definen una recta que divide el triángulo en dos partes. En una de ellas hay dos puntos y en la otra uno de los del conjunto de cinco puntos inicial. Estos dos puntos y los interiores forman automáticamente un cuadrilátero convexo.
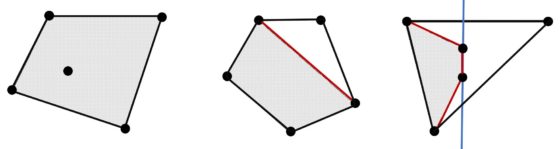 Los tres casos posibles de envolventes convexas y los cuadriláteros convexos obtenidos.
Los tres casos posibles de envolventes convexas y los cuadriláteros convexos obtenidos.
Como hemos comentado antes, Erdős y Szekeres publicaron en 1935 (ver [1]) una generalización del problema planteado por Esther Klein. El artículo comenzaba del siguiente modo:
El problema que nos ocupa ha sido sugerido por la señorita Esther Klein en relación con la siguiente proposición.
A partir de cinco puntos del plano de los cuales no hay tres en una misma línea recta, siempre es posible seleccionar cuatro puntos que determinan un cuadrilátero convexo.
[…] La señorita Klein sugirió el siguiente problema más general. Dado un entero positivo n, ¿es posible encontrar un número N(n) tal que de cualquier conjunto que contenga al menos N(n) puntos sea posible seleccionar n puntos que formen un polígono convexo?
Hay dos preguntas particulares: (1) ¿existe el número N(n) correspondiente a n? (2) Si es así, ¿cómo se determina el menor N(n) en función de n? (denotamos el menor N por N0(n)).
 Principio del artículo [1]
Principio del artículo [1]
En [1] los autores demostraban que el número N(n) existe (para n mayor que 2) y conjeturaban que
![]()
basándose en algún caso particular demostrado por otros autores. De hecho, es obvio que N0(3)=3, Esther Klein demostró que N0(4)=5 y en [1] se afirma que E Makai probó que N0(5)=9, aunque no existe evidencia escrita de ello. Años más tarde Szekeres y Lindsay Peters (ver [2]) demostraron con ayuda de un ordenador que N0(6)=17, reafirmando la conjetura.
Y, de momento nadie ha sido capaz de confirmar o refutar la conjetura. Pero la propuesta se ha reformulado proponiendo la alternativa siguiente (ver, por ejemplo, [4]):
![]()
donde la O mayúscula se refiere a la notación de Landau. Confiemos en que pronto se conocerá más sobre esta interesante acotación.
Por cierto, la historia de amor (el “final feliz” entre sus dos colegas, como lo denominaría Erdös) de Esther y George fue larga e incluso poética en su despedida: ambos fallecieron el 28 de agosto de 2005, con una hora de diferencia. Ella tenía 95 años, él 94… y ambos número de Erdös igual a 1.
Referencias
[1] Paul Erdös and George Szekeres, A combinatorial problem in geometry, Compositio Math. 2 (1935), 463-470.
[2] George Szekeres and Lindsay Peters, Computer solution to the 17-point Erdös-Szekeres problem, ANZIAM J. 48 (2006), 151-164
[3] Pierre-Alain Cherix, Shaula Fiorelli Vilmart, Pierre de la harpe, Polygones convexes : le problème de la fin heureuse, Images des Mathématiques, CNRS, 2014
[4] Sara Freyland, The Happy Ending Problem and its connection to Ramsey theory, Report Uppsala University, 2019
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo El problema del final feliz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El problema de la plantación de árboles en filas (2)
- Un dulce problema de Paul Erdös
- El problema de la plantación de árboles en filas
Superconductores
 El Shanghai Transrapid une el aeropuerto Shanghai Pudong con la estación de Longyang. Es un maglev comercial que alcanza los 431 km/h de velocidad de crucero. Fuente: Wikimedia Commons
El Shanghai Transrapid une el aeropuerto Shanghai Pudong con la estación de Longyang. Es un maglev comercial que alcanza los 431 km/h de velocidad de crucero. Fuente: Wikimedia CommonsLa teoría de la bandas ha sido sometida a pruebas experimentales muchas veces y ahora es el modelo de consenso para el comportamiento de conductores y aislantes. Pero tenemos que modificarla para poder explicar la superconductividad.
El modelo de Drude-Lorentz introdujo la idea de que la resistencia eléctrica se debe a colisiones de los electrones [1] con impurezas, imperfecciones y especialmente con las vibraciones reticulares del cristal. Las vibraciones reticulares del sólido disminuirán a medida que disminuya la temperatura, porque la entropía, que representa el desorden [2], también disminuye. Por lo tanto, la resistencia también debería disminuir. Esto es lo que se observa, y está bien explicado por la teoría cuántica de bandas. Pero a temperaturas muy bajas sucede algo extraño: la resistencia de algunos materiales cae repentinamente a cero a partir de cierta temperatura.
Estos materiales se convierten en superconductores, lo que significa que pueden conducir corrientes sin resistencia o, lo que es equivalente, sin pérdida de energía. La temperatura a partir de la que se produce la superconductividad se denomina temperatura crítica. Varía desde 0.015 K para el tungsteno [3], 160 K para ciertas cerámicas, hasta 250 K para algunas formas cristalinas de superhidruro de lantano [4][5].
Podemos imaginar algunas de las posibles ventajas de unos cables eléctricos con resistencia cero. Es como un movimiento sin fricción. Entre las muchas aplicaciones reales y potenciales están las líneas de transmisión eléctrica sin pérdida de energía, ordenadores más rápidas y electroimanes con una fuerza colosal. Estos últimos se usan actualmente en dispositivos de resonancia magnética (MRI), aceleradores de partículas de alta energía y trenes de levitación de alta velocidad, a menudo llamados «mag-lev» [6]. Dado que la temperatura de ebullición del nitrógeno líquido, que es abundante y relativamente fácil de producir, es de 77 K, los superconductores con temperaturas críticas superiores a 77 K pueden mantenerse lo suficientemente fríos manteniéndolos sumergidos en nitrógeno líquido. Sin embargo, un gran inconveniente de estos materiales es que son frágiles, no porque se puedan romper con facilidad, sino porque la superconductividad puede destruirse fácilmente por un campo magnético que no esté controlado. Como es lógico, se investiga intensamente para superar estos problemas y crear materiales superconductores con temperaturas de transición lo más cercanas que sea posible la temperatura ambiente (20 ° C o 293 K) [7].
El desarrollo de dispositivos superconductores tuvo un impulso enorme tras la aparición del modelo básico de la superconductividad propuesto en 1957 por John Bardeen, Leon Cooper y Robert Schrieffer. Los autores de la teoría BCS, como se le conoce, recibieron el Premio Nobel por su trabajo en 1972. Su teoría es altamente técnica, pero la idea básica es que las ondas de electrones en el estado superconductor ya no actúan de forma independiente, como en el modelo de Bloch. En cambio, se emparejan a la temperatura crítica de modo que sus funciones de onda actúan como una unidad a medida que interactúan con la red cristalina. Además, todos los pares de electrones se mueven juntos en un movimiento colectivo, de modo que si un solo electrón se dispersa por la red, su compañero “lo arrastra” hacia la corriente general, y si algún par de electrones se dispersa de alguna manera fuera de la ruta general, todos los demás pares “lo traen” de regreso al flujo colectivo. Como no hay dispersión o colisiones inelásticas, no hay resistencia y el material se convierte en un superconductor.
Aunque la teoría BCS explica bien en general ciertos sólidos cristalinos, se requieren más refinamientos del modelo para otros materiales [8] y para explicar el comportamiento de los superconductores en detalle.
Notas:
[1] Da igual si los tratamos como ondas o como corpúsculos.
[2] En puridad esto es una afirmación muy grosera, pero tolérese para poder visualizar lo que ocurre.
[3] En esta casa obedecemos las normas IUPAC.
[4] En concreto una forma del LaH10 altamente simétrica (grupo espacial Fm-3m), en la que una jaula de hidrógeno envuelve los átomos de lantano. Véase.
[5] Récord a la fecha de publicación. Cualquiera sabe cuando estés leyendo esto.
[6] De levitación magnética dicho en inglés.
[7] 20ºC es la temperatura ambiente estándar. Si nos fijamos ya se ha conseguido la superconductividad a temperatura ambiente en algunas regiones de la superficie del planeta Tierra en según qué épocas del año: 250 K son -23º C.
[8] Véase, por ejemplo, esto.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Superconductores se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Tipos de comportamiento conductor
- La ley del gas ideal y la tercera ley de la termodinámica
- El modelo clásico de electrones libres de Drude-Lorentz
A tomar el sol
 Foto: Mincho Kavaldzhiev / Unsplash
Foto: Mincho Kavaldzhiev / UnsplashEn las últimas décadas los expertos han recomendado evitar las exposiciones excesivas al sol pues son la principal causa de daños en la piel y, sobre todo, de la aparición de melanoma, un cáncer extendido y muy peligroso. La revisión, publicada en 2017, por Natalie Matthew y sus colegas, de la Universidad de Providence, en Estados Unidos, informa de que la incidencia del melanoma en todo el planeta ha crecido con rapidez en los últimos 50 años.
La tasa es mayor en personas de piel blanca y en zonas cercanas a los trópicos y al ecuador. Nuestra especie apareció en los trópicos del centro de África, un área geográfica con mucho sol. Homo necesita sol para el metabolismo de la vitamina D en la piel. Sin embargo, la exposición al sol es peligrosa por los rayos ultravioleta que tiene y, para evitarlos, apareció la melanina, el pigmento que oscurece la piel y evita los ultravioleta. Pero, cuando nuestra especie salió de África hacia el norte, hacia Eurasia, colonizó zonas con menos incidencia solar y, por tanto, menos producción de vitamina D en la piel. Se aclaró la piel y se seleccionó piel blanca, con poca melanina, que dejaba pasar la luz solar y permitía la síntesis de vitamina D. Pero, con el tiempo, los originarios de Eurasia se extendieron por todo el planeta, y, con su piel blanca, muchos volvieron a los trópicos, con demasiado sol para este tipo de piel con escasa melanina protectora. El exceso de sol, con su componente ultravioleta, produce daños en la piel y, en último término, la aparición del melanoma.
En conclusión, la relación de la piel de nuestra especie con el sol es complicada: buena para la vitamina D y dañina por el exceso con desarrollo de cáncer. Hasta ahora se ha intentado evitar el melanoma y, para conseguirlo, los protocolos de exposición al sol piden evitar el exceso y el uso de protectores solares.
Para explicar brevemente los efectos sobre la salud de la deficiencia en vitamina D, nos sirve la revisión publicada por Michael Holick, de la Universidad de Boston, el año pasado. Enumera, como consecuencia de la falta de vitamina D, a enfermedades agudas y crónicas como la caries en niños, osteoporosis, psoriasis, enfermedades autoinmunes, enfermedades cardiovasculares, algunos tipos de cáncer, diabetes tipo 2 y desordenes neurológicos.
Hay que tener mucho cuidado con el sol y, para tomarlo, no hacerlo a las horas centrales del día, cubierta la cabeza, con ropa adecuada y gafas de sol y, siempre, con protector solar, a ser posible con un factor superior a 30.
Pero, hemos visto que la vitamina D es esencial para muchas funciones del organismo y se sintetiza en la piel por la acción de los rayos ultravioleta solares. Eleni Linos y su equipo, de la Universidad de Stanford, aseguran que tanta protección frente al sol puede afectar a los niveles de vitamina D en el organismo. Esta deficiencia vitamínica, como hemos visto, aumenta el riesgo de varias enfermedades y en ello interviene el uso de los protectores solares.
Los protectores solares, en experimentos de laboratorio y en experimentos controlados, reducen los niveles de vitamina D. Ahora Eleni Linos pretende relacionar los niveles de vitamina D con el uso de protectores solares en la población en general y en situaciones de vida normal. A partir de una encuesta nacional sobre salud en Estados Unidos, con datos tomados de 2003 a 2006 a 5920 personas, consigue, por una parte, conocer el uso de protectores solares y, por otra, el nivel de vitamina D en sangre de los voluntarios (en realidad, del precursor 25-hidroxi-vitamina D que pasa a vitamina D en el riñón).
Al analizar los resultados, los autores encuentran que más de la mitad de los encuestados se protegen del sol de alguna manera, aunque el método varía según la raza, sobre todo en relación con los protectores solares: más de la mitad de los blancos (56%) los utilizan con frecuencia mientras que sólo lo hace un tercio de los hispanos (31%) y algo menos de la sexta parte de los negros (14%). Estar a la sombra, en cambio, es más frecuente en hispanos (37%) y negros (43%) que en blancos (25%). En cuanto al nivel de vitamina D en sangre, más del 70% de los que tienen deficiencia se protegen del sol a la sombra o usan la ropa adecuada (sobre todo las camisas de manga larga).
Las conclusiones son curiosas: la deficiencia en vitamina D la provoca la sombra y las mangas largas, no así los protectores solares que, según los investigadores, se utilizan poco o en poca cantidad y, por tanto, no protegen adecuadamente del sol y, de rebote, no provocan niveles bajos de vitamina D.
Hay que añadir que el grupo de Pelle Lindqvist, del Instituto Karolinska de Estocolmo, ha encontrado una relación entre evitar la exposición al sol y la tasa de mortalidad. Ha revisado datos de 29518 mujeres entre 1990 y la actualidad y que tenían de 25 a 64 años cuando se inició el estudio. Para este estudio, tomar poco el sol es, durante el verano, no tomarlo nunca, y tomarlo mucho es, en verano, hacerlo más de 30 veces.
Hasta 2011, fecha de la revisión de datos, habían muerto 2545 voluntarias. El número de fallecimientos es mayor cuanto menos se toma el sol. No hay que olvidar que los datos son de Suecia, un país al norte y con escasez de sol. Cuando se compara la mortalidad entre las que evitan el sol y las que lo toman, la tasa de mortalidad se dobla entre las que lo evitan. Para los autores, la causa está en la deficiencia en vitamina D, con las consecuencias para la salud que antes he mencionado. Conciliar el riesgo de melanoma con la deficiencia en vitamina D necesita un estudio más detallado y preciso para elaborar un protocolo adecuado.
El mismo grupo de Estocolmo estableció poco después que tomar el sol baja la tasa de mortalidad por enfermedades cardiovasculares y por otras enfermedades excepto cáncer. Calculan, por el contrario, que evitar el sol disminuye la esperanza de vida entre 0.6 y 2.1 años. Debido a la mayor esperanza de vida y a que evitan algunas enfermedades, las mujeres que toman el sol padecen cáncer años más tarde.
En conclusión, la radiación solar ultravioleta es esencial para la síntesis de vitamina D pero, a la vez, crece el riesgo de cáncer de piel, del peligroso melanoma. Sin embargo, cuando se ha buscado una relación entre el nivel de vitamina D con el riesgo de melanoma, no s eha encontrado. El estudio de Upekha Liyanage y su grupo, del Instituto de Investigación Médica Berghofer de Brisbane, en Australia, con datos de 36077 voluntarios, concluye que los niveles de vitamina D no se pueden asociar como causa y efecto con el riesgo de melanoma.
 Foto: Dimitris Vetsikas / Pixabay
Foto: Dimitris Vetsikas / PixabayQueda por mencionar un inesperado daño colateral en esta conducta de evitar el sol: la contaminación marina provocada por los protectores solares. Fue un grupo de las islas Baleares el primero en detectarlo en Mallorca.
El riesgo asociado a la exposición al sol ha llevado, en los últimos 80 años y según cuentan Antonio Tovar y sus colegas del Instituto Mediterráneo de Estudios Avanzados de Esporles, en Mallorca, a la invención, desarrollo y producción masiva de protectores solares. En consecuencia, también ha llegado su entrada masiva en el ambiente marino costero.
Su composición es compleja, con sustancias que filtran los rayos ultravioleta, algunas orgánicas como los aminobenzoatos, las benzofenonas, los derivados del alcanfor y muchos más, y otras inorgánicas como los óxidos de titanio o de zinc. Todas ellas reflejan y dispersan la radiación ultravioleta e impiden que llegue a la piel. Hay unos 45 compuestos de este tipo cuya producción está regulada en diferentes países.
Además de estas sustancias que actúan como filtros de ultravioleta, una crema solar lleva conservantes, colorantes, agentes que forman geles sobre la piel, controladores de viscosidad, fragancias, etcétera. Y todos ellos acaban, antes o después, en el ambiente, sobre todo en el mar.
El grupo de Antonio Tovar ha medido la presencia de alguno de estos compuestos en cinco puntos de tres zonas de costa de la isla de Mallorca con gran ocupación (entre 3 y 5 personas por metro de costa), en agosto y septiembre de 2011, temporada alta de turismo.
El análisis de las muestras de agua demuestra que los cuatro productos medidos están en el medio. Hay una benzofenona entre 53.6 y 577.5 nanogramos (millonésima parte del miligramo) por litro; un derivado del alcanfor entre 51.4 y 113.4 nanogramos por litro; óxido de titanio entre 6.9 y 37.6 microgramos (millonésima parte del gramo) por litro; y óxido de zinc entre 1.0 y 3.3 microgramos por litro. Estas concentraciones varían entre puntos de muestreo y, también a lo largo del día con el máximo entre las 14.00 y las 18.00 horas.
Para conseguir una primera aproximación de la posible influencia de estos compuestos en el medio marino, los ensayan sobre el crecimiento de un alga diatomea habitual en la zona, la Chaetoceras gracilis, y en ensayos cortos de 72 horas, en lo que se denomina toxicidad aguda. Con todos los compuestos hay una caída del crecimiento de la diatomea aunque las concentraciones necesarias son mucho más altas, a nivel de miligramos por litro, es decir, un millón de veces más altas que las encontradas en las playas. Pero no hay que olvidar que el periodo de exposición en el experimento era muy corto, solo 72 horas, y a más largo plazo, semanas, meses o años, incluso con concentraciones más bajas, no conocemos los efectos que provocan y los componentes de los protectores solares podrían ser peligrosos.
Referencias:
Holick, M.F. 2017. The vitamin D deficiency pandemic: Approaches for diagnosis, treatment and prevention. Reviews in Endocrine and Metabolic Disorders 18: 153-165.
Lindqvist, P.G. et al. 2014. Avoidance of sun exposure as a risk factor for all-cause mortality: results from the Melanoma in Southern Sweden cohort. Journal of Internal Medicine doi: 10.1111/joim.12251
Lindqvist, P.G. et al. 2016. Avoidance of sun exposure as a risk factor for major causes of death: a competing risk analysis of the Melanoma in Southern Sweden cohort. Journal of Internal Medicine doi: 10.1111/joim.12496
Linos, E. et al. 2012. Sun protective behaviors and vitamina D levels in the US population: NHANES 2003-2006. Cancer Causes Control 23: 133-140.
Liyanage, U.E. et al. 2020. Is there a causal relationship between vitamin D and melanoma risk? A Mendelian randomization study. British Journal of Dermatology 182: 97-103.
Matthews, N.H. et al. 2017. Epidemiology of melanoima. En “Cutaneous melanoma: ethology and therapy”, p. 3-22. Ed. por W.H. Ward & J.M. Farma. Codon Publ. Brisbane, Australia.
Tovar-Sánchez, A. et al. 2013. Sunscreen products as emerging pollutants to coastal waters. PLOS ONE 8: e6545
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo A tomar el sol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las mutaciones que aclaran la piel
- Biomarcadores para la detección precoz del melanoma
- Cómo nos ayuda la ciencia a tomar decisiones correctas
La hipótesis de la abuela
 Foto: djmboxsterman / Pixabay
Foto: djmboxsterman / PixabayLa menopausia es, desde una perspectiva evolutiva y en apariencia, una anomalía. De hecho, es un fenómeno muy poco frecuente en el mundo animal. En casi todas las especies las hembras se mantienen fértiles a lo largo de toda su vida. Nuestra especie forma parte de un pequeño grupo de mamíferos en los que la capacidad reproductiva se deteriora de forma acelerada con relación al declive orgánico general. El grupo lo forman, además de la especie humana, el calderón tropical, la beluga, el narval y la orca, todos ellos cetáceos odontocetos. Las hembras de esas especies pueden vivir décadas después de cesar de ovular y, por lo tanto, de poder procrear.
El biólogo norteamericano George C Williams propuso en 1957 que la menopausia podría ser, en realidad, una adaptación. Pensó que desde el punto de vista evolutivo, podría resultar más conveniente para las mujeres dedicar sus esfuerzos a apoyar a sus descendientes que tener ellas una progenie mayor. Conforme envejecemos aumenta la probabilidad de morir, por lo que si una mujer tiene descendencia a una edad avanzada, no sería improbable que sus últimos hijos no pudieran sobrevivir al morir ella. En tal caso, el esfuerzo que esa mujer hubiese dedicado a esos últimos hijos habría resultado baldío, pues sus genes no habrían podido replicarse y ser transmitidos a las siguientes generaciones a través de esos últimos descendientes. Por otro lado, que en una población haya individuos que no se reproducen carece de sentido desde un punto de vista evolutivo, pues esos individuos consumen unos recursos que podrían utilizar otros en beneficio de su propia progenie.
Por estas razones, Williams propuso que las mujeres de mayor edad contribuyen de una forma más efectiva a transmitir sus genes a las generaciones posteriores dedicando sus esfuerzos a los descendientes que ya forman parte del grupo, o sea, a sus nietos y nietas, en vez de hacerlo a los hijos e hijas que a una edad avanzada pudiera llegar a tener ellas mismas.
La “hipótesis de la abuela”, como se conoce en la actualidad la propuesta de Williams, cuenta con respaldo empírico en nuestra especie. Tanto en grupos de cazadores-recolectores, como en sociedades preindustriales se ha comprobado que las abuelas que no se reproducen aumentan la probabilidad de supervivencia de sus nietos. En otras palabras, su presencia en el grupo facilita que sus genes –los que han llegado hasta los nietos- perduren tras su propia muerte o, dicho en lenguaje darwinista, mejore su propia adecuación o éxito evolutivo (fitness) a través del cuidado que presta a sus nietos.
Hay especies, como el elefante asiático y posiblemente también los africanos, de las que sabemos que las abuelas mejoran la supervivencia de los nietos, aunque en este caso las abuelas se siguen reproduciendo. Pero aparte de la especie humana, en ningún otro animal se contaba con pruebas fehacientes en favor de la “hipótesis de la abuela”. Hasta hace unas semanas, pues se acaba de publicar un estudio con orcas –también llamadas, impropiamente, ballenas asesinas- que documenta el efecto positivo de abuelas que no se reproducen en la supervivencia de sus nietos. El estudio recién publicado no solo confirma ese efecto, también muestra que las abuelas que siguen procreando no prestan un apoyo similar al que brindan las orcas menopaúsicas.
La importancia que ese periodo posmenopáusico tan extenso tiene en seres humanos y en orcas habría impulsado, según los especialistas, un aumento en la longevidad de las dos especies, pues la mayor supervivencia de los nietos durante los años de vida añadidos habría compensado con creces, en términos evolutivos, el cese de la procreación.
Fuente: S. Nattrass et al (2019): Postreproductive killer whale grandmothers improve the survival of their grandoffspring. PNAS.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La hipótesis de la abuela se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- …
- hurrengoa ›
- azkena »

