El bienestar subjetivo es heredable, pero no en un alto grado
Al parecer, el sentimiento subjetivo de bienestar es un rasgo heredable, aunque en una pequeña medida. En otras palabras, aunque la herencia genética es responsable de una cierta fracción de la variabilidad de ese sentimiento de bienestar, esa fracción es pequeña; de hecho no supera un 25% de la variabilidad total.
 Foto: frank mckenna / Unsplash
Foto: frank mckenna / UnsplashEse es el principal resultado de un estudio basado en encuestas realizadas en Dinamarca y Holanda. A las personas incluidas en la muestra les hicieron dos preguntas. Una era si durante la semana anterior se había sentido contenta (happy), y la otra, si durante la semana anterior había disfrutado de la vida (enjoy).
Para su posterior tratamiento estadístico, transformaron las respuestas en variables binarias (mucho o no mucho) y, además, generaron una tercera variable, combinación de las dos anteriores, de manera que si las anteriores eran afirmativas, entonces la tercera (la combinación) también lo era, y era negativa en cualquier otro caso. El número total de individuos encuestados fue próximo a 11500. Y esos individuos fueron caracterizados genéticamente analizando alrededor de 850.000 polimorfismos de nucleótido único.
El equipo investigador estimó la denominada “heredabilidad estricta (o realizada) común” (o heredabilidad común en sentido estricto), que se define como la fracción de la varianza del carácter en cuestión que es atribuible a los efectos aditivos de los polimorfismos genéticos comunes. Ese término, –heredabilidad estricta–, se utiliza por oposición a la denominada “heredabilidad amplia” (o heredabilidad en sentido amplio), que incluye, además del efecto de los polimorfismos, el de las interacciones entre ellos (epistasia) y sus posibles efectos no lineales (dominancia).
Los especialistas consideran que la heredabilidad “estricta” es más relevante que la “amplia” a la hora de evaluar el poder predictivo de las técnicas de genética molecular, entre otras cosas porque se antoja extremadamente difícil delimitar el conjunto de interacciones epistáticas (interacciones entre los efectos lineales de los diferentes polimorfismos) susceptibles de tener algún efecto. Desde un punto de vista metodológico la tarea se presentaría ardua en extremo en caso de recurrir a la heredabilidad “amplia”, pues haría falta utilizar muestras poblacionales gigantescas para otorgar al análisis el necesario rigor estadístico.
El efecto de los factores genéticos, tal y como se ha determinado en este trabajo, es estadísticamente significativo para las respuestas a la pregunta de si había estado contento (happy) la semana pasada (p = 0,01), y algo menos significativo para la variable generada a partir de las dos primarias (happy y enjoy) (p = 0,03), y en ambos casos la proporción de la varianza explicada por los factores genéticos resultó de un 10% aproximadamente. Se trata de un valor muy bajo, inferior a las estimaciones que se han hecho para otros rasgos de personalidad o características psicológicas, y también por comparación con los obtenidos a partir de estudios de gemelos, hermanos y familiares próximos para este mismo rasgo, el del bienestar subjetivo.
Según los autores, ese bajo valor de heredabilidad se debe, en parte, al error que, por razones metodológicas, se comete en la determinación del sentimiento de bienestar. Una vez corregido el efecto de ese error, el porcentaje explicado por los factores genéticos resulta algo más alto: se encontraría en el rango 12-18%. En todo caso, sigue siendo un valor bajo si se compara con la heredabilidad de otros caracteres o con la heredabilidad “amplia”, que es la que se suele obtener en otros estudios. De hecho, es muy posible que, como ocurre con otros rasgos de personalidad (neuroticismo, apertura a la experiencia, simpatía), haya una importante componente de la heredabilidad no debida a factores aditivos (lo que antes hemos denominado interacciones epistáticas).
Cuando se ha medido la heredabilidad del modo en que se ha hecho en este trabajo, se han obtenido valores de 9% y 12% para el neuroticismo y la extroversión, respectivamente. También es baja la obtenida en este trabajo si se compara con la “heredabilidad estricta” que se determina en estudios con familiares próximos; estos han arrojado valores en el intervalo de 30-40%. Lo que ocurre es que estos estudios dan cuenta de “toda” la heredabilidad estricta, y la medida en este trabajo (heredabilidad estricta común) solo es, como se ha señalado antes, la debida a los polimorfismos comunes. Al corregir las estimaciones de este trabajo de manera que se incorpora el efecto de los polimorfismos raros, se obtienen valores en el entorno de 18%-27% de heredabilidad estricta, una estimación mucho más acorde con los valores obtenidos normalmente con rasgos de personalidad en estudios de familiares próximos.
Dado que la intervención para mejorar el bienestar subjetivo de las personas sólo se puede ejercer a través de factores ambientales (no heredables), es conveniente conocer los límites que pueden tener dichas intervenciones y para eso es esencial determinar, con la mayor precisión posible, las diferentes fuentes de variación, también la de origen genético. Es más, a partir de estos estudios pretenden llegar a identificar el conjunto de polimorfismos concretos que contribuyen de modo más decisivo al sentimiento de bienestar subjetivo.
No obstante, a la hora de valorar estos datos hay que ser cautelosos. Incluso cuando un rasgo es heredable en una alta proporción, ello no tendría por qué reducir la importancia de los factores ambientales. Los niveles basales de serotonina, así como la densidad de receptores de dopamina, inciden en la sensación de bienestar de forma directa, y están, en gran medida, condicionados genéticamente. Y hay otros factores genéticos que inciden en las preferencias, personalidad y habilidades de las personas, lo que influye en la elección de pareja y amistades, fecundidad, etc., elementos todos ellos de carácter ambiental.
Por tanto, los efectos de unos y otros factores son complejos y no es fácil establecer proporciones precisas, porque muchos actúan de modo interactivo. Y por otra parte, aunque estudios realizados en un momento y bajo ciertas condiciones arrojen unos determinados resultados de heredabilidad, esos resultados podrían ser distintos si el mismo estudio se realizase en un momento y bajo condiciones diferentes. Eso es así porque cuando las condiciones ambientales bajo las que se encuentran los sujetos son muy similares, la variabilidad registrada apenas sería atribuible a factores ambientales, de manera que habría de ser atribuida a factores hereditarios.
Para entender lo anterior, pensemos en dos poblaciones, de manera que todos los individuos de una de ellas estuviesen sometidos a restricciones nutricionales y todos los de la otra nadasen en la abundancia. Dentro de cada población se registraría una alta heredabilidad de rasgos tales como la altura o la obesidad, porque no habría apenas efecto de las condiciones alimenticias. Sin embargo, si se comparasen las dos poblaciones, se concluiría que el efecto de las condiciones nutricionales (ambientales) sería muy acusado, mucho más que el que se determina bajo condiciones relativamente homogéneas.
Fuente: Cornelius A. Rietveld, David Cesarini, Daniel J. Benjamin, Philipp D. Koellinger, Jan-Emmanuel De Neve, Henning Tiemeier, Magnus Johannesson, Patrik K. E. Magnusson, Nancy L. Pedersen, Robert F. Krueger, y Meike Bartels (2013): “Molecular genetics and subjective well-being” PNAS 110 (24).
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El bienestar subjetivo es heredable, pero no en un alto grado se ha escrito en Cuaderno de Cultura Científica.
¡Ciencia y humor, vaya par! (1)

La difusión del conocimiento de la ciencia se puede hacer a través de diferentes vías. Muchas veces son caminos que van más allá del ámbito académico y uno de ellos puede ser el uso del humor.
Con tiras publicadas en periódicos o revistas, a través de monólogos humorísticos y chistes o, por qué no, cantando coplas se puede hablar sobre ciencia. Todas estas estrategias son útiles y estas experiencias serán tema de conversación en la serie de conferencias Humor y ciencia, ¡vaya par!, organizadas dentro de Bilbo Zientzia Plaza.
Estas charlas suponen, además, la apertura de un nuevo curso del ciclo de conferencias Bidebarrieta Científica, organizado por la Cátedra de Cultura Científica de la Universidad del País Vasco y la Biblioteca Bidebarrieta.
El miércoles 20 de septiembre a las 19:00 de la tarde Eñaut Aiartzaguena Bravo, Irribarrez, ilustrador y autor de cómics, ofreció la charla Otso orojakilea (con traducción simultánea al castellano). Le acompañará Helena González Burón, doctora en Biomedicina y fundadora de Big Van Ciencia, que impartió la charla La ciencia hecha espectáculo.
Edición realizada por César Tomé López
El artículo ¡Ciencia y humor, vaya par! (1) se ha escrito en Cuaderno de Cultura Científica.
Una nueva plataforma de qubits creada átomo a átomo
Un equipo internacional de investigación liderado por Deung-Jang Choi y Cristina Mier, del Centro de Física de Materiales (CSIC-UPV/EHU) y del Donostia International Physics Center (DIPC), en colaboración con equipos de investigación de Corea, Japón y Estados Unidos, ha presentado una nueva plataforma cuántica que utiliza los espines de electrónicos de átomos individuales sobre una superficie sólida, logrando un sistema de qubits (bit cuántico) múltiple que utiliza tres espines de electrones simultaneamente. Los resultados se han publicado en Science.
La unidad fundamental para el almacenamiento de información y el cálculo en los ordenadores es el bit, que puede tener un valor de 0 ó 1. En cambio, los ordenadores cuánticos funcionan con qubits como unidad fundamental, que pueden realizar cálculos en una superposición de estados 0 y 1, lo que significa que pueden existir simultáneamente en ambos estados, como en la paradoja del gato de Schrodinger. Esta capacidad se traduce en una mejora significativa del rendimiento en términos de almacenamiento de información y velocidad de procesamiento en comparación con los ordenadores clásicos.
Para comercializar los ordenadores cuánticos, se han propuesto varios tipos de qubits utilizando uniones superconductoras, trampas de iones, puntos cuánticos y estados de fase cuánticos. Debido a la relativamente corta historia de la ciencia de la información cuántica, el reto de diseñar un sistema de qubits óptimo sigue pendiente. Durante décadas, los esfuerzos de la ciencia se han concentrado en construir una arquitectura cuántico-coherente a escala atómica, un reino donde las propiedades fundamentales de los átomos, como el espín de los electrones, se abran paso. Un logro así podría revolucionar la ciencia cuántica y la nanotecnología.
De hecho, continúa siendo necesaria una investigación científica fundamental para poner en marcha una nueva plataforma cuántica que subsane las deficiencias de los qubits existentes y, al mismo tiempo, aumente su integración y fiabilidad.
La microscopía de barrido de efecto túnel (STM) ha demostrado ser muy útil para medir y controlar los estados electrónicos de átomos individuales, aprovechando los fenómenos de la mecánica cuántica. En este trabajo, que combina la tecnología STM y la ESR (resonancia de espín electrónico), la proyección de pulsos de microondas sobre átomos individuales de titanio en la superficie permite controlar y medir con éxito los estados de espín. Como resultado, fue posible controlar con precisión el espín de un solo átomo y ajustarlo al estado cuántico deseado. El reto restante era implementar un sistema multiqubit capaz de controlar varios qubits simultáneamente. La plataforma de qubits presentada en este trabajo consiste en múltiples átomos de titanio colocados sobre la superficie de un fino aislante (óxido de magnesio) y ha superado con éxito el reto.
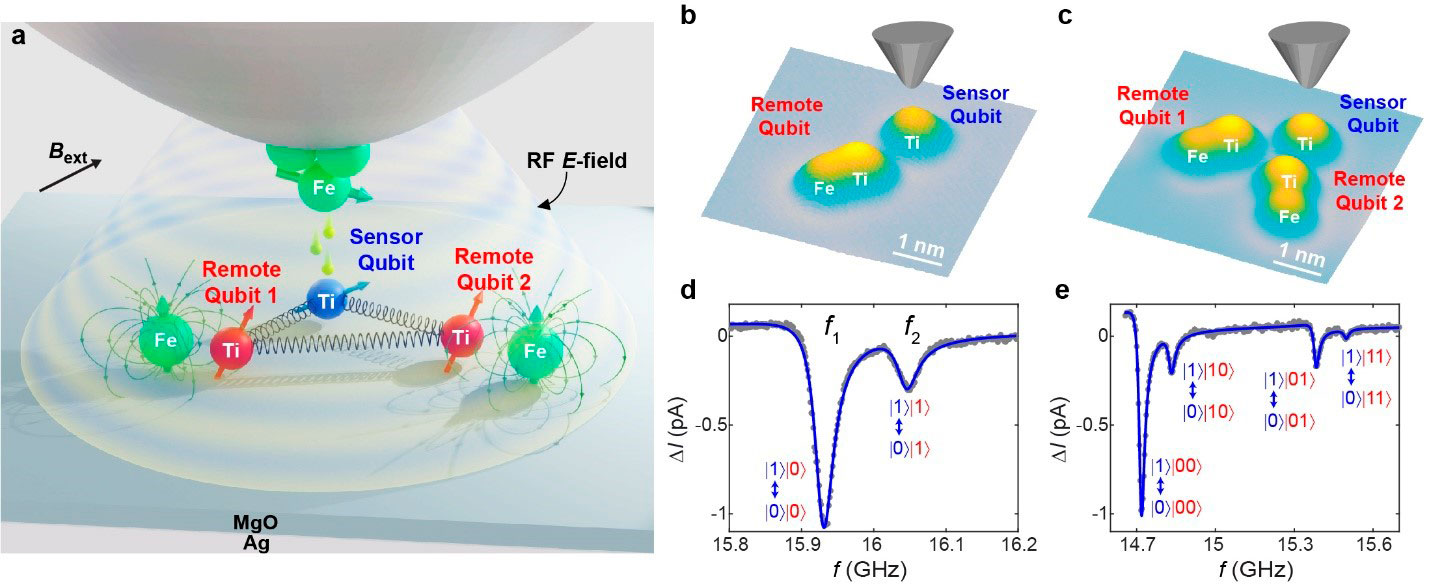
Las investigadoras utilizaron la sonda de un microscopio de barrido en túnel (STM) manipulando con precisión las posiciones de cada átomo, creando una estructura de múltiples átomos de titanio donde sus espines pueden interactuar. Posteriormente, aplicaron un método de control remoto al átomo de titanio que sirve de sensor (qubit sensor) y controlaron y midieron con éxito múltiples qubits (qubits remotos) colocados a distancia con una sola sonda.
Como cada qubit remoto interactúa con el qubit sensor, los cambios en el estado de espín de los qubits remotos afectan al qubit sensor, y este cambio se lee a través de la sonda. En este trabajo también implementaron las operaciones fundamentales del procesamiento cuántico de la información, las puertas «CNOT» (Controlled NOT gate) y «Toffoli», utilizando esta plataforma de qubits. La investigación se llevó a cabo a una temperatura de 0,4 K (-272,6 °C).
«Manipular múltiples qubits a distancia a nivel atómico es realmente extraordinario», afirmó una de las investigadoras. «Hasta ahora, solo podíamos controlar un único qubit en la superficie, pero gracias a esta investigación, hemos dado un salto significativo en la implementación de sistemas de qubits múltiples a nivel atómico».
La plataforma presentada en este estudio tiene la ventaja de controlar con precisión el intercambio de información entre qubits a nivel atómico. También se distingue de las plataformas de qubits existentes porque puede implementar circuitos cuánticos integrados con qubits individuales de menos de 1 nm. Además, a diferencia de otras plataformas que requieren materiales específicos (qubits de uniones superconductoras), permite seleccionar varios átomos como materiales de qubit, además del titanio.
En cuanto a la futura implementación y aplicación de estos resultados, la aplicación del sistema de qubits implementado para el procesamiento práctico de información cuántica, requerirá asegurar un tiempo de operación suficientemente largo para realizar diversas operaciones cuánticas de forma continua mientras se incrementa el número de qubits. Utilizando el método introducido en esta investigación, se espera que se puedan conectar y operar hasta 5-6 qubits, pero es necesario seguir investigando para desarrollar una plataforma que pueda controlar más de 10 qubits simultáneamente mejorando las conexiones y los métodos de medición entre qubits.
Referencia:
Yu Wang, Yi Chen, Hong T. Bui, Christoph Wolf, Masahiro Haze, Cristina Mier, Jinkyung Kim, Deung-Jang Choi, Christopher P. Lutz, Yujeong Bae, Soo-hyon Phark, and Andreas J. Heinrich (2023) An atomic-scale multi-qubit platform Science doi: 10.1126/science.ade5050
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Una nueva plataforma de qubits creada átomo a átomo se ha escrito en Cuaderno de Cultura Científica.
Islas, montañas que emergen del mar
De vez en cuando, los medios de comunicación emiten imágenes de esas acumulaciones de basura y desperdicios flotantes que hemos vertido a los océanos y las corrientes marinas han amontonado en ciertas zonas, a las que llamamos islas de plástico. Pues, aunque sea un nombre muy gráfico y llamativo, en realidad conduce a un error. Y no me refiero a lo de los plásticos, sino a lo de islas.
Asimilando conceptos, podemos llegar a pensar que las islas naturales son acumulaciones de tierra que están flotando en el mar, una idea que nos ha acompañado desde tiempos inmemoriales y que forma parte de muchas de nuestras mitologías. Desde Odiseo, más conocido por su nombre latinizado Ulises, teniendo que evitar con su barco unas enormes rocas erráticas que chocaban entre sí en algún lugar del mar Egeo, hasta Maui, que sacó un enorme trozo de tierra del fondo del mar utilizando su anzuelo mágico y que, al soltarlo y romperse en pedazos quedaron flotando en el océano dando lugar a las islas Hawaii. Por suerte, hoy en día, podemos acudir a la Geología para saber qué son y cómo se forman realmente las islas.
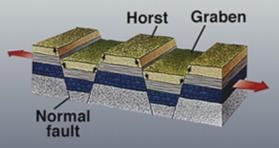 Mecanismo de extensión o separación de dos placas tectónicas (según las flechas rojas) en donde se produce una facturación de la litosfera a favor de fallas denominadas normales (normal fault en la imagen) que generan bloques levantados (horst) y bloques hundidos (graben). Imagen del Servicio Geológico de Estados Unidos de América (United States Geological Service)
Mecanismo de extensión o separación de dos placas tectónicas (según las flechas rojas) en donde se produce una facturación de la litosfera a favor de fallas denominadas normales (normal fault en la imagen) que generan bloques levantados (horst) y bloques hundidos (graben). Imagen del Servicio Geológico de Estados Unidos de América (United States Geological Service)Una isla es una porción de tierra emergida, es decir, que aparece en posición subaérea y está completamente rodeada de agua. Pero eso no quiere decir que flote sobre el mar, más bien todo lo contrario. Todas las islas están enraizadas en el fondo marino y no son más que la parte superior de grandes elevaciones que ascienden hacia la superficie hasta superar el nivel del mar, por lo que podemos verlas en el océano. Así que las islas no serían más que la parte superior de enormes montañas que crecen desde el suelo marino por encima del nivel del agua en ese momento. De hecho, el fondo oceánico no es una superficie plana, existen infinidad de elevaciones de tierra que no llegan a salir a superficie, formando lo que denominamos montes submarinos.
Generalizando un poco, las islas se pueden formar por dos procesos geológicos concretos. Por un lado tenemos los movimientos tectónicos. Como ya he comentado otras veces, la capa más externa, sólida y rígida de nuestro planeta, la litosfera, está partida en pedacitos llamados placas tectónicas. Estas placas se mueven sobre la capa inferior, la astenosfera, que es un sólido plástico. Cuando dos de estas placas se separan una de otra, la litosfera se va adelgazando y fracturando, dando lugar a una serie de bloques hundidos y elevados como si fuesen los peldaños de una escalera que se van a ir cubriendo de agua marina poco a poco. Si el nivel del mar no asciende lo suficiente, algunos de los bloques elevados pueden aflorar en superficie, formando islas.
Pero las placas tectónicas también pueden chocar entre sí. En esos casos, se produce la comprensión de las rocas, que se van levantando lentamente desde el fondo oceánico formando montañas que, de nuevo, pueden llegar a superar el nivel del agua del mar y generar islas en superficie. Para poneros un ejemplo conocido, estos procesos técnicos se produjeron durante el choque de la placa Ibérica con la placa Africana dando lugar a las Cordilleras Béticas y su continuación oriental submarina, las islas Baleares.
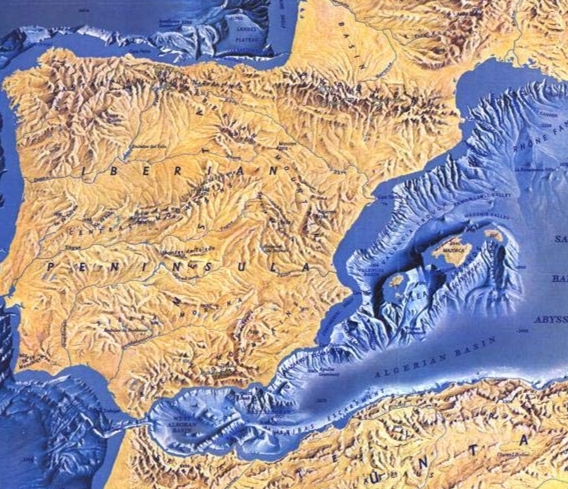 Mapa de la topografía submarina (batimetría) de la Península Ibérica donde se observa la elevación de las islas Baleares desde el fondo del Mediterráneo. Imagen modificada del mapa The Mediterranean seafloor, ilustrado por Tiborg G. Toth para la División Cartográfica de la Sociedad Geográfica Nacional de Estados Unidos de América (Cartographic Division, National Geographic Society).
Mapa de la topografía submarina (batimetría) de la Península Ibérica donde se observa la elevación de las islas Baleares desde el fondo del Mediterráneo. Imagen modificada del mapa The Mediterranean seafloor, ilustrado por Tiborg G. Toth para la División Cartográfica de la Sociedad Geográfica Nacional de Estados Unidos de América (Cartographic Division, National Geographic Society).El otro proceso geológico generador de islas más común es el vulcanismo submarino. En este caso, nos encontramos con una cámara magmática en un punto fijo por debajo del fondo oceánico que, en un momento puntual, entra en erupción formando un volcán submarino. Con sucesivas erupciones en la misma zona, ese volcán va a ir creciendo cada vez más hacia la superficie, pudiendo llegar a sobresalir por encima del agua. Entonces formará una isla de origen volcánico, como todas las del archipiélago de las Canarias.
Si los procesos geológicos que han dado lugar a la formación de las islas continúan en el tiempo, estás crecerán, tanto en altitud sobre el nivel del mar como en superficie expuesta de manera subaérea. Pero si dichos procesos se detienen, empezará a actuar la erosión, desmantelando los terrenos emergidos pudiendo llegar a desaparecer las islas quedando sólo unos pequeños remanentes en forma de montes submarinos. Incluso, debido a los ascensos y descensos del nivel marino, algunos territorios emergidos pueden quedar cubiertos por el agua y al revés, elevaciones submarinas pueden aparecer en superficie, encontrándonos con la formación y destrucción de islas de manera continua. Y eso sin entrar en la existencia de algunos eventos extremos que pueden provocar la creación o desmantelamiento de territorios emergidos de manera muy brusca, como la erupción explosiva del volcán Thera durante la época minoica, que se cargó más de la mitad de la isla de Santorini.
En definitiva, las islas, como el resto de montañas de nuestro planeta, no son puñados de tierra flotando en el agua, sino grandes aglomeraciones de rocas bien ancladas al fondo oceánico y que responden a procesos geológicos que modifican nuestro paisaje, también el submarino.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Islas, montañas que emergen del mar se ha escrito en Cuaderno de Cultura Científica.
Sorprendentes promedios
promedios
En la calle Acme 1 hay un edificio de dos plantas.

Las edades de las cinco personas que viven en la primera planta del edificio son 8, 14, 20, 23 y 35 años. Es decir, su edad promedio es:
(8 + 14 + 20 + 23 + 35) / 5 = 100 / 5 = 20 años.
Las seis personas que habitan en la segunda planta del inmueble tienen 25, 30, 35, 40, 45 y 59 años respectivamente. Por lo tanto, su edad promedio es
(25 + 30 + 35 + 40 + 45 + 59) / 6 = 235 / 6 = 39 años.
Juan vive en la primera planta. Tiene 35 años. Harto de soportar los ruidos de sus vecinos, decide mudarse a la segunda planta. Ahora la edad media en la primera planta de la calle Acme número 1 es:
(8 + 14 + 20 + 23) / 4 = 65 / 4 = 16,25 años,
y la edad media en la segunda planta pasa a ser (redondeando con dos decimales):
(25 + 30 + 35 + 35 + 40 + 45 + 59) / 7 = 269 / 7 = 38,43 años.
Sorprendentemente, las edades promedio en las dos plantas han disminuido.
Organizando movimientos de este tipo, ¿podríamos seguir reduciendo la edad media de todas las plantas del edificio y “rejuvenecer” de este modo (en media) a las personas residentes en el inmueble? ¿Qué cambios de este tipo consiguen reducir la edad promedio?
ExplicaciónEsta situación parece contradictoria: tenemos dos conjuntos de números, A y B y, moviendo un elemento de A a B, se ha reducido la media de ambos conjuntos. Raro, ¿no? Pero no hay errores de cálculo. Obviamente, el promedio de las edades de los once habitantes de las dos primeras plantas del edificio se ha mantenido; es:
(8 + 14 + 20 + 23 + 25 + 30 + 35 + 35 + 40 + 45 + 59) / 11 = 334 / 11 = 30,36.
La media ponderada de los dos primeros promedios es:
(5 / 11) x 20 + (6 / 11) x 39 = 334 / 11 = 30,36.
Y, por supuesto, coincide con la media ponderada de las edades tras el cambio de piso de Juan:
(4 / 11) x 16,25 + (7 / 11) x 38,43 = 334,01 / 11 = 30,36.
Esto es, de nuevo, bastante contraintuitivo: cuando tomamos el promedio ponderado de dos números puede permanecer constante, aunque cada uno de los dos números promediados disminuya…
Esta “paradoja” ha sucedido por el siguiente motivo: si en dos conjuntos de números A y B trasladamos de A a B un elemento x mayor que la media de A y menor que la media de B, entonces, las nuevas medias de A y B disminuirán. Pero los promedios ponderados antes y después del cambio permanecerán constantes.
En efecto, la media de los elementos de A disminuye porque se ha eliminado de A un número mayor que la media de A, y eso evidentemente baja su promedio. Además, se ha añadido al conjunto B un número inferior al promedio de los elementos de B; y obviamente esto baja la media de B.
En nuestro ejemplo, Juan tiene 35 años, cantidad que se sitúa entre los dos promedios del primer y el segundo piso (20 < 35 < 39), por eso su cambio de planta produce la disminución de las medias de edad en ambos pisos… ¡Aunque nadie se ha vuelto más joven!
Repitiendo el procesoPor supuesto, el anterior fenómeno no sucede siempre. Si tenemos dos conjuntos de números A y B, ambos con las mismas medias aritméticas, cualquier cambio de uno de los elementos (con valor diferente a la media) de uno a otro conjunto provocará que las medias resultantes varíen en direcciones opuestas.
En el caso de la calle Acme, tras el cambio de Juan, podrían volverse a reducir las edades medias si la persona de 23 años (16,25 < 23 < 38,43) de la primera planta se mudara a la segunda. La nueva edad media en la primera planta sería:
(8 + 14 + 20) / 3 = 42 / 3 = 14 años,
y la edad media en la segunda planta pasaría a ser:
(23 + 25 + 30 + 35 + 35 + 40 + 45 + 59) / 8 = 292 / 8 = 36,5 años.
Y podríamos realizar una nueva disminución de edad si la persona de 20 años del primer piso (14 < 20 < 36,5) se trasladara al segundo piso. La nueva edad media en la primera planta sería:
(8 + 14) / 2 = 22 / 2 = 11 años,
y la edad media en la segunda planta pasaría a ser (redondeando con dos cifras decimales):
(20 + 23 + 25 + 30 + 35 + 35 + 40 + 45 + 59) / 9 = 312 / 9 = 34,67 años.
De nuevo podríamos repetir este “juego” si la persona de 14 años del primer piso (11 < 14 < 34,67) se trasladara al segundo piso. La nueva edad media en la primera planta sería:
8 / 1 = 8 años,
y la edad media en la segunda planta pasaría a ser:
(14 + 20 + 23 + 25 + 30 + 35 + 35 + 40 + 45 + 59) / 10 = 326 / 10 = 32,6 años.
Aunque, por supuesto, la media ponderada en esta última etapa seguiría siendo la misma (redondeando con dos cifras decimales) que al principio:
(1 / 11) x 8 + (10 / 11) x 32,6 = 334 / 11 = 30,36.
Referencia
Jean-Paul Delahaye, Le déménagement miraculeux, Accromath 18.1, hiver – printemps 2023, 30-31.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Sorprendentes promedios se ha escrito en Cuaderno de Cultura Científica.
Un «demonio» invisible detectado en un raro superconductor
demonios
Los físicos han sospechado durante mucho tiempo que algunos trozos de metal podrían vibrar de una manera peculiar que sería casi invisible. Ahora los físicos han detectado estos «modos demoníacos».
Un artículo de Charlie Wood. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Los físicos han detectado una inusual onda «demonio» de electrones que es invisible a la radiación electromagnética. Fuente: Kristina Armitage / Quanta Magazine
Los físicos han detectado una inusual onda «demonio» de electrones que es invisible a la radiación electromagnética. Fuente: Kristina Armitage / Quanta MagazineEn 1956, David Pines formuló un fantasma. Predijo la existencia de mares de ondas eléctricas que podrían neutralizarse entre sí, dejando todo el océano inmóvil incluso cuando las olas individuales fluían y refluían. La rareza, que llegó a ser conocida como el demonio de Pines, sería eléctricamente neutra y, por lo tanto, invisible a la luz: la definición de difícil de detectar.
A lo largo de décadas, los físicos lograron vislumbrar variantes de demonios. Pero el demonio original de Pines, que surgiría naturalmente a partir de electrones en bloques metálicos, pasó desapercibido.
Ahora, un equipo de físicos de la Universidad de Illinois en Urbana-Champaign, parece haber detectado el demonio de Pines. Después de perfeccionar una técnica para rastrear con precisión los electrones cuando rebotan en un material, el equipo produjo y detectó una serie de ondas periódicas que se propagan a través de enjambres de electrones. Estas ondas, que los físicos llaman «modos», coinciden en gran medida con los cálculos de Pines. Los investigadores detallaron sus hallazgos en Nature en agosto.
«Estos modos no se habían visto en 70 años», explica Piers Coleman, físico teórico de la Universidad Rutgers. Pero este nuevo experimento, de alguna manera, «recoge estos modos demoníacos».
Imagina demoniosLa década de 1950 fue una época de auge para el estudio de los electrones en los metales. Los físicos ya habían desarrollado una teoría simplista que ignoraba la tendencia de los electrones a alejarse unos de otros, tratándolos colectivamente como si formaran una especie de gas que fluye libremente. En 1952, Pines y su director de tesis doctoral, David Bohm, dieron un paso más. Después de agregar las interacciones de los electrones a esta teoría del “gas de electrones”, descubrieron que los electrones podían agruparse en algunos lugares y dispersarse en otros. Estos electrones agrupados formaban ondas ordenadas de densidad mayor y menor alternadas (y, por lo tanto, regiones de carga eléctrica mayor y menor).
 Una onda de electrones (azul) con regiones alternas de alta y baja densidad. Fuente: Merrill Sherman / Revista Quanta
Una onda de electrones (azul) con regiones alternas de alta y baja densidad. Fuente: Merrill Sherman / Revista QuantaLuego, Pines llevaría más lejos aún más la nueva teoría. Imaginó un material que contenía dos gases, cada uno formado por un tipo diferente de partícula cargada. Específicamente, imaginó un metal con electrones «pesados» y electrones «ligeros». (Todos los electrones son idénticos en teoría, pero en el mundo real sus propiedades mensurables dependen de su entorno). Pines descubrió que las ondas del primer gas podían neutralizar las ondas del segundo; donde los electrones pesados se agrupaban, los electrones ligeros disminuían. Luego, a medida que los grupos de electrones pesados se dispersaban, los electrones más ligeros se reunían para llenar las zonas menos ocupadas. Debido a que un gas se espesaba precisamente donde el otro gas se diluía, la densidad electrónica total de ambos tipos juntos (y por lo tanto la carga y el campo eléctrico totales) permanecerían neutrales e invariables. «Las cosas pueden estar moviéndose incluso cuando parece que no lo están», explica Anshul Kogar, físico de materia condensada de la Universidad de California en Los Ángeles.
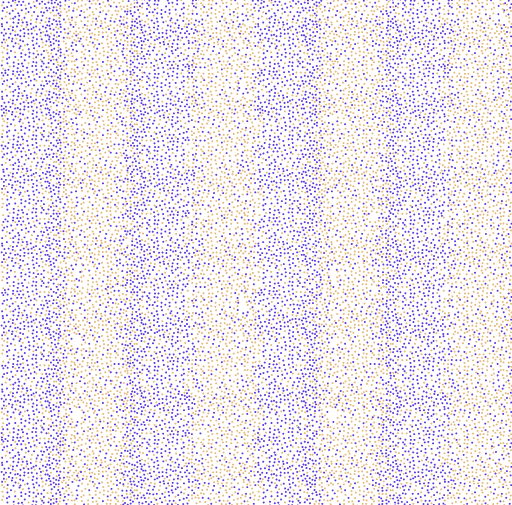 Ondas superpuestas de dos tipos de electrones (azul y dorado). La densidad de cada color varía, pero la densidad general de las partículas permanece igual en todas partes. Fuente: Merrill Sherman/Revista Quanta
Ondas superpuestas de dos tipos de electrones (azul y dorado). La densidad de cada color varía, pero la densidad general de las partículas permanece igual en todas partes. Fuente: Merrill Sherman/Revista QuantaLa luz se refleja sólo en objetos con una distribución desigual de carga eléctrica, por lo que la neutralidad de la vibración de Pines la hacía perfectamente invisible. La luz viene en paquetes de energía llamados fotones, y Pines bautizó los paquetes de energía de sus ondas como «demonios». El nombre era un guiño al experimento mental demoníaco de James Clerk Maxwell, un físico pionero que, se lamentó Pines, había vivido demasiado pronto como para que una partícula u onda llevara su nombre. «Sugiero que, en honor a Maxwell, y porque estamos tratando aquí con un caso de movimiento definido de electrones (o D.E.M. por sus siglas en inglés), llamemos a estas nuevas excitaciones ‘demonios'», escribió Pines en 1956.
A lo largo de las décadas, los físicos vieron ondas demoníacas en diversos materiales. En 1982, investigadores de los Laboratorios Bell detectaron ondas opuestas en láminas vecinas de arseniuro de galio. Y este año, un equipo dirigido por Feng Wang de la Universidad de California en Berkeley describió un experimento que capturó ondas casi invisibles de electrones latiendo en sincronía con ondas ligeramente más delgadas de objetos similares a partículas cargadas positivamente en una lámina de grafeno.
 David Pines predijo que podría surgir una onda «demonio» invisible en materiales con dos tipos de electrones. Foto: Minesh Bacrania para SFI
David Pines predijo que podría surgir una onda «demonio» invisible en materiales con dos tipos de electrones. Foto: Minesh Bacrania para SFIPero estos avistamientos ocurrieron en gran medida en sistemas bidimensionales donde una característica demoníaca definitoria era menos llamativa. Debido a una peculiaridad en la dimensionalidad, en 2D puedes desencadenar una onda de carga con un esfuerzo tan pequeño como quieras. Pero en 3D, iniciar una onda requiere una cantidad mínima de energía para que los electrones asociales se agrupen. Los demonios eléctricamente neutros se ahorran esta tarifa de energía 3D. «Ver al demonio en un sólido tridimensional es un poco especial», comenta Kogar, quien realizó su investigación doctoral con el grupo Urbana-Champaign.
Aquí hay demoniosEl equipo de Urbana-Champaign, dirigido por Peter Abbamonte, nunca fue a cazar demonios. El demonio de Pines vino directamente a su laboratorio.
En 2010, el grupo de Abbamonte comenzó a desarrollar una técnica para detectar pequeños temblores que se propagan a través de las hordas de electrones. Lanzaban electrones a un material y registraban con precisión la energía que transportaban y el camino que tomaban cuando rebotaban. Basándose en los detalles de esos rebotes el grupo pudo inferir cómo respondía el material a la colisión, lo que a su vez reveló las propiedades de las ondas creadas por la colisión. Era un poco como determinar si una bañera está llena de agua, miel o hielo arrojándole pelotas de pingpong.
 Peter Abbamonte, físico de la Universidad de Illinois, Urbana-Champaign, no fue a buscar al demonio de Pines. Su grupo se topó con esto mientras exploraba una nueva forma de estudiar materiales. Fuente: Universidad de Illinois
Peter Abbamonte, físico de la Universidad de Illinois, Urbana-Champaign, no fue a buscar al demonio de Pines. Su grupo se topó con esto mientras exploraba una nueva forma de estudiar materiales. Fuente: Universidad de IllinoisHace unos años, los investigadores decidieron poner en su punto de mira un metal superconductor llamado rutenato de estroncio. Su estructura es similar a la de una misteriosa clase de superconductores de “cuprato” a base de cobre, pero se puede fabricar de una manera más limpia. Si bien el equipo no aprendió los secretos de los cupratos, el material respondió de una manera que Ali Husain, quien había perfeccionado la técnica como parte de su doctorado, no entendía.
Husain descubrió que los electrones que rebotaban perdían su energía y su momento, lo que indicaba que estaban provocando ondas que drenaban energía en el rutenato de estroncio. Pero las ondas desafiaban sus expectativas: se movían 100 veces demasiado rápidas como para ser ondas sonoras (que se propagan a través de los núcleos atómicos) y 1.000 veces demasiado lentas como para ser ondas de carga propagándose por la superficie plana del metal. También tenían muy poca energía.
«Pensé que debía ser un artefacto», explica Husain. Entonces colocó otras muestras, probó otros voltajes e incluso hizo que diferentes personas tomaran las medidas.
 Ali Husain desarrolló una forma de medir con precisión las energías y las trayectorias de los electrones que rebotan; Estas observaciones revelaron modos demoníacos en el rutenato de estroncio. Foto: Mateo Mitrano
Ali Husain desarrolló una forma de medir con precisión las energías y las trayectorias de los electrones que rebotan; Estas observaciones revelaron modos demoníacos en el rutenato de estroncio. Foto: Mateo MitranoLas vibraciones no identificadas seguían ahí. Después de hacer los cálculos, el grupo se dio cuenta de que las energías y los momentos de las ondas encajaban mucho con la teoría de Pines. El grupo sabía que en el rutenato de estroncio los electrones viajan de un átomo a otro utilizando uno de tres canales distintos. El equipo concluyó que en dos de estos canales, los electrones se sincronizaban para neutralizar el movimiento de los otros, desempeñando el papel de los electrones «pesados» y «ligeros» del análisis original de Pines. Habían encontrado un metal con la capacidad de albergar al demonio de Pines.
«Es estable en el rutenato de estroncio», afirma Abbamonte. «Siempre está ahí».
Las ondulaciones no coinciden perfectamente con los cálculos de Pines. Y Abbamonte y sus colegas no pueden garantizar que no estén viendo una vibración diferente y más complicada. Pero en general, dicen otros investigadores, el grupo presenta argumentos sólidos de que han atrapado al demonio de Pines.
«Han hecho todas las comprobaciones de buena fe que pueden hacer», comenta Sankar Das Sarma, un teórico de la materia condensada de la Universidad de Maryland que ha sido pionero en el estudio de las vibraciones demoníacas.
Demonios desatadosAhora que los investigadores sospechan que el demonio existe en metales reales, algunos no pueden evitar preguntarse si los movimientos inmóviles tienen algún efecto en el mundo real. «No deberían ser raros y podrían hacer cosas», dice Abbamonte.
Por ejemplo, las ondas sonoras que se propagan a través de redes metálicas vinculan los electrones de una manera que conduce a la superconductividad, y en 1981, un grupo de físicos sugirió que las vibraciones demoníacas podrían conjurar la superconductividad de una manera similar. El grupo de Abbamonte eligió originalmente el rutenato de estroncio por su superconductividad poco ortodoxa. Quizás el demonio podría estar involucrado.
«En este momento se desconoce si el demonio juega un papel o no», explica Kogar, «pero es otra partícula en el juego». (Los físicos suelen considerar a las ondas con determinadas propiedades como partículas).
Pero la principal novedad de la investigación reside en detectar el tan esperado efecto metálico. Para los teóricos de la materia condensada, el hallazgo es una coda satisfactoria para una historia que comenzó hace 70 años.
«Es una posdata interesante de la historia temprana del gas de electrones», afirma Coleman.
Y para Husain, que terminó su carrera en 2020 y ahora trabaja en la empresa Quantinuum, la investigación sugiere que los metales y otros materiales están llenos de vibraciones extrañas que los físicos carecen de instrumentación para comprender.
“Simplemente están ahí sentadas”, dijo, “esperando a ser descubiertas”.
El artículo original, Invisible ‘Demon’ Discovered in Odd Superconductor, se publicó el 9 de octubre de 2023 en Quanta Magazine. Cuaderno de Cultura Científica tiene un acuerdo de distribución en castellano con Quanta Magazine.
Traducido por César Tomé López
El artículo Un «demonio» invisible detectado en un raro superconductor se ha escrito en Cuaderno de Cultura Científica.
Objetivo: Diezmar los mosquitos con caballos de Troya
Los animales que más vidas humanas se llevan por delante no son las serpientes, ni los perros y ni siquiera los propios seres humanos, sino diminutos insectos, en apariencia inofensivos, aunque letales: los mosquitos. Como vectores de multitud de enfermedades infecciosas (dengue, malaria, zika, fiebre amarilla, chikungunya, virus del Nilo Occidental…), estos insectos son unos de los principales enemigos de la Salud Pública mundial. Se calcula que diferentes especies de mosquito provocan, de forma indirecta, la muerte de en torno a 750.000 personas al año. Todo ello a pesar de las diversas medidas que se toman diariamente para limitar su número y evitar que piquen a los humanos: eliminación y tratamiento de aguas estancadas, mosquiteras, repelentes, insecticidas…
 Fuente: Pixabay
Fuente: PixabayPara empeorar aún más las cosas, la crisis climática está potenciando la expansión de los mosquitos a nuevos territorios. Las inundaciones y las olas de calor cada vez más frecuentes y graves en Europa, junto con unos veranos más cálidos y largos, crean unas condiciones más favorables para la expansión de los mosquitos invasores Aedes albopictus (más conocido como «mosquito tigre») y Aedes aegypti, que no son propios de esta zona del planeta. España atestigua la gran capacidad que tiene el mosquito tigre para extenderse: la primera vez que se detectó su presencia fue en Sant Cugat del Vallés en el verano de 2004, desde entonces este vector ha conseguido expandirse ya por casi todo el país.
En esta eterna lucha contra los mosquitos, los científicos llevan décadas investigando una solución más drástica para combatirlos: liberar individuos con ciertas características especiales para que se integren en las poblaciones de mosquitos y así destruirlas desde dentro, como si fueran caballos de Troya.
En ese sentido, una estrategia radical es modificar genéticamente a estos insectos para que se vuelvan estériles y así erradicar poblaciones completas al transmitir este rasgo entre los individuos a lo largo de sucesivas generaciones. Es algo que se ha conseguido ya en el laboratorio y que se ha probado en el mundo real. En 2019, por ejemplo, se liberaron por primera vez mosquitos macho genéticamente modificados para ser estériles en Burkina Faso. Los investigadores comprobaron que muchos de estos insectos murieron sin dejar descendencia, mientras que otros sí que fueron capaces de reproducirse con las hembras, pero sin llegar a tener descendencia viable. En conjunto, esto contribuyó a que el número total de mosquitos disminuyera de forma significativa en la zona.
Otra opción para diezmar a los mosquitos es la liberación de mosquitos portadores de bacterias Wolbachia. Este género de bacterias es muy común y se encuentra de forma natural en torno al 50-60 % de los insectos, incluyendo a algunas especies de mosquito, pero no todas. La especie Aedes aegypti, por ejemplo, vector principal de numerosas enfermedades infecciosas, no es portadora natural de Wolbachia. Sin embargo, es posible introducir estas bacterias a través de diferentes métodos, como depositarlas en los huevos.
El efecto positivo para los humanos es doble cuando se liberan mosquitos con Wolbachia en poblaciones de estos insectos. Por un lado, los mosquitos macho con estas bacterias que se aparean con los mosquitos hembra pueden dar como resultado huevos que no son viables. Este fenómeno, cuyos detalles siguen sin comprenderse todavía muy bien, se debe a que dichas bacterias causan una incompatibilidad citoplasmática entre los espermatozoides y los óvulos, de forma que los primeros son incapaces de fertilizar a los segundos.
Además de este efecto, cuando los mosquitos A. aegypti portan bacterias Wolbachia ocurre un hecho peculiar: estos microorganismos dificultan la transmisión de diferentes virus (como aquellos que causan dengue, zika, chikungunya, fiebre amarilla…) a través de su picadura. Estas bacterias compiten con los virus por los recursos biológicos en el interior de las células de los mosquitos y dificultan su multiplicación, por lo que el riesgo de contagio cuando una persona sufre una picadura con algún mosquito portador de Wolbachia y algún virus patológico es mucho menor. Además, los mosquitos con esta bacteria pueden ir transmitiéndola progresivamente con el paso del tiempo a sus compañeras, hasta que gran parte de la población sea portadora.
Esta última estrategia, la liberación de mosquitos con bacterias Wolbachia, se ha puesto a prueba en múltiples ocasiones en el mundo real (en un total de 13 países) con muy buenos resultados. Además, se ha comprobado que es una opción segura tanto para las personas como para el medio ambiente. Hace unos años, en Yumbo, Colombia, se liberaron mosquitos con estos microorganismos para limitar los casos de dengue en dicha zona. Más recientemente, Médicos Sin Fronteras ha puesto en marcha en Honduras, junto al Ministerio de Salud del país y el World Mosquito Program, la suelta de mosquitos A. aegypti con Wolbachia para reducir la capacidad de dichos insectos para transmitir diferentes tipos de virus como el que provoca el dengue.
La ventaja de este enfoque, a diferencia de extinguir poblaciones enteras de mosquitos al dejarles estériles mediante ingeniería genética, es que no existe el riesgo de alterar los ecosistemas en los que habitan los mosquitos. Aunque provoquen estragos en la salud del ser humano, los mosquitos también cumplen su papel en la naturaleza y eliminarlos podría provocar cambios perjudiciales sobre otras especies animales y vegetales. Al fin y al cabo, los mosquitos (hembra) no solo chupan la sangre, también polinizan plantas y son el alimento de multitud de animales como diferentes tipos de peces, aves, murciélagos, ranas o cangrejos.
Nuestra visión antropocéntrica (especialmente desde el punto de vista de la medicina) no debería hacernos olvidar que, por mucho odio que tengamos hacia el mosquito, este insecto simplemente se alimenta de nosotros para reproducirse (poner huevos) y tiene su función útil en los ecosistemas. Que sea portador de enfermedades infecciosas que matan a infinidad de personas cada año es un efecto colateral.
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo Objetivo: Diezmar los mosquitos con caballos de Troya se ha escrito en Cuaderno de Cultura Científica.
Aplaudir
aplaudir
Aplaudir. 1. Palmotear en señal de aprobación o entusiasmo. 2. Celebrar a alguien o algo con palabras u otras demostraciones.
Diccionario RAE.
Quiero medir por dónde deben ir mis pasos, condicionar cuál debe ser mi actitud, presentarme ante vosotros resistiendo hasta donde deba resistir los impulsos arrebatadores de vuestros aplausos, obedeciendo al mandato de mi conciencia.
Conferencia de Don Niceto Alcalá Zamora pronunciada en el Teatro de Apolo, de Valencia el día 13 de abril de 1930.
Doña Elena llegó sobre las 21.40 horas a la plaza de toros acompañada de su prima. Ambas entraron en el coliseo con discreción, pero la nube de fotógrafos y cámaras de televisión que las rodeaba advirtieron a los aficionados, que se encontraban en la plaza y que al reconocerla rompieron en un aplauso.
Entrada de Doña Elena en la Plaza de Toros de Palma el 13 de agosto de 2010.
Por su complejidad, utilidad y ubicuidad en contextos sociales y culturas, el interés por los aplausos podría extenderse a politólogos, historiadores, sociólogos, musicólogos, psicólogos, etólogos y todo observador humano curioso.
Alan Crawley, 2023.
 Foto: Valentin Lacoste / Unsplash
Foto: Valentin Lacoste / UnsplashHace unas semanas, en la retransmisión de las etapas del Tour de Francia o de la Vuelta a España y en los debates de investidura en el Congreso de Diputados, había multitud de personas aplaudiendo a ciclistas y diputados. Aplaudían todos, desde los bebés colocados en hombros de sus padres hasta los ancianos en silla de ruedas, incluso, y mucho, lo hacían los diputados cuando discurseaba su líder. Y, sin embargo, son escasos los estudios científicos y las hipótesis sobre el origen, función e intención de los aplausos, de la acción de aplaudir, del palmoteo en señal de aprobación o, incluso, de entusiasmo, como lo describe el Diccionario. Hoy los aplausos suceden a diario en miles de eventos, desde cumpleaños hasta actos políticos.
El aplauso, en general, es un refuerzo de la identidad de grupo, esencial en la conducta de la especie humana. Con ello se consolida el grupo, hacia su interior, y se evidencia su separación de otros grupos, hacia el exterior. Pero el aplauso requiere coordinación y es interesante conocer como se consigue.
La importancia del aplauso como señal de aprobación o reconocimiento es algo conocido desde la antigüedad. Por ejemplo, se cuenta que el emperador Nerón pagó a 5000 caballeros y soldados, los llamados Augustiani, para vitorear sus apariciones públicas con aplausos. Los directores de teatro y los empresarios descubrieron que podían hacer lo mismo en sus eventos, contratando gente para aplaudir; era y es la claque. En el siglo pasado, la televisión y los medios encontraron que podían copiar esta estrategia con la risa enlatada o, si se quiere, con el aplauso enlatado. Así incluso los políticos dan la apariencia de que más personas asistieron a sus mítines. Otra función social conjunta de los aplausos colectivos es habitual cuando un equipo de fútbol sale al campo de juego y el público recibe a los jugadores con cánticos, estruendo y aplausos. Aplaudir cumple dos funciones: expresar apoyo al equipo e intimidar al rival.
En fin, como escribe Alan Crowley, de la Universidad del Salvador en Buenos Aires, hoy en día, hay muchas preguntas sin resolver y grandes lagunas en el conocimiento como para afirmar que el comportamiento de los aplausos está poco estudiado, que la razón de los evidentes y extendidos aplausos en la especie humana es poco conocida.
Una definición de aplaudirEn primer lugar, la definición de aplauso. Para Alan Crowley, después de revisar la bibliografía, considera que no es fácil llegar a una conclusión. Este autor, después de debates y dudas, nos ofrece una definición realmente extensa y detallada:
Aplaudir es una acción corporal universal realizada conscientemente en la que los dos movimientos primarios son 1) el movimiento lateral hacia adentro de los antebrazos en el eje transversal, generalmente, hacia el centro del eje sagital y 2) la connivencia entre las manos abiertas izquierda y derecha contra cada una de ellas en una posición frecuente prototípica, con variaciones en las opciones de mano, brazo y postura, que produce a partir del golpe un sonido acústico humano ampliamente reconocible. El objetivo mecánico de tal acción es comprimir y explotar una pequeña burbuja de aire entre las palmas de las manos. Se realiza con una posterior repetición constante de la misma acción en la mayoría de los casos, siguiendo un ritmo relativamente estable con tendencia a aumentar o disminuir la cantidad de palmadas por minuto. Una cosa más es que los aplausos generalmente se realizan con la intención de comunicar algo.
Una definición compleja que merece meditación, debate y conclusiones. Además, hay que añadir que una persona puede aplaudir pero solo se convierte en aplauso cuando varias lo hacen repetidamente y al mismo tiempo.
Así, por ejemplo, el grupo de Z. Neda, desde la Universidad Babes-Bolyai de Cluj-Napoca, en Rumania, escribe que una audiencia expresa aprecio por una buena actuación por la fuerza y la naturaleza de sus aplausos. El estruendo de los primeros aplausos a menudo se convierte repentinamente en aplausos sincronizados, y esta sincronización puede desaparecer y reaparecer varias veces durante los aplausos. Primero, los aplausos iniciales no están sincronizados, pero se sincronizan eliminando, cada participante, el segundo golpe del aplauso. El fenómeno es una expresión de auto organización social que muestra un ejemplo a escala de la especie humana de los procesos de sincronización que ocurren en numerosos sistemas naturales, que van desde las luciérnagas asiáticas hasta las reacciones químicas oscilantes.
Por otra parte, es curioso, según los autores, que la sincronización es más habitual en los aplaudidores de Europa oriental mientras que solo se da esporádicamente en Europa occidental o en Norteamérica.
Es evidente que los políticos, o los actores, buscan el aplauso de su audiencia durante sus discursos. Peter Bull, de la Universidad de York, en Inglaterra, publicó una revisión de lo publicado sobre este tema hasta 2006. La primera conclusión es que se sobreestiman los trucos de los oradores para provocar el aplauso de sus seguidores. Y, por el contrario, hay otros dispositivos poco estudiados como, por ejemplo, los aplausos que no están sincronizados con el texto del discurso, el conocimiento previo por la audiencia del contenido del discurso, y, también, los aplausos no invitados, no preparados de antemano.
La falta de relación entre discurso y aplauso provoca que solo el 61% de los aplausos están verdaderamente sincronizados. Hay cuatro incidentes principales detrás de esta no sincronización: aplausos aislados y no del grupo, aplausos retrasados respecto del texto del discurso, aplausos que interrumpen al político y aplausos interrumpidos por el propio orador.
Para Crowley, aplaudir puede tener motivaciones muy antiguas en la historia de Homo sapiens:
1. Redirigir la atención de los compañeros hacia un evento o hacia el individuo mismo,
2. Señalar afiliación o no a través de momentos de entusiasmo que invitan a un encuentro lúdico,
3. Amenaza con códigos visuales y auditivos,
4. Mensaje afectivo,
5. Crear pertenencia colectiva al grupo con sincronización de conductas.
Y desde el significado cultural, el aplauso puede funcionar para:
1. Aprobación, con aplausos
2. Celebración, generalmente con aplausos
3. Apoyo, con aplausos
4. Cooperación, generalmente con aplausos
5. Intimidación, con aplausos
En conclusión, escribe Alan Crawley, aplaudir es una conducta con muchas variantes según los mensajes que se transmiten y según las formas de hacerlo. Aplaudir es una conducta típica que incluye significados positivos de apoyo y aprobación. El tipo de mensajes enviados con los aplausos quizá dependa de diferencias en la conducta de cada persona. Los aplausos se pueden realizar de diferentes maneras y con diferentes propósitos y significados y, por ello, los mensajes que se envían contienen mensajes no verbales polisémicos y multipropósito. Las funciones que cumple el aplauso podían ser una o varias de las siguientes: 1) atraer o redirigir la atención, 2) ser una invitación lúdica a participar en el juego, o 3) es amenaza visual y acústica ante cualquier alarma. Estas tres funciones se cumplen al menos en parte con los aplausos, tal como los utilizamos en este siglo en la mayoría de las situaciones sociales. Pero parece que el mensaje de aprobación del aplauso es la función principal del aplauso en nuestra cultura.
Aprender a aplaudirTodo lo anterior plantea una pregunta interesante: quizá aplaudir no sea un comportamiento innato sino adquirido durante el desarrollo. Si es así, ¿cuándo y cómo aprenden los humanos a aplaudir? ¿Aprendimos a aplaudir o es un legado biológico? Posiblemente, los humanos aprendan primero a aplaudir, y solo después del desarrollo de habilidades cognitivas específicas puedan usar el aplauso como tal, como aplauso.
Si el aplauso se adquiere durante la ontogenia, debe tener un origen accesible a toda la humanidad y ser fácil de aprender para justificar su distribución mundial. El Homo sapiens ha desarrollado una serie de patrones de conducta universales, como reír, bostezar y sonreír, presentes en las culturas más heterogéneas, todos los cuales tienen un repertorio con diferentes significados que pueden transmitir. Sin embargo, tienden a ocurrir transculturalmente con mayor frecuencia, en relación con un conjunto concreto de situaciones y significados. La cuestión es si el aplauso puede ser una conducta en esta misma categoría.
Para el inicio del aplauso solo se necesita que una persona comience a aplaudir para que este comportamiento sea adoptado y replicado por todos los demás. El hecho de que un solo individuo pueda provocar espontáneamente un acto cooperativo transitorio entre pocas o, incluso, miles de personas merece destacarse como una de las pocas conductas de nuestra especie que se copia e imita con tanta rapidez y participación. Quizá al ser un acto poco representativo de la identidad de cada individuo, puede aumentar la probabilidad de realizarlo con anonimato y, por tanto, es más fácil de utilizar para rituales sociales colectivos.
En el estudio de Paula Fitzpatrick y sus colegas, de la Universidad de Connecticut en Storrs, se muestra que los niños aprenden a aplaudir tarde durante el primer año de vida aunque no tienen la coordinación necesaria para producir una secuencia estable y predecible de palmadas, característica de la sincronía del aplauso. El grupo estudiado lo forman 20 niños de 3 a 7 años de edad. Parece que aplaudir es más difícil de aprender que otras actividades corporales básicas. El control motor óptimo necesario para producir un aplauso constante se desarrolla solo a partir de los siete años. Quizá el niño descubre el aplauso al chocar las palmas y se ayuda de la imitación de lo que observa en personas de más edad. Y, finalmente, se entrenará para conseguir un aplauso específico para conseguir un palmoteo concreto.
La hipótesis más aceptada es la que dice que aplaudir era un vehículo de comunicación cuando los ancestros de los primates carecían de aparatos vocales adecuados para producir el lenguaje en un momento dado de la evolución, pero tenían los músculos y la capacidad motora y estructural indispensables para producir palmas. Aplaudir es un modo de comunicación compartido con otros primates como, por ejemplo, los gorilas, tal como describen Ammie Kalan y Hugo Rainey, de la Universidad Brookes de Oxford y de la Sociedad de Conservación de la Vida Salvaje de Brazzaville, en la República del Congo, y es probable que la especie humana haya heredado esta conducta de algún predecesor primate. Para Kalan y Rainey, en los gorilas de Likouala, en el nordeste del Congo, aplaude una hembra adulta, da dos palmadas cada vez y parece un comportamiento que mantiene y refuerza la cohesión del grupo durante alguna amenaza. También se han detectado palmas en chimpancés de Guinea, en las montañas Nimba, para difundir alguna alarma en el grupo. Por otra parte, también las focas, otro grupo de mamíferos, aplauden con sus extremidades anteriores.
Todo lo anterior sobre la evolución del aplauso son especulaciones ya que las palmas son la señal no vocal con mayor volumen acústico y consiguen una capacidad muy eficaz de proyección de volumen. Esta es una acción simple, rápida y efectiva. Sin embargo, por ello mismo, su origen es borroso y siempre en debate.
La biología es la causa y el origen de muchos de nuestros comportamientos como especie. Cada gesto, expresión, postura o sonido que emitimos los humanos desde el principio hasta el final de nuestra vida está diseñado, influenciado, limitado y adquirido por nuestra biología y también moldeado por la cultura e individualidad humanas.
Los que hayan obtenido como producto de sus acciones, logros o reputación, y los aplausos de sus compañeros habrán experimentado satisfacción y disfrute. Dado que los aplausos provocan en la persona bienestar en la mayoría de los casos, es probable que los humanos hayan repetido conductas que impulsaron el aplauso de los demás hacia ellos. Quizás una parte de las conductas en los adultos venga de buscar la aprobación no verbal con el aplauso por parte de las personas influyentes más cercanas. Por ejemplo, después de completar una tarea, el niño que recibió una serie de aplausos puede intentar repetir ese comportamiento en el futuro para revivir el refuerzo positivo. En función del nivel de positividad experimentado tras la realización de la acción, el organismo tiende a repetir o no la acción.
Así, el lector puede deducir sus propias conclusiones hasta que no quede duda sobre el verdadero origen del aplauso. En la ciencia encontrará respuesta, pero mientras tanto, el conocimiento imperfecto es mejor que ninguno para navegar en las aguas de nuestro entorno social. Siempre es mejor tener una teoría para comprender un comportamiento de uso frecuente y ampliamente transcultural en lugar de no tener nada.
Referencias:
Bull, P. 2006. Invited and uninvited applause in political speeches. British Journal of Social Psychology 45: 563-578.
Bull, P. & M. Noordhuizen. 2000. The mistiming of applause in political speeches. Journal of Language and Social Psychology 19: 275-294.
Crawley, A. 2023. Clap, clap, clap – Unsystematic review essay on clapping and applause. Integrative Psychological and Behavioral Science doi: 10.1007/s12124-023-09786-9.
Fitzpatrick, P. et al. 1996. Dynamical patterns in the development of clapping. Child Development 67: 2691-2708-
Kalan, A. K. & H.J. Rainey. 2009. Hand-clapping as a communicative gesture by wild female swamp gorillas. Primates 50: 273-275.
Mouratidis, J. 1985. Nero: The artist, the athlete and his downfall. Journal of Sport History 12: 5-20.
Neda, Z. et al. 2000. The sound of many hands clapping. Nature 403: 849-850.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Aplaudir se ha escrito en Cuaderno de Cultura Científica.
¡Ups! La constante cosmológica
constante cosmológica
Hasta cuando se equivocaba, Einstein acertaba. En 1917, época en la que se daba por hecho que el universo era estacionario, las ecuaciones de Einstein predecían un universo dinámico. Convencido de que no podía ser así, añadió a la ecuación un elemento: la constante cosmológica. Años después tuvo que admitir que esta fue un error cuando tras varias observaciones astronómicas se confirmó que, efectivamente, el universo se expandía. Hoy sabemos que el universo se está expandiendo de forma acelerada. Y la culpable de esa aceleración es lo que llamamos energía oscura que, curiosamente, se comporta igual que la constante cosmológica.
Los vídeos de ¡UPS¡ presentan de forma breve y amena errores de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se han emitido en el programa de ciencia Órbita Laika (@orbitalaika_tve), en la 2 de RTVE.
Producción ejecutiva: Blanca Baena
Guion: José Antonio Pérez Ledo
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Doblaje: K 2000
Locución: José Antonio Pérez Ledo
El artículo ¡Ups! La constante cosmológica se ha escrito en Cuaderno de Cultura Científica.
Renovarse o morir: cuando se atasca el sistema de reciclaje cerebral
reciclaje
 Fuente: UC Regents Davis campus – http://brainmaps.org / Wikimedia Commons
Fuente: UC Regents Davis campus – http://brainmaps.org / Wikimedia CommonsLas células que componen nuestro cerebro son como pequeñas ciudades. En su interior hay una base, el núcleo, donde están codificadas la identidad y función de la célula en forma de genes y elementos regulatorios.
La información de este núcleo y los estímulos externos determinarán si la célula será una neurona, encargada de transmitir información nerviosa, o pertenecerá al linaje glial, el que se ocupa de acondicionar, facilitar y optimizar el trabajo neuronal. En cualquier caso, los datos codificados en el núcleo determinarán no solo el linaje, sino también el aspecto y la función de la célula.
El producto final de un gen es la proteína, el “ladrillo” básico de la vida. Existe una gran diversidad de proteínas en la célula, y su síntesis y procesamiento dependerá de su destino y ocupación final. Algunas llevarán a cabo una función de soporte estructural en las murallas o membranas celulares; otras participarán en la comunicación entre células, recibiendo, amplificando y enviando señales; y finalmente, algunas se especializarán en el plegamiento, transporte o ruptura de otras proteínas.
Por tanto, las proteínas no solo son las protagonistas principales de la actividad en la ciudad celular, sino también las dianas a intervenir con fármacos en caso de trastorno o enfermedad.
Reciclaje y renovaciónEl código proteico no es estático, es decir, las proteínas y las estructuras formadas con ellas, como las organelas celulares –mitocondrias, ribosomas, citoplasma…–, no se mantienen durante toda la vida de la célula. Al contrario, ambas se renuevan de forma gradual, como parte del mantenimiento de la maquinaria celular.
Tal renovación es posible debido al envío de estructuras macromoleculares al lisosoma –la “trituradora celular”– mediante un proceso denominado autofagia, palabra que significa “comerse a uno mismo”. Los lisosomas están equipados con ácidos y proteínas que destruyen todo tipo de macromoléculas –moléculas de gran tamaño– celulares, incluyendo grasas, azúcares, material genético y otras proteínas.
Este mecanismo, por tanto, permite la síntesis de nuevas proteínas tras su reciclaje. Por eso es clave en los procesos de mantenimiento y renovación celular en todas las etapas de vida del cerebro.
Problemas con el servicio de calidadCuando la trituradora celular falla, se acumulan las proteínas dañadas y otros desechos celulares. Es el desencadenante de las enfermedades de almacenamiento lisosomal, patologías raras que se transmiten por herencia genética. Debido a la importancia de la renovación celular desde edades tempranas, estas dolencias normalmente se manifiestan en la niñez.
Los organismos afectados pierden la capacidad de romper algún tipo de componente celular, normalmente proteínas y grasas con componentes azucarados, lo que facilita su acumulación en los compartimentos de los lisosomas. En consecuencia, se pierde la capacidad de renovación, lo que crea desorden y enfermedad.
Entre las patologías de almacenamiento lisosomal, la enfermedad de Gaucher es la más frecuente. Se hereda por mutaciones (presentes en ambos progenitores) en el gen con las instrucciones para producir la proteína glucocerebrosidasa (GBA). Esto causa una reducción significativa o una falta de actividad de la GBA, que se encarga de destruir grasas azucaradas.
En algunos casos, los desechos de grasa y azúcar se acumulan en células nerviosas, lo que produce un deterioro de las funciones cognitivas, motoras y autónomas (respiración, presión arterial…) cerebrales. Esto se debe principalmente a alteraciones en las conexiones locales o sinapsis neuronales, así como en las estructuras lipídicas que aíslan las prolongaciones neuronales y permiten la transmisión de alta velocidad. Son procesos que dependen del óptimo funcionamiento de las vías de renovación autofágicas y lisosomales.
Una nueva esperanza para el párkinsonEn los últimos años se ha descrito una conexión entre la enfermedad de Gaucher y la enfermedad de Parkinson. La mutación de una única copia del gen GBA no es suficiente para producir la primera, pero es el factor de riesgo genético más importante de sufrir párkinson.
Se estima que esta enfermedad afecta a más de 8,5 millones de personas en el mundo, lo que la convierte en el trastorno de movimiento más frecuente. Se desconoce la causa del 85 % de los casos, con la edad como principal factor de riesgo junto con otros factores desencadenantes genéticos y/o ambientales.
Los síntomas motores (temblor, rigidez, dificultades para iniciar movimientos…) son los más frecuentes, pero también puede afectar a funciones cognitivas y autónomas cerebrales, al igual que las enfermedades de almacenamiento lisosomal.
Entre los factores de riesgo genético que contribuyen de forma significativa al desarrollo del párkinson no solo se encuentra, como hemos señalado, la mutación del gen que codifica la proteína GBA, sino también otros genes relacionados con la regulación de las redes autofágicas y lisosomales. Esto refuerza la evidencia de que la alteración de esas vías contribuye a los déficits neurológicos causados por el párkinson esporádico.
La restauración de la función de proteínas relacionadas con la regulación de la trituradora cerebral –y más en concreto la GBA– podrían modificar el inicio y/o la progresión tanto del párkinson como de la enfermedad de Gaucher.
Y aquí podría venir en ayuda el ambroxol, un fármaco mucolítico clásico con capacidad de replegar la proteína GBA mutante. Diferentes investigaciones han mostrado que el ambroxol puede aumentar la actividad destructora de grasas azucaradas por la GBA, mejorando el flujo del tráfico de las redes autofágicas y lisosomales.
Ahora mismo se están haciendo ensayos clínicos para evaluar la eficacia del ambroxol, y en los próximos años sabremos si este esfuerzo de investigación mejorará la calidad de vida de los pacientes y sus familias.![]()
Sobre la autora: Ainhoa Plaza Zabala, Profesora e Investigadora en Biomedicina, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Renovarse o morir: cuando se atasca el sistema de reciclaje cerebral se ha escrito en Cuaderno de Cultura Científica.
La realidad resulta enigmática porque es no lineal
no lineal
Aunque el origen de la Dinámica se fundó a partir de los experimentos de Mecánica efectuados por Galileo Galilei, el cálculo infinitesimal -inventado por Isaac Newton y Gottfried Leibniz- permitió describir matemáticamente la evolución general de algunas de las más relevantes magnitudes de todas las ciencias. Las maravillosas ecuaciones diferenciales nos permiten describir, predecir e incluso controlar la dinámica de sistemas no sólo basados en las leyes de la mecánica clásica o relativista, el electromagnetismo o la mecánica cuántica, sino en todas las ciencias naturales y sociales, así como en todas las ingenierías.
El gran Henri Poincaré estableció a finales del siglo XIX las propiedades cualitativas de la teoría de ecuaciones diferenciales, con la Mecánica Celeste [1] como ejemplo de aplicación, pero más allá de esto, estableció su teoría matemática generalizada para fundar la Ciencia General de la Dinámica de Sistemas, aplicable a modelar, predecir su evolución en el tiempo y caracterizar las propiedades esenciales de cualquier efecto medible en cualquier tipo de realidad científica.
 El mundo a nuestro alrededor es mayormente no lineal. Foto: Jorge Fernández Salas / UnsplashEl principio de superposición
El mundo a nuestro alrededor es mayormente no lineal. Foto: Jorge Fernández Salas / UnsplashEl principio de superposición
La mayoría de los científicos naturales o sociales, muy a menudo consideramos verdadera la hipótesis de que la respuesta neta causada en un sistema por dos o más estímulos es la suma de las respuestas que habría causado cada estímulo por separado. Esto es el Principio de Superposición, que parece ser una cuestión casi de sentido común, y que muchas veces la asumimos sin demasiadas cautelas.
Una función matemática que satisface el principio de superposición se denomina función lineal. Estas funciones lineales, muy utilizadas con gran generalidad en todas las ciencias, incorporan dos propiedades matemáticas muy útiles como la aditividad y la homogeneidad, y nos permiten un análisis e interpretación muy profunda -y bastante sencilla- de leyes que establezcamos, experimentos que realicemos, generalizaciones que propongamos o conclusiones que extraigamos de una investigación.
El principio de superposición se aplica a cualquier sistema lineal, descrito mediante ecuaciones algebraicas o ecuaciones diferenciales lineales. Los estímulos sobre un sistema y las respuestas de éste pueden ser números, funciones, vectores, campos vectoriales, señales variables en el tiempo o cualquier otro objeto que cumpla ciertos axiomas muy comunes. Los Sistemas Lineales son una de las maneras más utilizadas para describir la realidad, aún estudiando situaciones complejas, como aquellas basadas en las leyes de Newton, las ecuaciones de Maxwell, la ecuación de Schrödinger o modelos en econometría, ecología, o cualquier tipo de ciencia para la que tratamos de expresar matemáticamente su funcionamiento. Una ventaja que tenemos es que, cuando escribimos un estímulo muy general en un sistema lineal como la superposición de estímulos de una forma específica y simple, a menudo la respuesta global resulta más fácil de calcular y predecir.
Modelos lineales ordinarios o extraordinariosMuchos sistemas dinámicos, basados en algunas de las leyes más valiosas de la historia de la ciencia, se pueden expresar mediante ecuaciones diferenciales ordinarias lineales con coeficientes constantes. Los matemáticos han suministrado para este tipo de sistemas -llamados autónomos- un verdadero arsenal de medios para resolverlos analíticamente, por muy complejos éstos sean. Por ejemplo, la conocida Transformada de Laplace reduce un complejo sistema de ecuaciones diferenciales ordinarias lineales en un sistema de ecuaciones algebraicas, mucho más fácil de solucionar. Ello además nos permite nos solo conocer al dedillo la evolución en el tiempo del sistema dinámico que hemos resuelto, sino también descubrir sus sorprendentes propiedades en el dominio de la frecuencia, extrayendo nuevo conocimiento que no pensábamos obtener de la mera integración de una sencilla ecuación diferencial.
Las ecuaciones diferenciales ordinarias son un caso particular de las ecuaciones en derivadas parciales, muy comunes también para describir la dinámica en todas las ciencias, y que, en contraposición con las anteriores más sencillas descripciones ordinarias, podemos denominar modelos extraordinarios. Aunque su resolución en este caso es algo más compleja, las ecuaciones diferenciales lineales, sean ordinarias o no, permitieron a los físicos expresar asuntos clave como la dinámica de los planetas, todo el electromagnetismo o la dualidad onda-corpúsculo, entre muchas otras cuestiones. Hoy día científicos e ingenieros de toda especie establecen modelos dinámicos para explicar por qué ocurre la realidad experimentada en su propio ámbito.
La realidad es no linealMuy pocos científicos utilizan ecuaciones diferenciales no lineales. Sentimos una cierta reacción alérgica a su empleo, quizás por la dificultad de resolver la matemática de estas ecuaciones o quizás por abandonar el principio de superposición que tanto apreciamos. En la teoría general de relatividad de Albert Einstein, las ecuaciones son no lineales, y su resolución casi siempre implican métodos matemáticos de linealización o de perturbaciones. Incluso para sistemas mucho más sencillos, descritos en simples ecuaciones diferenciales ordinarias no lineales, nuestra tendencia es linealizar el sistema en torno a unas ciertas condiciones y resolver ecuaciones lineales, para tratar de extraer información -al menos parcial- de la realidad que hemos modelado.
La cuestión es que la realidad es no lineal, y nuestras ecuaciones lineales pueden modelar bastante bien las cosas, pero en ocasiones ocurren fenómenos muy imprevisibles y no intuitivos, tanto en las ciencias naturales como en las ciencias sociales o en las ingenierías. Estos fenómenos no se producen en los modelos lineales, y son por tanto exclusivos de los sistemas no lineales.
Múltiples puntos de equilibrioLos puntos de equilibrio son las soluciones constantes en una ecuación diferencial. En sistemas lineales autónomos, el modelo tiende a un único punto de equilibrio. Uno de los ejemplos más sencillos podemos encontrarlo en la aproximada ley de enfriamiento de Newton: una simple ecuación diferencial lineal de primer orden que explica la transferencia de calor entre dos cuerpos partiendo de diferentes temperaturas. El punto de equilibrio es único y establece igualdad de temperaturas entre ambos cuerpos.
Si a esta sencilla ecuación diferencial añadimos un simple término cuadrático nos encontramos con un básico sistema no lineal, cuya resolución numérica puede observarse en la Figura 1.
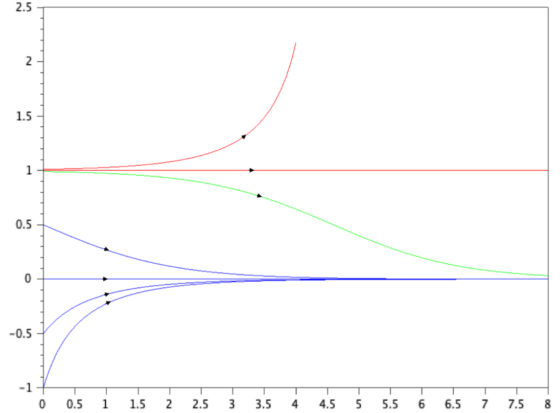 Figura 1: Dos puntos de equilibrio en una simple ecuación diferencial ordinaria autónoma no lineal de primer orden: punto de equilibrio estable en 0 y punto de equilibrio inestable en 1. Ecuación =-x+x2 . Fuente: [2] Cap. 1, pp.: 5-6.
Figura 1: Dos puntos de equilibrio en una simple ecuación diferencial ordinaria autónoma no lineal de primer orden: punto de equilibrio estable en 0 y punto de equilibrio inestable en 1. Ecuación =-x+x2 . Fuente: [2] Cap. 1, pp.: 5-6.Vemos que linealizando el sistema en torno a la temperatura 0, la solución (trayectorias azules) tienden al punto de equilibrio previsto por la ley de enfriamiento de Newton, si partimos de las inmediaciones en torno a la cual hemos linealizado. Pero si resolvemos el sistema no lineal completo, descubrimos que partir de otras condiciones iniciales nos puede dar lugar a otras soluciones radicalmente diferentes causadas por un segundo punto de equilibrio en 1. Cualquier perturbación partiendo de esta segunda temperatura hace que el sistema abandone la situación y, o bien tienda al anterior equilibrio 0 (trayectoria verde), o bien la temperatura crezca sin límite (trayectoria roja).
Ciclos límiteLos sistemas no lineales pueden oscilar sin excitación externa, con amplitud y frecuencia fijas. Las oscilaciones lineales como por ejemplo las de un péndulo linealizado en torno a la vertical, puede cambiar la amplitud de sus oscilaciones (por ejemplo, empujando más o menos un columpio). Balthasar Van der Pol, hacia 1920, añadió un término no lineal a la ecuación diferencial lineal del péndulo, haciendo depender su coeficiente de amortiguamiento con su posición. Se trata entonces de una sencilla ecuación diferencial ordinaria no lineal de segundo orden.
En sistemas dinámicos de orden dos o superior, se emplea muchas veces el espacio de fases para representar los grados de libertad del sistema. En la Figura 2 se muestra la solución de la ecuación de Van der Pol con dos condiciones iniciales diferentes.
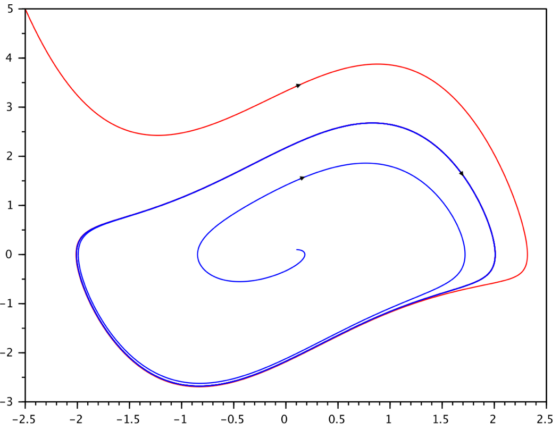 Figura 2: Ciclo límite estable en la ecuación de Van der Pol: solución representada en el plano de fase (posición-velocidad). Ecuación +(x2-1)+x=0 . Fuente [2] Cap 5, pp: 95-99.
Figura 2: Ciclo límite estable en la ecuación de Van der Pol: solución representada en el plano de fase (posición-velocidad). Ecuación +(x2-1)+x=0 . Fuente [2] Cap 5, pp: 95-99.Partiendo de posición y velocidad pequeñas (trayectoria azul inicialmente cerca de cero en la Figura 2), el sistema amplifica su oscilación sin excitación externa y tiende a cierta frecuencia y amplitud fijas (ciclo cerrado azul). Partiendo de posición y velocidad amplias (trayectoria roja) el sistema pierde energía y al final tiende a oscilar exactamente igual. En el plano fásico observamos el ciclo cerrado, llamado ciclo límite, efecto causado por la no linealidad añadida por Van der Pol. Ante cualquier perturbación creciente o decreciente que sufra la posición o velocidad de este especial péndulo no lineal, el dispositivo corregirá la situación y volverá a oscilar a la misma frecuencia y amplitud propias. Se trata de un sorprendente ciclo límite estable, exclusivo de los sistemas no lineales, y que nos lleva a un nuevo concepto de región de equilibrio estable, generalización del concepto de punto de equilibrio estable que hemos descrito arriba.
CaosEn sistemas dinámicos lineales estables, la ligera modificación de sus condiciones iniciales da lugar a ligeros cambios en su respuesta. Sin embargo, en sencillos sistemas no lineales se puede observar una extrema sensibilidad a las condiciones iniciales, propiedad exclusiva de la no linealidad, y que se denomina caos.
En la Figura 3 se muestran las soluciones de una ecuación diferencial ordinaria no lineal de segundo orden que modela un sistema mecánico con deflexiones elásticas no lineales y forzado con un coeficiente no constante ([2] p.7).
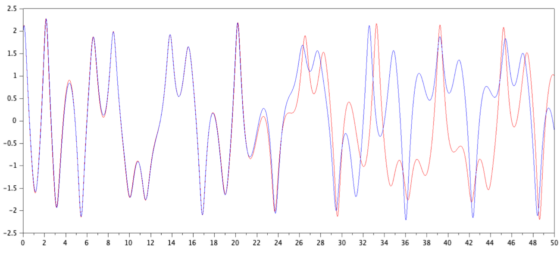 Figura 3: Evolución imprevisible de dos trayectorias en un simple sistema no lineal de segundo orden con dos condiciones iniciales casi idénticas. Ecuación +0,1+x5=6sen t. Fuente: [2] Cap. 1, pp.: 7-8.
Figura 3: Evolución imprevisible de dos trayectorias en un simple sistema no lineal de segundo orden con dos condiciones iniciales casi idénticas. Ecuación +0,1+x5=6sen t. Fuente: [2] Cap. 1, pp.: 7-8.Puede observarse que, ante condiciones iniciales casi idénticas, las dos trayectorias del sistema (azul y roja) son al principio iguales, pero en pocos instantes se produce una bifurcación radical en el comportamiento del sistema. Nuestro modelo es totalmente determinista, su ecuación puede ser exacta, pero su comportamiento es imprevisible: muy parecido a la imposible previsión del tiempo atmosférico que conocemos. Este ejemplo es aún más sencillo que el famoso modelo de dinámica atmosférica que presentó el conocido matemático y meteorólogo Edward Lorenz. En la Figura 4 se muestra una implementación física del atractor de Lorenz y su medida caótica en el laboratorio.
 Figura 4: Circuito electrónico que satisface el modelo del famoso atractor de Lorenz y medida de su respuesta caótica en el plano fásico. Fuente: Dept. de Electricidad y Electrónica UPV/EHU
Figura 4: Circuito electrónico que satisface el modelo del famoso atractor de Lorenz y medida de su respuesta caótica en el plano fásico. Fuente: Dept. de Electricidad y Electrónica UPV/EHU
La dinámica de la naturaleza y las sociedades es inherentemente no lineal. Los sistemas lineales deben entenderse como caso particular de los más generales sistemas no lineales. Los fenómenos impredecibles, anti-intuitivos o sorprendentes los podemos modelar, explicar, predecir, experimentar y controlar en el laboratorio, así como tratar de contribuir a descubrir o solucionar los enigmas de lo que llamamos realidad.
Referencias
[1] Henri Poincaré (1892-1893-1899) Les méthodes nouvelles de la mécanique céleste TOME I, II et III (PDF). Gauthier-Villars et fils, Paris
[2] Victor Etxebarria (1999) Sistemas de control no lineal y robótica. Servicio Editorial de la UPV/EHU, ISBN 8483731924 – 9788483731925, Bilbao
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo La realidad resulta enigmática porque es no lineal se ha escrito en Cuaderno de Cultura Científica.
El rompecabezas de los cuatro cubos de Nelson
En una reciente entrada de la sección Matemoción del Cuaderno de Cultura Científica, titulada Los cuadrados de MacMahon, estuvimos hablando de un interesante rompecabezas geométrico, cuyo nombre es precisamente el título de la misma. En esta entrada vamos a ir un poco más allá y con los cuadrados de ese juego de ingenio construiremos cubos que nos permitirán crear un nuevo rompecabezas, conocido primero con el nombre de “el rompecabezas de Nelson”, y después como “el rompecabezas de los cuatro cubos”.
 El rompecabezas de Nelson, con la firma de su creador Scott Nelson, comercializado en Japón por el inventor, coleccionista y comunicador de rompecabezas matemáticos y juegos de ingenio japonés Nob Yoshigahara (1936-2004). Imagen de la colección online de rompecabezas mecánicos de Jerry Slocum, cortesía de la Biblioteca Lilly de la Universidad de Indiana.Los cuadrados de MacMahon
El rompecabezas de Nelson, con la firma de su creador Scott Nelson, comercializado en Japón por el inventor, coleccionista y comunicador de rompecabezas matemáticos y juegos de ingenio japonés Nob Yoshigahara (1936-2004). Imagen de la colección online de rompecabezas mecánicos de Jerry Slocum, cortesía de la Biblioteca Lilly de la Universidad de Indiana.Los cuadrados de MacMahon
En primer lugar, recordemos el rompecabezas de los cuadrados de MacMahon, y más concretamente, las piezas con las que se juega al mismo. Percy Alexander MacMahon (1854–1929), que fue un militar y matemático británico, se planteó de cuántas formas distintas, salvo rotaciones, se puede colorear el cuadrado dividido en cuatro partes iguales por sus dos diagonales utilizando tres colores distintos y observó que es posible hacerlo de 24 maneras distintas. A partir de esta información, creó el rompecabezas que lleva su nombre, cuyas piezas, que vemos en la siguiente imagen (con los colores verde, azul y amarillo), son la realización de las 24 formas de colorear el cuadrado dividido en cuatro partes iguales por sus dos diagonales utilizando tres colores distintos.
 Las 24 fichas que componen el rompecabezas de “los cuadrados de MacMahon”
Las 24 fichas que componen el rompecabezas de “los cuadrados de MacMahon”
El rompecabezas consiste en construir un rectángulo de 4 filas y 6 columnas con las 24 fichas del mismo (si deseas imprimirlas te dejamos aquí el PDF con las 24 fichas), de manera que cuando dos fichas tienen un lado en común el color de las regiones triangulares que comparten ese lado, en los dos cuadrados, tienen que tener el mismo color y, además, todo el perímetro, es decir, todas las regiones triangulares que forman el perímetro del rectángulo, tiene que ser de un mismo color, ya sea este, verde, azul o amarillo (para más información sobre este juego de ingenio puede leerse la entrada Los cuadrados de MacMahon).
Con las 24 fichas se puede jugar al rompecabezas de MacMahon, pero también se pueden plantear otros juegos relacionados con el mismo. Por ejemplo, los miembros del Grupo Alquerque de Sevilla, los matemáticos Juan Antonio Hans Martín, José Muñoz Santonja y Antonio Fernández-Aliseda Redondo, plantearon diferentes retos, con diferentes niveles de dificultad, aunque más sencillos que el original (en los mismos solo se pide que se cumpla la primera condición, esto es, cuando dos fichas son adyacentes tienen el mismo color en las regiones de contacto) en su artículo «MacMahon y las matemáticas en colores», publicado en la revista SUMA. Estos problemas serían los siguientes:
A) de las 24 fichas del rompecabezas, separar las 9 que tienen los tres colores y con ellas formar un cuadrado de lado 3, es decir, con tres filas y tres columnas;
 Ejemplo de cuadrado de lado 3 formado por las 9 fichas que tienen los tres colores
Ejemplo de cuadrado de lado 3 formado por las 9 fichas que tienen los tres colores
B) con las 12 fichas que tienen sólo 2 colores construir un rectángulo 3 x 4, tres filas y cuatro columnas;
C) con las 12 fichas complementarias de las anteriores, luego las que tienen 1 o 3 colores, componer también un rectángulo 3 x 4;
D) con las 15 fichas que tienen 1 o 2 colores, construir un rectángulo 3 x 5;
E) con las 15 fichas anteriores (que tienen 1 o 2 colores) y otra cualquiera de las que tienen 3 colores, formar un rectángulo de lado 4, luego con cuatro filas y cuatro columnas;
F) dividiendo primero las 24 fichas en dos grupos de 12 fichas, componer dos rectángulos 3 x 4;
G) con todas las 24 fichas construir rectángulos de tamaños 2 x 12, 3 x 8 y 4 x 6 (si a estos últimos les añadimos la condición del perímetro tenemos el rompecabezas de MacMahon, aunque en los dos tamaños anteriores esta condición nos lleva a que no existan soluciones);
H) con todas las 24 fichas construir rectángulos huecos de tamaños 3 x 11, 4 x 10, 5 x 9, 6 x 8 y 7 x 7 (todos ellos de perímetro igual a 24, que son las piezas que tenemos para construirlos).
 Ejemplo de cuadrado hueco de lado 7 formado por las 24 fichas
Ejemplo de cuadrado hueco de lado 7 formado por las 24 fichasLos cubos de Nelson
El matemático, programador informático y diseñador de juegos de ingenio estadounidense Harry Lewis Nelson (1932), quien diseñó un juego basado en los cuadrados de MacMahon denominado Pohaku (véanse las siguientes imágenes), planteó la cuestión de si sería posible utilizar las 24 piezas cuadradas de MacMahon como las caras de cuatro cubos (como hay 6 caras por cubo, son 24 caras en total) de manera que, si dos caras comparten una arista, el color de las regiones triangulares de contacto sean del mismo color.
 Portada del juego Pohaku, inventado por el matemático estadounidense Harry L. Nelson y comercializado por Penny Norman, que consistía en 5 juegos, para jugar entre dos personas, que utilizaban los 24 cuadrados de MacMahon, denominados Domino Pohaku, Standard Pohaku, 5 x 5 Pohaku y Toroidal Pohaku. Imagen de eBay
Portada del juego Pohaku, inventado por el matemático estadounidense Harry L. Nelson y comercializado por Penny Norman, que consistía en 5 juegos, para jugar entre dos personas, que utilizaban los 24 cuadrados de MacMahon, denominados Domino Pohaku, Standard Pohaku, 5 x 5 Pohaku y Toroidal Pohaku. Imagen de eBay
 Reglas de los juegos Domino Pohaku, Standard Pohaku, 5 x 5 Pohaku y Toroidal Pohaku. Imagen de eBay
Reglas de los juegos Domino Pohaku, Standard Pohaku, 5 x 5 Pohaku y Toroidal Pohaku. Imagen de eBay
La cuestión planteada por el matemático fue resuelta por su hijo Scott Nelson en 1970, cuando tenía tan solo 9 años y fue el nacimiento de un nuevo rompecabezas. En la siguiente imagen se muestran los cuatro cubos, cumpliendo las condiciones de Harry Nelson, al desplegar en el plano las seis caras de los mismos.
¿En qué consiste el rompecabezas de Nelson? Se trata de crear formas tridimensionales con los cuatro cubos, como una fila de cuatro cubos o los cuatro cubos juntos formando una estructura cuadrada (véase la siguiente imagen), de manera que en las caras visibles se cumpla la condición de que las caras adyacentes tengan el mismo color en las regiones de contacto.
Por ejemplo, las soluciones a las dos figuras anteriores son las siguientes.

Las formas tridimensionales que aparecían en el juego comercial, divididas por nivel de dificultad, eran las siguientes. Nivel para principiantes:
Nivel intermedio:
Nivel experto:
Como cada vez que hablamos de rompecabezas, mi consejo es que construyáis los cuatro cubos de Nelson, cuyas caras son los 24 cuadrados de MacMahon, y disfrutéis del juego.
 El rompecabezas de Nelson fue comercializado como el rompecabezas de los cuatro cubos por la empresa Binary Arts, que hoy es ThinkFun. Imagen de la colección online de rompecabezas mecánicos de Jerry Slocum, cortesía de la Biblioteca Lilly de la Universidad de Indiana
El rompecabezas de Nelson fue comercializado como el rompecabezas de los cuatro cubos por la empresa Binary Arts, que hoy es ThinkFun. Imagen de la colección online de rompecabezas mecánicos de Jerry Slocum, cortesía de la Biblioteca Lilly de la Universidad de IndianaBibliografía
1.- Percy A. MacMahon, New Mathematical Pastimes, Cambridge University Press, 1921 (puede obtenerse una copia en pdf a través de la biblioteca digital Internet Archive [archive.org]).
2.- Martin Gardner, Nuevos pasatiempos matemáticos, Alianza editorial, 2018.
3.- Juan Antonio Hans Martín, José Muñoz Santonja y Antonio Fernández-Aliseda Redondo, MacMahon y las matemáticas en colores, SUMA 63, pp. 51-57, 2010.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El rompecabezas de los cuatro cubos de Nelson se ha escrito en Cuaderno de Cultura Científica.
Primera observación de la rotación de un agujero negro supermasivo
 Ilustración del modelo de disco de acreción inclinado. El eje de giro del agujero negro se alinea verticalmente y la dirección del chorro es casi perpendicular al disco. La desalineación entre el eje de giro del agujero negro y el eje de rotación del disco provocará la precesión (balanceo) del disco y del chorro. Fuente: Yuzhu Cui et al. 2023 / Intouchable Lab@Openverse / Zhejiang Lab
Ilustración del modelo de disco de acreción inclinado. El eje de giro del agujero negro se alinea verticalmente y la dirección del chorro es casi perpendicular al disco. La desalineación entre el eje de giro del agujero negro y el eje de rotación del disco provocará la precesión (balanceo) del disco y del chorro. Fuente: Yuzhu Cui et al. 2023 / Intouchable Lab@Openverse / Zhejiang LabUn equipo científico internacional, con participación del Instituto de Astrofísica de Andalucía (IAA-CSIC), ha analizado datos de 23 años del centro de la galaxia Messier 87 (M87), que alberga un agujero negro supermasivo (6.500 millones de veces más masivo que el Sol), el primero del que se obtuvo una imagen.
Los resultados revelan que el chorro que emerge del agujero negro a altísima velocidad oscila hacia arriba y hacia abajo con una amplitud de unos 10 grados, lo que a su vez confirma que el agujero negro se halla en rotación.
Los agujeros negros absorben grandes cantidades de material debido a su fuerza de gravedad, tan potente que ni siquiera la luz escapa de ellos, e impulsan un flujo de plasma en forma de chorro que se mueve casi a la velocidad de la luz y abarca enormes distancias. La galaxia M87, por ejemplo, presenta un chorro que emerge de sus regiones centrales y se extiende mucho más allá del tamaño de la propia galaxia.
Sin embargo, el mecanismo de transferencia de energía entre los agujeros negros supermasivos, los discos de acreción y los chorros aún se desconoce. La teoría predominante sugiere que se puede extraer energía de un agujero negro en rotación, permitiendo que parte del material que rodea el agujero negro sea expulsado a gran velocidad. A pesar de ello, la rotación de los agujeros negros supermasivos, un factor crucial en este proceso y el parámetro fundamental, además de la masa del agujero negro, nunca se ha observado directamente.
Un chorro en precesiónEl análisis del equipo de investigación, que incluye una comparación con una simulación teórica, indica que el eje de rotación del disco de acreción se desalinea con el eje de giro del agujero negro, lo que genera un chorro en precesión (como el balanceo de una peonza).
La detección de esta precesión constituye una evidencia inequívoca de que el agujero negro supermasivo de M87 se halla, en efecto, girando, lo que abre nuevas dimensiones en nuestra comprensión de la naturaleza de estos objetos.
La desalineación entre el agujero negro y el disco es relativamente pequeña y el período de precesión es de alrededor de once años, por lo que un análisis exhaustivo de los datos de alta resolución de la estructura de M87 acumulados durante dos décadas han sido suficientes para poder detectarla
Pero, ¿qué fuerza puede alterar la dirección de un chorro tan poderoso? La respuesta podría hallarse en el comportamiento del disco de acreción: a medida que los materiales que caen orbitan alrededor del agujero negro, forman una estructura de disco antes de girar gradualmente en espiral hasta que son absorbidos por el agujero negro. Pero si el agujero negro gira, ello ejerce un impacto significativo en el espacio-tiempo circundante, provocando que los objetos cercanos sean arrastrados a lo largo de su eje de rotación, es decir, produciendo el “arrastre de marco” (frame dragging) predicho por la Relatividad General de Einstein.
Si bien este estudio arroja luz sobre cómo funciona un agujero negro supermasivo, también abre grandes incógnitas. La estructura del disco y el valor exacto del giro del agujero negro supermasivo M87* son aún inciertos, y este trabajo predice que existen más factores que intervienen en esta configuración, lo que añade nuevos desafíos a la investigación.
Referencia:
Cui, Y., Hada, K., Kawashima, T. et al. (2023) Precessing jet nozzle connecting to a spinning black hole in M87 Nature doi: 10.1038/s41586-023-06479-6
Edición realizada por César Tomé López a partir de materiales suministrados por IAA-CSIC
El artículo Primera observación de la rotación de un agujero negro supermasivo se ha escrito en Cuaderno de Cultura Científica.
La importancia del dióxido de carbono en la dinámica geológica de Europa
En al menos tres ocasiones, en Planeta B hemos hablado sobre Europa, uno de los satélites más interesantes de Júpiter: “La evolución del interior de la luna Europa”, “Una tectónica de placas más allá de la Tierra” y “¿Y si pudiésemos llegar al océano de Europa sin necesidad de atravesar toda la corteza?”.
Y es que cuando lo miramos de cerca, su superficie atestigua una historia reciente de actividad geológica, quizás no solo pretérita, sino también en la actualidad, con la posible existencia de procesos que siguen rejuveneciendo el aspecto de este satélite. Además de esa juventud que aparenta en términos geológicos, el Hubble descubrió hace una década la posible existencia de penachos de agua que surgen de su superficie, lo que sería otra prueba a favor de ser un mundo activo, aunque estos serían bastante elusivos.
 Los penachos de vapor de agua en Europa tal y como los detectó el telescopio espacial Hubble, abajo a la izquierda, anotados por la palabra “Plumes”. Imagen cortesía de la NASA, ESA, W. Sparks (STScI) y USGS Astrogeology Science Center.
Los penachos de vapor de agua en Europa tal y como los detectó el telescopio espacial Hubble, abajo a la izquierda, anotados por la palabra “Plumes”. Imagen cortesía de la NASA, ESA, W. Sparks (STScI) y USGS Astrogeology Science Center.¿De dónde procede toda esta actividad geológica que observamos? Lo más probable es que el responsable directo sea un océano de agua líquida bastante salado -valga la redundancia- que a su vez está en contacto también con el núcleo rocoso del satélite, de donde procedería la energía para mantener líquido el océano. Este último serviría como una cinta transportadora de materia y energía desde el interior de Europa hacia el exterior, provocando esos cambios que observamos en su superficie.
Una manera indirecta de conocer con mayor grado de detalle la composición química del agua de ese posible océano sería si estuviese de algún modo conectado al exterior, ya que, de momento, carecemos de la tecnología para poder llegar hasta este, que requeriría una sonda capaz de atravesar varios kilómetros de hielo hasta llegar al agua.
Saber qué elementos y compuestos existen en el océano nos abre una puerta a saber si es un océano habitable -habitable para nuestros estándares- puesto que la existencia y abundancia de determinados elementos y compuestos puede ser crucial para el desarrollo de la vida. Por supuesto, esto no quiere decir que haya vida o se pueda haber desarrollado, pero si nos puede indicar si es un lugar hospitalario.
Los lugares más prometedores para “saborear” -me van a permitir que me tome una licencia literaria- este océano serían los penachos de vapor de agua (muestreándolos desde la órbita, por ejemplo- y por supuesto las zonas donde pueda existir actividad geológica reciente en Europa, ya que a través de las fisuras generadas como resultado de la dinámica del satélite podría haberse transportado material desde el océano hasta el exterior. Sería una manera indirecta, pero válida mientras no tengamos una tecnología capaz de llegar al océano.
Pero bueno, ¿qué se ha descubierto ahora que ha generado tanto revuelo? Lo cierto es que descubrir -gracias a Jesús Martínez-Frías por su corrección- no se ha descubierto nada en el sentido más estricto de la palabra, sino que se ha podido identificar mejor en que regiones de la superficie de Europa podemos encontrar dióxido de carbono, algo que ya contaba con detecciones previas como podemos leer en Hansen et al. (2008) y McCord et al. (1998).
El dióxido de carbono no es un compuesto que pueda ser estable a lo largo del tiempo geológico en las condiciones de presión y temperatura existentes en la superficie de Europa, por lo que cualquier cantidad de este que quede expuesta, debería de sublimarse y formar parte de la tenue atmósfera del satélite o escaparse al espacio, sin embargo, tanto las observaciones realizadas por la misión Galileo como con el telescopio espacial James Webb han sido capaces de detectar este compuesto en la superficie.
La diferencia entre el descubrimiento original del dióxido de carbono y los datos aportados en el reciente estudio publicado en Science por Trumbo et al. (2023) es principalmente una mejor localización espacial, así como aportar un contexto para su origen, ya que los datos de la Galileo tenían muy poca resolución en comparación con los del James Webb, que ha permitido adscribir la presencia de este compuesto en regiones muy concretas del satélite de Júpiter.
Lo cierto es que el dióxido de carbono no es un compuesto muy raro, y se había detectado previamente en otros lugares del sistema joviano así como en los satélites de Saturno, pero no con una asociación directa a zonas jóvenes de su superficie. Se sospecha que en algunos de estos casos la presencia de este dióxido de carbono podría deberse a factores externos como, por ejemplo, la aportación de compuestos orgánicos por parte de meteoritos o zonas ya ricas en compuestos orgánicos que sufren procesos de degradación a causa de la intensa radiación.
El caso de Europa es diferente, y las concentraciones de dióxido de carbono se encuentran fuertemente asociadas a regiones jóvenes con terreno de tipo chaos -los chaos, explicado de una manera sencilla, son zonas de la superficie de los planetas donde el terreno parece estar agrietado y desordenado- como son Tara Regio y Powys Regio. En el resto de satélites donde se ha detectado, el dióxido de carbono estaba asociado a zonas más oscuras ricas en compuestos orgánicos, cráteres de impacto o las zonas más afectadas por la radiación.
 Un detalle de la zona de Tara Regio capturado por la sonda Galileo en septiembre de 1998 a una resolución de 220 metros por píxel. Se aprecia perfectamente la existencia de juegos de grietas, crestas y una forma como de puzle desordenado. Cortesía de NASA/JPL/USGS.
Un detalle de la zona de Tara Regio capturado por la sonda Galileo en septiembre de 1998 a una resolución de 220 metros por píxel. Se aprecia perfectamente la existencia de juegos de grietas, crestas y una forma como de puzle desordenado. Cortesía de NASA/JPL/USGS.Esto nos lleva a la siguiente cuestión. Entonces, ¿de dónde sale el dióxido de carbono? Si en los párrafos anteriores hablábamos del posible origen exógeno -impactos de meteoritos y la degradación de los compuestos orgánicos-, ahora nos toca hablar del origen endógeno de este compuesto. Lo normal es que para que sea estable bajo las condiciones actuales, debe de encontrarse atrapado en el hielo.
Los científicos han estudiado otras posibilidades, como que el dióxido de carbono observado procediese de compuestos orgánicos o de minerales del grupo de los carbonatos, pero no se observan en los espectros señales que hagan pensar en estas dos últimas fuentes -sumada a la radiación- podrían ser una forma plausible de formar las concentraciones de dióxido de carbono encontrados tanto en la asociación a estas regiones jóvenes como en sus proporciones.
Así que solo nos queda una posibilidad, y es que el dióxido de carbono proceda directamente del interior de Europa como dióxido de carbono o como alguna otra molécula precursora de este compuesto desde el océano que hay bajo su superficie. Llegaría a la superficie durante la formación de estas zonas más jóvenes a través del ascenso de materiales del océano -ya sea en estado líquido o como masas de hielo con un comportamiento plástico-, por el colapso del hielo sobre zonas donde exista agua líquida bajo la superficie o por el ascenso de líquidos a través de grietas en la corteza.
Pero todavía hay más: y es que para que observemos las concentraciones de dióxido de carbono que vemos en la superficie, debe de haber un mecanismo continuo que vaya reponiendo este dióxido de carbono que se escapa a la atmósfera o bien la llegada de este compuesto a la superficie ha debido ocurrir en un lapso de tiempo muy reciente a escala geológica.
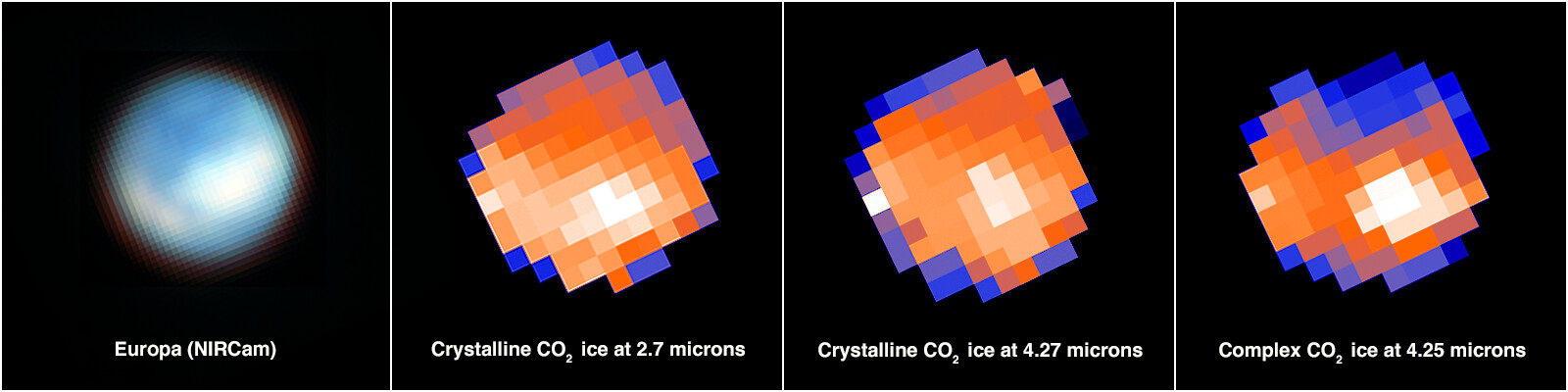 A la izquierda, una imagen de Europa tomada por el JWST. A la derecha, los mapas de concentración de CO2. Cortesía de NASA, ESA, CSA, G. Villanueva (NASA/GSFC), S. Trumbo (Cornell Univ.) y A. Pagan (STScI).
A la izquierda, una imagen de Europa tomada por el JWST. A la derecha, los mapas de concentración de CO2. Cortesía de NASA, ESA, CSA, G. Villanueva (NASA/GSFC), S. Trumbo (Cornell Univ.) y A. Pagan (STScI).Las implicaciones de estos resultados de cara a la astrobiología son muy importantes: el primero, que el carbono, que es un elemento que es necesario para la vida tal y como la conocemos, se encuentra presente en el océano de Europa, y también que este océano tendría unas condiciones ligeramente oxidantes, lo que coincidiría con una entrada al océano de compuestos oxidantes que se producen en la superficie a causa de la intensa radiación, completando también la cinta transportadora de materia desde la superficie hacia el océano y no solo desde dentro hacia afuera.
Un océano reductor, desde nuestro punto de vista, podría ser menos hospitalario para la vida, porque aunque haya organismos como los anaeróbicos que, capaces de realizar la respiración anaeróbica usando moléculas diferentes al oxígeno, o los quimioautótrofos, capaces de extraer su energía de compuestos inorgánicos, en nuestro planeta sabemos que la falta de oxígeno reduce las posibilidades de formas de vida más complejas.
Todos estos estudios son muy interesantes, ya que podrán servir de base a las futuras investigaciones de la sonda europea JUICE, que ya se dirige al sistema joviano, y la Europa Clipper de la NASA que, si todo va bien, despegará en octubre de 2024, desde donde poder verificar estas observaciones eso sí, desde mucho más cerca y aportarnos nuevos detalles de este cuerpo tan interesante.
Bibliografía:
Hansen, G. B., & McCord, T. B. (2008). Widespread CO2 and other non-ice compounds on the anti-Jovian and trailing sides of Europa from Galileo/NIMS observations. Geophysical Research Letters, 35(1), L01202. doi: 10.1029/2007GL031748
McCord, T. B., Hansen, G. B., Clark, R. N., Martin, P. D., Hibbitts, C. A., Fanale, F. P., Granahan, J. C., Segura, M., Matson, D. L., Johnson, T. V., Carlson, R. W., Smythe, W. D., & Danielson, G. E. (1998). Non‐water‐ice constituents in the surface material of the icy Galilean satellites from the Galileo near‐infrared mapping spectrometer investigation. Journal of Geophysical Research: Planets, 103(E4), 8603-8626. doi: 10.1029/98JE00788
Trumbo, S. K., & Brown, M. E. (2023). The distribution of CO 2 on Europa indicates an internal source of carbon. Science, 381(6664), 1308-1311. doi: 10.1126/science.adg4155
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo La importancia del dióxido de carbono en la dinámica geológica de Europa se ha escrito en Cuaderno de Cultura Científica.
Aburrimiento musical
José Manuel González Gamarro
La música, ese hecho cultural transversal a lo largo del planeta, esa gran invención humana que casi empuja a caer irremediablemente en lo interdisciplinar, ha sido estudiada de forma poliédrica. La extensísima literatura que aborda la investigación sobre música tiene casi tantos enfoques como disciplinas del conocimiento existen. Uno de los puntos que más consenso encuentra la investigación es el beneficio que aporta escucharla, estudiarla y/o practicarla. Hay quien, interesadamente sesgado, no duda en atribuirle propiedades casi mágicas con discursos grandilocuentes y atractivos titulares de prensa: «Quítele la pantalla y dele un instrumento musical a su hija o hijo», «La música te hace más inteligente», «¿Quiere envejecer mejor? Practique música», etc. Incluso el refranero popular nos dice que quien canta su mal espanta, pero, como todo en la vida, cabe un gran «depende» en todas estas afirmaciones.
 Foto: Manuel Nägeli / UnsplashEfectos negativos de la música
Foto: Manuel Nägeli / UnsplashEfectos negativos de la música
Todos los estudios en pos de los beneficios causados por la música o cómo ésta mejora la sociedad, tienen una consecuencia evidente: el número de estudios de los efectos negativos de la música es mucho menor y solo han suscitado interés en los últimos años. Uno de estos efectos “negativos” puede ser el aburrimiento. Este aburrimiento no siempre se puede considerar negativo ya que algunos autores1 lo consideran como una retroalimentación que provoca un cambio de tarea, por lo que cumple una función importante. Este estado emocional puede ocurrir cuando se interactúa con el arte. De hecho, ocurre con más frecuencia de la que se puede imaginar en un primer momento. Es por esto que un reciente estudio2 dirigido por la investigadora del Instituo Max Planck de Estética Empírica, Julia Merrill ha abordado esta cuestión, poniendo el foco de atención en investigar la prevalencia y las situaciones de aburrimiento al interactuar con la música. Aunque el estudio no es concluyente, aborda cuestiones poco exploradas, como qué características puede tener una música aburrida (por más que esto dependa del juicio del oyente), qué emociones se asocian a esta supuesta música aburrida, la importancia del contexto en la escucha musical, los rasgos de la personalidad del oyente o un constructo que se denomina “sofisticación musical” medida con una escala llamada Gold-MSI3 donde se autoevalúa el compromiso activo con la música, habilidades de percepción musical y la percepción de emociones al oír música.
Para arrojar luz sobre todas estas cuestiones, en el Instituto Max Planck se llevaron a cabo dos estudios diferentes y complementarios, atendiendo a métodos cualitativos y cuantitativos. Para el estudio cualitativo se formularon preguntas abiertas a 266 participantes sobre las situaciones en las que experimentaron aburrimiento al escuchar música atendiendo a la ubicación, el entorno, si estaban solos o acompañados, el tipo de música o la duración de ésta. También se formularon preguntas relativas a los sentimientos y emociones evocados al aburrirse y cómo reaccionaron ante esto. Otra de esas preguntas abiertas abordaba la cuestión de la definición de la música aburrida, es decir, qué características tiene la música con la que la gente se aburre. Para el estudio cuantitativo se usaron 719 participantes donde respondieron a una encuesta con tres preguntas: ¿Con qué frecuencia te aburres cuando escuchas música?, ¿con qué intensidad te aburres cuando escuchas música? y ¿Con qué frecuencia utilizas música para afrontar el aburrimiento? Usando en las respuestas una escala del 1 al 7, siendo el 1 nunca y el 7 siempre. Además, se realizó una lista con 14 estilos musicales que también fueron calificados desde el 1 (muy interesante) hasta el 7 (muy aburrido). A partir de estos datos se escogió el estilo más aburrido y uno ligeramente aburrido y se volvió a pedir a los participantes que valoraran estos dos estilos en la escala de 1 a 7, para a continuación presentar 16 razones por las que la música es aburrida con una escala de 5 puntos. A todos estos datos se le añaden los recopilados por la escala, anteriormente mencionada, Gold-MSI que mide la sofisticación musical de cada participante.
Aburrimiento musicalLos resultados del estudio cualitativo aportaron datos que revelan que, además de experimentar aburrimiento musical en situaciones con cierta monotonía como viajar en coche, en bus, etc. o no tener el control sobre qué música escuchar (bares, radio, etc.), también se experimenta aburrimiento cuando se está solo y la escucha es concentrada. El juicio estético influye de manera determinante cuando no se ajusta a las expectativas del oyente o bien la música no encaja con el estado de ánimo durante la escucha. Las estrategias para evitar el aburrimiento causado por la música dependen de las posibilidades del contexto de la escucha, dependiendo si se puede evitar la situación (salirse de un concierto o cambiar de música) o eso no es posible (ignorar la música o distraerse con otro estímulo). Uno de los resultados que arroja el estudio cuantitativo es el porcentaje de personas que experimentan aburrimiento al escuchar música. Aunque hay un porcentaje muy elevado (76,5 %) de personas que nunca o rara vez experimenta aburrimiento en la escucha, el porcentaje de personas que se aburren en diferentes grados de intensidad y frecuencia no es nada desdeñable.
En cuanto a las características musicales, el aburrimiento ocurre cuando existen ciertos aspectos generales de la música, como la repetición, la monotonía o las letras de las canciones, con una interesante relación entre aburrimiento y significado. Sin embargo, no solo la baja excitación y la subestimulación lo provocan, sino también la sobreestimualción y la alta excitación. La música con un mayor índice de complejidad, con mayor número de disonancias o caótica resulta aburrida por una sobreabundancia de características musicales muy intensa que provocan disgusto. Otra cuestión es que la música que no nos gusta la etiquetemos como aburrida y la identifiquemos como tal antes de su escucha. El gusto musical tiene mucho de vínculo y no tanto de observación y análisis, donde las cuestiones identitarias son un punto clave.
Experiencia estética fracasadaLa finalidad de la escucha musical, en numerosas ocasiones, es, precisamente, la de acabar con el aburrimiento o provocar en nosotros mismos emociones satisfactorias. Por lo tanto, según los autores del estudio se puede afirmar que, si la música nos provoca aburrimiento, es una experiencia estética fracasada con respecto al éxito de esta experiencia, que se produciría cuando hay un equilibrio entre el agrado, el placer, la excitación, la complejidad y la familiaridad. Sin embargo, este “fracaso” también puede significar éxito, puesto que existe el arte (y por lo tanto la música) deliberadamente aburrido4, es decir, algo creado con la firme intención de aburrir y motivado por diferentes razones.
Por otro lado, juzgar cualquier música como aburrida es controvertido, puesto que puede ser contraproducente tanto para el autor de la música como para la persona que la juzga. Se puede entender que una música es aburrida porque la compositora o compositor no ha sido capaz de crear algo emocionalmente satisfactorio, pero también puede ser negativo para quien juzga, por entenderse que no tiene la suficiente formación o sofisticación para comprender cierta música o sentir emociones satisfactorias al escucharla.
Es de suponer que la música con menos índice de aburrimiento, por decirlo de alguna manera, tendrá un mayor éxito en la sociedad. Sin embargo, como ya se ha advertido, el aburrimiento puede ser una consecuencia de escuchar música con unas ciertas características como una predisposición guiada por nuestro prejuicio y preferencia. Es por ello que también existen investigaciones5 que van más allá, buscando la sincronía neuronal en diferentes individuos al someterse a la escucha, con resultados que indican que a mayor sincronía, mayor éxito musical. Sea como fuere el aburrimiento musical y el fracaso de la escucha para evitarlo dependen en gran medida del concepto (filosófico) de belleza, que se podría establecer en la música como una relación compleja entre uniformidad y variedad. La investigación deberá seguir avanzando para tener una mayor comprensión de todos los factores que componen esta relación adversa con la música. Veremos.
Referencias:
1 Fahlman S. A., Mercer-Lynn K. B., Flora D. B., Eastwood J. D. (2013). Development and validation of the multidimensional state boredom scale. Assessment, 20(1), 68–85. https://doi.org/10.1177/1073191111421303
2 Merrill, J., & Niedecken, T. (2023). Music and Boredom: A First Insight Into an Unexplored Relationship. Music & Science, 6. https://doi.org/10.1177/20592043231181215
3 Müllensiefen D., Gingras B., Musil J., Stewart L. (2014). The musicality of non-musicians: An index for assessing musical sophistication in the general population. PLoS ONE, 9(2), 1–23. https://doi.org/10.1371/journal.pone.0089642
4 Elpidorou A., Gibson J. (2022). Really boring art. Ergo an Open Access Journal of Philosophy, 8(0). https://doi.org/10.3998/ergo.2231
5 Leeuwis, N., Pistone, D., Flick, N., & van Bommel, T. (2021). A sound prediction: EEG-based neural synchrony predicts online music streams. Frontiers in psychology, 12, 672980. https://doi.org/10.3389/fpsyg.2021.672980
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.
El artículo Aburrimiento musical se ha escrito en Cuaderno de Cultura Científica.
¡Ups! La fiebre amarilla

Aunque a día de hoy sabemos que la fiebre amarilla es una enfermedad vírica aguda y hemorrágica, ocasionada por arbovirus del género Flavivirus y transmitida por mosquitos infectados de los géneros Aedes y Haemogogus, no siempre ha sido así. Esta enfermedad acabó con el 10% de la población de Filadelfia en 1793. Tras aquello, el médico Stubbins Ffirth empezó a buscar la causa de la fiebre amarilla. Imprudentemente experimentó consigo mismo y después de restregarse los vómitos de enfermos e incluso bebérselos y no contagiarse, publicó en una tesis titulada ‘A Treatise on Malignant Fever’ en la que expuso que definitivamente la enfermedad no era contagiosa, un dato erróneo como sabemos actualmente.
Los vídeos de ¡UPS¡ presentan de forma breve y amena errores de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se han emitido en el programa de ciencia Órbita Laika (@orbitalaika_tve), en la 2 de RTVE.
Producción ejecutiva: Blanca Baena
Guion: José Antonio Pérez Ledo
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Doblaje: K 2000
Locución: José Antonio Pérez Ledo
Edición realizada por César Tomé López
El artículo ¡Ups! La fiebre amarilla se ha escrito en Cuaderno de Cultura Científica.
CartoCell o cómo detectar patrones ocultos en tejidos celulares
Una reciente colaboración entre el Instituto de Biomedicina de Sevilla con la Universidad del País Vasco, el Instituto Biofisika, el Donostia International Physics Center y otros prestigiosos centros nacionales e internacionales, han dado como resultado CartoCell, una herramienta de análisis de imágenes en 3D de alto contenido que revela patrones de morfología celular escondidos. Este software, de código abierto, tiene un gran potencial de aplicación tanto en ciencia básica, con la que ya ha sido probado, como para el desarrollo clínico y médico.
 CartoCell es una red neuronal artificial que procesa de forma automática epitelios en 3D, esto es, permite la reconstrucción automática en 3D de imágenes obtenidas por microscopía.En busca de patrones ocultos
CartoCell es una red neuronal artificial que procesa de forma automática epitelios en 3D, esto es, permite la reconstrucción automática en 3D de imágenes obtenidas por microscopía.En busca de patrones ocultos
Los animales y plantas, además de otras estructuras de la naturaleza, presentan patrones que podemos detectar fácilmente: las rayas de las cebras, los polígonos de la jirafa o en las conchas de las tortugas, por ejemplo. Todos estos patrones tienen en común que son macroscópicos. Sin embargo, este mismo fenómeno se da a nivel microscópico, en los tejidos. “Estos patrones también aparecen durante el desarrollo embrionario”, explica Luis M. Escudero, uno de los autores e investigador del Instituto de Biomedicina de Sevilla (IBiS) y profesor de la Universidad de Sevilla. “Por ejemplo, hay genes que se expresan en patrones alternos de rayas y que son fundamentales para establecer los segmentos de los insectos”. Muchos de dichos patrones son ya conocidos y muy estudiados, sin embargo, queda mucho por descubrir.
“En nuestro trabajo hemos encontrado patrones que aún estaban escondidos…. Y que solo han podido ser desvelados al usar herramientas de inteligencia artificial para el análisis de imágenes microscópicas de tejidos. Vemos que, incluso en estructuras muy simples, ya hay asimetrías en la morfología de las células. Esta es la forma en que comienza la morfogénesis”. La morfogénesis se refiere al proceso biológico que causa que un organismo desarrolle su forma y estructura. Es una de las etapas fundamentales durante el desarrollo embrionario y se refiere a la organización y distribución espacial de las células diferenciadas para formar estructuras específicas y eventualmente órganos completos.
CartoCell, una herramienta para cartografiar los tejidos epiteliales“CartoCell es una herramienta software que permite procesar de manera rápida y automática una gran cantidad de imágenes 3D obtenidas en el microscopio para la reconstrucción y el análisis de tejidos epiteliales a nivel celular”, prosigue el Dr. Escudero. En otras palabras, esta herramienta digital es capaz de trabajar de forma automática muchísima información, especializándose en buscar patrones, formas, distribuciones y estructuras en los tejidos a partir de imágenes.
Según aclara, CartoCell utiliza la potencia de las redes neuronales, específicamente una red neuronal artificial diseñada para optimizar la identificación de células tridimensionales en imágenes de microscopía. La principal ventaja de CartoCell es que puede identificar y estudiar la forma y distribución espacial de cada célula en el tejido epitelial, permitiendo descubrir patrones asociados a diferentes tipos de tejidos.
“Cada célula del tejido es reconstruida con una gran fidelidad, gracias a lo cual podemos estudiar tanto su forma como su distribución espacial. De este modo, CartoCell nos permite descubrir patrones asociados a los diferentes tipos de tejidos y células, así como estudiar sus reglas de empaquetamiento”. De momento, el software ha sido usado para estudios de ciencia básica, permitiendo cartografiar la morfología de las células con imágenes de diferentes tipos de tejidos. “De este modo, hemos podido encontrar patrones ocultos de una manera sencilla y muy visual”, continúa el investigador, “lo que es fundamental para estudiar la organización de tejidos epiteliales donde las células presentan un contacto estrecho”.
Pero, además de los patrones ocultos, y de la investigación biológica de tejidos, CartoCell también muestra un gran potencial de aplicación clínica. “En el ámbito biomédico, la posibilidad de analizar una gran cantidad de muestras de manera rápida y fiable, como hace CartoCell, es ideal para evaluar la reproducibilidad de cultivos de organoides [pequeños tejidos creados para simular un pequeño órgano] epiteliales y realizar comparativas detalladas entre condiciones normales y patológicas. Por poner un ejemplo sencillo”, continúa el investigador, “el testeo del efecto de fármacos en tejidos animales o humanos podría beneficiarse de nuestro método. Nuestro avanzado análisis de imágenes podría detectar cambios sutiles a nivel celular, que a la larga pueden ser importantes, del efecto de cada fármaco contra una determinada enfermedad”.
Redes neuronales y código abierto en su núcleoEl corazón de CartoCell es una red neuronal artificial. La arquitectura de la red fue diseñada partiendo de otros modelos desarrollados anteriormente por el grupo de investigación en visión artificial para bioimagen del Instituto Biofisika y el Donostia International Physics Center (DIPC), en el País Vasco, que participa en el proyecto. “Estos modelos ya habían demostrado gran versatilidad y robustez para problemas similares en imagen de microscopía de diferentes modalidades (microscopía electrónica y microscopía confocal, entre otras)”, explica el doctor Ignacio Arganda, líder de dicho grupo e investigador Ikerbasque afiliado también a la Facultad de Informática de la Universidad del País Vasco (UPV/EHU). “En concreto, la arquitectura y las imágenes de salida que genera fueron adaptadas para optimizar la identificación de células tridimensionales adquiridas mediante técnicas de microscopía”.
“Como toda red neuronal artificial”, continúa, “la nuestra necesita del conocido como conjunto de entrenamiento para aprender a realizar la tarea que le propongamos. En nuestro caso, dicha tarea se trata de la identificación (o “segmentación”) de células epiteliales en imágenes tridimensionales”. Normalmente, para que una red neuronal sea capaz de generalizar y realizar esta tarea con precisión, necesita un conjunto de datos muy grande y heterogéneo. Construir dicho conjunto requiere muchísimo trabajo manual, ya que habría que “pintar” una a una todas las células de las imágenes 3D de entrenamiento.
“Sin embargo”, aclara el experto, “CartoCell utiliza un conjunto de entrenamiento inicial de epitelios pintados muy pequeño. Con ese conjunto, entrenamos nuestra red neuronal una primera vez, e intentamos que prediga las identidades celulares en muchas otras imágenes de epitelios. Como es esperado, el resultado no es el ideal, pues muchas identidades no están completas, y quedan huecos entre las células. Para solucionarlo, empleamos un algoritmo de Voronoi que rellena los espacios vacíos entre las células identificadas, consiguiendo así que contacten entre ellas».
“Estas etiquetas celulares transformadas son las que llamamos weak labels [etiquetas débiles], y las utilizamos como nuestro nuevo conjunto de entrenamiento. Aunque estas etiquetas no son totalmente perfectas, capturan de una forma bastante realista la morfología celular (dado que las células epiteliales comparten algunas características de organización con los patrones de Voronoi). Además, al ser muchas y muy heterogéneas, ayudan a mejorar el proceso de re-entrenamiento de la red. Este paso es clave en CartoCell, ya que nos permite conseguir muy buenos resultados en segmentación sin tener que emplear un tiempo excesivo en etiquetar manualmente un conjunto de entrenamiento grande”, completa el investigador.
Una de las características de CartoCell es su versatilidad, según defiende el Dr. Pedro Gómez-Gálvez, autor también del trabajo y actualmente en el Departamento de Fisiología, Desarrollo y Neurociencia de la Universidad de Cambridge (Reino Unido). En concreto, su red neuronal se podría sustituir por cualquier modelo de segmentación del estado del arte (redes neuronales convolucionales 3D o cualquiera de sus variantes), siempre y cuando se utilice el concepto de etiquetado ligero o “weak labels” anteriormente descrito para mejorar el conjunto de entrenamiento. “De hecho, en nuestro artículo probamos con varias arquitecturas de red modernas y, con todas, los resultados fueron muy buenos tras el etiquetado ligero siguiendo el algoritmo de Voronoi”, confirma Gómez-Galvez.
Además, CartoCell es una herramienta de código abierto, lo que brinda la oportunidad a otros expertos de utilizar, mejorar o adaptar libremente su uso. “Todas las personas que hemos participado en la creación de CartoCell creemos firmemente en la idea de ciencia abierta. Consecuentemente, CartoCell ha sido implementado desde el primer día como código abierto, y siempre ha estado disponible para la comunidad. En ese sentido, nuestra intención ha sido crear una herramienta accesible, fácil de instalar y utilizar por personas no expertas, pero también adaptable y ampliable para quien quiera desarrollar nuevas soluciones sobre ella”, concluye.
Referencia:
Jesus A. Andres-San Roman, Carmen Gordillo-Vazquez, Daniel Franco-Barranco, Laura Morato, Cecilia H. Fernández-Espartero, Gabriel Baonza, Antonio Tagua, Pablo Vicente-Munuera, Ana M. Palacios, María P. Gavilán, Fernando Martín-Belmonte, Valentina Annese, Pedro Gómez-Gálvez, Ignacio Arganda-Carreras, Luis M. Escudero (2023) CartoCell, a high-content pipeline for 3D image analysis, unveils cell morphology patterns in epithelia Cell Reports Methods doi: 10.1016/j.crmeth.2023.100597
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo CartoCell o cómo detectar patrones ocultos en tejidos celulares se ha escrito en Cuaderno de Cultura Científica.
Minerales con brillo
brillo
Los minerales, esas sustancias sólidas naturales formadas por elementos químicos ordenados en estructuras cristalinas, presentan una serie de propiedades físicas y químicas que les son únicas y características, lo que nos permite utilizarlas como criterios identificativos y clasificatorios.
Dicho de otro modo y un poco más sencillo. Debido a la composición química de los minerales y la estructura interna que presentan esos elementos químicos, cada mineral tiene unas características concretas que se pueden observar a simple vista y que son propias de cada uno de ellos, lo que nos permite identificarlos rápidamente diferenciándolos de los demás. Si lo asimilamos a los seres humanos, serían esos caracteres heredados que sirven para describir a una persona sin confundirla con otra, como el color del pelo y de los ojos, el tono de la piel, la altura, la presencia de pecas y lunares o el rango de nuestra voz.
Esto nos da mucho juego cuando organizamos actividades de divulgación geológicas, ya que podemos plantear talleres de identificación de minerales de manera muy sencilla y utilizando artilugios de andar por casa, como un trozo de loza, una navaja o un vidrio, que suelen llamar mucho la atención del público asistente. Y, aunque la mayoría de las propiedades físicas y químicas a las que hacemos alusión son muy fáciles tanto de explicar cómo de entender, hay una que se le suele atragantar a la gente. Me estoy refiriendo al brillo.
 A) Ejemplar de galena, mineral con brillo metálico. B) Cristales de cuarzo, mineral con brillo no metálico.
A) Ejemplar de galena, mineral con brillo metálico. B) Cristales de cuarzo, mineral con brillo no metálico.En una definición rápida, el brillo es el aspecto que adquiere la superficie de un mineral cuando refleja la luz. Y de aquí viene la confusión. Cuando hablamos de reflejar la luz, nos imaginamos a las ondas luminosas rebotando con fuerza contra la cara del mineral y volviendo a la fuente de emisión como un nuevo haz de luz, casi como si ese mineral se convirtiese por sí mismo en emisor y produjese un destello luminoso. Esto es lo que vemos, por ejemplo, cuando el Sol incide en un objeto de metal en la calle, cuyo reflejo se convierte en un resplandor que nos marca exactamente su posición y nos molesta si lo miramos fijamente. Esto nos lleva a pensar que existen minerales que brillan, que serían aquellos que generan este efecto luminoso, y minerales que no brillan, entre los que incluiríamos todos aquellos que no provocan ese destello.
Pues este es el error que comentemos todas las personas la primera vez que nos enfrentamos a tener que describir esta propiedad óptica de los minerales, porque, en realidad, todos y cada uno de los minerales del planeta tienen brillo. Precisamente, esa apreciación visual que os he comentado en el párrafo anterior y que es totalmente intuitiva es la que nos permite clasificar el tipo de brillo de los minerales, diferenciando dos grandes grupos. Por un lado, aquellos minerales que tienen el aspecto brillante de un metal cuando les incide la luz decimos que tienen brillo metálico. Se trata de minerales de colores oscuros y opacos, es decir, que no dejan que les atraviese la luz, como la pirita (sulfuro de hierro, FeS2) o la galena (sulfuro de plomo, PbS). Y, por otro lado, tenemos los minerales de brillo no metálico, que son todos aquellos de colores claros y que se comportan como transparentes o translúcidos, por lo que transmiten la luz bien en parte o bien en su totalidad.
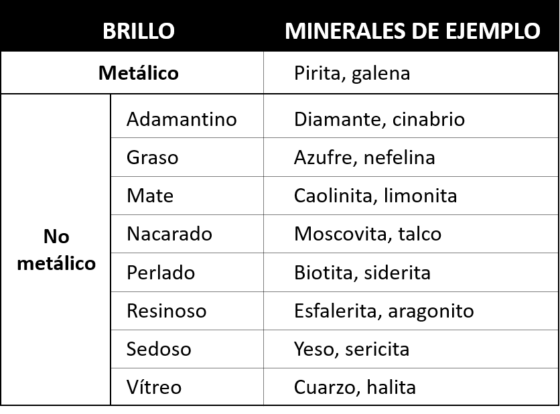 Tabla con la clasificación de los tipos (metálico y no metálico) y subtipos (adamantino, graso, mate, nacarado, perlado, resinoso, sedoso y vítreo) de brillo más comunes en los minerales, con algunos ejemplos característicos. Imagen modificada del original de Minerales de Visu / Universidad de Alicante
Tabla con la clasificación de los tipos (metálico y no metálico) y subtipos (adamantino, graso, mate, nacarado, perlado, resinoso, sedoso y vítreo) de brillo más comunes en los minerales, con algunos ejemplos característicos. Imagen modificada del original de Minerales de Visu / Universidad de AlicantePodemos encontrar diferentes subdivisiones o agrupaciones dentro de los minerales con brillo no metálico, como los de brillo vítreo porque nos recuerdan al brillo que presenta el vidrio de una ventana, que es lo que le ocurre al cuarzo (dióxido de silicio, SiO2), o los de brillo nacarado, que en este caso se asemeja a las irisaciones que se producen en las perlas y es característico del talco (silicato de magnesio hidratado, Mg3Si4O10(OH)2). Pero, por lo general, no entramos en tanto detalle a la hora de clasificar los minerales de acuerdo a su brillo, decimos simplemente que tienen brillo metálico o brillo no metálico.
Sé que he repetido la palabra clave brillo en demasiadas ocasiones a lo largo del texto, pero ha sido totalmente a posta para dejar las ideas bien claras de que todos los minerales tienen esta propiedad y que es una de las características físicas básicas para clasificarlos. Así, cuando os enfrentéis a un apasionante taller divulgativo de identificación de minerales, sabréis la diferencia entre brillo metálico y brillo no metálico y podréis seguir jugando con sus propiedades hasta que acertéis el nombre correcto del ejemplar que tengáis en la mano.
Agradecimiento:
Quiero dar las gracias a Ana Rodrigo, Directora del Museo Geominero del Instituto Geológico y Minero de España (IGME-CSIC), por darme la idea de escribir este artículo tras una interesante conversación sobre cómo mejorar nuestras actividades de divulgación geológicas, resaltando la problemática del público en general a la hora de entender algunas de las propiedades características de los minerales.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Minerales con brillo se ha escrito en Cuaderno de Cultura Científica.
Svetlana Jitomirskaya, la matemática que ganó la mitad de diez martinis
Ella era tan brillante que yo sabía que yo no lo era tanto.
Svetlana Jitomirskaya en [4].
En la anterior cita, la matemática Svetlana Jitomirskaya se refiere a Valentina Borok, su madre, que fue una destacada matemática ucraniana. De ella ya hablamos en este Cuaderno de Cultura Científica.
A pesar de lo brillante que era su madre, Svetlana Jitomirskaya no se queda atrás. Especialista en sistemas dinámicos y física matemática, en 2005 obtuvo el Premio Ruth Lyttle Satter en matemáticas por su trabajo pionero en su especialidad. Y, junto a Artur Ávila, resolvió en 2009 el conocido como problema de los diez martinis en el área de los sistemas dinámicos.
 Svetlana Jitomirskaya. Fuente: Springer.
Svetlana Jitomirskaya. Fuente: Springer.Una familia matemática
Svetlana Yakovlevna Jitomirskaya es la hija pequeña de los matemáticos Valentina Mikhailovna Borok y Yakov Yitomirski, que realizaron conjuntamente una parte importante de su investigación.
Su hermano mayor, Michail Zhitomirski (1958) también ha dedicado su vida profesional a las matemáticas. En este momento trabaja en teoría de variedades diferenciables en el Instituto Tecnológico de Israel en Haifa.
Svetlana Yakovlevna Jitomirskaya nació el 4 de junio de 1966 en Járkov (Ucrania). Comentaba sobre sus primeros años (ver [3]):
Cuando yo nací, mis padres ya eran catedráticos (en una sociedad en la que este título inspiraba mucho respeto). Mi madre era sin duda la matemática más destacada del país. Después de haber criado a mi hermano mayor, que estaba claramente dotado para las matemáticas, mis padres pensaron que un matemático más en nuestra familia sería demasiado. Me animaron a interesarme por cosas variadas, y empecé a inclinarme seriamente por las humanidades. Escribí poesía (premiada) y gané algunos concursos nacionales de bachillerato en literatura rusa. Planeé un futuro estudiando (si no escribiendo) poesía rusa.
A pesar de que ni ella ni su familia pensaban que se iba a dedicar a las matemáticas, Svetlana, a sus 14 años, se enamoró durante unas vacaciones de un chico que vivía en Moscú. Sabía que era difícil mantener una relación a distancia y, ya con 16 años, vio que la única manera que tenía de estar cerca de su amado era ingresando en la Universidad Estatal de Moscú. En aquella época esta institución limitaba el número de estudiantes judíos que podían acceder a sus enseñanzas. Para mantener esas cuotas limitantes los aspirantes judíos eran sometidos a preguntas exageradamente difíciles durante los exámenes orales de ingreso. De esta manera intentaban asegurar que el alumnado judío no constituyera más del 0,5 % del estudiantado total. Svetlana sabía que tenía muy pocas posibilidades de aprobar en cualquier disciplina, pero las matemáticas aparecieron como una opción mejor que las humanidades al haber una competencia mucho menor y una mayor objetividad.
Las matemáticas llegan de manera inesperadaCon esta idea en la cabeza dedicó su último año de instituto a preparar el examen oral de matemáticas. En sus propias palabras (ver [3]):
Creo que durante ese año resolví todos los problemas elementales complicados que había, y algunos más. Me tomaba cada problema como algo personal y lo atacaba como si mi felicidad futura dependiera de si lo resolvía o no. Me aceptaron en la Universidad Estatal de Moscú; sin embargo, no puedo considerarlo una victoria personal como me hubiera gustado. No llegué a mostrar ni una fracción de mis habilidades en aquel examen oral, ya que no me sometieron a ese trato «judío» (quizá, debido a las conexiones de mis padres). Sin embargo, algo me ocurrió durante esa extensa preparación, ya que empecé a amar el proceso.
Y de este modo consiguió acercarse a Moscú para no separarse de Vladimir A. Mandelshtam, quien posteriormente se dedicó a la química, con quien se casó en cuanto alcanzó su mayoría de edad.
Jitomirskaya terminó sus estudios universitarios en 1987, graduándose con matrícula de honor. Continuó con su formación doctoral en la Universidad Estatal de Moscú, bajo la supervisión de Yákov Grigórevich Sinái (1935), que también la había asesorado durante sus estudios universitarios. Sinái es un reconocido especialista en teoría de sistemas dinámicos, física matemática y teoría de la probabilidad. Reconocido con el Premio Abel en 2014, fue el principal artífice de la mayoría de los puentes que conectan el mundo de sistemas deterministas (dinámicos) con el mundo de los sistemas probabilísticos (estocásticos).
Svetlana presentó su tesis doctoral en 1991: Spectral and Statistical Properties of Lattice Hamiltonians. Ese mismo año, Vladimir finalizó también su trabajo doctoral.
Antes de finalizar su tesis, en 1990, comenzó a trabajar como investigadora en el Instituto Internacional de Teoría de la Predicción de Terremotos y Geofísica Matemática de Moscú, centro en el que ya trabajaba su marido.
Un año más tarde ofrecieron a Svetlana un puesto postdoctoral en la Universidad de California en Irvine y a Vladimir otro en la Universidad del Sur de California. Aceptaron ambas ofertas de trabajo porque estarían cerca, aunque no fuera en el mismo centro. Lo que pensaron que iba a ser una estancia de un año se convirtió en su lugar de trabajo y residencia definitivos.
Una matemática reconocidaJitomirskaya recibió el Premio Ruth Lyttle Satter 2005 de la American Mathematical Society. Este premio se concede cada dos años en reconocimiento a una contribución destacada a la investigación matemática realizada por una mujer en los cinco años anteriores. El comité de selección destacó (ver [1]):
El Premio Ruth Lyttle Satter de Matemáticas se concede a Svetlana Jitomirskaya por su trabajo pionero sobre la localización cuasiperiódica no perturbativa, en particular por los resultados de sus artículos (1) «Metal-insulator transition for the almost Mathieu operator«, Ann. of Math. (2) 150 (1999), no. 3, 1159-1175, y (2) con J. Bourgain, «Absolutely continuous spectrum for 1D quasiperiodic operators«, Invent. Math. 148 (2002), no. 3, 453-463. En su artículo de los Annals, desarrolló un enfoque no perturbativo de la localización cuasiperiódica y resolvió la vieja conjetura de Aubry-Andre sobre el operador casi Mathieu. Su artículo con Bourgain contiene el primer resultado general no perturbativo sobre el espectro absolutamente continuo.
Además, entre otros reconocimientos, Jitomirskaya ganó en 2020 del Premio Dannie Heineman de Física Matemática que se otorga cada año desde 1959 conjuntamente por la American Physical Society y el American Institute of Physics. Svetlana recibió este galardón:
Por su trabajo en la teoría espectral de operadores de Schrödinger casi periódicos y cuestiones relacionadas en sistemas dinámicos. En particular, por su papel en la solución del problema de los diez martinis, relativo a la naturaleza de conjunto de Cantor del espectro de todos los operadores casi Mathieu y en el desarrollo de los aspectos matemáticos fundamentales de los fenómenos de localización y transición metal-aislante.
El problema de los diez martinis lleva este nombre porque el especialista en teoría de la probabilidad Mark Kac (1914-1984) ofreció diez martinis a quien lo solucionara. Jitomirskaya lo resolvió junto al matemático Artur Avila (1979) en el artículo The Ten Martini Problem publicado en 2009.
A Svetlana Jitomirskaya aún le quedan muchos éxitos matemáticos por conseguir. Su madre fue un modelo extraordinario para ella. Al recibir el premio Ruth Lyttle Satter, comentó lo siguiente en su discurso de agradecimiento (ver [1]):
Debo decir que nunca me he sentido en desventaja por ser una mujer matemática; de hecho, hasta cierto punto ocurre lo contrario. Sin embargo, en comparación con la mayoría de las demás, tuve una ventaja única: un modelo fantástico desde muy pronto: mi madre, Valentina Borok, que habría sido mucho más merecedora de un premio así que yo ahora, si hubiera existido en su época. Para mí, recibir este premio es un homenaje especial a su memoria. Es un placer aprovechar esta oportunidad para darle las gracias.
Referencias
[1] AMS; 2005 Satter Prize, Notices of the AMS 52 (4) 447-448, 2005.
[2] Svetlana Jitomirskaya, Valentina Mikhailovna Borok, MacTutor History of Mathematics archive, University of St Andrews.
[3] John O’Connor and Edmund Robertson, Svetlana Yakovlevna Jitomirskaya, MacTutor History of Mathematics archive, University of St Andrews.
[4] Margarita Rodríguez, Svetlana Jitomirskaya, la matemática detrás de la solución a “el problema de los diez martinis” de la mecánica cuántica, BBC News, 10 de diciembre de 2022.
[5] Valentina Borok, Wikipedia.
[6] Svetlana Jitomirskaya, Wikipedia.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Svetlana Jitomirskaya, la matemática que ganó la mitad de diez martinis se ha escrito en Cuaderno de Cultura Científica.
La ‘repulsión de la especie’ permite una alta biodiversidad en los árboles tropicales
repulsión
Debido a que las plántulas de los árboles no crecen tan bien cuando están cerca de sus progenitores, se pueden concentrar más especies de árboles en los bosques tropicales.
Un artículo de Veronique Greenwood. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons
 Vista aérea del bosque tropical en la Isla de Barro Colorado. Fuente: Christian Ziegler / Wikimedia Commons / Gewin V, PLoS Biology Vol. 4/8/2006, e278 doi: 10.1371/journal.pbio.0040278
Vista aérea del bosque tropical en la Isla de Barro Colorado. Fuente: Christian Ziegler / Wikimedia Commons / Gewin V, PLoS Biology Vol. 4/8/2006, e278 doi: 10.1371/journal.pbio.0040278Para los ecólogos, las selvas tropicales encierran muchos enigmas. Una sola hectárea puede contener cientos de especies de árboles, muchas más que en los bosques más cercanos a los polos. De alguna manera estas especies coexisten en una abundancia tan vertiginosa que, como han señalado a veces los naturalistas y ecólogos, los bosques tropicales pueden parecer jardines botánicos, donde cada planta es algo nuevo.
Para que tal multitud de especies esté tan densamente agrupada deben coexistir en un equilibrio muy particular. La evolución parece no favorecer situaciones en las que una sola especie prospera de manera demasiado agresiva, sino que favorece aquellas en las que los organismos están rodeados de especies distintas a la suya. Conciliar estos hechos con lo que se sabe sobre cómo las especies se distribuyen, compiten e influyen entre sí es un desafío.
Para estudiar esta extraordinaria diversidad hace años los científicos comenzaron a establecer parcelas de bosque donde podían registrar y rastrear la ubicación y el estado de cada árbol durante décadas. Una de las primeras parcelas de este tipo, en la isla de Barro Colorado (IBC) en Panamá, tiene 500 metros de ancho por 1.000 metros de largo (el área de unos 70 campos de fútbol) y contiene más de 300 especies. Desde 1980, investigadores de todo el mundo han estudiado minuciosamente los registros detallados de sus habitantes.
En un artículo publicado recientemente en Science, investigadores de la Universidad de Texas en Austin modelaron varios escenarios de distribución y los compararon con datos de IBC. Descubrieron que los patrones en la dispersión de semillas por el viento o por las aves y otros animales salvajes, así como procesos más aleatorios, no eran suficientes para explicar la distribución de los árboles adultos en el bosque. Sugieren que esto es evidencia de una “repulsión específica de la especie”, una teoría de larga data de que los árboles de la misma especie se espacian naturalmente porque el ambiente que rodea inmediatamente a un árbol padre es específicamente hostil a la propia descendencia del árbol.
Distanciamiento social en árbolesEsta idea de repulsión, formalmente conocida como dependencia negativa de la densidad conespecífica, o CNDD (por sus siglas en inglés), se remonta a la década de 1970, cuando los ecólogos Daniel Janzen y Joseph Connell sugirieron de forma independiente que los insectos, herbívoros y patógenos que se alimentan selectivamente de una especie podrían hacer que el área alrededor de un árbol adulto fuese peligrosa para sus semillas. No se impediría con la misma eficacia que otras especies creciesen en la zona, aunque seguirían estando limitadas por problemas no específicos, como la falta de luz solar bajo la copa de un árbol adulto. El resultado sería que los árboles adultos de una especie tenderían a mantener una especie de “distancia social” mínima entre sí.
Los ensayos realizados en las últimas décadas, principalmente con plántulas, apoyan la CNDD, afirma Michael Kalyuzhny, autor principal del nuevo artículo, cuyo trabajo como investigador postdoctoral en la Universidad de Texas en Austin le ha llevado a abrir un laboratorio en la Universidad Hebrea de Jerusalén. Las semillas a menudo no crecen tan bien en el suelo tomado de lugares cercanos a sus árboles progenitores como en el suelo de lugares cercanos a árboles no relacionados.
Sin embargo, incluso una mirada superficial a los datos del IBC muestra que los árboles adultos en ese bosque no parecen repelerse entre sí. En cambio, los árboles se agrupan, formando grupos sueltos de la misma especie en toda la parcela.
Kalyuzhny y Annette Ostling, la ecóloga comunitaria que dirige el laboratorio donde trabaja Kalyuzhny, se propusieron modelar diferentes escenarios que podrían explicar las distribuciones de árboles observadas, para saber si algo podría estar dificultando el papel de la CNDD en el bosque.
El azar por sí solo no es la respuesta: cuando ejecutaron un modelo nulo, en el que los árboles estaban espaciados aleatoriamente, los árboles adultos de una especie se dispersaban demasiado.
Entonces los investigadores introdujeron el efecto de la dispersión de semillas en sus modelos, que podría ser por el viento, las aves y otros animales. Helene Muller-Landau y sus colaboradores de IBC han hecho estimaciones de lo lejos que puede viajar una semilla desde su fuente dentro de una parcela de 50 hectáreas, utilizando redes que capturan las semillas a medida que van a la deriva hacia el suelo del bosque. Las semillas se recolectan periódicamente y se calcula la distancia a sus progenitores. Kalyuzhny y sus colegas se han basado en estos datos para modelar disposiciones de los árboles determinadas únicamente por la limitación de la dispersión.
 Adult trees in tropical forests produce seeds and seed pods that have wildly diverse shapes, which allows them to be spread by wind or by animals in different ways. Foto: Christian Ziegler
Adult trees in tropical forests produce seeds and seed pods that have wildly diverse shapes, which allows them to be spread by wind or by animals in different ways. Foto: Christian ZieglerPero este modelo produjo árboles demasiado agrupados. Algo parecía estar actuando sobre la distribución producida por la limitación de la dispersión, dispersando los árboles. “Algo está creando esta repulsión. Y no podemos pensar en otra cosa que en la CNDD”, explica Kalyuzhny.
Cuando los investigadores calcularon lo específica que era la repulsión (cuánto peor era para un árbol estar cerca de su propia especie que de otra), descubrieron que habría tenido que ser bastante fuerte para producir el patrón observado. Esto confirmó un punto esencial de las ideas de Janzen y Connell: «Lo que sea que cree la CNDD tiene que ser específico de cada especie», añade Kalyuzhny.
La importancia de los eventos rarosRyan Chisholm, ecólogo teórico y profesor de la Universidad Nacional de Singapur que estudia la distribución de los árboles tropicales, está de acuerdo en que los hallazgos de Kalyuzhny encajan con trabajos anteriores sobre la CNDD. Sugiere, sin embargo, que los modelos podrían estar subestimando hasta qué punto los mecanismos de dispersión pueden propagar las semillas. Si los eventos de gran dispersión son raros, por ejemplo, podrían ser difíciles de ver en los datos de las trampas de semillas. Y si las semillas son transportadas más lejos de lo que los investigadores creen, eso podría explicar los grupos de árboles más dispersos en los bosques sin necesidad de repulsión.
«Lo que están diciendo aquí es que según su modelo de limitación de dispersión, los patrones que observan son imposibles», dijo Chisholm. «Yo diría que todavía no sabemos lo suficiente para decir eso».
Los eventos raros han sido importantes en la dispersión de especies de todo tipo: se cree que los monos, por ejemplo, llegaron a América desde África en balsas de vegetación, un evento tremendamente improbable que, sin embargo, tuvo consecuencias significativas. «Ocasionalmente, encontrarás ese pájaro que lleva la semilla muy lejos, o que queda atrapado por el viento y se lanza a la aventura», comenta Chisholm.
Señala que todavía no conocemos suficientemente bien la forma de la curva de distribución de semillas; no es una simple curva de campana, como podrían pensar los no expertos, porque parece tener una “cola muy gruesa” al final.
Si los ecólogos tuvieran datos a una escala mucho mayor que 50 hectáreas, algo que prometen las nuevas técnicas de estudio mediante las cuales los científicos pueden contar árboles desde el aire, podría surgir una nueva visión. Podría ser posible ver patrones que no se ven actualmente, lo que podría cambiar la comprensión del papel que desempeñan la CNDD y la limitación de la dispersión de semillas en la disposición de los bosques. «Esta era de simplemente contemplar una parcela de 50 hectáreas parecerá extremadamente pintoresca, como un telescopio portátil en comparación con el Hubble», predice Chisholm.
Por ahora, Kalyuzhny y sus colegas planean realizar análisis similares en otras parcelas de estudio en todo el mundo para ver qué patrones emergen: ahora hay más de 70 sitios en todo el mundo con parcelas de hasta 50 hectáreas de tamaño, todas monitoreadas como la parcela en IBC. También han realizado simulaciones en las que ajustan el alcance de la CNDD y han descubierto que incluso la repulsión en distancias relativamente cortas puede provocar grandes efectos a escala del bosque.
“Yo repelo a mis vecinos, y ellos repelen a sus vecinos, y ellos repelen a sus vecinos”, explica Kalyuzhny, describiendo cómo pueden surgir patrones a gran escala a partir de acciones a pequeña escala. «El bosque es un cristal desordenado».
El artículo original, ‘Species Repulsion’ Enables High Biodiversity in Tropical Trees, se publicó el 13 de septiembre de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo La ‘repulsión de la especie’ permite una alta biodiversidad en los árboles tropicales se ha escrito en Cuaderno de Cultura Científica.

