La paradoja del asno de Buridán
Jean Buridan (hacia 1292-hacia 1363) fue un filósofo escolástico francés, instigador del escepticismo religioso en Europa.
 Historieta satírica estadounidense (hacia 1900) sobre la indecisión del Congreso entre la elección de la ruta del canal de Panamá o del canal de Nicaragua y aludiendo a la paradoja de Buridán. Imagen: Wikimedia Commons.
Historieta satírica estadounidense (hacia 1900) sobre la indecisión del Congreso entre la elección de la ruta del canal de Panamá o del canal de Nicaragua y aludiendo a la paradoja de Buridán. Imagen: Wikimedia Commons.Una leyenda –propagada por la Balada de las damas de antaño del poeta François Villon (1431-1463¿?) y popularizada por el cantautor Georges Brassens– asociaba a Buridan –equivocadamente– con el escándalo de la torre de Nesle:
Y ¿dónde está, si no, la reina
que a Buridán hizo meter
en un saco y lo tiró al Sena?
¿Dónde están las nieves de ayer?
¿En un saco y lo tiró al Sena?
¿Dónde están las nieves de ayer?
Fragmento extraído de ‘Brassens en castellano’ (traducido por Ramón García Toga)
Su nombre se asocia también a un experimento mental conocido como ‘la paradoja del asno de Buridán’, a pesar de que no se recoge en ninguna de las obras conocidas de este filósofo. Sin embargo, un problema similar aparece en el tratado Sobre el cielo de Aristóteles (384 a. C.-322 a. C.), en un momento en el que su autor se preguntaba sobre cómo un hombre sediento y hambriento, situado a la misma distancia de una mesa llena de alimentos y otra llena de bebidas, se las arreglaría para escoger entre ambas ofertas… Y concluía que necesariamente, ¡se mantendría inmóvil!
En su comentario sobre el anterior tratado del polímata griego, Buridan cambiaba a la persona por un perro confrontado a este cruel dilema. Aludía a esta posibilidad como a la de una alternativa sin sentido comparable ‘a la que debería sopesar los méritos de la gravedad terrestre y del objeto pesado que se somete a ella.’
Buridan no discutió este problema en particular, pero aludía en su obra a la existencia de un determinismo moral en el que un ser humano que se enfrenta a posibles decisiones, siempre debe elegir el mayor bien, aunque la voluntad puede demorar la elección.
 L’âne de Buridan entre deux opinions (1859) por A-C-H de Noé. Imagen: Wikimedia Commons.
L’âne de Buridan entre deux opinions (1859) por A-C-H de Noé. Imagen: Wikimedia Commons.Posteriormente se satirizó esta visión por medio de la historia de un asno sediento y hambriento, situado a la misma distancia entre un cubo de agua y otro de avena… y que acababa muriendo, incapaz de elegir el cubo por el que le convenía.
Más que una paradoja, esta historia podría catalogarse como un dilema llevado al absurdo, ambos rasgos caracterizando el fenómeno del doble vínculo.
Parece que Baruch Spinoza (1632-1677) fue el primero en hablar de la Buridani asina –la asna de Buridán… en efecto, no el asno– en su Ethica (traducción de Vidal Peña):
[…] Puede objetarse que si el hombre no obra en virtud de la libertad de su voluntad, ¿qué sucederá si está en equilibrio, como el asna de Buridán? ¿Perecerá de hambre y sed? Si lo admito, parecería que pienso en un asno, o en una estatua de hombre, y no en un hombre, pero si lo niego, entonces el hombre se determinará a sí mismo y, por consiguiente, tendrá la facultad de dirigirse a donde quiera y hacer lo que quiera. […] Concedo por completo que un hombre, puesto en tal equilibrio (a saber, sin otras percepciones que las de la sed y el hambre, y las de tal y cual comida y bebida que están a igual distancia de él), perecerá de hambre y sed. Si me preguntan: ¿acaso tal hombre no debe ser estimado más bien como un asno que como un hombre?, respondo que no lo sé, como tampoco sé cómo ha de ser estimado el que se ahorca, o cómo han de ser estimados los niños, los necios, los locos, etc.
Buridan y Spinoza difieren en sus conclusiones. Para el primero, el asno moriría, pero un ser humano enfrentado a la misma situación sería capaz de elegir arbitrariamente… para el segundo el hombre actuaría de la misma manera que el animal… ¿Qué opináis?
Referencias:
Jean Buridan, Wikipédia (consultado el 19 de noviembre de 2018)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo La paradoja del asno de Buridán se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Fase y ecuación de onda
 En determinados estamentos se da mucha importancia al concepto de fase. Como en este caso muestran los cadetes de la Escuela de Suboficiales del Sargento 2° Daniel Rebolledo Sepúlveda (Chile).
En determinados estamentos se da mucha importancia al concepto de fase. Como en este caso muestran los cadetes de la Escuela de Suboficiales del Sargento 2° Daniel Rebolledo Sepúlveda (Chile).El concepto de fase no es en sí mismo complicado. La palabra fase suele emplearse habitualmente para indicar cada uno de los distintos estados sucesivos de un fenómeno natural (o histórico). Decimos habitualmente, pero hemos de ser conscientes de que no siempre para evitar errores. Así, por ejemplo, también se llama fase a una parte homogénea con límites bien definidos de un sistema heterogéneo, un concepto que, si bien tiene su origen en el uso habitual (el agua solida al calentarse pasa sucesivamente a una fase líquida y después a una fase vapor, por ejemplo), es un concepto actualmente independiente de la idea de estado sucesivo.
El concepto de fase es fundamental para entender el funcionamiento de una onda periódica. El siguiente diagrama representa una onda periódica que pasa a través de un medio. En él aparecen marcados conjuntos de puntos que se mueven “a la vez y de la misma forma” a medida que pasa la onda periódica. Los puntos cresta C y C’ han alcanzado posiciones máximas hacia arriba. Los puntos valle D y D’ han alcanzado posiciones máximas hacia abajo. Los puntos C y C’ tienen desplazamientos y velocidades idénticos en cualquier instante de tiempo. Sus vibraciones son idénticas y van al unísono. Lo mismo ocurre con los puntos D y D’. De hecho hay infinitos pares de puntos a lo largo del medio que vibran de manera idéntica cuando pasa esta onda. Démonos cuenta de que C y C’ están separados una distancia igual a una longitud de onda, λ, al igual que D y D’.
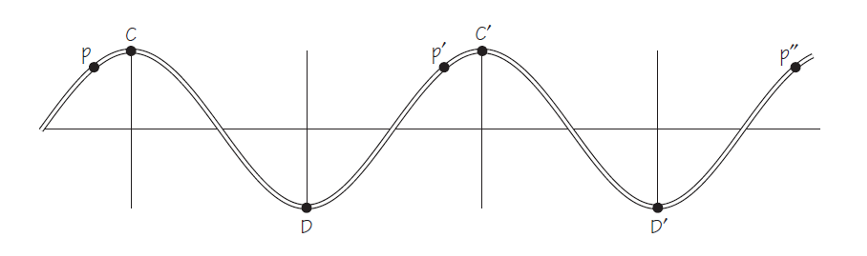
Los puntos que se mueven al unísono, como C y C’, se dice que están en fase entre sí. Los puntos D y D’ también se mueven en fase. De hecho, los puntos separados entre sí por distancias de λ, 2λ, 3λ,. . . o, en general, nλ (siendo n cualquier número entero) están todos en fase entre sí. Estos puntos pueden estar en cualquier lugar (fase) a lo largo de la longitud de la onda. No necesitan corresponderse solo con los puntos más altos o más bajos. Así, puntos como P, P’, P”, están todos en fase entre sí. Cada uno de estos puntos está separado por una distancia λ del siguiente que está en fase con él.
Por otro lado, también podemos ver que algunos pares de puntos están fuera de sincronía. Por ejemplo, el punto C alcanza su máximo desplazamiento hacia arriba al mismo tiempo que D alcanza su máximo desplazamiento hacia abajo. En el instante en que C comienza a bajar, D comienza a subir (y viceversa). Puntos como estos están medio período fuera de fase entre sí. C y D’ también están medio período fuera de fase. Cualquiera dos puntos separados entre sí por distancias de 1⁄2λ , 3/2λ , 5⁄2 λ, etc., están medio período fuera de fase.
En esta serie hacemos hincapié en las ideas, pero entendemos que las matemáticas son la mejor forma de expresarlas de forma eficaz y eficiente, auqnue no nos metamos a fondo con ellas. Si pretendemos representar una onda periódica y sus características en un plano XY, entonces la posición (x,y) de un punto cualquiera en función del tiempo, t, viene dada por la siguiente ecuación de onda:
y(x, t) = A sen (ωt + kx + δ),
donde A es la amplitud, ω es la velocidad angular dada por ω = 2π/T (donde T es el periodo), k es el número de onda dado por k = 2π/λ y δ el desfase. La fórmula parece que es ciencia infusa, pero con los conceptos que hemos visto y este fantástico vídeo de José Luis Crespo, la entenderás perfectamente (incluso sin tener ni idea de trigonometría):
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Fase y ecuación de onda se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Características de una onda periódica
- Propagación de una onda
- Incompletitud y medida en física cuántica (VI): la onda piloto
La boca
 Boca de una lamprea marina (Petromyzon marinus)
Boca de una lamprea marina (Petromyzon marinus)La boca es la entrada al sistema digestivo y puesto que hay una gran diversidad de modalidades de alimentación, existen también muy diferentes tipos de bocas. Los animales que se alimentan de fluidos biológicos tienen una anatomía bucal apta para succionar los líquidos (como algunos insectos fitófagos), aunque pueden necesitar también dispositivos adicionales para perforar tejidos e incluso para anestesiar a su huésped en el caso de los ectoparásitos de animales. Los micrófagos, como bivalvos, suelen tener aparatos filtradores para retener las minúsculas partículas en que consiste su alimento o, si comen sedimentos, dispositivos para seleccionar las de alto valor nutricional de las partículas de escaso o nulo valor. Hay animales macrófagos que engullen animales enteros, sin desmenuzarlos, como algunas serpientes, pero la mayoría han de fragmentar los pedazos de alimento y su boca suele estar dotada de dientes, con los que lo cortan en trozos pequeños. Las aves, sin embargo, han prescindido de los dientes y se han dotado de pico, una estructura dura con una diversidad anatómica y funcional enorme en las diferentes especies.
En los mamíferos la apertura bucal está bordeada por los labios, que aparte de para cerrar la boca o mantener sellado su contorno sobre la superficie mamaria en la lactación, también sirve a algunas especies como herramienta prensil. La bóveda de la cavidad bucal es el paladar, que la separa de las vías respiratorias nasales. La mayor parte de los anfibios, reptiles (aves incluidas) y mamíferos tienen lengua, que es una estructura muscular que cumple variadas funciones. En ciertas especies es el órgano que atrapa el alimento, como en algunas ranas y camaleones; en otras, como los rumiantes, sirve para coger el alimento; perros y gatos la utilizan para beber. Y a muchas especies, como la nuestra, les sirve para conducir el alimento y moverlo durante la masticación. En la lengua hay, además, un gran número de papilas gustativas, aunque también las hay en el paladar, y en la garganta.
El primer tratamiento que recibe la comida en la mayoría de macrófagos (no en las especies que engullen sus presas enteras) es la masticación. Masticando el alimento, se fragmenta en trozos muy pequeños, lo que además de aumentar la superficie expuesta a la acción digestiva1, facilita su posterior ingestión. Además, ayuda a mezclar la comida con la saliva. Y también estimula los receptores de las papilas gustativas, lo que desencadena reflejos de secreción de saliva en la cavidad bucal y de jugos gástricos, pancreáticos y biliares en órganos inferiores del sistema.
Los dientes de peces, anfibios y reptiles están especializados para sujetar y desgarrar los pedazos de alimento. Muchas especies renuevan sus piezas dentales a lo largo de la vida, como hacen tiburones, dinosaurios (estos hacían, claro) y reptiles no aviares (las aves carecen de dientes, como se ha dicho antes), aunque hay grandes diferencias de frecuencia de cambio entre unas especies y otras2. En las serpientes venenosas los colmillos contienen sendos depósitos de veneno. Y hay vertebrados (los misticetos) cuyos dientes vestigiales son reabsorbidos y sustituidos por las ballenas3, que utilizan como filtro para retener los crustáceos eufasiáceos (krill) que les sirve de alimento.
 La saliva de la boca de las sanguijuelas contiene apirasa, que impide la coagulación de la sangre en la herida.
La saliva de la boca de las sanguijuelas contiene apirasa, que impide la coagulación de la sangre en la herida.La saliva es producida por las glándulas salivares. Entre sus funciones se encuentran las siguientes:
(1) Humectación, para lubricar el alimento y facilitar su ingestión.
(2) Digestión, dado que en la mayor parte de animales la saliva contiene amilasa, la enzima que degrada el polisacárido almidón al disacárido maltosa.
(3) En algunas especies la saliva ejerce funciones de defensa, pues (a) contiene lisozima, una enzima que ataca las paredes bacterianas; (b) contiene aglutinina, una glucoproteína que forma complejos con anticuerpos IgA para unirse después a las bacterias; (c) lactoferrina, que se une al hierro que necesitan las bacterias para duplicarse; y (d) arrastrando material que podría ser fuente de alimento para las bacterias.
(4) La saliva es un disolvente para muchas moléculas que estimulan los receptores de las papilas gustativas. Si no están en disolución no surten efectos gustativos.
(5) Suele ser rica en tampón bicarbonato, por lo que neutraliza muchos ácidos de los alimentos, así como los que producen las bacterias.
(6) Puede cumplir también funciones de termorregulación en los animales que no recurren a la sudoración para disipar calor por evaporación en caso de necesidad. Hay animales que incluso impregnan de saliva su superficie corporal con ese propósito.
(7) La saliva de los ectoparásitos como vampiros, insectos y sanguijuelas contiene apirasa, que previene la agregación de plaquetas al degradar ADP; ejerce por lo tanto función anticoagulante.
(8) Las glándulas salivares de muchos insectos y algunos vertebrados liberan feromonas.
A diferencia del resto de secreciones digestivas, que están controladas por el sistema nervioso y el endocrino, la secreción de saliva en vertebrados4 está sometida a control nervioso únicamente. En los mamíferos, la estimulación permanente y de baja intensidad de las terminaciones nerviosas del subsistema parasimpático5 que inervan las glándulas salivares provoca la producción constante de saliva. Gracias a esa secreción la boca y la garganta se mantienen húmedas de forma permanente. La tasa basal de secreción de saliva en humanos es de 0,5 ml min-1, aunque puede elevarse rápidamente hasta los 5 ml min-1 bajo ciertos estímulos. Esas cifras, no obstante, empalidecen al lado de las de los rumiantes: una vaca produce 140 l de saliva diarios y la mitad del agua corporal pasa cada día de las glándulas salivares al rumen.
Además de la producción continua de un volumen limitado de saliva, hay dos reflejos que pueden provocar una elevación en su secreción. Uno es el reflejo simple o no-condicionado, que es el que se produce cuando los quimiorreceptores y barorreceptores de la cavidad bucal responden a la presencia de alimento. Esos receptores envían señales al centro salivar de la médula6 y esta, a su vez, responde enviando a las glándulas salivares las correspondientes señales para elevar la producción de saliva. El otro es el reflejo salivar condicionado, que ocurre sin que haya estimulación oral; es un reflejo aprendido que consiste en la insalivación en respuesta a un estímulo que indica que en breve habrá alimento disponible para comer.
Un rasgo que diferencia a las glándulas salivares del resto de órganos regulados por el sistema autónomo es que es el único caso en que los subsistemas simpático y parasimpático no tienen efectos antagonistas. Ambas divisiones estimulan la producción de saliva. La división parasimpática, que es dominante, provoca un aumento del flujo de sangre a las glándulas y, por consiguiente, da lugar a una abundante producción de saliva serosa. La simpática, sin embargo, reduce el flujo sanguíneo y, aunque mantiene un cierto nivel de producción salivar, esta es de menor volumen y de consistencia más mucosa. Bajo esa circunstancia suele experimentarse la sensación de boca seca característica de condiciones de estrés.
Fuente:
Lauralee Sherwood, Hillar Klandorf & Paul H. Yancey (2005): Animal Physiology: from genes to organisms. Brooks/Cole, Belmont.
Notas:
1 La superficie acumulada total de una misma masa o volumen de cualquier material es mayor cuando se encuentra fragmentada en muchos trozos de pequeño tamaño que en pocos de gran tamaño.
2 En la mayor parte de los tiburones se renuevan cada dos semanas, y en los cocodrilos cada dos años.
3 Las conocidas coloquialmente como barbas, que son largos filamentos de queratina dispuestos en paralelo.
4 Y con la excepción de los rumiantes, en los que la saliva es secretada de forma permanente por la glándula parótida sin que responda a estímulos nerviosos.
5 En la anotación dedicada al sistema nervioso periférico tratamos del subsistema parasimpático.
6 En El tronco encefálico y el cerebelo, hicimos referencia a la médula como parte del tronco encefálico.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La boca se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Modalidades de alimentación
- El balance energético animal
- Túbulos de Malpigio y recto, el sistema excretor de los insectos
Hace 16 años ya: el hundimiento del Prestige

“May day, may day. Soy el capitán del Prestige, un petrolero de 243 metros de eslora que transporta 77000 toneladas de fuel desde el Báltico con destino a Gibraltar. Perdimos el control y estamos escorados 25 grados a estribor. Necesito ayuda para evacuar a la tripulación.”
Capitán Apostolos Mangouras, 14.15 horas, 13 de noviembre de 2002.
El petrolero Prestige se hundió el 19 de noviembre de 2002, entre las 11.45 y las 16.18 horas.
“El último resto del Prestige yace bajo el fondo del mar desde las 16.18 de ayer, a unas 133 millas marinas (250 kilómetros) de la costa gallega… A las ocho de la mañana se partió en dos. A las 11.45 se hundió la popa, y cuatro horas y media después el Atlántico terminó de tragarse la proa.”
El País, 20 de noviembre de 2002.
“No se puede hablar de marea negra, son manchas negras y dispersas.”
José Luis López Sors, Director General de la Marina Mercante. 17 de noviembre de 2002.
“Se piensa que el fuel está aún enfriándose, salen unos pequeños hilitos, hay cuatro en concreto, los que se han visto, cuatro regueros solidificados con aspecto de plastilina en estiramiento vertical.”
Mariano Rajoy, Vicepresidente del Gobierno. 5 de diciembre de 2002.

El 13 de noviembre de 2002 se recibió el primer aviso del Prestige: fue la primera petición de ayuda. Se encontraba frente a las costas de Galicia, luchando con un fuerte temporal. Seis días más tarde, el 19 de noviembre, se hundió a unos 250 kilómetros al oeste de la costa gallega. Ahora, estos días de noviembre, celebramos el 16 aniversario de la catástrofe que provocó el vertido y el desastre ambiental que todos conocemos. Vamos a repasar algunos aspectos de las consecuencias que tuvo el accidente en el futuro o, mejor, en nuestro presente.
Hasta 2007, cinco años después del hundimiento, más de 300 investigadores de 42 centros de investigación colaboraron en proyectos relacionados con el Prestige. Organizaron 45 campañas de muestreos y recorrieron más de 2000 kilómetros de costa, en 10 barcos y durante 170 días. Nueve de esos investigadores eran de la UPV/EHU.
La primera conclusión de todos estos estudios, tal como cuentan Beatriz Morales Nin y sus colegas, de la Universidad de las Islas Baleares, es de sorpresa y alivio. A pesar de las alarmas que se activaron en muchos sectores afectados por el fuel vertido por el petrolero, el océano y las costas se recuperaron con una rapidez inesperada. Sin embargo, los científicos avisaron de que no hay que descuidar la vigilancia en el futuro pues, para esa fecha, en 2007, no se conocía, ni se conoce en la actualidad, donde están parte de las 77000 toneladas que llevaba el petrolero. Y pueden afectar a los ecosistemas en el futuro, aunque sea, como alguno aseguró en rueda de prensa, plastilina y no chapapote.
Galicia es una región a vigilar con un seguimiento continuo. Ha sufrido ocho episodios de vertidos de petróleo y productos químicos y, por ello, es la región costera del mundo con el mayor número de accidentes de este tipo. El primero de esta serie fue el Yanxilas en 1965, y el último el Prestige en 2002.

Entre los estudios sobre los efectos del fuel derramado por el Prestige, nos sirven de ejemplo los muestreos de mejillones que, desde el norte de Portugal, por el Cantábrico y hasta la costa de Francia, mostraron que el impacto más fuerte se detectó cerca de puertos como Avilés, Gijón, Santander o Bilbao, y en las zonas más cercanas al vertido, como la Costa da Morte y Corrubedo en Galicia. Pero la concentración de productos del fuel del Prestige descendió a los pocos meses del vertido. Además, no es posible comparar con datos anteriores al vertido para certificar la recuperación del medio pues esos datos, en la mayoría de los casos, no existen pues no había estudios ni seguimientos detallados anteriores.
A los dos años, en 2003 y 2004, los mejillones mostraban recuperación en varios marcadores de células y tejidos, según el grupo de Miren Cajaraville, de la UPV/EHU. Los animales proceden de 22 puntos de muestreo en las costas de Galicia y del Cantábrico. Una revisión de los datos del ecosistema marino recogidos entre 2003 y 2006, y con cinco índices diferentes de salud ambiental tratados en conjunto por el grupo de Ionan Marigómez, de la UPV/EHU, confirma la recuperación de los mejillones.
Esta disminución de concentraciones también la ha detectado el grupo de Dario Monaco, de la Universidad de Nápoles. Después del accidente, la concentración de petróleo en el fondo y en la superficie, en las costas de Galicia, era de 300 kilogramos por metro cuadrado en enero de 2003. Casi dos años después, en octubre de 2004, había bajado a 0.5 kilogramos por metro cuadrado. Como otras autores, avisan de que, aunque bajen las concentraciones, no se sabe donde está el petróleo que falta del vertido del Prestige, aunque, añaden, expertos y pescadores lo han visto en el fondo del mar y cerca de la costa.
Los autores han medido las concentraciones de hidrocarburos y metales pesados en las rías de Vigo y Pontevedra y en las islas Cíes. Los resultados indican que las mayores concentraciones se encuentran en la mitad interior de las rías y su origen está en la actividad humana habitual y no en vertidos grandes.
Un resultado similar ha encontrado en el estuario de Urdaibai el grupo de Eunate Puy, de la UPV/EHU. La contaminación por hidrocarburos en las rías de Galicia y en Urdaibai es habitual en muchos estuarios por la actividad humana. Los autores de la investigación de Galicia recomiendan un seguimiento continuo para detectar vertidos e iniciar, si se considera necesario, procesos de estudio y recuperación de los ecosistemas.
Entre los métodos de futuro, quizá ya en el presente, para el seguimiento y detectar y controlar los vertidos está la ciencia ciudadana tal como proponen Kieran Hyder y sus colegas, del Centro de Ciencias del Ambiente, Pesquerías y Acuicultura de Lowestoft, en Inglaterra. Los programas de detección de ciencia ciudadana, con la participación de muchas personas interesadas, son muy útiles para los vertidos en pequeña escala o los de mayor importancia pero con dispersión del contaminante en muchas manchas pequeñas, tal como ocurrió con el chapapote del Prestige (quizá a esto se refería López Sors en sus proféticas declaraciones). Estos vertidos dispersos a menudo no son detectados y son igualmente dañinos para el ambiente.

Siempre queda el riesgo de que la catástrofe se repita. Como decía al principio, entre 1965 y 2002, son ocho los vertidos graves desde buques que han contaminado las costas de Galicia. Es decir, uno cada casi cinco años y, por ello, estadísticamente ya toca otro accidente. Javier Fernández Macho, de la UPV/EHU, ha elaborado un índice que calcula el riesgo de vertidos en las costas europeas. Ha utilizado datos de 301 accidentes, ocurridos entre 1970 y 2014, en 156 regiones costeras de Europa.
De las 25 regiones con más riesgo, 20 están en Gran Bretaña, un grupo de islas cercano al continente y con muchos puertos y gran movimiento de barcos. Galicia y el estrecho de Gibraltar están entre las regiones con más riesgo de vertidos, también por el numeroso tráfico y, además, muchos de los barcos transportan productos contaminantes y peligrosos.
Para terminar, el coste económico del accidente del Prestige en Galicia tal como lo ha calculado María Loureiro y su grupo, de la Universidad de Santiago. Es un estudio fechado en 2006 y suma las pérdidas y gastos a corto plazo de los sectores económicos afectados, por la limpieza y recuperación, y por los daños ambientales conocidos en esa fecha.
El total es de algo más de 770 millones de euros, con el valor del euro de 2001. Recomiendan comparar esta cifra de gasto con los fondos que costaría la aplicación de medidas preventivas y de otros planes que eviten o mitiguen los vertidos. Otro estudio, publicado en las mismas fechas, y centrado en el sector pesquero de la Ría de Vigo, da cifras parecidas. Publicado por Dolores Garza y su grupo, de la Universidad de Vigo, calcula que, solo en el año 2003, las pérdidas alcanzan los 100 millones de euros.
Todavía quedan por conocer, y los grupos de investigación está en ello, los daños a largo plazo, tal como nos enseña el accidente del petrolero Exxon Valdez en las costas de Alaska, que ocurrió en 1989, y casi 30 años después todavía se observan daños en organismos marinos. Como recordaba antes, el petróleo del Prestige, o por lo menos mucho de ese petróleo, todavía está en el mar, casi seguro en el fondo, y sigue descargando compuestos peligrosos en el océano que, es fácil suponer, siguen influyendo en el funcionamiento de especies y ecosistemas.
Referencias:
Cajaraville, M.P. et al. 2006. Signs of recovery of mussels health two years after the Prestige oil spill. Marine Environmental Research Suppl 1: S337-S341.
Fernández Macho, J. 2016. Risk assessment for marine spills along European coast lines. Marine Pollution Bulletin doi: 10.1016/j.marpolbul.2016.09.015
Garza, M.D. et al. 2006. Assessment of economic damages from the Prestige oil spill. Marine Policy 30: 544-551.
Hyder, K. et al. 2017. The role of citizen science in monitoring small-scale pollution events. Marine Pollution Bulletin 120: 51-57.
Loureiro, M.L. et al. 2006. Estimated costs and admisible claims linked to the Prestige oil spill. Ecological Economics 59: 48-63.
Marigómez, I. et al. 2013. Marine ecosystem health status assessment through integrative biomarker indices: a comparative study after the Prestige oil spill “Mussel Watch”. Ecotoxicology 22: 486-505.
Monaco, D. et al. 2017. Spatial distribution of heavy hydrocarbons, PAHs and metals in polluted sea. The case of “Galicia”, Spain. Marine Pollution Bulletin doi: 10.1016/j.marpolbul.2017.06.003
Morales Nin, B. et al. 2007. Ciencia & Prestige. La investigación desarrollada a raíz del accidente del Prestige. Oficina Técnica de Vertidos Marinos. Universidad de Vigo. 67 pp.
Puy Azurmendi, E. et al. 2010. Origin and distribution of polycyclic aromatic hydrocarbon pollution in sediment and fish from the Biosphere Reserve of Urdaibai (Bay of Biscay, Basque country, Spain). Marine Environmental Research 70: 142-149.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Hace 16 años ya: el hundimiento del Prestige se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Prestige: impacto biológico
- El 70% de los varones del País Vasco desciende de un antepasado que vivió hace 4.500 años
- Flores en su tumba, hace 16.000 años
Diálogos en la frontera: Matemáticas y procesos creativos

Aunque la relación entre las diferentes formas de conocimiento puede parecer imposible, lo cierto es que en muchas ocasiones el vínculo entre ellas es necesario e inevitable. Las artes y las ciencias son el vivo ejemplo de la conexión que existe entre las distintas áreas de estudio. Y aunque puede resultar complicado pensar cómo pueden convivir la creación artística y la investigación científica, lo cierto es que hay profesionales que combinan estas disciplinas en su trabajo diario.
Ejemplo de ello son la artista donostiarra Esther Ferrer y el compositor minimalista estadounidense Tom Johnson, los protagonistas de la primera edición del programa “Diálogos en la frontera”, que se celebró el pasado 12 de marzo en la Biblioteca Bidebarrieta de Bilbao.
El evento, cuyo principal objetivo es crear un espacio para el diálogo entre las artes y las ciencias, congregó en la capital vizcaína a los profesores de la Universidad del País Vasco/Euskal Herriko Unibertsitatea Josu Rekalde (Bellas Artes) y Raúl Ibáñez (Ciencia y Tecnología), que conversaron con Ferrer y Johnson sobre la utilización de las matemáticas en los procesos creativos de ambos artistas.
El evento se enmarca dentro del ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
La artista donostiarra Esther Ferrer es pionera del arte de la performance y una de sus máximas representantes en España. Su trabajo ha sido reconocido con múltiples galardones como el Premio Nacional de Artes Plásticas (2008), el Premio Gure Artea (2012) y el premio Marie Claire de l’Art Contemporain (2014). En sus obras, expuestas por todo el mundo, aparecen múltiples referencias a las matemáticas (números primos, el infinito en el número pi, la geometría, espacio y tiempo…) y se relacionan con el minimalismo, el arte conceptual y el feminismo.
El músico Tom Johnson es un compositor minimalista y teórico de la música estadounidense. Para sus composiciones utiliza formas simples, escalas limitadas y elementos matemáticos como la combinatoria, las simetría, los números o los fractales. Entre sus obras destacan la famosa La ópera de las cuatro notas (1972), Melodías Racionales (1982) y Kientzy Loops, premiada con el premio nacional francés “Victoires de la musique 2000”; o melodías más recientes como Galileo (2001), Mosaicos (2002) o Ritmos de Vertmon (2008).
Edición realizada por César Tomé López.
El artículo Diálogos en la frontera: Matemáticas y procesos creativos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia, arte y cultura callejera: materiales y obra artística
- Ciencia, arte y cultura callejera: física y música
- Las matemáticas de la desigualdad
Vida artificial en un ordenador cuántico IBM
El grupo de investigación Quantum Technologies for Information Science (QUTIS), liderado por el Profesor Ikerbasque Enrique Solano del Departamento de Química Física de la UPV/EHU ha desarrollado un protocolo de biomimética que reproduce los procesos característicos de la evolución darwiniana adaptado a la computación cuántica. Los investigadores prevén que en el futuro se conjugarán el autoaprendizaje de las máquinas, la inteligencia artificial y la vida artificial a escala cuántica.

En un escenario de vida artificial los modelos de organismos simples serían capaces de experimentar las diferentes etapas de la vida en un entorno virtual controlado. Eso es lo que ha diseñado el grupo QUTIS pero en un escenario de ordenadores cuánticos: un protocolo de vida artificial, que codifica comportamientos propios de sistemas vivos, como la autorreplicación, la mutación, la interacción entre individuos, el nacimiento, la muerte, y lo ha ejecutado en el ordenador cuántico en la nube de IBM ibmqx4.
Se trata de la primera realización experimental de un algoritmo de vida artificial siguiendo las leyes evolutivas de Darwin en un ordenador cuántico. El algoritmo sigue un protocolo biomimético, que codifica comportamientos cuánticos simulando los mismos comportamientos de los sistemas vivos. La biomimética cuántica consiste en reproducir en sistemas cuánticos algunas propiedades exclusivas de los seres vivos, y este grupo de investigación anteriormente había conseguido imitar mediante sistemas cuánticos la vida, la selección natural, el aprendizaje y la memoria. El objetivo de esta investigación es, tal como relatan los propios autores, “diseñar una serie de algoritmos cuánticos basados en la imitación de procesos biológicos, que se dan en organismos complejos, y llevarlos a la escala cuántica, por lo que solamente tratamos de imitar los aspectos claves de estos procesos”.
En el escenario de vida artificial que han diseñado, una serie de modelos de organismos simples son capaces de llevar a cabo las fases más comunes de la vida en un entorno virtual controlado,. Los investigadores han probado que los sistemas cuánticos microscópicos pueden codificar características cuánticas y comportamientos biológicos que normalmente se asocian con sistemas vivos y la selección natural.
Los modelos de organismo se han diseñado como unidades de vida cuántica, cada una compuesta por dos cúbits, que hacen las veces de genotipo y fenotipo, respectivamente,. El genotipo contiene la información que describe el tipo de unidad viviente, información que se transmite de generación en generación, mientras que el fenotipo, las características que muestran efectivamente los individuos, viene determinado tanto por la información genética como por la interacción de los propios individuos con el medioambiente.
Las características básicas de la evolución darwiniana que han simulado con estos sistemas, para poder considerarlos como organismos de vida artificial, han sido el nacimiento, el desarrollo, la autorreplicación (que incluye las mutaciones, que se materializan en rotaciones al azar de cúbits individuales), la interacción entre los individuos y con el medioambiente. Esta interacción va degradando el fenotipo del individuo conforme va avanzando en edad hasta que llega a un estado que representa la muerte.
Esta prueba experimental representa la consolidación del marco teórico de la vida artificial cuántica en un sentido evolutivo, pero conforme vayan escalando el modelo a sistemas más complejos, podrán “realizar emulaciones cuánticas más precisas con una complejidad creciente hacia la supremacía cuántica”, tal como comentan los autores.
De la misma forma, esperan que estas unidades de vida artificial y sus posibles aplicaciones tengan profundas implicaciones en la comunidad de la simulación cuántica y la computación cuántica en diversidad de plataformas cuánticas, sean iones atrapados, sistemas fotónicos, átomos neutros o circuitos superconductores.
Según Enrique Solano “se han sentado las bases para plantearse diferentes niveles de complejidad clásica y cuántica. Por ejemplo, se podría considerar el crecimiento de poblaciones de individuos cuánticos con criterios de género, sus objetivos vitales tanto individuales como colectivos, comportamientos automatizados sin control externos, procesos de robótica cuántica, sistemas cuánticos inteligentes, hasta llegar a superar el umbral de la supremacía cuántica donde solo un ordenador cuántico podría llegar. A partir de allí surgen preguntas terriblemente arriesgadas como conjeturar el origen microscópico de la vida misma, el desarrollo inteligente de los individuos y sus sociedades, o plantearse el origen de la conciencia y la creatividad animal y humana. Esto es solo el principio, estamos a inicios del siglo XXI y tendremos muchos sueños y preguntas fantásticas que podremos responder”.
Referencia:
U. Alvarez-Rodriguez, M. Sanz, L. Lamata, E. Solano (2018) Quantum Artificial Life in an IBM Quantum Computer Scientific Reports doi: 10.1038/s41598-018-33125-3
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Vida artificial en un ordenador cuántico IBM se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La vida cuántica
- #Quantum13 El timo del ordenador cuántico comercial
- Un simulador cuántico de fenómenos imposibles
Pros y contras de los nuevos semáforos nutricionales

Las compañías Coca-Cola, Mondelez, Nestlé, Pepsico y Unilever se han puesto de acuerdo para incluir un nuevo etiquetado en el frontal de sus alimentos. Lo han llamado «Etiquetado Nutricional Evolucionado» (ENL en sus siglas en inglés) y recuerda al que se emplea en Reino Unido. El sistema de basa en una suerte de semáforo nutricional (verde, ámbar y rojo) que servirá como indicador de la cantidad de calorías, grasas, azúcares y sal presentes en una porción de alimento.
La iniciativa impulsada por estas cinco compañías llega en un momento en el que países como Francia o Bélgica ya han optado por apostar por otro sistema diferente llamado Nutri-Score. El Nutri-Score se basa en una calificación global de la calidad nutricional del alimento que va de la A a la E, siendo la A la mejor puntuación (color verde) y la E la peor posible (color rojo). Todas las medidas se presentan con respecto a 100 g de producto (no por porción) y hay elementos cuya presencia suma (frutas, verduras, frutos secos, fibra y proteínas) y otros que restan (grasas saturadas, azúcar, sal y calorías).
Los sistemas Nutri-Score y el ENL son de carácter voluntario a la espera de que la Comisión Europea armonice la información nutricional adicional. En España, el Ministerio de Sanidad, Consumo y Bienestar Social, ha informado recientemente que aplicará el modelo Nutri-Score.

Eroski lleva años utilizando el semáforo nutricional en sus alimentos de marca blanca. A finales de 2018 pretende añadir también el sistema Nutri-Score.
Para algunos, este colorido etiquetado frontal favorece la comprensión nutricional de los productos. Para otros, esto es un coladero que permitirá pasar por buenos a alimentos de escaso valor nutricional.
Estos etiquetados son un extra, puesto que la información obligatoria que debe presentar cualquier alimento envasado es la lista de ingredientes (ordenados de mayor a menor cantidad en el producto) y la tabla nutricional, en la que se desglosa, por cada 100 g de alimento, el aporte calórico, los carbohidratos (de los cuales se indica cuántos gramos son azúcares), las grasas (de las cuales de indica cuántas son saturadas), fibra, proteínas y sal.
Tampoco es obligatorio mostrar la tabla nutricional por porción de alimento, sino solo por cada 100 g de producto. La principal controversia del ENL surge precisamente de la definición de «porción de alimento». Por ejemplo, en el caso de un yogur o postre lácteo, la definición de «porción» es evidente, pero en el caso de cereales, galletas, frutos secos… u otros alimentos que se venden en paquetes grandes de los cuales tú eliges cuánto consumir, la elección del tamaño de la porción es arbitraria. Al ser arbitraria podríamos encontrarnos que un alimento con alto valor calórico, rico en grasas saturadas, azúcares y sal, como por ejemplo la mayoría de las galletas, podrían mostrar un semáforo nutricional en el que primase el verde y el ámbar. No porque sea un alimento saludable, sino porque la medida se ha hecho en función de una porción muy pequeña.
Además, la cantidad de azúcares, grasas o sal se compara con la «ingesta de referencia de un adulto medio», es decir, con el total de lo que podrías consumir en un día. Por este motivo, si la porción es de dos o tres galletas supondrá un porcentaje pequeño, lo que se traduce en un semáforo aparentemente benévolo.
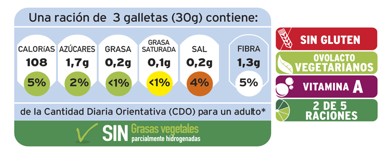
La solución a esto sería llegar a un consenso sobre qué es una «porción de alimento», para así poder comparar las cualidades nutricionales de diferentes cereales, panecillos, galletas, etc. Sin embargo, esto ya se hace al dorso: la tabla nutricional se hace obligatoriamente por 100 g de producto. Algunos fabricantes incluyen voluntariamente una columna más en la tabla nutricional «por ración». Esa ración puede ser un puñado de 30 g de avellanas o un envase de yogur de 125 g.
Con el sistema Nutri-Score, este problema desaparece, ya que siempre se da el dato con respecto a 100 g de producto.
Otra fuente de controversia es que podríamos entrar en comparaciones absurdas. Por ejemplo, en el semáforo nutricional ENL de la mayoría de los frutos secos aparecerá en rojo y ámbar el contenido calórico y de grasas. Los consumidores podrían pensar que se trata de un alimento insano, cuando la realidad es que los frutos secos son siempre una opción saludable.
Si comparásemos el semáforo nutricional de unas galletas con el de unas nueces, las nueces podrían parecer una opción menos saludable, ya que su contenido en grasas seguramente será mayor. La realidad es que unas nueces siempre serán una opción saludable, y unas galletas, salvo limitadas excepciones, no lo serán.

El sistema Nutri-Score no presenta este problema de comparaciones absurdas, ya que premia y penaliza por familia de alimentos. No analiza solo sus componentes, sino que tiene en cuenta el alimento completo. Los frutos secos tendrán buena calificación en Nutri-Score y la bollería no.
El contenido en azúcares también es complicado de evaluar con los semáforos nutricionales. Por ejemplo, un producto lácteo contendrá azúcares en forma de lactosa. Estos azúcares propios de la leche son saludables y no deberían condicionar la compra. Los azúcares añadidos son los que sí deberíamos evitar para mantener una alimentación saludable, no los que forman parte de la matriz del alimento.

Por ejemplo, el semáforo nutricional de un vaso de leche (200 ml), mostrará en ámbar los azúcares y en rojo las grasas, cuando ni los azúcares ni las grasas de la leche deberían preocuparnos, ya que la leche es un alimento a todas luces saludable. Por eso en el sistema Nutri-Score la leche tendrá una valoración positiva, mientras que con el ENL resulta engorroso saber si se trata o no de un buen alimento.
En la tabla nutricional obligatoria se indica qué cantidad de carbohidratos son azúcares, pero no se especifica si estos azúcares son añadidos o intrínsecos. Esto complica la elección de compra. Por ejemplo, un yogur natural sin azucarar contendrá entre 4 y 5 g de azúcares. Estos azúcares son la lactosa que contenía la leche con la que se fabricó el yogur, así que todos los yogures tendrán como mínimo entre 4 y 5 g de azúcares. Estos azúcares son saludables, pero en el semáforo y en la tabla nutricional suman como cualquier otro azúcar insalubre, lo que con frecuencia da lugar a malinterpretaciones.

Para saber si un yogur tiene azúcar añadido tenemos que buscar la palabra «azúcar» entre la lista de ingredientes. Si no aparece, quiere decir que ese yogur no tiene azúcar añadido. Si aparece la palabra «azúcar» (o equivalente, como jarabe de glucosa, miel, panela, etc.) tendremos que ir a la tabla nutricional para ver cuánto contiene. A esa cantidad le restamos unos 4-5 g, y ya tendremos la cantidad de azúcar añadido. Complicado.
Por este motivo algunos exigimos que en la tabla nutricional aparezca desglosado el azúcar en azúcar libre e intrínseco. Al igual que las grasas se desglosan en saturadas e insaturadas.
-
Conclusión
La incorporación de etiquetados frontales basados en el sistema de colores tipo semáforo nutricional como el ENL tiene pros y contras. Por un lado, nos permite saber de un vistazo si el contenido en grasas saturadas, azúcares, sal y calorías de un alimento es elevado. Por otro lado, este método puede inducir a error fácilmente, ya que una porción pequeña de un alimento insano puede mostrar un semáforo aparentemente benévolo. Tampoco sirve para diferenciar azúcares intrínsecos de azúcares añadidos, que es un problema todavía sin resolver en el etiquetado obligatorio basado en la lista de ingredientes y la tabla nutricional. También propicia comparaciones absurdas: unas galletas insanas pueden mostrar un semáforo más indulgente que el de unos frutos secos, aun cuando los frutos secos son una opción saludable.
La buena noticia es que el sistema Nutri-Score que ya han incorporado Bélgica y Francia, y al que pronto se sumará España, aunque no es perfecto, sí palía la mayor parte de los contras que presenta el semáforo nutricional ENL.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Pros y contras de los nuevos semáforos nutricionales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El azúcar oculto en los alimentos
- Miel y siropes, ¿son mejores que el azúcar?
- Lo dicen en la tele: un alimento natural no lleva aditivos
Construye tu propia calculadora de sumas y restas
Puede parecer raro que, en la actualidad, cuando tenemos calculadoras en nuestro teléfono móvil, tablet u ordenador, calculadoras on-line en internet que permiten realizar todo tipo de operaciones, ya sea con números, vectores o matrices, y sofisticadas calculadoras, que cada vez se parecen más a un ordenador de mano, planteemos en esta entrada del Cuaderno de Cultura Científica construir una calculadora mecánica para realizar sumas y restas.
 Máquina de sumar y restar, Addometer PAMOMA, modelo B estándar, construido en 1900 en Palma de Mallorca, 29 x 6 cm. Imagen de Antiguos instrumentos de cálculo
Máquina de sumar y restar, Addometer PAMOMA, modelo B estándar, construido en 1900 en Palma de Mallorca, 29 x 6 cm. Imagen de Antiguos instrumentos de cálculo Máquina de sumar y restar de mesa, Desk Calcumeter, diseñada en 1901 por el físico estadounidense James J. Walsh. Esta versión, con 6 diales, debe ser posterior, puesto que tiene tecla de “reseteado”. Imagen de Antiguos instrumentos de cálculo
Máquina de sumar y restar de mesa, Desk Calcumeter, diseñada en 1901 por el físico estadounidense James J. Walsh. Esta versión, con 6 diales, debe ser posterior, puesto que tiene tecla de “reseteado”. Imagen de Antiguos instrumentos de cálculoA finales del siglo XIX y principios del XX se diseñaron varias calculadoras mecánicas, del tipo de la Pascalina (máquina calculadora mecánica diseñada, haciendo uso de ruedas dentadas, por el matemático francés Blaise Pascal en 1642), de pequeño tamaño, que permitían realizar sumas y restas de forma sencilla, como las dos mostradas arriba.
Estas máquinas estaban diseñadas con una serie de ruedas dentadas, en las que se representaban las 10 cifras básicas de nuestro sistema de numeración, junto con un mecanismo sencillo, que variaba de unos diseños a otros, para incorporar la “llevada” de la suma al mecanismo.
Para explicar su funcionamiento, veamos un diseño simple de una máquina de sumar mecánica que podemos realizar en casa, o en clase, con algunos materiales que podemos tener a mano, como cartón, plástico o madera.
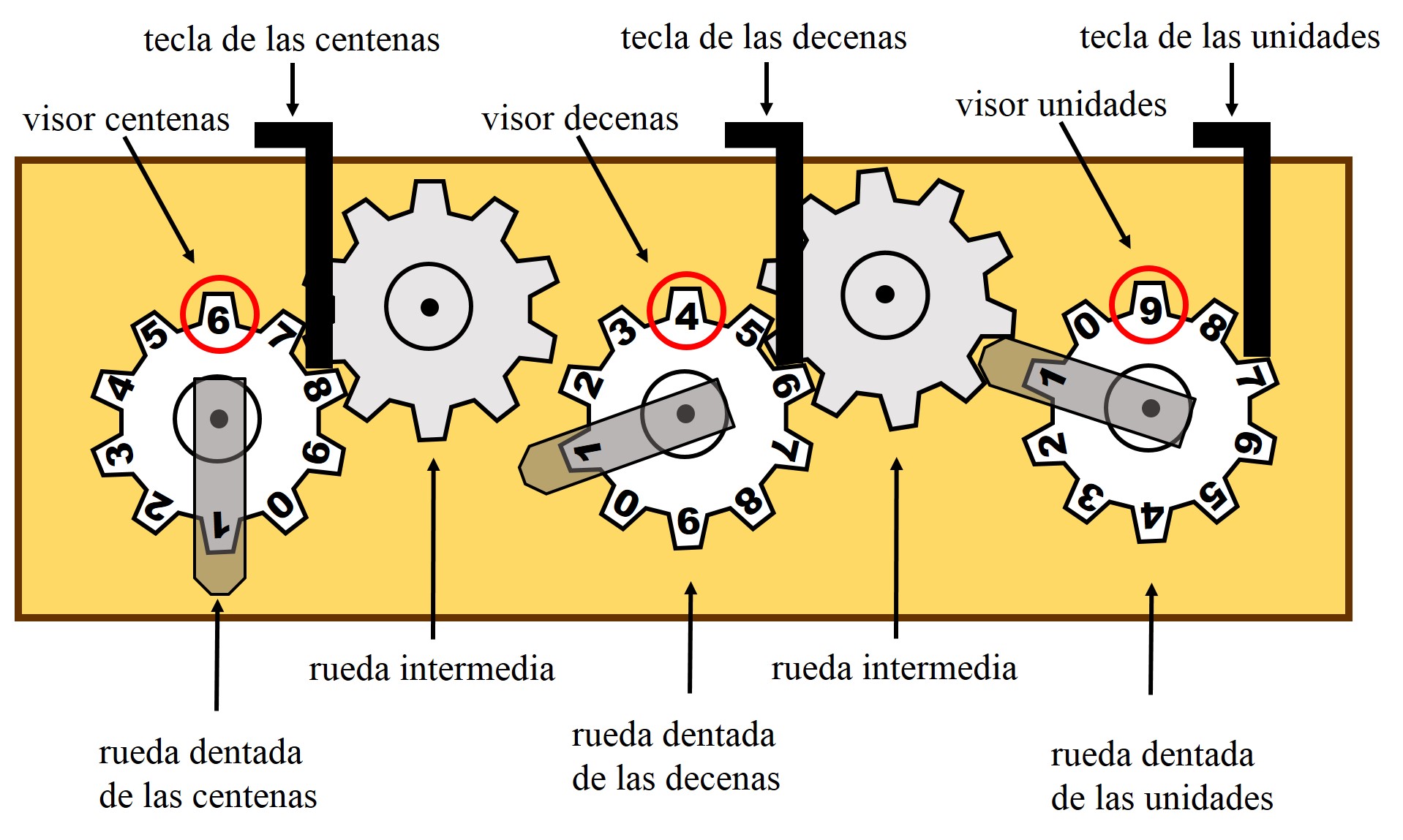 Diseño básico de una máquina de sumar mecánica, de tres ruedas dentadas, para construir uno mismo. Puede taparse el mecanismo, dejando libre la parte de las teclas, para poder accionarlas, y realizando unos agujeros en la parte de los visores para poder observar las cifras de las operaciones a realizar
Diseño básico de una máquina de sumar mecánica, de tres ruedas dentadas, para construir uno mismo. Puede taparse el mecanismo, dejando libre la parte de las teclas, para poder accionarlas, y realizando unos agujeros en la parte de los visores para poder observar las cifras de las operaciones a realizarComo vemos en la imagen anterior, esta calculadora mecánica de sumas está formada por tres ruedas dentadas con las diez cifras básicas, de 0 a 9, en cada una de ellas, lo que permite representar números de tres cifras. Aunque podemos construirla con más cantidad de ruedas dentadas, como en los ejemplos anteriores, para representar números mayores.
Para representar un número se presionan las teclas de las unidades, decenas y centenas, tantas veces como indique la cifra de la correspondiente posición. Así, para representar el número 649 que está en la imagen, se presiona 9 veces la tecla de las unidades, 4 la de las decenas y 6 la de las centenas (las ruedas dentadas girarán en el sentido de las agujas del reloj), viéndose en los visores de unidades, decenas y centenas las cifras del número 649.
Si ahora le queremos sumar el número 135 al número 649, es decir, queremos realizar la suma 649 + 135, se marcarán las cifras, desde las unidades a las centenas, con las correspondientes teclas, del número 135. ¿Qué es lo que va a ocurrir para que nos de la suma de esos dos números? Bastante simple. Al presionar 5 veces la tecla de las unidades, se están sumando las unidades, es decir, 9 + 5 (que son 14), de forma que cuando la rueda dentada da una vuelta completa, es decir, se pasa del 9 al 0 en el visor, la palanca alargada de la rueda de las unidades, que está colocada en el diente de la cifra 1, mueve la rueda dentada intermedia, la cual produce, a su vez, un movimiento de una posición en la rueda de las decenas (es la llevada de la suma de las unidades). Por lo tanto, en el visor de las unidades queda un 4, y en el de las decenas, se ha pasado del 4 al 5.
A continuación, se presiona 3 veces la tecla de las decenas, que pasa del 5 al 8, al sumar 3 al 5. Y finalmente, se presiona 1 vez la de las centenas, que pasa del 6 al 7. En los visores se verán las cifras 7 (centenas), 8 (decenas) y 4 (unidades), es decir, la suma es 784.
649 + 135 = 784.
La siguiente imagen es un ejemplo real de una máquina mecánica para sumar de este tipo. Es una máquina para realizar sumas rápidas para las compras, con los dos primeros números de la izquierda para los peniques y los dos siguientes para las libras. Teniendo en cuenta que cada libra son cien peniques, es como utilizar números de cuatro cifras en el sistema de numeración posicional decimal moderno, es decir, el sistema de numeración indo-arábigo que utilizamos en la actualidad.
 Sumador rápido para las compras, que cuenta libras y peniques. Fabricado en Hong Kong por FORDA, probablemente en la década de 1970. Es una máquina realmente pequeña, su tamaño es 7 x 3,5 x 1,5 cm. Imagen de Rechnen ohne Strom – Historische Rechenmaschinen
Sumador rápido para las compras, que cuenta libras y peniques. Fabricado en Hong Kong por FORDA, probablemente en la década de 1970. Es una máquina realmente pequeña, su tamaño es 7 x 3,5 x 1,5 cm. Imagen de Rechnen ohne Strom – Historische RechenmaschinenLa estructura interna de este pequeño sumador para las compras es similar a la del diseño básico explicado más arriba, aunque en este diseño se ahorran las ruedas intermedias al disponer las cifras en las ruedas dentadas en sentidos contrarios de forma alterna, unidades y centenas en el sentido contrario de las agujas del reloj, y decenas y unidades de mil, en el sentido de las agujas del reloj. De esta forma, la llevada se traslada directamente de una rueda dentada a la siguiente.
 Mecanismo interno del sumador rápido para las compras. Imagen de Rechnen ohne Strom – Historische Rechenmaschinen
Mecanismo interno del sumador rápido para las compras. Imagen de Rechnen ohne Strom – Historische Rechenmaschinen Con la máquina básica de sumas cuyo diseño hemos mostrado arriba, o con la que acabamos de mostrar para compras rápidas, se pueden realizar también restas. La idea para realizar una resta es considerar el complemento del sustraendo (el número que se resta) respecto a la potencia de 10 inmediatamente superior al minuendo (el número al que se le resta el sustraendo) y sumarlo al minuendo.
Veamos algún ejemplo. Para realizar la resta 93 – 57 en la sumadora anterior, se suma al sustraendo, 93, el complemento del minuendo, 57, respecto a 100, es decir, 43 (= 100 – 57). Al realizar la suma con la calculadora mecánica nos queda 93 + 43 = 136. No debemos de tener en cuenta el 1 inicial, que se corresponde con la llevada, y se obtiene el resultado, 36:
93 – 57 = 36.
Tengamos en cuenta que 93 + 43 = 93 + (100 – 57) = 100 + (93 – 57).
Otro ejemplo. Si queremos realizar la resta 723 – 235, debemos sumarle al sustraendo, 723, el complementario, respecto de 1000, del minuendo, 235, que es 1000 – 235 = 765. Por lo tanto, se realiza la suma 723 + 765 = 1488, y el resultado es 488.
723 – 235 = 488.
 Sumador rápido de pulsera. Frabricado en Hong Kong para la empresa estadounidense Kass Merchandise Co. Inc., en la década de 1970. Tamaño 6,5 x 5,5 x 2,3 cm y peso 39 gr. (con paquete). Imagen de Rechnen ohne Strom – Historische Rechenmaschinen
Sumador rápido de pulsera. Frabricado en Hong Kong para la empresa estadounidense Kass Merchandise Co. Inc., en la década de 1970. Tamaño 6,5 x 5,5 x 2,3 cm y peso 39 gr. (con paquete). Imagen de Rechnen ohne Strom – Historische RechenmaschinenEl problema de la resta es que tenemos que calcular el complementario del sustraendo, aunque realmente esto es fácil. Para calcular el complemento de un número respecto a una potencia de 10 más alta, solo hay que calcular el complemento de cada cifra, respecto a 9 o 10, dependiendo de su posición. Si la cifra es la de las unidades el complemento es respecto de 10, pero si es de las decenas, centenas o cualquier otra superior, el complemento es respecto de 9. Veamos algunos ejemplos.
El complemento del 75 respecto de 100 es 25, ya que 7 + 2 = 9 y 5 + 5 = 10; el complemento del 387 respecto de 1000 es 613, ya que 3 + 6 = 9, 8 + 1 = 9 y 7 + 3 = 10; o el complemento de 253 respecto de 10.000 es 9747, ya que 0 + 9 = 9, 2 + 7 = 9, 5 + 4 = 9 y 3 + 7 = 10.
 Antiguo teléfono con dial giratorio
Antiguo teléfono con dial giratorioEn el diseño básico de la máquina de sumar que hemos mostrado arriba, podemos sustituir las teclas para introducir las cifras de los números por discos con las diez cifras básicas sobre cada una de las ruedas de las unidades, las decenas, las centenas, etcétera. Más aún, estos discos, con los que introduciremos ahora las cifras de los números, pueden ser diales con diez agujeros, del tipo de un teléfono antiguo (como el que se muestra en la anterior imagen). Para introducir la cifra 3 giramos, mediante un dedo si los agujeros son grandes o mediante un lápiz si son pequeños, que suele ser el caso, en el sentido de las agujas del reloj, desde donde esté pintado el 3 hasta el tope, es decir, tres posiciones. Este es el diseño de la segunda calculadora que hemos mostrado en esta entrada.
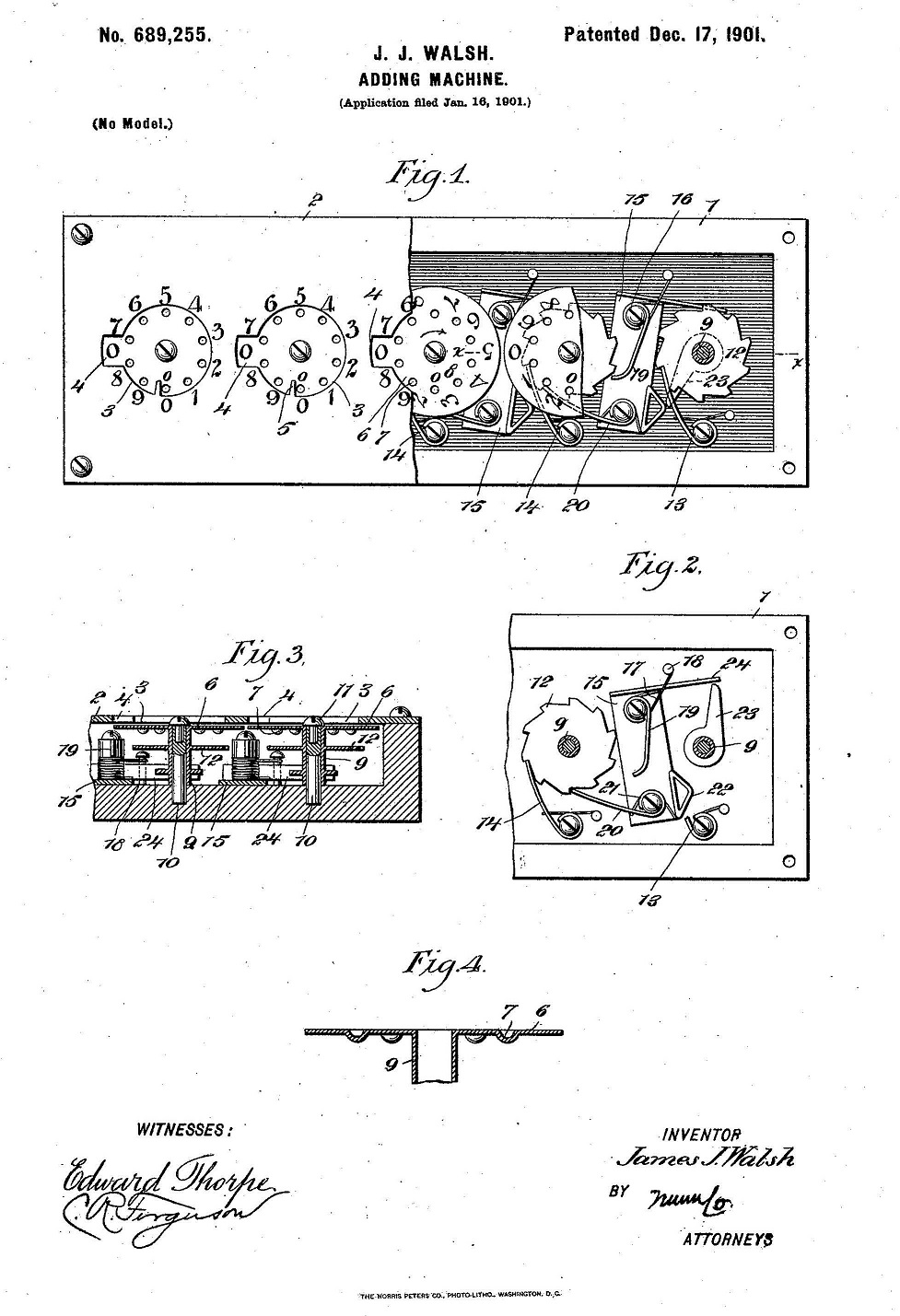 Página de la patente US 689.255 en Estados Unidos del “Calcumeter Desk”. Dispone de una rueda a la derecha para poner a cero el mecanismo. Imagen de History of computers.
Página de la patente US 689.255 en Estados Unidos del “Calcumeter Desk”. Dispone de una rueda a la derecha para poner a cero el mecanismo. Imagen de History of computers.En la siguiente imagen se muestra el diseño, para nuestra máquina mecánica básica de sumar mostrada arriba, de la rueda dentada con el dial para girar el disco y la tapa que iría delante de la rueda. Este diseño sería para cada rueda dentada.
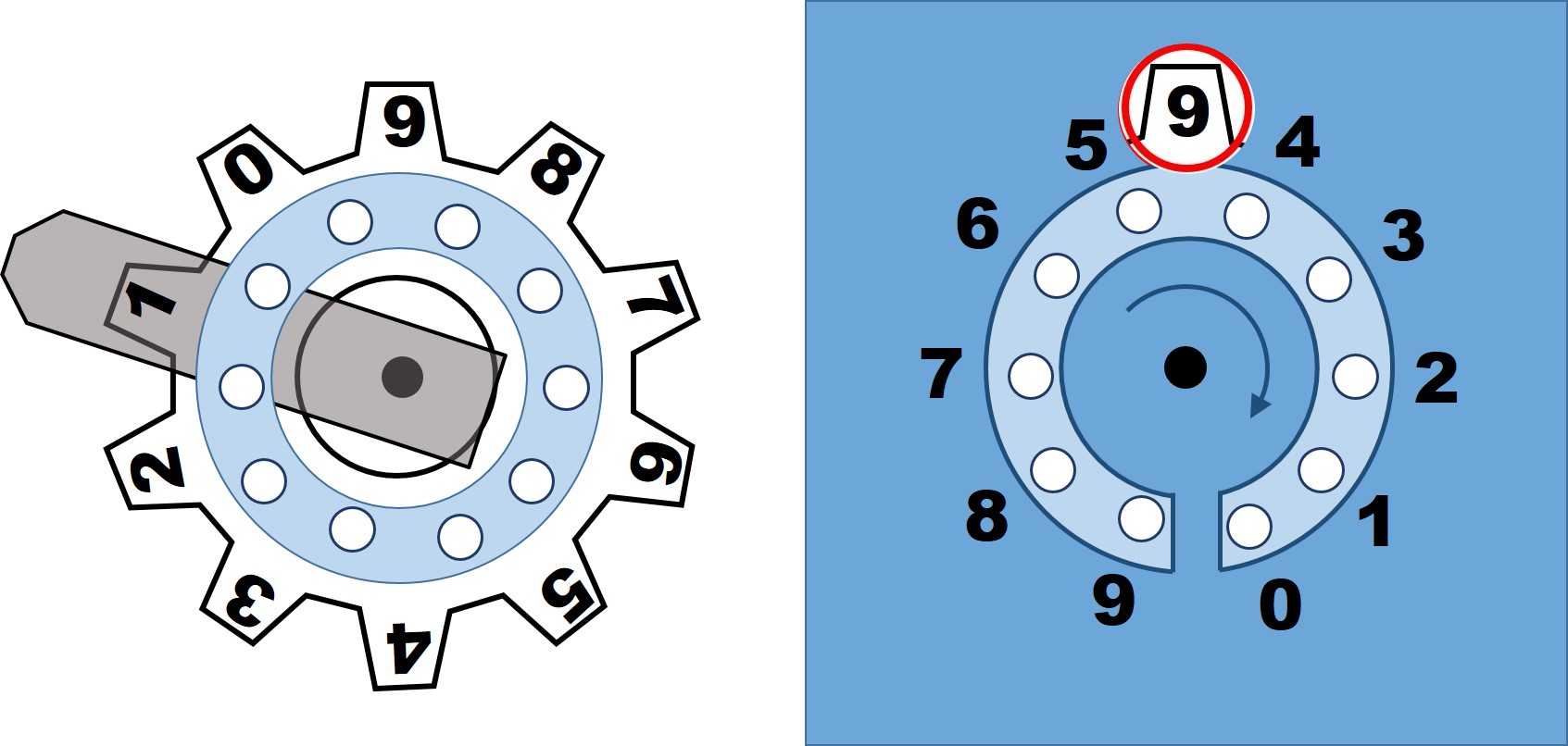 A la izquierda, el diseño de la rueda dentada de tipo dial correspondiente a nuestro diseño básico anterior de una máquina mecánica de sumar, y a la derecha, diseño de la tapa de la misma, donde se nos indican los números para el dial, desde donde se marca cada cifra como en un teléfono antiguo. La tapa nos deja ver la rueda dentada tanto por el visor, como en la parte central el dial con los diez agujeros
A la izquierda, el diseño de la rueda dentada de tipo dial correspondiente a nuestro diseño básico anterior de una máquina mecánica de sumar, y a la derecha, diseño de la tapa de la misma, donde se nos indican los números para el dial, desde donde se marca cada cifra como en un teléfono antiguo. La tapa nos deja ver la rueda dentada tanto por el visor, como en la parte central el dial con los diez agujeros Este sistema nos permite introducir cada cifra de una sola vez, mediante el dial, en cada rueda dentada y no hace falta estar presionando cada tecla tantas veces como indica la cifra correspondiente.
Además, una de las ventajas de este diseño de diales para introducir las cifras de nuestros números es que nos va a permitir realizar restas. Si para sumar en cada cifra, hay que girar el dial en el sentido de las agujas del reloj, utilizando para ello los números negros pintados en el exterior del dial), de forma que el mecanismo tiene en cuenta las llevadas, para la resta habrá que girar en el sentido contrario de las agujas del reloj, utilizando para ello los números rojos pintados en el interior del dial, y el mecanismo sigue teniendo en cuenta las llevadas para la resta.
 Diseño de la tapa de las ruedas dentadas de la máquina básica de sumar, con los números negros para sumar, girando el dial en el sentido de las agujas del reloj, y con los números rojos para restar, girando el dial en el sentido contrario a las agujas del reloj
Diseño de la tapa de las ruedas dentadas de la máquina básica de sumar, con los números negros para sumar, girando el dial en el sentido de las agujas del reloj, y con los números rojos para restar, girando el dial en el sentido contrario a las agujas del relojVeamos como realizar la resta 649 – 372 en nuestro mecanismo (véase en la siguiente imagen el interior del mecanismo en la versión de los diales, así como las tapas con los números en negro y rojo). Primero se introduce el número 649 en la calculadora mecánica. Se gira, en el sentido de las agujas del reloj, el dial de las unidades (el de la izquierda) desde el 9 negro, quedando marcado el 9 en el visor de arriba. Después se hace lo mismo para las decenas, segundo dial desde la derecha, girando en el sentido de las agujas del reloj desde el 4 negro. Y de forma similar el dial de las centenas, en el que se marca la cifra 6. Quedando en los visores el número 649, como en la imagen.
 Interior del diseño básico de una máquina de sumar mecánica, de tres ruedas dentadas, con diales para girar las ruedas dentadas, a derecha –para sumar– o izquierda –para restar–, como se indica en las tapas que irían sobre cada rueda dentada y que mostramos en la parte inferior de la imagen, utilizando los números negros y rojos como el dial de un teléfono antiguo que permite girar en los dos sentidos
Interior del diseño básico de una máquina de sumar mecánica, de tres ruedas dentadas, con diales para girar las ruedas dentadas, a derecha –para sumar– o izquierda –para restar–, como se indica en las tapas que irían sobre cada rueda dentada y que mostramos en la parte inferior de la imagen, utilizando los números negros y rojos como el dial de un teléfono antiguo que permite girar en los dos sentidosAhora le vamos a restar el número 372. Hay que tener en cuenta que como es una resta se utilizarán los números rojos y el giro es en el sentido contrario a las agujas del reloj. Como en las unidades del sustraendo tenemos un 2, giramos el dial de las unidades desde el 2 rojo en el sentido contrario a las agujas del reloj, quedando un 7 en el visor. En las decenas tenemos un 7, luego se gira el segundo dial desde el 7 rojo y en el sentido contrario a las agujas del reloj, en el visor se pasa del 4 al 7. Pero en este giro, cuando en el visor se pasa del 0 al 9 (es decir, necesitamos una llevada para la resta), la palanca que está en el 1, hace girar en el sentido de las agujas del reloj a la siguiente rueda dentada intermedia, que a su vez hace girar una posición a la rueda dentada de la izquierda (las centenas), en el sentido contrario a las agujas del reloj, y en el visor pasa del 6 al 5 (la llevada). Finalmente, en las centenas, que ahora hay un 5, se gira desde el 3 rojo, en el sentido contrario a las agujas del reloj, y queda un 2. Si miramos a los visores tendremos el resultado de la resta, 277.
649 – 372 = 277.
Una máquina calculadora mecánica para sumar y restar con ruedas dentadas y diales, como la que acabamos de describir, es la sumadora de bolsillo Kesling, también conocida, como sumadora de bolsillo Kes-Add, que fue diseñada en la década de 1940 por el dentista e inventor Elmer G. Kesling (1881-1961) y construida por la compañía The Hart Vance Company hacia 1954.
 Máquina mecánica de sumar, y restar, de bolsillo de Kelsing, construida hacia 1954 por la The Hart Vance Company, diseñada con ruedas dentadas y diales. Su tamaño es 1 x 13,7 x 5 cm. Esta acompañada de su lápiz para girar los diales a derecha o izquierda, y su bolsa para guardarla. Imagen de Jaap’s Mechanical Calculators Page
Máquina mecánica de sumar, y restar, de bolsillo de Kelsing, construida hacia 1954 por la The Hart Vance Company, diseñada con ruedas dentadas y diales. Su tamaño es 1 x 13,7 x 5 cm. Esta acompañada de su lápiz para girar los diales a derecha o izquierda, y su bolsa para guardarla. Imagen de Jaap’s Mechanical Calculators Page  Sumadora de bolsillo de Kesling desmontada. Se pueden observar las ruedas dentadas y el mecanismo de unión entre ellas para poder efectuar sumas y restas, como se ha descrito en esta entrada. Imagen de Aus der Rechenmaschinen-Werkstatt
Sumadora de bolsillo de Kesling desmontada. Se pueden observar las ruedas dentadas y el mecanismo de unión entre ellas para poder efectuar sumas y restas, como se ha descrito en esta entrada. Imagen de Aus der Rechenmaschinen-Werkstatt 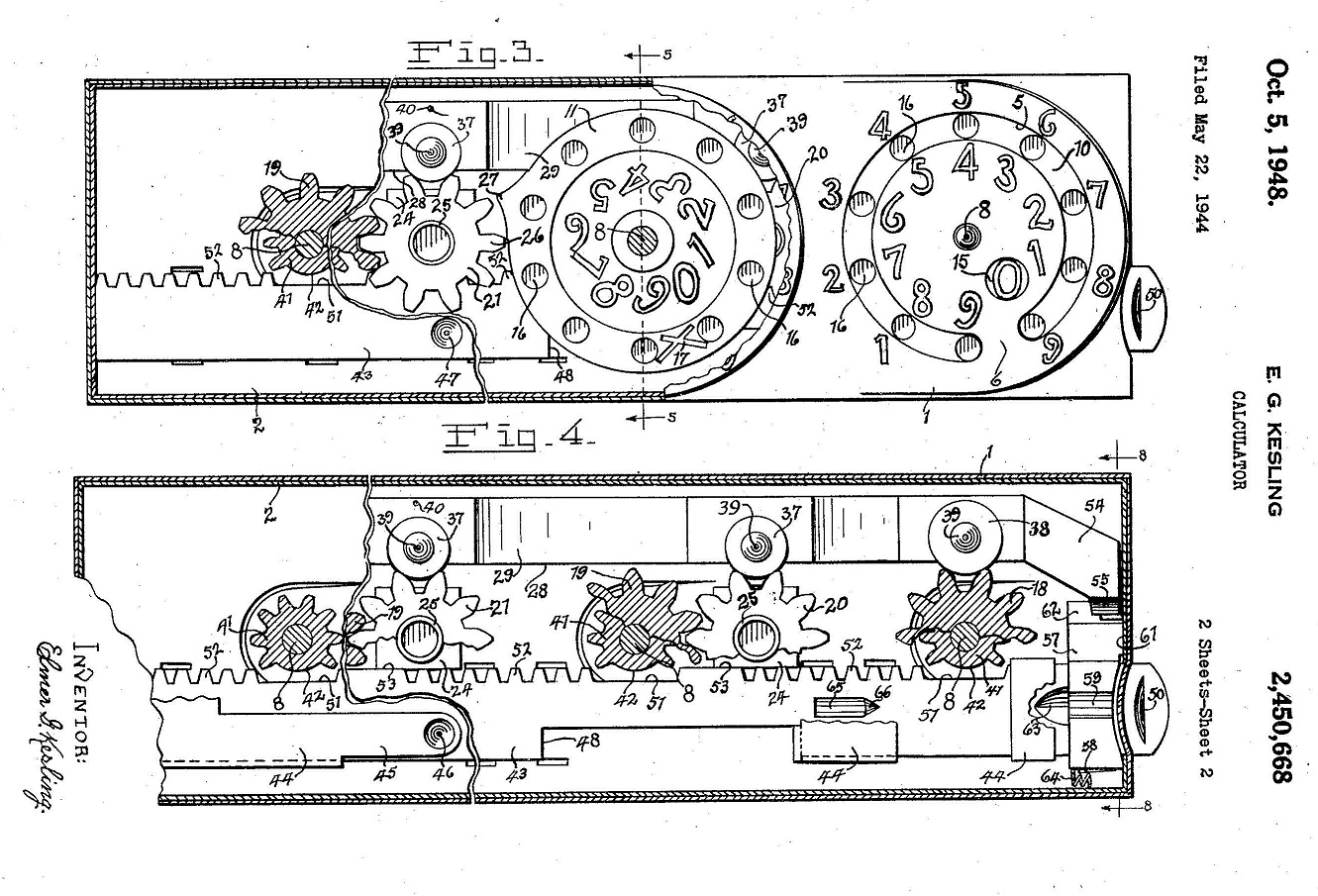 Página de la patente US 2.450.668 en Estados Unidos de la Sumadora de bolsillo de Kesling. Imagen de la página de patentes en Google
Página de la patente US 2.450.668 en Estados Unidos de la Sumadora de bolsillo de Kesling. Imagen de la página de patentes en GoogleY terminamos mostrando otra máquina similar, la máquina de sumar de Groesbeck, patentada en 1870 por John Groesbeck (1834-1884).
 Exterior e interior de la máquina de sumar de Groesbeck. Imagen de History of computers
Exterior e interior de la máquina de sumar de Groesbeck. Imagen de History of computers
Biblioteca
1.- Theodor Ziegler, Juegos de calcular, 38 sugerencias para utilizar el “Juego del ábaco”, Interduc/Schroedel, 1977.
2.- Antonio Pérez-Prados, Antiguos instrumentos de cálculo
3.- W. Denz, Rechnen ohne Strom – Historische Rechenmaschinen (Cálculo sin electricidad – Calculadoras históricas)
4.- Jaap Scherphuis, Jaap’s Mechanical Calculators Page
5.- Georgi Dalakov, History of computers
6.- Detlev Bölter, Aus der Rechenmaschinen-Werkstatt
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Construye tu propia calculadora de sumas y restas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Características de una onda periódica

Muchas de las perturbaciones que hemos considerado hasta ahora han sido repentinas y de corta duración, creadas por un breve movimiento como un latigazo en el extremo de una cuerda o un desplazamiento repentino en el extremo de un tren. En cada caso, vemos una onda que corre a lo largo del medio con una cierta velocidad. Ya hemos mencionado que este tipo de onda se llama pulso.
Consideremos ahora ondas periódicas, esto es, perturbaciones rítmicas regulares y continuas en un medio que resultan de la vibración periódica de una fuente. Un buen ejemplo de un objeto en vibración periódica es un péndulo oscilante. Dejando de lado los efectos de la resistencia del aire, cada oscilación es virtualmente idéntica a cualquier otra oscilación, y esta oscilación se repite una y otra vez en el tiempo.
Otro ejemplo es el movimiento hacia arriba y hacia abajo de un peso en el extremo de un muelle. En cada caso, el desplazamiento máximo desde la posición de equilibrio se llama amplitud, A, como se muestra en la imagen más abajo para el caso del muelle. El tiempo empleado en completar una vibración se denomina período, T, expresado habitualmente en segundos. El número de vibraciones por segundo se llama frecuencia, f. A la vista de estas definiciones debería ser evidente que T y f son recíprocos, es decir, T = 1 / f.
¿Qué sucede cuando se aplica una vibración periódica al extremo de una cuerda? Supongamos que el extremo izquierdo de una cuerda tensa se sujeta al peso oscilante (vibrante) que está en el extremo de un muelle vertical. A medida que el peso vibra hacia arriba y hacia abajo observamos una onda que se propaga a lo largo de la cuerda, como vemos en la siguiente imagen.

La onda toma la forma de una serie de crestas y valles a lo largo de la cuerda. La fuente ejecuta un movimiento armónico simple hacia arriba y hacia abajo. Idealmente, cada punto a lo largo de la cuerda ejecuta también un movimiento armónico simple. La onda viaja hacia la derecha a medida que crestas y valles se suceden. Cada punto o segmento pequeño a lo largo de la cuerda simplemente oscila hacia arriba y hacia abajo a la misma frecuencia que la fuente. La amplitud de la onda está representada por A. La distancia entre dos crestas consecutivas o dos depresiones consecutivas es la misma en toda la longitud de la cuerda. Esta distancia, llamada longitud de onda de la onda periódica, se representa convencionalmente por la letra griega λ (lambda).
La velocidad de una onda periódica se puede encontrar indirectamente si se puede medir su frecuencia y su longitud de onda. Para ilustrarlo usaremos el ejemplo de la onda en la cuerda. Sabemos que a medida que la onda avanza cada punto del medio oscila con la frecuencia y el período de la fuente. La imagen siguiente ilustra una onda periódica que se mueve hacia la derecha, representada por instantáneas tomadas cada cuarto de período, T.
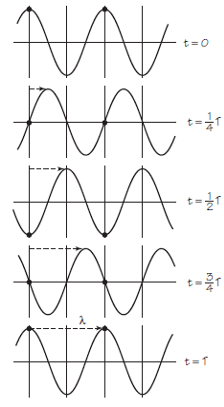
Sigamos el progreso de la cresta que comenzó desde el extremo izquierdo en el tiempo t = 0. El tiempo que tarda esta cresta en moverse una distancia de una longitud de onda es igual al tiempo requerido para una oscilación completa de la fuente, o de cualquier punto en la cuerda; es decir, la cresta mueve una longitud de onda durante un período de oscilación T. La velocidad v de la cresta, por lo tanto, viene dada por la ecuación v = distancia recorrida / tiempo empleado = λ / T.
Todas las partes de la forma de la onda se propagan con la misma velocidad a lo largo de la cuerda. Por lo tanto, la velocidad de cualquier cresta es la misma que la velocidad de la onda en su conjunto. Por lo tanto, la velocidad v de la onda también está dada por v = longitud de onda / periodo = λ / T.
Pero, hemos visto antes que T = 1 / f , lo que es equivalente a f = 1 / T, por tanto también podemos decir que la velocidad de una onda es v = λ· f. De aquí se sigue queλ = v / f y que f = v / λ. Estas expresiones muestran que, para ondas de la misma velocidad, la frecuencia y la longitud de onda son inversamente proporcionales; es decir, una onda con una frecuencia doble que otra que se desplaza a la misma velocidad tendría solo la mitad de la longitud de onda, y así sucesivamente. Esta relación inversa de frecuencia y longitud de onda es algo que es necesario tener siempre en mente cuando hablemos de ondas.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Características de una onda periódica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:¿Existe el derecho a un clima sostenible?
Estos jóvenes creen que sí y han demandado al gobierno de EEUU por ponerlo en peligro
 Manifestación para defender el derecho a un clima sostenible. Imagen: Our Children Trust.
Manifestación para defender el derecho a un clima sostenible. Imagen: Our Children Trust.El caso Julianna vs. Estados Unidos puede seguir adelante. Así lo anunció el pasado 2 de noviembre el Tribunal Supremo, después de que la administración Trump pidiese a este organismo que intercediese y lo desestimase. El tribunal ha desoído su petición.
En este caso, 21 jóvenes de entre 11 y 22 años se proponen pedir cuentas al gobierno de su país (tanto el actual como el anterior presidido por Barack Obama) porque consideran que ha puesto en peligro su derecho constitucional a la vida, la libertad y la propiedad privada al no haber evitado que el cambio climático alcanzase niveles peligrosos. Este impulso está basado en el concepto de que el gobierno tiene el control de los recursos naturales y debe gestionarlos teniendo en mente el beneficio común.
Afectados por sequías e inundaciones que ya se están produciendo
Los denunciantes aseguran que ya han sufrido las consecuencias. Uno de ellos, un chico de 17 años, tuvo que abandonar junto con su familia su hogar en la reserva de la Nación Navaja, en Arizona en 2011 porque los manantiales naturales de los que dependían para el consumo de agua ya habían comenzado a secarse. La casa de otro de ellos, situada en Luisiana, se vio afectada por las inundaciones de 2016, y el colegio de una tercera , situado en Nueva York tuvo que cerrar temporalmente en 2012 a causa del huracán Sandy.
Los demandantes quieren que el juzgado del distrito de Eugene, en Oregón, donde tendrá lugar el juicio, obligue al gobierno federal a implementar un plan orientado a reducir el nivel de partículas de dióxido de carbono en la atmósfera por debajo de 350 partes por millón en 2100 a partir de las 405 partes por millón que había de media en 2017.
Activistas en contra del cambio climático esperan que los demandantes de Julianna tengan éxito, pero en frente tienen a una administración que no se anda con chiquitas. El Departamento de Justicia defiende que no existe “el derecho a un sistema climático capaz de sostener la vida humana”, tal y como argumentan los impulsores del caso, y que en cualquier caso no está recogido como tal en la Quinta Enmienda, cuando se menciona el derecho a la vida, la libertad y la propiedad que enarbolan los denunciantes. El gobierno defiende también que el tribunal del distrito de Oregón no tiene competencia para este asunto.
Además, señala, y no sin razón, que no será posible una compensación significativa ya que una reducción drástica de las emisiones contaminantes por parte de Estados Unidos no tendría un impacto notable si los demás países no hacen lo mismo.
La lucha contra el cambio climático en los tribunales
No es la primera vez que la lucha contra el cambio climático se libra en los tribunales. Desde la década de los 80, cuando comenzábamos a ver las orejas al lobo, diversas iniciativas han tratado de lograr por la vía judicial las medidas y los planes de acción que ha sido tan difícil y lento alcanzar por la vía política, la mayor parte de las veces con poco éxito.
Recientemente las cosas han comenzado a cambiar y en 2015 la Fundación Urgenda logró una victoria histórica contra el gobierno holandés: el juez del caso obligó al país a reducir sus emisiones de gases con efecto invernadero al menos un 25% por debajo de las de 1990 antes de 2020 citando como motivo los posibles daños climáticos para las generaciones presentes y futuras de ciudadanos holandeses y el deber de su gobierno de prevenirlos.
 Manifestaciones juveniles por la ‘justicia climática’. Imagen: Our Children Trust
Manifestaciones juveniles por la ‘justicia climática’. Imagen: Our Children TrustEse caso, igual que el Julianna, se ha convertido en un modelo para otras demandas climáticas en otros países, en lo que ya se ha convertido en un fenómeno global. En enero de este año, 25 jóvenes colombianos denunciaron a su gobierno por no respetar su derecho a un medio ambiente sano y sostenible. El Tribunal Supremo de Colombia falló a su favor en abril. No solamente obligó al gobierno a tomar medidas para frenar la deforestación y el cambio climático, sino que determinó que la selva amazónica colombiana es sujeto de derecho y tiene derecho a “protección, conservación, mantenimiento y restauración”.
Según ese fallo, el gobierno no ha sido hasta ahora eficaz en los esfuerzos por proteger el Amazonas, poniendo en riesgo la calidad de vida de las generaciones actuales y futuras colombianas: “La imposibilidad de ejercer los derechos fundamentales al agua, a respirar aire puro y a disfrutar de un ambiente sano está enfermando a los colombianos, aumenta la carencia de agua dulce y disminuye las expectativas de vida digna”, se puede leer en este texto que explica la sentencia.
Referencias
US Supreme Court allows historic kids’ climate lawsuit to go forward – Nature
Anuncio del Tribunal Supremo del 3 de noviembre de 2018 sobre el caso Julianna vs USA
Europe braces for more climate litigation – Nature
En fallo histórico Corte Suprema concede tutela de cambio climático y generaciones futuras – Djusticia.org
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo ¿Existe el derecho a un clima sostenible? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La imperfección de los modelos del clima, por Manuel Toharia
- El clima, los informes y la política
- Del clima (y II)
Nos relacionamos con ciento cincuenta personas

Hace un cuarto de siglo, el científico británico Robin Dunbar propuso que el número de personas con el que nos relacionamos de forma habitual es de 150 aproximadamente. Algunos primatólogos habían observado que hay una relación entre el número de individuos con el que los primates se relacionan socialmente y el tamaño de su neocórtex cerebral, que está considerada, desde un punto de vista evolutivo, la parte más moderna del encéfalo. Según esas observaciones, la capacidad para relacionarse con más o menos individuos estaría limitada por el volumen de esa parte del cerebro puesto que ese volumen condicionaría la capacidad cognitiva. Dunbar estimó el número de 150 a partir de la relación citada utilizando datos correspondientes a 38 géneros de primates. Y desde entonces esa cifra, 150, ha sido denominada “número de Dunbar”.
También propuso que el tamaño de los grupos humanos reales solo llega a ser de 150 individuos cuando las condiciones en las que se desenvuelve el grupo son muy rigurosas y sus miembros tienen un fuerte incentivo para permanecer juntos. Solo grupos sometidos a una presión de supervivencia intensa, como aldeas de subsistencia, tribus nómadas y acantonamientos militares alcanzarían el número de 150. Cuando no se dan esas circunstancias, el grupo sería menor, aunque la capacidad para establecer relaciones seguiría estando en ese límite aproximado.
Investigadores de la Universidad Carlos III de Madrid y el propio Dunbar, de Oxford, han desarrollado un modelo teórico de relaciones sociales que parte de la base de que la capacidad para relacionarse con diferentes personas es limitada y que diferentes tipos de relaciones requieren diferentes grados de implicación. La teoría explica observaciones empíricas según las cuales las relaciones humanas normalmente se despliegan según una estructura en círculos. Lo normal es que nos relacionemos de forma estrecha con muy pocas personas, entre tres y cinco; en ese círculo se incluyen los familiares más cercanos y, en ocasiones, las amistades íntimas. El siguiente círculo lo forman otras diez personas, son buenos amigos. Algo más alejado hay un grupo de unas 30 a 35 personas, que son aquellas con quienes tratamos con frecuencia. Seguramente no es casual que las bandas de cazadores-recolectores en las que se estructuraban las poblaciones humanas durante la mayor parte de la historia de nuestra especie tuviesen, como mucho, unos 50 individuos; quizás esos tres primeros círculos sean reminiscentes de aquellas bandas. Y por último, tenemos un centenar de conocidos con los que nos relacionamos habitualmente.
Sin embargo, el modelo también da cuenta de una estructura social posible diferente, de configuración inversa a la que acabamos de ver. Ocurre, por ejemplo, cuando la comunidad a la que pertenece un individuo es pequeña (de menos de 55 personas); en ese caso, casi todas sus relaciones se encuentran en los primeros círculos, y el grupo tiene una gran cohesión. Esa estructura “inversa” es propia de individuos que, por su personalidad, tienen tendencia a relacionarse con muy pocas personas. O también cuando el individuo pertenece a comunidades especiales, de muy pocos efectivos, como las que forman ciertos grupos de inmigrantes.
Lo que parece deducirse de estos estudios es que tenemos una especie de capital cognitivo más o menos fijo, y que si dedicamos ese capital a relacionarnos con pocas personas, la relación con ellas puede ser muy intensa. Pero si, por nuestra personalidad o por otras circunstancias, tenemos tendencia o necesidad de relacionarnos con muchas personas, entonces no podremos dedicar a cada una de ellas más que una pequeña cantidad de capital cognitivo relacional. Y es que aunque tengamos un gran neocórtex, su volumen no es infinito.
Fuente: Ignacio Tamarit, José A. Cuesta, Robin I. M. Dunbar, and Angel Sánchez (2018): Cognitive resource allocation determines the organization of personal networks. PNAS.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 26 de agosto de 2018.
El artículo Nos relacionamos con ciento cincuenta personas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El método Feldenkreis y las personas con discapacidad intelectual
- ¡Préstame cincuenta dólares!
- Descartes se equivocó: “una persona es una persona a través de otras personas”
Ciencia, arte y cultura callejera: materiales y obra artística

La cultura se ha asociado históricamente con la actividad propiamente humana y en definitiva, con todas aquellas acciones que dan un sentido a la existencia del ser humano. En este sentido, todo lo que generamos para conocer el mundo, superarnos, deleitarnos o ensimismarnos, lo podemos definir como cultura.
Un término que abarca múltiples disciplinas y en el que el ser humano, en su afán por clasificar las diferentes formas de conocimiento y tratar de establecer una escala de relevancia, ha establecido una serie de fronteras delimitadoras. De la definición de estos límites surge el estereotipo de las dos culturas, las ciencias y las artes, así como la diferenciación entre las denominadas alta y baja cultura. Pero, ¿son realmente necesarias y útiles estas fronteras?
Con el objetivo de abordar este debate y mostrar una visión alternativa donde el arte y la ciencia se entrelazan, la Biblioteca Bidebarrieta de Bilbao acogió los pasados días 29 de mayo y 13 de junio el ciclo de conferencias “Ciencia, Arte y Cultura Callejera”.
El evento se enmarca dentro del ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
En esta segunga jornada la química Deborah García Bello, el profesor de la UPV/EHU Óscar González Mendia y la artista Nuria Mora hablaron sobre la ciencia que se esconde detrás de las técnicas del arte urbano.
Deborah García Bello es licenciada en Química y divulgadora científica. Ha escrito los libros Todo es cuestión de química y ¡Que se le van las vitaminas! y actualmente escribe en su blog Dimetilsulfuro, galardonado con el premio Bitácoras 2014. Recibió el premio Tesla de Divulgación Científica en 2016. García Bello colabora en diversos medios de comunicación (entre ellos, este Cuaderno) y es miembro de la Asociación Española de Comunicación Científica y de la Asociación de Comunicación Científica y Tecnológica.
Óscar González Mendia es doctor en Química Analítica y profesor en la Facultad de Ciencia y Tecnología de la Universidad del País Vasco (UPV/EHU). Aunque su investigación se centra en el análisis de fármacos y su metabolómica, desde hace tres años imparte también docencia en el Grado en Conservación y Restauración de Bienes Culturales de la Facultad de Bellas Artes de la UPV/EHU. Fruto de esta experiencia surgió su interés por indagar en la conexión entre ciencia y arte.
Nuria Mora es una artista contemporánea perteneciente a las corrientes del PostGraffiti y Street Art, siendo una de las precursoras de este último. Su obra ha sido expuesta en galerías y museos internacionales, entre los que destacan el Museo de Arte Contemporáneo de Johannesburgo y el Tate Modern de Londres.
El artículo Ciencia, arte y cultura callejera: materiales y obra artística se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia, arte y cultura callejera: física y música
- Arte & Ciencia: La relación entre el desarrollo de la ciencia y la creación artística
- Arte & Ciencia: Química y Arte, reacciones creativas
Buscando centinelas ambientales para las costas de Nicaragua
En colaboración con la Universidad Nacional Autónoma de Nicaragua, un grupo de investigación de la Estación Marina de Plentzia de la UPV/EHU ha estudiado los bivalvos de los manglares de las dos costas de Nicaragua con el fin de poder utilizarlos como centinelas (indicadores) de las alteraciones ambientales.
 Toma de muestras de bivalvos en los manglares nicaragüenses. Foto: Ionan Marigomez / UPV/EHU
Toma de muestras de bivalvos en los manglares nicaragüenses. Foto: Ionan Marigomez / UPV/EHUEl grupo de investigación Biología Celular en Toxicología Ambiental (CBET) cuenta con una amplia experiencia en la detección de las alteraciones que se dan en la salud de los ecosistemas mediante la medición de variables químicas y otra serie de parámetros en las células y tejidos de mejillones, bivalvos y peces. “Esas variables son como nuestra temperatura o pulso; el hecho de que cambien de alguna forma indica que algo está pasando”, explica Ionan Marigómez, director de la Estación Marina de Plentzia y catedrático de biología celular del grupo CBET.
En colaboración con la Universidad Nacional Autónoma de Nicaragua, el grupo abordó el estudio de los bivalvos que podían ser buenos indicadores del estado ambiental de los manglares nicaragüenses, tanto del Caribe como del Pacífico. Al pensar en el estado ambiental de las zonas tropicales, “existe mucha conciencia con el deterioro de los arrecifes de coral, y no está tan extendido fijarse en el estado de salud de los manglares. Pero los manglares protegen a los arrecifes, regulan la sedimentación y nutrientes que llegan desde tierra, y son el lugar de cría de muchas especies del arrecife”, aclara Marigómez.
En el caso concreto de Nicaragua, “la contaminación no es muy grande, pero existen varios factores de riesgo: los manglares reciben, entre otros, los pesticidas de todos los cultivos, o el mercurio que se vierte en las minas de oro. Además, no hay tratamiento de aguas”, continúa.
 Trabajo con el berberecho Larkinia grandis. Foto: Ionan Marigomez /UPV/EHU
Trabajo con el berberecho Larkinia grandis. Foto: Ionan Marigomez /UPV/EHUUna especie de almejas para el Caribe y dos de berberechos para el Pacífico
Una de las mejores candidatas para la monitorización de los ecosistemas de los manglares es la ostra Crassostrea rhizophorae. Sin embargo, Marigómez explica que “solamente se encuentra en los manglares de la costa caribeña, no en los del Pacífico; por tanto, queríamos encontrar especies sustitutas para la labor de centinela. Y para los manglares del lado del Caribe, además, vimos necesario buscar alguna otra especie adicional. Cada especie tiene una sensibilidad diferente ante los contaminantes, por lo que es conveniente realizar la biomonitorización con más de una especie simultáneamente”.
Para la investigación eligieron tres especies de bivalvos: para la costa atlántica, una especie de almeja, llamada Polymesoda arctata, como complementaria de la ostra que ya conocían, y para la costa Pacífica, dos especies de berberecho: Anadara tuberculosa y Larkinia grandis. En cada especie identificaron los parámetros de salud adecuados, como el nivel de contaminantes acumulados en sus tejidos, las variables biométricas con las que caracterizar el crecimiento y el estado de salud, los niveles de lesiones histopatológicas y de parásitos que presentan, y las anomalías en la reproducción, a través de los cuales poder deducir el estado de salud de los ecosistemas de los manglares en los que viven estos animales.
A pesar de contar con una larga experiencia en este tipo de tareas, Marigómez remarca que en Nicaragua no pudieron utilizar las técnicas y métodos habituales: “Aquel es otro mundo, y tienen unas normas muy rígida; por ejemplo, para llegar a los lugares de muestreo debíamos utilizar avionetas o lanchas motoras. Además, el uso de nitrógeno líquido y nieve carbónica está expresamente prohibido, y nuestra metodología de trabajo está basada principalmente en criotécnicas; debemos transportar las muestras congeladas obligatoriamente. Entonces, desde el punto de vista logístico, nos ha supuesto un gran reto el adaptar nuestra metodología de trabajo a esa realidad”.
“El trabajo realizado ha sido un bonito punto de partida, y nos ha motivado para poner en marcha otra investigación más adelante. El berberecho gigante L. grandis, que en Centroamérica conocen como casco de burro nos ha parecido muy adecuado para realizar la monitorización. Tiene una vida larga, por lo que reflejaría correctamente la evolución del lugar donde vive, y, además, tiene una distribución biogeográfica muy interesante: desde Baja California hasta el Ecuador. Sería bonito llevarla a cabo si consiguiéramos financiación a largo plazo, y crear una red para hacer el seguimiento en toda la región biogeográfica”.
El fin último de la monitorización es poder gestionar y proteger el medio ambiente. “En Europa el bienestar y uso de los ecosistemas se rige mediante dos directivas, la del agua y la de la estrategia marina, y en ambas se pide realizar la monitorización de los ecosistemas, para conocer en todo momento en qué estado se encuentran. En otras regiones del mundo, entre las que se encuentra Latinoamérica, sin embargo, la legislación de protección del medio ambiente no está tan desarrollada. Pero nuestro grupo, como creador y miembro de la Sociedad Iberoamericana de Contaminación y Toxicología Ambientales, mantiene relación con diferentes centros de investigación y universidades latinoamericanas, y nuestro propósito es ir superando los problemas técnicos existentes, para conseguir que la monitorización sea algo global”.
Referencia:
Javier R. Aguirre-Rubí, Maren Ortiz-Zarragoitia, Urtzi Izagirre, Nestor Etxebarria, Felix Espinoza, Ionan Marigómez. (2018) Prospective biomonitor and sentinel bivalve species for pollution monitoring and ecosystem health disturbance assessment in mangrove–lined Nicaraguan coasts Science of the Total Environment doi: 10.1016/j.scitotenv.2018.08.269
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Buscando centinelas ambientales para las costas de Nicaragua se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Riesgo de sufrir los efectos de un vertido de petróleo en el mar de las costas europeas
- Buscando la traducción automática perfecta
- Una nueva diana terapéutica para el neuroblastoma
Comienza Jakin-mina, el programa de conferencias para estudiantes de 4 de ESO
Jakin-mina es un programa de charlas organizado por Jakiunde cuyos destinatarios son estudiantes de cuarto curso de la ESO. La Cátedra de Cultura Científica de la UPV/EHU colabora con Jakiunde en la organización de este programa desde sus inicios.
El programa se desarrollará entre los meses de noviembre (2018) y marzo (2019) en diferentes localidades de la Comunidad Autónoma Vasca y la Comunidad Foral Navarra, y en él participan estudiantes seleccionados por los centros en los que estudian en función de su interés y motivación académica.

A los estudiantes se les ofrecen cinco conferencias de materias diversas, a cargo de especialistas, que se imparten en castellano, euskera e inglés. A cada conferencia asisten alrededor de 30 estudiantes. En la edición que comienza este mes de noviembre se ofrecerán diez ciclos de conferencias: tres en Bilbao, uno en Durango, uno en Arrasate, tres en Donostia-San Sebastián, uno en Pamplona, uno en Tudela y uno en Vitoria-Gasteiz. Todas las conferencias se celebran en viernes a las 17:30h.
Los y las estudiantes interesadas pueden inscribirse a través de sus centros. Los responsables de los centros que deseen inscribir a sus estudiantes en alguno de los ciclos, pueden enviar sus nombres y dos apellidos a akademia@jakiunde.eus. Para más información pueden llamar al 943 225773.
Conferencias Bilbao 1Lugar: Bizkaia Aretoa (Sala Arriaga), UPV/EHU, Avenida Abandoibarra 3, Bilbao.
23 de noviembre de 2018. Oskar Gonzalez (UPV/EHU): Zientziak agerian uzten duen artea
14 de diciembre de 2018. Mabel Marijuán (UPV/EHU): Las decisiones sanitarias: un reto personal, ético y político
11 de enero de 2018. Fernando Blanco (UD): The psychology of virtual reality
8 de febrero de 2019. Jordi Martí Carrera (Grupo init): Emprendimiento digital: cómo se hace el siguiente Instagram
22 de marzo de 2019. Ana Rodríguez (UPV/EHU): Gizaki eta roboten arteko elkarlanaren erronka: exoeskeletoak adibide
Bilbao 2Lugar: Bizkaia Aretoa (Sala Arriaga), UPV/EHU, Avenida Abandoibarra 3, Bilbao.
16 de noviembre de 2018. Eva Caballero (periodista, Radio Euskadi): La paradoja de Sagan
18 de enero de 2018. Ane Zabaleta (UPV/EHU): Uraren bide ezkutuak
22 de febrero de 2019. Nerea Toledo (UPV/EHU): How do trains talk to us?
22 de marzo de 2019. Guillermo Quindós (UPV/EHU): Viaje a nuestro mundo microbiano
5 de abril de 2019. Esteban Umerez (abogado): Lehenbiziko zeregina: abokatu guztiak akatu
Bilbao 3Lugar: La Comercial (Aula 06), Universidad de Deusto, Avenidad de las Universidades 24, Bilbao.
30 de noviembre de 2018. Esther Rebato (UPV/EHU): La dimensión sociocultural de los alimentos
14 de diciembre de 2018. Maider Huarte (UPV/EHU): Jokuak, sare sozialak, webguneak, bideoak… sakelekoan harrAPPatzen
25 de enero de 2018. Iñigo de Miguel Beriain (Ikerbasque; UPV/EHU): Why morals?
15 de febrero de 2019. Jon Irazusta (UPV/EHU): Muskuluak: osasunean baztertutako organoak
22 de marzo de 2019. Txani Rodríguez (escritora y periodista): La vocación literaria
DurangoLugar: Biblioteca Bizenta Mogel, Calle Komentukalea 8, Durango.
23 de noviembre 2018. Montse Hervella (UPV/EHU): ¿Llevamos un neandertal en nuestro interior?
25 de enero de 2019. Jesus Mari Lazkano (Jakiunde; UPV/EHU): Una mirada desde el arte
22 de febrero de 2019. Uxune Martínez (Euskampus Fundazioa): Internet, fauna bitxiaren bizileku
22 de marzo de 2019: Frederick Freundlich (MU): Do we (really) want to create more “employment”?
5 de abril de 2019. Gotzone Barandika (UPV/EHU): Bizirik edota naturalki?
ArrasateLugar: Goi-Eskola Politeknikoa, Mondragon Unibertsitatea, Loramendi 4, Arrasate.
30 de noviembre de 2018. Teresa del Valle (Jakiunde; catedrática emérita, UPV/EHU): ¿Pero, qué es el feminismo?
14 de diciembre de 2018. Jesus M. Ugalde (presidente de Jakiunde; UPV/EHU): Stardust: The origin of the matter that matters
18 de enero de 2019. Leire Legarreta (MU): 2002 jaiotzeko urterik onena izan zela ba al zenekien?
15 de febrero de 2019. Laura Pérez-Abad (MU): Ciencia y cocina: El Encuentro entre ambas disciplinas
22 de marzo de 2019. Jon Aurrekoetxea (MU): 3D inpresioa: ametsak eskuz ukitzeko aukera paregabea
Donostia-San Sebastián 1Lugares: Joxe Mari Korta Ikergunea, UPV/EHU, Tolosa hiribidea 72 / Musikene, Europa Plaza 2 / STM-San Telmo Museoa, Zuloaga plaza 1.
23 de noviembre de 2018 (Joxe Mari Korta Ikergunea). Aran Garcia-Lekue (Ikerbasque; DIPC): Surf eta zientzia
14 de diciembre de 2018 (Musikene): Josetxo Bretos (Musikene): La aventura de los instrumentos musicales
25 de enero de 2019 (San Telmo Museoa): Sonia Gaztambide (Jakiunde; Hospital Universitario de Cruces): Conozcamos la acromegalia (tras la conferencia, visita guiada para conocer los objetos personales del gigante de Altzo).
22 de febrero de 2019 (Joxe Mari Korta Ikergunea). Javier Aguirre (UPV/EHU). Zer da filosofia? Erantzun bat Grezia klasikotik
22 de marzo de 2019 (Joxe Mari Korta Ikergunea): Gemma Varona (IVC, UPV/EHU): The link between animal abuse and interpersonal violence
Donostia-San Sebastián 2Lugares: Joxe Mari Korta Ikergunea, UPV/EHU, Tolosa hiribidea 72 / STM-San Telmo Museoa, Zuloaga plaza 1.
16 de noviembre de 2018 (Joxe Mari Korta Ikergunea): Ekai Txapartegi (UPV/EHU): Filosofía eta enpresa
14 de diciembre de 2018 (Joxe Mari Korta Ikergunea). Eider San Sebastián (UPV/EHU): Phosphate wars oddisey
25 de enero de 2019 (San Telmo Museoa). Sonia Gaztambide (Jakiunde; Hospital Universitario de Cruces): Conozcamos la acromegalia (tras la conferencia, visita guiada para conocer los objetos personales del gigante de Altzo).
15 de febrero de 2019 (Joxe Mari Korta Ikergunea). Jon Maya (Jakiunde; Kukai Dantza taldea): Gurea gaur
29 de marzo de 2019 (Joxe Mari Korta Ikergunea). Iñaki Subijana (presidente de la Audiencia Provincial de Gipuzkoa): El acoso escolar en los centros educativos
Donostia-San Sebastián 3Lugares: Euskal Filmategia, Tabakalera, Andre zigarrogileak plaza 1 / CIC nanoGUNE, Tolosa Hiribidea 76 / STM-San Telmo Museoa, Zuloaga plaza 1.
30 de noviembre de 2018 (Euskal Filmategia, Tabakalera): José Luis Rebordinos (Director del Festival de Cine de San Sebastián): Tiempos de cambio en el audiovisual: nuevas formas de ver cine
14 de diciembre de 2018 (CICnanoGUNE). Joana Atxa (UPV/EHU): Dislexia, eod irkaruteza eizenzoka bliaaktzen deenan
25 de enero de 2019 (lugar: San Telmo Museoa). Sonia Gaztambide (Jakiunde; Hospital Universitario de Cruces): Conozcamos la acromegalia (tras la conferencia, visita guiada para conocer los objetos personales del gigante de Altzo).
22 de febrero de 2019 (CICnanoGUNE). Sara Barja (Ikerbasque; CFM – UPV/EHU; DIPC): The world of tiny things
22 de marzo de 2019 (CICnanoGUNE): Elena Lazkano (UPV/EHU): Robotak, nire lagun min onenak
Pamplona-IruñeaLugar: CIVICAN, Fundación Caja Navarra, Avda. de Pío XII 2, Pamplona-Iruñea.
23 de noviembre de 2018. Esperanza Rayón Valpuesta (UPNA): Cuidados y cuidadores en la sociedad actual
14 de diciembre de 2018. Ana Marta González (UN): La ética, una realidad cotidiana
11 de enero de 2019. Silvia Díaz Lucas (UPNA): Las mujeres en carreras STEM (Science, Technology, Engineering and Mathematics)
25 de enero de 2019. Adrián César Razquin (Universidad de Medicina de Viena, MUW; Austria): Pharmacogenomics and personalized medicine
8 de febrero de 2019. Juan Ignacio Pérez (Jakiunde; UPV/EHU): Animalien letrak
TudelaLugar: Sala de prensa Universidad Pública de Navarra, UPNA/NUP, Avda. de Tarazona s/n, Tudela.
16 de noviembre de 2018. Julia Pavón Benito (UN): El camino de Santiago: El peregrinaje y la formación de Europa en la Edad Media
14 de diciembre de 2018. Izaskun Berasategui Zabalza (dietista-nutricionista): Soy joven. Como lo que quiero
11 de enero de 2019. Mar Rubio Varas (UPNA): The next world: economic utopias and dystopias
15 de febrero de 2019. Inés Olza Moreno (UN): ¿Cómo nos convencen nuestros políticos? Discurso y retórica en el espacio público
22 de marzo de 2019. Ignacio López Goñi (UN): Microbiota, los microbios de tu organismo
Vitoria-GasteizLugar: Centro de investigación Lascaray y aulario Las Nieves , UPV/EHU, Miguel de Unamuno Etorbidea 3, Vitoria-Gasteiz.
16 de noviembre de 2018. Ana Iriarte (UPV/EHU): Diosas y dioses griegos
14 de diciembre de 2018. Aduna Badiola (UPV/EHU): Kirol-erakundeen antolakuntza-egitura eta hauen emaitzak
18 de enero de 2018. Eguzkiñe Iturrioz (meteoróloga, Tecnalia): Eguraldia, gu harritzeko prest!
15 de febrero de 2019 (salón de grados, aulario Las nieves). Iban Zaldua (UPV/EHU; escritor): Ese idioma raro y poderoso: la literatura vasca explicada en español
22 de marzo de 2019. Javier Garaizar (UPV/EHU): The Plague: a multidisciplinary approach
InscripcionesLos y las estudiantes interesadas deben inscribirse a través de sus centros. Los centros que deseen inscribir a sus estudiantes en alguno de los ciclos, pueden enviar sus nombres y dos apellidos a akademia@jakiunde.eus. Para más información pueden llamar al 943 225773.
El artículo Comienza Jakin-mina, el programa de conferencias para estudiantes de 4 de ESO se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ya está en marcha el programa Jakin-mina
- Ciencia Clip: un concurso de vídeos de ciencia para jóvenes estudiantes
- Conferencias plenarias #Quantum13 también en Bilbao
Tema y variaciones
La música es un ejercicio de aritmética inconsciente: la mente calcula sin saber que está calculando.
Gottfried Leibniz en una carta a Christian Goldbach, April 17, 1712
Os voy a contar la historia de una gran catedral sonora, la historia de (quizás) la melodía más repetida de la historia de la música occidental. Esa historia comienza, inevitablemente, donde yo la descubrí y fue aquí:
En 1995, Vangelis tuvo un éxito brutal con este tema. El músico griego lo había compuesto tres años antes para la banda sonora de “1492: The Conquest of Paradise” pero difícilmente podría haber anticipado el éxito que tendría. No sólo alcanzó la cima de los más vendidos en varios países europeos. Además, muchos otros artistas, decidieron hacer covers (repeticiones estilizadas, vaya) del archiconocido tema, incluido el mismísimo John Williams.
La cuestión es que… el tema de Vangelis no es, precisamente, original. A mí, en concreto, me recordó muchísimo a esta preciosa pieza para piano de Rachmaninov compuesta en 1931.
Fijaos, en concreto, en el tema inicial:
De hecho, las dos melodías están basadas en el mismo esquema armónico. Pero no es sólo eso. En realidad, las dos se construyen siguiendo la misma estructura: el mismo esquema de repeticiones, el mismo armazón rítmico… las dos se yerguen sobre los mismos huesos, por así decirlo. Y no es por casualidad.
La cuestión es que… el tema de Rachmaninov no es, precisamente, original. El mismo título de la obra así lo indica: para componer su Tema y variaciones, Sergei se inspiró en una sonata de Corelli del año 1700. Y la cuestión es que… el tema de Corelli tampoco era, precisamente, original. Los orígenes son bastante más antiguos y más interesantes. Pero, por ahora, dejemos de dar saltos atrás en el tiempo y permitidme que me detenga un rato en la repetición de 1931.
El Tema y variaciones sobre un tema de Corelli es la última pieza para piano solo de Rachmaninov que llevaba casi 15 años sin escribir nada para este instrumento. Curiosamente, nunca estuvo muy satisfecho con esta obra. Puede que fuese, en parte, por su propio carácter, tremendamente autocrítico. No era la primera partitura propia que criticaba duramente. Afirmó, por ejemplo, que su Sonata No.2 le parecía superflua y estuvo a punto de no componer su Concierto No.2 a causa de la depresión que le produjo el estreno de su primera Sinfonía (y menos mal que la superó). Hizo revisiones de muchas de sus primeras obras, a veces hasta 20 años después. Sin duda, un poquito perfeccionista sí que era.
Pero además, cuando escribió estas variaciones, se encontraba en un estado bastante depresivo. Ese año, Rachmaninov había escrito una carta criticando el régimen soviético, lo que provocó que su música fuese prohibida en Rusia hasta 1933. Rachmaninov, que hacía sonar su tierra natal en cada nota que escribía, no se debió de tomar muy bien esta noticia… y, por un motivo o por otro, terminó renegando de sus variaciones.
Sin embargo, yo quisiera reivindicar esta curiosa partitura. Empezando por su forma: el tema y variaciones. El nombre es bastante descriptivo: en este tipo de composición, se presenta un tema musical, sin florituras, que en sucesivas repeticiones va variando de distintas maneras: con adornos, cambiando de armonía, de ritmo o de textura… Cada variación debe ser consistente con el tema original y, más importante aún, con la norma interna que rige esa variación en concreto. Una posible norma sería, por ejemplo, duplicar la duración de todas las notas o al revés: acelerar el ritmo, añadiendo notas intermedias en la melodía. Otra podría ser cambiar todos los acordes mayores por acordes menores (equivalente a cambiar “el color” de una imagen). O desplazarlo todo medio pulso, de manera que la melodía suene desplazada en el tiempo (lo que en música se conoce como sincopada). Las posibilidades son infinitas. Rachmninov, en este caso, nos presenta hasta veinte (podéis encontrarlas descritas de una manera un poco más técnica, aquí).
Aunque a veces, las variaciones se han planteado como un mero ejercicio estilístico o académico, de hecho esta forma musical explota como ninguna otra nuestro gusto por la repetición en música. Como oyentes, el tema conductor nos permite generar expectativas, anticiparnos a lo que viene, reconociendo una y otra vez el patrón familiar: el tema que se quedará con nosotros en forma de melodía pegadiza.
Por su parte, las variaciones suelen tener caracteres sumamente diferenciados. Cada una nos descubre una nueva faceta de la música, nos sorprende y dirige nuestra atención hacia nuevas lecturas, hacia nuevos detalles que enriquecen la escucha: hacia esa nueva norma o forma de cambio que da consistencia a la variación. Nuestra cabeza, amante de los puzzles, se apresura a intentar adivinar la nueva música1 como un matemático deduciendo teoremas. Por su parte, la misma norma estimula la creatividad del compositor, que ahora debe reducir el tema a su esencia para poder cambiarlo sin perderlo.
Lo alucinante es que este juego de abstracción y adivinación sucede aunque no lo sepamos, aunque no seamos músicos, aunque nunca nos paremos a pensar en la música que nos llena los oídos. La norma está ahí y se hace perceptible como placer o como sorpresa (como expectativas que se frustran o se satisfacen) simplemente porque somos monos simbólicos, monos que abstraen y buscan patrones y anticipan continuamente las consecuencias de los patrones encontrados. Incluso cuando esas consecuencias son unas cuantas corcheas a destiempo.
El famoso tema de Vangelis, el tema que también fue de Rachmaninov y de Corelli, ha sido la base de variaciones o teoremas musicales durante al menos seis siglos de historia. Quizás no tan longevo como los axiomas de Euclides… pero mucho más bailable.
Referencia:
1 Eugene Narmour. Music Expectation by Cognitive Rule-Mapping. Music Perception: An Interdisciplinary Journal, 2000.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Tema y variaciones se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El arte de la repetición
- Variaciones artísticas del teorema de Napoleón
- La forma fractal de mapas y pulmones
Solomon Lefschetz, matemático ‘por accidente’
En los años cincuenta, en Princeton, se decía que había cuatro usos de la palabra ‘obvio’.
Algo es obvio en el sentido de Beckenbach, si es verdad y puedes verlo inmediatamente.
Algo es obvio en el sentido de Chevalley, si es verdad y te costará varias semanas verlo.
Algo es obvio en el sentido de Bochner, si es falso y te costará varias semanas verlo.
Algo es obvio en el sentido de Lefschetz, si es falso y puedes verlo inmediatamente.
Steven G. Krantz en [1]
Esta ocurrente cita nos la envío Natalia Castellana a un grupo de personas que habíamos compartido mesa –y animada conversación– en la cena del XXV Encuentro de Topología celebrado hace unas semanas en Barcelona. Nos comentaba que se la pasaba a su alumnado de topología… quizás para advertirles que eso de ser ‘obvio’ puede tener muchos matices.
Los matemáticos aludidos en esta cita de Steven G. Krantz son Edwin Ford Beckenbach (1906-1982), Claude Chevalley (1909-1984), Salomon Bochner (1899-1982) y Solomon Lefschetz (1884-1972). Todos ellos trabajaron en algún momento en la Universidad de Princeton, en la que Krantz realizó su tesis doctoral.
 Solomon Lefschetz. Imagen: Matemáticos en México
Solomon Lefschetz. Imagen: Matemáticos en MéxicoParece que Lefschetz era todo un personaje… De origen ruso, se formó como ingeniero en París y emigró a Estados Unidos. Pero un fatal accidente en el laboratorio en el que trabajaba –en la Westinghouse Electric Company– le hizo perder las dos manos en 1907. Este desafortunado percance provocó que sus intereses giraran hacia las matemáticas, convirtiéndose en un prolífico científico con especiales contribuciones a la topología algebraica y sus aplicaciones a la geometría algebraica.
En el lugar de sus manos llevaba unas prótesis cubiertas con unos guantes negros que escondían unas piezas bien formadas, pero que no tenían ninguna otra función. A primera hora de la mañana, uno de sus estudiantes se encargaba de encajar un trozo de tiza en su mano y retirarla al final del día.
Uno de sus resultados más conocidos es el teorema del punto fijo de Lefschetz (1926) que estudia los puntos fijos de un espacio topológico compacto en sí mismo usando técnicas de homología. En [1] se cuenta una anécdota sucedida en 1966 durante una mesa redonda que tuvo lugar tras una exposición por parte de Lefschetz de su famoso teorema. Alguien del público le recordó que, en los años 1940, habían coincidido en un tren y le preguntó por la diferencia entre el álgebra y la topología. Según esa persona, Lefschetz le había contestado: ‘Si solo se trata de girar la manivela, es álgebra; pero si hay una idea presente, entonces es topología’… el matemático, incómodo y sorprendido, se defendió afirmando que él no podría haber dicho nunca esas palabras.
Sin embargo, parece que Lefschetz tenía mucha seguridad en sí mismo y era bastante ‘temido’ por sus estudiantes y colegas. Prueba de ello es esta cantinela, un tanto cruel, que le dedicaba el alumnado de Princeton:
Here’s to Lefschetz, Solomon L.
Irrepressible as hell
When he’s at last beneath the sod
He’ll then begin to heckle God.
(Aquí está Lefschetz, Solomon L.
Incontrolable como el infierno
Cuando al fin esté bajo el césped
Entonces comenzará a molestar a Dios.)
A pesar de ese ‘miedo’ que provocaba entre algunos, fue un matemático sobresaliente, que dejó un importante legado científico y formó a un buen número de matemáticos. En particular, contribuyó a crear una potente escuela matemática en México, y por ello, el gobierno de este país le condecoró con la orden del Águila Azteca.
Krantz lo describe como ‘uno de esos matemáticos […] que podía dormir durante una conferencia y despertar al final con una pregunta brillante…’
Referencias
[1] Steven G. Krantz, Mathematical anecdotes, Math. Intelligencer 12 (4) (1990), 32-38
[2] Solomon Lefschetz, Fixed Points, Parts 1 and 2, Mathematical Association of America Lecture Films, 1966
[3] J J O’Connor and E F Robertson, Solomon Lefschetz, MacTutor History of Mathematics archive, University of St Andrews
[4] Solomon Lefschetz, Reminiscences of a mathematical immigrant in the United States, American Mathematical Monthly 77 (1970) 344-350
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Solomon Lefschetz, matemático ‘por accidente’ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ilustraciones artísticas de un matemático
- Un convite matemático ‘de altura’
- Pierre Fatou, un matemático poco (re)conocido
Propagación de una onda

El estudio de las ondas y su comportamiento puede que sea más intuitivo si pensamos en grandes modelos mecánicos y en ondas muy simples no periódicas, como los pulsos. Consideremos, por ejemplo, un tren de carga con muchos vagones unidos a una locomotora pero parado. Si la locomotora arranca bruscamente, su tracción sobre el el primer vagón envía una onda de desplazamiento que corre por la línea de vagones.
La perturbación del desplazamiento inicial procede de la locomotora que va haciendo chasquear los acoplamientos uno por uno. En este ejemplo, la locomotora es la fuente de la perturbación, mientras que los vagones de carga y sus acoplamientos son el medio. El “golpe” que viaja a lo largo de la línea de vagones es la onda. La perturbación se desplaza desde un extremo al otro del tren y con ella va la energía del desplazamiento y del movimiento. Sin embargo, ninguna partícula de materia se desplaza con la onda; cada vagón se mueve solo un poco hacia delante.
¿Cuánto tiempo tarda el efecto de la perturbación creada en un punto en llegar a un punto distante? El intervalo de tiempo depende, por supuesto, de la velocidad con la que se propaga la perturbación. Esta velocidad, a su vez, depende del tipo de onda y las características del medio. En cualquier caso, el efecto de una perturbación nunca se transmite instantáneamente. Cada componente del medio tiene inercia y cada parte del medio es compresible. Por lo tanto, se necesita tiempo para transferir energía de una parte a otra. Esto mismo aplica igualmente a las ondas transversales.
La serie de imágenes siguiente representa una onda, un pulso, en una cuerda. Pensemos en cada imagen como un fotograma de una película cinematográfica, y que daca una se ha tomado a intervalos de tiempo iguales. Ya sabemos que el material de la cuerda no viaja junto con la onda. Pero cada parte de la cuerda pasa se mueve hacia arriba y hacia abajo cuando la onda pasa. Cada trozo sufre exactamente el mismo movimiento que el trozo a su izquierda, excepto que lo hace un poco más tarde.
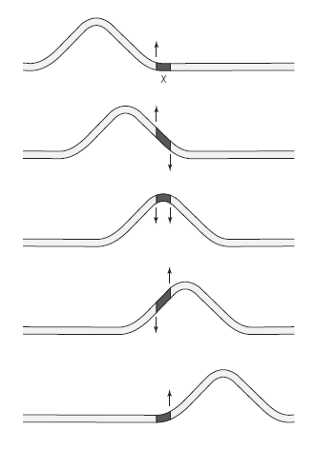
Fijémonos en el pequeño trozo de cuerda señalado con una X en el primer “fotograma”. Cuando el pulso que viaja por la cuerda alcanza X lo que está ocurriendo es que el trozo de cuerda justo a la izquierda de X ejerce una fuerza hacia arriba en X. Cuando X se mueve hacia arriba, el siguiente trozo ejerce una fuerza restauradora (una fuerza hacia abajo). Cuanto más se mueva X hacia arriba, mayores serán las fuerzas restauradoras. Llega un momento en que X deja de moverse hacia arriba y comienza a bajar de nuevo. La sección de la cuerda a la izquierda de X ahora ejerce una fuerza restauradora (hacia abajo), mientras que la sección de la derecha ejerce una fuerza hacia arriba. Por lo tanto, el movimiento hacia abajo es similar, pero opuesto, al movimiento hacia arriba. Finalmente, X regresa a la posición de equilibrio cuando ambas fuerzas han desaparecido.
El tiempo requerido para que X suba y baje, es decir, el tiempo requerido para que el pulso pase por esa parte de la cuerda, depende de dos factores. Estos factores son la magnitud de las fuerzas en X y la masa de X. Dicho de otra manera y en términos más generales: la velocidad con que se propaga una onda depende de la rigidez y de la densidad del medio. Cuanto más rígido sea el medio, mayor será la fuerza que cada sección ejerce sobre las secciones vecinas y, por tanto, mayor será la velocidad de propagación. Por otro lado, cuanto mayor sea la densidad del medio, menos responderá a las fuerzas* y, por tanto, más lenta será la propagación.
De hecho, la velocidad de propagación depende de la relación entre el factor de rigidez y el factor de densidad. El significado exacto “factor de rigidez” y “factor de densidad” es diferente para cada tipo de onda y para diferentes medios. Por ejemplo, para cuerdas tensas el factor de rigidez es la tensión T en la cuerda, y el factor de densidad es la masa por unidad de longitud, m / l, y la velocidad de propagación v viene dada por v = [T / (m / l)]½
Nota:
*Recordemos que F = m · a, es decir, para una fuerza constante, a mayor masa menor aceleración, que es el efecto que tiene una fuerza que actúa sobre una masa.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Propagación de una onda se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las ondas están por todas partes
- Incompletitud y medida en física cuántica (VI): la onda piloto
- Tipos de ondas
Tamaño corporal y función renal de aves y mamíferos
 Foto: Braden Tucker / flickr
Foto: Braden Tucker / flickrLos riñones de un ave o un mamífero de 1 kg no representan más de un 1% de su masa total. Por otro lado, la relación que mantienen la masa de los riñones con la del organismo es, como la de otros órganos, alométrica. Quiere esto decir que conforme aumenta el tamaño de un animal, también aumenta el de sus riñones, pero en diferente medida.
La masa de los riñones (Mrenal: g) de los mamíferos y de las aves depende de la masa corporal total (Mtotal: kg) de acuerdo con las siguientes ecuaciones:
Mrenal = 7.32 Mtotal0.85 (mamíferos) y
Mrenal = 8.68 Mtotal0.91 (aves).
Por otro lado, si se distingue dentro de las aves entre las que poseen glándulas de sal1 y las que no, las ecuaciones correspondientes son las siguientes:
Mrenal = 7,30 Mtotal0,93 (aves sin glándulas de sal) y
Mrenal = 11,27 Mtotal0,88 (aves con glándulas de sal).
De acuerdo con las expresiones anteriores, para un animal de 1 kg, la masa renal es ligeramente superior en el conjunto de las aves (8,7 g) que en los mamíferos (7,3 g), aunque es mayor el de aves con glándulas de sal (11,3 g) que el de las que carecen de tales órganos (7,3 g). Este hecho resulta paradójico, puesto que cabría pensar que al disponer de dispositivos adicionales para la regulación del balance osmótico (las glándulas de sal), los riñones podrían ser de menor tamaño, puesto que parte del trabajo ya lo hacen las glándulas. Sin embargo, la mayor parte de las aves con glándulas de sal son marinas, por lo que han de soportar mayores niveles de estrés osmótico. En otras palabras: la misma razón por la que han recurrido a dispositivos específicos para eliminar las sales sobrantes es probablemente la que ha conducido a dotarse de riñones de mayor tamaño relativo. En otras palabras, las aves marinas han de hacer un mayor trabajo osmótico, trabajo que se reparte entre las glándulas salinas y unos riñones de mayores dimensiones.
En lo relativo a la dependencia del tamaño renal con respecto al tamaño corporal, hay que fijarse en los valores de las potencias (o exponentes) de las correspondientes ecuaciones. Esos valores son algo superiores al valor esperable teniendo en cuenta que el metabolismo y la masa se relacionan de acuerdo con una ecuación cuya potencia vale 0,75. Para valorar correctamente el significado de los valores anteriores (0,93 y 0,88) conviene tener presente cuáles son las correspondientes relaciones de dependencia entre las funciones renales relevantes y el tamaño corporal.
La tasa de filtración glomerular (Vf.g.: ml min-1) depende del tamaño del organismo (Mtotal: kg) de acuerdo con las siguientes ecuaciones:
Vf.g. = 2,00 Mtotal0,73 (aves) y
Vf.g. = 5,36 Mtotal0,72 (mamíferos).
La tasa de filtración glomerular de un mamífero es, por lo tanto, aproximadamente el doble que la de un ave del mismo tamaño. Esa diferencia es consecuencia de la diferente forma en que aves y mamíferos producen orina. Las aves eliminan sus restos nitrogenados en forma de ácido úrico que, al ser virtualmente insoluble en las condiciones de la cloaca aviar, ejerce un efecto osmótico mínimo en la orina final; mientras que los mamíferos eliminan urea, lo que obliga a concentrar mucho la orina para evitar una pérdida excesiva de agua. Por lo anterior, las aves filtran un menor volumen de plasma y, de hecho, en caso de necesitar limitar la pérdida de agua, pueden reducir mucho y llegar a suprimir la filtración en los glomérulos de las nefronas que, como vimos aquí, carecen de asa de Henle y, por lo tanto, son incapaces de concentrar la orina. Como consecuencia de lo anterior, las aves, a pesar de tener tasas de filtración glomerular muy inferiores a las de los mamíferos, pueden eliminar la misma cantidad de restos nitrogenados que aquellos.
En todo caso, y al margen de las diferencias entre aves y mamíferos en lo que se refiere a los niveles absolutos de filtración glomerular, su dependencia con respecto al tamaño corporal viene expresada mediante una función alométrica en la que la potencia se aproxima mucho al valor de 0,75. Cabe, por tanto, atribuir esa dependencia al efecto del tamaño sobre el metabolismo global.
Y algo parecido cabe decir acerca de la tasa de producción de orina Vo (ml min-1), cuya dependencia con respecto a la masa corporal (Mtotal: kg) es la que, para los mamíferos, expresa la siguiente expresión:
Vo = 0,042 Mtotal0,75.
Por lo tanto, las tasas relevantes (de filtración glomerular y de producción de orina) se relacionan con el tamaño corporal de la misma forma que lo hace el metabolismo. Cabe concluir, por ello, que es la actividad metabólica, con su correspondiente generación de residuos nitrogenados, la que determina el modo en que el tamaño afecta al nivel de actividad renal. El hecho de que la masa renal dependa de la masa total a través de una potencia de valor algo superior a 0,75 es, muy probablemente, consecuencia de factores diferentes, más relacionados con la arquitectura de los riñones, los tejidos de soporte en los que se encuentran embebidas las nefronas con sus glomérulos y la forma en que todos esos elementos se empaquetan en los riñones.
Fuente:
William A. Calder III (1996): Size, Function, and Life History. Dover Publications Inc, Mineola, New York.
Nota:
1 Las glándulas de sal son glándulas tubulares que expulsan sales para evitar que se acumulen en los fluidos corporales.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Tamaño corporal y función renal de aves y mamíferos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La función del asa de Henle en el riñón de mamíferos
- La función respiratoria depende del tamaño de los animales
- La función renal en vertebrados
Carne bovina
“Las vacas domésticas ciertamente descienden de más de una forma salvaje… Los naturalistas generalmente han hecho dos principales divisiones del ganado vacuno: las clases jorobadas habitan los países tropicales, que en la India se llaman cebús, a los que se ha dado el nombre específico Bos indicus; y el ganado vacuno común no jorobado, generalmente incluidos bajo el nombre de Bos taurus.”
Charles Darwin, “La variación en los animales y las plantas domesticadas”, 1868.
 Uros (Bos primigenius) representados en la cueva de Lascaux (Francia)
Uros (Bos primigenius) representados en la cueva de Lascaux (Francia)Vacas, toros, terneras, bueyes,… y chuletones, todos y todas de la familia Bovidae, género Bos. De las siete especies domesticadas de este género hay dos que destacan: Bos taurus y Bos indicus. Ambas descienden del Bos primigenius, el ancestral y mítico uro cuyo último ejemplar del que tenemos constancia fue cazado en Polonia en 1627 y que tenía una distribución amplia por Eurasia, de este a oeste y del sur de la taiga al norte de los desiertos y del bosque tropical. Bos taurus es el ganado bovino europeo llevado a otros continentes y desde el Creciente Fértil en el Oriente Próximo y, quizá, con un proceso de domesticación independiente en África. Bos indicus es el cebú, el ganado bovino con joroba, que viene del sur de Asia, en concreto, del valle del Indo, hoy Pakistán, y se extendió por la India y, hace unos 3000 años, fue introducido en África.
 Toro retinto (Bos taurus). Fuente: MAPA
Toro retinto (Bos taurus). Fuente: MAPASon de los animales más importantes del planeta para la especie humana. Contribuyen con su potencia de tiro, carne, leche, pieles y estiércol. Además, al ser rumiantes, con su especial proceso digestivo, convierten la indigerible, para los humanos, celulosa de las plantas en productos asimilables como hidratos de carbono, grasa y proteínas En Mesopotamia, Egipto y el valle del Indo, el ganado bovino era esencial como fuerza de tiro para cultivar los terrenos regados del desierto y las regiones semiáridas. Criar el ganado suponía tiempo y esfuerzo pues necesitaba agua y forraje, que también había que cuidar o cultivar. Entonces era más importante como fuerza de tiro que como alimento. Durante la dinastía de Ur, en Mesopotamia, hace unos 4000 años, solo suponía el 10% de la carne de la alimentación.
 Cebú (Bos indicus). Fuente: Wikimedia Commons
Cebú (Bos indicus). Fuente: Wikimedia CommonsPara hacernos una idea de la importancia de los bovinos en la alimentación podemos citar que, en 2011, el censo mundial de bovinos era de 1347 millones de cabezas. De Brasil eran 175 millones, en la India se contaban 174 millones, en Estados Unidos llegaban a los 96 millones, en la Unión Europea 90 millones, y en China 82 millones y creciendo. La producción de carne de vacuno se repartía entre Estados Unidos con el 19.6%, Brasil con el 14.4%, la Unión Europea con el 12.8% y China con el 9.3%. España ocupaba el quinto lugar dentro de la Unión Europea, con un aumento del 40% en la primera década del siglo XXI. En aquel año, 2011, se consumieron 300 millones de kilogramos de carne de bovino en España, con el 75% de ternera. Donde más carne se consume es Castilla y León y donde menos en Extremadura.
 Hamburguesa neoyorkina. Fuente: Wikimedia Commons
Hamburguesa neoyorkina. Fuente: Wikimedia CommonsEn la actualidad y en todo el planeta una de las formas más consumidas de la carne de bovino es la hamburguesa. En Estados Unidos llega al 40% del total de carne para la alimentación humana. Es un icono de la cultura popular aunque tiene su origen en Hamburgo, Alemania. Carne “de Hamburgo” ya aparecía en la carta del restaurante Delmonico de Nueva York en 1836. En la Feria Mundial de St. Louis de 1904 se hicieron populares. Allí las preparaban y vendían inmigrantes alemanes.
Las hamburguesas son una consecuencia de la eficiencia típica de Estados Unidos. Se pueden cocinar en menos de ocho minutos y, en los restaurantes se preparan a pedido del cliente. Estos locales aparecen en la década de los veinte del siglo pasado y, años después, las grandes franquicias de la hamburguesa la han llevado a todo el planeta. Así comunican los valores del “American way of life” y, en concreto, de su dieta: eficiencia, servicio y limpieza. Sin embargo, para algunos críticos demuestran la escasa imaginación de la gastronomía de Estados Unidos.
 Toros de lidia en la dehesa de Salamanca (España). Hay quien afirma que el toro de lidia sería lo más parecido actualmente al uro primigenio.
Toros de lidia en la dehesa de Salamanca (España). Hay quien afirma que el toro de lidia sería lo más parecido actualmente al uro primigenio.El proceso de domesticación del ganado bovino comenzó hace unos 11000 años, aunque las pruebas directas del proceso que por ahora conocemos tienen fechas más cercanas, como unos 9000 años. En Catal Huyuk, en la actual Turquía, las excavaciones han demostrado el paso de uros, hace 8400 años, a ganado bovino, hace 7800 años. El ganado bovino supone del 20% al 25% de los huesos encontrados hace 8400 años, y se han identificado como de uro. También es bovino domesticado de fechas tempranas el que se ha encontrado en Grecia, en concreto, en Argissa, fechado hace 8500 años, y en Franchthi, hace 7000 años. El estudio genético de Ruth Bollongino y su grupo, del Museo Nacional de Historia Natural de Paris, con 15 muestras de 1500 a 8000 años de Irán, más 26 muestras de bovinos actuales de Turquía e Irak, permite a los autores sugerir que la primera población de bovinos domesticados tenía 80 hembras que, a pesar de ser un número pequeño, es el origen del Bos taurus actual.
 Fresco del salto del toro, que muestra a un acróbata sobre un toro con dos mujeres acróbatas a los lados. Palacio de Cnosos (Creta). Aproximadamente del 1450 a.e.c.
Fresco del salto del toro, que muestra a un acróbata sobre un toro con dos mujeres acróbatas a los lados. Palacio de Cnosos (Creta). Aproximadamente del 1450 a.e.c.Sin embargo, hay hallazgos en Chipre que plantean que hay que ajustar las fechas de la domesticación de animales. El uro no existía en la isla pero hay restos de bovinos de hace algo más de 10000 años. Esos bovinos solo pudieron llegar a Chipre si fueron transportados por nuestra especie y, se puede suponer, que o estaban domesticados o en proceso de domesticación.
Parece que la domesticación de los bovinos fue posterior a la de los cereales, las cabras y las ovejas. Además de las mencionadas domesticaciones del cebú y del bovino europeo en el valle del Indo y en el Creciente Fértil, parece que hubo otros procesos locales cuando era necesario y posible y en fechas diferentes. Por ejemplo, el poeta Virgilio cuenta que en la Roma imperial una virulenta enfermedad acabó con el ganado y los campesinos capturaron y domesticaron uros para reemplazarlo. Datos genéticos actuales indican que hubo cruces entre bovino domesticado y uros en las Islas Británicas y en la Península Ibérica.

Los estudios genéticos del bovino europeo y del cebú implican, por lo menos, a dos grupos distintos del uro en su origen y dos procesos de domesticación diferentes. Para el Bos taurus se han listado 480 razas de bovino en Europa y todas mantienen una continuidad genética con las razas seleccionadas en el Creciente Fértil. Los agricultores y ganaderos ancestrales se movieron en Europa desde el sudeste, el Creciente Fértil, hacia el noroeste, las Islas Británicas y Escandinavia, llevaban con ellos su ganado que se cruzó, no muy a menudo, con los uros salvajes de Europa. El ganado bovino se extendió por Europa a la vez que el arado de madera, esencial para el cultivo. Así aumentó el suelo dedicado a la agricultura. Además, para el uso del bovino como fuerza de tiro fue importante la castración de los machos y la aparición de los bueyes, fuertes, constantes, dóciles y manejables. Eran perfectos para acarrear y para el manejo del arado. Se han encontrado huesos de bueyes en yacimientos de hace 6000 años y, también, fragmentos de cerámica con figuras de bueyes y arados de hace 5000 años en Tsouginza, en Grecia.
En un estudio detallado de ADN del Bos taurus en Europa, Amelie Scheu y sus colegas, de la Universidad Johannes Gutenberg de Mainz, en Alemania, confirman que el bovino domesticado llegó desde Turquía e Irán hace 7000-8000 años y, como ocurre en los procesos de domesticación, la variabilidad genética disminuye con el aumento de la distancia al centro de origen de la especie domesticada. Cuanto más lejos, en Europa, del Creciente Fértil asiático, menos diversidad genética en los bovinos domesticados.

Viajemos a Inglaterra, al Condado de Wiltshire, a un lugar llamado Stonehenge, al conocido monumento megalítico con su extraordinario círculo de piedras. Cerca, a un par de kilómetros se ha descubierto y excavado un poblado, en un lugar llamado Durrington Walls, de hace unos 4000-5000 años. El grupo de Oliver Craig, de la Universidad de York, estudió el poblado y propuso que allí vivían los que construyeron y utilizaron el santuario de Stonehenge.
En las excavaciones encontraron gran cantidad de fragmentos de cerámica y muchos huesos de animales. Analizaron los lípidos adheridos a la cerámica y concluyeron que en esas vasijas se había cocinado carne de cerdo, hasta en un 80% del total de carne, y un 8% de bovino, todo ello en fiestas y banquetes al aire libre, con asados, y en interiores, por cocimiento. Por tanto, hace 5000 años se preparaba el estofado de buey, o de ternera o, quizá, de toro o , incluso, de uro. En la actualidad, en el Condado de Wiltshire todavía se cocina un estofado de bovino, que, quién sabe, quizá tiene reminiscencias de lo que comían los que construyeron Stonehenge.
Así es la receta del estofado de buey al estilo del Condado de Wiltshire:
“Picar una cebolla y dos tallos de apio y freírlos en aceite de colza, aunque por hacerlo más mediterráneo prefiero el aceite de oliva. Lo hacemos a fuego suave por unos cinco minutos. Añadimos un par de zanahorias en trozos, laurel y tomillo y dejamos otros dos minutos. Ahora juntamos tomate frito y salsa Worcestershire, que luego explicaré cómo hacer, y medio litro de agua hirviendo. Mezclamos y lo ponemos en una cazuela a cocer. Añadimos caldo de carne o un par de pastillas de caldo de carne. Sazonamos con pimienta.
En una sartén, freímos en aceite de oliva la carne, algo así como un kilo de falda, que hemos cortado antes en trozos. Cuando esté dorada echamos todo, con el aceite incluido, en la cazuela.
Dejamos cocer, a fuego suave, de ocho a diez horas, y, después, con fuego más fuerte, otras cuatro horas. Se aconseja que el estofado hay que prepararlo de un día para otro, que mejora mucho. Creo que con estos tiempos de cocimiento es inevitable, hay que cocinarlo el día anterior (al festejo, dirían en Durrington Walls).
Para la salsa Worcestershire, o se compra o se hace. Se junta vinagre de manzana, sala de soja, azúcar moreno, jengibre molido, mostaza, cebolla machacada, ajo en polvo, canela y pimienta negra. Mezclamos muy bien, hervimos revolviendo sin parar, cocinamos como un minuto a fuego suave y a la nevera.”
Es evidente que algunos de los ingredientes que he incluido en la receta todavía no habían llegado a Durrington Walls hace 5000 años pero, creo, nos podemos permitir la licencia.
En nuestro entorno más cercano, el ganado bovino aparece en el final del Neolítico y en la Edad del Bronce o Calcolítico, hace unos 5000 años, según Jesús Altuna, y en toda la cornisa cantábrica hay hallazgos de hace 6500 años. Anteriormente solo se encuentran fósiles de uro. Por ejemplo, se encontró un esqueleto casi completo de uro en el yacimiento de Sima Las Grajas, en la Sierra de Guibijo, en Álava, cerca del nacimiento del río Nervión. Se dató de hace algo más de 7000 años. Altuna menciona que hay una gran escasez de datos sobre el uro en toda esta zona. Relata, sin embargo, que en el siglo IV, hace 1600 años, el escritor romano Servio Gramático citó que había uros en el Pirineo.
En la época romana, el bovino era un importante proveedor de carne. También aparecen huesos de bovino en los yacimientos celtíberos y en las escasas excavaciones en el País Vasco de la época medieval que han estudiado los restos animales encontrados. Como ejemplo sirve la excavación del yacimiento de El Castillo, en Astúlez, Álava, con presencia de bovino desde el final de la Edad del Bronce hasta el siglo XIII. Y del siglo XI al XVIII se han estudiado los restos de ganado bovino en las ciudades del País Vasco. El ganado bovino es un componente importante de la dieta, sobre todo en Bilbao, seguida de Orduña y Vitoria. En Orduña han aparecido huesos grandes rotos en sentido longitudinal para la extracción del tuétano. Pero cambia el tamaño del bovino que se cría durante estos siglos. Hay una disminución después de la época romana en los siglos VIII y IX, y un aumento posterior hasta la actualidad.
Más o menos por esos años, hacia el siglo IX, los árabes trajeron a Al-Andalus la receta de un adobo de carne de bovino con fuerte influencia persa e hindú que, creo, merece la pena probar. Benavides Barajas nos lo cuenta así:
“Se corta la carne para guisar en trozos cuadrados y se limpia de grasas. La mezclamos con cebolla picada, dientes de ajo machacados, clavo, nuez moscada, jengibre, perejil, cardamomo en polvo, canela, azafrán, cúrcuma, sal, pimienta y vinagre, y todo en abundancia. Y aceite de oliva.
Se cubre con vinagre y se deja a la fresca, o en la nevera, por dos días. Después de pone en la cazuela a fuego suave. A las dos horas ya está cocinada y se añade tomate en salsa y agua con mostaza. Se calienta un poco y se retira del fuego.
La podemos guardar en la nevera un día y calentar para comer con arroz cocido y suelto y pasas. Si gusta, se puede añadir guindilla. Al recalentar, controlar que no se seque y añadir agua si es necesario.”
El estudio de Albano Beja Pereira y su grupo, de la Universidad de Oporto, con 27 colaboradores de otras 25 instituciones, analiza el ADN mitocondrial de cinco ejemplares de uro de Italia y lo compara con el ADN de más de 1000 ejemplares actuales de 51 razas de toda Europa. En el centro, norte y noroeste de Europa, casi todos los ADNs analizados son cercanos a uno de los tipos del Creciente Fértil, el llamado T3. En el norte de África, quizá desde Egipto, aparece otro grupo de ADN, el T1, que también se encuentra en las razas de los países ribereños del Mediterráneo. En la Península y en la muestra más cercana a nuestro entorno, casi todo el ADN viene del norte de África. Hay hallazgos recientes en Argelia y en el Sáhara oriental de un posible episodio de domesticación fechado hace 5000 años, y en el valle de Nilo desde hace 9500 años.
En África, los estudios genéticos recientes parece que indican dos grupos de bovinos con diferente origen. Hay un grupo con dotación genética como la de los bovinos del Creciente Fértil en el norte y noroeste, y otro grupo con similitud al cebú de Asia, quizá por paso a través del Índico y de la Península Arábica. Como aseguran Diane Gifford-Gonzalez y Olivier Hanotte, de las universidades de California en Santa Cruz y de Nottingham, una domesticación independiente de bovinos en África no está ni demostrada ni rechazada.
Para terminar una receta para cocinar carne de bovino, aunque sea una parte del animal que no se utiliza habitualmente. La he tomado de la Cocina para pobres, del Dr. Juderías, y es una receta autógrafa de la cocinera.
“Lávese y téngase en agua fría la ubre unas dos horas para que se limpie bien; póngase después un cuarto de hora en agua hirviendo y luego se deja enfriar, se saca, se corta y después se cuece y se guisa como los callos.”
Referencias:
Altuna, J. 1980. Historia de la domesticación animal en el País Vasco, desde sus orígenes hasta la romanización. Munibe 32: 1-163.
Beja-Pereira, A. et al. 2006. The origin of European cattle: Evidence from modern and ancient DNA. Proceedings of the National Academy of Sciences USA 103: 8113-8118.
Benavides Barajas, L. 1995. Nueva clásica cocina andalusí. Ed. Dulcinea. Granada. 328 pp.
Bollongino, R. et al. 2012. Modern taurine cattle descended from small number of Near-Eastern founders. Molecular Biology and Evolution 29: 2101-2104.
Castaños Ugarte, P.M. 1997. El pastoreo y la ganadería durante la romanización en el País Vasco. Isturitz 9: 659-668.
Craig, O.E. et al. 2015. Feeding Stonehenge: cuisine and consumption at the Late Neolithic of Durrington Walls. Antiquity 89: 1096-1109.
Gade, D.W. 2000. Cattle. En “The Cambridge World History of Food, vol. 1”, p. 489-496. Ed. por K.F. Kiple & K.C. Ornerlas. Cambridge University Press. Cambridge.
Gifford-Gonzalez, D. & O. Hanotte. 2011. Domesticating animals in Africa: Implications of genetic and archaeological findings. Journal of World Prehistory 24: 1-23.
Grau Sologestoa, I. 2015. Livestock management in Spain from Roman to post-medieval times: a biometrical analysis of cattle, sheep/goat and pig. Journal of Archaeological Science 54: 123-134.
Grau Sologestoa, I. 2016. Urban medieval and post-medieval zooarchaeology in the Basque Country: Meat supply and consumption. Quaternary International 399: 1-12.
Grau Sologestoa, I. 2017. Estudio de los materiales faunísticos del yacimiento de El Castillo (Astúlez, Valdegobía, Álava). Estudios de Arqueología Alavesa 27: 334-345.
Gupta, A.K. 2004. Origin of agricultura and domestication of plants and animals linked to early Holocene climate amelioration. Current Science 87: 54-59.
Juderías, A. 1994. Cocina para pobres. 11ª Ed. Ed. SETECO. Madrid.
Larson, G. & D.Q. Fuller. 2014. The evolution of animal domestication. Annual Review of Ecology, Evolution, and Systematics 45: 115-136.
Martín Cerdeño, V.J. 2011. Consumo de carne de vacuno en España. Distribución y Consumo Marzo-Abril: 95-98.
Orlando, L. 2015. The first aurochs genome reveals the breeding history of British and European cattle. Genome Biology 16: 225.
Park, S.D.E. et al. 2015. Genome sequencing of the extinct Eurasian wild aurochs, Bos primigenius, illuminates the phylogeography and evolution of cattle. Genome Biology 16: 234.
Russell, N. et al. 2005. Cattle domestication at Catalhoyuk revisited. Current Anthropology 46, Suppl.: S101-S108.
Scheu, A. et al. 2015. The genetic prehistory of domesticated cattle from their origin to the spread across Europe. BMC Genetics 16: 54.
Upadhyay, M.R. et al. 2017. Genetic origin, admixture and population history of aurochs (Bos primigenius) and primitive European cattle. Heredity 118: 169-176.
Vigne, J.-D. et al. 2011. The early process of mammal domestication in the Near East. New evidence from the Pre-Neolithic and pre-pottery Neolithic Cyprus. Current Anthropology 52, Suppl. 4: S255-S271.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Carne bovina se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ingredientes para la receta: el ajo
- Ingredientes para la receta: El conejo
- Ingredientes para la receta: El kiwi
Ciencia, arte y cultura callejera: física y música

La cultura se ha asociado históricamente con la actividad propiamente humana y en definitiva, con todas aquellas acciones que dan un sentido a la existencia del ser humano. En este sentido, todo lo que generamos para conocer el mundo, superarnos, deleitarnos o ensimismarnos, lo podemos definir como cultura.
Un término que abarca múltiples disciplinas y en el que el ser humano, en su afán por clasificar las diferentes formas de conocimiento y tratar de establecer una escala de relevancia, ha establecido una serie de fronteras delimitadoras. De la definición de estos límites surge el estereotipo de las dos culturas, las ciencias y las artes, así como la diferenciación entre las denominadas alta y baja cultura. Pero, ¿son realmente necesarias y útiles estas fronteras?
Con el objetivo de abordar este debate y mostrar una visión alternativa donde el arte y la ciencia se entrelazan, la Biblioteca Bidebarrieta de Bilbao acogió los pasados días 29 de mayo y 13 de junio el ciclo de conferencias “Ciencia, Arte y Cultura Callejera”.
El evento se enmarca dentro del ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
La primera jornada del ciclo de conferencias abordó el tema física y música desde un punto de vista multidisciplinar con la participación de los compositores Jaime Altozano y Sharif Fernández y la física y pianista Almudena Martín Castro. Se abordan las relaciones que existen hoy en día entre la física y la música, los aspectos elementales de la música, así como la relación entre el rap, la música y la poesía para abordar la brecha entre la alta y baja cultura.
Edición realizada por César Tomé López.
El artículo Ciencia, arte y cultura callejera: física y música se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: Analogías entre el arte y la ciencia como formas de conocimiento
- Arte & Ciencia: Sobre la dimensión cognitiva del arte en relación a la ciencia
- Arte & Ciencia: La importancia de la ciencia para la conservación del arte

