Tipos de ondas

Un muelle helicoidal muy popular como juguete (un Slinky) es un recurso fácil para visualizar los tres tipos diferentes de movimiento en el medio a través del que pasa una onda [1]. Primero movemos el extremo del muelle de lado a lado, o hacia arriba y hacia abajo como en la ilustración (a) de la figura de abajo. Observaremos que una onda de desplazamiento de lado a lado (o de arriba a abajo) viaja a lo largo del muelle. Ahora empujamos el extremo del muelle hacia adelante y hacia atrás, a lo largo de la dirección del propio muelle, como en la ilustración (b). Vemos ahora que una onda de desplazamiento de ida y vuelta viaja a lo largo del muelle. Finalmente, giramos el extremo del muelle rápidamente hacia la derecha y hacia la izquierda, como en la ilustración (c). En este caso una onda de desplazamiento angular se mueve a lo largo del muelle.
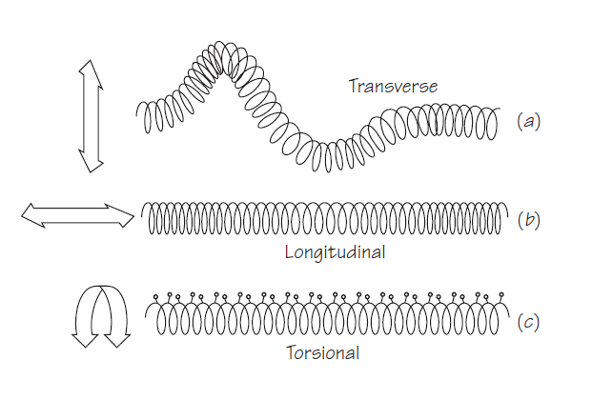
Las ondas como las de (a), en las que los desplazamientos son perpendiculares a la dirección en que viaja la onda, se denominan ondas transversales. Las ondas como las de (b), en las que los desplazamientos son en la dirección en la que se desplaza la onda, se denominan ondas longitudinales. A las ondas como las de (c), en las que los desplazamientos giran en un plano perpendicular a la dirección de la onda las llamaremos ondas torsionales.
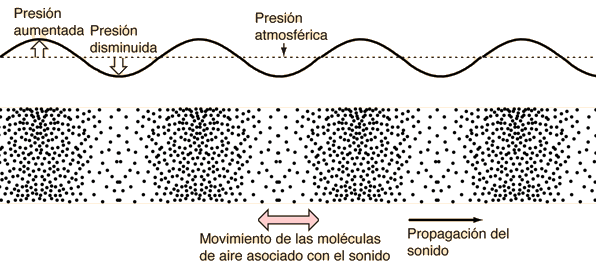
Los tres tipos de movimiento ondulatorio solo se encuentran a efectos prácticos en sólidos. Sin embargo, en los fluidos las ondas transversales y torsionales se extinguen muy rápidamente y, por lo general, no se pueden producir en absoluto salvo en la superficie. De aquí se deduce, por ejemplo, que las ondas sonoras en el aire y en el agua son longitudinales. Las moléculas del medio se desplazan hacia adelante y hacia atrás a lo largo de la dirección en la que viaja la energía del sonido [2].
Es habitual y muy útil hacer una gráfica para representar los patrones de una onda en un medio. Por supuesto, esto es muy fácil de hacer para las ondas transversales, pero no tanto para las ondas longitudinales o torsionales. Pero hay formas de conseguirlo. Por ejemplo, el gráfico siguiente representa el patrón de compresiones en un momento dado a medida que una onda de sonido (longitudinal) pasa por el aire. La línea del gráfico sube y baja porque el gráfico representa una instantánea del aumento y la disminución de la densidad del aire y de la presión asociada a lo largo de la trayectoria de la onda. No representa, y esto hay que recalcarlo, un movimiento hacia arriba y hacia abajo de las propias moléculas del aire.
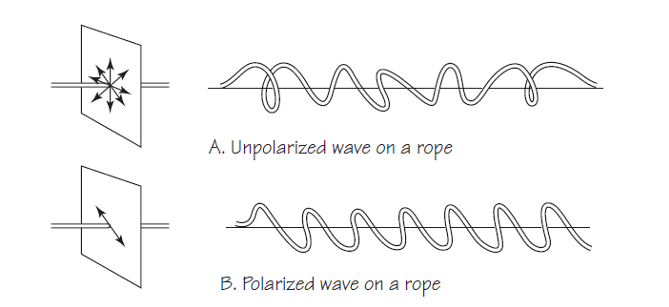
Para describir completamente las ondas transversales, como las de las cuerdas, se debe especificar la dirección del desplazamiento. Cuando el patrón de desplazamiento de una onda transversal está a lo largo de una línea en un plano perpendicular a la dirección del movimiento de la onda, se dice que la onda está polarizada. La polarización se suele asociar popularmente a las ondas electromagnéticas pero es un fenómeno que afecta, de hecho a todas las ondas transversales. En el gráfico siguiente se ve cómo se consigue la polarización cuando solo se permite una dirección del movimiento.
Estos tres tipos de ondas (longitudinal, transversal y torsional) tienen una característica importante en común. Las perturbaciones se alejan de sus fuentes a través del medio y continúan por sí mismas (aunque su amplitud puede disminuir debido a la pérdida de energía debido a la fricción y otras causas). Hacemos hincapié en esta característica concreta usando un verbo específico. Así, decimos que las ondas se propagan. Esto significa algo más que decir simplemente que “viajan” o “se mueven”.
 Campo de trigo con acianos (1890) de Vincent van Gogh. Óleo sobre lienzo. 60.0 x 81.0 cm. Fondation Beyeler (Suiza)
Campo de trigo con acianos (1890) de Vincent van Gogh. Óleo sobre lienzo. 60.0 x 81.0 cm. Fondation Beyeler (Suiza)Un ejemplo aclarará la diferencia entre las ondas que se propagan y las que no lo hacen. Es posible que hayas visto un campo de trigo o una pradera de hierba alta. Cuando el viento sopla se producen ondulaciones. El medio para estas “ondas” es el trigo o la hierba, y la perturbación es el movimiento oscilatorio de cada planta. Esta perturbación de hecho viaja, pero no se propaga; es decir, la perturbación no se origina en una fuente y luego continúa por sí misma. A diferencia de las ondas que estamos considerando, en los campos de trigo o en las praderas la ondulación tiene que alimentarse continuamente por la energía del viento. Cuando el viento cesa, la perturbación no continúa desplazándose, sino que también se detiene. Las ondulaciones viajeras del trigo oscilante no son en absoluto lo mismo que las ondas en una cuerda o en el agua. Las ondas son perturbaciones que se propagan en un medio [1].
Nota:
[1] En la primera parte de esta serie nos centramos en ondas mecánicas y todo lo que decimos, por defecto, se refiere exclusivamente a ondas mecánicas.
[2] Recordemos que las ondas son modos de transferencia de energía sin transferencia de materia.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Tipos de ondas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las ondas están por todas partes
- Ondas gravitacionales en la materia oscura
- La velocidad de las ondas electromagnéticas y la naturaleza de la luz
Una fórmula para dominar todos los mecanismos

En las entregas anteriores vimos cómo se definía el trabajo mecánico en física y cómo podía usarse la conservación de la energía para deducir la “ley de la palanca”.
En esta última entrega seguiremos el mismo procedimiento que en la anterior para derivar las “leyes” de otros mecanismos para mostrar cómo no son “leyes extra” de la física, sino el producto de la aplicación de la conservación de la energía.
Recordamos la técnica que usamos para la palanca:
-
Asumimos que no hay pérdidas de energía (rozamiento u otras)
-
Con argumentos geométricos vemos la diferencia de movimiento a la entrada y a la salida
-
Aplicando que el trabajo (la energía) debe ser igual en ambos extremos, obtenemos la variación en las fuerzas
Plano inclinado
Aunque no os parezca un mecanismo, es un dispositivo que me permite variar fuerza y distancia para ejercer un trabajo mecánico, así que, ahí va.
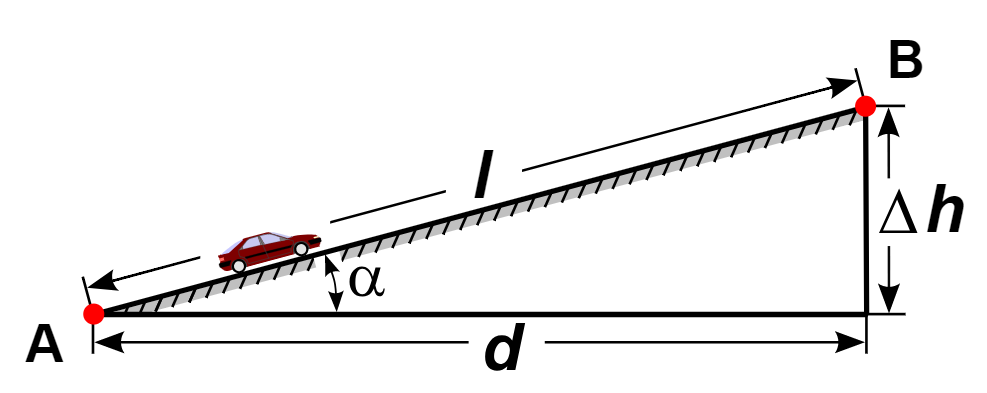
El objetivo es subir un objeto una determinada altura, bien puede ser el coche del dibujo, una caja que arrastremos, el carro de la compra. Aquello va a subir una altura Δh y podría hacerlo por dos caminos: directamente en vertical, desde la esquina inferior derecha hasta el punto B, o por la rampa, desde A hasta B.
Vayamos con nuestra técnica.
-
No tenemos en cuenta el rozamiento
-
Por geometría miremos la diferencia de camino recorrido
-
Por conservación de la energía estimamos la relación entre las fuerzas.
Llamemos 1 al trayecto por la rampa y 2 al trayecto vertical. En cualquier caso W1 = W2.
En el trayecto vertical la fuerza mínima que deberemos ejercer para elevar el objeto será el peso y la distancia Δh, la fuerza para movernos por la rampa no la sabemos, pero la distancia será L.
Recordamos una vez más que W = Fuerza·desplazamiento (si ambos alineadas)
F1 · despl1 = F2 · despl2
F1 · L = Peso · Δh
F1 = Peso · (Δh/L)
Resuelto. La fuerza que tengo que hacer es el peso multiplicado por un número que es menor que uno (fíjate que en un triángulo rectángulo así dispuesto, la altura siempre será menor que la rampa), por lo que la fuerza a hacer será una fracción del peso.
Cuanto menor sea la inclinación de la rampa o, si queréis verlo en función de d, cuanto mayor sea el desplazamiento horizontal de la rampa, menos fuerza tendré que hacer, pero más recorrido tendré que efectuar.
Para aquellos de vosotros que sepáis trigonometría, será claro que el factor reductor de la fuerza es el seno del ángulo alfa.
Vemos una vez más, que siempre tengo que “pagar” la misma energía. Estos sistemas nos permiten hacerlo a “plazos”, hago menos fuerza, pero tengo que ejercerla a lo largo de más distancia.
Tornillo
Este muchachito está muy infravalorado. Cuando decimos “tornillo” pensamos inmediatamente en esa pequeña punta con rosca que usamos para unir piezas, pero no es sólo eso, es el alma del tornillo de banco, los gatos de los carpinteros, algunos cascanueces (en realidad muchas herramientas de apriete), los sacacorchos y el gato con el que subimos el coche (¡de más de mil kilos!) usando una sola mano… deberíais gritar de asombro sólo con oír la palabra “¡Tornillo!”.
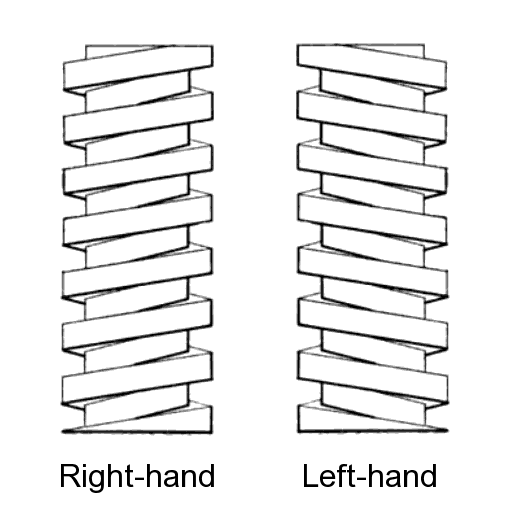
Un tornillo avanza linealmente cuando se le hace girar. Pueden ser a “derechas o izquierdas” según el sentido de giro para que avance, pero en ambos casos (y os lo pongo grande para que os lo imaginéis mejor) ¿no se trata realmente de un plano inclinado “enroscado” en un cilindro? Imaginaos subiendo por ahí.
 Eugene Wycliffe Kerr / Wikimedia Commons
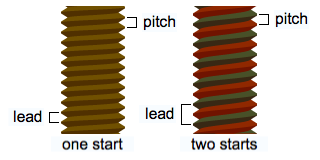
Eugene Wycliffe Kerr / Wikimedia CommonsLos tornillos a veces tienen más de un filete (la rampa), decimos que tienen varias entradas, lo veréis mejor en la siguiente imagen.
 Lambiam / Wikimedia Commons
Lambiam / Wikimedia CommonsMiremos el primer caso (una entrada), hay sólo una escalera, perdón, un filete, y cada vuelta que damos subimos una altura que coincide con la distancia entre roscas, que llamamos paso (pitch).
En el segundo caso (dos entradas), hay dos rampas que no se “mezclan”. Piensa en que son dos escaleras, la gris empieza en el primer piso y al cabo de una vuelta te deja acceder al tercer (!) piso, mientras que la roja va pasando por los pisos pares.
Ya sabes que a los que nos gustan las funciones de estado, como las energías, nos importan poco los caminos (bromas de físico, no se enfanden). Lo que me preocupa a mí es cuánto avanzo en cada vuelta que haga dar al tornillo con mi destornillador o manivela.
Pongamos un ejemplo viejuno
 Beat Rütti, Susanne Schenker (Museum Augusta Raurica) / Wikimedia Commons
Beat Rütti, Susanne Schenker (Museum Augusta Raurica) / Wikimedia CommonsImaginemos que la varilla está roscada y llamemos D a la distancia desde el eje al mango.
Vayamos a nuestra técnica
W1 = W2
F1 · despl1 = F2 · despl2
El desplazamiento de la manivela para una vuelta será la longitud de la circunferencia 2
Si estás embarazada, mejor no consumas alcohol

La exposición prenatal al alcohol tiene efectos negativos en el desarrollo del feto y, dependiendo de la dosis, puede dar lugar a alteraciones neurofisiológicas serias. Los efectos más severos de la exposición crónica a altas dosis provocan el llamado síndrome alcohólico fetal (SAF). El síndrome incluye déficits de crecimiento, rasgos faciales característicos y daños en el sistema nervioso central que conducen, inevitablemente, a dificultades de aprendizaje y problemas de comportamiento.
Aunque los efectos de la exposición a altas dosis de alcohol están bien establecidos, no se conocen igual de bien los de la exposición a niveles que no dan lugar al desarrollo de un SAF característico. Además, este ha sido un campo de estudio difícil porque casi toda la información se ha obtenido preguntando a las madres sobre su propio consumo durante el embarazo. Y por razones obvias, incluso cuando ha sido moderado, tienden a decir haber ingerido menos del que realmente han tomado. Por esa razón, unos investigadores alemanes ha recurrido al uso de etil glucurónido (EtG) como indicador. La degradación del alcohol en el hígado da lugar a la producción de EtG, que puede pasar a la sangre del feto de una mujer embarazada y, a través de la sangre, también a su intestino. Tiende por ello a acumularse junto con otros productos de desecho que han de ser expulsados al evacuarse el meconio, que es el primer excremento de los recién nacidos. La concentración de EtG puede medirse en volúmenes de meconio muy pequeños, aunque de su concentración no pueden deducirse niveles precisos de exposición prenatal al alcohol.
Los investigadores alemanes han observado que niños de entre 6 y 9 años de edad que habían dado positivo en EtG (de acuerdo con un umbral fiable para evitar falsos positivos) presentaban, en promedio, un cociente de inteligencia (IQ) 6 puntos inferior a los niños con niveles de EtG inferiores al valor umbral preestablecido (EtG negativo). También han encontrado una correlación positiva entre síntomas de trastorno por déficit de atención con hiperactividad (TDAH) -principalmente déficit de atención- y la concentración de EtG en meconio.
Como tenían la sospecha de que los efectos del alcohol se producen a través de lo que se conoce como mecanismos epigenéticos, analizaron también la metilación de ADN en muestras celulares de niños EtG positivos y EtG negativos. La metilación de ADN es un proceso por el que se añaden grupos metilo a la molécula de ADN y puede ocurrir por efecto de factores ambientales diversos. Como consecuencia, puede modificarse la actividad del segmento de ADN afectado y tener, por ello, consecuencias duraderas en los rasgos que dependen de esas zonas del genoma. Por esa razón, los investigadores estudiaron también la posible relación entre el déficit de atención de los niños EtG positivos y los genes que habían sido afectados por la metilación. Lo que observaron fue que los niños con muestras claras de haber sufrido exposición prenatal al alcohol presentaban 193 genes –agrupados en 19 asociaciones funcionales- cuya actividad había sido potencialmente modificada. Algunos de esos lotes de genes cumplen un papel crucial en la diferenciación, crecimiento y función neuronal. Todos los efectos se establecieron descontando el efecto del estatus socioeconómico de las madres.
Estas investigaciones no solo han establecido una relación entre la exposición prenatal al alcohol y el desarrollo de problemas cognitivos persistentes en los niñas y niños afectados, sino que han encontrado una asociación con efectos epigenéticos del alcohol. Dadas las consecuencias de tales efectos, toda insistencia en la importancia de evitar el consumo de alcohol por parte de las mujeres gestantes es poca.
Fuente:
Stefan Frey, Anna Eichler, Valeska Stonawski, Jennifer Kriebel, Simone Wahl, Sabina Gallati, Tamme W. Goecke, Peter A. Fasching, Matthias W. Beckmann, Oliver Kratz, Gunther H. Moll, Hartmut Heinrich, Johannes Kornhuber and Yulia Golub (2018): Prenatal Alcohol Exposure Is Associated With Adverse Cognitive Effects and Distinct Whole-Genome DNA Methylation Patterns in Primary School Children. Frontiers in Behavioral Neuroscience 12 (art. 125).
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 12 de agosto de 2018.
El artículo Si estás embarazada, mejor no consumas alcohol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Prevenir y tratar la enfermedad de Alzheimer: Una visión moderna
Actualmente, una de cada diez personas mayores de 65 años sufre alzhéimer, el tipo de demencia más común en ancianos. Se trata de una patología neurológica que conlleva un coste medio anual por paciente de aproximadamente 24.000 euros durante de 8 a 10 años. Es innegable que estamos ante un desafío sanitario, social y económico de primera magnitud.
En este contexto, el diagnóstico lo más temprano posible, el uso de las terapias y los tratamientos disponibles y la investigación en medidas de prevención primaria y secundaria son estrategias fundamentales para dar atención a las personas con demencia, optimizar su calidad de vida y la de sus familiares cuidadores e incluso reducir el número de enfermos a la mitad en una o dos décadas.
El neurólogo Pablo Martínez-Lange, director científico de la Fundación CITA Alzheimer, expuso los aspectos más relevantes asociados a esta patología en la conferencia titulada “Prevenir y tratar la enfermedad de Alzheimer: Una visión moderna”, que se celebró el pasado día 5 de marzo en la Biblioteca Bidebarrieta.
Entre otros aspectos, Martínez-Lange aborda en esta ponencia los mecanismos de esta enfermedad, los factores de riesgo y los tratamientos empleados en la actualidad para controlar o retrasar los síntomas de la misma. Así mismo analiza el papel que juegan hoy en día el diagnóstico precoz, los ensayos clínicos y la importancia de la prevención. la charla va seguida de un turno de preguntas.
Esta charla se enmarca dentro del ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
Edición realizada por César Tomé López.
El artículo Prevenir y tratar la enfermedad de Alzheimer: Una visión moderna se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El papel de la insulina en la enfermedad de Alzheimer
- #Naukas15 Alzhéimer
- Háblame y te digo si tienes alzhéimer
Cómo reducir el peso de un motor de aviación un 30 %
En la industria aeronáutica y aeroespacial se persigue no solo una mayor eficiencia de los motores como tales, sino también reducir las emisiones de CO2 y el consumo de combustible en términos absolutos. A esto último contribuye de manera significativa la disminución del peso de los motores de aviación. “Las aleaciones de titanio-aluminio (TiAl) muestran un gran potencial para satisfacer dichas demandas”, señala Leire Usategui Frias investigadora de la UPV/EHU.

Hasta ahora, las superaleaciones de base níquel han sido el material predominante en la fabricación de los álabes de las turbinas de los aviones, debido a su capacidad para soportar las elevadas cargas mecánicas y térmicas a las que se les somete en condiciones de servicio. Una desventaja de dichas superaleaciones es su alta densidad, y por tanto su peso, que en los TiAl queda reducida a casi la mitad.
“Además de ser más ligeras, las principales ventajas que presentan las aleaciones TiAl son una buena resistencia a la oxidación, al sobrecalentamiento y sobre todo a la fluencia (una deformación que tiene lugar cuando los materiales trabajan bajo tensión a alta temperatura y que es necesario evitar a toda costa)”, explica la doctora Usategui. Por ello, “las aleaciones TiAl se han convertido en la mejor alternativa para reemplazar las empleadas hasta ahora en las turbinas de aviación, ya que reducirían el peso de los motores entre un 20 y 30 % consiguiendo así un aumento significativo en el rendimiento del propio motor y una mayor eficiencia del combustible”, apunta la investigadora de la UPV/EHU.
Con el propósito de aumentar la temperatura de servicio de los componentes aeronáuticos, Usategui ha estudiado los efectos de la incorporación de distintos elementos químicos en las aleaciones TiAl. “Una de las aleaciones más relevantes y recientes, aparte de los elementos químicos principales (titanio y aluminio), presenta un contenido equilibrado de niobio y molibdeno y pequeñas cantidades de silicio y carbono”, explica la autora.
Se requiere una alta estabilidad estructural y un buen comportamiento de resistencia a la fluencia para que estas nuevas aleaciones cumplan los requerimientos de la ingeniería aeronáutica. Esas propiedades vienen controladas por los procesos de difusión y de deformación, por ello resulta crucial identificar los mecanismos atómicos que controlan esos procesos. “Hemos determinado, por ejemplo, que la presencia del carbono retarda los procesos de difusión”, señala Usategui. “Estamos hablando —añade la investigadora— de movimientos a nivel atómico que no son fáciles de detectar ni de analizar, pero que en este trabajo hemos conseguido estudiar con éxito mediante una compleja técnica experimental denominada espectroscopia mecánica. También hemos comprobado cómo se comporta el material a diferentes temperaturas, es decir, lo que le ocurriría a medida que el motor del avión se va calentando. Esta información es absolutamente necesaria para asegurar la fiabilidad y la eficiencia de los álabes que vayan a ser producidos con ese material, tanto en condiciones de vuelo como en reposo”, indica la doctora.
Así, “los resultados obtenidos han permitido conocer los efectos de añadir molibdeno, niobio, carbono y silicio en las aleaciones de TiAl y detectar cuándo y cómo se activa la difusión de esos elementos químicos. Ese conocimiento es indispensable para poder retrasar los procesos de difusión, lo que aseguraría retardar la deformación, así como incrementar las temperaturas a las que esas aleaciones podrían llegar a trabajar”, explica la investigadora de la UPV/EHU. “Además –concluye- el comportamiento mecánico y térmico que se ha medido en una de las aleaciones estudiadas, una aleación con microestructura nanolaminar, nos ha llevado a identificarla como una firme candidata para ser empleada en las turbinas de los aviones en los próximos años”.
Referencias:
L. Usategui et al (2017) Internal friction and atomic relaxation processes in an intermetallic Mo-rich Ti-44Al-7Mo (γ+βo) model alloy Materials Science and Engineering: A doi: 10.1016/j.msea.2017.06.014
T. Klein, L. Usategui et al (2017) Mechanical behavior and related microstructural aspects of a nano-lamellar TiAl alloy at elevated temperatures Acta Materialia doi: 10.1016/j.actamat.2017.02.050
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Cómo reducir el peso de un motor de aviación un 30 % se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo regular la velocidad de disolución de los biometales de las prótesis
- Cómo incorporar nanotubos de carbono a un plástico de aviación
- Una fibra óptica de plástico actúa como concentrador solar luminiscence
El arte de la repetición
 Martillos. Foto: Almudena M. Castro.
Martillos. Foto: Almudena M. Castro.“ Es una revelación cotejar el don Quijote de Menard con el de Cervantes. Éste, por ejemplo, escribió (Don Quijote, primera parte, noveno capítulo) :
… “la verdad, cuya madre es la historia, émula del tiempo, depósito de las acciones, testigo de lo pasado, ejemplo y aviso de lo presente, advertencia de lo por venir.”
Redactada en el siglo diecisiete, redactada por el “ingenio lego” Cervantes, esa enumeración es un mero elogio retórico de la historia. Menard, en cambio, escribe:
… la verdad, cuya madre es la historia, émula del tiempo, depósito de las acciones, testigo de lo pasado, ejemplo y aviso de lo presente, advertencia de lo por venir.
La historia, madre de la verdad; la idea es asombrosa. Menard, contemporáneo de William James, no define la historia como una indagación de la realidad sino como su origen. La verdad histórica, para él, no es lo que sucedió; es lo que juzgamos que sucedió. […] También es vívido el contraste de los estilos. El estilo arcaizante de Menard -extranjero al fin- adolece de alguna afectación. No así el del precursor, que maneja con desenfado el español corriente de su época.”
Jorge Luis Borges. Menard, autor del Quijote.
Jorge Luis Borges escribió la historia de Menard en 1962. Se trata de un relato ficticio camuflado en el comentario de un libro, también ficticio: El Quijote de Pierre Menard, escrito en el siglo XX. Borges cuenta cómo, siglos después de la publicación de la novela más célebre de la historia, un segundo autor llega a ella sin incurrir por ello en la copia o el plagio: Menard vuelve a escribir El Quijote, palabra por palabra, desde su propio tiempo y su propia inventiva. Como ello, argumenta Borges, “el texto de Cervantes y el de Menard son verbalmente idénticos, pero el segundo es casi infinitamente más rico”.
Algunas páginas más allá, otra de sus Ficciones nos lleva a La Biblioteca de Babel. También allí reside El Quijote. Pero en esta ocasión, la intención, el autor y el contexto de la novela quedan completamente borrados: en esta biblioteca, El Quijote es resultado de una permutación aleatoria (de entre las infinitas posibles) de todos los símbolos de nuestro abecedario.
Estos relatos, que parecen inverosímiles en el caso de la literatura, describen conflictos por copyright de lo más común en el mundo de la música. Por un lado, muchos compositores, por homenaje o por criptomnesia, terminan basándose en los mismos motivos musicales de los que los precedieron. Por otro, siendo la música un sistema de escritura basado en un número acotado de símbolos (12 notas en nuestra cultura, muchas menos que los signos ortográficos de la Biblioteca de Babel), es posible que las semejanzas a veces se presenten por pura casualidad.
Pero… no se trata sólo eso. Después de todo, la originalidad es una quimera en cualquier ámbito creativo. La imaginación -también lo decía Borges- “está hecha de convenciones de la memoria” y por eso crear consiste principalmente en copiar, repetir, recombinar… en apropiarse de todo un bagaje cultural previo y, sólo a veces, lograr hacer brillar algo que no estaba allí ya.
Sin embargo, la repetición en música no es sólo un recurso. Es aquello que la define.
Existe una ilusión auditiva, descrita por la profesora Diana Deutsch1, especialmente reveladora en este sentido. La ilusión del discurso convertido en canción (o Speech-to-Song illusion) consiste en un fragmento de audio hablado, relativamente breve, que se repite en bucle sin ninguna alteración. Sin embargo, al cabo de unas pocas repeticiones, los oyentes empiezan a percibirlo como música. De repente, la atención salta del significado de las palabras a las propiedades acústicas del habla como sonido y, entonces, se hacen evidentes ciertos patrones: el ritmo de las sílabas, las notas que marcan la entonación…
Esta frontera difusa entre lenguaje y canto está presente también en el mundo de la música. El rap es un buen ejemplo, quizás el primero que nos viene a la cabeza, seguido de cerca por la poesía, con sus rimas consonantes y sus rítmicas métricas. Pero podría especularse también que algunas formas de canto litúrgico nacieron de una oración repetida mil veces, y que fue esta repetición la que, poco a poco, dio lugar a un ritmo y una melodía procedentes del lenguaje mismo. Si te sabes alguna oración, pongamos, el Padre Nuestro, te reto a recitarla en voz alta y a observar tu propia entonación… y ahora, pregúntate qué haces tarareando una canción para saltar a la comba.
Otro claro ejemplo lo encontramos en la ópera. Por un lado, tenemos los recitativos, pasajes musicales que a veces son pura declamación, con un acompañamiento instrumental de lo más sencillo, un ritmo flexible, sin repeticiones y sin motivos musicales claramente reconocibles. Los recitativos son fundamentales para que la acción de la ópera avance, para poder seguir contando la historia de manera más o menos lineal. Por otra parte, están las arias, y las arias no sólo tienen más motivos musicales reconocibles y más melodías repetidas, sino que además solían interpretarse varias veces seguidas para mayor lucimiento del cantante o la cantante.
La repetición forma parte del ADN de la música porque es el ingrediente que nos permite encontrar los patrones presentes en el sonido y generar expectativas sobre lo que vendrá a continuación. Mientras escuchamos música, estamos constantemente intentando adivinar lo que viene a continuación y, en parte, es el hecho de acertar, el hecho de “sabernos” la canción y poder oírlo todo por anticipado en nuestra cabeza, lo que nos hace disfrutarla todavía más2. Por eso, sólo en música pasamos tanto tiempo escuchando canciones que ya habíamos oído previamente, y, por eso, algunas de esas canciones se quedan atrapadas en nuestra cabeza en forma de melodías pegadizas.
En el extremo opuesto, encontramos estilos musicales que deliberadamente huyen de patrones y repeticiones reconocibles para el oyente. Sucede con algunas de las vanguardias del s.XX: queriendo esquivar el lenguaje convencional de la música occidental, muchas dieron lugar a formas musicales donde las expectativas rehuyen al oyente. El resultado suele ser desconcertante, inesperado, confuso y, por ello, a menudo se ha utilizado en el cine acompañando situaciones de tensión psicológica o, directamente, en películas de terror. Pero basta añadir cierto grado de repetición para que también estos estilos se vuelvan más accesibles3. Esto fue lo que puso a prueba la investigadora Elizabeth Margullis. Ella tomó una pieza del compositor contemporáneo Luciano Berio (la Sequenza IX para clarinete) y, por métodos computacionales, añadió repeticiones de manera aleatoria. Cuando Margullis presentó la pieza original de Berio y la pieza generada por ordenador, los oyentes no sólo valoraron más la pieza con más repeticiones, sino que además creyeron que era la que había sido compuesta más probablemente por un ser humano.
Más allá de estos experimentos, casi cualquier forma musical implica algún tipo de repetición. Desde la fuga con sus sujetos y contrasujetos, a la sonata con sus temas alternantes y su reexposición, los leitmotivs wagnerianos o los estribillos del pop. No hay composición musical que no implique algún juego de espejos. Pero sí hay una forma que se basa, como ninguna otra, en este tipo de autorreferencia: es el tema con variaciones.
Referencias:
1 D. Deutsch, T. Henthorn and R. Lapidis. Illusory transformation from speech to song. Journal of the Acoustical Society of America, 2011.
2 David Huron. Sweet anticipation. 2006.
3 E. H. Margulis. Aesthetic Responses to Repetition in Unfamiliar Music. Empirical Studies of the Arts, 2013
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El arte de la repetición se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: Química y Arte, reacciones creativas
- Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte
- Arte & Ciencia: La importancia de la ciencia para la conservación del arte
‘La Historia es la ciencia de la desgracia de los hombres’
 Portadas de la primera edición (1966) y una reedición (2010)
Portadas de la primera edición (1966) y una reedición (2010)
La frase que da título a esta anotación está incluida en el ensayo Une histoire modèle –Una historia modelo– de Raymond Queneau. Esta consigna resume las reflexiones contenidas en el texto, que giran en torno a los infortunios de la vida.
En el prólogo de Une histoire modèle[1] Raymond Queneau explica que comenzó a escribir este ensayo en julio de 1942 y que lo quería titular, inspirándose en el matemático Girard Desargues (1591-1661)[2], Brouillon projet d’une atteinte à une science absolue de l’histoire[3] –Anteproyecto para un ensayo sobre una ciencia absoluta de la historia–. Aunque inacabado, abandonó este proyecto en octubre de ese mismo año, tras haber escrito los 96 primeros capítulos, algunos solo formados por unas pocas líneas. En 1966 decidió publicarlo tal y como lo había dejado en 1942, aunque cambiando su título.
Una historia modelo es una meditación de ‘aspecto’ matemático sobre la Historia, a la que el autor califica como: L’Histoire est la science du malheur des hommes –la Historia es la ciencia de la desgracia de los hombres–.
Comenta también Queneau en la introducción que sus fuentes son fácilmente identificables, entre ellas las Leçons sur la théorie mathématique de la lutte pour la vie (Gauthier-Villars, 1931) –Lecciones sobre la teoría matemática de la lucha por la vida–de Vito Volterra (1860-1940) y los escritos de otros autores que creyeron poder demostrar la existencia de ciclos a lo largo de la Historia.
Queneau opina que la Historia sólo existe porque existen guerras, revoluciones o diferentes catástrofes: de no producirse tales acontecimientos, tan sólo existirían, como mucho, Anales. Insiste además en que:
Como afirma la paremiología, los pueblos felices no tienen Historia. La Historia es la ciencia de la desgracia de los hombres.
Su objetivo con el libro es mostrar que la Historia es una ciencia, descubriendo la correlación entre fenómenos astronómicos, climáticos, etc. y los acontecimientos cíclicos.
Si no hubiera desgracias, no habría nada que contar. De otro modo, la felicidad es homogénea, la desgracia cambiante.
Habla, por ejemplo, de la Edad de Oro –los seres humanos obtienen alimentos sin trabajar y sin pensar que su comida puede llegar a faltar– y de las diferentes crisis que pueden llevar a que desaparezca. Incluso asigna a cada grupo humano un coeficiente que mide su capacidad para prevenir catástrofes: si su capacidad es nula, el grupo se llama ciego, y alude entonces al mito de Casandra. Entre las descripciones de la Edad de Oro que aparecen en el texto, una de ellas es la matemática (capítulo 21):
Sea N(t) el número de miembros del grupo en el tiempo t, Q(N) la cantidad de alimento consumida cada año por el grupo, Q la cantidad de comida absoluta obtenida sin trabajar en el territorio ocupado por el grupo, considerando que no posee vecinos y que no debe temer a otras especies animales. Hay crisis cuando Q(N)=Q, N(t) se supone creciente y por lo tanto Q(N). Sea T el tiempo de crisis, T’ el tiempo de Casandra (puramente hipotético durante esta primera época). Hay Edad de Oro mientras T’>T.
Otro ejemplo de modelización matemática se encuentra en el capítulo 30, en el que Queneau realiza un estudio matemático de dos especies, una voraz y la otra devorada: alude en este modelo de nuevo a los hombres y los vegetales.
La discusión continúa de este modo, realizando el autor un curioso análisis intentando encontrar patrones de los ciclos en la Historia de la humanidad y sus posibles causas…
Notas
[1] Este ensayo no está traducido al castellano.
[2] Queneau posee una especial predilección por las ‘traslaciones’ de textos matemáticos. Recordar, por ejemplo, Los fundamentos de la literatura según David Hilbert.
[3] Queneau alude al texto de Girard Desargues Brouillon project d’une atteinte aux événements des rencontres d’une cône avec un plan –Anteproyecto para un ensayo sobre los resultados obtenidos al realizar secciones planas sobre un cono– (1639) en el que su autor, considerado como el fundador de la geometría proyectiva, trata sobre secciones cónicas. Este texto, de difícil lectura, plantea los fundamentos de la geometría proyectiva, y por lo tanto la descriptiva.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo ‘La Historia es la ciencia de la desgracia de los hombres’ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (1): una historia que comienza en 1852
- 100 000 000 000 000 poemas
- Algunas observaciones someras relativas a las propiedades aerodinámicas de la suma
Las ondas están por todas partes
El universo está continuamente atravesado por ondas de todo tipo. Existen ondas hasta en el propio espaciotiempo. Tanto es así que es prácticamente imposible intentar conocer algún aspecto relevante del universo desde una perspectiva moderna sin poseer unos conocimientos básicos de lo que son las ondas. Esto es lo que pretendemos proporcionar en esta serie que hoy comenzamos, como siempre centrándonos en las ideas y empleando solo las matemáticas estrictamente imprescindibles y que no superen a las que se enseñan en la enseñanza secundaria obligatoria.
 Olas pasando la Isla de Ízaro, fotografiada desde Bermeo, y usarán los amantes del surf en Mundaka. Foto: Óscar Martínez
Olas pasando la Isla de Ízaro, fotografiada desde Bermeo, y usarán los amantes del surf en Mundaka. Foto: Óscar MartínezAntes de pensar en el universo en su conjunto quedémonos en una parte de él más familiar para las personas, la superficie del planeta Tierra. Estamos familiarizados con las ondas en el agua, ya sean las olas que llegan a Mundaka y que hacen las delicias de los surferos o las que forman las gotas de lluvia al caer sobre un charco. Pero no todas las ondas se producen en medios líquidos. También estamos familiarizados con el hecho de que los desplazamientos de la corteza de la Tierra causan temblores a miles de kilómetros de distancia producidos por ondas que se desplazan en un sólido. Y cuando un músico toca una guitarra, las ondas de sonido llegan a nuestros oídos tras desplazarse por el aire, un gas. También conocemos que las perturbaciones de las ondas pueden venir en forma de haces concentrados, como el frente de choque de un avión que vuela a velocidades supersónicas. O hacerlo en sucesión como el tren de ondas enviado desde una fuente en constante vibración, como una campana o una cuerda.
Todos los ejemplos anteriores son ondas mecánicas, en las que los cuerpos o las partículas se mueven físicamente de un lado a otro. Pero sabemos que existen ondas en campos eléctricos y magnéticos. Estas ondas son las responsables de lo que experimentamos como rayos X, la luz visible o las ondas de radio. Nos centraremos en la primera parte de la serie en las ondas mecánicas para tratar después las electromagnéticas.
Quizás contraintuitivamente, en todos los casos, los efectos de las ondas que observamos dependen del flujo de energía, no del de materia. Esto es importante: Las ondas son modos de transferencia de energía sin transferencia de materia.
Supongamos que dos personas sostienen los extremos opuestos de una cuerda tensa. De repente, una persona mueve la cuerda arriba y abajo rápidamente una vez. Eso “perturba” la cuerda y produce una “deformación” en ella que se desplaza a lo largo de la cuerda hacia la otra persona. La deformación viajera es un tipo de onda llamada pulso.
Originalmente, la cuerda estaba inmóvil. La altura sobre el suelo de cada punto de la cuerda dependía solo de su posición a lo largo de la cuerda y no cambiaba con el tiempo. Pero cuando la persona sacude la cuerda se crea un cambio rápido en la altura de un extremo. Luego, esta perturbación se aleja de su fuente y se desplaza por la cuerda hasta el otro extremo. La altura de cada punto en la cuerda ahora depende también del tiempo, ya que cada punto oscila hacia arriba y hacia abajo y vuelve a la posición inicial a medida que pasa el pulso. La perturbación es, por lo tanto, un patrón de desplazamiento que se mueve a lo largo de la cuerda. El movimiento del patrón de desplazamiento desde un extremo de la cuerda hacia el otro es un ejemplo de onda. La sacudida de un extremo es la fuente de la onda. La cuerda es el medio en el que se mueve la onda.

Consideremos otro ejemplo. Cuando una piedra cae en un estanque tranquilo, aparecen una serie de crestas circulares y valles que se extiende sobre la superficie. Este patrón de desplazamiento en la superficie del líquido es una onda. La piedra que cae es la fuente; el patrón en movimiento de crestas y valles es la onda; Y la superficie líquida es el medio. Las hojas u otros objetos que flotan en la superficie del líquido suben y bajan a medida que pasa cada onda. Pero en promedio no experimentan ningún desplazamiento neto. No se ha movido materia alguna desde la fuente de la onda junto con la onda, ya sea en la superficie o entre las partículas del líquido; solo se ha transmitido la energía y el momento contenidos en la perturbación. Lo mismo aplica a las ondas en una cuerda, a las ondas de sonido en el aire, o a las ondas sísmicas en un terremoto, etc.
Cuando cualquiera de estas ondas se mueve a través de un medio, la onda lo que produce es un desplazamiento que cambia en el tiempo de las partes sucesivas del medio. Por ello, podemos referirnos a estas ondas como ondas de desplazamiento. Si puedes ver el medio y reconocer los desplazamientos, entonces puedes ver las ondas. Pero también pueden existir ondas en medios que no puedes ver tan fácilmente, como el aire limpio; o pueden formarse como alteraciones de algo que no puedes detectar sin la ayuda de instrumentos específicos, como la presión o el campo eléctrico.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las ondas están por todas partes se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cuántica y relatividad por todas partes
- La existencia de ondas electromagnéticas
- Ondas gravitacionales en la materia oscura
Actividades digestivas y su regulación

Casi todos los animales1 tienen un sistema digestivo cuya función principal es digerir y absorber el alimento. Está formado por el tracto o tubo digestivo y diferentes órganos o estructuras auxiliares. A lo largo del tracto se diferencian varias áreas funcionales, cada una de las cuales desempeña una o varias tareas, normalmente distintas de las que se realizan en las demás áreas. Las actividades son de diferente naturaleza: movimiento, secreción de jugos digestivos, digestión propiamente dicha, y absorción.
En las sucesivas secciones, veremos de forma somera las actividades propias del sistema, la configuración básica de los sistemas digestivos, los elementos que intervienen en la regulación de sus actividades, así como el modo en que se relacionan entre sí esos elementos.
Procesos digestivos
Movimiento
El alimento que ingresa en el tracto digestivo ha de ser impulsado para que transite a su través. En algunos animales esa tarea corre a cargo de músculos que no forman parte del sistema, pero lo normal es que el tubo digestivo cuente con una musculatura lisa propia. Esa musculatura mantiene, por un lado, una cierta contracción de baja intensidad de forma permanente; ejerce así una ligera presión sobre los contenidos del tracto gastrointestinal e impide que éste se distienda en exceso. Y por el otro, experimenta series de contracciones más intensas que son las que sirven para impulsar el alimento a lo largo del tubo y para mezclar los jugos digestivos con el alimento sobre el que han de actuar.
El mecanismo principal de impulsión del alimento es el peristaltismo, que consiste en el desplazamiento a lo largo del tubo de una constricción de éste, de manera que el material que queda por delante es impulsado. La velocidad se ajusta de manera que el tiempo que el alimento permanece en cada área funcional es el adecuado para su digestión.
Los movimientos que propician la mezcla cumplen, a su vez, dos funciones. Por un lado hacen accesibles los alimentos a la acción de los jugos digestivos, principalmente en el estómago. Y también facilitan la absorción donde corresponde, al aproximar los productos de la digestión a los epitelios absortivos.
Secreción
Glándulas exocrinas ubicadas en diferentes posiciones secretan jugos digestivos. Los productos de secreción son variados: agua (mucha agua, de hecho), electrolitos (como Cl– y H+), enzimas, sales biliares o mucus. La producción y transporte de casi todas estas sustancias conlleva un importante gasto energético. En el del agua no hay gasto de energía, pero es, en sí misma, un compuesto normalmente valioso y sometido, por ello, a control fisiológico. Por esa razón casi todas ellas se reabsorben casi en su totalidad en un enclave u otro del tracto digestivo.
La liberación de los productos de secreción a la luz del tubo está sometida a control hormonal o nervioso, y está, lógicamente, acoplada al avance del contenido digestivo por su interior.
Digestión
La digestión es el proceso por medio del cual las grandes moléculas (macromoléculas), normalmente complejas, que constituyen el alimento (carbohidratos, proteínas, grasas y ácidos nucleicos, principalmente) son fragmentadas hasta rendir moléculas mucho más pequeñas. La digestión se produce mediante hidrólisis enzimática y, principalmente, en la zona anterior y media del sistema digestivo. Las enzimas hidrolíticas introducen agua (H2O) en las uniones químicas entre las subunidades que forman las macromoléculas, rompiendo el enlace que las une y liberando las pequeñas moléculas. De esa forma podrán ser absorbidas y transferidas al torrente circulatorio para su uso o almacenamiento.
Absorción
La absorción consiste en la transferencia de las pequeñas moléculas que resultan de la digestión del alimento ingerido desde la luz del tracto gastrointestinal hasta el sistema circulatorio. Normalmente se produce en la zona media y posterior del tubo. Junto a esas pequeñas moléculas, también se reabsorben agua, sales y vitaminas. Las superficies absortivas suelen ser muy grandes, lo que requiere de numerosos plegamientos del epitelio y estructuras celulares adecuadas, como vellosidades y microvellosidades.
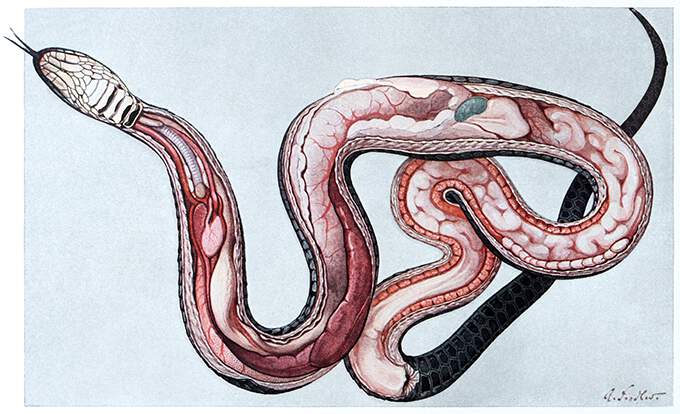
Organización básica de los sistemas digestivos
Hay una enorme variedad de configuraciones en los sistemas digestivos en el reino animal. En insectos (también en anélidos), por ejemplo, se diferencian tres grandes zonas: estomodeo, mesenterón y proctodeo. En insectos, el estomodeo es la zona anterior del tracto y contiene la boca, la faringe, el esófago, el buche y el proventrículo; es una zona especializada en la recepción y (a veces) almacenamiento del alimento. La válvula estomodeal da paso al mesenterón, o intestino medio, un tubo alargado en el que normalmente se pueden diferenciar dos secciones. En una de ellas se encuentran los ciegos gástricos y en la otra el estómago. El intestino medio cumple funciones digestivas principalmente, aunque también de almacenamiento (en menor medida). Tras la válvula pilórica viene el proctodeo o intestino posterior, con una sección anterior, el intestino, y otra posterior, el recto; el intestino posterior es un área de absorción, aunque el recto juega un papel crucial en la excreción de restos nitrogenados y la regulación hídrica y salina.
Por su parte, el tracto digestivo de la mayor parte de los vertebrados contiene las siguientes estructuras u órganos: boca (recepción del alimento), faringe, esófago (conducción), estómago y rumen [en rumiantes] o complejo proventrículo–molleja en aves (digestión inicial), intestino delgado (digestión final y absorción), intestino grueso (reabsorción de agua y otras sustancias) y ano (expulsión de restos fecales).
Además del tubo con sus correspondientes áreas funcionales, en muchos grupos hay órganos accesorios que colaboran en las tareas digestivas: glándulas salivares, páncreas exocrino y sistema biliar. Todos ellos son glándulas que vierten a la luz del tracto sus secreciones.
Regulación de la actividad digestiva
La regulación de las actividades digestivas corre a cargo de nervios intrínsecos (propios del sistema) y extrínsecos, así como de hormonas digestivas. Y como en el resto de sistemas reguladores, participan receptores sensoriales, sistemas de integración y efectores (células que ejecutan la respuesta reguladora). En los vertebrados, este sistema regulador se superpone a la actividad básica propia de la musculatura lisa del sistema digestivo, modulándola, además de ejercer otros efectos.
Las células de la musculatura lisa del sistema digestivo de los vertebrados desarrollan una actividad eléctrica espontánea denominada ritmo eléctrico básico. Ese ritmo puede dar lugar a que se desencadene una secuencia de potenciales de acción2, generando las correspondientes contracciones de las células musculares. Que se lleguen a producir los potenciales de acción o no depende del efecto de factores mecánicos, nerviosos y hormonales, y también del valor de potencial de membrana en torno al cual se producen las oscilaciones del ritmo eléctrico básico. En presencia de alimento en el tubo digestivo ese valor es más alto y, por lo tanto, es más probable que la oscilación alcance el valor de potencial de membrana umbral para que se desencadene el potencial de acción.
En la pared del tracto digestivo hay receptores sensoriales que responden a cambios químicos y mecánicos locales. Los quimiorreceptores son sensibles a las variaciones químicas que se producen en la luz del tubo. Los mecanorreceptores (barorreceptores, o receptores de presión) responden a la tensión de la pared o su grado de estiramiento. Y los osmorreceptores detectan variaciones en la concentración osmótica de la luz del tracto. Cuando estos receptores son estimulados, se desencadenan respuestas que consisten en reflejos nerviosos o secreción de hormonas a cargo de células endocrinas, y que provocan variaciones en el nivel de actividad de sus células diana, que son los efectores de este sistema. Estas pueden ser células de la musculatura lisa del sistema o glándulas exocrinas que liberan jugos digestivos.
La integración de la información procesada por los receptores sensoriales corre a cargo de dos redes o circuitos nerviosos y de las hormonas gastrointestinales.
Plexos nerviosos intrínsecos
En el sistema digestivo de los vertebrados hay dos plexos (o redes) nerviosos intrínsecos, el mientérico y el submucoso, ubicados ambos en la pared interna del tubo digestivo a lo largo de todo su recorrido. En conjunto reciben el nombre de sistema nervioso entérico y contiene, de hecho, más neuronas que la médula espinal. Los insectos tienen un sistema análogo, denominado sistema nervioso estomatogástrico. Estos plexos coordinan las actividades locales dentro del tracto digestivo y ejercen sus efectos en todas las facetas de su actividad.
Nervios extrínsecos
Se trata de fibras nerviosas pertenecientes a las dos divisiones del sistema nervioso autónomo, simpática y parasimpática. Modulan la actividad de los plexos nerviosos y pueden, incluso, inervar células de la musculatura lisa de forma directa. Como ocurre en otras actividades, también en el sistema digestivo las acciones de ambas divisiones suelen ser de sentido opuesto. El subsistema simpático provoca una disminución de la actividad digestiva y lo contrario ocurre con el parasimpático, cuyas señales llegan al sistema digestivo a través del nervio vago, principalmente.
Hormonas gastrointestinales
Son hormonas producidas por glándulas endocrinas que se encuentran en la mucosa de ciertas regiones del tracto digestivo y que son liberadas al sistema circulatorio en respuesta a ciertos estímulos. Ejercen sus efectos sobre la musculatura lisa del tracto y sobre glándulas exocrinas.
Reflejos
La activación de los receptores sensoriales del tracto digestivo puede provocar dos tipos de respuestas reflejas, cortas y largas. Los reflejos cortos se producen cuando los plexos intrínsecos responden a los estímulos locales y provocan respuestas a cargo de los correspondientes efectores; son cortos porque todos los elementos que participan se encuentran en el interior de la pared del tracto digestivo. Los reflejos largos, por el contrario, son aquellos en los que participan los nervios extrínsecos procedentes del sistema nervioso autónomo.
A los elementos anteriores, hay que añadir otras vías de regulación. La membrana plasmática de las células efectoras del sistema digestivo contienen proteínas receptoras que se unen y responden a hormonas gastrointestinales, neurotransmisores y otros mediadores químicos locales.
La regulación de la función gastrointestinal reviste, como se puede ver, una complejidad extraordinaria. Diferentes sistemas reguladores interactúan y se superponen unos a otros para ejercer un control estricto y dependiente, además, de diferentes estímulos (internos y externos al propio sistema) que no se produce en ninguna otra función animal. Las rutas regulatorias han evolucionado de manera que los organismos puedan obtener el máximo rendimiento posible del alimento ingerido a través de una secuencia finamente ajustada de procesos de digestión (que implican motilidad, secreciones y ataque enzimático a la comida) y absorción de los productos de la misma.
Fuente:
Lauralee Sherwood, Hillar Klandorf & Paul H. Yancey (2005): Animal Physiology: from genes to organisms. Brooks/Cole, Belmont.
Notas:
1 Como las esponjas (que realizan digestión intracelular), ciertos parásitos intestinales (que absorben los jugos ya digeridos por el hospedador) y animales de los surgimientos hidrotermales (que contienen microorganismos quimiolitotrofos simbiontes).
2 Los potenciales de acción son señales bioeléctricas todo o nada que se producen en axones neuronales y células musculares, y que constituyen el mecanismo básico de transmisión de información nerviosa y de contracción muscular.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Actividades digestivas y su regulación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las actividades animales
- La regulación de la diuresis en mamíferos
- La regulación osmótica de los animales de agua dulce
Las babosas y el undécimo aniversario
“Los limacos son muy listos”
Dicho popular muy apreciado en el Laboratorio de Citología e Histología donde hice la tesina y la tesis (y tengo copia de ambas), hacia 1975.
 Arion vulgaris
Arion vulgarisAcabo de descubrir, con sorpresa y el típico comentario de “que rápido pasa el tiempo”, que el 31 de octubre de 2007 publiqué las primeras entradas del blog “La Biología estupenda”. Es evidente que ya no puedo celebrar el décimo aniversario del blog y, qué remedio, celebraré el undécimo aniversario. No hay otra solución.
Transcribo no la primera entrada sino la segunda que incluye la explicación del origen del fantástico adjetivo de “estupenda” para la biología. Quizá se vea algo presuntuoso, incluso demasiado optimista para una ciencia pero, en fin, le debo el adjetivo a Arturo Pérez Reverte, a quien creo que llega el momento de agradecer públicamente el nombre de este blog. Va esa primera entrada que, en fin, era la segunda pero aquí he cambiado el orden.
La biología estupenda
Miércoles, 31 octubre 2007, 23:25
Arturo Pérez Reverte, en su columna de EL SEMANAL de fecha 8 de julio de 2007, publicó este texto:
“La ciencia -bombas atómicas y doctor Mengele aparte- es sin duda fuente de innumerables bienes para la Humanidad doliente; pero también, cuando se pone estupenda, termina convirtiéndose en una incómoda mosca cojonera.”
Quien haya leído la primera entrada de este blog entenderá porque lo he llamado La Biología Estupenda. Pérez Reverte me dio la idea; a él le corresponde la siembra y a mí, sólo a mí, la triste y desmedrada cosecha.
Hablaré de ciencia, pero de esa ciencia poco recompensada que aparece en los medios de comunicación casi como el chiste diario que hay que incluir porque es lo tradicional.
Y pondré citas más o menos divertidas y que tengan que ver con la ciencia, o con esa ciencia que debemos respetar pero, sobre todo, entender y criticar para que no se desmande, “bombas atómicas y doctor Mengele aparte” como nos decía don Arturo. Y habrá muchas citas, no por el sencillo experimento de copiar, sino por el ejercicio deliberado de humildad que significa aceptar que alguien dijo, y mucho mejor, la idea que intento expresar.
Amigos, bienvenidos a La Biología estupenda. Espero comentarios, críticas y correcciones. Adelante y a por ello.
Toda mi inspiración para este blog venía de años atrás, cuando no existía Internet y me peleaba con mi tesina y tesis doctoral, ambas sobre babosas o, como decimos aquí, limacos. Entonces, entre la bibliografía que consulté había un artículo del malacólogo suizo Lothar Forcart que aquí explico en mi primera entrada en el blog. Así comprenderán la convicción que defendíamos en el laboratorio pues creíamos, con absoluto convencimiento, que los limacos son muy listos. Creo que fue la primera y principal conclusión no escrita de mi tesis doctoral.
 Limax flavus
Limax flavus El turco y la babosa
Miércoles, 31 octubre 2007, 23:06
En 1949, un turco, cuyo nombre permanece en el anonimato, ingresó en un Hospital de Ankara, Turquía, con una fuerte gastritis que, en un momento dado y ya ingresado, le provocó un liberador vómito. Y en el vómito apareció una babosa viva y todo lo feliz que puede ser un bicho como este en medio de tanta sacudida. El animal lo conservó en alcohol el profesor A. Neuzat Tüzdul, de la Facultad de Veterinaria de Ankara. Como no era un experto en moluscos, envió el ejemplar al Dr. Lothar Forcart, del Museo de Historia Natural de Basilea, en Suiza. El Dr. Forcart, y este sí era un conocido malacólogo (es decir, estudioso de los moluscos), clasificó al animal como Limax flavus, babosa no muy abundante pero tampoco rara en los campos de Europa.
Forcart analizó, con la colaboración del profesor S. Scheidegger, del Instituto de Anatomía Patológica de la Universidad de Baale, el contenido del estómago de la babosa (no del turco, al que supongo aliviado, que recibió pronto el alta y reanudó su vida normal, y el resto del vómito quizás quedó depositado en Ankara por lo que, definitivamente, ambos desaparecen de nuestra historia). Scheidegger y Forcart encontraron en el estómago los típicos restos vegetales, habituales en la dieta de una babosa, aunque de alguna manera serían vegetales compartidos con el turco; pero, además, hallaron células epiteliales de origen animal que provenían del estómago del turco que, por lo visto al microscopio, compartía con su babosa algo más que la verdura, la fruta y las ensaladas: literalmente compartía su propio estómago, aunque supongo que involuntariamente. No es de extrañar que sufriera de gastritis.
Se supone que la babosa llegó al estómago del turco camuflada en alguna sabrosa ensalada, seguro que de lechuga, que encanta a estos animales. Cómo aguantaba la extrema acidez del estómago humano, no se sabe; quizá por la abundante secreción mucosa típica del tegumento de los moluscos. Seguro que no terminó la comida con un café pues la cafeína es un enérgico repelente de babosas y caracoles y, en altas concentraciones, funciona para ellos como una neurotoxina. En fin, café aparte, está claro que las babosas son muy listas y saben aprovechar las oportunidades según se presentan.
Hollingsworth, R.G., J.W. Armstrong & E. Campbell. 2002. Caffeine as a repellent for slugs and snails. Nature 417: 915.
Forcart, L. 1967. Un cas de pseudo-parasitisme de Limax flavus L. Journal de Conchiliologie 106: 129.
Para apoyar mi convencimiento de tantos años sobre lo listos que son los limacos, añado aquí las publicaciones del grupo de Bartosz Piechowicz, de la Universidad de Rzeszow, en Polonia, con el limaco Arion vulgaris (por cierto, sinónimo del Arion empiricorum, especie que estudié en mi tesina y tesis). A este limaco, considerado una especie invasora y una peste agrícola, sobre todo en Europa central, se le conoce, en su nombre vulgar, como babosa española (o Spanish slug en inglés), pues se considera que su origen está en el sudoeste francés y el norte español, o sea, más o menos, por aquí.
Pues bien, pocos molusquicidas, en concreto solo con dos principios activos, son eficaces contra la babosa española. Bartosz Piechowicz detectó que, en su entorno rural más próximo, había dueños de pequeñas huertas y jardines que utilizaban cerveza para atraer a esta peste agrícola. Los investigadores probaron seis marcas de cerveza compradas en el mercado local. Eran, por si alguien se interesa por este método de capturar limacos (o, sin más, por las cervezas), las marcas Goolman Premium, Harnas Jasue Pelne, Tatra Mocne, Kaztelan, Lezajsk y Wojak Jasny Pelny.

Colocaron las muestras de cerveza cerca de los limacos e hicieron correr aire por encima para que el aroma llegara a los animales y observaron si les atraía o no. También hicieron un estudio de campo con recipientes llenos de cerveza y, a los tres días, contaban los ejemplares que habían caído en las trampas.
Entre el 70% y el 80%, de media, de los limacos eligen cerveza de cualquier marca y parecidos resultados se dan en el experimento de campo. La Goolman Premium siempre supera el 80% de elección.
Es obvio que el siguiente paso en esta interesante investigación es utilizar la cerveza en trampas para cazar limacos y controlar la plaga que supone la babosa española. Utilizan cinco marcas locales de cerveza: Zurb, Warka Full, Karpackie Pils, Zywiec y Lezajsk Full.
Los limacos eligen para caer en la trampa la cerveza Lezajsk Full, seguida de Zurb. Los autores ensayan los compuestos químicos que forman parte del aroma de las cervezas para averiguar cuáles son los que más atraen a los limacos. El que mejor funciona es el ácido decanoico y, por el contrario, el que más rechazo provoca es el éster del ácido acrílico y el N-hidroxisuccinimida. Dejémoslo así, sin entrar en detalles de estos compuestos, pues los autores tampoco lo hacen.
Un curioso efecto colateral del gusto por la cerveza de la babosa española es que su metabolismo reacciona ante su aroma. Cuando el grupo de Bartosz Piechowicz mide la respiración de los limacos ante el olor de las cinco marcas de cerveza del experimento anterior detecta que los animales aumentan la emisión de dióxido de carbono. En algún caso incluso se triplica la emisión en los primeros cinco minutos después de oler la cerveza. Vaya resaca.
No lo aseguro, ni los autores lo hacen, que la unión de limaco y cerveza contribuye al aumento de dióxido de carbono en la atmósfera y al calentamiento global, o sea, al cambio climático. Recuerden aquello de los limacos son muy listos.
En fin, consideren celebrado el undécimo aniversario del blog “La Biología estupenda”.
Referencias:
Piechowicz, B. et al. 2014. Beer as olfactory attractant in the fight against harmful slugs Arion lusitanicus Mabille 1868. Chemistry Didactics Ecology Metrology 19: 119-125.
Piechowicz, B. et al. 2016. Beer as attractant for Arion vulgaris Moquin-Tandon, 1885 (Gastropoda: Pulmonata: Arionidae). Folia Malacologica 24: 193-200.
Piechowicz, B. et al. 2016. The smell of beer as a factor affecting the emission of carbon dioxide by Arion lusitanicus auct., non-Mabille. Annals of Animal Science 16: 463-476.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Las babosas y el undécimo aniversario se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El caso de Nikolái Ivánovich Vavílov
- La reproducción es obligatoria… en el método científico
- Una visión planetaria de la ciencia
Los primeros pasos de la evolución darwiniana y sesgos cognitivos y evolución (Día de Darwin 2018)

La Biblioteca Bidebarrieta de Bilbao se convertió el pasado 12 de febrero en el escenario de la duodécima edición del Día de Darwin, la celebración con la que anualmente se conmemora el nacimiento del autor de la teoría de la evolución por selección natural.
La jornada constó de dos charlas a cargo de Carlos Briones, investigador del Centro de Astrobiología (CSIC-INTA) y de Helena Matute, catedrática de psicología en la Universidad de Deusto. Tras las ponencias hubo un coloquio con participación del público.
La charla de Briones, titulada “Los primeros pasos de la evolución darwiniana”, trata sobre los avances científicos que se están produciendo en la investigación sobre el origen de los primeros seres vivos. El científico, especializado en el origen y la evolución temprana de la vida, muestra cómo los primeros pasos de la evolución darwiniana sentaron las bases para la construcción de esta biodiversidad de la que formamos parte.
Matute habla en “Sesgos cognitivos y evolución” sobre los errores que cometen todas las personas de manera sistemática y que dependen de cómo está configurada de serie la mente humana. La catedrática aborda en su charla los entresijos de estos “atajos” del pensamiento, que han surgido en un contexto evolutivo y tienen su propia razón de ser.
El periodista Alfonso Gámez se encargó de conducir estas charlas que se enmarcan dentro del ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
Edición realizada por César Tomé López.
El artículo Los primeros pasos de la evolución darwiniana y sesgos cognitivos y evolución (Día de Darwin 2018) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas14 Algunos trucos para reducir sesgos
- Cita con Charles Darwin en Bilbao
- La unidad de selección en la evolución y el origen del altruismo (1): En el comienzo fue Darwin
Una planta amazónica podría acabar con las células tumorales hepáticas
Un trabajo de investigación llevado a cabo por el grupo Radicales Libres y Estrés Oxidativo de la Facultad de Medicina y Enfermería de la UPV/EHU ha descifrado el mecanismo por el que Vismia baccifera, originaria del Amazonas colombiano, induce un estrés oxidativo en las células de cáncer de hígado humanas que acaba matándolas.
 Vismia baccifera
Vismia bacciferaLos productos derivados de plantas están recibiendo una atención cada vez mayor por la comunidad científica debido a su actividad antioxidante, antiinflamatoria y antitumoral; “actualmente hay mucho interés en identificar compuestos derivados de las plantas, que puedan ser utilizados como agentes quimioterapéuticos, con capacidad para parar el crecimiento de los tumores, o para tratar la metástasis, por ejemplo”, explica la doctora Jenifer Trepiana, una de las autoras del estudio.
Para su investigación, este grupo escogió la planta Vismia baccifera, que se recogió en la Amazonia de Colombia. “Las poblaciones indígenas la utilizan por su capacidad antiinflamatoria, o para enfermedades del tracto urinario, o enfermedades de la piel, pero nosotros la elegimos porque en estudios anteriores habíamos visto que es la que mayor capacidad antitumoral tiene en las células de cáncer de hígado que hemos utilizado”, comenta la investigadora.
El estudio fue realizado in vitro, con un modelo de células tumorales de hígado humanas, y se trataron las células con el extracto acuoso de hojas de Vismia baccifera, preparado en infusión, tal como se utiliza en la medicina tradicional indígena. Asimismo, trataron con ese mismo extracto células hepáticas humanas sanas, “para comprobar si las células sanas también se veían afectadas o no”, detalla la Dra. Trepiana.
Según han podido comprobar, el extracto de Vismia baccifera provoca una respuesta tóxica en las células tumorales. Concretamente, produce un aumento de radicales libres, y, en particular, de peróxido de hidrógeno, y eso termina provocando la muerte de las células tumorales. Entre los efectos que provoca el aumento del peróxido de hidrógeno, “se ha observado el bloqueo del ciclo celular (las células dejan de dividirse), daño en el material genético, y la activación de un proceso de muerte celular llamado apoptosis”, detalla la investigadora.
En la comparación entre la acción citotóxica de Vismia baccifera en células tumorales y células sanas, han visto que “solo se ven afectadas las células cancerosas; hemos probado que en las células de hígado humano sanas, y anteriormente en células de rata, no produce estos efectos —apunta—. Esto es de gran interés, porque lo más importante es que las células sanas no se vean afectadas”.
La investigadora valora “muy positivamente” estos resultados, el “conocer cómo afecta la planta dentro de las células. Lo ideal sería seguir adelante con la investigación, y pasar a hacer estudios in vivo, con modelos animales, para ir superando etapas hasta conseguir que sea utilizado como terapia contra el cáncer. Aunque sabemos que este camino es muy largo”, concluye.
Referencia:
Jenifer Trepiana, M. Begoña Ruiz-Larrea, José Ignacio Ruiz-Sanz (2018) Unraveling the in vitro antitumor activity of Vismia baccifera against HepG2: role of hydrogen peroxide Heliyon (2018) doi: 10.1016/j.heliyon.2018.e00675
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Una planta amazónica podría acabar con las células tumorales hepáticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Nanopartículas magnéticas contra células tumorales
- Medicina regenerativa: utilización de células madre para el tratamiento de enfermedades humanas
- Microcápsulas biomiméticas de células madre
Los champús sin sulfatos y la libertad de decidir

¿Hay razones por las que descartar los champús con sulfatos? ¿Qué función tienen en el producto? ¿Hay alternativas? ¿Son nocivos?
Los champús, geles de ducha y geles de limpieza en general, llevan tensioactivos (también llamados surfactantes) entre sus componentes mayoritarios. La razón es la más evidente de todas: sirven para limpiar. Los sulfatos presentes en estos cosméticos son un tipo de tensioactivos.
-
¿Qué son los tensioactivos?
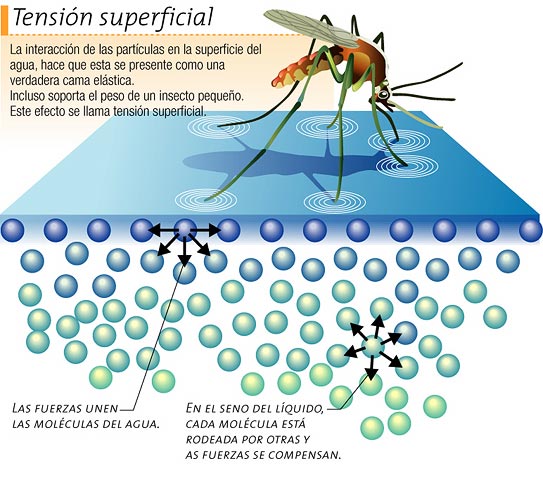
La tensión superficial es la fuerza que actúa en la superficie de un líquido y se dirige hacia su interior. El resultado es que la superficie del líquido presenta cierta contracción. La causa son las fuerzas de adhesión entre las moléculas del propio líquido. Así, la tensión superficial la podemos entender como la resistencia de un líquido contra una fuerza externa. Si esta fuerza es comparativamente pequeña, la superficie del líquido puede ser capaz de soportarla: por ejemplo, algunos insectos son capaces de posarse sobre el agua porque esta presenta una tensión superficial suficiente.
Los tensioactivos son sustancias que disminuyen la tensión superficial entre fases. Si tenemos dos fases inmiscibles, como el agua y el aceite, podemos conseguir que emulsionen (que se mezclen) añadiendo un tensioactivo.
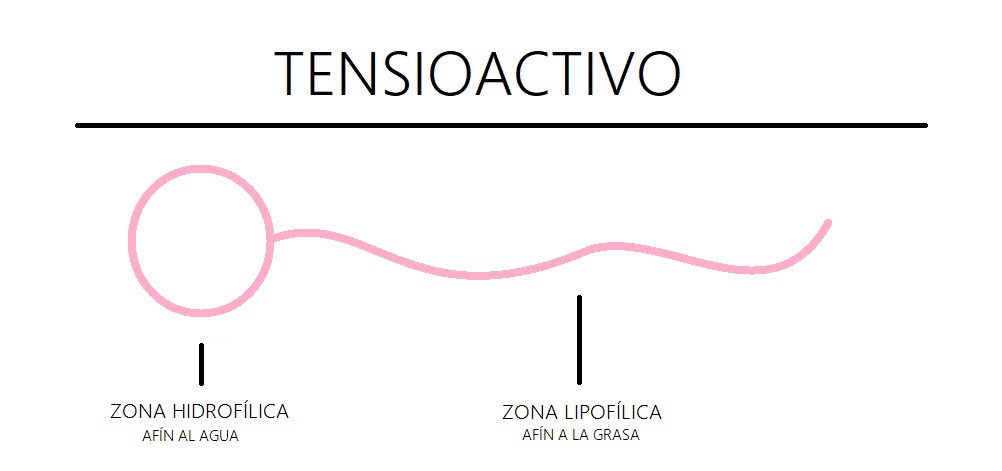
Podemos distinguir dos tipos de sustancias: hidrofílicas, con afinidad por el agua, y lipofílicas, con afinidad por las grasas. Las sustancias hidrofílicas y lipofílicas se repelen como en el caso del agua y el aceite. Pero si conseguimos rebajar lo suficiente la tensión superficial entre ellas el efecto final es que permanecen mezcladas.
Esto lo podemos observar si añadimos un tensioactivo (como el lavavajillas) en un vaso con agua y aceite y agitamos. Pasaremos de tener dos fases diferenciadas a una mezcla.
Lo que hacen los tensoactivos es colocarse en forma de capa monomolecular adsorbida en la superficie entre las fases hidrofílicas e hidrofóbicas. De hecho, los tensioactivos son sustancias que presentan una zona lipofílica y otra hidrofílica, de modo que se orientan generando una franja de contacto entre las dos fases. De esta manera, las moléculas de la superficie de las fases disminuyen la fuerza dirigida hacia el interior. El resultado es que los tensoactivos rebajan el fenómeno de tensión superficial.
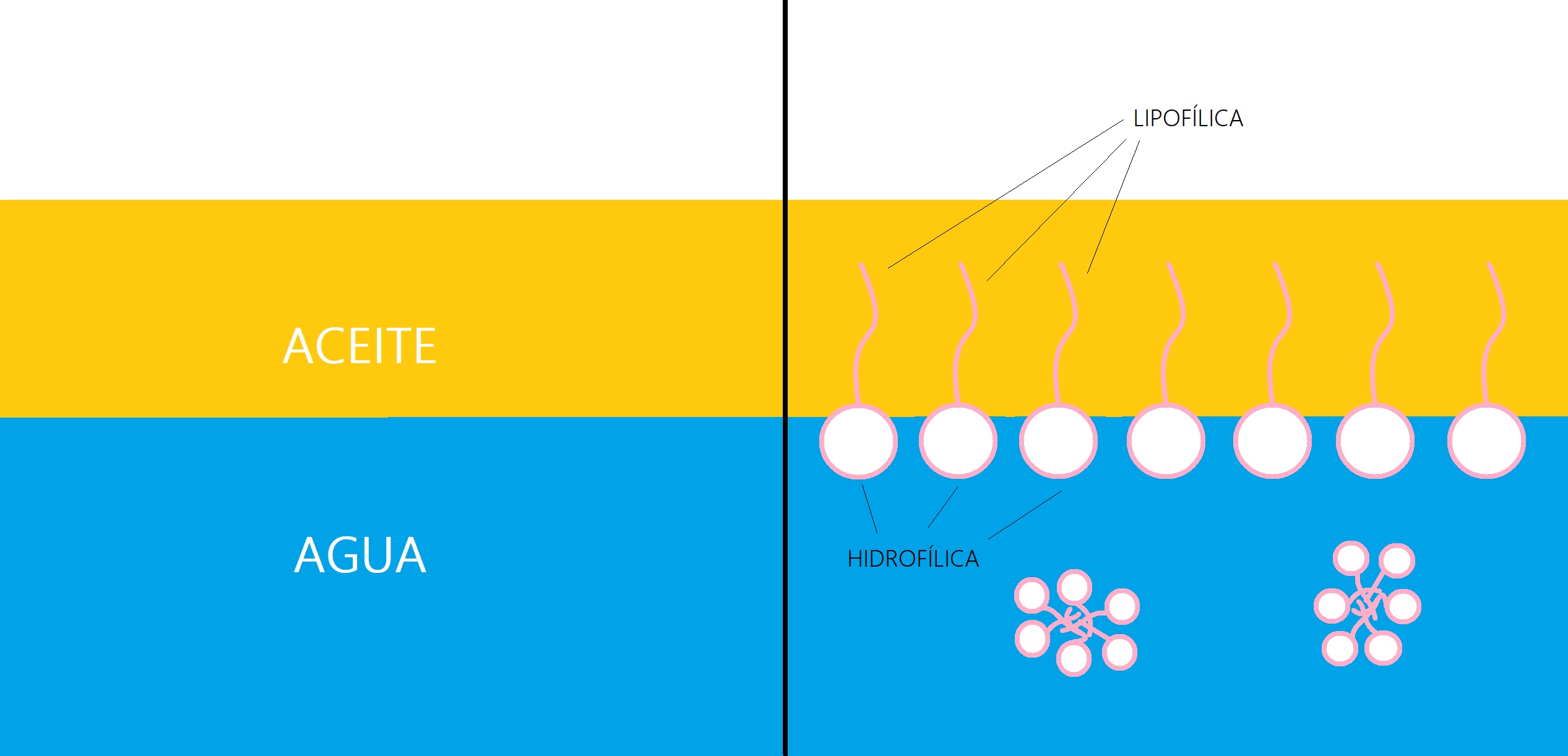 Tensioactivo formando una capa monomolecular entre las fases agua-aceite. Y tensioactivo rodeando pequeñas gotas de aceite dentro del agua en forma de micelas.
Tensioactivo formando una capa monomolecular entre las fases agua-aceite. Y tensioactivo rodeando pequeñas gotas de aceite dentro del agua en forma de micelas.
Existen diferentes tipos de tensioactivos. Según la naturaleza de su zona hidrofílica y de su zona lipofílica presentarán unas cualidades diferentes en el producto final. Según la naturaleza de sus zonas se establece el denominado equilibrio hidrofílico-lipofílico (HLB) por el que sabremos si un tensioactivo consigue emulsionar dos líquidos inmiscibles y de qué modo, si tiene capacidad de formar espumas, o cuánta detergencia presenta (capacidad de solubilizar la grasa, es decir, capacidad de limpieza).
-
Tipos de tensioactivos
La clasificación más habitual responde a cómo es la zona hidrofílica. Esta zona puede presentar carga eléctrica, así que los clasificamos en:
–Tensioactivos aniónicos, con carga negativa. Estos son los más habituales en cosméticos de limpieza, como champús y geles de ducha. Son buenos emulsionantes, generan espuma y presentan buena detergencia. Entre ellos encontramos los sulfatos (Sodium laureth sulphate, Sodium lauryl sulfate…), los carboxilatos (jabones), algunos sulfonatos (Sodium alkylbencene sulfonate, Dodecilbencene sulphonate…), tauratos (Sodium methyl cocoyl taurate), sulfosuccinatos (Disodium lauryl ether sulfosuccinate), etc.
-Tensioactivos catiónicos, con carga positiva. Estos se emplean en cosméticos que necesitan emulsión porque presentan dos fases (acuosa y oleosa) pero que no se destinan a limpieza, como pueden ser las mascarillas capilares y acondicionadores. Son buenos emulsionantes, humectantes y no generan espuma.
La fibra capilar presenta carga negativa, así que los tensioactivos catiónicos se adhieren a ella con facilidad. La función que tienen no es de limpieza, sino de lubricación, por lo que aportan brillo, suavidad y reducen la carga electrostática del cabello y, por tanto, el encrespamiento.
Entre ellos encontramos sobre todo sales de amonio cuaternarias (Quaternium-15, Quaternium-22, Quaternium-87, Cetrimonium chloride, Dicocodimonium chloride, Behentrimonium cloride, Behentrimonium methosulphate…) y esterquats, que también son sales cuaternarias de amonio pero con un enlace tipo éster (como el Distearoyleththydroxyethylmonium methosulphate). Este enlace tipo éster los hace menos irritantes, si cabe, y además los convierte en sustancias fácilmente biodegradables.
–Tensioactivos anfóteros, la carga cambia en función del pH. Sí se utilizan en cosméticos de limpieza, habitualmente acompañados por tensioactivos aniónicos, por lo que actúan como co-surfactantes. Resultan menos irritantes que los aniónicos, son más caros, y presentan buena generación de espuma, emulsión y detergencia. Son, por ejemplo, el Disodium cocoamphodiacetate, Cocamidopropyl betaine…
–Tensioactivos neutros o no iónicos, sin carga. Se utilizan como emulsionantes, no como agentes de limpieza. Entre ellos encontramos los PEG-n (propilen glicoles como el PEG-55 Prpylene glicol oleate, PEG-25 Propylene Glycol Stearate, PEG-75 Propylene Glycol Stearate) y el polioxiéter de alcohol láurico (Laureth-23, Laureth-4).
-
El agua no limpia, limpia el champú
El cabello se ensucia con la propia grasa de las glándulas sebáceas, por la descamación del cuero cabelludo y por contaminantes ambientales que se van acumulando en la cabeza. El agua no puede limpiar esta suciedad, precisamente porque no es capaz de mezclarse con ella. La suciedad es lipofílica mientras que el agua es hidrofílica.
El cabello sano tiene una superficie lipofílica (a la que se adhieren los lípidos pero que repele el agua). Por eso hacen falta los tensioactivos, para separar el sebo del cabello. La materia grasa se emulsiona con el champú y el agua y es arrastrada con el aclarado.
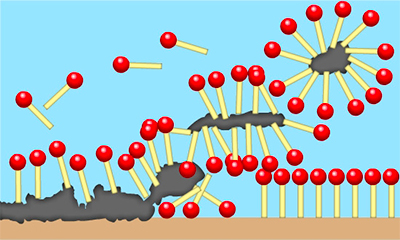
Los tensioactivos rodean la suciedad (lipofílica) orientando su zona lipofílica hacia ella y su zona hidrofílica hacia fuera, hacia el agua, de forma que la suciedad queda encapsulada y es fácil arrastrarla con el aclarado. A estas cápsulas las llamamos micelas.
-
¿Por qué un cosmético está formulado con unos tensioactivos y no otros?
Todos los cosméticos de limpieza incluirán en su formulación uno o varios tensioactivos aniónicos. Esto es así porque son las únicas sustancias capaces de arrastrar la suciedad.
También tienen otras virtudes, como la capacidad de formar espumas. El sodium lauryl sulphate (SLS), el sodium laureth sulphate (SLES), el jabón natural o el cocamidepropyl betaine, son agentes muy espumantes. La generación de espumas facilita el aclarado y, lo más importante, mejora la sensorialidad del producto; pero no hace que un champú limpie mejor, ni tampoco es indicativo de la presencia de sulfatos, ya que hay muchos otros tensioactivos que también son espumantes.
Los tensioactivos catiónicos solo se emplean en productos para el cabello que no limpian, como mascarillas o acondicionadores. Los champús, además de tensioactivos aniónicos podrán contener otros que faciliten la emulsión o que hagan que el producto sea más suave con la piel.
Los tensioactivos aniónicos pueden presentar mayor o menor detergencia, es decir, mayor o menor capacidad de arrastrar la suciedad y el sebo del cabello. Normalmente, si un tensioactivo presenta una alta detergencia, podría llegar a ser irritante. No obstante, los champús no están formados solo por agua y tensioactivos, sino que presentan toda una serie de sustancias que, como conjunto pueden dar fórmulas más o menos agresivas para el cuero cabelludo. Así que no debemos de juzgar la agresividad de un champú por los tensioactivos que contiene, porque estaríamos obviando cómo se comporta la fórmula completa.
Por norma general, la fórmula de un champú será un 75-90% agua, 10-25% tensioactivos, 1-5% emolientes e hidratantes, 1-2% conservantes y 1-2% otras sustancias, como controladores de pH, espesantes, perfumes y colorantes.
Por ejemplo, los carboxilatos, también denominados jabones, son tensioactivos aniónicos de elevada detergencia. Resultan los más irritantes para la piel y por eso es poco habitual encontrarlos en los champús, porque eliminarían sebo en exceso y terminarían por resecar el cabello, el cuero cabelludo e intensificarían problemas prexistentes de dermatitis. Aun así, los jabones combinados con emolientes y otros tensioactivos humectantes, sí podrían dar lugar a fórmulas suaves, por eso podemos encontrarlos en algunos geles de ducha y sobre todo en pastillas de jabón corporal.
-
Cómo saber si un champú lleva sulfatos
Los tensioactivos aniónicos más habituales de los champús son los sulfatos. Es fácil detectarlos porque los encontramos entre la lista de ingredientes con nombres terminados en -sulphate. Normalmente están entre los tres primeros ingredientes de la fórmula, es decir, entre los más abundantes. Recordemos que los ingredientes de un cosmético se ordenan de mayor a menor cantidad. Después del agua, que es el ingrediente mayoritario de los champús, aparecerán los tensioactivos.
-
No todos los sulfatos son iguales
Los sulfatos más habituales de los champús son el sodium lauryl sulfate (SLS), el sodium laureth sulphate (SLES) y el sodium coco sulphate (SCS).
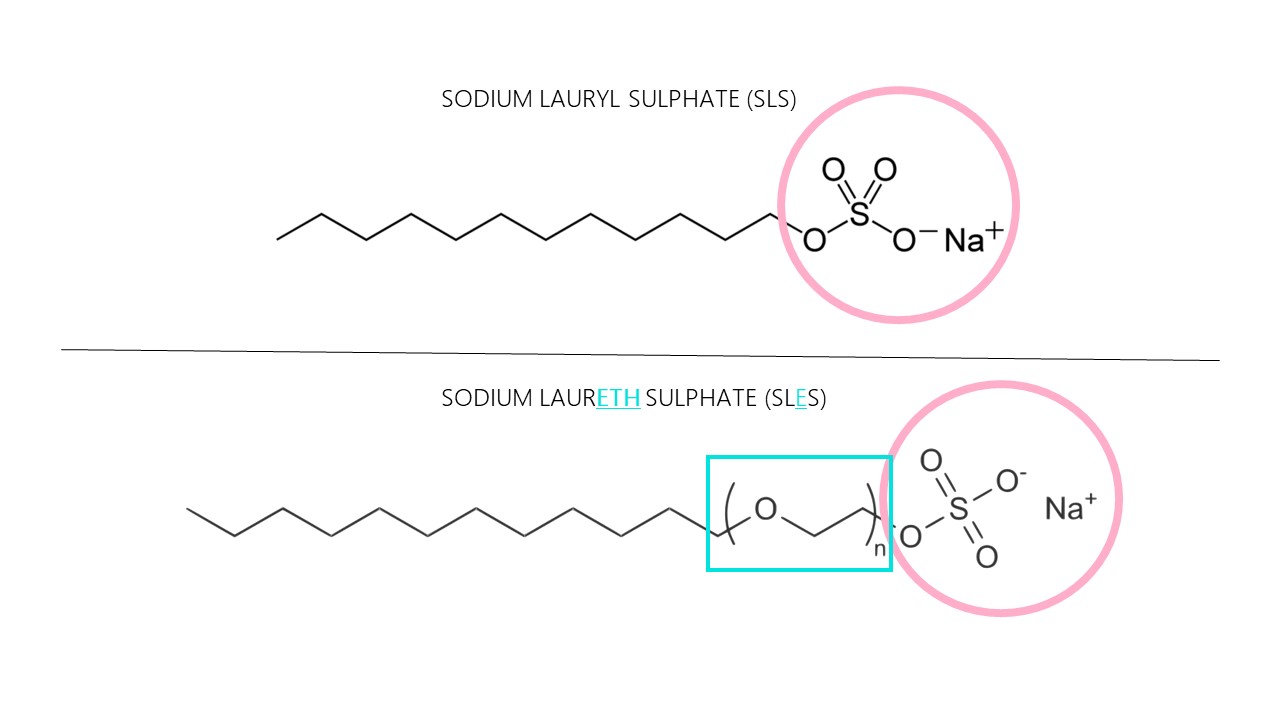
El sodium lauryl sulphate (SLS) es un tensioactivo aniónico de alta detergencia y puede resecar e irritar la piel. Es complicado formular champús con este tensioactivo que no resulten agresivos para el cuero cabelludo.
En cambio, el sodium laureth sulphate (SLES) es un tensioactivo aniónico que, aunque también tiene alta detergencia, es más suave para la piel y menos irritante gracias al enlace tipo éter que presenta la molécula. Por eso es común encontrarnos el SLES en champús con fórmulas respetuosas con el cuero cabelludo, incluyendo los champús formulados para pieles sensibles.
El sodium coco sulphate es otro tensioactivo aniónico de alta detergencia. Químicamente es mayoritariamente un lauryl, es decir, es un tensioactivo químicamente análogo al SLS cuyo nombre comercial alude al origen (aceite de coco) y por ello resulta más apetecible para el consumidor. Tanto el SLS como el SCS se obtienen a partir del aceite de coco en diferentes etapas del refinado, así que su procedencia “natural” no les convierte en mejores. La procedencia de una sustancia no es un buen criterio para escoger o descartar un producto cosmético.
-
La moda de los champús sin sulfatos
Hace tiempo que se ha puesto de moda el uso de champús sin sulfatos. Desgraciadamente estas modas no suelen ir acompañadas de hechos científicos que respalden las decisiones del consumidor, sino más bien responden a pulsiones derivadas de estrategias de márquetin como la moda del SIN. En general el SIN lo interpretamos como mejor, sin profundizar demasiado.
En el caso de los sulfatos, sí podríamos hacer la generalización de que, al tener alta detergencia, resultan más agresivos para la piel. Pero esa generalización no responde a la realidad, ya que un champú está formado por muchos otros ingredientes que pueden convertirlo en un producto respetuoso con la piel.
Es cierto que el SLS es un tensioactivo irritante y con una detergencia tan alta que limpia más de lo que necesitamos limpiar. Es decir, si nos lavamos el pelo con frecuencia, un tensioactivo como el SLS no es necesario. No da tiempo a que se acumule tanta suciedad en nuestro cabello. De hecho, resulta contraproducente arrastrar todo el sebo que lo recubre, ya que le resta elasticidad, brillo y aumenta su tendencia a encresparse.
En cambio, en SLES no presenta una detergencia tan alta y es más respetuoso con la piel. El sodium laureth sulphate (SLES) está especialmente indicado para limpiar bien el cabello si utilizamos lacas, espumas, gominas o pastas de peinado. También para pelos especialmente grasos que tienden a acumular suciedad. Es estos casos es indispensable usar un buen tensioactivo como el SLES, ya que los tensioactivos más suaves podrían no limpiar nuestro cabello en profundidad, lo que resulta peor para nuestra salud capilar.
Los productos para peinado, como lacas y pastas, contienen polímeros y siliconas que los tensioactivos más suaves no consiguen eliminar, por eso no podemos descartar el uso del SLES. Las personas que no emplean productos de peinado y que no tienen el pelo especialmente graso, pueden prescindir del SLES, o utilizar champús con SLES una o dos veces al mes.
-
Los sulfatos no son tóxicos ni cancerígenos
La American Cancer Society, la FDA, la comisión europea y la Agencia Española del Medicamento y el Producto Sanitario (AEMPS) permiten tanto el uso de SLS como SLES en productos cosméticos, y no hay estudios que vinculen el cáncer con su uso.
Sin embargo, en el proceso de fabricación del SLES se produce 1,4-dioxano como residuo. A determinadas dosis, este compuesto sí ha podido relacionarse con el cáncer hepático en ratones. Eso sí, a partir de ingestas de agua contaminada con 1 g de 1,4-dioxano por litro. Éste y otros estudios similares se han utilizado para tergiversar la realidad del uso del SLES en cosméticos. Los cosméticos con SLES no contienen 1,4-dioxano, ya que son dos sustancias diferentes y que sabemos separar. Además de lo obvio: no podemos extrapolar estudios en ratones a humanos, los cosméticos no se beben, el compuesto no tiene la misma capacidad de penetración a través de la piel que ingiriéndolo, y el 1,4-dioxano no está realmente presente en los cosméticos con SLES, ya que es un subproducto de síntesis, no es un ingrediente que se use en cosmética.
La realidad es que sabemos sintetizar SLES y purificarlo para que no contenga nada de 1,4-dioxano. Tanto es así que el Cosmetic Ingredient Review (CIR) Expert Panel estableció en el último estudio toxicológico que el 1,4-dioxano no supone un riesgo real, principalmente porque es indetectable en los productos finales.
-
Tengo el cuero cabelludo sensible, reactivo, con dermatitis ¿Podría usar sulfatos?
Sí. Hay champús con SLES formulados para cueros cabelludos sensibles, reactivos e incluso con dermatitis seborreica. Esto es así porque la fórmula del champú permite limpiar al mismo tiempo que hidrata, calma y regenera la piel. Esto se consigue gracias a la presencia de otras sustancias como el pantenol (provitamina B5), la sensirina, la piroctona olamina, que calman la piel, alivian la irritación, o la niacinamida, que restablece la barrera lipídica de la piel. Así que sí, es posible que el champú que mejor sienta a tu cuero cabelludo contenga SLES. No dejes de usarlo por ello.
También hay champús con alternativas al SLES, principalmente con tensioactivos aniónicos como los tauratos, los sulfonatos o sulfosuccinatos, con un poder de detergencia entre medio y bajo. Para personas con el cuero cabelludo sensibilizado que necesitan lavarse el pelo a diario, son una muy buena opción. Si lo necesitas, podrías combinarlos con champús calmantes con SLES una o dos veces al mes.
-
Si no disponemos de toda la información, ninguna de nuestras decisiones será libre
Esto es aplicable a todo, incluidas nuestras decisiones de compra. Quien decide comprar un champú sin sulfatos porque cree que son tóxicos, no sirven para nada, son irritantes, están de moda, es lo que usa tal famoso, está basando su decisión en sospechas, creencias y querencias. La realidad de la formulación de un buen cosmético va más allá de la presencia de un tipo de ingrediente. El “sin sulfatos”, igual que casi toda la cosmética “sin cosas”, responde más a una vaga estrategia de venta que a un hecho. Realmente esta estrategia se aprovecha de una triste realidad y la promueve: la incultura científica. Es una estrategia basada en pensar que los consumidores no sabemos qué es un sulfato, pero que si ponen “sin sulfato” asumiremos que es mejor. Es lo que sucede con el “sin parabenos” o con el “sin siliconas”. A esto además le sumamos toda la desinformación que circula por ahí acerca de la composición de los cosméticos. El consumidor demanda y los laboratorios fabrican. Y la bola se hace más grande.
La moda de los cosméticos SIN puede parecer inocua porque todos los cosméticos son seguros y pasan los controles de las autoridades sanitarias antes de salir a la venta, incluidos todos sus ingredientes. Pero la realidad es que la moda de lo SIN pone de manifiesto la desconfianza sobre el sector y la excesiva importancia que damos a las voces no autorizadas.
Como consumidora me gustan las estrategias de márquetin que me hablan de la realidad científica de un producto, de los ensayos clínicos, de los estudios que hay detrás, de los principios activos con evidencia científica. Me gustan los cosméticos que incluyen una suerte de prospecto. Eso es lo que espero de los laboratorios cosméticos. Si hacen ciencia, quiero que me la cuenten. La ciencia que hacen los laboratorios cosméticos es la propaganda que me resulta más convincente.
Si no lo publicitan así, será porque funcionaría para mí, que soy química, pero no para la mayoría de los consumidores y potenciales consumidores. O a lo mejor es que se han acostumbrado a que los consumidores seamos poco exigentes con la publicidad. O a lo mejor es que no tengo ni idea de márquetin.
Sin embargo, cada vez hay más gente que invierte su tiempo en tratar de descifrar la lista de ingredientes de un cosmético. Es una tarea casi imposible para alguien que no sepa de formulación cosmética, es decir, que no sepa de química. Quizá no sea una cuestión de exigencia. A lo mejor con tanto SIN y tanta desinformación, estamos paranoicos.
El conocimiento no solo hará que tu decisión sea más fácil, sino que hará que tu decisión sea más libre. Y esto aplica a los champús y los sulfatos como a cualquier otra esfera de la vida.
-
Conclusiones
– ¿Hay razones por las que descartar los champús con sulfatos? No. Los champús hay que juzgarlos por su fórmula. Un champú con sulfatos puede tener una fórmula específica para cueros cabelludos reactivos. Y un champú sin sulfatos, con una fórmula inadecuada, puede resultar irritante. Lo importante es la fórmula, no uno solo de sus ingredientes.
– ¿Qué función tienen en el producto? Los sulfatos son tensioactivos, sirven para encapsular la suciedad del pelo y arrastrarla con el aclarado. El agua por sí sola no es capaz de limpiar.
– ¿Hay alternativas? Sí, existen varios tensioactivos aniónicos en el mercado que no son sulfatos. Y entre los sulfatos, también hay diferencias. Es mucho más respetuoso con la piel y el pelo el sodium laureth sulphate (SLES) que el sodium lauryl sulphate (SLS).
– ¿Son nocivos? No. Los sulfatos son ingredientes autorizados por la Agencia Española del Medicamento y el Producto Sanitario, así que su uso es seguro.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Los champús sin sulfatos y la libertad de decidir se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Arte y geometría del triángulo rectángulo: Broken Lights
En la sección Matemoción del Cuaderno de Cultura Científica de la UPV/EHU nos gusta hablar de las diferentes formas en las que el arte y las matemáticas se relacionan entre sí. Hoy traemos a este espacio un nuevo y motivador ejemplo. Es la interesante exposición del artista brasileño Felipe Cohen, titulada Broken Lights, que la galería y editorial de libros de arte Ivorypress ha organizado en su espacio expositivo de Madrid, del 12 de septiembre al 3 de noviembre de 2018.
 Obra “Broken Lights Series #51” (2017), pintura acrílica sobre madera (24,6 24,6 cm), del artista brasileño Felipe Cohen, dentro de la exposición “Broken Lights” en la galería Ivorypress de Madrid. Imagen de Ivorypress
Obra “Broken Lights Series #51” (2017), pintura acrílica sobre madera (24,6 24,6 cm), del artista brasileño Felipe Cohen, dentro de la exposición “Broken Lights” en la galería Ivorypress de Madrid. Imagen de IvorypressEsta es una exposición a caballo entre la pintura y la escultura en la cual la geometría y el arte dialogan entre sí, y el artista Felipe Cohen hace partícipe al público de ese diálogo y de la belleza que emana del mismo.
Utilizando únicamente triángulos rectángulos, todos ellos con la misma forma pero de tres tamaños distintos, Felipe Cohen realiza hermosos, sugerentes e impactantes retratos de paisajes de la naturaleza. El artista brasileño trabaja con los módulos triangulares como si de un puzle geométrico, al estilo del Tangram (véase la entrada Tangram), se tratase.
En palabras del autor de la exposición:
“Mi principal objetivo era retratar la naturaleza como un campo de constante indeterminación y cambio, generado mediante sistemas. La construcción de la geometría y la repetición de módulos triangulares proporciona control y rigor, mientras que la apropiación de la naturaleza orgánica de las vetas de madera y el proceso con acuarela hace visible las marcas naturales del material, creando un efecto evocador, menos gráfico.”
 Obras “Broken Lights Series #43”, “Broken Lights Series #51” y “Broken Lights Series #45” (2017), pintura acrílica sobre madera (24,6 x 24,6 cm), del artista brasileño Felipe Cohen, dentro de la exposición “Broken Lights” en la galería Ivorypress de Madrid. Imagen de Ivorypress
Obras “Broken Lights Series #43”, “Broken Lights Series #51” y “Broken Lights Series #45” (2017), pintura acrílica sobre madera (24,6 x 24,6 cm), del artista brasileño Felipe Cohen, dentro de la exposición “Broken Lights” en la galería Ivorypress de Madrid. Imagen de IvorypressIvorypress es una editorial especializada en arte y en los libros de artista que fue fundada en 1996 por Elena Ochoa Foster. Entre las variadas actividades que incluye este proyecto están la organización de exposiciones de arte, como las organizadas en su galería de arte de Madrid, la publicación de diferentes colecciones de libros de arte y libros de artista, un programa educativo que pretende llevar el arte contemporáneo a la educación universitaria, proyectos audiovisuales relacionados con el arte y la arquitectura, y la activa librería de la galería de Madrid especializada en fotografía, arte contemporáneo y arquitectura.
Una de las señas de identidad de Ivorypress son sus exclusivos libros de artista. Entre los que ha publicado encontramos joyas artísticas como Reflections (2002), de Eduardo Chillida, Open Secret (2004), de Anthony Caro, Wound (2005), de Anish Kapoor, The Secrets Life of Plants (2008), de Anselm Kiefer, Becoming (2009), de Ai Weiwei, o Tummelplatz (2017), de William Kentridge, entre otros.
 Dos fotografías, una de Elena Ochoa Foster y el artista Isidoro Valcárcel Medina, frente a uno de los volúmenes del libro de artista “Ilimit” (2012), de Isidoro Valcárcel Medina, y la otra del artista trabajando en la página 6 de “Ilimit”. La edición consta de 9 volúmenes, más dos pruebas de artista, más una H.C. (siglas de Hors Commerce, prueba que está fuera de comercio). Como se explica en la página de Ivorypress, en “Ilimit” se “explora la contraposición entre los conceptos “limitado” e “ilimitado”, al tiempo que propone una reflexión acerca de los conceptos de seriación y exclusividad, tan recurrentes en el mundo del arte. Cada uno de los volúmenes es distinto y consta de 500 páginas. El contenido de estas páginas consiste únicamente en su numeración, correlativa volumen tras volumen desde la página 1 hasta la 6.000. Dicha paginación está escrita con numeración ordinal en distintos idiomas, escogidos aleatoriamente de entre una selección total de 58 lenguas”. Imágenes de Ivorypress
Dos fotografías, una de Elena Ochoa Foster y el artista Isidoro Valcárcel Medina, frente a uno de los volúmenes del libro de artista “Ilimit” (2012), de Isidoro Valcárcel Medina, y la otra del artista trabajando en la página 6 de “Ilimit”. La edición consta de 9 volúmenes, más dos pruebas de artista, más una H.C. (siglas de Hors Commerce, prueba que está fuera de comercio). Como se explica en la página de Ivorypress, en “Ilimit” se “explora la contraposición entre los conceptos “limitado” e “ilimitado”, al tiempo que propone una reflexión acerca de los conceptos de seriación y exclusividad, tan recurrentes en el mundo del arte. Cada uno de los volúmenes es distinto y consta de 500 páginas. El contenido de estas páginas consiste únicamente en su numeración, correlativa volumen tras volumen desde la página 1 hasta la 6.000. Dicha paginación está escrita con numeración ordinal en distintos idiomas, escogidos aleatoriamente de entre una selección total de 58 lenguas”. Imágenes de IvorypressPero volvamos a la exposición actual Broken Lights, del artista brasileño Felipe Cohen. Esta es la primera exposición individual en España del artista nacido en Sao Paolo (Brasil) en 1976, y que recibió en 2016 el premio illy SustainArt en la feria ARCOmadrid. Entre sus exposiciones individuales nos encontramos, entre otras, Ocidente en la Kubikgallery (Oporto, Portugal) en 2017 y en la Galeria Millan (São Paulo, Brasil) en 2016, Lapso en la Galeria Millan (São Paulo, Brasil) en 2013, Poente en Capela do Morumbi (São Paulo, Brasil) en 2013, Colagens en Anita Schwartz (Río de Janeiro, Brasil) en 2009 o A Gravidade e a Graça en la Galeria Virgílio (São Paulo, Brasil) en 2008, además de exposiciones colectivas a lo largo de todo el mundo. Sus obras se encuentran en colecciones como la Pinacoteca do Estado de São Paulo, Museu de Arte Moderna de São Paulo y Museu de Arte do Rio, Río de Janeiro.
 “Sin título” (2004), de Felipe Cohen, copa de vidrio y mármol, 7 x 6 x 6 cm. Imagen de la Galería Virgílio
“Sin título” (2004), de Felipe Cohen, copa de vidrio y mármol, 7 x 6 x 6 cm. Imagen de la Galería VirgílioFelipe Cohen utiliza todo tipo de materiales y medios para desarrollar su arte. Realiza esculturas con objetos encontrados, collages con diferentes materiales, como madera, papel o vidrio, instalaciones, videos y dibujos.
 “Catedral #2” (2010), de Felipe Cohen, pinza de la ropa de madera y travertino romano, 16,5 x 9,5 x 2 cm. Imagen de la Galería Estaçao
“Catedral #2” (2010), de Felipe Cohen, pinza de la ropa de madera y travertino romano, 16,5 x 9,5 x 2 cm. Imagen de la Galería EstaçaoEn la serie de obras Broken Lights, algunas de las cuales se exponen en la galería Ivorypress (Madrid), el artista Felipe Cohen trabaja uno de los temas centrales de la historia del arte, como es la representación de paisajes de la naturaleza, pero lo hace de una forma muy particular, a través de un proceso de geometrización del paisaje que quiere representar. Para realizar estos retratos utiliza una única figura geométrica, un triángulo rectángulo. Estas piezas triangulares se construyen en madera, de tres tamaños distintos, pero siempre la misma forma, y, además, algunas de ellas están pintadas con un color suave (cada pieza un único color). Mediante la combinación de diferentes triángulos se crea el retrato del rincón de la naturaleza que se desea representar, por ejemplo, una playa, un lago, un valle o una cueva.
 Vista de la exposición “Broken Lights”, de Felipe Cohen, en la galería Ivorypress, en la que se ven, de izquierda a derecha, las obras “Broken Lights Series #30, #29 y #28” (2017), pintura acrílica sobre madera. Imagen de Ivorypress
Vista de la exposición “Broken Lights”, de Felipe Cohen, en la galería Ivorypress, en la que se ven, de izquierda a derecha, las obras “Broken Lights Series #30, #29 y #28” (2017), pintura acrílica sobre madera. Imagen de IvorypressEl triángulo rectángulo utilizado por el artista de Sao Paolo es siempre el mismo, no se cambia su forma, aunque se utilizan tres tamaños distintos. Veamos qué triángulo es este.
Para empezar, el triángulo utilizado por Felipe Cohen es un triángulo rectángulo, luego con un ángulo recto, es decir, de 90º, que nos recuerda mucho a un cartabón. Recordemos que el cartabón es un instrumento de dibujo cuya forma es la de un triángulo rectángulo escaleno, sus lados son los tres de longitudes distintas, cuyos ángulos son 30º, 60º y 90º. Una de las propiedades del triángulo del cartabón es que, al colocar dos triángulos juntos, pegados por el cateto más largo, se forma un triángulo equilátero, con los tres lados iguales, y los tres ángulos también, de 60º.
 A la izquierda, un triángulo rectángulo escaleno de ángulos 30º, 60º y 90º, que es el que da lugar a la forma del cartabón, y a la derecha un triángulo equilátero, con los tres lados iguales, formado por la unión de dos triángulos como el anterior
A la izquierda, un triángulo rectángulo escaleno de ángulos 30º, 60º y 90º, que es el que da lugar a la forma del cartabón, y a la derecha un triángulo equilátero, con los tres lados iguales, formado por la unión de dos triángulos como el anteriorPero estos no son los triángulos rectángulos que utiliza Felipe Cohen. ¿Qué forma tienen, entonces, estos triángulos? Como podemos observar en las obras de la serie Broken Lights con cuatro triángulos rectángulos se forma un cuadrado (como se puede apreciar, por ejemplo, en la parte superior del primer cuadro, Broken Lights Series #51), por lo que la longitud del cateto mayor del triángulo rectángulo es igual al doble de la longitud del cateto menor. En la siguiente imagen hemos dibujado la forma de los triángulos que utiliza Felipe Cohen, el cateto grande el doble del cateto pequeño, y además hemos calculado, utilizando el teorema de Pitágoras, la longitud de la diagonal y, utilizando un poco de trigonometría, el valor exacto de los ángulos de ese triángulo.
 La geometría del triángulo rectángulo utilizado por el artista Felipe Cohen en la serie “Broken Lights”
La geometría del triángulo rectángulo utilizado por el artista Felipe Cohen en la serie “Broken Lights”  Comparativa de la forma del triángulo rectángulo del cartabón, a la izquierda, y del utilizado por Felipe Cohen, a la derecha
Comparativa de la forma del triángulo rectángulo del cartabón, a la izquierda, y del utilizado por Felipe Cohen, a la derechaLa obra Broken Lights Series #74, que sería la composición más sencilla de esta serie ya que todas las obras mantienen la forma rectangular o cuadrada clásica de un cuadro, está formada por dos triángulos rectángulos que forman un rectángulo de proporción 2, es decir, el largo es el doble que el ancho, de hecho, las medidas de la obra, sin el marco, son 6 cm de ancho y 12 cm de largo.
 Obra “Broken Lights Series #74” (2018), pintura acrílica sobre madera (6,5 12,5 cm), del artista brasileño Felipe Cohen, dentro de la exposición “Broken Lights” en la galería Ivorypress de Madrid. Imagen de Ivorypress
Obra “Broken Lights Series #74” (2018), pintura acrílica sobre madera (6,5 12,5 cm), del artista brasileño Felipe Cohen, dentro de la exposición “Broken Lights” en la galería Ivorypress de Madrid. Imagen de IvorypressY como hemos comentado, con cuatro triángulos de los utilizados por Felipe Cohen se puede formar un cuadrado, como se muestra en la siguiente imagen.

Además, en esta serie de obras se utilizan tres tamaños distintos de triángulos rectángulos. Los tres tamaños utilizados, dados por la longitud de sus catetos, son 6 x 12 cm, 12 x 24 cm y 18 x 36 cm, respectivamente, para que puedan encajar bien unos triángulos con otros.
En la obra Broken Lights Series #61 pueden verse los tres tamaños de triángulos utilizados. A continuación, mostramos la obra y la estructura de los triángulos de la misma.
 Obra “Broken Lights Series #61” (2017), pintura acrílica sobre madera (36,4 x 36,5 cm), del artista brasileño Felipe Cohen, dentro de la exposición “Broken Lights” en la galería Ivorypress de Madrid. Imagen de Ivorypress
Obra “Broken Lights Series #61” (2017), pintura acrílica sobre madera (36,4 x 36,5 cm), del artista brasileño Felipe Cohen, dentro de la exposición “Broken Lights” en la galería Ivorypress de Madrid. Imagen de Ivorypress  Estructura de los triángulos rectángulos de la obra “Broken Lights Series #61”, de Felipe Cohen
Estructura de los triángulos rectángulos de la obra “Broken Lights Series #61”, de Felipe CohenOtra de las peculiaridades de esta serie de obras, que conecta de nuevo con la historia del arte, es el uso del color para dotar de profundidad, de tridimensionalidad, a la pintura, que es una imagen bidimensional. Una de las obras en las que se aprecia muy bien este efecto es Broken Lights Series #73, que se muestra más abajo, la cual quizás podría representar la imagen de una cueva, mirando desde el interior hacia la salida. Otro de los elementos a destacar en esta obra es el uso de espirales mediante el contraste de color.
 Obra “Broken Lights Series #73” (2017), pintura acrílica sobre madera (36,6 x 36,6 cm), del artista brasileño Felipe Cohen, dentro de la exposición “Broken Lights” en la galería Ivorypress de Madrid. Imagen de Ivorypress
Obra “Broken Lights Series #73” (2017), pintura acrílica sobre madera (36,6 x 36,6 cm), del artista brasileño Felipe Cohen, dentro de la exposición “Broken Lights” en la galería Ivorypress de Madrid. Imagen de IvorypressAunque, la idea de utilizar triángulos rectángulos, a la manera de un puzle geométrico, como pueda ser el clásico y conocido Tangram u otros puzles similares, ya la utilizó el artista de Sao Paulo en su obra Chao ou Vao (2013), que consta de una serie de 140 triángulos rectángulos iguales de tres colores (blanco, gris y negro) que se pueden manipular para construir diferentes paisajes sobre el estuche rectangular con tapa transparente que hace las veces de cuadro, siendo por tanto una obra dinámica, nunca terminada y siempre dispuesta a ser modificada para crear la siguiente imagen.


 Tres imágenes de la obra “Chao ou Vao” (2013), del artista Felipe Cohen. Imagen de la galería Carbono
Tres imágenes de la obra “Chao ou Vao” (2013), del artista Felipe Cohen. Imagen de la galería CarbonoEn palabras del artista:
“A partir de juegos de madera como el Tangram y otros, que veía frecuentemente expuestos en el taller del carpintero con quien trabajo, empecé a pensar en la posibilidad de explorar la idea de collages no definitivos. A partir de esa idea central desarrollé la estructura de ese objeto/juego utilizando una malla geométrica formada por 140 triángulos de mdf de dimensiones iguales revestidos por formica por los dos lados, pero divididos en tres tonalidades: una más luminosa, próxima al color blanco, y las otras dos en tonos de gris, uno más claro y otro casi negro. Lo suficiente para hacer posible elaborar dentro de esa malla geométrica dibujos que sugieran profundidad. Las imágenes encontradas por mí por la combinación de estas piezas son paisajes abisales que sugieren agujeros y huecos a partir de la relación de las piezas más claras con las oscuras. Estas piezas se encajan en un estuche de madera con una tapa de acrílico, que permite el montaje de este juego en la pared, en una alusión directa al marco”.
Para terminar, simplemente recomendar a las personas que puedan pasarse por la galería Ivorypress de Madrid que visiten esta magnífica exposición y que disfruten del arte geométrico del artista brasileño Felipe Cohen, y para quienes no puedan visitarla, que entren en la página web de Ivorypress y/o compren el catálogo de Broken Lights.
Biblioteca
1.- Ivorypress, editorial y galería de arte
2.- Felipe Cohen, Broken Light, Ivorypress, 2018.
3.- Felipe Cohen, Trabalhos recentes, Galeria Marilia Razuk, 2012.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Arte y geometría del triángulo rectángulo: Broken Lights se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La geometría de la obsesión
- El tamaño sí importa, que se lo pregunten a Colón (o de la geometría griega para medir el diámetro de la Tierra)
- Arte cartográfico, arte con mapas
Contra la meritocracia
En una gran organización la gente viene y va. Siempre hay decisiones que tomar sobre a quien se promociona, las nuevas promesas recién llegadas frente a los cuadros medios experimentados, mientras todo el mundo espera el ascenso. Dados dos candidatos para un puesto, uno muy competente en su trabajo actual y el otro más errático y, en general, con menos éxito, la mayoría de la gente considera una obviedad que debe ascender el primero y no el segundo. Sin embargo, en 1969, Laurence Peter introdujo el famoso principio que lleva su nombre, que afirma que cada nuevo miembro de una organización jerárquica asciende en la jerarquía hasta que alcanza su nivel de máxima incompetencia. Una afirmación que está en contra, aparentemente, del sentido común y de lo que ha dado en llamarse meritocracia, que muchos citan como un chiste… pero que es muy probable que no lo sea.
 Imagen: Truman Show HDR by Maximes21500 (DeviantArt)
Imagen: Truman Show HDR by Maximes21500 (DeviantArt)Efectivamente, un resultado obvio de la estrategia promocional basada en el sentido común de ascender al competente es que todo el mundo promocionará hasta que llegue a un trabajo para el que no sea bueno. En ese momento dejará de ascender y la organización tenderá a tener incompetentes en cada puesto [asumimos que el departamento de recursos humanos ya es incompetente, no es consciente de esta situación por una variante del efecto Dunning-Kruger, y es incapaz de intervenir eficazmente]. La eficiencia de la organización disminuye. A esto es a lo que se refería Peter cuando afirmaba que cada nuevo miembro de la organización asciende hasta alcanzar su máximo nivel de incompetencia.
El principio de Peter se basa en que el departamento de recursos humanos tiene poco que decir más allá de administrar las nominas. Dicho de forma más técnica, Peter asume la hipótesis, no necesariamente cierta, de que existe poca o ninguna correlación entre las competencias necesarias para desempeñar un puesto y el nivel en la organización. Aquí chocamos de nuevo con el sentido común que afirma que sí existe esa correlación. Sin embargo, el hecho empírico es que existe un patrón de promoción en las organizaciones que hace que las personas que son buenas haciendo determinadas cosas alcancen puestos en los que ya no se hacen esas cosas: en muchos casos pasan a “administrar” personas que las hacen. Es decir, en muchas organizaciones se actúa de hecho como si no existiese correlación entre competencias y nivel jerárquico. Veamos algunos ejemplos familiares: los buenos profesores dando clase no suelen ser buenos directores de instituto, futbolistas de mucho éxito no siempre se convierten en buenos directores deportivos, magníficos investigadores es probable que no sean buenos decanos, estupendos atletas puede que no sean buenos entrenadores, vendedores superlativos casi nunca son buenos jefes de ventas y extraordinarios estudiantes con notas magníficas puede que no sean buenos médicos.
Un grupo de investigadores de la Universidad de Catania, encabezados por Alessandro Pluchino, fue un paso más allá y estudió las distintas políticas de promoción usando modelos computacionales de distintas organizaciones con distintos niveles a los que promocionar. Increíblemente (o no), encontraron que la política de ascender siempre a la persona menos competente puede maximizar la competencia general de la empresa, mientras que ascender al más competente puede disminuirla significativamente. La investigación fue merecedora de un Ig-Nobel en 2010.
Los investigadores compararon los cambios en la organización en su conjunto con tres políticas de promoción distintas (al mejor, al peor, al azar) aplicadas en los dos supuestos de que hay o no hay correlación entre las capacidades necesarias para realizar tu trabajo actual y aquel al que se te promociona.
Sus resultados son contundentes. Si, tal y como asume Peter, no existe correlación entre trabajos nuevos y antiguos entonces “al mejor” lleva, efectivamente, a una pérdida del 10% en la eficiencia de la organización. Ello se debe a la gente que es mucho menos competente en sus nuevos trabajos que en los anteriores. Por otra parte, “al peor” lleva a una ganancia del 12%, ya que la gente que era mala en un puesto lo hará igual de mal o mejor. En el caso de que exista correlación, “al mejor” lleva a una ganancia del 9% y “al peor” a una pérdida del 5 %.
La cuestión es que en una organización nada es blanco o negro, y la correlación estará en algún punto intermedio. El reto para el departamento de recursos humanos y para el máximo ejecutivo está en superar los resultados al azar: si no hay correlación la promoción al azar incrementa la efectividad de la organización en un 2% y si la hay en un 1%. No parecen grandes números, pero para superarlos el departamento de RR.HH. debe ser, primero, muy competente y, segundo, que su labor no sea interferida por asuntos políticos ajenos a las valoraciones técnicas. Ambos supuestos, mucho nos tememos, es muy improbable que se den completamente. Paradójicamente, por tanto, puede que la mejor decisión para mejorar la eficiencia de la organización sea dejar de gestionar los recursos humanos y ahorrarse el coste de un departamento y sus reuniones y papeleos asociados.
Habrá quien argumente que promocionar al azar disminuye la moral y los incentivos para el trabajo duro. Pero esto tiene fácil solución: primero, negarlo taxativamente y, segundo, un uso adecuado de la propaganda interna. Lo importante no es la realidad, sino lo que las personas crean que es la realidad.
Referencia:
Pluchino, A., Rapisarda, A., & Garofalo, C. (2010). The Peter principle revisited: A computational study Physica A: Statistical Mechanics and its Applications, 389 (3), 467-472 doi: 10.1016/j.physa.2009.09.045
Una versión anterior de este texto se publicó en Experientia docet el 9 de noviembre de 2011 con el título Más allá del principio de Peter: el azar como política de recursos humanos.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Contra la meritocracia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Una fórmula para dominarlos a todos: La conservación de la energía y la ley de la palanca
 Representación de la frase de Arquímedes “Dadme un punto de apoyo y moveré el mundo”, que ejemplifica la ley de la palanca, en la decoración del techo del “Stanzino delle Matematiche” de la Galleria degli Uffizzi (Florencia). Obra de Giulio Parigi (1599-1600)
Representación de la frase de Arquímedes “Dadme un punto de apoyo y moveré el mundo”, que ejemplifica la ley de la palanca, en la decoración del techo del “Stanzino delle Matematiche” de la Galleria degli Uffizzi (Florencia). Obra de Giulio Parigi (1599-1600)En la entrega anterior vimos cómo la definición del trabajo en la física era mucho más comprensible y de “sentido común” de lo que suele apreciarse.
Hasta aquí estupendo, pero, ¿qué tiene que ver esto con la energía y los mecanismos?
La primera ley de la termodinámica nos dice que la variación de energía (ΔU) de un sistema se produce por el intercambio de calor (Q) y de trabajo (W).
ΔU = Q + W
No nos meteremos aquí con el asunto del calor, estamos pensando en mecanismos que cambian tipos de movimiento y su velocidad, entenderemos que habrá pérdidas por rozamiento, pero consideraremos el caso ideal sin pérdidas (recordad que soy físico).
Así que elijamos un mecanismo, una palanca, por ejemplo.
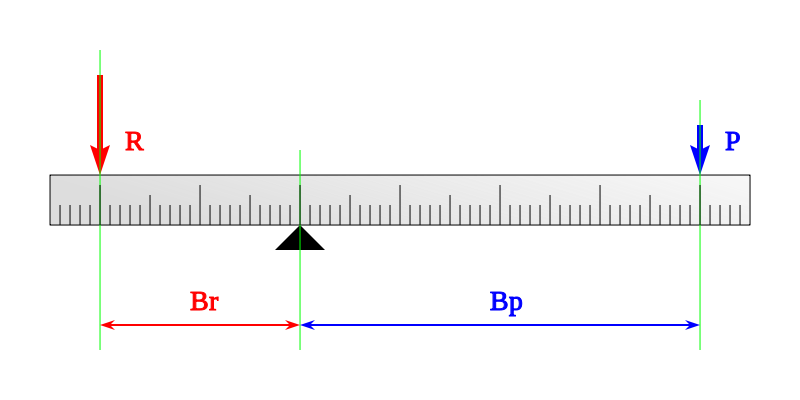 Fuente: Dnu72 / Wikimedia Commons
Fuente: Dnu72 / Wikimedia Commons
No hay más aportes de energía que la que hacemos en un extremo mediante nuestra fuerza y eso es todo lo que tendremos a la salida. La energía que entra será la que salga, y ambas serán trabajo (ya, ya, salvo pérdidas).
Así que podemos decir que
W1 = W2
Como hemos visto, nuestro trabajo tiene dos factores, la fuerza y la distancia (supongamos alineación entre ellos). Por lo que podríamos conseguir 10 J (unidades de trabajo) de muchas maneras, por ejemplo:
W = F · d
1 · 10 = 10 J
2 · 5 = 10 J
5 · 2 = 10 J
10 · 1 = 10 J
…
Mandaremos la misma energía (trabajo) de un extremo al otro del mecanismo, pero podemos hacerlo con más fuerza y menos recorrido o al revés, según nos interese.
¿Podría ser entonces que en un extremo del mecanismo tuviéramos más fuerza que en el otro? Por supuesto, no existe nada parecido a un “principio de conservación de la fuerza”. Tú puedes multiplicar tu fuerza lo que desees (idealmente, claro). De ahí viene la expresión “Dadme un punto de apoyo y moveré el mundo”.
Supongo que ya te habrás dado cuenta de que ese aumento de fuerza tiene un precio. Tendrás que reducir el recorrido en la misma proporción, de forma que la energía se mantenga constante, porque para la energía sí tenemos una ley de conservación.
Así que, sin más, podemos afirmar que si en un mecanismo el recorrido que se hace a la salida es la mitad que el que se hace a la entrada, la fuerza será el doble. No necesitamos saber nada más de lo que ocurre en el interior del mecanismo. Estoy haciendo balance de energía a la entrada y a la salida, punto. Pura conservación de la energía que no se la salta nadie, primera ley de la termodinámica.
Volvamos a nuestra palanca, mediante argumentos geométricos podemos saber qué relación hay entre las distancias recorridas a un lado y a otro, y eso nos llevará, vía conservación de la energía, a concluir la relación entre las fuerzas a ambos extremos. Vaya, llegaremos a la “ley de la palanca”.
La Palanca
 Fuente: Dnu72 / Wikimedia Commons
Fuente: Dnu72 / Wikimedia Commons
 Fuente: Silver Spoon / Wikimedia Commons
Fuente: Silver Spoon / Wikimedia CommonsVemos que los extremos de la palanca recorren ambos un arco de circunferencia, cuyos radios son Br y Bp, y son obviamente distintos en longitud, así que ya estamos en condiciones de afirmar que las fuerzas a ambos lados también lo serán.
Fíjate que los ángulos recorridos en ambos extremos son iguales, en caso contrario la barra se doblaría.
Pero a nosotros nos interesa la distancia (para la fórmula del trabajo), así que pensemos en la longitud del arco de circunferencia que se recorre.
Esa longitud de arco es proporcional al radio y al ángulo. Si recordáis la popular fórmula para la longitud de la circunferencia completa L = (2π)·r es justo esa proporcionalidad para un ángulo de 2π radianes, lo que en grados sería 360º.
Por lo tanto, para un arco cualquiera sería:
arco = ángulo · radio de giro
Sigamos adelante, comparemos trabajos:
W1 = W2
W = F·d (suponiendo fuerzas alineadas con el desplazamiento)
R · arco1= P · arco2
R · ángulo · Br = P · ángulo · Bp (ya que los radios de giro son Br y Bp)
Como los ángulos son iguales, si la barra no se dobla, podemos simplificar
R · Br = P · Bp
¡Hecho! Fuerza por su brazo igual a fuerza por su brazo. La ley de la palanca.
Vemos que simplemente hemos aplicado argumentos geométricos para averiguar la distancia recorrida al principio y al final del mecanismo y después la conservación de la energía para ver la relación entre las fuerzas.
En la próxima entrega haremos los cálculos para varios mecanismos, pero os animamos a que lo probéis vosotros y, si sois docentes, que se lo pongáis a vuestros (pobres) alumnos como ejercicio.
El artículo Una fórmula para dominarlos a todos: La conservación de la energía y la ley de la palanca se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una fórmula para dominarlos a todos: El trabajo
- Se establece el principio de conservación de la energía
- El modelo cuántico de Rabi, un sencillo modelo para dominarlos a todos
El Imperio Romano extendió la tuberculosis

La tuberculosis es una enfermedad que afecta principalmente a los pulmones y que se contagia fácilmente a través del aire. De no ser tratada correctamente provoca tos continua, fiebre, pérdida de peso, debilidad y finalmente, la muerte. Ha sido y es una de las mayores causas de muerte infecciosa en el mundo; cada año se producen entre 10 y 11 millones de nuevos casos y provoca entre 1,5 y 1,8 millones de muertes.
El equipo de Caitilin Pepperell, de la Universidad de Wisconsin-Madison (EEUU), ha analizado el genoma de 552 muestras de la bacteria que produce la tuberculosis, Mycobacterium tuberculosis, obtenidas de personas de diferentes lugares del Mundo, salvo del continente americano (la bacteria llegó a América con los europeos en el siglo XV). A partir del origen geográfico de las muestras y teniendo en cuenta la velocidad a que cambia el genoma bacteriano por efecto de las mutaciones, el grupo de la Dra. Pepperell ha reconstruido el árbol de linajes de la bacteria. Como ya se sabía, hay siete familias principales de Mycobacterium tuberculosis. El último ancestro común a esas siete familias surgió probablemente en el Oeste de África hace unos cinco mil años, y tres de ellas no han salido nunca del continente africano.
Al parecer, una de esas familias se extendió al Sudeste asiático más de tres siglos antes del comienzo de nuestra era. Había entonces un intenso tráfico de mercancías –especias, principalmente- por las costas del Océano Índico, y ello propició que ese linaje de Mycobacterium tuberculosis llegase incluso a la isla de Papua Nueva Guinea.
Sin embargo, la variedad que ha alcanzado mayor extensión es la que se propagó en el primer siglo desde la cuenca del Mediterráneo hacia casi toda Europa, las estepas rusas, Asia y, retornando a la zona donde surgió, África también. La época en la que se produjo esa expansión coincide con el periodo en que el Imperio Romano alcanzó su máxima extensión, por lo que aumentaron los desplazamientos, creció mucho el transporte de mercancías en el interior de sus fronteras, y se intensificó el comercio con los pueblos del entorno e, incluso, con el mismísimo Imperio Chino. Se pusieron así en contacto personas de muy diferentes orígenes, pertenecientes a pueblos que no habían tenido relación directa con anterioridad. Además, las ciudades adquirieron una gran importancia. Roma llegó a tener entonces un millón de habitantes, una cifra que en Europa solo alcanzaría Londres durante la revolución industrial. A Roma y de Roma viajaban en todas las direcciones miles de personas cada año. Muchas de esas personas llevaban consigo unos cuantos miles de ejemplares de Mycobacterium tuberculosis. Además, algunos hábitos que los romanos extendieron allí donde llegaban, como la vida en grandes barracones militares o el uso de los populares baños públicos, proporcionaban condiciones ideales para la transmisión de estos microbios de unas personas a otras.
De los romanos heredamos las lenguas que hablamos muchos europeos y gran parte del vocabulario de las demás lenguas de Europa, incluida la vasca. Construyeron, además, carreteras, acueductos, aseos públicos, teatros, circos y otras infraestructuras que fueron los cimientos materiales de su civilización. Nos legaron el derecho que hoy conocemos precisamente como romano, y sentaron las bases del calendario que utilizamos en la actualidad; en otras palabras, organizamos nuestra vida y convivencia de acuerdo con normas creadas por ellos. Y a todo lo anterior y muchas otras cosas hay que añadir que facilitaron la expansión de la bacteria que causa la tuberculosis, la enfermedad que, de acuerdo con estimaciones recientes, más muertes ha provocado en la historia de la humanidad.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 29 de julio de 2018.
El artículo El Imperio Romano extendió la tuberculosis se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las contorsiones de una enzima clave para la tuberculosis
- El arte de abrir cráneos: neurocirugía y trepanaciones durante el imperio inca
- Superbacterias
Medicina regenerativa: utilización de células madre para el tratamiento de enfermedades humanas
Las investigaciones realizadas en los últimos veinte años han demostrado la capacidad de regeneración de los tejidos dañados asociada a la presencia de células madre específicas. Esta es precisamente la premisa sobre la que trabaja la medicina regenerativa y la terapia celular, basada en el uso de medicamentos de terapia avanzada para el tratamiento de ciertas enfermedades humanas.
Pero, ¿cuáles son los principios científicos que justifican la utilización de estos medicamentos y las dificultades regulatorias y científicas a las que hay que hacer frente para llevarlos a la práctica clínica? El doctor Felipe Prósper Cardoso, director del Área de Terapia Celular y codirector de Hematología de la Clínica Universidad de Navarra, abordó las realidades y los retos de futuro de las terapias celulares en una conferencia titulada “Medicina regenerativa: utilización de células madre para el tratamiento de enfermedades humanas”, que se celebró el pasado 31 de enero en la Biblioteca Bidebarrieta de Bilbao.
Esta charla que se enmarca dentro del ciclo “Bidebarrieta Científica” una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
Edición realizada por César Tomé López.
El artículo Medicina regenerativa: utilización de células madre para el tratamiento de enfermedades humanas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Microcápsulas biomiméticas de células madre
- Naukas Pro 2017: Manuel Collado y las células madre
- El Nobel de Medicina de 2013: Logística de prefabricados de construcción (en las células)
El modelo cuántico de Rabi, un sencillo modelo para dominarlos a todos
Sofisticados modelos matemáticos que se usan para describir fenómenos físicos muy diferentes estrían integrados en el sencillo modelo cuántico de Rabi, que describe la interacción entre un sistema muy simple, de solo dos niveles, y un campo electromagnético.
 I.I. Rabi ganó el premio Nobel por el descubrimiento de la resonancia magnética nuclear. Este sistema se describe usando su modelo cuántico, en el que los dos estados del sistema son los dos valores del espín y el campo aplicado un campo magnético externo.
I.I. Rabi ganó el premio Nobel por el descubrimiento de la resonancia magnética nuclear. Este sistema se describe usando su modelo cuántico, en el que los dos estados del sistema son los dos valores del espín y el campo aplicado un campo magnético externo.La mecánica cuántica ha revolucionado el mundo de las comunicaciones y los ordenadores con la introducción de algoritmos mucho más veloces y seguros en la trasferencia de la información. “El modelo cuántico de Rabi es un modelo fundamental que aparece en muchos sistemas físicos, incluyendo plataformas cuánticas como iones atrapados o circuitos superconductores, que en un futuro más o menos cercano podrían utilizarse como hardware de un ordenador cuántico”, explica Jorge Casanova quien desarrolló este trabajo mientras trabajaba en Universidad de Ulm (Alemania) y que es actualmente investigador Juan de la Cierva en el grupo de investigación Quantum Technologies for Information Science (QUTIS) del Departamento de Química Física de la UPV/EHU. “Se trata del modelo matemático más sencillo que tenemos para describir los procesos de interacción entre la luz y la materia. Es decir, el modelo cuántico de Rabi es el mecanismo que la materia y la luz (la radiación) han elegido para comunicarse”, comenta el investigador de la UPV/EHU.
Este trabajo ha demostrado por primera vez que varios modelos matemáticos muy sofisticados que se usan para describir fenómenos físicos diferentes, se encuentran dentro del mismo modelo cuántico de Rabi. “Es como si el modelo cuántico de Rabi fuera la raíz de un conjunto mucho más avanzado de modelos matemáticos”, dice Casanova. “Esto significa que si uno interpreta los resultados que el modelo cuántico de Rabi predice, tendría acceso directo a las predicciones de otros modelos más complejos”, señala el investigador. Básicamente, “hemos conectado el modelo cuántico de Rabi con otros modelos matemáticos más sofisticados que se creían muy diferentes, todo esto mediante un algoritmo matemático, es decir, mediante una serie de reglas que, además, son bastante sencillas”, añade.
Por lo tanto, “una comprensión más profunda del mecanismo operacional del modelo cuántico de Rabi nos permitiría, por un lado, lidiar de manera más precisa con los problemas técnicos que tiene el desarrollo de un ordenador cuántico”, subraya el autor del trabajo. Por otra parte, “dado que ahora tendríamos acceso de manera directa a otros modelos más allá del modelo cuántico de Rabi —comenta Casanova—, también tendríamos acceso directo a cambiar el mecanismo operacional más básico de las anteriormente citadas plataformas cuánticas, y por consiguiente de un futuro ordenador cuántico”.
Jorge Casanova señala que “más allá de las posibles aplicaciones prácticas que puedan derivarse y que sin duda son muy interesantes, como físico me parece increíble que un modelo tan sencillo siga escondiendo secretos como el que hemos encontrado”. “Es un avance inesperado, del que todavía tenemos que aprender y extraer toda la información posible para abrir nuevas vías de desarrollo en el campo de la computación cuántica”, añade el investigador de la UPV/EHU.
Referencia:
Jorge Casanova, Ricardo Puebla, Hector Moya-Cessa, Martin B. Plenio (2018) Connecting nth order generalised quantum Rabi models: Emergence of nonlinear spin-boson coupling via spin rotations Npj Quantum Information volume 4, Article number: 47 (2018) doi: 10.1038/s41534-018-0096-9
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El modelo cuántico de Rabi, un sencillo modelo para dominarlos a todos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una fórmula para dominarlos a todos: El trabajo
- Física de partículas en un simulador cuántico
- Entrelazamiento cuántico entre dos nubes de átomos ultrafríos
La forma fractal de mapas y pulmones
Los mapas isócronos son mapas que representan tiempos: en general, el tiempo que se tarda en llegar de un lugar a otro. Distintos tonos de color corresponden a distintos valores de tiempo y, en consecuencia, dos puntos del mapa del mismo color están a la misma “distancia temporal” de otro que se haya tomado como origen.
Si la superficie representada en el mapa fuese la de un terreno liso, igualmente transitable en todas las direcciones, podríamos esperar que un mapa isócrono fuese, sencillamente, una especie de diana: círculos concéntricos trazados a partir del origen elegido. En lugar de eso, el patrón que nos encontramos es este:
El vídeo, publicado por Alberto Hernando de Castro, muestra un mapa isócrono de España con origen en la Plaza Mayor de Madrid, creado con herramientas de software libre (el autor explica cómo aquí, por si queréis jugar). Pero existe una galería completa de mapas isócronos que podéis consultar: Estados Unidos, Japón, Brasil… y todos ellos tienen la misma forma. Una forma que recuerda poderosamente a la de un fractal.
No es casualidad, claro. Esta es la forma que tienen, en general, los caminos construidos por humanos mirados desde un único punto de origen (o de destino). Pero también; la forma que adopta nuestro sistema circulatorio. O las ramificaciones de nuestros pulmones. O las raíces de un árbol… Todos estos sistemas se parecen porque todos dan solución a un problema muy concreto: el problema del transporte, o de cómo cubrir una superficie (léase, un objeto de dimensión n) usando sólo líneas (de dimensión n-1).
 Todos los caminos llevan a Roma… formando un precioso fractal. Fuente: Moovel Lab
Todos los caminos llevan a Roma… formando un precioso fractal. Fuente: Moovel LabLos fractales son, quizás, una de las estrellas pop de la matemática moderna y, francamente, no me extraña. Presentan un equilibrio intrigante de sencillez y complejidad, como los mejores puzzles de lógica: una premisa aparentemente fácil va escalando poco a poco y da lugar a una trama mucho más rica y minuciosa. Puede que su atractivo visual algo que ver con esto. O puede que nos hechice saber que ninguna de sus líneas se debe al capricho: cada una obedece un camino preciso, exacto, sin que ningún diseñador haya tenido que trazarlo, sin que ningún espectador vaya a poder recorrerlo por completo jamás.
A pesar de su encanto y su fama, los fractales son también grandes incomprendidos: la idea popular los pinta como objetos idénticos a sí mismos a distintas escalas. Sin embargo, esta no es una característica compartida por todos los fractales, sólo por los llamados autosimilares. Como definición, resultaría demasiado restrictiva, demasiado “ideal”. Los fractales, en cambio, nacieron en los años 70 con la ambición de describir objetos muy reales de la naturaleza, que no podían ser delimitados por las líneas suaves a las que nos tenía acostumbrado el cálculo, o la geometría. Lo que Mandelbrot tenía en mente era capturar la idea de rugosidad: como la de la costa de Gran Bretaña o, sí, como el contorno de una carretera. Para representar esta idea matemáticamente, podemos utilizar el concepto de dimensión fractal.
Fácil y divertido. O… no tanto. Veamos qué es esto: ¿qué es una dimensión?
A todos nos suena más o menos, aunque sólo sea como salmodia, que “un punto no tiene dimensiones”, que una línea recta es un objeto unidimensional, una superficie tiene dos dimensiones y los volúmenes que nos rodean ocupan un espacio de tres dimensiones (4 si consideramos el tiempo). De manera intuitiva, podemos decir que una dimensión es un parámetro de cambio que puede ser fijado mediante una coordenada. Por lo tanto, el número de dimensiones de un objeto será igual al número de coordenadas necesarias para definir un punto sobre el mismo.
Ahora bien, tomemos un fractal e intentemos poner a prueba esta idea: por simplicidad, elegiremos un fractal de los más populares, autosimilar, como el copo de nieve de Koch. A primera vista, parece ser una línea (unidimensional), por lo que debería bastar una única coordenada para definir un punto sobre ella. En este caso, claro, al no estar sobre una línea recta, nuestra coordenada será una especie de “punto kilométrico” sobre la curva.
Bien, imaginemos que buscamos el punto “1,5” de la curva, siendo sus segmentos rectos de longitud 1. Para ello, hacemos zoom y nos quedamos con un fragmento lo más sencillo posible del copo de nieve. Algo como esto:

Lo dicho ¡fácil y divertido! O… no tanto. En realidad, al intentar simplificar el problema, hemos hecho una pequeña trampa. Hemos eliminado, precisamente, la rugosidad del fractal. De hecho, si nos fijamos un poco mejor y añadimos más detalle a la curva de Koch, nos encontramos con que el punto 1,5 ya no donde lo habíamos encontrado:
Y con una tercera iteración, el punto se desplaza todavía más:
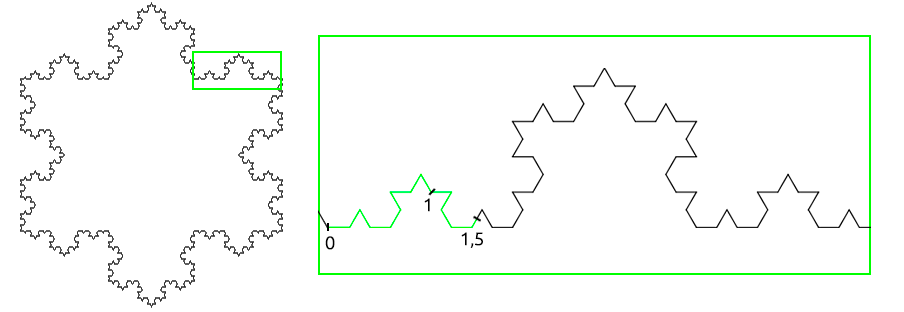
Supongo que veis adónde va a parar esto. Realmente, no es posible localizar nuestro punto de esta manera porque la longitud un fragmento cualquiera de la curva de Koch es infinito.
Como lo sería (figuradamente) el contorno de Gran Bretaña medido alrededor de cada grano de arena de su costa (o del peinado de Boris Johnson). El detalle de nuestra medida, la “escala” elegida, altera la medida misma. Esto es lo que se conoce como el efecto Richardson.
Nuestro primer intento, por tanto, no ha funcionado. Pensemos en otra manera de entender la dimensión de un objeto. Partamos, de nuevo, ejemplos conocidos: un fragmento de recta, un cuadrado, un cubo e imaginemos que queremos “pesarlos”. En este caso, se tratará de un peso imaginario, intuitivo. Podemos usar una báscula matemática de masas platónicas para medirlo, si queréis. En concreto, nos interesa saber cómo cambia la masa de estos objetos al cambiar su escala y multiplicarla por 3.
Bien: si tomamos la recta y multiplicamos su tamaño por 3, su masa se multiplicará también por 3. En el caso del cuadrado, al triplicar su escala, obtendremos un peso 9 veces mayor (dicho de otro modo: el cuadrado original cabe 9 veces en el ampliado). El cubo, pasará a pesar 27 veces más… Supongo el patrón es fácil de ver: 3=31, 9=32, 27=33. La dimensión de cada objeto nos indica a qué número debemos elevar el cambio de escala (3) para obtener el valor de la nueva masa.
¿Qué sucede entonces con la curva de Koch? Bien, en este caso, si ampliamos un fragmento de nuestro copo por 3, obtenemos un fragmento que contiene 4 veces al fragmento original. Es decir: su peso se multiplicará por 4.
Siguiendo el razonamiento del párrafo anterior, podemos calcular cuánto vale la dimensión del fractal, encontrando el valor de este exponente (x): 3x=4
¿A cuánto hay que elevar el factor de escala (3) para que el peso se multiplique por 4? La solución de la ecuación, x = log4 / log3 nos indica que la dimensión fractal de la curva de Koch no es ni 1 ni 2: es, aproximadamente, 1,26.
Esta es la magia de los fractales: su dimensión puede ser un número no entero. El infinito que llevan en su ADN (infinitas torsiones, infinitas ramificaciones) los coloca a mitad de camino entre líneas y superficies, o superficies y volúmenes. Existen, incluso, curvas ¡de dimensión fractal 2! capaces de llenar el plano. Este es el caso de la curva de Hilbert, por ejemplo, pero existen muchas otras.

Pero volvamos a los ejemplos reales. Ciertamente, nuestros pulmones no se ramifican de manera infinita ni tienen una masa platónica. Sin embargo, es precisamente su parecido con un fractal lo que les permite maximizar su superficie siguiendo un patrón de crecimiento relativamente sencillo (similar a distintas escalas). Los pulmones, como árboles invertidos (y los árboles, como pulmones invertidos), intercambian gases en la punta de cada rama, donde se encuentran los alvéolos (las hojas). La cantidad de gases que consiguen aprovechar es directamente proporcional a su superficie total. Y aquí es donde viene el dato sorprendente: aunque el volumen de los pulmones humanos es apenas de unos 4 a 6 litros, su superficie ronda los 140 metros cuadrados1, algo más de media cancha de tenis. En esto consiste, precisamente, la idea de rugosidad. Para cuantificarla, eso sí, pueden tomarse distintas aproximaciones: en el caso de los pulmones, la dimensión fractal varía, según distintos autores, entre 2,26 y 2,882.
 Pulmones humanos (con sistema circulatorio a la derecha). Fotografía de Ewald Weibel, Institute of Anantomy, University of Berne.
Pulmones humanos (con sistema circulatorio a la derecha). Fotografía de Ewald Weibel, Institute of Anantomy, University of Berne.Volviendo a las líneas del precioso mapa isócrono que, sin quererlo, se han ramificado hasta dar forma a esta digresión: se ha estimado que podrían tener una dimensión de 1,83. Resulta difícil asegurar si la fractalidad de estas carreteras se debe, quizás, a la rugosidad del propio terreno sobre el que se construyen. O si el truco radica en tomar un punto de origen sobre una red mucho más compleja. En cualquier caso, es bonito pensar que nuestros caminos son, de hecho, equivalentes a pulmones, o al sistema circulatorio de un organismo inmenso del que, sin saberlo, formamos parte. Un organismo vivo que nosotros mismos hemos ido construyendo.
Bonus track: Este es el aspecto de los ríos y sus afluentes
Referencias:
1 E.N. Marieb, K.N. Hoehn. Human anatomy and physiology.
2 K. Lamrini Uahabi and M. Atounti. New approach to the calculation of fractal dimension of the lungs
3 P. Pavón et al. Multifractal approach for comparing road transport network geometry: The case of Spain
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo La forma fractal de mapas y pulmones se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia en la cocina: Fractal de cochinilla
- Frank Stella, la forma del lienzo
- La nueva forma de enfriar que lo cambiará todo

